Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T08:52:13.710Z Has data issue: false hasContentIssue false
  • English
  • Français

On 3-Manifolds with Sufficiently Large Decompositions

Published online by Cambridge University Press:  20 November 2018

Wolfgang Heil
Wolfgang Heil*
Affiliation:
Florida State University, Tallahassee, Florida
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6] it is shown that two (compact) orientable 3-manifolds which are irreducible, boundary irreducible and sufficiently large are homeomorphic if and only if there exists an isomorphism between the fundamental groups which respects the peripheral structure. In this note we extend this theorem to reducible 3-manifolds.

Any compact 3-manifold M has a decomposition into prime manifolds [1; 4].

1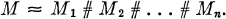

Here the connected sum of two bounded manifolds N1, N2 is denned by removing 3-balls B1 B2 in int N1, int N2, respectively, and glueing the resulting boundary spheres together. The M1's which occur in the decomposition (1) are either irreducible or handles (i.e., a fibre bundle over S1 with fibre S2). If (1) contains a fake 3-sphere, we assume it to be Mn.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 4 , August 1971 , pp. 746 - 748
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Haken, W., Ein Verfahren zur Aufspaltung einer 3-Mannigfaltigkeit in irreduzible 3-Mannigfaltigkeiten, Math. Z. 76 (1961), 427–467.Google Scholar
2. Heil, W. H., On P2-irreducible 3-manifolds, Bull. Amer. Math. Soc. 75 (1969), 772–775.Google Scholar
3. Heil, W. H., On Kneser's conjecture for bounded 3-manifolds (to appear).Google Scholar
4. Milnor, J., A unique decomposition theorem for 3-manifolds, Amer. J. Math. 84 (1962), 1–7.Google Scholar
5. Stallings, J., Grushko's theorem II. Kneser's conjecture, Notices Amer. Math. Soc. 6 (1959), Abstract 559-165, 531–532.Google Scholar
6. Waldhausen, F., On irreducible 3-manifolds which are sufficiently large, Ann. Math. 87 (1968), 56–88.Google Scholar