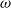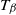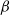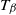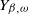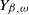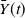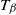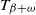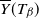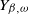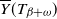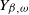1. Introduction
We consider a general real-valued Lévy process
![]() $Y \equiv \{Y(t), \, t \geqslant 0\}$
that is inspected at the epochs
$Y \equiv \{Y(t), \, t \geqslant 0\}$
that is inspected at the epochs
![]() $I_1,I_2,\dots$
of an independently evolving Poisson process with intensity
$I_1,I_2,\dots$
of an independently evolving Poisson process with intensity
![]() $\omega>0$
. Our aim is to compare the distributions of the running maximum of the Lévy process under continuous observation and its counterpart at the inspection epochs. We do this until an, independently sampled, exp(
$\omega>0$
. Our aim is to compare the distributions of the running maximum of the Lévy process under continuous observation and its counterpart at the inspection epochs. We do this until an, independently sampled, exp(
![]() $\beta$
)-distributed ‘killing time’
$\beta$
)-distributed ‘killing time’
![]() $T_\beta$
(for
$T_\beta$
(for
![]() $\beta\geqslant 0$
). This also covers the case of an infinite time horizon: let
$\beta\geqslant 0$
). This also covers the case of an infinite time horizon: let
![]() $\beta$
go to 0, imposing the additional assumption of the Lévy process’s mean being negative to avoid the running maximum drifting to
$\beta$
go to 0, imposing the additional assumption of the Lévy process’s mean being negative to avoid the running maximum drifting to
![]() $\infty$
.
$\infty$
.
The motivation behind our study lies in the fact that in many real-life situations the stochastic process under study is not, or cannot, be continuously observed, but is rather inspected at discrete times. Examples abound in reliability and healthcare, where an object or person is checked regularly during their lifetime. Our interest in this topic mainly stems from an application in insurance risk, and in particular from the classical Cramér–Lundberg model. That model represents the surplus process of an insurance company that earns money (at a constant rate) via premiums, and that pays claims to its clients according to a compound Poisson process. The main quantity of interest is the ruin probability p(u), i.e. the probability that the surplus level becomes negative when starting with initial capital
![]() $u>0$
. This model was relaxed in [Reference Albrecher, Gerber and Shiu3], which observed that companies can sometimes continue doing business even when they are technically ruined. More specifically, it distinguished between ruin and bankruptcy, the latter occurring when the surplus is negative at an inspection epoch. It is obvious that the probability of bankruptcy
$u>0$
. This model was relaxed in [Reference Albrecher, Gerber and Shiu3], which observed that companies can sometimes continue doing business even when they are technically ruined. More specifically, it distinguished between ruin and bankruptcy, the latter occurring when the surplus is negative at an inspection epoch. It is obvious that the probability of bankruptcy
![]() $\tilde{p}(u)$
is smaller than p(u), but we would like to quantify the difference. The bankruptcy probability in the Cramér–Lundberg setting with exponentially distributed claim sizes was determined in [Reference Albrecher and Lautscham6]; in [Reference Boxma, Essifi and Janssen10] this was generalized to the case of generally distributed claim sizes. In both papers, the inspection rate was allowed to depend on the current surplus level. In [Reference Albrecher, Boxma, Essifi and Kuijstermans2, Reference Boxma, Essifi and Janssen10], a related queueing (or inventory) model was also studied, where a server works even when there are no customers (or orders), building up storage that is removed at the Poisson inspection epochs.
$\tilde{p}(u)$
is smaller than p(u), but we would like to quantify the difference. The bankruptcy probability in the Cramér–Lundberg setting with exponentially distributed claim sizes was determined in [Reference Albrecher and Lautscham6]; in [Reference Boxma, Essifi and Janssen10] this was generalized to the case of generally distributed claim sizes. In both papers, the inspection rate was allowed to depend on the current surplus level. In [Reference Albrecher, Boxma, Essifi and Kuijstermans2, Reference Boxma, Essifi and Janssen10], a related queueing (or inventory) model was also studied, where a server works even when there are no customers (or orders), building up storage that is removed at the Poisson inspection epochs.
While the results in the present paper allow us to get a better insight into the relation between the ruin and bankruptcy probabilities in the Cramér–Lundberg model and some of its (Lévy) generalizations, our motivation is also to a large extent theoretical. We prove that there is a remarkably simple relation between the running maximum
![]() $\overline{Y}(T_{\beta})$
of the supremum of the Lévy process Y until the exp(
$\overline{Y}(T_{\beta})$
of the supremum of the Lévy process Y until the exp(
![]() $\beta$
) killing epoch and the running maximum
$\beta$
) killing epoch and the running maximum
![]() $Y_{\beta,\omega}$
of Y at inspection epochs until that killing: our main result (Theorem 2.2) is that
$Y_{\beta,\omega}$
of Y at inspection epochs until that killing: our main result (Theorem 2.2) is that
the two quantities on the right-hand side being independent. The proof of this result relies on known results from the Wiener–Hopf theory for Lévy processes, and is surprisingly straightforward.
Our main result, the decomposition in (1.1), is proved in Section 2, where we also show how it can, alternatively, be obtained by applying results from [Reference Albrecher and Ivanovs4]. The latter paper also served as an important source of inspiration for us, as it presents several beautiful identities relating exit problems for Lévy processes under permanent observation and their counterparts under Poisson inspections; see also [Reference Albrecher, Ivanovs and Zhou5]. While Section 2 focuses on a general Lévy process, we restrict ourselves in Section 3 to spectrally one-sided Lévy processes. In the spectrally positive case, we succeed in expressing the transform of
![]() $Y_{\beta,\omega}$
explicitly in terms of the Laplace exponent of the driving Lévy process Y. In the spectrally negative case we prove that
$Y_{\beta,\omega}$
explicitly in terms of the Laplace exponent of the driving Lévy process Y. In the spectrally negative case we prove that
![]() $Y_{\beta,\omega}$
is exponentially distributed, with an atom at zero. As an illustration of the application potential of our results, we study in Section 4 the asymptotics (for large initial capital u, that is) of the bankruptcy probability in the setting of the Cramér–Lundberg model, distinguishing between the cases of light-tailed and heavy-tailed claim sizes. At various places we explicitly exploit the relation between fluctuation-theoretic concepts and their queueing counterparts, effectively resting on a duality between Lévy-type insurance risk models and corresponding queueing models; regarding this duality, see, e.g., the account in [Reference Asmussen and Albrecher7, Section III.2]. In addition, we frequently use the fact that, due to the Wiener–Hopf decomposition, the increment of Y between two inspection epochs can be written as the difference between two independent positive random variables, which enables us to write the quantities under study in terms of waiting times in associated queueing models.
$Y_{\beta,\omega}$
is exponentially distributed, with an atom at zero. As an illustration of the application potential of our results, we study in Section 4 the asymptotics (for large initial capital u, that is) of the bankruptcy probability in the setting of the Cramér–Lundberg model, distinguishing between the cases of light-tailed and heavy-tailed claim sizes. At various places we explicitly exploit the relation between fluctuation-theoretic concepts and their queueing counterparts, effectively resting on a duality between Lévy-type insurance risk models and corresponding queueing models; regarding this duality, see, e.g., the account in [Reference Asmussen and Albrecher7, Section III.2]. In addition, we frequently use the fact that, due to the Wiener–Hopf decomposition, the increment of Y between two inspection epochs can be written as the difference between two independent positive random variables, which enables us to write the quantities under study in terms of waiting times in associated queueing models.
2. Decomposition
This section establishes the decomposition in (1.1), and relates it to results that have recently appeared in [Reference Albrecher and Ivanovs4].
2.1. The main decomposition result
Let
![]() $Y\equiv \{Y(t), \, t \geqslant 0\} $
be a general real-valued Lévy process. In addition, let
$Y\equiv \{Y(t), \, t \geqslant 0\} $
be a general real-valued Lévy process. In addition, let
![]() $\bar Y$
be the associated running maximum process,
$\bar Y$
be the associated running maximum process,
![]() $\overline Y(t) \,:\!=\, \sup_{s \in [0,t]} Y(s)$
. We consider the setting in which, for some intensity
$\overline Y(t) \,:\!=\, \sup_{s \in [0,t]} Y(s)$
. We consider the setting in which, for some intensity
![]() $\omega>0$
, the Lévy process is inspected at Poisson(
$\omega>0$
, the Lévy process is inspected at Poisson(
![]() $\omega$
) moments
$\omega$
) moments
![]() $I_1,I_2,\dots$
, so that the number of inspections up to time t has a Poisson distribution with mean
$I_1,I_2,\dots$
, so that the number of inspections up to time t has a Poisson distribution with mean
![]() $\omega t$
. We consider the resulting inspected process until ‘killing’, which happens at an exponentially distributed time
$\omega t$
. We consider the resulting inspected process until ‘killing’, which happens at an exponentially distributed time
![]() $T_\beta$
with parameter
$T_\beta$
with parameter
![]() $\beta\geqslant 0$
, sampled independently from Y.
$\beta\geqslant 0$
, sampled independently from Y.
To analyze the process Y at inspection moments, we denote by
![]() $Z_m$
the increment of the Lévy process Y(t) between the two consecutive inspection times
$Z_m$
the increment of the Lévy process Y(t) between the two consecutive inspection times
![]() $I_{m-1}$
and
$I_{m-1}$
and
![]() $I_m$
(with
$I_m$
(with
![]() $I_0 \,:\!=\,0$
), conditioned on the process not having been killed. We also define
$I_0 \,:\!=\,0$
), conditioned on the process not having been killed. We also define
![]() $S_0\,:\!=\,0$
,
$S_0\,:\!=\,0$
,
![]() $S_n\,:\!=\,\sum_{m=1}^n Z_m$
for
$S_n\,:\!=\,\sum_{m=1}^n Z_m$
for
![]() $n\in{\mathbb N}$
, and the corresponding running maximum process
$n\in{\mathbb N}$
, and the corresponding running maximum process
![]() $\overline S_n\,:\!=\,\max\{S_0,S_1,\ldots,S_n\}$
. We wish to analyze the running maximum of the inspected process until killing. The number of inspections
$\overline S_n\,:\!=\,\max\{S_0,S_1,\ldots,S_n\}$
. We wish to analyze the running maximum of the inspected process until killing. The number of inspections
![]() $N_{\beta,\omega}$
before killing is shifted-geometric, with the ‘killing probability’ given by
$N_{\beta,\omega}$
before killing is shifted-geometric, with the ‘killing probability’ given by
![]() $\beta/(\beta+\omega)$
:
$\beta/(\beta+\omega)$
:
The random variable of interest is
Observe that we have the identity
Theorem 2.1. For any
![]() $\alpha>0$
,
$\alpha>0$
,
Proof. As pointed out in [Reference Kyprianou18], applying the Wiener–Hopf theory for random walks,
 \begin{equation*} \sum_{n=0}^\infty (1-p)^n p \,{\mathbb E}\,{\rm e}^{-\alpha \overline S_n} = \exp\Bigg({-}\int_{(0,\infty)} \sum_{n=1}^\infty \frac{1}{n} (1-{\rm e}^{-\alpha x})(1-p)^n\,{\mathbb P}(S_n\in {\rm d}x)\Bigg);\end{equation*}
\begin{equation*} \sum_{n=0}^\infty (1-p)^n p \,{\mathbb E}\,{\rm e}^{-\alpha \overline S_n} = \exp\Bigg({-}\int_{(0,\infty)} \sum_{n=1}^\infty \frac{1}{n} (1-{\rm e}^{-\alpha x})(1-p)^n\,{\mathbb P}(S_n\in {\rm d}x)\Bigg);\end{equation*}
see also, e.g., [Reference Debicki and Mandjes13, Section 3.3]. As a consequence,
 \begin{equation*} {\mathbb E}\,{\rm e}^{-\alpha Y_{\beta,\omega}} = \exp\Bigg({-}\int_{(0,\infty)} \sum_{n=1}^\infty \frac{1}{n} (1-{\rm e}^{-\alpha x})\bigg(\frac{\omega}{\beta+\omega}\bigg)^n\,{\mathbb P}(S_n\in {\rm d}x)\Bigg).\end{equation*}
\begin{equation*} {\mathbb E}\,{\rm e}^{-\alpha Y_{\beta,\omega}} = \exp\Bigg({-}\int_{(0,\infty)} \sum_{n=1}^\infty \frac{1}{n} (1-{\rm e}^{-\alpha x})\bigg(\frac{\omega}{\beta+\omega}\bigg)^n\,{\mathbb P}(S_n\in {\rm d}x)\Bigg).\end{equation*}
Now realize that, with
![]() ${\rm E}(n,a)$
an Erlang random variable with shape parameter
${\rm E}(n,a)$
an Erlang random variable with shape parameter
![]() $n\in{\mathbb N}$
and scale parameter
$n\in{\mathbb N}$
and scale parameter
![]() $a>0$
, conditional on the process not having been killed,
$a>0$
, conditional on the process not having been killed,
![]() $S_n\stackrel{\rm d} = Y({\rm E}(n, \beta+\omega))$
, so that
$S_n\stackrel{\rm d} = Y({\rm E}(n, \beta+\omega))$
, so that
We thus obtain
 \begin{align*} {\mathbb E}\,{\rm e}^{-\alpha Y_{\beta,\omega}} & = \exp\Bigg({-}\int_0^\infty\int_{(0,\infty)} \frac{1}{t}\sum_{n=1}^\infty \frac{1}{n!} (1-{\rm e}^{-\alpha x})({\omega}t)^n\,{\rm e}^{-(\beta+\omega)t}\,{\mathbb P}(Y(t)\in {\rm d}x)\, {\rm d}t\Bigg) \\ & = \exp\bigg({-}\int_0^\infty\int_{(0,\infty)} \frac{1}{t}({\rm e}^{\omega t}-1) (1-{\rm e}^{-\alpha x})\,{\rm e}^{-(\beta+\omega)t} \,{\mathbb P}(Y(t)\in {\rm d}x)\,{\rm d}t\bigg) \\ & = \exp\bigg({-}\int_0^\infty\int_{(0,\infty)} \frac{1}{t} {\rm e}^{-\beta t}(1-{\rm e}^{-\omega t}) (1-{\rm e}^{-\alpha x})\, \,{\mathbb P}(Y(t)\in {\rm d}x)\,{\rm d}t\bigg).\end{align*}
\begin{align*} {\mathbb E}\,{\rm e}^{-\alpha Y_{\beta,\omega}} & = \exp\Bigg({-}\int_0^\infty\int_{(0,\infty)} \frac{1}{t}\sum_{n=1}^\infty \frac{1}{n!} (1-{\rm e}^{-\alpha x})({\omega}t)^n\,{\rm e}^{-(\beta+\omega)t}\,{\mathbb P}(Y(t)\in {\rm d}x)\, {\rm d}t\Bigg) \\ & = \exp\bigg({-}\int_0^\infty\int_{(0,\infty)} \frac{1}{t}({\rm e}^{\omega t}-1) (1-{\rm e}^{-\alpha x})\,{\rm e}^{-(\beta+\omega)t} \,{\mathbb P}(Y(t)\in {\rm d}x)\,{\rm d}t\bigg) \\ & = \exp\bigg({-}\int_0^\infty\int_{(0,\infty)} \frac{1}{t} {\rm e}^{-\beta t}(1-{\rm e}^{-\omega t}) (1-{\rm e}^{-\alpha x})\, \,{\mathbb P}(Y(t)\in {\rm d}x)\,{\rm d}t\bigg).\end{align*}
This proves the claim.
We can let
![]() $\omega \rightarrow \infty$
in the above theorem to recover a classical Wiener–Hopf factorization result for general Lévy process Y.
$\omega \rightarrow \infty$
in the above theorem to recover a classical Wiener–Hopf factorization result for general Lévy process Y.
We now state and prove our main result, a decomposition theorem for a Lévy process with Poisson inspection epochs.
Theorem 2.2. The following distributional equality applies:
with the two terms on the right-hand side being independent.
Proof. By applying the Wiener–Hopf theory for Lévy processes, as presented in, e.g., [Reference Kyprianou17, Theorem 6.15] or [Reference Debicki and Mandjes13, Section 3.3], for any
![]() $\zeta>0$
,
$\zeta>0$
,
Taking
![]() $\zeta=\beta$
and
$\zeta=\beta$
and
![]() $\zeta = \beta + \omega$
, and using Theorem 2.1, we obtain
$\zeta = \beta + \omega$
, and using Theorem 2.1, we obtain
![]() ${\mathbb E} \,{\rm e}^{-\alpha \overline Y({T_\beta})} = {\mathbb E}\,{\rm e}^{-\alpha Y_{\beta,\omega}}\cdot {\mathbb E} \,{\rm e}^{-\alpha \overline Y({T_{\beta+\omega}})}$
, which implies the stated result.
${\mathbb E} \,{\rm e}^{-\alpha \overline Y({T_\beta})} = {\mathbb E}\,{\rm e}^{-\alpha Y_{\beta,\omega}}\cdot {\mathbb E} \,{\rm e}^{-\alpha \overline Y({T_{\beta+\omega}})}$
, which implies the stated result.
Remark 2.1. A striking aspect of the decomposition, besides its remarkably straightforward proof, is that the impact of
![]() $\omega$
in the first term on the right-hand side of (2.4) apparently equals the impact of
$\omega$
in the first term on the right-hand side of (2.4) apparently equals the impact of
![]() $\omega$
in the second term, but ‘with opposite sign’; to this end, observe that the left-hand side of (2.4) does not involve
$\omega$
in the second term, but ‘with opposite sign’; to this end, observe that the left-hand side of (2.4) does not involve
![]() $\omega$
at all. Observe that the first term on the right-hand side is increasing in
$\omega$
at all. Observe that the first term on the right-hand side is increasing in
![]() $\omega$
(as the inspection process takes place at an increasingly high frequency, with the length of the interval held fixed), whereas the second term is decreasing in
$\omega$
(as the inspection process takes place at an increasingly high frequency, with the length of the interval held fixed), whereas the second term is decreasing in
![]() $\omega$
(as a supremum over an increasingly small interval is taken).
$\omega$
(as a supremum over an increasingly small interval is taken).
Remark 2.2. As is to be expected,
![]() $S_{N_{\beta,\omega}}$
can also be decomposed as the sum of
$S_{N_{\beta,\omega}}$
can also be decomposed as the sum of
![]() $\overline S_{N_{\beta,\omega}}$
and
$\overline S_{N_{\beta,\omega}}$
and
![]() $\underline S_{N_{\beta,\omega}} \,:\!=\, \inf_{n=0,1,\ldots,N_{\beta,\omega}} S_n$
, with the latter two quantities being independent. To verify this, first observe that
$\underline S_{N_{\beta,\omega}} \,:\!=\, \inf_{n=0,1,\ldots,N_{\beta,\omega}} S_n$
, with the latter two quantities being independent. To verify this, first observe that
![]() ${\mathbb E} \, {\rm e}^{\alpha {\rm i} Z_m} = (\beta + \omega)/\big(\beta + \omega - {\rm log} \, {\mathbb E} \, {\rm e}^{\alpha{\rm i} Y(1)}\big)$
. Hence,
${\mathbb E} \, {\rm e}^{\alpha {\rm i} Z_m} = (\beta + \omega)/\big(\beta + \omega - {\rm log} \, {\mathbb E} \, {\rm e}^{\alpha{\rm i} Y(1)}\big)$
. Hence,
 \begin{align*} {\mathbb E}\,e^{\alpha{\rm i} S_{N_{\beta,\omega}}} & = \frac{\beta}{\beta+\omega -\omega\, {\mathbb E}\,{\mathrm{e}}^{\alpha{\rm i}Z}} = \frac{1 + \omega/(\beta - {\rm log} \, {\mathbb E} \, {\rm e}^{\alpha{\rm i} Y(1)})}{1 + \omega/\beta} \\ & = \exp\bigg({-}\int_0^\infty\int_{({-}\infty,\infty)} \frac{1}{t} {\rm e}^{-\beta t}(1-{\rm e}^{-\omega t}) (1-{\rm e}^{\alpha{\rm i} x})\, \,{\mathbb P}(Y(t)\in {\rm d}x)\,{\rm d}t\bigg). \end{align*}
\begin{align*} {\mathbb E}\,e^{\alpha{\rm i} S_{N_{\beta,\omega}}} & = \frac{\beta}{\beta+\omega -\omega\, {\mathbb E}\,{\mathrm{e}}^{\alpha{\rm i}Z}} = \frac{1 + \omega/(\beta - {\rm log} \, {\mathbb E} \, {\rm e}^{\alpha{\rm i} Y(1)})}{1 + \omega/\beta} \\ & = \exp\bigg({-}\int_0^\infty\int_{({-}\infty,\infty)} \frac{1}{t} {\rm e}^{-\beta t}(1-{\rm e}^{-\omega t}) (1-{\rm e}^{\alpha{\rm i} x})\, \,{\mathbb P}(Y(t)\in {\rm d}x)\,{\rm d}t\bigg). \end{align*}
In the last step we have used the Frullani integral [Reference Kyprianou17, Lemma 1.7],
with both
![]() $a = \beta$
and
$a = \beta$
and
![]() $a = \beta - \log {\mathbb E}\,{\mathrm{e}}^{\alpha{\rm i} Y(1)}$
. Finally, observe that, by symmetry, the running minimum can be dealt with in precisely the same manner as the running maximum, in that the transform of
$a = \beta - \log {\mathbb E}\,{\mathrm{e}}^{\alpha{\rm i} Y(1)}$
. Finally, observe that, by symmetry, the running minimum can be dealt with in precisely the same manner as the running maximum, in that the transform of
![]() $\underline S_{N_{\beta,\omega}}$
is as given in (2.3), but with the integration interval
$\underline S_{N_{\beta,\omega}}$
is as given in (2.3), but with the integration interval
![]() $(0,\infty)$
replaced by
$(0,\infty)$
replaced by
![]() $({-}\infty,0)$
.
$({-}\infty,0)$
.
2.2. Relation to a result in [Reference Albrecher and Ivanovs4]
In this subsection we outline the relation between Theorem 2.2 and some results from [Reference Albrecher and Ivanovs4]. In preparation, we take a closer look at the increments
![]() $Z_m$
between inspection epochs, and we mention the powerful concept of Wiener–Hopf factorization for Lévy processes; see, e.g., [Reference Kyprianou17, Chapter 6] or [Reference Debicki and Mandjes13, Section 3.3].
$Z_m$
between inspection epochs, and we mention the powerful concept of Wiener–Hopf factorization for Lévy processes; see, e.g., [Reference Kyprianou17, Chapter 6] or [Reference Debicki and Mandjes13, Section 3.3].
The Wiener–Hopf decomposition entails each
![]() $Z_m$
being written as
$Z_m$
being written as
![]() $Z_m = Z_m^+ - Z_m^-$
, with
$Z_m = Z_m^+ - Z_m^-$
, with
![]() $Z_m^+$
and
$Z_m^+$
and
![]() $Z_m^-$
independent and both non-negative. Here,
$Z_m^-$
independent and both non-negative. Here,
![]() $Z_m^+$
(resp.
$Z_m^+$
(resp.
![]() $Z_m^-$
) is distributed as the supremum (resp. minus the infimum) of the Lévy process Y, when started anew at zero at inspection epoch
$Z_m^-$
) is distributed as the supremum (resp. minus the infimum) of the Lévy process Y, when started anew at zero at inspection epoch
![]() $I_{m-1}$
, over the interval between
$I_{m-1}$
, over the interval between
![]() $I_{m-1}$
and
$I_{m-1}$
and
![]() $I_m$
(whose length is exp(
$I_m$
(whose length is exp(
![]() ${\beta+\omega}$
)). To get some feeling for this property, it is useful to observe that a time-reversibility argument for Lévy processes implies that, with
${\beta+\omega}$
)). To get some feeling for this property, it is useful to observe that a time-reversibility argument for Lévy processes implies that, with
![]() $\underline Y(t)$
denoting the running minimum process, we have
$\underline Y(t)$
denoting the running minimum process, we have
(but, evidently, for a given t,
![]() $\underline Y(t)$
and
$\underline Y(t)$
and
![]() $\overline{Y}(t)$
are not independent). In the following,
$\overline{Y}(t)$
are not independent). In the following,
![]() $Z^+$
(resp.
$Z^+$
(resp.
![]() $Z^-$
) is a generic random variable distributed as
$Z^-$
) is a generic random variable distributed as
![]() $Z_m^+$
(resp.
$Z_m^+$
(resp.
![]() $Z_m^-$
).
$Z_m^-$
).
Albrecher and Ivanovs [Reference Albrecher and Ivanovs4] considered a Lévy process
![]() $X\equiv \{X(t),\, t\geqslant 0\}$
, starting at u, which is also being inspected at Poisson(
$X\equiv \{X(t),\, t\geqslant 0\}$
, starting at u, which is also being inspected at Poisson(
![]() $\omega$
) epochs
$\omega$
) epochs
![]() $I_0=0,I_1,\dots$
If X attains a negative value, then ruin is said to occur, whereas if it is negative at an inspection epoch, then bankruptcy is said to occur. Recall that the all-time ruin probability starting at surplus level u is denoted by p(u), and the (obviously smaller) corresponding bankruptcy probability by
$I_0=0,I_1,\dots$
If X attains a negative value, then ruin is said to occur, whereas if it is negative at an inspection epoch, then bankruptcy is said to occur. Recall that the all-time ruin probability starting at surplus level u is denoted by p(u), and the (obviously smaller) corresponding bankruptcy probability by
![]() $\tilde{p}(u)$
. The starting point in [Reference Albrecher and Ivanovs4] is their elegant Proposition 1, which (in our notation) states that
$\tilde{p}(u)$
. The starting point in [Reference Albrecher and Ivanovs4] is their elegant Proposition 1, which (in our notation) states that
where the process X relates to our Y through the relation
![]() $X(t)=u-Y(t)$
for
$X(t)=u-Y(t)$
for
![]() $t\geqslant 0$
. The focus in [Reference Albrecher and Ivanovs4] lies not on deriving decompositions, but the proof of (2.6) in fact implicitly reveals such a decomposition, which can be used to rederive our decomposition of Theorem 2.2. They introduced (again adapted to our notation) the partial sums, for
$t\geqslant 0$
. The focus in [Reference Albrecher and Ivanovs4] lies not on deriving decompositions, but the proof of (2.6) in fact implicitly reveals such a decomposition, which can be used to rederive our decomposition of Theorem 2.2. They introduced (again adapted to our notation) the partial sums, for
![]() $i=1,2,\dots$
,
$i=1,2,\dots$
,
 \begin{alignat*}{2} \hat{\sigma}_0 & \,:\!=\, 0, & \hat{\sigma}_i & \,:\!=\, - \sum_{j=1}^i Z_j, \\
\sigma_0 & \,:\!=\, -Z_1^+, \qquad & \sigma_i & \,:\!=\, - \sum_{j=1}^i \big(Z_{j+1}^+ -Z_j^-\big) , \end{alignat*}
\begin{alignat*}{2} \hat{\sigma}_0 & \,:\!=\, 0, & \hat{\sigma}_i & \,:\!=\, - \sum_{j=1}^i Z_j, \\
\sigma_0 & \,:\!=\, -Z_1^+, \qquad & \sigma_i & \,:\!=\, - \sum_{j=1}^i \big(Z_{j+1}^+ -Z_j^-\big) , \end{alignat*}
and then concluded that
![]() $\{\hat{\sigma}_i -Z^+ \}_{i=0,1,\ldots} \stackrel{{\rm d}} = \{\sigma_i\}_{i=0,1,\ldots}$
, and hence
$\{\hat{\sigma}_i -Z^+ \}_{i=0,1,\ldots} \stackrel{{\rm d}} = \{\sigma_i\}_{i=0,1,\ldots}$
, and hence
![]() $p(u) = {\mathbb P}({-} \min_{i \geqslant 0} \sigma_i \geqslant u) = {\mathbb P}\big({-} \min_{i \geqslant 0} \hat{\sigma}_i + Z_1^+ \geqslant u\big) = {\mathbb E} \,\tilde{p}\big(u-Z_1^+\big)$
. Observe that this identity implicitly entails the decomposition
$p(u) = {\mathbb P}({-} \min_{i \geqslant 0} \sigma_i \geqslant u) = {\mathbb P}\big({-} \min_{i \geqslant 0} \hat{\sigma}_i + Z_1^+ \geqslant u\big) = {\mathbb E} \,\tilde{p}\big(u-Z_1^+\big)$
. Observe that this identity implicitly entails the decomposition
![]() $- \min_{i=0,1,\ldots} \sigma_i \stackrel{{\rm d}} = - \min_{i =0,1,\ldots} \hat{\sigma}_i + Z_1^+$
.
$- \min_{i=0,1,\ldots} \sigma_i \stackrel{{\rm d}} = - \min_{i =0,1,\ldots} \hat{\sigma}_i + Z_1^+$
.
Let us now turn to the case with ‘killing’, as considered in Theorem 2.2, i.e. the process ends at
![]() $T_\beta \sim {\rm exp}(\beta)$
. We note that [Reference Albrecher and Ivanovs4, Remark 3] briefly mentions the option of killing, at an inspection epoch
$T_\beta \sim {\rm exp}(\beta)$
. We note that [Reference Albrecher and Ivanovs4, Remark 3] briefly mentions the option of killing, at an inspection epoch
![]() $I_i$
. It is stated there, without proof, that the finite-time ruin and bankruptcy probabilities before inspection time
$I_i$
. It is stated there, without proof, that the finite-time ruin and bankruptcy probabilities before inspection time
![]() $I_i$
are related via
$I_i$
are related via
 \begin{align} p(u,I_i) & = {\mathbb P}\Big({-} \min_{j=0,1,\ldots, i-1} \sigma_j \geqslant u\Big) \nonumber \\
& = {\mathbb P}\Big({-} \min_{j=0,1,\ldots, i-1} \hat{\sigma}_j + Z_1^+ \geqslant u\Big) = {\mathbb E} \,\tilde{p}\big(u-Z_1^+,I_{i-1}\big) ;\end{align}
\begin{align} p(u,I_i) & = {\mathbb P}\Big({-} \min_{j=0,1,\ldots, i-1} \sigma_j \geqslant u\Big) \nonumber \\
& = {\mathbb P}\Big({-} \min_{j=0,1,\ldots, i-1} \hat{\sigma}_j + Z_1^+ \geqslant u\Big) = {\mathbb E} \,\tilde{p}\big(u-Z_1^+,I_{i-1}\big) ;\end{align}
here, p(u, t) (resp.
![]() $\tilde p(u,t)$
) is the probability of ruin (resp. bankruptcy) before time t, given an initial surplus u. To translate this observation to the setting of Theorem 2.2, let us assume that the system is inspected at the Poisson(
$\tilde p(u,t)$
) is the probability of ruin (resp. bankruptcy) before time t, given an initial surplus u. To translate this observation to the setting of Theorem 2.2, let us assume that the system is inspected at the Poisson(
![]() $\beta+\omega$
) epochs
$\beta+\omega$
) epochs
![]() $I_0=0,I_1,\dots$
The inspection intervals now are exp(
$I_0=0,I_1,\dots$
The inspection intervals now are exp(
![]() $\beta+\omega$
) distributed and, accordingly, in the distributions of the
$\beta+\omega$
) distributed and, accordingly, in the distributions of the
![]() $Z^+$
and
$Z^+$
and
![]() $Z^-$
the parameter
$Z^-$
the parameter
![]() $\omega$
should be replaced by
$\omega$
should be replaced by
![]() $\beta + \omega$
. The ‘
$\beta + \omega$
. The ‘
![]() $\beta$
-inspection’ is preceded by
$\beta$
-inspection’ is preceded by
![]() $N_{\beta,\omega}$
‘
$N_{\beta,\omega}$
‘
![]() $\omega$
-inspections’ at epochs
$\omega$
-inspections’ at epochs
![]() $I_1,\dots,I_{N_{\beta,\omega}}$
. Now consider the three terms in Theorem 2.2, and compare them with the three main random elements featuring in (2.7). Firstly, observe that
$I_1,\dots,I_{N_{\beta,\omega}}$
. Now consider the three terms in Theorem 2.2, and compare them with the three main random elements featuring in (2.7). Firstly, observe that
as both are distributed as the supremum of the Lévy process Y over an exp(
![]() $\beta + \omega$
) interval. Secondly, noticing that if
$\beta + \omega$
) interval. Secondly, noticing that if
![]() $I_i = T_\beta$
then
$I_i = T_\beta$
then
![]() $N_{\beta,\omega} = i-1$
, we have
$N_{\beta,\omega} = i-1$
, we have
 \begin{equation*} - \min_{j=0,1, \ldots, N_{\beta,\omega}} \hat{\sigma}_j = \sup_{j=0,1, \ldots, N_{\beta,\omega}} \sum_{k=0}^j Z_k \stackrel{{\rm d}} = \overline{Y}_{\beta,\omega} .\end{equation*}
\begin{equation*} - \min_{j=0,1, \ldots, N_{\beta,\omega}} \hat{\sigma}_j = \sup_{j=0,1, \ldots, N_{\beta,\omega}} \sum_{k=0}^j Z_k \stackrel{{\rm d}} = \overline{Y}_{\beta,\omega} .\end{equation*}
Thirdly,
 \begin{equation*} - \min_{j=0,1, \ldots, N_{\beta,\omega}} \sigma_j = \sup_{j=0,1, \ldots, N_{\beta,\omega}} \sum_{k=0}^j \big(Z_{k+1}^+ - Z_k^-\big) \stackrel{{\rm d}} = \overline{Y}(T_\beta) ,\end{equation*}
\begin{equation*} - \min_{j=0,1, \ldots, N_{\beta,\omega}} \sigma_j = \sup_{j=0,1, \ldots, N_{\beta,\omega}} \sum_{k=0}^j \big(Z_{k+1}^+ - Z_k^-\big) \stackrel{{\rm d}} = \overline{Y}(T_\beta) ,\end{equation*}
as the latter supremum is the supremum of the Y process until
![]() $T_\beta$
. We thus conclude that Theorem 2.2 can be recovered in this way from the middle equality in (2.7).
$T_\beta$
. We thus conclude that Theorem 2.2 can be recovered in this way from the middle equality in (2.7).
3. The two spectrally one-sided cases
In this section we consider two special cases for which the various components of Theorem 2.2 can be obtained through an explicit characterization. Section 3.1 considers the case that the driving Lévy process Y is spectrally positive, and Section 3.2 its spectrally negative counterpart.
3.1. The spectrally positive case
Suppose that Y is spectrally positive, i.e. it has no downward jumps. Define its Laplace exponent by
![]() $\varphi(\alpha)\,:\!=\, \log {\mathbb E}\exp({-}\alpha Y(1))$
, and
$\varphi(\alpha)\,:\!=\, \log {\mathbb E}\exp({-}\alpha Y(1))$
, and
![]() $\psi(\beta)$
its right-inverse; cf. [Reference Kyprianou17, Section 3.3]. It is well known [Reference Kyprianou17, Section 6.5.2] that, for
$\psi(\beta)$
its right-inverse; cf. [Reference Kyprianou17, Section 3.3]. It is well known [Reference Kyprianou17, Section 6.5.2] that, for
![]() $\zeta\geqslant 0$
,
$\zeta\geqslant 0$
,
By substituting first
![]() $\zeta = \beta$
and then
$\zeta = \beta$
and then
![]() $\zeta = \beta + \omega$
, we obtain from (3.1) and Theorem 2.2 the following expression for the Laplace–Stieltjes transform (LST) of
$\zeta = \beta + \omega$
, we obtain from (3.1) and Theorem 2.2 the following expression for the Laplace–Stieltjes transform (LST) of
![]() $Y_{\beta,\omega}$
.
$Y_{\beta,\omega}$
.
Proposition 3.1. If Y is spectrally positive, then, for
![]() $\alpha\geqslant 0$
,
$\alpha\geqslant 0$
,
Remark 3.1. We also provide an alternative derivation of Proposition 3.1, using a relation with an associated queueing model. First observe that
![]() $Z^-$
is minus the running minimum of Y over an interval between two successive Poisson(
$Z^-$
is minus the running minimum of Y over an interval between two successive Poisson(
![]() $\omega$
) inspection epochs, given that the latter epoch occurs before the killing epoch
$\omega$
) inspection epochs, given that the latter epoch occurs before the killing epoch
![]() $T_\beta$
; such an inspection interval is exp(
$T_\beta$
; such an inspection interval is exp(
![]() $\beta+\omega$
) distributed. Hence,
$\beta+\omega$
) distributed. Hence,
![]() $Z^-$
is exp(
$Z^-$
is exp(
![]() $\psi(\beta+\omega)$
) distributed, just like
$\psi(\beta+\omega)$
) distributed, just like
![]() $-\underline{Y}(T_{\beta+\omega})$
; see, e.g., [Reference Kyprianou17, Section 6.5.2]. Furthermore,
$-\underline{Y}(T_{\beta+\omega})$
; see, e.g., [Reference Kyprianou17, Section 6.5.2]. Furthermore,
Hence, because
![]() $Z = Z^+ - Z^-$
, with
$Z = Z^+ - Z^-$
, with
![]() $Z^+$
and
$Z^+$
and
![]() $Z^-$
being independent,
$Z^-$
being independent,
indeed, cf. (3.1),
![]() $Z^+ \stackrel{{\rm d}} = \overline{Y}(T_{\beta+\omega})$
, as we already noticed in (2.8). Now observe, cf. (2.1), that
$Z^+ \stackrel{{\rm d}} = \overline{Y}(T_{\beta+\omega})$
, as we already noticed in (2.8). Now observe, cf. (2.1), that
![]() $Y_{\beta,\omega}$
can be interpreted as the waiting time of the
$Y_{\beta,\omega}$
can be interpreted as the waiting time of the
![]() $N_{\beta,\omega}$
th customer of an M/G/1 queue with generic interarrival time
$N_{\beta,\omega}$
th customer of an M/G/1 queue with generic interarrival time
![]() $Z^-$
and generic service time
$Z^-$
and generic service time
![]() $Z^+$
, with the first customer arriving in an empty system. Its LST is given by
$Z^+$
, with the first customer arriving in an empty system. Its LST is given by
with
![]() $W_n$
denoting the waiting time of the nth such customer. The next step is to use the expression from [Reference Cohen12, (II.4.77)] for the generating function of
$W_n$
denoting the waiting time of the nth such customer. The next step is to use the expression from [Reference Cohen12, (II.4.77)] for the generating function of
![]() ${\mathbb E} \,{\rm e}^{-\alpha W_n}$
. After some elementary calculations, (3.2) is recovered.
${\mathbb E} \,{\rm e}^{-\alpha W_n}$
. After some elementary calculations, (3.2) is recovered.
Remark 3.2. Considering the special case that the spectrally positive Lévy process is a compound Poisson process, our model corresponds to the Cramér–Lundberg insurance risk model. In particular, taking
![]() $\varphi'(0)>0$
so that eventual ruin is not certain, the LST of
$\varphi'(0)>0$
so that eventual ruin is not certain, the LST of
![]() $Y_{\beta,\omega}$
with
$Y_{\beta,\omega}$
with
![]() $\beta = 0$
immediately yields the LST of the (all-time) bankruptcy probability in the Cramér–Lundberg model with initial capital u. That quantity was studied in [Reference Albrecher and Lautscham6] for exponentially distributed claim sizes, and in [Reference Boxma, Essifi and Janssen10] for generally distributed claim sizes.
$\beta = 0$
immediately yields the LST of the (all-time) bankruptcy probability in the Cramér–Lundberg model with initial capital u. That quantity was studied in [Reference Albrecher and Lautscham6] for exponentially distributed claim sizes, and in [Reference Boxma, Essifi and Janssen10] for generally distributed claim sizes.
Through the duality relation between the Cramér–Lundberg model and its queueing counterpart, our results also provide insight into the M/G/1 queue. In particular, Theorem 2.2 entails for the special case
![]() $\beta=0$
and
$\beta=0$
and
![]() $\varphi'(0)>0$
that the steady-state workload is distributed as the sum of two independent quantities: (i)
$\varphi'(0)>0$
that the steady-state workload is distributed as the sum of two independent quantities: (i)
![]() $\overline{Y}(T_\omega)$
, the supremum of the workload until the first Poisson(
$\overline{Y}(T_\omega)$
, the supremum of the workload until the first Poisson(
![]() $\omega$
) inspection epoch, and (ii)
$\omega$
) inspection epoch, and (ii)
![]() $\overline{Y}_{0,\omega}$
, the steady-state workload (or waiting time) in an M/G/1 queue with
$\overline{Y}_{0,\omega}$
, the steady-state workload (or waiting time) in an M/G/1 queue with
![]() ${\rm exp}(\psi(\omega))$
-distributed interarrival times and service times distributed as the
${\rm exp}(\psi(\omega))$
-distributed interarrival times and service times distributed as the
![]() $Z^+$
defined above (with
$Z^+$
defined above (with
![]() $\beta=0$
).
$\beta=0$
).
Remark 3.3. In many real-life applications, it may be more natural to have inspection intervals that are constant, or at least have a small coefficient of variation, instead of being exponentially distributed. In this remark we outline how we can use the alternative derivation of Proposition 3.1, as described in Remark 3.1, to determine the LST of the running maximum at Erlang(
![]() $k,k \omega$
)-distributed inspection moments, with
$k,k \omega$
)-distributed inspection moments, with
![]() $k\in{\mathbb N}$
. Note that the mean inspection interval still equals
$k\in{\mathbb N}$
. Note that the mean inspection interval still equals
![]() $1/\omega$
, and that its squared coefficient of variation equals
$1/\omega$
, and that its squared coefficient of variation equals
![]() $1/k$
, so that the case of a large k emulates constant inspection intervals. We shall again denote by
$1/k$
, so that the case of a large k emulates constant inspection intervals. We shall again denote by
![]() $Y_{\beta,\omega}$
the running maximum at inspection moments until killing epoch
$Y_{\beta,\omega}$
the running maximum at inspection moments until killing epoch
![]() $T_\beta \sim {\rm exp}(\beta)$
, and by
$T_\beta \sim {\rm exp}(\beta)$
, and by
![]() $N_{\beta,\omega}$
the number of inspections before killing. We now have
$N_{\beta,\omega}$
the number of inspections before killing. We now have
Indeed, the first factor on the right-hand side denotes the probability that at least kn intervals
![]() $ \sim {\rm exp}(k \omega)$
occur before
$ \sim {\rm exp}(k \omega)$
occur before
![]() $T_\beta$
, while the second factor denotes the probability that, subsequently, less than k such exp
$T_\beta$
, while the second factor denotes the probability that, subsequently, less than k such exp
![]() $(k \omega)$
intervals occur, i.e. the (
$(k \omega)$
intervals occur, i.e. the (
![]() $n+1$
)th inspection does not occur before
$n+1$
)th inspection does not occur before
![]() $T_\beta$
.
$T_\beta$
.
Denote by
![]() $Z_1^-,\dots,Z_k^-$
the negatives of the running minima, and by
$Z_1^-,\dots,Z_k^-$
the negatives of the running minima, and by
![]() $Z_1^+,\dots,Z_k^+$
the running maxima, over k consecutive exp(
$Z_1^+,\dots,Z_k^+$
the running maxima, over k consecutive exp(
![]() $k \omega$
) intervals which together compose one inspection interval. Since Y is a spectrally positive Lévy process, it follows that
$k \omega$
) intervals which together compose one inspection interval. Since Y is a spectrally positive Lévy process, it follows that
![]() $Z_1^-,\dots,Z_k^-$
are independent and identically distributed (i.i.d.) exp
$Z_1^-,\dots,Z_k^-$
are independent and identically distributed (i.i.d.) exp
![]() $(\psi(\beta + k \omega))$
distributed. We furthermore note that
$(\psi(\beta + k \omega))$
distributed. We furthermore note that
![]() $Z_1^+,\dots,Z_k^+$
are i.i.d., and the reasoning leading to (3.3) shows that their LST is given by
$Z_1^+,\dots,Z_k^+$
are i.i.d., and the reasoning leading to (3.3) shows that their LST is given by
Moreover, all the
![]() $Z_i^-$
and
$Z_i^-$
and
![]() $Z_j^+$
are independent. Now
$Z_j^+$
are independent. Now
![]() $Y_{\beta,\omega}$
, as a supremum of partial sums
$Y_{\beta,\omega}$
, as a supremum of partial sums
![]() $S_n = \sum_{m=1}^n Z_m$
with
$S_n = \sum_{m=1}^n Z_m$
with
![]() $Z_m = \sum_{i=1}^k Z_{m,i}^+ - \sum_{i=1}^k Z_{m,i}^-$
, can be interpreted as the waiting time of the
$Z_m = \sum_{i=1}^k Z_{m,i}^+ - \sum_{i=1}^k Z_{m,i}^-$
, can be interpreted as the waiting time of the
![]() $N_{\beta,\omega}$
th customer of an E
$N_{\beta,\omega}$
th customer of an E
![]() $_k$
/G/1 queue with generic interarrival time
$_k$
/G/1 queue with generic interarrival time
![]() $\sum_{i=1}^k Z_i^-$
and generic service time
$\sum_{i=1}^k Z_i^-$
and generic service time
![]() $\sum_{i=1}^k Z_i^+$
, with the first customer arriving in an empty system. Its LST, and hence the LST of
$\sum_{i=1}^k Z_i^+$
, with the first customer arriving in an empty system. Its LST, and hence the LST of
![]() $Y_{\beta,\omega}$
, is given by
$Y_{\beta,\omega}$
, is given by
 \begin{equation*} \sum_{n=1}^{\infty} {\mathbb P}(N_{\beta,\omega}=n) \,{\mathbb E} \,{\rm e}^{-\alpha W_n} = \bigg(1 - \bigg(\frac{k \omega}{\beta+k \omega}\bigg)^k \bigg) \sum_{n=1}^{\infty} \bigg(\frac{k \omega}{\beta+k \omega}\bigg)^{kn} {\mathbb E} \,{\rm e}^{-\alpha W_n}. \end{equation*}
\begin{equation*} \sum_{n=1}^{\infty} {\mathbb P}(N_{\beta,\omega}=n) \,{\mathbb E} \,{\rm e}^{-\alpha W_n} = \bigg(1 - \bigg(\frac{k \omega}{\beta+k \omega}\bigg)^k \bigg) \sum_{n=1}^{\infty} \bigg(\frac{k \omega}{\beta+k \omega}\bigg)^{kn} {\mathbb E} \,{\rm e}^{-\alpha W_n}. \end{equation*}
Finally, we can use [Reference Prabhu20, Theorem 25, p. 44] for the generating function of
![]() ${\mathbb E} \,{\rm e}^{-\alpha W_n}$
in the E
${\mathbb E} \,{\rm e}^{-\alpha W_n}$
in the E
![]() $_k$
/G/1 queue.
$_k$
/G/1 queue.
We close this remark by once more focusing on the bankruptcy probability in insurance risk. In Section 2.2 we saw that the probability of bankruptcy before
![]() $T_\beta$
is given by
$T_\beta$
is given by
![]() $\tilde{p}(u,T_\beta) = {\mathbb P}(Y_{\beta, \omega} > u)$
. Hence, the LST of the bankruptcy probability, in the case of a spectrally positive Lévy process and Erlang(
$\tilde{p}(u,T_\beta) = {\mathbb P}(Y_{\beta, \omega} > u)$
. Hence, the LST of the bankruptcy probability, in the case of a spectrally positive Lévy process and Erlang(
![]() $k,k \omega$
) inspection intervals, immediately follows from the LST of
$k,k \omega$
) inspection intervals, immediately follows from the LST of
![]() $Y_{\beta,\omega}$
.
$Y_{\beta,\omega}$
.
Remark 3.4. The decomposition can be used to determine all moments of
![]() $Y_{\beta,\omega}$
from the (known) corresponding moments of
$Y_{\beta,\omega}$
from the (known) corresponding moments of
![]() $\overline Y(T_\beta)$
and
$\overline Y(T_\beta)$
and
![]() $\overline Y(T_{\beta+\omega})$
. In this remark we demonstrate this by providing such a computation for the mean and variance of
$\overline Y(T_{\beta+\omega})$
. In this remark we demonstrate this by providing such a computation for the mean and variance of
![]() $Y_{\beta,\omega}$
. Clearly, it suffices to be able to determine the mean and variance of
$Y_{\beta,\omega}$
. Clearly, it suffices to be able to determine the mean and variance of
![]() $\overline{Y}(T_{\zeta})$
for some
$\overline{Y}(T_{\zeta})$
for some
![]() $\zeta>0$
:
$\zeta>0$
:
 \begin{align} {\mathbb E} \,\overline{Y}(T_\zeta) & = \frac{1}{\psi(\zeta)} - \frac{\varphi'(0)}{\zeta} ,\\[3pt]
{\mathbb V}{\rm ar}\, \overline{Y}(T_\zeta) & = \frac{\varphi''(0)}{\zeta} + \bigg(\frac{\varphi'(0)}{\zeta}\bigg)^2 - \bigg(\frac{1}{\psi(\zeta)}\bigg)^2. \nonumber\end{align}
\begin{align} {\mathbb E} \,\overline{Y}(T_\zeta) & = \frac{1}{\psi(\zeta)} - \frac{\varphi'(0)}{\zeta} ,\\[3pt]
{\mathbb V}{\rm ar}\, \overline{Y}(T_\zeta) & = \frac{\varphi''(0)}{\zeta} + \bigg(\frac{\varphi'(0)}{\zeta}\bigg)^2 - \bigg(\frac{1}{\psi(\zeta)}\bigg)^2. \nonumber\end{align}
Due to the independence of the terms on the right-hand side of the decomposition of Theorem 2.2, the mean and variance of
![]() $Y_{\beta,\omega}$
immediately follow by successively plugging in
$Y_{\beta,\omega}$
immediately follow by successively plugging in
![]() $\zeta = \beta$
and
$\zeta = \beta$
and
![]() $\zeta = \beta + \omega$
, and subtracting the resulting expressions.
$\zeta = \beta + \omega$
, and subtracting the resulting expressions.
3.2. The spectrally negative case
Suppose that Y is spectrally negative, i.e. it has no upward jumps. Consider an exp(
![]() $\zeta$
)-distributed interval. Define the cumulant
$\zeta$
)-distributed interval. Define the cumulant
![]() $\Phi(\alpha) \,:\!=\, \log {\mathbb E} \exp({\alpha Y(1)})$
and its right-inverse
$\Phi(\alpha) \,:\!=\, \log {\mathbb E} \exp({\alpha Y(1)})$
and its right-inverse
![]() $\Psi(\beta)$
. As follows directly from, e.g., [Reference Kyprianou17, Section 6.5.2], the running maximum
$\Psi(\beta)$
. As follows directly from, e.g., [Reference Kyprianou17, Section 6.5.2], the running maximum
![]() $\overline Y (T_\zeta)$
is exponentially distributed with rate
$\overline Y (T_\zeta)$
is exponentially distributed with rate
![]() $\Psi(\zeta)$
. Using this result with
$\Psi(\zeta)$
. Using this result with
![]() $\zeta = \beta$
and
$\zeta = \beta$
and
![]() $\zeta = \beta + \omega$
, and applying Theorem 2.2, we obtain an expression for the LST of
$\zeta = \beta + \omega$
, and applying Theorem 2.2, we obtain an expression for the LST of
![]() $Y_{\beta,\omega}$
in the spectrally negative case.
$Y_{\beta,\omega}$
in the spectrally negative case.
Proposition 3.2. If Y is spectrally negative, then, for
![]() $\alpha\geqslant 0$
,
$\alpha\geqslant 0$
,
Using Proposition 3.2, an elementary computation reveals that
![]() $Y_{\beta,\omega}$
has an atom at zero, i.e.
$Y_{\beta,\omega}$
has an atom at zero, i.e.
and is exp(
![]() $\Psi(\beta)$
) distributed with the complementary probability
$\Psi(\beta)$
) distributed with the complementary probability
![]() $1-{\mathbb P}(Y_{\beta,\omega} = 0)$
.
$1-{\mathbb P}(Y_{\beta,\omega} = 0)$
.
Remark 3.5. Just like in Remark 3.1, we could also have obtained the LST of
![]() $Y_{\beta,\omega}$
by observing that
$Y_{\beta,\omega}$
by observing that
![]() $Y_{\beta,\omega}$
can be interpreted as the waiting time of the
$Y_{\beta,\omega}$
can be interpreted as the waiting time of the
![]() $N_{\beta,\omega}$
th customer in a single-server queue with generic interarrival time
$N_{\beta,\omega}$
th customer in a single-server queue with generic interarrival time
![]() $Z^-$
and generic service time
$Z^-$
and generic service time
![]() $Z^+$
, with the first customer arriving in an empty system. In this case
$Z^+$
, with the first customer arriving in an empty system. In this case
![]() $Z^+$
is exp(
$Z^+$
is exp(
![]() $\Psi(\beta + \omega)$
) distributed. Hence, we can now use [Reference Cohen12, (II.3.100)] for the generating function
$\Psi(\beta + \omega)$
) distributed. Hence, we can now use [Reference Cohen12, (II.3.100)] for the generating function
![]() $\sum_{n=1}^{\infty} r^n \mathbb{P}(W_n < s)$
, with
$\sum_{n=1}^{\infty} r^n \mathbb{P}(W_n < s)$
, with
![]() $W_n$
denoting the waiting time of the nth customer in the G/M/1 queue. We close this remark by observing that
$W_n$
denoting the waiting time of the nth customer in the G/M/1 queue. We close this remark by observing that
![]() $Y_{0,\omega}$
is distributed as the steady-state waiting time (if it exists) in the above-described G/M/1 queue; that waiting time is also exponentially distributed with an atom at zero.
$Y_{0,\omega}$
is distributed as the steady-state waiting time (if it exists) in the above-described G/M/1 queue; that waiting time is also exponentially distributed with an atom at zero.
4. Asymptotics in the compound Poisson setting
In this section we demonstrate the potential of our results by using them to establish the asymptotics of the bankruptcy probability for large initial capital u. The driving Lévy process is a compound Poisson process with drift, characterized through its Laplace exponent
![]() $\varphi(\alpha) = r \alpha - \lambda(1-b(\alpha))$
; here,
$\varphi(\alpha) = r \alpha - \lambda(1-b(\alpha))$
; here,
![]() $\lambda$
can be viewed as the claim arrival rate, r as the premium rate, and
$\lambda$
can be viewed as the claim arrival rate, r as the premium rate, and
![]() $b({\cdot})$
as the LST of a generic claim size B. We are interested in the behavior of
$b({\cdot})$
as the LST of a generic claim size B. We are interested in the behavior of
![]() $\tilde p(u)={\mathbb P}(Y_{0,\omega} > u)$
for large u, which can be interpreted as the bankruptcy probability in the Cramér–Lundberg insurance risk model for large initial capital u. We assume that
$\tilde p(u)={\mathbb P}(Y_{0,\omega} > u)$
for large u, which can be interpreted as the bankruptcy probability in the Cramér–Lundberg insurance risk model for large initial capital u. We assume that
![]() $\lambda \,{\mathbb E} B < r$
, as otherwise ruin and bankruptcy are certain. Section 4.1 treats the case of a light-tailed jump-size distribution, and Section 4.2 that of a heavy-tailed jump-size distribution. Here, light-tailed means that
$\lambda \,{\mathbb E} B < r$
, as otherwise ruin and bankruptcy are certain. Section 4.1 treats the case of a light-tailed jump-size distribution, and Section 4.2 that of a heavy-tailed jump-size distribution. Here, light-tailed means that
![]() $b(\alpha)$
is finite for some
$b(\alpha)$
is finite for some
![]() $\alpha <0$
or, equivalently, that
$\alpha <0$
or, equivalently, that
![]() ${\mathbb P}(B>x) = O({\rm e}^{-ax})$
for some
${\mathbb P}(B>x) = O({\rm e}^{-ax})$
for some
![]() $a>0$
. Heavy-tailed means that
$a>0$
. Heavy-tailed means that
![]() $b(\alpha)$
is infinite for all
$b(\alpha)$
is infinite for all
![]() $\alpha <0$
; we shall restrict ourselves to the well-known subclass
$\alpha <0$
; we shall restrict ourselves to the well-known subclass
![]() ${\mathscr S}^\star$
.
${\mathscr S}^\star$
.
4.1. The bankruptcy probability in the light-tailed case
We assume in this subsection that B is light-tailed in the sense that there is a unique strictly positive solution
![]() $\theta^\star$
of the equation
$\theta^\star$
of the equation
![]() $\varphi({-}\theta^\star)=0$
. Our aim is to identify the asymptotic behavior of
$\varphi({-}\theta^\star)=0$
. Our aim is to identify the asymptotic behavior of
![]() $\tilde p(u)$
, and to compare it to the classic result for the asymptotic ruin probability p(u) in the same model (which coincides with the asymptotic behavior of the waiting-time tail in the dual M/G/1 queue). The well-known Cramér–Lundberg approximation [Reference Asmussen and Albrecher7, Theorem 5.3] states that
$\tilde p(u)$
, and to compare it to the classic result for the asymptotic ruin probability p(u) in the same model (which coincides with the asymptotic behavior of the waiting-time tail in the dual M/G/1 queue). The well-known Cramér–Lundberg approximation [Reference Asmussen and Albrecher7, Theorem 5.3] states that
with
![]() $f(u)\sim g(u)$
denoting
$f(u)\sim g(u)$
denoting
![]() $f(u)/g(u)\to 1$
as
$f(u)/g(u)\to 1$
as
![]() $u\to\infty$
, and
$u\to\infty$
, and
To determine the asymptotics of
![]() $\tilde{p}(u)$
we return to an observation made in Remark 3.1:
$\tilde{p}(u)$
we return to an observation made in Remark 3.1:
![]() $Y_{\beta,\omega}$
can be interpreted as the waiting time of the
$Y_{\beta,\omega}$
can be interpreted as the waiting time of the
![]() $N_{\beta,\omega}$
th customer of an M/G/1 queue with generic (exponentially distributed) interarrival time
$N_{\beta,\omega}$
th customer of an M/G/1 queue with generic (exponentially distributed) interarrival time
![]() $Z^-$
and generic service time
$Z^-$
and generic service time
![]() $Z^+$
. For
$Z^+$
. For
![]() $\beta=0$
,
$\beta=0$
,
![]() $Y_{0,\omega}$
becomes the steady-state waiting time for that queue. Notice that
$Y_{0,\omega}$
becomes the steady-state waiting time for that queue. Notice that
![]() ${\mathbb E}Z^- = 1/\psi(\omega)$
while, as
${\mathbb E}Z^- = 1/\psi(\omega)$
while, as
![]() $Z^+$
is distributed as
$Z^+$
is distributed as
![]() $\overline{Y}(T_{\omega})$
, it follows from (3.4) that
$\overline{Y}(T_{\omega})$
, it follows from (3.4) that
![]() ${\mathbb E}Z^+ = 1/\psi(\omega) - \varphi'(0)/\omega$
. As
${\mathbb E}Z^+ = 1/\psi(\omega) - \varphi'(0)/\omega$
. As
![]() $\varphi'(0) = r-\lambda {\mathbb E} B > 0$
, we have
$\varphi'(0) = r-\lambda {\mathbb E} B > 0$
, we have
![]() ${\mathbb E} Z^- > {\mathbb E} Z^+$
, so the steady-state waiting-time distribution indeed exists. As a consequence, we can (again) rely on the Cramér–Lundberg approximation, or (equivalently) the tail asymptotics of the M/G/1 queue with generic interarrival time
${\mathbb E} Z^- > {\mathbb E} Z^+$
, so the steady-state waiting-time distribution indeed exists. As a consequence, we can (again) rely on the Cramér–Lundberg approximation, or (equivalently) the tail asymptotics of the M/G/1 queue with generic interarrival time
![]() $Z^-$
and generic service time
$Z^-$
and generic service time
![]() $Z^+$
, cf. (4.1):
$Z^+$
, cf. (4.1):
![]() $\tilde{p}(u) \sim \tilde{\gamma} {\rm e}^{-\tilde{\theta}^\star u}$
,
$\tilde{p}(u) \sim \tilde{\gamma} {\rm e}^{-\tilde{\theta}^\star u}$
,
![]() $u \rightarrow \infty$
. Our next task is to determine the constants
$u \rightarrow \infty$
. Our next task is to determine the constants
![]() $\tilde{\theta}^\star$
and
$\tilde{\theta}^\star$
and
![]() $\tilde{\gamma}$
. The customer arrival rate in the auxiliary M/G/1 queue is
$\tilde{\gamma}$
. The customer arrival rate in the auxiliary M/G/1 queue is
![]() $1/{\mathbb E}Z^- = \psi(\omega$
), the generic service time
$1/{\mathbb E}Z^- = \psi(\omega$
), the generic service time
![]() $Z^+$
has LST (cf. (3.3))
$Z^+$
has LST (cf. (3.3))
and the service speed or premium rate equals one. Hence,
![]() $\tilde{\theta}^\star$
is the unique positive solution of
$\tilde{\theta}^\star$
is the unique positive solution of
![]() $\tilde{\varphi}({-}\tilde{\theta}^\star)=0$
, with
$\tilde{\varphi}({-}\tilde{\theta}^\star)=0$
, with
![]() $\tilde{\varphi}(\alpha) \,:\!=\, \alpha - \psi(\omega)(1 - {\mathbb E}\,{\rm e}^{-\alpha Z^+})$
:
$\tilde{\varphi}(\alpha) \,:\!=\, \alpha - \psi(\omega)(1 - {\mathbb E}\,{\rm e}^{-\alpha Z^+})$
:
It readily follows that
![]() $\tilde{\theta}^\star = \theta^\star$
satisfies this equation (as
$\tilde{\theta}^\star = \theta^\star$
satisfies this equation (as
![]() $\varphi({-}\theta^\star)=0$
), while otherwise there is only the negative solution
$\varphi({-}\theta^\star)=0$
), while otherwise there is only the negative solution
![]() $\tilde{\theta}^\star = - \psi(\omega)$
. The implication is that the bankruptcy probability
$\tilde{\theta}^\star = - \psi(\omega)$
. The implication is that the bankruptcy probability
![]() $\tilde{p}(u)$
has the same decay rate
$\tilde{p}(u)$
has the same decay rate
![]() $\theta^\star$
as the ruin probability p(u).
$\theta^\star$
as the ruin probability p(u).
Let us now determine the prefactor
![]() $\tilde{\gamma}$
. Using (4.2) with
$\tilde{\gamma}$
. Using (4.2) with
![]() $\varphi(\alpha)$
replaced by
$\varphi(\alpha)$
replaced by
![]() $\tilde{\varphi}(\alpha)$
, we find:
$\tilde{\varphi}(\alpha)$
, we find:
A brief calculation, using (4.2), results in
We have established the main result of this subsection.
Proposition 4.1. Assume B is light-tailed. As
![]() $u\to\infty$
,
$u\to\infty$
,
This result shows that
![]() $\gamma^\star_\omega\uparrow 1$
as the inspection rate
$\gamma^\star_\omega\uparrow 1$
as the inspection rate
![]() $\omega$
grows large. In addition, using that
$\omega$
grows large. In addition, using that
![]() $\varphi(\alpha)-r\alpha +\lambda\to 0$
as
$\varphi(\alpha)-r\alpha +\lambda\to 0$
as
![]() $\alpha\to\infty$
implies that
$\alpha\to\infty$
implies that
![]() $\psi(\theta)- (\theta+\lambda)/r\to 0$
as
$\psi(\theta)- (\theta+\lambda)/r\to 0$
as
![]() $\theta\to\infty$
, it can be verified that
$\theta\to\infty$
, it can be verified that
![]() $\lim_{\omega\to\infty}\omega(1-\gamma^\star_\omega) = r\theta^\star$
, which means that, for
$\lim_{\omega\to\infty}\omega(1-\gamma^\star_\omega) = r\theta^\star$
, which means that, for
![]() $\omega$
large,
$\omega$
large,
![]() $\gamma^\star_\omega$
behaves as
$\gamma^\star_\omega$
behaves as
![]() $1- r\theta^\star/\omega$
. This relation can be used to determine a ‘rule of thumb’ by which one can determine the minimally required inspection rate
$1- r\theta^\star/\omega$
. This relation can be used to determine a ‘rule of thumb’ by which one can determine the minimally required inspection rate
![]() $\omega$
such that the information loss due to Poisson inspection is below a given threshold.
$\omega$
such that the information loss due to Poisson inspection is below a given threshold.
4.2. The bankruptcy probability in the heavy-tailed case
In this subsection we study the asymptotic behavior of the bankruptcy probability when B is heavy-tailed. More specifically, we assume that
![]() $B \in {\mathscr S}^\star$
, a class introduced in [Reference Klüppelberg16]. A random variable U on
$B \in {\mathscr S}^\star$
, a class introduced in [Reference Klüppelberg16]. A random variable U on
![]() ${\mathbb R}$
belongs to
${\mathbb R}$
belongs to
![]() ${\mathscr S}^\star$
if and only if its complementary distribution function
${\mathscr S}^\star$
if and only if its complementary distribution function
![]() $\overline F_U(x)\,:\!=\,{\mathbb P}(U>x)$
is positive for all x, and
$\overline F_U(x)\,:\!=\,{\mathbb P}(U>x)$
is positive for all x, and
![]() $\int_0^x \overline{F}_U(x-y) \overline{F}_U(y) \,{\rm d}y \sim 2 m_U\, \overline{F}_U(x)$
as
$\int_0^x \overline{F}_U(x-y) \overline{F}_U(y) \,{\rm d}y \sim 2 m_U\, \overline{F}_U(x)$
as
![]() $x \rightarrow \infty$
; here,
$x \rightarrow \infty$
; here,
![]() $m_U$
denotes the mean of U, restricted to the positive half-axis.
$m_U$
denotes the mean of U, restricted to the positive half-axis.
![]() ${\mathscr S}^\star$
is a class that is contained in, but is also very close to, the well-known class
${\mathscr S}^\star$
is a class that is contained in, but is also very close to, the well-known class
![]() ${\mathscr S}$
of subexponential distributions. The class
${\mathscr S}$
of subexponential distributions. The class
![]() ${\mathscr S}^\star$
has the convenient property that if
${\mathscr S}^\star$
has the convenient property that if
![]() $U \in {\mathscr S}^\star$
then both U and
$U \in {\mathscr S}^\star$
then both U and
![]() $U^{{\rm res}}$
, the latter random variable being characterized through
$U^{{\rm res}}$
, the latter random variable being characterized through
are subexponential.
In our analysis of the asymptotics of
![]() $\tilde p(u)$
, we shall use a well-known result from [Reference Embrechts, Klüppelberg and Mikosch14] concerning the supremum
$\tilde p(u)$
, we shall use a well-known result from [Reference Embrechts, Klüppelberg and Mikosch14] concerning the supremum
![]() $M_{\sigma}$
of a random walk
$M_{\sigma}$
of a random walk
![]() $\{S_n\}_{n\in{\mathbb N}}$
over an interval
$\{S_n\}_{n\in{\mathbb N}}$
over an interval
![]() $[0,\sigma]$
, with
$[0,\sigma]$
, with
![]() $\sigma$
some random variable (see also [Reference Foss and Zachary15, Theorem 1] for the more general case of
$\sigma$
some random variable (see also [Reference Foss and Zachary15, Theorem 1] for the more general case of
![]() $\sigma$
being a stopping time, and [Reference Asmussen and Albrecher7, p. 309] for the special case of a constant
$\sigma$
being a stopping time, and [Reference Asmussen and Albrecher7, p. 309] for the special case of a constant
![]() $\sigma$
). If the increments of the random walk are in
$\sigma$
). If the increments of the random walk are in
![]() ${\mathscr S}^\star$
, with distribution function
${\mathscr S}^\star$
, with distribution function
![]() $F({\cdot})$
and complementary distribution function
$F({\cdot})$
and complementary distribution function
![]() $\overline F({\cdot})$
, then
$\overline F({\cdot})$
, then
Notice that the increments attain values in
![]() ${\mathbb R}$
, i.e. not necessarily in
${\mathbb R}$
, i.e. not necessarily in
![]() ${\mathbb R}^+$
. If we take
${\mathbb R}^+$
. If we take
![]() $F({\cdot})$
to be the distribution function of a claim size minus a claim interarrival time, then we can apply (4.4) by considering the random number of claim arrivals in an exp(
$F({\cdot})$
to be the distribution function of a claim size minus a claim interarrival time, then we can apply (4.4) by considering the random number of claim arrivals in an exp(
![]() $\omega$
) interval. This yields:
$\omega$
) interval. This yields:
In order to use this result to determine the asymptotic behavior of the bankruptcy probability, we observe the following:
-
(i)
 $\overline{Y}(T_\omega)$
has the same distribution as
$\overline{Y}(T_\omega)$
has the same distribution as
 $Z^+$
, cf. (2.8) with
$Z^+$
, cf. (2.8) with
 $\beta = 0$
. Hence,
$\beta = 0$
. Hence,
 $Z^+ \in {\mathscr S}^\star$
, and
$Z^+ \in {\mathscr S}^\star$
, and
 $Z^{+,{\rm res}}$
is subexponential.
$Z^{+,{\rm res}}$
is subexponential. -
(ii)
 $Y_{0,\omega}$
can be viewed as the steady-state waiting time in an M/G/1 queue with generic service time
$Y_{0,\omega}$
can be viewed as the steady-state waiting time in an M/G/1 queue with generic service time
 $Z^+$
and arrival rate
$Z^+$
and arrival rate
 $\psi(\omega)$
, so with load
$\psi(\omega)$
, so with load
 $\rho \,:\!=\, {\mathbb E}Z^+/{\mathbb E}Z^-$
. Hence, we can use a standard result for the waiting-time tail in the M/G/1 queue, in which the residual service time
$\rho \,:\!=\, {\mathbb E}Z^+/{\mathbb E}Z^-$
. Hence, we can use a standard result for the waiting-time tail in the M/G/1 queue, in which the residual service time
 $Z^{+,{\rm res}}$
is subexponential:
This result holds equivalently for the ruin probability in the dual Cramér–Lundberg model, see, e.g., [Reference Asmussen and Albrecher7, Theorem X.2.1], and hence we conclude that
$Z^{+,{\rm res}}$
is subexponential:
This result holds equivalently for the ruin probability in the dual Cramér–Lundberg model, see, e.g., [Reference Asmussen and Albrecher7, Theorem X.2.1], and hence we conclude that \begin{equation*} {\mathbb P}(Y_{0,\omega} >u) \sim \frac{\rho}{1-\rho} {\mathbb P}(Z^{+,{\rm res}}>u). \end{equation*}
Here, the last equality follows using
\begin{equation*} {\mathbb P}(Y_{0,\omega} >u) \sim \frac{\rho}{1-\rho} {\mathbb P}(Z^{+,{\rm res}}>u). \end{equation*}
Here, the last equality follows using \begin{align*} \tilde{p}(u) = {\mathbb P}(Y_{0,\omega} >u) & \sim \frac{{\mathbb E} Z^+}{{\mathbb E}Z^- - {\mathbb E} Z^+} {\mathbb P}(Z^{+,{\rm res}} >u) \\ & = \frac{1}{{\mathbb E}Z^- - {\mathbb E}Z^+} \int_u^{\infty} {\mathbb P}(Z^+ >y)\, {\rm d} y \\ & = \frac{\omega}{r - \lambda {\mathbb E}B} \int_u^{\infty} \frac{\lambda}{\omega}\, {\mathbb P}(B>y)\, {\rm d} y . \end{align*}
\begin{align*} \tilde{p}(u) = {\mathbb P}(Y_{0,\omega} >u) & \sim \frac{{\mathbb E} Z^+}{{\mathbb E}Z^- - {\mathbb E} Z^+} {\mathbb P}(Z^{+,{\rm res}} >u) \\ & = \frac{1}{{\mathbb E}Z^- - {\mathbb E}Z^+} \int_u^{\infty} {\mathbb P}(Z^+ >y)\, {\rm d} y \\ & = \frac{\omega}{r - \lambda {\mathbb E}B} \int_u^{\infty} \frac{\lambda}{\omega}\, {\mathbb P}(B>y)\, {\rm d} y . \end{align*}
 ${\mathbb E}Z^- = 1/\psi(\omega)$
and (cf. (3.4))
${\mathbb E}Z^- = 1/\psi(\omega)$
and (cf. (3.4))
 ${\mathbb E}Z^+ = 1/\psi(\omega) - \varphi'(0)/\omega$
with
${\mathbb E}Z^+ = 1/\psi(\omega) - \varphi'(0)/\omega$
with
 $\varphi'(0) = r-\lambda {\mathbb E}B >0$
, and applying (4.5).
$\varphi'(0) = r-\lambda {\mathbb E}B >0$
, and applying (4.5).
Combining (i) and (ii) yields the main result of this subsection.
Proposition 4.2. Assume
![]() $B\in {\mathscr S}^\star$
. As
$B\in {\mathscr S}^\star$
. As
![]() $u\to\infty$
,
$u\to\infty$
,
Notice, looking at the statement in (ii) above regarding the tail behavior in an M/G/1 queue, that
![]() $\tilde p(u)$
has the exact same tail asymptotics as p(u). In particular, the asymptotics of
$\tilde p(u)$
has the exact same tail asymptotics as p(u). In particular, the asymptotics of
![]() $\tilde p(u)$
do not depend on the inspection rate
$\tilde p(u)$
do not depend on the inspection rate
![]() $\omega$
. This may look surprising at first sight, but realize that for
$\omega$
. This may look surprising at first sight, but realize that for
![]() $B\in {\mathscr S}^\star$
there is the intuition that ‘a single big jump’ is responsible (with overwhelming probability as
$B\in {\mathscr S}^\star$
there is the intuition that ‘a single big jump’ is responsible (with overwhelming probability as
![]() $u\to\infty$
) for exceeding a high level. This suggests that when ruin occurs, it is highly likely that the capital is still below zero at the next inspection moment.
$u\to\infty$
) for exceeding a high level. This suggests that when ruin occurs, it is highly likely that the capital is still below zero at the next inspection moment.
Remark 4.1. In the special heavy-tailed case of regularly varying claim sizes, we can identify the tail asymptotics of
![]() $\tilde{p}(u)$
in a more straightforward way by applying [Reference Bingham, Goldie and Teugels9, Theorem 8.1.6] to the LST of
$\tilde{p}(u)$
in a more straightforward way by applying [Reference Bingham, Goldie and Teugels9, Theorem 8.1.6] to the LST of
![]() $Y_{0,\omega}$
(as given by (3.5) with
$Y_{0,\omega}$
(as given by (3.5) with
![]() $\beta=0$
).
$\beta=0$
).
Remark 4.2. As suggested in [Reference Albrecher1], we could alternatively obtain the asymptotics of this section via [Reference Albrecher and Ivanovs4, (2)], which in our notation reads as
![]() $\tilde{p}(u) = {\mathbb E} \, p(u+Z^-)$
(see also (2.6)). Use dominated convergence to take the limit inside the expectation of this equation, and observe that
$\tilde{p}(u) = {\mathbb E} \, p(u+Z^-)$
(see also (2.6)). Use dominated convergence to take the limit inside the expectation of this equation, and observe that
![]() $Z^-$
is exp
$Z^-$
is exp
![]() $(\psi(\omega))$
distributed in this spectrally positive case. In the light-tailed case we can then see that
$(\psi(\omega))$
distributed in this spectrally positive case. In the light-tailed case we can then see that
![]() $\tilde{\theta}^\star = \theta^\star$
and that
$\tilde{\theta}^\star = \theta^\star$
and that
![]() $\tilde{\gamma} = \gamma {\mathbb E} \,{\rm e}^{-\theta^\star Z^-}$
, thus yielding (4.3). In the heavy-tailed case the following holds for a subexponential random variable
$\tilde{\gamma} = \gamma {\mathbb E} \,{\rm e}^{-\theta^\star Z^-}$
, thus yielding (4.3). In the heavy-tailed case the following holds for a subexponential random variable
![]() $X\,:\,{\mathbb P}(X>u) \sim {\mathbb P}(X>u+Z^-)$
, and hence the subexponential asymptotics for the continuously observed and discretely observed processes are the same.
$X\,:\,{\mathbb P}(X>u) \sim {\mathbb P}(X>u+Z^-)$
, and hence the subexponential asymptotics for the continuously observed and discretely observed processes are the same.
5. Discussion and concluding remarks
The main finding presented in this work is a decomposition result involving the running maximum value of a Lévy process at Poisson inspection times as well as the running maximum of the continuously observed process. It allows the translation of known results for the continuously observed process in terms of the Poisson-observed process; such a translation procedure has been followed to find an explicit characterization of the running maximum value of spectrally one-sided Lévy processes at Poisson inspection times, and to find tail asymptotics of the bankruptcy probability in the celebrated Cramér–Lundberg model.
Many extensions can be conceived. In the first place, we could think of the inter-inspection times being phase-type; to this end, ideas from [Reference Boxma and Mandjes11, Section 5.1] and [Reference Asmussen and Ivanovs8] could potentially be used. It would also be interesting to see whether we can have similar decompositions to Theorem 2.2 for overshoots, cf. [Reference Albrecher and Ivanovs4]. From a practical perspective, it would further be relevant to allow the inspection rate to depend on the process level. Finally, the connection with Poisson-observed Lévy-driven storage systems can be explored, e.g. to study whether the results in the present paper can be used for hypothesis testing purposes [Reference Mandjes and Ravner19].
Acknowledgement
The authors thank Hansjoerg Albrecher and Jevgenijs Ivanovs for various useful comments.
Funding information
This research is partly funded by the NWO Gravitation project Networks, grant number 024.002.003.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.