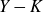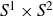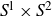Null-homotopic knots have Property R

Abstract

We prove that if K is a nontrivial null-homotopic knot in a closed oriented 3–manfiold Y such that $Y-K$ does not have an $S^1\times S^2$ summand, then the zero surgery on K does not have an $S^1\times S^2$ summand. This generalises a result of Hom and Lidman, who proved the case when Y is an irreducible rational homology sphere.

1. Introduction

Given a null-homologous knot K in a 3–manifold Y and a slope $p/q\in\mathbb Q\cup\{\infty\}$ , let $Y_{p/q}(K)$ be the $p/q$ –surgery on K. Gabai’s famous Property R Theorem [ 6 ] asserts, among others, that if K is a nontrivial knot in $S^3$ , then $S^3_0(K)$ is irreducible. In particular, $S^3_0(K)$ does not have an $S^1\times S^2$ summand.

In recently years, many generalisations of this theorem have been proved using Heegaard Floer homology. See, for example, the overview in [ 14 ]. Hom and Lidman [ 9 ] proved two generalisations of Property R. One result they proved is, if K is a nontrivial null-homotopic knot in an irreducible rational homology sphere Y, then $Y_0(K)$ does not have an $S^1\times S^2$ summand. The aim of this paper to remove the restrictions on the ambient manifold.

Theorem 1·1. Let Y be a closed, oriented, connected 3–manifold, and $K\subset Y$ be a nontrivial null-homotopic knot such that $Y-K$ does not have an $S^1\times S^2$ summand, then $Y_0(K)$ does not have an $S^1\times S^2$ summand.

In Gabai’s work [ 6 ], it is proved that $S^3_0(K)$ remembers the information of K about the genus and fiberedness. Motivated by this result, a concept “Property G” was introduced in [ 13 ] as a generalisation of Property R. Known results on Property G are summarised in [ 14 ]. We will not give the complete definition of Property G here. Instead, we just state the explicit result for genus–1 null-homotopic knot.

Corollary 1·2. Let $K\subset Y$ be a genus–1 null-homotopic knot, then K has Property G. That is, if F is a genus–1 Seifert surface bounded by K, and $\widehat{F}\subset Y_0(K)$ is the torus obtained by capping off $\partial F$ with a disk, then $[\widehat F]\in H_2(Y_0(K))$ is not represented by a sphere. Moreover, if $Y_0(K)$ is a torus bundle over $S^1$ with fiber $\widehat{F}$ , then K is a fibered knot with fiber F.

Corollary 1·2 answers the genus–1 case of a question of Boileau [ 10 , problem 1·80C]. There are easy counterexamples to the original question of Boileau, so one should modify the question to add the condition on the fiber of the zero surgery. See [ 12 ] for more details.

The strategy of the proof of Theorem 1·1 is as follows. If $b_1(Y)>0$ , the theorem easily follows from a result of Lackenby [ 11 ] and Gabai [ 5 ]. If $b_1(Y)=0$ , we use results about degree-one maps and a result in [ 4 ] to show that if $Y_0(K)=Z\#(S^1\times S^2)$ then $\pi_1(Z)\cong\pi_1(Y)$ . Theorem 1·1 then follows from work of Hom and Lidman [ 9 ].

We will use the following notation. If N is a submanifold of a manifold M, let $\nu(N)$ be a closed tubular neighbourhood of N, and let $\nu^{\circ}(N)$ be the interior of $\nu(N)$ . If X, Y are two spaces, $f\,{:}\,X\to Y$ is a continuous map, let $f_*\,{:}\,\pi_1(X)\to \pi_1(Y)$ be the induced map. We will always suppress the base point in the notation when we talk about fundamental groups.

This paper is organised as follows. In Section 2, we prove general results about degree-one maps with certain properties on the induced homomorphisms on $\pi_1$ . In Section 3, we prove that if the zero surgery on a knot in Y is $Z\#(S^1\times S^2)$ , then $\pi_1(Z)\cong\pi_1(Y)$ . In Section 4, we use work of Lackenby [ 11 ] and Hom–Lidman [ 9 ] to prove Theorem 1·1. Corollary 1·2 is also proved as an application of this theorem.

2. Degree-one maps which induce surface-group injective homomorphisms

In this section, we will prove results about degree-one maps which induce surface-group injective homomorphisms on $\pi_1$ .

A group $\Gamma$ is a surface group if it is isomorphic to the fundamental group of a closed orientable surface. Let $\varphi\,{:}\, G\to H$ be a group homomorphism. We say $\varphi$ is surface-group injective, if the restriction of $\varphi$ to every surface subgroup of G is injective.

Lemma 2·1. Let $\varphi\,{:}\, G_1*G_2\to H$ be a group homomorphism. If both $\varphi|_{G_1}$ and $\varphi|_{G_2}$ are surface-group injective, then $\varphi$ is also surface-group injective.

Proof. Let $\Gamma$ be a surface subgroup of $G_1*G_2$ . By the Kurosh Subgroup Theorem [ 8 , theorem 8·3], $\Gamma$ is the free product of a free group and conjugates of subgroups of $G_i$ , $i=1,2$ . Since $\Gamma$ is not a nontrivial free product, it is conjugated to a subgroup of $G_i$ for some i. Since $\varphi|_{G_i}$ is surface-group injective, $\varphi$ is also injective on $\Gamma$ .

The importance of the concept of surface-group injective maps is illustrated by the next lemma.

Lemma 2·2. Let X, Y be closed, oriented, connected 3–manifolds, $f\,{:}\,X\to Y$ be a surjective map such that $f_*$ is surface-group injective. Let $S\subset Y$ be a separating 2–sphere, and assume that $R=f^{-1}(S)$ is a closed, oriented, connected surface. Then there exists a separating 2–sphere $E\subset X$ so that R is obtained by adding tubes to E.

Proof. Let $\iota\,{:}\, R\to X$ be the inclusion map. Since $f(R)=S$ is a sphere,

\begin{align*}\iota_*(\pi_1(R))\subset\ker f_*.\end{align*}

If R is not a sphere, since $f_*$ is surface-group injective, R must be compressible. Let R $^{\prime}$ be the surface obtained by compressing R, then R can be obtained from R $^{\prime}$ by adding a tube. Let $R_1^{\prime}$ be a component of R $^{\prime}$ , let $\iota'\,{:}\, R_1^{\prime}\to X$ be the inclusion map, then

\begin{align*}\iota^{\prime}_*(\pi_1(R_1^{\prime}))=\iota_*(\pi_1(R_1^{\prime}\cap R))\subset\iota_*(\pi_1(R))\subset\ker f_*.\end{align*}

If R $^{\prime}$ does not consist of spheres, since $f_*$ is surface-group injective, R $^{\prime}$ must be compressible. So R $^{\prime}$ can be obtained from another surface R $^{\prime\prime}$ by adding a tube.

Continue with the above process, we conclude that R can be obtained from some spheres by adding tubes. We can rearrange the order of the tubes, so that some tubes connecting different spheres are added first to get a single sphere E, then R is obtained by adding other tubes to E.

Let $y_1,y_2\in Y$ be two points separated by S. Since f is surjective, both $f^{-1}(y_1)$ and $f^{-1}(y_2)$ are non-empty. These two sets are clearly separated by R, so R is separating. The process of compressing a surface does not change the homology class of the surface, hence E is also separating.

In the rest of this section, let Y be a 3–manifold which has no $S^1\times S^2$ summand, $S_1,S_2,\dots,S_n$ be a collection of disjoint 2–spheres in Y satisfying the following conditions: $Y\setminus (\cup_{i=1}^n S_i)$ has $n+1$ components whose closures are $\check Y_1,\check Y_2,\dots,\check Y_n,\check Y_{n+1}$ , where $\check Y_{n+1}$ is $S^3$ with n open balls removed, and a closed irreducible manifold $Y_i\ne S^3$ can be obtained from $\check Y_i$ by capping off $\partial\check Y_i=S_i$ with a ball $B_i$ , $1\le i\le n$ . Then

\begin{align*}Y=\#_{i=1}^nY_i.\end{align*}

When Y is irreducible, it is understood that $n=0$ .

Proposition 2·3. Let X be a closed, oriented, connected 3–manifold, and $f\,{:}\,X\to Y$ be a degree-one map such that $f_*$ is surface-group injective. Then there exists a degree-one map $g\,{:}\, X\to Y$ satisfying $g_*=f_*$ , and each $E_i=g^{-1}(S_i)$ is a 2–sphere.

Proof. We induct on n. When $n=0$ , there is nothing to prove. So we assume $n>0$ and the result is proved for $n-1$ .

Using [ 17 , theorem 1·1], we may assume $R_1=f^{-1}(S_1)$ is a connected surface. Let $\check Y_0=\overline{Y\setminus\check Y_1}$ , and let $Y_0$ be obtained by capping off $\partial \check Y_0$ with a ball $B_0$ . Let $U_i=f^{-1}(\check Y_i)$ , $i=0,1$ . Then $\partial U_1=\partial U_0=R_1$ .

By Lemma 2·2, there exists a separating 2–sphere $E_1\subset X$ , so that $R_1$ is obtained by adding tubes to $E_1$ . Now $E_1$ splits X into two parts $\check X_1,\check X_0$ , so that $\check X_i$ can be obtained from $U_i$ by adding 1–handles and digging tunnels, $i=0,1$ . Let $X_i$ be the closed manifold obtained by capping off $\partial\check X_i$ with a ball, $i=0,1$ .

We claim that each map $f|_{U_i}\,{:}\,U_i\to \check Y_i$ can be extended to a degree-one map $f_i\,{:}\, X_i\to Y_i$ . In fact, the manifold $X_i$ can be obtained from $U_i$ by gluing a 3–manifold $V_i$ which is obtained from $B^3$ by digging tunnels and adding 1–handles. Since $B_i$ is a ball which is contractible, we can extend $f|_{U_i}\,{:}\,U_i\to \check Y_i$ to a map $f_i\,{:}\, X_i\to Y_i$ by sending $V_i$ to $B_i$ . The degree of $f_i$ is 1 since the degree of $f|_{U_i}$ is 1.

Since $\deg f_i=1$ , after a homotopy supported in $V_i$ , we may assume there exists a ball $B^{\prime}_i\subset\mathrm{int}(B_i)$ , such that $f_i$ sends $B^{\star}_i=f_i^{-1}(B^{\prime}_i)$ homeomorphically onto $B_i^{\prime}$ . Now we can glue $X_i\setminus\mathrm{int}(B_i^{\star})$ , $i=0,1$ , together along their boundary, to get back

\begin{align*}X=(X_0\setminus\mathrm{int}(B_0^{\star}))\cup_{S^2} (X_1\setminus\mathrm{int}(B_1^{\star})),\end{align*}

and define a map

\begin{align*}f_0\#f_1\,{:}\,X\to Y=(Y_0\setminus\mathrm{int}(B_0^{\prime}))\cup_{S^2} (Y_1\setminus\mathrm{int}(B_1^{\prime}))\end{align*}

by gluing the restrictions of $f_0,f_1$ . We rename

\begin{align*}S_1=\partial (Y_0\setminus\mathrm{int}(B_0^{\prime})), E_1=\partial (X_0\setminus\mathrm{int}(B_0^{\star})),\end{align*}

then $E_1=(f_0\#f_1)^{-1}(S_1)$ .

We claim that $(f_0\#f_1)_*=f_*$ . Let $D\subset E_1$ be a disk such that all tubes in $S_1$ are added to the interior of D, and let $D^c=\overline{E_1\setminus D}$ . Let $V\subset X$ be the handlebody obtained by adding the 1–handles bounded by the tubes to $\nu(D)$ . Since $\pi_1(V)$ is a quotient of $\pi_1(\partial V)$ , the map $X\setminus V\to X$ induces a surjective map on $\pi_1$ . To prove $(f_0\#f_1)_*=f_*$ , we only need to prove that $(f_0\#f_1)_*(\alpha)=f_*(\alpha)$ when $\alpha$ is a homotopy class represented by a loop in $X\setminus V$ . We observe that $f_0\#f_1=f$ on $X\setminus(V\cup\nu(D^c))$ , and $\pi_1(X\setminus V)$ is the free product of the $\pi_1$ of the two components of $X\setminus(V\cup\nu(D^c))$ , so $(f_0\#f_1)_*(\alpha)=f_*(\alpha)$ .

By the induction hypothesis, there exists a map $g_0\,{:}\,X_0\to Y_0$ , such that $g_1^{-1}(S_i)$ is a sphere for $2\le i\le n$ , and $(g_1)_*=(f_0)_*$ . We can define a map $g=g_0\#f_1$ in a similar way as $f_0\#f_1$ , then $g^{-1}(S_i)$ is a sphere for $1\le i\le n$ , and

\begin{align*}g_*=(g_0\#f_1)_*=(f_0\#f_1)_*=f_*.\end{align*}

This finishes the induction step.

3. Zero surgery on a null-homotopic knot

The aim of this section is to prove the following proposition.

Proposition 3·1. Let Y be a closed, connected, oriented 3–manifold which does not have an $S^1\times S^2$ summand, and $K\subset Y$ be a null-homotopic knot. If $Y_0(K)=Z\#(S^1\times S^2)$ , then $\pi_1(Z)\cong\pi_1(Y)$ .

We first prove a general result about surgery on null-homotopic knots.

Lemma 3·2. Let Y be a closed, oriented, connected 3–manifold, and $K\subset Y$ be a null-homotopic knot. Let V be the 2–handle cobordism from Y to $Y_m(K)$ for some integer m. Then there exists a retraction $p\,{:}\,V\to Y$ , so that $p|_{Y_m(K)}\,{:}\,Y_m(K)\to Y$ is a degree-one map.

Proof. The cobordism V deformation retracts to the space V $^{\prime}$ obtained from Y by adding a 2–cell $e^2$ along K. Since K is null-homotopic, the identity map on Y can be extended over $e^2$ . Hence we have a retraction $V'\to Y$ , which implies the existence of the retraction $p\,{:}\,V\to Y$ . The degree of the restriction $p|_{Y_m(K)}\,{:}\,Y_m(K)\to Y$ is 1 since it induces an isomorphism on $H_3$ .

The existence of the above degree-one map is a well-known result. See [ 3 , Proposition 3·2] and [ 7 ].

In the rest of this section, let V be the 2–handle cobordism from Y to $X=Y_0(K)$ , $p\,{:}\,V\to Y$ be the retraction in Lemma 3·2, and $f=p|_{Y_0(K)}$ . Moreover, we assume $Y_0(K)=Z\#(S^1\times S^2)$ . Let $\check Z$ be the submanifold of $Y_0(K)$ which is Z with a ball removed. Since $Y_0(K)=Z\#(S^1\times S^2)$ , we can add a 3–handle to V to get a cobordism $W\,{:}\,Y\to Z$ .

Lemma 3·3. The restriction of $f_*$ to $\pi_1(\check Z)$ is injective.

Proof. Consider the following commutative diagram, where all maps except p are inclusions:

Then $f=p\circ\iota_0$ .

Since the 2–handle in V is added along the null-homotopic knot K, the inclusion $\iota_Y\,{:}\,Y\to V$ induces an isomorphism on $\pi_1$ . Since $p\circ\iota_Y=\mathrm{id}_Y$ , $p_*$ is an isomorphism.

Since W is obtained from V by adding a 3–handle, the inclusion $V\subset W$ induces an isomorphism on $\pi_1$ . We have the commutative diagram

The manifold W (after being turned up-side-down) can be obtained from $Z\times I$ by adding a 1–handle and a 2–handle, and the 2–handle cobordism is exactly V being turned up-side-down. By [ 4 , Proposition 2·1], $(\iota_Z)_*$ is injective, so $(\iota_{\check Z})_*$ is also injective.

Now consider the commutative diagram

The restriction of $f_*$ to $\pi_1(\check Z)$ is just $p_*\circ(\iota_{\check Z})_*$ , which is injective since $(\iota_{\check Z})_*$ is injective and $p_*$ is an isomorphism.

Corollary 3·4. The induced map $f_*\,{:}\,\pi_1(Y_0(K))\to \pi_1(Y)$ is surface-group injective.

Proof. This follows from Lemmas 2·1 and 3·3.

Proof of Proposition 3·1. We will use the notations in Section 2. Since $f_*$ is surface-group injective, we can apply Proposition 2·3 to get a degree-one map $g\,{:}\,X=Y_0(K)\to Y$ so that $g_*=f_*$ and $g^{-1}(S_i)=E_i$ is a separating sphere whenever $1\le i\le n$ .

Since X has an $S^1\times S^2$ summand, by the uniqueness part of the Kneser–Milnor theorem, one component of $X\setminus(\cup_{i=1}^n E_i)$ has an $S^1\times S^2$ summand.

If the $S^1\times S^2$ summand is in $g^{-1}(\check Y_{n+1})$ , then $g_*(S^1\times\{point\})$ is null-homotopic. It follows that

\begin{align*}g_*(\pi_1(X)=g_*(\pi_1(Z\#(S^1\times S^2)))=g_*(\pi_1(Z)).\end{align*}

Since $\deg g=1$ , $g_*$ is surjective. So $g_*|_{\pi_1(Z)}$ is surjective. Our result follows from Lemma 3·3 since $g_*=f_*$ .

If $\check X_i=g^{-1}(\check Y_i)$ has an $S^1\times S^2$ summand for some i satisfying $1\le i\le n$ , without loss of generality, we may assume $i=1$ . The map $g|_{\check X_1}$ extends to a map $g_1\,{:}\,X_1\to Y_1$ . Suppose that $X_1=Z_1\#(S^1\times S^2)$ , let $P\subset X_1$ be $\{\mathrm{point}\}\times S^2$ . Then $X_{1}\setminus \nu^{\circ}(P)$ is homeomorphic to $Z_1$ with two open balls removed. Since $\pi_2(Y_1)=0$ , $(g_1)|_P$ is null-homotopic in $Y_1$ . We can then extend $g_1|_{X_1\setminus \nu^{\circ}(P)}$ to a map $h_1\,{:}\, Z_1\to Y_1$ . The new map $h_1$ is again a degree-one map, so $(h_1)_*$ is surjective.

Using Lemma 3·3, we see that $g_*$ is injective on $\pi_1(X_0\#Z_1)$ . (Recall that $X_0$ is obtained from X by replacing $\check X_1$ with a ball.) In particular, $(h_1)_*$ is injective, so

\begin{align*}\pi_1(Z_1)\cong\pi_1(Y_1).\end{align*}

We also get that $g_*$ is injective on $\pi_1(X_0)$ . Since $g|_{\check X_0}\,{:}\,\check X_0\to\check Y_0$ is a degree-one proper map, $(g|_{\check X_0})*$ is surjective. So

\begin{align*}\pi_1(X_0)\cong \pi_1(Y_0).\end{align*}

Since $Z\cong X_0\#Z_1$ , $Y=Y_0\#Y_1$ , we have

\begin{align*}\pi_1(Z)\cong\pi_1(X_0)*\pi_1(Z_1)\cong\pi_1(Y_0)*\pi_1(Y_1)\cong\pi_1(Y).\end{align*}

4. Proof of the main theorem

In this section, we will prove Theorem 1·1 and Corollary 1·2.

Proof of Theorem 1·1. when $b_1(Y)>0$ Without loss of generality, we may assume $M=Y\setminus\nu^{\circ}(K)$ is irreducible. Since $b_1(Y)>0$ , there exists a closed, oriented, connected surface S in the interior of M, so that S is taut in M. Notice that for the $\infty$ slope on K, the core of the surgery solid torus, which is K, is null-homotopic. Using [ 11 , theorem A.21], which is a stronger version of the main result in [ 5 ], we conclude that each 2–sphere in $Y_0(K)$ bounds a rational homology ball. Hence $Y_0(K)$ does not have an $S^1\times S^2$ summand.

Proposition 4·1. Let $Y_1,Y_2$ be two closed, oriented, connected 3–manifolds. If $\pi_1(Y_1)\cong\pi_2(Y_2)$ , then

\begin{align*}\mathrm{rank}\widehat{HF}(Y_1)=\mathrm{rank}\widehat{HF}(Y_2).\end{align*}

Proof. This is a well-known consequence of the Geometrisation Theorem. As in [ 2 , theorem 2·1·3], if $\pi_1(Y_1)\cong\pi_2(Y_2)$ , then there is a one-to-one correspondence between the summands of $Y_1$ and the summands of $Y_2$ , such that any pair of summands in the correspondence consists of either homeomorphic manifolds, (the homemorphism does not necessarily preserve the orientation), or lens spaces with the same $H_1$ . Our result then follows from basic properties of Heegaard Floer homology [ 15, 16 ].

Proof of Theorem 1·1. when $b_1(Y)=0$ Without loss of generality, we may assume $Y\setminus K$ is irreducible. Assume that $Y_0(K)=Z\#(S^1\times S^2)$ . By Proposition 3·1, $\pi_1(Y)\cong\pi_1(Z)$ . Using Proposition 4·1, we get $\mathrm{rank}\widehat{HF}(Y)=\mathrm{rank}\widehat{HF}(Z)$ . Our conclusion follows from [ 9 , theorem 1·1].

Proof of Corollary 1·2. The first statement follows from Theorem 1·1. We only need to prove the second statement. In this case, $Y_0(K)$ is a torus bundle over $S^1$ . By Lemma 3·2, there exists a degree-one map $f\,{:}\,Y_0(K)\to Y$ . Then $f_*$ is surjective. We claim that Y is $S^1\times S^2,\mathbb RP^3\#\mathbb RP^3$ or a spherical manifold. Then our conclusion follows from [ 1 ].

If Y is reducible, then either $Y=S^1\times S^2$ or Y is a nontrivial connected sum. If $Y=S^1\times S^2$ , we are done. Now we assume Y is a nontrivial connected sum, so $\pi_1(Y)\cong A*B$ with A, B nontrivial. Let T be a fiber of $Y_0(K)$ , then $f_*(\pi_1(T))$ is an abelian normal subgroup of $\pi_1(Y)=f_*(\pi_1(Y_0(K)))$ . By the Kurosh Subgroup Theorem [ 8 , theorem 8·3], $f_*(\pi_1(T))$ is also a free product of free groups and conjugates of subgroups of A, B. Since $f_*(\pi_1(T))$ is abelian, it must be either a subgroup of $\mathbb Z$ or the conjugate of a subgroup of A or B. Since $f_*(\pi_1(T))$ is a normal subgroup of $\pi_1(Y)\cong A*B$ , the latter case cannot happen.

Now $f_*(\pi_1(T))$ is a subgroup of $\mathbb Z$ . Since $f_*$ is surjective, $\pi_1(Y)/f_*(\pi_1(T))$ is a cyclic group. If $f_*(\pi_1(T))=\{1\}$ , then $\pi_1(Y)$ is cyclic, a contradiction to $\pi_1(Y)\cong A*B$ . So $f_*(\pi_1(T))\cong\mathbb Z$ .

If $\pi_1(Y)/f_*(\pi_1(T))\cong\mathbb Z$ , then $\pi_1(Y)$ contains $\mathbb Z^2$ as a finite index subgroup, which is not possible since $\mathbb Z^2$ is not the fundamental group of any closed 3–manifold. If $\pi_1(Y)/f_*(\pi_1(T))$ is finite, then $\pi_1(Y)$ contains $\mathbb Z$ as a finite index subgroup. It follows that Y is finitely covered by $S^1\times S^2$ , thus it must be $S^1\times S^2$ or $\mathbb RP^3\#\mathbb RP^3$ .

Now we consider the case Y is irreducible. If Y is a spherical manifold, we are done. If Y is irreducible and not a spherical manifold, then $f_*$ is injective by [ 18 , theorem 4]. So $f_*$ is an isomorphism, a contradiction to the fact that $b_1(Y_0(K))>b_1(Y)$ .