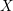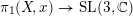1 Introduction
The main examples of local systems in complex algebraic geometry are those that come from families of varieties. Suppose
![]() $f:Z\rightarrow X$
is a smooth projective morphism of algebraic varieties. Then the
$f:Z\rightarrow X$
is a smooth projective morphism of algebraic varieties. Then the
![]() $i$
th higher direct image of the constant sheaf
$i$
th higher direct image of the constant sheaf
![]() $\mathbb{C}_{Z}$
is a semi-simple local system
$\mathbb{C}_{Z}$
is a semi-simple local system
![]() $R^{i}f_{\ast }(\mathbb{C}_{Z})$
on
$R^{i}f_{\ast }(\mathbb{C}_{Z})$
on
![]() $X$
. It furthermore has a structure of polarized
$X$
. It furthermore has a structure of polarized
![]() $\mathbb{Z}$
-variation of Hodge structure with integral structure given by the image of the map
$\mathbb{Z}$
-variation of Hodge structure with integral structure given by the image of the map
![]() $R^{i}f_{\ast }(\mathbb{Z}_{Z})\rightarrow R^{i}f_{\ast }(\mathbb{C}_{Z})$
. We will view all the irreducible direct factors of such local systems as coming from geometry.
$R^{i}f_{\ast }(\mathbb{Z}_{Z})\rightarrow R^{i}f_{\ast }(\mathbb{C}_{Z})$
. We will view all the irreducible direct factors of such local systems as coming from geometry.
Somewhat more generally, over a smooth variety
![]() $X$
we say that an irreducible
$X$
we say that an irreducible
![]() $\mathbb{C}$
-local system
$\mathbb{C}$
-local system
![]() $L$
is of geometric origin if there is a Zariski open dense subset
$L$
is of geometric origin if there is a Zariski open dense subset
![]() $U\subset X$
and a smooth projective family
$U\subset X$
and a smooth projective family
![]() $f:Z\rightarrow U$
such that
$f:Z\rightarrow U$
such that
![]() $L|_{U}$
is a direct factor of
$L|_{U}$
is a direct factor of
![]() $R^{i}f_{\ast }(\mathbb{C}_{Z})$
for some
$R^{i}f_{\ast }(\mathbb{C}_{Z})$
for some
![]() $i$
. See §§ 2.5 and 7 for a further discussion of possible variants of this notion.
$i$
. See §§ 2.5 and 7 for a further discussion of possible variants of this notion.
Local systems of geometric origin are
![]() $\mathbb{C}$
-variations of Hodge structure. Furthermore, from the
$\mathbb{C}$
-variations of Hodge structure. Furthermore, from the
![]() $R^{i}f_{\ast }(\mathbb{Z}_{Z})$
they inherit integral structure, in the sense that the traces of monodromy matrices are algebraic integers. Local systems of geometric origin also have a Galois descent property when viewed as
$R^{i}f_{\ast }(\mathbb{Z}_{Z})$
they inherit integral structure, in the sense that the traces of monodromy matrices are algebraic integers. Local systems of geometric origin also have a Galois descent property when viewed as
![]() $\mathbb{Q}_{\ell }$
-local systems over an arithmetic model of
$\mathbb{Q}_{\ell }$
-local systems over an arithmetic model of
![]() $X$
, as described in [Reference SimpsonSim92, Theorem 4].
$X$
, as described in [Reference SimpsonSim92, Theorem 4].
Several natural questions may be posed. For instance, does an integral local system underlying a
![]() $\mathbb{C}$
-variation of Hodge structure have geometric origin?
$\mathbb{C}$
-variation of Hodge structure have geometric origin?
Recall from Mostow–Margulis rigidity theorems that many local systems naturally occurring over higher-dimensional varieties are rigid, i.e. they have no non-trivial deformations. One can easily see that rigid
![]() $\mathbb{Q}_{\ell }$
-local systems automatically have the Galois descent property mentioned above. Furthermore, it is a consequence of Corlette’s theorem that rigid local systems are
$\mathbb{Q}_{\ell }$
-local systems automatically have the Galois descent property mentioned above. Furthermore, it is a consequence of Corlette’s theorem that rigid local systems are
![]() $\mathbb{C}$
-variations of Hodge structure. It is natural to formulate the following conjecture.
$\mathbb{C}$
-variations of Hodge structure. It is natural to formulate the following conjecture.
Conjecture 1.1. Over a smooth projective variety
![]() $X$
, any rigid local system
$X$
, any rigid local system
![]() $L$
is of geometric origin.
$L$
is of geometric origin.
This conjecture was proven for local systems on root stacks over
![]() $\mathbb{P}^{1}$
by Katz [Reference KatzKaz96], who gives a complete classification and inductive description of rigid local systems in that case. For local systems of rank
$\mathbb{P}^{1}$
by Katz [Reference KatzKaz96], who gives a complete classification and inductive description of rigid local systems in that case. For local systems of rank
![]() $2$
it was proven by Corlette and the second author [Reference Corlette and SimpsonCS08] who also prove a stronger classification result.
$2$
it was proven by Corlette and the second author [Reference Corlette and SimpsonCS08] who also prove a stronger classification result.
A consequence of the conjecture would be the following subsidiary statement.
Conjecture 1.2. Over a smooth projective variety
![]() $X$
, any rigid local system is integral.Footnote
1
$X$
, any rigid local system is integral.Footnote
1
In this paper we consider the case of rank
![]() $3$
, and obtain the following main theorem.
$3$
, and obtain the following main theorem.
Theorem 1.3. Let
![]() $X$
be a smooth complex projective variety with basepoint
$X$
be a smooth complex projective variety with basepoint
![]() $x$
. Then every rigid integral irreducible representation
$x$
. Then every rigid integral irreducible representation
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
is of geometric origin.
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
is of geometric origin.
Our techniques will not address the question of proving that a local system is integral, so we have included integrality as a hypothesis. Consequently, our theorem does not provide a complete answer to Conjecture 1.1 in the rank
![]() $3$
case, but it does show for rank
$3$
case, but it does show for rank
![]() $3$
that Conjecture 1.2 implies Conjecture 1.1.
$3$
that Conjecture 1.2 implies Conjecture 1.1.
On the other hand, for varieties with no symmetric differentials in some range, Conjecture 1.2 was proven by Klingler in [Reference KlinglerKli13]. Together with Theorem 1.3 his results imply the following corollary.
Corollary 1.4. Let
![]() $X$
be a smooth projective variety with
$X$
be a smooth projective variety with
![]() $H^{0}(X,\operatorname{Sym}^{i}\unicode[STIX]{x1D6FA}_{X})=0$
for
$H^{0}(X,\operatorname{Sym}^{i}\unicode[STIX]{x1D6FA}_{X})=0$
for
![]() $i=1,2,3$
. Then any representation
$i=1,2,3$
. Then any representation
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(3,\mathbb{C})$
is of geometric origin.
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(3,\mathbb{C})$
is of geometric origin.
We now explain the main ideas of the proof of Theorem 1.3. We say that a variation of Hodge structure (VHS for short) is of weight one if its Hodge types are contained in the set
![]() $\{(1,0),(0,1)\}$
. It is well-known that a polarizable weight-one
$\{(1,0),(0,1)\}$
. It is well-known that a polarizable weight-one
![]() $\mathbb{Z}$
-VHS comes from an algebraic smooth family of abelian varieties. Therefore, if we can construct such a VHS then we obtain an algebraic family and the underlying local system is of geometric origin. A refined version of this observation, which one can learn for example from Deligne’s [Reference DeligneDel71], goes as follows. Start with a local system
$\mathbb{Z}$
-VHS comes from an algebraic smooth family of abelian varieties. Therefore, if we can construct such a VHS then we obtain an algebraic family and the underlying local system is of geometric origin. A refined version of this observation, which one can learn for example from Deligne’s [Reference DeligneDel71], goes as follows. Start with a local system
![]() $L$
of complex vector spaces, but assume that
$L$
of complex vector spaces, but assume that
![]() $L$
is rigid. Then it is defined over some algebraic number field
$L$
is rigid. Then it is defined over some algebraic number field
![]() $K\subset \mathbb{C}$
. If we also assume that
$K\subset \mathbb{C}$
. If we also assume that
![]() $L$
is integral, then Bass–Serre theory says that there is a local system of projective
$L$
is integral, then Bass–Serre theory says that there is a local system of projective
![]() ${\mathcal{O}}_{K}$
-modules
${\mathcal{O}}_{K}$
-modules
![]() $L_{{\mathcal{O}}_{K}}$
with
$L_{{\mathcal{O}}_{K}}$
with
The local system
![]() $L_{{\mathcal{O}}_{K}}$
may be viewed as a local system of abelian groups, and hence of (free)
$L_{{\mathcal{O}}_{K}}$
may be viewed as a local system of abelian groups, and hence of (free)
![]() $\mathbb{Z}$
-modules. Now
$\mathbb{Z}$
-modules. Now
where
![]() $L^{\unicode[STIX]{x1D70E}}$
is the
$L^{\unicode[STIX]{x1D70E}}$
is the
![]() $\mathbb{C}$
-local system obtained by extension of scalars using the embedding
$\mathbb{C}$
-local system obtained by extension of scalars using the embedding
![]() $\unicode[STIX]{x1D70E}$
. In order to give our
$\unicode[STIX]{x1D70E}$
. In order to give our
![]() $\mathbb{Z}$
-local system a structure of polarized weight-one
$\mathbb{Z}$
-local system a structure of polarized weight-one
![]() $\mathbb{Z}$
-VHS, we should therefore give each complex local system
$\mathbb{Z}$
-VHS, we should therefore give each complex local system
![]() $L^{\unicode[STIX]{x1D70E}}$
a structure of polarized
$L^{\unicode[STIX]{x1D70E}}$
a structure of polarized
![]() $\mathbb{C}$
-VHS of weight one. Adjusting these together in order to have the required properties to get a family of abelian varieties, will be discussed in more detail in § 7.
$\mathbb{C}$
-VHS of weight one. Adjusting these together in order to have the required properties to get a family of abelian varieties, will be discussed in more detail in § 7.
Our original local system
![]() $L$
is one of the factors
$L$
is one of the factors
![]() $L^{\unicode[STIX]{x1D70E}_{0}}$
corresponding to the initially given embedding
$L^{\unicode[STIX]{x1D70E}_{0}}$
corresponding to the initially given embedding
![]() $\unicode[STIX]{x1D70E}_{0}:K{\hookrightarrow}\mathbb{C}$
. The plan to show that
$\unicode[STIX]{x1D70E}_{0}:K{\hookrightarrow}\mathbb{C}$
. The plan to show that
![]() $L$
is of geometric origin is therefore to try to put weight-one VHSs on each
$L$
is of geometric origin is therefore to try to put weight-one VHSs on each
![]() $L^{\unicode[STIX]{x1D70E}}$
. Assuming
$L^{\unicode[STIX]{x1D70E}}$
. Assuming
![]() $L$
is irreducible, so all these local systems are irreducible, if they have VHSs then these structures are unique up to translation of Hodge types. The existence of weight-one structures is therefore a property of the
$L$
is irreducible, so all these local systems are irreducible, if they have VHSs then these structures are unique up to translation of Hodge types. The existence of weight-one structures is therefore a property of the
![]() $L^{\unicode[STIX]{x1D70E}}$
.
$L^{\unicode[STIX]{x1D70E}}$
.
In the case
![]() $\text{rk}(L)=2$
, this property is automatic. Indeed the only two possibilities for the Hodge numbers are a single Hodge number equal to
$\text{rk}(L)=2$
, this property is automatic. Indeed the only two possibilities for the Hodge numbers are a single Hodge number equal to
![]() $2$
, a case we denote
$2$
, a case we denote
![]() $(2)$
, or two adjacent Hodge numbers equal to
$(2)$
, or two adjacent Hodge numbers equal to
![]() $1$
, a case we denote
$1$
, a case we denote
![]() $(1,1)$
. Notice that if the non-zero Hodge numbers are not adjacent then the Kodaira–Spencer map (Higgs field) must be zero and the system becomes reducible. This explains in a nutshell the procedure that was used in [Reference Corlette and SimpsonCS08] to treat the rigid and integral local systems of rank
$(1,1)$
. Notice that if the non-zero Hodge numbers are not adjacent then the Kodaira–Spencer map (Higgs field) must be zero and the system becomes reducible. This explains in a nutshell the procedure that was used in [Reference Corlette and SimpsonCS08] to treat the rigid and integral local systems of rank
![]() $2$
.
$2$
.
In the case of local systems of rank
![]() $3$
, there are four possibilities for the type of VHS: either
$3$
, there are four possibilities for the type of VHS: either
![]() $(3)$
corresponding to unitary ones, or
$(3)$
corresponding to unitary ones, or
![]() $(1,2)$
or
$(1,2)$
or
![]() $(2,1)$
corresponding to weight-one VHS (with Hodge numbers
$(2,1)$
corresponding to weight-one VHS (with Hodge numbers
![]() $h^{1,0}=1,h^{0,1}=2$
or
$h^{1,0}=1,h^{0,1}=2$
or
![]() $h^{1,0}=2,h^{0,1}=1$
respectively); or the last case
$h^{1,0}=2,h^{0,1}=1$
respectively); or the last case
![]() $(1,1,1)$
when the Hodge bundles are three line bundles. The unitary type
$(1,1,1)$
when the Hodge bundles are three line bundles. The unitary type
![]() $(3)$
can be considered as having weight one in two different ways. Thus we have the following lemma which is implicit in the proof of [Reference Corlette and SimpsonCS08, Theorem 8.1].
$(3)$
can be considered as having weight one in two different ways. Thus we have the following lemma which is implicit in the proof of [Reference Corlette and SimpsonCS08, Theorem 8.1].
Lemma 1.5. Suppose
![]() $V$
is an irreducible rank
$V$
is an irreducible rank
![]() $3$
local system on a smooth quasi-projective variety
$3$
local system on a smooth quasi-projective variety
![]() $X$
. If
$X$
. If
![]() $V$
is rigid then it underlies either a complex VHS of weight one or a complex VHS of type
$V$
is rigid then it underlies either a complex VHS of weight one or a complex VHS of type
![]() $(1,1,1)$
.
$(1,1,1)$
.
The reasoning up until now has been well-known and standard. The main idea of the present paper is that we can use substantial arguments in birational geometry to rule out the case of VHS type
![]() $(1,1,1)$
, unless some special behaviour occurs; namely factorization through a curve. In turn, the case of factorization through a curve can be shown, again by standard arguments using Katz’s theorem, to lead to local systems of geometric origin under the hypothesis of rigidity. We show the following main theorem. See Theorem 5.1 for a more detailed version of part (1) of the conclusion.
$(1,1,1)$
, unless some special behaviour occurs; namely factorization through a curve. In turn, the case of factorization through a curve can be shown, again by standard arguments using Katz’s theorem, to lead to local systems of geometric origin under the hypothesis of rigidity. We show the following main theorem. See Theorem 5.1 for a more detailed version of part (1) of the conclusion.
Theorem 1.6. Let
![]() $X$
be a smooth complex projective variety with basepoint
$X$
be a smooth complex projective variety with basepoint
![]() $x$
and let
$x$
and let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
be an irreducible representation coming from a complex variation of Hodge structure of type
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
be an irreducible representation coming from a complex variation of Hodge structure of type
![]() $(1,1,1)$
. Let
$(1,1,1)$
. Let
![]() $V_{\unicode[STIX]{x1D70C}}$
denote the corresponding local system. Then one of the following holds:
$V_{\unicode[STIX]{x1D70C}}$
denote the corresponding local system. Then one of the following holds:
(i) the image of
 $\unicode[STIX]{x1D70C}$
is not Zariski-dense in
$\unicode[STIX]{x1D70C}$
is not Zariski-dense in
 $\operatorname{SL}(3,\mathbb{C})$
; or
$\operatorname{SL}(3,\mathbb{C})$
; or(ii)
 $\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
$\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
Once we have this theorem, the proof of Theorem 1.3 follows the outline described above: the case of factorization through a curve is treated on the side, and otherwise the theorem rules out having a VHS of type
![]() $(1,1,1)$
. Therefore, all of our local systems
$(1,1,1)$
. Therefore, all of our local systems
![]() $L^{\unicode[STIX]{x1D70E}}$
underlie VHS of weight one, and these may be put together into a polarized
$L^{\unicode[STIX]{x1D70E}}$
underlie VHS of weight one, and these may be put together into a polarized
![]() $\mathbb{Z}$
-VHS of weight one corresponding to a family of abelian varieties. The details are described in § 7.
$\mathbb{Z}$
-VHS of weight one corresponding to a family of abelian varieties. The details are described in § 7.
We note that Theorem 1.6 generalizes Klingler’s result [Reference KlinglerKli03, Proposition 3.3] which had as the hypothesis that the Neron–Severi group be of rank 1.
Let us now explain briefly how we can use arguments from birational geometry to rule out the case of VHS of type
![]() $(1,1,1)$
. Such a VHS corresponds to a Higgs bundle of the form
$(1,1,1)$
. Such a VHS corresponds to a Higgs bundle of the form
with
![]() $E^{p,q}$
line bundles, and the Higgs field consists of
$E^{p,q}$
line bundles, and the Higgs field consists of
![]() $\unicode[STIX]{x1D703}:E^{2,0}\rightarrow E^{1,1}~\otimes ~\unicode[STIX]{x1D6FA}_{X}^{1}$
and
$\unicode[STIX]{x1D703}:E^{2,0}\rightarrow E^{1,1}~\otimes ~\unicode[STIX]{x1D6FA}_{X}^{1}$
and
![]() $\unicode[STIX]{x1D703}:E^{1,1}\rightarrow E^{0,2}~\otimes ~\unicode[STIX]{x1D6FA}_{X}^{1}$
. In terms of the VHS
$\unicode[STIX]{x1D703}:E^{1,1}\rightarrow E^{0,2}~\otimes ~\unicode[STIX]{x1D6FA}_{X}^{1}$
. In terms of the VHS
![]() $(V,F^{\cdot },\unicode[STIX]{x1D6FB})$
, the line bundles are the Hodge bundles
$(V,F^{\cdot },\unicode[STIX]{x1D6FB})$
, the line bundles are the Hodge bundles
![]() $E^{p,q}=F^{p}V/F^{p+1}V$
and the
$E^{p,q}=F^{p}V/F^{p+1}V$
and the
![]() $\unicode[STIX]{x1D703}$
are the Kodaira–Spencer maps induced by
$\unicode[STIX]{x1D703}$
are the Kodaira–Spencer maps induced by
![]() $\unicode[STIX]{x1D6FB}$
. Since the
$\unicode[STIX]{x1D6FB}$
. Since the
![]() $E^{p,q}$
are line bundles, locally
$E^{p,q}$
are line bundles, locally
![]() $\unicode[STIX]{x1D703}$
looks like a collection of sections of
$\unicode[STIX]{x1D703}$
looks like a collection of sections of
![]() $\unicode[STIX]{x1D6FA}_{X}^{1}$
and the integrability condition
$\unicode[STIX]{x1D6FA}_{X}^{1}$
and the integrability condition
![]() $\unicode[STIX]{x1D703}\wedge \unicode[STIX]{x1D703}=0$
implies that these local sections are proportional where non-vanishing. They generate a saturated subline bundle
$\unicode[STIX]{x1D703}\wedge \unicode[STIX]{x1D703}=0$
implies that these local sections are proportional where non-vanishing. They generate a saturated subline bundle
![]() $M\subset \unicode[STIX]{x1D6FA}_{X}^{1}$
.
$M\subset \unicode[STIX]{x1D6FA}_{X}^{1}$
.
For simplicity, let us here assume that
![]() $X$
is a surface. Consider the line bundles
$X$
is a surface. Consider the line bundles
![]() $L_{1}=E^{2,0}~\otimes ~(E^{1,1})^{\ast }$
and
$L_{1}=E^{2,0}~\otimes ~(E^{1,1})^{\ast }$
and
![]() $L_{2}=E^{1,1}~\otimes ~(E^{0,2})^{\ast }$
. The sections
$L_{2}=E^{1,1}~\otimes ~(E^{0,2})^{\ast }$
. The sections
![]() $\unicode[STIX]{x1D703}$
may be viewed as inclusions
$\unicode[STIX]{x1D703}$
may be viewed as inclusions
![]() $L_{i}{\hookrightarrow}M\subset \unicode[STIX]{x1D6FA}_{X}^{1}$
. Write
$L_{i}{\hookrightarrow}M\subset \unicode[STIX]{x1D6FA}_{X}^{1}$
. Write
with
![]() $B_{i}$
effective divisors. Bogomolov’s lemma (see [Reference BogomolovBog78, Theorem 4]) says that
$B_{i}$
effective divisors. Bogomolov’s lemma (see [Reference BogomolovBog78, Theorem 4]) says that
![]() $M$
cannot be big. We know that the Higgs bundle
$M$
cannot be big. We know that the Higgs bundle
![]() $(E,\unicode[STIX]{x1D703})$
is stable, and its rational Chern classes vanish. We are able to conclude several fairly strong properties:
$(E,\unicode[STIX]{x1D703})$
is stable, and its rational Chern classes vanish. We are able to conclude several fairly strong properties:
∙ the line bundles
 $L_{i}$
both lie on the same line in
$L_{i}$
both lie on the same line in
 $NS(X)_{\mathbb{Q}}$
;
$NS(X)_{\mathbb{Q}}$
;∙ at least one of
 $L_{i}$
is nef of strictly positive degree; and
$L_{i}$
is nef of strictly positive degree; and∙
 $L_{i}^{2}=0$
.
$L_{i}^{2}=0$
.
That happens in § 4. The technique is to play off the numerical properties given by stability and vanishing of Chern classes, against the fact that we have effective divisors
![]() $B_{i}$
such that
$B_{i}$
such that
![]() $L_{i}+B_{i}$
are contained in
$L_{i}+B_{i}$
are contained in
![]() $\unicode[STIX]{x1D6FA}_{X}^{1}$
and not big by Bogomolov’s lemma.
$\unicode[STIX]{x1D6FA}_{X}^{1}$
and not big by Bogomolov’s lemma.
Then in § 5, assuming for example that
![]() $L_{1}$
is nef of strictly positive degree, we write
$L_{1}$
is nef of strictly positive degree, we write
![]() $L_{2}=a.L_{1}$
in the rational Neron–Severi group, with
$L_{2}=a.L_{1}$
in the rational Neron–Severi group, with
![]() $a\in \mathbb{Q}$
, and we try to get information about
$a\in \mathbb{Q}$
, and we try to get information about
![]() $a$
. Notice that having
$a$
. Notice that having
![]() $L_{1}^{2}=0$
and
$L_{1}^{2}=0$
and
![]() $L_{1}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}^{1}$
allows us to create the rank
$L_{1}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}^{1}$
allows us to create the rank
![]() $2$
Higgs bundle
$2$
Higgs bundle
![]() ${\mathcal{O}}_{X}\oplus L_{1}$
corresponding to a projectively flat connection. We would like to view
${\mathcal{O}}_{X}\oplus L_{1}$
corresponding to a projectively flat connection. We would like to view
![]() $E$
as being the symmetric square of this rank
$E$
as being the symmetric square of this rank
![]() $2$
bundle. In other words, we would like to show that
$2$
bundle. In other words, we would like to show that
![]() $a=1$
and moreover
$a=1$
and moreover
![]() $L_{1}=L_{2}$
.
$L_{1}=L_{2}$
.
Part of the difficulty is that there exist VHSs over a curve where
![]() $a$
could be somewhat arbitrary, including being negative. Therefore, our strategy is to show that either
$a$
could be somewhat arbitrary, including being negative. Therefore, our strategy is to show that either
![]() $a=1$
, or else our VHS factors through a map to a curve. In the case
$a=1$
, or else our VHS factors through a map to a curve. In the case
![]() $a=1$
, again with some further arguments assuming that there is no factorization through a curve, we finally conclude that
$a=1$
, again with some further arguments assuming that there is no factorization through a curve, we finally conclude that
![]() $L_{1}=L_{2}$
and indeed our VHS was a symmetric square of a rank
$L_{1}=L_{2}$
and indeed our VHS was a symmetric square of a rank
![]() $2$
local system. These arguments use various aspects of the theory of factorization of representations. We include a proof that several different statements of the property ‘factors through a curve’ are equivalent, in Appendix A. The proof of Theorem 1.6 is concluded at the end of § 5.
$2$
local system. These arguments use various aspects of the theory of factorization of representations. We include a proof that several different statements of the property ‘factors through a curve’ are equivalent, in Appendix A. The proof of Theorem 1.6 is concluded at the end of § 5.
Section 6 contains some remarks about the possible extension of this discussion to VHSs of type
![]() $(1,1,\ldots ,1)$
in higher ranks, and § 6 derives the corollaries about local systems of geometric origin leading to the proof of Theorem 1.3.
$(1,1,\ldots ,1)$
in higher ranks, and § 6 derives the corollaries about local systems of geometric origin leading to the proof of Theorem 1.3.
1.1 Notation
Let us recall that a Higgs bundle is a pair
![]() $(E,\unicode[STIX]{x1D703})$
consisting of a locally free
$(E,\unicode[STIX]{x1D703})$
consisting of a locally free
![]() ${\mathcal{O}}_{X}$
-module and an
${\mathcal{O}}_{X}$
-module and an
![]() ${\mathcal{O}}_{X}$
-linear map
${\mathcal{O}}_{X}$
-linear map
![]() $\unicode[STIX]{x1D703}:E\rightarrow E~\otimes ~\unicode[STIX]{x1D6FA}_{X}$
such that
$\unicode[STIX]{x1D703}:E\rightarrow E~\otimes ~\unicode[STIX]{x1D6FA}_{X}$
such that
![]() $\unicode[STIX]{x1D703}\wedge \unicode[STIX]{x1D703}=0$
. A system of Hodge bundles is a Higgs bundle
$\unicode[STIX]{x1D703}\wedge \unicode[STIX]{x1D703}=0$
. A system of Hodge bundles is a Higgs bundle
![]() $(E,\unicode[STIX]{x1D703})$
with a decomposition
$(E,\unicode[STIX]{x1D703})$
with a decomposition
![]() $E=\bigoplus E^{p,q}$
such that
$E=\bigoplus E^{p,q}$
such that
![]() $\unicode[STIX]{x1D703}$
maps
$\unicode[STIX]{x1D703}$
maps
![]() $E^{p,q}$
into
$E^{p,q}$
into
![]() $E^{p-1,q+1}~\otimes ~\unicode[STIX]{x1D6FA}_{X}$
. We say that a system of Hodge bundles
$E^{p-1,q+1}~\otimes ~\unicode[STIX]{x1D6FA}_{X}$
. We say that a system of Hodge bundles
![]() $(E,\unicode[STIX]{x1D703})$
is of type
$(E,\unicode[STIX]{x1D703})$
is of type
![]() $(i_{0},\ldots ,i_{n})$
if
$(i_{0},\ldots ,i_{n})$
if
and all the maps
![]() $\unicode[STIX]{x1D703}:E^{m-q,q}\rightarrow E^{m-q-1,q+1}~\otimes ~\unicode[STIX]{x1D6FA}_{X}$
are non-zero for
$\unicode[STIX]{x1D703}:E^{m-q,q}\rightarrow E^{m-q-1,q+1}~\otimes ~\unicode[STIX]{x1D6FA}_{X}$
are non-zero for
![]() $q=0,\ldots ,n-1$
. Similarly, replacing
$q=0,\ldots ,n-1$
. Similarly, replacing
![]() $\unicode[STIX]{x1D6FA}_{X}$
with
$\unicode[STIX]{x1D6FA}_{X}$
with
![]() $\unicode[STIX]{x1D6FA}_{X}(\log D)$
one can define logarithmic systems of Hodge bundles.
$\unicode[STIX]{x1D6FA}_{X}(\log D)$
one can define logarithmic systems of Hodge bundles.
In the following we make the convention that complex variation of VHS always means polarizable VHS. Giving an irreducible VHS on a smooth complex projective variety is equivalent to giving a stable system of Hodge bundles with vanishing rational Chern classes.
We say that a complex VHS is of type
![]() $(i_{0},\ldots ,i_{n})$
if the corresponding system of Hodge bundles is of type
$(i_{0},\ldots ,i_{n})$
if the corresponding system of Hodge bundles is of type
![]() $(i_{0},\ldots ,i_{n})$
.
$(i_{0},\ldots ,i_{n})$
.
Let
![]() $X$
be a smooth complex projective variety. Let us recall that a line bundle is called nef if it has a non-negative degree on every irreducible projective curve in
$X$
be a smooth complex projective variety. Let us recall that a line bundle is called nef if it has a non-negative degree on every irreducible projective curve in
![]() $X$
. Let us recall that after Miles Reid, ‘nef’ stands for ‘numerically eventually free’. A line bundle
$X$
. Let us recall that after Miles Reid, ‘nef’ stands for ‘numerically eventually free’. A line bundle
![]() $L$
is called big if its Iitaka’s dimension
$L$
is called big if its Iitaka’s dimension
![]() $\unicode[STIX]{x1D705}(L)$
is equal to the dimension of
$\unicode[STIX]{x1D705}(L)$
is equal to the dimension of
![]() $X$
.
$X$
.
A
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $D$
is called effective if it can be written as
$D$
is called effective if it can be written as
![]() $D=\sum a_{i}D_{i}$
, where
$D=\sum a_{i}D_{i}$
, where
![]() $D_{i}$
are prime divisors and
$D_{i}$
are prime divisors and
![]() $a_{i}$
are non-negative rational numbers. We write
$a_{i}$
are non-negative rational numbers. We write
![]() $D_{1}\geqslant D_{2}$
for two
$D_{1}\geqslant D_{2}$
for two
![]() $\mathbb{Q}$
-divisors
$\mathbb{Q}$
-divisors
![]() $D_{1},D_{2}$
, if their difference
$D_{1},D_{2}$
, if their difference
![]() $(D_{1}-D_{2})$
is an effective
$(D_{1}-D_{2})$
is an effective
![]() $\mathbb{Q}$
-divisor.
$\mathbb{Q}$
-divisor.
If
![]() $L_{1}$
and
$L_{1}$
and
![]() $L_{2}$
are line bundles then we write
$L_{2}$
are line bundles then we write
![]() $L_{1}\geqslant L_{2}$
if
$L_{1}\geqslant L_{2}$
if
![]() $H^{0}(L_{1}~\otimes ~L_{2}^{-1})\neq 0$
.
$H^{0}(L_{1}~\otimes ~L_{2}^{-1})\neq 0$
.
For various other definitions and properties of line bundles we refer the reader to [Reference LazarsfeldLaz04, Theorem 2.2.16]. Let us just mention that if
![]() $L$
is nef then it is big if and only if
$L$
is nef then it is big if and only if
![]() $L^{\dim X}>0$
.
$L^{\dim X}>0$
.
A morphism
![]() $f:X\rightarrow Y$
between smooth quasi-projective varieties (or just orbifolds) is called a fibration if it is surjective and the fibers of
$f:X\rightarrow Y$
between smooth quasi-projective varieties (or just orbifolds) is called a fibration if it is surjective and the fibers of
![]() $f$
are connected.
$f$
are connected.
A morphism
![]() $f:X\rightarrow Y$
is called an alteration if
$f:X\rightarrow Y$
is called an alteration if
![]() $X$
is smooth and
$X$
is smooth and
![]() $f$
is proper, surjective and generically finite.
$f$
is proper, surjective and generically finite.
In the following we often abuse notation and we do not distinguish between an algebraic variety and the underlying analytic space. For example, the fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}(X)$
and cohomology groups
$\unicode[STIX]{x1D70B}_{1}(X)$
and cohomology groups
![]() $H^{\ast }(X,\mathbb{Q})$
of an algebraic variety
$H^{\ast }(X,\mathbb{Q})$
of an algebraic variety
![]() $X$
always denote the corresponding notion for the underlying analytic space. Similarly, essentially all varieties, bundles and maps are algebraic. In the projective case this convention is harmless due to GAGA-type theorems but in general this could lead to some confusion so in case we use non-algebraic structures we explicitly say so (see the use of analytic maps in the proof of Theorem 5.1).
$X$
always denote the corresponding notion for the underlying analytic space. Similarly, essentially all varieties, bundles and maps are algebraic. In the projective case this convention is harmless due to GAGA-type theorems but in general this could lead to some confusion so in case we use non-algebraic structures we explicitly say so (see the use of analytic maps in the proof of Theorem 5.1).
Let
![]() $X$
be a smooth complex quasi-projective variety. Let us fix a smooth projective compactification
$X$
be a smooth complex quasi-projective variety. Let us fix a smooth projective compactification
![]() $\bar{X}$
of
$\bar{X}$
of
![]() $X$
such that
$X$
such that
![]() $D=\bar{X}-X$
is a simple normal crossing divisor. Let
$D=\bar{X}-X$
is a simple normal crossing divisor. Let
![]() $\{\unicode[STIX]{x1D6FE}_{i}\}$
be loops going around the irreducible components of
$\{\unicode[STIX]{x1D6FE}_{i}\}$
be loops going around the irreducible components of
![]() $D$
. Let
$D$
. Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
be a representation of
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
be a representation of
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
in some reductive group
$\unicode[STIX]{x1D70B}_{1}(X,x)$
in some reductive group
![]() $G$
and let us assume that all
$G$
and let us assume that all
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{i})$
are quasi-unipotent. Let us denote by
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{i})$
are quasi-unipotent. Let us denote by
![]() $C_{i}$
the closure of the conjugacy class of
$C_{i}$
the closure of the conjugacy class of
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{i})$
. We say that
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{i})$
. We say that
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
is rigid if it represents an isolated point in the moduli space
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
is rigid if it represents an isolated point in the moduli space
![]() $M(X,G,\{C_{i}\})$
of representations of
$M(X,G,\{C_{i}\})$
of representations of
![]() $\unicode[STIX]{x1D70F}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
with conjugacy classes of
$\unicode[STIX]{x1D70F}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
with conjugacy classes of
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FE}_{i})$
contained in
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FE}_{i})$
contained in
![]() $C_{i}$
.
$C_{i}$
.
2 Preliminaries
2.1 Homotopy exact sequence
Let
![]() $C$
be a smooth complex quasi-projective curve and let
$C$
be a smooth complex quasi-projective curve and let
![]() $X$
be a smooth complex quasi-projective variety. Let
$X$
be a smooth complex quasi-projective variety. Let
![]() $f:X\rightarrow C$
be a fibration and let
$f:X\rightarrow C$
be a fibration and let
![]() $c$
be a closed point of
$c$
be a closed point of
![]() $C$
. Let us recall that the multiplicity of a fiber
$C$
. Let us recall that the multiplicity of a fiber
![]() $F=\sum a_{i}F_{i}$
, where
$F=\sum a_{i}F_{i}$
, where
![]() $F_{i}$
are irreducible components of
$F_{i}$
are irreducible components of
![]() $F$
, is equal to the greatest common divisor of the coefficients
$F$
, is equal to the greatest common divisor of the coefficients
![]() $a_{i}$
. Let
$a_{i}$
. Let
![]() $p_{1},\ldots ,p_{k}$
be all the points of
$p_{1},\ldots ,p_{k}$
be all the points of
![]() $C$
at which the fiber of
$C$
at which the fiber of
![]() $f$
is multiple (i.e., it has multiplicity at least
$f$
is multiple (i.e., it has multiplicity at least
![]() $2$
) and let
$2$
) and let
![]() $m_{j}$
denote the multiplicity of the fiber of
$m_{j}$
denote the multiplicity of the fiber of
![]() $f$
over
$f$
over
![]() $p_{j}$
. Let
$p_{j}$
. Let
![]() $c$
be a point of
$c$
be a point of
![]() $C$
over which the fiber of
$C$
over which the fiber of
![]() $f$
has multiplicity
$f$
has multiplicity
![]() $1$
.
$1$
.
We define the orbifold fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}^{\operatorname{orb}}(C_{f},c)$
of
$\unicode[STIX]{x1D70B}_{1}^{\operatorname{orb}}(C_{f},c)$
of
![]() $C$
with respect to
$C$
with respect to
![]() $f$
as the quotient of
$f$
as the quotient of
![]() $\unicode[STIX]{x1D70B}_{1}(C-\{p_{1},\ldots ,p_{k}\},c)$
by the normal subgroup generated by all the elements of the form
$\unicode[STIX]{x1D70B}_{1}(C-\{p_{1},\ldots ,p_{k}\},c)$
by the normal subgroup generated by all the elements of the form
![]() $\unicode[STIX]{x1D6FE}_{j}^{m_{j}}$
, where
$\unicode[STIX]{x1D6FE}_{j}^{m_{j}}$
, where
![]() $\unicode[STIX]{x1D6FE}_{j}$
is a simple loop going around the point
$\unicode[STIX]{x1D6FE}_{j}$
is a simple loop going around the point
![]() $p_{j}$
.
$p_{j}$
.
The following theorem is well-known.
Theorem 2.1. Let
![]() $c\in C-\{p_{1},\ldots ,p_{k}\}$
and let
$c\in C-\{p_{1},\ldots ,p_{k}\}$
and let
![]() $x$
be a closed point of the fiber
$x$
be a closed point of the fiber
![]() $X_{c}$
of
$X_{c}$
of
![]() $f$
over
$f$
over
![]() $c$
. Let us assume that either
$c$
. Let us assume that either
![]() $f$
is proper or
$f$
is proper or
![]() $c\in C$
is general. Then the following sequence of groups is exact:
$c\in C$
is general. Then the following sequence of groups is exact:
In particular, if we also assume that
![]() $f$
has no multiple fibers then the sequence
$f$
has no multiple fibers then the sequence
is exact.
Proof. If all the fibers of
![]() $f$
have at least one smooth point then the theorem is due to Nori [Reference NoriNor83, Lemma 1.5] (for general fiber) with a small improvement due to Debarre [Reference DebarreDeb05, Lemma 8.11] allowing arbitrary fibers to be dealt with in the proper case. Nori’s proof with appropriate changes as in [Reference XiaoXia91] works also for general fibers even without assumption that all the fibers have at least one smooth point. In the general proper case, the assertion comes from [Reference XiaoXia91, Lemmas 1–3] in the surface case, but Xiao’s proof also works in the general case. Alternatively, for smooth fibers the general case can be reduced to the surface case by the Lefschetz hyperplane theorem. Namely, if
$f$
have at least one smooth point then the theorem is due to Nori [Reference NoriNor83, Lemma 1.5] (for general fiber) with a small improvement due to Debarre [Reference DebarreDeb05, Lemma 8.11] allowing arbitrary fibers to be dealt with in the proper case. Nori’s proof with appropriate changes as in [Reference XiaoXia91] works also for general fibers even without assumption that all the fibers have at least one smooth point. In the general proper case, the assertion comes from [Reference XiaoXia91, Lemmas 1–3] in the surface case, but Xiao’s proof also works in the general case. Alternatively, for smooth fibers the general case can be reduced to the surface case by the Lefschetz hyperplane theorem. Namely, if
![]() $\dim X\geqslant 3$
then by Bertini’s theorem we can find a very ample divisor
$\dim X\geqslant 3$
then by Bertini’s theorem we can find a very ample divisor
![]() $H$
such that both
$H$
such that both
![]() $X_{c}~\cap ~H$
and
$X_{c}~\cap ~H$
and
![]() $H$
are smooth and connected. Since, by the Lefschetz hyperplane theorem, the map
$H$
are smooth and connected. Since, by the Lefschetz hyperplane theorem, the map
![]() $\unicode[STIX]{x1D70B}_{1}(X_{c}~\cap ~H)\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{c})$
is surjective and the map
$\unicode[STIX]{x1D70B}_{1}(X_{c}~\cap ~H)\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{c})$
is surjective and the map
![]() $\unicode[STIX]{x1D70B}_{1}(H)\rightarrow \unicode[STIX]{x1D70B}_{1}(X)$
is an isomorphism, exactness of the homotopy sequence for
$\unicode[STIX]{x1D70B}_{1}(H)\rightarrow \unicode[STIX]{x1D70B}_{1}(X)$
is an isomorphism, exactness of the homotopy sequence for
![]() $f$
follows from exactness of the homotopy sequence for
$f$
follows from exactness of the homotopy sequence for
![]() $f|_{H}:H\rightarrow C$
. Now the required assertion follows from the surface case by induction.◻
$f|_{H}:H\rightarrow C$
. Now the required assertion follows from the surface case by induction.◻
Remark 2.2. If
![]() $f$
is not proper then the homotopy sequence from the above theorem need not be exact even if we assume that all the fibers of
$f$
is not proper then the homotopy sequence from the above theorem need not be exact even if we assume that all the fibers of
![]() $f$
are smooth. One can easily construct examples when this sequence is not exact by blowing up a smooth surface fibered over a curve and removing non-exceptional components in the fiber over the blown-up point.
$f$
are smooth. One can easily construct examples when this sequence is not exact by blowing up a smooth surface fibered over a curve and removing non-exceptional components in the fiber over the blown-up point.
2.2 Intersection pairing
Let
![]() $X$
be a smooth complex projective variety of dimension
$X$
be a smooth complex projective variety of dimension
![]() $d\geqslant 2$
. Let
$d\geqslant 2$
. Let
![]() $A$
be a fixed very ample divisor on
$A$
be a fixed very ample divisor on
![]() $X$
. Then we use intersection pairing on
$X$
. Then we use intersection pairing on
![]() $\mathbb{Q}$
-divisors given by
$\mathbb{Q}$
-divisors given by
We will often use the fact that if
![]() $D.A=D^{2}=0$
then the class of
$D.A=D^{2}=0$
then the class of
![]() $D$
in
$D$
in
![]() $H^{2}(X,\mathbb{Q})$
is
$H^{2}(X,\mathbb{Q})$
is
![]() $0$
. To prove that note that if
$0$
. To prove that note that if
![]() $Y\in |A|\cap \cdots \cap |A|$
denotes a general complete intersection surface in
$Y\in |A|\cap \cdots \cap |A|$
denotes a general complete intersection surface in
![]() $X$
then the class of
$X$
then the class of
![]() $D|_{Y}$
in
$D|_{Y}$
in
![]() $H^{2}(Y,\mathbb{Q})$
is zero by the Hodge index theorem. But by the Lefschetz hyperplane theorem the restriction
$H^{2}(Y,\mathbb{Q})$
is zero by the Hodge index theorem. But by the Lefschetz hyperplane theorem the restriction
![]() $H^{2}(X,\mathbb{Q})\rightarrow H^{2}(Y,\mathbb{Q})$
is injective so the class of
$H^{2}(X,\mathbb{Q})\rightarrow H^{2}(Y,\mathbb{Q})$
is injective so the class of
![]() $D$
in
$D$
in
![]() $H^{2}(X,\mathbb{Q})$
is also zero.
$H^{2}(X,\mathbb{Q})$
is also zero.
In the following we write
![]() $D_{1}\equiv D_{2}$
, if for every
$D_{1}\equiv D_{2}$
, if for every
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $D$
we have
$D$
we have
![]() $D_{1}.D=D_{2}.D$
. In that case the Lefschetz hyperplane theorem implies that the class of
$D_{1}.D=D_{2}.D$
. In that case the Lefschetz hyperplane theorem implies that the class of
![]() $(D_{1}-D_{2})$
in
$(D_{1}-D_{2})$
in
![]() $H^{2}(X,\mathbb{Q})$
is equal to zero.
$H^{2}(X,\mathbb{Q})$
is equal to zero.
![]() $L_{1}\equiv L_{2}$
for line bundles
$L_{1}\equiv L_{2}$
for line bundles
![]() $L_{1}$
and
$L_{1}$
and
![]() $L_{2}$
denotes equality
$L_{2}$
denotes equality
![]() $c_{1}(L_{1})\equiv c_{1}(L_{2})$
in
$c_{1}(L_{1})\equiv c_{1}(L_{2})$
in
![]() $H^{2}(X,\mathbb{Q})$
. In that case
$H^{2}(X,\mathbb{Q})$
. In that case
![]() $L_{1}~\otimes ~L_{2}^{-1}\in \operatorname{Pic}^{\unicode[STIX]{x1D70F}}X$
.
$L_{1}~\otimes ~L_{2}^{-1}\in \operatorname{Pic}^{\unicode[STIX]{x1D70F}}X$
.
If
![]() $\dim X=2$
then an effective
$\dim X=2$
then an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $N=\sum a_{i}N_{i}$
, where
$N=\sum a_{i}N_{i}$
, where
![]() $a_{i}>0$
and
$a_{i}>0$
and
![]() $N_{i}$
are prime, is called negative if the intersection matrix
$N_{i}$
are prime, is called negative if the intersection matrix
![]() $[N_{i}.N_{j}]$
is negative definite. It is called semi-negative if the matrix
$[N_{i}.N_{j}]$
is negative definite. It is called semi-negative if the matrix
![]() $[N_{i}.N_{j}]$
is negative semi-definite. By convention, the zero divisor is both negative and semi-negative.
$[N_{i}.N_{j}]$
is negative semi-definite. By convention, the zero divisor is both negative and semi-negative.
2.3 Zariski semi-decomposition
Let
![]() $X$
be a smooth complex projective surface. We say that the degree of a
$X$
be a smooth complex projective surface. We say that the degree of a
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $L$
on
$L$
on
![]() $X$
is strictly positive if for every ample divisor
$X$
is strictly positive if for every ample divisor
![]() $H$
we have
$H$
we have
![]() $L.H>0$
.
$L.H>0$
.
Lemma 2.3. Let
![]() $L$
be a
$L$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. Assume that
$X$
. Assume that
![]() $L.A>0$
for some ample
$L.A>0$
for some ample
![]() $A$
and
$A$
and
![]() $L^{2}\geqslant 0$
. If
$L^{2}\geqslant 0$
. If
![]() $L$
is not big then
$L$
is not big then
![]() $L$
is nef,
$L$
is nef,
![]() $L^{2}=0$
and the degree of
$L^{2}=0$
and the degree of
![]() $L$
is strictly positive.
$L$
is strictly positive.
Proof. Let us first note that
![]() $L$
is pseudoeffective, i.e., its intersection with any nef divisor is non-negative. Indeed, if
$L$
is pseudoeffective, i.e., its intersection with any nef divisor is non-negative. Indeed, if
![]() $L.H<0$
for some nef
$L.H<0$
for some nef
![]() $H$
then there exists a positive rational number
$H$
then there exists a positive rational number
![]() $a$
such that
$a$
such that
![]() $L.(A+aH)=0$
. Since
$L.(A+aH)=0$
. Since
![]() $A+aH$
is ample, by the Hodge index theorem we get
$A+aH$
is ample, by the Hodge index theorem we get
![]() $L^{2}<0$
, a contradiction.
$L^{2}<0$
, a contradiction.
Now recall that pseudoeffective divisors admit the so-called Zariski decomposition. This means that
![]() $L$
can be written as a sum
$L$
can be written as a sum
![]() $P+N$
, where
$P+N$
, where
![]() $P$
is a nef
$P$
is a nef
![]() $\mathbb{Q}$
-divisor and
$\mathbb{Q}$
-divisor and
![]() $N$
is a negative effective
$N$
is a negative effective
![]() $\mathbb{Q}$
-divisor with
$\mathbb{Q}$
-divisor with
![]() $P.N=0$
. Since
$P.N=0$
. Since
![]() $L$
is not big,
$L$
is not big,
![]() $P$
is also not big which implies that
$P$
is also not big which implies that
![]() $P^{2}=0$
. But in this case if
$P^{2}=0$
. But in this case if
![]() $N\neq 0$
then
$N\neq 0$
then
![]() $L^{2}=N^{2}<0$
, a contradiction. Therefore
$L^{2}=N^{2}<0$
, a contradiction. Therefore
![]() $L=P$
so
$L=P$
so
![]() $L$
is nef with
$L$
is nef with
![]() $L^{2}=0$
.
$L^{2}=0$
.
To prove that the degree of
![]() $L$
is strictly positive it is sufficient to show that there are no ample divisors
$L$
is strictly positive it is sufficient to show that there are no ample divisors
![]() $H$
with
$H$
with
![]() $L.H=0$
. But if such a divisor
$L.H=0$
. But if such a divisor
![]() $H$
exists then by the Hodge index theorem
$H$
exists then by the Hodge index theorem
![]() $L$
is numerically trivial contradicting inequality
$L$
is numerically trivial contradicting inequality
![]() $L.A>0$
.◻
$L.A>0$
.◻
Lemma 2.4. Let
![]() $C$
be a
$C$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. Assume that
$X$
. Assume that
![]() $C=L+B$
, where
$C=L+B$
, where
![]() $L$
is nef and
$L$
is nef and
![]() $B$
is effective. If
$B$
is effective. If
![]() $C$
is not big then the following conditions are satisfied:
$C$
is not big then the following conditions are satisfied:
(i)
 $L^{2}=0$
;
$L^{2}=0$
;(ii)
 $B$
is semi-negative;
$B$
is semi-negative;(iii)
 $L.B=0$
. In particular, if we write
$L.B=0$
. In particular, if we write
 $B=\sum a_{i}C_{i}$
, where
$B=\sum a_{i}C_{i}$
, where
 $a_{i}>0$
and
$a_{i}>0$
and
 $C_{i}$
are prime divisors, then
$C_{i}$
are prime divisors, then
 $L.C_{i}=0$
for every
$L.C_{i}=0$
for every
 $i$
.
$i$
.
In this case we say that
![]() $C=L+B$
is a Zariski semi-decomposition of
$C=L+B$
is a Zariski semi-decomposition of
![]() $C$
.
$C$
.
Note that unlike the usual Zariski decomposition, Zariski semi-decomposition need not be unique, i.e., one divisor can have many different Zariski semi-decompositions.
Proof. Since
![]() $L$
is nef we have
$L$
is nef we have
![]() $L^{2}\geqslant 0$
. If
$L^{2}\geqslant 0$
. If
![]() $L^{2}>0$
then
$L^{2}>0$
then
![]() $L$
is big. But then
$L$
is big. But then
![]() $C$
is big, contradicting our assumption. This proves the first assertion.
$C$
is big, contradicting our assumption. This proves the first assertion.
To prove the second one, it is sufficient to take any combination
![]() $\sum \unicode[STIX]{x1D6FC}_{i}C_{i}$
with rational numbers
$\sum \unicode[STIX]{x1D6FC}_{i}C_{i}$
with rational numbers
![]() $\unicode[STIX]{x1D6FC}_{i}\in [0,a_{i}]$
and prove that
$\unicode[STIX]{x1D6FC}_{i}\in [0,a_{i}]$
and prove that
![]() $(\sum \unicode[STIX]{x1D6FC}_{i}C_{i})^{2}\leqslant 0$
.
$(\sum \unicode[STIX]{x1D6FC}_{i}C_{i})^{2}\leqslant 0$
.
Let us take a rational number
![]() $\unicode[STIX]{x1D6FD}\in [0,1]$
. Since
$\unicode[STIX]{x1D6FD}\in [0,1]$
. Since
![]() $(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i})\leqslant C$
and
$(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i})\leqslant C$
and
![]() $C$
is not big, the
$C$
is not big, the
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i})$
is not big. But
$(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i})$
is not big. But
![]() $(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i}).A\geqslant 0$
, so we have
$(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i}).A\geqslant 0$
, so we have
![]() $(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i})^{2}\leqslant 0$
. Putting
$(\unicode[STIX]{x1D6FD}L+\sum \unicode[STIX]{x1D6FC}_{i}C_{i})^{2}\leqslant 0$
. Putting
![]() $\unicode[STIX]{x1D6FD}=0$
, we get the required inequality.
$\unicode[STIX]{x1D6FD}=0$
, we get the required inequality.
Putting
![]() $\unicode[STIX]{x1D6FD}=1$
we see that for any
$\unicode[STIX]{x1D6FD}=1$
we see that for any
![]() $\unicode[STIX]{x1D716}\in [0,1]$
, we have
$\unicode[STIX]{x1D716}\in [0,1]$
, we have
![]() $(L+\unicode[STIX]{x1D716}B)^{2}\leqslant 0$
. Since
$(L+\unicode[STIX]{x1D716}B)^{2}\leqslant 0$
. Since
![]() $L^{2}=0$
, this gives
$L^{2}=0$
, this gives
![]() $2L.B+\unicode[STIX]{x1D716}B^{2}\leqslant 0$
. Passing with
$2L.B+\unicode[STIX]{x1D716}B^{2}\leqslant 0$
. Passing with
![]() $\unicode[STIX]{x1D716}$
to
$\unicode[STIX]{x1D716}$
to
![]() $0$
we get
$0$
we get
![]() $L.B\leqslant 0$
. But
$L.B\leqslant 0$
. But
![]() $L$
is nef and
$L$
is nef and
![]() $B$
is effective so we get
$B$
is effective so we get
![]() $L.B=0$
.◻
$L.B=0$
.◻
2.4 Lifting representations of the fundamental group
Let
![]() $G/\mathbb{C}$
be a connected, semi-simple group and let
$G/\mathbb{C}$
be a connected, semi-simple group and let
![]() $\unicode[STIX]{x1D6E4}$
be a group. A homomorphism of groups
$\unicode[STIX]{x1D6E4}$
be a group. A homomorphism of groups
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}\rightarrow G$
is called irreducible if the Zariski closure of the image of
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}\rightarrow G$
is called irreducible if the Zariski closure of the image of
![]() $\unicode[STIX]{x1D6E4}$
is not contained in any proper parabolic subgroup of
$\unicode[STIX]{x1D6E4}$
is not contained in any proper parabolic subgroup of
![]() $G$
. In the case
$G$
. In the case
![]() $G=\operatorname{SL}(n,\mathbb{C})$
, this notion is equivalent to the usual notion of an irreducible representation.
$G=\operatorname{SL}(n,\mathbb{C})$
, this notion is equivalent to the usual notion of an irreducible representation.
Let us recall the following definition (cf. [Reference de JongdJo01, 2.14]).
Definition 2.5. A homomorphism
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}\rightarrow G$
is called Lie irreducible if it is irreducible and remains so on all finite index subgroups of
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}\rightarrow G$
is called Lie irreducible if it is irreducible and remains so on all finite index subgroups of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}\rightarrow G$
be an irreducible homomorphism and let
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}\rightarrow G$
be an irreducible homomorphism and let
![]() $G_{\unicode[STIX]{x1D70C}}\subset G$
be the Zariski closure of the image of
$G_{\unicode[STIX]{x1D70C}}\subset G$
be the Zariski closure of the image of
![]() $\unicode[STIX]{x1D70C}$
. Then
$\unicode[STIX]{x1D70C}$
. Then
![]() $\unicode[STIX]{x1D70C}$
is Lie irreducible if and only if the inclusion of the connected component
$\unicode[STIX]{x1D70C}$
is Lie irreducible if and only if the inclusion of the connected component
![]() $G_{\unicode[STIX]{x1D70C}}^{0}$
of
$G_{\unicode[STIX]{x1D70C}}^{0}$
of
![]() $G_{\unicode[STIX]{x1D70C}}$
into
$G_{\unicode[STIX]{x1D70C}}$
into
![]() $G$
is irreducible. In that case
$G$
is irreducible. In that case
![]() $G_{\unicode[STIX]{x1D70C}}$
is semi-simple and its centralizer in
$G_{\unicode[STIX]{x1D70C}}$
is semi-simple and its centralizer in
![]() $G$
is finite.
$G$
is finite.
The following lemma is a stronger version of [Reference CousinCou15, Theorem 3.1].
Lemma 2.6. Let
![]() $X$
be a smooth, complex, quasi-projective variety and let
$X$
be a smooth, complex, quasi-projective variety and let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
be a homomorphism into a complex, linear algebraic group
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
be a homomorphism into a complex, linear algebraic group
![]() $G$
and let
$G$
and let
![]() $\tilde{G}\rightarrow G$
be a central isogeny. Then there exists a finite surjective morphism
$\tilde{G}\rightarrow G$
be a central isogeny. Then there exists a finite surjective morphism
![]() $p:Z\rightarrow X$
such that
$p:Z\rightarrow X$
such that
![]() $p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
lifts to
$p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
lifts to
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \tilde{G}$
. Moreover, for any completion
$\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \tilde{G}$
. Moreover, for any completion
![]() $X\subset \bar{X}$
there exists an alteration
$X\subset \bar{X}$
there exists an alteration
![]() $\bar{p}:\bar{Z}\rightarrow \bar{X}$
, such that
$\bar{p}:\bar{Z}\rightarrow \bar{X}$
, such that
![]() $\bar{Z}$
is smooth and projective,
$\bar{Z}$
is smooth and projective,
![]() $D=\bar{Z}-Z$
is a simple normal crossing divisor and the restriction
$D=\bar{Z}-Z$
is a simple normal crossing divisor and the restriction
![]() $p=\bar{p}|_{p^{-1}X}:Z=p^{-1}(X)\rightarrow X$
is such that
$p=\bar{p}|_{p^{-1}X}:Z=p^{-1}(X)\rightarrow X$
is such that
![]() $p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
can be lifted to
$p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
can be lifted to
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \tilde{G}$
.
$\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \tilde{G}$
.
Proof. Let
![]() $A$
be the finite abelian group defined by the short exact sequence
$A$
be the finite abelian group defined by the short exact sequence
Since
![]() $A$
is contained in the center of
$A$
is contained in the center of
![]() $\tilde{G}$
, this sequence induces an exact sequence
$\tilde{G}$
, this sequence induces an exact sequence
By the comparison theorem, for a finite abelian group
![]() $A$
we have a natural isomorphism
$A$
we have a natural isomorphism
![]() $H^{2}(X,A)\simeq H_{\acute{e} t}^{2}(X,A)$
of the complex cohomology group with an étale cohomology group. By [Reference BhattBha12, Theorem 1.1] there exists a finite surjective morphism
$H^{2}(X,A)\simeq H_{\acute{e} t}^{2}(X,A)$
of the complex cohomology group with an étale cohomology group. By [Reference BhattBha12, Theorem 1.1] there exists a finite surjective morphism
![]() $p:Z\rightarrow X$
such that the image of the obstruction class
$p:Z\rightarrow X$
such that the image of the obstruction class
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D70C}])$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D70C}])$
in
![]() $H_{\acute{e} t}^{2}(Z,A)$
vanishes. This shows that
$H_{\acute{e} t}^{2}(Z,A)$
vanishes. This shows that
![]() $p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
can be lifted to a homomorphism
$p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
can be lifted to a homomorphism
![]() $\unicode[STIX]{x1D70C}_{Z}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \tilde{G}$
.
$\unicode[STIX]{x1D70C}_{Z}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \tilde{G}$
.
The second part of the lemma follows from the first one and from existence of log resolution of singularities of the normalization of
![]() $\bar{X}$
in the function field of
$\bar{X}$
in the function field of
![]() $Z$
.◻
$Z$
.◻
Let us recall that a linear algebraic group is called almost-simple, if it does not contain any Zariski closed, connected normal subgroups of positive dimension. Clearly, an almost-simple group is semi-simple and connected.
Proposition 2.7. Let
![]() $X$
be a smooth complex quasi-projective variety and let
$X$
be a smooth complex quasi-projective variety and let
![]() $G/\mathbb{C}$
be a connected, semi-simple group. Let
$G/\mathbb{C}$
be a connected, semi-simple group. Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
be an irreducible homomorphism. Then one of the following holds:
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
be an irreducible homomorphism. Then one of the following holds:
(i) there exists a finite étale covering
 $p:Z\rightarrow X$
such that
$p:Z\rightarrow X$
such that
 $p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,~z)\rightarrow G$
is not irreducible;
$p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,~z)\rightarrow G$
is not irreducible;(ii) there exists a finite étale covering
 $p:Z\rightarrow X$
such that the Zariski closure of the image of
$p:Z\rightarrow X$
such that the Zariski closure of the image of
 $p^{\ast }\unicode[STIX]{x1D70C}$
in
$p^{\ast }\unicode[STIX]{x1D70C}$
in
 $G$
is almost-simple and irreducible;
$G$
is almost-simple and irreducible;(iii) there exists a finite surjective morphism
 $p:Z\rightarrow X$
and simple, simply connected groups
$p:Z\rightarrow X$
and simple, simply connected groups
 $H_{1},\ldots ,H_{m}$
,
$H_{1},\ldots ,H_{m}$
,
 $m\geqslant 2$
, such that
$m\geqslant 2$
, such that
 $p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
factors through a homomorphism
$p^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow G$
factors through a homomorphism
 $\unicode[STIX]{x1D70F}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow H_{1}\times \cdots \times H_{m}$
with a Zariski-dense image.
$\unicode[STIX]{x1D70F}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow H_{1}\times \cdots \times H_{m}$
with a Zariski-dense image.
Proof. There exists a finite étale covering
![]() $Z\rightarrow X$
such that
$Z\rightarrow X$
such that
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)$
maps into the connected component
$\unicode[STIX]{x1D70B}_{1}(Z,z)$
maps into the connected component
![]() $H=G_{\unicode[STIX]{x1D70C}}^{0}$
of the Zariski closure of the image of
$H=G_{\unicode[STIX]{x1D70C}}^{0}$
of the Zariski closure of the image of
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)$
in
$\unicode[STIX]{x1D70B}_{1}(Z,z)$
in
![]() $G$
. If
$G$
. If
![]() $H\subset G$
is not irreducible then we are in the first case. So let us assume that
$H\subset G$
is not irreducible then we are in the first case. So let us assume that
![]() $H\subset G$
is irreducible. Then
$H\subset G$
is irreducible. Then
![]() $H$
has a canonical decomposition into an almost direct product of its almost-simple factors (see [Reference BorelBor91, Theorem 22.10]). More precisely, let
$H$
has a canonical decomposition into an almost direct product of its almost-simple factors (see [Reference BorelBor91, Theorem 22.10]). More precisely, let
![]() $H_{1},\ldots ,H_{m}$
be the minimal elements among the closed, connected normal subgroups of
$H_{1},\ldots ,H_{m}$
be the minimal elements among the closed, connected normal subgroups of
![]() $H$
of positive dimension. Then all
$H$
of positive dimension. Then all
![]() $H_{i}$
are almost-simple and the isogeny
$H_{i}$
are almost-simple and the isogeny
![]() $H_{1}\times \cdots \times H_{m}\rightarrow H$
is central (with finite kernel). If
$H_{1}\times \cdots \times H_{m}\rightarrow H$
is central (with finite kernel). If
![]() $m=1$
then we are in the second case. If
$m=1$
then we are in the second case. If
![]() $m\geqslant 2$
then we can pass to the universal covering of the product
$m\geqslant 2$
then we can pass to the universal covering of the product
![]() $H_{1}\times \cdots \times H_{m}$
and we are in the last case by Lemma 2.6.◻
$H_{1}\times \cdots \times H_{m}$
and we are in the last case by Lemma 2.6.◻
Remark 2.8. The second case of the above proposition is particularly interesting in the presence of fibrations. More precisely, if
![]() $f:X\rightarrow Y$
is a fibration,
$f:X\rightarrow Y$
is a fibration,
![]() $G$
is almost-simple and
$G$
is almost-simple and
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
has a Zariski-dense image, then the image of the restriction of
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
has a Zariski-dense image, then the image of the restriction of
![]() $\unicode[STIX]{x1D70C}$
to a smooth fiber of
$\unicode[STIX]{x1D70C}$
to a smooth fiber of
![]() $f$
is either Zariski-dense in
$f$
is either Zariski-dense in
![]() $G$
or it is finite (see [Reference ZuoZuo99, Proposition 2.2.2]). In the second case, after some blowing up and taking a finite étale cover, one can factor
$G$
or it is finite (see [Reference ZuoZuo99, Proposition 2.2.2]). In the second case, after some blowing up and taking a finite étale cover, one can factor
![]() $\unicode[STIX]{x1D70C}$
through the induced fibration (see [Reference ZuoZuo99, Lemma 2.2.3]).
$\unicode[STIX]{x1D70C}$
through the induced fibration (see [Reference ZuoZuo99, Lemma 2.2.3]).
2.5 Representations of geometric origin
Let
![]() $X$
be a smooth complex quasi-projective variety and let
$X$
be a smooth complex quasi-projective variety and let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be a semi-simple representation. Let us recall the following definition from the introduction.
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be a semi-simple representation. Let us recall the following definition from the introduction.
Definition 2.9. We say that a semi-simple representation
![]() $\unicode[STIX]{x1D70C}$
and its associated local system
$\unicode[STIX]{x1D70C}$
and its associated local system
![]() $V$
are of geometric origin if there exists a dense Zariski open subset
$V$
are of geometric origin if there exists a dense Zariski open subset
![]() $U\subset X$
and a smooth projective morphism
$U\subset X$
and a smooth projective morphism
![]() $f:Z\rightarrow U$
such that
$f:Z\rightarrow U$
such that
![]() $V|_{U}$
occurs as a subquotient of the local system
$V|_{U}$
occurs as a subquotient of the local system
![]() $R^{i}f_{\ast }(\mathbb{C}_{Z})$
for some
$R^{i}f_{\ast }(\mathbb{C}_{Z})$
for some
![]() $i$
.
$i$
.
Proposition 2.10. If
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are local systems then
$V_{2}$
are local systems then
![]() $V_{1}\oplus V_{2}$
is of geometric origin if and only if
$V_{1}\oplus V_{2}$
is of geometric origin if and only if
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are. If
$V_{2}$
are. If
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are of geometric origin then so is
$V_{2}$
are of geometric origin then so is
![]() $V_{1}~\otimes ~V_{2}$
. A rank
$V_{1}~\otimes ~V_{2}$
. A rank
![]() $1$
local system is of geometric origin if and only if it is of finite order.
$1$
local system is of geometric origin if and only if it is of finite order.
If
![]() $p:Y\rightarrow X$
is a generically surjective map between irreducible varieties, and
$p:Y\rightarrow X$
is a generically surjective map between irreducible varieties, and
![]() $V$
is a semi-simple local system on
$V$
is a semi-simple local system on
![]() $X$
, then
$X$
, then
![]() $V$
is of geometric origin if and only if
$V$
is of geometric origin if and only if
![]() $p^{\ast }(V)$
is of geometric origin.
$p^{\ast }(V)$
is of geometric origin.
Suppose that
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
are two irreducible representations with determinants of finite order, whose projectivizations are isomorphic. Then
$\unicode[STIX]{x1D70C}_{2}$
are two irreducible representations with determinants of finite order, whose projectivizations are isomorphic. Then
![]() $\unicode[STIX]{x1D70C}_{1}$
is of geometric origin if and only if
$\unicode[STIX]{x1D70C}_{1}$
is of geometric origin if and only if
![]() $\unicode[STIX]{x1D70C}_{2}$
is.
$\unicode[STIX]{x1D70C}_{2}$
is.
Proof. Given families for
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
we can take a disjoint union of products with fixed varieties for
$V_{2}$
we can take a disjoint union of products with fixed varieties for
![]() $V_{1}\oplus V_{2}$
. One may also stay within the world of fibrations with connected fibers by then embedding the resulting family in a big projective space and blowing up along that locus. If
$V_{1}\oplus V_{2}$
. One may also stay within the world of fibrations with connected fibers by then embedding the resulting family in a big projective space and blowing up along that locus. If
![]() $V_{1}\oplus V_{2}$
is of geometric origin then
$V_{1}\oplus V_{2}$
is of geometric origin then
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are so by definition. If
$V_{2}$
are so by definition. If
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are of geometric origin, taking the fiber product of the families results, by the Künneth formula, in a family for
$V_{2}$
are of geometric origin, taking the fiber product of the families results, by the Künneth formula, in a family for
![]() $V_{1}~\otimes ~V_{2}$
.
$V_{1}~\otimes ~V_{2}$
.
A rank
![]() $1$
system of finite order is a direct factor in the
$1$
system of finite order is a direct factor in the
![]() $0$
th direct image of a finite ramified cover. In the other direction, let
$0$
th direct image of a finite ramified cover. In the other direction, let
![]() $V$
be a rank
$V$
be a rank
![]() $1$
local system of geometric origin. Let
$1$
local system of geometric origin. Let
![]() $f:Z\rightarrow U\subset X$
be the corresponding map. Note that
$f:Z\rightarrow U\subset X$
be the corresponding map. Note that
![]() $R^{i}f_{\ast }\mathbb{C}_{Z}$
comes with an integral structure given by the image of
$R^{i}f_{\ast }\mathbb{C}_{Z}$
comes with an integral structure given by the image of
![]() $R^{i}f_{\ast }\mathbb{Z}_{Z}\rightarrow R^{i}f_{\ast }\mathbb{C}_{Z}$
. Hence the eigenvalues of all monodromy transformations are algebraic integers, so any direct summand of
$R^{i}f_{\ast }\mathbb{Z}_{Z}\rightarrow R^{i}f_{\ast }\mathbb{C}_{Z}$
. Hence the eigenvalues of all monodromy transformations are algebraic integers, so any direct summand of
![]() $R^{i}f_{\ast }\mathbb{C}_{Z}$
is integral. The action of
$R^{i}f_{\ast }\mathbb{C}_{Z}$
is integral. The action of
![]() $\text{Gal}\,(\mathbb{C}/\mathbb{Q})$
takes one direct summand to another. Now existence of a polarization implies that any rank
$\text{Gal}\,(\mathbb{C}/\mathbb{Q})$
takes one direct summand to another. Now existence of a polarization implies that any rank
![]() $1$
direct summand is unitary. Thus,
$1$
direct summand is unitary. Thus,
![]() $V$
and all its
$V$
and all its
![]() $\text{Gal}\,(\mathbb{C}/\mathbb{Q})$
-conjugates are integral and unitary. But by Kronecker’s theorem, an algebraic integer all of whose conjugates have absolute value
$\text{Gal}\,(\mathbb{C}/\mathbb{Q})$
-conjugates are integral and unitary. But by Kronecker’s theorem, an algebraic integer all of whose conjugates have absolute value
![]() $1$
is a root of unity, so
$1$
is a root of unity, so
![]() $V$
is of finite order (not only on
$V$
is of finite order (not only on
![]() $U$
but also on
$U$
but also on
![]() $X$
).
$X$
).
Suppose
![]() $p:Y\rightarrow X$
is a generically surjective map and
$p:Y\rightarrow X$
is a generically surjective map and
![]() $V$
a local system on
$V$
a local system on
![]() $X$
. If
$X$
. If
![]() $V$
is of geometric origin on
$V$
is of geometric origin on
![]() $X$
then since the image of
$X$
then since the image of
![]() $p$
intersects the open set
$p$
intersects the open set
![]() $U\subset X$
on which
$U\subset X$
on which
![]() $V$
is defined, we get a family over
$V$
is defined, we get a family over
![]() $p^{-1}(U)$
showing that
$p^{-1}(U)$
showing that
![]() $p^{\ast }(V)$
is of geometric origin.
$p^{\ast }(V)$
is of geometric origin.
In the other direction, suppose
![]() $p^{\ast }(V)$
is of geometric origin coming from a family
$p^{\ast }(V)$
is of geometric origin coming from a family
![]() $f:Z\rightarrow U$
with
$f:Z\rightarrow U$
with
![]() $U\subset Y$
. Choose a subvariety
$U\subset Y$
. Choose a subvariety
![]() $Y^{\prime }\subset U$
which is quasi-finite over
$Y^{\prime }\subset U$
which is quasi-finite over
![]() $X$
. By replacing
$X$
. By replacing
![]() $Y^{\prime }$
by a Zariski open subset, we may assume that
$Y^{\prime }$
by a Zariski open subset, we may assume that
![]() $p^{\prime }:Y^{\prime }\rightarrow U^{\prime }$
is a finite étale map to a dense open subset
$p^{\prime }:Y^{\prime }\rightarrow U^{\prime }$
is a finite étale map to a dense open subset
![]() $U^{\prime }\subset X$
. Let
$U^{\prime }\subset X$
. Let
![]() $Z^{\prime }\subset Z$
be the inverse image of
$Z^{\prime }\subset Z$
be the inverse image of
![]() $Y^{\prime }$
, and denote by
$Y^{\prime }$
, and denote by
![]() $f^{\prime }:Z^{\prime }\rightarrow Y^{\prime }$
the map. Under our suppositions, it is smooth and projective, hence also the composed map
$f^{\prime }:Z^{\prime }\rightarrow Y^{\prime }$
the map. Under our suppositions, it is smooth and projective, hence also the composed map
is smooth and projective. By the decomposition theorem,
![]() $R^{i}(f^{\prime })_{\ast }(\mathbb{C}_{Z^{\prime }})$
is semi-simple so a subquotient may be viewed as a direct factor. Thus, we may assume given an injective map
$R^{i}(f^{\prime })_{\ast }(\mathbb{C}_{Z^{\prime }})$
is semi-simple so a subquotient may be viewed as a direct factor. Thus, we may assume given an injective map
![]() $(p^{\prime })^{\ast }(V)\rightarrow R^{i}(f^{\prime })_{\ast }(\mathbb{C}_{Z^{\prime }})$
which gives by composition, in turn, an injective map
$(p^{\prime })^{\ast }(V)\rightarrow R^{i}(f^{\prime })_{\ast }(\mathbb{C}_{Z^{\prime }})$
which gives by composition, in turn, an injective map
showing that
![]() $V$
is of geometric origin.
$V$
is of geometric origin.
For the last part, suppose given two irreducible representations
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
whose determinants are of finite order. Let
$\unicode[STIX]{x1D70C}_{2}$
whose determinants are of finite order. Let
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
respectively denote the corresponding local systems. Suppose the projectivizations of
$V_{2}$
respectively denote the corresponding local systems. Suppose the projectivizations of
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
are isomorphic, and fix bases for
$\unicode[STIX]{x1D70C}_{2}$
are isomorphic, and fix bases for
![]() $(V_{1})_{x}$
and
$(V_{1})_{x}$
and
![]() $(V_{2})_{x}$
at the basepoint
$(V_{2})_{x}$
at the basepoint
![]() $x\in X$
that are compatible with the isomorphism of projectivizations. For any
$x\in X$
that are compatible with the isomorphism of projectivizations. For any
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(X,x)$
we may then write
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(X,x)$
we may then write
with
![]() $a(\unicode[STIX]{x1D6FE})$
a diagonal matrix. Now
$a(\unicode[STIX]{x1D6FE})$
a diagonal matrix. Now
![]() $a:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \mathbb{C}^{\ast }$
is a rank
$a:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \mathbb{C}^{\ast }$
is a rank
![]() $1$
representation corresponding to a rank
$1$
representation corresponding to a rank
![]() $1$
local system
$1$
local system
![]() $A$
, and we have
$A$
, and we have
![]() $V_{2}=A~\otimes ~V_{1}$
. If
$V_{2}=A~\otimes ~V_{1}$
. If
![]() $r=\text{rk}(V_{1})$
then
$r=\text{rk}(V_{1})$
then
From the hypothesis,
![]() $A^{\otimes r}$
is of finite order, so
$A^{\otimes r}$
is of finite order, so
![]() $A$
is of finite order. Hence,
$A$
is of finite order. Hence,
![]() $A$
is of geometric origin. It follows that
$A$
is of geometric origin. It follows that
![]() $V_{2}$
is of geometric origin if and only if
$V_{2}$
is of geometric origin if and only if
![]() $V_{1}$
is.◻
$V_{1}$
is.◻
Concerning the second paragraph, it is also true that any pullback of a system of geometric origin, is of geometric origin. For the case of pullback along a map that goes into the complement of the open set
![]() $U$
over which the smooth family is given, this requires using the theory of perverse sheaves and applying the decomposition theorem; we do not treat that here.
$U$
over which the smooth family is given, this requires using the theory of perverse sheaves and applying the decomposition theorem; we do not treat that here.
The converse to the part about
![]() $V_{1}~\otimes ~V_{2}$
looks like an interesting question: if
$V_{1}~\otimes ~V_{2}$
looks like an interesting question: if
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are irreducible local systems with trivial determinant such that
$V_{2}$
are irreducible local systems with trivial determinant such that
![]() $V_{1}~\otimes ~V_{2}$
is of geometric origin then are
$V_{1}~\otimes ~V_{2}$
is of geometric origin then are
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
of geometric origin?
$V_{2}$
of geometric origin?
Our definition of local systems of geometric origin is rather large, and one can envision a couple of strengthenings. The following remarks on this point are not needed in the rest of the paper: we refer everywhere only to the notion of Definition 2.9, and leave open the question of obtaining the stronger properties we now mention.
First, one could ask for
![]() $U=X$
, that is to say one could ask for a smooth family extending over
$U=X$
, that is to say one could ask for a smooth family extending over
![]() $X$
. We might say in that case that
$X$
. We might say in that case that
![]() $V$
is smoothly of geometric origin. This looks to be a very strong condition, and it is difficult to predict when it should be satisfied. There are natural examples of local systems coming from families of varieties, such that the local system extends to a larger subset than the subset of definition of the smooth family. Indeed, any even-dimensional Lefschetz pencil has order two monodromy around the singularities, so after pulling back to a twofold cover of the base ramified at the singular points, the local system extends. It is highly unclear whether to expect the existence of a smooth globally defined family realizing the same monodromy representation.
$V$
is smoothly of geometric origin. This looks to be a very strong condition, and it is difficult to predict when it should be satisfied. There are natural examples of local systems coming from families of varieties, such that the local system extends to a larger subset than the subset of definition of the smooth family. Indeed, any even-dimensional Lefschetz pencil has order two monodromy around the singularities, so after pulling back to a twofold cover of the base ramified at the singular points, the local system extends. It is highly unclear whether to expect the existence of a smooth globally defined family realizing the same monodromy representation.
In particular, Katz’s theorem that rigid local systems over the orbifold projective line are of geometric origin, does not give smooth geometric origin. The discussion of the notion of geometric origin in [Reference TotaroTot07] should probably be modified accordingly.
Another point is the question of whether the projector to our direct factor is motivic. Say that a local system
![]() $V$
is strongly of geometric origin if there exists a proper morphism
$V$
is strongly of geometric origin if there exists a proper morphism
![]() $f:Z\rightarrow X$
and an algebraic cycle representing a projector
$f:Z\rightarrow X$
and an algebraic cycle representing a projector
![]() $\unicode[STIX]{x1D70B}:Rf_{\ast }(\mathbb{Z}_{Z})\rightarrow Rf_{\ast }(\mathbb{Z}_{Z})$
such that
$\unicode[STIX]{x1D70B}:Rf_{\ast }(\mathbb{Z}_{Z})\rightarrow Rf_{\ast }(\mathbb{Z}_{Z})$
such that
![]() $V$
is the image of
$V$
is the image of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
One would need at least the Hodge conjecture to go from our (weak) notion of geometric origin to this notion of strong geometric origin, but in fact it does not even seem clear that the Hodge conjecture would be sufficient for that.
For instance one would like to answer the following question (a punctual analogue of the converse question for tensor products of local systems mentioned above): given
![]() $\mathbb{Z}$
-Hodge structures
$\mathbb{Z}$
-Hodge structures
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
with trivial determinants such that
$V_{2}$
with trivial determinants such that
![]() $V_{1}~\otimes ~V_{2}$
is a motive, are
$V_{1}~\otimes ~V_{2}$
is a motive, are
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
motives?
$V_{2}$
motives?
If we do not know the answer to that question, but do assume the Hodge conjecture, then one might be able to show that
![]() $V$
of weak geometric origin implies that some
$V$
of weak geometric origin implies that some
![]() $V^{\oplus k}$
is of strong geometric origin. Some understanding of algebraic cycles and the decomposition theorem would also clearly be needed.
$V^{\oplus k}$
is of strong geometric origin. Some understanding of algebraic cycles and the decomposition theorem would also clearly be needed.
In the context of the present paper, our main constructions provide smooth families of abelian varieties, and hence give smooth geometric origin in some cases. One can envision looking at the question of strong geometric origin for those cases – that would require delving into the endomorphism algebras of the families of abelian varieties we construct. We do not make any claims about that here.
3 Factorization through orbicurves
An orbicurve
![]() $C$
is a smooth one-dimensional Deligne–Mumford stack whose generic stabilizer group is trivial. The coarse moduli space
$C$
is a smooth one-dimensional Deligne–Mumford stack whose generic stabilizer group is trivial. The coarse moduli space
![]() $C^{\text{coarse}}$
is a smooth curve having a collection of points
$C^{\text{coarse}}$
is a smooth curve having a collection of points
![]() $p_{1},\ldots ,p_{k}$
such that there exist strictly positive integers
$p_{1},\ldots ,p_{k}$
such that there exist strictly positive integers
![]() $n_{1},\ldots ,n_{k}$
such that
$n_{1},\ldots ,n_{k}$
such that
is the root stack. The fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}(C,y)$
is the same as the orbifold fundamental group considered in § 2.1 (with
$\unicode[STIX]{x1D70B}_{1}(C,y)$
is the same as the orbifold fundamental group considered in § 2.1 (with
![]() $n_{i}$
equal to multiplicities of the fibers over
$n_{i}$
equal to multiplicities of the fibers over
![]() $p_{i}$
).
$p_{i}$
).
The goal of this subsection is to prove the equivalence of several different notions of factorization through orbicurves.
Definition 3.1. Let
![]() $X$
be a smooth complex quasi-projective variety. Suppose that
$X$
be a smooth complex quasi-projective variety. Suppose that
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
is an irreducible representation.
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
is an irreducible representation.
(i) We say that
 $\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve if there is an orbicurve
$\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve if there is an orbicurve
 $C$
, a fibration
$C$
, a fibration
 $f:X\rightarrow C$
, and the following commutative diagram.
$f:X\rightarrow C$
, and the following commutative diagram. 
(ii) We say that
 $\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve if there is an alteration
$\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve if there is an alteration
 $p:Z\rightarrow X$
such that
$p:Z\rightarrow X$
such that
 $p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
$p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
Definition 3.2. Let
![]() $X$
be a smooth complex quasi-projective variety. We say that an irreducible representation
$X$
be a smooth complex quasi-projective variety. We say that an irreducible representation
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
is tensor decomposable if the associated local system
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
is tensor decomposable if the associated local system
![]() $V_{\unicode[STIX]{x1D70C}}$
can be written as a tensor product
$V_{\unicode[STIX]{x1D70C}}$
can be written as a tensor product
![]() $V_{1}~\otimes ~V_{2}$
of two local systems of rank
$V_{1}~\otimes ~V_{2}$
of two local systems of rank
![]() ${\geqslant}2$
. Say that
${\geqslant}2$
. Say that
![]() $\unicode[STIX]{x1D70C}$
is virtually tensor decomposable if there exists an alteration
$\unicode[STIX]{x1D70C}$
is virtually tensor decomposable if there exists an alteration
![]() $p:Z\rightarrow X$
such that
$p:Z\rightarrow X$
such that
![]() $p^{\ast }\unicode[STIX]{x1D70C}$
is tensor decomposable.
$p^{\ast }\unicode[STIX]{x1D70C}$
is tensor decomposable.
Say that
![]() $\unicode[STIX]{x1D70C}$
is virtually reducible if there is an alteration
$\unicode[STIX]{x1D70C}$
is virtually reducible if there is an alteration
![]() $p:Z\rightarrow X$
such that
$p:Z\rightarrow X$
such that
![]() $p^{\ast }\unicode[STIX]{x1D70C}$
is reducible, i.e. it decomposes into a non-trivial direct sum.
$p^{\ast }\unicode[STIX]{x1D70C}$
is reducible, i.e. it decomposes into a non-trivial direct sum.
Let us note that a representation
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
is virtually reducible if and only if it is not Lie irreducible. Indeed, if
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
is virtually reducible if and only if it is not Lie irreducible. Indeed, if
![]() $p:Z\rightarrow X$
is an alteration then the image of
$p:Z\rightarrow X$
is an alteration then the image of
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \unicode[STIX]{x1D70B}_{1}(X,x)$
has finite index in
$\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \unicode[STIX]{x1D70B}_{1}(X,x)$
has finite index in
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
. So if
$\unicode[STIX]{x1D70B}_{1}(X,x)$
. So if
![]() $\unicode[STIX]{x1D70C}$
is virtually reducible then it is not Lie irreducible. The implication in the other direction follows from the fact that a finite index subgroup in
$\unicode[STIX]{x1D70C}$
is virtually reducible then it is not Lie irreducible. The implication in the other direction follows from the fact that a finite index subgroup in
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
gives rise to a finite étale covering.
$\unicode[STIX]{x1D70B}_{1}(X,x)$
gives rise to a finite étale covering.
For the proof of the following factorization theorem we refer to Appendix A (see Theorem A.4).
Theorem 3.3. Let
![]() $X$
be a smooth complex projective variety. Let us fix an irreducible representation
$X$
be a smooth complex projective variety. Let us fix an irreducible representation
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
for some
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
for some
![]() $n\geqslant 2$
. Suppose that
$n\geqslant 2$
. Suppose that
![]() $\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable, and not virtually reducible. Then the following conditions are equivalent:
$\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable, and not virtually reducible. Then the following conditions are equivalent:
(i)
 $\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve;
$\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve;(ii)
 $\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve;
$\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve;(iii) there exists a map
 $f:X\rightarrow C$
to an orbicurve and a fiber
$f:X\rightarrow C$
to an orbicurve and a fiber
 $F=f^{-1}(y)$
, such that the restriction of
$F=f^{-1}(y)$
, such that the restriction of
 $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
 $\unicode[STIX]{x1D70B}_{1}(F)$
becomes reducible;
$\unicode[STIX]{x1D70B}_{1}(F)$
becomes reducible;(iv) there exists an alteration
 $p:Z\rightarrow X$
such that the previous condition holds for the pullback
$p:Z\rightarrow X$
such that the previous condition holds for the pullback
 $p^{\ast }\unicode[STIX]{x1D70C}$
.
$p^{\ast }\unicode[STIX]{x1D70C}$
.
Lemma 3.4. Suppose
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
is an irreducible representation of rank
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
is an irreducible representation of rank
![]() $n\leqslant 3$
. Then
$n\leqslant 3$
. Then
![]() $\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable. If
$\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable. If
![]() $\unicode[STIX]{x1D70C}$
is virtually reducible then it has image either in a finite subgroup, or in the normalizer of a maximal torus. If
$\unicode[STIX]{x1D70C}$
is virtually reducible then it has image either in a finite subgroup, or in the normalizer of a maximal torus. If
![]() $\unicode[STIX]{x1D70C}$
is virtually reducible and underlies a VHS then it is unitary with a single Hodge type.
$\unicode[STIX]{x1D70C}$
is virtually reducible and underlies a VHS then it is unitary with a single Hodge type.
Proof. Clearly
![]() $\unicode[STIX]{x1D70C}$
cannot be virtually tensor decomposable because then it should have rank
$\unicode[STIX]{x1D70C}$
cannot be virtually tensor decomposable because then it should have rank
![]() ${\geqslant}4$
. Suppose
${\geqslant}4$
. Suppose
![]() $\unicode[STIX]{x1D70C}$
is virtually reducible, becoming reducible upon pullback to
$\unicode[STIX]{x1D70C}$
is virtually reducible, becoming reducible upon pullback to
![]() $p:Z\rightarrow X$
. The image of
$p:Z\rightarrow X$
. The image of
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)$
is of finite index in
$\unicode[STIX]{x1D70B}_{1}(Z,z)$
is of finite index in
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
and the restriction of
$\unicode[STIX]{x1D70B}_{1}(X,x)$
and the restriction of
![]() $\unicode[STIX]{x1D70C}$
to this subgroup is reducible. Therefore we may replace
$\unicode[STIX]{x1D70C}$
to this subgroup is reducible. Therefore we may replace
![]() $Z$
by the finite étale covering corresponding to this subgroup, in other words, we may suppose that
$Z$
by the finite étale covering corresponding to this subgroup, in other words, we may suppose that
![]() $p$
is finite étale. We may furthermore suppose it is Galois with group
$p$
is finite étale. We may furthermore suppose it is Galois with group
![]() $G$
. Write the decomposition into isotypical components
$G$
. Write the decomposition into isotypical components
where
![]() $V_{i}$
are irreducible local systems on
$V_{i}$
are irreducible local systems on
![]() $Z$
and
$Z$
and
![]() $W_{i}$
are vector spaces. The Galois group acts on
$W_{i}$
are vector spaces. The Galois group acts on
![]() $\{V_{i}\}$
. This action is transitive, otherwise
$\{V_{i}\}$
. This action is transitive, otherwise
![]() $\unicode[STIX]{x1D70C}$
would be reducible. In particular, all of the
$\unicode[STIX]{x1D70C}$
would be reducible. In particular, all of the
![]() $V_{i}$
and all of the
$V_{i}$
and all of the
![]() $W_{i}$
have the same rank.
$W_{i}$
have the same rank.
Suppose there is more than one isotypical component. Then
![]() $V_{i}$
and
$V_{i}$
and
![]() $W_{i}$
must be of rank
$W_{i}$
must be of rank
![]() $1$
and
$1$
and
![]() $G$
acts on the set of isotypical components by permutation. Since the subgroup of
$G$
acts on the set of isotypical components by permutation. Since the subgroup of
![]() $\operatorname{SL}(n,\mathbb{C})$
fixing the decomposition of
$\operatorname{SL}(n,\mathbb{C})$
fixing the decomposition of
![]() $V_{\unicode[STIX]{x1D70C}}|_{Z}$
into isotypical components is a maximal torus, the image of
$V_{\unicode[STIX]{x1D70C}}|_{Z}$
into isotypical components is a maximal torus, the image of
![]() $\unicode[STIX]{x1D70C}$
is contained in the normalizer of a maximal torus. Furthermore, assume that
$\unicode[STIX]{x1D70C}$
is contained in the normalizer of a maximal torus. Furthermore, assume that
![]() $\unicode[STIX]{x1D70C}$
underlies a VHS. The Galois action preserves the Hodge type, and there is a single Hodge type for the rank
$\unicode[STIX]{x1D70C}$
underlies a VHS. The Galois action preserves the Hodge type, and there is a single Hodge type for the rank
![]() $1$
isotypical component (note that the isotypical decomposition is compatible with the Hodge structure). Therefore
$1$
isotypical component (note that the isotypical decomposition is compatible with the Hodge structure). Therefore
![]() $\unicode[STIX]{x1D70C}$
has only a single Hodge type and it is unitary. This proves the lemma in the case of several isotypical components.
$\unicode[STIX]{x1D70C}$
has only a single Hodge type and it is unitary. This proves the lemma in the case of several isotypical components.
We may now assume
![]() $V_{\unicode[STIX]{x1D70C}}|_{Z}=V_{1}~\otimes ~W_{1}$
. Since the rank is
$V_{\unicode[STIX]{x1D70C}}|_{Z}=V_{1}~\otimes ~W_{1}$
. Since the rank is
![]() ${\leqslant}3$
, and by hypothesis
${\leqslant}3$
, and by hypothesis
![]() $V_{\unicode[STIX]{x1D70C}}|_{Z}$
is reducible so the rank of
$V_{\unicode[STIX]{x1D70C}}|_{Z}$
is reducible so the rank of
![]() $V_{1}$
is strictly smaller than
$V_{1}$
is strictly smaller than
![]() $n$
, we get that
$n$
, we get that
![]() $V_{1}$
has rank
$V_{1}$
has rank
![]() $1$
. It means that the restriction and projection to a representation
$1$
. It means that the restriction and projection to a representation
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \operatorname{PGL}(n,\mathbb{C})$
is trivial. Since by hypothesis our representation is into
$\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \operatorname{PGL}(n,\mathbb{C})$
is trivial. Since by hypothesis our representation is into
![]() $\operatorname{SL}(n,\mathbb{C})$
we get that
$\operatorname{SL}(n,\mathbb{C})$
we get that
![]() $\unicode[STIX]{x1D70C}$
has finite image. In particular it is unitary, and a unitary irreducible VHS can have only a single Hodge type. This completes the proof of the lemma.◻
$\unicode[STIX]{x1D70C}$
has finite image. In particular it is unitary, and a unitary irreducible VHS can have only a single Hodge type. This completes the proof of the lemma.◻
Corollary 3.5. Let
![]() $X$
be a smooth complex projective variety, and suppose
$X$
be a smooth complex projective variety, and suppose
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
is an irreducible representation of rank
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
is an irreducible representation of rank
![]() $3$
underlying a VHS with more than a single Hodge type. Then the conditions listed in Theorem 3.3 are equivalent.
$3$
underlying a VHS with more than a single Hodge type. Then the conditions listed in Theorem 3.3 are equivalent.
Proof. By the above lemma,
![]() $\unicode[STIX]{x1D70C}$
is not tensor decomposable and not virtually reducible.◻
$\unicode[STIX]{x1D70C}$
is not tensor decomposable and not virtually reducible.◻
4 Structure of complex VHS of type
 $(1,1,1)$
$(1,1,1)$
In this section we study general complex VHS of type
![]() $(1,1,1)$
on quasi-projective varieties. The main aim is to prove that every complex VHS of type
$(1,1,1)$
on quasi-projective varieties. The main aim is to prove that every complex VHS of type
![]() $(1,1,1)$
or its dual can be constructed analogously to the following example.
$(1,1,1)$
or its dual can be constructed analogously to the following example.
Example 4.1. Let
![]() $X$
be a smooth complex projective surface. Let
$X$
be a smooth complex projective surface. Let
![]() $L_{1}$
be a nef line bundle with strictly positive degree,
$L_{1}$
be a nef line bundle with strictly positive degree,
![]() $L_{1}^{2}=0$
and fixed inclusion
$L_{1}^{2}=0$
and fixed inclusion
![]() $j_{1}:L_{1}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}$
. Let us fix a line bundle
$j_{1}:L_{1}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}$
. Let us fix a line bundle
![]() $j_{2}:L_{2}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}$
generically the same as
$j_{2}:L_{2}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}$
generically the same as
![]() $j_{1}(L_{1})$
such that
$j_{1}(L_{1})$
such that
![]() $c_{1}(L_{2})=a\,c_{1}(L_{1})$
in
$c_{1}(L_{2})=a\,c_{1}(L_{1})$
in
![]() $H^{2}(X,\mathbb{Q})$
for some (rational)
$H^{2}(X,\mathbb{Q})$
for some (rational)
![]() $a\in (-\frac{1}{2},1]$
. Finally, let us fix a line bundle
$a\in (-\frac{1}{2},1]$
. Finally, let us fix a line bundle
![]() $L_{0}$
such that
$L_{0}$
such that
![]() $3c_{1}(L_{0})=(2+a)c_{1}(L_{1})$
in
$3c_{1}(L_{0})=(2+a)c_{1}(L_{1})$
in
![]() $H^{2}(X,\mathbb{Q})$
.
$H^{2}(X,\mathbb{Q})$
.
Let us consider the system of Hodge bundles defined by
with
![]() $\unicode[STIX]{x1D703}$
given by inclusions
$\unicode[STIX]{x1D703}$
given by inclusions
![]() $j_{i}:L_{i}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}$
tensored with identity on
$j_{i}:L_{i}{\hookrightarrow}\unicode[STIX]{x1D6FA}_{X}$
tensored with identity on
![]() $E^{p,q}$
for
$E^{p,q}$
for
![]() $(p,q)=(2,0),(1,1)$
. Then for any ample line bundle
$(p,q)=(2,0),(1,1)$
. Then for any ample line bundle
![]() $A$
the pair
$A$
the pair
![]() $(E,\unicode[STIX]{x1D703})$
is an
$(E,\unicode[STIX]{x1D703})$
is an
![]() $A$
-stable system of Hodge bundles with vanishing rational Chern classes.
$A$
-stable system of Hodge bundles with vanishing rational Chern classes.
Later we will see that if
![]() $a\neq 1$
then this system of Hodge bundles comes from an orbicurve (see Theorem 5.1).
$a\neq 1$
then this system of Hodge bundles comes from an orbicurve (see Theorem 5.1).
Let
![]() $X$
be a smooth complex quasi-projective variety of dimension
$X$
be a smooth complex quasi-projective variety of dimension
![]() $d\geqslant 2$
. Let us fix a smooth projective variety
$d\geqslant 2$
. Let us fix a smooth projective variety
![]() $\bar{X}$
containing
$\bar{X}$
containing
![]() $X$
as an open subset and such that
$X$
as an open subset and such that
![]() $D=\bar{X}-X$
is a simple normal crossing divisor. In this section, we consider the quasi-projective case for future reference, although afterwards in the present paper we shall assume
$D=\bar{X}-X$
is a simple normal crossing divisor. In this section, we consider the quasi-projective case for future reference, although afterwards in the present paper we shall assume
![]() $D=\emptyset$
.
$D=\emptyset$
.
Let
![]() $A$
be a fixed very ample divisor on
$A$
be a fixed very ample divisor on
![]() $\bar{X}$
. In the following we use the intersection pairing of
$\bar{X}$
. In the following we use the intersection pairing of
![]() $\mathbb{Q}$
-divisors on the polarized variety
$\mathbb{Q}$
-divisors on the polarized variety
![]() $(\bar{X},A)$
as defined in § 2.2.
$(\bar{X},A)$
as defined in § 2.2.
Remark 4.2. Technically speaking, one should make a distinction between a line bundle and its corresponding divisor class. In the subsequent numerical calculations that would add burdensome extra notation, so we make the convention that a symbol such as, typically,
![]() $L_{i}$
can either mean the line bundle or the corresponding divisor class, according to context. In particular, we usually use the tensor product
$L_{i}$
can either mean the line bundle or the corresponding divisor class, according to context. In particular, we usually use the tensor product
![]() $L_{1}~\otimes ~L_{2}$
but in computation of intersection numbers we use divisor classes and write, e.g.,
$L_{1}~\otimes ~L_{2}$
but in computation of intersection numbers we use divisor classes and write, e.g.,
![]() $(L_{1}+2L_{2}).A$
instead of
$(L_{1}+2L_{2}).A$
instead of
![]() $(L_{1}~\otimes ~L_{2}^{\otimes 2}).A$
.
$(L_{1}~\otimes ~L_{2}^{\otimes 2}).A$
.
Let us recall that by Bertini’s theorem the general complete intersection surface
![]() $\bar{Y}$
in
$\bar{Y}$
in
![]() $\bar{X}$
is smooth and irreducible. We can also assume that
$\bar{X}$
is smooth and irreducible. We can also assume that
![]() $D_{Y}=\bar{Y}~\cap ~D$
is a simple normal crossing divisor on
$D_{Y}=\bar{Y}~\cap ~D$
is a simple normal crossing divisor on
![]() $\bar{Y}$
. Let us set
$\bar{Y}$
. Let us set
![]() $Y:=\bar{Y}-D_{Y}$
.
$Y:=\bar{Y}-D_{Y}$
.
Let
![]() $(E=\bigoplus _{p+q=2}E^{p,q},\unicode[STIX]{x1D703})$
be a rank
$(E=\bigoplus _{p+q=2}E^{p,q},\unicode[STIX]{x1D703})$
be a rank
![]() $3$
logarithmic system of Hodge bundles of type
$3$
logarithmic system of Hodge bundles of type
![]() $(1,1,1)$
. Recall that this definition includes the condition that both Kodaira–Spencer maps
$(1,1,1)$
. Recall that this definition includes the condition that both Kodaira–Spencer maps
![]() $\unicode[STIX]{x1D703}$
be non-zero, so they induce injections of rank
$\unicode[STIX]{x1D703}$
be non-zero, so they induce injections of rank
![]() $1$
sheaves
$1$
sheaves
and
The proof of the following proposition is inspired by the proof of [Reference Langer and BeltramettiLan02, Theorem 4.2].
Proposition 4.3. Assume that
![]() $E$
has vanishing rational Chern classes and that
$E$
has vanishing rational Chern classes and that
![]() $(E,\unicode[STIX]{x1D703})$
is slope
$(E,\unicode[STIX]{x1D703})$
is slope
![]() $A$
-stable. Then the following conditions are satisfied:
$A$
-stable. Then the following conditions are satisfied:
(i)
 $c_{1}(E^{p,q}).c_{1}(E^{p^{\prime },q^{\prime }})=0$
for all pairs
$c_{1}(E^{p,q}).c_{1}(E^{p^{\prime },q^{\prime }})=0$
for all pairs
 $(p,q)$
and
$(p,q)$
and
 $(p^{\prime },q^{\prime })$
;
$(p^{\prime },q^{\prime })$
;(ii) the classes of
 $L_{1}$
and
$L_{1}$
and
 $L_{2}$
lie on the same line in the vector space
$L_{2}$
lie on the same line in the vector space
 $H^{2}(\bar{X},\mathbb{Q})$
;
$H^{2}(\bar{X},\mathbb{Q})$
;(iii) there exist effective divisors
 $B_{1}$
and
$B_{1}$
and
 $B_{2}$
such that
$B_{2}$
such that
 $M:=L_{1}(B_{1})=L_{2}(B_{2})$
is a saturation of both
$M:=L_{1}(B_{1})=L_{2}(B_{2})$
is a saturation of both
 $L_{1}$
and
$L_{1}$
and
 $L_{2}$
in
$L_{2}$
in
 $\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
. Moreover, we have
$\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
. Moreover, we have
 $L_{i}.M=0$
and
$L_{i}.M=0$
and
 $L_{i}.B_{j}=0$
for all
$L_{i}.B_{j}=0$
for all
 $i$
and
$i$
and
 $j$
;
$j$
;(iv) either
 $L_{1}|_{\bar{Y}}$
or
$L_{1}|_{\bar{Y}}$
or
 $L_{2}|_{\bar{Y}}$
is nef with self intersection zero and strictly positive degree.
$L_{2}|_{\bar{Y}}$
is nef with self intersection zero and strictly positive degree.
Proof. We claim that the map
induced from
![]() $\unicode[STIX]{x1D703}$
has rank
$\unicode[STIX]{x1D703}$
has rank
![]() $1$
. Indeed, in the local coordinates
$1$
. Indeed, in the local coordinates
![]() $\unicode[STIX]{x1D6FC}$
is given by two logarithmic
$\unicode[STIX]{x1D6FC}$
is given by two logarithmic
![]() $1$
-forms
$1$
-forms
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $\unicode[STIX]{x1D714}_{2}$
and the integrability of
$\unicode[STIX]{x1D714}_{2}$
and the integrability of
![]() $\unicode[STIX]{x1D703}$
implies that
$\unicode[STIX]{x1D703}$
implies that
![]() $\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}=0$
, so they are proportional and
$\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}=0$
, so they are proportional and
![]() $\unicode[STIX]{x1D6FC}$
has rank
$\unicode[STIX]{x1D6FC}$
has rank
![]() $1$
. Let
$1$
. Let
![]() $M$
be the saturation of the image of
$M$
be the saturation of the image of
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
![]() $\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
(i.e., the largest rank
$\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
(i.e., the largest rank
![]() $1$
subsheaf of
$1$
subsheaf of
![]() $\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
containing the image of
$\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
containing the image of
![]() $\unicode[STIX]{x1D6FC}$
). Then
$\unicode[STIX]{x1D6FC}$
). Then
![]() $M$
is a line bundle (as it is a rank
$M$
is a line bundle (as it is a rank
![]() $1$
reflexive
$1$
reflexive
![]() ${\mathcal{O}}_{X}$
-module on a smooth variety) such that
${\mathcal{O}}_{X}$
-module on a smooth variety) such that
![]() $\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)/M$
is torsion-free.
$\unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)/M$
is torsion-free.
By construction we have inclusions
![]() $L_{1}\subset M$
and
$L_{1}\subset M$
and
![]() $L_{2}\subset M$
defining effective divisors
$L_{2}\subset M$
defining effective divisors
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
, respectively. Let us set
$B_{2}$
, respectively. Let us set
![]() $e^{p,q}=c_{1}(E^{p,q})$
,
$e^{p,q}=c_{1}(E^{p,q})$
,
![]() $l_{i}=c_{1}(L_{i})$
and
$l_{i}=c_{1}(L_{i})$
and
![]() $b_{i}=c_{1}(B_{i})$
. Then we can write
$b_{i}=c_{1}(B_{i})$
. Then we can write
By assumption we have
in the rational cohomology
![]() $H^{2}(\bar{X},\mathbb{Q})$
, so the classes
$H^{2}(\bar{X},\mathbb{Q})$
, so the classes
![]() $e^{p,q}$
can be written in terms of
$e^{p,q}$
can be written in terms of
![]() $l_{1}$
and
$l_{1}$
and
![]() $l_{2}$
in the following way:
$l_{2}$
in the following way:
Therefore
In particular, we have
![]() $m\geqslant -e^{0,2}$
. Similarly, we have
$m\geqslant -e^{0,2}$
. Similarly, we have
so
![]() $m\geqslant e^{2,0}$
.
$m\geqslant e^{2,0}$
.
The following lemma is a corollary of the well-known Bogomolov’s lemma.
Lemma 4.4. For any line bundle
![]() $N\subset \unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
the restriction
$N\subset \unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)$
the restriction
![]() $N|_{\bar{Y}}$
is not big on
$N|_{\bar{Y}}$
is not big on
![]() $\bar{Y}$
.
$\bar{Y}$
.
Proof. We have a short exact sequence
Let us consider the composition
![]() $N|_{\bar{Y}}\rightarrow \unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)|_{\bar{Y}}\rightarrow \unicode[STIX]{x1D6FA}_{\bar{Y}}(\log D_{Y})$
. By Bogomolov’s lemma (see [Reference BogomolovBog78, Theorem 4] and [Reference Esnault and ViehwegEV92, Corollary 6.9])
$N|_{\bar{Y}}\rightarrow \unicode[STIX]{x1D6FA}_{\bar{X}}(\log D)|_{\bar{Y}}\rightarrow \unicode[STIX]{x1D6FA}_{\bar{Y}}(\log D_{Y})$
. By Bogomolov’s lemma (see [Reference BogomolovBog78, Theorem 4] and [Reference Esnault and ViehwegEV92, Corollary 6.9])
![]() $\unicode[STIX]{x1D6FA}_{\bar{Y}}(\log D_{Y})$
does not contain big line bundles. So if this composition is non-zero then
$\unicode[STIX]{x1D6FA}_{\bar{Y}}(\log D_{Y})$
does not contain big line bundles. So if this composition is non-zero then
![]() $N|_{\bar{Y}}$
is not big.
$N|_{\bar{Y}}$
is not big.
If the map
![]() $N|_{\bar{Y}}\rightarrow \unicode[STIX]{x1D6FA}_{\bar{Y}}(\log D_{Y})$
is zero then by the above exact sequence
$N|_{\bar{Y}}\rightarrow \unicode[STIX]{x1D6FA}_{\bar{Y}}(\log D_{Y})$
is zero then by the above exact sequence
![]() $N|_{\bar{Y}}$
is contained in
$N|_{\bar{Y}}$
is contained in
![]() ${\mathcal{O}}_{\bar{Y}}(-A)^{n-2}$
, so
${\mathcal{O}}_{\bar{Y}}(-A)^{n-2}$
, so
![]() $\unicode[STIX]{x1D705}(N|_{\bar{Y}})=-\infty$
.◻
$\unicode[STIX]{x1D705}(N|_{\bar{Y}})=-\infty$
.◻
Slope
![]() $A$
-stability of
$A$
-stability of
![]() $(E,\unicode[STIX]{x1D703})$
implies that
$(E,\unicode[STIX]{x1D703})$
implies that
and
If
![]() $(e^{0,2})^{2}>0$
then, thanks to Lemma 2.3, the first inequality implies that
$(e^{0,2})^{2}>0$
then, thanks to Lemma 2.3, the first inequality implies that
![]() $-e^{0,2}|_{\bar{Y}}$
is big. But then
$-e^{0,2}|_{\bar{Y}}$
is big. But then
![]() $M|_{\bar{Y}}$
is big, which contradicts the above lemma. Therefore
$M|_{\bar{Y}}$
is big, which contradicts the above lemma. Therefore
Similarly, if
![]() $(e^{2,0})^{2}>0$
then
$(e^{2,0})^{2}>0$
then
![]() $e^{2,0}|_{\bar{Y}}$
is big. But then
$e^{2,0}|_{\bar{Y}}$
is big. But then
![]() $M|_{\bar{Y}}$
is big, a contradiction. Therefore
$M|_{\bar{Y}}$
is big, a contradiction. Therefore
Let us also recall that
Therefore
Similarly, we have
From stability of
![]() $E$
we get
$E$
we get
![]() $(L_{1}+2L_{2}).A=-3e^{0,2}.A>0$
and hence there exists
$(L_{1}+2L_{2}).A=-3e^{0,2}.A>0$
and hence there exists
![]() $i$
with
$i$
with
![]() $L_{i}.A>0$
. Lemmas 2.3 and 4.4 imply that
$L_{i}.A>0$
. Lemmas 2.3 and 4.4 imply that
![]() $L_{i}|_{\bar{Y}}$
is nef with
$L_{i}|_{\bar{Y}}$
is nef with
![]() $L_{i}^{2}=0$
and the degree of
$L_{i}^{2}=0$
and the degree of
![]() $L_{i}|_{\bar{Y}}$
is strictly positive.
$L_{i}|_{\bar{Y}}$
is strictly positive.
Lemma 4.5. We have
![]() $L_{1}^{2}=L_{1}.L_{2}=L_{2}^{2}=0$
.
$L_{1}^{2}=L_{1}.L_{2}=L_{2}^{2}=0$
.
Proof. Let us first assume that
![]() $i=1$
, i.e.,
$i=1$
, i.e.,
![]() $L_{1}|_{\bar{Y}}$
is nef with
$L_{1}|_{\bar{Y}}$
is nef with
![]() $L_{1}^{2}=0$
. Since
$L_{1}^{2}=0$
. Since
![]() $B_{2}$
is effective, we have
$B_{2}$
is effective, we have
![]() $L_{1}.B_{2}\geqslant 0$
. By the Lefschetz hyperplane theorem for quasi-projective varieties (see [Reference Hamm and LêHL85, Theorem 1.1.3]) we have
$L_{1}.B_{2}\geqslant 0$
. By the Lefschetz hyperplane theorem for quasi-projective varieties (see [Reference Hamm and LêHL85, Theorem 1.1.3]) we have
![]() $\unicode[STIX]{x1D70B}_{1}(Y)\simeq \unicode[STIX]{x1D70B}_{1}(X)$
. So by functoriality of the correspondence between representations and Higgs bundles, the restriction
$\unicode[STIX]{x1D70B}_{1}(Y)\simeq \unicode[STIX]{x1D70B}_{1}(X)$
. So by functoriality of the correspondence between representations and Higgs bundles, the restriction
of
![]() $(E,\unicode[STIX]{x1D703})$
to
$(E,\unicode[STIX]{x1D703})$
to
![]() $\bar{Y}$
is
$\bar{Y}$
is
![]() $A$
-stable (one can also give a direct proof of this fact: see [Reference LangerLan15, Theorem 12] and [Reference LangerLan16]). Since the rational Chern classes of
$A$
-stable (one can also give a direct proof of this fact: see [Reference LangerLan15, Theorem 12] and [Reference LangerLan16]). Since the rational Chern classes of
![]() $E|_{\bar{Y}}$
vanish,
$E|_{\bar{Y}}$
vanish,
![]() $(E|_{\bar{Y}},\unicode[STIX]{x1D703}_{Y})$
is stable with respect to every stable polarization and semi-stable with respect to every nef polarization. In particular,
$(E|_{\bar{Y}},\unicode[STIX]{x1D703}_{Y})$
is stable with respect to every stable polarization and semi-stable with respect to every nef polarization. In particular,
![]() $L_{1}|_{\bar{Y}}$
-semi-stability of
$L_{1}|_{\bar{Y}}$
-semi-stability of
![]() $(E|_{\bar{Y}},\unicode[STIX]{x1D703}_{Y})$
implies that
$(E|_{\bar{Y}},\unicode[STIX]{x1D703}_{Y})$
implies that
![]() $L_{1}.(L_{1}+2L_{2})\geqslant 0$
. Therefore we have
$L_{1}.(L_{1}+2L_{2})\geqslant 0$
. Therefore we have
![]() $L_{1}.L_{2}\geqslant 0$
.
$L_{1}.L_{2}\geqslant 0$
.
Applying Lemma 2.4 to
![]() $M=L_{1}+B_{1}$
we see that
$M=L_{1}+B_{1}$
we see that
![]() $L_{1}^{2}=0$
,
$L_{1}^{2}=0$
,
![]() $L_{1}.B_{1}=0$
and
$L_{1}.B_{1}=0$
and
![]() $L_{1}.M=0$
. Using
$L_{1}.M=0$
. Using
![]() $M=L_{2}+B_{2}$
we get equalities
$M=L_{2}+B_{2}$
we get equalities
![]() $L_{1}.L_{2}=L_{1}.B_{2}=0$
. But then
$L_{1}.L_{2}=L_{1}.B_{2}=0$
. But then
implies that
![]() $L_{2}^{2}=-L_{1}.L_{2}=0$
.
$L_{2}^{2}=-L_{1}.L_{2}=0$
.
The proof in the case
![]() $i=2$
is analogous.◻
$i=2$
is analogous.◻
This lemma finishes the proof of assertions (i) and (iv) of the proposition. To prove (ii), let us consider
![]() $i^{\prime }$
such that
$i^{\prime }$
such that
![]() $\{i,i^{\prime }\}=\{1,2\}$
. Let us choose a rational
$\{i,i^{\prime }\}=\{1,2\}$
. Let us choose a rational
![]() $a$
such that
$a$
such that
![]() $(L_{i^{\prime }}-aL_{i}).A=0$
. Since
$(L_{i^{\prime }}-aL_{i}).A=0$
. Since
![]() $(L_{i^{\prime }}-aL_{i})^{2}=0$
this implies that
$(L_{i^{\prime }}-aL_{i})^{2}=0$
this implies that
![]() $l_{i^{\prime }}=al_{i}$
in
$l_{i^{\prime }}=al_{i}$
in
![]() $H^{2}(X,\mathbb{Q})$
.
$H^{2}(X,\mathbb{Q})$
.
Assertion (iii) of the proposition follows from the proof of Lemma 4.5. More precisely, if
![]() $i=1$
then this proof shows that
$i=1$
then this proof shows that
![]() $L_{1}.M=L_{1}.B_{1}=L_{1}.B_{2}=0$
. So (ii) implies that
$L_{1}.M=L_{1}.B_{1}=L_{1}.B_{2}=0$
. So (ii) implies that
![]() $L_{2}.M=L_{2}.B_{1}=L_{2}.B_{2}=0$
. The proof in the case
$L_{2}.M=L_{2}.B_{1}=L_{2}.B_{2}=0$
. The proof in the case
![]() $i=2$
is analogous.◻
$i=2$
is analogous.◻
Remark 4.6. Let us remark that stability of
![]() $E$
implies that
$E$
implies that
![]() $(L_{1}+2L_{2}).A>0$
and
$(L_{1}+2L_{2}).A>0$
and
![]() $(2L_{1}+L_{2}).A>0$
so that
$(2L_{1}+L_{2}).A>0$
so that
![]() $a>-\frac{1}{2}$
in the notation of the above proof. In fact, this condition is sufficient to define a stable rank
$a>-\frac{1}{2}$
in the notation of the above proof. In fact, this condition is sufficient to define a stable rank
![]() $3$
logarithmic system of Hodge bundles.
$3$
logarithmic system of Hodge bundles.
Let us recall that a smooth log pair is a pair consisting of a smooth variety and a (reduced) simple normal crossing divisor. A morphism of log pairs
![]() $\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
is a proper morphism of normal varieties such that
$\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
is a proper morphism of normal varieties such that
![]() $\bar{f}(D_{Z})=D$
. For a morphism of smooth projective log pairs
$\bar{f}(D_{Z})=D$
. For a morphism of smooth projective log pairs
![]() $\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
, we write
$\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
, we write
![]() $Z:=\bar{Z}-D_{Z}$
, we choose a point
$Z:=\bar{Z}-D_{Z}$
, we choose a point
![]() $z$
over
$z$
over
![]() $x$
and we set
$x$
and we set
![]() $f=\bar{f}|_{\bar{Z}-D_{Z}}$
.
$f=\bar{f}|_{\bar{Z}-D_{Z}}$
.
Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be an irreducible representation with quasi-unipotent monodromy at infinity (i.e., such that
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be an irreducible representation with quasi-unipotent monodromy at infinity (i.e., such that
![]() $\unicode[STIX]{x1D70C}$
has quasi-unipotent monodromies along small simple loops around all irreducible components of
$\unicode[STIX]{x1D70C}$
has quasi-unipotent monodromies along small simple loops around all irreducible components of
![]() $D$
). Then by Kawamata’s covering trick there exists a finite flat morphism of smooth projective log pairs
$D$
). Then by Kawamata’s covering trick there exists a finite flat morphism of smooth projective log pairs
![]() $\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
such that
$\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
such that
![]() $(\bar{f}^{\ast }D)_{\text{red}}=D_{Z}$
and
$(\bar{f}^{\ast }D)_{\text{red}}=D_{Z}$
and
![]() $f^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \operatorname{SL}(n,\mathbb{C})$
has unipotent monodromy at infinity, i.e.,
$f^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \operatorname{SL}(n,\mathbb{C})$
has unipotent monodromy at infinity, i.e.,
![]() $f^{\ast }\unicode[STIX]{x1D70C}$
has unipotent local monodromies along all irreducible components of
$f^{\ast }\unicode[STIX]{x1D70C}$
has unipotent local monodromies along all irreducible components of
![]() $D_{Z}$
. This implies that the residues of Deligne’s canonical extension of the flat bundle associated to
$D_{Z}$
. This implies that the residues of Deligne’s canonical extension of the flat bundle associated to
![]() $f^{\ast }\unicode[STIX]{x1D70C}$
are nilpotent (since all the eigenvalues of the residues are zero) and we are interested in bundles with trivial parabolic structure.
$f^{\ast }\unicode[STIX]{x1D70C}$
are nilpotent (since all the eigenvalues of the residues are zero) and we are interested in bundles with trivial parabolic structure.
More precisely, let us consider a vector bundle with connection
![]() $(V,\unicode[STIX]{x1D6FB})$
with regular singularities and rational residues in
$(V,\unicode[STIX]{x1D6FB})$
with regular singularities and rational residues in
![]() $[0,1)$
along the irreducible components of
$[0,1)$
along the irreducible components of
![]() $D$
, that corresponds to the representation
$D$
, that corresponds to the representation
![]() $\unicode[STIX]{x1D70C}$
. This bundle comes equipped with a canonical parabolic structure, which makes the corresponding parabolic flat bundle stable with vanishing parabolic Chern classes (cf. [Reference MochizukiMoc06, Reference MochizukiMoc09] and [Reference Iyer and SimpsonIS07, Lemma 3.3]).
$\unicode[STIX]{x1D70C}$
. This bundle comes equipped with a canonical parabolic structure, which makes the corresponding parabolic flat bundle stable with vanishing parabolic Chern classes (cf. [Reference MochizukiMoc06, Reference MochizukiMoc09] and [Reference Iyer and SimpsonIS07, Lemma 3.3]).
If we assume the local system
![]() $V_{\unicode[STIX]{x1D70C}}$
underlies a complex variation of Hodge structure then
$V_{\unicode[STIX]{x1D70C}}$
underlies a complex variation of Hodge structure then
![]() $f^{\ast }\unicode[STIX]{x1D70C}$
also underlies a complex VHS. The logarithmic parabolic Higgs bundle corresponding to
$f^{\ast }\unicode[STIX]{x1D70C}$
also underlies a complex VHS. The logarithmic parabolic Higgs bundle corresponding to
![]() $\unicode[STIX]{x1D70C}$
is stable and it has vanishing parabolic first and second Chern classes (see [Reference MochizukiMoc06, Reference MochizukiMoc09]). The pullback of this logarithmic parabolic Higgs bundle to
$\unicode[STIX]{x1D70C}$
is stable and it has vanishing parabolic first and second Chern classes (see [Reference MochizukiMoc06, Reference MochizukiMoc09]). The pullback of this logarithmic parabolic Higgs bundle to
![]() $(\bar{Z},D_{Z})$
(cf. [Reference Iyer and SimpsonIS07, Lemma 3.7]) becomes a stable logarithmic system of Hodge bundles (with trivial parabolic structure) which has vanishing all rational Chern classes (by functoriality of the Kobayashi–Hitchin correspondence, the Higgs bundle associated to the pullback
$(\bar{Z},D_{Z})$
(cf. [Reference Iyer and SimpsonIS07, Lemma 3.7]) becomes a stable logarithmic system of Hodge bundles (with trivial parabolic structure) which has vanishing all rational Chern classes (by functoriality of the Kobayashi–Hitchin correspondence, the Higgs bundle associated to the pullback
![]() $f^{\ast }\unicode[STIX]{x1D70C}$
corresponds to a complex VHS, so it is a system of Hodge bundles). Thus, we have the following lemma.
$f^{\ast }\unicode[STIX]{x1D70C}$
corresponds to a complex VHS, so it is a system of Hodge bundles). Thus, we have the following lemma.
Lemma 4.7. Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be an irreducible representation with quasi-unipotent monodromy at infinity. If
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be an irreducible representation with quasi-unipotent monodromy at infinity. If
![]() $\unicode[STIX]{x1D70C}$
underlies a complex VHS then there exists a finite flat morphism of smooth projective log pairs
$\unicode[STIX]{x1D70C}$
underlies a complex VHS then there exists a finite flat morphism of smooth projective log pairs
![]() $\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
such that
$\bar{f}:(\bar{Z},D_{Z})\rightarrow (\bar{X},D)$
such that
![]() $f^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \operatorname{SL}(n,\mathbb{C})$
has unipotent monodromy at infinity. To this representation the Kobayashi–Hitchin correspondence associates a stable rank
$f^{\ast }\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Z,z)\rightarrow \operatorname{SL}(n,\mathbb{C})$
has unipotent monodromy at infinity. To this representation the Kobayashi–Hitchin correspondence associates a stable rank
![]() $n$
system of logarithmic Hodge sheaves with vanishing rational Chern classes.
$n$
system of logarithmic Hodge sheaves with vanishing rational Chern classes.
In case the underlying rank
![]() $3$
logarithmic system of Hodge bundles on
$3$
logarithmic system of Hodge bundles on
![]() $(\bar{Z},D_{Z})$
is of type
$(\bar{Z},D_{Z})$
is of type
![]() $(1,1,1)$
, we can apply Proposition 4.3.
$(1,1,1)$
, we can apply Proposition 4.3.
Remark 4.8. If
![]() $\unicode[STIX]{x1D70C}$
is a rigid irreducible representation with quasi-unipotent monodromy at infinity, then it underlies a complex VHS (this part of [Reference Corlette and SimpsonCS08, Theorem 8.1] works in any rank) and we can apply the above lemma to such representations.
$\unicode[STIX]{x1D70C}$
is a rigid irreducible representation with quasi-unipotent monodromy at infinity, then it underlies a complex VHS (this part of [Reference Corlette and SimpsonCS08, Theorem 8.1] works in any rank) and we can apply the above lemma to such representations.
5 Geometry of complex VHS of type
 $(1,1,1)$
$(1,1,1)$
Let
![]() $X$
be a smooth complex projective variety. If
$X$
be a smooth complex projective variety. If
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
is a representation then the induced projective representation
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
is a representation then the induced projective representation
![]() $\unicode[STIX]{x1D70B}_{1}(X)\rightarrow \operatorname{PGL}(n,\mathbb{C})$
is denoted by
$\unicode[STIX]{x1D70B}_{1}(X)\rightarrow \operatorname{PGL}(n,\mathbb{C})$
is denoted by
![]() $\bar{\unicode[STIX]{x1D70C}}$
.
$\bar{\unicode[STIX]{x1D70C}}$
.
Theorem 5.1. Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
be an irreducible representation coming from a complex variation of Hodge structure of type
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
be an irreducible representation coming from a complex variation of Hodge structure of type
![]() $(1,1,1)$
. Let
$(1,1,1)$
. Let
![]() $V_{\unicode[STIX]{x1D70C}}$
denote the corresponding local system. Then one of the following holds.
$V_{\unicode[STIX]{x1D70C}}$
denote the corresponding local system. Then one of the following holds.
(i) There exists a projective representation
 $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{PGL}(2,\mathbb{C})$
which induces
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{PGL}(2,\mathbb{C})$
which induces
 $\bar{\unicode[STIX]{x1D70C}}$
via the homomorphism
$\bar{\unicode[STIX]{x1D70C}}$
via the homomorphism
 $\operatorname{PGL}(2,\mathbb{C})\rightarrow \operatorname{PGL}(3,\mathbb{C})$
given by second symmetric power. Moreover, there exists a finite covering
$\operatorname{PGL}(2,\mathbb{C})\rightarrow \operatorname{PGL}(3,\mathbb{C})$
given by second symmetric power. Moreover, there exists a finite covering
 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
from a smooth projective variety
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
from a smooth projective variety
 $Y$
, a rank
$Y$
, a rank
 $1$
local system
$1$
local system
 $W_{1}$
on
$W_{1}$
on
 $X$
such that
$X$
such that
 $W_{1}^{\otimes 3}$
is trivial and a rank
$W_{1}^{\otimes 3}$
is trivial and a rank
 $2$
local system
$2$
local system
 $W_{2}$
on
$W_{2}$
on
 $Y$
such that
$Y$
such that
 $\unicode[STIX]{x1D70B}^{\ast }V_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70B}^{\ast }W_{1}~\otimes ~\operatorname{Sym}^{2}W_{2}$
.
$\unicode[STIX]{x1D70B}^{\ast }V_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70B}^{\ast }W_{1}~\otimes ~\operatorname{Sym}^{2}W_{2}$
.(ii)
 $\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
$\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
Proof. We can assume that
![]() $X$
has dimension at least
$X$
has dimension at least
![]() $2$
as otherwise there is nothing to be proven. Therefore the complex variation of Hodge structure corresponding to
$2$
as otherwise there is nothing to be proven. Therefore the complex variation of Hodge structure corresponding to
![]() $\unicode[STIX]{x1D70C}$
is of the form described in Proposition 4.3. Let us write
$\unicode[STIX]{x1D70C}$
is of the form described in Proposition 4.3. Let us write
![]() $L_{2}\equiv aL_{1}$
. Since the assertion for a representation is equivalent to the assertion for its dual, we can assume that for a general complete intersection surface
$L_{2}\equiv aL_{1}$
. Since the assertion for a representation is equivalent to the assertion for its dual, we can assume that for a general complete intersection surface
![]() $S\subset X$
the restriction
$S\subset X$
the restriction
![]() $L_{1}|_{S}$
is nef with strictly positive degree and
$L_{1}|_{S}$
is nef with strictly positive degree and
![]() $a\leqslant 1$
.
$a\leqslant 1$
.
In the notation of Proposition 4.3 we have
![]() $M=L_{1}(B_{1})=L_{2}(B_{2})$
. Let us write
$M=L_{1}(B_{1})=L_{2}(B_{2})$
. Let us write
![]() $B_{1}=B+B_{1}^{\prime }$
and
$B_{1}=B+B_{1}^{\prime }$
and
![]() $B_{2}=B+B_{2}^{\prime }$
, where
$B_{2}=B+B_{2}^{\prime }$
, where
![]() $B$
,
$B$
,
![]() $B_{1}^{\prime }$
,
$B_{1}^{\prime }$
,
![]() $B_{2}^{\prime }$
are effective and
$B_{2}^{\prime }$
are effective and
![]() $B_{1}^{\prime }$
and
$B_{1}^{\prime }$
and
![]() $B_{2}^{\prime }$
have no common irreducible components. Recall that
$B_{2}^{\prime }$
have no common irreducible components. Recall that
![]() $L_{1}.B=L_{1}.B_{1}^{\prime }=0$
and
$L_{1}.B=L_{1}.B_{1}^{\prime }=0$
and
![]() $L_{2}.B=L_{2}.B_{2}^{\prime }=0$
. We set
$L_{2}.B=L_{2}.B_{2}^{\prime }=0$
. We set
![]() $M^{\prime }:=M(-B)$
. This line bundle has a canonical inclusion into
$M^{\prime }:=M(-B)$
. This line bundle has a canonical inclusion into
![]() $\unicode[STIX]{x1D6FA}_{X}$
given by composing
$\unicode[STIX]{x1D6FA}_{X}$
given by composing
![]() $M(-B)\subset M$
with
$M(-B)\subset M$
with
![]() $M\rightarrow \unicode[STIX]{x1D6FA}_{X}$
. By definition we also have
$M\rightarrow \unicode[STIX]{x1D6FA}_{X}$
. By definition we also have
![]() $M^{\prime }=L_{1}(B_{1}^{\prime })=L_{2}(B_{2}^{\prime })$
. Intersecting both sides of equality
$M^{\prime }=L_{1}(B_{1}^{\prime })=L_{2}(B_{2}^{\prime })$
. Intersecting both sides of equality
![]() $L_{1}+B_{1}^{\prime }=L_{2}+B_{2}^{\prime }$
with
$L_{1}+B_{1}^{\prime }=L_{2}+B_{2}^{\prime }$
with
![]() $B_{1}^{\prime }$
we get
$B_{1}^{\prime }$
we get
(here we use that
![]() $L_{2}.B_{1}^{\prime }=aL_{1}.B_{1}^{\prime }=0$
, and since
$L_{2}.B_{1}^{\prime }=aL_{1}.B_{1}^{\prime }=0$
, and since
![]() $B_{1}^{\prime }$
and
$B_{1}^{\prime }$
and
![]() $B_{2}^{\prime }$
have no common components their intersection is positive). But Lemma 2.4 implies that
$B_{2}^{\prime }$
have no common components their intersection is positive). But Lemma 2.4 implies that
![]() $(B_{1}^{\prime })^{2}\leqslant 0$
, so we have
$(B_{1}^{\prime })^{2}\leqslant 0$
, so we have
![]() $(B_{1}^{\prime })^{2}=B_{1}^{\prime }.B_{2}^{\prime }=0$
. Hence, we also get
$(B_{1}^{\prime })^{2}=B_{1}^{\prime }.B_{2}^{\prime }=0$
. Hence, we also get
![]() $(B_{2}^{\prime })^{2}=0$
. There exists also some non-negative
$(B_{2}^{\prime })^{2}=0$
. There exists also some non-negative
![]() $\unicode[STIX]{x1D6FC}_{1}$
such that
$\unicode[STIX]{x1D6FC}_{1}$
such that
![]() $(B_{1}^{\prime }-\unicode[STIX]{x1D6FC}_{1}L_{1}).A=0$
. Since
$(B_{1}^{\prime }-\unicode[STIX]{x1D6FC}_{1}L_{1}).A=0$
. Since
![]() $(B_{1}^{\prime }-\unicode[STIX]{x1D6FC}_{1}L_{1})^{2}=0$
, we have
$(B_{1}^{\prime }-\unicode[STIX]{x1D6FC}_{1}L_{1})^{2}=0$
, we have
![]() $B_{1}^{\prime }\equiv \unicode[STIX]{x1D6FC}_{1}L_{1}$
. Similarly, there exists some non-negative
$B_{1}^{\prime }\equiv \unicode[STIX]{x1D6FC}_{1}L_{1}$
. Similarly, there exists some non-negative
![]() $\unicode[STIX]{x1D6FC}_{2}$
such that
$\unicode[STIX]{x1D6FC}_{2}$
such that
![]() $B_{2}^{\prime }\equiv \unicode[STIX]{x1D6FC}_{2}L_{1}$
. Note also that
$B_{2}^{\prime }\equiv \unicode[STIX]{x1D6FC}_{2}L_{1}$
. Note also that
![]() $B_{i}^{\prime }=0$
is equivalent to
$B_{i}^{\prime }=0$
is equivalent to
![]() $\unicode[STIX]{x1D6FC}_{i}=0$
, since if
$\unicode[STIX]{x1D6FC}_{i}=0$
, since if
![]() $B_{i}^{\prime }$
is a non-zero effective divisor then
$B_{i}^{\prime }$
is a non-zero effective divisor then
![]() $B_{i}^{\prime }.A>0$
. Let us recall that
$B_{i}^{\prime }.A>0$
. Let us recall that
![]() $L_{1}+B_{1}^{\prime }=L_{2}+B_{2}^{\prime }$
, so
$L_{1}+B_{1}^{\prime }=L_{2}+B_{2}^{\prime }$
, so
![]() $(1+\unicode[STIX]{x1D6FC}_{1})L_{1}\equiv (a+\unicode[STIX]{x1D6FC}_{2})L_{1}$
. But
$(1+\unicode[STIX]{x1D6FC}_{1})L_{1}\equiv (a+\unicode[STIX]{x1D6FC}_{2})L_{1}$
. But
![]() $L_{1}.A>0$
, so
$L_{1}.A>0$
, so
![]() $1+\unicode[STIX]{x1D6FC}_{1}=a+\unicode[STIX]{x1D6FC}_{2}$
. Since
$1+\unicode[STIX]{x1D6FC}_{1}=a+\unicode[STIX]{x1D6FC}_{2}$
. Since
![]() $a\leqslant 1$
, this implies that
$a\leqslant 1$
, this implies that
![]() $0\leqslant \unicode[STIX]{x1D6FC}_{1}\leqslant \unicode[STIX]{x1D6FC}_{2}$
.
$0\leqslant \unicode[STIX]{x1D6FC}_{1}\leqslant \unicode[STIX]{x1D6FC}_{2}$
.
We consider two cases depending on whether
![]() $B_{2}^{\prime }$
is zero or not.
$B_{2}^{\prime }$
is zero or not.
If
![]() $B_{2}^{\prime }=0$
then
$B_{2}^{\prime }=0$
then
![]() $\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}_{1}=0$
,
$\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}_{1}=0$
,
![]() $B_{1}^{\prime }=0$
and
$B_{1}^{\prime }=0$
and
![]() $L:=L_{1}=L_{2}$
with the same map to
$L:=L_{1}=L_{2}$
with the same map to
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D6FA}_{X}$
. In this case we set
$\unicode[STIX]{x1D6FA}_{X}$
. In this case we set
![]() $N:=E^{2,0}~\otimes ~L_{1}^{-1}$
. Since
$N:=E^{2,0}~\otimes ~L_{1}^{-1}$
. Since
![]() $\det E=N^{\otimes 3}$
, the line bundle
$\det E=N^{\otimes 3}$
, the line bundle
![]() $N$
is
$N$
is
![]() $3$
-torsion. Therefore
$3$
-torsion. Therefore
![]() $(E,\unicode[STIX]{x1D703})\simeq (N,0)~\otimes ~\operatorname{Sym}^{2}(F)~\otimes ~\det (F)^{-1}$
, where
$(E,\unicode[STIX]{x1D703})\simeq (N,0)~\otimes ~\operatorname{Sym}^{2}(F)~\otimes ~\det (F)^{-1}$
, where
![]() $F=(F^{1,0}~\oplus ~F^{0,1},\unicode[STIX]{x1D703}_{F})$
is a system of Hodge bundles with
$F=(F^{1,0}~\oplus ~F^{0,1},\unicode[STIX]{x1D703}_{F})$
is a system of Hodge bundles with
![]() $F^{1,0}=L$
,
$F^{1,0}=L$
,
![]() $F^{0,1}={\mathcal{O}}_{X}$
and the Higgs field
$F^{0,1}={\mathcal{O}}_{X}$
and the Higgs field
![]() $\unicode[STIX]{x1D703}_{F}$
given by the inclusion
$\unicode[STIX]{x1D703}_{F}$
given by the inclusion
![]() $L\rightarrow \unicode[STIX]{x1D6FA}_{X}$
. Note that
$L\rightarrow \unicode[STIX]{x1D6FA}_{X}$
. Note that
![]() $F$
is an
$F$
is an
![]() $A$
-stable system of Hodge bundles but it does not have vanishing Chern classes so it does not underlie a rank
$A$
-stable system of Hodge bundles but it does not have vanishing Chern classes so it does not underlie a rank
![]() $2$
representation of
$2$
representation of
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
. But it comes from a projective representation
$\unicode[STIX]{x1D70B}_{1}(X,x)$
. But it comes from a projective representation
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{PGL}(2,\mathbb{C})$
. There exists a finite covering
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{PGL}(2,\mathbb{C})$
. There exists a finite covering
![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$
such that
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
such that
![]() $\unicode[STIX]{x1D70B}^{\ast }L=M^{\otimes 2}$
for some line bundle
$\unicode[STIX]{x1D70B}^{\ast }L=M^{\otimes 2}$
for some line bundle
![]() $M$
on
$M$
on
![]() $Y$
. Then
$Y$
. Then
![]() $\unicode[STIX]{x1D70B}^{\ast }(E,\unicode[STIX]{x1D703})\simeq \unicode[STIX]{x1D70B}^{\ast }(N,0)~\otimes ~\operatorname{Sym}^{2}(F_{Y})$
, where
$\unicode[STIX]{x1D70B}^{\ast }(E,\unicode[STIX]{x1D703})\simeq \unicode[STIX]{x1D70B}^{\ast }(N,0)~\otimes ~\operatorname{Sym}^{2}(F_{Y})$
, where
![]() $F_{Y}=(F_{Y}^{1,0}\oplus F_{Y}^{1,0},\unicode[STIX]{x1D703}_{Y})$
is a system of Hodge bundles with
$F_{Y}=(F_{Y}^{1,0}\oplus F_{Y}^{1,0},\unicode[STIX]{x1D703}_{Y})$
is a system of Hodge bundles with
![]() $F_{Y}^{1,0}=M$
,
$F_{Y}^{1,0}=M$
,
![]() $F_{Y}^{0,1}=M^{-1}$
and the Higgs field
$F_{Y}^{0,1}=M^{-1}$
and the Higgs field
![]() $\unicode[STIX]{x1D703}_{Y}$
given by the inclusion
$\unicode[STIX]{x1D703}_{Y}$
given by the inclusion
![]() $\unicode[STIX]{x1D70B}^{\ast }L\rightarrow \unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FA}_{X}\rightarrow \unicode[STIX]{x1D6FA}_{Y}$
.
$\unicode[STIX]{x1D70B}^{\ast }L\rightarrow \unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FA}_{X}\rightarrow \unicode[STIX]{x1D6FA}_{Y}$
.
This corresponds to case (i) of the theorem.
If
![]() $B_{2}^{\prime }\neq 0$
, then by the Hodge index theorem there exist positive integers
$B_{2}^{\prime }\neq 0$
, then by the Hodge index theorem there exist positive integers
![]() $b$
and
$b$
and
![]() $c$
such that
$c$
such that
![]() $bM^{\prime }\equiv cB_{2}^{\prime }$
. The idea is now to say that
$bM^{\prime }\equiv cB_{2}^{\prime }$
. The idea is now to say that
![]() $M^{\prime }$
looks like an effective divisor. Roughly speaking, we try to get a section of
$M^{\prime }$
looks like an effective divisor. Roughly speaking, we try to get a section of
![]() $M^{\prime }$
and then argue using this differential form. In practice we need to extract a root, and we only have numerical information so, in the case where the Picard scheme has positive dimension, we need to deal with several cases.
$M^{\prime }$
and then argue using this differential form. In practice we need to extract a root, and we only have numerical information so, in the case where the Picard scheme has positive dimension, we need to deal with several cases.
Start by noting that
![]() $U:=bM^{\prime }-cB_{2}^{\prime }\in \operatorname{Pic}^{\unicode[STIX]{x1D70F}}(X)$
. Multiplying
$U:=bM^{\prime }-cB_{2}^{\prime }\in \operatorname{Pic}^{\unicode[STIX]{x1D70F}}(X)$
. Multiplying
![]() $b$
and
$b$
and
![]() $c$
by the same positive integer we can assume that in fact
$c$
by the same positive integer we can assume that in fact
![]() $U\in \operatorname{Pic}^{0}(X)$
. Therefore we have a non-zero map
$U\in \operatorname{Pic}^{0}(X)$
. Therefore we have a non-zero map
determined by the divisor
![]() $cB_{2}^{\prime }$
. We can write
$cB_{2}^{\prime }$
. We can write
![]() $U=V^{\otimes b}$
for some
$U=V^{\otimes b}$
for some
![]() $V\in \operatorname{Pic}^{0}(X)$
and hence we get a section
$V\in \operatorname{Pic}^{0}(X)$
and hence we get a section
![]() $\unicode[STIX]{x1D702}\in H^{0}(X,(M^{\prime }~\otimes ~V^{\ast })^{\otimes b})$
(whose divisor is
$\unicode[STIX]{x1D702}\in H^{0}(X,(M^{\prime }~\otimes ~V^{\ast })^{\otimes b})$
(whose divisor is
![]() $cB_{2}^{\prime }$
).
$cB_{2}^{\prime }$
).
Let
![]() $p:Z\rightarrow X$
be a desingularization of the ramified covering defined by taking the
$p:Z\rightarrow X$
be a desingularization of the ramified covering defined by taking the
![]() $b$
th root of
$b$
th root of
![]() $\unicode[STIX]{x1D702}$
. Over
$\unicode[STIX]{x1D702}$
. Over
![]() $Z$
we have a tautological section
$Z$
we have a tautological section
![]() $\unicode[STIX]{x1D6FC}\in H^{0}(Z,p^{\ast }(M^{\prime }~\otimes ~V^{\ast }))$
such that
$\unicode[STIX]{x1D6FC}\in H^{0}(Z,p^{\ast }(M^{\prime }~\otimes ~V^{\ast }))$
such that
![]() $\unicode[STIX]{x1D6FC}^{\otimes b}=p^{\ast }\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D6FC}^{\otimes b}=p^{\ast }\unicode[STIX]{x1D702}$
.
In particular,
![]() $\unicode[STIX]{x1D6FC}\in H^{0}(Z,\unicode[STIX]{x1D6FA}_{Z}^{1}~\otimes ~p^{\ast }V^{\ast })$
, which means that
$\unicode[STIX]{x1D6FC}\in H^{0}(Z,\unicode[STIX]{x1D6FA}_{Z}^{1}~\otimes ~p^{\ast }V^{\ast })$
, which means that
![]() $p^{\ast }V^{\ast }\in \operatorname{Pic}^{0}(Z)$
is in the jump-locus for twisted sections of
$p^{\ast }V^{\ast }\in \operatorname{Pic}^{0}(Z)$
is in the jump-locus for twisted sections of
![]() $\unicode[STIX]{x1D6FA}_{Z}^{1}$
:
$\unicode[STIX]{x1D6FA}_{Z}^{1}$
:
The irreducible components of this jump-locus are translates of abelian subvarieties of
![]() $\text{Pic}^{0}(Z)$
by torsion points. The fact that the components are translates of abelian varieties was proved in [Reference Green and LazarsfeldGL91] and the assertion about torsion was proved in [Reference SimpsonSim93b]. We distinguish two cases depending on whether
$\text{Pic}^{0}(Z)$
by torsion points. The fact that the components are translates of abelian varieties was proved in [Reference Green and LazarsfeldGL91] and the assertion about torsion was proved in [Reference SimpsonSim93b]. We distinguish two cases depending on whether
![]() $p^{\ast }V^{\ast }$
is a torsion point or not.
$p^{\ast }V^{\ast }$
is a torsion point or not.
Case 1: let us assume that
![]() $p^{\ast }V^{\ast }$
is a torsion point of
$p^{\ast }V^{\ast }$
is a torsion point of
![]() $\text{Pic}^{0}(Z)$
. Then the line bundle
$\text{Pic}^{0}(Z)$
. Then the line bundle
![]() $p^{\ast }V^{\ast }$
defines a finite étale covering
$p^{\ast }V^{\ast }$
defines a finite étale covering
![]() $q:Z^{\prime }\rightarrow Z$
such that
$q:Z^{\prime }\rightarrow Z$
such that
![]() $V^{\ast }$
becomes trivial after pulling back to
$V^{\ast }$
becomes trivial after pulling back to
![]() $Z^{\prime }$
. Let
$Z^{\prime }$
. Let
![]() $p^{\prime }$
denote the composition of
$p^{\prime }$
denote the composition of
![]() $q:Z^{\prime }\rightarrow Z$
with
$q:Z^{\prime }\rightarrow Z$
with
![]() $p:Z\rightarrow X$
. Then over
$p:Z\rightarrow X$
. Then over
![]() $Z^{\prime }$
we get a non-zero section
$Z^{\prime }$
we get a non-zero section
![]() $\unicode[STIX]{x1D709}\in H^{0}(Z^{\prime },\unicode[STIX]{x1D6FA}_{Z^{\prime }}^{1})$
given by the composition of
$\unicode[STIX]{x1D709}\in H^{0}(Z^{\prime },\unicode[STIX]{x1D6FA}_{Z^{\prime }}^{1})$
given by the composition of
![]() $q^{\ast }\unicode[STIX]{x1D6FC}:{\mathcal{O}}_{Z^{\prime }}\rightarrow q^{\ast }(p^{\ast }(M^{\prime }~\otimes ~V^{\ast }))\simeq q^{\ast }(p^{\ast }(M^{\prime }))=(p^{\prime })^{\ast }M^{\prime }$
with the canonical map
$q^{\ast }\unicode[STIX]{x1D6FC}:{\mathcal{O}}_{Z^{\prime }}\rightarrow q^{\ast }(p^{\ast }(M^{\prime }~\otimes ~V^{\ast }))\simeq q^{\ast }(p^{\ast }(M^{\prime }))=(p^{\prime })^{\ast }M^{\prime }$
with the canonical map
![]() $(p^{\prime })^{\ast }M^{\prime }\rightarrow (p^{\prime })^{\ast }\unicode[STIX]{x1D6FA}_{X}\rightarrow \unicode[STIX]{x1D6FA}_{Z^{\prime }}^{1}$
.
$(p^{\prime })^{\ast }M^{\prime }\rightarrow (p^{\prime })^{\ast }\unicode[STIX]{x1D6FA}_{X}\rightarrow \unicode[STIX]{x1D6FA}_{Z^{\prime }}^{1}$
.
The line bundle
![]() $(p^{\prime })^{\ast }M^{\prime }\subset \unicode[STIX]{x1D6FA}_{Z^{\prime }}^{1}$
is generically generated by this section
$(p^{\prime })^{\ast }M^{\prime }\subset \unicode[STIX]{x1D6FA}_{Z^{\prime }}^{1}$
is generically generated by this section
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
We can look at the Albanese map defined by
![]() $\unicode[STIX]{x1D709}$
(see [Reference SimpsonSim93a, p. 101]). This is the map
$\unicode[STIX]{x1D709}$
(see [Reference SimpsonSim93a, p. 101]). This is the map
![]() $\unicode[STIX]{x1D713}:Z^{\prime }\rightarrow A=\operatorname{Alb}(Z^{\prime })/B$
, where
$\unicode[STIX]{x1D713}:Z^{\prime }\rightarrow A=\operatorname{Alb}(Z^{\prime })/B$
, where
![]() $B$
is the sum of all abelian subvarieties of
$B$
is the sum of all abelian subvarieties of
![]() $\operatorname{Alb}(Z^{\prime })$
on which
$\operatorname{Alb}(Z^{\prime })$
on which
![]() $\unicode[STIX]{x1D709}$
vanishes. By construction
$\unicode[STIX]{x1D709}$
vanishes. By construction
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D713}^{\ast }(\unicode[STIX]{x1D709}_{A})$
for some
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D713}^{\ast }(\unicode[STIX]{x1D709}_{A})$
for some
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D709}_{A}$
on
$\unicode[STIX]{x1D709}_{A}$
on
![]() $A$
such that the restriction of
$A$
such that the restriction of
![]() $\unicode[STIX]{x1D709}_{A}$
to any non-trivial abelian subvariety of
$\unicode[STIX]{x1D709}_{A}$
to any non-trivial abelian subvariety of
![]() $A$
is non-zero.
$A$
is non-zero.
We distinguish two subcases depending on the dimension of
![]() $\unicode[STIX]{x1D713}(Z^{\prime })$
.
$\unicode[STIX]{x1D713}(Z^{\prime })$
.
Subcase 1.1: the image of
![]() $\unicode[STIX]{x1D713}$
is a curve. In this case taking the Stein factorization of
$\unicode[STIX]{x1D713}$
is a curve. In this case taking the Stein factorization of
![]() $Z^{\prime }\rightarrow \unicode[STIX]{x1D713}(Z^{\prime })$
, we get a fibration
$Z^{\prime }\rightarrow \unicode[STIX]{x1D713}(Z^{\prime })$
, we get a fibration
![]() $f:Z^{\prime }\rightarrow C$
over a smooth projective curve and a
$f:Z^{\prime }\rightarrow C$
over a smooth projective curve and a
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D709}_{C}$
on
$\unicode[STIX]{x1D709}_{C}$
on
![]() $C$
such that
$C$
such that
![]() $\unicode[STIX]{x1D709}=f^{\ast }\unicode[STIX]{x1D709}_{C}$
. Considering
$\unicode[STIX]{x1D709}=f^{\ast }\unicode[STIX]{x1D709}_{C}$
. Considering
![]() $\unicode[STIX]{x1D709}$
as a map
$\unicode[STIX]{x1D709}$
as a map
![]() ${\mathcal{O}}_{Z^{\prime }}\rightarrow \unicode[STIX]{x1D6FA}_{Z^{\prime }}$
, this means that the map factors through
${\mathcal{O}}_{Z^{\prime }}\rightarrow \unicode[STIX]{x1D6FA}_{Z^{\prime }}$
, this means that the map factors through
![]() $f^{\ast }\unicode[STIX]{x1D709}_{C}:{\mathcal{O}}_{Z^{\prime }}=f^{\ast }{\mathcal{O}}_{C}\rightarrow f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
. Therefore
$f^{\ast }\unicode[STIX]{x1D709}_{C}:{\mathcal{O}}_{Z^{\prime }}=f^{\ast }{\mathcal{O}}_{C}\rightarrow f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
. Therefore
![]() $(p^{\prime })^{\ast }M$
is contained in the saturation of
$(p^{\prime })^{\ast }M$
is contained in the saturation of
![]() $f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
in
$f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
in
![]() $\unicode[STIX]{x1D6FA}_{Z^{\prime }}$
. If
$\unicode[STIX]{x1D6FA}_{Z^{\prime }}$
. If
![]() $F$
is a smooth fiber of
$F$
is a smooth fiber of
![]() $f$
(or just a multiplicity
$f$
(or just a multiplicity
![]() $1$
irreducible component of a fiber of
$1$
irreducible component of a fiber of
![]() $f$
) then this shows that the canonical map
$f$
) then this shows that the canonical map
![]() $(p^{\prime })^{\ast }M|_{F}\rightarrow \unicode[STIX]{x1D6FA}_{Z^{\prime }/C}|_{F}=\unicode[STIX]{x1D6FA}_{F}$
is zero. This implies that the Kodaira–Spencer maps of our variation of Hodge structures restricted to the fiber
$(p^{\prime })^{\ast }M|_{F}\rightarrow \unicode[STIX]{x1D6FA}_{Z^{\prime }/C}|_{F}=\unicode[STIX]{x1D6FA}_{F}$
is zero. This implies that the Kodaira–Spencer maps of our variation of Hodge structures restricted to the fiber
![]() $F$
, vanish. Each Hodge subbundle is therefore a flat subbundle. Hence, the restriction of our variation of Hodge structures to
$F$
, vanish. Each Hodge subbundle is therefore a flat subbundle. Hence, the restriction of our variation of Hodge structures to
![]() $F$
splits into a direct sum of three rank
$F$
splits into a direct sum of three rank
![]() $1$
variations of Hodge structure at the three different Hodge types. Clearly,
$1$
variations of Hodge structure at the three different Hodge types. Clearly,
![]() $\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable. It is also not virtually reducible as the Kodaira–Spencer maps remain non-zero under alterations. So by Theorem 3.3 (
$\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable. It is also not virtually reducible as the Kodaira–Spencer maps remain non-zero under alterations. So by Theorem 3.3 (
![]() $4\Rightarrow 1$
),
$4\Rightarrow 1$
),
![]() $\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
$\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve.
Subcase 1.2: the dimension of the image
![]() $\unicode[STIX]{x1D713}(Z^{\prime })$
is at least
$\unicode[STIX]{x1D713}(Z^{\prime })$
is at least
![]() $2$
. Let
$2$
. Let
![]() $\tilde{A}\rightarrow A$
be the universal covering of
$\tilde{A}\rightarrow A$
be the universal covering of
![]() $A$
(treated as a complex vector space). This map is only analytic and not algebraic. Let
$A$
(treated as a complex vector space). This map is only analytic and not algebraic. Let
![]() $\tilde{Z}:=Z^{\prime }\times _{A}\tilde{A}$
be the covering of
$\tilde{Z}:=Z^{\prime }\times _{A}\tilde{A}$
be the covering of
![]() $Z^{\prime }$
defined by the Albanese map
$Z^{\prime }$
defined by the Albanese map
![]() $\unicode[STIX]{x1D713}$
and let
$\unicode[STIX]{x1D713}$
and let
![]() $\unicode[STIX]{x1D70B}:\tilde{Z}\rightarrow Z^{\prime }$
be the projection on the first factor and
$\unicode[STIX]{x1D70B}:\tilde{Z}\rightarrow Z^{\prime }$
be the projection on the first factor and
![]() $\tilde{\unicode[STIX]{x1D713}}:\tilde{Z}\rightarrow \tilde{A}$
on the second factor (these maps are also only analytic). Let us fix a point
$\tilde{\unicode[STIX]{x1D713}}:\tilde{Z}\rightarrow \tilde{A}$
on the second factor (these maps are also only analytic). Let us fix a point
![]() $\tilde{z}_{0}\in \tilde{Z}$
. There exists a unique linear function
$\tilde{z}_{0}\in \tilde{Z}$
. There exists a unique linear function
![]() $g_{\tilde{A}}:\tilde{A}\rightarrow \mathbb{C}$
such that
$g_{\tilde{A}}:\tilde{A}\rightarrow \mathbb{C}$
such that
![]() $g_{\tilde{A}}(\tilde{\unicode[STIX]{x1D713}}(\tilde{z}_{0}))=0$
and
$g_{\tilde{A}}(\tilde{\unicode[STIX]{x1D713}}(\tilde{z}_{0}))=0$
and
![]() $dg_{\tilde{A}}=\unicode[STIX]{x1D709}_{A}$
. Let
$dg_{\tilde{A}}=\unicode[STIX]{x1D709}_{A}$
. Let
![]() $g:\tilde{Z}\rightarrow \mathbb{C}$
be the composition of
$g:\tilde{Z}\rightarrow \mathbb{C}$
be the composition of
![]() $g_{\tilde{A}}$
with
$g_{\tilde{A}}$
with
![]() $\tilde{\unicode[STIX]{x1D713}}$
. Then the Lefschetz theorem (see [Reference SimpsonSim93a, Theorem 1]; since
$\tilde{\unicode[STIX]{x1D713}}$
. Then the Lefschetz theorem (see [Reference SimpsonSim93a, Theorem 1]; since
![]() $\dim (\unicode[STIX]{x1D713}(Z^{\prime }))\geqslant 2$
the assumptions of this theorem are satisfied) says that for any fiber
$\dim (\unicode[STIX]{x1D713}(Z^{\prime }))\geqslant 2$
the assumptions of this theorem are satisfied) says that for any fiber
![]() $F$
of
$F$
of
![]() $g$
(or, in other words, a possibly non-compact leaf of the foliation defined by
$g$
(or, in other words, a possibly non-compact leaf of the foliation defined by
![]() $\unicode[STIX]{x1D709}$
), the map
$\unicode[STIX]{x1D709}$
), the map
![]() $\unicode[STIX]{x1D70B}_{1}(F,\tilde{z}_{0})\rightarrow \unicode[STIX]{x1D70B}_{1}(\tilde{Z},\tilde{z}_{0})$
is surjective.
$\unicode[STIX]{x1D70B}_{1}(F,\tilde{z}_{0})\rightarrow \unicode[STIX]{x1D70B}_{1}(\tilde{Z},\tilde{z}_{0})$
is surjective.
Note that by our construction the restriction
![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D709}|_{F}$
is zero. Choosing
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D709}|_{F}$
is zero. Choosing
![]() $F$
so that it does not lie in the preimage of
$F$
so that it does not lie in the preimage of
![]() $B_{2}^{\prime }$
, the inclusion
$B_{2}^{\prime }$
, the inclusion
![]() $M^{\prime }\rightarrow \unicode[STIX]{x1D6FA}_{X}$
becomes zero after pulling back to
$M^{\prime }\rightarrow \unicode[STIX]{x1D6FA}_{X}$
becomes zero after pulling back to
![]() $F$
and composing with the canonical map to
$F$
and composing with the canonical map to
![]() $\unicode[STIX]{x1D6FA}_{F}$
. So our variation of Hodge structure splits on
$\unicode[STIX]{x1D6FA}_{F}$
. So our variation of Hodge structure splits on
![]() $F$
into a direct sum of three line bundles. In this case the image of the representation
$F$
into a direct sum of three line bundles. In this case the image of the representation
![]() $\unicode[STIX]{x1D70B}_{1}(F,\tilde{z}_{0})\rightarrow \operatorname{SL}(3,\mathbb{C})$
is contained in a maximal torus. Therefore the monodromy representation is abelian on
$\unicode[STIX]{x1D70B}_{1}(F,\tilde{z}_{0})\rightarrow \operatorname{SL}(3,\mathbb{C})$
is contained in a maximal torus. Therefore the monodromy representation is abelian on
![]() $\unicode[STIX]{x1D70B}_{1}(\tilde{Z},\tilde{z}_{0})$
. But
$\unicode[STIX]{x1D70B}_{1}(\tilde{Z},\tilde{z}_{0})$
. But
![]() $\unicode[STIX]{x1D70B}_{1}(Z^{\prime },\tilde{\unicode[STIX]{x1D713}}(\tilde{z}_{0}))/\unicode[STIX]{x1D70B}_{1}(\tilde{Z},\tilde{z}_{0})$
is an abelian group, so the monodromy of our original VHS would be solvable. Then the Zariski closure
$\unicode[STIX]{x1D70B}_{1}(Z^{\prime },\tilde{\unicode[STIX]{x1D713}}(\tilde{z}_{0}))/\unicode[STIX]{x1D70B}_{1}(\tilde{Z},\tilde{z}_{0})$
is an abelian group, so the monodromy of our original VHS would be solvable. Then the Zariski closure
![]() $G\subset \operatorname{SL}(3,\mathbb{C})$
of
$G\subset \operatorname{SL}(3,\mathbb{C})$
of
![]() $\text{im}\,\unicode[STIX]{x1D70C}$
is also solvable (this follows from [Reference BorelBor91, I.2.4 Proposition]). On the other hand, since
$\text{im}\,\unicode[STIX]{x1D70C}$
is also solvable (this follows from [Reference BorelBor91, I.2.4 Proposition]). On the other hand, since
![]() $\unicode[STIX]{x1D70C}$
is irreducible, the connected component
$\unicode[STIX]{x1D70C}$
is irreducible, the connected component
![]() $G^{0}$
is reductive. Hence,
$G^{0}$
is reductive. Hence,
![]() $G^{0}$
is contained in a maximal torus of
$G^{0}$
is contained in a maximal torus of
![]() $\operatorname{SL}(3,\mathbb{C})$
. Taking the étale covering
$\operatorname{SL}(3,\mathbb{C})$
. Taking the étale covering
![]() $q:\tilde{X}\rightarrow X$
corresponding to the image of
$q:\tilde{X}\rightarrow X$
corresponding to the image of
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G/G^{0}$
, we see that the monodromy of
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G/G^{0}$
, we see that the monodromy of
![]() $q^{\ast }V_{\unicode[STIX]{x1D70C}}$
is contained in the maximal torus of
$q^{\ast }V_{\unicode[STIX]{x1D70C}}$
is contained in the maximal torus of
![]() $\operatorname{SL}(3,\mathbb{C})$
. But then the corresponding pullback of the system of Hodge bundles is a direct sum of line bundles with trivial maps between the components, contradicting the fact that the original VHS was of type
$\operatorname{SL}(3,\mathbb{C})$
. But then the corresponding pullback of the system of Hodge bundles is a direct sum of line bundles with trivial maps between the components, contradicting the fact that the original VHS was of type
![]() $(1,1,1)$
.
$(1,1,1)$
.
Case 2: assume that
![]() $p^{\ast }V^{\ast }$
is not a torsion point. Then an irreducible component of
$p^{\ast }V^{\ast }$
is not a torsion point. Then an irreducible component of
![]() $S(Z)$
containing this point has dimension
$S(Z)$
containing this point has dimension
![]() ${\geqslant}1$
.
${\geqslant}1$
.
Let us recall that for a line bundle
![]() $N\in \operatorname{Pic}^{0}(Z)$
we have an isomorphism of complex vector spaces
$N\in \operatorname{Pic}^{0}(Z)$
we have an isomorphism of complex vector spaces
so
Beauville proves in [Reference BeauvilleBea92] that the positive-dimensional components of this set all come from maps to orbicurves. More precisely, [Reference BeauvilleBea92, Corollaire 2.3] says that there exists a fibration
![]() $f:Z\rightarrow C$
over a smooth projective curve of genus
$f:Z\rightarrow C$
over a smooth projective curve of genus
![]() $g\geqslant 1$
such that
$g\geqslant 1$
such that
![]() $p^{\ast }V^{\ast }$
is trivial on every smooth fiber of
$p^{\ast }V^{\ast }$
is trivial on every smooth fiber of
![]() $f$
.
$f$
.
The proof of the following lemma is modelled on the proof of [Reference BeauvilleBea92, Proposition 1.10].
Lemma 5.2. Let
![]() $Z$
be a smooth complex projective variety and let
$Z$
be a smooth complex projective variety and let
![]() $C$
be a smooth complex projective curve. Let
$C$
be a smooth complex projective curve. Let
![]() $f:Z\rightarrow C$
be a fibration with reduced fibers. Let
$f:Z\rightarrow C$
be a fibration with reduced fibers. Let
![]() $L\in \operatorname{Pic}^{\unicode[STIX]{x1D70F}}Z$
be a non-torsion line bundle, which is trivial on some smooth fiber of
$L\in \operatorname{Pic}^{\unicode[STIX]{x1D70F}}Z$
be a non-torsion line bundle, which is trivial on some smooth fiber of
![]() $f$
. If
$f$
. If
![]() $0\neq \unicode[STIX]{x1D6FC}\in H^{0}(\unicode[STIX]{x1D6FA}_{Z}~\otimes ~L^{-1})$
then there exists a line bundle
$0\neq \unicode[STIX]{x1D6FC}\in H^{0}(\unicode[STIX]{x1D6FA}_{Z}~\otimes ~L^{-1})$
then there exists a line bundle
![]() $L_{C}$
on
$L_{C}$
on
![]() $C$
and
$C$
and
![]() $\unicode[STIX]{x1D6FD}\in H^{0}(\unicode[STIX]{x1D6FA}_{C}~\otimes ~L_{C}^{-1})=\operatorname{Hom}(L_{C},\unicode[STIX]{x1D6FA}_{C})$
such that
$\unicode[STIX]{x1D6FD}\in H^{0}(\unicode[STIX]{x1D6FA}_{C}~\otimes ~L_{C}^{-1})=\operatorname{Hom}(L_{C},\unicode[STIX]{x1D6FA}_{C})$
such that
![]() $L=f^{\ast }L_{C}$
and the composition
$L=f^{\ast }L_{C}$
and the composition
corresponds to
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Proof. First let us recall that existence of
![]() $L_{C}$
such that
$L_{C}$
such that
![]() $L=f^{\ast }L_{C}$
follows from [Reference BeauvilleBea92, Proposition 1.2]. We have a short exact sequence
$L=f^{\ast }L_{C}$
follows from [Reference BeauvilleBea92, Proposition 1.2]. We have a short exact sequence
coming from the Leray spectral sequence. Using the isomorphisms
![]() $H^{1}(Z,L)\simeq \overline{H^{0}(Z,\unicode[STIX]{x1D6FA}_{Z}^{1}~\otimes ~L^{-1})}$
and
$H^{1}(Z,L)\simeq \overline{H^{0}(Z,\unicode[STIX]{x1D6FA}_{Z}^{1}~\otimes ~L^{-1})}$
and
![]() $H^{1}(C,L_{C})\simeq \overline{H^{0}(C,\unicode[STIX]{x1D6FA}_{C}^{1}~\otimes ~L_{C}^{-1})}$
, it is sufficient to show that
$H^{1}(C,L_{C})\simeq \overline{H^{0}(C,\unicode[STIX]{x1D6FA}_{C}^{1}~\otimes ~L_{C}^{-1})}$
, it is sufficient to show that
![]() $H^{0}(C,R^{1}f_{\ast }L)=0$
. But
$H^{0}(C,R^{1}f_{\ast }L)=0$
. But
![]() $H^{0}(C,R^{1}f_{\ast }L)=H^{0}(C,L_{C}~\otimes ~R^{1}f_{\ast }{\mathcal{O}}_{Z})$
and
$H^{0}(C,R^{1}f_{\ast }L)=H^{0}(C,L_{C}~\otimes ~R^{1}f_{\ast }{\mathcal{O}}_{Z})$
and
![]() $R^{1}f_{\ast }{\mathcal{O}}_{Z}$
is dual to
$R^{1}f_{\ast }{\mathcal{O}}_{Z}$
is dual to
![]() $f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
, so we need to check that
$f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
, so we need to check that
![]() $\operatorname{Hom}(f_{\ast }\unicode[STIX]{x1D714}_{Z/C},L_{C})=0$
. Let us recall that by [Reference FujitaFuj78, Theorem] (see also [Reference Catanese and DettweilerCD17, Theorem 17]),
$\operatorname{Hom}(f_{\ast }\unicode[STIX]{x1D714}_{Z/C},L_{C})=0$
. Let us recall that by [Reference FujitaFuj78, Theorem] (see also [Reference Catanese and DettweilerCD17, Theorem 17]),
![]() $f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
is a direct sum of an ample vector bundle and a direct sum of stable vector bundles of degree zero. Therefore
$f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
is a direct sum of an ample vector bundle and a direct sum of stable vector bundles of degree zero. Therefore
![]() $\operatorname{Hom}(f_{\ast }\unicode[STIX]{x1D714}_{Z/C},L_{C})\neq 0$
if and only if
$\operatorname{Hom}(f_{\ast }\unicode[STIX]{x1D714}_{Z/C},L_{C})\neq 0$
if and only if
![]() $L_{C}$
is isomorphic to one of the direct summands of
$L_{C}$
is isomorphic to one of the direct summands of
![]() $f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
. But by Deligne’s result, the rank
$f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
. But by Deligne’s result, the rank
![]() $1$
summands of
$1$
summands of
![]() $f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
are torsion (see [Reference Catanese and DettweilerCD17, Corollary 21]) and
$f_{\ast }\unicode[STIX]{x1D714}_{Z/C}$
are torsion (see [Reference Catanese and DettweilerCD17, Corollary 21]) and
![]() $L_{C}$
is not torsion, so we get a contradiction.◻
$L_{C}$
is not torsion, so we get a contradiction.◻
Taking a semi-stable reduction of
![]() $f$
we can assume that all the fibers of
$f$
we can assume that all the fibers of
![]() $f$
are reduced. Then, by the above lemma, there exists a line bundle
$f$
are reduced. Then, by the above lemma, there exists a line bundle
![]() $L_{C}\in \operatorname{Pic}^{0}(C)$
such that
$L_{C}\in \operatorname{Pic}^{0}(C)$
such that
![]() $p^{\ast }V=f^{\ast }L_{C}$
and the section
$p^{\ast }V=f^{\ast }L_{C}$
and the section
![]() $\unicode[STIX]{x1D6FC}$
comes from a section of
$\unicode[STIX]{x1D6FC}$
comes from a section of
![]() $H^{0}(C,\unicode[STIX]{x1D6FA}_{C}^{1}~\otimes ~L_{C}^{\ast })$
. This shows that
$H^{0}(C,\unicode[STIX]{x1D6FA}_{C}^{1}~\otimes ~L_{C}^{\ast })$
. This shows that
![]() $p^{\ast }V^{\ast }\rightarrow f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
is an isomorphism at the generic point of
$p^{\ast }V^{\ast }\rightarrow f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
is an isomorphism at the generic point of
![]() $Z$
. Since
$Z$
. Since
![]() $p^{\ast }V\rightarrow p^{\ast }M$
is also an isomorphism at the generic point of
$p^{\ast }V\rightarrow p^{\ast }M$
is also an isomorphism at the generic point of
![]() $Z$
, the sheaf
$Z$
, the sheaf
![]() $p^{\ast }M$
is contained in
$p^{\ast }M$
is contained in
![]() $f^{\ast }\unicode[STIX]{x1D6FA}_{C}\subset \unicode[STIX]{x1D6FA}_{Z}$
(since the fibers of
$f^{\ast }\unicode[STIX]{x1D6FA}_{C}\subset \unicode[STIX]{x1D6FA}_{Z}$
(since the fibers of
![]() $f$
are reduced,
$f$
are reduced,
![]() $f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
is saturated in
$f^{\ast }\unicode[STIX]{x1D6FA}_{C}$
is saturated in
![]() $\unicode[STIX]{x1D6FA}_{Z}$
).
$\unicode[STIX]{x1D6FA}_{Z}$
).
As before this implies that the pullback of our variation of Hodge structure to a fiber of
![]() $f$
splits into a direct sum of three rank
$f$
splits into a direct sum of three rank
![]() $1$
variations of Hodge structure. Therefore Corollary 3.5 implies that
$1$
variations of Hodge structure. Therefore Corollary 3.5 implies that
![]() $\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve. Alternatively, the same arguments as before show that
$\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve. Alternatively, the same arguments as before show that
![]() $((p^{\prime })^{\ast }M^{\prime })^{\otimes b}$
is a line bundle associated to a certain sum of rational multiples of fibers of
$((p^{\prime })^{\ast }M^{\prime })^{\otimes b}$
is a line bundle associated to a certain sum of rational multiples of fibers of
![]() $f$
(but not necessarily positive). Then by passing to a certain cover
$f$
(but not necessarily positive). Then by passing to a certain cover
![]() $Z^{\prime \prime }\rightarrow Z^{\prime }$
we conclude that the pullback of our original variation of Hodge structure to
$Z^{\prime \prime }\rightarrow Z^{\prime }$
we conclude that the pullback of our original variation of Hodge structure to
![]() $Z^{\prime \prime }$
is isomorphic to the pullback of a variation of Hodge structure on a certain curve
$Z^{\prime \prime }$
is isomorphic to the pullback of a variation of Hodge structure on a certain curve
![]() $C^{\prime }$
. So
$C^{\prime }$
. So
![]() $\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve and we can again conclude by Corollary 3.5. This completes the proof of Theorem 4.1.◻
$\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve and we can again conclude by Corollary 3.5. This completes the proof of Theorem 4.1.◻
6 Some remarks on the case
 $(1,1,\ldots ,1)$
$(1,1,\ldots ,1)$
In this section we consider the possibility of generalization of the results of § 4 to the case
![]() $(1,1,\ldots ,1)$
. For simplicity of notation, we consider only the case when
$(1,1,\ldots ,1)$
. For simplicity of notation, we consider only the case when
![]() $X$
is a smooth projective variety (i.e.,
$X$
is a smooth projective variety (i.e.,
![]() $\bar{X}=X$
).
$\bar{X}=X$
).
Let
![]() $n$
be a positive integer and let
$n$
be a positive integer and let
![]() $(E=\bigoplus _{p+q=n}E^{p,q},\unicode[STIX]{x1D703})$
be a rank
$(E=\bigoplus _{p+q=n}E^{p,q},\unicode[STIX]{x1D703})$
be a rank
![]() $(n+1)$
system of Hodge bundles of type
$(n+1)$
system of Hodge bundles of type
![]() $(1,\ldots ,1)$
. Then
$(1,\ldots ,1)$
. Then
![]() $\unicode[STIX]{x1D703}$
induces injections
$\unicode[STIX]{x1D703}$
induces injections
for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
Lemma 6.1. Assume that
![]() $c_{1}(E)=0$
and
$c_{1}(E)=0$
and
![]() $(E,\unicode[STIX]{x1D703})$
is slope
$(E,\unicode[STIX]{x1D703})$
is slope
![]() $A$
-stable. Let us set
$A$
-stable. Let us set
for
![]() $i=1,\ldots ,n$
. Then for all non-negative real numbers
$i=1,\ldots ,n$
. Then for all non-negative real numbers
![]() $x_{1},\ldots ,x_{n}$
we have
$x_{1},\ldots ,x_{n}$
we have
Proof. We claim that for all
![]() $i=1,\ldots ,n-1$
the map
$i=1,\ldots ,n-1$
the map
induced from
![]() $\unicode[STIX]{x1D703}$
has rank
$\unicode[STIX]{x1D703}$
has rank
![]() $1$
. Indeed, in the local coordinates
$1$
. Indeed, in the local coordinates
![]() $\unicode[STIX]{x1D6FC}$
is given by two
$\unicode[STIX]{x1D6FC}$
is given by two
![]() $1$
-forms
$1$
-forms
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $\unicode[STIX]{x1D714}_{2}$
and the integrability of
$\unicode[STIX]{x1D714}_{2}$
and the integrability of
![]() $\unicode[STIX]{x1D703}$
implies that
$\unicode[STIX]{x1D703}$
implies that
![]() $\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}=0$
, so they are proportional and
$\unicode[STIX]{x1D714}_{1}\wedge \unicode[STIX]{x1D714}_{2}=0$
, so they are proportional and
![]() $\unicode[STIX]{x1D6FC}_{i}$
has rank
$\unicode[STIX]{x1D6FC}_{i}$
has rank
![]() $1$
. It follows that the map
$1$
. It follows that the map
also has rank
![]() $1$
. Let
$1$
. Let
![]() $M$
be the saturation of the image of
$M$
be the saturation of the image of
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
![]() $\unicode[STIX]{x1D6FA}_{X}$
(i.e., the largest rank
$\unicode[STIX]{x1D6FA}_{X}$
(i.e., the largest rank
![]() $1$
subsheaf of
$1$
subsheaf of
![]() $\unicode[STIX]{x1D6FA}_{X}$
containing the image of
$\unicode[STIX]{x1D6FA}_{X}$
containing the image of
![]() $\unicode[STIX]{x1D6FC}$
). Then
$\unicode[STIX]{x1D6FC}$
). Then
![]() $M$
is a line bundle such that
$M$
is a line bundle such that
![]() $\unicode[STIX]{x1D6FA}_{X}/M$
is torsion-free.
$\unicode[STIX]{x1D6FA}_{X}/M$
is torsion-free.
By construction we have inclusions
![]() $L_{i}\subset M$
defining effective divisors
$L_{i}\subset M$
defining effective divisors
![]() $B_{i}$
. Let us set
$B_{i}$
. Let us set
![]() $e^{p,q}=c_{1}(E^{p,q})$
,
$e^{p,q}=c_{1}(E^{p,q})$
,
![]() $l_{i}=c_{1}(L_{i})$
and
$l_{i}=c_{1}(L_{i})$
and
![]() $b_{i}=c_{1}(B_{i})$
. Then we can write
$b_{i}=c_{1}(B_{i})$
. Then we can write
By assumption we have
in the rational cohomology
![]() $H^{2}(X,\mathbb{Q})$
, so the classes
$H^{2}(X,\mathbb{Q})$
, so the classes
![]() $e^{p,q}$
can be written in terms of
$e^{p,q}$
can be written in terms of
![]() $l_{i}$
in the following way:
$l_{i}$
in the following way:
for
![]() $i=0,\ldots ,n$
.
$i=0,\ldots ,n$
.
Slope
![]() $A$
-stability of
$A$
-stability of
![]() $(E,\unicode[STIX]{x1D703})$
implies that
$(E,\unicode[STIX]{x1D703})$
implies that
for
![]() $i=0,\ldots ,n-1$
. This is equivalent to
$i=0,\ldots ,n-1$
. This is equivalent to
for
![]() $i=1,\ldots ,n$
. Rewriting these inequalities in terms of
$i=1,\ldots ,n$
. Rewriting these inequalities in terms of
![]() $L_{i}$
we get
$L_{i}$
we get
for
![]() $i=1,\ldots ,n$
. Since
$i=1,\ldots ,n$
. Since
![]() $L_{i}\leqslant M$
we have
$L_{i}\leqslant M$
we have
for all non-negative rational numbers
![]() $x_{1},\ldots ,x_{n}$
. But by Lemma 4.4,
$x_{1},\ldots ,x_{n}$
. But by Lemma 4.4,
![]() $M|_{Y}$
is not big and hence the
$M|_{Y}$
is not big and hence the
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\sum _{i=1}^{n}x_{i}N_{i}$
restricted to
$\sum _{i=1}^{n}x_{i}N_{i}$
restricted to
![]() $Y$
is also not big. Therefore we have
$Y$
is also not big. Therefore we have
for all non-negative rational numbers
![]() $x_{1},\ldots ,x_{n}$
(so also for all non-negative real numbers
$x_{1},\ldots ,x_{n}$
(so also for all non-negative real numbers
![]() $x_{1},\ldots ,x_{n}$
).◻
$x_{1},\ldots ,x_{n}$
).◻
This lemma gives many inequalities. Unfortunately, when
![]() $n\geqslant 3$
vanishing of higher Chern classes of
$n\geqslant 3$
vanishing of higher Chern classes of
![]() $E$
does not seem to give any particularly useful information. For example for
$E$
does not seem to give any particularly useful information. For example for
![]() $n=3$
in dimension
$n=3$
in dimension
![]() $2$
it gives
$2$
it gives
Since
 $$\begin{eqnarray}\displaystyle N_{1} & = & \displaystyle 3L_{1}+2L_{2}+L_{3},\nonumber\\ \displaystyle N_{2} & = & \displaystyle 2L_{1}+4L_{2}+2L_{3},\nonumber\\ \displaystyle N_{1} & = & \displaystyle L_{1}+2L_{2}+3L_{3},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{1} & = & \displaystyle 3L_{1}+2L_{2}+L_{3},\nonumber\\ \displaystyle N_{2} & = & \displaystyle 2L_{1}+4L_{2}+2L_{3},\nonumber\\ \displaystyle N_{1} & = & \displaystyle L_{1}+2L_{2}+3L_{3},\nonumber\end{eqnarray}$$
![]() $E$
is
$E$
is
![]() $A$
-stable if
$A$
-stable if
![]() $L_{2}.A$
is large and
$L_{2}.A$
is large and
![]() $L_{1}.A$
and
$L_{1}.A$
and
![]() $L_{3}.A$
are not too negative. In that case
$L_{3}.A$
are not too negative. In that case
![]() $L_{1}^{2}$
can be positive and we do not get an analogue of Proposition 4.3.
$L_{1}^{2}$
can be positive and we do not get an analogue of Proposition 4.3.
7 Corollaries
Recall that our variations of Hodge structure are always considered to be polarizable. We say that a VHS is of weight
![]() $k$
if its Hodge decomposition takes the form
$k$
if its Hodge decomposition takes the form
![]() $V=\bigoplus _{p+q=k,p,q\geqslant 0}V^{p,q}$
.
$V=\bigoplus _{p+q=k,p,q\geqslant 0}V^{p,q}$
.
Proposition 7.1. Let
![]() $X$
be a smooth complex quasi-projective variety. Suppose
$X$
be a smooth complex quasi-projective variety. Suppose
![]() $\unicode[STIX]{x1D70C}_{K}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,K)$
is an absolutely irreducible representation defined over an algebraic number field, such that for each embedding
$\unicode[STIX]{x1D70C}_{K}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,K)$
is an absolutely irreducible representation defined over an algebraic number field, such that for each embedding
![]() $\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the associated
$\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the associated
![]() $\mathbb{C}$
-local system
$\mathbb{C}$
-local system
![]() $V_{\unicode[STIX]{x1D70E}}$
underlies a polarized complex VHS of weight
$V_{\unicode[STIX]{x1D70E}}$
underlies a polarized complex VHS of weight
![]() $k$
. Then there is a totally imaginary quadratic extension
$k$
. Then there is a totally imaginary quadratic extension
![]() $L$
of a totally real algebraic number field
$L$
of a totally real algebraic number field
![]() $F$
, with
$F$
, with
![]() $L$
Galois over
$L$
Galois over
![]() $\mathbb{Q}$
, and a representation
$\mathbb{Q}$
, and a representation
![]() $\unicode[STIX]{x1D70C}_{L}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,L)$
, together with an extension
$\unicode[STIX]{x1D70C}_{L}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,L)$
, together with an extension
![]() $K^{\prime }$
containing both
$K^{\prime }$
containing both
![]() $K$
and
$K$
and
![]() $L$
such that the extensions of scalars of
$L$
such that the extensions of scalars of
![]() $\unicode[STIX]{x1D70C}_{K}$
and
$\unicode[STIX]{x1D70C}_{K}$
and
![]() $\unicode[STIX]{x1D70C}_{L}$
to
$\unicode[STIX]{x1D70C}_{L}$
to
![]() $K^{\prime }$
are isomorphic (i.e. conjugate). Let
$K^{\prime }$
are isomorphic (i.e. conjugate). Let
![]() $V_{L}$
denote the
$V_{L}$
denote the
![]() $L$
-local system corresponding to
$L$
-local system corresponding to
![]() $\unicode[STIX]{x1D70C}_{L}$
and let
$\unicode[STIX]{x1D70C}_{L}$
and let
![]() $V_{L/\mathbb{Q}}$
denote the same local system considered as a local system of
$V_{L/\mathbb{Q}}$
denote the same local system considered as a local system of
![]() $\mathbb{Q}$
-vector spaces by restriction of scalars. We may arrange things so that
$\mathbb{Q}$
-vector spaces by restriction of scalars. We may arrange things so that
![]() $V_{L/\mathbb{Q}}$
underlies a polarizable
$V_{L/\mathbb{Q}}$
underlies a polarizable
![]() $\mathbb{Q}$
-variation of Hodge structure of weight
$\mathbb{Q}$
-variation of Hodge structure of weight
![]() $k$
.
$k$
.
Proof. This is discussed in [Reference Corlette and SimpsonCS08, § 10] and [Reference SimpsonSim92, Theorem 5]. The basic idea goes back at least to Deligne’s ‘Travaux de Shimura’ [Reference DeligneDel71].
The discussion in the third and following paragraphs of the proof of Theorem 5 in [Reference SimpsonSim92] does not use the rigidity hypothesis of that theorem, but only the statement that for every embedding
![]() $\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the induced local system
$\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the induced local system
![]() $V_{\unicode[STIX]{x1D70E}}$
is a polarizable VHS. One should assume there that
$V_{\unicode[STIX]{x1D70E}}$
is a polarizable VHS. One should assume there that
![]() $K$
is a Galois extension of
$K$
is a Galois extension of
![]() $\mathbb{Q}$
(we can make that hypothesis), and the discussion gives the conclusion that the subfield
$\mathbb{Q}$
(we can make that hypothesis), and the discussion gives the conclusion that the subfield
![]() $L\subset K$
generated by the traces of monodromy elements, has a uniquely defined complex conjugation operation.
$L\subset K$
generated by the traces of monodromy elements, has a uniquely defined complex conjugation operation.
We recall the reason. The field of traces that was denoted by
![]() $L$
in [Reference SimpsonSim92] will be denoted by
$L$
in [Reference SimpsonSim92] will be denoted by
![]() $L^{\text{tr}}$
here, and the extension that we are looking for, denoted
$L^{\text{tr}}$
here, and the extension that we are looking for, denoted
![]() $L^{\prime }$
in [Reference SimpsonSim92], will be denoted by
$L^{\prime }$
in [Reference SimpsonSim92], will be denoted by
![]() $L$
here.
$L$
here.
Since
![]() $V_{\unicode[STIX]{x1D70E}}$
is polarizable, its complex conjugate is isomorphic to its dual. As we assume
$V_{\unicode[STIX]{x1D70E}}$
is polarizable, its complex conjugate is isomorphic to its dual. As we assume
![]() $V$
is absolutely irreducible, each
$V$
is absolutely irreducible, each
![]() $V_{\unicode[STIX]{x1D70E}}$
is irreducible so this isomorphism is unique up to a scalar.
$V_{\unicode[STIX]{x1D70E}}$
is irreducible so this isomorphism is unique up to a scalar.
Let
![]() $c:\mathbb{C}\rightarrow \mathbb{C}$
denote complex conjugation. It means that
$c:\mathbb{C}\rightarrow \mathbb{C}$
denote complex conjugation. It means that
![]() $V_{c\circ \unicode[STIX]{x1D70E}}\cong (V_{\unicode[STIX]{x1D70E}})^{\ast }$
. Suppose
$V_{c\circ \unicode[STIX]{x1D70E}}\cong (V_{\unicode[STIX]{x1D70E}})^{\ast }$
. Suppose
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(X,x)$
, and let
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(X,x)$
, and let
![]() $\unicode[STIX]{x1D70C}_{K}^{\ast }$
denote the dual representation. Recall that
$\unicode[STIX]{x1D70C}_{K}^{\ast }$
denote the dual representation. Recall that
![]() $\unicode[STIX]{x1D70C}_{K}^{\ast }(\unicode[STIX]{x1D6FE})=(\unicode[STIX]{x1D70C}_{K}(\unicode[STIX]{x1D6FE})^{-1})^{t}$
, so
$\unicode[STIX]{x1D70C}_{K}^{\ast }(\unicode[STIX]{x1D6FE})=(\unicode[STIX]{x1D70C}_{K}(\unicode[STIX]{x1D6FE})^{-1})^{t}$
, so
![]() $\text{Tr}(\unicode[STIX]{x1D70C}_{K}^{\ast }(\unicode[STIX]{x1D6FE}))=\text{Tr}(\unicode[STIX]{x1D70C}_{K}(\unicode[STIX]{x1D6FE}^{-1}))$
. From the isomorphism
$\text{Tr}(\unicode[STIX]{x1D70C}_{K}^{\ast }(\unicode[STIX]{x1D6FE}))=\text{Tr}(\unicode[STIX]{x1D70C}_{K}(\unicode[STIX]{x1D6FE}^{-1}))$
. From the isomorphism
![]() $V_{c\circ \unicode[STIX]{x1D70E}}\cong (V_{\unicode[STIX]{x1D70E}})^{\ast }$
we therefore get
$V_{c\circ \unicode[STIX]{x1D70E}}\cong (V_{\unicode[STIX]{x1D70E}})^{\ast }$
we therefore get
As we are assuming that
![]() $K$
is a Galois extension of
$K$
is a Galois extension of
![]() $\mathbb{Q}$
, the image of
$\mathbb{Q}$
, the image of
![]() $c\circ \unicode[STIX]{x1D70E}$
is equal to the image of
$c\circ \unicode[STIX]{x1D70E}$
is equal to the image of
![]() $\unicode[STIX]{x1D70E}$
and it makes sense to write
$\unicode[STIX]{x1D70E}$
and it makes sense to write
![]() $\unicode[STIX]{x1D70E}^{-1}\circ c\circ \unicode[STIX]{x1D70E}:K\rightarrow K$
(this notational shortcut was used without explanation in [Reference SimpsonSim92] and required the hypothesis that
$\unicode[STIX]{x1D70E}^{-1}\circ c\circ \unicode[STIX]{x1D70E}:K\rightarrow K$
(this notational shortcut was used without explanation in [Reference SimpsonSim92] and required the hypothesis that
![]() $K$
be Galois). We obtain
$K$
be Galois). We obtain
It follows that on the subfield
![]() $L^{\text{tr}}\subset K$
generated by the traces of monodromy elements, the map
$L^{\text{tr}}\subset K$
generated by the traces of monodromy elements, the map
is well-defined and independent of
![]() $\unicode[STIX]{x1D70E}$
. In other words,
$\unicode[STIX]{x1D70E}$
. In other words,
![]() $L^{\text{tr}}$
has a well-defined complex conjugation operation.
$L^{\text{tr}}$
has a well-defined complex conjugation operation.
Therefore,
![]() $L^{\text{tr}}$
is either a totally real field, if
$L^{\text{tr}}$
is either a totally real field, if
![]() $c_{L^{\text{tr}}}$
is the identity, or a totally imaginary quadratic extension of a totally real field
$c_{L^{\text{tr}}}$
is the identity, or a totally imaginary quadratic extension of a totally real field
![]() $F:=(L^{\text{tr}})^{c_{L^{\text{tr}}}}$
otherwise.
$F:=(L^{\text{tr}})^{c_{L^{\text{tr}}}}$
otherwise.
Larsen’s lemma [Reference SimpsonSim92, Lemma 4.8] says that we can extend
![]() $L^{\text{tr}}$
to
$L^{\text{tr}}$
to
![]() $L$
(as said before, that was denoted
$L$
(as said before, that was denoted
![]() $L^{\prime }$
there), a totally imaginary quadratic extension of a totally real field, such that
$L^{\prime }$
there), a totally imaginary quadratic extension of a totally real field, such that
![]() $V$
may be defined over
$V$
may be defined over
![]() $L$
. The proof uses a consideration of Brauer groups, and we refer to the discussion in [Reference SimpsonSim92, Lemma 4.8].
$L$
. The proof uses a consideration of Brauer groups, and we refer to the discussion in [Reference SimpsonSim92, Lemma 4.8].
We have
If
![]() $\unicode[STIX]{x1D70E}:L\rightarrow \mathbb{C}$
then it extends to
$\unicode[STIX]{x1D70E}:L\rightarrow \mathbb{C}$
then it extends to
![]() $\unicode[STIX]{x1D70E}_{K^{\prime }}:K^{\prime }\rightarrow \mathbb{C}$
which then restricts to an embedding
$\unicode[STIX]{x1D70E}_{K^{\prime }}:K^{\prime }\rightarrow \mathbb{C}$
which then restricts to an embedding
![]() $\unicode[STIX]{x1D70E}_{K}:K\rightarrow \mathbb{C}$
, and
$\unicode[STIX]{x1D70E}_{K}:K\rightarrow \mathbb{C}$
, and
![]() $V_{\unicode[STIX]{x1D70E}}\cong V_{\unicode[STIX]{x1D70E}_{K}}$
. Therefore, our hypothesis that the
$V_{\unicode[STIX]{x1D70E}}\cong V_{\unicode[STIX]{x1D70E}_{K}}$
. Therefore, our hypothesis that the
![]() $V_{\unicode[STIX]{x1D70E}_{K}}$
are VHS of weight
$V_{\unicode[STIX]{x1D70E}_{K}}$
are VHS of weight
![]() $k$
implies that the
$k$
implies that the
![]() $V_{\unicode[STIX]{x1D70E}}$
are VHS of weight
$V_{\unicode[STIX]{x1D70E}}$
are VHS of weight
![]() $k$
.
$k$
.
Our hypothesis says that for any
![]() $\unicode[STIX]{x1D70E}$
, the Hodge types of
$\unicode[STIX]{x1D70E}$
, the Hodge types of
![]() $V_{\unicode[STIX]{x1D70E}}$
can be chosen within
$V_{\unicode[STIX]{x1D70E}}$
can be chosen within
![]() $\{(p,q):\,p+q=k\text{ and }p,q\geqslant 0\}$
. There could be a choice to be made in assigning the Hodge types, for instance if
$\{(p,q):\,p+q=k\text{ and }p,q\geqslant 0\}$
. There could be a choice to be made in assigning the Hodge types, for instance if
![]() $V_{\unicode[STIX]{x1D70E}}$
is unitary then it has only a single Hodge type and that could be put at any
$V_{\unicode[STIX]{x1D70E}}$
is unitary then it has only a single Hodge type and that could be put at any
![]() $(p,q)$
in the desired set.
$(p,q)$
in the desired set.
As noted in the discussion of [Reference Corlette and SimpsonCS08, § 10.2] we may choose the Hodge types in such a way that there is a
![]() $\mathbb{Q}$
-polarization. We may do the analogue of [Reference Corlette and SimpsonCS08, Lemma 10.3] for the general case as follows. Let
$\mathbb{Q}$
-polarization. We may do the analogue of [Reference Corlette and SimpsonCS08, Lemma 10.3] for the general case as follows. Let
![]() $c_{L}:L\rightarrow L$
and
$c_{L}:L\rightarrow L$
and
![]() $c:\mathbb{C}\rightarrow \mathbb{C}$
denote the complex conjugation automorphisms. For
$c:\mathbb{C}\rightarrow \mathbb{C}$
denote the complex conjugation automorphisms. For
![]() $\unicode[STIX]{x1D70E}:L\rightarrow \mathbb{C}$
put
$\unicode[STIX]{x1D70E}:L\rightarrow \mathbb{C}$
put
![]() $\overline{\unicode[STIX]{x1D70E}}:=c\circ \unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}\circ c_{L}$
. Choose a collection of embeddings
$\overline{\unicode[STIX]{x1D70E}}:=c\circ \unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}\circ c_{L}$
. Choose a collection of embeddings
![]() $\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{d}:L\rightarrow \mathbb{C}$
such that the
$\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{d}:L\rightarrow \mathbb{C}$
such that the
![]() $\overline{\unicode[STIX]{x1D70E}_{i}}$
are distinct from the
$\overline{\unicode[STIX]{x1D70E}_{i}}$
are distinct from the
![]() $\unicode[STIX]{x1D70E}_{j}$
and the collection
$\unicode[STIX]{x1D70E}_{j}$
and the collection
is equal to the full collection of embeddings. For each
![]() $i$
choose a structure of VHS for
$i$
choose a structure of VHS for
![]() $V_{\unicode[STIX]{x1D70E}_{i}}$
, and then put
$V_{\unicode[STIX]{x1D70E}_{i}}$
, and then put
This determines the structures of VHS for
![]() $V_{\overline{\unicode[STIX]{x1D70E}}_{i}}$
in such a way that the property of [Reference Corlette and SimpsonCS08, Lemma 10.3] holds.
$V_{\overline{\unicode[STIX]{x1D70E}}_{i}}$
in such a way that the property of [Reference Corlette and SimpsonCS08, Lemma 10.3] holds.
As in [Reference Corlette and SimpsonCS08, Proposition 10.2], there is a form
which is
![]() $\mathbb{Q}$
-bilinear, and
$\mathbb{Q}$
-bilinear, and
![]() $L$
-linear in the first variable and
$L$
-linear in the first variable and
![]() $L$
-
$L$
-
![]() $c_{L}$
-antilinear in the second variable that is to say
$c_{L}$
-antilinear in the second variable that is to say
![]() $\unicode[STIX]{x1D6F7}(u,\unicode[STIX]{x1D706}v)=c_{L}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D6F7}(u,v)$
. Also we may assume that it is
$\unicode[STIX]{x1D6F7}(u,\unicode[STIX]{x1D706}v)=c_{L}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D6F7}(u,v)$
. Also we may assume that it is
![]() $c_{L}$
-
$c_{L}$
-
![]() $(-1)^{k}$
-symmetric:
$(-1)^{k}$
-symmetric:
![]() $\unicode[STIX]{x1D6F7}(v,u)=(-1)^{k}c_{L}\unicode[STIX]{x1D6F7}(u,v)$
by multiplying by a purely imaginary element if necessary to get this sign right. The form
$\unicode[STIX]{x1D6F7}(v,u)=(-1)^{k}c_{L}\unicode[STIX]{x1D6F7}(u,v)$
by multiplying by a purely imaginary element if necessary to get this sign right. The form
![]() $\unicode[STIX]{x1D6F7}$
is unique up to multiplying by an element of
$\unicode[STIX]{x1D6F7}$
is unique up to multiplying by an element of
![]() $F^{\ast }$
.
$F^{\ast }$
.
Put
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{Q}}:=\text{Tr}_{L/\mathbb{Q}}\circ \unicode[STIX]{x1D6F7}$
, giving a
$\unicode[STIX]{x1D6F7}_{\mathbb{Q}}:=\text{Tr}_{L/\mathbb{Q}}\circ \unicode[STIX]{x1D6F7}$
, giving a
![]() $\mathbb{Q}$
-bilinear form
$\mathbb{Q}$
-bilinear form
that is
![]() $(-1)^{k}$
-symmetric. This will be our polarization form, after having first adjusted
$(-1)^{k}$
-symmetric. This will be our polarization form, after having first adjusted
![]() $\unicode[STIX]{x1D6F7}$
by multiplying by an appropriate element of
$\unicode[STIX]{x1D6F7}$
by multiplying by an appropriate element of
![]() $F^{\ast }$
to be chosen below. Let
$F^{\ast }$
to be chosen below. Let
be the induced
![]() $\mathbb{C}$
-bilinear form. We would like to say that
$\mathbb{C}$
-bilinear form. We would like to say that
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{C}}$
pairs
$\unicode[STIX]{x1D6F7}_{\mathbb{C}}$
pairs
![]() $V_{\unicode[STIX]{x1D70E}}$
with
$V_{\unicode[STIX]{x1D70E}}$
with
![]() $V_{\overline{\unicode[STIX]{x1D70E}}}$
.
$V_{\overline{\unicode[STIX]{x1D70E}}}$
.
To see this, let
![]() $v\mapsto z.v$
be the action of
$v\mapsto z.v$
be the action of
![]() $z\in L$
upon
$z\in L$
upon
![]() $v\in V_{L/\mathbb{Q}}$
. This extends to an action of
$v\in V_{L/\mathbb{Q}}$
. This extends to an action of
![]() $L$
on
$L$
on
![]() $V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
by
$V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
by
![]() $\mathbb{C}$
-linear automorphisms. Then
$\mathbb{C}$
-linear automorphisms. Then
![]() $V_{\unicode[STIX]{x1D70E}}\subset V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
is the subset of vectors such that
$V_{\unicode[STIX]{x1D70E}}\subset V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
is the subset of vectors such that
for
![]() $z\in L$
. We have
$z\in L$
. We have
Thus, if
![]() $u\in V_{\unicode[STIX]{x1D70E}}$
and
$u\in V_{\unicode[STIX]{x1D70E}}$
and
![]() $v\in V_{\unicode[STIX]{x1D70F}}$
then
$v\in V_{\unicode[STIX]{x1D70F}}$
then
Therefore, if
![]() $\unicode[STIX]{x1D70E}(z)\neq \overline{\unicode[STIX]{x1D70F}}(z)$
then this expression must be zero. For
$\unicode[STIX]{x1D70E}(z)\neq \overline{\unicode[STIX]{x1D70F}}(z)$
then this expression must be zero. For
![]() $\unicode[STIX]{x1D70E}\neq \overline{\unicode[STIX]{x1D70F}}$
there is a
$\unicode[STIX]{x1D70E}\neq \overline{\unicode[STIX]{x1D70F}}$
there is a
![]() $z\in L$
with
$z\in L$
with
![]() $\unicode[STIX]{x1D70E}(z)\neq \overline{\unicode[STIX]{x1D70F}}(z)$
and we obtain
$\unicode[STIX]{x1D70E}(z)\neq \overline{\unicode[STIX]{x1D70F}}(z)$
and we obtain
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{C}}(u,v)=0$
. We conclude that
$\unicode[STIX]{x1D6F7}_{\mathbb{C}}(u,v)=0$
. We conclude that
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{C}}$
pairs
$\unicode[STIX]{x1D6F7}_{\mathbb{C}}$
pairs
![]() $V_{\unicode[STIX]{x1D70E}}$
with
$V_{\unicode[STIX]{x1D70E}}$
with
![]() $V_{\overline{\unicode[STIX]{x1D70E}}}$
.
$V_{\overline{\unicode[STIX]{x1D70E}}}$
.
The complex conjugation on
![]() $V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
also sends
$V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
also sends
![]() $V_{\unicode[STIX]{x1D70E}}$
to
$V_{\unicode[STIX]{x1D70E}}$
to
![]() $V_{\overline{\unicode[STIX]{x1D70E}}}$
, indeed if
$V_{\overline{\unicode[STIX]{x1D70E}}}$
, indeed if
![]() $z.v=\unicode[STIX]{x1D70E}(z)v$
then
$z.v=\unicode[STIX]{x1D70E}(z)v$
then
![]() $z.\overline{v}=\overline{z.v}=\overline{\unicode[STIX]{x1D70E}(z)v}=\overline{\unicode[STIX]{x1D70E}}(z)v$
.
$z.\overline{v}=\overline{z.v}=\overline{\unicode[STIX]{x1D70E}(z)v}=\overline{\unicode[STIX]{x1D70E}}(z)v$
.
The Hodge types on
![]() $V_{\mathbb{C}}:=V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
are defined by
$V_{\mathbb{C}}:=V_{L/\mathbb{Q}}~\otimes _{\mathbb{Q}}~\mathbb{C}$
are defined by
With our choice of Hodge types satisfying the property of [Reference Corlette and SimpsonCS08, Lemma 10.3], the complex conjugation operation satisfies
![]() $\overline{V_{\mathbb{C}}^{p,q}}=V_{\mathbb{C}}^{q,p}$
.
$\overline{V_{\mathbb{C}}^{p,q}}=V_{\mathbb{C}}^{q,p}$
.
We get the hermitian form
![]() $(u,v)\mapsto \unicode[STIX]{x1D6F7}_{\mathbb{C}}(u,\overline{v})$
on
$(u,v)\mapsto \unicode[STIX]{x1D6F7}_{\mathbb{C}}(u,\overline{v})$
on
![]() $V_{\unicode[STIX]{x1D70E}}$
induced by
$V_{\unicode[STIX]{x1D70E}}$
induced by
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{Q}}$
. As the hermitian forms on the irreducible local system
$\unicode[STIX]{x1D6F7}_{\mathbb{Q}}$
. As the hermitian forms on the irreducible local system
![]() $V_{\unicode[STIX]{x1D70E}}$
are unique up to multiplication by a real scalar, we deduce that this hermitian form is either a polarization, or minus a polarization of the complex VHS
$V_{\unicode[STIX]{x1D70E}}$
are unique up to multiplication by a real scalar, we deduce that this hermitian form is either a polarization, or minus a polarization of the complex VHS
![]() $V_{\unicode[STIX]{x1D70E}}$
. By uniqueness, the hermitian form has a pure Hodge type, and this type has to be
$V_{\unicode[STIX]{x1D70E}}$
. By uniqueness, the hermitian form has a pure Hodge type, and this type has to be
![]() $(k,k)$
otherwise the Hodge types of
$(k,k)$
otherwise the Hodge types of
![]() $V_{\unicode[STIX]{x1D70E}}$
and
$V_{\unicode[STIX]{x1D70E}}$
and
![]() $V_{\overline{\unicode[STIX]{x1D70E}}}$
could not be symmetric under
$V_{\overline{\unicode[STIX]{x1D70E}}}$
could not be symmetric under
![]() $(p,q)\mapsto (q,p)$
.
$(p,q)\mapsto (q,p)$
.
In order for
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{Q}}$
to define a polarization to get a
$\unicode[STIX]{x1D6F7}_{\mathbb{Q}}$
to define a polarization to get a
![]() $\mathbb{Q}$
-variation of Hodge structure on
$\mathbb{Q}$
-variation of Hodge structure on
![]() $V_{L/\mathbb{Q}}$
, we need these forms on
$V_{L/\mathbb{Q}}$
, we need these forms on
![]() $V_{\unicode[STIX]{x1D70E}}$
to define polarizations rather than minus polarizations. This problem of fixing the sign, by multiplying our original form
$V_{\unicode[STIX]{x1D70E}}$
to define polarizations rather than minus polarizations. This problem of fixing the sign, by multiplying our original form
![]() $\unicode[STIX]{x1D6F7}$
by an element of the totally real field
$\unicode[STIX]{x1D6F7}$
by an element of the totally real field
![]() $F^{\ast }$
, was discussed in [Reference Corlette and SimpsonCS08, Lemma 10.4] and we refer there for the proof, which just uses the fact that
$F^{\ast }$
, was discussed in [Reference Corlette and SimpsonCS08, Lemma 10.4] and we refer there for the proof, which just uses the fact that
![]() $F$
is dense in
$F$
is dense in
![]() $F~\otimes _{\mathbb{Q}}~\mathbb{R}$
.
$F~\otimes _{\mathbb{Q}}~\mathbb{R}$
.
Once this adjustment has been made, we obtain a polarization form
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{Q}}$
, such that with our choice of Hodge decompositions we obtain a
$\unicode[STIX]{x1D6F7}_{\mathbb{Q}}$
, such that with our choice of Hodge decompositions we obtain a
![]() $\mathbb{Q}$
-variation of Hodge structure
$\mathbb{Q}$
-variation of Hodge structure
![]() $V_{L/\mathbb{Q}}$
of weight
$V_{L/\mathbb{Q}}$
of weight
![]() $k$
.◻
$k$
.◻
Remark.
In the situation of the proposition, notice that the original irreducible local systems
![]() $V_{\unicode[STIX]{x1D70E}_{K}}$
for
$V_{\unicode[STIX]{x1D70E}_{K}}$
for
![]() $\unicode[STIX]{x1D70E}_{K}:K\rightarrow \mathbb{C}$
, are among the complex direct factors
$\unicode[STIX]{x1D70E}_{K}:K\rightarrow \mathbb{C}$
, are among the complex direct factors
![]() $V_{\unicode[STIX]{x1D70E}}$
of the
$V_{\unicode[STIX]{x1D70E}}$
of the
![]() $\mathbb{Q}$
-variation that was constructed. That was pointed out during the proof.
$\mathbb{Q}$
-variation that was constructed. That was pointed out during the proof.
Lemma 7.2. Suppose in the situation of the previous proposition, that we know furthermore the traces
![]() $\text{Tr}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}))$
are algebraic integers for
$\text{Tr}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}))$
are algebraic integers for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(X,x)$
. Then the
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(X,x)$
. Then the
![]() $\mathbb{Q}$
-VHS constructed there is a
$\mathbb{Q}$
-VHS constructed there is a
![]() $\mathbb{Z}$
-VHS.
$\mathbb{Z}$
-VHS.
Proof. By Bass–Serre theory [Reference BassBas80], there is a projective
![]() ${\mathcal{O}}_{L}$
-module
${\mathcal{O}}_{L}$
-module
![]() $P$
such that
$P$
such that
![]() $V_{L}=P~\otimes _{{\mathcal{O}}_{L}}~L$
(speaking here about the fiber over the basepoint which is a representation of
$V_{L}=P~\otimes _{{\mathcal{O}}_{L}}~L$
(speaking here about the fiber over the basepoint which is a representation of
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
). Then
$\unicode[STIX]{x1D70B}_{1}(X,x)$
). Then
![]() $P$
gives a local system of free
$P$
gives a local system of free
![]() $\mathbb{Z}$
-modules forming a lattice inside the
$\mathbb{Z}$
-modules forming a lattice inside the
![]() $\mathbb{Q}$
-local system
$\mathbb{Q}$
-local system
![]() $V_{L/\mathbb{Q}}$
.◻
$V_{L/\mathbb{Q}}$
.◻
Corollary 7.3. Let
![]() $X$
be a smooth complex projective variety. Suppose
$X$
be a smooth complex projective variety. Suppose
![]() $V$
is a rank
$V$
is a rank
![]() $3$
local system over an algebraic number field
$3$
local system over an algebraic number field
![]() $K$
such that:
$K$
such that:
(i) the monodromy group is Zariski-dense in
 $\operatorname{SL}(3,\overline{K})$
;
$\operatorname{SL}(3,\overline{K})$
;(ii)
 $V$
is integral, in the sense that
$V$
is integral, in the sense that
 $\text{Tr}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}))\in {\mathcal{O}}_{K}$
for any group element
$\text{Tr}(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}))\in {\mathcal{O}}_{K}$
for any group element
 $\unicode[STIX]{x1D6FE}$
(here
$\unicode[STIX]{x1D6FE}$
(here
 $\unicode[STIX]{x1D70C}$
being the monodromy representation); and
$\unicode[STIX]{x1D70C}$
being the monodromy representation); and(iii) for any
 $\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the induced
$\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the induced
 $\mathbb{C}$
-local system
$\mathbb{C}$
-local system
 $V_{\unicode[STIX]{x1D70E}}$
is a VHS.
$V_{\unicode[STIX]{x1D70E}}$
is a VHS.
Then either
![]() $V$
projectively factors through an orbicurve, or else the
$V$
projectively factors through an orbicurve, or else the
![]() $V_{\unicode[STIX]{x1D70E}}$
are direct factors of the monodromy of a family of abelian varieties.
$V_{\unicode[STIX]{x1D70E}}$
are direct factors of the monodromy of a family of abelian varieties.
Proof. Assume that
![]() $V$
does not projectively factor through an orbicurve. The same holds for each
$V$
does not projectively factor through an orbicurve. The same holds for each
![]() $V_{\unicode[STIX]{x1D70E}}$
. Then by Theorem 5.1, we can conclude that the VHS
$V_{\unicode[STIX]{x1D70E}}$
. Then by Theorem 5.1, we can conclude that the VHS
![]() $V_{\unicode[STIX]{x1D70E}}$
are not of type
$V_{\unicode[STIX]{x1D70E}}$
are not of type
![]() $(1,1,1)$
, because the first case of the theorem is ruled out by our hypothesis that the monodromy group is Zariski-dense.
$(1,1,1)$
, because the first case of the theorem is ruled out by our hypothesis that the monodromy group is Zariski-dense.
Therefore, the VHS
![]() $V_{\unicode[STIX]{x1D70E}}$
may be chosen to have a set of Hodge types contained in
$V_{\unicode[STIX]{x1D70E}}$
may be chosen to have a set of Hodge types contained in
![]() $\{(1,0),(0,1)\}$
. Indeed, if
$\{(1,0),(0,1)\}$
. Indeed, if
![]() $V_{\unicode[STIX]{x1D70E}}$
is unitary we can just choose one of them; if not, it must have Hodge numbers
$V_{\unicode[STIX]{x1D70E}}$
is unitary we can just choose one of them; if not, it must have Hodge numbers
![]() $(1,2)$
or
$(1,2)$
or
![]() $(2,1)$
since
$(2,1)$
since
![]() $(1,1,1)$
is ruled out. In either case we can arrange the Hodge types within
$(1,1,1)$
is ruled out. In either case we can arrange the Hodge types within
![]() $\{(1,0),(0,1)\}$
. In other words, each
$\{(1,0),(0,1)\}$
. In other words, each
![]() $V_{\unicode[STIX]{x1D70E}}$
has a structure of VHS of weight
$V_{\unicode[STIX]{x1D70E}}$
has a structure of VHS of weight
![]() $1$
.
$1$
.
We may now apply Proposition 7.1 to conclude that the
![]() $V_{\unicode[STIX]{x1D70E}}$
is a direct factor in the monodromy of a
$V_{\unicode[STIX]{x1D70E}}$
is a direct factor in the monodromy of a
![]() $\mathbb{Q}$
-VHS of weight
$\mathbb{Q}$
-VHS of weight
![]() $1$
denoted
$1$
denoted
![]() $V_{L/\mathbb{Q}}$
. By Lemma 7.2 using our hypothesis (i), it is a polarized
$V_{L/\mathbb{Q}}$
. By Lemma 7.2 using our hypothesis (i), it is a polarized
![]() $\mathbb{Z}$
-VHS of weight
$\mathbb{Z}$
-VHS of weight
![]() $1$
. This corresponds to a family of abelian varieties [Reference DeligneDel71].◻
$1$
. This corresponds to a family of abelian varieties [Reference DeligneDel71].◻
Remark 7.4. Let
![]() $V$
be a rank
$V$
be a rank
![]() $1$
local system defined over an algebraic number field
$1$
local system defined over an algebraic number field
![]() $K$
, integral and such that for each embedding
$K$
, integral and such that for each embedding
![]() $\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the associated local system
$\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the associated local system
![]() $V_{\unicode[STIX]{x1D70E}}$
is a polarizable VHS. Then
$V_{\unicode[STIX]{x1D70E}}$
is a polarizable VHS. Then
![]() $V_{\unicode[STIX]{x1D70E}}$
is unitary so Kronecker’s theorem implies that the monodromies of
$V_{\unicode[STIX]{x1D70E}}$
is unitary so Kronecker’s theorem implies that the monodromies of
![]() $V$
are roots of unity. In other words,
$V$
are roots of unity. In other words,
![]() $V$
is of finite order (cf. proof of Proposition 2.10).
$V$
is of finite order (cf. proof of Proposition 2.10).
Lemma 7.5. If for some
![]() $n\geqslant 1$
there exists a rigid representation
$n\geqslant 1$
there exists a rigid representation
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
then the moduli space of rank
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
then the moduli space of rank
![]() $1$
local systems is a torsion abelian group. In particular, a rigid local system of rank
$1$
local systems is a torsion abelian group. In particular, a rigid local system of rank
![]() $1$
is of finite order.
$1$
is of finite order.
Proof. If the moduli space of rank
![]() $1$
local systems has positive dimension then its connected component of identity is divisible by
$1$
local systems has positive dimension then its connected component of identity is divisible by
![]() $n$
and there exists a non-isotrivial family of rank
$n$
and there exists a non-isotrivial family of rank
![]() $1$
local systems
$1$
local systems
![]() $W$
containing the trivial system and such that
$W$
containing the trivial system and such that
![]() $W^{\otimes n}$
is also a non-isotrivial family. If
$W^{\otimes n}$
is also a non-isotrivial family. If
![]() $V_{\unicode[STIX]{x1D70C}}~\otimes ~W_{1}\simeq V_{\unicode[STIX]{x1D70C}}~\otimes ~W_{2}$
for some rank
$V_{\unicode[STIX]{x1D70C}}~\otimes ~W_{1}\simeq V_{\unicode[STIX]{x1D70C}}~\otimes ~W_{2}$
for some rank
![]() $1$
local systems
$1$
local systems
![]() $W_{1}$
and
$W_{1}$
and
![]() $W_{2}$
then the determinants coincide and
$W_{2}$
then the determinants coincide and
![]() $W_{1}^{\otimes n}\simeq W_{2}^{\otimes n}$
. Therefore the family
$W_{1}^{\otimes n}\simeq W_{2}^{\otimes n}$
. Therefore the family
![]() $V_{\unicode[STIX]{x1D70C}}~\otimes ~W$
of rank
$V_{\unicode[STIX]{x1D70C}}~\otimes ~W$
of rank
![]() $n$
local systems is non-isotrivial. Since it contains
$n$
local systems is non-isotrivial. Since it contains
![]() $V_{\unicode[STIX]{x1D70C}}$
, we get a contradiction with rigidity of
$V_{\unicode[STIX]{x1D70C}}$
, we get a contradiction with rigidity of
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
It follows that
![]() $H^{1}(X,\mathbb{Q})=0$
and the moduli space of rank
$H^{1}(X,\mathbb{Q})=0$
and the moduli space of rank
![]() $1$
local systems is a torsion abelian group, so for any rigid
$1$
local systems is a torsion abelian group, so for any rigid
![]() $\unicode[STIX]{x1D70C}$
the system
$\unicode[STIX]{x1D70C}$
the system
![]() $\det V_{\unicode[STIX]{x1D70C}}$
is of finite order.◻
$\det V_{\unicode[STIX]{x1D70C}}$
is of finite order.◻
Definition 7.6. Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
be a representation. The geometric monodromy group
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
be a representation. The geometric monodromy group
![]() $M_{\text{geom}}(\unicode[STIX]{x1D70C})$
of
$M_{\text{geom}}(\unicode[STIX]{x1D70C})$
of
![]() $\unicode[STIX]{x1D70C}$
is the Zariski closure of the image of
$\unicode[STIX]{x1D70C}$
is the Zariski closure of the image of
![]() $\unicode[STIX]{x1D70C}$
in
$\unicode[STIX]{x1D70C}$
in
![]() $\operatorname{GL}(n,\mathbb{C})$
. We say that
$\operatorname{GL}(n,\mathbb{C})$
. We say that
![]() $\unicode[STIX]{x1D70C}$
is properly rigid if
$\unicode[STIX]{x1D70C}$
is properly rigid if
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow M_{\text{geom}}(\unicode[STIX]{x1D70C})$
is rigid.
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow M_{\text{geom}}(\unicode[STIX]{x1D70C})$
is rigid.
Note that any rigid representation is properly rigid. On the other hand, a properly rigid representation might be non-rigid. For example, it could happen that
![]() $H^{1}(X,\mathbb{Q})\neq 0$
. Therefore, it is more general to consider properly rigid representations.
$H^{1}(X,\mathbb{Q})\neq 0$
. Therefore, it is more general to consider properly rigid representations.
Given a rigid representation into
![]() $\operatorname{GL}(n,\mathbb{C})$
, by the previous lemma the identity component
$\operatorname{GL}(n,\mathbb{C})$
, by the previous lemma the identity component
![]() $M_{\text{geom}}(\unicode[STIX]{x1D70C})^{0}$
of its geometric monodromy group is contained in
$M_{\text{geom}}(\unicode[STIX]{x1D70C})^{0}$
of its geometric monodromy group is contained in
![]() $\operatorname{SL}(n,\mathbb{C})$
. In the following we are interested in properly rigid representations with the largest possible geometric monodromy group. More precisely, we are interested in representations
$\operatorname{SL}(n,\mathbb{C})$
. In the following we are interested in properly rigid representations with the largest possible geometric monodromy group. More precisely, we are interested in representations
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
which satisfy one of the following equivalent conditions:
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(n,\mathbb{C})$
which satisfy one of the following equivalent conditions:
(i)
 $M_{\text{geom}}(\unicode[STIX]{x1D70C})$
contains
$M_{\text{geom}}(\unicode[STIX]{x1D70C})$
contains
 $\operatorname{SL}(n,\mathbb{C})$
as a subgroup of finite index;
$\operatorname{SL}(n,\mathbb{C})$
as a subgroup of finite index;(ii)
 $M_{\text{geom}}(\unicode[STIX]{x1D70C})^{0}=\operatorname{SL}(n,\mathbb{C})$
;
$M_{\text{geom}}(\unicode[STIX]{x1D70C})^{0}=\operatorname{SL}(n,\mathbb{C})$
;(iii)
 $\text{Lie}\,M_{\text{geom}}(\unicode[STIX]{x1D70C})=\mathfrak{sl}(n,\mathbb{C})$
.
$\text{Lie}\,M_{\text{geom}}(\unicode[STIX]{x1D70C})=\mathfrak{sl}(n,\mathbb{C})$
.
If any of these conditions is satisfied then the composition
maps onto the group of
![]() $m$
th roots of unity
$m$
th roots of unity
![]() $\unicode[STIX]{x1D707}_{m}$
, where
$\unicode[STIX]{x1D707}_{m}$
, where
![]() $m$
is the index of
$m$
is the index of
![]() $M_{\text{geom}}(\unicode[STIX]{x1D70C})^{0}$
in
$M_{\text{geom}}(\unicode[STIX]{x1D70C})^{0}$
in
![]() $M_{\text{geom}}(\unicode[STIX]{x1D70C})$
. Then the surjection
$M_{\text{geom}}(\unicode[STIX]{x1D70C})$
. Then the surjection
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \unicode[STIX]{x1D707}_{m}$
gives rise to a degree
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \unicode[STIX]{x1D707}_{m}$
gives rise to a degree
![]() $m$
étale Galois covering
$m$
étale Galois covering
![]() $f:Z\rightarrow X$
such that
$f:Z\rightarrow X$
such that
![]() $M_{\text{geom}}(f^{\ast }(\unicode[STIX]{x1D70C}))=\operatorname{SL}(n,\mathbb{C})$
.
$M_{\text{geom}}(f^{\ast }(\unicode[STIX]{x1D70C}))=\operatorname{SL}(n,\mathbb{C})$
.
Corollary 7.7. Let
![]() $V$
be an irreducible complex local system of rank
$V$
be an irreducible complex local system of rank
![]() $3$
. Assume that the corresponding representation is integral, properly rigid and that the geometric monodromy group of
$3$
. Assume that the corresponding representation is integral, properly rigid and that the geometric monodromy group of
![]() $V$
contains
$V$
contains
![]() $\operatorname{SL}(3,\mathbb{C})$
as a subgroup of finite index. Then either
$\operatorname{SL}(3,\mathbb{C})$
as a subgroup of finite index. Then either
![]() $V$
projectively factors through an orbicurve, or
$V$
projectively factors through an orbicurve, or
![]() $V$
comes as a direct factor in the monodromy of a family of abelian varieties.
$V$
comes as a direct factor in the monodromy of a family of abelian varieties.
Proof. Rigidity implies that
![]() $V$
is defined over an algebraic number field
$V$
is defined over an algebraic number field
![]() $K$
and it implies that for any
$K$
and it implies that for any
![]() $\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the induced local system
$\unicode[STIX]{x1D70E}:K\rightarrow \mathbb{C}$
the induced local system
![]() $V_{\unicode[STIX]{x1D70E}}$
is a VHS (see [Reference SimpsonSim92, Lemma 4.5]). By the above, we can find a finite étale covering
$V_{\unicode[STIX]{x1D70E}}$
is a VHS (see [Reference SimpsonSim92, Lemma 4.5]). By the above, we can find a finite étale covering
![]() $f:Z\rightarrow X$
such that
$f:Z\rightarrow X$
such that
![]() $M_{\text{geom}}(f^{\ast }(\unicode[STIX]{x1D70C}))=\operatorname{SL}(n,\mathbb{C})$
. Therefore
$M_{\text{geom}}(f^{\ast }(\unicode[STIX]{x1D70C}))=\operatorname{SL}(n,\mathbb{C})$
. Therefore
![]() $f^{\ast }(\unicode[STIX]{x1D70C})$
satisfies Hypothesis (i) of Corollary 7.3. Clearly,
$f^{\ast }(\unicode[STIX]{x1D70C})$
satisfies Hypothesis (i) of Corollary 7.3. Clearly,
![]() $f^{\ast }V_{\unicode[STIX]{x1D70E}}$
is also a VHS for any
$f^{\ast }V_{\unicode[STIX]{x1D70E}}$
is also a VHS for any
![]() $\unicode[STIX]{x1D70E}$
so
$\unicode[STIX]{x1D70E}$
so
![]() $f^{\ast }(\unicode[STIX]{x1D70C})$
also satisfies Hypothesis (iii). Hypothesis (ii) is provided by our assumption that
$f^{\ast }(\unicode[STIX]{x1D70C})$
also satisfies Hypothesis (iii). Hypothesis (ii) is provided by our assumption that
![]() $V$
is integral. Hence, Corollary 7.3 implies that
$V$
is integral. Hence, Corollary 7.3 implies that
![]() $f^{\ast }V$
projectively factors through an orbicurve, or else the
$f^{\ast }V$
projectively factors through an orbicurve, or else the
![]() $f^{\ast }V_{\unicode[STIX]{x1D70E}}$
are direct factors of the monodromy of a family of abelian varieties.
$f^{\ast }V_{\unicode[STIX]{x1D70E}}$
are direct factors of the monodromy of a family of abelian varieties.
We may descend these conclusions back to
![]() $X$
. Lemma A.6 says that if
$X$
. Lemma A.6 says that if
![]() $f^{\ast }V$
projectively factors through an orbicurve, then
$f^{\ast }V$
projectively factors through an orbicurve, then
![]() $V$
does so. If on the other hand
$V$
does so. If on the other hand
![]() $f^{\ast }V$
comes from a family of abelian varieties, then taking the product of the Galois conjugates of the family gives a family which descends back to
$f^{\ast }V$
comes from a family of abelian varieties, then taking the product of the Galois conjugates of the family gives a family which descends back to
![]() $X$
, and
$X$
, and
![]() $V$
is a direct factor in the monodromy of this family.◻
$V$
is a direct factor in the monodromy of this family.◻
Corollary 7.8. If
![]() $V$
is any local system of rank
$V$
is any local system of rank
![]() $3$
for which the geometric monodromy group contains
$3$
for which the geometric monodromy group contains
![]() $\operatorname{SL}(3,\mathbb{C})$
as a subgroup of finite index, then either it projectively factors through an orbicurve, or it comes from a family of abelian varieties, or else there is a non-constant equivariant map from the universal cover of
$\operatorname{SL}(3,\mathbb{C})$
as a subgroup of finite index, then either it projectively factors through an orbicurve, or it comes from a family of abelian varieties, or else there is a non-constant equivariant map from the universal cover of
![]() $X$
to a two-dimensional building.
$X$
to a two-dimensional building.
Proof. If the representation is non-rigid, or non-integral, then there is a non-constant equivariant map from the universal cover of
![]() $X$
to a two-dimensional building (see [Reference Gromov and SchoenGS92] and [Reference Corlette and SimpsonCS08, § 4]). Otherwise, the previous corollary applies.◻
$X$
to a two-dimensional building (see [Reference Gromov and SchoenGS92] and [Reference Corlette and SimpsonCS08, § 4]). Otherwise, the previous corollary applies.◻
Let us recall that by Lemma 7.5 a rigid local system
![]() $V$
has
$V$
has
![]() $\det (V)$
of finite order.
$\det (V)$
of finite order.
Corollary 7.9. Suppose
![]() $V$
is an irreducible rank
$V$
is an irreducible rank
![]() $3$
local system. If
$3$
local system. If
![]() $V$
is integral and properly rigid with
$V$
is integral and properly rigid with
![]() $\det (V)$
of finite order, then it is of geometric origin.
$\det (V)$
of finite order, then it is of geometric origin.
Proof. Let us first assume that the geometric monodromy group contains
![]() $\operatorname{SL}(3,\mathbb{C})$
as a subgroup of finite index. If
$\operatorname{SL}(3,\mathbb{C})$
as a subgroup of finite index. If
![]() $V$
projectively factors through an orbicurve, then the factoring representation is rigid. As was shown in [Reference Corlette and SimpsonCS08] using Katz’s theorem, it follows that the factoring representation is of geometric origin. Let us recall briefly the argument here. If an orbicurve admits a rigid representation, then its coarse moduli space is the projective line and there is an open subset of the orbicurve that is isomorphic to
$V$
projectively factors through an orbicurve, then the factoring representation is rigid. As was shown in [Reference Corlette and SimpsonCS08] using Katz’s theorem, it follows that the factoring representation is of geometric origin. Let us recall briefly the argument here. If an orbicurve admits a rigid representation, then its coarse moduli space is the projective line and there is an open subset of the orbicurve that is isomorphic to
![]() $\mathbb{P}^{1}-\{t_{1},\ldots ,t_{k}\}$
. By modifying the monodromy at one point, we may assume that we have an
$\mathbb{P}^{1}-\{t_{1},\ldots ,t_{k}\}$
. By modifying the monodromy at one point, we may assume that we have an
![]() $\operatorname{SL}(3,\mathbb{C})$
-local system on the orbicurve, pulling back to a local system projectively equivalent to our original one. It is still rigid as a local system on the orbicurve, which implies also that it is rigid as a local system on
$\operatorname{SL}(3,\mathbb{C})$
-local system on the orbicurve, pulling back to a local system projectively equivalent to our original one. It is still rigid as a local system on the orbicurve, which implies also that it is rigid as a local system on
![]() $\mathbb{P}^{1}-\{t_{1},\ldots ,t_{k}\}$
with fixed (semi-simple, finite-order) monodromy transformations at the points
$\mathbb{P}^{1}-\{t_{1},\ldots ,t_{k}\}$
with fixed (semi-simple, finite-order) monodromy transformations at the points
![]() $t_{i}$
. Therefore, Katz’s theorem [Reference KatzKaz01] says that the new local system has geometric origin. We may now complete the proof of this case: the last part of Proposition 2.10 shows that our original representation was of geometric origin.
$t_{i}$
. Therefore, Katz’s theorem [Reference KatzKaz01] says that the new local system has geometric origin. We may now complete the proof of this case: the last part of Proposition 2.10 shows that our original representation was of geometric origin.
If
![]() $V$
does not projectively factor through an orbicurve then Corollary 7.7 implies that
$V$
does not projectively factor through an orbicurve then Corollary 7.7 implies that
![]() $V$
is a direct factor in the monodromy of a family of abelian varieties, so it is of geometric origin.
$V$
is a direct factor in the monodromy of a family of abelian varieties, so it is of geometric origin.
If the geometric monodromy group is not a group containing
![]() $\operatorname{SL}(3,\mathbb{C})$
then it is either finite, isogenous to
$\operatorname{SL}(3,\mathbb{C})$
then it is either finite, isogenous to
![]() $\operatorname{SL}(2,\mathbb{C})$
, or isogenous to a positive-dimensional torus. Note however that in the case of a monodromy group isogenous to a positive-dimensional torus, the representation is not rigid, indeed a rigid representation to a finite extension of a torus must have finite image. A representation with finite monodromy group has geometric origin, see Proposition 2.10. For monodromy groups isogenous to
$\operatorname{SL}(2,\mathbb{C})$
, or isogenous to a positive-dimensional torus. Note however that in the case of a monodromy group isogenous to a positive-dimensional torus, the representation is not rigid, indeed a rigid representation to a finite extension of a torus must have finite image. A representation with finite monodromy group has geometric origin, see Proposition 2.10. For monodromy groups isogenous to
![]() $\operatorname{SL}(2,\mathbb{C})$
the result of [Reference Corlette and SimpsonCS08] shows that rigid integral local systems are of geometric origin.◻
$\operatorname{SL}(2,\mathbb{C})$
the result of [Reference Corlette and SimpsonCS08] shows that rigid integral local systems are of geometric origin.◻
Proof of Theorem 1.3.
We note that the statement of Theorem 1.3 is a special case of Corollary 7.9. Indeed, assume the hypotheses of Theorem 1.3 hold, then since any rigid representation is properly rigid, and a representation into
![]() $\operatorname{SL}(3,\mathbb{C})$
automatically has determinant of finite order, the hypotheses of Corollary 7.9 hold so the local system is of geometric origin.◻
$\operatorname{SL}(3,\mathbb{C})$
automatically has determinant of finite order, the hypotheses of Corollary 7.9 hold so the local system is of geometric origin.◻
We leave it to the reader to formulate some other variants on these corollaries. For instance, one could say that a rigid integral representation of rank
![]() $3$
comes (projectively) by pullback from a curve or a Shimura modular variety.
$3$
comes (projectively) by pullback from a curve or a Shimura modular variety.
The hypothesis of rigidity could be replaced by a hypothesis that the representation is a point of a zero-dimensional stratum of a stratification by, say, dimensions of cohomology groups or singularities of the moduli space.
We do not know how to show the conjecture ‘rigid implies integral’. One could hope that in some kind of very heuristic sense the argument for the
![]() $(1,1,1)$
case could motivate us to analyze what happens when we have a map to a two-dimensional building.
$(1,1,1)$
case could motivate us to analyze what happens when we have a map to a two-dimensional building.
Corollary 7.10. Let
![]() $X$
be a smooth projective variety such that for
$X$
be a smooth projective variety such that for
![]() $i=1,2,3$
we have
$i=1,2,3$
we have
![]() $H^{0}(X,\operatorname{Sym}^{i}\unicode[STIX]{x1D6FA}_{X})=0$
. Then any representation
$H^{0}(X,\operatorname{Sym}^{i}\unicode[STIX]{x1D6FA}_{X})=0$
. Then any representation
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(3,\mathbb{C})$
is of geometric origin.
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(3,\mathbb{C})$
is of geometric origin.
Proof. If
![]() $X$
is a smooth projective variety such that
$X$
is a smooth projective variety such that
![]() $H^{0}(X,\operatorname{Sym}^{i}\unicode[STIX]{x1D6FA}_{X})=0$
for
$H^{0}(X,\operatorname{Sym}^{i}\unicode[STIX]{x1D6FA}_{X})=0$
for
![]() $i=1,2,3$
, then any representation
$i=1,2,3$
, then any representation
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(3,\mathbb{C})$
is rigid and integral (see [Reference KlinglerKli13, Theorem 1.6 and Corollary 1.8]). Corollary 7.9 implies that it is of geometric origin.◻
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{GL}(3,\mathbb{C})$
is rigid and integral (see [Reference KlinglerKli13, Theorem 1.6 and Corollary 1.8]). Corollary 7.9 implies that it is of geometric origin.◻
Interesting examples of such varieties come from [Reference KlinglerKli13, Theorem 1.11]. Namely we can take the ball quotient
![]() $\unicode[STIX]{x1D6E4}\backslash \mathbf{B}_{\mathbb{C}}^{n}$
for a torsion-free Kottwitz lattice
$\unicode[STIX]{x1D6E4}\backslash \mathbf{B}_{\mathbb{C}}^{n}$
for a torsion-free Kottwitz lattice
![]() $\unicode[STIX]{x1D6E4}\subset \text{SU}(n,1)$
for
$\unicode[STIX]{x1D6E4}\subset \text{SU}(n,1)$
for
![]() $n\geqslant 4$
such that
$n\geqslant 4$
such that
![]() $n+1$
is prime. But these varieties are simple Shimura varieties, so probably for such varieties our result follows easily in a different way.
$n+1$
is prime. But these varieties are simple Shimura varieties, so probably for such varieties our result follows easily in a different way.
Our results give geometric origin for two-dimensional ball quotients (that is to say, any smooth projective surfaces of general type with
![]() $c_{1}^{2}=3c_{2}$
), provided we know integrality.
$c_{1}^{2}=3c_{2}$
), provided we know integrality.
Corollary 7.11. Suppose
![]() $\unicode[STIX]{x1D6E4}\subset \text{PU}(2,1)$
is a torsion-free cocompact lattice that is integral, i.e. such that the traces of its elements are algebraic integers. Let
$\unicode[STIX]{x1D6E4}\subset \text{PU}(2,1)$
is a torsion-free cocompact lattice that is integral, i.e. such that the traces of its elements are algebraic integers. Let
![]() $X=B^{2}/\unicode[STIX]{x1D6E4}$
be the ball quotient which is a smooth projective variety. Then the standard representation of
$X=B^{2}/\unicode[STIX]{x1D6E4}$
be the ball quotient which is a smooth projective variety. Then the standard representation of
![]() $\unicode[STIX]{x1D70B}_{1}(X)=\unicode[STIX]{x1D6E4}$
is of geometric origin.
$\unicode[STIX]{x1D70B}_{1}(X)=\unicode[STIX]{x1D6E4}$
is of geometric origin.
Proof. The standard representation
![]() $\unicode[STIX]{x1D70C}$
is cohomologically rigid (see below), by [Reference WeilWei62], so all of its conjugates
$\unicode[STIX]{x1D70C}$
is cohomologically rigid (see below), by [Reference WeilWei62], so all of its conjugates
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}$
for
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}$
for
![]() $\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{C}/\mathbb{Q})$
are cohomologically rigid, and hence they are variations of Hodge structure. There exists a finite possibly ramified covering
$\unicode[STIX]{x1D70E}\in \text{Gal}(\mathbb{C}/\mathbb{Q})$
are cohomologically rigid, and hence they are variations of Hodge structure. There exists a finite possibly ramified covering
![]() $Z\rightarrow X$
such that
$Z\rightarrow X$
such that
![]() $\unicode[STIX]{x1D70C}_{Z}=\unicode[STIX]{x1D70C}|_{\unicode[STIX]{x1D70B}_{1}(Z)}$
lifts to
$\unicode[STIX]{x1D70C}_{Z}=\unicode[STIX]{x1D70C}|_{\unicode[STIX]{x1D70B}_{1}(Z)}$
lifts to
![]() $\text{SU}(2,1)$
(Lemma 2.6), in other words, it is a rank
$\text{SU}(2,1)$
(Lemma 2.6), in other words, it is a rank
![]() $3$
local system. It is clearly Zariski-dense. Furthermore,
$3$
local system. It is clearly Zariski-dense. Furthermore,
![]() $\unicode[STIX]{x1D70C}_{Z}$
is a variation of Hodge structure where the period map is the composition
$\unicode[STIX]{x1D70C}_{Z}$
is a variation of Hodge structure where the period map is the composition
in particular the differential of this period map at a general point has rank
![]() $2$
. Therefore,
$2$
. Therefore,
![]() $\unicode[STIX]{x1D70C}_{Z}$
cannot factor through an orbicurve. Now apply Corollary 7.3 to get that
$\unicode[STIX]{x1D70C}_{Z}$
cannot factor through an orbicurve. Now apply Corollary 7.3 to get that
![]() $\unicode[STIX]{x1D70C}_{Z}$
has geometric origin, and by Proposition 2.10
$\unicode[STIX]{x1D70C}_{Z}$
has geometric origin, and by Proposition 2.10
![]() $\unicode[STIX]{x1D70C}$
is of geometric origin (meaning that its composition with any linear representation of
$\unicode[STIX]{x1D70C}$
is of geometric origin (meaning that its composition with any linear representation of
![]() $\text{PU}(2,1)$
has geometric origin).◻
$\text{PU}(2,1)$
has geometric origin).◻
Remark 7.12. A vector bundle
![]() $E$
with an integrable connection
$E$
with an integrable connection
![]() $\unicode[STIX]{x1D6FB}$
on
$\unicode[STIX]{x1D6FB}$
on
![]() $X/\mathbb{C}$
is called cohomologically rigid if
$X/\mathbb{C}$
is called cohomologically rigid if
![]() $H^{1}(X,{\mathcal{E}}nd^{0}(E,\unicode[STIX]{x1D6FB}))=0$
. A local system is cohomologically rigid if the corresponding vector bundle with an integrable connection is cohomologically rigid. Esnault and Groechenig prove that a cohomologically rigid local system is integral [Reference Esnault and GroechenigEG17]. This means that in many of our statements above we can remove the integrality hypothesis if we assume cohomological rigidity.
$H^{1}(X,{\mathcal{E}}nd^{0}(E,\unicode[STIX]{x1D6FB}))=0$
. A local system is cohomologically rigid if the corresponding vector bundle with an integrable connection is cohomologically rigid. Esnault and Groechenig prove that a cohomologically rigid local system is integral [Reference Esnault and GroechenigEG17]. This means that in many of our statements above we can remove the integrality hypothesis if we assume cohomological rigidity.
An important special case is that this allows us to remove the hypothesis of integrality in Corollary 7.11. Indeed for two-dimensional ball quotients the standard representation
![]() $\unicode[STIX]{x1D6E4}\rightarrow \text{PU}(2,1)$
is cohomologically rigid by [Reference WeilWei62], therefore [Reference Esnault and GroechenigEG17] applies to provide the hypothesis of integrality needed to apply Corollary 7.11. We conclude that the standard representation is of geometric origin, for any smooth projective surface of general type with
$\unicode[STIX]{x1D6E4}\rightarrow \text{PU}(2,1)$
is cohomologically rigid by [Reference WeilWei62], therefore [Reference Esnault and GroechenigEG17] applies to provide the hypothesis of integrality needed to apply Corollary 7.11. We conclude that the standard representation is of geometric origin, for any smooth projective surface of general type with
![]() $c_{1}^{2}=3c_{2}$
.
$c_{1}^{2}=3c_{2}$
.
Acknowledgements
The authors would like to thank the referees for their remarks. This collaboration started during the first author’s visit to Université de Nice – Sophia Antipolis in May–June 2015. The visit was supported by the Szolem Mandelbrojt prize awarded to the first author by the French Mathematical Society (SMF) and Institute Français in Poland.
Appendix A The factorization theorem
The main aim of this appendix is to prove Theorem 3.3. Before giving a proof of this theorem, we need a few auxiliary results. The first one is a strong version of Proposition 2.7 and Remark 2.8 in case of representations into
![]() $\operatorname{SL}(n,\mathbb{C})$
.
$\operatorname{SL}(n,\mathbb{C})$
.
Proposition A.1. Let
![]() $X$
be a smooth complex quasi-projective variety with an irreducible representation
$X$
be a smooth complex quasi-projective variety with an irreducible representation
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
. Suppose
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
. Suppose
![]() $f:X\rightarrow C$
is a fibration (cf. § 1.1) over an orbicurve such that for a general fiber
$f:X\rightarrow C$
is a fibration (cf. § 1.1) over an orbicurve such that for a general fiber
![]() $F=f^{-1}(c)$
, the restriction of
$F=f^{-1}(c)$
, the restriction of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $F$
is reducible. Then one of the following holds:
$F$
is reducible. Then one of the following holds:
(i)
 $\unicode[STIX]{x1D70C}$
projectively factors through
$\unicode[STIX]{x1D70C}$
projectively factors through
 $f$
;
$f$
;(ii) there exists a finite étale cover
 $C_{Z}\rightarrow C$
, which by base change induces a finite étale cover
$C_{Z}\rightarrow C$
, which by base change induces a finite étale cover
 $p:Z\rightarrow X$
such that
$p:Z\rightarrow X$
such that
 $p^{\ast }\unicode[STIX]{x1D70C}$
is tensor decomposable. In particular,
$p^{\ast }\unicode[STIX]{x1D70C}$
is tensor decomposable. In particular,
 $\unicode[STIX]{x1D70C}$
is virtually tensor decomposable;
$\unicode[STIX]{x1D70C}$
is virtually tensor decomposable;(iii) there exists a finite étale cover
 $C_{Z}\rightarrow C$
, which induces a finite étale cover
$C_{Z}\rightarrow C$
, which induces a finite étale cover
 $p:Z\rightarrow X$
such that
$p:Z\rightarrow X$
such that
 $p^{\ast }\unicode[STIX]{x1D70C}$
is reducible. In particular,
$p^{\ast }\unicode[STIX]{x1D70C}$
is reducible. In particular,
 $\unicode[STIX]{x1D70C}$
is virtually reducible.
$\unicode[STIX]{x1D70C}$
is virtually reducible.
Proof. Some arguments in the following proof are similar to the one used, e.g. in [Reference KatzKaz01, pp. 92–93].
Let
![]() $V_{\unicode[STIX]{x1D70C}}$
denote the local system associated to
$V_{\unicode[STIX]{x1D70C}}$
denote the local system associated to
![]() $\unicode[STIX]{x1D70C}$
. Write the isotypical decomposition
$\unicode[STIX]{x1D70C}$
. Write the isotypical decomposition
where
![]() $V_{i}$
are distinct irreducible representations of
$V_{i}$
are distinct irreducible representations of
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)$
and
$\unicode[STIX]{x1D70B}_{1}(F,x)$
and
![]() $W_{i}$
are vector spaces. By hypothesis, either there is more than one factor, or there is a single factor but
$W_{i}$
are vector spaces. By hypothesis, either there is more than one factor, or there is a single factor but
![]() $W_{1}$
has dimension
$W_{1}$
has dimension
![]() ${>}1$
.
${>}1$
.
Use the homotopy exact sequence (Theorem 2.1), assuming that
![]() $C$
has the maximal orbifold structure such that
$C$
has the maximal orbifold structure such that
![]() $f$
is a morphism, and letting
$f$
is a morphism, and letting
![]() $x\in F$
. Let
$x\in F$
. Let
![]() $\unicode[STIX]{x1D6F7}$
denote the image of
$\unicode[STIX]{x1D6F7}$
denote the image of
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)$
in
$\unicode[STIX]{x1D70B}_{1}(F,x)$
in
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
, which is also the kernel of
$\unicode[STIX]{x1D70B}_{1}(X,x)$
, which is also the kernel of
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \unicode[STIX]{x1D70B}_{1}(C,c)$
. Then
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \unicode[STIX]{x1D70B}_{1}(C,c)$
. Then
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
acts by outer automorphisms on
$\unicode[STIX]{x1D70B}_{1}(C,c)$
acts by outer automorphisms on
![]() $\unicode[STIX]{x1D6F7}$
(more precisely, we have a homomorphism from
$\unicode[STIX]{x1D6F7}$
(more precisely, we have a homomorphism from
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
to the group of outer automorphisms of
$\unicode[STIX]{x1D70B}_{1}(C,c)$
to the group of outer automorphisms of
![]() $\unicode[STIX]{x1D6F7}$
). The above isotypical decomposition is a decomposition of the restriction of
$\unicode[STIX]{x1D6F7}$
). The above isotypical decomposition is a decomposition of the restriction of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $\unicode[STIX]{x1D6F7}$
, and inner automorphisms of
$\unicode[STIX]{x1D6F7}$
, and inner automorphisms of
![]() $\unicode[STIX]{x1D6F7}$
preserve the isomorphism type of the
$\unicode[STIX]{x1D6F7}$
preserve the isomorphism type of the
![]() $V_{i}$
. Therefore,
$V_{i}$
. Therefore,
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
acts on the set of isotypical components
$\unicode[STIX]{x1D70B}_{1}(C,c)$
acts on the set of isotypical components
![]() $\{V_{i}\}$
by its conjugation action.
$\{V_{i}\}$
by its conjugation action.
Assume that there is more than one different isotypical component. As there are only finitely many isotypical components, there exists a subgroup of finite index in
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
that stabilizes each isotypical component. Therefore there exists a finite étale covering
$\unicode[STIX]{x1D70B}_{1}(C,c)$
that stabilizes each isotypical component. Therefore there exists a finite étale covering
![]() $p:Z\rightarrow X$
obtained by base change from a finite étale covering
$p:Z\rightarrow X$
obtained by base change from a finite étale covering
![]() $C_{Z}\rightarrow C$
defined by the above subgroup, such that when we pull back the above picture to
$C_{Z}\rightarrow C$
defined by the above subgroup, such that when we pull back the above picture to
![]() $Z$
, the isotypical components are preserved by the action of
$Z$
, the isotypical components are preserved by the action of
![]() $\unicode[STIX]{x1D70B}_{1}(C_{Z},c^{\prime })$
. Then the decomposition is preserved by the full monodromy action of
$\unicode[STIX]{x1D70B}_{1}(C_{Z},c^{\prime })$
. Then the decomposition is preserved by the full monodromy action of
![]() $\unicode[STIX]{x1D70B}_{1}(Z,z)$
. So
$\unicode[STIX]{x1D70B}_{1}(Z,z)$
. So
![]() $V_{\unicode[STIX]{x1D70C}}|_{Z}$
becomes reducible, and in that case
$V_{\unicode[STIX]{x1D70C}}|_{Z}$
becomes reducible, and in that case
![]() $\unicode[STIX]{x1D70C}$
is virtually reducible.
$\unicode[STIX]{x1D70C}$
is virtually reducible.
We may therefore now suppose that there is only a single isotypical component in the above decomposition, that is to say
where
![]() $n_{1}=\operatorname{rk}V_{1}\geqslant 1$
and
$n_{1}=\operatorname{rk}V_{1}\geqslant 1$
and
![]() $m_{1}=\dim W_{1}\geqslant 2$
.
$m_{1}=\dim W_{1}\geqslant 2$
.
Lemma A.2. There exists a finite étale covering
![]() $C_{Z}\rightarrow C$
of the orbicurve
$C_{Z}\rightarrow C$
of the orbicurve
![]() $C$
such that for the induced étale covering
$C$
such that for the induced étale covering
![]() $p:Z\rightarrow X$
inducing
$p:Z\rightarrow X$
inducing
![]() $p_{F}:F_{Z}\rightarrow F$
, the local system
$p_{F}:F_{Z}\rightarrow F$
, the local system
![]() $p_{F}^{\ast }(V_{1})$
extends to a local system
$p_{F}^{\ast }(V_{1})$
extends to a local system
![]() $V_{1}^{\prime }$
on
$V_{1}^{\prime }$
on
![]() $Z$
.
$Z$
.
Proof. Let
![]() $\unicode[STIX]{x1D6F7}\subset \unicode[STIX]{x1D70B}_{1}(X,x)$
be the image of
$\unicode[STIX]{x1D6F7}\subset \unicode[STIX]{x1D70B}_{1}(X,x)$
be the image of
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)$
and let
$\unicode[STIX]{x1D70B}_{1}(F,x)$
and let
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6F7}\rightarrow \operatorname{GL}(n_{1},\mathbb{C})$
be the irreducible representation corresponding to
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6F7}\rightarrow \operatorname{GL}(n_{1},\mathbb{C})$
be the irreducible representation corresponding to
![]() $V_{1}$
. The homomorphism
$V_{1}$
. The homomorphism
![]() $\unicode[STIX]{x1D711}$
factors through the almost-simple subgroup
$\unicode[STIX]{x1D711}$
factors through the almost-simple subgroup
![]() $G:=\{A\in \operatorname{GL}(n_{1},\mathbb{C}):\,(\det A)^{m_{1}}=1\}$
. For each element
$G:=\{A\in \operatorname{GL}(n_{1},\mathbb{C}):\,(\det A)^{m_{1}}=1\}$
. For each element
![]() $g\in \unicode[STIX]{x1D70B}_{1}(X,x)$
we can consider the representation
$g\in \unicode[STIX]{x1D70B}_{1}(X,x)$
we can consider the representation
![]() $\unicode[STIX]{x1D711}_{g}:\unicode[STIX]{x1D6F7}\rightarrow G\subset \operatorname{GL}(n_{1},\mathbb{C})$
given by
$\unicode[STIX]{x1D711}_{g}:\unicode[STIX]{x1D6F7}\rightarrow G\subset \operatorname{GL}(n_{1},\mathbb{C})$
given by
![]() $\unicode[STIX]{x1D711}_{g}(h)=\unicode[STIX]{x1D711}(ghg^{-1})$
and the corresponding
$\unicode[STIX]{x1D711}_{g}(h)=\unicode[STIX]{x1D711}(ghg^{-1})$
and the corresponding
![]() $\unicode[STIX]{x1D6F7}$
-module
$\unicode[STIX]{x1D6F7}$
-module
![]() $V_{\unicode[STIX]{x1D711}_{g}}$
. By definition,
$V_{\unicode[STIX]{x1D711}_{g}}$
. By definition,
![]() $V_{\unicode[STIX]{x1D711}}~\otimes ~W\simeq V_{\unicode[STIX]{x1D711}_{g}}~\otimes ~W$
and
$V_{\unicode[STIX]{x1D711}}~\otimes ~W\simeq V_{\unicode[STIX]{x1D711}_{g}}~\otimes ~W$
and
![]() $V_{\unicode[STIX]{x1D711}}$
is a simple
$V_{\unicode[STIX]{x1D711}}$
is a simple
![]() $\unicode[STIX]{x1D6F7}$
-module. Therefore there exists a non-zero map from one of the simple factors in the Jordan–Hölder filtration of
$\unicode[STIX]{x1D6F7}$
-module. Therefore there exists a non-zero map from one of the simple factors in the Jordan–Hölder filtration of
![]() $V_{\unicode[STIX]{x1D711}_{g}}$
to
$V_{\unicode[STIX]{x1D711}_{g}}$
to
![]() $V_{\unicode[STIX]{x1D711}}$
. By Schur’s lemma, this factor is isomorphic to
$V_{\unicode[STIX]{x1D711}}$
. By Schur’s lemma, this factor is isomorphic to
![]() $V_{\unicode[STIX]{x1D711}}$
. But
$V_{\unicode[STIX]{x1D711}}$
. But
![]() $V_{\unicode[STIX]{x1D711}}$
and
$V_{\unicode[STIX]{x1D711}}$
and
![]() $V_{\unicode[STIX]{x1D711}_{g}}$
have the same dimension over
$V_{\unicode[STIX]{x1D711}_{g}}$
have the same dimension over
![]() $\mathbb{C}$
, so
$\mathbb{C}$
, so
![]() $V_{\unicode[STIX]{x1D711}_{g}}$
is simple and the
$V_{\unicode[STIX]{x1D711}_{g}}$
is simple and the
![]() $\unicode[STIX]{x1D6F7}$
-modules
$\unicode[STIX]{x1D6F7}$
-modules
![]() $V_{\unicode[STIX]{x1D711}}$
and
$V_{\unicode[STIX]{x1D711}}$
and
![]() $V_{\unicode[STIX]{x1D711}_{g}}$
are isomorphic. Therefore for each fixed
$V_{\unicode[STIX]{x1D711}_{g}}$
are isomorphic. Therefore for each fixed
![]() $g\in \unicode[STIX]{x1D70B}_{1}(X,x)$
, we can choose
$g\in \unicode[STIX]{x1D70B}_{1}(X,x)$
, we can choose
![]() $A_{g}$
in
$A_{g}$
in
![]() $G\subset \operatorname{GL}(n_{1},\mathbb{C})$
such that
$G\subset \operatorname{GL}(n_{1},\mathbb{C})$
such that
for all
![]() $h\in \unicode[STIX]{x1D6F7}$
. The map
$h\in \unicode[STIX]{x1D6F7}$
. The map
![]() $\bar{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{PGL}(n_{1},\mathbb{C})$
defined by sending
$\bar{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{PGL}(n_{1},\mathbb{C})$
defined by sending
![]() $g$
to the class of
$g$
to the class of
![]() $A_{g}$
, is a projective representation extending the projective representation
$A_{g}$
, is a projective representation extending the projective representation
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)\rightarrow \operatorname{PGL}(n_{1},\mathbb{C})$
associated to
$\unicode[STIX]{x1D70B}_{1}(F,x)\rightarrow \operatorname{PGL}(n_{1},\mathbb{C})$
associated to
![]() $V_{1}$
.
$V_{1}$
.
We distinguish two cases. By [Reference Behrend and NoohiBN06, Proposition 5.5] (see also [Reference Corlette and SimpsonCS08, 2.2]), either the orbicurve is spherical, or it has a finite étale covering that is a usual curve with infinite fundamental group.
In the spherical case, there is a finite étale covering of
![]() $C$
whose fundamental group is trivial. After pulling back to this covering we are in the situation where
$C$
whose fundamental group is trivial. After pulling back to this covering we are in the situation where
![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D70B}_{1}(X,x)$
and the claim follows.
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D70B}_{1}(X,x)$
and the claim follows.
We may therefore assume that there is a finite étale covering of
![]() $C$
that is a usual curve not equal to
$C$
that is a usual curve not equal to
![]() $\mathbb{P}^{1}$
or
$\mathbb{P}^{1}$
or
![]() $\mathbb{A}^{1}$
. Pulling everything back to this covering, we may assume that
$\mathbb{A}^{1}$
. Pulling everything back to this covering, we may assume that
![]() $C$
has no orbifold structure.
$C$
has no orbifold structure.
We can choose an analytic neighborhood
![]() $U\subset C$
of
$U\subset C$
of
![]() $c=f(x)$
isomorphic to a disk and such that the induced fibration
$c=f(x)$
isomorphic to a disk and such that the induced fibration
![]() $f^{-1}(U)\rightarrow U$
is trivial in the usual topology (cf. [Reference NoriNor83, Lemma 1.5A]). If
$f^{-1}(U)\rightarrow U$
is trivial in the usual topology (cf. [Reference NoriNor83, Lemma 1.5A]). If
![]() $C$
is compact then we choose a point
$C$
is compact then we choose a point
![]() $c^{\prime }\in U-\{c\}$
. The fiber
$c^{\prime }\in U-\{c\}$
. The fiber
![]() $F^{\prime }$
of
$F^{\prime }$
of
![]() $f$
over
$f$
over
![]() $c^{\prime }$
is smooth and homeomorphic to
$c^{\prime }$
is smooth and homeomorphic to
![]() $F$
. Then we define the Zariski open subcurve
$F$
. Then we define the Zariski open subcurve
![]() $C^{\ast }=C-\{c^{\prime }\}\subset C$
. In case
$C^{\ast }=C-\{c^{\prime }\}\subset C$
. In case
![]() $C$
is non-complete we set
$C$
is non-complete we set
![]() $C^{\ast }=C$
. Let us also set
$C^{\ast }=C$
. Let us also set
![]() $X^{\ast }=f^{-1}(C^{\ast })$
. By construction, the fundamental group
$X^{\ast }=f^{-1}(C^{\ast })$
. By construction, the fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}(C^{\ast },c)$
is free.
$\unicode[STIX]{x1D70B}_{1}(C^{\ast },c)$
is free.
Now for some elements
![]() $g_{1},\ldots ,g_{s}\in \unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
whose images are free generators of
$g_{1},\ldots ,g_{s}\in \unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
whose images are free generators of
![]() $\unicode[STIX]{x1D70B}_{1}(C^{\ast },c)$
, we can consider the semi-direct product
$\unicode[STIX]{x1D70B}_{1}(C^{\ast },c)$
, we can consider the semi-direct product
with
![]() $g_{i}$
acting on
$g_{i}$
acting on
![]() $\unicode[STIX]{x1D6F7}$
by conjugation. This group is isomorphic to
$\unicode[STIX]{x1D6F7}$
by conjugation. This group is isomorphic to
![]() $\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
. Then we can extend
$\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
. Then we can extend
![]() $\unicode[STIX]{x1D711}$
to a representation
$\unicode[STIX]{x1D711}$
to a representation
![]() $\tilde{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)\rightarrow G$
by setting
$\tilde{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)\rightarrow G$
by setting
The short exact sequence
where
![]() $l=n_{1}m_{1}$
, leads to an exact sequence of (non-abelian) group cohomology
$l=n_{1}m_{1}$
, leads to an exact sequence of (non-abelian) group cohomology
where the map
![]() $\unicode[STIX]{x1D6FF}$
sends the 1-cocyle
$\unicode[STIX]{x1D6FF}$
sends the 1-cocyle
![]() $[\bar{\unicode[STIX]{x1D70F}}]=\{A_{g}\}_{g\in G}$
to the 2-cocycle
$[\bar{\unicode[STIX]{x1D70F}}]=\{A_{g}\}_{g\in G}$
to the 2-cocycle
![]() $[~]:\unicode[STIX]{x1D70B}_{1}(X)\times \unicode[STIX]{x1D70B}_{1}(X)\rightarrow \unicode[STIX]{x1D707}_{l}$
given by
$[~]:\unicode[STIX]{x1D70B}_{1}(X)\times \unicode[STIX]{x1D70B}_{1}(X)\rightarrow \unicode[STIX]{x1D707}_{l}$
given by
The sequence above shows that this 2-cocycle is the obstruction to lifting
![]() $\bar{\unicode[STIX]{x1D70F}}$
to a representation
$\bar{\unicode[STIX]{x1D70F}}$
to a representation
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
.
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
.
Let
![]() $\unicode[STIX]{x1D6F7}^{\ast }\subset \unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
be the image of
$\unicode[STIX]{x1D6F7}^{\ast }\subset \unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
be the image of
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)$
. We claim that the canonical surjection
$\unicode[STIX]{x1D70B}_{1}(F,x)$
. We claim that the canonical surjection
![]() $\unicode[STIX]{x1D6F7}^{\ast }\rightarrow \unicode[STIX]{x1D6F7}$
is in fact an isomorphism. By van Kampen’s theorem
$\unicode[STIX]{x1D6F7}^{\ast }\rightarrow \unicode[STIX]{x1D6F7}$
is in fact an isomorphism. By van Kampen’s theorem
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
is isomorphic to the amalgamated product of
$\unicode[STIX]{x1D70B}_{1}(X,x)$
is isomorphic to the amalgamated product of
![]() $\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
and
$\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)$
and
![]() $\unicode[STIX]{x1D70B}_{1}(f^{-1}(U),x)\simeq \unicode[STIX]{x1D70B}_{1}(F,x)$
over
$\unicode[STIX]{x1D70B}_{1}(f^{-1}(U),x)\simeq \unicode[STIX]{x1D70B}_{1}(F,x)$
over
![]() $\unicode[STIX]{x1D70B}_{1}(X^{\ast }~\cap ~f^{-1}(U),x)\simeq \unicode[STIX]{x1D70B}_{1}(F,x)\times \mathbb{Z}$
. This implies that
$\unicode[STIX]{x1D70B}_{1}(X^{\ast }~\cap ~f^{-1}(U),x)\simeq \unicode[STIX]{x1D70B}_{1}(F,x)\times \mathbb{Z}$
. This implies that
![]() $\unicode[STIX]{x1D6F7}^{\ast }\simeq \unicode[STIX]{x1D6F7}$
.
$\unicode[STIX]{x1D6F7}^{\ast }\simeq \unicode[STIX]{x1D6F7}$
.
Therefore we have a commutative diagram

that leads to the following commutative diagram.

Note that the class
![]() $\unicode[STIX]{x1D6FF}([\bar{\unicode[STIX]{x1D70F}}])|_{X^{\ast }}\in H^{2}(\unicode[STIX]{x1D70B}_{1}(X^{\ast },x);\unicode[STIX]{x1D707}_{l})$
is zero, since the representation
$\unicode[STIX]{x1D6FF}([\bar{\unicode[STIX]{x1D70F}}])|_{X^{\ast }}\in H^{2}(\unicode[STIX]{x1D70B}_{1}(X^{\ast },x);\unicode[STIX]{x1D707}_{l})$
is zero, since the representation
![]() $\bar{\unicode[STIX]{x1D70F}}|_{X^{\ast }}:\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)\rightarrow \operatorname{PGL}(n_{1},\mathbb{C})$
lifts to
$\bar{\unicode[STIX]{x1D70F}}|_{X^{\ast }}:\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)\rightarrow \operatorname{PGL}(n_{1},\mathbb{C})$
lifts to
![]() $\tilde{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)\rightarrow G$
. Therefore the above diagram shows that
$\tilde{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D70B}_{1}(X^{\ast },x)\rightarrow G$
. Therefore the above diagram shows that
![]() $\unicode[STIX]{x1D6FF}([\bar{\unicode[STIX]{x1D70F}}])$
lifts to a class
$\unicode[STIX]{x1D6FF}([\bar{\unicode[STIX]{x1D70F}}])$
lifts to a class
![]() $\unicode[STIX]{x1D702}$
in the kernel of
$\unicode[STIX]{x1D702}$
in the kernel of
![]() $\operatorname{res}$
. Now, by the Lyndon–Hochschild–Serre spectral sequence
$\operatorname{res}$
. Now, by the Lyndon–Hochschild–Serre spectral sequence
so this kernel fits into the following commutative diagram.

Now we need to kill
![]() $\unicode[STIX]{x1D716}(\unicode[STIX]{x1D702})$
by passing to a finite étale cover of
$\unicode[STIX]{x1D716}(\unicode[STIX]{x1D702})$
by passing to a finite étale cover of
![]() $C$
. Let us first remark that
$C$
. Let us first remark that
![]() $A:=H^{1}(\unicode[STIX]{x1D6F7};\unicode[STIX]{x1D707}_{l})=\operatorname{Hom}(\unicode[STIX]{x1D6F7};\unicode[STIX]{x1D707}_{l})=\operatorname{Hom}(\unicode[STIX]{x1D6F7}/[\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7}];\unicode[STIX]{x1D707}_{l})$
is a finite abelian group. This is clear since
$A:=H^{1}(\unicode[STIX]{x1D6F7};\unicode[STIX]{x1D707}_{l})=\operatorname{Hom}(\unicode[STIX]{x1D6F7};\unicode[STIX]{x1D707}_{l})=\operatorname{Hom}(\unicode[STIX]{x1D6F7}/[\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7}];\unicode[STIX]{x1D707}_{l})$
is a finite abelian group. This is clear since
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)$
, and hence also
$\unicode[STIX]{x1D70B}_{1}(F,x)$
, and hence also
![]() $\unicode[STIX]{x1D6F7}$
, are finitely generated. Passing to the finite étale covering defined by the finite index subgroup
$\unicode[STIX]{x1D6F7}$
, are finitely generated. Passing to the finite étale covering defined by the finite index subgroup
![]() $\bigcap _{a\in A}\unicode[STIX]{x1D70B}_{1}(C,c)_{a}\subset \unicode[STIX]{x1D70B}_{1}(C,c)$
obtained by intersecting all the stabilizers of
$\bigcap _{a\in A}\unicode[STIX]{x1D70B}_{1}(C,c)_{a}\subset \unicode[STIX]{x1D70B}_{1}(C,c)$
obtained by intersecting all the stabilizers of
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
-action on
$\unicode[STIX]{x1D70B}_{1}(C,c)$
-action on
![]() $A$
, we can assume that
$A$
, we can assume that
![]() $A$
is a trivial
$A$
is a trivial
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
-module. Then
$\unicode[STIX]{x1D70B}_{1}(C,c)$
-module. Then
is a finite abelian group. Let us consider a finite index subgroup of
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
defined by
$\unicode[STIX]{x1D70B}_{1}(C,c)$
defined by
It is clear from the definition that the induced restriction map
![]() $H^{1}(\unicode[STIX]{x1D70B}_{1}(C,c),A)\rightarrow H^{1}(H;A)$
is zero, so
$H^{1}(\unicode[STIX]{x1D70B}_{1}(C,c),A)\rightarrow H^{1}(H;A)$
is zero, so
![]() $H\subset \unicode[STIX]{x1D70B}_{1}(C,c)$
defines a finite étale cover of
$H\subset \unicode[STIX]{x1D70B}_{1}(C,c)$
defines a finite étale cover of
![]() $C$
which kills the class
$C$
which kills the class
![]() $\unicode[STIX]{x1D716}(\unicode[STIX]{x1D702})$
. Therefore we can assume that
$\unicode[STIX]{x1D716}(\unicode[STIX]{x1D702})$
. Therefore we can assume that
![]() $\unicode[STIX]{x1D702}$
lifts to a class
$\unicode[STIX]{x1D702}$
lifts to a class
![]() $\tilde{\unicode[STIX]{x1D702}}\in H^{2}(\unicode[STIX]{x1D70B}_{1}(C,c);\unicode[STIX]{x1D707}_{l})$
.
$\tilde{\unicode[STIX]{x1D702}}\in H^{2}(\unicode[STIX]{x1D70B}_{1}(C,c);\unicode[STIX]{x1D707}_{l})$
.
By assumption
![]() $C$
is not spherical, so the universal cover
$C$
is not spherical, so the universal cover
![]() $\tilde{C}$
of
$\tilde{C}$
of
![]() $C$
is contractible. So the spectral sequence
$C$
is contractible. So the spectral sequence
degenerates to
![]() $H^{p}(\unicode[STIX]{x1D70B}_{1}(C,c);\unicode[STIX]{x1D707}_{l})=H^{p}(C,\unicode[STIX]{x1D707}_{l})$
.
$H^{p}(\unicode[STIX]{x1D70B}_{1}(C,c);\unicode[STIX]{x1D707}_{l})=H^{p}(C,\unicode[STIX]{x1D707}_{l})$
.
If
![]() $C$
is not projective then there is nothing to prove as
$C$
is not projective then there is nothing to prove as
![]() $H^{2}(C,\unicode[STIX]{x1D707}_{l})=0$
. So we can assume that
$H^{2}(C,\unicode[STIX]{x1D707}_{l})=0$
. So we can assume that
![]() $C$
is projective of genus
$C$
is projective of genus
![]() $g\geqslant 1$
. For any finite abelian group
$g\geqslant 1$
. For any finite abelian group
![]() $A$
any element
$A$
any element
![]() $\unicode[STIX]{x1D6FC}\in H^{2}(C,A)$
can be killed after passing to a finite étale cover
$\unicode[STIX]{x1D6FC}\in H^{2}(C,A)$
can be killed after passing to a finite étale cover
![]() $\unicode[STIX]{x1D70B}:C^{\prime }\rightarrow C$
. This follows from the fact that
$\unicode[STIX]{x1D70B}:C^{\prime }\rightarrow C$
. This follows from the fact that
![]() $H^{2}(C,A)\simeq A$
and
$H^{2}(C,A)\simeq A$
and
![]() $\unicode[STIX]{x1D70B}^{\ast }:H^{2}(C,A)\rightarrow H^{2}(C^{\prime },A)$
is multiplication by the degree of
$\unicode[STIX]{x1D70B}^{\ast }:H^{2}(C,A)\rightarrow H^{2}(C^{\prime },A)$
is multiplication by the degree of
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
has a subgroup of index equal to the order of
$\unicode[STIX]{x1D70B}_{1}(C,c)$
has a subgroup of index equal to the order of
![]() $A$
. But
$A$
. But
![]() $\unicode[STIX]{x1D70B}_{1}(C,c)$
contains subgroups of arbitrary finite index, so applying the above remark to the class
$\unicode[STIX]{x1D70B}_{1}(C,c)$
contains subgroups of arbitrary finite index, so applying the above remark to the class
![]() $\tilde{\unicode[STIX]{x1D702}}$
, we can find a connected degree
$\tilde{\unicode[STIX]{x1D702}}$
, we can find a connected degree
![]() $n$
finite étale covering
$n$
finite étale covering
![]() $C_{Z}\rightarrow C$
such that the pullback of
$C_{Z}\rightarrow C$
such that the pullback of
![]() $\tilde{\unicode[STIX]{x1D702}}$
is zero in
$\tilde{\unicode[STIX]{x1D702}}$
is zero in
![]() $H^{2}(\unicode[STIX]{x1D70B}_{1}(C_{Z},c^{\prime });\unicode[STIX]{x1D707}_{l})=H^{2}(C_{Z},\unicode[STIX]{x1D707}_{l})$
. So letting
$H^{2}(\unicode[STIX]{x1D70B}_{1}(C_{Z},c^{\prime });\unicode[STIX]{x1D707}_{l})=H^{2}(C_{Z},\unicode[STIX]{x1D707}_{l})$
. So letting
![]() $Z$
be the pullback of this covering over
$Z$
be the pullback of this covering over
![]() $X$
we get that our class in
$X$
we get that our class in
![]() $H^{2}(\unicode[STIX]{x1D70B}_{1}(X,x);\unicode[STIX]{x1D707}_{l})$
pulls back to the zero class in
$H^{2}(\unicode[STIX]{x1D70B}_{1}(X,x);\unicode[STIX]{x1D707}_{l})$
pulls back to the zero class in
![]() $H^{2}(\unicode[STIX]{x1D70B}_{1}(Z,z);\unicode[STIX]{x1D707}_{l})$
. Therefore, when pulled back to
$H^{2}(\unicode[STIX]{x1D70B}_{1}(Z,z);\unicode[STIX]{x1D707}_{l})$
. Therefore, when pulled back to
![]() $Z$
, the representation lifts to
$Z$
, the representation lifts to
![]() $G$
.◻
$G$
.◻
Let
![]() $f_{Z}$
denote the map from
$f_{Z}$
denote the map from
![]() $Z$
to
$Z$
to
![]() $C_{Z}$
. Let us consider
$C_{Z}$
. Let us consider
Note that
![]() $V_{1}^{\prime }|_{F_{Z}}$
is irreducible, since
$V_{1}^{\prime }|_{F_{Z}}$
is irreducible, since
![]() $p_{F}:F_{Z}\rightarrow F$
is an isomorphism (this is why we need
$p_{F}:F_{Z}\rightarrow F$
is an isomorphism (this is why we need
![]() $p:Z\rightarrow X$
to be induced from a finite covering of the curves
$p:Z\rightarrow X$
to be induced from a finite covering of the curves
![]() $C_{Z}\rightarrow C$
). So after restricting the above map to the fiber
$C_{Z}\rightarrow C$
). So after restricting the above map to the fiber
![]() $F_{Z}$
we get an isomorphism. Since this map is a map of local systems on
$F_{Z}$
we get an isomorphism. Since this map is a map of local systems on
![]() $Z$
, it must be an isomorphism.
$Z$
, it must be an isomorphism.
If the rank of
![]() $V_{1}^{\prime }$
is
$V_{1}^{\prime }$
is
![]() ${\geqslant}2$
this gives a tensor decomposition over
${\geqslant}2$
this gives a tensor decomposition over
![]() $Z$
so
$Z$
so
![]() $\unicode[STIX]{x1D70C}$
is virtually tensor decomposable. Finally, if
$\unicode[STIX]{x1D70C}$
is virtually tensor decomposable. Finally, if
![]() $V_{1}^{\prime }$
has rank
$V_{1}^{\prime }$
has rank
![]() $1$
then
$1$
then
![]() $V_{1}$
has rank
$V_{1}$
has rank
![]() $1$
, so the restriction of
$1$
, so the restriction of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)$
projects to the trivial representation in
$\unicode[STIX]{x1D70B}_{1}(F,x)$
projects to the trivial representation in
![]() $\operatorname{PGL}(n,\mathbb{C})$
. This means that
$\operatorname{PGL}(n,\mathbb{C})$
. This means that
![]() $\unicode[STIX]{x1D70C}$
projectively factors through
$\unicode[STIX]{x1D70C}$
projectively factors through
![]() $f$
. This finishes proof of Proposition A.1.◻
$f$
. This finishes proof of Proposition A.1.◻
The proof of the next lemma uses projectivity of the base manifold.
Lemma A.3. Let
![]() $X$
be a smooth complex projective variety of dimension
$X$
be a smooth complex projective variety of dimension
![]() ${\geqslant}2$
. Let
${\geqslant}2$
. Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be a representation with an infinite image. Assume that
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
be a representation with an infinite image. Assume that
![]() $\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve. Then there exists a fibration
$\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve. Then there exists a fibration
![]() $h:X\rightarrow B$
over a smooth projective curve
$h:X\rightarrow B$
over a smooth projective curve
![]() $B$
such that the restriction of
$B$
such that the restriction of
![]() $V_{\unicode[STIX]{x1D70C}}$
to a general fiber of
$V_{\unicode[STIX]{x1D70C}}$
to a general fiber of
![]() $h$
has finite monodromy.
$h$
has finite monodromy.
Proof. By assumption there exists an alteration
![]() $p:Z\rightarrow X$
for which
$p:Z\rightarrow X$
for which
![]() $p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through a fibration
$p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through a fibration
![]() $f:Z\rightarrow C$
over an orbicurve
$f:Z\rightarrow C$
over an orbicurve
![]() $C$
. Let
$C$
. Let
![]() $Z_{y}\subset Z$
denote the fiber over
$Z_{y}\subset Z$
denote the fiber over
![]() $y\in C$
. Choose
$y\in C$
. Choose
![]() $a\in C$
at which the stabilizer group is trivial and the fiber
$a\in C$
at which the stabilizer group is trivial and the fiber
![]() $Z_{a}$
is smooth.
$Z_{a}$
is smooth.
Let us consider
![]() $g=(p,f):Z\rightarrow X\times C$
. Let
$g=(p,f):Z\rightarrow X\times C$
. Let
![]() $Y\subset X\times C$
be the image of
$Y\subset X\times C$
be the image of
![]() $g$
and let
$g$
and let
![]() $r_{1}:Y\rightarrow X$
and
$r_{1}:Y\rightarrow X$
and
![]() $r_{2}:Y\rightarrow C$
denote the corresponding projections.
$r_{2}:Y\rightarrow C$
denote the corresponding projections.
Claim. We have
![]() $p(Z_{a})~\cap ~p(Z_{y})=\emptyset$
for general
$p(Z_{a})~\cap ~p(Z_{y})=\emptyset$
for general
![]() $y\in C$
.
$y\in C$
.
Proof. Assume that
![]() $p(Z_{a})~\cap ~p(Z_{y})\neq \emptyset$
for general
$p(Z_{a})~\cap ~p(Z_{y})\neq \emptyset$
for general
![]() $y\in C$
. Then
$y\in C$
. Then
![]() $Y~\cap ~(p(Z_{a})\times C)$
contains an irreducible component that dominates
$Y~\cap ~(p(Z_{a})\times C)$
contains an irreducible component that dominates
![]() $C$
. So we can choose a complete irreducible curve
$C$
. So we can choose a complete irreducible curve
![]() $D\subset Z$
such that
$D\subset Z$
such that
![]() $g(D)$
is contained in
$g(D)$
is contained in
![]() $Y~\cap ~(p(Z_{a})\times C)$
and
$Y~\cap ~(p(Z_{a})\times C)$
and
![]() $f(D)=C$
. Let
$f(D)=C$
. Let
![]() $\unicode[STIX]{x1D708}:\tilde{D}\rightarrow D{\hookrightarrow}Z$
be composition of the normalization of
$\unicode[STIX]{x1D708}:\tilde{D}\rightarrow D{\hookrightarrow}Z$
be composition of the normalization of
![]() $D$
with the canonical inclusion. Then
$D$
with the canonical inclusion. Then
![]() $\tilde{D}$
is a smooth projective curve,
$\tilde{D}$
is a smooth projective curve,
![]() $p\circ \unicode[STIX]{x1D708}$
maps
$p\circ \unicode[STIX]{x1D708}$
maps
![]() $\tilde{D}$
into
$\tilde{D}$
into
![]() $p(Z_{a})$
but
$p(Z_{a})$
but
![]() $f\circ \unicode[STIX]{x1D708}:\tilde{D}\rightarrow C$
is surjective. The situation can be summed up in the following diagram.
$f\circ \unicode[STIX]{x1D708}:\tilde{D}\rightarrow C$
is surjective. The situation can be summed up in the following diagram.

If
![]() $p(D)$
is a point then
$p(D)$
is a point then
![]() $\unicode[STIX]{x1D708}^{\ast }p^{\ast }(V_{\unicode[STIX]{x1D70C}})$
is a local system with finite (in fact, trivial) monodromy on
$\unicode[STIX]{x1D708}^{\ast }p^{\ast }(V_{\unicode[STIX]{x1D70C}})$
is a local system with finite (in fact, trivial) monodromy on
![]() $\tilde{D}$
. If
$\tilde{D}$
. If
![]() $D^{\prime }:=p(D)$
is a curve then we can choose an irreducible curve
$D^{\prime }:=p(D)$
is a curve then we can choose an irreducible curve
![]() $D^{\prime \prime }\subset Z_{a}$
mapping onto
$D^{\prime \prime }\subset Z_{a}$
mapping onto
![]() $D^{\prime }$
. Since
$D^{\prime }$
. Since
![]() $p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through
$p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through
![]() $f$
, the monodromy of the pullback of
$f$
, the monodromy of the pullback of
![]() $V_{\unicode[STIX]{x1D70C}}$
to
$V_{\unicode[STIX]{x1D70C}}$
to
![]() $Z_{a}$
is contained in the center of
$Z_{a}$
is contained in the center of
![]() $\operatorname{SL}(n,\mathbb{C})$
, so it is finite. Therefore the monodromy of the pullback of
$\operatorname{SL}(n,\mathbb{C})$
, so it is finite. Therefore the monodromy of the pullback of
![]() $V_{\unicode[STIX]{x1D70C}}$
to the normalization
$V_{\unicode[STIX]{x1D70C}}$
to the normalization
![]() $\widetilde{D^{\prime \prime }}$
of
$\widetilde{D^{\prime \prime }}$
of
![]() $D^{\prime \prime }$
is also finite. Since
$D^{\prime \prime }$
is also finite. Since
![]() $\widetilde{D^{\prime \prime }}\rightarrow Z\rightarrow X$
factors through the normalization
$\widetilde{D^{\prime \prime }}\rightarrow Z\rightarrow X$
factors through the normalization
![]() $\widetilde{D^{\prime }}$
of
$\widetilde{D^{\prime }}$
of
![]() $D^{\prime }$
, the image of
$D^{\prime }$
, the image of
![]() $\unicode[STIX]{x1D70B}_{1}(\widetilde{D^{\prime \prime }})$
in
$\unicode[STIX]{x1D70B}_{1}(\widetilde{D^{\prime \prime }})$
in
![]() $\unicode[STIX]{x1D70B}_{1}(\widetilde{D^{\prime }})$
has finite index. Therefore the local system
$\unicode[STIX]{x1D70B}_{1}(\widetilde{D^{\prime }})$
has finite index. Therefore the local system
![]() $V_{\unicode[STIX]{x1D70C}}$
, pulled back to the normalization
$V_{\unicode[STIX]{x1D70C}}$
, pulled back to the normalization
![]() $\widetilde{D^{\prime }}$
, has finite monodromy. The map
$\widetilde{D^{\prime }}$
, has finite monodromy. The map
![]() $p\circ \unicode[STIX]{x1D708}:\tilde{D}\rightarrow X$
factors through
$p\circ \unicode[STIX]{x1D708}:\tilde{D}\rightarrow X$
factors through
![]() $\widetilde{D^{\prime }}$
. Therefore, also in this case
$\widetilde{D^{\prime }}$
. Therefore, also in this case
![]() $\unicode[STIX]{x1D708}^{\ast }p^{\ast }(V_{\unicode[STIX]{x1D70C}})$
is a local system with finite monodromy on
$\unicode[STIX]{x1D708}^{\ast }p^{\ast }(V_{\unicode[STIX]{x1D70C}})$
is a local system with finite monodromy on
![]() $\tilde{D}$
.
$\tilde{D}$
.
On the other hand, the image of
![]() $\unicode[STIX]{x1D70B}_{1}(\tilde{D})$
in
$\unicode[STIX]{x1D70B}_{1}(\tilde{D})$
in
![]() $\unicode[STIX]{x1D70B}_{1}(C)$
has finite index (since
$\unicode[STIX]{x1D70B}_{1}(C)$
has finite index (since
![]() $f\circ g:\tilde{D}\rightarrow C$
is surjective), the image of
$f\circ g:\tilde{D}\rightarrow C$
is surjective), the image of
![]() $\unicode[STIX]{x1D70C}$
is infinite and
$\unicode[STIX]{x1D70C}$
is infinite and
![]() $p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through
$p^{\ast }\unicode[STIX]{x1D70C}$
projectively factors through
![]() $f$
. Therefore the image of
$f$
. Therefore the image of
![]() $\unicode[STIX]{x1D70B}_{1}(\tilde{D})$
in
$\unicode[STIX]{x1D70B}_{1}(\tilde{D})$
in
![]() $\text{SL}(n,\mathbb{C})$
cannot be finite, a contradiction.◻
$\text{SL}(n,\mathbb{C})$
cannot be finite, a contradiction.◻
By the above claim, we can choose three distinct, smooth fibers
![]() $Z_{a}$
,
$Z_{a}$
,
![]() $Z_{b}$
,
$Z_{b}$
,
![]() $Z_{c}$
of
$Z_{c}$
of
![]() $f$
such that their images in
$f$
such that their images in
![]() $X$
are pairwise disjoint divisors. Since
$X$
are pairwise disjoint divisors. Since
![]() $Z_{a}$
,
$Z_{a}$
,
![]() $Z_{b}$
and
$Z_{b}$
and
![]() $Z_{c}$
are algebraically equivalent, the corresponding cycles
$Z_{c}$
are algebraically equivalent, the corresponding cycles
![]() $p_{\ast }Z_{a}$
,
$p_{\ast }Z_{a}$
,
![]() $p_{\ast }Z_{b}$
and
$p_{\ast }Z_{b}$
and
![]() $p_{\ast }Z_{c}$
are also algebraically equivalent. In particular, the corresponding cohomology classes of
$p_{\ast }Z_{c}$
are also algebraically equivalent. In particular, the corresponding cohomology classes of
![]() $p(Z_{a})$
,
$p(Z_{a})$
,
![]() $p(Z_{b})$
and
$p(Z_{b})$
and
![]() $p(Z_{c})$
lie on the same line in
$p(Z_{c})$
lie on the same line in
![]() $H^{2}(X,\mathbb{Q})$
. Therefore by [Reference TotaroTot00, Theorem 2.1] there exists a fibration
$H^{2}(X,\mathbb{Q})$
. Therefore by [Reference TotaroTot00, Theorem 2.1] there exists a fibration
![]() $h:X\rightarrow B$
over a smooth curve
$h:X\rightarrow B$
over a smooth curve
![]() $B$
such that
$B$
such that
![]() $p(Z_{a})$
,
$p(Z_{a})$
,
![]() $p(Z_{b})$
and
$p(Z_{b})$
and
![]() $p(Z_{c})$
are fibers of
$p(Z_{c})$
are fibers of
![]() $h$
. Moreover, by [Reference TotaroTot00, Lemma 2.2] for general
$h$
. Moreover, by [Reference TotaroTot00, Lemma 2.2] for general
![]() $y\in C$
, the image
$y\in C$
, the image
![]() $p(Z_{y})$
is a fiber of
$p(Z_{y})$
is a fiber of
![]() $h$
. In particular,
$h$
. In particular,
![]() $p(Z_{y})$
is smooth for general
$p(Z_{y})$
is smooth for general
![]() $y\in C$
. Since the monodromy group of the pullback of
$y\in C$
. Since the monodromy group of the pullback of
![]() $V_{\unicode[STIX]{x1D70C}}$
to
$V_{\unicode[STIX]{x1D70C}}$
to
![]() $Z_{y}$
is finite and
$Z_{y}$
is finite and
![]() $\unicode[STIX]{x1D70B}_{1}(Z_{y})$
has finite index in
$\unicode[STIX]{x1D70B}_{1}(Z_{y})$
has finite index in
![]() $\unicode[STIX]{x1D70B}_{1}(p(Z_{y}))$
, we conclude that the restriction of
$\unicode[STIX]{x1D70B}_{1}(p(Z_{y}))$
, we conclude that the restriction of
![]() $V_{\unicode[STIX]{x1D70C}}$
to a general fiber of
$V_{\unicode[STIX]{x1D70C}}$
to a general fiber of
![]() $h$
has finite monodromy.◻
$h$
has finite monodromy.◻
Now we can prove Theorem 3.3, which we recall as follows.
Theorem A.4. Let
![]() $X$
be a smooth complex projective variety. Let us fix an irreducible representation
$X$
be a smooth complex projective variety. Let us fix an irreducible representation
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
for some
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \operatorname{SL}(n,\mathbb{C})$
for some
![]() $n\geqslant 2$
. Suppose that
$n\geqslant 2$
. Suppose that
![]() $\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable, and not virtually reducible. Then the following conditions are equivalent:
$\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable, and not virtually reducible. Then the following conditions are equivalent:
(i)
 $\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve;
$\unicode[STIX]{x1D70C}$
projectively factors through an orbicurve;(ii)
 $\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve;
$\unicode[STIX]{x1D70C}$
virtually projectively factors through an orbicurve;(iii) there exists a non-constant map
 $f:X\rightarrow C$
to an orbicurve and a smooth fiber
$f:X\rightarrow C$
to an orbicurve and a smooth fiber
 $F=f^{-1}(y)$
, such that the restriction of
$F=f^{-1}(y)$
, such that the restriction of
 $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
 $\unicode[STIX]{x1D70B}_{1}(F,x)$
becomes reducible;
$\unicode[STIX]{x1D70B}_{1}(F,x)$
becomes reducible;(iv) there exists an alteration
 $p:Z\rightarrow X$
such that the previous condition holds for the pullback
$p:Z\rightarrow X$
such that the previous condition holds for the pullback
 $p^{\ast }\unicode[STIX]{x1D70C}$
.
$p^{\ast }\unicode[STIX]{x1D70C}$
.
Proof. Let us first remark that the image of
![]() $\unicode[STIX]{x1D70C}$
is infinite. Indeed, if the image of
$\unicode[STIX]{x1D70C}$
is infinite. Indeed, if the image of
![]() $\unicode[STIX]{x1D70C}$
is finite then there exists a finite étale covering
$\unicode[STIX]{x1D70C}$
is finite then there exists a finite étale covering
![]() $X^{\prime }\rightarrow X$
such that the pullback of
$X^{\prime }\rightarrow X$
such that the pullback of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $X^{\prime }$
is trivial, contradicting our assumption that
$X^{\prime }$
is trivial, contradicting our assumption that
![]() $\unicode[STIX]{x1D70C}$
is not virtually reducible. In the following we assume that
$\unicode[STIX]{x1D70C}$
is not virtually reducible. In the following we assume that
![]() $X$
has dimension
$X$
has dimension
![]() ${\geqslant}2$
, as otherwise the theorem is trivial. Clearly, the implications (i)
${\geqslant}2$
, as otherwise the theorem is trivial. Clearly, the implications (i)
![]() $\Rightarrow$
(ii) and (iii)
$\Rightarrow$
(ii) and (iii)
![]() $\Rightarrow$
(iv) are trivial. Let us assume (ii). Then by Lemma A.3 there is a map
$\Rightarrow$
(iv) are trivial. Let us assume (ii). Then by Lemma A.3 there is a map
![]() $h:X\rightarrow B$
to an orbicurve, such that the restriction of
$h:X\rightarrow B$
to an orbicurve, such that the restriction of
![]() $V_{\unicode[STIX]{x1D70C}}$
to a general fiber of
$V_{\unicode[STIX]{x1D70C}}$
to a general fiber of
![]() $h$
has finite monodromy. Apply the homotopy exact sequence (Theorem 2.1), making sure that the orbicurve structure of
$h$
has finite monodromy. Apply the homotopy exact sequence (Theorem 2.1), making sure that the orbicurve structure of
![]() $B$
is the necessary one so that it works. Let
$B$
is the necessary one so that it works. Let
![]() $F$
denote a general fiber. Assume that the basepoint
$F$
denote a general fiber. Assume that the basepoint
![]() $x$
belongs to
$x$
belongs to
![]() $F$
and denote by
$F$
and denote by
![]() $b:=f(x)$
the basepoint in
$b:=f(x)$
the basepoint in
![]() $B$
. We get the exact sequence
$B$
. We get the exact sequence
Now we need the following group-theoretic lemma.
Lemma A.5. If
![]() $H\subset \operatorname{SL}(n,\mathbb{C})$
is finite and irreducible then the normalizer of
$H\subset \operatorname{SL}(n,\mathbb{C})$
is finite and irreducible then the normalizer of
![]() $H$
in
$H$
in
![]() $\operatorname{SL}(n,\mathbb{C})$
is finite.
$\operatorname{SL}(n,\mathbb{C})$
is finite.
Proof. Since
![]() $H$
is a closed subgroup of
$H$
is a closed subgroup of
![]() $\operatorname{SL}(n,\mathbb{C})$
, its normalizer
$\operatorname{SL}(n,\mathbb{C})$
, its normalizer
![]() $G:=N_{H}\operatorname{SL}(n,\mathbb{C})$
is also closed in
$G:=N_{H}\operatorname{SL}(n,\mathbb{C})$
is also closed in
![]() $\operatorname{SL}(n,\mathbb{C})$
. Let us fix an element
$\operatorname{SL}(n,\mathbb{C})$
. Let us fix an element
![]() $h\in H$
. Since the identity component
$h\in H$
. Since the identity component
![]() $G^{0}$
normalizes
$G^{0}$
normalizes
![]() $H$
, the map
$H$
, the map
![]() $\unicode[STIX]{x1D711}_{h}:G^{0}\rightarrow \operatorname{SL}(n,\mathbb{C})$
defined by
$\unicode[STIX]{x1D711}_{h}:G^{0}\rightarrow \operatorname{SL}(n,\mathbb{C})$
defined by
![]() $\unicode[STIX]{x1D711}_{h}(g)=ghg^{-1}h^{-1}$
has image in
$\unicode[STIX]{x1D711}_{h}(g)=ghg^{-1}h^{-1}$
has image in
![]() $H$
. Since
$H$
. Since
![]() $G^{0}$
is connected and
$G^{0}$
is connected and
![]() $H$
is finite,
$H$
is finite,
![]() $\unicode[STIX]{x1D711}_{h}$
is constant. Hence,
$\unicode[STIX]{x1D711}_{h}$
is constant. Hence,
![]() $G^{0}$
commutes with
$G^{0}$
commutes with
![]() $H$
. Since
$H$
. Since
![]() $H$
is irreducible, elements commuting with
$H$
is irreducible, elements commuting with
![]() $H$
are contained in the center
$H$
are contained in the center
![]() $Z(\operatorname{SL}(n,\mathbb{C}))$
of
$Z(\operatorname{SL}(n,\mathbb{C}))$
of
![]() $\operatorname{SL}(n,\mathbb{C})$
. Therefore
$\operatorname{SL}(n,\mathbb{C})$
. Therefore
![]() $G^{0}$
is finite. Since
$G^{0}$
is finite. Since
![]() $G^{0}$
is of finite index in
$G^{0}$
is of finite index in
![]() $G$
,
$G$
,
![]() $G$
is also finite.◻
$G$
is also finite.◻
Let
![]() $\unicode[STIX]{x1D6F7}\subset \unicode[STIX]{x1D70B}_{1}(X,x)$
denote the image of
$\unicode[STIX]{x1D6F7}\subset \unicode[STIX]{x1D70B}_{1}(X,x)$
denote the image of
![]() $\unicode[STIX]{x1D70B}_{1}(F,x)$
. Suppose that the restriction
$\unicode[STIX]{x1D70B}_{1}(F,x)$
. Suppose that the restriction
![]() $\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D70C}|_{\unicode[STIX]{x1D6F7}}$
is irreducible and let
$\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D70C}|_{\unicode[STIX]{x1D6F7}}$
is irreducible and let
![]() $H\subset \operatorname{SL}(n,\mathbb{C})$
denote the image of
$H\subset \operatorname{SL}(n,\mathbb{C})$
denote the image of
![]() $\unicode[STIX]{x1D711}$
. Since
$\unicode[STIX]{x1D711}$
. Since
![]() $\unicode[STIX]{x1D6F7}$
is a normal subgroup of
$\unicode[STIX]{x1D6F7}$
is a normal subgroup of
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)$
, for any
$\unicode[STIX]{x1D70B}_{1}(X,x)$
, for any
![]() $s\in \unicode[STIX]{x1D70B}_{1}(X,x)$
,
$s\in \unicode[STIX]{x1D70B}_{1}(X,x)$
,
![]() $\unicode[STIX]{x1D70C}(s)$
is contained in the normalizer of
$\unicode[STIX]{x1D70C}(s)$
is contained in the normalizer of
![]() $H$
in
$H$
in
![]() $\operatorname{SL}(n,\mathbb{C})$
. Therefore, by the above lemma, the image of
$\operatorname{SL}(n,\mathbb{C})$
. Therefore, by the above lemma, the image of
![]() $\unicode[STIX]{x1D70C}$
is finite, contradicting our hypothesis.
$\unicode[STIX]{x1D70C}$
is finite, contradicting our hypothesis.
Thus the restriction
![]() $V_{\unicode[STIX]{x1D70C}}|_{F}$
to a general fiber is reducible, proving the implication (ii)
$V_{\unicode[STIX]{x1D70C}}|_{F}$
to a general fiber is reducible, proving the implication (ii)
![]() $\Rightarrow$
(iii).
$\Rightarrow$
(iii).
Now let us assume (iii). Passing to the Stein factorization and using Theorem 2.1, we can assume that
![]() $f$
is a fibration over an orbicurve, and the restriction
$f$
is a fibration over an orbicurve, and the restriction
![]() $V_{\unicode[STIX]{x1D70C}}|_{F}$
to a general fiber of
$V_{\unicode[STIX]{x1D70C}}|_{F}$
to a general fiber of
![]() $f$
is reducible. In view of the hypothesis that
$f$
is reducible. In view of the hypothesis that
![]() $\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable and not virtually reducible, Proposition A.1 implies that
$\unicode[STIX]{x1D70C}$
is not virtually tensor decomposable and not virtually reducible, Proposition A.1 implies that
![]() $\unicode[STIX]{x1D70C}$
projectively factors through
$\unicode[STIX]{x1D70C}$
projectively factors through
![]() $f$
. This completes the proof of the implication (iii)
$f$
. This completes the proof of the implication (iii)
![]() $\Rightarrow$
(i).
$\Rightarrow$
(i).
The fact that (iii)
![]() $\Rightarrow$
(i) shows that (iv)
$\Rightarrow$
(i) shows that (iv)
![]() $\Rightarrow$
(ii). Indeed, in the situation of (iv), the pullback of
$\Rightarrow$
(ii). Indeed, in the situation of (iv), the pullback of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $Z$
satisfies all the hypotheses: it is irreducible because we assumed that
$Z$
satisfies all the hypotheses: it is irreducible because we assumed that
![]() $\unicode[STIX]{x1D70C}$
was not virtually reducible, and the hypotheses of not being virtually tensor decomposable and not being virtually reducible are conserved. Over
$\unicode[STIX]{x1D70C}$
was not virtually reducible, and the hypotheses of not being virtually tensor decomposable and not being virtually reducible are conserved. Over
![]() $Z$
we are in the situation of (iii) so we have shown that
$Z$
we are in the situation of (iii) so we have shown that
![]() $\unicode[STIX]{x1D70C}|_{Z}$
factors through an orbicurve. This shows (iv)
$\unicode[STIX]{x1D70C}|_{Z}$
factors through an orbicurve. This shows (iv)
![]() $\Rightarrow$
(ii) which completes the proof.◻
$\Rightarrow$
(ii) which completes the proof.◻
In order to optimize the statements of our corollaries in § 7, we need a result concerning groups lying between
![]() $\operatorname{SL}(3,\mathbb{C})$
and
$\operatorname{SL}(3,\mathbb{C})$
and
![]() $\operatorname{GL}(3,\mathbb{C})$
. For notational reasons we do this separately here, rather than modifying the previous discussion to take into account such groups. However, one can easily check that the proofs of Proposition A.1 and Theorem A.4 work also in this more general case with just minor notational changes.
$\operatorname{GL}(3,\mathbb{C})$
. For notational reasons we do this separately here, rather than modifying the previous discussion to take into account such groups. However, one can easily check that the proofs of Proposition A.1 and Theorem A.4 work also in this more general case with just minor notational changes.
Suppose
![]() $G\subset \operatorname{GL}(3,\mathbb{C})$
is a subgroup such that
$G\subset \operatorname{GL}(3,\mathbb{C})$
is a subgroup such that
![]() $\operatorname{SL}(3,\mathbb{C})\subset G$
is of finite index. Let
$\operatorname{SL}(3,\mathbb{C})\subset G$
is of finite index. Let
![]() $\unicode[STIX]{x1D707}_{m}:=G/\operatorname{SL}(3,\mathbb{C})$
denote the quotient group which is a finite cyclic group of some order
$\unicode[STIX]{x1D707}_{m}:=G/\operatorname{SL}(3,\mathbb{C})$
denote the quotient group which is a finite cyclic group of some order
![]() $m$
.
$m$
.
Lemma A.6. Suppose
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
is a representation with Zariski-dense image. Let
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow G$
is a representation with Zariski-dense image. Let
![]() $Z\rightarrow X$
be the cyclic covering determined by the composed representation
$Z\rightarrow X$
be the cyclic covering determined by the composed representation
![]() $\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \unicode[STIX]{x1D707}_{m}$
, and let
$\unicode[STIX]{x1D70B}_{1}(X,x)\rightarrow \unicode[STIX]{x1D707}_{m}$
, and let
denote the pullback representation. If
![]() $\unicode[STIX]{x1D70C}_{Z}$
projectively factors through a map to an orbicurve then
$\unicode[STIX]{x1D70C}_{Z}$
projectively factors through a map to an orbicurve then
![]() $\unicode[STIX]{x1D70C}$
projectively factors through a map to an orbicurve.
$\unicode[STIX]{x1D70C}$
projectively factors through a map to an orbicurve.
Proof. Consider the composed representation
where the last arrow is the adjoint action on the Lie algebra
![]() $\mathfrak{sl}(3)\cong \mathbb{C}^{8}$
. Call this representation
$\mathfrak{sl}(3)\cong \mathbb{C}^{8}$
. Call this representation
![]() $\unicode[STIX]{x1D701}$
. Our hypothesis tells us that the monodromy group of
$\unicode[STIX]{x1D701}$
. Our hypothesis tells us that the monodromy group of
![]() $\unicode[STIX]{x1D701}$
is
$\unicode[STIX]{x1D701}$
is
![]() $\operatorname{PGL}(3,\mathbb{C})$
, and that its restriction
$\operatorname{PGL}(3,\mathbb{C})$
, and that its restriction
![]() $\unicode[STIX]{x1D701}_{Z}$
to
$\unicode[STIX]{x1D701}_{Z}$
to
![]() $Z$
factors through an orbicurve. As
$Z$
factors through an orbicurve. As
![]() $\operatorname{PGL}(3,\mathbb{C})$
has no finite-index subgroups, the monodromy group of any pullback to a finite cover is still
$\operatorname{PGL}(3,\mathbb{C})$
has no finite-index subgroups, the monodromy group of any pullback to a finite cover is still
![]() $\operatorname{PGL}(3,\mathbb{C})$
. In particular,
$\operatorname{PGL}(3,\mathbb{C})$
. In particular,
![]() $\unicode[STIX]{x1D701}$
is not virtually reducible, and not virtually tensor decomposable. By Theorem A.4 we conclude that
$\unicode[STIX]{x1D701}$
is not virtually reducible, and not virtually tensor decomposable. By Theorem A.4 we conclude that
![]() $\unicode[STIX]{x1D701}$
projectively factors through an orbicurve. However, the composed map
$\unicode[STIX]{x1D701}$
projectively factors through an orbicurve. However, the composed map
is injective. Therefore,
![]() $\unicode[STIX]{x1D701}$
factors through an orbicurve. This factorization gives the projective factorization of
$\unicode[STIX]{x1D701}$
factors through an orbicurve. This factorization gives the projective factorization of
![]() $\unicode[STIX]{x1D70C}$
through an orbicurve, that we are looking for.◻
$\unicode[STIX]{x1D70C}$
through an orbicurve, that we are looking for.◻