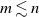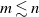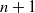1. Introduction
Parking functions are an established area of research in combinatorics, with connections to labeled trees and forests (Chassaing and Marckert [Reference Chassaing and Marckert4]), non-crossing partitions and hyperplane arrangements (Stanley [Reference Stanley18, Reference Stanley19]), symmetric functions (Haiman [Reference Haiman12]), abelian sandpiles (Cori and Rossin [Reference Cori and Rossin6]), and other topics.
Consider a parking lot with n parking spots placed sequentially along a one-way street. A line of ![]() $m \leq n$ cars enters the lot, one by one. The ith car drives to its preferred spot
$m \leq n$ cars enters the lot, one by one. The ith car drives to its preferred spot ![]() $\pi_i$ and parks there if possible; if the spot is already occupied then the car parks in the first available spot after that. The list of preferences
$\pi_i$ and parks there if possible; if the spot is already occupied then the car parks in the first available spot after that. The list of preferences ![]() ${\boldsymbol \pi}=(\pi_1,\dots,\pi_m)$ is called a generalized parking function if all cars successfully park. (This generalizes the term parking function, which classically refers to the case
${\boldsymbol \pi}=(\pi_1,\dots,\pi_m)$ is called a generalized parking function if all cars successfully park. (This generalizes the term parking function, which classically refers to the case ![]() $m=n$. When there is no risk of confusion we will drop the modifier ‘generalized’ and simply refer to both of these cases as parking functions.) We denote the set of parking functions by
$m=n$. When there is no risk of confusion we will drop the modifier ‘generalized’ and simply refer to both of these cases as parking functions.) We denote the set of parking functions by ![]() ${\text{PF}}(m, n)$, where m is the number of cars and n is the number of parking spots. The total number of parking functions is
${\text{PF}}(m, n)$, where m is the number of cars and n is the number of parking spots. The total number of parking functions is ![]() $|{\text{PF}}(m, n)|=(n-m+1)(n+1)^{m-1}$ (Pitman and Stanley [Reference Pitman and Stanley16]). Using the pigeonhole principle, we see that a parking function
$|{\text{PF}}(m, n)|=(n-m+1)(n+1)^{m-1}$ (Pitman and Stanley [Reference Pitman and Stanley16]). Using the pigeonhole principle, we see that a parking function ![]() ${\boldsymbol \pi}\in {\text{PF}}(m, n)$ must have at most one value
${\boldsymbol \pi}\in {\text{PF}}(m, n)$ must have at most one value ![]() $=n$, at most two values
$=n$, at most two values ![]() $\geq n-1$, and for each k at most k values
$\geq n-1$, and for each k at most k values ![]() $\ge n-k+1$, and any such function is a parking function. Equivalently,
$\ge n-k+1$, and any such function is a parking function. Equivalently, ![]() ${\boldsymbol \pi}$ is a parking function if and only if
${\boldsymbol \pi}$ is a parking function if and only if
Note that parking functions are invariant under the action of ![]() ${\mathfrak{S}}_m$ by permuting cars.
${\mathfrak{S}}_m$ by permuting cars.
In our previous work [Reference Kenyon and Yin13], we investigated various probabilistic properties of a parking function chosen uniformly at random from ![]() ${\text{PF}}(m, n)$, giving a formula for the law of a single coordinate. Adapting known results on random linear probes, we further deduced the covariance between two coordinates in the special situation
${\text{PF}}(m, n)$, giving a formula for the law of a single coordinate. Adapting known results on random linear probes, we further deduced the covariance between two coordinates in the special situation ![]() $m=n$. This paper will delve deeper into the properties of a uniform parking function in the generic situation
$m=n$. This paper will delve deeper into the properties of a uniform parking function in the generic situation ![]() $m \lesssim n$. Our probabilistic results rely on an original combinatorial construction which we term a parking function multi-shuffle, and our novel asymptotic calculation utilizes the multi-dimensional Cauchy product of the tree function
$m \lesssim n$. Our probabilistic results rely on an original combinatorial construction which we term a parking function multi-shuffle, and our novel asymptotic calculation utilizes the multi-dimensional Cauchy product of the tree function ![]() $F(z) = \sum_{s=0}^\infty\! (s+1)^{s-1}\frac{z^s}{s!}$, a variant of the Lambert function, and its generalizations. We will give all moments of multiple coordinates and deduce all possible covariances: between two coordinates, between a coordinate and an unattempted spot, and between two unattempted spots.
$F(z) = \sum_{s=0}^\infty\! (s+1)^{s-1}\frac{z^s}{s!}$, a variant of the Lambert function, and its generalizations. We will give all moments of multiple coordinates and deduce all possible covariances: between two coordinates, between a coordinate and an unattempted spot, and between two unattempted spots.
The multi-shuffle construction allows us to compute the number of parking functions ![]() ${\text{PF}}(m, n)$ where the parking preferences of
${\text{PF}}(m, n)$ where the parking preferences of ![]() $l\leq m$ cars are arbitrarily specified. Alternatively, by permutation symmetry, we can think that l spots are already taken along a one-way street with n parking spots, and we want to count the possible preferences for the remaining
$l\leq m$ cars are arbitrarily specified. Alternatively, by permutation symmetry, we can think that l spots are already taken along a one-way street with n parking spots, and we want to count the possible preferences for the remaining ![]() $m-l$ cars allowing them all to park successfully. In the parking function literature, the successful preference sequences for the
$m-l$ cars allowing them all to park successfully. In the parking function literature, the successful preference sequences for the ![]() $m-l$ cars that enter the street later are referred to as parking completions for
$m-l$ cars that enter the street later are referred to as parking completions for ![]() ${\boldsymbol \tau}=(\tau_1, \dots, \tau_l)$, where the entries of
${\boldsymbol \tau}=(\tau_1, \dots, \tau_l)$, where the entries of ![]() ${\boldsymbol \tau}$ denote the l spots that are already taken, arranged in increasing order.
${\boldsymbol \tau}$ denote the l spots that are already taken, arranged in increasing order.
This parking scenario and its variations, such as defective parking functions where some drivers fail to park (Cameron et al. [Reference Cameron, Johannsen, Prellberg and Schweitzer3]), have generated significant interest over the years. Much progress has been made for the special case ![]() $m=n$ of parking functions. Parking completions with a single spot taken (
$m=n$ of parking functions. Parking completions with a single spot taken (![]() ${\boldsymbol \tau}=(\tau_1)$ arbitrary) were enumerated by Diaconis and Hicks [Reference Diaconis and Hicks7]. The case in which the taken spots form a contiguous block starting from the first spot in the linear car park,
${\boldsymbol \tau}=(\tau_1)$ arbitrary) were enumerated by Diaconis and Hicks [Reference Diaconis and Hicks7]. The case in which the taken spots form a contiguous block starting from the first spot in the linear car park, ![]() ${\boldsymbol \tau}=(1, \dots, l)$, was first considered by Yan [Reference Yan20], with an explicit formula given in a follow-up work by Gessel and Seo [Reference Gessel and Seo11]. The formula was generalized by Ehrenborg and Happ [Reference Ehrenborg and Happ9] to take into account cars of different sizes. More recently, Adeniran et al. [Reference Adeniran1] unified prior work on parking completions for
${\boldsymbol \tau}=(1, \dots, l)$, was first considered by Yan [Reference Yan20], with an explicit formula given in a follow-up work by Gessel and Seo [Reference Gessel and Seo11]. The formula was generalized by Ehrenborg and Happ [Reference Ehrenborg and Happ9] to take into account cars of different sizes. More recently, Adeniran et al. [Reference Adeniran1] unified prior work on parking completions for ![]() ${\text{PF}}(n, n)$ and computed the number of parking functions
${\text{PF}}(n, n)$ and computed the number of parking functions ![]() ${\text{PF}}(n, n)$ where the parking preferences of
${\text{PF}}(n, n)$ where the parking preferences of ![]() $l\leq n$ cars are arbitrarily specified utilizing a pair of operations termed Join and Split. The multi-shuffle construction introduced in this paper builds upon our prior single-shuffle construction [Reference Kenyon and Yin13] and is a further generalization of the above-mentioned work, being applicable for general m and n. Recognizing that unattempted parking spots break up a parking function into non-interacting pieces, the multi-shuffle construction also sheds light on the correlation between the coordinates of parking functions and unattempted spots.
$l\leq n$ cars are arbitrarily specified utilizing a pair of operations termed Join and Split. The multi-shuffle construction introduced in this paper builds upon our prior single-shuffle construction [Reference Kenyon and Yin13] and is a further generalization of the above-mentioned work, being applicable for general m and n. Recognizing that unattempted parking spots break up a parking function into non-interacting pieces, the multi-shuffle construction also sheds light on the correlation between the coordinates of parking functions and unattempted spots.
Given a positive-integer-valued vector ![]() ${\textbf{u}}=(u_1, \dots, u_m)$ with
${\textbf{u}}=(u_1, \dots, u_m)$ with ![]() $u_1 \leq \cdots \leq u_m$, a
$u_1 \leq \cdots \leq u_m$, a ![]() ${\textbf{u}}$-parking function of length m is a sequence
${\textbf{u}}$-parking function of length m is a sequence ![]() $(\pi_1, \dots, \pi_m)$ of positive integers whose non-decreasing rearrangement
$(\pi_1, \dots, \pi_m)$ of positive integers whose non-decreasing rearrangement ![]() $(\lambda_1, \dots, \lambda_m)$ satisfies
$(\lambda_1, \dots, \lambda_m)$ satisfies ![]() $\lambda_i\leq u_i$ for all
$\lambda_i\leq u_i$ for all ![]() $1\leq i\leq m$. Via a switch of coordinates in (1.1), we see that the parking function
$1\leq i\leq m$. Via a switch of coordinates in (1.1), we see that the parking function ![]() ${\text{PF}}(m, n)$ investigated in this paper may be alternatively posed as a
${\text{PF}}(m, n)$ investigated in this paper may be alternatively posed as a ![]() ${\textbf{u}}$-parking function, where the vector
${\textbf{u}}$-parking function, where the vector ![]() ${\textbf{u}}$ is an arithmetic progression:
${\textbf{u}}$ is an arithmetic progression: ![]() ${\textbf{u}}=(n-m+1, \dots, n)$. As we will see in Section 2.1, more generally, a parking completion for
${\textbf{u}}=(n-m+1, \dots, n)$. As we will see in Section 2.1, more generally, a parking completion for ![]() ${\text{PF}}(m, n)$ may be interpreted as a
${\text{PF}}(m, n)$ may be interpreted as a ![]() ${\textbf{u}}$-parking function, where the vector
${\textbf{u}}$-parking function, where the vector ![]() ${\textbf{u}}$ need not consist of consecutive numbers. Knowledge about
${\textbf{u}}$ need not consist of consecutive numbers. Knowledge about ![]() ${\text{PF}}(m, n)$ with specified parking preferences of
${\text{PF}}(m, n)$ with specified parking preferences of ![]() $l\leq m$ cars therefore adds to the understanding of
$l\leq m$ cars therefore adds to the understanding of ![]() ${\textbf{u}}$-parking functions as well. In particular, our enumeration of parking completions provides a different perspective on the volume formula for Pitman–Stanley polytopes [Reference Pitman and Stanley16], and our mixed moment calculations for multiple coordinates of parking functions extend those of Kung and Yan [Reference Kung and Yan14], who give explicit formulas for the first and second factorial moments and a general form for the higher factorial moments of sums of
${\textbf{u}}$-parking functions as well. In particular, our enumeration of parking completions provides a different perspective on the volume formula for Pitman–Stanley polytopes [Reference Pitman and Stanley16], and our mixed moment calculations for multiple coordinates of parking functions extend those of Kung and Yan [Reference Kung and Yan14], who give explicit formulas for the first and second factorial moments and a general form for the higher factorial moments of sums of ![]() ${\textbf{u}}$-parking functions.
${\textbf{u}}$-parking functions.
This paper is organized as follows. Section 2 illustrates the notion of a parking function multi-shuffle, which decomposes a parking function into smaller components (Definition 1). This construction leads to an explicit characterization of multiple coordinates ![]() $\pi_1, \dots, \pi_l\in[n]$ of parking functions (Theorems 1 and 2). For the case in which
$\pi_1, \dots, \pi_l\in[n]$ of parking functions (Theorems 1 and 2). For the case in which ![]() $\pi_1, \dots, \pi_l$ form a contiguous block, a simplified characterization is given in Proposition 2. Section 3 uses the multi-shuffle construction introduced in Section 2 to investigate various properties of a parking function chosen uniformly at random from
$\pi_1, \dots, \pi_l$ form a contiguous block, a simplified characterization is given in Proposition 2. Section 3 uses the multi-shuffle construction introduced in Section 2 to investigate various properties of a parking function chosen uniformly at random from ![]() ${\text{PF}}(m, n)$. We compute asymptotics of all moments of multiple coordinates in Theorem 5 in the generic situation
${\text{PF}}(m, n)$. We compute asymptotics of all moments of multiple coordinates in Theorem 5 in the generic situation ![]() $m \lesssim n$ and give complete technical details for all moments of two coordinates (Theorem 4). We further derive all possible covariances involving coordinates of parking functions and unattempted spots in Propositions 6, 8, and 9. The asymptotic scenario in the generic situation
$m \lesssim n$ and give complete technical details for all moments of two coordinates (Theorem 4). We further derive all possible covariances involving coordinates of parking functions and unattempted spots in Propositions 6, 8, and 9. The asymptotic scenario in the generic situation ![]() $m \lesssim n$ is contrasted with that of the special situation
$m \lesssim n$ is contrasted with that of the special situation ![]() $m=n$ in Section 3.5. Finally, Section 4 studies a generalization of parking functions called interval parking functions, in which each driver is willing to park only in a fixed interval of spots. We construct a family of bijections between interval parking functions
$m=n$ in Section 3.5. Finally, Section 4 studies a generalization of parking functions called interval parking functions, in which each driver is willing to park only in a fixed interval of spots. We construct a family of bijections between interval parking functions ![]() ${\text{IPF}}(n, n)$ and edge-labeled spanning trees
${\text{IPF}}(n, n)$ and edge-labeled spanning trees ![]() ${\mathscr F}^e(n+1)$ (Theorem 10).
${\mathscr F}^e(n+1)$ (Theorem 10).
Notation
Let ![]() $\mathbb{N}$ be the set of non-negative integers. For
$\mathbb{N}$ be the set of non-negative integers. For ![]() $m, n \in \mathbb{N}$, we write [m, n] for the set of integers
$m, n \in \mathbb{N}$, we write [m, n] for the set of integers ![]() $\{m, \dots, n\}$ and
$\{m, \dots, n\}$ and ![]() $[n]=[1, n]$. For vectors
$[n]=[1, n]$. For vectors ![]() ${\textbf{a}}, {\textbf{b}} \in [n]^m$, we write
${\textbf{a}}, {\textbf{b}} \in [n]^m$, we write ![]() ${\textbf{a}}\leq_C {\textbf{b}}$ if
${\textbf{a}}\leq_C {\textbf{b}}$ if ![]() $a_i\leq b_i$ for all
$a_i\leq b_i$ for all ![]() $i\in [m]$; this is the componentwise partial order on
$i\in [m]$; this is the componentwise partial order on ![]() $[n]^m$. In a similar fashion, we write
$[n]^m$. In a similar fashion, we write ![]() ${\textbf{a}} <_C {\textbf{b}}$ if
${\textbf{a}} <_C {\textbf{b}}$ if ![]() $a_i\leq b_i$ for all
$a_i\leq b_i$ for all ![]() $i\in [m]$ and there is at least one
$i\in [m]$ and there is at least one ![]() $j \in [m]$ such that
$j \in [m]$ such that ![]() $a_j<b_j$. For
$a_j<b_j$. For ![]() ${\textbf{b}} \in [n]^m$, we write
${\textbf{b}} \in [n]^m$, we write ![]() $[{\textbf{b}}]$ for the set of
$[{\textbf{b}}]$ for the set of ![]() ${\textbf{a}} \in [n]^m$ with
${\textbf{a}} \in [n]^m$ with ![]() ${\textbf{a}} \leq_C {\textbf{b}}$. The conjugate (or reverse complement) of
${\textbf{a}} \leq_C {\textbf{b}}$. The conjugate (or reverse complement) of ![]() ${\textbf{x}}\in[n]^m$ is the vector
${\textbf{x}}\in[n]^m$ is the vector ![]() ${\textbf{x}}^*=(n+1-x_m, \dots, n+1-x_1)$.
${\textbf{x}}^*=(n+1-x_m, \dots, n+1-x_1)$.
2. Parking function multi-shuffle
In this section we explore the properties of parking functions through a parking function multi-shuffle construction. For explicitness, we will write our results in terms of parking coordinates ![]() $\pi_1, \dots, \pi_l$, where
$\pi_1, \dots, \pi_l$, where ![]() $1\leq l \leq m$ is any integer. However, by permutation symmetry, they may be interpreted for any coordinates. Temporarily fix
$1\leq l \leq m$ is any integer. However, by permutation symmetry, they may be interpreted for any coordinates. Temporarily fix ![]() $\pi_{l+1}, \dots, \pi_m$. Let
$\pi_{l+1}, \dots, \pi_m$. Let
Via a switch of coordinates in (1.1), we see that ![]() ${\boldsymbol \pi}=(u_1, \dots, u_l, \pi_{l+1}, \dots, \pi_{m})\in {\text{PF}}(m, n)$ if and only if its non-decreasing rearrangement
${\boldsymbol \pi}=(u_1, \dots, u_l, \pi_{l+1}, \dots, \pi_{m})\in {\text{PF}}(m, n)$ if and only if its non-decreasing rearrangement ![]() ${\boldsymbol \lambda}=(\lambda_1, \dots, \lambda_m)$ satisfies
${\boldsymbol \lambda}=(\lambda_1, \dots, \lambda_m)$ satisfies ![]() $\lambda_i \leq n-m+i$ for all
$\lambda_i \leq n-m+i$ for all ![]() $1\leq i\leq m$. From the parking scheme, we may assume that
$1\leq i\leq m$. From the parking scheme, we may assume that ![]() ${\textbf{u}}=(u_1, \dots, u_l)$ is in strictly increasing order, so that
${\textbf{u}}=(u_1, \dots, u_l)$ is in strictly increasing order, so that ![]() $u_i=\lambda_j \geq \lambda_i$ for some
$u_i=\lambda_j \geq \lambda_i$ for some ![]() $j\geq i$. This implies that if
$j\geq i$. This implies that if ![]() $A_{\pi_{l+1}, \dots, \pi_m}$ is non-empty, then there is a unique maximal element (in the componentwise partial order)
$A_{\pi_{l+1}, \dots, \pi_m}$ is non-empty, then there is a unique maximal element (in the componentwise partial order) ![]() ${\textbf{u}} \in [n]^l$ with
${\textbf{u}} \in [n]^l$ with ![]() $u_i \geq n-m+i$ for all
$u_i \geq n-m+i$ for all ![]() $1\leq i\leq l$ and
$1\leq i\leq l$ and ![]() $A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$. Therefore, given the last
$A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$. Therefore, given the last ![]() $m-l$ parking preferences, it is sufficient to identify the largest feasible first l preferences (if any exist).
$m-l$ parking preferences, it is sufficient to identify the largest feasible first l preferences (if any exist).
Example 1. Take ![]() $m=4$,
$m=4$, ![]() $n=6$,
$n=6$, ![]() $\pi_3=2$, and
$\pi_3=2$, and ![]() $\pi_4=6$. Then
$\pi_4=6$. Then ![]() $A_{\pi_3, \pi_4}=[{\textbf{u}}]=[(4, 5)]$.
$A_{\pi_3, \pi_4}=[{\textbf{u}}]=[(4, 5)]$.
Definition 1. Take ![]() $1\leq l \leq m$ any integer. Let
$1\leq l \leq m$ any integer. Let ![]() ${\textbf{u}}=(u_1, \dots, u_l) \in [n]^l$ be in increasing order with
${\textbf{u}}=(u_1, \dots, u_l) \in [n]^l$ be in increasing order with ![]() $u_i\geq n-m+i$ for all
$u_i\geq n-m+i$ for all ![]() $1\leq i\leq l$. Say that
$1\leq i\leq l$. Say that ![]() $\pi_{l+1}, \dots, \pi_m$ is a parking function multi-shuffle of
$\pi_{l+1}, \dots, \pi_m$ is a parking function multi-shuffle of ![]() $l+1$ parking functions
$l+1$ parking functions ![]() ${\boldsymbol \alpha}_1 \in {{PF}}(m-n+u_1-1, u_1-1), {\boldsymbol \alpha}_2 \in {{PF}}(u_2-u_1-1, u_2-u_1-1), \dots, {\boldsymbol \alpha}_l \in {{PF}}(u_l-u_{l-1}-1, u_l-u_{l-1}-1)$, and
${\boldsymbol \alpha}_1 \in {{PF}}(m-n+u_1-1, u_1-1), {\boldsymbol \alpha}_2 \in {{PF}}(u_2-u_1-1, u_2-u_1-1), \dots, {\boldsymbol \alpha}_l \in {{PF}}(u_l-u_{l-1}-1, u_l-u_{l-1}-1)$, and ![]() ${\boldsymbol \alpha}_{l+1} \in {{PF}}(n-u_l, n-u_l)$ if
${\boldsymbol \alpha}_{l+1} \in {{PF}}(n-u_l, n-u_l)$ if ![]() $\pi_{l+1}, \dots, \pi_m$ is any permutation of the union of the
$\pi_{l+1}, \dots, \pi_m$ is any permutation of the union of the ![]() $l+1$ words
$l+1$ words ![]() ${\boldsymbol \alpha}_1, {\boldsymbol \alpha}_2+(u_1, \dots, u_1), \dots, {\boldsymbol \alpha}_{l+1}+(u_l, \dots, u_l)$. We will denote this by
${\boldsymbol \alpha}_1, {\boldsymbol \alpha}_2+(u_1, \dots, u_1), \dots, {\boldsymbol \alpha}_{l+1}+(u_l, \dots, u_l)$. We will denote this by ![]() $(\pi_{l+1}, \dots, \pi_m) \in {\text{MS}}(m-n+u_1-1, u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
$(\pi_{l+1}, \dots, \pi_m) \in {\text{MS}}(m-n+u_1-1, u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
Example 2. Take ![]() $m=8$,
$m=8$, ![]() $n=10$,
$n=10$, ![]() $u_1=6$, and
$u_1=6$, and ![]() $u_2=8$. Take
$u_2=8$. Take ![]() ${\boldsymbol \alpha}_1=(2, 1, 2) \in {\text{PF}}(3, 5)$,
${\boldsymbol \alpha}_1=(2, 1, 2) \in {\text{PF}}(3, 5)$, ![]() ${\boldsymbol \alpha}_2=(1) \in {\text{PF}}(1, 1)$, and
${\boldsymbol \alpha}_2=(1) \in {\text{PF}}(1, 1)$, and ![]() ${\boldsymbol \alpha}_3=(2, 1) \in {\text{PF}}(2, 2)$. Then
${\boldsymbol \alpha}_3=(2, 1) \in {\text{PF}}(2, 2)$. Then ![]() $(2, \overline{7},2, \underline{9}, \underline{10},1) \in {\text{MS}}(3, 5, 1, 2)$ is a multi-shuffle of the three words (2, 1, 2), (7), and (10, 9).
$(2, \overline{7},2, \underline{9}, \underline{10},1) \in {\text{MS}}(3, 5, 1, 2)$ is a multi-shuffle of the three words (2, 1, 2), (7), and (10, 9).
Theorem 1. Take ![]() $1\leq l \leq m$ any integer. Let
$1\leq l \leq m$ any integer. Let ![]() ${\textbf{u}}=(u_1, \dots, u_l) \in [n]^l$ be in increasing order with
${\textbf{u}}=(u_1, \dots, u_l) \in [n]^l$ be in increasing order with ![]() $u_i\geq n-m+i$ for all
$u_i\geq n-m+i$ for all ![]() $1\leq i\leq l$. Then
$1\leq i\leq l$. Then ![]() $A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$ if and only if
$A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$ if and only if ![]() $(\pi_{l+1}, \dots, \pi_m) \in {\text{MS}}(m-n+u_1-1, u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
$(\pi_{l+1}, \dots, \pi_m) \in {\text{MS}}(m-n+u_1-1, u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
Proof. ![]() $\Longrightarrow$: The statement
$\Longrightarrow$: The statement ![]() $A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$ is equivalent to saying that
$A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$ is equivalent to saying that ![]() ${\boldsymbol \pi}=\big(u_1, \dots, u_l,$
${\boldsymbol \pi}=\big(u_1, \dots, u_l,$ ![]() $\pi_{l+1}, \dots, \pi_m\big)$ is a parking function, but
$\pi_{l+1}, \dots, \pi_m\big)$ is a parking function, but ![]() ${\boldsymbol \pi}^i=(u_1, \dots, u_{i-1}, u_i+1, u_{i+1}, \dots, u_l,$
${\boldsymbol \pi}^i=(u_1, \dots, u_{i-1}, u_i+1, u_{i+1}, \dots, u_l,$ ![]() $\pi_{l+1}, \dots, \pi_m)$ is not, for any
$\pi_{l+1}, \dots, \pi_m)$ is not, for any ![]() $1 \leq i\leq l$. By (1.1), this can only happen when
$1 \leq i\leq l$. By (1.1), this can only happen when ![]() $\#\{k\,:\, \pi_k \leq u_i\}=m-n+u_i$ for all
$\#\{k\,:\, \pi_k \leq u_i\}=m-n+u_i$ for all ![]() $1\leq i\leq l$. We claim that none of the subsequent
$1\leq i\leq l$. We claim that none of the subsequent ![]() $m-l$ cars can have preference
$m-l$ cars can have preference ![]() $u_1, \dots, u_l$. Suppose otherwise, so that there is a later car with preference
$u_1, \dots, u_l$. Suppose otherwise, so that there is a later car with preference ![]() $u_i$. Such a car would necessarily park in spots
$u_i$. Such a car would necessarily park in spots ![]() $u_i+1, \dots, n$ for
$u_i+1, \dots, n$ for ![]() ${\boldsymbol \pi}$, and consequently it could change places with car i in
${\boldsymbol \pi}$, and consequently it could change places with car i in ![]() ${\boldsymbol \pi}^i$, contradicting the statement that
${\boldsymbol \pi}^i$, contradicting the statement that ![]() $\pi_i=u_i$ is allowed but
$\pi_i=u_i$ is allowed but ![]() $\pi^i_i=u_i+1$ is not allowed. Hence, excluding the first l cars,
$\pi^i_i=u_i+1$ is not allowed. Hence, excluding the first l cars, ![]() ${\boldsymbol \pi}$ has exactly
${\boldsymbol \pi}$ has exactly ![]() $m-n+u_1-1$ cars with value
$m-n+u_1-1$ cars with value ![]() $\leq u_1-1$, exactly
$\leq u_1-1$, exactly ![]() $u_2-u_1-1$ cars with value
$u_2-u_1-1$ cars with value ![]() $\geq u_1+1$ and
$\geq u_1+1$ and ![]() $\leq u_2-1$,
$\leq u_2-1$, ![]() $\dots$, exactly
$\dots$, exactly ![]() $u_l-u_{l-1}-1$ cars with value
$u_l-u_{l-1}-1$ cars with value ![]() $\geq u_{l-1}+1$ and
$\geq u_{l-1}+1$ and ![]() $\leq u_l-1$, and exactly
$\leq u_l-1$, and exactly ![]() $n-u_l$ cars with value
$n-u_l$ cars with value ![]() $\geq u_l+1$.
$\geq u_l+1$.
Let ![]() ${\boldsymbol \alpha}_1$ be the subsequence of
${\boldsymbol \alpha}_1$ be the subsequence of ![]() $(\pi_{l+1}, \dots, \pi_m)$ with value
$(\pi_{l+1}, \dots, \pi_m)$ with value ![]() $\leq u_1-1$,
$\leq u_1-1$, ![]() ${\boldsymbol \alpha}^{\prime}_2$ the subsequence with value
${\boldsymbol \alpha}^{\prime}_2$ the subsequence with value ![]() $\geq u_1+1$ and
$\geq u_1+1$ and ![]() $\leq u_2-1$,
$\leq u_2-1$, ![]() $\dots$,
$\dots$, ![]() ${\boldsymbol \alpha}^{\prime}_l$ the subsequence with value
${\boldsymbol \alpha}^{\prime}_l$ the subsequence with value ![]() $\geq u_{l-1}+1$ and
$\geq u_{l-1}+1$ and ![]() $\leq u_l-1$, and
$\leq u_l-1$, and ![]() ${\boldsymbol \alpha}^{\prime}_{l+1}$ the subsequence with value
${\boldsymbol \alpha}^{\prime}_{l+1}$ the subsequence with value ![]() $\geq u_l+1$. Construct
$\geq u_l+1$. Construct ![]() ${\boldsymbol \alpha}_2={\boldsymbol \alpha}^{\prime}_2 -(u_1, \dots, u_1), \dots, {\boldsymbol \alpha}_{l+1}={\boldsymbol \alpha}^{\prime}_{l+1} -(u_l, \dots, u_l)$. It is clear from the above reasoning that
${\boldsymbol \alpha}_2={\boldsymbol \alpha}^{\prime}_2 -(u_1, \dots, u_1), \dots, {\boldsymbol \alpha}_{l+1}={\boldsymbol \alpha}^{\prime}_{l+1} -(u_l, \dots, u_l)$. It is clear from the above reasoning that ![]() ${\boldsymbol \alpha}_1 \in {\text{PF}}(m-n+u_1-1, u_1-1)$,
${\boldsymbol \alpha}_1 \in {\text{PF}}(m-n+u_1-1, u_1-1)$, ![]() ${\boldsymbol \alpha}_2 \in {\text{PF}}(u_2-u_1-1, u_2-u_1-1)$,
${\boldsymbol \alpha}_2 \in {\text{PF}}(u_2-u_1-1, u_2-u_1-1)$, ![]() $\dots,$
$\dots,$ ![]() ${\boldsymbol \alpha}_l \in {\text{PF}}(u_l-u_{l-1}-1, u_l-u_{l-1}-1)$, and
${\boldsymbol \alpha}_l \in {\text{PF}}(u_l-u_{l-1}-1, u_l-u_{l-1}-1)$, and ![]() ${\boldsymbol \alpha}_{l+1} \in {\text{PF}}(n-u_l, n-u_l)$. By Definition 1,
${\boldsymbol \alpha}_{l+1} \in {\text{PF}}(n-u_l, n-u_l)$. By Definition 1, ![]() $(\pi_{l+1}, \dots, \pi_m) \in {\text{MS}}(m-n+u_1-1, u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
$(\pi_{l+1}, \dots, \pi_m) \in {\text{MS}}(m-n+u_1-1, u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
![]() $\Longleftarrow$: We first show that
$\Longleftarrow$: We first show that ![]() ${\boldsymbol \pi}=(u_1, \dots, u_l, \pi_{l+1}, \dots, \pi_m)$ is a parking function. This is clear, since from Definition 1,
${\boldsymbol \pi}=(u_1, \dots, u_l, \pi_{l+1}, \dots, \pi_m)$ is a parking function. This is clear, since from Definition 1, ![]() ${\boldsymbol \pi}$ can be decomposed into
${\boldsymbol \pi}$ can be decomposed into ![]() $2l+1$ parts: a subsequence
$2l+1$ parts: a subsequence ![]() ${\boldsymbol \alpha}_1$ of length
${\boldsymbol \alpha}_1$ of length ![]() $m-n+u_1-1$ with entries
$m-n+u_1-1$ with entries ![]() $\leq u_1-1$, one entry
$\leq u_1-1$, one entry ![]() $u_1$, a subsequence
$u_1$, a subsequence ![]() ${\boldsymbol \alpha}^{\prime}_2 $ of length
${\boldsymbol \alpha}^{\prime}_2 $ of length ![]() $u_2-u_1-1$ with entries
$u_2-u_1-1$ with entries ![]() $\geq u_1+1$ and
$\geq u_1+1$ and ![]() $\leq u_2-1$, one entry
$\leq u_2-1$, one entry ![]() $u_2$,
$u_2$, ![]() $\dots$, a subsequence
$\dots$, a subsequence ![]() ${\boldsymbol \alpha}^{\prime}_l$ of length
${\boldsymbol \alpha}^{\prime}_l$ of length ![]() $u_l-u_{l-1}-1$ with entries
$u_l-u_{l-1}-1$ with entries ![]() $\geq u_{l-1}+1$ and
$\geq u_{l-1}+1$ and ![]() $\leq u_l-1$, one entry
$\leq u_l-1$, one entry ![]() $u_l$, and a subsequence
$u_l$, and a subsequence ![]() ${\boldsymbol \alpha}^{\prime}_{l+1} $ of length
${\boldsymbol \alpha}^{\prime}_{l+1} $ of length ![]() $n-u_l$ with entries
$n-u_l$ with entries ![]() $\geq u_l+1$. Moreover,
$\geq u_l+1$. Moreover, ![]() ${\boldsymbol \alpha}_1, {\boldsymbol \alpha}_2={\boldsymbol \alpha}^{\prime}_2 -(u_1, \dots, u_1), \dots, {\boldsymbol \alpha}_{l+1}={\boldsymbol \alpha}^{\prime}_{l+1} -(u_l, \dots, u_l)$ are
${\boldsymbol \alpha}_1, {\boldsymbol \alpha}_2={\boldsymbol \alpha}^{\prime}_2 -(u_1, \dots, u_1), \dots, {\boldsymbol \alpha}_{l+1}={\boldsymbol \alpha}^{\prime}_{l+1} -(u_l, \dots, u_l)$ are ![]() $l+1$ parking functions.
$l+1$ parking functions.
Next we show that ![]() ${\boldsymbol \pi}^i=(u_1, \dots, u_{i-1}, u_i+1, u_{i+1}, \dots, u_l, \pi_{l+1}, \dots, \pi_m)$ is not a parking function for any
${\boldsymbol \pi}^i=(u_1, \dots, u_{i-1}, u_i+1, u_{i+1}, \dots, u_l, \pi_{l+1}, \dots, \pi_m)$ is not a parking function for any ![]() $1 \leq i\leq l$. But this is immediate: since the only entries of
$1 \leq i\leq l$. But this is immediate: since the only entries of ![]() ${\boldsymbol \pi}^i$ that are bounded above by
${\boldsymbol \pi}^i$ that are bounded above by ![]() $u_i$ are those from
$u_i$ are those from ![]() ${\boldsymbol \alpha}_1, {\boldsymbol \alpha}^{\prime}_2, \dots, {\boldsymbol \alpha}^{\prime}_i $ and
${\boldsymbol \alpha}_1, {\boldsymbol \alpha}^{\prime}_2, \dots, {\boldsymbol \alpha}^{\prime}_i $ and ![]() $u_1, \dots, u_{i-1}$, we have
$u_1, \dots, u_{i-1}$, we have
a contradiction.
Combining, we have ![]() $A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$.
$A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$.
Theorem 2. Take ![]() $1\leq l \leq m$ any integer. Let
$1\leq l \leq m$ any integer. Let ![]() ${\textbf{v}}=(v_1, \dots, v_l) \in [n]^l$ be in increasing order. The number of parking functions
${\textbf{v}}=(v_1, \dots, v_l) \in [n]^l$ be in increasing order. The number of parking functions ![]() ${\boldsymbol \pi}\in {{PF}}(m, n)$ with
${\boldsymbol \pi}\in {{PF}}(m, n)$ with ![]() $\pi_1=v_1, \dots, \pi_l=v_l$ is
$\pi_1=v_1, \dots, \pi_l=v_l$ is
 \begin{equation}(n-m+1) \sum_{{\textbf{s}} \in S_l({\textbf{v}})} \binom{m-l}{{\textbf{s}}} (s_1+1+n-m)^{s_1-1}\prod_{i=2}^{l+1} (s_i+1)^{s_i-1},\end{equation}
\begin{equation}(n-m+1) \sum_{{\textbf{s}} \in S_l({\textbf{v}})} \binom{m-l}{{\textbf{s}}} (s_1+1+n-m)^{s_1-1}\prod_{i=2}^{l+1} (s_i+1)^{s_i-1},\end{equation}
where
Note that this quantity stays constant if all ![]() $v_i \leq n-m+i$ and decreases as each
$v_i \leq n-m+i$ and decreases as each ![]() $v_i$ increases past
$v_i$ increases past ![]() $n-m+i$, as there are fewer resulting summands.
$n-m+i$, as there are fewer resulting summands.
Proof. If ![]() $\pi_i=v_i$ for
$\pi_i=v_i$ for ![]() $1\leq i\leq l$, then
$1\leq i\leq l$, then ![]() $A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$ where
$A_{\pi_{l+1}, \dots, \pi_m}=[{\textbf{u}}]$ where ![]() $u_i\geq \max\!(v_i, n-m+i)$. Thus, from Theorem 1, the number of parking functions with
$u_i\geq \max\!(v_i, n-m+i)$. Thus, from Theorem 1, the number of parking functions with ![]() $\pi_1=v_1, \dots, \pi_l=v_l$ is
$\pi_1=v_1, \dots, \pi_l=v_l$ is
 \begin{align}&\sum_{u_i=\max\!(v_i, n-m+i) \quad \forall i\in [l]}^{n-l+i} \binom{m-l}{{\textbf{s}}} |{\text{PF}}(m-n+u_1-1, u_1-1)| \cdot \notag \\
& \cdot \prod_{i=2}^l |{\text{PF}}(u_i-u_{i-1}-1, u_i-u_{i-1}-1)||{\text{PF}}(n-u_l, n-u_l)| \notag \\
&=\sum_{u_i=\max\!(v_i, n-m+i) \quad \forall i\in [l]}^{n-l+i} \binom{m-l}{{\textbf{s}}} (n-m+1) u_1^{m-n+u_1-2}\nonumber\\
& \qquad \prod_{i=2}^l (u_i-u_{i-1})^{u_i-u_{i-1}-2}(n-u_l+1)^{n-u_l-1} \notag \\
&=(n-m+1) \sum_{{\textbf{s}} \in S_l({\textbf{v}})} \binom{m-l}{{\textbf{s}}} (s_1+1+n-m)^{s_1-1}\prod_{i=2}^{l+1} (s_i+1)^{s_i-1}, \end{align}
\begin{align}&\sum_{u_i=\max\!(v_i, n-m+i) \quad \forall i\in [l]}^{n-l+i} \binom{m-l}{{\textbf{s}}} |{\text{PF}}(m-n+u_1-1, u_1-1)| \cdot \notag \\
& \cdot \prod_{i=2}^l |{\text{PF}}(u_i-u_{i-1}-1, u_i-u_{i-1}-1)||{\text{PF}}(n-u_l, n-u_l)| \notag \\
&=\sum_{u_i=\max\!(v_i, n-m+i) \quad \forall i\in [l]}^{n-l+i} \binom{m-l}{{\textbf{s}}} (n-m+1) u_1^{m-n+u_1-2}\nonumber\\
& \qquad \prod_{i=2}^l (u_i-u_{i-1})^{u_i-u_{i-1}-2}(n-u_l+1)^{n-u_l-1} \notag \\
&=(n-m+1) \sum_{{\textbf{s}} \in S_l({\textbf{v}})} \binom{m-l}{{\textbf{s}}} (s_1+1+n-m)^{s_1-1}\prod_{i=2}^{l+1} (s_i+1)^{s_i-1}, \end{align}
where ![]() ${\textbf{s}}=(m-n+u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
${\textbf{s}}=(m-n+u_1-1, u_2-u_1-1, \dots, u_l-u_{l-1}-1, n-u_l)$.
For the special case ![]() $l=0$ and
$l=0$ and ![]() ${\textbf{v}}=()$ (where no parking preferences are specified), we recover the total number of parking functions
${\textbf{v}}=()$ (where no parking preferences are specified), we recover the total number of parking functions ![]() $|{\text{PF}}(m, n)|=(n-m+1)(n+1)^{m-1}$. We describe an alternative characterization of this number in the following.
$|{\text{PF}}(m, n)|=(n-m+1)(n+1)^{m-1}$. We describe an alternative characterization of this number in the following.
Proposition 1. The number of parking functions ![]() $|{{PF}}(m, n)|$ satisfies
$|{{PF}}(m, n)|$ satisfies
 \begin{equation}|{{PF}}(m, n)|=\sum_{{\textbf{s}} \models m} \binom{m}{{\textbf{s}}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1},\end{equation}
\begin{equation}|{{PF}}(m, n)|=\sum_{{\textbf{s}} \models m} \binom{m}{{\textbf{s}}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1},\end{equation}
where ![]() ${\textbf{s}}=(s_1, \dots, s_{n-m+1})$ is a composition of m.
${\textbf{s}}=(s_1, \dots, s_{n-m+1})$ is a composition of m.
Proof. For a parking function ![]() ${\boldsymbol \pi}\in {\text{PF}}(m, n)$, there are
${\boldsymbol \pi}\in {\text{PF}}(m, n)$, there are ![]() $n-m$ parking spots that are never attempted by any car. Let
$n-m$ parking spots that are never attempted by any car. Let ![]() $k_i({\boldsymbol \pi})$ for
$k_i({\boldsymbol \pi})$ for ![]() $i=1, \dots, n-m$ represent these spots, so that
$i=1, \dots, n-m$ represent these spots, so that ![]() $0\,:\!=\,k_0<k_1<\cdots<k_{n-m}<k_{n-m+1}\,:\!=\,n+1$. This separates
$0\,:\!=\,k_0<k_1<\cdots<k_{n-m}<k_{n-m+1}\,:\!=\,n+1$. This separates ![]() ${\boldsymbol \pi}$ into
${\boldsymbol \pi}$ into ![]() $n-m+1$ disjoint non-interacting segments (some segments might be empty), with each segment a classical parking function of length
$n-m+1$ disjoint non-interacting segments (some segments might be empty), with each segment a classical parking function of length ![]() $(k_{i}-k_{i-1}-1)$ after translation. We have
$(k_{i}-k_{i-1}-1)$ after translation. We have
 \begin{align}&|{\text{PF}}(m, n)|=\sum_{k} \prod_{i=1}^{n-m+1} (k_{i}-k_{i-1})^{k_{i}-k_{i-1}-2} \binom{m}{k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1} \notag \\&=\sum_{{\textbf{s}} \models m} \binom{m}{s_1, \dots, s_{n-m+1}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1},\end{align}
\begin{align}&|{\text{PF}}(m, n)|=\sum_{k} \prod_{i=1}^{n-m+1} (k_{i}-k_{i-1})^{k_{i}-k_{i-1}-2} \binom{m}{k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1} \notag \\&=\sum_{{\textbf{s}} \models m} \binom{m}{s_1, \dots, s_{n-m+1}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1},\end{align}
where ![]() ${\textbf{s}}=(k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1)$ and
${\textbf{s}}=(k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1)$ and ![]() $\sum_{i=1}^{n-m+1} s_i=m$.
$\sum_{i=1}^{n-m+1} s_i=m$.
Building upon Theorem 2 and Proposition 1, we specialize to the case where the specified parking preferences of the first l cars form a contiguous block.
Proposition 2. Take ![]() $1\leq l \leq m$ any integer. Let
$1\leq l \leq m$ any integer. Let ![]() $1\leq k\leq n-l+1$. The number of parking functions
$1\leq k\leq n-l+1$. The number of parking functions ![]() ${\boldsymbol \pi}\in {{PF}}(m, n)$ with
${\boldsymbol \pi}\in {{PF}}(m, n)$ with ![]() $\pi_1=k, \dots, \pi_l=k+l-1$ is
$\pi_1=k, \dots, \pi_l=k+l-1$ is
 \begin{equation}(n-m+1) \sum_{s=0}^{\min\!(n-k-l+1, m-l)}\binom{m-l}{s} (n-s+1-l)^{m-s-l-1} l (s+l)^{s-1}.\end{equation}
\begin{equation}(n-m+1) \sum_{s=0}^{\min\!(n-k-l+1, m-l)}\binom{m-l}{s} (n-s+1-l)^{m-s-l-1} l (s+l)^{s-1}.\end{equation}
Note that this quantity stays constant for ![]() $k\leq n-m+1$ and decreases as k increases past
$k\leq n-m+1$ and decreases as k increases past ![]() $n-m+1$, as there are fewer resulting summands.
$n-m+1$, as there are fewer resulting summands.
Proof. We take ![]() $v_i=k+i-1$ for
$v_i=k+i-1$ for ![]() $1\leq i\leq l$ in Theorem 2 and extract
$1\leq i\leq l$ in Theorem 2 and extract ![]() $s_1$ from the multinomial coefficient
$s_1$ from the multinomial coefficient ![]() $\binom{m-l}{{\textbf{s}}}$:
$\binom{m-l}{{\textbf{s}}}$:
 \begin{multline}(n-m+1) \sum_{s_1=\max\!(0, m-n+k-1)}^{m-l} \binom{m-l}{s_1} (s_1+1+n-m)^{s_1-1} \cdot \\ \cdot \sum_{(s_2, \dots, s_{l+1}) \models m-l-s_1} \binom{m-l-s_1}{s_2, \dots, s_{l+1}} \prod_{i=2}^{l+1} (s_i+1)^{s_i-1}.\end{multline}
\begin{multline}(n-m+1) \sum_{s_1=\max\!(0, m-n+k-1)}^{m-l} \binom{m-l}{s_1} (s_1+1+n-m)^{s_1-1} \cdot \\ \cdot \sum_{(s_2, \dots, s_{l+1}) \models m-l-s_1} \binom{m-l-s_1}{s_2, \dots, s_{l+1}} \prod_{i=2}^{l+1} (s_i+1)^{s_i-1}.\end{multline}
Using Proposition 1 and simplifying, we find that this becomes
 \begin{align}&(n-m+1) \sum_{s_1=\max\!(0, m-n+k-1)}^{m-l} \binom{m-l}{s_1} (s_1+1+n-m)^{s_1-1} |{\text{PF}}(m-l-s_1, m-1-s_1)| \notag \\&=(n-m+1) \sum_{s_1=\max\!(0, m-n+k-1)}^{m-l} \binom{m-l}{s_1} (s_1+1+n-m)^{s_1-1} l (m-s_1)^{m-l-s_1-1} \notag \\&=(n-m+1) \sum_{s=0}^{\min\!(n-k-l+1, m-l)} \binom{m-l}{s} (n-s+1-l)^{m-s-l-1} l (s+l)^{s-1},\end{align}
\begin{align}&(n-m+1) \sum_{s_1=\max\!(0, m-n+k-1)}^{m-l} \binom{m-l}{s_1} (s_1+1+n-m)^{s_1-1} |{\text{PF}}(m-l-s_1, m-1-s_1)| \notag \\&=(n-m+1) \sum_{s_1=\max\!(0, m-n+k-1)}^{m-l} \binom{m-l}{s_1} (s_1+1+n-m)^{s_1-1} l (m-s_1)^{m-l-s_1-1} \notag \\&=(n-m+1) \sum_{s=0}^{\min\!(n-k-l+1, m-l)} \binom{m-l}{s} (n-s+1-l)^{m-s-l-1} l (s+l)^{s-1},\end{align}
where the last equality comes from a change of variables ![]() $s=m-l-s_1$.
$s=m-l-s_1$.
If we sum over all possible contiguous blocks that the first l cars may occupy, the result simplifies nicely.
Proposition 3. Take ![]() $1\leq l \leq m$ any integer. Then
$1\leq l \leq m$ any integer. Then
 \begin{equation}\sum_{k=1}^{n-l+1} \#\{{\boldsymbol \pi}\in {{PF}}(m, n)\,:\, \pi_1=k, \dots, \pi_l=k+l-1\}=(n-m+1)(n+1)^{m-l}.\end{equation}
\begin{equation}\sum_{k=1}^{n-l+1} \#\{{\boldsymbol \pi}\in {{PF}}(m, n)\,:\, \pi_1=k, \dots, \pi_l=k+l-1\}=(n-m+1)(n+1)^{m-l}.\end{equation}
Proof. The proof relies on an extension of Pollak’s circle argument [Reference Foata and Riordan10]. Add an additional space ![]() $n+1$, and arrange the spaces in a circle. Allow
$n+1$, and arrange the spaces in a circle. Allow ![]() $n+1$ also to be a preferred space. We first select a contiguous block of length l for the first l cars, which can be done in
$n+1$ also to be a preferred space. We first select a contiguous block of length l for the first l cars, which can be done in ![]() $n+1$ ways. Then, for the remaining
$n+1$ ways. Then, for the remaining ![]() $m-l$ cars, there are
$m-l$ cars, there are ![]() $(n+1)^{m-l}$ possible preference sequences. Note that
$(n+1)^{m-l}$ possible preference sequences. Note that ![]() ${\boldsymbol \pi}$ is a parking function if and only if the spot
${\boldsymbol \pi}$ is a parking function if and only if the spot ![]() $n+1$ is left open. For
$n+1$ is left open. For ![]() $j \in \mathbb{Z}/(n+1)\mathbb{Z}$, the preference sequence
$j \in \mathbb{Z}/(n+1)\mathbb{Z}$, the preference sequence ![]() $\pi+j(1, \dots, 1)$ (modulo
$\pi+j(1, \dots, 1)$ (modulo ![]() $n+1$) gives an assignment whose missing spaces are the rotations by j of the missing spaces for the assignment of
$n+1$) gives an assignment whose missing spaces are the rotations by j of the missing spaces for the assignment of ![]() ${\boldsymbol \pi}$. Since there are
${\boldsymbol \pi}$. Since there are ![]() $n-m+1$ missing spaces for the assignment of any preference sequence, any preference sequence
$n-m+1$ missing spaces for the assignment of any preference sequence, any preference sequence ![]() ${\boldsymbol \pi}$ has
${\boldsymbol \pi}$ has ![]() $n-m+1$ rotations which are parking functions. Therefore
$n-m+1$ rotations which are parking functions. Therefore
 \begin{align}\sum_{k=1}^{n-l+1} \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=k, \dots, \pi_l=k+l-1\}&=\frac{n-m+1}{n+1}(n+1)(n+1)^{m-l}\notag\\&=(n-m+1)(n+1)^{m-l}.\end{align}
\begin{align}\sum_{k=1}^{n-l+1} \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=k, \dots, \pi_l=k+l-1\}&=\frac{n-m+1}{n+1}(n+1)(n+1)^{m-l}\notag\\&=(n-m+1)(n+1)^{m-l}.\end{align}
For the special case ![]() $l=1$, Proposition 3 reduces to the decomposition of parking functions
$l=1$, Proposition 3 reduces to the decomposition of parking functions ![]() ${\text{PF}}(m, n)$ according to the parking preference of the first car
${\text{PF}}(m, n)$ according to the parking preference of the first car ![]() $\pi_1$.
$\pi_1$.
2.1. Connections with Pitman–Stanley polytopes
Denote the set of ![]() ${\textbf{u}}$-parking functions by
${\textbf{u}}$-parking functions by ![]() ${\text{PF}}({\textbf{u}})$. The following propositions are direct consequences of the parking criterion (1.1) and are equivalent in nature. See the beginning of Section 2 for more explanation.
${\text{PF}}({\textbf{u}})$. The following propositions are direct consequences of the parking criterion (1.1) and are equivalent in nature. See the beginning of Section 2 for more explanation.
Proposition 4. Take ![]() $1\leq l\leq m$ any integer. Let
$1\leq l\leq m$ any integer. Let ![]() ${\textbf{v}}=(v_1, \dots, v_l) \in [n]^l$ be in increasing order. Then
${\textbf{v}}=(v_1, \dots, v_l) \in [n]^l$ be in increasing order. Then ![]() ${\boldsymbol \pi}=(v_1, \dots, v_l, \pi_{l+1}, \dots, \pi_{m}) \in {{PF}}(m, n)$ if and only if
${\boldsymbol \pi}=(v_1, \dots, v_l, \pi_{l+1}, \dots, \pi_{m}) \in {{PF}}(m, n)$ if and only if ![]() $(\pi_{l+1}, \dots, \pi_{m}) \in {{PF}}({\textbf{u}})$, where the
$(\pi_{l+1}, \dots, \pi_{m}) \in {{PF}}({\textbf{u}})$, where the ![]() $u_i$ are the largest
$u_i$ are the largest ![]() $m-l$ numbers in
$m-l$ numbers in ![]() , arranged in increasing order.
, arranged in increasing order.
Proposition 5. Let ![]() ${\textbf{u}}=(u_1, \dots, u_m)$ be a positive-integer-valued vector with
${\textbf{u}}=(u_1, \dots, u_m)$ be a positive-integer-valued vector with ![]() $u_1 < \cdots < u_m$. Let
$u_1 < \cdots < u_m$. Let ![]() , arranged in increasing order. Then
, arranged in increasing order. Then ![]() ${\boldsymbol \pi}=(v_1, \dots, v_l, \pi_1, \dots, \pi_m) \in {{PF}}(u_m-u_1+1, u_m)$ if and only if
${\boldsymbol \pi}=(v_1, \dots, v_l, \pi_1, \dots, \pi_m) \in {{PF}}(u_m-u_1+1, u_m)$ if and only if ![]() $(\pi_1, \dots, \pi_m) \in {{PF}}({\textbf{u}})$.
$(\pi_1, \dots, \pi_m) \in {{PF}}({\textbf{u}})$.
Knowledge about ![]() ${\text{PF}}({\textbf{u}})$ thus yields knowledge about
${\text{PF}}({\textbf{u}})$ thus yields knowledge about ![]() ${\text{PF}}(m, n)$ where the first l cars have specified parking preferences, with l depending on the gaps in
${\text{PF}}(m, n)$ where the first l cars have specified parking preferences, with l depending on the gaps in ![]() ${\textbf{u}}$, and vice versa. In [Reference Pitman and Stanley16], Pitman and Stanley introduced an m-dimensional polytope
${\textbf{u}}$, and vice versa. In [Reference Pitman and Stanley16], Pitman and Stanley introduced an m-dimensional polytope ![]() $\Pi_m$ and related the number of
$\Pi_m$ and related the number of ![]() ${\textbf{u}}$-parking functions to the volume polynomial of
${\textbf{u}}$-parking functions to the volume polynomial of ![]() $\Pi_m$. Let
$\Pi_m$. Let ![]() ${\textbf{x}}=(x_1, \dots, x_m)$ with
${\textbf{x}}=(x_1, \dots, x_m)$ with ![]() $x_i>0$ for all i. Let
$x_i>0$ for all i. Let
The m-dimensional volume ![]() $V_m({\textbf{x}})=\text{Vol}(\Pi_m({\textbf{x}}))$ is a homogeneous polynomial of degree m in the variables
$V_m({\textbf{x}})=\text{Vol}(\Pi_m({\textbf{x}}))$ is a homogeneous polynomial of degree m in the variables ![]() $x_1, \dots, x_m$, and is called the volume polynomial of the Pitman–Stanley polytope. The definition of volume may be extended to when some of the
$x_1, \dots, x_m$, and is called the volume polynomial of the Pitman–Stanley polytope. The definition of volume may be extended to when some of the ![]() $x_i$ equal zero for
$x_i$ equal zero for ![]() $2\leq i\leq m$. Trivially, we take
$2\leq i\leq m$. Trivially, we take ![]() $V_m({\textbf{x}})=0$ if
$V_m({\textbf{x}})=0$ if ![]() $x_1=0$.
$x_1=0$.
Theorem 3. (Adapted from Pitman and Stanley [Reference Pitman and Stanley16].) Take ![]() $m\geq 1$ any integer. Let
$m\geq 1$ any integer. Let ![]() ${\textbf{u}}=(u_1, \dots, u_m) \in \mathbb{N}^m$ with
${\textbf{u}}=(u_1, \dots, u_m) \in \mathbb{N}^m$ with ![]() $u_1 \leq \cdots \leq u_m$. Let
$u_1 \leq \cdots \leq u_m$. Let ![]() ${\textbf{x}}=\Delta {\textbf{u}}=(u_1, u_2-u_1, \dots, u_m-u_{m-1}) \in \mathbb{N}^m$. The number of
${\textbf{x}}=\Delta {\textbf{u}}=(u_1, u_2-u_1, \dots, u_m-u_{m-1}) \in \mathbb{N}^m$. The number of ![]() ${\textbf{u}}$-parking functions
${\textbf{u}}$-parking functions ![]() $|{{PF}}({\textbf{u}})|=m!V_m({\textbf{x}})$, where the volume polynomial
$|{{PF}}({\textbf{u}})|=m!V_m({\textbf{x}})$, where the volume polynomial
 \begin{equation}V_m({\textbf{x}})=\sum_{{\textbf{k}} \in K_m} \prod_{i=1}^m \frac{x_i^{k_i}}{k_i!}=\frac{1}{m!} \sum_{{\textbf{k}} \in K_m} \binom{m}{k_1, \dots, k_m} x_1^{k_1} \dots x_m^{k_m},\end{equation}
\begin{equation}V_m({\textbf{x}})=\sum_{{\textbf{k}} \in K_m} \prod_{i=1}^m \frac{x_i^{k_i}}{k_i!}=\frac{1}{m!} \sum_{{\textbf{k}} \in K_m} \binom{m}{k_1, \dots, k_m} x_1^{k_1} \dots x_m^{k_m},\end{equation}
and ![]() $K_m$ is the set of balanced vectors of length m, i.e.
$K_m$ is the set of balanced vectors of length m, i.e.
Though the index set and summation formula in Theorem 3 resemble those of Theorem 2, we will show via an example that they are not parallel interpretations for parking functions, but rather are complementary to each other.
Example 3. Take ![]() $m=4$,
$m=4$, ![]() $n=5$,
$n=5$, ![]() ${\textbf{u}}=(2, 5)$,
${\textbf{u}}=(2, 5)$, ![]() ${\textbf{v}}=(3, 4)$, and
${\textbf{v}}=(3, 4)$, and ![]() ${\textbf{x}}=\Delta {\textbf{u}}=(2, 3)$. Then by Propositions 4 and 5,
${\textbf{x}}=\Delta {\textbf{u}}=(2, 3)$. Then by Propositions 4 and 5, ![]() $(v_1, v_2, \pi_1, \pi_2) \in {\text{PF}}(4, 5)$ and
$(v_1, v_2, \pi_1, \pi_2) \in {\text{PF}}(4, 5)$ and ![]() $(\pi_1, \pi_2) \in {\text{PF}}({\textbf{u}})$ both satisfy
$(\pi_1, \pi_2) \in {\text{PF}}({\textbf{u}})$ both satisfy
From Theorem 2,
From Theorem 3,
We see that neither of the compositions of ![]() $|A|$ refines the other.
$|A|$ refines the other.
3. Properties of random parking functions
In this section we use the multi-shuffle construction introduced in Section 2 to investigate various properties of a parking function chosen uniformly at random from ![]() ${\text{PF}}(m, n)$. Sections 3.1 through 3.4 discuss the generic situation
${\text{PF}}(m, n)$. Sections 3.1 through 3.4 discuss the generic situation ![]() $m \lesssim n$, with Section 3.1 focusing on mixed moments of multiple coordinates and Sections 3.2 through 3.4 focusing on covariances. Section 3.5 discusses the special situation
$m \lesssim n$, with Section 3.1 focusing on mixed moments of multiple coordinates and Sections 3.2 through 3.4 focusing on covariances. Section 3.5 discusses the special situation ![]() $m=n$. We will write our results in terms of coordinates
$m=n$. We will write our results in terms of coordinates ![]() $\pi_1, \dots, \pi_l$ of parking functions, where
$\pi_1, \dots, \pi_l$ of parking functions, where ![]() $1\leq l\leq m$ is any integer, and unattempted parking spots, which we denote by
$1\leq l\leq m$ is any integer, and unattempted parking spots, which we denote by ![]() $k_i({\boldsymbol \pi})$ for
$k_i({\boldsymbol \pi})$ for ![]() $i=1, \dots, n-m$. The parking coordinates satisfy permutation symmetry while the unattempted parking spots do not, so the statements in this section may be interpreted for any coordinates but are specific to the unattempted spots.
$i=1, \dots, n-m$. The parking coordinates satisfy permutation symmetry while the unattempted parking spots do not, so the statements in this section may be interpreted for any coordinates but are specific to the unattempted spots.
3.1. Mixed moments of multiple coordinates
We begin with an asymptotic result for the mixed moments of two coordinates.
Theorem 4. Take ![]() $p,q \geq 1$ any integer. Take m and n large with
$p,q \geq 1$ any integer. Take m and n large with ![]() $m=cn$ for some
$m=cn$ for some ![]() $0<c<1$. For a parking function
$0<c<1$. For a parking function ![]() ${\boldsymbol \pi}$ chosen uniformly at random from
${\boldsymbol \pi}$ chosen uniformly at random from ![]() ${{PF}}(m, n)$, we have
${{PF}}(m, n)$, we have
and
The proof of Theorem 4 will utilize the following lemma.
Lemma 1. Take ![]() $l \geq 1$ any integer and n large. For
$l \geq 1$ any integer and n large. For ![]() $1\leq i\leq l$, take
$1\leq i\leq l$, take ![]() $p_i \geq 1$ any integer and
$p_i \geq 1$ any integer and ![]() $a_i \sim n$ with
$a_i \sim n$ with ![]() $a_1<\cdots<a_l$. Then
$a_1<\cdots<a_l$. Then
 \begin{align}\sum_{\substack{\#\{i\,:\, \pi_i \leq a_k\} \geq k \\ \forall k \in [l]}} \prod_{i=1}^l \pi_i^{p_i}=\frac{a_l^{\sum_{i=1}^l p_i+l}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}\right)+O\!\left(\frac{1}{n^2}\right)\right).\end{align}
\begin{align}\sum_{\substack{\#\{i\,:\, \pi_i \leq a_k\} \geq k \\ \forall k \in [l]}} \prod_{i=1}^l \pi_i^{p_i}=\frac{a_l^{\sum_{i=1}^l p_i+l}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}\right)+O\!\left(\frac{1}{n^2}\right)\right).\end{align}
Proof. Notice that the left side of (3.3) may be alternatively computed in stages.
Stage 1: We sum up ![]() $\prod_{i=1}^l \pi_i^{p_i}$, where the
$\prod_{i=1}^l \pi_i^{p_i}$, where the ![]() $\pi_i$ all range from 1 to
$\pi_i$ all range from 1 to ![]() $a_l$.
$a_l$.
Stage 2: We subtract the sum of ![]() $\prod_{i=1}^l \pi_i^{p_i}$, where the
$\prod_{i=1}^l \pi_i^{p_i}$, where the ![]() $\pi_i$ all range from
$\pi_i$ all range from ![]() $a_1+1$ to
$a_1+1$ to ![]() $a_l$ (so none of the
$a_l$ (so none of the ![]() $\pi_i$ is
$\pi_i$ is ![]() $\leq a_1$).
$\leq a_1$).
Stage 3: We subtract the sum of ![]() $\prod_{i=1}^l \pi_i^{p_i}$, where one of the
$\prod_{i=1}^l \pi_i^{p_i}$, where one of the ![]() $\pi_i$ ranges from 1 to
$\pi_i$ ranges from 1 to ![]() $a_1$, while the others all range from
$a_1$, while the others all range from ![]() $a_2+1$ to
$a_2+1$ to ![]() $a_l$ (so only one of the
$a_l$ (so only one of the ![]() $\pi_i$ is
$\pi_i$ is ![]() $\leq a_2$).
$\leq a_2$).
![]() $\vdots$
$\vdots$
Stage l: We subtract the sum of ![]() $\prod_{i=1}^l \pi_i^{p_i}$, where one of the
$\prod_{i=1}^l \pi_i^{p_i}$, where one of the ![]() $\pi_i$ ranges from 1 to
$\pi_i$ ranges from 1 to ![]() $a_1$, one ranges from 1 to
$a_1$, one ranges from 1 to ![]() $a_2$,
$a_2$, ![]() $\dots$, one ranges from 1 to
$\dots$, one ranges from 1 to ![]() $a_{l-2}$, and the two remaining
$a_{l-2}$, and the two remaining ![]() $\pi_i$ both range from
$\pi_i$ both range from ![]() $a_{l-1}+1$ to
$a_{l-1}+1$ to ![]() $a_l$ (so only
$a_l$ (so only ![]() $l-2$ of the
$l-2$ of the ![]() $\pi_i$ are
$\pi_i$ are ![]() $\leq a_{l-1}$).
$\leq a_{l-1}$).
For illustration, we perform this alternative procedure when ![]() $l=3$:
$l=3$:
 \begin{align}&\sum_{\pi_1=1}^{a_3} \sum_{\pi_2=1}^{a_3} \sum_{\pi_3=1}^{a_3} \pi_1^{p_1}\pi_2^{p_2}\pi_3^{p_3}-\sum_{\pi_1=a_1+1}^{a_3} \sum_{\pi_2=a_1+1}^{a_3} \sum_{\pi_3=a_1+1}^{a_3} \pi_1^{p_1}\pi_2^{p_2}\pi_3^{p_3}\notag \\
&-\left(\sum_{\pi_1=1}^{a_1} \pi_1^{p_1} \sum_{\pi_2=a_2+1}^{a_3} \sum_{\pi_3=a_2+1}^{a_3} \pi_2^{p_2} \pi_3^{p_3}+\sum_{\pi_2=1}^{a_1} \pi_2^{p_2} \sum_{\pi_1=a_2+1}^{a_3} \sum_{\pi_3=a_2+1}^{a_3} \pi_1^{p_1} \pi_3^{p_3}\right.\notag \\
&\qquad\qquad\qquad \left.+\sum_{\pi_3=1}^{a_1} \pi_3^{p_3} \sum_{\pi_1=a_2+1}^{a_3} \sum_{\pi_2=a_2+1}^{a_3} \pi_1^{p_1} \pi_2^{p_2}\right).\end{align}
\begin{align}&\sum_{\pi_1=1}^{a_3} \sum_{\pi_2=1}^{a_3} \sum_{\pi_3=1}^{a_3} \pi_1^{p_1}\pi_2^{p_2}\pi_3^{p_3}-\sum_{\pi_1=a_1+1}^{a_3} \sum_{\pi_2=a_1+1}^{a_3} \sum_{\pi_3=a_1+1}^{a_3} \pi_1^{p_1}\pi_2^{p_2}\pi_3^{p_3}\notag \\
&-\left(\sum_{\pi_1=1}^{a_1} \pi_1^{p_1} \sum_{\pi_2=a_2+1}^{a_3} \sum_{\pi_3=a_2+1}^{a_3} \pi_2^{p_2} \pi_3^{p_3}+\sum_{\pi_2=1}^{a_1} \pi_2^{p_2} \sum_{\pi_1=a_2+1}^{a_3} \sum_{\pi_3=a_2+1}^{a_3} \pi_1^{p_1} \pi_3^{p_3}\right.\notag \\
&\qquad\qquad\qquad \left.+\sum_{\pi_3=1}^{a_1} \pi_3^{p_3} \sum_{\pi_1=a_2+1}^{a_3} \sum_{\pi_2=a_2+1}^{a_3} \pi_1^{p_1} \pi_2^{p_2}\right).\end{align}
Since ![]() $a_i \sim n$, the sums subtracted in Stages 2 through l are all of lower order than the sum in Stage 1. The conclusion then follows from standard asymptotic analysis on the leading-order term.
$a_i \sim n$, the sums subtracted in Stages 2 through l are all of lower order than the sum in Stage 1. The conclusion then follows from standard asymptotic analysis on the leading-order term.
Proof of Theorem 4. We convert the parking preferences of the first two cars to an equivalent increasing order:
 \begin{multline}\sum_{j=1}^n \sum_{k=1}^n j^p k^q \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=k\}=\sum_{j=1}^{n-1} j^{p+q} \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=j+1\}\\+\sum_{j=1}^{n-1} \sum_{k=j+1}^n \big(j^p k^q+j^qk^p\big) \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=k\}.\end{multline}
\begin{multline}\sum_{j=1}^n \sum_{k=1}^n j^p k^q \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=k\}=\sum_{j=1}^{n-1} j^{p+q} \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=j+1\}\\+\sum_{j=1}^{n-1} \sum_{k=j+1}^n \big(j^p k^q+j^qk^p\big) \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=k\}.\end{multline}
By Theorem 2, the second term of (3.5) is
 \begin{align}&(n-m+1) \sum_{j=1}^{n-1} \sum_{k=j+1}^n \big(j^p k^q+j^qk^p\big) \sum_{s_1=\max\!(0, m-n+j-1)}^{m-2} \sum_{s_2=\max\!(0, m-n+k-2-s_1)}^{m-2-s_1}\notag\\
& \binom{m-2}{s_1, s_2, m-2-s_1-s_2} (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1}\notag \\
&=(n-m+1) \sum_{s_1=0}^{m-2} \sum_{s_2=0}^{m-2-s_1} \binom{m-2}{s_1, s_2, m-2-s_1-s_2} (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} \cdot \notag \\
&\quad \cdot (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1} \sum_{j=1}^{n-m+1+s_1} \sum_{k=j+1}^{n-m+2+s_1+s_2} \big(j^p k^q+j^qk^p\big).\end{align}
\begin{align}&(n-m+1) \sum_{j=1}^{n-1} \sum_{k=j+1}^n \big(j^p k^q+j^qk^p\big) \sum_{s_1=\max\!(0, m-n+j-1)}^{m-2} \sum_{s_2=\max\!(0, m-n+k-2-s_1)}^{m-2-s_1}\notag\\
& \binom{m-2}{s_1, s_2, m-2-s_1-s_2} (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1}\notag \\
&=(n-m+1) \sum_{s_1=0}^{m-2} \sum_{s_2=0}^{m-2-s_1} \binom{m-2}{s_1, s_2, m-2-s_1-s_2} (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} \cdot \notag \\
&\quad \cdot (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1} \sum_{j=1}^{n-m+1+s_1} \sum_{k=j+1}^{n-m+2+s_1+s_2} \big(j^p k^q+j^qk^p\big).\end{align}
We make a change of variables: ![]() $s=s_2$ and
$s=s_2$ and ![]() $t=m-2-s_1-s_2$. Then (3.6) becomes
$t=m-2-s_1-s_2$. Then (3.6) becomes
 \begin{align}&(n-m+1) \sum_{s=0}^{m-2} \sum_{t=0}^{m-2-s} \binom{m-2}{s, t, m-2-s-t} (n-1-s-t)^{m-3-s-t} \cdot \notag \\&\quad \cdot (s+1)^{s-1}(t+1)^{t-1} \sum_{j=1}^{n-1-s-t} \sum_{k=j+1}^{n-t} \big(j^p k^q+j^qk^p\big).\end{align}
\begin{align}&(n-m+1) \sum_{s=0}^{m-2} \sum_{t=0}^{m-2-s} \binom{m-2}{s, t, m-2-s-t} (n-1-s-t)^{m-3-s-t} \cdot \notag \\&\quad \cdot (s+1)^{s-1}(t+1)^{t-1} \sum_{j=1}^{n-1-s-t} \sum_{k=j+1}^{n-t} \big(j^p k^q+j^qk^p\big).\end{align}
Similarly, by Proposition 2, the first term of (3.5) is
 \begin{align}&(n-m+1) \sum_{j=1}^{n-1} j^{p+q} \sum_{s_1=\max\!(0, m-n+j-1)}^{m-2} \sum_{s_2=0}^{m-2-s_1} \binom{m-2}{s_1, s_2, m-2-s_1-s_2} \cdot \notag \\&\quad \cdot (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1}\notag \\&=(n-m+1) \sum_{s_1=0}^{m-2} \sum_{s_2=0}^{m-2-s_1} \binom{m-2}{s_1, s_2, m-2-s_1-s_2} (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} \cdot \notag \\ &\quad \cdot (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1} \sum_{j=1}^{n-m+1+s_1} j^{p+q}.\end{align}
\begin{align}&(n-m+1) \sum_{j=1}^{n-1} j^{p+q} \sum_{s_1=\max\!(0, m-n+j-1)}^{m-2} \sum_{s_2=0}^{m-2-s_1} \binom{m-2}{s_1, s_2, m-2-s_1-s_2} \cdot \notag \\&\quad \cdot (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1}\notag \\&=(n-m+1) \sum_{s_1=0}^{m-2} \sum_{s_2=0}^{m-2-s_1} \binom{m-2}{s_1, s_2, m-2-s_1-s_2} (s_1+1+n-m)^{s_1-1} (s_2+1)^{s_2-1} \cdot \notag \\ &\quad \cdot (m-2-s_1-s_2+1)^{m-2-s_1-s_2-1} \sum_{j=1}^{n-m+1+s_1} j^{p+q}.\end{align}
We make a change of variables: ![]() $s=s_2$ and
$s=s_2$ and ![]() $t=m-2-s_1-s_2$. Then (3.8) becomes
$t=m-2-s_1-s_2$. Then (3.8) becomes
 \begin{align}&(n-m+1) \sum_{s=0}^{m-2} \sum_{t=0}^{m-2-s} \binom{m-2}{s, t, m-2-s-t} (n-1-s-t)^{m-3-s-t} \cdot \notag \\&\quad \cdot (s+1)^{s-1}(t+1)^{t-1} \sum_{j=1}^{n-1-s-t} j^{p+q}.\end{align}
\begin{align}&(n-m+1) \sum_{s=0}^{m-2} \sum_{t=0}^{m-2-s} \binom{m-2}{s, t, m-2-s-t} (n-1-s-t)^{m-3-s-t} \cdot \notag \\&\quad \cdot (s+1)^{s-1}(t+1)^{t-1} \sum_{j=1}^{n-1-s-t} j^{p+q}.\end{align}
Using Lemma 1, for ![]() $p, q \geq 1$, (3.7)+(3.9) is asymptotically
$p, q \geq 1$, (3.7)+(3.9) is asymptotically
 \begin{align}&\frac{n-m+1}{(p+1)(q+1)} \sum_{s=0}^{m-2} \sum_{t=0}^{m-2-s} \frac{m^{s+t}}{s! t!} n^{m-s-t+p+q-1} e^{-c(s+t+1)} (s+1)^{s-1}(t+1)^{t-1} \cdot \notag \\
&\cdot \left(1-\frac{(s+t)(s+t+3)}{2cn}+\frac{(s+t+1)(s+t+3)}{n}-\frac{t(p+q+2)}{n}\right.\notag \\
& \qquad\qquad\qquad \left.-\frac{c(s+t+1)^2}{2n}+\frac{p+q+2}{2n}+O\big(n^{-2}\big)\right).\end{align}
\begin{align}&\frac{n-m+1}{(p+1)(q+1)} \sum_{s=0}^{m-2} \sum_{t=0}^{m-2-s} \frac{m^{s+t}}{s! t!} n^{m-s-t+p+q-1} e^{-c(s+t+1)} (s+1)^{s-1}(t+1)^{t-1} \cdot \notag \\
&\cdot \left(1-\frac{(s+t)(s+t+3)}{2cn}+\frac{(s+t+1)(s+t+3)}{n}-\frac{t(p+q+2)}{n}\right.\notag \\
& \qquad\qquad\qquad \left.-\frac{c(s+t+1)^2}{2n}+\frac{p+q+2}{2n}+O\big(n^{-2}\big)\right).\end{align}
The tree function ![]() $F(z) = \sum_{s=0}^\infty \frac{z^s}{s!}(s+1)^{s-1}$ is related to the Lambert W function via
$F(z) = \sum_{s=0}^\infty \frac{z^s}{s!}(s+1)^{s-1}$ is related to the Lambert W function via ![]() $F(z)=-W(-z)/z$, and satisfies
$F(z)=-W(-z)/z$, and satisfies ![]() $F\big(ce^{-c}\big) = e^c$. By the chain rule its first and second derivatives therefore satisfy
$F\big(ce^{-c}\big) = e^c$. By the chain rule its first and second derivatives therefore satisfy
We recognize that (3.10) is in the form of a Cauchy product, and converges to
 \begin{align}&\frac{n-m+1}{(p+1)(q+1)} n^{m+p+q-1}e^{-c} \sum_{s=0}^{\infty} \sum_{t=0}^{\infty}\frac{\big(ce^{-c}\big)^{s+t}}{s! t!} (s+1)^{s-1} (t+1)^{t-1} \cdot \notag \\& \quad \cdot \left(1+\frac{1}{n} (A+Bs+Ct+Ds^2+Et^2+Fst)+O\big(n^{-2}\big)\right),\end{align}
\begin{align}&\frac{n-m+1}{(p+1)(q+1)} n^{m+p+q-1}e^{-c} \sum_{s=0}^{\infty} \sum_{t=0}^{\infty}\frac{\big(ce^{-c}\big)^{s+t}}{s! t!} (s+1)^{s-1} (t+1)^{t-1} \cdot \notag \\& \quad \cdot \left(1+\frac{1}{n} (A+Bs+Ct+Ds^2+Et^2+Fst)+O\big(n^{-2}\big)\right),\end{align}
where
 \begin{align}A & =-\frac{c}{2}+3+\frac{p+q+2}{2}, \quad B=-c-\frac{3}{2c}+4, \quad C=-c-\frac{3}{2c}-p-q+2,\nonumber\\
D & =-\frac{c}{2}-\frac{1}{2c}+1, \quad E=-\frac{c}{2}-\frac{1}{2c}+1, \quad F=-c-\frac{1}{c}+2.\end{align}
\begin{align}A & =-\frac{c}{2}+3+\frac{p+q+2}{2}, \quad B=-c-\frac{3}{2c}+4, \quad C=-c-\frac{3}{2c}-p-q+2,\nonumber\\
D & =-\frac{c}{2}-\frac{1}{2c}+1, \quad E=-\frac{c}{2}-\frac{1}{2c}+1, \quad F=-c-\frac{1}{c}+2.\end{align}
Using F(z) this can be written as follows (with ![]() $z=ce^{-c}$):
$z=ce^{-c}$):
 \begin{align}&\frac{n-m+1}{(p+1)(q+1)} n^{m+p+q-1} \cdot \notag \\&\cdot \left[F(z)+\frac1n\left(AF(z)+(B+C)zF^{\prime}(z)+(D+E)\big(z^2F^{\prime\prime}(z)+zF^{\prime}(z)\big)+Fz^2 F^{\prime}(z) \frac{F^{\prime}(z)}{F(z)}\right)+O\big(n^{-2}\big)\right].\end{align}
\begin{align}&\frac{n-m+1}{(p+1)(q+1)} n^{m+p+q-1} \cdot \notag \\&\cdot \left[F(z)+\frac1n\left(AF(z)+(B+C)zF^{\prime}(z)+(D+E)\big(z^2F^{\prime\prime}(z)+zF^{\prime}(z)\big)+Fz^2 F^{\prime}(z) \frac{F^{\prime}(z)}{F(z)}\right)+O\big(n^{-2}\big)\right].\end{align}
Dividing by ![]() $|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
$|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
for the generic (p, q)th mixed moment.
For the special case ![]() $p\geq 1$ and
$p\geq 1$ and ![]() $q=0$, a similar asymptotic calculation gives the pth moment as
$q=0$, a similar asymptotic calculation gives the pth moment as
Extending the asymptotic expansion approach in the proof of Theorem 4, we have the following more general result.
Theorem 5. Take ![]() $l\geq 1$ any integer. For
$l\geq 1$ any integer. For ![]() $1\leq i\leq l$, take
$1\leq i\leq l$, take ![]() $p_i \geq 1$ any integer. Take m and n large with
$p_i \geq 1$ any integer. Take m and n large with ![]() $m=cn$ for some
$m=cn$ for some ![]() $0<c<1$. For a parking function
$0<c<1$. For a parking function ![]() ${\boldsymbol \pi}$ chosen uniformly at random from
${\boldsymbol \pi}$ chosen uniformly at random from ![]() ${{PF}}(m, n)$, we have
${{PF}}(m, n)$, we have
 \begin{equation}{\mathbb E}\!\left(\prod_{i=1}^l \pi_i^{p_i}\right)=\frac{n^{\sum_{i=1}^l p_i}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}-\frac{c\sum_{i=1}^l p_i}{1-c}\right)+O\!\left(\frac{1}{n^2}\right)\right).\end{equation}
\begin{equation}{\mathbb E}\!\left(\prod_{i=1}^l \pi_i^{p_i}\right)=\frac{n^{\sum_{i=1}^l p_i}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}-\frac{c\sum_{i=1}^l p_i}{1-c}\right)+O\!\left(\frac{1}{n^2}\right)\right).\end{equation}
Proof. We will not include all technical details as in the ![]() $l=1, 2$ case, but point out some key facts. As in the proof of Theorem 4, using Theorem 2 and Proposition 2 and interchanging the order of summation, we have
$l=1, 2$ case, but point out some key facts. As in the proof of Theorem 4, using Theorem 2 and Proposition 2 and interchanging the order of summation, we have
 \begin{align}&\sum \!\left(\prod_{i=1}^l \pi_i^{p_i}\right) \{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_i \text{ specified } \forall i \in [l]\} \notag \\&=(n-m+1) \sum_{s_1=0}^{m-l} \cdots \sum_{s_l=0}^{m-l-s_1-\cdots-s_{l-1}} \binom{m-l}{s_1, \dots, s_l, m-l-s_1-\cdots-s_l} \cdot \notag \\&\cdot (n-l+1-s_1-\cdots-s_l)^{m-l-1-s_1-\cdots-s_l} \prod_{i=1}^l (s_i+1)^{s_i-1} \left[\sum_{\substack{\#\big\{i\,:\, \pi_i \leq n-l+k-\sum_{j=k}^l s_j\big\} \geq k \\ \forall k \in [l]}} \prod_{i=1}^l \pi_i^{p_i}\right].\end{align}
\begin{align}&\sum \!\left(\prod_{i=1}^l \pi_i^{p_i}\right) \{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_i \text{ specified } \forall i \in [l]\} \notag \\&=(n-m+1) \sum_{s_1=0}^{m-l} \cdots \sum_{s_l=0}^{m-l-s_1-\cdots-s_{l-1}} \binom{m-l}{s_1, \dots, s_l, m-l-s_1-\cdots-s_l} \cdot \notag \\&\cdot (n-l+1-s_1-\cdots-s_l)^{m-l-1-s_1-\cdots-s_l} \prod_{i=1}^l (s_i+1)^{s_i-1} \left[\sum_{\substack{\#\big\{i\,:\, \pi_i \leq n-l+k-\sum_{j=k}^l s_j\big\} \geq k \\ \forall k \in [l]}} \prod_{i=1}^l \pi_i^{p_i}\right].\end{align}
By Lemma 1, for ![]() $p_i\geq 1$, (3.18) is asymptotically
$p_i\geq 1$, (3.18) is asymptotically
 \begin{align}&\frac{n-m+1}{\prod_{i=1}^l (p_i+1)} \sum_{s_1=0}^{m-l} \cdots \sum_{s_l=0}^{m-l-s_1-\cdots-s_{l-1}} \frac{m^{\sum_{i=1}^l s_i}}{\prod_{i=1}^l s_i!} n^{m-1+\sum_{i=1}^l (p_i-s_i)} e^{-c\!\left(l-1+\sum_{i=1}^l s_i\right)} \prod_{i=1}^l (s_i+1)^{s_i-1} \cdot \notag \\&\cdot \left(1-\frac{\left(\sum_{i=1}^l s_i\right)\left(2l-1+\sum_{i=1}^l s_i\right)}{2cn}+\frac{\left(l-1+\sum_{i=1}^l s_i\right)\left(l+1+\sum_{i=1}^l s_i\right)}{n}-\frac{s_l\left(\sum_{i=1}^l p_i+l\right)}{n}\right.\notag \\& \quad \left.-\frac{c\!\left(l-1+\sum_{i=1}^l s_i\right)^2}{2n}+\frac{\sum_{i=1}^l p_i+l}{2n}+O\!\left(n^{-2}\right)\right). \end{align}
\begin{align}&\frac{n-m+1}{\prod_{i=1}^l (p_i+1)} \sum_{s_1=0}^{m-l} \cdots \sum_{s_l=0}^{m-l-s_1-\cdots-s_{l-1}} \frac{m^{\sum_{i=1}^l s_i}}{\prod_{i=1}^l s_i!} n^{m-1+\sum_{i=1}^l (p_i-s_i)} e^{-c\!\left(l-1+\sum_{i=1}^l s_i\right)} \prod_{i=1}^l (s_i+1)^{s_i-1} \cdot \notag \\&\cdot \left(1-\frac{\left(\sum_{i=1}^l s_i\right)\left(2l-1+\sum_{i=1}^l s_i\right)}{2cn}+\frac{\left(l-1+\sum_{i=1}^l s_i\right)\left(l+1+\sum_{i=1}^l s_i\right)}{n}-\frac{s_l\left(\sum_{i=1}^l p_i+l\right)}{n}\right.\notag \\& \quad \left.-\frac{c\!\left(l-1+\sum_{i=1}^l s_i\right)^2}{2n}+\frac{\sum_{i=1}^l p_i+l}{2n}+O\!\left(n^{-2}\right)\right). \end{align}
Let ![]() $F(z) = \sum_{s=0}^\infty \frac{z^s}{s!}(s+1)^{s-1}$. An application of the tree function method shows that (3.19) converges to
$F(z) = \sum_{s=0}^\infty \frac{z^s}{s!}(s+1)^{s-1}$. An application of the tree function method shows that (3.19) converges to
 \begin{align}&\frac{n-m+1}{\prod_{i=1}^l (p_i+1)} n^{m-1+\sum_{i=1}^l p_i} \cdot \notag \\&\cdot \Bigg[F(z)+\frac1n\left(AF(z)+\left(Bl-\sum_{i=1}^l p_i-l\right)zF^{\prime}(z)+Cl\big(z^2F^{\prime\prime}(z)+zF^{\prime}(z)\big)+D\binom{l}{2}z^2 F^{\prime}(z) \frac{F^{\prime}(z)}{F(z)}\right)\notag \\&\quad +O\big(n^{-2}\big)\Bigg],\end{align}
\begin{align}&\frac{n-m+1}{\prod_{i=1}^l (p_i+1)} n^{m-1+\sum_{i=1}^l p_i} \cdot \notag \\&\cdot \Bigg[F(z)+\frac1n\left(AF(z)+\left(Bl-\sum_{i=1}^l p_i-l\right)zF^{\prime}(z)+Cl\big(z^2F^{\prime\prime}(z)+zF^{\prime}(z)\big)+D\binom{l}{2}z^2 F^{\prime}(z) \frac{F^{\prime}(z)}{F(z)}\right)\notag \\&\quad +O\big(n^{-2}\big)\Bigg],\end{align}
where
 \begin{align}A & =-\frac{c(l-1)^2}{2}+(l^2-1)+\frac{\sum_{i=1}^l p_i+l}{2}, \quad B=-c(l-1)-\frac{2l-1}{2c}+2l,\nonumber\\
C & =-\frac{c}{2}-\frac{1}{2c}+1, \quad D=-c-\frac{1}{c}+2.\end{align}
\begin{align}A & =-\frac{c(l-1)^2}{2}+(l^2-1)+\frac{\sum_{i=1}^l p_i+l}{2}, \quad B=-c(l-1)-\frac{2l-1}{2c}+2l,\nonumber\\
C & =-\frac{c}{2}-\frac{1}{2c}+1, \quad D=-c-\frac{1}{c}+2.\end{align}
Dividing by ![]() $|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
$|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
 \begin{equation}\frac{n^{\sum_{i=1}^l p_i}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}-\frac{c\sum_{i=1}^l p_i}{1-c}\right)+O\!\left(\frac{1}{n^2}\right)\right)\end{equation}
\begin{equation}\frac{n^{\sum_{i=1}^l p_i}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}-\frac{c\sum_{i=1}^l p_i}{1-c}\right)+O\!\left(\frac{1}{n^2}\right)\right)\end{equation}
for the generic mixed moment.
Record the parking outcome of ![]() ${\boldsymbol \pi}\in {\text{PF}}(m, n)$ as
${\boldsymbol \pi}\in {\text{PF}}(m, n)$ as ![]() ${\boldsymbol \tau}({\boldsymbol \pi})=(\tau_1, \dots, \tau_m)$, where the ith car parks in spot
${\boldsymbol \tau}({\boldsymbol \pi})=(\tau_1, \dots, \tau_m)$, where the ith car parks in spot ![]() $\tau_i$ with
$\tau_i$ with ![]() $1\leq \tau_i\leq n$. An asymptotic argument similar to the one in the proof of Theorems 4 and 5 leads to the following.
$1\leq \tau_i\leq n$. An asymptotic argument similar to the one in the proof of Theorems 4 and 5 leads to the following.
Theorem 6. Take ![]() $l\geq 1$ any integer. For
$l\geq 1$ any integer. For ![]() $1\leq i\leq l$, take
$1\leq i\leq l$, take ![]() $p_i \geq 1$ any integer. Take m and n large with
$p_i \geq 1$ any integer. Take m and n large with ![]() $m=cn$ for some
$m=cn$ for some ![]() $0<c<1$. For a parking function
$0<c<1$. For a parking function ![]() ${\boldsymbol \pi}$ chosen uniformly at random from
${\boldsymbol \pi}$ chosen uniformly at random from ![]() ${{PF}}(m, n)$, we have
${{PF}}(m, n)$, we have
 \begin{equation}{\mathbb E}\Bigg(\prod_{i=1}^l \tau_i^{p_i}\Bigg)=\frac{n^{\sum_{i=1}^l p_i}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}-\frac{c\sum_{i=1}^l p_i}{1-c}\right)+O\!\left(\frac{1}{n^2}\right)\right),\end{equation}
\begin{equation}{\mathbb E}\Bigg(\prod_{i=1}^l \tau_i^{p_i}\Bigg)=\frac{n^{\sum_{i=1}^l p_i}}{\prod_{i=1}^l (p_i+1)} \left(1+\frac{1}{n}\left(\frac{\sum_{i=1}^l p_i+l}{2}-\frac{c\sum_{i=1}^l p_i}{1-c}\right)+O\!\left(\frac{1}{n^2}\right)\right),\end{equation}
where ![]() ${\boldsymbol \tau}$ is the parking outcome of
${\boldsymbol \tau}$ is the parking outcome of ![]() ${\boldsymbol \pi}$. In particular, for any finite i,
${\boldsymbol \pi}$. In particular, for any finite i,
We will now deduce all possible covariances of parking functions: between two coordinates, between a coordinate and an unattempted spot, and between two unattempted spots. As for the mixed moment calculations in Section 3.1, combinatorial considerations and asymptotic expansion will be the central ingredients in our derivations.
3.2. Covariance between two coordinates
Proposition 6. Take m and n large with ![]() $m=cn$ for some
$m=cn$ for some ![]() $0<c<1$. For a parking function
$0<c<1$. For a parking function ![]() ${\boldsymbol \pi}$ chosen uniformly at random from
${\boldsymbol \pi}$ chosen uniformly at random from ![]() ${{PF}}(m, n)$, we have
${{PF}}(m, n)$, we have
Proof. For ![]() $p=q=1$, performing asymptotic expansion as in the proof of Theorem 4 but keeping more lower-order terms, we have that
$p=q=1$, performing asymptotic expansion as in the proof of Theorem 4 but keeping more lower-order terms, we have that
 \begin{align*}\sum_{j=1}^n \sum_{k=1}^n jk \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=k\}\end{align*}
\begin{align*}\sum_{j=1}^n \sum_{k=1}^n jk \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, \pi_2=k\}\end{align*}
converges to
 \begin{align*}&\frac{n-m+1}{4} n^{m+1}e^{-c} \sum_{s=0}^{\infty} \sum_{t=0}^{\infty} \frac{\big(ce^{-c}\big)^{s+t}}{s! t!} (s+1)^{s-1} (t+1)^{t-1} \cdot \notag \\
&\cdot \left(1+\Big(A_1+A_2s+A_3t+A_4s^2+A_5t^2+A_6st\Big)\frac{1}{n}+\Big(B_1+B_2s+B_3t+B_4s^2+B_5t^2+B_6st+ \right. \notag \\
&\left.+B_7s^2t+B_8st^2+B_9s^3+B_{10}t^3+B_{11}s^3t+B_{12}st^3+B_{13}s^2t^2+B_{14}s^4+B_{15}t^4\Big)\frac{1}{n^2} +O\big(n^{-3}\big) \right)\!,\end{align*}
\begin{align*}&\frac{n-m+1}{4} n^{m+1}e^{-c} \sum_{s=0}^{\infty} \sum_{t=0}^{\infty} \frac{\big(ce^{-c}\big)^{s+t}}{s! t!} (s+1)^{s-1} (t+1)^{t-1} \cdot \notag \\
&\cdot \left(1+\Big(A_1+A_2s+A_3t+A_4s^2+A_5t^2+A_6st\Big)\frac{1}{n}+\Big(B_1+B_2s+B_3t+B_4s^2+B_5t^2+B_6st+ \right. \notag \\
&\left.+B_7s^2t+B_8st^2+B_9s^3+B_{10}t^3+B_{11}s^3t+B_{12}st^3+B_{13}s^2t^2+B_{14}s^4+B_{15}t^4\Big)\frac{1}{n^2} +O\big(n^{-3}\big) \right)\!,\end{align*}
where
A more involved application of the tree function method then yields
The same approach also yields
The claimed asymptotics are then immediate.
3.3. Covariance between a coordinate and an unattempted spot
Recall that for a parking function ![]() ${\boldsymbol \pi}\in {\text{PF}}(m, n)$, there are
${\boldsymbol \pi}\in {\text{PF}}(m, n)$, there are ![]() $n-m$ parking spots that are never attempted by any car. Let
$n-m$ parking spots that are never attempted by any car. Let ![]() $k_i({\boldsymbol \pi})$ for
$k_i({\boldsymbol \pi})$ for ![]() $i=1, \dots, n-m$ represent these spots, so that
$i=1, \dots, n-m$ represent these spots, so that ![]() $0\,:\!=\,k_0<k_1<\cdots<k_{n-m}<k_{n-m+1}\,:\!=\,n+1$. Let
$0\,:\!=\,k_0<k_1<\cdots<k_{n-m}<k_{n-m+1}\,:\!=\,n+1$. Let
consisting of parking functions where the ith empty spot is fixed at k. The unattempted spot k ranges from i to ![]() $m+i$ and breaks up the parking function
$m+i$ and breaks up the parking function ![]() ${\boldsymbol \pi}$ into two components
${\boldsymbol \pi}$ into two components ![]() ${\boldsymbol \alpha}$ and
${\boldsymbol \alpha}$ and ![]() ${\boldsymbol \beta}$, with
${\boldsymbol \beta}$, with ![]() ${\boldsymbol \alpha} \in {\text{PF}}(k-i, k-1)$ and
${\boldsymbol \alpha} \in {\text{PF}}(k-i, k-1)$ and ![]() ${\boldsymbol \beta} \in {\text{PF}}(m-k+i, n-k)$, and
${\boldsymbol \beta} \in {\text{PF}}(m-k+i, n-k)$, and ![]() ${\boldsymbol \pi}$ a shuffle of the two. From the parking scheme, if
${\boldsymbol \pi}$ a shuffle of the two. From the parking scheme, if ![]() $j<k$ and
$j<k$ and ![]() ${\boldsymbol \pi}=(j, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$, then
${\boldsymbol \pi}=(j, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$, then ![]() ${\boldsymbol \pi}^{\prime}=(l, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$ for all
${\boldsymbol \pi}^{\prime}=(l, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$ for all ![]() $1\leq l\leq j$, while if
$1\leq l\leq j$, while if ![]() $j>k$ and
$j>k$ and ![]() ${\boldsymbol \pi}=(j, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$, then
${\boldsymbol \pi}=(j, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$, then ![]() ${\boldsymbol \pi}^{\prime}=(l, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$ for all
${\boldsymbol \pi}^{\prime}=(l, \pi_2, \dots, \pi_m) \in {\text{PF}}(m, n;\, i, k)$ for all ![]() $k+1\leq l\leq j$. This implies that given the last
$k+1\leq l\leq j$. This implies that given the last ![]() $m-1$ parking preferences, it is sufficient to identify the largest feasible first preference (if any exists).
$m-1$ parking preferences, it is sufficient to identify the largest feasible first preference (if any exists).
Theorem 7. We have that ![]() ${\boldsymbol \pi}=(j, \pi_2, \dots, \pi_m)$ is in
${\boldsymbol \pi}=(j, \pi_2, \dots, \pi_m)$ is in ![]() ${{PF}}(m, n;\, i, k)$ but
${{PF}}(m, n;\, i, k)$ but ![]() ${\boldsymbol \pi}^{\prime}=(j+1, \pi_2, \dots, \pi_m)$ is not if and only if either
${\boldsymbol \pi}^{\prime}=(j+1, \pi_2, \dots, \pi_m)$ is not if and only if either ![]() $(1)\ i\leq j\leq k-1$ and
$(1)\ i\leq j\leq k-1$ and ![]() $(\pi_2, \dots, \pi_m)$ is a multi-shuffle of
$(\pi_2, \dots, \pi_m)$ is a multi-shuffle of ![]() ${\boldsymbol \alpha} \in {{PF}}(j-i, j-1)$,
${\boldsymbol \alpha} \in {{PF}}(j-i, j-1)$, ![]() ${\boldsymbol \beta} \in {{PF}}(k-j-1, k-j-1)$, and
${\boldsymbol \beta} \in {{PF}}(k-j-1, k-j-1)$, and ![]() ${\boldsymbol \gamma} \in {{PF}}(m-k+i, n-k)$; or
${\boldsymbol \gamma} \in {{PF}}(m-k+i, n-k)$; or ![]() $(2)\ j \geq n-m-i+k+1$ and
$(2)\ j \geq n-m-i+k+1$ and ![]() $(\pi_2, \dots, \pi_m)$ is a multi-shuffle of
$(\pi_2, \dots, \pi_m)$ is a multi-shuffle of ![]() ${\boldsymbol \alpha} \in {{PF}}(k-i, k-1)$,
${\boldsymbol \alpha} \in {{PF}}(k-i, k-1)$, ![]() ${\boldsymbol \beta} \in {{PF}}(j-k-1-n+m+i, j-k-1)$, and
${\boldsymbol \beta} \in {{PF}}(j-k-1-n+m+i, j-k-1)$, and ![]() ${\boldsymbol \gamma} \in {{PF}}(n-j, n-j)$.
${\boldsymbol \gamma} \in {{PF}}(n-j, n-j)$.
Proof. The proof builds upon Theorem 1.
First suppose ![]() $j<k$. Then
$j<k$. Then ![]() $(\pi_2, \dots, \pi_m)=(\delta_1, \dots, \delta_{k-i-1}, \gamma_1, \dots, \gamma_{m-k+i})\,:\!=\,({\boldsymbol \delta}, {\boldsymbol \gamma})$, where
$(\pi_2, \dots, \pi_m)=(\delta_1, \dots, \delta_{k-i-1}, \gamma_1, \dots, \gamma_{m-k+i})\,:\!=\,({\boldsymbol \delta}, {\boldsymbol \gamma})$, where ![]() ${\boldsymbol \delta}$ consists of cars with preference
${\boldsymbol \delta}$ consists of cars with preference ![]() $\leq k-1$ and
$\leq k-1$ and ![]() ${\boldsymbol \gamma}$ consists of cars with preference
${\boldsymbol \gamma}$ consists of cars with preference ![]() $\geq k+1$. It is clear that
$\geq k+1$. It is clear that ![]() $(\pi_1, {\boldsymbol \delta}) \in {\text{PF}}(k-i, k-1)$ and
$(\pi_1, {\boldsymbol \delta}) \in {\text{PF}}(k-i, k-1)$ and ![]() ${\boldsymbol \gamma} \in {\text{PF}}(m-k+i, n-k)$. The statement of the theorem is equivalent to identifying j such that
${\boldsymbol \gamma} \in {\text{PF}}(m-k+i, n-k)$. The statement of the theorem is equivalent to identifying j such that ![]() $A_{{\boldsymbol \delta}}=[j]$. From Theorem 1,
$A_{{\boldsymbol \delta}}=[j]$. From Theorem 1, ![]() $j \geq i$ and
$j \geq i$ and ![]() ${\boldsymbol \delta}$ is a shuffle of
${\boldsymbol \delta}$ is a shuffle of ![]() ${\boldsymbol \alpha} \in {\text{PF}}(j-i, j-1)$ and
${\boldsymbol \alpha} \in {\text{PF}}(j-i, j-1)$ and ![]() ${\boldsymbol \beta} \in {\text{PF}}(k-j-1, k-j-1)$.
${\boldsymbol \beta} \in {\text{PF}}(k-j-1, k-j-1)$.
Next suppose ![]() $j>k$. Then
$j>k$. Then ![]() $(\pi_2, \dots, \pi_m)=(\alpha_1, \dots, \alpha_{k-i}, \delta_1, \dots, \delta_{m-k+i-1})\,:\!=\,({\boldsymbol \alpha}, {\boldsymbol \delta})$, where
$(\pi_2, \dots, \pi_m)=(\alpha_1, \dots, \alpha_{k-i}, \delta_1, \dots, \delta_{m-k+i-1})\,:\!=\,({\boldsymbol \alpha}, {\boldsymbol \delta})$, where ![]() ${\boldsymbol \alpha}$ consists of cars with preference
${\boldsymbol \alpha}$ consists of cars with preference ![]() $\leq k-1$ and
$\leq k-1$ and ![]() ${\boldsymbol \delta}$ consists of cars with preference
${\boldsymbol \delta}$ consists of cars with preference ![]() $\geq k+1$. It is clear that
$\geq k+1$. It is clear that ![]() ${\boldsymbol \alpha} \in {\text{PF}}(k-i, k-1)$ and
${\boldsymbol \alpha} \in {\text{PF}}(k-i, k-1)$ and ![]() $(\pi_1, {\boldsymbol \delta}) \in {\text{PF}}(m-k+i, n-k)$. The statement of the theorem is equivalent to identifying j such that
$(\pi_1, {\boldsymbol \delta}) \in {\text{PF}}(m-k+i, n-k)$. The statement of the theorem is equivalent to identifying j such that ![]() $A_{{\boldsymbol \delta}}=[j-k]$. From Theorem 1,
$A_{{\boldsymbol \delta}}=[j-k]$. From Theorem 1, ![]() $j-k \geq n-m-i+1$ and
$j-k \geq n-m-i+1$ and ![]() ${\boldsymbol \delta}$ is a shuffle of
${\boldsymbol \delta}$ is a shuffle of ![]() ${\boldsymbol \beta} \in {\text{PF}}(j-k-1-n+m+i, j-k-1)$ and
${\boldsymbol \beta} \in {\text{PF}}(j-k-1-n+m+i, j-k-1)$ and ![]() ${\boldsymbol \gamma} \in {\text{PF}}(n-j, n-j)$.
${\boldsymbol \gamma} \in {\text{PF}}(n-j, n-j)$.
Proposition 7. Take ![]() $1\leq i \leq n-m$ any integer. Take
$1\leq i \leq n-m$ any integer. Take ![]() $i \leq k \leq m+i$ any integer. For
$i \leq k \leq m+i$ any integer. For ![]() $j<k$, the number of parking functions
$j<k$, the number of parking functions ![]() ${\boldsymbol \pi}\in {{PF}}(m, n)$ with
${\boldsymbol \pi}\in {{PF}}(m, n)$ with ![]() $\pi_1=j$ and
$\pi_1=j$ and ![]() $k_i=k$ is
$k_i=k$ is
 \begin{align}& \binom{m-1}{m-k+i} i(n-m-i+1) (n-k+1)^{m-k+i-1} \sum_{s=0}^{\min\!(k-i-1, k-j-1)}\nonumber\\
&\qquad\qquad\qquad\qquad\qquad\qquad \binom{k-i-1}{s} (k-1-s)^{k-i-s-2} (s+1)^{s-1}.\end{align}
\begin{align}& \binom{m-1}{m-k+i} i(n-m-i+1) (n-k+1)^{m-k+i-1} \sum_{s=0}^{\min\!(k-i-1, k-j-1)}\nonumber\\
&\qquad\qquad\qquad\qquad\qquad\qquad \binom{k-i-1}{s} (k-1-s)^{k-i-s-2} (s+1)^{s-1}.\end{align}
Note that this quantity stays constant for ![]() $j \leq i$ and decreases as j increases past i, as there are fewer resulting summands. For
$j \leq i$ and decreases as j increases past i, as there are fewer resulting summands. For ![]() $j>k$, the number of parking functions
$j>k$, the number of parking functions ![]() ${\boldsymbol \pi}\in {{PF}}(m, n)$ with
${\boldsymbol \pi}\in {{PF}}(m, n)$ with ![]() $\pi_1=j$ and
$\pi_1=j$ and ![]() $k_i=k$ is
$k_i=k$ is
 \begin{equation}\binom{m-1}{k-i} i k^{k-i-1} (n-m-i+1) \sum_{s=0}^{\min\!(m+i-k-1, n-j)} \binom{m-k+i-1}{s} (n-k-s)^{m+i-k-s-2} (s+1)^{s-1}.\end{equation}
\begin{equation}\binom{m-1}{k-i} i k^{k-i-1} (n-m-i+1) \sum_{s=0}^{\min\!(m+i-k-1, n-j)} \binom{m-k+i-1}{s} (n-k-s)^{m+i-k-s-2} (s+1)^{s-1}.\end{equation}
Note that this quantity stays constant for ![]() $j \leq n-m-i+k+1$ and decreases as j increases past
$j \leq n-m-i+k+1$ and decreases as j increases past ![]() $n-m-i+k+1$, as there are fewer resulting summands.
$n-m-i+k+1$, as there are fewer resulting summands.
Proof. If ![]() $\pi_1=j<k$, then the maximal
$\pi_1=j<k$, then the maximal ![]() $\pi_1$ consistent with
$\pi_1$ consistent with ![]() $\pi_2, \dots, \pi_m$ and
$\pi_2, \dots, \pi_m$ and ![]() $k_i$ is some
$k_i$ is some ![]() $l \geq \max\!(j, i)$ and
$l \geq \max\!(j, i)$ and ![]() $\leq k-1$. Thus, from Theorem 7, the number of parking functions with
$\leq k-1$. Thus, from Theorem 7, the number of parking functions with ![]() $\pi_1=j$ and
$\pi_1=j$ and ![]() $k_i=k$ is
$k_i=k$ is
 \begin{align}&\sum_{l=\max\!(j, i)}^{k-1} \binom{m-1}{l-i, k-l-1, m-k+i} |{\text{PF}}(l-i, l-1)| \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad\qquad \cdot |{\text{PF}}(k-l-1, k-l-1)| |{\text{PF}}(m-k+i, n-k)| \notag \\[3pt]
&=\sum_{l=\max\!(j, i)}^{k-1} \binom{m-1}{l-i, k-l-1, m-k+i} i(n-m-i+1) l^{l-i-1} (k-l)^{k-l-2} (n-k+1)^{m-k+i-1} \notag \\[3pt]
&=\binom{m-1}{m-k+i} i(n-m-i+1) (n-k+1)^{m-k+i-1} \cdot \notag \\[3pt]
& \qquad\qquad\qquad\quad \cdot \sum_{s=0}^{\min\!(k-i-1, k-j-1)} \binom{k-i-1}{s} (k-1-s)^{k-i-s-2} (s+1)^{s-1},\end{align}
\begin{align}&\sum_{l=\max\!(j, i)}^{k-1} \binom{m-1}{l-i, k-l-1, m-k+i} |{\text{PF}}(l-i, l-1)| \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad\qquad \cdot |{\text{PF}}(k-l-1, k-l-1)| |{\text{PF}}(m-k+i, n-k)| \notag \\[3pt]
&=\sum_{l=\max\!(j, i)}^{k-1} \binom{m-1}{l-i, k-l-1, m-k+i} i(n-m-i+1) l^{l-i-1} (k-l)^{k-l-2} (n-k+1)^{m-k+i-1} \notag \\[3pt]
&=\binom{m-1}{m-k+i} i(n-m-i+1) (n-k+1)^{m-k+i-1} \cdot \notag \\[3pt]
& \qquad\qquad\qquad\quad \cdot \sum_{s=0}^{\min\!(k-i-1, k-j-1)} \binom{k-i-1}{s} (k-1-s)^{k-i-s-2} (s+1)^{s-1},\end{align}
where the last equality comes from a change of variables ![]() $s=k-l-1$.
$s=k-l-1$.
If ![]() $\pi_1=j>k$, then the maximal
$\pi_1=j>k$, then the maximal ![]() $\pi_1$ consistent with
$\pi_1$ consistent with ![]() $\pi_2, \dots, \pi_m$ and
$\pi_2, \dots, \pi_m$ and ![]() $k_i$ is some
$k_i$ is some ![]() $l \geq \max\!(j, n-m-i+k+1)$. Thus, from Theorem 7, the number of parking functions with
$l \geq \max\!(j, n-m-i+k+1)$. Thus, from Theorem 7, the number of parking functions with ![]() $\pi_1=j$ and
$\pi_1=j$ and ![]() $k_i=k$ is
$k_i=k$ is
 \begin{align*}&\sum_{l=\max\!(j, n-m-i+k+1)}^n \binom{m-1}{k-i, l-k-1-n+m+i, n-l} |{\text{PF}}(k-i, k-1)| \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad \cdot |{\text{PF}}(l-k-1-n+m+i, l-k-1)| |{\text{PF}}(n-l, n-l)| \notag \\[3pt]
&=\sum_{l=\max\!(j, n-m-i+k+1)}^n \binom{m-1}{k-i, l-k-1-n+m+i, n-l} i k^{k-i-1} (n-m-i+1) \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad \cdot (l-k)^{l-k-n+m+i-2} (n-l+1)^{n-l-1} \notag \\[3pt]
&=\binom{m-1}{k-i} i k^{k-i-1} (n-m-i+1) \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad \cdot \sum_{s=0}^{\min\!(m+i-k-1, n-j)} \binom{m-k+i-1}{s} (n-k-s)^{m+i-k-s-2} (s+1)^{s-1},\end{align*}
\begin{align*}&\sum_{l=\max\!(j, n-m-i+k+1)}^n \binom{m-1}{k-i, l-k-1-n+m+i, n-l} |{\text{PF}}(k-i, k-1)| \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad \cdot |{\text{PF}}(l-k-1-n+m+i, l-k-1)| |{\text{PF}}(n-l, n-l)| \notag \\[3pt]
&=\sum_{l=\max\!(j, n-m-i+k+1)}^n \binom{m-1}{k-i, l-k-1-n+m+i, n-l} i k^{k-i-1} (n-m-i+1) \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad \cdot (l-k)^{l-k-n+m+i-2} (n-l+1)^{n-l-1} \notag \\[3pt]
&=\binom{m-1}{k-i} i k^{k-i-1} (n-m-i+1) \cdot \notag \\[3pt]
& \qquad\qquad\qquad\qquad\qquad \cdot \sum_{s=0}^{\min\!(m+i-k-1, n-j)} \binom{m-k+i-1}{s} (n-k-s)^{m+i-k-s-2} (s+1)^{s-1},\end{align*}
where the last equality comes from a change of variables ![]() $s=n-l$.
$s=n-l$.
Proposition 8. Take ![]() $i \geq 1$ any integer. Take m and n large with
$i \geq 1$ any integer. Take m and n large with ![]() $m=cn$ for some
$m=cn$ for some ![]() $0<c<1$. For a parking function
$0<c<1$. For a parking function ![]() ${\boldsymbol \pi}$ chosen uniformly at random from
${\boldsymbol \pi}$ chosen uniformly at random from ![]() ${{PF}}(m, n)$, we have
${{PF}}(m, n)$, we have
Proof. From Proposition 7 and interchanging the order of summation, we have
 \begin{align}&\sum_{k=i}^{m+i} k \!\left(\sum_{j=1}^{k-1} j \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, k_i=k\}+\sum_{j=k+1}^{n} j \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, k_i=k\}\right) \notag \\
&=\frac{1}{2}i(n-m-i+1) \left[\sum_{s=0}^{m-1} \sum_{k=i+1+s}^{m+i} \binom{m-1}{m-k+i, s, k-i-s-1}k (n-k+1)^{m-k+i-1} \cdot\right. \notag \\
& \qquad\qquad\qquad\qquad\qquad\qquad \cdot (k-1-s)^{k-i-s} (s+1)^{s-1} \left(1+\frac{1}{k-1-s}\right) \notag \\&\left.+\sum_{s=0}^{m-1} \sum_{k=i}^{m+i-1-s} \binom{m-1}{k-i, s, m-k+i-1-s} k^{k-i} (n-k-s)^{m+i-k-s} (s+1)^{s-1}\left(1+\frac{2k+1}{n-k-s}\right)\right].\end{align}
\begin{align}&\sum_{k=i}^{m+i} k \!\left(\sum_{j=1}^{k-1} j \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, k_i=k\}+\sum_{j=k+1}^{n} j \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, \pi_1=j, k_i=k\}\right) \notag \\
&=\frac{1}{2}i(n-m-i+1) \left[\sum_{s=0}^{m-1} \sum_{k=i+1+s}^{m+i} \binom{m-1}{m-k+i, s, k-i-s-1}k (n-k+1)^{m-k+i-1} \cdot\right. \notag \\
& \qquad\qquad\qquad\qquad\qquad\qquad \cdot (k-1-s)^{k-i-s} (s+1)^{s-1} \left(1+\frac{1}{k-1-s}\right) \notag \\&\left.+\sum_{s=0}^{m-1} \sum_{k=i}^{m+i-1-s} \binom{m-1}{k-i, s, m-k+i-1-s} k^{k-i} (n-k-s)^{m+i-k-s} (s+1)^{s-1}\left(1+\frac{2k+1}{n-k-s}\right)\right].\end{align}
We make a change of variables: ![]() $t=k-i-s-1$ in the first sum and
$t=k-i-s-1$ in the first sum and ![]() $t=k-i$ in the second sum. Then (3.34) becomes
$t=k-i$ in the second sum. Then (3.34) becomes
 \begin{align}&\frac{1}{2}i(n-m-i+1) \sum_{s=0}^{m-1} \sum_{t=0}^{m-1-s} \binom{m-1}{s, t, m-1-s-t} (n-i-s-t)^{m-s-t-2} (s+1)^{s-1} \cdot \notag \\& \quad \cdot \left[(s+t+i+1)(t+i)^{t+1} \left(1+\frac{1}{t+i}\right)+(t+i)^{t} (n-i-s-t)^{2} \left(1+\frac{2(t+i)+1}{n-i-s-t}\right)\right] \notag \\&= \frac{1}{2}i(n-m-i+1) n^{m} e^{-ic} \sum_{s=0}^{m-1} \sum_{t=0}^{m-1-s} \frac{\big(ce^{-c}\big)^{s+t}}{s!t!} (s+1)^{s-1} (t+i)^{t} \cdot \notag \\&\quad \cdot \left(1-\frac{(s+t)(s+t+1)}{2cn}-\frac{c(s+t+i)^2}{2n}+\frac{(s+t+i)(s+t)}{n}+\frac{2(t+i)+1}{n}+O\!\left(n^{-2}\right)\right).\end{align}
\begin{align}&\frac{1}{2}i(n-m-i+1) \sum_{s=0}^{m-1} \sum_{t=0}^{m-1-s} \binom{m-1}{s, t, m-1-s-t} (n-i-s-t)^{m-s-t-2} (s+1)^{s-1} \cdot \notag \\& \quad \cdot \left[(s+t+i+1)(t+i)^{t+1} \left(1+\frac{1}{t+i}\right)+(t+i)^{t} (n-i-s-t)^{2} \left(1+\frac{2(t+i)+1}{n-i-s-t}\right)\right] \notag \\&= \frac{1}{2}i(n-m-i+1) n^{m} e^{-ic} \sum_{s=0}^{m-1} \sum_{t=0}^{m-1-s} \frac{\big(ce^{-c}\big)^{s+t}}{s!t!} (s+1)^{s-1} (t+i)^{t} \cdot \notag \\&\quad \cdot \left(1-\frac{(s+t)(s+t+1)}{2cn}-\frac{c(s+t+i)^2}{2n}+\frac{(s+t+i)(s+t)}{n}+\frac{2(t+i)+1}{n}+O\!\left(n^{-2}\right)\right).\end{align}
The generalized tree function ![]() $F_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s-1}$ is related to the tree function
$F_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s-1}$ is related to the tree function ![]() $F_1(z)$ via
$F_1(z)$ via ![]() $F_i(z)=(F_1(z))^i/i$, and satisfies
$F_i(z)=(F_1(z))^i/i$, and satisfies ![]() $F_i\big(ce^{-c}\big)=e^{ic}/i$. Furthermore,
$F_i\big(ce^{-c}\big)=e^{ic}/i$. Furthermore, ![]() $G_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s}=(F_{i-1}(z))^{\prime}$. By the chain rule, the first and second derivatives of
$G_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s}=(F_{i-1}(z))^{\prime}$. By the chain rule, the first and second derivatives of ![]() $F_1(z)$ and
$F_1(z)$ and ![]() $G_i(z)$ therefore respectively satisfy
$G_i(z)$ therefore respectively satisfy
 \begin{align}F^{\prime}_1\big(ce^{-c}\big) & = \frac{e^{2c}}{1-c}, \quad F^{\prime\prime}_1 \big(ce^{-c}\big) = \frac{3-2c}{(1-c)^3}e^{3c},\nonumber\\
G_i\big(ce^{-c}\big) & = \frac{e^{ic}}{1-c}, \quad G^{\prime}_i\big(ce^{-c}\big) = \frac{i+1-ic}{(1-c)^3}e^{(i+1)c},\\
G^{\prime\prime}_i \big(ce^{-c}\big) & = \frac{(1-c)^2i^2+(1-c)(4-c)i+(4-c)}{(1-c)^5} e^{(i+2)c}.\nonumber\end{align}
\begin{align}F^{\prime}_1\big(ce^{-c}\big) & = \frac{e^{2c}}{1-c}, \quad F^{\prime\prime}_1 \big(ce^{-c}\big) = \frac{3-2c}{(1-c)^3}e^{3c},\nonumber\\
G_i\big(ce^{-c}\big) & = \frac{e^{ic}}{1-c}, \quad G^{\prime}_i\big(ce^{-c}\big) = \frac{i+1-ic}{(1-c)^3}e^{(i+1)c},\\
G^{\prime\prime}_i \big(ce^{-c}\big) & = \frac{(1-c)^2i^2+(1-c)(4-c)i+(4-c)}{(1-c)^5} e^{(i+2)c}.\nonumber\end{align}
We recognize that (3.35) is in the form of a Cauchy product, and converges to
 \begin{align*}&\frac{1}{2}i(n-m-i+1) n^{m} e^{-ic} \sum_{s=0}^{\infty} \sum_{t=0}^{\infty}\frac{\big(ce^{-c}\big)^{s+t}}{s! t!} (s+1)^{s-1} (t+i)^{t} \cdot \notag \\
& \qquad\qquad\qquad \cdot \left(1+\frac{1}{n} (A+Bs+Ct+Ds^2+Et^2+Fst)+O\big(n^{-2}\big)\right),\end{align*}
\begin{align*}&\frac{1}{2}i(n-m-i+1) n^{m} e^{-ic} \sum_{s=0}^{\infty} \sum_{t=0}^{\infty}\frac{\big(ce^{-c}\big)^{s+t}}{s! t!} (s+1)^{s-1} (t+i)^{t} \cdot \notag \\
& \qquad\qquad\qquad \cdot \left(1+\frac{1}{n} (A+Bs+Ct+Ds^2+Et^2+Fst)+O\big(n^{-2}\big)\right),\end{align*}
where
 \begin{align}A =1+2i-\frac{ci^2}{2}, \quad B=-\frac{1}{2c}+i-ci,\quad\nonumber\\
C =-\frac{1}{2c}+i-ci+2, \quad D=1-\frac{1}{2c}-\frac{c}{2},\\
E =1-\frac{1}{2c}-\frac{c}{2}, \quad F=2-\frac{1}{c}-c.\ \ \ \quad\nonumber\end{align}
\begin{align}A =1+2i-\frac{ci^2}{2}, \quad B=-\frac{1}{2c}+i-ci,\quad\nonumber\\
C =-\frac{1}{2c}+i-ci+2, \quad D=1-\frac{1}{2c}-\frac{c}{2},\\
E =1-\frac{1}{2c}-\frac{c}{2}, \quad F=2-\frac{1}{c}-c.\ \ \ \quad\nonumber\end{align}
Using ![]() $F_1(z)$ and
$F_1(z)$ and ![]() $G_i(z)$, this can be written as follows (with
$G_i(z)$, this can be written as follows (with ![]() $z=ce^{-c}$):
$z=ce^{-c}$):
 \begin{align}&\frac{1}{2}i(n-m-i+1) n^{m} e^{-ic} \left[F_1(z)G_i(z)+\frac1n\Big(AF_1(z)G_i(z)+BzF^{\prime}_1(z)G_i(z)+CzF_1(z)G^{\prime}_i(z)+\Big.\right. \notag \\
&\left.\Big.D\big(z^2F^{\prime\prime}_1 (z)+zF^{\prime}_1(z)\big)G_i(z)+EF_1(z)\big(z^2G^{\prime\prime}_i (z)+zG^{\prime}_i(z)\big)+Fz^2 F^{\prime}_1(z)G^{\prime}_i(z)\Big)+O\!\left(\frac{1}{n^2}\right)\right].\end{align}
\begin{align}&\frac{1}{2}i(n-m-i+1) n^{m} e^{-ic} \left[F_1(z)G_i(z)+\frac1n\Big(AF_1(z)G_i(z)+BzF^{\prime}_1(z)G_i(z)+CzF_1(z)G^{\prime}_i(z)+\Big.\right. \notag \\
&\left.\Big.D\big(z^2F^{\prime\prime}_1 (z)+zF^{\prime}_1(z)\big)G_i(z)+EF_1(z)\big(z^2G^{\prime\prime}_i (z)+zG^{\prime}_i(z)\big)+Fz^2 F^{\prime}_1(z)G^{\prime}_i(z)\Big)+O\!\left(\frac{1}{n^2}\right)\right].\end{align}
Dividing by ![]() $|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
$|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
The same approach also yields
If we combine these with Theorem 4, the claimed asymptotics are then immediate.
3.4. Covariance between two unattempted spots
Proposition 9. Take ![]() $1\leq i<j$ any pair of distinct integers. Take m and n large with
$1\leq i<j$ any pair of distinct integers. Take m and n large with ![]() $m=cn$ for some
$m=cn$ for some ![]() $0<c<1$. For a parking function
$0<c<1$. For a parking function ![]() ${\boldsymbol \pi}$ chosen uniformly at random from
${\boldsymbol \pi}$ chosen uniformly at random from ![]() ${{PF}}(m, n)$, we have
${{PF}}(m, n)$, we have
Proof. Take ![]() $k_i({\boldsymbol \pi})=k$ and
$k_i({\boldsymbol \pi})=k$ and ![]() $k_j({\boldsymbol \pi})=l$. The unattempted spot k ranges from i to
$k_j({\boldsymbol \pi})=l$. The unattempted spot k ranges from i to ![]() $m+i$, and the unattempted spot l ranges from
$m+i$, and the unattempted spot l ranges from ![]() $k-i+j$ to
$k-i+j$ to ![]() $m+j$. The two unattempted spots break up the parking function
$m+j$. The two unattempted spots break up the parking function ![]() ${\boldsymbol \pi}$ into three components
${\boldsymbol \pi}$ into three components ![]() ${\boldsymbol \alpha}$,
${\boldsymbol \alpha}$, ![]() ${\boldsymbol \beta}$, and
${\boldsymbol \beta}$, and ![]() ${\boldsymbol \gamma}$, with
${\boldsymbol \gamma}$, with ![]() ${\boldsymbol \alpha} \in {\text{PF}}(k-i, k-1)$,
${\boldsymbol \alpha} \in {\text{PF}}(k-i, k-1)$, ![]() ${\boldsymbol \beta} \in {\text{PF}}(l-k-j+i, l-k-1)$, and
${\boldsymbol \beta} \in {\text{PF}}(l-k-j+i, l-k-1)$, and ![]() ${\boldsymbol \gamma} \in {\text{PF}}(m-l+j, n-l)$, and
${\boldsymbol \gamma} \in {\text{PF}}(m-l+j, n-l)$, and ![]() ${\boldsymbol \pi}$ a multi-shuffle of the three. We have
${\boldsymbol \pi}$ a multi-shuffle of the three. We have
 \begin{align}&\sum_{k=i}^{m+i} k\sum_{l=k-i+j}^{m+j} l \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, k_i=k, k_j=l\}\notag \\
&=\sum_{k=i}^{m+i} k\sum_{l=k-i+j}^{m+j} l \binom{m}{k-i, l-k-j+i, m-l+j} i k^{k-i-1} \cdot \notag \\
&\qquad\qquad\qquad \cdot (j-i) (l-k)^{l-k-j+i-1} (n-m-j+1) (n-l+1)^{m-l+j-1}.\end{align}
\begin{align}&\sum_{k=i}^{m+i} k\sum_{l=k-i+j}^{m+j} l \#\{{\boldsymbol \pi}\in {\text{PF}}(m, n)\,:\, k_i=k, k_j=l\}\notag \\
&=\sum_{k=i}^{m+i} k\sum_{l=k-i+j}^{m+j} l \binom{m}{k-i, l-k-j+i, m-l+j} i k^{k-i-1} \cdot \notag \\
&\qquad\qquad\qquad \cdot (j-i) (l-k)^{l-k-j+i-1} (n-m-j+1) (n-l+1)^{m-l+j-1}.\end{align}
We make a change of variables: ![]() $s=k-i$ and
$s=k-i$ and ![]() $t=l-k-j+i$. Then (3.42) becomes
$t=l-k-j+i$. Then (3.42) becomes
 \begin{align}&i(j-i)(n-m-j+1) \sum_{s=0}^m \sum_{t=0}^{m-s} \binom{m}{s, t, m-s-t} (s+i)^s (t+j-i)^{t-1} \cdot \notag \\
&\qquad\qquad \cdot (j+s+t)(n-j-s-t+1)^{m-s-t-1} \notag \\
&= i(j-i)(n-m-j+1) n^{m-1} e^{-c(j-1)} \sum_{s=0}^m \sum_{t=0}^{m-s} \frac{\big(ce^{-c}\big)^{s+t}}{s!t!} \cdot \notag \\
&\qquad\qquad \cdot \Big[(s+i)^{s+1} (t+j-i)^{t-1}+(s+i)^s (t+j-i)^t \Big] \left(1+O\!\left(n^{-1}\right)\right).\end{align}
\begin{align}&i(j-i)(n-m-j+1) \sum_{s=0}^m \sum_{t=0}^{m-s} \binom{m}{s, t, m-s-t} (s+i)^s (t+j-i)^{t-1} \cdot \notag \\
&\qquad\qquad \cdot (j+s+t)(n-j-s-t+1)^{m-s-t-1} \notag \\
&= i(j-i)(n-m-j+1) n^{m-1} e^{-c(j-1)} \sum_{s=0}^m \sum_{t=0}^{m-s} \frac{\big(ce^{-c}\big)^{s+t}}{s!t!} \cdot \notag \\
&\qquad\qquad \cdot \Big[(s+i)^{s+1} (t+j-i)^{t-1}+(s+i)^s (t+j-i)^t \Big] \left(1+O\!\left(n^{-1}\right)\right).\end{align}
The generalized tree function ![]() $F_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s-1}$ is related to the tree function
$F_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s-1}$ is related to the tree function ![]() $F_1(z)$ via
$F_1(z)$ via ![]() $F_i(z)=(F_1(z))^i/i$, and satisfies
$F_i(z)=(F_1(z))^i/i$, and satisfies ![]() $F_i\big(ce^{-c}\big)=e^{ic}/i$. Furthermore,
$F_i\big(ce^{-c}\big)=e^{ic}/i$. Furthermore, ![]() $G_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s}=(F_{i-1}(z))^{\prime}$ and
$G_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s}=(F_{i-1}(z))^{\prime}$ and ![]() $H_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s+1}=(F_{i-2}(z))^{\prime\prime}$. By the chain rule,
$H_i(z)=\sum_{s=0}^\infty \frac{z^s}{s!} (s+i)^{s+1}=(F_{i-2}(z))^{\prime\prime}$. By the chain rule, ![]() $G_i(z)$ and
$G_i(z)$ and ![]() $H_i(z)$ therefore respectively satisfy
$H_i(z)$ therefore respectively satisfy
We recognize that (3.43) is in the form of a Cauchy product, and converges to
 \begin{align*}&i(j-i)(n-m-j+1) n^{m-1} e^{-c(j-1)} \cdot \notag \\& \cdot \sum_{s=0}^{\infty} \sum_{t=0}^{\infty}\frac{\big(ce^{-c}\big)^{s+t}}{s! t!} \Big[(s+i)^{s+1} (t+j-i)^{t-1}+(s+i)^s (t+j-i)^t \Big] \left(1+O\!\left(n^{-1}\right)\right).\end{align*}
\begin{align*}&i(j-i)(n-m-j+1) n^{m-1} e^{-c(j-1)} \cdot \notag \\& \cdot \sum_{s=0}^{\infty} \sum_{t=0}^{\infty}\frac{\big(ce^{-c}\big)^{s+t}}{s! t!} \Big[(s+i)^{s+1} (t+j-i)^{t-1}+(s+i)^s (t+j-i)^t \Big] \left(1+O\!\left(n^{-1}\right)\right).\end{align*}
Using ![]() $F_i(z)$,
$F_i(z)$, ![]() $G_i(z)$, and
$G_i(z)$, and ![]() $H_i(z)$, this can be written as follows (with
$H_i(z)$, this can be written as follows (with ![]() $z=ce^{-c}$):
$z=ce^{-c}$):
Dividing by ![]() $|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
$|{\text{PF}}(m,n)|=(n-m+1)(n+1)^{m-1}$ and simplifying, we get
The same approach also yields
If we combine these with (3.40), the claimed asymptotics are then immediate.
3.5. The special situation  $m\, \textrm{=}\, n$
$m\, \textrm{=}\, n$
The asymptotic moment calculations in Sections 3.1, 3.2, 3.3, and 3.4 could alternatively be approached via Abel’s multinomial theorem. Unlike the tree function method, which fails for the case ![]() $m=n$ because of divergence, Abel’s multinomial theorem applies broadly, whether in the generic case
$m=n$ because of divergence, Abel’s multinomial theorem applies broadly, whether in the generic case ![]() $m \lesssim n$ or in the special case
$m \lesssim n$ or in the special case ![]() $m=n$. However, calculation-wise, it is in general more cumbersome to apply Abel’s multinomial theorem than the tree function method, so we only use this alternative approach when
$m=n$. However, calculation-wise, it is in general more cumbersome to apply Abel’s multinomial theorem than the tree function method, so we only use this alternative approach when ![]() $m=n$.
$m=n$.
Theorem 8. (Abel’s multinomial theorem, derived from Pitman [Reference Pitman15] and Riordan [Reference Riordan17].) Let
 \begin{equation}A_n(x_1, \dots, x_m;\, p_1, \dots, p_m)=\sum \binom{n}{{\textbf{s}}} \prod_{j=1}^m (x_j+s_j)^{s_j+p_j},\end{equation}
\begin{equation}A_n(x_1, \dots, x_m;\, p_1, \dots, p_m)=\sum \binom{n}{{\textbf{s}}} \prod_{j=1}^m (x_j+s_j)^{s_j+p_j},\end{equation}
where ![]() ${\textbf{s}}=(s_1, \dots, s_m)$ and
${\textbf{s}}=(s_1, \dots, s_m)$ and ![]() $\sum_{i=1}^m s_i=n$. Then
$\sum_{i=1}^m s_i=n$. Then
 \begin{align}
& A_n(x_1, \dots, x_m;\, p_1, \dots, p_m)\nonumber\\
& \qquad =\sum_{i=1}^m A_{n-1}(x_1, \dots, x_{i-1}, x_i+1, x_{i+1}, \dots, x_m;\, p_1, \dots, p_{i-1}, p_i+1, p_{i+1}, \dots, p_m);\end{align}
\begin{align}
& A_n(x_1, \dots, x_m;\, p_1, \dots, p_m)\nonumber\\
& \qquad =\sum_{i=1}^m A_{n-1}(x_1, \dots, x_{i-1}, x_i+1, x_{i+1}, \dots, x_m;\, p_1, \dots, p_{i-1}, p_i+1, p_{i+1}, \dots, p_m);\end{align}
Moreover, the following special instances hold via the basic recurrences listed above:
We recognize that in computing ![]() ${\mathbb E}\big(\prod_{i=1}^l \pi_i^{p_i}\big)$ in Theorem 5, (3.18) is asymptotically
${\mathbb E}\big(\prod_{i=1}^l \pi_i^{p_i}\big)$ in Theorem 5, (3.18) is asymptotically

This is a general formula that works for any m, n, and l. When ![]() $m=n$, taking
$m=n$, taking ![]() $l=1, 2$, we have
$l=1, 2$, we have
These asymptotic results are in sharp contrast with the case ![]() $m=cn$ for some
$m=cn$ for some ![]() $0<c<1$. As
$0<c<1$. As ![]() $c \rightarrow 1$, the correction terms in (3.27) and (3.28) blow up, contributing to the difference between the asymptotic orders in the generic situation
$c \rightarrow 1$, the correction terms in (3.27) and (3.28) blow up, contributing to the difference between the asymptotic orders in the generic situation ![]() $m \lesssim n$ and the special situation
$m \lesssim n$ and the special situation ![]() $m=n$.
$m=n$.
4. Interval parking functions
In this section we study a generalization of the parking functions ![]() ${\text{PF}}(m, n)$ in which the ith car is willing to park only in an interval
${\text{PF}}(m, n)$ in which the ith car is willing to park only in an interval ![]() $[a_i,b_i]\subseteq\{1,\dots,n\}$. If all cars can successfully park then we say that the pair
$[a_i,b_i]\subseteq\{1,\dots,n\}$. If all cars can successfully park then we say that the pair ![]() $({\textbf{a}},{\textbf{b}})=((a_1,\dots,a_m), (b_1,\dots,b_m))$ is an interval parking function with m cars and n spots, or
$({\textbf{a}},{\textbf{b}})=((a_1,\dots,a_m), (b_1,\dots,b_m))$ is an interval parking function with m cars and n spots, or ![]() ${\text{IPF}}(m, n)$. If
${\text{IPF}}(m, n)$. If ![]() $b_i=n$ for all i, then we recover a parking function
$b_i=n$ for all i, then we recover a parking function ![]() ${\text{PF}}(m, n)$.
${\text{PF}}(m, n)$.
Let ![]() ${\boldsymbol \tau}({\cdot})$ denote the parking outcome of either a parking function or an interval parking function. The following propositions for
${\boldsymbol \tau}({\cdot})$ denote the parking outcome of either a parking function or an interval parking function. The following propositions for ![]() ${\text{IPF}}(m, n)$ generalize the corresponding results for the special case
${\text{IPF}}(m, n)$ generalize the corresponding results for the special case ![]() ${\text{IPF}}(n, n)$ discussed in [Reference Colaric, DeMuse, Martin and Yin5].
${\text{IPF}}(n, n)$ discussed in [Reference Colaric, DeMuse, Martin and Yin5].
Proposition 10. Let ![]() ${\textbf{a}}, {\textbf{b}} \in [n]^m$. Then the following hold:
${\textbf{a}}, {\textbf{b}} \in [n]^m$. Then the following hold:
1.
 ${\textbf{a}} \in {{PF}}(m, n)$ if and only if
${\textbf{a}} \in {{PF}}(m, n)$ if and only if  $({\textbf{a}},(n,\dots,n))\in{{IPF}}(m, n)$.
$({\textbf{a}},(n,\dots,n))\in{{IPF}}(m, n)$.2.
 $({\textbf{a}}, {\textbf{b}})\in{{IPF}}(m, n)$ if and only if
$({\textbf{a}}, {\textbf{b}})\in{{IPF}}(m, n)$ if and only if  ${\textbf{a}}\in{{PF}}(m, n)$ and
${\textbf{a}}\in{{PF}}(m, n)$ and  ${\boldsymbol \tau}({\textbf{a}}) \le_C {\textbf{b}}$.
${\boldsymbol \tau}({\textbf{a}}) \le_C {\textbf{b}}$.
Proof. These equivalences follow directly from the definition.
Proposition 11. Let ![]() ${\textbf{c}}=({\textbf{a}}, {\textbf{b}}) \in {{IPF}}(m, n)$. Then the following hold:
${\textbf{c}}=({\textbf{a}}, {\textbf{b}}) \in {{IPF}}(m, n)$. Then the following hold:
1.
 ${\textbf{b}}^* \in {{PF}}(m, n)$.
${\textbf{b}}^* \in {{PF}}(m, n)$.2.
 ${\textbf{a}} \leq_C {\boldsymbol \tau}({\textbf{c}}) \leq_C {\textbf{b}}$ and
${\textbf{a}} \leq_C {\boldsymbol \tau}({\textbf{c}}) \leq_C {\textbf{b}}$ and  ${\boldsymbol \tau}({\textbf{b}}^*)^* \leq_C {\textbf{b}}$.
${\boldsymbol \tau}({\textbf{b}}^*)^* \leq_C {\textbf{b}}$.
Proof. Evidently ![]() ${\textbf{a}} \leq_C {\boldsymbol \tau}({\textbf{c}}) \leq_C {\textbf{b}}$. Since
${\textbf{a}} \leq_C {\boldsymbol \tau}({\textbf{c}}) \leq_C {\textbf{b}}$. Since ![]() ${\boldsymbol \tau}({\textbf{c}})$ is a parking outcome, it consists of distinct entries, and so its non-decreasing rearrangement
${\boldsymbol \tau}({\textbf{c}})$ is a parking outcome, it consists of distinct entries, and so its non-decreasing rearrangement ![]() ${\boldsymbol \lambda}=(\lambda_1, \dots, \lambda_m)$ satisfies
${\boldsymbol \lambda}=(\lambda_1, \dots, \lambda_m)$ satisfies ![]() $\lambda_i \geq i$ for all
$\lambda_i \geq i$ for all ![]() $1\leq i\leq m$. It follows that
$1\leq i\leq m$. It follows that ![]() ${\boldsymbol \tau}({\textbf{c}})^*$ also consists of distinct entries, and its non-decreasing rearrangement
${\boldsymbol \tau}({\textbf{c}})^*$ also consists of distinct entries, and its non-decreasing rearrangement ![]() ${\boldsymbol \lambda}^*=(\lambda_1^*, \dots, \lambda_m^*)=(n+1-\lambda_m, \dots, n+1-\lambda_1)$ satisfies
${\boldsymbol \lambda}^*=(\lambda_1^*, \dots, \lambda_m^*)=(n+1-\lambda_m, \dots, n+1-\lambda_1)$ satisfies ![]() $\lambda_i^* \leq n-m+i$ for all
$\lambda_i^* \leq n-m+i$ for all ![]() $1\leq i\leq m$. Therefore
$1\leq i\leq m$. Therefore ![]() ${\boldsymbol \tau}({\textbf{c}})^* \in {{PF}}(m, n)$. From
${\boldsymbol \tau}({\textbf{c}})^* \in {{PF}}(m, n)$. From ![]() ${\boldsymbol \tau}({\textbf{c}}) \leq_C {\textbf{b}}$, one has
${\boldsymbol \tau}({\textbf{c}}) \leq_C {\textbf{b}}$, one has ![]() ${\textbf{b}}^* \leq_C {\boldsymbol \tau}({\textbf{c}})^*$. Hence
${\textbf{b}}^* \leq_C {\boldsymbol \tau}({\textbf{c}})^*$. Hence ![]() ${\textbf{b}}^* \in {\text{PF}}(m, n)$. This implies that
${\textbf{b}}^* \in {\text{PF}}(m, n)$. This implies that ![]() ${\textbf{b}}^* \leq_C {\boldsymbol \tau}({\textbf{b}}^*)$, and further implies that
${\textbf{b}}^* \leq_C {\boldsymbol \tau}({\textbf{b}}^*)$, and further implies that ![]() ${\boldsymbol \tau}({\textbf{b}}^*)^* \leq_C {\textbf{b}}$.
${\boldsymbol \tau}({\textbf{b}}^*)^* \leq_C {\textbf{b}}$.
Proposition 12. The number of interval parking functions ![]() $|{{IPF}}(m, n)|$ satisfies
$|{{IPF}}(m, n)|$ satisfies
 \begin{equation}|{{IPF}}(m, n)|=\sum_{{\textbf{s}} \models m} \binom{m}{{\textbf{s}}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1} \frac{n!}{\prod_{i=1}^{n-m} (n-i+1-s_1-\cdots-s_i)},\end{equation}
\begin{equation}|{{IPF}}(m, n)|=\sum_{{\textbf{s}} \models m} \binom{m}{{\textbf{s}}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1} \frac{n!}{\prod_{i=1}^{n-m} (n-i+1-s_1-\cdots-s_i)},\end{equation}
where ![]() ${\textbf{s}}=(s_1, \dots, s_{n-m+1})$ is a composition of m. In particular,
${\textbf{s}}=(s_1, \dots, s_{n-m+1})$ is a composition of m. In particular,
Proof. For an interval parking function ![]() ${\textbf{c}}=({\textbf{a}}, {\textbf{b}}) \in {\text{IPF}}(m, n)$, there are
${\textbf{c}}=({\textbf{a}}, {\textbf{b}}) \in {\text{IPF}}(m, n)$, there are ![]() $n-m$ parking spots that are never attempted by any car. Let
$n-m$ parking spots that are never attempted by any car. Let ![]() $k_i({\boldsymbol \pi})$ for
$k_i({\boldsymbol \pi})$ for ![]() $i=1, \dots, n-m$ represent these spots, so that
$i=1, \dots, n-m$ represent these spots, so that ![]() $0\,:\!=\,k_0<k_1<\cdots<k_{n-m}<k_{n-m+1}\,:\!=\,n+1$. This separates
$0\,:\!=\,k_0<k_1<\cdots<k_{n-m}<k_{n-m+1}\,:\!=\,n+1$. This separates ![]() ${\textbf{a}} \in {\text{PF}}(m, n)$ into
${\textbf{a}} \in {\text{PF}}(m, n)$ into ![]() $n-m+1$ disjoint non-interacting segments (some segments might be empty), with each segment a classical parking function of length
$n-m+1$ disjoint non-interacting segments (some segments might be empty), with each segment a classical parking function of length ![]() $(k_{i}-k_{i-1}-1)$ after translation. The parking outcome is
$(k_{i}-k_{i-1}-1)$ after translation. The parking outcome is ![]() ${\boldsymbol \tau}({\textbf{c}})={\boldsymbol \tau}({\textbf{a}})$, and for every
${\boldsymbol \tau}({\textbf{c}})={\boldsymbol \tau}({\textbf{a}})$, and for every ![]() ${\textbf{a}} \in {\text{PF}}(m, n)$, there are precisely
${\textbf{a}} \in {\text{PF}}(m, n)$, there are precisely ![]() $n!/\prod_{i=1}^{n-m} (n-k_i+1)$ choices for
$n!/\prod_{i=1}^{n-m} (n-k_i+1)$ choices for ![]() ${\textbf{b}}$ such that
${\textbf{b}}$ such that ![]() $({\textbf{a}}, {\textbf{b}}) \in {\text{IPF}}(m, n)$. We have
$({\textbf{a}}, {\textbf{b}}) \in {\text{IPF}}(m, n)$. We have
 \begin{align}&|{\text{IPF}}(m, n)|=\sum_{k} \prod_{i=1}^{n-m+1} (k_{i}-k_{i-1})^{k_{i}-k_{i-1}-2}\frac{n!}{\prod_{i=1}^{n-m} (n-k_i+1)} \cdot \notag \\
& \qquad\qquad \cdot \binom{m}{k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1} \notag \\
&=\sum_{{\textbf{s}} \models m} \binom{m}{s_1, \dots, s_{n-m+1}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1} \frac{n!}{\prod_{i=1}^{n-m} (n-i+1-s_1-\cdots-s_i)},\end{align}
\begin{align}&|{\text{IPF}}(m, n)|=\sum_{k} \prod_{i=1}^{n-m+1} (k_{i}-k_{i-1})^{k_{i}-k_{i-1}-2}\frac{n!}{\prod_{i=1}^{n-m} (n-k_i+1)} \cdot \notag \\
& \qquad\qquad \cdot \binom{m}{k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1} \notag \\
&=\sum_{{\textbf{s}} \models m} \binom{m}{s_1, \dots, s_{n-m+1}} \prod_{i=1}^{n-m+1} (s_i+1)^{s_i-1} \frac{n!}{\prod_{i=1}^{n-m} (n-i+1-s_1-\cdots-s_i)},\end{align}
where ![]() ${\textbf{s}}=(k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1)$ and
${\textbf{s}}=(k_1-k_0-1, \dots, k_{n-m+1}-k_{n-m}-1)$ and ![]() $\sum_{i=1}^{n-m+1} s_i=m$.
$\sum_{i=1}^{n-m+1} s_i=m$.
From (4.2), we recognize that the number of interval parking functions ![]() ${\text{IPF}}(n, n)$ coincides with the number of edge-labeled spanning trees of
${\text{IPF}}(n, n)$ coincides with the number of edge-labeled spanning trees of ![]() $K_{n+1}$. The rest of Section 4 will focus on this combinatorial implication. We first present some background material on the symmetric group.
$K_{n+1}$. The rest of Section 4 will focus on this combinatorial implication. We first present some background material on the symmetric group.
4.1. The symmetric group as a Coxeter system
Denote by ![]() ${\mathfrak{S}}_n$ the symmetric group on n letters. We set
${\mathfrak{S}}_n$ the symmetric group on n letters. We set ![]() $e=(1,\dots,n)$ (the identity permutation) and
$e=(1,\dots,n)$ (the identity permutation) and ![]() $w_0=(n,n-1,\dots,1)$. We denote by
$w_0=(n,n-1,\dots,1)$. We denote by ![]() $t_{ij}$ the permutation transposing i and j and fixing all other values, and take
$t_{ij}$ the permutation transposing i and j and fixing all other values, and take ![]() $s_i=t_{i,i+1}$. The elements
$s_i=t_{i,i+1}$. The elements ![]() $s_1,\dots,s_{n-1}$ are termed the standard generators. Our convention for multiplication is right to left, which is consistent with treating permutations as bijective functions from
$s_1,\dots,s_{n-1}$ are termed the standard generators. Our convention for multiplication is right to left, which is consistent with treating permutations as bijective functions from ![]() $[n]\to [n]$. Thus
$[n]\to [n]$. Thus ![]() $t_{ij}x$ is obtained by transposing the digits i,j wherever they appear in x, while
$t_{ij}x$ is obtained by transposing the digits i,j wherever they appear in x, while ![]() $x t_{ij}$ is obtained by transposing the digits in the ith and jth positions.
$x t_{ij}$ is obtained by transposing the digits in the ith and jth positions.
The theory of normal forms in a Coxeter system was introduced by du Cloux [Reference Du Cloux8] and is elaborated in Björner and Brenti [Reference Björner and Brenti2]. The symmetric group ![]() ${\mathfrak{S}}_n$ may be viewed as a Coxeter system of type A, with generators
${\mathfrak{S}}_n$ may be viewed as a Coxeter system of type A, with generators ![]() $S=\{s_1,\dots,s_{n-1}\}$. The length l(x) of
$S=\{s_1,\dots,s_{n-1}\}$. The length l(x) of ![]() $x\in{\mathfrak{S}}_n$ is the smallest number k such that x can be written as a product
$x\in{\mathfrak{S}}_n$ is the smallest number k such that x can be written as a product ![]() $s_{i_1}\cdots s_{i_k}$ of standard generators; in this case
$s_{i_1}\cdots s_{i_k}$ of standard generators; in this case ![]() $s_{i_1}\cdots s_{i_k}$ is called a reduced word for x. It is a standard fact that length equals number of inversions:
$s_{i_1}\cdots s_{i_k}$ is called a reduced word for x. It is a standard fact that length equals number of inversions:
Let ![]() $\sigma_k=s_k\cdots s_1$. Every
$\sigma_k=s_k\cdots s_1$. Every ![]() $x\in{\mathfrak{S}}_n$ has a unique normal form: a reduced word N(x) of the form
$x\in{\mathfrak{S}}_n$ has a unique normal form: a reduced word N(x) of the form ![]() $v_1 \cdots v_{n-1}$, where
$v_1 \cdots v_{n-1}$, where ![]() $v_k=e$ or
$v_k=e$ or ![]() $v_k=s_k \cdots s_j$ for some
$v_k=s_k \cdots s_j$ for some ![]() $1\leq j\leq k$ is a prefix of
$1\leq j\leq k$ is a prefix of ![]() $\sigma_k$. For example,
$\sigma_k$. For example, ![]() $l(e)=0$,
$l(e)=0$, ![]() $N(e)=e$, and
$N(e)=e$, and ![]() $l(w_0)=n(n-1)/2$,
$l(w_0)=n(n-1)/2$, ![]() $N(w_0)=\sigma_1\cdots\sigma_{n-1}$. It is straightforward to obtain the permutation x given its normal form N(x). Conversely, since
$N(w_0)=\sigma_1\cdots\sigma_{n-1}$. It is straightforward to obtain the permutation x given its normal form N(x). Conversely, since ![]() $xv_{n-1}^{-1} \cdots v_1^{-1}=e$, we may interpret the normal-form decomposition of x in an alternative way: start with the permutation x. Then
$xv_{n-1}^{-1} \cdots v_1^{-1}=e$, we may interpret the normal-form decomposition of x in an alternative way: start with the permutation x. Then ![]() $v_{n-1}^{-1}$ corresponds to a sequence of adjacent transpositions that moves the value n in x to the right until it is in the last position (if n is already in the last position, then
$v_{n-1}^{-1}$ corresponds to a sequence of adjacent transpositions that moves the value n in x to the right until it is in the last position (if n is already in the last position, then ![]() $v_{n-1}^{-1}=e$). Similarly,
$v_{n-1}^{-1}=e$). Similarly, ![]() $v_{n-2}^{-1}$ corresponds to a sequence of adjacent transpositions that moves the value
$v_{n-2}^{-1}$ corresponds to a sequence of adjacent transpositions that moves the value ![]() $n-1$ in
$n-1$ in ![]() $xv_{n-1}^{-1}$ to the right until it is in the next-to-last position (if
$xv_{n-1}^{-1}$ to the right until it is in the next-to-last position (if ![]() $n-1$ is already in the next-to-last position, then
$n-1$ is already in the next-to-last position, then ![]() $v_{n-2}^{-1}=e$); and so on. Thus x is fully characterized by the sequence
$v_{n-2}^{-1}=e$); and so on. Thus x is fully characterized by the sequence
This describes an explicit bijection between ![]() ${\mathfrak{S}}_n$ and
${\mathfrak{S}}_n$ and ![]() $C_2 \times \cdots \times C_n$, where
$C_2 \times \cdots \times C_n$, where ![]() $C_i$ is a chain with i elements.
$C_i$ is a chain with i elements.
4.2. One-to-one correspondence between interval parking functions  ${\text{IPF}}(n, n)$ and edge-labeled spanning trees of
${\text{IPF}}(n, n)$ and edge-labeled spanning trees of  $K_{n\,\mathrm{+}\,\mathrm{1}}$
$K_{n\,\mathrm{+}\,\mathrm{1}}$
Recall the classical result that there exists a bijection between parking functions ![]() ${\text{PF}}(n, n)$ and spanning trees of
${\text{PF}}(n, n)$ and spanning trees of ![]() $K_{n+1}$, using the concepts of specification and order permutation. Building upon this result, we will construct a bijection between interval parking functions
$K_{n+1}$, using the concepts of specification and order permutation. Building upon this result, we will construct a bijection between interval parking functions ![]() ${\text{IPF}}(n, n)$ and edge-labeled spanning trees of
${\text{IPF}}(n, n)$ and edge-labeled spanning trees of ![]() $K_{n+1}$, where the vertices are labeled 0 through n (vertex 0 is the root) and the edges are labeled 1 through n.
$K_{n+1}$, where the vertices are labeled 0 through n (vertex 0 is the root) and the edges are labeled 1 through n.
As illustrated in Chassaing and Marckert [Reference Chassaing and Marckert4] and Yan [Reference Yan21], a parking function ![]() ${\boldsymbol \pi} \in {\text{PF}}(n, n)$ may be uniquely determined by its associated specification
${\boldsymbol \pi} \in {\text{PF}}(n, n)$ may be uniquely determined by its associated specification ![]() ${\textbf{r}}({\boldsymbol \pi})$ and order permutation
${\textbf{r}}({\boldsymbol \pi})$ and order permutation ![]() $\sigma({\boldsymbol \pi})$. Here the specification is
$\sigma({\boldsymbol \pi})$. Here the specification is ![]() ${\textbf{r}}({\boldsymbol \pi})=(r_1, \dots, r_n)$, where
${\textbf{r}}({\boldsymbol \pi})=(r_1, \dots, r_n)$, where ![]() $r_k=\#\{i\,:\, \pi_i=k\}$ records the number of cars whose first preference is spot k. The order permutation
$r_k=\#\{i\,:\, \pi_i=k\}$ records the number of cars whose first preference is spot k. The order permutation ![]() $\sigma({\boldsymbol \pi}) \in {\mathfrak{S}}_n$, on the other hand, is defined by
$\sigma({\boldsymbol \pi}) \in {\mathfrak{S}}_n$, on the other hand, is defined by
and so is the permutation that orders the list, without switching elements which are the same. In words, ![]() $\sigma_i$ is the position of the entry
$\sigma_i$ is the position of the entry ![]() $\pi_i$ in the non-decreasing rearrangement of
$\pi_i$ in the non-decreasing rearrangement of ![]() ${\boldsymbol \pi}$. Conversely, we can easily recover a parking function
${\boldsymbol \pi}$. Conversely, we can easily recover a parking function ![]() ${\boldsymbol \pi}$ by replacing i in
${\boldsymbol \pi}$ by replacing i in ![]() $\sigma({\boldsymbol \pi})$ with the ith smallest term in the sequence
$\sigma({\boldsymbol \pi})$ with the ith smallest term in the sequence ![]() $1^{r_1}\dots n^{r_n}$.
$1^{r_1}\dots n^{r_n}$.
However, not every pair of a length-n vector ![]() ${\textbf{r}}$ and a permutation
${\textbf{r}}$ and a permutation ![]() $\sigma \in {\mathfrak{S}}_n$ can be the specification and the order permutation of a parking function from
$\sigma \in {\mathfrak{S}}_n$ can be the specification and the order permutation of a parking function from ![]() ${\text{PF}}(n, n)$. The vector and the permutation must be compatible with each other, in the sense that the terms
${\text{PF}}(n, n)$. The vector and the permutation must be compatible with each other, in the sense that the terms ![]() $1+\sum_{i=1}^{k-1} r_i, \dots, \sum_{i=1}^{k} r_i$ appear from left to right in
$1+\sum_{i=1}^{k-1} r_i, \dots, \sum_{i=1}^{k} r_i$ appear from left to right in ![]() $\sigma$ for every k to satisfy the non-decreasing rearrangement requirement of
$\sigma$ for every k to satisfy the non-decreasing rearrangement requirement of ![]() ${\boldsymbol \pi}$. Moreover, the specification
${\boldsymbol \pi}$. Moreover, the specification ![]() ${\textbf{r}}$ should satisfy a balance condition:
${\textbf{r}}$ should satisfy a balance condition:
 \begin{align}\sum_{s=1}^{j} r_s \geq j, \quad \forall 1 \leq j \leq n, \quad \sum_{s=1}^n r_s=n.\end{align}
\begin{align}\sum_{s=1}^{j} r_s \geq j, \quad \forall 1 \leq j \leq n, \quad \sum_{s=1}^n r_s=n.\end{align}
Let ![]() ${\mathscr C}(n)$ be the set of all compatible pairs.
${\mathscr C}(n)$ be the set of all compatible pairs.
Denote by ![]() ${\mathscr F}(n+1)$ the set of spanning trees of
${\mathscr F}(n+1)$ the set of spanning trees of ![]() $K_{n+1}$, where the vertices are labeled 0 through n and vertex 0 is the root. Furthermore, denote by
$K_{n+1}$, where the vertices are labeled 0 through n and vertex 0 is the root. Furthermore, denote by ![]() ${\mathscr F}^e(n+1)$ the set of edge-labeled spanning trees of
${\mathscr F}^e(n+1)$ the set of edge-labeled spanning trees of ![]() $K_{n+1}$, where the edges, in addition to the vertices, are also labeled 1 through n.
$K_{n+1}$, where the edges, in addition to the vertices, are also labeled 1 through n.
Theorem 9. (Adapted from Yan [Reference Yan21].) The set ![]() ${\mathscr C}(n)$ is in one-to-one correspondence with
${\mathscr C}(n)$ is in one-to-one correspondence with ![]() ${{PF}}(n, n)$, and is also in one-to-one correspondence with
${{PF}}(n, n)$, and is also in one-to-one correspondence with ![]() ${\mathscr F}(n+1)$.
${\mathscr F}(n+1)$.
Theorem 10. There is a one-to-one correspondence between ![]() ${{IPF}}(n, n)$ and
${{IPF}}(n, n)$ and ![]() ${\mathscr F}^e(n+1)$, the set of edge-labeled spanning trees of
${\mathscr F}^e(n+1)$, the set of edge-labeled spanning trees of ![]() $K_{n+1}$.
$K_{n+1}$.
Proof. By Proposition 10, ![]() $({\textbf{a}}, {\textbf{b}}) \in {\text{IPF}}(n, n)$ is equivalent to
$({\textbf{a}}, {\textbf{b}}) \in {\text{IPF}}(n, n)$ is equivalent to ![]() ${\textbf{a}}\in {\text{PF}}(n, n)$ and
${\textbf{a}}\in {\text{PF}}(n, n)$ and ![]() ${\boldsymbol \tau}({\textbf{a}}) \leq_C {\textbf{b}}$. Using Theorem 9,
${\boldsymbol \tau}({\textbf{a}}) \leq_C {\textbf{b}}$. Using Theorem 9, ![]() ${\textbf{a}}$ is in one-to-one correspondence with a spanning tree of
${\textbf{a}}$ is in one-to-one correspondence with a spanning tree of ![]() $K_{n+1}$, where
$K_{n+1}$, where ![]() ${\textbf{a}}$ determines the shape and vertex labels of the spanning tree. Since
${\textbf{a}}$ determines the shape and vertex labels of the spanning tree. Since ![]() ${\boldsymbol \tau}({\textbf{a}})$ is a permutation on n letters,
${\boldsymbol \tau}({\textbf{a}})$ is a permutation on n letters, ![]() ${\textbf{b}}-{\boldsymbol \tau}({\textbf{a}})$ takes values in
${\textbf{b}}-{\boldsymbol \tau}({\textbf{a}})$ takes values in ![]() $C_1 \times \cdots \times C_n$, where
$C_1 \times \cdots \times C_n$, where ![]() $C_i$ is a chain of length i (after reordering the indices). Using the results on Coxeter systems from Section 4.1, this gives an association between
$C_i$ is a chain of length i (after reordering the indices). Using the results on Coxeter systems from Section 4.1, this gives an association between ![]() ${\textbf{b}}$ and the edge labels of the spanning tree.
${\textbf{b}}$ and the edge labels of the spanning tree.
We illustrate the map with a representative example. See Figure 1, which represents an element of ![]() ${\mathscr F}^e(10)$. We read the vertices in ‘breadth-first search’ (BFS) order:
${\mathscr F}^e(10)$. We read the vertices in ‘breadth-first search’ (BFS) order: ![]() $v_{0}, \dots, v_{9}=0,2,5,9,6,1,8,4,7,3$. That is, read the root vertex first, then all vertices at level one (distance one from the root), then those at level two (distance two from the root), and so on, where vertices at a given level are naturally ordered in order of increasing predecessor, and, if they have the same predecessor, increasing order. We let
$v_{0}, \dots, v_{9}=0,2,5,9,6,1,8,4,7,3$. That is, read the root vertex first, then all vertices at level one (distance one from the root), then those at level two (distance two from the root), and so on, where vertices at a given level are naturally ordered in order of increasing predecessor, and, if they have the same predecessor, increasing order. We let ![]() $\sigma=259618473$ be this vertex ordering once we remove the root vertex. We also record the edges incident with the vertices as
$\sigma=259618473$ be this vertex ordering once we remove the root vertex. We also record the edges incident with the vertices as ![]() $x=569341827$, with associated normal form
$x=569341827$, with associated normal form ![]() ${\boldsymbol \lambda}(x)=(0, 2, 2, 4, 4, 0, 2, 6) \in C_2 \times \cdots \times C_9$. We let
${\boldsymbol \lambda}(x)=(0, 2, 2, 4, 4, 0, 2, 6) \in C_2 \times \cdots \times C_9$. We let ![]() $r_i$ record the number of successors of
$r_i$ record the number of successors of ![]() $v_i$; that is,
$v_i$; that is, ![]() ${\textbf{r}}=(3, 1, 2, 1, 1, 0, 1, 0, 0)$. Now
${\textbf{r}}=(3, 1, 2, 1, 1, 0, 1, 0, 0)$. Now ![]() ${\textbf{r}}$ is balanced and
${\textbf{r}}$ is balanced and ![]() $\sigma^{-1}=519724863$ is compatible with
$\sigma^{-1}=519724863$ is compatible with ![]() ${\textbf{r}}$, by virtue of the fact that vertices with the same predecessor are read in increasing order. The corresponding parking function is
${\textbf{r}}$, by virtue of the fact that vertices with the same predecessor are read in increasing order. The corresponding parking function is ![]() ${\textbf{a}}=(3, 1, 7, 4, 1, 2, 5, 3, 1)$, with parking outcome
${\textbf{a}}=(3, 1, 7, 4, 1, 2, 5, 3, 1)$, with parking outcome ![]() ${\boldsymbol \tau}({\textbf{a}})=(3, 1, 7, 4, 2, 5, 6, 8, 9)$. Thus
${\boldsymbol \tau}({\textbf{a}})=(3, 1, 7, 4, 2, 5, 6, 8, 9)$. Thus ![]() ${\textbf{b}}-{\boldsymbol \tau}({\textbf{a}}) \in C_7 \times C_9 \times C_3 \times C_6 \times C_8 \times C_5 \times C_4 \times C_2 \times C_1$. Reordering the indices in
${\textbf{b}}-{\boldsymbol \tau}({\textbf{a}}) \in C_7 \times C_9 \times C_3 \times C_6 \times C_8 \times C_5 \times C_4 \times C_2 \times C_1$. Reordering the indices in ![]() ${\boldsymbol \lambda}(x)$ and adding an extra 0 (for
${\boldsymbol \lambda}(x)$ and adding an extra 0 (for ![]() $C_1$), we have
$C_1$), we have ![]() ${\textbf{b}}-{\boldsymbol \tau}({\textbf{a}})=(0, 6, 2, 4, 2, 4, 2, 0, 0)$. Hence
${\textbf{b}}-{\boldsymbol \tau}({\textbf{a}})=(0, 6, 2, 4, 2, 4, 2, 0, 0)$. Hence ![]() ${\textbf{b}}=(3, 7, 9, 8, 4, 9, 8, 8, 9)$. The interval parking function connected with this edge-labeled spanning tree is
${\textbf{b}}=(3, 7, 9, 8, 4, 9, 8, 8, 9)$. The interval parking function connected with this edge-labeled spanning tree is ![]() ${\textbf{c}}=({\textbf{a}}, {\textbf{b}})=((3, 1, 7, 4, 1, 2, 5, 3, 1), (3, 7, 9, 8, 4, 9, 8, 8, 9))$.
${\textbf{c}}=({\textbf{a}}, {\textbf{b}})=((3, 1, 7, 4, 1, 2, 5, 3, 1), (3, 7, 9, 8, 4, 9, 8, 8, 9))$.
The above one-to-one correspondence between edge-labeled spanning trees and interval parking functions does not depend on using the BFS algorithm; any other algorithm which builds up a tree one edge at a time through a sequence of growing subtrees will give an alternative bijection. Generally, an algorithm checks the vertices of the tree one by one, starting with the root. At each step, we pick a new vertex and connect it to the checked vertices. The choice function (which defines the algorithm) tells us which new vertex to pick.

Figure 1. Edge-labeled spanning tree of complete graph.
Equivalently, we could view the edge-labeled spanning tree of ![]() $K_{n+1}$ as the spanning tree of a complete bipartite graph of
$K_{n+1}$ as the spanning tree of a complete bipartite graph of ![]() $K_{n, n+1}$ where the first group has n vertices labeled 1 through n and the second group has
$K_{n, n+1}$ where the first group has n vertices labeled 1 through n and the second group has ![]() $n+1$ vertices labeled 0 through n, and every vertex in the first group has two incident edges. Two vertices i and j of
$n+1$ vertices labeled 0 through n, and every vertex in the first group has two incident edges. Two vertices i and j of ![]() $K_{n+1}$ are connected with edge label k if and only if vertices i and j in the second group of
$K_{n+1}$ are connected with edge label k if and only if vertices i and j in the second group of ![]() $K_{n, n+1}$ are both connected to vertex k in the first group. This is a one-to-one correspondence, since vertex k must be unique, as otherwise this creates a cycle in
$K_{n, n+1}$ are both connected to vertex k in the first group. This is a one-to-one correspondence, since vertex k must be unique, as otherwise this creates a cycle in ![]() $K_{n, n+1}$. See Figure 2 for a transformed view of Figure 1.
$K_{n, n+1}$. See Figure 2 for a transformed view of Figure 1.

Figure 2. Spanning tree of complete bipartite graph.
The author acknowledges helpful conversations with Jeremy L. Martin, and is particularly thankful to Richard Kenyon for many enlightening comments.
Funding information
The author’s research was supported in part by the University of Denver’s Faculty Research Fund 84688-145601 and Professional Research Opportunities for Faculty Fund 80369-145601.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.