Published online by Cambridge University Press: 19 October 2021
We will show that almost all nonassociative relation algebras are symmetric and integral (in the sense that the fraction of both labelled and unlabelled structures that are symmetric and integral tends to
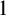 $1$
), and using a Fraïssé limit, we will establish that the classes of all atom structures of nonassociative relation algebras and relation algebras both have
$1$
), and using a Fraïssé limit, we will establish that the classes of all atom structures of nonassociative relation algebras and relation algebras both have
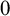 $0$
–
$0$
–
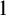 $1$
laws. As a consequence, we obtain improved asymptotic formulas for the numbers of these structures and broaden some known probabilistic results on relation algebras.
$1$
laws. As a consequence, we obtain improved asymptotic formulas for the numbers of these structures and broaden some known probabilistic results on relation algebras.