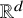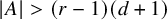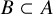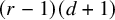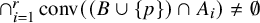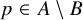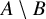Extensions of the colorful Helly theorem for d-collapsible and d-Leray complexes

Abstract

We present extensions of the colorful Helly theorem for d-collapsible and d-Leray complexes, providing a common generalization to the matroidal versions of the theorem due to Kalai and Meshulam, the ‘very colorful’ Helly theorem introduced by Arocha, Bárány, Bracho, Fabila and Montejano and the ‘semi-intersecting’ colorful Helly theorem proved by Montejano and Karasev.

As an application, we obtain the following extension of Tverberg’s theorem: Let A be a finite set of points in ${\mathbb R}^d$ with $|A|>(r-1)(d+1)$. Then, there exist a partition $A_1,\ldots ,A_r$ of A and a subset $B\subset A$ of size $(r-1)(d+1)$ such that $\cap _{i=1}^r \operatorname {\mathrm {\text {conv}}}( (B\cup \{p\})\cap A_i)\neq \emptyset $ for all $p\in A\setminus B$. That is, we obtain a partition of A into r parts that remains a Tverberg partition even after removing all but one arbitrary point from $A\setminus B$.

1 Introduction

Let $\mathcal {F}$ be a family of (not necessarily distinct) sets, colored with r colors. Formally, we have a partition $\mathcal {F}=\mathcal {F}_1\cup \cdots \cup \mathcal {F}_r$ . We call the subfamilies $\mathcal {F}_i$ the color classes of $\mathcal {F}$ . We say that a subfamily $\mathcal {F}'\subset \mathcal {F}$ is colorful if it contains at least one set from each color class. We say that $\mathcal {F}'$ is intersecting if $\cap _{F\in \mathcal {F}'} F\neq \emptyset $ . The colorful Helly theorem, observed by Lovász, asserts the following:

Theorem 1.1 (Lovász’s colorful Helly theorem (see [4])).

Let $\mathcal {C}$ be a finite family of convex sets in ${\mathbb R}^d$ colored with $d+1$ colors. If all colorful subfamilies of $\mathcal {F}$ of size $d+1$ are intersecting, then one of the color classes is intersecting.

Many combinatorial properties of families of convex sets, and in particular Helly-type results like Theorem 1.1, can be described in terms of the nerve of the family. Given a finite family $\mathcal {F}$ of sets, the nerve of $\mathcal {F}$ is the simplicial complex on vertex set $\mathcal {F}$ whose simplices are the subfamilies $\mathcal {F}'\subset \mathcal {F}$ that are intersecting. We say that a simplicial complex X is d-representable if it is isomorphic to the nerve of some family of convex sets in ${\mathbb R}^d$ .

Two related notions are those of d-collapsibility and d-Lerayness, introduced by Wegner in [24]. Let X be a simplicial complex. A simplex $\sigma \in X$ is called a free face of X if $\sigma $ is contained in a unique maximal face $\tau $ (possibly equal to $\sigma $ ) of X. Given a free face $\sigma $ of size at most d in X, an elementary d-collapse is the operation of removing from X all the simplices containing $\sigma $ (and contained in $\tau $ ). We say that X is d-collapsible if there is a sequence of elementary d-collapses reducing X to the void complex $\emptyset $ . A simplicial complex X is called d-Leray if all induced subcomplexes of X, including X itself, have trivial homology groups in dimensions d and higher.

Wegner showed in [24] that every d-representable complex is d-collapsible and that every d-collapsible complex is d-Leray. Many interesting results about the intersection patterns of a family of convex sets can be obtained from the fact that the nerve of such a family is d-collapsible (or d-Leray). For example, in [9], Kalai and Meshulam proved the following generalizations of Theorem 1.1.

Theorem 1.2 [9, Theorem 2.1].

Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid on V of rank r, with rank function $\rho $ such that $M\subset X$ . Then, there is some $\tau \in X$ such that $\rho (\tau )=r$ and $\rho (V\setminus \tau )\leq d$ .

Theorem 1.3 [9, Theorem 1.6].

Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid on V of rank r, with rank function $\rho $ such that $M\subset X$ . Then, there is some $\tau \in X$ such that $\rho (V\setminus \tau )\leq d$ .

Theorem 1.1 can be deduced from either Theorem 1.2 or 1.3 by taking X to be the nerve of the family of convex sets, and M to be a ‘partition matroid’ corresponding to the coloring of the family (see Section 6 for more details).

Generalizations of Theorem 1.1 in a different direction were presented by Arocha et al. in [3] and by Montejano and Karasev in [13].

Theorem 1.4 (Very colorful Helly theorem [3, Theorem 10]).

Let $1\leq k\leq d+1$ , and let $\mathcal {C}$ be a finite family of convex sets in ${\mathbb R}^d$ colored with $d+1$ colors. If every subfamily $\mathcal {C}'\subset \mathcal {C}$ of size $d+1$ having at least k different colors is intersecting, then there are $d+2-k$ color classes whose union is intersecting.

Theorem 1.5 (‘Semi-intersecting’ colorful Helly theorem [13, Lemma 2]).

Let $\mathcal {C}$ be a finite family of convex sets in ${\mathbb R}^d$ colored with $d+2$ colors. If every colorful subfamily of size $d+2$ has at most one nonintersecting subfamily of size $d+1$ , then one of the color classes is intersecting.

Our main results consist of the following common generalizations of Theorem 1.4, Theorem 1.5 and Theorem 1.2 (Theorem 1.3, respectively).

Theorem 1.6. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ be integers. Let V be a finite set with $|V|\geq \max \{m+d,r\}$ . Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function $\rho $ .

Assume that, for every $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$ with $\rho (U)\geq k$ , there is some $i\in [m]$ such that $\{u_1,\ldots ,u_d,v_i\}\in X$ . Then, there is some $\tau \in X$ such that $\rho (\tau )\geq r+1-m$ and $\rho (V\setminus \tau )\leq k-1$ .

Under the weaker assumption of d-Lerayness, we obtain a weaker conclusion:

Theorem 1.7. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ be integers. Let V be a finite set with $|V|\geq \max \{m+d,r\}$ . Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function $\rho $ .

Assume that for every $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-1}\}\subset V$ with $\rho (U)\geq k$ , either $\{u_1,\ldots ,u_{d+1}\}\in X$ or there exists $j\in [m-1]$ such that $\sigma \cup \{v_j\}\in X$ for every $\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$ . Then, there is some $\tau \in X$ such that $\rho (V\setminus \tau ) \leq k-1$ .

Remark 1.8. Note that the condition in Theorem 1.6 is implied by the condition in Theorem 1.7 and that both conditions are implied by the following stronger (but perhaps more natural) condition: ‘For every subset U of V of size $d+m$ with $\rho (U) \geq k$ , all but possibly at most $m-1$ of the the subsets of U of size $d+1$ are simplices in X’. Moreover, note that all three conditions are equivalent for $m\leq 2$ .

As an immediate consequence of Theorem 1.6, we obtain the following:

Theorem 1.9. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ . Let $\mathcal {C}$ be a finite family of convex sets in ${\mathbb R}^d$ , colored with r different colors, of size $|\mathcal {C}|\geq \max \{m+d,r\}$ . Assume that for every family $\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset \mathcal {C}$ , colored with at least k different colors, at least one of the subfamilies of the form $\{A_1,\ldots ,A_d,B_i\}$ , for $i\in [m]$ , is intersecting. Then, there are $r-k+1$ color classes whose union is intersecting.

In the special case $m=1$ and $r=d+1$ , we recover Theorem 1.4. For $m=2$ and $r=k=d+2$ , we recover Theorem 1.5.

As an application of Theorem 1.9, we obtain the following extension of Tverberg’s theorem [23].

Let $A\subset {\mathbb R}^d$ be a finite set of points, and let $A=A_1\cup \ldots \cup A_r$ be a partition of A. We say that $A_1,\ldots , A_r$ is a Tverberg partition of A if $\cap _{i=1}^r \operatorname {\mathrm {\text {conv}}}(A_i)\neq \emptyset $ . Let $B\subset A$ . We say that $B\subsetneq A$ is a Tverberg center for the partition $A=A_1\cup \cdots \cup A_r$ if, for every $p\in A\setminus B$ , $ \bigcap _{i=1}^r \operatorname {\mathrm {\text {conv}}}\left ((B\cup \{p\})\cap A_i\right )\neq \emptyset. $ In other words, B is a Tverberg center for $A=A_1\cup \ldots \cup A_r$ if, for every $p\in A\setminus B$ , the partition of $B\cup \{p\}$ induced by $A_1,\ldots ,A_r$ is a Tverberg partition.

Theorem 1.10. Let $d\geq 1$ , $r\geq 2$ , and let $n=(r-1)(d+1)$ . Let $A\subset {\mathbb R}^d$ be a finite set of points of size larger than n. Then, there exists a partition $A_1,\ldots ,A_r$ of A that has a Tverberg center of size n.

For $|A|=n+1$ , this is exactly Tverberg’s theorem. Theorem 1.10 is sharp in the sense that we cannot guarantee a Tverberg center of size smaller than $(r-1)(d+1)$ : Let A be a generic set of points in ${\mathbb R}^d$ (in the sense that the $d|A|$ coordinates of A are algebraically independent over the rationals). Assume for contradiction that A has a partition $A_1,\ldots , A_r$ with a Tverberg center B of size $k<(r-1)(d+1)$ . Then, for every $p\in A\setminus B$ , $B'=B\cup \{p\}$ is a generic set of $k+1\leq (r-1)(d+1)$ points in ${\mathbb R}^d$ , with a Tverberg partition into r parts. However, it is well known that such a set does not have a Tverberg partition into r parts (see, e.g., [23]). In fact, the condition of genericity can be replaced by the weaker property of ‘strong general position’ introduced by Reay in [18] (under the name ‘strong independence’); see also [16, 17].

Theorem 1.10 is closely related to the ‘tolerant Tverberg theorem’ (see, e.g., [12, 6, 21, 7, 8]). Using Theorem 1.10, we obtain a new proof of the following result from [21]:

Theorem 1.11 (Soberón–Strausz [21, Theorem 1]).

Let $d\geq 1$ , $r\geq 2$ and $t\geq 0$ . Let $A\subset {\mathbb R}^d$ be a finite set of points of size at least $(t+1)(r-1)(d+1)+1$ . Then, there exists a partition $A_1,\ldots ,A_r$ of A such that, for any $C\subset A$ of size t,

$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\setminus C)\neq\emptyset. \end{align*}$$

Our paper is organized as follows. In Section 2, we present some basic facts about simplicial complexes and matroids that we will use later. In Section 3, we introduce the notion of ‘tolerance complexes’ of matroids, which is used in the proofs of our main results. In Section 4, we present the proof of Theorem 1.6, and in Section 5, we present the proof of Theorem 1.7. Section 6 deals with the geometric applications of our results and contains the proofs of Theorems 1.9, 1.10 and 1.11. We conclude in Section 7 with some open problems arising from our work.

2 Preliminaries

2.1 Simplicial complexes

A simplicial complex X is a family of subsets of some finite set V such that for every $\sigma \in X$ and $\sigma '\subset \sigma $ , we have $\sigma '\in X$ . The set $V = V(X)$ is called the vertex set of X. The sets in X are called the simplices or faces of the complex. The dimension of a simplex $\sigma \in X$ is $|\sigma |-1$ , and the dimension of X, denoted by $\dim (X)$ , is the maximal dimension of a simplex in X. We denote by $2^V=\{\sigma :\, \sigma \subset U\}$ the complete complex on vertex set V.

A subcomplex of X is a simplicial complex $X'$ such that each simplex of $X'$ is also a simplex of X. For $U\subset V$ , the subcomplex of X induced by U is the complex

$$\begin{align*}X[U]=\{\sigma\in X:\, \sigma\subset U\}. \end{align*}$$

Let $\sigma $ be a simplex in X. We define the link of $\sigma $ in X to be the subcomplex

$$\begin{align*}\operatorname{\mathrm{lk}}(X,\sigma)= \{\tau\in X: \, \sigma\cap\tau=\varnothing,\, \sigma\cup\tau \in X\}, \end{align*}$$

and the costar of $\sigma $ in X to be the subcomplex

$$\begin{align*}\operatorname{\mathrm{cost}}(X,\sigma) = \{\tau\in X:\, \sigma \not\subset\tau\}. \end{align*}$$

If $\sigma $ is a zero-dimensional simplex, that is, if $\sigma = \{v\}$ for some vertex $v \in V$ , we simply write $\operatorname {\mathrm {lk}}(X,v)=\operatorname {\mathrm {lk}}(X,\{v\})$ , and $X\setminus v= \operatorname {\mathrm {cost}}(X,\{v\})=X[V\setminus \{v\}]$ .

Let X and Y be simplicial complexes on disjoint vertex sets. The join of X and Y is the simplicial complex on $V(X) \cup V(Y)$ defined as

$$\begin{align*}X \ast Y= \{ \sigma\cup \tau:\, \sigma\in X, \tau\in Y\}. \end{align*}$$

The following well-known special case of the Mayer–Vietoris exact sequence relates the homology of a complex X to that of the link and costar of one of its vertices (see, e.g., [11, Theorem 2.2] for a detailed proof).

Theorem 2.1. Let X be a simplicial complex on vertex set V, and let $v\in V$ . Then, there is an exact sequence

$$\begin{align*}\cdots\to \tilde{H}_{k}\left(\operatorname{\mathrm{lk}}(X,v)\right) \to \tilde{H}_{k}\left(X\setminus v\right)\to \tilde{H}_{k}\left(X\right)\to \tilde{H}_{k-1}\left(\operatorname{\mathrm{lk}}(X,v)\right)\to \cdots \end{align*}$$

We will need the following equivalent definition of d-Leray complexes due to Kalai and Meshulam.

Lemma 2.2 [10, Proposition 3.1].

A simplicial complex X is d-Leray if and only if $\tilde {H}_k(\operatorname {\mathrm {lk}}(X,\sigma ))=0$ for all $\sigma \in X$ and $k\geq d$ .

Recall that, given a free face $\sigma \in X$ of size $|\sigma |\leq d$ , an elementary d-collapse is the operation consisting of removing $\sigma $ and all simplices containing it from X. Note that the complex obtained after this operation is exactly $\operatorname {\mathrm {cost}}(X,\sigma )$ . We denote such an elementary d-collapse by $X\to X'=\operatorname {\mathrm {cost}}(X,\sigma )$ . The following equivalent definition of d-collapsibility was observed by Tancer in [22] (see also [24, Lemma 1] for a similar statement):

Lemma 2.3 [22, Lemma 5.2].

A simplicial complex X is d-collapsible if and only if there is a sequence of elementary d-collapses

$$\begin{align*}X=X_1\to X_2\to \cdots\to X_t\end{align*}$$

such that the free face in each elementary d-collapse is of size exactly d, and $\dim (X_t)< d-1$ .

2.2 Matroids

A family M of subsets of a nonempty set V is a matroid if it satisfies

1. (i) $\emptyset \in M$ ,

2. (ii) for all $A' \subset A \subset V$ , if $A \in M$ , then $A' \in M$ , and

3. (iii) if $A, B \in M$ and $|A| < |B|$ , then there exists $x \in B \setminus A$ such that $A \cup \{x\} \in M$ .

The elements of M are usually called the independent sets of M, and the maximal elements are called the bases of M. The rank function of a matroid M on V is a function $\rho : 2^V \to \mathbb {N}$ such that for every $W \subset V$ , $\rho (W)$ equals the maximal size of a set $W' \subset W$ with $W' \in M$ . The rank of the matroid M is defined as $\rho (V)$ . The span of a set $U\subset V$ is defined as

$$\begin{align*}\text{span}_M(U)= \{v\in V:\, \rho(U\cup\{v\})=\rho(U)\}. \end{align*}$$

Note that the conditions (i) and (ii) allow us to regard a matroid M as a simplicial complex. Moreover, condition (iii), sometimes called the ‘exchange property’ for independent sets, implies that M is a pure simplicial complex – that is, all the bases of M are of the same size (equal to the rank of M). See, for example, [15] for more background on matroids.

We will need the following very simple auxiliary results about matroids.

Lemma 2.4. Let M be a rank r matroid on vertex set V, and let $\rho $ be its rank function. Then, for each $0\leq t\leq |V|$ , there exists $U\subset V$ such that $|U|=t$ and $\rho (U)\geq \min \{t,r\}$ .

Proof. If $t\leq r$ , let U be any independent set of M of size t. If $t\geq r$ , let $U\subset V$ be any set of size t containing a basis of M.

Lemma 2.5. Let M be a matroid on vertex set V with rank function $\rho $ . Let $U\subset W\subset V$ . Then

$$\begin{align*}\rho(U)\geq \rho(W)-|W\setminus U|. \end{align*}$$

Proof. By definition of the rank function, W contains an independent set $W'$ of size $\rho (W)$ . Then, $W'\cap U$ is an independent set of size at least $|W'|-|W\setminus U|=\rho (W)-|W\setminus U|$ . So $\rho (U)\geq \rho (W)-|W\setminus U|$ .

3 Tolerance complexes of matroids

Let M be a matroid with rank function $\rho $ on vertex set V. Let $r=\rho (V)$ be the rank of M. For $0\leq t\leq r$ , let

$$\begin{align*}M^t= \{\sigma\subset V:\, \rho(\sigma)\geq |\sigma|-t\}. \end{align*}$$

In particular, for $t=0$ we have $M^0=M$ . Note that $M^t$ is exactly the ‘t-tolerance complex’ of M, as defined in [11].

Lemma 3.1. Let $0\leq t\leq r$ . Then, $M^t$ is a matroid.

Proof. First, note that $M^t$ is a simplicial complex: If $\sigma \in M^t$ and $\sigma '\subset \sigma $ , then, by Lemma 2.5,

$$\begin{align*}\rho(\sigma')\geq \rho(\sigma)-|\sigma\setminus\sigma'| \geq |\sigma|-|\sigma\setminus\sigma'|-t =|\sigma'|-t, \end{align*}$$

and therefore $\sigma '\in M^t$ .

We will show that $M^t$ satisfies the exchange property for independent sets: Let $\sigma ,\tau \in M^t$ such that $|\tau |>|\sigma |$ . We have to show that there is a vertex $v\in \tau \setminus \sigma $ such that $\sigma \cup \{v\}\in M^t$ .

Since $\sigma \in M^t$ , we have $\rho (\sigma )\geq |\sigma |-t$ . If $\rho (\sigma )>|\sigma |-t$ , then for all $v\in V\setminus \sigma $ we have $\rho (\sigma \cup \{v\})\geq \rho (\sigma ) \geq |\sigma \cup \{v\}|-t$ , as wanted. If $\rho (\sigma )=|\sigma |-t$ , then, since $\tau \in M^t$ ,

$$\begin{align*}\rho(\tau)\geq |\tau|-t> |\sigma|-t =\rho(\sigma). \end{align*}$$

Let $\tau '\subset \tau $ such that $|\tau '|=\rho (\tau )$ and $\tau '\in M$ , and let $\sigma '\subset \sigma $ such that $|\sigma '|=\rho (\sigma )$ and $\sigma '\in M$ . Then, since $|\tau '|>|\sigma '|$ , there exists $v\in \tau '\setminus \sigma '$ such that $\sigma '\cup \{v\}\in M$ . Note that $v\in \tau \setminus \sigma $ (otherwise, $\sigma '\cup \{v\}\subset \sigma $ , in contradiction to $\rho (\sigma )=|\sigma '|$ ). We obtain

$$\begin{align*}\rho(\sigma\cup\{v\})\geq \rho(\sigma)+1 =|\sigma\cup\{v\}|-t, \end{align*}$$

and therefore, $\sigma \cup \{v\}\in M^t$ . Hence, $M^t$ is a matroid.

Lemma 3.2. Let $0\leq t\leq r$ . Denote the rank function of $M^t$ by $\rho ^t$ . Then, for every $A\subset V$ ,

$$\begin{align*}\rho^t(A)= \min\{ |A|,\rho(A)+t\}. \end{align*}$$

Proof. Assume first that $|A|\leq \rho (A)+t$ . Then $\rho (A) \geq |A|-t$ , and therefore $A\in M^t$ . In particular, $\rho ^t(A)=|A|$ .

Assume now that $|A|\geq \rho (A)+t$ . Let $I\subset A$ such that $|I|=\rho (A)$ and $I\in M$ . Then, any $U\subset A$ of size $\rho (A)+t$ containing I satisfies

$$\begin{align*}\rho(U)\geq \rho(I)=\rho(A) = (\rho(A)+t)-t= |U|-t, \end{align*}$$

and therefore belongs to $M^t$ . Thus, $\rho ^t(A)\geq \rho (A)+t$ . On the other hand, every $U\subset A$ such that $U\in M^t$ satisfies $\rho (U)\geq |U|-t$ , and therefore $|U|\leq \rho (U)+t\leq \rho (A)+t$ . So $\rho ^t(A)\leq \rho (A)+t$ .

Remark 3.3. Given two matroids $M_1$ and $M_2$ on vertex set V, the matroid union of $M_1$ and $M_2$ is defined as $M_1\vee M_2=\{\sigma \cup \tau :\, \sigma \in M_1,\, \tau \in M_2\}$ . The matroid union theorem (see, e.g., [15, Sec. 11.3]) states that $M_1\vee M_2$ is a matroid, with rank function $\rho _{12}$ satisfying

$$\begin{align*}\rho_{12}(A)=\min\{\rho_1(B)+\rho_2(B)+|A\setminus B| :\, B\subset A\} \end{align*}$$

for every $A\subset V$ , where $\rho _1$ and $\rho _2$ are the rank functions of $M_1$ and $M_2$ , respectively.

Note that $M^t$ is the matroid union of M and the uniform matroid $\{A\subset V:\, |A|\leq t\}$ . Therefore, Lemma 3.1 and Lemma 3.2 can also be obtained as a consequence of the matroid union theorem.

4 Proof of Theorem 1.6

In this section, we prove Theorem 1.6. Our proof extends the argument for the case $m=1, k=d+1$ given by Kalai and Meshulam in [9, Theorem 2.1].

Theorem 1.6. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ be integers. Let V be a finite set with $|V|\geq \max \{m+d,r\}$ . Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function $\rho $ .

Assume that, for every $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$ with $\rho (U)\geq k$ , there is some $i\in [m]$ such that $\{u_1,\ldots ,u_d,v_i\}\in X$ . Then, there is some $\tau \in X$ such that $\rho (\tau )\geq r+1-m$ and $\rho (V\setminus \tau )\leq k-1$ .

Proof of Theorem 1.6.

Let

$$ \begin{align*} \mathcal{R} &=\{\eta\in X:\, |\eta|\geq d+1,\, \rho(\eta)\geq k-m-d+|\eta|\} \\&= \{\eta\in X\cap M^{d+m-k} : \, |\eta|\geq d+1\}. \end{align*} $$

By Lemma 2.4, there is some $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_{m}\}\subset V$ with $\rho (U)\geq \min \{m+d,r\}\geq k$ . Then, there is some $i\in [m]$ such that $\sigma _i=\{u_1,\ldots ,u_d,v_i\}\in X$ . Note that $\sigma _i\subset U\in M^{d+m-k}$ , so $\sigma _i\in \mathcal {R}$ , and in particular $\mathcal {R}\neq \emptyset $ .

By Lemma 2.3, there is a sequence of elementary d-collapses $X=X_1\to X_2\to \cdots \to X_t$ such that the free faces collapsed at each step are of size exactly d, and $X_t$ satisfies $\dim (X_t)< d-1$ .

By definition, $\mathcal {R}\subset X=X_1$ , and clearly $\mathcal {R}\not \subset X_t$ . Let $1\leq n<t$ be the maximal index such that $\mathcal {R}\subset X_n$ . Let $\sigma $ be the free face of size d in the elementary d-collapse $X_n\to X_{n+1}$ , and let $\tau $ be the unique maximal face of $X_n$ containing $\sigma $ .

Since $\mathcal {R}\subset X_n$ but $\mathcal {R}\not \subset X_{n+1}$ , there is some $\sigma \subset \sigma '\subset \tau $ such that $\sigma '\in M^{d+m-k}$ . In particular, we have $\sigma \in M^{d+m-k}$ . Let

$$\begin{align*}\mathcal{A}= \{ \eta\subset V\setminus \sigma :\, \sigma\cup \eta \in M^{d+m-k}, \, \sigma\cup\{u\}\notin X_n \text{ for all } u\in \eta \}. \end{align*}$$

Note that, since $\sigma \in M^{d+m-k}$ , we have $\emptyset \in \mathcal {A}$ , and therefore $\mathcal {A}\neq \emptyset $ . Let $\eta $ be a maximal element of $\mathcal {A}$ .

First, note that $|\eta |\leq m-1$ . Otherwise, let $v_1,\ldots ,v_m\in \eta $ , and let $U=\sigma \cup \{v_1,\ldots ,v_m\}$ . Then $U \subset \sigma \cup \eta \in M^{d+m-k}$ , and therefore

$$\begin{align*}\rho(U)\geq |U|-(d+m-k)= (d+m)-(d+m-k)=k. \end{align*}$$

Therefore, there is some $i\in [m]$ such that $\sigma _i=\sigma \cup \{v_i\}\in X$ . Since $\sigma _i\subset \sigma \cup \eta \in M^{d+m-k}$ , we also have $\sigma _i\in M^{d+m-k}$ . Thus, $\sigma _i\in \mathcal {R}$ , and therefore $\sigma _i=\sigma \cup \{v_i\}\in X_n$ , in contradiction to $\eta \in \mathcal {A}$ .

Next, note that, for all $v\in V\setminus \text {span}_M(\sigma \cup \eta )$ , we have $\sigma \cup \{v\}\in X_n$ . Otherwise, we would have

$$\begin{align*}\rho(\sigma\cup\eta\cup\{v\})=\rho(\sigma\cup\eta)+1 \geq |\sigma\cup\eta|-(d+m-k)+1 = |\sigma\cup\eta\cup\{v\}|-(d+m-k). \end{align*}$$

So $\sigma \cup \eta \cup \{v\}\in M^{d+m-k}$ , and therefore $\eta \cup \{v\}\in \mathcal {A}$ , in contradiction the the maximality of $\eta $ . Therefore, since $\sigma $ is contained in the unique maximal face $\tau $ of $X_n$ , we obtain

(4.1) $$ \begin{align} V\setminus \text{span}_M(\sigma\cup\eta) \subset \tau, \end{align} $$

or equivalently,

$$\begin{align*}V\setminus \tau \subset \text{span}_M(\sigma\cup\eta). \end{align*}$$

We divide into two cases: If $\rho (\sigma \cup \eta )=|\sigma \cup \eta |-(d+m-k)= k-m+|\eta |$ , then

$$\begin{align*}\rho(V\setminus \tau)\leq \rho(\sigma\cup\eta) = k-m+|\eta|\leq k-1, \end{align*}$$

as wanted.

If $\rho (\sigma \cup \eta )\geq |\sigma \cup \eta |-(d+m-k)+1$ , then for every $v\in V\setminus (\sigma \cup \eta )$ , we have

$$\begin{align*}\rho(\sigma\cup\eta\cup\{v\})\geq \rho(\sigma\cup\eta) \geq |\sigma\cup\eta\cup\{v\}| -(d+m-k). \end{align*}$$

So $\sigma \cup \eta \cup \{v\}\in M^{d+m-k}$ , and therefore, by the maximality of $\eta $ in $\mathcal {A}$ , we must have $\sigma \cup \{v\}\in X_n$ . Hence, since $\sigma $ is contained in the unique maximal face $\tau $ of $X_n$ , we have $V\setminus \eta \subset \tau $ (actually, $V\setminus \eta = \tau $ since $\sigma \cup \{u\}\notin X_n$ for all $u\in \eta $ by the definition of $\mathcal {A}$ ). Thus,

$$\begin{align*}\rho(V\setminus \tau)= \rho(\eta) \leq |\eta|\leq m-1 \leq k-1. \end{align*}$$

Finally, let $v\in V$ . If $v\in \text {span}_M(\sigma \cup \eta )$ , then, since $\sigma \subset \tau $ , we have $v\in \text {span}_M(\tau \cup \eta )$ . If $v\notin \text {span}_M(\sigma \cup \eta )$ , then by Equation (4.1), $v\in \tau \subset \text {span}_M(\tau \cup \eta )$ . Thus, $\text {span}_M(\tau \cup \eta )=V$ , and therefore $\rho (\tau \cup \eta )=\rho (V)=r$ . Hence, by Lemma 2.5, we obtain

$$\begin{align*}\rho(\tau)\geq r-|\eta|\geq r-m+1.\\[-38pt] \end{align*}$$

5 Proof of Theorem 1.7

First, we prove the $m=1$ case of Theorem 1.7:

Theorem 5.1. Let X be a d-Leray simplicial complex on vertex set V. Let M be a matroid on V of rank $r\geq d+1$ . Denote by $\rho $ the rank function of M. Let $1\leq k\leq d+1$ .

Assume that X contains all the sets $\sigma \subset V$ of size $d+1$ such that $\rho (\sigma )\geq k$ . Then, there is some $\tau \in X$ such that $\rho (V\setminus \tau )\leq k-1$ .

The main tool we will need for the proof is the following result by Kalai and Meshulam (implicit in the proof of [9, Thm 1.6]; see also [2, Theorem 3] for a similar statement and [1, Theorem 4.5] for an equivalent dual version).

Lemma 5.2 (Kalai–Meshulam [9]).

Let X be a simplicial complex and M a matroid with rank function $\rho $ on the same vertex set V. For each $\sigma \in X$ , let

$$\begin{align*}\ell_{\sigma}=\min\{k\geq -1:\, \tilde{H}_i(\operatorname{\mathrm{lk}}(X,\sigma))=0\,\, \forall i\geq k\}. \end{align*}$$

If for all $\sigma \in X$ ,

$$\begin{align*}\rho(V\setminus \sigma)\geq \ell_{\sigma}+1, \end{align*}$$

then $M\not \subset X$ .

We will also need the following well-known simple result.

Lemma 5.3 (Helly’s theorem for d-Leray complexes).

Let X be a d-Leray complex on vertex set V, and let $U\subset V$ be a set of size at least $d+1$ . Assume that every subset of U of size $d+1$ is a simplex of X. Then, $U\in X$ .

Proof. Assume for contradiction that $U\notin X$ . Let $S\subset U$ be an inclusion minimal set such that $S\notin X$ . By the assumption of the lemma, we must have $|S|\geq d+2$ . But then, by the minimality of S, $X[S]$ is just the boundary of a $(|S|-1)$ -dimensional simplex, which has nontrivial homology in dimension $|S|-2 \geq d$ . This is a contradiction to the assumption that X is d-Leray.

Proof of Theorem 5.1.

Assume for contradiction that for all $\sigma \in X$ , $\rho (V\setminus \sigma )\geq k$ . In particular, we have $|V\setminus \sigma |\geq k$ for all $\sigma \in X$ .

Recall that we defined, for $\sigma \in X$ ,

$$\begin{align*}\ell_{\sigma}=\min\{n\geq -1:\, \tilde{H}_i(\operatorname{\mathrm{lk}}(X,\sigma))=0\, \forall i\geq n\}. \end{align*}$$

Let $t=d+1-k$ . In order to apply Lemma 5.2, we will show that $\rho ^t(V\setminus \sigma )\geq \ell _{\sigma }+1$ for all $\sigma \in X$ .

Let $\sigma \in X$ . By Lemma 3.2, we have

$$\begin{align*}\rho^t(V\setminus\sigma)\geq \min\{|V\setminus\sigma|,t+k\}= \min\{|V\setminus\sigma|,d+1\}. \end{align*}$$

We divide into two cases:

First, assume $|V\setminus \sigma |\geq d+1$ . Then, since X is d-Leray, we have, by Lemma 2.2, $\ell _{\sigma }\leq d$ , and therefore

$$\begin{align*}\rho^t(V\setminus\sigma)\geq \min\{|V\setminus\sigma|,d+1\}= d+1 \geq \ell_{\sigma}+1. \end{align*}$$

Now, assume $|V\setminus \sigma |\leq d$ . Then, we have $\rho ^t(V\setminus \sigma )=|V\setminus \sigma |$ . Since $|V\setminus \sigma '|\geq k$ for all $\sigma '\in X$ , we must have $\dim (X)\leq |V|-k-1$ , and therefore

$$\begin{align*}\dim(\operatorname{\mathrm{lk}}(X,\sigma))\leq |V\setminus\sigma|-k-1. \end{align*}$$

In particular, $\ell _{\sigma }\leq |V\setminus \sigma |-k$ . We obtain

$$\begin{align*}\rho^t(V\setminus\sigma)=|V\setminus\sigma|\geq \ell_{\sigma}+k\geq \ell_{\sigma}+1. \end{align*}$$

Hence, by Lemma 5.2, we have $M^t\not \subset X$ . That is, there is some $\tau \in M^t$ such that $\tau \notin X$ . If $|\tau |\geq d+1$ then, by Lemma 5.3, there is some $\tau '\subset \tau $ of size $d+1$ such that $\tau '\notin X$ . If $|\tau |<d+1$ , then, since $M^t$ is a matroid of rank $r\geq d+1>|\tau |$ , there is some $\tau '\supset \tau $ of size $d+1$ such that $\tau '\in M^t$ , and, since $\tau \notin X$ , we also have $\tau '\notin X$ .

In both cases, since $\tau '\in M^t$ , we have

$$\begin{align*}\rho(\tau')\geq |\tau'|-t= d+1-t= k, \end{align*}$$

but this is a contradiction to the assumption of the theorem.

For the proof of Theorem 1.7, we will need the following Lemma about d-Leray complexes.

Lemma 5.4. Let X be a d-Leray complex on vertex set V, and let $A\subset d+1$ such that $A\notin X$ . Let

$$\begin{align*}U=\{ v\in V\setminus A:\, v\cup \sigma\in X:\, \text{ for all } \sigma\subset A, |\sigma|=d\}. \end{align*}$$

Assume that $U\neq \emptyset $ . Then, for every $a\in A$ , $U\cup A\setminus \{a\}\in X$ .

Proof. Given a set $B\subset V$ and $i\geq 0$ , we denote by $\binom {B}{i}$ the family of all subsets of B of size i, and we denote by $\partial 2^B$ the boundary of the simplex on vertex set B, that is, the simplicial complex consisting of all proper subsets of B.

First, note that, since $U\neq \emptyset $ , we must have $\sigma \in X$ for every $\sigma \subsetneq A$ . That is, $\partial 2^A\subset X$ . We will show that, for every $1\leq i\leq |U|$ and $W \in \binom {U}{i}$ , $X[A\cup W] = \partial 2^A\ast 2^{W}$ . We argue by induction on i. The base case $i=1$ is obvious by the definition of U. Suppose, for some $1\leq i<|U|$ , that $X[A\cup T] =\partial 2^A\ast 2^{T}$ for every $T \in \binom {U}{i}$ . Let $W = \{u_1,u_2,\ldots ,u_{i+1}\} \subset U$ .

Consider

$$\begin{align*}L = \operatorname{\mathrm{lk}}(X[A\cup W], \{u_1,u_2,\ldots,u_{i-1}\}).\end{align*}$$

Note that, by Lemma 2.2, $\tilde {H}_j(L) = 0$ for every $j \geq d$ . Furthermore, by the induction hypothesis, we have $X[A\cup (W\setminus \{u_{i}\})]=\partial 2^A \ast 2^{W\setminus \{u_{i}\}}$ , and therefore $L \setminus u_{i} = \partial 2^A\ast 2^{\{u_{i+1}\}}$ . In particular, $L\setminus u_i$ contractible, and thus $\tilde {H}_j(L\setminus u_i)=0$ for all $j\geq 0$ . By Theorem 2.1, there exists a long exact sequence

$$\begin{align*}\cdots \to \tilde{H}_j(L)\to \tilde{H}_{j-1}(\operatorname{\mathrm{lk}}(L,u_i))\to \tilde{H}_{j-1}(L\setminus u_i)\to\cdots \end{align*}$$

We obtain that

$$\begin{align*}\tilde{H}_j(\operatorname{\mathrm{lk}}(L, u_i)) = 0\;\;\text{for all}\;\;j \geq d-1.\end{align*}$$

Since $\partial 2^A \subset \operatorname {\mathrm {lk}}(L, u_i)=\operatorname {\mathrm {lk}}(X[A\cup W], \{u_1,u_2,\ldots ,u_{i}\})$ , there must be a d-dimensional chain in $\operatorname {\mathrm {lk}}(L, u_i)$ whose boundary equals to $\partial 2^A$ . For each $(d-1)$ -dimensional simplex $\sigma $ in $\partial 2^A$ , the only possible d-dimensional simplex of $\operatorname {\mathrm {lk}}(L, u_i)$ containing $\sigma $ is $\sigma \cup \{u_{i+1}\}$ . This shows $\partial 2^A \ast 2^{\{u_{i+1}\}}\subset \operatorname {\mathrm {lk}}(L,u_i)$ . Since $A\notin \operatorname {\mathrm {lk}}(L,u_i)$ , we must actually have $\operatorname {\mathrm {lk}}(L, u_i) = \partial 2^A\ast 2^{\{u_{i+1}\}} $ , and hence we have $X[A\cup W] = \partial 2^A \ast 2^W$ .

Finally, letting $i=|U|$ , we obtain that $\partial 2^A\ast 2^U \subset X$ , as desired.

Theorem 1.7. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ be integers. Let V be a finite set with $|V|\geq \max \{m+d,r\}$ . Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function $\rho $ .

Assume that for every $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-1}\}\subset V$ with $\rho (U)\geq k$ , either $\{u_1,\ldots ,u_{d+1}\}\in X$ or there exists $j\in [m-1]$ such that $\sigma \cup \{v_j\}\in X$ for every $\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$ . Then, there is some $\tau \in X$ such that $\rho (V\setminus \tau ) \leq k-1$ .

Proof. We argue by induction on m. For $m=1$ the claim holds by Theorem 5.1. Let $m>1$ , and assume that the claim holds for $m-1$ .

If for all $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2}\}\subset V$ with $\rho (U)\geq k-1$ , either $\{u_1,\ldots ,u_{d+1}\}\in X$ or there is some $1\leq j\leq m-2$ such that $\sigma \cup \{v_j\}\in X$ for all $\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$ , then by the induction hypothesis there is some $\tau \in X$ such that $\rho (V\setminus \tau )\leq k-2\leq k-1$ , as wanted.

Otherwise, there exists $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2}\}\subset V$ with $\rho (U)\geq k-1$ such that $A=\{u_1,\ldots ,u_{d+1}\}\notin X$ and for every $1\leq j\leq m-2$ there is some $\sigma _j\subsetneq A$ such that $\sigma _j\cup \{v_j\}\notin X$ . We divide into two cases: First, assume that $\rho (U)=k-1$ . Then, for any $v\in V\setminus \text {span}_M(U)$ , we have $\rho (\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2},v\})\geq k$ , and therefore by the assumption of the theorem we must have $\sigma \cup \{v\}\in X$ for all $\sigma \subsetneq A$ . Note that, since $\rho (V)=r \geq k>\rho (U)$ , we must have $V\setminus \text {span}_M(U)\neq \emptyset $ . Hence, by Lemma 5.4, we have $\tau =V\setminus \text {span}_M(U)\in X$ . Note that $\rho (V\setminus \tau )=\rho (U)= k-1$ , as desired.

Next, assume that $\rho (U)\geq k$ . Then, for any $v\in V\setminus U$ , we have $\rho (\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2},v\})\geq \rho (U)\geq k$ , and therefore by the assumption of the theorem, we must have $\sigma \cup \{v\}\in X$ for every $\sigma \subsetneq A$ . Note that, since $|V|\geq d+m \geq |U|+1$ , we must have $V\setminus U\neq \emptyset $ . So, by Lemma 5.4, we have $\tau =(V\setminus U)\cup \{u_1,\ldots ,u_d\}\in X$ . Since $\rho (V\setminus \tau )=\rho (\{u_{d+1},v_1,\ldots ,v_{m-2})\leq m-1\leq k-1$ , we are done.

6 Geometric applications

6.1 Colorful Helly and Carathéodory theorems

In this section, we present a proof of Theorem 1.9 and show how to derive from it an analogous extension of Bárány’s colorful Carathéodory theorem [4]. The arguments in this section are standard and well known (see, e.g., [9, 4]), but we include detailed proofs for completeness.

Theorem 1.9. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ . Let $\mathcal {C}$ be a finite family of convex sets in ${\mathbb R}^d$ , colored with r different colors, of size $|\mathcal {C}|\geq \max \{m+d,r\}$ . Assume that, for every family $\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset \mathcal {C}$ , colored with at least k different colors, at least one of the subfamilies of the form $\{A_1,\ldots ,A_d,B_i\}$ , for $i\in [m]$ , is intersecting. Then, there are $r-k+1$ color classes whose union is intersecting.

Proof. Let X be the nerve of the family $\mathcal {C}$ . By Wegner’s theorem [24], X is d-collapsible. Let $\mathcal {C}_1,\ldots ,\mathcal {C}_r$ be the color classes of $\mathcal {C}$ . Let M be the partition matroid on vertex set $\mathcal {C}$ , corresponding to the partition $\mathcal {C}=\mathcal {C}_1\cup \cdots \cup \mathcal {C}_r$ . That is, the independent sets of M are exactly the colorful subfamilies of $\mathcal {C}$ , and the rank function $\rho $ satisfies

$$\begin{align*}\rho(\mathcal{C}')= |\{i\in[r]:\, \mathcal{C}'\cap \mathcal{C}_i\neq \emptyset\}| \end{align*}$$

for all $\mathcal {C}'\subset \mathcal {C}$ . That is, $\rho (\mathcal {C}')$ is the number of different colors appearing in $\mathcal {C}'$ .

Let $U=\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset V$ be a subfamily colored with at least k different colors (or equivalently, satisfying $\rho (U)\geq k$ ). Then, there is some $i\in [m]$ such that $\{A_1,\ldots ,A_d,B_i\}$ is intersecting. In other words, $\{A_1,\ldots ,A_d,B_i\}\in X$ . Therefore, by Theorem 1.6, there is some $\tau \in X$ such that $\rho (V\setminus \tau )\leq k-1$ . That is, $\tau \subset \mathcal {C}$ is an intersecting subfamily, whose complement intersects at most $k-1$ color classes. This means that $\tau $ contains at least $r-k+1$ entire color classes, as wanted.

Theorem 6.1. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ . Let P be a finite family of points in ${\mathbb R}^d$ colored with r colors of size $|P|\geq \max \{m+d,r\}$ .

Assume that the convex hull of the union of every $r-k+1$ color classes contains the origin. Then, there is some $\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$ , colored with at least k different colors, such that $0\in \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$ for all $i\in [m]$ .

Proof. For each $p\in P$ , let $H_p\subset {\mathbb R}^d$ be defined as

$$\begin{align*}H_p=\{ x\in {\mathbb R}^d :\, x\cdot p>0\}. \end{align*}$$

Note that, for $p\neq 0$ , $H_p$ is an open half-space, and for $p=0$ , $H_p=\emptyset $ . In particular, $H_p$ is convex for all $p\in P$ .

It is a well-known fact that for any $P'\subset P$ , $0\in \operatorname {\mathrm {\text {conv}}}(P')$ if and only if $\cap _{p\in P'} H_p=\emptyset $ . Indeed, assume first that $\cap _{p\in P'} H_p\neq \emptyset $ . That is, there is some $x\in {\mathbb R}^d$ such that $x\cdot p>0$ for all $p\in P'$ . Let $\{t_p\}_{p\in P'}$ be nonnegative real numbers such that $\sum _{p\in P'} t_p=1$ . Then, there is some $p_0\in P'$ such that $t_{p_0}>0$ . Thus, we obtain

$$\begin{align*}\left(\sum_{p\in P'} t_p p\right) \cdot x = \sum_{p\in P'} t_p (p\cdot x)\geq t_{p_0}(p_0\cdot x)>0. \end{align*}$$

Therefore, $0\notin \operatorname {\mathrm {\text {conv}}}(P')$ . In the other direction, assume that $0\notin \operatorname {\mathrm {\text {conv}}}(P')$ . Then, there is some hyperplane separating $0$ from $ \operatorname {\mathrm {\text {conv}}}(P')$ . In other words, there exists $x\in {\mathbb R}^d$ such that $x\cdot y>0$ for all $y\in \operatorname {\mathrm {\text {conv}}}(P')$ . In particular, $x\in H_p$ for all $p\in P'$ . Therefore, $\cap _{p\in P'} H_p\neq \emptyset $ .

We color the family $\mathcal {H}=\{H_p\}_{p\in P}$ in r colors, each set $H_p$ colored with the color of p. Assume for contradiction that for all $\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$ , colored with at least k colors, $0\notin \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$ for some $i\in [m]$ . Equivalently, for all $\{H_{u_1},\ldots ,H_{u_d},H_{v_1},\ldots ,H_{v_m}\}\subset \mathcal {H}$ , colored with at least k colors, $\{ H_{u_1},\ldots ,H_{u_d},H_{v_i}\}$ is intersecting for some $i\in [m]$ .

By Theorem 1.9, there are $r-k+1$ color classes in $\mathcal {H}$ whose union is intersecting. Equivalently, there are $r-k+1$ color classes in P that do not contain the origin in the convex hull of their union. But this is a contradiction to the assumption of the theorem.

For the next section, we will need the special case $r=k=d+m$ of Theorem 6.1:

Theorem 6.2. Let $d\geq 1$ and $m\geq 1$ . Let P be a finite family of points in ${\mathbb R}^d$ colored with $d+m$ colors. Assume that the convex hull of every color class contains the origin. Then, there is some colorful set $\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$ such that $0\in \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$ for all $i\in [m]$ .

6.2 Tverberg centers for large point sets

In this section, we prove Theorem 1.10. Theorem 1.10 follows from Theorem 6.2 by a straightforward adaptation of Sarkaria’s proof of Tverberg’s theorem via the colorful Carathéodory theorem [19]. For completeness, we write down the argument, closely following the exposition in [3] (which in turn is based on Bárány and Onn’s variant of Sarkaria’s proof given in [5]).

First, we will need the following Lemma:

Lemma 6.3 (Sarkaria (see, e.g., [3, Lemma 2])).

Let $P_1,\ldots ,P_r$ be finite sets of points in ${\mathbb R}^d$ . Let $v_1,\ldots ,v_r\in {\mathbb R}^{r-1}$ be the vertices of the standard $(r-1)$ -dimensional simplex. Define

$$\begin{align*}\bar{P}= \left\{ \begin{pmatrix} x\\1 \end{pmatrix}\otimes v_j :\, j\in[r],\, x\in P_j\right\}\subset {\mathbb R}^{(r-1)(d+1)}, \end{align*}$$

where $\otimes $ denotes the Kronecker product. Then $\cap _{j=1}^r \operatorname {\mathrm {\text {conv}}}(P_j)=\emptyset $ if and only if $0\notin \operatorname {\mathrm {\text {conv}}}(\bar {P})$ .

Theorem 1.10. Let $d\geq 1$ , $r\geq 2$ , and let $n=(r-1)(d+1)$ . Let $A\subset {\mathbb R}^d$ be a finite set of points of size larger than n. Then, there exists a partition $A_1,\ldots ,A_r$ of A that has a Tverberg center of size n.

Proof. Let $n=(r-1)(d+1)$ and $m=|A|-n$ . Write $A=\{x_1,\ldots ,x_{n+m}\}$ . For $1\leq i\leq m+n$ and $1\leq j\leq r$ , let $x_i^j$ be a copy of the point $x_i$ . For $1\leq j\leq r$ , let $P_j=\{x_1^j,\ldots ,x_{n+m}^j\}$ , and let $P=P_1\cup \cdots \cup P_r$ . Let $v_1,\ldots ,v_r\in {\mathbb R}^{r-1}$ be the vertices of the standard simplex, and define for each $1\leq i\leq n+m$ and $1\leq j\leq r$ ,

$$\begin{align*}\bar{x}_i^j = \begin{pmatrix} x_i^j\\1 \end{pmatrix}\otimes v_j\in {\mathbb R}^n. \end{align*}$$

Let $\bar {P}=\{\bar {x}_i^j :\, 1\leq i\leq n+m, 1\leq j\leq r\}$ . We color the points in P with $|A|=n+m$ colors, where, for $1\leq i\leq n+m$ and $1\leq j\leq r$ , $x_i^j$ is colored with color i. Similarly, we color $\bar {P}$ with $n+m$ colors, where, for $1\leq i\leq n+m$ and $1\leq j\leq r$ , $\bar {x}_i^j$ is colored with color i.

Note that for each color class $C_i=\{x_i^j :\, 1\leq j\leq r\}$ , $1\leq i\leq n+m$ , we have $\cap _{j=1}^r \operatorname {\mathrm {\text {conv}}}(C_i\cap P_j)=\cap _{j=1}^r\operatorname {\mathrm {\text {conv}}}(\{x_i^j\})= \{x_i\}\neq \emptyset $ . So, by Lemma 6.3, we have

$$\begin{align*}0 \in \operatorname{\mathrm{\text{conv}}}(\{\bar{x}_i^j :\, 1\leq j\leq r\}) \end{align*}$$

for all $1\leq i\leq n+m$ . That is, the convex hull of each of the color classes of $\bar {P}$ contains the origin. Therefore, by Theorem 6.2, there is a colorful set $U=\{\bar {x}_{a_1}^{b_1},\ldots ,\bar {x}_{a_{n+m}}^{b_{n+m}}\}\subset \bar {P}$ such that

(6.1) $$ \begin{align} 0\in \operatorname{\mathrm{\text{conv}}}(\{\bar{x}_{a_1}^{b_1},\ldots,\bar{x}_{a_n}^{b_n},\bar{x}_{a_{n+i}}^{b_{n+i}}\}) \end{align} $$

for all $1\leq i\leq m$ . Since U is colorful, the index set $\{a_1,\ldots ,a_{n+m}\}$ is a permutation of $[n+m]$ . Therefore, we can define a partition $A=A_1\cup \cdots \cup A_r$ by

$$\begin{align*}A_j= \{x_{a_i} : \, b_i=j\} \end{align*}$$

for $1\leq j\leq r$ . Let $B=\{ x_{a_1},\ldots ,x_{a_n}\}\subset A$ . By Lemma 6.3, Equation (6.1) implies that for all $1\leq i\leq m$ ,

$$\begin{align*}\bigcap_{j=1}^r \operatorname{\mathrm{\text{conv}}}\left(\{x_{a_1}^{b_1},\ldots,x_{a_n}^{b_n},x_{a_{n+i}}^{b_{n+i}}\}\cap P_j\right) = \bigcap_{j=1}^r \operatorname{\mathrm{\text{conv}}}\left((B\cup \{x_{a_{n+i}}\})\cap A_j\right)\neq \emptyset, \end{align*}$$

as wanted.

Remark 6.4. For any point set in ${\mathbb R}^d$ of size larger than $(r-1)(d+1)$ , Theorem 1.10 guarantees the existence of a partition into r parts with Tverberg center of size at most $(r-1)(d+1)$ . Note, however, that the same point set may have other Tverberg partitions without such a center (see Figure 1).

Figure 1 Two Tverberg partitions of nine points in the plane into three parts. The partition on the left does not have a Tverberg center of size $6$ , while the partition on the right has one: $\{v_2,v_4,v_5,v_6,v_7,v_9\}$ .

Let $A\subset {\mathbb R}^d$ be a finite set of points. We say that a partition $A_1,\ldots ,A_r$ of A is a Tverberg partition with tolerance t if

$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\setminus C)\neq\emptyset, \end{align*}$$

for any $C\subset A$ of size at most t. In other words, the partition has tolerance t if it remains a Tverberg partition even after removing any t points from A. Larman showed in [12] that any $2d+3$ points in ${\mathbb R}^d$ have a Tverberg partition into two parts (that is, a Radon partition) with tolerance $1$ . This was later extended by García-Colín ([6, 7]) who showed that any $(t+1)(d+1)+1$ points in ${\mathbb R}^d$ have a Radon partition with tolerance t, and by Soberón and Strausz in [21], who showed that any $(t+1)(r-1)(d+1)+1$ points in ${\mathbb R}^d$ have a Tverberg partition into r parts with tolerance t. Note that this bound is not sharp in general: In [8], it was shown that any set of $rt+o(t)$ points in ${\mathbb R}^d$ has a Tverberg partition into r parts with tolerance t, giving an improved bound for large values of t (see [20] for a further improvement of this bound). In [14], an improved bound was given in the case $d=1$ , and in the case $d=2$ for some values of $r,t$ .

It was brought to our attention by Andreas Holmsen that one can recover Soberón and Strausz’s result as a consequence of Theorem 1.10, in the following way:

Theorem 1.11 (Soberón-Strausz [21, Theorem 1]).

Let $d\geq 1$ , $r\geq 2$ and $t\geq 0$ . Let $A\subset {\mathbb R}^d$ be finite set of points of size at least $(t+1)(r-1)(d+1)+1$ . Then, A has a Tverberg partition into r parts with tolerance t.

Proof. We argue by induction on t. For $t=0$ , the claim is just Tverberg’s theorem. Assume $t\geq 1$ . By Theorem 1.10, there exists a partition $A_1,\ldots ,A_r$ of A and a set $B\subset A$ of size $(r-1)(d+1)$ such that

$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}((B\cup\{p\})\cap A_i)\neq\emptyset \end{align*}$$

for any $p\in A\setminus B$ . Note that $|A\setminus B|\geq t(r-1)(d+1)+1$ . Therefore, by the induction hypothesis, there is a Tverberg partition $B_1,\ldots ,B_r$ of $A\setminus B$ with tolerance $t-1$ .

We denote by $S_r$ the set of permutations of $[r]$ . Since $|A\setminus B|> t(r-1)(d+1)\geq tr$ , we have

$$ \begin{align*} \frac{1}{r!}\sum_{\pi\in S_r} |\cup_{i=1}^r A_i\cap B_{\pi(i)}| &=\frac{1}{r!}\sum_{\pi\in S_r} \sum_{i=1}^r |A_i\cap B_{\pi(i)}| =\frac{1}{r!} \sum_{i=1}^r \sum_{\pi\in S_r} |A_i\cap B_{\pi(i)}| \\ &=\frac{1}{r!} \sum_{i=1}^r (r-1)! |A_i\setminus B| = \frac{|A\setminus B|}{r}>t. \end{align*} $$

Therefore, there is some $\pi \in S_r$ such that $|\cup _{i=1}^r A_i\cap B_{\pi (i)}|\geq t+1$ . Let $D=\cup _{i=1}^r A_i\cap B_{\pi (i)}$ . We define a new partition $\tilde {A}_1,\ldots ,\tilde {A}_r$ of A by

$$\begin{align*}\tilde{A}_i = (A_i\cap B)\cup (B_{\pi(i)}\cap(A\setminus B)) \end{align*}$$

for all $1\leq i\leq r$ . Note that $\tilde {A}_i\cap D=A_i\cap D$ for all i.

We are left to show that $\tilde {A}_1,\ldots ,\tilde {A}_r$ is a Tverberg partition of A with tolerance t. Let $C\subset A$ be a subset of size at most t. We divide into two cases. First, assume that C is disjoint from B. Then, since $|C|\leq t$ and $|D|\geq t+1$ , there is some $p\in D\setminus C$ . We obtain

$$ \begin{align*} \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(\tilde{A_i}\setminus C) \supset \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}&((\tilde{A_i}\cap (B\cup D))\setminus C) \\ & = \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}((A_i\cap(B\cup D) )\setminus C) \supset \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\cap(B\cup \{p\}))\neq \emptyset, \end{align*} $$

as desired. Next, assume that $C\cap B\neq \emptyset $ . Let $C'=C\cap (A\setminus B)$ . Then $|C'|\leq t-1$ , and therefore, since $B_1,\ldots ,B_r$ is a Tverberg partition of $A\setminus B$ with tolerance $t-1$ , we obtain

$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(\tilde{A_i}\setminus C) \supset \bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}((\tilde{A_i}\cap (A\setminus B))\setminus C') =\bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}( B_{\pi(i)}\setminus C') =\bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}( B_{i}\setminus C') \neq \emptyset. \end{align*}$$

Thus, $\tilde {A}_1,\ldots ,\tilde {A}_r$ is a Tverberg partition of A with tolerance t, as wanted.

7 Concluding remarks

It would be interesting to prove a stronger version of Theorem 1.7, analogous to Theorem 1.6:

Conjecture 7.1. Let $d\geq 1$ , $r\geq d+1$ , $1\leq m\leq r$ and $m\leq k\leq \min \{m+d,r\}$ be integers. Let V be a finite set with $|V|\geq \max \{m+d,r\}$ . Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function $\rho $ .

Assume that for every $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$ with $\rho (U)\geq k$ , there is some $i\in [m]$ such that $\{u_1,\ldots ,u_d,v_i\}\in X$ . Then, there is some $\tau \in X$ such that $\rho (V\setminus \tau )\leq k-1$ .

Another interesting question, suggested to us by Florian Frick, is whether a version of Theorem 1.10 holds in the context of the topological Tverberg theorem. That is,

Conjecture 7.2. Let $d\geq 1$ , $r\geq 2$ a prime power, and $n=(r-1)(d+1)$ . Let $N>n$ , and let $\Delta _N$ be the N-dimensional simplex. Then, for every continuous map $ f: \Delta _N\to {\mathbb R}^d, $ there exist r pairwise disjoint faces $F_1,\ldots ,F_r$ of $\Delta _N$ , and an $(n-1)$ -dimensional face F of $\Delta _N$ such that, for each n-dimensional face $F'$ of $\Delta _N$ containing F, $\cap _{i=1}^r f(F_i\cap F')\neq \emptyset $ .