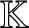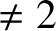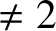1 Introduction
The semi-infinite flag varieties are variants of affine flag varieties that encode the modular representation theory of a semi-simple Lie algebra, representation theory of a quantum group at roots of unity and representation theory of an affine Lie algebra at the critical level. They originate from the ideas of Lusztig [Reference Lusztig64] and Drinfeld, put forward by Feigin and Frenkel [Reference Feigin and Frenkel24] and subsequently polished by the work of Braverman, Finkelberg, and their collaborators [Reference Finkelberg and Mirković29, Reference Feigin, Finkelberg, Kuznetsov and Mirković23, Reference Arkhipov, Bezrukavnikov, Braverman, Gaitsgory and Mirković2, Reference Braverman7, Reference Braverman, Feigin, Finkelberg and Rybnikov8, Reference Braverman and Finkelberg9, Reference Braverman and Finkelberg10, Reference Braverman and Finkelberg11]. They (mainly) used the ind-model of semi-infinite flag varieties, and achieved spectacular success on the geometric Langlands correspondence [Reference Arkhipov, Bezrukavnikov, Braverman, Gaitsgory and Mirković2, Reference Braverman, Finkelberg, Gaitsgory and Mirković12], the quantum K-groups of flag manifolds [Reference Braverman and Finkelberg9] and their (conjectural) relation to the finite ![]() $\mathcal W$-algebras [Reference Braverman, Feigin, Finkelberg and Rybnikov8].
$\mathcal W$-algebras [Reference Braverman, Feigin, Finkelberg and Rybnikov8].
In [Reference Kato, Naito and Sagaki51], we initiated the study of the formal model of a semi-infinite flag variety (over ![]() ${\mathbb C}$) that follows the classical description of flag varieties [Reference Kumar57, Reference Mathieu69, Reference Littelmann63, Reference Kumar and Littelmann58] more closely than the works already cited. We refer to this formal model of a semi-infinite flag variety as a ‘semi-infinite flag manifold’, since we hope to justify that it is ‘smooth’ in a sense. However, the analysis in [Reference Kato, Naito and Sagaki51] has two defects: the relation with the ind-models of semi-infinite flag varieties is unclear, and the treatment there is rather ad hoc (it is just an ind-scheme whose set of
${\mathbb C}$) that follows the classical description of flag varieties [Reference Kumar57, Reference Mathieu69, Reference Littelmann63, Reference Kumar and Littelmann58] more closely than the works already cited. We refer to this formal model of a semi-infinite flag variety as a ‘semi-infinite flag manifold’, since we hope to justify that it is ‘smooth’ in a sense. However, the analysis in [Reference Kato, Naito and Sagaki51] has two defects: the relation with the ind-models of semi-infinite flag varieties is unclear, and the treatment there is rather ad hoc (it is just an ind-scheme whose set of ![]() ${\mathbb C}$-valued points have the desired property, and lacks a characterisation as a functor; compare [Reference Beauville and Laszlo3, Reference Faltings22]). The first defect produces difficulty in discussing deep properties on the identification between the equivariant K-group of a semi-infinite flag manifold and the equivariant quantum K-group of a flag manifold [Reference Kato47], which is in turn inspired by the works of Givental and Lee [Reference Givental32, Reference Givental and Lee33]. The goal of this paper is to study semi-infinite flag manifolds in characteristic
${\mathbb C}$-valued points have the desired property, and lacks a characterisation as a functor; compare [Reference Beauville and Laszlo3, Reference Faltings22]). The first defect produces difficulty in discussing deep properties on the identification between the equivariant K-group of a semi-infinite flag manifold and the equivariant quantum K-group of a flag manifold [Reference Kato47], which is in turn inspired by the works of Givental and Lee [Reference Givental32, Reference Givental and Lee33]. The goal of this paper is to study semi-infinite flag manifolds in characteristic ![]() $\neq 2$ from scratch, and resolve these defects. In particular, we verify that the scheme in [Reference Kato, Naito and Sagaki51] is universal one among all the ind-schemes with similar set-theoretic properties, and provide new proofs of the normality of Zastava spaces [Reference Braverman and Finkelberg9] and the semi-infinite flag manifolds [Reference Kato, Naito and Sagaki51].
$\neq 2$ from scratch, and resolve these defects. In particular, we verify that the scheme in [Reference Kato, Naito and Sagaki51] is universal one among all the ind-schemes with similar set-theoretic properties, and provide new proofs of the normality of Zastava spaces [Reference Braverman and Finkelberg9] and the semi-infinite flag manifolds [Reference Kato, Naito and Sagaki51].
It is possible to regard our work ([Reference Kato46, Reference Kato49, Reference Kato, Naito and Sagaki51, Reference Kato47, Reference Kato48]) as part of catch-up of Peterson’s original construction [Reference Peterson74] of his isomorphism [Reference Lam and Shimozono61] between the quantum cohomology of a flag manifold and the cohomology of an affine Grassmannian in the K-theoretic setting. From this viewpoint, this paper provides some varieties considered in [Reference Peterson74, Lecture 11] with their appropriate compactifications. Hence, though there are still some missing pieces to complete the original program along the lines in [Reference Peterson74], this paper provides a step to fully examine Peterson’s ideas.
To explain our results more precisely, we introduce more notation: Let ![]() $\mathfrak {g}$ denote a simple Lie algebra (given in terms of root data and the Chevalley generators) over an algebraically closed field
$\mathfrak {g}$ denote a simple Lie algebra (given in terms of root data and the Chevalley generators) over an algebraically closed field ![]() ${\mathbb K}$ of characteristic
${\mathbb K}$ of characteristic ![]() $\neq 2$. Let G denote the connected simply connected algebraic group over
$\neq 2$. Let G denote the connected simply connected algebraic group over ![]() ${\mathbb K}$ such that
${\mathbb K}$ such that ![]() $\mathfrak {g} = \mathrm {Lie}\, G$. Let
$\mathfrak {g} = \mathrm {Lie}\, G$. Let ![]() $H \subset G$ be a Cartan subgroup and N be an unipotent radical of G that is normalised by H. We set
$H \subset G$ be a Cartan subgroup and N be an unipotent radical of G that is normalised by H. We set ![]() $B:= HN$ and
$B:= HN$ and ![]() $\mathscr {B} := G / B$ (the flag manifold of G). Let
$\mathscr {B} := G / B$ (the flag manifold of G). Let ![]() $\mathbf {I}^+ \subset G ( {\mathbb K} [\![ z ]\!] )$ denote the Iwahori subgroup that contains B, and let
$\mathbf {I}^+ \subset G ( {\mathbb K} [\![ z ]\!] )$ denote the Iwahori subgroup that contains B, and let  $\mathbf {I}^- \subset G \left ( {\mathbb K} \left [z^{-1}\right ]\right )$ be its opposite Iwahori subgroup. Let
$\mathbf {I}^- \subset G \left ( {\mathbb K} \left [z^{-1}\right ]\right )$ be its opposite Iwahori subgroup. Let ![]() $\widetilde {\mathfrak {g}}$ denote the untwisted affine Kac–Moody algebra associated to
$\widetilde {\mathfrak {g}}$ denote the untwisted affine Kac–Moody algebra associated to ![]() $\mathfrak {g}$, and let W and
$\mathfrak {g}$, and let W and ![]() $W_{\mathrm {af}}$ be the finite Weyl group and the affine Weyl group of
$W_{\mathrm {af}}$ be the finite Weyl group and the affine Weyl group of ![]() $\mathfrak {g}$, respectively. The coroot lattice
$\mathfrak {g}$, respectively. The coroot lattice ![]() $Q^{\vee }$ of
$Q^{\vee }$ of ![]() $\mathfrak {g}$ yields a natural subgroup
$\mathfrak {g}$ yields a natural subgroup  $\left \{ t_{\beta } \right \}_{\beta \in Q^{\vee }} \subset W_{\mathrm {af}}$. Let
$\left \{ t_{\beta } \right \}_{\beta \in Q^{\vee }} \subset W_{\mathrm {af}}$. Let ![]() $w_0 \in W$ be the longest element.
$w_0 \in W$ be the longest element.
Our first main result is as follows:
Theorem A  $\doteq $ Theorem 4.18 and Proposition 4.26
$\doteq $ Theorem 4.18 and Proposition 4.26
There is an ind-scheme ![]() $\mathbf {Q}_G ^{\mathrm {rat}}$ with the following properties:
$\mathbf {Q}_G ^{\mathrm {rat}}$ with the following properties:
1. It is expressed as the union of infinite-type integral schemes flat over
 $\mathbb {Z}$.
$\mathbb {Z}$.2. If we set
 $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K} := \mathbf {Q}_G ^{\mathrm {rat}} \otimes _{\mathbb {Z}} {\mathbb K}$, we have which intertwines the natural
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K} := \mathbf {Q}_G ^{\mathrm {rat}} \otimes _{\mathbb {Z}} {\mathbb K}$, we have which intertwines the natural $$ \begin{align*}\left( \mathbf{Q}_G ^{\mathrm{rat}} \right)_{\mathbb K} ( {\mathbb K} ) \cong G ( {\mathbb K} (\!(z)\!)) / ( H ( {\mathbb K} ) N ( {\mathbb K} (\!(z)\!)) ),\end{align*} $$
$$ \begin{align*}\left( \mathbf{Q}_G ^{\mathrm{rat}} \right)_{\mathbb K} ( {\mathbb K} ) \cong G ( {\mathbb K} (\!(z)\!)) / ( H ( {\mathbb K} ) N ( {\mathbb K} (\!(z)\!)) ),\end{align*} $$ $G ( {\mathbb K} (\!(z)\!) ) \ltimes \mathbb {G}_m ( {\mathbb K} )$-actions on both sides, where
$G ( {\mathbb K} (\!(z)\!) ) \ltimes \mathbb {G}_m ( {\mathbb K} )$-actions on both sides, where  $\mathbb {G}_m$ is the loop rotation.
$\mathbb {G}_m$ is the loop rotation.3. The functor
is coarsely ind-representable by $$ \begin{align*}A\!f\!\!f^{op}_{{\mathbb K}} \ni R \mapsto G ( R (\!(z)\!)) / ( H ( R ) N ( R (\!(z)\!)) )\in \mathrm{Sets}\end{align*} $$
$$ \begin{align*}A\!f\!\!f^{op}_{{\mathbb K}} \ni R \mapsto G ( R (\!(z)\!)) / ( H ( R ) N ( R (\!(z)\!)) )\in \mathrm{Sets}\end{align*} $$ $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ (see Section 4.3 for the convention).
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ (see Section 4.3 for the convention).
One can equip  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K} ( {\mathbb K} )$ with an ind-scheme structure using the arc scheme of the basic affine space
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K} ( {\mathbb K} )$ with an ind-scheme structure using the arc scheme of the basic affine space ![]() $\overline {G/N}$. Such an ind-scheme cannot coincide with ours (in general), by the appearance of the nontrivial nilradicals [Reference Mustata71, Reference Feigin and Makedonskyi27, Reference Feigin and Makedonskyi26]. In fact, such an ind-scheme defines a radicial thickening of
$\overline {G/N}$. Such an ind-scheme cannot coincide with ours (in general), by the appearance of the nontrivial nilradicals [Reference Mustata71, Reference Feigin and Makedonskyi27, Reference Feigin and Makedonskyi26]. In fact, such an ind-scheme defines a radicial thickening of  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$.
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$.
The set of ![]() $H \times \mathbb {G}_m$-fixed points of
$H \times \mathbb {G}_m$-fixed points of  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ is in bijection with
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ is in bijection with ![]() $W_{\mathrm {af}}$. Let
$W_{\mathrm {af}}$. Let  $p_w \in \big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ be the point corresponding to
$p_w \in \big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ be the point corresponding to ![]() $w \in W_{\mathrm {af}}$. We set
$w \in W_{\mathrm {af}}$. We set ![]() $\mathbb {O} ( w ) := \mathbf {I}^+ p_w$ and
$\mathbb {O} ( w ) := \mathbf {I}^+ p_w$ and ![]() $\mathbb {O}^- ( w ) := \mathbf {I}^- p_w$ for each
$\mathbb {O}^- ( w ) := \mathbf {I}^- p_w$ for each ![]() $w \in W_{\mathrm {af}}$.
$w \in W_{\mathrm {af}}$.
Theorem A has some applications to the theory of quasi-map spaces from ![]() $\mathbb {P}^1$ to
$\mathbb {P}^1$ to ![]() $\mathscr {B}$ presented in [Reference Finkelberg and Mirković29, Reference Feigin, Finkelberg, Kuznetsov and Mirković23, Reference Braverman and Finkelberg9, Reference Braverman and Finkelberg10, Reference Braverman and Finkelberg11] as follows:
$\mathscr {B}$ presented in [Reference Finkelberg and Mirković29, Reference Feigin, Finkelberg, Kuznetsov and Mirković23, Reference Braverman and Finkelberg9, Reference Braverman and Finkelberg10, Reference Braverman and Finkelberg11] as follows:
Theorem B. In the foregoing settings, the following hold:
1. (Corollary 3.38 and Theorem 4.30) If
 $\mathsf {char}\, {\mathbb K}> 0$, then the scheme
$\mathsf {char}\, {\mathbb K}> 0$, then the scheme  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ admits an
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ admits an  $\mathbf {I}^{\pm }$-canonical Frobenius splitting that is compatible with
$\mathbf {I}^{\pm }$-canonical Frobenius splitting that is compatible with  $\overline {\mathbb {O} ( w )}$s and
$\overline {\mathbb {O} ( w )}$s and  $\overline {\mathbb {O} ^- ( v )}$s
$\overline {\mathbb {O} ^- ( v )}$s  $(w, v \in W_{\mathrm {af}})$.
$(w, v \in W_{\mathrm {af}})$.2. (Corollary 4.10 and Remark 4.13) For each
 $w, v \in W_{\mathrm {af}}$, the intersection
$w, v \in W_{\mathrm {af}}$, the intersection  $\mathscr {Q} ( v, w ) := \overline {\mathbb {O} ( w )} \cap \overline {\mathbb {O} ^- ( v )}$ is reduced. It is irreducible when
$\mathscr {Q} ( v, w ) := \overline {\mathbb {O} ( w )} \cap \overline {\mathbb {O} ^- ( v )}$ is reduced. It is irreducible when  $v = w_0 t_{\beta }$ for some
$v = w_0 t_{\beta }$ for some  $\beta \in Q^{\vee }$.
$\beta \in Q^{\vee }$.3. (Lemma 4.7 and Corollary 5.24) For each
 $w, v \in W_{\mathrm {af}}$, the scheme
$w, v \in W_{\mathrm {af}}$, the scheme  $\mathscr {Q} ( v, w )$ is weakly normal. It is normal (and irreducible) when
$\mathscr {Q} ( v, w )$ is weakly normal. It is normal (and irreducible) when  $\mathsf {char}\, {\mathbb K} = 0$ or
$\mathsf {char}\, {\mathbb K} = 0$ or  $\mathsf {char}\, {\mathbb K} \gg 0$.
$\mathsf {char}\, {\mathbb K} \gg 0$.4. (Lemma 4.28) For each
 $\beta \in Q^{\vee }_+$, the set of
$\beta \in Q^{\vee }_+$, the set of  ${\mathbb K}$-valued points of the scheme
${\mathbb K}$-valued points of the scheme  $\mathscr {Q} \left ( w_0 t_{\beta }, e \right )$ is in bijection with the set of (
$\mathscr {Q} \left ( w_0 t_{\beta }, e \right )$ is in bijection with the set of ( ${\mathbb K}$-valued) Drinfeld–Plücker data. In particular,
${\mathbb K}$-valued) Drinfeld–Plücker data. In particular,  $\mathscr {Q} \left ( w_0 t_{\beta }, e \right )$ is isomorphic to the quasi-map space in [Reference Finkelberg and Mirković29] when
$\mathscr {Q} \left ( w_0 t_{\beta }, e \right )$ is isomorphic to the quasi-map space in [Reference Finkelberg and Mirković29] when  ${\mathbb K} = {\mathbb C}$.
${\mathbb K} = {\mathbb C}$.
Theorem B is a key result at the deepest part (correspondence between natural bases) in our proof ([Reference Kato47]) of a conjecture of Lam, Li, Mihalcea and Shimozono [Reference Lam, Li, Mihalcea and Shimozono60] about the comparison between the equivariant K-group of the affine Grassmannian of G and the equivariant small quantum K-group of ![]() $\mathscr {B}$. In [Reference Kato47], we also prove that
$\mathscr {B}$. In [Reference Kato47], we also prove that ![]() $\mathscr {Q} \left ( w_0 t_{\beta }, w \right )$ admits only rational singularities (and hence it is Cohen–Macaulay) when
$\mathscr {Q} \left ( w_0 t_{\beta }, w \right )$ admits only rational singularities (and hence it is Cohen–Macaulay) when ![]() ${\mathbb K} = {\mathbb C}$ on the basis of Theorem B. We remark that Theorem B(3) is proved in [Reference Braverman and Finkelberg9, Reference Braverman and Finkelberg10] when
${\mathbb K} = {\mathbb C}$ on the basis of Theorem B. We remark that Theorem B(3) is proved in [Reference Braverman and Finkelberg9, Reference Braverman and Finkelberg10] when ![]() $v = w_0 t_{\beta }$,
$v = w_0 t_{\beta }$, ![]() $w = e$ and
$w = e$ and ![]() ${\mathbb K} = {\mathbb C}$.
${\mathbb K} = {\mathbb C}$.
Our proof of Theorem B(1) is not at all standard, and in fact it forms the core of the technical contributions in this paper. To appreciate its contents, let us recall that there are two standard ways to construct a Frobenius splitting of ![]() $\mathscr {B}$ ([Reference Brion and Kumar14]): One is to consider the Bott–Samelson–Demazure–Hansen resolution of
$\mathscr {B}$ ([Reference Brion and Kumar14]): One is to consider the Bott–Samelson–Demazure–Hansen resolution of ![]() $\mathscr {B}$, which reduces the assertion to the case of a point, which is a Schubert variety with trivial Frobenius splitting. The other is to analyse the space of global sections of (some power of) the canonical bundle of
$\mathscr {B}$, which reduces the assertion to the case of a point, which is a Schubert variety with trivial Frobenius splitting. The other is to analyse the space of global sections of (some power of) the canonical bundle of ![]() $\mathscr {B}$.
$\mathscr {B}$.
However, neither of these proof strategies works for ![]() $\mathbf {Q}_G^{\mathrm {rat}}$. The first one fails because any Schubert variety of
$\mathbf {Q}_G^{\mathrm {rat}}$. The first one fails because any Schubert variety of ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ is infinite-dimensional, and carries rich internal structure by itself. The second one fails because the canonical bundle of
$\mathbf {Q}_G^{\mathrm {rat}}$ is infinite-dimensional, and carries rich internal structure by itself. The second one fails because the canonical bundle of ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ simply does not make sense, at least naively. These require some new ideas to prove Theorem B(1). Our idea here is as follows: An interpretation of the filtrations in [Reference Kato and Loktev50] reduces the existence of a Frobenius splitting of
$\mathbf {Q}_G^{\mathrm {rat}}$ simply does not make sense, at least naively. These require some new ideas to prove Theorem B(1). Our idea here is as follows: An interpretation of the filtrations in [Reference Kato and Loktev50] reduces the existence of a Frobenius splitting of ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ to a property of the Frobenius splitting of the corresponding thick affine flag manifold [Reference Kato49, Corollary B]. This property can be seen as a special case of some homological property in the representation theory of affine Lie algebras ([Reference Chari and Ion18, Reference Cherednik and Kato20]), but it is proved only for characteristic
$\mathbf {Q}_G^{\mathrm {rat}}$ to a property of the Frobenius splitting of the corresponding thick affine flag manifold [Reference Kato49, Corollary B]. This property can be seen as a special case of some homological property in the representation theory of affine Lie algebras ([Reference Chari and Ion18, Reference Cherednik and Kato20]), but it is proved only for characteristic ![]() $0$. Thus, we use Kashiwara’s theory of global basis ([Reference Kashiwara43, Reference Kashiwara44]) to transfer such a homological property into the positive-characteristic setting (Proposition 3.19).
$0$. Thus, we use Kashiwara’s theory of global basis ([Reference Kashiwara43, Reference Kashiwara44]) to transfer such a homological property into the positive-characteristic setting (Proposition 3.19).
In the rest of this introduction, we assume ![]() ${\mathbb K} = {\mathbb C}$ for the sake of simplicity. Let P be the weight lattice of H, and let
${\mathbb K} = {\mathbb C}$ for the sake of simplicity. Let P be the weight lattice of H, and let ![]() $P_+ \subset P$ denote its subset corresponding to dominant weights. For each
$P_+ \subset P$ denote its subset corresponding to dominant weights. For each ![]() $\lambda \in P$, we have an equivariant line bundle
$\lambda \in P$, we have an equivariant line bundle  ${\mathcal O}_{\mathbf {Q}_G^{\mathrm {rat}}} ( \lambda )$ on
${\mathcal O}_{\mathbf {Q}_G^{\mathrm {rat}}} ( \lambda )$ on ![]() $\mathbf {Q}_G^{\mathrm {rat}}$, whose restriction to
$\mathbf {Q}_G^{\mathrm {rat}}$, whose restriction to ![]() $\mathscr {Q} ( v, w )$ is denoted by
$\mathscr {Q} ( v, w )$ is denoted by ![]() ${\mathcal O}_{\mathscr {Q} \left ( v, w \right )} ( \lambda )$. Associated to
${\mathcal O}_{\mathscr {Q} \left ( v, w \right )} ( \lambda )$. Associated to ![]() $\lambda \in P_{+}$, we have a level
$\lambda \in P_{+}$, we have a level ![]() $0$ extremal weight module
$0$ extremal weight module ![]() $\mathbb {X} ( \lambda )$ of
$\mathbb {X} ( \lambda )$ of ![]() $U \left ( \widetilde {\mathfrak {g}} \right )$ in the sense of Kashiwara [Reference Kashiwara44]. We know that
$U \left ( \widetilde {\mathfrak {g}} \right )$ in the sense of Kashiwara [Reference Kashiwara44]. We know that ![]() $\mathbb {X} ( \lambda )$ is equipped with two kinds of Demazure modules and a distinguished basis (the global basis).
$\mathbb {X} ( \lambda )$ is equipped with two kinds of Demazure modules and a distinguished basis (the global basis).
Corollary C  $\doteq $ Theorem 4.33
$\doteq $ Theorem 4.33
Set ![]() $w, v \in W_{\mathrm {af}}$. For each
$w, v \in W_{\mathrm {af}}$. For each ![]() $\lambda \in P_{+}$, we have
$\lambda \in P_{+}$, we have
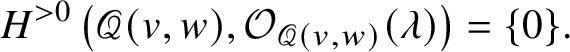 $$ \begin{align*}H^{>0} \left( \mathscr{Q} ( v, w ), {\mathcal O}_{\mathscr{Q} \left( v, w \right)} ( \lambda )\right) = \{ 0 \}.\end{align*} $$
$$ \begin{align*}H^{>0} \left( \mathscr{Q} ( v, w ), {\mathcal O}_{\mathscr{Q} \left( v, w \right)} ( \lambda )\right) = \{ 0 \}.\end{align*} $$The space  $H^0 \left ( \mathscr {Q} ( v, w ), {\mathcal O}_{\mathscr {Q} \left ( v, w \right )} ( \lambda )\right )^{\vee }$ is the intersection of two Demazure modules of
$H^0 \left ( \mathscr {Q} ( v, w ), {\mathcal O}_{\mathscr {Q} \left ( v, w \right )} ( \lambda )\right )^{\vee }$ is the intersection of two Demazure modules of ![]() $\mathbb {X} ( \lambda )$ spanned by a subset of the global basis of
$\mathbb {X} ( \lambda )$ spanned by a subset of the global basis of ![]() $\mathbb {X} ( \lambda )$ if
$\mathbb {X} ( \lambda )$ if ![]() $\lambda $ is strictly dominant. If we have
$\lambda $ is strictly dominant. If we have ![]() $w',v' \in W_{\mathrm {af}}$ such that
$w',v' \in W_{\mathrm {af}}$ such that ![]() $\mathscr {Q} ( v',w' ) \subset \mathscr {Q} ( v, w )$, then the restriction map
$\mathscr {Q} ( v',w' ) \subset \mathscr {Q} ( v, w )$, then the restriction map
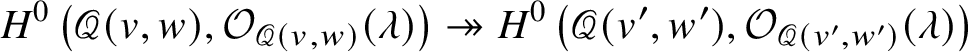 $$ \begin{align*}H^0 \left( \mathscr{Q} ( v, w ), {\mathcal O}_{\mathscr{Q} \left( v, w \right)} ( \lambda )\right) \twoheadrightarrow H^0 \left( \mathscr{Q} ( v', w' ), {\mathcal O}_{\mathscr{Q} \left( v', w' \right)} ( \lambda )\right)\end{align*} $$
$$ \begin{align*}H^0 \left( \mathscr{Q} ( v, w ), {\mathcal O}_{\mathscr{Q} \left( v, w \right)} ( \lambda )\right) \twoheadrightarrow H^0 \left( \mathscr{Q} ( v', w' ), {\mathcal O}_{\mathscr{Q} \left( v', w' \right)} ( \lambda )\right)\end{align*} $$is surjective.
Note that Corollary C adds new vanishing region to [Reference Braverman and Finkelberg10, Theorem 3.1 1)]. We also provide parabolic versions of Theorems A and B and Corollary C. We have a description of  $H^0 \left ( \mathscr {Q} ( v, w ), {\mathcal O}_{\mathscr {Q} \left ( v, w \right )} ( \lambda )\right )$ for general
$H^0 \left ( \mathscr {Q} ( v, w ), {\mathcal O}_{\mathscr {Q} \left ( v, w \right )} ( \lambda )\right )$ for general ![]() $\lambda \in P_+$ that is more complicated (Theorem B.6).
$\lambda \in P_+$ that is more complicated (Theorem B.6).
Let ![]() $\mathscr {B}_{2,\beta }$ be the space of genus
$\mathscr {B}_{2,\beta }$ be the space of genus ![]() $0$ stable maps with two marked points to
$0$ stable maps with two marked points to ![]() $\mathscr {B}$ with the class of its image
$\mathscr {B}$ with the class of its image ![]() $\beta \in Q^{\vee }_+ \subset Q^{\vee } \cong H_2 ( \mathscr {B}, \mathbb {Z} )$. We have evaluation maps
$\beta \in Q^{\vee }_+ \subset Q^{\vee } \cong H_2 ( \mathscr {B}, \mathbb {Z} )$. We have evaluation maps ![]() $\mathtt {e}_j : \mathscr {B}_{2,\beta } \to \mathscr {B}$ for
$\mathtt {e}_j : \mathscr {B}_{2,\beta } \to \mathscr {B}$ for ![]() $j = 1,2$. The following purely geometric result is a by-product of our proof that may be of independent interest:
$j = 1,2$. The following purely geometric result is a by-product of our proof that may be of independent interest:
Corollary D  $\doteq $ Corollary 5.19
$\doteq $ Corollary 5.19
Set ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $x, y \in \mathscr {B}$. The space
$x, y \in \mathscr {B}$. The space  $\left ( \mathtt {e}_1^{-1} ( x ) \cap \mathtt {e}_2^{-1} \left ( \overline {B y} \right ) \right )$ is connected if it is nonempty.
$\left ( \mathtt {e}_1^{-1} ( x ) \cap \mathtt {e}_2^{-1} \left ( \overline {B y} \right ) \right )$ is connected if it is nonempty.
Note that Corollary D is contained in [Reference Buch, Chaput, Mihalcea and Perrin16] whenever ![]() $\{x\},\overline {By} \subset \mathscr {B}$ are in general position.
$\{x\},\overline {By} \subset \mathscr {B}$ are in general position.
The plan of this paper is as follows: In Section 2, we collect basic material needed in what follows. In Section 3, after recalling generalities on Frobenius splitting and representation theory of quantum loop algebras, we construct the ind-scheme ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ and equip it with a Frobenius splitting (Corollary 3.38). In Section 4, we first interpret
$\mathbf {Q}_G^{\mathrm {rat}}$ and equip it with a Frobenius splitting (Corollary 3.38). In Section 4, we first interpret ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ as an ind-scheme (coarsely) representing the coset
$\mathbf {Q}_G^{\mathrm {rat}}$ as an ind-scheme (coarsely) representing the coset ![]() $G ( {\mathbb K} (\!(z)\!) ) / (H ( {\mathbb K} ) N ( {\mathbb K} (\!(z)\!) ))$ (Theorem A). Using this, we identify some Richardson varieties of
$G ( {\mathbb K} (\!(z)\!) ) / (H ( {\mathbb K} ) N ( {\mathbb K} (\!(z)\!) ))$ (Theorem A). Using this, we identify some Richardson varieties of ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ with quasi-map spaces (Theorem 4.30) and present their cohomological properties (Theorem 4.33), and hence prove (large parts of) Theorem B and Corollary C. Since our construction equips quasi-map spaces with Frobenius splittings (Lemma 4.7), they are automatically weakly normal. Moreover, we explain how to connect characteristic
$\mathbf {Q}_G^{\mathrm {rat}}$ with quasi-map spaces (Theorem 4.30) and present their cohomological properties (Theorem 4.33), and hence prove (large parts of) Theorem B and Corollary C. Since our construction equips quasi-map spaces with Frobenius splittings (Lemma 4.7), they are automatically weakly normal. Moreover, we explain how to connect characteristic ![]() $0$ and positive characteristic (Section 4.5). In Section 5, we analyse the fibres of the graph-space resolutions of quasi-map spaces and deduce that Richardson varieties of semi-infinite flag manifolds (over
$0$ and positive characteristic (Section 4.5). In Section 5, we analyse the fibres of the graph-space resolutions of quasi-map spaces and deduce that Richardson varieties of semi-infinite flag manifolds (over ![]() ${\mathbb C}$) are normal based on the weak normality proved in the previous section. This proves the remaining part of Theorem B. Our analysis here contains an inductive proof that the fibres of the evaluation maps of the space of genus
${\mathbb C}$) are normal based on the weak normality proved in the previous section. This proves the remaining part of Theorem B. Our analysis here contains an inductive proof that the fibres of the evaluation maps of the space of genus ![]() $0$ stable maps to flag varieties are connected (Corollary D). In Appendix A, we give a proof of the normality of (the ind-pieces of)
$0$ stable maps to flag varieties are connected (Corollary D). In Appendix A, we give a proof of the normality of (the ind-pieces of) ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ (which works also in the positive characteristic setting) and present an analogue of the Kempf vanishing theorem [Reference Kempf52] for
$\mathbf {Q}_G^{\mathrm {rat}}$ (which works also in the positive characteristic setting) and present an analogue of the Kempf vanishing theorem [Reference Kempf52] for ![]() $\mathbf {Q}_G^{\mathrm {rat}}$. Appendix B exhibits the structure of global sections of nef line bundles of Richardson varieties of
$\mathbf {Q}_G^{\mathrm {rat}}$. Appendix B exhibits the structure of global sections of nef line bundles of Richardson varieties of ![]() $\mathbf {Q}_G^{\mathrm {rat}}$.
$\mathbf {Q}_G^{\mathrm {rat}}$.
Note that Theorem B equips a quasi-map space from ![]() $\mathbb {P}^1$ to
$\mathbb {P}^1$ to ![]() $\mathscr {B}$ with a Frobenius splitting compatible with the boundaries. However, the notion of a boundary in quasi-map spaces depends on a configuration of points in
$\mathscr {B}$ with a Frobenius splitting compatible with the boundaries. However, the notion of a boundary in quasi-map spaces depends on a configuration of points in ![]() $\mathbb {P}^1$ (we implicitly set them to
$\mathbb {P}^1$ (we implicitly set them to ![]() $\{0,\infty \} \subset \mathbb {P}^1$ throughout this paper). This makes our analogues of open Richardson varieties not necessarily smooth, contrary to the original case [Reference Richardson76] (see also [Reference Finkelberg and Mirković29, §8.4.1]). We hope to give a further account of this, as well as the factorisation structure ([Reference Finkelberg and Mirković29, §6.3]) from the viewpoint presented in this paper, in future work.
$\{0,\infty \} \subset \mathbb {P}^1$ throughout this paper). This makes our analogues of open Richardson varieties not necessarily smooth, contrary to the original case [Reference Richardson76] (see also [Reference Finkelberg and Mirković29, §8.4.1]). We hope to give a further account of this, as well as the factorisation structure ([Reference Finkelberg and Mirković29, §6.3]) from the viewpoint presented in this paper, in future work.
2 Preliminaries
We work over an algebraically closed field ![]() ${\mathbb K}$ unless stated otherwise. A vector space is a
${\mathbb K}$ unless stated otherwise. A vector space is a ![]() ${\mathbb K}$-vector space, and a graded vector space refers to a
${\mathbb K}$-vector space, and a graded vector space refers to a ![]() $\mathbb {Z}$-graded vector space whose graded pieces are finite-dimensional and whose grading is bounded from above or from below. Tensor products are taken over
$\mathbb {Z}$-graded vector space whose graded pieces are finite-dimensional and whose grading is bounded from above or from below. Tensor products are taken over ![]() ${\mathbb K}$ unless specified otherwise.
${\mathbb K}$ unless specified otherwise.
Let A be a principal ideal domain. For a graded free A-module ![]() $M = \bigoplus _{m \in \mathbb {Z}} M_m$, we set
$M = \bigoplus _{m \in \mathbb {Z}} M_m$, we set ![]() $M^{\vee } := \bigoplus _{m \in \mathbb {Z}} \mathrm {Hom}_A ( M_m, A )$, where
$M^{\vee } := \bigoplus _{m \in \mathbb {Z}} \mathrm {Hom}_A ( M_m, A )$, where ![]() $\mathrm {Hom}_A ( M_m, A )$ is understood to have degree
$\mathrm {Hom}_A ( M_m, A )$ is understood to have degree ![]() $-m$.
$-m$.
As a rule, we suppress ![]() $\emptyset $ and associated parentheses from notation. This particularly applies to
$\emptyset $ and associated parentheses from notation. This particularly applies to ![]() $\emptyset = \mathtt J \subset \mathtt I$, frequently used to specify parabolic subgroups.
$\emptyset = \mathtt J \subset \mathtt I$, frequently used to specify parabolic subgroups.
2.1 Groups, root systems and Weyl groups
We refer to [Reference Chriss and Ginzburg21, Reference Kumar57] for precise expositions of general material presented in this subsection.
Let G be a connected, simply connected simple algebraic group of rank r over an algebraically closed field ![]() ${\mathbb K}$, and let B and H be a Borel subgroup and a maximal torus of G such that
${\mathbb K}$, and let B and H be a Borel subgroup and a maximal torus of G such that ![]() $H \subset B$. We set
$H \subset B$. We set ![]() $N (= [B,B])$ to be the unipotent radical of B and let
$N (= [B,B])$ to be the unipotent radical of B and let ![]() $N^-$ be the opposite unipotent subgroup of N with respect to H. We denote the Lie algebra of an algebraic group by the corresponding German (Fraktur) small letter. We have a (finite) Weyl group
$N^-$ be the opposite unipotent subgroup of N with respect to H. We denote the Lie algebra of an algebraic group by the corresponding German (Fraktur) small letter. We have a (finite) Weyl group ![]() $W := N_G ( H ) / H$. For an algebraic group E, we denote its set of
$W := N_G ( H ) / H$. For an algebraic group E, we denote its set of ![]() ${\mathbb K} [z]$-valued points by
${\mathbb K} [z]$-valued points by ![]() $E [z]$, its set of
$E [z]$, its set of ![]() ${\mathbb K} [\![z]\!]$-valued points by
${\mathbb K} [\![z]\!]$-valued points by ![]() $E [\![z]\!]$, and its set of
$E [\![z]\!]$, and its set of ![]() ${\mathbb K} (\!(z)\!)$-valued points by
${\mathbb K} (\!(z)\!)$-valued points by ![]() $E (\!(z)\!)$, and so on. Let
$E (\!(z)\!)$, and so on. Let ![]() $\mathbf I \subset G [\![z]\!]$ be the preimage of
$\mathbf I \subset G [\![z]\!]$ be the preimage of ![]() $B \subset G$ via the evaluation at
$B \subset G$ via the evaluation at ![]() $z = 0$ (the Iwahori subgroup of
$z = 0$ (the Iwahori subgroup of ![]() $G [\![z]\!]$). We set
$G [\![z]\!]$). We set  $\mathbf {I}^- \subset G \left [z^{-1}\right ]$ as the opposite Iwahori subgroup of
$\mathbf {I}^- \subset G \left [z^{-1}\right ]$ as the opposite Iwahori subgroup of ![]() $\mathbf {I}$ in
$\mathbf {I}$ in ![]() $G (\!(z)\!)$ with respect to H. By abuse of notation, we might consider
$G (\!(z)\!)$ with respect to H. By abuse of notation, we might consider ![]() $\mathbf {I}$ and
$\mathbf {I}$ and ![]() $G [\![z]\!]$ as proalgebraic groups over
$G [\![z]\!]$ as proalgebraic groups over ![]() ${\mathbb K}$ whose
${\mathbb K}$ whose ![]() ${\mathbb K}$-valued points are given as these.
${\mathbb K}$-valued points are given as these.
Let ![]() $P := \mathrm {Hom} _{gr} ( H, \mathbb {G}_m )$ be the weight lattice of H,
$P := \mathrm {Hom} _{gr} ( H, \mathbb {G}_m )$ be the weight lattice of H, ![]() $\Delta \subset P$ be the set of roots,
$\Delta \subset P$ be the set of roots, ![]() $\Delta _+ \subset \Delta $ be the set of roots that yield root subspaces in
$\Delta _+ \subset \Delta $ be the set of roots that yield root subspaces in ![]() $\mathfrak {b}$ and
$\mathfrak {b}$ and ![]() $\Pi \subset \Delta _+$ be the set of simple roots. We set
$\Pi \subset \Delta _+$ be the set of simple roots. We set ![]() $\Delta _- := - \Delta _+$. Let
$\Delta _- := - \Delta _+$. Let ![]() $Q^{\vee }$ be the dual lattice of P with a natural pairing
$Q^{\vee }$ be the dual lattice of P with a natural pairing ![]() $\langle \bullet , \bullet \rangle : Q^{\vee } \times P \rightarrow \mathbb {Z}$. We define
$\langle \bullet , \bullet \rangle : Q^{\vee } \times P \rightarrow \mathbb {Z}$. We define ![]() $\Pi ^{\vee } \subset Q ^{\vee }$ to be the set of positive simple coroots and let
$\Pi ^{\vee } \subset Q ^{\vee }$ to be the set of positive simple coroots and let ![]() $Q_+^{\vee } \subset Q ^{\vee }$ be the set of nonnegative integer spans of
$Q_+^{\vee } \subset Q ^{\vee }$ be the set of nonnegative integer spans of ![]() $\Pi ^{\vee }$. For
$\Pi ^{\vee }$. For ![]() $\beta , \gamma \in Q^{\vee }$, we define
$\beta , \gamma \in Q^{\vee }$, we define ![]() $\beta \ge \gamma $ if and only if
$\beta \ge \gamma $ if and only if ![]() $\beta - \gamma \in Q^{\vee }_+$. We set
$\beta - \gamma \in Q^{\vee }_+$. We set ![]() $P_+ := \left \{ \lambda \in P \mid \left \langle \alpha ^{\vee }, \lambda \right \rangle \ge 0, \ \forall \alpha ^{\vee } \in \Pi ^{\vee } \right \}$ and
$P_+ := \left \{ \lambda \in P \mid \left \langle \alpha ^{\vee }, \lambda \right \rangle \ge 0, \ \forall \alpha ^{\vee } \in \Pi ^{\vee } \right \}$ and ![]() $P_{++} := \left \{ \lambda \in P \mid \left \langle \alpha ^{\vee }, \lambda \right \rangle> 0, \ \forall \alpha ^{\vee } \in \Pi ^{\vee } \right \}$. Define
$P_{++} := \left \{ \lambda \in P \mid \left \langle \alpha ^{\vee }, \lambda \right \rangle> 0, \ \forall \alpha ^{\vee } \in \Pi ^{\vee } \right \}$. Define ![]() $\mathtt I := \{1,2,\ldots ,r\}$. We fix bijections
$\mathtt I := \{1,2,\ldots ,r\}$. We fix bijections ![]() $\mathtt I \cong \Pi \cong \Pi ^{\vee }$ such that
$\mathtt I \cong \Pi \cong \Pi ^{\vee }$ such that ![]() $i \in \mathtt I$ corresponds to
$i \in \mathtt I$ corresponds to ![]() $\alpha _i \in \Pi $, its coroot
$\alpha _i \in \Pi $, its coroot ![]() $\alpha _i^{\vee } \in \Pi ^{\vee }$ and a simple reflection
$\alpha _i^{\vee } \in \Pi ^{\vee }$ and a simple reflection ![]() $s_i \in W$ corresponding to
$s_i \in W$ corresponding to ![]() $\alpha _i$. Let
$\alpha _i$. Let ![]() $\{\varpi _i\}_{i \in \mathtt I} \subset P_+$ be the set of fundamental weights
$\{\varpi _i\}_{i \in \mathtt I} \subset P_+$ be the set of fundamental weights  $\left (\text {i.e., }\left \langle \alpha _i^{\vee }, \varpi _j \right \rangle = \delta _{ij}\right )$ and
$\left (\text {i.e., }\left \langle \alpha _i^{\vee }, \varpi _j \right \rangle = \delta _{ij}\right )$ and  $\rho := \sum _{i \in \mathtt I} \varpi _i = \frac {1}{2}\sum _{\alpha \in \Delta ^+} \alpha \in P_+$.
$\rho := \sum _{i \in \mathtt I} \varpi _i = \frac {1}{2}\sum _{\alpha \in \Delta ^+} \alpha \in P_+$.
For a subset ![]() $\mathtt J \subset \mathtt I$, we define
$\mathtt J \subset \mathtt I$, we define ![]() $P ( \mathtt J )$ as the standard parabolic subgroup of G corresponding to
$P ( \mathtt J )$ as the standard parabolic subgroup of G corresponding to ![]() $\mathtt J$ – that is, we have
$\mathtt J$ – that is, we have ![]() $\mathfrak {b} \subset \mathfrak p (\mathtt J) \subset \mathfrak {g}$, and
$\mathfrak {b} \subset \mathfrak p (\mathtt J) \subset \mathfrak {g}$, and ![]() $\mathfrak p (\mathtt J)$ contains the root subspace corresponding to
$\mathfrak p (\mathtt J)$ contains the root subspace corresponding to ![]() $- \alpha _i$ (
$- \alpha _i$ (![]() $i \in \mathtt I$) if and only if
$i \in \mathtt I$) if and only if ![]() $i \in \mathtt J$. Let
$i \in \mathtt J$. Let ![]() $H \subset L ( \mathtt J ) \subset P ( \mathtt J )$ be the standard Levi subgroup (which is isomorphic to the quotient of
$H \subset L ( \mathtt J ) \subset P ( \mathtt J )$ be the standard Levi subgroup (which is isomorphic to the quotient of ![]() $P ( \mathtt J )$ by its unipotent radical). Then the set of characters of
$P ( \mathtt J )$ by its unipotent radical). Then the set of characters of ![]() $P ( \mathtt J )$ is identified with
$P ( \mathtt J )$ is identified with ![]() $P_{\mathtt J} := \sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z} \varpi _i$. We also set
$P_{\mathtt J} := \sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z} \varpi _i$. We also set ![]() $P_{\mathtt J, +} := \sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z}_{\ge 0} \varpi _i = P_+ \cap P_{\mathtt J}$ and
$P_{\mathtt J, +} := \sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z}_{\ge 0} \varpi _i = P_+ \cap P_{\mathtt J}$ and ![]() $P_{\mathtt J, ++} := \sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z}_{\ge 1} \varpi _i = P_{++} \cap P_{\mathtt J}$. We define
$P_{\mathtt J, ++} := \sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z}_{\ge 1} \varpi _i = P_{++} \cap P_{\mathtt J}$. We define ![]() $W_{\mathtt J} \subset W$ to be the reflection subgroup generated by
$W_{\mathtt J} \subset W$ to be the reflection subgroup generated by ![]() $\{s_i\}_{i \in \mathtt J}$. It is the Weyl group of
$\{s_i\}_{i \in \mathtt J}$. It is the Weyl group of ![]() $[L ( \mathtt J ), L (\mathtt J) ]$ and
$[L ( \mathtt J ), L (\mathtt J) ]$ and ![]() $L ( \mathtt J )$. We define
$L ( \mathtt J )$. We define ![]() $\rho _{\mathtt J}$ to be the half-sum of positive roots whose root spaces are contained in the unipotent radical of
$\rho _{\mathtt J}$ to be the half-sum of positive roots whose root spaces are contained in the unipotent radical of ![]() $\mathfrak p ( \mathtt J )$.
$\mathfrak p ( \mathtt J )$.
Let ![]() $\Delta _{\mathrm {af}} := \Delta \times \mathbb {Z} \delta \cup \{m \delta \}_{m \neq 0}$ be the untwisted affine root system of
$\Delta _{\mathrm {af}} := \Delta \times \mathbb {Z} \delta \cup \{m \delta \}_{m \neq 0}$ be the untwisted affine root system of ![]() $\Delta $ with its positive part
$\Delta $ with its positive part ![]() $\Delta _+ \subset \Delta _{\mathrm {af}, +}$. We set
$\Delta _+ \subset \Delta _{\mathrm {af}, +}$. We set ![]() $\alpha _0 := - \vartheta + \delta $,
$\alpha _0 := - \vartheta + \delta $, ![]() $\Pi _{\mathrm {af}} := \Pi \cup \{ \alpha _0 \}$ and
$\Pi _{\mathrm {af}} := \Pi \cup \{ \alpha _0 \}$ and ![]() $\mathtt I_{\mathrm {af}} := \mathtt I \cup \{ 0 \}$, where
$\mathtt I_{\mathrm {af}} := \mathtt I \cup \{ 0 \}$, where ![]() $\vartheta $ is the highest root of
$\vartheta $ is the highest root of ![]() $\Delta _+$. We set
$\Delta _+$. We set ![]() $W _{\mathrm {af}} := W \ltimes Q^{\vee }$ and call it the affine Weyl group. It is a reflection group generated by
$W _{\mathrm {af}} := W \ltimes Q^{\vee }$ and call it the affine Weyl group. It is a reflection group generated by ![]() $\{s_i \mid i \in \mathtt I_{\mathrm {af}} \}$, where
$\{s_i \mid i \in \mathtt I_{\mathrm {af}} \}$, where ![]() $s_0$ is the reflection with respect to
$s_0$ is the reflection with respect to ![]() $\alpha _0$. We also have a reflection
$\alpha _0$. We also have a reflection ![]() $s_{\alpha } \in W_{\mathrm {af}}$ corresponding to
$s_{\alpha } \in W_{\mathrm {af}}$ corresponding to ![]() $\alpha \in \Delta \times \mathbb {Z} \delta \subsetneq \Delta ^{\mathrm {af}}$. Let
$\alpha \in \Delta \times \mathbb {Z} \delta \subsetneq \Delta ^{\mathrm {af}}$. Let ![]() $\ell : W_{\mathrm {af}} \rightarrow \mathbb {Z}_{\ge 0}$ be the length function and
$\ell : W_{\mathrm {af}} \rightarrow \mathbb {Z}_{\ge 0}$ be the length function and ![]() $w_0 \in W$ be the longest element in
$w_0 \in W$ be the longest element in ![]() $W \subset W_{\mathrm {af}}$. Together with the normalisation
$W \subset W_{\mathrm {af}}$. Together with the normalisation ![]() $t_{- \vartheta ^{\vee }} := s_{\vartheta } s_0$ (for the coroot
$t_{- \vartheta ^{\vee }} := s_{\vartheta } s_0$ (for the coroot ![]() $\vartheta ^{\vee }$ of
$\vartheta ^{\vee }$ of ![]() $\vartheta $), we introduce the translation element
$\vartheta $), we introduce the translation element ![]() $t_{\beta } \in W _{\mathrm {af}}$ for each
$t_{\beta } \in W _{\mathrm {af}}$ for each ![]() $\beta \in Q^{\vee }$.
$\beta \in Q^{\vee }$.
For each ![]() $i \in \mathtt I_{\mathrm {af}}$, we have a connected algebraic group
$i \in \mathtt I_{\mathrm {af}}$, we have a connected algebraic group ![]() $\mathop {\textit{SL}} ( 2, i )$ that is isomorphic to
$\mathop {\textit{SL}} ( 2, i )$ that is isomorphic to ![]() $\mathop {\textit{SL}} ( 2 )$ equipped with an inclusion
$\mathop {\textit{SL}} ( 2 )$ equipped with an inclusion ![]() $\mathop {\textit{SL}} ( 2, i ) ( {\mathbb K} ) \subset G (\!(z)\!)$ as groups corresponding to
$\mathop {\textit{SL}} ( 2, i ) ( {\mathbb K} ) \subset G (\!(z)\!)$ as groups corresponding to ![]() $\pm \alpha _i \in \mathtt I_{\mathrm {af}}$. Let
$\pm \alpha _i \in \mathtt I_{\mathrm {af}}$. Let ![]() $\rho _{\pm \alpha _i} : \mathbb {G}_m \rightarrow \mathop {\textit{SL}} ( 2, i )$ denote the unipotent one-parameter subgroup corresponding to
$\rho _{\pm \alpha _i} : \mathbb {G}_m \rightarrow \mathop {\textit{SL}} ( 2, i )$ denote the unipotent one-parameter subgroup corresponding to ![]() $\pm \alpha _i \in \Delta _{\mathrm {af}}$. We set
$\pm \alpha _i \in \Delta _{\mathrm {af}}$. We set ![]() $B_i := \mathop {\textit{SL}} ( 2, i ) \cap \mathbf I$, which is a Borel subgroup of
$B_i := \mathop {\textit{SL}} ( 2, i ) \cap \mathbf I$, which is a Borel subgroup of ![]() $\mathop {\textit{SL}} ( 2, i )$. For each
$\mathop {\textit{SL}} ( 2, i )$. For each ![]() $i \in \mathtt I$, we set
$i \in \mathtt I$, we set ![]() $P_i := P ( \{ i \} )$. For each
$P_i := P ( \{ i \} )$. For each ![]() $i \in \mathtt I_{\mathrm {af}}$, we set
$i \in \mathtt I_{\mathrm {af}}$, we set ![]() $\mathbf {I} ( i ) := \mathop {\textit{SL}} ( 2, i ) \mathbf {I}$. Each
$\mathbf {I} ( i ) := \mathop {\textit{SL}} ( 2, i ) \mathbf {I}$. Each ![]() $\mathbf {I} (i)$ can be regarded as a proalgebraic group.
$\mathbf {I} (i)$ can be regarded as a proalgebraic group.
As a variation of [Reference Kumar57, Chapter VI], we say an ind-scheme ![]() $\mathfrak X$ over
$\mathfrak X$ over ![]() ${\mathbb K}$ admits a
${\mathbb K}$ admits a ![]() $G(\!(z)\!)$-action if it admits an action of
$G(\!(z)\!)$-action if it admits an action of ![]() $\mathbf {I}$ and
$\mathbf {I}$ and ![]() $\mathop {\textit{SL}} ( 2, i )$ (
$\mathop {\textit{SL}} ( 2, i )$ (![]() $i \in \mathtt I_{\mathrm {af}}$) as (ind-)schemes over
$i \in \mathtt I_{\mathrm {af}}$) as (ind-)schemes over ![]() ${\mathbb K}$ that coincides on
${\mathbb K}$ that coincides on ![]() $B_i = ( \mathbf {I} \cap \mathop {\textit{SL}} ( 2, i ) )$ and they generate a
$B_i = ( \mathbf {I} \cap \mathop {\textit{SL}} ( 2, i ) )$ and they generate a ![]() $G(\!(z)\!)$-action on the set of closed points of
$G(\!(z)\!)$-action on the set of closed points of ![]() $\mathfrak X$ (the latter is a group action on a set). We consider the notion of
$\mathfrak X$ (the latter is a group action on a set). We consider the notion of ![]() $G(\!(z)\!)$-equivariant morphisms accordingly.
$G(\!(z)\!)$-equivariant morphisms accordingly.
We set
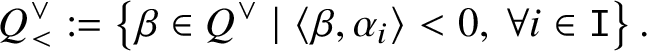 $$ \begin{align*}Q^{\vee}_< := \left\{\beta \in Q^{\vee} \mid \left\langle \beta, \alpha_i \right\rangle < 0, \ \forall i \in \mathtt I \right\}.\end{align*} $$
$$ \begin{align*}Q^{\vee}_< := \left\{\beta \in Q^{\vee} \mid \left\langle \beta, \alpha_i \right\rangle < 0, \ \forall i \in \mathtt I \right\}.\end{align*} $$ Let ![]() $\le $ be the Bruhat order of
$\le $ be the Bruhat order of ![]() $W_{\mathrm {af}}$. In other words,
$W_{\mathrm {af}}$. In other words, ![]() $w \le v$ holds if and only if a subexpression of a reduced decomposition of v yields a reduced decomposition of w. We define the generic (semi-infinite) Bruhat order
$w \le v$ holds if and only if a subexpression of a reduced decomposition of v yields a reduced decomposition of w. We define the generic (semi-infinite) Bruhat order ![]() $\le _{\frac {\infty }{2}}$ as
$\le _{\frac {\infty }{2}}$ as
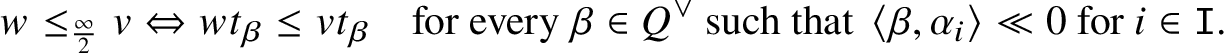 $$ \begin{align} w \le_{\frac{\infty}{2}} v \Leftrightarrow w t_{\beta} \le v t_{\beta} \quad \text{for every } \beta \in Q^{\vee} \text{ such that } \left\langle \beta, \alpha_i \right\rangle \ll 0 \text{ for } i \in \mathtt I. \end{align} $$
$$ \begin{align} w \le_{\frac{\infty}{2}} v \Leftrightarrow w t_{\beta} \le v t_{\beta} \quad \text{for every } \beta \in Q^{\vee} \text{ such that } \left\langle \beta, \alpha_i \right\rangle \ll 0 \text{ for } i \in \mathtt I. \end{align} $$By [Reference Lusztig64], this defines a preorder on ![]() $W_{\mathrm {af}}$. Here we remark that
$W_{\mathrm {af}}$. Here we remark that ![]() $w \le v$ if and only if
$w \le v$ if and only if ![]() $w \ge _{\frac {\infty }{2}} v$ for
$w \ge _{\frac {\infty }{2}} v$ for ![]() $w, v \in W$. We also have
$w, v \in W$. We also have
For proofs and related results, we refer to [Reference Kato, Naito and Sagaki51, §2.2] and [Reference Peterson74, Lecture 13].
For each ![]() $u \in W$ and
$u \in W$ and ![]() $\beta \in Q^{\vee }$, we set
$\beta \in Q^{\vee }$, we set
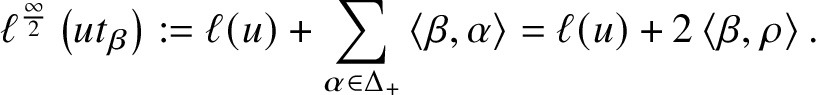 $$ \begin{align*}\ell^{\frac{\infty}{2}} \left( u t_{\beta} \right) := \ell ( u ) + \sum_{\alpha \in \Delta_+} \left\langle \beta, \alpha \right\rangle = \ell ( u ) + 2 \left\langle \beta, \rho \right\rangle.\end{align*} $$
$$ \begin{align*}\ell^{\frac{\infty}{2}} \left( u t_{\beta} \right) := \ell ( u ) + \sum_{\alpha \in \Delta_+} \left\langle \beta, \alpha \right\rangle = \ell ( u ) + 2 \left\langle \beta, \rho \right\rangle.\end{align*} $$Theorem 2.1 [Reference Lusztig64]; compare [Reference Lam and Shimozono61]
For each ![]() $w, v \in W_{\mathrm {af}}$ such that
$w, v \in W_{\mathrm {af}}$ such that ![]() $w \le _{\frac {\infty }{2}} v$, there exists
$w \le _{\frac {\infty }{2}} v$, there exists ![]() $\alpha \in \Delta _+^{\mathrm {af}}$ such that
$\alpha \in \Delta _+^{\mathrm {af}}$ such that ![]() $ w \le _{\frac {\infty }{2}} s_{\alpha } v \le _{\frac {\infty }{2}} v$ and
$ w \le _{\frac {\infty }{2}} s_{\alpha } v \le _{\frac {\infty }{2}} v$ and ![]() $\ell ^{\frac {\infty }{2}} ( s_{\alpha } v ) = \ell ^{\frac {\infty }{2}} ( v ) + 1$.
$\ell ^{\frac {\infty }{2}} ( s_{\alpha } v ) = \ell ^{\frac {\infty }{2}} ( v ) + 1$.
For each ![]() $\lambda \in P_+$, we denote the corresponding Weyl module by
$\lambda \in P_+$, we denote the corresponding Weyl module by ![]() $V ( \lambda )$ (see, e.g. [Reference Andersen, Polo and Wen1, Proposition 1.22] and [Reference Kashiwara41, Theorem 5]). By convention,
$V ( \lambda )$ (see, e.g. [Reference Andersen, Polo and Wen1, Proposition 1.22] and [Reference Kashiwara41, Theorem 5]). By convention, ![]() $V ( \lambda )$ is a finite-dimensional indecomposable G-module with a cyclic B-eigenvector
$V ( \lambda )$ is a finite-dimensional indecomposable G-module with a cyclic B-eigenvector ![]() $\mathbf {v}_\lambda ^0$ (highest weight vector) with H-weight
$\mathbf {v}_\lambda ^0$ (highest weight vector) with H-weight ![]() $\lambda $ whose character obeys the Weyl character formula. For a semisimple H-module V, we set
$\lambda $ whose character obeys the Weyl character formula. For a semisimple H-module V, we set
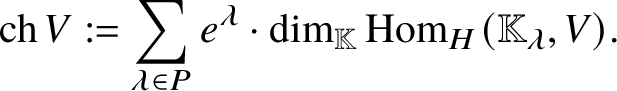 $$ \begin{align*}\mathrm{ch}\, V := \sum_{\lambda \in P} e^\lambda \cdot \dim _{{\mathbb K}} \mathrm{Hom}_H ( {\mathbb K}_\lambda, V ).\end{align*} $$
$$ \begin{align*}\mathrm{ch}\, V := \sum_{\lambda \in P} e^\lambda \cdot \dim _{{\mathbb K}} \mathrm{Hom}_H ( {\mathbb K}_\lambda, V ).\end{align*} $$If V is a ![]() $\mathbb {Z}$-graded H-module in addition, then we set
$\mathbb {Z}$-graded H-module in addition, then we set
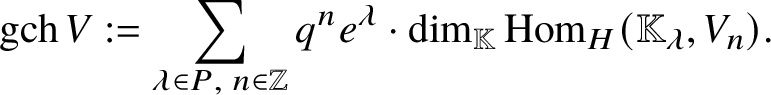 $$ \begin{align} \mathrm{gch}\, V := \sum_{\lambda \in P, \; n \in \mathbb{Z}} q^n e^\lambda \cdot \dim _{{\mathbb K}} \mathrm{Hom}_H ( {\mathbb K}_\lambda, V_n ). \end{align} $$
$$ \begin{align} \mathrm{gch}\, V := \sum_{\lambda \in P, \; n \in \mathbb{Z}} q^n e^\lambda \cdot \dim _{{\mathbb K}} \mathrm{Hom}_H ( {\mathbb K}_\lambda, V_n ). \end{align} $$ Define ![]() $\mathscr {B} := G / B$ and call it the flag manifold of G. We have the Bruhat decomposition
$\mathscr {B} := G / B$ and call it the flag manifold of G. We have the Bruhat decomposition
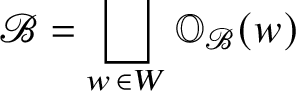 $$ \begin{align} \mathscr{B} = \bigsqcup _{w \in W} \mathbb{O}_{\mathscr{B}} ( w ) \end{align} $$
$$ \begin{align} \mathscr{B} = \bigsqcup _{w \in W} \mathbb{O}_{\mathscr{B}} ( w ) \end{align} $$into B-orbits such that ![]() $\dim \, \mathbb {O}_{\mathscr {B}} ( w ) = \ell ( w _0 ) - \ell ( w )$ for each
$\dim \, \mathbb {O}_{\mathscr {B}} ( w ) = \ell ( w _0 ) - \ell ( w )$ for each ![]() $w \in W \subset W_{\mathrm {af}}$. We set
$w \in W \subset W_{\mathrm {af}}$. We set ![]() $\mathscr {B} ( w ) := \overline {\mathbb O_{\mathscr {B}} ( w )} \subset \mathscr {B}$.
$\mathscr {B} ( w ) := \overline {\mathbb O_{\mathscr {B}} ( w )} \subset \mathscr {B}$.
For each ![]() $\lambda \in P$, we have a line bundle
$\lambda \in P$, we have a line bundle ![]() ${\mathcal O} _{\mathscr {B}} ( \lambda )$ such that
${\mathcal O} _{\mathscr {B}} ( \lambda )$ such that
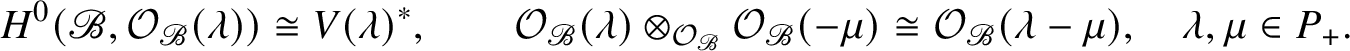 $$ \begin{align*}H ^0 ( \mathscr{B}, {\mathcal O}_{\mathscr{B}} ( \lambda ) ) \cong V ( \lambda )^*, \qquad {\mathcal O}_{\mathscr{B}} ( \lambda ) \otimes_{{\mathcal O}_{\mathscr{B}}} {\mathcal O} _{\mathscr{B}} ( - \mu ) \cong {\mathcal O}_{\mathscr{B}} ( \lambda - \mu ), \quad \lambda, \mu \in P_+.\end{align*} $$
$$ \begin{align*}H ^0 ( \mathscr{B}, {\mathcal O}_{\mathscr{B}} ( \lambda ) ) \cong V ( \lambda )^*, \qquad {\mathcal O}_{\mathscr{B}} ( \lambda ) \otimes_{{\mathcal O}_{\mathscr{B}}} {\mathcal O} _{\mathscr{B}} ( - \mu ) \cong {\mathcal O}_{\mathscr{B}} ( \lambda - \mu ), \quad \lambda, \mu \in P_+.\end{align*} $$ For each ![]() $w \in W$, let
$w \in W$, let ![]() $p_w \in \mathbb {O}_{\mathscr {B}} ( w )$ be the unique H-fixed point. We normalise
$p_w \in \mathbb {O}_{\mathscr {B}} ( w )$ be the unique H-fixed point. We normalise ![]() $p_w$ (and hence
$p_w$ (and hence ![]() $\mathbb {O}_{\mathscr {B}} ( w )$) so that the restriction of
$\mathbb {O}_{\mathscr {B}} ( w )$) so that the restriction of ![]() ${\mathcal O}_{\mathscr {B}} ( \lambda )$ to
${\mathcal O}_{\mathscr {B}} ( \lambda )$ to ![]() $p_w$ is isomorphic to
$p_w$ is isomorphic to ![]() ${\mathbb K}_{- w w_0 \lambda }$ for every
${\mathbb K}_{- w w_0 \lambda }$ for every ![]() $\lambda \in P_+$. (Here we warn that the convention differs from [Reference Kato47].)
$\lambda \in P_+$. (Here we warn that the convention differs from [Reference Kato47].)
2.2 Representations of affine and current algebras
In the rest of this section, we work over ![]() ${\mathbb K} = {\mathbb C}$, the field of complex numbers. Material in this subsection without a reference can be found in [Reference Kac40, Reference Kashiwara41]. Every result in this subsection is transferred to an arbitrary field in Section 3.2.
${\mathbb K} = {\mathbb C}$, the field of complex numbers. Material in this subsection without a reference can be found in [Reference Kac40, Reference Kashiwara41]. Every result in this subsection is transferred to an arbitrary field in Section 3.2.
Let ![]() $\widetilde {\mathfrak {g}}$ denote the untwisted affine Kac–Moody algebra associated to
$\widetilde {\mathfrak {g}}$ denote the untwisted affine Kac–Moody algebra associated to ![]() $\mathfrak {g}$ – that is, we have
$\mathfrak {g}$ – that is, we have
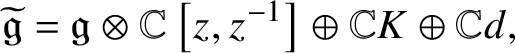 $$ \begin{align*}\widetilde{\mathfrak{g}} = \mathfrak{g} \otimes {\mathbb C} \left[z, z^{-1}\right] \oplus {\mathbb C} K \oplus {\mathbb C} d,\end{align*} $$
$$ \begin{align*}\widetilde{\mathfrak{g}} = \mathfrak{g} \otimes {\mathbb C} \left[z, z^{-1}\right] \oplus {\mathbb C} K \oplus {\mathbb C} d,\end{align*} $$where K is central, ![]() $[d, X \otimes z^m] = m X \otimes z ^m$ for each
$[d, X \otimes z^m] = m X \otimes z ^m$ for each ![]() $X \in \mathfrak {g}$ and
$X \in \mathfrak {g}$ and ![]() $m \in \mathbb {Z}$ and, for each
$m \in \mathbb {Z}$ and, for each ![]() $X, Y \in \mathfrak {g}$ and
$X, Y \in \mathfrak {g}$ and  $f, g \in {\mathbb C} \left [z^{\pm 1}\right ]$, we have
$f, g \in {\mathbb C} \left [z^{\pm 1}\right ]$, we have
 $$ \begin{align*}[X \otimes f , Y \otimes g ] = [X, Y] \otimes f g + ( X, Y )_{\mathfrak{g}} \cdot K \cdot \mathrm{Res}_{z = 0} f \frac{\partial g}{\partial z},\end{align*} $$
$$ \begin{align*}[X \otimes f , Y \otimes g ] = [X, Y] \otimes f g + ( X, Y )_{\mathfrak{g}} \cdot K \cdot \mathrm{Res}_{z = 0} f \frac{\partial g}{\partial z},\end{align*} $$where ![]() $(\bullet , \bullet )_{\mathfrak {g}}$ denotes the G-invariant bilinear form such that
$(\bullet , \bullet )_{\mathfrak {g}}$ denotes the G-invariant bilinear form such that ![]() $\left ( \alpha ^{\vee }, \alpha ^{\vee }\right )_{\mathfrak {g}} = 2$ for a long simple root
$\left ( \alpha ^{\vee }, \alpha ^{\vee }\right )_{\mathfrak {g}} = 2$ for a long simple root ![]() $\alpha $. Let
$\alpha $. Let ![]() $E_i, F_i$ (
$E_i, F_i$ (![]() $i \in \mathtt I_{\mathrm {af}}$) denote the Kac–Moody generators of
$i \in \mathtt I_{\mathrm {af}}$) denote the Kac–Moody generators of ![]() $\widetilde {\mathfrak {g}}$ corresponding to
$\widetilde {\mathfrak {g}}$ corresponding to ![]() $\alpha _i$. We set
$\alpha _i$. We set ![]() $\widetilde {\mathfrak {h}} := \mathfrak {h} \oplus {\mathbb C} K \oplus {\mathbb C} d$. Let
$\widetilde {\mathfrak {h}} := \mathfrak {h} \oplus {\mathbb C} K \oplus {\mathbb C} d$. Let ![]() $\mathfrak {I}$ be the Lie subalgebra of
$\mathfrak {I}$ be the Lie subalgebra of ![]() $\widetilde {\mathfrak {g}}$ generated by
$\widetilde {\mathfrak {g}}$ generated by ![]() $E_i$ (
$E_i$ (![]() $i \in \mathtt I_{\mathrm {af}}$) and
$i \in \mathtt I_{\mathrm {af}}$) and ![]() $\widetilde {\mathfrak {h}}$, and
$\widetilde {\mathfrak {h}}$, and ![]() $\mathfrak {I}^-$ be the Lie subalgebra of
$\mathfrak {I}^-$ be the Lie subalgebra of ![]() $\widetilde {\mathfrak {g}}$ generated by
$\widetilde {\mathfrak {g}}$ generated by ![]() $F_i$ (
$F_i$ (![]() $i \in \mathtt I_{\mathrm {af}}$) and
$i \in \mathtt I_{\mathrm {af}}$) and ![]() $\widetilde {\mathfrak {h}}$. For each
$\widetilde {\mathfrak {h}}$. For each ![]() $i \in \mathtt I_{\mathrm {af}}$ and
$i \in \mathtt I_{\mathrm {af}}$ and ![]() $n \ge 0$, we set
$n \ge 0$, we set  $E_i^{(n)} := \frac {1}{n!} E_i^n$ and
$E_i^{(n)} := \frac {1}{n!} E_i^n$ and  $F_i^{(n)} := \frac {1}{n!} F_i^n$.
$F_i^{(n)} := \frac {1}{n!} F_i^n$.
We define
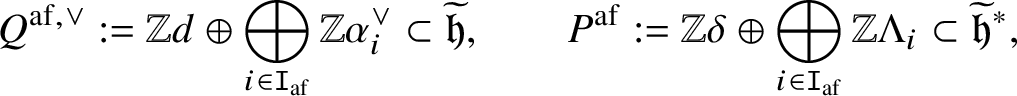 $$ \begin{align*}Q^{\mathrm{af}, \vee} := \mathbb{Z} d \oplus \bigoplus_{i \in \mathtt I_{\mathrm{af}}} \mathbb{Z} \alpha^{\vee}_i \subset \widetilde{\mathfrak{h}}, \qquad P^{\mathrm{af}} := \mathbb{Z} \delta \oplus \bigoplus_{i \in \mathtt I_{\mathrm{af}}} \mathbb{Z} \Lambda_i \subset \widetilde{\mathfrak{h}}^*,\end{align*} $$
$$ \begin{align*}Q^{\mathrm{af}, \vee} := \mathbb{Z} d \oplus \bigoplus_{i \in \mathtt I_{\mathrm{af}}} \mathbb{Z} \alpha^{\vee}_i \subset \widetilde{\mathfrak{h}}, \qquad P^{\mathrm{af}} := \mathbb{Z} \delta \oplus \bigoplus_{i \in \mathtt I_{\mathrm{af}}} \mathbb{Z} \Lambda_i \subset \widetilde{\mathfrak{h}}^*,\end{align*} $$and a pairing ![]() $Q^{\mathrm {af}, \vee } \times P^{\mathrm {af}} \rightarrow \mathbb {Z}$ such that
$Q^{\mathrm {af}, \vee } \times P^{\mathrm {af}} \rightarrow \mathbb {Z}$ such that
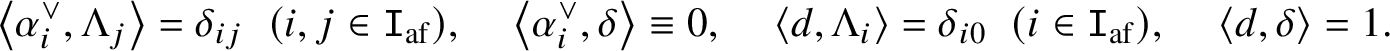 $$ \begin{align*}\left\langle \alpha_i^{\vee}, \Lambda_j \right\rangle = \delta_{ij} \hskip 2mm (i,j \in \mathtt I_{\mathrm{af}}), \hskip 4mm \left\langle \alpha^{\vee}_i, \delta \right\rangle \equiv 0, \hskip 4mm \left\langle d, \Lambda_i \right\rangle = \delta_{i0} \hskip 2mm (i \in \mathtt I_{\mathrm{af}}), \hskip 4mm \left\langle d, \delta \right\rangle = 1.\end{align*} $$
$$ \begin{align*}\left\langle \alpha_i^{\vee}, \Lambda_j \right\rangle = \delta_{ij} \hskip 2mm (i,j \in \mathtt I_{\mathrm{af}}), \hskip 4mm \left\langle \alpha^{\vee}_i, \delta \right\rangle \equiv 0, \hskip 4mm \left\langle d, \Lambda_i \right\rangle = \delta_{i0} \hskip 2mm (i \in \mathtt I_{\mathrm{af}}), \hskip 4mm \left\langle d, \delta \right\rangle = 1.\end{align*} $$We have a projection map
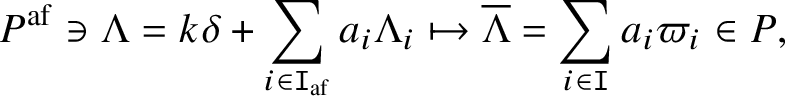 $$ \begin{align*}P^{\mathrm{af}} \ni \Lambda = k \delta + \sum_{i \in \mathtt I_{\mathrm{af}}} a_i \Lambda_i \mapsto \overline{\Lambda} = \sum_{i \in \mathtt I} a_i \varpi_i \in P,\end{align*} $$
$$ \begin{align*}P^{\mathrm{af}} \ni \Lambda = k \delta + \sum_{i \in \mathtt I_{\mathrm{af}}} a_i \Lambda_i \mapsto \overline{\Lambda} = \sum_{i \in \mathtt I} a_i \varpi_i \in P,\end{align*} $$which has a unique splitting ![]() $P \subset P^{\mathrm {af}}$ whose image is orthogonal to
$P \subset P^{\mathrm {af}}$ whose image is orthogonal to ![]() $d,K \in \widetilde {\mathfrak {h}}$. We set
$d,K \in \widetilde {\mathfrak {h}}$. We set  $P^{\mathrm {af}}_+ := \sum _{i \in \mathtt I_{\mathrm {af}}} \mathbb {Z}_{\ge 0} \Lambda _i$. Each
$P^{\mathrm {af}}_+ := \sum _{i \in \mathtt I_{\mathrm {af}}} \mathbb {Z}_{\ge 0} \Lambda _i$. Each ![]() $\Lambda \in P^{\mathrm {af}}_+$ defines an irreducible integrable highest weight module
$\Lambda \in P^{\mathrm {af}}_+$ defines an irreducible integrable highest weight module ![]() $L ( \Lambda )$ of
$L ( \Lambda )$ of ![]() $\widetilde {\mathfrak {g}}$ with its highest weight vector
$\widetilde {\mathfrak {g}}$ with its highest weight vector ![]() $\mathbf {v}_{\Lambda }$. In addition, each
$\mathbf {v}_{\Lambda }$. In addition, each ![]() $\lambda \in P_+$ defines a level
$\lambda \in P_+$ defines a level ![]() $0$ extremal weight module
$0$ extremal weight module ![]() $\mathbb {X} ( \lambda )$ of
$\mathbb {X} ( \lambda )$ of ![]() $\widetilde {\mathfrak {g}}$ by means of the specialisation of the quantum parameter
$\widetilde {\mathfrak {g}}$ by means of the specialisation of the quantum parameter ![]() $\mathsf q = 1$ in [Reference Kashiwara43, Proposition 8.2.2] and [Reference Kashiwara44, §5.1], which is integrable, and K acts by
$\mathsf q = 1$ in [Reference Kashiwara43, Proposition 8.2.2] and [Reference Kashiwara44, §5.1], which is integrable, and K acts by ![]() $0$. The module
$0$. The module ![]() $\mathbb {X} ( \lambda )$ carries a cyclic
$\mathbb {X} ( \lambda )$ carries a cyclic ![]() $\widetilde {\mathfrak {h}}$-weight vector
$\widetilde {\mathfrak {h}}$-weight vector ![]() $\mathbf {v}_{\lambda }$ such that
$\mathbf {v}_{\lambda }$ such that
(We can deduce that ![]() $\mathbb {X} ( \lambda )$ is the maximal integrable
$\mathbb {X} ( \lambda )$ is the maximal integrable ![]() $\widetilde {\mathfrak {g}}$-module that possesses a cyclic vector with these properties [Reference Kashiwara43, §8.1].) Moreover, each
$\widetilde {\mathfrak {g}}$-module that possesses a cyclic vector with these properties [Reference Kashiwara43, §8.1].) Moreover, each ![]() $w = u t_{\beta } \in W_{\mathrm {af}}$ (
$w = u t_{\beta } \in W_{\mathrm {af}}$ (![]() $u \in W, \beta \in Q^{\vee }$) defines an element
$u \in W, \beta \in Q^{\vee }$) defines an element ![]() $\mathbf {v}_{w \lambda } \in \mathbb {X} ( \lambda )$ such that
$\mathbf {v}_{w \lambda } \in \mathbb {X} ( \lambda )$ such that
up to sign [Reference Kashiwara43, §8.1]. We call a vector in ![]() $\{\mathbf {v}_{w\lambda }\}_{w \in W_{\mathrm {af}}}$ an extremal weight vector of
$\{\mathbf {v}_{w\lambda }\}_{w \in W_{\mathrm {af}}}$ an extremal weight vector of ![]() $\mathbb {X} ( \lambda )$.
$\mathbb {X} ( \lambda )$.
We set ![]() $\mathfrak {g} [z] := \mathfrak {g} \otimes _{\mathbb C} {\mathbb C} [z]$ and regard it as a Lie subalgebra of
$\mathfrak {g} [z] := \mathfrak {g} \otimes _{\mathbb C} {\mathbb C} [z]$ and regard it as a Lie subalgebra of ![]() $\widetilde {\mathfrak {g}}$. We have
$\widetilde {\mathfrak {g}}$. We have ![]() $\mathfrak {I} \subset \mathfrak {g} [z] + {\mathbb C} K + {\mathbb C} d$. The Lie algebra
$\mathfrak {I} \subset \mathfrak {g} [z] + {\mathbb C} K + {\mathbb C} d$. The Lie algebra ![]() $\mathfrak {g} [z]$ is graded, and its grading is the internal grading of
$\mathfrak {g} [z]$ is graded, and its grading is the internal grading of ![]() $\widetilde {\mathfrak {g}}$ given by d.
$\widetilde {\mathfrak {g}}$ given by d.
For each ![]() $\lambda \in P_+$, we set
$\lambda \in P_+$, we set
These are the ![]() $\mathsf q = 1$ cases of the Demazure modules of
$\mathsf q = 1$ cases of the Demazure modules of ![]() $\mathbb {X} ( \lambda )$, as well as the generalised global Weyl modules in the sense of [Reference Feigin, Makedonskyi and Orr28]. We set
$\mathbb {X} ( \lambda )$, as well as the generalised global Weyl modules in the sense of [Reference Feigin, Makedonskyi and Orr28]. We set ![]() $\mathbb {W} ( \lambda ) := \mathbb {W}_{w_0} ( \lambda )$. By construction, both
$\mathbb {W} ( \lambda ) := \mathbb {W}_{w_0} ( \lambda )$. By construction, both ![]() $\mathbb {X} ( \lambda )$ and
$\mathbb {X} ( \lambda )$ and ![]() $\mathbb {W} _w ( \lambda )$ are semisimple as
$\mathbb {W} _w ( \lambda )$ are semisimple as ![]() $( H \times \mathbb {G}_m )$-modules, where
$( H \times \mathbb {G}_m )$-modules, where ![]() $\mathbb {G}_m$ acts on z by
$\mathbb {G}_m$ acts on z by ![]() $a : z^m \mapsto a^{m} z^m$ (
$a : z^m \mapsto a^{m} z^m$ (![]() $m \in \mathbb {Z}$).
$m \in \mathbb {Z}$).
Theorem 2.2 [Reference Lenart, Naito, Sagaki, Schilling and Shimozono62]; compare [Reference Kato46]
For each ![]() $\lambda \in P_+$, the
$\lambda \in P_+$, the ![]() $\mathfrak {I}$-action on
$\mathfrak {I}$-action on ![]() $\mathbb {W} ( \lambda )$ prolongs to
$\mathbb {W} ( \lambda )$ prolongs to ![]() $\mathfrak {g} [z]$ and is isomorphic to the global Weyl module of
$\mathfrak {g} [z]$ and is isomorphic to the global Weyl module of ![]() $\mathfrak {g} [z]$ in the sense of Chari and Pressley [Reference Chari and Pressley19]. Moreover,
$\mathfrak {g} [z]$ in the sense of Chari and Pressley [Reference Chari and Pressley19]. Moreover, ![]() $\mathbb {W} ( \lambda )$ is a projective module in the category of
$\mathbb {W} ( \lambda )$ is a projective module in the category of ![]() $\mathfrak {g}[z]$-modules whose restriction to
$\mathfrak {g}[z]$-modules whose restriction to ![]() $\mathfrak {g}$ is a direct sum of modules in
$\mathfrak {g}$ is a direct sum of modules in ![]() $\{ V ( \mu )\}_{\mu \le \lambda }$.
$\{ V ( \mu )\}_{\mu \le \lambda }$.
Theorem 2.3 [Reference Kato46]
Set ![]() $\lambda , \mu \in P_+$ and
$\lambda , \mu \in P_+$ and ![]() $w \in W$. We have a unique
$w \in W$. We have a unique ![]() $($up to scalar
$($up to scalar![]() $)$ injective degree
$)$ injective degree ![]() $0\; \mathfrak {I}$-module map
$0\; \mathfrak {I}$-module map
Proof Sketch of proof.
For each ![]() $\lambda , \mu \in P_+$, the projectivity of
$\lambda , \mu \in P_+$, the projectivity of ![]() $\mathbb {W} ( \lambda + \mu )$ in the sense of Theorem 2.2 yields a unique graded
$\mathbb {W} ( \lambda + \mu )$ in the sense of Theorem 2.2 yields a unique graded ![]() $\mathfrak {g} [z]$-module map
$\mathfrak {g} [z]$-module map
of degree ![]() $0$. This map is injective by examining the specialisations to local Weyl modules (for their definitions, see [Reference Kato46, Theorem 1.4] or Lemma 3.20 and Remark 3.21). Examining the
$0$. This map is injective by examining the specialisations to local Weyl modules (for their definitions, see [Reference Kato46, Theorem 1.4] or Lemma 3.20 and Remark 3.21). Examining the ![]() $\mathfrak {I}$-cyclic vectors, it uniquely restricts to a map
$\mathfrak {I}$-cyclic vectors, it uniquely restricts to a map
up to scalar. Because the ambient map is injective, this map must be also.
2.3 Semi-infinite flag manifolds
We work over ![]() ${\mathbb C}$ as in the previous subsection. Material in this section is re-proved in the setting of characteristic
${\mathbb C}$ as in the previous subsection. Material in this section is re-proved in the setting of characteristic ![]() $\neq 2$ in Sections 3.4 and 4.2 (compare Section 4.3). We define the semi-infinite flag manifold as the reduced ind-scheme such that both of the following are true:
$\neq 2$ in Sections 3.4 and 4.2 (compare Section 4.3). We define the semi-infinite flag manifold as the reduced ind-scheme such that both of the following are true:
• We have a closed embedding
 $$ \begin{align*}\mathbf{Q}_G^{\mathrm{rat}} \subset \prod_{i \in \mathtt I} \mathbb{P} ( V ( \varpi_i ) \otimes {\mathbb C} (\!(z)\!) ).\end{align*} $$
$$ \begin{align*}\mathbf{Q}_G^{\mathrm{rat}} \subset \prod_{i \in \mathtt I} \mathbb{P} ( V ( \varpi_i ) \otimes {\mathbb C} (\!(z)\!) ).\end{align*} $$• We have an equality
 $\mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb C} ) = G (\!(z)\!) / \left ( H ( {\mathbb C} ) \cdot N (\!(z)\!) \right )$.
$\mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb C} ) = G (\!(z)\!) / \left ( H ( {\mathbb C} ) \cdot N (\!(z)\!) \right )$.
This is a pure ind-scheme of ind-infinite type [Reference Kato, Naito and Sagaki51]. Note that the group ![]() $Q^{\vee } \subset H (\!(z)\!) / H ( {\mathbb C} )$ acts on
$Q^{\vee } \subset H (\!(z)\!) / H ( {\mathbb C} )$ acts on ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ from the right. The ind-scheme
$\mathbf {Q}_G^{\mathrm {rat}}$ from the right. The ind-scheme ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ is equipped with a
$\mathbf {Q}_G^{\mathrm {rat}}$ is equipped with a ![]() $G (\!(z)\!)$-equivariant line bundle
$G (\!(z)\!)$-equivariant line bundle  ${\mathcal O} _{\mathbf {Q}_G^{\mathrm {rat}}} ( \lambda )$ for each
${\mathcal O} _{\mathbf {Q}_G^{\mathrm {rat}}} ( \lambda )$ for each ![]() $\lambda \in P$. Here we normalised so that
$\lambda \in P$. Here we normalised so that  $\Gamma \left ( \mathbf {Q}_G^{\mathrm {rat}}, {\mathcal O}_{\mathbf {Q}_G^{\mathrm {rat}}} ( \lambda ) \right )$ is
$\Gamma \left ( \mathbf {Q}_G^{\mathrm {rat}}, {\mathcal O}_{\mathbf {Q}_G^{\mathrm {rat}}} ( \lambda ) \right )$ is ![]() $B^- (\!(z)\!)$-cocyclic to an H-weight vector with its H-weight
$B^- (\!(z)\!)$-cocyclic to an H-weight vector with its H-weight ![]() $- \lambda $. We warn that this convention is twisted by
$- \lambda $. We warn that this convention is twisted by ![]() $-w_0$ from that of [Reference Kato47], and complies with [Reference Kato, Naito and Sagaki51].
$-w_0$ from that of [Reference Kato47], and complies with [Reference Kato, Naito and Sagaki51].
Theorem 2.4 [Reference Finkelberg and Mirković29, Reference Feigin, Finkelberg, Kuznetsov and Mirković23, Reference Kato, Naito and Sagaki51, Reference Lusztig64]
We have an ![]() $\mathbf {I}$-orbit decomposition
$\mathbf {I}$-orbit decomposition
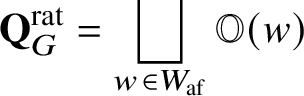 $$ \begin{align*}\mathbf{Q}_G^{\mathrm{rat}} = \bigsqcup_{w \in W_{\mathrm{af}}} \mathbb{O} ( w )\end{align*} $$
$$ \begin{align*}\mathbf{Q}_G^{\mathrm{rat}} = \bigsqcup_{w \in W_{\mathrm{af}}} \mathbb{O} ( w )\end{align*} $$with the following properties:
1. Each
 $\mathbb O ( w )$ is isomorphic to
$\mathbb O ( w )$ is isomorphic to  ${\mathbb A}^{\infty }$ and has a unique
${\mathbb A}^{\infty }$ and has a unique  $(H \times \mathbb {G}_m)$-fixed point.
$(H \times \mathbb {G}_m)$-fixed point.2. The right action of
 $\gamma \in Q^{\vee }$ on
$\gamma \in Q^{\vee }$ on  $\mathbf {Q}_G^{\mathrm {rat}}$ yields the translation
$\mathbf {Q}_G^{\mathrm {rat}}$ yields the translation  $\mathbb O ( w ) \mapsto \mathbb O ( w t_{\gamma })$.
$\mathbb O ( w ) \mapsto \mathbb O ( w t_{\gamma })$.3. We have
 $\mathbb O ( w ) \subset \overline {\mathbb O ( v )}$ if and only if
$\mathbb O ( w ) \subset \overline {\mathbb O ( v )}$ if and only if  $w \le _{\frac {\infty }{2}} v$.
$w \le _{\frac {\infty }{2}} v$.4. The relative dimension of
 $\mathbb {O} \left ( u t_{\beta } \right )$ (
$\mathbb {O} \left ( u t_{\beta } \right )$ ( $u \in W, \beta \in Q^{\vee }$) and
$u \in W, \beta \in Q^{\vee }$) and  $\mathbb {O} ( e )$, counted as the difference of the cardinality of the maximal chain of intermediate
$\mathbb {O} ( e )$, counted as the difference of the cardinality of the maximal chain of intermediate  $\mathbf {I}$-orbits to a common smaller
$\mathbf {I}$-orbits to a common smaller  $\mathbf {I}$-orbit, is
$\mathbf {I}$-orbit, is  $\ell ^{\frac {\infty }{2}} \left ( u t_{\beta } \right )$.
$\ell ^{\frac {\infty }{2}} \left ( u t_{\beta } \right )$.
For each ![]() $w \in W_{\mathrm {af}}$, let
$w \in W_{\mathrm {af}}$, let ![]() $\mathbf {Q}_G ( w )$ denote the closure of
$\mathbf {Q}_G ( w )$ denote the closure of ![]() $\mathbb {O} ( w )$. We refer to
$\mathbb {O} ( w )$. We refer to ![]() $\mathbf {Q}_G ( w )$ as a Schubert variety of
$\mathbf {Q}_G ( w )$ as a Schubert variety of ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ (corresponding to
$\mathbf {Q}_G^{\mathrm {rat}}$ (corresponding to ![]() $w \in W_{\mathrm {af}}$).
$w \in W_{\mathrm {af}}$).
Let  $S = \bigoplus _{\lambda \in P_{\mathtt J,+}} S ( \lambda )$ be a
$S = \bigoplus _{\lambda \in P_{\mathtt J,+}} S ( \lambda )$ be a ![]() $P_{\mathtt J,+}$-graded commutative ring such that
$P_{\mathtt J,+}$-graded commutative ring such that ![]() $S ( 0 ) = A$ is a principal ideal domain and S is torsion-free over A and generated by
$S ( 0 ) = A$ is a principal ideal domain and S is torsion-free over A and generated by  $\bigoplus _{i \in \mathtt I \setminus \mathtt J} S ( \varpi _i )$. We define
$\bigoplus _{i \in \mathtt I \setminus \mathtt J} S ( \varpi _i )$. We define
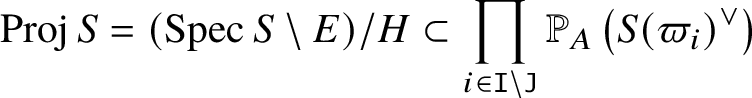 $$ \begin{align} \mathrm{Proj}\, S = ( \mbox{Spec}\, S \setminus E ) / H \subset \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_A \left( S ( \varpi_i )^{\vee} \right) \end{align} $$
$$ \begin{align} \mathrm{Proj}\, S = ( \mbox{Spec}\, S \setminus E ) / H \subset \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_A \left( S ( \varpi_i )^{\vee} \right) \end{align} $$as the ![]() $P_{\mathtt J,+}$-graded proj over
$P_{\mathtt J,+}$-graded proj over ![]() $\mbox {Spec}\, A$, where E is the locus where all of
$\mbox {Spec}\, A$, where E is the locus where all of ![]() $S ( \varpi _i )$ vanishes for some
$S ( \varpi _i )$ vanishes for some ![]() $i \in \mathtt I \setminus \mathtt J$ (the irrelevant locus).
$i \in \mathtt I \setminus \mathtt J$ (the irrelevant locus).
Theorem 2.5 [Reference Kato, Naito and Sagaki51]
For each ![]() $w \in W_{\mathrm {af}}$, we have
$w \in W_{\mathrm {af}}$, we have
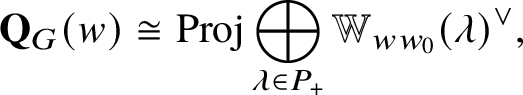 $$ \begin{align*}\mathbf{Q}_G ( w ) \cong \mathrm{Proj} \bigoplus _{\lambda \in P_+} \mathbb{W} _{ww_0} ( \lambda )^{\vee},\end{align*} $$
$$ \begin{align*}\mathbf{Q}_G ( w ) \cong \mathrm{Proj} \bigoplus _{\lambda \in P_+} \mathbb{W} _{ww_0} ( \lambda )^{\vee},\end{align*} $$where the multiplication of the ring ![]() $\bigoplus _\lambda \mathbb {W} _{ww_0} ( \lambda )^{\vee }$ is given by Theorem 2.3.
$\bigoplus _\lambda \mathbb {W} _{ww_0} ( \lambda )^{\vee }$ is given by Theorem 2.3.
2.4 Quasi-map spaces and Zastava spaces
We work over ![]() ${\mathbb C}$ as in the previous subsection. Here we recall basics of quasi-map spaces from [Reference Finkelberg and Mirković29, Reference Feigin, Finkelberg, Kuznetsov and Mirković23].
${\mathbb C}$ as in the previous subsection. Here we recall basics of quasi-map spaces from [Reference Finkelberg and Mirković29, Reference Feigin, Finkelberg, Kuznetsov and Mirković23].
We have W-equivariant isomorphisms ![]() $H^2 ( \mathscr {B}, \mathbb {Z} ) \cong P$ and
$H^2 ( \mathscr {B}, \mathbb {Z} ) \cong P$ and ![]() $H_2 ( \mathscr {B}, \mathbb {Z} ) \cong Q ^{\vee }$. This identifies the (integral points of the) nef cone of
$H_2 ( \mathscr {B}, \mathbb {Z} ) \cong Q ^{\vee }$. This identifies the (integral points of the) nef cone of ![]() $\mathscr {B}$ with
$\mathscr {B}$ with ![]() $P_+ \subset P$ and the effective cone of
$P_+ \subset P$ and the effective cone of ![]() $\mathscr {B}$ with
$\mathscr {B}$ with ![]() $Q_+^{\vee }$. A quasi-map
$Q_+^{\vee }$. A quasi-map ![]() $( f, D )$ is a map
$( f, D )$ is a map ![]() $f : \mathbb {P} ^1 \rightarrow \mathscr {B}$ together with a
$f : \mathbb {P} ^1 \rightarrow \mathscr {B}$ together with a ![]() $\Pi ^{\vee }$-coloured effective divisor
$\Pi ^{\vee }$-coloured effective divisor
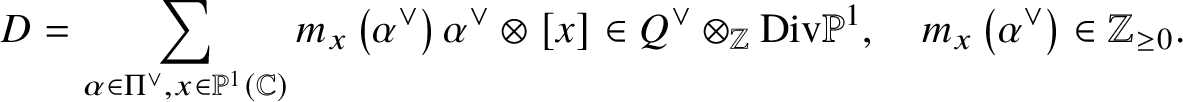 $$ \begin{align*}D = \sum_{\alpha \in \Pi^{\vee}, x \in \mathbb{P}^1 ({\mathbb C})} m_x \left(\alpha^{\vee}\right) \alpha^{\vee} \otimes [x] \in Q^{\vee} \otimes_{\mathbb{Z}} \mathrm{Div} \mathbb{P}^1, \quad m_x \left(\alpha^{\vee}\right) \in \mathbb{Z}_{\ge 0}.\end{align*} $$
$$ \begin{align*}D = \sum_{\alpha \in \Pi^{\vee}, x \in \mathbb{P}^1 ({\mathbb C})} m_x \left(\alpha^{\vee}\right) \alpha^{\vee} \otimes [x] \in Q^{\vee} \otimes_{\mathbb{Z}} \mathrm{Div} \mathbb{P}^1, \quad m_x \left(\alpha^{\vee}\right) \in \mathbb{Z}_{\ge 0}.\end{align*} $$For ![]() $i \in \mathtt I$, we set
$i \in \mathtt I$, we set ![]() $D_i := \left \langle D, \varpi _i \right \rangle \in \mathrm {Div} \, \mathbb {P}^1$. We call D the defect of the quasi-map
$D_i := \left \langle D, \varpi _i \right \rangle \in \mathrm {Div} \, \mathbb {P}^1$. We call D the defect of the quasi-map ![]() $(f, D)$. Here we define the (total) degree of the defect by
$(f, D)$. Here we define the (total) degree of the defect by
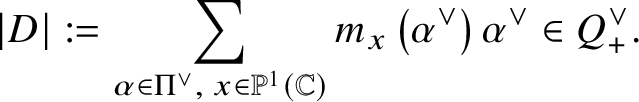 $$ \begin{align*}\lvert D\rvert := \sum_{\alpha \in \Pi^{\vee}, \; x \in \mathbb{P}^1 ({\mathbb C})} m_x \left(\alpha^{\vee}\right) \alpha^{\vee} \in Q_+^{\vee}.\end{align*} $$
$$ \begin{align*}\lvert D\rvert := \sum_{\alpha \in \Pi^{\vee}, \; x \in \mathbb{P}^1 ({\mathbb C})} m_x \left(\alpha^{\vee}\right) \alpha^{\vee} \in Q_+^{\vee}.\end{align*} $$ For each ![]() $\beta \in Q_+^{\vee }$, we set
$\beta \in Q_+^{\vee }$, we set
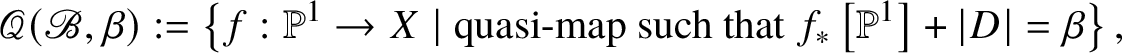 $$ \begin{align*}\mathscr{Q} ( \mathscr{B}, \beta ) : = \left\{ f : \mathbb{P} ^1 \rightarrow X \mid \text{quasi-map such that } f _* \left[ \mathbb{P}^1 \right] + \lvert D \rvert = \beta \right\},\end{align*} $$
$$ \begin{align*}\mathscr{Q} ( \mathscr{B}, \beta ) : = \left\{ f : \mathbb{P} ^1 \rightarrow X \mid \text{quasi-map such that } f _* \left[ \mathbb{P}^1 \right] + \lvert D \rvert = \beta \right\},\end{align*} $$where  $f_* \left [\mathbb {P}^1\right ]$ is the class of the image of
$f_* \left [\mathbb {P}^1\right ]$ is the class of the image of ![]() $\mathbb {P}^1$ multiplied by the degree of
$\mathbb {P}^1$ multiplied by the degree of ![]() $\mathbb {P}^1 \to \mathrm {Im} f$. We denote
$\mathbb {P}^1 \to \mathrm {Im} f$. We denote ![]() $\mathscr {Q} ( \mathscr {B}, \beta )$ by
$\mathscr {Q} ( \mathscr {B}, \beta )$ by ![]() $\mathscr {Q} ( \beta )$ when there is no danger of confusion.
$\mathscr {Q} ( \beta )$ when there is no danger of confusion.
Definition 2.6. Drinfeld–Plücker data
Consider a collection  $\mathcal L = \left \{\left ( \psi _{\lambda }, \mathcal L^{\lambda } \right ) \right \}_{\lambda \in P_+}$ of inclusions
$\mathcal L = \left \{\left ( \psi _{\lambda }, \mathcal L^{\lambda } \right ) \right \}_{\lambda \in P_+}$ of inclusions ![]() $\psi _{\lambda } : \mathcal L ^{\lambda } \hookrightarrow V ( \lambda ) \otimes _{{\mathbb C}} \mathcal O _{\mathbb {P}^1}$ of line bundles
$\psi _{\lambda } : \mathcal L ^{\lambda } \hookrightarrow V ( \lambda ) \otimes _{{\mathbb C}} \mathcal O _{\mathbb {P}^1}$ of line bundles ![]() $\mathcal L ^{\lambda }$ over
$\mathcal L ^{\lambda }$ over ![]() $\mathbb {P}^1$. The data
$\mathbb {P}^1$. The data ![]() $\mathcal L$ are called Drinfeld–Plücker data (DP-data) if the canonical inclusion of G-modules
$\mathcal L$ are called Drinfeld–Plücker data (DP-data) if the canonical inclusion of G-modules
induces an isomorphism
 $$ \begin{align*}\eta_{\lambda, \mu} \otimes \mathrm{id} : \psi_{\lambda + \mu} \left( \mathcal L ^{\lambda + \mu} \right) \stackrel{\cong}{\longrightarrow} \psi _{\lambda} \left( \mathcal L^{\lambda} \right) \otimes_{{\mathcal O}_{\mathbb{P}^1}} \psi_{\mu} \left( \mathcal L^{\mu} \right)\end{align*} $$
$$ \begin{align*}\eta_{\lambda, \mu} \otimes \mathrm{id} : \psi_{\lambda + \mu} \left( \mathcal L ^{\lambda + \mu} \right) \stackrel{\cong}{\longrightarrow} \psi _{\lambda} \left( \mathcal L^{\lambda} \right) \otimes_{{\mathcal O}_{\mathbb{P}^1}} \psi_{\mu} \left( \mathcal L^{\mu} \right)\end{align*} $$for every ![]() $\lambda , \mu \in P_+$.
$\lambda , \mu \in P_+$.
Theorem 2.7 Drinfeld; see [Reference Finkelberg and Mirković29]
The variety ![]() $\mathscr {Q} ( \beta )$ is isomorphic to the variety formed by isomorphism classes of the DP-data
$\mathscr {Q} ( \beta )$ is isomorphic to the variety formed by isomorphism classes of the DP-data  $\mathcal L = \left \{\left ( \psi _{\lambda }, \mathcal L^{\lambda } \right ) \right \}_{\lambda \in P_+}$ such that
$\mathcal L = \left \{\left ( \psi _{\lambda }, \mathcal L^{\lambda } \right ) \right \}_{\lambda \in P_+}$ such that ![]() $\deg \mathcal L ^{\lambda } = \left \langle w_0 \beta , \lambda \right \rangle $. In addition,
$\deg \mathcal L ^{\lambda } = \left \langle w_0 \beta , \lambda \right \rangle $. In addition, ![]() $\mathscr {Q} ( \beta )$ is an irreducible variety of dimension
$\mathscr {Q} ( \beta )$ is an irreducible variety of dimension ![]() $2 \left \langle \rho , \beta \right \rangle + \ell ( w_0 )$.
$2 \left \langle \rho , \beta \right \rangle + \ell ( w_0 )$.
For each ![]() $w \in W$, let
$w \in W$, let ![]() $\mathscr {Z} ( \beta , w ) \subset \mathscr {Q} ( \beta )$ be the locally closed subset consisting of quasi-maps that are defined at
$\mathscr {Z} ( \beta , w ) \subset \mathscr {Q} ( \beta )$ be the locally closed subset consisting of quasi-maps that are defined at ![]() $z = 0$, and their values at
$z = 0$, and their values at ![]() $z = 0$ are contained in
$z = 0$ are contained in ![]() $\mathscr {B} ( w ) \subset \mathscr {B}$. We set
$\mathscr {B} ( w ) \subset \mathscr {B}$. We set ![]() $\mathscr {Q} ( \beta , w ) := \overline {\mathscr {Z} ( \beta , w )}$. (Hence, we have
$\mathscr {Q} ( \beta , w ) := \overline {\mathscr {Z} ( \beta , w )}$. (Hence, we have ![]() $\mathscr {Q} ( \beta ) = \mathscr {Q} ( \beta , e)$.)
$\mathscr {Q} ( \beta ) = \mathscr {Q} ( \beta , e)$.)
Theorem 2.8 [Reference Finkelberg and Mirković29]
Let ![]() ${\mathbb K}$ be an algebraically closed field (not necessarily of characteristic
${\mathbb K}$ be an algebraically closed field (not necessarily of characteristic ![]() $0$), and let
$0$), and let ![]() $\mathscr {Q} ( \beta )_{{\mathbb K}}$ and
$\mathscr {Q} ( \beta )_{{\mathbb K}}$ and ![]() $\mathscr {Z} ( \beta , w_0 )_{{\mathbb K}}$ be the spaces obtained by replacing the base field
$\mathscr {Z} ( \beta , w_0 )_{{\mathbb K}}$ be the spaces obtained by replacing the base field ![]() ${\mathbb C}$ with
${\mathbb C}$ with ![]() ${\mathbb K}$ in Definition 2.6. For each
${\mathbb K}$ in Definition 2.6. For each ![]() $\beta \in Q^{\vee }_+$, the space
$\beta \in Q^{\vee }_+$, the space ![]() $\mathscr {Z} ( \beta , w_0 )_{{\mathbb K}}$ is an irreducible affine scheme equipped with an action of
$\mathscr {Z} ( \beta , w_0 )_{{\mathbb K}}$ is an irreducible affine scheme equipped with an action of ![]() $( B \times \mathbb {G}_m )$ over
$( B \times \mathbb {G}_m )$ over ![]() ${\mathbb K}$. In addition, this action has a unique fixed point.
${\mathbb K}$. In addition, this action has a unique fixed point.
Proof Remarks on the proof.
Theorem 2.8 is proved in [Reference Finkelberg and Mirković29] for ![]() ${\mathbb K} = {\mathbb C}$ using [Reference Mirković and Vilonen70], and in the current setting in [Reference Braverman, Finkelberg, Gaitsgory and Mirković12] using [Reference Braverman and Gaitsgory13]. One can also replace the usage of [Reference Mirković and Vilonen70] with [Reference Zhu81, Corollary 5.3.8] along the lines of [Reference Finkelberg and Mirković29].
${\mathbb K} = {\mathbb C}$ using [Reference Mirković and Vilonen70], and in the current setting in [Reference Braverman, Finkelberg, Gaitsgory and Mirković12] using [Reference Braverman and Gaitsgory13]. One can also replace the usage of [Reference Mirković and Vilonen70] with [Reference Zhu81, Corollary 5.3.8] along the lines of [Reference Finkelberg and Mirković29].
For each ![]() $\lambda \in P$ and
$\lambda \in P$ and ![]() $w \in W$, we have a G-equivariant line bundle
$w \in W$, we have a G-equivariant line bundle ![]() ${\mathcal O} _{\mathscr {Q} \left ( \beta , w \right )} ( \lambda )$ (and its pro-object
${\mathcal O} _{\mathscr {Q} \left ( \beta , w \right )} ( \lambda )$ (and its pro-object ![]() ${\mathcal O} _{\mathscr {Q}} ( \lambda )$) obtained by the (tensor products of the) pullbacks
${\mathcal O} _{\mathscr {Q}} ( \lambda )$) obtained by the (tensor products of the) pullbacks ![]() ${\mathcal O} _{\mathscr {Q} \left ( \beta , w \right )}( \varpi _i )$ of the ith
${\mathcal O} _{\mathscr {Q} \left ( \beta , w \right )}( \varpi _i )$ of the ith ![]() ${\mathcal O} ( 1 )$ via the embedding
${\mathcal O} ( 1 )$ via the embedding
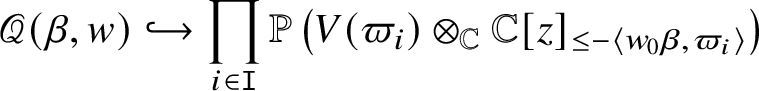 $$ \begin{align} \mathscr{Q} ( \beta, w ) \hookrightarrow \prod_{i \in \mathtt I} \mathbb{P} \left( V ( \varpi_i ) \otimes_{{\mathbb C}} {\mathbb C} [z] _{\le - \left\langle w_0 \beta, \varpi_i \right\rangle} \right) \end{align} $$
$$ \begin{align} \mathscr{Q} ( \beta, w ) \hookrightarrow \prod_{i \in \mathtt I} \mathbb{P} \left( V ( \varpi_i ) \otimes_{{\mathbb C}} {\mathbb C} [z] _{\le - \left\langle w_0 \beta, \varpi_i \right\rangle} \right) \end{align} $$for each ![]() $\beta \in Q_+^{\vee }$.
$\beta \in Q_+^{\vee }$.
We have embeddings ![]() $\mathscr {B} \subset \mathscr {Q} ( \beta ) \subset \mathbf {Q}_G ( e )$ such that the line bundles
$\mathscr {B} \subset \mathscr {Q} ( \beta ) \subset \mathbf {Q}_G ( e )$ such that the line bundles ![]() ${\mathcal O} ( \lambda )$ (
${\mathcal O} ( \lambda )$ (![]() $\lambda \in P$) correspond to each other by restrictions ([Reference Braverman and Finkelberg10, Reference Kato46, Reference Kato, Naito and Sagaki51]).
$\lambda \in P$) correspond to each other by restrictions ([Reference Braverman and Finkelberg10, Reference Kato46, Reference Kato, Naito and Sagaki51]).
3 Semi-infinite flag manifolds over  $\mathbb {Z} \left [\frac {1}{2}\right ]$
$\mathbb {Z} \left [\frac {1}{2}\right ]$
We keep the settings of the previous section. In this section, we sometimes work over a (commutative) ring or a non-algebraically closed field. For a ring S or a scheme ![]() $\mathfrak {X}$, we may write
$\mathfrak {X}$, we may write ![]() $S_{A}$ or
$S_{A}$ or ![]() $\mathfrak {X}_{A}$ if it is defined over A. In addition, we may consider their scalar extensions
$\mathfrak {X}_{A}$ if it is defined over A. In addition, we may consider their scalar extensions ![]() $S_{B} := S_A \otimes _A B$ and
$S_{B} := S_A \otimes _A B$ and ![]() $\mathfrak {X}_{B}$ for a ring map
$\mathfrak {X}_{B}$ for a ring map ![]() $A \to B$.
$A \to B$.
3.1 Frobenius splittings
Let ![]() $\Bbbk $ be a field and p be a prime. We assume
$\Bbbk $ be a field and p be a prime. We assume ![]() $\mathsf {char}\, \Bbbk = p$,
$\mathsf {char}\, \Bbbk = p$, ![]() $\Bbbk \subset {\mathbb K}$ and that the pth power map is invertible on
$\Bbbk \subset {\mathbb K}$ and that the pth power map is invertible on ![]() $\Bbbk $ (e.g.,
$\Bbbk $ (e.g., ![]() $\Bbbk = \mathbb F_p$ or
$\Bbbk = \mathbb F_p$ or ![]() $\overline {\mathbb F}_p$) throughout this subsection.
$\overline {\mathbb F}_p$) throughout this subsection.
We follow the generality on Frobenius splittings in [Reference Brion and Kumar14], which considers separated schemes of finite type. We sometimes use the assertions from [Reference Brion and Kumar14] without the finite-type assumption when the assertion is independent of that; typical disguises are properness, finite generation and the Serre vanishing theorem.
Definition 3.1. Frobenius splitting of a ring
Let R be a commutative ring over ![]() $\Bbbk $, and let
$\Bbbk $, and let ![]() $R^{(1)}$ denote the set R equipped with the map
$R^{(1)}$ denote the set R equipped with the map
This equips ![]() $R^{(1)}$ with an R-module structure over
$R^{(1)}$ with an R-module structure over ![]() $\Bbbk $ (the
$\Bbbk $ (the ![]() $\Bbbk $-vector space structure on
$\Bbbk $-vector space structure on ![]() $R^{(1)}$ is also twisted by the pth power operation), together with a map
$R^{(1)}$ is also twisted by the pth power operation), together with a map ![]() $\imath : R. 1 \rightarrow R^{(1)}$. An R-module map
$\imath : R. 1 \rightarrow R^{(1)}$. An R-module map ![]() $\phi : R^{(1)} \to R$ is said to be a Frobenius splitting if
$\phi : R^{(1)} \to R$ is said to be a Frobenius splitting if ![]() $\phi \circ \imath $ is an identity.
$\phi \circ \imath $ is an identity.
Note that ![]() $\imath $ in Definition 3.1 must be an inclusion if we have a Frobenius splitting
$\imath $ in Definition 3.1 must be an inclusion if we have a Frobenius splitting ![]() $\phi $. Since the pth power map in
$\phi $. Since the pth power map in ![]() $\Bbbk $ is invertible, we can twist the (scalar multiplication part of the)
$\Bbbk $ is invertible, we can twist the (scalar multiplication part of the) ![]() $\Bbbk $-vector space structure of R (
$\Bbbk $-vector space structure of R (![]() $\cong R^{(1)}$ as sets) to make
$\cong R^{(1)}$ as sets) to make ![]() $\imath $ into a
$\imath $ into a ![]() $\Bbbk $-linear map without making it into an R-linear map (when
$\Bbbk $-linear map without making it into an R-linear map (when ![]() $R \neq \Bbbk $).
$R \neq \Bbbk $).
Definition 3.2. Frobenius splitting of a scheme
Let ![]() $\mathfrak X$ be a separated scheme defined over
$\mathfrak X$ be a separated scheme defined over ![]() $\Bbbk $. Let
$\Bbbk $. Let ![]() $\mathsf {Fr}$ be the (relative) Frobenius endomorphism of
$\mathsf {Fr}$ be the (relative) Frobenius endomorphism of ![]() $\mathfrak X$ (which induces a
$\mathfrak X$ (which induces a ![]() $\Bbbk $-linear endomorphism). We have a natural inclusion
$\Bbbk $-linear endomorphism). We have a natural inclusion ![]() $\imath : {\mathcal O}_{\mathfrak X} \rightarrow \mathsf {Fr}_{*} {\mathcal O}_{\mathfrak X}$. A Frobenius splitting of
$\imath : {\mathcal O}_{\mathfrak X} \rightarrow \mathsf {Fr}_{*} {\mathcal O}_{\mathfrak X}$. A Frobenius splitting of ![]() $\mathfrak X$ is a
$\mathfrak X$ is a ![]() ${\mathcal O}_{\mathfrak X}$-linear morphism
${\mathcal O}_{\mathfrak X}$-linear morphism ![]() $\phi : \mathsf {Fr}_{*} {\mathcal O}_{\mathfrak X} \rightarrow {\mathcal O}_{\mathfrak X}$ such that the composition
$\phi : \mathsf {Fr}_{*} {\mathcal O}_{\mathfrak X} \rightarrow {\mathcal O}_{\mathfrak X}$ such that the composition ![]() $\phi \circ \imath $ is the identity.
$\phi \circ \imath $ is the identity.
Definition 3.3. Compatible splitting
Let ![]() $\mathfrak {Y} \subset \mathfrak {X}$ be a closed immersion of separated schemes defined over
$\mathfrak {Y} \subset \mathfrak {X}$ be a closed immersion of separated schemes defined over ![]() $\Bbbk $. A Frobenius splitting
$\Bbbk $. A Frobenius splitting ![]() $\phi $ of
$\phi $ of ![]() $\mathfrak {X}$ is said to be compatible with
$\mathfrak {X}$ is said to be compatible with ![]() $\mathfrak {Y}$ if
$\mathfrak {Y}$ if ![]() $\phi \left (\mathsf {Fr}_* \mathcal I _{\mathfrak {Y}} \right ) \subset \mathcal I_{\mathfrak {Y}}$, where
$\phi \left (\mathsf {Fr}_* \mathcal I _{\mathfrak {Y}} \right ) \subset \mathcal I_{\mathfrak {Y}}$, where ![]() $\mathcal I _{\mathfrak {Y}} := \ker \left ( {\mathcal O}_{\mathfrak {X}} \to {\mathcal O}_{\mathfrak {Y}} \right )$. Compatible Frobenius splitting of a pair of a commutative ring and its quotient ring is defined through their spectra.
$\mathcal I _{\mathfrak {Y}} := \ker \left ( {\mathcal O}_{\mathfrak {X}} \to {\mathcal O}_{\mathfrak {Y}} \right )$. Compatible Frobenius splitting of a pair of a commutative ring and its quotient ring is defined through their spectra.
Remark 3.4. A Frobenius splitting of ![]() $\mathfrak {X}$ compatible with
$\mathfrak {X}$ compatible with ![]() $\mathfrak {Y}$ induces a Frobenius splitting of
$\mathfrak {Y}$ induces a Frobenius splitting of ![]() $\mathfrak {Y}$ (see, e.g., [Reference Brion and Kumar14, Remark 1.1.4 (ii)]).
$\mathfrak {Y}$ (see, e.g., [Reference Brion and Kumar14, Remark 1.1.4 (ii)]).
Theorem 3.5 [Reference Brion and Kumar14]
Let ![]() $\mathfrak X$ be a separated scheme of finite type over
$\mathfrak X$ be a separated scheme of finite type over ![]() $\Bbbk $ with semiample line bundles
$\Bbbk $ with semiample line bundles ![]() $\mathcal L_1,\ldots , \mathcal L_r$. If
$\mathcal L_1,\ldots , \mathcal L_r$. If ![]() $\mathfrak X$ admits a Frobenius splitting, then the multisection ring
$\mathfrak X$ admits a Frobenius splitting, then the multisection ring
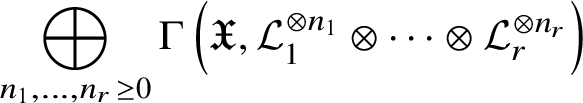 $$ \begin{align*}\bigoplus_{n_1,\ldots,n_r \ge 0} \Gamma \left( \mathfrak X, \mathcal L_1 ^{\otimes n_1} \otimes \cdots \otimes \mathcal L_r ^{\otimes n_r} \right)\end{align*} $$
$$ \begin{align*}\bigoplus_{n_1,\ldots,n_r \ge 0} \Gamma \left( \mathfrak X, \mathcal L_1 ^{\otimes n_1} \otimes \cdots \otimes \mathcal L_r ^{\otimes n_r} \right)\end{align*} $$admits a Frobenius splitting ![]() $\phi $. Moreover, a closed subscheme
$\phi $. Moreover, a closed subscheme ![]() $\mathfrak {Y} \subset \mathfrak {X} = \mathrm {Proj}\, R$ admits a compatible Frobenius splitting if and only if the homogeneous ideal
$\mathfrak {Y} \subset \mathfrak {X} = \mathrm {Proj}\, R$ admits a compatible Frobenius splitting if and only if the homogeneous ideal ![]() $I _{\mathfrak {Y}} \subset R$ that defines
$I _{\mathfrak {Y}} \subset R$ that defines ![]() $\mathfrak {Y}$ satisfies
$\mathfrak {Y}$ satisfies ![]() $\phi \left ( I_{\mathfrak {Y}} \right ) \subset I_{\mathfrak {Y}}$ – that is, the pair
$\phi \left ( I_{\mathfrak {Y}} \right ) \subset I_{\mathfrak {Y}}$ – that is, the pair ![]() $\left (R, R / I _{\mathfrak {Y}}\right )$ admits a compatible Frobenius splitting
$\left (R, R / I _{\mathfrak {Y}}\right )$ admits a compatible Frobenius splitting ![]() $\phi $.
$\phi $. ![]() $\Box $
$\Box $
Definition 3.6. Canonical splitting
Let ![]() $\mathfrak {X}$ be a separated scheme over
$\mathfrak {X}$ be a separated scheme over ![]() $\Bbbk $ equipped with a B-action. A Frobenius splitting
$\Bbbk $ equipped with a B-action. A Frobenius splitting ![]() $\phi $ is said to be B-canonical if it is H-fixed and each
$\phi $ is said to be B-canonical if it is H-fixed and each ![]() $i \in \mathtt I$ yields
$i \in \mathtt I$ yields
 $$ \begin{align} \rho_{\alpha_i} ( z^p ) \phi \left( \rho_{\alpha_i} ( - z ) f \right) = \sum_{j = 0}^{p-1} \frac{z^j}{j!} \phi_{i, j} ( f ), \quad z \in \Bbbk, \end{align} $$
$$ \begin{align} \rho_{\alpha_i} ( z^p ) \phi \left( \rho_{\alpha_i} ( - z ) f \right) = \sum_{j = 0}^{p-1} \frac{z^j}{j!} \phi_{i, j} ( f ), \quad z \in \Bbbk, \end{align} $$where ![]() $\phi _{i, j} \in \mbox {Hom}_{{\mathcal O}_{\mathfrak X}} ( \mathsf {Fr}_{*} {\mathcal O}_{\mathfrak X}, {\mathcal O}_{\mathfrak X} )$. We similarly define the notion of
$\phi _{i, j} \in \mbox {Hom}_{{\mathcal O}_{\mathfrak X}} ( \mathsf {Fr}_{*} {\mathcal O}_{\mathfrak X}, {\mathcal O}_{\mathfrak X} )$. We similarly define the notion of ![]() $B^-$-canonical splitting (resp.,
$B^-$-canonical splitting (resp., ![]() $\mathbf {I}$-canonical splitting and
$\mathbf {I}$-canonical splitting and ![]() $\mathbf {I}^-$-canonical splitting) by using
$\mathbf {I}^-$-canonical splitting) by using  $\left \{ \rho _{-\alpha _i} \right \}_{i \in \mathtt I}$ (resp.,
$\left \{ \rho _{-\alpha _i} \right \}_{i \in \mathtt I}$ (resp.,  $\left \{ \rho _{\alpha _i} \right \}_{i \in \mathtt I_{\mathrm {af}}}$ and
$\left \{ \rho _{\alpha _i} \right \}_{i \in \mathtt I_{\mathrm {af}}}$ and  $\left \{ \rho _{-\alpha _i} \right \}_{i \in \mathtt I_{\mathrm {af}}}$) instead. Canonical splitting of a commutative ring S over
$\left \{ \rho _{-\alpha _i} \right \}_{i \in \mathtt I_{\mathrm {af}}}$) instead. Canonical splitting of a commutative ring S over ![]() $\Bbbk $ is defined through its spectrum.
$\Bbbk $ is defined through its spectrum.
Proposition 3.7. Compare [Reference Brion and Kumar14]
Let ![]() $S = \bigoplus _{m \ge 0} S_m$ be a graded ring with
$S = \bigoplus _{m \ge 0} S_m$ be a graded ring with ![]() $S_0 = \Bbbk $ such that
$S_0 = \Bbbk $ such that
• S is equipped with a degree-preserving
 $\mathbf {I}$-action,
$\mathbf {I}$-action,• each
 $S_m$ is a graded
$S_m$ is a graded  $\Bbbk $-vector space compatible with the multiplication and
$\Bbbk $-vector space compatible with the multiplication and• we have an
 $\mathbf {I}$-canonical Frobenius splitting
$\mathbf {I}$-canonical Frobenius splitting  $\phi : S^{(1)} \to S$.
$\phi : S^{(1)} \to S$.
Then the induced map
 $$ \begin{align*}\phi^{\vee} : S_{m}^{\vee} \longrightarrow S_{pm}^{\vee}, \quad m \in \mathbb{Z}_{\ge 0},\end{align*} $$
$$ \begin{align*}\phi^{\vee} : S_{m}^{\vee} \longrightarrow S_{pm}^{\vee}, \quad m \in \mathbb{Z}_{\ge 0},\end{align*} $$satisfies
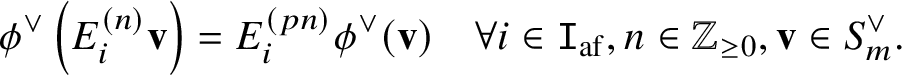 $$ \begin{align*}\phi^{\vee} \left( E_i^{(n)} \mathbf{v} \right) = E_i^{(pn)} \phi^{\vee} ( \mathbf{v} ) \quad \forall i \in \mathtt I_{\mathrm{af}}, n \in \mathbb{Z}_{\ge 0}, \mathbf{v} \in S_m^{\vee}.\end{align*} $$
$$ \begin{align*}\phi^{\vee} \left( E_i^{(n)} \mathbf{v} \right) = E_i^{(pn)} \phi^{\vee} ( \mathbf{v} ) \quad \forall i \in \mathtt I_{\mathrm{af}}, n \in \mathbb{Z}_{\ge 0}, \mathbf{v} \in S_m^{\vee}.\end{align*} $$Similar results hold for the ![]() $\mathbf {I}^-$- and
$\mathbf {I}^-$- and ![]() $B^{\pm }$-actions.
$B^{\pm }$-actions.
Remark 3.8. In our opinion, one merit of Proposition 3.7 over [Reference Brion and Kumar14, Proposition 4.1.8] is that it becomes obvious that a projective variety ![]() $\mathfrak X$ with a B-action has at most one B-canonical splitting whenever the space of global sections of all ample line bundles is (or can be made) B-cocyclic compatible with multiplications (compare [Reference Brion and Kumar14, Theorem 4.1.15] and Corollary 3.35).
$\mathfrak X$ with a B-action has at most one B-canonical splitting whenever the space of global sections of all ample line bundles is (or can be made) B-cocyclic compatible with multiplications (compare [Reference Brion and Kumar14, Theorem 4.1.15] and Corollary 3.35).
Proof Proof of Proposition 3.7.
The condition that ![]() $S_m$ is a graded vector space implies
$S_m$ is a graded vector space implies  $S_m \stackrel {\cong }{\longrightarrow }\left (S_m^{\vee }\right )^{\vee }$ for each
$S_m \stackrel {\cong }{\longrightarrow }\left (S_m^{\vee }\right )^{\vee }$ for each ![]() $m \in \mathbb {Z}_{\ge 0}$. By [Reference Brion and Kumar14, Proposition 4.1.8], each
$m \in \mathbb {Z}_{\ge 0}$. By [Reference Brion and Kumar14, Proposition 4.1.8], each  $\mathbf {w} \in S_{pm} \subset S^{(1)}$ satisfies
$\mathbf {w} \in S_{pm} \subset S^{(1)}$ satisfies  $\phi \left ( E_i^{(pn)} \mathbf {w} \right ) = E_i^{(n)} \phi ( \mathbf {w} )$ for
$\phi \left ( E_i^{(pn)} \mathbf {w} \right ) = E_i^{(n)} \phi ( \mathbf {w} )$ for ![]() $i \in \mathtt I_{\mathrm {af}}$ and
$i \in \mathtt I_{\mathrm {af}}$ and ![]() $n \ge 0$. Using the natural nondegenerate invariant pairing
$n \ge 0$. Using the natural nondegenerate invariant pairing ![]() $\left \langle \bullet , \bullet \right \rangle $ between
$\left \langle \bullet , \bullet \right \rangle $ between ![]() $S_m^{\vee }$ and
$S_m^{\vee }$ and ![]() $S_m$, we compute the leftmost term of
$S_m$, we compute the leftmost term of
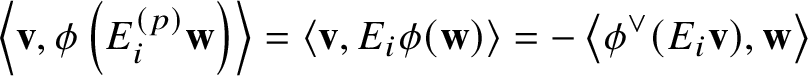 $$ \begin{align*}\left\langle \mathbf{v}, \phi \left( E^{(p)}_i \mathbf{w} \right) \right\rangle = \left\langle \mathbf{v}, E_i \phi ( \mathbf{w} ) \right\rangle = - \left\langle \phi^{\vee} ( E_i \mathbf{v} ), \mathbf{w} \right\rangle\end{align*} $$
$$ \begin{align*}\left\langle \mathbf{v}, \phi \left( E^{(p)}_i \mathbf{w} \right) \right\rangle = \left\langle \mathbf{v}, E_i \phi ( \mathbf{w} ) \right\rangle = - \left\langle \phi^{\vee} ( E_i \mathbf{v} ), \mathbf{w} \right\rangle\end{align*} $$by using the invariance under the corresponding unipotent action, yielding
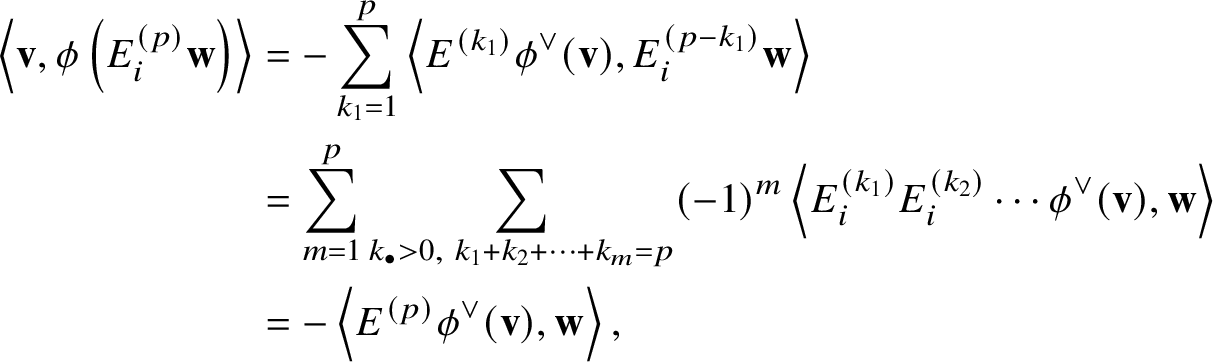 $$ \begin{align*} \left\langle \mathbf{v}, \phi \left( E^{(p)}_i \mathbf{w} \right) \right\rangle & = - \sum_{k_1 = 1}^{p} \left\langle E^{\left(k_1\right)}\phi^{\vee} ( \mathbf{v} ), E^{\left(p-k_1\right)}_i \mathbf{w} \right\rangle\\ & = \sum_{m=1}^p \sum_{k_\bullet> 0, \; k_1 + k_2 +\cdots + k_m = p} (-1)^m \left\langle E^{\left(k_1\right)}_i E^{\left(k_2\right)}_i \cdots \phi^{\vee} ( \mathbf{v} ), \mathbf{w} \right\rangle\\ & = - \left\langle E^{(p)} \phi^{\vee} ( \mathbf{v} ), \mathbf{w} \right\rangle, \end{align*} $$
$$ \begin{align*} \left\langle \mathbf{v}, \phi \left( E^{(p)}_i \mathbf{w} \right) \right\rangle & = - \sum_{k_1 = 1}^{p} \left\langle E^{\left(k_1\right)}\phi^{\vee} ( \mathbf{v} ), E^{\left(p-k_1\right)}_i \mathbf{w} \right\rangle\\ & = \sum_{m=1}^p \sum_{k_\bullet> 0, \; k_1 + k_2 +\cdots + k_m = p} (-1)^m \left\langle E^{\left(k_1\right)}_i E^{\left(k_2\right)}_i \cdots \phi^{\vee} ( \mathbf{v} ), \mathbf{w} \right\rangle\\ & = - \left\langle E^{(p)} \phi^{\vee} ( \mathbf{v} ), \mathbf{w} \right\rangle, \end{align*} $$since we have  $E^{\left (k_1\right )}_i E^{\left (k_2\right )}_i \cdots E^{\left (k_m\right )}_i \in p \mathbb {Z} E^{(p)}_i$ except for
$E^{\left (k_1\right )}_i E^{\left (k_2\right )}_i \cdots E^{\left (k_m\right )}_i \in p \mathbb {Z} E^{(p)}_i$ except for ![]() $k_1 = p$,
$k_1 = p$, ![]() $0 = k_2 = \cdots $. This implies the case when
$0 = k_2 = \cdots $. This implies the case when ![]() $n = 1$.
$n = 1$.
Similarly, we have
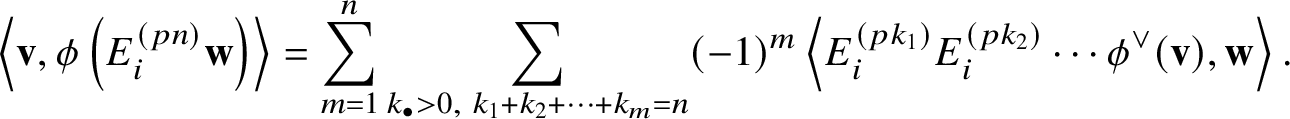 $$ \begin{align*}\left\langle \mathbf{v}, \phi \left( E^{(pn)}_i \mathbf{w} \right) \right\rangle = \sum_{m=1}^n \sum_{k_\bullet> 0, \; k_1 + k_2 +\cdots + k_m = n} (-1)^m \left\langle E^{\left(pk_1\right)}_i E^{\left(pk_2\right)}_i \cdots \phi^{\vee} ( \mathbf{v} ), \mathbf{w} \right\rangle.\end{align*} $$
$$ \begin{align*}\left\langle \mathbf{v}, \phi \left( E^{(pn)}_i \mathbf{w} \right) \right\rangle = \sum_{m=1}^n \sum_{k_\bullet> 0, \; k_1 + k_2 +\cdots + k_m = n} (-1)^m \left\langle E^{\left(pk_1\right)}_i E^{\left(pk_2\right)}_i \cdots \phi^{\vee} ( \mathbf{v} ), \mathbf{w} \right\rangle.\end{align*} $$Compared with
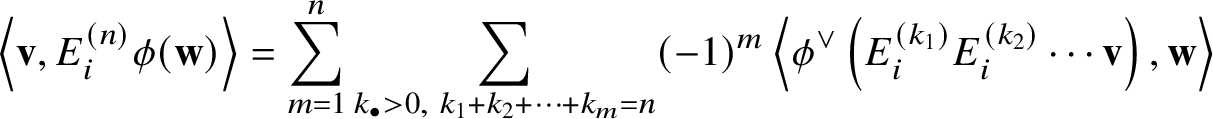 $$ \begin{align*}\left\langle \mathbf{v}, E^{(n)}_i \phi ( \mathbf{w} ) \right\rangle = \sum_{m=1}^n \sum_{k_\bullet> 0, \; k_1 + k_2 +\cdots + k_m = n} (-1)^m \left\langle \phi^{\vee} \left( E^{\left(k_1\right)}_i E^{\left(k_2\right)}_i \cdots\mathbf{v} \right), \mathbf{w} \right\rangle\end{align*} $$
$$ \begin{align*}\left\langle \mathbf{v}, E^{(n)}_i \phi ( \mathbf{w} ) \right\rangle = \sum_{m=1}^n \sum_{k_\bullet> 0, \; k_1 + k_2 +\cdots + k_m = n} (-1)^m \left\langle \phi^{\vee} \left( E^{\left(k_1\right)}_i E^{\left(k_2\right)}_i \cdots\mathbf{v} \right), \mathbf{w} \right\rangle\end{align*} $$using induction on n, we conclude the result.
3.2 Representations of affine Lie algebras over  $\mathbb {Z}$
$\mathbb {Z}$
In this section, we systematically use global basis theory [Reference Kashiwara41, Reference Kashiwara43, Reference Kashiwara44, Reference Kashiwara45, Reference Lusztig65, Reference Grojnowski and Lusztig35] by specialising the quantum parameter ![]() $\mathsf q$ to
$\mathsf q$ to ![]() $1$. Therefore, we might refer to these references without an explicit declaration that we specialise
$1$. Therefore, we might refer to these references without an explicit declaration that we specialise ![]() $\mathsf q$.
$\mathsf q$.
We consider the Kostant–Lusztig ![]() $\mathbb {Z}$-form
$\mathbb {Z}$-form ![]() $U ^+ _{\mathbb {Z}}$ (resp.,
$U ^+ _{\mathbb {Z}}$ (resp., ![]() $U^-_{\mathbb {Z}}$) of
$U^-_{\mathbb {Z}}$) of ![]() $U ( [\mathfrak {I},\mathfrak {I}] )$ (resp.,
$U ( [\mathfrak {I},\mathfrak {I}] )$ (resp., ![]() $U ( [\mathfrak {I}^-,\mathfrak {I}^-] )$) obtained as the specialisation
$U ( [\mathfrak {I}^-,\mathfrak {I}^-] )$) obtained as the specialisation ![]() $\mathsf q = 1$ of the
$\mathsf q = 1$ of the  $\mathbb {Z} \left [\mathsf q,\mathsf q^{-1}\right ]$-integral form of the quantised enveloping algebras [Reference Lusztig66, §23.2].
$\mathbb {Z} \left [\mathsf q,\mathsf q^{-1}\right ]$-integral form of the quantised enveloping algebras [Reference Lusztig66, §23.2].
Remark 3.9. We remark that ![]() $U ^\pm _{\mathbb {Z}}$ are the same integral forms dealt with in [Reference Garland31], and also coincide with the integral forms obtained through the Drinfeld presentation ([Reference Beck, Chari and Pressley4, §2] and [Reference Naoi73, Lemma 2.5]).
$U ^\pm _{\mathbb {Z}}$ are the same integral forms dealt with in [Reference Garland31], and also coincide with the integral forms obtained through the Drinfeld presentation ([Reference Beck, Chari and Pressley4, §2] and [Reference Naoi73, Lemma 2.5]).
Note that ![]() $U^{\pm }_{\mathbb {Z}}$ are equipped with the
$U^{\pm }_{\mathbb {Z}}$ are equipped with the ![]() $\mathbb {Z}$-bases
$\mathbb {Z}$-bases ![]() ${\mathbf B} ( \mp \infty )$ obtained by the specialisation
${\mathbf B} ( \mp \infty )$ obtained by the specialisation ![]() $\mathsf q = 1$ of the lower global basis [Reference Kashiwara41] (see also [Reference Lusztig66, §25]). In view of [Reference Lusztig65, Reference Kashiwara43], we have an idempotent
$\mathsf q = 1$ of the lower global basis [Reference Kashiwara41] (see also [Reference Lusztig66, §25]). In view of [Reference Lusztig65, Reference Kashiwara43], we have an idempotent ![]() $\mathbb {Z}$-integral form
$\mathbb {Z}$-integral form
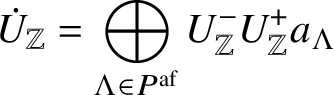 $$ \begin{align*} \dot{U}_{\mathbb{Z}} = \bigoplus_{\Lambda \in P^{\mathrm{af}}} U ^- _{\mathbb{Z}} U ^+ _{\mathbb{Z}} a_{\Lambda} \end{align*} $$
$$ \begin{align*} \dot{U}_{\mathbb{Z}} = \bigoplus_{\Lambda \in P^{\mathrm{af}}} U ^- _{\mathbb{Z}} U ^+ _{\mathbb{Z}} a_{\Lambda} \end{align*} $$such that
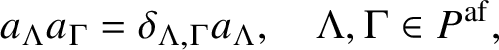 $$ \begin{align*} a_{\Lambda} a_{\Gamma} = \delta_{\Lambda, \Gamma} a_{\Lambda}, \quad \Lambda, \Gamma \in P^{\mathrm{af}}, \end{align*} $$
$$ \begin{align*} a_{\Lambda} a_{\Gamma} = \delta_{\Lambda, \Gamma} a_{\Lambda}, \quad \Lambda, \Gamma \in P^{\mathrm{af}}, \end{align*} $$and
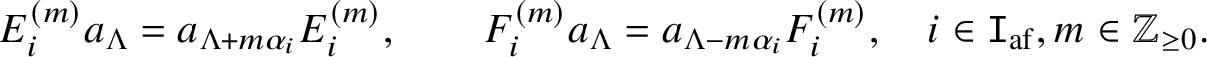 $$ \begin{align*} E_i^{(m)} a_{\Lambda} = a_{\Lambda + m \alpha_i} E_i^{(m)}, \qquad F_i^{(m)} a_{\Lambda} = a_{\Lambda - m \alpha_i} F_i^{(m)}, \quad i \in \mathtt I_{\mathrm{af}}, m \in \mathbb{Z}_{\ge 0}. \end{align*} $$
$$ \begin{align*} E_i^{(m)} a_{\Lambda} = a_{\Lambda + m \alpha_i} E_i^{(m)}, \qquad F_i^{(m)} a_{\Lambda} = a_{\Lambda - m \alpha_i} F_i^{(m)}, \quad i \in \mathtt I_{\mathrm{af}}, m \in \mathbb{Z}_{\ge 0}. \end{align*} $$We set  $\dot {U}^{\ge 0}_{\mathbb {Z}} \subset \dot {U}_{\mathbb {Z}}$ to be the subalgebra generated by
$\dot {U}^{\ge 0}_{\mathbb {Z}} \subset \dot {U}_{\mathbb {Z}}$ to be the subalgebra generated by  $\left \{F_i^{(m)}\right \}_{i \in \mathtt I, m \in \mathbb {Z}_{\ge 0}}$,
$\left \{F_i^{(m)}\right \}_{i \in \mathtt I, m \in \mathbb {Z}_{\ge 0}}$, ![]() $\{a _{\Lambda }\}_{\Lambda \in P^{\mathrm {af}}}$ and
$\{a _{\Lambda }\}_{\Lambda \in P^{\mathrm {af}}}$ and ![]() $U_{\mathbb {Z}}^+$.
$U_{\mathbb {Z}}^+$.
If a ![]() $\dot {U}_{\mathbb {Z}}$-module M admits a decomposition
$\dot {U}_{\mathbb {Z}}$-module M admits a decomposition
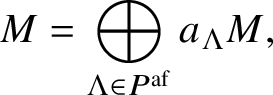 $$ \begin{align*}M = \bigoplus_{\Lambda \in P^{\mathrm{af}}} a_{\Lambda} M,\end{align*} $$
$$ \begin{align*}M = \bigoplus_{\Lambda \in P^{\mathrm{af}}} a_{\Lambda} M,\end{align*} $$then we call this the ![]() $P^{\mathrm {af}}$-weight decomposition. If
$P^{\mathrm {af}}$-weight decomposition. If ![]() $\Lambda \in P^{\mathrm {af}}$ satisfies
$\Lambda \in P^{\mathrm {af}}$ satisfies ![]() $a_{\Lambda } M \neq 0$, then we call
$a_{\Lambda } M \neq 0$, then we call ![]() $\Lambda $ a
$\Lambda $ a ![]() $P^{\mathrm {af}}$-weight of M. When M is defined over a field
$P^{\mathrm {af}}$-weight of M. When M is defined over a field ![]() $\Bbbk $, we define the
$\Bbbk $, we define the ![]() $P^{\mathrm {af}}$-character of M as
$P^{\mathrm {af}}$-character of M as
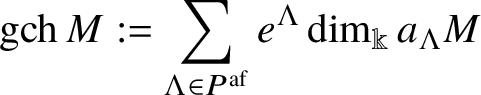 $$ \begin{align*}\mathrm{gch}\, M := \sum _{\Lambda \in P^{\mathrm{af}}} e^{\Lambda} \dim_{\Bbbk} a_{\Lambda} M\end{align*} $$
$$ \begin{align*}\mathrm{gch}\, M := \sum _{\Lambda \in P^{\mathrm{af}}} e^{\Lambda} \dim_{\Bbbk} a_{\Lambda} M\end{align*} $$whenever the right-hand side makes sense. For each ![]() $n \in \mathbb {Z}$, we set
$n \in \mathbb {Z}$, we set
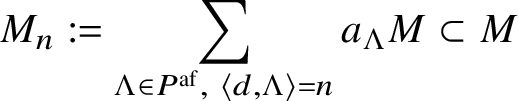 $$ \begin{align*}M_n := \sum_{\Lambda \in P^{\mathrm{af}}, \; \left\langle d, \Lambda \right\rangle = n} a_\Lambda M \subset M\end{align*} $$
$$ \begin{align*}M_n := \sum_{\Lambda \in P^{\mathrm{af}}, \; \left\langle d, \Lambda \right\rangle = n} a_\Lambda M \subset M\end{align*} $$and call it the d-degree n-part of M. Note that these are consistent with formula (2.3) through the identification ![]() $q = e^{\delta }$.
$q = e^{\delta }$.
For each ![]() $\lambda \in P$, we set
$\lambda \in P$, we set
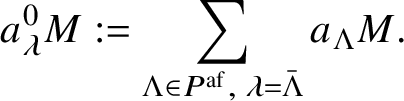 $$ \begin{align}a_{\lambda}^0 M := \sum_{\Lambda \in P^{\mathrm{af}}, \; \lambda = \bar{\Lambda}} a_{\Lambda} M.\end{align} $$
$$ \begin{align}a_{\lambda}^0 M := \sum_{\Lambda \in P^{\mathrm{af}}, \; \lambda = \bar{\Lambda}} a_{\Lambda} M.\end{align} $$We call the decomposition
 $$\begin{align*}M = \bigoplus_{\lambda \in P} a_{\lambda}^0 M\end{align*}$$
$$\begin{align*}M = \bigoplus_{\lambda \in P} a_{\lambda}^0 M\end{align*}$$the P-weight decomposition. We call a nonzero element of ![]() $a_{\Lambda } M$ (resp.,
$a_{\Lambda } M$ (resp.,  $a^0 _\lambda M$) a
$a^0 _\lambda M$) a ![]() $P^{\mathrm {af}}$-weight vector of M (resp., a P-weight vector of M). We also call
$P^{\mathrm {af}}$-weight vector of M (resp., a P-weight vector of M). We also call ![]() $\lambda \in P$ with
$\lambda \in P$ with  $a_{\lambda }^0 M \neq \{ 0 \}$ a P-weight of M.
$a_{\lambda }^0 M \neq \{ 0 \}$ a P-weight of M.
Similarly, we have the Kostant–Lusztig ![]() $\mathbb {Z}$-form
$\mathbb {Z}$-form  $U ^{0, +} _{\mathbb {Z}}$ (resp.,
$U ^{0, +} _{\mathbb {Z}}$ (resp.,  $U^{0,- }_{\mathbb {Z}}$) of
$U^{0,- }_{\mathbb {Z}}$) of ![]() $U ( \mathfrak {n} )$ (resp.,
$U ( \mathfrak {n} )$ (resp., ![]() $U ( \mathfrak {n}^- )$). We have
$U ( \mathfrak {n}^- )$). We have  $U^{0,+}_{\mathbb {Z}} \subset U^{+}_{\mathbb {Z}}$ and
$U^{0,+}_{\mathbb {Z}} \subset U^{+}_{\mathbb {Z}}$ and  $U^{0,-}_{\mathbb {Z}} \subset U^{-}_{\mathbb {Z}}$. In view of the characterisation of global bases ([Reference Kashiwara41]), we find that
$U^{0,-}_{\mathbb {Z}} \subset U^{-}_{\mathbb {Z}}$. In view of the characterisation of global bases ([Reference Kashiwara41]), we find that  ${\mathbf B}^0 ( \mp \infty ) := {\mathbf B} ( \mp \infty ) \cap U^{0,\pm }_{\mathbb {Z}}$ define
${\mathbf B}^0 ( \mp \infty ) := {\mathbf B} ( \mp \infty ) \cap U^{0,\pm }_{\mathbb {Z}}$ define ![]() $\mathbb {Z}$-bases of
$\mathbb {Z}$-bases of ![]() $U^{0,\pm }$.
$U^{0,\pm }$.
We set  $\dot {U}^{0}_{\mathbb {Z}} \subset \dot {U}_{\mathbb {Z}}$ to be the subalgebra of
$\dot {U}^{0}_{\mathbb {Z}} \subset \dot {U}_{\mathbb {Z}}$ to be the subalgebra of ![]() $\dot {U}_{\mathbb {Z}}$ generated by
$\dot {U}_{\mathbb {Z}}$ generated by  $\left \{E_i^{(m)}, F_i^{(m)}\right \}_{i \in \mathtt I, m \in \mathbb {Z}_{\ge 0}}$,
$\left \{E_i^{(m)}, F_i^{(m)}\right \}_{i \in \mathtt I, m \in \mathbb {Z}_{\ge 0}}$, ![]() $\{a _{\Lambda } \}_{\Lambda \in P^{\mathrm {af}}}$. For a field
$\{a _{\Lambda } \}_{\Lambda \in P^{\mathrm {af}}}$. For a field ![]() $\Bbbk $, a
$\Bbbk $, a  $\dot {U}_{\Bbbk }^{\ge 0}$-module M with a
$\dot {U}_{\Bbbk }^{\ge 0}$-module M with a ![]() $P^{\mathrm {af}}$-weight decomposition is said to be
$P^{\mathrm {af}}$-weight decomposition is said to be ![]() $\dot {U}^0_\Bbbk $-integrable if its
$\dot {U}^0_\Bbbk $-integrable if its  $\left \{ E^{(m)}_i, F^{(m)}_i \right \}_{m \ge 0}$-action induces an
$\left \{ E^{(m)}_i, F^{(m)}_i \right \}_{m \ge 0}$-action induces an ![]() $\mathop {\textit{SL}} ( 2, i )_\Bbbk $-action whose
$\mathop {\textit{SL}} ( 2, i )_\Bbbk $-action whose ![]() $( \mathop {\textit{SL}} ( 2, i ) \cap H )_\Bbbk $-eigenvalues are given by the P-weights for each
$( \mathop {\textit{SL}} ( 2, i ) \cap H )_\Bbbk $-eigenvalues are given by the P-weights for each ![]() $i \in \mathtt I$.
$i \in \mathtt I$.
Note that if a ![]() $U \left ( \widetilde {\mathfrak {g}}_{\mathbb C} \right )$-module V over
$U \left ( \widetilde {\mathfrak {g}}_{\mathbb C} \right )$-module V over ![]() ${\mathbb C}$ carries a cyclic
${\mathbb C}$ carries a cyclic ![]() $\widetilde {\mathfrak {h}}_{\mathbb C}$-weight vector whose weight belongs to
$\widetilde {\mathfrak {h}}_{\mathbb C}$-weight vector whose weight belongs to ![]() $P^{\mathrm {af}}$ and each of its
$P^{\mathrm {af}}$ and each of its ![]() $\widetilde {\mathfrak {h}}_{\mathbb C}$-weight spaces is finite-dimensional, then we have a
$\widetilde {\mathfrak {h}}_{\mathbb C}$-weight spaces is finite-dimensional, then we have a ![]() $\dot {U}_{\mathbb {Z}}$-lattice
$\dot {U}_{\mathbb {Z}}$-lattice ![]() $V_{\mathbb {Z}}$ inside V. In such a case, the module
$V_{\mathbb {Z}}$ inside V. In such a case, the module ![]() $V_{\mathbb {Z}} \otimes _{\mathbb {Z}} \Bbbk $ admits
$V_{\mathbb {Z}} \otimes _{\mathbb {Z}} \Bbbk $ admits ![]() $P^{\mathrm {af}}$- or P-weight decompositions.
$P^{\mathrm {af}}$- or P-weight decompositions.
The Chevalley involution of ![]() $\dot {U}_{\mathbb {Z}}$ is defined as
$\dot {U}_{\mathbb {Z}}$ is defined as
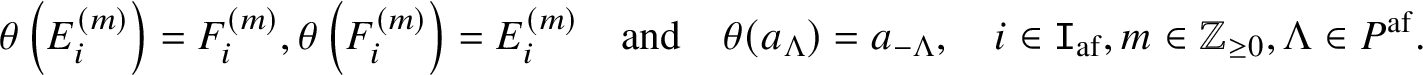 $$ \begin{align*}\theta \left( E_i ^{(m)}\right) = F_i ^{(m)}, \theta \left( F_i ^{(m)}\right) = E_i ^{(m)} \quad \text{and} \quad \theta ( a _{\Lambda} ) = a_{- \Lambda}, \quad i \in \mathtt I_{\mathrm{af}}, m \in \mathbb{Z}_{\ge 0}, \Lambda \in P^{\mathrm{af}}.\end{align*} $$
$$ \begin{align*}\theta \left( E_i ^{(m)}\right) = F_i ^{(m)}, \theta \left( F_i ^{(m)}\right) = E_i ^{(m)} \quad \text{and} \quad \theta ( a _{\Lambda} ) = a_{- \Lambda}, \quad i \in \mathtt I_{\mathrm{af}}, m \in \mathbb{Z}_{\ge 0}, \Lambda \in P^{\mathrm{af}}.\end{align*} $$Definition 3.10 [Reference Kashiwara45]
A ![]() $U \left ( \widetilde {\mathfrak {g}}_{{\mathbb C}} \right )$-module V over
$U \left ( \widetilde {\mathfrak {g}}_{{\mathbb C}} \right )$-module V over ![]() ${\mathbb C}$ with a cyclic
${\mathbb C}$ with a cyclic ![]() $\widetilde {\mathfrak {h}}_{{\mathbb C}}$-weight vector
$\widetilde {\mathfrak {h}}_{{\mathbb C}}$-weight vector ![]() $\mathbf {v}$ is said to be compatible with the negative global basis if we have
$\mathbf {v}$ is said to be compatible with the negative global basis if we have
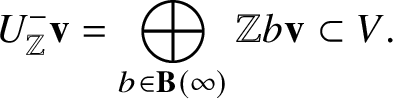 $$ \begin{align*}U ^{-}_{\mathbb{Z}} \mathbf{v} = \bigoplus _{b \in {\mathbf B} ( \infty )} \mathbb{Z} b \mathbf{v} \subset V.\end{align*} $$
$$ \begin{align*}U ^{-}_{\mathbb{Z}} \mathbf{v} = \bigoplus _{b \in {\mathbf B} ( \infty )} \mathbb{Z} b \mathbf{v} \subset V.\end{align*} $$ If ![]() $(V,\mathbf {v})$ is compatible with the negative global basis, then we set
$(V,\mathbf {v})$ is compatible with the negative global basis, then we set
and refer to them as the negative global basis of V.
Compatibility with the positive global basis and the positive global basis ![]() ${\mathbf B} ^{+} ( V ) = {\mathbf B} ^{+} ( V, \mathbf {v} )$ of V is defined similarly.
${\mathbf B} ^{+} ( V ) = {\mathbf B} ^{+} ( V, \mathbf {v} )$ of V is defined similarly.
Theorem 3.11 [Reference Kashiwara41]
We have the following:
1. For each
 $\Lambda \in P^{\mathrm {af}}_+$, the
$\Lambda \in P^{\mathrm {af}}_+$, the  $\widetilde {\mathfrak {g}}_{{\mathbb C}}$-module
$\widetilde {\mathfrak {g}}_{{\mathbb C}}$-module  $L ( \Lambda )_{\mathbb C}$ is compatible with the negative global basis.
$L ( \Lambda )_{\mathbb C}$ is compatible with the negative global basis.2. For each
 $\lambda \in P_+$, we have
$\lambda \in P_+$, we have  $$ \begin{align*}V ( \lambda )_{\mathbb C} = \bigoplus _{b \in {\mathbf B}^0 ( \infty )} {\mathbb C} b \mathbf{v}_{\lambda}^0.\end{align*} $$
$$ \begin{align*}V ( \lambda )_{\mathbb C} = \bigoplus _{b \in {\mathbf B}^0 ( \infty )} {\mathbb C} b \mathbf{v}_{\lambda}^0.\end{align*} $$
We set ![]() ${\mathbf B} ( \Lambda ) := {\mathbf B}^- ( L ( \Lambda )_{\mathbb C}, \mathbf {v}_{\Lambda } )$ for each
${\mathbf B} ( \Lambda ) := {\mathbf B}^- ( L ( \Lambda )_{\mathbb C}, \mathbf {v}_{\Lambda } )$ for each ![]() $\Lambda \in P^{\mathrm {af}}_+$.
$\Lambda \in P^{\mathrm {af}}_+$.
For each ![]() $\Lambda \in P^{\mathrm {af}}_+$ and
$\Lambda \in P^{\mathrm {af}}_+$ and ![]() $\lambda \in P_+$, we set
$\lambda \in P_+$, we set
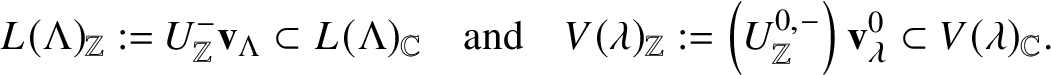 $$ \begin{align*}L ( \Lambda )_{\mathbb{Z}} := U _{\mathbb{Z}}^- \mathbf{v}_{\Lambda} \subset L ( \Lambda )_{\mathbb C} \quad \text{and} \quad V ( \lambda )_{\mathbb{Z}} := \left( U _{\mathbb{Z}}^{0,-} \right) \mathbf{v}_{\lambda}^0 \subset V ( \lambda )_{\mathbb C}.\end{align*} $$
$$ \begin{align*}L ( \Lambda )_{\mathbb{Z}} := U _{\mathbb{Z}}^- \mathbf{v}_{\Lambda} \subset L ( \Lambda )_{\mathbb C} \quad \text{and} \quad V ( \lambda )_{\mathbb{Z}} := \left( U _{\mathbb{Z}}^{0,-} \right) \mathbf{v}_{\lambda}^0 \subset V ( \lambda )_{\mathbb C}.\end{align*} $$ Here ![]() $V ( \lambda )_{\mathbb {Z}}$ acquires the action of
$V ( \lambda )_{\mathbb {Z}}$ acquires the action of ![]() $\dot {U}^0_{\mathbb {Z}}$ thanks to the splitting
$\dot {U}^0_{\mathbb {Z}}$ thanks to the splitting ![]() $P \hookrightarrow P^{\mathrm {af}}$.
$P \hookrightarrow P^{\mathrm {af}}$.
Corollary 3.12. We have the following:
1. For each
 $\Lambda , \Gamma \in P^{\mathrm {af}}_+$, we have a natural inclusion
$\Lambda , \Gamma \in P^{\mathrm {af}}_+$, we have a natural inclusion  $L ( \Lambda + \Gamma )_{\mathbb {Z}} \hookrightarrow L ( \Lambda )_{\mathbb {Z}} \otimes _{\mathbb {Z}} L ( \Gamma )_{\mathbb {Z}}$ of
$L ( \Lambda + \Gamma )_{\mathbb {Z}} \hookrightarrow L ( \Lambda )_{\mathbb {Z}} \otimes _{\mathbb {Z}} L ( \Gamma )_{\mathbb {Z}}$ of  $\dot {U}_{\mathbb {Z}}$-modules, which is a direct summand as
$\dot {U}_{\mathbb {Z}}$-modules, which is a direct summand as  $\mathbb {Z}$-modules.
$\mathbb {Z}$-modules.2. For each
 $\lambda ,\mu \in P_+$, we have a natural inclusion
$\lambda ,\mu \in P_+$, we have a natural inclusion  $V ( \lambda + \mu )_{\mathbb {Z}} \hookrightarrow V ( \lambda )_{\mathbb {Z}} \otimes _{\mathbb {Z}} V ( \mu )_{\mathbb {Z}}$ of
$V ( \lambda + \mu )_{\mathbb {Z}} \hookrightarrow V ( \lambda )_{\mathbb {Z}} \otimes _{\mathbb {Z}} V ( \mu )_{\mathbb {Z}}$ of  $\dot {U}_{\mathbb {Z}}^0$-modules, which is a direct summand as
$\dot {U}_{\mathbb {Z}}^0$-modules, which is a direct summand as  $\mathbb {Z}$-modules.
$\mathbb {Z}$-modules.
Proof. Since the two cases are completely parallel, we prove only the first case. The ![]() $\widetilde {\mathfrak {g}}$-module
$\widetilde {\mathfrak {g}}$-module ![]() $L ( \Lambda )_{\mathbb C} \otimes _{\mathbb C} L ( \Gamma )_{\mathbb C}$ decomposes into the direct sum of integrable highest weight modules ([Reference Kac40, Proposition 9.10]), with a direct summand
$L ( \Lambda )_{\mathbb C} \otimes _{\mathbb C} L ( \Gamma )_{\mathbb C}$ decomposes into the direct sum of integrable highest weight modules ([Reference Kac40, Proposition 9.10]), with a direct summand ![]() $L ( \Lambda + \Gamma )_{\mathbb C}$. In view of [Reference Kashiwara41, Theorem 3], it gives rise to the
$L ( \Lambda + \Gamma )_{\mathbb C}$. In view of [Reference Kashiwara41, Theorem 3], it gives rise to the ![]() $\mathbb {Z} [\mathsf q]$-lattice of the quantised version of
$\mathbb {Z} [\mathsf q]$-lattice of the quantised version of ![]() $L ( \Lambda ) \otimes L ( \Gamma )$ compatible with those of
$L ( \Lambda ) \otimes L ( \Gamma )$ compatible with those of ![]() $L ( \Lambda + \Gamma )$ via the natural embedding. By setting
$L ( \Lambda + \Gamma )$ via the natural embedding. By setting ![]() $\mathsf q = 1$, we obtain a direct sum decomposition of
$\mathsf q = 1$, we obtain a direct sum decomposition of ![]() $L ( \Lambda )_{\mathbb {Z}} \otimes _{\mathbb {Z}} L ( \Gamma )_{\mathbb {Z}}$ as
$L ( \Lambda )_{\mathbb {Z}} \otimes _{\mathbb {Z}} L ( \Gamma )_{\mathbb {Z}}$ as ![]() $\mathbb {Z}$-modules with its direct summand
$\mathbb {Z}$-modules with its direct summand ![]() $L ( \Lambda + \Gamma )_{\mathbb {Z}}$.
$L ( \Lambda + \Gamma )_{\mathbb {Z}}$.
Theorem 3.13 [Reference Kashiwara43]
For each ![]() $\lambda \in P_+$, the
$\lambda \in P_+$, the ![]() $\widetilde {\mathfrak {g}}_{\mathbb C}$-module
$\widetilde {\mathfrak {g}}_{\mathbb C}$-module ![]() $\mathbb {X} ( \lambda )_{\mathbb C}$ is compatible with the negative/positive global basis (for every extremal weight vector).
$\mathbb {X} ( \lambda )_{\mathbb C}$ is compatible with the negative/positive global basis (for every extremal weight vector).
For each ![]() $\lambda \in P_+$, we set
$\lambda \in P_+$, we set
Theorem 3.14 [Reference Kashiwara45]
Set ![]() $\lambda \in P_+$. There exists a
$\lambda \in P_+$. There exists a ![]() $\mathbb {Z}$-basis
$\mathbb {Z}$-basis ![]() ${\mathbf B} ( \mathbb {X} ( \lambda ) )$ of
${\mathbf B} ( \mathbb {X} ( \lambda ) )$ of ![]() $\mathbb {X} ( \lambda )_{\mathbb {Z}}$ that contains the negative/positive global basis of
$\mathbb {X} ( \lambda )_{\mathbb {Z}}$ that contains the negative/positive global basis of ![]() $\mathbb {X} ( \lambda )_{\mathbb {Z}}$ constructed from every extremal weight vector of
$\mathbb {X} ( \lambda )_{\mathbb {Z}}$ constructed from every extremal weight vector of ![]() $\mathbb {X} ( \lambda )_{\mathbb C}$.
$\mathbb {X} ( \lambda )_{\mathbb C}$.
Proof. We set ![]() ${\mathbf B} ( \mathbb {X} ( \lambda ) )$ to be the specialisation of the global basis of a quantum loop algebra module [Reference Kashiwara43, Proposition 8.2.2]. Then it is compatible with the global basis generated from extremal weight vectors by [Reference Kashiwara45, Theorem 3.3].
${\mathbf B} ( \mathbb {X} ( \lambda ) )$ to be the specialisation of the global basis of a quantum loop algebra module [Reference Kashiwara43, Proposition 8.2.2]. Then it is compatible with the global basis generated from extremal weight vectors by [Reference Kashiwara45, Theorem 3.3].
For each ![]() $\lambda \in P_+$ and
$\lambda \in P_+$ and ![]() $w \in W_{\mathrm {af}}$, we define
$w \in W_{\mathrm {af}}$, we define
We set ![]() $\mathbb {W} ( \lambda )_{\mathbb {Z}} := \mathbb {W} _{w_0} ( \lambda )_{\mathbb {Z}}$ and
$\mathbb {W} ( \lambda )_{\mathbb {Z}} := \mathbb {W} _{w_0} ( \lambda )_{\mathbb {Z}}$ and ![]() $\mathbb {W} ^-( \lambda )_{\mathbb {Z}} := \mathbb {W} _{e} ^- ( \lambda )_{\mathbb {Z}}$.
$\mathbb {W} ^-( \lambda )_{\mathbb {Z}} := \mathbb {W} _{e} ^- ( \lambda )_{\mathbb {Z}}$.
Lemma 3.15 Naito and Sagaki
For each ![]() $\lambda \in P_+$ and
$\lambda \in P_+$ and ![]() $w,v \in W_{\mathrm {af}}$, we have
$w,v \in W_{\mathrm {af}}$, we have ![]() $\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{vw_0} ( \lambda )_{\mathbb {Z}}$ if
$\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{vw_0} ( \lambda )_{\mathbb {Z}}$ if ![]() $w \le _{\frac {\infty }{2}} v$. If we have
$w \le _{\frac {\infty }{2}} v$. If we have ![]() $\lambda \in P_{++}$ in addition, then we have
$\lambda \in P_{++}$ in addition, then we have ![]() $\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{vw_0} ( \lambda )_{\mathbb {Z}}$ if and only if
$\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{vw_0} ( \lambda )_{\mathbb {Z}}$ if and only if ![]() $w \le _{\frac {\infty }{2}} v$.
$w \le _{\frac {\infty }{2}} v$.
Proof. Apply the inclusion relation of the (labels of the) global basis in [Reference Naito and Sagaki72, Corollary 5.2.5] (see also [Reference Kashiwara45, §2.8]).
Corollary 3.16. For each ![]() $\lambda \in P_+$,
$\lambda \in P_+$, ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $i \in \mathtt I_{\mathrm {af}}$, we have
$i \in \mathtt I_{\mathrm {af}}$, we have ![]() $\mathbb {W} _{s_i ww_0} ( \lambda )_{{\mathbb K}} \subset \mathbb {W} _{ww_0} ( \lambda )_{{\mathbb K}}$ if
$\mathbb {W} _{s_i ww_0} ( \lambda )_{{\mathbb K}} \subset \mathbb {W} _{ww_0} ( \lambda )_{{\mathbb K}}$ if ![]() $s_i w \le _{\frac {\infty }{2}} w$. In this case,
$s_i w \le _{\frac {\infty }{2}} w$. In this case, ![]() $\mathbb {W} _{ww_0} ( \lambda )_{{\mathbb K}}$ inherits an action of
$\mathbb {W} _{ww_0} ( \lambda )_{{\mathbb K}}$ inherits an action of ![]() $\mathop {\textit{SL}} (2,i)_{{\mathbb K}}$ from
$\mathop {\textit{SL}} (2,i)_{{\mathbb K}}$ from ![]() $\mathbb {X} ( \lambda )_{{\mathbb K}}$.
$\mathbb {X} ( \lambda )_{{\mathbb K}}$.
Proof. The first part of the assertion is the special case of Lemma 3.15. Given this, it remains to notice that a lift of ![]() $s_i \in W_{\mathrm {af}}$ sends
$s_i \in W_{\mathrm {af}}$ sends ![]() $\mathbf {v}_{ww_0 \lambda }$ to
$\mathbf {v}_{ww_0 \lambda }$ to ![]() $\pm \mathbf {v}_{s_iww_0 \lambda }$, and hence the Bruhat decomposition of
$\pm \mathbf {v}_{s_iww_0 \lambda }$, and hence the Bruhat decomposition of ![]() $\mathbf {I} ( i )_{{\mathbb K}}$ (into two
$\mathbf {I} ( i )_{{\mathbb K}}$ (into two ![]() $\mathbf {I}_{{\mathbb K}}$-double cosets) implies that
$\mathbf {I}_{{\mathbb K}}$-double cosets) implies that ![]() $\mathbb {W} _{ww_0} ( \lambda )_{{\mathbb K}}$ is stable under
$\mathbb {W} _{ww_0} ( \lambda )_{{\mathbb K}}$ is stable under ![]() $\mathbf {I} ( i )_{{\mathbb K}}$.
$\mathbf {I} ( i )_{{\mathbb K}}$.
Lemma 3.17. For each ![]() $\lambda \in P_+$ and
$\lambda \in P_+$ and ![]() $w \in W_{\mathrm {af}}$, we have the following:
$w \in W_{\mathrm {af}}$, we have the following:
1. Each
 $\beta \in Q^{\vee }$ defines a
$\beta \in Q^{\vee }$ defines a  $\dot {U}_{\mathbb {Z}}$-module automorphism
$\dot {U}_{\mathbb {Z}}$-module automorphism  $\tau _\beta $ on
$\tau _\beta $ on  $\mathbb {X} ( \lambda )_{\mathbb {Z}}$ determined by
$\mathbb {X} ( \lambda )_{\mathbb {Z}}$ determined by  $\tau _{\beta }( \mathbf {v}_{\lambda } ) := \mathbf {v}_{t_{\beta } \lambda }$. Moreover,
$\tau _{\beta }( \mathbf {v}_{\lambda } ) := \mathbf {v}_{t_{\beta } \lambda }$. Moreover,  $\tau _{\beta }{\mathbf B} ( \mathbb {X} ( \lambda ) ) = {\mathbf B} ( \mathbb {X} ( \lambda ) )$.
$\tau _{\beta }{\mathbf B} ( \mathbb {X} ( \lambda ) ) = {\mathbf B} ( \mathbb {X} ( \lambda ) )$.2.
 $\theta ^* ( \mathbb {X} ( \lambda )_{\mathbb {Z}} ) \cong \mathbb {X} ( - w_0 \lambda )_{\mathbb {Z}}$ as
$\theta ^* ( \mathbb {X} ( \lambda )_{\mathbb {Z}} ) \cong \mathbb {X} ( - w_0 \lambda )_{\mathbb {Z}}$ as  $\dot {U}_{\mathbb {Z}}$-modules. Moreover,
$\dot {U}_{\mathbb {Z}}$-modules. Moreover,  $\theta ^* {\mathbf B} ( \mathbb {X} ( \lambda ) ) = {\mathbf B} ( \mathbb {X} ( - w_0 \lambda ) )$.
$\theta ^* {\mathbf B} ( \mathbb {X} ( \lambda ) ) = {\mathbf B} ( \mathbb {X} ( - w_0 \lambda ) )$.3.
 $\mathbb {W} _w ( \lambda ) _{\mathbb {Z}} = \mathbb {W} _w ( \lambda )_{\mathbb C} \cap \mathbb {X} ( \lambda )_{\mathbb {Z}}$.
$\mathbb {W} _w ( \lambda ) _{\mathbb {Z}} = \mathbb {W} _w ( \lambda )_{\mathbb C} \cap \mathbb {X} ( \lambda )_{\mathbb {Z}}$.4. There is a
 $U_{\mathbb {Z}}^-$-cyclic vector of
$U_{\mathbb {Z}}^-$-cyclic vector of  $\theta ^* (\mathbb {W} _w ( \lambda ) _{\mathbb {Z}} )$ with weight
$\theta ^* (\mathbb {W} _w ( \lambda ) _{\mathbb {Z}} )$ with weight  $- w \lambda = w w_0 ( - w_0 \lambda )$. In particular,
$- w \lambda = w w_0 ( - w_0 \lambda )$. In particular,  $$ \begin{align*}\theta^* ( \mathbb{W}_w ( \lambda )_{\mathbb{Z}} ) \cong \mathbb{W}_{ww_0}^- ( -w_0 \lambda )_{\mathbb{Z}} \quad \text{and} \quad \theta^* \left( \mathbb{W}_w^- ( \lambda )_{\mathbb{Z}} \right) \cong \mathbb{W}_{ww_0} ( -w_0 \lambda )_{\mathbb{Z}}.\end{align*} $$
$$ \begin{align*}\theta^* ( \mathbb{W}_w ( \lambda )_{\mathbb{Z}} ) \cong \mathbb{W}_{ww_0}^- ( -w_0 \lambda )_{\mathbb{Z}} \quad \text{and} \quad \theta^* \left( \mathbb{W}_w^- ( \lambda )_{\mathbb{Z}} \right) \cong \mathbb{W}_{ww_0} ( -w_0 \lambda )_{\mathbb{Z}}.\end{align*} $$
Proof. We borrow the setting of [Reference Kashiwara43, §8.1 and §8.2].
We prove the first assertion. Since ![]() $\mathbf {v}_{\lambda }$ and
$\mathbf {v}_{\lambda }$ and ![]() $\mathbf {v}_{t_{\beta } \lambda }$ obey the same relation,
$\mathbf {v}_{t_{\beta } \lambda }$ obey the same relation, ![]() $\tau _\beta $ defines an automorphism as
$\tau _\beta $ defines an automorphism as ![]() $\widetilde {\mathfrak {g}}_{\mathbb C}$-modules. The latter assertion follows from Theorem 3.14.
$\widetilde {\mathfrak {g}}_{\mathbb C}$-modules. The latter assertion follows from Theorem 3.14.
We prove the second assertion. The defining equation of ![]() $\theta ^* ( \mathbf {v}_{\lambda } )$ is the same as the cyclic vector
$\theta ^* ( \mathbf {v}_{\lambda } )$ is the same as the cyclic vector ![]() $\mathbf {v}_{- w_0 \lambda } \in \mathbb {X} ( - w_0 \lambda )_{\mathbb C}$ as
$\mathbf {v}_{- w_0 \lambda } \in \mathbb {X} ( - w_0 \lambda )_{\mathbb C}$ as ![]() $\widetilde {\mathfrak {g}}_{\mathbb C}$-modules. This yields a
$\widetilde {\mathfrak {g}}_{\mathbb C}$-modules. This yields a ![]() $\widetilde {\mathfrak {g}}_{\mathbb C}$-module isomorphism
$\widetilde {\mathfrak {g}}_{\mathbb C}$-module isomorphism ![]() $\eta : \theta ^* ( \mathbb {X} ( \lambda )_{\mathbb C} ) \longrightarrow \mathbb {X} ( - w_0 \lambda )_{\mathbb C}$. Since
$\eta : \theta ^* ( \mathbb {X} ( \lambda )_{\mathbb C} ) \longrightarrow \mathbb {X} ( - w_0 \lambda )_{\mathbb C}$. Since ![]() $\theta $ exchanges
$\theta $ exchanges ![]() $U^\pm _{\mathbb {Z}}$ and
$U^\pm _{\mathbb {Z}}$ and ![]() $\mathbf {v}_\lambda $ is cyclic, we deduce that
$\mathbf {v}_\lambda $ is cyclic, we deduce that ![]() $\eta ( \theta ^* ( \mathbb {X} ( \lambda )_{\mathbb {Z}} ) ) = \dot {U}_{\mathbb {Z}} \mathbf {v}_{- \lambda } \subset \mathbb {X} ( - w_0 \lambda )_{\mathbb C}$. By Theorem 3.14, we conclude
$\eta ( \theta ^* ( \mathbb {X} ( \lambda )_{\mathbb {Z}} ) ) = \dot {U}_{\mathbb {Z}} \mathbf {v}_{- \lambda } \subset \mathbb {X} ( - w_0 \lambda )_{\mathbb C}$. By Theorem 3.14, we conclude ![]() $\theta ^* {\mathbf B} ( \mathbb {X} ( \lambda ) ) = {\mathbf B} ( \mathbb {X} ( - w_0 \lambda ) )$, as required.
$\theta ^* {\mathbf B} ( \mathbb {X} ( \lambda ) ) = {\mathbf B} ( \mathbb {X} ( - w_0 \lambda ) )$, as required.
We prove the third assertion. By Theorem 3.14, the ![]() $\mathbb {Z}$-basis of
$\mathbb {Z}$-basis of ![]() $\mathbb {W} ( \lambda ) _{\mathbb {Z}}$ is formed by the nonzero elements of
$\mathbb {W} ( \lambda ) _{\mathbb {Z}}$ is formed by the nonzero elements of ![]() ${\mathbf B} ( - \infty ) \mathbf {v}_{w_0 \lambda }$ and forms a direct summand of
${\mathbf B} ( - \infty ) \mathbf {v}_{w_0 \lambda }$ and forms a direct summand of ![]() $\mathbb {X} ( \lambda )_{\mathbb {Z}}$ as
$\mathbb {X} ( \lambda )_{\mathbb {Z}}$ as ![]() $\mathbb {Z}$-modules. Hence, the case where
$\mathbb {Z}$-modules. Hence, the case where ![]() $w = w_0$ follows. For
$w = w_0$ follows. For ![]() $w \in W$, we apply [Reference Kashiwara43, Lemma 8.2.1] repeatedly to deduce the assertion from the
$w \in W$, we apply [Reference Kashiwara43, Lemma 8.2.1] repeatedly to deduce the assertion from the ![]() $w = w_0$ case by using
$w = w_0$ case by using ![]() ${\mathbf B} ( - \infty ) \mathbf {v}_{w \lambda } \subset {\mathbf B} ( - \infty ) \mathbf {v}_{w_0 \lambda }$. For
${\mathbf B} ( - \infty ) \mathbf {v}_{w \lambda } \subset {\mathbf B} ( - \infty ) \mathbf {v}_{w_0 \lambda }$. For ![]() $w = u t_{\beta } \in W_{\mathrm {af}}$ with
$w = u t_{\beta } \in W_{\mathrm {af}}$ with ![]() $u \in W, \beta \in Q^{\vee }$, we additionally apply
$u \in W, \beta \in Q^{\vee }$, we additionally apply ![]() $\tau _{w_0 \beta }$ to conclude the assertion.
$\tau _{w_0 \beta }$ to conclude the assertion.
We prove the fourth assertion. The vector ![]() $\theta ^* ( \mathbf {v}_{w \lambda } )$ is a
$\theta ^* ( \mathbf {v}_{w \lambda } )$ is a ![]() $U_{\mathbb {Z}}^-$-cyclic vector of
$U_{\mathbb {Z}}^-$-cyclic vector of ![]() $\theta ^* (\mathbb {W} _w ( \lambda ) _{\mathbb {Z}} )$, and its weight is
$\theta ^* (\mathbb {W} _w ( \lambda ) _{\mathbb {Z}} )$, and its weight is
Hence, we conclude the assertion (using the fact that ![]() $\theta $ is an involution).
$\theta $ is an involution).
Theorem 3.18 [Reference Kashiwara44] and [Reference Beck and Nakajima5]
Set ![]() $\lambda \in P_+$. The unique (d-degree
$\lambda \in P_+$. The unique (d-degree ![]() $0$)
$0$)  $\dot {U}^{\ge 0}_{\mathbb {Z}}$-module map
$\dot {U}^{\ge 0}_{\mathbb {Z}}$-module map
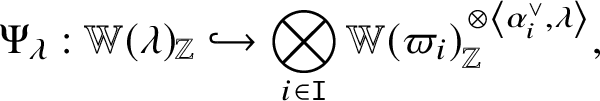 $$ \begin{align} \Psi_\lambda : \mathbb{W} ( \lambda )_{\mathbb{Z}} \hookrightarrow \bigotimes _{i \in \mathtt I} \mathbb{W} ( \varpi_i )_{\mathbb{Z}}^{\otimes \left\langle \alpha_i^{\vee}, \lambda \right\rangle}, \end{align} $$
$$ \begin{align} \Psi_\lambda : \mathbb{W} ( \lambda )_{\mathbb{Z}} \hookrightarrow \bigotimes _{i \in \mathtt I} \mathbb{W} ( \varpi_i )_{\mathbb{Z}}^{\otimes \left\langle \alpha_i^{\vee}, \lambda \right\rangle}, \end{align} $$which sends ![]() $\mathbf {v}_\lambda $ to the tensor product of
$\mathbf {v}_\lambda $ to the tensor product of  $\left \{\mathbf {v}_{\varpi _i}\right \}_{i \in \mathtt I}$s, is injective and defines a direct summand as
$\left \{\mathbf {v}_{\varpi _i}\right \}_{i \in \mathtt I}$s, is injective and defines a direct summand as ![]() $\mathbb {Z}$-modules.
$\mathbb {Z}$-modules.
Proof. We set  $\mathbb {X}^{\otimes } := \bigotimes _{i \in \mathtt I} \mathbb {X} ( \varpi _i )_{\mathbb {Z}}^{\otimes \left \langle \alpha _i^{\vee }, \lambda \right \rangle }$. The map
$\mathbb {X}^{\otimes } := \bigotimes _{i \in \mathtt I} \mathbb {X} ( \varpi _i )_{\mathbb {Z}}^{\otimes \left \langle \alpha _i^{\vee }, \lambda \right \rangle }$. The map ![]() $\Psi _\lambda $ exists, as
$\Psi _\lambda $ exists, as  $\bigotimes _{i \in \mathtt I} \mathbf {v}_{\varpi _i}^{\otimes \left \langle \alpha _i^{\vee }, \lambda \right \rangle }$ obeys the same defining condition as the extremal weight vector
$\bigotimes _{i \in \mathtt I} \mathbf {v}_{\varpi _i}^{\otimes \left \langle \alpha _i^{\vee }, \lambda \right \rangle }$ obeys the same defining condition as the extremal weight vector ![]() $\mathbf {v}_{\lambda } \in \mathbb {X} ( \lambda )_{\mathbb {Z}}$, and the comultiplication of
$\mathbf {v}_{\lambda } \in \mathbb {X} ( \lambda )_{\mathbb {Z}}$, and the comultiplication of ![]() $\widetilde {\mathfrak {g}}$ induces an algebra map
$\widetilde {\mathfrak {g}}$ induces an algebra map ![]() ${\triangle}{\kern-0.5pt}{:}{\kern1.5pt} \dot {U}_{\mathbb {Z}} \subset \dot {U}_{\mathbb {Z}} \otimes \dot {U}_{\mathbb {Z}}$ ([Reference Lusztig66, §23.1.5]).
${\triangle}{\kern-0.5pt}{:}{\kern1.5pt} \dot {U}_{\mathbb {Z}} \subset \dot {U}_{\mathbb {Z}} \otimes \dot {U}_{\mathbb {Z}}$ ([Reference Lusztig66, §23.1.5]).
The map ![]() $\Psi _\lambda $ is injective by [Reference Beck and Nakajima5, Corollary 4.15 and Remark 4.17]. By [Reference Kashiwara44, Theorem 8.5], the
$\Psi _\lambda $ is injective by [Reference Beck and Nakajima5, Corollary 4.15 and Remark 4.17]. By [Reference Kashiwara44, Theorem 8.5], the ![]() $\mathsf {q} = 1$ specialisations of the global bases yield the
$\mathsf {q} = 1$ specialisations of the global bases yield the ![]() $\dot {U}_{\mathbb {Z}}$-spans of the extremal weight vectors in
$\dot {U}_{\mathbb {Z}}$-spans of the extremal weight vectors in ![]() $\mathbb {X} ( \lambda )_{\mathbb {Z}}$ and
$\mathbb {X} ( \lambda )_{\mathbb {Z}}$ and ![]() $\mathbb {X}^{\otimes }$ up to the action of some rings of (partially symmetric) polynomials with integer coefficients, respectively. This yields a splitting of
$\mathbb {X}^{\otimes }$ up to the action of some rings of (partially symmetric) polynomials with integer coefficients, respectively. This yields a splitting of ![]() $\Psi _\lambda $ as
$\Psi _\lambda $ as ![]() $\mathbb {Z}$-modules, where the
$\mathbb {Z}$-modules, where the ![]() $\mathbb {Z}$-module structure of the right-hand side comes from the crystal lattice of (the
$\mathbb {Z}$-module structure of the right-hand side comes from the crystal lattice of (the ![]() $\mathsf q$-version of)
$\mathsf q$-version of) ![]() $\mathbb {X}^{\otimes }$ (as in [Reference Kashiwara44, (8.8)]). We call this crystal lattice
$\mathbb {X}^{\otimes }$ (as in [Reference Kashiwara44, (8.8)]). We call this crystal lattice ![]() $\mathsf L_1$.
$\mathsf L_1$.
We have another ![]() $\mathbb {Z} [\mathsf q]$-lattice inside (the
$\mathbb {Z} [\mathsf q]$-lattice inside (the ![]() $\mathsf q$-version of)
$\mathsf q$-version of) ![]() $\mathbb {X}^{\otimes }$ obtained by the tensor product of the crystal lattices of (the
$\mathbb {X}^{\otimes }$ obtained by the tensor product of the crystal lattices of (the ![]() $\mathsf q$-versions of)
$\mathsf q$-versions of) ![]() $\mathbb {X} ( \varpi _i )$s. We call this
$\mathbb {X} ( \varpi _i )$s. We call this ![]() $\mathbb {Z} [\mathsf q]$-lattice
$\mathbb {Z} [\mathsf q]$-lattice ![]() $\mathsf L_2$.
$\mathsf L_2$.
By [Reference Kashiwara44, Proposition 8.6], the global basis of ![]() $\mathsf L_1$ is written in terms of the (tensor product) global bases of
$\mathsf L_1$ is written in terms of the (tensor product) global bases of ![]() $\mathsf L_2$ by an upper-unitriangular matrix
$\mathsf L_2$ by an upper-unitriangular matrix ![]() $\mathsf C$ (valued in
$\mathsf C$ (valued in ![]() $\mathbb {Q} [ \mathsf q ]$, with finitely many nonzero entries in each row). Hence, the corresponding bases in
$\mathbb {Q} [ \mathsf q ]$, with finitely many nonzero entries in each row). Hence, the corresponding bases in ![]() $\mathbb {X}^{\otimes }$ are related by an upper-unitriangular matrix C obtained as the
$\mathbb {X}^{\otimes }$ are related by an upper-unitriangular matrix C obtained as the ![]() $\mathsf {q} = 1$ specialisation of
$\mathsf {q} = 1$ specialisation of ![]() $\mathsf C$ (valued in
$\mathsf C$ (valued in ![]() $\mathbb {Q}$). In view of the fact that
$\mathbb {Q}$). In view of the fact that ![]() $\triangle $ is an algebra morphism (and [Reference Kashiwara44, Theorem 8.5]), we deduce
$\triangle $ is an algebra morphism (and [Reference Kashiwara44, Theorem 8.5]), we deduce ![]() $\mathsf L_1 \subset \mathsf L_2$. Hence, we have
$\mathsf L_1 \subset \mathsf L_2$. Hence, we have ![]() $\mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_1 \subset \mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_2 \subset \mathbb {X}^{\otimes }$. In particular, the matrix C must be valued in
$\mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_1 \subset \mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_2 \subset \mathbb {X}^{\otimes }$. In particular, the matrix C must be valued in ![]() $\mathbb {Z}$. This implies
$\mathbb {Z}$. This implies ![]() $\mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_1 = \mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_2$.
$\mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_1 = \mathbb {Z} \otimes _{\mathbb {Z} [\mathsf q]} \mathsf L_2$.
Hence, the ![]() $\mathbb {Z}$-module splitting in the second paragraph is indeed what we wanted.
$\mathbb {Z}$-module splitting in the second paragraph is indeed what we wanted.
3.3 Projectivity of the module  $\mathbb {W} ( \lambda )_{\Bbbk }$
$\mathbb {W} ( \lambda )_{\Bbbk }$
Let ![]() $\Bbbk $ be a field. We equip
$\Bbbk $ be a field. We equip  $\mathring {U}^+_\Bbbk := \bigoplus _{\lambda \in P} U^+_\Bbbk a_{\lambda }^0$ with the structure of an algebra by setting
$\mathring {U}^+_\Bbbk := \bigoplus _{\lambda \in P} U^+_\Bbbk a_{\lambda }^0$ with the structure of an algebra by setting  $a_{\lambda }^0 a_{\mu }^0 = \delta _{\lambda , \mu } a_{\lambda }^0 (\lambda , \mu \in P)$,
$a_{\lambda }^0 a_{\mu }^0 = \delta _{\lambda , \mu } a_{\lambda }^0 (\lambda , \mu \in P)$,
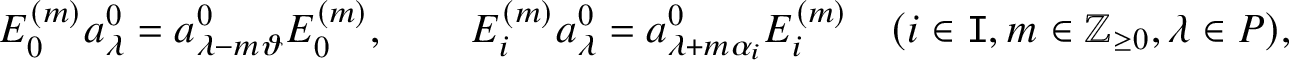 $$ \begin{align*}E_0^{(m)} a_{\lambda}^0 = a_{\lambda - m \vartheta}^0 E_0^{(m)}, \qquad E_i^{(m)} a_{\lambda}^0 = a_{\lambda + m \alpha_i}^0 E_i^{(m)} \quad (i \in \mathtt I, m \in \mathbb{Z}_{\ge 0}, \lambda \in P),\end{align*} $$
$$ \begin{align*}E_0^{(m)} a_{\lambda}^0 = a_{\lambda - m \vartheta}^0 E_0^{(m)}, \qquad E_i^{(m)} a_{\lambda}^0 = a_{\lambda + m \alpha_i}^0 E_i^{(m)} \quad (i \in \mathtt I, m \in \mathbb{Z}_{\ge 0}, \lambda \in P),\end{align*} $$and require
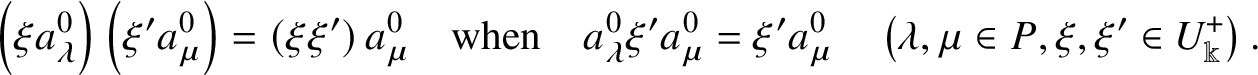 $$ \begin{align*}\left( \xi a_{\lambda}^0 \right) \left( \xi' a_{\mu}^0 \right) = \left( \xi \xi' \right) a_{\mu}^0 \quad \text{when} \quad a_{\lambda}^0 \xi' a_{\mu}^0 = \xi' a_{\mu}^0 \quad \left( \lambda, \mu \in P, \xi, \xi' \in U^+_{\Bbbk} \right).\end{align*} $$
$$ \begin{align*}\left( \xi a_{\lambda}^0 \right) \left( \xi' a_{\mu}^0 \right) = \left( \xi \xi' \right) a_{\mu}^0 \quad \text{when} \quad a_{\lambda}^0 \xi' a_{\mu}^0 = \xi' a_{\mu}^0 \quad \left( \lambda, \mu \in P, \xi, \xi' \in U^+_{\Bbbk} \right).\end{align*} $$Similarly, we define
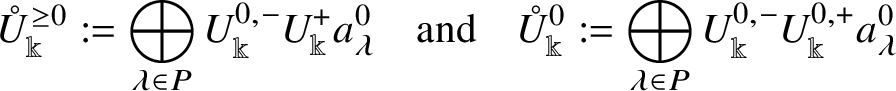 $$ \begin{align*}\mathring{U}^{\ge 0}_\Bbbk:= \bigoplus_{\lambda \in P} U^{0,-}_{\Bbbk} U^{+}_\Bbbk a_{\lambda}^0 \quad \text{and} \quad \mathring{U}^{0}_\Bbbk:= \bigoplus_{\lambda \in P} U^{0,-}_{\Bbbk} U^{0,+}_\Bbbk a_{\lambda}^0\end{align*} $$
$$ \begin{align*}\mathring{U}^{\ge 0}_\Bbbk:= \bigoplus_{\lambda \in P} U^{0,-}_{\Bbbk} U^{+}_\Bbbk a_{\lambda}^0 \quad \text{and} \quad \mathring{U}^{0}_\Bbbk:= \bigoplus_{\lambda \in P} U^{0,-}_{\Bbbk} U^{0,+}_\Bbbk a_{\lambda}^0\end{align*} $$and regard them as subalgebras of the completions of  $\dot {U}^{\ge 0}_\Bbbk $ and
$\dot {U}^{\ge 0}_\Bbbk $ and ![]() $\dot {U}^{0}_\Bbbk $ with respect to the idempotents by setting
$\dot {U}^{0}_\Bbbk $ with respect to the idempotents by setting
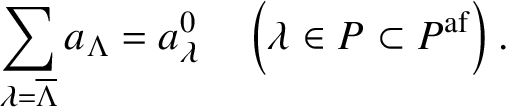 $$ \begin{align*}\sum_{\lambda = \overline{\Lambda}}a_{\Lambda} = a_{\lambda}^0 \quad \left(\lambda \in P \subset P^{\mathrm{af}}\right).\end{align*} $$
$$ \begin{align*}\sum_{\lambda = \overline{\Lambda}}a_{\Lambda} = a_{\lambda}^0 \quad \left(\lambda \in P \subset P^{\mathrm{af}}\right).\end{align*} $$The eigendecomposition with respect to ![]() $d \in \widetilde {\mathfrak {h}}$ now becomes an external grading of algebras
$d \in \widetilde {\mathfrak {h}}$ now becomes an external grading of algebras ![]() $\mathring {U}^+_\Bbbk $ and
$\mathring {U}^+_\Bbbk $ and  $\mathring {U}^{\ge 0}_\Bbbk $. We have algebra inclusions
$\mathring {U}^{\ge 0}_\Bbbk $. We have algebra inclusions
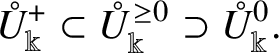 $$ \begin{align*}\mathring{U}^+_\Bbbk \subset \mathring{U}^{\ge 0}_\Bbbk \supset \mathring{U}^0_\Bbbk.\end{align*} $$
$$ \begin{align*}\mathring{U}^+_\Bbbk \subset \mathring{U}^{\ge 0}_\Bbbk \supset \mathring{U}^0_\Bbbk.\end{align*} $$Note that we have a surjective algebra map  $\dot {U}^{\ge 0}_{\mathbb {Z}} \rightarrow \dot {U}^0_{\mathbb {Z}}$, since
$\dot {U}^{\ge 0}_{\mathbb {Z}} \rightarrow \dot {U}^0_{\mathbb {Z}}$, since  $a_{\Lambda } \dot {U}^{\ge 0}_{\mathbb {Z}} a_{\Gamma } \neq 0$ implies
$a_{\Lambda } \dot {U}^{\ge 0}_{\mathbb {Z}} a_{\Gamma } \neq 0$ implies ![]() $\left \langle d, \Lambda \right \rangle \ge \left \langle d, \Gamma \right \rangle $ and
$\left \langle d, \Lambda \right \rangle \ge \left \langle d, \Gamma \right \rangle $ and  $a_{\Lambda } \dot {U}^{0}_{\mathbb {Z}} a_{\Gamma } \neq 0$ implies
$a_{\Lambda } \dot {U}^{0}_{\mathbb {Z}} a_{\Gamma } \neq 0$ implies ![]() $\left \langle d, \Lambda \right \rangle = \left \langle d, \Gamma \right \rangle $ for
$\left \langle d, \Lambda \right \rangle = \left \langle d, \Gamma \right \rangle $ for ![]() $\Lambda , \Gamma \in P^{\mathrm {af}}$. This induces a surjective algebra map
$\Lambda , \Gamma \in P^{\mathrm {af}}$. This induces a surjective algebra map  $\mathring {U}^{\ge 0}_{\mathbb {Z}} \rightarrow \mathring {U}^0_{\mathbb {Z}}$, which specialises to
$\mathring {U}^{\ge 0}_{\mathbb {Z}} \rightarrow \mathring {U}^0_{\mathbb {Z}}$, which specialises to  $\mathring {U}^{\ge 0}_\Bbbk \rightarrow \mathring {U}^0_\Bbbk $.
$\mathring {U}^{\ge 0}_\Bbbk \rightarrow \mathring {U}^0_\Bbbk $.
We sometimes regard ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ (
$\mathbb {W} ( \lambda )_{\Bbbk }$ (![]() $\lambda \in P_+$) as a
$\lambda \in P_+$) as a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\mathring {U}^+_\Bbbk $-module or a
$\mathring {U}^+_\Bbbk $-module or a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded  $\mathring {U}^{\ge 0}_\Bbbk $-module by means of (3.2), whose gradings are given by the d-degrees.
$\mathring {U}^{\ge 0}_\Bbbk $-module by means of (3.2), whose gradings are given by the d-degrees.
Proposition 3.19. Let ![]() $\Bbbk $ be a field and set
$\Bbbk $ be a field and set ![]() $\lambda \in P_+$. The module
$\lambda \in P_+$. The module ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ is the projective cover of
$\mathbb {W} ( \lambda )_{\Bbbk }$ is the projective cover of ![]() $V ( \lambda )_{\Bbbk }$ in the category of
$V ( \lambda )_{\Bbbk }$ in the category of  $\dot {U}_\Bbbk ^{\ge 0}$-modules that are
$\dot {U}_\Bbbk ^{\ge 0}$-modules that are ![]() $\dot {U}_\Bbbk ^0$-integrable and whose P-weights are contained in
$\dot {U}_\Bbbk ^0$-integrable and whose P-weights are contained in ![]() $\mathrm {Conv} W \lambda \subset P \otimes _{\mathbb {Z}} \mathbb {R}$, where
$\mathrm {Conv} W \lambda \subset P \otimes _{\mathbb {Z}} \mathbb {R}$, where ![]() $\mathrm {Conv}$ denotes the
$\mathrm {Conv}$ denotes the ![]() $\mathbb {R}$-convex hull.
$\mathbb {R}$-convex hull.
Lemma 3.20. For each ![]() $\lambda \in P_+$, the module
$\lambda \in P_+$, the module ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ is free over a polynomial ring and we have a finite-dimensional quotient
$\mathbb {W} ( \lambda )_{\Bbbk }$ is free over a polynomial ring and we have a finite-dimensional quotient ![]() $W ( \lambda )_{\Bbbk }$ with
$W ( \lambda )_{\Bbbk }$ with  $\dim _{\Bbbk } a^0_\lambda W ( \lambda )_{\Bbbk } = 1$.
$\dim _{\Bbbk } a^0_\lambda W ( \lambda )_{\Bbbk } = 1$.
Remark 3.21. The modules ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ and
$\mathbb {W} ( \lambda )_{\Bbbk }$ and ![]() $W ( \lambda )_{\Bbbk }$ (
$W ( \lambda )_{\Bbbk }$ (![]() $\lambda \in P_+$) are analogues of global and local Weyl modules in [Reference Chari and Pressley19, Reference Lenart, Naito, Sagaki, Schilling and Shimozono62, Reference Chari and Ion18] (compare Theorem 2.2). By construction, their characters are the same as those defined over
$\lambda \in P_+$) are analogues of global and local Weyl modules in [Reference Chari and Pressley19, Reference Lenart, Naito, Sagaki, Schilling and Shimozono62, Reference Chari and Ion18] (compare Theorem 2.2). By construction, their characters are the same as those defined over ![]() ${\mathbb C}$ (see [Reference Kato46, §1] for more discussion).
${\mathbb C}$ (see [Reference Kato46, §1] for more discussion).
Proof of Lemma 3.20. Note that the endomorphism ![]() $\tau _{\beta }$ in Lemma 3.17 induces an endomorphism of
$\tau _{\beta }$ in Lemma 3.17 induces an endomorphism of ![]() $\mathbf B ( \mathbb X ( \varpi_i ))$ for each
$\mathbf B ( \mathbb X ( \varpi_i ))$ for each ![]() $\beta \in Q$ and
$\beta \in Q$ and ![]() $i \in \mathtt I$, and hence we know the existence of the injective endomorphisms of
$i \in \mathtt I$, and hence we know the existence of the injective endomorphisms of ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ that form a polynomial algebra whose graded dimension is equal to
$\mathbb {W} ( \lambda )_{\Bbbk }$ that form a polynomial algebra whose graded dimension is equal to
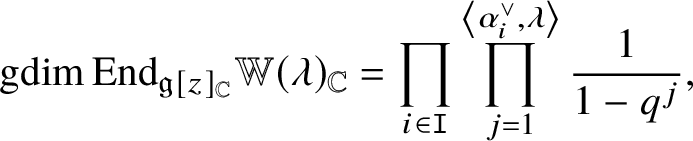 $$ \begin{align*}\mathrm{gdim}\, \mathrm{End}_{\mathfrak{g} [z]_{\mathbb C}} \mathbb{W} ( \lambda )_{\mathbb C} = \prod_{i \in \mathtt I} \prod_{j=1}^{\left\langle \alpha_i^{\vee}, \lambda \right\rangle}\frac{1}{1-q^j},\end{align*} $$
$$ \begin{align*}\mathrm{gdim}\, \mathrm{End}_{\mathfrak{g} [z]_{\mathbb C}} \mathbb{W} ( \lambda )_{\mathbb C} = \prod_{i \in \mathtt I} \prod_{j=1}^{\left\langle \alpha_i^{\vee}, \lambda \right\rangle}\frac{1}{1-q^j},\end{align*} $$which can be read off from [Reference Beck and Nakajima5, Proposition 4.13] (or [Reference Kato46, Theorem 1.4]), through Theorem 3.18. By [Reference Beck and Nakajima5, Reference Chari and Ion18, Reference Kato46], it exhausts the P-weight ![]() $\lambda $-part of
$\lambda $-part of ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$, which generates
$\mathbb {W} ( \lambda )_{\Bbbk }$, which generates ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ as a
$\mathbb {W} ( \lambda )_{\Bbbk }$ as a  $\mathring {U}^{\ge 0}_\Bbbk $-module. Therefore, we conclude the result.
$\mathring {U}^{\ge 0}_\Bbbk $-module. Therefore, we conclude the result.
The rest of this subsection is devoted to the proof of Proposition 3.19.
We consider the Demazure functor ![]() $\mathscr D_{w}$ for
$\mathscr D_{w}$ for ![]() $w \in W_{\mathrm {af}}$ with respect to
$w \in W_{\mathrm {af}}$ with respect to ![]() $\mathring {U}^+_\Bbbk $ (compare [Reference Joseph39, Reference Kato46, Reference Cherednik and Kato20]). In view of [Reference Kashiwara45, §2.8], the character part of the calculation in [Reference Kato46, Theorem 4.13] carries over to our setting, and hence we have
$\mathring {U}^+_\Bbbk $ (compare [Reference Joseph39, Reference Kato46, Reference Cherednik and Kato20]). In view of [Reference Kashiwara45, §2.8], the character part of the calculation in [Reference Kato46, Theorem 4.13] carries over to our setting, and hence we have
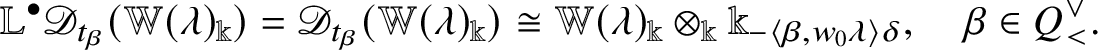 $$ \begin{align*}\mathbb L^{\bullet} \mathscr D_{t_{\beta}} ( \mathbb{W} ( \lambda )_{\Bbbk}) = \mathscr D_{t_{\beta}} ( \mathbb{W} ( \lambda )_{\Bbbk}) \cong \mathbb{W} ( \lambda )_{\Bbbk} \otimes_{\Bbbk} \Bbbk_{- \left\langle \beta, w_0 \lambda \right\rangle \delta}, \quad \beta \in Q^{\vee}_<.\end{align*} $$
$$ \begin{align*}\mathbb L^{\bullet} \mathscr D_{t_{\beta}} ( \mathbb{W} ( \lambda )_{\Bbbk}) = \mathscr D_{t_{\beta}} ( \mathbb{W} ( \lambda )_{\Bbbk}) \cong \mathbb{W} ( \lambda )_{\Bbbk} \otimes_{\Bbbk} \Bbbk_{- \left\langle \beta, w_0 \lambda \right\rangle \delta}, \quad \beta \in Q^{\vee}_<.\end{align*} $$From this, we also derive
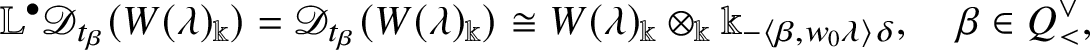 $$ \begin{align*}\mathbb L^{\bullet} \mathscr D_{t_{\beta}} ( W ( \lambda )_{\Bbbk}) = \mathscr D_{t_{\beta}} ( W ( \lambda )_{\Bbbk}) \cong W ( \lambda )_{\Bbbk} \otimes_{\Bbbk} \Bbbk_{- \left\langle \beta, w_0 \lambda \right\rangle \delta}, \quad \beta \in Q^{\vee}_<,\end{align*} $$
$$ \begin{align*}\mathbb L^{\bullet} \mathscr D_{t_{\beta}} ( W ( \lambda )_{\Bbbk}) = \mathscr D_{t_{\beta}} ( W ( \lambda )_{\Bbbk}) \cong W ( \lambda )_{\Bbbk} \otimes_{\Bbbk} \Bbbk_{- \left\langle \beta, w_0 \lambda \right\rangle \delta}, \quad \beta \in Q^{\vee}_<,\end{align*} $$using the Koszul resolution as in [Reference Cherednik and Kato20, §5.1.4] by Lemma 3.20.
The d-gradings of  $\mathring {U}^+_\Bbbk , \mathbb {W} ( \lambda )$ and
$\mathring {U}^+_\Bbbk , \mathbb {W} ( \lambda )$ and ![]() $W ( \mu )_{\Bbbk }$ are concentrated in nonnegative degrees. It follows that the d-grading of
$W ( \mu )_{\Bbbk }$ are concentrated in nonnegative degrees. It follows that the d-grading of  $\mathrm {Ext}^{\bullet } _{\mathring {U}^+_\Bbbk } \left ( \mathbb {W} ( \lambda ), W ( \mu )_{\Bbbk }^* \right )$ is bounded from above. Moreover, we have
$\mathrm {Ext}^{\bullet } _{\mathring {U}^+_\Bbbk } \left ( \mathbb {W} ( \lambda ), W ( \mu )_{\Bbbk }^* \right )$ is bounded from above. Moreover, we have
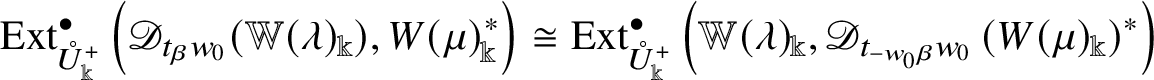 $$ \begin{align*}\mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} \left( \mathscr D_{t_{\beta}w_0} ( \mathbb{W} ( \lambda )_{\Bbbk}), W ( \mu )_{\Bbbk}^* \right) \cong \mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} \left( \mathbb{W} ( \lambda )_{\Bbbk}, \mathscr D_{t_{-w_0 \beta}w_0} \left( W ( \mu )_{\Bbbk} \right)^* \right)\end{align*} $$
$$ \begin{align*}\mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} \left( \mathscr D_{t_{\beta}w_0} ( \mathbb{W} ( \lambda )_{\Bbbk}), W ( \mu )_{\Bbbk}^* \right) \cong \mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} \left( \mathbb{W} ( \lambda )_{\Bbbk}, \mathscr D_{t_{-w_0 \beta}w_0} \left( W ( \mu )_{\Bbbk} \right)^* \right)\end{align*} $$for every ![]() $\lambda , \mu \in P_+$ and
$\lambda , \mu \in P_+$ and ![]() $\beta \in Q^{\vee }_<$ by repeated application of [Reference Feigin, Kato and Makedonskyi25, Proposition 5.7] (the argument of which carries over to our setting). By varying
$\beta \in Q^{\vee }_<$ by repeated application of [Reference Feigin, Kato and Makedonskyi25, Proposition 5.7] (the argument of which carries over to our setting). By varying ![]() $\beta $, we conclude that
$\beta $, we conclude that
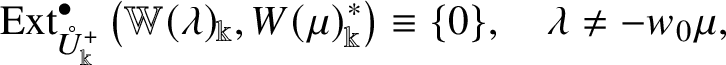 $$ \begin{align} \mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} \left( \mathbb{W} ( \lambda )_{\Bbbk}, W ( \mu )_{\Bbbk}^* \right) \equiv \{ 0 \}, \quad \lambda \neq -w_0 \mu, \end{align} $$
$$ \begin{align} \mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} \left( \mathbb{W} ( \lambda )_{\Bbbk}, W ( \mu )_{\Bbbk}^* \right) \equiv \{ 0 \}, \quad \lambda \neq -w_0 \mu, \end{align} $$since ![]() $- \left \langle \beta , w_0 \lambda \right \rangle \neq - \left \langle - w_0 \beta , w_0 \mu \right \rangle = \left \langle \beta , \mu \right \rangle $ for some choice of
$- \left \langle \beta , w_0 \lambda \right \rangle \neq - \left \langle - w_0 \beta , w_0 \mu \right \rangle = \left \langle \beta , \mu \right \rangle $ for some choice of ![]() $\beta $.
$\beta $.
Consider the simple integrable ![]() $\mathring {U}_{\Bbbk }^0$-module quotient
$\mathring {U}_{\Bbbk }^0$-module quotient ![]() $L ( \lambda )_{\Bbbk }$ of
$L ( \lambda )_{\Bbbk }$ of ![]() $V ( \lambda )_{\Bbbk }$ for each
$V ( \lambda )_{\Bbbk }$ for each ![]() $\lambda \in P_+$.
$\lambda \in P_+$.
Lemma 3.22. The set ![]() $\left \{L ( \lambda )_{\Bbbk }\right \}_{\lambda \in P_+}$ is the complete collection of the isomorphism classes of the irreducible d-graded
$\left \{L ( \lambda )_{\Bbbk }\right \}_{\lambda \in P_+}$ is the complete collection of the isomorphism classes of the irreducible d-graded ![]() $\mathring {U}_{\Bbbk }^0$-integrable
$\mathring {U}_{\Bbbk }^0$-integrable  $\mathring {U}^{\ge 0}_{\Bbbk }$-modules
$\mathring {U}^{\ge 0}_{\Bbbk }$-modules ![]() $($up to d-grading shifts
$($up to d-grading shifts![]() $)$.
$)$.
Proof. Since ![]() $V ( \lambda )_{\Bbbk }$ surjects onto every irreducible
$V ( \lambda )_{\Bbbk }$ surjects onto every irreducible ![]() $\mathring {U}_{\Bbbk }^0$-module with highest weight
$\mathring {U}_{\Bbbk }^0$-module with highest weight ![]() $\lambda $ ([Reference Andersen, Polo and Wen1, §1.20]), it follows that it surjects onto every irreducible d-graded
$\lambda $ ([Reference Andersen, Polo and Wen1, §1.20]), it follows that it surjects onto every irreducible d-graded  $\mathring {U}^{\ge 0}_{\Bbbk }$-module with highest weight
$\mathring {U}^{\ge 0}_{\Bbbk }$-module with highest weight ![]() $\lambda $. Since the P-weight
$\lambda $. Since the P-weight ![]() $\lambda $-part of
$\lambda $-part of ![]() $V ( \lambda )_{\Bbbk }$ is one-dimensional, we conclude the result.
$V ( \lambda )_{\Bbbk }$ is one-dimensional, we conclude the result.
We return to the proof of Proposition 3.19. We have
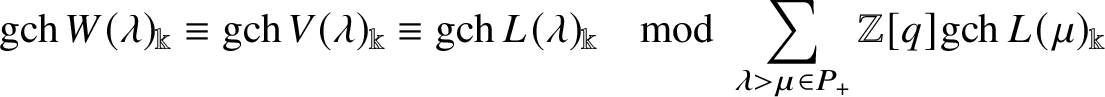 $$ \begin{align*}\mathrm{gch}\, W ( \lambda )_{\Bbbk} \equiv \mathrm{gch}\, V ( \lambda )_{\Bbbk} \equiv \mathrm{gch}\, L ( \lambda )_{\Bbbk} \mod \sum_{\lambda> \mu \in P_+} \mathbb{Z} [q] \mathrm{gch}\, L ( \mu )_{\Bbbk}\end{align*} $$
$$ \begin{align*}\mathrm{gch}\, W ( \lambda )_{\Bbbk} \equiv \mathrm{gch}\, V ( \lambda )_{\Bbbk} \equiv \mathrm{gch}\, L ( \lambda )_{\Bbbk} \mod \sum_{\lambda> \mu \in P_+} \mathbb{Z} [q] \mathrm{gch}\, L ( \mu )_{\Bbbk}\end{align*} $$by [Reference Lenart, Naito, Sagaki, Schilling and Shimozono62] (compare [Reference Chari and Ion18]). Therefore, ![]() $W ( \lambda )_{\Bbbk }$ admits a (d-graded) Jordan–Hölder series as a
$W ( \lambda )_{\Bbbk }$ admits a (d-graded) Jordan–Hölder series as a  $\mathring {U}^{\ge 0}_\Bbbk $-module whose irreducible constituents are of the form
$\mathring {U}^{\ge 0}_\Bbbk $-module whose irreducible constituents are of the form ![]() $\{L ( \mu )_{\Bbbk }\}_{\mu \le \lambda }$ (up to d-grading shifts). It follows that
$\{L ( \mu )_{\Bbbk }\}_{\mu \le \lambda }$ (up to d-grading shifts). It follows that
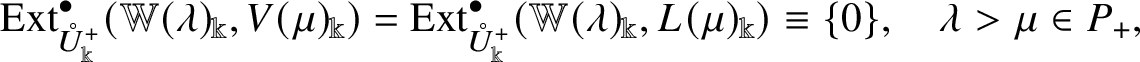 $$ \begin{align*}\mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, V ( \mu )_{\Bbbk} ) = \mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, L ( \mu )_{\Bbbk} ) \equiv \{ 0 \}, \quad \lambda> \mu \in P_+,\end{align*} $$
$$ \begin{align*}\mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, V ( \mu )_{\Bbbk} ) = \mathrm{Ext}^{\bullet} _{\mathring{U}^+_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, L ( \mu )_{\Bbbk} ) \equiv \{ 0 \}, \quad \lambda> \mu \in P_+,\end{align*} $$by a repeated application of the short exact sequences to formula (3.4). Since both ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ and
$\mathbb {W} ( \lambda )_{\Bbbk }$ and ![]() $L ( \lambda )_{\Bbbk }$ are
$L ( \lambda )_{\Bbbk }$ are ![]() $\dot {U}^0_\Bbbk $-integrable, we find
$\dot {U}^0_\Bbbk $-integrable, we find
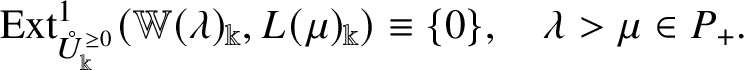 $$ \begin{align*}\mathrm{Ext}^{1} _{\mathring{U}^{\ge 0}_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, L ( \mu )_{\Bbbk} ) \equiv \{ 0 \}, \quad \lambda> \mu \in P_+.\end{align*} $$
$$ \begin{align*}\mathrm{Ext}^{1} _{\mathring{U}^{\ge 0}_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, L ( \mu )_{\Bbbk} ) \equiv \{ 0 \}, \quad \lambda> \mu \in P_+.\end{align*} $$From these, it suffices to prove
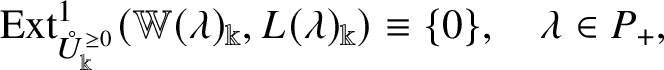 $$ \begin{align} \mathrm{Ext}^{1} _{\mathring{U}^{\ge 0}_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, L ( \lambda )_{\Bbbk} ) \equiv \{ 0 \}, \quad \lambda \in P_+, \end{align} $$
$$ \begin{align} \mathrm{Ext}^{1} _{\mathring{U}^{\ge 0}_\Bbbk} ( \mathbb{W} ( \lambda )_{\Bbbk}, L ( \lambda )_{\Bbbk} ) \equiv \{ 0 \}, \quad \lambda \in P_+, \end{align} $$to deduce the assertion.
In view of the fact that ![]() $\lambda + \alpha _i$ (
$\lambda + \alpha _i$ (![]() $i \in \mathtt I$) is not a P-weight of
$i \in \mathtt I$) is not a P-weight of ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$, the Drinfeld presentation of
$\mathbb {W} ( \lambda )_{\Bbbk }$, the Drinfeld presentation of  $\mathring {U}^{\ge 0}_\Bbbk $ ([Reference Beck and Nakajima5, §3]) forces the space of
$\mathring {U}^{\ge 0}_\Bbbk $ ([Reference Beck and Nakajima5, §3]) forces the space of  $\mathring {U}^{\ge 0}_\Bbbk $-module endomorphisms of
$\mathring {U}^{\ge 0}_\Bbbk $-module endomorphisms of ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ to be generated by the images of the imaginary weight vectors
$\mathbb {W} ( \lambda )_{\Bbbk }$ to be generated by the images of the imaginary weight vectors ![]() $\tilde {P}_{i,m\delta }$ for
$\tilde {P}_{i,m\delta }$ for ![]() $i \in \mathtt I$ and
$i \in \mathtt I$ and ![]() $m> 0$ (defined in [Reference Beck and Nakajima5, (3.7)]). In view of its descriptions ([Reference Beck and Nakajima5, Proposition 3.17] or [Reference Chari, Fourier and Khandai17, Lemma 4.5]), we find that
$m> 0$ (defined in [Reference Beck and Nakajima5, (3.7)]). In view of its descriptions ([Reference Beck and Nakajima5, Proposition 3.17] or [Reference Chari, Fourier and Khandai17, Lemma 4.5]), we find that ![]() $\tilde {P}_{i,m}$ acts on
$\tilde {P}_{i,m}$ acts on ![]() $\mathbf {v}_\lambda \in \mathbb {W} ( \lambda )_{\Bbbk }$ by zero if
$\mathbf {v}_\lambda \in \mathbb {W} ( \lambda )_{\Bbbk }$ by zero if  $\left \langle \alpha ^{\vee }_i, \lambda \right \rangle> m$. From this, we derive that the P-weight
$\left \langle \alpha ^{\vee }_i, \lambda \right \rangle> m$. From this, we derive that the P-weight ![]() $\lambda $-part of
$\lambda $-part of ![]() $\mathbb {W} ( \lambda )_{\Bbbk }$ is maximal possible as a cyclic module with a cyclic vector of P-weight
$\mathbb {W} ( \lambda )_{\Bbbk }$ is maximal possible as a cyclic module with a cyclic vector of P-weight ![]() $\lambda $ in the category of
$\lambda $ in the category of  $\mathring {U}_\Bbbk ^{\ge 0}$-modules that are
$\mathring {U}_\Bbbk ^{\ge 0}$-modules that are ![]() $\mathring {U}_\Bbbk ^0$-integrable and whose P-weights are contained in
$\mathring {U}_\Bbbk ^0$-integrable and whose P-weights are contained in ![]() $\mathrm {Conv} W \lambda \subset P \otimes _{\mathbb {Z}} \mathbb {R}$. Therefore, formula (3.5) vanishes and we conclude Proposition 3.19.
$\mathrm {Conv} W \lambda \subset P \otimes _{\mathbb {Z}} \mathbb {R}$. Therefore, formula (3.5) vanishes and we conclude Proposition 3.19.
3.4 Frobenius splitting of  $\mathbf {Q}_{G,\mathtt J}$
$\mathbf {Q}_{G,\mathtt J}$
Theorem 3.23. For each ![]() $\Lambda \in P^{\mathrm {af}}_+$, we have a surjective map
$\Lambda \in P^{\mathrm {af}}_+$, we have a surjective map ![]() $L ( \Lambda )_{\mathbb C} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb C}$ of
$L ( \Lambda )_{\mathbb C} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb C}$ of  $\mathfrak {g} \left [z^{-1}\right ]_{\mathbb C}$-modules. In addition, this map yields a surjection
$\mathfrak {g} \left [z^{-1}\right ]_{\mathbb C}$-modules. In addition, this map yields a surjection ![]() $L ( \Lambda )_{\mathbb {Z}} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb {Z}}$ of
$L ( \Lambda )_{\mathbb {Z}} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb {Z}}$ of ![]() $U^-_{\mathbb {Z}}$-modules.
$U^-_{\mathbb {Z}}$-modules.
Proof. By [Reference Kato and Loktev50, Theorem A], the graded ![]() $\mathfrak {g} [z]_{\mathbb C}$-module
$\mathfrak {g} [z]_{\mathbb C}$-module ![]() $\theta ^* ( L ( \Lambda )_{\mathbb C} )$ admits a filtration by the grading shifts of
$\theta ^* ( L ( \Lambda )_{\mathbb C} )$ admits a filtration by the grading shifts of ![]() $\{ \mathbb {W} ( \mu )_{\mathbb C} \}_{\mu \in P_+}$. Since the (d-)degrees of
$\{ \mathbb {W} ( \mu )_{\mathbb C} \}_{\mu \in P_+}$. Since the (d-)degrees of ![]() $L ( \Lambda )_{\mathbb C}$ are concentrated in
$L ( \Lambda )_{\mathbb C}$ are concentrated in ![]() $\mathbb {Z}_{\le 0}$ and the degree
$\mathbb {Z}_{\le 0}$ and the degree ![]() $0$ part of
$0$ part of ![]() $L ( \Lambda )_{\mathbb C}$ is
$L ( \Lambda )_{\mathbb C}$ is ![]() $V (\bar{\Lambda})_{\mathbb C}$, the first quotient of
$V (\bar{\Lambda})_{\mathbb C}$, the first quotient of ![]() $\theta ^* ( L ( \Lambda )_{\mathbb C} )$ in our filtration must be
$\theta ^* ( L ( \Lambda )_{\mathbb C} )$ in our filtration must be ![]() $\theta ^* \left ( \mathbb {W}^- (\bar{\Lambda})_{\mathbb C} \right )$. Hence we obtain the surjection
$\theta ^* \left ( \mathbb {W}^- (\bar{\Lambda})_{\mathbb C} \right )$. Hence we obtain the surjection ![]() $\eta : L ( \Lambda )_{\mathbb C} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb C}$ of
$\eta : L ( \Lambda )_{\mathbb C} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb C}$ of  $\mathfrak {g} \left [z^{-1}\right ]_{\mathbb C}$-modules.
$\mathfrak {g} \left [z^{-1}\right ]_{\mathbb C}$-modules.
Since both modules share the ![]() $U^-_{\mathbb C}$-cyclic vector and are compatible with the negative global basis, we conclude that the
$U^-_{\mathbb C}$-cyclic vector and are compatible with the negative global basis, we conclude that the ![]() $\mathbb {Z}$-basis of
$\mathbb {Z}$-basis of ![]() $\mathbb {W}^- (\bar{\Lambda})_{\mathbb {Z}}$ is obtained as a
$\mathbb {W}^- (\bar{\Lambda})_{\mathbb {Z}}$ is obtained as a ![]() $\mathbb {Z}$-basis of
$\mathbb {Z}$-basis of ![]() $L ( \Lambda )_{\mathbb {Z}}$ that is not annihilated by
$L ( \Lambda )_{\mathbb {Z}}$ that is not annihilated by ![]() $\eta $. Hence we conclude that
$\eta $. Hence we conclude that ![]() $\eta $ induces a surjection
$\eta $ induces a surjection ![]() $L ( \Lambda )_{\mathbb {Z}} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb {Z}}$ of
$L ( \Lambda )_{\mathbb {Z}} \rightarrow \mathbb {W}^- (\bar{\Lambda})_{\mathbb {Z}}$ of ![]() $U^-_{\mathbb {Z}}$-modules.
$U^-_{\mathbb {Z}}$-modules.
Corollary 3.24. Let ![]() $\Bbbk $ be a field. For
$\Bbbk $ be a field. For ![]() $\Lambda \in P^{\mathrm {af}}_+$, we have a
$\Lambda \in P^{\mathrm {af}}_+$, we have a ![]() $U^-_\Bbbk $-module generator set
$U^-_\Bbbk $-module generator set ![]() $\{ \mathbf {u} _m \}_{m \in \mathbb {Z}_{\ge 0}}$ of
$\{ \mathbf {u} _m \}_{m \in \mathbb {Z}_{\ge 0}}$ of ![]() $\ker \left ( L ( \Lambda )_\Bbbk \rightarrow \mathbb {W}^- (\bar{\Lambda})_\Bbbk \right )$ that satisfies the following:
$\ker \left ( L ( \Lambda )_\Bbbk \rightarrow \mathbb {W}^- (\bar{\Lambda})_\Bbbk \right )$ that satisfies the following:
• Each element
 $\mathbf {u}_m$ satisfies
$\mathbf {u}_m$ satisfies  $a_{\Lambda _m} \mathbf {u}_m = \mathbf {u}_m$ for some
$a_{\Lambda _m} \mathbf {u}_m = \mathbf {u}_m$ for some  $\Lambda _m \in P^{\mathrm {af}}$.
$\Lambda _m \in P^{\mathrm {af}}$.• For each
 $m \in \mathbb {Z}_{\ge 0}$, we have
$m \in \mathbb {Z}_{\ge 0}$, we have  $\overline {\Lambda }_m \not \in \mathrm {Conv} W \overline {\Lambda } \subset P \otimes _{\mathbb {Z}} \mathbb {R}$.
$\overline {\Lambda }_m \not \in \mathrm {Conv} W \overline {\Lambda } \subset P \otimes _{\mathbb {Z}} \mathbb {R}$.
Proof. Note that ![]() $L ( \Lambda )_\Bbbk $ has at most countable rank over
$L ( \Lambda )_\Bbbk $ has at most countable rank over ![]() $\Bbbk $, which implies that the generator set is at most countable. As both
$\Bbbk $, which implies that the generator set is at most countable. As both ![]() $L ( \Lambda )_\Bbbk $ and
$L ( \Lambda )_\Bbbk $ and ![]() $\mathbb {W}^- (\bar{\Lambda})_\Bbbk $ admit
$\mathbb {W}^- (\bar{\Lambda})_\Bbbk $ admit ![]() $P^{\mathrm {af}}$-weight decompositions, we deduce the first assertion. Since both modules are
$P^{\mathrm {af}}$-weight decompositions, we deduce the first assertion. Since both modules are ![]() $\dot {U}^0_\Bbbk $-integrable and
$\dot {U}^0_\Bbbk $-integrable and ![]() $U^-_\Bbbk $-cyclic, the second assertion follows by Proposition 3.19.
$U^-_\Bbbk $-cyclic, the second assertion follows by Proposition 3.19.
Proposition 3.25. For each ![]() $\Lambda , \Gamma \in P^{\mathrm {af}}_+$, we have the following commutative diagram of
$\Lambda , \Gamma \in P^{\mathrm {af}}_+$, we have the following commutative diagram of ![]() $U^-_{\mathbb {Z}}$-modules:
$U^-_{\mathbb {Z}}$-modules:

Moreover, all the maps define direct summands as ![]() $\mathbb {Z}$-modules.
$\mathbb {Z}$-modules.
Proof. The injectivity of the top horizontal arrow and the fact that it defines a direct summand as ![]() $\mathbb {Z}$-modules are Corollary 3.12.
$\mathbb {Z}$-modules are Corollary 3.12.
The surjectivity of the vertical arrows is Theorem 3.23. Since they are obtained by annihilating parts of ![]() $\mathbb {Z}$-bases, these maps define direct summands as
$\mathbb {Z}$-bases, these maps define direct summands as ![]() $\mathbb {Z}$-modules.
$\mathbb {Z}$-modules.
Since all the modules are generated by the cyclic vectors ![]() $\mathbf {v}_{\Lambda + \Gamma }$ or
$\mathbf {v}_{\Lambda + \Gamma }$ or ![]() $\mathbf {v}_{\Lambda } \otimes \mathbf {v}_{\Gamma }$ as
$\mathbf {v}_{\Lambda } \otimes \mathbf {v}_{\Gamma }$ as  $\mathfrak {g} \left [z^{-1}\right ]_{\mathbb C}$-modules or
$\mathfrak {g} \left [z^{-1}\right ]_{\mathbb C}$-modules or  $\mathfrak {g} \left [z^{-1}\right ]^{\oplus 2}_{\mathbb C}$-modules, Theorem 2.3 (twisted by
$\mathfrak {g} \left [z^{-1}\right ]^{\oplus 2}_{\mathbb C}$-modules, Theorem 2.3 (twisted by ![]() $\theta $) implies the injectivity of
$\theta $) implies the injectivity of ![]() $\mathsf {m}$ after extending the scalar to
$\mathsf {m}$ after extending the scalar to ![]() ${\mathbb C}$. Hence we deduce
${\mathbb C}$. Hence we deduce
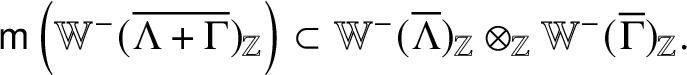 $$ \begin{align} \mathsf{m} \left( \mathbb{W}^- (\overline{\Lambda + \Gamma})_{\mathbb{Z}} \right) \subset \mathbb{W}^- (\overline{\Lambda})_{\mathbb{Z}} \otimes_{\mathbb{Z}} \mathbb{W}^- (\overline{\Gamma})_{\mathbb{Z}}. \end{align} $$
$$ \begin{align} \mathsf{m} \left( \mathbb{W}^- (\overline{\Lambda + \Gamma})_{\mathbb{Z}} \right) \subset \mathbb{W}^- (\overline{\Lambda})_{\mathbb{Z}} \otimes_{\mathbb{Z}} \mathbb{W}^- (\overline{\Gamma})_{\mathbb{Z}}. \end{align} $$ Therefore, to complete the proof it suffices to prove that formula (3.6) has torsion-free cokernel (as a ![]() $\mathbb {Z}$-module). By a repeated use of formula (3.6), we arrive the setting of Theorem 3.18 in view of Theorem 2.3. Thus, the map
$\mathbb {Z}$-module). By a repeated use of formula (3.6), we arrive the setting of Theorem 3.18 in view of Theorem 2.3. Thus, the map ![]() $\mathsf {m}$ defines a direct summand of
$\mathsf {m}$ defines a direct summand of ![]() $\mathbb {W} (\overline{\Lambda})_{\mathbb {Z}} \otimes _{\mathbb {Z}} \mathbb {W} (\overline{\Gamma})_{\mathbb {Z}}$ as
$\mathbb {W} (\overline{\Lambda})_{\mathbb {Z}} \otimes _{\mathbb {Z}} \mathbb {W} (\overline{\Gamma})_{\mathbb {Z}}$ as ![]() $\mathbb {Z}$-modules.
$\mathbb {Z}$-modules.
Corollary 3.26. For each ![]() $\lambda , \mu \in P_+$ and
$\lambda , \mu \in P_+$ and ![]() $w \in W$, we have the following commutative diagram of
$w \in W$, we have the following commutative diagram of ![]() $U_{\mathbb {Z}}^+$-modules:
$U_{\mathbb {Z}}^+$-modules:
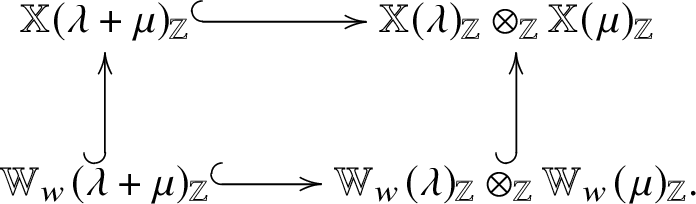
The vertical inclusions are compatible with positive global basis, and the horizontal inclusions define direct summands as ![]() $\mathbb {Z}$-modules. In addition, all the inclusions commute with the automorphism
$\mathbb {Z}$-modules. In addition, all the inclusions commute with the automorphism ![]() $\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ of
$\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ of ![]() $\mathbb {X} ( \lambda )_{\mathbb {Z}}, \mathbb {X} ( \mu )_{\mathbb {Z}}$ and
$\mathbb {X} ( \lambda )_{\mathbb {Z}}, \mathbb {X} ( \mu )_{\mathbb {Z}}$ and ![]() $\mathbb {X} ( \lambda + \mu )_{\mathbb {Z}}$.
$\mathbb {X} ( \lambda + \mu )_{\mathbb {Z}}$.
Proof. In view of Proposition 3.25, the ![]() $w = w_0$ case follows from Lemma 3.17(1). Thanks to Theorem 2.3 and Lemma 3.17(3), we deduce the general case from the
$w = w_0$ case follows from Lemma 3.17(1). Thanks to Theorem 2.3 and Lemma 3.17(3), we deduce the general case from the ![]() $w = w_0$ case.
$w = w_0$ case.
Set ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$. We define
$\mathtt J \subset \mathtt I$. We define ![]() $P_+$- and
$P_+$- and ![]() $P_{\mathtt J,+}$- graded
$P_{\mathtt J,+}$- graded ![]() $\mathbb {Z}$-modules
$\mathbb {Z}$-modules
 $$ \begin{align*}R ^{\mathrm{af}} := \bigoplus_{\Lambda \in P_+^{\mathrm{af}}} L ( \Lambda )_{\mathbb{Z}} ^{\vee} \quad \text{and} \quad R _{w}( \mathtt J ) := \bigoplus_{\lambda \in P_{\mathtt J,+}} \mathbb{W}_{ww_0} ( \lambda )_{\mathbb{Z}} ^{\vee}.\end{align*} $$
$$ \begin{align*}R ^{\mathrm{af}} := \bigoplus_{\Lambda \in P_+^{\mathrm{af}}} L ( \Lambda )_{\mathbb{Z}} ^{\vee} \quad \text{and} \quad R _{w}( \mathtt J ) := \bigoplus_{\lambda \in P_{\mathtt J,+}} \mathbb{W}_{ww_0} ( \lambda )_{\mathbb{Z}} ^{\vee}.\end{align*} $$Lemma 3.27. The ![]() $\mathbb {Z}$-duals of the horizontal maps in Proposition 3.25 equip
$\mathbb {Z}$-duals of the horizontal maps in Proposition 3.25 equip ![]() $R ^{\mathrm {af}}$ and
$R ^{\mathrm {af}}$ and ![]() $R _{w}( \mathtt J )$ structures of (
$R _{w}( \mathtt J )$ structures of (![]() $P_+$- and
$P_+$- and ![]() $P_{\mathtt J,+}$-)graded commutative rings.
$P_{\mathtt J,+}$-)graded commutative rings.
Proof. The maps in Proposition 3.25 are characterised as the d-degree ![]() $0$ maps of cyclic
$0$ maps of cyclic ![]() $U^-_{\mathbb {Z}}$-modules, which are unique up to a scalar. Therefore, the composition
$U^-_{\mathbb {Z}}$-modules, which are unique up to a scalar. Therefore, the composition
is the same map as
for every ![]() $\lambda , \mu , \gamma \in P_+$, as the images of the cyclic vectors are the same. Taking their restricted duals implies the associativity of the multiplication of
$\lambda , \mu , \gamma \in P_+$, as the images of the cyclic vectors are the same. Taking their restricted duals implies the associativity of the multiplication of ![]() $R _{e}( \mathtt J )$. In view of Lemma 3.17(1) and Corollary 3.26, we deduce the associativity of the multiplication of
$R _{e}( \mathtt J )$. In view of Lemma 3.17(1) and Corollary 3.26, we deduce the associativity of the multiplication of ![]() $R _{w}( \mathtt J )$ for each
$R _{w}( \mathtt J )$ for each ![]() $w \in W_{\mathrm {af}}$. The associativity of
$w \in W_{\mathrm {af}}$. The associativity of ![]() $R ^{\mathrm {af}}$ is proved similarly (compare [Reference Kato49]). The commutativity of
$R ^{\mathrm {af}}$ is proved similarly (compare [Reference Kato49]). The commutativity of ![]() $R ^{\mathrm {af}}$ and
$R ^{\mathrm {af}}$ and ![]() $R _{w}( \mathtt J )$ follow, as the
$R _{w}( \mathtt J )$ follow, as the ![]() $\mathsf {q} = 1$ coproduct of
$\mathsf {q} = 1$ coproduct of ![]() $\dot {U}_{\mathbb {Z}}$ is symmetric ([Reference Lusztig66, Lemma 3.1.4, §23.1.5]).
$\dot {U}_{\mathbb {Z}}$ is symmetric ([Reference Lusztig66, Lemma 3.1.4, §23.1.5]).
Corollary 3.28 Corollary of the proof of Lemma 3.27
For each ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $\beta \in Q^{\vee }$, we have an isomorphism of
$\beta \in Q^{\vee }$, we have an isomorphism of ![]() $( R_w )_{\mathbb {Z}}$ and
$( R_w )_{\mathbb {Z}}$ and  $\left ( R_{wt_{\beta }} \right )_{\mathbb {Z}}$ as graded commutative rings equipped with
$\left ( R_{wt_{\beta }} \right )_{\mathbb {Z}}$ as graded commutative rings equipped with ![]() $U_{\mathbb {Z}}^+$-actions up to grading twists (given by Lemma 3.17).
$U_{\mathbb {Z}}^+$-actions up to grading twists (given by Lemma 3.17).
We set ![]() $R := R_e$. Note that
$R := R_e$. Note that ![]() $R_{w} ( \mathtt J )\subset R_w$ is a subring. We also define
$R_{w} ( \mathtt J )\subset R_w$ is a subring. We also define
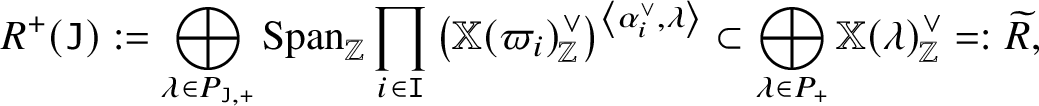 $$ \begin{align*}R^+ ( \mathtt J ) := \bigoplus_{\lambda \in P_{\mathtt J, +}} \mathrm{Span}_{\mathbb{Z}} \prod_{i \in \mathtt I} \left( \mathbb{X} ( \varpi_i )_{\mathbb{Z}}^{\vee} \right)^{\left\langle \alpha_i^{\vee}, \lambda \right\rangle} \subset \bigoplus_{\lambda \in P_+} \mathbb{X} ( \lambda )_{\mathbb{Z}} ^{\vee} =: \widetilde{R},\end{align*} $$
$$ \begin{align*}R^+ ( \mathtt J ) := \bigoplus_{\lambda \in P_{\mathtt J, +}} \mathrm{Span}_{\mathbb{Z}} \prod_{i \in \mathtt I} \left( \mathbb{X} ( \varpi_i )_{\mathbb{Z}}^{\vee} \right)^{\left\langle \alpha_i^{\vee}, \lambda \right\rangle} \subset \bigoplus_{\lambda \in P_+} \mathbb{X} ( \lambda )_{\mathbb{Z}} ^{\vee} =: \widetilde{R},\end{align*} $$where the multiplication is defined through the projective limit formed by the duals of Corollary 3.26. Here we warn that the (![]() $\mathbb {Z}$-)rank of some
$\mathbb {Z}$-)rank of some ![]() $P^{\mathrm {af}}$-weight space of
$P^{\mathrm {af}}$-weight space of ![]() $\mathbb {X} ( \lambda )_{\mathbb {Z}}$ can be infinity, and hence the inclusion
$\mathbb {X} ( \lambda )_{\mathbb {Z}}$ can be infinity, and hence the inclusion ![]() $R^+ \subsetneq \widetilde {R}$ has a huge cokernel. Note that the rank of the
$R^+ \subsetneq \widetilde {R}$ has a huge cokernel. Note that the rank of the ![]() $P^{\mathrm {af}}$-weight spaces of
$P^{\mathrm {af}}$-weight spaces of ![]() $\mathbb {X} ( \varpi _i )_{\mathbb {Z}}$ is bounded for each
$\mathbb {X} ( \varpi _i )_{\mathbb {Z}}$ is bounded for each ![]() $i \in \mathtt I$ ([Reference Kashiwara44, Proposition 5.16]), and hence
$i \in \mathtt I$ ([Reference Kashiwara44, Proposition 5.16]), and hence ![]() $R^+ ( \mathtt J )$ has only countably many generators of
$R^+ ( \mathtt J )$ has only countably many generators of ![]() $P_{\mathtt J,+}$-degrees
$P_{\mathtt J,+}$-degrees ![]() $\{ \varpi _i \}_{i \in \mathtt I \setminus \mathtt J}$.
$\{ \varpi _i \}_{i \in \mathtt I \setminus \mathtt J}$.
By construction, the rings ![]() $R ^{\mathrm {af}}, R _{w}( \mathtt J )$ and
$R ^{\mathrm {af}}, R _{w}( \mathtt J )$ and ![]() $R^+ ( \mathtt J )$ are free over
$R^+ ( \mathtt J )$ are free over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
For each ![]() $\lambda \in P_+$ and
$\lambda \in P_+$ and ![]() $w \in W_{\mathrm {af}}$, we have a unique
$w \in W_{\mathrm {af}}$, we have a unique ![]() $P^{\mathrm {af}}$-weight vector
$P^{\mathrm {af}}$-weight vector
with paring ![]() $1$ with
$1$ with ![]() $\mathbf {v}_{w\lambda } \in \mathbb {W}_w ( \lambda )_{\mathbb {Z}}$. This vector
$\mathbf {v}_{w\lambda } \in \mathbb {W}_w ( \lambda )_{\mathbb {Z}}$. This vector ![]() $\mathbf {v}_{w\lambda }^{\vee }$ yields a
$\mathbf {v}_{w\lambda }^{\vee }$ yields a ![]() $U^+_{\Bbbk }$-cocyclic vector of
$U^+_{\Bbbk }$-cocyclic vector of ![]() $\mathbb {W}_w ( \lambda )_{\Bbbk }^{\vee }$ for a field
$\mathbb {W}_w ( \lambda )_{\Bbbk }^{\vee }$ for a field ![]() $\Bbbk $. By the construction of the ring structure on
$\Bbbk $. By the construction of the ring structure on ![]() $R_w$, we have
$R_w$, we have  $\mathbf {v}_{ww_0\lambda }^{\vee } \cdot \mathbf {v}_{ww_0\mu }^{\vee } = \mathbf {v}_{ww_0(\lambda +\mu )}^{\vee }$ in
$\mathbf {v}_{ww_0\lambda }^{\vee } \cdot \mathbf {v}_{ww_0\mu }^{\vee } = \mathbf {v}_{ww_0(\lambda +\mu )}^{\vee }$ in ![]() $R_w$ for every
$R_w$ for every ![]() $\lambda , \mu \in P_+$.
$\lambda , \mu \in P_+$.
Lemma 3.29. For each ![]() $w,v\in W_{\mathrm {af}}$ and
$w,v\in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$, the ring
$\mathtt J \subset \mathtt I$, the ring ![]() $R_{w}( \mathtt J )$ is a quotient of
$R_{w}( \mathtt J )$ is a quotient of ![]() $R_{v}( \mathtt J )$ if
$R_{v}( \mathtt J )$ if ![]() $w \le _{\frac {\infty }{2}} v$. In addition, the ring
$w \le _{\frac {\infty }{2}} v$. In addition, the ring ![]() $R_{w}$ is a quotient of
$R_{w}$ is a quotient of ![]() $R_{v}$ if and only if
$R_{v}$ if and only if ![]() $w \le _{\frac {\infty }{2}} v$.
$w \le _{\frac {\infty }{2}} v$.
Proof. We have ![]() $\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{vw_0} ( \lambda )_{\mathbb {Z}}$ if and only if
$\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{vw_0} ( \lambda )_{\mathbb {Z}}$ if and only if ![]() $\mathbf {v}_{w w_0 \lambda } \in \mathbb {W}_{vw_0} ( \lambda )_{\mathbb {Z}}$. Now we apply Lemma 3.15 to deduce the result.
$\mathbf {v}_{w w_0 \lambda } \in \mathbb {W}_{vw_0} ( \lambda )_{\mathbb {Z}}$. Now we apply Lemma 3.15 to deduce the result.
Lemma 3.30. We have morphisms of rings with ![]() $U^+_{\mathbb {Z}}$-actions
$U^+_{\mathbb {Z}}$-actions
that admit ![]() $\mathbb {Z}$-module splittings, where the
$\mathbb {Z}$-module splittings, where the ![]() $\dot {U}_{\mathbb {Z}}$-action on
$\dot {U}_{\mathbb {Z}}$-action on ![]() $R^{\mathrm {af}}$ is twisted by
$R^{\mathrm {af}}$ is twisted by ![]() $\theta $.
$\theta $.
For each ![]() $w \in W$ and
$w \in W$ and ![]() $\mathtt J \subset \mathtt I$, we set
$\mathtt J \subset \mathtt I$, we set
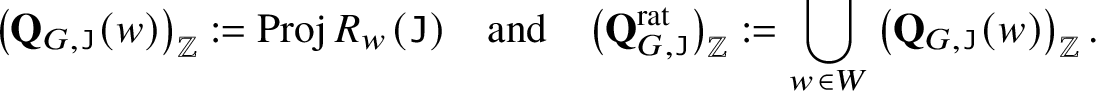 $$ \begin{align*}\left( \mathbf{Q}_{G, \mathtt J} ( w ) \right)_{\mathbb{Z}} := \mathrm{Proj}\, R_{w}( \mathtt J ) \quad \text{and} \quad \big( \mathbf{Q}_{G, \mathtt J}^{\mathrm{rat}} \big)_{\mathbb{Z}} := \bigcup _{w \in W} \left( \mathbf{Q}_{G, \mathtt J} ( w ) \right)_{\mathbb{Z}}.\end{align*} $$
$$ \begin{align*}\left( \mathbf{Q}_{G, \mathtt J} ( w ) \right)_{\mathbb{Z}} := \mathrm{Proj}\, R_{w}( \mathtt J ) \quad \text{and} \quad \big( \mathbf{Q}_{G, \mathtt J}^{\mathrm{rat}} \big)_{\mathbb{Z}} := \bigcup _{w \in W} \left( \mathbf{Q}_{G, \mathtt J} ( w ) \right)_{\mathbb{Z}}.\end{align*} $$These schemes and ind-schemes are flat over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Remark 3.31. In view of equation (2.5), we have embeddings
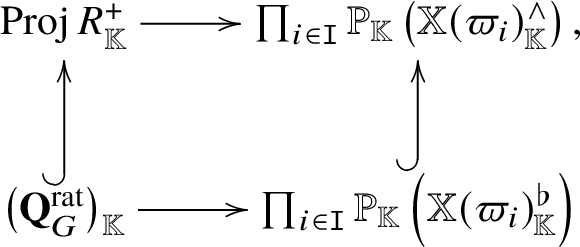
where we set
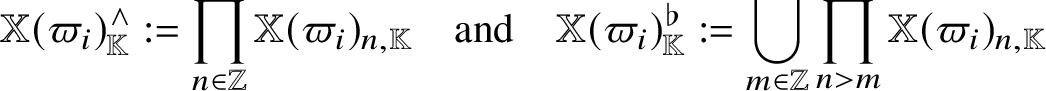 $$ \begin{align*}\mathbb{X} ( \varpi_i )_{{\mathbb K}}^{\wedge} := \prod_{n \in \mathbb{Z}} \mathbb{X} ( \varpi_i )_{n, {\mathbb K}} \quad \text{and} \quad \mathbb{X} ( \varpi_i )_{{\mathbb K}}^{\flat} := \bigcup_{m \in \mathbb{Z}} \prod_{n> m} \mathbb{X} ( \varpi_i )_{n, {\mathbb K}}\end{align*} $$
$$ \begin{align*}\mathbb{X} ( \varpi_i )_{{\mathbb K}}^{\wedge} := \prod_{n \in \mathbb{Z}} \mathbb{X} ( \varpi_i )_{n, {\mathbb K}} \quad \text{and} \quad \mathbb{X} ( \varpi_i )_{{\mathbb K}}^{\flat} := \bigcup_{m \in \mathbb{Z}} \prod_{n> m} \mathbb{X} ( \varpi_i )_{n, {\mathbb K}}\end{align*} $$for each ![]() $i \in \mathtt I$. Here all the spaces in diagram (3.8) admit actions of
$i \in \mathtt I$. Here all the spaces in diagram (3.8) admit actions of ![]() $\mathop {\textit{SL}}( 2,i )_{{\mathbb K}}$ (
$\mathop {\textit{SL}}( 2,i )_{{\mathbb K}}$ (![]() $i \in \mathtt I$), while only the bottom two spaces admit actions of
$i \in \mathtt I$), while only the bottom two spaces admit actions of ![]() $G [\![z]\!]_{{\mathbb K}}$. Nevertheless, the top two spaces have some advantages, since they are
$G [\![z]\!]_{{\mathbb K}}$. Nevertheless, the top two spaces have some advantages, since they are ![]() $\theta $-stable (unlike the bottom two) and consequently also contain
$\theta $-stable (unlike the bottom two) and consequently also contain  $\theta \left ( \big( \mathbf {Q}_{G}^{\mathrm {rat}} \big)_{{\mathbb K}} \right )$.
$\theta \left ( \big( \mathbf {Q}_{G}^{\mathrm {rat}} \big)_{{\mathbb K}} \right )$.
Theorem 3.32 [Reference Kato49]
Let p be a prime. Then the ring  $R^{\mathrm {af}} _{\mathbb F_p}$ admits a Frobenius splitting that is
$R^{\mathrm {af}} _{\mathbb F_p}$ admits a Frobenius splitting that is ![]() $\mathbf {I}$- and
$\mathbf {I}$- and ![]() $\mathbf {I}^-$-canonically split.
$\mathbf {I}^-$-canonically split.
Theorem 3.33. Let p be a prime. The ring ![]() $R _{\mathbb F_p}$ admits a Frobenius splitting that is
$R _{\mathbb F_p}$ admits a Frobenius splitting that is ![]() $\mathbf {I}$-canonically split.
$\mathbf {I}$-canonically split.
Proof. The ![]() $\mathbf {I}$-canonical Frobenius splitting
$\mathbf {I}$-canonical Frobenius splitting ![]() $\phi $ of
$\phi $ of ![]() $R^{\mathrm {af}}$ gives rise to the following maps, whose composition is the identity:
$R^{\mathrm {af}}$ gives rise to the following maps, whose composition is the identity:
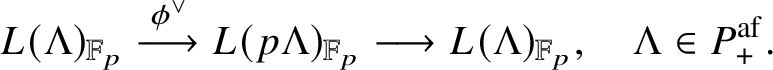 $$ \begin{align*}L ( \Lambda )_{\mathbb F_p} \stackrel{\phi^{\vee}}{\longrightarrow} L ( p \Lambda )_{\mathbb F_p} \longrightarrow L ( \Lambda )_{\mathbb F_p}, \quad \Lambda \in P^{\mathrm{af}}_+.\end{align*} $$
$$ \begin{align*}L ( \Lambda )_{\mathbb F_p} \stackrel{\phi^{\vee}}{\longrightarrow} L ( p \Lambda )_{\mathbb F_p} \longrightarrow L ( \Lambda )_{\mathbb F_p}, \quad \Lambda \in P^{\mathrm{af}}_+.\end{align*} $$In view of Proposition 3.25, this prolongs to
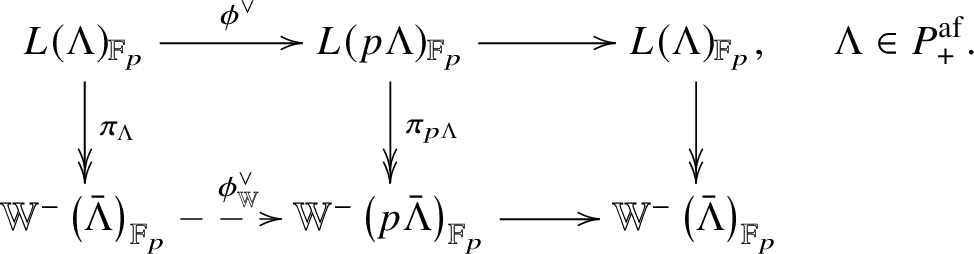
The right square is automatic (and is canonically defined) from the adjunction of the Frobenius push-forward (by taking the restricted dual). In order to show that ![]() $\phi $ descends to a Frobenius splitting of
$\phi $ descends to a Frobenius splitting of ![]() $R_{\mathbb F_p}$, it suffices to show that the dotted map
$R_{\mathbb F_p}$, it suffices to show that the dotted map ![]() $\phi ^{\vee }_{\mathbb {W}}$ is a well-defined linear map (induced from
$\phi ^{\vee }_{\mathbb {W}}$ is a well-defined linear map (induced from ![]() $\phi ^{\vee }$ and such that the left square is commutative).
$\phi ^{\vee }$ and such that the left square is commutative).
By Corollary 3.24, ![]() $\ker \pi _{\Lambda }$ is generated by the P-weight
$\ker \pi _{\Lambda }$ is generated by the P-weight ![]() $\left ( P \setminus \mathrm {Conv} W \bar {\Lambda } \right )$-part of
$\left ( P \setminus \mathrm {Conv} W \bar {\Lambda } \right )$-part of ![]() $L ( \Lambda )_{\mathbb F_p}$. By the cyclicity of
$L ( \Lambda )_{\mathbb F_p}$. By the cyclicity of ![]() $L ( \Lambda )_{\mathbb F_p}$ as
$L ( \Lambda )_{\mathbb F_p}$ as ![]() $U^-_{\mathbb {Z}}$-modules and Proposition 3.7, we deduce that
$U^-_{\mathbb {Z}}$-modules and Proposition 3.7, we deduce that ![]() $\phi ^{\vee } ( \ker \, \pi _{\Lambda } )$ is contained in the
$\phi ^{\vee } ( \ker \, \pi _{\Lambda } )$ is contained in the  $U^-_{\mathbb F_p}$-submodule of
$U^-_{\mathbb F_p}$-submodule of ![]() $L ( p \Lambda )_{\mathbb F_p}$ generated by the P-weight
$L ( p \Lambda )_{\mathbb F_p}$ generated by the P-weight ![]() $p \left ( P \setminus \mathrm {Conv} W \bar {\Lambda } \right )$-part of
$p \left ( P \setminus \mathrm {Conv} W \bar {\Lambda } \right )$-part of ![]() $L ( p \Lambda )_{\mathbb F_p}$. The latter is contained in
$L ( p \Lambda )_{\mathbb F_p}$. The latter is contained in ![]() $\ker \, \pi _{p\Lambda }$ by
$\ker \, \pi _{p\Lambda }$ by
Therefore, we conclude that ![]() $\phi ^{\vee }_{\mathbb {W}}$ is a well-defined linear map, and hence
$\phi ^{\vee }_{\mathbb {W}}$ is a well-defined linear map, and hence  $\theta ^* \left ( R_{\mathbb F_p} \right )$ admits a Frobenius splitting induced from
$\theta ^* \left ( R_{\mathbb F_p} \right )$ admits a Frobenius splitting induced from ![]() $\phi $. The unipotent part of the
$\phi $. The unipotent part of the ![]() $\mathbf {I}^-$-canonical splitting condition is in common with subrings. It remains to twist the grading given by
$\mathbf {I}^-$-canonical splitting condition is in common with subrings. It remains to twist the grading given by ![]() $\alpha _0^{\vee }$ with that given by
$\alpha _0^{\vee }$ with that given by ![]() $- \vartheta ^{\vee }$ and twist the
$- \vartheta ^{\vee }$ and twist the ![]() $\mathbf {I}^-$-action into the
$\mathbf {I}^-$-action into the ![]() $\mathbf {I}$-action by
$\mathbf {I}$-action by ![]() $\theta $ to conclude that our Frobenius splitting on
$\theta $ to conclude that our Frobenius splitting on ![]() $R_{\mathbb F_p}$ is
$R_{\mathbb F_p}$ is ![]() $\mathbf {I}$-canonical.
$\mathbf {I}$-canonical.
Corollary 3.34. Let p be a prime and set ![]() $w \in W$. The
$w \in W$. The ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $R_{\mathbb F_p}$ obtained in Theorem 3.33 induces an
$R_{\mathbb F_p}$ obtained in Theorem 3.33 induces an ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $( R_w ) _{\mathbb F_p}$.
$( R_w ) _{\mathbb F_p}$.
Proof. We set ![]() $L^{ww_0} ( \Lambda )_{\mathbb {Z}} := U^-_{\mathbb {Z}} \mathbf {v}_{ww_0 \Lambda }$, where
$L^{ww_0} ( \Lambda )_{\mathbb {Z}} := U^-_{\mathbb {Z}} \mathbf {v}_{ww_0 \Lambda }$, where ![]() $\mathbb {Z} \mathbf {v}_{ww_0 \Lambda }$ is the
$\mathbb {Z} \mathbf {v}_{ww_0 \Lambda }$ is the ![]() $P^{\mathrm {af}}$-weight
$P^{\mathrm {af}}$-weight ![]() $ww_0 \Lambda $-part of
$ww_0 \Lambda $-part of ![]() $L ( \Lambda )_{\mathbb {Z}}$, which has rank
$L ( \Lambda )_{\mathbb {Z}}$, which has rank ![]() $1$ over
$1$ over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
The subspace ![]() $\mathbb {W} _{ww_0}^- ( \lambda )_{\mathbb {Z}} \subset \mathbb {W}^- ( \lambda )_{\mathbb {Z}}$ is the image of
$\mathbb {W} _{ww_0}^- ( \lambda )_{\mathbb {Z}} \subset \mathbb {W}^- ( \lambda )_{\mathbb {Z}}$ is the image of ![]() $L^{ww_0} ( \Lambda )_{\mathbb {Z}} \subset L ( \Lambda )_{\mathbb {Z}}$ (with
$L^{ww_0} ( \Lambda )_{\mathbb {Z}} \subset L ( \Lambda )_{\mathbb {Z}}$ (with ![]() $\lambda = \bar {\Lambda }$) under Theorem 3.23, since
$\lambda = \bar {\Lambda }$) under Theorem 3.23, since ![]() $L^{ww_0} ( \Lambda )_{\mathbb {Z}}$ is spanned by a subset of
$L^{ww_0} ( \Lambda )_{\mathbb {Z}}$ is spanned by a subset of ![]() \mathbf {B} ( \Lambda )$ ([Reference Kashiwara43, (0.3)]). Our Frobenius splitting
\mathbf {B} ( \Lambda )$ ([Reference Kashiwara43, (0.3)]). Our Frobenius splitting ![]() $\phi $ is obtained from that of
$\phi $ is obtained from that of  $R^{\mathrm {af}}_{\mathbb F_p}$, which is compatible with
$R^{\mathrm {af}}_{\mathbb F_p}$, which is compatible with  $\bigoplus _{\lambda \in P_+} L^{ww_0} ( \Lambda )_{\mathbb F_p}^{\vee }$ by [Reference Kato49, Corollary B]. Applying
$\bigoplus _{\lambda \in P_+} L^{ww_0} ( \Lambda )_{\mathbb F_p}^{\vee }$ by [Reference Kato49, Corollary B]. Applying ![]() $\theta $, we conclude that
$\theta $, we conclude that ![]() $\phi $ must descend to a Frobenius splitting of
$\phi $ must descend to a Frobenius splitting of ![]() $( R_{w} ) _{\mathbb F_p}$.
$( R_{w} ) _{\mathbb F_p}$.
Corollary 3.35. An ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $R_{\mathbb F_p}$ is unique.
$R_{\mathbb F_p}$ is unique.
Proof. The behaviour of the vectors in formula (3.7) (with ![]() $w = e$) under an
$w = e$) under an ![]() $\mathbf {I}$-canonical Frobenius splitting is uniquely determined, as they form a polynomial ring isomorphic to
$\mathbf {I}$-canonical Frobenius splitting is uniquely determined, as they form a polynomial ring isomorphic to ![]() $\mathbb F_p P_+$ such that each of its (
$\mathbb F_p P_+$ such that each of its (![]() $P_+$-)graded components is a multiplicity-free
$P_+$-)graded components is a multiplicity-free ![]() $P^{\mathrm {af}}$-weight space in
$P^{\mathrm {af}}$-weight space in  $\mathbb {W} ( \lambda )_{\mathbb F_p}^{\vee }$s. By Proposition 3.7, this completely determines the behaviour of our splitting (through its dual map).
$\mathbb {W} ( \lambda )_{\mathbb F_p}^{\vee }$s. By Proposition 3.7, this completely determines the behaviour of our splitting (through its dual map).
Corollary 3.36. An ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $R_{\mathbb F_p}$ is compatible with
$R_{\mathbb F_p}$ is compatible with ![]() $(R_w)_{\mathbb F_p}$ for every
$(R_w)_{\mathbb F_p}$ for every ![]() $w \in W_{\mathrm {af}}$ such that
$w \in W_{\mathrm {af}}$ such that ![]() $w \le _{\frac {\infty }{2}} e$.
$w \le _{\frac {\infty }{2}} e$.
Proof. By [Reference Brion and Kumar14, Proposition 4.1.17 and Remark 4.1.18 (i)] and [Reference Kato46, Theorem 4.12] (the algebraic portion of the latter stemming from [Reference Kashiwara45, Lemma 2.6], which carries over to this setting; compare [Reference Kato46, Lemma 4.4 and Theorem 4.7]), we derive that an ![]() $\mathbf {I}$-canonical Frobenius splitting of
$\mathbf {I}$-canonical Frobenius splitting of ![]() $( R_{w} )_{\mathbb F_p}$ (
$( R_{w} )_{\mathbb F_p}$ (![]() $w \in W$) gives rise to an
$w \in W$) gives rise to an ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $R_{\mathbb F_p}$ that is compatible with
$R_{\mathbb F_p}$ that is compatible with ![]() $( R_{w} )_{\mathbb F_p}$ (arguing by restricting to the
$( R_{w} )_{\mathbb F_p}$ (arguing by restricting to the ![]() $\mathop {\textit{SL}} ( 2, i )$-actions for each
$\mathop {\textit{SL}} ( 2, i )$-actions for each ![]() $i \in \mathtt I$). In particular, the
$i \in \mathtt I$). In particular, the ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $(R_w)_{\mathbb F_p}$ (
$(R_w)_{\mathbb F_p}$ (![]() $w \in W$) also uniquely exists and is compatible with that of
$w \in W$) also uniquely exists and is compatible with that of ![]() $R_{\mathbb F_p}$ by Corollaries 3.34 and 3.35. By Corollary 3.28, we further deduce that the
$R_{\mathbb F_p}$ by Corollaries 3.34 and 3.35. By Corollary 3.28, we further deduce that the ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $(R_w)_{\mathbb F_p}$ (
$(R_w)_{\mathbb F_p}$ (![]() $w \in W_{\mathrm {af}}$) uniquely exists.
$w \in W_{\mathrm {af}}$) uniquely exists.
Set ![]() $w \in W$ such that
$w \in W$ such that ![]() $s_0 w = s_{\vartheta } w t_{- w^{-1} \vartheta ^{\vee }} \le _{\frac {\infty }{2}} w$. Then
$s_0 w = s_{\vartheta } w t_{- w^{-1} \vartheta ^{\vee }} \le _{\frac {\infty }{2}} w$. Then ![]() $R_{s_0w}$ is a quotient of
$R_{s_0w}$ is a quotient of ![]() $R_w$. Again by [Reference Brion and Kumar14, Proposition 4.1.17 and Remark 4.1.18 (i)], the set of
$R_w$. Again by [Reference Brion and Kumar14, Proposition 4.1.17 and Remark 4.1.18 (i)], the set of ![]() $\mathbf {I}$-canonical splittings of
$\mathbf {I}$-canonical splittings of  $\left ( R_{s_0w} \right )_{\mathbb F_p}$ is in bijection with that of
$\left ( R_{s_0w} \right )_{\mathbb F_p}$ is in bijection with that of ![]() $( R_{w} )_{\mathbb F_p}$ that are compatible with
$( R_{w} )_{\mathbb F_p}$ that are compatible with  $\left ( R_{s_0 w} \right )_{\mathbb F_p}$. By Corollary 3.28 and the previous paragraph, we find that the (unique)
$\left ( R_{s_0 w} \right )_{\mathbb F_p}$. By Corollary 3.28 and the previous paragraph, we find that the (unique) ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of  $\left ( R_{s_0 w} \right )_{\mathbb F_p}$ is compatible with
$\left ( R_{s_0 w} \right )_{\mathbb F_p}$ is compatible with ![]() $( R_w )_{\mathbb F_p}$, and hence also compatible with
$( R_w )_{\mathbb F_p}$, and hence also compatible with ![]() $R_{\mathbb F_p}$ and
$R_{\mathbb F_p}$ and  $\big( R_{t_{- w^{-1} \vartheta ^{\vee }}} \big)_{\mathbb F_p}$. This forces the
$\big( R_{t_{- w^{-1} \vartheta ^{\vee }}} \big)_{\mathbb F_p}$. This forces the ![]() $\mathbf {I}$-canonical splitting of
$\mathbf {I}$-canonical splitting of ![]() $R_{\mathbb F_p}$ to be compatible with that of
$R_{\mathbb F_p}$ to be compatible with that of  $\big( R_{u t_{- w^{-1} \vartheta ^{\vee }}} \big)_{\mathbb F_p}$ for every
$\big( R_{u t_{- w^{-1} \vartheta ^{\vee }}} \big)_{\mathbb F_p}$ for every ![]() $u,w \in W$ such that
$u,w \in W$ such that ![]() $-w^{-1}\vartheta ^{\vee } \in \Delta _+^{\vee }$.
$-w^{-1}\vartheta ^{\vee } \in \Delta _+^{\vee }$.
The set  $\left ( \left \{ -w^{-1}\vartheta ^{\vee } \right \}_{w \in W} \cap Q^{\vee }_+ \right )$ is precisely the set of short positive coroots in
$\left ( \left \{ -w^{-1}\vartheta ^{\vee } \right \}_{w \in W} \cap Q^{\vee }_+ \right )$ is precisely the set of short positive coroots in ![]() $\Delta _+^{\vee }$. This spans
$\Delta _+^{\vee }$. This spans ![]() $Q^{\vee }_+$ as monoids, by inspection. Since
$Q^{\vee }_+$ as monoids, by inspection. Since ![]() $w \in W_{\mathrm {af}}$ with
$w \in W_{\mathrm {af}}$ with ![]() $w \le _{\frac {\infty }{2}} e$ is written as
$w \le _{\frac {\infty }{2}} e$ is written as ![]() $w = u t_{\beta }$ for some
$w = u t_{\beta }$ for some ![]() $u \in W$ and
$u \in W$ and ![]() $\beta \in Q^{\vee }_+$ ([Reference Peterson74, Lecture 13, Proposition 1]), we conclude the assertion.
$\beta \in Q^{\vee }_+$ ([Reference Peterson74, Lecture 13, Proposition 1]), we conclude the assertion.
Theorem 3.37. Let p be a prime and set ![]() $\mathtt J \subset \mathtt I$. The ring
$\mathtt J \subset \mathtt I$. The ring ![]() $R^+ ( \mathtt J )_{\mathbb F_p}$ admits a Frobenius splitting that is
$R^+ ( \mathtt J )_{\mathbb F_p}$ admits a Frobenius splitting that is ![]() $\mathbf {I}$- and
$\mathbf {I}$- and ![]() $\mathbf {I}^-$-canonically split. This splitting is compatible with
$\mathbf {I}^-$-canonically split. This splitting is compatible with ![]() $R_{w}( \mathtt J )_{\mathbb F_p}$ and the image of
$R_{w}( \mathtt J )_{\mathbb F_p}$ and the image of  $R^+( \mathtt J )_{\mathbb F_p} \subset R^+ _{\mathbb F_p}$ under the quotient map
$R^+( \mathtt J )_{\mathbb F_p} \subset R^+ _{\mathbb F_p}$ under the quotient map  $R^+_{\mathbb F_p} \rightarrow \!\!\!\!\! \rightarrow \theta ^* \left ( \left ( R _{ww_0} \right )_{\mathbb F_p} \right )$ for each
$R^+_{\mathbb F_p} \rightarrow \!\!\!\!\! \rightarrow \theta ^* \left ( \left ( R _{ww_0} \right )_{\mathbb F_p} \right )$ for each ![]() $w \in W_{\mathrm {af}}$.
$w \in W_{\mathrm {af}}$.
Proof. Since the case of ![]() $\mathtt J \neq \emptyset $ follows by the restriction to a part of the
$\mathtt J \neq \emptyset $ follows by the restriction to a part of the ![]() $P_+$-grading, we concentrate on the case where
$P_+$-grading, we concentrate on the case where ![]() $\mathtt J = \emptyset $.
$\mathtt J = \emptyset $.
The ring structure of  $R^+_{\mathbb F_p}$ is determined by
$R^+_{\mathbb F_p}$ is determined by ![]() $R_{\mathbb F_p}$ through the application of
$R_{\mathbb F_p}$ through the application of ![]() $U^-_{\mathbb {Z}}$ before taking duals. By Corollary 3.36 (and its proof), it defines an
$U^-_{\mathbb {Z}}$ before taking duals. By Corollary 3.36 (and its proof), it defines an ![]() $\mathbf {I}$-canonical splitting
$\mathbf {I}$-canonical splitting ![]() $\phi $ of
$\phi $ of  $R^+_{\mathbb F_p}$ compatible with
$R^+_{\mathbb F_p}$ compatible with ![]() $( R_w )_{\mathbb F_p}$ for each
$( R_w )_{\mathbb F_p}$ for each ![]() $w \in W_{\mathrm {af}}$. The ring
$w \in W_{\mathrm {af}}$. The ring  $R^+_{\mathbb F_p}$ admits an
$R^+_{\mathbb F_p}$ admits an ![]() $\mathop {\textit{SL}} ( 2, i )_{\mathbb F_p}$-action that integrates the actions of
$\mathop {\textit{SL}} ( 2, i )_{\mathbb F_p}$-action that integrates the actions of  $E_i^{(n)}$ and
$E_i^{(n)}$ and  $F_i^{(n)}$ (
$F_i^{(n)}$ (![]() $n \in \mathbb {Z}_{>0}$) for each
$n \in \mathbb {Z}_{>0}$) for each ![]() $i \in \mathtt I_{\mathrm {af}}$. By [Reference Brion and Kumar14, Proposition 2.10], this splitting
$i \in \mathtt I_{\mathrm {af}}$. By [Reference Brion and Kumar14, Proposition 2.10], this splitting ![]() $\phi $ is also
$\phi $ is also ![]() $\mathbf {I}^-$-canonical.
$\mathbf {I}^-$-canonical.
The ![]() $\mathbf {I}$-cocyclic
$\mathbf {I}$-cocyclic ![]() $P^{\mathrm {af}}$-weight vector
$P^{\mathrm {af}}$-weight vector  $\mathbf {v}_{w w_0\lambda }^{\vee } \in \mathbb {W} _{ww_0} ( \lambda )^{\vee }_{\mathbb F_p}$ is uniquely characterised by its
$\mathbf {v}_{w w_0\lambda }^{\vee } \in \mathbb {W} _{ww_0} ( \lambda )^{\vee }_{\mathbb F_p}$ is uniquely characterised by its ![]() $P^{\mathrm {af}}$-weight. Hence we obtain a map
$P^{\mathrm {af}}$-weight. Hence we obtain a map
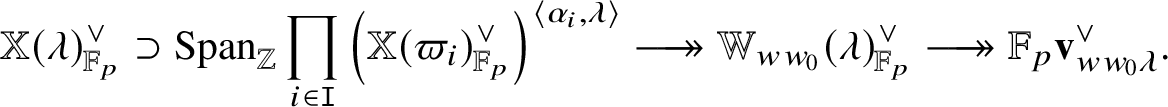 $$ \begin{align*}\mathbb{X} ( \lambda )^{\vee}_{\mathbb F_p} \supset \mathrm{Span}_{\mathbb{Z}} \prod_{i \in \mathtt I} \left( \mathbb{X} ( \varpi_i)_{\mathbb F_p}^{\vee} \right)^{\left\langle \alpha_i, \lambda \right\rangle} \longrightarrow \!\!\!\!\! \rightarrow \mathbb{W} _{ww_0} ( \lambda )_{\mathbb F_p}^{\vee} \longrightarrow \!\!\!\!\! \rightarrow \mathbb F_p \mathbf{v}_{ww_0\lambda}^{\vee}.\end{align*} $$
$$ \begin{align*}\mathbb{X} ( \lambda )^{\vee}_{\mathbb F_p} \supset \mathrm{Span}_{\mathbb{Z}} \prod_{i \in \mathtt I} \left( \mathbb{X} ( \varpi_i)_{\mathbb F_p}^{\vee} \right)^{\left\langle \alpha_i, \lambda \right\rangle} \longrightarrow \!\!\!\!\! \rightarrow \mathbb{W} _{ww_0} ( \lambda )_{\mathbb F_p}^{\vee} \longrightarrow \!\!\!\!\! \rightarrow \mathbb F_p \mathbf{v}_{ww_0\lambda}^{\vee}.\end{align*} $$It gives rise to the ring surjections
 $$ \begin{align*}R^+_{\mathbb F_p} \longrightarrow \!\!\!\!\! \rightarrow ( R_w )_{\mathbb F_p} \longrightarrow \!\!\!\!\! \rightarrow \bigoplus_{\lambda \in P_+} \mathbb F_p \mathbf{v}_{w w_0 \lambda}^{\vee},\end{align*} $$
$$ \begin{align*}R^+_{\mathbb F_p} \longrightarrow \!\!\!\!\! \rightarrow ( R_w )_{\mathbb F_p} \longrightarrow \!\!\!\!\! \rightarrow \bigoplus_{\lambda \in P_+} \mathbb F_p \mathbf{v}_{w w_0 \lambda}^{\vee},\end{align*} $$which are compatible with ![]() $\phi $ by construction in the first surjection and by examining the
$\phi $ by construction in the first surjection and by examining the ![]() $P^{\mathrm {af}}$-weights in the second (we denote this composition surjective ring map by
$P^{\mathrm {af}}$-weights in the second (we denote this composition surjective ring map by ![]() $\xi $). Consider the ideal
$\xi $). Consider the ideal
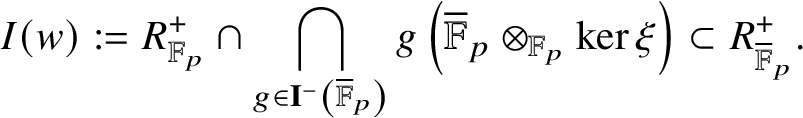 $$ \begin{align*}I (w) := R^+_{\mathbb F_p} \cap \bigcap _{g \in \mathbf{I}^- \left( \overline{\mathbb F}_p \right)} g \left( \overline{\mathbb F}_p \otimes_{\mathbb F_p} \ker \xi \right)\subset R^+_{\overline{\mathbb F}_p}.\end{align*} $$
$$ \begin{align*}I (w) := R^+_{\mathbb F_p} \cap \bigcap _{g \in \mathbf{I}^- \left( \overline{\mathbb F}_p \right)} g \left( \overline{\mathbb F}_p \otimes_{\mathbb F_p} \ker \xi \right)\subset R^+_{\overline{\mathbb F}_p}.\end{align*} $$(Here the action of  $\mathbf {I}^- \big( \overline {\mathbb F}_p \big)$ is obtained by the unipotent one-parameter subgroups
$\mathbf {I}^- \big( \overline {\mathbb F}_p \big)$ is obtained by the unipotent one-parameter subgroups  $\left \{ \rho _{-\alpha _i}\right \}_{i \in \mathtt I_{\mathrm {af}}}$ defined through the exponentials, which are well defined, as we have all the divided powers. The passage from
$\left \{ \rho _{-\alpha _i}\right \}_{i \in \mathtt I_{\mathrm {af}}}$ defined through the exponentials, which are well defined, as we have all the divided powers. The passage from ![]() $\mathbb F_p$ to
$\mathbb F_p$ to ![]() $\overline {\mathbb F}_p$ is necessary to ensure scheme-theoretic invariance, since we want an intersection that is equivalent to the geometric
$\overline {\mathbb F}_p$ is necessary to ensure scheme-theoretic invariance, since we want an intersection that is equivalent to the geometric ![]() $\mathbb {G}_a$-actions through
$\mathbb {G}_a$-actions through ![]() $\rho _{- \alpha _i}$ for all
$\rho _{- \alpha _i}$ for all ![]() $i \in \mathtt I_{\mathrm {af}}$ by finding the Zariski dense subsets of
$i \in \mathtt I_{\mathrm {af}}$ by finding the Zariski dense subsets of ![]() $\mathbb {G}_a$. For this purpose, we want the image of each
$\mathbb {G}_a$. For this purpose, we want the image of each ![]() $\rho _{-\alpha _i}$ to be infinite, which cannot be achieved by sending
$\rho _{-\alpha _i}$ to be infinite, which cannot be achieved by sending ![]() $\mathbb {G}_a \left ( \mathbb F_p \right ) \cong \mathbb F_p$.) This ideal is the maximal
$\mathbb {G}_a \left ( \mathbb F_p \right ) \cong \mathbb F_p$.) This ideal is the maximal  $U_{\mathbb F_p}^-$-invariant ideal of
$U_{\mathbb F_p}^-$-invariant ideal of  $R^+_{\mathbb F_p}$ that is contained in
$R^+_{\mathbb F_p}$ that is contained in ![]() $\ker \xi $. Let us denote the quotient ring by
$\ker \xi $. Let us denote the quotient ring by
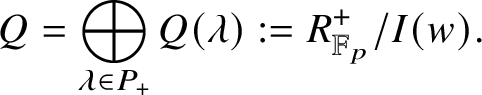 $$ \begin{align*}Q = \bigoplus_{\lambda \in P_+} Q ( \lambda ) := R^+_{\mathbb F_p} / I ( w ).\end{align*} $$
$$ \begin{align*}Q = \bigoplus_{\lambda \in P_+} Q ( \lambda ) := R^+_{\mathbb F_p} / I ( w ).\end{align*} $$By the construction of ![]() $I (w)$, we deduce that
$I (w)$, we deduce that
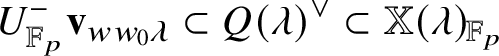 $$ \begin{align*}U_{\mathbb F_p}^- \mathbf{v} _{w w_0 \lambda} \subset Q ( \lambda )^{\vee}\subset \mathbb{X} ( \lambda )_{\mathbb F_p}\end{align*} $$
$$ \begin{align*}U_{\mathbb F_p}^- \mathbf{v} _{w w_0 \lambda} \subset Q ( \lambda )^{\vee}\subset \mathbb{X} ( \lambda )_{\mathbb F_p}\end{align*} $$for each ![]() $\lambda \in P_+$ (otherwise we can differentiate a vector in
$\lambda \in P_+$ (otherwise we can differentiate a vector in ![]() $I ( w )$ to obtain a nonzero element of
$I ( w )$ to obtain a nonzero element of  $\bigoplus _{\lambda \in P_+} \mathbb F_p \mathbf {v}_{w w_0 \lambda }^{\vee }$). Since
$\bigoplus _{\lambda \in P_+} \mathbb F_p \mathbf {v}_{w w_0 \lambda }^{\vee }$). Since  $\theta ^* \left ( \mathbb {W} _{ww_0} ( - w_0 \lambda )_{\mathbb F_p} \right )$ is a cyclic
$\theta ^* \left ( \mathbb {W} _{ww_0} ( - w_0 \lambda )_{\mathbb F_p} \right )$ is a cyclic  $U_{\mathbb F_p}^-$-submodule of
$U_{\mathbb F_p}^-$-submodule of ![]() $\mathbb {X} ( \lambda )_{\mathbb F_p}$, we have
$\mathbb {X} ( \lambda )_{\mathbb F_p}$, we have  $U_{\mathbb F_p}^- \mathbf {v} _{w w_0 \lambda } = \theta ^* \left ( \mathbb {W} _{ww_0} ( - w_0 \lambda )_{\mathbb F_p} \right )$. In particular, we deduce a vector space surjection
$U_{\mathbb F_p}^- \mathbf {v} _{w w_0 \lambda } = \theta ^* \left ( \mathbb {W} _{ww_0} ( - w_0 \lambda )_{\mathbb F_p} \right )$. In particular, we deduce a vector space surjection
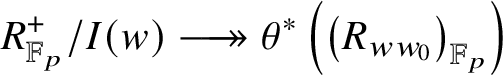 $$ \begin{align*}R^+_{\mathbb F_p} / I ( w ) \longrightarrow \!\!\!\!\! \rightarrow \theta^* \left( \left( R _{ww_0} \right)_{\mathbb F_p} \right)\end{align*} $$
$$ \begin{align*}R^+_{\mathbb F_p} / I ( w ) \longrightarrow \!\!\!\!\! \rightarrow \theta^* \left( \left( R _{ww_0} \right)_{\mathbb F_p} \right)\end{align*} $$(compare Corollary 3.26). Since the right-hand side is naturally a ring, we conclude
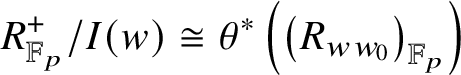 $$ \begin{align*}R^+_{\mathbb F_p} / I ( w ) \cong \theta^* \left( \left( R _{ww_0} \right)_{\mathbb F_p} \right)\end{align*} $$
$$ \begin{align*}R^+_{\mathbb F_p} / I ( w ) \cong \theta^* \left( \left( R _{ww_0} \right)_{\mathbb F_p} \right)\end{align*} $$by the maximality of ![]() $I ( w )$.
$I ( w )$.
The ideal  $I (w) \subset R^+_{\mathbb F_p}$ also splits compatibly by
$I (w) \subset R^+_{\mathbb F_p}$ also splits compatibly by ![]() $\phi $ (since
$\phi $ (since ![]() $\phi $ is
$\phi $ is ![]() $\mathbf {I}^-$-canonical and
$\mathbf {I}^-$-canonical and ![]() $\ker \xi $ splits compatibly). In particular, each
$\ker \xi $ splits compatibly). In particular, each  $\theta ^* \left ( \left ( R_{ww_0} \right )_{\mathbb F_p} \right )$ compatibly splits under
$\theta ^* \left ( \left ( R_{ww_0} \right )_{\mathbb F_p} \right )$ compatibly splits under ![]() $\phi $, as required.
$\phi $, as required.
Corollary 3.38. For each ![]() $\mathtt J \subset \mathtt I$, the ind-scheme
$\mathtt J \subset \mathtt I$, the ind-scheme  $\big( \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}} \big)_{\mathbb F_p}$ admits an
$\big( \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}} \big)_{\mathbb F_p}$ admits an ![]() $\mathbf {I}$- and
$\mathbf {I}$- and ![]() $\mathbf {I}^-$-canonical Frobenius splitting that is compatible with
$\mathbf {I}^-$-canonical Frobenius splitting that is compatible with ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ for each
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ for each ![]() $w \in W_{\mathrm {af}}$.
$w \in W_{\mathrm {af}}$.
Proof. The condition of the canonical splitting can be checked by line bundle twists, and hence we only need to show whether the Frobenius splitting of ![]() $R_w (\mathtt J) _{\mathbb F_p}$ descends to
$R_w (\mathtt J) _{\mathbb F_p}$ descends to ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ for each
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ for each ![]() $w \in W_{\mathrm {af}}$. Since
$w \in W_{\mathrm {af}}$. Since ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is the quotient of an open subset of
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is the quotient of an open subset of ![]() $X := \mathrm {Spec} \, R_w (\mathtt J) _{\mathbb F_p}$ by H (corresponding to the
$X := \mathrm {Spec} \, R_w (\mathtt J) _{\mathbb F_p}$ by H (corresponding to the ![]() $P_{\mathtt J,+}$-grading), and our Frobenius splitting is H-fixed, it suffices to see whether the localisation to the nonirrelevant locus preserves the Frobenius splitting. This follows if the localisation of
$P_{\mathtt J,+}$-grading), and our Frobenius splitting is H-fixed, it suffices to see whether the localisation to the nonirrelevant locus preserves the Frobenius splitting. This follows if the localisation of ![]() $\mathsf {Fr}_* \mathcal O_X = \mathcal O_{X^{(1)}}$ as a
$\mathsf {Fr}_* \mathcal O_X = \mathcal O_{X^{(1)}}$ as a ![]() $\mathsf {Fr}_* \mathcal O_X$-module and as an
$\mathsf {Fr}_* \mathcal O_X$-module and as an ![]() $\mathcal O_X$-module are the same. This holds, as localisation by a multiplicative set S is the same as localisation by
$\mathcal O_X$-module are the same. This holds, as localisation by a multiplicative set S is the same as localisation by ![]() $S^p$.
$S^p$.
Recall that a scheme X defined over a field ![]() $\Bbbk $ is called weakly normal if every finite bijective birational (
$\Bbbk $ is called weakly normal if every finite bijective birational (![]() $\Bbbk $-)morphism
$\Bbbk $-)morphism ![]() $f : Y \rightarrow X$ from a (reduced) scheme over
$f : Y \rightarrow X$ from a (reduced) scheme over ![]() $\Bbbk $ is in fact an isomorphism ([Reference Manaresi68] and [Reference Brion and Kumar14, §1.2.3]).
$\Bbbk $ is in fact an isomorphism ([Reference Manaresi68] and [Reference Brion and Kumar14, §1.2.3]).
Corollary 3.39. For each ![]() $\mathtt J \subset \mathtt I$, the ind-scheme
$\mathtt J \subset \mathtt I$, the ind-scheme  $\big( \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}} \big)_{\mathbb F_p}$ and the schemes
$\big( \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}} \big)_{\mathbb F_p}$ and the schemes ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ (
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ (![]() $w \in W_{\mathrm {af}}$) are reduced. In addition,
$w \in W_{\mathrm {af}}$) are reduced. In addition, ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is weakly normal.
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is weakly normal.
Proof. For the first assertion, apply [Reference Brion and Kumar14, Proposition 1.2.1] to Corollary 3.38. For the second assertion, apply [Reference Brion and Kumar14, Proposition 1.2.5] to Corollary 3.34.
4 Frobenius splitting of quasi-map spaces
We retain the settings of the previous section. In particular, we sometimes work over a ring or a nonalgebraically closed field. Moreover, the notational conventions explained in the beginning of Section 3 continue to apply.
4.1 The scheme  $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ and its Frobenius splitting
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ and its Frobenius splitting
Set ![]() $v,w \in W_{\mathrm {af}}$ and
$v,w \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$. We set
$\mathtt J \subset \mathtt I$. We set
where we have ![]() $\ker \left ( R^+ ( \mathtt J ) \to \theta ^* \left ( R _{vw_0} \left ( \mathtt J' \right ) \right ) \right ) = \ker \left ( R^+ ( \mathtt J ) \to \theta ^* \left ( R _{vw_0} \right ) \right )$ for
$\ker \left ( R^+ ( \mathtt J ) \to \theta ^* \left ( R _{vw_0} \left ( \mathtt J' \right ) \right ) \right ) = \ker \left ( R^+ ( \mathtt J ) \to \theta ^* \left ( R _{vw_0} \right ) \right )$ for
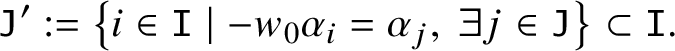 $$ \begin{align*}\mathtt J' := \left\{i \in \mathtt I \mid -w_0 \alpha_i = \alpha_j, \ \exists j \in \mathtt J \right\} \subset \mathtt I.\end{align*} $$
$$ \begin{align*}\mathtt J' := \left\{i \in \mathtt I \mid -w_0 \alpha_i = \alpha_j, \ \exists j \in \mathtt J \right\} \subset \mathtt I.\end{align*} $$By construction, ![]() $R ^v _w ( \mathtt J )$ is a
$R ^v _w ( \mathtt J )$ is a ![]() $P_{\mathtt J,+}$-graded ring. We set
$P_{\mathtt J,+}$-graded ring. We set
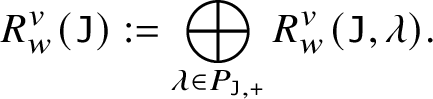 $$ \begin{align*}R ^v _w ( \mathtt J ) := \bigoplus_{\lambda \in P_{\mathtt J,+}} R ^v _w ( \mathtt J, \lambda ).\end{align*} $$
$$ \begin{align*}R ^v _w ( \mathtt J ) := \bigoplus_{\lambda \in P_{\mathtt J,+}} R ^v _w ( \mathtt J, \lambda ).\end{align*} $$Lemma 4.1. For each ![]() $w, v \in W_{\mathrm {af}}$ and
$w, v \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$, the multiplication map
$\mathtt J \subset \mathtt I$, the multiplication map
is surjective.
Proof. We have a quotient
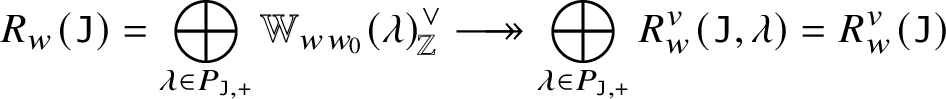 $$ \begin{align*}R _w ( \mathtt J ) = \bigoplus_{\lambda \in P_{\mathtt J,+}} \mathbb{W}_{ww_0} ( \lambda )^{\vee}_{\mathbb{Z}} \longrightarrow \!\!\!\!\! \rightarrow \bigoplus_{\lambda \in P_{\mathtt J,+}} R ^v _w ( \mathtt J, \lambda ) = R ^v _w ( \mathtt J )\end{align*} $$
$$ \begin{align*}R _w ( \mathtt J ) = \bigoplus_{\lambda \in P_{\mathtt J,+}} \mathbb{W}_{ww_0} ( \lambda )^{\vee}_{\mathbb{Z}} \longrightarrow \!\!\!\!\! \rightarrow \bigoplus_{\lambda \in P_{\mathtt J,+}} R ^v _w ( \mathtt J, \lambda ) = R ^v _w ( \mathtt J )\end{align*} $$of homogeneous rings. Corollary 3.26 implies that the multiplication map of ![]() $R _w ( \mathtt J )$ is surjective. Hence so is the quotient ring.
$R _w ( \mathtt J )$ is surjective. Hence so is the quotient ring.
We set
where our definition of ![]() $\mathrm {Proj}$ is equation (2.5). In case where
$\mathrm {Proj}$ is equation (2.5). In case where ![]() $v = w_0 t_{\beta }$ for
$v = w_0 t_{\beta }$ for ![]() $\beta \in Q^{\vee }$, we may write
$\beta \in Q^{\vee }$, we may write ![]() $R ^v _w ( \mathtt J )$ and
$R ^v _w ( \mathtt J )$ and ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ as
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ as  $R ^\beta _w ( \mathtt J )$ and
$R ^\beta _w ( \mathtt J )$ and ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , w )$, respectively.
$\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , w )$, respectively.
Lemma 4.2. For each ![]() $w, v \in W$, the Chevalley involution induces an isomorphism
$w, v \in W$, the Chevalley involution induces an isomorphism
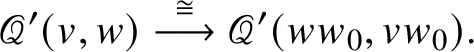 $$ \begin{align*}\mathscr{Q}' ( v, w ) \stackrel{\cong}{\longrightarrow} \mathscr{Q}' ( w w_0, v w_0 ).\end{align*} $$
$$ \begin{align*}\mathscr{Q}' ( v, w ) \stackrel{\cong}{\longrightarrow} \mathscr{Q}' ( w w_0, v w_0 ).\end{align*} $$Proof. Apply Lemma 3.17 to the construction of ![]() $R ^v _w$ to deduce an isomorphism
$R ^v _w$ to deduce an isomorphism
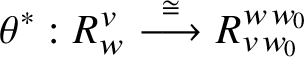 $$ \begin{align*}\theta^* : R ^v _w \stackrel{\cong}{\longrightarrow}R ^{ww_0} _{vw_0}\end{align*} $$
$$ \begin{align*}\theta^* : R ^v _w \stackrel{\cong}{\longrightarrow}R ^{ww_0} _{vw_0}\end{align*} $$of graded rings, which yields the assertion.
Lemma 4.3. For each ![]() $w,v \in W_{\mathrm {af}}$ and
$w,v \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$, the scheme
$\mathtt J \subset \mathtt I$, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is flat over
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is flat over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Proof. The ring ![]() $R^+ ( \mathtt J )$ has a
$R^+ ( \mathtt J )$ has a ![]() $\mathbb {Z}$-basis that is dual to
$\mathbb {Z}$-basis that is dual to ![]() $\bigsqcup _{\lambda \in P_{\mathtt J,+}} {\mathbf B} ( \mathbb {X} ( \lambda ) )$. The rings
$\bigsqcup _{\lambda \in P_{\mathtt J,+}} {\mathbf B} ( \mathbb {X} ( \lambda ) )$. The rings ![]() $R _w ( \mathtt J )$ and
$R _w ( \mathtt J )$ and ![]() $\mathrm {Im} \left ( R^+ ( \mathtt J ) \rightarrow \theta ^* \left ( R _{vw_0} \right ) \right )$ are quotients by subsets of such basis elements, by Lemma 3.17. Hence we have a free
$\mathrm {Im} \left ( R^+ ( \mathtt J ) \rightarrow \theta ^* \left ( R _{vw_0} \right ) \right )$ are quotients by subsets of such basis elements, by Lemma 3.17. Hence we have a free ![]() $\mathbb {Z}$-basis of
$\mathbb {Z}$-basis of ![]() $R ^v _w( \mathtt J )$, as required.
$R ^v _w( \mathtt J )$, as required.
Lemma 4.4. For each ![]() $w, v \in W_{\mathrm {af}}$ and
$w, v \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$, the scheme
$\mathtt J \subset \mathtt I$, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is projective
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is projective ![]() $($of finite type
$($of finite type![]() $)$ over
$)$ over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Proof. By [Reference Kashiwara44, Proposition 5.16], we have ![]() $\mathrm {rank}_{\mathbb {Z}} R ^v _w ( \varpi _i ) < \infty $ for each
$\mathrm {rank}_{\mathbb {Z}} R ^v _w ( \varpi _i ) < \infty $ for each ![]() $i \in \mathtt I$. By Lemma 4.1, this forces
$i \in \mathtt I$. By Lemma 4.1, this forces ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ to be a projective scheme (which usually implies finite type by definition; here we explicitly include it, since our
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ to be a projective scheme (which usually implies finite type by definition; here we explicitly include it, since our ![]() $\mathrm {Proj}$ does not yield a finite-type scheme in general), as required.
$\mathrm {Proj}$ does not yield a finite-type scheme in general), as required.
Lemma 4.5. Set ![]() $\mathtt J \subset \mathtt I$. We have
$\mathtt J \subset \mathtt I$. We have ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w ) \neq \emptyset $ if
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w ) \neq \emptyset $ if ![]() $v \le _{\frac {\infty }{2}} w$.
$v \le _{\frac {\infty }{2}} w$.
Proof. We have ![]() $R ^v _w ( \mathtt J, \lambda ) \neq \{ 0 \}$ if
$R ^v _w ( \mathtt J, \lambda ) \neq \{ 0 \}$ if ![]() $\mathbf {v}_{v w_0 \lambda } \in \mathbb {W}_{ww_0} ( \lambda )_{\mathbb {Z}}$ by Lemma 3.17(4). Here
$\mathbf {v}_{v w_0 \lambda } \in \mathbb {W}_{ww_0} ( \lambda )_{\mathbb {Z}}$ by Lemma 3.17(4). Here ![]() $\mathbf {v}_{v w_0 \lambda } \in \mathbb {W}_{ww_0} ( \lambda )_{\mathbb {Z}}$ is equivalent to
$\mathbf {v}_{v w_0 \lambda } \in \mathbb {W}_{ww_0} ( \lambda )_{\mathbb {Z}}$ is equivalent to ![]() $\mathbb {W}_{vw_0} ( \lambda )_{\mathbb {Z}}\subset \mathbb {W}_{ww_0} ( \lambda )_{\mathbb {Z}}$. Now apply Lemma 3.15 to obtain the assertion.
$\mathbb {W}_{vw_0} ( \lambda )_{\mathbb {Z}}\subset \mathbb {W}_{ww_0} ( \lambda )_{\mathbb {Z}}$. Now apply Lemma 3.15 to obtain the assertion.
Lemma 4.6. Set ![]() $v,w \in W_{\mathrm {af}}$,
$v,w \in W_{\mathrm {af}}$, ![]() $\beta \in Q^{\vee }$ and
$\beta \in Q^{\vee }$ and ![]() $\mathtt J \subset \mathtt I$. We have
$\mathtt J \subset \mathtt I$. We have ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w ) \cong \mathscr {Q}^{\prime }_{\mathtt J} \left ( vt_{\beta }, w t_{\beta } \right )$.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w ) \cong \mathscr {Q}^{\prime }_{\mathtt J} \left ( vt_{\beta }, w t_{\beta } \right )$.
Proof. We borrow notation from Lemma 3.17. By the definition of our ring ![]() $R^v_w ( \mathtt J )$, the assertion follows if
$R^v_w ( \mathtt J )$, the assertion follows if
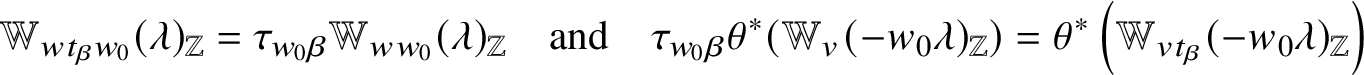 $$ \begin{align*}\mathbb{W} _{wt_{\beta}w_0}( \lambda )_{\mathbb{Z}} = \tau_{w_0\beta} \mathbb{W} _{ww_0}( \lambda )_{\mathbb{Z}} \quad \text{and} \quad \tau_{w_0 \beta} \theta^* ( \mathbb{W} _{v}( -w_0 \lambda )_{\mathbb{Z}} ) = \theta^* \left( \mathbb{W} _{vt_{\beta}}( -w_0 \lambda )_{\mathbb{Z}} \right)\end{align*} $$
$$ \begin{align*}\mathbb{W} _{wt_{\beta}w_0}( \lambda )_{\mathbb{Z}} = \tau_{w_0\beta} \mathbb{W} _{ww_0}( \lambda )_{\mathbb{Z}} \quad \text{and} \quad \tau_{w_0 \beta} \theta^* ( \mathbb{W} _{v}( -w_0 \lambda )_{\mathbb{Z}} ) = \theta^* \left( \mathbb{W} _{vt_{\beta}}( -w_0 \lambda )_{\mathbb{Z}} \right)\end{align*} $$hold for each ![]() $w,v \in W_{\mathrm {af}}$,
$w,v \in W_{\mathrm {af}}$, ![]() $\beta \in Q^{\vee }$ and
$\beta \in Q^{\vee }$ and ![]() $\lambda \in P_+$. These assertions themselves follow by chasing the weights of the cyclic vectors.
$\lambda \in P_+$. These assertions themselves follow by chasing the weights of the cyclic vectors.
Lemma 4.7. Let p be a prime and set ![]() $\mathtt J \subset \mathtt I$. For each
$\mathtt J \subset \mathtt I$. For each ![]() $w,v \in W_{\mathrm {af}}$, the ring
$w,v \in W_{\mathrm {af}}$, the ring ![]() $R ^v _w ( \mathtt J )_{\mathbb F_p}$ admits a Frobenius splitting that is compatible with the quotient
$R ^v _w ( \mathtt J )_{\mathbb F_p}$ admits a Frobenius splitting that is compatible with the quotient  $R^{v'}_{w'} ( \mathtt J ) _{\mathbb F_p}$ for
$R^{v'}_{w'} ( \mathtt J ) _{\mathbb F_p}$ for ![]() $v',w' \in W_{\mathrm {af}}$ such that
$v',w' \in W_{\mathrm {af}}$ such that ![]() $v \le _{\frac {\infty }{2}} v' \le _{\frac {\infty }{2}} w' \le _{\frac {\infty }{2}} w$. In particular, the scheme
$v \le _{\frac {\infty }{2}} v' \le _{\frac {\infty }{2}} w' \le _{\frac {\infty }{2}} w$. In particular, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ is reduced and weakly normal.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ is reduced and weakly normal.
Proof. By construction,  $\ker \left ( R^+ ( \mathtt J )_{\mathbb F_p} \to ( R _w )_{\mathbb F_p} \right )$ and
$\ker \left ( R^+ ( \mathtt J )_{\mathbb F_p} \to ( R _w )_{\mathbb F_p} \right )$ and  $\ker \left ( R^+ ( \mathtt J )_{\mathbb F_p} \to \theta ^* \left ( \left ( R _{vw_0} \right )_{\mathbb F_p} \right ) \right )$ are ideals of a ring
$\ker \left ( R^+ ( \mathtt J )_{\mathbb F_p} \to \theta ^* \left ( \left ( R _{vw_0} \right )_{\mathbb F_p} \right ) \right )$ are ideals of a ring ![]() $R^+ ( \mathtt J )_{\mathbb F_p}$ that are compatible with the canonical Frobenius splitting of
$R^+ ( \mathtt J )_{\mathbb F_p}$ that are compatible with the canonical Frobenius splitting of ![]() $R^+ ( \mathtt J )_{\mathbb F_p}$ by Theorem 3.37. Hence so is their sum. It must be compatible with every quotient of the form
$R^+ ( \mathtt J )_{\mathbb F_p}$ by Theorem 3.37. Hence so is their sum. It must be compatible with every quotient of the form  $R^{v'}_{w'} ( \mathtt J ) _{\mathbb F_p}$ with the given condition, Corollary 3.34 and Lemmas 3.17(4), 3.29 and 4.5. This proves the first assertion. We apply [Reference Brion and Kumar14, Proposition 1.2.1 and 1.2.5] to deduce the second assertion.
$R^{v'}_{w'} ( \mathtt J ) _{\mathbb F_p}$ with the given condition, Corollary 3.34 and Lemmas 3.17(4), 3.29 and 4.5. This proves the first assertion. We apply [Reference Brion and Kumar14, Proposition 1.2.1 and 1.2.5] to deduce the second assertion.
Corollary 4.8. Let p be a prime. For each ![]() $w, v \in W$, the scheme
$w, v \in W$, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ admits a Frobenius splitting compatible with
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ admits a Frobenius splitting compatible with ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v', w' )_{\mathbb F_p}$ for every
$\mathscr {Q}^{\prime }_{\mathtt J} ( v', w' )_{\mathbb F_p}$ for every ![]() $w',v' \in W_{\mathrm {af}}$ such that
$w',v' \in W_{\mathrm {af}}$ such that ![]() $v \le _{\frac {\infty }{2}} v' \le _{\frac {\infty }{2}} w' \le _{\frac {\infty }{2}} w$.
$v \le _{\frac {\infty }{2}} v' \le _{\frac {\infty }{2}} w' \le _{\frac {\infty }{2}} w$.
Remark 4.9. Unlike the case of Corollary 3.38, the space ![]() $\mathrm {Spec}\, R ^v _w ( \mathtt J )_{\mathbb F_p}$ is not irreducible in general. In fact, we discard some of its irreducible components from Lemma 4.7 to Corollary 4.8.
$\mathrm {Spec}\, R ^v _w ( \mathtt J )_{\mathbb F_p}$ is not irreducible in general. In fact, we discard some of its irreducible components from Lemma 4.7 to Corollary 4.8.
Corollary 4.10. The ring ![]() $R^v_w ( \mathtt J )$ is reduced. In particular, the scheme
$R^v_w ( \mathtt J )$ is reduced. In particular, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is reduced.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is reduced.
4.2 Modular interpretation of  $\mathbf {Q}_{G,\mathtt J}^{\mathrm {rat}}$
$\mathbf {Q}_{G,\mathtt J}^{\mathrm {rat}}$
We have an identification
regardless of the (algebraically closed) base field ![]() ${\mathbb K}$. We denote a lift of
${\mathbb K}$. We denote a lift of ![]() $w \in W_{\mathrm {af}}$ in
$w \in W_{\mathrm {af}}$ in ![]() $N_{G (\!(z)\!)} ( H ( {\mathbb K} ) ) / H ( {\mathbb K} )$ by
$N_{G (\!(z)\!)} ( H ( {\mathbb K} ) ) / H ( {\mathbb K} )$ by ![]() $\dot {w}$.
$\dot {w}$.
Lemma 4.11. For each ![]() $w \in W$ and
$w \in W$ and ![]() $\mathtt J \subset \mathtt I$, the scheme
$\mathtt J \subset \mathtt I$, the scheme ![]() $\mathbf {Q}_{G,\mathtt J} ( w )_{\mathbb K}$ contains an affine Zariski open
$\mathbf {Q}_{G,\mathtt J} ( w )_{\mathbb K}$ contains an affine Zariski open ![]() $\mathbf {I}_{\mathbb K}$-orbit
$\mathbf {I}_{\mathbb K}$-orbit ![]() $\mathbb {O} ( \mathtt J, w )_{\mathbb K}$ that is isomorphic to
$\mathbb {O} ( \mathtt J, w )_{\mathbb K}$ that is isomorphic to
as a scheme over ![]() ${\mathbb K}$. (By abuse of notation, here we identify the set of
${\mathbb K}$. (By abuse of notation, here we identify the set of ![]() ${\mathbb K}$-valued points
${\mathbb K}$-valued points ![]() $( \mathrm {Ad} ( \dot {w}\dot {w}_0 ) ( [P (\mathtt J),P(\mathtt J)] (\!(z)\!) ) \cap \mathbf {I}_{\mathbb K})$ with its Zariski closure in
$( \mathrm {Ad} ( \dot {w}\dot {w}_0 ) ( [P (\mathtt J),P(\mathtt J)] (\!(z)\!) ) \cap \mathbf {I}_{\mathbb K})$ with its Zariski closure in ![]() $\mathbf {I}_{\mathbb K}$.) It is an open neighbourhood of the unique
$\mathbf {I}_{\mathbb K}$.) It is an open neighbourhood of the unique ![]() $(H \times \mathbb {G}_m)_{\mathbb K}$-fixed point of
$(H \times \mathbb {G}_m)_{\mathbb K}$-fixed point of ![]() $\mathbb {O} ( \mathtt J, w )_{\mathbb K}$.
$\mathbb {O} ( \mathtt J, w )_{\mathbb K}$.
Proof. Recall that  $\mathbf {v}_{ww_0\lambda }^{\vee } \cdot \mathbf {v}_{ww_0\mu }^{\vee } = \mathbf {v}_{ww_0(\lambda + \mu )}^{\vee }$ for each
$\mathbf {v}_{ww_0\lambda }^{\vee } \cdot \mathbf {v}_{ww_0\mu }^{\vee } = \mathbf {v}_{ww_0(\lambda + \mu )}^{\vee }$ for each ![]() $\lambda , \mu \in P_+$. Since
$\lambda , \mu \in P_+$. Since ![]() $\mathbb {W}_{ww_0} ( \lambda )$ is compatible with the positive global basis, the ring
$\mathbb {W}_{ww_0} ( \lambda )$ is compatible with the positive global basis, the ring
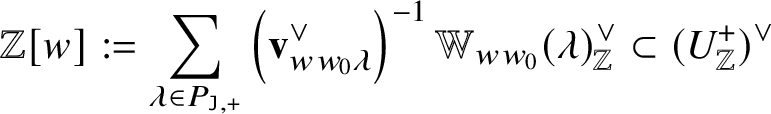 $$ \begin{align} \mathbb{Z} [w] := \sum_{\lambda \in P_{\mathtt J,+}} \left( \mathbf{v}_{ww_0\lambda}^{\vee} \right)^{-1} \mathbb{W}_{ww_0} ( \lambda )^{\vee} _{\mathbb{Z}} \subset ( U _{\mathbb{Z}}^+ )^{\vee} \end{align} $$
$$ \begin{align} \mathbb{Z} [w] := \sum_{\lambda \in P_{\mathtt J,+}} \left( \mathbf{v}_{ww_0\lambda}^{\vee} \right)^{-1} \mathbb{W}_{ww_0} ( \lambda )^{\vee} _{\mathbb{Z}} \subset ( U _{\mathbb{Z}}^+ )^{\vee} \end{align} $$admits its dual basis. By construction, ![]() $\mathbb {Z} [w]$ is the coordinate ring of an affine Zariski open set of
$\mathbb {Z} [w]$ is the coordinate ring of an affine Zariski open set of ![]() $\mathbf {Q} _G ( w )_{\mathbb {Z}}$. In addition, it inherits a natural
$\mathbf {Q} _G ( w )_{\mathbb {Z}}$. In addition, it inherits a natural ![]() $P^{\mathrm {af}}$-grading from
$P^{\mathrm {af}}$-grading from ![]() $R_{w} ( \mathtt J )$. Therefore,
$R_{w} ( \mathtt J )$. Therefore, ![]() $\mathbb {Z} [w]$ defines an open neighbourhood of an
$\mathbb {Z} [w]$ defines an open neighbourhood of an ![]() $(H \times \mathbb {G}_m)$-fixed point of
$(H \times \mathbb {G}_m)$-fixed point of ![]() $\mathbf {Q}_{G,\mathtt J} ( w )$ obtained by the linear forms
$\mathbf {Q}_{G,\mathtt J} ( w )$ obtained by the linear forms  $\left \{\mathbf {v}_{ww_0\lambda }\right \}_\lambda $. We set
$\left \{\mathbf {v}_{ww_0\lambda }\right \}_\lambda $. We set ![]() ${\mathbb C} [w] := {\mathbb C} \otimes _{\mathbb {Z}} \mathbb {Z} [w]$ and
${\mathbb C} [w] := {\mathbb C} \otimes _{\mathbb {Z}} \mathbb {Z} [w]$ and ![]() ${\mathbb K} [w] := {\mathbb K} \otimes _{\mathbb {Z}} \mathbb {Z} [w]$.
${\mathbb K} [w] := {\mathbb K} \otimes _{\mathbb {Z}} \mathbb {Z} [w]$.
The defining relation of ![]() $( {\mathbb C} [e] )^{\vee }$ in terms of the
$( {\mathbb C} [e] )^{\vee }$ in terms of the ![]() $U_{\mathbb C}^+$-action is
$U_{\mathbb C}^+$-action is
by (the limit of) Chari, Fourier and Khandai [Reference Chari, Fourier and Khandai17, Proposition 3.3]. Since ![]() $\mathbb {W} _{uw_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{w_0} ( \lambda )_{\mathbb {Z}}$ for each
$\mathbb {W} _{uw_0} ( \lambda )_{\mathbb {Z}} \subset \mathbb {W} _{w_0} ( \lambda )_{\mathbb {Z}}$ for each ![]() $u \in W$, the defining relation of
$u \in W$, the defining relation of ![]() $( {\mathbb C} [u] )^{\vee }$ in terms of the
$( {\mathbb C} [u] )^{\vee }$ in terms of the ![]() $U_{\mathbb C}^+$-action is
$U_{\mathbb C}^+$-action is
by applying the action of ![]() $\dot {u} \in N_G ( H )_{\mathbb C}$ that lifts
$\dot {u} \in N_G ( H )_{\mathbb C}$ that lifts ![]() $u \in W$. In particular, we have
$u \in W$. In particular, we have
as schemes over ![]() ${\mathbb C}$. We put
${\mathbb C}$. We put  $\mathbf {I}_{\mathbb {Z}} ^1 := [ \mathbf {I}_{\mathbb {Z}}, \mathbf {I}_{\mathbb {Z}}]$. Let
$\mathbf {I}_{\mathbb {Z}} ^1 := [ \mathbf {I}_{\mathbb {Z}}, \mathbf {I}_{\mathbb {Z}}]$. Let ![]() $\mathbf L_{{\mathbb C}}$ and
$\mathbf L_{{\mathbb C}}$ and ![]() $\mathbf R_{{\mathbb C}}$ be prounipotent subgroups of
$\mathbf R_{{\mathbb C}}$ be prounipotent subgroups of ![]() $\mathbf {I}_{\mathbb C} ^1$ whose closed points are
$\mathbf {I}_{\mathbb C} ^1$ whose closed points are
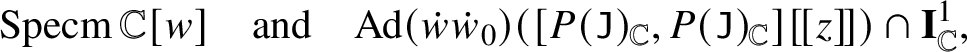 $$ \begin{align*}\mathrm{Specm}\, {\mathbb C} [w] \quad \text{and} \quad \mathrm{Ad} ( \dot{w} \dot{w}_0 ) ( [P ( \mathtt J )_{\mathbb C}, P ( \mathtt J )_{\mathbb C}][\![z]\!] ) \cap \mathbf{I}^1_{\mathbb C},\end{align*} $$
$$ \begin{align*}\mathrm{Specm}\, {\mathbb C} [w] \quad \text{and} \quad \mathrm{Ad} ( \dot{w} \dot{w}_0 ) ( [P ( \mathtt J )_{\mathbb C}, P ( \mathtt J )_{\mathbb C}][\![z]\!] ) \cap \mathbf{I}^1_{\mathbb C},\end{align*} $$respectively, and they are stable by the natural ![]() $( H \times \mathbb {G}_m )_{\mathbb C}$-action on
$( H \times \mathbb {G}_m )_{\mathbb C}$-action on ![]() $\mathbf {I}_{\mathbb C}$. The isomorphism (4.2) gives rise to an isomorphism
$\mathbf {I}_{\mathbb C}$. The isomorphism (4.2) gives rise to an isomorphism
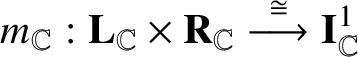 $$ \begin{align} m_{\mathbb C} : \mathbf L_{{\mathbb C}} \times \mathbf R_{{\mathbb C}} \stackrel{\cong}{\longrightarrow} \mathbf{I}_{\mathbb C} ^1 \end{align} $$
$$ \begin{align} m_{\mathbb C} : \mathbf L_{{\mathbb C}} \times \mathbf R_{{\mathbb C}} \stackrel{\cong}{\longrightarrow} \mathbf{I}_{\mathbb C} ^1 \end{align} $$of schemes over ![]() ${\mathbb C}$, where
${\mathbb C}$, where ![]() $m_{\mathbb C}$ is the multiplication map, as all the groups are prounipotent and the isomorphism between the sets of closed points is compatible with truncations by
$m_{\mathbb C}$ is the multiplication map, as all the groups are prounipotent and the isomorphism between the sets of closed points is compatible with truncations by ![]() $P^{\mathrm {af}}$-weight considerations. The Hopf algebra
$P^{\mathrm {af}}$-weight considerations. The Hopf algebra  $\mathbb {Z} \left [\mathbf {I} ^1_{\mathbb {Z}}\right ] := \left ( U ^+_{\mathbb {Z}} \right )^{\vee }$ is the coordinate ring of
$\mathbb {Z} \left [\mathbf {I} ^1_{\mathbb {Z}}\right ] := \left ( U ^+_{\mathbb {Z}} \right )^{\vee }$ is the coordinate ring of ![]() $\mathbf {I}^1_{\mathbb {Z}}$ (compare [Reference Kato49, Theorem 1.3]). Sending
$\mathbf {I}^1_{\mathbb {Z}}$ (compare [Reference Kato49, Theorem 1.3]). Sending  $\mathbb {Z} \left [\mathbf {I} ^1\right ]$ by the restriction morphisms
$\mathbb {Z} \left [\mathbf {I} ^1\right ]$ by the restriction morphisms  ${\mathbb C} \left [\mathbf {I} ^1_{{\mathbb C}}\right ] \to {\mathbb C} [\mathbf L_{{\mathbb C}}]$ and
${\mathbb C} \left [\mathbf {I} ^1_{{\mathbb C}}\right ] \to {\mathbb C} [\mathbf L_{{\mathbb C}}]$ and  ${\mathbb C} \left [\mathbf {I} ^1_{{\mathbb C}}\right ] \to {\mathbb C} [\mathbf R_{{\mathbb C}}]$, we have the corresponding group schemes
${\mathbb C} \left [\mathbf {I} ^1_{{\mathbb C}}\right ] \to {\mathbb C} [\mathbf R_{{\mathbb C}}]$, we have the corresponding group schemes ![]() $\mathbf L_{\mathbb {Z}}$ and
$\mathbf L_{\mathbb {Z}}$ and ![]() $\mathbf R_{\mathbb {Z}}$ over
$\mathbf R_{\mathbb {Z}}$ over ![]() $\mathbb {Z}$ (we denote their coordinate rings as
$\mathbb {Z}$ (we denote their coordinate rings as ![]() $\mathbb {Z} [\mathbf L]$ and
$\mathbb {Z} [\mathbf L]$ and ![]() $\mathbb {Z} [\mathbf R]$, respectively). For each real root
$\mathbb {Z} [\mathbf R]$, respectively). For each real root ![]() $\alpha \in \Delta _{\mathrm {af}, +}$, one of the restricted dual rings
$\alpha \in \Delta _{\mathrm {af}, +}$, one of the restricted dual rings ![]() ${\mathbb C} [\mathbf L_{{\mathbb C}}]^{\vee }$ or
${\mathbb C} [\mathbf L_{{\mathbb C}}]^{\vee }$ or ![]() ${\mathbb C} [\mathbf R_{{\mathbb C}}]^{\vee }$ contains the image of a primitive element of
${\mathbb C} [\mathbf R_{{\mathbb C}}]^{\vee }$ contains the image of a primitive element of ![]() $U^+_{\mathbb {Z}}$ with
$U^+_{\mathbb {Z}}$ with ![]() $\widetilde {\mathfrak {h}}$-weight
$\widetilde {\mathfrak {h}}$-weight ![]() $\alpha $ (obtained by conjugations of
$\alpha $ (obtained by conjugations of ![]() $\{E_i\}_{i \in \mathtt I_{\mathrm {af}}}$s; compare [Reference Lusztig66, Proposition 40.1.3] or [Reference Garland31, Lemma 6.6]), and hence the corresponding one-parameter subgroup lands in either
$\{E_i\}_{i \in \mathtt I_{\mathrm {af}}}$s; compare [Reference Lusztig66, Proposition 40.1.3] or [Reference Garland31, Lemma 6.6]), and hence the corresponding one-parameter subgroup lands in either ![]() $\mathbf L_{\mathbb {Z}}$ or
$\mathbf L_{\mathbb {Z}}$ or ![]() $\mathbf R_{\mathbb {Z}}$. In view of [Reference Beck and Nakajima5, Theorem 3.13] (or [Reference Garland31, Theorem 5.8]), they generate a closed normal subgroup scheme
$\mathbf R_{\mathbb {Z}}$. In view of [Reference Beck and Nakajima5, Theorem 3.13] (or [Reference Garland31, Theorem 5.8]), they generate a closed normal subgroup scheme ![]() $\mathbf N_{\mathbb {Z}}^-$ of
$\mathbf N_{\mathbb {Z}}^-$ of ![]() $\mathbf L_{\mathbb {Z}}$ that is a projective limit of extensions of
$\mathbf L_{\mathbb {Z}}$ that is a projective limit of extensions of ![]() $\mathbb {G}_a$ over
$\mathbb {G}_a$ over ![]() $\mathbb {Z}$. (The same is true and exhausts the whole of
$\mathbb {Z}$. (The same is true and exhausts the whole of ![]() $\mathbf R_{\mathbb {Z}}$ if
$\mathbf R_{\mathbb {Z}}$ if ![]() $\mathtt J = \emptyset $.)
$\mathtt J = \emptyset $.)
We examine the action of the imaginary Poincaré–Birkhoff–Witt generators  $\left \{ \tilde {P}_{i,m\delta }\right \}_{i \in \mathtt I \setminus \mathtt J, m> 0}$ (the weight of
$\left \{ \tilde {P}_{i,m\delta }\right \}_{i \in \mathtt I \setminus \mathtt J, m> 0}$ (the weight of ![]() $\tilde {P}_{i,m\delta }$ is
$\tilde {P}_{i,m\delta }$ is ![]() $m \delta $) in [Reference Beck and Nakajima5, (3.7)]. By applying them on the direct sum of P-weight
$m \delta $) in [Reference Beck and Nakajima5, (3.7)]. By applying them on the direct sum of P-weight ![]() $\lambda $-parts of
$\lambda $-parts of ![]() $\mathbb {X} ( \lambda )_{\mathbb C}$ for all
$\mathbb {X} ( \lambda )_{\mathbb C}$ for all ![]() $\lambda \in P_{\mathtt J, +}$, we obtain a quotient group scheme
$\lambda \in P_{\mathtt J, +}$, we obtain a quotient group scheme ![]() $\mathbf L_{\mathbb {Z}} \to \mathbf T_{\mathbb {Z}}$ whose kernel is
$\mathbf L_{\mathbb {Z}} \to \mathbf T_{\mathbb {Z}}$ whose kernel is ![]() $\mathbf N_{\mathbb {Z}}^-$. By [Reference Beck and Nakajima5, Proposition 3.22], the group scheme
$\mathbf N_{\mathbb {Z}}^-$. By [Reference Beck and Nakajima5, Proposition 3.22], the group scheme  $\mbox {Spec}\, \mathbb {Z} \left [\tilde {P}_{i,m\delta }\mid m> 1\right ]^{\vee }$ for each
$\mbox {Spec}\, \mathbb {Z} \left [\tilde {P}_{i,m\delta }\mid m> 1\right ]^{\vee }$ for each ![]() $i \in \mathtt I$ is isomorphic to a projective limit of extensions of
$i \in \mathtt I$ is isomorphic to a projective limit of extensions of ![]() $\mathbb {G}_a$ (given by truncations with respect to the duals of
$\mathbb {G}_a$ (given by truncations with respect to the duals of  $\left \{ \tilde {P}_{i,m\delta } \right \}_{m> N}$ for
$\left \{ \tilde {P}_{i,m\delta } \right \}_{m> N}$ for ![]() $N \in \mathbb {Z}_{> 0}$), which is flat over
$N \in \mathbb {Z}_{> 0}$), which is flat over ![]() $\mathbb {Z}$. Thus so is
$\mathbb {Z}$. Thus so is ![]() $\mathbf T_{\mathbb {Z}}$.
$\mathbf T_{\mathbb {Z}}$.
From these, we deduce that  $\mathbf L_{\mathbb {Z}} \subset \mathbf {I}_{\mathbb {Z}}^1$ defines a group subscheme over
$\mathbf L_{\mathbb {Z}} \subset \mathbf {I}_{\mathbb {Z}}^1$ defines a group subscheme over ![]() $\mathbb {Z}$ such that
$\mathbb {Z}$ such that  $\mathbb {Z} \left [\mathbf {I}_{\mathbb {Z}}^1\right ] \rightarrow \mathbb {Z} [\mathbf L]$ splits as
$\mathbb {Z} \left [\mathbf {I}_{\mathbb {Z}}^1\right ] \rightarrow \mathbb {Z} [\mathbf L]$ splits as ![]() $\mathbb {Z}$-modules. The P-weight decomposition of the coordinate ring defines a splitting
$\mathbb {Z}$-modules. The P-weight decomposition of the coordinate ring defines a splitting  $\mathbf T_{\mathbb {Z}} \subset \mathbf L_{\mathbb {Z}} \subset \mathbf {I}^1_{\mathbb {Z}}$. Since
$\mathbf T_{\mathbb {Z}} \subset \mathbf L_{\mathbb {Z}} \subset \mathbf {I}^1_{\mathbb {Z}}$. Since ![]() $[L ( \mathtt J ), L ( \mathtt J )]$ defines a product of connected and simply connected simple algebraic groups, its (prounipotent part of the) Iwahori subgroup (we take the product over simple factors) defines a subgroup scheme
$[L ( \mathtt J ), L ( \mathtt J )]$ defines a product of connected and simply connected simple algebraic groups, its (prounipotent part of the) Iwahori subgroup (we take the product over simple factors) defines a subgroup scheme  $\mathbf R^0_{\mathbb {Z}} \subset \mathbf R_{\mathbb {Z}}$ such that
$\mathbf R^0_{\mathbb {Z}} \subset \mathbf R_{\mathbb {Z}}$ such that
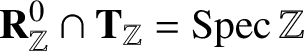 $$ \begin{align} \mathbf R^0_{\mathbb{Z}} \cap \mathbf T_{\mathbb{Z}} = \mbox{Spec}\, \mathbb{Z} \end{align} $$
$$ \begin{align} \mathbf R^0_{\mathbb{Z}} \cap \mathbf T_{\mathbb{Z}} = \mbox{Spec}\, \mathbb{Z} \end{align} $$(scheme-theoretically). Since ![]() $[L ( \mathtt J ), L ( \mathtt J )] \subset G$ defines a closed group subscheme over
$[L ( \mathtt J ), L ( \mathtt J )] \subset G$ defines a closed group subscheme over ![]() $\mathbb {Z}$ (thanks to the fact that the corresponding modified enveloping algebras share the same
$\mathbb {Z}$ (thanks to the fact that the corresponding modified enveloping algebras share the same ![]() $\mathbb {Z}$-basis, by [Reference Kashiwara41, Reference Kashiwara43, Reference Lusztig67]), we deduce that the map
$\mathbb {Z}$-basis, by [Reference Kashiwara41, Reference Kashiwara43, Reference Lusztig67]), we deduce that the map  $\mathbb {Z} \left [\mathbf {I}_{\mathbb {Z}}^1\right ] \rightarrow \mathbb {Z} \left [\mathbf R^0_{\mathbb {Z}}\right ]$ must be surjective. The one-parameter subgroups corresponding to the unipotent radical of
$\mathbb {Z} \left [\mathbf {I}_{\mathbb {Z}}^1\right ] \rightarrow \mathbb {Z} \left [\mathbf R^0_{\mathbb {Z}}\right ]$ must be surjective. The one-parameter subgroups corresponding to the unipotent radical of ![]() $P ( \mathtt J )$ generate a subgroup
$P ( \mathtt J )$ generate a subgroup  $\mathbf R^+_{\mathbb {Z}} \subset \mathbf R_{\mathbb {Z}} \subset \mathbf {I}_{\mathbb {Z}}^1$ such that
$\mathbf R^+_{\mathbb {Z}} \subset \mathbf R_{\mathbb {Z}} \subset \mathbf {I}_{\mathbb {Z}}^1$ such that  $\mathbb {Z} \left [\mathbf {I}_{\mathbb {Z}}^1\right ] \rightarrow \mathbb {Z} \left [\mathbf R^+_{\mathbb {Z}}\right ]$ is surjective. In view of the P-weight decomposition, we deduce that
$\mathbb {Z} \left [\mathbf {I}_{\mathbb {Z}}^1\right ] \rightarrow \mathbb {Z} \left [\mathbf R^+_{\mathbb {Z}}\right ]$ is surjective. In view of the P-weight decomposition, we deduce that  $\mathbf R^0_{\mathbb {Z}} \times \mathbf R^+_{\mathbb {Z}} \cong \mathbf R_{\mathbb {Z}}$. From equation (4.4), we derive
$\mathbf R^0_{\mathbb {Z}} \times \mathbf R^+_{\mathbb {Z}} \cong \mathbf R_{\mathbb {Z}}$. From equation (4.4), we derive ![]() $\mathbb {Z} [\mathbf L] \cap \mathbb {Z} [\mathbf R] = \mathbb {Z}$. Therefore, we have a surjection
$\mathbb {Z} [\mathbf L] \cap \mathbb {Z} [\mathbf R] = \mathbb {Z}$. Therefore, we have a surjection
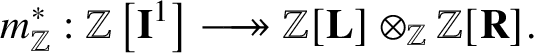 $$ \begin{align*}m^*_{\mathbb{Z}} : \mathbb{Z} \left[\mathbf{I}^1\right] \longrightarrow\!\!\!\!\!\rightarrow \mathbb{Z} [\mathbf L] \otimes_{\mathbb{Z}} \mathbb{Z}[\mathbf R].\end{align*} $$
$$ \begin{align*}m^*_{\mathbb{Z}} : \mathbb{Z} \left[\mathbf{I}^1\right] \longrightarrow\!\!\!\!\!\rightarrow \mathbb{Z} [\mathbf L] \otimes_{\mathbb{Z}} \mathbb{Z}[\mathbf R].\end{align*} $$The ideal ![]() $\ker m^*_{\mathbb {Z}}$ must be flat over
$\ker m^*_{\mathbb {Z}}$ must be flat over ![]() $\mathbb {Z}$, and hence
$\mathbb {Z}$, and hence ![]() $\ker m^*_{\mathbb C} \neq 0$ if
$\ker m^*_{\mathbb C} \neq 0$ if ![]() $\ker m^*_{\mathbb {Z}} \neq 0$. We know that
$\ker m^*_{\mathbb {Z}} \neq 0$. We know that ![]() $m^*_{\mathbb C}$ must be an isomorphism by formula (4.3). This is a contradiction, and hence
$m^*_{\mathbb C}$ must be an isomorphism by formula (4.3). This is a contradiction, and hence ![]() $m^*_{\mathbb {Z}}$ must be an isomorphism (compare [Reference Garland31, Theorem 5.8]).
$m^*_{\mathbb {Z}}$ must be an isomorphism (compare [Reference Garland31, Theorem 5.8]).
In view of the flatness of the group schemes over ![]() $\mathbb {Z}$ afforded by the foregoing, we conclude that
$\mathbb {Z}$ afforded by the foregoing, we conclude that
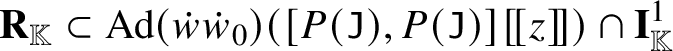 $$ \begin{align*}\mathbf R_{{\mathbb K}} \subset \mathrm{Ad} ( \dot{w} \dot{w}_0 ) ( [P ( \mathtt J ), P ( \mathtt J )][\![z]\!] ) \cap \mathbf{I}^1_{{\mathbb K}}\end{align*} $$
$$ \begin{align*}\mathbf R_{{\mathbb K}} \subset \mathrm{Ad} ( \dot{w} \dot{w}_0 ) ( [P ( \mathtt J ), P ( \mathtt J )][\![z]\!] ) \cap \mathbf{I}^1_{{\mathbb K}}\end{align*} $$is in fact an isomorphism as schemes. By construction, ![]() $\mathbb {Z} [w]$ is precisely the subring of
$\mathbb {Z} [w]$ is precisely the subring of  $\mathbb {Z} \left [\mathbf {I}^1_{\mathbb K}\right ]$ that is invariant under the
$\mathbb {Z} \left [\mathbf {I}^1_{\mathbb K}\right ]$ that is invariant under the ![]() $\mathbf R_{\mathbb {Z}}$-action. It follows that the image of the composition map
$\mathbf R_{\mathbb {Z}}$-action. It follows that the image of the composition map
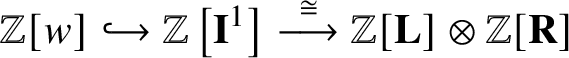 $$ \begin{align*}\mathbb{Z} [w] \hookrightarrow \mathbb{Z} \left[\mathbf{I}^1\right] \stackrel{\cong}{\longrightarrow} \mathbb{Z} [ \mathbf L ] \otimes \mathbb{Z} [ \mathbf R ]\end{align*} $$
$$ \begin{align*}\mathbb{Z} [w] \hookrightarrow \mathbb{Z} \left[\mathbf{I}^1\right] \stackrel{\cong}{\longrightarrow} \mathbb{Z} [ \mathbf L ] \otimes \mathbb{Z} [ \mathbf R ]\end{align*} $$is equal to ![]() $\mathbb {Z} [ \mathbf L ] \otimes _{\mathbb {Z}} \mathbb {Z}$. Hence we have
$\mathbb {Z} [ \mathbf L ] \otimes _{\mathbb {Z}} \mathbb {Z}$. Hence we have
Therefore, each ![]() $\mathbf {Q}_G ( w )_{\mathbb K}$ contains
$\mathbf {Q}_G ( w )_{\mathbb K}$ contains ![]() $\mathrm {Spec}\, {\mathbb K} [w]$ as a Zariski open
$\mathrm {Spec}\, {\mathbb K} [w]$ as a Zariski open ![]() $\mathbf {I}$-orbit, and it admits a unique
$\mathbf {I}$-orbit, and it admits a unique ![]() $(H \times \mathbb {G}_m)_{\mathbb K}$-fixed point, as required.
$(H \times \mathbb {G}_m)_{\mathbb K}$-fixed point, as required.
Corollary 4.12. The ring ![]() $R ( \mathtt J )_{\mathbb K}$ is integral for each
$R ( \mathtt J )_{\mathbb K}$ is integral for each ![]() $\mathtt J \subset \mathtt I$.
$\mathtt J \subset \mathtt I$.
Proof. Proof of Corollary 4.12.
It suffices to prove the case where ![]() $\mathtt J = \emptyset $, since a subring of an integral ring is integral. We borrow notation from the proof of Lemma 4.11. We have an inclusion
$\mathtt J = \emptyset $, since a subring of an integral ring is integral. We borrow notation from the proof of Lemma 4.11. We have an inclusion
 $$ \begin{align*}R _e = \bigoplus_{\lambda \in P_+} \mathbb{W} ( \lambda )_{\mathbb{Z}}^{\vee} \hookrightarrow \mathbb{Z} [e] \otimes \bigoplus_{\lambda \in P_+} \mathbb{Z} \mathbf{v}_{w_0 \lambda}^{\vee}\end{align*} $$
$$ \begin{align*}R _e = \bigoplus_{\lambda \in P_+} \mathbb{W} ( \lambda )_{\mathbb{Z}}^{\vee} \hookrightarrow \mathbb{Z} [e] \otimes \bigoplus_{\lambda \in P_+} \mathbb{Z} \mathbf{v}_{w_0 \lambda}^{\vee}\end{align*} $$as the Rees construction of formula (4.1). Taking the tensor product ![]() ${\mathbb K} \otimes _{\mathbb {Z}} \bullet $ preserves the inclusion in view of the definition of
${\mathbb K} \otimes _{\mathbb {Z}} \bullet $ preserves the inclusion in view of the definition of ![]() $\mathbb {Z} [e]$. Hence,
$\mathbb {Z} [e]$. Hence, ![]() $( R_e )_{{\mathbb K}}$ is integral as a subring of an integral ring.
$( R_e )_{{\mathbb K}}$ is integral as a subring of an integral ring.
Proposition 4.14. Set ![]() $\mathtt J \subset \mathtt I$. The ind-scheme
$\mathtt J \subset \mathtt I$. The ind-scheme  $\big( \mathbf {Q}_{G,\mathtt J} ^{\mathrm {rat}} \big)_{\mathbb K}$ admits a
$\big( \mathbf {Q}_{G,\mathtt J} ^{\mathrm {rat}} \big)_{\mathbb K}$ admits a ![]() $G (\!(z)\!)$-action. We have a subset
$G (\!(z)\!)$-action. We have a subset ![]() $\mathbf {Q}_{\mathbb K}'$ of the set of
$\mathbf {Q}_{\mathbb K}'$ of the set of ![]() ${\mathbb K}$-valued points of
${\mathbb K}$-valued points of  $\big( \mathbf {Q}_{G,\mathtt J} ^{\mathrm {rat}} \big)_{\mathbb K}$ that is in bijection with
$\big( \mathbf {Q}_{G,\mathtt J} ^{\mathrm {rat}} \big)_{\mathbb K}$ that is in bijection with
Proof. In view of Lemma 4.11, the proof for general ![]() $\mathtt J$ is completely parallel to the case of
$\mathtt J$ is completely parallel to the case of ![]() $\mathtt J = \emptyset $. Hence we concentrate in this proof on the case where
$\mathtt J = \emptyset $. Hence we concentrate in this proof on the case where ![]() $\mathtt J = \emptyset $.
$\mathtt J = \emptyset $.
Set ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $\beta \in Q^{\vee }$. We have an isomorphism
$\beta \in Q^{\vee }$. We have an isomorphism ![]() $R_w \cong R_{w t_{\beta }}$ as rings with
$R_w \cong R_{w t_{\beta }}$ as rings with ![]() $U_{\mathbb {Z}}^+$-action, by Corollary 3.28.
$U_{\mathbb {Z}}^+$-action, by Corollary 3.28.
In particular, we have an isomorphism ![]() $\mathbf {Q}_G ( w )_{\mathbb K} \cong \mathbf {Q}_G \left ( w t_{\beta } \right )_{\mathbb K}$ of schemes with
$\mathbf {Q}_G ( w )_{\mathbb K} \cong \mathbf {Q}_G \left ( w t_{\beta } \right )_{\mathbb K}$ of schemes with ![]() $\mathbf {I}$-actions for each
$\mathbf {I}$-actions for each ![]() $\beta \in Q^{\vee }$. This implies that
$\beta \in Q^{\vee }$. This implies that ![]() $\mathbf {Q}_G \left ( w t_{\beta } \right )_{\mathbb K}$ has a Zariski open subset of the shape
$\mathbf {Q}_G \left ( w t_{\beta } \right )_{\mathbb K}$ has a Zariski open subset of the shape
where we used the fact that ![]() $\mathrm {Ad} ( \dot {w}_0 ) ( N (\!(z)\!) )$ is invariant under the
$\mathrm {Ad} ( \dot {w}_0 ) ( N (\!(z)\!) )$ is invariant under the ![]() $\mathrm {Ad} \left ( \dot {t}_{\beta } \right )$-action.
$\mathrm {Ad} \left ( \dot {t}_{\beta } \right )$-action.
The ring ![]() $( R_{w} )_{{\mathbb K}}$ admits an action of
$( R_{w} )_{{\mathbb K}}$ admits an action of ![]() $\mathop {\textit{SL}} ( 2, i )$ whenever
$\mathop {\textit{SL}} ( 2, i )$ whenever ![]() $s_i w \le _{\frac {\infty }{2}} w$ (
$s_i w \le _{\frac {\infty }{2}} w$ (![]() $i \in \mathtt I_{\mathrm {af}}$), since each
$i \in \mathtt I_{\mathrm {af}}$), since each ![]() $\mathbb {W}_{ww_0} ( \lambda )_{{\mathbb K}}$ (
$\mathbb {W}_{ww_0} ( \lambda )_{{\mathbb K}}$ (![]() $\lambda \in P_+$) admits an action of
$\lambda \in P_+$) admits an action of ![]() $\mathop {\textit{SL}} ( 2, i )$ by Corollary 3.16. Hence,
$\mathop {\textit{SL}} ( 2, i )$ by Corollary 3.16. Hence, ![]() $\mathrm {Proj} (R_{w})_{{\mathbb K}}$ admits an action of
$\mathrm {Proj} (R_{w})_{{\mathbb K}}$ admits an action of ![]() $\mathop {\textit{SL}} ( 2, i )$ if
$\mathop {\textit{SL}} ( 2, i )$ if ![]() $s_i w \le _{\frac {\infty }{2}} w$. In particular, the proalgebraic group
$s_i w \le _{\frac {\infty }{2}} w$. In particular, the proalgebraic group ![]() $\mathbf {I} ( i )$ acts on
$\mathbf {I} ( i )$ acts on ![]() $\mathrm {Proj} ( R_{w} )_{{\mathbb K}}$ if
$\mathrm {Proj} ( R_{w} )_{{\mathbb K}}$ if ![]() $s_i w \le _{\frac {\infty }{2}} w$. Hence the ind-limit
$s_i w \le _{\frac {\infty }{2}} w$. Hence the ind-limit
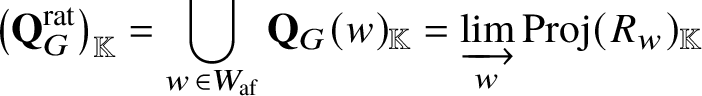 $$ \begin{align*}\left( \mathbf{Q}_G^{\mathrm{rat}} \right)_{\mathbb K} = \bigcup_{w \in W_{\mathrm{af}}} \mathbf{Q}_G ( w )_{{\mathbb K}} = \varinjlim_w \mathrm{Proj} (R_{w} )_{\mathbb K}\end{align*} $$
$$ \begin{align*}\left( \mathbf{Q}_G^{\mathrm{rat}} \right)_{\mathbb K} = \bigcup_{w \in W_{\mathrm{af}}} \mathbf{Q}_G ( w )_{{\mathbb K}} = \varinjlim_w \mathrm{Proj} (R_{w} )_{\mathbb K}\end{align*} $$admits an action of ![]() $\mathbf {I} ( i )$ for each
$\mathbf {I} ( i )$ for each ![]() $i \in \mathtt I_{\mathrm {af}}$ (which coincide on
$i \in \mathtt I_{\mathrm {af}}$ (which coincide on ![]() $\mathbf {I}$). By rank
$\mathbf {I}$). By rank ![]() $2$ calculations, they induce an action of
$2$ calculations, they induce an action of ![]() $N_{G(\!(z)\!)} ( H ( {\mathbb K} ) )$ on
$N_{G(\!(z)\!)} ( H ( {\mathbb K} ) )$ on  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$. The intersections of
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$. The intersections of ![]() $N_{G(\!(z)\!)} ( H ( {\mathbb K} ) )$ and
$N_{G(\!(z)\!)} ( H ( {\mathbb K} ) )$ and ![]() $\mathbf {I} ( {\mathbb K} )$ or
$\mathbf {I} ( {\mathbb K} )$ or ![]() $\mathbf {I} ( i ) ( {\mathbb K})$ (
$\mathbf {I} ( i ) ( {\mathbb K})$ (![]() $i \in \mathtt I_{\mathrm {af}}$) inside
$i \in \mathtt I_{\mathrm {af}}$) inside ![]() $G (\!(z)\!)$ define common actions on
$G (\!(z)\!)$ define common actions on  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$. The system of groups
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$. The system of groups ![]() $\left (\mathbf {I} ({\mathbb K}), N_{G(\!(z)\!)} ( H ( {\mathbb K} ) ), \mathbf {I}(i) ({\mathbb K}); i \in \mathtt I_{\mathrm {af}} \right )$ (in the sense of [Reference Kumar57, Definition 5.1.6]) admits a map from the system of groups in [Reference Kumar57, §6.1.16] for
$\left (\mathbf {I} ({\mathbb K}), N_{G(\!(z)\!)} ( H ( {\mathbb K} ) ), \mathbf {I}(i) ({\mathbb K}); i \in \mathtt I_{\mathrm {af}} \right )$ (in the sense of [Reference Kumar57, Definition 5.1.6]) admits a map from the system of groups in [Reference Kumar57, §6.1.16] for ![]() $\widetilde {\mathfrak {g}}$ (with exponential maps replaced by one-parameter subgroups). Hence, [Reference Kumar57, Theorem 6.1.17] asserts that
$\widetilde {\mathfrak {g}}$ (with exponential maps replaced by one-parameter subgroups). Hence, [Reference Kumar57, Theorem 6.1.17] asserts that ![]() $G(\!(z)\!)$ acts on
$G(\!(z)\!)$ acts on  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$.
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$.
The Bruhat decomposition of ![]() $\mathop {\textit{SL}} ( 2, i )$ asserts that
$\mathop {\textit{SL}} ( 2, i )$ asserts that ![]() $\mathbb {O} ( w )_{{\mathbb K}} \sqcup \mathbb {O} ( s_i w )_{{\mathbb K}}$ admits an
$\mathbb {O} ( w )_{{\mathbb K}} \sqcup \mathbb {O} ( s_i w )_{{\mathbb K}}$ admits an ![]() $\mathop {\textit{SL}} ( 2, i )$-action. This induces an action of
$\mathop {\textit{SL}} ( 2, i )$-action. This induces an action of ![]() $\mathop {\textit{SL}} ( 2, i ) ( {\mathbb K} )$ (
$\mathop {\textit{SL}} ( 2, i ) ( {\mathbb K} )$ (![]() $i \in \mathtt I_{\mathrm {af}}$) on the union
$i \in \mathtt I_{\mathrm {af}}$) on the union
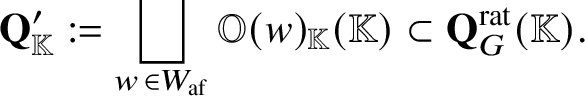 $$ \begin{align*}\mathbf{Q}_{\mathbb K}' := \bigsqcup_{w \in W_{\mathrm{af}}} \mathbb{O} ( w )_{{\mathbb K}} ( {\mathbb K} ) \subset \mathbf{Q}_G^{\mathrm{rat}}( {\mathbb K} ).\end{align*} $$
$$ \begin{align*}\mathbf{Q}_{\mathbb K}' := \bigsqcup_{w \in W_{\mathrm{af}}} \mathbb{O} ( w )_{{\mathbb K}} ( {\mathbb K} ) \subset \mathbf{Q}_G^{\mathrm{rat}}( {\mathbb K} ).\end{align*} $$Taking into account the fact that each ![]() $\mathbb {O} ( w )_{{\mathbb K}}$ admits an
$\mathbb {O} ( w )_{{\mathbb K}}$ admits an ![]() $\mathbf {I}$-action (Lemma 4.11), we conclude that
$\mathbf {I}$-action (Lemma 4.11), we conclude that ![]() $\mathbf {Q}_{\mathbb K}'$ admits an action of
$\mathbf {Q}_{\mathbb K}'$ admits an action of ![]() $G (\!(z)\!)$ thanks to the Iwasawa decomposition (compare [Reference Iwahori and Matsumoto38, Theorem 2.5])
$G (\!(z)\!)$ thanks to the Iwasawa decomposition (compare [Reference Iwahori and Matsumoto38, Theorem 2.5])
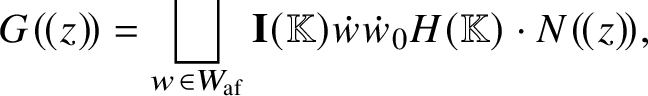 $$ \begin{align*}G (\!(z)\!) = \bigsqcup_{w \in W_{\mathrm{af}}} \mathbf{I} ( {\mathbb K} ) \dot{w} \dot{w}_0 H ( {\mathbb K} ) \cdot N (\!(z)\!),\end{align*} $$
$$ \begin{align*}G (\!(z)\!) = \bigsqcup_{w \in W_{\mathrm{af}}} \mathbf{I} ( {\mathbb K} ) \dot{w} \dot{w}_0 H ( {\mathbb K} ) \cdot N (\!(z)\!),\end{align*} $$as required.
For ![]() $\lambda ,\mu \in P_+$, we have a unique injective
$\lambda ,\mu \in P_+$, we have a unique injective ![]() $\dot {U}_{\mathbb {Z}}^0$-module map
$\dot {U}_{\mathbb {Z}}^0$-module map
obtained by sending  $\mathbf {v}^0_{\lambda + \mu }$ to
$\mathbf {v}^0_{\lambda + \mu }$ to  $\mathbf {v}^0_\lambda \otimes \mathbf {v}^0_{\mu }$, which is in fact a
$\mathbf {v}^0_\lambda \otimes \mathbf {v}^0_{\mu }$, which is in fact a ![]() $\mathbb {Z}$-direct summand (Corollary 3.12). By extending the scalar, we obtain a unique injective
$\mathbb {Z}$-direct summand (Corollary 3.12). By extending the scalar, we obtain a unique injective  $\left (\dot {U}_{\mathbb K}^0, {\mathbb K} [\![z]\!]\right )$-bimodule map
$\left (\dot {U}_{\mathbb K}^0, {\mathbb K} [\![z]\!]\right )$-bimodule map
Lemma 4.15. For each ![]() $\lambda , \mu , \gamma \in P_+$, we have
$\lambda , \mu , \gamma \in P_+$, we have
Proof. This is straightforward from the construction (compare Lemma 3.27).
Proposition 4.16. Assume that ![]() $\mathsf {char}\, {\mathbb K} \neq 2$. For each
$\mathsf {char}\, {\mathbb K} \neq 2$. For each ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$, we have an
$\mathtt J \subset \mathtt I$, we have an ![]() $\mathbf {I}$-equivariant rational map
$\mathbf {I}$-equivariant rational map
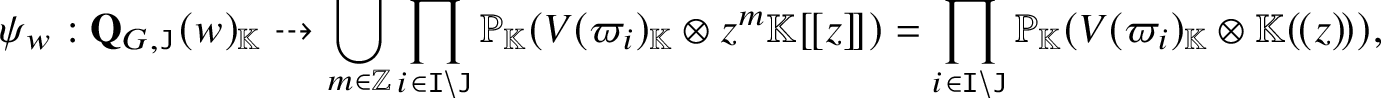 $$ \begin{align*}\psi_w : \mathbf{Q}_{G,\mathtt J} ( w )_{{\mathbb K}} \dashrightarrow \bigcup_{m \in \mathbb{Z}} \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb K} ( V ( \varpi_i ) _{\mathbb K} \otimes z^m {\mathbb K} [\![z]\!]) = \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb K} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!)),\end{align*} $$
$$ \begin{align*}\psi_w : \mathbf{Q}_{G,\mathtt J} ( w )_{{\mathbb K}} \dashrightarrow \bigcup_{m \in \mathbb{Z}} \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb K} ( V ( \varpi_i ) _{\mathbb K} \otimes z^m {\mathbb K} [\![z]\!]) = \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb K} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!)),\end{align*} $$which gives rise to a ![]() $G(\!(z)\!)$-equivariant rational map
$G(\!(z)\!)$-equivariant rational map
 $$ \begin{align*}\psi : \big( \mathbf{Q}_{G,\mathtt J} ^{\mathrm{rat}} \big)_{{\mathbb K}} \dashrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb K} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!)).\end{align*} $$
$$ \begin{align*}\psi : \big( \mathbf{Q}_{G,\mathtt J} ^{\mathrm{rat}} \big)_{{\mathbb K}} \dashrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb K} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!)).\end{align*} $$In addition, the set ![]() $( \mathrm {Im} \, \psi ) ( {\mathbb K} )$ defines a closed
$( \mathrm {Im} \, \psi ) ( {\mathbb K} )$ defines a closed ![]() $($ind-
$($ind-![]() $)$subscheme of
$)$subscheme of ![]() $\prod _{i \in \mathtt I \setminus \mathtt J} \mathbb {P}_{\mathbb K} ( V ( \varpi _i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!))$.
$\prod _{i \in \mathtt I \setminus \mathtt J} \mathbb {P}_{\mathbb K} ( V ( \varpi _i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!))$.
Proof. We have a surjective map
as  $\dot {U}^{\ge 0}_{\mathbb K}$-modules, since we have the corresponding map over
$\dot {U}^{\ge 0}_{\mathbb K}$-modules, since we have the corresponding map over  $\dot {U}^{\ge 0}_{\mathbb {Z}}$ such that the P-weight
$\dot {U}^{\ge 0}_{\mathbb {Z}}$ such that the P-weight ![]() $\varpi _i$-part is the same (and
$\varpi _i$-part is the same (and ![]() $V ( \varpi _i )_{\mathbb K}$ is cyclic as a
$V ( \varpi _i )_{\mathbb K}$ is cyclic as a ![]() $\dot {U}^{0}_{\mathbb K}$-module). The identification of the P-weight
$\dot {U}^{0}_{\mathbb K}$-module). The identification of the P-weight ![]() $\varpi _i$-part also implies that this map commutes with the action of
$\varpi _i$-part also implies that this map commutes with the action of ![]() $\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ and extends to a surjective map
$\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ and extends to a surjective map
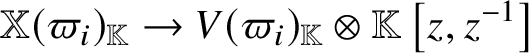 $$ \begin{align*}\mathbb{X} ( \varpi_i )_{\mathbb K}\rightarrow V ( \varpi_i )_{\mathbb K} \otimes {\mathbb K} \left[z,z^{-1}\right]\end{align*} $$
$$ \begin{align*}\mathbb{X} ( \varpi_i )_{\mathbb K}\rightarrow V ( \varpi_i )_{\mathbb K} \otimes {\mathbb K} \left[z,z^{-1}\right]\end{align*} $$of ![]() $\dot {U}_{\mathbb K}$-modules.
$\dot {U}_{\mathbb K}$-modules.
This gives a rational map
and its graded completion
Taking Corollary 3.26 into account, we have an embedding
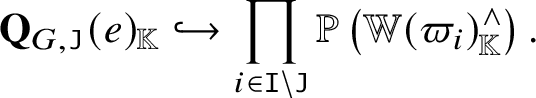 $$ \begin{align} \mathbf{Q}_{G,\mathtt J} ( e )_{\mathbb K} \hookrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} \left( \mathbb{W} ( \varpi_i )_{{\mathbb K}}^{\wedge} \right). \end{align} $$
$$ \begin{align} \mathbf{Q}_{G,\mathtt J} ( e )_{\mathbb K} \hookrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} \left( \mathbb{W} ( \varpi_i )_{{\mathbb K}}^{\wedge} \right). \end{align} $$This yields a rational map
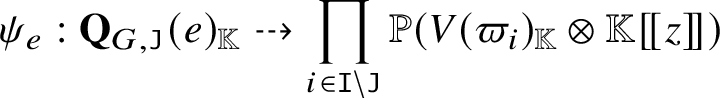 $$ \begin{align*}\psi_e : \mathbf{Q}_{G,\mathtt J} ( e )_{\mathbb K} \dashrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i )_{\mathbb K} \otimes {\mathbb K} [\![z]\!] )\end{align*} $$
$$ \begin{align*}\psi_e : \mathbf{Q}_{G,\mathtt J} ( e )_{\mathbb K} \dashrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i )_{\mathbb K} \otimes {\mathbb K} [\![z]\!] )\end{align*} $$as a composition. This map is ![]() $G [\![z]\!]$-equivariant by construction.
$G [\![z]\!]$-equivariant by construction.
For each ![]() $w \in W$, we can choose
$w \in W$, we can choose ![]() $\beta \in Q^{\vee }_+$ such that
$\beta \in Q^{\vee }_+$ such that ![]() $\mathbf {Q}_{G,\mathtt J} ( w )_{\mathbb K} \cong \mathbf {Q}_{G,\mathtt J} \left ( w t_{\beta } \right )_{\mathbb K} \subset \mathbf {Q} _{G,\mathtt J}( e )_{\mathbb K}$, by Corollary 3.28 and Lemma 3.29. Hence we obtain the map
$\mathbf {Q}_{G,\mathtt J} ( w )_{\mathbb K} \cong \mathbf {Q}_{G,\mathtt J} \left ( w t_{\beta } \right )_{\mathbb K} \subset \mathbf {Q} _{G,\mathtt J}( e )_{\mathbb K}$, by Corollary 3.28 and Lemma 3.29. Hence we obtain the map ![]() $\psi _w$ for every
$\psi _w$ for every ![]() $w \in W_{\mathrm {af}}$ as the composition of the foregoing maps (up to grading shifts). We fix the effect of grading shifts from
$w \in W_{\mathrm {af}}$ as the composition of the foregoing maps (up to grading shifts). We fix the effect of grading shifts from ![]() $\psi _w$ to
$\psi _w$ to ![]() $\psi _{wt_{\beta }}$ by applying
$\psi _{wt_{\beta }}$ by applying ![]() $\tau _{w_0 \beta }$ on
$\tau _{w_0 \beta }$ on ![]() $\mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ for each
$\mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ for each ![]() $i \in \mathtt I \setminus \mathtt J$ in formula (4.6). Then the
$i \in \mathtt I \setminus \mathtt J$ in formula (4.6). Then the ![]() $\tau _{w_0\beta }$-action (on the completions of
$\tau _{w_0\beta }$-action (on the completions of ![]() $\{ \mathbb {X} ( \varpi _i )_{{\mathbb K}}\}_{i \in \mathtt I \setminus \mathtt J}$) transfers
$\{ \mathbb {X} ( \varpi _i )_{{\mathbb K}}\}_{i \in \mathtt I \setminus \mathtt J}$) transfers ![]() $\psi _w$ to
$\psi _w$ to ![]() $\psi _{wt_{\beta }}$ for each
$\psi _{wt_{\beta }}$ for each ![]() $\beta \in Q^{\vee }$, and is compatible with the restrictions to
$\beta \in Q^{\vee }$, and is compatible with the restrictions to ![]() $\mathbf {Q}_G ( \bullet )$s by Lemma 3.17(1). Hence, we obtain the map
$\mathbf {Q}_G ( \bullet )$s by Lemma 3.17(1). Hence, we obtain the map ![]() $\psi $ of ind-schemes. This map is
$\psi $ of ind-schemes. This map is ![]() $G (\!(z)\!)$-equivariant in our sense. This proves the first assertion.
$G (\!(z)\!)$-equivariant in our sense. This proves the first assertion.
From now on, we concentrate on the second assertion.
Each ![]() $(H \times \mathbb {G}_m)$-fixed point of
$(H \times \mathbb {G}_m)$-fixed point of ![]() $\mathbb {O} ( w )_{{\mathbb K}}$ (
$\mathbb {O} ( w )_{{\mathbb K}}$ (![]() $w \in W_{\mathrm {af}}$) is contained in the domain of
$w \in W_{\mathrm {af}}$) is contained in the domain of ![]() $\psi $, and their images are distinct by inspection. It follows that
$\psi $, and their images are distinct by inspection. It follows that ![]() $\mathbf {Q}_{\mathbb K}'$ is contained in the domain of
$\mathbf {Q}_{\mathbb K}'$ is contained in the domain of ![]() $\psi $, and the restriction of
$\psi $, and the restriction of ![]() $\psi $ to
$\psi $ to ![]() $\mathbf {Q}_{\mathbb K}'$ is injective by examining the stabiliser of the
$\mathbf {Q}_{\mathbb K}'$ is injective by examining the stabiliser of the ![]() $\mathbf {I} ( {\mathbb K} )$-actions at each
$\mathbf {I} ( {\mathbb K} )$-actions at each ![]() $(H \times \mathbb {G}_m)$-fixed point.
$(H \times \mathbb {G}_m)$-fixed point.
In view of Theorem 3.18, the maps  $\left \{\eta _{\lambda ,\mu }\right \}_{\lambda ,\mu }$ (
$\left \{\eta _{\lambda ,\mu }\right \}_{\lambda ,\mu }$ (![]() $\lambda ,\mu \in P_{\mathtt J,+}$) induce a commutative diagram of
$\lambda ,\mu \in P_{\mathtt J,+}$) induce a commutative diagram of  $\dot {U}^{\ge 0}_{{\mathbb K}}$-modules:
$\dot {U}^{\ge 0}_{{\mathbb K}}$-modules:
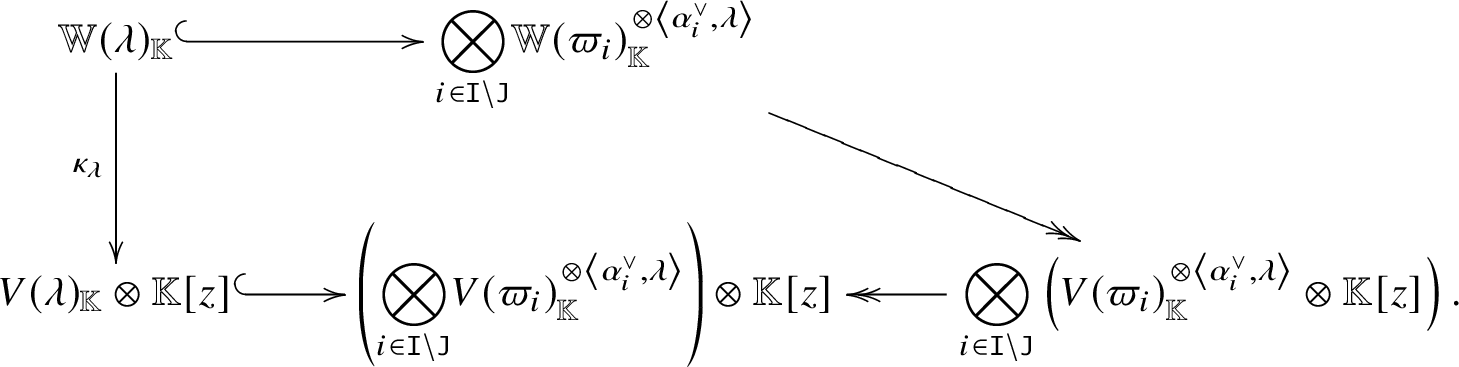
Here the map ![]() $\kappa _\lambda $ is well defined by examination of the degree
$\kappa _\lambda $ is well defined by examination of the degree ![]() $0$ part and the action of
$0$ part and the action of ![]() $E_0 = F_{\vartheta } \otimes z$ (where
$E_0 = F_{\vartheta } \otimes z$ (where ![]() $F_{\vartheta }$ is a nonzero vector in the
$F_{\vartheta }$ is a nonzero vector in the ![]() $- \vartheta $-weight space of
$- \vartheta $-weight space of ![]() $\mathfrak {n}^-$). This commutative diagram also commutes with the translation by
$\mathfrak {n}^-$). This commutative diagram also commutes with the translation by ![]() $\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ by construction. Moreover, we have
$\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ by construction. Moreover, we have ![]() $\kappa _\lambda ( \mathbf {v}_{w \lambda } ) \neq 0$ for each
$\kappa _\lambda ( \mathbf {v}_{w \lambda } ) \neq 0$ for each ![]() $w \in W_{\mathrm {af}}$. Therefore, the map
$w \in W_{\mathrm {af}}$. Therefore, the map ![]() $\kappa _\lambda $ must be surjective whenever its d-degree belongs to
$\kappa _\lambda $ must be surjective whenever its d-degree belongs to  $\sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z} \left \langle \alpha _i^{\vee }, \lambda \right \rangle $.
$\sum _{i \in \mathtt I \setminus \mathtt J} \mathbb {Z} \left \langle \alpha _i^{\vee }, \lambda \right \rangle $.
For each ![]() $i \in \mathtt I \setminus \mathtt J$, the
$i \in \mathtt I \setminus \mathtt J$, the  $\mathbb {Z} \left [\frac {1}{2}\right ]$-integral structure of
$\mathbb {Z} \left [\frac {1}{2}\right ]$-integral structure of  $V ( 2 \varpi _i ) \otimes _{{\mathbb C}} {\mathbb C} \left [z,z^{-1}\right ]$ at the odd degree and even degree must be the same as
$V ( 2 \varpi _i ) \otimes _{{\mathbb C}} {\mathbb C} \left [z,z^{-1}\right ]$ at the odd degree and even degree must be the same as ![]() $\dot {U}_{\mathbb {Z}}$-modules (as we can connect the extremal weight vectors of the even-degree and odd-degree parts using the
$\dot {U}_{\mathbb {Z}}$-modules (as we can connect the extremal weight vectors of the even-degree and odd-degree parts using the ![]() $\mathfrak {sl} ( 2 )$-strings of length
$\mathfrak {sl} ( 2 )$-strings of length ![]() $3$). Therefore, for
$3$). Therefore, for ![]() $\lambda = \varpi _i, \varpi _i + \varpi _j, 2 \varpi _i$ (
$\lambda = \varpi _i, \varpi _i + \varpi _j, 2 \varpi _i$ (![]() $i,j \in \mathtt I \setminus \mathtt J$), the map
$i,j \in \mathtt I \setminus \mathtt J$), the map ![]() $\kappa _{\lambda }$ is surjective.
$\kappa _{\lambda }$ is surjective.
Consider a (representative of the) image
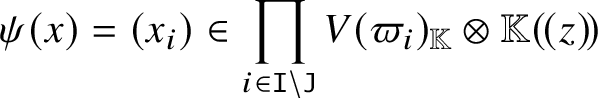 $$ \begin{align*}\psi ( x ) = (x_i) \in \prod_{i \in \mathtt I \setminus \mathtt J} V ( \varpi_i ) _{{\mathbb K}} \otimes {\mathbb K} (\!(z)\!)\end{align*} $$
$$ \begin{align*}\psi ( x ) = (x_i) \in \prod_{i \in \mathtt I \setminus \mathtt J} V ( \varpi_i ) _{{\mathbb K}} \otimes {\mathbb K} (\!(z)\!)\end{align*} $$of a ![]() ${\mathbb K}$-valued point
${\mathbb K}$-valued point ![]() $x \in \mathbf {Q}_{G, \mathtt J} ( e )_{\mathbb K}$ under
$x \in \mathbf {Q}_{G, \mathtt J} ( e )_{\mathbb K}$ under ![]() $\psi $. We consider its lifts
$\psi $. We consider its lifts ![]() $\widetilde {x}_i \in \mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ and
$\widetilde {x}_i \in \mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ and ![]() $\widetilde {x}_j \in \mathbb {W} ( \varpi _j )_{{\mathbb K}}^{\wedge }$. They must belong to
$\widetilde {x}_j \in \mathbb {W} ( \varpi _j )_{{\mathbb K}}^{\wedge }$. They must belong to
 $$ \begin{align*}\mathrm{Im} \left( \mathbb{W} \left( \varpi_i + \varpi_j \right)_{{\mathbb K}}^{\wedge} \longrightarrow \left( \mathbb{W} ( \varpi_i )_{{\mathbb K}} \otimes \mathbb{W} \left( \varpi_j \right)_{{\mathbb K}} \right)^{\wedge} \right)\end{align*} $$
$$ \begin{align*}\mathrm{Im} \left( \mathbb{W} \left( \varpi_i + \varpi_j \right)_{{\mathbb K}}^{\wedge} \longrightarrow \left( \mathbb{W} ( \varpi_i )_{{\mathbb K}} \otimes \mathbb{W} \left( \varpi_j \right)_{{\mathbb K}} \right)^{\wedge} \right)\end{align*} $$in order to satisfy the defining relations of ![]() $R_{{\mathbb K}}$. In view of the commutative diagram (4.7) for
$R_{{\mathbb K}}$. In view of the commutative diagram (4.7) for ![]() $\lambda = \varpi _i + \varpi _j$, we deduce an equation
$\lambda = \varpi _i + \varpi _j$, we deduce an equation
Since the relation of the ring  $\bigoplus _{\lambda \in P_{\mathtt J,+}} V ( \lambda )^*_{{\mathbb K}}$ is generated by P-degrees
$\bigoplus _{\lambda \in P_{\mathtt J,+}} V ( \lambda )^*_{{\mathbb K}}$ is generated by P-degrees ![]() $2 \varpi _i$ and
$2 \varpi _i$ and ![]() $\varpi _i + \varpi _j$ for
$\varpi _i + \varpi _j$ for ![]() $i,j \in \mathtt I$ ([Reference Brion and Kumar14, Theorem 3.5.3]), this defines an element of
$i,j \in \mathtt I$ ([Reference Brion and Kumar14, Theorem 3.5.3]), this defines an element of
through quadratic relations [Reference Finkelberg and Mirković29, §4], where
is the basic affine space. Therefore, applying some ![]() $\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ if necessary, we conclude that if a
$\tau _{\beta } \left (\beta \in Q^{\vee }\right )$ if necessary, we conclude that if a ![]() ${\mathbb K}$-valued point x of
${\mathbb K}$-valued point x of  $\mathbf {Q}_{G, \mathtt J} ^{\mathrm {rat}}$ belongs to the domain of
$\mathbf {Q}_{G, \mathtt J} ^{\mathrm {rat}}$ belongs to the domain of ![]() $\psi $, then
$\psi $, then ![]() $\psi ( x )$ belongs to the set of
$\psi ( x )$ belongs to the set of ![]() ${\mathbb K}$-valued points of the image given by formula (4.9). Taking Proposition 4.14 (and its
${\mathbb K}$-valued points of the image given by formula (4.9). Taking Proposition 4.14 (and its ![]() $G(\!(z)\!)$-action) and formula (4.8) into account, we conclude the second assertion.
$G(\!(z)\!)$-action) and formula (4.8) into account, we conclude the second assertion.
Corollary 4.17. Keep the setting of Proposition 4.16. The map ![]() $\psi $ induces a bijection of
$\psi $ induces a bijection of ![]() ${\mathbb K}$-valued points between the domain and the range.
${\mathbb K}$-valued points between the domain and the range.
Proof. By abuse of convention, we regard ![]() $\mathbf {Q}^{\prime }_{{\mathbb K}}$ as subsets of both
$\mathbf {Q}^{\prime }_{{\mathbb K}}$ as subsets of both ![]() $\mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb K} )$ and
$\mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb K} )$ and ![]() $( \mathrm {Im} \, \psi ) ( {\mathbb K} )$. Let
$( \mathrm {Im} \, \psi ) ( {\mathbb K} )$. Let ![]() $x' \in \mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb K} )$ be a preimage of an
$x' \in \mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb K} )$ be a preimage of an ![]() $( H \times \mathbb {G}_m ) ( {\mathbb K} )$-fixed point
$( H \times \mathbb {G}_m ) ( {\mathbb K} )$-fixed point ![]() $x \in \mathbf {Q}^{\prime }_{{\mathbb K}}$ through
$x \in \mathbf {Q}^{\prime }_{{\mathbb K}}$ through ![]() $\psi $. Consider the embedding
$\psi $. Consider the embedding
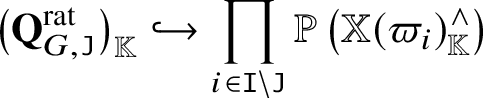 $$ \begin{align*}\big( \mathbf{Q}_{G,\mathtt J} ^{\mathrm{rat}} \big)_{\mathbb K} \hookrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} \left( \mathbb{X} ( \varpi_i )_{{\mathbb K}}^{\wedge} \right)\end{align*} $$
$$ \begin{align*}\big( \mathbf{Q}_{G,\mathtt J} ^{\mathrm{rat}} \big)_{\mathbb K} \hookrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} \left( \mathbb{X} ( \varpi_i )_{{\mathbb K}}^{\wedge} \right)\end{align*} $$that prolongs formula (4.6). Let  $x' = \left ( x^{\prime }_i \right )_{i \in \mathtt I \setminus \mathtt J}$ (resp.,
$x' = \left ( x^{\prime }_i \right )_{i \in \mathtt I \setminus \mathtt J}$ (resp., ![]() $x = ( x_i )_{i \in \mathtt I \setminus \mathtt J}$) be the coordinate of
$x = ( x_i )_{i \in \mathtt I \setminus \mathtt J}$) be the coordinate of ![]() $x'$ (resp., x) through this embedding. We can regard
$x'$ (resp., x) through this embedding. We can regard ![]() $x^{\prime }_i \in \mathbb {X} ( \varpi _i )_{{\mathbb K}}^{\wedge }$, which admits a decomposition
$x^{\prime }_i \in \mathbb {X} ( \varpi _i )_{{\mathbb K}}^{\wedge }$, which admits a decomposition
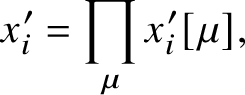 $$ \begin{align*}x^{\prime}_i = \prod_{\mu} x^{\prime}_i [\mu],\end{align*} $$
$$ \begin{align*}x^{\prime}_i = \prod_{\mu} x^{\prime}_i [\mu],\end{align*} $$where ![]() $\mu \in P$ runs over the P-weights of
$\mu \in P$ runs over the P-weights of ![]() $\mathbb {X} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ (or
$\mathbb {X} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ (or ![]() $\mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge }$). Let
$\mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge }$). Let ![]() $d^{\prime }_i [\mu ]$ be the degree of the lowest d-degree nonzero contribution of
$d^{\prime }_i [\mu ]$ be the degree of the lowest d-degree nonzero contribution of ![]() $x^{\prime }_i [\mu ]$ (or
$x^{\prime }_i [\mu ]$ (or ![]() $\infty $ if
$\infty $ if ![]() $x^{\prime }_i [\mu ] = 0$) for each
$x^{\prime }_i [\mu ] = 0$) for each ![]() $i \in \mathtt I \setminus \mathtt J$ and
$i \in \mathtt I \setminus \mathtt J$ and ![]() $\mu \in P$. Let
$\mu \in P$. Let ![]() $d_i$ be the d-degree of
$d_i$ be the d-degree of ![]() $x_i$ for each
$x_i$ for each ![]() $i \in \mathtt I \setminus \mathtt J$ (remember that x is
$i \in \mathtt I \setminus \mathtt J$ (remember that x is ![]() $( H \times \mathbb {G}_m ) ( {\mathbb K} )$-fixed). Note that we have
$( H \times \mathbb {G}_m ) ( {\mathbb K} )$-fixed). Note that we have ![]() $x_i [u \varpi _i] = x^{\prime }_i [u \varpi _i]$ for every
$x_i [u \varpi _i] = x^{\prime }_i [u \varpi _i]$ for every ![]() $i \in \mathtt I$ and
$i \in \mathtt I$ and ![]() $u \in W$, since
$u \in W$, since
For each ![]() $\gamma \in Q^{\vee }$, we have a collection of the automorphisms of the vector spaces
$\gamma \in Q^{\vee }$, we have a collection of the automorphisms of the vector spaces ![]() $\{\mathbb {X} ( \lambda )_{{\mathbb K}}\}_{\lambda \in P_+}$ by shifting the (d-)gradings of the weight
$\{\mathbb {X} ( \lambda )_{{\mathbb K}}\}_{\lambda \in P_+}$ by shifting the (d-)gradings of the weight ![]() $\mu $ parts by
$\mu $ parts by ![]() $\left \langle \gamma , \mu \right \rangle $ (
$\left \langle \gamma , \mu \right \rangle $ (![]() $\mu \in P$). This defines an automorphism of
$\mu \in P$). This defines an automorphism of ![]() $R^+_{\mathbb K}$, and hence defines an automorphism of
$R^+_{\mathbb K}$, and hence defines an automorphism of ![]() $\mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb K} )$. By using this twist for an appropriate
$\mathbf {Q}_G^{\mathrm {rat}} ( {\mathbb K} )$. By using this twist for an appropriate ![]() $\gamma \in Q^{\vee }$, we can assume that
$\gamma \in Q^{\vee }$, we can assume that
for each ![]() $i \in \mathtt I \setminus \mathtt J$ and fixed
$i \in \mathtt I \setminus \mathtt J$ and fixed ![]() $u \in W$, from the fact that every P-weight of
$u \in W$, from the fact that every P-weight of ![]() $W ( \varpi _i )_{{\mathbb K}}$ is
$W ( \varpi _i )_{{\mathbb K}}$ is ![]() $\le \varpi _i$. We have
$\le \varpi _i$. We have ![]() $x_i \in \mathbb {W}_{ww_0} ( \varpi _i )_{{\mathbb K}}$ for some
$x_i \in \mathbb {W}_{ww_0} ( \varpi _i )_{{\mathbb K}}$ for some ![]() $w \in W_{\mathrm {af}}$ and all
$w \in W_{\mathrm {af}}$ and all ![]() $i \in \mathtt I \setminus \mathtt J$. Formula (4.11) implies
$i \in \mathtt I \setminus \mathtt J$. Formula (4.11) implies ![]() $x_i' \in \mathbb {W}_{ww_0} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ for all
$x_i' \in \mathbb {W}_{ww_0} ( \varpi _i )_{{\mathbb K}}^{\wedge }$ for all ![]() $i \in \mathtt I \setminus \mathtt J$ ([Reference Kashiwara44, Theorem 5.17]). Hence, we have
$i \in \mathtt I \setminus \mathtt J$ ([Reference Kashiwara44, Theorem 5.17]). Hence, we have ![]() $x' \in \mathbf {Q}_{G, \mathtt J} ( w )_{{\mathbb K}}$ for
$x' \in \mathbf {Q}_{G, \mathtt J} ( w )_{{\mathbb K}}$ for ![]() $w \in W_{\mathrm {af}}$ such that x is the unique
$w \in W_{\mathrm {af}}$ such that x is the unique ![]() $( H \times \mathbb {G}_m )$-fixed point of
$( H \times \mathbb {G}_m )$-fixed point of ![]() $\mathbb {O} ( \mathtt J, w )_{{\mathbb K}}$.
$\mathbb {O} ( \mathtt J, w )_{{\mathbb K}}$.
From fact (4.10), the ![]() $( H \times \mathbb {G}_m )$-action shrinks
$( H \times \mathbb {G}_m )$-action shrinks ![]() $x'$ to x. In view of its proof, the Zariski open set
$x'$ to x. In view of its proof, the Zariski open set ![]() $\mathbb {O} ( \mathtt J, w )_{{\mathbb K}}$ in Lemma 4.11 is obtained by localising along the vectors
$\mathbb {O} ( \mathtt J, w )_{{\mathbb K}}$ in Lemma 4.11 is obtained by localising along the vectors  $\left \{ \mathbf {v}_{ww_0\lambda }^{\vee } \right \}_{\lambda \in P_{\mathtt J,+}}$, which pairs nontrivially with
$\left \{ \mathbf {v}_{ww_0\lambda }^{\vee } \right \}_{\lambda \in P_{\mathtt J,+}}$, which pairs nontrivially with ![]() $x'$. Therefore, we necessarily have
$x'$. Therefore, we necessarily have ![]() $x' \in \mathbb {O} ( \mathtt J, w )_{{\mathbb K}} ( {\mathbb K} )$. As
$x' \in \mathbb {O} ( \mathtt J, w )_{{\mathbb K}} ( {\mathbb K} )$. As ![]() $\mathbb {O} ( \mathtt J, w )_{{\mathbb K}} ( {\mathbb K} ) \subset \mathbf {Q}^{\prime }_{{\mathbb K}}$ by Proposition 4.14 and its proof, we deduce
$\mathbb {O} ( \mathtt J, w )_{{\mathbb K}} ( {\mathbb K} ) \subset \mathbf {Q}^{\prime }_{{\mathbb K}}$ by Proposition 4.14 and its proof, we deduce ![]() $x = x'$. Since
$x = x'$. Since ![]() $\mathbf {Q}^{\prime }_{{\mathbb K}}$ is stable under the action of
$\mathbf {Q}^{\prime }_{{\mathbb K}}$ is stable under the action of ![]() $Q^{\vee }$, as well as
$Q^{\vee }$, as well as ![]() $G (\!(z)\!)$, we conclude that
$G (\!(z)\!)$, we conclude that ![]() $x = x'$ holds for a preimage of
$x = x'$ holds for a preimage of ![]() $x'$ of every
$x'$ of every ![]() $x \in \mathbf {Q}^{\prime }_{{\mathbb K}}$, as required.
$x \in \mathbf {Q}^{\prime }_{{\mathbb K}}$, as required.
Theorem 4.18. Assume that ![]() $\mathsf {char}\, {\mathbb K} \neq 2$. For each
$\mathsf {char}\, {\mathbb K} \neq 2$. For each ![]() $\mathtt J \subset \mathtt I$, we have a closed immersion of ind-schemes
$\mathtt J \subset \mathtt I$, we have a closed immersion of ind-schemes
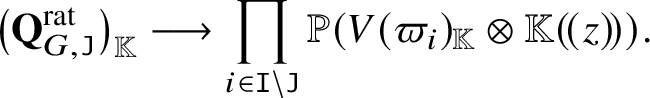 $$ \begin{align*}\big( \mathbf{Q}_{G,\mathtt J} ^{\mathrm{rat}} \big)_{{\mathbb K}} \longrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i )_{\mathbb K} \otimes {\mathbb K} (\!(z)\!) ).\end{align*} $$
$$ \begin{align*}\big( \mathbf{Q}_{G,\mathtt J} ^{\mathrm{rat}} \big)_{{\mathbb K}} \longrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i )_{\mathbb K} \otimes {\mathbb K} (\!(z)\!) ).\end{align*} $$In particular, the set of ![]() ${\mathbb K}$-valued points of the ind-scheme
${\mathbb K}$-valued points of the ind-scheme  $\big( \mathbf {Q}_{G,\mathtt J} ^{\mathrm {rat}} \big)_{\mathbb K}$ is in bijection with
$\big( \mathbf {Q}_{G,\mathtt J} ^{\mathrm {rat}} \big)_{\mathbb K}$ is in bijection with
Proof. By construction, the locus  $E \subset \mathbf {Q}_{G,\mathtt J}^{\mathrm {rat}}$ on which
$E \subset \mathbf {Q}_{G,\mathtt J}^{\mathrm {rat}}$ on which ![]() $\psi $ (borrowed from Proposition 4.16) is not defined is an ind-subscheme. The map
$\psi $ (borrowed from Proposition 4.16) is not defined is an ind-subscheme. The map ![]() $\psi $ is
$\psi $ is ![]() $G (\!(z)\!)$-equivariant. It follows that E admits a
$G (\!(z)\!)$-equivariant. It follows that E admits a ![]() $G (\!(z)\!)$-action as ind-schemes. The map
$G (\!(z)\!)$-action as ind-schemes. The map
(borrowed from the proof of Proposition 4.16) sends an irreducible component of ![]() $\left ( E \cap \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}} \right )$ onto a closed subscheme of
$\left ( E \cap \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}} \right )$ onto a closed subscheme of ![]() $\mathbb {P} \left ( \ker \left ( \mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge } \to V ( \varpi _i )_{{\mathbb K}} \otimes {\mathbb K} [\![z]\!]\right )\right )$ for some
$\mathbb {P} \left ( \ker \left ( \mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge } \to V ( \varpi _i )_{{\mathbb K}} \otimes {\mathbb K} [\![z]\!]\right )\right )$ for some ![]() $i \in \mathtt I \setminus \mathtt J$. In particular,
$i \in \mathtt I \setminus \mathtt J$. In particular, ![]() $\left ( E \cap \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}} \right ) \subset \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}}$ is a closed subscheme. Taking into account the
$\left ( E \cap \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}} \right ) \subset \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}}$ is a closed subscheme. Taking into account the  $\left \{ \tau _{\beta } \right \}_{\beta }$-actions (Lemma 3.17), we have
$\left \{ \tau _{\beta } \right \}_{\beta }$-actions (Lemma 3.17), we have ![]() $E \neq \emptyset $ if and only if
$E \neq \emptyset $ if and only if ![]() $\left ( E \cap \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}} \right ) \neq \emptyset $, and
$\left ( E \cap \mathbf {Q}_{G,\mathtt J} ( e )_{{\mathbb K}} \right ) \neq \emptyset $, and ![]() $\psi $ is a closed immersion if and only if
$\psi $ is a closed immersion if and only if ![]() $\psi _e$ is a closed immersion (compare Lemma 3.29).
$\psi _e$ is a closed immersion (compare Lemma 3.29).
The one-parameter subgroup ![]() $a = ( \xi , 1 ) : \mathbb {G}_m \to ( H \times \mathbb {G}_m )$ for
$a = ( \xi , 1 ) : \mathbb {G}_m \to ( H \times \mathbb {G}_m )$ for ![]() $\xi \in Q^{\vee }_<$ attracts every point of
$\xi \in Q^{\vee }_<$ attracts every point of ![]() $\mathbb {P} ( \mathbb {W} ( \varpi _i )_{{\mathbb K}})$ into its
$\mathbb {P} ( \mathbb {W} ( \varpi _i )_{{\mathbb K}})$ into its ![]() $( H \times \mathbb {G}_m )$-fixed points (by setting
$( H \times \mathbb {G}_m )$-fixed points (by setting ![]() $t \to 0$). In particular, E has an
$t \to 0$). In particular, E has an ![]() $( H \times \mathbb {G}_m )$-fixed point that is not realised by
$( H \times \mathbb {G}_m )$-fixed point that is not realised by ![]() $\mathbf {Q}_{\mathbb K}'$. Since the
$\mathbf {Q}_{\mathbb K}'$. Since the ![]() $( H \times \mathbb {G}_m )$-fixed point of bounded d-degree is captured by the corresponding degree terms of
$( H \times \mathbb {G}_m )$-fixed point of bounded d-degree is captured by the corresponding degree terms of ![]() $R_{{\mathbb K}}$, it follows that the ind-scheme E intersects with
$R_{{\mathbb K}}$, it follows that the ind-scheme E intersects with ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ for some
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ for some ![]() $v \in W_{\mathrm {af}}$. The intersection of
$v \in W_{\mathrm {af}}$. The intersection of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$ and
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$ and ![]() $\mathbf {Q}_{\mathbb K}'$ (as the set of
$\mathbf {Q}_{\mathbb K}'$ (as the set of ![]() ${\mathbb K}$-valued points) defines a closed subset Y of (a product of) a finite-dimensional projective space, by Proposition 4.16 and Corollary 4.17. In particular, Y acquires the structure of a proper scheme through
${\mathbb K}$-valued points) defines a closed subset Y of (a product of) a finite-dimensional projective space, by Proposition 4.16 and Corollary 4.17. In particular, Y acquires the structure of a proper scheme through ![]() $\psi $. From this viewpoint, Corollary 4.17 provides a
$\psi $. From this viewpoint, Corollary 4.17 provides a ![]() $\psi $-section of Y that defines a bijection of
$\psi $-section of Y that defines a bijection of ![]() ${\mathbb K}$-valued points with a Zariski open subset
${\mathbb K}$-valued points with a Zariski open subset ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}\setminus E$ of
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}\setminus E$ of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$. Since
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$. Since ![]() $\mathbf {Q}_{\mathbb K}'$ admits a homogeneous
$\mathbf {Q}_{\mathbb K}'$ admits a homogeneous ![]() $G (\!(z)\!)$-action, we can think of
$G (\!(z)\!)$-action, we can think of ![]() $\psi $ as an everywhere-defined section of a vector bundle over the image (whose fibre is a product of
$\psi $ as an everywhere-defined section of a vector bundle over the image (whose fibre is a product of ![]() $\ker \left ( \mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge } \to V ( \varpi _i )_{{\mathbb K}} \otimes {\mathbb K} [\![z]\!]\right )$s). This implies that
$\ker \left ( \mathbb {W} ( \varpi _i )_{{\mathbb K}}^{\wedge } \to V ( \varpi _i )_{{\mathbb K}} \otimes {\mathbb K} [\![z]\!]\right )$s). This implies that ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}\setminus E$ can be seen as an everywhere-defined section of a vector bundle over the image (whose fibre is a product of finite-dimensional subspaces of
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}\setminus E$ can be seen as an everywhere-defined section of a vector bundle over the image (whose fibre is a product of finite-dimensional subspaces of ![]() $\ker \, ( \mathbb {W} ( \varpi _i )_{{\mathbb K}} \to V ( \varpi _i )_{{\mathbb K}} \otimes {\mathbb K} [z])$s). Since
$\ker \, ( \mathbb {W} ( \varpi _i )_{{\mathbb K}} \to V ( \varpi _i )_{{\mathbb K}} \otimes {\mathbb K} [z])$s). Since ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$ is a finite-type scheme defined over an algebraically closed field
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$ is a finite-type scheme defined over an algebraically closed field ![]() ${\mathbb K}$, it has a dense subset formed by its
${\mathbb K}$, it has a dense subset formed by its ![]() ${\mathbb K}$-valued points ([Reference Grothendieck36, Corollarie 10.4.8]). Thus, the section
${\mathbb K}$-valued points ([Reference Grothendieck36, Corollarie 10.4.8]). Thus, the section ![]() $\psi $ can be seen as that of schemes. Therefore,
$\psi $ can be seen as that of schemes. Therefore, ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}} \setminus E$ is proper by itself. In conclusion,
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}} \setminus E$ is proper by itself. In conclusion, ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}} \setminus E$ can be seen as a connected component of
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}} \setminus E$ can be seen as a connected component of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$ (as being an open and closed subset) which does not intersect with E. It follows that if
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )_{{\mathbb K}}$ (as being an open and closed subset) which does not intersect with E. It follows that if ![]() $E \neq \emptyset $ as a scheme, then the scheme
$E \neq \emptyset $ as a scheme, then the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ must have at least two connected components. Therefore, the projective coordinate ring
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ must have at least two connected components. Therefore, the projective coordinate ring ![]() $R^v_e ( \mathtt J )_{{\mathbb K}}$ of
$R^v_e ( \mathtt J )_{{\mathbb K}}$ of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ must be nonintegral. The same is true if we replace v with a smaller element with respect to
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ must be nonintegral. The same is true if we replace v with a smaller element with respect to ![]() $<_{\frac {\infty }{2}}$.
$<_{\frac {\infty }{2}}$.
Hence, we can find ![]() $f,g \in R^v_e ( \mathtt J )_{{\mathbb K}} \setminus \{ 0 \}$ such that
$f,g \in R^v_e ( \mathtt J )_{{\mathbb K}} \setminus \{ 0 \}$ such that ![]() $fg = 0$ for
$fg = 0$ for ![]() $v \ll _{\frac {\infty }{2}} e$. Since E and its complement are
$v \ll _{\frac {\infty }{2}} e$. Since E and its complement are ![]() $\mathbb {G}_m$-stable, we can assume that f and g are
$\mathbb {G}_m$-stable, we can assume that f and g are ![]() $\mathbb {G}_m$-eigenfunctions. Since E defines a connected component of
$\mathbb {G}_m$-eigenfunctions. Since E defines a connected component of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ for every
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, e )$ for every ![]() $v \ll _{\frac {\infty }{2}} e$, we can fix the degrees of f and g for every
$v \ll _{\frac {\infty }{2}} e$, we can fix the degrees of f and g for every ![]() $v \ll _{\frac {\infty }{2}} e$. For a fixed degree, the d-graded component of
$v \ll _{\frac {\infty }{2}} e$. For a fixed degree, the d-graded component of ![]() $R^v_e ( \mathtt J )_{{\mathbb K}}$ and
$R^v_e ( \mathtt J )_{{\mathbb K}}$ and ![]() $R_e ( \mathtt J )_{{\mathbb K}}$ are in common for
$R_e ( \mathtt J )_{{\mathbb K}}$ are in common for ![]() $v \ll _{\frac {\infty }{2}} e$. Since
$v \ll _{\frac {\infty }{2}} e$. Since ![]() $R^v_e ( \mathtt J )_{{\mathbb K}}$ is a quotient ring of
$R^v_e ( \mathtt J )_{{\mathbb K}}$ is a quotient ring of ![]() $R_e ( \mathtt J )_{{\mathbb K}}$, we can find
$R_e ( \mathtt J )_{{\mathbb K}}$, we can find ![]() $\mathbb {G}_m$-eigenfunctions
$\mathbb {G}_m$-eigenfunctions ![]() $f,g \in R_e ( \mathtt J )_{{\mathbb K}} \setminus \{ 0 \}$ such that
$f,g \in R_e ( \mathtt J )_{{\mathbb K}} \setminus \{ 0 \}$ such that ![]() $fg = 0$. This implies that the ring
$fg = 0$. This implies that the ring ![]() $R_{\mathbb K}$ is also nonintegral. This contradicts Corollary 4.12, and hence we deduce
$R_{\mathbb K}$ is also nonintegral. This contradicts Corollary 4.12, and hence we deduce ![]() $E = \emptyset $ as an ind-scheme. Therefore, we conclude that
$E = \emptyset $ as an ind-scheme. Therefore, we conclude that ![]() $\psi $ is in fact a genuine morphism (instead of a rational map) of ind-schemes.
$\psi $ is in fact a genuine morphism (instead of a rational map) of ind-schemes.
Next we prove that ![]() $\psi $ (or rather
$\psi $ (or rather ![]() $\psi _e$) defines a closed immersion. By Lemma 4.11 and the fact that
$\psi _e$) defines a closed immersion. By Lemma 4.11 and the fact that ![]() $\psi $ is a morphism, we deduce that
$\psi $ is a morphism, we deduce that ![]() $\psi $ induces an isomorphism between the function fields of
$\psi $ induces an isomorphism between the function fields of ![]() $\mathbf {Q}_{G, \mathtt J} ( e )_{{\mathbb K}}$ and its image under
$\mathbf {Q}_{G, \mathtt J} ( e )_{{\mathbb K}}$ and its image under ![]() $\psi $. An irreducible component Z of a reduced scheme
$\psi $. An irreducible component Z of a reduced scheme ![]() $\mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}}$ shares a Zariski dense subset with a unique orbit
$\mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}}$ shares a Zariski dense subset with a unique orbit ![]() $\mathbb {O} ( \mathtt J, w )_{\mathbb K}$ (
$\mathbb {O} ( \mathtt J, w )_{\mathbb K}$ (![]() $w \in W_{\mathrm {af}}$). Hence the variety
$w \in W_{\mathrm {af}}$). Hence the variety ![]() $( Z \cap \mathbb {O} ( \mathtt J, w )_{\mathbb K} )$ and its image under
$( Z \cap \mathbb {O} ( \mathtt J, w )_{\mathbb K} )$ and its image under ![]() $\psi $ are presented by the quotients of a common polynomial ring
$\psi $ are presented by the quotients of a common polynomial ring ![]() ${\mathbb K} [\mathbb {O} ( \mathtt J, w )_{\mathbb K}]$ of infinite variables. In view of the d-degree bounds from above and below offered by
${\mathbb K} [\mathbb {O} ( \mathtt J, w )_{\mathbb K}]$ of infinite variables. In view of the d-degree bounds from above and below offered by ![]() $\mathbb {W} _{vw_0}^- ( \varpi _i )_{{\mathbb K}}$ and
$\mathbb {W} _{vw_0}^- ( \varpi _i )_{{\mathbb K}}$ and ![]() $\mathbb {W} _{w_0} ( \varpi _i )_{{\mathbb K}}$ for each
$\mathbb {W} _{w_0} ( \varpi _i )_{{\mathbb K}}$ for each ![]() $i \in \mathtt I \setminus \mathtt J$, these two quotients of
$i \in \mathtt I \setminus \mathtt J$, these two quotients of ![]() ${\mathbb K} [\mathbb {O} ( \mathtt J, w )_{\mathbb K}]$ factor through a common polynomial ring of finite variables. Thus, we deduce that
${\mathbb K} [\mathbb {O} ( \mathtt J, w )_{\mathbb K}]$ factor through a common polynomial ring of finite variables. Thus, we deduce that ![]() $\psi $ also induces an isomorphism between the function fields of Z and
$\psi $ also induces an isomorphism between the function fields of Z and ![]() $\psi ( Z )$. Once we fix an integer
$\psi ( Z )$. Once we fix an integer ![]() $d_0$, two rings
$d_0$, two rings ![]() $R^v_e ( \mathtt J )_{{\mathbb K}}$ and
$R^v_e ( \mathtt J )_{{\mathbb K}}$ and ![]() $R_e ( \mathtt J )_{{\mathbb K}}$ share the same (d-)grading
$R_e ( \mathtt J )_{{\mathbb K}}$ share the same (d-)grading ![]() $d_0$-part for
$d_0$-part for ![]() $v \ll _{\frac {\infty }{2}} e$. Hence, it suffices to prove that
$v \ll _{\frac {\infty }{2}} e$. Hence, it suffices to prove that ![]() $\psi $ restricts to a closed immersion of
$\psi $ restricts to a closed immersion of ![]() $\mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}}$ for
$\mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}}$ for ![]() $v \ll _{\frac {\infty }{2}} e$. Here
$v \ll _{\frac {\infty }{2}} e$. Here ![]() $R^v_e ( \mathtt J )_{{\mathbb K}}$ is weakly normal by Lemma 4.7. Let
$R^v_e ( \mathtt J )_{{\mathbb K}}$ is weakly normal by Lemma 4.7. Let ![]() $R'$ be the multihomogeneous coordinate ring of the (reduced induced structure of the) closed subscheme of
$R'$ be the multihomogeneous coordinate ring of the (reduced induced structure of the) closed subscheme of ![]() $\prod _{i \in \mathtt I \setminus \mathtt J} \mathbb {P} ( V ( \varpi _i )_{\mathbb K} \otimes {\mathbb K} (\!(z)\!) )$ defined by
$\prod _{i \in \mathtt I \setminus \mathtt J} \mathbb {P} ( V ( \varpi _i )_{\mathbb K} \otimes {\mathbb K} (\!(z)\!) )$ defined by ![]() $\psi \left ( \mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}} \right )$. Then if we consider each maximal integral quotient, we deduce that the weak normalisation of
$\psi \left ( \mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}} \right )$. Then if we consider each maximal integral quotient, we deduce that the weak normalisation of ![]() $R'$ is precisely
$R'$ is precisely ![]() $R^v_e ( \mathtt J )_{{\mathbb K}}$ (up to irrelevant locus). This implies that
$R^v_e ( \mathtt J )_{{\mathbb K}}$ (up to irrelevant locus). This implies that ![]() $\psi \left ( \mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}} \right )$ defines a closed subscheme for each
$\psi \left ( \mathscr {Q}_{\mathtt J}' ( v, e )_{{\mathbb K}} \right )$ defines a closed subscheme for each ![]() $v \in W_{\mathrm {af}}$ as required.
$v \in W_{\mathrm {af}}$ as required.
Since ![]() $\psi $ is a closed immersion, the rest of the assertion follows from Proposition 4.16. This completes the proof.
$\psi $ is a closed immersion, the rest of the assertion follows from Proposition 4.16. This completes the proof.
Corollary 4.19 Corollary of the proof of Theorem 4.18
Set ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$. Every two rational functions on
$\mathtt J \subset \mathtt I$. Every two rational functions on ![]() $\mathbf {Q}_{G,\mathtt J} ( w )_{{\mathbb K}}$ are distinguished by a pair of
$\mathbf {Q}_{G,\mathtt J} ( w )_{{\mathbb K}}$ are distinguished by a pair of ![]() ${\mathbb K}$-valued points of
${\mathbb K}$-valued points of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ for some
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ for some ![]() $v \in W_{\mathrm {af}}$. In particular, the union
$v \in W_{\mathrm {af}}$. In particular, the union ![]() $\bigcup _{v \in W_{\mathrm {af}}} \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is Zariski dense in
$\bigcup _{v \in W_{\mathrm {af}}} \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is Zariski dense in ![]() $\mathbf {Q}_{G,\mathtt J} ( w )_{{\mathbb K}}$.
$\mathbf {Q}_{G,\mathtt J} ( w )_{{\mathbb K}}$.
Corollary 4.20. The conclusions of Theorems 2.4 and 2.5 hold when we replace ![]() ${\mathbb C}$ with an algebraically closed field
${\mathbb C}$ with an algebraically closed field ![]() ${\mathbb K}$ of characteristic
${\mathbb K}$ of characteristic ![]() $\neq 2$.
$\neq 2$.
Proof. In view of Theorem 4.18, all the results in Theorems 2.4 and 2.5 are consequences of the corresponding set-theoretic considerations.
Corollary 4.21. We have ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}} \neq \emptyset $ if and only if
$\mathscr {Q}' ( v, w )_{{\mathbb K}} \neq \emptyset $ if and only if ![]() $v \le _{\frac {\infty }{2}} w$.
$v \le _{\frac {\infty }{2}} w$.
Proof. By Lemma 4.5, it remains to prove that ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}} = \emptyset $ if
$\mathscr {Q}' ( v, w )_{{\mathbb K}} = \emptyset $ if ![]() $v \not {\le }_{\frac {\infty }{2}} w$. By Theorem 4.18 and the definition of
$v \not {\le }_{\frac {\infty }{2}} w$. By Theorem 4.18 and the definition of ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$, the
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$, the ![]() $(H \times \mathbb {G}_m)$-fixed point of
$(H \times \mathbb {G}_m)$-fixed point of ![]() $\mathbb {O} ( u )_{{\mathbb K}}$ is contained in
$\mathbb {O} ( u )_{{\mathbb K}}$ is contained in ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ (
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ (![]() $v,w\in W_{\mathrm {af}}$) only if
$v,w\in W_{\mathrm {af}}$) only if ![]() $v \le _{\frac {\infty }{2}} u \le _{\frac {\infty }{2}} w$. Since
$v \le _{\frac {\infty }{2}} u \le _{\frac {\infty }{2}} w$. Since ![]() $\le _{\frac {\infty }{2}}$ is a partial order, the condition
$\le _{\frac {\infty }{2}}$ is a partial order, the condition ![]() $v \not {\le }_{\frac {\infty }{2}} w$ implies that
$v \not {\le }_{\frac {\infty }{2}} w$ implies that ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ has no
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ has no ![]() $(H \times \mathbb {G}_m)$-fixed point. Since
$(H \times \mathbb {G}_m)$-fixed point. Since ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is projective by Lemma 4.4, it carries an
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is projective by Lemma 4.4, it carries an ![]() $(H \times \mathbb {G}_m)$-fixed point if it is nonempty. Thus, we conclude
$(H \times \mathbb {G}_m)$-fixed point if it is nonempty. Thus, we conclude ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}} = \emptyset $ as required.
$\mathscr {Q}' ( v, w )_{{\mathbb K}} = \emptyset $ as required.
4.3 Coarse representability of the scheme  $\mathbf {Q}_G^{\mathrm {rat}}$
$\mathbf {Q}_G^{\mathrm {rat}}$
Material in this subsection is rather special in this paper, and is irrelevant to the arguments in the later part such as the normality of quasi-map spaces.
In this subsection, we assume that ![]() $\mathsf {char}\, {\mathbb K} \neq 2$, and we drop subscripts
$\mathsf {char}\, {\mathbb K} \neq 2$, and we drop subscripts ![]() ${\mathbb K}$ from
${\mathbb K}$ from  $\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ and its subschemes to simplify notation.
$\big( \mathbf{Q}_G ^{\mathrm{rat}} \big)_{\mathbb K}$ and its subschemes to simplify notation.
Let ![]() $A\!f\!\!f _{\mathbb K}$ be the category of affine schemes over
$A\!f\!\!f _{\mathbb K}$ be the category of affine schemes over ![]() ${\mathbb K}$. We identify
${\mathbb K}$. We identify  $A\!f\!\!f _{\mathbb K}^{op}$ with the category of commutative rings over
$A\!f\!\!f _{\mathbb K}^{op}$ with the category of commutative rings over ![]() ${\mathbb K}$. Let
${\mathbb K}$. Let ![]() $Zar _{\mathbb K}$ denote a big Zariski site over
$Zar _{\mathbb K}$ denote a big Zariski site over ![]() ${\mathbb K}$ [77, Section 020N]. For
${\mathbb K}$ [77, Section 020N]. For ![]() $X \in Zar_{\mathbb K}$, the assignment
$X \in Zar_{\mathbb K}$, the assignment
defines a sheaf ![]() $h_X$ on
$h_X$ on ![]() $Zar_{{\mathbb K}}$ [77, Definition 00WR].
$Zar_{{\mathbb K}}$ [77, Definition 00WR].
For the definition on the coarse moduli functors, we refer to [Reference Viehweg78, Definition 1.10]. However, we use some modified definitions:
Definition 4.22 Strict ind-scheme
Let ![]() $\mathfrak X = \bigcup _{n \ge 0} X_n$ be an increasing union of schemes in
$\mathfrak X = \bigcup _{n \ge 0} X_n$ be an increasing union of schemes in ![]() $Zar_{{\mathbb K}}$. We call
$Zar_{{\mathbb K}}$. We call ![]() $( \mathfrak X, \{ X_n \}_n )$ (or simply
$( \mathfrak X, \{ X_n \}_n )$ (or simply ![]() $\mathfrak X$) a strict ind-scheme if each inclusion
$\mathfrak X$) a strict ind-scheme if each inclusion ![]() $X_k \subset X_{k+1}$ (
$X_k \subset X_{k+1}$ (![]() $k \ge 0$) is a closed immersion.
$k \ge 0$) is a closed immersion.
Definition 4.23 Filtered sheaf on  $Zar_{{\mathbb K}}$
$Zar_{{\mathbb K}}$
A filtered (pre)sheaf ![]() $( \mathcal F, \{ \mathcal F_n \}_{n\ge 0} )$ on
$( \mathcal F, \{ \mathcal F_n \}_{n\ge 0} )$ on ![]() $Zar_{{\mathbb K}}$ is a family of (pre)sheaves such that
$Zar_{{\mathbb K}}$ is a family of (pre)sheaves such that ![]() $\mathcal F_k \subset \mathcal F_{k+1}$ for each
$\mathcal F_k \subset \mathcal F_{k+1}$ for each ![]() $k \in \mathbb {Z}_{\ge 0}$ and
$k \in \mathbb {Z}_{\ge 0}$ and ![]() $\mathcal F = \bigcup _{n} \mathcal F_n$. Let
$\mathcal F = \bigcup _{n} \mathcal F_n$. Let ![]() $( \mathcal F, \{ \mathcal F_n \}_{n\ge 0} )$ and
$( \mathcal F, \{ \mathcal F_n \}_{n\ge 0} )$ and ![]() $( \mathcal G, \{ \mathcal G_n \}_{n\ge 0} )$ be filtered (pre)sheaves on
$( \mathcal G, \{ \mathcal G_n \}_{n\ge 0} )$ be filtered (pre)sheaves on ![]() $Zar_{{\mathbb K}}$. A morphism
$Zar_{{\mathbb K}}$. A morphism ![]() $f : \mathcal F \rightarrow \mathcal G$ of (pre)sheaves is said to be continuous if for each
$f : \mathcal F \rightarrow \mathcal G$ of (pre)sheaves is said to be continuous if for each ![]() $n \in \mathbb {Z}_{\ge 0}$, there is some
$n \in \mathbb {Z}_{\ge 0}$, there is some ![]() $m \in \mathbb {Z}_{\ge 0}$ such that
$m \in \mathbb {Z}_{\ge 0}$ such that
Let ![]() $( \mathfrak F, \{F_n\}_n )$ be a strict ind-scheme. Then we call
$( \mathfrak F, \{F_n\}_n )$ be a strict ind-scheme. Then we call  $h_{\mathfrak F} := \left ( \bigcup _{n} h_{F_n}, \left \{h_{F_n}\right \}_{n\ge 0} \right )$ the filtered sheaf associated to
$h_{\mathfrak F} := \left ( \bigcup _{n} h_{F_n}, \left \{h_{F_n}\right \}_{n\ge 0} \right )$ the filtered sheaf associated to ![]() $\mathfrak F$.
$\mathfrak F$.
Definition 4.24 Coarse ind-representability
Let ![]() $\mathcal X$ be a filtered (pre)sheaf on
$\mathcal X$ be a filtered (pre)sheaf on ![]() $Zar_{{\mathbb K}}$. Let
$Zar_{{\mathbb K}}$. Let ![]() $\mathfrak X$ be a strict ind-scheme over
$\mathfrak X$ be a strict ind-scheme over ![]() ${\mathbb K}$. We say that
${\mathbb K}$. We say that ![]() $\mathcal X$ is coarsely ind-representable by
$\mathcal X$ is coarsely ind-representable by ![]() $\mathfrak X$ if the following conditions hold:
$\mathfrak X$ if the following conditions hold:
• We have a continuous morphism
 $u : \mathcal X \rightarrow h_{\mathfrak X}$ of filtered (pre)sheaves.
$u : \mathcal X \rightarrow h_{\mathfrak X}$ of filtered (pre)sheaves.•
 $\mathcal X ( \Bbbk ) = h_{\mathfrak X} ( \Bbbk )$ for an overfield
$\mathcal X ( \Bbbk ) = h_{\mathfrak X} ( \Bbbk )$ for an overfield  $\Bbbk \supset {\mathbb K}$.
$\Bbbk \supset {\mathbb K}$.• If
 $\mathfrak Y$ is a strict ind-scheme and we have a continuous morphism
$\mathfrak Y$ is a strict ind-scheme and we have a continuous morphism  $f : \mathcal X \rightarrow h_{\mathfrak Y}$, it factors aswhere g is a morphism of presheaves. It is automatic that g is continuous, and hence is induced by a morphism of ind-schemes.
$f : \mathcal X \rightarrow h_{\mathfrak Y}$, it factors aswhere g is a morphism of presheaves. It is automatic that g is continuous, and hence is induced by a morphism of ind-schemes.
We consider the assignment ![]() $\mathcal Q$ on
$\mathcal Q$ on  $A\!f\!\!f^{op}_{\mathbb K}$ defined as
$A\!f\!\!f^{op}_{\mathbb K}$ defined as
For each ![]() $n \in \mathbb {Z}_{\ge 0}$, we consider an assignment
$n \in \mathbb {Z}_{\ge 0}$, we consider an assignment
where
The assignments ![]() $( \mathcal Q, \{ \mathcal Q_n \}_n)$ define a filtered presheaf on
$( \mathcal Q, \{ \mathcal Q_n \}_n)$ define a filtered presheaf on ![]() $Zar_{\mathbb K}$ that we denote by
$Zar_{\mathbb K}$ that we denote by ![]() $\mathcal Q$.
$\mathcal Q$.
Lemma 4.25. The ind-scheme ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ defines a filtered sheaf on
$\mathbf {Q}_G^{\mathrm {rat}}$ defines a filtered sheaf on ![]() $Zar_{\mathbb K}$ given by a strict ind-scheme structure.
$Zar_{\mathbb K}$ given by a strict ind-scheme structure.
Proof. A scheme over ![]() ${\mathbb K}$ defines a sheaf over
${\mathbb K}$ defines a sheaf over ![]() $Zar_{\mathbb K}$, and so is its increasing union. In view of Proposition 4.16, the pole order n condition amounts to choosing the
$Zar_{\mathbb K}$, and so is its increasing union. In view of Proposition 4.16, the pole order n condition amounts to choosing the ![]() $\mathbf {I}$-orbits
$\mathbf {I}$-orbits ![]() $\mathbb {O} \left (u t_{\beta } \right ) \left (u \in W, \beta \in Q^{\vee }\right )$ such that
$\mathbb {O} \left (u t_{\beta } \right ) \left (u \in W, \beta \in Q^{\vee }\right )$ such that ![]() $\left \langle \beta , \varpi _i \right \rangle \ge - n$ (for every
$\left \langle \beta , \varpi _i \right \rangle \ge - n$ (for every ![]() $i \in \mathtt I$), which makes the smaller one a closed subscheme of the larger one (compare Lemma 3.29).
$i \in \mathtt I$), which makes the smaller one a closed subscheme of the larger one (compare Lemma 3.29).
Proposition 4.26. The scheme ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ coarsely ind-represents the presheaf
$\mathbf {Q}_G^{\mathrm {rat}}$ coarsely ind-represents the presheaf ![]() $\mathcal Q$.
$\mathcal Q$.
Proof. We first construct an injective continuous morphism  $\mathcal Q \rightarrow h_{\mathbf {Q}_G^{\mathrm {rat}}}$ as filtered presheaves on
$\mathcal Q \rightarrow h_{\mathbf {Q}_G^{\mathrm {rat}}}$ as filtered presheaves on ![]() $Zar_{\mathbb K}$ such that
$Zar_{\mathbb K}$ such that  $\mathcal Q ( \Bbbk ) = h_{\mathbf {Q}_G^{\mathrm {rat}}} ( \Bbbk )$ for an overfield
$\mathcal Q ( \Bbbk ) = h_{\mathbf {Q}_G^{\mathrm {rat}}} ( \Bbbk )$ for an overfield ![]() $\Bbbk \supset {\mathbb K}$.
$\Bbbk \supset {\mathbb K}$.
For  $R \in A\!f\!\!f_{\mathbb K}^{op}$, the set
$R \in A\!f\!\!f_{\mathbb K}^{op}$, the set ![]() $\mathcal Q ( R )$ is represented by a class of
$\mathcal Q ( R )$ is represented by a class of ![]() $g \in G ( R (\!(z)\!))$ modulo the right action of
$g \in G ( R (\!(z)\!))$ modulo the right action of ![]() $H ( R ) N ( R (\!(z)\!) )$. It defines a point of
$H ( R ) N ( R (\!(z)\!) )$. It defines a point of ![]() $\mathbf {Q}_G^{\mathrm {rat}} ( R )$ by applying g on
$\mathbf {Q}_G^{\mathrm {rat}} ( R )$ by applying g on  $\left \{\left [\mathbf {v}_{\varpi _i}\right ]\right \} _{i \in \mathtt I} \in \prod _{i \in \mathtt I} \mathbb {P} _{R} ( V ( \varpi _i )_{\mathbb {Z}} \otimes _{\mathbb {Z}} R (\!(z)\!) )$. Since the
$\left \{\left [\mathbf {v}_{\varpi _i}\right ]\right \} _{i \in \mathtt I} \in \prod _{i \in \mathtt I} \mathbb {P} _{R} ( V ( \varpi _i )_{\mathbb {Z}} \otimes _{\mathbb {Z}} R (\!(z)\!) )$. Since the ![]() $G(R(\!(z)\!))$-stabiliser of
$G(R(\!(z)\!))$-stabiliser of ![]() $\mathbf {v}_{\varpi _i}$ is precisely
$\mathbf {v}_{\varpi _i}$ is precisely ![]() $H ( R ) N ( R (\!(z)\!) )$, we conclude an inclusion
$H ( R ) N ( R (\!(z)\!) )$, we conclude an inclusion  $\mathcal Q ( R ) \subset h_{\mathbf {Q}_G^{\mathrm {rat}}} ( R )$. By examining the construction, we deduce that this defines an injective continuous morphism of filtered presheaves.
$\mathcal Q ( R ) \subset h_{\mathbf {Q}_G^{\mathrm {rat}}} ( R )$. By examining the construction, we deduce that this defines an injective continuous morphism of filtered presheaves.
By the Bruhat decomposition, we have
for an overfield ![]() $\Bbbk \supset {\mathbb K}$ (and hence
$\Bbbk \supset {\mathbb K}$ (and hence ![]() $\Bbbk (\!(z)\!)$ is a field). In view of Theorem 4.18, we conclude that
$\Bbbk (\!(z)\!)$ is a field). In view of Theorem 4.18, we conclude that  $\mathcal Q \subset h_{\mathbf {Q}_G^{\mathrm {rat}}}$ is an inclusion of filtered presheaves with
$\mathcal Q \subset h_{\mathbf {Q}_G^{\mathrm {rat}}}$ is an inclusion of filtered presheaves with  $\mathcal Q ( \Bbbk ) = h_{\mathbf {Q}_G^{\mathrm {rat}}} ( \Bbbk )$ when
$\mathcal Q ( \Bbbk ) = h_{\mathbf {Q}_G^{\mathrm {rat}}} ( \Bbbk )$ when ![]() $\Bbbk \supset {\mathbb K}$ is an overfield.
$\Bbbk \supset {\mathbb K}$ is an overfield.
We verify the versality property. Suppose that we have a strict ind-scheme ![]() $( \mathfrak X, \{ X_n \}_n )$ and a continuous morphism
$( \mathfrak X, \{ X_n \}_n )$ and a continuous morphism ![]() $\mathcal Q \rightarrow h_{\mathfrak X}$. By Lemma 4.11, we deduce that each
$\mathcal Q \rightarrow h_{\mathfrak X}$. By Lemma 4.11, we deduce that each ![]() $\mathbf {I}$-orbit of
$\mathbf {I}$-orbit of ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ defines a subfunctor of
$\mathbf {Q}_G^{\mathrm {rat}}$ defines a subfunctor of ![]() $\mathcal Q_n$ for some
$\mathcal Q_n$ for some ![]() $n \ge 0$. The zeroth ind-piece
$n \ge 0$. The zeroth ind-piece  $\big( \mathbf {Q}_G^{\mathrm {rat}} \big)_0$ in Lemma 4.25 is
$\big( \mathbf {Q}_G^{\mathrm {rat}} \big)_0$ in Lemma 4.25 is ![]() $\mathbf {Q}_G ( e )$.
$\mathbf {Q}_G ( e )$.
For each  $t_{\beta } \le _{\frac {\infty }{2}} e \left (\beta \in Q^{\vee }_+\right )$, we find a reduced expression
$t_{\beta } \le _{\frac {\infty }{2}} e \left (\beta \in Q^{\vee }_+\right )$, we find a reduced expression  $t_{\beta }^{-1} = s_{i_1} \cdots s_{i_{\ell }}$ (which we record as
$t_{\beta }^{-1} = s_{i_1} \cdots s_{i_{\ell }}$ (which we record as ![]() ${\mathbf i} := (i_1,\ldots , i_{\ell })$) and form a scheme
${\mathbf i} := (i_1,\ldots , i_{\ell })$) and form a scheme
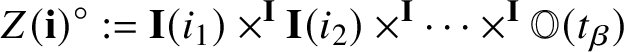 $$ \begin{align*}Z ( {\mathbf i} )^{\circ} := \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbb{O} ( t_{\beta} )\end{align*} $$
$$ \begin{align*}Z ( {\mathbf i} )^{\circ} := \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbb{O} ( t_{\beta} )\end{align*} $$and the map
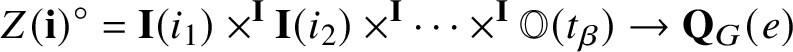 $$ \begin{align*}Z ( {\mathbf i} )^{\circ} = \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbb{O} ( t_{\beta} ) \rightarrow \mathbf{Q}_G ( e )\end{align*} $$
$$ \begin{align*}Z ( {\mathbf i} )^{\circ} = \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbb{O} ( t_{\beta} ) \rightarrow \mathbf{Q}_G ( e )\end{align*} $$(see, e.g., [Reference Kumar57, Chapter VIII]; compare [Reference Kato46, §6]). In view of Lemma 4.11, the image of this map contains an open neighbourhood of ![]() $\mathbb {O} \left ( t_{\beta } \right )$. In view of the
$\mathbb {O} \left ( t_{\beta } \right )$. In view of the ![]() $G(\!(z)\!)$-action (or the various
$G(\!(z)\!)$-action (or the various ![]() $\mathop {\textit{SL}} ( 2, i )$-actions for
$\mathop {\textit{SL}} ( 2, i )$-actions for ![]() $i \in \mathtt I_{\mathrm {af}}$) on
$i \in \mathtt I_{\mathrm {af}}$) on ![]() $\mathbf {Q}_G^{\mathrm {rat}}$ and
$\mathbf {Q}_G^{\mathrm {rat}}$ and ![]() $\mathcal Q$, we have a morphism
$\mathcal Q$, we have a morphism
By varying ![]() ${\mathbf i}$ (and consequently varying
${\mathbf i}$ (and consequently varying ![]() $t_{\beta } \le _{\frac {\infty }{2}} e$), we deduce that the union of the image of the morphisms
$t_{\beta } \le _{\frac {\infty }{2}} e$), we deduce that the union of the image of the morphisms ![]() $\{ f_{{\mathbf i}} \}_{{\mathbf i}}$ exhausts
$\{ f_{{\mathbf i}} \}_{{\mathbf i}}$ exhausts ![]() $\mathcal Q_0 ( \Bbbk )$ for an overfield
$\mathcal Q_0 ( \Bbbk )$ for an overfield ![]() $\Bbbk \supset {\mathbb K}$. From the Yoneda embedding, we derive a map
$\Bbbk \supset {\mathbb K}$. From the Yoneda embedding, we derive a map
of schemes for some fixed ![]() $n \in \mathbb {Z}$. This map factors through a scheme Z that glues (among
$n \in \mathbb {Z}$. This map factors through a scheme Z that glues (among ![]() ${\mathbf i}$s) all the closed points that map to the same points in
${\mathbf i}$s) all the closed points that map to the same points in ![]() $\mathcal Q_0$. Such a scheme is integral, as
$\mathcal Q_0$. Such a scheme is integral, as ![]() $Z ( {\mathbf i} )^{\circ }$s are integral, and the gluing identifies the Zariski open dense subset
$Z ( {\mathbf i} )^{\circ }$s are integral, and the gluing identifies the Zariski open dense subset ![]() $\mathbb {O} ( e )$ for distinct
$\mathbb {O} ( e )$ for distinct ![]() ${\mathbf i}$s. In addition, we have a birational map
${\mathbf i}$s. In addition, we have a birational map ![]() $\pi : Z \rightarrow \mathbf {Q}_G ( e )$, and hence we have
$\pi : Z \rightarrow \mathbf {Q}_G ( e )$, and hence we have
We prove that ![]() $Z = \mathbf {Q}_G ( e )$ by induction. For each
$Z = \mathbf {Q}_G ( e )$ by induction. For each ![]() $m \in \mathbb {Z}_{\ge 0}$, let
$m \in \mathbb {Z}_{\ge 0}$, let ![]() $\mathbf {Q}_G ( e ) _{<m}$ (resp.,
$\mathbf {Q}_G ( e ) _{<m}$ (resp., ![]() $\mathbf {Q}_G ( e ) _{\le m}$) be the union of
$\mathbf {Q}_G ( e ) _{\le m}$) be the union of ![]() $\mathbf {I}$-orbits in
$\mathbf {I}$-orbits in ![]() $\mathbf {Q}_G ( e )$ of the shape
$\mathbf {Q}_G ( e )$ of the shape ![]() $\mathbb {O} ( v )$ for
$\mathbb {O} ( v )$ for ![]() $\ell ^{\frac {\infty }{2}} ( v ) < m$ (resp.,
$\ell ^{\frac {\infty }{2}} ( v ) < m$ (resp., ![]() $\le m$).
$\le m$).
Assume that the map ![]() $\pi $ is an isomorphism when restricted to
$\pi $ is an isomorphism when restricted to ![]() $\mathbf {Q}_G ( e ) _{<m}$; we prove the same is true when restricted to
$\mathbf {Q}_G ( e ) _{<m}$; we prove the same is true when restricted to ![]() $\mathbf {Q}_G ( e ) _{\le m}$. The
$\mathbf {Q}_G ( e ) _{\le m}$. The ![]() $m = 1$ case is afforded by
$m = 1$ case is afforded by ![]() $\mathbb {O} ( e ) \subset Z$, already used in the foregoing construction.
$\mathbb {O} ( e ) \subset Z$, already used in the foregoing construction.
We have a partial compactification ![]() $Z ( {\mathbf i} )$ of
$Z ( {\mathbf i} )$ of ![]() $Z ( {\mathbf i} )^{\circ }$ with a map
$Z ( {\mathbf i} )^{\circ }$ with a map ![]() $f^+_{{\mathbf i}}$:
$f^+_{{\mathbf i}}$:
 $$ \begin{align*}Z ( {\mathbf i} ) := \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{Q}_G \left( t_{\beta} \right) \stackrel{f^+_{{\mathbf i}}}{\longrightarrow} \mathbf{Q}_G ( e ).\end{align*} $$
$$ \begin{align*}Z ( {\mathbf i} ) := \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{Q}_G \left( t_{\beta} \right) \stackrel{f^+_{{\mathbf i}}}{\longrightarrow} \mathbf{Q}_G ( e ).\end{align*} $$Note that we have a surjective morphism induced by ![]() $\mathbb {O} ( t_{\beta } ) \to \mbox {Spec}\, {\mathbb K}$:
$\mathbb {O} ( t_{\beta } ) \to \mbox {Spec}\, {\mathbb K}$:
where we denote the image (the right-hand side) by ![]() $Z' ( {\mathbf i} )$. Since
$Z' ( {\mathbf i} )$. Since ![]() $Z' ( {\mathbf i} )$ is a finite successive
$Z' ( {\mathbf i} )$ is a finite successive ![]() $\mathbb {P}^1$-fibration, it is proper. The map
$\mathbb {P}^1$-fibration, it is proper. The map ![]() $f_{{\mathbf i}}^+$ is proper, as the product map
$f_{{\mathbf i}}^+$ is proper, as the product map
is a closed immersion. In view of the isomorphism ![]() $\mathbf {Q}_G \left ( t_{\beta } \right ) \cong \mathbf {Q}_G ( e )$, we transplant
$\mathbf {Q}_G \left ( t_{\beta } \right ) \cong \mathbf {Q}_G ( e )$, we transplant ![]() $\mathbf {Q}_G ( e )_{< m}$ to
$\mathbf {Q}_G ( e )_{< m}$ to  $\mathbf {Q}_G \left ( t_{\beta } \right )_{< m}$.
$\mathbf {Q}_G \left ( t_{\beta } \right )_{< m}$.
Claim A. For each closed point ![]() $x \in \mathbf {Q}_G ( e )_{\le m}$, the scheme
$x \in \mathbf {Q}_G ( e )_{\le m}$, the scheme
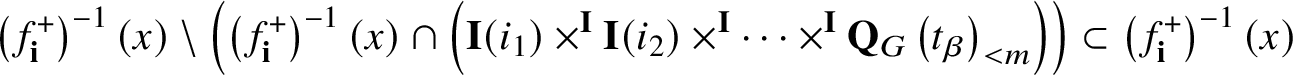 $$ \begin{align*}\left( f_{{\mathbf i}}^+ \right)^{-1} ( x ) \setminus \left( \left( f_{{\mathbf i}}^+ \right)^{-1} ( x ) \cap \left( \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{Q}_G \left( t_{\beta} \right)_{<m} \right) \right) \subset \left( f_{{\mathbf i}}^+ \right)^{-1} ( x )\end{align*} $$
$$ \begin{align*}\left( f_{{\mathbf i}}^+ \right)^{-1} ( x ) \setminus \left( \left( f_{{\mathbf i}}^+ \right)^{-1} ( x ) \cap \left( \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{Q}_G \left( t_{\beta} \right)_{<m} \right) \right) \subset \left( f_{{\mathbf i}}^+ \right)^{-1} ( x )\end{align*} $$is a closed subscheme that is zero-dimensional. In other words, it is a finite union of points (potentially an empty set).
Proof. For each sequence ![]() $(j_1,\ldots ,j_s) \in \mathtt I_{\mathrm {af}}^s$ (
$(j_1,\ldots ,j_s) \in \mathtt I_{\mathrm {af}}^s$ (![]() $s \in \mathbb {Z}_{> 0}$) and
$s \in \mathbb {Z}_{> 0}$) and ![]() $v\le _{\frac {\infty }{2}} e$ such that
$v\le _{\frac {\infty }{2}} e$ such that ![]() $\ell ^{\frac {\infty }{2}} ( v ) = \ell $, the image of the map
$\ell ^{\frac {\infty }{2}} ( v ) = \ell $, the image of the map
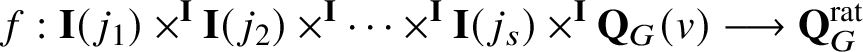 $$ \begin{align*}f : \mathbf{I} ( j_1 ) \times^{\mathbf{I}} \mathbf{I} ( j_2 ) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{I} ( j_s ) \times^{\mathbf{I}} \mathbf{Q}_G ( v ) \longrightarrow \mathbf{Q}_G^{\mathrm{rat}}\end{align*} $$
$$ \begin{align*}f : \mathbf{I} ( j_1 ) \times^{\mathbf{I}} \mathbf{I} ( j_2 ) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{I} ( j_s ) \times^{\mathbf{I}} \mathbf{Q}_G ( v ) \longrightarrow \mathbf{Q}_G^{\mathrm{rat}}\end{align*} $$induced by the multiplication is a union of ![]() $\mathbf {I}$-orbits
$\mathbf {I}$-orbits ![]() $\mathbb {O} ( v' )$ with
$\mathbb {O} ( v' )$ with ![]() $\ell ^{\frac {\infty }{2}} ( v' ) \ge \ell - s$ (as we have
$\ell ^{\frac {\infty }{2}} ( v' ) \ge \ell - s$ (as we have  $\ell ^{\frac {\infty }{2}} ( s_i w ) \in \left \{\ell ^{\frac {\infty }{2}} ( w ) \pm 1 \right \}$ for each
$\ell ^{\frac {\infty }{2}} ( s_i w ) \in \left \{\ell ^{\frac {\infty }{2}} ( w ) \pm 1 \right \}$ for each ![]() $i \in \mathtt I_{\mathrm {af}}$ and
$i \in \mathtt I_{\mathrm {af}}$ and ![]() $w \in W_{\mathrm {af}}$ by [Reference Peterson74, Lecture 13, Proposition
$w \in W_{\mathrm {af}}$ by [Reference Peterson74, Lecture 13, Proposition ![]() ${\ell}_s$]). In addition, if the image of the map f contains
${\ell}_s$]). In addition, if the image of the map f contains ![]() $\mathbb {O} ( v' )$ for
$\mathbb {O} ( v' )$ for ![]() $\ell ^{\frac {\infty }{2}} ( v' ) = \ell - s$, then f is an isomorphism along
$\ell ^{\frac {\infty }{2}} ( v' ) = \ell - s$, then f is an isomorphism along ![]() $\mathbb {O} ( v' )$ (as the isomorphism between open subsets). By collecting these for
$\mathbb {O} ( v' )$ (as the isomorphism between open subsets). By collecting these for ![]() $\mathbf {I}$-orbits in the closed subset
$\mathbf {I}$-orbits in the closed subset  $\mathbf {Q}_G \left ( t_{\beta } \right ) \setminus \mathbf {Q}_G \left ( t_{\beta } \right )_{<m}$ of
$\mathbf {Q}_G \left ( t_{\beta } \right ) \setminus \mathbf {Q}_G \left ( t_{\beta } \right )_{<m}$ of ![]() $\mathbf {Q}_G \left ( t_{\beta } \right )$ in the construction of the (proper) map
$\mathbf {Q}_G \left ( t_{\beta } \right )$ in the construction of the (proper) map ![]() $f_{{\mathbf i}}^+$, we conclude the result.
$f_{{\mathbf i}}^+$, we conclude the result.
We return to the proof of Proposition 4.26. By Claim A, we deduce that
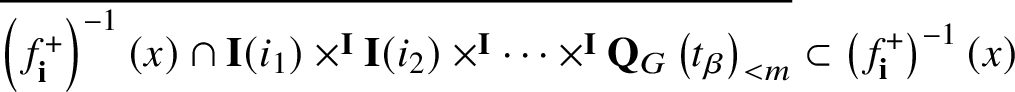 $$ \begin{align*}\overline{\left( f_{{\mathbf i}}^+ \right)^{-1} ( x ) \cap \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{Q}_G \left( t_{\beta} \right)_{<m}} \subset \left( f_{{\mathbf i}}^+ \right)^{-1} ( x )\end{align*} $$
$$ \begin{align*}\overline{\left( f_{{\mathbf i}}^+ \right)^{-1} ( x ) \cap \mathbf{I} (i_1)\times^{\mathbf{I}} \mathbf{I} (i_2) \times^{\mathbf{I}} \cdots \times^{\mathbf{I}} \mathbf{Q}_G \left( t_{\beta} \right)_{<m}} \subset \left( f_{{\mathbf i}}^+ \right)^{-1} ( x )\end{align*} $$is a union of connected components of  $\left ( f_{{\mathbf i}}^+ \right )^{-1} ( x )$ for each closed point
$\left ( f_{{\mathbf i}}^+ \right )^{-1} ( x )$ for each closed point ![]() $x \in \mathbf {Q}_G ( e )_{\le m}$.
$x \in \mathbf {Q}_G ( e )_{\le m}$.
Requiring regular functions on  $\left ( f_{{\mathbf i}}^+ \right )^{-1} ( \mathbf {Q}_G ( e )_{\le m} )$ to be constant along all the fibres yields sections in
$\left ( f_{{\mathbf i}}^+ \right )^{-1} ( \mathbf {Q}_G ( e )_{\le m} )$ to be constant along all the fibres yields sections in  $\left (f^+_{\mathbf i}\right )_* {\mathcal O}_{Z ( {\mathbf i} )}$. From this (for arbitrary
$\left (f^+_{\mathbf i}\right )_* {\mathcal O}_{Z ( {\mathbf i} )}$. From this (for arbitrary ![]() $t_{\beta } \le _{\frac {\infty }{2}} e$ and
$t_{\beta } \le _{\frac {\infty }{2}} e$ and ![]() ${\mathbf i}$) and the induction hypothesis, we conclude that
${\mathbf i}$) and the induction hypothesis, we conclude that ![]() $\pi ^{-1} ( \mathbf {Q}_G ( e )_{\le m} ) \subset Z$ is a union of proper schemes over
$\pi ^{-1} ( \mathbf {Q}_G ( e )_{\le m} ) \subset Z$ is a union of proper schemes over ![]() $\mathbf {Q}_G ( e )_{\le m}$ that contains a Zariski open subset
$\mathbf {Q}_G ( e )_{\le m}$ that contains a Zariski open subset ![]() $\mathbf {Q}_G ( e )_{< m}$. In view of Corollary 3.39 (when
$\mathbf {Q}_G ( e )_{< m}$. In view of Corollary 3.39 (when ![]() $\mathsf {char}\, {\mathbb K}> 0$) or Proposition A.1 (when
$\mathsf {char}\, {\mathbb K}> 0$) or Proposition A.1 (when ![]() $\mathsf {char}\, {\mathbb K} = 0$; compare [Reference Kato, Naito and Sagaki51, Theorem A]), we deduce that
$\mathsf {char}\, {\mathbb K} = 0$; compare [Reference Kato, Naito and Sagaki51, Theorem A]), we deduce that
defines an isomorphism as schemes (as ![]() $\pi ^{-1} ( \mathbf {Q}_G ( e )_{\le m} ) \to \mathbf {Q}_G ( e )_{\le m}$ is finite bijective and birational; compare [77, Section 02LQ]). Therefore, induction on m proceeds and we conclude
$\pi ^{-1} ( \mathbf {Q}_G ( e )_{\le m} ) \to \mathbf {Q}_G ( e )_{\le m}$ is finite bijective and birational; compare [77, Section 02LQ]). Therefore, induction on m proceeds and we conclude ![]() $Z \cong \mathbf {Q}_G ( e )$ as schemes. Thus we obtain a morphism
$Z \cong \mathbf {Q}_G ( e )$ as schemes. Thus we obtain a morphism ![]() $\mathbf {Q}_G ( e ) \to X_n$ of schemes.
$\mathbf {Q}_G ( e ) \to X_n$ of schemes.
Rearranging ![]() $\mathbf {Q}_G( e )$ by the right
$\mathbf {Q}_G( e )$ by the right ![]() $Q^{\vee }$-translations, we deduce a morphism
$Q^{\vee }$-translations, we deduce a morphism ![]() $\mathbf {Q}_G ^{\mathrm {rat}} \to \mathfrak X$ as ind-schemes. This yields a continuous morphism
$\mathbf {Q}_G ^{\mathrm {rat}} \to \mathfrak X$ as ind-schemes. This yields a continuous morphism  $h_{\mathbf {Q}_G^{\mathrm {rat}}} \to h_{\mathfrak X}$. Therefore,
$h_{\mathbf {Q}_G^{\mathrm {rat}}} \to h_{\mathfrak X}$. Therefore,  $h_{\mathbf {Q}_G^{\mathrm {rat}}}$ is an initial object in the category of sheaves on
$h_{\mathbf {Q}_G^{\mathrm {rat}}}$ is an initial object in the category of sheaves on ![]() $Zar_{\mathbb K}$ ind-representable by strict ind-schemes that admits a continuous morphism from
$Zar_{\mathbb K}$ ind-representable by strict ind-schemes that admits a continuous morphism from ![]() $\mathcal Q$, as required.
$\mathcal Q$, as required.
Corollary 4.27. For each ![]() $\mathtt J \subset \mathtt I$, the scheme
$\mathtt J \subset \mathtt I$, the scheme  $\mathbf {Q}_{G,\mathtt J}^{\mathrm {rat}}$ coarsely ind-represents the filtered presheaf
$\mathbf {Q}_{G,\mathtt J}^{\mathrm {rat}}$ coarsely ind-represents the filtered presheaf ![]() $\mathcal Q_{\mathtt J}$ defined by
$\mathcal Q_{\mathtt J}$ defined by
Proof. By construction, we have a continuous morphism of presheaves ![]() $\mathcal Q \rightarrow \mathcal Q_{\mathtt J}$ (by transplanting subsheaves
$\mathcal Q \rightarrow \mathcal Q_{\mathtt J}$ (by transplanting subsheaves ![]() $\mathcal Q_n$ to
$\mathcal Q_n$ to ![]() $\mathcal Q_{\mathtt J}$ via this map). Thus, the coarse ind-representability of
$\mathcal Q_{\mathtt J}$ via this map). Thus, the coarse ind-representability of ![]() $\mathbf {Q}_{G}^{\mathrm {rat}}$ implies that the maximal ind-scheme X obtained by gluing points of
$\mathbf {Q}_{G}^{\mathrm {rat}}$ implies that the maximal ind-scheme X obtained by gluing points of ![]() $\mathbf {Q}_{G}^{\mathrm {rat}}$ admits a continuous morphism
$\mathbf {Q}_{G}^{\mathrm {rat}}$ admits a continuous morphism ![]() $\mathcal Q_{\mathtt J} \rightarrow h_X$ that coarsely ind-represents the filtered presheaf
$\mathcal Q_{\mathtt J} \rightarrow h_X$ that coarsely ind-represents the filtered presheaf ![]() $\mathcal Q_{\mathtt J}$. Every two rational functions on
$\mathcal Q_{\mathtt J}$. Every two rational functions on ![]() $\mathbf {Q}_{G}(w)$ (
$\mathbf {Q}_{G}(w)$ (![]() $w \in W_{\mathrm {af}}$) are distinguished by some pair of
$w \in W_{\mathrm {af}}$) are distinguished by some pair of ![]() ${\mathbb K}$-valued points (Corollary 4.19). Since we have
${\mathbb K}$-valued points (Corollary 4.19). Since we have  $\mathcal Q_{\mathtt J} ( {\mathbb K} ) = \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}} ( {\mathbb K} )$, we conclude that
$\mathcal Q_{\mathtt J} ( {\mathbb K} ) = \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}} ( {\mathbb K} )$, we conclude that  $X = \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}}$.
$X = \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}}$.
4.4 The properties of the schemes  $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$
In the rest of this section, we assume ![]() $\mathsf {char}\, {\mathbb K} \neq 2$.
$\mathsf {char}\, {\mathbb K} \neq 2$.
Lemma 4.28. Set ![]() $\mathtt J \subset \mathtt I$. For each
$\mathtt J \subset \mathtt I$. For each ![]() $\beta \in Q^{\vee }_+$, the set of
$\beta \in Q^{\vee }_+$, the set of ![]() ${\mathbb K}$-valued points of
${\mathbb K}$-valued points of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , e )_{{\mathbb K}}$ is in bijection with the collection
$\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , e )_{{\mathbb K}}$ is in bijection with the collection ![]() $\{u_\lambda ( z )\}_{\lambda \in P_{\mathtt J,+}}$ such that
$\{u_\lambda ( z )\}_{\lambda \in P_{\mathtt J,+}}$ such that
•
 $u_{\lambda } ( z ) \in V ( \lambda )_{{\mathbb K}} \otimes \bigoplus _{j = 0}^{- \left \langle w_0 \beta , \lambda \right \rangle } {\mathbb K} z^j$ and
$u_{\lambda } ( z ) \in V ( \lambda )_{{\mathbb K}} \otimes \bigoplus _{j = 0}^{- \left \langle w_0 \beta , \lambda \right \rangle } {\mathbb K} z^j$ and• for each
 $\lambda , \mu \in P_+$, we have
$\lambda , \mu \in P_+$, we have  $\eta _{\lambda , \mu } \left ( u_{\lambda } ( z ) \otimes u_{\mu } ( z ) \right ) = u _{\lambda + \mu } ( z )$.
$\eta _{\lambda , \mu } \left ( u_{\lambda } ( z ) \otimes u_{\mu } ( z ) \right ) = u _{\lambda + \mu } ( z )$.
Proof. We have
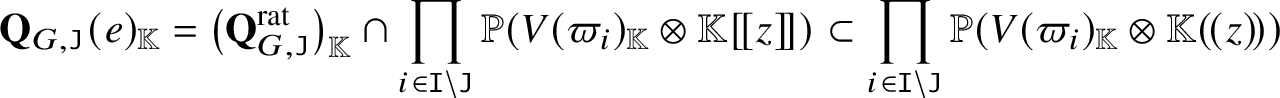 $$ \begin{align*}\mathbf{Q}_{G,\mathtt J} ( e )_{{\mathbb K}} = \big( \mathbf{Q}_{G,\mathtt J}^{\mathrm{rat}} \big)_{{\mathbb K}} \cap \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} [\![z]\!]) \subset \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!))\end{align*} $$
$$ \begin{align*}\mathbf{Q}_{G,\mathtt J} ( e )_{{\mathbb K}} = \big( \mathbf{Q}_{G,\mathtt J}^{\mathrm{rat}} \big)_{{\mathbb K}} \cap \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} [\![z]\!]) \subset \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} (\!(z)\!))\end{align*} $$by Theorem 4.18. By the symmetry of the construction of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , e )$ in terms of
$\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , e )$ in terms of ![]() $\theta $ (compare Remark 3.31), we conclude that
$\theta $ (compare Remark 3.31), we conclude that
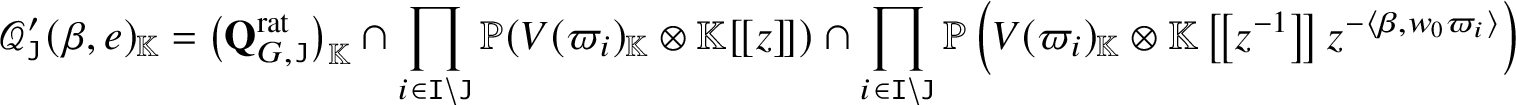 $$ \begin{align*}\mathscr{Q}^{\prime}_{\mathtt J} ( \beta, e )_{\mathbb K} = \big( \mathbf{Q}_{G,\mathtt J}^{\mathrm{rat}} \big)_{{\mathbb K}} \cap \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} [\![z]\!]) \cap \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} \left( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} \left[\!\left[z^{-1}\right]\!\right] z^{- \left\langle \beta, w_0 \varpi_i \right\rangle} \right)\end{align*} $$
$$ \begin{align*}\mathscr{Q}^{\prime}_{\mathtt J} ( \beta, e )_{\mathbb K} = \big( \mathbf{Q}_{G,\mathtt J}^{\mathrm{rat}} \big)_{{\mathbb K}} \cap \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} ( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} [\![z]\!]) \cap \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P} \left( V ( \varpi_i ) _{\mathbb K} \otimes {\mathbb K} \left[\!\left[z^{-1}\right]\!\right] z^{- \left\langle \beta, w_0 \varpi_i \right\rangle} \right)\end{align*} $$inside  $\prod _{i \in \mathtt I \setminus \mathtt J} \mathbb {P} \left ( V ( \varpi _i ) _{\mathbb K} \otimes {\mathbb K} \left [\!\left [z, z^{-1}\right ]\!\right ] \right )$, which is our degree bound. In view of this, it suffices to remember that the second condition is the same as the Plücker relation that defines
$\prod _{i \in \mathtt I \setminus \mathtt J} \mathbb {P} \left ( V ( \varpi _i ) _{\mathbb K} \otimes {\mathbb K} \left [\!\left [z, z^{-1}\right ]\!\right ] \right )$, which is our degree bound. In view of this, it suffices to remember that the second condition is the same as the Plücker relation that defines ![]() $G (\!(z)\!) / H ( {\mathbb K} ) \cdot [P( \mathtt J ), P( \mathtt J )] (\!(z)\!)$ in the last two paragraphs of the proof of Proposition 4.16.
$G (\!(z)\!) / H ( {\mathbb K} ) \cdot [P( \mathtt J ), P( \mathtt J )] (\!(z)\!)$ in the last two paragraphs of the proof of Proposition 4.16.
Set ![]() $w,v \in W_{\mathrm {af}}$ and
$w,v \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$. For each
$\mathtt J \subset \mathtt I$. For each ![]() $\lambda \in P_{\mathtt J, +}$, we have a line bundle
$\lambda \in P_{\mathtt J, +}$, we have a line bundle ![]() ${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \lambda )$ on
${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \lambda )$ on ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ such that we have a map
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ such that we have a map
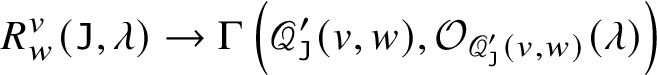 $$ \begin{align*}R ^v _w ( \mathtt J, \lambda ) \rightarrow \Gamma \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w ), {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} ( v, w )} ( \lambda ) \right)\end{align*} $$
$$ \begin{align*}R ^v _w ( \mathtt J, \lambda ) \rightarrow \Gamma \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w ), {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} ( v, w )} ( \lambda ) \right)\end{align*} $$that commutes with the multiplications. This yields ![]() ${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \lambda )$ for each
${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \lambda )$ for each ![]() $\lambda \in P_{\mathtt J}$ by tensor products.
$\lambda \in P_{\mathtt J}$ by tensor products.
Lemma 4.29. For each ![]() $w, v \in W_{\mathrm {af}}$, the line bundle
$w, v \in W_{\mathrm {af}}$, the line bundle ![]() ${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \lambda )$ is very ample if
${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \lambda )$ is very ample if  $\left \langle \alpha _i^{\vee }, \lambda \right \rangle> 0$ for every
$\left \langle \alpha _i^{\vee }, \lambda \right \rangle> 0$ for every ![]() $i \in \mathtt I \setminus \mathtt J$.
$i \in \mathtt I \setminus \mathtt J$.
Proof. We can assume that ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w ) \neq \emptyset $ without the loss of generality.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w ) \neq \emptyset $ without the loss of generality.
By Lemma 4.1, we have
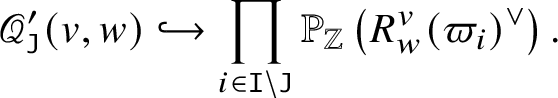 $$ \begin{align*}\mathscr{Q}^{\prime}_{\mathtt J} ( v, w ) \hookrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb{Z}} \left( R ^v _w ( \varpi_i )^{\vee} \right).\end{align*} $$
$$ \begin{align*}\mathscr{Q}^{\prime}_{\mathtt J} ( v, w ) \hookrightarrow \prod_{i \in \mathtt I \setminus \mathtt J} \mathbb{P}_{\mathbb{Z}} \left( R ^v _w ( \varpi_i )^{\vee} \right).\end{align*} $$From this and again by Lemma 4.1, we deduce that the following diagram is commutative:
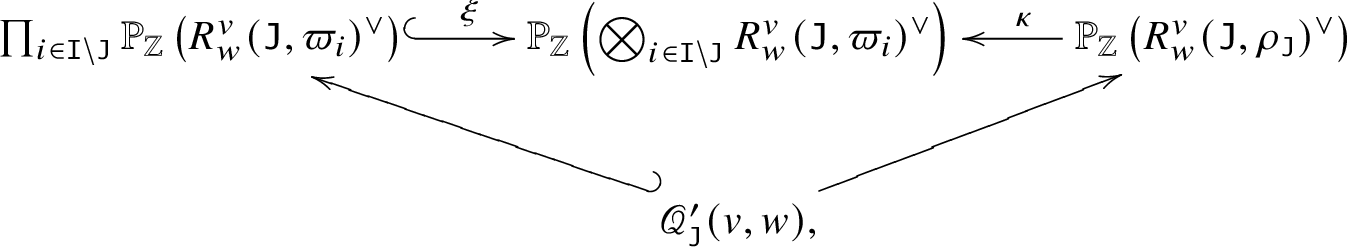
where ![]() $\xi $ is the Veronese embedding and
$\xi $ is the Veronese embedding and ![]() $\kappa $ is induced from the multiplication map. The ring
$\kappa $ is induced from the multiplication map. The ring ![]() $R ^v _w ( \mathtt J )$ is reduced by Corollary 4.10. Since
$R ^v _w ( \mathtt J )$ is reduced by Corollary 4.10. Since  $\left \langle \alpha _i^{\vee }, \rho _{\mathtt J} \right \rangle> 0$ for every
$\left \langle \alpha _i^{\vee }, \rho _{\mathtt J} \right \rangle> 0$ for every ![]() $i \in \mathtt I \setminus \mathtt J$ and the multiplication maps are surjective, a nonzero element of
$i \in \mathtt I \setminus \mathtt J$ and the multiplication maps are surjective, a nonzero element of ![]() $R ^v _w ( \mathtt J, \rho _{\mathtt J} )$ is not supported in the irrelevant locus. It follows that
$R ^v _w ( \mathtt J, \rho _{\mathtt J} )$ is not supported in the irrelevant locus. It follows that  $R ^v _w ( \mathtt J, \rho _{\mathtt J} ) \subset H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w ), {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )} ( \rho _{\mathtt J} ) \right )$ and it is spanned by a product of linear functions that separates closed points of
$R ^v _w ( \mathtt J, \rho _{\mathtt J} ) \subset H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w ), {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )} ( \rho _{\mathtt J} ) \right )$ and it is spanned by a product of linear functions that separates closed points of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$. In particular,
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$. In particular, ![]() ${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \rho _{\mathtt J} )$ is very ample. Since we have embeddings
${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )} ( \rho _{\mathtt J} )$ is very ample. Since we have embeddings
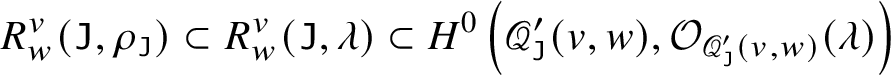 $$ \begin{align*}R ^v _w ( \mathtt J, \rho_{\mathtt J} ) \subset R ^v _w ( \mathtt J, \lambda ) \subset H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w ), {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)} ( \lambda ) \right)\end{align*} $$
$$ \begin{align*}R ^v _w ( \mathtt J, \rho_{\mathtt J} ) \subset R ^v _w ( \mathtt J, \lambda ) \subset H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w ), {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)} ( \lambda ) \right)\end{align*} $$obtained through multiplications corresponding to the duals of extremal weight vectors (so that the image is base-point free along an ![]() $( H \times \mathbb {G}_m)$-stable Zariski open neighbourhood of each
$( H \times \mathbb {G}_m)$-stable Zariski open neighbourhood of each ![]() $( H \times \mathbb {G}_m)$-fixed point of a projective variety), we conclude that
$( H \times \mathbb {G}_m)$-fixed point of a projective variety), we conclude that ![]() ${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )} ( \lambda )$ is also very ample, as required.
${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )} ( \lambda )$ is also very ample, as required.
Theorem 4.30. For each ![]() $w = u t_{\beta '} \in W_{\mathrm {af}} \left (u \in W, \beta ' \in Q^{\vee }\right )$ and
$w = u t_{\beta '} \in W_{\mathrm {af}} \left (u \in W, \beta ' \in Q^{\vee }\right )$ and ![]() $\beta \in Q^{\vee }_+$, we have an isomorphism
$\beta \in Q^{\vee }_+$, we have an isomorphism ![]() $\mathscr {Q}' ( \beta , w )_{\mathbb C} \cong \mathscr {Q} ( \beta - \beta ', u )$ as varieties. Moreover,
$\mathscr {Q}' ( \beta , w )_{\mathbb C} \cong \mathscr {Q} ( \beta - \beta ', u )$ as varieties. Moreover, ![]() $\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible, and its dimension is given as
$\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible, and its dimension is given as
Proof. By Lemma 4.7, we know that  $\left ( R ^ \beta _ v \right )_{{\mathbb K}}$ is a quotient of
$\left ( R ^ \beta _ v \right )_{{\mathbb K}}$ is a quotient of  $\left ( R ^ \beta _ w \right )_{{\mathbb K}}$ for
$\left ( R ^ \beta _ w \right )_{{\mathbb K}}$ for ![]() $v \in W_{\mathrm {af}}$ such that
$v \in W_{\mathrm {af}}$ such that ![]() $v \le _{\frac {\infty }{2}} w$. Hence, we have
$v \le _{\frac {\infty }{2}} w$. Hence, we have ![]() $\mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbf {Q}_G ( v )_{{\mathbb K}} = \mathscr {Q}' ( \beta , v )_{{\mathbb K}}$. By Lemma 4.6, the scheme
$\mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbf {Q}_G ( v )_{{\mathbb K}} = \mathscr {Q}' ( \beta , v )_{{\mathbb K}}$. By Lemma 4.6, the scheme ![]() $\mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}}$ is isomorphic to
$\mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}}$ is isomorphic to ![]() $\mathscr {Q}' ( \beta - \gamma , u' )_{{\mathbb K}} \cap \mathbb {O} ( u' )_{{\mathbb K}}$, where
$\mathscr {Q}' ( \beta - \gamma , u' )_{{\mathbb K}} \cap \mathbb {O} ( u' )_{{\mathbb K}}$, where ![]() $v = u' t_{\gamma } \left (u' \in W, \gamma \in Q_+^{\vee }\right )$. By Lemma 4.28 and Theorem 2.8, we have the following:
$v = u' t_{\gamma } \left (u' \in W, \gamma \in Q_+^{\vee }\right )$. By Lemma 4.28 and Theorem 2.8, we have the following:
•
 $( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}} ) = ( \mathscr {Q}' ( \beta , v )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}} )$ for each
$( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}} ) = ( \mathscr {Q}' ( \beta , v )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}} )$ for each  $v \in W_{\mathrm {af}}$ such that
$v \in W_{\mathrm {af}}$ such that  $v \le _{\frac {\infty }{2}} w$.
$v \le _{\frac {\infty }{2}} w$.• The variety
 $( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}} )$ is irreducible for every
$( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( v )_{{\mathbb K}} )$ is irreducible for every  $v \in W_{\mathrm {af}}$.
$v \in W_{\mathrm {af}}$.
We have
for ![]() $v = u' t_{\gamma } \left (u' \in W, \gamma \in Q^{\vee }_+\right )$ by Lemma 4.28 and Theorem 2.7 (whenever
$v = u' t_{\gamma } \left (u' \in W, \gamma \in Q^{\vee }_+\right )$ by Lemma 4.28 and Theorem 2.7 (whenever ![]() $\mathscr {Q}' ( \beta , w )_{\mathbb C} \cap \mathbb {O} ( v )_{\mathbb C} \neq \emptyset $). In addition, Lemma 4.3 implies
$\mathscr {Q}' ( \beta , w )_{\mathbb C} \cap \mathbb {O} ( v )_{\mathbb C} \neq \emptyset $). In addition, Lemma 4.3 implies
•
 $\dim \, \mathscr {Q}' ( \beta , w ) _{\mathbb C} = \dim \, \mathscr {Q}' ( \beta , w )_{{\mathbb K}}$.
$\dim \, \mathscr {Q}' ( \beta , w ) _{\mathbb C} = \dim \, \mathscr {Q}' ( \beta , w )_{{\mathbb K}}$.
In particular, we have the desired dimension formula if ![]() $\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible with its Zariski open dense subset
$\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible with its Zariski open dense subset ![]() $( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )$.
$( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )$.
Since ![]() $\mathscr {Q} ( \beta , w )$ and
$\mathscr {Q} ( \beta , w )$ and ![]() $\mathscr {Q}' ( \beta , w )_{\mathbb C}$ share an open subset and the former is irreducible, we have
$\mathscr {Q}' ( \beta , w )_{\mathbb C}$ share an open subset and the former is irreducible, we have ![]() $\mathscr {Q} ( \beta , w ) = \mathscr {Q}' ( \beta , w )_{\mathbb C}$ as closed subvarieties of
$\mathscr {Q} ( \beta , w ) = \mathscr {Q}' ( \beta , w )_{\mathbb C}$ as closed subvarieties of  $\big( \mathbf {Q} _G^{\mathrm {rat}} \big)_{\mathbb C}$ if
$\big( \mathbf {Q} _G^{\mathrm {rat}} \big)_{\mathbb C}$ if ![]() $\mathscr {Q}' ( \beta , w )_{\mathbb C}$ is irreducible.
$\mathscr {Q}' ( \beta , w )_{\mathbb C}$ is irreducible.
Therefore, it suffices to prove that ![]() $\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible (with its Zariski open dense subset
$\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible (with its Zariski open dense subset ![]() $( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )$). By Theorem 2.1 and Corollary 4.21, it suffices to prove that
$( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )$). By Theorem 2.1 and Corollary 4.21, it suffices to prove that
for every ![]() $w \in W_{\mathrm {af}}$ and every reflection
$w \in W_{\mathrm {af}}$ and every reflection ![]() $s \in W_{\mathrm {af}}$ such that
$s \in W_{\mathrm {af}}$ such that ![]() $\ell ^{\frac {\infty }{2}} ( s w ) = \ell ^{\frac {\infty }{2}} ( w ) + 1$ and
$\ell ^{\frac {\infty }{2}} ( s w ) = \ell ^{\frac {\infty }{2}} ( w ) + 1$ and ![]() $w_0 t_{\beta } \le _{\frac {\infty }{2}} s w \le _{\frac {\infty }{2}} w$. Here
$w_0 t_{\beta } \le _{\frac {\infty }{2}} s w \le _{\frac {\infty }{2}} w$. Here ![]() $\mathbf {Q}_G ( s v )_{{\mathbb K}} \subset \mathbf {Q} _G ( v )_{{\mathbb K}}$ is an irreducible component of the boundary by Theorem 2.4(3) (compare Corollary 4.20). This boundary component is these cut out as (a part of) the zero of
$\mathbf {Q}_G ( s v )_{{\mathbb K}} \subset \mathbf {Q} _G ( v )_{{\mathbb K}}$ is an irreducible component of the boundary by Theorem 2.4(3) (compare Corollary 4.20). This boundary component is these cut out as (a part of) the zero of  $\mathbf {v}_{v w_0 \lambda }^{\vee } \in \mathbb {W}_{vw_0} ( \lambda )^{\vee }$ (
$\mathbf {v}_{v w_0 \lambda }^{\vee } \in \mathbb {W}_{vw_0} ( \lambda )^{\vee }$ (![]() $\lambda \in P_+$). Thus, we deduce that
$\lambda \in P_+$). Thus, we deduce that ![]() $\overline {( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( s w )_{{\mathbb K}} )}$ contains an irreducible component of
$\overline {( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( s w )_{{\mathbb K}} )}$ contains an irreducible component of
for some single equation f (an instance of  $\mathbf {v}_{vw_0 \lambda }^{\vee }$s) if it is nonempty. By comparison of dimensions, this forces
$\mathbf {v}_{vw_0 \lambda }^{\vee }$s) if it is nonempty. By comparison of dimensions, this forces
to be an irreducible component if the left-hand side is nonempty. Consider the ![]() $( H \times \mathbb {G}_m )$-invariant curve C that connects the (unique)
$( H \times \mathbb {G}_m )$-invariant curve C that connects the (unique) ![]() $( H \times \mathbb {G}_m )$-fixed points
$( H \times \mathbb {G}_m )$-fixed points ![]() $p_{sw}$ in
$p_{sw}$ in ![]() $\mathbb {O} ( s w )_{{\mathbb K}}$ and
$\mathbb {O} ( s w )_{{\mathbb K}}$ and ![]() $p_w$ in
$p_w$ in ![]() $\mathbb {O} ( w )_{{\mathbb K}}$. The curve C is the closure of the orbit of a one-parameter unipotent subgroup action corresponding to a root in
$\mathbb {O} ( w )_{{\mathbb K}}$. The curve C is the closure of the orbit of a one-parameter unipotent subgroup action corresponding to a root in ![]() $\Delta _{\mathrm {af},+}$ applied to
$\Delta _{\mathrm {af},+}$ applied to ![]() $p_w$. In particular, we have
$p_w$. In particular, we have ![]() $C \subset \mathbb {O} (sw)_{{\mathbb K}} \sqcup \mathbb {O} ( w )_{{\mathbb K}}$. By the degree bound (from above) offered by Lemma 4.28, we conclude that
$C \subset \mathbb {O} (sw)_{{\mathbb K}} \sqcup \mathbb {O} ( w )_{{\mathbb K}}$. By the degree bound (from above) offered by Lemma 4.28, we conclude that ![]() $C \subset \overline {(\mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )}$. Therefore, the left-hand side of formula (4.13) is nonempty. Hence, the irreducibility of
$C \subset \overline {(\mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )}$. Therefore, the left-hand side of formula (4.13) is nonempty. Hence, the irreducibility of ![]() $( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( s w )_{{\mathbb K}} )$ forces
$( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( s w )_{{\mathbb K}} )$ forces
Therefore, we conclude formula (4.12). This implies ![]() $\mathscr {Q} ( \beta - \beta ', u ) = \mathscr {Q}' ( \beta , w )_{{\mathbb C}}$ as an irreducible (reduced) closed subvariety of
$\mathscr {Q} ( \beta - \beta ', u ) = \mathscr {Q}' ( \beta , w )_{{\mathbb C}}$ as an irreducible (reduced) closed subvariety of  $\big ( \mathbf {Q}_G^{\mathrm {rat}} \big )_{\mathbb C}$, and
$\big ( \mathbf {Q}_G^{\mathrm {rat}} \big )_{\mathbb C}$, and ![]() $\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible in general. Its dimension
$\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$ is irreducible in general. Its dimension ![]() $\dim \mathscr {Q} ( \beta - \beta ', u )$ comes from the dimension of
$\dim \mathscr {Q} ( \beta - \beta ', u )$ comes from the dimension of ![]() $( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )$, which is a Zariski open dense subset of
$( \mathscr {Q}' ( \beta , w )_{{\mathbb K}} \cap \mathbb {O} ( w )_{{\mathbb K}} )$, which is a Zariski open dense subset of ![]() $\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$.
$\mathscr {Q}' ( \beta , w )_{{\mathbb K}}$.
Corollary 4.31. For each ![]() $w,v \in W_{\mathrm {af}}$, the dimension of an irreducible component of
$w,v \in W_{\mathrm {af}}$, the dimension of an irreducible component of ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is ![]() $\ell ^{\frac {\infty }{2}} ( v ) - \ell ^{\frac {\infty }{2}} ( w )$ if
$\ell ^{\frac {\infty }{2}} ( v ) - \ell ^{\frac {\infty }{2}} ( w )$ if ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}} \neq \emptyset $ (which is equivalent to
$\mathscr {Q}' ( v, w )_{{\mathbb K}} \neq \emptyset $ (which is equivalent to ![]() $v \le _{\frac {\infty }{2}} w$ by Corollary 4.21). In particular,
$v \le _{\frac {\infty }{2}} w$ by Corollary 4.21). In particular, ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is equidimensional.
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is equidimensional.
Proof. The case where ![]() $v = w_0 t_{\beta }$ with
$v = w_0 t_{\beta }$ with ![]() $\beta \in Q^{\vee }$ follows from Theorem 4.30. We have
$\beta \in Q^{\vee }$ follows from Theorem 4.30. We have ![]() $\mathscr {Q}' ( w, w )_{{\mathbb K}} = \mbox {Spec}\, {\mathbb K}$ (
$\mathscr {Q}' ( w, w )_{{\mathbb K}} = \mbox {Spec}\, {\mathbb K}$ (![]() $w \in W_{\mathrm {af}}$), since
$w \in W_{\mathrm {af}}$), since ![]() $\dim \mathbb {W}_{ww_0} ( \lambda )_{{\mathbb K}} \cap \mathbb {W}^- _{ww_0} ( \lambda )_{{\mathbb K}} = 1$ for every
$\dim \mathbb {W}_{ww_0} ( \lambda )_{{\mathbb K}} \cap \mathbb {W}^- _{ww_0} ( \lambda )_{{\mathbb K}} = 1$ for every ![]() $\lambda \in P_+$ by
$\lambda \in P_+$ by ![]() $P^{\mathrm {af}}$-weight comparison.
$P^{\mathrm {af}}$-weight comparison.
Let ![]() $v = u t_{\beta }$ (
$v = u t_{\beta }$ (![]() $u \in W$). In view of the proof of Theorem 4.30, the variety
$u \in W$). In view of the proof of Theorem 4.30, the variety ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is obtained from
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is obtained from ![]() $\mathscr {Q}' \left ( w_0 t_{\beta }, w \right )_{{\mathbb K}}$ by
$\mathscr {Q}' \left ( w_0 t_{\beta }, w \right )_{{\mathbb K}}$ by ![]() $( \ell ( w_0 ) - \ell ( u ) )$-successive hyperplane cuts by the
$( \ell ( w_0 ) - \ell ( u ) )$-successive hyperplane cuts by the ![]() $\theta $-twists of the
$\theta $-twists of the ![]() $\mathbf {I}$-stable boundaries of
$\mathbf {I}$-stable boundaries of ![]() $\mathbf {Q}_G ( \bullet )_{{\mathbb K}}$ (compare Remark 3.31). Each of these hyperplane cuts lowers the dimension of an irreducible component by at most
$\mathbf {Q}_G ( \bullet )_{{\mathbb K}}$ (compare Remark 3.31). Each of these hyperplane cuts lowers the dimension of an irreducible component by at most ![]() $1$ if the intersection is nonempty. Since
$1$ if the intersection is nonempty. Since  $\ell ( w_0 ) - \ell ( u ) = \ell ^{\frac {\infty }{2}} \left ( w_0t_{\beta } \right ) - \ell ^{\frac {\infty }{2}} ( v )$, the dimension inequality
$\ell ( w_0 ) - \ell ( u ) = \ell ^{\frac {\infty }{2}} \left ( w_0t_{\beta } \right ) - \ell ^{\frac {\infty }{2}} ( v )$, the dimension inequality ![]() $\ge $ always holds.
$\ge $ always holds.
Every irreducible component of ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ is ![]() $(H \times \mathbb {G}_m)$-stable by construction. Since we have only one
$(H \times \mathbb {G}_m)$-stable by construction. Since we have only one ![]() $(H \times \mathbb {G}_m)$-fixed point in each
$(H \times \mathbb {G}_m)$-fixed point in each ![]() $\mathbf {I}$-orbit of
$\mathbf {I}$-orbit of  $\big( \mathbf {Q}^{\mathrm {rat}}_G \big)_{{\mathbb K}}$, all but one
$\big( \mathbf {Q}^{\mathrm {rat}}_G \big)_{{\mathbb K}}$, all but one ![]() $( H \times \mathbb {G}_m)$-fixed point of
$( H \times \mathbb {G}_m)$-fixed point of ![]() $\mathbf {Q}_G(w)_{{\mathbb K}}$ (
$\mathbf {Q}_G(w)_{{\mathbb K}}$ (![]() $w \in W_{\mathrm {af}}$) lie in the boundary. Thus, if an irreducible component of
$w \in W_{\mathrm {af}}$) lie in the boundary. Thus, if an irreducible component of ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ does not meet any
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ does not meet any ![]() $\mathbf {I}$-stable boundary divisors of
$\mathbf {I}$-stable boundary divisors of ![]() $\mathbf {Q}_G ( w )_{{\mathbb K}}$ or the
$\mathbf {Q}_G ( w )_{{\mathbb K}}$ or the ![]() $\theta $-twists of any
$\theta $-twists of any ![]() $\mathbf {I}$-stable boundary divisors of
$\mathbf {I}$-stable boundary divisors of ![]() $\mathbf {Q}_G ( vw_0 )_{{\mathbb K}}$, then such an irreducible component does not contain an
$\mathbf {Q}_G ( vw_0 )_{{\mathbb K}}$, then such an irreducible component does not contain an ![]() $(H \times \mathbb {G}_m)$-fixed point unless
$(H \times \mathbb {G}_m)$-fixed point unless ![]() $v = w$. This is a contradiction (of the properness of
$v = w$. This is a contradiction (of the properness of ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$). Hence, every irreducible component of
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$). Hence, every irreducible component of ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$ meets its boundary cut out by an
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$ meets its boundary cut out by an ![]() $\mathbf {I}$-stable boundary divisor of
$\mathbf {I}$-stable boundary divisor of ![]() $\mathbf {Q}_G(w)_{{\mathbb K}}$ or the
$\mathbf {Q}_G(w)_{{\mathbb K}}$ or the ![]() $\theta $-twist of an
$\theta $-twist of an ![]() $\mathbf {I}$-stable boundary divisor of
$\mathbf {I}$-stable boundary divisor of ![]() $\mathbf {Q}_G ( vw_0 )_{{\mathbb K}}$.
$\mathbf {Q}_G ( vw_0 )_{{\mathbb K}}$.
Assume the contrary to deduce a contradiction. Then we have ![]() $\mathscr {Q}' ( v, w )_{{\mathbb K}}$, whose irreducible components have dimension
$\mathscr {Q}' ( v, w )_{{\mathbb K}}$, whose irreducible components have dimension  $\left (\ell ^{\frac {\infty }{2}} ( v ) - \ell ^{\frac {\infty }{2}} ( w )\right )$, but one of its irreducible components is in fact contained in
$\left (\ell ^{\frac {\infty }{2}} ( v ) - \ell ^{\frac {\infty }{2}} ( w )\right )$, but one of its irreducible components is in fact contained in ![]() $\mathscr {Q}' ( v', w' )_{{\mathbb K}}$ with
$\mathscr {Q}' ( v', w' )_{{\mathbb K}}$ with ![]() $\mathscr {Q}' ( v', w' )_{{\mathbb K}} \subsetneq \mathscr {Q}' ( v, w )_{{\mathbb K}}$ for
$\mathscr {Q}' ( v', w' )_{{\mathbb K}} \subsetneq \mathscr {Q}' ( v, w )_{{\mathbb K}}$ for ![]() $v', w' \in W_{\mathrm {af}}$, and hence it gives an irreducible component of
$v', w' \in W_{\mathrm {af}}$, and hence it gives an irreducible component of ![]() $\mathscr {Q}' ( v', w' )_{{\mathbb K}}$ with dimension
$\mathscr {Q}' ( v', w' )_{{\mathbb K}}$ with dimension  $> \left (\ell ^{\frac {\infty }{2}} ( v' ) - \ell ^{\frac {\infty }{2}} ( w' )\right )$. From this, we can lower the dimension of an irreducible component of
$> \left (\ell ^{\frac {\infty }{2}} ( v' ) - \ell ^{\frac {\infty }{2}} ( w' )\right )$. From this, we can lower the dimension of an irreducible component of ![]() $\mathscr {Q}' ( v', w' )_{{\mathbb K}}$ by intersecting with a divisor to raise
$\mathscr {Q}' ( v', w' )_{{\mathbb K}}$ by intersecting with a divisor to raise ![]() $v'$ or lower
$v'$ or lower ![]() $w'$ successively to reach the case
$w'$ successively to reach the case ![]() $v' = w'$ (as in the second paragraph). Since the dimension drops at most
$v' = w'$ (as in the second paragraph). Since the dimension drops at most ![]() $1$ in each step, we find that
$1$ in each step, we find that ![]() $\dim \mathscr {Q}' ( w, w )_{{\mathbb K}}> 0$ for some
$\dim \mathscr {Q}' ( w, w )_{{\mathbb K}}> 0$ for some ![]() $w \in W_{\mathrm {af}}$. This is a contradiction, and hence this case does not happen.
$w \in W_{\mathrm {af}}$. This is a contradiction, and hence this case does not happen.
These imply that the dimension equality always holds, as required.
Remark 4.32. The analogous assertions from Theorem 4.30 and Corollary 4.31 hold for the case where ![]() $\mathtt J \subsetneq \mathtt I$ (compare Corollaries 5.21 and 5.22).
$\mathtt J \subsetneq \mathtt I$ (compare Corollaries 5.21 and 5.22).
Theorem 4.33. For each ![]() $w, v \in W_{\mathrm {af}}$,
$w, v \in W_{\mathrm {af}}$, ![]() $\mathtt J \subset \mathtt I$ and
$\mathtt J \subset \mathtt I$ and ![]() $\lambda \in P_{\mathtt J,+}$, we have
$\lambda \in P_{\mathtt J,+}$, we have
 $$ \begin{align*}H^i \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \cong \begin{cases} R ^v _w ( \lambda )_{{\mathbb K}}, & i = 0, \lambda \in P_{\mathtt J,++},\\ \{ 0 \}, & i \neq 0. \end{cases}\end{align*} $$
$$ \begin{align*}H^i \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \cong \begin{cases} R ^v _w ( \lambda )_{{\mathbb K}}, & i = 0, \lambda \in P_{\mathtt J,++},\\ \{ 0 \}, & i \neq 0. \end{cases}\end{align*} $$Moreover, if ![]() $w',v' \in W_{\mathrm {af}}$ satisfies
$w',v' \in W_{\mathrm {af}}$ satisfies ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v', w' ) \subset \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ and
$\mathscr {Q}^{\prime }_{\mathtt J} ( v', w' ) \subset \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ and ![]() $\lambda \in P_{\mathtt J,+}$, then the restriction map induces a surjection
$\lambda \in P_{\mathtt J,+}$, then the restriction map induces a surjection
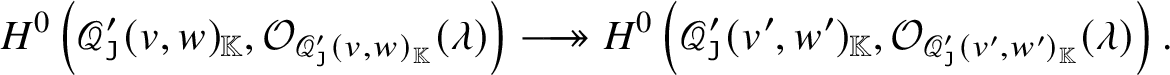 $$ \begin{align*}H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \longrightarrow \!\!\!\!\! \rightarrow H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v', w' )_{{\mathbb K}}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v', w' \right)_{{\mathbb K}}} ( \lambda ) \right).\end{align*} $$
$$ \begin{align*}H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \longrightarrow \!\!\!\!\! \rightarrow H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v', w' )_{{\mathbb K}}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v', w' \right)_{{\mathbb K}}} ( \lambda ) \right).\end{align*} $$Remark 4.34. The strict dominance condition in Theorem 4.33 cannot be removed naively. For ![]() $G = \mathop {\textit{SL}} ( 3 )$,
$G = \mathop {\textit{SL}} ( 3 )$, ![]() ${\mathbb K} = {\mathbb C}$ and
${\mathbb K} = {\mathbb C}$ and ![]() $w = e$, we have
$w = e$, we have
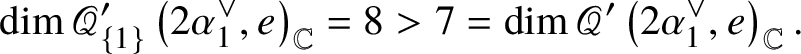 $$ \begin{align*}\dim \mathscr{Q}^{\prime}_{\{1\}} \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}} = 8> 7 = \dim \mathscr{Q}' \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}.\end{align*} $$
$$ \begin{align*}\dim \mathscr{Q}^{\prime}_{\{1\}} \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}} = 8> 7 = \dim \mathscr{Q}' \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}.\end{align*} $$This results in the noninjectivity of the pullback map
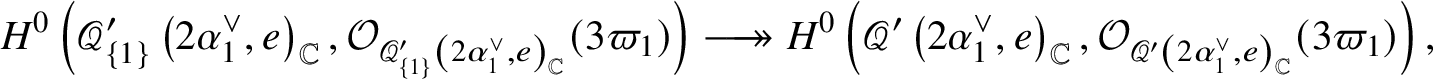 $$ \begin{align*}H^0 \left( \mathscr{Q}^{\prime}_{\{1\}} \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}, {\mathcal O}_{\mathscr{Q}^{\prime}_{\{1\}} \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}} ( 3 \varpi_1 ) \right) \longrightarrow\!\!\!\!\!\rightarrow H^0 \left( \mathscr{Q}' \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}, {\mathcal O}_{\mathscr{Q}' \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}} ( 3 \varpi_1 ) \right),\end{align*} $$
$$ \begin{align*}H^0 \left( \mathscr{Q}^{\prime}_{\{1\}} \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}, {\mathcal O}_{\mathscr{Q}^{\prime}_{\{1\}} \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}} ( 3 \varpi_1 ) \right) \longrightarrow\!\!\!\!\!\rightarrow H^0 \left( \mathscr{Q}' \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}, {\mathcal O}_{\mathscr{Q}' \left( 2 \alpha_1^{\vee}, e \right)_{{\mathbb C}}} ( 3 \varpi_1 ) \right),\end{align*} $$where the left-hand side is  $R^{2 \alpha _1^{\vee }}_e ( 3 \varpi _1 )_{{\mathbb C}} = R^{2 \alpha _1^{\vee }}_e (\{ 1 \}, 3 \varpi _1 )_{{\mathbb C}} \cong S^3 \left ( {\mathbb C}^3 \oplus {\mathbb C}^3 z \oplus {\mathbb C}^3 z^2 \right )^{\vee }$ and the right-hand side is its quotient by the G-invariants of
$R^{2 \alpha _1^{\vee }}_e ( 3 \varpi _1 )_{{\mathbb C}} = R^{2 \alpha _1^{\vee }}_e (\{ 1 \}, 3 \varpi _1 )_{{\mathbb C}} \cong S^3 \left ( {\mathbb C}^3 \oplus {\mathbb C}^3 z \oplus {\mathbb C}^3 z^2 \right )^{\vee }$ and the right-hand side is its quotient by the G-invariants of  $\left ( {\mathbb C}^3 \otimes {\mathbb C}^3 z \otimes {\mathbb C}^3 z^2 \right )^{\vee }\subset S^3 \left ( {\mathbb C}^3 \oplus {\mathbb C}^3 z \oplus {\mathbb C}^3 z^2 \right )^{\vee }$. In fact, the ring
$\left ( {\mathbb C}^3 \otimes {\mathbb C}^3 z \otimes {\mathbb C}^3 z^2 \right )^{\vee }\subset S^3 \left ( {\mathbb C}^3 \oplus {\mathbb C}^3 z \oplus {\mathbb C}^3 z^2 \right )^{\vee }$. In fact, the ring  $\left ( R ^{2 \alpha _1^{\vee }} _e \right )_{{\mathbb C}}$ is reduced but not integral, and the extra irreducible component is contained in the irrelevant locus.
$\left ( R ^{2 \alpha _1^{\vee }} _e \right )_{{\mathbb C}}$ is reduced but not integral, and the extra irreducible component is contained in the irrelevant locus.
Proof of Theorem 4.33. We first observe that it is enough to show the surjectivity part of the assertion only for the ![]() $w = w'$ case, since the
$w = w'$ case, since the ![]() $v = v'$ case follows by applying
$v = v'$ case follows by applying ![]() $\theta $ (and the rest of the cases follow by repeated applications of the two cases).
$\theta $ (and the rest of the cases follow by repeated applications of the two cases).
Since ![]() $\mathbb {O} ( \mathtt J, w )_{\mathbb F_p} \subset \mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is affine, the union Z of codimension one
$\mathbb {O} ( \mathtt J, w )_{\mathbb F_p} \subset \mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is affine, the union Z of codimension one ![]() $\mathbf {I}$-orbits contains the support of an ample divisor. The reduced union of the irreducible components of Z affords a Weil divisor D (by Corollary A.2). Since our Frobenius splitting of
$\mathbf {I}$-orbits contains the support of an ample divisor. The reduced union of the irreducible components of Z affords a Weil divisor D (by Corollary A.2). Since our Frobenius splitting of ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is ![]() $\mathbf {I}$-canonical and compatible with the
$\mathbf {I}$-canonical and compatible with the ![]() $\mathbf {I}$-orbit closures (Corollary 3.38), we deduce that
$\mathbf {I}$-orbit closures (Corollary 3.38), we deduce that ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is D-split in the sense of [Reference Brion and Lakshmibai15, Definition 3] (compare [Reference Ramanathan75, Definition 1.2]). Each irreducible component of Z intersects properly with
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb F_p}$ is D-split in the sense of [Reference Brion and Lakshmibai15, Definition 3] (compare [Reference Ramanathan75, Definition 1.2]). Each irreducible component of Z intersects properly with ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v', w )_{\mathbb F_p} \subset \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ (
$\mathscr {Q}^{\prime }_{\mathtt J} ( v', w )_{\mathbb F_p} \subset \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ (![]() $v' \in W_{\mathrm {af}}$) whenever the intersection is nonempty, by Corollary 4.31 (and Remark 4.32). Thus, we deduce that
$v' \in W_{\mathrm {af}}$) whenever the intersection is nonempty, by Corollary 4.31 (and Remark 4.32). Thus, we deduce that ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ admits a Frobenius D-splitting compatible with
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}$ admits a Frobenius D-splitting compatible with ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v', w )_{\mathbb F_p}$ (
$\mathscr {Q}^{\prime }_{\mathtt J} ( v', w )_{\mathbb F_p}$ (![]() $v' \in W_{\mathrm {af}}$). Therefore, the cohomology vanishing part of the assertion and the surjectivity part (for
$v' \in W_{\mathrm {af}}$). Therefore, the cohomology vanishing part of the assertion and the surjectivity part (for ![]() $w' = w$) follow from [Reference Ramanathan75, Proposition 1.13 (ii)]. The cohomology vanishing part lifts to
$w' = w$) follow from [Reference Ramanathan75, Proposition 1.13 (ii)]. The cohomology vanishing part lifts to ![]() $\mathsf {char}\, {\mathbb K} = 0$ by [Reference Brion and Kumar14, Proposition 1.6.2]. The surjectivity part lifts to
$\mathsf {char}\, {\mathbb K} = 0$ by [Reference Brion and Kumar14, Proposition 1.6.2]. The surjectivity part lifts to ![]() $\mathsf {char}\, {\mathbb K} = 0$ by [Reference Brion and Kumar14, Corollary 1.6.3] and Lemma 4.3.
$\mathsf {char}\, {\mathbb K} = 0$ by [Reference Brion and Kumar14, Corollary 1.6.3] and Lemma 4.3.
It remains to calculate  $H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda ) \right )$ for each
$H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda ) \right )$ for each ![]() $\lambda \in P_{\mathtt J, ++}$. Here
$\lambda \in P_{\mathtt J, ++}$. Here  $H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda ) \right )$ is obtained as the degree
$H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O} _{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda ) \right )$ is obtained as the degree ![]() $\lambda $ part of the (graded) normalisation of the ring
$\lambda $ part of the (graded) normalisation of the ring ![]() $\left ( R ^v _w ( \mathtt J ) \right )_{{\mathbb K}}$. For each prime p, our ring
$\left ( R ^v _w ( \mathtt J ) \right )_{{\mathbb K}}$. For each prime p, our ring  $\left (R ^v _w ( \mathtt J )\right )_{\mathbb F_p}$ is weakly normal by Lemma 4.7. Let us consider the
$\left (R ^v _w ( \mathtt J )\right )_{\mathbb F_p}$ is weakly normal by Lemma 4.7. Let us consider the ![]() $P_{\mathtt J,+}$-graded quotient
$P_{\mathtt J,+}$-graded quotient  $R' = \bigoplus _{\lambda \in P_{\mathtt J,+}} R' ( \lambda )$ of
$R' = \bigoplus _{\lambda \in P_{\mathtt J,+}} R' ( \lambda )$ of ![]() $R ^v _w ( \mathtt J, \lambda )_{\mathbb F_p}$ that annihilates all the irrelevant irreducible components. Since
$R ^v _w ( \mathtt J, \lambda )_{\mathbb F_p}$ that annihilates all the irrelevant irreducible components. Since ![]() $R ^v _w ( \mathtt J )_{\mathbb F_p}$ is a reduced ring, we have
$R ^v _w ( \mathtt J )_{\mathbb F_p}$ is a reduced ring, we have ![]() $R ^v _w ( \mathtt J, \lambda )_{\mathbb F_p} = R' ( \lambda )$ for
$R ^v _w ( \mathtt J, \lambda )_{\mathbb F_p} = R' ( \lambda )$ for ![]() $\lambda \in P_{\mathtt J,++}$. The ring
$\lambda \in P_{\mathtt J,++}$. The ring ![]() $R'$ is generated by
$R'$ is generated by  $\bigoplus _{i \in \mathtt I \setminus \mathtt J} R' ( \varpi _i )$, because
$\bigoplus _{i \in \mathtt I \setminus \mathtt J} R' ( \varpi _i )$, because ![]() $R ^v _w ( \mathtt J )_{\mathbb F_p}$ is. We have
$R ^v _w ( \mathtt J )_{\mathbb F_p}$ is. We have
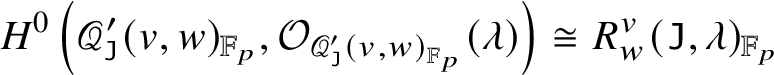 $$ \begin{align} H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{\mathbb F_p}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{\mathbb F_p}} ( \lambda ) \right) \cong R ^v _w ( \mathtt J, \lambda )_{\mathbb F_p} \end{align} $$
$$ \begin{align} H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{\mathbb F_p}, {\mathcal O} _{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{\mathbb F_p}} ( \lambda ) \right) \cong R ^v _w ( \mathtt J, \lambda )_{\mathbb F_p} \end{align} $$for sufficiently large ![]() $\lambda \in P_{\mathtt J, +}$ (see, e.g., [Reference Hartshorne37, II Excecise 5.9]). In other words, formula (4.14) holds for
$\lambda \in P_{\mathtt J, +}$ (see, e.g., [Reference Hartshorne37, II Excecise 5.9]). In other words, formula (4.14) holds for ![]() $m \lambda $, where
$m \lambda $, where ![]() $\lambda \in P_{\mathtt J, ++}$ is arbitrary and
$\lambda \in P_{\mathtt J, ++}$ is arbitrary and ![]() $m \gg 0$.
$m \gg 0$.
Define  $R^\sharp ( \lambda ) := H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}, {\mathcal O} _{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{\mathbb F_p}} ( \lambda ) \right )$ for
$R^\sharp ( \lambda ) := H^0 \left ( \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb F_p}, {\mathcal O} _{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{\mathbb F_p}} ( \lambda ) \right )$ for ![]() $\lambda \in P_{\mathtt J, ++}$. We set
$\lambda \in P_{\mathtt J, ++}$. We set  $R^\sharp [\lambda ] : = \mathbb F_p 1 \oplus \bigoplus _{m \ge 1} R^\sharp ( m \lambda )$ and
$R^\sharp [\lambda ] : = \mathbb F_p 1 \oplus \bigoplus _{m \ge 1} R^\sharp ( m \lambda )$ and ![]() $R'[\lambda ] := \bigoplus _{m \ge 0} R' ( m \lambda ) \subset R'$ for
$R'[\lambda ] := \bigoplus _{m \ge 0} R' ( m \lambda ) \subset R'$ for ![]() $\lambda \in P_{\mathtt J, ++}$. Both are naturally rings. Then we have a ring extension
$\lambda \in P_{\mathtt J, ++}$. Both are naturally rings. Then we have a ring extension ![]() $R' [ \lambda ] \subset R^\sharp [ \lambda ]$ such that their degree
$R' [ \lambda ] \subset R^\sharp [ \lambda ]$ such that their degree ![]() $m \gg 0$ parts are the same.
$m \gg 0$ parts are the same.
We prove ![]() $R' ( \lambda ) = R^\sharp ( \lambda )$. The ring
$R' ( \lambda ) = R^\sharp ( \lambda )$. The ring ![]() $R'[\lambda ]$ is weakly normal, as we have an inclusion
$R'[\lambda ]$ is weakly normal, as we have an inclusion ![]() $R'[\lambda ] \hookrightarrow R ^v _w ( \mathtt J )_{\mathbb F_p}$ (and the reasoning that
$R'[\lambda ] \hookrightarrow R ^v _w ( \mathtt J )_{\mathbb F_p}$ (and the reasoning that ![]() $R ^v _w ( \mathtt J )_{\mathbb F_p}$ is weakly normal equally applies to
$R ^v _w ( \mathtt J )_{\mathbb F_p}$ is weakly normal equally applies to ![]() $R' [\lambda ]$). Since it is generated by
$R' [\lambda ]$). Since it is generated by ![]() $R' ( \lambda )$, we deduce that the rings
$R' ( \lambda )$, we deduce that the rings ![]() $R'[\lambda ]$ and
$R'[\lambda ]$ and ![]() $R^\sharp [\lambda ]$ share the same spectrum (the irrelevant locus of
$R^\sharp [\lambda ]$ share the same spectrum (the irrelevant locus of ![]() $R'[\lambda ]$ is one point, as it is a
$R'[\lambda ]$ is one point, as it is a ![]() $\mathbb {Z}_{\ge 0}$-graded ring, and other points are just the same). This forces
$\mathbb {Z}_{\ge 0}$-graded ring, and other points are just the same). This forces ![]() $R' ( \lambda ) = R^\sharp ( \lambda )$ by the weak normality of
$R' ( \lambda ) = R^\sharp ( \lambda )$ by the weak normality of ![]() $R'[\lambda ]$.
$R'[\lambda ]$.
This yields the ![]() $H^0$-part of the assertion for
$H^0$-part of the assertion for ![]() $\mathsf {char}\, {\mathbb K}> 0$ through the extension of scalars. The
$\mathsf {char}\, {\mathbb K}> 0$ through the extension of scalars. The ![]() $H^0$-part of the assertion for
$H^0$-part of the assertion for ![]() $\mathsf {char}\, {\mathbb K} = 0$ is obtained by taking the generic specialisation of the base scheme
$\mathsf {char}\, {\mathbb K} = 0$ is obtained by taking the generic specialisation of the base scheme ![]() $\mathrm {Spec}\, \mathbb {Z}$ of
$\mathrm {Spec}\, \mathbb {Z}$ of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$.
Corollary 4.35. Set ![]() $w, v \in W_{\mathrm {af}}$ and
$w, v \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$. Assume that the map
$\mathtt J \subset \mathtt I$. Assume that the map ![]() $\Pi _{\mathtt J} : \mathscr {Q}' ( v, w )_{{\mathbb K}} \rightarrow \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ defined through the projective coordinate ring is surjective. We have
$\Pi _{\mathtt J} : \mathscr {Q}' ( v, w )_{{\mathbb K}} \rightarrow \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ defined through the projective coordinate ring is surjective. We have
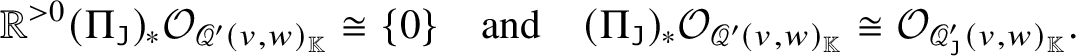 $$ \begin{align*}\mathbb{R}^{>0} ( \Pi_{\mathtt J} )_* {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} \cong \{ 0 \} \quad \text{and} \quad ( \Pi_{\mathtt J} )_* {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} \cong {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}}.\end{align*} $$
$$ \begin{align*}\mathbb{R}^{>0} ( \Pi_{\mathtt J} )_* {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} \cong \{ 0 \} \quad \text{and} \quad ( \Pi_{\mathtt J} )_* {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} \cong {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}}.\end{align*} $$Remark 4.36. Since the map  $\mathbf {Q}_G^{\mathrm {rat}} \to \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}}$ is surjective, we can replace v with
$\mathbf {Q}_G^{\mathrm {rat}} \to \mathbf {Q}_{G, \mathtt J}^{\mathrm {rat}}$ is surjective, we can replace v with ![]() $v t_{\beta }$ for some
$v t_{\beta }$ for some  $\beta \in \sum _{j \in \mathtt J} \mathbb {Z}_{\ge 0} \alpha _j^{\vee }$ to obtain a surjection
$\beta \in \sum _{j \in \mathtt J} \mathbb {Z}_{\ge 0} \alpha _j^{\vee }$ to obtain a surjection
For ![]() $v = w_0$ and
$v = w_0$ and ![]() $w = e$, there is an optimal choice of
$w = e$, there is an optimal choice of ![]() $\beta $, which is sometimes referred to as the Peterson–Woodward threshold ([Reference Woodward79]).
$\beta $, which is sometimes referred to as the Peterson–Woodward threshold ([Reference Woodward79]).
Proof. Proof of Corollary 4.35.
Thanks to Lemma 4.29 and [Reference Kumar57, Lemma A.31], it suffices to prove
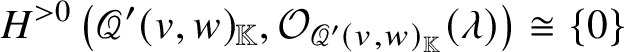 $$ \begin{align*} H^{>0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \cong \{ 0 \} \end{align*} $$
$$ \begin{align*} H^{>0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \cong \{ 0 \} \end{align*} $$and
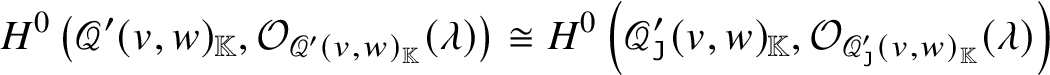 $$ \begin{align*} H^{0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \cong H^{0} \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \end{align*} $$
$$ \begin{align*} H^{0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \cong H^{0} \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) \end{align*} $$for each ![]() $\lambda \in P_{\mathtt J,++}$. The
$\lambda \in P_{\mathtt J,++}$. The ![]() $H^{>0}$-part of the assertion follow from Theorem 4.33. The
$H^{>0}$-part of the assertion follow from Theorem 4.33. The ![]() $H^0$-part of the assertion follows as in the latter part of the proof of Theorem 4.33, since the surjectivity of
$H^0$-part of the assertion follows as in the latter part of the proof of Theorem 4.33, since the surjectivity of ![]() $\Pi _{\mathtt J}$ guarantees that every nonzero element of
$\Pi _{\mathtt J}$ guarantees that every nonzero element of ![]() $R ^v _w ( \lambda )_{\mathbb F_p}$ is supported outside of the irrelevant locus by pullback, and that the (graded) normalisation of the ring
$R ^v _w ( \lambda )_{\mathbb F_p}$ is supported outside of the irrelevant locus by pullback, and that the (graded) normalisation of the ring ![]() $R ^v _w ( \mathtt J )_{\mathbb F_p}$ is the degree
$R ^v _w ( \mathtt J )_{\mathbb F_p}$ is the degree ![]() $P_{\mathtt J, +}$ part of the (graded) normalisation of the ring
$P_{\mathtt J, +}$ part of the (graded) normalisation of the ring  $\left ( R ^v _w \right )_{\mathbb F_p}$ by the degree reasons.
$\left ( R ^v _w \right )_{\mathbb F_p}$ by the degree reasons.
Corollary 4.37. Set ![]() $\lambda \in P_{+}$ and
$\lambda \in P_{+}$ and ![]() $w, v \in W_{\mathrm {af}}$. We set
$w, v \in W_{\mathrm {af}}$. We set  $\mathtt J := \left \{i \in \mathtt I \mid \left \langle \alpha _i^{\vee }, \lambda \right \rangle = 0 \right \}$. Assume that
$\mathtt J := \left \{i \in \mathtt I \mid \left \langle \alpha _i^{\vee }, \lambda \right \rangle = 0 \right \}$. Assume that ![]() $\Pi _{\mathtt J} ( \mathscr {Q}' ( v, w )_{{\mathbb K}} ) = \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$. Then we have
$\Pi _{\mathtt J} ( \mathscr {Q}' ( v, w )_{{\mathbb K}} ) = \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$. Then we have
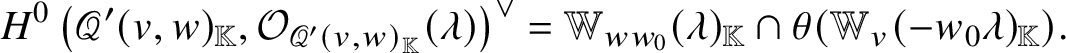 $$ \begin{align*}H^{0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right)^{\vee} = \mathbb{W} _{ww_0} ( \lambda )_{{\mathbb K}} \cap \theta ( \mathbb{W} _{v} ( -w_0 \lambda )_{{\mathbb K}} ).\end{align*} $$
$$ \begin{align*}H^{0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right)^{\vee} = \mathbb{W} _{ww_0} ( \lambda )_{{\mathbb K}} \cap \theta ( \mathbb{W} _{v} ( -w_0 \lambda )_{{\mathbb K}} ).\end{align*} $$Proof. Combine Theorem 4.33 for ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ and Corollary 4.35.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ and Corollary 4.35.
Lemma 4.38. Set ![]() $w,v \in W_{\mathrm {af}}$ and
$w,v \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$. For each
$\mathtt J \subset \mathtt I$. For each ![]() $i \in \mathtt I_{\mathrm {af}}$ such that
$i \in \mathtt I_{\mathrm {af}}$ such that ![]() $s_i w>_{\frac {\infty }{2}} w$ and
$s_i w>_{\frac {\infty }{2}} w$ and ![]() $s_i v>_{\frac {\infty }{2}} v$, the variety
$s_i v>_{\frac {\infty }{2}} v$, the variety ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ is
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ is ![]() $B_i$-stable. In addition, we have a morphism
$B_i$-stable. In addition, we have a morphism
The map ![]() $\pi _i$ is a
$\pi _i$ is a ![]() $\mathbb {P}^1$-fibration if
$\mathbb {P}^1$-fibration if ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ is
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ is ![]() $\mathop {\textit{SL}} ( 2, i )$-stable
$\mathop {\textit{SL}} ( 2, i )$-stable ![]() $($this never happens under our assumption when
$($this never happens under our assumption when ![]() $\mathtt J = \emptyset )$. In general, the fibre of
$\mathtt J = \emptyset )$. In general, the fibre of ![]() $\pi _i$ is either a point or
$\pi _i$ is either a point or ![]() $\mathbb {P}^1$ if it is nonempty.
$\mathbb {P}^1$ if it is nonempty.
Proof. For each ![]() $\lambda \in P_{\mathtt J,++}$, the module
$\lambda \in P_{\mathtt J,++}$, the module ![]() $\mathbb {W} _{v} ( - w_0 \lambda )_{\mathbb K}$ is
$\mathbb {W} _{v} ( - w_0 \lambda )_{\mathbb K}$ is ![]() $\mathbf {I} ( i )$-stable by Corollary 3.16 and formula (2.2), and the module
$\mathbf {I} ( i )$-stable by Corollary 3.16 and formula (2.2), and the module ![]() $\mathbb {W} _{ww_0} ( \lambda )_{\mathbb K}$ is
$\mathbb {W} _{ww_0} ( \lambda )_{\mathbb K}$ is ![]() $\mathbf {I}$-stable. In particular,
$\mathbf {I}$-stable. In particular,
is ![]() $B_i$-stable. It follows that the ring
$B_i$-stable. It follows that the ring ![]() $R ^v _w ( \mathtt J )_{\mathbb K}$ is
$R ^v _w ( \mathtt J )_{\mathbb K}$ is ![]() $B_i$-stable. Hence the scheme
$B_i$-stable. Hence the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ is also
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ is also ![]() $B_i$-stable.
$B_i$-stable.
The map ![]() $\pi _i$ is a
$\pi _i$ is a ![]() $\mathbb {P}^1$-fibration if
$\mathbb {P}^1$-fibration if ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is ![]() $\mathop {\textit{SL}} ( 2, i )$-stable, since in this case we have
$\mathop {\textit{SL}} ( 2, i )$-stable, since in this case we have ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , w )_{{\mathbb K}} = \mathscr {Q}^{\prime }_{\mathtt J} ( \beta , s_i w )_{{\mathbb K}}$ (which in turn holds if and only if
$\mathscr {Q}^{\prime }_{\mathtt J} ( \beta , w )_{{\mathbb K}} = \mathscr {Q}^{\prime }_{\mathtt J} ( \beta , s_i w )_{{\mathbb K}}$ (which in turn holds if and only if ![]() $\mathbb {W} _{s_iw w_0} ( \lambda )_{{\mathbb K}} = \mathbb {W} _{w w_0} ( \lambda )_{{\mathbb K}}$ for
$\mathbb {W} _{s_iw w_0} ( \lambda )_{{\mathbb K}} = \mathbb {W} _{w w_0} ( \lambda )_{{\mathbb K}}$ for ![]() $\lambda \in P_{\mathtt J,++}$, since
$\lambda \in P_{\mathtt J,++}$, since ![]() $\mathbb {W}^- _{vw_0} ( \lambda )_{\mathbb K}$ is
$\mathbb {W}^- _{vw_0} ( \lambda )_{\mathbb K}$ is ![]() $\mathop {\textit{SL}} ( 2, i )$-stable; hence it never happens when
$\mathop {\textit{SL}} ( 2, i )$-stable; hence it never happens when ![]() $\mathtt J = \emptyset $, by Lemma 3.15). The fibre of the map
$\mathtt J = \emptyset $, by Lemma 3.15). The fibre of the map ![]() $\pi _i$ is either a point or
$\pi _i$ is either a point or ![]() $\mathbb {P}^1$ if
$\mathbb {P}^1$ if ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is not
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is not ![]() $\mathop {\textit{SL}} ( 2, i )$-stable, as the corresponding statement holds true for
$\mathop {\textit{SL}} ( 2, i )$-stable, as the corresponding statement holds true for ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{{\mathbb K}} \subset \mathbf {Q}_{G, \mathtt J} ( s_i w )_{{\mathbb K}}$ by a set-theoretic consideration (and it carries over to any
$\mathbf {Q}_{G, \mathtt J} ( w )_{{\mathbb K}} \subset \mathbf {Q}_{G, \mathtt J} ( s_i w )_{{\mathbb K}}$ by a set-theoretic consideration (and it carries over to any ![]() $B_i$-stable locus). Therefore, we conclude the result.
$B_i$-stable locus). Therefore, we conclude the result.
Proposition 4.39. Set ![]() $w,v \in W_{\mathrm {af}}$ and
$w,v \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$. For each
$\mathtt J \subset \mathtt I$. For each ![]() $i \in \mathtt I_{\mathrm {af}}$ such that
$i \in \mathtt I_{\mathrm {af}}$ such that ![]() $s_i w>_{\frac {\infty }{2}} w$ and
$s_i w>_{\frac {\infty }{2}} w$ and ![]() $s_i v>_{\frac {\infty }{2}} v$, we have a surjective map
$s_i v>_{\frac {\infty }{2}} v$, we have a surjective map
such that  $(\pi _i)_* {\mathcal O}_{\mathop {\textit{SL}} \left ( 2, i \right ) \times ^{B_i} \mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{\mathbb K}} \cong {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, s_i w \right )_{\mathbb K}}$ and
$(\pi _i)_* {\mathcal O}_{\mathop {\textit{SL}} \left ( 2, i \right ) \times ^{B_i} \mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{\mathbb K}} \cong {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, s_i w \right )_{\mathbb K}}$ and
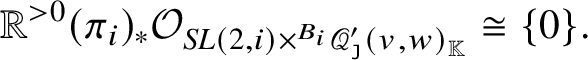 $$ \begin{align*}\mathbb{R}^{>0} (\pi_i)_* {\mathcal O}_{\mathop{\textit{SL}} \left( 2, i \right) \times^{B_i} \mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{\mathbb K}} \cong \{ 0 \}.\end{align*} $$
$$ \begin{align*}\mathbb{R}^{>0} (\pi_i)_* {\mathcal O}_{\mathop{\textit{SL}} \left( 2, i \right) \times^{B_i} \mathscr{Q}^{\prime}_{\mathtt J} \left( v, w \right)_{\mathbb K}} \cong \{ 0 \}.\end{align*} $$Proof. For each ![]() $\lambda \in P_{\mathtt J,++}$, the
$\lambda \in P_{\mathtt J,++}$, the ![]() $\lambda $-graded component
$\lambda $-graded component
of the coordinate ring of ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is obtained as the
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is obtained as the ![]() $\mathbb {Z}$-span of a subset of positive global basis of
$\mathbb {Z}$-span of a subset of positive global basis of ![]() $\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}}$.
$\mathbb {W} _{ww_0} ( \lambda )_{\mathbb {Z}}$.
We set ![]() $\mathscr {Q}^+ _{\mathtt J} ( v, w )_{\mathbb K}:= \mathop {\textit{SL}} ( 2, i ) \times ^{B_i} \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ for simplicity in what follows.
$\mathscr {Q}^+ _{\mathtt J} ( v, w )_{\mathbb K}:= \mathop {\textit{SL}} ( 2, i ) \times ^{B_i} \mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb K}$ for simplicity in what follows.
In view of [Reference Naito and Sagaki72, Theorem 4.2.1] (compare Corollary 3.16), the basis elements of ![]() $\theta ^* ( \mathbb {W} _{v} ( - w_0 \lambda )_{\mathbb {Z}} )$ afforded by the negative global basis, regarded as a subset of the
$\theta ^* ( \mathbb {W} _{v} ( - w_0 \lambda )_{\mathbb {Z}} )$ afforded by the negative global basis, regarded as a subset of the ![]() $\widetilde {\mathfrak {g}}$-crystal
$\widetilde {\mathfrak {g}}$-crystal ![]() ${\mathbf B} ( \mathbb {X} (\lambda ) )$, decompose into the disjoint union of connected
${\mathbf B} ( \mathbb {X} (\lambda ) )$, decompose into the disjoint union of connected ![]() $\mathfrak {sl} ( 2, i )$-crystals (which is the set of labels of a basis of an irreducible
$\mathfrak {sl} ( 2, i )$-crystals (which is the set of labels of a basis of an irreducible ![]() $\mathfrak {sl} ( 2 )$-module equipped with combinatorial operations
$\mathfrak {sl} ( 2 )$-module equipped with combinatorial operations ![]() $\widetilde {e}_i$ and
$\widetilde {e}_i$ and ![]() $\widetilde {f}_i$ corresponding to
$\widetilde {f}_i$ corresponding to  $E^{(\bullet )}_i$ and
$E^{(\bullet )}_i$ and  $F^{(\bullet )}_i$ – see, e.g., [Reference Kashiwara41, Definition 2.3.1]; it is the i-string in [Reference Kashiwara42, Reference Kashiwara45]). Moreover, the basis elements of
$F^{(\bullet )}_i$ – see, e.g., [Reference Kashiwara41, Definition 2.3.1]; it is the i-string in [Reference Kashiwara42, Reference Kashiwara45]). Moreover, the basis elements of ![]() $\mathbb {W} _{s_iww_0} ( \lambda )_{\mathbb {Z}}$ afforded by the positive global basis, regarded as a subset of the
$\mathbb {W} _{s_iww_0} ( \lambda )_{\mathbb {Z}}$ afforded by the positive global basis, regarded as a subset of the ![]() $\widetilde {\mathfrak {g}}$-crystal
$\widetilde {\mathfrak {g}}$-crystal ![]() ${\mathbf B} ( \mathbb {X} ( \lambda ) )$, also decompose into the disjoint union of
${\mathbf B} ( \mathbb {X} ( \lambda ) )$, also decompose into the disjoint union of ![]() $\mathfrak {sl} ( 2, i )$-crystals ([Reference Kashiwara45, Reference Kato46]), and the set S of basis elements corresponding to each connected
$\mathfrak {sl} ( 2, i )$-crystals ([Reference Kashiwara45, Reference Kato46]), and the set S of basis elements corresponding to each connected ![]() $\mathfrak {sl} ( 2, i )$-crystal satisfies
$\mathfrak {sl} ( 2, i )$-crystal satisfies
where ![]() $\mathbf {v} \in S$ is the highest weight vector as a
$\mathbf {v} \in S$ is the highest weight vector as a ![]() $\mathfrak {sl} ( 2, i )$-crystal, which has dominant weight as a weight of
$\mathfrak {sl} ( 2, i )$-crystal, which has dominant weight as a weight of ![]() $\mathfrak {sl} ( 2, i )$ ([Reference Kashiwara45, Lemma 2.6]). In particular, we have
$\mathfrak {sl} ( 2, i )$ ([Reference Kashiwara45, Lemma 2.6]). In particular, we have
Therefore, a reinterpretation of [Reference Kashiwara42, (0.5)] using Theorem 4.33 (compare [Reference Joseph39, Reference Kato46]) reads as
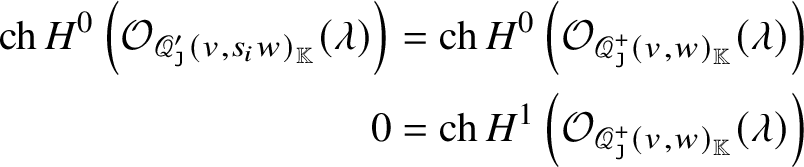 $$ \begin{align*} \mathrm{ch}\, H^0 \left( {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, s_i w \right)_{\mathbb K}} ( \lambda ) \right) & = \mathrm{ch}\, H^0 \left( {\mathcal O}_{\mathscr{Q}^+ _{\mathtt J} \left( v, w \right)_{\mathbb K}} ( \lambda ) \right)\\ 0 & = \mathrm{ch}\, H^1 \left( {\mathcal O}_{\mathscr{Q}^+ _{\mathtt J} \left( v, w \right)_{\mathbb K}} ( \lambda ) \right) \end{align*} $$
$$ \begin{align*} \mathrm{ch}\, H^0 \left( {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, s_i w \right)_{\mathbb K}} ( \lambda ) \right) & = \mathrm{ch}\, H^0 \left( {\mathcal O}_{\mathscr{Q}^+ _{\mathtt J} \left( v, w \right)_{\mathbb K}} ( \lambda ) \right)\\ 0 & = \mathrm{ch}\, H^1 \left( {\mathcal O}_{\mathscr{Q}^+ _{\mathtt J} \left( v, w \right)_{\mathbb K}} ( \lambda ) \right) \end{align*} $$for each ![]() $\lambda \in P_{\mathtt J,++}$. Since the zeroth part of the Demazure functor is the same as taking the maximal integrable
$\lambda \in P_{\mathtt J,++}$. Since the zeroth part of the Demazure functor is the same as taking the maximal integrable ![]() $\mathop {\textit{SL}} ( 2,i )$-inflation of a (weight-semisimple)
$\mathop {\textit{SL}} ( 2,i )$-inflation of a (weight-semisimple) ![]() $B_i$-module, we conclude that the inclusion
$B_i$-module, we conclude that the inclusion ![]() $R ^v _w ( \mathtt J, \lambda )^{\vee }_{{\mathbb K}} \subset R ^v _{s_i w} ( \mathtt J, \lambda )^{\vee }_{{\mathbb K}}$ induces a natural inclusion
$R ^v _w ( \mathtt J, \lambda )^{\vee }_{{\mathbb K}} \subset R ^v _{s_i w} ( \mathtt J, \lambda )^{\vee }_{{\mathbb K}}$ induces a natural inclusion
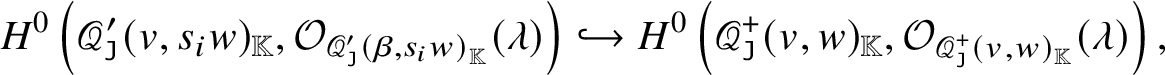 $$ \begin{align} H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, s_i w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( \beta, s_i w \right)_{{\mathbb K}}} ( \lambda ) \right) \hookrightarrow H^0 \left( \mathscr{Q}^+_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}^+_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right), \end{align} $$
$$ \begin{align} H^0 \left( \mathscr{Q}^{\prime}_{\mathtt J} ( v, s_i w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( \beta, s_i w \right)_{{\mathbb K}}} ( \lambda ) \right) \hookrightarrow H^0 \left( \mathscr{Q}^+_{\mathtt J} ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}^+_{\mathtt J} \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right), \end{align} $$which is an isomorphism by the character comparison. Thus, Lemma 4.29 implies
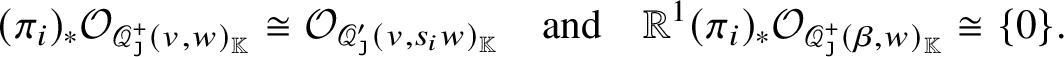 $$ \begin{align*}(\pi_i)_* {\mathcal O}_{\mathscr{Q}^+_{\mathtt J} \left( v, w \right)_{\mathbb K}} \cong {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, s_i w \right)_{\mathbb K}} \quad \text{and} \quad \mathbb{R}^1 (\pi_i)_* {\mathcal O}_{\mathscr{Q}^{+}_{\mathtt J} \left( \beta, w \right)_{\mathbb K}} \cong \{ 0 \}.\end{align*} $$
$$ \begin{align*}(\pi_i)_* {\mathcal O}_{\mathscr{Q}^+_{\mathtt J} \left( v, w \right)_{\mathbb K}} \cong {\mathcal O}_{\mathscr{Q}^{\prime}_{\mathtt J} \left( v, s_i w \right)_{\mathbb K}} \quad \text{and} \quad \mathbb{R}^1 (\pi_i)_* {\mathcal O}_{\mathscr{Q}^{+}_{\mathtt J} \left( \beta, w \right)_{\mathbb K}} \cong \{ 0 \}.\end{align*} $$Since we have  $\mathbb {R}^{\ge 2} (\pi _i)_* {\mathcal O}_{\mathscr {Q}^+_{\mathtt J} \left ( v, w \right )_{\mathbb K}} \cong \{ 0 \}$ by dimension reasons, we conclude the result.
$\mathbb {R}^{\ge 2} (\pi _i)_* {\mathcal O}_{\mathscr {Q}^+_{\mathtt J} \left ( v, w \right )_{\mathbb K}} \cong \{ 0 \}$ by dimension reasons, we conclude the result.
A particular case of Proposition 4.39 is worth noting:
Corollary 4.40. Set ![]() $\beta \in Q^{\vee }$,
$\beta \in Q^{\vee }$, ![]() $w \in W$ and
$w \in W$ and ![]() $\mathtt J \subset \mathtt I$. For each
$\mathtt J \subset \mathtt I$. For each ![]() $i \in \mathtt I$ such that
$i \in \mathtt I$ such that ![]() $s_i w < w$, we have a surjective map
$s_i w < w$, we have a surjective map
such that  $\mathbb {R}^{\bullet }(\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q}^{\prime }_{\mathtt J} \left ( \beta , w \right )_{\mathbb K}} \cong {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( \beta , s_i w \right )_{\mathbb K}}$.
$\mathbb {R}^{\bullet }(\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q}^{\prime }_{\mathtt J} \left ( \beta , w \right )_{\mathbb K}} \cong {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( \beta , s_i w \right )_{\mathbb K}}$.
4.5 Lifting to and from characteristic  $0$
$0$
Theorem 4.41. Let ![]() $\mathfrak {X}$ be a Noetherian scheme flat over
$\mathfrak {X}$ be a Noetherian scheme flat over ![]() $\mathbb {Z}$. If
$\mathbb {Z}$. If ![]() $\mathfrak {X} _{\mathbb F_p}$ is weakly normal for
$\mathfrak {X} _{\mathbb F_p}$ is weakly normal for ![]() $p \gg 0$, then
$p \gg 0$, then ![]() $\mathfrak {X}_{\mathbb C}$ is also weakly normal.
$\mathfrak {X}_{\mathbb C}$ is also weakly normal.
Proof. Since the weak normalisation commutes with localisation [Reference Manaresi68, Theorem IV.3], we can argue locally. Let ![]() $( S,\mathfrak {m} )$ be a local ring of
$( S,\mathfrak {m} )$ be a local ring of  $\mathfrak {X} _{\overline {\mathbb {Q}}}$ and let
$\mathfrak {X} _{\overline {\mathbb {Q}}}$ and let ![]() $S^-$ be the weak normalisation of S ([Reference Yanagihara80, Remark 1]). By the Noetherian hypothesis, we can invert finitely many primes and take a finite algebraic extension of
$S^-$ be the weak normalisation of S ([Reference Yanagihara80, Remark 1]). By the Noetherian hypothesis, we can invert finitely many primes and take a finite algebraic extension of ![]() $\mathbb {Z}$ to obtain a ring A such that we have a commutative ring
$\mathbb {Z}$ to obtain a ring A such that we have a commutative ring ![]() $S_A$ over A and its ideal
$S_A$ over A and its ideal ![]() $\mathfrak {m}_A$ with the following properties:
$\mathfrak {m}_A$ with the following properties:
•
 $\left ( S_A \otimes _A \overline {\mathbb {Q}}, \mathfrak {m}_{A} \otimes _A \overline {\mathbb Q}\right ) \cong ( S,\mathfrak {m} )$.
$\left ( S_A \otimes _A \overline {\mathbb {Q}}, \mathfrak {m}_{A} \otimes _A \overline {\mathbb Q}\right ) \cong ( S,\mathfrak {m} )$.• The A-modules
 $S_A, \mathfrak {m}_A$ and
$S_A, \mathfrak {m}_A$ and  $S_A / \mathfrak {m}_A$ are torsion free.
$S_A / \mathfrak {m}_A$ are torsion free.• The specialisation of A to the algebraic closure of a finite field yields a weakly normal (local) ring ([Reference Manaresi68, Theorem V.2]).
As A is a Dedekind domain, we find that ![]() $S_A, \mathfrak {m}_A$ and
$S_A, \mathfrak {m}_A$ and ![]() $S_A / \mathfrak {m}_A$ are flat over A.
$S_A / \mathfrak {m}_A$ are flat over A.
We have ![]() $S^- = S [f_1,\ldots ,f_n]$, where
$S^- = S [f_1,\ldots ,f_n]$, where ![]() $f_1,\ldots ,f_n$ are integral elements. Multiplying with elements in
$f_1,\ldots ,f_n$ are integral elements. Multiplying with elements in ![]() $\overline {\mathbb {Q}}$, we can assume that
$\overline {\mathbb {Q}}$, we can assume that ![]() $f_1,\ldots ,f_n$ are integral over
$f_1,\ldots ,f_n$ are integral over ![]() $S_A$. By inverting additional primes in
$S_A$. By inverting additional primes in ![]() $\mathbb {Z}$ if necessary (to assume that the denominator of
$\mathbb {Z}$ if necessary (to assume that the denominator of ![]() $f_i$ in
$f_i$ in ![]() $\mathrm {Frac} ( S )$ does not vanish along specialisations and achieve the conditions in the following), we can further assume that
$\mathrm {Frac} ( S )$ does not vanish along specialisations and achieve the conditions in the following), we can further assume that ![]() $S_A^- := S_A [f_1,\ldots ,f_n]$ is flat over A and is integral for every specialisation of A to a field.
$S_A^- := S_A [f_1,\ldots ,f_n]$ is flat over A and is integral for every specialisation of A to a field.
The ring  $\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) \otimes _A {\mathbb C}$ is a finite-dimensional local commutative
$\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) \otimes _A {\mathbb C}$ is a finite-dimensional local commutative ![]() ${\mathbb C}$-algebra by the weak normality assumption on
${\mathbb C}$-algebra by the weak normality assumption on ![]() $S^-$ [Reference Yanagihara80, Remark 1]. In particular, the multiplication action of each element of
$S^-$ [Reference Yanagihara80, Remark 1]. In particular, the multiplication action of each element of  $\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) \otimes _A {\mathbb C}$ has a unique eigenvalue. Hence, if we present
$\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) \otimes _A {\mathbb C}$ has a unique eigenvalue. Hence, if we present  $\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) = A [X_1,\ldots ,X_m] / \sim $ (where
$\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) = A [X_1,\ldots ,X_m] / \sim $ (where ![]() $\sim $ contains the minimal polynomials of the A-valued matrix
$\sim $ contains the minimal polynomials of the A-valued matrix ![]() $X_i$), then the minimal polynomial of
$X_i$), then the minimal polynomial of ![]() $X_i$ is of the form
$X_i$ is of the form ![]() $( T - a_i )^{m_i}$ (
$( T - a_i )^{m_i}$ (![]() $a_i \in A$). Therefore, we can assume that each
$a_i \in A$). Therefore, we can assume that each ![]() $X_i$ is nilpotent by changing
$X_i$ is nilpotent by changing ![]() $X_i$ to
$X_i$ to ![]() $X_i + a_i$ if necessary. Hence, we conclude that
$X_i + a_i$ if necessary. Hence, we conclude that  $(X_1,\ldots ,X_m) \subset \left ( S_A^- / \mathfrak {m}_A S_A^- \right )$ have eigenvalues
$(X_1,\ldots ,X_m) \subset \left ( S_A^- / \mathfrak {m}_A S_A^- \right )$ have eigenvalues ![]() $0$ after specialising to
$0$ after specialising to ![]() $\overline {\mathbb F}_p$.
$\overline {\mathbb F}_p$.
By assumption,  $( S_A ) \otimes _A \overline {\mathbb F}_p$ is weakly normal for every possible prime p and every ring homomorphism
$( S_A ) \otimes _A \overline {\mathbb F}_p$ is weakly normal for every possible prime p and every ring homomorphism  $A \to \overline {\mathbb F}_p$. Hence, the specialisation
$A \to \overline {\mathbb F}_p$. Hence, the specialisation  $\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) \otimes _A \overline {\mathbb F}_p$ must contain
$\left ( S_A^- / \mathfrak {m}_A S_A^- \right ) \otimes _A \overline {\mathbb F}_p$ must contain ![]() $\overline {\mathbb F}_p$ as its ring direct summand (if it is nonzero). This forces
$\overline {\mathbb F}_p$ as its ring direct summand (if it is nonzero). This forces  $\mathrm {rank} \left ( S_A^- / \mathfrak {m}_A S_A^- \right ) = 1$, since we cannot have two linearly independent idempotents that have distinct eigenspaces, by the previous paragraph.
$\mathrm {rank} \left ( S_A^- / \mathfrak {m}_A S_A^- \right ) = 1$, since we cannot have two linearly independent idempotents that have distinct eigenspaces, by the previous paragraph.
Therefore, we deduce that ![]() $S_A^- = S_A$, which implies that
$S_A^- = S_A$, which implies that ![]() $( S, \mathfrak {m} )$ is itself weakly normal. In view of [Reference Manaresi68, Theorem V.2 and Corollary V.3], we conclude the assertion.
$( S, \mathfrak {m} )$ is itself weakly normal. In view of [Reference Manaresi68, Theorem V.2 and Corollary V.3], we conclude the assertion.
Corollary 4.42. For each ![]() $\mathtt J \subset \mathtt I$,
$\mathtt J \subset \mathtt I$, ![]() $w,v\in W_{\mathrm {af}}$, the scheme
$w,v\in W_{\mathrm {af}}$, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v,w )_{\mathbb C}$ is weakly normal.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v,w )_{\mathbb C}$ is weakly normal.
Proposition 4.43. For each ![]() $\mathtt J \subset \mathtt I$,
$\mathtt J \subset \mathtt I$, ![]() $v,w \in W$, the variety
$v,w \in W$, the variety  $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb F}_p}$ is normal for
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb F}_p}$ is normal for ![]() $p \gg 0$, provided
$p \gg 0$, provided ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb C}$ is normal. The same is true for irreducibility.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb C}$ is normal. The same is true for irreducibility.
Proof. Since ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is defined over
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )$ is defined over ![]() $\mathbb {Z}$, the scheme
$\mathbb {Z}$, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb C}$ is a scalar extension of
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb C}$ is a scalar extension of  $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb {Q}}}$. By [77, Lemma 038P], we deduce that
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb {Q}}}$. By [77, Lemma 038P], we deduce that  $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb {Q}}}$ is normal. We apply [77, Lemma 0364] to derive the irreducibility of
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb {Q}}}$ is normal. We apply [77, Lemma 0364] to derive the irreducibility of  $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb {Q}}}$. Now apply [Reference Grothendieck36, Proposition 9.9.4 and Théorème 9.7.7] to
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb {Q}}}$. Now apply [Reference Grothendieck36, Proposition 9.9.4 and Théorème 9.7.7] to ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb {Z}} \to \mbox {Spec}\, \mathbb {Z}$.
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\mathbb {Z}} \to \mbox {Spec}\, \mathbb {Z}$.
5 Normality of quasi-map spaces
In this section, we continue to work in the setting of the previous section, with the exception that ![]() ${\mathbb K} = {\mathbb C}$. Also, a point of a scheme (over
${\mathbb K} = {\mathbb C}$. Also, a point of a scheme (over ![]() ${\mathbb C}$) means a closed point unless stated otherwise.
${\mathbb C}$) means a closed point unless stated otherwise.
5.1 Graph-space resolution of  $\mathscr {Q} ( \beta )$
$\mathscr {Q} ( \beta )$
We refer to [Reference Kontsevich and Manin56, Reference Fulton and Pandharipande30, Reference Behrend and Manin6, Reference Feigin, Finkelberg, Kuznetsov and Mirković23, Reference Givental and Lee33] for precise explanations of the material in this subsection. For each nonnegative integer n and ![]() $\beta \in Q^{\vee }_+$, we set
$\beta \in Q^{\vee }_+$, we set ![]() ${\mathscr{GB}}_{n, \beta }$ to be the space of stable maps of genus
${\mathscr{GB}}_{n, \beta }$ to be the space of stable maps of genus ![]() $0$ curves with n-parked points to
$0$ curves with n-parked points to ![]() $\left ( \mathbb {P}^1 \times \mathscr {B} \right )$ of bidegree
$\left ( \mathbb {P}^1 \times \mathscr {B} \right )$ of bidegree ![]() $( 1, \beta )$, which is also called the graph space of
$( 1, \beta )$, which is also called the graph space of ![]() $\mathscr {B}$. A point of
$\mathscr {B}$. A point of ![]() ${\mathscr{GB}}_{n, \beta }$ represents a genus
${\mathscr{GB}}_{n, \beta }$ represents a genus ![]() $0$ curve C with n-marked points, together with a map to
$0$ curve C with n-marked points, together with a map to ![]() $\mathbb {P}^1$ of degree
$\mathbb {P}^1$ of degree ![]() $1$ (obtained by composing the map from C to
$1$ (obtained by composing the map from C to ![]() $\mathbb {P}^1 \times \mathscr {B}$ with the first projection of the target). Hence, we have a unique
$\mathbb {P}^1 \times \mathscr {B}$ with the first projection of the target). Hence, we have a unique ![]() $\mathbb {P}^1$-component of C that maps isomorphically onto
$\mathbb {P}^1$-component of C that maps isomorphically onto ![]() $\mathbb {P}^1$. We call this component the main component of C and denote it by
$\mathbb {P}^1$. We call this component the main component of C and denote it by ![]() $C_0$. The space
$C_0$. The space ![]() ${\mathscr{GB}}_{n, \beta }$ is a normal projective variety by [Reference Fulton and Pandharipande30, Theorem 2], which has at worst quotient singularities arising from the automorphism of curves (and hence is smooth as an orbifold). The natural
${\mathscr{GB}}_{n, \beta }$ is a normal projective variety by [Reference Fulton and Pandharipande30, Theorem 2], which has at worst quotient singularities arising from the automorphism of curves (and hence is smooth as an orbifold). The natural ![]() $( H \times \mathbb {G}_m)$-action on
$( H \times \mathbb {G}_m)$-action on ![]() $\left ( \mathbb {P}^1 \times \mathscr {B} \right )$ induces a natural
$\left ( \mathbb {P}^1 \times \mathscr {B} \right )$ induces a natural ![]() $( H \times \mathbb {G}_m)$-action on
$( H \times \mathbb {G}_m)$-action on ![]() ${\mathscr{GB}}_{n, \beta }$.
${\mathscr{GB}}_{n, \beta }$.
We have a morphism ![]() $\pi _{n, \beta } : {\mathscr{GB}}_{n, \beta } \rightarrow \mathscr {Q} ( \beta )$ that factors through
$\pi _{n, \beta } : {\mathscr{GB}}_{n, \beta } \rightarrow \mathscr {Q} ( \beta )$ that factors through ![]() $\mathscr G \mathscr B_{0, \beta }$ (Givental’s main lemma [Reference Givental34]; see [Reference Feigin, Finkelberg, Kuznetsov and Mirković23, §8.3]). Let
$\mathscr G \mathscr B_{0, \beta }$ (Givental’s main lemma [Reference Givental34]; see [Reference Feigin, Finkelberg, Kuznetsov and Mirković23, §8.3]). Let ![]() $\mathtt {e}_j : \mathscr {B}_{n, \beta } \to \mathscr {B}$ (
$\mathtt {e}_j : \mathscr {B}_{n, \beta } \to \mathscr {B}$ (![]() $1 \le j \le n$) be the evaluation at the jth marked point, and let
$1 \le j \le n$) be the evaluation at the jth marked point, and let ![]() $\mathtt {ev}_j : {\mathscr{GB}}_{n, \beta } \to \mathscr {B}$ be the jth evaluation map to
$\mathtt {ev}_j : {\mathscr{GB}}_{n, \beta } \to \mathscr {B}$ be the jth evaluation map to ![]() $\mathbb {P}^1 \times \mathscr {B}$ composed with the second projection.
$\mathbb {P}^1 \times \mathscr {B}$ composed with the second projection.
Since ![]() $\mathscr {Q} ( \beta )$ is irreducible (Theorem 2.7), [Reference Feigin, Finkelberg, Kuznetsov and Mirković23, §8.3] asserts that
$\mathscr {Q} ( \beta )$ is irreducible (Theorem 2.7), [Reference Feigin, Finkelberg, Kuznetsov and Mirković23, §8.3] asserts that ![]() ${\mathscr{GB}}_{n,\beta }$ is irreducible (as a special feature of flag varieties; see [Reference Fulton and Pandharipande30, §1.2] and [Reference Kim and Pandharipande53]).
${\mathscr{GB}}_{n,\beta }$ is irreducible (as a special feature of flag varieties; see [Reference Fulton and Pandharipande30, §1.2] and [Reference Kim and Pandharipande53]).
5.2 The variety  $\mathscr {Q} ( \beta , v, w )$
$\mathscr {Q} ( \beta , v, w )$
Let  ${\mathscr{GB}}_{2,\beta }^{\flat }$ denote the subvariety of
${\mathscr{GB}}_{2,\beta }^{\flat }$ denote the subvariety of ![]() ${\mathscr{GB}}_{2,\beta }$ consisting of points such that the first marked point projects to
${\mathscr{GB}}_{2,\beta }$ consisting of points such that the first marked point projects to ![]() $0 \in \mathbb {P}^1$ and the second projects to
$0 \in \mathbb {P}^1$ and the second projects to ![]() $\infty \in \mathbb {P}^1$ through the projection of quasi-stable curves C to their main component
$\infty \in \mathbb {P}^1$ through the projection of quasi-stable curves C to their main component ![]() $C_0 \cong \mathbb {P}^1$. Let us denote the restrictions of
$C_0 \cong \mathbb {P}^1$. Let us denote the restrictions of ![]() $\mathtt {ev}_i (i=1,2)$ and
$\mathtt {ev}_i (i=1,2)$ and ![]() $\pi _{2,\beta }$ to
$\pi _{2,\beta }$ to  ${\mathscr{GB}}_{2,\beta }^{\flat }$ by the same letter. By [Reference Braverman and Finkelberg9, Reference Braverman and Finkelberg10],
${\mathscr{GB}}_{2,\beta }^{\flat }$ by the same letter. By [Reference Braverman and Finkelberg9, Reference Braverman and Finkelberg10],  ${\mathscr{GB}}_{2,\beta }^{\flat }$ gives a resolution of singularities of
${\mathscr{GB}}_{2,\beta }^{\flat }$ gives a resolution of singularities of ![]() $\mathscr {Q} ( \beta )$ (in an orbifold sense).
$\mathscr {Q} ( \beta )$ (in an orbifold sense).
Recall that each Schubert cell ![]() $\mathbb {O}_{\mathscr {B}} ( w )$ contains a unique H-fixed point
$\mathbb {O}_{\mathscr {B}} ( w )$ contains a unique H-fixed point ![]() $p_w$. For each
$p_w$. For each ![]() $w \in W$, we set
$w \in W$, we set
 $$ \begin{align*}\mathbb{O}_{\mathscr{B}} ^{\mathrm{op}} ( w ) := N^- p_w \subset \mathscr{B}, \qquad \mathscr{B}^{\mathrm{op}} ( w ) := \overline{\mathbb{O}_{\mathscr{B}} ^{\mathrm{op}} ( w )} = \overline{N^- p_w} \subset \mathscr{B}.\end{align*} $$
$$ \begin{align*}\mathbb{O}_{\mathscr{B}} ^{\mathrm{op}} ( w ) := N^- p_w \subset \mathscr{B}, \qquad \mathscr{B}^{\mathrm{op}} ( w ) := \overline{\mathbb{O}_{\mathscr{B}} ^{\mathrm{op}} ( w )} = \overline{N^- p_w} \subset \mathscr{B}.\end{align*} $$For ![]() $w,v \in W$, we define
$w,v \in W$, we define
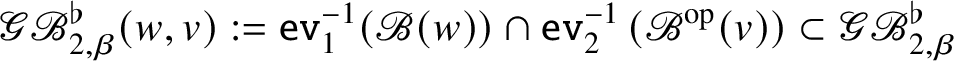 $$ \begin{align*}{\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) := \mathtt{ev}_1^{-1} ( \mathscr{B} ( w ) ) \cap \mathtt{ev}_2^{-1} \left( \mathscr{B}^{\mathrm{op}} ( v ) \right) \subset {\mathscr{GB}}_{2,\beta}^{\flat}\end{align*} $$
$$ \begin{align*}{\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) := \mathtt{ev}_1^{-1} ( \mathscr{B} ( w ) ) \cap \mathtt{ev}_2^{-1} \left( \mathscr{B}^{\mathrm{op}} ( v ) \right) \subset {\mathscr{GB}}_{2,\beta}^{\flat}\end{align*} $$and
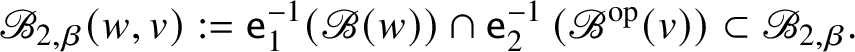 $$ \begin{align*}\mathscr{B}_{2,\beta} ( w, v ) := \mathtt{e}_1^{-1} ( \mathscr{B} ( w ) ) \cap \mathtt{e}_2^{-1} \left( \mathscr{B}^{\mathrm{op}} ( v ) \right) \subset \mathscr{B}_{2,\beta}.\end{align*} $$
$$ \begin{align*}\mathscr{B}_{2,\beta} ( w, v ) := \mathtt{e}_1^{-1} ( \mathscr{B} ( w ) ) \cap \mathtt{e}_2^{-1} \left( \mathscr{B}^{\mathrm{op}} ( v ) \right) \subset \mathscr{B}_{2,\beta}.\end{align*} $$Theorem 5.1 [Reference Buch, Chaput, Mihalcea and Perrin16]
For each ![]() $v,w \in W$ and
$v,w \in W$ and ![]() $\beta \in Q^{\vee }_+$, the variety
$\beta \in Q^{\vee }_+$, the variety  ${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ is either empty or a unirational
${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ is either empty or a unirational ![]() $($and hence connected and irreducible
$($and hence connected and irreducible![]() $)$ variety that has rational singularities. The same is true for
$)$ variety that has rational singularities. The same is true for ![]() $\mathscr {B}_{2,\beta } ( w, v )$. In particular, they are normal.
$\mathscr {B}_{2,\beta } ( w, v )$. In particular, they are normal.
Proof. Since both cases are parallel, we concentrate on the case of  ${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$.
${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$.
As ![]() $\mathbb {P}^1 \times \mathscr {B}$ is a homogeneous variety under the group action of
$\mathbb {P}^1 \times \mathscr {B}$ is a homogeneous variety under the group action of ![]() $(\mathop {\textit{SL}} ( 2 ) \times G)$, [Reference Kim and Pandharipande53, Theorem 2 and Theorem 3] apply and hence
$(\mathop {\textit{SL}} ( 2 ) \times G)$, [Reference Kim and Pandharipande53, Theorem 2 and Theorem 3] apply and hence ![]() ${\mathscr{GB}}_{2,\beta }$ is a rational variety. Then a pair of Schubert subvarieties (with respect to a pair of opposite Borel subgroups of
${\mathscr{GB}}_{2,\beta }$ is a rational variety. Then a pair of Schubert subvarieties (with respect to a pair of opposite Borel subgroups of ![]() $\mathop {\textit{SL}} ( 2 ) \times G$) of
$\mathop {\textit{SL}} ( 2 ) \times G$) of ![]() $\mathbb {P}^1 \times \mathscr {B}$ presented as
$\mathbb {P}^1 \times \mathscr {B}$ presented as ![]() $\{ 0 \} \times \mathscr {B} ( w )$ and
$\{ 0 \} \times \mathscr {B} ( w )$ and ![]() $\{ \infty \} \times \mathscr {B}^{\mathrm {op}} ( v )$ is used to define
$\{ \infty \} \times \mathscr {B}^{\mathrm {op}} ( v )$ is used to define  ${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$. Hence, [Reference Buch, Chaput, Mihalcea and Perrin16, Proposition 3.2 c)] implies that
${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$. Hence, [Reference Buch, Chaput, Mihalcea and Perrin16, Proposition 3.2 c)] implies that  ${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ is either empty or unirational (and hence connected). Since a pair of Schubert varieties with respect to the opposite Borel subgroups forms the dense subset of the pair of translations of Schubert varieties by applying the G-action, it must contain a pair of Schubert varieties in general position. Therefore, [Reference Buch, Chaput, Mihalcea and Perrin16, Corollary 3.1] implies that
${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ is either empty or unirational (and hence connected). Since a pair of Schubert varieties with respect to the opposite Borel subgroups forms the dense subset of the pair of translations of Schubert varieties by applying the G-action, it must contain a pair of Schubert varieties in general position. Therefore, [Reference Buch, Chaput, Mihalcea and Perrin16, Corollary 3.1] implies that  ${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ has rational singularity. The last assertion is a well-known property of rational singularities [Reference Kollár, Mori, Clemens and Corti55, Definition 5.8].
${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ has rational singularity. The last assertion is a well-known property of rational singularities [Reference Kollár, Mori, Clemens and Corti55, Definition 5.8].
Corollary 5.2. In the setting of Theorem 5.1, we additionally assume that  ${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ is nonempty. Then we have
${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ is nonempty. Then we have
 $$ \begin{align*}\dim {\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) = \dim \mathscr{Q} ( \beta ) - \ell ( w ) - \ell ( vw_0 ).\end{align*} $$
$$ \begin{align*}\dim {\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) = \dim \mathscr{Q} ( \beta ) - \ell ( w ) - \ell ( vw_0 ).\end{align*} $$Proof. By [Reference Buch, Chaput, Mihalcea and Perrin16, Proposition 3.2 b)], the dimension count of (a Zariski open subset of)  ${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ can be borrowed from [Reference Kleiman54, Theorem 2] applied to the
${\mathscr{GB}}_{2,\beta }^{\flat } ( w, v )$ can be borrowed from [Reference Kleiman54, Theorem 2] applied to the ![]() $( \mathop {\textit{SL}} ( 2 ) \times G )$-action on
$( \mathop {\textit{SL}} ( 2 ) \times G )$-action on ![]() $\mathbb {P}^1 \times \mathscr {B}$. In addition, the map
$\mathbb {P}^1 \times \mathscr {B}$. In addition, the map ![]() $\pi _{2,\beta }$ is birational. Therefore, we have
$\pi _{2,\beta }$ is birational. Therefore, we have
 $$ \begin{align*} \dim {\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) & = \dim \mathscr{Q} ( \beta ) - \mathrm{codim}_{\mathscr{B}} \mathscr{B} ( w ) - \mathrm{codim}_{\mathscr{B}} \mathscr{B}^{\mathrm{op}} ( v )\\ & = \dim \mathscr{Q} ( \beta ) - \ell ( w ) - \ell ( vw_0 ), \end{align*} $$
$$ \begin{align*} \dim {\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) & = \dim \mathscr{Q} ( \beta ) - \mathrm{codim}_{\mathscr{B}} \mathscr{B} ( w ) - \mathrm{codim}_{\mathscr{B}} \mathscr{B}^{\mathrm{op}} ( v )\\ & = \dim \mathscr{Q} ( \beta ) - \ell ( w ) - \ell ( vw_0 ), \end{align*} $$as required.
Proposition 5.3. For each ![]() $v,w \in W$ and
$v,w \in W$ and ![]() $\beta \in Q^{\vee }_+$, the variety
$\beta \in Q^{\vee }_+$, the variety  $\mathscr {Q}' \left ( v t_{\beta }, w \right )_{\mathbb C}$ is irreducible.
$\mathscr {Q}' \left ( v t_{\beta }, w \right )_{\mathbb C}$ is irreducible.
Proof. We define
 $$ \begin{align*}\mathring{\mathscr{Q}}'\left( vt_{\beta}, w \right)_{\mathbb C} := \mathscr{Q}'\left( vt_{\beta}, w \right)_{\mathbb C} \setminus \left( \left( \bigcup_{w'<_{\frac{\infty}{2}} w} \mathscr{Q}'\left( vt_{\beta}, w' \right)_{\mathbb C} \right) \cup \bigcup_{v'>_{\frac{\infty}{2}} v} \mathscr{Q}'\left( v't_{\beta}, w \right)_{\mathbb C} \right).\end{align*} $$
$$ \begin{align*}\mathring{\mathscr{Q}}'\left( vt_{\beta}, w \right)_{\mathbb C} := \mathscr{Q}'\left( vt_{\beta}, w \right)_{\mathbb C} \setminus \left( \left( \bigcup_{w'<_{\frac{\infty}{2}} w} \mathscr{Q}'\left( vt_{\beta}, w' \right)_{\mathbb C} \right) \cup \bigcup_{v'>_{\frac{\infty}{2}} v} \mathscr{Q}'\left( v't_{\beta}, w \right)_{\mathbb C} \right).\end{align*} $$In view of Corollary 4.31, every irreducible component of  $\mathscr {Q}' \left ( vt_{\beta }, w \right )_{\mathbb C}$ has dimension
$\mathscr {Q}' \left ( vt_{\beta }, w \right )_{\mathbb C}$ has dimension  $\ell ^{\frac {\infty }{2}} \left ( v t_{\beta } \right ) - \ell ^{\frac {\infty }{2}} ( w )$ if it is nonempty. We have
$\ell ^{\frac {\infty }{2}} \left ( v t_{\beta } \right ) - \ell ^{\frac {\infty }{2}} ( w )$ if it is nonempty. We have  $\mathscr {Q}' \left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $ if and only if
$\mathscr {Q}' \left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $ if and only if ![]() $vt_{\beta }\le _{\frac {\infty }{2}} w$, by Corollary 4.21. In particular, we find that
$vt_{\beta }\le _{\frac {\infty }{2}} w$, by Corollary 4.21. In particular, we find that  $\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $ if
$\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $ if ![]() $vt_{\beta } \le _{\frac {\infty }{2}} w$, and in that case all of its irreducible components have dimension
$vt_{\beta } \le _{\frac {\infty }{2}} w$, and in that case all of its irreducible components have dimension
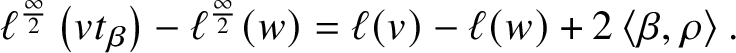 $$ \begin{align} \ell^{\frac{\infty}{2}} \left( v t_{\beta} \right) - \ell^{\frac{\infty}{2}} ( w ) = \ell ( v ) - \ell ( w ) + 2 \left\langle \beta, \rho \right\rangle. \end{align} $$
$$ \begin{align} \ell^{\frac{\infty}{2}} \left( v t_{\beta} \right) - \ell^{\frac{\infty}{2}} ( w ) = \ell ( v ) - \ell ( w ) + 2 \left\langle \beta, \rho \right\rangle. \end{align} $$A point of  $\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ can be seen as a quasi-map of degree
$\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ can be seen as a quasi-map of degree ![]() $\beta $ with no defects at
$\beta $ with no defects at ![]() $0$ and
$0$ and ![]() $\infty $ (Theorem 4.30). In particular,
$\infty $ (Theorem 4.30). In particular,  ${\mathscr{GB}}_{2,\beta }^\flat ( w, v ) \neq \emptyset $ if
${\mathscr{GB}}_{2,\beta }^\flat ( w, v ) \neq \emptyset $ if  $\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $. When
$\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $. When  $\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $, we have
$\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $, we have
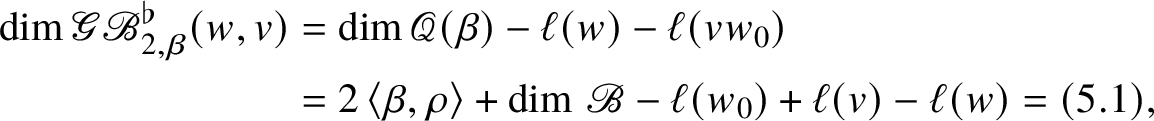 $$ \begin{align}\nonumber \dim {\mathscr{GB}}_{2,\beta}^\flat ( w, v ) & = \dim \mathscr{Q} ( \beta ) - \ell ( w ) - \ell ( vw_0 )\\ & = 2 \left\langle \beta, \rho \right\rangle + \dim \, \mathscr{B} - \ell ( w_0 ) + \ell ( v ) - \ell ( w ) = (5.1), \end{align} $$
$$ \begin{align}\nonumber \dim {\mathscr{GB}}_{2,\beta}^\flat ( w, v ) & = \dim \mathscr{Q} ( \beta ) - \ell ( w ) - \ell ( vw_0 )\\ & = 2 \left\langle \beta, \rho \right\rangle + \dim \, \mathscr{B} - \ell ( w_0 ) + \ell ( v ) - \ell ( w ) = (5.1), \end{align} $$where the first equality follows from Corollary 5.2 and the second follows from Theorem 2.7. By the surjectivity of ![]() $\pi _{2,\beta }$ and equation (5.2), we find that the rational map
$\pi _{2,\beta }$ and equation (5.2), we find that the rational map  ${\mathscr{GB}}_{2,\beta }^\flat ( w, v ) \dashrightarrow \mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ is surjective and generically finite (it is in fact birational, by Theorem 5.7 and Proposition 5.11). In view of Theorem 5.1, the variety
${\mathscr{GB}}_{2,\beta }^\flat ( w, v ) \dashrightarrow \mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ is surjective and generically finite (it is in fact birational, by Theorem 5.7 and Proposition 5.11). In view of Theorem 5.1, the variety  ${\mathscr{GB}}_{2,\beta }^\flat ( w, v )$ is irreducible if it is nonempty. Therefore,
${\mathscr{GB}}_{2,\beta }^\flat ( w, v )$ is irreducible if it is nonempty. Therefore,  $\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $ implies that
$\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C} \neq \emptyset $ implies that  $\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ is irreducible. Again by Corollary 4.31, we conclude that
$\mathring {\mathscr {Q}}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ is irreducible. Again by Corollary 4.31, we conclude that  $\mathscr {Q}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ has a unique irreducible component, as required.
$\mathscr {Q}'\left ( vt_{\beta }, w \right )_{\mathbb C}$ has a unique irreducible component, as required.
In view of Proposition 5.3, we set  $\mathscr {Q}_{\mathtt J} ( \beta , v, w ) := \mathscr {Q}^{\prime }_{\mathtt J} \left ( v t_{\beta }, w \right )_{\mathbb C}$ for each
$\mathscr {Q}_{\mathtt J} ( \beta , v, w ) := \mathscr {Q}^{\prime }_{\mathtt J} \left ( v t_{\beta }, w \right )_{\mathbb C}$ for each ![]() $\mathtt J \subset \mathtt I$,
$\mathtt J \subset \mathtt I$, ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $v,w \in W$ in what follows (see also Corollary 5.21). We have
$v,w \in W$ in what follows (see also Corollary 5.21). We have ![]() $\mathscr {Q} ( \beta , w_0, w ) = \mathscr {Q} ( \beta , w )$ by Theorem 4.30.
$\mathscr {Q} ( \beta , w_0, w ) = \mathscr {Q} ( \beta , w )$ by Theorem 4.30.
Corollary 5.4 Corollary of the proof of Proposition 5.3
For each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $v,w \in W$, the scheme
$v,w \in W$, the scheme ![]() $\mathscr {Q} ( \beta , v, w )$ is nonempty if and only if
$\mathscr {Q} ( \beta , v, w )$ is nonempty if and only if ![]() $v t_{\beta } \le _{\frac {\infty }{2}} w$. If it is nonempty, then it has dimension
$v t_{\beta } \le _{\frac {\infty }{2}} w$. If it is nonempty, then it has dimension ![]() $\ell ( v ) - \ell ( w ) + 2 \left \langle \beta , \rho \right \rangle $. Moreover, the space
$\ell ( v ) - \ell ( w ) + 2 \left \langle \beta , \rho \right \rangle $. Moreover, the space ![]() $\mathscr {Q} ( \beta , v, w )$ (viewed as a subspace of
$\mathscr {Q} ( \beta , v, w )$ (viewed as a subspace of ![]() $\mathscr {Q} ( \beta ))$ contains a quasi-map with no defects at
$\mathscr {Q} ( \beta ))$ contains a quasi-map with no defects at ![]() $0$ and
$0$ and ![]() $\infty $.
$\infty $. ![]() $\Box $
$\Box $
Remark 5.5. Corollary 5.4 removes the condition ![]() $\gamma \gg 0$ from [Reference Finkelberg and Mirković29, Lemma 8.5.2].
$\gamma \gg 0$ from [Reference Finkelberg and Mirković29, Lemma 8.5.2].
Thanks to Proposition 5.3 and its proof, we deduce that the map ![]() $\pi _{2,\beta }$ restricts to an
$\pi _{2,\beta }$ restricts to an ![]() $( H \times \mathbb {G}_m)$-equivariant birational proper map
$( H \times \mathbb {G}_m)$-equivariant birational proper map
 $$ \begin{align*}\pi_{\beta, w,v} : {\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) \to \mathscr{Q} ( \beta, v, w ),\end{align*} $$
$$ \begin{align*}\pi_{\beta, w,v} : {\mathscr{GB}}_{2,\beta}^{\flat} ( w, v ) \to \mathscr{Q} ( \beta, v, w ),\end{align*} $$by inspection.
5.3 From Givental’s main lemma
For each ![]() $w, v \in W$, we define subvarieties of
$w, v \in W$, we define subvarieties of ![]() $\mathscr {B}_{2,\beta }$ as
$\mathscr {B}_{2,\beta }$ as
 $$ \begin{align*}\mathscr{B}_{2, \beta} [ w ] := \mathtt{e}_1^{-1} ( p_w ), \qquad \mathscr{B}_{2, \beta} [ w, v ] := \mathtt{e}_1^{-1} ( p_w ) \cap \mathtt{e}_2^{-1} ( p_v ).\end{align*} $$
$$ \begin{align*}\mathscr{B}_{2, \beta} [ w ] := \mathtt{e}_1^{-1} ( p_w ), \qquad \mathscr{B}_{2, \beta} [ w, v ] := \mathtt{e}_1^{-1} ( p_w ) \cap \mathtt{e}_2^{-1} ( p_v ).\end{align*} $$Similarly, we set
 $$ \begin{align*}{\mathscr{GB}}^{\flat}_{2, \beta} [ w, v ] := \mathtt{ev}_1^{-1} ( p_w ) \cap \mathtt{ev}_2^{-1} ( p_v ) \subset {\mathscr{GB}}_{2,\beta}^{\flat}, \qquad \mathscr{B}_{1, \beta} [ w ] := \mathtt{e}_1^{-1} ( p_w ) \subset \mathscr{B}_{1, \beta} [ w ].\end{align*} $$
$$ \begin{align*}{\mathscr{GB}}^{\flat}_{2, \beta} [ w, v ] := \mathtt{ev}_1^{-1} ( p_w ) \cap \mathtt{ev}_2^{-1} ( p_v ) \subset {\mathscr{GB}}_{2,\beta}^{\flat}, \qquad \mathscr{B}_{1, \beta} [ w ] := \mathtt{e}_1^{-1} ( p_w ) \subset \mathscr{B}_{1, \beta} [ w ].\end{align*} $$Lemma 5.6. For each ![]() $x,y \in \mathscr {B}$ and
$x,y \in \mathscr {B}$ and ![]() $\beta \in Q^{\vee }_+$, there exists
$\beta \in Q^{\vee }_+$, there exists ![]() $w \in W$ such that
$w \in W$ such that
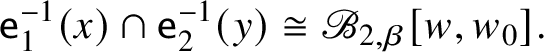 $$ \begin{align*}\mathtt{e}_1^{-1} ( x ) \cap \mathtt{e}_2^{-1} ( y ) \cong \mathscr{B}_{2, \beta} [ w, w_0 ].\end{align*} $$
$$ \begin{align*}\mathtt{e}_1^{-1} ( x ) \cap \mathtt{e}_2^{-1} ( y ) \cong \mathscr{B}_{2, \beta} [ w, w_0 ].\end{align*} $$The same is true for ![]() $\mathtt {ev}$ and
$\mathtt {ev}$ and ![]() ${\mathscr{GB}}$.
${\mathscr{GB}}$.
Proof. We consider only the case of ![]() $\mathtt {e}$ and
$\mathtt {e}$ and ![]() $\mathscr {B}$, as the other case is completely parallel. Since
$\mathscr {B}$, as the other case is completely parallel. Since ![]() $(x,y) \in \mathscr {B} \times \mathscr {B}$ and the G-action on
$(x,y) \in \mathscr {B} \times \mathscr {B}$ and the G-action on ![]() $\mathscr {B}$ is transitive, we can assume
$\mathscr {B}$ is transitive, we can assume ![]() $y = p_{w_0}$. Since we have
$y = p_{w_0}$. Since we have ![]() $\mathsf {Stab}_G y = B$, we can further rearrange
$\mathsf {Stab}_G y = B$, we can further rearrange ![]() $x = p_w$ for some
$x = p_w$ for some ![]() $w \in W$ by equation (2.4).
$w \in W$ by equation (2.4).
Theorem 5.7 Givental’s main lemma [Reference Givental34]; see [Reference Feigin, Finkelberg, Kuznetsov and Mirković23]
Set ![]() $\beta \in Q^{\vee }_+$. Let
$\beta \in Q^{\vee }_+$. Let ![]() $(f, D) \in \mathscr {Q} ( \beta )$ be a quasi-map with defect
$(f, D) \in \mathscr {Q} ( \beta )$ be a quasi-map with defect ![]() $D = \sum _{x \in \mathbb {P}^1 ( {\mathbb C} )} \beta _x \otimes [x]$. Then we have
$D = \sum _{x \in \mathbb {P}^1 ( {\mathbb C} )} \beta _x \otimes [x]$. Then we have
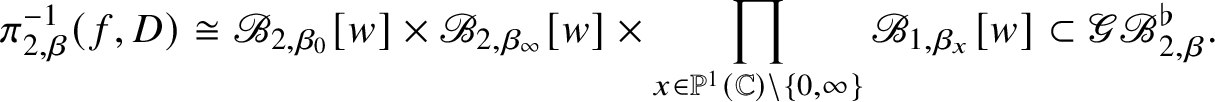 $$ \begin{align*}\pi_{2,\beta}^{-1} (f, D) \cong \mathscr{B} _{2,\beta_0} [ w ] \times \mathscr{B} _{2,\beta_\infty} [ w ] \times \prod_{x \in \mathbb{P}^1 ( {\mathbb C} ) \setminus \{0,\infty\}} \mathscr{B} _{1,\beta_x} [ w ] \subset {\mathscr{GB}}_{2,\beta}^{\flat}.\end{align*} $$
$$ \begin{align*}\pi_{2,\beta}^{-1} (f, D) \cong \mathscr{B} _{2,\beta_0} [ w ] \times \mathscr{B} _{2,\beta_\infty} [ w ] \times \prod_{x \in \mathbb{P}^1 ( {\mathbb C} ) \setminus \{0,\infty\}} \mathscr{B} _{1,\beta_x} [ w ] \subset {\mathscr{GB}}_{2,\beta}^{\flat}.\end{align*} $$In particular, the map ![]() $\pi _{2,\beta }$ is an isomorphism along the locus with
$\pi _{2,\beta }$ is an isomorphism along the locus with ![]() $D = 0$.
$D = 0$. ![]() $\Box $
$\Box $
Remark 5.8. In Theorem 5.7, the first marked points of (the stable maps in)  ${\mathscr{GB}}_{2,\beta }^{\flat }$ (the marked points at
${\mathscr{GB}}_{2,\beta }^{\flat }$ (the marked points at ![]() $0 \in \mathbb {P}^1$; i.e., the image of
$0 \in \mathbb {P}^1$; i.e., the image of ![]() $\mathsf {ev}_1$) are identified with the second marked points of (the stable maps in)
$\mathsf {ev}_1$) are identified with the second marked points of (the stable maps in) ![]() $\mathscr {B} _{2,\beta _0} [ w ]$ (i.e., the image of
$\mathscr {B} _{2,\beta _0} [ w ]$ (i.e., the image of ![]() $\mathsf {e}_2$), and the second marked points of
$\mathsf {e}_2$), and the second marked points of  ${\mathscr{GB}}_{2,\beta }^{\flat }$ (the marked points at
${\mathscr{GB}}_{2,\beta }^{\flat }$ (the marked points at ![]() $\infty \in \mathbb {P}^1$) are identified with the second marked points of
$\infty \in \mathbb {P}^1$) are identified with the second marked points of ![]() $\mathscr {B} _{2,\beta _\infty } [ w ]$. (Other marked points are used to glue pieces of stable maps together.)
$\mathscr {B} _{2,\beta _\infty } [ w ]$. (Other marked points are used to glue pieces of stable maps together.)
Lemma 5.9 [Reference Finkelberg and Mirković29]
For each ![]() $\beta \in Q^{\vee }_+$ such that
$\beta \in Q^{\vee }_+$ such that ![]() $\left \langle \beta , \alpha _i \right \rangle \ge 1$ for all
$\left \langle \beta , \alpha _i \right \rangle \ge 1$ for all ![]() $i \in \mathtt I$, the evaluation map
$i \in \mathtt I$, the evaluation map
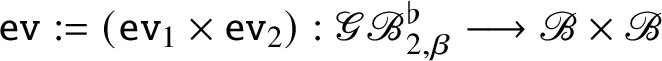 $$ \begin{align*}\mathtt{ev} := ( \mathtt{ev}_1 \times \mathtt{ev}_2 ) : {\mathscr{GB}}^{\flat}_{2, \beta} \longrightarrow \mathscr{B} \times \mathscr{B}\end{align*} $$
$$ \begin{align*}\mathtt{ev} := ( \mathtt{ev}_1 \times \mathtt{ev}_2 ) : {\mathscr{GB}}^{\flat}_{2, \beta} \longrightarrow \mathscr{B} \times \mathscr{B}\end{align*} $$is surjective.
Proof. Taking into account the fact that  ${\mathscr{GB}}^{\flat }_{2, \beta }$ is projective, it suffices to prove that the tangent map associated to
${\mathscr{GB}}^{\flat }_{2, \beta }$ is projective, it suffices to prove that the tangent map associated to ![]() $\mathtt {ev}$ is surjective on a dense open subset of
$\mathtt {ev}$ is surjective on a dense open subset of  ${\mathscr{GB}}^{\flat }_{2, \beta }$.
${\mathscr{GB}}^{\flat }_{2, \beta }$.
Since the map ![]() $\pi _{2,\beta }$ is birational by Theorem 5.7, we replace the problem with the case of a genuine map
$\pi _{2,\beta }$ is birational by Theorem 5.7, we replace the problem with the case of a genuine map ![]() $f : \mathbb {P}^1 \rightarrow \mathscr {B}$. Thanks to [Reference Finkelberg and Mirković29, Proposition 3.5],
$f : \mathbb {P}^1 \rightarrow \mathscr {B}$. Thanks to [Reference Finkelberg and Mirković29, Proposition 3.5], ![]() $\mathscr {Q} ( \beta )$ and hence
$\mathscr {Q} ( \beta )$ and hence  ${\mathscr{GB}}^{\flat }_{2, \beta }$ are smooth at f. Moreover, its tangent space is described as
${\mathscr{GB}}^{\flat }_{2, \beta }$ are smooth at f. Moreover, its tangent space is described as
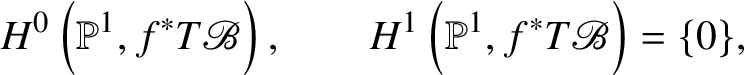 $$ \begin{align*}H^0 \left( \mathbb{P}^1, f^* T \mathscr{B} \right), \qquad H^1 \left( \mathbb{P}^1, f^* T \mathscr{B} \right) = \{ 0 \},\end{align*} $$
$$ \begin{align*}H^0 \left( \mathbb{P}^1, f^* T \mathscr{B} \right), \qquad H^1 \left( \mathbb{P}^1, f^* T \mathscr{B} \right) = \{ 0 \},\end{align*} $$and the filtration of ![]() $T \mathscr {B}$ as G-equivariant line bundles yields the associated graded
$T \mathscr {B}$ as G-equivariant line bundles yields the associated graded
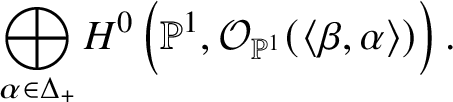 $$ \begin{align*}\bigoplus_{\alpha \in \Delta_+} H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle ) \right).\end{align*} $$
$$ \begin{align*}\bigoplus_{\alpha \in \Delta_+} H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle ) \right).\end{align*} $$(Here we used ![]() $\left \langle \beta , \alpha _i \right \rangle \ge -1$ for each
$\left \langle \beta , \alpha _i \right \rangle \ge -1$ for each ![]() $i \in \mathtt I$.) In particular, we have
$i \in \mathtt I$.) In particular, we have
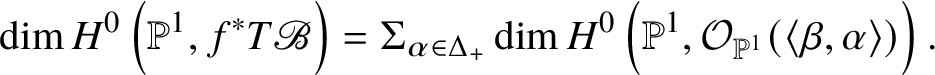 $$ \begin{align*}\dim H^0 \left( \mathbb{P}^1, f^* T \mathscr{B} \right) = \Sigma_{\alpha \in \Delta_+} \dim H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle ) \right).\end{align*} $$
$$ \begin{align*}\dim H^0 \left( \mathbb{P}^1, f^* T \mathscr{B} \right) = \Sigma_{\alpha \in \Delta_+} \dim H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle ) \right).\end{align*} $$The effect of fixing the image of two points ![]() $0, \infty \in \mathbb {P}^1$ corresponds to imposing a divisor twist by
$0, \infty \in \mathbb {P}^1$ corresponds to imposing a divisor twist by ![]() ${\mathcal O}_{\mathbb {P}^1} ( - [0] - [\infty ] )$. We have
${\mathcal O}_{\mathbb {P}^1} ( - [0] - [\infty ] )$. We have
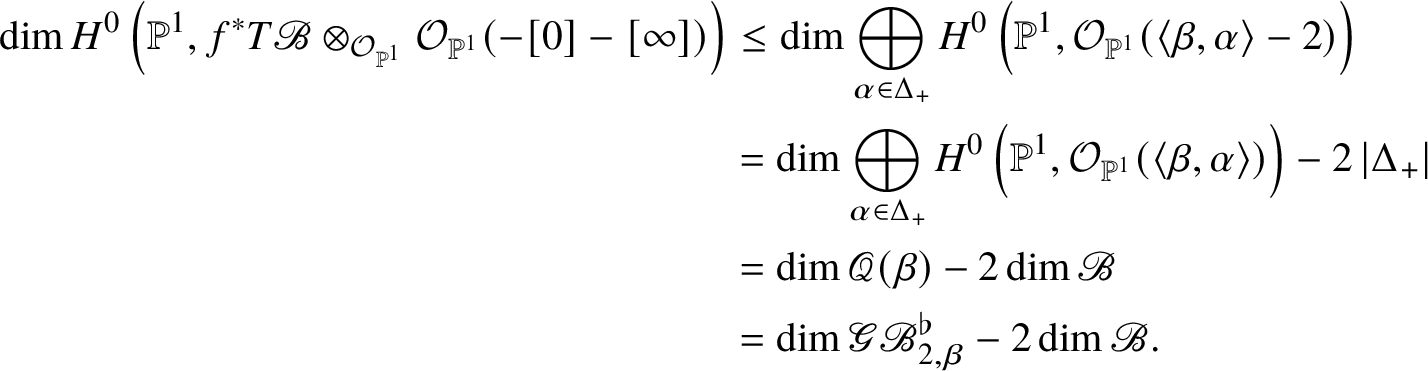 $$ \begin{align*} \dim H^0 \left( \mathbb{P}^1, f^* T \mathscr{B} \otimes_{{\mathcal O}_{\mathbb{P}^1}} {\mathcal O}_{\mathbb{P}^1} ( - [0] - [\infty] ) \right) & \le \dim \bigoplus_{\alpha \in \Delta_+} H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle - 2 )\right)\\ & = \dim \bigoplus_{\alpha \in \Delta_+} H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle )\right) - 2 \left\lvert\Delta_+\right\rvert\\ & = \dim \mathscr{Q} ( \beta ) - 2 \dim \mathscr{B} \\ & = \dim {\mathscr{GB}}^{\flat}_{2, \beta} - 2 \dim \mathscr{B}. \end{align*} $$
$$ \begin{align*} \dim H^0 \left( \mathbb{P}^1, f^* T \mathscr{B} \otimes_{{\mathcal O}_{\mathbb{P}^1}} {\mathcal O}_{\mathbb{P}^1} ( - [0] - [\infty] ) \right) & \le \dim \bigoplus_{\alpha \in \Delta_+} H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle - 2 )\right)\\ & = \dim \bigoplus_{\alpha \in \Delta_+} H^0 \left( \mathbb{P}^1, {\mathcal O}_{\mathbb{P}^1} ( \left\langle \beta, \alpha \right\rangle )\right) - 2 \left\lvert\Delta_+\right\rvert\\ & = \dim \mathscr{Q} ( \beta ) - 2 \dim \mathscr{B} \\ & = \dim {\mathscr{GB}}^{\flat}_{2, \beta} - 2 \dim \mathscr{B}. \end{align*} $$Here the first inequality comes from the short exact sequences, the equality that follows is ![]() $\left \langle \beta , \alpha _i \right \rangle \ge 1$ for each
$\left \langle \beta , \alpha _i \right \rangle \ge 1$ for each ![]() $i \in \mathtt I$, the next equality is the smoothness of
$i \in \mathtt I$, the next equality is the smoothness of ![]() $\mathscr {Q} ( \beta )$ at f and
$\mathscr {Q} ( \beta )$ at f and ![]() $\left \lvert \Delta _+\right \rvert = \dim \mathscr {B}$ and the final equality is the birationality of
$\left \lvert \Delta _+\right \rvert = \dim \mathscr {B}$ and the final equality is the birationality of ![]() $\pi _{2,\beta }$ (restricted to
$\pi _{2,\beta }$ (restricted to  ${\mathscr{GB}}^\flat _{2,\beta } \subset {\mathscr{GB}}_{2,\beta }$).
${\mathscr{GB}}^\flat _{2,\beta } \subset {\mathscr{GB}}_{2,\beta }$).
From this, we deduce that ![]() $d \pi _{2,\beta }$ is generically surjective, as required.
$d \pi _{2,\beta }$ is generically surjective, as required.
Proposition 5.10. For each ![]() $\beta \in Q^{\vee }_{+}$ such that
$\beta \in Q^{\vee }_{+}$ such that ![]() $\left \langle \beta , \alpha _i \right \rangle \ge 1$ for all
$\left \langle \beta , \alpha _i \right \rangle \ge 1$ for all ![]() $i \in \mathtt I$ and
$i \in \mathtt I$ and ![]() $w, v \in W$, the scheme
$w, v \in W$, the scheme  ${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ]$ is connected and nonempty.
${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ]$ is connected and nonempty.
Proof. The map ![]() $\mathtt {ev}$ borrowed from Lemma 5.9 is G-equivariant, and
$\mathtt {ev}$ borrowed from Lemma 5.9 is G-equivariant, and ![]() $( \mathscr {B} \times \mathscr {B} )$ admits an open dense G-orbit
$( \mathscr {B} \times \mathscr {B} )$ admits an open dense G-orbit ![]() $\mathbf O$ by the Bruhat decomposition. Since
$\mathbf O$ by the Bruhat decomposition. Since  ${\mathscr{GB}}^{\flat }_{2, \beta }$ is an irreducible variety, so is its Zariski open set
${\mathscr{GB}}^{\flat }_{2, \beta }$ is an irreducible variety, so is its Zariski open set ![]() $\mathtt {ev}^{-1} ( \mathbf O )$. If we consider
$\mathtt {ev}^{-1} ( \mathbf O )$. If we consider ![]() $x \in \mathbf O$, then the irreducible components of
$x \in \mathbf O$, then the irreducible components of ![]() $\mathtt {ev}^{-1} ( x )$ (which must be finite, as we consider varieties that are finite types) must be permuted by
$\mathtt {ev}^{-1} ( x )$ (which must be finite, as we consider varieties that are finite types) must be permuted by ![]() $\mathsf {Stab} _G x \cong H$. Since H is connected, we cannot have a nontrivial action. Therefore, the irreducible component of
$\mathsf {Stab} _G x \cong H$. Since H is connected, we cannot have a nontrivial action. Therefore, the irreducible component of ![]() $\mathtt {ev}^{-1} ( x )$ must be unique. Thanks to the Stein factorisation theorem [77, Theorem 03H0], the map
$\mathtt {ev}^{-1} ( x )$ must be unique. Thanks to the Stein factorisation theorem [77, Theorem 03H0], the map ![]() $\mathtt {ev}$ factors through the normalisation Y of
$\mathtt {ev}$ factors through the normalisation Y of ![]() $( \mathscr {B} \times \mathscr {B} )$ inside (the function field of)
$( \mathscr {B} \times \mathscr {B} )$ inside (the function field of)  ${\mathscr{GB}}^{\flat }_{2, \beta }$, and the map
${\mathscr{GB}}^{\flat }_{2, \beta }$, and the map  ${\mathscr{GB}}^{\flat }_{2, \beta } \to Y$ has connected fibre. Since the general fibre of
${\mathscr{GB}}^{\flat }_{2, \beta } \to Y$ has connected fibre. Since the general fibre of ![]() $\mathtt {ev}$ is connected, so is the map
$\mathtt {ev}$ is connected, so is the map ![]() $Y \rightarrow ( \mathscr {B} \times \mathscr {B} )$. It follows that
$Y \rightarrow ( \mathscr {B} \times \mathscr {B} )$. It follows that ![]() $Y \rightarrow ( \mathscr {B} \times \mathscr {B} )$ is a birational map (which is also finite, by the Stein factorisation theorem). This implies that Y and
$Y \rightarrow ( \mathscr {B} \times \mathscr {B} )$ is a birational map (which is also finite, by the Stein factorisation theorem). This implies that Y and ![]() $(\mathscr {B} \times \mathscr {B} )$ share the same function field. Thus, we conclude that
$(\mathscr {B} \times \mathscr {B} )$ share the same function field. Thus, we conclude that ![]() $Y \cong ( \mathscr {B} \times \mathscr {B} )$ by the normality of
$Y \cong ( \mathscr {B} \times \mathscr {B} )$ by the normality of ![]() $( \mathscr {B} \times \mathscr {B} )$. This particularly means that every fibre of
$( \mathscr {B} \times \mathscr {B} )$. This particularly means that every fibre of ![]() $\mathtt {ev}$ is connected. Therefore, the assertion follows by choosing
$\mathtt {ev}$ is connected. Therefore, the assertion follows by choosing ![]() $(H \times H)$-fixed points in
$(H \times H)$-fixed points in ![]() $( \mathscr {B} \times \mathscr {B} )$ as particular cases.
$( \mathscr {B} \times \mathscr {B} )$ as particular cases.
Proposition 5.11. For each ![]() $\beta \in Q^{\vee }_+$ such that
$\beta \in Q^{\vee }_+$ such that ![]() $\left \langle \beta , \alpha _i \right \rangle \ge 1$ for all
$\left \langle \beta , \alpha _i \right \rangle \ge 1$ for all ![]() $i \in \mathtt I$ and
$i \in \mathtt I$ and ![]() $w, v \in W$, the scheme
$w, v \in W$, the scheme ![]() $\mathscr {B} _{2,\beta } [ w, v ]$ is connected and nonempty. For each
$\mathscr {B} _{2,\beta } [ w, v ]$ is connected and nonempty. For each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w \in W$, the schemes
$w \in W$, the schemes ![]() $\mathscr {B} _{1,\beta } [ w ]$ and
$\mathscr {B} _{1,\beta } [ w ]$ and ![]() $\mathscr {B} _{2,\beta } [ w ]$ are connected and nonempty.
$\mathscr {B} _{2,\beta } [ w ]$ are connected and nonempty.
Proof. We prove the first assertion. We have a rational map  ${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ] \rightarrow \mathscr {B} _{2,\beta } [ w, v ]$ obtained by forgetting the map to
${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ] \rightarrow \mathscr {B} _{2,\beta } [ w, v ]$ obtained by forgetting the map to ![]() $\mathbb {P}^1$. Moreover, the locus of this map is not defined consists of stable maps whose main components have degree
$\mathbb {P}^1$. Moreover, the locus of this map is not defined consists of stable maps whose main components have degree ![]() $0$ and have only two marked points. By modifying the universal family by adjoining two such marked points in such a degree
$0$ and have only two marked points. By modifying the universal family by adjoining two such marked points in such a degree ![]() $0$ component, we conclude that
$0$ component, we conclude that  ${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ] \rightarrow \mathscr {B} _{2,\beta } [ w, v ]$ extends to a map of topological spaces. By examining the condition to be a stable map [Reference Fulton and Pandharipande30, §1.1], we deduce that this map is surjective onto the image. Therefore, the connectedness and nonemptiness of
${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ] \rightarrow \mathscr {B} _{2,\beta } [ w, v ]$ extends to a map of topological spaces. By examining the condition to be a stable map [Reference Fulton and Pandharipande30, §1.1], we deduce that this map is surjective onto the image. Therefore, the connectedness and nonemptiness of  ${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ]$ imply that
${\mathscr{GB}}^{\flat }_{2, \beta } [ w, v ]$ imply that ![]() $\mathscr {B} _{2,\beta } [ w, v ]$ is likewise connected and nonempty – which is the first assertion.
$\mathscr {B} _{2,\beta } [ w, v ]$ is likewise connected and nonempty – which is the first assertion.
The second assertion is straightforward from the irreducibility of ![]() $\mathscr {B} _{n,\beta }$, together with the fact that
$\mathscr {B} _{n,\beta }$, together with the fact that ![]() $\mathtt {e}_1$ is a G-equivariant fibre bundle over
$\mathtt {e}_1$ is a G-equivariant fibre bundle over ![]() $\mathscr {B}$ (see the proof of Proposition 5.10).
$\mathscr {B}$ (see the proof of Proposition 5.10).
Lemma 5.12. Set ![]() $\beta \in Q^{\vee }_+$. Let
$\beta \in Q^{\vee }_+$. Let ![]() $(f, D) \in \mathscr {Q} ( \beta )$ be a quasi-map with defect D with the following properties:
$(f, D) \in \mathscr {Q} ( \beta )$ be a quasi-map with defect D with the following properties:
•
 $D = \sum _{x \in \mathbb {P}^1 ( {\mathbb C} )} \beta _x \otimes [x]$.
$D = \sum _{x \in \mathbb {P}^1 ( {\mathbb C} )} \beta _x \otimes [x]$.•
 $\left \langle \beta _0, \alpha _i \right \rangle \ge 1$ and
$\left \langle \beta _0, \alpha _i \right \rangle \ge 1$ and  $\left \langle \beta _\infty , \alpha _i \right \rangle \ge 1$ for each
$\left \langle \beta _\infty , \alpha _i \right \rangle \ge 1$ for each  $i \in \mathtt I$.
$i \in \mathtt I$.
Then  $\pi _{\beta , w,v}^{-1} (f, D)$ is connected for every
$\pi _{\beta , w,v}^{-1} (f, D)$ is connected for every ![]() $w,v \in W$ if it is nonempty.
$w,v \in W$ if it is nonempty.
Proof. By Proposition 5.11 and Theorem 5.7, we can forget about the contribution of ![]() $\mathscr {B} _{1,\beta _x} [ w ]$ when
$\mathscr {B} _{1,\beta _x} [ w ]$ when ![]() $x \neq 0,\infty $. By our assumption and Proposition 5.11, we know that
$x \neq 0,\infty $. By our assumption and Proposition 5.11, we know that
which are nonempty and connected for each ![]() $u,w',v' \in W$. Since
$u,w',v' \in W$. Since ![]() $\mathscr {B} _{2,\beta _0}$ and
$\mathscr {B} _{2,\beta _0}$ and ![]() $\mathscr {B} _{2,\beta _\infty }$ are proper, we always find a limit point with respect to the H-action. It follows that
$\mathscr {B} _{2,\beta _\infty }$ are proper, we always find a limit point with respect to the H-action. It follows that  $\mathscr {B} _{2,\beta _0} [ u ] \cap \mathtt {e}_2^{-1} ( \mathscr {B} ( u' ) )$ (resp.,
$\mathscr {B} _{2,\beta _0} [ u ] \cap \mathtt {e}_2^{-1} ( \mathscr {B} ( u' ) )$ (resp.,  $\mathscr {B} _{2,\beta _\infty } [ u ] \cap \mathtt {e}_2^{-1} ( \mathscr {B}^{\mathrm {op}} ( u' ) )$) is connected for each
$\mathscr {B} _{2,\beta _\infty } [ u ] \cap \mathtt {e}_2^{-1} ( \mathscr {B}^{\mathrm {op}} ( u' ) )$) is connected for each ![]() $u,u' \in W$, as we can connect every two points by appropriately sending to or from H-limit points that are contained in a connected component of the form
$u,u' \in W$, as we can connect every two points by appropriately sending to or from H-limit points that are contained in a connected component of the form ![]() $\mathscr {B} _{2,\beta _0} [u,w']$ (
$\mathscr {B} _{2,\beta _0} [u,w']$ (![]() $w' \in W$). Thanks to Theorem 5.7, we conclude the assertion.
$w' \in W$). Thanks to Theorem 5.7, we conclude the assertion.
5.4 Normality of  $\mathscr {Q} ( \beta , v, w )$
$\mathscr {Q} ( \beta , v, w )$
Let ![]() $\mathscr {Q}^+ ( \beta , v, w )$ be the normalisation of
$\mathscr {Q}^+ ( \beta , v, w )$ be the normalisation of ![]() $\mathscr {Q} ( \beta , v, w )$ for each
$\mathscr {Q} ( \beta , v, w )$ for each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $v, w \in W$. We denote the normalisation map by
$v, w \in W$. We denote the normalisation map by ![]() $\eta _{\beta , v, w} : \mathscr {Q}^+ ( \beta , v, w ) \to \mathscr {Q} ( \beta , v, w )$.
$\eta _{\beta , v, w} : \mathscr {Q}^+ ( \beta , v, w ) \to \mathscr {Q} ( \beta , v, w )$.
Proposition 5.13. For each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w, v \in W$, the variety
$w, v \in W$, the variety ![]() $\mathscr {Q} ( \beta , v, w )$ is normal if and only if every fibre of
$\mathscr {Q} ( \beta , v, w )$ is normal if and only if every fibre of ![]() $\pi _{\beta ,v,w}$ is connected.
$\pi _{\beta ,v,w}$ is connected.
Proof. As  ${\mathscr{GB}}_{2,\beta }^{\flat } ( v, w )$ is normal and
${\mathscr{GB}}_{2,\beta }^{\flat } ( v, w )$ is normal and ![]() $\pi _{\beta ,v,w}$ is proper, we know that
$\pi _{\beta ,v,w}$ is proper, we know that
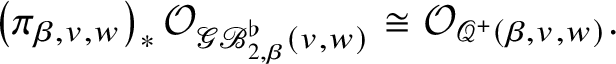 $$ \begin{align*}\left( \pi_{\beta, v, w} \right) _* {\mathcal O}_{{\mathscr{GB}}_{2,\beta}^{\flat} \left( v, w \right)} \cong {\mathcal O}_{\mathscr{Q}^+ \left( \beta, v, w \right)}.\end{align*} $$
$$ \begin{align*}\left( \pi_{\beta, v, w} \right) _* {\mathcal O}_{{\mathscr{GB}}_{2,\beta}^{\flat} \left( v, w \right)} \cong {\mathcal O}_{\mathscr{Q}^+ \left( \beta, v, w \right)}.\end{align*} $$The properness of ![]() $\pi _{\beta ,v,w}$ also implies that
$\pi _{\beta ,v,w}$ also implies that ![]() ${\mathcal O}_{\mathscr {Q}^+ \left ( \beta , v, w \right )}$ is a coherent sheaf on
${\mathcal O}_{\mathscr {Q}^+ \left ( \beta , v, w \right )}$ is a coherent sheaf on ![]() $\mathscr {Q} ( \beta , v, w )$. For each closed point x of
$\mathscr {Q} ( \beta , v, w )$. For each closed point x of ![]() $\mathscr {Q} ( \beta , v, w )$, we set
$\mathscr {Q} ( \beta , v, w )$, we set
By the Stein factorisation theorem, the map ![]() $\eta _{\beta , v, w}$ is finite. By Corollary 4.42 and Section 5.2, we know that the variety
$\eta _{\beta , v, w}$ is finite. By Corollary 4.42 and Section 5.2, we know that the variety ![]() $\mathscr {Q} ( \beta , v, w )$ is weakly normal. From this, we deduce that
$\mathscr {Q} ( \beta , v, w )$ is weakly normal. From this, we deduce that  $\Theta (x) = \# \eta _{\beta ,v,w}^{-1} ( x )$ (compare [Reference Yanagihara80, Remark 1]). Moreover, it counts the number of irreducible components of the fibre of
$\Theta (x) = \# \eta _{\beta ,v,w}^{-1} ( x )$ (compare [Reference Yanagihara80, Remark 1]). Moreover, it counts the number of irreducible components of the fibre of ![]() $\eta _{\beta ,v,w}$.
$\eta _{\beta ,v,w}$.
The coherence of ![]() ${\mathcal O}_{\mathscr {Q}^+ ( \beta , v, w )}$ implies that the right-hand side of formula (5.3) is an upper-semicontinuous function on
${\mathcal O}_{\mathscr {Q}^+ ( \beta , v, w )}$ implies that the right-hand side of formula (5.3) is an upper-semicontinuous function on ![]() $\mathscr {Q} ( \beta , v, w )$, and hence so is
$\mathscr {Q} ( \beta , v, w )$, and hence so is ![]() $\Theta $.
$\Theta $.
If we have ![]() $\Theta \equiv 1$ on
$\Theta \equiv 1$ on ![]() $\mathscr {Q} ( \beta , v, w )$, then we have
$\mathscr {Q} ( \beta , v, w )$, then we have ![]() $\mathscr {Q}^+ ( \beta , v, w ) = \mathscr {Q} ( \beta , v, w )$ by the weak normality of the latter (compare [Reference Yanagihara80, Remark 1]). Therefore, the ‘if’ part of the assertion follows.
$\mathscr {Q}^+ ( \beta , v, w ) = \mathscr {Q} ( \beta , v, w )$ by the weak normality of the latter (compare [Reference Yanagihara80, Remark 1]). Therefore, the ‘if’ part of the assertion follows.
If we have ![]() $\Theta \not \equiv 1$ on
$\Theta \not \equiv 1$ on ![]() $\mathscr {Q} ( \beta , v, w )$, then we have
$\mathscr {Q} ( \beta , v, w )$, then we have ![]() $\mathscr {Q}^+ ( \beta , v, w ) \neq \mathscr {Q} ( \beta , v, w )$. Hence, the ‘only if’ part of the assertion follows.
$\mathscr {Q}^+ ( \beta , v, w ) \neq \mathscr {Q} ( \beta , v, w )$. Hence, the ‘only if’ part of the assertion follows.
These complete the proof of the proposition.
Corollary 5.14. Braverman and Finkelberg
For each ![]() $\beta \in Q^{\vee }_+$, the variety
$\beta \in Q^{\vee }_+$, the variety ![]() $\mathscr {Q} ( \beta )$ is normal.
$\mathscr {Q} ( \beta )$ is normal.
Remark 5.15. Our proof of Corollary 5.14 is independent of [Reference Braverman and Finkelberg9] (although based on common earlier papers [Reference Finkelberg and Mirković29, Reference Feigin, Finkelberg, Kuznetsov and Mirković23]). Hence, we obtain a new proof of the normality of ![]() $\mathscr {Q} ( \beta )$ and
$\mathscr {Q} ( \beta )$ and ![]() $\mathscr {Z} ( \beta , w_0 )$. Together with Theorem 4.33, Corollary 5.14 also makes the contents of [Reference Kato, Naito and Sagaki51] logically independent of [Reference Braverman and Finkelberg9] (compare Appendix A).
$\mathscr {Z} ( \beta , w_0 )$. Together with Theorem 4.33, Corollary 5.14 also makes the contents of [Reference Kato, Naito and Sagaki51] logically independent of [Reference Braverman and Finkelberg9] (compare Appendix A).
Proof. Proof of Corollary 5.14.
Recall that ![]() $\mathscr {Q} ( \beta ) = \mathscr {Q} ( \beta , w_0, e )$. We borrow the upper-semicontinuous function
$\mathscr {Q} ( \beta ) = \mathscr {Q} ( \beta , w_0, e )$. We borrow the upper-semicontinuous function ![]() $\Theta $ that counts the number of connected components of the fibre of
$\Theta $ that counts the number of connected components of the fibre of ![]() $\eta _{\beta , w_0, e}$ from formula (5.3) in the proof of Proposition 5.13.
$\eta _{\beta , w_0, e}$ from formula (5.3) in the proof of Proposition 5.13.
By Proposition 5.13, it suffices to prove that ![]() $\Theta \equiv 1$ on
$\Theta \equiv 1$ on ![]() $\mathscr {Q} ( \beta )$. In other words, it suffices to prove that the fibre
$\mathscr {Q} ( \beta )$. In other words, it suffices to prove that the fibre  $\eta _{\beta , w_0, e}^{-1} ( x )$ is connected for each
$\eta _{\beta , w_0, e}^{-1} ( x )$ is connected for each ![]() $x \in \mathscr {Q} ( \beta )$.
$x \in \mathscr {Q} ( \beta )$.
By Theorem 5.7, we deduce that the set of connected components of  $\eta _{\beta ,w_0,e}^{-1} ( x )$ is in bijection with the set of connected components of
$\eta _{\beta ,w_0,e}^{-1} ( x )$ is in bijection with the set of connected components of ![]() $\prod _{y \in \mathbb {P}^1 ( {\mathbb C} )} \mathscr {B}_{\beta _y} [w]$. By Proposition 5.11, this latter space is connected.
$\prod _{y \in \mathbb {P}^1 ( {\mathbb C} )} \mathscr {B}_{\beta _y} [w]$. By Proposition 5.11, this latter space is connected.
Therefore, we conclude the result.
Theorem 5.16. For each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w \in W$, the varieties
$w \in W$, the varieties ![]() $\mathscr {Q} ( \beta , w_0, w_0 )$ and
$\mathscr {Q} ( \beta , w_0, w_0 )$ and ![]() $\mathscr {Q} ( \beta , e, w_0 )$ are normal.
$\mathscr {Q} ( \beta , e, w_0 )$ are normal.
Proof. We set ![]() $(v,w) = (w_0,w_0)$ or
$(v,w) = (w_0,w_0)$ or ![]() $(e,w_0)$. We borrow the upper-semicontinuous function
$(e,w_0)$. We borrow the upper-semicontinuous function ![]() $\Theta $ that counts the number of connected components of the fibre of
$\Theta $ that counts the number of connected components of the fibre of ![]() $\eta _{\beta , v, w}$ from formula (5.3) in the proof of Proposition 5.13.
$\eta _{\beta , v, w}$ from formula (5.3) in the proof of Proposition 5.13.
By Proposition 5.13, it suffices to prove that ![]() $\Theta \equiv 1$ on
$\Theta \equiv 1$ on ![]() $\mathscr {Q} ( \beta , v, w )$ by assuming the contrary to deduce a contradiction. For each
$\mathscr {Q} ( \beta , v, w )$ by assuming the contrary to deduce a contradiction. For each ![]() $x \in \mathscr {Q} ( \beta , v, w )$ such that
$x \in \mathscr {Q} ( \beta , v, w )$ such that ![]() $\Theta ( x ) \ge 2$, the fibre
$\Theta ( x ) \ge 2$, the fibre  $\eta _{\beta , w_0, e}^{-1} ( x )$ is disconnected.
$\eta _{\beta , w_0, e}^{-1} ( x )$ is disconnected.
By our choice of ![]() $(v,w)$ and Theorem 5.7 (compare Proposition 5.11 and Corollary 5.14), we deduce that the set of connected components of
$(v,w)$ and Theorem 5.7 (compare Proposition 5.11 and Corollary 5.14), we deduce that the set of connected components of  $\eta _{\beta , v, w}^{-1} ( x )$ is in bijection with the set of connected components of
$\eta _{\beta , v, w}^{-1} ( x )$ is in bijection with the set of connected components of ![]() $\mathscr {B} _{2,\beta _0} [ u, w_0 ]$ or
$\mathscr {B} _{2,\beta _0} [ u, w_0 ]$ or ![]() $\mathscr {B} _{2,\beta _0} [ u, w_0 ] \times \mathscr {B}_{2,\beta _{\infty }} [u',w_0]$ for some
$\mathscr {B} _{2,\beta _0} [ u, w_0 ] \times \mathscr {B}_{2,\beta _{\infty }} [u',w_0]$ for some ![]() $u,u' \in W$.
$u,u' \in W$.
To see whether this is the case, we specialise to the case of ![]() $(v, w ) = ( w_0, w_0 )$ (to guarantee that the contribution at
$(v, w ) = ( w_0, w_0 )$ (to guarantee that the contribution at ![]() $\infty \in \mathbb {P}^1$ in Theorem 5.7 is the same as the points in
$\infty \in \mathbb {P}^1$ in Theorem 5.7 is the same as the points in ![]() ${\mathbb C}^{\times } \subset \mathbb {P}^1$, which are connected by Proposition 5.11). We can choose
${\mathbb C}^{\times } \subset \mathbb {P}^1$, which are connected by Proposition 5.11). We can choose ![]() $\beta _0 < \beta _0' \in Q^{\vee }_+$ such that
$\beta _0 < \beta _0' \in Q^{\vee }_+$ such that  $\left \langle \alpha _i^{\vee }, \beta _0' \right \rangle \ge 1$ for every
$\left \langle \alpha _i^{\vee }, \beta _0' \right \rangle \ge 1$ for every ![]() $i \in \mathtt I$. By Proposition 5.11, we deduce that the fibre of the locus
$i \in \mathtt I$. By Proposition 5.11, we deduce that the fibre of the locus ![]() $\mathscr {Z}$ of
$\mathscr {Z}$ of ![]() $\mathscr {Q} ( \beta , w_0 )$ whose points have defect
$\mathscr {Q} ( \beta , w_0 )$ whose points have defect ![]() $\beta _0'$ along
$\beta _0'$ along ![]() $0$ is connected (if it is nonempty) for every
$0$ is connected (if it is nonempty) for every ![]() $\beta \in Q^{\vee }$. Hence we have
$\beta \in Q^{\vee }$. Hence we have ![]() $\Theta ( y ) = 1$ for each
$\Theta ( y ) = 1$ for each ![]() $y \in \mathscr {Z}$.
$y \in \mathscr {Z}$.
For each  $\tilde {x} \in {\mathscr{GB}}_ {2, \beta }^{\flat }$ such that
$\tilde {x} \in {\mathscr{GB}}_ {2, \beta }^{\flat }$ such that ![]() $x = \pi _{2,\beta } ( \tilde {x} ) \in \mathscr {Q} ( \beta , w_0 )$ has defect
$x = \pi _{2,\beta } ( \tilde {x} ) \in \mathscr {Q} ( \beta , w_0 )$ has defect ![]() $\beta _0$ at
$\beta _0$ at ![]() $0$, we can replace
$0$, we can replace ![]() $\beta $ with
$\beta $ with ![]() $\beta + \beta _0' - \beta _0$ and add additional irreducible components
$\beta + \beta _0' - \beta _0$ and add additional irreducible components ![]() $C'$ to the main component
$C'$ to the main component ![]() $\mathbb {P}^1$ of
$\mathbb {P}^1$ of ![]() $\tilde {x}$ (as quasi-stable curves) outside of
$\tilde {x}$ (as quasi-stable curves) outside of ![]() $0 \in \mathbb {P}^1$ (whose images to
$0 \in \mathbb {P}^1$ (whose images to ![]() $\mathscr {B}$ have their degrees sum up to
$\mathscr {B}$ have their degrees sum up to ![]() $(\beta _0' - \beta _0)$). (This does not change the defect of x at
$(\beta _0' - \beta _0)$). (This does not change the defect of x at ![]() $0$, and also does not change
$0$, and also does not change ![]() $\Theta ( x )$.) Then we shrink all the inserting points of
$\Theta ( x )$.) Then we shrink all the inserting points of ![]() $C'$ on
$C'$ on ![]() $\mathbb {P}^1$ to
$\mathbb {P}^1$ to ![]() $0$ to obtain
$0$ to obtain  $\tilde {x}' \in {\mathscr{GB}}_ {2, \beta }^{\flat }$ in the limit, which exists by the valuative criterion of properness, as
$\tilde {x}' \in {\mathscr{GB}}_ {2, \beta }^{\flat }$ in the limit, which exists by the valuative criterion of properness, as  ${\mathscr{GB}}_ {2, \beta }^{\flat }$ is projective. By examining the images of this family on
${\mathscr{GB}}_ {2, \beta }^{\flat }$ is projective. By examining the images of this family on ![]() $\mathscr {Q} ( \beta , w_0 )$ via
$\mathscr {Q} ( \beta , w_0 )$ via ![]() $\pi _{2,\beta }$, we deduce
$\pi _{2,\beta }$, we deduce ![]() $y = \pi _{2,\beta } \left ( \tilde {x}' \right ) \in \mathscr {Z}$. Therefore, the semicontinuity of
$y = \pi _{2,\beta } \left ( \tilde {x}' \right ) \in \mathscr {Z}$. Therefore, the semicontinuity of ![]() $\Theta $ implies that
$\Theta $ implies that ![]() $\Theta ( x ) \le \Theta ( y ) = 1$ – that is,
$\Theta ( x ) \le \Theta ( y ) = 1$ – that is, ![]() $\Theta ( x ) = 1$. Hence,
$\Theta ( x ) = 1$. Hence, ![]() $\mathscr {B} _{2,\beta _0} [ w, w_0 ]$ must be connected. This is a contradiction, and we conclude that
$\mathscr {B} _{2,\beta _0} [ w, w_0 ]$ must be connected. This is a contradiction, and we conclude that ![]() $\Theta \equiv 1$ (for general
$\Theta \equiv 1$ (for general ![]() $(v,w) \in \{ (e,w_0),(w_0,w_0)\}$ by the previous two paragraphs).
$(v,w) \in \{ (e,w_0),(w_0,w_0)\}$ by the previous two paragraphs).
Therefore, Proposition 5.13 implies the result.
Corollary 5.17. Set ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w \in W$. For each
$w \in W$. For each ![]() $i \in \mathtt I$ such that
$i \in \mathtt I$ such that ![]() $s_i w < w$, we have a surjective map
$s_i w < w$, we have a surjective map
such that ![]() $(\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q} \left ( \beta , w \right )} \cong {\mathcal O}_{\mathscr {Q} \left ( \beta , s_i w \right )}$ and
$(\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q} \left ( \beta , w \right )} \cong {\mathcal O}_{\mathscr {Q} \left ( \beta , s_i w \right )}$ and  $\mathbb {R}^{>0} (\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q} \left ( \beta , w \right )} \cong \{ 0 \}$.
$\mathbb {R}^{>0} (\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q} \left ( \beta , w \right )} \cong \{ 0 \}$.
Proof. Combine Corollary 4.40 with Theorem 4.30 (and take the generic localisations over ![]() $\mathbb {Z}$).
$\mathbb {Z}$).
Corollary 5.18. For each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w \in W$, the variety
$w \in W$, the variety ![]() $\mathscr {Q} ( \beta , w )$ is normal.
$\mathscr {Q} ( \beta , w )$ is normal.
Proof. The case ![]() $w = w_0$ is in Theorem 5.16. Assume that the assertion holds for w. Set
$w = w_0$ is in Theorem 5.16. Assume that the assertion holds for w. Set ![]() $i \in \mathtt I$ such that
$i \in \mathtt I$ such that ![]() $s_i w < w$. Then Corollary 5.17 implies that
$s_i w < w$. Then Corollary 5.17 implies that ![]() ${\mathcal O}_{\mathscr {Q} \left ( \beta , s_i w \right )}$ is isomorphic to the normal sheaf of rings
${\mathcal O}_{\mathscr {Q} \left ( \beta , s_i w \right )}$ is isomorphic to the normal sheaf of rings ![]() $(\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q} \left ( \beta , w \right )}$. Hence the assertion holds for
$(\pi _i)_* {\mathcal O}_{P_i \times ^B \mathscr {Q} \left ( \beta , w \right )}$. Hence the assertion holds for ![]() $s_i w < w$. This proceeds to the induction, and we conclude the result.
$s_i w < w$. This proceeds to the induction, and we conclude the result.
Corollary 5.19. For each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w, v \in W$, the subspace
$w, v \in W$, the subspace
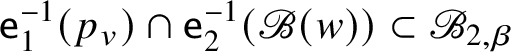 $$ \begin{align*}\mathtt{e}_1^{-1} ( p_v ) \cap \mathtt{e}_2^{-1} ( \mathscr{B} ( w ) ) \subset \mathscr{B}_{2,\beta}\end{align*} $$
$$ \begin{align*}\mathtt{e}_1^{-1} ( p_v ) \cap \mathtt{e}_2^{-1} ( \mathscr{B} ( w ) ) \subset \mathscr{B}_{2,\beta}\end{align*} $$is connected.
Proof. This space appears in the fibre of ![]() $\pi _{\beta , w_0, w}$ along the constant quasi-map
$\pi _{\beta , w_0, w}$ along the constant quasi-map ![]() $\mathbb {P}^1 \rightarrow \{ p_v \} \subset \mathscr {B}$ with its defect concentrated in
$\mathbb {P}^1 \rightarrow \{ p_v \} \subset \mathscr {B}$ with its defect concentrated in ![]() $0 \in \mathbb {P}^1$. Hence, the assertion follows from Corollary 5.18 and Proposition 5.13.
$0 \in \mathbb {P}^1$. Hence, the assertion follows from Corollary 5.18 and Proposition 5.13.
Theorem 5.20. For each ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w, v \in W$, the scheme
$w, v \in W$, the scheme ![]() $\mathscr {Q} ( \beta , v, w )$ is normal.
$\mathscr {Q} ( \beta , v, w )$ is normal.
Proof. The combination of Theorem 5.7 and Corollary 5.19 implies that every fibre of ![]() $\pi _{\beta , v, w}$ is connected. Thus, Proposition 5.13 implies the result.
$\pi _{\beta , v, w}$ is connected. Thus, Proposition 5.13 implies the result.
Corollary 5.21. For each ![]() $\mathtt J \subset \mathtt I$,
$\mathtt J \subset \mathtt I$, ![]() $\beta \in Q^{\vee }_+$ and
$\beta \in Q^{\vee }_+$ and ![]() $w,v \in W$, the variety
$w,v \in W$, the variety ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ is irreducible and normal.
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ is irreducible and normal.
Proof. By Corollary 4.35 and Remark 4.36, we can rearrange the map ![]() $\Pi _{\mathtt J}$ to be surjective with connected fibres. Hence, Proposition 5.3 implies the irreducibility of
$\Pi _{\mathtt J}$ to be surjective with connected fibres. Hence, Proposition 5.3 implies the irreducibility of ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$. By the Stein factorisation theorem applied to the composition map
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$. By the Stein factorisation theorem applied to the composition map ![]() $\Pi _{\mathtt J} \circ \pi _{\beta , v, w}$, we deduce that the normalisation of
$\Pi _{\mathtt J} \circ \pi _{\beta , v, w}$, we deduce that the normalisation of ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ is bijective to
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ is bijective to ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$. Therefore, the weak normality of
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$. Therefore, the weak normality of ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ (Corollary 4.42) implies the result.
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ (Corollary 4.42) implies the result.
We set ![]() $W^{\mathtt J} := W / w_0 W_{\mathtt J} w_0$ and identify it with the set of their minimal length representatives in W. Recall that
$W^{\mathtt J} := W / w_0 W_{\mathtt J} w_0$ and identify it with the set of their minimal length representatives in W. Recall that ![]() $2 \rho _{\mathtt J}$ is the sum of the positive roots that belong to the unipotent radical of
$2 \rho _{\mathtt J}$ is the sum of the positive roots that belong to the unipotent radical of ![]() $\mathfrak p ( \mathtt J )$.
$\mathfrak p ( \mathtt J )$.
Corollary 5.22. For each ![]() $\mathtt J \subset \mathtt I$,
$\mathtt J \subset \mathtt I$, ![]() $\beta \in Q^{\vee }_+$ such that
$\beta \in Q^{\vee }_+$ such that  $-w_0 \beta \in Q^{\vee }_{\mathtt J, +}$,
$-w_0 \beta \in Q^{\vee }_{\mathtt J, +}$, ![]() $w \in W^{\mathtt J}$ and
$w \in W^{\mathtt J}$ and ![]() $v \in W$ such that
$v \in W$ such that ![]() $w_0 v \in W^{\mathtt J}$, the variety
$w_0 v \in W^{\mathtt J}$, the variety ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ has dimension
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ has dimension
if it is nonempty. When ![]() $v = w_0$, the variety
$v = w_0$, the variety ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ is always nonempty. In addition,
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ is always nonempty. In addition, ![]() $\mathscr {Q}_{\mathtt J} ( \beta , w_0, e )$ is the collection of DP-data as in Definition 2.6, with the data and compatibility conditions only for
$\mathscr {Q}_{\mathtt J} ( \beta , w_0, e )$ is the collection of DP-data as in Definition 2.6, with the data and compatibility conditions only for ![]() $\lambda \in P_{\mathtt J, +}$.
$\lambda \in P_{\mathtt J, +}$.
Remark 5.23. If we replace the labels of  $\mathscr {Q}_{\mathtt J} ( \beta , v, w ) = \mathscr {Q}^{\prime }_{\mathtt J} \left ( vt_{\beta }, w \right )_{{\mathbb C}}$ with the labels of parabolic semi-infinite Bruhat order as in [Reference Lam and Shimozono61, §10.3], then we can write the condition of
$\mathscr {Q}_{\mathtt J} ( \beta , v, w ) = \mathscr {Q}^{\prime }_{\mathtt J} \left ( vt_{\beta }, w \right )_{{\mathbb C}}$ with the labels of parabolic semi-infinite Bruhat order as in [Reference Lam and Shimozono61, §10.3], then we can write the condition of ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ to be nonempty by the order relation, just as in Corollary 4.21.
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ to be nonempty by the order relation, just as in Corollary 4.21.
Proof of Corollary 5.22. By [Reference Braverman, Finkelberg, Gaitsgory and Mirković12], the collection of DP-data in Definition 2.6 with the compatibility condition imposed only for ![]() $\lambda \in P_{\mathtt J, +}$ (without nondefining points) represents the (closure of the) space of maps
$\lambda \in P_{\mathtt J, +}$ (without nondefining points) represents the (closure of the) space of maps ![]() $\mathbb {P}^1 \rightarrow G / P ( \mathtt J )$ such that the image of
$\mathbb {P}^1 \rightarrow G / P ( \mathtt J )$ such that the image of  $\left [\mathbb {P}^1\right ]$ in
$\left [\mathbb {P}^1\right ]$ in ![]() $\mathscr {B}$ is
$\mathscr {B}$ is ![]() $- w_0 \beta \in H_2 ( \mathscr {B}, \mathbb {Z} )$. Thus, we conclude the last assertion.
$- w_0 \beta \in H_2 ( \mathscr {B}, \mathbb {Z} )$. Thus, we conclude the last assertion.
The dimension of ![]() $\mathscr {Q}_{\mathtt J} ( \beta , w_0, e )$ is given by
$\mathscr {Q}_{\mathtt J} ( \beta , w_0, e )$ is given by ![]() $\dim G / P ( \mathtt J ) - 2 \left \langle w_0 \beta , \rho _{\mathtt J} \right \rangle $, since the first Chern class of the tangent bundle of
$\dim G / P ( \mathtt J ) - 2 \left \langle w_0 \beta , \rho _{\mathtt J} \right \rangle $, since the first Chern class of the tangent bundle of ![]() $G / P ( \mathtt J )$ is
$G / P ( \mathtt J )$ is ![]() $2 \rho _{\mathtt J}$ (compare [Reference Finkelberg and Mirković29, Proposition 3.5]). In particular, the dimension of
$2 \rho _{\mathtt J}$ (compare [Reference Finkelberg and Mirković29, Proposition 3.5]). In particular, the dimension of ![]() $\mathscr {Q}_{\mathtt J} ( \beta , w_0, e )$ is formula (5.4) in this case.
$\mathscr {Q}_{\mathtt J} ( \beta , w_0, e )$ is formula (5.4) in this case.
Since imposing a hyperplane section in the image of ![]() $G/P(\mathtt J)$ through the (generically defined) evaluation map at
$G/P(\mathtt J)$ through the (generically defined) evaluation map at ![]() $0 \in \mathbb {P}^1$ (which is surjective as being G-equivariant)
$0 \in \mathbb {P}^1$ (which is surjective as being G-equivariant)
lowers the dimension by exactly ![]() $1$, we deduce that
$1$, we deduce that ![]() $\mathscr {Q}_{\mathtt J} ( \beta , w_0, w )$ has an irreducible component of expected dimension. From this and Corollary 5.21, we conclude that
$\mathscr {Q}_{\mathtt J} ( \beta , w_0, w )$ has an irreducible component of expected dimension. From this and Corollary 5.21, we conclude that ![]() $\mathscr {Q}_{\mathtt J} ( \beta , w_0, w )$ is nonempty and its dimension is given by formula (5.4).
$\mathscr {Q}_{\mathtt J} ( \beta , w_0, w )$ is nonempty and its dimension is given by formula (5.4).
We consider the dimension estimate in the general case.
Since ![]() $\mathscr {Q}_{\mathtt J} ( \beta , s_i v, w ) \subsetneq \mathscr {Q}_{\mathtt J} ( \beta , v, w )$ (
$\mathscr {Q}_{\mathtt J} ( \beta , s_i v, w ) \subsetneq \mathscr {Q}_{\mathtt J} ( \beta , v, w )$ (![]() $i \in \mathtt I$) implies
$i \in \mathtt I$) implies ![]() $s_i v>_{\frac {\infty }{2}} v$ (
$s_i v>_{\frac {\infty }{2}} v$ (![]() $\Leftrightarrow s_i v < v$) when
$\Leftrightarrow s_i v < v$) when ![]() $w_0 s_i v \in W^{\mathtt J}$, we find that they are the images of
$w_0 s_i v \in W^{\mathtt J}$, we find that they are the images of ![]() $\mathscr {Q} ( \beta ', s_i v, w ) \subsetneq \mathscr {Q} ( \beta ', v, w )$ for some
$\mathscr {Q} ( \beta ', s_i v, w ) \subsetneq \mathscr {Q} ( \beta ', v, w )$ for some  $\beta ' \in \beta + \sum _{j \in \mathtt J} \mathbb {Z}_{\ge 0} \alpha _j^{\vee }$ (see Remark 4.36). In particular,
$\beta ' \in \beta + \sum _{j \in \mathtt J} \mathbb {Z}_{\ge 0} \alpha _j^{\vee }$ (see Remark 4.36). In particular, ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ has dimension of at least formula (5.4) in general, by induction from the case when
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ has dimension of at least formula (5.4) in general, by induction from the case when ![]() $v = w_0$.
$v = w_0$.
Let Z denote the space of genus ![]() $0$ stable maps to
$0$ stable maps to ![]() $\mathbb {P}^1 \times G/P ( \mathtt J )$ of bidegree
$\mathbb {P}^1 \times G/P ( \mathtt J )$ of bidegree ![]() $(1,\beta )$ with two marked points such that the first and second marked points correspond to
$(1,\beta )$ with two marked points such that the first and second marked points correspond to ![]() $0, \infty \in \mathbb {P}^1$, respectively (parabolic analogue of
$0, \infty \in \mathbb {P}^1$, respectively (parabolic analogue of  ${\mathscr{GB}}^\flat _{2,\beta }$). Then we have a resolution
${\mathscr{GB}}^\flat _{2,\beta }$). Then we have a resolution ![]() $\pi : Z \rightarrow \mathscr {Q} _{\mathtt J} ( \beta , w_0, e )$ (which shares genuine maps
$\pi : Z \rightarrow \mathscr {Q} _{\mathtt J} ( \beta , w_0, e )$ (which shares genuine maps ![]() $\mathbb {P}^1 \to G/P(\mathtt J)$ in their common open dense subset). Let
$\mathbb {P}^1 \to G/P(\mathtt J)$ in their common open dense subset). Let ![]() $\eta : \mathscr {B} = G / B \rightarrow G/P(\mathtt J)$ be the projection. By our choices of
$\eta : \mathscr {B} = G / B \rightarrow G/P(\mathtt J)$ be the projection. By our choices of ![]() $v,w$, we find
$v,w$, we find
respectively. We have the evaluation map of two points ![]() $\mathtt {z} : Z \rightarrow ( G/P(\mathtt J))^2$. We set
$\mathtt {z} : Z \rightarrow ( G/P(\mathtt J))^2$. We set ![]() $Z_{v,w} := \mathtt {z}^{-1} ( \eta ( \mathscr {B} ( w )) \times \eta ( \mathscr {B}^{\mathrm {op}} ( v )))$. By [Reference Buch, Chaput, Mihalcea and Perrin16, Propostion 3.2 b)] (see also the proof of Corollary 5.2), we find that
$Z_{v,w} := \mathtt {z}^{-1} ( \eta ( \mathscr {B} ( w )) \times \eta ( \mathscr {B}^{\mathrm {op}} ( v )))$. By [Reference Buch, Chaput, Mihalcea and Perrin16, Propostion 3.2 b)] (see also the proof of Corollary 5.2), we find that
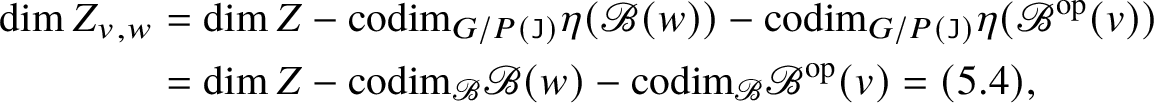 $$ \begin{align*} \dim Z_{v,w} & = \dim Z - \mathrm{codim} _{G/P(\mathtt J)} \eta ( \mathscr{B} ( w ) ) - \mathrm{codim} _{G/P(\mathtt J)} \eta ( \mathscr{B}^{\mathrm{op}} ( v ) )\\ & = \dim Z - \mathrm{codim} _{\mathscr{B}} \mathscr{B} ( w ) - \mathrm{codim} _{\mathscr{B}} \mathscr{B}^{\mathrm{op}} ( v ) = (5.4), \end{align*} $$
$$ \begin{align*} \dim Z_{v,w} & = \dim Z - \mathrm{codim} _{G/P(\mathtt J)} \eta ( \mathscr{B} ( w ) ) - \mathrm{codim} _{G/P(\mathtt J)} \eta ( \mathscr{B}^{\mathrm{op}} ( v ) )\\ & = \dim Z - \mathrm{codim} _{\mathscr{B}} \mathscr{B} ( w ) - \mathrm{codim} _{\mathscr{B}} \mathscr{B}^{\mathrm{op}} ( v ) = (5.4), \end{align*} $$and ![]() $Z_{v,w}$ is irreducible (if it is nonempty). Since
$Z_{v,w}$ is irreducible (if it is nonempty). Since ![]() $G / P ( \mathtt J )$ is homogeneous, we find that
$G / P ( \mathtt J )$ is homogeneous, we find that ![]() $G \cdot \pi \left ( Z_{w_0,w} \right ) \subset Z$ is Zariski dense. Hence,
$G \cdot \pi \left ( Z_{w_0,w} \right ) \subset Z$ is Zariski dense. Hence, ![]() $Z_{w_0,w}$ contains an open dense subset whose points are genuine maps
$Z_{w_0,w}$ contains an open dense subset whose points are genuine maps ![]() $\mathbb {P}^1 \to G/P (\mathtt J)$. In conjunction with the irreducibility of
$\mathbb {P}^1 \to G/P (\mathtt J)$. In conjunction with the irreducibility of ![]() $Z_{w_0,w}$ and
$Z_{w_0,w}$ and ![]() $\mathscr {Q} _{\mathtt J} (\beta ,w_0,w )$, we find
$\mathscr {Q} _{\mathtt J} (\beta ,w_0,w )$, we find ![]() $\pi ^{-1} ( \mathscr {Q} _{\mathtt J} (\beta ,w_0,w ) ) = Z_{w_0,w}$. Similarly, we have
$\pi ^{-1} ( \mathscr {Q} _{\mathtt J} (\beta ,w_0,w ) ) = Z_{w_0,w}$. Similarly, we have ![]() $\pi ^{-1} ( \mathscr {Q} _{\mathtt J} (\beta ,v,e ) ) = Z_{v,e}$. Therefore, we conclude that
$\pi ^{-1} ( \mathscr {Q} _{\mathtt J} (\beta ,v,e ) ) = Z_{v,e}$. Therefore, we conclude that ![]() $Z_{v,w}$ surjects onto
$Z_{v,w}$ surjects onto ![]() $\mathscr {Q} _{\mathtt J} (\beta ,v,w )$ by the restriction of
$\mathscr {Q} _{\mathtt J} (\beta ,v,w )$ by the restriction of ![]() $\pi $. In particular,
$\pi $. In particular, ![]() $\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ has dimension of at most formula (5.4) in general.
$\mathscr {Q}_{\mathtt J} ( \beta , v, w )$ has dimension of at most formula (5.4) in general.
Therefore, our dimension estimate must be strict in general.
Corollary 5.24. For each ![]() $\mathtt J \subset \mathtt I$ and
$\mathtt J \subset \mathtt I$ and ![]() $w,v \in W_{\mathrm {af}}$, the scheme
$w,v \in W_{\mathrm {af}}$, the scheme  $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb F}_p}$ is irreducible and normal for
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{\overline {\mathbb F}_p}$ is irreducible and normal for ![]() $p \gg 0$.
$p \gg 0$.
Corollary 5.25. Let ![]() ${\mathbb K}$ be an algebraically closed field of characteristic
${\mathbb K}$ be an algebraically closed field of characteristic ![]() $0$ or
$0$ or ![]() $p \gg 0$. For each
$p \gg 0$. For each ![]() $\mathtt J \subset \mathtt I$ and
$\mathtt J \subset \mathtt I$ and ![]() $w,v \in W_{\mathrm {af}}$, the scheme
$w,v \in W_{\mathrm {af}}$, the scheme ![]() $\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is projectively normal with respect to a line bundle
$\mathscr {Q}^{\prime }_{\mathtt J} ( v, w )_{{\mathbb K}}$ is projectively normal with respect to a line bundle ![]() ${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda )$ (
${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda )$ (![]() $\lambda \in P_{\mathtt J, ++}$).
$\lambda \in P_{\mathtt J, ++}$).
Proof. In view of Lemmas 4.1 and 4.3 and Theorem 4.33, the multiplication of the section ring afforded by  $\left \{ {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( m \lambda ) \right \}_{m \ge 0}$ is surjective. Therefore, Corollaries 5.21 and 5.24 imply the result.
$\left \{ {\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( m \lambda ) \right \}_{m \ge 0}$ is surjective. Therefore, Corollaries 5.21 and 5.24 imply the result.
A Some properties of  $\mathbf {Q}_G ( w )$ in positive characteristic
$\mathbf {Q}_G ( w )$ in positive characteristic
We work in the setting of Section 4.2. Let ![]() ${\mathbb K}$ be an algebraically closed field of characteristic
${\mathbb K}$ be an algebraically closed field of characteristic ![]() $\neq 2$. The aim of this appendix is twofold: to show that our scheme
$\neq 2$. The aim of this appendix is twofold: to show that our scheme ![]() $\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb K}$ is (projectively) normal and to present an analogue of the Kempf vanishing theorem for
$\mathbf {Q}_{G, \mathtt J} ( w )_{\mathbb K}$ is (projectively) normal and to present an analogue of the Kempf vanishing theorem for ![]() $\mathbf {Q}_G ( w )_{\mathbb K}$. Both results are proved in [Reference Kato, Naito and Sagaki51] for the case when
$\mathbf {Q}_G ( w )_{\mathbb K}$. Both results are proved in [Reference Kato, Naito and Sagaki51] for the case when ![]() ${\mathbb K} = {\mathbb C}$. Our proof of the former is new and does not depend on [Reference Kato, Naito and Sagaki51] (when
${\mathbb K} = {\mathbb C}$. Our proof of the former is new and does not depend on [Reference Kato, Naito and Sagaki51] (when ![]() $w = e$), while our proof of the latter depends on the results and arguments in [Reference Kato, Naito and Sagaki51] in an essential way.
$w = e$), while our proof of the latter depends on the results and arguments in [Reference Kato, Naito and Sagaki51] in an essential way.
Proposition A.1. For each ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $\mathtt J \subset \mathtt I$, the ring
$\mathtt J \subset \mathtt I$, the ring ![]() $R_w ( \mathtt J )_{{\mathbb K}}$ is normal.
$R_w ( \mathtt J )_{{\mathbb K}}$ is normal.
Proof. We first prove the case where ![]() $w = e$ and
$w = e$ and ![]() $\mathtt J = \emptyset $. Let
$\mathtt J = \emptyset $. Let ![]() $\mathring {\mathbf {Q}}_G$ denote the open
$\mathring {\mathbf {Q}}_G$ denote the open ![]() $G [\![z]\!]$-orbit of
$G [\![z]\!]$-orbit of ![]() $\mathbf {Q}_G ( e )_{\mathbb K}$ obtained by the G-translation of Lemma 4.11.
$\mathbf {Q}_G ( e )_{\mathbb K}$ obtained by the G-translation of Lemma 4.11.
We have an inclusion
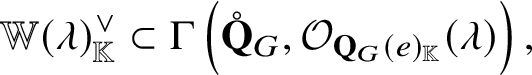 $$ \begin{align} \mathbb{W} ( \lambda )^{\vee}_{\mathbb K} \subset \Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right), \end{align} $$
$$ \begin{align} \mathbb{W} ( \lambda )^{\vee}_{\mathbb K} \subset \Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right), \end{align} $$since ![]() $R _{{\mathbb K}}$ is integral (Corollary 4.12). We also have an inclusion
$R _{{\mathbb K}}$ is integral (Corollary 4.12). We also have an inclusion
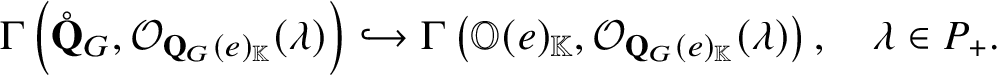 $$ \begin{align*}\Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right) \hookrightarrow \Gamma \left( \mathbb{O} ( e )_{\mathbb K}, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right), \quad \lambda \in P_+.\end{align*} $$
$$ \begin{align*}\Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right) \hookrightarrow \Gamma \left( \mathbb{O} ( e )_{\mathbb K}, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right), \quad \lambda \in P_+.\end{align*} $$Thanks to Lemma 4.11 and its proof, we deduce
which is cocyclic as a ![]() $U^{+}_{{\mathbb K}}$-module. Since the G-action on
$U^{+}_{{\mathbb K}}$-module. Since the G-action on  $\Gamma \left ( \mathring {\mathbf {Q}}_G, {\mathcal O}_{\mathbf {Q}_G (e)_{\mathbb K}} ( \lambda )\right )$ is algebraic, we deduce that
$\Gamma \left ( \mathring {\mathbf {Q}}_G, {\mathcal O}_{\mathbf {Q}_G (e)_{\mathbb K}} ( \lambda )\right )$ is algebraic, we deduce that
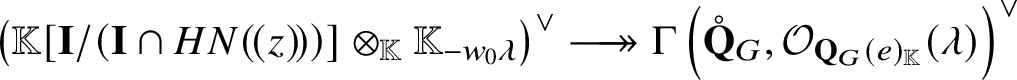 $$ \begin{align*}\left( {\mathbb K} [\mathbf{I} / \left( \mathbf{I} \cap H N (\!(z)\!) \right)] \otimes_{{\mathbb K}} {\mathbb K}_{-w_0\lambda} \right) ^{\vee} \longrightarrow \!\!\!\!\! \rightarrow \Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right)^{\vee}\end{align*} $$
$$ \begin{align*}\left( {\mathbb K} [\mathbf{I} / \left( \mathbf{I} \cap H N (\!(z)\!) \right)] \otimes_{{\mathbb K}} {\mathbb K}_{-w_0\lambda} \right) ^{\vee} \longrightarrow \!\!\!\!\! \rightarrow \Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right)^{\vee}\end{align*} $$is a ![]() $\dot {U}_{\mathbb K}^0$-integrable quotient. By Proposition 3.19, we conclude a surjection
$\dot {U}_{\mathbb K}^0$-integrable quotient. By Proposition 3.19, we conclude a surjection
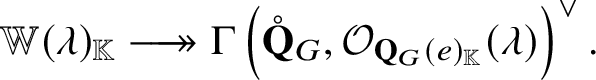 $$ \begin{align*}\mathbb{W} ( \lambda )_{{\mathbb K}} \longrightarrow \!\!\!\!\! \rightarrow \Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right)^{\vee}.\end{align*} $$
$$ \begin{align*}\mathbb{W} ( \lambda )_{{\mathbb K}} \longrightarrow \!\!\!\!\! \rightarrow \Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right)^{\vee}.\end{align*} $$Compared with formula (A.1), we conclude the isomorphism
 $$ \begin{align*}\Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right) \stackrel{\cong}{\longrightarrow} \Gamma \left( \mathbf{Q}_G ( e )_{\mathbb K}, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right), \quad \lambda \in P_+,\end{align*} $$
$$ \begin{align*}\Gamma \left( \mathring{\mathbf{Q}}_G, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right) \stackrel{\cong}{\longrightarrow} \Gamma \left( \mathbf{Q}_G ( e )_{\mathbb K}, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right), \quad \lambda \in P_+,\end{align*} $$since the space of sections supported on a dense open Zarsiki subset must be larger than (or equal to) the space of sections supported on the whole space for an integral scheme. In other words, ![]() $R _{{\mathbb K}}$ is the maximal
$R _{{\mathbb K}}$ is the maximal ![]() $\dot {U}_{\mathbb K}^0$-integrable
$\dot {U}_{\mathbb K}^0$-integrable ![]() $U^+_{{\mathbb K}}$-stable subring of
$U^+_{{\mathbb K}}$-stable subring of
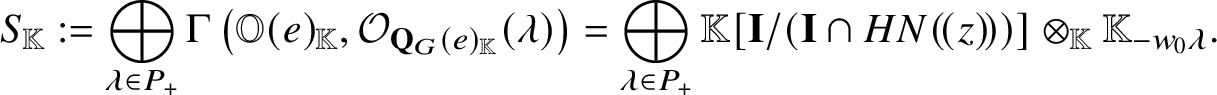 $$ \begin{align*}S_{{\mathbb K}} := \bigoplus_{\lambda \in P_+} \Gamma \left( \mathbb{O} ( e )_{\mathbb K}, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right) = \bigoplus_{\lambda \in P_+} {\mathbb K} [\mathbf{I} / \left( \mathbf{I} \cap H N (\!(z)\!) \right)] \otimes_{{\mathbb K}} {\mathbb K}_{-w_0\lambda}.\end{align*} $$
$$ \begin{align*}S_{{\mathbb K}} := \bigoplus_{\lambda \in P_+} \Gamma \left( \mathbb{O} ( e )_{\mathbb K}, {\mathcal O}_{\mathbf{Q}_G (e)_{\mathbb K}} ( \lambda )\right) = \bigoplus_{\lambda \in P_+} {\mathbb K} [\mathbf{I} / \left( \mathbf{I} \cap H N (\!(z)\!) \right)] \otimes_{{\mathbb K}} {\mathbb K}_{-w_0\lambda}.\end{align*} $$The ring ![]() $S_{{\mathbb K}}$ is integrally closed, as it is a polynomial ring (of countably many variables). Hence, the integral closure
$S_{{\mathbb K}}$ is integrally closed, as it is a polynomial ring (of countably many variables). Hence, the integral closure ![]() $R^+$ of the ring
$R^+$ of the ring ![]() $R _{{\mathbb K}}$ is also a subring of
$R _{{\mathbb K}}$ is also a subring of ![]() $S_{{\mathbb K}}$. In view of the
$S_{{\mathbb K}}$. In view of the ![]() $\dot {U}_{\mathbb K}^0$-integrability, the ring
$\dot {U}_{\mathbb K}^0$-integrability, the ring ![]() $R_{{\mathbb K}}$ admits an algebraic G-action. By the canonical nature of the normalisation, we deduce that
$R_{{\mathbb K}}$ admits an algebraic G-action. By the canonical nature of the normalisation, we deduce that ![]() $R^+$ admits an algebraic G-action (note that we can approximate
$R^+$ admits an algebraic G-action (note that we can approximate ![]() $R_{{\mathbb K}}$ as a union of Noetherian rings with algebraic G-actions). However,
$R_{{\mathbb K}}$ as a union of Noetherian rings with algebraic G-actions). However, ![]() $R_{{\mathbb K}}$ is already the maximal
$R_{{\mathbb K}}$ is already the maximal ![]() $\dot {U}_{\mathbb K}^0$-integrable
$\dot {U}_{\mathbb K}^0$-integrable ![]() $U^+_{{\mathbb K}}$-stable subring of
$U^+_{{\mathbb K}}$-stable subring of ![]() $S_{{\mathbb K}}$. Hence, we necessarily have
$S_{{\mathbb K}}$. Hence, we necessarily have ![]() $R^+ = R_{{\mathbb K}}$. Thus, the case of
$R^+ = R_{{\mathbb K}}$. Thus, the case of ![]() $w = e$ and
$w = e$ and ![]() $\mathtt J = \emptyset $ follows.
$\mathtt J = \emptyset $ follows.
The case of arbitrary ![]() $w \in W_{\mathrm {af}}$ follows from the case of
$w \in W_{\mathrm {af}}$ follows from the case of ![]() $w = e$ as in [Reference Kato46, §4]. As the fraction field of
$w = e$ as in [Reference Kato46, §4]. As the fraction field of ![]() $R_w ( \mathtt J )_{{\mathbb K}}$ is a subfield of the fraction field of
$R_w ( \mathtt J )_{{\mathbb K}}$ is a subfield of the fraction field of ![]() $( R_w )_{{\mathbb K}}$ and
$( R_w )_{{\mathbb K}}$ and ![]() $P_{\mathtt J, +} \subset P_+$ forms (the set of integral points of) a face, we conclude the general case by restriction.
$P_{\mathtt J, +} \subset P_+$ forms (the set of integral points of) a face, we conclude the general case by restriction.
Corollary A.2. The scheme ![]() $\mathbf {Q} _{G, \mathtt J} ( w )_{{\mathbb K}}$ is normal.
$\mathbf {Q} _{G, \mathtt J} ( w )_{{\mathbb K}}$ is normal.
Corollary A.3. For each ![]() $\lambda \in P_{\mathtt J,+}$, we have
$\lambda \in P_{\mathtt J,+}$, we have
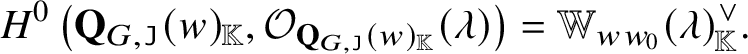 $$ \begin{align*}H^0 \left( \mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}} ( \lambda ) \right) = \mathbb{W}_{ww_0} ( \lambda )_{{\mathbb K}} ^{\vee}.\end{align*} $$
$$ \begin{align*}H^0 \left( \mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}} ( \lambda ) \right) = \mathbb{W}_{ww_0} ( \lambda )_{{\mathbb K}} ^{\vee}.\end{align*} $$Proof. Because finding ![]() $H^0$ from
$H^0$ from ![]() $R_w ( \mathtt J )_{{\mathbb K}}$ can be seen as finding graded pieces of the normalisation, the assertion follows from Proposition A.1.
$R_w ( \mathtt J )_{{\mathbb K}}$ can be seen as finding graded pieces of the normalisation, the assertion follows from Proposition A.1.
Proposition A.4 [Reference Kato, Naito and Sagaki51]
Assume that ![]() $\mathsf {char}\, {\mathbb K} \neq 2$. Set
$\mathsf {char}\, {\mathbb K} \neq 2$. Set ![]() $w \in W$ and
$w \in W$ and ![]() $\mathtt J \subset \mathtt I$. Then an
$\mathtt J \subset \mathtt I$. Then an ![]() $\mathbf {I}$-equivariant line bundle on
$\mathbf {I}$-equivariant line bundle on ![]() $\mathbf {Q} _{G, \mathtt J} ( w )_{{\mathbb K}}$ is a character twist of
$\mathbf {Q} _{G, \mathtt J} ( w )_{{\mathbb K}}$ is a character twist of  $\left \{{\mathcal O}_{\mathbf {Q} _{G, \mathtt J} ( w )_{{\mathbb K}}} ( \lambda )\right \}_{\lambda \in P_{\mathtt J}}$.
$\left \{{\mathcal O}_{\mathbf {Q} _{G, \mathtt J} ( w )_{{\mathbb K}}} ( \lambda )\right \}_{\lambda \in P_{\mathtt J}}$.
Proof. Taking Corollaries 4.20 and A.2 into account, the proof in [Reference Kato, Naito and Sagaki51, Proposition 5.1] works in this setting.
Theorem A.5. Set ![]() $w \in W$ and
$w \in W$ and ![]() $\mathtt J \subset \mathtt I$. For each
$\mathtt J \subset \mathtt I$. For each ![]() $\lambda \in P_{\mathtt J}$, we have
$\lambda \in P_{\mathtt J}$, we have
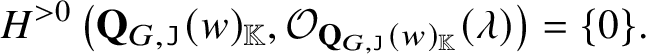 $$ \begin{align*}H^{> 0} \left( \mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}} ( \lambda ) \right) = \{ 0 \} .\end{align*} $$
$$ \begin{align*}H^{> 0} \left( \mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}} ( \lambda ) \right) = \{ 0 \} .\end{align*} $$Proof. Assume that ![]() $w = e$. We consider the subring defined by
$w = e$. We consider the subring defined by
 $$ \begin{align*}T_{\mathtt J} := \bigoplus_{\lambda \in P_{\mathtt J, +}} T_{\mathtt J} (\lambda) \subset \bigoplus_{\lambda \in P_{\mathtt J, +}} \mathbb{W} ( \lambda )_{{\mathbb K}}^{\vee} = \bigoplus_{\lambda \in P_{\mathtt J, +}} \mathbb{W}_{w_0} ( \lambda )_{{\mathbb K}}^{\vee} = R_{\mathtt J},\end{align*} $$
$$ \begin{align*}T_{\mathtt J} := \bigoplus_{\lambda \in P_{\mathtt J, +}} T_{\mathtt J} (\lambda) \subset \bigoplus_{\lambda \in P_{\mathtt J, +}} \mathbb{W} ( \lambda )_{{\mathbb K}}^{\vee} = \bigoplus_{\lambda \in P_{\mathtt J, +}} \mathbb{W}_{w_0} ( \lambda )_{{\mathbb K}}^{\vee} = R_{\mathtt J},\end{align*} $$where ![]() $T_{\mathtt J} (\lambda ) \subset \mathbb {W} ( \lambda )_{{\mathbb K}}^{\vee }$ is the P-weight
$T_{\mathtt J} (\lambda ) \subset \mathbb {W} ( \lambda )_{{\mathbb K}}^{\vee }$ is the P-weight ![]() $( - \lambda )$-part of
$( - \lambda )$-part of ![]() $\mathbb {W} ( \lambda )_{{\mathbb K}}^{\vee }$. They are generated by the duals of
$\mathbb {W} ( \lambda )_{{\mathbb K}}^{\vee }$. They are generated by the duals of  $\widetilde {P}_{i,m\delta } \mathbf {v}_{\varpi _i} \in \mathbb {W} ( \varpi _i )_{{\mathbb K}}$ (
$\widetilde {P}_{i,m\delta } \mathbf {v}_{\varpi _i} \in \mathbb {W} ( \varpi _i )_{{\mathbb K}}$ (![]() $i \in \mathtt I \setminus \mathtt J, m \in \mathbb {Z}_{>0}$; see [Reference Beck and Nakajima5, (3.18)] for the definition of
$i \in \mathtt I \setminus \mathtt J, m \in \mathbb {Z}_{>0}$; see [Reference Beck and Nakajima5, (3.18)] for the definition of ![]() $\widetilde {P}_{i,m\delta }$). In view of [Reference Beck and Nakajima5, Proposition 3.18], the ring
$\widetilde {P}_{i,m\delta }$). In view of [Reference Beck and Nakajima5, Proposition 3.18], the ring ![]() $T_{\mathtt J}$ is a polynomial ring. The actions of
$T_{\mathtt J}$ is a polynomial ring. The actions of  $\left \{\widetilde {P}_{i,m\delta }\right \}_{i \in ( \mathtt I \setminus \mathtt J ), m> 0}$ define endomorphisms of the module
$\left \{\widetilde {P}_{i,m\delta }\right \}_{i \in ( \mathtt I \setminus \mathtt J ), m> 0}$ define endomorphisms of the module ![]() $\mathbb {W} ( \lambda )_{{\mathbb K}}$ (
$\mathbb {W} ( \lambda )_{{\mathbb K}}$ (![]() $\lambda \in P_{\mathtt J,+}$), each of which is either an injection or zero (compare the proof of Proposition 3.19). It follows that the action of
$\lambda \in P_{\mathtt J,+}$), each of which is either an injection or zero (compare the proof of Proposition 3.19). It follows that the action of ![]() $T_{\mathtt J}$ on
$T_{\mathtt J}$ on ![]() $R_{\mathtt J}$ is torsion free.
$R_{\mathtt J}$ is torsion free.
Thanks to [Reference Kato, Naito and Sagaki51, Corollary 4.29], the character comparison forces the torsion-free action of ![]() $T_{\mathtt J}$ on
$T_{\mathtt J}$ on ![]() $R_{\mathtt J}$ to be free. Therefore, the proof of [Reference Kato, Naito and Sagaki51, Theorem 4.30] works in a verbatim way. This proves the case when
$R_{\mathtt J}$ to be free. Therefore, the proof of [Reference Kato, Naito and Sagaki51, Theorem 4.30] works in a verbatim way. This proves the case when ![]() $w = e$. The general case can be easily deduced from the
$w = e$. The general case can be easily deduced from the ![]() $w = e$ case as in [Reference Kato, Naito and Sagaki51, Corollary 4.31].
$w = e$ case as in [Reference Kato, Naito and Sagaki51, Corollary 4.31].
B An application of the Pieri–Chevalley formula
We work in the setting of Section 4.4. The aim of this appendix is to present a method (Theorem B.6) to describe the global sections of nef line bundles on ![]() $\mathscr {Q}' ( v,w )_{{\mathbb K}}$ for
$\mathscr {Q}' ( v,w )_{{\mathbb K}}$ for ![]() $v,w \in W_{\mathrm {af}}$ and an algebraically closed field
$v,w \in W_{\mathrm {af}}$ and an algebraically closed field ![]() ${\mathbb K}$ of characteristic
${\mathbb K}$ of characteristic ![]() $\neq 2$.
$\neq 2$.
For each ![]() $\mu \in P_{+}$, we have an extremal weight module
$\mu \in P_{+}$, we have an extremal weight module ![]() $\mathbb {X} ( \mu )_{{\mathbb K}}$ and its global base
$\mathbb {X} ( \mu )_{{\mathbb K}}$ and its global base ![]() ${\mathbf B} ( \mathbb {X} ( \mu ) )$ borrowed from Theorem 3.14.
${\mathbf B} ( \mathbb {X} ( \mu ) )$ borrowed from Theorem 3.14.
Lemma B.1. Set ![]() $\mathtt J \subset \mathtt I$ and
$\mathtt J \subset \mathtt I$ and ![]() $\mu \in P_{\mathtt J, +}$. A subset of
$\mu \in P_{\mathtt J, +}$. A subset of ![]() ${\mathbf B} ( \mathbb {X} ( \mu ) )$ spans
${\mathbf B} ( \mathbb {X} ( \mu ) )$ spans
 $$ \begin{align*} H^{0} \left( \mathbf{Q}_{G} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G} ( w )_{{\mathbb K}}} ( \mu ) \right)^{\vee} = & H^{0} \left( \mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}} ( \mu ) \right)^{\vee} \subset \mathbb{X} ( \mu )_{{\mathbb K}} \end{align*} $$
$$ \begin{align*} H^{0} \left( \mathbf{Q}_{G} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G} ( w )_{{\mathbb K}}} ( \mu ) \right)^{\vee} = & H^{0} \left( \mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \mathtt J} ( w )_{{\mathbb K}}} ( \mu ) \right)^{\vee} \subset \mathbb{X} ( \mu )_{{\mathbb K}} \end{align*} $$and
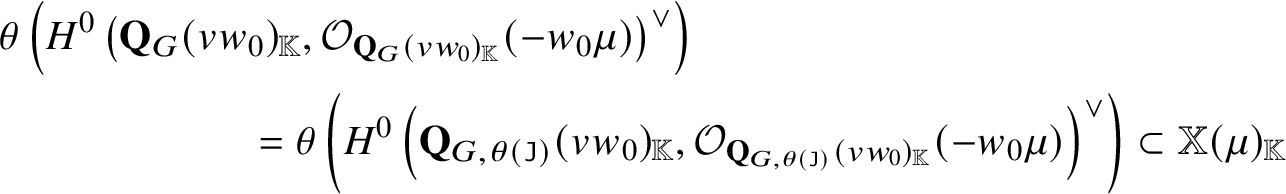 $$ \begin{align*} &\theta \left( H^{0} \left( {\mathbf{Q}}_{G} ( vw_0 )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G} ( vw_0 )_{{\mathbb K}}} ( -w_0\mu ) \right)^{\vee} \right)\\ {} &\qquad\qquad\qquad= \theta \left( H^{0} \left( \mathbf{Q}_{G, \theta ( \mathtt J )} ( vw_0 )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \theta ( \mathtt J )} ( vw_0 )_{\mathbb K}} ( - w_0 \mu ) \right)^{\vee} \right) \subset \mathbb{X} ( \mu )_{\mathbb K} \end{align*} $$
$$ \begin{align*} &\theta \left( H^{0} \left( {\mathbf{Q}}_{G} ( vw_0 )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G} ( vw_0 )_{{\mathbb K}}} ( -w_0\mu ) \right)^{\vee} \right)\\ {} &\qquad\qquad\qquad= \theta \left( H^{0} \left( \mathbf{Q}_{G, \theta ( \mathtt J )} ( vw_0 )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G, \theta ( \mathtt J )} ( vw_0 )_{\mathbb K}} ( - w_0 \mu ) \right)^{\vee} \right) \subset \mathbb{X} ( \mu )_{\mathbb K} \end{align*} $$for each ![]() $w,v \in W_{\mathrm {af}}$.
$w,v \in W_{\mathrm {af}}$.
Corollary A.3 combined with Theorem 4.33 yields
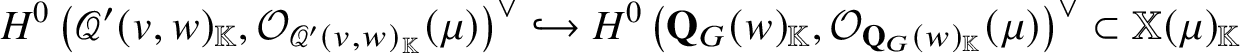 $$ \begin{align} H^{0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \mu ) \right)^{\vee} \hookrightarrow H^{0} \left( \mathbf{Q}_{G} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G} ( w )_{{\mathbb K}}} ( \mu ) \right)^{\vee} \subset \mathbb{X} ( \mu )_{{\mathbb K}} \end{align} $$
$$ \begin{align} H^{0} \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \mu ) \right)^{\vee} \hookrightarrow H^{0} \left( \mathbf{Q}_{G} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_{G} ( w )_{{\mathbb K}}} ( \mu ) \right)^{\vee} \subset \mathbb{X} ( \mu )_{{\mathbb K}} \end{align} $$for each ![]() $w,v \in W_{\mathrm {af}}$.
$w,v \in W_{\mathrm {af}}$.
Lemma B.2. Set ![]() $\mu \in P_{++}$. For each
$\mu \in P_{++}$. For each ![]() $b \in {\mathbf B} ( \mathbb {X} ( \mu ) )$, there exist unique elements
$b \in {\mathbf B} ( \mathbb {X} ( \mu ) )$, there exist unique elements ![]() $\kappa ( b ), \imath ( b ) \in W_{\mathrm {af}}$ with the following properties:
$\kappa ( b ), \imath ( b ) \in W_{\mathrm {af}}$ with the following properties:
1.
 $b \in H^{0} \left ( \mathbf {Q}_{G} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf {Q}_{G} ( w )_{{\mathbb K}}} ( \mu ) \right )^{\vee }$ for
$b \in H^{0} \left ( \mathbf {Q}_{G} ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf {Q}_{G} ( w )_{{\mathbb K}}} ( \mu ) \right )^{\vee }$ for  $w \in W_{\mathrm {af}}$ if and only if
$w \in W_{\mathrm {af}}$ if and only if  $\kappa ( b ) \le _{\frac {\infty }{2}} w$.
$\kappa ( b ) \le _{\frac {\infty }{2}} w$.2.
 $b \in \theta \left ( H^{0} ( \mathbf {Q}_{G} ( vw_0 )_{{\mathbb K}}, {\mathcal O}_{\mathbf {Q}_{G} ( vw_0 )_{{\mathbb K}}} ( -w_0 \mu ) )^{\vee } \right )$ for
$b \in \theta \left ( H^{0} ( \mathbf {Q}_{G} ( vw_0 )_{{\mathbb K}}, {\mathcal O}_{\mathbf {Q}_{G} ( vw_0 )_{{\mathbb K}}} ( -w_0 \mu ) )^{\vee } \right )$ for  $v \in W_{\mathrm {af}}$ if and only if
$v \in W_{\mathrm {af}}$ if and only if  $\imath ( b ) \ge _{\frac {\infty }{2}} v$.
$\imath ( b ) \ge _{\frac {\infty }{2}} v$.
Proof. In view of Corollary A.3, the first assertion is a rephrasing of Lemma 3.15. The second assertion is obtained from the first in view of Lemma 3.17 and formula (2.2).
Corollary B.3. The functions ![]() $\kappa $ and
$\kappa $ and ![]() $\imath $ play the same role as the same-named functions in [Reference Kato, Naito and Sagaki51, (2.17)] (with the opposite convention on the order
$\imath $ play the same role as the same-named functions in [Reference Kato, Naito and Sagaki51, (2.17)] (with the opposite convention on the order ![]() $\le _{\frac {\infty }{2}}$).
$\le _{\frac {\infty }{2}}$).
Proof. Compare Lemma B.2 with [Reference Kato, Naito and Sagaki51, Theorem 2.8].
Corollary B.4. Set ![]() $\mu \in P_{++}$ and
$\mu \in P_{++}$ and ![]() $v,w \in W_{\mathrm {af}}$. The space
$v,w \in W_{\mathrm {af}}$. The space  $H^{0} \left ( \mathscr {Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr {Q}' \left ( v, w \right )_{{\mathbb K}}} ( \mu ) \right )^{\vee }$ is spanned by the subset of
$H^{0} \left ( \mathscr {Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr {Q}' \left ( v, w \right )_{{\mathbb K}}} ( \mu ) \right )^{\vee }$ is spanned by the subset of ![]() $b \in {\mathbf B} ( \mathbb {X} ( \mu ) )$ that satisfies
$b \in {\mathbf B} ( \mathbb {X} ( \mu ) )$ that satisfies ![]() $w \ge _{\frac {\infty }{2}} \kappa ( b ) \ge _{\frac {\infty }{2}} \imath ( b ) \ge _{\frac {\infty }{2}} v$.
$w \ge _{\frac {\infty }{2}} \kappa ( b ) \ge _{\frac {\infty }{2}} \imath ( b ) \ge _{\frac {\infty }{2}} v$.
Proof. This is a rephrasing of Theorem 4.33 for ![]() $\mathtt J = \emptyset $.
$\mathtt J = \emptyset $.
Theorem B.5 [Reference Kato, Naito and Sagaki51]
Set ![]() $w \in W_{\mathrm {af}}$ and
$w \in W_{\mathrm {af}}$ and ![]() $\lambda \in P_+$. There exists a unique collection of elements
$\lambda \in P_+$. There exists a unique collection of elements  $a^u_w ( \lambda ) \in \mathbb {Z} \left [q^{-1}\right ][H] (u \in W_{\mathrm {af}})$ such that
$a^u_w ( \lambda ) \in \mathbb {Z} \left [q^{-1}\right ][H] (u \in W_{\mathrm {af}})$ such that
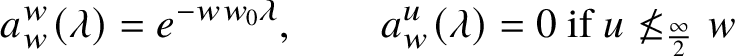 $$ \begin{align*}a^w_w ( \lambda ) = e^{- w w_0\lambda}, \qquad a^u_w ( \lambda ) = 0 \text{ if } u \not\le_{\frac{\infty}{2}} w\end{align*} $$
$$ \begin{align*}a^w_w ( \lambda ) = e^{- w w_0\lambda}, \qquad a^u_w ( \lambda ) = 0 \text{ if } u \not\le_{\frac{\infty}{2}} w\end{align*} $$and
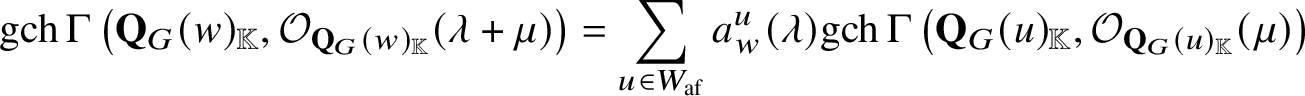 $$ \begin{align*}\mathrm{gch}\, \Gamma \left( \mathbf{Q}_G ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_G ( w )_{{\mathbb K}}} ( \lambda + \mu ) \right) = \sum_{u \in W_{\mathrm{af}}} a^u_w ( \lambda ) \mathrm{gch}\, \Gamma \left( \mathbf{Q}_G ( u )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_G ( u )_{{\mathbb K}}} ( \mu ) \right)\end{align*} $$
$$ \begin{align*}\mathrm{gch}\, \Gamma \left( \mathbf{Q}_G ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_G ( w )_{{\mathbb K}}} ( \lambda + \mu ) \right) = \sum_{u \in W_{\mathrm{af}}} a^u_w ( \lambda ) \mathrm{gch}\, \Gamma \left( \mathbf{Q}_G ( u )_{{\mathbb K}}, {\mathcal O}_{\mathbf{Q}_G ( u )_{{\mathbb K}}} ( \mu ) \right)\end{align*} $$for every ![]() $\mu \in P_{++}$.
$\mu \in P_{++}$.
The goal of this appendix is to prove the following:
Theorem B.6. Set ![]() $w,v \in W_{\mathrm {af}}$ and
$w,v \in W_{\mathrm {af}}$ and ![]() $\lambda \in P_+$. Let
$\lambda \in P_+$. Let  $\left \{ a^v_w ( \lambda ) \right \}_{v \in W_{\mathrm {af}}}$ be the collection of elements in Theorem B.5. Then we have
$\left \{ a^v_w ( \lambda ) \right \}_{v \in W_{\mathrm {af}}}$ be the collection of elements in Theorem B.5. Then we have
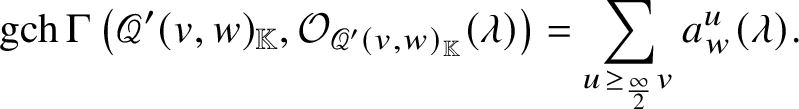 $$ \begin{align*}\mathrm{gch}\, \Gamma \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) = \sum_{u \ge_{\frac{\infty}{2}} v} a^u_w ( \lambda ).\end{align*} $$
$$ \begin{align*}\mathrm{gch}\, \Gamma \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda ) \right) = \sum_{u \ge_{\frac{\infty}{2}} v} a^u_w ( \lambda ).\end{align*} $$Proof. The proof of the numerical part of Theorem B.5 is [Reference Kato, Naito and Sagaki51, Theorem 3.5] (proved in [Reference Kato, Naito and Sagaki51, §8.1]), and it counts the elements of ![]() ${\mathbf B} ( \mathbb {X} ( \lambda + \mu ) )$ that contribute
${\mathbf B} ( \mathbb {X} ( \lambda + \mu ) )$ that contribute  $\Gamma \left ( \mathbf {Q}_G ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf {Q}_G ( w )_{{\mathbb K}}} ( \lambda + \mu ) \right )^{\vee } = \mathbb {W} _{ww_0} ( \lambda + \mu )_{{\mathbb K}}$ in two ways. In particular, we can additionally impose the condition
$\Gamma \left ( \mathbf {Q}_G ( w )_{{\mathbb K}}, {\mathcal O}_{\mathbf {Q}_G ( w )_{{\mathbb K}}} ( \lambda + \mu ) \right )^{\vee } = \mathbb {W} _{ww_0} ( \lambda + \mu )_{{\mathbb K}}$ in two ways. In particular, we can additionally impose the condition ![]() $\imath ( \bullet ) \ge _{\frac {\infty }{2}} v$ for
$\imath ( \bullet ) \ge _{\frac {\infty }{2}} v$ for ![]() ${\mathbf B} ( \mathbb {X} ( \lambda + \mu ) )$ to deduce that
${\mathbf B} ( \mathbb {X} ( \lambda + \mu ) )$ to deduce that
 $$ \begin{align*}\mathrm{gch}\, \Gamma \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda + \mu ) \right) = \sum_{u \le_{\frac{\infty}{2}} v} a^u_w ( \lambda ) \mathrm{gch}\, \Gamma \left( \mathscr{Q}' ( u, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( u, w \right)_{{\mathbb K}}} ( \mu ) \right)\end{align*} $$
$$ \begin{align*}\mathrm{gch}\, \Gamma \left( \mathscr{Q}' ( v, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( v, w \right)_{{\mathbb K}}} ( \lambda + \mu ) \right) = \sum_{u \le_{\frac{\infty}{2}} v} a^u_w ( \lambda ) \mathrm{gch}\, \Gamma \left( \mathscr{Q}' ( u, w )_{{\mathbb K}}, {\mathcal O}_{\mathscr{Q}' \left( u, w \right)_{{\mathbb K}}} ( \mu ) \right)\end{align*} $$for every ![]() $\mu \in P_{++}$ in view of Corollary B.4. The (
$\mu \in P_{++}$ in view of Corollary B.4. The (![]() $H \times \mathbb {G}_m$)-equivariant Euler characteristic of
$H \times \mathbb {G}_m$)-equivariant Euler characteristic of ![]() ${\mathcal O}_{\mathscr {Q}' \left ( v, w \right )_{{\mathbb K}}} ( \mu )$ (
${\mathcal O}_{\mathscr {Q}' \left ( v, w \right )_{{\mathbb K}}} ( \mu )$ (![]() $\mu \in P$) is a rational function on the characters of H, and we can specialise to
$\mu \in P$) is a rational function on the characters of H, and we can specialise to ![]() $\mu = 0$. Now we apply Theorem 4.33 to deduce
$\mu = 0$. Now we apply Theorem 4.33 to deduce
for every ![]() $\mu \in P_+$. This implies the desired equality.
$\mu \in P_+$. This implies the desired equality.
1. In view of Corollary 4.35 and Remark 4.36, Theorem B.6 describes the space of global sections of
 ${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda )$ for every
${\mathcal O}_{\mathscr {Q}^{\prime }_{\mathtt J} \left ( v, w \right )_{{\mathbb K}}} ( \lambda )$ for every  $w,v \in W_{\mathrm {af}}$,
$w,v \in W_{\mathrm {af}}$,  $\mathtt J \subset \mathtt I$ and
$\mathtt J \subset \mathtt I$ and  $\lambda \in P_{\mathtt J,+}$.
$\lambda \in P_{\mathtt J,+}$.2. In conjunction with Theorem 4.33, Theorem B.6 can be seen as an analogue of [Reference Lakshmibai and Littelmann59, Theorem 34] for semi-infinite flag manifolds.
3. Thanks to [Reference Kato, Naito and Sagaki51, §3], we have a combinatorial rule to express
 $a^u_w ( \lambda )$s.
$a^u_w ( \lambda )$s.
Acknowledgments
The author would like to thank Prakash Belkale, Ievgen Makedonskyi, Leonardo Mihalcea, Katsuyuki Naoi and Daisuke Sagaki for helpful discussions. This work was supported in part by JSPS KAKENHI grants JP26287004 and JP19H01782.
Conflict of Interest:
None.