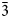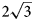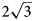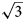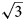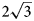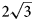Introduction
Charmarite, ideally Mn4Al2(OH)12CO3⋅3H2O, is a member of the quintinite group (with the ratio between di- and trivalent cations equal to M2+:M3+ = 2:1), which is a part of the hydrotalcite supergroup (Mills et al., Reference Mills, Christy, Génin, Kameda and Colombo2012), a natural branch of the layered double hydroxide (LDH) family (Rives, Reference Rives2001; Evans and Slade, Reference Evans, Slade, Duan and Evans2005). Layered double hydroxides are united by a common structural motif in which brucite-like metal-hydroxyl layers (or octahedral sheets) formed by di- and trivalent (in specific cases also monovalent) metals and interlayers alternate (Rives, Reference Rives2001). The positive charge of the brucite-like metal-hydroxide layers is compensated by the negatively charged interlayer species. In some cases, metal-hydroxide layers are gibbsite-based (formed primarily by trivalent cations), where monovalent cations [or divalent cations as shown by synthetic materials (Andersen et al., Reference Andersen, Henriksen, Wang, Ravnsbæk, Hansen and Nielsen2021)] produce the positive charge of the layers (Serna et al., Reference Serna1982; Sissoko et al., Reference Sissoko, Iyagba, Sahai and Biloen1985; Britto and Kamath, Reference Britto and Kamath2011; Karpenko et al., Reference Karpenko, Zhitova, Pautov, Agakhanov, Siidra, Krzhizhanovskaya, Rassulov and Bocharov2020). Layered double hydroxides are used in catalytic (Karim et al., Reference Karim, Hassani, Eghbali and Nidheesh2022; Xu and Wei, Reference Xu and Wei2018; Bosa et al., Reference Bosa, Silva, Brito, Terzi, Wypych and Nakagaki2023) and pharmaceutical (Guilherme et al., Reference Guilherme, Cunha, de Paula, de Araujo and Constantino2022) applications, are of interest from the material science point of view as sorbents and ion exchangers (Forano et al., Reference Forano, Hibino, Leroux and Taviot-Guého2006), and are useful for the design of new materials (Sotiles and Wypych, Reference Sotiles and Wypych2019). The synthetic analogue of charmarite can be obtained by co-precipitation and may be of interest for catalytic applications (Grand et al., Reference Grand, Palmer and Frost2010).
Charmarite was first described in well-shaped hexagonal crystals from the Mont Saint-Hilaire alkaline complex, Québec, Canada in two polytypic modifications, 2H and 3T (Chao and Gault, Reference Chao and Gault1997). In the cited paper, charmarite was described together with two other new minerals that have the same stoichiometry: its Mg-analogue quintinite, Mg4Al2(OH)12CO3⋅3H2O, and its Fe2+-analogue caresite, Fe2+4Al2(OH)12CO3⋅3H2O. The work by Chao and Gault (Reference Chao and Gault1997) turned out to be pioneering in the approach to quintinite (and, consequently, quintinite-group minerals), which has been finally separated from hydrotalcite after 155 years, during which time two phases of different stoichiometry and properties where under the common name ‘hydrotalcite’. Later studies showed a wider distribution of quintinite compared to hydrotalcite and fundamental structural differences between the two minerals, especially with respect to the layer charge densities and associated properties (Wang et al., Reference Wang, Liu, Wang, Chuang and Chiang2009; Mills et al., Reference Mills, Christy and Schmitt2016; Zhitova et al., Reference Zhitova, Krivovichev, Pekov, Yakovenchuk and Pakhomovsky2016, Reference Zhitova, Krivovichev, Yakovenchuk, Ivanyuk, Pakhomovsky and Mikhailova2018).
Crystal structures of most LDHs remain unknown, owing to the absence of single crystals for synthetic materials and, as a result, the absence of starting crystal-structure models for the refinement of powder X-ray diffraction data. In contrast, a number of structure models for synthetic LDHs have been studied based on investigations of their natural analogues (see summary in Mills et al., Reference Mills, Christy, Génin, Kameda and Colombo2012 and Zhitova et al., Reference Zhitova, Krivovichev, Pekov and Greenwell2019a).
To date, charmarite is an endemic mineral with an unknown crystal structure. Charmarite is closely related to quintinite and caresite in terms of stoichiometry and, in general, chemistry. This prompts us to discuss these minerals together. In the work of Chao and Gault (Reference Chao and Gault1997) the unit-cell parameters of quintinite, caresite and charmarite have been determined by single-crystal photographic methods and refined by least-squares methods using powder XRD data (Table 1). Based on the single-crystal X-ray photographs Chao and Gault (Reference Chao and Gault1997) suggested the presence of a 2$\sqrt 3 a{\rm ^{\prime}}\;\times 2\sqrt 3 a{\rm ^{\prime}}\;( {\rm or}$![]() $\sqrt {12} a{\rm ^{\prime}}$
$\sqrt {12} a{\rm ^{\prime}}$![]() × $\sqrt {12} a{\rm ^{\prime}})$
× $\sqrt {12} a{\rm ^{\prime}})$![]() superstructure in all three minerals interpreted as ordering of di- and trivalent cations (Mills et al., Reference Mills, Christy, Génin, Kameda and Colombo2012). The first crystal structure determination of quintinite (Arakcheeva et al., Reference Arakcheeva, Pushcharovskii, Rastsvetaeva, Atencio and Lubman1996) proposed the presence of only the $\sqrt 3 a{\rm ^{\prime}}\;\times \sqrt 3 a{\rm ^{\prime}}$
superstructure in all three minerals interpreted as ordering of di- and trivalent cations (Mills et al., Reference Mills, Christy, Génin, Kameda and Colombo2012). The first crystal structure determination of quintinite (Arakcheeva et al., Reference Arakcheeva, Pushcharovskii, Rastsvetaeva, Atencio and Lubman1996) proposed the presence of only the $\sqrt 3 a{\rm ^{\prime}}\;\times \sqrt 3 a{\rm ^{\prime}}$![]() superstructure (a’ is not listed further in designation of superstructures) due to the ordered arrangement of di- and trivalent cations. Systematic studies of crystal structures of quintinite from different worldwide localities indicated the existence of at least five polytypes differing by the presence or absence of $\sqrt 3 \;\times \sqrt 3$
superstructure (a’ is not listed further in designation of superstructures) due to the ordered arrangement of di- and trivalent cations. Systematic studies of crystal structures of quintinite from different worldwide localities indicated the existence of at least five polytypes differing by the presence or absence of $\sqrt 3 \;\times \sqrt 3$![]() Mg–Al ordering combined with different stacking sequences (Krivovichev et al., Reference Krivovichev, Yakovenchuk, Zhitova, Zolotarev, Pakhomovsky and Ivanyuk2010a, Reference Krivovichev, Yakovenchuk, Zhitova, Zolotarev, Pakhomovsky and Ivanyuk2010b; Zhitova et al., Reference Zhitova, Yakovenchuk, Krivovichev, Zolotarev, Pakhomovsky and Ivanyuk2010, Reference Zhitova, Krivovichev, Yakovenchuk, Ivanyuk, Pakhomovsky and Mikhailova2018, Reference Zhitova, Sheveleva, Zolotarev and Krivovichev2023a) (Table 1). The 2$\sqrt 3 \;\times 2\sqrt 3 \;( {\rm or}$
Mg–Al ordering combined with different stacking sequences (Krivovichev et al., Reference Krivovichev, Yakovenchuk, Zhitova, Zolotarev, Pakhomovsky and Ivanyuk2010a, Reference Krivovichev, Yakovenchuk, Zhitova, Zolotarev, Pakhomovsky and Ivanyuk2010b; Zhitova et al., Reference Zhitova, Yakovenchuk, Krivovichev, Zolotarev, Pakhomovsky and Ivanyuk2010, Reference Zhitova, Krivovichev, Yakovenchuk, Ivanyuk, Pakhomovsky and Mikhailova2018, Reference Zhitova, Sheveleva, Zolotarev and Krivovichev2023a) (Table 1). The 2$\sqrt 3 \;\times 2\sqrt 3 \;( {\rm or}$![]() $\sqrt {12}$
$\sqrt {12}$![]() × $\sqrt {12} )$
× $\sqrt {12} )$![]() structure was not determined and refined for any LDH (for almost 30 years after the first report) and was considered questionable. Moreover, the crystal chemical mechanism of potential formation of the $2\sqrt 3 \;\times 2\sqrt 3 \;$
structure was not determined and refined for any LDH (for almost 30 years after the first report) and was considered questionable. Moreover, the crystal chemical mechanism of potential formation of the $2\sqrt 3 \;\times 2\sqrt 3 \;$![]() superstructure in LDHs remained unclear, as experimental observations have shown that the ordering of di- and trivalent cations (rather common for LDHs) do not result in such long-periodic (within xy plane) structures (e.g. Walenta Reference Walenta1984; Bonaccorsi et al., Reference Bonaccorsi, Merlino and Orlandi2007). This attracted our attention to the crystal chemical investigation of charmarite, which is a subject of this work.
superstructure in LDHs remained unclear, as experimental observations have shown that the ordering of di- and trivalent cations (rather common for LDHs) do not result in such long-periodic (within xy plane) structures (e.g. Walenta Reference Walenta1984; Bonaccorsi et al., Reference Bonaccorsi, Merlino and Orlandi2007). This attracted our attention to the crystal chemical investigation of charmarite, which is a subject of this work.
Table 1. Unit-cell parameters of quintinite-group minerals: charmarite, caresite and quintinite.

(1) a’ is the distance between two neighbouring M cations;
(2) d 00n is the distance between two neighbouring octahedral sheets.
Materials
The charmarite studied in this work originates from the Mont Saint-Hilaire alkaline complex. The specimen was collected in 2004 and is in a private collection. The mineral occurs as hexagonal yellowish crystals and curved colourless hexagonal plates up to 0.05 mm in size (Fig. 1), grouped chaotically in clusters that overgrow dark-brown tabular laverovite crystals (1 cm × 1 cm in size) in association with white albite.

Figure 1. Back-scattered electron image of a bunch of charmarite crystals studied in this work.
Methods
Chemical composition
The chemical analyses (5 points) were carried out with a Hitachi FlexSEM 1000 scanning electron microscope equipped with energy-dispersive spectrometry (EDS) Xplore Contact 30 detector and Oxford AZtecLive STD system of analysis. Analytical conditions were: accelerating voltage 15 kV, beam current 5 nA and beam size 2 μm. The standards used are given in Table 2.
Table 2. Chemical composition of charmarite.

(1) calculated by charge balance;
(2) calculated from the ideal stoichiometry of charmarite.
S.D. – standard deviation
Single-crystal X-ray diffraction
The single-crystal X-ray diffraction (SCXRD) data have been obtained from tabular hexagonal crystals of reddish colour. The experiment was carried out with MoKα radiation by means of a Bruker Apex II Duo diffractometer (Bruker, Billerica, MA, USA) operated at 50 kV/1 mA and equipped with a charge coupled device (CCD) area detector.
The unit-cell check based on 250 reflections indicated the trigonal symmetry of the mineral (P cell) with a = b = 10.97 and c = 15.08 Å. The full SCXRD data set was collected and separately processed using Bruker and CrysAlis software in automatic and manual (including a check for twin domains) mode. The intensity data were reduced and corrected for Lorentz, polarisation, and background effects using the CrysAlis PRO program (CrysAlis PRO, 2014). A semi-empirical absorption-correction based upon the intensities of equivalent reflections was applied (Bruker-AXS, 2014, Sheldrick, Reference Sheldrick2015). The unit-cell parameters were refined by the least-squares methods. Using Olex2 (Dolomanov et al., Reference Dolomanov, Blake, Champness and Schröder2009), the structure was solved with the SHELXS (Sheldrick, Reference Sheldrick2008) structure solution program using direct methods and refined with the SHELXL (Sheldrick, Reference Sheldrick2015) refinement package using least squares minimisation. The two-component twinning by matrix {$\bar{1}$![]() 0 0 / 0 $\bar{1}$
0 0 / 0 $\bar{1}$![]() 0 / 0 0 1} was applied to the structure refinement. Crystal structures were visualised using the Vesta program (Momma and Izumi, Reference Momma and Izumi2011). All procedures resulted in the confirmation of the aforementioned lattice. The topology of the model obtained was reasonable and the search for a higher symmetry using the Platon software (Spek, Reference Spek2003) confirmed the correct choice of the space-group symmetry. Note that we have also obtained structure models in the space groups P3, P $\bar{3}$
0 / 0 0 1} was applied to the structure refinement. Crystal structures were visualised using the Vesta program (Momma and Izumi, Reference Momma and Izumi2011). All procedures resulted in the confirmation of the aforementioned lattice. The topology of the model obtained was reasonable and the search for a higher symmetry using the Platon software (Spek, Reference Spek2003) confirmed the correct choice of the space-group symmetry. Note that we have also obtained structure models in the space groups P3, P $\bar{3}$![]() m1 and P $\bar{6}$
m1 and P $\bar{6}$![]() 2m, but none of these provided an improvement over the P $\bar{3}$
2m, but none of these provided an improvement over the P $\bar{3}$![]() model. The alternative refinements in space group P $\bar{3}$
model. The alternative refinements in space group P $\bar{3}$![]() m1 resulted in R 1 = 0.1883 based on 2222 unique observed reflections and without considerable structural difference and in the space group P $\bar{6}$
m1 resulted in R 1 = 0.1883 based on 2222 unique observed reflections and without considerable structural difference and in the space group P $\bar{6}$![]() 2m the refinement converged to R 1 = 0.0827 based on 2202 unique observed reflections with non-equivalent interlayers that seemed to us crystal chemically unreasonable.
2m the refinement converged to R 1 = 0.0827 based on 2202 unique observed reflections with non-equivalent interlayers that seemed to us crystal chemically unreasonable.
Powder X-ray diffraction
Powder XRD data were collected from an intergrowth of lamellar charmarite crystals up to 0.2 mm in size using a Rigaku R-Axis Rapid II diffractometer (Debye-Sсherrer geometry and d = 127.4 mm) equipped with a rotating anode X-ray source (CoKα and λ = 1.79021 Å) and a curved image plate detector. The data were integrated using the software package Osc2Tab/SQRay (Britvin et al., Reference Britvin, Dolivo-Dobrovolsky and Krzhizhanovskaya2017) and processed using the International Centre for Diffraction Data (ICDD) database incorporated into the PDXL program (Rigaku, Reference Rigaku2018). The h, k and l values were calculated using the software package VESTA (Momma and Izumi, Reference Momma and Izumi2011) from the crystal structure model of charmarite obtained in this work. The unit-cell parameters of charmarite were refined by the Le Bail method implemented in Topas software (Bruker-AXS, 2009) using the starting structural model of charmarite reported therein. The refinement was based on the reflections in the 2θ region from 10 to 80°. The background was modelled by a Chebyshev polynomial approximation of the 12-th order; preferred orientation of the sample along the [002] direction was confirmed during the refinement.
Raman spectroscopy
The Raman spectrum of charmarite was obtained by Horiba Jobin-Yvon LabRam HR800 spectrometer, equipped with a solid-state laser (λ = 532 nm) at 50 mW output power and ~6 mW power at the sample surface for an area of 2 μm × 2 μm. The spectrum was recorded with resolution 2 cm–1 at room temperature on the plate used previously for powder XRD data collection that had been placed on a glass slide. The plate had been cleared of paratone oil (used for sample attachment in the powder XRD experiment), but some traces may remain. The spectrum was further processed using LabSpec (Horiba) software.
Results
Chemical composition
The chemical composition of charmarite in wt.% is given in Table 2. The empirical formula calculated on the basis of the sum of all metal cations = 6 apfu and OH = 12 apfu is: (Mn3.94Mg0.03Fe0.01)Σ3.98Al2.01(OH)12CO3⋅3H2O. The CO2 content has been calculated by charge balance. The OH and H2O content has been calculated from stoichiometry of charmarite.
Single-crystal X-ray diffraction data
The data obtained for charmarite were indexed in the trigonal cell, space group P $\bar{3}$![]() with the following unit-cell parameters: a = 10.9630(4), c = 15.0732(5) Å and V = 1568.89(12) Å3. The correct choice of the unit cell is supported by the analysis of the reconstructed reciprocal space slices where regular superstructure reflections are clearly visible (Fig. 2). The crystal structure was solved and refined in the space group P $\bar{3}$
with the following unit-cell parameters: a = 10.9630(4), c = 15.0732(5) Å and V = 1568.89(12) Å3. The correct choice of the unit cell is supported by the analysis of the reconstructed reciprocal space slices where regular superstructure reflections are clearly visible (Fig. 2). The crystal structure was solved and refined in the space group P $\bar{3}$![]() to R 1 = 0.075 for 3801 unique observed reflections with F o > 2σ(F o) (Table 3). Atom coordinates, site occupancies and displacement parameters are given in Table 4. Selected bond lengths and angles are listed in Table 5, the hydrogen bonding scheme is shown in Table 6. The anisotropic displacement parameters are given in Table S1. The crystallographic information file (cif) has been deposited (1) via the joint Cambridge Crystal Data Centre CCDC/FIZ Karlsruhe deposition service; the deposition number is CSD 2285202 and (2) with the Principal Editor of Mineralogical Magazine and is available as Supplementary Material (see below).
to R 1 = 0.075 for 3801 unique observed reflections with F o > 2σ(F o) (Table 3). Atom coordinates, site occupancies and displacement parameters are given in Table 4. Selected bond lengths and angles are listed in Table 5, the hydrogen bonding scheme is shown in Table 6. The anisotropic displacement parameters are given in Table S1. The crystallographic information file (cif) has been deposited (1) via the joint Cambridge Crystal Data Centre CCDC/FIZ Karlsruhe deposition service; the deposition number is CSD 2285202 and (2) with the Principal Editor of Mineralogical Magazine and is available as Supplementary Material (see below).

Figure 2. The reciprocal space slices of charmarite: (a) hk0 section; (b) h0l section; (c) enlarged part of hk0 section, indexed; (d) enlarged part of h0l section, indexed; and (e) juxtaposition of hk0 and 0kl sections.
Table 3. Crystal data, data collection information and structure refinement details for charmarite-2T.

* for the formula Mn3.7Al2.3(OH)12CO3⋅1.9H2O.
Table 4. Atom coordinates, equivalent isotropic displacement parameters (Å2), site occupancies and assigned site populations for charmarite-2T.

* epfu – electrons per formula unit; epfu for Mn8Al4 (as in ideal formula) is 126 e –.
**Note: [(CO3)(H2O)3.5]2
s.o.f – site occupation factor;
Table 5. Selected bond distances (in Å) for charmarite-2T.

Table 6. Hydrogen bonding scheme for charmarite-2T.

Juxtaposition of the hk0 and 0kl reciprocal space sections is shown in Fig. 2e that outlines possible unit cells based on main and superstructure reflections and justifies the choice of lattice with the 2$\sqrt 3$![]() × 2$\sqrt 3$
× 2$\sqrt 3$![]() (or 2$\sqrt 3$
(or 2$\sqrt 3$![]() a’) supercell. The analysis of spots along l (stacking direction) shows that (1) a two-layer hexagonal cell is well sustained (k = 0, 6); (2) spots with k = 1 and 3 are characterised by some diffuse scattering, but are clearly separated and assigned to the 2$\sqrt 3$
a’) supercell. The analysis of spots along l (stacking direction) shows that (1) a two-layer hexagonal cell is well sustained (k = 0, 6); (2) spots with k = 1 and 3 are characterised by some diffuse scattering, but are clearly separated and assigned to the 2$\sqrt 3$![]() × 2$\sqrt 3$
× 2$\sqrt 3$![]() ordering along the stacking direction; and (3) the strongest diffuse scattering is observed for the spots with k = 2 and 4 that mainly refer to the $\sqrt 3$
ordering along the stacking direction; and (3) the strongest diffuse scattering is observed for the spots with k = 2 and 4 that mainly refer to the $\sqrt 3$![]() × $\sqrt 3$
× $\sqrt 3$![]() superstructure. Possibly, the diffuse character of the spots with k = 2 and 4 reflects partial Mn–Al disorder in the octahedral sites along the stacking direction (with formation of mixed-occupied positions in some layers) as observed herein.
superstructure. Possibly, the diffuse character of the spots with k = 2 and 4 reflects partial Mn–Al disorder in the octahedral sites along the stacking direction (with formation of mixed-occupied positions in some layers) as observed herein.
Powder X-ray diffraction data
Powder XRD data are provided in Table 7, the XRD pattern is presented in Fig. 3. The powder XRD pattern obtained of charmarite is very similar to that from the ICDD card #00-051-1529 (Chao and Gault, Reference Chao and Gault1997), which corresponds to the original description of charmarite-2H (crystal structure undetermined, see comparison in Table 7). The polytype notation by Ramsdell (Reference Ramsdell1947) is based on the number of layers within the unit cell and symmetry of the crystal structure. In LDHs there are two main types of layer stacking sequences: hexagonal that normally results in two-layer cells and rhombohedral that normally results in three-layer cells with symmetry reduction from trigonal to monoclinic one-layer cells being also rather widespread (Krivovichev et al., Reference Krivovichev, Yakovenchuk, Zhitova, Zolotarev, Pakhomovsky and Ivanyuk2010a, Reference Krivovichev, Yakovenchuk, Zhitova, Zolotarev, Pakhomovsky and Ivanyuk2010b; Zhitova et al., Reference Zhitova, Krivovichev, Yakovenchuk, Ivanyuk, Pakhomovsky and Mikhailova2018). From powder XRD data and preliminary SCXRD data the layer stacking sequence can be determined: hexagonal or rhombohedral, commonly interpreted as 2H and 3T/3R polytypes, respectively. However, the full symmetry of the crystal structure (e.g. T, H or M) can be affected by cation and/or anion ordering and requires detailed structure analysis. In the original work by Chao and Gault (Reference Chao and Gault1997) the polytypes for charmarite, caresite and quintinite were determined as 2H and 3T. This study shows (by structure refinement using SCXRD data) cation and anion ordering for charmarite with the hexagonal layer stacking sequence resulting in a trigonal cell and polytype notation as 2T. The difference in the suffix for polytype notation of 2T for charmarite compared to the 2H used by Chao and Gault (Reference Chao and Gault1997) is not due to any structure differences, but due to structure peculiarities revealed by SCXRD herein. The refined unit-cell parameters of charmarite-2T from the powder XRD data are as follows: a = 10.9934(6), c = 15.1426(11) Å and V = 1584.9(2) Å3.

Figure 3. The powder XRD pattern for charmarite.
Table 7. Powder X-ray diffraction data obtained for charmarite-2T compared to the original data for charmarite-2H provided by Chao and Gault (Reference Chao and Gault1997)*.

* Charmarite-2H, ICDD # 00-051-1529; n.p. – not provided by Chao and Gault (Reference Chao and Gault1997). The five strongest reflections are highlighted in bold type.
For the easier comparison of the lattice parameters obtained by different methods we have reduced them to the sublattice, i.e. the distance between the two nearest metal atoms (a’) and the distance between two octahedral layers (d 00n). The obtained values are a’ = a/2/$\sqrt 3$![]() = 3.17 Å obtained by powder XRD versus 3.16 Å obtained by single-crystal X-ray diffraction and d 00n = c/2 = 7.57 Å obtained by powder X-ray diffraction versus 7.54 Å obtained by single-crystal X-ray diffraction. The comparison shows that isomorphic substitution (influencing the in-plane a’ parameter) is negligible. The difference in the c parameter (d 00n) is larger, but also insignificant for layered compounds and fluctuates around the value of 7.56 Å, which is most often found in stoichiometric quintinite. In view of the insignificance of these changes in d 00n, it seems that they may be more likely to be associated with a change in the height of the octahedral layer due distortions of the octahedra, rather than the change in stoichiometry (variations in the M 2+:M 3+ ratio), as the second factor usually causes more significant changes in the interlayer distance, but the height of the octahedral layer fluctuates within 0.0n Å (Zhitova et al., Reference Zhitova, Krivovichev, Pekov, Yakovenchuk and Pakhomovsky2016). Finally, unit-cell parameters determined by single-crystal and powder X-ray diffraction differ by ~1% (due to multiplication of these small differences), which is a good agreement, taking into account that different crystals of charmarite were studied by these diffraction techniques.
= 3.17 Å obtained by powder XRD versus 3.16 Å obtained by single-crystal X-ray diffraction and d 00n = c/2 = 7.57 Å obtained by powder X-ray diffraction versus 7.54 Å obtained by single-crystal X-ray diffraction. The comparison shows that isomorphic substitution (influencing the in-plane a’ parameter) is negligible. The difference in the c parameter (d 00n) is larger, but also insignificant for layered compounds and fluctuates around the value of 7.56 Å, which is most often found in stoichiometric quintinite. In view of the insignificance of these changes in d 00n, it seems that they may be more likely to be associated with a change in the height of the octahedral layer due distortions of the octahedra, rather than the change in stoichiometry (variations in the M 2+:M 3+ ratio), as the second factor usually causes more significant changes in the interlayer distance, but the height of the octahedral layer fluctuates within 0.0n Å (Zhitova et al., Reference Zhitova, Krivovichev, Pekov, Yakovenchuk and Pakhomovsky2016). Finally, unit-cell parameters determined by single-crystal and powder X-ray diffraction differ by ~1% (due to multiplication of these small differences), which is a good agreement, taking into account that different crystals of charmarite were studied by these diffraction techniques.
Raman spectroscopy
The Raman spectrum of charmarite-2T is shown in Fig. 4a,b and compared with the Raman spectra of quintinite and caresite in Fig. 4 and Table 8. The spectrum contains bands of O–H stretching vibrations and symmetric C–O stretching vibrations that are in agreement with charmarite chemistry in terms of light elements (C, H), the determination of which is problematic by other methods. In general, the Raman spectra of charmarite, quintinite and caresite are similar (Table 8), which confirms their structural and chemical similarity.

Figure 4. Raman spectrum of charmarite obtained therein: (a) 4000–2500 cm–1 range and (b) 1500–0 cm–1 range compared to Raman spectra of caresite available in the RRUFF database (under ID: R120028): (c) 4000–2500 cm–1 range and (d) 1500–0 cm–1 range and quintinite (e,f).
Table 8. Raman bands observed in the spectra of charmarite, caresite and quintinite and their assignments.

* https://rruff.info/Caresite, accessed on 15 July 2023, Lafuente et al. (Reference Lafuente, Downs, Yang, Stone, Armbruster and Danisi2015).
sh – shoulder; w – weak
Discussion
The crystal structure of charmarite consists of two types of metal-hydroxide layers located at the levels z = 0 (type 1) and ½ (type 2) and two interlayers located at the levels of z = ¼ and ¾ (Fig. 5). Each metal-hydroxide layer consists of four metal sites M(1–4) for octahedral sheet 1 and M(5–8) for octahedral sheet 2 (Fig. 6). Each M site is octahedrally coordinated by OH groups. The M(OH)6 octahedra are edge-shared to form brucite-type sheets.

Figure 5. The crystal structure of charmarite-2T: (a) projected perpendicular to the stacking direction and (b) within the xy plane showing superstructure meshes [the unit cell is outlined by a solid black line; the 2 × 2 superstructure of interlayer carbonate groups (z = 0.75) is shown by a blue dashed line; the $\sqrt 3$![]() × $\sqrt 3$
× $\sqrt 3$![]() superstructure of M 2+ and M 3+ cations within the octahedral sheet (z = 0.5) is outlined by an orange dashed line] (see explanations in the text). Crystal structures were visualised using the Vesta program (Momma and Izumi, Reference Momma and Izumi2011).
superstructure of M 2+ and M 3+ cations within the octahedral sheet (z = 0.5) is outlined by an orange dashed line] (see explanations in the text). Crystal structures were visualised using the Vesta program (Momma and Izumi, Reference Momma and Izumi2011).

Figure 6. The crystal structure of charmarite-2T: (a) octahedral sheet type 1; (b) interlayer at z = ¼; (c) octahedral sheet type 2; and (d) interlayer at z = ¾. Crystal structures were visualised using the Vesta program (Momma and Izumi, Reference Momma and Izumi2011).
The octahedral sheets of type 2 are characterised by the contrasting occupancy of the M sites: the M(5) and M(6) sites are nearly fully occupied by Mn, while the M(7) and M(8) sites are almost completely occupied by Al. This agrees well with the average M‒O distances and the polyhedral volumes of the respective octahedra: the Mn-occupied octahedra (both M(5)- and M(6)-centred) have an average M(5,6)‒O distance of 2.18 Å (and polyhedral volumes of 12.8–12.9 Å3), while the Al-centred octahedra have <M(7)‒O> = 1.92 Å and <M(8)‒O> = 1.90 Å (with polyhedral volumes equal to 9.3 and 9.1 Å3, respectively). The Mn-centred octahedra exhibit significant angular distortion (Table 9) in order to fit to the lengths of shared edges with neighbouring small Al(OH)6 octahedra (the shared edge of ~2.58 Å) and large Mn(OH)6 octahedra (the shared edge of ~2.99 Å) (Fig. 6c). The geometry of the Al(OH)6 octahedra seems to be unaffected by distortion (Table 9). The total occupancy of the M(5–8) sites agrees with charmarite ideal stoichiometry Mn2Al with a small amount of a lighter cation, possibly Mg (total electrons per formula unit = 121(3) e –, while the ratio Mn:Al = 2:1 suggesting the ideal epfu value of 126 e –; see Table 5).
Table 9. Some geometrical parameters for MO6 octahedra and occupancies of M sites.

Quadratic elongation, bond angle variance, distortion index and polyhedral volume were introduced by Robinson et al. (Reference Robinson, Gibbs and Ribbe1971) and have been calculated using Vesta software (Momma and Izumi, Reference Momma and Izumi2011).
The octahedral sheets of type 1 are characterised by the mixed occupancy of the M(1–4) sites: the M(1) and M(2) sites have higher numbers of electrons per formula unit (epfu) in comparison to the M(3) and M(4) sites. The occupancies agree well with the average M‒O bond lengths: 2.12 Å for the M(1)- and M(2)-centred octahedra, 2.05 Å for the M(3)-centred octahedra, and 2.03 Å for the M(4)-centred octahedra. The general tendency is that the M(1) and M(2) octahedra are occupied preferentially by Mn, while the M(3) and M(4) octahedra are occupied preferentially by Al. The layer topology of the octahedral sheet of type 1 agrees with the topology of the octahedral sheet 2 in the position of Mn- and Al-centred octahedra, whereas occupancies of Mn- and Al-centred octahedra are different. The total occupancy of the M(1–4) sites is in agreement with the ideal charmarite stoichiometry Mn2Al as 125(3) e – versus ideal value of 126 e – (Table 5).
The interlayers accommodate carbonate groups and H2O molecules in-between the octahedral sheets. The C(2)O3 carbonate groups concentrate in the trigonal prism formed by M(8) (i.e. Al) sites from the adjacent sheets, whereas the C(1)O3 and C(3)O3 carbonate groups are in the trigonal prisms formed by M(1) (Mn) and M(5) (Mn) sites from the adjacent sheets (Fig. 6b,d). The interaction between the interlayer (CO3)2– anions and (OH)– groups of metal-hydroxide layers is realised through O–H···OCO2 hydrogen bonds. The H atoms not involved in the bonding between OH groups and (CO3)2– anions form hydrogen bonds to interlayer H2O molecules (Fig. 5). Octahedral sheets are linked by weak hydrogen bonding to carbonate groups (O⋅⋅⋅O ≈ 2.90 Å) and H2O molecules (O⋅⋅⋅O ≈ 2.6–2.8 Å). The general tendency in the localisation of (CO3)2– groups is that they do not occur in the neighbouring trigonal prisms of H atoms (Fig. 6b,d). There is some disorder associated with the carbonate and H2O molecules in interlayers reflected by partial occupancies of the interlayer C and O sites. There are three C sites in the interlayer (Figs 5, 6), however in accord with charge requirements and taking into account two interlayers per unit cell, only two (CO3)2– groups are needed per one interlayer (per unit-cell mesh) to compensate the charge leading to some statistical disorder in their localisation. The same is also true about the occupancy of interlayer O atoms, some of which belong to (CO3)2– groups, whereas the rest belongs to H2O molecules. The local position of H2O molecules is sensitive to localisation of the (CO3)2– group and compensates with spare bond strengths of metal-hydroxide layers.
The observed herein 2$\sqrt 3$![]() × 2$\sqrt 3$
× 2$\sqrt 3$![]() superstructure agrees with the arrangement of symmetrically independent Al sites [i.e. M(7) and M(8) in one sheet]. However, the differences in the geometry of symmetrically independent Al-occupied sites (measured by bond lengths and polyhedral distortions) is small (Table 9), which indicates that these differences are hardly responsible for the doubling of the a unit-cell parameter. The position of the interlayer components is more remarkable. The analysis of the localisation of the (CO3)2– anions shows that they are arranged according to the 2 × 2 superstructure (in which each second trigonal prism is empty) (Fig. 6b,d). At the same time Mn and Al atoms are arranged according to the $\sqrt 3$
superstructure agrees with the arrangement of symmetrically independent Al sites [i.e. M(7) and M(8) in one sheet]. However, the differences in the geometry of symmetrically independent Al-occupied sites (measured by bond lengths and polyhedral distortions) is small (Table 9), which indicates that these differences are hardly responsible for the doubling of the a unit-cell parameter. The position of the interlayer components is more remarkable. The analysis of the localisation of the (CO3)2– anions shows that they are arranged according to the 2 × 2 superstructure (in which each second trigonal prism is empty) (Fig. 6b,d). At the same time Mn and Al atoms are arranged according to the $\sqrt 3$![]() × $\sqrt 3$
× $\sqrt 3$![]() superstructure. The combination of these superstructures leads to the formation of the 2$\sqrt 3$
superstructure. The combination of these superstructures leads to the formation of the 2$\sqrt 3$![]() × 2$\sqrt 3$
× 2$\sqrt 3$![]() superstructure that allows ordering of both (1) Mn and Al cations in octahedral sheets and (2) (CO3)2– anions in the interlayers. The answer to the question then on why the 2$\sqrt 3$
superstructure that allows ordering of both (1) Mn and Al cations in octahedral sheets and (2) (CO3)2– anions in the interlayers. The answer to the question then on why the 2$\sqrt 3$![]() × 2$\sqrt 3$
× 2$\sqrt 3$![]() superstructure has not been previously observed in carbonate and other LDHs may lie in the specific chemical composition of the mineral. According to the data on ionic radii (Shannon, Reference Shannon1976), a six-coordinated Mn2+ cation has the radius of 0.81 Å (low spin) or 0.97 Å (high spin). In the crystal structure of charmarite, the M(5) site is occupied nearly exclusively by Mn with the M(5)–O distance of 2.18 Å. Taking into account the O2– radius of 1.22 Å (Shannon, Reference Shannon1976), the M(5)–O distance corresponds to the ionic radius of the high-spin Mn2+ ion (0.97 Å). The ionic radius of Al3+ is 0.675 Å, while Mg (dominant divalent cation in quintinite) has the crystal radius of 0.86 Å. So, the species-forming cations Mn2+ and Al in charmarite have a more significant difference in the size than Mg and Al in quintinite. Hypothetically, this should lead to the higher tendency of Mn and Al to order as di- and trivalent cations. The higher degree of ordering of di- and trivalent cations within octahedral sheets is responsible for the ordering of interlayer components that follows the scheme of charge distribution. The general tendency revealed recently for Cl-dominant LDHs shows that a higher degree of ordering of di- and trivalent cations leads to the higher degree of ordering of interlayer components, which has been reflected by the occupancy of interlayer Cl and O (of H2O) sites in chlormagaluminite and dritsite with the $\sqrt 3$
superstructure has not been previously observed in carbonate and other LDHs may lie in the specific chemical composition of the mineral. According to the data on ionic radii (Shannon, Reference Shannon1976), a six-coordinated Mn2+ cation has the radius of 0.81 Å (low spin) or 0.97 Å (high spin). In the crystal structure of charmarite, the M(5) site is occupied nearly exclusively by Mn with the M(5)–O distance of 2.18 Å. Taking into account the O2– radius of 1.22 Å (Shannon, Reference Shannon1976), the M(5)–O distance corresponds to the ionic radius of the high-spin Mn2+ ion (0.97 Å). The ionic radius of Al3+ is 0.675 Å, while Mg (dominant divalent cation in quintinite) has the crystal radius of 0.86 Å. So, the species-forming cations Mn2+ and Al in charmarite have a more significant difference in the size than Mg and Al in quintinite. Hypothetically, this should lead to the higher tendency of Mn and Al to order as di- and trivalent cations. The higher degree of ordering of di- and trivalent cations within octahedral sheets is responsible for the ordering of interlayer components that follows the scheme of charge distribution. The general tendency revealed recently for Cl-dominant LDHs shows that a higher degree of ordering of di- and trivalent cations leads to the higher degree of ordering of interlayer components, which has been reflected by the occupancy of interlayer Cl and O (of H2O) sites in chlormagaluminite and dritsite with the $\sqrt 3$![]() × $\sqrt 3$
× $\sqrt 3$![]() superstructure versus iowaite that shows the 1 × 1 (disordered) unit cell (Zhitova et al., Reference Zhitova, Krivovichev, Pekov and Yapaskurt2019b, Reference Zhitova, Pekov, Chaikovskiy, Chirkova, Yapaskurt, Bychkova, Belakovsky, Chukanov, Zubkova, Krivovichev and Bocharov2019c; Reference Zhitova, Chukanov, Pekov, Zolotarev, Shilovskikh and Bocharov2023b).
superstructure versus iowaite that shows the 1 × 1 (disordered) unit cell (Zhitova et al., Reference Zhitova, Krivovichev, Pekov and Yapaskurt2019b, Reference Zhitova, Pekov, Chaikovskiy, Chirkova, Yapaskurt, Bychkova, Belakovsky, Chukanov, Zubkova, Krivovichev and Bocharov2019c; Reference Zhitova, Chukanov, Pekov, Zolotarev, Shilovskikh and Bocharov2023b).
Perhaps, a role may be played by the possibility of detecting weak superstructure reflections and superstructures, which is influenced by factors such as the scattering power of atoms (which is more than twice higher for Mn than for Mg), the crystal quality, and the detector sensitivity. The previous studies of quintinite and chlormagaluminite (Zhitova et al., Reference Zhitova, Krivovichev, Yakovenchuk, Ivanyuk, Pakhomovsky and Mikhailova2018, Reference Zhitova, Krivovichev, Pekov and Yapaskurt2019b) were performed on the same diffractometer as the one used for the study of charmarite. Therefore, we believe that, among the listed factors, technical reasons are the least likely cause of differences.
Acknowledgements
This research was supported by the Russian Science Foundation (project no. 22-77-10036 for ESZ, AAZ and RMS). Technical support of the St. Petersburg State University Resource Centres “X-ray diffraction research methods” and “Geomodel” is carried out within the framework of SPbSU, grants No. AAAA-A19-119091190094 and No. 116234388, for both Resource Centres, respectively. We would like to thank the reviewers for constructive comments.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1180/mgm.2024.11.
Competing interests
The authors declare none.