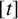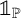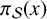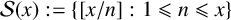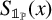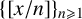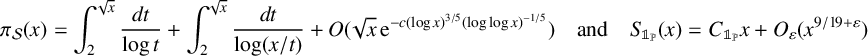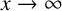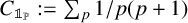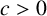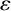ON THE PRIMES IN FLOOR FUNCTION SETS

Abstract

Let $[t]$ be the integral part of the real number t and let $\mathbb {1}_{{\mathbb P}}$ be the characteristic function of the primes. Denote by $\pi _{\mathcal {S}}(x)$ the number of primes in the floor function set $\mathcal {S}(x) := \{[{x}/{n}] : 1\leqslant n\leqslant x\}$ and by $S_{\mathbb {1}_{{\mathbb P}}}(x)$ the number of primes in the sequence $\{[{x}/{n}]\}_{n\geqslant 1}$. Improving a result of Heyman [‘Primes in floor function sets’, Integers 22 (2022), Article no. A59], we show

$$ \begin{align*} \pi_{\mathcal{S}}(x) = \int_2^{\sqrt{x}} \frac{d t}{\log t} + \int_2^{\sqrt{x}} \frac{d t}{\log(x/t)} + O(\sqrt{x}\,\mathrm{e}^{-c(\log x)^{3/5}(\log\log x)^{-1/5}}) \quad\mbox{and}\quad S_{\mathbb{1}_{{\mathbb P}}}(x) = C_{\mathbb{1}_{{\mathbb P}}} x + O_{\varepsilon}(x^{9/19+\varepsilon}) \end{align*} $$

for $x\to \infty $, where $C_{\mathbb {1}_{{\mathbb P}}} := \sum _{p} {1}/{p(p+1)}$, $c>0$ is a positive constant and $\varepsilon $ is an arbitrarily small positive number.

1 Introduction

The distribution of prime numbers is one of the most important problems in number theory. Denote by $\pi (x)$ the number of primes $p\leqslant x$ . The prime number theorem states that

$$ \begin{align*} \pi(x) = \frac{x}{\log x} + O\bigg(\frac{x}{(\log x)^2}\bigg) \quad (x\to\infty). \end{align*} $$

A strong form of this theorem is

(1.1) $$ \begin{align} \pi(x) = {\mathrm{Li}}(x) + O(x \exp(-c(\log x)^{3/5}(\log_2x)^{-1/5})) \quad (x\to\infty), \end{align} $$

where c is a positive constant, $\log _2$ denotes the iterated logarithm function and

$$ \begin{align*} {\mathrm{Li}}(x) := \int_2^x \frac{d t}{\log t}. \end{align*} $$

The Riemann hypothesis is equivalent to the asymptotic formula

(1.2) $$ \begin{align} \pi(x) = {\mathrm{Li}}(x) + O_{\varepsilon}(x^{1/2+\varepsilon}) \quad\; (x\to\infty), \end{align} $$

where $\varepsilon $ is an arbitrarily small positive number. More generally, let $\mathcal {N}(x)$ be a set of integers of $[1, x]$ and let $\mathcal {N}_{{\mathbb P}}(x)$ be the set of prime numbers in $\mathcal {N}(x)$ . We expect that

(1.3) $$ \begin{align} |\mathcal{N}_{{\mathbb P}}(x)|\sim \frac{|\mathcal{N}(x)|}{\log |\mathcal{N}(x)|} \quad (x\to \infty), \end{align} $$

provided $\mathcal {N}(x)$ is rather regular and is not too sparse. Some well-known examples are

$$ \begin{align*} \{qn+a\leqslant x\}, \;\; \{[n^c]\leqslant x\}, \;\; \{m^2+n^4\leqslant x\}, \;\; \{m^3+2n^3\leqslant x\}, \;\; \{x<n\leqslant x+x^{7/12+\varepsilon}\}, \end{align*} $$

the respective densities for which are

$$ \begin{align*} x/\varphi(q) \quad &(q\leqslant (\log x)^A, \text{Walfisz--Siegel } [3]), \\ x^{1/c} \quad &\bigg(c\leqslant \dfrac{2817}{2426}, \text{Rivat--Sargos } [12]\bigg), \\ x^{3/4} \quad &(\text{Friedlander--Iwaniec } [4]), \\ x^{2/3} \quad &(\text{Heath-Brown } [5]), \\ x^{7/12+\varepsilon} \quad &(\text{Huxley } [8]), \end{align*} $$

where $[t]$ is the integral part of the real number t, $\varphi (q)$ is the Euler function, A is any positive constant and $\varepsilon>0$ is an arbitrarily small positive number.

Recently, Bordellès et al. [2] investigated the asymptotic behaviour of the summative function

$$ \begin{align*} S_f(x) := \sum_{n\leqslant x} f\bigg(\bigg[\frac{x}{n}\bigg]\bigg) \end{align*} $$

under some simple hypothesis on the growth of f and there are a number of further developments on this theme. If we use $\Lambda (n)$ to denote the von Mangoldt function, then [13, Theorem 1.2(i)] or [15, Theorem 1] give us immediately

(1.4) $$ \begin{align} S_{\Lambda}(x) = C_{\Lambda} x + O_{\varepsilon}(x^{1/2+\varepsilon}), \end{align} $$

for any $\varepsilon>0$ and $x\to \infty $ , where $C_{\Lambda } := \sum _{n\geqslant 1} {\Lambda (n)}/{n(n+1)}$ . Ma and Wu [11] applied the Vaughan identity and the technique of one-dimensional exponential sums to break the $\tfrac 12$ -barrier by establishing

(1.5) $$ \begin{align} S_{\Lambda}(x) = C_{\Lambda} x + O_{\varepsilon}(x^{35/71+\varepsilon}). \end{align} $$

This result seems rather interesting if we compare it with (1.2). The exponent ${35}/{71}$ has been improved to ${97}/{203}$ by Bordellès [1] and ${9}/{19}$ by Liu et al. [10], using more sophisticated techniques of multiple exponential sums. Obviously, (1.5) is the prime number theorem for the floor function set

$$ \begin{align*} \mathcal{S}(x) := \bigg\{\bigg[\frac{x}{n}\bigg] : 1\leqslant n\leqslant x\bigg\} \end{align*} $$

considered as the weighted count of prime powers. Very recently, Heyman [7] examined the number of primes in the floor function set $\mathcal {S}(x)$ without the multiplicity. The principal result of Heyman [7, Theorem 1] is the asymptotic formula

(1.6) $$ \begin{align} \pi_{\mathcal{S}}(x) := \sum_{\substack{p\leqslant x\\ \exists\,n\,\text{such that}\; [x/n]=p}} 1 = \frac{4\sqrt{x}}{\log x} + O\bigg(\frac{\sqrt{x}}{(\log x)^2}\bigg) \quad(x\to\infty). \end{align} $$

Since Heyman [6, Theorems 1 and 2] proved that

(1.7) $$ \begin{align} |\mathcal{S}(x)| = 2\sqrt{x} + O(1) \quad(x\to\infty). \end{align} $$

it follows from (1.6) that (1.3) holds for this sparse set $\mathcal {S}(x)$ . This may be the first example of such a sparse subset of $[1, x]\cap {\mathbb N}$ (of density $x^{1/2}$ ) for which the prime number theorem holds.

It seems natural and interesting to establish an analogue of the strong form of the prime number theorem in (1.1) for the set $\mathcal {S}(x)$ . We prove such a result.

Theorem 1.1. (i) For $x\to \infty $ ,

(1.8) $$ \begin{align} \pi_{\mathcal{S}}(x) = {\mathrm{Li}}_{\mathcal{S}}(x) + O(\sqrt{x} \exp(-c'(\log x)^{3/5}(\log_2x)^{-1/5})), \end{align} $$

where $c'>0$ is a positive constant and

$$ \begin{align*} {\mathrm{Li}}_{\mathcal{S}}(x) := \int_2^{\sqrt{x}} \frac{d t}{\log t} + \int_2^{\sqrt{x}} \frac{d t}{\log(x/t)}\cdot \end{align*} $$

(ii) There is a real sequence $\{a_n\}_{n\geqslant 1}$ with $a_1=4$ such that for any positive integer $N\geqslant 1$ ,

$$ \begin{align*} \pi_{\mathcal{S}}(x) = \sqrt{x} \sum_{n=1}^{N} \frac{a_n}{(\log x)^n} + O_N\bigg(\frac{\sqrt{x}}{(\log x)^{N+1}}\bigg) \quad (x\to\infty). \end{align*} $$

Let ${\mathbb P}$ be the set of all primes and let ${{\mathbb P}}_{\mathrm {ower}}$ be the set of all prime powers. Denote by $\mathbb {1}_{{\mathbb P}}$ and $\mathbb {1}_{{{\mathbb P}}_{\mathrm {ower}}}$ their characteristic functions. Define

$$ \begin{align*} S_{\mathbb{1}_{{\mathbb P}}}(x) := \sum_{n\leqslant x} \mathbb{1}_{{\mathbb P}}\bigg(\bigg[\frac{x}{n}\bigg]\bigg), \quad S_{\mathbb{1}_{{{\mathbb P}}_{\mathrm{ower}}}}(x) := \sum_{n\leqslant x} \mathbb{1}_{{{\mathbb P}}_{\mathrm{ower}}}\bigg(\bigg[\frac{x}{n}\bigg]\bigg). \end{align*} $$

Theorems 5 and 7 of [7] can be stated as follows:

(1.9) $$ \begin{align} S_{\mathbb{1}_{{\mathbb P}}}(x) & = C_{\mathbb{1}_{{\mathbb P}}} x + O(x^{1/2}), \end{align} $$

(1.10) $$ \begin{align} S_{\mathbb{1}_{{{\mathbb P}}_{\mathrm{ower}}}}(x) & = C_{\mathbb{1}_{{{\mathbb P}}_{\mathrm{ower}}}} x + O(x^{1/2}), \end{align} $$

where $C_{\mathbb {1}_{{\mathbb P}}} := \sum _{p} {1}/{p(p+1)}$ and $C_{\mathbb {1}_{{{\mathbb P}}_{\mathrm {ower}}}} := \sum _{p, \, \nu \geqslant 1} {1}/{p^{\nu }(p^{\nu }+1)}$ . Similar to (1.4), these are immediate consequences of [13, Theorem 1.2(i)] or [15, Theorem 1]. Heyman [7, Theorem 6] also proved that there is a positive constant $B>0$ such that the inequality

(1.11) $$ \begin{align} S_{\mathbb{1}_{{\mathbb P}}}(x) \geqslant C_{\mathbb{1}_{{\mathbb P}}} x - \frac{Bx^{1/2}}{\log x} \end{align} $$

for $x\geqslant 2$ . We improve these results by breaking the $\tfrac 12$ -barrier in the error terms of (1.9), (1.10) and (1.11).

Theorem 1.2. For any $\varepsilon>0$ ,

(1.12) $$ \begin{align} S_{\mathbb{1}_{{\mathbb P}}}(x) & = C_{\mathbb{1}_{{\mathbb P}}} x + O_{\varepsilon}(x^{9/19+\varepsilon}), \end{align} $$

(1.13) $$ \begin{align} S_{\mathbb{1}_{{{\mathbb P}}_{\mathrm{ower}}}}(x) & = C_{\mathbb{1}_{{{\mathbb P}}_{\mathrm{ower}}}} x + O_{\varepsilon}(x^{9/19+\varepsilon}), \end{align} $$

as $x\to \infty $ , where the implied constants depend on $\varepsilon $ .

Remark 1.3. It is possible to improve the error terms in (1.12) and (1.13). It seems interesting to prove $\Omega $ -results for the error terms in (1.8), (1.12) and (1.13). We shall return to this problem in forthcoming work.

Very recently, Yu and Wu [14] generalised Heyman’s (1.7) by showing

$$ \begin{align*} \mathcal{S}(x; q, a) := \sum_{\substack{m\in \mathcal{S}(x)\\ m\equiv a \,(\mathrm{mod}\,q)}} 1 = \frac{2\sqrt{x}}{q} + O((x/q)^{1/3}\log x) \end{align*} $$

uniformly for $x\geqslant 3$ , $1\leqslant q\leqslant x^{1/4}/(\log x)^{3/2}$ and $1\leqslant a\leqslant q$ , where the implied constant is absolute. This confirms a numerical test of Heyman.

2 Proof of Theorem 1.1

We begin by following the argument of [7]. First, we note that

$$ \begin{align*} \mathcal{S}(x) = \bigg\{p\in \mathbb{P} : \exists \; n\in [1, x] \;\text{such that}\; \bigg[\frac{x}{n}\bigg]=p\bigg\}. \end{align*} $$

Further, if $[{x}/{n}] = p\in \mathbb {P}$ , then $x/(p+1)<n\leqslant x/p$ . Thus, we can write

(2.1) $$ \begin{align} \pi_{\mathcal{S}}(x) = \sum_{p\leqslant x} \mathbb{1}\bigg(\bigg[\frac{x}{p}\bigg]-\bigg[\frac{x}{p+1}\bigg]>0\bigg) = G_1(x) + G_2(x), \end{align} $$

where $\mathbb {1}(Q)=1$ if the statement Q is true and 0 otherwise, and

$$ \begin{align*} G_1(x) & := \sum_{p\leqslant \sqrt{x}} \mathbb{1}\bigg(\bigg[\frac{x}{p}\bigg]-\bigg[\frac{x}{p+1}\bigg]>0\bigg), \\ G_2(x) & := \sum_{\sqrt{x}<p\leqslant x} \mathbb{1}\bigg(\bigg[\frac{x}{p}\bigg]-\bigg[\frac{x}{p+1}\bigg]>0\bigg). \end{align*} $$

For $p\leqslant \sqrt {x}-1$ ,

$$ \begin{align*} \bigg[\frac{x}{p}\bigg]-\bigg[\frac{x}{p+1}\bigg]>\frac{x}{p(p+1)}-1 >0. \end{align*} $$

Thus, the prime number theorem (1.1) gives us

(2.2) $$ \begin{align} G_1(x) = \pi(\sqrt{x}) + O(1) = {\mathrm{Li}}(\sqrt{x}) + O(\sqrt{x} \exp(-c'(\log x)^{3/5}(\log_2x)^{-1/5})) \end{align} $$

for $x\geqslant 3$ , where $c'>0$ is a positive constant.

Next, we treat $G_2(x)$ . Noticing that

$$ \begin{align*} 0<\frac{x}{p}-\frac{x}{p+1}=\frac{x}{p(p+1)}<1 \end{align*} $$

for $p>\sqrt {x}$ , the quantity $[{x}/{p}]-[{x}/{p+1}]$ can only equal 0 or 1. However, for $p>x^{10/19}$ , we have $p=[{x}/{n}]$ for some $n\leqslant x^{9/19}$ . Thus, we can write

(2.3) $$ \begin{align} \begin{aligned} G_2(x) & = \sum_{x^{1/2}<p\leqslant x^{10/19}} \bigg(\bigg[\frac{x}{p}\bigg]-\bigg[\frac{x}{p+1}\bigg]\bigg) + O(x^{9/19}) \\ & = \sum_{x^{1/2}<p\leqslant x^{10/19}} \bigg(\frac{x}{p}-\frac{x}{p+1}-\psi\bigg(\frac{x}{p}\bigg)+\psi\bigg(\frac{x}{p+1}\bigg)\bigg) + O(x^{9/19}) \\ & = G_{2, 1}(x) - G_{2, 2}^{\langle 0\rangle}(x) + G_{2, 2}^{\langle 1\rangle}(x) + O(x^{9/19}), \end{aligned} \end{align} $$

where $\psi (t):=t-[t]-\tfrac 12$ and

$$ \begin{align*} G_{2, 1}(x) & := \sum_{x^{1/2}<p\leqslant x^{10/19}} \bigg(\frac{x}{p}-\frac{x}{p+1}\bigg), \\ G_{2, 2}^{\langle\delta\rangle}(x) & := \sum_{x^{1/2}<p\leqslant x^{10/19}} \psi\bigg(\frac{x}{p+\delta}\bigg) \quad (\delta=0, 1). \end{align*} $$

With the help of the prime number theorem (1.1), a simple partial integration gives

$$ \begin{align*} G_{2, 1}(x) & = \sum_{x^{1/2}<p\leqslant x/2} \frac{x}{p^2} + O(x^{9/19}) = x \int_{\sqrt{x}}^{x/2} \frac{d \pi(t)}{t^2} + O(x^{9/19}) \\ & = x \int_{\sqrt{x}}^{x/2} \frac{d t}{t^2\log t} + O(\sqrt{x}\exp(-c'(\log x)^{3/5}(\log_2x)^{-1/5}), \end{align*} $$

where $c'>0$ is a positive constant. Making the change of variables $t\to x/t$ in the last integral, it follows that

(2.4) $$ \begin{align} G_{2, 1}(x) = \int_2^{\sqrt{x}} \frac{d t}{\log(x/t)} + O(\sqrt{x}\exp(-c'(\log x)^{3/5}(\log_2x)^{-1/5}) \end{align} $$

for $x\to \infty $ .

It remains to bound $G_{2, 2}^{\langle \delta \rangle }(x)$ . Similar to [10], define

$$ \begin{align*} \mathfrak{S}_{\delta}(x; D, D') := \sum_{D<d\leqslant D'} \Lambda(d) \psi\bigg(\frac{x}{d+\delta}\bigg). \end{align*} $$

According to [10, (4.3)], for any $\varepsilon>0$ ,

$$ \begin{align*} \mathfrak{S}_{\delta}(x; D, 2D) \ll_{\varepsilon} (x^2 D^7)^{1/12} x^{\varepsilon} \end{align*} $$

uniformly for $x\geqslant 3$ and $x^{6/13}\leqslant D\leqslant x^{2/3}$ . The same proof shows that for any $\varepsilon>0$ ,

(2.5) $$ \begin{align} \mathfrak{S}_{\delta}(x; D, D') \ll_{\varepsilon} (x^2 D^7)^{1/12} x^{\varepsilon} \end{align} $$

uniformly for $x\geqslant 3$ , $x^{6/13}\leqslant D\leqslant x^{2/3}$ and $D<D'\leqslant 2D$ . Since we have trivially

$$ \begin{align*} \sum_{D<p^{\nu}\leqslant D', \, \nu\geqslant 2} \Lambda(p^{\nu}) \psi\bigg(\frac{x}{p^{\nu}+\delta}\bigg) \ll \sum_{p\leqslant (2D)^{1/2}} \sum_{\nu\leqslant (\log 2D)/\log p} \log p \ll D^{1/2}, \end{align*} $$

the inequality (2.5) implies that the bound

(2.6) $$ \begin{align} \sum_{D<p\leqslant D'} (\log p) \psi\bigg(\frac{x}{p+\delta}\bigg) \ll_{\varepsilon} (x^2 D^7)^{1/12} x^{\varepsilon} \end{align} $$

holds uniformly for $x\geqslant 3$ , $x^{6/13}\leqslant D\leqslant x^{2/3}$ and $D<D'\leqslant 2D$ . Using (2.6),

(2.7) $$ \begin{align} \begin{aligned} G_{2, 2}^{\langle\delta\rangle}(x) & \ll \max_{x^{1/2}<D\leqslant x^{10/19}} \sum_{D<p\leqslant 2D} \psi\bigg(\frac{x}{p+\delta}\bigg) \\ & \ll \max_{x^{1/2}<D\leqslant x^{10/19}} \int_D^{2D} \frac{1}{\log t} \,d \bigg(\sum_{D<p\leqslant t} (\log p) \psi\bigg(\frac{x}{p+\delta}\bigg)\bigg) \\ & \ll_{\varepsilon} \max_{x^{1/2}<D\leqslant x^{10/19}} (x^2 D^7)^{1/12} x^{\varepsilon} \\ & \ll_{\varepsilon} x^{9/19+\varepsilon}. \end{aligned} \end{align} $$

Inserting (2.4) and (2.7) into (2.3), we find that

(2.8) $$ \begin{align} G_2(x) = \int_2^{\sqrt{x}} \frac{d t}{\log(x/t)} + O(\sqrt{x}\exp(-c'(\log x)^{3/5}(\log_2x)^{-1/5}). \end{align} $$

Now the required result (1.8) follows from (2.1), (2.2) and (2.8).

The second assertion is an immediate consequence of the first one thanks to a simple partial integration.

3 Proof of Theorem 1.2

We begin by following the argument of [9]. Let $f=\mathbb {1}_{{\mathbb P}}$ or $\mathbb {1}_{{{\mathbb P}}_{\mathrm {ower}}}$ and let $N\in [x^{1/3}, x^{1/2})$ be a parameter which can be chosen later. First, we write

(3.1) $$ \begin{align} S_f(x) = \sum_{n\leqslant x} f\bigg(\bigg[\frac{x}{n}\bigg]\bigg) = S_f^{\dagger}(x)+S_f^{\sharp}(x) \end{align} $$

with

$$ \begin{align*} S_f^{\dagger}(x):=\sum_{n\leqslant N} f\bigg(\bigg[\frac{x}{n}\bigg]\bigg), \quad S_f^{\sharp}(x):=\sum_{N<n\leqslant x} f\bigg(\bigg[\frac{x}{n}\bigg]\bigg). \end{align*} $$

We have trivially

(3.2) $$ \begin{align} S_f^{\dagger}(x) \ll N. \end{align} $$

To bound $S_f^{\sharp }(x)$ , we put $d=[x/n]$ . Noticing that

$$ \begin{align*} x/n-1<d\leqslant x/n \Leftrightarrow x/(d+1)<n\leqslant x/d, \end{align*} $$

we see that

(3.3) $$ \begin{align} \begin{aligned} S_f^{\sharp}(x) & = \sum_{d\leqslant x/N} f(d) \sum_{x/(d+1)<n\leqslant x/d} 1 \\ & = \sum_{d\leqslant x/N} f(d) \bigg(\frac{x}{d}-\psi\bigg(\frac{x}{d}\bigg)-\frac{x}{d+1}+\psi\bigg(\frac{x}{d+1} \bigg) \bigg) \\ & = x \sum_{d\geqslant 1} \frac{f(d)}{d(d+1)} + \mathcal{R}_1^{f}(x, N) - \mathcal{R}_0^{f}(x, N) + O(N), \end{aligned} \end{align} $$

where we have used the bounds

$$ \begin{align*} x \sum_{d>x/N} \frac{f(d)}{d(d+1)}\ll N, \quad \sum_{d\leqslant N} f(d)\bigg(\psi\bigg(\frac{x}{d+1}\bigg) - \psi\bigg(\frac{x}{d}\bigg)\bigg) \ll N \end{align*} $$

and

$$ \begin{align*} \mathcal{R}_{\delta}^{f}(x, N) = \sum_{N<d\leqslant x/N} f(d) \psi\bigg(\frac{x}{d+\delta}\bigg). \end{align*} $$

Combining (3.1), (3.2) and (3.3), it follows that

$$ \begin{align*} S_f(x) = x \sum_{d\geqslant 1} \frac{f(d)}{d(d+1)} + O_{\varepsilon}(|\mathcal{R}_1^{f}(x, N)| + |\mathcal{R}_0^{f}(x, N)| + N). \end{align*} $$

However,

$$ \begin{align*} \mathcal{R}_{\delta}^{\mathbb{1}_{{{\mathbb P}}_{\mathrm{ower}}}}(x, N) = \sum_{N<p^{\nu}\leqslant x/N} \psi\bigg(\frac{x}{p^{\nu}+\delta}\bigg) = \mathcal{R}_{\delta}^{\mathbb{1}_{{\mathbb P}}}(x, N) + O((x/N)^{1/2}). \end{align*} $$

Thus, to prove Theorem 1.2, it suffices to show that

$$ \begin{align*} \mathcal{R}_{\delta}^{\mathbb{1}_{{\mathbb P}}}(x, N)\ll_{\varepsilon} N x^{\varepsilon} \quad (x\geqslant 1) \end{align*} $$

for $N=x^{9/19}$ . This can be done exactly as for (2.7) by using (2.6):

$$ \begin{align*} \mathcal{R}_{\delta}^{\mathbb{1}_{{\mathbb P}}}(x, N) & \ll x^{\varepsilon} \max_{x^{9/19}<D\leqslant x^{10/19}} \sum_{D<p\leqslant 2D} \psi\bigg(\frac{x}{p+\delta}\bigg) \\ & \ll x^{\varepsilon} \max_{x^{9/19}<D\leqslant x^{10/19}} \int_D^{2D} \frac{1}{\log t} \,d \bigg(\sum_{D<p\leqslant t} (\log p) \psi\bigg(\frac{x}{p+\delta}\bigg)\bigg) \\ & \ll_{\varepsilon} \max_{x^{9/19}<D\leqslant x^{10/19}} (x^2 D^7)^{1/12} x^{\varepsilon} \\ & \ll_{\varepsilon} x^{9/19+\varepsilon}. \end{align*} $$

This completes the proof.