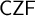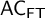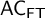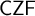1 Introduction
In this paper, we prove that extensional generic realizability [Reference Frittaion and Rathjen17] validates the natural extension of
![]() $\mathsf { AC}_{\mathsf {FT}}$
(the axiom of choice in finite types) and
$\mathsf { AC}_{\mathsf {FT}}$
(the axiom of choice in finite types) and
![]() $\mathsf {RDC}_{\mathsf {FT}}$
(relativized dependent choice in finite types) to transfinite dependent types. By routinely combining extensional generic realizability with a Beeson-style forcing construction, along the lines of [Reference Friedman and Ščedrov15, Section 5], we also show that T augmented with such choice principles is conservative over T for arithmetic sentences, for a host of intuitionistic set theories T. In particular, we extend Friedman and Ščedrov’s result [Reference Friedman and Ščedrov15] that
$\mathsf {RDC}_{\mathsf {FT}}$
(relativized dependent choice in finite types) to transfinite dependent types. By routinely combining extensional generic realizability with a Beeson-style forcing construction, along the lines of [Reference Friedman and Ščedrov15, Section 5], we also show that T augmented with such choice principles is conservative over T for arithmetic sentences, for a host of intuitionistic set theories T. In particular, we extend Friedman and Ščedrov’s result [Reference Friedman and Ščedrov15] that
![]() $\mathsf {IZF}$
augmented with
$\mathsf {IZF}$
augmented with
![]() $\mathsf {CAC}_{\mathsf {FT}}$
(finite type countable choice) and
$\mathsf {CAC}_{\mathsf {FT}}$
(finite type countable choice) and
![]() $\mathsf {DC}_{\mathsf {FT}}$
(finite type dependent choice) is arithmetically conservative over
$\mathsf {DC}_{\mathsf {FT}}$
(finite type dependent choice) is arithmetically conservative over
![]() $\mathsf {IZF}$
.Footnote
1
$\mathsf {IZF}$
.Footnote
1
Generic realizabilityFootnote
2
is distinguished by its treatment of unbounded quantifiers: a realizer of
![]() $\forall x\, \varphi (x)$
(resp.
$\forall x\, \varphi (x)$
(resp.
![]() $\exists x\, \varphi (x)$
) must be a realizer of
$\exists x\, \varphi (x)$
) must be a realizer of
![]() $\varphi (x)$
for every x (resp. some x). This strain of realizability goes back to Kreisel and Troelstra’s realizability for theories of elementary analysis with species variables [Reference Kreisel and Troelstra21, Section 3.7]. A direct descendant of Kreisel and Troelstra’s realizability was applied to nonextensional theories of higher order arithmetic and set theory by Friedman [Reference Friedman14] and Beeson [Reference Beeson5, Reference Beeson7]. McCarty [Reference McCarty22, Reference McCarty23] developed a version of generic realizability that applies directly to the extensional set theory
$\varphi (x)$
for every x (resp. some x). This strain of realizability goes back to Kreisel and Troelstra’s realizability for theories of elementary analysis with species variables [Reference Kreisel and Troelstra21, Section 3.7]. A direct descendant of Kreisel and Troelstra’s realizability was applied to nonextensional theories of higher order arithmetic and set theory by Friedman [Reference Friedman14] and Beeson [Reference Beeson5, Reference Beeson7]. McCarty [Reference McCarty22, Reference McCarty23] developed a version of generic realizability that applies directly to the extensional set theory
![]() $\mathsf {IZF}$
. He also employed, inspired by Feferman [Reference Feferman12], arbitrary partial combinatory algebras, rather than just natural numbers. Whereas McCarty’s approach is geared towards
$\mathsf {IZF}$
. He also employed, inspired by Feferman [Reference Feferman12], arbitrary partial combinatory algebras, rather than just natural numbers. Whereas McCarty’s approach is geared towards
![]() $\mathsf {IZF}$
, it was shown in [Reference Rathjen30] that
$\mathsf {IZF}$
, it was shown in [Reference Rathjen30] that
![]() $\mathsf {CZF}$
suffices for a formalization of generic realizability, thus providing a self-validating semantics for
$\mathsf {CZF}$
suffices for a formalization of generic realizability, thus providing a self-validating semantics for
![]() $\mathsf {CZF}$
and other fragments of
$\mathsf {CZF}$
and other fragments of
![]() $\mathsf {IZF}$
.
$\mathsf {IZF}$
.
In [Reference Frittaion and Rathjen17], we added an extra layer of extensionality to McCarty’s generic realizability, and thus obtained inner models of both
![]() $\mathsf {CZF}$
and
$\mathsf {CZF}$
and
![]() $\mathsf {IZF}$
that further validate
$\mathsf {IZF}$
that further validate
![]() $\mathsf {AC}_{\mathsf {FT}}$
.Footnote
3
In the present paper, we show that extensional generic realizability yields an interpretation of
$\mathsf {AC}_{\mathsf {FT}}$
.Footnote
3
In the present paper, we show that extensional generic realizability yields an interpretation of
-
•
 $T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
in T, and
$T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
in T, and -
•
 $T+\mathsf {REA}+ {\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger } +{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
in
$T+\mathsf {REA}+ {\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger } +{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
in
 $T+\mathsf {REA}$
,
$T+\mathsf {REA}$
,
where T can be either
![]() $\mathsf {CZF}$
,
$\mathsf {CZF}$
,
![]() $\mathsf {IZF}$
or an extension thereof with other choice axioms. We will introduce this family of choice principles for dependent types in Section 2. Suffice it to say here that
$\mathsf {IZF}$
or an extension thereof with other choice axioms. We will introduce this family of choice principles for dependent types in Section 2. Suffice it to say here that
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf { AC}^{\dagger }$
and
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf { AC}^{\dagger }$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
are closely related to, and in fact follow from, Aczel’s
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
are closely related to, and in fact follow from, Aczel’s
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}$
and
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}$
. The latter are validated by the type-theoretic interpretations of
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}$
. The latter are validated by the type-theoretic interpretations of
![]() $\mathsf {CZF}$
[Reference Aczel1, Reference Aczel2] and
$\mathsf {CZF}$
[Reference Aczel1, Reference Aczel2] and
![]() $\mathsf {CZF}+\mathsf {REA}$
[Reference Aczel3], respectively. Our interpretation does not appear to validate
$\mathsf {CZF}+\mathsf {REA}$
[Reference Aczel3], respectively. Our interpretation does not appear to validate
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}$
and relatives, even if we assume it in the background theory. We will see in Section 4.4 that extensional generic realizability refutes the statement that every set is an image of a
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}$
and relatives, even if we assume it in the background theory. We will see in Section 4.4 that extensional generic realizability refutes the statement that every set is an image of a
![]() ${\Pi }{\Sigma }\mathrm {I}$
-set (
${\Pi }{\Sigma }\mathrm {I}$
-set (
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-set), which instead holds true in Aczel’s type-theoretic interpretation of
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-set), which instead holds true in Aczel’s type-theoretic interpretation of
![]() $\mathsf {CZF}$
(
$\mathsf {CZF}$
(
![]() $\mathsf {CZF}+\mathsf {REA}$
).
$\mathsf {CZF}+\mathsf {REA}$
).
The basic plan for interpreting choice via extensional generic realizability can be easily described as follows. Consider the
![]() ${\Pi }{\Sigma }\mathrm {I}$
case. We start out with a realizability universe
${\Pi }{\Sigma }\mathrm {I}$
case. We start out with a realizability universe
![]() $\mathrm {V_{ext}}(A)$
, which is built on top of a given partial combinatory algebra A. We then construct an extensional type structure on A (Definition 4.3). In particular, types are elements of A. Next, we single out nice sets of
$\mathrm {V_{ext}}(A)$
, which is built on top of a given partial combinatory algebra A. We then construct an extensional type structure on A (Definition 4.3). In particular, types are elements of A. Next, we single out nice sets of
![]() $\mathrm {V_{ext}}(A)$
of the form
$\mathrm {V_{ext}}(A)$
of the form
![]() $X_{\sigma }$
, where
$X_{\sigma }$
, where
![]() $\sigma $
runs over all types (Definition 4.9). We think of these sets as the extensions of the corresponding types. With this identification in mind, we show that
$\sigma $
runs over all types (Definition 4.9). We think of these sets as the extensions of the corresponding types. With this identification in mind, we show that
![]() $\mathsf {AC}_{\sigma ,\tau }$
and
$\mathsf {AC}_{\sigma ,\tau }$
and
![]() $\mathsf {RDC}_{\sigma }$
hold in
$\mathsf {RDC}_{\sigma }$
hold in
![]() $\mathrm {V_{ext}}(A)$
(Theorems 4.17 and 4.18). Finally, we prove that every
$\mathrm {V_{ext}}(A)$
(Theorems 4.17 and 4.18). Finally, we prove that every
![]() ${\Pi }{\Sigma }\mathrm {I}$
-set of
${\Pi }{\Sigma }\mathrm {I}$
-set of
![]() $\mathrm {V_{ext}}(A)$
is nicely represented (Theorems 4.14 and 4.16). Niceness is captured by a suitable notion of being injectively presented in
$\mathrm {V_{ext}}(A)$
is nicely represented (Theorems 4.14 and 4.16). Niceness is captured by a suitable notion of being injectively presented in
![]() $\mathrm {V_{ext}}(A)$
(similar notions can be encountered in [Reference Aczel2, Reference Aczel3, Reference Rathjen27–Reference Rathjen29]). It will be crucial to work with extensional type structures.
$\mathrm {V_{ext}}(A)$
(similar notions can be encountered in [Reference Aczel2, Reference Aczel3, Reference Rathjen27–Reference Rathjen29]). It will be crucial to work with extensional type structures.
2 Preliminaries
2.1
 $\mathsf {CZF}$
and
$\mathsf {CZF}$
and
 $\mathsf {IZF}$
$\mathsf {IZF}$
In this paper, we will be concerned with (extensions of)
![]() $\mathsf {CZF}$
(constructive Zermelo–Fraenkel set theory) and
$\mathsf {CZF}$
(constructive Zermelo–Fraenkel set theory) and
![]() $\mathsf {IZF}$
(intuitionistic Zermelo–Fraenkel set theory). The logic is intuitionistic first order logic with equality in the language of classical
$\mathsf {IZF}$
(intuitionistic Zermelo–Fraenkel set theory). The logic is intuitionistic first order logic with equality in the language of classical
![]() $\mathsf {ZF}$
. As usual, a formula is bounded, or
$\mathsf {ZF}$
. As usual, a formula is bounded, or
![]() $\Delta _0$
, if all quantifiers appear in the form
$\Delta _0$
, if all quantifiers appear in the form
![]() $\forall x\in y$
and
$\forall x\in y$
and
![]() $\exists x\in y$
.
$\exists x\in y$
.
The theory
![]() $\mathsf {CZF}$
consists of the following axioms:
$\mathsf {CZF}$
consists of the following axioms:

![]() $^{\ast} $
Let
$^{\ast} $
Let
![]() $x=0$
be
$x=0$
be
![]() $\forall y\in x\, (y\notin x)$
and
$\forall y\in x\, (y\notin x)$
and
![]() $x=y\cup \{y\}$
be
$x=y\cup \{y\}$
be
![]() $\forall z\kern-1pt \in\kern-1pt x\, (z\kern-1pt \in\kern-1pt y\lor z\kern-1pt =\kern-1pt y)\land \forall z\kern-1pt \in\kern-1pt y\, (z\in x)\land y\kern-1pt \in\kern-1pt x$
.
$\forall z\kern-1pt \in\kern-1pt x\, (z\kern-1pt \in\kern-1pt y\lor z\kern-1pt =\kern-1pt y)\land \forall z\kern-1pt \in\kern-1pt y\, (z\in x)\land y\kern-1pt \in\kern-1pt x$
.
The theory
![]() $\mathsf {IZF}$
consists of extensionality, pairing, union, infinity, induction,
$\mathsf {IZF}$
consists of extensionality, pairing, union, infinity, induction,

Thus
![]() $\mathsf {IZF}$
is
$\mathsf {IZF}$
is
![]() $\mathsf {CZF}$
with bounded separation replaced by full separation and subset collection replaced by powerset. Note that powerset implies subset collection, and strong collection follows from separation and collection. It is well known that
$\mathsf {CZF}$
with bounded separation replaced by full separation and subset collection replaced by powerset. Note that powerset implies subset collection, and strong collection follows from separation and collection. It is well known that
![]() $\mathsf { CZF}$
with classical logic, and hence
$\mathsf { CZF}$
with classical logic, and hence
![]() $\mathsf {IZF}$
with classical logic, is equivalent to
$\mathsf {IZF}$
with classical logic, is equivalent to
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
2.2 Countable and dependent choice
The full axiom of choice
![]() $\mathsf {AC}$
is known to imply forms of excluded middle [Reference Diaconescu11]. For example,
$\mathsf {AC}$
is known to imply forms of excluded middle [Reference Diaconescu11]. For example,
![]() $\mathsf {CZF}+\mathsf {AC}+\text { separation}=\mathsf {IZF}+\mathsf {AC}=\mathsf {ZFC}$
(cf. [Reference Aczel and Rathjen4]). Nevertheless, countable choice and several forms of dependent choice are deemed constructively acceptable. Note that
$\mathsf {CZF}+\mathsf {AC}+\text { separation}=\mathsf {IZF}+\mathsf {AC}=\mathsf {ZFC}$
(cf. [Reference Aczel and Rathjen4]). Nevertheless, countable choice and several forms of dependent choice are deemed constructively acceptable. Note that
![]() $\mathsf {RDC}$
is an axiom of Myhill’s
$\mathsf {RDC}$
is an axiom of Myhill’s
![]() $\mathsf {CST}$
(constructive set theory) [Reference Myhill24], which provides a standard set-theoretical framework for Bishop-style constructive mathematics [Reference Bishop9]. Dependent choice also features in Brouwer’s intuitionistic analysis (cf. [Reference Troelstra and van Dalen34]).
$\mathsf {CST}$
(constructive set theory) [Reference Myhill24], which provides a standard set-theoretical framework for Bishop-style constructive mathematics [Reference Bishop9]. Dependent choice also features in Brouwer’s intuitionistic analysis (cf. [Reference Troelstra and van Dalen34]).
Countable choice (
![]() $\mathsf {AC}_{\omega }$
): if
$\mathsf {AC}_{\omega }$
): if
![]() $\forall n\in \omega \, \exists y\, \varphi (n,y)$
, then there exists a function f with
$\forall n\in \omega \, \exists y\, \varphi (n,y)$
, then there exists a function f with
![]() $\operatorname {{\mathrm {dom}}}(f)=\omega $
such that
$\operatorname {{\mathrm {dom}}}(f)=\omega $
such that
![]() $\forall n\in \omega \, \varphi (n,f(n))$
, for all formulae
$\forall n\in \omega \, \varphi (n,f(n))$
, for all formulae
![]() $\varphi $
.
$\varphi $
.
Dependent choice (
![]() $\mathsf {DC}$
): if
$\mathsf {DC}$
): if
![]() $\forall x\, \exists y\, \varphi (x,y)$
, then for every x there is a function f with
$\forall x\, \exists y\, \varphi (x,y)$
, then for every x there is a function f with
![]() $\operatorname {{\mathrm {dom}}}(f)=\omega $
such that
$\operatorname {{\mathrm {dom}}}(f)=\omega $
such that
![]() $f(0)=x$
and
$f(0)=x$
and
![]() $\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
$\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
![]() $\varphi $
.
$\varphi $
.
Limited dependent choice (
![]() $\mathsf {DC}^{\dagger }$
): if X is a set and
$\mathsf {DC}^{\dagger }$
): if X is a set and
![]() $\forall x\in X\, \exists y\in X\, \varphi (x,y)$
, then for every
$\forall x\in X\, \exists y\in X\, \varphi (x,y)$
, then for every
![]() $x\in X$
there is a function
$x\in X$
there is a function
![]() $f\colon \omega \to X$
such that
$f\colon \omega \to X$
such that
![]() $f(0)=x$
and
$f(0)=x$
and
![]() $\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
$\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
![]() $\varphi $
.
$\varphi $
.
Relativized dependent choice (
![]() $\mathsf {RDC}$
): if
$\mathsf {RDC}$
): if
![]() $\forall x\, (\psi (x)\rightarrow \exists y\, (\psi (y)\land \varphi (x,y)))$
, then for every x such that
$\forall x\, (\psi (x)\rightarrow \exists y\, (\psi (y)\land \varphi (x,y)))$
, then for every x such that
![]() $\psi (x)$
, there is a function f with
$\psi (x)$
, there is a function f with
![]() $\operatorname {{\mathrm {dom}}}(f)=\omega $
such that
$\operatorname {{\mathrm {dom}}}(f)=\omega $
such that
![]() $f(0)=x$
and
$f(0)=x$
and
![]() $\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
$\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
.
$\varphi $
.
Limited relativized dependent choice (
![]() $\mathsf {RDC}^{\dagger }$
): if X is a set and
$\mathsf {RDC}^{\dagger }$
): if X is a set and
![]() $\forall x\in X\, (\psi (x)\rightarrow \exists y\in X\, (\psi (y)\land \varphi (x,y)))$
, then for every
$\forall x\in X\, (\psi (x)\rightarrow \exists y\in X\, (\psi (y)\land \varphi (x,y)))$
, then for every
![]() $x\in X$
such that
$x\in X$
such that
![]() $\psi (x)$
, there is a function
$\psi (x)$
, there is a function
![]() $f\colon \omega \to X$
such that
$f\colon \omega \to X$
such that
![]() $f(0)=x$
and
$f(0)=x$
and
![]() $\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
$\forall n\in \omega \, \varphi (f(n),f(n+1))$
, for all formulae
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
.
$\varphi $
.
Note that classically, say over
![]() $\mathsf {ZF}$
, the above forms of dependent choice are all equivalent to one another. Over
$\mathsf {ZF}$
, the above forms of dependent choice are all equivalent to one another. Over
![]() $\mathsf {CZF}$
,
$\mathsf {CZF}$
,
![]() $\mathsf {RDC}\rightarrow \mathsf {DC}$
and
$\mathsf {RDC}\rightarrow \mathsf {DC}$
and
![]() $\mathsf {RDC}\rightarrow \mathsf {RDC}^{\dagger }\rightarrow \mathsf {DC}^{\dagger }\rightarrow \mathsf { AC}_{\omega }$
. Over
$\mathsf {RDC}\rightarrow \mathsf {RDC}^{\dagger }\rightarrow \mathsf {DC}^{\dagger }\rightarrow \mathsf { AC}_{\omega }$
. Over
![]() $\mathsf {IZF}$
, due to separation,
$\mathsf {IZF}$
, due to separation,
![]() $\mathsf {RDC}^{\dagger }\leftrightarrow \mathsf {DC}^{\dagger }$
.
$\mathsf {RDC}^{\dagger }\leftrightarrow \mathsf {DC}^{\dagger }$
.
2.3 Inductive definitions and the regular extension axiom
The theory
![]() $\mathsf {CZF}$
allows for a smooth treatment of inductively defined classes [Reference Aczel3, Reference Aczel and Rathjen4].
$\mathsf {CZF}$
allows for a smooth treatment of inductively defined classes [Reference Aczel3, Reference Aczel and Rathjen4].
Definition 2.1. An inductive definition is a class
![]() $\Phi $
of ordered pairs. In other words, any formula
$\Phi $
of ordered pairs. In other words, any formula
![]() $\Phi (X,x)$
is an inductive definition. We write
$\Phi (X,x)$
is an inductive definition. We write
or simply
![]() $(X,x)\in \Phi $
, in place of
$(X,x)\in \Phi $
, in place of
![]() $\Phi (X,x)$
. A class I is closed under
$\Phi (X,x)$
. A class I is closed under
![]() $\Phi $
if, whenever
$\Phi $
if, whenever
![]() $(X,x)\in \Phi $
and
$(X,x)\in \Phi $
and
![]() $X\subseteq I$
, we have
$X\subseteq I$
, we have
![]() $x\in I$
.
$x\in I$
.
Theorem 2.2. Given an inductive definition
![]() $\Phi $
, there exists a class
$\Phi $
, there exists a class
![]() $I(\Phi )$
such that
$I(\Phi )$
such that
![]() $\mathsf {CZF}$
proves that
$\mathsf {CZF}$
proves that
![]() $I(\Phi )$
is closed under
$I(\Phi )$
is closed under
![]() $\Phi $
, and for every class J,
$\Phi $
, and for every class J,
![]() $\mathsf {CZF}$
proves that if J is closed under
$\mathsf {CZF}$
proves that if J is closed under
![]() $\Phi $
, then
$\Phi $
, then
![]() $I\subseteq J$
. We say that
$I\subseteq J$
. We say that
![]() $I(\Phi )$
is inductively defined by
$I(\Phi )$
is inductively defined by
![]() $\Phi $
.
$\Phi $
.
Proof See, e.g., [Reference Aczel and Rathjen4] for details. The class
![]() $I(\Phi )$
is defined as follows. A set of ordered pairs Z is called an iteration set for
$I(\Phi )$
is defined as follows. A set of ordered pairs Z is called an iteration set for
![]() $\Phi $
if for every
$\Phi $
if for every
![]() $\langle {u,x}\rangle \in Z$
there exists
$\langle {u,x}\rangle \in Z$
there exists
![]() $(X,x)\in \Phi $
such that
$(X,x)\in \Phi $
such that
![]() $X\subseteq \bigcup _{v\in u}\{z\mid \langle {v,z}\rangle \in Z\}$
. Let
$X\subseteq \bigcup _{v\in u}\{z\mid \langle {v,z}\rangle \in Z\}$
. Let
To prove that
![]() $I(\Phi )$
is closed under
$I(\Phi )$
is closed under
![]() $\Phi $
we invoke strong collection. The fact that
$\Phi $
we invoke strong collection. The fact that
![]() $I(\Phi )$
is the smallest class closed under
$I(\Phi )$
is the smallest class closed under
![]() $\Phi $
is proved by induction.
$\Phi $
is proved by induction.
Theorem 2.3 (Induction on the inductive definition
 $\Phi $
).
$\Phi $
).
![]() $\mathsf {CZF}$
proves
$\mathsf {CZF}$
proves
for every formula
![]() $\varphi $
.
$\varphi $
.
Proof Obvious.
In the presence of Aczel’s
![]() $\mathsf {REA}$
(regular extension axiom), one can show that many inductively defined classes exist as sets.
$\mathsf {REA}$
(regular extension axiom), one can show that many inductively defined classes exist as sets.
Definition 2.4 (Regular).
A set X is regular if it is transitive and, whenever
![]() $x\in X$
and R is a set such that
$x\in X$
and R is a set such that
![]() $\forall u\in x\, \exists v\in X\, (\langle {u,v}\rangle \in R)$
, then there is a
$\forall u\in x\, \exists v\in X\, (\langle {u,v}\rangle \in R)$
, then there is a
![]() $y\in X$
such that
$y\in X$
such that
In particular, if
![]() $R\colon x\to X$
is a function, then
$R\colon x\to X$
is a function, then
![]() $\operatorname {{\mathrm {ran}}}(R)\in X$
.
$\operatorname {{\mathrm {ran}}}(R)\in X$
.
Regular extension axiom (
![]() $\mathsf {REA}$
): every set is a subset of a regular set.
$\mathsf {REA}$
): every set is a subset of a regular set.
Definition 2.5. An inductive definition
![]() $\Phi $
is bounded if:
$\Phi $
is bounded if:
-
• the class
 $\{x\mid (X,x)\in \Phi \}$
is a set for every set X;
$\{x\mid (X,x)\in \Phi \}$
is a set for every set X; -
• there is a set B such that whenever
 $(X,x)\in \Phi $
, then X is an image of a set in B, that is, there is a function f from Y onto X for some
$(X,x)\in \Phi $
, then X is an image of a set in B, that is, there is a function f from Y onto X for some
 $Y\in B$
. The set B is called a bound for
$Y\in B$
. The set B is called a bound for
 $\Phi $
.
$\Phi $
.
Theorem 2.6 (
 $\mathsf {CZF}+\mathsf {REA}$
).
$\mathsf {CZF}+\mathsf {REA}$
).
If
![]() $\Phi $
is a bounded inductive definition, then the class
$\Phi $
is a bounded inductive definition, then the class
![]() $I(\Phi )$
is a set.
$I(\Phi )$
is a set.
Proof See [Reference Aczel3, Theorem 5.2].
2.4 Dependent type constructions
The usual type constructors
![]() ${\Pi }$
(dependent product),
${\Pi }$
(dependent product),
![]() ${\Sigma }$
(dependent sum),
${\Sigma }$
(dependent sum),
![]() $\mathrm {I}$
(identity), and
$\mathrm {I}$
(identity), and
![]() $\mathrm {W}$
have obvious set-theoretic analogues.
$\mathrm {W}$
have obvious set-theoretic analogues.
Definition 2.7 (
 $\mathsf {CZF}$
).
$\mathsf {CZF}$
).
Let F be a function with
![]() $\operatorname {{\mathrm {dom}}}(F)=X$
. Let
$\operatorname {{\mathrm {dom}}}(F)=X$
. Let
 $$ \begin{align*} {\Pi}(X,F)&= \prod_{x\in X}F(x)=\{f\colon X\to \bigcup_{x\in X}F(x)\mid \forall x\in X\, (f(x)\in F(x))\} && ({{Cartesian\ product}}), \\ {\Sigma}(X,F)&=\sum_{x\in X}F(x)=\{ \langle{x,y}\rangle\mid x\in X\land y\in F(x)\} && ({{disjoint\ union}}). \end{align*} $$
$$ \begin{align*} {\Pi}(X,F)&= \prod_{x\in X}F(x)=\{f\colon X\to \bigcup_{x\in X}F(x)\mid \forall x\in X\, (f(x)\in F(x))\} && ({{Cartesian\ product}}), \\ {\Sigma}(X,F)&=\sum_{x\in X}F(x)=\{ \langle{x,y}\rangle\mid x\in X\land y\in F(x)\} && ({{disjoint\ union}}). \end{align*} $$
For x, y sets, let
![]() $\mathrm {I}(x,y)=\{z\in \{0\}\mid x=y\}$
.
$\mathrm {I}(x,y)=\{z\in \{0\}\mid x=y\}$
.
Remark 2.8. Set exponentiation
![]() $X\to Y$
and the binary Cartesian product
$X\to Y$
and the binary Cartesian product
![]() $X\times Y$
are special instances of
$X\times Y$
are special instances of
![]() ${\Pi }(X,F)$
and
${\Pi }(X,F)$
and
![]() ${\Sigma }(X,F)$
respectively, with
${\Sigma }(X,F)$
respectively, with
![]() $F(x)=Y$
.
$F(x)=Y$
.
Definition 2.9 (
 $\mathsf {CZF}$
).
$\mathsf {CZF}$
).
If F is a function with
![]() $\operatorname {{\mathrm {dom}}}(F)=X$
, then
$\operatorname {{\mathrm {dom}}}(F)=X$
, then
![]() $\mathrm {W}(X,F)$
is the smallest class W such that
$\mathrm {W}(X,F)$
is the smallest class W such that
-
• if
 $x\in X$
and
$x\in X$
and
 $f\colon F(x)\to W$
, then
$f\colon F(x)\to W$
, then
 $\langle {x,f}\rangle \in W$
.
$\langle {x,f}\rangle \in W$
.
Remark 2.10.
![]() $\mathrm {W}(X,F)$
is the class of well-founded rooted trees with labels in X such that the arity of a node with label x is the set
$\mathrm {W}(X,F)$
is the class of well-founded rooted trees with labels in X such that the arity of a node with label x is the set
![]() $F(x)$
.
$F(x)$
.
Theorem 2.11 (
 $\mathsf {CZF}+\mathsf {REA}$
).
$\mathsf {CZF}+\mathsf {REA}$
).
The class
![]() $\mathrm {W}(X,F)$
is a set.
$\mathrm {W}(X,F)$
is a set.
Proof By Theorem 2.6, since
![]() $\mathrm {W}(X,F)$
is bounded inductively definable.
$\mathrm {W}(X,F)$
is bounded inductively definable.
Definition 2.12 (
 $\mathsf {CZF}$
).
$\mathsf {CZF}$
).
The class
![]() $I={\Pi }{\Sigma }$
is inductively defined by clauses:
$I={\Pi }{\Sigma }$
is inductively defined by clauses:
-
(i)
 $n\in I$
for every
$n\in I$
for every
 $n\in \omega $
;
$n\in \omega $
; -
(ii)
 $\omega \in I$
;
$\omega \in I$
; -
(iii) if
 $X\in I$
and
$X\in I$
and
 $F\colon X\to I$
, then
$F\colon X\to I$
, then
 ${\Pi }(X,F),{\Sigma }(X,F)\in I$
.
${\Pi }(X,F),{\Sigma }(X,F)\in I$
.
The class
![]() $I={\Pi }{\Sigma }\mathrm {I}$
is inductively defined by clauses (i), (ii), (iii), and
$I={\Pi }{\Sigma }\mathrm {I}$
is inductively defined by clauses (i), (ii), (iii), and
-
(iv) if
 $X\in I$
and
$X\in I$
and
 $x,y\in X$
, then
$x,y\in X$
, then
 $\mathrm {I}(x,y)\in I$
.
$\mathrm {I}(x,y)\in I$
.
Definition 2.13 (
 $\mathsf {CZF}+\mathsf {REA}$
).
$\mathsf {CZF}+\mathsf {REA}$
).
The class
![]() $I={\Pi }{\Sigma }\mathrm {W}$
is inductively defined by clauses (i), (ii), (iii), and
$I={\Pi }{\Sigma }\mathrm {W}$
is inductively defined by clauses (i), (ii), (iii), and
-
(v) if
 $X\in I$
and
$X\in I$
and
 $F\colon X\to I$
, then
$F\colon X\to I$
, then
 $\mathrm {W}(X,F)\in I$
.
$\mathrm {W}(X,F)\in I$
.
The class
![]() $I={\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
is inductively defined by clauses (i)–(v).
$I={\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
is inductively defined by clauses (i)–(v).
Given a class I, we say that x is an I-set if x belongs to I.
2.5 Choice for dependent types
Definition 2.14 (Base).
A set X is a base if for every relation R such that
![]() $\forall x\in X\, \exists y\, (\langle {x,y}\rangle \in R)$
, there exists a function f with domain X such that
$\forall x\in X\, \exists y\, (\langle {x,y}\rangle \in R)$
, there exists a function f with domain X such that
![]() $\forall x\in X\, (\langle {x,f(x)}\rangle \in R)$
.Footnote
4
$\forall x\in X\, (\langle {x,f(x)}\rangle \in R)$
.Footnote
4
Presentation axiom (
![]() $\mathsf {PAx}$
): every set is an image of a base.
$\mathsf {PAx}$
): every set is an image of a base.
![]() ${\Pi }{\Sigma }$
axiom of choice (
${\Pi }{\Sigma }$
axiom of choice (
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}$
): every
${\Pi }{\Sigma }\text {-}\mathsf {AC}$
): every
![]() ${\Pi }{\Sigma }$
-set is a base.
${\Pi }{\Sigma }$
-set is a base.
![]() ${\Pi }{\Sigma }$
presentation axiom (
${\Pi }{\Sigma }$
presentation axiom (
![]() ${\Pi }{\Sigma }\text {-}\mathsf {PAx}$
): every set is an image of a
${\Pi }{\Sigma }\text {-}\mathsf {PAx}$
): every set is an image of a
![]() ${\Pi }{\Sigma }$
-set and every
${\Pi }{\Sigma }$
-set and every
![]() ${\Pi }{\Sigma }$
-set is a base.
${\Pi }{\Sigma }$
-set is a base.
We have analogue axioms for
![]() ${\Pi }{\Sigma }\mathrm {I}$
and relatives. A simple argument shows that
${\Pi }{\Sigma }\mathrm {I}$
and relatives. A simple argument shows that
![]() $\mathsf {CZF}+\mathsf {PAx}\vdash \mathsf { DC}^{\dagger }$
(cf. [Reference Aczel1, p. 65] and [Reference Aczel2, p. 27]). Aczel’s interpretation of
$\mathsf {CZF}+\mathsf {PAx}\vdash \mathsf { DC}^{\dagger }$
(cf. [Reference Aczel1, p. 65] and [Reference Aczel2, p. 27]). Aczel’s interpretation of
![]() $\mathsf {CZF}$
in type theory [Reference Aczel1] validates
$\mathsf {CZF}$
in type theory [Reference Aczel1] validates
![]() $\mathsf {RDC}$
[Reference Aczel1, Theorem 7.1], [Reference Aczel2, Theorem 5.7] and
$\mathsf {RDC}$
[Reference Aczel1, Theorem 7.1], [Reference Aczel2, Theorem 5.7] and
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {PAx}$
[Reference Aczel2, Theorem 7.4]. In [Reference Aczel3], the type-theoretic interpretation of
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {PAx}$
[Reference Aczel2, Theorem 7.4]. In [Reference Aczel3], the type-theoretic interpretation of
![]() $\mathsf {CZF}+\mathsf {REA}$
(by using
$\mathsf {CZF}+\mathsf {REA}$
(by using
![]() $\mathrm {W}$
-types) is shown to validate
$\mathrm {W}$
-types) is shown to validate
![]() $\mathsf {RDC}$
and
$\mathsf {RDC}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {PAx}$
[Reference Aczel3, Theorem 5.6].Footnote
5
Similarly, Rathjen’s formulae-as-classes interpretation provides a model of
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {PAx}$
[Reference Aczel3, Theorem 5.6].Footnote
5
Similarly, Rathjen’s formulae-as-classes interpretation provides a model of
![]() $\mathsf {CZF}+\mathsf { RDC}+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}$
in
$\mathsf {CZF}+\mathsf { RDC}+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}$
in
![]() $\mathsf {CZF}_{\mathsf {exp}}$
[Reference Rathjen29, Theorem 4.13] and of
$\mathsf {CZF}_{\mathsf {exp}}$
[Reference Rathjen29, Theorem 4.13] and of
![]() $\mathsf {CZF}+\mathsf {REA}+\mathsf {RDC}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}$
in
$\mathsf {CZF}+\mathsf {REA}+\mathsf {RDC}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}$
in
![]() $\mathsf {CZF}_{\mathsf { exp}}+\mathsf {REA}$
[Reference Rathjen29, Theorem 4.33], where
$\mathsf {CZF}_{\mathsf { exp}}+\mathsf {REA}$
[Reference Rathjen29, Theorem 4.33], where
![]() $\mathsf {CZF}_{\mathsf {exp}}$
is
$\mathsf {CZF}_{\mathsf {exp}}$
is
![]() $\mathsf {CZF}$
with exponentiation in lieu of subset collection.
$\mathsf {CZF}$
with exponentiation in lieu of subset collection.
We introduce the following natural extensions of
![]() $\mathsf {AC}_{\mathsf {FT}}$
and
$\mathsf {AC}_{\mathsf {FT}}$
and
![]() $\mathsf {RDC}_{\mathsf {FT}}$
.
$\mathsf {RDC}_{\mathsf {FT}}$
.
![]() ${\Pi }{\Sigma }$
limited axiom of choice (
${\Pi }{\Sigma }$
limited axiom of choice (
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
): if X and Y are
${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
): if X and Y are
![]() ${\Pi }{\Sigma }$
-sets and
${\Pi }{\Sigma }$
-sets and
![]() $\forall x\in X\, \exists y\in Y\, \varphi (x,y)$
, then there is a function
$\forall x\in X\, \exists y\in Y\, \varphi (x,y)$
, then there is a function
![]() $f\colon X\to Y$
such that
$f\colon X\to Y$
such that
![]() $\forall x\in X\, \varphi (x,f(x))$
, for all formulae
$\forall x\in X\, \varphi (x,f(x))$
, for all formulae
![]() $\varphi $
.
$\varphi $
.
![]() ${\Pi }{\Sigma }$
limited relativized dependent choice (
${\Pi }{\Sigma }$
limited relativized dependent choice (
![]() ${\Pi }{\Sigma }\text {-}\mathsf {RDC}^{\dagger }$
): this is just
${\Pi }{\Sigma }\text {-}\mathsf {RDC}^{\dagger }$
): this is just
![]() $\mathsf { RDC}^{\dagger }$
restricted to
$\mathsf { RDC}^{\dagger }$
restricted to
![]() ${\Pi }{\Sigma }$
-sets.
${\Pi }{\Sigma }$
-sets.
We have similar axioms for
![]() ${\Pi }{\Sigma }\mathrm {I}$
and relatives. Each schema can be replaced by a single axiom over say
${\Pi }{\Sigma }\mathrm {I}$
and relatives. Each schema can be replaced by a single axiom over say
![]() $\mathsf { IZF}+\mathsf {REA}$
. This is just an upper bound. For example, over
$\mathsf { IZF}+\mathsf {REA}$
. This is just an upper bound. For example, over
![]() $\mathsf {CZF}$
,
$\mathsf {CZF}$
,
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
is equivalent to:
${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
is equivalent to:
If X and Y are
![]() ${\Pi }{\Sigma }$
-sets, then for every relation R such that
${\Pi }{\Sigma }$
-sets, then for every relation R such that
![]() $\forall x\in X\, \exists y\in Y\, (\langle {x,y}\rangle \in R)$
, there is a function
$\forall x\in X\, \exists y\in Y\, (\langle {x,y}\rangle \in R)$
, there is a function
![]() $f\colon X\to Y$
such that
$f\colon X\to Y$
such that
![]() $\forall x\in X\, (\langle {x,f(x)}\rangle \in R)$
.
$\forall x\in X\, (\langle {x,f(x)}\rangle \in R)$
.
Clearly,
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
follows from
${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
follows from
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}$
, and similarly for
${\Pi }{\Sigma }\text {-}\mathsf {AC}$
, and similarly for
![]() ${\Pi }{\Sigma }\mathrm {I}$
and the like. Note that
${\Pi }{\Sigma }\mathrm {I}$
and the like. Note that
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
already includes the axiom of choice for all finite types.
${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
already includes the axiom of choice for all finite types.
Theorem 2.15. Over
![]() $\mathsf {CZF}$
,
$\mathsf {CZF}$
,
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}\leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {AC}$
and
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}\leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {AC}$
and
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {PAx} \ \leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {PAx}$
.
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {PAx} \ \leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {PAx}$
.
Over
![]() $\mathsf {CZF}+\mathsf {REA}$
,
$\mathsf {CZF}+\mathsf {REA}$
,
![]() ${\Pi }{\Sigma }\mathrm {W}\text {-}\mathsf {AC}\leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {AC}$
and
${\Pi }{\Sigma }\mathrm {W}\text {-}\mathsf {AC}\leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {AC}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\text {-}\mathsf {PAx}\leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {PAx}$
.
${\Pi }{\Sigma }\mathrm {W}\text {-}\mathsf {PAx}\leftrightarrow {\Pi }{\Sigma }\text {-}\mathsf {PAx}$
.
Proof See [Reference Aczel3, Theorems 3.7 and 5.9].
Theorem 2.15 does not translate to
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
and relatives. For example, the proof of [Reference Aczel3, Theorem 3.7] consists in showing, under
${\Pi }{\Sigma }\text {-}\mathsf {AC}^{\dagger }$
and relatives. For example, the proof of [Reference Aczel3, Theorem 3.7] consists in showing, under
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}$
, that every set in
${\Pi }{\Sigma }\text {-}\mathsf {AC}$
, that every set in
![]() ${\Pi }{\Sigma }\mathrm {I}$
is in bijection with a set in
${\Pi }{\Sigma }\mathrm {I}$
is in bijection with a set in
![]() ${\Pi }{\Sigma }$
. The use of
${\Pi }{\Sigma }$
. The use of
![]() ${\Pi }{\Sigma }\text {-}\mathsf {AC}$
is essential. The proof of the following is trivial.
${\Pi }{\Sigma }\text {-}\mathsf {AC}$
is essential. The proof of the following is trivial.
Theorem 2.16. Over
![]() $\mathsf {CZF} +$
“every set is an image of a
$\mathsf {CZF} +$
“every set is an image of a
![]() ${\Pi }{\Sigma }\mathrm {I}$
-set,”
${\Pi }{\Sigma }\mathrm {I}$
-set,”
![]() $ {\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC} \leftrightarrow {\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
. Similarly for
$ {\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC} \leftrightarrow {\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
. Similarly for
![]() $\mathsf {CZF}+\mathsf {REA}$
and
$\mathsf {CZF}+\mathsf {REA}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
in place of
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
in place of
![]() $\mathsf {CZF}$
and
$\mathsf {CZF}$
and
![]() ${\Pi }{\Sigma }\mathrm {I}$
respectively.
${\Pi }{\Sigma }\mathrm {I}$
respectively.
3 Extensional generic realizability
3.1 Partial combinatory algebras
Generic realizability is based on the notion of partial combinatory algebra. Let us review some basic facts. For more information, we refer the reader to [Reference Beeson7, Reference Feferman12, Reference Feferman13, Reference van Oosten26].
Definition 3.1. Application terms, or simply terms, over a set A are defined by clauses:
-
(i) variables
 $x_1,x_2,\ldots $
are terms;
$x_1,x_2,\ldots $
are terms; -
(ii) elements of A are terms;
-
(iii) if t and s are terms,
 $(ts)$
is also a term.
$(ts)$
is also a term.
Definition 3.2. A partial algebra is a set A together with a partial binary operation
![]() $\cdot $
on A.
$\cdot $
on A.
Every partial algebra A induces a partial interpretation of closed applications terms over A by elements of A in the obvious way.
Notation 3.3. Let
![]() $a,b,c\in A$
and
$a,b,c\in A$
and
![]() $t,s$
be closed terms over A. Instead of
$t,s$
be closed terms over A. Instead of
![]() $a\cdot b$
we just write
$a\cdot b$
we just write
![]() $ab$
. We also employ the association to the left convention, meaning that
$ab$
. We also employ the association to the left convention, meaning that
![]() $abc$
stands for
$abc$
stands for
![]() $(ab)c$
. The relation
$(ab)c$
. The relation
![]() $t\downarrow a$
is defined by clauses: (i)
$t\downarrow a$
is defined by clauses: (i)
![]() $a\downarrow a$
and (ii)
$a\downarrow a$
and (ii)
![]() $(ts)\downarrow a$
if
$(ts)\downarrow a$
if
![]() $t\downarrow b$
,
$t\downarrow b$
,
![]() $s\downarrow c$
, and
$s\downarrow c$
, and
![]() $bc=a$
for some
$bc=a$
for some
![]() $b,c\in A$
. We write
$b,c\in A$
. We write
![]() $t\downarrow $
for
$t\downarrow $
for
![]() $\exists a\, (t\downarrow a)$
. We use Kleene equality
$\exists a\, (t\downarrow a)$
. We use Kleene equality
![]() $t\simeq s$
to express that either both sides are undefined, or else they are both defined and equal. In the second case, we write
$t\simeq s$
to express that either both sides are undefined, or else they are both defined and equal. In the second case, we write
![]() $t=s$
.
$t=s$
.
Definition 3.4. A partial algebra
![]() $(A,\cdot )$
with at least two elements is a partial combinatory algebra (pca) if there are elements
$(A,\cdot )$
with at least two elements is a partial combinatory algebra (pca) if there are elements
![]() $\mathbf k$
and
$\mathbf k$
and
![]() $\mathbf s$
in A such that for all
$\mathbf s$
in A such that for all
![]() $a,b,c\in A$
:
$a,b,c\in A$
:
-
•
 $\mathbf ka b\simeq a$
;
$\mathbf ka b\simeq a$
; -
•
 $\mathbf sab\downarrow $
and
$\mathbf sab\downarrow $
and
 $\mathbf sabc\simeq ac(bc)$
.
$\mathbf sabc\simeq ac(bc)$
.
The combinators
![]() $\mathbf k$
and
$\mathbf k$
and
![]() $\mathbf s$
are due to Schönfinkel [Reference Schönfinkel31] and the defining equations, although formulated just in the total case, are due to Curry [Reference Curry10]. The name combinatory stems from the property known as combinatory completeness. Informally, this means that we can form
$\mathbf s$
are due to Schönfinkel [Reference Schönfinkel31] and the defining equations, although formulated just in the total case, are due to Curry [Reference Curry10]. The name combinatory stems from the property known as combinatory completeness. Informally, this means that we can form
![]() $\lambda $
-terms.
$\lambda $
-terms.
Lemma 3.5 (
 $\lambda $
-abstraction).
$\lambda $
-abstraction).
Let A be a pca. For every term
![]() $t(x,x_1,\ldots ,x_n)$
, one can find (in an effective way) a new term
$t(x,x_1,\ldots ,x_n)$
, one can find (in an effective way) a new term
![]() $s(x_1,\ldots ,x_n)$
, denoted
$s(x_1,\ldots ,x_n)$
, denoted
![]() $\lambda x.t$
, such that for all
$\lambda x.t$
, such that for all
![]() $a_1,\ldots ,a_n\in A$
:
$a_1,\ldots ,a_n\in A$
:
-
•
 $s(a_1,\ldots ,a_n)\downarrow $
;
$s(a_1,\ldots ,a_n)\downarrow $
; -
•
 $s(a_1,\ldots ,a_n)a\simeq t(a,a_1,\ldots ,a_n)$
.
$s(a_1,\ldots ,a_n)a\simeq t(a,a_1,\ldots ,a_n)$
.
Remark 3.6. The term
![]() $\lambda x.t$
is built solely with the aid of
$\lambda x.t$
is built solely with the aid of
![]() $\mathbf k$
,
$\mathbf k$
,
![]() $\mathbf s$
, and symbols occurring in t. Also, the construction of this term is uniform in the given pca.
$\mathbf s$
, and symbols occurring in t. Also, the construction of this term is uniform in the given pca.
An immediate consequence of
![]() $\lambda $
-abstraction is the existence of pairing and unpairing combinators
$\lambda $
-abstraction is the existence of pairing and unpairing combinators
![]() $\mathbf p$
,
$\mathbf p$
,
![]() $\mathbf {p_0}$
, and
$\mathbf {p_0}$
, and
![]() $\mathbf {p_1}$
such that
$\mathbf {p_1}$
such that
![]() $\mathbf pab\downarrow $
and
$\mathbf pab\downarrow $
and
![]() $\mathbf {p_i}(\mathbf pa_0a_1)\simeq a_i$
.Footnote
6
A more remarkable application of
$\mathbf {p_i}(\mathbf pa_0a_1)\simeq a_i$
.Footnote
6
A more remarkable application of
![]() $\lambda $
-abstraction is the recursion theorem for pca’s.
$\lambda $
-abstraction is the recursion theorem for pca’s.
Lemma 3.7 (Recursion theorem).
There exists a closed term
![]() $\mathbf f$
such that for all
$\mathbf f$
such that for all
![]() $a,b\in A$
we have
$a,b\in A$
we have
![]() $\mathbf f a\downarrow $
and
$\mathbf f a\downarrow $
and
![]() $\mathbf f ab\simeq a(\mathbf fa) b$
.
$\mathbf f ab\simeq a(\mathbf fa) b$
.
It is worth considering some additional structure (see however Remark 3.9).
Definition 3.8. We say that A is a pca over
![]() $\omega $
if there are combinators
$\omega $
if there are combinators
![]() $\mathbf {succ}, \mathbf {pred}$
(successor and predecessor combinators),
$\mathbf {succ}, \mathbf {pred}$
(successor and predecessor combinators),
![]() $\mathbf d$
(definition by cases combinator), and a map
$\mathbf d$
(definition by cases combinator), and a map
![]() $n\mapsto \bar n$
from
$n\mapsto \bar n$
from
![]() $\omega $
to A such that for all
$\omega $
to A such that for all
![]() $n\in \omega $
$n\in \omega $
 $$ \begin{align*} \operatorname{\mathrm{\mathbf{succ}}} \bar n&\simeq \overline{n+1}, & \operatorname{\mathrm{\mathbf{pred}}}\overline{n+1}&\simeq \bar n, & \mathbf d\bar n\bar mab\simeq \begin{cases} a, & n=m,\\ b, & n\neq m. \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\mathbf{succ}}} \bar n&\simeq \overline{n+1}, & \operatorname{\mathrm{\mathbf{pred}}}\overline{n+1}&\simeq \bar n, & \mathbf d\bar n\bar mab\simeq \begin{cases} a, & n=m,\\ b, & n\neq m. \end{cases} \end{align*} $$
One then defines
![]() $\mathbf 0=_{\mathrm {def}}\bar 0$
and
$\mathbf 0=_{\mathrm {def}}\bar 0$
and
![]() ${\mathbf 1}=_{\mathrm {def}}\bar 1$
.
${\mathbf 1}=_{\mathrm {def}}\bar 1$
.
For the rest of the paper, by a pca we really mean a pca over
![]() $\omega $
. The only closed terms we ever need are built up by using the combinators
$\omega $
. The only closed terms we ever need are built up by using the combinators
![]() $\mathbf k$
,
$\mathbf k$
,
![]() $\mathbf s$
,
$\mathbf s$
,
![]() $\mathbf p$
,
$\mathbf p$
,
![]() $\mathbf {p_0}$
,
$\mathbf {p_0}$
,
![]() $\mathbf {p_1}$
,
$\mathbf {p_1}$
,
![]() $\mathbf 0$
,
$\mathbf 0$
,
![]() ${\mathbf 1}$
,
${\mathbf 1}$
,
![]() $\mathbf {succ}$
,
$\mathbf {succ}$
,
![]() $\mathbf {pred}$
, and
$\mathbf {pred}$
, and
![]() $\mathbf d$
.
$\mathbf d$
.
Note that one can do without
![]() $\mathbf k$
by letting
$\mathbf k$
by letting
![]() $\mathbf k=_{\mathrm {def}}\mathbf d\mathbf 0\mathbf 0$
. The existence of
$\mathbf k=_{\mathrm {def}}\mathbf d\mathbf 0\mathbf 0$
. The existence of
![]() $\mathbf d$
implies that the map
$\mathbf d$
implies that the map
![]() $n\mapsto \bar n$
is one-to-one. In fact, suppose
$n\mapsto \bar n$
is one-to-one. In fact, suppose
![]() $\bar n=\bar m$
but
$\bar n=\bar m$
but
![]() $n\neq m$
. Then
$n\neq m$
. Then
![]() $\mathbf d\bar n\bar n\simeq \mathbf d\bar n\bar m$
. It then follows that
$\mathbf d\bar n\bar n\simeq \mathbf d\bar n\bar m$
. It then follows that
![]() $a\simeq \mathbf d\bar n\bar nab\simeq \mathbf d\bar n\bar mab\simeq b$
for all
$a\simeq \mathbf d\bar n\bar nab\simeq \mathbf d\bar n\bar mab\simeq b$
for all
![]() $a,b$
. On the other hand, by our definition, every pca contains at least two elements.
$a,b$
. On the other hand, by our definition, every pca contains at least two elements.
Remark 3.9. Every pca can be turned into a pca over
![]() $\omega $
. For example, one can define Curry numerals and construct by
$\omega $
. For example, one can define Curry numerals and construct by
![]() $\lambda $
-abstraction a combinator
$\lambda $
-abstraction a combinator
![]() $\mathbf d$
for this representation of natural numbers. In practice, however, all natural examples of pca come already equipped with a canonical copy of the natural numbers and pertaining combinators.
$\mathbf d$
for this representation of natural numbers. In practice, however, all natural examples of pca come already equipped with a canonical copy of the natural numbers and pertaining combinators.
3.2 Defining realizability
Definition 3.10 (
 $\mathsf {CZF}$
).
$\mathsf {CZF}$
).
Given a pca A, the class
![]() $\mathrm {V_{ext}}(A)$
is inductively defined by the clause:
$\mathrm {V_{ext}}(A)$
is inductively defined by the clause:
-
• if
 $x\subseteq A\times A\times \mathrm {V_{ext}}(A)$
, then
$x\subseteq A\times A\times \mathrm {V_{ext}}(A)$
, then
 $x\in \mathrm {V_{ext}}(A)$
.
$x\in \mathrm {V_{ext}}(A)$
.
The inductive definition of
![]() $\mathrm {V_{ext}}(A)$
within
$\mathrm {V_{ext}}(A)$
within
![]() $\mathsf {CZF}$
is on par with that of
$\mathsf {CZF}$
is on par with that of
![]() $\mathrm {V}(A)$
[Reference Rathjen30,Lemma 3.4].
$\mathrm {V}(A)$
[Reference Rathjen30,Lemma 3.4].
Notation 3.11. We use
![]() $(a)_i$
or simply
$(a)_i$
or simply
![]() $a_i$
for
$a_i$
for
![]() $\mathbf {p_i}a$
. Whenever we write a term t, we assume that it is defined. In other words, a formula
$\mathbf {p_i}a$
. Whenever we write a term t, we assume that it is defined. In other words, a formula
![]() $\varphi (t)$
stands for
$\varphi (t)$
stands for
![]() $\exists a\, (t\downarrow a\land \varphi (a))$
.
$\exists a\, (t\downarrow a\land \varphi (a))$
.
Definition 3.12 (Extensional realizability).
We define the relation
![]() $a=b\Vdash \varphi $
, where
$a=b\Vdash \varphi $
, where
![]() $a,b\in A$
and
$a,b\in A$
and
![]() $\varphi $
is a realizability formula with parameters in
$\varphi $
is a realizability formula with parameters in
![]() $\mathrm {V_{ext}}(A)$
. The atomic cases fall under the scope of definitions by transfinite recursion.
$\mathrm {V_{ext}}(A)$
. The atomic cases fall under the scope of definitions by transfinite recursion.
 $$ \begin{align*} a=b&\Vdash x\in y && \Leftrightarrow && \exists z\, (\langle (a)_0,(b)_0,z\rangle \in y\land (a)_1=(b)_1\Vdash x=z),\\ a=b& \Vdash x=y && \Leftrightarrow &&\forall \langle c,d,z\rangle \in x\, ((ac)_0=(bd)_0\Vdash z\in y) \text{ and } \\ &&&&& \forall \langle c,d,z\rangle \in y\, ((ac)_1=(bd)_1\Vdash z\in x),\\ a=b& \Vdash \varphi\land \psi && \Leftrightarrow && (a)_0=(b)_0\Vdash \varphi \land (a)_1=(b)_1\Vdash \psi, \\ a=b& \Vdash \varphi\lor\psi && \Leftrightarrow && (a)_0=(b)_0=\mathbf 0\land (a)_1=(b)_1\Vdash \varphi \text{ or } \\ &&&&& (a)_0=(b)_0={\mathbf 1}\land (a)_1=(b)_1\Vdash \psi, \\ a=b&\Vdash \neg\varphi && \Leftrightarrow && \forall c, d\, \neg (c=d\Vdash \varphi), \\ a=b&\Vdash \varphi\rightarrow\psi && \Leftrightarrow && \forall c,d\, (c=d\Vdash \varphi\rightarrow ac=bd\Vdash \psi), \\ a=b& \Vdash \forall x\in y\, \varphi && \Leftrightarrow && \forall \langle c,d,x\rangle\in y\, (ac=bd\Vdash \varphi), \\ a=b&\Vdash \exists x\in y\, \varphi && \Leftrightarrow && \exists x\, (\langle (a)_0,(b)_0,x\rangle \in y\land (a)_1=(b)_1\Vdash \varphi),\\ a=b& \Vdash \forall x\, \varphi && \Leftrightarrow && \forall x\in \mathrm{V_{ext}}(A)\, (a=b\Vdash \varphi), \\ a=b& \Vdash \exists x\, \varphi && \Leftrightarrow && \exists x\in \mathrm{V_{ext}}(A)\, (a=b\Vdash \varphi). \end{align*} $$
$$ \begin{align*} a=b&\Vdash x\in y && \Leftrightarrow && \exists z\, (\langle (a)_0,(b)_0,z\rangle \in y\land (a)_1=(b)_1\Vdash x=z),\\ a=b& \Vdash x=y && \Leftrightarrow &&\forall \langle c,d,z\rangle \in x\, ((ac)_0=(bd)_0\Vdash z\in y) \text{ and } \\ &&&&& \forall \langle c,d,z\rangle \in y\, ((ac)_1=(bd)_1\Vdash z\in x),\\ a=b& \Vdash \varphi\land \psi && \Leftrightarrow && (a)_0=(b)_0\Vdash \varphi \land (a)_1=(b)_1\Vdash \psi, \\ a=b& \Vdash \varphi\lor\psi && \Leftrightarrow && (a)_0=(b)_0=\mathbf 0\land (a)_1=(b)_1\Vdash \varphi \text{ or } \\ &&&&& (a)_0=(b)_0={\mathbf 1}\land (a)_1=(b)_1\Vdash \psi, \\ a=b&\Vdash \neg\varphi && \Leftrightarrow && \forall c, d\, \neg (c=d\Vdash \varphi), \\ a=b&\Vdash \varphi\rightarrow\psi && \Leftrightarrow && \forall c,d\, (c=d\Vdash \varphi\rightarrow ac=bd\Vdash \psi), \\ a=b& \Vdash \forall x\in y\, \varphi && \Leftrightarrow && \forall \langle c,d,x\rangle\in y\, (ac=bd\Vdash \varphi), \\ a=b&\Vdash \exists x\in y\, \varphi && \Leftrightarrow && \exists x\, (\langle (a)_0,(b)_0,x\rangle \in y\land (a)_1=(b)_1\Vdash \varphi),\\ a=b& \Vdash \forall x\, \varphi && \Leftrightarrow && \forall x\in \mathrm{V_{ext}}(A)\, (a=b\Vdash \varphi), \\ a=b& \Vdash \exists x\, \varphi && \Leftrightarrow && \exists x\in \mathrm{V_{ext}}(A)\, (a=b\Vdash \varphi). \end{align*} $$
Notation 3.13. We write
![]() $\Vdash \varphi $
in place of
$\Vdash \varphi $
in place of
![]() $\exists a,b\in A\, (a=b\Vdash \varphi )$
and
$\exists a,b\in A\, (a=b\Vdash \varphi )$
and
![]() $a\Vdash \varphi $
for
$a\Vdash \varphi $
for
![]() $a=a\Vdash \varphi $
.
$a=a\Vdash \varphi $
.
We will repeatedly use the following internal pairing function
![]() $\langle {x,y}\rangle _{\!A}$
in
$\langle {x,y}\rangle _{\!A}$
in
![]() $\mathrm {V_{ext}}(A)$
.
$\mathrm {V_{ext}}(A)$
.
Definition 3.14 (Pairing).
For
![]() $x,y\in \mathrm {V_{ext}}(A)$
, let
$x,y\in \mathrm {V_{ext}}(A)$
, let
 $$ \begin{align*} \{{x}\}_{A}&=\{\langle{\mathbf 0,\mathbf 0,x}\rangle\}, \\ \{{x,y}\}_{A}&=\{\langle{\mathbf 0,\mathbf 0,x}\rangle,\langle{{\mathbf 1},{\mathbf 1},y}\rangle\}, \\ \langle{x,y}\rangle_{\!A}&=\{\langle{\mathbf 0,\mathbf 0,\{{x}\}_{A}}\rangle, \langle{{\mathbf 1},{\mathbf 1},\{{x,y}\}_{A}}\rangle\}. \end{align*} $$
$$ \begin{align*} \{{x}\}_{A}&=\{\langle{\mathbf 0,\mathbf 0,x}\rangle\}, \\ \{{x,y}\}_{A}&=\{\langle{\mathbf 0,\mathbf 0,x}\rangle,\langle{{\mathbf 1},{\mathbf 1},y}\rangle\}, \\ \langle{x,y}\rangle_{\!A}&=\{\langle{\mathbf 0,\mathbf 0,\{{x}\}_{A}}\rangle, \langle{{\mathbf 1},{\mathbf 1},\{{x,y}\}_{A}}\rangle\}. \end{align*} $$
Note that all these sets are in
![]() $\mathrm {V_{ext}}(A)$
.
$\mathrm {V_{ext}}(A)$
.
We use
![]() $\operatorname {{\mathrm {OP}}}(z,x,y)$
as abbreviation for the set-theoretic formula expressing that z is the ordered pair of x and y. In standard notation,
$\operatorname {{\mathrm {OP}}}(z,x,y)$
as abbreviation for the set-theoretic formula expressing that z is the ordered pair of x and y. In standard notation,
![]() $z=\langle {x,y}\rangle $
. Ordered pairs can be defined as usual as
$z=\langle {x,y}\rangle $
. Ordered pairs can be defined as usual as
![]() $\langle {x,y}\rangle =_{\mathrm {def}}\{\{x\},\{x,y\}\}$
.
$\langle {x,y}\rangle =_{\mathrm {def}}\{\{x\},\{x,y\}\}$
.
Lemma 3.15. There are closed terms
![]() ${\mathbf u}_i$
such that
${\mathbf u}_i$
such that
![]() $\mathsf {CZF}$
proves
$\mathsf {CZF}$
proves
 $$ \begin{align*} {\mathbf u}_0 & \Vdash \operatorname{{\mathrm{OP}}}(\langle{x,y}\rangle_{\!A},x,y),\\ {\mathbf u}_1 & \Vdash \langle{x,y}\rangle_{\!A}=\langle{u,v}\rangle_{\!A}\rightarrow x=u\land y=v, \\ {\mathbf u}_2 &\Vdash \operatorname{{\mathrm{OP}}}(z,x,y) \rightarrow z=\langle{x,y}\rangle_{\!A}. \end{align*} $$
$$ \begin{align*} {\mathbf u}_0 & \Vdash \operatorname{{\mathrm{OP}}}(\langle{x,y}\rangle_{\!A},x,y),\\ {\mathbf u}_1 & \Vdash \langle{x,y}\rangle_{\!A}=\langle{u,v}\rangle_{\!A}\rightarrow x=u\land y=v, \\ {\mathbf u}_2 &\Vdash \operatorname{{\mathrm{OP}}}(z,x,y) \rightarrow z=\langle{x,y}\rangle_{\!A}. \end{align*} $$
Proof This is similar to [Reference McCarty22, Lemmas 3.2 and 3.4].
Theorem 3.16 [Reference Frittaion and Rathjen17].
For every theorem
![]() $\varphi $
of
$\varphi $
of
![]() $\mathsf {CZF}+\mathsf {AC}_{\mathsf {FT}}$
, there is a closed term
$\mathsf {CZF}+\mathsf {AC}_{\mathsf {FT}}$
, there is a closed term
![]() ${\mathbf t}$
such that
${\mathbf t}$
such that
![]() $\mathsf { CZF}$
proves
$\mathsf { CZF}$
proves
![]() ${\mathbf t}\Vdash \varphi $
. The same for
${\mathbf t}\Vdash \varphi $
. The same for
![]() $\mathsf {IZF}$
.
$\mathsf {IZF}$
.
Remark 3.17. The realizability relation
![]() $\Vdash $
uses A as a parameter. We should then write
$\Vdash $
uses A as a parameter. We should then write
![]() $\Vdash _A$
. The soundness theorem claims that for every theorem
$\Vdash _A$
. The soundness theorem claims that for every theorem
![]() $\varphi $
of T there is a closed term
$\varphi $
of T there is a closed term
![]() ${\mathbf t}$
such that
${\mathbf t}$
such that
![]() $T\vdash \forall A\, (A\text { is a pca}\rightarrow {\mathbf t}\Vdash _A \varphi )$
. For special cases, where the pca A is definable as a set in T and
$T\vdash \forall A\, (A\text { is a pca}\rightarrow {\mathbf t}\Vdash _A \varphi )$
. For special cases, where the pca A is definable as a set in T and
![]() $T\vdash A \text { is a pca}$
, we obtain
$T\vdash A \text { is a pca}$
, we obtain
![]() $T\vdash {\mathbf t}\Vdash _A \varphi $
. For instance, in the case of Kleene’s first algebra, we have that for every theorem
$T\vdash {\mathbf t}\Vdash _A \varphi $
. For instance, in the case of Kleene’s first algebra, we have that for every theorem
![]() $\varphi $
, there is a closed term
$\varphi $
, there is a closed term
![]() ${\mathbf t}$
such that
${\mathbf t}$
such that
![]() $T\vdash \exists n\in \omega \, ({\mathbf t}\downarrow n\land n\Vdash \varphi )$
.
$T\vdash \exists n\in \omega \, ({\mathbf t}\downarrow n\land n\Vdash \varphi )$
.
Definition 3.18. Write
![]() $T\models \varphi $
for
$T\models \varphi $
for
![]() $T\vdash \exists a,b\in A\, (a=b\Vdash \varphi )$
. In general, we write
$T\vdash \exists a,b\in A\, (a=b\Vdash \varphi )$
. In general, we write
![]() $T\models S$
if
$T\models S$
if
![]() $T\models \varphi $
for every sentence
$T\models \varphi $
for every sentence
![]() $\varphi $
of S. We say that T is self-validating if
$\varphi $
of S. We say that T is self-validating if
![]() $T\models T$
.
$T\models T$
.
Theorem 3.19. Let T be any of the theories obtained by appending to either
![]() $\mathsf {CZF}$
or
$\mathsf {CZF}$
or
![]() $\mathsf {IZF}$
some or all of the axioms
$\mathsf {IZF}$
some or all of the axioms
![]() $\mathsf { REA}$
,
$\mathsf { REA}$
,
![]() $\mathsf {AC}_{\omega }$
,
$\mathsf {AC}_{\omega }$
,
![]() $\mathsf {DC}$
,
$\mathsf {DC}$
,
![]() $\mathsf {DC}^{\dagger }$
,
$\mathsf {DC}^{\dagger }$
,
![]() $\mathsf {RDC}$
,
$\mathsf {RDC}$
,
![]() $\mathsf {RDC}^{\dagger }$
, and
$\mathsf {RDC}^{\dagger }$
, and
![]() $\mathsf {PAx}$
. Then T is self-validating.
$\mathsf {PAx}$
. Then T is self-validating.
Proof This holds in the case of generic realizability. See [Reference Rathjen30, Theorem 6.2] for
![]() $\mathsf {REA}$
and [Reference Rathjen30, Theorem 10.1] for
$\mathsf {REA}$
and [Reference Rathjen30, Theorem 10.1] for
![]() $\mathsf {DC}^{\dagger }$
(there called
$\mathsf {DC}^{\dagger }$
(there called
![]() $\mathsf {DC}$
),
$\mathsf {DC}$
),
![]() $\mathsf {RDC}$
, and
$\mathsf {RDC}$
, and
![]() $\mathsf { PAx}$
. The other axioms are treated in a similar way. In the case of extensional generic realizability, the proof is a nearly verbatim copy of that for generic realizability.
$\mathsf { PAx}$
. The other axioms are treated in a similar way. In the case of extensional generic realizability, the proof is a nearly verbatim copy of that for generic realizability.
Let us sketch a proof for
![]() $\mathsf {PAx}$
. We wish to find a closed term
$\mathsf {PAx}$
. We wish to find a closed term
![]() ${\mathbf e}$
such that, over
${\mathbf e}$
such that, over
![]() $\mathsf {CZF}+\mathsf {PAx}$
,
$\mathsf {CZF}+\mathsf {PAx}$
,
By definition, this means that for every
![]() $y\in \mathrm {V_{ext}}(A)$
there are
$y\in \mathrm {V_{ext}}(A)$
there are
![]() $x,f\in \mathrm {V_{ext}}(A)$
such that
$x,f\in \mathrm {V_{ext}}(A)$
such that
Let
![]() $y\in \mathrm {V_{ext}}(A)$
. By
$y\in \mathrm {V_{ext}}(A)$
. By
![]() $\mathsf {PAx}$
in the background universe, there exists a base B and a function F from B onto y. Say
$\mathsf {PAx}$
in the background universe, there exists a base B and a function F from B onto y. Say
![]() $F(u)=\langle {a_u,b_u,z_u}\rangle \in y$
for
$F(u)=\langle {a_u,b_u,z_u}\rangle \in y$
for
![]() $u\in B$
. By transfinite recursion, define
$u\in B$
. By transfinite recursion, define
Then for every set u,
![]() $\check u\in \mathrm {V_{ext}}(A)$
. Moreover, by induction, one can show that these names are absolute, namely,
$\check u\in \mathrm {V_{ext}}(A)$
. Moreover, by induction, one can show that these names are absolute, namely,
Let
 $$ \begin{align*} x&=\{\langle{a_u,b_u,\check u}\rangle\mid u\in B\},\\[5pt] f&=\{\langle{a_u,b_u,\langle{\check u,z_u}\rangle_{\!A}}\rangle\mid u\in B\}, \end{align*} $$
$$ \begin{align*} x&=\{\langle{a_u,b_u,\check u}\rangle\mid u\in B\},\\[5pt] f&=\{\langle{a_u,b_u,\langle{\check u,z_u}\rangle_{\!A}}\rangle\mid u\in B\}, \end{align*} $$
where
![]() $\langle {u,v}\rangle _{\!A}$
is the internal pair in
$\langle {u,v}\rangle _{\!A}$
is the internal pair in
![]() $\mathrm {V_{ext}}(A)$
from Definition 3.14. One can find a closed term
$\mathrm {V_{ext}}(A)$
from Definition 3.14. One can find a closed term
![]() $\mathbf f$
such that
$\mathbf f$
such that
![]() $\mathbf f \Vdash \operatorname {{\mathrm {Fun}}}(f)$
thanks to the absoluteness of
$\mathbf f \Vdash \operatorname {{\mathrm {Fun}}}(f)$
thanks to the absoluteness of
![]() $\check {}$
names. It is not difficult to build a closed term
$\check {}$
names. It is not difficult to build a closed term
![]() ${\mathbf t}$
such that
${\mathbf t}$
such that
![]() ${\mathbf t} \Vdash f\colon x\twoheadrightarrow y$
. Finally, it is straightforward to cook up a closed term
${\mathbf t} \Vdash f\colon x\twoheadrightarrow y$
. Finally, it is straightforward to cook up a closed term
![]() $\mathbf b$
and show that
$\mathbf b$
and show that
![]() $\mathbf b\Vdash x \text { is a base}$
, by using the fact that B is a base.
$\mathbf b\Vdash x \text { is a base}$
, by using the fact that B is a base.
In view of Definition 3.18, our goal is to show that:
-
•
 $T\models T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
,
$T\models T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
, -
•
 $T+\mathsf {REA}\models T+\mathsf {REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf { AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
,
$T+\mathsf {REA}\models T+\mathsf {REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf { AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
,
where T is as in Theorem 3.19.
4 Realizing choice for dependent types
4.1 Dependent types over partial combinatory algebras
Given a pca A, we wish to define extensional type structures on A, that is, structures of the form
where
![]() $\sim $
is a partial equivalence relation on A and
$\sim $
is a partial equivalence relation on A and
![]() $\sim _{\sigma }$
is a partial equivalence relation on A for every
$\sim _{\sigma }$
is a partial equivalence relation on A for every
![]() $\sigma $
such that
$\sigma $
such that
![]() $\sigma \sim \sigma $
. Then
$\sigma \sim \sigma $
. Then
![]() $\mathbb {T}=\{\sigma \in A\mid \sigma \sim \sigma \}$
and
$\mathbb {T}=\{\sigma \in A\mid \sigma \sim \sigma \}$
and
![]() $A_{\sigma }=\{a\in A\mid a\sim _{\sigma } a\}$
for every
$A_{\sigma }=\{a\in A\mid a\sim _{\sigma } a\}$
for every
![]() $\sigma \in \mathbb {T}$
. Clearly, we want equivalent types to have the same elements. We must then ensure that if
$\sigma \in \mathbb {T}$
. Clearly, we want equivalent types to have the same elements. We must then ensure that if
![]() $\sigma \sim \tau $
, then
$\sigma \sim \tau $
, then
![]() $a\sim _{\sigma } b$
iff
$a\sim _{\sigma } b$
iff
![]() $a\sim _{\tau } b$
.
$a\sim _{\tau } b$
.
Definition 4.1. We say that
![]() $\sigma $
is a type if
$\sigma $
is a type if
![]() $\sigma \in \mathbb {T}$
. We say that
$\sigma \in \mathbb {T}$
. We say that
![]() $a\in A$
has type
$a\in A$
has type
![]() $\sigma $
if
$\sigma $
if
![]() $a\in A_{\sigma }$
.
$a\in A_{\sigma }$
.
From now on, definitions and theorems take place in
![]() $\mathsf {CZF}$
, unless we are dealing with
$\mathsf {CZF}$
, unless we are dealing with
![]() $\mathrm {W}$
-types, in which case we work in
$\mathrm {W}$
-types, in which case we work in
![]() $\mathsf {CZF}+\mathsf {REA}$
.
$\mathsf {CZF}+\mathsf {REA}$
.
Notation 4.2. Given a pca A,
![]() $a,b,c\in A$
, and
$a,b,c\in A$
, and
![]() $n\in \omega $
, we write:
$n\in \omega $
, we write:
 $$ \begin{align*} \mathsf{N}_n&=_{\mathrm{def}} \mathbf p \bar 0\bar n, & \mathsf{N}&=_{\mathrm{def}}\mathbf p\bar 1\mathbf 0, \\ {\Pi}_ab&=_{\mathrm{def}} \mathbf p \bar 2(\mathbf pab), & {\Sigma}_ab&=_{\mathrm{def}}\mathbf p \bar 3(\mathbf pab), \\ \mathrm{I}_c(a,b)&=_{\mathrm{def}} \mathbf p \bar 4(\mathbf p c(\mathbf pab)), & \mathrm{W}_ab &=_{\mathrm{def}}\mathbf p \bar 5(\mathbf p ab). \end{align*} $$
$$ \begin{align*} \mathsf{N}_n&=_{\mathrm{def}} \mathbf p \bar 0\bar n, & \mathsf{N}&=_{\mathrm{def}}\mathbf p\bar 1\mathbf 0, \\ {\Pi}_ab&=_{\mathrm{def}} \mathbf p \bar 2(\mathbf pab), & {\Sigma}_ab&=_{\mathrm{def}}\mathbf p \bar 3(\mathbf pab), \\ \mathrm{I}_c(a,b)&=_{\mathrm{def}} \mathbf p \bar 4(\mathbf p c(\mathbf pab)), & \mathrm{W}_ab &=_{\mathrm{def}}\mathbf p \bar 5(\mathbf p ab). \end{align*} $$
This ensures unique readability. For example,
![]() $\mathsf {N}\neq {\Pi }_a b$
, and
$\mathsf {N}\neq {\Pi }_a b$
, and
![]() ${\Pi }_ab={\Pi }_cd$
implies
${\Pi }_ab={\Pi }_cd$
implies
![]() $a=b$
and
$a=b$
and
![]() $c=d$
.
$c=d$
.
Definition 4.3 (
 ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types).
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types).
Given a pca A, we inductively define the
![]() ${\Pi }{\Sigma }$
type structure by clauses:
${\Pi }{\Sigma }$
type structure by clauses:
-
(i)
 $\mathsf {N}_n\sim \mathsf {N}_n$
and
$\mathsf {N}_n\sim \mathsf {N}_n$
and
 $a\sim _{\mathsf {N}_n} b$
iff
$a\sim _{\mathsf {N}_n} b$
iff
 $a=b=\bar m$
for some
$a=b=\bar m$
for some
 $m<n$
;
$m<n$
; -
(ii)
 $\mathsf {N}\sim \mathsf {N}$
and
$\mathsf {N}\sim \mathsf {N}$
and
 $a\sim _{\mathsf {N}} b$
iff
$a\sim _{\mathsf {N}} b$
iff
 $a=b=\bar n$
for some
$a=b=\bar n$
for some
 $n\in \omega $
;
$n\in \omega $
; -
(iii) if
 $\sigma \sim \tau $
, and
$\sigma \sim \tau $
, and
 $a\sim _{\sigma } b$
implies
$a\sim _{\sigma } b$
implies
 $ia\sim jb$
, then:
$ia\sim jb$
, then:-
•
 $\alpha ={\Pi }_{\sigma } i\sim {\Pi }_{\tau } j$
;
$\alpha ={\Pi }_{\sigma } i\sim {\Pi }_{\tau } j$
; -
•
 $f\sim _{\alpha } g$
iff
$f\sim _{\alpha } g$
iff
 $fa\sim _{ia} gb$
whenever
$fa\sim _{ia} gb$
whenever
 $a\sim _{\sigma } b$
; and
$a\sim _{\sigma } b$
; and -
•
 $\beta ={\Sigma }_{\sigma } i\sim {\Sigma }_{\tau } j$
;
$\beta ={\Sigma }_{\sigma } i\sim {\Sigma }_{\tau } j$
; -
•
 $a\sim _{\beta } b$
iff
$a\sim _{\beta } b$
iff
 $a_0\sim _{\sigma } b_0$
and
$a_0\sim _{\sigma } b_0$
and
 $a_1\sim _{ia_0} b_1$
.
$a_1\sim _{ia_0} b_1$
.
-
The
![]() $\Pi {\Sigma }\mathrm {I}$
type structure is inductively defined by adding the clause:
$\Pi {\Sigma }\mathrm {I}$
type structure is inductively defined by adding the clause:
-
(iv) if
 $\sigma \sim \tau $
,
$\sigma \sim \tau $
,
 $a\sim _{\sigma } \breve a$
, and
$a\sim _{\sigma } \breve a$
, and
 $b\sim _{\sigma } \breve b$
, then:
$b\sim _{\sigma } \breve b$
, then:-
•
 $\gamma =\mathrm {I}_{\sigma }(a,b)\sim \mathrm {I}_{\tau }(\breve a,\breve b)$
;
$\gamma =\mathrm {I}_{\sigma }(a,b)\sim \mathrm {I}_{\tau }(\breve a,\breve b)$
; -
•
 $c\sim _{\gamma } d$
iff
$c\sim _{\gamma } d$
iff
 $c=d=\mathbf 0$
and
$c=d=\mathbf 0$
and
 $a\sim _{\sigma } b$
.
$a\sim _{\sigma } b$
.
-
The
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
type structure is inductively defined by clauses (i), (ii), (iii), (iv), and
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
type structure is inductively defined by clauses (i), (ii), (iii), (iv), and
-
(v) if
 $\sigma \sim \tau $
, and
$\sigma \sim \tau $
, and
 $a\sim _{\sigma } b$
implies
$a\sim _{\sigma } b$
implies
 $ia\sim jb$
, then:
$ia\sim jb$
, then:-
•
 $\delta =\mathrm {W}_{\sigma } i\sim \mathrm {W}_{\tau } j$
;
$\delta =\mathrm {W}_{\sigma } i\sim \mathrm {W}_{\tau } j$
; -
•
 $c\sim _{\delta } d$
iff
$c\sim _{\delta } d$
iff
 $c_0\sim _{\sigma } d_0$
and
$c_0\sim _{\sigma } d_0$
and
 $c_1p\sim _{\delta } d_1q$
whenever
$c_1p\sim _{\delta } d_1q$
whenever
 $p\sim _{ic_0} q$
.
$p\sim _{ic_0} q$
.
-
Remark 4.4. To be precise, each type structure from Definition 4.3 is an inductively defined class I of triples
![]() $\langle {\sigma ,\tau ,B}\rangle $
. The intended meaning is
$\langle {\sigma ,\tau ,B}\rangle $
. The intended meaning is
![]() $\sigma \sim \tau $
and
$\sigma \sim \tau $
and
![]() $a\sim _{\sigma } b$
iff
$a\sim _{\sigma } b$
iff
![]() $\langle {a,b}\rangle \in B$
. For instance, the rules for the introduction of
$\langle {a,b}\rangle \in B$
. For instance, the rules for the introduction of
![]() ${\Pi }$
-types and
${\Pi }$
-types and
![]() $\mathrm {W}$
-types are
$\mathrm {W}$
-types are

where
![]() $\sigma ,\tau ,i,j\in A$
, and for some set
$\sigma ,\tau ,i,j\in A$
, and for some set
![]() $B\subseteq A\times A$
and some function F with
$B\subseteq A\times A$
and some function F with
![]() $\operatorname {{\mathrm {dom}}}(F)=B$
, we have:
$\operatorname {{\mathrm {dom}}}(F)=B$
, we have:
-
•
 $\{\langle {\sigma ,\tau ,B}\rangle \}\cup \{\langle {ia,jb,F(a,b)}\rangle \mid \langle {a,b}\rangle \in B\}\subseteq X$
,
$\{\langle {\sigma ,\tau ,B}\rangle \}\cup \{\langle {ia,jb,F(a,b)}\rangle \mid \langle {a,b}\rangle \in B\}\subseteq X$
, -
•
 $C=\{\langle {f,g}\rangle \in A\times A\mid \forall \langle {a,b}\rangle \in B\, (\langle {fa,gb}\rangle \in F(a,b))\}$
,
$C=\{\langle {f,g}\rangle \in A\times A\mid \forall \langle {a,b}\rangle \in B\, (\langle {fa,gb}\rangle \in F(a,b))\}$
, -
•
 $D=\{\langle {c,d}\rangle \in A\times A\mid \langle {c_0,d_0}\rangle \in B\land \forall \langle {p,q}\rangle \in F(c_0,d_0)\, \langle {c_1p,d_1p}\rangle \in D\}$
.
$D=\{\langle {c,d}\rangle \in A\times A\mid \langle {c_0,d_0}\rangle \in B\land \forall \langle {p,q}\rangle \in F(c_0,d_0)\, \langle {c_1p,d_1p}\rangle \in D\}$
.
It is not difficult to see that D has a bounded inductive definition, and therefore by Theorem 2.6 is a set in
![]() $\mathsf { CZF}+\mathsf {REA}$
.
$\mathsf { CZF}+\mathsf {REA}$
.
By induction on the inductive definition of I, one may show that if
![]() $\langle {\sigma ,\tau _0,B_0}\rangle \in I$
and
$\langle {\sigma ,\tau _0,B_0}\rangle \in I$
and
![]() $\langle {\sigma ,\tau _1,B_1}\rangle \in I$
, then
$\langle {\sigma ,\tau _1,B_1}\rangle \in I$
, then
![]() $B_0=B_1$
. Hence, by letting
$B_0=B_1$
. Hence, by letting
 $$ \begin{align*} \sim &=_{\mathrm{def}} \{\langle{\sigma,\tau}\rangle\mid \exists B\, \langle{\sigma,\tau,B}\rangle\in I\}, \\ \sim_{\sigma} &=_{\mathrm{def}} \bigcup\{ B\mid \exists \tau\, \langle{\sigma,\tau,B}\rangle\in I\}, \end{align*} $$
$$ \begin{align*} \sim &=_{\mathrm{def}} \{\langle{\sigma,\tau}\rangle\mid \exists B\, \langle{\sigma,\tau,B}\rangle\in I\}, \\ \sim_{\sigma} &=_{\mathrm{def}} \bigcup\{ B\mid \exists \tau\, \langle{\sigma,\tau,B}\rangle\in I\}, \end{align*} $$
we obtain in particular that if
![]() $\langle {\sigma ,\tau ,B}\rangle \in I$
, then
$\langle {\sigma ,\tau ,B}\rangle \in I$
, then
![]() $B=\bigcup \{B\mid \exists \tau \, \langle {\sigma ,\tau ,B}\rangle \in I\}$
is a set, and so
$B=\bigcup \{B\mid \exists \tau \, \langle {\sigma ,\tau ,B}\rangle \in I\}$
is a set, and so
![]() $\sim _{\sigma }$
is a set as well.
$\sim _{\sigma }$
is a set as well.
Lemma 4.5. Suppose
![]() $\sigma \sim \tau $
and
$\sigma \sim \tau $
and
![]() $\tau \sim \rho $
. Then:
$\tau \sim \rho $
. Then:
-
(i)
 $\sigma \sim \sigma $
,
$\sigma \sim \sigma $
,
 $\tau \sim \sigma $
, and
$\tau \sim \sigma $
, and
 $\sigma \sim \rho $
;
$\sigma \sim \rho $
; -
(ii)
 $a\sim _{\sigma } b$
iff
$a\sim _{\sigma } b$
iff
 $a\sim _{\tau } b$
;
$a\sim _{\tau } b$
; -
(iii)
 $a\sim _{\sigma } b$
and
$a\sim _{\sigma } b$
and
 $b\sim _{\sigma } c$
implies
$b\sim _{\sigma } c$
implies
 $a\sim _{\sigma } a$
,
$a\sim _{\sigma } a$
,
 $b\sim _{\sigma } a$
, and
$b\sim _{\sigma } a$
, and
 $a\sim _{\sigma } c$
.
$a\sim _{\sigma } c$
.
In other words,
![]() $\sim $
and
$\sim $
and
![]() $\sim _{\sigma }$
are partial equivalence relations on A.
$\sim _{\sigma }$
are partial equivalence relations on A.
Proof By induction on the (inductive definition of the) type structure. The case of
![]() $\mathrm {W}_{\sigma } i$
is dealt with a further induction on the given
$\mathrm {W}_{\sigma } i$
is dealt with a further induction on the given
![]() $\mathrm {W}$
-type.
$\mathrm {W}$
-type.
4.2 Representing
 ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
Definition 4.6. Given a type structure on A and a type
![]() $\sigma $
, we say that
$\sigma $
, we say that
![]() $i\in A$
is a family of types over
$i\in A$
is a family of types over
![]() $\sigma $
if
$\sigma $
if
![]() $ia\sim ib$
whenever
$ia\sim ib$
whenever
![]() $a\sim _{\sigma } b$
. If
$a\sim _{\sigma } b$
. If
![]() $\sigma $
is a type and
$\sigma $
is a type and
![]() $ia\sim jb$
whenever
$ia\sim jb$
whenever
![]() $a\sim _{\sigma } b$
, we write
$a\sim _{\sigma } b$
, we write
![]() $i\approx _{\sigma } j$
.
$i\approx _{\sigma } j$
.
Note that in any of the type structures here considered, if i is a family of types over
![]() $\sigma $
, then
$\sigma $
, then
![]() ${\Pi }_{\sigma } i$
and
${\Pi }_{\sigma } i$
and
![]() ${\Sigma }_{\sigma } i$
are types. Moreover, if
${\Sigma }_{\sigma } i$
are types. Moreover, if
![]() $\sigma \sim \tau $
and
$\sigma \sim \tau $
and
![]() $i\approx _{\sigma } j$
, then
$i\approx _{\sigma } j$
, then
![]() $i\approx _{\tau } j$
.
$i\approx _{\tau } j$
.
Definition 4.7 (Mapping typed elements of A in
 $\mathrm {V_{ext}}(A)$
).
$\mathrm {V_{ext}}(A)$
).
For
![]() $n\in \omega $
, let
$n\in \omega $
, let
For every
![]() ${\Pi }{\Sigma }\mathrm {I}$
-type
${\Pi }{\Sigma }\mathrm {I}$
-type
![]() $\sigma $
, we inductively define
$\sigma $
, we inductively define
![]() $a^{\sigma }\in \mathrm {V_{ext}}(A)$
for every a of type
$a^{\sigma }\in \mathrm {V_{ext}}(A)$
for every a of type
![]() $\sigma $
by:
$\sigma $
by:
-
• if
 $\sigma =\mathsf {N}_n$
or
$\sigma =\mathsf {N}_n$
or
 $\sigma =\mathsf {N}$
, let
$\sigma =\mathsf {N}$
, let
 $a^{\sigma }=\dot m$
, where
$a^{\sigma }=\dot m$
, where
 $a=\bar m$
;
$a=\bar m$
; -
• if
 $\alpha ={\Pi }_{\sigma } i$
, let
$\alpha ={\Pi }_{\sigma } i$
, let
 $ f^{\alpha }=\{\langle {a,b,\langle {a^{\sigma },(fa)^{\tau }}\rangle _{\!A}}\rangle \mid a\sim _{\sigma } b\land ia=\tau \}$
;
$ f^{\alpha }=\{\langle {a,b,\langle {a^{\sigma },(fa)^{\tau }}\rangle _{\!A}}\rangle \mid a\sim _{\sigma } b\land ia=\tau \}$
; -
• if
 $\beta ={\Sigma }_{\sigma } i$
, let
$\beta ={\Sigma }_{\sigma } i$
, let
 $ a^{\beta }=\langle {(a_0)^{\sigma },(a_1)^{\tau }}\rangle _{\!A}$
, where
$ a^{\beta }=\langle {(a_0)^{\sigma },(a_1)^{\tau }}\rangle _{\!A}$
, where
 $ia_0= \tau $
;
$ia_0= \tau $
; -
• if
 $\gamma =\mathrm {I}_{\sigma }(a,b)$
, let
$\gamma =\mathrm {I}_{\sigma }(a,b)$
, let
 $ c^{\gamma }=0 $
.
$ c^{\gamma }=0 $
.
For
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types, we add the clause:
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types, we add the clause:
-
• if
 $\delta =\mathrm {W}_{\sigma } i$
, let
$\delta =\mathrm {W}_{\sigma } i$
, let
 $c^{\delta }=\langle {a^{\sigma },\{\langle {p,q,\langle {p^{ia},(c_1p)^{\delta }}\rangle _{\!A}}\rangle \mid p\sim _{ia} q\}}\rangle _{\!A}$
, where
$c^{\delta }=\langle {a^{\sigma },\{\langle {p,q,\langle {p^{ia},(c_1p)^{\delta }}\rangle _{\!A}}\rangle \mid p\sim _{ia} q\}}\rangle _{\!A}$
, where
 $a=c_0$
.
$a=c_0$
.
Remark 4.8. A comment on the above definition may be in order. The class function
![]() $(\sigma ,a)\mapsto a^{\sigma }$
is obtained by defining a class E of pairs
$(\sigma ,a)\mapsto a^{\sigma }$
is obtained by defining a class E of pairs
![]() $\langle {\sigma ,e_{\sigma }}\rangle $
, the intended meaning of which is
$\langle {\sigma ,e_{\sigma }}\rangle $
, the intended meaning of which is
![]() $e_{\sigma }=\{\langle {a,a^{\sigma }}\rangle \mid a\in A_{\sigma }\}$
, where
$e_{\sigma }=\{\langle {a,a^{\sigma }}\rangle \mid a\in A_{\sigma }\}$
, where
![]() $A_{\sigma }=\{a\in A\mid a\text { has type } \sigma \}$
. Note that
$A_{\sigma }=\{a\in A\mid a\text { has type } \sigma \}$
. Note that
![]() $A_{\sigma }$
is a set. Hence,
$A_{\sigma }$
is a set. Hence,
![]() $a^{\sigma }$
is really
$a^{\sigma }$
is really
![]() $e_{\sigma }(a)$
. For example, the rules for
$e_{\sigma }(a)$
. For example, the rules for
![]() ${\Sigma }$
-types and
${\Sigma }$
-types and
![]() $\mathrm {W}$
-types are
$\mathrm {W}$
-types are

where
![]() $\sigma $
is type, i is a family of types over
$\sigma $
is type, i is a family of types over
![]() $\sigma $
, and there exist functions
$\sigma $
, and there exist functions
![]() $e_{\sigma }$
and f on
$e_{\sigma }$
and f on
![]() $A_{\sigma }$
such that:
$A_{\sigma }$
such that:
-
•
 $\operatorname {{\mathrm {Fun}}}(f(a))\land \operatorname {{\mathrm {dom}}}(f(a))=A_{ia}$
, for every
$\operatorname {{\mathrm {Fun}}}(f(a))\land \operatorname {{\mathrm {dom}}}(f(a))=A_{ia}$
, for every
 $a\in A_{\sigma }$
,
$a\in A_{\sigma }$
, -
•
 $X=\{\langle {\sigma ,e_{\sigma }}\rangle \}\cup \{\langle {ia,f(a)}\rangle \mid a\in A_{\sigma }\}$
,
$X=\{\langle {\sigma ,e_{\sigma }}\rangle \}\cup \{\langle {ia,f(a)}\rangle \mid a\in A_{\sigma }\}$
, -
•
 $e_{\beta }=\{\langle {a,\langle {e_{\sigma }(a_0),f(a_0,a_1)}\rangle _{\!A}}\rangle \mid a\text { has type } {\Sigma }_{\sigma } i\}$
,
$e_{\beta }=\{\langle {a,\langle {e_{\sigma }(a_0),f(a_0,a_1)}\rangle _{\!A}}\rangle \mid a\text { has type } {\Sigma }_{\sigma } i\}$
,
and
![]() $e_{\delta }$
is inductively defined by the clause:
$e_{\delta }$
is inductively defined by the clause:
-
• if c has type
 $\mathrm {W}_{\sigma } i$
and there exists a function k with
$\mathrm {W}_{\sigma } i$
and there exists a function k with
 $\operatorname {{\mathrm {dom}}}(k)=A_{ic_0}$
such that
$\operatorname {{\mathrm {dom}}}(k)=A_{ic_0}$
such that
 $\langle {c_1p,k(p)}\rangle \in e_{\delta }$
for every
$\langle {c_1p,k(p)}\rangle \in e_{\delta }$
for every
 $p\in \operatorname {{\mathrm {dom}}}(k)$
, then
$p\in \operatorname {{\mathrm {dom}}}(k)$
, then  $$\begin{align*}\langle{c,\langle{e_{\sigma}(c_0),\{\langle{p,q,\langle{f(c_0,p), k(p)}\rangle_{\!A}}\rangle\mid p\sim_{ic_0} q\}}\rangle_{\!A}}\rangle \in e_{\delta}. \end{align*}$$
$$\begin{align*}\langle{c,\langle{e_{\sigma}(c_0),\{\langle{p,q,\langle{f(c_0,p), k(p)}\rangle_{\!A}}\rangle\mid p\sim_{ic_0} q\}}\rangle_{\!A}}\rangle \in e_{\delta}. \end{align*}$$
By induction on the inductive definition of E, one shows that E is a class function on
![]() $\mathbb {T}$
, and
$\mathbb {T}$
, and
![]() $E(\sigma )=e_{\sigma }\colon A_{\sigma }\to \mathrm {V_{ext}}(A)$
, for every type
$E(\sigma )=e_{\sigma }\colon A_{\sigma }\to \mathrm {V_{ext}}(A)$
, for every type
![]() $\sigma $
. Note that
$\sigma $
. Note that
![]() $e_{\delta }$
has a bounded inductive definition and so is a set in
$e_{\delta }$
has a bounded inductive definition and so is a set in
![]() $\mathsf {CZF}+\mathsf {REA}$
.
$\mathsf {CZF}+\mathsf {REA}$
.
Definition 4.9 (Canonical
 ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets in
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets in
 $\mathrm {V_{ext}}(A)$
).
$\mathrm {V_{ext}}(A)$
).
Given a type
![]() $\sigma $
and a family i of types over
$\sigma $
and a family i of types over
![]() $\sigma $
, we define sets
$\sigma $
, we define sets
![]() $X_{\sigma }, F_{\sigma ,i}\in \mathrm {V_{ext}}(A)$
by:
$X_{\sigma }, F_{\sigma ,i}\in \mathrm {V_{ext}}(A)$
by:
-
•
 $X_{\sigma }=\{\langle {a,b,a^{\sigma }}\rangle \mid a \sim _{\sigma } b\}$
;
$X_{\sigma }=\{\langle {a,b,a^{\sigma }}\rangle \mid a \sim _{\sigma } b\}$
; -
•
 $F_{\sigma ,i}=\{\langle {a,b,\langle {a^{\sigma },X_{\tau }}\rangle _{\!A}}\rangle \mid a\sim _{\sigma } b\land ia= \tau \}$
.
$F_{\sigma ,i}=\{\langle {a,b,\langle {a^{\sigma },X_{\tau }}\rangle _{\!A}}\rangle \mid a\sim _{\sigma } b\land ia= \tau \}$
.
Remark 4.10. The set
![]() $X_{\mathsf {N}_n}=\dot n$
is the canonical name for
$X_{\mathsf {N}_n}=\dot n$
is the canonical name for
![]() $n\in \omega $
, and
$n\in \omega $
, and
![]() $X_{\mathsf {N}}=\dot \omega =\{\langle {\bar n,\bar n, \dot n}\rangle \mid n\in \omega \}$
is the canonical name for
$X_{\mathsf {N}}=\dot \omega =\{\langle {\bar n,\bar n, \dot n}\rangle \mid n\in \omega \}$
is the canonical name for
![]() $\omega $
.
$\omega $
.
Lemma 4.11 (Absoluteness and uniqueness up to extensional equality).
Let
![]() $\sigma \sim \tau $
and
$\sigma \sim \tau $
and
![]() $a,b$
of type
$a,b$
of type
![]() $\sigma $
. Then:
$\sigma $
. Then:
-
•
 $\Vdash a^{\sigma }=b^{\tau }$
implies
$\Vdash a^{\sigma }=b^{\tau }$
implies
 $a\sim _{\sigma } b$
;
$a\sim _{\sigma } b$
; -
•
 $a\sim _{\sigma } b$
implies
$a\sim _{\sigma } b$
implies
 $a^{\sigma }=b^{\tau }$
.
$a^{\sigma }=b^{\tau }$
.
Proof By induction on the (inductive definition of the) type structure. The cases
![]() $\sigma =\tau =\mathsf {N}_n$
and
$\sigma =\tau =\mathsf {N}_n$
and
![]() $\sigma =\tau =\mathsf {N}$
are straightforward.
$\sigma =\tau =\mathsf {N}$
are straightforward.
Let
![]() $\alpha ={\Pi }_{\sigma } i\sim {\Pi }_{\tau } j=\gamma $
and
$\alpha ={\Pi }_{\sigma } i\sim {\Pi }_{\tau } j=\gamma $
and
![]() $f,g\in A_{\alpha }$
. Recall that:
$f,g\in A_{\alpha }$
. Recall that:
 $$ \begin{align*} f^{\alpha}&=\{\langle{a,b,\langle{a^{\sigma},(fa)^{ia}}\rangle_{\!A}}\rangle\mid a\sim_{\sigma} b\};\\ g^{\gamma}&=\{\langle{a,b,\langle{a^{\tau},(ga)^{ja}}\rangle_{\!A}}\rangle\mid a\sim_{\tau} b\}. \end{align*} $$
$$ \begin{align*} f^{\alpha}&=\{\langle{a,b,\langle{a^{\sigma},(fa)^{ia}}\rangle_{\!A}}\rangle\mid a\sim_{\sigma} b\};\\ g^{\gamma}&=\{\langle{a,b,\langle{a^{\tau},(ga)^{ja}}\rangle_{\!A}}\rangle\mid a\sim_{\tau} b\}. \end{align*} $$
Suppose
![]() $\Vdash f^{\alpha }=g^{\gamma }$
. Let us show that
$\Vdash f^{\alpha }=g^{\gamma }$
. Let us show that
![]() $f\sim _{\alpha } g$
. Let
$f\sim _{\alpha } g$
. Let
![]() $a\sim _{\sigma } b$
. We want to prove
$a\sim _{\sigma } b$
. We want to prove
![]() $fa\sim _{\rho } gb$
, where
$fa\sim _{\rho } gb$
, where
![]() $\rho =ia$
. By definition of realizability, we have that
$\rho =ia$
. By definition of realizability, we have that
for some
![]() $\breve {a}\in A_{\tau }$
, where
$\breve {a}\in A_{\tau }$
, where
![]() $\eta =j\breve {a}$
. Then
$\eta =j\breve {a}$
. Then
![]() $\Vdash a^{\sigma }=\breve a^{\tau }$
and
$\Vdash a^{\sigma }=\breve a^{\tau }$
and
![]() $\Vdash (fa)^{\rho }=(g\breve a)^{\eta }$
. By induction,
$\Vdash (fa)^{\rho }=(g\breve a)^{\eta }$
. By induction,
![]() $a\sim _{\sigma } \breve a$
and
$a\sim _{\sigma } \breve a$
and
![]() $fa\sim _{\rho } g\breve a$
. By Lemma 4.5,
$fa\sim _{\rho } g\breve a$
. By Lemma 4.5,
![]() $\breve a\sim _{\sigma } b$
. Hence,
$\breve a\sim _{\sigma } b$
. Hence,
![]() $\breve a\sim _{\tau } b$
, and therefore
$\breve a\sim _{\tau } b$
, and therefore
![]() $g\breve a\sim _{\eta } gb$
. Since
$g\breve a\sim _{\eta } gb$
. Since
![]() $i\approx _{\sigma } j$
, it also follows from
$i\approx _{\sigma } j$
, it also follows from
![]() $a\sim _{\sigma } \breve a$
that
$a\sim _{\sigma } \breve a$
that
![]() $\rho \sim \eta $
. Thus
$\rho \sim \eta $
. Thus
![]() $g\breve a\sim _{\rho } gb$
. By transitivity,
$g\breve a\sim _{\rho } gb$
. By transitivity,
![]() $fa\sim _{\rho } gb$
.
$fa\sim _{\rho } gb$
.
Now suppose
![]() $f\sim _{\alpha } g$
. We wish to show that
$f\sim _{\alpha } g$
. We wish to show that
![]() $f^{\alpha }=g^{\gamma }$
. Since
$f^{\alpha }=g^{\gamma }$
. Since
![]() $\sigma \sim \tau $
, it suffices to show that if
$\sigma \sim \tau $
, it suffices to show that if
![]() $a\in A_{\sigma }$
, then
$a\in A_{\sigma }$
, then
![]() $a^{\sigma }=a^{\tau }$
and
$a^{\sigma }=a^{\tau }$
and
![]() $(fa)^{ia}=(ga)^{ja}$
. This follows by induction since
$(fa)^{ia}=(ga)^{ja}$
. This follows by induction since
![]() $\sigma \sim \tau $
,
$\sigma \sim \tau $
,
![]() $a\sim _{\sigma } a$
,
$a\sim _{\sigma } a$
,
![]() $ia\sim ja$
, and
$ia\sim ja$
, and
![]() $fa\sim _{ia} ga$
.
$fa\sim _{ia} ga$
.
The cases
![]() ${\Sigma }_{\sigma } i$
,
${\Sigma }_{\sigma } i$
,
![]() $\mathrm {I}_{\sigma }(a,b)$
and
$\mathrm {I}_{\sigma }(a,b)$
and
![]() $\mathrm {W}_{\sigma } i$
are left as an exercise.
$\mathrm {W}_{\sigma } i$
are left as an exercise.
By virtue of Lemmas 4.5 and 4.11, every
![]() $X_{\sigma }$
is injectively presented in the following sense.
$X_{\sigma }$
is injectively presented in the following sense.
Definition 4.12. A set
![]() $x\in \mathrm {V_{ext}}(A)$
is injectively presented if
$x\in \mathrm {V_{ext}}(A)$
is injectively presented if
where
![]() $\sim $
is a partial equivalence relation on A and f is a (definable) function from the domain of
$\sim $
is a partial equivalence relation on A and f is a (definable) function from the domain of
![]() $\sim $
to
$\sim $
to
![]() $\mathrm {V_{ext}}(A)$
such that:
$\mathrm {V_{ext}}(A)$
such that:
-
•
 $\Vdash f(a)=f(b)$
implies
$\Vdash f(a)=f(b)$
implies
 $a\sim b$
;
$a\sim b$
; -
•
 $a\sim b$
implies
$a\sim b$
implies
 $f(a)=f(b)$
.
$f(a)=f(b)$
.
This property will ensure the validity of choice for names of the form
![]() $X_{\sigma }$
(see Theorem 4.17).
$X_{\sigma }$
(see Theorem 4.17).
Lemma 4.13. Let
![]() $\sigma \sim \tau $
and
$\sigma \sim \tau $
and
![]() $i\approx _{\sigma } j$
. Then
$i\approx _{\sigma } j$
. Then
![]() $X_{\sigma }=X_{\tau }$
and
$X_{\sigma }=X_{\tau }$
and
![]() $F_{\sigma ,i}=F_{\tau ,j}$
.
$F_{\sigma ,i}=F_{\tau ,j}$
.
Proof By Lemma 4.11.
Theorem 4.14. There are closed terms such that:
where
![]() $\sigma $
is a type, i is a family of types over
$\sigma $
is a type, i is a family of types over
![]() $\sigma $
, and
$\sigma $
, and
![]() $a,b$
have type
$a,b$
have type
![]() $\sigma $
.
$\sigma $
.
Remark 4.15.
![]() $\mathsf {CZF}$
proves (i)–(v) for
$\mathsf {CZF}$
proves (i)–(v) for
![]() ${\Pi }{\Sigma }\mathrm {I}$
-types.
${\Pi }{\Sigma }\mathrm {I}$
-types.
![]() $\mathsf {CZF}+\mathsf {REA}$
proves (i)–(vi) for
$\mathsf {CZF}+\mathsf {REA}$
proves (i)–(vi) for
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types.
Theorem 4.16. There are closed terms
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
such that:
${\mathbf e}$
such that:
for every
![]() $X\in \mathrm {V_{ext}}(A)$
. The same for
$X\in \mathrm {V_{ext}}(A)$
. The same for
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
.
4.3 Realizing choice
Theorem 4.17 (
 $\mathsf {AC}_{\sigma ,\tau }$
).
$\mathsf {AC}_{\sigma ,\tau }$
).
There is a closed term
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
![]() $\mathsf {CZF}$
proves
$\mathsf {CZF}$
proves
for all
![]() ${\Pi }{\Sigma }\mathrm {I}$
-types
${\Pi }{\Sigma }\mathrm {I}$
-types
![]() $\sigma ,\tau $
and for every formula
$\sigma ,\tau $
and for every formula
![]() $\varphi $
. The same for
$\varphi $
. The same for
![]() $\mathsf {CZF}+\mathsf {REA}$
and
$\mathsf {CZF}+\mathsf {REA}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types.
Proof Suppose
![]() $c=d\Vdash \forall x\in X_{\sigma }\, \exists y\in X_{\tau }\, \varphi (x,y)$
. Then, whenever
$c=d\Vdash \forall x\in X_{\sigma }\, \exists y\in X_{\tau }\, \varphi (x,y)$
. Then, whenever
![]() $a\sim _{\sigma } b$
, we have
$a\sim _{\sigma } b$
, we have
![]() $(ca)_0\sim _{\tau } (db)_0$
and
$(ca)_0\sim _{\tau } (db)_0$
and
![]() $(ca)_1=(db)_1\Vdash \varphi (a^{\sigma },e^{\tau })$
, where
$(ca)_1=(db)_1\Vdash \varphi (a^{\sigma },e^{\tau })$
, where
![]() $e=(ca)_0$
. Let
$e=(ca)_0$
. Let
Then
![]() $f\in \mathrm {V_{ext}}(A)$
. We wish to find
$f\in \mathrm {V_{ext}}(A)$
. We wish to find
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
It suffices to look for closed terms
![]() $\mathbf {r},\mathbf {c},\mathbf {f}$
such that:
$\mathbf {r},\mathbf {c},\mathbf {f}$
such that:
where
![]() $f\subseteq X_{\sigma }\times X_{\tau }$
stands for
$f\subseteq X_{\sigma }\times X_{\tau }$
stands for
![]() $\forall z\in f\, \exists x\in X_{\sigma }\, \exists y\in X_{\tau }\, \operatorname {{\mathrm {OP}}}(z,x,y)$
, and f is functional stands for
$\forall z\in f\, \exists x\in X_{\sigma }\, \exists y\in X_{\tau }\, \operatorname {{\mathrm {OP}}}(z,x,y)$
, and f is functional stands for
(1) and (2) are straightforward. (3) Let
![]() $a\sim _{\sigma } b$
and
$a\sim _{\sigma } b$
and
![]() $\breve a\sim _{\sigma } \breve b$
. We want
$\breve a\sim _{\sigma } \breve b$
. We want
for all
![]() $x,y_0,y_1\in \mathrm {V_{ext}}(A)$
, where
$x,y_0,y_1\in \mathrm {V_{ext}}(A)$
, where
![]() $e=(ca)_0$
and
$e=(ca)_0$
and
![]() $\breve e=(c\breve a)_0$
. Suppose
$\breve e=(c\breve a)_0$
. Suppose
In particular,
![]() $\Vdash a^{\sigma }=\breve a^{\sigma }$
. By Lemma 4.11,
$\Vdash a^{\sigma }=\breve a^{\sigma }$
. By Lemma 4.11,
![]() $a\sim _{\sigma } \breve a$
. By Lemma 4.5, since
$a\sim _{\sigma } \breve a$
. By Lemma 4.5, since
![]() $(ca)_0\sim _{\tau } (da)_0$
and
$(ca)_0\sim _{\tau } (da)_0$
and
![]() $(c\breve a)_0\sim _{\tau } (da)_0$
, it follows that
$(c\breve a)_0\sim _{\tau } (da)_0$
, it follows that
![]() $(ca)_0\sim _{\tau } (c\breve a)_0$
. That is,
$(ca)_0\sim _{\tau } (c\breve a)_0$
. That is,
![]() $e\sim _{\tau } \breve e$
. By Lemma 4.11 again, we get
$e\sim _{\tau } \breve e$
. By Lemma 4.11 again, we get
![]() $e^{\tau }=\breve e^{\tau }$
. By the properties of equality, there is a closed term
$e^{\tau }=\breve e^{\tau }$
. By the properties of equality, there is a closed term
![]() $\mathbf q$
such that
$\mathbf q$
such that
![]() $\mathbf q\breve c=\mathbf q\breve d\Vdash y_0=y_1$
. We may let
$\mathbf q\breve c=\mathbf q\breve d\Vdash y_0=y_1$
. We may let
![]() $\mathbf f=_{\mathrm {def}}\lambda ca\breve a\breve c. \mathbf q\breve c$
.
$\mathbf f=_{\mathrm {def}}\lambda ca\breve a\breve c. \mathbf q\breve c$
.
Theorem 4.18 (
 $\mathsf {RDC}_{\sigma }$
).
$\mathsf {RDC}_{\sigma }$
).
There is a closed term
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
![]() $\mathsf {CZF}$
proves
$\mathsf {CZF}$
proves
 $$ \begin{align*} {\mathbf e} \Vdash \forall x\in X_{\sigma}\, &(\psi(x)\rightarrow \exists y\in X_{\sigma}\, (\psi(x)\land \varphi(x,y))) \rightarrow \forall x\in X_{\sigma}\, (\psi(x)\rightarrow \\ &\qquad\qquad\qquad\exists f\colon \omega\to X_{\sigma}\, (f(0)=x\land \forall n\in\omega\, \varphi(f(n),f(n+1)))), \end{align*} $$
$$ \begin{align*} {\mathbf e} \Vdash \forall x\in X_{\sigma}\, &(\psi(x)\rightarrow \exists y\in X_{\sigma}\, (\psi(x)\land \varphi(x,y))) \rightarrow \forall x\in X_{\sigma}\, (\psi(x)\rightarrow \\ &\qquad\qquad\qquad\exists f\colon \omega\to X_{\sigma}\, (f(0)=x\land \forall n\in\omega\, \varphi(f(n),f(n+1)))), \end{align*} $$
for every
![]() ${\Pi }{\Sigma }\mathrm {I}$
-type
${\Pi }{\Sigma }\mathrm {I}$
-type
![]() $\sigma $
and for every formula
$\sigma $
and for every formula
![]() $\varphi $
. The same for
$\varphi $
. The same for
![]() $\mathsf {CZF}+\mathsf {REA}$
and
$\mathsf {CZF}+\mathsf {REA}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-types.
Proof Suppose
![]() $\mathring a\sim _{\sigma } \mathring b$
and
$\mathring a\sim _{\sigma } \mathring b$
and
![]() $\mathring c=\mathring d\Vdash \psi (a^{\sigma })$
. We search for
$\mathring c=\mathring d\Vdash \psi (a^{\sigma })$
. We search for
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
By (1), whenever
![]() $a\sim _{\sigma } b$
and
$a\sim _{\sigma } b$
and
![]() $\breve c=\breve d\Vdash \psi (a^{\sigma })$
, we have
$\breve c=\breve d\Vdash \psi (a^{\sigma })$
, we have
In every pca one can simulate primitive recursion. We thus have a closed term
![]() $\mathbf r$
satisfying the following equations, where r is an abbreviation for
$\mathbf r$
satisfying the following equations, where r is an abbreviation for
![]() $\mathbf rc\mathring a\mathring c$
:
$\mathbf rc\mathring a\mathring c$
:
 $$ \begin{align*} r\mathbf 0&\simeq \mathbf p \mathring a(\mathbf p\mathring c\mathbf 0);\\ r\overline{n+1}&\simeq \mathbf p (c(r\bar n)_0(r\bar n)_{10} )_0 (c(r\bar n)_0(r\bar n)_{10})_1. \end{align*} $$
$$ \begin{align*} r\mathbf 0&\simeq \mathbf p \mathring a(\mathbf p\mathring c\mathbf 0);\\ r\overline{n+1}&\simeq \mathbf p (c(r\bar n)_0(r\bar n)_{10} )_0 (c(r\bar n)_0(r\bar n)_{10})_1. \end{align*} $$
By induction, owing to (2) and (3), one can verify that for every
![]() $n\in \omega $
,
$n\in \omega $
,
Note that
![]() $\mathring a=(\mathbf rc\mathring a\mathring c \mathbf 0)_0\sim _{\sigma } (\mathbf rd\mathring b\mathring d \mathbf 0)_0=\mathring b$
, and
$\mathring a=(\mathbf rc\mathring a\mathring c \mathbf 0)_0\sim _{\sigma } (\mathbf rd\mathring b\mathring d \mathbf 0)_0=\mathring b$
, and
![]() $\mathring c=(\mathbf rc\mathring a\mathring c \mathbf 0)_{10}= (\mathbf rd\mathring b\mathring d \bar 0)_{10}=\mathring d \Vdash \psi (\mathring a^{\sigma })$
. Let
$\mathring c=(\mathbf rc\mathring a\mathring c \mathbf 0)_{10}= (\mathbf rd\mathring b\mathring d \bar 0)_{10}=\mathring d \Vdash \psi (\mathring a^{\sigma })$
. Let
Then
![]() $f\in \mathrm {V_{ext}}(A)$
. By using
$f\in \mathrm {V_{ext}}(A)$
. By using
![]() $\mathbf r$
, it is not difficult to build
$\mathbf r$
, it is not difficult to build
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
Theorem 4.19. There is a closed term
![]() $\mathbf c$
such that
$\mathbf c$
such that
![]() $\mathsf {CZF}$
proves
$\mathsf {CZF}$
proves
![]() $\mathbf c\Vdash \chi $
, for every instance
$\mathbf c\Vdash \chi $
, for every instance
![]() $\chi $
of
$\chi $
of
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
. The same for
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
. The same for
![]() ${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
. Similarly, there is a closed term
${\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
. Similarly, there is a closed term
![]() $\mathbf c$
such that
$\mathbf c$
such that
![]() $\mathsf {CZF}+\mathsf {REA}$
proves
$\mathsf {CZF}+\mathsf {REA}$
proves
![]() $\mathbf c\Vdash \chi $
, for every instance
$\mathbf c\Vdash \chi $
, for every instance
![]() $\chi $
of
$\chi $
of
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
. The same for
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
. The same for
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
.
Corollary 4.20. It thus follows by Theorem 3.19 that:
-
(i)
 $T\models T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf { RDC}^{\dagger }$
,
$T\models T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf { RDC}^{\dagger }$
, -
(ii)
 $T+\mathsf {REA}\models T+\mathsf {REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf { AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
,
$T+\mathsf {REA}\models T+\mathsf {REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf { AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
,
for every theory T obtained by appending to either
![]() $\mathsf {CZF}$
or
$\mathsf {CZF}$
or
![]() $\mathsf {IZF}$
some or all of the axioms
$\mathsf {IZF}$
some or all of the axioms
![]() $\mathsf { AC}_{\omega }$
,
$\mathsf { AC}_{\omega }$
,
![]() $\mathsf {DC}$
,
$\mathsf {DC}$
,
![]() $\mathsf {DC}^{\dagger }$
,
$\mathsf {DC}^{\dagger }$
,
![]() $\mathsf {RDC}$
,
$\mathsf {RDC}$
,
![]() $\mathsf {RDC}^{\dagger }$
, and
$\mathsf {RDC}^{\dagger }$
, and
![]() $\mathsf {PAx}$
.
$\mathsf {PAx}$
.
4.4 Failure of presentation
The interpretations of
![]() $\mathsf {CZF}$
and
$\mathsf {CZF}$
and
![]() $\mathsf {CZF}+\mathsf {REA}$
in type theory validate strong presentation axioms (see Section 2.5). It is natural to ask whether extensional generic realizability validates the statement that every set is an image of a
$\mathsf {CZF}+\mathsf {REA}$
in type theory validate strong presentation axioms (see Section 2.5). It is natural to ask whether extensional generic realizability validates the statement that every set is an image of a
![]() ${\Pi }{\Sigma }\mathrm {I}$
-set, even under the assumption that this holds in the background universe. If it did, in view of Theorems 2.16 and 4.19, we would obtain that
${\Pi }{\Sigma }\mathrm {I}$
-set, even under the assumption that this holds in the background universe. If it did, in view of Theorems 2.16 and 4.19, we would obtain that
![]() $T+\text {every set is an image of a } {\Pi }{\Sigma }\mathrm {I}\text {-set} \models {\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {PAx}$
, and similarly for
$T+\text {every set is an image of a } {\Pi }{\Sigma }\mathrm {I}\text {-set} \models {\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {PAx}$
, and similarly for
![]() $T+\mathsf {REA}$
and
$T+\mathsf {REA}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets. However, the answer is negative.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets. However, the answer is negative.
Theorem 4.21. The following holds.
Similarly for
![]() $\mathsf {CZF}+\mathsf {REA}$
and
$\mathsf {CZF}+\mathsf {REA}$
and
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets.
Proof Let
![]() $y=\{\langle {\mathbf 0,\mathbf 0,\dot 0}\rangle ,\langle {\mathbf 0,\mathbf 0,\dot 1}\rangle \}\in \mathrm {V_{ext}}(A)$
. Although y is in bijection with
$y=\{\langle {\mathbf 0,\mathbf 0,\dot 0}\rangle ,\langle {\mathbf 0,\mathbf 0,\dot 1}\rangle \}\in \mathrm {V_{ext}}(A)$
. Although y is in bijection with
![]() $2=\{0,1\}$
, this fact is not realizable. The proof is the same in both cases. Let us consider the
$2=\{0,1\}$
, this fact is not realizable. The proof is the same in both cases. Let us consider the
![]() ${\Pi }{\Sigma }\mathrm {I}$
case and show that
${\Pi }{\Sigma }\mathrm {I}$
case and show that
Towards a contradiction, suppose
![]() $\Vdash X\in {\Pi }{\Sigma }\mathrm {I}\land f\colon X \twoheadrightarrow y$
, for some
$\Vdash X\in {\Pi }{\Sigma }\mathrm {I}\land f\colon X \twoheadrightarrow y$
, for some
![]() $X,f\in \mathrm {V_{ext}}(A)$
. By soundness and Theorem 4.16, there is a
$X,f\in \mathrm {V_{ext}}(A)$
. By soundness and Theorem 4.16, there is a
![]() ${\Pi }{\Sigma }\mathrm {I}$
-type
${\Pi }{\Sigma }\mathrm {I}$
-type
![]() $\sigma $
such that
$\sigma $
such that
![]() $\Vdash f\colon X_{\sigma } \twoheadrightarrow y$
. In particular, there are
$\Vdash f\colon X_{\sigma } \twoheadrightarrow y$
. In particular, there are
![]() $a,b$
such that
$a,b$
such that
By unpacking the definition, we must have
![]() $\breve a= (a\mathbf 0)_0\sim _{\sigma }(b\mathbf 0)_0=\breve b$
and
$\breve a= (a\mathbf 0)_0\sim _{\sigma }(b\mathbf 0)_0=\breve b$
and
where
![]() $x=\breve a^{\sigma }$
. From
$x=\breve a^{\sigma }$
. From
![]() $\Vdash \operatorname {{\mathrm {Fun}}}(f)$
, we then obtain
$\Vdash \operatorname {{\mathrm {Fun}}}(f)$
, we then obtain
![]() $\Vdash \dot 0=\dot 1$
, which implies
$\Vdash \dot 0=\dot 1$
, which implies
![]() $0=1$
, for the desired contradiction.
$0=1$
, for the desired contradiction.
5 Far beyond Goodman’s theorem
Goodman [Reference Goodman18, Reference Goodman19] proved that intuitionistic finite type arithmetic
![]() $\mathsf {HA}^{\omega }$
augmented with the axiom of choice in all finite types
$\mathsf {HA}^{\omega }$
augmented with the axiom of choice in all finite types
![]() $\mathsf {AC}_{\mathsf {FT}}$
is conservative over
$\mathsf {AC}_{\mathsf {FT}}$
is conservative over
![]() $\mathsf {HA}$
. This still holds in the presence of extensionality, that is,
$\mathsf {HA}$
. This still holds in the presence of extensionality, that is,
![]() $\mathsf {HA}^{\omega }+\mathsf {EXT}+\mathsf {AC_{\mathsf {FT}}}$
is conservative over
$\mathsf {HA}^{\omega }+\mathsf {EXT}+\mathsf {AC_{\mathsf {FT}}}$
is conservative over
![]() $\mathsf {HA}$
(cf. [Reference Beeson6, Reference Beeson7]). Since
$\mathsf {HA}$
(cf. [Reference Beeson6, Reference Beeson7]). Since
![]() $\mathsf {HA}^{\omega }$
and
$\mathsf {HA}^{\omega }$
and
![]() $\mathsf {HA}^{\omega } +\mathsf {EXT}$
are easily seen to be conservative over
$\mathsf {HA}^{\omega } +\mathsf {EXT}$
are easily seen to be conservative over
![]() $\mathsf{HA}$
(via the models
$\mathsf{HA}$
(via the models
![]() ${\mathsf{HRO}}$
and
${\mathsf{HRO}}$
and
![]() $\mathsf {HEO}$
respectively; cf. [Reference Troelstra32]), Goodman’s theorem is the prototypical example of arithmetical conservativity of (some) choice over a given theory T. Goodman-type results have been proved for a variety of set theories and choice principles at finite types. Write
$\mathsf {HEO}$
respectively; cf. [Reference Troelstra32]), Goodman’s theorem is the prototypical example of arithmetical conservativity of (some) choice over a given theory T. Goodman-type results have been proved for a variety of set theories and choice principles at finite types. Write
![]() $T=_{arith}S$
to convey that T and S prove the same arithmetic sentences.
$T=_{arith}S$
to convey that T and S prove the same arithmetic sentences.
Theorem 5.1. This much (as a minimum) is known:
-
•
 $T =_{arith}T+\mathsf {CAC}_{\mathsf {FT}}+{\mathsf {DC}}_{\mathsf {FT}}$
for
$T =_{arith}T+\mathsf {CAC}_{\mathsf {FT}}+{\mathsf {DC}}_{\mathsf {FT}}$
for
 $T=\mathsf {IZF}$
and extensions of
$T=\mathsf {IZF}$
and extensions of
 $\mathsf {IZF}$
by large set axioms; see [Reference Friedman and Ščedrov15, Theorem 5.1];
$\mathsf {IZF}$
by large set axioms; see [Reference Friedman and Ščedrov15, Theorem 5.1]; -
•
 $T =_{arith}T+\mathsf {AC}_{\mathsf {FT}}$
for
$T =_{arith}T+\mathsf {AC}_{\mathsf {FT}}$
for
 $T=\mathsf {CZF}$
and fragments thereof; see [Reference Gordeev20, p. 25].
$T=\mathsf {CZF}$
and fragments thereof; see [Reference Gordeev20, p. 25].
We are going to further extend such results and in particular make good on the claim in [Reference Frittaion and Rathjen17] that extensional realizability may be used to show arithmetical conservativity of
![]() $\mathsf {AC}_{\mathsf {FT}}$
over
$\mathsf {AC}_{\mathsf {FT}}$
over
![]() $\mathsf {IZF}$
(as well as
$\mathsf {IZF}$
(as well as
![]() $\mathsf {CZF}$
).
$\mathsf {CZF}$
).
Theorem 5.2. Let T be any of the theories obtained by appending to either
![]() $\mathsf {CZF}$
or
$\mathsf {CZF}$
or
![]() $\mathsf {IZF}$
some or all of the axioms
$\mathsf {IZF}$
some or all of the axioms
![]() $\mathsf { AC}_{\omega }$
,
$\mathsf { AC}_{\omega }$
,
![]() $\mathsf {DC}$
,
$\mathsf {DC}$
,
![]() $\mathsf {DC}^{\dagger }$
,
$\mathsf {DC}^{\dagger }$
,
![]() $\mathsf {RDC}$
,
$\mathsf {RDC}$
,
![]() $\mathsf {RDC}^{\dagger }$
, and
$\mathsf {RDC}^{\dagger }$
, and
![]() $\mathsf {PAx}$
. Then:
$\mathsf {PAx}$
. Then:
-
•
 $T =_{arith}T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger } $
;
$T =_{arith}T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger } $
; -
•
 $T +\mathsf {REA} =_{arith}T+\mathsf {REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+ {\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
.
$T +\mathsf {REA} =_{arith}T+\mathsf {REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+ {\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
.
One can allow type
![]() $1$
parameters. Namely, we have conservativity for sentences of the form
$1$
parameters. Namely, we have conservativity for sentences of the form
where
![]() $\varphi $
is arithmetic (relative to
$\varphi $
is arithmetic (relative to
![]() $f_1,\ldots ,f_n$
).
$f_1,\ldots ,f_n$
).
Remark 5.3. Of course, some of the theories to the left reduce to
![]() $T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
and
$T+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
and
![]() $T+\mathsf { REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
respectively.
$T+\mathsf { REA}+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }$
respectively.
Friedman and Ščedrov’s [Reference Friedman and Ščedrov15] versions of generic realizability and forcing only work for set theories without extensionality. We show how to adapt the argument to an extensional setting. Definition 5.4 fully specifies our forcing relation. It is a routine although tedious matter to check all the details. By the way, one should also prove that every theory T as above is self-validating with respect to forcing. This is not difficult to see.
It is convenient to work in a conservative extension S of T obtained by adding the constant symbol
![]() $\omega $
and an axiom saying that
$\omega $
and an axiom saying that
![]() $\omega $
is the set of natural numbers.Footnote
7
Now, we can clearly identify number quantifiers with bounded quantifiers of the form
$\omega $
is the set of natural numbers.Footnote
7
Now, we can clearly identify number quantifiers with bounded quantifiers of the form
![]() $\forall x\in \omega $
and
$\forall x\in \omega $
and
![]() $\exists x\in \omega $
. On the other hand, every primitive recursive number-theoretic function and hence relation is canonically definable by a
$\exists x\in \omega $
. On the other hand, every primitive recursive number-theoretic function and hence relation is canonically definable by a
![]() $\Sigma $
formula in the language of set theory (with just
$\Sigma $
formula in the language of set theory (with just
![]() $\in $
as primitive).Footnote
8
We call such formulas primitive recursive. Kleene’s T-predicate
$\in $
as primitive).Footnote
8
We call such formulas primitive recursive. Kleene’s T-predicate
![]() $T(e,x,z)$
and the function
$T(e,x,z)$
and the function
![]() $U(z)$
are among them. We then say that a formula is arithmetic if it is built up from primitive recursive formulas by using
$U(z)$
are among them. We then say that a formula is arithmetic if it is built up from primitive recursive formulas by using
![]() $\land $
,
$\land $
,
![]() $\lor $
,
$\lor $
,
![]() $\neg $
,
$\neg $
,
![]() $\rightarrow $
, and number quantifiers
$\rightarrow $
, and number quantifiers
![]() $\forall x\in \omega $
and
$\forall x\in \omega $
and
![]() $\exists x\in \omega $
.
$\exists x\in \omega $
.
Proof of Theorem 5.2
We first consider the case without parameters. The goal is to show that for every arithmetic sentence
![]() $\varphi $
of S,
$\varphi $
of S,
-
• if
 $S+\Phi \vdash \varphi $
, then
$S+\Phi \vdash \varphi $
, then
 $S\vdash \varphi $
,
$S\vdash \varphi $
, -
• if
 $S+\mathsf {REA}+\Psi \vdash \varphi $
, then
$S+\mathsf {REA}+\Psi \vdash \varphi $
, then
 $S+\mathsf {REA}\vdash \varphi $
,
$S+\mathsf {REA}\vdash \varphi $
,
where
![]() $\Phi ={\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
and
$\Phi ={\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {I}\text {-}\mathsf {RDC}^{\dagger }$
and
![]() $\Psi ={\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf { RDC}^{\dagger }$
.
$\Psi ={\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf {AC}^{\dagger }+{\Pi }{\Sigma }\mathrm {W}\mathrm {I}\text {-}\mathsf { RDC}^{\dagger }$
.
Step 1. Let
![]() $S^g$
be the theory obtained from S by adjoining a new constant symbol g and an axiom saying the g is a partial function from
$S^g$
be the theory obtained from S by adjoining a new constant symbol g and an axiom saying the g is a partial function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
. Within
$\omega $
. Within
![]() $S^g$
, one can define extensional generic realizability
$S^g$
, one can define extensional generic realizability
![]() $a=b\Vdash _{\omega } \varphi $
, where
$a=b\Vdash _{\omega } \varphi $
, where
![]() $a,b\in \omega $
and
$a,b\in \omega $
and
![]() $\varphi $
is a formula of T with parameters in
$\varphi $
is a formula of T with parameters in
![]() $\mathrm {V_{ext}}(\omega )$
, by using partial recursive application relative to the generic oracle g. To be precise, we use Kleene’s relativized T-predicate
$\mathrm {V_{ext}}(\omega )$
, by using partial recursive application relative to the generic oracle g. To be precise, we use Kleene’s relativized T-predicate
![]() $T(e,x,z,f)$
, where f is a partial function from
$T(e,x,z,f)$
, where f is a partial function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
. So, for example, the clause for implication reads as follows:
$\omega $
. So, for example, the clause for implication reads as follows:
For
![]() $\land $
and
$\land $
and
![]() $\lor $
, we may use a primitive recursive pairing function
$\lor $
, we may use a primitive recursive pairing function
![]() $(n,m)$
on natural numbers with primitive recursive projections
$(n,m)$
on natural numbers with primitive recursive projections
![]() $(n)_0$
and
$(n)_0$
and
![]() $(n)_1$
. So, for example, we let
$(n)_1$
. So, for example, we let
One can lift the realizability interpretation to every formula
![]() $\varphi $
of S by interpreting
$\varphi $
of S by interpreting
![]() $\omega $
with
$\omega $
with
![]() $\dot \omega \in \mathrm {V_{ext}}(\omega )$
. Here,
$\dot \omega \in \mathrm {V_{ext}}(\omega )$
. Here,
![]() $\dot \omega =\{\langle {n,n,\dot n}\rangle \mid n\in \omega \}$
, where
$\dot \omega =\{\langle {n,n,\dot n}\rangle \mid n\in \omega \}$
, where
![]() $\dot n=\{\langle {m,m,\dot m}\rangle \mid m\in n\}$
.
$\dot n=\{\langle {m,m,\dot m}\rangle \mid m\in n\}$
.
One proves that
Similarly for
![]() $S+\mathsf {REA}+\Psi $
and
$S+\mathsf {REA}+\Psi $
and
![]() $(S+\mathsf {REA})^g$
. This concludes the realizability part.
$(S+\mathsf {REA})^g$
. This concludes the realizability part.
Step 2. Next, within S, given any definable set
![]() $\mathbb {P}$
of partial functions from
$\mathbb {P}$
of partial functions from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
such that
$\omega $
such that
![]() $0\in \mathbb {P}$
, one defines a forcing interpretation
$0\in \mathbb {P}$
, one defines a forcing interpretation
![]() $p\Vdash _{\mathbb {P}} \varphi $
, where
$p\Vdash _{\mathbb {P}} \varphi $
, where
![]() $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
![]() $\varphi $
is a formula of T with parameters in
$\varphi $
is a formula of T with parameters in
![]() $\mathrm {V}(\mathbb {P})$
. The universe
$\mathrm {V}(\mathbb {P})$
. The universe
![]() $\mathrm {V}(\mathbb {P})$
is inductively defined by the clause:
$\mathrm {V}(\mathbb {P})$
is inductively defined by the clause:
-
• if
 $x\subseteq \mathbb {P}\times \mathrm {V}(\mathbb {P})$
and
$x\subseteq \mathbb {P}\times \mathrm {V}(\mathbb {P})$
and
 $\langle {q,z}\rangle \in x$
whenever
$\langle {q,z}\rangle \in x$
whenever
 $\langle {p,z}\rangle \in x$
with
$\langle {p,z}\rangle \in x$
with
 $q\supseteq p$
, then
$q\supseteq p$
, then
 $x\in \mathrm {V}(\mathbb {P})$
.
$x\in \mathrm {V}(\mathbb {P})$
.
In
![]() $\mathrm {V}(\mathbb {P})$
, we have a canonical name
$\mathrm {V}(\mathbb {P})$
, we have a canonical name
![]() $\mathring g$
for the generic g defined as
$\mathring g$
for the generic g defined as
where
![]() $\check n=\{\langle {p,\check m}\rangle \mid p\in \mathbb {P}\land m\in n\}$
, and
$\check n=\{\langle {p,\check m}\rangle \mid p\in \mathbb {P}\land m\in n\}$
, and
![]() $\langle {x,y}\rangle _{\mathbb {P}}$
is some suitable pairing function in
$\langle {x,y}\rangle _{\mathbb {P}}$
is some suitable pairing function in
![]() $\mathrm {V}(\mathbb {P})$
. In particular, every natural number
$\mathrm {V}(\mathbb {P})$
. In particular, every natural number
![]() $n\in \omega $
has a canonical name
$n\in \omega $
has a canonical name
![]() $\check n$
in
$\check n$
in
![]() $\mathrm {V}(\mathbb {P})$
. A canonical name
$\mathrm {V}(\mathbb {P})$
. A canonical name
![]() $\check \omega $
for
$\check \omega $
for
![]() $\omega $
is given by
$\omega $
is given by
![]() $ \check \omega =\{\langle {p,\check n}\rangle \mid p\in \mathbb {P}\land n\in \omega \}$
.
$ \check \omega =\{\langle {p,\check n}\rangle \mid p\in \mathbb {P}\land n\in \omega \}$
.
One can then extend the forcing interpretation
![]() $p\Vdash _{\mathbb {P}} \varphi $
to formulas of
$p\Vdash _{\mathbb {P}} \varphi $
to formulas of
![]() $S^g$
by interpreting g with
$S^g$
by interpreting g with
![]() $\mathring g$
and
$\mathring g$
and
![]() $\omega $
with
$\omega $
with
![]() $\check \omega $
. The basic idea however is that
$\check \omega $
. The basic idea however is that
![]() $p\Vdash _{\mathbb {P}} g(\check n)=\check m$
iff
$p\Vdash _{\mathbb {P}} g(\check n)=\check m$
iff
![]() $\langle {n,m}\rangle \in p$
. Moreover,
$\langle {n,m}\rangle \in p$
. Moreover,
-
• if
 $\{e\}^p(a)\simeq b$
, then
$\{e\}^p(a)\simeq b$
, then
 $p\Vdash \{\check e\}^g(\check a)\simeq \check b$
,
$p\Vdash \{\check e\}^g(\check a)\simeq \check b$
, -
• if
 $p\Vdash \{\check e\}^g(\check a)\simeq \check b$
, then for every
$p\Vdash \{\check e\}^g(\check a)\simeq \check b$
, then for every
 $q\supseteq p$
, there is an
$q\supseteq p$
, there is an
 $r\supseteq q$
such that
$r\supseteq q$
such that
 $\{e\}^r(a)\simeq b$
.
$\{e\}^r(a)\simeq b$
.
Then one shows that
Similarly for
![]() $S^g+\mathsf {REA}$
and
$S^g+\mathsf {REA}$
and
![]() $S+\mathsf {REA}$
. In particular, we must have that
$S+\mathsf {REA}$
. In particular, we must have that
Moreover, forcing is absolute for arithmetic sentences, namely,
for every arithmetic sentence
![]() $\varphi $
of S. This is the forcing part.
$\varphi $
of S. This is the forcing part.
Finally, one shows that if
![]() $\varphi $
is an arithmetic sentence, then there exists a forcing notion
$\varphi $
is an arithmetic sentence, then there exists a forcing notion
![]() $\mathbb {P}$
such that
$\mathbb {P}$
such that
Step 3. By putting all together, the arguments run as follows. If
![]() $S+\Phi \vdash \varphi $
, with
$S+\Phi \vdash \varphi $
, with
![]() $\varphi $
arithmetic, let
$\varphi $
arithmetic, let
![]() $\mathbb {P}$
be as in (4). By (1),
$\mathbb {P}$
be as in (4). By (1),
![]() $S^g\vdash \exists e\in \omega \, (e\Vdash _{\omega }\varphi )$
. By (2),
$S^g\vdash \exists e\in \omega \, (e\Vdash _{\omega }\varphi )$
. By (2),
![]() $S\vdash \forall p\, \exists q\supseteq p\, (q\Vdash _{\mathbb {P}} \exists e\in \omega \, (e\Vdash _{\omega }\varphi ))$
. We now reason in S. By the soundness of forcing and (4), we can find
$S\vdash \forall p\, \exists q\supseteq p\, (q\Vdash _{\mathbb {P}} \exists e\in \omega \, (e\Vdash _{\omega }\varphi ))$
. We now reason in S. By the soundness of forcing and (4), we can find
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
![]() $p\Vdash _{\mathbb {P}} \varphi $
. By (3), we finally obtain
$p\Vdash _{\mathbb {P}} \varphi $
. By (3), we finally obtain
![]() $\varphi $
.
$\varphi $
.
Definition 5.4 (Forcing).
We define the relation
![]() $p\Vdash _{\mathbb {P}} \varphi $
, where
$p\Vdash _{\mathbb {P}} \varphi $
, where
![]() $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
![]() $\varphi $
is a formula of T with parameters in
$\varphi $
is a formula of T with parameters in
![]() $\mathrm {V}(\mathbb {P})$
. The atomic cases are defined by transfinite recursion.
$\mathrm {V}(\mathbb {P})$
. The atomic cases are defined by transfinite recursion.
 $$ \begin{align*} p &\Vdash_{\mathbb{P}} x\in y && \Leftrightarrow && \exists z\in\mathrm{V}(\mathbb{P})\, (\langle{p,z}\rangle\in y\land p\Vdash_{\mathbb{P}} x=z), \\ p & \Vdash_{\mathbb{P}} x=y && \Leftrightarrow && \forall \langle q,z\rangle \in x\, (q\supseteq p\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} z\in y)) \text{ and } \\ &&&&& \forall \langle q,z\rangle \in y\, (q\supseteq p\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} z\in x)),\\ p& \Vdash_{\mathbb{P}} \varphi\land \psi && \Leftrightarrow && p\Vdash_{\mathbb{P}} \varphi \land p\Vdash_{\mathbb{P}} \psi, \\ p & \Vdash_{\mathbb{P}} \varphi\lor\psi && \Leftrightarrow && p\Vdash_{\mathbb{P}} \varphi \lor p\Vdash_{\mathbb{P}} \psi, \\ p &\Vdash_{\mathbb{P}} \neg\varphi && \Leftrightarrow && \forall q\supseteq p\, \neg (q\Vdash_{\mathbb{P}} \varphi), \\ p &\Vdash_{\mathbb{P}} \varphi\rightarrow\psi && \Leftrightarrow && \forall q\supseteq p\, (q\Vdash_{\mathbb{P}} \varphi\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} \psi)), \\ p& \Vdash_{\mathbb{P}} \forall x\in y\, \varphi && \Leftrightarrow && \forall \langle{q,x}\rangle\in y\, (q\supseteq p\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} \varphi)), \\ p &\Vdash_{\mathbb{P}} \exists x\in y\, \varphi && \Leftrightarrow && \exists x\in\mathrm{V}(\mathbb{P})\, (\langle{p,x}\rangle\in y\land p\Vdash_{\mathbb{P}} \varphi),\\ p& \Vdash_{\mathbb{P}} \forall x\, \varphi && \Leftrightarrow && \forall x\in\mathrm{V}(\mathbb{P})\, \forall q\supseteq p\, \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} \varphi), \\ p & \Vdash_{\mathbb{P}} \exists x\, \varphi && \Leftrightarrow && \exists x\in\mathrm{V}(\mathbb{P})\, (p\Vdash_{\mathbb{P}} \varphi). \end{align*} $$
$$ \begin{align*} p &\Vdash_{\mathbb{P}} x\in y && \Leftrightarrow && \exists z\in\mathrm{V}(\mathbb{P})\, (\langle{p,z}\rangle\in y\land p\Vdash_{\mathbb{P}} x=z), \\ p & \Vdash_{\mathbb{P}} x=y && \Leftrightarrow && \forall \langle q,z\rangle \in x\, (q\supseteq p\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} z\in y)) \text{ and } \\ &&&&& \forall \langle q,z\rangle \in y\, (q\supseteq p\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} z\in x)),\\ p& \Vdash_{\mathbb{P}} \varphi\land \psi && \Leftrightarrow && p\Vdash_{\mathbb{P}} \varphi \land p\Vdash_{\mathbb{P}} \psi, \\ p & \Vdash_{\mathbb{P}} \varphi\lor\psi && \Leftrightarrow && p\Vdash_{\mathbb{P}} \varphi \lor p\Vdash_{\mathbb{P}} \psi, \\ p &\Vdash_{\mathbb{P}} \neg\varphi && \Leftrightarrow && \forall q\supseteq p\, \neg (q\Vdash_{\mathbb{P}} \varphi), \\ p &\Vdash_{\mathbb{P}} \varphi\rightarrow\psi && \Leftrightarrow && \forall q\supseteq p\, (q\Vdash_{\mathbb{P}} \varphi\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} \psi)), \\ p& \Vdash_{\mathbb{P}} \forall x\in y\, \varphi && \Leftrightarrow && \forall \langle{q,x}\rangle\in y\, (q\supseteq p\rightarrow \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} \varphi)), \\ p &\Vdash_{\mathbb{P}} \exists x\in y\, \varphi && \Leftrightarrow && \exists x\in\mathrm{V}(\mathbb{P})\, (\langle{p,x}\rangle\in y\land p\Vdash_{\mathbb{P}} \varphi),\\ p& \Vdash_{\mathbb{P}} \forall x\, \varphi && \Leftrightarrow && \forall x\in\mathrm{V}(\mathbb{P})\, \forall q\supseteq p\, \exists r\supseteq q\, (r\Vdash_{\mathbb{P}} \varphi), \\ p & \Vdash_{\mathbb{P}} \exists x\, \varphi && \Leftrightarrow && \exists x\in\mathrm{V}(\mathbb{P})\, (p\Vdash_{\mathbb{P}} \varphi). \end{align*} $$
Forcing is monotone, that is, if
![]() $p\Vdash _{\mathbb {P}} \varphi $
and
$p\Vdash _{\mathbb {P}} \varphi $
and
![]() $q\supseteq p$
, then
$q\supseteq p$
, then
![]() $q\Vdash _{\mathbb {P}} \varphi $
.
$q\Vdash _{\mathbb {P}} \varphi $
.
All the ingredients are in place to carry out a proof of (1)–(4). Here we give some clues.
On absoluteness
For every set x, define by transfinite recursion the name
![]() $\check x\in \mathrm {V}(\mathbb {P})$
by
$\check x\in \mathrm {V}(\mathbb {P})$
by
![]() $\check x=\{\langle {p,\check y}\rangle \mid p\in \mathbb {P} \land y\in x\}$
. We set out to prove that for every arithmetic formula
$\check x=\{\langle {p,\check y}\rangle \mid p\in \mathbb {P} \land y\in x\}$
. We set out to prove that for every arithmetic formula
![]() $\varphi (x_1,\ldots ,x_n)$
,
$\varphi (x_1,\ldots ,x_n)$
,
The absoluteness of arithmetic sentences in the sense of (3) then follows.
It is an easy exercise to show that (5) is preserved under logical connectives and number quantifiers. It is thus sufficient to show that for every primitive recursive function
![]() $f(x_1,\ldots ,x_n)$
, the primitive recursive formula
$f(x_1,\ldots ,x_n)$
, the primitive recursive formula
![]() $\varphi _f(x_1,\ldots ,x_n,y)$
defining f satisfies (5). This is proved by (an external) induction on the generation of f.
$\varphi _f(x_1,\ldots ,x_n,y)$
defining f satisfies (5). This is proved by (an external) induction on the generation of f.
For example, suppose
![]() $f(x_1,\ldots ,x_n,x)$
is defined by primitive recursion from
$f(x_1,\ldots ,x_n,x)$
is defined by primitive recursion from
![]() $g(x_1,\ldots ,x_n)$
and
$g(x_1,\ldots ,x_n)$
and
![]() $h(x_1,\ldots ,x_n,x,y)$
, namely,
$h(x_1,\ldots ,x_n,x,y)$
, namely,
 $$ \begin{align*} f(x_1,\ldots,x_n,0)&=g(x_1,\ldots,x_n);\\ f(x_1,\ldots,x_n,x+1)&=h(x_1,\ldots,x_n,x,f(x_1,\ldots,x_n,x)). \end{align*} $$
$$ \begin{align*} f(x_1,\ldots,x_n,0)&=g(x_1,\ldots,x_n);\\ f(x_1,\ldots,x_n,x+1)&=h(x_1,\ldots,x_n,x,f(x_1,\ldots,x_n,x)). \end{align*} $$
Define
![]() $\varphi _f(x_1,\ldots ,x_n,x,y)$
as
$\varphi _f(x_1,\ldots ,x_n,x,y)$
as
![]() $\exists z\, (\psi (z) \land z(x)=y)$
, where
$\exists z\, (\psi (z) \land z(x)=y)$
, where
![]() $\psi (z)$
is
$\psi (z)$
is
 $$ \begin{align*} \operatorname{{\mathrm{Fun}}}(z)&\land \operatorname{{\mathrm{dom}}}(z) \in\omega \land (0\in\operatorname{{\mathrm{dom}}}(z)\rightarrow \varphi_g(x_1,\ldots,x_n,z(0))) \\ &\land \forall n\in\operatorname{{\mathrm{dom}}}(z)\, \forall m\in n\, (n=m+1\rightarrow \varphi_h(x_1,\ldots,x_n,n,z(m),z(n))). \end{align*} $$
$$ \begin{align*} \operatorname{{\mathrm{Fun}}}(z)&\land \operatorname{{\mathrm{dom}}}(z) \in\omega \land (0\in\operatorname{{\mathrm{dom}}}(z)\rightarrow \varphi_g(x_1,\ldots,x_n,z(0))) \\ &\land \forall n\in\operatorname{{\mathrm{dom}}}(z)\, \forall m\in n\, (n=m+1\rightarrow \varphi_h(x_1,\ldots,x_n,n,z(m),z(n))). \end{align*} $$
(Note that
![]() $\varphi _f$
is equivalent to a
$\varphi _f$
is equivalent to a
![]() $\Sigma $
formula if
$\Sigma $
formula if
![]() $\varphi _g$
and
$\varphi _g$
and
![]() $\varphi _h$
are also
$\varphi _h$
are also
![]() $\Sigma $
definable.) One shows that (5) holds for
$\Sigma $
definable.) One shows that (5) holds for
![]() $\varphi _f(x_1,\ldots ,x_n,x,y)$
, by assuming that it holds for
$\varphi _f(x_1,\ldots ,x_n,x,y)$
, by assuming that it holds for
![]() $\varphi _g$
and
$\varphi _g$
and
![]() $\varphi _h$
. The left-to-right direction of (5) requires some standard absoluteness arguments. For the right-to-left direction, one also uses the fact that, for every primitive recursive function
$\varphi _h$
. The left-to-right direction of (5) requires some standard absoluteness arguments. For the right-to-left direction, one also uses the fact that, for every primitive recursive function
![]() $f(x_1,\ldots ,x_n)$
,
$f(x_1,\ldots ,x_n)$
,
 $$ \begin{align*} S&\vdash \forall x_1\in\omega\cdots \forall x_n\in\omega\, (\exists y\in\omega \, \varphi_f(x_1,\ldots,x_n,y) \\ & \qquad \land \forall y_0\, \forall y_1\, (\varphi_f(x_1,\ldots,x_n,y_0)\land \varphi_f(x_1,\ldots,x_n,y_1)\rightarrow y_0=y_1)), \end{align*} $$
$$ \begin{align*} S&\vdash \forall x_1\in\omega\cdots \forall x_n\in\omega\, (\exists y\in\omega \, \varphi_f(x_1,\ldots,x_n,y) \\ & \qquad \land \forall y_0\, \forall y_1\, (\varphi_f(x_1,\ldots,x_n,y_0)\land \varphi_f(x_1,\ldots,x_n,y_1)\rightarrow y_0=y_1)), \end{align*} $$
and thereby this is forced in S.
On forcing self-realizability
To obtain (4), one shows that for every arithmetic formula
![]() $\varphi (x_1,\ldots ,x_n)$
there is a
$\varphi (x_1,\ldots ,x_n)$
there is a
![]() $\mathbb {P}$
such that S proves:
$\mathbb {P}$
such that S proves:
-
(i) there is
 $e\in \omega $
such that for every p there is a
$e\in \omega $
such that for every p there is a
 $q\supseteq p$
forcing
$q\supseteq p$
forcing  $$ \begin{align*} & \forall a_1\in\omega\cdots\forall a_n\in\omega\, (\varphi(a_1,\ldots,a_n)\rightarrow \\ & \qquad\qquad\qquad \exists b\in\omega\, (\{\check e\}^g(a_1,\ldots,a_n,0)=b\land b\Vdash_{\omega} \varphi(\dot a_1,\ldots,\dot a_n))); \end{align*} $$
$$ \begin{align*} & \forall a_1\in\omega\cdots\forall a_n\in\omega\, (\varphi(a_1,\ldots,a_n)\rightarrow \\ & \qquad\qquad\qquad \exists b\in\omega\, (\{\check e\}^g(a_1,\ldots,a_n,0)=b\land b\Vdash_{\omega} \varphi(\dot a_1,\ldots,\dot a_n))); \end{align*} $$
-
(ii) for every p there is a
 $q\supseteq p$
forcing
$q\supseteq p$
forcing  $$\begin{align*}\forall a_1\in\omega\cdots\forall a_n\in\omega\, \forall a,b\in\omega\, ((a=b\Vdash_{\omega} \varphi(\dot a_1,\ldots,\dot a_n))\rightarrow \varphi(a_1,\ldots,a_n)). \end{align*}$$
$$\begin{align*}\forall a_1\in\omega\cdots\forall a_n\in\omega\, \forall a,b\in\omega\, ((a=b\Vdash_{\omega} \varphi(\dot a_1,\ldots,\dot a_n))\rightarrow \varphi(a_1,\ldots,a_n)). \end{align*}$$
Here,
![]() $\{e\}^f(a,b)$
stands for
$\{e\}^f(a,b)$
stands for
![]() $\{\{e\}^f(a)\}^f(b)$
, and so on and so forth. On a technical note, the dummy argument for
$\{\{e\}^f(a)\}^f(b)$
, and so on and so forth. On a technical note, the dummy argument for
![]() $0$
is used to handle the case where
$0$
is used to handle the case where
![]() $\varphi $
is closed.
$\varphi $
is closed.
Now, let
![]() $\varphi (x_1,\ldots ,x_n)$
be arithmetic. We define
$\varphi (x_1,\ldots ,x_n)$
be arithmetic. We define
![]() $\mathbb {P}$
as follows. First, let
$\mathbb {P}$
as follows. First, let
![]() $\mathbb {Q}$
be the set of partial functions p from
$\mathbb {Q}$
be the set of partial functions p from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
such that
$\omega $
such that
![]() $\operatorname {{\mathrm {dom}}}(p)$
is an image of a natural number. The point of this definition is just to make sure that, within
$\operatorname {{\mathrm {dom}}}(p)$
is an image of a natural number. The point of this definition is just to make sure that, within
![]() $\mathsf {CZF}$
, the class
$\mathsf {CZF}$
, the class
![]() $\mathbb {Q}$
exists as a set and the domain of every
$\mathbb {Q}$
exists as a set and the domain of every
![]() $p\in \mathbb {Q}$
is decidable, in the sense that
$p\in \mathbb {Q}$
is decidable, in the sense that
Note that if we are working in
![]() $\mathsf {IZF}$
, we can directly define the set
$\mathsf {IZF}$
, we can directly define the set
![]() $\mathbb {Q}$
of all partial functions from
$\mathbb {Q}$
of all partial functions from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
with decidable domain. Enumerate all subformulas
$\omega $
with decidable domain. Enumerate all subformulas
![]() $\varphi _1,\ldots ,\varphi _k$
of
$\varphi _1,\ldots ,\varphi _k$
of
![]() $\varphi $
starting from the primitive recursive ones. Let
$\varphi $
starting from the primitive recursive ones. Let
![]() $\mathbb {P}$
be the set of
$\mathbb {P}$
be the set of
![]() $p\in \mathbb {Q}$
such that for every subformula
$p\in \mathbb {Q}$
such that for every subformula
![]() $\varphi _i(y_1,\ldots , y_{j}) $
of the form
$\varphi _i(y_1,\ldots , y_{j}) $
of the form
![]() $\psi _0\lor \psi _1$
, for every
$\psi _0\lor \psi _1$
, for every
![]() $a_1,\ldots ,a_j\in \omega $
, if
$a_1,\ldots ,a_j\in \omega $
, if
![]() $a=(i,a_1,\ldots ,a_j)\in \operatorname {{\mathrm {dom}}}(p)$
, then
$a=(i,a_1,\ldots ,a_j)\in \operatorname {{\mathrm {dom}}}(p)$
, then
![]() $p(a)=0\land \psi _0(a_1,\ldots ,a_j)$
or
$p(a)=0\land \psi _0(a_1,\ldots ,a_j)$
or
![]() $p(a)=1\land \psi _0(a_1,\ldots ,a_j)$
, and for every subformula
$p(a)=1\land \psi _0(a_1,\ldots ,a_j)$
, and for every subformula
![]() $\varphi _i(y_1,\ldots ,y_j)$
of the form
$\varphi _i(y_1,\ldots ,y_j)$
of the form
![]() $\exists x\, \psi (x,y_1,\ldots ,y_j)$
, for every
$\exists x\, \psi (x,y_1,\ldots ,y_j)$
, for every
![]() $a_1,\ldots ,a_j\in \omega $
, if
$a_1,\ldots ,a_j\in \omega $
, if
![]() $a=(i,a_1,\ldots ,a_j)\in \operatorname {{\mathrm {dom}}}(p)$
, then
$a=(i,a_1,\ldots ,a_j)\in \operatorname {{\mathrm {dom}}}(p)$
, then
![]() $\psi (p(a),a_1,\ldots ,a_j)$
.
$\psi (p(a),a_1,\ldots ,a_j)$
.
One can write down a formula defining
![]() $\mathbb {P}$
as there are standard finitely many subformulas of
$\mathbb {P}$
as there are standard finitely many subformulas of
![]() $\varphi $
. Here,
$\varphi $
. Here,
![]() $(a_1,\ldots ,a_j)$
is a primitive recursive coding of sequences of natural numbers. One then shows (i) and (ii) for every subformula of
$(a_1,\ldots ,a_j)$
is a primitive recursive coding of sequences of natural numbers. One then shows (i) and (ii) for every subformula of
![]() $\varphi $
.
$\varphi $
.
If
![]() $\varphi $
is primitive recursive, then one can find a number e such that
$\varphi $
is primitive recursive, then one can find a number e such that
where we identify e with the corresponding numeral. This fact can be gleaned from [Reference McCarty22, Chapter 4, Theorem 2.6] in the case of
![]() $\mathsf {IZF}$
. The same holds for
$\mathsf {IZF}$
. The same holds for
![]() $\mathsf {CZF}$
[Reference Rathjen30, Proposition 8.5]. We can then use the soundness of forcing to get (i) and (ii).
$\mathsf {CZF}$
[Reference Rathjen30, Proposition 8.5]. We can then use the soundness of forcing to get (i) and (ii).
The index of complex subformulas is computed according to the following table. Let i be the number of the given subformula according to our enumeration. Write
![]() $\vec {a}$
for the tuple
$\vec {a}$
for the tuple
![]() $a_1,\ldots ,a_j$
.
$a_1,\ldots ,a_j$
.
 $$ \begin{align*} \{e_{\varphi\land\psi}\}^f(\vec a,0)&\simeq (\{e_{\varphi}\}^f(\vec a,0),\{e_{\psi}\}^f(\vec a,0)), \\ \{e_{\varphi\lor\psi}\}^f(\vec a,0)&\simeq \begin{cases} \{e_{\varphi}\}^f(\vec a,0), & \text{if } f(i,\vec a)=0, \\ \{e_{\psi}\}^f(\vec a,0),& \text{if } f(i,\vec a)=1, \end{cases} \\ \{e_{\forall x\in\omega\, \varphi(x)}\}^f(\vec a,0,b)&\simeq \{e_{\varphi}\}^f(\vec a,b,0),\\ \{e_{\exists x\in\omega\, \varphi(x)}\}^f(\vec a,0)&\simeq (f(i,\vec a),\{e_{\varphi}\}^f(\vec a,f(i,\vec a),0)). \end{align*} $$
$$ \begin{align*} \{e_{\varphi\land\psi}\}^f(\vec a,0)&\simeq (\{e_{\varphi}\}^f(\vec a,0),\{e_{\psi}\}^f(\vec a,0)), \\ \{e_{\varphi\lor\psi}\}^f(\vec a,0)&\simeq \begin{cases} \{e_{\varphi}\}^f(\vec a,0), & \text{if } f(i,\vec a)=0, \\ \{e_{\psi}\}^f(\vec a,0),& \text{if } f(i,\vec a)=1, \end{cases} \\ \{e_{\forall x\in\omega\, \varphi(x)}\}^f(\vec a,0,b)&\simeq \{e_{\varphi}\}^f(\vec a,b,0),\\ \{e_{\exists x\in\omega\, \varphi(x)}\}^f(\vec a,0)&\simeq (f(i,\vec a),\{e_{\varphi}\}^f(\vec a,f(i,\vec a),0)). \end{align*} $$
By way of example, let us illustrate how to obtain (i) in the existential case. For simplicity, suppose we have a subformula of the form
![]() $\exists y\in \omega \, \varphi (x,y)$
. We work in S. We have already found an index
$\exists y\in \omega \, \varphi (x,y)$
. We work in S. We have already found an index
![]() $e_{\varphi }$
for
$e_{\varphi }$
for
![]() $\varphi $
. So, let e be such that
$\varphi $
. So, let e be such that
Let
![]() $p\in \mathbb {P}$
. We search for a
$p\in \mathbb {P}$
. We search for a
![]() $q\supseteq p$
such that
$q\supseteq p$
such that
Notice that, within
![]() $S^g$
,
$S^g$
,
and thereby this is forced in S. It is then enough to find an extension
![]() $q\supseteq p$
such that
$q\supseteq p$
such that
 $$ \begin{align} q&\Vdash_{\mathbb{P}} \forall a\in\omega\, (\exists y\in\omega\, \varphi(a,y)\rightarrow \exists c\in\omega\, \exists b\in\omega\, (\{\check e\}^g(a,0)\simeq c \notag \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \land (c)_0=b \land (c)_1\Vdash_{\omega} \varphi(\dot a,\dot b))). \end{align} $$
$$ \begin{align} q&\Vdash_{\mathbb{P}} \forall a\in\omega\, (\exists y\in\omega\, \varphi(a,y)\rightarrow \exists c\in\omega\, \exists b\in\omega\, (\{\check e\}^g(a,0)\simeq c \notag \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \land (c)_0=b \land (c)_1\Vdash_{\omega} \varphi(\dot a,\dot b))). \end{align} $$
We claim that p already satisfies (1). Let
![]() $a\in \omega $
,
$a\in \omega $
,
![]() $q\supseteq p$
, and suppose
$q\supseteq p$
, and suppose
![]() $q\Vdash _{\mathbb {P}} \exists y\in \omega \, \varphi (\check a,y)$
. We are clear if we find
$q\Vdash _{\mathbb {P}} \exists y\in \omega \, \varphi (\check a,y)$
. We are clear if we find
![]() $r\supseteq q$
such that
$r\supseteq q$
such that
 $$ \begin{align} r&\Vdash_{\mathbb{P}} \exists c\in\omega\, \exists b\in\omega\, (\{\check e\}^g(\check a,0)\simeq c\land (c)_0=b \notag \\ & \qquad\qquad \land \forall x\, (i(\check a,x)\rightarrow (c)_1\Vdash_{\omega} \varphi(x,\dot b))), \end{align} $$
$$ \begin{align} r&\Vdash_{\mathbb{P}} \exists c\in\omega\, \exists b\in\omega\, (\{\check e\}^g(\check a,0)\simeq c\land (c)_0=b \notag \\ & \qquad\qquad \land \forall x\, (i(\check a,x)\rightarrow (c)_1\Vdash_{\omega} \varphi(x,\dot b))), \end{align} $$
where the formula
![]() $i(x,y)$
expresses that
$i(x,y)$
expresses that
![]() $y=\dot x$
for
$y=\dot x$
for
![]() $x\in \omega $
. By definition, there is a
$x\in \omega $
. By definition, there is a
![]() $b\in \omega $
such that
$b\in \omega $
such that
![]() $q\Vdash _{\mathbb {P}} \varphi (\check a,\check b)$
. By absoluteness,
$q\Vdash _{\mathbb {P}} \varphi (\check a,\check b)$
. By absoluteness,
![]() $\varphi (a,b)$
holds. Now, we can decide whether
$\varphi (a,b)$
holds. Now, we can decide whether
![]() $(i,a)\in \operatorname {{\mathrm {dom}}}(q)$
. If not, we can take
$(i,a)\in \operatorname {{\mathrm {dom}}}(q)$
. If not, we can take
![]() $q'=q\cup \{\langle {(i,a),b}\rangle \}$
. By the assumption on
$q'=q\cup \{\langle {(i,a),b}\rangle \}$
. By the assumption on
![]() $e_{\varphi }$
, there is an
$e_{\varphi }$
, there is an
![]() $s\supseteq q'$
such that
$s\supseteq q'$
such that
 $$ \begin{align} & s\Vdash_{\mathbb{P}} \exists c_1\in\omega\, (\{\check e_{\varphi}\}^g(\check a,\check b,0)\simeq c_1 \notag \\ & \qquad\qquad\qquad \land \forall x\, \forall y\, (i(\check a,x)\land i(\check b,y) \rightarrow c_1\Vdash_{\omega} \varphi(x,y))). \end{align} $$
$$ \begin{align} & s\Vdash_{\mathbb{P}} \exists c_1\in\omega\, (\{\check e_{\varphi}\}^g(\check a,\check b,0)\simeq c_1 \notag \\ & \qquad\qquad\qquad \land \forall x\, \forall y\, (i(\check a,x)\land i(\check b,y) \rightarrow c_1\Vdash_{\omega} \varphi(x,y))). \end{align} $$
One can see that
![]() $s\Vdash _{\mathbb {P}} \{\check e\}^g(\check a,0)\simeq (\check b,\{\check e_{\varphi }\}^g(\check a,\check b,0))$
. By (3) and soundness, one can finally find an
$s\Vdash _{\mathbb {P}} \{\check e\}^g(\check a,0)\simeq (\check b,\{\check e_{\varphi }\}^g(\check a,\check b,0))$
. By (3) and soundness, one can finally find an
![]() $r\supseteq s$
satisfying (2), as desired.
$r\supseteq s$
satisfying (2), as desired.
Adding parameters
We briefly discuss how to generalize such conservation result to arithmetic formulas with type
![]() $1$
parameters. For example, suppose
$1$
parameters. For example, suppose
![]() $S+\Phi \vdash \forall f\in \omega ^{\omega }\, \varphi (f)$
. Then
$S+\Phi \vdash \forall f\in \omega ^{\omega }\, \varphi (f)$
. Then
![]() $(S+\Phi )_f\vdash \varphi (f)$
, where, in general,
$(S+\Phi )_f\vdash \varphi (f)$
, where, in general,
![]() $T_f$
is obtained from T by adjoining a constant symbol f and an axiom saying that f is a function from
$T_f$
is obtained from T by adjoining a constant symbol f and an axiom saying that f is a function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
. It clearly suffices to show that
$\omega $
. It clearly suffices to show that
![]() $S_f\vdash \varphi (f)$
. If we do so, then
$S_f\vdash \varphi (f)$
. If we do so, then
![]() $S\vdash \forall f\in \omega ^{\omega }\, \varphi (f)$
$S\vdash \forall f\in \omega ^{\omega }\, \varphi (f)$
Now consider the theory
![]() $(S_f)^g$
obtained from
$(S_f)^g$
obtained from
![]() $S_f$
by further extending the language with a constant symbol g and an axiom saying that g is a partial function from
$S_f$
by further extending the language with a constant symbol g and an axiom saying that g is a partial function from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
. Within
$\omega $
. Within
![]() $(S_f)^g$
, consider extensional generic realizability
$(S_f)^g$
, consider extensional generic realizability
![]() $a=b\Vdash _{\omega } \varphi $
, where
$a=b\Vdash _{\omega } \varphi $
, where
![]() $a,b\in \omega $
and
$a,b\in \omega $
and
![]() $\varphi $
is a formula of
$\varphi $
is a formula of
![]() $S_f$
, by using partial recursive application relative to the oracle
$S_f$
, by using partial recursive application relative to the oracle
![]() $f\oplus g=\{\langle {2n,f(n)}\rangle \mid n\in \omega \}\cup \{\langle {2n+1,g(n)}\rangle \mid n\in \operatorname {{\mathrm {dom}}}(g)\}$
. Use the name
$f\oplus g=\{\langle {2n,f(n)}\rangle \mid n\in \omega \}\cup \{\langle {2n+1,g(n)}\rangle \mid n\in \operatorname {{\mathrm {dom}}}(g)\}$
. Use the name
![]() $\dot f=\{\langle {n,n,\langle {\dot n,\dot m}\rangle _{\omega }}\rangle \mid f(n)=m\}\in \mathrm {V_{ext}}(\omega )$
to define realizability on formulas containing f. Note that we could extend the interpretation to every formula of
$\dot f=\{\langle {n,n,\langle {\dot n,\dot m}\rangle _{\omega }}\rangle \mid f(n)=m\}\in \mathrm {V_{ext}}(\omega )$
to define realizability on formulas containing f. Note that we could extend the interpretation to every formula of
![]() $(S_f)^g$
by interpreting g with
$(S_f)^g$
by interpreting g with
![]() $\dot g$
, which is defined in a similar way as
$\dot g$
, which is defined in a similar way as
![]() $\dot f$
. Show that
$\dot f$
. Show that
Similarly for
![]() $(S+\mathsf {REA}+\Psi )_f$
and
$(S+\mathsf {REA}+\Psi )_f$
and
![]() $(S_f+\mathsf {REA})^g$
. In particular, we must have
$(S_f+\mathsf {REA})^g$
. In particular, we must have
This is the realizability part.
In
![]() $S_f$
, given any definable set
$S_f$
, given any definable set
![]() $\mathbb {P}$
of partial functions from
$\mathbb {P}$
of partial functions from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
, where now we can use the parameter f in defining
$\omega $
, where now we can use the parameter f in defining
![]() $\mathbb {P}$
, we extend the forcing interpretation
$\mathbb {P}$
, we extend the forcing interpretation
![]() $p\Vdash _{\mathbb {P}} \varphi $
of Definition 5.4 to formulas of
$p\Vdash _{\mathbb {P}} \varphi $
of Definition 5.4 to formulas of
![]() $(S_f)^g$
by interpreting g with
$(S_f)^g$
by interpreting g with
![]() $\mathring g$
, like before, and f with
$\mathring g$
, like before, and f with
![]() $\check f$
. Note that
$\check f$
. Note that
![]() $\check f=\{\langle {p,\check z}\rangle \mid p\in \mathbb {P}\land z\in f\}=\{\langle {p,\langle {\check n,\check m}\rangle _{\mathbb {P}}}\rangle \mid p\in \mathbb {P}\land f(n)=m\}$
. The rest of the argument is roughly as before, but with everything relativized to the parameter f. In particular, one must show that arithmetic (in f) formulas are absolute for forcing. Finally, given
$\check f=\{\langle {p,\check z}\rangle \mid p\in \mathbb {P}\land z\in f\}=\{\langle {p,\langle {\check n,\check m}\rangle _{\mathbb {P}}}\rangle \mid p\in \mathbb {P}\land f(n)=m\}$
. The rest of the argument is roughly as before, but with everything relativized to the parameter f. In particular, one must show that arithmetic (in f) formulas are absolute for forcing. Finally, given
![]() $\varphi (f)$
, one defines
$\varphi (f)$
, one defines
![]() $\mathbb {P}$
as before, but relative to f, and show that in
$\mathbb {P}$
as before, but relative to f, and show that in
![]() $\mathrm {V}(\mathbb {P})$
,
$\mathrm {V}(\mathbb {P})$
,
![]() $\varphi (f)$
is self-realizing.⊣
$\varphi (f)$
is self-realizing.⊣
6 Appendix
The proofs of Theorems 4.14 and 4.16 will rely on the following two facts.
Theorem 6.1 (
 $\mathsf {CZF}$
).
$\mathsf {CZF}$
).
There is a formula
![]() $\vartheta (u,Y)$
, such that
$\vartheta (u,Y)$
, such that
 $$\begin{align*}{\Pi}{\Sigma}\mathrm{I}=\{Y\mid \exists u\, \vartheta(u,Y)\}\ \ \text{and}\ \ \vartheta(u,Y)\leftrightarrow \bigvee_{i=0}^4 \vartheta_{i}(u,Y), \end{align*}$$
$$\begin{align*}{\Pi}{\Sigma}\mathrm{I}=\{Y\mid \exists u\, \vartheta(u,Y)\}\ \ \text{and}\ \ \vartheta(u,Y)\leftrightarrow \bigvee_{i=0}^4 \vartheta_{i}(u,Y), \end{align*}$$
where
 $$ \begin{align*} & \vartheta_0(u,Y) && \Leftrightarrow && Y\in\omega, \\ &\vartheta_1(u,Y) && \Leftrightarrow && Y=\omega, \\ &\vartheta_2(u,Y) && \Leftrightarrow && \exists X\, \exists F\, (\psi(u,X,F)\land Y={\Pi}(X,F)), \\ &\vartheta_3(u,Y) && \Leftrightarrow && \exists X\, \exists F\, (\psi(u,X,F)\land Y={\Sigma}(X,F)), \\ & \vartheta_4(u,Y) && \Leftrightarrow && \exists X\, (\exists v\in u\, \vartheta(v,X)\land \exists x\in X\, \exists y\in X\, (Y=\mathrm{I}(x,y))), \end{align*} $$
$$ \begin{align*} & \vartheta_0(u,Y) && \Leftrightarrow && Y\in\omega, \\ &\vartheta_1(u,Y) && \Leftrightarrow && Y=\omega, \\ &\vartheta_2(u,Y) && \Leftrightarrow && \exists X\, \exists F\, (\psi(u,X,F)\land Y={\Pi}(X,F)), \\ &\vartheta_3(u,Y) && \Leftrightarrow && \exists X\, \exists F\, (\psi(u,X,F)\land Y={\Sigma}(X,F)), \\ & \vartheta_4(u,Y) && \Leftrightarrow && \exists X\, (\exists v\in u\, \vartheta(v,X)\land \exists x\in X\, \exists y\in X\, (Y=\mathrm{I}(x,y))), \end{align*} $$
with
![]() $\psi (u,X,F)$
being a shorthand for
$\psi (u,X,F)$
being a shorthand for
Similarly, there is a formula
![]() $\vartheta ^*(u,Y)$
, such that
$\vartheta ^*(u,Y)$
, such that
 $$\begin{align*}{\Pi}{\Sigma}\mathrm{W}\mathrm{I}=\{Y\mid \exists u\, \vartheta^*(u,Y)\} \ \ \text{and}\ \ \vartheta^*(u,Y)\leftrightarrow \bigvee_{i=0}^5 \vartheta^*_{i}(u,Y), \end{align*}$$
$$\begin{align*}{\Pi}{\Sigma}\mathrm{W}\mathrm{I}=\{Y\mid \exists u\, \vartheta^*(u,Y)\} \ \ \text{and}\ \ \vartheta^*(u,Y)\leftrightarrow \bigvee_{i=0}^5 \vartheta^*_{i}(u,Y), \end{align*}$$
where
![]() $\vartheta ^*_i$
for
$\vartheta ^*_i$
for
![]() $i=0,\ldots ,4$
is defined in a similar fashion as
$i=0,\ldots ,4$
is defined in a similar fashion as
![]() $\vartheta _i$
, and
$\vartheta _i$
, and
 $$ \begin{align*} &\vartheta^*_5(u,Y) && \Leftrightarrow && \exists X\, \exists F\, (\exists v\in u\, \vartheta^*(v,X)\land \operatorname{{\mathrm{Fun}}}(F) \land \operatorname{{\mathrm{dom}}}(F)=X\land \\ &&&&& \forall x\in X\, \exists v\in u\, \vartheta^*(v,F(x))\land Y=\mathrm{W}(X,F)). \end{align*} $$
$$ \begin{align*} &\vartheta^*_5(u,Y) && \Leftrightarrow && \exists X\, \exists F\, (\exists v\in u\, \vartheta^*(v,X)\land \operatorname{{\mathrm{Fun}}}(F) \land \operatorname{{\mathrm{dom}}}(F)=X\land \\ &&&&& \forall x\in X\, \exists v\in u\, \vartheta^*(v,F(x))\land Y=\mathrm{W}(X,F)). \end{align*} $$
Theorem 6.2 (
 $\mathsf {CZF}+\mathsf {REA}$
).
$\mathsf {CZF}+\mathsf {REA}$
).
If F is a function with domain X, then for every set Y,
 $$ \begin{align*} Y&=\mathrm{W}(X,F) \leftrightarrow \forall y\, (y\in Y\leftrightarrow \exists x\in X\, \exists f\, (y=\langle{x,f}\rangle\land \operatorname{{\mathrm{Fun}}}(f)\land \\ & \qquad \qquad \operatorname{{\mathrm{dom}}}(f)=F(x)\land \forall u\in\operatorname{{\mathrm{dom}}}(f)\, (f(u)\in Y))). \end{align*} $$
$$ \begin{align*} Y&=\mathrm{W}(X,F) \leftrightarrow \forall y\, (y\in Y\leftrightarrow \exists x\in X\, \exists f\, (y=\langle{x,f}\rangle\land \operatorname{{\mathrm{Fun}}}(f)\land \\ & \qquad \qquad \operatorname{{\mathrm{dom}}}(f)=F(x)\land \forall u\in\operatorname{{\mathrm{dom}}}(f)\, (f(u)\in Y))). \end{align*} $$
Proof of Theorem 4.14
From now on, let
(i) A closed term
![]() $\mathbf o$
such that
$\mathbf o$
such that
![]() $\mathbf o\Vdash X_{\mathsf {N}}=\omega $
is given in the proof of Theorem 3.16. In fact, the set
$\mathbf o\Vdash X_{\mathsf {N}}=\omega $
is given in the proof of Theorem 3.16. In fact, the set
![]() $X_{\mathsf {N}}=\dot \omega $
is the canonical name for
$X_{\mathsf {N}}=\dot \omega $
is the canonical name for
![]() $\omega $
used to realize infinity.
$\omega $
used to realize infinity.
(ii) We aim for
![]() $\mathbf {fun}\Vdash \operatorname {{\mathrm {Fun}}}(F)\land \operatorname {{\mathrm {dom}}}(F) = X_{\sigma }$
. It suffices to look for closed terms
$\mathbf {fun}\Vdash \operatorname {{\mathrm {Fun}}}(F)\land \operatorname {{\mathrm {dom}}}(F) = X_{\sigma }$
. It suffices to look for closed terms
![]() $\mathbf r,\mathbf f, {\mathbf t}$
such that:
$\mathbf r,\mathbf f, {\mathbf t}$
such that:
 $$ \begin{align*} \mathbf r&\Vdash \forall z\in F\, \exists x\in X_{\sigma}\, \exists y\, \operatorname{{\mathrm{OP}}}(z,x,y) \quad (\text{namely, } F\text{ is a relation }\land \operatorname{{\mathrm{dom}}}(F)\subseteq X_{\sigma}), \\ {\mathbf t}& \Vdash \forall x\in X_{\sigma}\, \exists y\, \exists z\in F\, \operatorname{{\mathrm{OP}}}(z,x,y) \quad (\text{namely, } X_{\sigma}\subseteq \operatorname{{\mathrm{dom}}}(F)), \\ \mathbf f &\Vdash F \text{ is functional.} & \end{align*} $$
$$ \begin{align*} \mathbf r&\Vdash \forall z\in F\, \exists x\in X_{\sigma}\, \exists y\, \operatorname{{\mathrm{OP}}}(z,x,y) \quad (\text{namely, } F\text{ is a relation }\land \operatorname{{\mathrm{dom}}}(F)\subseteq X_{\sigma}), \\ {\mathbf t}& \Vdash \forall x\in X_{\sigma}\, \exists y\, \exists z\in F\, \operatorname{{\mathrm{OP}}}(z,x,y) \quad (\text{namely, } X_{\sigma}\subseteq \operatorname{{\mathrm{dom}}}(F)), \\ \mathbf f &\Vdash F \text{ is functional.} & \end{align*} $$
We can easily arrange for
![]() $\mathbf r$
and
$\mathbf r$
and
![]() ${\mathbf t}$
. Let us find
${\mathbf t}$
. Let us find
![]() $\mathbf f$
. By unraveling the definition, we want
$\mathbf f$
. By unraveling the definition, we want
![]() $\mathbf f$
such that, if
$\mathbf f$
such that, if
![]() $a\sim _{\sigma } b $
,
$a\sim _{\sigma } b $
,
![]() $\breve a\sim _{\sigma } \breve b$
and
$\breve a\sim _{\sigma } \breve b$
and
where
![]() $ia=\tau $
and
$ia=\tau $
and
![]() $i\breve a=\breve \tau $
, then
$i\breve a=\breve \tau $
, then
![]() $\mathbf fa\breve ac=\mathbf fb\breve bd\Vdash y_0=y_1$
. By the properties of pairing, from c and d as above we get
$\mathbf fa\breve ac=\mathbf fb\breve bd\Vdash y_0=y_1$
. By the properties of pairing, from c and d as above we get
![]() $\Vdash a^{\sigma }=\breve a^{\sigma }$
. By Lemma 4.11, we must have
$\Vdash a^{\sigma }=\breve a^{\sigma }$
. By Lemma 4.11, we must have
![]() $a\sim _{\sigma } \breve a$
. Since i is a family of types over
$a\sim _{\sigma } \breve a$
. Since i is a family of types over
![]() $\sigma $
,
$\sigma $
,
![]() $ia\sim i\breve a$
. That is,
$ia\sim i\breve a$
. That is,
![]() $\tau \sim \breve \tau $
. By Lemma 4.13,
$\tau \sim \breve \tau $
. By Lemma 4.13,
![]() $X_{\tau }=X_{\breve \tau }$
. As in the proof of Theorem 4.17, by the properties of equality, there is a closed term
$X_{\tau }=X_{\breve \tau }$
. As in the proof of Theorem 4.17, by the properties of equality, there is a closed term
![]() $\mathbf q$
such that
$\mathbf q$
such that
![]() $\mathbf q c=\mathbf q d\Vdash y_0=y_1$
. We may let
$\mathbf q c=\mathbf q d\Vdash y_0=y_1$
. We may let
![]() $\mathbf f=_{\mathrm {def}}\lambda a\breve ac. \mathbf q c$
.
$\mathbf f=_{\mathrm {def}}\lambda a\breve ac. \mathbf q c$
.
(iii) We aim for
![]() $\mathbf {prod}\Vdash X_{{\Pi }_{\sigma } i}={\Pi }(X_{\sigma }, F)$
. We abbreviate
$\mathbf {prod}\Vdash X_{{\Pi }_{\sigma } i}={\Pi }(X_{\sigma }, F)$
. We abbreviate
 $$ \begin{align*} &\vartheta_r(f,X,F) && \Leftrightarrow && f\subseteq {\Sigma}(X,F)\\&&&\Leftrightarrow && \forall z\in f\, \exists x\in X\, \exists y\, \exists Z\in F\, \exists Y\, (\operatorname{{\mathrm{OP}}}(z,x,y)\land \operatorname{{\mathrm{OP}}}(Z,x,Y)\land y\in Y), \\&\vartheta_t(X,f) && \Leftrightarrow && X\subseteq\operatorname{{\mathrm{dom}}}(f) \\&&&\Leftrightarrow && \forall x\in X\, \exists z\in f\, \exists y\, \operatorname{{\mathrm{OP}}}(z,x,y), \\&\vartheta_f(f) && \Leftrightarrow && f \text{ is functional}\\&&& \Leftrightarrow && \forall z_0\in f\, \forall z_1\in f\, \forall x\, \forall y_0\, \forall y_1\, (\operatorname{{\mathrm{OP}}}(z_0,x,y_0)\land \operatorname{{\mathrm{OP}}}(z_1,x,y_1)\rightarrow y_0=y_1). \end{align*} $$
$$ \begin{align*} &\vartheta_r(f,X,F) && \Leftrightarrow && f\subseteq {\Sigma}(X,F)\\&&&\Leftrightarrow && \forall z\in f\, \exists x\in X\, \exists y\, \exists Z\in F\, \exists Y\, (\operatorname{{\mathrm{OP}}}(z,x,y)\land \operatorname{{\mathrm{OP}}}(Z,x,Y)\land y\in Y), \\&\vartheta_t(X,f) && \Leftrightarrow && X\subseteq\operatorname{{\mathrm{dom}}}(f) \\&&&\Leftrightarrow && \forall x\in X\, \exists z\in f\, \exists y\, \operatorname{{\mathrm{OP}}}(z,x,y), \\&\vartheta_f(f) && \Leftrightarrow && f \text{ is functional}\\&&& \Leftrightarrow && \forall z_0\in f\, \forall z_1\in f\, \forall x\, \forall y_0\, \forall y_1\, (\operatorname{{\mathrm{OP}}}(z_0,x,y_0)\land \operatorname{{\mathrm{OP}}}(z_1,x,y_1)\rightarrow y_0=y_1). \end{align*} $$
Let
![]() $\alpha ={\Pi }_{\sigma } i$
. For the direction left to right, it suffices to look for closed terms
$\alpha ={\Pi }_{\sigma } i$
. For the direction left to right, it suffices to look for closed terms
![]() $\mathbf r$
,
$\mathbf r$
,
![]() ${\mathbf t}$
, and
${\mathbf t}$
, and
![]() $\mathbf f$
such that whenever
$\mathbf f$
such that whenever
![]() $f\sim _{\alpha } g$
, then
$f\sim _{\alpha } g$
, then
For the direction right to left, we look for a closed term
![]() $\mathbf c$
such that, for every
$\mathbf c$
such that, for every
![]() $h\in \mathrm {V_{ext}}(A)$
, if
$h\in \mathrm {V_{ext}}(A)$
, if
![]() $c=d\Vdash \vartheta _r(h,X_{\sigma },F)\land \vartheta _t(X_{\sigma },h)\land \vartheta _f(h)$
, then
$c=d\Vdash \vartheta _r(h,X_{\sigma },F)\land \vartheta _t(X_{\sigma },h)\land \vartheta _f(h)$
, then
![]() $\mathbf c c=\mathbf c d\Vdash h\in X_{{\Pi }_{\sigma } i}$
.
$\mathbf c c=\mathbf c d\Vdash h\in X_{{\Pi }_{\sigma } i}$
.
Let us start with the forward direction.
(1) Let
![]() $f\sim _{\alpha } g$
,
$f\sim _{\alpha } g$
,
![]() $a\sim _{\sigma } b$
,
$a\sim _{\sigma } b$
,
![]() $ia=\tau $
, and
$ia=\tau $
, and
![]() $fa=e$
. We want
$fa=e$
. We want
We let
![]() $(\mathbf rfa)_0=a$
and set out for
$(\mathbf rfa)_0=a$
and set out for
We let
![]() $(\mathbf rfa)_{10}=a$
,
$(\mathbf rfa)_{10}=a$
,
![]() $Y=X_{\tau }$
and set out for
$Y=X_{\tau }$
and set out for
Let
![]() $(\mathbf rfa)_{110}=(\mathbf rfa)_{1110}={\mathbf v}$
, where
$(\mathbf rfa)_{110}=(\mathbf rfa)_{1110}={\mathbf v}$
, where
![]() ${\mathbf v}\Vdash \operatorname {{\mathrm {OP}}}(\langle {x,y}\rangle _{\!A},x,y)$
exists by Lemma 3.15. Let
${\mathbf v}\Vdash \operatorname {{\mathrm {OP}}}(\langle {x,y}\rangle _{\!A},x,y)$
exists by Lemma 3.15. Let
![]() $(\mathbf rfa)_{1111}=\mathbf p(ca)\mathbf i$
, where
$(\mathbf rfa)_{1111}=\mathbf p(ca)\mathbf i$
, where
![]() $\mathbf i\Vdash \forall x\, (x=x)$
. Then
$\mathbf i\Vdash \forall x\, (x=x)$
. Then
![]() $\langle {fa,gb,e^{\tau }}\rangle \in X_{\tau }$
and
$\langle {fa,gb,e^{\tau }}\rangle \in X_{\tau }$
and
is as desired.
(2) Exercise.
(3) Let
![]() $f\sim _{\alpha } g$
. Let
$f\sim _{\alpha } g$
. Let
![]() $a_j\sim _{\sigma } b_j$
,
$a_j\sim _{\sigma } b_j$
,
![]() $ia_j=\tau _j$
, and
$ia_j=\tau _j$
, and
![]() $fa_j=e_j$
for
$fa_j=e_j$
for
![]() $j=0,1$
. We wish to find
$j=0,1$
. We wish to find
![]() $\mathbf f$
such that, if
$\mathbf f$
such that, if
![]() $c=d\Vdash \operatorname {{\mathrm {OP}}}(\langle {a_0^{\sigma },e_0^{\tau _0}}\rangle _{\!A},x,y_0)\land \operatorname {{\mathrm {OP}}}(\langle {a_1^{\sigma },e_1^{\tau _1}}\rangle _{\!A},x,y_1)$
, then
$c=d\Vdash \operatorname {{\mathrm {OP}}}(\langle {a_0^{\sigma },e_0^{\tau _0}}\rangle _{\!A},x,y_0)\land \operatorname {{\mathrm {OP}}}(\langle {a_1^{\sigma },e_1^{\tau _1}}\rangle _{\!A},x,y_1)$
, then
![]() $\mathbf ffa_0a_1c=\mathbf fgb_0b_1d\Vdash y_0=y_1$
, for all
$\mathbf ffa_0a_1c=\mathbf fgb_0b_1d\Vdash y_0=y_1$
, for all
![]() $x,y_0,y_1\in \mathrm {V_{ext}}(A)$
. Suppose we have c and d as above. Then in particular
$x,y_0,y_1\in \mathrm {V_{ext}}(A)$
. Suppose we have c and d as above. Then in particular
![]() $\Vdash a_0^{\sigma }=a_1^{\sigma }$
. By Lemma 4.11, it follows that
$\Vdash a_0^{\sigma }=a_1^{\sigma }$
. By Lemma 4.11, it follows that
![]() $a_0\sim _{\sigma } a_1$
, and hence
$a_0\sim _{\sigma } a_1$
, and hence
![]() $\tau _0\sim \tau _1$
and
$\tau _0\sim \tau _1$
and
![]() $e_0\sim _{\tau _0} e_1$
. Thus by Lemma 4.11 again,
$e_0\sim _{\tau _0} e_1$
. Thus by Lemma 4.11 again,
![]() $y=e_0^{\tau _0}=e_1^{\tau _1}$
. Then
$y=e_0^{\tau _0}=e_1^{\tau _1}$
. Then
![]() $c=d\Vdash \operatorname {{\mathrm {OP}}}(\langle {a_0^{\sigma },y}\rangle _{\!A},x,y_0)\land \operatorname {{\mathrm {OP}}}(\langle {a_1^{\sigma },y}\rangle _{\!A},x,y_1)$
. By soundness and the properties of pairing,
$c=d\Vdash \operatorname {{\mathrm {OP}}}(\langle {a_0^{\sigma },y}\rangle _{\!A},x,y_0)\land \operatorname {{\mathrm {OP}}}(\langle {a_1^{\sigma },y}\rangle _{\!A},x,y_1)$
. By soundness and the properties of pairing,
![]() $\mathbf q c=\mathbf qd\Vdash y_0=y_1$
, for some closed term
$\mathbf q c=\mathbf qd\Vdash y_0=y_1$
, for some closed term
![]() $\mathbf q$
. Thus
$\mathbf q$
. Thus
![]() $\mathbf f=_{\mathrm {def}}\lambda f\lambda a_0\lambda a_1\lambda c. \mathbf qc$
is as desired.
$\mathbf f=_{\mathrm {def}}\lambda f\lambda a_0\lambda a_1\lambda c. \mathbf qc$
is as desired.
Conversely, let
![]() $h\in \mathrm {V_{ext}}(A)$
and suppose
$h\in \mathrm {V_{ext}}(A)$
and suppose
We wish to find
![]() $\mathbf c$
such that
$\mathbf c$
such that
![]() $\mathbf c c=\mathbf c d\Vdash h\in X_{{\Pi }_{\sigma } i}$
. We thus aim for
$\mathbf c c=\mathbf c d\Vdash h\in X_{{\Pi }_{\sigma } i}$
. We thus aim for
![]() $f=(\mathbf cc)_0\sim _{\alpha } (\mathbf cd)_0=g$
and
$f=(\mathbf cc)_0\sim _{\alpha } (\mathbf cd)_0=g$
and
![]() $(\mathbf cc)_1=(\mathbf cd)_1\Vdash h=f^{\alpha }$
. Let us first find f and g. If
$(\mathbf cc)_1=(\mathbf cd)_1\Vdash h=f^{\alpha }$
. Let us first find f and g. If
![]() $a\sim _{\sigma } b$
, then by (5) there are
$a\sim _{\sigma } b$
, then by (5) there are
![]() $z,y\in \mathrm {V_{ext}}(A)$
such that
$z,y\in \mathrm {V_{ext}}(A)$
such that
From (4) and (7), it follows that
and for some
![]() $\breve {y},Y\in \mathrm {V_{ext}}(A)$
,
$\breve {y},Y\in \mathrm {V_{ext}}(A)$
,
where
![]() $\tilde \tau =i \tilde {a}$
. Now, by (8) and (9) we obtain
$\tilde \tau =i \tilde {a}$
. Now, by (8) and (9) we obtain
![]() $\Vdash a^{\sigma }=\breve {a}^{\sigma }$
and
$\Vdash a^{\sigma }=\breve {a}^{\sigma }$
and
![]() $\Vdash \tilde {a}^{\sigma }=\breve {a}^{\sigma }$
, and hence by Lemma 4.11 we have
$\Vdash \tilde {a}^{\sigma }=\breve {a}^{\sigma }$
, and hence by Lemma 4.11 we have
![]() $a\sim _{\sigma } \breve {a}\sim _{\sigma } \tilde {a}$
. Therefore,
$a\sim _{\sigma } \breve {a}\sim _{\sigma } \tilde {a}$
. Therefore,
![]() $a^{\sigma }=\breve a^{\sigma }$
,
$a^{\sigma }=\breve a^{\sigma }$
,
![]() $\tau =ia\sim i\breve {a}=\breve {\tau }$
, and
$\tau =ia\sim i\breve {a}=\breve {\tau }$
, and
![]() $X_{\tau }=X_{\breve {\tau }}$
. By the properties of pairing and equality, from (8) and (9) we obtain
$X_{\tau }=X_{\breve {\tau }}$
. By the properties of pairing and equality, from (8) and (9) we obtain
![]() $\mathbf q ca=\mathbf q db\Vdash y\in X_{\tau }$
, for some closed term
$\mathbf q ca=\mathbf q db\Vdash y\in X_{\tau }$
, for some closed term
![]() $\mathbf q$
. Hence
$\mathbf q$
. Hence
Therefore, by (10), by letting
![]() $(\mathbf c c)_0=\lambda a.(\mathbf qca)_0$
, we have
$(\mathbf c c)_0=\lambda a.(\mathbf qca)_0$
, we have
It remains to show
![]() $(\mathbf c c)_1=(\mathbf c d)_1\Vdash h=f^{\alpha }$
.
$(\mathbf c c)_1=(\mathbf c d)_1\Vdash h=f^{\alpha }$
.
For the right to left inclusion, let
![]() $a\sim _{\sigma } b$
,
$a\sim _{\sigma } b$
,
![]() $e=fa$
, and
$e=fa$
, and
![]() $\tau =ia$
. We want
$\tau =ia$
. We want
By the foregoing discussion, we have that (7), (8), and (11) hold true for some
![]() $z,y\in \mathrm {V_{ext}}(A)$
. By the properties of pairing and equality, it follows from (8) and (11) that
$z,y\in \mathrm {V_{ext}}(A)$
. By the properties of pairing and equality, it follows from (8) and (11) that
![]() $\mathbf rca=\mathbf rdb\Vdash \langle {a^{\sigma },e^{\tau }}\rangle _{\!A}=z$
, for some closed term
$\mathbf rca=\mathbf rdb\Vdash \langle {a^{\sigma },e^{\tau }}\rangle _{\!A}=z$
, for some closed term
![]() $\mathbf r$
. We may then let
$\mathbf r$
. We may then let
![]() $((\mathbf c c)_1a)_{1}=\mathbf p (c_{10}a)_0 (\mathbf rca)$
.
$((\mathbf c c)_1a)_{1}=\mathbf p (c_{10}a)_0 (\mathbf rca)$
.
The left to right inclusion is treated in a similar manner. Suppose
![]() $\langle {\breve c,\breve d,\breve z}\rangle \in h$
. By (4),
$\langle {\breve c,\breve d,\breve z}\rangle \in h$
. By (4),
![]() $a=(c_0\breve c)_0\sim _{\sigma } (d_0\breve d)_0=b$
, and for some
$a=(c_0\breve c)_0\sim _{\sigma } (d_0\breve d)_0=b$
, and for some
![]() $\breve y\in \mathrm {V_{ext}}(A)$
,
$\breve y\in \mathrm {V_{ext}}(A)$
,
![]() $(c_0\breve c)_{110}= (d_0\breve d)_{110}\Vdash \operatorname {{\mathrm {OP}}}(\breve z,a^{\sigma },\breve y)$
. As before, there are
$(c_0\breve c)_{110}= (d_0\breve d)_{110}\Vdash \operatorname {{\mathrm {OP}}}(\breve z,a^{\sigma },\breve y)$
. As before, there are
![]() $z,y\in \mathrm {V_{ext}}(A)$
such that (7), (8), and (11) hold true of a and b. On account of (6), it follows from (7), (8), and (11) that
$z,y\in \mathrm {V_{ext}}(A)$
such that (7), (8), and (11) hold true of a and b. On account of (6), it follows from (7), (8), and (11) that
![]() $\mathbf l c\breve c=\mathbf ld\breve d\Vdash \breve z=\langle {a^{\sigma },(fa)^{\tau }}\rangle _{\!A}$
, for some closed term
$\mathbf l c\breve c=\mathbf ld\breve d\Vdash \breve z=\langle {a^{\sigma },(fa)^{\tau }}\rangle _{\!A}$
, for some closed term
![]() $\mathbf l$
. Then
$\mathbf l$
. Then
![]() $\mathbf c$
such that
$\mathbf c$
such that
![]() $((\mathbf c c)_1\breve c)_0=\mathbf p (c_0\breve c)_0 (\mathbf lc\breve c)$
does the job.
$((\mathbf c c)_1\breve c)_0=\mathbf p (c_0\breve c)_0 (\mathbf lc\breve c)$
does the job.
(iv) We aim for
![]() $\mathbf {sum}\Vdash X_{{\Sigma }_{\sigma } i}={\Sigma }(X_{\sigma }, F)$
. Let
$\mathbf {sum}\Vdash X_{{\Sigma }_{\sigma } i}={\Sigma }(X_{\sigma }, F)$
. Let
![]() $\beta ={\Sigma }_{\sigma } i$
. For the direction from left to right, we ask for a closed term
$\beta ={\Sigma }_{\sigma } i$
. For the direction from left to right, we ask for a closed term
![]() $\mathbf l$
such that
$\mathbf l$
such that
Let
![]() $a\sim _{\beta } b$
. We want
$a\sim _{\beta } b$
. We want
where
![]() $\tau =ia_0$
. By definition,
$\tau =ia_0$
. By definition,
![]() $a_0\sim _{\sigma } b_0$
. Let
$a_0\sim _{\sigma } b_0$
. Let
![]() $(\mathbf l a)_0=a_0$
. Then we aim for
$(\mathbf l a)_0=a_0$
. Then we aim for
for some
![]() $y,Y\in \mathrm {V_{ext}}(A)$
. Let
$y,Y\in \mathrm {V_{ext}}(A)$
. Let
![]() $y=a_1^{\tau }$
, and
$y=a_1^{\tau }$
, and
![]() $Y=X_{\tau }$
. Note that
$Y=X_{\tau }$
. Note that
![]() $\langle {a_0,b_0,\langle {a_0^{\sigma },X_{\tau }}\rangle _{\!A}}\rangle \in F$
. Set
$\langle {a_0,b_0,\langle {a_0^{\sigma },X_{\tau }}\rangle _{\!A}}\rangle \in F$
. Set
![]() $(\mathbf la)_{10}=a_0$
. We thus want
$(\mathbf la)_{10}=a_0$
. We thus want
By the properties of pairing, we just need to worry about the last conjunct. Now,
![]() $a_1\sim _{\tau } b_1$
, and thereby
$a_1\sim _{\tau } b_1$
, and thereby
![]() $\langle {a_1,b_1,a_1^{\tau }}\rangle \in X_{\tau }$
. Therefore,
$\langle {a_1,b_1,a_1^{\tau }}\rangle \in X_{\tau }$
. Therefore,
![]() $\mathbf p a_1\mathbf i=\mathbf p b_1\mathbf i\Vdash a_1^{\tau }\in X_{\tau }$
, where
$\mathbf p a_1\mathbf i=\mathbf p b_1\mathbf i\Vdash a_1^{\tau }\in X_{\tau }$
, where
![]() $\mathbf i\Vdash \forall x\, (x=x)$
.
$\mathbf i\Vdash \forall x\, (x=x)$
.
We now consider the converse direction. We look for a closed term
![]() $\mathbf r$
such that
$\mathbf r$
such that
Let
![]() $z,y\in \mathrm {V_{ext}}(A)$
and
$z,y\in \mathrm {V_{ext}}(A)$
and
![]() $\breve a\sim _{\sigma }\breve b$
. We want
$\breve a\sim _{\sigma }\breve b$
. We want
Let
![]() $a\sim _{\sigma } b$
and
$a\sim _{\sigma } b$
and
![]() $\tau =ia$
. We set out for
$\tau =ia$
. We set out for
for every
![]() $Y\in \mathrm {V_{ext}}(A)$
. Fix a
$Y\in \mathrm {V_{ext}}(A)$
. Fix a
![]() $Y\in \mathrm {V_{ext}}(A)$
and suppose
$Y\in \mathrm {V_{ext}}(A)$
and suppose
By the properties of pairing and equality, we have
![]() $\Vdash a^{\sigma }=\breve a^{\sigma }$
and
$\Vdash a^{\sigma }=\breve a^{\sigma }$
and
for some closed term
![]() $\mathbf q$
. By Lemma 4.11, we then obtain
$\mathbf q$
. By Lemma 4.11, we then obtain
![]() $a^{\sigma }=\breve a^{\sigma }$
. Therefore,
$a^{\sigma }=\breve a^{\sigma }$
. Therefore,
By the usual properties of pairing and equality, we have
![]() $\mathbf z c=\mathbf z d\Vdash z=\langle {a^{\sigma },\mathring c^{\tau }}\rangle _{\!A}$
, for some closed term
$\mathbf z c=\mathbf z d\Vdash z=\langle {a^{\sigma },\mathring c^{\tau }}\rangle _{\!A}$
, for some closed term
![]() $\mathbf z$
. Now,
$\mathbf z$
. Now,
![]() $\mathbf p a\mathring c\sim _{\beta }\mathbf p b\mathring d$
, and so
$\mathbf p a\mathring c\sim _{\beta }\mathbf p b\mathring d$
, and so
![]() $\langle {\mathbf p a\mathring c,\mathbf p b\mathring d, \langle {a^{\sigma },\mathring c^{\tau }}\rangle _{\!A}}\rangle \in X_{{\Sigma }_{\sigma } i}$
. Therefore,
$\langle {\mathbf p a\mathring c,\mathbf p b\mathring d, \langle {a^{\sigma },\mathring c^{\tau }}\rangle _{\!A}}\rangle \in X_{{\Sigma }_{\sigma } i}$
. Therefore,
Then
![]() $\mathbf r$
such that
$\mathbf r$
such that
![]() $\mathbf r\breve a ac=\mathbf p(\mathbf p a(\mathbf q c)_{10})(\mathbf z c)$
does the job.
$\mathbf r\breve a ac=\mathbf p(\mathbf p a(\mathbf q c)_{10})(\mathbf z c)$
does the job.
(v) We aim for
![]() $\mathbf {id}\Vdash X_{\mathrm {I}_{\sigma }(a,b)}=\mathrm {I}(a^{\sigma },b^{\sigma })$
. For the left to right direction, we want a closed term
$\mathbf {id}\Vdash X_{\mathrm {I}_{\sigma }(a,b)}=\mathrm {I}(a^{\sigma },b^{\sigma })$
. For the left to right direction, we want a closed term
![]() $\mathbf l$
such that whenever
$\mathbf l$
such that whenever
![]() $\langle {c,d,z}\rangle \in X_{\mathrm {I}_{\sigma }(a,b)}$
, then
$\langle {c,d,z}\rangle \in X_{\mathrm {I}_{\sigma }(a,b)}$
, then
![]() $\mathbf {l}c=\mathbf ld\Vdash \nu (z)\land a^{\sigma }=b^{\sigma }$
, where
$\mathbf {l}c=\mathbf ld\Vdash \nu (z)\land a^{\sigma }=b^{\sigma }$
, where
![]() $\nu (z)$
expresses that
$\nu (z)$
expresses that
![]() $z=0$
. Suppose
$z=0$
. Suppose
![]() $\langle {c,d,z}\rangle \in X_{\mathrm {I}_{\sigma }(a,b)}$
. By definition,
$\langle {c,d,z}\rangle \in X_{\mathrm {I}_{\sigma }(a,b)}$
. By definition,
![]() $c=d=\mathbf 0$
,
$c=d=\mathbf 0$
,
![]() $z=0$
, and
$z=0$
, and
![]() $a\sim _{\sigma } b$
. It is easy to find
$a\sim _{\sigma } b$
. It is easy to find
![]() ${\mathbf t}$
such that
${\mathbf t}$
such that
![]() ${\mathbf t}\Vdash \nu (0)$
. On the other hand, by Lemma 4.11, from
${\mathbf t}\Vdash \nu (0)$
. On the other hand, by Lemma 4.11, from
![]() $a\sim _{\sigma } b$
we obtain
$a\sim _{\sigma } b$
we obtain
![]() $a^{\sigma }=b^{\sigma }$
. Let
$a^{\sigma }=b^{\sigma }$
. Let
![]() $\mathbf l=_{\mathrm {def}}\lambda c.\mathbf p\mathbf q\mathbf i$
, where
$\mathbf l=_{\mathrm {def}}\lambda c.\mathbf p\mathbf q\mathbf i$
, where
![]() $\mathbf i\Vdash \forall x\, (x=x)$
.
$\mathbf i\Vdash \forall x\, (x=x)$
.
For the right to left direction, we aim for a closed term
![]() $\mathbf r$
such that for every
$\mathbf r$
such that for every
![]() $z\in \mathrm {V_{ext}}(A)$
,
$z\in \mathrm {V_{ext}}(A)$
,
![]() $\mathbf r\Vdash \nu (z)\land a^{\sigma }=b^{\sigma } \rightarrow z\in X_{\mathrm {I}_{\sigma }(a,b)}$
. Note that
$\mathbf r\Vdash \nu (z)\land a^{\sigma }=b^{\sigma } \rightarrow z\in X_{\mathrm {I}_{\sigma }(a,b)}$
. Note that
![]() $\Vdash \nu (z)$
implies
$\Vdash \nu (z)$
implies
![]() $z=0$
. By Lemma 4.11,
$z=0$
. By Lemma 4.11,
![]() $\Vdash a^{\sigma }=b^{\sigma }$
implies
$\Vdash a^{\sigma }=b^{\sigma }$
implies
![]() $a\sim _{\sigma } b$
. Thus let
$a\sim _{\sigma } b$
. Thus let
![]() $\mathbf r=_{\mathrm {def}}\lambda c.\mathbf p\mathbf 0\mathbf i$
, where
$\mathbf r=_{\mathrm {def}}\lambda c.\mathbf p\mathbf 0\mathbf i$
, where
![]() $\mathbf i$
is as before.
$\mathbf i$
is as before.
(vi) We aim for
![]() $\mathbf w\Vdash X_{\mathrm {W}_{\sigma } i}=\mathrm {W}(X_{\sigma },F)$
. Set
$\mathbf w\Vdash X_{\mathrm {W}_{\sigma } i}=\mathrm {W}(X_{\sigma },F)$
. Set
![]() $\delta =\mathrm {W}_{\sigma } i$
. By Theorem 6.2, it suffices to find closed terms
$\delta =\mathrm {W}_{\sigma } i$
. By Theorem 6.2, it suffices to find closed terms
![]() $\mathbf l$
and
$\mathbf l$
and
![]() $\mathbf r$
such that
$\mathbf r$
such that
 $$ \begin{align*} \mathbf l &\Vdash \forall y\in X_{\delta}\, \exists x\in X_{\sigma}\, \exists f\, \vartheta(y,x,f), \\ \mathbf r &\Vdash \forall y\, (\exists x\in X_{\sigma}\, \exists f\, \vartheta(y,x,f)\rightarrow y\in X_{\delta}), \end{align*} $$
$$ \begin{align*} \mathbf l &\Vdash \forall y\in X_{\delta}\, \exists x\in X_{\sigma}\, \exists f\, \vartheta(y,x,f), \\ \mathbf r &\Vdash \forall y\, (\exists x\in X_{\sigma}\, \exists f\, \vartheta(y,x,f)\rightarrow y\in X_{\delta}), \end{align*} $$
where
![]() $\vartheta (y,x,f) \Leftrightarrow \operatorname {{\mathrm {OP}}}(y,x,f)\land \vartheta _0(x,f)\land \vartheta _1(f)\land \vartheta _2(f)$
, with
$\vartheta (y,x,f) \Leftrightarrow \operatorname {{\mathrm {OP}}}(y,x,f)\land \vartheta _0(x,f)\land \vartheta _1(f)\land \vartheta _2(f)$
, with
 $$ \begin{align*} &\vartheta_0(x,f) && \Leftrightarrow && f \text{ is a relation}\land \operatorname{{\mathrm{dom}}}(f)=F(x) \\ & && \Leftrightarrow && \forall Z\in F\, \forall X\, (\operatorname{{\mathrm{OP}}}(Z,x,X)\rightarrow \forall v\in f\, \exists u\in X\, \exists z\, \operatorname{{\mathrm{OP}}}(v,u,z)\land \\ &&&&& \qquad\qquad\qquad\qquad\qquad\qquad\qquad \forall u\in X\, \exists z\, \exists v\in f\, \operatorname{{\mathrm{OP}}}(v,u,z)),\\ &\vartheta_1(f) && \Leftrightarrow && f \text{ is functional} \\ &&& \Leftrightarrow && \forall v_0\in f\, \forall v_1\in f\, \forall u\, \forall z_0\, \forall z_1\, (\operatorname{{\mathrm{OP}}}(v_0,u,z_0)\land \operatorname{{\mathrm{OP}}}(v_1,u,z_1)\rightarrow z_0=z_1), \\ &\vartheta_2(f) && \Leftrightarrow && \operatorname{{\mathrm{ran}}}(f)\subseteq X_{\delta} \\ &&& \Leftrightarrow && \forall v\in f\, \forall u\, \forall z\, (\operatorname{{\mathrm{OP}}}(v,u,z)\rightarrow z\in X_{\delta}). \end{align*} $$
$$ \begin{align*} &\vartheta_0(x,f) && \Leftrightarrow && f \text{ is a relation}\land \operatorname{{\mathrm{dom}}}(f)=F(x) \\ & && \Leftrightarrow && \forall Z\in F\, \forall X\, (\operatorname{{\mathrm{OP}}}(Z,x,X)\rightarrow \forall v\in f\, \exists u\in X\, \exists z\, \operatorname{{\mathrm{OP}}}(v,u,z)\land \\ &&&&& \qquad\qquad\qquad\qquad\qquad\qquad\qquad \forall u\in X\, \exists z\, \exists v\in f\, \operatorname{{\mathrm{OP}}}(v,u,z)),\\ &\vartheta_1(f) && \Leftrightarrow && f \text{ is functional} \\ &&& \Leftrightarrow && \forall v_0\in f\, \forall v_1\in f\, \forall u\, \forall z_0\, \forall z_1\, (\operatorname{{\mathrm{OP}}}(v_0,u,z_0)\land \operatorname{{\mathrm{OP}}}(v_1,u,z_1)\rightarrow z_0=z_1), \\ &\vartheta_2(f) && \Leftrightarrow && \operatorname{{\mathrm{ran}}}(f)\subseteq X_{\delta} \\ &&& \Leftrightarrow && \forall v\in f\, \forall u\, \forall z\, (\operatorname{{\mathrm{OP}}}(v,u,z)\rightarrow z\in X_{\delta}). \end{align*} $$
Remember that
 $$ \begin{align*} F&=F_{\sigma,i}=\{\langle{a,b,\langle{a^{\sigma},X_{ia}}\rangle_{\!A}}\rangle\mid a\sim_{\sigma} b\}, \\ X_{\delta}&=\{\langle{c,d,c^{\delta}}\rangle\mid c\sim_{\delta} d\}, \\ c^{\delta}&=\langle{c_0^{\sigma},f_c}\rangle_{\!A}, \ \ \text{where } f_c=\{\langle{p,q,\langle{p^{ic_0},(c_1p)^{\delta}}\rangle_{\!A}}\rangle\mid p\sim_{ic_0} q\}, \\ c\sim_{\delta} d&\leftrightarrow c_0\sim_{\sigma} d_0\land \forall p\, \forall q\, (p\sim_{ic_0}q\rightarrow c_1p\sim_{\delta} d_1q). \end{align*} $$
$$ \begin{align*} F&=F_{\sigma,i}=\{\langle{a,b,\langle{a^{\sigma},X_{ia}}\rangle_{\!A}}\rangle\mid a\sim_{\sigma} b\}, \\ X_{\delta}&=\{\langle{c,d,c^{\delta}}\rangle\mid c\sim_{\delta} d\}, \\ c^{\delta}&=\langle{c_0^{\sigma},f_c}\rangle_{\!A}, \ \ \text{where } f_c=\{\langle{p,q,\langle{p^{ic_0},(c_1p)^{\delta}}\rangle_{\!A}}\rangle\mid p\sim_{ic_0} q\}, \\ c\sim_{\delta} d&\leftrightarrow c_0\sim_{\sigma} d_0\land \forall p\, \forall q\, (p\sim_{ic_0}q\rightarrow c_1p\sim_{\delta} d_1q). \end{align*} $$
From left to right, note that if
![]() $c\sim _{\delta } d$
, then
$c\sim _{\delta } d$
, then
![]() $c_0\sim _{\sigma } d_0$
. Let
$c_0\sim _{\sigma } d_0$
. Let
![]() $(\mathbf lc)_0=c_0$
. We then want
$(\mathbf lc)_0=c_0$
. We then want
![]() $(\mathbf lc)_1=(\mathbf ld)_1\Vdash \exists f\, \vartheta (c^{\delta },c_0^{\sigma },f)$
. The obvious candidate for f is
$(\mathbf lc)_1=(\mathbf ld)_1\Vdash \exists f\, \vartheta (c^{\delta },c_0^{\sigma },f)$
. The obvious candidate for f is
![]() $f_c$
. The details are tedious but straightforward.
$f_c$
. The details are tedious but straightforward.
Let us consider the slightly more interesting direction. Let
![]() $y\in \mathrm {V_{ext}}(A)$
and suppose
$y\in \mathrm {V_{ext}}(A)$
and suppose
The goal is to find
![]() $\mathbf r$
such that
$\mathbf r$
such that
![]() $\mathbf ra=\mathbf rb\Vdash y\in X_{\delta }$
. By undoing (16), we obtain
$\mathbf ra=\mathbf rb\Vdash y\in X_{\delta }$
. By undoing (16), we obtain
for some
![]() $f\in \mathrm {V_{ext}}(A)$
. It follows from the second half of (17) that
$f\in \mathrm {V_{ext}}(A)$
. It follows from the second half of (17) that
![]() $a_{10}=b_{10}\Vdash \operatorname {{\mathrm {OP}}}(y,a_0^{\sigma },f)$
. Also, we can find closed terms
$a_{10}=b_{10}\Vdash \operatorname {{\mathrm {OP}}}(y,a_0^{\sigma },f)$
. Also, we can find closed terms
![]() $\mathbf q_0,\mathbf q_1,\mathbf q_2$
such that
$\mathbf q_0,\mathbf q_1,\mathbf q_2$
such that
![]() $\mathbf q_0a=\mathbf q_0b\Vdash \vartheta _0(a_0^{\sigma },f)$
and
$\mathbf q_0a=\mathbf q_0b\Vdash \vartheta _0(a_0^{\sigma },f)$
and
![]() $\mathbf q_ia=\mathbf q_ib\Vdash \vartheta _i(f)$
for
$\mathbf q_ia=\mathbf q_ib\Vdash \vartheta _i(f)$
for
![]() $i=1,2$
. Because
$i=1,2$
. Because
![]() $a_0\sim _{\sigma } b_0$
by the first half of (17), we can apply
$a_0\sim _{\sigma } b_0$
by the first half of (17), we can apply
![]() $\mathbf q_0$
and obtain
$\mathbf q_0$
and obtain
where
By the properties of pairing with
![]() $X=X_{ia_0}$
, it follows from (18) that
$X=X_{ia_0}$
, it follows from (18) that
for some closed term
![]() ${\mathbf t}$
. Suppose
${\mathbf t}$
. Suppose
![]() $p\sim _{ia_0} q$
. By (19),
$p\sim _{ia_0} q$
. By (19),
![]() $(\mathbf ta)_1p=({\mathbf t} b)_1q\Vdash \exists z\, \exists v\in f \operatorname {{\mathrm {OP}}}(v,p^{ia_0},z)$
, and hence for some
$(\mathbf ta)_1p=({\mathbf t} b)_1q\Vdash \exists z\, \exists v\in f \operatorname {{\mathrm {OP}}}(v,p^{ia_0},z)$
, and hence for some
![]() $z,v\in \mathrm {V_{ext}}(A)$
,
$z,v\in \mathrm {V_{ext}}(A)$
,
Write
![]() $\langle {\breve p,\breve q,v}\rangle $
for
$\langle {\breve p,\breve q,v}\rangle $
for
![]() $\langle {((\mathbf ta)_1p)_0, (({\mathbf t} b)_1q)_0,v}\rangle $
. Now,
$\langle {((\mathbf ta)_1p)_0, (({\mathbf t} b)_1q)_0,v}\rangle $
. Now,
![]() $\mathbf q_2a=\mathbf q_2b\Vdash \vartheta _2(f)$
. It then follows from (20) that
$\mathbf q_2a=\mathbf q_2b\Vdash \vartheta _2(f)$
. It then follows from (20) that
By (21) and (22), we get
![]() $\mathbf q_2a\breve p((\mathbf ta)_1p)_1=\mathbf q_2b\breve q(({\mathbf t} b)_1q)_1 \Vdash z\in X_{\delta }$
, and so we can construct a closed term
$\mathbf q_2a\breve p((\mathbf ta)_1p)_1=\mathbf q_2b\breve q(({\mathbf t} b)_1q)_1 \Vdash z\in X_{\delta }$
, and so we can construct a closed term
![]() $\mathbf f$
such that
$\mathbf f$
such that
The foregoing discussion also shows that, if we let
![]() $(\mathbf ra)_0=\mathbf p a_0(\lambda p.(\mathbf fap)_0)$
, then
$(\mathbf ra)_0=\mathbf p a_0(\lambda p.(\mathbf fap)_0)$
, then
![]() $c= (\mathbf ra)_0\sim _{\delta } (\mathbf rb)_0=d$
. We then wish to find
$c= (\mathbf ra)_0\sim _{\delta } (\mathbf rb)_0=d$
. We then wish to find
![]() $\mathbf r$
such that
$\mathbf r$
such that
![]() $(\mathbf ra)_1=(\mathbf rb)_1\Vdash y=c^{\delta }$
. For this one needs to show that
$(\mathbf ra)_1=(\mathbf rb)_1\Vdash y=c^{\delta }$
. For this one needs to show that
![]() $\mathbf ha=\mathbf hb\Vdash f=f_c$
for some closed term
$\mathbf ha=\mathbf hb\Vdash f=f_c$
for some closed term
![]() $\mathbf h$
. Since this is similar to the proof of the right to left direction of (iii), we leave the details to the reader.
$\mathbf h$
. Since this is similar to the proof of the right to left direction of (iii), we leave the details to the reader.
Proof of Theorem 4.16
We have to provide closed terms
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
for every
![]() $X\in \mathrm {V_{ext}}(A)$
. The same task for
$X\in \mathrm {V_{ext}}(A)$
. The same task for
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets.
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
-sets.
Let
![]() $\vartheta (u,Y)$
be as in Theorem 6.1. Thus
$\vartheta (u,Y)$
be as in Theorem 6.1. Thus
![]() ${\Pi }{\Sigma }\mathrm {I}=\{Y\mid \exists u\, \vartheta (u,Y)\}$
. We want
${\Pi }{\Sigma }\mathrm {I}=\{Y\mid \exists u\, \vartheta (u,Y)\}$
. We want
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
such that for every
${\mathbf e}$
such that for every
![]() $u,Y\in \mathrm {V_{ext}}(A)$
,
$u,Y\in \mathrm {V_{ext}}(A)$
,
The closed terms
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
are obtained by means of the recursion theorem for pca’s. The verification is done by induction on u. First, by soundness, there is a closed term
${\mathbf e}$
are obtained by means of the recursion theorem for pca’s. The verification is done by induction on u. First, by soundness, there is a closed term
![]() $\mathbf {t}$
such that
$\mathbf {t}$
such that
![]() $c=d\Vdash \vartheta (u,Y)$
implies
$c=d\Vdash \vartheta (u,Y)$
implies
 $$\begin{align*}{\mathbf t} c={\mathbf t} d\Vdash \bigvee_{i=0}^4 \vartheta_{i}(u,Y). \end{align*}$$
$$\begin{align*}{\mathbf t} c={\mathbf t} d\Vdash \bigvee_{i=0}^4 \vartheta_{i}(u,Y). \end{align*}$$
By using the definition by cases combinator
![]() $\mathbf d$
, we can find closed terms
$\mathbf d$
, we can find closed terms
![]() $\mathbf {c}$
and
$\mathbf {c}$
and
![]() ${\mathbf t}_i$
for
${\mathbf t}_i$
for
![]() $i<4$
such that if
$i<4$
such that if
![]() $c=d\Vdash \vartheta (u,Y)$
, then for some
$c=d\Vdash \vartheta (u,Y)$
, then for some
![]() $i<5$
,
$i<5$
,
Case 0. If
![]() $\mathbf c c=\mathbf 0$
, then
$\mathbf c c=\mathbf 0$
, then
![]() ${\mathbf t}_0 c={\mathbf t}_0 d\Vdash Y\in \omega $
. By Theorem 4.14, we have a closed term
${\mathbf t}_0 c={\mathbf t}_0 d\Vdash Y\in \omega $
. By Theorem 4.14, we have a closed term
![]() $\mathbf o$
such that
$\mathbf o$
such that
![]() $\mathbf o\Vdash X_{\mathsf {N}}=\omega $
. By soundness, there is a closed term
$\mathbf o\Vdash X_{\mathsf {N}}=\omega $
. By soundness, there is a closed term
![]() ${\mathbf v}_0$
such that
${\mathbf v}_0$
such that
![]() ${\mathbf v}_0c={\mathbf v}_0d\Vdash Y\in X_{\mathsf {N}}$
. This means that, for some
${\mathbf v}_0c={\mathbf v}_0d\Vdash Y\in X_{\mathsf {N}}$
. This means that, for some
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $({\mathbf v}_0c)_0=({\mathbf v}_0d)_0=\bar n$
and
$({\mathbf v}_0c)_0=({\mathbf v}_0d)_0=\bar n$
and
![]() $({\mathbf v}_0c)_1=({\mathbf v}_0d)_1\Vdash Y=\dot n$
. Now,
$({\mathbf v}_0c)_1=({\mathbf v}_0d)_1\Vdash Y=\dot n$
. Now,
![]() $\mathsf {N}_n=\mathbf p \mathbf 0\bar n$
and
$\mathsf {N}_n=\mathbf p \mathbf 0\bar n$
and
![]() $X_{\mathsf {N}_n}=\dot n$
. Therefore, in this case, meaning
$X_{\mathsf {N}_n}=\dot n$
. Therefore, in this case, meaning
![]() $\mathbf c c=\mathbf 0$
, we look for
$\mathbf c c=\mathbf 0$
, we look for
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
![]() $\mathbf ic=\mathbf p\mathbf 0({\mathbf v}_0c)_0$
and
$\mathbf ic=\mathbf p\mathbf 0({\mathbf v}_0c)_0$
and
![]() $\mathbf ec=({\mathbf v}_0c)_1$
.
$\mathbf ec=({\mathbf v}_0c)_1$
.
Case 1. If
![]() $\mathbf cc={\mathbf 1}$
, then
$\mathbf cc={\mathbf 1}$
, then
![]() ${\mathbf t}_1c={\mathbf t}_1d\Vdash Y=\omega $
. As before, by soundness, there is a closed term
${\mathbf t}_1c={\mathbf t}_1d\Vdash Y=\omega $
. As before, by soundness, there is a closed term
![]() ${\mathbf v}_1$
such that
${\mathbf v}_1$
such that
![]() ${\mathbf v}_1c={\mathbf v}_1d\Vdash Y=X_{\mathsf {N}}$
. Therefore, in this case, meaning
${\mathbf v}_1c={\mathbf v}_1d\Vdash Y=X_{\mathsf {N}}$
. Therefore, in this case, meaning
![]() $\mathbf cc={\mathbf 1}$
, we look for
$\mathbf cc={\mathbf 1}$
, we look for
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
![]() $\mathbf ic=o$
and
$\mathbf ic=o$
and
![]() $\mathbf ec={\mathbf v}_1c$
.
$\mathbf ec={\mathbf v}_1c$
.
Case 2. Suppose
![]() $\mathbf c c=\mathbf 2$
. We are in the case where
$\mathbf c c=\mathbf 2$
. We are in the case where
 $$ \begin{align} {\mathbf t}_2 c={\mathbf t}_2 d&\Vdash \exists v\in u\, \vartheta(v,X)\land \operatorname{{\mathrm{Fun}}}(F) \land \operatorname{{\mathrm{dom}}}(F)=X\land \nonumber \\ & \qquad \forall x\in X\, \exists v\in u\, \vartheta(v,F(x))\land Y={\Pi}(X,F), \end{align} $$
$$ \begin{align} {\mathbf t}_2 c={\mathbf t}_2 d&\Vdash \exists v\in u\, \vartheta(v,X)\land \operatorname{{\mathrm{Fun}}}(F) \land \operatorname{{\mathrm{dom}}}(F)=X\land \nonumber \\ & \qquad \forall x\in X\, \exists v\in u\, \vartheta(v,F(x))\land Y={\Pi}(X,F), \end{align} $$
for some
![]() $X,F\in \mathrm {V_{ext}}(A)$
. By undoing (1), we get that for some
$X,F\in \mathrm {V_{ext}}(A)$
. By undoing (1), we get that for some
![]() $\langle {\mathring {c},\mathring {d},v}\rangle \in u$
,
$\langle {\mathring {c},\mathring {d},v}\rangle \in u$
,
![]() $({\mathbf t}_2 c)_{01}=({\mathbf t}_2 d)_{01} \Vdash \vartheta (v,X)$
. By induction, we can assume
$({\mathbf t}_2 c)_{01}=({\mathbf t}_2 d)_{01} \Vdash \vartheta (v,X)$
. By induction, we can assume
By the properties of equality, on account of (1) and (3), we can find closed terms
![]() $\mathbf q_0,\mathbf q_1,\mathbf q_2$
such that
$\mathbf q_0,\mathbf q_1,\mathbf q_2$
such that
Suppose
![]() $a\sim _{\sigma } b$
. By using (4), we can obtain a closed term
$a\sim _{\sigma } b$
. By using (4), we can obtain a closed term
![]() $\mathbf r$
such that
$\mathbf r$
such that
Therefore, there are
![]() $Z,\mathring {X}\in \mathrm {V_{ext}}(A)$
such that
$Z,\mathring {X}\in \mathrm {V_{ext}}(A)$
such that
![]() $\mathbf r\mathbf eca=\mathbf r\mathbf edb\Vdash Z\in F\land \operatorname {{\mathrm {OP}}}(Z,a^{\sigma },\mathring {X})$
. On the other hand, it follows from (5) that
$\mathbf r\mathbf eca=\mathbf r\mathbf edb\Vdash Z\in F\land \operatorname {{\mathrm {OP}}}(Z,a^{\sigma },\mathring {X})$
. On the other hand, it follows from (5) that
In particular, for some
![]() $\langle {\mathring c,\mathring d,v}\rangle \in u$
,
$\langle {\mathring c,\mathring d,v}\rangle \in u$
,
![]() $(\mathbf q_1\mathbf eca)_1(\mathbf r\mathbf eca)=(\mathbf q_1\mathbf edb)_1(\mathbf r\mathbf edb)\Vdash \vartheta (v,\mathring {X})$
. To ease notation, let
$(\mathbf q_1\mathbf eca)_1(\mathbf r\mathbf eca)=(\mathbf q_1\mathbf edb)_1(\mathbf r\mathbf edb)\Vdash \vartheta (v,\mathring {X})$
. To ease notation, let
![]() $r({\mathbf e},c,a)=(\mathbf q_1\mathbf eca)_1(\mathbf r\mathbf eca)$
. By induction, we can assume that
$r({\mathbf e},c,a)=(\mathbf q_1\mathbf eca)_1(\mathbf r\mathbf eca)$
. By induction, we can assume that
![]() $\rho =\mathbf i r({\mathbf e},c,a)\sim \mathbf i r({\mathbf e},d,b)$
and
$\rho =\mathbf i r({\mathbf e},c,a)\sim \mathbf i r({\mathbf e},d,b)$
and
![]() ${\mathbf e} r({\mathbf e},c,a)={\mathbf e} r({\mathbf e},d,b)\Vdash \mathring X=X_{\rho }$
. We have just shown that if
${\mathbf e} r({\mathbf e},c,a)={\mathbf e} r({\mathbf e},d,b)\Vdash \mathring X=X_{\rho }$
. We have just shown that if
![]() $a\sim _{\sigma } b$
then
$a\sim _{\sigma } b$
then
![]() $ia\sim jb$
, where
$ia\sim jb$
, where
![]() $i=\lambda a.\mathbf i r({\mathbf e},c,a)$
and
$i=\lambda a.\mathbf i r({\mathbf e},c,a)$
and
![]() $j=\lambda b.\mathbf i r({\mathbf e},d,b)$
. By (2), we thus have
$j=\lambda b.\mathbf i r({\mathbf e},d,b)$
. By (2), we thus have
![]() ${\Pi }_{\sigma } i\sim {\Pi }_{\tau } j$
.
${\Pi }_{\sigma } i\sim {\Pi }_{\tau } j$
.
Let
![]() $\mathbf {prod}$
be as in Theorem 4.14. That is,
$\mathbf {prod}$
be as in Theorem 4.14. That is,
![]() $\mathbf {prod}\Vdash X_{{\Pi }_{\sigma } i}={\Pi }(X_{\sigma },F_{\sigma ,i})$
. We aim to show that for some closed term
$\mathbf {prod}\Vdash X_{{\Pi }_{\sigma } i}={\Pi }(X_{\sigma },F_{\sigma ,i})$
. We aim to show that for some closed term
![]() $\mathbf f$
,
$\mathbf f$
,
![]() $\mathbf f \mathbf ec=\mathbf f \mathbf ed\Vdash F=F_{\sigma ,i}$
. If we do so, owing to the soundness, we can cook up, by using (6) and
$\mathbf f \mathbf ec=\mathbf f \mathbf ed\Vdash F=F_{\sigma ,i}$
. If we do so, owing to the soundness, we can cook up, by using (6) and
![]() $\mathbf {prod}$
, a closed term
$\mathbf {prod}$
, a closed term
![]() ${\mathbf v}_2$
such that
${\mathbf v}_2$
such that
![]() ${\mathbf v}_2\mathbf ec={\mathbf v}_2\mathbf ed\Vdash Y=X_{{\Pi }_{\sigma } i}$
. In this case, meaning
${\mathbf v}_2\mathbf ec={\mathbf v}_2\mathbf ed\Vdash Y=X_{{\Pi }_{\sigma } i}$
. In this case, meaning
![]() $\mathbf c c=\mathbf 2$
, we thus want
$\mathbf c c=\mathbf 2$
, we thus want
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
Let us show how to find
![]() $\mathbf f$
. By Theorem 4.14,
$\mathbf f$
. By Theorem 4.14,
![]() $\mathbf {fun}\Vdash \operatorname {{\mathrm {Fun}}}(F_{\sigma ,i})\land \operatorname {{\mathrm {dom}}}(F)=X_{\sigma }$
. By (4), it then suffices to look for a closed term
$\mathbf {fun}\Vdash \operatorname {{\mathrm {Fun}}}(F_{\sigma ,i})\land \operatorname {{\mathrm {dom}}}(F)=X_{\sigma }$
. By (4), it then suffices to look for a closed term
![]() $\mathbf {h}$
such that
$\mathbf {h}$
such that
Let
![]() $a\sim _{\sigma } b$
. We aim for
$a\sim _{\sigma } b$
. We aim for
![]() $\mathbf h \mathbf eca=\mathbf h \mathbf edb\Vdash \langle {a^{\sigma },X_{\rho }}\rangle _{\!A}\in F$
, where
$\mathbf h \mathbf eca=\mathbf h \mathbf edb\Vdash \langle {a^{\sigma },X_{\rho }}\rangle _{\!A}\in F$
, where
![]() $\rho =i a$
. As before, we know that for some
$\rho =i a$
. As before, we know that for some
![]() $Z,\mathring X\in \mathrm {V_{ext}}(A)$
,
$Z,\mathring X\in \mathrm {V_{ext}}(A)$
,
![]() $\mathbf r\mathbf eca=\mathbf r\mathbf edb \Vdash Z\in F\land \operatorname {{\mathrm {OP}}}(Z,a^{\sigma },\mathring {X})$
and
$\mathbf r\mathbf eca=\mathbf r\mathbf edb \Vdash Z\in F\land \operatorname {{\mathrm {OP}}}(Z,a^{\sigma },\mathring {X})$
and
![]() ${\mathbf e} r({\mathbf e},c,a)={\mathbf e} r({\mathbf e},d,b) \Vdash \mathring X=X_{\rho }$
. By the properties of equality and pairing, we can easily arrange for such
${\mathbf e} r({\mathbf e},c,a)={\mathbf e} r({\mathbf e},d,b) \Vdash \mathring X=X_{\rho }$
. By the properties of equality and pairing, we can easily arrange for such
![]() $\mathbf h$
.
$\mathbf h$
.
Case 3. The case
![]() $\mathbf c c=\mathbf 3$
is treated similarly.
$\mathbf c c=\mathbf 3$
is treated similarly.
Case 4. Suppose
![]() $\mathbf cc={\mathbf 4}$
. In this case,
$\mathbf cc={\mathbf 4}$
. In this case,
for some
![]() $X\in \mathrm {V_{ext}}(A)$
. As in Case 2, we can assume
$X\in \mathrm {V_{ext}}(A)$
. As in Case 2, we can assume
By the properties of equality, owing to (7) and (8), we thus have a closed term
![]() $\mathbf q$
such that
$\mathbf q$
such that
![]() $\mathbf q\mathbf ec=\mathbf q\mathbf ed\Vdash \exists x\in X_{\sigma }\, \exists y\in X_{\sigma }\, (Y=\mathrm {I}(x,y))$
. By unfolding the definition, we obtain
$\mathbf q\mathbf ec=\mathbf q\mathbf ed\Vdash \exists x\in X_{\sigma }\, \exists y\in X_{\sigma }\, (Y=\mathrm {I}(x,y))$
. By unfolding the definition, we obtain
By using
![]() $\mathbf {id}\Vdash X_{\mathrm {I}_{\sigma }(a,b)}=\mathrm {I}(a^{\sigma },b^{\sigma })$
from Theorem 4.14, we then obtain by soundness a closed term
$\mathbf {id}\Vdash X_{\mathrm {I}_{\sigma }(a,b)}=\mathrm {I}(a^{\sigma },b^{\sigma })$
from Theorem 4.14, we then obtain by soundness a closed term
![]() ${\mathbf v}_4$
such that
${\mathbf v}_4$
such that
![]() ${\mathbf v}_4\mathbf ec={\mathbf v}_4\mathbf ed\Vdash Y=X_{\mathrm {I}_{\sigma }(a,b)}$
. In this case, meaning
${\mathbf v}_4\mathbf ec={\mathbf v}_4\mathbf ed\Vdash Y=X_{\mathrm {I}_{\sigma }(a,b)}$
. In this case, meaning
![]() $\mathbf c c={\mathbf 4}$
, we thus want
$\mathbf c c={\mathbf 4}$
, we thus want
![]() $\mathbf i$
and
$\mathbf i$
and
![]() ${\mathbf e}$
such that
${\mathbf e}$
such that
In the
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
case, one considers
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}$
case, one considers
![]() $\vartheta ^*(u,Y)$
as in Theorem 6.1. Thus
$\vartheta ^*(u,Y)$
as in Theorem 6.1. Thus
![]() ${\Pi }{\Sigma }\mathrm {W}\mathrm {I}=\{Y\mid \exists u\, \vartheta ^*(u,Y)\}$
. The proof then proceeds exactly as before, except that now we also need to deal with
${\Pi }{\Sigma }\mathrm {W}\mathrm {I}=\{Y\mid \exists u\, \vartheta ^*(u,Y)\}$
. The proof then proceeds exactly as before, except that now we also need to deal with
![]() $\mathrm {W}$
-types. On the other hand, the treatment of
$\mathrm {W}$
-types. On the other hand, the treatment of
![]() $\mathrm {W}$
-types is completely analogous to that of
$\mathrm {W}$
-types is completely analogous to that of
![]() ${\Pi }$
-types and
${\Pi }$
-types and
![]() ${\Sigma }$
-types. The reader can easily fill in the gaps using Case 2 as template.
${\Sigma }$
-types. The reader can easily fill in the gaps using Case 2 as template.
Acknowledgment
The author’s research was funded by the Alexander von Humboldt foundation.