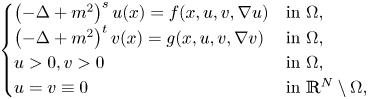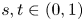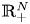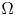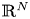Liouville-type results for positive solutions of pseudo-relativistic Schrödinger system

Abstract

In this paper, we are concerned with the physically engaging pseudo-relativistic Schrödinger system:

\[ \begin{cases} \left(-\Delta+m^{2}\right)^{s}u(x)=f(x,u,v,\nabla u) & \hbox{in } \Omega,\\ \left(-\Delta+m^{2}\right)^{t}v(x)=g(x,u,v,\nabla v) & \hbox{in } \Omega,\\ u>0,v>0 & \hbox{in } \Omega, \\ u=v\equiv 0 & \hbox{in } \mathbb{R}^{N}\setminus\Omega, \end{cases} \]

where $s,t\in (0,1)$ and the mass $m>0.$ By using the direct method of moving plane, we prove the strict monotonicity, symmetry and uniqueness for positive solutions to the above system in a bounded domain, unbounded domain, $\mathbb {R}^{N}$, $\mathbb {R}^{N}_{+}$ and a coercive epigraph domain $\Omega$ in $\mathbb {R}^{N}$, respectively.

1. Introduction

We consider the following generalized pseudo-relativistic Schrödinger system:

(1.1)\begin{equation} \begin{cases}\left(-\Delta+m^{2}\right)^{s}u(x)=f(x,u,v,\nabla u) & \hbox{in } \Omega,\\ \left(-\Delta+m^{2}\right)^{t}v(x)=g(x,u,v,\nabla v) & \hbox{in } \Omega,\\ u>0,v>0 & \hbox{in } \Omega, \\ u=v\equiv 0 & \hbox{in } \mathbb{R}^{N}\setminus\Omega, \end{cases}\end{equation}

where $(-\Delta +m^{2})^{s}$ is the generalized pseudo-relativistic Schrödinger operator, $\Omega$ may be bounded domain, unbounded domain, $\mathbb {R}^{N}_+$, $\mathbb {R}^{N}$ or a coercive epigraph domain $\Omega$ in $\mathbb {R}^{N}.$

System (1.1) is closely related to the pseudo-relativistic Schrödinger equations:

(1.2)\begin{equation} \textrm{i}\frac{\partial \Psi}{\partial t}=\left({-}c^{2}\Delta+m^{2}c^{4}\right)^{{1}/{2}}\Psi-mc^{2}\Psi-f(|\Psi(t, x)|^{2})\Psi, \forall (t,x)\in \mathbb{R}_+{\times} \mathbb{R}^{N}, \end{equation}

where $c$ denotes the speed of the light, $m>0$ represents the particle mass, $\Psi (t, x)$ is a complex-valued wave field and $f:[0, 1)\to \mathbb {R}$ is a nonlinear function describing the dynamics of the system consisting of identical spin-$0$ bosons whose motions are relativistic (see [32, 33]), such as boson stars. If we consider the standing waves solution $\Psi (t, x)=e^{i\omega t}u(x)$ to (1.2), where $\omega \in \mathbb {R}$ is the frequency and $u(x)$ is real-valued, then equation (1.2) becomes a static semi-linear elliptic equation:

(1.3)\begin{equation} \left({-}c^{2}\Delta+m^{2}c^{4}\right)^{{1}/{2}}u(x)-(\omega-mc^{2})u(x)=f(|u(x)|^{2})u(x), \quad \forall x\in \mathbb{R}^{N}. \end{equation}

Recall that the pseudo-relativistic operators $(-\Delta +m^{2})^{s}$ in $\mathbb {R}^{N}$ is defined by (see [1, 7])

(1.4)\begin{align} \left(-\Delta+m^{2}\right)^{s}u(x)& :=c_{N,s} m^{{{N}/{2}+s}} P.V. \int_{\mathbb{R}^{N}} \frac{u(x)-u(y)}{|x-y|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}(m|x-y|)\,\textrm{d} y\notag\\ & \quad +m^{2 s}u(x), \end{align}

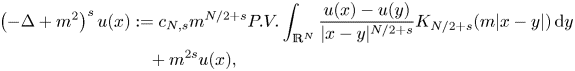
where $s\in (0, 1)$, $P.V.$ stands for Cauchy principal value, and

(1.5)\begin{equation} c_{N, s}=2^{1-{N}/{2}+s}\pi^{-{N}/{2}}\frac{s(1-s)}{\Gamma(2-s)}, \end{equation}

$K_{\nu }$ denotes the modified Bessel function with order $\nu$, which solves the equation

(1.6)\begin{equation} r^{2} K_{\nu}^{\prime \prime}+r K_{\nu}^{\prime}-\left(r^{2}+\nu^{2}\right) K_{\nu}=0, \end{equation}

and satisfies the following integral representation

\[ K_{\nu}(r)=\displaystyle\int_{0}^{\infty} \textrm{e}^{{-}r \cosh t} \cosh (\nu t) \,\textrm{d}t. \]

It is easy to verify that $K_{\nu }(r)$ is a real and positive function satisfying $K'_{\nu }(r)<0$ for all $r>0$, $K_{\nu }=K_{-\nu }$ for $\nu <0$. Moreover, for $\nu >0$, it holds that (see [26–28, 31])

(1.7)\begin{equation} \lim_{r\rightarrow 0}\frac{K_{\nu}(r)}{\frac{\Gamma(\nu)}{2}\left(\frac{r}{2}\right)^{-\nu}}=1. \end{equation}

Hence there exists a small $r_0>0$ and two constants $C_0>c_0>0$ such that

(1.8)\begin{equation} \frac{c_0}{r^{\nu}}\leq K_\nu(r)\leq\frac{C_0}{r^{\nu}},\quad \hbox{for all } r\leq r_0. \end{equation}

Next, for $\nu >0$, we can also derive that

(1.9)\begin{equation} \frac{ K_{\nu}(r)}{\frac{\sqrt{\pi}}{\sqrt{2}} r^{{-}1/2} \textrm{e}^{{-}r}}\to 1, \quad\hbox{as } r \rightarrow\infty. \end{equation}

Hence there exists a large $R_\infty >0$ and two constants $C_\infty >c_\infty >0$ such that

(1.10)\begin{equation} \frac{c_\infty}{r^{1/2}\textrm{e}^{r}}\leq K_\nu(r)\leq\frac{C_\infty}{r^{1/2}\textrm{e}^{r}},\quad \hbox{for all } r\geq R_\infty. \end{equation}

Let

(1.11)\begin{equation} \mathcal{L}_s(\mathbb{R}^{N}):=\left\{u : \mathbb{R}^{N} \rightarrow \mathbb{R} \left|\, \int_{\mathbb{R}^{N}} \frac{\textrm{e}^{-|x|}|u(x)|}{1+|x|^{({N+1})/{2}+s}}\,\textrm{d}x<{+}\infty\right.\right\}. \end{equation}

Then it is easy to verify that for any $u \in \mathcal {L}_s(\mathbb {R}^{N})\cap C_{\text {loc }}^{1,1}(\mathbb {R}^{N})$, the integral on the right-hand side of the definition (1.4) is well-defined. Hence $(-\Delta +m^{2})^{s}u$ makes sense for all functions $u \in \mathcal {L}_s(\mathbb {R}^{N})\cap C_{\text {loc}}^{1,1}(\mathbb {R}^{N})$. We would like to mention that the generalized pseudo-relativistic operators $(-\Delta +m^{2})^{s}$ can also be expressed equivalently via the extension method. For more details, we refer to [27, 28] and the references therein.

Besides its physical background, we see that the generalized pseudo-relativistic operators $(-\Delta +m^{2})^{s}$ become the fractional Laplacian $(-\Delta )^{s}$ as $m\rightarrow 0+$, which is a nonlocal pseudo-differential operator defined by (see e.g. [8, 10, 11, 13, 15, 22, 35, 36])

(1.12)\begin{equation} (-\Delta)^{s} u(x) = C_{N, s} \, P.V. \int_{\mathbb{R}^{N}} \frac{u(x)-u(y)}{|x-y|^{N+2s}}\, \textrm{d}y, \end{equation}

where $0< s<1$, $C_{N,s}=(\int _{\mathbb {R}^{N}}(({{1-\cos (2\pi y_{1}))}/{|y|^{N+2s}})\,\textrm {d}y})^{-1}$. Fractional Laplacian $(-\Delta )^{s}$ is well-defined for any $u\in C^{1,1}_{loc}(\mathbb {R}^{N})\cap \dot {L}_{s}(\mathbb {R}^{N})$ with the function spaces

\[ \dot{L}_{s}(\mathbb{R}^{N}):=\left\{ u: \mathbb{R}^{N} \rightarrow \mathbb{R} \left| \,\int_{\mathbb{R}^{N}} \frac{|u(x)|}{1 + |x|^{N+2s}}\,\textrm{d}x <{+}\infty \right.\right\}. \]

It can also be defined equivalently through Caffarelli and Silvestre's extension method (see [3]).

Due to its various applications in fluid mechanics, molecular dynamics, relativistic quantum mechanics of stars (see [6, 18]), in conformal geometry (see [11]) and in probability and finance (see [2, 4]). Problems involving fractional operators have attracted more and more attention in recent years. Note that the equations with general pseudo-relativistic Schrödinger operator $(-\Delta +m^{2})^{s}$ with $m\geq 0$ are inhomogeneous in general. Therefore scaling invariance does not hold for this kind of problem. To overcome this difficulty, there are two basic approaches in the literature. One approach is to define the operators $(-\Delta +m^{2})^{s}$ via the extension method and reduce the nonlocal problem into a local one in higher dimension space. Another way is to use the integral representation formulae of solutions [11, 12]. By establishing the equivalence between the fractional order equation and its corresponding integral equation (with Bessel kernel if $m > 0$, Riesz kernel if $m = 0$), one can apply the method of moving planes (spheres) in integral forms, the method of scaling spheres or regularity lifting methods to study various properties of solutions. These two methods have been applied successfully to study the problems involving fractional operators $(-\Delta )^{s} (0< s<1)$, and a series of fruitful results have been achieved (see [3–5, 9, 12, 14, 16, 17, 19–21, 24, 25, 29, 30, 34, 37] and the references therein). The disadvantage of the approaches mentioned above is that one needs to impose some additional conditions on the solutions. Recently, Dai et al. [23] established a direct method for the general pseudo-relativistic Schrödinger operators.

The present paper aims to extend the direct method of moving planes for a generalized fractional pseudo-relativistic nonlinear Schrödinger system. The nonlinearities depend not only on $u$ but also depend on $\nabla u.$ We first establish maximum principles such as narrow region principle and decay at infinity, then combine these results with the direct method of moving plane. We derive the symmetry and monotonicity of solutions to the pseudo-relativistic Schrödinger system in various domains, including bounded domain, unbounded domain and epigraph $\Omega$ in $\mathbb {R}^{N}.$ And then, we derive Liouville-type results in $\mathbb {R}^{N}$ and $\mathbb {R}^{N}_+$.

In the following, we denote $({\partial u}/{\partial x_{1}},{\partial u}/{\partial x_{2}},\ldots,{\partial u}/{\partial x_{N}})$ by $\mathbf {p}$ and $({\partial v}/{\partial x_{1}},{\partial v}/{\partial x_{2}},\ldots,{\partial v}/{\partial x_{N}})$ by $\mathbf {q}$,

We say a function $f(x, u, v,\mathbf {p}): \, \Omega \times \mathbb {R}\times \mathbb {R}\times \mathbb {R}^{n}\rightarrow \mathbb {R}$ is locally Lipschitz in $u$, uniformly in $\mathbf {p}$ and locally uniformly in $x$: for any $M>0$ and any compact subset $K\subset \bar {\Omega }$, there exists $C_{K,M}>0$ such that, $\forall \, u_1,u_2\in [-M, M]$, $\forall \, x\in K$ and $\forall \, \mathbf {p}\in \mathbb {R}^{N}$,

\[ |f(x, u_1, v, \mathbf{p})-f(x, u_2, v, \mathbf{p})|\leq C_{K,M}|u_1-u_2|. \]

We assume the following conditions on the nonlinearity $f$ and $g$:

\[ (\mathbf{F}_\textbf{{1}}):\quad \frac{\partial f}{\partial v}>0,\quad \frac{\partial g}{\partial u}>0,\quad \frac{\partial f}{\partial u} < m^{2s},\quad \frac{\partial g}{\partial v} < m^{2t}. \]

More precisely, we first concerned the generalized pseudo-relativistic Schrödinger system (1.1) in bounded domain and unbounded domain, the main results are as follows.

Theorem 1.1 Let $\Omega \subset \mathbb {R}^{N}$ be a bounded domain which is convex in $x_1$-direction and symmetric about $\{x\in \mathbb {R}^{N} \mid x_{1}=0\}$. Suppose that $u\in C^{1,1}_{loc}(\Omega )\cap C(\bar {\Omega })$, $v\in C^{1,1}_{loc}(\Omega )\cap C(\bar {\Omega })$ solve system (1.19), $f(x, u, v,\mathbf {p}), g(x, u, v,\mathbf {q})$ are Lipschitz continuous with respect to $u,v$. If $f(x,u,v,\mathbf {q})$, $g(x,u,v,\mathbf {q})$ satisfy conditions $\mathbf {F_1}$ and

(1.13)\begin{equation} \begin{cases}f(x_1, x', u, v, p_1, p_2,\dots, p_N)\leq f(\bar{x}_1, x', u, v, -p_1, p_2,\dots, p_N),\\ g(x_1, x', u, v, q_1, q_2,\dots, q_N)\leq g(\bar{x}_1, x', u, v, -q_1, q_2,\dots, q_N),\\ \qquad \forall \ - x_1\geq 0, p_1\geq 0, q_1\geq 0,\ x_1\leq \bar{x}_1\leq{-}x_1. \end{cases}\end{equation}

Then $u(x_1, x')$ and $v(x_1, x')$ are strictly increasing in the left half of $\Omega$ in $x_1$-direction and

\[ u(x_1, x')\leq u({-}x_1, x'),\quad v(x_1, x')\leq v({-}x_1, x'),\quad \forall \ x_1<0, \ (x_1,x')\in \Omega. \]

Moreover, if

(1.14)\begin{equation} \begin{cases}f(x_1, x', u, p_1, p_2,\dots, p_N)=f({-}x_{1}, x', u, -p_1, p_2,\dots, p_N),\\ g(x_1, x', u, q_1, q_2,\dots, q_N)=g({-}x_{1}, x', u, -q_1, q_2,\dots, q_N),\\ \qquad \forall \ x_{1}p_{1}\leq 0,\ x_{1}q_{1}\leq 0, \end{cases}\end{equation}

then we have

\[ u(x_1, x')=u({-}x_1, x'),\quad v(x_1, x')=v({-}x_1, x'), \quad \forall \ x_1<0, \ (x_1,x')\in \Omega. \]

To state our monotonicity and symmetry results for unbounded domain $\Omega$, we need to impose a growth condition on $f(x,u,v,\mathbf {p})$ and $g(x,u,v,\mathbf {q})$: for some $\beta _{1}, \beta _{2}>0$, there exists a positive constant $C$ such that

(1.15)\begin{align} \frac{|f(x, u_1,v, \mathbf{p})-f(x, u_2,v, \mathbf{p})|}{|u_1-u_2|}& \leq C(|u_1|^{\beta_{1}}+|u_2|^{\beta_{1}}), \quad \text{as}\ u_1, u_2\rightarrow 0, \end{align}

(1.16)\begin{align} \frac{|g(x, u, v_1, \mathbf{q})-g(x, u, v_2, \mathbf{q})|}{|v_1-v_2|}& \leq C(|v_1|^{\beta_{2}}+|v_2|^{\beta_{2}}), \quad \text{as}\ v_1, v_2\rightarrow 0. \end{align}

Theorem 1.2 Let $\Omega$ be a unbounded domain in $\mathbb {R}^{N}$ which is convex in $x_1$-direction and symmetric with respect to $\{x\in \mathbb {R}^{N} \mid x_1 = 0\}$. Suppose that $u\in C^{1,1}_{loc}(\Omega )\cap C(\bar {\Omega })\cap \mathcal {L}_{s}(\mathbb {R}^{N})$, $v\in C^{1,1}_{loc}(\Omega )\cap C(\bar {\Omega })\cap \mathcal {L}_{t}(\mathbb {R}^{N})$ solve the system (1.19) and $f, g$ are Lipschitz continuous with respect to $u,v$. If $f(x, u, v,\mathbf {p}), g(x, u, v,\mathbf {q})$ satisfy $\mathbf {F}_{\mathbf {1}}$, (1.13), (1.15), (1.16) and $u(x), v(x)$ satisfy the following asymptotic properties:

(1.17)\begin{equation} \limsup_{\substack{|x|\rightarrow\infty \\ x\in\Omega, \, x_1<0}}\left[u(x)\right]^{\beta_{1}}<\frac{m^{2s}}{4C},\quad \limsup_{\substack{|x|\rightarrow\infty \\ x\in\Omega, \, x_1<0}}\left[v(x)\right]^{\beta_{2}}<\frac{m^{2t}}{4C}, \end{equation}

and

(1.18)\begin{equation} \min_{\bar{\Omega}}\left(m^{2s}-2C\left[u(x)\right]^{\beta_{1}}\right)\min_{\bar{\Omega}}\left(m^{2t}-2C\left[v(x)\right]^{\beta_{2}}\right) \geq\max_{\bar{\Omega}}\frac{\partial f}{\partial v}\cdot \max_{\bar{\Omega}} \frac{\partial g}{\partial u}, \end{equation}

where $C$ is the constant in assumption (1.15). Then we have

1. (i) If there exists a line $\mathcal {L}$ parallel to $x_{1}$-axis satisfying $\mathcal {L}\cap \Omega \neq \emptyset$ such that $\mathcal {L}\cap \Omega ^{c}\neq \emptyset$, then $u(x_1, x')$, $v(x_1, x')$ are strictly increasing in the left half of $\Omega$ in $x_1$-direction and

   \[ u(x_1, x')\leq u({-}x_1, x'),\quad v(x_1, x')\leq v({-}x_1, x'), \quad \forall \ x_1<0, \ (x_1,x')\in \Omega. \]

2. (ii) If any line $\mathcal {L}$ parallel to $x_{1}$-axis such that $\mathcal {L}\cap \Omega \neq \emptyset$ must satisfy $\mathcal {L}\cap \Omega ^{c}=\emptyset$, then there exists $\mu _{0}\leq 0$ such that $u(x_1, x'), v(x_1, x')$ are strictly increasing in $\Omega \cap \{x_{1}<\mu _{0}\}$ in $x_1$-direction and

   \begin{align*} \text{if} \ \mu_{0}=0, \quad u(x_1, x')& \leq u({-}x_1, x'),\ v(x_1, x')\leq v({-}x_1, x'),\\ & \qquad \forall \ x_1<0, \ (x_1,x')\in \Omega, \end{align*}
   \begin{align*}\text{if} \ \mu_{0}<0, \quad u(x_1, x')& =u(2\mu_{0}-x_1, x'),\ v(x_1, x')=v(2\mu_{0}-x_1, x'),\\ & \qquad \forall \ x_1<\mu_{0}, \ (x_1,x')\in \Omega. \end{align*}

Secondly, we concerned with the following generalized pseudo-relativistic Schrödinger system in $\mathbb {R}^{N}$:

(1.19)\begin{equation} \begin{cases} \left(-\Delta+m^{2}\right)^{s}u(x)=f(x,u,v,\nabla u), & \hbox{ in }\mathbb{R}^{N}, \\ \left(-\Delta+m^{2}\right)^{t}v(x)=g(x,u,v,\nabla v), & \hbox{ in }\mathbb{R}^{N}, \end{cases} \end{equation}

where $s,t\in (0,1)$ and $m>0$. Then we derive the following Liouville-type result in $\mathbb {R}^{N}$.

Theorem 1.3 Liouville theorem in $\mathbb {R}^{N}$

Assume that $u \in \mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N})$, $v \in \mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N})$ be a pair of nonnegative solutions to generalized pseudo-relativistic Schrödinger system (1.19), $f(x, u, v,\mathbf {p}), g(x, u, v,\mathbf {q})$ are Lipschitz continuous about $u,v$ and satisfy assumption $\mathbf {F_1}$ and (1.14). Suppose that $(u,v)$ are bounded and $f,g$ satisfy

\[ (\mathbf{F_{2}}):\quad \min_{\mathbb{R}^{N}}\left(m^{2s}-\frac{\partial f}{\partial u}\right)\min_{\mathbb{R}^{N}}\left(m^{2t}-\frac{\partial g}{\partial v}\right)\geq\max_{\mathbb{R}^{N}}\frac{\partial f}{\partial v}\cdot\max_{\mathbb{R}^{N}}\frac{\partial g}{\partial u}, \]

then we have

\[(u,v)\equiv (C_{1},C_{2}). \]

Thirdly, we consider the generalized pseudo-relativistic Schrödinger system (1.19) in a coercive epigraph $\Omega$. We say a domain $\Omega \subseteq \mathbb {R}^{N}$ is coercive epigraph if there exists a continuous function $\varphi : \mathbb {R}^{N-1}\rightarrow \mathbb {R}$ satisfying

(1.20)\begin{equation} \lim_{|x'|\rightarrow +\infty}\varphi(x')={+}\infty, \end{equation}

such that $\Omega =\{x=(x',x_N)\in \mathbb {R}^{N}|x_N>\varphi (x')\}$. Our main result for generalized pseudo-relativistic Schrödinger system (1.19) in a coercive epigraph $\Omega$ is as follows.

Theorem 1.4 Assume that $u\in \mathcal {L}_{s}(\mathbb {R}^{N})\cap C^{1,1}_{loc}(\Omega )\cap C(\bar {\Omega })$, $v\in \mathcal {L}_{t}(\mathbb {R}^{N})\cap C^{1,1}_{loc}(\Omega )\cap C(\bar {\Omega })$ be a pair of nonnegative solution to system (1.1), $f(x, u, v,\mathbf {p}), g(x, u, v,\mathbf {q})$ are Lipschitz continuous with respect to $u,v$. Further suppose that $f,g$ satisfy condition $\mathbf {F_{1}}$ and

(1.21)\begin{equation} \begin{cases}f(x', x_{N}, u, v, p_1, p_2,\dots, p_N)\leq f(x', \bar{x}_{N}, u, v, p_1, p_2,\dots, -p_N),\\ g(x', x_{N}, u, v, q_1, q_2,\dots, p_N)\leq g(x', \bar{x}_{N}, u, v, q_1, q_2,\dots, -q_N),\\ \qquad \forall \ x_N\geq\min_{\mathbb{R}^{N-1}}\varphi, \ p_N\geq 0, \ q_N\geq 0, \ \bar{x}_{N}\geq x_{N}. \end{cases}\end{equation}

Then $(u,v)$ are strictly monotone increasing with respect to the $x_{N}$-axis.

Finally, we shall consider the generalized pseudo-relativistic Schrödinger system (1.1) in $\mathbb {R}^{N}_{+}$. By applying theorem 1.4, we prove the following result.

Theorem 1.5 Liouville theorem in $\mathbb {R}^{N}_{+}$

Assume that $u \in \mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N}_{+})$, $v \in \mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N}_{+})$ be a pair of nonnegative solutions of

(1.22)\begin{equation} \begin{cases} \left(-\Delta+m^{2}\right)^{s}u(x)=f(x,u,v,\nabla u), & \forall x\in \mathbb{R}^{N}_{+}, \\ \left(-\Delta+m^{2}\right)^{t}v(x)=g(x,u,v,\nabla v), & \forall x\in \mathbb{R}^{N}_{+}, \\ u=v=0, & \forall x \notin \mathbb{R}^{N}_{+}, \end{cases} \end{equation}

where $f(x, u, v,\mathbf {p}), g(x, u, v,\mathbf {q})$ are Lipschitz continuous about $u,v$ and satisfy condition $\mathbf {F_{1}}$, (1.21) with $x_N\geq \min _{\mathbb {R}^{N-1}}\varphi =0$. Suppose that

\[ \lim_{|x|\rightarrow+\infty}(u(x),v(x))=(0,0),\quad f(x,0,0,0)=g(x,0,0,0)=0. \]

Then we have

\[(u,v)\equiv (0,0).\]

Our paper is organized as follows. In § 2, we establish the narrow region principle for the generalized pseudo-relativistic Schrödinger system (1.1) and give the decay at infinity. The proof of theorem 1.1 and theorem 1.2 will be provided in §§ 3 and 4, respectively. In § 5, we prove the Liouville-type results for the generalized pseudo-relativistic Schrödinger system in $\mathbb {R} ^{N}$. In the last section, we study the strictly monotone and Liouville-type results for the generalized pseudo-relativistic Schrödinger system in a coercive epigraph domain $\Omega$ and the half-space $\mathbb {R}^{N}_+,$ respectively.

2. Narrow region principle and decay at infinity

This section establishes the narrow region principle and study the decay at infinity for a anti-symmetric system. These principles are crucial in applying the direct method of moving planes for the pseudo-relativistic Schrödinger system.

We first introduce the following notations. For arbitrary $\lambda \in \mathbb {R}$, let

\[ T_{\lambda}:=\left\{x \in \mathbb{R}^{N} | x_{1}=\lambda\right\} \]

be the moving planes, and let

(2.1)\begin{equation} \Sigma_{\lambda}:=\left\{x \in \mathbb{R}^{N} | x_{1}<\lambda\right\} \end{equation}

be the region to the left of the plane, and set

\[ x^{\lambda}:=\left(2 \lambda-x_{1}, x_{2}, \dots, x_{N}\right) \]

be the reflection of $x$ about the plane $T_{\lambda }$. Let $(u,v) \in \{\mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N})\}\times \{\mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N})\}$ be a pair of nonnegative solutions to the pseudo-relativistic Schrödinger system (1.19), we denote the reflected functions by $u_{\lambda }(x):=u(x^{\lambda })$ and $v_{\lambda }(x):=v(x^{\lambda })$. Moreover, we define

(2.2)\begin{equation} \left\{\begin{aligned} U_{\lambda}(x) & :=u\left(x^{\lambda}\right)-u(x) \\ V_{\lambda}(x) & :=v\left(x^{\lambda}\right)-v(x) \end{aligned}\right. \end{equation}

to be the comparison between the values of $u(x), u(x^{\lambda })$ and $v(x), v(x^{\lambda })$. Evidently, $U_{\lambda }$ and $V_{\lambda }$ are anti-symmetric functions. From now on and in the following of the paper, we always use the same $C$ denotes a constant whose value may be different from line to line, and only the relevant dependence is specified.

Proposition 2.1 Narrow region principle

Let $\Omega$ be a bounded open set in $\Sigma _{\lambda }$ which is contained in the region between $T_{\lambda }$ and $T_{\Omega }$, where $T_{\Omega }$ is a hyper-plane that is parallel to $T_{\lambda }$. Let $d(\Omega ):=dist(T_{\lambda },T_{\Omega })$. Suppose that $(U_{\lambda },V_{\lambda })\in \{\mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\Omega )\}\times \{\mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\Omega )\}$, $U_{\lambda }$, $V_{\lambda }$ are lower semi-continuous on $\bar {\Omega }$, and satisfy

(2.3)\begin{equation} \begin{cases}{(-\Delta+m^{2})^{s} U_{\lambda}(x)+c_{1}(x)U_{\lambda}(x)+c_{2}(x)V_{\lambda}(x)\geq 0} & {\text{in } \Omega}, \\ {(-\Delta+m^{2})^{t} V_{\lambda}(x)+c_{3}(x)V_{\lambda}(x)+c_{4}(x)U_{\lambda}(x)\geq 0} & {\text {in } \Omega}, \\ {U_{\lambda}(x) \geq 0, V_{\lambda}(x) \geq 0} & {\text {in } \Sigma_{\lambda} \backslash \Omega}, \\ {U_{\lambda}(x^{\lambda})={-}U_{\lambda}(x), V_{\lambda}(x^{\lambda})={-}V_{\lambda}(x)} & {\text{in } \Sigma_{\lambda},}\end{cases} \end{equation}

where $c_{1}(x), c_{2}(x), c_{3}(x), c_{4}(x)$ are uniformly bounded from below about $d(\Omega )$ and $c_{2}(x), c_{4}(x)<0$. We assume $\Omega$ is narrow in the sense that, $d(\Omega )\leq {r_{0}}/{4m}$, $r_{0}$ is given by (1.8), and there exists $C_{N,s}>0$ and $C_{N,t}>0$ such that

(2.4)\begin{equation} \inf_{\left\{x\in\Omega\,|\,U_{\lambda}(x)<0\right\}}c_{1}(x)+m^{2s}>{-}\frac{C_{N,s}}{d(\Omega)^{2s}},\quad \inf_{\left\{x\in\Omega\,|\,V_{\lambda}(x)<0\right\}}c_{3}(x)+m^{2t}>{-}\frac{C_{N,t}}{d(\Omega)^{2t}}. \end{equation}

Then we have either

(2.5)\begin{equation} U_{\lambda}(x)> 0,\ V_{\lambda}(x)> 0 \text{ in } \Omega\quad \text{or}\quad U_{\lambda}=V_{\lambda}=0 \quad \text{almost everywhere in} \ \mathbb{R}^{N}. \end{equation}

These conclusions hold for unbounded open set $\Omega$ if we further assume that

\[ \varliminf_{|x| \rightarrow \infty} U_{\lambda}(x)\geq 0,\quad \varliminf_{|x| \rightarrow \infty}V_{\lambda}(x) \geq 0. \]

Proof. Without loss of generalities, we may assume that

\[ T_{\lambda}=\{x\in\mathbb{R}^{N}\,|\,x_{1}=0\} \quad \text{and} \quad \Sigma_{\lambda}=\{x\in\mathbb{R}^{N}\,|\,x_{1}<0\}, \]

and hence $\Omega \subseteq \{x\in \mathbb {R}^{N}\,|-d(\Omega )< x_{1}<0\}$.

If $U_{\lambda }$ or $V_{\lambda }$ is not nonnegative in $\Omega$, we assume there exists a $\bar {x}\in \bar {\Omega }$ such that

\[ U_{\lambda}\left(\bar{x}\right)=\min_{\bar{\Omega}} U_{\lambda}<0. \]

Otherwise, the same arguments as follows can also yield a contradiction for the case that $V_{\lambda }(\bar {x})<0$.

First, we will prove that

(2.6)\begin{equation} U_{\lambda}(x)\geq 0,\quad V_{\lambda}(x)\geq 0 \text{ in } \Omega. \end{equation}

One can further deduce from (2.3) that $\bar {x}$ is in the interior of $\Omega$. It follows that

(2.7)\begin{align} & (-\Delta+m^{2})^{s} U_{\lambda}\left(\bar{x}\right) \nonumber\\ & \quad=c_{N,s}m^{{N}/{2}+s}P.V.\int_{\mathbb{R}^{N}}\frac{U_{\lambda}\left(\bar{x}\right) -U_{\lambda}(y)}{\left|\bar{x}-y\right|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}\left(m\left|\bar{x}-y\right|\right)\textrm{d}y+m^{2s}U_{\lambda}\left(\bar{x}\right) \nonumber\\ & \quad =c_{N,s}m^{{N}/{2}+s}P.V.\left\{\int_{\Sigma_\lambda} \frac{U_{\lambda}\left(\bar{x}\right)-U_{\lambda}(y)}{\left|\bar{x}-y\right|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}\left(m\left|\bar{x}-y\right|\right) \textrm{d}y\right.\nonumber\\ & \qquad +\left.\int_{\Sigma_\lambda}\frac{U_{\lambda}\left(\bar{x}\right)+U_{\lambda}(y)}{ \left|\bar{x}-{y}^{\lambda}\right|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}\left(m\left|\bar{x}-{y}^{\lambda}\right|\right) \textrm{d}y \right\}+m^{2s}U_{\lambda}\left(\bar{x}\right) \nonumber\\ & \quad \leq c_{N,s}m^{{N}/{2}+s} \int_{\Sigma_\lambda}\left\{\frac{U_{\lambda}\left(\bar{x}\right)-U_{\lambda}(y)}{\left|\bar{x}-{y}^{\lambda}\right|^{{{N}/{2}+s}}} +\frac{U_{\lambda}\left(\bar{x}\right)+U_{\lambda}(y)}{\left|\bar{x}-{y}^{\lambda}\right|^{{{N}/{2}+s}}}\right\}\notag\\ & \qquad \times K_{{{N}/{2}+s}} \left(m\left|\bar{x}-{y}^{\lambda}\right|\right)\textrm{d}y +m^{2s}U_{\lambda}\left(\bar{x}\right) \nonumber\\ & \quad =c_{N,s}m^{{N}/{2}+s}\int_{\Sigma_\lambda}\frac{2U_{\lambda}\left(\bar{x}\right)}{\left| \bar{x}-{y}^{\lambda}\right|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}\left(m\left|\bar{x}-{y}^{\lambda}\right|\right)\textrm{d}y +m^{2s}U_{\lambda}\left(\bar{x}\right). \end{align}

Let

\[ D:=\left\{y=(y_1,y')\in\mathbb{R}^{N} \mid d(\Omega)< y_{1}-(\bar{x})_{1}<2d(\Omega),\left|y^{\prime}-\left(\bar{x}\right)^{\prime}\right|<\displaystyle\frac{r_{0}}{2m}\right\}, \]

where $(x)^{\prime }=(x_2,x_3,\ldots,x_N)$, then $m|y-\bar {x}|< r_0,$ for all $y\in D$. Denote $t:=y_{1}-(\bar {x})_{1}$, $\tau :=\left |y^{\prime }-(\bar {x})^{\prime }\right |$. Using (1.8), we have

(2.8)\begin{align} & m^{{N}/{2}+s}\int_{\Sigma_\lambda}\frac{1}{\left|\bar{x}-{y}^{\lambda}\right|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}\left(m\left|\bar{x}-\tilde{y}\right|\right)\textrm{d}y \nonumber\\ & \quad \geq m^{{N}/{2}+s}\int_{D}\frac{1}{\left|\bar{x}-y\right|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}\left(m\left|\bar{x}-y\right|\right)\textrm{d}y \nonumber\\ & \quad \geq c_{0}\int_{D}\frac{1}{\left|\bar{x}-y\right|^{N+2s}}\,\textrm{d}y \nonumber\\ & \quad =c_{0}\int_{d(\Omega)}^{2d(\Omega)}\int_{0}^{{r_0}/{2m}}\frac{\sigma_{N-1}\tau^{N-2}\,\textrm{d}\tau}{ \left(t^{2}+\tau^{2}\right)^{{{N}/{2}+s}}}\,\textrm{d}t\nonumber\\ & \quad=c_{0}\int_{d(\Omega)}^{2d(\Omega)}\int_{0}^{{r_0}/{2mt}}\frac{\sigma_{N-1}(t\rho)^{N-2}t \,\textrm{d}\rho}{t^{N+2s}\left(1+\rho^{2}\right)^{{{N}/{2}+s}}}\,\textrm{d}t \nonumber\\ & \quad=c_{0}\int_{d(\Omega)}^{2d(\Omega)}\frac{1}{t^{1+2s}}\int_{0}^{{r_0}/{2mt}}\frac{\sigma_{N-1}\rho^{N-2} \,\textrm{d}\rho}{\left(1+\rho^{2}\right)^{{{N}/{2}+s}}}\,\textrm{d}t\nonumber\\ & \quad \geq c_{0}\int_{d(\Omega)}^{2d(\Omega)}\frac{1}{t^{1+2s}}\int_{0}^{1}\frac{\sigma_{N-1}\rho^{N-2} \,\textrm{d}\rho}{\left(1+\rho^{2}\right)^{{{N}/{2}+s}}}\,\textrm{d}t\nonumber\\ & \quad \geq C_{N,s}\int_{d(\Omega)}^{2d(\Omega)}\frac{1}{t^{1+2s}}\,\textrm{d}t=\frac{C_{N,s}}{d(\Omega)^{2s}}, \end{align}

where we have used the substitution $\rho :=\tau /t$ and $\sigma _{N-1}$ denotes the area of the unit sphere in $\mathbb {R}^{N-1}$. Since $c_{1}(x)$ has lower bound, it follows from (2.4), (2.7) and (2.8) that

\begin{align*} & (-\Delta+m^{2})^{s} U_{\lambda}\left(\bar{x}\right)+c_{1}\left(\bar{x}\right)U_{\lambda}\left(\bar{x}\right) \\ & \quad \leq\left[\displaystyle\frac{C_{N,s}}{d(\Omega)^{2s}}+\inf_{\{x\in\Omega\,|\,U_{\lambda}(x)<0\}}c_{1}(x)+m^{2s}\right]U_{\lambda}\left(\bar{x}\right)<0. \end{align*}

By (2.3), we have

(2.9)\begin{equation} c_{2}(\bar{x})V_{\lambda}\left(\bar{x}\right)\geq{-}(-\Delta+m^{2})^{s} U_{\lambda}\left(\bar{x}\right)-c_{1}\left(\bar{x}\right)U_{\lambda}\left(\bar{x}\right)>0. \end{equation}

Since $c_{2}(x)<0$, we deduce from (2.9) that $V_{\lambda }(\bar {x})<0$. We can infer from the lower semi-continuous of $V_{\lambda }$ that there exists some $\tilde {x}$ such that

\[ V_{\lambda}\left(\tilde{x}\right)=\min_{\bar{\Omega}} V_{\lambda}<0. \]

By using the similar arguments as used in (2.7) and (2.8), we can also get

\begin{align*} & (-\Delta+m^{2})^{t} V_{\lambda}\left(\tilde{x}\right)+c_{3}\left(\bar{x}\right)V_{\lambda}\left(\tilde{x}\right) \\ & \quad \leq\left[\displaystyle\frac{C_{N,t}}{d(\Omega)^{2t}}+\inf_{\{x\in\Omega\,|\,V_{\lambda}(x)<0\}}c_{3}(x)+m^{2t}\right]V_{\lambda}\left(\tilde{x}\right)<0. \end{align*}

Note that

(2.10)\begin{equation} \nabla U_{\lambda}\left(\bar{x}\right)=0. \end{equation}

By Taylor expansion, we have

(2.11)\begin{equation} 0=U_{\lambda}\left(x^{0}\right)=U_{\lambda}\left(\bar{x}\right)+\nabla U_{\lambda}\left(\bar{x}\right)\left(x^{0}-\bar{x}\right)+o\left(\left|\bar{x}-x^{0}\right|\right), \end{equation}

where $x^{0}=(0, \bar {x}_{2}, \ldots, \bar {x}_{N}) \in T_{\lambda }$. Hence, we obtain that

(2.12)\begin{equation} U_{\lambda}\left(\bar{x}\right)=o(1) \delta_{\bar{x}}, \end{equation}

for sufficiently small $\delta _{\bar {x}}.$

Thus a combination of (2.11), (2.12), and the assumption (2.4) deduces that

\begin{align*} 0 & \leq(-\Delta+m^{2})^{t} V_{\lambda}\left(\tilde{x}\right)+c_{3}\left(\tilde{x}\right)V_{\lambda}\left(\tilde{x}\right)+c_{4}\left(\tilde{x}\right)U_{\lambda}\left(\tilde{x}\right) \\ & \leq\left[\displaystyle\frac{C_{N,t}}{d(\Omega)^{2t}}+\inf_{\{x\in\Omega\,|\,V_{\lambda}(x)<0\}}c_{3}(x)+m^{2t}\right]V_{\lambda}\left(\tilde{x}\right)+c_{4}\left(\tilde{x}\right)U_{\lambda}\left(\bar{x}\right) \\ & \leq\left[\frac{C_{N,t}}{d(\Omega)^{2t}}+\inf_{\{x\in\Omega\,|\,V_{\lambda}(x)<0\}}c_{3}(x)+m^{2t}\right]V_{\lambda}\left(\tilde{x}\right)+c_{4}\left(\tilde{x}\right)o(1) \delta_{\bar{x}} \\ & <0, \end{align*}

which contradicts (2.3). Thus, equation (2.6) holds.

Subsequently, if there is some point $\bar {x}\in \Omega$ such that

\[ U_{\lambda}\left(\bar{x}\right)=0 \quad \text{or}\quad V_{\lambda}\left(\bar{x}\right)=0. \]

Without loss of generality, we assume

(2.13)\begin{equation} U_{\lambda}\left(\bar{x}\right)=0. \end{equation}

Otherwise, the same arguments as follows can also yield a contradiction for the case that $V_{\lambda }(\bar {x})=0$.

Now we must have

(2.14)\begin{equation} U_{\lambda}=V_{\lambda}=0 \quad \text{almost everywhere in} \ \mathbb{R}^{N}. \end{equation}

If not, we can directly calculate that

(2.15)\begin{align} & \left(-\Delta+m^{2}\right)^{s}U_{\lambda}(\bar{x}) \nonumber\\ & \quad = c_{N,s} m^{{{N}/{2}+s}} P.V. \int_{\mathbb{R}^{N}} \frac{U_{\lambda}(\bar{x})-U_{\lambda}(y)}{|\bar{x}-y|^{{{N}/{2}+s}}} K_{{{N}/{2}+s}}(m|\bar{x}-y|)\,\textrm{d}y+m^{2s}U_{\lambda}(\bar{x}) \nonumber\\ & \quad ={-}c_{N, s} m^{{{N}/{2}+s}} P.V. \int_{\mathbb{R}^{N}} \frac{U_{\lambda}(y)}{|\bar{x}-y|^{{{N}/{2}+s}}} K_{{{N}/{2}+s}}(m|\bar{x}-y|)\,\textrm{d}y \nonumber\\ & \quad = c_{N, s} m^{{{N}/{2}+s}} P.V. \int_{\Sigma_{\lambda}}\left(\frac{K_{{{N}/{2}+s}}(m|\bar{x}-{y}^{\lambda}|)}{|\bar{x}-{y}^{\lambda}|^{{{N}/{2}+s}}}- \frac{K_{{{N}/{2}+s}}(m|\bar{x}-y|)} {|\bar{x}-y|^{{{N}/{2}+s}}}\right)U_{\lambda}(y)\,\textrm{d}y\nonumber\\ & \quad \leq 0 . \end{align}

Combining the above inequality with (2.3) and $c_{2}(x)<0$, we derive that

(2.16)\begin{equation} V_{\lambda}(\bar{x}) \leq 0. \end{equation}

By (2.5), we have $V_{\lambda }(\bar {x}) = 0$.

So, we get

\begin{align*} 0& \leq(-\Delta+m^{2})^{s} U_{\lambda}(\bar{x})+c_{1}(\bar{x})U_{\lambda}(\bar{x})+c_{2}(\bar{x})V_{\lambda}(\bar{x}) \\ & =c_{N, s} m^{{{N}/{2}+s}} P.V. \int_{\Sigma_{\lambda}} \left(\frac{K_{{{N}/{2}+s}}(m|x-{y}^{\lambda}|)}{|x-{y}^{\lambda}|^{{{N}/{2}+s}}}-\frac{K_{{{N}/{2}+s}}(m|x-y|)}{|x-y|^{{{N}/{2}+s}}}\right)U_{\lambda}(y)\,\textrm{d}y \\ & \leq 0, \end{align*}

which implies that $U_{\lambda }=0$ almost everywhere in $\Sigma _{\lambda }$ and hence $U_{\lambda }=0$ almost everywhere in $\mathbb {R}^{N}$.

Similarly, we have

\begin{align*} 0& \leq(-\Delta+m^{2})^{t} V_{\lambda}(\bar{x})+c_{3}(\bar{x})V_{\lambda}(\bar{x})+c_{4}(\bar{x})U_{\lambda}(\bar{x}) \\ & =(-\Delta+m^{2})^{t} V_{\lambda}(\bar{x})\\ & =c_{N, t} m^{{N}/{2}+t} P.V. \int_{\Sigma_{\lambda}} \left(\frac{K_{{N}/{2}+t}(m|x-{y}^{\lambda}|)}{|x-{y}^{ \lambda}|^{{N}/{2}+t}}-\frac{K_{{N}/{2}+t}(m|x-y|)}{|x-y|^{{N}/{2}+t}}\right)V_{\lambda}(y)\,\textrm{d}y\\ & \leq 0. \end{align*}

And it turns out that $V_{\lambda }=0$ almost everywhere in $\mathbb {R}^{N}$.

This finishes the proof of proposition 2.1.

Remark 2.2 It is easy to see from the proof of proposition 2.1, the assumptions ‘$U_{\lambda }$, $V_{\lambda }$ are lower semi-continuous on $\bar {\Omega }$’ and ‘$U_{\lambda }\geq 0$ and $V_{\lambda }\geq 0$, in $\Sigma \setminus \Omega$’ can be weakened into: ‘if $U_{\lambda }<0$ somewhere in $\Sigma _{\lambda }$, then the minimum negative $\inf _{\Sigma _{\lambda }}U_{\lambda }(x)$ is attained in $\Omega$’ and ‘if $V_{\lambda }<0$ somewhere in $\Sigma _{\lambda }$, then the minimum negative $\inf _{\Sigma _{\lambda }}V_{\lambda }(x)$ is attained in $\Omega$’, the same conclusions are still correct.

In order to carry on the direct method of moving planes in $\mathbb {R}^{N}$, we need to the decay at infinity for the solutions to generalized pseudo-relativistic Schrödinger system. We have

Proposition 2.3 Decay at infinity

Let $\Omega$ be an unbounded open set in $\Sigma _{\lambda }$. Assume $U_{\lambda }\in \mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\Omega )$, $V_{\lambda }\in \mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\Omega )$, $(U_{\lambda },V_{\lambda })$ is a pair of solutions to

(2.17)\begin{equation} \begin{cases}{(-\Delta+m^{2})^{s} U_{\lambda}(x)+c_{1}(x)U_{\lambda}(x)+c_{2}(x)V_{\lambda}(x)\geq 0} & {\text{in } \Omega}, \\ {(-\Delta+m^{2})^{t} V_{\lambda}(x)+c_{3}(x)V_{\lambda}(x)+c_{4}(x)U_{\lambda}(x)\geq 0} & {\text{in } \Omega}, \\ {U_{\lambda}(x) \geq 0, V_{\lambda}(x) \geq 0} & {\text {in } \Sigma_{\lambda} \backslash \Omega}, \\ {U_{\lambda}(x^{\lambda})={-}U_{\lambda}(x), V_{\lambda}(x^{\lambda})={-}V_{\lambda}(x)} & {\text{in } \Sigma_{\lambda},} \end{cases} \end{equation}

with

(2.18)\begin{equation} \liminf_{\substack{x\in\Sigma_{\lambda} \\ |x| \rightarrow+\infty}}\left(c_{1}(x)+m^{2s}\right)> 0,\quad \liminf_{\substack{x\in\Sigma_{\lambda} \\ |x| \rightarrow+\infty}} \left(c_{3}(x)+m^{2t}\right)> 0, \end{equation}

where $c_{i}(x)\ (i=1,2,3,4)$ have lower bounds, $c_{2}(x)<0$, $c_{4}(x)<0$ and

\[ \min_{\bar{\Omega}}(c_{1}(x)+m^{2s}) \min_{\bar{\Omega}}(c_{3}(x)+m^{2t})\geq \min_{\bar{\Omega}}c_{2}(x)\min_{\bar{\Omega}}c_{4}(x). \]

If there exists a constant $R_{0}>0$ (depending only on $c_{1}(x)$, $c_{2}(x)$, $c_{3}(x)$, $c_{4}(x)$, $m$, $N$, $s$ and $t$, but independent of $U_{\lambda }$, $V_{\lambda }$ and $\Sigma _{\lambda }$) such that, if $\hat {x}\in \Omega$ satisfying

\[ U_{\lambda}\left(\hat{x}\right)=\min _{\bar{\Omega}} U_{\lambda}(x)<0\quad \text{or}\quad V_{\lambda}\left(\hat{x}\right)=\min _{\bar{\Omega}} V_{\lambda}(x)<0, \]

then $\left |\hat {x}\right |\leq R_{0}$.

Proof. Without loss of generalities, we may assume that, for some $\lambda \leq 0$,

\[ T_{\lambda}=\{x\in\mathbb{R}^{N}\,|\,x_{1}=\lambda\} \quad \text{and} \quad \Sigma_{\lambda}=\{x\in\mathbb{R}^{N}\,|\,x_{1}<\lambda\}. \]

Note that $U_{\lambda }\in \mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\Omega )$, $V_{\lambda }\in \mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\Omega )$ and $\hat {x}\in \Omega$ satisfying

\[ U_{\lambda}\left(\hat{x}\right)=\min _{\bar{\Omega}} U_{\lambda}(x)<0 \quad \hbox{or}\quad V_{\lambda}\left(\hat{x}\right)=\min _{\bar{\Omega}} V_{\lambda}(x)<0. \]

We assume that

\[ U_{\lambda}\left(\hat{x}\right)=\min _{\bar{\Omega}} U_{\lambda}(x)<0. \]

Otherwise, the same arguments as follows can also yield a contradiction for the case that $V_{\lambda }(\hat {x})=\min _{\bar {\Omega }} V_{\lambda }(x)<0$.

By using similar arguments as in the proof of (2.7), we have

(2.19)\begin{align} (-\Delta+m^{2})^{s} U_{\lambda}\left(\hat{x}\right) & \leq c_{N,s}m^{{N}/{2}+s}\int_{\Sigma_{\lambda}}\frac{2U_{\lambda}\left(\hat{x}\right)}{\left|\hat{x}-{y}^{ \lambda}\right|^{{{N}/{2}+s}}}K_{{{N}/{2}+s}}\left(m\left|\hat{x}-{y}^{\lambda}\right|\right) \textrm{d}y\notag\\ & \quad +m^{2s}U_{\lambda}\left(\hat{x}\right). \end{align}

Note that $\lambda \leq 0$ and $\hat {x}\in \Omega$, it follows that

\[ B_{\left|\hat{x}\right|}\left(\bar{x}\right) \subset \left\{x \in \mathbb{R}^{N} | x_{1}>\lambda\right\}, \]

where $\bar {x}:=(2\left |\hat {x}\right |+(\hat {x})_{1},(\hat {x})^{\prime })$, $(\hat {x})^{\prime }=((\hat {x})_{2},\ldots,(\hat {x})_{N})$.

Thus we derive that, if $|\hat {x}|\geq {R_{\infty }}/{3m}$ ($R_{\infty }$ is same as (1.10)),

(2.20)\begin{align} & m^{{N}/{2}+s}\int_{\Sigma_{\lambda}}\frac{K_{{{N}/{2}+s}}\left(m\left|\hat{x}-{y}^{\lambda}\right|\right)}{\left|\hat{x}-{y}^{\lambda}\right|^{{{N}/{2}+s}}}\,\textrm{d}y\nonumber\\ & \quad \geq m^{{N}/{2}+s}\int_{B_{|\hat{x}|}\left(\bar{x}\right)}\frac{K_{{{N}/{2}+s}}\left(m\left|\hat{x}-y\right|\right)} {\left|\hat{x}-y\right|^{{{N}/{2}+s}}} \,\textrm{d}y\nonumber\\ & \quad \geq m^{{N}/{2}+s}\int_{B_{\left|\hat{x}\right|}\left(\bar{x}\right)}\frac{K_{{{N}/{2}+s}}\left(3m\left|\hat{x}\right|\right)} {3^{{{N}/{2}+s}}\left|\hat{x}\right|^{{{N}/{2}+s}}} \,\textrm{d}y \nonumber\\ & \quad \geq\frac{c_{\infty}m^{({N-1})/{2}+s}\omega_N}{3^{({N+1})/{2}+s}\left|\hat{x}\right|^{s+1/2-{N}/{2}}\textrm{e}^{3m\left|\hat{x}\right|}}, \end{align}

where $\omega _{N}:=|B_{1}(0)|$ denotes the volume of the unit ball in $\mathbb {R}^{N}$. Then we can deduce from (2.17), (2.19), and (2.20) that

(2.21)\begin{align} 0& \leq(-\Delta+m^{2})^{s} U_{\lambda}(\hat{x})+c_{1}(\hat{x})U_{\lambda}(\hat{x})+c_{2}(\hat{x})V_{\lambda}(\hat{x}) \nonumber\\ & \leq\left[\frac{2c_{N,s}c_{\infty}\omega_{N}m^{({N-1})/{2}+s}}{3^{({N+1})/{2}+s} \left|\hat{x}\right|^{s+1/2-{N}/{2}}\textrm{e}^{3m\left|\hat{x}\right|}} +c_{1}(\hat{x})+m^{2s}\right]U_{\lambda}(\hat{x})+c_{2}(\hat{x})V_{\lambda}(\hat{x})\nonumber\\ & =:\left[A_{1}(\hat{x})+c_{1}(\hat{x})+m^{2s}\right]U_{\lambda}(\hat{x})+c_{2}(\hat{x})V_{\lambda}(\hat{x}), \end{align}

where $A_{1}(\hat {x})=({2c_{N,s}c_{\infty }\omega _{N}m^{({N-1})/{2}+s}})/({3^{({N+1})/{2}+s} \left |\hat {x}\right |^{s+1/2-{N}/{2}}\textrm {e}^{3m\left |\hat {x}\right |}})$. From (2.18), we infer that there exists a $R_{1}$ sufficiently large such that, for any $|x|>R_{1}$,

(2.22)\begin{equation} |x|^{s+{1}/{2}-{N}/{2}}\textrm{e}^{3m|x|}\left(c_{1}(x)+m^{2s}\right)>0>{-} \frac{2c_{N,s}c_{\infty}\omega_{N}m^{({N-1})/{2}+s}}{3^{({N+1})/{2}+s}}, \end{equation}

and

(2.23)\begin{equation} |x|^{t+{1}/{2}-{N}/{2}}\textrm{e}^{3m|x|}\left(c_{3}(x)+m^{2t}\right)>0>{-}\frac{2c_{N,t}c_{\infty} \omega_{N}m^{({N-1})/{2}+t}}{3^{({N+1})/{2}+t}}. \end{equation}

Therefore, take $R_{0}:=\max \{{R_{\infty }}/{3m},R_{1}\}$, if $|\hat {x}|>R_{0}$, both (2.21), (2.22), and (2.23) are established. Combine with (2.21), we get

(2.24)\begin{equation} U_{\lambda}(\hat{x})\geq{-}\frac{c_{2}(\hat{x})V_{\lambda}(\hat{x})}{\left[A_{1}+c_{1}(\hat{x})+m^{2s}\right]}. \end{equation}

Next, we will prove that $|\hat {x}|\leq R_{0}$.

If not, then it follows from (2.21), (2.22), and $c_{2}(x)<0$ that

(2.25)\begin{equation} V_{\lambda}\left(\hat{x}\right)<0. \end{equation}

Using the lower semi-continuous of $V_{\lambda }$ that there exists some $\bar {x}$ such that

\[ V_{\lambda}\left(\bar{x}\right)=\min_{\bar{\Omega}} V_{\lambda}<0. \]

Through a computation similar to (2.7), we have

\begin{align*} & (-\Delta+m^{2})^{t} V_{\lambda}\left(\bar{x}\right) \\ & \quad =c_{N,t}m^{{N}/{2}+t}P.V.\int_{\mathbb{R}^{N}}\frac{V_{\lambda}\left(\bar{x}\right) -V_{\lambda}(y)}{\left|\bar{x}-y\right|^{{N}/{2}+t}}K_{{N}/{2}+t}\left(m\left|\bar{x}-y\right|\right) \textrm{d}y+m^{2t}V_{\lambda}\left(\bar{x}\right) \\ & \quad =c_{N,t}m^{{N}/{2}+t}P.V.\left\{\int_{\Sigma_\lambda} \frac{V_{\lambda}\left(\bar{x}\right)- V_{\lambda}(y)}{\left|\bar{x}-y\right|^{{N}/{2}+t}}K_{{N}/{2}+t}\left(m\left|\bar{x}-y\right|\right) \textrm{d}y\right. \\ & \qquad +\left.\int_{\Sigma_\lambda}\frac{V_{\lambda}\left(\bar{x}\right)+V_{\lambda}(y)}{ \left|\bar{x}-{y}^{\lambda}\right|^{{N}/{2}+t}}K_{{N}/{2}+t}\left(m\left|\bar{x}-{y}^{\lambda}\right|\right) \textrm{d}y \right\}+m^{2t}V_{\lambda}\left(\bar{x}\right) \\ & \quad \leq c_{N,t}m^{{N}/{2}+t} \int_{\Sigma_\lambda}\left\{\frac{V_{\lambda}\left(\bar{x}\right)-V_{\lambda}(y)}{\left|\bar{x}-{y}^{\lambda} \right|^{{N}/{2}+t}}+\frac{V_{\lambda}\left(\bar{x}\right)+V_{\lambda}(y)}{\left|\bar{x}-{y}^{\lambda}\right|^{ {N}/{2}+t}}\right\}\\ & \qquad \times K_{{N}/{2}+t}\left(m\left|\bar{x}-{y}^{\lambda}\right|\right)\textrm{d}y +m^{2t}V_{\lambda}\left(\bar{x}\right) \\ & \quad =c_{N,t}m^{{N}/{2}+s}\int_{\Sigma_\lambda}\frac{2V_{\lambda}\left(\bar{x}\right)}{\left|\bar{x}-{y}^{\lambda} \right|^{{N}/{2}+t}}K_{{N}/{2}+t}\left(m\left|\bar{x}-{y}^{\lambda}\right|\right)\textrm{d}y +m^{2t}V_{\lambda}\left(\bar{x}\right)\\ & \quad \leq m^{2t}V_{\lambda}\left(\bar{x}\right). \end{align*}

Similar to (2.20), (2.21), combine with $\min _{\bar {\Omega }}(c_{1}(x)+m^{2s}) \min _{\bar {\Omega }}(c_{3}(x)+m^{2t})\geq \min _{\bar {\Omega }}c_{2}(x)\min _{\bar {\Omega }}c_{4}(x)$. We have, if $|\hat {x}|>R_{0}$,

(2.26)\begin{align} 0& \leq(-\Delta+m^{2})^{t} V_{\lambda}(\bar{x})+c_{3}(\bar{x})V_{\lambda}(\bar{x})+c_{4}(\bar{x})U_{\lambda}(\bar{x})\nonumber\\ & \leq\left[c_{3}(\bar{x})+m^{2t}\right]V_{\lambda}(\bar{x})+c_{4}(\bar{x})U_{\lambda}(\hat{x})\nonumber\\ & \leq \left[c_{3}(\bar{x})+m^{2t}-\frac{c_{2}(\hat{x})c_{4}(\bar{x})}{A_{1}(\bar{x})+c_{1}(\hat{x})+m^{2s}}\right]V_{\lambda}(\bar{x}) \nonumber\\ & \leq \left[\frac{(A_{1}(\bar{x})+c_{1}(\hat{x})+m^{2s})(c_{3}(\bar{x})+m^{2t})-c_{2}(\hat{x})c_{4}(\bar{x})}{A_{1}(\bar{x})+c_{1}(\hat{x})+m^{2s}}\right]V_{\lambda}(\bar{x}) \nonumber\\ & < 0. \end{align}

That is impossible. So we have $|\hat {x}|\leq R_{0}$.

This completes the proof of proposition 2.3.

Remark 2.4 We point out that in both propositions 2.1 and 2.3, we actually only need $(-\Delta +m^{2})^{s} U_{\lambda }(x)+c_{1}(x)U_{\lambda }(x)+c_{2}(x)V_{\lambda }(x)\geq 0$ and $(-\Delta +m^{2})^{t} V_{\lambda }(x)+c_{3}(x)V_{\lambda }(x)+c_{4}(x)U_{\lambda }(x)\geq 0$ holds for $x\in \{x\in \Omega |U_{\lambda }(x)<0\}$ or $x\in \{x\in \Omega |V_{\lambda }(x)<0\}$, not for all $x\in \Omega$; For simplicity and convenience, we assume it hold for all $x\in \Omega$.

3. Proof of theorem 1.1

In this section, we will use the direct method of moving plane to prove the strictly monotonicity and symmetry of nonnegative solutions to generalized pseudo-relativistic Schrödinger system (1.19) in a bounded domain.

Choose an arbitrary direction to be the $x_{1}$-direction and keep the notations $T_{\lambda }$, $\Sigma _{\lambda }$, $x_{\lambda }$, $U_{\lambda }$ and $V_{\lambda }$ defined in § 2.

Proof. Since $\Omega$ is bounded, we may assume that $\Omega \subset \{|x_1|\leq 1\}$ and $\partial \Omega \cap \{x_1=-1\}\neq \emptyset$. Our goal is to show that $U_{\lambda }>0$ and $V_{\lambda }>0$ in $\Sigma _{\lambda }\cap \Omega$ for any $\lambda \in (-1,0)$.

We carry out the direct method of moving planes procedure in two steps.

Step 1. We shall show that there exists $\epsilon >0$ small enough such that, for any $-1<\lambda \leq -1+\epsilon$,

(3.1)\begin{equation} U_\lambda(x)\geq 0,\ V_\lambda(x)\geq 0, \quad \forall \ x\in\Sigma_\lambda\cap\Omega. \end{equation}

Suppose (3.1) is not true, there exists a sequence $\{\lambda _{k}\}\subset (-1,0)$ satisfying $\lambda _k\rightarrow -1$ as $k\rightarrow +\infty$ such that

(3.2)\begin{equation} \inf_{\Sigma_{\lambda_{k}}\cap\Omega}U_{\lambda_{k}}=\inf_{\lambda\in({-}1,\lambda_{k}]}\inf_{x\in\Sigma_\lambda}U_\lambda(x)<0. \end{equation}

Otherwise, the same arguments as follows can also yield a contradiction for the case that

\[ \inf_{\Sigma_{\lambda_{k}}\cap\Omega}V_{\lambda_{k}}=\inf_{\lambda\in({-}1,\lambda_{k}]}\inf_{x\in\Sigma_\lambda}V_\lambda(x)<0. \]

Consequently, there exists $x^{k}\in \Sigma _{\lambda _{k}}\cap \Omega$ such that

(3.3)\begin{equation} w_{\lambda_{k}}(x^{k})=\inf_{\Sigma_{\lambda_{k}}\cap\Omega}w_{\lambda_{k}}=\inf_{\Sigma_{\lambda_{k}}}w_{\lambda_{k}}<0. \end{equation}

It follows directly from (3.2) and (3.3) that ${\partial U_{\lambda }}/{\partial \lambda }|_{\lambda =\lambda _k}(x^{k})\leq 0$, and hence $(\partial _{x_1}u)[(x^{k})^{\lambda _k}]\leq 0$. Note that $x^{k}$ is the interior minimum of $U_{\lambda _k}(x)$, then one has $\nabla _{x}U_{\lambda _k}(x^{k})=0$, i.e.,

(3.4)\begin{equation} (\nabla_{x}u_{\lambda_k})(x^{k})=(\nabla_{x}u)(x^{k}). \end{equation}

By the assumption (1.13) in theorem 1.1, we have

(3.5)\begin{align} & \left(-\Delta+m^{2}\right)^{s}U_{\lambda_{k}}(x^{k})\nonumber\\ & \quad =\left(-\Delta+m^{2}\right)^{s}u_{\lambda_k}(x^{k})-\left(-\Delta+m^{2}\right)^{s}u(x^{k})\nonumber\\ & \quad=f\left((x^{k})^{\lambda_k},u_{\lambda_k}(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_{x}u)((x^{k})^{\lambda_k})\right) =f\left(x^{k},u(x^{k}),v(x^{k}),(\nabla_{x}u)(x^{k})\right)\nonumber\\ & \quad \geq f\left(x^{k},u_{\lambda_k}(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_{x}u)(x^{k})\right)- f\left(x^{k},u(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_{x}u)(x^{k})\right)\nonumber\\ & \qquad+f\left(x^{k},u(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_{x}u)(x^{k})\right)-f \left(x^{k},u(x^{k}),v(x^{k}),(\nabla_{x}u)(x^{k})\right)\nonumber\\ & \quad =:-c_{1}(x^{k})U_{\lambda_k}(x^{k})-c_{2}(x^{k})V_{\lambda_k}(x^{k}), \end{align}

where

(3.6)\begin{equation} c_{1}(x^{k}):={-}\frac{f(x^{k},u_{\lambda_k}(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_xu)(x^{k}))-f(x^{k},u(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_xu)(x^{k}))}{u_{\lambda_k}(x^{k})-u(x^{k})} \end{equation}

and

(3.7)\begin{equation} c_{2}(x^{k}):={-}\frac{f\left(x^{k},u(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_xu)(x^{k})\right)-f\left(x^{k},u(x^{k}),v(x^{k}),(\nabla_xu)(x^{k})\right)}{v_{\lambda_k}(x^{k})-v(x^{k})}. \end{equation}

Similarly, we can get $(-\Delta +m^{2})^{s}U_{\lambda _{k}}(x^{k})=c_{3}(x^{k})V_{\lambda _k}(x^{k})+c_{4}(x^{k})U_{\lambda _k}(x^{k})$, where

(3.8)\begin{equation} c_{3}(x^{k}):={-}\frac{g\left(x^{k},u_{\lambda_k}(x^{k}),v_{\lambda_k}(x^{k}),(\nabla_xv)(x^{k})\right)-g\left(x^{k},u_{\lambda_k}(x^{k}),v(x^{k}),(\nabla_xv)(x^{k})\right)}{v_{\lambda_k}(x^{k})-v(x^{k})} \end{equation}

and

(3.9)\begin{align} c_{4}(x^{k}):={-}\frac{g\left(x^{k},u_{\lambda_k}(x^{k}),v(x^{k}),(\nabla_xv)(x^{k})\right)-g\left(x^{k},u(x^{k}),v(x^{k}),(\nabla_xu)(x^{k})\right)}{u_{\lambda_k}(x^{k})-u(x^{k})}. \end{align}

Since $u,v \in C(\mathbb {R}^{N})$ with compact supports and $f(x, u, v, \mathbf {p})$, $g(x, u, v, \mathbf {q})$ are Lipschitz continuous about $u,v$, so $c_{i}(x) (i=1,2,3,4)$ are uniformly bounded independent of $k$. By using the assumption $\mathbf {F_{1}}$, we know $c_{i}(x)$ satisfy the condition of proposition 2.1.

Note that $\Sigma _{\lambda _{k}}\cap \Omega$ is a narrow region for $k$ large enough and $U_{\lambda },V_{\lambda } \not \equiv 0$. From (3.5)–(3.9) and the Narrow region principle proposition 2.1, one can derive that, for $k$ sufficiently large,

(3.10)\begin{equation} U_{\lambda_{k}}>0,\ V_{\lambda_{k}}>0,\quad \text{in} \ \Sigma_{\lambda_{k}}\cap\Omega, \end{equation}

which yields a contradiction with (3.2). Hence there exists an $\epsilon >0$ small enough such that, (3.1) holds for any $-1<\lambda \leq -1+\epsilon$.

Furthermore, suppose there exist $\hat {\lambda }\in (-1,-1+\epsilon ]$ and $\hat {x}\in \Sigma _{\hat {\lambda }}\cap \Omega$ such that

\[U_{\hat{\lambda}}(\hat{x})=0\quad \text{or}\quad V_{\hat{\lambda}}(\hat{x})=0. \]

For simplify, here we assume that $U_{\hat {\lambda }}(\hat {x})=0$. On the one hand, similar to (3.5), we can infer from the assumption (1.13) in theorem 1.1 that

(3.11)\begin{align} & \left(-\Delta+m^{2}\right)^{s}U_{\hat{\lambda}}(\hat{x})\nonumber\\ & \quad =\left(-\Delta+m^{2}\right)^{s}u_{\hat{\lambda}}(\hat{x})-\left(-\Delta+m^{2}\right)^{s}u(\hat{x})\nonumber\\ & \quad =f\left((\hat{x})^{\hat{\lambda}},u_{\hat{\lambda}}(\hat{x}),v_{\hat{\lambda}}(\hat{x}),(\nabla_{x}u)((\hat{x})^{\hat{\lambda}})\right) -f\left(\hat{x},u(\hat{x}),v(\hat{x}),(\nabla_{x}u)(\hat{x})\right)\nonumber\\ & \quad \geq f\left(\hat{x},u_{\hat{\lambda}}(\hat{x}),v_{\hat{\lambda}}(\hat{x}),(\nabla_{x}u)(\hat{x})\right) -f\left(\hat{x},u(\hat{x}),v(\hat{x}),(\nabla_{x}u)(\hat{x})\right)\nonumber\\ & \quad ={-}c_{2}(\hat{x})V_{\hat{\lambda}}(\hat{x}). \end{align}

On the other hand, we can deduce from (2.15) that

(3.12)\begin{equation} \left(-\Delta+m^{2}\right)^{s}U_{\hat{\lambda}}(\hat{x})\leq 0. \end{equation}

Then it follows from (3.11), (3.12) and $c_{2}(x)>0$ that $V_{\hat {\lambda }}(\hat {x})=0$. Combing (3.11) and the definition of $(-\Delta +m^{2})^{s}$, we can derive that $U_{\lambda }=V_{\lambda }=0$ a.e. in $\mathbb {R}^{N}$. Since $\Omega$ is convex in $x_1$-direction and symmetric about $T_{0}$, $u,v$ satisfy system (1.1), one has $U_{\lambda }\geq 0$, $V_{\lambda }\geq 0$ in $\Sigma _{\lambda }\setminus \Omega$, $U_{\lambda }\not \equiv 0$ or $V_{\lambda }\not \equiv 0$ in $\Sigma _{\lambda }\setminus \Omega$ for any $\lambda \in (-\infty,0)$. That is a contradiction. Therefore, we have, for any $-1<\lambda \leq -1+\epsilon$,

(3.13)\begin{equation} U_\lambda(x)>0,\ V_\lambda(x)>0, \quad \forall \ x\in\Sigma_\lambda\cap\Omega. \end{equation}

Step 2. Step 1 provides a starting point, from which we can now move the plane $T_\lambda$, as long as (3.13) holds, to its limiting position. To this end, let us define

(3.14)\begin{equation} \lambda_{0}:=\sup\left\{\lambda\in\mathbb{R} \mid U_{\mu}> 0\ \textrm{and}\ V_{\mu}> 0,\ \text{in} \ \Sigma_{\mu}\cap\Omega, \ \forall - 1<\mu<\lambda\right\}. \end{equation}

Our goal is to show that $\lambda _{0}=0$.

To prove it, we use the contraction and suppose $\lambda _{0}<0$, then we can infer from (1.1) that $U_{\lambda _{0}}>0$, $U_{\lambda _{0}}>0$ in $(\Omega ^{\lambda _{0}}\setminus \Omega )\cap \Sigma _{\lambda _{0}}$ ($A^{\lambda }$ denotes the reflection of a set $A$ about $T_{\lambda }$), then we must have

(3.15)\begin{equation} U_{\lambda_{0}}(x)>0,\ V_{\lambda_{0}}(x)>0, \quad \forall \ x\in\Sigma_{\lambda_{0}}\cap\Omega. \end{equation}

Otherwise, we assume that there exists $x_{0}\in \Sigma _{\lambda _{0}}\cap \Omega$ such that $U_{\lambda _{0}}(x_{0})=0$ (the same arguments as follows can also yield a contradiction for the case that $V_{\lambda _{0}}(x_{0})=0$). Then from step 1, we have

(3.16)\begin{equation} \left(-\Delta+m^{2}\right)^{s}U_{\lambda_{0}}(x)\geq 0, \quad \forall \ x\in\Sigma_{\lambda_{0}}\cap\Omega. \end{equation}

By the definition of $(-\Delta +m^{2})^{s}$, we have

(3.17)\begin{align} & \left(-\Delta+m^{2}\right)^{s}U_{\lambda_{0}}(x) \nonumber\\ & \quad = c_{N, s} m^{{{N}/{2}+s}} P.V.\int_{\Sigma_{\lambda}}\left(\frac{K_{{{N}/{2}+s}}(m|\bar{x}-{y}^{\lambda}|)}{|\bar{x}-{y}^{\lambda}|^{{{N}/{2}+s}}}-\frac{K_{{{N}/{2}+s}}(m|\bar{x}-y|)} {|\bar{x}-y|^{{{N}/{2}+s}}}\right)\notag\\ & \qquad \times U_{\lambda}(y)\,\textrm{d}y<0. \end{align}

This contradicts (3.16). Hence (3.15) must hold.

Thanks to (3.15), so there exists a compact subset $K\subset \subset \Omega ^{\lambda _{0}}\cap \Sigma _{\lambda _{0}}$ and a constant $c>0$ such that

(3.18)\begin{equation} U_{\lambda_{0}}(x)\geq c>0,\ V_{\lambda_{0}}(x)\geq c>0, \quad \forall \ x\in K\cap\Omega, \end{equation}

and $(\Sigma _{\lambda _{0}}\cap \Omega )\setminus (K\cap \Omega )$ is a narrow region. Since the continuity of $w_{\lambda }$ about $\lambda$, then there exists a sufficiently small $0<\epsilon <\min \{-\lambda _{0},\lambda _{0}+1\}$ such that, for any $\lambda \in [\lambda _{0},\lambda _{0}+\epsilon ]$,

(3.19)\begin{equation} U_{\lambda}(x)>0,\ V_{\lambda}(x)>0, \quad \forall \ x\in K\cap\Omega, \end{equation}

and $(\Sigma _{\lambda _{0}+\epsilon }\cap \Omega )\setminus (K\cap \Omega )$ is also a narrow region.

Next, we will show that

(3.20)\begin{equation} U_{\lambda}(x)\geq 0,\ V_{\lambda}(x)\geq 0, \quad \forall \ x\in(\Sigma_{\lambda}\cap\Omega)\setminus(K\cap\Omega). \end{equation}

If (3.20) is not valid, we may assume that there exists a $\tilde {\lambda }\in (\lambda _{0},\lambda _{0}+\epsilon ]$ (depending on $\epsilon$) such that

(3.21)\begin{equation} \inf_{(\Sigma_{\tilde{\lambda}}\cap\Omega)\setminus(K\cap\Omega)}U_{\tilde{\lambda}}=\inf_{\Sigma_{\tilde{\lambda}}\cap\Omega}U_{\tilde{\lambda}} =\inf_{\lambda\in(\lambda_{0},\tilde{\lambda}]}\inf_{x\in\Sigma_\lambda}U_\lambda(x)<0. \end{equation}

Consequently, there exists $\tilde {x}\in (\Sigma _{\tilde {\lambda }}\cap \Omega )\setminus (K\cap \Omega )$ such that

(3.22)\begin{equation} U_{\tilde{\lambda}}(\tilde{x})=\inf_{(\Sigma_{\tilde{\lambda}}\cap\Omega)\setminus(K\cap\Omega)}U_{\tilde{\lambda}} =\inf_{\Sigma_{\tilde{\lambda}}\cap\Omega}U_{\tilde{\lambda}}=\inf_{\Sigma_{\tilde{\lambda}}}U_{\tilde{\lambda}}<0. \end{equation}

Then we can infer from (3.5)–(3.9) and Narrow region principle proposition 2.1 that

(3.23)\begin{equation} U_{\tilde{\lambda}}>0,\quad V_{\tilde{\lambda}}>0 \quad \text{in} \ (\Sigma_{\tilde{\lambda}}\cap\Omega)\setminus(K\cap\Omega), \end{equation}

which yields a contradiction with (3.21). As a consequence, we have, for any $\lambda \in [\lambda _{0},\lambda _{0}+\epsilon ]$, (3.20) holds. Furthermore, it follows from (3.16) and (3.17) that

(3.24)\begin{equation} U_{\lambda}(x)>0,\ V_{\lambda}(x)>0, \quad \forall \ x\in(\Sigma_{\lambda}\cap\Omega)\setminus(K\cap\Omega), \end{equation}

and hence, for any $\lambda \in [\lambda _{0},\lambda _{0}+\epsilon ]$,

(3.25)\begin{equation} U_{\lambda}(x)>0,\ V_{\lambda}(x)>0, \quad \forall \ x\in\Sigma_{\lambda}\cap\Omega. \end{equation}

This contradicts the definition of $\lambda _{0}$. Thus $\lambda _{0}=0$.

By choosing $(x_1,x')$, $(\bar {x}_1,x')\in \Omega$ with $0>x_1>\bar {x}_1$ and $\lambda =({x_{1}+\bar {x}_{1}})/{2}$, then we get

\[ u(x_{1},x')>u(\bar{x}_{1},x'),\quad v(x_{1},x')>v(\bar{x}_{1},x'), \]

and hence $u(x_{1},x')$ and $v(x_{1},x')$ are strictly increasing in the left half of $\Omega$ in $x_{1}$-direction. Moreover, if $f(x_1, x', u, p_1, p_2,\dots, p_n)= f(-x_{1}, x', u, -p_1, p_2,\dots, p_n)$, then $\hat {u}(x_{1},x'):=u(-x_{1},x')$ and $\hat {v}(x_{1},x'):=v(-x_{1},x')$ also solves system (1.1). Thus we have derived that

(3.26)\begin{equation} \hat{u}(x_1,x')\leq \hat{u}({-}x_1, x'),\ \hat{v}(x_1,x')\leq \hat{v}({-}x_1, x'), \quad \forall \ (x_1,x')\in \Omega, \ x_{1}<0. \end{equation}

Equation (3.26) is equivalent to

(3.27)\begin{equation} u(x_1, x')\geq u({-}x_1, x'),\ v(x_1, x')\geq v({-}x_1, x'), \quad \forall \ (x_1,x')\in \Omega, \ x_{1}<0. \end{equation}

Combining this with $u(x_1, x')\leq u(-x_1, x')$, $u(x_1, x')\leq u(-x_1, x')$ yields that

(3.28)\begin{equation} u(x_1, x')=u({-}x_1, x'),\ v(x_1, x')=v({-}x_1, x'), \quad \forall \ (x_1,x')\in \Omega, \ x_{1}<0, \end{equation}

we see $u$ and $v$ are symmetric in the $x_1$ direction about $\{x\in \mathbb {R}^{N} \mid x_{1}=0\}$. This completes the proof of theorem 1.1.

4. Proof of theorem 1.2

In this section, we will use the direct method of moving plane to prove the strictly monotonicity and symmetry of nonnegative solutions to generalized pseudo-relativistic Schrödinger system (1.19) in an unbounded domain.

Choose an arbitrary direction to be the $x_{1}$-direction and keep the notations $T_{\lambda }$, $\Sigma _{\lambda }$, $x_{\lambda }$, $U_{\lambda }$ and $V_{\lambda }$ defined in § 2.

We carry out the direct method of moving planes procedure in two steps.

Proof. Step 1. We show that, for sufficiently negative $\lambda$,

(4.1)\begin{equation} U_{\lambda}(x)\geq 0\quad \text{and}\quad V_{\lambda}(x)\geq 0, \quad \forall \ x\in\Sigma_{\lambda}. \end{equation}

If (4.1) does not hold, then

\[ \inf_{\Sigma_{\lambda}}U_{\lambda}<0 \quad \text{or}\quad \inf_{\Sigma_{\lambda}}V_{\lambda}<0. \]

Let's suppose $\inf _{\Sigma _{\lambda }}U_{\lambda }<0$. The same arguments as follows can also yield a contradiction for the case that $\inf _{\Sigma _{\lambda }}V_{\lambda }<0$. Then there exists a sequence $\lambda _k\rightarrow -\infty$ as $k\rightarrow +\infty$ such that

(4.2)\begin{equation} \inf_{x\in\Sigma_{\lambda_{k}}\cap\Omega}U_{\lambda_{k}}(x)=\inf_{\lambda \leq\lambda_k}\inf_{x\in\Sigma_\lambda}U_\lambda(x)<0, \end{equation}

for every $k=1,2,\dots$. Moreover, for every $k=1,2,\dots$, $\inf _{\Sigma _{\lambda _{k}}\cap \Omega }U_{\lambda _{k}}$ is attained at some $x^{k}\in \Sigma _{\lambda _{k}}\cap \Omega$, that is,

(4.3)\begin{equation} U_{\lambda_{k}}(x^{k})=\inf_{\Sigma_{\lambda_{k}}\cap\Omega}U_{\lambda_{k}}=\inf_{\Sigma_{\lambda_{k}}}U_{\lambda_{k}}<0. \end{equation}

Using the assumption (1.13), $F_{1}$, $F_2$, (1.15), (1.16) and the asymptotic property (1.17), we have, for $k$ large enough, at any points $x\in \Sigma _{\lambda _{k}}\cap \Omega$ where $U_{\lambda _{k}}(x)<0$,

(4.4)\begin{equation} |c_{1}(x)|\leq C\left(|u_{\lambda_k}(x)|^{\beta_{1}}+|u(x)|^{\beta_1}\right)\leq 2C\left[u(x)\right]^{\beta_{1}}, \end{equation}

and hence

(4.5)\begin{equation} \liminf_{\substack{x\in\Sigma_{\lambda_{k}}\cap\Omega, U_{\lambda_{k}}<0 \\ |x|\rightarrow+\infty}}c_{1}(x)+m^{2s}\geq{-}2C\cdot \limsup_{\substack{x\in\Sigma_{\lambda_{k}}\cap\Omega, U_{\lambda_{k}}<0 \\ |x|\rightarrow+\infty}}\left[u(x)\right]^{\beta_{1}}+m^{2s}>0. \end{equation}

Similarly, we can infer from the asymptotic property (1.17) that

(4.6)\begin{equation} \liminf_{\substack{x\in\Sigma_{\lambda_{k}}\cap\Omega, V_{\lambda_{k}}<0 \\ |x|\rightarrow+\infty}}c_{4}(x)+m^{2t}\geq{-}2C\cdot \limsup_{\substack{x\in\Sigma_{\lambda_{k}}\cap\Omega, V_{\lambda_{k}}<0 \\ |x|\rightarrow+\infty}}\left[v(x)\right]^{\beta_{2}}+m^{2t}>0. \end{equation}

Combining (4.5), (4.6) and (4.6) the assumption $F_{1}$, $F_2$, we know $c_{i}(x) (i=1,2,3,4)$ satisfy the condition of proposition 2.3. By the Decay at infinity proposition 2.3, it is easy to deduce, and there exists a $R_{0}>0$ such that

(4.7)\begin{equation} |x^{k}|\leq R_{0}, \end{equation}

This will lead to a contradiction provided that $\lambda _{k}\leq -R_{0}$ as $k\rightarrow \infty$. Thus (4.1) holds.

Since $u(x), v(x)\rightarrow 0$ as $|x|\rightarrow +\infty$ and $x\in \Sigma _{0}$, we can actually deduce that $U_{\lambda }\not \equiv 0$ or $V_{\lambda }\not \equiv 0$ in $\Sigma _{\lambda }$ for any $\lambda \leq -R_{0}$ by choosing $R_{0}$ larger. Then, similar to (3.13) in step 1 in the proof of theorem 1.1, we can also get

(4.8)\begin{equation} U_\lambda>0,\ V_\lambda>0, \quad \text{in} \ \Sigma_\lambda\cap\Omega, \quad \forall \ \lambda\leq{-}R_0. \end{equation}

Step 2. Step 1 provides a starting point, from which we can now move the plane $T_\lambda$, as long as (4.8) holds, to its limiting position. To this end, let us define

(4.9)\begin{equation} \lambda_{0}:=\sup\left\{\lambda\in(-\infty,0] \mid U_{\mu}> 0\ \text{and} \ V_{\mu}> 0,\ \text{in} \ \Sigma_{\mu}, \ \forall \ \mu \leq \lambda\right\}. \end{equation}

It follows from step 1 that $-R_{0}\leq \lambda _{0}\leq 0$. One can easily verify that

(4.10)\begin{equation} U_{\lambda_{0}}(x)\geq 0\quad \text{and}\quad V_{\lambda_{0}}(x)\geq 0 \quad \forall \ x\in\Sigma_{\lambda_{0}}. \end{equation}

Case (i). There exists a line $\mathcal {L}$ parallel to $x_{1}$-axis satisfying $\mathcal {L}\cap \Omega \neq \emptyset$ such that $\mathcal {L}\cap \Omega ^{c}\neq \emptyset$. In this case, we will show that

\[\lambda_0=0. \]

Now suppose on the contrary that $\lambda _{0}<0$. Note that $U_{\lambda _{0}}\not \equiv 0$ or $V_{\lambda _{0}}\not \equiv 0$ in $\Sigma _{\lambda _{0}}$, then from the step 1 in the proof of theorem 1.1, we can derive that

(4.11)\begin{equation} U_{\lambda_0}>0,\ U_{\lambda_0}>0, \quad \text{in} \ \Omega\cap\Sigma_{\lambda_0}. \end{equation}

Next, we will show that the plane $T_{\lambda }$ can be moved a little bit further from $T_{\lambda _{0}}$ to the right. More precisely, we will show that there exists a $\varepsilon >0$, such that for any $\lambda \in [\lambda _{0},\lambda _{0}+\varepsilon ]$, it holds

(4.12)\begin{equation} U_\lambda\geq 0,\ V_\lambda\geq 0, \quad \text{in} \ \Sigma_\lambda, \quad \forall \ \lambda_{0}<\lambda\leq\lambda_0+\varepsilon. \end{equation}

To prove (4.12), we shall use the Narrow region principle proposition 2.1 and the Decay at Infinity proposition 2.3.

Suppose (4.12) is not true, for convenience, we assume that there exists a sequence $\{\lambda _{k}\}\subset (\lambda _{0},0)$ satisfying $\lambda _k\rightarrow \lambda _{0}$ as $k\rightarrow +\infty$ such that

(4.13)\begin{equation} \inf_{x\in\Sigma_{\lambda_{k}}\cap\Omega}U_{\lambda_{k}}(x)=\inf_{\lambda \leq\lambda_k}\inf_{x\in\Sigma_\lambda}U_\lambda(x)<0 \end{equation}

Moreover, for every $k=1,2,\dots$, $\inf _{\Sigma _{\lambda _{k}}\cap \Omega }w_{\lambda _{k}}$ can be attained at some $x^{k}\in \Sigma _{\lambda _{k}}\cap \Omega$, that is,

(4.14)\begin{equation} U_{\lambda_{k}}(x^{k})=\inf_{\Sigma_{\lambda_{k}}\cap\Omega}U_{\lambda_{k}}=\inf_{\Sigma_{\lambda_{k}}}U_{\lambda_{k}}<0. \end{equation}

We can deduce the proof of proposition 2.3 that $V_{\lambda _{k}}(x^{k})<0$, and hence there exists some $x^{j}\in \Sigma _{\lambda _{k}}\cap \Omega$ such that $V_{\lambda _{k}}(x^{j})=\inf _{\Sigma _{\lambda _{k}}\cap \Omega }V_{\lambda _{k}}=\inf _{\Sigma _{\lambda _{k}}}V_{\lambda _{k}}<0$. Through direct calculation, we get

(4.15)\begin{equation} \left\{\begin{aligned} (-\Delta+m^{2})^{s} U_{\lambda_{k}}(x^{k})+c_{1}(x)U_{\lambda_{k}}(x)+c_{2}(x)V_{\lambda_{k}}(x)=0,\\ (-\Delta+m^{2})^{t} V_{\lambda_{k}}(x^{k})+c_{3}(x)V_{\lambda_{k}}(x)+c_{4}(x)U_{\lambda_{k}}(x)=0, \end{aligned}\right. \end{equation}

where $c_i(x)$ is the same as (3.6)–(3.9). Now we shall show that $\{x^{k}\}$ is bounded.

If $\{x^{k}\}$ is not bounded, then up to a subsequence (still denote by $\{x^{k}\}$), $|x^{k}|\rightarrow +\infty$ as $k\rightarrow +\infty$. By the assumption (1.15) and (1.16), we have, for $k$ large enough,

(4.16)\begin{equation} |c_{1}(x^{k})|\leq 2C\left[u(x^{k})\right]^{\beta_{1}},\quad|c_{3}(x^{k})|\leq 2C\left[v(x^{k})\right]^{\beta_{2}}. \end{equation}

From (2.21) and (2.26) in Decay at infinity proposition 2.3, we infer that

(4.17)\begin{align} 0& \leq(-\Delta+m^{2})^{t} V_{\lambda_{k}}(x^{j})+c_{3}(x^{j})V_{\lambda_{k}}(x^{j})+c_{4}(x^{j})U_{\lambda_{k}}(x^{j})\nonumber\\ & \leq\left[\frac{(A_{1}(x^{k})+c_{1}(x^{k})+m^{2s})(c_{3}(x^{j})+m^{2t})-c_{2}(x^{k})c_{4}(x^{j})}{A_{1}(x^{k})+c_{1}(x^{k})+m^{2s}}\right]V_{\lambda_{k}}(x^{j})\nonumber\\ & \leq\left[\frac{(A_{1}(x^{k})-2C\left[u(x^{k})\right]^{\beta_{1}}+m^{2s})({-}2C\left[v(x^{j})\right]^{\beta_{2}}+m^{2t})-c_{2}(x^{k})c_{4}(x^{j})}{A_{1}(x^{k})+c_{1}(x^{k})+m^{2s}}\right]V_{\lambda_{k}}(x^{j})\nonumber\\ & <0, \end{align}

where $A_{1}(x)$ is the same to proposition 2.3, the last equation holds because of the assumption (1.18). This leads to a contradiction. Thus there exists $R_{\ast }>0$ such that $|x^{k}|< R_{\ast }$.

In fact, since $\lambda _{0}<0$, one can infer from (1.1) that $U_{\lambda _{0}}>0$, $V_{\lambda _{0}}>0$ in $(\Omega ^{\lambda _{0}}\setminus \Omega )\cap \Sigma _{\lambda _{0}}$ ($A^{\lambda }$ denotes the reflection of a set $A$ about $T_{\lambda }$), and hence (4.11) yields that $U_{\lambda _{0}}>0$, $V_{\lambda _{0}}>0$ in $\Omega ^{\lambda _{0}}\cap \Sigma _{\lambda _{0}}$. So there exists a compact subset $K\subset \subset \Omega ^{\lambda _{0}}\cap \Sigma _{\lambda _{0}}$ and a constant $c>0$ such that

(4.18)\begin{equation} U_{\lambda_{0}}(x)\geq c>0,\ V_{\lambda_{0}}(x)\geq c>0, \quad \forall \ x\in K\cap\Omega\cap B_{R_{{\ast}}}(0), \end{equation}

and $(\Sigma _{\lambda _{0}}\cap \Omega \cap B_{R_{\ast }}(0))\setminus (K\cap \Omega \cap B_{R_{\ast }}(0))$ is a narrow region. Hence we choose sufficiently small $0<\varepsilon <\min \{-\lambda _{0},\lambda _{0}+1\}$ such that, for any $\lambda \in [\lambda _{0},\lambda _{0}+\varepsilon ]$,

(4.19)\begin{equation} U_{\lambda}(x)>0,\ V_{\lambda}(x)>0, \quad \forall \ x\in K\cap\Omega\cap B_{R_{{\ast}}}(0), \end{equation}

and $(\Sigma _{\lambda _{0}+\varepsilon }\cap \Omega \cap B_{R_{\ast }}(0))\setminus (K\cap \Omega \cap B_{R_{\ast }}(0))$ is also a narrow region. Inequality (4.19) imply $x^{k}\in (\Sigma _{\lambda _{0}+\varepsilon }\cap \Omega \cap B_{R_{\ast }}(0))\setminus (K\cap \Omega \cap B_{R_{\ast }}(0))$. From the Lipschitz continuous of $f,g$ with respect to $u,v$, we have $c_{i}(x^{k})$ are uniformly bounded. Since $(\Sigma _{\lambda _{k}}\cap \Omega \cap B_{R_{\ast }}(0))\setminus (K\cap \Omega \cap B_{R_{\ast }}(0))$ is a narrow region. We can infer from the assumption of $c_{i}(x)$ and Narrow region principle proposition 2.1 that

(4.20)\begin{equation} U_{\lambda_{k}}>0,\ V_{\lambda_{k}}>0 \quad \text{in} \ (\Sigma_{\lambda_{k}}\cap\Omega\cap B_{R_{{\ast}}}(0))\setminus(K\cap\Omega\cap B_{R_{{\ast}}}(0))\quad \text{as}\ k\rightarrow\infty, \end{equation}

which yields a contradiction with (4.14). Thus we have derived (4.12).

From step 1 in the proof of 1.1, we have either $U_{\lambda }>0$, $V_{\lambda }>0$, or $U_{\lambda }=V_{\lambda }\equiv 0$ in $\Omega \cap \Sigma _{\lambda }$. Furthermore, since $U_{\lambda _{0}}>0$ in $\Omega \cap \Sigma _{\lambda _{0}}$, by continuity, choosing $\varepsilon >0$ smaller if necessary, we actually have

(4.21)\begin{equation} U_\lambda>0,\ V_{\lambda}>0 \quad \text{in} \ \Omega\cap\Sigma_\lambda, \quad \forall \ \lambda_{0}\leq\lambda\leq\lambda_0+\varepsilon. \end{equation}

This contradicts the definition of $\lambda _{0}$. Thus $\lambda _{0}=0$. The strict monotonicity follows from $U_\lambda >0$ and $V_\lambda >0$ in $\Sigma _\lambda \cap \Omega$ for any $\lambda <\lambda _0$.

Case (ii). Any line $\mathcal {L}$ parallel to $x_{1}$-axis such that $\mathcal {L}\cap \Omega \neq \emptyset$ must satisfy $\mathcal {L}\cap \Omega ^{c}=\emptyset$. We will show that either $\lambda _{0}=0$ or $\lambda _{0}<0$ and $U_{\lambda _{0}}=V_{\lambda _{0}}\equiv 0$ in $\Sigma _{\lambda _{0}}$.

Assume that $\lambda _{0}<0$ but $U_{\lambda _{0}}\not \equiv 0$ or $V_{\lambda _{0}}\not \equiv 0$ in $\Sigma _{\lambda _{0}}$. Then, similar to (4.11), we can derive that

(4.22)\begin{equation} U_{\lambda_0}>0,\ V_{\lambda_0}>0, \quad \text{in} \ \Omega\cap\Sigma_{\lambda_0}. \end{equation}

Next, similar to (4.21), we can show that, there exists $\varepsilon >0$ small enough such that

(4.23)\begin{equation} U_\lambda>0,\ V_\lambda>0, \quad \text{in} \ \Omega\cap\Sigma_\lambda, \quad \forall \ \lambda_{0}\leq\lambda\leq\lambda_0+\varepsilon, \end{equation}

which contradicts the definition of $\lambda _{0}$. As a consequence, $\lambda _{0}=0$ is correct. This completes the proof of theorem 1.2.

5. Proof of theorem 1.3

In this section, we shall prove theorem 1.3. For this purpose, we first establish a maximum principle for the anti-symmetric system in an unbounded domain.

Lemma 5.1 For any function $\phi \in C^{1,1}(\mathbb {R}^{N})$ with $\|\phi \|_{C^{1,1}(\mathbb {R}^{N})}<+\infty$ and any $r>0$, set $\phi _r(x):=\phi (\frac {x}{r})$. Then,

\[ \left|\left[\left(-\Delta+m^{2}\right)^{s}-m^{2s}\right]\phi_r(x)\right|\leq \frac{C}{r^{2s}}, \quad \forall\ x\in\mathbb{R}^{N}, \]

where $C>0$ is a constant depending on $N$, $s$ and $\|\phi \|_{C^{1,1}(\mathbb {R}^{N})}$, but independent of $r$.

The proof of lemma 5.1, please refer to lemma 2.10 in [23].

For simplicity reason, in this section, we will use $\Sigma$ to stand for $\Sigma _\lambda$, use $T$ to stand for $T_\lambda$, and use $(U,V)$ to stand for $(U_\lambda,V_\lambda )$, that is

(5.1)\begin{equation} \left\{\begin{aligned} U(x) & :=u\left(x^{\lambda}\right)-u(x) \\ V(x) & :=v\left(x^{\lambda}\right)-v(x). \end{aligned}\right. \end{equation}

Proposition 5.2 Maximum principles for anti-symmetric system in a unbounded domain

Assume that $U \in \mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N})$, $V \in \mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{loc}^{1,1}(\mathbb {R}^{N})$ are bounded from above, $U({x^{\lambda }})=-U(x)$ and $V({x^{\lambda }})=-V(x)$ in $\Sigma$, where ${x^{\lambda }}$ is the reflection point of $x$ with respect to $T$. Suppose that

(5.2)\begin{align} \begin{cases}{(-\Delta+m^{2})^{s} U(x)+c_{1}(x)U(x)+c_{2}(x)V(x)\leq 0} & x\in\{x\in \Omega| U(x)>0\} \\ {(-\Delta+m^{2})^{t} V(x)+c_{3}(x)V(x)+c_{4}(x)U(x)\leq 0} & x\in\{x\in \Omega| V(x)>0\}, \end{cases} \end{align}

where $c_{2}(x)<0$, $c_{4}(x)<0$, $c_{1}(x)$ and $c_{3}(x)$ satisfy

(5.3)\begin{equation} \inf_{\{x\in\Sigma \mid U(x)>0\}}\,c_{1}(x)>{-}m^{2s}\quad \text{and}\quad \inf_{\{x\in\Sigma \mid V(x)>0\}}\,c_{3}(x)>{-}m^{2t}, \end{equation}

meanwhile

\[ \left(\inf_{\{x\in\Sigma \mid U(x)>0\}}\,c_{1}(x)+m^{2s}\right)\left(\inf_{\{x\in\Sigma \mid V(x)>0\}}\,c_{3}(x)+m^{2t}\right)>\inf_{\Sigma}c_{2}(x) \cdot\inf_{\Sigma}c_{4}(x). \]

Then, we have

(5.4)\begin{equation} U(x) \leq 0,\quad V(x) \leq 0, \quad \forall\ x \in\Sigma. \end{equation}

Proof. Suppose that (5.4) is false, then we have

\[\sup_{\Sigma} U(x)>0 \quad \text{or}\quad \sup_{\Sigma} V(x)>0. \]

We may assume

\[ \sup_{\Sigma} U(x)>0. \]

The same arguments as follows can also yield a contradiction for the case that $\sup _{\Sigma } V(x)>0$.

Since $U$ is bounded from above, we have

\[ M:=\sup_{\Sigma} U(x)>0. \]

Noting that $\Sigma$ is unbounded domain, hence $\sup _{\Sigma } U(x)$ may not be attained. So, there exists sequences $x^{k}\in \Sigma$ and $0<\beta _k<1$ with $\beta _k\rightarrow 1$ as $k\rightarrow \infty,$ such that

(5.5)\begin{equation} U(x^{k})\geq \beta_k M. \end{equation}

Now we denote

\[T=\{x\in\mathbb{R}^{N}| x_1=0\}, \quad \Sigma=\{x\in\mathbb{R}^{N}| x_1<0\}. \]

Let $d_k:=dist(x^{k}, T)$ and

\[ \psi(x)=\begin{cases}\textrm{e}^{{|x|^{2}}/{|x|^{2}-1}}, & |x|<1\\ 0, & |x|\geq 1.\end{cases} \]

Then we see that $\psi \in C_0^{\infty }(\mathbb {R}^{N})$ and $|(-\Delta +m^{2})^{s}\psi (x)|\leq C$ for all $x \in \mathbb {R}^{N}$. Moreover, $(-\Delta +m^{2})^{s}\psi (x)$ is monotone decreasing with respect to $|x|$ and

\[ \displaystyle\frac{\left(-\Delta+m^{2}\right)^{s}\psi(x)}{|x|^{-({N+1})/{2}-s}\textrm{e}^{-|x|}}\to 1,\quad \hbox{as } |x|\rightarrow +\infty. \]

Set

\[\psi_k(x):=\psi\left(\displaystyle\frac{x-{(x^{k})^{\lambda}}}{d_k}\right) \quad \text{and} \quad \tilde{\psi_k}(x)=\psi_k({x}^{\lambda})=\psi\left(\frac{x-x^{k}}{d_k}\right), \]

where ${x}^{\lambda }=(-x_1, x_2,\ldots, x_N)$ is the anti-symmetry point of $x$ with respect to $x_1$ direction.

Obviously $\tilde {\psi _k}-\psi _k$ is anti-symmetric with respect to $T$. Let $\varepsilon _k=(1-\beta _k)M$, we have

\[ U(x^{k})+\varepsilon_k[\tilde{\psi_k}-\psi_k](x^{k})\geq M. \]

We denote

\[U_k(x):=U(x)+\varepsilon_k[\tilde{\psi_k}-\psi_k](x). \]

Then $U_k$ is also anti-symmetric with respect to $T$.

Noting that for any $x\in \Sigma \setminus B_{d_k}(x^{k})$, $U(x)\leq M$ and $\tilde {\psi _k}(x)=\psi _k(x)=0$, we have

\[ U_k(x^{k})\geq U_k(x), \quad \forall \ x\in\Sigma\setminus B_{d_k}(x^{k}). \]

Hence the supremum of $U_k(x)$ in $\Sigma$ is achieved in $B_{d_k}(x^{k})$. Consequently, there exists a point $\overline {x}^{k}\in B_{d_k}(x^{k})$ such that

(5.6)\begin{equation} U_k(\overline{x}^{k})=\sup_{x\in\Sigma} U_k(x)\geq M. \end{equation}

By the choice of $\varepsilon _k$, it is easy to verify that $U(\bar {x}^{k})\geq \beta _k M>0$.

Next, we will evaluate the upper and lower bound of $(-\Delta +m^{2})^{s}U_k(\bar {x}^{k})$. In fact, we can obtain from (5.2) and lemma 5.1 that

(5.7)\begin{equation} \left(-\Delta+m^{2}\right)^{s}U_{k}(\bar{x}^{k})\leq{-}c_{1}(\bar{x}^{k})U(\bar{x}^{k})-c_{2}(\bar{x}^{k})V(\bar{x}^{k})+C\left(\frac{1}{d_k^{2s}}+1\right)\varepsilon_k. \end{equation}

On the other hand, combine with the following facts

\[ \displaystyle\frac{K_{{N}/{2}+s}(m|\bar{x}^{k}-y|)}{|\bar{x}^{k}-y|^{{N}/{2}+s}}> \frac{K_{{N}/{2}+s}(m|\bar{x}^{k}-{y}^{\lambda}|)}{|\bar{x}^{k}-{y}^{\lambda}|^{{n}/{2}+s}}, \quad \forall \ y\in \Sigma, \]

and

\[ U_k(\bar{x}^{k})\geq U_k(y),\quad \forall \ y\in \Sigma. \]

We can derive the following lower bound

(5.8)\begin{align} & \left(-\Delta+m^{2}\right)^{s}U_k(\bar{x}^{k}) \nonumber\\ & \quad =c_{N,s} m^{{N}/{2}+s} P.V.\int_{\mathbb{R}^{N}}\frac{U_k(\bar{x}^{k})-U_k(y)}{|\bar{x}^{k}-y|^{{N}/{2}+s}} K_{{N}/{2}+s}\left(m|\bar{x}^{k}-y|\right)\textrm{d}y+m^{2 s} U_k(\bar{x}^{k}) \nonumber\\ & \quad =c_{N, s}m^{{N}/{2}+s}P.V. \int_{\Sigma}\left[\frac{U_k(\bar{x}^{k})-U_k(y)}{|\bar{x}^{k}-y|^{{N}/{2}+s}} K_{{N}/{2}+s}(m|\bar{x}^{k}-y|)\right. \nonumber\\ & \qquad \left.+\frac{U_k(\bar{x}^{k})+U_k(y)}{|\bar{x}^{k}-{y}^{\lambda}|^{{N}/{2}+s}}K_{{N}/{2}+s} (m|\bar{x}^{k}-{y}^{\lambda}|)\right]dy+m^{2s}U_k(\bar{x}^{k})\nonumber\\ & \quad =c_{N,s} m^{{N}/{2}+s} P.V.\int_{\Sigma}\left(\frac{K_{{N}/{2}+s}(m|\bar{x}^{k}-y|)}{|\bar{x}^{k}-y|^{{N}/{2}+s}} -\frac{K_{{N}/{2}+s}(m|\bar{x}^{k}-{y}^{\lambda}|)}{|\bar{x}^{k}-{y}^{\lambda}|^{{N}/{2}+s}}\right) \notag\\ & \qquad \times (U_k(\bar{x}^{k})-U_k(y))\,\textrm{d}y \nonumber\\ & \qquad +2c_{N,s}m^{{N}/{2}+s} U_k(\bar{x}^{k})\int_{\Sigma} \frac{K_{{N}/{2}+s}(m|\bar{x}^{k}-{y}^{\lambda}|)}{|\bar{x}^{k}-{y}^{\lambda}|^{{N}/{2}+s}}\,\textrm{d}y+m^{2s} U_k(\bar{x}^{k}) \nonumber\\ & \quad >m^{2s}U_k(\bar{x}^{k}). \end{align}

Combining (5.7) and (5.8), we derive

\begin{align*} m^{2 s}U(\bar{x}^{k})& \leq m^{2 s}U_k(\bar{x}^{k})\leq{-}\left(\inf_{\{x\in\Sigma \mid U(x)>0\}}\, c_{1}(x)\right)U(\bar{x}^{k})-c_{2}(\bar{x}^{k})V(\bar{x}^{k})\\ & \quad +C\left(\frac{1}{d_k^{2s}}+1\right)\varepsilon_k. \end{align*}

Now we choose $k$ large enough such that $\beta _{k}>\frac {1}{2}$, then we have

(5.9)\begin{equation} \left(\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{1}(x)+m^{2s}\right)\beta_{k}+c_{2}(\bar{x}^{k})\frac{V(\bar{x}^{k})}{M}\leq 2C(1-\beta_k), \end{equation}

which implies

(5.10)\begin{equation} \left(\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{1}(x)+m^{2s}\right)\beta_{k}+c_{2}(\bar{x}^{k})\frac{V(\bar{x}^{k})}{U(\bar{x}^{k})}\leq 2C(1-\beta_k). \end{equation}

If we take the limit $k\rightarrow +\infty$, apply the fact of $c_{2}<0$ and

\[\inf_{\{x\in\Sigma \mid U(x)>0\}}\,c_{1}(x)>{-}m^{2s},\]

we deduce that

\[ V(\bar{x}^{k})>0. \]

Since $V$ is bounded from above, we have

\[ M_{1}:=\sup_{\Sigma} V(x)>0. \]

Hence, there exists sequences $x^{l}\in \Sigma$ and $0<\beta _l<1$ with $\beta _l\rightarrow 1$ as $l\rightarrow \infty$ such that

(5.11)\begin{equation} U(x^{l})\geq \beta_l M_{1}. \end{equation}

By using the similar arguments as above, we can get the following upper bound

(5.12)\begin{equation} \left(-\Delta+m^{2}\right)^{t}V_{l}(\bar{x}^{l})\leq{-}c_{3}(\bar{x}^{l})V(\bar{x}^{l})-c_{4}(\bar{x}^{l})U(\bar{x}^{l})+C\left(\frac{1}{d_l^{2t}}+1\right)\varepsilon_l. \end{equation}

where

\[ d_l:=dist(x^{l}, T)\quad \text{and}\quad \varepsilon_l=(1-\beta_l)M_{1}, \]

\[ V_l(x):=V(x)+\varepsilon_l[\tilde{\psi_l}-\psi_l](x), \]

and

\[ V_l(\overline{x}^{l})=\sup_{x\in\Sigma} V_l(x)\geq M_{1}. \]

Similar to (5.8), we can also derive the following lower bound

(5.13)\begin{equation} \left(-\Delta+m^{2}\right)^{t}V_l(\bar{x}^{l})>m^{2t}V_l(\bar{x}^{l}). \end{equation}

Combine (5.12) and (5.13), we have

(5.14)\begin{equation} \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}V(\bar{x}^{l})+c_{4}(\bar{x}^{l}){U(\bar{x}^{l})}\leq C\left(\frac{1}{d_l^{2t}}+1\right)\varepsilon_l. \end{equation}

If we take the limit $k\rightarrow +\infty$, by (5.10), we have

(5.15)\begin{equation} U(\bar{x}^{k})\leq{-}\frac{c_{2}(\bar{x}^{k})}{\left(\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{1}(x)+m^{2s}\right)}V(\bar{x}^{k}). \end{equation}

Next, let us choose $l$ large enough such that $\beta _{l}>\frac {1}{2}$, then (5.12) becomes

(5.16)\begin{equation} \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}+c_{4}(\bar{x}^{l})\frac{U(\bar{x}^{l})}{M_{1}}\leq 2C(1-\beta_l). \end{equation}

Let $k,l\rightarrow \infty$ in (5.15) and (5.16), we get

\begin{align*} & \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}M_{1}+c_{4}(\bar{x}^{l}){U(\bar{x}^{l})} \\ & \quad \geq \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}{V(\bar{x}^{l})}+c_{4}(\bar{x}^{l}){U(\bar{x}^{l})} \\ & \quad \geq \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}{V(\bar{x}^{l})}+c_{4}(\bar{x}^{l}){U(\bar{x}^{k})} \\ & \quad \geq \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}{V(\bar{x}^{l})}-\displaystyle\frac{c_{2}(\bar{x}^{k})c_{4}(\bar{x}^{l})}{\left(\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{1}(x)+m^{2s}\right)}V(\bar{x}^{k})\\ & \quad \geq \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}{V(\bar{x}^{l})}-\frac{c_{2}(\bar{x}^{k})c_{4}(\bar{x}^{l})}{\left(\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{1}(x)+m^{2s}\right)}V(\bar{x}^{l}). \end{align*}

Hence,

\begin{align*} & \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right)\beta_{l}{V(\bar{x}^{l})}-\displaystyle\frac{c_{2}(\bar{x}^{k})c_{4}(\bar{x}^{l})}{\left(\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{1}(x)+m^{2s}\right)}V(\bar{x}^{l})\\ & \quad \leq 2C(1-\beta_l)M_{1}. \end{align*}

Taking the limit $k,l \rightarrow +\infty$, we have

\[ 0< \left(\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{3}(x)+m^{2t}\right){V(\bar{x}^{l})}-\displaystyle\frac{c_{2}(\bar{x}^{k})c_{4}(\bar{x}^{l})}{\left(\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{1}(x)+m^{2s}\right)}V(\bar{x}^{l})\leq 0. \]

The left inequality used the fact $c_{1}, c_{2}>0$ and

\begin{align*} & \left(\inf_{\{x\in\Sigma \mid U(x)>0\}}\,c_{1}(x)+m^{2s}\right)\left(\inf_{\{x\in\Sigma \mid V(x)>0\}}\,c_{3}(x)+m^{2t}\right)\\ & \quad >\inf_{\{x\in\Sigma \mid U(x)>0\}}c_{2}(x) \cdot\inf_{\{x\in\Sigma \mid V(x)>0\}}c_{4}(x). \end{align*}

That is impossible. So we have

\[ U(x)\leq 0 \quad \text{and}\quad V(x)\leq 0\ \text{in}\ \Sigma. \]

Proof of theorem 1.3. Let $T$ be any hyper-plane, $\Sigma$ be the half space on one side of the plane $T$ and $x_{N}$ be any given direction in $\mathbb {R}^{N}$. Set

\[ U(x)=u({x}^{\lambda})-u(x), \ V(x)=v(x^{\lambda})-v(x),\quad \hbox{ for all } x\in \Sigma,\]

and

\[ T:=\left\{x \in \mathbb{R}^{N} | x_{N}=\lambda \text { for any }\lambda \in \mathbb{R}^{N}\right\}, \]

where $x^{\lambda }$ is the reflection of $x$ with respect to $T$. We shall show that $u$ and $v$ are symmetric with respect to any hyper-plane $T$.

From the assumption in theorem 1.3, we have $U \in \mathcal {L}_{s}(\mathbb {R}^{N})\cap C_{\text {loc}}^{1,1}(\mathbb {R}^{N})$ and $V \in \mathcal {L}_{t}(\mathbb {R}^{N})\cap C_{\text {loc}}^{1,1}(\mathbb {R}^{N})$ are bounded. By a direct calculation, we get

(5.17)\begin{align} & \left(-\Delta+m^{2}\right)^{s}U(x)\nonumber\\ & \quad =f(x^{\lambda},u_{\lambda},v_{\lambda}, \nabla u(x^{\lambda}))-f(x,u,v,\nabla u(x)) \nonumber\\ & \quad \geq f(x,u_{\lambda},v_{\lambda}, \nabla u(x))-f(x,u,v,\nabla u(x)) \nonumber\\ & \quad = f(x,u_{\lambda},v_{\lambda}, \nabla u(x))- f(x,u,v_{\lambda}, \nabla u(x))\notag\\ & \qquad + f(x,u,v_{\lambda}, \nabla u(x))-f(x,u,v,\nabla u(x)) \nonumber\\ & \quad = \frac{\partial f}{\partial u}(x,\xi_{1},v_{\lambda},\nabla u(x))U(x)+\frac{\partial f}{\partial v}(x,u,\eta_{1},\nabla u(x))V(x) \nonumber\\ & \quad ={-}c_{1}(x)U(x)-c_{2}(x)V(x), \end{align}

and

(5.18)\begin{align} & \left(-\Delta+m^{2}\right)^{t}V(x) \nonumber\\ & \quad =g(x^{\lambda},u_{\lambda},v_{\lambda}, \nabla v(x^{\lambda}))-g(x,u,v,\nabla v(x)) \nonumber\\ & \quad \geq g(x,u_{\lambda},v_{\lambda}, \nabla v(x))-g(x,u,v,\nabla v(x)) \nonumber\\ & \quad = g(x,u_{\lambda},v_{\lambda}, \nabla v(x))- g(x,u,v_{\lambda}, \nabla v(x))+ g(x,u,v_{\lambda}, \nabla v(x))-g(x,u,v,\nabla v) \nonumber\\ & \quad =\frac{\partial g}{\partial u}(x,\xi_{2},v_{\lambda},\nabla v(x))U(x)+\frac{\partial g}{\partial v}(x,u,\eta_{2},\nabla u(x))V(x)\nonumber\\ & \quad ={-}c_{3}(x)V(x)-c_{4}(x)U(x), \end{align}

where $\xi _{1}, \xi _{2}$ are the values between $u(x)$ and $u_{\lambda }(x)$, $\eta _{1}, \eta _{2}$ are the values between $v(x)$ and $v_{\lambda }(x)$. Since $f(x, u, v,\mathbf {p}), g(x, u, v,\mathbf {q})$ are Lipschitz continuous with respect to $u,v$, we have $c_i(x)$(i=1,2,3,4) are bounded. By the assumptions of theorem 1.3, we have

\[ \inf_{\{x\in\Sigma \mid U(x)>0\}}\,c_{1}(x)>{-}m^{2s}\quad \text{and}\quad \inf_{\{x\in\Sigma \mid V(x)>0\}}\,c_{3}(x)>{-}m^{2t}, \]

and

\[ \left(\inf_{\{x\in\Sigma \mid U(x)>0\}}\,c_{1}(x)+m^{2s}\right)\left(\inf_{\{x\in\Sigma \mid V(x)>0\}}\,c_{3}(x)+m^{2t}\right)>\inf_{\Sigma} c_{2}(x)\cdot\inf_{\Sigma}c_{4}(x). \]

It follows from proposition 5.2 that

\[ U\leq 0 \quad \hbox{and}\quad V\leq 0\quad \text{in}\ {\Sigma}. \]

In a similar way, we can also prove that $U\leq 0, V\leq 0$ in $\mathbb {R}^{N}\setminus \Sigma$. Hence

(5.19)\begin{equation} U=V \equiv 0\quad \text{in} \ \mathbb{R}^{N}. \end{equation}

This implies that $u$ and $v$ are symmetric with respect to $T$ for any $\lambda$. Since the $x_{N}$-direction can be chosen arbitrarily, (5.19) suggests $u$ and $v$ are radially symmetric about any point. It follows that

\[ (u,v)\equiv (C_{1},C_{2})\quad \text{in}\ \mathbb{R}^{N}. \]

The proof of theorem 1.3 is completed.

6. Proof of theorems 1.4 and 1.5

In this section, by using the direct method of moving plane, we shall first prove the strict monotonicity for system (1.1) in coercive epigraph domain.

Proof of theorem 1.4. Without loss of generality, we assume

\[ \inf_{x\in\Omega}x_N=0. \]

First, let us introduce the following notations

\[ T_{\lambda}:=\left\{x \in \mathbb{R}_{+}^{N} | x_{N}=\lambda, \text{ for some } \lambda \in \mathbb{R}_{+}\right\},\]

\[\Sigma_{\lambda}:=\left\{x \in \mathbb{R}_{+}^{N} | x_{N}<\lambda\right\}. \]

And denoting the reflection of $x$ about the moving plane $T_{\lambda }$ by $x^{\lambda }:=(x_{1}, x_{2}, \ldots, 2 \lambda -x_{N})$. $U_\lambda (x), V_\lambda (x)$ are defined as in § 2.

Next, we carry out the moving planes procedure in two steps.

Step 1. We show that, for $\lambda >0$ sufficiently closing to $0$,

(6.1)\begin{equation} U_{\lambda}(x)>0,\ V_{\lambda}(x) > 0, \quad x \in \Sigma_{\lambda}\cap \Omega. \end{equation}

First, we shall prove that

(6.2)\begin{equation} U_{\lambda}(x)\geq 0,\ V_{\lambda}(x)\geq 0, \quad x \in \Sigma_{\lambda}\cap \Omega. \end{equation}

If (6.2) does not hold, for simplicity, we assume that there exists a sequence $\{\lambda _{k}\}$ and $x^{k}\in \Sigma _{\lambda _{k}}\cap \Omega$ satisfying $\lambda _{k}>0$ and $\lambda _k\rightarrow 0$ as $k\rightarrow +\infty$ such that

(6.3)\begin{equation} U_{\lambda_{k}}(x^{k})=\inf_{\Sigma_{\lambda_{k}}\cap\Omega}U_{\lambda_{k}}=\inf_{\lambda\in(0,\lambda_{k}]}\inf_{x\in\Sigma_\lambda}U_\lambda(x)<0. \end{equation}

It follows directly from (6.3) that ${\partial U_{\lambda }}/{\partial \lambda }|_{\lambda =\lambda _k}(x^{k})\leq 0$, and hence $(\partial _{x_{n}}u) [(x^{k})^{\lambda _k}]\leq 0$. Note that $x^{k}$ is the interior minimum of $U_{\lambda _k}(x)$, then one has $\nabla _{x}U_{\lambda _k}(x^{k})=0$, i.e.,

(6.4)\begin{equation} (\nabla_{x}u_{\lambda_k})(x^{k})=(\nabla_{x}u)(x^{k}). \end{equation}

Through a direct calculation, we get

(6.5)\begin{equation} \left\{\begin{array}{l} (-\Delta+m^{2})^{s} U_{\lambda_{k}}(x)+c_{1}(x)U_{\lambda_{k}}(x)+c_{2}(x)V_{\lambda_{k}}(x)=0,\\ (-\Delta+m^{2})^{t} V_{\lambda_{k}}(x)+c_{3}(x)V_{\lambda_{k}}(x)+c_{4}(x)U_{\lambda_{k}}(x)=0, \end{array}\right. \end{equation}

where $c_i(x)$ is same to (3.6)–(3.9). Due to the Lipschitz continuous of $u,v$, we have $c_{i}(i=1,2,3,4)$ are bounded. We can also infer from $\mathbf {F_{1}}$ that $c_{2}(x)<0, c_{4}(x)<0$ and $-c_{1}(x)+m^{2s}\geq 0$, $-c_{3}(x)+m^{2t}\geq 0$. Since $\Omega$ is a coercive epigraph, $\Sigma _{\lambda }\cap \Omega$ is always is a bounded narrow region for $k$ large enough. In addition, one can easily obtain from system (1.1) that

(6.6)\begin{equation} U_{\lambda}(x)\geq 0,\ V_{\lambda}(x)\geq 0, \quad U_{\lambda}(x)\not\equiv 0 \ \text{or}\ V_{\lambda}(x)\not\equiv 0 \quad \text{in}\ \Sigma_{\lambda}\setminus \Omega. \end{equation}

By the assumption of theorem 1.4 and applying the Narrow region principle proposition 2.1, we can conclude the assertion (6.1).

Step 2. We continue to move the plane $T_{\lambda }$ along the $x_{N}$ -axis until its limiting position as long as (6.1) holds. More precisely, let

(6.7)\begin{equation} \lambda_{0}:=\sup \left\{\lambda>0 | U_{\mu}(x) > 0\ \text{and}\ V_{\mu}(x) > 0, x \in \Sigma_{\mu}\cap \Omega, \mu \leq \lambda\right\}. \end{equation}

We shall show that

(6.8)\begin{equation} \lambda_{0}={+}\infty. \end{equation}

If $\lambda _{0}<+\infty$, we shall show that the plane $T_{\lambda _0}$ can be moved upward a little bit more, that is, there exists an $\varepsilon >0$ small enough such that

(6.9)\begin{equation} U_{\lambda}>0 \quad \text{and}\quad V_{\lambda}>0 \quad \text{in} \ \Sigma_{\lambda}\cap\Omega, \quad \forall \ \lambda_{0}\leq\lambda\leq\lambda_{0}+\varepsilon, \end{equation}

which contradicts the definition (6.7) of $\lambda _{0}$.

Indeed, by the definition of $\lambda _{0}$, we have

\[ U_{\lambda_{0}}\geq 0\quad \text{and}\quad V_{\lambda_{0}}\geq 0 \quad \text{in}\ \Sigma_{\lambda_0}\cap\Omega. \]

Since $u,v>0$ in $\Omega$ and $u=v \equiv 0$ in $\mathbb {R}^{N}\setminus \Omega$, we have $U_{\lambda _{0}}>0, V_{\lambda _{0}}> 0$ for any $x\in \Omega ^{\lambda _{0}}\setminus \Omega$, where the notation $\Omega ^{\lambda }$ denotes the reflection of a given set $\Omega$ with respect to the plane $T_{\lambda }$. Then, we obtain from proposition 2.1 that

\[ U_{\lambda_{0}}>0,\ V_{\lambda_{0}} >0\quad \text{in}\ \Sigma_{\lambda_0}\cap\Omega. \]

Now we choose $\varepsilon _1>0$ sufficiently small such that $(\Sigma _{\lambda _{0}+\varepsilon _1}\setminus \overline {\Sigma _{\lambda _{0}-\varepsilon _1}})\cap \Omega$ is a bounded narrow region. By the fact that $U_{\lambda _{0}}(x)>0, V_{\lambda _{0}}(x)>0$ for $x\in \Omega ^{\lambda _{0}}\cap \Sigma _{\lambda _{0}}$ and the continuity of $U_{\lambda _{0}}$ and $V_{\lambda _{0}}$, there exists $c_0>0$ such that

\[ U_{\lambda_{0}}(x)> c_0, \quad V_{\lambda_{0}}(x)> c_0,\quad \forall \ x\in\overline{\Sigma_{\lambda_0-\varepsilon_1}}\cap \Omega. \]

Therefore, we can choose $0<\varepsilon _2<\varepsilon _1$ sufficiently small such that

(6.10)\begin{equation} U_{\lambda}(x)>\frac{c_0}{2}>0,\quad V_{\lambda}(x)>\frac{c_0}{2}>0,\quad \forall \ x\in\overline{\Sigma_{\lambda_0-\varepsilon_1}}\cap \Omega, \end{equation}

for every $\lambda _0\leq \lambda \leq \lambda _0+\varepsilon _2$. Since $(\Sigma _{\lambda }\setminus \overline {\Sigma _{\lambda _{0}-\varepsilon _1}})\cap \Omega$ is also a bounded narrow region. From the assumption $\mathbf {F}_{\mathbf {1}}$, we know $c_{i}(x)$ satisfy the condition of Narrow region principle proposition 2.1. Thus we can deduce from proposition 2.1 that

\[ U_{\lambda}>0,\ V_{\lambda}>0 \quad \text{in} \ \left(\Sigma_{\lambda}\setminus\overline{\Sigma_{\lambda_{0}-\varepsilon_1}}\right)\cap \Omega, \quad \forall \ \lambda_{0}\leq\lambda\leq\lambda_{0}+\varepsilon_2, \]

and hence

\[ U_{\lambda}>0,\ V_{\lambda}>0 \quad \text{in} \ \Sigma_{\lambda}\cap\Omega, \quad \forall \ \lambda_{0}\leq\lambda\leq\lambda_{0}+\varepsilon_2, \]

which contradicts the definition of $\lambda _{0}$ (6.7). Thus, we have $\lambda _0=+\infty$. Hence, $u$ and $v$ are increasing with respect to the $x_{N}$-axis. This completes the proof of theorem 1.4.

Now we are in the position to prove that the Liouville-type theorem for generalized pseudo-relativistic Schrödinger system (1.22) in $\mathbb {R}^{N}_{+}.$

Proof of theorem 1.5. We first show that if there exists $x_{0} \in \mathbb {R}_{+}^{N}$ such that $u(x_{0})=0$. Then, we have

(6.11)\begin{equation} u(x)\equiv v(x) \equiv 0\quad \text{in } \mathbb{R}_{+}^{N}. \end{equation}

Note that, $u$ is a nonnegative solution of system (1.1) and $u(x_{0})=0$, so we have $\nabla u(x_{0})=0$. On one hand, if $u(x) \not \equiv 0,$ we have

(6.12)\begin{align} & \left(-\Delta+m^{2}\right)^{s}u(x_{0}) \nonumber\\ & \quad = c_{N,s} m^{{{N}/{2}+s}} P.V. \int_{\mathbb{R}^{N}} \frac{u(x_{0})-u(y)}{|x-y|^{{{N}/{2}+s}}} K_{{{N}/{2}+s}}(m|x-y|)\,\textrm{d}y \nonumber\\ & \quad ={-}c_{N, s} m^{{{N}/{2}+s}} P.V. \int_{\mathbb{R}^{N}} \frac{u(y)}{|x-y|^{{{N}/{2}+s}}} K_{{{N}/{2}+s}}(m|x-y|)\,\textrm{d}y < 0. \end{align}

On the other hand, since ${\partial f}/{\partial v}>0$, we have

(6.13)\begin{equation} (-\Delta+m^{2})^{s} u\left(x_{0}\right)=f\left(x,0, v(x_{0}),\quad\nabla u\left(x_{0}\right)\right)> f(x,0,0,0)=0. \end{equation}

This is a contradiction, which implies that $u(x) \equiv 0$ in $\mathbb {R}_{+}^{N}$. Combining this truth with the first equation in (1.1), we must have $f(x, 0, v, \nabla u)=f(x, 0, v, 0)=0$. Hence, if $u(x)\not \equiv 0$,

(6.14)\begin{equation} 0=f(x, 0, v, 0)> f(x, 0, 0, 0)=0. \end{equation}

We can deduce that $v(x) \equiv 0$ in $\mathbb {R}_{+}^{N}$. Thus, we have

\[ u(x)=v(x)=0 \quad \text{in } \mathbb{R}_{+}^{N}. \]

If there exists $x_{0} \in \mathbb {R}_{+}^{N}$ such that $v(x_{0})=0$, we can use the same arguments as above to yield a contradiction by using the fact of ${\partial g}/{\partial u}>0$ and $g(x,0,0,0)=0$.

In the following, we always assume that $u(x)>0$ and $v(x)>0$. Then, we carry out the moving planes procedure in two steps.

Step 1. We shall show that, for $\lambda >0$ sufficiently closing to $0$,

(6.15)\begin{equation} U_{\lambda}(x)\geq 0,\ V_{\lambda}(x) \geq 0, \quad x \in \Sigma_{\lambda}. \end{equation}

Combining the assumption (iii) of theorem 1.5 with $u>0$, $v>0$, we have

\[ \varliminf_{|x| \rightarrow \infty} U_{\lambda}(x) \geq 0 \quad \text{and} \quad \varliminf_{|x| \rightarrow \infty} V_{\lambda}(x) \geq 0. \]

Then similar to the proof of theorem 1.4, by applying proposition 2.1, we get (6.15).

Step 2. We continue to move the plane $T_{\lambda }$ along the $x_{N}$ -axis until its limiting position as long as (6.15) holds. More precisely, let

(6.16)\begin{equation} \lambda_{0}:=\sup \left\{\lambda>0 | U_{\mu}(x) > 0\ \text{and}\ V_{\mu}(x) > 0, x \in \Sigma_{\mu}, \mu \leq \lambda\right\}. \end{equation}

Now we show that

(6.17)\begin{equation} \lambda_{0}={+}\infty. \end{equation}

If (6.17) is not true. Similar to the proof of theorem 1.4, we can derive either

(6.18)\begin{equation} U_{\lambda_{0}}(x)=0,\ V_{\lambda_{0}}(x)=0,\quad x \in {\Sigma}_{\lambda_{0}}, \end{equation}

or

(6.19)\begin{equation} U_{\lambda_{0}}(x)>0\quad \textrm{and}\quad V_{\lambda_{0}}(x)>0, \quad x \in {\Sigma}_{\lambda_{0}}. \end{equation}

If (6.19) is true, by the similar argument as proof of theorem 1.4, we will show that the plane $T_{\lambda _{0}}$ can be moved upward a little more, which contradicts the definition (6.16) of $\lambda _{0}$. Hence, (6.18) is true. It reveals that

\[ u(x_{1},x_{2},\ldots,x_{N-1},2\lambda_{0})=u(x_{1},x_{2},\ldots,x_{N-1},0)=0 \]

and

\[ v(x_{1},x_{2},\ldots,x_{N-1},2\lambda_{0})=v(x_{1},x_{2},\ldots,x_{N-1},0)=0. \]

That is a contradiction with $u,v>0$. So (6.17) holds.

Therefore, $u$ and $v$ are increasing concerning the $x_{N}$-axis. In terms of the assumption $\lim _{|x|\rightarrow +\infty }(u(x),v(x))=(0,0)$, we know that is impossible. So $u(x)= v(x) \equiv 0 \text { in } \mathbb {R}_+^{N}$.

We complete the proof of theorem 1.5.