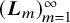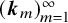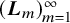New parameters and Lebesgue-type estimates in greedy approximation

Abstract

The purpose of this paper is to quantify the size of the Lebesgue constants $(\boldsymbol {L}_m)_{m=1}^{\infty }$ associated with the thresholding greedy algorithm in terms of a new generation of parameters that modulate accurately some features of a general basis. This fine tuning of constants allows us to provide an answer to the question raised by Temlyakov in 2011 to find a natural sequence of greedy-type parameters for arbitrary bases in Banach (or quasi-Banach) spaces which combined linearly with the sequence of unconditionality parameters $(\boldsymbol {k}_m)_{m=1}^{\infty }$ determines the growth of $(\boldsymbol {L}_m)_{m=1}^{\infty }$ . Multiple theoretical applications and computational examples complement our study.

1 Introduction and background

Let $\mathbb {X}$ be an infinite-dimensional separable Banach space (or, more generally, a quasi-Banach space) over the real or complex field $\mathbb {F}$ , and let $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ be a basis in $\mathbb {X}$ , that is, $(\boldsymbol {x}_n)_{n=1}^{\infty }$ is a norm-bounded sequence that generates the entire space $\mathbb {X}$ , in the sense that

$$\begin{align*}\overline{\operatorname{\mathrm{span}}(\boldsymbol{x}_n \colon n\in\mathbb{N})}=\mathbb{X}, \end{align*}$$

and for which there is a (unique) norm-bounded sequence $\mathcal {X}^*=(\boldsymbol {x}_n^*)_{n=1}^{\infty }$ in the dual space $\mathbb {X}^*$ such that $(\boldsymbol {x}_n, \boldsymbol {x}_n^*)_{n=1}^{\infty }$ is a biorthogonal system. The sequence $\mathcal {X}^*$ will be called the dual basis of $\mathcal {X}$ .

For each $m\in \mathbb {N}$ , we let $\Sigma _m[\mathcal {X}, \mathbb {X}]$ denote the collection of all f in $\mathbb {X}$ which can be expressed as a linear combination of m elements of $\mathcal {X}$ , that is,

$$\begin{align*}\Sigma_m[\mathcal{X}, \mathbb{X}]= \left\lbrace\sum_{n\in A} a_n\, \boldsymbol{x}_n \colon A\subseteq \mathbb{N},\, \left\lvert A\right\rvert = m,\; a_n\in\mathbb{F}\right\rbrace, \quad m=1,2,\dots \end{align*}$$

A fundamental question in nonlinear approximation theory using bases is how to construct for each $f\in \mathbb {X}$ and each $m\in \mathbb {N}$ an element $g_m$ in $\Sigma _m$ so that the error of the approximation of f by $g_m$ is as small as possible. To that end we need, on one hand, an easy way to build for all $m\in \mathbb {N}$ an m-term approximant of any function (or signal) $f\in \mathbb {X}$ and, on the other hand, a way to measure the efficiency of our approximation.

Konyagin and Temlyakov [34] introduced in 1999 the thresholding greedy algorithm (TGA for short) $(\mathcal {G}_m)_{m=1}^{\infty }$ , where $\mathcal {G}_m(f)$ is obtained by choosing the first m terms in decreasing order or magnitude from the formal series expansion $\sum _{n=1}^{\infty }\boldsymbol {x}_n^*(f)\, \boldsymbol {x}_n$ of f with respect to $\mathcal {X}$ , with the agreement that when two terms are of equal size we take them in the basis order. By our assumptions on the dual basis $\mathcal {X}^*$ , the coefficient transform

$$\begin{align*}\mathcal{F}\colon\mathbb{X}\to\mathbb{F}^{\mathbb{N}}, \quad \mathcal{F}(f)=(\boldsymbol{x}_n^*(f))_{n=1}^{\infty}, \quad f\in\mathbb{X}, \end{align*}$$

is a bounded map from $\mathbb {X}$ into $c_0$ so that the maps $\mathcal {G}_m\colon \mathbb {X}\to \mathbb {X}$ are well defined for all $m\in \mathbb {N}$ ; however, the operators $(\mathcal {G}_m)_{m=1}^{\infty }$ are not linear nor continuous.

To measure the performance of the greedy algorithm, we compare the error $\left \lVert f-\mathcal {G}_m(f)\right \rVert $ in the approximation of any $f\in \mathbb {X}$ by $\mathcal {G}_m(f)$ , with the best m-term approximation error, given by

$$\begin{align*}\sigma_m[\mathcal{X}, \mathbb{X}](f):=\sigma_m(f) =\inf\lbrace \left\lVert f -g \right\rVert \colon g\in \Sigma_m\rbrace. \end{align*}$$

An upper estimate for the rate $\left \lVert f- \mathcal {G}_m(f)\right \rVert /\sigma _m(f)$ is usually called a Lebesgue-type inequality for the TGA (see [44, Chapter 2]). Obtaining Lebesgue-type inequalities is tantamount to finding upper bounds for the Lebesgue constants of the basis, given for $m\in \mathbb {N}$ by

$$\begin{align*}\boldsymbol{L}_m=\boldsymbol{L}_m[\mathcal{X},\mathbb{X}]=\sup\left\lbrace\frac{\left\lVert f- \mathcal{G}_m(f)\right\rVert}{\sigma_m(f)}\colon f\in \mathbb{X}\setminus \Sigma_m\right\rbrace. \end{align*}$$

By definition, the basis $\mathcal {X}$ is greedy [34] if and only if

$$\begin{align*}\boldsymbol{C}_g=\boldsymbol{C}_g[\mathcal{X},\mathbb{X}]:=\sup_m \boldsymbol{L}_m<\infty. \end{align*}$$

Certain important bases, such as the Haar system in $L_p$ , $1<p<\infty $ , or the Haar system in $H_p$ , $0<p\le 1$ , are known to be greedy (see [45, 55, 4]). In the literature, we also find instances where the Lebesgue constants have been computed or estimated for special nongreedy bases in important spaces:

• ○ In [40], the Lebesgue constants of the Haar basis in the spaces $\mathrm {BMO}$ and dyadic $\mathrm {BMO}$ were computed.

• ○ More recently, in [50, 49], the Lebesgue constants for tensor product bases in $L_{p}$ -spaces (in particular, for the multi-Haar basis) were calculated.

• ○ The Lebesgue constants for the trigonometric basis in $L_p$ are also known (see [46]).

• ○ The paper [23] estimates the Lebesgue constants for bases in $L_{p}$ -spaces with specific properties (such as being uniformly bounded).

• ○ Lebesgue constants for redundant dictionaries are studied in [48, Section 2.6].

Calculating the exact value of the Lebesgue constants can be in general a difficult task, so to study the efficiency of nongreedy bases, we must settle for obtaining easy-to-handle estimates that control the asymptotic growth of $(\boldsymbol {L}_m)_{m=1}^{\infty }$ . To center the problem, we shall introduce some preliminary notation.

1.1 Unconditionality parameters and democracy parameters

Konyagin and Temlyakov [34] characterized greedy bases as those bases that are simultaneously unconditional and democratic. Thus, in order to find bounds for the Lebesgue constants, it is only natural to quantify the unconditionality and the democracy of a basis and study their relation with $\boldsymbol {L}_m$ .

For finite $A\subseteq \mathbb {N}$ , we let $S_A=S_A[\mathcal {X},\mathbb {X}]\colon \mathbb {X} \to \mathbb {X}$ denote the coordinate projection on the set A, that is,

$$\begin{align*}S_A(f)=\sum_{n\in A} \boldsymbol{x}_n^*(f)\, \boldsymbol{x}_n,\quad f\in \mathbb{X}. \end{align*}$$

The norms of the coordinate projections associated to a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ are quantified by the unconditionality parameters

$$\begin{align*}\boldsymbol{k}_m=\boldsymbol{k}_m[\mathcal{X},\mathbb{X}] :=\sup_{\left\lvert A\right\rvert= m} \left\lVert S_A\right\rVert, \quad m\in\mathbb{N}, \end{align*}$$

and by the complemented unconditionality parameters,

$$\begin{align*}{\boldsymbol{k}^{\boldsymbol{c}}_m}={\boldsymbol{k}^{\boldsymbol{c}}_m}[\mathcal{X},\mathbb{X}] :=\sup_{\left\lvert A\right\rvert= m} \left\lVert \mathrm{Id}_{\mathbb{X}}-S_A\right\rVert, \quad m\in\mathbb{N}. \end{align*}$$

Note that, if $\mathbb {X}$ is a p-Banach space, $0<p\le 1$ , then

(1.1) $$ \begin{align} (\boldsymbol{k}_m)^p\le 1+({\boldsymbol{k}^{\boldsymbol{c}}_m})^p,\quad ({\boldsymbol{k}^{\boldsymbol{c}}_m})^p\le 1+(\boldsymbol{k}_m)^p, \end{align} $$

and $(\boldsymbol {k}_{2m})^p \le 2 (\boldsymbol {k}_m)^p$ for all $m\in \mathbb {N}$ .

We also define the mth democracy parameter of the basis as

where

A basis is unconditional if and only if $\sup _m\boldsymbol {k}_m<\infty $ , and it is democratic if and only if $\sup _m \boldsymbol {\mu }_m<\infty $ . A reproduction of the original proof of the above-mentioned characterization of greedy bases from [34] for general bases, where we pay close attention to the dependency on m in the constants involved, yields the following upper and lower bounds for the Lebesgue constants in terms of $\boldsymbol {k}_m$ and $\boldsymbol {\mu }_m$ :

(1.2) $$ \begin{align} \frac{1}{C_2} \max\left\lbrace \boldsymbol{k}_m, \boldsymbol{\mu}_m\right\rbrace \le \boldsymbol{L}_m \le C_1 \boldsymbol{k}_m\, \boldsymbol{\mu}_m, \end{align} $$

where $C_1$ and $C_2$ depend only on the modulus of concavity of the space $\mathbb {X}$ (see [13, Proposition 1.1] and [4, Theorem 7.2]). However, since the function on the left is not the same as the function on the right, these bounds are not optimal, and as a consequence, when applying them, we lose accuracy in estimating the size of $\boldsymbol {L}_m$ .

The investigation of Lebesgue constants for greedy algorithms dates back to the initial stages of the theory, with some relevant ideas appearing already in [34]. Oswald gave in [40, Theorem 1] the correct asymptotic behavior for the quantities $\boldsymbol {L}_m$ in the general case replacing $(\boldsymbol {\mu }_m)_{m=1}^{\infty }$ with other parameters. However, its application to particular systems is tedious due the complicated, implicit definitions of the parameters his estimates rely on.

Other authors have approached the subject by imposing extra conditions on the basis which permit to obtain sharp estimates for $(\boldsymbol {L}_m)_{m=1}^{\infty }$ . The first movers in this direction were Garrigós et al., who in 2013 gave optimal estimates for the Lebesgue constants of quasi-greedy bases, that is, bases for which the operators $(\mathcal {G}_m)_{m=1}^{\infty }$ are uniformly bounded (or, equivalently, bases for which $\mathcal {G}_m(f)$ converges to f for all $f\in \mathbb {X}$ ).

Theorem 1.1 ([29, Theorem 1.1])

If the basis $\mathcal {X}$ is quasi-greedy, then there is a constant C such that

$$ \begin{align*} \frac{1}{C} \max\lbrace\boldsymbol{\mu}_m, \boldsymbol{k}_m\rbrace\le \boldsymbol{L}_m\le C \max\lbrace\boldsymbol{\mu}_m, \boldsymbol{k}_m\rbrace, \quad m\in \mathbb{N}. \end{align*} $$

Thus, in the particular case that $\mathcal {X}$ is unconditional, $(\boldsymbol {L}_m)_{m=1}^{\infty }$ is asymptotically of the same order as $(\boldsymbol {\mu }_m)_{m=1}^{\infty }$ .

In this paper, we seek sharp estimates for the Lebesgue constants in the general case. For that, we introduce a sequence of greedy-like parameters $\boldsymbol {\lambda }_m=\boldsymbol {\lambda }_m[\mathcal {X},\mathbb {X}]$ , which we call the squeeze-symmetry parameters and which allow proving the estimate

(1.3) $$ \begin{align} \boldsymbol{L}_m \approx \max\lbrace\boldsymbol{\lambda}_m, \boldsymbol{k}_m\rbrace, \quad m\in\mathbb{N}, \end{align} $$

for the Lebesgue constants of any basis $\mathcal {X}$ of any quasi-Banach space $\mathbb {X}$ .

Section 3 concentrates on the introduction of the new parameters $\boldsymbol {\lambda }_m$ and the proof of the promised estimate for $\boldsymbol {L}_m$ . In Section 4, we will also show the almost greedy analogue of equation (1.3), which in this case involves the almost greedy constants, the quasi-greedy parameters and some relatives of the squeeze-symmetry parameters (see Theorem 4.2). In Sections 5, 6 and 7, we investigate the theoretical applications of the new Lebesgue constants and the new Lebesgue-type estimates derived from them. In particular, we compare equation (1.3) with other bounds for the Lebesgue constants that can be found in the literature. As a matter of fact, as we will see, most known estimates for the Lebesgue constants can be deduced from estimate (1.3). For instance, Theorem 1.1 can be deduced from Theorem 5.3. Since the practical interest of our results depend on the ability to estimate the squeeze-symmetry parameters, we devote Section 8 to relating these parameters with other parameters that quantify different degrees of democracy. In Section 9, we compute the Lebesgue constants and obtain Lebesgue-type estimates in some important examples. These examples suggest the pattern that the Lebesgue constants grow linearly with the unconditionality parameters and the democracy parameters. However, to dispel doubts about the optimality of equation (1.3) and the convenience of introducing the squeeze-symmetry parameters $\boldsymbol {\lambda }_{m}$ , in the last section of the paper we provide an example of a basis that shows that $\max \lbrace \boldsymbol {\mu }_m, \boldsymbol {k}_m\rbrace $ could be asymptotically strictly smaller than $\boldsymbol {L}_m$ .

2 Terminology and notation

Throughout this paper, we use standard facts and notation from Banach spaces and approximation theory (see, e.g., [9]). The reader will find the required specialized background and notation on greedy-like bases in quasi-Banach spaces in the recent article [4]; however, a few remarks are in order.

Let us first recall that a quasi-Banach space is a vector space $\mathbb {X}$ over the real or complex field $\mathbb {F}$ equipped with a map $\left \lVert \cdot \right \rVert \colon \mathbb {X}\to [0,\infty )$ , called a quasi-norm, which satisfies all the usual properties of the norm with the exception that the triangle law is replaced with the inequality

(2.1) $$ \begin{align} \left\lVert f+g\right\rVert \leq \kappa( \left\lVert f\right\rVert + \left\lVert g\right\rVert ),\quad f,g\in \mathbb{X} \end{align} $$

for some $\kappa \ge 1$ independent of f and g, and moreover $(\mathbb {X},\left \lVert \cdot \right \rVert )$ is complete. The modulus of concavity of the quasi-norm is the smallest constant $\kappa \ge 1$ in equation (2.1). Given $0<p\le 1$ , a p-Banach space will be a quasi-Banach space whose quasi-norm is p-subadditive, that is,

$$\begin{align*}\left\lVert f+g\right\rVert^p \le \left\lVert f\right\rVert^p +\left\lVert g \right\rVert^p, \quad f,g\in\mathbb{X}. \end{align*}$$

Any p-Banach space has modulus of concavity at most $2^{1/p-1}$ . Conversely, by the Aoki–Rolewicz theorem [12, 42], any quasi-Banach space with modulus of concavity at most $2^{1/p-1}$ is p-Banach under an equivalent quasi-norm. So, we will suppose that all quasi-Banach spaces are p-Banach spaces for some $0<p\le 1$ . As a consequence of this assumption, all quasi-norms will be continuous.

The linear space of all eventually null sequences will be denoted by $c_{00}$ , and $c_0$ will be the Banach space consisting of all null sequences. Let $0<q< \infty $ and $\boldsymbol {w}=(w_n)_{n=1}^{\infty }$ be a weight, that is, a sequence of nonnegative scalars with $w_1>0$ . Let $(s_m)_{m=1}^{\infty }$ be the primitive weight of $\boldsymbol {w}$ . We will denote by $d_{1,q}(\boldsymbol {w})$ the Lorentz sequence space consisting of all $f\in c_0$ whose nonincreasing rearrangement $(a_n)_{n=1}^{\infty }$ satisfies

$$\begin{align*}\left\lVert f\right\rVert_{d_{1,q}(\boldsymbol{w})}=\left( \sum_{n=1}^{\infty} a_n^q s_n^{q-1}w_n\right)^{1/q}<\infty. \end{align*}$$

If $q=\infty $ , the corresponding weak Lorentz space $d_{1,\infty }(\boldsymbol {w})$ is defined by means of the quasi-norm

$$\begin{align*}\left\lVert f\right\rVert_{d_{1,\infty}(\boldsymbol{w})}=\sup_{n\in\mathbb{N}} a_n s_n. \end{align*}$$

If $\boldsymbol {\sigma }=(s_m)_{m=1}^{\infty }$ is doubling, that is, there exists a constant C such that $s_{2m} \le C s_m$ for all $m \in \mathbb {N}$ , $d_{1,q}(\boldsymbol {w})$ is a quasi-Banach space. Moreover, if $\boldsymbol {\sigma }$ is doubling, the unit vector system is a $1$ -symmetric basis of its closed linear span, and, if $q<\infty $ , the aforementioned closed linear span is $d_{1,q}(\boldsymbol {w})$ . Regardless of the value of q, the fundamental function of the unit vector system of $d_{1,q}(\boldsymbol {w})$ is of the same order as $(s_m)_{m=1}^{\infty }$ . We refer the reader to [4, Section 9.2] for a concise introduction to Lorentz sequence spaces.

The norm of an operator T from a quasi-Banach space $\mathbb {X}$ into a quasi-Banach space $\mathbb {Y}$ will be denoted by $\left \lVert T\right \rVert _{\mathbb {X}\to \mathbb {Y}}$ or simply $\left \lVert T\right \rVert $ if the spaces are clear from context. A sequence $(\boldsymbol {x}_n)_{n=1}^{\infty }$ in a quasi-Banach space $\mathbb {X}$ is said to be seminormalized if

$$\begin{align*}0 < \inf_{n\in\mathbb{N}} \left\lVert \boldsymbol{x}_n\right\rVert \le \sup_{n\in\mathbb{N}} \left\lVert \boldsymbol{x}_n\right\rVert<\infty. \end{align*}$$

We will only deal with biorthogonal systems $(\boldsymbol {x}_n,\boldsymbol {x}_n^*)_{n=1}^{\infty }$ for which the democracy and the unconditionality parameters of $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ are finite. Note that

$$\begin{align*}\boldsymbol{k}_1[\mathcal{X},\mathbb{X}]=\sup_{n\in\mathbb{N}} \left\lVert \boldsymbol{x}_n\right\rVert \, \left\lVert \boldsymbol{x}_n^*\right\rVert, \end{align*}$$

and that, if $\boldsymbol {k}_1<\infty $ , then $\boldsymbol {k}_m<\infty $ for all $m\in \mathbb {N}$ . In turn, taking into account that

$$ \begin{align*} \boldsymbol{\mu}_1[\mathcal{X},\mathbb{X}] =\frac{\sup_n \left\lVert \boldsymbol{x}_n\right\rVert}{\inf_n \left\lVert \boldsymbol{x}_n\right\rVert}, \end{align*} $$

we infer that, if $\boldsymbol {\mu }_1$ and $\boldsymbol {k}_1$ are both finite, then $\boldsymbol {\mu }_m<\infty $ for all $m\in \mathbb {N}$ . Indeed, if $\mathbb {X}$ is a p-Banach space and $\left \lvert A\right \rvert =\left \lvert B\right \rvert \le m$ ,

Finally, we note that $\max \lbrace \boldsymbol {\mu }_1,\boldsymbol {k}_1\rbrace <\infty $ if and only if

(2.2) $$ \begin{align} C[\mathcal{X}]:=\sup_{n\in\mathbb{N}} \max\lbrace\left\lVert \boldsymbol{x}_n\right\rVert, \left\lVert \boldsymbol{x}_n^*\right\rVert \rbrace<\infty, \end{align} $$

in which case both $\mathcal {X}$ and $\mathcal {X}^*=(\boldsymbol {x}_n^*)_{n=1}^{\infty }$ are seminormalized.

Given a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ of a quasi-Banach space $\mathbb {X}$ , $f\in \mathbb {X}$ and $f^*\in \mathbb {X}^*$ , we define sequences $\varepsilon (f)$ and $\varepsilon (f^*)$ in $\mathbb {E}^{\mathbb {N}}$ by

$$ \begin{align*} \varepsilon(f)&=(\varepsilon_n(f))_{n=1}^{\infty}=( \operatorname{\mathrm{sign}} (\boldsymbol{x}_n^*(f)))_{n=1}^{\infty},\\ \varepsilon(f^*)&=(\varepsilon_n(f^*))_{n=1}^{\infty}=( \operatorname{\mathrm{sign}} (f^*(\boldsymbol{x}_n))_{n=1}^{\infty}, \end{align*} $$

where $\operatorname {\mathrm {sign}}(0)=1$ and $\operatorname {\mathrm {sign}}(a)=a/\left \lvert a\right \rvert $ if $a\not =0$ .

We say that a set of integers A is a greedy set of $f\in \mathbb {X}$ (relative to the basis $\mathcal {X}$ ) if

$$\begin{align*}\left\lvert\boldsymbol{x}_n^*(f)\right\rvert\ge \left\lvert\boldsymbol{x}_k^*(f)\right\rvert, \quad n\in A,\; k\in\mathbb{N}\setminus A, \end{align*}$$

in which case $S_A(f)$ is called a greedy sum of order $m :=\left \lvert A\right \rvert $ of f. The greedy sums of a function f need not be unique. In this regard, the thresholding greedy algorithm $(\mathcal {G}_m(f))_{m=1}^{\infty }$ is a natural way to construct for each m a greedy sum of f. Indeed, we can use the natural ordering of $\mathbb {N}$ to recursively define for each $f\in \mathbb {X}$ and $m\in \mathbb {N}$ a greedy set $A_m(f)$ of cardinality m as follows. Assuming that $A_{m-1}(f)$ is defined, we put

$$\begin{align*}\textstyle k(A,m)=\min\lbrace k \in \mathbb{N}\setminus A_{m-1}(f) \colon \left\lvert\boldsymbol{x}_k^*(f)\right\rvert= \max_{n\notin A_{m-1}(f)} \left\lvert\boldsymbol{x}_n^*(f)\right\rvert \rbrace, \end{align*}$$

and $A_m(f)=A_{m-1}(f)\cup \lbrace k(A,m)\rbrace $ . With this agreement, we have

$$\begin{align*}\mathcal{G}_m[\mathcal{X}, \mathbb{X}](f):=\mathcal{G}_m(f) = S_{A_m(f)}(f), \quad f\in \mathbb{X}, \; m\in\mathbb{N}. \end{align*}$$

The continuity of the quasi-norm combined with a standard perturbation technique yield that the mth Lebesgue constant $\boldsymbol {L}_m$ of the basis $\mathcal {X}$ is the smallest constant C such that

$$\begin{align*}\left\lVert f-S_A(f)\right\rVert \le C \sigma_m(f), \quad f\in\mathbb{X},\; A \text{ greedy set of } f,\; \left\lvert A\right\rvert\le m. \end{align*}$$

Thus, we infer that the sequence $(\boldsymbol {L}_m)_{m=1}^{\infty }$ is nonincreasing. Standard approximation arguments also give that we can equivalently define $\boldsymbol {L}_m$ , $\boldsymbol {k}_m$ and ${\boldsymbol{k}^{\boldsymbol{c}}_m}$ by restricting us to finitely supported functions. Using this, it is easy to deduce that $(\boldsymbol {k}_m)_{m=1}^{\infty }$ , and $({\boldsymbol{k}^{\boldsymbol{c}}_m})_{m=1}^{\infty }$ are also nondecreasing.

Given two sequences of parameters $(\alpha _m)_{m=1}^{\infty }$ and $(\beta _m)_{m=1}^{\infty }$ related to bases of quasi-Banach spaces, the symbol $\alpha _m\lesssim C\beta _m$ will mean that for every $0<p\le 1$ there is a constant C such that $\alpha _m[\mathcal {X},\mathbb {X}] \le C \beta _m[\mathcal {X},\mathbb {X}]$ for all $m\in \mathbb {N}$ and for all bases $\mathcal {X}$ of a p-Banach space $\mathbb {X}$ .

3 Lower and upper bounds for the Lebesgue constants

Inequalities (1.2) are a quantitative reformulation of Konyagin and Temlyakov’s characterization of greedy bases. Since the function on the right of equation (1.2) does not depend linearly on the unconditionality and democracy parameters, a natural question raised by Temlyakov [47] is to find parameters related to the unconditionality and the democracy of the basis whose maximum value grows as the Lebesgue constant. This section is geared towards the introduction of a new breed of parameters with the aim to provide a satisfactory answer to Temlyakov’s aforementioned question. For that, we will adopt a view point that regards certain Lebesgue-type parameters as quantifiers of the different degrees of symmetry that can be found in a basis.

3.1 Towards new parameters in greedy approximation

Recall that a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ of $\mathbb {X}$ is symmetric if it is equivalent to all its permutations, that is, there is a constant $C\ge 1$ such that

(3.1) $$ \begin{align} \frac{1}{C} \left\lVert \sum_{n=1}^{\infty} a_n \, \boldsymbol{x}_n\right\rVert \le \left\lVert \sum_{n=1}^{\infty} a_n \, \boldsymbol{x}_{\pi(n)}\right\rVert \le C \left\lVert \sum_{n=1}^{\infty} a_n \, \boldsymbol{x}_n\right\rVert \end{align} $$

for all $(a_n)_{n=1}^{\infty }\in c_{00}$ and all permutations $\pi $ on $\mathbb {N}$ . Democracy is the weakest symmetry condition that a basis can have, where we demand to a basis to verify equation (3.1) when all coefficients $a_{n}$ of $f\in \mathbb {X}$ are equal (without loss of generality) to 1.

Symmetric bases are in particular unconditional, which permits improving the previous inequality to have

(3.2) $$ \begin{align} \frac{1}{C} \left\lVert \sum_{n=1}^{\infty} a_n \, \boldsymbol{x}_n\right\rVert \le \left\lVert \sum_{n=1}^{\infty} \varepsilon_n\, a_{n} \, \boldsymbol{x}_{\pi(n)}\right\rVert \le C \left\lVert \sum_{n=1}^{\infty} a_n \, \boldsymbol{x}_n\right\rVert \end{align} $$

for all $(\varepsilon _n)_{n=1}^{\infty }\in \mathbb {E}^{\mathbb {N}}$ , where $\mathbb {E}$ denotes the subset of $\mathbb {F}$ consisting of all scalars of modulus $1$ , for a possibly larger constant C. If a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ of $\mathbb {X}$ satisfies equation (3.2) when all coefficients $a_{n}$ are 1 it is called superdemocratic. To quantify the superdemocracy of $\mathcal {X}$ , we use the mth superdemocracy parameter,

where

so that $\mathcal {X}$ is superdemocratic if $\sup _m {\boldsymbol{\mu}^{\boldsymbol{s}}_m}<\infty $ .

Although the parameters $({\boldsymbol{\mu}^{\boldsymbol{s}}_m})_{m=1}^{\infty }$ are one step up in the scale of symmetry, in practice they do not provide asymptotically better estimates than $(\boldsymbol {\mu }_m)_{m=1}^{\infty }$ for $(\boldsymbol {L}_m)_{m=1}^{\infty }$ . Indeed, with a smaller constant $C_1$ and a larger constant $C_2$ , we have

$$\begin{align*}\frac{1}{C_2} \max\left\lbrace \boldsymbol{k}_m, \boldsymbol{\mu}^{\boldsymbol{s}}_m\right\rbrace \le \boldsymbol{L}_m \le C_1 \boldsymbol{k}_m \, \boldsymbol{\mu}^{\boldsymbol{s}}_m, \quad m\in\mathbb{N} \end{align*}$$

(cf. [13, Proposition 1.1]).

Another condition related to symmetry which has been successfully implemented in the theory is the so-called symmetry for largest coefficients. Let

$$\begin{align*}\operatorname{\mathrm{supp}}(f)=\lbrace n\in\mathbb{N} \colon \boldsymbol{x}_n^*(f) \not=0\rbrace \end{align*}$$

denote the support of $f\in \mathbb {X}$ with respect to the basis $\mathcal {X}$ . We define

the supremum being taken over all finite subsets A, B of $\mathbb {N}$ with $ \left \lvert A\right \rvert =\left \lvert B\right \rvert \le m$ , all signs $\varepsilon \in \mathbb {E}^{A}$ and $\delta \in \mathbb {E}^{B}$ and all $f\in \mathbb {X}$ with $\left \lVert f\right \rVert _{\infty }\le 1$ and $\operatorname {\mathrm {supp}}(f)\cap (A\cup B)=\emptyset $ . A basis $\mathcal {X}$ is symmetric for largest coefficients (SLC for short) if $\sup _m \boldsymbol {\nu }_m<\infty $ . Imposing the extra assumption $A\cap B=\emptyset $ in the definition, we obtain the ‘disjoint’ counterpart of the SLC parameters, herein denoted by ${\boldsymbol{\nu}^{\boldsymbol{d}}_m}={\boldsymbol{\nu}^{\boldsymbol{d}}_m}[\mathcal {X},\mathbb {X}]$ .

Bases with $\sup _m \boldsymbol {\nu }_m=1$ were first considered in [10], where they were called bases with Property (A). The parameters that quantify the symmetry for largest coefficients of a basis appear naturally when looking for estimates for the Lebesgue constants that are close to one (see [10, 22, 20, 7]). In fact, if we put

$$\begin{align*}A_p=(2^p-1)^{1/p}, \quad 0<p\le 1, \end{align*}$$

and $\mathbb {X}$ is a p-Banach space,

(3.3) $$ \begin{align} \max\left\lbrace {\boldsymbol{k}^{\boldsymbol{c}}_m}, {\boldsymbol{\nu}^{\boldsymbol{d}}_m}\right\rbrace \le \boldsymbol{L}_m \le A_p^2 \boldsymbol{k}^{\boldsymbol{c}}_{2m} {\boldsymbol{\nu}^{\boldsymbol{d}}_m}, \quad m\in\mathbb{N}, \end{align} $$

(see [13, Proposition 1.1] and [4, Theorem 7.2]).

Thus, since ${\boldsymbol{\nu}^{\boldsymbol{d}}_m}\le \boldsymbol {\nu }_m \le ({\boldsymbol{\nu}^{\boldsymbol{d}}_m})^2$ , in the case when $\mathbb {X}$ is a Banach space, $\boldsymbol {C}_g=1$ if and only if ${\boldsymbol{k}^{\boldsymbol{c}}_m}=\boldsymbol {\nu }_m=1$ for all $m\in \mathbb {N}$ . Taking into account that for some constant C,

$$\begin{align*}\boldsymbol{\nu}_m\le C {\boldsymbol{\nu}^{\boldsymbol{d}}_m},\quad m\in \mathbb{N}, \end{align*}$$

(see Proposition 8.1 below), equation (3.3) yields

$$\begin{align*}\frac{1}{ C_1} \max\left\lbrace \boldsymbol{k}_m, \boldsymbol{\nu}_m \right\rbrace \le \boldsymbol{L}_m \le C_2 \boldsymbol{k}_m \, \boldsymbol{\nu}_m, \quad m\in\mathbb{N}, \end{align*}$$

for some constants $C_1$ and $C_2$ . Thus, again, the attempt to obtain better asymptotic estimates for $(\boldsymbol {L}_m)_{m=1}^{\infty }$ using parameters larger than $(\boldsymbol {\mu }_m)_{m=1}^{\infty }$ is futile.

The vestiges of symmetry found in some bases can also be measured qualitatively by means of the upper and lower democracy functions and using the concept of dominance between bases.

The upper superdemocracy function, also known as fundamental function, of a basis $\mathcal {X}$ of a quasi-Banach space $\mathbb {X}$ is defined as

(3.4)

while the lower superdemocracy function of $\mathcal {X}$ is

A basis $\mathcal {Y}=(\boldsymbol {y}_n)_{n=1}^{\infty }$ of a quasi-Banach space $\mathbb {Y}$ is said to dominate a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ of a quasi-Banach space $\mathbb {X}$ if there is a bounded linear map $S\colon \mathbb {X}\to \mathbb {Y}$ such that $S(\boldsymbol {x}_n)=\boldsymbol {y}_n$ for all $n\in \mathbb {N}$ . If $\left \lVert S\right \rVert \le D$ , we will say that $\mathcal {Y} \ D$ -dominates $\mathcal {X}$ .

Roughly speaking, we are interested in bases that can be ‘squeezed’ (using domination) between two symmetric bases with equivalent fundamental functions.

Definition 3.1. A basis $\mathcal {X}$ of a quasi-Banach space $\mathbb {X}$ is said to be squeeze-symmetric if there are quasi-Banach spaces $\mathbb {X}_1$ and $\mathbb {X}_2$ with symmetric bases $\mathcal {X}_1$ and $\mathcal {X}_2$ respectively such that

1. (a) $\boldsymbol {\varphi _u}[\mathcal {X}_1,\mathbb {X}_1]\le \boldsymbol {\varphi _l}[\mathcal {X}_2,\mathbb {X}_2]$ ,

2. (b) $\mathcal {X}_1$ dominates $\mathcal {X}$ and

3. (c) $\mathcal {X}$ dominates $\mathcal {X}_2$ .

Squeeze-symmetry guarantees in a certain sense the optimality of the compression algorithms with respect to the basis (see [24]). For an approach to squeeze-symmetric bases from this angle, we refer the reader to [1, 55, 17]. Squeeze-symmetry also serves in some situations as a tool to derive other properties of the bases like being quasi-greedy for instance (see [34, 18, 13, 14, 6, 56]).

Although it was not originally given this name, squeeze-symmetry was introduced in [4] to highlight a feature that had been implicit in greedy approximation with respect to bases since the early stages of the theory. The techniques developed in [4, Section 9] show that squeeze-symmetric bases are closely related to embeddings involving Lorentz sequence spaces. Before providing a precise formulation of this connection, we recall that if a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ of $\mathbb {X}$ is $1$ -symmetric, that is, equation (3.2) holds with $C_1=C_2=1$ , then $\boldsymbol {\varphi _u}[\mathcal {X},\mathbb {X}]=\boldsymbol {\varphi _l}[\mathcal {X},\mathbb {X}]$ . Note also that every symmetric basis is $1$ -symmetric under a suitable renorming of the space; thus, there is no real restriction in assuming that all symmetric bases are $1$ -symmetric.

Recall that a weight $\boldsymbol {\sigma }=(s_m)_{m=1}^{\infty }$ is the primitive weight of a weight $\boldsymbol {w}=(w_n)_{n=1}^{\infty }$ , in which case we say that $\boldsymbol {w}$ is the discrete derivative of $\boldsymbol {\sigma }$ , if $s_m=\sum _{n=1}^m w_n$ for all $m\in \mathbb {N}$ .

Theorem 3.2 (see [4, Equation (9.4), Lemma 9.3 and Theorem 9.12])

Let $\mathbb {X}$ be a quasi-Banach space with a basis $\mathcal {X}$ . Let $\boldsymbol {w}$ be the discrete derivative of the fundamental function of $\mathcal {X}$ . Then, $\mathcal {X}$ is squeeze-symmetric if and only if the coefficient transform defines a bounded linear operator from $\mathbb {X}$ into $d_{1,\infty }(\boldsymbol {w})$ . Quantitatively, if we set $\Gamma =\inf D_1 D_2$ , where the infimum is taken over all $1$ -symmetric bases $\mathcal {X}_1$ and $\mathcal {X}_2$ of quasi-Banach spaces $\mathbb {X}_1$ and $\mathbb {X}_2$ such that $\mathcal {X}_1 \ D_1$ -dominates $\mathcal {X}$ , $\mathcal {X} \ D_2$ -dominates $\mathcal {X}_2$ , and $\boldsymbol {\varphi _u}[\mathcal {X}_1,\mathbb {X}_1]\le \boldsymbol {\varphi _u}[\mathcal {X}_2,\mathbb {X}_2]$ , then there are constants $C_1$ and $C_2$ depending only on the modulus of concavity of $\mathbb {X}$ such that

$$\begin{align*}\frac{1}{C_2} \Gamma \le \left\lVert \mathcal{F}\right\rVert_{\mathbb{X}\to d_{1,\infty}(\boldsymbol{w})} \le C_2 \Gamma. \end{align*}$$

Theorem 3.2 serves as motivation to define a new kind of Lebesgue constants associated with an arbitrary basis $\mathcal {X}$ , which will eventually be key in solving Temlyakov’s problem.

For each $f\in \mathbb {X}$ , let $(\boldsymbol {a}_m(f))_{m=1}^{\infty }$ be the nonincreasing rearrangement of $\left \lvert \mathcal {F}(f)\right \rvert $ . Note that, if we put

(3.5) $$ \begin{align} \boldsymbol{\psi}_m= \boldsymbol{\psi}_m[\mathcal{X},\mathbb{X}]=\sup_{f\in\mathbb{X}\setminus\lbrace0\rbrace} \frac{\boldsymbol{a}_m(f)}{\left\lVert f\right\rVert}, \quad m\in\mathbb{N}, \end{align} $$

then the norm of the coefficient transform as an operator from $\mathbb {X}$ into $d_{1,\infty }(\boldsymbol {w})$ is $\sup _m \boldsymbol {\psi }_m \boldsymbol {\varphi _u}(m)$ . So, for $m\in \mathbb {N}$ , we define the mth squeeze-symmetry parameter of $\mathcal {X}$ ,

$$\begin{align*}\boldsymbol{\lambda}_m=\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}]= \boldsymbol{\psi}_m[\mathcal{X},\mathbb{X}] \boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m). \end{align*}$$

We can also approach the definition of the squeeze-symmetry parameters from a functional angle. If for $A\subseteq \mathbb {N}$ finite, we denote by $\mathcal {F}_A$ the projection of the coefficient transform onto A,

$$\begin{align*}\mathcal{F}_A\colon\mathbb{X} \to \mathbb{F}^{\mathbb{N}}, \quad f\mapsto \mathcal{F}(f) \chi_A, \end{align*}$$

then

$$\begin{align*}\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] = \sup \lbrace \left\lVert \mathcal{F}_A\right\rVert_{\mathbb{X}\to d_{1,\infty}(\boldsymbol{w})} \colon \left\lvert A\right\rvert\le m\rbrace. \end{align*}$$

Using that $(\boldsymbol {a}_m(f))_{m=1}^{\infty }$ is nonincreasing for all $f\in \mathbb {X}$ yields the properties of $(\boldsymbol {\lambda }_m)_{m=1}^{\infty }$ gathered in the following lemma for further reference.

Lemma 3.3. Let $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ be a basis of a quasi-Banach space $\mathbb {X}$ with coordinate functionals $(\boldsymbol {x}_n^*)_{n=1}^{\infty }$ , and let $m\in \mathbb {N}$ .

1. (i) $1/\boldsymbol {\psi }_m$ is the infimum value of $\left \lVert f\right \rVert $ , where f runs over all functions in $\mathbb {X}$ with

   $$\begin{align*}\left\lvert\lbrace n\in\mathbb{N}\colon \left\lvert\boldsymbol{x}_n^*(f)\right\rvert\ge 1\rbrace\right\rvert\ge m. \end{align*}$$

2. (ii) $\boldsymbol {\lambda }_m[\mathcal {X},\mathbb {X}]$ is the smallest constant C such that whenever $t\in [0,\infty )$ , $f\in \mathbb {X}$ , $A\subseteq \mathbb {N}$ and $\varepsilon \in \mathbb {E}^A$ satisfy

   $$\begin{align*}\left\lvert A\right\rvert\le\min\lbrace m,\left\lvert\lbrace n\in\mathbb{N}\colon \left\lvert\boldsymbol{x}_n^*(f)\right\rvert\ge t\rbrace\right\rvert\rbrace. \end{align*}$$

3. (iii) $\boldsymbol {\lambda }_m[\mathcal {X},\mathbb {X}]$ is the smallest constant C such that

   

   whenever $A\subseteq \mathbb {N}$ , $\varepsilon \in \mathbb {E}^A$ and B is a greedy set of $f\in \mathbb {X}$ with $\left \lvert A\right \rvert = \left \lvert B\right \rvert \le m$ .

In particular, the sequence $(\boldsymbol {\psi }_m)_{m=1}^{\infty }$ is nonincreasing and $(\boldsymbol {\lambda }_m)_{m=1}^{\infty }$ is nondecreasing.

Although the parameters $\boldsymbol {\lambda }_m$ could appear to be nonintuitive at first glance, it should be understood that they capture a very natural feature of a basis, namely, the inverse of $\boldsymbol {\lambda }_m$ is the optimal constant which bounds below the norm of vectors whose coefficients are greater than $1/\boldsymbol {\varphi _u}(m)$ on a set of cardinality m. In other words, $\boldsymbol {\lambda }_m$ is the inverse of the distance from the origin to such set of vectors.

3.2 Optimal estimates in terms of the squeeze-symmetry parameters

We get started with a lemma which connects some important constants that we will need by using the p-convexitity techniques developed in [4, Section 2]. The symbol ${\boldsymbol {\Upsilon }}$ stands for $2$ if $\mathbb {F}=\mathbb {R}$ , and for $4$ if $\mathbb {F}=\mathbb {C}$ .

Lemma 3.4. Let $0<p\le 1$ , and let $\mathcal {X}$ be a basis of a p-Banach space $\mathbb {X}$ . Given $A\subseteq \mathbb {N}$ finite, $f\in \mathbb {X}$ and $\delta =(\delta _n)_{n\in A}\in \mathbb {E}^A$ , we put

Set $C_p={\boldsymbol {\Upsilon }}^{1/p}$ if $f=0$ and $C_p=(1+{\boldsymbol {\Upsilon }})^{1/p}$ otherwise. Then:

$$ \begin{align*} K[A,f]&\le \min\lbrace C_p\, M[\delta,A,f], A_p\, L[A,f]\rbrace \text{ and }\\ M[\delta,A,f]&\le A_p\, N[\delta,A,f]. \end{align*} $$

Proof. In the case when $\mathbb {F}=\mathbb {C}$ , set $\gamma _j=i^j$ for $j=1$ , $2$ , $3$ , $4$ . In the case when $\mathbb {F}=\mathbb {R}$ , set $\gamma _j=(-1)^j$ for $j=1$ , $2$ . Given $(a_n)_{n\in A}\in \mathbb {F}^A$ with $\left \lvert a_n\right \rvert \le 1$ , there are $(a_{j,n})_{n\in A}\in \mathbb {F}^A$ , $j\in \mathbb {N}$ , $1\le j\le {\boldsymbol {\Upsilon }}$ , in $[0,1]$ such that $a_n=\sum _{j=1}^4 \gamma _j a_{j,n}$ . The identity

$$\begin{align*}g:= f+ \sum_{n\in A} a_n\,\boldsymbol{x}_n=f+ \sum_{j=1}^{\boldsymbol{\Upsilon}} \gamma_j \left( f+ \sum_{n\in A} a_{j,n}\,\boldsymbol{x}_n\right) \end{align*}$$

gives $\left \lVert g \right \rVert \le C_p M[\delta ,A,f]$ . The other inequalities follow readily from [4, Corollary 2.3].

With all the previous ingredients, we are now in a position to provide a satisfactory answer to Temlyakov’s question by means of the squeeze-symmetry parameters.

Theorem 3.5. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . There are constants $C_1$ and $C_2$ (depending only on the modulus of concavity of $\mathbb {X}$ ) such that

$$\begin{align*}\frac{1}{C_1} \boldsymbol{L}_m[\mathcal{X},\mathbb{X}] \le \max\lbrace\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}], \boldsymbol{k}_m[\mathcal{X},\mathbb{X}]\rbrace\le C_2 \, \boldsymbol{L}_m[\mathcal{X},\mathbb{X}], \quad m\in\mathbb{N}. \end{align*}$$

Proof. Let us first note that by equation (1.1), we can replace $\boldsymbol {k}_m$ with ${\boldsymbol{k}^{\boldsymbol{c}}_m}$ . The inequality

(3.6) $$ \begin{align} {\boldsymbol{k}^{\boldsymbol{c}}_m} \le \boldsymbol{L}_m, \quad m\in\mathbb{N}, \end{align} $$

can be deduced from the fact that, given $f\in \mathbb {X}$ and $A\subseteq \mathbb {N}$ finite, there is $h\in \operatorname {\mathrm {span}}(\boldsymbol {x}_n \colon n\in A)$ such that A is a greedy set of $f+h$ (see [29]). Thus, to complete the proof it suffices to show that

(3.7) $$ \begin{align} \boldsymbol{L}_m\le C_1 \max\lbrace\boldsymbol{\lambda}_m,{\boldsymbol{k}^{\boldsymbol{c}}_m}\rbrace \end{align} $$

and

(3.8) $$ \begin{align} \boldsymbol{\lambda}_m\le C_2 \max\lbrace{\boldsymbol{k}^{\boldsymbol{c}}_m},\boldsymbol{L}_m\rbrace \end{align} $$

for all $m\in \mathbb {N}$ and some constants $C_1$ and $C_2$ .

To show equation (3.7), assume that $\mathbb {X}$ is a p-Banach space, $0<p\le 1$ . Let A be a greedy set of $f\in \mathbb {X}$ with $\left \lvert A\right \rvert =m<\infty $ , and pick $z=\sum _{n\in B}a_n\, \boldsymbol {x}_n$ with $\left \lvert B\right \rvert =\left \lvert A\right \rvert $ . Notice that

$$ \begin{align*} \max_{n\in B\setminus A}\left\lvert\boldsymbol{x}_n^*(f)\right\rvert\le\min_{n\in A\setminus B}\left\lvert\boldsymbol{x}_n^*(f)\right\rvert =\min_{n\in A\setminus B}\left\lvert\boldsymbol{x}_n^*(f-z)\right\rvert. \end{align*} $$

Set $k=\left \lvert B\setminus A\right \rvert =\left \lvert A\setminus B\right \rvert $ . On one hand, by Lemma 3.3 (ii) and Lemma 3.4,

$$\begin{align*}\left\lVert S_{B\setminus A}(f)\right\rVert \le A_p \boldsymbol{\lambda}_m \left\lVert f-z\right\rVert. \end{align*}$$

On the other hand, since $\left \lvert A\cup B\right \rvert =m+k$ ,

$$\begin{align*}\left\lVert (f-z) -S_{A\cup B)}(f-z)\right\rVert\le {\boldsymbol{k}^{\boldsymbol{c}}_{m+k}} \left\lVert f -z\right\rVert\le {\boldsymbol{k}^{\boldsymbol{c}}_{2m}}\left\lVert f -z\right\rVert. \end{align*}$$

Since

$$\begin{align*}f- S_A(f) = (f-z)-S_{A\cup B}(f-z) + S_{B\setminus A}(f), \end{align*}$$

combining both inequalities gives

$$ \begin{align*} \left\lVert f- S_A(f)\right\rVert^p &\le \left(({\boldsymbol{k}^{\boldsymbol{c}}_{2m}})^p + (A_p \boldsymbol{\lambda}_m)^p\right)\left\lVert f\right\rVert^p\\ &\le \left( 1+2 (\boldsymbol{k}_m)^p + (A_p \boldsymbol{\lambda}_m)^p\right)\left\lVert f\right\rVert^p. \end{align*} $$

Let us now prove inequality (3.8). In order to apply Lemma 3.3 (iii), we pick $A\subseteq \mathbb {N}$ , $f\in \mathbb {X}$ and B greedy set of f with $\left \lvert A\right \rvert =\left \lvert B\right \rvert \le m$ . Set $t=\min _{n\in B} \left \lvert \boldsymbol {x}_n^*(f)\right \rvert $ , and pick $(a_n)_{n\in A\cup B}$ in $[0,t]$ . Let us put

$$\begin{align*}y=\sum_{n\in B} a_n \, \varepsilon_n(f)\, \boldsymbol{x}_n, \quad z=\sum_{n\in A\setminus B} a_n \, \varepsilon_n(f)\, \boldsymbol{x}_n \end{align*}$$

and $g=f-z$ . On the one hand, since $\left \lvert A\setminus B\right \rvert \le \left \lvert B\right \rvert $ , B is a greedy set of g and $g-S_B(g)=f-S_B(f)-z$ , we have

$$\begin{align*}\left\lVert f-S_B(f)-z\right\rVert\le\boldsymbol{L}_m \left\lVert g+z\right\rVert=\boldsymbol{L}_m \left\lVert f\right\rVert. \end{align*}$$

On the other hand, since $\left \lvert \boldsymbol {x}_n^*(f-y)\right \rvert \le \left \lvert \boldsymbol {x}_n^*(f)\right \rvert $ and $\operatorname {\mathrm {sign}}(\boldsymbol {x}_n^*(f-y))=\operatorname {\mathrm {sign}}(\boldsymbol {x}_n^*(f))$ for all $n\in B$ , applying [4, Corollary 2.3] yields

$$\begin{align*}\left\lVert f-S_{B}(f) +y \right\rVert =\left\lVert f-S_{B}(f-y) \right\rVert \le A_p {\boldsymbol{k}^{\boldsymbol{c}}_m} \left\lVert f \right\rVert. \end{align*}$$

Combining both estimates, we obtain

$$\begin{align*}\left\lVert y-z \right\rVert \le \left((A_p\, ({\boldsymbol{k}^{\boldsymbol{c}}_m})^p + (\boldsymbol{L}_m)^p\right)^{1/p} \left\lVert f \right\rVert. \end{align*}$$

Hence, by Lemma 3.4,

$$\begin{align*}\left\lVert \sum_{n\in A\cup B} b_n\, \boldsymbol{x}_n \right\rVert \le {\boldsymbol{\Upsilon}}^{1/p} \left( (A_p\, {\boldsymbol{k}^{\boldsymbol{c}}_m})^p + (\boldsymbol{L}_m)^p\right)^{1/p}\left\lVert f\right\rVert. \end{align*}$$

Applying this inequality with $b_n=0$ for all $n\in B\setminus A$ and $\left \lvert b_n\right \rvert =1$ for all $n\in A$ , we are done.

4 Almost greedy Lebesgue constants

In greedy approximation with respect to bases, it is also of interest to compare the error $\left \lVert f-\mathcal {G}_m(f)\right \rVert $ with the best error in the approximation of f by m-term coordinate projections. Thus, given a basis $\mathcal {X}$ of a quasi-Banach space $\mathbb {X}$ , for $m\in \mathbb {N}$ we put

$$\begin{align*}\widetilde{\sigma}_m[\mathcal{X}, \mathbb{X}](f):=\widetilde{\sigma}_m(f) = \inf\lbrace \left\lVert f - S_A(f) \right\rVert \colon \left\lvert A\right\rvert =m\rbrace \end{align*}$$

and define the mth almost greedy constant as

$$\begin{align*}{\boldsymbol{L}^{\boldsymbol{a}}_m}={\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X},\mathbb{X}]=\sup\left\lbrace \frac{\left\lVert f-\mathcal{G}_m(f)\right\rVert}{\widetilde{\sigma}_m(f)} \colon f\in\mathbb{X}\setminus\Sigma_m\right\rbrace. \end{align*}$$

By definition [19], the basis $\mathcal {X}$ is almost greedy if and only if $\sup _m {\boldsymbol{L}^{\boldsymbol{a}}_m}<\infty $ . Roughly speaking, if the Lebesgue constants $\boldsymbol {L}_m$ measure how far a basis is from being greedy, it could be said that the parameters ${\boldsymbol{L}^{\boldsymbol{a}}_m}$ quantify how far a basis is from being almost greedy. In this section, we estimate the size of these parameters in terms of the squeeze-symmetry parameters and the so-called quasi-greedy parameters, which in turn measure how far a basis is from being quasi-greedy.

Similarly to the Lebesgue constant $\boldsymbol {L}_m$ , the almost greedy constant ${\boldsymbol{L}^{\boldsymbol{a}}_m}$ is the optimal constant C such that

(4.1) $$ \begin{align} \left\lVert f-S_A(f)\right\rVert \le C \widetilde{\sigma}_k(f), \; A \text{ greedy set of } f,\; k\le \left\lvert A\right\rvert\le m, \end{align} $$

(see [2, Lemma 2.2] and [4, Lemma 6.1]), and this implies that the sequence $({\boldsymbol{L}^{\boldsymbol{a}}_m})_{m=1}^{\infty }$ is nonincreasing.

The mth quasi-greedy constant $\boldsymbol {g}_m$ and its complemented counterpart ${\boldsymbol{g}^{\boldsymbol{c}}_m}$ are defined by

$$\begin{align*}\boldsymbol{g}_m=\sup_{1\le k \le m} \left\lVert \mathcal{G}_{k}\right\rVert, \quad {\boldsymbol{g}^{\boldsymbol{c}}_m}=\sup_{1\le k \le m} \left\lVert \mathrm{Id}_{\mathbb{X}}- \mathcal{G}_{k}\right\rVert. \end{align*}$$

Similarly to the unconditionality parameters, in the case when $\mathbb {X}$ is a p-Banach space, these parameters are related by the inequalities

$$\begin{align*}(\boldsymbol{g}_m)^p\le 1+({\boldsymbol{g}^{\boldsymbol{c}}_m})^p \quad \mbox{and}\quad ({\boldsymbol{g}^{\boldsymbol{c}}_m})^p\le 1+(\boldsymbol{g}_m)^p. \end{align*}$$

A perturbation technique similar to the one used when dealing with the Lebesgue and the almost greedy constants gives that ${\boldsymbol{g}^{\boldsymbol{c}}_m}$ is the smallest constant C such that

$$ \begin{align*} \left\lVert f-S_A(f)\right\rVert \le C \left\lVert f \right\rVert,\; A \ \mbox{greedy set of} \ f, \; \left\lvert A\right\rvert\le m, \end{align*} $$

and the quasi-greedy constant $\boldsymbol {g}_m$ is the smallest constant C such that

(4.2) $$ \begin{align} \left\lVert S_A(f)\right\rVert \le C \left\lVert f \right\rVert,\; A \ \mbox{greedy set of} \ f, \; \left\lvert A\right\rvert\le m. \end{align} $$

Since a basis is almost greedy if and only if it is quasi-greedy and democratic (see [19, Theorem 3.3] and [4, Theorem 6.3]), it seems natural to look for democracy-like parameters which, when combined with the quasi-greediness parameters, provide optimal bounds for the growth of the almost greedy constants. For this purpose, we define the disjoint squeeze-symmetry parameter ${\boldsymbol{\lambda}^{\boldsymbol{d}}_m}={\boldsymbol{\lambda}^{\boldsymbol{d}}_m}[\mathcal {X},\mathbb {X}]$ as the smallest constant C such that

whenever $A\subseteq \mathbb {N}$ , $\varepsilon \in \mathbb {E}^A$ and B greedy set of $f\in \mathbb {X}$ satisfy $A\cap \operatorname {\mathrm {supp}}(f)=\emptyset $ and $\left \lvert A\right \rvert = \left \lvert B\right \rvert \le m$ . The following estimates imply that a basis is squeeze-symmetric if and only if $\sup _m {\boldsymbol{\lambda}^{\boldsymbol{d}}_m}<\infty $ .

Lemma 4.1. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . Then

$$\begin{align*}{\boldsymbol{\lambda}^{\boldsymbol{d}}_m}[\mathcal{X},\mathbb{X}] \le \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] \le ({\boldsymbol{\lambda}^{\boldsymbol{d}}_m}[\mathcal{X},\mathbb{X}])^2. \end{align*}$$

Proof. Lemma 3.3 (iii) yields the left-hand side inequality. Let A and B be disjoint sets with $\left \lvert A\right \rvert =\left \lvert B\right \rvert =m$ . Then

for all $\varepsilon \in \mathbb {E}^A$ and $\delta \in \mathbb {E}^B$ . Since we can restrict ourselves to finitely supported vectors, combining this fact with Lemma 3.3 (iii) yields the right-hand side inequality.

Theorem 4.2. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . There are constants $C_1$ and $C_2$ depending only on the modulus of concavity of $\mathbb {X}$ such that

$$\begin{align*}\frac{1}{C_1} {\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X},\mathbb{X}] \le \max\lbrace{\boldsymbol{\lambda}^{\boldsymbol{d}}_m}[\mathcal{X},\mathbb{X}], \boldsymbol{g}_m[\mathcal{X},\mathbb{X}]\rbrace\le C_2 {\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X},\mathbb{X}], \quad m\in\mathbb{N}. \end{align*}$$

Proof. Assume that $\mathbb {X}$ is a p-Banach space, $0<p\le 1$ . Inequality (4.1) yields ${\boldsymbol{g}^{\boldsymbol{c}}_m} \le {\boldsymbol{L}^{\boldsymbol{a}}_m}$ (see [13, Proposition 1.1]). To conclude the proof of the right side estimate, we pick $A\subseteq \mathbb {N}$ , $\varepsilon \in \mathbb {E}^A$ , $f\in \mathbb {X}$ and B greedy set of f with $\left \lvert A\right \rvert =\left \lvert B\right \rvert \le m$ and $A\cap \operatorname {\mathrm {supp}}(f)=\emptyset $ . Set $t=\min _{n\in B} \left \lvert \boldsymbol {x}_n^*(f)\right \rvert $ . Taking into account that B is a greedy set of

and that

, we obtain

To prove the left side estimate, we pick a greedy set A of $f\in \mathbb {X}$ and $B\subseteq \mathbb {N}$ with $\left \lvert A\right \rvert =\left \lvert B\right \rvert = m$ . Notice that $\left \lvert A\setminus B\right \rvert =\left \lvert B\setminus A\right \rvert \le m$ , that $A\setminus B$ is a greedy set of $g:=f-S_B(f)$ , that

$$\begin{align*}g-S_{A\setminus B}(g)=f-S_{A\cup B}(f)\; \mbox{ and }\; f -S_A(f)= f-S_{A\cup B}(f) + S_{B\setminus A}(f) \end{align*}$$

and that

$$\begin{align*}\max_{n\in A\setminus B} \left\lvert\boldsymbol{x}_n^*(f)\right\rvert\le \min_{n\in B\setminus A} \left\lvert\boldsymbol{x}_n^*(g)\right\rvert. \end{align*}$$

Hence, applying Lemma 3.4 we obtain

$$\begin{align*}\left\lVert f -S_A(f) \right\rVert^p = \left\lVert f-S_{A\cup B}(f)\right\rVert^p + \left\lVert S_{B\setminus A}(f) \right\rVert^p\le C^p \left\lVert g\right\rVert^p, \end{align*}$$

where $C^p=({\boldsymbol{g}^{\boldsymbol{c}}_m})^p + (A_p {\boldsymbol{\lambda}^{\boldsymbol{d}}_m})^p$ . Consequently, ${\boldsymbol{L}^{\boldsymbol{a}}_m} \le C$ .

5 Lebesgue-type inequalities for truncation quasi-greedy bases

Democracy and unconditionality are a priori independent properties of each other, so we can regard them as the disjoint components of greedy bases. In the same way, quasi-greediness is a weakened form of unconditionality which complements democracy to give almost greedy bases. The overlapping between squeeze-symmetry and unconditionality can also be identified. For that, let us first introduce the corresponding unconditionality-like property.

Given a basis $\mathcal {X}$ is a quasi-Banach space $\mathbb {X}$ , and $A\subseteq \mathbb {N}$ finite, we consider the nonlinear operator

Now, for $m\in \mathbb {N}$ , we define the mth restricted truncation operator of the basis $\mathcal {X}$ as

$$\begin{align*}\mathcal{R}_m\colon\mathbb{X}\to \mathbb{X}, \quad f\mapsto \mathcal{R}_{A_m(f)}(f) \end{align*}$$

and the mth-truncation quasi-greedy parameter as

$$\begin{align*}\boldsymbol{r}_m=\boldsymbol{r}_m[\mathcal{X},\mathbb{X}] =\sup_{1\le k\le m} \left\lVert \mathcal{R}_k\right\rVert. \end{align*}$$

Those bases for which the restricted truncations operators are uniformly bounded, that is, $\sup _m \boldsymbol {r}_m<\infty $ , will be called truncation quasi-greedy. A standard approximation argument gives

$$\begin{align*}\boldsymbol{r}_m=\sup\left\lbrace \frac{ \left\lVert \mathcal{R}_A(f) \right\rVert}{\left\lVert f \right\rVert } \colon A \mbox{ greedy set of } f\in\mathbb{X}\setminus\lbrace0\rbrace,\; \left\lvert A\right\rvert\le m\right\rbrace. \end{align*}$$

Hence, $(\boldsymbol {r}_m)_{m=1}^{\infty }$ is nondecreasing.

Quasi-greedy bases are truncation quasi-greedy. This result, and the quantitative estimates associated with it, deserve a detailed explanation. If $\mathbb {X}$ is a Banach space, for $m\in \mathbb {N}$ ,

(5.1) $$ \begin{align} \boldsymbol{r}_m[\mathcal{X},\mathbb{X}]\le \boldsymbol{g}_m[\mathcal{X},\mathbb{X}] \end{align} $$

(see the proofs of [55, Theorem 3], [19, Lemma 2.2] or [2, Theorem 2.4]). However, the argument that shows inequality (5.1) does not transfer to nonlocally convex quasi-Banach spaces. The authors circumvented in [4] the use of convexity at the cost of getting worse estimates. In fact, if $\mathbb {X}$ is a p-Banach space, $0<p<1$ , the proof of [4, Theorem 4.8] gives

$$\begin{align*}\boldsymbol{r}_m\le \boldsymbol{g}_m \eta_p(\boldsymbol{g}_m),\quad m\in\mathbb{N}, \end{align*}$$

where $\eta _p$ is the function defined in [4, Equation (4.5)]. Hence, (see [4, Remark 4.9]) there is a constant C (independent of p) such that

(5.2) $$ \begin{align} \boldsymbol{r}_m[\mathcal{X},\mathbb{X}]\le C (\boldsymbol{g}_m[\mathcal{X},\mathbb{X}])^{1+1/p},\; m\in\mathbb{N},\; 0<p<1,\; \mathbb{X}\ p\mbox{-Banach}. \end{align} $$

With an eye to relating the truncation quasi-greedy and democracy parameters with the squeeze-symmetry parameters, we write down a general lemma that will be useful in applications.

Lemma 5.1. Let $0<p,q\le 1$ . Assume that a basis $\mathcal {Y}$ of a q-Banach space $\mathbb {Y} \ C$ -dominates a basis $\mathcal {X}$ of a p-Banach space $\mathbb {X}$ . Then

$$\begin{align*}\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] \le {\boldsymbol{\Upsilon}}^{1/p+1/q} A_p A_q C \theta_m \boldsymbol{r}_m[\mathcal{Y},\mathbb{Y}] , \quad m\in\mathbb{N}, \end{align*}$$

where

Proof. Let $A\subseteq \mathbb {N}$ , $\varepsilon \in \mathbb {E}^A$ , $f\in \mathbb {X}$ finitely supported and B a greedy set of f with $\left \lvert A\right \rvert = \left \lvert B\right \rvert \le m$ . Set $t=\min _{n\in B} \left \lvert \boldsymbol {x}_n^*(f)\right \rvert $ . Applying Lemma 3.4 we obtain

$$\begin{align*}\left\lVert\sum_{n\in B} a_n \, \boldsymbol{y}_n \right\rVert\le {\boldsymbol{\Upsilon}}^{1/q} A_q \boldsymbol{r}_m[\mathcal{Y},\mathbb{Y}] \left\lVert S(f) \right\rVert, \quad \left\lvert a_n\right\rvert\le t. \end{align*}$$

Hence,

We get the desired inequality by applying again Lemma 3.4.

The quantitative estimates we obtain in Proposition 5.2 imply that a basis is squeeze-symmetric if and only if it is truncation quasi-greedy and democratic (see [4, Proposition 9.4 and Corollary 9.15]).

Proposition 5.2. Let $\mathcal {X}$ be a basis of a p-Banach space, $0<p\le 1$ . Then, for all $m\in \mathbb {N}$ ,

(5.3) $$ \begin{align} \boldsymbol{\mu}_m \le {\boldsymbol{\lambda}^{\boldsymbol{d}}_m} \; \mbox{ and }\; \boldsymbol{r}_m \le \boldsymbol{\lambda}_m \le {\boldsymbol{\Upsilon}}^{2/p} A_p^2 \boldsymbol{r}_m \boldsymbol{\mu}_m. \end{align} $$

Proof. Using Lemma 5.1 with $\mathcal {X}=\mathcal {Y}$ and $\mathbb {X}=\mathbb {Y}$ yields the right-hand side of the second inequality. The other two inequalities are straightforward.

Proposition 5.2 yields in particular that the squeeze-symmetry parameters and the democracy parameters of truncation quasi-greedy bases are of the same order. Thus, combining that with Theorem 3.5 gives the following improvement of Theorem 1.1.

Theorem 5.3. Let $\mathcal {X}$ be an truncation quasi-greedy basis of a quasi-Banach space $\mathbb {X}$ . There are constants $C_1$ and $C_2$ depending on the modulus of concavity of $\mathbb {X}$ and the truncation quasi-greedy constant of $\mathcal {X}$ such that

$$\begin{align*}\frac{1}{C_1}\boldsymbol{L}_m \le \max\lbrace\boldsymbol{k}_m,\boldsymbol{\mu}_m\rbrace \le C_2 \boldsymbol{L}_m, \quad m\in\mathbb{N}. \end{align*}$$

We close this section with the almost greedy counterpart of Theorem 5.3.

Theorem 5.4. Let $\mathcal {X}$ be a truncation quasi-greedy basis of a quasi-Banach space $\mathbb {X}$ . There are constants $C_1$ and $C_2$ depending on the modulus of concavity of $\mathbb {X}$ and the truncation quasi-greedy constant of $\mathcal {X}$ such that

$$\begin{align*}\frac{1}{C_1}{\boldsymbol{L}^{\boldsymbol{a}}_m} \le \max\lbrace\boldsymbol{g}_m,\boldsymbol{\mu}_m\rbrace \le C_2 {\boldsymbol{L}^{\boldsymbol{a}}_m}, \quad m\in\mathbb{N}. \end{align*}$$

Proof. It follows by combining Theorem 4.2 with Proposition 5.2.

6 Squeeze-symmetry versus unconditionality

Proposition 5.2 shows that squeeze-symmetry and unconditionality are intertwined. This overlapping can be regarded from a different angle since squeezing a basis $\mathcal {X}$ between two symmetric bases yields estimates for the unconditionality parameters of $\mathcal {X}$ . To give a precise formulation of this analysis, we introduce some additional terminology.

Given two bases $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ and $\mathcal {Y}=(\boldsymbol {y}_n)_{n=1}^{\infty }$ of quasi-Banach spaces $\mathbb {X}$ and $\mathbb {Y}$ , $\boldsymbol {\delta }_m[\mathcal {X}, \mathcal {Y}]$ will denote for each $m\in \mathbb {N}$ the smallest constant C such that

$$\begin{align*}\left\lVert\sum_{n\in A} \boldsymbol{y}_n^*(f) \, \boldsymbol{x}_n\right\rVert \le C \left\lVert f \right\rVert, \quad \left\lvert A\right\rvert=m, \; f\in\mathbb{Y}. \end{align*}$$

Notice that $\boldsymbol {k}_m[\mathcal {X},\mathbb {X}]=\boldsymbol {\delta }_m[\mathcal {X},\mathcal {X}]$ .

Thanks to these parameters, we can give an alternative reinterpretation of the fundamental function of a basis $\mathcal {X}$ . In fact, if $\mathbb {X}$ is a p-Banach space, by Lemma 3.4,

(6.1) $$ \begin{align} \boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m) \le \boldsymbol{\delta}_m[\mathcal{X},\ell_{\infty}] \le A_p\, \boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m), \quad m\in\mathbb{N}. \end{align} $$

Here and subsequently, whenever the unit vector system $\mathcal {B}=(\boldsymbol {e}_{n})_{n=1}^{\infty }$ is a basis of a quasi-Banach space $\mathbb {Y}$ , we will write $\boldsymbol {\delta }_m[\mathcal {X},\mathbb {Y}]$ instead of $\boldsymbol {\delta }_m[\mathcal {X},\mathcal {B}]$ ; we will proceed analogously when $\mathcal {X}$ is the unit vector system of $\mathbb {X}$ .

In the case when the bases $\mathcal {X}$ and $\mathcal {Y}$ are $1$ -symmetric or, more generally, $1$ -subsymmetric (see [11]), $\boldsymbol {\delta }_m[\mathcal {X}, \mathcal {Y}]$ is the smallest constant C such that

$$\begin{align*}\left\lVert\sum_{n=1}^m a_n\, \boldsymbol{y}_n\right\rVert \le C \left\lVert\sum_{n=1}^m a_n\, \boldsymbol{x}_n\right\rVert, \quad a_n\ge 0. \end{align*}$$

Lemma 6.1. Let $\mathcal {X}$ , $\mathcal {X}_1$ and $\mathcal {X}_2$ be bases of a quasi-Banach spaces $\mathbb {X}$ , $\mathbb {X}_1$ and $\mathbb {X}_2$ respectively. Suppose that $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty } \ D$ -dominates $\mathcal {X}_2$ . For each $A\subseteq \mathbb {N}$ finite, let $T_A\colon \mathbb {X}_1 \to \mathbb {X}$ be the operator given by

$$\begin{align*}T_A(f)=\sum_{n\in A} a_n\, \boldsymbol{x}_n, \ (a_n)_{n=1}^{\infty}=\mathcal{F}[\mathcal{X}_1,\mathbb{X}_1](f). \end{align*}$$

Set $\zeta _m=\sup _{\left \lvert A\right \rvert \le m} \left \lVert T_A \right \rVert $ . Then, for $m\in \mathbb {N}$ ,

$$ \begin{align*} \boldsymbol{k}_m[\mathcal{X},\mathbb{X}] & \le D \zeta_m \boldsymbol{\delta}_m[\mathcal{X}_1,\mathcal{X}_2], \mbox{ and}\\ \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}]& \le D \zeta_m \boldsymbol{\lambda}_m[\mathcal{X}_1,\mathbb{X}_1] \, \boldsymbol{\delta}_m[\mathcal{X}_1,\mathcal{X}_2]. \end{align*} $$

Proof. We will only prove the second inequality because it is more general. Given $f\in \mathbb {X}$ , let $g\in \mathbb {X}_1$ be such that $\mathcal {F}(g)=\mathcal {F}(f)\chi _A$ , and let $h\in \mathbb {X}_2$ be such that $\mathcal {F}(h)=\mathcal {F}(f)$ . We have

$$\begin{align*}\left\lVert g \right\rVert \le \boldsymbol{\delta}_m[\mathcal{X}_1,\mathcal{X}_2]\left\lVert h \right\rVert, \ \left\lVert h \right\rVert \le D \boldsymbol{\delta}_m[\mathcal{X}_1,\mathcal{X}_2] \left\lVert f \right\rVert \end{align*}$$

and, since $S_A(f)=T_A(g)$ ,

$$\begin{align*}\left\lVert S_A(f)\right\rVert\le \zeta_m \left\lVert g \right\rVert. \end{align*}$$

Finally, if A is a greedy set of f and $\left \lvert B\right \rvert =\left \lvert A\right \rvert $ ,

Despite the fact that we stated Lemma 6.1 in wide generality, in practice we will only apply it in the case when $\mathcal {X}_1$ and $\mathcal {X}_2$ are $1$ -symmetric, in which case $\boldsymbol {\lambda }_m[\mathcal {X}_1,\mathbb {X}_1]=1$ and therefore the parameters $\boldsymbol {\delta }_m$ are easy to compute. We also point out that the best-case scenario occurs when $\mathcal {X}_1$ dominates $\mathcal {X}$ so that $\sup _m \zeta _m<\infty $ . With an eye to applying Lemma 6.1 to estimating Lebesgue constants, we record the parameters $\boldsymbol {\delta }_m$ in some important situations.

(6.2) $$ \begin{align} \boldsymbol{\delta}_m[\ell_p,\ell_q]=m^{1/p-1/q}, \quad m\in\mathbb{N}, \; p\le q. \end{align} $$

Given a nondecreasing weight $\boldsymbol {\sigma }= (s_m)_{m=1}^{\infty }$ , we set

$$\begin{align*}H_m[\boldsymbol{\sigma}]=\sum_{n=1}^m \frac{s_n-s_{n-1}}{s_n}. \end{align*}$$

If $\boldsymbol {w}$ is a weight whose primitive weight $\boldsymbol {\sigma }$ is doubling, then for any $0<p<\infty $ ,

(6.3) $$ \begin{align} \boldsymbol{\delta}_m[d_{1,p}(\boldsymbol{w}), d_{1,\infty}(\boldsymbol{w})]=(H_m[\boldsymbol{\sigma}])^{1/p}, \quad m\in\mathbb{N}. \end{align} $$

Remark 6.2. A weight $\boldsymbol {\sigma }= (s_m)_{m=1}^{\infty }$ is said to have the upper regularity property (URP for short) if there is $r\in \mathbb {N}$ such that

$$\begin{align*}s_{rm}\le \frac{1}{2} r s_m, \quad m\in\mathbb{N}, \end{align*}$$

and is said to have the lower regularity property (LRP for short) if there is $r\in \mathbb {N}$ such that

$$\begin{align*}s_{rm}\ge 2 s_m, \quad m\in\mathbb{N}. \end{align*}$$

The weight $\boldsymbol {\sigma }$ has the LRP if and only if $\boldsymbol {\sigma }^*=(m/s_m)_{m=1}^{\infty }$ has the URP. Moreover, if $\boldsymbol {\sigma }$ has the URP, there is a constant C such that

$$\begin{align*}\sum_{n=1}^m \frac{1}{s_n} \le C \frac{m}{s_m}, \quad m\in\mathbb{N}, \end{align*}$$

(see [19, Section 4]). Hence, if $\boldsymbol {\sigma }$ has the LRP, there is a constant C such that

$$\begin{align*}\sum_{n=1}^m \frac{s_n}{n} \le C s_m= \sum_{n=1}^m s_n-s_{n-1}, \quad m\in\mathbb{N}. \end{align*}$$

Using that $1/s_{n}$ is nonincreasing, we infer that

$$\begin{align*}H_m:=\sum_{n=1}^m \frac{1}{n}= \sum_{n=1}^m \frac{s_n}{n}\frac{1}{s_n} \le C H_m[\boldsymbol{\sigma}],\quad m\in\mathbb{N}. \end{align*}$$

The reverse inequality holds for general doubling weights. Indeed, since $\inf _n s_n/s_{n+1}>0$ , for every $\alpha>0$ there is a constant $C_1$ such that

$$\begin{align*}\frac{s_n-s_{n-1}}{s_n} \le C_1 \frac{s_n^{\alpha} -s_{n-1}^{\alpha}}{s_n^{\alpha}}, \quad n\in\mathbb{N}. \end{align*}$$

Moreover, for $\alpha $ small enough,

$$\begin{align*}C_2:=\sup_{n\le m} \frac{n}{m} \frac{s_m^{\alpha}}{s_n^{\alpha}}<\infty. \end{align*}$$

Therefore,

$$\begin{align*}s_m^{\alpha} \le C_2 \sum_{n=1}^m \frac{s_n^{\alpha}}{n},\quad m\in\mathbb{N}. \end{align*}$$

Summing up,

$$ \begin{align*} H_m[\boldsymbol{\sigma}] \le C_1 \sum_{n=1}^m \frac{s_n^{\alpha} -s_{n-1}^{\alpha}}{s_n^{\alpha}} \le C_1 C_2 H_m, \quad m\in\mathbb{N}. \end{align*} $$

7 The thresholding greedy algorithm, greedy parameters and duality

An important research topic in approximation theory using bases is the study of the duality properties of the TGA. This section is motivated by the attempt to make headway in the following general question: If a basis $\mathcal {X}$ enjoys some greedy-like property, what can be said about its dual basis $\mathcal {X}^*$ in this regard? To that end, we need to introduce the bidemocracy parameters of $\mathcal {X}$ ,

$$\begin{align*}\boldsymbol{B}_m[\mathcal{X},\mathbb{X}]= \frac{1}{m} \boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m) \boldsymbol{\varphi_u}[\mathcal{X}^*,\mathbb{X}^*](m), \quad m\in\mathbb{N}. \end{align*}$$

The basis $\mathcal {X}$ is bidemocratic [19] if and only if $\sup _m \boldsymbol {B}_m<\infty $ (see, e.g., [4, Lemma 5.5]).

Proposition 7.1. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . Then

$$\begin{align*}\max\lbrace \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] , \boldsymbol{\lambda}_m[\mathcal{X}^*,\mathbb{X}^*]\rbrace \le \boldsymbol{B}_m[\mathcal{X},\mathbb{X}], \quad m\in\mathbb{N}. \end{align*}$$

Proof. Let $f\in \mathbb {X}$ , $f^*\in \mathbb {X}^*$ and $B\subseteq \mathbb {N}$ with $\left \lvert B\right \rvert =m$ . We have

Thus, if $\left \lvert \lbrace n\colon \left \lvert \boldsymbol {x}_n^*(f)\right \rvert \ge 1\rbrace \right \rvert \ge m$ and $\left \lvert \lbrace n\colon \left \lvert f^*(\boldsymbol {x}_n)\right \rvert \ge 1\rbrace \right \rvert \ge m$ , we deduce that

$$\begin{align*}\left\lVert f\right\rVert \ge \frac{m}{\boldsymbol{\varphi_u}[\mathcal{X}^*,\mathbb{X}^*](m)}, \quad \left\lVert f^*\right\rVert \ge \frac{m}{\boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m)}. \end{align*}$$

We conclude the proof by applying Lemma 3.3 (i).

Proposition 7.1 is a quantitative version of [4, Proposition 5.7]. When combined with Theorem 3.5 and Theorem 4.2, it leads to linear estimates for the Lebesgue constants in terms of the bidemocracy parameters.

Theorem 7.2. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . Then there are constants C and D such that, for all $m\in \mathbb {N}$ ,

(7.1) $$ \begin{align} \boldsymbol{L}_m \le C \max\lbrace \boldsymbol{k}_m, \boldsymbol{B}_m\rbrace,\end{align} $$

and

$$\begin{align*}{\boldsymbol{L}^{\boldsymbol{a}}_m} \le D \max\lbrace \boldsymbol{g}_m, \boldsymbol{B}_m\rbrace. \end{align*}$$

Inequality (7.1) was proved in the locally convex setting in [3, Theorem 2.3 and Theorem 1.3] with the purpose of finding bounds for the growth of the greedy constant of the $L_p$ -normalized Haar system as p either increases to $\infty $ or decreases to $1$ .

Since the unconditionality parameters are defined in terms of linear operators, they dualize as expected, that is,

$$\begin{align*}\boldsymbol{k}_m[\mathcal{X}^*,\mathbb{X}^*]\le \boldsymbol{k}_m[\mathcal{X},\mathbb{X}], \quad m\in\mathbb{N}. \end{align*}$$

The reverse inequality also holds in the case when $\mathbb {X}$ is a Banach space. Consequently, by Theorem 3.5, for $m\in \mathbb {N}$ ,

(7.2) $$ \begin{align} \boldsymbol{L}_m[\mathcal{X}^*,\mathbb{X}^*]\le C\max\lbrace \boldsymbol{\lambda}_m[\mathcal{X}^*,\mathbb{X}^*], \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}], \boldsymbol{k}_m[\mathcal{X},\mathbb{X}]\rbrace, \end{align} $$

where the constant C depends only on the modulus of concavity of $\mathbb {X}$ . Our next goal is to obtain duality results for the almost greedy and quasi-greedy parameters.

Proposition 7.3. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . Then for $m\in \mathbb {N}$ ,

$$ \begin{align*} {\boldsymbol{g}^{\boldsymbol{c}}_m}[\mathcal{X}^*,\mathbb{X}^*] &\le \boldsymbol{g}_m[\mathcal{X},\mathbb{X}] +\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}]+\boldsymbol{\lambda}_m[\mathcal{X}^*,\mathbb{X}^*]\mbox{ and }\\ \boldsymbol{g}_m[\mathcal{X}^*,\mathbb{X}^*] &\le {\boldsymbol{g}^{\boldsymbol{c}}_m}[\mathcal{X},\mathbb{X}] +\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}]+\boldsymbol{\lambda}_m[\mathcal{X}^*,\mathbb{X}^*]. \end{align*} $$

Proof. Given $D\subseteq \mathbb {N}$ , put $S_D=S_D[\mathcal {X},\mathbb {X}]$ . Let A be a greedy set of $f^*\in \mathbb {X}^*$ , and let B be a greedy set of $f\in \mathbb {X}$ . Assume that $\left \lvert A\right \rvert =\left \lvert B\right \rvert \le m$ . Then

Similarly, switching the roles of $\mathcal {X}$ and $\mathcal {X}^*$ , we obtain

$$\begin{align*}\left\lvert S_{A}^*(f^*)(S_{B^c}(f))\right\rvert\le \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] \left\lVert f^*\right\rVert \, \left\lVert f\right\rVert. \end{align*}$$

Applying these inequalities to the identities

$$ \begin{align*} S_{A^c}^*(f^*)(f) &=f^*(S_{B^c}(f))+ S_{A^c}^*(f^*)(S_B(f))- S_{A}^*(f^*)(S_{B^c}(f)),\\ S_{A}^*(f^*)(f)&= f^*(S_{B}(f))- S_{A^c}^*(f^*)(S_B(f)) + S_{A}^*(f^*)(S_{B^c}(f)) \end{align*} $$

leads to the desired inequalities.

Proposition 7.4. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . There is a constant C, depending only on the modulus of concavity of $\mathbb {X}$ , such that

$$\begin{align*}{\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X}^*,\mathbb{X}^*]\le C\max\lbrace \boldsymbol{\lambda}_m[\mathcal{X}^*,\mathbb{X}^*], \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}], \boldsymbol{g}_m[\mathcal{X},\mathbb{X}]\rbrace, \quad m\in\mathbb{N}. \end{align*}$$

Proof. Just combine Theorem 4.2 with Proposition 7.3.

We make a stop en route to gather some consequences of combining Theorem 3.5, Theorem 4.2, Proposition 7.1, Proposition 7.3, Proposition 7.4 and inequality (7.2).

Theorem 7.5. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . There are constants $C_1$ , $C_2$ and $C_3$ , depending only on the modulus of concavity of $\mathbb {X}$ , such that

(7.3) $$ \begin{align} \begin{aligned} \boldsymbol{g}_m[\mathcal{X}^*,\mathbb{X}^*] &\le C_1 \max\lbrace\boldsymbol{B}_m [\mathcal{X},\mathbb{X}],\boldsymbol{g}_m[\mathcal{X},\mathbb{X}]\rbrace, \\ {\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X}^*,\mathbb{X}^*] &\le C_2 \max\lbrace\boldsymbol{B}_m[\mathcal{X},\mathbb{X}],{\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X},\mathbb{X}]\rbrace, \mbox{ and } \\ \boldsymbol{L}_m[\mathcal{X}^*,\mathbb{X}^*] &\le C_3 \max\lbrace\boldsymbol{B}_m[\mathcal{X},\mathbb{X}],\boldsymbol{L}_m[\mathcal{X},\mathbb{X}]\rbrace. \end{aligned} \end{align} $$

Note that equation (7.3) is a quantitative version of [19, Theorem 5.4] (see also [4, Corollary 6.8]).

Inequality (7.2), Proposition 7.3 and Proposition 7.4 justify the quest to find upper estimates for the squeeze-symmetry parameters of the dual basis. We tackle this problem with the help of the bidemocracy paremeters.

Given a nondecreasing sequence $\boldsymbol {\sigma }= (s_m)_{m=1}^{\infty }$ , we set

$$\begin{align*}R_m[\boldsymbol{\sigma}]=\frac{s_m}{m}\sum_{n=1}^m \frac{1}{s_n}, \quad m\in\mathbb{N}. \end{align*}$$

If $\boldsymbol {\sigma }$ has the URP, $\sup _m R_m[\boldsymbol {\sigma }]<\infty $ . Thus, the sequence $(R_m[\boldsymbol {\sigma }])_{m=1}^{\infty }$ could be said to measure the regularity of $\boldsymbol {\sigma }$ . Note that, in the case when the dual weight $\boldsymbol {\sigma }^*$ is also nondecreasing,

$$\begin{align*}R_m[\boldsymbol{\sigma}]\le H_m, \quad m\in\mathbb{N}. \end{align*}$$

Theorem 7.6. Let $0<p\le 1$ , and let $\boldsymbol {\sigma }$ be the fundamental function of a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ of a p-Banach space $\mathbb {X}$ . Then there are constants $C_1$ and $C_2$ depending only on p such that

$$ \begin{align*} \boldsymbol{B}_m[\mathcal{X},\mathbb{X}] & \le C_1 \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] R_m[\boldsymbol{\sigma}], \mbox{ and }\\ \boldsymbol{k}_m[\mathcal{X},\mathbb{X}] &\le C_2 \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] (H_m[\boldsymbol{\sigma}])^{1/p}, \quad m\in\mathbb{N}. \end{align*} $$

Proof. Let $A\subseteq \mathbb {N}$ with $\left \lvert A\right \rvert \le m$ . Dualizing the operator $\mathcal {F}_A$ and taking into consideration [15, Theorem 2.4.14], we obtain that the operator

$$\begin{align*}T_A \colon d_{1,1}(1/\boldsymbol{\sigma}) \to \mathbb{X}^*, \quad (a_n)_{n=1}^{\infty} \mapsto \sum_{n\in A} a_n\, \boldsymbol{x}_n^* \end{align*}$$

satisfies $ \left \lVert T_A\right \rVert \le \boldsymbol {\lambda }_m$ . In particular,

This yields the estimate for the bidemocracy parameters. Now, by [4, Theorem 9.12], the unit vector system of $d_{1,p}(\boldsymbol {w})$ dominates $\mathcal {X}$ . Appealing to Lemma 6.1 and to the identity (6.3), we obtain the estimate for the unconditionality parameters.

To finish this section, we will obtain estimates for the squeeze-symmetry parameters in some particular situations that occur naturally in applications. Let us introduce a mild condition on bases.

Definition 7.7. We say that a basis has the upper gliding hump property for constant coefficients if there is a constant C such that for every A and $D\subseteq \mathbb {N}$ finite there is $B\subseteq \mathbb {N}$ with $A\cap D=\emptyset $ , $\left \lvert B\right \rvert \le \left \lvert A\right \rvert $ and .

For instance, the trigonometric system in $L_1(\mathbb {T})$ or, more generally, in any translation invariant quasi-Banach space over $\mathbb {T}$ , has the upper gliding hump property for constant coefficients. Similarly, any wavelet basis in a translation invariant quasi-Banach space over $\mathbb {R}^d$ has the upper gliding hump property for constant coefficients.

Lemma 7.8. Suppose that a basis $\mathcal {X}$ of a quasi-Banach space $\mathbb {X}$ has the upper gliding hump property for constant coefficients. Then there is a constant C such that $\boldsymbol {\lambda }_m[\mathcal {X},\mathbb {X}]\le C {\boldsymbol{\lambda}^{\boldsymbol{d}}_m}[\mathcal {X},\mathbb {X}]$ for all $m\in \mathbb {N}$ .

Proof. Let C be as in Definition 7.7, and set $C_1=\left \lVert \mathcal {F}\right \rVert _{\mathbb {X}\to c_0}$ . Given $f\in \mathbb {X}$ and $t>0$ , let $B=\lbrace n\in \mathbb {N} \colon \left \lvert \boldsymbol {x}_n^*(f)\right \rvert \ge t\rbrace $ , $s=\max \lbrace n\in \mathbb {N} \setminus B \colon \left \lvert \boldsymbol {x}_n^*(f)\right \rvert \rbrace $ . Suppose that $\left \lvert B\right \rvert \ge m$ . Pick $A\subseteq \mathbb {N}$ finite with $\left \lvert A\right \rvert \le \left \lvert B\right \rvert $ and $\epsilon>0$ . There is $0<\epsilon _1 < (t-s)/(2C_1)$ such that $\left \lVert g\right \rVert \le \left \lVert f \right \rVert +\epsilon /(C{\boldsymbol{\lambda}^{\boldsymbol{d}}_m})$ whenever $\left \lVert f -g\right \rVert \le \epsilon _1$ . Use density to choose $g\in \mathbb {X}$ with finite support. Then B is a greedy set of g. Moreover, there is $D\subseteq \mathbb {N}$ with $\left \lvert D\right \rvert \le \left \lvert A\right \rvert $ , $D\cap \operatorname {\mathrm {supp}}(g)=\emptyset $ and

. Therefore,

Since $\epsilon $ is arbitrary, applying Lemma 3.4 puts an end to the proof.

Proposition 7.9. Let $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ be a basis of a p-Banach space $\mathbb {X}$ , $0<p\le 1$ . Suppose that $\mathcal {X}$ has the upper gliding hump property for constant coefficients. Then, there is a constant C depending only on p such that $\boldsymbol {L}_m \le C {\boldsymbol{L}^{\boldsymbol{a}}_m} (\log m)^{1/p}$ for all $m\ge 2$ .

Proof. Just combine Lemma 7.8, Theorem 7.6, Theorem 3.5 and Theorem 4.2.

Given a basis $\mathcal {X}$ of a quasi-Banach space $\mathbb {X}$ , the identity

yields

$$\begin{align*}m \le \boldsymbol{\varphi_l}[\mathcal{X},\mathbb{X}](m) \boldsymbol{\varphi_u}[\mathcal{X}^*,\mathbb{X}^*](m), \quad m\in\mathbb{N}. \end{align*}$$

To quantify the optimality of this inequality, we introduce the parameters

$$\begin{align*}{\boldsymbol{B}^{\boldsymbol{w}}_m}[\mathcal{X},\mathbb{X}]= \frac{1}{m} \boldsymbol{\varphi_l}[\mathcal{X},\mathbb{X}](m) \boldsymbol{\varphi_u}[\mathcal{X}^*,\mathbb{X}^*](m), \quad m\in\mathbb{N}. \end{align*}$$

Since there are quite a few bases that satisfy the condition $\sup _m {\boldsymbol{B}^{\boldsymbol{w}}_m}<\infty $ , called property ( $ \boldsymbol {D}^*$ ) in [14], the following elementary lemma could be of interest.

Lemma 7.10. Let $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ be a basis of a quasi-Banach space $\mathbb {X}$ . Then,

$$\begin{align*}\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] \le {\boldsymbol{B}^{\boldsymbol{w}}_m}[\mathcal{X},\mathbb{X}]\, \boldsymbol{\mu}^{\boldsymbol{s}}_m[\mathcal{X},\mathbb{X}], \quad m \in\mathbb{N}. \end{align*}$$

Proof. Let B be a greedy set of cardinality m of $f\in \mathbb {X}$ . Set $t=\min _{n\in B} \left \lvert \boldsymbol {x}_n^*(f)\right \rvert $ . Let A and D be subsets of $\mathbb {N}$ of cardinality m, and let $\varepsilon \in \mathbb {E}^A$ and $\delta \in \mathbb {E}^D$ . Then,

Taking the infimum on D and $\delta $ , we obtain the desired inequality.

Let us record an easy criterium for property ( $ \boldsymbol {D}^*$ ).

Lemma 7.11. Let $\mathcal {X}$ a basis of a quasi-Banach space $\mathbb {X}$ which dominates a symmetric basis $\mathcal {X}_1$ of a Banach space $\mathbb {X}_1$ . Suppose that there is a sequence $(A_m)_{m=1}^{\infty }$ in $\mathbb {N}$ with $\left \lvert A_m\right \rvert =m$ for all $m\in \mathbb {N}$ , and

Then $\mathcal {X}$ has property ( $ \boldsymbol {D}^*$ ).

Proof. Just dualize the operator from $\mathbb {X}$ into $\mathbb {X}_1$ provided by the domination hypothesis, and use that any symmetric basis of a locally convex space is bidemocratic (see [36, Proposition 3.a.6]).

For instance, in the case when $\max \lbrace p,q\rbrace \ge 1$ , the unit vector system of the mix-norm spaces $\ell _p\oplus \ell _q$ , $(\bigoplus _{n=1}^{\infty } \ell _q^n)_{\ell _p}$ and $\ell _p(\ell _q)$ fulfils the above criterium. The trigonometric system in $L_p(\mathbb {T})$ , $1<p\le \infty $ , also does.

Remark 7.12. If a basis is democratic, its squeeze-symmetry parameters and the truncation quasi-greedy parameters are of the same order. If a basis is either truncation quasi-greedy or has property ( $ \boldsymbol {D}^*$ ), then its squeeze-symmetry parameters and the superdemocracy parameters are of the same order. Hence, the combination of Theorem 3.5, Theorem 4.2, Proposition 7.1, Proposition 7.3, Proposition 7.4, equation (7.2) and Theorem 7.6 overrides [14, Corollaries 7.2, 7.5 and 7.6].

8 The spectrum of Lebesgue-type parameters associated with democratic bases

In greedy approximation theory, democracy can be regarded as an atomic property of bases, in the sense that it cannot be broken into (or it implies) other properties of interest in the theory. When combined with other (especially, unconditionality-like) properties of bases, democracy gives rise to a spectrum of molecular, more complex types of bases, such as greedy, almost greedy and squeeze-symmetric bases.

Let us define other unconditionality-like properties of interest in approximation theory. If we restrict inequality (4.2) defining the quasi-greedy parameters only to functions f such that $\left \lvert \mathcal {F}(f)\right \rvert $ is constant on A, we will denote by $\boldsymbol {q}_m$ the corresponding parameter and will call it the mth quasi-greedy parameter for largest coefficients, or mth quasi-greedy bases for large coefficients (QGLC) parameter for short. Finally, the mth unconditionality parameter for constant coefficients, or mth UCC parameter for short, denoted $\boldsymbol {u}_m$ , is defined by imposing condition (4.2) only to functions f with $\left \lvert \mathcal {F}(f)\right \rvert $ constant and $\left \lvert \operatorname {\mathrm {supp}}(f)\right \rvert \le m$ . A basis is quasi-greedy for largest coefficients (resp., unconditional for constant coefficients) if the corresponding sequence of parameters is uniformly bounded.

Superdemocratic bases share with unconditional bases the feature of being unconditional for constant coefficients. And, the other way around, a basis is superdemocratic if and only if it is simultaneously democratic and UCC (see [18]). Similarly, a basis is SLC if and only if it is democratic and QGLC (see [4, Proposition 5.3]). The following diagram summarizes the hierarchy of all the bases we deal with in this paper. A dashed arrow means that when a property on the right-hand side column amalgamates with democracy it is transformed in the corresponding property on its left.

(✠)

Quantitatively, each implication in equation (✠) follows as a result of an estimate between the Lebesgue-type parameters associated with each property. Let us write down the relations between any two parameters associated with the properties from the right column of equation (✠), that is, the unconditionality-like parameters. Any basis of a p-Banach space, $0<p\le 1$ , satisfies

(8.1) $$ \begin{align} \boldsymbol{u}_m\le \boldsymbol{q}_m \le \min\lbrace\boldsymbol{r}_m, \boldsymbol{g}_m\rbrace, \quad \max\lbrace A_p^{-1} \boldsymbol{r}_m, \boldsymbol{g}_m\rbrace\le \boldsymbol{k}_m, \end{align} $$

and inequalities (5.1) and (5.2) complete the picture. As far as the relations between parameters associated with properties from the left column of equation (✠) is concerned, it is clear that

(8.2) $$ \begin{align} \boldsymbol{\mu}_m\le \boldsymbol{\mu}^{\boldsymbol{s}}_m\le\ & \boldsymbol{\nu}_m,\; \mbox{ and that }\qquad\qquad\qquad\quad \end{align} $$

(8.3) $$ \begin{align} &\ \ \qquad\qquad{\boldsymbol{\nu}^{\boldsymbol{d}}_m} \le {\boldsymbol{L}^{\boldsymbol{a}}_m} \le \boldsymbol{L}_m,\quad m\in\mathbb{N}. \end{align} $$

Inequalities (8.2) and (8.3) will be connected using the equivalence between the SLC parameters and the disjoint SLC parameters provided by the following proposition.

Proposition 8.1. Let $\mathcal {X}$ be a basis of a p-Banach space $\mathbb {X}$ , $0<p\le 1$ . Then

(8.4) $$ \begin{align} \boldsymbol{\nu}_m[\mathcal{X},\mathbb{X}]\le 2^{1/p-1} (1+{\boldsymbol{\Upsilon}})^{1/p} A_p {\boldsymbol{\nu}^{\boldsymbol{d}}_m}[\mathcal{X},\mathbb{X}], \quad m\in\mathbb{N}. \end{align} $$

Proof. Let $B\subseteq \mathbb {N}$ with $\left \lvert B\right \rvert \le m$ , $\delta \in \mathbb {E}^B$ and $f\in \mathbb {X}$ be finitely supported with $B\cap \operatorname {\mathrm {supp}}(f)=\emptyset $ . Pick an arbitrary extension of $\delta $ to $\mathbb {E}^{\mathbb {N}}$ , which we still denote by $\delta $ . Given $D\subseteq \mathbb {N}$ with $\left \lvert D\right \rvert \le \left \lvert B\right \rvert $ and $D\cap \operatorname {\mathrm {supp}}(f)=\emptyset $ , we pick $E\subseteq \mathbb {N}\setminus (B\cup D\cup \operatorname {\mathrm {supp}}(f))$ with $\left \lvert E\right \rvert =\left \lvert B\right \rvert -\left \lvert D\right \rvert $ . Set

. Since the sets $D\setminus B$ , E, $B\setminus D$ and $\operatorname {\mathrm {supp}}(g)$ are pairwise disjoint, and $\left \lvert D\setminus B\right \rvert +\left \lvert E\right \rvert =\left \lvert D\setminus B\right \rvert $ ,

Therefore, applying Lemma 3.4 gives the desired inequality.

Next, we compare the SLC parameters and the squeeze-symmetry parameters. To that end, we will use the relation between the QGLC and the truncation quasi-greedy parameters.

Proposition 8.2. Let $\mathcal {X}$ be a basis of a p-Banach space $\mathbb {X}$ , $0<p\le 1$ . Then,

(8.5) $$ \begin{align} \boldsymbol{\nu}_m[\mathcal{X},\mathbb{X}]\le 2^{1/p} \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}], \quad m\in\mathbb{N}. \end{align} $$

Proof. Applying the p-triangle law gives $(\boldsymbol {\nu }_m)^p \le (\boldsymbol {\lambda }_m)^p+(\boldsymbol {q}_m)^p$ . Combining this inequality with equations (8.1) and (5.3), we are done.

Combining equations (8.2), (8.3), (8.4) and (8.5) yields

(8.6) $$ \begin{align} \boldsymbol{\mu}_m\lesssim \boldsymbol{\mu}^{\boldsymbol{s}}_m \lesssim \boldsymbol{\nu}_m \lesssim\min\lbrace\boldsymbol{\lambda}_m, {\boldsymbol{L}^{\boldsymbol{a}}_m}\rbrace \le \max\lbrace\boldsymbol{\lambda}_m, {\boldsymbol{L}^{\boldsymbol{a}}_m}\rbrace\lesssim \boldsymbol{L}_m. \end{align} $$

The only pathway for connecting with implications the squeeze-symmetry parameters and the almost greediness parameters seems to be through the corresponding unconditionality-like properties. Indeed, combining equations (5.3), (8.3), (5.1) and (5.2) yields, for every basis $\mathcal {X}$ of a p-Banach space $\mathbb {X}$ ,

$$\begin{align*}\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}] \le C ({\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X},\mathbb{X}])^{\alpha}, \end{align*}$$

where

$$\begin{align*}\alpha=\begin{cases} 2 & \mbox{ if } p=1, \\ 2+1/p & \mbox{ if } p<1,\end{cases} \end{align*}$$

and the constant C depends only on p. Thus, the question is whether this asymptotic estimate can be improved.

Question 8.3. Given $0<p\le 1$ , is there a constant C such that $\boldsymbol {\lambda }_m\le C {\boldsymbol{L}^{\boldsymbol{a}}_m}$ for every basis of a p-Banach space?

Note that an (unlikely) positive answer to Question 8.3 would allow replacing $({\boldsymbol{\lambda}^{\boldsymbol{d}}_m})_{m=1}^{\infty }$ with $(\boldsymbol {\lambda }_m)_{m=1}^{\infty }$ in Theorem 4.2. It would also provide an alternative proof to the estimate $\boldsymbol {\lambda }_m\lesssim \boldsymbol {L}_m$ (see Theorem 3.5). In the same line of thought, we wonder about the relation between the squeeze-symmetry parameters and their disjoint counterpart, as well as where to place the latter in inequality (8.6).

Question 8.4. By Lemma 4.1, $\boldsymbol {\lambda }_m \lesssim ({\boldsymbol{\lambda}^{\boldsymbol{d}}_m})^2$ . Hence, by equation (8.6), $\boldsymbol {\nu }_m\lesssim ({\boldsymbol{\lambda}^{\boldsymbol{d}}_m})^2$ , ${\boldsymbol{\mu}^{\boldsymbol{s}}_m}\lesssim ({\boldsymbol{\lambda}^{\boldsymbol{d}}_m})^2$ and $\boldsymbol {\mu }_m\lesssim ({\boldsymbol{\lambda}^{\boldsymbol{d}}_m})^2$ . Can any of these asymptotic estimates be improved?

To finish this section, we see the quantitative estimates associated with each row in equation (✠). Inequalities (1.2) and (5.3) do the job for the first and the third rows, respectively. As far as the fifth row is concerned, it readily follows from [4, Lemma 2.2] that

(8.7) $$ \begin{align} \max\lbrace \boldsymbol{\mu}_m, \boldsymbol{u}_m\rbrace \lesssim \boldsymbol{\mu}^{\boldsymbol{s}}_m \lesssim \boldsymbol{\mu}_m \boldsymbol{u}_m,\quad m\in\mathbb{N}. \end{align} $$

The following result takes care of the estimates involving the parameters in the fourth row.

Proposition 8.5. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . There are constants $C_1$ and $C_2$ depending only on the modulus of concavity of $\mathbb {X}$ such that

$$ \begin{align*} \frac{1}{C_2} \max\lbrace \boldsymbol{\mu}_m, \boldsymbol{q}_m\rbrace \le \boldsymbol{\nu}_m \le C_1\boldsymbol{\mu}_m \boldsymbol{q}_m, \quad m\in\mathbb{N}. \end{align*} $$

Proof. Assume that $\mathbb {X}$ is a p-Banach space. Let $f\in \mathbb {X}$ with $\left \lVert \mathcal {F}(f)\right \rVert _{\infty }\le 1$ , let $A\subseteq \mathbb {N}$ with $A\cap \operatorname {\mathrm {supp}}(f)=\emptyset $ and $\left \lvert A\right \rvert \le m$ and let $\varepsilon =(\varepsilon _n)_{n\in A}\in \mathbb {E}^A$ . We have

This yields $\boldsymbol {q}_m\le 2^{1/p-1}\boldsymbol {\nu }_m$ . Thus, by equation (8.2), the proof of the left side inequality is over.

For every $D\subseteq A$ ,

Therefore, by Lemma 3.4,

Consequently, for any $E\subseteq \mathbb {N}$ with $\left \lvert E\right \rvert \le \left \lvert A\right \rvert $ ,

Applying again Lemma 3.4 puts an end to the proof.

Finally, we tackle the quantitative estimates for the parameters in the second row of equation (✠). Combining Theorem 4.2 with inequalities (5.1), (5.2) and (5.3) gives

$$\begin{align*}\max\lbrace \boldsymbol{\mu}_m, \boldsymbol{g}_m\rbrace \lesssim {\boldsymbol{L}^{\boldsymbol{a}}_m} \lesssim \boldsymbol{\mu}_m (\boldsymbol{g}_m)^{\beta},\; \mbox{ where }\; \beta=\begin{cases} 1 & \mbox{ if } p=1, \\ 1+1/p & \mbox{ if } p<1.\end{cases} \end{align*}$$

Notice that the relations between the Lebesgue constants involved in the properties from the second row follow the same pattern as the relations of the parameters of the other rows in the diagram (✠) only in the locally convex setting.

9 Examples

Before we study the applicability of our estimates to important examples in Analysis, we need to introduce another type of democracy functions.

Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . Lemma 3.4 implies that if we modify definition (3.4) by taking the supremum only over sets $A$ with $\left \lvert A\right \rvert =m$ , we obtain a function equivalent to the upper democracy function; and the same occurs if we restrict ourselves to $\varepsilon =1$ . In contrast, the function

can be much smaller than $\boldsymbol {\varphi _u}[\mathcal {X},\mathbb {X}]$ , whereas the nondecreasing function

can be much larger than $\boldsymbol {\varphi _l}[\mathcal {X},\mathbb {X}]$ (see [57]). Lemma 3.4 also gives the inequality

(9.1) $$ \begin{align} \boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m) \le \Upsilon^{1/p} \boldsymbol{\mu}_m[\mathcal{X},\mathbb{X}]\, \underline{\boldsymbol{\varphi}}[\mathcal{X},\mathbb{X}](m), \quad m\in\mathbb{N}, \end{align} $$

for any basis $\mathcal {X}$ of a p-Banach space $\mathbb {X}$ , $0<p\le 1$ .

Given $p\in [1,\infty ]$ , we will denote by $p'$ its conjugate exponent, determined by the identity $1/p'=1-1/p$ . We also set $p^*=\max \lbrace p,p'\rbrace $ .

9.1 Orthogonal systems as bases of $L_p$

Let $(\Omega ,\Sigma ,\mu )$ be a finite measure space, and let $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ be an orthogonal basis of $L_2(\mu )$ . Given $1\le p\le \infty $ such that $ \mathcal {X}\subseteq L_{p^*}(\mu ), $ $\mathcal {X}$ is also a basis of $L_p(\mu )$ (a basis of its closed linear span if $r=\infty $ ).

Lemma 9.1. Let $\mathcal {X}$ be an orthonormal basis of $L_2(\mu )$ , where $(\Omega ,\Sigma ,\mu )$ is a finite measure space. Let $1\le q<2< p\le \infty $ , and suppose that the unit vector system of $\ell _q$ dominates $\mathcal {X}$ regarded as a sequence in $L_p(\mu )$ . Given $0\le \lambda \le 1$ , we define $p_{\lambda }^+\in [2,p]$ , $p_{\lambda }^-\in [p',2]$ , $q_{\lambda }^+\in [q,2]$ and $q_{\lambda }^-\in [2,q']$ by

$$\begin{align*}\frac{1}{p_{\lambda}^+}=(1-\lambda)\frac{1}{p} +\frac{\lambda}{2},\quad p_{\lambda}^-=(p_{\lambda}^+)', \quad \frac{1}{q_{\lambda}^+}=(1-\lambda)\frac{1}{q} +\frac{\lambda}{2},\quad q_{\lambda}^-=(q_{\lambda}^+)'. \end{align*}$$

Then there is a constant C such that, for all $\lambda \in [0,1]$ and $\varepsilon =\pm 1$ ,

$$\begin{align*}\max\lbrace\boldsymbol{k}_m[\mathcal{X},L_{p_{\lambda}^{\varepsilon}}(\mu)], \boldsymbol{\lambda}_m[\mathcal{X}, L_{p_{\lambda}^{\varepsilon}}(\mu)]\rbrace \le C m^{(1-\lambda)(1/q-1/2)}, \quad m\in\mathbb{N}. \end{align*}$$

Proof. We denote by $\mathcal {X}_{(r)}$ the system $\mathcal {X}$ regarded as a basic sequence in $L_r(\mu )$ , $1\le r\le \infty $ . By Riesz–Thorin’s interpolation theorem (see, e.g., [31]), the unit vector system of $\ell _{q_{\lambda }^+}$ dominates $\mathcal {X}_{(p_{\lambda }^+)}$ . In turn, since $L_{p_{\lambda }^+}(\mu )$ is continuously included in $L_2(\mu )$ , $\mathcal {X}_{(p_{\lambda }^+)}$ dominates the unit vector system of $\ell _2$ . By duality, the unit vector system of $\ell _2$ dominates $\mathcal {X}_{(p_{\lambda }^-)}$ , which, in turn, dominates the unit vector system of $\ell _{q_{\lambda }^-}$ . Applying Lemma 6.1, and taking into account equation (6.2), yields the desired result.

For uniformly bounded orthogonal systems, we obtain the following.

Lemma 9.2. Let $(\Omega ,\Sigma ,\mu )$ be a finite measure space and $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ be an orthonormal basis of $L_2(\mu )$ with $\sup _n \left \lVert \boldsymbol {x}_n\right \rVert _{\infty }<\infty $ . There is a constant C such that, for all $1\le p \le \infty $ ,

$$\begin{align*}\frac{1}{C}\max\lbrace\boldsymbol{k}_m[\mathcal{X},L_p(\mu)], \boldsymbol{\lambda}_m[\mathcal{X}, L_p(\mu)]\rbrace \le \Phi_p(m):=m^{\left\lvert1/p-1/2\right\rvert}, \quad m\in\mathbb{N}. \end{align*}$$

Proof. Just apply Lemma 9.1, taking into account that the unit vector system of $\ell _1$ dominates $\mathcal {X}_{(\infty )}$ .

Let us obtain lower estimates for the parameters.

Lemma 9.3. Let $\mathcal {X}$ be an orthogonal basis of $L_2(\mu )$ , where $(\Omega ,\Sigma ,\mu )$ is a finite measure space. Let $1\le p\le \infty $ be such that $\mathcal {X}\subseteq L_{p^*}(\mu )$ .

1. (i) If $1\le p \le 2$ , there is a constant C such that

   $$ \begin{align*} \boldsymbol{u}_m[\mathcal{X},L_{p}(\mu)]&\ge \frac{1}{C} \frac{m^{1/2}}{\boldsymbol{\varphi_l}[\mathcal{X},L_{p}(\mu)](m)} \mbox{ and }\\ \boldsymbol{\mu}_m[\mathcal{X},L_{p}(\mu)]&\ge \frac{1}{C} \frac{m^{1/2}}{\underline{\boldsymbol{\varphi}}[\mathcal{X},L_{p}(\mu)](m)}, \quad m\in\mathbb{N}. \end{align*} $$

   Moreover, $\mathcal {X}$ has the upper gliding hump property for constant coefficients.

2. (ii) If $2\le p <\infty $ , there is a constant C such that

   $$ \begin{align*} \boldsymbol{u}_m[\mathcal{X},L_p(\mu)] & \ge \frac{1}{C} \frac{ \boldsymbol{\varphi_u}[\mathcal{X},L_p(\mu)](m) }{ m^{1/2}} \mbox{ and}\\ \boldsymbol{\mu}_m[\mathcal{X},L_p(\mu)]&\ge \frac{1}{C} \frac{ \overline{\boldsymbol{\varphi}}[\mathcal{X},L_p(\mu)](m) }{ m^{1/2}}, \quad m\in\mathbb{N}. \end{align*} $$

3. (iii) There is a constant C such that

   $$\begin{align*}\boldsymbol{u}_m[\mathcal{X},L_{\infty}(\mu)]\ge \frac{1}{C} \frac{m}{\boldsymbol{\varphi_l}[\mathcal{X},L_{\infty}(\mu)](m)}, \quad m\in\mathbb{N}. \end{align*}$$

Proof. If $1\le p< \infty $ , by Kahane–Khintchine’s inequalities and [5, Proposition 2.4], there is a constant $C_1$ such that

Combining these inequalities with Lemma 3.4 yields (i) and the estimate for $\boldsymbol {u}_m$ in (ii). In the case when $2< p<\infty $ , by [33, Corollary 7], $\mathcal {X}$ has a subsequence equivalent to the unit vector system of $\ell _2$ . We infer that the estimate for $\boldsymbol {\mu }_m$ in (ii) holds. If $p=\infty $ , since $c=\inf _n \left \lVert \boldsymbol {x}_n\right \rVert _1>0$ (see, e.g., [5, Lemma 2.7]),

$$\begin{align*}\int_{\Omega} \left(\sum_{n\in A} \left\lvert x_n\right\rvert\right)\, d\mu \ge c \left\lvert A\right\rvert, \end{align*}$$

whence

for all $A\subseteq \mathbb {N}$ finite. We deduce that (iii) holds.

9.2 The trigonometric system over $\mathbb {T}^d$

Temlyakov [46, Theorem 2.1 and Remark 2] established the growth of the Lebesgue constants of the trigonometric system in $L_p$ . Later on, Wojtaszczyk [55, Corollary (a)] and Blasco et al. [14, Proposition 8.6] revisited this result. Our discussion here uses Theorem 3.5 and, more specifically, the estimates obtained in Sections 9.1. Note that Lemmas 9.2 and 9.3 apply, in particular, to the trigonometric system $\mathcal {T}^d$ over $\mathbb {T}^d:=\mathbb {R}^d/\mathbb {Z}^d$ .

Using Shapiro’s polynomials, we obtain for each $m\in \mathbb {N}$ a set $A_m$ of cardinality m with for a suitable $\varepsilon \in \mathbb {E}^{A_m}$ (see [43]). Hence, there is a constant $C_1$ such that

$$\begin{align*}\boldsymbol{u}_m[\mathcal{T}^d,L_{\infty}(\mathbb{T}^d)] \ge \frac{1}{C_1} \left\lvert m\right\rvert^{1/2}, \quad m\in\mathbb{N}. \end{align*}$$

In the case when $1<p<\infty $ , Dirichlet’s kernel (see e.g. [31]) shows the existence of a constant $C_2$ such that, for the same sets $A_m$ ,

Therefore, for each $1<p< \infty $ there is a constant $C_3$ such that

$$\begin{align*}\min\lbrace \boldsymbol{\mu}_m[\mathcal{T}^d,L_p(\mathbb{T}^d)] , \boldsymbol{u}_m[\mathcal{T}^d,L_p(\mathbb{T}^d)]\rbrace \ge \frac{1}{C_3} \Phi_p(m), \quad m\in\mathbb{N}. \end{align*}$$

In the case when $p=1$ , we have

for all $m\ge 2$ and a suitable constant $C_4$ . Thus, the same argument gives

$$\begin{align*}C_5 \min\lbrace \boldsymbol{\mu}_m[\mathcal{T}^d,L_1(\mathbb{T}^d)], \boldsymbol{u}_m[\mathcal{T}^d,L_1(\mathbb{T}^d)]\rbrace \ge \Psi(m):= \frac{m^{1/2}}{\log m}, \quad m\ge 2, \end{align*}$$

for a suitable constant $C_5$ . This estimate is optimal. Indeed, applying induction on d and using Fubini’s theorem, we infer from [38, Theorem 2.1] that there is a constant $C_6$ such that

Therefore, using the aforementioned bounded linear map from $\ell _2$ into $L_1(\mathbb {T}^d)$ ,

$$\begin{align*}\boldsymbol{\mu}^{\boldsymbol{s}}_m[\mathcal{T}^d,L_1(\mathbb{T}^d)]\le C_6 \Psi(m), \quad m\ge 2. \end{align*}$$

To obtain sharp estimates for the squeeze-symmetry parameters and the unconditionality parameters in the case $p=1$ , we invoke the De La Vallée–Pousin’s kernel, which yields, for each $m\in \mathbb {N}$ and $s>1$ , a function $v_{m,s}$ with $\left \lVert v_{m,s} \right \rVert _1 \le 1+s$ and

$$\begin{align*}\chi_{A_m} \le \mathcal{F}(v_{m,s}) \le 1, \end{align*}$$

(see, e.g., [39]). Since there exists a constant $C_7$ such that, for each $m\in \mathbb {N}$ there is $\varepsilon \in \mathbb {E}^{A_m}$ with

, applying Lemma 3.4, we obtain

$$\begin{align*}C_7\min\lbrace {\boldsymbol{\lambda}^{\boldsymbol{d}}_m} [\mathcal{T}^d,L_1(\mathbb{T}^d)] , {\boldsymbol{\Upsilon}} \boldsymbol{q}_m [\mathcal{T}^d,L_1(\mathbb{T}^d)] \rbrace \ge m^{1/2}, \quad m\in\mathbb{N}. \end{align*}$$

Summing up, the democracy, superdemocracy, SLC, disjoint squeeze-symmetry, squeeze-symmetry, almost greediness, Lebesgue, unconditionality, quasi-greediness, truncation quasi-greedy, QGLC and UCC parameters of the trigonometric system in $L_p(\mathbb {T}^d)$ grow as $(\Phi _p(m))_{m=1}^{\infty }$ for all $1\le p \le \infty $ with the following exceptions in the case $p=1$ : The democracy, superdemocracy and the UCC parameters of the trigonometric system in $L_1(\mathbb {T}^d)$ grow as $(\Psi (m))_{m=2}^{\infty }$ , and in the case $p=\infty $ , $\mathcal {T}^d$ is democratic in $L_{\infty }(\mathbb {T}^d)$ .

9.3 The trigonometric system in Hardy spaces

Fix $0<p<1$ . If for $n\in \mathbb {N}\cup \lbrace 0\rbrace $ we set

$$\begin{align*}\tau_n(\theta)=e^{2\pi i \theta}, \quad -1/2\le\theta\le 1/2, \end{align*}$$

the sequence $\mathcal {T}=(\tau _n)_{n=0}^{\infty }$ is a basis of $H_p(\mathbb {T})$ whose biorthogonal functionals are the members of the sequence $(\overline {\tau }_n)_{n=0}^{\infty }$ under the natural dual mapping. Since $H_2(\mathbb {T})\subseteq H_p(\mathbb {T})$ , the unit vector system of $\ell _2$ dominates $\mathcal {T}$ regarded as basis of $H_p(\mathbb {T})$ . In turn, since the dual basis is uniformly bounded (see [25]), $\mathcal {T}$ dominates the unit vector system of $c_0$ . We infer from Lemma 6.1 that there is a constant C such that

$$\begin{align*}\max\lbrace\boldsymbol{k}_m[\mathcal{T},H_p(\mathbb{T})], \boldsymbol{\lambda}_m[\mathcal{T},H_p(\mathbb{T})]\rbrace \le C m^{1/2}, \quad m\in\mathbb{N}. \end{align*}$$

This estimates are optimal. Indeed, the Dirichlet kernel $\sum _{k=0}^{n-1}\tau _k$ , $n\in \mathbb {N}$ , is uniformly bounded in $H_p(\mathbb {T})$ , and Khintchine’s inequalities yield a constant $C_1$ such that

Therefore, for some constant $C_2$ ,

$$\begin{align*}\min\lbrace\boldsymbol{\mu}_m[\mathcal{T},H_p(\mathbb{T})], \boldsymbol{u}_m[\mathcal{T},H_p(\mathbb{T})]\rbrace \ge\frac{1}{C_2} m^{1/2}, \quad m\in\mathbb{N}. \end{align*}$$

9.4 Jacobi polynomials

Given scalars $\alpha $ , $\beta>-1$ , the Jacobi polynomials

$$\begin{align*}\mathcal{J}(\alpha,\beta)=(p_n^{(\alpha,\beta)})_{n=0}^{\infty} \end{align*}$$

appear as the orthonormal polynomials associated with the measure $\mu _{\alpha ,\beta }$ given by

$$ \begin{align*} d\mu_{\alpha,\beta}(x)=(1-x)^{\alpha} (1+x)^{\beta} \chi_{(-1,1)} (x) \, dx. \end{align*} $$

In the case when $\gamma _0:=\min \lbrace \alpha ,\beta \rbrace> -1/2$ , we set $\gamma =\max \lbrace \alpha ,\beta \rbrace $ and

$$\begin{align*}\underline{p}=\underline{p}(\alpha,\beta)=\frac{4(\gamma+1)}{2\gamma+3}, \quad \overline{p}=\overline{p}(\alpha,\beta)=\frac{4(\gamma+1)}{2 \gamma +1}. \end{align*}$$

Notice that $\underline {p}$ and $\overline {p}$ are conjugate exponents. Given $p\in (\underline {p},\overline {p})$ , we define $q(p,\alpha ,\beta )\in (1,\infty )$ by

$$\begin{align*}\frac{1}{q(p,\alpha,\beta)}=\lambda, \end{align*}$$

where $\lambda \in [0,1]$ is such that

$$\begin{align*}p=(1-\lambda)\underline{p}(\alpha,\beta)+\lambda \overline{p}(\alpha,\beta). \end{align*}$$

A routine computation yields

$$\begin{align*}\frac{1}{q(p,\alpha,\beta)}=\frac{2\gamma+3}{2}-\frac{2(\gamma+1)}{p}, \quad \underline{p}(\alpha,\beta) <p< \overline{p}(\alpha,\beta). \end{align*}$$

We also define $r=r(p,\alpha ,\beta )$ by

$$\begin{align*}\frac{1}{r(p,\alpha,\beta)}=\frac{2\gamma_0+3}{2}-\frac{2(\gamma_0+1)}{p}, \quad \underline{p}(\alpha,\beta) <p< \overline{p}(\alpha,\beta). \end{align*}$$

Theorem 9.4. Let $\alpha $ and $\beta $ be such that $\min \lbrace \alpha ,\beta \rbrace> -1/2$ . Given $p\in (\underline {p}(\alpha ,\beta ),\overline {p}(\alpha ,\beta ))$ , set $q=q(p,\alpha ,\beta )$ . In the case when $p\le 2$ , the unit vector system of $\ell _q$ dominates $\mathcal {J}(\alpha ,\beta )$ regarded as sequence in $L_p(\mu _{\alpha ,\beta })$ and, in the case when $p\ge 2$ , $\mathcal {J}(\alpha ,\beta )$ , regarded as sequence in $L_p(\mu _{\alpha ,\beta })$ , dominates the unit vector system of $\ell _q$ .

Proof. This result could be derived from [53]. Here, we present an alternative proof. Using Marcinkiewicz’s interpolation theorem (see, e.g., [31]) and duality, it suffices to prove that the unit vector system of $\ell _1$ dominates $(p_n^{(\alpha ,\beta )})_{n=0}^{\infty }$ regarded as a sequence in $\mathbb {X}:=L_{\overline {p},\infty } (\mu _{\alpha ,\beta })$ . Since $\mathbb {X}$ is locally convex, we must prove that $\sup _n \left \lVert p_n^{(\alpha ,\beta )}\right \rVert _{\overline {p},\infty } <\infty $ . This can be deduced from classical estimates for Jacobi polynomials (see [5, Theorem 3.2 and Lemma 3.3]) or from the fact that the partial sums of Jacobi–Fourier series $(J_n)_{n=1}^{\infty }$ are uniformly bounded when regarded as operators from $L_{\overline {p},1}(\mu _{\alpha ,\beta })$ into $L_{\overline {p},\infty }(\mu _{\alpha ,\beta })$ (see [32]). Indeed, taking into account that the dual of $L_{\overline {p},1}(\mu _{\alpha ,\beta })$ is $L_{\underline {p},\infty }(\mu _{\alpha ,\beta })$ under the natural dual pairing, the uniform boundedness of the operators $(J_n-J_{n-1})_{n=0}^{\infty }$ yields

$$\begin{align*}\sup_{n\in\mathbb{N}} \left\lVert p_n^{(\alpha,\beta)}\right\rVert_{\underline{p},\infty} \left\lVert p_n^{(\alpha,\beta)}\right\rVert_{\overline{p},\infty}<\infty. \end{align*}$$

Since $L_{\overline {p},\infty }(\mu _{\alpha ,\beta })\subseteq L_1(\mu _{\alpha ,\beta })$ and $\inf _n \left \lVert p_n^{(\alpha ,\beta )}\right \rVert _1>0$ (see, e.g., [5, Equation (3.4)]), we are done.

Theorem 9.5. Let $\alpha $ and $\beta $ be such that $\min \lbrace \alpha ,\beta \rbrace> -1/2$ . Given $p\in [2,\overline {p}(\alpha ,\beta ))$ , set $q=q(p,\alpha ,\beta )$ and $r=r(p,\alpha ,\beta )$ . Then:

1. (i) If $p\ge 2$ , there is a constant $C_1$ such that

   $$\begin{align*}\overline{\boldsymbol{\varphi}}[\mathcal{J}(\alpha,\beta),L_p(\mu_{\alpha,\beta})](m)\ge \frac{1}{C_1} m^{1/q}, \quad m\in\mathbb{N}, \end{align*}$$

2. (ii) If $p\le 2$ , there is a constant $C_2$ such that

   $$\begin{align*}\boldsymbol{\varphi_l}[\mathcal{J}(\alpha,\beta),L_p(\mu_{\alpha,\beta})](m)\le C_2 m^{1/r}, \quad m\in\mathbb{N}. \end{align*}$$

Proof. It follows by combining [5, Proposition 3.8], Lemma 3.4 and the fact that $\mathcal {J}(\alpha ,\beta )$ is a Schauder basis of $L_p(\mu _{\alpha ,\beta })$ (see [41]).

Theorem 9.6. Let $\alpha $ and $\beta $ be such that $\min \lbrace \alpha ,\beta \rbrace> -1/2$ . Set $\gamma _0=\min \lbrace \alpha ,\beta \rbrace $ and $\gamma =\max \lbrace \alpha ,\beta \rbrace $ .

1. (i) If $p\in [2,\overline {p}(\alpha ,\beta ))$ , the democracy, superdemocracy, SLC, disjoint squeeze-symmetry, squeeze-symmetry, almost greediness, Lebesgue, unconditionality, quasi-greediness, truncation quasi-greedy, QGLC and UCC parameters of $\mathcal {J}(\alpha ,\beta )$ regarded as a basis of $L_p(\mu _{\alpha ,\beta })$ grow as

   $$\begin{align*}\Phi(m)=m^{(1+\gamma)\left\lvert1-2/p\right\rvert}, \quad m\in\mathbb{N}. \end{align*}$$

2. (ii) If $p\in (\underline {p},2]$ , the Lebesgue constants and the unconditionality parameters of $\mathcal {J}(\alpha ,\beta )$ regarded as a basis of $L_p(\mu _{\alpha ,\beta })$ grow as the sequence $(\Phi (m))_{m=1}^{\infty }$ ; the almost greedy constants, the squeeze-symmetry and the disjoint squeeze-symmetry parameters grow at least as

   $$\begin{align*}\frac{\Phi(m)}{\log m}, \quad m\ge 2 \end{align*}$$

   and the superdemocracy, SLC, quasi-greediness, truncation quasi-greedy, QGLC and UCC parameters grow as least as

   $$\begin{align*}m^{(1+\gamma_0)\left\lvert1-2/p\right\rvert}, \quad m\in\mathbb{N}. \end{align*}$$

Proof. Just combine Theorems 9.5 and 9.4, Lemmas 9.1 and 9.3 and Proposition 7.9.

9.5 Lindenstrauss dual bases

Let $\delta =(d_n)_{n=1}^{\infty }$ be a nondecreasing sequence in $\mathbb {N}$ with $d_n\geq 2$ for all $n\in \mathbb {N}$ . Set

$$ \begin{align*} \quad \sigma(k)=2+\sum_{j=1}^{k-1} d_j, \quad k\in\mathbb{N}. \end{align*} $$

Let $\Gamma \colon \mathbb {N}\to \mathbb {N}\cup \lbrace 0\rbrace $ be the left inverse of the function defined by $n\mapsto \sigma ^{(n)}(1)$ , $n\in \mathbb {N}\cup \lbrace 0\rbrace $ . In [8], it was constructed an almost greedy basis $\mathcal {X}_{\delta }$ of a subspace $\mathbb {X}_{\delta }$ of $\ell _1$ with

$$\begin{align*}\frac{1}{4}(1+\Gamma(m)) \le \boldsymbol{k}_m[\mathcal{X}_{\delta},\mathbb{X}_{\delta}] \le 2 (1+\Gamma(m)), \quad m\in\mathbb{N}. \end{align*}$$

In the case when $d_n=2$ for $n\in \mathbb {N}$ , the resulting space is the classical Lindesntrauss space, say $\mathbb {X}$ , built in [35]. Moreover, $\mathbb {X}_{\delta }$ is isomporphic to $\mathbb {X}$ regardless the choice of $\delta $ . The dual space of $\mathbb {X}_{\delta }$ is isomorphic to $\ell _{\infty }$ , and the dual basis $\mathcal {X}_{\delta }^*$ spans a space isomorphic to $c_0$ . In [8], it is also proved that for each increasing concave function $\phi \colon [0,\infty ) \to [0,\infty )$ with $\phi (0)=0$ , we can choose $\delta $ so that $\Gamma $ grows as $(\phi (\log (m)))_{m=2}^{\infty }$ . By [8, Proposition 4.4 and Lemma 7.3],

$$\begin{align*}\boldsymbol{B}_m[\mathcal{X}_{\delta}, \mathbb{X}_{\delta}]\le 2 (1+\Gamma(m)), \quad m\in\mathbb{N}. \end{align*}$$

Thus, by equation (7.2) and Proposition 7.1, there is a constant C such that $\boldsymbol {L}_m[\mathcal {X}_{\delta }^*, \mathbb {X}_{\delta }^*]\le C\Gamma (m)$ for all $m\ge 2$ .

As far as lower bounds is concerned, combining [8, Lemma 7.1 and Lemma 7.2] yields

$$\begin{align*}\boldsymbol{\mu}_m[\mathcal{X}_{\delta}^*, \mathbb{X}_{\delta}^*]\ge \frac{1}{2} \Gamma(m), \quad m\in\mathbb{N}, \end{align*}$$

and the proof of [8, Lemma 7.1] gives

$$\begin{align*}\boldsymbol{u}_m[\mathcal{X}_{\delta}^*, \mathbb{X}_{\delta}^*]\ge\frac{1}{8} \Gamma(m), \quad m\in\mathbb{N}. \end{align*}$$

9.6 Bases with large greedy-like parameters

The unconditionality constants of truncation quasi-greedy bases grow slowly. Indeed, if $\mathbb {X}$ is a p-Banach space, $0<p\le 1$ ,

(9.2) $$ \begin{align} \boldsymbol{k}_m \le C (\log m)^{1/p},\quad m\ge 2, \end{align} $$

(see [18, Lemma 8.2], [29, Theorem 5.1] and [8, Theorem 5.1]). Hence, if $\mathcal {X}$ is quasi-greedy and democratic there is a constant C such that

$$ \begin{align*} \boldsymbol{L}_m \le C (\log m)^{1/p},\quad m\ge 2. \end{align*} $$

In general, the unconditionality parameters of a basis $\mathcal {X}=(\boldsymbol {x}_n)_{n=1}^{\infty }$ of a p-Banach space $\mathbb {X}$ can grow much faster. Notice that $\mathcal {X}$ satisfies equation (2.2), then

$$\begin{align*}\max\lbrace \boldsymbol{k}_m[\mathcal{X},\mathbb{X}], \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}]\rbrace \le (C[\mathcal{X}])^2 m^{1/p}, \quad m\in\mathbb{N}. \end{align*}$$

Consequently, there is a constant C such that $\boldsymbol {L}_m[\mathcal {X},\mathbb {X}]\le C m^{1/p}$ for all $m\in \mathbb {N}$ . There are bases for which $\boldsymbol {k}_m\approx m^{1/p}$ so that this estimate is optimal. Take, for instance, the difference basis $\mathcal {D}=(\boldsymbol {d}_n)_{n=1}^{\infty }$ in $\ell _p$ given by

$$\begin{align*}\boldsymbol{d}_n=\boldsymbol{e}_n-\boldsymbol{e}_{n-1},\quad n\in \mathbb{N}, \end{align*}$$

where $(\boldsymbol {e}_n)_{n=1}^{\infty }$ is the unit vector system and $\boldsymbol {e}_0=0$ . For $0<p\le 1$ , $\mathcal {D}$ is a Schauder basis of $\ell _p$ whose dual basis is (naturally identified with) the summing basis $\mathcal {S}=(\boldsymbol {s}_n)_{n=1}^{\infty }$ of $c_0$ given by

$$\begin{align*}\boldsymbol{s}_n=\sum_{k=1}^n \boldsymbol{e}_k,\quad n\in \mathbb{N}. \end{align*}$$

Since $\left \lVert \sum _{n=1}^m \boldsymbol {d}_n\right \rVert _p=1$ and $\left \lVert \sum _{n=1}^{m} \boldsymbol {d}_{2n} \right \rVert _p=(2m)^{1/p}$ for all $m\in \mathbb {N}$ , we have

$$\begin{align*}\boldsymbol{\mu}_m[\mathcal{D},\ell_p]\ge (2m)^{1/p},\quad m\in \mathbb{N}, \end{align*}$$

and

$$\begin{align*}\boldsymbol{u}_m[\mathcal{D},\ell_p]\ge m^{1/p}, \quad m\in \mathbb{N}. \end{align*}$$

As for the dual basis, we have

$$\begin{align*}\left\lVert \sum_{n=1}^m \boldsymbol{s}_n\right\rVert_{\infty}=m,\;\mbox{ and }\; \left\lVert \sum_{n=1}^m (-1)^n\boldsymbol{s}_n\right\rVert_{\infty}=1, \end{align*}$$

whence $\boldsymbol {u}_m[\mathcal {S},c_0]\ge m$ , for all $m\in \mathbb {N}$ . Notice that the summing basis of $c_0$ is democratic.

Another classical basis with large greedy-like parameters is the $L_1$ -normalized Haar system $\mathcal {H}$ . It is essentially known that

$$\begin{align*}\boldsymbol{\mu}_m[\mathcal{H},L_1([0,1])]\ge m, \quad m\in\mathbb{N}, \end{align*}$$

and

$$\begin{align*}\boldsymbol{u}_{2m}[\mathcal{H},L_1([0,1])\ge m/4,\quad m\in\mathbb{N} \end{align*}$$

(see [21]). Nonetheless, certain subbases of $\mathcal {H}$ are quasi-greedy basic sequences in $L_1([0,1])$ [21, 30].

9.7 Tsirelson’s space

The space $\mathcal {T}^*$ constructed by Tsirelson [52] to prove the existence of a Banach space that contains no copy of $\ell _p$ or $c_0$ is the dual of the Tsirelson space $\mathcal {T}$ defined by Figiel and Johnson [26]. The unit vector system $\mathcal {B}=(\boldsymbol {e}_n)_{n=1}^{\infty }$ is a greedy basis of $\mathcal {T}$ whose fundamental function is equivalent to the fundamental function of the unit vector system of $\ell _1$ (see [22]). Although $\mathcal {T}$ contains no copy of $\ell _1$ , its unit vector system contains finite subbases uniformly equivalent to the unit vector system of $\ell _1^n$ for all $n\in \mathbb {N}$ (see [16, Proposition I.2]). Thus, the unit vector system of the original Tsirelson space $\mathcal {T}^*$ contains finite subbases uniformly equivalent to the unit vector system of $\ell _{\infty }^n$ for all $n\in \mathbb {N}$ . In particular, $\underline {\boldsymbol {\varphi }}[\mathcal {B},\mathcal {T}^*]$ is bounded. With an eye to studying the TGA with respect to the canonical basis of the original Tsirelson space $\mathcal {T}^*$ we give a general lemma.

Lemma 9.7. Let $\mathcal {X}$ be a basis of a quasi-Banach space $\mathbb {X}$ . Suppose that $\underline {\boldsymbol {\varphi }}[\mathcal {X}^*,\mathbb {X}^*]$ is bounded and that $\mathcal {X}^{**}$ is equivalent to $\mathcal {X}$ . Then

$$ \begin{align*} \boldsymbol{B}_m[\mathcal{X},\mathbb{X}] &\approx{\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{X}^*,\mathbb{X}^*] \approx \boldsymbol{\lambda}_m[\mathcal{X}^*,\mathbb{X}^*] \approx {\boldsymbol{\lambda}^{\boldsymbol{d}}_m}[\mathcal{X}^*,\mathbb{X}^*] \approx\boldsymbol{\varphi_u}[\mathcal{X}^*,\mathbb{X}^*]\\ &\approx \boldsymbol{\mu}_m[\mathcal{X}^*,\mathbb{X}^*] \approx\boldsymbol{\delta}_m[\mathcal{X}^*,c_0] \approx \boldsymbol{\delta}_m[\ell_1,\mathcal{X}]. \end{align*} $$

Proof. The equivalence $\boldsymbol {\delta }_m[\mathcal {X}^*,c_0]\approx \boldsymbol {\delta }_m[\ell _1,\mathcal {X}]$ follows by duality. The inequality

$$\begin{align*}\boldsymbol{B}_m[\mathcal{X},\mathbb{X}]\le \boldsymbol{\varphi_u}[\mathcal{X}^*,\mathbb{X}^*](m) \sup_n\left\lVert \boldsymbol{x}_n\right\rVert \end{align*}$$

holds for any basis of any Banach space. Combining Lemma 3.3, Propositions 5.2 and 7.1 and inequalities (6.1) and (9.1) concludes the proof.

Loosely speaking, Lemma 9.7 says that, for bases close to canonical $\ell _1$ -basis, the squeeze-symmetry parameters of their dual basis measure how far the basis is from the unit vector system of $\ell _1$ . We note that this applies in particular to the Lindenstrauss bases we considered in §9.5.

By Theorem 7.6, the dual basis $\mathcal {X}^*$ of any squeeze-symmetric basis $\mathcal {X}$ of as quasi-Banach space $\mathbb {X}$ satisfies $\boldsymbol {L}_m[\mathcal {X}^*,\mathbb {X}^*]=O(\log m)$ . For the canonical basis of the original Tsirelson space (which is not greedy), this general estimate is far from being optimal. To write down a precise statement of this estimate, we recursively define $\log ^{(k)}\colon (e^{k-1},\infty ) \to (0,\infty )$ by $\log ^{(1)}=\log $ and

$$\begin{align*}\log^{(k)}=\log^{(k-1)} \circ \log. \end{align*}$$

Since $\mathcal {B}$ is an unconditional basis of $\mathcal {T}^*$ , applying Lemma 9.7 to the canonical basis of $\mathcal {T}$ yields $\boldsymbol {L}_m[\mathcal {B},\mathcal {T}^*]\approx \boldsymbol {\delta }_m[\ell _1,\mathcal {T}]$ . Moreover, by [16, Proposition I.9.3],

$$\begin{align*}\boldsymbol{\delta}_m[\ell_1,\mathcal{T}]\approx\sup\left\lbrace\sum_{n=1}^m \left\lvert a_n\right\rvert \colon \left\lVert \sum_{n=1}^m a_n \boldsymbol{e}_n \right\rVert_{\mathcal{T}} \le 1\right\rbrace, \quad m\in\mathbb{N}. \end{align*}$$

Then, by [16, Proposition IV.b.3],

$$\begin{align*}\lim_m \frac{\boldsymbol{L}_m[\mathcal{B},\mathcal{T}^*]}{\log^{(k)}(m)}=0 \end{align*}$$

for all $k\in \mathbb {N}$ .

9.8 The dual basis of the Haar system in $\mathrm {BV}(\mathbb {R}^d)$

Given $d\in \mathbb {N}$ , $d\ge 2$ , let $\mathscr {D}$ denote the set consisting of all dyadic cubes in the Euclidean space $\mathbb {R}^d$ . If $Q\in \mathscr {D}$ there is a unique $k=k(Q)\in \mathbb {Z}$ such that $\left \lvert Q\right \rvert =2^{-kd}$ . Given $P\in \mathscr {D}$ and $k\in \mathbb {Z}$ , we define

$$\begin{align*}\mathscr{R}[P,k]=\lbrace Q\in \mathscr{D} \colon Q\subseteq P,\; k(Q)=k\rbrace. \end{align*}$$

Of course, $\mathscr {R}[P,k]=\emptyset $ for all $k<k(P)$ . Set also

$$\begin{align*}\mathscr{D}[P,k]=\bigcup_{j=k(P)}^{k-1} \mathscr{R}[P,j], \quad k>k(P). \end{align*}$$

Given an interval $J\subseteq \mathbb {R}$ , we denote by $J_{l}$ its left half and by $J_{r}$ its right half, and we set $h_I^0=\chi _I$ and $h_J^1=-\chi _{J_{l}}+\chi _{J_{r}}$ . For $\theta =(\theta _i)_{i=1}^d\in \Theta _d:=\lbrace 0,1\rbrace ^d\setminus \lbrace 0\rbrace $ and $Q\in \prod _{i=1}^d J_i\in \mathscr {D}$ put

$$\begin{align*}h_{Q,\theta}=\left\lvert Q\right\rvert^{(1-d)/d}\prod_{j=1}^d h_{J_i}^{\theta_i}, \quad h_{Q,\theta}^*=\left\lvert Q\right\rvert^{-1/d}\prod_{i=1}^d h_{J_i}^{\theta_i}, \end{align*}$$

and we denote by $\mathbb {X}$ be the subspace of $\mathrm {BV}(\mathbb {R}^d)$ spanned by

$$\begin{align*}\mathcal{H}=(h_{Q,\theta})_{(Q,\theta)\in\mathscr{D}\times\Theta_d}. \end{align*}$$

Let $\operatorname *{\mathrm {Ave}}(f;Q)$ denote average value of $f\in L_1(\mathbb {R}^d)$ over the cube Q. For every $f\in \mathrm {BV}(\mathbb {R}^d)$ , $P\in \mathscr {D}$ and $k\in \mathbb {Z}$ , $k> k(P)$ , we have

$$ \begin{align*} T_{P,k}(f)&:= \sum_{Q\in\mathscr{D}[P,k]}\sum_{\theta\in\Theta_d} h_{Q,\theta} \int_{\mathbb{R}^d} f(x)\, h_{Q,\theta}^*(x)\, dx\\ &=-\operatorname*{\mathrm{Ave}}(f;P)\chi_P+ \sum_{Q\in\mathscr{R}[P,k]} \operatorname*{\mathrm{Ave}}(f;Q) \chi_Q. \end{align*} $$

Hence, if $\pi \colon \mathbb {N}\to \mathscr {D}\times \Theta _d$ is a bijection such that the sets

$$\begin{align*}\pi^{-1}(\lbrace p\rbrace\times \Theta_d) \;\mbox{ and }\; \pi^{-1}(\mathscr{R}[P,k(P)+1]\times \Theta_d) \end{align*}$$

are integer intervals for every $P\in \mathscr {D}$ , applying [56, Corollary 12] gives that $(h_{\pi (n)})_{n=1}^{\infty }$ is a seminormalized Schauder basis of $\mathbb {X}$ . By [17, Theorem 8.1 and Remark 8.1], $\mathcal {H}$ is a squeeze-symmetric basis whose fundamental function is of the same order as $(m)_{m=1}^{\infty }$ . By [56, Theorem 10], $\mathcal {H}$ is a quasi-greedy basis of $\mathbb {X}$ . Pick a sequence $(Q_j)_{j=1}^{\infty }$ of pairwise disjoint dyadic cubes such that $k(Q_{j+1})=1+k(Q_j)$ , and pick an arbitrary sequence $(\theta _j)_{j=1}^{\infty }$ in $\Theta _d$ . By [18, Corollary 8.6], $(h_{Q_j,\theta _j})_{j=1}^{\infty }$ is equivalent to the unit vector system of $\ell _1$ . By Lemma 9.7 and Theorem 7.6, the dual basis

$$\begin{align*}\mathcal{H}^*=(h_{Q,\theta}^*)_{(Q,\theta)\in\mathscr{D}\times\Theta_d} \end{align*}$$

of $\mathcal {H}$ satisfies

$$\begin{align*}{\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{H}^*,\mathbb{X}^*]\approx \boldsymbol{\lambda}_m[\mathcal{H}^*,\mathbb{X}^*] \approx {\boldsymbol{\lambda}^{\boldsymbol{d}}_m}[\mathcal{H}^*,\mathbb{X}^*]\approx \boldsymbol{\mu}_m[\mathcal{H}^*,\mathbb{X}^*] \end{align*}$$

and $\boldsymbol {L}_m[\mathcal {H}^*,\mathbb {X}^*] =O( \log m)$ . We will prove that

$$\begin{align*}\boldsymbol{L}_m[\mathcal{H}^*,\mathbb{X}^*]\approx {\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{H}^*,\mathbb{X}^*]\approx \boldsymbol{g}_m[\mathcal{H}^*,\mathbb{X}^*] \approx \log m. \end{align*}$$

To that end, it suffices to show that $\log m=O( \boldsymbol {\varphi _u}[\mathcal {H}^*,\mathbb {X}^*](m))$ and $\log m=O( \boldsymbol {u}[\mathcal {H}^*,\mathbb {X}^*](m))$ .

For each $k\in \mathbb {N}$ , we define $f_k^*\in (\mathrm {BV}(\mathbb {R}^d))^*$ by

$$\begin{align*}f_k^*(f)= \frac{\partial}{\partial x_1} \left(T_{[0,1]^d,k}(f)\right)\left( \left[ \frac{1}{3},\infty\right)\times\mathbb{R}^{d-1}\right). \end{align*}$$

It is clear that $\left \lVert f_k^*\right \rVert =\left \lVert f_k^*|_{\mathbb {X}}\right \rVert $ for all $k\in \mathbb {N}$ , and $\sup _k \left \lVert f_k^*\right \rVert <\infty $ . Note that for each $j\in \mathbb {N}\cup \lbrace 0\rbrace $ there is a unique dyadic interval $I_j$ with $\left \lvert I_j\right \rvert =2^{-j}$ and $1/3\in I_j$ . Let $A_k$ (resp. $B_k$ ) be the subset of $\mathscr {D}\times \Theta _d$ defined by $(Q,\theta )\in A_k$ (resp. $(Q,\theta )\in B_k$ ) if and only if $\theta =(1,0,\dots ,0)$ , $Q=\prod _{i=1}^d J_i\subseteq [0,1)^d$ and $J_1=I_j$ for some even (resp. odd) integer $j\in [0,k-1]$ . A routine computation yields

$$\begin{align*}f_k^*(h_{Q,\theta})= \begin{cases} 0 & \mbox{ if } (Q,\theta)\notin A_k\cup B_k,\\ 1 & \mbox{ if } (Q,\theta)\in A_k \mbox{ and} \\ -1 & \mbox{ if } (Q,\theta)\in B_k \\ \end{cases} \end{align*}$$

(cf. [29, Example 2]). In other words,

. Set $f=\chi _{[0,1/3)\times [0,1)^{d-1}}$ . The arguments in [29, Example 2] also give

Since

$$\begin{align*}\left\lvert A_k\cup B_k\right\rvert=\frac{ 2^{(d-1)k}-1}{2^{d-1}-1}, \end{align*}$$

we are done. Note that this yields $\boldsymbol {k}_m[\mathcal {H},\mathbb {X}]=\boldsymbol {k}_m[\mathcal {H}^*,\mathbb {X}^*]\approx \log m$ .

9.9 The Franklin system as a basis of $\mathrm {VMO}$

As in §9.8, we denote by $\mathscr {D}$ the set consisting of all d-dimensional dyadic cubes, $d\in \mathbb {N}$ . The homogeneous Triebel–Lizorkin sequence space $\skew6\mathring {\boldsymbol {f}}_{p,q}^{d}$ of indices $p,q\in (0,\infty )$ consists of all scalar sequences $f=(a_Q)_{Q\in \mathscr {D}}$ for which

$$\begin{align*}\left\lVert f \right\rVert_{ \boldsymbol{f}_{p,q}^{d}}= \left\lVert \left(\sum_{Q\in\mathscr{D}} \left\lvert Q\right\rvert^{-q/p} \left\lvert a_Q\right\rvert^q \chi_{Q}\right)^{1/q}\right\rVert_p<\infty. \end{align*}$$

By definition, the unit vector system $\mathcal {B}=(\boldsymbol {e}_Q)_{Q\in \mathscr {D}}$ is a normalized unconditional basis of $\skew6\mathring {\boldsymbol {f}}_{p,q}^{d}$ . Moreover, it is a democratic (hence greedy) basis whose fundamental function is of the same order as $(m^{1/p})_{m=1}^{\infty }$ (see [4, Section 11.3]). Let $\mathscr {D}_0$ denote the set consisting of all dyadic cubes contained in $[0,1]^d$ , and consider the subbasis $\mathcal {B}_0=(\boldsymbol {e}_Q)_{Q\in \mathscr {D}_0}$ of $\mathcal {B}$ . It is known that certain wavelet bases of homogeneous (resp. inhomogenous) Triebel–Lizorkin function spaces $\skew6\mathring {F}_{p,q}^{s}(\mathbb {R}^d)$ (resp. $F_{p,q}^{s}(\mathbb {R}^d)$ ) of smoothness $s\in \mathbb {R}$ are equivalent to $\mathcal {B}$ (resp. $\mathcal {B}_0$ ) regarded as a basis (resp. basic sequence) of $\skew6\mathring {\boldsymbol {f}}_{p,q}^{d}$ (see [28, Theorem 7.20] for the homogeneous case and [51, Theorem 3.5] for the inhomogenous case). In the particular case that $p=1$ , $q=2$ and $d=1$ , $\mathcal {B}_0$ is equivalent to both the Franklin system in the Hardy space $H_1$ and the Haar system in the dyadic Hardy space $H_1(\delta )$ (see [37, 54]). Consequently, the dual basis of $\mathcal {B}_0$ is equivalent to both the Franklin system regarded as a basis of $\mathrm {VMO}$ and the Haar system regarded as a basic sequence in dyadic $\mathrm {BMO}$ .

Suppose that $1<q<\infty $ and $r=q'$ . Consider the space $\skew6\mathring {\boldsymbol {f}}_{\infty ,r}^{d}$ consisting of all sequences $f=(a_{\lambda })_{Q\in \mathscr {D}}$ satisfying the Carleson-type condition

$$\begin{align*}\left\lVert f \right\rVert_{ \boldsymbol{f}_{\infty,r}^d}= \sup_{P\in\mathscr{D}} \left(\frac{1}{\left\lvert P\right\rvert} \sum_{\substack{Q\in\mathscr{D}\\ Q\subseteq P}} \left\lvert Q\right\rvert\, \left\lvert a_Q\right\rvert^2 \right)^{1/2}<\infty. \end{align*}$$

It is known that the dual space of $\skew6\mathring {\boldsymbol {f}}_{1,q}^{d}$ is $\skew6\mathring {\boldsymbol {f}}_{\infty ,r}^{d}$ under the natural pairing (see [27, Equation (5.2)]. Our analysis of the unit vector system of $\skew6\mathring {\boldsymbol {f}}_{\infty ,r}^{d}$ relies on the following lemma.

Lemma 9.8. Let $d\in \mathbb {N}$ . There is a constant C such that for every $\mathcal {A}\subseteq \mathscr {D}$ and $P\in \mathscr {D}$

$$\begin{align*}L(\mathcal{A},P):= \sum_{\substack{Q\in \mathcal{A} \\ Q\subseteq P}} \left\lvert Q\right\rvert \le C \left\lvert P\right\rvert \log(1+\left\lvert\mathcal{A}\right\rvert). \end{align*}$$

Moreover, for every $P\in \mathscr {D}$ and $m\in \mathbb {N}$ there is $\mathcal {A}\subseteq \mathscr {D}$ with $\left \lvert \mathcal {A}\right \rvert = m$ and $ \log (1+m)\le C \, L(\mathcal {A},P)$ .

Proof. By homogeneity, we can assume that $P=[0,1]^d$ . Given $k\in \mathbb {N}$ we set

$$\begin{align*}\mathcal{A}_k=\lbrace Q\in\mathscr{D} \colon Q\subseteq[0,1]^d,\; \left\lvert Q\right\rvert\ge 2^{-k+1}\rbrace. \end{align*}$$

We have $L(\mathcal {A}_k,[0,1]^d)=k$ and

$$\begin{align*}\left\lvert\mathcal{A}_k\right\rvert=m(k):=\frac{2^{dk}-1}{2^d-1}, \quad k\in\mathbb{N}. \end{align*}$$

Given $\mathcal {A}\subseteq \mathscr {D}$ , let $k\in \mathbb {N}$ be such that $m(k)\le \left \lvert \mathcal {A}\right \rvert <m(k+1)$ . Set $\mathcal {A}'=\lbrace Q\in \mathcal {A} \colon \left \lvert Q\right \rvert \le 2^{-kd}\rbrace $ . We have

$$ \begin{align*} L(\mathcal{A},[0,1]^d) &\le L(\mathcal{A}_k,[0,1]^d)+ S(\mathcal{A}',[0,1]^d)\\ &\le k + 2^{-kd} \left\lvert\mathcal{A}\right\rvert\\ &\le k +2^{-kd} m(k+1)\\ &\le k+\frac{2^d}{2^d -1}. \end{align*} $$

Since $\sup _k (k+(1-2^{-d})^{-1})/\log (1+m(k))<\infty $ , we are done. For the ‘moreover’ part, we pick $k\in \mathbb {N}$ such that $m(k)\le m < m(k+1)$ and $\mathcal {A}\supseteq \mathcal {A}_{k}$ with $\left \lvert \mathcal {A}\right \rvert =m$ . Then,

$$\begin{align*}L(\mathcal{A},[0,1]^d)\ge L(\mathcal{A}_{k},[0,1]^d)=k\ge c \log(1+m), \end{align*}$$

where $c=\inf _k k/\log (m(k+1))>0$ .

Finally, we are in a position to estimate the constants of the unit vector system of $\skew6\mathring {\boldsymbol {f}}_{\infty ,r}^{d}$ . If $\mathscr {D}_1\subseteq \mathscr {D}$ consists of pairwise disjoint dyadic cubes, then $(\boldsymbol {e}_Q)_{Q\in \mathscr {D}_1}$ is, when regarded as a basic sequence in $\skew6\mathring {\boldsymbol {f}}_{1,q}^{d}$ , isometrically equivalent to the unit vector system of $\ell _1$ . Therefore, we can apply Lemma 9.8 to obtain that $\boldsymbol {\varphi _u}[\mathcal {B},\skew6\mathring {\boldsymbol {f}}_{\infty ,r}^{d}]$ and $\boldsymbol {\varphi _u}[\mathcal {B}_0,\skew6\mathring {\boldsymbol {f}}_{\infty ,r}^{d}]$ grow as $((\log m)^{1/r})_{m=2}^{\infty }$ Therefore, applying Lemma 9.7 gives that

$$ \begin{align*} \boldsymbol{L}_m[\mathcal{B},\skew6\mathring{\boldsymbol{f}}_{\infty,r}^{d}] &\approx \boldsymbol{L}_m[\mathcal{B}_0,\skew6\mathring{\boldsymbol{f}}_{\infty,r}^{d}] \approx{\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{B},\skew6\mathring{\boldsymbol{f}}_{\infty,r}^{d}] \approx {\boldsymbol{L}^{\boldsymbol{a}}_m}[\mathcal{B}_0,\skew6\mathring{\boldsymbol{f}}_{\infty,r}^{d}]\\ &\approx ((\log m)^{1/r})_{m=2}^{\infty}. \end{align*} $$

9.10 Direct sums of bases

Given bases $\mathcal {X}$ and $\mathcal {Y}$ of respective quasi-Banach spaces $\mathbb {X}$ and $\mathbb {Y}$ , its direct sum $\mathcal {X}\oplus \mathcal {Y}$ is a basis in $\mathbb {X}\oplus \mathbb {Y}$ whose dual basis is $\mathcal {X}^*\oplus \mathcal {Y}^*$ , via the natural identification of the dual space of $\mathbb {X}\oplus \mathbb {Y}$ with $\mathbb {X}^*\oplus \mathbb {Y}^*$ .

The growth of the unconditionality-like parameters of $\mathcal {X}\oplus \mathcal {Y}$ is linearly determined by the growth of the unconditionality-like parameters of its summands $\mathcal {X}$ and $\mathcal {Y}$ . For instance,

(9.3) $$ \begin{align} \boldsymbol{k}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}]&\approx \max\lbrace \boldsymbol{k}_m[\mathcal{X},\mathbb{X}], \boldsymbol{k}_m[\mathcal{Y},\mathbb{Y}]\rbrace, \end{align} $$

(9.4) $$ \begin{align} \boldsymbol{r}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}]&\approx \max\lbrace \boldsymbol{r}_m[\mathcal{X},\mathbb{X}], \boldsymbol{r}_m[\mathcal{Y},\mathbb{Y}]\rbrace \end{align} $$

for $m\in \mathbb {N}$ . The behavior of the democracy-like parameters is more involved. Here, we study the squeeze-symmetry parameters of direct sums of bases.

To that end, we notice that for any basis $\mathcal {X}$ of a quasi-Banach space $\mathbb {X}$ the parameters $(\boldsymbol {\psi }_m)_{m=1}^{\infty }$ defined in equation (3.5) satisfy

$$\begin{align*}\boldsymbol{\psi}_{\left\lceil m/2\right\rceil} \lesssim \boldsymbol{\psi}_m, \quad m\in\mathbb{N}. \end{align*}$$

Indeed, if $\kappa $ is the modulus of concavity of $\mathbb {X}$ ,

$$\begin{align*}\boldsymbol{\psi}_{\left\lceil m/2\right\rceil}=\frac{\boldsymbol{\lambda}_{\left\lceil m/2\right\rceil}}{\boldsymbol{\varphi_u}(\left\lceil m/2\right\rceil)}\le \frac{\boldsymbol{\lambda}_m}{\boldsymbol{\varphi_u}(\left\lceil m/2\right\rceil)} \le \frac{\kappa\boldsymbol{\lambda}_m}{\boldsymbol{\varphi_u}(m)}=\kappa \boldsymbol{\psi}_m. \end{align*}$$

Let us consider $\mathbb {X}\oplus \mathbb {Y}$ endowed with the maximum norm. We deduce from Lemma 3.3 (i) that

$$\begin{align*}\boldsymbol{\rho}_m:=\max\lbrace \boldsymbol{\psi}_m[\mathcal{X},\mathbb{X}], \boldsymbol{\psi}_m[\mathcal{Y},\mathbb{Y}]\rbrace \le \boldsymbol{\psi}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}] \le \boldsymbol{\rho}_{\left\lceil m/2\right\rceil} \end{align*}$$

for all $m\in \mathbb {N}$ . In turn, it is well known (see [29]) that

$$\begin{align*}\boldsymbol{\varphi_u}(m):=\max\lbrace \boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m), \boldsymbol{\varphi_u}[\mathcal{Y},\mathbb{Y}](m)\rbrace = \boldsymbol{\varphi_u}[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}](m). \end{align*}$$

Hence, $\boldsymbol {\lambda }_m[\mathcal {X}\oplus \mathcal {Y},\mathbb {X}\oplus \mathbb {Y}]$ grows as

$$\begin{align*}\max\lbrace \boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m), \boldsymbol{\varphi_u}[\mathcal{Y},\mathbb{Y}](m)\rbrace \max\left\lbrace \frac{ \boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}]}{\boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m)}, \frac{ \boldsymbol{\lambda}_m[\mathcal{Y},\mathbb{Y}]}{\boldsymbol{\varphi_u}[\mathcal{Y},\mathbb{Y}](m)}\right\rbrace. \end{align*}$$

That is, if

$$\begin{align*}\boldsymbol{\xi}_m[\mathcal{X},\mathcal{Y}]=\max\left\lbrace 1, \frac{\boldsymbol{\varphi_u}[\mathcal{Y},\mathbb{Y}](m)}{\boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}](m)}\right\rbrace\boldsymbol{\lambda}_m[\mathcal{X},\mathbb{X}], \end{align*}$$

then

(9.5) $$ \begin{align} \boldsymbol{\lambda}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}]\approx \max\lbrace \boldsymbol{\xi}_m[\mathcal{X},\mathcal{Y}], \boldsymbol{\xi}_m[\mathcal{Y},\mathcal{X}]\rbrace, \quad m\in\mathbb{N}. \end{align} $$

9.11 The Lebesgue constants do not grow linearly with the democracy parameters and the unconditionality parameters

Let $\mathcal {X}$ and $\mathcal {Y}$ be bases of quasi-Banach spaces $\mathbb {X}$ and $\mathbb {Y}$ , respectively. Suppose that $\mathcal {X}$ and $\mathcal {Y}$ are superdemocratic and that

$$\begin{align*}h=\frac{\boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}]}{\boldsymbol{\varphi_u}[\mathcal{Y},\mathbb{Y}]} \end{align*}$$

is equivalent to a nondecreasing function. Then,

$$\begin{align*}\boldsymbol{\mu}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}] \approx \boldsymbol{\mu}^{\boldsymbol{s}}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}] \approx h(m),\quad m\in\mathbb{N}. \end{align*}$$

Suppose also that $\mathcal {Y}$ is truncation quasi-greedy and that $\mathbb {Y}$ is r-Banach, $0<r\le 1$ . By equations (9.2) and (9.3),

$$\begin{align*}\boldsymbol{k}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}] \lesssim \max\lbrace \boldsymbol{k}_m[\mathcal{X},\mathbb{X}],\log (1+m)^{1/r}\rbrace, \quad m\in\mathbb{N}. \end{align*}$$

In turn, by equation (9.5) and Proposition 5.2,

$$\begin{align*}\boldsymbol{\lambda}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}]\approx h(m) \boldsymbol{r}_m[\mathcal{X},\mathbb{X}], \quad m\in\mathbb{N}. \end{align*}$$

If the function h controls the growth of both the powers of the logarithmic function and the unconditionality parameters of $\mathcal {X}$ , then

$$ \begin{align*} \boldsymbol{L}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}] &\approx h(m) \boldsymbol{r}_m[\mathcal{X},\mathbb{X}],\\ \max\lbrace \boldsymbol{\mu^s}[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}] ,\boldsymbol{k}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus \mathbb{Y}] \rbrace &\approx h(m) \end{align*} $$

for $m\in \mathbb {N}$ . If $\mathcal {X}$ is not truncation quasi-greedy, then

$$\begin{align*}\boldsymbol{L}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus\mathbb{Y}]\not\approx \max\lbrace\boldsymbol{\mu}^{\boldsymbol{s}}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus\mathbb{Y}],\boldsymbol{k}_m[\mathcal{X}\oplus\mathcal{Y},\mathbb{X}\oplus\mathbb{Y}]\rbrace. \end{align*}$$

To look for bases where this situation occurs, we appeal to [4, Example 11.6]. The computations therein show that the basis $\mathcal {X}$ constructed there for $\mathbb {X}=\ell _p\oplus \ell _q$ , $0<p<q\le \infty $ , is superdemocratic and satisfies

$$\begin{align*}\boldsymbol{\varphi_u}[\mathcal{X},\mathbb{X}] \approx m^{1/p}\quad \mbox{ and } \quad \boldsymbol{q}_m[\mathcal{X},\mathbb{X}] \gtrsim m^{1/p-1/q} \quad m\in\mathbb{N}. \end{align*}$$

Besides, it is easily checked that $\mathcal {X}$ dominates the unit vector system of $\ell _q$ and it is dominated by the unit vector system of $\ell _p$ . Therefore,

$$\begin{align*}\boldsymbol{k}_m[\mathcal{X},\mathbb{X}] \lesssim m^{1/p-1/q}, \quad m\in\mathbb{N}. \end{align*}$$

Hence,

$$\begin{align*}\boldsymbol{q}_m[\mathcal{X},\mathbb{X}] \approx \boldsymbol{r}_m[\mathcal{X},\mathbb{X}] \approx \boldsymbol{k}_m[\mathcal{X},\mathbb{X}] \approx m^{1/p-1/q}, \quad m\in\mathbb{N}. \end{align*}$$

Now, it suffices to pick a squeeze-symmetric basis $\mathcal {Y}$ of a quasi-Banach space $\mathbb {Y}$ which satisfies

$$\begin{align*}\boldsymbol{\varphi_u}[\mathcal{Y},\mathbb{Y}] \approx m^{1/s}, \quad m\in\mathbb{N}, \end{align*}$$

for some $s\in (0,\infty )$ with $1/s>2/p-1/q$ . Take, for instance, the unit vector system of $\ell _{s}$ .

Note that the right-hand side estimate of equation (1.2) is optimal for the basis of $\ell _p \oplus \ell _q \oplus \ell _s$ that we have constructed.