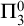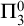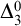A RECURSIVE COLORING FUNCTION WITHOUT $ \Pi _3^0$ SOLUTIONS FOR HINDMAN’S THEOREM

Abstract

We show that there exists a recursive coloring function c such that any $\Pi ^0_3$ set is not a solution to c for Hindman’s theorem. We also show that there exists a recursive coloring function c such that any $\Delta ^0_3$ set is not a solution to c for Hindman’s theorem restricted to sums of at most three numbers.

1. Introduction

Reverse mathematics is a branch of mathematical logic. Its aim is to determine the strength of theorems which axioms are needed to prove these theorems. Among all axiom systems, reverse mathematics mainly focuses on five subsystems of second-order arithmetic, known as the Big Five:

$$ \begin{align*}\textrm{RCA}_0, \textrm{WKL}_0, \textrm{ACA}_0, \textrm{ATR}_0, \Pi^1_1\textrm{-CA}_0. \end{align*} $$

The results of this paper are about $\textrm {ACA}_0$ , which is equivalent to say that the Turing jump exists for every set of natural numbers.

One of the most important topics in reverse mathematics is Ramsey’s theorem and its variants. The version of Ramsey’s theorem studied in reverse mathematics is the infinite countable version of the finite Ramsey’s theorem from finite combinatorics. This theorem states that, for any finite coloring function c on $[\mathbb {N}]^n$ , there exists an infinite set H that $[H]^n$ is monochromatic [12]. This infinite set is called a solution to c.

The strategy for analyzing these theorems is to study the computational complexity of their solutions. Jockusch proves that every recursive instance of $\mathrm {RT}^n_2$ ( $n> 1$ ) has a $\Pi ^0_n$ solution and some recursive instance of $\mathrm {RT}^3_2$ only has solutions computing the halting problem.

In this paper, we will discuss Hindman’s theorem. Hindman’s theorem is a Ramsey-type combinatorial theorem about finite sums:

Theorem 1.1 (Hindman [9]).

For any coloring function $c:\mathbb {N}\rightarrow r$ , where $r\geq 2$ is a natural number, there exists an infinite set $H\subset \mathbb {N}$ such that $FS(H)$ is monochromatic under c where $FS(H)$ is the set consisting of all finite sums of different numbers from H:

$$ \begin{align*} FS(H)=\left\{\sum_{x\in F}x:F\subset H, F\text{ is finite and nonempty}\right\}. \end{align*} $$

For convenience, we call such a set H in the above theorem a solution to c for Hindman’s theorem. In this paper, Hindman’s theorem will be abbreviated as $\textrm {HT}$ .

The study of the reverse mathematics of Hindman’s theorem began with the paper by Blass, Hirst, and Simpson in 1987 [2]. They established some fundamental results about the complexity of solutions of Hindman’s theorem:

Theorem 1.2 (Blass, Hirst, and Simpson [2]).

1. For any coloring function $c:\mathbb {N}\rightarrow r$ , where $r \geq 2$ is a natural number, there exists a solution to c for Hindman’s theorem that is recursive in $c^{(\omega +1)}$ , the $(\omega +1)$ th Turing jump of c.

2. There exists a recursive coloring function c such that any solution to c can compute $c'$ , the Turing jump of c; this result can be relativized to any degree.

Based on these results about the complexity of solutions, they showed that the strength of Hindman’s theorem is between $\mathrm {ACA}_{0}$ and $\mathrm {ACA}_{0}^{+}$ : $\mathrm {ACA}_{0}$ is necessary and $\mathrm {ACA}_{0}^{+}$ is sufficient. Simply speaking, $\mathrm {ACA}_{0}^{+}$ is to say the $\omega $ th Turing jump of every set exists. However, this result has not been improved since 1987.

In addition, before presenting their main results, Blass, Hirst, and Simpson provided another theorem as an example, which gives a lower bound on the complexity of a solution for Hindman’s theorem. That is the following:

Theorem 1.3 (Blass, Hirst, and Simpson [2]).

There exists a recursive coloring function c in two colors without any $\Delta ^0_2$ solutions for Hindman’s theorem.

We may call Theorem 1.3 the $\Delta _2^0$ -unsolvability of Hindman’s theorem.

For the meaning of Hindman’s theorem in reverse mathematics, see Montalbans’ paper [13]. For more information on reverse mathematics of Hindman’s theorem, see the references [7, 11].

In this paper, we will prove the $\Pi _3^0$ -unsolvability of Hindman’s theorem:

Theorem 1.4. There exists a recursive coloring function c in finitely many colors without any $\Pi _3^0$ solutions for Hindman’s theorem.

Restricted versions of Hindman’s theorem has received some attention in recent years. This idea comes from Blass’ paper [1]. The most common restricted Hindman’s theorem is the following theorem, denoted $\textrm {HT}^{\leq k}_r$ :

Theorem 1.5 (Restricted Hindman’s theorem $\textrm {HT}^{\leq k}_r$ for fixed numbers $r,k$ ).

Suppose $r,k>0$ are two fixed natural numbers. For any coloring function $c:\mathbb {N}\rightarrow r$ , there exists an infinite set $H\subset \mathbb {N}$ such that $FS^{\leq k}(H)$ is monochromatic under c. Here, $FS^{\leq k}(H)$ is defined as follows:

$$ \begin{align*} FS^{\leq k}(H)=\left\{\sum_{x\in F}x:F\subset H, |F|\leq k\text{ is and nonempty}\right\}. \end{align*} $$

We omit to mention colors when we are not interested in their number. There are plenty of results about the restricted Hindman’s theorems $\textrm {HT}^{\leq k}_r$ , see [3, 4, 6]. However, even for such apparently weak theorems, we do not know much about their exact strength. For example, we do not know if $\mathrm {ACA}_{0}$ can prove any such restricted Hindman’s theorem, even the weakest $\textrm {HT}^{\leq 2}_2$ . Meanwhile, the question of whether $\textrm {HT}^{\leq 2}_2$ is provable in $\mathrm {ACA}_0$ , and whether it separates from $\mathrm {HT}$ is interestingly related to a combinatorial open question asked by Hindman, Leader, and Strauss in 2003 [10].

In Section 2, we will prove the $\Delta _3^0$ -unsolvability for $\textrm {HT}$ and $\mathrm {HT}^{\leq 3}_2$ . In Section 3, we will prove the $\Pi ^3_0$ -unsolvability for $\textrm {HT}$ with weak apartness (defined in Section 2). In Section 4, we will prove the $\Delta _3^0$ -unsolvability for $\textrm {HT}^{\leq 3}$ and $\Pi _3^0$ -unsolvability for $\textrm {HT}$ without weak apartness. In Section 5, we will prove $\Pi _3^0$ -unsolvability without weak apartness using only four colors.

2. Proof of $\Delta _3^0$ unsolvability

In this section, we will construct a coloring function c in two colors such that any infinite $\Delta _3^0$ set is not a solution to c for $\mathrm {HT}$ . First, we list some notations. Some of them are from Blass, Hirst, and Simpson’s paper [2], Hindman’s paper [8, 9], and Carlucci’s paper [3].

Definition 2.1.

1. 1. We define two functions $\mu (x),\lambda (x)$ on $\mathbb {Z^+}$ as follows:

   If $x=2^{n_0}+\dots +2^{n_k}\in \mathbb {Z^+}$ , where $n_0<\cdots <n_k\in \mathbb {N}$ , then $\mu (x)=n_k,\lambda (x)=n_0$ . If $x=2^{n_0}$ , then $\mu (x)=\lambda (x)=n_0$ .

2. 2. For two positive integers $x<y$ , we write that $x\ll y$ or $y\gg x$ if $\mu (x)<\lambda (y)$ . A set A has apartness (or is with apartness; this concept origins from Hindman’s paper [8], and this name apartness is from [3]) if for any $x<y$ in A, $x\ll y$ . A number $x\gg Y$ for a set Y means that for any $y\in Y$ , $x\gg y$ .

3. 3. For each natural number n, we define that

   $$ \begin{align*} B^n=\{x\in \mathbb{Z^+}:\mu(x)=n\}\text{ and }B^{\leq n}=\{x\in \mathbb{Z^+}: \mu(x)\leq n\}. \end{align*} $$

4. 4. A set A has weak apartness if: (1) For any natural number m, $B^m\cap A$ contains at most one element. (2) for any natural number l, there are at most two numbers x in A satisfying $\lambda (x)=l$ ; therefore, if a set A has weak apartness, then for any natural number L, there exists M such that for any $x>M$ in A, $\lambda (x)>L$ .

In addition to the above definitions, for convenience, we also have some other conventions. 1. For a set A, we use $A(x)$ to denote its characteristic function. 2. We say that a coloring c or a construction of a coloring c kills a set A, or a set A is killed, if $FS(A)$ is not monochromatic (under c). 3. In this paper, all variables are natural numbers, any quantifier without specified range is over the set of natural numbers $\mathbb {N}$ , and all intervals are intervals of natural numbers. For example, $\forall x \phi $ means that for any $x\in \mathbb {N}$ , $\phi $ holds, and $n\in (a,b),n\in (a,b],n\in [a,b)$ means that n is an integer between integers a and b. 4. Limit notations such as $\lim _x f(x)$ or $\lim \limits _{x}f(x)$ , mean: $\lim \limits _{x\rightarrow \infty }f(x)$ .

2.1. Strategy

A naive strategy is to set infinitely many requests $\langle x,y\rangle \in \mathbb {N}^2$ and each such request means that we let x be colored in one color, say Red, and let y be colored in another color, say Green. But this strategy does not succeed. Instead, we try a different approach using a new type of request. A request $\langle w,x\rangle $ means that $w+x$ and w need to have different colors. We must limit the number of requests we set. For example, if we set requests $\langle 4,2\rangle ,\langle 4,3\rangle $ , and $\langle 6,1\rangle $ , then because $4+2=6, 4+3=7,6+1=7$ , all three numbers $4,6,7$ need to have different colors, which contradicts the condition that c has only two colors.

Example 2.2. Consider a set of requests $\{\langle w,2^n\rangle :\lambda (w)>n\}$ . We want to find a coloring function $c:\mathbb {N}\rightarrow \{0,1\}$ such that for any two numbers w,n such that $\lambda (w)>n$ (i.e., w is divisible by $2^{n+1}$ ), w and $w+2^n$ have different colors.

We can find a simple solution: let $c(w)$ be the number of digits $1$ mod 2 in the binary representation of w: for example, $c(2)=c(10_2)=1$ , $c(3)=c(11_2)=0$ , $c(4)=c(100_2)=1$ , $c(5)=c(101_2)=0$ and so on.

We will construct a recursive function $R(n,w)$ from a recursive subset of $\mathbb {N}^2$ to $\mathbb {N}$ to represent the desired request set: each pair $\langle w, R(n,w)\rangle $ will be a request. This function $R(n,w)$ will satisfy two conditions:

C1. There exists a recursive coloring function $c:\mathbb {N}\rightarrow \{0,1\}$ such that for any w and n, if $R(n,w)$ is defined, then $c(w)\neq c(R(n,w)+w)$ .

C2. For every infinite $\Delta _3^0$ set A with weak apartness, there exists $w\in FS(A)$ and n such that $R(n,w)$ is defined, $R(n,w)\in A$ and $R(n,w)+w\in FS(A)$ .

The following lemma provides a sufficient condition for $R(n,w)$ to satisfy C1.

Lemma 2.3. Let R be a function from a recursive subset of $\mathbb {N}^2$ to $\mathbb {N}$ such that $R(n,w)\in B^n$ . There exists a coloring function $c:\mathbb {N}\rightarrow \{0,1\}$ recursive in R and its domain such that for any w and $n<\lambda (w)$ , if $R(n,w)$ is defined, then

$$ \begin{align*} c(w)\neq c(R(n,w)+w). \end{align*} $$

Moreover, c is uniformly recursive in R and its domain: there exists a recursive functional $\Phi ^X$ such that $\Phi ^{R\oplus \mathrm {dom}(R)}=c$ .

Proof Because the domain of $R(n,w)$ is recursive, first we extend R to the whole of $\mathbb {N}^2$ : for $n,w$ , $R(n,w)$ has not been defined, let $R(n,w)=2^n$ . The extended $R(n,w)$ is still a recursive function.

We construct the coloring function c stage by stage. At stage s, we color numbers in $B^s$ . For each s, we will create a graph with vertex set $B^s$ and edges depending on the function $R(n,w)$ so that this graph is a tree. So for any $w_1,w_2\in B^s$ , there exists a unique path P from $w_1$ to $w_2$ .

Fix a stage s. For each $w\in B^s$ and $n< \lambda (w)$ , We add one edge between $w+R(n,w)$ and w and call it $e_{w,w+R(n,w)}$ . This graph does not contain any multiple edges or self-loops. We show that this graph is a tree by induction.

For every $w\in B^s$ and $n<\lambda (w)$ , define the vertex set

$$ \begin{align*} T_{w,n}=\{w+x:0\leq x<2^{n+1}\}, \end{align*} $$

and consider the corresponding induced subgraph. By definition, $T_{w_1,n_1}=T_{w_2,n_2}$ iff $ \langle w_1,n_1\rangle =\langle w_2,n_2 \rangle $ ; and if $n_1=n_2$ but $w_1\neq w_2$ , then $T_{w_1,n_1},T_{w_2,n_2}$ are disjoint.

If we write integers in binary representation, then the vertex set $T_{w,n}$ looks like

$$ \begin{align*} T_{w,n}=\{(w_sw_{s-1}\dots w_{n+1}x_n\dots x_{0})_2:x_0,\dots,x_n\in\{0,1\}\}, \end{align*} $$

where $w_sw_{s-1}\dots w_{n+1}$ is the highest $s-n$ many digits of w and it is the common part of all numbers in the vertex set $T_{w,n}$ . All other digits of w are $0$ . By definition, for $n\geq 1$ ,

$$ \begin{align*} T_{w,n}&=\{w+x:0\leq x<2^{n+1}\}\\ &=\{w+x:0\leq x<2^{n}\}\cup \{w+x:2^n\leq x<2^{n+1}\}\\ &=\{w+x:0\leq x<2^{n}\}\cup \{w+2^n+x:0\leq x<2^{n}\}\\ &=T_{w,n-1}\cup T_{w+2^n,n-1}. \end{align*} $$

The two sets $T_{w,n-1}$ and $T_{w+2^n,n-1}$ look like

$$ \begin{align*} T_{w,n-1}&=\{(w_sw_{s-1}\dots w_{n+1} 0 x_{n-1}\dots x_{0})_2:x_0,\dots,x_n\in\{0,1\}\}\\ T_{w+2^n,n-1}&=\{(w_sw_{s-1}\dots w_{n+1} 1 x_{n-1}\dots x_{0})_2:x_0,\dots,x_n\in\{0,1\}\}, \end{align*} $$

where, $w_s,w_{s-1},\dots ,w_{n+1}$ are the first a few digits of w. They are disjoint. The induced subgraph of $T_{w,n}$ is equal to the union of the induced subgraphs of $T_{w,n-1},T_{w+2^n,n-1}$ plus the edges between vertices in $T_{w,n-1}$ and vertices in $T_{w+2^n,n-1}$ . We claim that there exists exactly one edge between two vertex sets $T_{w,n-1},T_{w+2^n,n-1}$ .

Suppose there is an edge $e'$ from $w'\in T_{w,n-1}$ to $w'+R(n',w')\in T_{w+2^n,n-1}$ . Since $\mu (R(n',w'))=n'<\lambda (w')$ by hypothesis on R and choice of n, if $n'<n$ , then $w'+R(n',w')$ is still in $T_{w,n-1}$ ; if $n'>n$ , then $w'+R(n',w')$ is greater than all numbers in $T_{w+2^n,n-1}$ . Therefore, $n'=n$ . Because $n=n'<\lambda (w')$ , $w'=w$ , otherwise $w'$ is not in $T_{w,n-1}$ . Therefore such edge is unique and the claim is true.

We now show by induction on n that all induced graphs of $T_{w,n}$ are trees. For $n=0$ and any w such that $\lambda (w)>0$ , $T_{w,0}$ has a single vertex and the induced graph is a tree. For $n>0$ , by the construction of edges, for any $w\in B^s$ that $\lambda (w)>n$ , there is an edge $w,w+R(n,w)$ between $T_{w,n-1}$ and $T_{w+2^n,n-1}$ ; because $T_{w,n}$ is the union of two trees (induced graphs of $T_{w,n-1}$ and $T_{w+2^n,n-1}$ ) plus one edge between two trees, it is a tree. Finally, since $B^s=T_{2^s,s-1}$ , the whole graph with $B^s$ as the vertex set is also a tree.

We now define the coloring function c. Let $c(2^s)=0$ . For $w \in B^s$ other than $2^s$ , because the graph is a tree, we find the unique path P from $2^{s}$ to w, and let $c(w)$ be the length of P mod 2. This definition is uniformly recursive in R.

Verification: Let $P_w$ be a path from $2^s$ to w and $x=R(n,w)$ . If $w+x$ is a vertex in $P_w$ , then it must be the vertex in $P_w$ immediately preceding w, since otherwise there would be two paths from w to $w+x$ . Then $c(w+x)\equiv |P_w|-1\ \mod 2$ which is not equal to $c(w)$ . If $w+x$ is not in the path, then the path $P_w$ plus $e_{w,w+x}$ is a path from $2^s$ to $w+x$ , and $c(w+x)\equiv |P_w|+1\ \mod 2$ , which is not equal to $c(w)$ . In both cases, we can see that $c(w) \neq c(w+x)$ , which completes the verification.

Once we have Lemma 2.3, our task becomes to construct a function $R(n,w)$ defined on a recursive subset of $\{\langle n,w\rangle :n<\lambda (w)\}$ such that $R(n,w)\in B^n$ if defined, and satisfying the condition C2 $^*$ :

C2 $^*$ . For every infinite $\Delta _3^0$ set A with weak apartness, there exists $w\in FS(A)$ and $n<\lambda (w)$ such that $R(n,w)$ is defined and in A.

The construction will use approximations of $\Delta _3^0$ sets. By recursion theory [14], a set A is $\Delta _3^0$ iff $A\leq _T \emptyset "$ , and $A\leq _T B'$ iff there exists a function $\tilde {A}(x,k)\leq _T B$ such that $\lim _k \tilde {A}(x,k)=A$ . More precisely, we will use the following lemma.

Lemma 2.4. There exists a recursive list of total recursive functions $\{A_i(x,k,s)\}_{i\in \mathbb {N}}$ taking values in $\{0,1\}$ such that for any $\Delta _3^0$ set A, there exists a function $A_i(x,k,s)$ in the list such that for any x,

$$ \begin{align*}\lim_{y}\lim_s A_i(x,k,s)=A(x).\end{align*} $$

Proof If a set A is $\Delta _3^0$ , then $A\leq _T \emptyset "$ , and there exists a function $\tilde {A}(x,k)\leq _T \emptyset '$ such that $\lim _k \tilde {A}(x,k)=A(x)$ . Let $\tilde {A}(x,k)=\Phi ^{\emptyset '}_i(x,k)$ , where $\Phi _i$ is the ith two variable recursive function with oracle. Consider $\Phi _i^{\emptyset '[s]}(x,k)[s]$ . We will show that for every x, $\lim _{k}\lim _s \Phi _i^{\emptyset '[s]}(x,k)[s]$ is defined and equal $A(x)$ .

By definition, there exists $k_0$ such that for any $k>k_0$ , $\tilde {A}(x,k)$ is defined and equal to $A(x)$ , written as $\tilde {A}(x,k)\downarrow =A(x)$ . Now for any number $k>k_0$ , we show that $\lim _s\Phi _i^{\emptyset '[s]}(x,k)[s]=\tilde {A}(x,k)$ . Because $\tilde {A}(x,k)=\Phi _i^{\emptyset '}(x,k)$ is defined, there exists s such that $\Phi ^{\emptyset '[s]}(x,k)[s]\downarrow =\tilde {A}(x,k)$ and the use of $\emptyset '$ in this computation will never change from stage s on. Hence for any $s'>s$ , this computation still holds and $\Phi ^{\emptyset '[s']}(x,k)[s']=\tilde {A}(x,k)$ . Therefore, $\lim _s\Phi ^{\emptyset '[s]}(x,k)[s]=\tilde {A}(x,k)$ and $\lim _{k}\lim _s \Phi _i^{\emptyset '[s]}(x,k)[s]=A(x)$ .

So we define the list as follows: for each number j, define the jth function in the list

$$ \begin{align*}A_j(x,k,s)=\Phi_j^{\emptyset'[s]}(x,k)[s],\end{align*} $$

if the value of right-hand side is $0$ or $1$ ; otherwise $A_j(x,k,s)=0$ . This is a total recursive function and this list is also recursive.

Therefore, when discussing all $\Delta _3^0$ sets, we can focus on $\Delta _3^0$ sets in this list.

2.2. Strategy of killing one set

Assuming A is an infinite $\Delta _3^0$ set with weak apartness, we show how to kill A by constructing the function $R(n,w)$ . If for this $R(n,w)$ , condition C2 $^*$ holds for set A, then, by Lemma 2.3, we can construct a coloring function c that kills the set A.

Our strategy is to guess which number is in $A\cap B^n$ (by weak apartness, $A\cap B^n$ contains at most one element) and let $R(n,w)$ be this element. We can use the approximation of A, $A(x,k,s)$ as a guessing function.

We use a guessing function to construct the function $R(n,w)$ . For numbers $n,w$ , we compute $A(x,\lambda (w),\mu (w))$ for all $x\in B^n$ and check if there exists any x in $B^n$ such that

$$ \begin{align*}A(x,\lambda(w),\mu(w))=1,\end{align*} $$

which suggests that $x\in B^n\cap A$ ; if such x exists, then we guess $B^n\cap A\neq \emptyset $ and let $R(n,w)$ be the minimal one among all such x; if such x does not exist, let $R(n,w)=2^{n+1}-1$ , i.e.:

$$ \begin{align*}R(n,w)=\min(\{x\in B^n:A(x,\lambda(w),\mu(w))=1\}\cup\{2^{n+1}-1\}).\end{align*} $$

We show that this construction kills set A. Because A is infinite, there exists n such that $B^n\cap A$ is nonempty. Let x be the unique element in $B^n\cap A$ . By Lemma 2.4, for any number y in $B^n$ , $\lim _k\lim _s A(y,k,s)=A(y)$ . Because $B^n$ is finite, $\lim _k\lim _s (A(\cdot ,k,s)\restriction B^n)=A(\cdot )\restriction B^n$ ; for any natural numbers $k,s$ , if $ A(\cdot ,k,s)\restriction B^n=A(\cdot )\restriction B^n$ , then $A(x,k,s)=1$ and for any $y\in B^n\setminus \{x\}$ , $A(y,k,s)=0$ .

Now, look for a number K such that for any $k>K$ , $\lim _s (A(\cdot ,k,s)\restriction B^n)=A(\cdot )\restriction B^n$ , and choose a number $w_1\in A$ such that $\lambda (w_1)$ is greater than K and n; let $k=\lambda (w_1)$ . Next, for the fixed number k, look for a number $s_k$ such that for any $s>s_k$ , $A(\cdot ,k,s)\restriction B^n=A(\cdot )\restriction B^n$ , and choose another number $w_2\gg w_1$ from A such that $\mu (w_2)>s_k$ .

Let $w=w_1+w_2$ , then $\lambda (w)=\lambda (w_1)=k>K$ and $\mu (w)=\mu (w_2)>s_k$ . Combining all discussions above, $A(\cdot ,\lambda (w),\mu (w))\restriction B^n=A(\cdot )\restriction B^n$ . This means $A(x,\lambda (w),\mu (w))=1$ while for any $y\in B^n\setminus \{x\}$ , $A(y,\lambda (w),\mu (w))=0$ . By the definition of function $R(n,w)$ , $R(n,w_1+w_2)=x\in A$ . All three numbers $x\ll w_1\ll w_2$ are in A. By Lemma 2.3, there exists a recursive function c such that $c(w_1+w_2)\neq c(x+w_1+w_2)$ where both $w_1+w_2$ and $x+w_1+w_2$ are in $FS(A)$ .

2.3. Strategy for killing infinitely many sets

The strategy of killing infinitely many sets is based on the strategy of killing a single set. Now, condition C2 $^*$ , as defined earlier, becomes: for any $\Delta _3^0$ infinite set $A_i$ with weak apartness in the list of Lemma 2.4, there exist numbers $w\in FS(A_i)$ and $n<\lambda (w)$ such that $R(n,w)\in A_i$ . We will continue to use the construction of the previous subsection with one more step: first, we need to choose a set $A_i$ among all $\Delta _3^0$ sets in the list of Lemma 2.4 by a priority argument, and then apply the construction introduced earlier. To do this, we first guess which $A_i$ have nonempty intersection with $B^n$ , and then choose one such set among them. To use this argument, we need a function which guesses, for a number n and a set $A_i$ , whether $A_i\cap B^n$ is empty or not. For a set $A_i$ , a number w, and a number $n<\lambda (w)$ , we check if there exists $x\in B^n$ such that $A_i(x,\lambda (w),\mu (w))=1$ and use a function $a_i(n,k,s)$ to denote this check:

$$ \begin{align*} a_i(n,k,s)=\max\{A_i(x,k,s):x\in B^n\}=\left\{\!\!\!\begin{array}{l} 1, \text{ if }\exists x\in B^n\ A_i(x,k,s)=1; \\ 0, \text{ otherwise.} \\ \end{array} \right. \end{align*} $$

Because $B^n=\{x:\mu (x)=n\}$ is finite, this function is also recursive and total. If $a_i(n,\lambda (w),\mu (w))=1$ , which means that there exists a number $x\in B^n$ such that $A_i(x,\lambda (w),\mu (w))=1$ , then we guess $A_i\cap B^n$ is nonempty; otherwise, we guess $A_i\cap B^n$ is empty.

We cannot recursively list all infinite $\Delta _3^0$ sets, but by Proposition 2.4, we have a recursive list of some total recursive functions $A_i(x,k,s)$ such that every $\Delta _3^0$ set is represented in the list. This list contains approximations of all infinite $\Delta _3^0$ sets. However, some functions in the list may not correspond to an infinite $\Delta _3^0$ set, a set with weak apartness or even a set.

So we need to use some restrictions from Jockusch’s argument [12] for Ramsey’s theorem, which Blass, Hirst, and Simpson adapt to Hindman’s theorem [2]. During the construction, for any function $A_i(x,k,s)$ and any pair $k,s$ , we will choose at most $2^i$ many numbers $n\in (i,s)$ and call them the candidates of $A_i$ for $k,s$ . For any $k,s$ , any set $A_i$ has at most $2^i$ many candidates. When defining $R(n,w)$ , only if n is a candidate of $A_i$ for $k=\lambda (w),s=\mu (w)$ , $A_i$ may be chosen to apply the construction of killing one set.

2.4. Construction

We use the recursive list $\{A_i(x,k,s)\}_{i\in \mathbb {N}}$ from Lemma 2.4.

Part 1: For each $A_i(x,k,s)$ in the list, define $a_i(n,k,s)=\max \{A_i(x,k,s):x\in B^n\}$ as mentioned earlier. $\langle a_i(n,k,s)\rangle _{i\in \mathbb {N}}$ is also a recursive list of total recursive functions. For each i and for each $k,s$ , define a candidate set $C_i(k,s)$ to be the set of first $2^i$ numbers $n\in (i,s)$ such that $a_i(n,k,s)=1$ . If there are not $2^i$ many such numbers n, then let $C_i(k,s)$ be all $n\in (i,s)$ such that $a_i(n,k,s)=1$ . These sets $C_i(k,s)$ are uniformly recursive in $i,k,s$ .

Part 2: For each $n,w$ such that $n<\lambda (w)$ , compute the set

$$ \begin{align*}\{i< n: n\in C_i(\lambda(w),\mu(w))\},\end{align*} $$

the index set of sets $A_i$ such that $C_i(\lambda (w),\mu (w))$ contains n, which means that we guess $A_i\cap B^n\neq \emptyset $ . Let $j=\min (\{i< n: n\in C_i(\lambda (w),\mu (w))\}\cup \{n\}))$ and

$$ \begin{align*}R(n,w)=\min(\{x\in B^n:A_j(x,\lambda(w),\mu(w))=1\}\cup\{2^{n+1}-1\})\end{align*} $$

as killing one set in previous subsection. This is the construction of function $R(n,w)$ .

$R(n,w)$ is a recursive function with recursive domain. By Lemma 2.3, we can construct a coloring function c uniformly recursive in $R(n,w)$ that satisfies the condition C1: for any w and $n<\lambda (w)$ , $c(w)\neq c(w+R(n,w))$ . The only remaining task is to verify condition C2 $^*$ for $R(n,w)$ .

2.5. Verification

In this subsection, we show that the above construction satisfies condition C2 $^*$ . By Proposition 2.4, every $\Delta _3^0$ set is contained in the list of Lemma 2.4, so we only need to consider sets in this list. We use $A_i$ to denote the set represented by $A_i(x,k,s)$ if that set is defined. First, we have the following lemma.

Lemma 2.5. Let $C_i(k,s)$ be the function in our construction. For any infinite $\Delta _3^0$ set $A_i$ with weak apartness, there exists a finite set $C_i$ of size $2^i$ such that $\lim _k\lim _sC_i(k,s)\downarrow =C_i$ .

Proof Because $A_i$ is infinite and has weak apartness, there are infinitely many $n>i$ such that $A_i\cap B^n$ is nonempty. Let N be the $2^i$ th such n.

By definition, for any x in $B^{\leq N}$ , $\lim _{k}\lim _s A_i(x,k,s)=A_i(x)$ . Because $B^{\leq N}$ is finite, by the properties of the limit operation, we also have

$$ \begin{align*}\lim_{k}\lim_s (A_i(\cdot,k,s)\restriction B^{\leq N})=A_i(\cdot)\restriction B^{\leq N}.\end{align*} $$

Hence for any sufficiently large k, there exists $s_k$ such that for any $s>s_k$ and every $n\leq N$ , $a_i(n,k,s)=\max \{A_i(x,k,s):x\in B^n\}=\max \{A(x):x\in B^n \}$ . This means that, for $n\leq N$ , $a_i(n,k,s)=1$ iff $B^n\cap A_i$ is nonempty. Because N is the $2^i$ th number $n>i$ such that $B^n\cap A_i$ is nonempty, there exists $2^i$ numbers $n\leq N$ greater than i such that $B^n\cap A_i$ is nonempty and hence $a_i(n,k,s)=1$ . By definition, $C_i(k,s)$ is the set of first $2^i$ elements $n\in (i,s)$ such that $a_i(n,k,s)=1$ ; hence for those k and s, $C_i(k,s)$ is equal to the set of first $2^i$ number $n>i$ such that $B^n\cap A_i\neq \emptyset $ .

So we can conclude that, for any sufficiently large k, there exists $s_k$ such that for any $s>s_k$ , $C_i(k,s)$ exactly contains first $2^i$ number $n>i$ such that $B^n\cap A_i\neq \emptyset $ . This means $\lim _{k}\lim _s C_i(k,s)\downarrow =C_i$ for a fixed set $C_i$ .

Next, we have the following lemma:

Lemma 2.6. Let $R(n,k)$ be the function in our construction. For any $\Delta _3^0$ infinite set $A_i$ with weak apartness, there exists a finite set $X_i\subset A_i$ such that

$$ \begin{align*} \exists K\forall k>K\exists s_k\forall s>s_k\forall w\Big(\lambda(w)=k\wedge\mu(w)=s\longrightarrow \exists x\in X_i (R(\mu(x),w)=x)\Big). \end{align*} $$

Proof Consider limits $\lim _k\lim _sC_i(k,s)\downarrow =C_i$ and $\lim _{k}\lim _s A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$ in the proof of Lemma 2.5 and let $X_i=\cup _{n\in C_i}B^n\cap A_i$ . Using these two limits, there exists a number K such that for any $k>K$ , there exists a number $s_k$ such that for any $s>s_k$ , $C_i(k,s)=C_i$ and $A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$ . We show that if for numbers $k,s$ , these two equations hold, then for any w such that $k=\lambda (w),s=\mu (w)$ , there exists $x\in X_i$ such that $R(\mu (x),w)=x$ and therefore this lemma is true.

We claim that for these $k,s$ , for at least one $n\in C_i(k,s)=C_i$ ,

$$ \begin{align*}i=\min(\{j< n: n\in C_j(k,s)\}\cup\{n\})).\end{align*} $$

By definition, for any $j<i$ , $|C_j(k,s)|\leq 2^j$ . So $|\cup _{j<i}C_j(k,s)|<2^i$ . If this claim is not true, then for every $n\in C_i(k,s)$ , there exists $j<i$ such that $n\in C_j(k,s)$ . This means that $\cup _{j<i}C_j(k,s)\supseteq C_i(k,s)$ , which is impossible because $|\cup _{j<i}C_j(k,s)|<2^i=|C_i(k,s)|$ . So the claim is true.

Let $n\in C_i$ be a number such that $i=\min (\{j<n: n\in C_j(k,s)\}\cup \{n\})).$ For any w such that $\lambda (w)=k\wedge \mu (w)=s$ , by definition,

$$ \begin{align*}R(n,w)=\min(\{x\in B^n:A_i(x,\lambda(w),\mu(w))=1\}\cup\{2^{n+1}-1\}).\end{align*} $$

Because for $k,s$ , $A_i(x,k,s)=A_i(x)$ for all $x\in B^n$ , $\min \{x\in B^n: A_i(x,k,s)=1\}$ is defined and is just the unique element in $B^n\cap A_i$ . Hence $R(n,w)$ is the unique element in $B^n\cap A_i$ and is in $X_i$ .

So for those $k,s$ such that $C_i(k,s)=C_i$ and $A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$ , for any w such that $\lambda (w)=k,\mu (w)=s$ , there exists $x\in X_i$ such that $R(\mu (x),w)=x$ . This finishes the proof.

Now we can get the following result.

Theorem 2.7. There exists a recursive coloring function c such that for any infinite $\Delta _3^0$ set A with weak apartness, there exist $x\ll w_1\ll w_2$ in A such that

$$ \begin{align*} c(w_1+w_2)\neq c(x+w_1+w_2). \end{align*} $$

Hence $FS^{\leq 3}(A)$ is not monochromatic under c.

Proof Choose the coloring function c in our construction. For an infinite $\Delta _3^0$ set A with weak apartness, there exists a set $A_i$ in the list of Lemma 2.4 such that $A=A_i$ . We apply Lemma 2.6 to $A_i$ and get $X_i\subseteq A_i$ and K.

Choose a sufficiently large number $w_1\gg X_i$ in $A_i$ such that $\lambda (w_1)>K$ ; let $k=\lambda (w_1)$ . For this fixed k, find $s_k$ by Lemma 2.6 and choose a sufficiently large $w_2\gg w_1$ in $A_i$ such that $\mu (w_2)>s_k$ ; let $s=\mu (w_2)$ . Because $w_2\gg w_1$ , $\lambda (w_1+w_2)=\lambda (w_1)=k,\mu (w_1+w_2)=\mu (w_2)=s$ . Hence by Lemma 2.6, there exists a number $x\in X_i$ such that $R(\mu (x),w_1+w_2)=x$ . By the construction and Lemma 2.3, $c(w_1+w_2)\neq c(x+w_1+w_2)$ .

Theorem 2.7 shows that there exists a recursive coloring function c such that for any infinite $\Delta _3^0$ set A with weak apartness, $FS^{\leq 3}(A)$ is not monochromatic. This theorem is close to our aim, except the requirement of weak apartness. We can use the following fact proved by Hindman:

Lemma 2.8 [9].

For any infinite set A, there exists an infinite set $B\leq _T A$ such that B has apartness and $FS(B)\subseteq FS(A)$ .

So for the same coloring function c in Theorem 2.7, if it has any infinite $\Delta _3^0$ solution A, then A can compute an infinite solution B with apartness and hence weak apartness. Since A is $\Delta _3^0$ and $B\leq _T A$ , B is also $\Delta _3^0$ . However, this is impossible. Now we have achieved our aim for this section:

Theorem 2.9. There exists a recursive coloring function c without any $\Delta _3^0$ solution for Hindman’s theorem.

Moreover, we can use Lemma 2.7 and nearby propositions from the paper of Carlucci et al. [5]. From these results, we know that for any n, for any recursive coloring function c of k many colors, there exists a recursive coloring function d of many $2k$ colors such that any solution B to d for $\mathrm {HT}^{\leq n}$ can compute a solution A to c for $\mathrm {HT}^{\leq n}$ with apartness.

Therefore, applying these results to our coloring function c, we get a coloring function d of four colors. Then if d has a $\Delta _3^0$ solution for $\mathrm {HT}^{\leq 3}$ , c will also have a $\Delta _3^0$ solution for $\mathrm {HT}^{\leq 3}$ with apartness, which is impossible. Hence we can get the following theorem:

Theorem 2.10. There exists a recursive coloring function d of four colors without any $\Delta _3^0$ solution for $\mathrm {HT}^{\leq 3}$ .

3. Proof of $\Pi _3^0$ unsolvability with weak apartness

3.1. General preparation

To prove the $\Pi ^0_3$ case of unsolvability, we will use more than one function similar to $R(n,w)$ , denoted as $R,Q$ . In addition, we need to generalize Lemma 2.3:

Lemma 3.1. Let $r>1$ and $R(n,w)$ be a function with recursive domain such that $R(n,w)\in B^n$ if it is defined. There exists a coloring function $c:\mathbb {N}\rightarrow r$ uniformly recursive in R such that for any w and any $n<\lambda (w)$ , if $R(n,w)$ is defined, then

$$ \begin{align*} \ c(w+R(n,w))\equiv c(w)+1\quad \mod r. \end{align*} $$

Proof This proof is very similar to the proof of Lemma 2.3. Just like in Lemma 2.3, we start by extending the domain of function R to whole $\mathbb {N}^2$ .

For each number s, we create a graph with vertex set $B^s$ as in Lemma 2.3. As shown in Lemma 2.3, this graph is a tree: there exists a unique path from one vertex to another.

Definition of the coloring: Let $c(2^s)=0$ . For another vertex w, since the graph is a tree, find the unique path P from $2^{s}$ to w. Even though the graph is undirected, we will still note the direction of this path, since it allows us to keep track of the order in which vertices are visited. An edge $e_{w',w'+R(n',w')}$ in the path is considered a positive edge if the direction from $w'$ to $w'+R(n',w')$ is the same as the direction from $2^{s}$ to w, and negative otherwise. We count the number of positive edges as a and the numbers of negative edges as b. We then let the color of w be $a-b\ \mod r$ . This process is uniformly recursive in R.

Verification: Similar to Lemma 2.3, let $P_w$ be the unique path from $2^s$ to w, and $x=R(n,w)$ . If $w+x$ is a vertex in $P_w$ , then it must be the vertex in $P_w$ immediately preceding w; and because the direction of edge $e_{w,w+x}$ is from w to $w+x$ , $P_w$ is $P_{w+x}$ plus a negative direction edge. So $c(w)\equiv c(x+w)-1\ \mod r$ . If $w+x$ is not in the path, then the path obtained by adding the edge $e_{w,w+x}$ to $P_w$ is a path from $2^s$ to $w+x$ ; because the direction of edge $e_{w,w+x}$ is from w to $w+x$ , $P_{w+x}$ is $P_{w}$ plus a positive direction edge; so $c(w)+1\equiv c(x+w)\ \mod r$ . In either case, we have $c(w)+1\equiv c(x+w)\ \mod r$ .

We will use two special forms of this lemma. The first special form is when $r=2$ , it corresponds to Lemma 2.3. The second special form is when the function $R(n,w)$ only depends on $\lambda (w)$ , $\mu (w)$ in addition to n: for example, the function in the last section,

$$ \begin{align*}R(n,w)=\min(\{x\in B^n:A_j(x,\lambda(w),\mu(w))=1\}\cup\{2^{n+1}-1\}).\end{align*} $$

For $w_1\neq w_2$ , if $\lambda (w_1)=\lambda (w_2)$ and $\mu (w_1)=\mu (w_2)$ , then $R(n,w_1)=R(n,w_2)$ . In this case, we treat these functions as three-variable functions like $R(n,k,s), Q(n,k,s):$

Corollary 1. Let $r>1$ and Q be a function from a recursive subset of $\mathbb {N}^3$ to $\mathbb {N}$ such that $Q(n,k,s)\in B^n$ . There exists a coloring function $c:\mathbb {N}\rightarrow r$ uniformly recursive in Q such that for any w and $n<\lambda (w)$ , if $Q(n,\lambda (w),\mu (w))$ is defined, then: $\ c(w+Q(n,\lambda (w),\mu (w)))\equiv c(w)+1\ \mod r.$

Similar to last section, we need to choose a list of approximation of $\Pi _3^0$ sets. By definition, every $\Pi _3^0$ set A can be represented as $x\in A\leftrightarrow \forall y\ \Phi (x,y)$ by a $\Sigma _2^0$ formula $\Phi (x,y)$ . By recursion theory [14], there exists a total recursive function $g(i,x,y)$ such that if $\Phi _i(x,y)$ is the ith $\Sigma _2^0$ formula, then $\Phi _i(x,y)$ holds iff $W_{g(i,x,y)}$ , the $g(i,x,y)$ th r.e. set. And this is equivalent to the fact that $\lim _{s} |W_{g(i,x,y),s}|$ is finite, where $W_{g(i,x,y),s}$ is the sth stage of $W_{g(i,x,y)}$ and is a recursive finite set.

So we consider a function

$$ \begin{align*}F(i,x,y,s)=\max\limits_{y'\leq y} |W_{g(i,x,y'),s}|,\end{align*} $$

the max value of sizes of $W_{g(i,x,y')}$ at stage s for all $y'\leq y$ . If $x\in A$ , then because for any y, $W_{g(i,x,y)}$ is finite, $F(i,x,y,s)\leq \max _{y'\leq y} |W_{g(i,x,y'),s}|$ and hence $\lim _s F(i,x,y,s)$ exists and is finite; if $x\notin A$ , then there exists $y_0$ such that $|W_{g(i,x,y_0)}|=\infty $ and $\lim _s |W_{g(i,x,y_0),s}|=\infty $ , so for any $y\geq y_0$ , $\lim _s F(i,x,y,s)=\infty $ . We collect these observations in the following lemma:

Lemma 3.2. There exists a total recursive function $F(i,x,y,s)$ such that:

1. 1. The function $F(i,x,y,s)$ is non-decreasing with respect to y and s separately. Therefore for any $i,x$ and y, the limit $\lim _s F(i,x,y,s)$ is defined $($ can be infinite $)$ and this limit is non-decreasing with respect to y.

2. 2. For each i, let $A_i=\{x:\forall y\ \lim _s F(i,x,y,s)\text { is finite}\}$ . Then $A_i$ is a $\Pi _3^0$ set. Moreover, $A_i^c=\{x:\exists y_0 \forall y>y_0\ \lim _s F(i,x,y,s)\text { is infinite}\}$

3. 3. For any $\Pi _3^0$ set A, there exists i such that $A=A_i$ , where $A_i$ is defined as in 2.

Therefore, the function $F(i,x,y,s)$ defines a list $\langle A_i\rangle _{i\in \mathbb {N}}$ of $\Pi ^0_3$ sets that includes all $\Pi _3^0$ sets (finite and infinite, with apartness and without apartness).

3.2. Strategy

As in the $\Delta _3^0$ section, to define the recursive coloring function c, we will construct a recursive function $R(n,w)$ and apply Lemma 3.1. Similar to the $\Delta _3^0$ section, function $R(n,w)$ must satisfy the condition that, for any infinite $\Pi _3^0$ set $A_i$ with weak apartness in the list, there exists $w\in FS(A_i)$ and $n< \lambda (w)$ such that $R(n,w)\in A_i$ . Constructing such a function $R(n,w)$ is the key part of this strategy.

In the construction of the $\Delta _3^0$ section, for each n, we guess and choose a specific set $A_i$ such that $A_i\cap B^n\neq \emptyset $ by a priority argument. We then try to construct a function $R(n,w)$ such that for sufficiently many w, $R(n,w)$ is an element in $A_i$ .

In the $\Pi _3^0$ section, we will use a modified strategy. In this construction, for a fixed n, we guess and choose a specific set $A_i$ such that $A_i\cap B^n\neq \emptyset $ by a priority argument, and aim to make it so that the value of $R(n,w)$ can be any number in $B^n$ when w goes through the set $FS(A_i)$ . If so, there exists a number $w\in FS(A_i)$ such that $R(n,w)\in A_i$ .

In other words, for a fixed n, we can regard $R(n,\cdot )$ as a coloring function sending $w\in \mathbb {N}$ to a number $R(n,w)\in B^n$ , one of $|B^n|$ many colors. Our aim is to let $FS(A_i)$ includes all colors under the coloring function $R(n,\cdot )$ . We can use Corollary 1 to do this.

For each fixed n, to construct such a function $R(n,\cdot )$ , we construct a recursive function $Q_n(y,k,s):D\subseteq \mathbb {N}^3\rightarrow \mathbb {N}$ such that $Q_n(y,k,s)\in B^y$ . Later we will apply Corollary 1 to $Q_n(y,k,s)$ and $r=|B^n|$ to get our desired function $R(n,\cdot )$ . The construction of $Q_n(y,k,s)$ depends on the choice of set $A_i$ . If we choose a set $A_i$ , then our aim is ensure that for sufficiently many sufficiently large $y,k,s$ , $Q_n(y,k,s)$ is in $A_i$ .

In this way, we can find sufficiently many sufficiently large $w\in A_i$ such that $w=Q_n(y,k,s)$ for some $y,k,s$ . Moreover, we can find an arbitrarily long sequence of such w:

$$ \begin{align*}w_1\ll w_2\ll\dots\ll w_k\ll w_{k+1}\ll\dots\ll w_L\end{align*} $$

all in $A_i$ and (because of Corollary 1) for any $1\leq k<L$

$$ \begin{align*} R(n,w_k+w_{k+1}+\cdots+w_L)\equiv R(n,w_{k+1}+\dots+w_L)+1\quad \mod r. \end{align*} $$

Therefore, for each k, $R(n,w_k+\dots +w_L)$ has a distinct value. If we choose $L>r=|B^n|$ , then for every number $x\in B^n$ , we can find $k'$ such that

$$ \begin{align*}R(n,w_{k'}+\dots+w_L)=x.\end{align*} $$

3.3. Preparation for the construction

We need to guess two things: whether $B^n\cap A_i$ is empty or not and if $B^n\cap A_i$ is nonempty, which element is in $B^n\cap A_i$ .

First, we guess which element is in $B^n\cap A_i$ if assuming it is nonempty. If $x\in B^n\cap A_i$ , then for any y, $\lim _s F(i,x,y,s)$ is finite, and if $x\in B^n$ but $x\notin A_i$ , then for almost all y, $\lim _s F(i,x,y,s)$ is infinite. So we define the guessing function $x(i,n,y,s)$ to be the element $x\in B^n$ with minimal $F(i,x,y,s)$ value:

$$ \begin{align*}x(i,n,y,s)=\min\{x\in B^n:\forall x'\in B^n\ F(i,x,y,s)\leq F(i,x',y,s)\}.\end{align*} $$

Here the $\min $ function means that if more than one element x in $B^n\cap A_i$ have the minimal $F(i,x,y,s)$ value, then we choose the least one. Because $F(i,x,y,s)$ is a total recursive function, $x(i,n,y,s)$ is also a total recursive function.

Lemma 3.3 (Guessing a single set).

Let n be a natural number and $A_i$ be an infinite $\Pi _3^0$ set with weak apartness in the list of Lemma 3.2 such that $A_i\cap B^{n}$ is nonempty, then $\lim _{y}\lim _s x(i,n,y,s)$ exists and equals the unique element in $A_i\cap B^n$ .

Proof Since $A_i\cap B^n\neq \emptyset $ , we choose a number $x_0\in A_i\cap B^n$ . Because $A_i$ has weak apartness, $x_0$ is the unique element in $B^n\cap A_i$ and $B^n\setminus A_i=B^n\setminus \{x_0\}$ . So for any $x\in B^n\setminus \{x_0\}$ , there exists $y_x$ such that $\lim _s F(i,x,y,s)=\infty $ for any $y>y_x$ . Let $y_0=\max \{y_x:x\in B^n\setminus \{x_0\}\}$ .

For any $y>y_0$ , there exists a number $k_y$ such that $\lim _s F(i,x_0,y,s)=k_y$ . And for each $x\in B^n\setminus \{x_0\}$ , $ \lim _sF(i,x,y,s)$ is infinite. So for any $y>y_0$ , for any sufficiently large number s, $x(i,n,y,s)=x_0$ .

Next we define a function to guess whether $A_i\cap B^n$ is empty or not.

Lemma 3.4. For every set $A_i$ in the list of Lemma 3.2, let

$$ \begin{align*} B(i,n,y,s)=\min\{F(i,x,y,s):x\in B^n\}. \end{align*} $$

Then if $A_i\cap B^n$ is nonempty, then $\forall y \lim _s B(i,n,y,s)<\infty $ ; and if $A_i\cap B^n$ is empty, then $\exists y_0\forall y>y_0 \lim _s B(i,n,y,s)=\infty $ .

Proof By Lemma 3.2 and property of limit.

We use the function $B(i,n,y,s)$ to guess whether $A_i\cap B^n$ is empty or not. Specifically, for a given number k, if $B(i,n,y,s)<k$ , we guess the $A_i\cap B^n$ is nonempty at “stage” k and s.

3.4. Construction

The construction consists of two parts:

Part 1: First, we define a function $I(n,y,k,s)$ which indicates the index of the choice $A_i$ as mentioned earlier and is a recursive function with recursive domain. For numbers $n<y\leq k\leq s$ , if for all $m<n$ , $I(m,y,k,s)$ is defined, then

$$ \begin{align*}I(n,y,k,s)=\min(\{i<n: B(i,n,y,s)<k \wedge \forall m<n (I(m,y,k,s)\neq i)\}\cup\{\infty\}).\end{align*} $$

Part 2: Define $Q_n(y,k,s)$ : if $I(n,y,k,s)\neq \infty $ , let $j=I(n,y,k,s)$ , and let

$$ \begin{align*}Q_n(y,k,s)=x(j,y,k,s);\end{align*} $$

otherwise let $Q_n(y,k,s)=2^{y}$ .

For each n, the function $Q_n(y,k,s)$ is recursive with a recursive domain. We can apply Corollary 1 to $Q_n(y,k,s)$ and $r=|B^n|$ to obtain a function $R_0(n,\cdot )$ with range $\{0,\dots ,r-1\}$ . Because $R(n,w)$ has a range $B^n$ , we define $R(n,w)$ to be the $R_0(n,w)$ th number in $B^n$ .

The sequence $\langle Q_n(y,k,s)\rangle _{n\in \mathbb {N}}$ is a recursive sequence. Because the function in Corollary 1 is uniformly recursive in $Q_n(y,k,s)$ , $\langle R(n,\cdot )\rangle _{n\in \mathbb {N}}$ is a recursive sequence and the function $R(n,w)$ is recursive.

3.5. Verification, part 1

In this subsection, we will show that for any infinite $\Pi _3^0$ set $A_i$ (with or without weak apartness) in the list of Lemma 3.2, there exists n such that $\lim _y\lim _k\lim _s I(n,y,k,s)=i$ .

Lemma 3.5. For any n, $\lim _y\lim _k\lim _s I(n,y,k,s)$ is defined. Moreover, if we let

$$ \begin{align*}I(n)=\lim_y\lim_k\lim_s I(n,y,k,s),\end{align*} $$

$$ \begin{align*}H(n)=\{i<n:\exists m<n, I(m)=i\},\end{align*} $$

and

$$ \begin{align*}Z(n)=\{i<n: \exists x\in B^n\ x\in A_i\},\end{align*} $$

then for any n,

$$ \begin{align*}I(n)=\min (Z(n)\setminus H(n)\cup\{\infty\}).\end{align*} $$

Proof We prove this lemma by induction on n. For a number n, we assume that for any $m<n$ , $I(m)$ is defined and $I(m)=\min (Z(m)\setminus H(m)\cup \{\infty \})$ .

By definition, for each $y,k,s$ ,

$$ \begin{align*}I(n,y,k,s)=\min(\{i<n:B(i,n,y,s)<k \wedge \forall m<n\ (I(m,y,k,s)\neq i)\}\cup\{\infty\}).\end{align*} $$

Consider the following set in above definition:

$$ \begin{align*}\{i<n:B(i,n,y,s)<k\wedge\forall m<n( I(m,y,k,s)\neq i)\},\end{align*} $$

which is the set $\{i<n:B(i,n,y,s)<k\}$ minus $\{i<n:\exists m<n\ I(m,y,k,s)=i\}$ . We claim that

(3.1) $$ \begin{align} \lim_y\lim_k\lim_s \{i<n:B(i,n,y,s)<k\}=Z(n) \end{align} $$

and

(3.2) $$ \begin{align} \lim_y\lim_k\lim_s \{i<n:\exists m<n\ I(m,y,k,s)=i\}=H(n). \end{align} $$

To prove equation (2.2.1), we use the definition of $Z(n)$ and $B(i,n,y,s)$ . By Lemma 3.4 and property of limit, there exists $y_1$ such that for any $y>y_1$ and any k, there exists $s_{y,k}$ such that for any $s>s_{y,k}$ and any $i\in n\setminus Z(n)$ , $B(i,n,y,s)>k$ . Similarly, for any y there exists $k_y$ such that for any s and any $i\in Z(n)$ , $B(i,n,y,s)<k_y$ . Hence:

$$ \begin{align*} \lim_y\lim_k\lim_s \{i<n:B(i,n,y,s)<k\}&\subseteq Z(n)\\ \lim_y\lim_k\lim_s \{i<n:B(i,n,y,s)<k\}&\supseteq Z(n). \end{align*} $$

Equation (2.2.1) is true.

We now prove equation (2.2.2). By the Induction Hypothesis, for any $m<n$ , $I(m)$ is defined. Using property of limit, we can find $y_0$ such that for any $y>y_0$ , there exists $k_y$ such that any $k>k_y$ , there exists $s_{y,k}$ such that for any $s>s_{y,k}$ and any $m<n$ , $I(m,y,k,s)=I(m)$ . Thus, for those $y,k,s$ , we have that

$$ \begin{align*}\{i<n:\exists m<n\ I(m,y,k,s)=i\}=\{i<n:\exists m<n\ I(m)=i\}.\end{align*} $$

The right-hand side of this equation is equal to $H(n)$ . Therefore, we conclude that $\lim _y\lim _k\lim _s \{i<n:\exists m<n,I(m,y,k,s)=i\}=H(n)$ .

Since equations (2.2.1) and (2.2.2) hold, by the properties of the limit operation,

$$ \begin{align*} &I(n)=\lim_y\lim_k\lim_s\ I(n,y,k,s)\\ =&\lim_y\lim_k\lim_s\ \min(\{i<n:B(i,n,y,s)<k \wedge \forall m<n (I(m,y,k,s)\neq i)\}\cup\{\infty\})\\ =&\lim_y\lim_k\lim_s\ \min(\{i<n:B(i,n,y,s)<k\}\setminus\{i<n:\exists m<n(I(m,y,k,s)=i)\}\cup\{\infty\})\\ =&\min(Z(n)\setminus H(n)\cup\{\infty\}). \end{align*} $$

This concludes the proof.

Lemma 3.6. For any infinite $\Pi _3^0$ set $A_i$ in the list of Lemma 3.2, there exists n such that $I(n)=i$ .

Proof We prove this lemma by induction on i. For each i, if $A_i$ is infinite, there exist infinitely many n such that $A_i\cap B^n\neq \emptyset $ . For any $j<i$ , if $A_j$ is finite, there exists $n_j$ such that for any $n>n_j$ , $A_j\cap B^n=\emptyset $ ; and for any $j<i$ , if $A_j$ is infinite, by induction hypothesis, there exists $n_j$ such that $I(n_j)=j$ . So we choose a number N sufficiently large such that $A_i\cap B^N$ is nonempty and for any $j<i$ , either $A_j\cap B^N=\emptyset $ or $\exists m<N, I(m)=j$ .

If there exists $n<N$ such that $I(n)=i$ , the we are done. Otherwise by the definition of $H(N)$ , we have $i\notin H(N)$ ; since $B^n\cap A_i\neq \emptyset $ , we have $i\in Z(N)$ . Therefore $i\in Z(N)\setminus H(N)$ . For any $j<i$ , if $A_j$ is finite, then $A_j\cap B^N=\emptyset $ , and $j\notin Z(N)$ ; if $A_j$ is infinite, then $\exists m<N, I(m)=j$ and hence $j\in H(N)$ . Thus for any $j<i$ , we have $j\notin Z(N)\setminus H(N)$ . Therefore $i=\min (Z(N)\setminus H(N)\cup \{\infty \})$ and by Lemma 3.5, $I(N)=i$ .

Therefore, there exists $n\leq N$ such that $I(n)=i$ .

3.6. Verification: part 2

In this subsection, we will finish the verification.

Lemma 3.7. Let $A_i$ be an infinite $\Pi _3^0$ set with weak apartness and n be a number such that $I(n)=i$ . Then for any $r>1$ and Y, there exists a sequence

$$ \begin{align*}x_1\ll x_2\ll\cdots\ll x_r\end{align*} $$

all in $A_i$ such that:

(1) $\lambda (x_1)>Y$ .

(2) For any $g\in (0,r)$ , $\lim _sQ_n(\mu (x_{g}),\lambda (x_{g+1}),s)=x_{g}.$

Proof Because $I(n)=i$ , $\lim _y\lim _k\lim _s I(n,y,k,s)=i$ . We will prove this lemma by induction on r.

Because $I(n)=i$ and $A_i$ has weak apartness, by Lemma 3.3, there exists $Y_0$ such that for any $Y_1>Y_0$ , $\lim _k\lim _s I(n,Y_1,k,s)=i$ and if $B^{Y_1}\cap A_i$ is nonempty, then $B^{Y_1}\cap A_i$ contains exactly one element and $\lim _{k}\lim _s x(i,{Y_1},k,s)\in A_i$ . Because $\lim _k\lim _s I(n,Y_1,k,s)=i$ , $\lim _{k}\lim _s Q_n(Y_1,k,s)=\lim _{k}\lim _s x(i,Y_1,k,s)$ is defined and equal to the unique element $x\in A_i\cap B^{Y_1}$ . Without loss of generality, we assume that $Y>Y_0$ .

For the case $r=2$ : in this case, g can only be $1$ . We choose $x_1\in A_i$ such that $\lambda (x_1)>Y$ . Since $ A_i\cap B^{\mu (x_1)}$ contains $x_1$ , it is nonempty, and thus

$$ \begin{align*}\lim_k\lim_s Q_n(\mu(x_1),k,s)=x_1.\end{align*} $$

Then we choose $k_0$ such that for any $k>k_0$ , $\lim _s Q_n(\mu (x_1),k,s)=x_1$ , and choose a number $x_2\gg x_1$ in $A_i$ such that $\lambda (x_2)>k_0$ . Then lim_s Q _n (μ(x ₁), λ(x ₂), s) = x ₁. It follows that two numbers $x_2\gg x_1$ satisfy our requirements.

Suppose we have proved case $r\geq 2$ , by the Induction Hypothesis, for Y and r, there exists a sequence $x_1\ll \cdots \ll x_r$ that satisfies the lemma for $Y,r$ :

$$ \begin{align*}\forall g\in(0,r), \lim_sQ_n(\mu(x_{g}),\lambda(x_{g+1}),s)=x_{g},\end{align*} $$

and $\lambda (x_1)>Y$ . We need to find $x_{r+1}$ such that $\lim _s Q_n(\mu (x_r),\lambda (x_{r+1}),s)=x_r$ . Since $B^{\mu (x_r)}\cap A_i$ is nonempty, $\lim _{k}\lim _s Q_n(\mu (x_r),k,s)=x_r$ ; therefore we only need to choose $x_{r+1}$ such that $\lambda (x_{r+1})$ is sufficiently large. Choose a sufficiently large $x_{r+1}\gg x_{r}$ in $A_i$ such that $\lim _s Q_n(\mu (x_r),\lambda (x_{r+1}),s)=x_r$ . The sequence $x_1\ll x_2\cdots \ll x_{r+1}$ satisfies this lemma.

Lemma 3.8. Let $A_i$ be an infinite $\Pi _3^0$ set with weak apartness, n be a natural number such that $I(n)=i$ and $R(n,w)$ be the function in our construction. For any $r>1$ , there exist r different numbers $w_h, 0< h\leq r$ in $FS(A_i)$ such that:

(1) each $w_h$ is sum of finitely many numbers x in $A_i$ such that $\lambda (x)>n$ ;

(2) for any two different $w_{h_1}$ and $w_{h_2}$ , $R(n,w_{h_1})\neq R(n,w_{h_2})$ .

Proof By Lemma 3.7, there exists a sequence $x_1\ll x_2\ll \cdots \ll x_r$ such that $\lambda (x_1)>n$ and

$$ \begin{align*}\forall g\in(0,r), \lim_sQ_n(\mu(x_{g}),\lambda(x_{g+1}),s)=x_{g}.\end{align*} $$

Choose a sufficiently large $x_{r+1}\in A_i$ such that $x_{r+1}\gg x_r$ and

$$ \begin{align*}\forall g\in(0,r), Q_n(\mu(x_{g}),\lambda(x_{g+1}),\mu(x_{r+1}))=x_{g}.\end{align*} $$

For $ h\in (0,r]$ , let $w_h=\sum _{g=h}^{r+1}x_g$ . This is a sum of finitely many numbers $x_g$ in $A_i$ such that $\lambda (x_g)>n$ . We show that for $0< h_2<h_1\leq r$ , $R(n,w_{h_1})\neq R(n,w_{h_2})$ . For each $w_h$ , $\mu (w_h)=\mu (x_{r+1})$ and $\lambda (w_h)=\lambda (x_h)$ . So by Lemma 3.7 and our assumption, $Q_n(\mu (x_{h}),\lambda (w_{h+1}),\mu (w_{h+1}))=x_{h}$ . Then by the construction and Corollary 1:

$$ \begin{align*} R_0(n,w_{h+1})+1&\equiv R_0(n,Q_n(\mu(x_{h}),\lambda(w_{h+1}),\mu(w_{h+1}))+w_{h+1})\quad \mod r\\ &\equiv R_0(n,x_{h}+w_{h+1})\quad \mod r\\ &\equiv R_0(n,w_{h})\quad \mod r. \end{align*} $$

So, $R_0(n,w_{h_1})\equiv R_0(n,w_{h_2})-(h_1-h_2)\ \mod r$ and each $w_h$ has a distinct $R(n,w_h)$ value.

Lemma 3.9. Let $A_i$ be an infinite $\Pi _3^0$ set with weak apartness in the list of Lemma 3.2 and $R(n,w)$ be the function in our construction. There exists n, $x\in B^n\cap A_i$ and $w\in FS(A_i)$ such that $\lambda (w)>n$ , $x+w\in FS(A_i)$ and

$$ \begin{align*} R(n,w)=x. \end{align*} $$

Proof By Lemma 3.6, there exists n such that $I(n)=i$ and by Lemma 3.8, for $r=|B^n|$ , there exist numbers $w_h,1\leq h\leq r$ all in $FS(A_i)$ such that each $w_h$ is a sum of finitely many numbers $x'\in A_i$ such that $\lambda (x')>n$ (hence $x+w_h\in FS(A_i)$ for any $x\in B^n$ ), and each $w_h$ has a distinct $R(n,w_h)$ value. Because $R(n,w_h)\in B^n$ for any such $w_h$ , for any $x\in B^n$ , there exists one $w_h$ such that $R(n,w_h)=x$ .

By Lemma 3.5, $i=I(n)=\min \{Z(n)\setminus H(n)\cup \{\infty \}\}.$ Because i is a number rather than $\infty $ , $i\in Z(n)=\{i<n:A_i\cap B^n\neq \emptyset \}$ . Hence $A_i\cap B^n\neq \emptyset $ .

Therefore we can find $x\in B^n\cap A_i$ and $w_h$ such that $R(n,w_h)=x$ and these $n,w_h,x$ are what we need.

Theorem 3.10. There exists a recursive coloring function $c:\mathbb {N}\rightarrow 2$ such that for any infinite $\Pi _3^0$ set A with weak apartness, there exist $w_1,w_2\in FS(A)$ such that $c(w_1)\neq c(w_2)$ .

Proof Use the function $R(n,w)$ in our construction and apply Corollary 1 to $R(n,w)$ to get a coloring function c. We show that c is what we need.

Because any infinite $\Pi _3^0$ set A with weak apartness is equal to a set $A_i$ in the list of Lemma 3.2, by Lemma 3.9, there exists numbers $n,x,w$ such that $x\in B^n\cap A_i$ , $w\in FS(A_i)$ , $\lambda (w)>n$ , $x+w\in FS(A_i)$ and $R(n,w)=x$ . By Corollary 1, $c(w)\neq c(w+R(n,w))$ if $n<\lambda (w)$ . So, $c(w)\neq c(w+x)$ . Because $\lambda (w)>n=\mu (x)$ , both w and $w+x$ are in $FS(A_i)$ . Two numbers $w,w+x$ are both in $FS(A_i)$ , and hence $c(w)\neq c(w+x)$ . This concludes the proof.

4. Unsolvabilities without apartness

In this section, we will prove $\Pi _3^0$ unsolvability for $\mathrm {HT}$ without weak apartness. We use the idea of getting rid of apartness/weak apartness from paper by Dzhafarov et al. [6], and also in Lemma 2.7 from the paper by Carlucci et al. [5]. While $\Delta _3^0$ unsolvability without apartness can be directly proved using results in the paper Carlucci et al. [5], for $\Pi _3^0$ unsolvability, we need to write more details because $A\leq _T B$ and B is $\Pi _3^0$ do not imply that A is also $\Pi _3^0$ .

Lemma 4.1. There exists a recursive coloring function $c_0:\mathbb {N}\rightarrow \{0,1\}^2$ such that for any infinite set A, if it does not have weak apartness, then it is not a solution to c for $\mathrm {HT}^{\leq 2}$ .

Proof We define two coloring functions $c_1,c_2:\mathbb {N}\rightarrow \{0,1\}$ :

$$ \begin{align*} c_1(x) \equiv \mu(x)\quad \mod 2;\\ c_2(x) \equiv \lambda(x)\quad \mod 2. \end{align*} $$

We show that for $c_0=c_1\times c_2$ , if an infinite set A does not have weak apartness, then it is not monochromatic under $c_0$ . If A has not weak apartness, there are two cases.

The first case is that, there are two numbers $x_1,x_2$ such that $\mu (x_1)=\mu (x_2)=m$ . This means these two numbers are in the interval $[2^m,2^{m+1})$ . Thus $\mu (x_1+x_2)=m+1$ , and $c_1(x_1)\neq c_1(x_1+x_2)$ . Therefore, $FS^{\leq 2}(A)$ is not monochromatic.

The second case is that, there are three number $x_1,x_2,x_3$ such that $\lambda (x_1)=\lambda (x_2)=\lambda (x_3)=l$ . In this case, all three numbers are divisible by $2^l$ and not by $2^{l+1}$ . So for any X among these three numbers, $X\equiv 2^l \text { or }2^{l+1}+2^l\ \mod 2^{l+2}$ and there must be two number $X_1,X_2$ among $x_1,x_2,x_3$ such that $X_1\equiv X_2\ \mod 2^{l+2}$ . Hence $X_1+X_2$ is divisible by $2^{l+1}$ but not $2^{l+2}$ and $\lambda (X_1+X_2)=l+1$ . Since $\lambda (x_1)=l$ , $c_2(X_1+X_2)\neq c_2(x_1)$ and $FS^{\leq 2}(A)$ is not monochromatic.

In each case, $FS^{\leq 2}(A)$ is not monochromatic. Therefore, if A does not have weak apartness, then it is not a solution to $c_0=c_1\times c_2$ .

Using Lemma 4.1, we can prove our theorem.

Theorem 4.2. There exists a recursive coloring function $c:\mathbb {N}\rightarrow \{0,1\}^3$ such that any infinite $\Pi _3^0$ set A is not a solution to c for $\mathrm {HT}$ .

Proof By Theorem 3.10, there exists a recursive coloring $c_2:\mathbb {N}\rightarrow \{0,1\}$ such that any infinite $\Pi _3^0$ set with weak apartness is not a solution to $c_2$ for $\mathrm {HT}$ .

Let $c=c_2\times c_0$ where $c_0$ is the coloring function in Lemma 4.1. We claim that this coloring function is what we want.

For any infinite $\Pi ^0_3$ set A, if it has weak apartness, then it is not a solution to $c_2$ for $\mathrm {HT}$ ; if it does not have weak apartness, then it is not a solution to $c_0$ for $\mathrm {HT}^{\leq 2}$ (and hence $\mathrm {HT}$ ). So in either case, A is not a solution to $c=c_2\times c_0$ for $\mathrm {HT}$ .

5. $\Pi _3^0$ -unsolvability with four colors

In this section, we will prove the $\Pi ^0_3$ -unsolvability with only four colors, i.e., the following theorem:

Theorem 5.1. There exists a recursive coloring function $c:\mathbb {N}\rightarrow \{0,1\}^2$ such that any infinite $\Pi _3^0$ set A is not a solution to c for $\mathrm {HT}$ .

This theorem is an improvement of 4.2 because the number of colors also matters in reverse mathematics investigations on Hindman’s theorem. For example, $\mathrm {HT}^{\leq 2}_4$ implies $\mathrm {ACA}_0$ , but for $\mathrm {HT}^{\leq 2}_2$ it is unknown, see [5].

Recall that, the definition of weak apartness has two properties, and each one requires a $\times 2$ factor for the number of colors of the final coloring function. However, one property is not necessary to prove $\Pi ^0_3$ -unsolvability. We can use the following even weaker notion of apartness:

Definition 5.2. (1) An infinite set A has weak–weak-apartness if for any number L, there are only finitely many x such that $\lambda (x)\leq L$ .

(2) For an infinite set A with weak–weak-apartness, we define a function $p_A$ from $\mathbb {N}$ to $\mathbb {N}$ : $p_A(m)$ is the least value $\lambda (w)$ when $\mu (w)\geq m$ .

Lemma 5.3. Let A be an infinite set with weak–weak-apartness, then:

(1) For any number L, there exists M such that for any $x>M$ in A, $\lambda (x)>L$ . And similarly, there exists M such that for any x, if $\mu (x)>M$ , then $\lambda (x)>L$ ; then we define a function $b_A(L)$ to be the least such M.

(2) $p_A$ is well-defined and $\lim _m p_A(m)=\infty $ .

Proof Both parts are quite obvious.

(1) By definition, there are only finitely many x in A that $\lambda (x)\leq L$ . If there does not exist such x, then let $M=0$ and any x has that $\lambda (x)>L$ . If there exists at least one such x, we choose the largest number x and let $M=x$ , then for any $x>M$ in A, not $\lambda (x)\leq L$ and hence $\lambda (x)>L$ . Similarly, we choose the largest $\mu (x)$ and let $M=\mu (x)$ , then for any x in A such that $\mu (x)>M$ , we have $\lambda (x)>L$ .

(2) The reason $p_A$ is well-defined is simply because A is infinite. This implies that for any m, there exists $x\in A$ such that $\mu (x)\geq m$ . Thus, we can conclude that the least value of $\lambda (w)$ exists.

$\lim _m p_A(m)=\infty $ because for any L, by (1), there exists M such that for any $x>M$ in A, $\lambda (x)>L$ . So for any x in A, if $\mu (x)>M+1$ , because $\mu (x)\leq x-1$ , we have that $\lambda (x)>L$ and hence $p_A(M+1)>L$ . So $\lim _m p_A(m)=\infty $ .

We will show that the construction of Section 2.2 also kills all infinite $\Pi _3^0$ sets with weak–weak-apartness without any other modification. This is because the construction, definitions in verification part 1, and Lemma 3.6 all do not rely on apartness or weak-apartness. So we only need to modify and prove the conclusions in verification part 2 of Section 2.2.

For convenience, in this section, if $f(s)$ is a function with finite range and A is a set, then $\lim _s f(s)\in A$ means that there exists a number S such that for any $s>S$ , $f(s)\in A$ . We will use this expression frequently. In this case, it is possible that $\lim _s f(s)$ does not exist. We introduce a generalization of Lemma 3.3.

Lemma 5.4 (Guessing a single set).

Let n be a natural number and $A_i$ be an infinite $\Pi _3^0$ set in the list of Lemma 3.2 such that $A_i\cap B^{n}$ is nonempty, then $\lim _{y}\lim _s x(i,n,y,s)\in A_i$ .

Proof Since $A_i\cap B^n\neq \emptyset $ , we choose a number $x_0\in A_i\cap B^n$ . For any $x\in B^n\setminus A_i$ , there exists $y_x$ such that $\lim _s F(i,x,y,s)=\infty $ for any $y>y_x$ . Let $y_0=\max \{y_x:x\in B^n\setminus A_i\}$ .

For any $y>y_0$ , there exists a number $k_y$ such that $\lim _s F(i,x_0,y,s)=k_y$ . And for each $x\in B^n\setminus A_i$ , $ \lim _sF(i,x,y,s)$ is infinite. So for any $y>y_0$ , for any sufficiently large number s, $x(i,n,y,s)\in A_i$ .

Lemma 5.5. Let $A_i$ be an infinite $\Pi _3^0$ set in the list with weak–weak-apartness, and n be an number such that $I(n)=i$ . Then for any $r>1$ and any Y, there exists a sequence $m_1<\cdots <m_g\cdots <m_r$ such that:

(1) For any $g\in (0,r]$ , $B^{m_g}\cap A_i\neq \emptyset $ .

(2) $p_{A_i}(m_1)>Y$ and for any $g\in (0,r)$ , $p_{A_{i}}(m_{g+1})>m_g$ .

(3) For any $g\in (0,r)$ and any $l\in [p_{A_i}(m_{g+1}),m_{g+1}]$ ,

$$ \begin{align*}\lim_s\ Q_n(m_{g},l,s)\in A_i.\end{align*} $$

Proof This proof is similar to Lemma 3.7 but more complex. By Lemma 5.4, for any sufficiently large M such that $B^M\cap A_i$ is nonempty,

$$ \begin{align*}\lim_{k}\lim_s x(i,M,k,s)\in A_i,\end{align*} $$

where the limit may not exist. And because $\lim _k\lim _s I(n,M,k,s)=i$ , we have that

$$ \begin{align*}\lim_{k}\lim_s Q_n(M,k,s)\in A_i\cap B^M\end{align*} $$

for any sufficiently large M. Based on this, we prove the lemma by induction on r.

For $r=2$ : In this case, g can only be $1$ . Let Y be given, and without loss of generality, we assume that Y is sufficiently large:

$$ \begin{align*} \forall M>Y (B^M\cap A_i\neq\emptyset\rightarrow\lim_{k}\lim_s Q_n(M,k,s)\in A_i\cap B^M). \end{align*} $$

By Lemma 5.3, we choose a number $m_1$ such that $p_{A_{i}}(m_1)>Y$ , and $ A_i\cap B^{m_1}$ is nonempty. Hence

$$ \begin{align*}\lim_k\lim_s Q_n(m_1,k,s)\in A_i.\end{align*} $$

Then we choose a number $k_0$ such that

$$ \begin{align*}\forall k>k_0\ \lim_s Q_n(m_1,k,s)\in A_i,\end{align*} $$

and a number $m_2$ such that $ A_i\cap B^{m_2}$ is nonempty and $p_{A_{i}}(m_2)>m_1,k_0$ . Then lim_s Q _n (m ₁, l, s) ∈ A _i for any l in $[p_{A_i}(m_2),m_2]$ . This sequence $m_1<m_2$ satisfies our requirements.

For $r+1$ when $r\geq 2$ : Again, let Y be the given number that is sufficiently large. Applying the Induction Hypothesis for r and Y, there exists a sequence $m_1<\cdots <m_r$ such that:

(1) for any $g\in (0,r]$ , $B^{m_g}\cap A_i\neq \emptyset $ ;

(2) $p_{A_i}(m_1)>Y$ and for any $g\in (0,r)$ , $p_{A_{i}}(m_{g+1})>m_g$ ;

(3) for any $g\in (0,r)$ and any $l\in [p_{A_i}(m_{g+1}),m_{g+1}]$ ,

$$ \begin{align*}\lim_s\ Q_n(m_{g},l,s)\in A_i.\end{align*} $$

Because $A_i\cap B^{m_r}\neq \emptyset $ , $m_r>Y$ and Y is sufficiently large,

$$ \begin{align*}\lim_k\lim_s Q_n(m_{r},k,s)\in A_i.\end{align*} $$

So we choose a number $k_0$ such that for any $k>k_0, \lim _s Q_n(m_{r},k,s)\in A_i$ and choose a number $m_{r+1}$ such that $ A_i\cap B^{m_{r+1}}\neq \emptyset $ and $p_{A_{i}}(m_{r+1})>m_r,k_0$ . Then for any $l\in [p_{A_{i}}(m_{r+1}),m_{r+1}]$ ,

$$ \begin{align*}\lim_s Q_n(m_r,l,s)\in A_i.\end{align*} $$

We can see that this new the sequence $m_1<\cdots <m_r<m_{r+1}$ is what we want.

Lemma 5.6. Let $A_i$ be a infinite $\Pi _3^0$ set with weak–weak-apartness, and n be a number such that $I(n)=i$ . Then for any $r>1$ and any number Y, there exists a sequence $x_1\ll x_2\ll \cdots \ll x_r\ll x_{r+1}$ all in $A_i$ such that $\lambda (x_1)>Y$ and for any $g\in (0,r)$ ,

$$ \begin{align*}Q_n(\mu(x_{g}),\lambda(x_{g+1}),\mu(x_{r+1}))=x_{g}.\end{align*} $$

Proof First of all, by Lemma 5.5, for r and Y, choose a sequence $\langle m_g\rangle , g\in [1,r]$ satisfying those properties, especially, for any $g\in [1,r-1]$ ,

$$ \begin{align*} \forall l\in[p_{A_i}(m_{g+1}),m_{g+1}]\ \lim_s\ Q_n(m_{g},l,s)\in A_i. \end{align*} $$

So we choose a number $x_{r+1}\in A_i$ sufficiently large such that $\lambda (x_{r+1})>m_r$ and for any $g\in [1,r-1]$ ,

$$ \begin{align*} \forall l\in[p_{A_i}(m_{g+1}),m_{g+1}]\ Q_n(m_{g},l,\mu(x_{r+1}))\in A_i. \end{align*} $$

Then we choose a number $x_r\in A_i$ such that $\mu (x_r)=m_r$ .

Now we inductively construct the sequence $x_1\ll \cdots \ll x_r\ll x_{r+1}$ from $x_r$ to $x_1$ satisfying the requirements of this lemma and $\mu (x_h)=m_h$ for each $h\in [1,r]$ .

Suppose for a number $h\in [2,r]$ , we have constructed a sequence $x_h\ll \cdots \ll x_r\ll x_{r+1}$ satisfying our requirements, then by the properties of the sequence $\langle m_g\rangle _{g\in [1,r]}$ and because $p_{A_i}(m_{h})\leq \lambda (x_{h})\leq m_h$ , we have that

$$ \begin{align*}Q_n(m_{h-1},\lambda(x_{h}),\mu(x_{r+1}))\in A_i.\end{align*} $$

So we can choose a number $x_{h-1}\in B^{m_{h-1}}\cap A_i$ such that

$$ \begin{align*}Q_n(\mu(x_{h-1}),\lambda(x_{h}),\mu(x_{r+1}))=x_{h-1}.\end{align*} $$

We add $x_{h-1}$ to the sequence. We can see this new sequence satisfies our requirements. This finishes the induction step. Finally, we show that $\lambda (x_1)>Y$ . This is simply because $p_{A_i}(m_1)>Y$ and $x_1\in B^{m_1}$ . This finishes the proof of this lemma.

Lemma 5.7. Let $R(n,w)$ be the function in previous construction, $A_i$ be an infinite $\Pi _3^0$ set with weak–weak-apartness and n be a number such that $I(n)=i$ . Then, for $r=|B^n|$ , there exist r many numbers $w_j\in FS(A_i)$ , with $j\in [1,r]$ , such that each $w_h$ is sum of finitely many numbers x in $A_i$ such that $\lambda (x)>n$ and has a distinct $R(n,w_j)$ value.

Proof This proof is almost the same as the proof of Lemma 3.8.

Apply Lemma 5.6 for $Y=n$ and r, there exists a sequence $\langle x_g\rangle $ with $g\in [1,r+1]$ such that $\lambda (x_1)>n$ and for any $h\in [2,r]$ ,

$$ \begin{align*} Q_n(\mu(x_{h-1}),\lambda(x_{h}),\mu(x_{r+1}))=x_{h-1}. \end{align*} $$

Now for $ h\in [1,r]$ , let $w_h=\sum _{g=h}^{r+1}x_g$ . It is obvious that $\lambda (w_h)>n$ for any $h\in [1,r]$ . We show that for $1\leq h_2<h_1\leq r$ ,

$$ \begin{align*}R(n,w_{h_1})\neq R(n,w_{h_2}).\end{align*} $$

For each $w_h$ , $\mu (w_h)=\mu (x_{r+1})$ and $\lambda (w_h)=\lambda (x_h)$ . So by our assumption, for $h\in [1,r]$

$$ \begin{align*} Q_n(\mu(x_{h-1}),\lambda(w_{h}),\mu(w_{h}))=x_{h-1}. \end{align*} $$

Then by the construction and Corollary 1, for $h\in [2,r]$

$$ \begin{align*} R_0(n,w_{h})+1&\equiv R_0(n,Q_n(\mu(x_{h-1}),\lambda(w_{h}),\mu(w_{h}))+w_{h})\quad \mod r\\ &\equiv R_0(n,x_{h-1}+w_{h})\quad \mod r\\ &\equiv R_0(n,w_{h-1})\quad \mod r. \end{align*} $$

So $R_0(n,w_{h_1})\equiv R_0(n,w_{h_2})-(h_1-h_2)\ \mod r$ and each $w_h$ has a distinct $R(n,w_h)$ value. This finishes the proof.

Lemma 5.8. Let $A_i$ be an infinite $\Pi _3^0$ set with weak–weak apartness in the list of Lemma 3.2 and $R(n,w)$ be the function in our construction. There exists n, $x\in B^n\cap A_i$ and $w\in FS(A_i)$ such that $x+w\in FS(A_i)n$ and

$$ \begin{align*} R(n,w)=x. \end{align*} $$

Proof This proof is very similar to the proof of Lemma 3.9.

By Lemma 3.6, there exists n such that $I(n)=i$ and by Lemma 5.7, for $r=|B^n|$ , there exist numbers $w_h,1\leq h\leq r$ all in $FS(A_i)$ such that each $w_h$ is sum of finitely many numbers x in $A_i$ such that $\lambda (x)>n$ , and each $w_h$ has a distinct $R(n,w_h)$ value. Because $R(n,w_h)\in B^n$ for any such $w_h$ , for any $x\in B^n$ , there exists one $w_h$ such that $R(n,w_h)=x$ .

By Lemma 3.5, $i=I(n)=\min \{Z(n)\setminus H(n)\cup \{\infty \}\}.$ Because i is a number rather than $\infty $ , $i\in Z(n)=\{i<n:A_i\cap B^n\neq \emptyset \}$ . Hence $A_i\cap B^n\neq \emptyset $ .

Therefore we can find $x\in B^n\cap A_i$ and $w_h$ such that $R(n,w_h)=x$ and these $n,w_h,x$ are what we need.

Theorem 5.9. There exists a recursive coloring function $c:\mathbb {N}\rightarrow \{0,1\}$ such that any infinite $\Pi _3^0$ set with weak–weak-apartness is not a solution of c for Hindman’s theorem.

Proof We show that the coloring function c in Section 2.2, Theorem 3.10 is a witness for this theorem. This is almost the same as the proof of Theorem 3.10. Use the function $R(n,w)$ in our construction and apply Corollary 1 to $R(n,w)$ to get a coloring function c. We show that c is what we need.

Because any infinite $\Pi _3^0$ set A is equal to a set $A_i$ in the list of Lemma 3.2, by Lemma 5.8, there exists numbers $n,x,w$ such that $x\in B^n\cap A_i$ , $w\in FS(A_i)$ , $\lambda (w)>n$ , $x+w\in FS(A_i)$ and $R(n,w)=x$ . By Corollary 1, $c(w)\neq c(w+R(n,w))$ if $n<\lambda (w)$ . So $c(w)\neq c(w+x)$ . Because $\lambda (w)>n=\mu (x)$ , both w and $w+x$ are in $FS(A_i)$ . Two numbers $w,w+x$ are both in $FS(A_i)$ and $c(w)\neq c(w+x)$ . This concludes the proof.

Lemma 5.10. There exists a recursive coloring function $c_0:\mathbb {N}\rightarrow \{0,1\}$ such that for any infinite set A, if it does not have weak–weak-apartness, then it is not a solution to c for $\mathrm {HT}^{\leq 2}$ .

Proof This proof is just a subset of the proof of Lemma 4.1.

We define a coloring function $c_0:\mathbb {N}\rightarrow \{0,1\}$ :

$$ \begin{align*} c_0(x) \equiv \lambda(x)\quad \mod 2. \end{align*} $$

We show that if an infinite set A does not have weak–weak-apartness, then it is not monochromatic under $c_0$ . If A has not weak–weak-apartness, then there are three different numbers $x_1,x_2,x_3$ such that $\lambda (x_1)=\lambda (x_2)=\lambda (x_3)=l$ ; otherwise there are at most $2L$ numbers x that satisfies $\lambda (x)\leq L$ , contradict to the assumption of weak–weak-apartness. All three numbers are divisible by $2^l$ and not by $2^{l+1}$ . So for any X among these three numbers, $X\equiv 2^l \text { or }2^{l+1}+2^l\ \mod 2^{l+2}$ and there must be two number $X_1,X_2$ among $x_1,x_2,x_3$ such that $X_1\equiv X_2\ \mod 2^{l+2}$ . Hence $X_1+X_2$ is divisible by $2^{l+1}$ but not $2^{l+2}$ and $\lambda (X_1+X_2)=l+1$ . Since $\lambda (x_1)=l$ , $c_2(X_1+X_2)\neq c_2(x_1)$ and $FS^{\leq 2}(A)$ is not monochromatic.

Therefore, if A does not have weak apartness, then it is not a solution to $c_0$ .

Now we can show the main theorem of this section.

Theorem 5.11. There exists a recursive coloring function $c:\mathbb {N}\rightarrow \{0,1\}^2$ such that any infinite $\Pi _3^0$ set is not a solution of c for Hindman’s theorem.

Proof From Lemmas 5.9 and 5.10, we can get recursive colorings $c_1,c_2$ such that any infinite $\Pi ^0_3$ set with weak–weak-apartness is not monochromatic for $c_1$ , and any infinite $\Pi ^0_3$ set without weak–weak-apartness is not monochromatic for $c_2$ .

Define the coloring $c=c_1\times c_2$ . We can easily see that any infinite $\Pi ^0_3$ set is not monochromatic for c. Hence, any infinite $\Pi _3^0$ set is not a solution of c for Hindman’s theorem.

6. Conclusion

We end with a few questions for further investigation. Some open questions are mentioned in [6] or [4]. In this paper, we proved the $\Pi _3^0$ -unsolvability of $\textrm {HT}$ . So the first question is about the $\Delta _4^0$ -unsolvability:

Question 6.1. Is there any recursive coloring without any $\Delta _4^0$ solution for Hindman’s theorem?

Similarly, in this paper, we proved the $\Delta _3^0$ -unsolvability of $\textrm {HT}^{\leq 3}$ . However, we have not been able to prove the same theorem for the $\Pi _3^0$ case so far. Therefore, we pose the following question:

Question 6.2. Is there any recursive coloring such that any infinite $\Pi _3^0$ sets is not a solution for $\textrm {HT}^{\leq 3}$ ?

It is known from the literature that the weakest restriction of Hindman’s theorem that codes the jump (as the full version does) is $\mathrm {HT}^{\leq 2}_4$ , the restriction to sums of at most two numbers [5]. So, a natural question is whether our result is also true of the restriction to sums of at most 2.

Question 6.3. Is there any recursive coloring such that any infinite $\Delta _3^0$ sets is not a solution for $\textrm {HT}^{\leq 2}$ ?

And similarly, we can ask the following questions:

Question 6.4. Is there any recursive 2-coloring such that any infinite $\Delta _3^0$ sets is not a solution for $\textrm {HT}^{\leq 3}$ ?

Question 6.5. Is there any recursive 2-coloring such that any infinite $\Pi _3^0$ sets is not a solution for Hindman’s theorem?

An end to all these types of questions is to find a coloring without any arithmetic solution. However, there is currently no mainstream consensus on whether Hindman’s theorem has arithmetical solutions. It is even possible that every coloring function has a $\Delta _4^0$ solution.