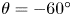Guiding-centre orbit-following simulations of charge exchange loss of NBI ions with the finite Larmor radius effect

Abstract

Guiding-centre orbit-following simulations of the charge exchange (CX) loss of neutral beam injection (NBI) ions are presented. The finite Larmor radius (FLR) effect in the fast ion–neutral collision can be included in guiding-centre orbit-following simulations by using the gyroaverage method. It is proved that the neutralization probability of fast ions computed by using the gyroaverage method in the guiding-centre orbit simulation is roughly the same as that computed in the full-orbit simulation when the time step in the guiding-centre simulation is the order of the gyroperiod. The CX losses of NBI fast ions for two NBIs in the EAST tokamak have been simulated by the guiding-centre orbit-following code GYCAVA, and the FLR effect in the fast ion–neutral collision on CX losses has been numerically studied. The CX effect of the fast ion–neutral collision can significantly enhance NBI ion losses on EAST. The FLR effect in the fast ion–neutral collision can enhance the CX loss. Vertical asymmetry of localized heat loads induced by CX losses is found, which is related to the FLR effect of fast ions and the strong radial gradient of the neutral density near the plasma edge. Heat loads induced by CX losses are localized in the regions near the poloidal angle $\theta =-60^\circ$, because the likelihood of exchanging charge is the largest at gyrophase $\xi ={\rm \pi}$, and this leads to fast downwards moving neutrals. Fast ion loss fractions induced by CX increase with the neutral density increasing.

1. Introduction

The confinement of fast ions is important in a magnetically confined plasma (Heidbrink & Sadler 1994; Jacquinot et al. 1999; Fasoli et al. 2007; Gorelenkov, Pinches & Toi 2014; Pinches et al. 2015). A major source of fast ions in a tokamak is neutral beam injection (NBI) which is used for heating the plasma and driving plasma rotation and current. The NBI fast ion losses can damage the plasma facing component surfaces of a tokamak and can reduce the NBI heating efficiency.

In this paper, we consider two kinds of collisions between fast ions and other particles. One is the Coulomb collision between fast ions and background charged particles. The other is the collision between fast ions and neutrals which are mainly located in the region outside the last closed flux surface (LCFS). Due to the magnetic drift effect and transport induced by collision or electromagnetic perturbations, fast ions in the plasma region can move across the LCFS and enter the gap between the LCFS and the first wall. While most of the fast ions will either re-enter the plasma or hit the first wall, it is possible that, due to the existence of neutrals in the gap, they also undergo charge exchange (CX) reactions. After CX reactions, fast ions become fast neutrals. They will hit the first wall or move back to the plasma region. The CX effect between fast ions and neutrals can impact fast ion losses. Fast neutrals re-entering a plasma will be reionized if fast neutrals collide with charged particles in a plasma. The reionization of fast neutrals also can impact fast ion losses. In the reionization, the CX reaction between fast neutrals and thermal ions is one of the basic atomic processes. Therefore, the CX effect on fast particle losses is related to the fast ion–neutral collision and the fast neutral–plasma collision, that is, the reionization collision.

In most of the previous orbit-following simulations of the fast ion behaviour, the CX effect on fast ion losses was not considered. The CX losses of NBI fast ions in tokamaks have been numerically studied by using guiding-centre orbit codes or full orbit codes. Effects of resonant magnetic perturbations and CX on the fast ion behaviour (McClements et al. 2018) in MAST (mega ampere spherical tokamak) have been simulated by the guiding-centre and full orbit code OMFC (Tani et al. 2016). The TRANSP (Goldston et al. 1981) code with its guiding-centre orbit-following module NUBEAM (Pankin et al. 2004a,b), has been used to compute CX losses of fast ions in MAST (Tournianski et al. 2005) and MAST-U (Ollus et al. 2022). The impact of CX on NBI ion losses has been simulated in MAST-U (Ollus et al. 2022) by using the ASCOT (Hirvijoki et al. 2014) code. The NBI ion losses induced by CX has also been simulated in COMPASS (Jaulmes, Westerhof & de Blank 2014) by using the full orbit code EBdyna (Jaulmes et al. 2021). These numerical results show that NBI fast ion losses due to the CX effect are important in a tokamak for a significant neutral density near the edge.

Hot spots induced by fast particles in EAST (experimental advanced superconducting tokamak) have been found to limit the improvement of the plasma performance (Li et al. 2018). The CX losses of NBI fast ions may produce hot spots in EAST. There are four NBIs in EAST. In order to reduce NBI fast ion losses, the original two counter-current NBIs were changed to cocurrent NBIs in the previous upgrade of the EAST tokamak. Now all NBIs in EAST are in the cocurrent direction. The CX losses of NBI ions have been simply analysed in EAST (Wang et al. 2016) by the TRANSP code with the NUBEAM module. It is necessary to investigate the CX effect on NBI ion losses in detail in EAST.

We have developed a guiding-centre orbit-following code GYCAVA (Xu et al. 2019) based on the gyrokinetic theory (Frieman & Chen 1982; Brizard & Hahm 2007) for investigating the behaviour of NBI ions (Xu et al. 2020; XU et al. 2021) in EAST and alpha particles (Xu et al. 2022) in CFETR in the presence of the electromagnetic perturbations. It is of interest to add the CX module in the GYCAVA code for studying CX losses of NBI ions in EAST.

In this paper, simulations of NBI fast ion loss with the CX effect in the EAST tokamak by using the guiding-centre code GYCAVA are presented. In order to study CX losses of fast ions, a neutral collision module related to deuterium has been added in the latest version of the GYCAVA code. The neutral collision module includes the CX collision between fast deuterium ions and deuterium neutrals, and the reionization collision between fast deuterium neutrals and background charged particles. In these two collisions related to neutrals, the CX effect is important. In order to investigate the finite Larmor radius (FLR) effect of fast ion–neutral collision on CX losses, the GYCAVA code used the gyroaverage method to treat this FLR effect in guiding-centre orbit simulations. For simplicity, the electromagnetic perturbations including the toroidal field ripple were not considered.

The structure of the paper is as follows. The unperturbed guiding-centre Hamilton equations and two kinds of collisions used in the orbit-following code GYCAVA are introduced in § 2. Collisions include the Coulomb collision between fast ions and background charged particles, and the neutral collision between fast particles and background particles. In the latter collision, the CX effect is dominant. Guiding-centre orbit-following simulations with the FLR effect of the fast ion–neutral collision based on the gyroaverage method is discussed. The simulation set-up is given in § 3. Numerical results of NBI fast ion losses in the presence of the CX effect on EAST computed by the GYCAVA code are presented in § 4. In § 5, a summary is given.

2. Guiding-centre Hamilton equations and collisions

2.1. Guiding-centre Hamilton equations

In order to study NBI ion losses with collision effects in EAST, we use the GYCAVA code for computing guiding-centre orbits of fast ions and simulating collisions of fast particles.

Guiding-centre orbits of NBI ions were computed by using the unperturbed guiding-centre Hamilton equations in cylindrical coordinates, which can be written as $Y^i=J^{ij}\partial _j H$ with $\boldsymbol {Y}=(R,Z,\phi,v_\parallel )$. The explicit form of the unperturbed guiding-centre equations of motion can be written as

(2.1)\begin{gather} \dot{R} = J^{RZ}\partial_Z H + J^{Rv_{{\parallel}}}\partial_{v_{{\parallel}}}H, \end{gather}

(2.2)\begin{gather}\dot{Z} = J^{ZR}\partial_R H + J^{Zv_{{\parallel}}}\partial_{v_{{\parallel}}}H, \end{gather}

(2.3)\begin{gather}\dot{\phi} = J^{\phi R}\partial_R H + J^{\phi Z}\partial_Z H + J^{\phi v_{{\parallel}}}\partial_{v_{{\parallel}}}H, \end{gather}

(2.4)\begin{gather}\dot{v}_{{\parallel} } = J^{v_{{\parallel}}R}\partial_R H + J^{v_{{\parallel}}Z}\partial_{Z}H. \end{gather}

Here, $H$ is the unperturbed guiding-centre Hamiltonian. The components of the Poisson matrix $J^{ij}$ can be obtained from the unperturbed guiding-centre equations of motion,

(2.5)\begin{gather} \dot{\boldsymbol{X}} = \frac{\boldsymbol{b}}{e_{f}B_{{\parallel} }^{*}}\times \boldsymbol{\nabla} H + \frac{\boldsymbol{B}^{*}}{m_{f} B_{{\parallel} }^{*}} \frac{\partial H}{\partial v_{{\parallel}}}, \end{gather}

(2.6)\begin{gather}\dot{v}_{{\parallel}} = \frac{\boldsymbol{B}^{*}}{m_{f}B_{{\parallel} }^{*}}\boldsymbol{\cdot}\boldsymbol{\nabla} H. \end{gather}

Here, $\boldsymbol {X}$ is the guiding-centre position, $\boldsymbol {B}^{*} = \boldsymbol {B} + ({m_{f}}/{e_{f}})v_{\parallel }\boldsymbol {\nabla }\times \boldsymbol {b}$ and $B^{*}_{\parallel }=\boldsymbol {B}^{*}\boldsymbol {\cdot } \boldsymbol {b}$ and $\boldsymbol {b} = \boldsymbol {B}/B$. The subscript $f$ denotes a fast particle. The equilibrium magnetic field can be written as

(2.7)\begin{equation} \boldsymbol{B}=g(\psi)\boldsymbol{\nabla} \phi + \boldsymbol{\nabla}\phi \times \boldsymbol{\nabla}\psi. \end{equation}

Here, $\psi$ is the poloidal magnetic flux.

2.2. Coulomb collision

The Coulomb collision between fast ions and background charged particles includes the slowing down effect and the pitch angle scattering effect. The slowing down of fast ions by background electrons and ions is governed by (Xu et al. 2019)

(2.8)\begin{equation} \frac{{\rm d} v}{{\rm d} t}={-}\nu_{s}(1+v^3_{c}/v^{3})v. \end{equation}

Here, $\nu _{s}$ is the slowing down collision rate and $v_{c}$ is the critical velocity. The critical energy $E_c$ ($E_c=\frac {1}{2}mv_c^2$) for a deuterium ion is approximately $19T_{e}$. The critical energy near the edge where $T_{e}\leq 0.5\,{\rm keV}$ is smaller than 9.3 keV. It means that NBI ions with the injection energy of 55 keV near the plasma edge are mainly slowed down by background electrons when the fast ion energy is larger than 9.3 keV. The pitch angle scattering of a fast ion is governed by (Boozer & Kuo-Petravic 1981)

(2.9)\begin{equation} \lambda_{\rm new} = \lambda_{\rm old}(1-2\nu_{d} {\rm \Delta} t) \pm \sqrt{(1-\lambda_{\rm old}^2)2\nu_{d} {\rm \Delta} t}. \end{equation}

Here, $\lambda =v_{\parallel }/v$ is the particle pitch and $\nu _{d}$ is the pitch angle scattering rate expressed as (Xu et al. 2020)

(2.10)\begin{equation} \nu_{d} = Z_{\rm eff} \frac{v_{c}^{3}}{2v^{3}}\nu_{s} \end{equation}

and ${\rm \Delta} t$ is the time step. The effective charge number used in our simulations was chosen as $Z_{\rm eff}=2$. Equations (2.8)–(2.9) can be derived by assuming that the distributions of background ions and electrons are Maxwellian velocity distributions and $v_{i} \ll v \ll v_{e}$. Here, $v_{i,e}$ are thermal velocities of background ions and electrons, respectively.

2.3. Neutral collision

In order to study CX losses of fast ions, we have recently added the neutral collision effect in the GYCAVA code. Now collisions in the GYCAVA code contain the Coulomb collision and the neutral collision.

The neutral collision effect in the GYCAVA code includes the CX collision between fast deuterium ions and deuterium neutrals, and the reionization collision between fast deuterium neutrals and background charged particles. The first wall of EAST is the metal wall, for which the number of deuterium molecules is much smaller than that of deuterium atoms near the LCFS (Stangeby & McCracken 1990). For simplicity, neutrals used in our EAST simulations are only deuterium atoms. In other words, deuterium molecules $D_{2}$ are neglected. The CX reaction between a fast deuterium ion $D_{f}^+$ and a deuterium neutral $D$ is

(2.11)\begin{equation} D_{f}^+{+} D \rightarrow D_{f} + D^+ . \end{equation}

A fast deuterium neutral and a deuterium ion are produced in this CX process. In a short time ${\rm \Delta} t$, a fast ion moves along the full orbit a short distance, that is, $v {\rm \Delta} t$. The corresponding neutralization probability $P_{n}$, can be expressed as

(2.12)\begin{equation} P_{n}(\boldsymbol{r}^{\rm full},E) = n_{n}(\boldsymbol{r}^{\rm full})\sigma_{\rm cx}(E)v {\rm \Delta} t. \end{equation}

Here, $n_{n}$ is the neutral density and $\sigma _{\rm cx}$ is the cross-section of CX and $\boldsymbol {r}^{\rm full}$ is the particle space position obtained from the full-orbit computation and $E$ is the fast ion energy. Note that the time step used in guiding-centre orbit computation is much larger than that used in the full orbit computation. In order to keep the FLR effect in our guiding-centre orbit computation, the neutralization probability $P_{n}(\boldsymbol {X},E)$ in the guiding-centre position is used in the GYCAVA, expressed as

(2.13)\begin{equation} P_{n}(\boldsymbol{X},E) = \langle P_{n}(\boldsymbol{r},E) \rangle = \langle n_{n}(\boldsymbol{X}+\boldsymbol{\rho})\rangle \sigma_{\rm cx}(E)v {\rm \Delta} t. \end{equation}

Here, the lowest-order inverse guiding-centre transformation $\boldsymbol {r}=\boldsymbol {X}+\boldsymbol {\rho }$ has been used and $\boldsymbol {\rho }$ is the gyroradius and $\boldsymbol {r}$ is the particle space position obtained from the guiding-centre orbit computation. The finite temperature effect of background particles was neglected. The gyroaverage of the neutral density $\langle n _{n}\rangle$ can be numerically solved by an $m$-point discrete sum method, that is,

(2.14)\begin{equation} \langle n_{n}(\boldsymbol{X}+\boldsymbol{\rho})\rangle = \frac{1}{m}\sum_{i=1}^{m}n _{n}(\boldsymbol{X}+\boldsymbol{\rho}_{i}). \end{equation}

Here, $\boldsymbol {\rho }_{i}=\boldsymbol {\rho }(\boldsymbol {X},\mu,\xi _{i})$ with $\mu$ being the magnetic moment and the gyrophase $\xi _{i}=2 (i-1){\rm \pi} /m$. The gyroradius can be written as

(2.15)\begin{equation} \boldsymbol{\rho} =\rho(\cos\xi \boldsymbol{e}_{1} - \sin\xi \boldsymbol{e}_{2}). \end{equation}

Here, $\boldsymbol {e}_{1} = \boldsymbol {\nabla }\psi /|\boldsymbol {\nabla }\psi |$ and $\boldsymbol {e}_{2} = \boldsymbol {b}\times \boldsymbol {e}_{1}$. Then the contravariant components of $\boldsymbol {\rho }$ in the cylindrical coordinates can be written as

(2.16)\begin{gather} \rho^{R}=\rho\left(\frac{\partial_R\psi}{|\boldsymbol{\nabla}\psi|}\cos\xi + \frac{g\partial_Z \psi}{|\boldsymbol{\nabla}\psi|BR}\sin\xi\right), \end{gather}

(2.17)\begin{gather}\rho^{Z}=\rho\left(\frac{\partial_Z\psi}{|\boldsymbol{\nabla}\psi|}\cos\xi - \frac{g\partial_R \psi}{|\boldsymbol{\nabla}\psi|BR}\sin\xi\right), \end{gather}

(2.18)\begin{gather}\rho^{\phi}=\frac{\rho|\boldsymbol{\nabla}\psi|}{BR^{2}}\sin\xi. \end{gather}

The neutralization probability $P_{n}(\boldsymbol {X},E)$ (2.13) can be rewritten as

(2.19)\begin{equation} P_{n}(\boldsymbol{X},E) = \sum _{i=1}^{m} P^{i}_{n}(\boldsymbol{X},E). \end{equation}

Here, $P^{i}_{n}(\boldsymbol {X},E)$ depends on the gyroradius $\rho _{i}$, expressed as

(2.20)\begin{equation} P^{i}_{n}(\boldsymbol{X},E) = n_{n}(\boldsymbol{X}+\boldsymbol{\rho}_{i}) \sigma_{\rm cx}(E)v {\rm \Delta} t/m. \end{equation}

The guiding-centre coordinates of a fast ion are transformed into the particle coordinates by the lowest-order inverse guiding-centre transformation, that is, $\boldsymbol {r}=\boldsymbol {X}+\boldsymbol {\rho }$, when it becomes a neutral in the CX process. In the GYCAVA code, the probability $P^{i}_{n}$ with the superscript $i$ chosen as $i=1,\ldots,m$ is used to judge whether a fast ion with the gyrophase $\xi _{i}$ becomes a neutral or not, and the discrete and uniform gyrophases, that is, $\xi _{i}=2(i-1){\rm \pi} /m$, are used. Then the particle phase-space coordinates $(R,Z,\phi,v_{\parallel },\mu,\xi _{i})$ are transformed into Cartesian coordinates $(X,Y,Z,v_{X},v_{Y},v_{Z})$ to compute the motion of a neutral.

The computation of the neutralization probability by using the gyroaverage method in the guiding-centre orbit simulation is roughly equivalent to the computation of the neutralization probability in the full orbit simulation. We use $\delta t$ to represent the time step in the full orbit simulation and let $\delta t=T_{\rm gyro}/m$. Here, $T_{\rm gyro}$ is the gyroperiod. From (2.12), we can compute the neutralization probability in a gyroperiod,

(2.21)\begin{equation} P_{n}^{\rm full} =\sum_{i=1}^{m}n_{n}(\boldsymbol{r}_{i}^{\rm full})\sigma_{\rm cx}(E)v \delta t = \sum_{i=1}^{m}n_{n}(\boldsymbol{r}_{i}^{\rm full})\sigma_{\rm cx}(E)v T_{\rm gyro}/m. \end{equation}

Here, the change of particle energy in a gyroperiod is neglected. $\boldsymbol {r}_{i}$ is the particle position where the gyrophase is $\xi _{i}$. Then we use ${\rm \Delta} t$ to represent the time step in the guiding-centre simulation and let ${\rm \Delta} t =T_{{\rm gyro}}$. From (2.19)–(2.20), we can compute the neutralization probability in a gyroperiod by using the gyroaverage method,

(2.22)\begin{equation} P_{n}^{\rm gc} = \sum_{i=1}^{m}n_{n}(\boldsymbol{X}+\boldsymbol{\rho}_{i}) \sigma_{\rm cx}(E)v T_{\rm gyro}/m. \end{equation}

Here $\boldsymbol {r}_{i}^{\rm full}$ and $\boldsymbol {r}_i$ are the particle space positions obtained from the full-orbit and guiding-centre orbit computation, respectively. We have $\boldsymbol {r}_{i}^{\rm full}\boldsymbol {\cdot } \boldsymbol {b} \neq \boldsymbol {r}_i\boldsymbol {\cdot } \boldsymbol {b}=\boldsymbol {X}\boldsymbol {\cdot } \boldsymbol {b}$. Then we have $n_{n}(\boldsymbol {r}_{i}^{\rm full}) \simeq n_{n}(\boldsymbol {r}_{i}) = n_{n}(\boldsymbol {X}+\boldsymbol {\rho }_{i})$ because the change of $n_{n}$ in the parallel direction is small. Therefore, $P_{n}(\boldsymbol {r}^{\rm full}_{i},E) \simeq P^{i}_{n}(\boldsymbol {X},E)$ and $P_{n}^{\rm full} \simeq P_{n}^{\rm gc}$. Note that the time step used in our guiding-centre orbit simulations is approximately one gyroperiod.

The GYCAVA code can neglect the FLR effect in the fast ion–neutral collision by setting $\rho =0$ in the computation of the probability $P^{i}_{n}$ and the inverse guiding-centre transformation. It allows us to investigate the FLR effect in the fast ion–neutral collision on CX losses of fast ions.

The reionization collision of fast neutrals includes three atomic processes in the GYCAVA code. They are CX with thermal ions, ionization by thermal ions and ionization by thermal electrons, which are written as

(2.23)\begin{gather} D_{f} + D^+ \rightarrow D_{f}^+{+} D, \end{gather}

(2.24)\begin{gather}D_{f} + D^+ \rightarrow D_{f}^+{+} D^+{+} e, \end{gather}

(2.25)\begin{gather}D_{f} + e \rightarrow D_{f}^+{+} 2e. \end{gather}

The analytic fitting functions of the cross-section of CX, and ionization by thermal ions adopted in the GYCAVA code can be seen in Janev & Smith (1993) and the cross-section data of ionization by electrons are from the ADAS database (https://open.adas.ac.uk/). In a short time ${\rm \Delta} t$, a fast neutral moves straight a short distance $v {\rm \Delta} t$ and the ionization probability $P_{i}$, which is similar to the neutral probability, can be expressed as

(2.26)\begin{equation} P_{i}(\boldsymbol{r},E) = n_{e}(\boldsymbol{r})\sigma_{i}(\boldsymbol{r},E)v {\rm \Delta} t. \end{equation}

Here, $n_{e}$ is the electron density and $\sigma _{i}$ is the ionization cross-section, that is, the sum of three cross-sections, expressed as

(2.27)\begin{equation} \sigma_{i}(\boldsymbol{r},E) = \sigma_{\rm cx}(E) + \sigma_{ii}(E) + \sigma_{\rm ie}(T_{e}(\boldsymbol{r}),E). \end{equation}

Here, $\sigma _{{\rm ii}}$ and $\sigma _{{\rm ie}}$ are cross-sections of ionization by thermal ions and electrons, respectively; $\sigma _{{\rm ie}}$ is inversely proportional to the fast particle velocity and depends on the local electron temperature $T_{e}(\boldsymbol {r})$. In the GYCAVA code, the particle coordinates of a fast neutral are transformed from Cartesian coordinates $(X,Y,Z,v_{X},v_{Y},v_{Z})$ to cylindrical coordinates $(R,Z,\phi,v_{R},v_{Z},v_{\phi })$. Then the particle coordinates are transformed into the guiding-centre coordinates $(R,Z,\phi,v_{\parallel },\mu )$ by using the lowest-order guiding-centre transformation, that is, $\boldsymbol {X}=\boldsymbol {r}-\boldsymbol {\rho }$, when it becomes a fast ion. Here, the gyroradius in the cylindrical coordinates is computed by $\boldsymbol \rho = \boldsymbol {v} \times \boldsymbol {b}/\omega _{c}$ with $\omega _{c}$ being the gyrofrequency.

The CX cross-section of a fast ion is smaller than the cross-section of ionization of a fast neutral and the neutral density is much smaller than the electron density. Therefore, $P_{n}/{\rm \Delta} t \ll P_{i}/{\rm \Delta} t$. However, the CX effect of a fast ion may still be important. It is because the orbits of a fast neutral and a fast ion are different, a fast neutral moves in a straight line and collides with the local charged particles only once, but a fast ion moves in a roughly closed orbit in the poloidal cross-section and can move through the neutral region many times. In other words, the total length of ionization for a fast neutral is much smaller than that of CX for a fast ion.

The full energy of NBI in our simulations was chosen as 55 keV. For this energy, the CX cross-section is much larger than the cross-sections of ionization by ions and electrons. Therefore, the CX collision between fast neutrals and thermal ions is dominant in the three ionization collisions.

3. Simulation set-up

The magnetic equilibrium configuration, plasma parameter profiles and birth distributions of NBI ions in EAST are presented. In our NBI fast ion loss simulations, the equilibrium data of EAST discharge no. $102391$ were used. The equilibrium configuration was obtained by the EFIT (Lao et al. 1985) code. Figure 1 shows the magnetic configuration and shapes of the first wall and the LCFS. The toroidal plasma current is approximately 450 kA and in the anticlockwise direction from the top view. The toroidal magnetic field is in the clockwise direction from the top view and its value at the magnetic axis is 2.3 T. Profiles of the safety factor, the electron density and the electron and ion temperatures for EAST discharge no. $102391$ are shown in figure 2. The safety factor at the magnetic axis is $q_0=3$ and its value at the $95\,\%$ poloidal magnetic flux is $q_{95}=5.9$. The electron density at the magnetic axis is $n_{e0}=5.4\times 10^{19}\,{\rm m}^{-3}$. The electron and ion temperatures at the magnetic axis are $T_{e0}=2.1$ and $T_{\rm i0}=1.6\,{\rm keV}$, respectively.

Figure 1. The magnetic equilibrium configuration and shapes of the LCFS (blue) and the first wall (black) for EAST discharge no. $102391$. The magenta lines denote contours of the poloidal magnetic flux. The black straight lines denote contours of the poloidal angle.

Figure 2. Profiles of the safety factor (a), the electron density (b), the temperatures of electron (c) and ion (d) for EAST discharge no. $102391$. The square of $\rho _{t}$ is the normalized toroidal flux of the magnetic field.

The neutralization probability of a fast ion linearly depends on the local neutral density, which can be seen from (2.12). Therefore, the amplitude and profile of the neutral density can affect CX losses of fast ions, which will be discussed in the next section. However, it is difficult to measure the neutral density in tokamak experiments. For simplicity, an analytical neutral density was adopted in our NBI ion loss simulations, which is shown in figure 3. The neutral density outside the LCFS ($\rho _{t}>1$), that is, $n_{n0}$, is constant. The analytical form of the neutral density $n_{n}$ inside the LCFS ($\rho _{t}<1$) is expressed as

(3.1)\begin{equation} n_{n} = n_{n0}\exp{[-(1-\rho_{t})/\varDelta_{\rho}]}. \end{equation}

Here, the square of $\rho _{t}$ is the normalized toroidal flux of the magnetic field and the parameter $\varDelta _\rho$ was chosen as $\varDelta _{\rho }=0.015$. Most of neutrals are outside the LCFS and a few neutrals are inside the LCFS near the edge of plasma, which can be seen from figure 3. However, most of NBI fast ions are inside the LCFS. Therefore, the collision between fast ions and neutrals inside the LCFS may not be neglected. This collision was also considered in our fast ion loss simulations to make the results of CX losses more accurate. According to some previous estimations of the neutral density in the tokamak plasma edge (Carreras et al. 1998; Colchin et al. 2000; Viezzer et al. 2011; Zhang et al. 2011; Stotler et al. 2015), the range of the neutral density outside the LCFS is $n_{n0} = 10^{15}\unicode{x2013}10^{19}\,{\rm m}^{-3}$. The default value of $n_{n0}$ is chosen as $n_{n0}=10^{17}\,{\rm m}^{-3}$ in the following simulations. The neutral density in the core region of a tokamak is very small and generally smaller than $10^{14}\,{\rm m}^{-3}$ (Dnestrovskij, Lysenko & Kislyakov 1979). Therefore, the effect of the neutral density in the core region on the fast ion loss can be neglected.

Figure 3. The neutral density profile.

Two NBIs in EAST were used in our fast ion loss simulations. They are both in the cocurrent direction and are injected in the midplane $(Z\sim 0)$. One NBI is in the nearly tangential direction. The tangential radius of this cocurrent tangential (co-tang) NBI is $R^{\text {co-tang}}_{\rm tan}=1.26\,{\rm m}$. The other NBI is in the nearly perpendicular direction. The tangential radius of this cocurrent perpendicular (co-perp) NBI is $R^{\text {co-perp}}_{\rm tan}=0.73\,{\rm m}$. The NBI power injected into a plasma was chosen as 1 MW. Here 50 000 markers were used as test neutral beam particles in each simulation. We have performed two fast ion loss simulations by using 100 000 markers. Using 100 000 markers, particle loss fractions of co-perp and co-tang NBI ions in the presence of the Coulomb collision and the neutral collision are within $2\,\%$ of the results using 50 000 markers. It means that 50 000 markers are enough. Three components of beam particles with different energies are included. The current fractions with full, a half and a third energy are $80\,\%:14\,\%:6\,\%$, respectively. The initial phase space positions of the test NBI fast ions were computed by the NBI code TGCO (Hu et al. 2021). Birth distributions of NBI ions in the poloidal cross-section and from the top view are shown in figure 4. We can see that birth distributions in the poloidal cross-section of co-perp and co-tang NBIs are similar. When fast neutral particles are deposited into the plasma, fast ions are produced by ionization reactions. More NBI ions are produced on the low field side in contrast to the high field side.

Figure 4. The NBI deposition in the EAST plasma: birth distributions in the poloidal cross-section of co-perp (a) and co-tang (b) NBIs and birth distributions from the top view of these two NBIs (c).

Test NBI fast ions are launched at the initial time and then they are traced by the orbit code GYCAVA. The slowing-down time near the plasma edge is approximately 10 ms. The simulation time is approximately 50 ms in each simulation. The test particles will not be followed if they are thermalized. The fast particle behaviour is independent of the initial time in our simulations, therefore, it is not necessary to launch new test particles to replace the thermal particles (Xu et al. 2020, 2021). In this simulation time, NBI fast ion losses can reach a steady state when the Coulomb collision is present.

4. Numerical results of NBI ion losses with the CX effect in EAST

In this section, we present numerical results of NBI ion losses with the collision effects in EAST. The collision effects include the Coulomb collision between fast ions and background charged particles, and the neutral collision. The neutral collision contains the collision between fast ions and neutrals and the reionization collision between fast neutrals and background charged particles. The collision between fast ions and neutrals is the CX reaction. In the reionization, the CX reaction is the dominant reaction in our simulations with the injection energy of NBI ions chosen as 55 keV. Therefore, the CX effect is dominant in the neutral collision. The slowing-down time near the plasma edge is $t_{s}\sim 10\,{\rm ms}$ in our simulations. The characteristic CX time $t_{\rm cx}$, defined as $t_{\rm cx}=1/(n_{n0}\sigma _{\rm cx}v)$, is $t_{\rm cx} \sim 0.2\,{\rm ms}$ with $n_{n0}$ chosen as $10^{17}\,{\rm m}^{-3}$. In fact, a fast ion near the edge can collide with neutrals only in a part of the fast ion orbit, therefore, $t_{\rm cx}$ should be much larger and is estimated as $t_{\rm cx} \sim 1\,{\rm ms}$. It means that the slowing-down time is much larger than the CX time for $n_{n0}=10^{17}\,{\rm m}^{-3}$. We focus on the CX effect on NBI ion losses in the following simulations.

In order to investigate the CX effect related to the neutral collision, NBI ion loss simulations were performed in four cases, which are shown in figures 5–8 and 10–11. Only the neutral collision, that is, the fast ion–neutral collision and the fast neutral–plasma collision, is considered in the first case. Only the Coulomb collision, that is, the fast ion–plasma collision, is included in the second case. In the third and fourth cases, both of the neutral collision and the Coulomb collision are included. The FLR effect in the fast ion–neutral collision is included in the third case, while it is not included in the fourth case. The neutral density outside the LCFS was chosen as $n_{n0}=10^{17}\,{\rm m}^{-3}$. The parameter $m$ in the gyroaverage, which is related to the FLR effect, was chosen as $m=8$ in our simulations. Using $m=16$, particle loss fractions of co-perp and co-tang NBI ions in the presence of the Coulomb collision and the neutral collision are within $3\,\%$ of the results using $m=8$.

Figure 5. Time histories of particle (a) and power (b) loss fraction of co-tang NBI ions in the four cases: (blue dash line) with only the neutral collision effect (the fast ion–neutral collision and the fast neutral–plasma collision); (red dash–dotted line) with the Coulomb collision effect; and (black solid line) with the neutral collision and the Coulomb collision; (magenta solid line) with the neutral collision and the Coulomb collision but without the FLR effect in the fast ion–neutral collision.

Figure 6. Time histories of particle loss fraction (a) and power loss fraction (b) of co-perp NBI ions in the four cases.

Temporal evolutions of loss fraction of the co-tang and co-perp NBI fast ions in the four cases are shown in figures 5–6, respectively. Fast ion losses with only the neutral collision, that is, the CX effect, are much larger than those with only the Coulomb collision, that is, neoclassical losses, which include losses induced by the pitch-angle scattering and first-orbit losses. Note that the three-dimensional magnetic field effect, such as the toroidal field ripple, has not been included in our simulations. Beam ions, especially from the perpendicular beam, are prone to ripple diffusion and ripple well trapping. These loss channels should increase the neoclassical losses. In the presence of the neutral collision and the Coulomb collision, the fast ion loss fractions can reach a steady state in the simulation time of approximately 50 ms due to the slowing down effect of the Coulomb collision. The fast ion loss fractions with the FLR effect are larger than those without the FLR effect. It means that the FLR effect enhances the CX loss. In the presence of the neutral collision and the Coulomb collision, the fractions of particle loss and power loss of co-tang NBI ions are $8.6\,\%$ and $6.4\,\%$, respectively, while the fractions of particle loss and power loss of co-perp NBI ions are $17.5\,\%$ and $12.5\,\%$, respectively. The loss fractions of co-perp NBI ions are much larger than those of co-tang NBI ions. It is because more trapped ions are born for the co-perp NBI and they are more easily lost due to the pitch angle scattering or exchange charge with neutrals more likely in contrast to passing ions. We can see from figures 5–6 that the synergetic effect of the neutral collision and the Coulomb collision on the particle loss fractions for the co-perp NBI is more significant than that for the co-tang NBI. This synergetic effect is mainly related to CX between trapped fast ions and neutrals and the pitch angle scattering of trapped fast ions. In the simulation time of approximately 2 ms, which is similar to the CX time but is much smaller than the slowing-down time, NBI fast ion losses are mainly due to the CX effect. The power loss fraction with the neutral collision and the Coulomb collision is smaller than that with only the neutral collision for the co-tang NBI. It is because the slowing-down effect reduces the fast ion energy and thus reduces the power loss fraction induced by CX. The reduction of the power loss fraction by the slowing-down effect is larger than the enhancement of the power loss fraction by the pitch-angle scattering effect for the co-tang NBI.

Figures 7–8 show birth distributions of lost fast ions produced by the co-tang and co-perp NBIs, respectively. From figures 7(a,b) and 8(a,b), we can see that both of the neutral collision and the Coulomb collision can make NBI ions born on the low field side near the plasma edge become lost. The widths of loss regions with only the neutral collision are much wider than those with only the Coulomb collision. It is shown in figures 7(c) and 8(c) that loss regions in the case with the neutral collision and the Coulomb collision are located on the left- and right-hand sides of the plasma edge. Loss regions in the case without the FLR effect (figures 7d and 8d) are slightly smaller than those in the case with the FLR effect (figures 7c and 8c). It is related to the fact that the FLR effect enhances the CX loss. From figures 7(a) and 8(a), we can see that CX losses are significant when neutrals are present. The CX-induced fast ion losses are related to the fast ion–neutral collision. In the case with the neutral collision, loss regions on the high field side are much wider than those on the low field side. The major reason is that fast ions born on the high field side near the edge move across the LCFS and then collide with neutrals on the low field side and finally get lost. It can be seen from the typical orbit of a fast particle launched from the high field side in the presence of the neutral collision, which is shown in figure 9. In the case with only the neutral collision, loss regions on the high field side are wider in contrast to the case with only the Coulomb collision shown in figures 7(b) and 8(b). It means that the CX loss is the dominant fast ion loss mechanism for NBI ions born on the high field side.

Figure 7. Initial distributions (normalized by the maximal value) of co-tang NBI lost fast ions in the four cases. The corresponding loss fractions of particle and power can be seen in figure 5.

Figure 8. Initial distributions (normalized by the maximal value) of co-perp NBI lost fast ions in the four cases. The corresponding loss fractions of particle and power can be seen in figure 6.

Figure 9. The typical orbit (red) of a lost fast particle in the presence of the neutral collision. The cross and plus symbols denote the initial position of the fast particle and the magnetic axis.

Figure 10. Heat loads induced by co-tang NBI ions in the four cases. The corresponding fractions of particle loss and power loss can be seen in figure 5. The injected power of NBI is 1 MW.

Figure 11. Heat loads induced by co-perp NBI ions in the four cases. The corresponding fractions of particle loss and power loss can be seen in figure 6.

Figure 12. Distributions (normalized by the maximal value) of CX reactions of fast ions in the presence of the Coulomb collision in the four cases: (a) the co-tang NBI with the FLR effect; (b) co-tang NBI without the FLR effect; (c) the co-perp NBI with the FLR effect; (d) the co-perp NBI without the FLR effect.

Figure 13. Gyrophases and directions of the gyroradius (2.15) and the perpendicular velocity in an ion gyro-orbit. Here $\boldsymbol {e}_{1} = \boldsymbol {\nabla }\psi /|\boldsymbol {\nabla }\psi |$ and $\boldsymbol {e}_{2} = \boldsymbol {b}\times \boldsymbol {e}_{1}$. Four gyrophases $\xi _{1}=0$, $\xi _{2}={\rm \pi} /2$, $\xi _{3}={\rm \pi}$ and $\xi _{4}=3{\rm \pi} /2$ are marked.

Figure 14. Typical orbits of fast particle undergoing a CX reaction outside the LCFS with four gyrophases: (a) $\xi ^*=0$; (b) $\xi ^*={\rm \pi} /2$; (c) $\xi ^*={\rm \pi}$;(d) $\xi ^*=3{\rm \pi} /2$.

Figure 15. Heat loads induced by the co-perp NBI ions in the presence of the neutral collision and the Coulomb collision in the four cases: $\xi ^{*}=0$; $\xi ^{*}={\rm \pi} /2$;$\xi ^{*}={\rm \pi}$; $\xi ^{*}=3{\rm \pi} /2$. We artificially set that all gyrophases of fast ions in CX reactions between fast ions and background neutrals are the same, that is, $\xi ^{*}$.

Loss regions of co-perp and co-tang NBI ions are similar in the case with only the neutral collision effect. The loss region on the low field side for the co-perp NBI is wider than that for the co-tang NBI in the presence of a Coulomb collision whether or not the neutral collision is present. It is due to the fact that in contrast to the co-tang NBI more trapped ions on the low field side near the edge are produced by the co-perp NBI. These trapped ions are more easily lost due to the pitch angle scattering or exchange charge with neutrals more likely in contrast to passing ions.

Figures 10–11 show heat loads induced by co-tang and co-perp NBI fast ions in the four cases, respectively. Heat load distributions for co-tang and co-perp NBIs are similar in each case. The peak heat load for the co-perp NBI is much larger than that for the co-tang NBI in the case with the neutral collision and the Coulomb collision. In the case with only the Coulomb collision, heat loads of NBI ions are in the lower divertor and the first wall near the midplane. In the case with the neutral collision and the Coulomb collision, heat loads are mainly located in the regions that the poloidal angle $\theta$ is near $-60^\circ$ when the FLR effect is present, while heat loads are mainly located in the $|\theta | \sim 60^\circ$ regions when the FLR effect is absent. Although the wall shape can affect heat loads to some degree, the localization of heat loads in the region with $|\theta | \sim 60^\circ$ is mainly related to the distributions of CX reaction in the fast ion–neutral collision. Vertical asymmetry of heat loads in the case with the FLR effect is related to the strong radial gradient of neutral density near the edge. These will be explained in the following.

Figure 12 shows distributions of CX reactions in the fast ion–neutral collision for co-tang and co-perp NBIs with and without the FLR effect. A few fast ions can exchange charge with neutrals and be reionized several times. Only the final time of CX was recorded in our simulations. Distributions of CX reactions with and without the FLR effect are similar and they are near the LCFS on the low field side. The number of CX reactions in the fast ion–neutral collision for the co-perp NBI are larger than that for the co-tang NBI. These distributions are narrow in the $R$ direction but is wide in the $Z$ direction. The shape of these distributions leads to peaks of heat loads near ${\pm }60^{\circ }$. The FLR effect on distributions of CX reactions is small.

In order to study the relation between the heat load and the FLR effect, gyrophases and directions of the gyroradius and the perpendicular velocity in an ion gyro-orbit are plotted in figure 13. The unit vector $\boldsymbol {e}_{1}={\boldsymbol {\nabla }\psi }/{|\boldsymbol {\nabla }\psi |}$ is towards the magnetic axis because the toroidal plasma current is in the anticlockwise direction from the top view in our simulations. For simplicity, we consider four gyrophases, that is, $\xi _{1}=0$, $\xi _{2}={\rm \pi} /2$, $\xi _{3}={\rm \pi}$ and $\xi _{4}=3{\rm \pi} /2$. For fast particles near the midplane on the low field side, the perpendicular velocities $\boldsymbol {v}_{\perp }$ at $\xi _{1}=0$ and $\xi _{2}={\rm \pi} /2$ are upwards and towards the outside, respectively. Here $\boldsymbol {v}_{\perp }$ at $\xi _{3}={\rm \pi}$ and $\xi _{4}=3{\rm \pi} /2$ are downwards and towards the inside, respectively. Typical orbits of fast particle undergoing a CX reaction outside the LCFS with four gyrophases $\xi ^{*}=\xi _{i}$ ($i=1,2,3,4$) are shown in figure 14. These gyrophases are artificially set in order to compute the path of the fast neutral when the CX reaction occurs. We can see that fast particle orbits are the same before the CX reaction. After the CX reaction, the paths of fast neutrals with different gyrophases are different. The direction of the fast neutral motion is mainly determined by the gyrophase or the perpendicular velocity direction of the fast ion when the CX reaction occurs. For $\xi ^*=0$ and $\xi ^*={\rm \pi}$, the fast neutrals move upwards and downwards, respectively. For $\xi ^*={\rm \pi} /2$, the fast neutral moves outwards and upwards. For $\xi ^*=3{\rm \pi} /2$, the fast neutral moves inwards and upwards and enters the plasma. Then the fast neutral is ionized and becomes a fast ion. The partially upwards motion direction of the fast neutrals with $\xi ^*=0$ and $\xi ^*={\rm \pi}$ is related to the parallel velocity of the fast ion when the CX reaction occurs. We have performed four fast particle loss simulations by artificially setting the gyrophase of all fast ions in the CX processes $\xi ^{*}=\xi _{i}$ ($i=1,2,3,4$) for co-perp NBI ions. The corresponding heat loads are shown in figure 15. For $\xi ^{*}=0$ and $\xi ^{*}={\rm \pi}$, heat loads are mainly near $50^{\circ }$ and $-50^{\circ }$, respectively. For $\xi ^{*}={\rm \pi} /2$, heat loads are mainly on the low field side of the first wall. For $\xi ^{*}=3{\rm \pi} /2$, heat loads near the midplane are very small because fast neutrals re-enter the plasma and most of them are ionized. Heat loads with $\xi ^{*}=0$ and $\xi ^{*}={\rm \pi}$ have peaks but the heat load distribution with $\xi ^{*}={\rm \pi} /2$ is flat, because the CX distribution is narrow in the $R$ direction but is wide in the $Z$ direction, which can be seen from figure 12. For each gyrophase, the typical fast particle orbit shown in figure 14 can illustrate the heat load distribution shown in figure 15.

Figure 16. Energy spectra (normalized by the maximal value) of lost fast neutrals for the co-tang and co-perp NBIs in the presence of the neutral collision and the Coulomb collision. Here, $E_0$ is the full energy of beam particles, that is, $E_0=55\,{\rm keV}$.

Figure 17. Time histories of particle loss fraction (a) and power loss fraction (b) of the co-tang NBI ions for different neutral densities with the neutral collision and the Coulomb collision (solid line) and with only the neutral collision (dash line).

Figure 18. Time histories of particle loss fraction (a) and power loss fraction (b) of the co-perp NBI ions in the six cases same as figure 17.

Due to the strong radial gradient of the neutral density near the LCFS, the neutral densities and the corresponding neutralization probabilities at different gyrophases in the same gyro-orbit are different. It can lead to that the heat load distribution with the FLR effect is asymmetrical in the vertical direction. The CX reactions of fast ions mainly occur near the LCFS on the low field side. Then for the same fast ion gyro-orbit near the LCFS on the low field side, the neutral density at $\xi =0$ is the smallest one among all gyrophases and the neutral density at $\xi ={\rm \pi}$ is the largest one due to the strong radial gradient of the neutral density near the LCFS. It means that CX reactions between fast ions and background neutrals mainly occur at $\xi ={\rm \pi}$. The perpendicular velocity of a fast particle near the midplane on the low field side at $\xi ={\rm \pi}$ is downwards. Then most fast neutrals move downwards and hit the first wall where the poloidal angle is near $-60^\circ$. Therefore, the heat load distribution with the FLR effect is asymmetrical in the vertical direction and mainly near $-60^{\circ }$, which can be seen in figures 10–11.

In the case without the FLR effect ($\rho =0$), the neutralization probabilities at different gyrophases are the same. Then the heat load distribution without the FLR effect is roughly symmetrical in the vertical direction, which can also be seen in figures 10–11.

Energy spectra of lost fast neutrals for co-tang and co-perp NBIs in the presence of the neutral collision and the Coulomb collision are shown in figure 16. We can clearly see three peaks at $E/E_0 \simeq 1,1/2,1/3$ for the co-perp NBI, which are related to three components of beam particles with full, a half and a third energy. For the co-tang NBI, the peak at $E/E_0\simeq 1$ can be clearly seen. Lost fast particles with $E/E_0\simeq 1$ stayed in the plasma for a short time, which is much smaller than the slowing-down time. In contrast to the co-tang NBI, the number of lost fast particles with $E/E_0< 0.9$ is larger for the co-perp NBI. It is related to the fact that the co-perp NBI produces more trapped ions near the edge, which are more easily lost due to the pitch angle scattering or exchange charge with neutrals more likely in contrast to passing ions.

The neutral density can directly impact CX losses of NBI ions by the fast ion–neutral collision. Time histories of the loss fraction of co-tang and co-perp NBI fast ions for different neutral densities in the presence of the neutral collision with and without the Coulomb collision are shown in figures 17–18. We can see that fast ion loss fractions in the presence of the neutral collision decrease with the neutral density decreasing. At the early stage, the loss rate is positively related to the neutral density because the CX loss is dominant. The particle loss fractions of co-perp NBI ions with the neutral collision and the Coulomb collision are larger than those with only the neutral collision, which is due to the pitch-angle scattering effect. For the co-tang NBI, the power loss fractions of NBI ions with only the neutral collision are larger than those with the neutral collision and the Coulomb collision, which is due to the slowing down effect of the Coulomb collision. For the co-perp NBI, the power loss fractions with the neutral collision and the Coulomb collision are larger in contrast to the case with only the neutral collision when the neutral density is significant.

5. Conclusion

Guiding-centre orbit-following simulations of the CX loss of NBI ions with the FLR effect based on a gyroaverage method are presented. The FLR effect in the fast ion–neutral collision can be included in guiding-centre orbit-following simulations by using the gyroaverage method. It is proved that the neutralization probability of fast ions computed by using the gyroaverage method in the guiding-centre orbit simulation is roughly the same as that computed in the full orbit simulation when the time step in the guiding-centre simulation is the order of the gyroperiod.

The NBI ion losses in the presence of background neutrals in EAST have been computed by the guiding-centre orbit code GYCAVA. The CX effect on loss regions, loss fractions and heat loads of fast ions has been numerically investigated for co-tang and co-perp NBIs. Loss fractions of fast ions produced by the co-perp NBI are much larger than those produced by the co-tang NBI, which is due to the fact that more trapped ions are produced by the co-perp NBI. Fast ion losses induced by CX increase with the neutral density increasing. The CX effect is included in the fast ion–neutral collision and the reionization collision. The FLR effect in the fast ion–neutral collision can enhance the CX loss. This was explained as being caused by the radial gradient of the neutral density, so the fast ions are observing higher neutral density and thus are more likely to undergo CX when the FLR effect is accounted for.

Heat loads induced by the CX loss are asymmetrical in the vertical direction and are localized in the regions near $\theta =-60^\circ$. It is related to the FLR effect of fast ions and the strong radial gradient of the neutral density near the plasma edge. For the same gyro-orbit, the neutral density at $\xi ={\rm \pi}$ is the largest among all gyrophases. In other words, the likelihood of exchanging charge is the largest at gyrophase $\xi ={\rm \pi}$. Therefore, fast ions near the gyrophase $\xi ={\rm \pi}$ are most easily neutralized and become fast neutrals due to the strong radial gradient of the neutral density near the LCFS. These fast neutrals finally hit the first wall where $\theta \sim -60^\circ$.

In this work, the toroidal field ripple was not included for simplicity. We will simulate fast ion losses and steady-state distributions of NBI fast ions with the toroidal field ripple and the CX effect by the GYCAVA code in the future.