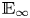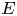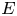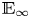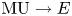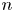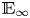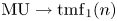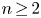1. Introduction
Complex-oriented ring spectra play a central role in the chromatic approach to homotopy theory. Given a homotopy associative ring spectrum ![]() $E$, recall that a complex orientation is a choice of class
$E$, recall that a complex orientation is a choice of class ![]() $u \in \widetilde {E}^2 (\mathbb {CP}^\infty )$ with the property that its restriction along
$u \in \widetilde {E}^2 (\mathbb {CP}^\infty )$ with the property that its restriction along ![]() $S^2 \cong \mathbb {CP}^1 \hookrightarrow \mathbb {CP}^\infty$ is the unit
$S^2 \cong \mathbb {CP}^1 \hookrightarrow \mathbb {CP}^\infty$ is the unit ![]() $1 \in E^0 (\ast ) \cong \widetilde {E}^{2} (S^2)$. A complex orientation determines an isomorphism of graded rings
$1 \in E^0 (\ast ) \cong \widetilde {E}^{2} (S^2)$. A complex orientation determines an isomorphism of graded rings
Complex orientations may also be described in terms of the complex cobordism spectrum ![]() $\mathrm {MU}$: complex orientations of
$\mathrm {MU}$: complex orientations of ![]() $E$ are in natural bijection with maps of homotopy associative ring spectra
$E$ are in natural bijection with maps of homotopy associative ring spectra ![]() $\mathrm {MU} \to E$. For more background on complex orientations, we refer the reader to [Reference AdamsAda74, Part II].
$\mathrm {MU} \to E$. For more background on complex orientations, we refer the reader to [Reference AdamsAda74, Part II].
The complex cobordism spectrum ![]() $\mathrm {MU}$ admits much more structure than that of a homotopy associative ring spectrum: it is an
$\mathrm {MU}$ admits much more structure than that of a homotopy associative ring spectrum: it is an ![]() $\mathbb {E}_\infty$-ring spectrum. When
$\mathbb {E}_\infty$-ring spectrum. When ![]() $E$ also admits the structure of an
$E$ also admits the structure of an ![]() $\mathbb {E}_\infty$-ring spectrum, it is natural to ask whether a given complex orientation is induced by a map of
$\mathbb {E}_\infty$-ring spectrum, it is natural to ask whether a given complex orientation is induced by a map of ![]() $\mathbb {E}_\infty$-ring spectra
$\mathbb {E}_\infty$-ring spectra
We will call such maps ![]() $\mathbb {E}_\infty$-complex orientations. The
$\mathbb {E}_\infty$-complex orientations. The ![]() $\mathbb {E}_\infty$-complex orientations of an
$\mathbb {E}_\infty$-complex orientations of an ![]() $\mathbb {E}_\infty$-ring may be viewed as particularly canonical complex orientations.
$\mathbb {E}_\infty$-ring may be viewed as particularly canonical complex orientations.
Indeed, many of the most familiar (not necessarily complex) orientations admit lifts to ![]() $\mathbb {E}_\infty$-orientations. For example, the Atiyah–Bott–Shapiro orientations [Reference Atiyah, Bott and ShapiroABS64]
$\mathbb {E}_\infty$-orientations. For example, the Atiyah–Bott–Shapiro orientations [Reference Atiyah, Bott and ShapiroABS64]
were refined to ![]() $\mathbb {E}_\infty$-orientations by Joachim [Reference JoachimJoa04], who gave an explicit geometric construction of such an
$\mathbb {E}_\infty$-orientations by Joachim [Reference JoachimJoa04], who gave an explicit geometric construction of such an ![]() $\mathbb {E}_\infty$-orientation. Indeed, one expects that any orientation of geometric origin may, with enough care, be refined to an
$\mathbb {E}_\infty$-orientation. Indeed, one expects that any orientation of geometric origin may, with enough care, be refined to an ![]() $\mathbb {E}_\infty$-orientation. A more sophisticated example is the Ando–Hopkins–Rezk
$\mathbb {E}_\infty$-orientation. A more sophisticated example is the Ando–Hopkins–Rezk ![]() $\mathbb {E}_\infty$-String orientation of the connective
$\mathbb {E}_\infty$-String orientation of the connective ![]() $\mathbb {E}_\infty$-ring of topological modular forms
$\mathbb {E}_\infty$-ring of topological modular forms ![]() $\mathrm {tmf}$ (see [Reference Ando, Hopkins and RezkAHR10])
$\mathrm {tmf}$ (see [Reference Ando, Hopkins and RezkAHR10])
which refines the Witten genus [Reference WittenWit87, Reference WittenWit88]. While it is expected that this ![]() $\mathbb {E}_\infty$-orientation has a geometric origin, and much work has gone into developing such a viewpoint (for a small sampling, see [Reference Stolz and TeichnerST04, Reference Stolz and TeichnerST11, Reference CostelloCos10, Reference CostelloCos11, Reference Douglas and HenriquesDH11, Reference Berwick-EvansBE21]), such a description has so far remained elusive. In Theorem 1.7, we will prove that the Hirzebruch level
$\mathbb {E}_\infty$-orientation has a geometric origin, and much work has gone into developing such a viewpoint (for a small sampling, see [Reference Stolz and TeichnerST04, Reference Stolz and TeichnerST11, Reference CostelloCos10, Reference CostelloCos11, Reference Douglas and HenriquesDH11, Reference Berwick-EvansBE21]), such a description has so far remained elusive. In Theorem 1.7, we will prove that the Hirzebruch level ![]() $n$ elliptic genera [Reference HirzebruchHir88], [Reference WittenWit88, § 5] for
$n$ elliptic genera [Reference HirzebruchHir88], [Reference WittenWit88, § 5] for ![]() $n \geq 2$ may be lifted to
$n \geq 2$ may be lifted to ![]() $\mathbb {E}_\infty$-complex orientations
$\mathbb {E}_\infty$-complex orientations
1.1 The Ando criterion
An algebraic approximation of what it means for a complex orientation ![]() $\mathrm {MU} \to E$ to be
$\mathrm {MU} \to E$ to be ![]() $\mathbb {E}_\infty$ is given by the Ando criterion. It asks that the complex orientation be compatible in a suitable sense with the power operations in
$\mathbb {E}_\infty$ is given by the Ando criterion. It asks that the complex orientation be compatible in a suitable sense with the power operations in ![]() $E$. In many cases, the Ando criterion is equivalent to the property that the complex orientation
$E$. In many cases, the Ando criterion is equivalent to the property that the complex orientation ![]() $\mathrm {MU} \to E$ be a map of
$\mathrm {MU} \to E$ be a map of ![]() $\mathbb {H}_\infty$-ring spectra (see, e.g., [Reference Ando, Hopkins and StricklandAHS04, Proposition 6.1]).
$\mathbb {H}_\infty$-ring spectra (see, e.g., [Reference Ando, Hopkins and StricklandAHS04, Proposition 6.1]).
Now let ![]() $E$ denote an
$E$ denote an ![]() $\mathbb {E}_\infty$, or more generally an
$\mathbb {E}_\infty$, or more generally an ![]() $\mathbb {H}_\infty$-ring spectrum, with a fixed complex orientation
$\mathbb {H}_\infty$-ring spectrum, with a fixed complex orientation ![]() $u$.
$u$.
Notation 1.1 Given a complex vector bundle ![]() $V \to X$ of dimension
$V \to X$ of dimension ![]() $d$, we let
$d$, we let ![]() $t_u (V) \in E^{2d} (\mathrm {Th}(V))$ denote the Thom class of
$t_u (V) \in E^{2d} (\mathrm {Th}(V))$ denote the Thom class of ![]() $V$.
$V$.
Fix a prime ![]() $p$, let
$p$, let ![]() $\rho$ denote the vector bundle over
$\rho$ denote the vector bundle over ![]() $\mathrm {BC}_p$ corresponding to the complex regular representation of
$\mathrm {BC}_p$ corresponding to the complex regular representation of ![]() $C_p$, and let
$C_p$, and let ![]() $\gamma _1$ denote the tautological bundle over
$\gamma _1$ denote the tautological bundle over ![]() $\mathbb {CP}^\infty$. Let
$\mathbb {CP}^\infty$. Let ![]() $I_{\rm tr} \subset E^* (\mathrm {BC}_p)$ denote the transfer ideal. Recall from [Reference Hopkins and LawsonHL18, § 7] that there are additive power operations
$I_{\rm tr} \subset E^* (\mathrm {BC}_p)$ denote the transfer ideal. Recall from [Reference Hopkins and LawsonHL18, § 7] that there are additive power operations
Definition 1.2 We say that a complex orientation of ![]() $E$ satisfies the Ando criterion at the prime
$E$ satisfies the Ando criterion at the prime ![]() $p$ if
$p$ if
in ![]() $E^{2p} (\mathrm {Th}(\rho \boxtimes \gamma _1))/I_{\rm tr}$. We say that a complex orientation of
$E^{2p} (\mathrm {Th}(\rho \boxtimes \gamma _1))/I_{\rm tr}$. We say that a complex orientation of ![]() $E$ satisfies the Ando criterion if it satisfies the Ando criterion for all primes
$E$ satisfies the Ando criterion if it satisfies the Ando criterion for all primes ![]() $p$.
$p$.
Remark 1.3 If ![]() $E$ is
$E$ is ![]() $p$-local, then
$p$-local, then ![]() $E^* (\mathrm {BC}_\ell ) / I_{\rm tr} = 0$ for all primes
$E^* (\mathrm {BC}_\ell ) / I_{\rm tr} = 0$ for all primes ![]() $\ell \neq p$. Therefore, a complex orientation of a
$\ell \neq p$. Therefore, a complex orientation of a ![]() $p$-local
$p$-local ![]() $\mathbb {E}_\infty$-ring satisfies the Ando criterion if and only if it satisfies the Ando criterion at
$\mathbb {E}_\infty$-ring satisfies the Ando criterion if and only if it satisfies the Ando criterion at ![]() $p$.
$p$.
The complex cobordism spectrum ![]() $\mathrm {MU}$, equipped with the canonical complex orientation, satisfies the Ando criterion.Footnote 1 It follows that any
$\mathrm {MU}$, equipped with the canonical complex orientation, satisfies the Ando criterion.Footnote 1 It follows that any ![]() $\mathbb {E}_\infty$-complex orientation, or more generally any
$\mathbb {E}_\infty$-complex orientation, or more generally any ![]() $\mathbb {H}_\infty$-complex orientation, satisfies the Ando criterion.
$\mathbb {H}_\infty$-complex orientation, satisfies the Ando criterion.
1.2 Results
The first main theorem of this paper states that for many ![]() $\mathbb {E}_\infty$-rings of height at most two, this condition is sufficient, and that the resulting
$\mathbb {E}_\infty$-rings of height at most two, this condition is sufficient, and that the resulting ![]() $\mathbb {E}_\infty$-complex orientations are determined up to homotopy by their underlying complex orientations.
$\mathbb {E}_\infty$-complex orientations are determined up to homotopy by their underlying complex orientations.
Theorem 1.4 Let ![]() $E$ denote a height at most two Landweber exact
$E$ denote a height at most two Landweber exact ![]() $\mathbb {E}_\infty$-ring whose homotopy is concentrated in even degrees. Then any complex orientation
$\mathbb {E}_\infty$-ring whose homotopy is concentrated in even degrees. Then any complex orientation ![]() $\mathrm {MU} \to E$ which satisfies the Ando criterion lifts uniquely up to homotopy to an
$\mathrm {MU} \to E$ which satisfies the Ando criterion lifts uniquely up to homotopy to an ![]() $\mathbb {E}_\infty$-ring map
$\mathbb {E}_\infty$-ring map ![]() $\mathrm {MU} \to E$.
$\mathrm {MU} \to E$.
In the above theorem, we say that a Landweber exact ring spectrum ![]() $E$ is of height at most
$E$ is of height at most ![]() $n$ if
$n$ if ![]() $v_n \in \pi _* (E) / (p, v_1, \ldots, v_{n-1})$ is a unit for all primes
$v_n \in \pi _* (E) / (p, v_1, \ldots, v_{n-1})$ is a unit for all primes ![]() $p$.Footnote 2 As a corollary, we obtain the following result for height at most two Lubin–Tate theories.Footnote 3
$p$.Footnote 2 As a corollary, we obtain the following result for height at most two Lubin–Tate theories.Footnote 3
Corollary 1.5 Let ![]() $k \subseteq \overline {\mathbb {F}}_p$ denote a field of characteristic
$k \subseteq \overline {\mathbb {F}}_p$ denote a field of characteristic ![]() $p > 0$ which is algebraic over the prime field
$p > 0$ which is algebraic over the prime field ![]() $\mathbb {F}_p$, and let
$\mathbb {F}_p$, and let ![]() $\mathbb {G}$ denote a formal group of height at most two over
$\mathbb {G}$ denote a formal group of height at most two over ![]() $k$. Then any complex orientation of the associated
$k$. Then any complex orientation of the associated ![]() $2$-periodic Morava
$2$-periodic Morava ![]() $K$-theory
$K$-theory ![]() $K(k,\mathbb {G})$ lifts uniquely up to homotopy to an
$K(k,\mathbb {G})$ lifts uniquely up to homotopy to an ![]() $\mathbb {E}_\infty$-complex orientation of
$\mathbb {E}_\infty$-complex orientation of ![]() $E(k, \mathbb {G})$
$E(k, \mathbb {G})$
Proof. This follows immediately from Theorem 1.4 and [Reference ZhuZhu20, Theorem 1.2], which implies that every complex orientation of ![]() $K(k,\mathbb {G})$ admits a unique lift to a complex orientation of
$K(k,\mathbb {G})$ admits a unique lift to a complex orientation of ![]() $E(k,\mathbb {G})$ which satisfies the Ando criterion whenever
$E(k,\mathbb {G})$ which satisfies the Ando criterion whenever ![]() $k$ is algebraic over
$k$ is algebraic over ![]() $\mathbb {F}_p$.
$\mathbb {F}_p$.
Remark 1.6 Theorem 1.4 was inspired by recent work of Balderrama [Reference BalderramaBal21, Theorem 6.5.3]. Balderrama showed that every periodic complex orientation of a Lubin–Tate theory of height at most two satisfying an analogue of the Ando criterion lifts to an ![]() $\mathbb {E}_\infty$-orientation. He also showed that
$\mathbb {E}_\infty$-orientation. He also showed that ![]() $\mathbb {E}_\infty$-refinements of periodic complex orientations of even periodic
$\mathbb {E}_\infty$-refinements of periodic complex orientations of even periodic ![]() $K(1)$-local
$K(1)$-local ![]() $\mathbb {E}_\infty$-rings exist whenever the Ando criterion is satisfied and are unique up to homotopy.
$\mathbb {E}_\infty$-rings exist whenever the Ando criterion is satisfied and are unique up to homotopy.
The key observation he made is the presence of evenness in the Goerss–Hopkins obstruction theory for (periodic) ![]() $\mathbb {E}_\infty$-complex orientations, which implies that the obstructions to existence and uniqueness appearing in his theorem vanish for formal reasons. Our results about existence of
$\mathbb {E}_\infty$-complex orientations, which implies that the obstructions to existence and uniqueness appearing in his theorem vanish for formal reasons. Our results about existence of ![]() $\mathbb {E}_\infty$-complex orientations will be obtained by observing a similar evenness in the Hopkins–Lawson obstruction theory [Reference Hopkins and LawsonHL18].
$\mathbb {E}_\infty$-complex orientations will be obtained by observing a similar evenness in the Hopkins–Lawson obstruction theory [Reference Hopkins and LawsonHL18].
In contrast to Theorem 1.4, Balderrama did not obtain any uniqueness results at height ![]() $2$ (see [Reference BalderramaBal21, Remark 6.5.4]). In Remark 3.6, we will prove that
$2$ (see [Reference BalderramaBal21, Remark 6.5.4]). In Remark 3.6, we will prove that ![]() $\mathbb {E}_\infty$-refinements of periodic complex orientations of height
$\mathbb {E}_\infty$-refinements of periodic complex orientations of height ![]() $2$ Lubin–Tate theories are unique.
$2$ Lubin–Tate theories are unique.
Our second main theorem uses Theorem 1.4 to give a simple proof of the following theorem.
Theorem 1.7 For ![]() $n \geq 2$, the Hirzebruch level
$n \geq 2$, the Hirzebruch level ![]() $n$ elliptic genus lifts uniquely up to homotopy to a map of
$n$ elliptic genus lifts uniquely up to homotopy to a map of ![]() $\mathbb {E}_\infty$-rings
$\mathbb {E}_\infty$-rings
While Theorem 1.4 does not apply directly to ![]() $\mathrm {tmf}_1 (n)$, it does apply to
$\mathrm {tmf}_1 (n)$, it does apply to ![]() $\mathrm {TMF}_1 (n)$, and it is not hard to upgrade the resulting
$\mathrm {TMF}_1 (n)$, and it is not hard to upgrade the resulting ![]() $\mathbb {E}_\infty$-complex orientation to one of
$\mathbb {E}_\infty$-complex orientation to one of ![]() $\mathrm {tmf}_1 (n)$. This reduces us to verifying the Ando criterion, which may be done following the strategy of Ando, Hopkins, and Strickland [Reference Ando, Hopkins and StricklandAHS04].
$\mathrm {tmf}_1 (n)$. This reduces us to verifying the Ando criterion, which may be done following the strategy of Ando, Hopkins, and Strickland [Reference Ando, Hopkins and StricklandAHS04].
Remark 1.8 During the writing process, [Reference AbsmeierAbs21] has also appeared, which follows the strategy of Ando, Hopkins, and Rezk [Reference Ando, Hopkins and RezkAHR10] to prove a similar result to Theorem 1.7 for ![]() $\mathrm {Tmf}_1 (n)$. Our method is rather different from that of Absmeier and completely avoids the consideration of
$\mathrm {Tmf}_1 (n)$. Our method is rather different from that of Absmeier and completely avoids the consideration of ![]() $p$-adic Eisenstein measures.
$p$-adic Eisenstein measures.
1.3 Further questions
One of the key inputs in our proof of Theorem 1.4 is Theorem 2.11, which states that the Morava ![]() $K$-theory of certain finite groups is concentrated in even degrees. This is closely related to these groups being good in the sense of Hopkins, Kuhn, and Ravenel [Reference Hopkins, Kuhn and RavenelHKR00, § 7].
$K$-theory of certain finite groups is concentrated in even degrees. This is closely related to these groups being good in the sense of Hopkins, Kuhn, and Ravenel [Reference Hopkins, Kuhn and RavenelHKR00, § 7].
These groups come in a family, and to see that the Hopkins–Lawson obstruction theory is concentrated in even degrees one would like to show that the entire family has Morava ![]() $K$-theory concentrated in even degrees; see Remark 2.13.
$K$-theory concentrated in even degrees; see Remark 2.13.
Question 1.9 Is the Morava ![]() $K$-theory of the groups
$K$-theory of the groups ![]() $\Gamma _k ^{(n)}$ of Definition 2.7 concentrated in even degrees for
$\Gamma _k ^{(n)}$ of Definition 2.7 concentrated in even degrees for ![]() $k > 2$, at least for
$k > 2$, at least for ![]() $n \gg 0$? The groups
$n \gg 0$? The groups ![]() $\Gamma _k ^{(1)}$ are the extraspecial
$\Gamma _k ^{(1)}$ are the extraspecial ![]() $p$-groups of type
$p$-groups of type ![]() $p^{1+2k} _+$.
$p^{1+2k} _+$.
One could also ask about ![]() $C_2$-equivariant refinement of our results.
$C_2$-equivariant refinement of our results.
Question 1.10 The complex cobordism spectrum may be refined to a ![]() $C_2$-equivariant
$C_2$-equivariant ![]() $\mathbb {E}_\infty$-ring
$\mathbb {E}_\infty$-ring ![]() $\mathrm {MU}_\mathbb {R}$, and
$\mathrm {MU}_\mathbb {R}$, and ![]() $\mathrm {tmf}_1 (n)$ admits the natural structure of a
$\mathrm {tmf}_1 (n)$ admits the natural structure of a ![]() $C_2$-equivariant
$C_2$-equivariant ![]() $\mathbb {E}_\infty$-ring [Reference MeierMei21, Theorem 2.20]. Moreover, the Hirzebruch level
$\mathbb {E}_\infty$-ring [Reference MeierMei21, Theorem 2.20]. Moreover, the Hirzebruch level ![]() $n$ elliptic genus admits a refinement to a map of homotopy
$n$ elliptic genus admits a refinement to a map of homotopy ![]() $C_2$-ring spectra
$C_2$-ring spectra ![]() $\mathrm {MU}_\mathbb {R} \to \mathrm {tmf}_1 (n)$ (see [Reference MeierMei21, Theorem 3.5]). Is there a suitable
$\mathrm {MU}_\mathbb {R} \to \mathrm {tmf}_1 (n)$ (see [Reference MeierMei21, Theorem 3.5]). Is there a suitable ![]() $C_2$-equivariant analogue of Theorem 1.4 which may be used to prove a
$C_2$-equivariant analogue of Theorem 1.4 which may be used to prove a ![]() $C_2$-equivariant refinement of Theorem 1.7? See [Reference Hopkins and LawsonHL18, Remark 13] for a comment on a
$C_2$-equivariant refinement of Theorem 1.7? See [Reference Hopkins and LawsonHL18, Remark 13] for a comment on a ![]() $C_2$-equivariant version of the Hopkins–Lawson obstruction theory.
$C_2$-equivariant version of the Hopkins–Lawson obstruction theory.
On the other hand, it would be very interesting to study ![]() $\mathbb {E}_\infty$-complex orientations at heights
$\mathbb {E}_\infty$-complex orientations at heights ![]() $3$ and above. A natural choice of spectra to study would be Lubin–Tate spectra. Since the obstruction groups do not vanish for formal reasons at these heights, it seems likely that this will require an explicit analysis of the Goerss–Hopkins obstruction theory for
$3$ and above. A natural choice of spectra to study would be Lubin–Tate spectra. Since the obstruction groups do not vanish for formal reasons at these heights, it seems likely that this will require an explicit analysis of the Goerss–Hopkins obstruction theory for ![]() $\mathbb {E}_\infty$-maps
$\mathbb {E}_\infty$-maps ![]() $\mathrm {MU} \to E(k,\mathbb {G})$. In particular, one would have to compute the
$\mathrm {MU} \to E(k,\mathbb {G})$. In particular, one would have to compute the ![]() $\mathrm {E}_2$-page.
$\mathrm {E}_2$-page.
Problem 1.11 Compute the Goerss–Hopkins obstruction groups for ![]() $\mathbb {E}_\infty$-maps
$\mathbb {E}_\infty$-maps ![]() $\mathrm {MU} \to E(k,\mathbb {G})$ for height
$\mathrm {MU} \to E(k,\mathbb {G})$ for height ![]() $3$ and above Lubin–Tate theories
$3$ and above Lubin–Tate theories ![]() $E(k,\mathbb {G})$.
$E(k,\mathbb {G})$.
2. Existence of  $\mathbb {E}_\infty$-orientations
$\mathbb {E}_\infty$-orientations
In this section, we will prove the half of Theorem 1.4 concerning the existence of ![]() $\mathbb {E}_\infty$-complex orientations. The main tool that we will utilize is an obstruction theory for
$\mathbb {E}_\infty$-complex orientations. The main tool that we will utilize is an obstruction theory for ![]() $\mathbb {E}_\infty$-complex orientations studied by Hopkins and Lawson [Reference Hopkins and LawsonHL18]. Given this obstruction theory, the existence half of Theorem 1.4 reduces to the statement that certain obstruction groups vanish. Using work of Arone and Lesh [Reference Arone and LeshAL07], this can be further reduced to the evenness of the Morava
$\mathbb {E}_\infty$-complex orientations studied by Hopkins and Lawson [Reference Hopkins and LawsonHL18]. Given this obstruction theory, the existence half of Theorem 1.4 reduces to the statement that certain obstruction groups vanish. Using work of Arone and Lesh [Reference Arone and LeshAL07], this can be further reduced to the evenness of the Morava ![]() $K$-theory of certain extraspecial
$K$-theory of certain extraspecial ![]() $p$-groups and related groups, which we are able to extract from the literature.
$p$-groups and related groups, which we are able to extract from the literature.
2.1 Hopkins–Lawson obstruction theory
We begin by summarizing the main results of the Hopkins–Lawson obstruction theory [Reference Hopkins and LawsonHL18]. First, a definition.
Definition 2.1 Let ![]() $E$ denote a homotopy commutative ring spectrum. We let
$E$ denote a homotopy commutative ring spectrum. We let ![]() $\mathrm {Or}(E)$ denote the space of complex orientations of
$\mathrm {Or}(E)$ denote the space of complex orientations of ![]() $E$, i.e. the fiber
$E$, i.e. the fiber
above the unit map ![]() $\mathbb {S} \to E$.
$\mathbb {S} \to E$.
Theorem 2.2 [Reference Hopkins and LawsonHL18, Theorems 1 and 32]
There exists a diagram of ![]() $\mathbb {E}_\infty$-ring spectra
$\mathbb {E}_\infty$-ring spectra
such that the following hold:
(i) the natural map
 $\varinjlim \mathrm {MX}_n \to \mathrm {MU}$ is an equivalence;
$\varinjlim \mathrm {MX}_n \to \mathrm {MU}$ is an equivalence;(ii) the
 $\mathbb {E}_\infty$-ring
$\mathbb {E}_\infty$-ring  $\mathrm {MX}_1$ is equipped with a natural complex orientation inducing an equivalence
$\mathrm {MX}_1$ is equipped with a natural complex orientation inducing an equivalence  $\mathrm {Map}_{\mathbb {E}_\infty } (\mathrm {MX}_1, E) \xrightarrow {\sim } \mathrm {Or}(E)$ for each
$\mathrm {Map}_{\mathbb {E}_\infty } (\mathrm {MX}_1, E) \xrightarrow {\sim } \mathrm {Or}(E)$ for each  $\mathbb {E}_\infty$-ring
$\mathbb {E}_\infty$-ring  $E$;
$E$;(iii) given
 $m > 0$ and an
$m > 0$ and an  $\mathbb {E}_\infty$-ring
$\mathbb {E}_\infty$-ring  $E$, there is a pullback square
where
$E$, there is a pullback square
where
 $F_m$ is a pointed space described in Recollection 2.6;
$F_m$ is a pointed space described in Recollection 2.6;(iv) the map
 $\mathrm {MX}_{m-1} \to \mathrm {MX}_m$ is a rational equivalence if
$\mathrm {MX}_{m-1} \to \mathrm {MX}_m$ is a rational equivalence if  $m > 1$, a
$m > 1$, a  $p$-local equivalence if
$p$-local equivalence if  $m$ is not a power of
$m$ is not a power of  $p$, and a
$p$, and a  $K(n)$-local equivalence if
$K(n)$-local equivalence if  $m > p^n$;
$m > p^n$;(v) let
 $E$ denote an
$E$ denote an  $\mathbb {E}_\infty$-ring such that
$\mathbb {E}_\infty$-ring such that  $\pi _* E$ is
$\pi _* E$ is  $p$-local and
$p$-local and  $p$-torsion free. Then an
$p$-torsion free. Then an  $\mathbb {E}_\infty$-map
$\mathbb {E}_\infty$-map  $\mathrm {MX}_1 \to E$ extends to an
$\mathrm {MX}_1 \to E$ extends to an  $\mathbb {E}_\infty$-map
$\mathbb {E}_\infty$-map  $\mathrm {MX}_p \to E$ if and only if the corresponding complex orientation of
$\mathrm {MX}_p \to E$ if and only if the corresponding complex orientation of  $E$ satisfies the Ando criterion.
$E$ satisfies the Ando criterion.
Using this theorem, we will reduce the proof of Theorem 1.4 to the following.
Lemma 2.3 Let ![]() $E$ denote a
$E$ denote a ![]() $p$-complete Landweber exact ring spectrum with homotopy concentrated in even degrees. Then
$p$-complete Landweber exact ring spectrum with homotopy concentrated in even degrees. Then ![]() $E^{2n} (F_p) \cong E^{2n+1} (F_{p^2}) \cong 0$ for all
$E^{2n} (F_p) \cong E^{2n+1} (F_{p^2}) \cong 0$ for all ![]() $n \in \mathbb {Z}$.
$n \in \mathbb {Z}$.
Remark 2.4 In fact, we only need that ![]() $E^{2n+1} (F_{p^2}) \cong 0$. However, we include the statement
$E^{2n+1} (F_{p^2}) \cong 0$. However, we include the statement ![]() $E^{2n} (F_p) \cong 0$ since it is no harder for us to prove. This extra evenness implies uniqueness up to homotopy for
$E^{2n} (F_p) \cong 0$ since it is no harder for us to prove. This extra evenness implies uniqueness up to homotopy for ![]() $\mathbb {E}_\infty$-refinements of complex orientations of height at most one. However, we will prove uniqueness in a different way in § 3.
$\mathbb {E}_\infty$-refinements of complex orientations of height at most one. However, we will prove uniqueness in a different way in § 3.
Question 2.5 Given a ![]() $p$-complete Landweber exact ring spectrum
$p$-complete Landweber exact ring spectrum ![]() $E$ with homotopy concentrated in even degrees, is
$E$ with homotopy concentrated in even degrees, is ![]() $E^{2*+k-1} (F_{p^k}) \cong 0$ for
$E^{2*+k-1} (F_{p^k}) \cong 0$ for ![]() $k \geq 3$?
$k \geq 3$?
Proof Proof of existence in Theorem 1.4 assuming Lemma 2.3
We begin by reducing to the case where ![]() $E$ is
$E$ is ![]() $p$-complete for some prime
$p$-complete for some prime ![]() $p$. We make use of the following fracture square (see [Reference BousfieldBou79, Proposition 2.9]).
$p$. We make use of the following fracture square (see [Reference BousfieldBou79, Proposition 2.9]).

Note that ![]() $E^{\wedge } _p$ is again even and Landweber exact; see Appendix A.
$E^{\wedge } _p$ is again even and Landweber exact; see Appendix A.
By Theorem 2.2, we have ![]() $\mathrm {Map}_{\mathbb {E}_\infty } (\mathrm {MU}, R) \simeq \mathrm {Or}(R)$ for a rational
$\mathrm {Map}_{\mathbb {E}_\infty } (\mathrm {MU}, R) \simeq \mathrm {Or}(R)$ for a rational ![]() $\mathbb {E}_\infty$-ring
$\mathbb {E}_\infty$-ring ![]() $R$; it follows further that
$R$; it follows further that ![]() $\pi _1 \mathrm {Map}_{\mathbb {E}_\infty } (\mathrm {MU}, R) \cong \pi _1 \mathrm {Or}(R) \cong 0$ if
$\pi _1 \mathrm {Map}_{\mathbb {E}_\infty } (\mathrm {MU}, R) \cong \pi _1 \mathrm {Or}(R) \cong 0$ if ![]() $R$ has homotopy concentrated in even degrees. As a consequence, there are pullback squares of sets:
$R$ has homotopy concentrated in even degrees. As a consequence, there are pullback squares of sets:

and

To lift a complex orientation of ![]() $E$ to an
$E$ to an ![]() $\mathbb {E}_\infty$-complex orientation, it therefore suffices to lift the induced complex orientation of
$\mathbb {E}_\infty$-complex orientation, it therefore suffices to lift the induced complex orientation of ![]() $E^{\wedge }_p$. We may therefore assume that
$E^{\wedge }_p$. We may therefore assume that ![]() $E$ is
$E$ is ![]() $p$-complete.
$p$-complete.
Let ![]() $E$ now denote an
$E$ now denote an ![]() $p$-complete Landweber exact
$p$-complete Landweber exact ![]() $\mathbb {E}_\infty$-ring with homotopy concentrated in even degrees. Using Theorem 2.2, we see that it suffices to show that
$\mathbb {E}_\infty$-ring with homotopy concentrated in even degrees. Using Theorem 2.2, we see that it suffices to show that
is surjective.
By Theorem 2.2, there is a fiber sequence
Now, there are equivalences
where in the second equivalence we have used the fact that ![]() $\Sigma ^\infty F_m$ is
$\Sigma ^\infty F_m$ is ![]() $(2m-1)$-connected by [Reference Hopkins and LawsonHL18, Corollary 4(5)]. It therefore follows from the above fiber sequence that it suffices to show that
$(2m-1)$-connected by [Reference Hopkins and LawsonHL18, Corollary 4(5)]. It therefore follows from the above fiber sequence that it suffices to show that
Since ![]() $E$ is
$E$ is ![]() $p$-complete, this follows from Lemma 2.3.
$p$-complete, this follows from Lemma 2.3.
2.2 Proof of Lemma 2.3
In the remainder of this section, we will prove Lemma 2.3. First, we must recall the definition of the spaces ![]() $F_m$.
$F_m$.
Recollection 2.6 Let ![]() $L_m$ denote the nerve of the topologized poset of proper direct-sum decompositions of
$L_m$ denote the nerve of the topologized poset of proper direct-sum decompositions of ![]() $\mathbb {C}^m$, and let
$\mathbb {C}^m$, and let ![]() $(L_m)^{\diamond }$ denote its unreduced suspension. The natural action of
$(L_m)^{\diamond }$ denote its unreduced suspension. The natural action of ![]() $U(m)$ on
$U(m)$ on ![]() $\mathbb {C}^m$ endows
$\mathbb {C}^m$ endows ![]() $L_m$ and
$L_m$ and ![]() $(L_m)^{\diamond }$ with the structure of
$(L_m)^{\diamond }$ with the structure of ![]() $U(m)$-spaces.
$U(m)$-spaces.
Furthermore, view ![]() $S^{2m}$ as a
$S^{2m}$ as a ![]() $U(m)$-space via its identification with the one-point compactification of
$U(m)$-space via its identification with the one-point compactification of ![]() $\mathbb {C}^m$, viewed as the fundamental representation of
$\mathbb {C}^m$, viewed as the fundamental representation of ![]() $U(m)$. Then
$U(m)$. Then ![]() $F_m$ is given by
$F_m$ is given by
To prove Lemma 2.3, we will use a result of Arone–Lesh to reduce the study of the ![]() $E$-cohomology of
$E$-cohomology of ![]() $F_m$ to the
$F_m$ to the ![]() $E$-cohomology of certain groups
$E$-cohomology of certain groups ![]() $\Gamma _k$, whose definition we now recall.
$\Gamma _k$, whose definition we now recall.
Definition 2.7 [Reference OliverOli94, Definition 1]
Let ![]() $\sigma _0, \ldots, \sigma _{k-1} \in \Sigma _{p^k}$ denote the permutations
$\sigma _0, \ldots, \sigma _{k-1} \in \Sigma _{p^k}$ denote the permutations
 \[ \sigma_r (i) = \begin{cases} i + p^r & \text{ if } i \equiv 1, \ldots, (p-1)p^r \mod p^{r+1}, \\ i-(p-1) p^r & \text{ if } i \equiv (p-1)p^r +1, \ldots, p^{r+1} \mod p^{r+1}. \end{cases} \]
\[ \sigma_r (i) = \begin{cases} i + p^r & \text{ if } i \equiv 1, \ldots, (p-1)p^r \mod p^{r+1}, \\ i-(p-1) p^r & \text{ if } i \equiv (p-1)p^r +1, \ldots, p^{r+1} \mod p^{r+1}. \end{cases} \]
We let ![]() $\Gamma _k \subset U(p^k)$ denote the subgroup generated by the permutation matrices corresponding to
$\Gamma _k \subset U(p^k)$ denote the subgroup generated by the permutation matrices corresponding to ![]() $\sigma _0, \ldots, \sigma _{k-1}$, the central
$\sigma _0, \ldots, \sigma _{k-1}$, the central ![]() $S^1$, and the diagonal matrices
$S^1$, and the diagonal matrices ![]() $A_0, \ldots, A_{k-1}$ given by
$A_0, \ldots, A_{k-1}$ given by
where ![]() $\zeta _p$ is a primitive
$\zeta _p$ is a primitive ![]() $p$th root of unity. Then
$p$th root of unity. Then ![]() $\Gamma _k$ lies in a central extension
$\Gamma _k$ lies in a central extension
For each ![]() $n \geq 1$, there is a normal subgroup
$n \geq 1$, there is a normal subgroup ![]() $\Gamma _k ^{(n)} \subset \Gamma _k$ which only contains the central
$\Gamma _k ^{(n)} \subset \Gamma _k$ which only contains the central ![]() $p^{n}$th roots of unity instead of the full
$p^{n}$th roots of unity instead of the full ![]() $S^1$. Then there are central extensions
$S^1$. Then there are central extensions
and exact sequences
Remark 2.8 The groups ![]() $\Gamma _k ^{(1)}$ are examples of extraspecial
$\Gamma _k ^{(1)}$ are examples of extraspecial ![]() $p$-groups, and in this language are commonly denoted by
$p$-groups, and in this language are commonly denoted by ![]() $p^{1+2k} _+$.
$p^{1+2k} _+$.
Proposition 2.9 [Reference Arone and LeshAL07, Propositions 9.6 and 10.3]
The ![]() $p$-completion of the spectrum
$p$-completion of the spectrum
is null unless ![]() $m = p^k$, in which case it is a summand of the
$m = p^k$, in which case it is a summand of the ![]() $p$-completion of
$p$-completion of
where ![]() $\Gamma _k$ acts on
$\Gamma _k$ acts on ![]() $S^{2p^k}$ via the inclusion
$S^{2p^k}$ via the inclusion ![]() $\Gamma _k \subset U(p^k)$.
$\Gamma _k \subset U(p^k)$.
Now, ![]() $(S^{2p^k})_{h\Gamma _k}$ may also be described as the Thom spectrum associated to the composition
$(S^{2p^k})_{h\Gamma _k}$ may also be described as the Thom spectrum associated to the composition
from which it follows that
Lemma 2.3 therefore reduces to the following lemma.
Lemma 2.10 Let ![]() $E$ denote a
$E$ denote a ![]() $p$-local Landweber exact ring spectrum whose homotopy is concentrated in even degrees. Then, for
$p$-local Landweber exact ring spectrum whose homotopy is concentrated in even degrees. Then, for ![]() $k \leq 2$,
$k \leq 2$, ![]() $E^* (B\Gamma _k\!)$ is concentrated in even degrees.
$E^* (B\Gamma _k\!)$ is concentrated in even degrees.
We will deduce Lemma 2.10 from the following Morava ![]() $K$-theory computations.
$K$-theory computations.
Theorem 2.11 For all ![]() $n \geq 0$, the following groups are concentrated in even degrees:
$n \geq 0$, the following groups are concentrated in even degrees:
(i) (Tezuka and Yagita [Reference Tezuka and YagitaTY89, Theorem 4.2])
 $K(n)^* (B\Gamma _1 ^{(1)})$ at all primes
$K(n)^* (B\Gamma _1 ^{(1)})$ at all primes  $p$;
$p$;(ii) (Schuster and Yagita [Reference Schuster and YagitaSY04, Theorem 5.4])
 $K(n)^* (B\Gamma _2 ^{(1)})$ at the prime
$K(n)^* (B\Gamma _2 ^{(1)})$ at the prime  $2$;
$2$;(iii) (Yagita [Reference YagitaYag05, Theorem 1.2])
 $K(n)^* (B\Gamma _2 ^{(2)})$ at odd primes
$K(n)^* (B\Gamma _2 ^{(2)})$ at odd primes  $p$.
$p$.
A lemma of Strickland which builds on the work of Ravenel, Wilson, and Yagita [Reference Ravenel, Wilson and YagitaRWY98] allows us to transport this evenness from Morava ![]() $K$-theory to
$K$-theory to ![]() $E$-cohomology.
$E$-cohomology.
Corollary 2.12 Given a ![]() $p$-local Landweber exact ring spectrum
$p$-local Landweber exact ring spectrum ![]() $E$ whose homotopy is concentrated in even degrees, the following groups are concentrated in even degrees:
$E$ whose homotopy is concentrated in even degrees, the following groups are concentrated in even degrees:
(i)
 $E^* (B\Gamma _1 ^{(1)})$ at all primes
$E^* (B\Gamma _1 ^{(1)})$ at all primes  $p$;
$p$;(ii)
 $E^* (B\Gamma _2 ^{(1)})$ at the prime
$E^* (B\Gamma _2 ^{(1)})$ at the prime  $2$;
$2$;(iii)
 $E^* (B\Gamma _2 ^{(2)})$ at odd primes
$E^* (B\Gamma _2 ^{(2)})$ at odd primes  $p$.
$p$.
Proof. Combine Theorem 2.11 with [Reference StricklandStr99, Lemma 8.25].Footnote 4![]() $^,$Footnote 5
$^,$Footnote 5
Proof of Lemma 2.10 The short exact sequence
induces a fiber sequence
Using the associated Atiyah–Hirzebruch spectral sequence
we find that if ![]() $E^* (B\Gamma _k ^{(n)})$ is even for some
$E^* (B\Gamma _k ^{(n)})$ is even for some ![]() $n$, then
$n$, then ![]() $E^* (B\Gamma _k)$ must be as well. Therefore, Lemma 2.10 follows from Corollary 2.12.
$E^* (B\Gamma _k)$ must be as well. Therefore, Lemma 2.10 follows from Corollary 2.12.
Remark 2.13 By the same arguments, to give a positive answer to Question 2.5 it suffices to show that ![]() $K(n)^* (B\Gamma _k ^{(i_k)})$ is concentrated in even degrees for a fixed
$K(n)^* (B\Gamma _k ^{(i_k)})$ is concentrated in even degrees for a fixed ![]() $i_k$ not depending on
$i_k$ not depending on ![]() $n$. This is closely related to the question of whether
$n$. This is closely related to the question of whether ![]() $\Gamma _k ^{(i_k)}$ is a good group in the sense of Hopkins, Kuhn, and Ravenel [Reference Hopkins, Kuhn and RavenelHKR00, § 7].
$\Gamma _k ^{(i_k)}$ is a good group in the sense of Hopkins, Kuhn, and Ravenel [Reference Hopkins, Kuhn and RavenelHKR00, § 7].
3. Uniqueness of  $\mathbb {E}_\infty$-orientations
$\mathbb {E}_\infty$-orientations
Our goal in this section is to prove the following result.
Theorem 3.1 Let ![]() $E$ denote an
$E$ denote an ![]() $L_2$-localFootnote 6 complex orientable
$L_2$-localFootnote 6 complex orientable ![]() $\mathbb {E}_\infty$-ring with the property that
$\mathbb {E}_\infty$-ring with the property that ![]() $K(1)_* E$ and
$K(1)_* E$ and ![]() $K(1)_* L_{K(2)} E$ are concentrated in even degrees at all primes
$K(1)_* L_{K(2)} E$ are concentrated in even degrees at all primes ![]() $p$. Then each complex orientation of
$p$. Then each complex orientation of ![]() $E$ admits at most one refinement to an
$E$ admits at most one refinement to an ![]() $\mathbb {E}_\infty$-complex orientation up to homotopy.
$\mathbb {E}_\infty$-complex orientation up to homotopy.
Example 3.2 Any Landweber exact ring spectrum ![]() $E$ of height at most two whose homotopy is concentrated in even degrees satisfies the hypotheses of Theorem 3.1. By Lemma A.1,
$E$ of height at most two whose homotopy is concentrated in even degrees satisfies the hypotheses of Theorem 3.1. By Lemma A.1, ![]() $L_{K(2)} E$ is again Landweber exact and has homotopy concentrated in even degrees. It therefore suffices to show that
$L_{K(2)} E$ is again Landweber exact and has homotopy concentrated in even degrees. It therefore suffices to show that ![]() $K(1)_* E$ is concentrated in even degrees. This is true because
$K(1)_* E$ is concentrated in even degrees. This is true because ![]() $K(1)_* E \cong K(1)_* \mathrm {MU} \otimes _{\pi _* \mathrm {MU}} \pi _* E$, and
$K(1)_* E \cong K(1)_* \mathrm {MU} \otimes _{\pi _* \mathrm {MU}} \pi _* E$, and ![]() $K(1)_* \mathrm {MU}$ is concentrated in even degrees.
$K(1)_* \mathrm {MU}$ is concentrated in even degrees.
Combining Theorem 3.1 with Example 3.2, we obtain the uniqueness half of Theorem 1.4.
Example 3.3 The ring spectra ![]() $\mathrm {Tmf}_1 (n)$ satisfy the hypotheses of Theorem 3.1. This follows from [Reference WilsonWil15, Propositions 2.4 and 2.6], which imply that the
$\mathrm {Tmf}_1 (n)$ satisfy the hypotheses of Theorem 3.1. This follows from [Reference WilsonWil15, Propositions 2.4 and 2.6], which imply that the ![]() $p$-complete complex
$p$-complete complex ![]() $K$-theory of these spectra and their
$K$-theory of these spectra and their ![]() $K(2)$-localizations is
$K(2)$-localizations is ![]() $p$-torsionfree and concentrated in even degrees. The proof is exactly the same as the case without level structure, which is treated in [Reference Behrens, Douglas, Francis, Henriques and HillBeh14]. The key point is that the Igusa tower becomes formally affine at a finite stage.
$p$-torsionfree and concentrated in even degrees. The proof is exactly the same as the case without level structure, which is treated in [Reference Behrens, Douglas, Francis, Henriques and HillBeh14]. The key point is that the Igusa tower becomes formally affine at a finite stage.
Our proof of Theorem 3.1 will be based on the orientation theory of [Reference Ando, Blumberg, Gepner, Hopkins and RezkABGHR14] and the following lemma.
Lemma 3.4 Let ![]() $E$ denote an
$E$ denote an ![]() $\mathrm {MU}$-module with the property that
$\mathrm {MU}$-module with the property that ![]() $K(1)_* E$ is concentrated in even degrees. Then
$K(1)_* E$ is concentrated in even degrees. Then ![]() $[\mathrm {KU}_p, L_{K(1)} E]$ is torsionfree and
$[\mathrm {KU}_p, L_{K(1)} E]$ is torsionfree and ![]() $[\Sigma \mathrm {KU}_p, L_{K(1)} E] = 0$.
$[\Sigma \mathrm {KU}_p, L_{K(1)} E] = 0$.
Definition 3.5 We say that a ![]() $(\mathrm {KU}_p)_*$-module is pro-free if it is the
$(\mathrm {KU}_p)_*$-module is pro-free if it is the ![]() $p$-completion of a free module. Moreover, given a spectrum
$p$-completion of a free module. Moreover, given a spectrum ![]() $X$, we write
$X$, we write ![]() $\mathrm {KU}^{\vee }_* (X)$ for
$\mathrm {KU}^{\vee }_* (X)$ for ![]() $\pi _* L_{K(1)} (\mathrm {KU} \otimes X)$.
$\pi _* L_{K(1)} (\mathrm {KU} \otimes X)$.
Proof. Since ![]() $K(1)_* (\mathrm {KU}_p)$ is even,
$K(1)_* (\mathrm {KU}_p)$ is even, ![]() $\mathrm {KU}^{\vee } _* (\mathrm {KU}_p)$ is pro-free by [Reference Hovey and StricklandHSt99, Proposition 8.4(f)]. Therefore, by [Reference Barthel and HeardBH16, Proposition 1.14], there is an isomorphism
$\mathrm {KU}^{\vee } _* (\mathrm {KU}_p)$ is pro-free by [Reference Hovey and StricklandHSt99, Proposition 8.4(f)]. Therefore, by [Reference Barthel and HeardBH16, Proposition 1.14], there is an isomorphism
By assumption, ![]() $K(1)_* (E)$ is even and, hence,
$K(1)_* (E)$ is even and, hence, ![]() $\mathrm {KU}^{\vee } _* (E)$ is even and pro-free by [Reference Hovey and StricklandHSt99, Proposition 8.4(f)]. In particular, it is torsionfree, so that
$\mathrm {KU}^{\vee } _* (E)$ is even and pro-free by [Reference Hovey and StricklandHSt99, Proposition 8.4(f)]. In particular, it is torsionfree, so that ![]() $\mathrm {Hom}_{(\mathrm {KU}_p)_*} (\mathrm {KU}^{\vee } _* (\mathrm {KU}_p), \mathrm {KU}^{\vee } _* (E))$ is even and torsionfree.
$\mathrm {Hom}_{(\mathrm {KU}_p)_*} (\mathrm {KU}^{\vee } _* (\mathrm {KU}_p), \mathrm {KU}^{\vee } _* (E))$ is even and torsionfree.
The result then follows from the following facts.
(i) Since
 $E$ is an
$E$ is an  $\mathrm {MU}$-module, the unit map
$\mathrm {MU}$-module, the unit map  $L_{K(1)} E \to L_{K(1)} (\mathrm {MU} \otimes E)$ admits a splitting given by the module structure map.
$L_{K(1)} E \to L_{K(1)} (\mathrm {MU} \otimes E)$ admits a splitting given by the module structure map.(ii) There is a splitting of the map
 $L_{K(1)} \mathrm {MU} \to L_{K(1)} E(1)$ which is compatible with the unit map [Reference Hovey and SadofskyHSa99, Theorem 4.1].
$L_{K(1)} \mathrm {MU} \to L_{K(1)} E(1)$ which is compatible with the unit map [Reference Hovey and SadofskyHSa99, Theorem 4.1].(iii) There is an equivalence of spectra
 $\mathrm {KU}_p \simeq \bigoplus _{i=0} ^{p-2} \Sigma ^{2i} L_{K(1)} E(1)$.
$\mathrm {KU}_p \simeq \bigoplus _{i=0} ^{p-2} \Sigma ^{2i} L_{K(1)} E(1)$.
Proof of Theorem 3.1 Using the pullback square of sets (1), we may assume that ![]() $E$ is
$E$ is ![]() $p$-complete.
$p$-complete.
Recall the map ![]() $\Sigma ^{\infty } \mathbb {CP}^{\infty } \to \mathrm {bu}$ which is adjoint to the canonical map
$\Sigma ^{\infty } \mathbb {CP}^{\infty } \to \mathrm {bu}$ which is adjoint to the canonical map ![]() $\mathbb {CP}^\infty \to \mathrm {BU}$. By orientation theory [Reference Ando, Blumberg, Gepner, Hopkins and RezkABGHR14], we must show that
$\mathbb {CP}^\infty \to \mathrm {BU}$. By orientation theory [Reference Ando, Blumberg, Gepner, Hopkins and RezkABGHR14], we must show that
is injective. Since ![]() $E$ is
$E$ is ![]() $p$-complete,
$p$-complete, ![]() $\mathrm {gl}_1 (E)$ agrees with
$\mathrm {gl}_1 (E)$ agrees with ![]() $\mathrm {gl}_1 (E)^{\wedge } _p$ in degrees
$\mathrm {gl}_1 (E)^{\wedge } _p$ in degrees ![]() ${\geq }2$, so we may as well replace the former by the latter. Letting
${\geq }2$, so we may as well replace the former by the latter. Letting ![]() $F$ denote the fiber of the map
$F$ denote the fiber of the map ![]() $\mathrm {gl}_1 (E) \to L_2 \mathrm {gl}_1 (E)$, we find that there is a fiber sequence
$\mathrm {gl}_1 (E) \to L_2 \mathrm {gl}_1 (E)$, we find that there is a fiber sequence
It therefore suffices to show that
and
are injective. The first is injective because ![]() $F^{\wedge } _p$ is
$F^{\wedge } _p$ is ![]() $3$-coconnective by [Reference Ando, Hopkins and RezkAHR10, Theorem 4.11] and the cofiber of
$3$-coconnective by [Reference Ando, Hopkins and RezkAHR10, Theorem 4.11] and the cofiber of ![]() $\Sigma ^{\infty } \mathbb {CP}^{\infty } \to \mathrm {bu}$ is
$\Sigma ^{\infty } \mathbb {CP}^{\infty } \to \mathrm {bu}$ is ![]() $4$-connective.
$4$-connective.
To prove that the second is injective, we first note that the Bousfield–Kuhn functor [Reference BousfieldBou87, Reference KuhnKuh89] and the chromatic fracture square for ![]() $L_{K(1) \oplus K(2)} \mathrm {gl}_1 (E)$ imply that there is an exact sequence
$L_{K(1) \oplus K(2)} \mathrm {gl}_1 (E)$ imply that there is an exact sequence
Applying Lemma 3.4, we learn that ![]() $[\mathrm {bu}, L_{K(2) \oplus K(1)} E]$ is torsionfree. It therefore injects into its rationalization, so that the result follows from the fact that
$[\mathrm {bu}, L_{K(2) \oplus K(1)} E]$ is torsionfree. It therefore injects into its rationalization, so that the result follows from the fact that ![]() $\Sigma ^{\infty } \mathbb {CP}^{\infty } \to \mathrm {bu}$ is a rational equivalence.
$\Sigma ^{\infty } \mathbb {CP}^{\infty } \to \mathrm {bu}$ is a rational equivalence.
Remark 3.6 Balderrama has shown that periodic complex orientations of height ![]() $2$ Lubin–Tate theories
$2$ Lubin–Tate theories ![]() $E(k,\mathbb {G})$ which satisfy a version of the Ando criterion admit lifts to periodic
$E(k,\mathbb {G})$ which satisfy a version of the Ando criterion admit lifts to periodic ![]() $\mathbb {E}_\infty$-complex orientations
$\mathbb {E}_\infty$-complex orientations ![]() $\mathrm {MUP} \to E(k,\mathbb {G})$ (see [Reference BalderramaBal21, Theorem 6.5.3(3)]). In this remark, we prove that such lifts are unique up to homotopy.
$\mathrm {MUP} \to E(k,\mathbb {G})$ (see [Reference BalderramaBal21, Theorem 6.5.3(3)]). In this remark, we prove that such lifts are unique up to homotopy.
We begin with a result which has been proven by Rezk at height ![]() $2$ (which is the case that we use) [Reference RezkRez13] and in general is an unpublished theorem of Hopkins and Lurie that has now appeared in work of Burklund, Schlank, and Yuan [Reference Burklund, Schlank and YuanBSY22, Theorem H]. Let
$2$ (which is the case that we use) [Reference RezkRez13] and in general is an unpublished theorem of Hopkins and Lurie that has now appeared in work of Burklund, Schlank, and Yuan [Reference Burklund, Schlank and YuanBSY22, Theorem H]. Let ![]() $\overline {k}$ denote the algebraic closure of
$\overline {k}$ denote the algebraic closure of ![]() $k$. Then we have
$k$. Then we have
 \[ \pi_* \mathbb{G}_m (E(\overline{k}, \mathbb{G})) := \pi_* \mathrm{Map} (\mathbb{Z}, \mathrm{gl}_1 (E(\overline{k}, \mathbb{G}))) \cong \begin{cases} \overline{k}^{\times} & *=0 ,\\ \mathbb{Z}_p & *=3, \\ 0 & \text{otherwise}. \end{cases} \]
\[ \pi_* \mathbb{G}_m (E(\overline{k}, \mathbb{G})) := \pi_* \mathrm{Map} (\mathbb{Z}, \mathrm{gl}_1 (E(\overline{k}, \mathbb{G}))) \cong \begin{cases} \overline{k}^{\times} & *=0 ,\\ \mathbb{Z}_p & *=3, \\ 0 & \text{otherwise}. \end{cases} \]
On ![]() $\pi _0$, the map
$\pi _0$, the map ![]() $\mathbb {Z} \to \mathrm {gl}_1 (E(\overline {k}, \mathbb {G}))$ corresponding to
$\mathbb {Z} \to \mathrm {gl}_1 (E(\overline {k}, \mathbb {G}))$ corresponding to ![]() $a \in \overline {k}^{\times }$ picks out the Teichmuller lift
$a \in \overline {k}^{\times }$ picks out the Teichmuller lift ![]() $[a]$.
$[a]$.
Since ![]() $\mathrm {Gal}(k)$ has
$\mathrm {Gal}(k)$ has ![]() $p$-cohomological dimension at most
$p$-cohomological dimension at most ![]() $1$ (see [Reference Gille and SzamuelyGS06, Proposition 6.1.9]), it follows that
$1$ (see [Reference Gille and SzamuelyGS06, Proposition 6.1.9]), it follows that
In particular, the map ![]() $\pi _0 \mathbb {G}_m (E(k,\mathbb {G})) \to \pi _0 \mathrm {gl}_1 (E(k,\mathbb {G}))$ is injective. Now, by orientation theory it suffices to show that
$\pi _0 \mathbb {G}_m (E(k,\mathbb {G})) \to \pi _0 \mathrm {gl}_1 (E(k,\mathbb {G}))$ is injective. Now, by orientation theory it suffices to show that
is injective. By what we have proven above about uniqueness of ![]() $\mathbb {E}_\infty$-complex orientations, it suffices to show that
$\mathbb {E}_\infty$-complex orientations, it suffices to show that
is injective, which is what we showed above.
As noted in [Reference BalderramaBal21, Remark 6.5.4], this implies that the Goerss–Hopkins obstruction group ![]() $\mathrm {Ext}^2_{\Delta } (\hat {Q}(E(k,\mathbb {G})_0 ^{\wedge } \mathrm {MUP}), \omega )$ is equal to
$\mathrm {Ext}^2_{\Delta } (\hat {Q}(E(k,\mathbb {G})_0 ^{\wedge } \mathrm {MUP}), \omega )$ is equal to ![]() $0$.
$0$.
4. The level  $n$ elliptic genus
$n$ elliptic genus
Convention 4.1 In this section ![]() $n$ will denote an integer greater than or equal to
$n$ will denote an integer greater than or equal to ![]() $2$.
$2$.
In this section, we will prove Theorem 1.7, which states that the Hirzebruch level ![]() $n$ elliptic genus lifts uniquely up to homotopy to an
$n$ elliptic genus lifts uniquely up to homotopy to an ![]() $\mathbb {E}_\infty$-complex orientation
$\mathbb {E}_\infty$-complex orientation ![]() $\mathrm {MU} \to \mathrm {tmf}_1 (n)$.
$\mathrm {MU} \to \mathrm {tmf}_1 (n)$.
We will begin by recalling some background material about ![]() $\mathbb {E}_\infty$-rings of topological modular forms with level-
$\mathbb {E}_\infty$-rings of topological modular forms with level-![]() $\Gamma _1 (n)$ structures in § 4.1. In § 4.2, we recall from [Reference Ando, Hopkins and StricklandAHS01, Reference Ando, Hopkins and StricklandAHS04] how complex orientations may be described in terms of
$\Gamma _1 (n)$ structures in § 4.1. In § 4.2, we recall from [Reference Ando, Hopkins and StricklandAHS01, Reference Ando, Hopkins and StricklandAHS04] how complex orientations may be described in terms of ![]() $\Theta ^1$-structures. We then describe the level
$\Theta ^1$-structures. We then describe the level ![]() $n$ elliptic genus in this language, following Meier [Reference MeierMei21, § 3]. In § 4.3, we show that a complex orientation for
$n$ elliptic genus in this language, following Meier [Reference MeierMei21, § 3]. In § 4.3, we show that a complex orientation for ![]() $\mathrm {TMF}_1 (n)$ satisfies the Ando criterion at
$\mathrm {TMF}_1 (n)$ satisfies the Ando criterion at ![]() $p$ if and only if its composition along a map
$p$ if and only if its composition along a map ![]() $\mathrm {TMF}_1 (n) \to E(k, \mathbb {G})$ to a Lubin–Tate theory does.
$\mathrm {TMF}_1 (n) \to E(k, \mathbb {G})$ to a Lubin–Tate theory does.
In § 4.4, we recall from [Reference Ando, Hopkins and StricklandAHS04] how the Ando criterion for Lubin–Tate theories may be rephrased in terms of ![]() $\Theta ^1$-structures. We then prove that the Hirzebruch level
$\Theta ^1$-structures. We then prove that the Hirzebruch level ![]() $n$ genus satisfies the Ando criterion. As a consequence of Theorem 1.4, it lifts uniquely up to homotopy to an
$n$ genus satisfies the Ando criterion. As a consequence of Theorem 1.4, it lifts uniquely up to homotopy to an ![]() $\mathbb {E}_\infty$-ring map
$\mathbb {E}_\infty$-ring map ![]() $\mathrm {MU} \to \mathrm {TMF}_1 (n)$. Finally, in § 4.5, we prove that this
$\mathrm {MU} \to \mathrm {TMF}_1 (n)$. Finally, in § 4.5, we prove that this ![]() $\mathbb {E}_\infty$-ring map admits a unique up to homotopy lift to an
$\mathbb {E}_\infty$-ring map admits a unique up to homotopy lift to an ![]() $\mathbb {E}_\infty$-ring map
$\mathbb {E}_\infty$-ring map ![]() $\mathrm {MU} \to \mathrm {tmf}_1 (n)$, completing the proof of Theorem 1.7.
$\mathrm {MU} \to \mathrm {tmf}_1 (n)$, completing the proof of Theorem 1.7.
4.1 Topological modular forms with level structures
In this section, we will recall some basic facts about the ![]() $\mathbb {E}_\infty$-rings
$\mathbb {E}_\infty$-rings ![]() $\mathrm {tmf}_1 (n)$,
$\mathrm {tmf}_1 (n)$, ![]() $\mathrm {Tmf}_1 (n)$ and
$\mathrm {Tmf}_1 (n)$ and ![]() $\mathrm {TMF}_1 (n)$ of topological modular forms with level-
$\mathrm {TMF}_1 (n)$ of topological modular forms with level-![]() $\Gamma _1 (n)$ structure. We begin by recalling the algebraic background.
$\Gamma _1 (n)$ structure. We begin by recalling the algebraic background.
Definition 4.2 We let ![]() $\mathcal {M}_1 (n)$ denote the Deligne–Mumford moduli stack of elliptic curves with level
$\mathcal {M}_1 (n)$ denote the Deligne–Mumford moduli stack of elliptic curves with level ![]() $\Gamma _1 (n)$ structure over
$\Gamma _1 (n)$ structure over ![]() $\mathbb {Z}[ {1}/{n}]$. Concretely, given a scheme
$\mathbb {Z}[ {1}/{n}]$. Concretely, given a scheme ![]() $S$ on which
$S$ on which ![]() $n$ is invertible, we have
$n$ is invertible, we have
Moreover, we write ![]() $\overline {\mathcal {M}_1} (n)$ for the Deligne–Rapoport moduli stack of generalized elliptic curves with level
$\overline {\mathcal {M}_1} (n)$ for the Deligne–Rapoport moduli stack of generalized elliptic curves with level ![]() $\Gamma _1 (n)$ structure [Reference Deligne and RapoportDR73]. This is again a Deligne–Mumford stack over
$\Gamma _1 (n)$ structure [Reference Deligne and RapoportDR73]. This is again a Deligne–Mumford stack over ![]() $\mathbb {Z}[ {1}/{n}]$, and
$\mathbb {Z}[ {1}/{n}]$, and ![]() $\mathcal {M}_1 (n) \subset \overline {\mathcal {M}_1} (n)$ is an open substack.
$\mathcal {M}_1 (n) \subset \overline {\mathcal {M}_1} (n)$ is an open substack.
We denote the universal family of curves by ![]() $\pi : \mathcal {C} \to \overline {\mathcal {M}_1} (n)$, and write
$\pi : \mathcal {C} \to \overline {\mathcal {M}_1} (n)$, and write ![]() $\pi ^{\mathrm {sm}} : \mathcal {C}^{\mathrm {sm}} \to \overline {\mathcal {M}_1} (n)$ for the smooth locus. Then
$\pi ^{\mathrm {sm}} : \mathcal {C}^{\mathrm {sm}} \to \overline {\mathcal {M}_1} (n)$ for the smooth locus. Then ![]() $\mathcal {C}^{\mathrm {sm}}$ admits a natural structure of a group scheme, and we write
$\mathcal {C}^{\mathrm {sm}}$ admits a natural structure of a group scheme, and we write ![]() $\omega$ for the line bundle of invariant differentials.
$\omega$ for the line bundle of invariant differentials.
Finally, we write ![]() $\mathcal {M} = \mathcal {M}_1 (1)$ and
$\mathcal {M} = \mathcal {M}_1 (1)$ and ![]() $\overline {\mathcal {M}} = \overline {\mathcal {M}_1} (1)$ for the moduli stacks of (generalized) elliptic curves without level structure.
$\overline {\mathcal {M}} = \overline {\mathcal {M}_1} (1)$ for the moduli stacks of (generalized) elliptic curves without level structure.
Recollection 4.3 (Goerss, Hopkins, and Miller [Reference Douglas, Francis, Henriques and HillDFHH14, Chapter 12], Lurie [Reference LurieLur18b], and Hill and Lawson [Reference Hill and LawsonHL16])
There is a sheaf ![]() $\mathcal {O}^{\mathrm {top}}_{\overline {\mathcal {M}}}$ of
$\mathcal {O}^{\mathrm {top}}_{\overline {\mathcal {M}}}$ of ![]() $\mathbb {E}_\infty$-ring spectra on the Kummer log-étale site of
$\mathbb {E}_\infty$-ring spectra on the Kummer log-étale site of ![]() $\overline {\mathcal {M}}$ with the following properties.
$\overline {\mathcal {M}}$ with the following properties.
(i) There is a natural isomorphism of sheaves
 $\pi _0 \mathcal {O}^{\mathrm {top}}_{\overline {\mathcal {M}}} \cong \mathcal {O}_{\overline {\mathcal {M}}}$.
$\pi _0 \mathcal {O}^{\mathrm {top}}_{\overline {\mathcal {M}}} \cong \mathcal {O}_{\overline {\mathcal {M}}}$.(ii) There are natural isomorphisms of quasicoherent sheaves
 $\pi _{2i} \mathcal {O}^{\mathrm {top}} _{\overline {\mathcal {M}}} \cong \omega ^{i}$ and
$\pi _{2i} \mathcal {O}^{\mathrm {top}} _{\overline {\mathcal {M}}} \cong \omega ^{i}$ and  $\pi _{2i+1} \mathcal {O}^{\mathrm {top}}_{\overline {\mathcal {M}}} \cong 0$.
$\pi _{2i+1} \mathcal {O}^{\mathrm {top}}_{\overline {\mathcal {M}}} \cong 0$.(iii) Write
 $\widehat {\pi ^{\mathrm {sm}}} : \widehat {\mathcal {C}^{\mathrm {sm}}} \to \overline {\mathcal {M}}$ for the completion of
$\widehat {\pi ^{\mathrm {sm}}} : \widehat {\mathcal {C}^{\mathrm {sm}}} \to \overline {\mathcal {M}}$ for the completion of  $\pi ^{\mathrm {sm}} : \mathcal {C}^{\mathrm {sm}} \to \overline {\mathcal {M}}$ along the zero section. There is a natural isomorphism of sheaves of rings
$\pi ^{\mathrm {sm}} : \mathcal {C}^{\mathrm {sm}} \to \overline {\mathcal {M}}$ along the zero section. There is a natural isomorphism of sheaves of rings  $\pi _0 \mathrm {Hom} (\Sigma ^\infty _+ \mathbb {CP}^{\infty }, \mathcal {O}^{\mathrm {top}}) \cong (\widehat {\pi ^{\mathrm {sm}}})_* \mathcal {O}_{\widehat {\mathcal {C}^{\mathrm {sm}}}}$.
$\pi _0 \mathrm {Hom} (\Sigma ^\infty _+ \mathbb {CP}^{\infty }, \mathcal {O}^{\mathrm {top}}) \cong (\widehat {\pi ^{\mathrm {sm}}})_* \mathcal {O}_{\widehat {\mathcal {C}^{\mathrm {sm}}}}$.
Since the natural morphisms ![]() $\overline {\mathcal {M}_1} (n) \to \overline {\mathcal {M}}$ are Kummer log-étale (we refer the reader to [Reference Hill and LawsonHL16] for more details), we may define
$\overline {\mathcal {M}_1} (n) \to \overline {\mathcal {M}}$ are Kummer log-étale (we refer the reader to [Reference Hill and LawsonHL16] for more details), we may define ![]() $\mathbb {E}_\infty$-rings:
$\mathbb {E}_\infty$-rings:
and
By definition, there are spectral sequences
and
Remark 4.4 Let ![]() $n \geq 2$. It follows from [Reference MeierMei22a, Proposition 2.4(4)] that
$n \geq 2$. It follows from [Reference MeierMei22a, Proposition 2.4(4)] that ![]() $\mathrm {H}^s (\mathcal {M}_1 (n), \omega ^i) = 0$ for all
$\mathrm {H}^s (\mathcal {M}_1 (n), \omega ^i) = 0$ for all ![]() $s > 0$, so that
$s > 0$, so that ![]() $\mathrm {TMF}_1 (n)$ has homotopy groups concentrated in even degrees and that there are natural isomorphisms
$\mathrm {TMF}_1 (n)$ has homotopy groups concentrated in even degrees and that there are natural isomorphisms
Moreover, ![]() $\mathrm {TMF}_1 (n)$ is Landweber exact. Indeed, this is a consequence of flatness of
$\mathrm {TMF}_1 (n)$ is Landweber exact. Indeed, this is a consequence of flatness of ![]() $\mathcal {M}_1 (n)$ over
$\mathcal {M}_1 (n)$ over ![]() $\mathbb {Z}[ {1}/{n}]$, the integrality of
$\mathbb {Z}[ {1}/{n}]$, the integrality of ![]() $\mathcal {M}_1 (n)_{\mathbb {F}_p}$ and the fact that the formal group of an elliptic curve is of height at most two.
$\mathcal {M}_1 (n)_{\mathbb {F}_p}$ and the fact that the formal group of an elliptic curve is of height at most two.
However, because the groups ![]() $\mathrm {H}^1 (\overline {\mathcal {M}_1}, \omega ^i)$ do not in general vanish, we do not have a similar theorem for
$\mathrm {H}^1 (\overline {\mathcal {M}_1}, \omega ^i)$ do not in general vanish, we do not have a similar theorem for ![]() $\mathrm {Tmf}_1 (n)$. Instead, we have the
$\mathrm {Tmf}_1 (n)$. Instead, we have the ![]() $\mathbb {E}_\infty$-ring spectrum
$\mathbb {E}_\infty$-ring spectrum ![]() $\mathrm {tmf}_1 (n)$ from [Reference MeierMei21].
$\mathrm {tmf}_1 (n)$ from [Reference MeierMei21].
Recollection 4.5 [Reference MeierMei21, Theorem 1.1]
There is an essentially unique connective ![]() $\mathbb {E}_\infty$-ring spectrum
$\mathbb {E}_\infty$-ring spectrum ![]() $\mathrm {tmf}_1 (n)$ whose homotopy groups are concentrated in even degrees and which is equipped with an
$\mathrm {tmf}_1 (n)$ whose homotopy groups are concentrated in even degrees and which is equipped with an ![]() $\mathbb {E}_\infty$-ring map
$\mathbb {E}_\infty$-ring map
such that the induced maps
are isomorphisms.
Remark 4.6 There is a sequence of natural maps
4.2  $\Theta ^1$-structures
$\Theta ^1$-structures
In this section, we describe complex orientations in terms of ![]() $\Theta ^1$-structures and give a description of the Hirzebruch level
$\Theta ^1$-structures and give a description of the Hirzebruch level ![]() $n$ genus in this language.
$n$ genus in this language.
Suppose that we are given a base Deligne–Mumford stack ![]() $S$ and a formal group or generalized elliptic curve
$S$ and a formal group or generalized elliptic curve ![]() $G$ over
$G$ over ![]() $S$. We denote the structure map by
$S$. We denote the structure map by ![]() $p : G \to S$ and the zero section by
$p : G \to S$ and the zero section by ![]() $0 : S \to G$. Given a line bundle
$0 : S \to G$. Given a line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $G$, we set
$G$, we set
There is a canonical trivialization ![]() $0^* \Theta ^1 (\mathcal {L}) \cong \mathcal {O}_{S}$.
$0^* \Theta ^1 (\mathcal {L}) \cong \mathcal {O}_{S}$.
Definition 4.7 A ![]() $\Theta ^1$-structure on a line bundle
$\Theta ^1$-structure on a line bundle ![]() $\mathcal {L}$ over
$\mathcal {L}$ over ![]() $G$ is a trivialization of
$G$ is a trivialization of ![]() $\Theta ^1 (\mathcal {L})$ which pulls back to the canonical trivialization of
$\Theta ^1 (\mathcal {L})$ which pulls back to the canonical trivialization of ![]() $0^* \Theta ^1 (\mathcal {L})$.
$0^* \Theta ^1 (\mathcal {L})$.
Equivalently, a ![]() $\Theta ^1$-structure on
$\Theta ^1$-structure on ![]() $\mathcal {L}$ is an isomorphism
$\mathcal {L}$ is an isomorphism ![]() $p^* 0^* \mathcal {L} \cong \mathcal {L}$ which pulls back to the canonical isomorphism
$p^* 0^* \mathcal {L} \cong \mathcal {L}$ which pulls back to the canonical isomorphism ![]() $0^* p^* 0^* \mathcal {L} \cong 0^* \mathcal {L}$.
$0^* p^* 0^* \mathcal {L} \cong 0^* \mathcal {L}$.
Remark 4.8 It is clear from the definition that there is a natural bijection between ![]() $\Theta ^1$-structures on
$\Theta ^1$-structures on ![]() $\mathcal {L}$ and
$\mathcal {L}$ and ![]() $\mathcal {L}^{-1}$.
$\mathcal {L}^{-1}$.
Remark 4.9 Note that a line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $G$ admits a
$G$ admits a ![]() $\Theta ^1$-structure if and only if it is pulled back from a line bundle on
$\Theta ^1$-structure if and only if it is pulled back from a line bundle on ![]() $S$ via the structure map
$S$ via the structure map ![]() $p$.
$p$.
When ![]() $G$ is a generalized elliptic curve,
$G$ is a generalized elliptic curve, ![]() $\Theta ^1$-structures are unique when they exist.
$\Theta ^1$-structures are unique when they exist.
Lemma 4.10 Suppose that ![]() $G$ is a generalized elliptic curve. Then the set of
$G$ is a generalized elliptic curve. Then the set of ![]() $\Theta ^1$-structures on a line bundle
$\Theta ^1$-structures on a line bundle ![]() $\mathcal {L}$ over
$\mathcal {L}$ over ![]() $G$ is either empty or consists of a single element.
$G$ is either empty or consists of a single element.
Proof. The set of isomorphisms ![]() $p^* 0^* \mathcal {L} \cong \mathcal {L}$ is a torsor for
$p^* 0^* \mathcal {L} \cong \mathcal {L}$ is a torsor for ![]() $\mathcal {O}_G (G)^{\times }$, whereas the set of isomorphisms
$\mathcal {O}_G (G)^{\times }$, whereas the set of isomorphisms ![]() $0^* p^* 0^* \mathcal {L} \cong 0^* \mathcal {L}$ is a torsor for
$0^* p^* 0^* \mathcal {L} \cong 0^* \mathcal {L}$ is a torsor for ![]() $\mathcal {O}_S (S)^{\times }$. It therefore suffices to show that the map
$\mathcal {O}_S (S)^{\times }$. It therefore suffices to show that the map ![]() $\mathcal {O}_G (G) \to \mathcal {O}_S (S)$ induced by pulling back along the zero section is an isomorphism. This follows from [Sta23, Tag 0E0L].
$\mathcal {O}_G (G) \to \mathcal {O}_S (S)$ induced by pulling back along the zero section is an isomorphism. This follows from [Sta23, Tag 0E0L].
Now let ![]() $E$ denote an even weakly periodic homotopy commutative ring spectrum, and let
$E$ denote an even weakly periodic homotopy commutative ring spectrum, and let ![]() $\mathbb {G}_E = \mathrm {Spf} E^0 (\mathbb {CP}^\infty )$ denote the associated formal group over
$\mathbb {G}_E = \mathrm {Spf} E^0 (\mathbb {CP}^\infty )$ denote the associated formal group over ![]() $\text {Spec}\ \pi _0 E$. We denote by
$\text {Spec}\ \pi _0 E$. We denote by ![]() $\gamma _1$ the canonical line bundle over
$\gamma _1$ the canonical line bundle over ![]() $\mathbb {CP}^\infty$ and let
$\mathbb {CP}^\infty$ and let ![]() $\mathcal {O}_{\mathbb {G}_E} (1)$ denote the line bundle over
$\mathcal {O}_{\mathbb {G}_E} (1)$ denote the line bundle over ![]() $\mathbb {G}_E$ corresponding to
$\mathbb {G}_E$ corresponding to
Then we have the following theorem.
Proposition 4.11 [Reference Ando, Hopkins and StricklandAHS01, Theorem 2.48]
There is a natural bijection between complex orientations of ![]() $E$ and
$E$ and ![]() $\Theta ^1$-structures on
$\Theta ^1$-structures on ![]() $\mathcal {O}_{\mathbb {G}_E} (1)$.
$\mathcal {O}_{\mathbb {G}_E} (1)$.
Proof. Recall that a complex orientation of ![]() $E$ consists of an element of
$E$ consists of an element of ![]() $\widetilde {E^2} (\mathbb {CP}^{\infty })$ which restricts to the unit along the map
$\widetilde {E^2} (\mathbb {CP}^{\infty })$ which restricts to the unit along the map ![]() $\widetilde {E^2} (\mathbb {CP}^\infty ) \to \widetilde {E^2} (\mathbb {CP}^1) \cong \pi _0 E$. Since the map
$\widetilde {E^2} (\mathbb {CP}^\infty ) \to \widetilde {E^2} (\mathbb {CP}^1) \cong \pi _0 E$. Since the map ![]() $E^0 (\mathbb {CP}^\infty ) \to \pi _0 E$ is an infinitesimal thickening, complex orientations of
$E^0 (\mathbb {CP}^\infty ) \to \pi _0 E$ is an infinitesimal thickening, complex orientations of ![]() $E$ may be identified with
$E$ may be identified with ![]() $E^0 (\mathbb {CP}^\infty )$-module isomorphisms
$E^0 (\mathbb {CP}^\infty )$-module isomorphisms ![]() $E^0 (\mathbb {CP}^{\infty }) \cong \widetilde {E^2} (\mathbb {CP}^{\infty })$ that become equal to the canonical isomorphism
$E^0 (\mathbb {CP}^{\infty }) \cong \widetilde {E^2} (\mathbb {CP}^{\infty })$ that become equal to the canonical isomorphism ![]() $\widetilde {E^2} (\mathbb {CP}^1) \cong \pi _0 E$ after tensoring down along
$\widetilde {E^2} (\mathbb {CP}^1) \cong \pi _0 E$ after tensoring down along ![]() $E^0 (\mathbb {CP}^\infty ) \to \pi _0 E$.
$E^0 (\mathbb {CP}^\infty ) \to \pi _0 E$.
By Remark 4.8, we may replace ![]() $\mathcal {O}_{\mathbb {G}_E} (1)$ with
$\mathcal {O}_{\mathbb {G}_E} (1)$ with ![]() $\mathcal {O}_{\mathbb {G}_E} (1)^{-1}$ in the statement of the proposition. To prove the proposition, it therefore suffices to identify the global sections of
$\mathcal {O}_{\mathbb {G}_E} (1)^{-1}$ in the statement of the proposition. To prove the proposition, it therefore suffices to identify the global sections of ![]() $\Theta ^1 (\mathcal {O}_{\mathbb {G}_E} (1)^{-1})$ with
$\Theta ^1 (\mathcal {O}_{\mathbb {G}_E} (1)^{-1})$ with ![]() $\widetilde {E^2} (\mathbb {CP}^{\infty })$ and pullback along the zero section with
$\widetilde {E^2} (\mathbb {CP}^{\infty })$ and pullback along the zero section with ![]() $\widetilde {E^2} (\mathbb {CP}^\infty ) \to \widetilde {E^2} (\mathbb {CP}^1) \cong \pi _0 E$. This is an immediate consequence of the definitions.
$\widetilde {E^2} (\mathbb {CP}^\infty ) \to \widetilde {E^2} (\mathbb {CP}^1) \cong \pi _0 E$. This is an immediate consequence of the definitions.
Even though ![]() $\mathrm {tmf}_1 (n)$ is not weakly even periodic, Meier has shown that its complex orientations may still be described in terms of
$\mathrm {tmf}_1 (n)$ is not weakly even periodic, Meier has shown that its complex orientations may still be described in terms of ![]() $\Theta ^1$-structures.
$\Theta ^1$-structures.
Proposition 4.12 [Reference MeierMei21, Lemma 3.2]
There is a natural bijection between complex orientations of ![]() $\mathrm {tmf}_1 (n)$ and
$\mathrm {tmf}_1 (n)$ and ![]() $\Theta ^1$-structures on
$\Theta ^1$-structures on ![]() $\mathcal {O}_{\widehat {\mathcal {C}}} (1)$ over
$\mathcal {O}_{\widehat {\mathcal {C}}} (1)$ over ![]() $\widehat {C} \to \overline {\mathcal {M}_1} (n)$.
$\widehat {C} \to \overline {\mathcal {M}_1} (n)$.
We now recall the treatment of Hirzebruch's level ![]() $n$ elliptic genus from [Reference MeierMei21, § 3]. The following proposition is a mild rephrasing of [Reference MeierMei21, Lemma 3.3].
$n$ elliptic genus from [Reference MeierMei21, § 3]. The following proposition is a mild rephrasing of [Reference MeierMei21, Lemma 3.3].
Proposition 4.13 Let ![]() $P : \overline {\mathcal {M}_1} (n) \to \mathcal {C}^{\mathrm {sm}}$ denote the universal level
$P : \overline {\mathcal {M}_1} (n) \to \mathcal {C}^{\mathrm {sm}}$ denote the universal level ![]() $\Gamma _1 (n)$ structure.
$\Gamma _1 (n)$ structure.
(i) The pullback of the line bundle
 $\mathcal {O}_{\mathcal {C}} ([0] - [P])$ on
$\mathcal {O}_{\mathcal {C}} ([0] - [P])$ on  $\mathcal {C}$ to
$\mathcal {C}$ to  $\widehat {\mathcal {C}}$ is naturally isomorphic to
$\widehat {\mathcal {C}}$ is naturally isomorphic to  $\mathcal {O}_{\widehat {\mathcal {C}}} (1)$.
$\mathcal {O}_{\widehat {\mathcal {C}}} (1)$.(ii) There is a degree
 $n$ étale cover
$n$ étale cover  $q : \mathcal {C}' \to \mathcal {C}$ of generalized elliptic curves so that
$q : \mathcal {C}' \to \mathcal {C}$ of generalized elliptic curves so that  $q^* \mathcal {O}_{\mathcal {C}} ([0] - [P])$ admits a (necessarily unique)
$q^* \mathcal {O}_{\mathcal {C}} ([0] - [P])$ admits a (necessarily unique)  $\Theta ^1$-structure.
$\Theta ^1$-structure.
Since the induced map ![]() $\widehat {q} : \widehat {\mathcal {C}'} \xrightarrow {\sim } \widehat {\mathcal {C}}$ is an isomorphism, we obtain a
$\widehat {q} : \widehat {\mathcal {C}'} \xrightarrow {\sim } \widehat {\mathcal {C}}$ is an isomorphism, we obtain a ![]() $\Theta ^1$-structure on
$\Theta ^1$-structure on ![]() $\mathcal {O}_{\widehat {C}} (1)$ and, hence, by Proposition 4.12 a complex orientation of
$\mathcal {O}_{\widehat {C}} (1)$ and, hence, by Proposition 4.12 a complex orientation of ![]() $\mathrm {tmf}_1 (n)$. This is the complex orientation corresponding to the Hirzebruch level
$\mathrm {tmf}_1 (n)$. This is the complex orientation corresponding to the Hirzebruch level ![]() $n$ elliptic genus.
$n$ elliptic genus.
4.3 Reduction to Lubin–Tate theory
Our goal in this section is to prove Proposition 4.16. This proposition implies that to verify the Ando criterion for the Hirzebruch level ![]() $n$ elliptic genus, it suffices to verify the Ando criterion after composition with a map
$n$ elliptic genus, it suffices to verify the Ando criterion after composition with a map ![]() $\mathrm {TMF}_1 (n) \to E(k, \mathbb {G})$ to a Lubin–Tate theory. This will be useful to us because work of Ando, Hopkins, and Strickland [Reference Ando, Hopkins and StricklandAHS04] rephrases the Ando criterion for Lubin–Tate theories in terms of
$\mathrm {TMF}_1 (n) \to E(k, \mathbb {G})$ to a Lubin–Tate theory. This will be useful to us because work of Ando, Hopkins, and Strickland [Reference Ando, Hopkins and StricklandAHS04] rephrases the Ando criterion for Lubin–Tate theories in terms of ![]() $\Theta ^1$-structures.
$\Theta ^1$-structures.
We begin by recalling some basic facts about Lubin–Tate theories.
Recollection 4.14 (Goerss and Hopkins [Reference Goerss and HopkinsGH04] and Lurie [Reference LurieLur18b])
Let ![]() $k$ denote a perfect field of characteristic
$k$ denote a perfect field of characteristic ![]() $p > 0$ and let
$p > 0$ and let ![]() $\mathbb {G}$ denote a formal group of finite height
$\mathbb {G}$ denote a formal group of finite height ![]() $h$ over
$h$ over ![]() $k$. To the pair
$k$. To the pair ![]() $(k, \mathbb {G})$ one may associate an
$(k, \mathbb {G})$ one may associate an ![]() $\mathbb {E}_\infty$-ring spectrum
$\mathbb {E}_\infty$-ring spectrum ![]() $E(k,\mathbb {G})$, known as the Lubin–Tate spectrum of
$E(k,\mathbb {G})$, known as the Lubin–Tate spectrum of ![]() $(k,\mathbb {G})$. The ring
$(k,\mathbb {G})$. The ring ![]() $\pi _0 E(k,\mathbb {G})$ is naturally isomorphic to the universal deformation ring of
$\pi _0 E(k,\mathbb {G})$ is naturally isomorphic to the universal deformation ring of ![]() $(k,\mathbb {G})$, which is non-canonically isomorphic to
$(k,\mathbb {G})$, which is non-canonically isomorphic to ![]() $\mathbb {W}(k) [\![u_1, \ldots, u_{h-1}]\!]$. We let
$\mathbb {W}(k) [\![u_1, \ldots, u_{h-1}]\!]$. We let ![]() $\mathbb {G}^{\mathrm {univ}}$ denote the universal deformation of
$\mathbb {G}^{\mathrm {univ}}$ denote the universal deformation of ![]() $\mathbb {G}$ over
$\mathbb {G}$ over ![]() $\pi _0 E(k, \mathbb {G})$, and denote by
$\pi _0 E(k, \mathbb {G})$, and denote by ![]() $\omega _{\mathbb {G}^{\mathrm {univ}}}$ its module of invariant differentials. There are natural isomorphisms of
$\omega _{\mathbb {G}^{\mathrm {univ}}}$ its module of invariant differentials. There are natural isomorphisms of ![]() $\pi _{2i} E(k,\mathbb {G})$ with
$\pi _{2i} E(k,\mathbb {G})$ with ![]() $\omega ^{i} _{\mathbb {G}^{\mathrm {univ}}}$.
$\omega ^{i} _{\mathbb {G}^{\mathrm {univ}}}$.
Construction 4.15 Let ![]() $k$ denote a perfect field of characteristic
$k$ denote a perfect field of characteristic ![]() $p > 0$. Associated to a supersingular
$p > 0$. Associated to a supersingular ![]() $k$-point
$k$-point ![]() $(E, \alpha \in E[n] (k))$ of
$(E, \alpha \in E[n] (k))$ of ![]() $\mathcal {M}_1 (n)$, there is a map of
$\mathcal {M}_1 (n)$, there is a map of ![]() $\mathbb {E}_\infty$-ring spectra
$\mathbb {E}_\infty$-ring spectra ![]() $\mathrm {TMF}_1 (n) \to E(k, \widehat {E})$. Indeed, this follows from the description of
$\mathrm {TMF}_1 (n) \to E(k, \widehat {E})$. Indeed, this follows from the description of ![]() $E(k, \widehat {E})$ as an oriented deformation ring [Reference LurieLur18b, § 6], Lurie's Serre–Tate theorem for strict abelian varieties [Reference LurieLur18a, § 7], and the universal property of
$E(k, \widehat {E})$ as an oriented deformation ring [Reference LurieLur18b, § 6], Lurie's Serre–Tate theorem for strict abelian varieties [Reference LurieLur18a, § 7], and the universal property of ![]() $\mathrm {TMF}_1 (n)$.
$\mathrm {TMF}_1 (n)$.
Proposition 4.16 Let ![]() $k$ denote a perfect field of characteristic
$k$ denote a perfect field of characteristic ![]() $p$ and let
$p$ and let ![]() $(E, \alpha \in E[n](k))$ denote an object of
$(E, \alpha \in E[n](k))$ denote an object of ![]() $\mathcal {M}_1 (n)(k)$ with
$\mathcal {M}_1 (n)(k)$ with ![]() $E$ a supersingular elliptic curve. Then a complex orientation of
$E$ a supersingular elliptic curve. Then a complex orientation of ![]() $\mathrm {TMF}_1 (n)$ satisfies the Ando criterion at
$\mathrm {TMF}_1 (n)$ satisfies the Ando criterion at ![]() $p$ if and only if its composite with the canonical map
$p$ if and only if its composite with the canonical map ![]() $\mathrm {TMF}_1 (n) \to E(k, \widehat {E})$ does.
$\mathrm {TMF}_1 (n) \to E(k, \widehat {E})$ does.
Our proof of Proposition 4.16 rests on the following lemma.
Lemma 4.17 Let ![]() $E \to F$ denote a map of complex orientable homotopy commutative ring spectra. Suppose that
$E \to F$ denote a map of complex orientable homotopy commutative ring spectra. Suppose that ![]() $\pi _* E$ and
$\pi _* E$ and ![]() $\pi _* F$ are
$\pi _* F$ are ![]() $p$-torsionfree and that the induced map
$p$-torsionfree and that the induced map ![]() $\pi _* E / p \to \pi _* F / p$ is an injection. Then the map
$\pi _* E / p \to \pi _* F / p$ is an injection. Then the map ![]() $E^* (\mathrm {BC}_p)/ I_{\rm tr} \to F^* (\mathrm {BC}_p)/ I_{\rm tr}$ is an injection.
$E^* (\mathrm {BC}_p)/ I_{\rm tr} \to F^* (\mathrm {BC}_p)/ I_{\rm tr}$ is an injection.
Proof. Since ![]() $\pi _* E$ is
$\pi _* E$ is ![]() $p$-torsionfree, a choice of complex orientation gives rise to an isomorphism (see [Reference QuillenQui71, Proposition 4.2]):
$p$-torsionfree, a choice of complex orientation gives rise to an isomorphism (see [Reference QuillenQui71, Proposition 4.2]):
where ![]() $\lvert t \rvert = 2$,
$\lvert t \rvert = 2$, ![]() $\langle p \rangle (t) = {[p](t)}/{t}$, and
$\langle p \rangle (t) = {[p](t)}/{t}$, and ![]() $[p] (t)$ is the
$[p] (t)$ is the ![]() $p$-series of the formal group on
$p$-series of the formal group on ![]() $E^*$. Moreover, since
$E^*$. Moreover, since ![]() $\pi _* E$ is
$\pi _* E$ is ![]() $p$-torsionfree, we may identify
$p$-torsionfree, we may identify ![]() $t^{n-1} E^* [[t]] / (\langle p \rangle (t), t^n)$ with a shift of
$t^{n-1} E^* [[t]] / (\langle p \rangle (t), t^n)$ with a shift of ![]() $E^* / p$. The analogous statements for
$E^* / p$. The analogous statements for ![]() $F$ also hold.
$F$ also hold.
Taking the induced complex orientation of ![]() $F$, we identify
$F$, we identify ![]() $E^* (\mathrm {BC}_p) / I_{\rm tr} \to F^* (\mathrm {BC}_p) / I_{\rm tr}$ with the natural map
$E^* (\mathrm {BC}_p) / I_{\rm tr} \to F^* (\mathrm {BC}_p) / I_{\rm tr}$ with the natural map ![]() $E^* [[t]] / \langle p \rangle (t) \to F^* [[t]] / \langle p \rangle (t)$. To show that this map is injective, it suffices to show that it is injection on the associated graded for the
$E^* [[t]] / \langle p \rangle (t) \to F^* [[t]] / \langle p \rangle (t)$. To show that this map is injective, it suffices to show that it is injection on the associated graded for the ![]() $t$-adic filtration. This identifies with a shift of the natural map
$t$-adic filtration. This identifies with a shift of the natural map ![]() $E^* / p \to F^* / p$ in each degree, which is an injection by hypothesis.
$E^* / p \to F^* / p$ in each degree, which is an injection by hypothesis.
Proof of Proposition 4.16 It is clear that if a complex orientation of ![]() $\mathrm {TMF}_1 (n)$ satisfies the Ando criterion at
$\mathrm {TMF}_1 (n)$ satisfies the Ando criterion at ![]() $p$, so does the induced complex orientation of
$p$, so does the induced complex orientation of ![]() $E(k, \widehat {E})$. To prove the converse, it suffices to show that the induced map
$E(k, \widehat {E})$. To prove the converse, it suffices to show that the induced map
is an injection. We begin by reducing to the case ![]() $n \geq 5$. Any map
$n \geq 5$. Any map ![]() $\text {Spec}\ k \to \mathcal {M}_1 (n)$ fits into a diagram
$\text {Spec}\ k \to \mathcal {M}_1 (n)$ fits into a diagram

for ![]() $k'$ a finite separable extension of
$k'$ a finite separable extension of ![]() $k$. It follows that there is a diagram
$k$. It follows that there is a diagram

so that it suffices to show that
and
are injective.
We may therefore assume that ![]() $n \geq 5$ if we can show that the first map is an injection. Both
$n \geq 5$ if we can show that the first map is an injection. Both ![]() $\pi _* \mathrm {TMF}_1 (n)$ and
$\pi _* \mathrm {TMF}_1 (n)$ and ![]() $\pi _* \mathrm {TMF}_1 (n^2)$ are
$\pi _* \mathrm {TMF}_1 (n^2)$ are ![]() $p$-torsionfree, and
$p$-torsionfree, and
is an injection since ![]() $\mathcal {M}_1 (n^2)_{\mathbb {F}_p} \to \mathcal {M}_1 (n)_{\mathbb {F}_p}$ is a finite étale cover. Therefore, we may apply Lemma 4.17 to show that the first map above is an injection.
$\mathcal {M}_1 (n^2)_{\mathbb {F}_p} \to \mathcal {M}_1 (n)_{\mathbb {F}_p}$ is a finite étale cover. Therefore, we may apply Lemma 4.17 to show that the first map above is an injection.
We may now assume that ![]() $n \geq 5$, so that
$n \geq 5$, so that ![]() $\mathcal {M}_1 (n)$ is represented by an affine scheme
$\mathcal {M}_1 (n)$ is represented by an affine scheme ![]() $\text {Spec}\ R_n$ (see [Reference MeierMei22a, Proposition 2.4(2)]). Let
$\text {Spec}\ R_n$ (see [Reference MeierMei22a, Proposition 2.4(2)]). Let ![]() $\mathfrak {m} \subset R_n$ denote the kernel of the map
$\mathfrak {m} \subset R_n$ denote the kernel of the map ![]() $R_n \to k$. Then
$R_n \to k$. Then ![]() $R_n / \mathfrak {m}$ is a finite field (hence, perfect), and the pair
$R_n / \mathfrak {m}$ is a finite field (hence, perfect), and the pair ![]() $(E, P \in E[n](k))$ descends to
$(E, P \in E[n](k))$ descends to ![]() $R_n/ \mathfrak {m}$. As a consequence, there is a factorization
$R_n/ \mathfrak {m}$. As a consequence, there is a factorization ![]() $\mathrm {TMF}_1 (n) \to E(R_n/ \mathfrak {m}, \widehat {E}) \to E(k, \widehat {E})$. It follows immediately from Lemma 4.17 that the induced map
$\mathrm {TMF}_1 (n) \to E(R_n/ \mathfrak {m}, \widehat {E}) \to E(k, \widehat {E})$. It follows immediately from Lemma 4.17 that the induced map
is an injection, so that it suffices to show that
is an injection. To apply Lemma 4.17, we need to show that ![]() $\pi _{*} \mathrm {TMF}_1 (n) / p \to \pi _{*} E(R_n / \mathfrak {m}, \widehat {E}) / p$ is an injection. By abuse of notation, we let
$\pi _{*} \mathrm {TMF}_1 (n) / p \to \pi _{*} E(R_n / \mathfrak {m}, \widehat {E}) / p$ is an injection. By abuse of notation, we let ![]() $\omega$ denote the invertible
$\omega$ denote the invertible ![]() $R_n$-module corresponding to the line bundle
$R_n$-module corresponding to the line bundle ![]() $\omega$ on
$\omega$ on ![]() $\mathcal {M}_1 (n)$. Then the above map can be identified with the
$\mathcal {M}_1 (n)$. Then the above map can be identified with the ![]() $\mathfrak {m}$-adic completion map
$\mathfrak {m}$-adic completion map ![]() $(\omega ^{*/2} / p) \to (\omega ^{*/2} / p)^{\wedge } _\mathfrak {m}$. This is an injection by the Krull intersection theorem, since
$(\omega ^{*/2} / p) \to (\omega ^{*/2} / p)^{\wedge } _\mathfrak {m}$. This is an injection by the Krull intersection theorem, since ![]() $\mathcal {M}_1 (n)_{\mathbb {F}_p}$ is an integral scheme.
$\mathcal {M}_1 (n)_{\mathbb {F}_p}$ is an integral scheme.
4.4 The Ando criterion and  $\Theta ^1$-structures
$\Theta ^1$-structures
In this section, we recall from the work of Ando, Hopkins, and Strickland how the Ando criterion for Lubin–Tate theories may be rephrased in terms of ![]() $\Theta ^1$-structures. We refer the reader to [Reference Ando, Hopkins and StricklandAHS04] for proofs and further details. We then combine this rephrasing with Proposition 4.16 to prove that the Hirzebruch level
$\Theta ^1$-structures. We refer the reader to [Reference Ando, Hopkins and StricklandAHS04] for proofs and further details. We then combine this rephrasing with Proposition 4.16 to prove that the Hirzebruch level ![]() $n$ elliptic genus satisfies the Ando criterion. Finally, we deduce from Theorem 1.4 that the Hirzebruch level
$n$ elliptic genus satisfies the Ando criterion. Finally, we deduce from Theorem 1.4 that the Hirzebruch level ![]() $n$ elliptic genus lifts uniquely up to homotopy to an
$n$ elliptic genus lifts uniquely up to homotopy to an ![]() $\mathbb {E}_\infty$-ring map
$\mathbb {E}_\infty$-ring map
We begin by recalling from [Reference Ando, Hopkins and StricklandAHS04, § 14] how ![]() $\Theta ^1$-structures may be normed along isogenies.
$\Theta ^1$-structures may be normed along isogenies.
Recollection 4.18 [Reference Ando, Hopkins and StricklandAHS04, § 14]
Suppose we are given an isogeny ![]() $G \to G'$ of formal groups or elliptic curves. Given a line bundle
$G \to G'$ of formal groups or elliptic curves. Given a line bundle ![]() $\mathcal {L}$ over
$\mathcal {L}$ over ![]() $G$, there is a line bundle
$G$, there is a line bundle ![]() $N(\mathcal {L})$ over
$N(\mathcal {L})$ over ![]() $G'$, called the norm of
$G'$, called the norm of ![]() $\mathcal {L}$. Moreover, given a
$\mathcal {L}$. Moreover, given a ![]() $\Theta ^1$-structure
$\Theta ^1$-structure ![]() $s$ on
$s$ on ![]() $\mathcal {L}$, there is an associated
$\mathcal {L}$, there is an associated ![]() $\Theta ^1$-structure
$\Theta ^1$-structure ![]() $N(s)$ on
$N(s)$ on ![]() $N(\mathcal {L})$, called the norm of
$N(\mathcal {L})$, called the norm of ![]() $s$.
$s$.
Remark 4.19 Given an isogeny of formal groups ![]() $\mathbb {G} \to \widetilde {\mathbb {G}}$, there is a natural isomorphism of line bundles
$\mathbb {G} \to \widetilde {\mathbb {G}}$, there is a natural isomorphism of line bundles ![]() $N(\mathcal {O}_\mathbb {G} (1)) \cong \mathcal {O}_{\widetilde {\mathbb {G}}} (1)$.
$N(\mathcal {O}_\mathbb {G} (1)) \cong \mathcal {O}_{\widetilde {\mathbb {G}}} (1)$.
Remark 4.20 Suppose that we are given an elliptic curve ![]() $E$ with a point
$E$ with a point ![]() $P$ of exact order
$P$ of exact order ![]() $n$, i.e. a level
$n$, i.e. a level ![]() $\Gamma _1 (n)$ structure, and an isogeny
$\Gamma _1 (n)$ structure, and an isogeny ![]() $E \to \widetilde {E}$ of degree
$E \to \widetilde {E}$ of degree ![]() $p$ coprime to
$p$ coprime to ![]() $n$. Then the image
$n$. Then the image ![]() $\widetilde {P}$ of
$\widetilde {P}$ of ![]() $P$ in
$P$ in ![]() $\widetilde {E}$ is again a point of exact order
$\widetilde {E}$ is again a point of exact order ![]() $n$, and there is a natural isomorphism of line bundles
$n$, and there is a natural isomorphism of line bundles ![]() $N (\mathcal {O}_E ([0] - [P])) \cong \mathcal {O}_{\widetilde {E}} ([0] - [\widetilde {P}])$.
$N (\mathcal {O}_E ([0] - [P])) \cong \mathcal {O}_{\widetilde {E}} ([0] - [\widetilde {P}])$.
Following [Reference Ando, Hopkins and StricklandAHS04], we may now use this language to rephrase the Ando criterion for Lubin–Tate theory. We begin with some setup.
Recollection 4.21 Let ![]() $k$ denote a perfect field of characteristic
$k$ denote a perfect field of characteristic ![]() $p > 0$ and let
$p > 0$ and let ![]() $\mathbb {G}$ denote a formal group of finite height over
$\mathbb {G}$ denote a formal group of finite height over ![]() $k$, so that we have an associated Lubin–Tate theory
$k$, so that we have an associated Lubin–Tate theory ![]() $E(k,\mathbb {G})$. Then there are two ring maps
$E(k,\mathbb {G})$. Then there are two ring maps ![]() $i, \psi : \pi _0 E(k, \mathbb {G}) \to E(k,\mathbb {G})^0 (\mathrm {BC}_p) / I_{\rm tr}$. The first,
$i, \psi : \pi _0 E(k, \mathbb {G}) \to E(k,\mathbb {G})^0 (\mathrm {BC}_p) / I_{\rm tr}$. The first, ![]() $i$, is induced by the projection
$i$, is induced by the projection ![]() $\mathrm {BC}_p \to \ast$. The second
$\mathrm {BC}_p \to \ast$. The second ![]() $\psi$, is the total power operation. Over the ring
$\psi$, is the total power operation. Over the ring ![]() $E(k,\mathbb {G})^0 (\mathrm {BC}_p) /I_{\rm tr}$, there is a degree
$E(k,\mathbb {G})^0 (\mathrm {BC}_p) /I_{\rm tr}$, there is a degree ![]() $p$ isogeny
$p$ isogeny
induced by the total power operation on ![]() $E(k, \mathbb {G})^0 (\mathbb {CP}^\infty )$.
$E(k, \mathbb {G})^0 (\mathbb {CP}^\infty )$.
Given a ![]() $\Theta ^1$-structure
$\Theta ^1$-structure ![]() $s$ on
$s$ on ![]() $\mathcal {O}_{\mathbb {G}^{\mathrm {univ}}} (1)$, there are therefore two naturally induced
$\mathcal {O}_{\mathbb {G}^{\mathrm {univ}}} (1)$, there are therefore two naturally induced ![]() $\Theta ^1$-structures on
$\Theta ^1$-structures on ![]() $\mathcal {O}_{\psi ^* \mathbb {G}^{\mathrm {univ}}} (1) \cong N(\mathcal {O}_{i^* \mathbb {G}^{\mathrm {univ}}} (1))$: the pullback
$\mathcal {O}_{\psi ^* \mathbb {G}^{\mathrm {univ}}} (1) \cong N(\mathcal {O}_{i^* \mathbb {G}^{\mathrm {univ}}} (1))$: the pullback ![]() $\psi ^* (s)$ and the norm
$\psi ^* (s)$ and the norm ![]() $N(i^* (s))$.
$N(i^* (s))$.
Definition 4.22 We say that a ![]() $\Theta ^1$-structure
$\Theta ^1$-structure ![]() $s$ on
$s$ on ![]() $\mathbb {G}^{\mathrm {univ}}$ satisfies the Ando criterion if
$\mathbb {G}^{\mathrm {univ}}$ satisfies the Ando criterion if ![]() $\psi ^* (s) = N(i^* (s))$.
$\psi ^* (s) = N(i^* (s))$.
It follows from [Reference Ando, Hopkins and StricklandAHS04, § 5] that this is compatible with our previous definition of the Ando criterion.
Proposition 4.23 A complex orientation of ![]() $E(k, \mathbb {G})$ satisfies the Ando criterion if and only if the associated
$E(k, \mathbb {G})$ satisfies the Ando criterion if and only if the associated ![]() $\Theta ^1$-structure on
$\Theta ^1$-structure on ![]() $\mathcal {O}_{\widetilde {\mathbb {G}}} (1)$ satisfies the Ando criterion.
$\mathcal {O}_{\widetilde {\mathbb {G}}} (1)$ satisfies the Ando criterion.
We are now able to prove the main theorem of this section.
Theorem 4.24 The Hirzebruch level ![]() $n$ elliptic genus
$n$ elliptic genus ![]() $\mathrm {MU} \to \mathrm {tmf}_1 (n) \to \mathrm {TMF}_1 (n)$ satisfies the Ando criterion. As a consequence of Theorem 1.4 and Remark 4.4, it lifts uniquely up to homotopy to an
$\mathrm {MU} \to \mathrm {tmf}_1 (n) \to \mathrm {TMF}_1 (n)$ satisfies the Ando criterion. As a consequence of Theorem 1.4 and Remark 4.4, it lifts uniquely up to homotopy to an ![]() $\mathbb {E}_\infty$-complex orientation
$\mathbb {E}_\infty$-complex orientation
Proof. Choose, for each ![]() $p$ not dividing
$p$ not dividing ![]() $n$,
$n$, ![]() $(E, P \in E[n] (k)) \in \mathcal {M}_1 (n)(k)$ with
$(E, P \in E[n] (k)) \in \mathcal {M}_1 (n)(k)$ with ![]() $E$ supersingular and
$E$ supersingular and ![]() $k$ a perfect field of characteristic
$k$ a perfect field of characteristic ![]() $p$. By Proposition 4.16, it suffices to show that the induced complex orientation of
$p$. By Proposition 4.16, it suffices to show that the induced complex orientation of ![]() $E(k,\widehat {E})$ satisfies the Ando criterion.
$E(k,\widehat {E})$ satisfies the Ando criterion.
By the Serre–Tate theorem [Reference KatzKat81, § 1], ![]() $\pi _0 E(k, \widehat {E})$ is the universal deformation ring of
$\pi _0 E(k, \widehat {E})$ is the universal deformation ring of ![]() $E$. We let
$E$. We let ![]() $E^{\mathrm {univ}}$ denote the universal deformation of
$E^{\mathrm {univ}}$ denote the universal deformation of ![]() $E$ over
$E$ over ![]() $\pi _0 E(k, \widehat {E})$, and let
$\pi _0 E(k, \widehat {E})$, and let ![]() $P^\mathrm {univ} \in E^{\mathrm {univ}}[n](\pi _0 E(k,\mathbb {G}))$ denote the unique lift of
$P^\mathrm {univ} \in E^{\mathrm {univ}}[n](\pi _0 E(k,\mathbb {G}))$ denote the unique lift of ![]() $P$. The associated formal group
$P$. The associated formal group ![]() $\widehat {E^{\mathrm {univ}}}$ is a universal deformation of
$\widehat {E^{\mathrm {univ}}}$ is a universal deformation of ![]() $\widehat {E}$.
$\widehat {E}$.
Applying Proposition 4.23, we must show that the ![]() $\Theta ^1$-structure
$\Theta ^1$-structure ![]() $s$ on
$s$ on ![]() $\mathcal {O}_{\widehat {E^\mathrm {univ}}} (1)$ corresponding to the level
$\mathcal {O}_{\widehat {E^\mathrm {univ}}} (1)$ corresponding to the level ![]() $n$ elliptic genus satisfies the Ando criterion, i.e. that
$n$ elliptic genus satisfies the Ando criterion, i.e. that ![]() $\psi ^* (s) = N(i^* (s))$. By the definition of the level
$\psi ^* (s) = N(i^* (s))$. By the definition of the level ![]() $n$ elliptic genus, there is a degree
$n$ elliptic genus, there is a degree ![]() $n$ étale isogeny
$n$ étale isogeny ![]() $q: (E^{\mathrm {univ}})' \to E^\mathrm {univ}$ and a
$q: (E^{\mathrm {univ}})' \to E^\mathrm {univ}$ and a ![]() $\Theta ^1$-structure
$\Theta ^1$-structure ![]() $\overline {s}$ on
$\overline {s}$ on ![]() $q^* \mathcal {O}_{E^{\mathrm {univ}}} ([0] - [P^{\mathrm {univ}}])$ which induces
$q^* \mathcal {O}_{E^{\mathrm {univ}}} ([0] - [P^{\mathrm {univ}}])$ which induces ![]() $s$. By the Serre–Tate theorem, the isogeny of formal groups
$s$. By the Serre–Tate theorem, the isogeny of formal groups
over ![]() $E(k, \widehat {E})^0 (\mathrm {BC}_p)/ I_{\rm tr}$ lifts to the following diagram of isogenies of elliptic curves.
$E(k, \widehat {E})^0 (\mathrm {BC}_p)/ I_{\rm tr}$ lifts to the following diagram of isogenies of elliptic curves.

Let ![]() $\overline {P^{\mathrm {univ}}}$ denote the image of
$\overline {P^{\mathrm {univ}}}$ denote the image of ![]() $i^*(P^\mathrm {univ} )$ in
$i^*(P^\mathrm {univ} )$ in ![]() $\psi ^* E^\mathrm {univ}$. From the above diagram, we obtain
$\psi ^* E^\mathrm {univ}$. From the above diagram, we obtain ![]() $\Theta ^1$-structures
$\Theta ^1$-structures ![]() $\psi ^* (\overline {s})$ and
$\psi ^* (\overline {s})$ and ![]() $N(i^* (\overline {s}))$ on
$N(i^* (\overline {s}))$ on
As these induce ![]() $\psi ^* (s)$ and
$\psi ^* (s)$ and ![]() $N( i^* (s))$, it suffices to show that
$N( i^* (s))$, it suffices to show that ![]() $\psi ^* (\overline {s}) = N(i^* (\overline {s}))$. But this follows immediately from the uniqueness of
$\psi ^* (\overline {s}) = N(i^* (\overline {s}))$. But this follows immediately from the uniqueness of ![]() $\Theta ^1$-structures over elliptic curves proven in Lemma 4.10.
$\Theta ^1$-structures over elliptic curves proven in Lemma 4.10.
4.5 Lift to  $\mathrm {tmf}_1 (n)$
$\mathrm {tmf}_1 (n)$
In this section, we will complete the proof of Theorem 1.7 by proving the following two lemmas.
Lemma 4.25 Suppose that we are given a complex orientation ![]() $\mathrm {MU} \to \mathrm {Tmf}_1 (n)$ with the property that the composite
$\mathrm {MU} \to \mathrm {Tmf}_1 (n)$ with the property that the composite
lifts to an ![]() $\mathbb {E}_\infty$-ring map. Then this complex orientation lifts uniquely to an
$\mathbb {E}_\infty$-ring map. Then this complex orientation lifts uniquely to an ![]() $\mathbb {E}_\infty$-complex orientation
$\mathbb {E}_\infty$-complex orientation ![]() $\mathrm {MU} \to \mathrm {Tmf}_1 (n)$.
$\mathrm {MU} \to \mathrm {Tmf}_1 (n)$.
Lemma 4.26 Any ![]() $\mathbb {E}_\infty$-complex orientation of
$\mathbb {E}_\infty$-complex orientation of ![]() $\mathrm {Tmf}_1 (n)$ lifts uniquely to an
$\mathrm {Tmf}_1 (n)$ lifts uniquely to an ![]() $\mathbb {E}_\infty$-complex orientation of
$\mathbb {E}_\infty$-complex orientation of ![]() $\mathrm {tmf}_1 (n)$.
$\mathrm {tmf}_1 (n)$.
Proof of Lemma 4.25 The uniqueness will follow from Theorem 3.1 and Example 3.3 once we know that a complex orientation of ![]() $\mathrm {Tmf}_1 (n)$ is determined by the induced complex orientation of
$\mathrm {Tmf}_1 (n)$ is determined by the induced complex orientation of ![]() $\mathrm {TMF}_1 (n)$. This follows from the fact that the map
$\mathrm {TMF}_1 (n)$. This follows from the fact that the map ![]() $\pi _* \mathrm {Tmf}_1 (n) \to \pi _* \mathrm {TMF}_1 (n)$ is injective in even degrees by [Reference MeierMei22b, Proposition 2.5] and the descent spectral sequence.
$\pi _* \mathrm {Tmf}_1 (n) \to \pi _* \mathrm {TMF}_1 (n)$ is injective in even degrees by [Reference MeierMei22b, Proposition 2.5] and the descent spectral sequence.
It therefore suffices to show that the ![]() $\mathbb {E}_\infty$-map
$\mathbb {E}_\infty$-map ![]() $\mathrm {MU} \to \mathrm {TMF}_1 (n)$ lifts to an
$\mathrm {MU} \to \mathrm {TMF}_1 (n)$ lifts to an ![]() $\mathbb {E}_\infty$-map
$\mathbb {E}_\infty$-map ![]() $\mathrm {MU} \to \mathrm {Tmf}_1 (n)$. We begin with the pullback square of
$\mathrm {MU} \to \mathrm {Tmf}_1 (n)$. We begin with the pullback square of ![]() $\mathbb {E}_\infty$-rings coming from [Reference Hill and LawsonHL16]:
$\mathbb {E}_\infty$-rings coming from [Reference Hill and LawsonHL16]:

This square satisfies the following properties.
(i) The
 $\mathbb {E}_\infty$-rings
$\mathbb {E}_\infty$-rings  $K^{\mathrm {cusp}}_1 (n)$ and
$K^{\mathrm {cusp}}_1 (n)$ and  $\Delta ^{-1} K^{\mathrm {cusp}} _1 (n)$ are Landweber exact and of height at most one.
$\Delta ^{-1} K^{\mathrm {cusp}} _1 (n)$ are Landweber exact and of height at most one.(ii) The induced map
 $\pi _* K^{\mathrm {cusp}}_1 (n)/p \to \pi _* \Delta ^{-1} K^{\mathrm {cusp}} _1 (n)/p$ is injective for all
$\pi _* K^{\mathrm {cusp}}_1 (n)/p \to \pi _* \Delta ^{-1} K^{\mathrm {cusp}} _1 (n)/p$ is injective for all  $p$.
$p$.
It follows that to construct an ![]() $\mathbb {E}_\infty$-lifting
$\mathbb {E}_\infty$-lifting ![]() $\mathrm {MU} \to \mathrm {Tmf}_1 (n)$, it suffices to lift the composite
$\mathrm {MU} \to \mathrm {Tmf}_1 (n)$, it suffices to lift the composite
to an ![]() $\mathbb {E}_\infty$-map
$\mathbb {E}_\infty$-map
By the uniqueness in Theorem 1.4 and (i) above, it suffices to lift the complex orientation and verify that it satisfies the Ando criterion. However, we are given a lift of the complex orientation by assumption, and it follows from Lemma 4.17 and (ii) above that it satisfies the Ando criterion.
Proof of Lemma 4.26 For this, we use orientation theory [Reference Ando, Blumberg, Gepner, Hopkins and RezkABGHR14]. We have the sequence of maps
and ![]() $\mathbb {E}_\infty$-complex orientations of
$\mathbb {E}_\infty$-complex orientations of ![]() $\mathrm {tmf}_1$ and
$\mathrm {tmf}_1$ and ![]() $\mathrm {Tmf}_1 (n)$ correspond to nullhomotopies of the respective composites. Since
$\mathrm {Tmf}_1 (n)$ correspond to nullhomotopies of the respective composites. Since ![]() $\mathrm {bu}$ is
$\mathrm {bu}$ is ![]() $2$-connective, we may as well replace all occurrences of
$2$-connective, we may as well replace all occurrences of ![]() $\mathrm {bgl}_1$ with
$\mathrm {bgl}_1$ with ![]() $\mathrm {bsl}_1 := \tau _{\geq 2} \mathrm {bgl}_1$.
$\mathrm {bsl}_1 := \tau _{\geq 2} \mathrm {bgl}_1$.
Now, it follows from the definition of ![]() $\mathrm {tmf}_1 (n)$ (see [Reference MeierMei21]) that the map
$\mathrm {tmf}_1 (n)$ (see [Reference MeierMei21]) that the map ![]() $\mathrm {tmf}_1 (n) \to \tau _{\geq 0} \mathrm {Tmf}_1 (n)$ fits into the following pullback square.
$\mathrm {tmf}_1 (n) \to \tau _{\geq 0} \mathrm {Tmf}_1 (n)$ fits into the following pullback square.

As a consequence, ![]() $\mathrm {tmf}_1 (n) \to \mathrm {Tmf}_1 (n)$ induces an isomorphism on
$\mathrm {tmf}_1 (n) \to \mathrm {Tmf}_1 (n)$ induces an isomorphism on ![]() $\pi _k$ for
$\pi _k$ for ![]() $k \geq 2$. Since
$k \geq 2$. Since ![]() $\pi _1 \mathrm {tmf}_1 (n) = 0$, it follows that the composite
$\pi _1 \mathrm {tmf}_1 (n) = 0$, it follows that the composite
is an equivalence, so that there is a splitting
from which the lemma follows.
Acknowledgements
The author would like to thank Robert Burklund and Jeremy Hahn for useful comments on a draft.
Conflicts of Interest
None.
Appendix A.  $K(n)$-localizations of Landweber exact ring spectra
$K(n)$-localizations of Landweber exact ring spectra
In this appendix, we prove the following lemma, which the author was unable to find a reference for in the literature.
Lemma A.1 Let ![]() $E$ denote a Landweber exact ring spectrum whose homotopy is concentrated in even degrees. Then
$E$ denote a Landweber exact ring spectrum whose homotopy is concentrated in even degrees. Then ![]() $L_{K(n)} E$ is also a Landweber exact ring spectrum whose homotopy is concentrated in even degrees.
$L_{K(n)} E$ is also a Landweber exact ring spectrum whose homotopy is concentrated in even degrees.
Before we proceed to the proof of Lemma A.1, we need a lemma from commutative algebra.
Lemma A.2 Let ![]() $R_*$ denote a graded commutative ring and let
$R_*$ denote a graded commutative ring and let ![]() $x_1, \ldots, x_n \in R_*$ denote a regular sequence of homogeneous elements. Then the sequence
$x_1, \ldots, x_n \in R_*$ denote a regular sequence of homogeneous elements. Then the sequence ![]() $x_1, \ldots, x_n$ remains regular in the completion
$x_1, \ldots, x_n$ remains regular in the completion ![]() $(R_*) ^{\wedge } _{(x_1, \ldots x_n)}$.
$(R_*) ^{\wedge } _{(x_1, \ldots x_n)}$.
Proof. Let ![]() $I = (x_1, \ldots x_n)$. We claim that there are short exact sequences
$I = (x_1, \ldots x_n)$. We claim that there are short exact sequences
for all ![]() $k \geq 1$. Supposing this for the moment, we find by taking the limit that
$k \geq 1$. Supposing this for the moment, we find by taking the limit that
is short exact. In particular, we find that ![]() $x_1$ is a regular element in
$x_1$ is a regular element in ![]() $(R_*)^{\wedge } _I$ and that
$(R_*)^{\wedge } _I$ and that ![]() $(R_*)^{\wedge } _I / x_1 \cong (R_* / x_1)^{\wedge } _I$. Taking
$(R_*)^{\wedge } _I / x_1 \cong (R_* / x_1)^{\wedge } _I$. Taking ![]() $R_* / x_1$ as our new ring and the image of
$R_* / x_1$ as our new ring and the image of ![]() $x_2, \ldots, x_n$ in
$x_2, \ldots, x_n$ in ![]() $R_* / x_1$ as our exact sequence, we may conclude by induction on the length of our regular sequence.
$R_* / x_1$ as our exact sequence, we may conclude by induction on the length of our regular sequence.
It remains to establish (A.1). It is sufficient to prove that (A.1) is exact on the associated graded of the ![]() $I$-adic filtration where
$I$-adic filtration where ![]() $x_1$ is considered as a map of
$x_1$ is considered as a map of ![]() $I$-adic filtration degree
$I$-adic filtration degree ![]() $1$. Since
$1$. Since ![]() $x_1, \ldots, x_n$ is regular, this associated graded may be identified with the sequence
$x_1, \ldots, x_n$ is regular, this associated graded may be identified with the sequence

which is easily verified to be short exact.
Proof Proof of Lemma A.1
By abuse of notation, we let ![]() $v_i \in \pi _* E$ inductively denote an arbitrary lift of the class
$v_i \in \pi _* E$ inductively denote an arbitrary lift of the class ![]() $v_i \in \pi _* E / (p, \ldots, v_{i-1})$. Given a positive integer
$v_i \in \pi _* E / (p, \ldots, v_{i-1})$. Given a positive integer ![]() $k$, let
$k$, let ![]() $I_k = (p, v_1, \ldots, v_{k-1})$ and let
$I_k = (p, v_1, \ldots, v_{k-1})$ and let ![]() $I_0 = (0)$. It follows from [Reference Hovey and StricklandHSt99, Proposition 7.10] that
$I_0 = (0)$. It follows from [Reference Hovey and StricklandHSt99, Proposition 7.10] that ![]() $\pi _* L_{K(n)} E \cong (v_n ^{-1} \pi _* E)^{\wedge } _{I_n}$. In particular,
$\pi _* L_{K(n)} E \cong (v_n ^{-1} \pi _* E)^{\wedge } _{I_n}$. In particular, ![]() $\pi _{2*-1} L_{K(n)} E = 0$. It is clear that the operation of inverting
$\pi _{2*-1} L_{K(n)} E = 0$. It is clear that the operation of inverting ![]() $v_n ^{-1}$ preserves Landweber exactness, so that it suffices to prove that completion with respect to
$v_n ^{-1}$ preserves Landweber exactness, so that it suffices to prove that completion with respect to ![]() $I_n$ does as well. However, this follows immediately from Lemma A.2.
$I_n$ does as well. However, this follows immediately from Lemma A.2.