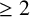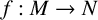Sampson [Reference Sampson4] proved a unique continuation theorem for harmonic mappings of Riemannian manifolds. Siu [Reference Siu5] showed that a harmonic mapping of connected Kähler manifolds
![]() $f: M\to N$
is holomorphic whenever
$f: M\to N$
is holomorphic whenever
![]() $f\vert _U$
is holomorphic for some nonempty open set
$f\vert _U$
is holomorphic for some nonempty open set
![]() $U\subset M$
. It is not difficult to see that, in general, U cannot be replaced by an analytic hypersurface
$U\subset M$
. It is not difficult to see that, in general, U cannot be replaced by an analytic hypersurface
![]() $V\subset M$
. For example, take
$V\subset M$
. For example, take
![]() $f= \phi \times \psi $
, where
$f= \phi \times \psi $
, where
![]() $\phi : X\to Y$
is a holomorphic mapping of connected Kähler manifolds and
$\phi : X\to Y$
is a holomorphic mapping of connected Kähler manifolds and
![]() $\psi :S\to Y$
is a harmonic map from a Riemann surface S. If
$\psi :S\to Y$
is a harmonic map from a Riemann surface S. If
![]() $\psi $
is not holomorphic, then f is not holomorphic, but
$\psi $
is not holomorphic, then f is not holomorphic, but
![]() $f\vert _{X\times \{p\}}$
is holomorphic for every
$f\vert _{X\times \{p\}}$
is holomorphic for every
![]() $p\in S$
.
$p\in S$
.
Siu’s unique continuation theorem is a basic ingredient in the proof of the strong rigidity theorem for compact Kähler manifolds [Reference Siu5, Theorem 2]. Suppose
![]() $M\subset \mathbb {P}^k$
is a projective manifold of dimension
$M\subset \mathbb {P}^k$
is a projective manifold of dimension
![]() $\geq 2$
and V is a smooth hyperplane section of M. We shall see that if
$\geq 2$
and V is a smooth hyperplane section of M. We shall see that if
![]() $f:M\to N$
is a pluriharmonic map into a Kähler manifold N such that
$f:M\to N$
is a pluriharmonic map into a Kähler manifold N such that
![]() $f\vert _V$
is holomorphic, then f is holomorphic. This result is motivated by the application of Toledo’s theorem on plurisubharmonicity of the energy to rigidity theory [Reference Gromov, Pardalos and Rassias2, Reference Toledo6]. Note that we may weaken the assumption that
$f\vert _V$
is holomorphic, then f is holomorphic. This result is motivated by the application of Toledo’s theorem on plurisubharmonicity of the energy to rigidity theory [Reference Gromov, Pardalos and Rassias2, Reference Toledo6]. Note that we may weaken the assumption that
![]() $f\vert _V$
is holomorphic by applying Siu’s unique continuation theorem.
$f\vert _V$
is holomorphic by applying Siu’s unique continuation theorem.
The main purpose of this note is to establish the following result.
Proposition 1. Suppose
![]() $f:M\to N$
is a pluriharmonic map from a projective manifold M into a Kähler manifold N, with
$f:M\to N$
is a pluriharmonic map from a projective manifold M into a Kähler manifold N, with
![]() ${dim}\, M \geq 2$
. Suppose
${dim}\, M \geq 2$
. Suppose
![]() $D=\sum _{i=1}^k a_i V_i$
is an ample divisor in M, where
$D=\sum _{i=1}^k a_i V_i$
is an ample divisor in M, where
![]() $a_i\in \mathbb {Z}$
,
$a_i\in \mathbb {Z}$
,
![]() $a_i\neq 0$
, and
$a_i\neq 0$
, and
![]() $V_i$
is an irreducible hypersurface in M, for
$V_i$
is an irreducible hypersurface in M, for
![]() $i=1,\ldots ,k$
. Let V be the support of D and let U be an open set in M such that
$i=1,\ldots ,k$
. Let V be the support of D and let U be an open set in M such that
![]() $V_i\hspace {0.02cm}\cap \hspace {0.02cm} U\neq \emptyset $
for each i. If
$V_i\hspace {0.02cm}\cap \hspace {0.02cm} U\neq \emptyset $
for each i. If
![]() $f\vert _{V\,\cap \, U}$
is holomorphic, then f is holomorphic.
$f\vert _{V\,\cap \, U}$
is holomorphic, then f is holomorphic.
Remark 2. Proposition 1 generalises the following result due to Gromov [Reference Gromov, Pardalos and Rassias2, Section 4.6] (see also [Reference Toledo6, Theorem 5]). Suppose
![]() $f:M\to N$
is a pluriharmonic map from a smooth projective surface M into a quotient
$f:M\to N$
is a pluriharmonic map from a smooth projective surface M into a quotient
![]() $N=\Omega \,/\,\Gamma $
of an irreducible bounded symmetric domain
$N=\Omega \,/\,\Gamma $
of an irreducible bounded symmetric domain
![]() $\Omega $
. If
$\Omega $
. If
![]() $f\vert _V$
is holomorphic for some general element V of a Lefschetz pencil on M, then f is holomorphic.
$f\vert _V$
is holomorphic for some general element V of a Lefschetz pencil on M, then f is holomorphic.
Proof of Proposition 1.
Let
![]() $\omega $
be a Kähler form on M representing the first Chern class
$\omega $
be a Kähler form on M representing the first Chern class
![]() $c_1(\mathcal {O}(D))$
associated to D and let
$c_1(\mathcal {O}(D))$
associated to D and let
![]() $\omega _N = \sqrt {-1}\, h_{\alpha \overline {\beta }} \,dw^\alpha \wedge d \overline {w^\beta }$
denote the Kähler form on N. If
$\omega _N = \sqrt {-1}\, h_{\alpha \overline {\beta }} \,dw^\alpha \wedge d \overline {w^\beta }$
denote the Kähler form on N. If
![]() $\phi :X\to N$
is a smooth map from an n-dimensional complex submanifold
$\phi :X\to N$
is a smooth map from an n-dimensional complex submanifold
![]() $X\subset M$
into N, we let
$X\subset M$
into N, we let
![]() $\omega _X=\omega \vert _X$
and
$\omega _X=\omega \vert _X$
and
![]() $\varepsilon "(\phi )= \sqrt {-1}\, h_{\alpha \overline {\beta }} \,\partial \overline {\phi ^\beta }\wedge \overline {\partial } \phi ^\alpha $
, which are real
$\varepsilon "(\phi )= \sqrt {-1}\, h_{\alpha \overline {\beta }} \,\partial \overline {\phi ^\beta }\wedge \overline {\partial } \phi ^\alpha $
, which are real
![]() $(1,1)$
-forms on X such that
$(1,1)$
-forms on X such that
and we define
![]() $E"(\phi )=\int _X\,\vert \overline {\partial }\phi \vert ^2\,dV_{\omega _X}$
provided that the integral is finite.
$E"(\phi )=\int _X\,\vert \overline {\partial }\phi \vert ^2\,dV_{\omega _X}$
provided that the integral is finite.
Since
![]() $c_1(\mathcal {O}(D))=[\omega ]$
is the Poincaré dual of the fundamental homology class
$c_1(\mathcal {O}(D))=[\omega ]$
is the Poincaré dual of the fundamental homology class
![]() $[D]$
of D,
$[D]$
of D,
 $$ \begin{align} E"(f)=\int_M\, \varepsilon"({f})\wedge\frac{\omega^{m-1}}{(m-1)!}=\sum_{i=1}^k\,a_i\cdot\int_{D_i}\,\hspace{-0.02cm} \varepsilon"(f\vert_{D_i})\wedge\frac{\omega_{D_i}^{m-2}}{(m-2)!}=\sum_{i=1}^k a_i E"(f\vert_{D_i}), \end{align} $$
$$ \begin{align} E"(f)=\int_M\, \varepsilon"({f})\wedge\frac{\omega^{m-1}}{(m-1)!}=\sum_{i=1}^k\,a_i\cdot\int_{D_i}\,\hspace{-0.02cm} \varepsilon"(f\vert_{D_i})\wedge\frac{\omega_{D_i}^{m-2}}{(m-2)!}=\sum_{i=1}^k a_i E"(f\vert_{D_i}), \end{align} $$
where
![]() $m=\text {dim}\, M$
and
$m=\text {dim}\, M$
and
![]() $D_i$
is the smooth locus of
$D_i$
is the smooth locus of
![]() $V_i$
for
$V_i$
for
![]() $1\leq i\leq k$
. Note that
$1\leq i\leq k$
. Note that
![]() $\varepsilon "(f\vert _{D_i})= \varepsilon "(f)\vert _{D_i}$
for each i, and that
$\varepsilon "(f\vert _{D_i})= \varepsilon "(f)\vert _{D_i}$
for each i, and that
![]() $\varepsilon "(f)$
is closed because f is pluriharmonic [Reference Ohnita and Udagawa3, Lemma 3.10]. Since
$\varepsilon "(f)$
is closed because f is pluriharmonic [Reference Ohnita and Udagawa3, Lemma 3.10]. Since
![]() $f\vert _{V\,\cap \, U}$
is holomorphic,
$f\vert _{V\,\cap \, U}$
is holomorphic,
![]() $f\vert _{D_i}$
is holomorphic for each i (see [Reference Siu5, pages 88–89]) and we conclude from (1) that f is holomorphic.
$f\vert _{D_i}$
is holomorphic for each i (see [Reference Siu5, pages 88–89]) and we conclude from (1) that f is holomorphic.
We shall see that the analogue of (1) holds for the Dirichlet energy
![]() $E(f)$
. Suppose that
$E(f)$
. Suppose that
![]() $f: M\to N$
is a pluriharmonic map from a projective manifold M of dimension
$f: M\to N$
is a pluriharmonic map from a projective manifold M of dimension
![]() $m\geq 2$
into a Riemannian manifold
$m\geq 2$
into a Riemannian manifold
![]() $(N, h=h_{ij}\,dy^i\otimes dy^{\,j})$
. We fix a Kähler form
$(N, h=h_{ij}\,dy^i\otimes dy^{\,j})$
. We fix a Kähler form
![]() $\omega $
on M with integral cohomology class and choose a divisor
$\omega $
on M with integral cohomology class and choose a divisor
![]() $D=\sum _{i=1}^k a_i V_i$
such that
$D=\sum _{i=1}^k a_i V_i$
such that
![]() $c_1(\mathcal {O}(D))=[\omega ]$
, where
$c_1(\mathcal {O}(D))=[\omega ]$
, where
![]() $a_i$
is a nonzero integer and
$a_i$
is a nonzero integer and
![]() $V_i$
is an irreducible hypersurface in M with smooth locus
$V_i$
is an irreducible hypersurface in M with smooth locus
![]() $D_i$
for each i.
$D_i$
for each i.
Recall that if
![]() $\phi :X\to N$
is a smooth map from a Kähler submanifold
$\phi :X\to N$
is a smooth map from a Kähler submanifold
![]() $X\subset M$
, with Kähler form
$X\subset M$
, with Kähler form
![]() $\omega _X=\omega \vert _X$
, then the energy density
$\omega _X=\omega \vert _X$
, then the energy density
![]() $e(\phi )$
of
$e(\phi )$
of
![]() $\phi $
is given by
$\phi $
is given by
![]() $e(\phi ) = \tfrac 12\vert {d}\phi \vert ^2=\langle \varepsilon (\phi ), \omega _X\rangle $
, where
$e(\phi ) = \tfrac 12\vert {d}\phi \vert ^2=\langle \varepsilon (\phi ), \omega _X\rangle $
, where
![]() $\varepsilon (\phi )=\sqrt {-1}\,h_{ij}\,\partial \phi ^i\wedge \overline {\partial }\phi ^{\,j}$
is a real (1,1)-form on X, and the energy
$\varepsilon (\phi )=\sqrt {-1}\,h_{ij}\,\partial \phi ^i\wedge \overline {\partial }\phi ^{\,j}$
is a real (1,1)-form on X, and the energy
![]() $E(\phi )$
of
$E(\phi )$
of
![]() $\phi $
is given by
$\phi $
is given by
![]() $E(\phi )=\int _X e(\phi )\,d V_{\omega _X}$
.
$E(\phi )=\int _X e(\phi )\,d V_{\omega _X}$
.
Since f is pluriharmonic, the
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\varepsilon (f)$
is closed (see, for example, [Reference Ohnita and Udagawa3, Lemma 2.2]). For
$\varepsilon (f)$
is closed (see, for example, [Reference Ohnita and Udagawa3, Lemma 2.2]). For
![]() $i=1,\ldots ,k$
,
$i=1,\ldots ,k$
,
![]() $\varepsilon (f)\vert _{D_i}= \varepsilon (f\vert _{D_i})$
. Since
$\varepsilon (f)\vert _{D_i}= \varepsilon (f\vert _{D_i})$
. Since
![]() $c_1(\mathcal {O}(D))=[\omega ]$
is the Poincaré dual of
$c_1(\mathcal {O}(D))=[\omega ]$
is the Poincaré dual of
![]() $[D]$
, it follows that
$[D]$
, it follows that
 $$ \begin{align} E(f)=\int_M\, \varepsilon({f})\wedge\frac{\omega^{m-1}}{(m-1)!}=\sum_{i=1}^k\,a_i\cdot\int_{D_i}\,\hspace{-0.02cm} \varepsilon(f\vert_{D_i})\wedge\frac{\omega_{D_i}^{m-2}}{(m-2)!}=\sum_{i=1}^k a_i E(f\vert_{D_i}). \end{align} $$
$$ \begin{align} E(f)=\int_M\, \varepsilon({f})\wedge\frac{\omega^{m-1}}{(m-1)!}=\sum_{i=1}^k\,a_i\cdot\int_{D_i}\,\hspace{-0.02cm} \varepsilon(f\vert_{D_i})\wedge\frac{\omega_{D_i}^{m-2}}{(m-2)!}=\sum_{i=1}^k a_i E(f\vert_{D_i}). \end{align} $$
Example 3. Suppose S is a compact Riemann surface of genus
![]() $g\geq 2$
. The Jacobian
$g\geq 2$
. The Jacobian
![]() $J(S)$
of S is an Abelian variety with a principal polarisation
$J(S)$
of S is an Abelian variety with a principal polarisation
![]() $[\omega ]=c_1(\mathcal {O}(\Theta ))$
, where
$[\omega ]=c_1(\mathcal {O}(\Theta ))$
, where
![]() $\Theta $
is a theta divisor in
$\Theta $
is a theta divisor in
![]() $J(S)$
, that is, a translate of the zero locus of the Riemann theta function. Put
$J(S)$
, that is, a translate of the zero locus of the Riemann theta function. Put
![]() $M=J(S)$
and let
$M=J(S)$
and let
![]() $f: M\to N$
be a pluriharmonic map into a Kähler manifold N. Then Proposition 1 shows that if
$f: M\to N$
be a pluriharmonic map into a Kähler manifold N. Then Proposition 1 shows that if
![]() $f\vert _G$
is holomorphic for some nonempty open subset G of
$f\vert _G$
is holomorphic for some nonempty open subset G of
![]() $\Theta $
, then f is holomorphic.
$\Theta $
, then f is holomorphic.
Let
![]() $W=\mu (S)$
be the image of S under the Abel–Jacobi map
$W=\mu (S)$
be the image of S under the Abel–Jacobi map
![]() $\mu : S\to J(S)$
. We have
$\mu : S\to J(S)$
. We have
 $$ \begin{align*}E"(f)=\int_M\, \varepsilon"({f})\wedge\frac{\omega^{g-1}}{(g-1)!}=\int_{W}\,\hspace{-0.02cm} \varepsilon"(f\vert_{W})= E"(f\vert_{W}), \end{align*} $$
$$ \begin{align*}E"(f)=\int_M\, \varepsilon"({f})\wedge\frac{\omega^{g-1}}{(g-1)!}=\int_{W}\,\hspace{-0.02cm} \varepsilon"(f\vert_{W})= E"(f\vert_{W}), \end{align*} $$
since
![]() $[({1}/{(g-1)!})\,\omega ^{g-1}]$
is the Poincaré dual of
$[({1}/{(g-1)!})\,\omega ^{g-1}]$
is the Poincaré dual of
![]() $[W]$
(see, for example, [Reference Griffiths and Harris1, page 350]). Similarly,
$[W]$
(see, for example, [Reference Griffiths and Harris1, page 350]). Similarly,
![]() $E(f)=E(f\vert _W)$
. Using (1) and (2), we conclude that
$E(f)=E(f\vert _W)$
. Using (1) and (2), we conclude that
where
![]() $\Theta ^*$
denotes the smooth locus of
$\Theta ^*$
denotes the smooth locus of
![]() $\Theta $
. As in the proof of Proposition 1, it follows that if
$\Theta $
. As in the proof of Proposition 1, it follows that if
![]() $f\vert _G$
is holomorphic for some nonempty open subset G of W, then f is holomorphic.
$f\vert _G$
is holomorphic for some nonempty open subset G of W, then f is holomorphic.