No CrossRef data available.
Published online by Cambridge University Press: 24 May 2022
It is standard in chemistry to represent a sequence of reactions by a single overall reaction, often called a complex reaction in contrast to an elementary reaction. Photosynthesis
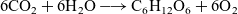 $6 \text{CO}_2+6 \text{H}_2\text{O} \longrightarrow \text{C}_6\text{H}_{12}\text{O}_6 + 6 \text{O}_2$
is an example of such complex reaction. We introduce a mathematical operation that corresponds to summing two chemical reactions. Specifically, we define an associative and non-communicative operation on the product space
$6 \text{CO}_2+6 \text{H}_2\text{O} \longrightarrow \text{C}_6\text{H}_{12}\text{O}_6 + 6 \text{O}_2$
is an example of such complex reaction. We introduce a mathematical operation that corresponds to summing two chemical reactions. Specifically, we define an associative and non-communicative operation on the product space
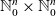 ${\mathbb{N}}_0^n\times {\mathbb{N}}_0^n$
(representing the reactant and the product of a chemical reaction, respectively). The operation models the overall effect of two reactions happening in succession, one after the other. We study the algebraic properties of the operation and apply the results to stochastic reaction networks (RNs), in particular to reachability of states, and to reduction of RNs.
${\mathbb{N}}_0^n\times {\mathbb{N}}_0^n$
(representing the reactant and the product of a chemical reaction, respectively). The operation models the overall effect of two reactions happening in succession, one after the other. We study the algebraic properties of the operation and apply the results to stochastic reaction networks (RNs), in particular to reachability of states, and to reduction of RNs.