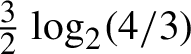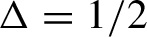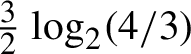A complete proof that square ice entropy is $\tfrac 32\log _{2} (4/3)$

Abstract

In this text, we provide a fully rigorous and complete proof of E.H. Lieb’s statement that (topological) entropy of square ice (or six-vertex model, XXZ spin chain for anisotropy parameter $\Delta =1/2$ ) is equal to $\tfrac 32\log _{2} (4/3)$ .

1 Introduction

1.1 Computing entropy of multidimensional subshifts of finite type

This work is the consequence of a renewal of interest from the fields of symbolic dynamics to entropy computation methods developed in quantum and statistical physics for lattice models. This interest comes from constructive methods for multidimensional subshifts of finite type (some equivalent formulation in symbolic dynamics of lattice models) that are involved in the characterization by Hochman and Meyerovitch [HM10] of the possible values of topological entropy for these dynamical systems (where the dynamics are provided by the action of the $\mathbb {Z}^{2}$ shift action) with a recursion-theoretic criterion. The consequences of this theorem are not only that entropy may be algorithmically uncomputable for a multidimensional subshift of finite type (SFT), which was previously proved for cellular automata [HKC92], but also strong evidence that the study of these systems as a class is intertwined with computability theory. Moreover, it is an important tool to localize sub-classes for which the entropy is computable in a uniform way, as ones defined by strong dynamical constraints [PS15]. Some current research attempts have been made to understand the frontier between the uncomputability and the computability of entropy for a multidimensional SFT. For instance, approaching the frontier from the uncomputable domain, the author, together with Sablik [GS17], proved that the characterization of Hochman and Meyerovitch stands under a relaxed form of the constraint studied in [PS15], which includes notably all exactly solvable models considered in statistical and quantum physics. To approach the frontier from the computable domain, it is natural to attempt to understand (in particular, prove) and extend the computation methods developed for these models.

1.2 Content of this text

Our study in the present text focuses on square ice (or equivalently, the six-vertex model or the XXZ spin chain for anisotropy parameter $\Delta =1/2$ ). Since it is central among exactly solvable models in quantum physics [B82], this work will serve as a ground for further connections between entropy computation methods and constructive methods coming from symbolic dynamics. The entropy of square ice was argued by Lieb [L67] to be exactly $\tfrac 32 \log _{2} ( \tfrac 43 )$ . However, his proof was not complete, as it relied on a non-verified hypothesis (the condensation of Bethe roots, see §6). Moreover, various other arguments involved in Lieb’s argumentation and later developments have not yet received full rigorous treatment. In this text, we fill the holes and propose a (complete) proof of the following theorem.

Theorem 1. The entropy of square ice is equal to $\tfrac 32 \log _{2} ( \tfrac 43 )$ .

For completeness, we include some exposition of what can be considered as background material. The proof is thus self-contained, except for the use of the coordinate Bethe ansatz, for which we rely on another paper by Duminil-Copin et al. [DGHMT18].

One can find an overview of the proof in §3, presented after some definitions related to symbolic dynamics and representations of square ice in §2.

2 Background: square ice and its entropy

2.1 Subshifts of finite type

2.1.1 Definitions

Let $\mathcal {A}$ be some finite set, called the alphabet. For all $d \ge 1$ , the set $\mathcal {A}^{\mathbb Z^{d}}\!$ , whose elements are called configurations, is a topological space with the infinite power of the discrete topology on $\mathcal {A}$ . Let us denote by $\sigma $ the shift action of $\mathbb Z^{d}$ on this space defined by the following equality for all $\textbf {u} \in \mathbb Z^{d}$ and x element of the space: $(\sigma ^{\textbf {u}} (x) )_{\textbf {v}} = x_{\textbf {v}+\textbf {u}}.$ A compact subset X of this space is called a d-dimensional subshift when this subset is stable under the action of the shift, which means that for all $\textbf {u} \in \mathbb Z^{d}$ , $\sigma ^{\textbf {u}}(X) \subset X.$ For any finite subset $\mathbb {U}$ of $\mathbb Z^{d}$ , an element p of $\mathcal {A}^{\mathbb {U}}$ is called a pattern on the alphabet $\mathcal {A}$ and on support $\mathbb {U}$ . We say that this pattern appears in a configuration x when there exists a translate $\mathbb {V}$ of $\mathbb {U}$ such that $x_{\mathbb {V}}=p$ . We say that it appears in another pattern q on a support containing $\mathbb {U}$ such that the restriction of q on $\mathbb {U}$ is p. We say that it appears in a subshift X when it appears in a configuration of X. Such a pattern is also called globally admissible for X. For all $d \ge 1$ , the number of patterns on support that appear in a d-dimensional subshift X is denoted by $\mathcal {N}_{N} (X)$ . When $d=2$ , the number of patterns on support that appear in X is denoted by $\mathcal {N}_{M,N}(X)$ . A d-dimensional subshift X defined by forbidding patterns in some finite set $\mathcal {F}$ to appear in the configurations, formally

$$ \begin{align*}X= \{ x \in \mathcal{A}^{\mathbb Z^{d}} : \text{for all } \mathbb{U} \subset \mathbb{Z}^{d}, x_{\mathbb{U}} \notin \mathcal{F} \},\end{align*} $$

is called a subshift of finite type (SFT). In a context where the set of forbidden patterns defining the SFT is fixed, a pattern is called locally admissible for this SFT when no forbidden pattern appears in it. A morphism between two $\mathbb Z^{d}$ -subshifts $X,Z$ is a continuous map $\varphi : X \rightarrow Z$ such that $\varphi \circ \sigma ^{\textbf {v}} = \sigma ^{\textbf {v}} \circ \varphi $ for all $\textbf {v} \in \mathbb Z^{d}$ (the map commutes with the shift action). An isomorphism is an invertible morphism.

2.1.2 Topological entropy

Definition 1. Let X be a d-dimensional subshift. The topological entropy of X is defined as

$$ \begin{align*}h (X) \equiv \inf_{N \ge 1} \frac{\log_{2} (\mathcal{N}_{N} (X))}{N^{d}}. \end{align*} $$

It is a well-known fact in topological dynamics that this infimum is a limit:

$$ \begin{align*}{h (X) = \lim_{N \ge 1} \frac{\log_{2} (\mathcal{N}_{N} (X))}{N^{d}}}. \end{align*} $$

It is a topological invariant, meaning that when there is an isomorphism between two subshifts, these two subshifts have the same entropy [LM95].

Definition 2. Let X be a bidimensional subshift ( $d=2$ ). For all $n \ge 1$ , we denote by $X_{N}$ the subshift obtained from X by restricting to the width N infinite strip $\{1,\ldots ,N\} \times \mathbb {Z}$ . Formally, this subshift is defined on alphabet $\mathcal {A}^{N}$ and by that $z \in X_{N}$ if and only if there exists $x \in X$ such that for all $k \in \mathbb {Z}$ , $z_{k} = (x_{1,k},\ldots ,x_{N,k})$ . See Figure 1.

Figure 1 Illustration of Definition 2 for $N=3$ .

In the following, we will use the following proposition.

Proposition 1. The entropy of X can be computed through the sequence $(h(X_{N}))_{N}$ :

$$ \begin{align*}{h(X)= \lim_{N} \frac{h(X_{N})}{N}}.\end{align*} $$

We include a proof of this statement, for completeness.

Proof. From the definition of $X_{N}$ ,

$$ \begin{align*}h(X)= \lim_{N} \lim_{M} \frac{\log_{2}(\mathcal{N}_{M,N} (X))}{NM}.\end{align*} $$

We prove this via an upper bound on the $\limsup _{N}$ and a lower bound on the $\liminf _{N}$ of the sequence in this formula.

Upper bound by decomposing squares into rectangles. Since for any $M,N,k$ , the set $\mathbb {U}^{(2)}_{kM,kN}$ is the union of $MN$ translates of $\mathbb {U}^{(2)}_{k}$ , a pattern on support $\mathbb {U}^{(2)}_{kM,kN}$ can be seen as an array of patterns on $\mathbb {U}^{(2)}_{k}$ . As a consequence,

$$ \begin{align*}\mathcal{N}_{kM,kN} (X)\le (\mathcal{N}_{k,k} (X)) {}^{MN},\end{align*} $$

and using this inequality, we get

$$ \begin{align*}\lim_{M} \frac{\log_{2}(\mathcal{N}_{M,N} (X))}{NM} &= \lim_{M} \frac{\log_{2}(\mathcal{N}_{kM,kN} (X))}{k^{2} NM}\\ &\le \lim_{M} \frac{\log_{2}(\mathcal{N}_{k,k} (X))}{k^{2}} = \frac{\log_{2} (\mathcal{N}_{k,k} (X))}{k^{2}}.\end{align*} $$

As a consequence, for all k,

$$ \begin{align*}\limsup_{N} \lim_{M} \frac{\log_{2} (\mathcal{N}_{M,N} (X))}{NM} \le \frac{\log_{2} (\mathcal{N}_{k,k} (X))}{k^{2}},\end{align*} $$

and this implies

(1) $$ \begin{align} \limsup_{N} \lim_{M} \frac{\log_{2} (\mathcal{N}_{M,N} (X))}{NM} \le h(X), \end{align} $$

by taking $ k \rightarrow + \infty $ in the last inequality.

Lower bound by decomposing rectangles into squares. For all $M,N$ , by considering a pattern on $\mathbb {U}^{(2)}_{MN,NM}$ as an array of patterns on $\mathbb {U}^{(2)}_{M,N}$ , we get that

$$ \begin{align*}\mathcal{N}_{MN,NM} (X)\le (\mathcal{N}_{M,N} (X)) {}^{MN}.\end{align*} $$

Thus,

$$ \begin{align*}h(X) = \lim_{M} \frac{\log_{2} (\mathcal{N}_{MN,NM} (X))}{M^{2} N^{2}} \le \lim_{M} \frac{\log_{2}(\mathcal{N}_{M,N} (X))}{M N}.\end{align*} $$

As a consequence,

(2) $$ \begin{align} h(X) \le \liminf_{N} \lim_{M} \frac{\log_{2} (\mathcal{N}_{M,N} (X))}{NM}. \end{align} $$

The two inequalities in equations (1) and (2) imply that the sequence $( {h(X_{N})}/{N} )_{N}$ converges and that the limit is $h(X)$ .

In the following, for all N and M, we assimilate patterns of $X_{N}$ on $\mathbb {U}^{(1)}_{M}$ with patterns of X on $\mathbb {U}^{(2)}_{M,N}$ .

2.2 Representations of square ice

The square ice can be defined as an isomorphic class of subshifts of finite type, whose elements can be thought of as various representations of the same object. The most widely used is the six-vertex model (whose name derives from the fact that the elements of the alphabet represent vertices of a regular grid) and is presented in §2.2.1. In this text, we will use another representation, presented in §2.2.2, whose configurations consist of drifting discrete curves, representing possible particle trajectories. In §2.2.3, we provide a proof that one can restrict to a subset of the total set of patterns considered to compute entropy of square ice.

2.2.1 The six-vertex model

The six-vertex model is the subshift of finite type described as follows.

Symbols: .

Local rules: Considering two adjacent positions in $\mathbb {Z}^{2}$ , the arrows corresponding to the common edge of the symbols on the two positions have to be directed the same way. For instance, the pattern is allowed, while is not.

Global behavior: The symbols draw a lattice whose edges are oriented in such a way that all the vertices have two incoming arrows and two outgoing ones. This is called an Eulerian orientation of the square lattice. See an example of an admissible pattern in Figure 2.

Figure 2 An example of locally and thus globally admissible pattern of the six-vertex model.

Remark 1. The name of square ice of the considered class of SFT appears clearly when considering the following application on the alphabet of the six-vertex model to local configurations of dihydrogen monoxide:

2.2.2 Drifting discrete curves

From the six-vertex model, we derive another representation of square ice through an isomorphism, which consists in transforming the letters via an application $\pi _{s}$ on the alphabet of the six-vertex model, described as follows:

For instance, the pattern in Figure 2 corresponds, after application of $\pi _{s}$ , to that in Figure 3. In this SFT, the local rules consist in forcing that any segment of the curve in a symbol extends in the positions that it directs to (in the fifth symbol in the above list, we consider that there are only two segments).

Figure 3 Representation of pattern in Figure 2.

In the following, we denote by $X^{s}$ this SFT.

Remark 2. One can see straightforwardly that locally admissible patterns of this SFT are always globally admissible, since any locally admissible pattern can be extended into a configuration by extending the curves in a straight way.

2.2.3 Entropy of $X^{s}$ and cylindrical stripes subshifts of square ice

Consider some alphabet $\mathcal {A}$ , and X a bidimensional subshift of finite type on this alphabet. For all $N \ge 1$ , we set $\Pi _{N}= \mathbb {Z} / (N\mathbb {Z}) \times \mathbb {Z}$ . Let us also denote by and the canonical projections. Formally, for all and ,

$$ \begin{align*}(\phi_{N} (x))_{\pi_{N} (\textbf{u})} = x_{\textbf{u}}. \end{align*} $$

We say that a pattern p on support appears in a configuration $\overline {x}$ on $\Pi _{N}$ when there exists a configuration in $X_{N}$ whose image by $\pi _{N}$ is $\overline {x}$ , and there exists an element $\textbf {u} \in \Pi _{N}$ such that for all $\textbf {v} \in \mathbb {U}, {\overline {x}}_{\textbf {u}+\pi _{N} (\textbf {v})}=x_{\textbf {v}}$ .

Notation 1. Let us denote by $\overline {X}_{N}$ the set of configurations in $X_{N}$ whose image by $\phi _{N}$ does not contain any forbidden pattern for X (in other words, this pattern can be wrapped on an infinite cylinder without breaking the rules defining X).

Similarly, we call $(M,N)$ -cylindrical pattern of X a pattern on $\mathbb {U}_{M,N}$ that can be wrapped on a finite cylinder $\mathbb {Z}/N\mathbb {Z} \times \{1,\ldots ,M\}$ . Let us prove a preliminary result on the entropy of square ice, which relates the entropy of $X^{s}$ to the sequence $(h(\overline {X}^{s}_{N}))_{N}$ .

Lemma 1. The subshift $X^{s}$ has entropy equal to

$$ \begin{align*}{h (X^{s}) = \lim_{N} \frac{h(\overline{X}^{s}_{N})}{N}}.\end{align*} $$

Remark 3. To prove this lemma, we use a technique that first appeared in a work of Friedland [F97], which relies on a symmetry of the alphabet and rules of the SFT.

Proof. (1) Lower bound: Since for all N, $\overline {X}^{s}_{N} \subset X^{s}_{N}$ , then $h(\overline {X}^{s}_{N}) \le h(X^{s}_{N})$ . We deduce by Proposition 1 that

$$ \begin{align*}\limsup_{N} \frac{h(\overline{X}^{s}_{N})}{N} \le h(X^{s}).\end{align*} $$

(2) Upper bound: Consider the transformation $\tau $ on the six-vertex model alphabet that consists in a horizontal symmetry of the symbols and then the inversion of all the arrows. The symmetry can be represented as follows:

The inversion is represented by

As a consequence, $\tau $ is

We define then a horizontal symmetry operation $\mathcal {T}_{N}$ (see Figure 4 for an illustration) on patterns p whose support is some $\mathbb {U}^{(2)}_{M,N}$ , with $M \ge 1$ .

Figure 4 Illustration of the definition of $\mathcal {T}_{3}$ : the pattern on the left (on support $\mathbb {U}^{(2)}_{3,4}$ ) is transformed into the pattern on the right via this transformation.

For all such M and p, $\mathcal {T}_{M} (p)$ has also support $\mathbb {U}^{(2)}_{M,N}$ and for all $(i,j) \in \mathbb {U}^{(2)}_{M,N}$ ,

$$ \begin{align*}\mathcal{T}_{N}(p)_{i,j} = \tau (p_{N-i,j}).\end{align*} $$

We define also the applications $\partial ^{r}_{N}$ (respectively, $\partial ^{l}_{N}$ , $\partial ^{t}_{N}$ ) that acts on patterns of the six-vertex model whose support is some $\mathbb {U}^{(2)}_{M,N}$ , $M\ge 1$ and such that for all $M \ge 1$ and p on support $\mathbb {U}^{(2)}_{M,N}$ , $\partial ^{r}_{N} (p)$ (respectively, $\partial ^{l}_{N} (p)$ ) is a length M (respectively, M, N) word and for all j between $1$ and M (respectively, M), $\partial ^{r}_{N} (p)_{j}$ (respectively, $\partial ^{l}_{N} (p)_{j}$ ) is the east (respectively, west) arrow in the symbol $p_{N,j}$ (respectively, $p_{1,j}$ ). For instance, if p is the pattern on the left in Figure 4, then $\partial ^{r}_{N} (p)$ (respectively, $\partial ^{l}_{N} (p)$ ) is the word:

$$ \begin{align*}\leftarrow \leftarrow \rightarrow \leftarrow \quad (\text{respectively,} \rightarrow \rightarrow \rightarrow \rightarrow).\end{align*} $$

For the purpose of notation, we denote also by $\pi _{s}$ the application that transforms patterns of the six-vertex model into patterns of $X_{s}$ via the application of $\pi _{s}$ letter by letter. Let us consider the transformation $ \mathcal {T}^{s}_{N} \equiv \pi _{s} \circ \mathcal {T}_{N} \circ \pi _{s}^{-1}$ on patterns of $X^{s}$ on some $\mathbb {U}^{(2)}_{M,N}$ . We also denote by $\partial _{N}^{l,s} \equiv \partial _{N}^{l} \circ \pi _{s}^{-1}$ , $\partial _{N}^{r,s} \equiv \partial _{N}^{r} \circ \pi _{s}^{-1}$ . Let us prove some properties of these transformations. For any word $\textbf {w}$ on the alphabet $\{\leftarrow ,\rightarrow \}$ or $\{\uparrow ,\downarrow \}$ , we denote by $\overline {\textbf {w}}$ the word obtained by exchanging the two letters in the word $\textbf {w}$ .

1. (a) Preservation of global admissibility: For any p globally admissible, $\mathcal {T}_{N} (p)$ is also locally admissible, and as a consequence globally admissible; indeed, it is sufficient to check that for all $u,v$ in the alphabet, if $uv$ is not a forbidden pattern in the six-vertex model, then $\tau (v) \tau (u)$ is also not a forbidden pattern and that if $\begin {smallmatrix} u \\ v \end {smallmatrix}$ is not forbidden, then $\begin {smallmatrix} \tau (u) \\ \tau (v) \end {smallmatrix}$ is also not forbidden.

   The first assertion is verified because $u v$ is not forbidden if and only if the arrows of these symbols attached to their adjacent edge are pointing in the same direction, and this property is preserved when changing $uv$ into $\tau (v)\tau (u)$ . The second one is verified for a similar reason.

2. (b) Gluing patterns: Let us consider any $N,M \ge 1$ and $p,p^{\prime }$ two patterns of $X^{s}$ on support $\mathbb {U}^{(2)}_{M,N}$ , such that $\partial _{N}^{r,s} (p) = \partial _{N}^{r,s} (p^{\prime }) $ and $\partial _{N}^{l,s} (p) = \partial _{N}^{l,s} (p^{\prime })$ . Let us denote by pattern $p^{\prime \prime }$ on support $\mathbb {U}^{(2)}_{M,2N}$ such that the restriction of $p^{\prime \prime }$ on $\mathbb {U}^{(2)}_{M,N}$ is p and the restriction on $(0,N) + \mathbb {U}^{(2)}_{M,N}$ is $\mathcal {T}_{N} (p^{\prime })$ .

   • • This pattern is admissible (locally and thus globally). Indeed, this is sufficient to check that gluing the two patterns p and $p^{\prime }$ does not make forbidden patterns appear, and this comes from that for all letter u, $ u \tau (u)$ is not forbidden. This can be checked directly, letter by letter.

   • • Moreover, ${p}^{\prime \prime }$ is in ${\mathcal {N}_{M} (\overline {X}_{2N})}$ . Indeed, this pattern can be wrapped on a cylinder, and this comes from the fact that if u is a symbol of the six-vertex model, $\tau (u) u$ is not forbidden.

(3) From the gluing property to an upper bound: Given $\textbf {w} = (\textbf {w}^{l},\textbf {w}^{r})$ as some pair of words on $\{\rightarrow ,\leftarrow \}$ , we denote by $\mathcal {N}^{\textbf {w}}_{M,N}$ the number of patterns of $X^{s}$ on support $\mathbb {U}^{(2)}_{M,N}$ such that $\partial _{N}^{l,s}=\textbf {w}^{l}$ and $\partial _{N}^{r,s}=\textbf {w}^{r}$ . Since $\mathcal {T}_{N}$ is a bijection, denoting $\overline {\textbf {w}} = (\overline {\textbf {w}^{l}},\overline {\textbf {w}^{r}})$ , we have

$$ \begin{align*}\mathcal{N}_{M,N}^{\textbf{w}} = \mathcal{N}_{M,N}^{\overline{\textbf{w}}}.\end{align*} $$

From the last point, for all $\textbf {w}$ ,

$$ \begin{align*}\mathcal{N}_{M} (\overline{X}^{s}_{2N}) \ge \mathcal{N}_{M,N}^{\textbf{w}}. \mathcal{N}_{M,N}^{\overline{\textbf{w}}} = (\mathcal{N}_{M,N}^{\textbf{w}})^{2}\end{align*} $$

$$ \begin{align*}(\mathcal{N}_{M} (\overline{X}^{s}_{2N}))^{{1}/{2}} \ge \mathcal{N}_{M,N}^{\textbf{w}}.\end{align*} $$

By summing over all possible $\textbf {w}$ :

$$ \begin{align*}2^{2M} \cdot (\mathcal{N}_{M}(\overline{X}^s_{2N}))^{{1}/{2}} = \sum_{\textbf{w}} (\mathcal{N}_{M} (\overline{X}^s_{2N}))^{{1}/{2}} \ge \sum_{\textbf{w}} \mathcal{N}_{M,N}^{\textbf{w}} = \mathcal{N}_{M,N} (X^s).\end{align*} $$

As a consequence, for all N,

$$ \begin{align*}2 + \frac{1}{2} h(\overline{X}^{s}_{2N}) \ge h(X^{s}_{N}).\end{align*} $$

This implies that

$$ \begin{align*}\liminf_{N} \frac{h(\overline{X}^{s}_{2N})}{2N} \ge \liminf_{N} \frac{h(X^{s}_{N})}{N} = h(X^{s}).\end{align*} $$

For similar reasons,

$$ \begin{align*}\liminf_{N} \frac{h(\overline{X}^{s}_{2N+1})}{2N+1} \ge \liminf_{N} \frac{h(X^{s}_{N})}{N} = h(X^{s}),\end{align*} $$

and thus,

$$ \begin{align*}\liminf_{N} \frac{h(\overline{X}^{s}_{N})}{N} \ge \liminf_{N} \frac{h(X^{s}_{N})}{N} = h(X^{s}).\\[-34pt]\end{align*} $$

3 Overview of the proof

In the following, we provide a complete proof of the following theorem.

Theorem 2. The entropy of square ice is equal to

$$ \begin{align*}{h(X^{s})= \tfrac{3}{2} \log_{2} \big( \tfrac{4}{3} \big)}.\end{align*} $$

The proof of Theorem 2 can be summarized as follows. Some of the terms will be defined in the text; however, this overview will provide us with a way in which to situate every argument in the overall strategy, which consists of:

1. (1) finding a formula for $h(\overline {X}^{s}_{N})$ for all N (in practice for all N odd);

2. (2) then using Lemma 1 to compute $h(X^{s})$ .

• • The first point is done using the transfer matrix method, which allows us to express $h(\overline {X}^{s}_{N})$ with a formula involving a sequence of numbers defined implicitly through a system of nonlinear equations called Bethe equations. This method itself consists of several steps.

  1. (1) Formulation with transfer matrices [§4]: it is usual, when dealing with unidimensional subshifts of finite type, to express their entropy as the greatest eigenvalue of the adjacency matrix, which tells which couples of symbols (which are rows of symbols in the case of stripe subshifts) can be adjacent. In this text, we use the adjacency matrix $V_{N}^{*}$ of a subshift which is isomorphic to $\overline {X}_{N}$ , and see the matrix of a linear operator on $\Omega _{N} = \mathbb {C}^{2} \otimes \cdots \otimes \mathbb {C}^{2}$ .

  2. (2) Lieb path—transport of information through analyticity [§4]: In quantum physics, transfer matrices, which are complexifications of the adjacency matrices in a local way (in the sense that the coefficient relative to a couple of rows is the product of some coefficients in $\mathbb {C}$ relative to the symbols in the two rows) are used to derive properties of the system. In this text, we will see the adjacency matrix as a particular value of an analytic path of such transfer matrices, $t \in \mathbb {R} \mapsto V_{N} (t)$ such that for all t, $V_{N} (t)$ is an irreducible non-negative and symmetric matrix, and such that $V_{N} (1) = V_{N}^{*}$ —we will call such a path a Lieb path in the following. The analyticity is used here to gain some information on the whole path, including on $V_{N}(1)$ , from information on a segment of the path. This part is contained in §4 and is a detailed exposition of notions defined in the article of Lieb [L67].

  3. (3) Coordinate Bethe ansatz [§5]: We use the coordinate Bethe ansatz (due originally to Hans Bethe and exposed recently in [DGHMT18] and related in the present text), which consists in a clever guess on the form of potential eigenvectors, and actually provides some candidates, for the matrices $V_{N}(t)$ . In practice, we apply this on each of the subspaces $\Omega ^{(n)}_{N}$ of a decomposition of $\Omega _{N}$ :

     $$ \begin{align*}\Omega_{N} = \bigoplus_{n=0}^{N} \Omega^{(n)}_{N}.\end{align*} $$
     The candidate eigenvectors and eigenvalues depend each on a solution $(p_{j})_{j=1\ldots n}$ of a nonlinear system of equations, with parameter t, called Bethe equations.

     It is shown that the system of Bethe equations admits a unique solution for each n,N and t, which we denote by $({\kern1pt}\textbf{p}_{j} (t))_{j}$ for all $t \in (0,\sqrt {2})$ , in a context where $n,N$ are fixed, using convexity arguments on an auxiliary function. The analyticity of the Lieb path and the convexity of the auxiliary function ensure together that $t \mapsto ({\kern1pt}\textbf{p}_{j} (t))_{j}$ is analytic. This part completes the proof of an argument left incomplete in [YY66a]. To identify the greatest eigenvalue of $V_{N}(t)$ for all t, we use the fact that $V_{N} (\sqrt {2})$ commutes with some Hamiltonian $H_{N}$ that is completely diagonalized (following [LSM61]). The consequence of this fact is that $V_{N} (\sqrt {2})$ and $H_{N}$ have a common base of eigenvectors. The candidate eigenvector provided by the Bethe ansatz on this point is proved not to be null and associated to the maximal eigenvalue of $H_{N}$ on $\Omega _{N}^{(n)}$ . By Perron–Frobenius theorem, the vector has positive coordinates, and by the same theorem (uniqueness part), it is an eigenvector of $V_{N} (\sqrt {2})$ and is associated with the maximal eigenvalue of this matrix on $\Omega _{N}^{(n)}$ . By continuity, this is true also for t in a neighborhood of $\sqrt {2}$ , and by analyticity, this identity is true for all $t \in (0,\sqrt {2})$ .

• • The second point is derived in two steps:

  1. (1) Asymptotic condensation of Bethe roots [§6]: The sequences $({\kern1pt}\textbf{p}_{j} (t))_{j}$ are transformed into sequences $(\boldsymbol {\alpha }_{j} (t))_{j}$ through an analytic bijection. The values of these second sequences are in $\mathbb {R}$ and are called Bethe roots.

     We first prove that the sequences of Bethe roots are condensed according to a density function $\rho _{t}$ over $\mathbb {R}$ , relative to any continuous decreasing and integrable function $f : (0,+\infty ) \rightarrow (0,+\infty )$ , which means that the Cesàro mean of the finite sequence $(f(\boldsymbol {\alpha }_{j} (t)))_{j}$ converges towards $\int \rho _{t} (x) f(x) \,dx$ . This part involves rigorous proofs, some simplifications and adaptations of arguments that appeared in [K18]. The density $\rho _{t}$ is defined as the solution of a Fredholm integral equation which can be thought of as the asymptotic version of Bethe equations. This equation is solved through Fourier analysis, following a computation done in [YY66b].

  2. (2) Computation of integrals [§7]: The condensation property proved in the last point implies that the formula obtained for $\frac {1}{N} h(\overline {X}^{s}_{N})$ converges to an integral involving $\rho _{1}$ . The formula obtained for $\rho _{1}$ allows the computation of this integral, via loop integrals techniques. This part is a detailed version of computations exposed in [L67].

For the purpose of clarity, we will begin each section with a paragraph beginning with $\triangleright $ relating the section to this overview.

4 A Lieb path for square ice

$\triangleright $ In this section, we define the matrices $V_{N}^{*}$ [§4.1], the Lieb paths $t \mapsto V_{N} (t)$ that we will use in the following [§4.2] and prove that $V_{N} (1) = V^{*}_{N}$ [§4.3].

4.1 The interlacing relation and the matrices $V_{N}^{*}$

$\triangleright $ The definition of the matrix $V_{N}^{*}$ relies on a relation between words on $\{0,1\}$ having length N. In this section, we prove the properties of this relation which will be translated later into properties of the matrices $V_{N}(t)$ , and in particular $V_{N}^{*}$ .

In the following, for a square matrix M, we will denote by $M[u,v]$ its entry on $(u,v)$ . Moreover, we denote by $\{0,1\}^{*}_{N}$ the set of length N words on $\{0,1\}$ .

Notation 2. Consider $\textbf {u},\textbf {v}$ two words in $\{0,1\}^{*}_{N}$ , and w some $(N,1)$ -cylindrical pattern of the subshift X. We say that the pattern w connects $\textbf {u}$ to $\textbf {v}$ , and we denote this by $\textbf {u} \mathcal {R}[w] \textbf {v}$ , when for all , $\textbf {u}_{k} = 1$ (respectively, $\textbf {v}_{k}=1$ ) if and only if w has an incoming (respectively, outgoing) curve on the bottom (respectively, top) of its kth symbol. This notation is illustrated in Figure 5.

Figure 5 Illustration for the definition of the notation $\boldsymbol {u} \mathcal {R}[w] \boldsymbol {v}$ .

Definition 3. Let us denote by $\mathcal {R} \subset \{0,1\}^{N} \times \{0,1\}^{N}$ the relation defined by $\boldsymbol {u} \mathcal {R} \boldsymbol {v}$ if and only if there exists an $(N,1)$ -cylindrical pattern w of the discrete curves shift $X^{s}$ such that $\boldsymbol {u} \mathcal {R}[w] \boldsymbol {v}$ .

Notation 3. Let $N \ge 1$ be an integer and $t>0$ . Let us denote by $\Omega _{N}$ the space $\mathbb {C}^{2} \bigotimes \cdots \bigotimes \mathbb {C}^{2}$ , the tensor product of N copies of $\mathbb {C}^{2}$ , whose canonical basis elements are denoted indifferently by $\boldsymbol {\epsilon }= \lvert {\boldsymbol {\epsilon }_{1} \cdots \boldsymbol {\epsilon }_{N}}\rangle $ or the words $\boldsymbol {\epsilon }_{1} \cdots \boldsymbol {\epsilon }_{N}$ , for $(\boldsymbol {\epsilon }_{1}, \ldots , \boldsymbol {\epsilon }_{N}) \in \{0,1\}^{N}$ , according to quantum mechanics notation, to distinguish them from the coordinate definition of vectors of $\Omega _{N}$ . For the definition of the matrices, we order the elements of this basis with the lexicographic order.

Definition 4. Let us define $V_{N}^{*} \in \mathcal {M}_{2^{N}}(\mathbb {C})$ the matrix such that for all $\boldsymbol {\epsilon },\boldsymbol {\eta } \in {0,1}^{*}_{N}$ , $V_{N}[\boldsymbol {\epsilon },\boldsymbol {\eta }]$ is the number of w such that $\boldsymbol {\epsilon }\mathcal {R}[w]\boldsymbol {\eta }$ .

Notation 4. For all $\textbf {u} \in \{0,1\}_{N}^{*}$ , we denote by $|\textbf {u}|_{1}$ the number of such that $\textbf {u}_{k} = 1$ . If $|\textbf {u}|_{1} =n$ , we denote by $q_{1} [\textbf {u}]< \cdots < q_{n} [\textbf {u}]$ the integers such that $\textbf {u}_{k} = 1$ if and only if $k=q_{i}[\textbf {u}]$ for some .

Let us also notice that $\textbf {u} \mathcal {R} \textbf {v}$ implies that the number of $1$ symbols in $\textbf {u}$ is equal to the number of $1$ symbols in $\textbf {v}$ .

Definition 5. We say that two words $\textbf {u},\textbf {v}$ in $\{0,1\}^{*}_{N}$ such that $|\textbf {u}|_{1}=|\textbf {v}|_{1} \equiv n$ are interlaced when one of the two following conditions is satisfied:

$$ \begin{align*}q_{1} [\boldsymbol{u}] \le q_{1} [\boldsymbol{v}] \le q_{2} [\boldsymbol{u}] \le \cdots \le q_{n} [\boldsymbol{u}] \le q_{n} [\boldsymbol{v}],\end{align*} $$

$$ \begin{align*}q_{1} [\boldsymbol{v}] \le q_{1} [\boldsymbol{u}] \le q_{2} [\boldsymbol{v}] \le \cdots \le q_{n} [\boldsymbol{v}] \le q_{n} [\boldsymbol{u}].\end{align*} $$

Proposition 2. For two length N words $\textbf {u},\textbf {v}$ , we have $\textbf {u} \mathcal {R} \textbf {v}$ if and only if $|\textbf {u}|_{1} = |\textbf {v}|_{1} \equiv n$ and $\textbf {u},\textbf {v}$ are interlaced.

Proof. $(\Rightarrow )$ : assume that $\boldsymbol {u} \mathcal {R}[w] \boldsymbol {v}$ for some w.

First, since w is an $(N,1)$ -cylindrical pattern, each of the curves that cross its bottom side also crosses its top side, which implies that $|\boldsymbol {u}|_{1} = |\boldsymbol {v}|_{1}$ .

We assume that $q_{1} [\boldsymbol {u}] \le q_{1} [\boldsymbol {v}]$ (the other case is processed similarly).

1. (1) The position ${q_{1}} \boldsymbol {[u]}$ is connected to ${q_{1}} \boldsymbol {[v]}$ or ${q_{1}} \boldsymbol {[u]} = {q_{1}} \boldsymbol {[v]}$ : Let us assume that $q_{1} [\boldsymbol {u}] \neq q_{1} [\boldsymbol {v}]$ and $q_{1} [\boldsymbol {u}]$ is not connected to $q_{1} [\boldsymbol {v}]$ . Then because $\boldsymbol {u} \mathcal {R}[w] \boldsymbol {v}$ , another curve would have to connect another position $q_{k} [\boldsymbol {u}]$ , $k \neq 1$ of $\boldsymbol {u}$ to $q_{1} [\boldsymbol {v}]$ . Since $q_{k} [\boldsymbol {u}]> q_{1} [\boldsymbol {u}]$ (by definition), this curve would cross the left border of w. It would imply that in the $q_{1} [\boldsymbol {u}]$ th symbol of w, two pieces of curves would appear: one horizontal, corresponding to the curve connecting the position $q_{k} [\boldsymbol {u}]$ to $q_{1} [\boldsymbol {v}]$ , and the one that connects $q_{1} [\boldsymbol {u}]$ to another position in $\boldsymbol {u}$ , which is not possible, by the definition of the alphabet of $X^{s}$ . This is illustrated in Figure 6.

   

   Figure 6 Illustration of (impossible) crossing situation, which would imply non-authorized symbols.

2. (2) $q_{1} \boldsymbol {[v]} \le q_{2} \boldsymbol {[u]} \le q_{2} \boldsymbol {[v]}$ : In both cases, this derives from similar arguments.

3. (3) Repetition: We can then repeat these arguments to obtain:

   $$ \begin{align*}q_{1} [\boldsymbol{u}] \le q_{1} [\boldsymbol{v}] \le q_{2} [\boldsymbol{u}] \le \cdots \le q_{n} [\boldsymbol{u}] \le q_{n} [\boldsymbol{v}],\end{align*} $$
   meaning that $\boldsymbol {u}$ and $\boldsymbol {v}$ are interlaced.

$(\Leftarrow )$ : if $|\boldsymbol {u}|_{1} = \boldsymbol {v}_{1}$ and $\boldsymbol {u},\boldsymbol {v}$ are interlaced, then we define w by connecting $q_{i} [\boldsymbol {u}]$ to $q_{i} [\boldsymbol {v}]$ for all . We thus have directly $\boldsymbol {u} \mathcal {R} [w] \boldsymbol {v}$ .

Proposition 3. When $\textbf {u} \mathcal {R} \textbf {v}$ and $\textbf {u} \neq \textbf {v}$ , there exists a unique w such that $\textbf {u} \mathcal {R} [w] \textbf {v}$ . When $\textbf {u} = \textbf {v}$ , there are exactly two possibilities, either the word w that connects $q_{i} [\textbf {u}]$ to itself for all i, or the one connecting $q_{i} [\textbf {u}]$ to $q_{i+1} [\textbf {u}]$ for all i.

Proof. Consider words $\boldsymbol {u} \neq \boldsymbol {v}$ and w, such that $\boldsymbol {u} \mathcal {R}[w] \boldsymbol {v}$ . Because of Proposition 2, $\boldsymbol {u}$ and $\boldsymbol {v}$ are interlaced. Let us assume that we have (the other case is processed similarly)

$$ \begin{align*}q_{1} [\boldsymbol{u}] \le q_{1} [\boldsymbol{v}] \le q_{2} [\boldsymbol{u}] \le \cdots \le q_{n} [\boldsymbol{u}] \le q_{n} [\boldsymbol{v}].\end{align*} $$

Because the words are different, there is some j such that the position $q_{j} [\boldsymbol {u}]$ is connected to $q_{j} [\boldsymbol {v}]$ . This forces that the position $q_{j+1} [\boldsymbol {u}]$ is connected to $q_{j+1} [\boldsymbol {v}]$ if $j<n$ . If n, $q_{1} [\boldsymbol {u}]$ is connected to $q_{1} [\boldsymbol {v}]$ . By repeating this, we obtain that for all i, $q_{i} [\boldsymbol {u}]$ is connected to $q_{i} [\boldsymbol {v}]$ . This determines w, which implies that there is a unique w such that $\boldsymbol {u} \mathcal {R}[w] \boldsymbol {v}$ .

When $\boldsymbol {u} = \boldsymbol {v}$ , it is clear that there is a unique w connecting position $q_{i} [\boldsymbol {u}]$ to $q_{i} [\boldsymbol {v}]$ for all i. Any other w connecting $\boldsymbol {u}$ to $\boldsymbol {v}$ connects $q_{i} [\boldsymbol {u}]$ to $q_{j} [\boldsymbol {v}]$ for some $j \neq i$ . This j is forced to be $i+1$ (for similar arguments as in the first point of the proof of Proposition 2) and for similar arguments as above, this forces that $q_{i} [\boldsymbol {u}]$ to $q_{i+1} [\boldsymbol {v}]$ for all $i \le n$ and connects $q_{n} [\boldsymbol {u}]$ to $q_{1} [\boldsymbol {v}]$ .

4.2 The Lieb path $t \mapsto V_{N} (t)$

$\triangleright $ In this section, we define the matrices $V_{N}(t)$ . This definition is similar to that of $V_{N}^{*}$ , and relies in particular on the interlacing relation and on an additional parameter t. We prove here properties of matrices $V_{N}(t)$ , symmetry and irreducibility, which derive from properties of the relation $\mathcal {R}$ . These properties are essential to apply later the Perron–Frobenius theorem, which we recall here.

Notation 5. For all N and $(N,1)$ -cylindrical pattern w, let us denote by $|w|$ the number of symbols

in this pattern. For instance, for the word w in Figure 5, $|w|=6$ .

Definition 6. For all $t \ge 0$ , let us define $V_{N} (t) \in \mathcal {M}_{2^{N}} (\mathbb {C})$ the matrix such that for all $\boldsymbol {\epsilon },\boldsymbol {\eta } \in \{0,1\}^{*}_{N}$ ,

$$ \begin{align*}V_{N} (t) [\boldsymbol{\epsilon},\boldsymbol{\eta}] =\displaystyle{\sum_{\boldsymbol{\epsilon} \mathcal{R}[w] \boldsymbol{\eta}}} t^{|w|}.\end{align*} $$

It is immediate that $V_{N}^{*}$ is equal to $V_{N}(1)$ .

For all N and $n \le N$ , let us denote by $\Omega _{N}^{(n)} \subset \Omega _{N}$ the vector space generated by the $\boldsymbol {\epsilon }=\lvert {\boldsymbol {\epsilon }_{1} \cdots \boldsymbol {\epsilon }_{N}}\rangle $ such that $|\boldsymbol {\epsilon }|_{1} = n$ .

Proposition 4. For all N and $n \le N$ , the matrix $V_{N} (t)$ stabilizes the vector subspaces $\Omega _{N}^{(n)}$ :

$$ \begin{align*}V_{N} (t). \Omega_{N}^{(n)} \subset \Omega_{N}^{(n)}.\end{align*} $$

Proof. This is a direct consequence of Proposition 2, since if $V_{N} (t) [\boldsymbol {\epsilon }, \boldsymbol {\eta }] \neq 0$ for $\boldsymbol {\epsilon },\boldsymbol {\eta }$ , two elements of the canonical basis of $\Omega _{N}$ , then $|\boldsymbol {\epsilon }|_{1} = |\boldsymbol {\eta }|_{1}$ .

Let us recall that a non-negative matrix A is called irreducible when there exists some $k \ge 1$ such that all the coefficients of $A^{k}$ are positive. Let us also recall the Perron–Frobenius theorem for symmetric, non-negative and irreducible matrices.

Theorem 2. (Perron–Frobenius)

Let A be a symmetric, non-negative and irreducible matrix. Then A has a positive eigenvalue $\lambda $ such that any other eigenvalue $\mu $ of A satisfies $|\mu | \le \lambda $ . Moreover, there exists some eigenvector u for the eigenvalue $\lambda $ with positive coordinates such that if v is another eigenvector (not necessarily for $\lambda $ ) with positive coordinates, then $v= \alpha .u$ for some $\alpha> 0$ .

Let us prove the uniqueness of the positive eigenvector up to a multiplicative constant.

Proof. Let us denote by $u \in \Omega _{N}$ the Perron–Frobenius eigenvector and $v \in \Omega _{N}$ another vector whose coordinates are all positive, associated to the eigenvalue $\mu $ . Then

$$ \begin{align*}\mu u^{t}.v = (Au)^{t}. v = u^{t} A v = \lambda u^{t}.v.\end{align*} $$

Thus, since $u^{t}.v>0$ , then $\mu = \lambda $ , and by (usual version of) Perron–Frobenius, there exists some $\alpha \in \mathbb {R}$ such that $v= \alpha .u$ . Since v has positive coordinates, $\alpha>0$ .

Lemma 2. The matrix $V_{N} (t)$ is symmetric, non-negative (all its coefficients are non-negative numbers) when $t\ge 0$ and for all $n \le N$ , its restriction to $\Omega _{N}^{(n)}$ is irreducible whenever $t>0$ .

Proof. The non-negativity of the matrix is immediate when $t \ge 0$ is immediate. Let us prove the other properties.

Symmetry: since the interlacing relation is symmetric, for all $\boldsymbol {\epsilon },\boldsymbol {\eta } \in \{0,1\}^{*}_{N}$ , we have that $V_{N} (t) [\boldsymbol {\epsilon },\boldsymbol {\eta }]>0$ if and only if $V_{N} (t) [\boldsymbol {\eta },\boldsymbol {\epsilon }]>0$ . When this is the case, and $\boldsymbol {\epsilon } \neq \boldsymbol {\eta }$ (the case $\boldsymbol {\epsilon }=\boldsymbol {\eta }$ is trivial), there exists a unique (Proposition 3) w connecting $\boldsymbol {\epsilon }$ to $\boldsymbol {\eta }$ . The coefficient of this word is exactly $t^{2(n-|\{k: \boldsymbol {\epsilon }_{k} = \boldsymbol {\eta }_{k} = 1\}|)}$ , where $n= |\{k:\boldsymbol {\epsilon }_{k}=1\}|=|\{k:\boldsymbol {\eta }_{k}=1\}|$ , and this coefficient is indifferent to the exchange of $\boldsymbol {\epsilon }$ and $\boldsymbol {\eta }$ . This implies that $V_{N} (t) [\boldsymbol {\epsilon },\boldsymbol {\eta }] = V_{N} (t) [\boldsymbol {\eta },\boldsymbol {\epsilon }]$ . As a consequence, $V_{N}(t)$ is symmetric.

Irreducibility: Let $\boldsymbol {\epsilon }$ , $\boldsymbol {\eta }$ be two elements of the canonical basis of $\Omega _{N}$ such that $|\boldsymbol {\epsilon }|_{1} = |\boldsymbol {\eta }|_{1} = n$ . We shall prove that $V_{N}^{N^{n}} (t) [\boldsymbol {\epsilon },\boldsymbol {\eta }]>0$ .

1. (1) Interlacing case: If we have $\boldsymbol {\epsilon } \mathcal {R} \boldsymbol {\eta }$ , then $V_{N} (t) [\boldsymbol {\epsilon },\boldsymbol {\eta }]>0$ . Since $V_{N} (t) [\boldsymbol {\eta },\boldsymbol {\eta }]>0$ and $V_{N}(t)$ is non-negative, for all $k\ge 1$ ,

   $$ \begin{align*}V_{N} (t)^{k} [\boldsymbol{\epsilon},\boldsymbol{\eta}] \ge V_{N}(t) [\boldsymbol{\epsilon},\boldsymbol{\eta}] (V_{N} (t) [\boldsymbol{\eta},\boldsymbol{\eta}])^{k-1}>0.\end{align*} $$

   In particular, $V_{N} (t)^{N^{n}} [\boldsymbol {\epsilon },\boldsymbol {\eta }]>0$ .

2. (2) Non-interlacing case:

   • • Decreasing the interlacing degree: If we do not have the relation $\boldsymbol {\epsilon } \mathcal {R} \boldsymbol {\eta }$ , let us denote by $\omega (\boldsymbol {\epsilon },\boldsymbol {\eta })$ the following quantity (interlacing degree):

     
     Since the relation $\boldsymbol {\epsilon } \mathcal {R} \boldsymbol {\eta }$ does not hold, $\omega (\boldsymbol {\epsilon },\boldsymbol {\eta }) \ge 2$ . Let us also denote by $\lambda (\boldsymbol {\epsilon },\boldsymbol {\eta })$ the number of integers i such that i realizes the maximum in the definition of $\omega (\boldsymbol {\epsilon },\boldsymbol {\eta })$ .

     Let us see that there exists some $\boldsymbol {\epsilon }^{\prime }$ such that $\boldsymbol {\epsilon } \mathcal {R} \boldsymbol {\epsilon }^{\prime }$ and $\lambda (\boldsymbol {\epsilon }^{\prime },\boldsymbol {\eta }) < \lambda (\boldsymbol {\epsilon },\boldsymbol {\eta })$ if $\lambda (\boldsymbol {\epsilon },\boldsymbol {\eta }) \ge 2$ and otherwise $\omega (\boldsymbol {\epsilon }^{\prime },\boldsymbol {\eta }) < \omega (\boldsymbol {\epsilon },\boldsymbol {\eta })$ .

     Since $|\boldsymbol {\epsilon }|_{1} = |\boldsymbol {\eta }|_{1}$ , there exist i and $i^{\prime }$ such that is maximal and is equal to $0$ . Let us assume that $i < i^{\prime }$ (the other case is processed similarly). We can also assume that there is no $i^{\prime \prime }$ such that $i < i^{\prime \prime }<i^{\prime }$ such that is equal to  $0$ .

     Let us denote $j_{0}$ and $j_{1}$ such that $q_{j_{0}} [\boldsymbol {\epsilon }]$ and $q_{j_{1}} [\boldsymbol {\epsilon }]$ are respectively the maxima of the sets and . There is a word w which connects $q_{j}[\boldsymbol {\epsilon }]$ to $q_{j+1}[\boldsymbol {\epsilon }]$ for all , and fixes $q_{j}[\boldsymbol {\epsilon }]$ for all other j. The words w thus connects $\epsilon $ to $\epsilon ^{\prime }$ which satisfies the above properties.

   • • A sequence with decreasing interlacing degree: As a consequence, since $\omega (\boldsymbol {\epsilon },\boldsymbol {\eta }) \le N$ , one can construct a finite sequence of words $\boldsymbol {\epsilon }^{(k)}$ , $k=1\ldots m$ such that $m \le N^{n}$ , $\boldsymbol {\epsilon }^{(1)} = \boldsymbol {\epsilon }$ , $\boldsymbol {\epsilon }^{(m)}$ and $\boldsymbol {\eta }$ are interlaced, and for all ${k <m}$ , $\boldsymbol {\epsilon }^{(k)} \mathcal {R} \boldsymbol {\epsilon }^{(k+1)}$ . This means that for all $k<m$ , $V_{N}[\boldsymbol {\epsilon }^{(k)}, \boldsymbol {\epsilon }^{(k+1)}]>0$ and $V_{N}[\boldsymbol {\epsilon }^{(m)},\boldsymbol {\eta }]>0$ . As a consequence, $V_{N} (t)^{N^{n}} [\boldsymbol {\epsilon },\boldsymbol {\eta }]>0$ .

This implies that $V_{N} (t)$ is irreducible on $\Omega _{N}^{(n)}$ for all $n \le N$ .

4.3 Relation between $h(X^{s})$ and the matrices $V_{N} (1)$

$\triangleright $ We know that the entropy of $X^{s}$ can be obtained out of the sequence $h(\overline {X}_{N}^{s})$ . In this section, we prove that the $h(\overline {X}_{N}^{s})$ is related to the eigenvalues of $V_{N}(1)$ , which enables us to use linear algebra to compute the entropy of $X^{s}$ .

Notation 6. For all N and $n \le N$ , let us denote by $\overline {X}^{s}_{n,N}$ the subset (which is also a subshift) of $\overline {X}^{s}_{N}$ which consists in the set of configurations of $\overline {X}^{s}_{N}$ such that the number of curves that cross each of its rows is n, and $\overline {X}_{n,N}$ the subset of $\overline {X}_{N}$ such that the number of arrows pointing south in the south part of the symbols in any raw is n.

Notation 7. Let us denote, for all N and $n \le N$ , by $\lambda _{n,N} (t)$ the greatest eigenvalue of $V_{N} (t)$ on $\Omega _{N}^{(n)}$ .

Proposition 5. For all N and $n \le N$ , $h(\overline {X}^{s}_{n,N}) = \log _{2} (\lambda _{n,N} (1))$ .

Proof. Correspondence between elements of ${\overline {X}}^{{s}}_{{n,N}}$ and trajectories under action of ${V_{N}(1)}$ : Since for all N, $n \le N$ and $\boldsymbol {\epsilon },\boldsymbol {\eta }$ in the canonical basis of $\Omega _{N}^{(n)}$ , $V_{N} (1) [\boldsymbol {\epsilon },\boldsymbol {\eta }]$ is the number of ways to connect $\boldsymbol {\epsilon }$ to $\boldsymbol {\eta }$ by an $(N,1)$ -cylindrical pattern, and that there is a natural invertible map from the set of $(M,N)$ -cylindrical patterns to the sequences $(w_{i})_{i=1\ldots M}$ of $(N,1)$ -cylindrical patterns such that there exists some $(\boldsymbol {\epsilon }_{i})_{i=1\ldots M+1}$ such that for all i, $|\boldsymbol {\epsilon }_{i}|=n$ and for all $i \le M$ , $\boldsymbol {\epsilon }_{i} \mathcal {R}[w_{i}]\boldsymbol {\epsilon }_{i+1}$ ,

$$ \begin{align*}\|(V_{N}(1)_{\Omega_{N}^{(n)}}^{M})\|_{1}=\mathcal{N}_{M} (\overline{X}^{s}_{n,N}).\end{align*} $$

Gelfand’s formula: It is known (Gelfand’s formula) that $\|(V_{N} (1)_{\Omega _{N}^{(n)}}^{M})\|_{1}^{1/M} \rightarrow \lambda _{n,N} (1).$

As a consequence of the first point, $h (\overline {X}^{s}_{n,N}) = \log _{2} (\lambda _{n,N} (1)).$

Proposition 6. For all N, $h (X^{s}) = \lim _{N} ({1}/{N}) \max _{n \le N} h(\overline {X}^{s}_{n,N})$ .

Proof. We have the decomposition

$$ \begin{align*}\overline{X}^{s}_{N} = \displaystyle{\bigcup_{n=0}^{N}} \overline{X}^{s}_{n,N}.\end{align*} $$

Moreover, these subshifts are disjoint. As a consequence,

$$ \begin{align*}h(\overline{X}^{s}_{N}) = \max_{n \le N} h(\overline{X}^{s}_{n,N}).\end{align*} $$

From this, we deduce the statement.

Lemma 3. For all $N \ge 1$ and $n \le N$ , $h(\overline {X}^{s}_{n,N}) = h(\overline {X}^{s}_{N-n,N})$ .

Proof. For the purpose of notation, we also denote by $\pi _{s}$ the application from $\overline {X}_{n,N}$ to $\overline {X}^{s}_{n,N}$ that consists in an application of $\pi _{s}$ letter by letter. This map is invertible. Let us consider the application $\overline {\mathcal {T}}_{n,N}$ from $\overline {X}_{n,N}$ to $\overline {X}_{N-n,N}$ that inverts all the arrows. This map is an isomorphism, and thus the map $\pi _{s} \circ \overline {X}_{n,N} \circ \pi _{s}^{-1}$ is also an isomorphism from $\overline {X}^{s}_{n,N}$ to $\overline {X}^{s}_{N-n,N}$ . As a consequence, the two subshifts have the same entropy:

$$ \begin{align*}h(\overline{X}^{s}_{n,N}) = h(\overline{X}^{s}_{N-n,N}).\\[-40pt]\end{align*} $$

The following corollary is a straightforward consequence of Lemma 3.

Corollary 1. The entropy of $X^{s}$ is given by the following formula:

$$ \begin{align*}h(X^{s}) = \lim_{N} \frac{1}{2N}\displaystyle{\max_{n \le N}} \log_{2} (\lambda_{n,2N} (1)).\end{align*} $$

Lemma 4. We deduce that

$$ \begin{align*}{h(X^{s}) = \lim_{N} \frac{1}{2N}\displaystyle{\max_{2n+1 \le N}} \log_{2} (\lambda_{2n+1,2N} (1))}.\end{align*} $$

Proof. Let us fix some integer N and for all n between $1$ and $N/2+1$ , and consider the application that the set of patterns of $\overline {X}^{s}_{n,N}$ on $\mathbb {U}^{(1)}_{M}$ associates a pattern of $\overline {X}^{s}_{n-1,N}$ on $\mathbb {U}^{(1)}_{M}$ by suppressing the curve that crosses the leftmost symbol in the bottom row of the pattern crossed by a curve [see the schema in Figure 7].

Figure 7 Illustration of the curve suppressing operation; the leftmost position of the bottom row crossed by a curve is colored gray on the left pattern.

For each pattern of $\overline {X}^{s}_{n-1,N}$ , the number of patterns in its preimage by this transformation is bounded from above by $N^{M}$ . As a consequence, for all M:

$$ \begin{align*}\mathcal{N}_{M} (\overline{X}^{s}_{n-1,N}). N^{M} \ge \mathcal{N}_{M} (\overline{X}^{s}_{n,N}),\end{align*} $$

and thus

$$ \begin{align*}h(\overline{X}^{s}_{n-1,N}) + \log_{2} (N) \ge h(\overline{X}^{s}_{n,N}).\end{align*} $$

As a consequence,

$$ \begin{align*} h(X^{s}) & = \lim_{N} \frac{1}{2N} \max ( \max_{2n+1 \le N} h(\overline{X}^{s}_{2n+1,2N}), \max_{2n \le N} h(\overline{X}^{s}_{2n,2N}) ) \nonumber \\& \le \lim_{N} \frac{1}{2N} \max ( \max_{2n+1 \le N} h(\overline{X}^{s}_{2n+1,2N}), \max_{2n \le N} h(\overline{X}^{s}_{2n-1,2N}) + \log_{2} (N) )\\ & \le \lim_{N} \frac{1}{2N} \max_{2n+1 \le N} h(\overline{X}^{s}_{2n+1,2N}). \end{align*} $$

Moreover, it is straightforward that

$$ \begin{align*}h(X^{s}) \ge \lim_{N} \frac{1}{2N} \max_{2n+1 \le N} h(\overline{X}^{s}_{2n+1,2N}),\end{align*} $$

thus we have the following equality:

$$ \begin{align*}h(X^{s}) = \lim_{N} \frac{1}{2N}\displaystyle{\max_{2n +1 \le N}} \log_{2} (\lambda_{2n+1,2N} (1)).\\[-3.6pc]\end{align*} $$

5 Coordinate Bethe ansatz

$\triangleright $ Let us remember that we proved in the last section that the entropy of $X^{s}$ can be computed out of the eigenvalues of the matrices $V_{2N}(1)$ . Ideally, we would like to diagonalize these matrices, which is in fact very difficult. The purpose of the (coordinate) Bethe ansatz [§5.2] is to provide instead candidate eigenvectors for the matrix $V_{2N}(t)$ for all t on all $\Omega _{2N}^{(n)}$ , whose formulation relies on some solution of the system of Bethe equations $(E_{j}) [t,n,N]$ , $j \le n$ (see §5.2). We prove the existence unicity and analyticity relative to the parameter t of the solutions of the system in §5.3. For the statement of the ansatz, we need to introduce some auxiliary functions [§5.1] which are involved in its formulation, and prove some properties they satisfy which will be useful in particular to prove the existence and analyticity of the solutions of the system of Bethe equations $(E_{j}) [t,n,N]$ , $j \le n$ . We will prove that the candidate eigenvalue corresponding to the candidate eigenvector is the maximal eigenvalue of $V_{2N}(t)$ on $\Omega _{2N}^{(2n+1)}$ for $2n+1 \le N$ , for t close to $\sqrt {2}$ , in §5.5. This relies on the diagonalization of the Hamiltonian mentioned in the overview [§5.4]. The analyticity of the solutions to the system of Bethe equations implies that this is true for all $t \in (0,\sqrt {2})$ .

5.1 Auxiliary functions

$\triangleright $ The purpose of the present section is to introduce the functions $\Theta $ and $\kappa $ (respectively, Notation 8 and Notation 9) which will be used in the statement of the ansatz and then through the whole article. The reader may skip the details of computations done in this section. We provide them because they were not properly proven and may ultimately help to understand under which conditions it is possible to use an argument similar to Bethe ansatz in order to compute entropy for other multidimensional SFT.

5.1.1 Notation

Let us denote by $\mu : (-1,1) \rightarrow (0,\pi )$ the inverse of the function $\cos : (0,\pi ) \rightarrow (-1,1)$ . For all $t \in (0,\sqrt {2})$ , we will set $\Delta _{t} = ({2-t^{2}})/{2}$ , $\mu _{t} = \mu (-\Delta _{t})$ and $I_{t} = (-(\pi -\mu _{t}), (\pi -\mu _{t}))$ .

Notation 8. Let us denote by $\Theta $ the unique analytic function $(t,x,y) \mapsto \Theta _{t} (x,y)$ from the set $\{(t,x,y): x,y \in I_{t}\}$ to $\mathbb {R}$ such that $\Theta _{\sqrt {2}} (0,0) = 0$ and for all $t,x,y$ ,

$$ \begin{align*}{\exp(-i\Theta_{t} (x,y)) = \exp(i(x-y))\cdot \frac{e^{-ix} + e^{iy} - 2 \Delta_{t}}{e^{-iy} + e^{ix} - 2 \Delta_{t}}}.\end{align*} $$

By a unicity argument, one can see that for all $t,x,y$ , $\Theta _{t}(x,y) = - \Theta _{t}(y,x).$ As a consequence, for all x, $\Theta _{t} (x,x) = 0$ . For the same reason, $\Theta _{t}(x,-y)= -\Theta _{t}(-x,y)$ and $\Theta _{t} (-x,-y) = - \Theta _{t} (x,y)$ . Moreover, $\Theta _{t}$ and all its derivatives can be extended by continuity on $I_{t}^{2} \backslash \{(x,x): x \in \partial I_{t}\}$ . For the purpose of notation, we will also denote by $\Theta _{t}$ the extended function. We will use the following.

Computation 1. For all $y \neq (\pi -\mu _{t})$ , $\Theta _{t} ((\pi -\mu _{t}),y) = 2\mu _{t} - \pi $ .

Proof. From the definition of $\mu _{t}$ , $\Delta _{t} = -\cos (\mu _{t}) = - ({e^{i\mu _{t}}+e^{-i\mu _{t}}})/{2}$ . As a consequence, from the definition of $\Theta _{t}$ ,

$$ \begin{align*}\exp(-i\Theta_{t} ((\pi-\mu_{t}),y)) = e^{i(\pi-\mu_{t}-y)} \cdot \frac{e^{iy} - e^{i\mu_{t}} - 2 \Delta_{t}}{e^{-iy} - e^{-i\mu_{t}} - 2 \Delta_{t}} = e^{i(\pi-\mu_{t}-y)} \cdot \frac{e^{iy} + e^{-i\mu_{t}}}{e^{-iy} + e^{i\mu_{t}}}. \end{align*} $$

As a consequence,

$$ \begin{align*}\exp(-i\Theta_{t} ((\pi-\mu_{t}),y)) = e^{i(\pi-\mu_{t}-y)}\cdot \frac{e^{iy}}{e^{i\mu_{t}}} \frac{1+ e^{-i(\mu_{t} + y)}}{e^{-i(y+\mu_{t})}+1} = e^{i(\pi-2\mu_{t})}.\end{align*} $$

This yields the statement as a consequence.

Notation 9. Let us denote by $\kappa $ the unique analytic map $(t,\alpha ) \mapsto \kappa _{t} (\alpha )$ from $(0,\sqrt {2}) \times \mathbb {R}$ to $\mathbb {R}$ such that $\kappa _{\sqrt {2}/2} (0)=0$ and for all $t,\alpha $ ,

$$ \begin{align*}{e^{i\kappa_{t} (\alpha)} = \frac{e^{i\mu_{t}}-e^{\alpha}}{e^{i\mu_{t}+\alpha} - 1}}.\end{align*} $$

With the argument of uniqueness, we have that for all $t,\alpha $ , $\kappa _{t} (-\alpha ) = -\kappa _{t} (\alpha )$ , and as a consequence, $\kappa _{t} (0) = 0$ . We also set for all $t,\alpha ,\beta $ ,

$$ \begin{align*}\theta_{t} (\alpha,\beta) = \Theta_{t} (\kappa_{t} (\alpha),\kappa_{t} (\beta)).\end{align*} $$

5.1.2 Properties of the auxiliary functions

$\triangleright $ In this section, we prove some properties of the functions $\Theta $ and $\kappa $ (computation of derivatives, invertibility, and a relation between $\Theta $ and $\kappa $ ), which will be used later.

Computation of the derivative $\kappa ^{\prime }_{t}$

Computation 2. Let us fix some $t \in (0,\sqrt {2})$ . For all $\alpha \in \mathbb {R}$ ,

$$ \begin{align*}{\kappa^{\prime}_{t}(\alpha) = \frac{\sin(\mu_{t})}{\cosh(\alpha)-\cos(\mu_{t})}.}\end{align*} $$

Proof. Computation of ${\cos }({\kappa }_{{t}}({\alpha }))$ and ${\sin }({\kappa }_{{t}}({\alpha }))$ : By definition of $\kappa $ (for the first equality, we multiply both numerator and denominator by $(e^{-i\mu _{t} +\alpha }-1)$ ),

$$ \begin{align*}e^{i\kappa_{t} (\alpha)} = \frac{(e^{-i\mu_{t} +\alpha}-1)(e^{i\mu_{t}}-e^{\alpha})}{|e^{i\mu_{t}+\alpha}-1|^{2}} = \frac{e^{\alpha} - e^{2\alpha} e^{-i\mu_{t}} - e^{i\mu_{t}} + e^{\alpha}}{(\cos(\mu_{t})e^{\alpha}-1)^{2}+(\sin(\mu_{t})e^{\alpha})^{2}}.\end{align*} $$

Thus by taking the real part,

$$ \begin{align*}\cos(\kappa_{t}(\alpha)) = \frac{2e^{\alpha} - (e^{2\alpha}+1)\cos(\mu_{t})}{\cos^{2}(\mu_{t})e^{2\alpha} - 2\cos(\mu_{t}) e^{\alpha} + 1 + (1- \cos^{2} (\mu_{t}))e^{2\alpha}}, \end{align*} $$

$$ \begin{align*}\cos(\kappa_{t}(\alpha)) = \frac{2e^{\alpha} - (e^{2\alpha}+1)\cos(\mu_{t})}{e^{2\alpha} - 2\cos(\mu_{t}) e^{\alpha} + 1} = \frac{1 - \cos(\mu_{t})\cosh(\alpha)}{\cosh(\alpha)-\cos(\mu_{t})},\end{align*} $$

where we factorized by $2e^{\alpha }$ for the second equality. As a consequence,

(3) $$ \begin{align}\cos(\kappa_{t}(\alpha)) &=\frac{\sin^{2}(\mu_{t})+\cos^{2}(\mu_{t})-\cos(\mu_{t}) \cosh(\alpha)}{\cosh(\alpha)-\cos(\mu_{t})}\nonumber\\ &= \frac{\sin^{2}(\mu_{t})}{\cosh(\alpha)-\cos(\mu_{t})} - \cos(\mu_{t}). \end{align} $$

A similar computation gives

(4) $$ \begin{align}\sin(\kappa_{t}(\alpha)) = \frac{\sin(\mu_{t}) \sinh(\alpha)}{\cosh(\alpha)-\cos(\mu_{t})}. \end{align} $$

Deriving the expression ${\cos (\kappa _{t}(\alpha ))}$ : By deriving equation (3), for all $\alpha $ ,

$$ \begin{align*}-\kappa'_t(\alpha) \sin(\kappa_t(\alpha)) = - \frac{\sin^2 (\mu_t) \sinh(\alpha)}{(\cosh(\alpha)-\cos(\mu_t))^2} = -\frac{\sin(\kappa_t(\alpha))^2}{\sinh(\alpha)},\end{align*} $$

where we used equation (4) for the second equality.

Thus, for all $\alpha $ but in a discrete subset of $\mathbb {R}$ ,

$$ \begin{align*}\kappa^{\prime}_{t}(\alpha) = \frac{\sin(\mu_{t})}{\cosh(\alpha)-\cos(\mu_{t})}.\end{align*} $$

This identity is thus verified on all $\mathbb {R}$ by continuity.

Domain and invertibility

Let us remember that $I_{t} = (-(\pi -\mu _{t}),(\pi -\mu _{t}))$ .

Proposition 7. For all t, $\kappa _{t} (\mathbb {R}) \subset I_{t}$ . Moreover, $\kappa _{t}$ , considered as a function from $\mathbb {R}$ to $I_{t}$ , is bijective.

Proof. Injectivity: Since $\mu _{t} \in (0,\pi )$ , then $\sin (\mu _{t})> 0$ and we have the inequality $\cosh (\alpha ) \ge 1> \cos (\mu _{t})$ . As a consequence of Computation 2, $\kappa _{t}$ is strictly increasing, and thus injective.

The equality ${\kappa _{t}(\alpha )=n\pi }$ implies ${\alpha =0}$ : Assume that for some $\alpha $ , $\kappa _{t}(\alpha ) = n \pi $ for some integer n. By definition of $\kappa $ ,

$$ \begin{align*}e^{i n\pi} = \frac{e^{i\mu_{t}}-e^{\alpha}}{e^{i\mu_{t}+\alpha} -1}.\end{align*} $$

If n was odd, then

$$ \begin{align*}e^{\alpha} - e^{i\mu_{t}} = e^{i\mu_{t}+\alpha} -1,\end{align*} $$

$$ \begin{align*}e^{\alpha}+1 = e^{i\mu_{t}}\cdot (e^{\alpha}+1),\end{align*} $$

and thus $e^{i\mu _{t}}=1$ , which is impossible, since $\mu _{t} \in (0,\pi )$ . Thus n is even, and then

$$ \begin{align*}-e^{\alpha} + e^{i\mu_t} = e^{i\mu_t+\alpha} -1.\end{align*} $$

As a consequence, since $e^{i\mu _{t}} \neq -1$ , we have $e^{\alpha }=1$ , and thus $\alpha =0$ .

Extension of the images: Since when $\alpha $ tends towards $+\infty $ (respectively, $-\infty $ ), $({e^{i\mu _{t}}-e^{\alpha }})/({e^{i\mu _{t}+\alpha } -1})$ tends towards $-e^{i\mu _{t}}$ (respectively, $e^{i\mu _{t}}$ ), $\kappa _{t}(\alpha )$ tends towards some $n\pi -\mu _{t}$ (respectively, $m\pi +\mu _{t}$ ). and from the last point, $n=1$ (respectively, $m=-1$ ). Thus the image of $\kappa _{t}$ is the set $I_{t}$ .

Thus $\kappa _{t}$ is an invertible map from $\mathbb {R}$ to $I_{t}$ .

A relation between $\theta _{t}$ and $\kappa _{t}$

The following equality originates in [YY66a]. We provide some details of a relatively simple way to compute it.

Computation 3. For any numbers $t,\alpha ,\beta $ ,

$$ \begin{align*}{ \frac{\partial \theta_{t}}{\partial \alpha} (\alpha,\beta) = - \frac{\partial \theta_{t}}{\partial \beta} (\alpha,\beta) = - \frac{\sin(2\mu_{t})}{\cosh(\alpha-\beta) - \cos(2\mu_{t})}}.\end{align*} $$

Proof. Deriving the equation that defines ${\Theta _{t}}$ : Let us set, for all $x,y$ ,

$$ \begin{align*}G_{t} (x,y) = \frac{x(1-2\Delta_{t} y)+y}{x+y-2\Delta_{t}}.\end{align*} $$

Then we have that for all $x,y$ ,

$$ \begin{align*}\frac{\partial G_{t}}{\partial x} (x,y) = \frac{(1-2\Delta_{t} y) \cdot (x+y-2\Delta_{t}) - (x(1-2\Delta_{t} y) + y)}{(x+y-2\Delta_{t})^{2}}.\end{align*} $$

Then,

(5) $$ \begin{align} \frac{\partial G_{t}}{\partial x} (x,y) = -2\Delta_{t} \frac{1 +y^{2} - 2\Delta_{t} y}{(x+y-2\Delta_{t})^{2}}. \end{align} $$

For all $t,\alpha $ , let us set $\alpha _{t} \equiv \kappa _{t} (\alpha )$ . By definition of $\Theta _{t}$ , for all $\alpha ,\beta $ ,

(6) $$ \begin{align}\exp(-i \Theta_{t} (\alpha_{t},\beta_{t})) = G(e^{i\alpha_{t}},e^{-i\beta_{t}}). \end{align} $$

Thus we have, by deriving the equality in equation (6),

$$ \begin{align*}-i\frac{d}{d\alpha} (\Theta_t (\alpha_t,\beta_t)) \exp(-i \Theta_t (\alpha_t,\beta_t)) = i\kappa'_t(\alpha) e^{i\alpha_t} \frac{\partial}{\partial x} G_t (e^{i\alpha_t},e^{-i\beta_t}).\end{align*} $$

Then,

$$ \begin{align*}\frac{d}{d\alpha} (\Theta_{t} (\alpha_{t},\beta_{t})) = - \kappa^{\prime}_{t}(\alpha)e^{i\alpha_{t}} \frac{({\partial}/{\partial x}) G_{t} (e^{i\alpha_{t}},e^{-i\beta_{t}})}{G_{t}(e^{i\alpha_{t}},e^{-i\beta_{t}})},\end{align*} $$

and thus, using equation (5),

$$ \begin{align*}\frac{d}{d\alpha} \Theta_{t} (\alpha_{t},\beta_{t}) = \frac{(\kappa^{\prime}_{t} (\alpha) 2\Delta e^{i\alpha_{t}})(1+e^{-2i\beta_{t}}-2\Delta e^{-i\beta_{t}})}{(e^{i\alpha_{t}}+e^{-i\beta_{t}}-2\Delta_{t})(e^{i\alpha_{t}}+e^{-i\beta_{t}}-2\Delta_{t} .e^{i(\alpha_{t}-\beta_{t})})}.\end{align*} $$

Factoring by $e^{i(\alpha _{t}-\beta _{t})}$ ,

(7) $$ \begin{align}\frac{d}{d\alpha} \Theta_{t} (\alpha_{t},\beta_{t}) = 2\Delta_{t} \kappa^{\prime}_{t}(\alpha)\cdot \frac{e^{i\beta_{t}} + e^{-i\beta_{t}} - 2\Delta_{t}}{(e^{i\alpha_{t}}+e^{-i\beta_{t}}-2\Delta_{t})(e^{i\beta_{t}}+e^{-i\alpha_{t}}-2\Delta_{t})}. \end{align} $$

Simplification of the term ${e^{i\alpha _{t}}+ e^{-i\beta _{t}} - 2\Delta _{t}}$ in equation (7): Let us denote the function F defined on $\alpha ,\beta $ by

(8) $$ \begin{align} F_{t}(\alpha,\beta) = e^{i\alpha_{t}}+ e^{-i\beta_{t}} - 2\Delta_{t}. \end{align} $$

By definition of $\kappa _{t}$ and $-2\Delta _{t}=e^{-i\mu _{t}}+e^{i\mu _{t}}$ , we have

$$ \begin{align*}F_{t}(\alpha,\beta) = \frac{e^{i\mu_{t}} -e^{\alpha}}{e^{i\mu_{t}+\alpha} -1} + \frac{ e^{i\mu_{t}+\beta} -1}{e^{i\mu_{t}} -e^{\beta}} + e^{i\mu_{t}} + e^{-i\mu_{t}}.\end{align*} $$

Thus $F_{t}(\alpha ,\beta )$ is equal to

$$ \begin{align*}\frac{(e^{i\mu_{t}} -e^{\alpha})(e^{i\mu_{t}} -e^{\beta}) + (e^{i\mu_{t}+\alpha} -1)(e^{i\mu_{t}+\beta} -1)+ (e^{i\mu_{t}}+e^{-i\mu_{t}})\cdot(e^{i\mu_{t}+\alpha} -1)(e^{i\mu_{t}} -e^{\beta})}{(e^{i\mu_{t}+\alpha} -1)(e^{i\mu_{t}} -e^{\beta})}.\end{align*} $$

Finally,

(9) $$ \begin{align} F_{t}(\alpha,\beta) = \frac{e^{3i\mu_{t}+\alpha} +e^{\beta-i\mu_{t}} - e^{i\mu_{t}}\cdot (e^{\alpha}+e^{\beta})}{(e^{i\mu_{t}+\alpha} -1)(e^{i\mu_{t}} -e^{\beta})}. \end{align} $$

Simplification of the derivative of ${\Theta _{t}}$ : For all $\alpha ,\beta $ , we have, using equations (7) and (8),

$$ \begin{align*}\frac{1}{\kappa^{\prime}_{t}(\alpha)} \frac{d}{d\alpha} \Theta_{t}(\alpha,\beta) = 2\Delta_{t} \frac{F_{t}(\beta,\beta)}{ F_{t}(\alpha,\beta)\cdot F_{t}(\beta,\alpha)}.\end{align*} $$

As a consequence of equation (9),

$$ \begin{align*}&\frac{1}{\kappa^{\prime}_{t}(\alpha)} \frac{d}{d\alpha} \Theta_{t}( \alpha_{t},\beta_{t})\\ &\quad= \frac{-(e^{i\mu_{t}+\alpha} -1)(e^{i\mu_{t}}-e^{\alpha})(e^{-i\mu_{t}}+e^{i\mu_{t}})(e^{3i\mu_{t}+\beta} +e^{\beta-i\mu_{t}} - 2e^{i\mu_{t}}.e^{\beta})}{(e^{3i\mu_{t}+\alpha} +e^{\beta-i\mu_{t}} - e^{i\mu_{t}}.(e^{\alpha}+e^{\beta}))(e^{3i\mu_{t}+\beta} +e^{\alpha-i\mu_{t}} - e^{i\mu_{t}}.(e^{\beta}+e^{\alpha}))},\end{align*} $$

and thus

$$ \begin{align*}&\frac{1}{\kappa^{\prime}_{t}(\alpha)} \frac{d}{d\alpha} \Theta_{t}(\alpha_{t},\beta_{t})\\ &\quad= - \frac{(e^{i\mu_{t}+\alpha} -1)(e^{i\mu_{t}}-e^{\alpha})e^{\beta} \cdot (e^{2i\mu_{t}}-1)\cdot(e^{2i\mu_{t}}-e^{-2i\mu_{t}})}{e^{2i\mu_{t}}(e^{2i\mu_{t}+\alpha} +e^{\beta-2i\mu_{t}} - (e^{\alpha}+e^{\beta}))(e^{2i\mu_{t}+\beta} +e^{\alpha-2i\mu_{t}} - (e^{\beta}+e^{\alpha}))}.\end{align*} $$

Since in the denominator of the fraction is the square of the modulus of some number, we rewrite it.

$$ \begin{align*}\frac{1}{\kappa^{\prime}_{t}(\alpha)} \frac{d}{d\alpha} \Theta_{t}(\alpha_{t},\beta_{t}) = - \frac{(e^{i\mu_{t}+\alpha} -1)(e^{i\mu_{t}}-e^{\alpha}) e^{\beta} \cdot (e^{2i\mu_{t}}-1)\cdot(e^{2i\mu_{t}}-e^{-2i\mu_{t}})}{e^{2i\mu_{t}} ((e^{\alpha}+e^{\beta})^{2} (\cos(2\mu_{t})-1)^{2} + (e^{\alpha}-e^{\beta})^{2} \sin^{2} (2\mu_{t}))}.\end{align*} $$

We rewrite also the other terms, by splitting the $e^{2i\mu _{t}}$ in the denominator in two parts, one makes $\sin (\mu _{t})$ appear and the other one the square modulus in the following formula:

$$ \begin{align*}&\frac{1}{\kappa^{\prime}_{t}(\alpha)} \frac{d}{d\alpha} \Theta_{t} (\alpha_{t},\beta_{t})\\ &\quad= -4|e^{i\mu_{t}+\alpha} -1|^{2} \frac{e^{\beta} \cdot \sin(\mu_{t})\cdot\sin(2\mu_{t})}{(e^{\alpha}+e^{\beta})^{2} (\cos(2\mu_{t})-1)^{2} + (e^{\alpha}-e^{\beta})^{2} \sin^{2} (2\mu_{t})}.\end{align*} $$

By writing $\sin ^{2}(2\mu _{t})=1-\cos ^{2}(2\mu _{t})$ and then factoring by $1-\cos (2\mu _{t})$ ,

$$ \begin{align*}&\frac{1}{\kappa^{\prime}_{t}(\alpha)} \frac{d}{d\alpha} \Theta_{t}(\alpha_{t},\beta_{t})\\ &\quad= -4\frac{|e^{i\mu_{t}+\alpha} -1|^{2}}{1-\cos(2\mu_{t})} \cdot \frac{e^{\beta} \cdot \sin(\mu_{t})\cdot \sin(2\mu_{t})}{(e^{\alpha}+e^{\beta})^{2} (1-\cos(2\mu_{t})) + (e^{\alpha}-e^{\beta})^{2} (1+\cos(2\mu_{t}))}.\end{align*} $$

Simplifying the denominator and factoring it by $4e^{\alpha +\beta }$ , we obtain

$$ \begin{align*}\frac{1}{\kappa^{\prime}_{t}(\alpha)} \frac{d}{d\alpha} \Theta_{t}(\alpha_{t},\beta_{t}) = -\frac{|e^{i\mu_{t}+\alpha} -1|^{2}}{e^{\alpha}(1-\cos(2\mu_{t}))}\cdot \frac{\sin(\mu_{t})\cdot \sin(2\mu_{t})}{\cosh(\alpha-\beta)- \cos(2\mu_{t})}.\end{align*} $$

We have left to see that

$$ \begin{align*}\frac{\sin(\mu_{t}) \kappa^{\prime}_{t}(\alpha)\cdot|e^{i\mu_{t}+\alpha} -1|^{2}}{e^{\alpha}(1-\cos(2\mu_{t}))} = 1.\end{align*} $$

This derives directly from $1-\cos (2\mu _{t}) = 2\sin ^{2}(\mu _{t})$ and the value of $\kappa ^{\prime }_{t}(\alpha )$ given by Computation 2.

We thus have the stated formula of ${\partial \theta _{t}}/{\partial \alpha } (\alpha ,\beta ) = {d}/{d\alpha } (\Theta _{t}(\alpha _{t},\beta _{t}))$ .

The other equality: We obtain the value of ${\partial \theta _{t}}/{\partial \beta } (\alpha ,\beta ) = {d}/{d\beta } (\Theta _{t}(\alpha _{t},\beta _{t}))$ through the equality $\Theta _{t}(x,y) = -\Theta _{t}(y,x)$ for all $x,y$ (§5.1.1).

Lemma 5. For all $t,\alpha ,\beta $ ,

$$ \begin{align*}\theta_{t} (\alpha+\beta,\alpha) = \theta_{t} (\beta,0).\end{align*} $$

Proof. Let us fix some $\alpha \in \mathbb {R}$ . By Computation 3, the derivative of the function $\beta \mapsto \theta _{t} (\alpha +\beta ,\alpha )$ is equal to the derivative of the function $\beta \mapsto \theta _{t} (\beta ,0)$ . As a consequence, these two functions differ by a constant. Since they have the same value 0 in $\beta =0$ (§5.1.1), they are equal.

5.2 Statement of the ansatz

$\triangleright $ In this section, we state of the coordinate Bethe ansatz in Theorem 3 (let us remember that this provides candidate eigenvectors and eigenvalues for $V_{N}(t)$ for all N and t).

Notation 10. For all $(p_{1},\ldots ,p_{n}) \in I_{t}^{n}$ , let us denote by $\psi _{\mu _{t},n,N} (p_{1},\ldots ,p_{n})$ the vector in $\Omega _{N}$ such that for all $\boldsymbol {\epsilon } \in \{0,1\}^{*}_{N}$ ,

$$ \begin{align*}\psi_{\mu_{t},n,N}(p_{1},\ldots,p_{n})[\boldsymbol{\epsilon}] = \sum_{\sigma \in \Sigma_{n}} C_{\sigma} (t) [p_{1},\ldots,p_{n}] \prod_{k=1}^{n} e^{ip_{\sigma(k)} q_{k} [\boldsymbol{\epsilon}]},\end{align*} $$

where, denoting by $\epsilon (\sigma )$ the signature of $\sigma $ ,

$$ \begin{align*}C_{\sigma} (t) [p_{1},\ldots,p_{n}] = \epsilon(\sigma)\prod_{1 \le k <l\le n} ( 1 + e^{i(p_{\sigma(k)}+p_{\sigma(l)})} - 2\Delta_{t} e^{ip_{\sigma(k)}}).\end{align*} $$

Definition 7. We say that $p_{1},\ldots ,p_{n} \in I_{t}$ satisfy the system of Bethe equations when for all j,

$$ \begin{align*}(E_{j})[t,n,N]: Np_{j} = 2\pi j - (n+1)\pi - \sum_{k=1}^{n} \Theta_{t} (p_{j},p_{k}).\end{align*} $$

Theorem 3. For all N and $n \le N/2$ , and $p_{1},\ldots ,p_{n} \in I_{t}$ distinct which satisfy the system of Bethe equations, we have

$$ \begin{align*}V_{N} (t)\cdot \psi_{n,N} (p_{1},\ldots,p_{n}) = \Lambda_{n,N} (t) [p_{1},\ldots,p_{n}] \cdot \psi_{n,N} (p_{1},\ldots,p_{n}),\end{align*} $$

where $\Lambda _{n,N} (t) [p_{1},\ldots ,p_{n}]$ is equal to

$$ \begin{align*}\prod_{k=1}^{n} L_{t} (e^{ip_{k}}) + \prod_{k=1}^{n} M_{t} (e^{ip_{k}})\end{align*} $$

when all the $p_{k}$ are distinct from $0$ . Else, it is equal to

$$ \begin{align*}\bigg( 2 + t^{2} (N-1) + \sum_{k \neq l} \frac{\partial \Theta_{t}}{\partial x} (0,p_{k})\bigg)\prod_{k=1}^{n} M_{t} (e^{ip_{k}})\end{align*} $$

for l such that $p_{l} = 0$ .

In [DGHMT18] (Theorem 2.2), the equations (BE) are implied by the equations $(E_{j})[t,n,N]$ in Theorem 3 by taking the exponential of the members of $(BE)$ . To make the connection easier with [DGHMT18], here is a list of correspondences between the notation: in [DGHMT18], the notation t corresponds to c, and it is fixed in the formulation of the theorem. Thus, $\Delta _{t}$ corresponds to $\Delta $ , $\mathcal {I}_{t}$ to $\mathcal {D}_{\Delta }$ , $V_{N} (t)$ to V, $\psi _{t,n,N} (p_{1},\ldots ,p_{n})$ to $\psi $ , $L_{t}$ and $M_{t}$ to L and M, $\Theta _{t}$ to $\Theta $ , $\Lambda _{n,N} (t)[p_{1},\ldots ,p_{n}]$ to $\Lambda $ , $C_{\sigma } (t) [p_{1},\ldots ,p_{n}]$ to $A_{\sigma }$ and the sequence $(x_{k})_{k}$ to the sequence $(q_{k} [\boldsymbol {\epsilon }])_{k}$ for some $\boldsymbol {\epsilon }$ .

5.3 Existence of solutions of Bethe equations and analyticity

$\triangleright $ As a matter of fact, the Bethe ansatz presented in §5.2 provides a candidate eigenvector on the condition that there exists a solution to the system of Bethe equations. We prove that this is the case for all N and t and that this solution is unique. Furthermore, we will need that this solution is analytic relative to t for all N. These statements are encompassed in the following theorem, whose proof is a rigorous and complete version of an argument in [YY66a].

Theorem 4. There exists a unique sequence of analytic functions $\textbf {p}_{j} : (0,\sqrt {2}) \mapsto (-\pi ,\pi )$ such that for all $t \in (0,\sqrt {2})$ , $\textbf {p}_{j} (t) \in I_{t} $ and we have the system of Bethe equations:

$$ \begin{align*}(E_{j})[t,n,N]: N p_{j} (t) = 2\pi j - (n+1)\pi - \sum_{k=1}^{n} \Theta_{t} (p_{j}(t) ,p_{k}(t)).\end{align*} $$

Moreover, for all t and j, $\textbf {p}_{n-j+1} (t) = -\textbf {p}_{j} (t)$ ; for all t, the $\textbf {p}_{j} (t)$ are all distinct.

Idea of the proof: Following Yang and Yang [YY66a], we use an auxiliary multivariate function $\zeta _{t}$ whose derivative is zero exactly when the equations $(E_{j}) [t,n,N]$ are verified. We prove that up to a monotonous change of variable, this function is convex, which implies that it admits a unique local (and thus global) minimum (this relies on the properties of $\theta _{t}$ and $\kappa _{t}$ ). Since we rule out the possibility that the minimum is on the border of the domain, this function admits a point where its derivative is zero, and thus the system of equations $(E_{j})[t,n,N]$ admits a unique solution. To prove the analyticity, we then define a function of t that verifies an analytic differential equation (and thus is analytic), whose value in some point coincides with the minimum of $\zeta _{t}$ . Since the differential equation ensures that $\zeta ^{\prime }_{t}$ is null on the values of this function, this means that for all t, its value in t is the minimum of $\zeta _{t}$ .

Proof. The solutions are critical points of an auxiliary function ${\zeta _{t}}$ : Let us set, for all $t,p_{1},\ldots ,p_{n}$ (in the third sum, both k and j are arguments of the sum),

$$ \begin{align*} \zeta_{t} (p_{1},\ldots,p_{n}) & = N \sum_{j=1}^{n} \int_{0}^{\kappa^{-1}_{t} (p_{j})} \kappa_{t} (x) \,dx + \pi (n+1-2j)\sum_{j=1}^{n} \kappa_{t}^{-1} (p_{j})\\ &\quad + \sum_{k < j} \int_{0}^{\kappa_{t} {}^{-1} (p_{j})-\kappa_{t} {}^{-1} (p_{k})} \theta_{t} (x,0)\,dx. \end{align*} $$

The interest of this function lies in the fact that for all j (here the argument in each of the sums is k),

(10) $$ \begin{align} \frac{\partial \zeta_{t}}{\partial p_{j}} (p_{1}, \ldots, p_{n}) & = ( \kappa_{t}^{-1} )^{\prime} (p_{j}). \bigg( N p_{j} - 2\pi j + (n+1)\pi\nonumber\\ &\quad - \!\sum_{k < j}\! \theta_{t} (\kappa_{t} {}^{-1} (p_{j})-\kappa_{t} {}^{-1} (p_{k}),0) \bigg) + \!\sum_{k> j}\! \theta_{t} (\kappa_{t} {}^{-1} (p_{k})-\kappa_{t} {}^{-1} (p_{j}),0) .\nonumber\\ & = ( \kappa_{t}^{-1} )^{\prime} (p_{j}). \bigg( N p_{j} - 2\pi j + (n+1)\pi - \!\sum_{k < j } \theta_{t} (\kappa_{t} {}^{-1} (p_{k}),\kappa_{t} {}^{-1} (p_{j})) \bigg) \nonumber\\ &\quad + \sum_{k> j} \theta_{t} (\kappa_{t} {}^{-1} (p_{j}),\kappa_{t} {}^{-1} (p_{k})).\nonumber\\ \frac{\partial \zeta_{t}}{\partial p_{j}} (p_{1}, \ldots, p_{n}) & = ( \kappa_{t}^{-1} )^{\prime} (p_{j}). \bigg( N p_{j} - 2\pi j + (n+1)\pi + \sum_{k} \Theta_{t} (p_{j},p_{k})\bigg), \end{align} $$

since for all $x,y$ , $\Theta _{t} (x,y) = - \Theta _{t} (y,x)$ and for all x, $\Theta _{t}(x,x)=0$ (§5.1.1).

Hence, the system of Bethe equations is verified for the sequence $(p_{j})_{j}$ if and only for all j, $ {\partial \zeta _{t} }/{\partial p_{j}} (p_{1}, \ldots , p_{n} )=0$ .

Uniqueness of the local minimum of ${\zeta _{t}}$ using convexity: Let us set $\tilde {\zeta }_{t} : \mathbb {R}^{n} \rightarrow \mathbb {R}$ such that for all $\alpha _{1}, \ldots , \alpha _{n}$ :

$$ \begin{align*}\tilde{\zeta}_{t} (\alpha_{1} , \ldots , \alpha_{n}) = \zeta_{t} (\kappa_{t} (\alpha_{1}), \ldots , \kappa_{t} (\alpha_{n})).\end{align*} $$

From equation (10), we have that for all sequence $(\alpha _{k})_{k}$ and all j,

$$ \begin{align*}\frac{\partial \tilde{\zeta}_{t}}{\partial p_{j}} (\alpha_{1}, \ldots , \alpha_{n}) = N \kappa_{t} (\alpha_{j}) - 2\pi j + (n+1)\pi + \sum_{k} \theta_{t} (\alpha_{j},\alpha_{k}).\end{align*} $$

As a consequence, using Computation 3, for all $k \neq j$ ,

(11) $$ \begin{align}\frac{\partial {}^{2} \tilde{\zeta}_{t}}{\partial p_{k} \partial p_{j}} (\alpha_{1}, \ldots , \alpha_{n}) = \frac{\partial \theta_{t}}{\partial \beta} (\alpha_{j},\alpha_{k}) = \frac{\sin(2\mu_{t})}{\cosh(\alpha_{j}-\alpha_{k}) - \cos(2\mu_{t})}. \end{align} $$

Moreover, for all j,

(12) $$ \begin{align} \frac{\partial^{2} \tilde{\zeta}_{t}}{\partial^{2} p_{j}} (\alpha_{1}, \ldots , \alpha_{n} , t) = N \kappa^{\prime}_{t} (\alpha_{j}) + \sum_{k \neq j} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha_{j}, \alpha_{k}) = N \kappa^{\prime}_{t} (\alpha_{j}) - \sum_{k \neq j} \frac{\partial \theta_{t}}{\partial \beta} (\alpha_{j}, \alpha_{k}). \end{align} $$

Let us denote by $\tilde {H}_{t} (\alpha _{1} , \ldots , \alpha _{n})$ the Hessian matrix of $\tilde {\zeta }_{t}$ . For any $(x_{1}, \ldots , x_{n}) \in \mathbb {R}^{n}$ , we have, from equations (11) and (12),

$$ \begin{align*} |&|(x_{1},\ldots,x_{n}) \cdot \tilde{H}_{t} (\alpha_{1} , \ldots , \alpha_{n} ) \cdot (x_{1},\ldots,x_{n})^{t} \\ &\quad= N \sum_{j} \kappa^{\prime}_{t} (\alpha_{j}) x_{j} {}^{2} - \sum_{j \neq k} \bigg( \frac{\partial \theta_{t}}{\partial \beta} (\alpha_{j}, \alpha_{k}) x_{j} (x_{j}-x_{k}).\bigg)\\ &\quad = N \sum_{j} \kappa^{\prime}_{t} (\alpha_{j}) x_{j} {}^{2} - \sum_{j < k} \bigg( \frac{\partial \theta_{t}}{\partial \beta} (\alpha_{j}, \alpha_{k}) x_{j} (x_{j}-x_{k}) \bigg)\\ & \qquad - \sum_{j < k} \bigg( \frac{\partial \theta_{t}}{\partial \beta} (\alpha_{k}, \alpha_{j}) x_{k} (x_{k}-x_{j}) \bigg)\\ &\quad = N \sum_{j} \kappa^{\prime}_{t} (\alpha_{j}) x_{j} {}^{2} - \sum_{j < k} \bigg( \frac{\partial \theta_{t}}{\partial \beta} (\alpha_{j}, \alpha_{k}) (x_{j}-x_{k})^{2} \bigg)> 0. \end{align*} $$

As a consequence, $\tilde {\zeta }_{t}$ is a convex function. Thus, if it has a local minimum, it is unique. Since $\kappa _{t}$ is increasing, this property is also true for $\zeta _{t}$ . The function ${\zeta _{t}}$ has a minimum in ${I_{t}^{n}}$ : Let us consider $(C_{l})_{l}$ as an increasing sequence of compact intervals such that $\bigcup _{l} C_{l} = I_{t}$ .

Let us assume that $\zeta _{t}$ has no local minimum in $I_{t}^{n}$ . As a consequence, for all j, the minimum $\textbf {p}^{(l)}$ of $\zeta _{t}$ on $(C_{l})^{n}$ is on its border. Without loss of generality, we can assume that there exists some $\textbf {p}^{(\infty )} \in \overline {I_{t}}^{n}$ such that $\textbf {p}^{(l)} \rightarrow \textbf {p}^{(\infty )} $ .

We can assume without loss of generality that there exists some such that $j \le j_{0}$ if and only if $\textbf {p}^{(\infty )}_{j} = \pi -\mu _{t}$ . The number $j_{0}$ is the number of j such that $\textbf {p}^{(\infty )}_{j} = \pi -\mu _{t}$ . We can assume furthermore that $j_{0} \le n/2$ : if it is not the case, then we use a reasoning similar to the one that follows, replacing $\pi -\mu _{t}$ by $-(\pi -\mu _{t})$ .

Thus, there exists $l_{0}$ such that for all l and $j \le j_{0}$ , $\textbf {p}_{j}^{(l)} \ge 0$ . Since $\tilde {\zeta }_{t}$ is convex and that $\textbf {p}^{(l)}$ is a minimum for this function on the compact set $(C_{l})^{n}$ , then for all $j \le j_{0}$ ,

(13)j $$\begin{align} \frac{\partial \zeta_{t}}{\partial p_{j}} ({\kern1pt}\textbf{p}^{(l)}_{1}, \ldots , \textbf{p}^{(l)}_{n}) \le 0. \end{align}$$

This is a particular case of the fact that for a convex and continuously differentiable function $f : I \mapsto \mathbb {R}$ , where I is a compact interval of $\mathbb {R}$ , if its minimum on I occurs at maximal element of I, then $f^{\prime }$ is non-positive on this point, as illustrated in Figure 8.

Figure 8 Illustration of the fact that the minimum of a convex continuously differentiable function on a real compact interval has non-positive derivative.

Since $\Theta _{t}$ cannot be defined on $\{(x,x): x \in \partial I_{t}\}$ , to have an inequality that can be transformed by continuity into an inequality on $\textbf {p}$ , we sum the inequalities in equation (13) _j :

$$ \begin{align*}\sum_{j=1}^{j_{0}} \frac{\partial \zeta_{t}}{\partial p_{j}} ({\kern1pt}\textbf{p}^{(l)}_{1}, \ldots , \textbf{p}^{(l)}_{n}) \le 0.\end{align*} $$

According to the first point of the proof (equation (10)), this inequality can be re-written:

$$ \begin{align*}N \sum_{j=1}^{j_{0}} \textbf{p}_{j} - 2\pi \sum_{j=1}^{j_{0}} j + j_{0} (n+1) \pi + \sum_{j=1}^{j_{0}} \sum_{k} \Theta_{t} ({\kern1pt}\textbf{p}_{j}^{(l)}, \textbf{p}_{k}^{(l)}) \le 0.\end{align*} $$

For all $j,j^{\prime } \le j_{0}$ , the terms $\Theta _{t} ({\kern1pt}\textbf{p}_{j}^{(l)},\textbf {p}_{j^{\prime }}^{(l)})$ and $\Theta _{t} ({\kern1pt}\textbf{p}_{j^{\prime }}^{(l)},\textbf {p}_{j}^{(l)})$ cancel out in this sum. As a consequence,

$$ \begin{align*}N \sum_{j=1}^{j_{0}} \textbf{p}_{j} - 2\pi \sum_{j=1}^{j_{0}} j + j_{0} (n+1) \pi + \sum_{j=1}^{j_{0}} \sum_{k>j_{0}} \Theta_{t} ({\kern1pt}\textbf{p}_{j}^{(l)}, \textbf{p}_{k}^{(l)}) \le 0.\end{align*} $$

This time, the inequality can be extended by continuity and we obtain

$$ \begin{align*}N \sum_{j=1}^{j_{0}} \textbf{p}_{j} - 2\pi \sum_{j=1}^{j_{0}} j + j_{0} (n+1) \pi + \sum_{j=1}^{j_{0}} \sum_{k>j_{0}} \Theta_{t} ({\kern1pt}\textbf{p}_{j}^{(\infty)}, \textbf{p}_{k}^{(\infty)}) \le 0.\end{align*} $$

From Computation 1, we have

$$ \begin{align*}N j_{0} (\pi-\mu_{t}) - 2\pi \sum_{j=1}^{j_{0}} j + j_{0} (n+1) \pi + j_{0} (n-j_{0})\cdot (2\mu_{t} - \pi) \le 0.\end{align*} $$

Thus,

$$ \begin{align*}j_{0} (n+1) \pi + j_{0} (n-j_{0})\pi + (N j_{0}- 2j_{0} (n-j_{0})) (\pi-\mu_{t} ) \le 2\pi \sum_{j=1}^{j_{0}} j.\end{align*} $$

Since $\mu _{t} \le \pi $ and that $2j_{0} (n-j_{0}) - Nj_{0} = -2 j_{0}^{2} < 0$ , this last inequality implies

(14) $$ \begin{align} j_{0} (n+1) \pi + j_{0} (n-j_{0}) \pi \le 2\pi \sum_{j=1}^{j_{0}} j. \end{align} $$

However, we have

(15) $$ \begin{align} \sum_{j=1}^{j_{0}} j \le n j_{0} - \sum_{j=1}^{j_{0}} j = nj_{0} - \frac{j_{0} (j_{0}+1)}{2}.\end{align} $$

As a consequence of equations (14) and (15),

$$ \begin{align*} j_{0} (n+1) \pi + j_{0} (n-j_{0})\cdot \pi & \le 2\pi n j_{0} - j_{0} (j_{0} +1) \pi\\ (2n+1) j_{0} \pi - j_{0} {}^{2} \pi & \le 2\pi n j_{0} - j_{0} {}^{2} \pi - j_{0} \pi \\ j_{0} \pi & \le -j_{0} \pi. \end{align*} $$

Since this last inequality is impossible, this means that $\zeta _{t}$ has a minimum in $I_{t}^{n}$ .

Characterization of the solutions with an analytic differential equation: Let us denote by $\textbf {p} (t) = ({\kern1pt}\textbf{p}_{1} (t) , \ldots , \textbf {p}_{n} (t))$ , for all $t \in (0, \sqrt {2})$ , the unique minimum of the function $\zeta _{t}$ in $I_{t}^{n}$ . Let us denote by $t \mapsto \textbf {s} (t) = (\textbf {s}_{1} (t), \ldots , \textbf {s}_{n} (t))$ the unique solution of the differential equation:

(16) $$ \begin{align} {\textbf{s}}^{\prime}(t) = -( H_{t} (\textbf{s}_{1} (t) , \ldots , \textbf{s}_{n} (t))) {}^{-1} \cdot \bigg( \frac{\partial^{2} \zeta_{t}} {\partial t \partial p_{j} } (\textbf{s}_{1} (t), \ldots , \textbf{s}_{n} (t)) \bigg)_{j}, \end{align} $$

such that $\textbf {s}(t)$ is the minimum of the function $\zeta _{t}$ when $t=\sqrt {2}/2$ , where $H_{t}$ is the Hessian matrix of $\zeta _{t}$ (existence and uniqueness are provided by classical theorems on first-order nonlinear differential equations). Since this is an analytic differential equation, its solution $\textbf {s}$ is analytic.

Let us rewrite equation (16):

$$ \begin{align*}H_{t} (\textbf{s}_{1} (t) , \ldots , \textbf{s}_{n} (t)) \cdot \textbf{s}^{\prime}(t) = -\bigg(\frac{\partial^{2} \zeta_{t}} {\partial t \partial p_{j} } (\textbf{s}_{1} (t), \ldots , \textbf{s}_{n} (t)) \bigg)_{j} \end{align*} $$

$$ \begin{align*}\frac{\partial^{2} \zeta_{t}} {\partial t \partial p_{j} } (\textbf{s}_{1} (t), \ldots , \textbf{s}_{n} (t)) + \sum_{k} \textbf{s}^{\prime}_{k} (t) \cdot \frac{\partial^{2} \zeta_{t}} {\partial p_{k} \partial p_{j} } (\textbf{s}_{1} (t), \ldots , \textbf{s}_{n} (t)) = 0. \end{align*} $$

This means that for all j,

$$ \begin{align*}\frac{\partial \zeta_{t}} {\partial p_{j} } (\textbf{s}_{1} (t), \ldots , \textbf{s}_{n} (t) )\end{align*} $$

is a constant. Since $\textbf {s}(t)$ is the minimum of $\zeta _{t}$ when $t=\sqrt {2}/2$ , this constant is zero. As a consequence, by uniqueness of the minimum of $\zeta _{t}$ for all t, $\textbf {s}(t) = \textbf {p}(t)$ . This means that $t \mapsto \textbf {p} (t)$ is analytic.

Antisymmetry of the solutions: For all $t,j$ , since $\textbf {p} (t)$ is the minimum of $\zeta _{t}$ , using equation (10) and the fact that $\kappa _{t}$ is increasing, we can write successively the following equations:

$$ \begin{align*} N\textbf{p}_{n-j+1} - 2\pi (n-j+1) + (n+1)\pi +\sum_{k} \Theta_{k} ({\kern1pt}\textbf{p}_{n-j+1}, \textbf{p}_{n-k+1}) & = 0;\\ N\textbf{p}_{n-j+1} + 2\pi j - (n+1)\pi +\sum_{k} \Theta_{k} ({\kern1pt}\textbf{p}_{n-j+1}, \textbf{p}_{n-k+1}) & = 0;\\ -N\textbf{p}_{n-j+1} - 2\pi j + (n+1)\pi -\sum_{k} \Theta_{k} ({\kern1pt}\textbf{p}_{n-j+1}, \textbf{p}_{n-k+1}) & = 0;\\ -N\textbf{p}_{n-j+1} - 2\pi j + (n+1)\pi +\sum_{k} \Theta_{k} (-\textbf{p}_{n-j+1}, -\textbf{p}_{n-k+1}) & = 0. \end{align*} $$

This means that the sequence $(-\textbf {p}_{n-j+1} (t))_{j}$ is a minimum for $\zeta _{t}$ , and as a consequence, for all j, $\textbf {p}_{n-j+1} = - \textbf {p}_{j}$ .

The numbers $\textbf {p}_{{j(t)}}$ , ${j \le n}$ , are all distinct: Let us consider the function

$$ \begin{align*}\chi_{t} : \alpha \mapsto N \kappa_{t} (\alpha) + \sum_{k=1}^{n} \theta_{t} (\alpha,\boldsymbol{\alpha}_{k} (t)),\end{align*} $$

where for all k, $\boldsymbol {\alpha }_{k} (t)$ is equal to $\kappa _{t}^{-1} ({\kern1pt}\textbf{p}_{k} (t))$ . For all j, this function has value ${\pi (2j-(n+1))}$ in $\boldsymbol {\alpha }_{j} (t)$ (by the Bethe equations). The finite sequence ${(\pi (2j-(n+1)))_{j}}$ is increasing, thus it is sufficient to prove that the function $\chi _{t}$ is increasing. Its derivative is

$$ \begin{align*}\chi^{\prime}_{t} : \alpha \mapsto N \kappa^{\prime}_{t} (\alpha) + \sum_{k=1}^{n} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha, \boldsymbol{\alpha}_{k} (t)).\end{align*} $$

Since $t \in (0,\sqrt {2})$ , $\sin (\mu _{t})<0$ , and thus this function is positive. As a consequence, $\chi _{t}$ is increasing.

5.4 Diagonalization of some Heisenberg Hamiltonian

$\triangleright $ Now that we have proved that the system of Bethe equations has a unique solution, the Bethe ansatz effectively provides a candidate eigenvector and eigenvalue for $V_{N}(t)$ for each of the sub-spaces $\Omega _{N}^{(n)}$ . In the following, we will focus on $t=\sqrt {2}$ and show that the candidate eigenvalue is indeed the maximal eigenvalue of $V_{N}(t)$ on the corresponding sub-space, for all t sufficiently close to $\sqrt {2}$ (let us remember that the analyticity of the solutions of Bethe equations will imply that this is also the case away from $\sqrt {2}$ ). For this purpose, we will need first to introduce a Hamiltonian $H_{N}$ which we diagonalize completely, following Lieb, Schultz and Mattis [LSM61]. The term ‘Hamiltonian’ is only borrowed from the article [LSM61]. In this paper, it is sufficient to see $H_{N}$ as a matrix acting on $\Omega _{N}$ .

5.4.1 Bosonic creation and annihilation operators

$\triangleright $ The Hamiltonian $H_{N}$ is expressed by elementary operators which are defined in this section. We also prove the usefulness of their properties as Bosonic creation and annihilation operators. The Hamiltonian itself will be defined in the next section.

Let us recall that $\Omega _{N} = \mathbb {C}^{2} \otimes \cdots \otimes \mathbb {C}^{2}$ . In this section, for the purpose of notation, we identify $\{1,\ldots ,N\}$ with $\mathbb {Z}/N\mathbb {Z}$ .

Notation 11. Let us denote by a and $a^{*}$ the matrices in $\mathcal {M}_{2} (\mathbb {C})$ equal to

$$ \begin{align*} a := \left(\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right), \quad a^{*} := \left(\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right)\kern-2pt.\end{align*} $$

For all $j \in \mathbb {Z}/N\mathbb {Z}$ , we denote by $a_{j}$ (creation operator at position j) and $a^{*}_{j}$ (annihilation operator at position j) the matrices in $\mathcal {M}_{2^{N}}(\mathbb {C})$ equal to

$$ \begin{align*}a_{j} := \mathrm{id} \otimes \cdots \otimes a \otimes \cdots \otimes \mathrm{id}, \quad a^{*}_{j} := \mathrm{id} \otimes \cdots \otimes a^{*} \otimes \cdots \otimes \mathrm{id}.\end{align*} $$

where $\mathrm {id}$ is the identity, and a acts on the jth copy of $\mathbb {C}^{2}$ .

In other words, the image of a vector $\lvert {\boldsymbol {\epsilon }_{1} \cdots \boldsymbol {\epsilon }_{N}}\rangle $ in the basis of $\Omega _{N}$ by $a_{j}$ (respectively, $a^{*}_{j}$ ) is as follows:

• • if $\boldsymbol {\epsilon }_{j}=0$ (respectively, $\boldsymbol {\epsilon }_{j} = 1$ ), then the image vector is $\textbf {0}$ ;

• • if $\boldsymbol {\epsilon }_{j}=1$ (respectively, $\boldsymbol {\epsilon }_{j} = 0$ ), then the image vector is $\lvert {\boldsymbol {\eta }_{1} \cdots \boldsymbol {\eta }_{N}}\rangle $ such that $\boldsymbol {\eta }_{j} = 0$ (respectively, $\boldsymbol {\eta }_{j} = 1$ ) and for all $k \neq j$ , $\boldsymbol {\eta }_{k} = \boldsymbol {\epsilon }_{k}$ .

Remark 4. The term creation (respectively, annihilation) refers to the fact that for two elements $\boldsymbol {\epsilon }$ , $\boldsymbol {\eta }$ of the basis of $\Omega _{N}$ , $a_{j} [\boldsymbol {\epsilon },\boldsymbol {\eta }] \neq 0$ (respectively, $a_{j}^{*} [\boldsymbol {\epsilon },\boldsymbol {\eta }] \neq 0$ ) implies that $|\boldsymbol {\eta }|_{1} = |\boldsymbol {\epsilon }|_{1}+1$ (respectively, $|\boldsymbol {\eta }|_{1} = |\boldsymbol {\epsilon }|_{1}-1$ ). If we think of $1$ symbols as particles, this operator acts by creating (respectively, annihilating) a particle.

Lemma 6. The matrices $a_{j}$ and $a^{*}_{j}$ satisfy the following properties, for all j and $k \neq j$ :

1. (1) $a_{j} a^{*}_{j} + a^{*}_{j} a_{j} = {\mathrm {id}}$ ;

2. (2) $a_{j}^{2} = {a^{*}_{j}}^{2} = 0$ ;

3. (3) $a_{j}$ , $a^{*}_{j}$ commute both with $a_{k}$ and $a^{*}_{k}$ .

Proof. (1) By straightforward computation, we get

$$ \begin{align*}a a^{*} = \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right) \left( \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right) = \left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array}\right)\end{align*} $$

and

$$ \begin{align*}a^{*} a = \left( \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right)\left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right)\kern-2pt.\end{align*} $$

Thus $a a^{*} + a^{*} a$ is the identity of $\mathbb {C}^{2}$ . As a consequence, for all j,

$$ \begin{align*}a_{j} a {}^{*}_{j} + a^{*}_{j} a_{j} = \mathrm{id} \otimes \cdots \otimes \mathrm{id},\end{align*} $$

which is the identity of $\Omega _{N}$ .

(2) The second set of equalities comes directly from

$$ \begin{align*}a {}^{2} = \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right) \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right) = \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right), \end{align*} $$

$$ \begin{align*}\left({a^{*}}\right) {}^{2} = \left( \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right) \left( \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right) = \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right)\kern-2pt.\end{align*} $$

(3) The last set derives from the fact that any operator on $\mathbb {C}^{2}$ commutes with the identity.

5.4.2 Definition and properties of the Heisenberg Hamiltonian

Notation 12. Let us denote by $H_{N}$ the matrix in $\mathcal {M}_{2^{N}} (\mathbb {C})$ defined as

$$ \begin{align*}H_{N} = \displaystyle{\sum_{j \in \mathbb{Z}/N\mathbb{Z}} (a^{*}_{j} a_{j+1} + a_{j} a^{*}_{j+1})}.\end{align*} $$

Lemma 7. This matrix $H_{N}$ is non-negative, symmetric and for all n, its restriction to $\Omega _{N}^{(n)}$ is irreducible.

The proof of Lemma 7 is similar to that of Lemma 2, following the interpretation of the action of $H_{N}$ described in Remark 5.

Remark 5. For all j, $a^{*}_{j} a_{j+1} + a_{j} a^{*}_{j+1}$ acts on a vector $\boldsymbol {\epsilon }$ on the basis of $\Omega _{N}$ by exchanging the symbols in positions j and $j+1$ if they are different. If they are not, the image of $\boldsymbol {\epsilon }$ by this matrix is $\textit {0}$ . As a consequence, for two vectors $\boldsymbol {\epsilon }$ and $\boldsymbol {\eta }$ on the basis of $\Omega _{N}$ , $H_{N}[\boldsymbol {\epsilon },\boldsymbol {\eta }] \neq 0$ if and only if $\boldsymbol {\eta }$ is obtained from $\boldsymbol {\epsilon }$ by exchanging a $1$ symbol of $\boldsymbol {\epsilon }$ with a $0$ in its neighborhood. The Hamiltonian $H_{N}$ thus corresponds to H in [DGHMT18] for $\Delta =0$ .

5.4.3 Fermionic creation and annihilation operators

$\triangleright $ The reason for defining the Hamiltonian, as in the last section, comes from the way it is obtained in the first place. We will not provide details on this here, and only rewrite the definition using other operators, called Fermionic creation and annihilation operators. This rewriting, exposed in the present section, will help diagonalize the matrix $H_{N}$ .

Notation 13. Let us denote by $\sigma $ the matrix of $\mathcal {M}_{2} (\mathbb {C})$ defined as

$$ \begin{align*}\sigma = \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right)\kern-2pt.\end{align*} $$

Let us denote, for all $j \in \mathbb {Z}/N\mathbb {Z}$ , by $c_{j}$ and $c^{*}_{j}$ the matrices

$$ \begin{align*}c_{j} = \sigma \otimes \cdots \sigma \otimes a \otimes \mathrm{id} \otimes \cdots \otimes \mathrm{id}, \quad c^{*}_{j} = \sigma \otimes \cdots \sigma \otimes a^{*} \otimes \mathrm{id} \otimes \cdots \otimes \mathrm{id}.\end{align*} $$

Let us recall that two matrices $P,Q$ anti-commute when $PQ = - QP$ .

Lemma 8. These operators verify the following properties for all j and $k \neq j$ :

1. (1) $c_{j} c^{*}_{j} + c^{*}_{j} c_{j} = {\mathrm {id}}$ ;

2. (2) $c^{*}_{j}$ and $c_{j}$ anti-commute with both $c^{*}_{k}$ and $c_{k}$ ;

3. (3) $a^{*}_{j+1} a_{j} = - c^{*}_{j+1} c_{j}$ and $a^{*}_{j} a_{j+1} = - c^{*}_{j} c_{j+1}$ .

Proof. (1) Since $\sigma ^ 2 = \mathrm {id}$ , for all j,

$$ \begin{align*}c_{j} c^{*}_{j} + c^{*}_{j} c_{j} = a_{j} a^{*}_{j} + a^{*}_{j} a_{j}.\end{align*} $$

From Lemma 6, we know that this operator is equal to identity.

(2) We can assume without loss of generality that $j <k$ . Let us prove that $c_{j}$ anti-commutes with $c_{k}$ (the other cases are similar):

$$ \begin{align*}c_{j} c_{k} = \mathrm{id} \otimes \cdots \otimes a \sigma \otimes \sigma \otimes \cdots \otimes \sigma \otimes \sigma a \otimes \mathrm{id} \otimes \cdots \otimes \mathrm{id},\end{align*} $$

$$ \begin{align*}c_{j} c_{k} = \mathrm{id} \otimes \cdots \otimes \sigma a \otimes \sigma \otimes \cdots \otimes \sigma \otimes a \sigma \otimes \mathrm{id} \otimes \cdots \otimes \mathrm{id}.\end{align*} $$

Hence it is sufficient to see

$$ \begin{align*}\sigma a = \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right) = \left( \begin{array}{cc} 0 & 0 \\ -1 & 0 \end{array}\right),\end{align*} $$

$$ \begin{align*}a \sigma = \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right) \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) = \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right)= - \sigma a.\end{align*} $$

(3) Let us prove the first equality (the other one is similar),

$$ \begin{align*}c^{*}_{j+1} c_{j} = \mathrm{id} \otimes \cdots \otimes \mathrm{id} \otimes \sigma a \otimes a^{*} \otimes \mathrm{id} \otimes \cdots \otimes \mathrm{id}.\end{align*} $$

We have just seen in the last point that $\sigma a = - a$ . As a consequence, $c^{*}_{j+1} c_{j} = - a^{*}_{j+1} a_{j}$ .

5.4.4 Action of a symmetric orthogonal matrix

$\triangleright $ In this section, we consider some operators derived from the Fermionic operators introduced in the last section by the action of a symmetric and orthogonal matrix. We also prove some of their properties. Using these new operators, we define a family of vectors that we prove in the next section to be a basis of eigenvectors for $H_{N}$ .

Let us denote by $c^{*}$ the vector $(c^{*}_{1}, \ldots , c^{*}_{N})$ and $c^{t}$ is the transpose of the vector $(c_{1}, \ldots , c_{N})$ . Let us consider a symmetric and orthogonal matrix $U= ( u_{i,j} )_{i,j}$ in $\mathcal {M}_{N} (\mathbb {R})$ and denote by b and $b^{*}$ the matrices

$$ \begin{align*}b = U\cdot c^{t} = (b_{1}, \ldots , b_{N}), \quad b^{*} = c^{*} \cdot U^{t} = (b^{*}_{1} , \ldots , b^{*}_{N}).\end{align*} $$

Notation 14. For all $\alpha \in \{0,1\}^{N}$ , we set

$$ \begin{align*}\psi_{\alpha} = (b^{*}_{1})^{\alpha_{1}} \ldots (b^{*}_{N})^{\alpha_{N}} \cdot \boldsymbol{\nu}_{N},\end{align*} $$

where $\boldsymbol {\nu }_{N} = \lvert {0,\ldots ,0}\rangle $ .

Lemma 9. For all j and $k \neq j$ :

• (1) $b_{j}$ and $b^{*}_{j}$ anti-commute with both $b_{k}$ and $b^{*}_{k}$ and $b_{j} b^{*}_{j} + b^{*}_{j} b_{j} = \mathrm {id}$ ;

• (2) for all $\alpha \in \{0,1\}^{N}$ , $\psi _{\alpha } \neq {0}$ ;

• (3) for all j and $\alpha $ , we have:

  1. (i) $b^{*}_{j} b_{j} \psi _{\alpha } = {0}$ if $\alpha _{j} = 0$ ;

  2. (ii) $b^{*}_{j} b_{j} \psi _{\alpha } = \psi _{\alpha }$ if $\alpha _{j} = 1$ .

Proof. (1) Anti-commutation relations: Let us prove that $b_{j}$ and $b^{*}_{k}$ anti-commute (the other statements of the first point have a similar proof). We rewrite the definition of $b_{j}$ and  $b^{*}_{k}$ :

$$ \begin{align*}b_{j} = \sum_{i} u_{i,j} c_{i}\quad \text{and} \quad b^{*}_{k} = \sum_{i} u_{k,i} c^{*}_{i} = \sum_{i} u_{i,k} c^{*}_{i}.\end{align*} $$

Thus,

$$ \begin{align*}b_{j} b^{*}_{k} = \sum_{i} \sum_{l \neq i} u_{i,j} u_{l,k} c_{i} c^{*}_{l} + \sum_{i} u_{i,j} u_{i,k} c_{i} c^{*}_{i}.\end{align*} $$

From Lemma 8,

$$ \begin{align*}b_{j} b^{*}_{k} = - \sum_{l} \sum_{i \neq l} u_{i,j} u_{l,k} c^{*}_{l} c_{i} + \sum_{i} u_{i,j} u_{i,k} ( \mathrm{id} - c^{*}_{i} c_{i}).\end{align*} $$

Since the matrix U is orthogonal,

$$ \begin{align*}b_{j} b^{*}_{k} = - \sum_{l} \sum_{i \neq l} u_{i,j} u_{l,k} c^{*}_{l} c_{i} - \sum_{i} u_{i,j} u_{i,k} c^{*}_{i} c_{i} = - b^{*}_{k} b_{j}.\end{align*} $$

Let us notice that this step is the reason why we use the operators $c_{i}$ instead of the operators  $a_{i}$ .

(2) For all k, $b^{*}_{k} = \sum _{l} u_{k,l} a^{*}_{l}.$ As a consequence, for a sequence $k_{1}, \ldots , k_{s}$ ,

$$ \begin{align*}b^{*}_{k_{1}} \ldots b^{*}_{k_{s}} \cdot \boldsymbol{\nu}_{N} = \sum_{l_{1}} \cdots \sum_{l_{s}} \bigg(\prod_{j=1}^{s} u_{k_{j},l_{j}} \bigg) \bigg(\prod_{j=1}^{s} a^{*}_{l_{j}}\bigg).\boldsymbol{\nu}_{N}.\end{align*} $$

Since $(a^{*})^{2} = 0$ , the sum can be considered on the integers $l_{1},\ldots ,l_{s}$ such that they are two by two distinct. The operator $a^{*}_{l_{1}} \ldots a^{*}_{l_{s}}$ acts on $\boldsymbol {\nu }_{N}$ by changing the $0$ on positions $l_{1}, \ldots , l_{s}$ into symbols $1$ . The coefficient of the image of $\boldsymbol {\nu }_{N}$ by this operator in the vector $b^{*}_{k_{1}} \ldots b^{*}_{k_{s}} \cdot \boldsymbol {\nu }_{N}$ is thus:

$$ \begin{align*}\sum_{\sigma \in \Sigma_{s}} \prod_{j=1}^{s} u_{k_{j},l_{\sigma(j)}}.\end{align*} $$

If this coefficient was equal to zero for all $\sigma $ , it would mean that all $s \times s$ sub-matrices of U have determinant equal to zero, which is impossible since U is orthogonal, and thus invertible (this derives from iterating Laplace expansion of the determinant of U). As a consequence, none of the vectors $\psi _{\alpha }$ is equal to zero.

(3) When $\alpha _{j} = 0$ , from the fact that when $j \neq k$ , $b_{j}$ and $b^{*}_{k}$ anti-commute, we get that

$$ \begin{align*}b_{j} \psi_{\alpha} = (-1)^{|\alpha|_{1}} (b^{*}_{1})^{\alpha_{1}} \ldots (b^{*}_{N})^{\alpha_{N}} b_{j} \boldsymbol{\nu}_{N},\end{align*} $$

and $b_{j} \boldsymbol {\nu }_{N} = \textbf {0}$ , since for all j, $a_{j} \boldsymbol {\nu }_{N} = \textbf {0}$ . As a consequence, $b^{*}_{j} b_{j} \boldsymbol {\nu }_{N} = \textbf {0}$ . When ${\alpha _{j} = 1}$ , by the anti-commutation relations,

$$ \begin{align*}b^{*}_{j} b_{j} \psi_{\alpha} = (b^{*}_{1})^{\alpha_{1}} \cdots (b^{*}_{j-1})^{\alpha_{j-1}} b^{*}_{j} b_{j} b^{*}_{j} (b^{*}_{j+1})^{\alpha_{j+1}} \cdots (b^{*}_{N})^{\alpha_{N}} \boldsymbol{\nu}_{N},\end{align*} $$

since the coefficients $-1$ introduced by anti-commutation are canceled out by the fact that we use it for $b_{j}$ and $b^{*}$ . From the first point,

$$ \begin{align*}b^{*}_{j} b_{j} \psi_{\alpha} = (b^{*}_{1})^{\alpha_{1}} \cdots (b^{*}_{j-1})^{\alpha_{j-1}} b^{*}_{j} ( \mathrm{id}- b^{*}_{j} b_{j}) (b^{*}_{j+1})^{\alpha_{j+1}} \cdots (b^{*}_{N})^{\alpha_{N}}.\end{align*} $$

$$ \begin{align*} b^{*}_{j} b_{j} \psi_{\alpha} & = (b^{*}_{1})^{\alpha_{1}} \cdots (b^{*}_{j-1})^{\alpha_{j-1}} b^{*}_{j} ( \mathrm{id}- b^{*}_{j} b_{j}) (b^{*}_{j+1})^{\alpha_{j+1}} \cdots (b^{*}_{N})^{\alpha_{N}} \\[2pt] & = \psi_{\alpha} - (b^{*}_{1})^{\alpha_{1}} \cdots (b^{*}_{N})^{\alpha_{N}} b_{j} \boldsymbol{\nu}_{N} \\[2pt] & = \psi_{\alpha}.\\[-3pc] \end{align*} $$

5.4.5 Diagonalization of the Hamiltonian

$\triangleright $ In this section, we diagonalize $H_{N}$ using the last section. Since we will only use its eigenvalues, we formulate the following.

Theorem 5. The eigenvalues of $H_{N}$ are exactly the numbers

$$ \begin{align*}2 \sum_{\alpha_{j} =1} \cos\bigg(\frac{2\pi j }{N}\bigg),\end{align*} $$

for $\alpha \in \{0,1\}^{N}$ .

Proof. (1) Rewriting ${H_{N}}$ : From Lemma 8, we can write $H_{N}$ as

$$ \begin{align*}H_{N} = \sum_{j} c^{*}_{j} c_{j+1} + c^{*}_{j+1} c_{j}.\end{align*} $$

The Hamiltonian $H_{N}$ can be then rewritten as $H_{N}= c^{*} M c^{t}$ , where M is the matrix defined by blocks

$$ \begin{align*}M = \frac{1}{2} \left( \begin{array}{cccc} \textbf{0} & \mathrm{id} & & \mathrm{id} \\[2pt] \mathrm{id} & \ddots & \ddots & \\[2pt] & \ddots & \ddots & \mathrm{id} \\[3pt] \mathrm{id} & & \mathrm{id} & \textbf{0} \end{array}\right),\end{align*} $$

where $\mathrm {id}$ is the identity matrix on $\mathbb {C}^{2}$ , and 0 is the null matrix. Let us denote by $M^{\prime }$ the matrix of $\mathcal {M}_{2^{N}} (\mathbb {R})$ obtained from M by replacing $\textbf {0},\mathrm {id}$ by $0,1$ .

(2) Diagonalization of ${M}$ : The matrix $M^{\prime }$ is symmetric and thus can be diagonalized in $\mathcal {M}_{2^{N}} (\mathbb {R})$ in an orthogonal basis. It is rather straightforward to see that the vectors $\psi ^{k}$ , $k \in \{0,\ldots ,N-1\}$ form an orthonormal family of eigenvectors of $M^{\prime }$ for the eigenvalue $\lambda _{k} = \cos ({2\pi k}/{N})$ , where for all $j \in \{1,\ldots ,N\}$ ,

$$ \begin{align*}\psi^{k}_{j} = \sqrt{\frac{2}{N}} \bigg(\sin(\frac{2\pi kj}{N}),\cos(\frac{2\pi kj}{N})\bigg).\end{align*} $$

This comes from the equalities

$$ \begin{align*}\cos(x-y)+\cos(x+y) = 2\cos(x)\cos(y), \end{align*} $$

$$ \begin{align*}\sin(x-y)+\sin(x+y) = 2\cos(x)\sin(y),\end{align*} $$

applied to $x=k(j-1)$ and $y=k(j+1)$ . This family of vectors is linearly independent, since the Vandermonde matrix with coefficients $e^{2\pi kj/N}$ is invertible. As a consequence, one can write

$$ \begin{align*}U^{\prime} M^{\prime} {U^{\prime}}^{t} = D^{\prime},\end{align*} $$

where $D^{\prime }$ is the diagonal matrix whose diagonal coefficients are the numbers $\lambda _{k}$ , and $U^{\prime }$ is the orthogonal matrix given by the vectors $\psi ^{k}$ . Replacing any coefficient of these matrices by the product of this coefficient with the identity, one gets an orthogonal matrix U and a diagonal one D such that

$$ \begin{align*}U M U^{t} = D.\end{align*} $$

(3) Some eigenvectors of ${H_{N}}$ : Let us consider the vectors $\psi _{\alpha }$ constructed in §5.4.4 for the matrix U of the last point, which is symmetric and orthogonal. From the expression of $H_{N}$ , we get that

$$ \begin{align*}H_{N} \psi_{\alpha} = \bigg(2 \sum_{j:\alpha_{j} = 1} \cos\bigg( \frac{2\pi j}{N} \bigg)\bigg) \cdot \psi_{\alpha}.\end{align*} $$

Since $\psi _{\alpha }$ is non-zero, this is an eigenvector of $H_{N}$ .

(4) The family ${(\psi _{\alpha })}$ is a basis of ${\Omega _{N}}$ : From cardinality of this family (the number of possible $\alpha $ , equal to $2^{N}$ ), it is sufficient to prove that this family is linearly independent. For this purpose, let us assume that there exists a sequence $(x_{\alpha })_{\alpha \in \{0,1\}}$ such that

$$ \begin{align*}\sum_{\alpha \in \{0,1\}^{N}} x_{\alpha}\cdot \psi_{\alpha} = \textbf{0}.\end{align*} $$

We apply first $b^{*}_{1} b_{1} \cdots. b^{*}_{N} b_{N}$ and get that $x_{(1,\ldots ,1)} \psi _{(1,\ldots ,1)} = 0,$ and thus $x_{(1,\ldots ,1)}=0$ (by Lemma 9, the vector $\psi _{(1,\ldots ,1)}$ is not equal to zero). Then we apply successively the operators $\prod _{j\neq k} b^{*}_{j} b_{j}$ for all k, and obtain that for all $\alpha \in \{0,1\}_{N}$ such that $|\alpha |_{1} = N-1$ , $x_{\alpha }=0$ . By repeating this argument, we obtain that all the coefficient $x_{\alpha }$ are null. As a consequence, $(\psi _{\alpha })_{\alpha }$ is a base of eigenvectors for $H_{H}$ , and the eigenvalues obtained in the last point cover all the eigenvalues of $H_{N}$ .

5.5 Identification

$\triangleright $ In this section, we use the diagonalization sub-spaces $\Omega _{N}^{(2n+1)}$ for $t \in (0,\sqrt {2})$ and $2n+1 \le N/2$ . of $H_{N}$ and a commutation relation between $H_{N}$ and $V_{N}(\sqrt {2})$ to prove that the candidate eigenvalue is the maximal eigenvalue of $V_{N}(t)$ for each of the The proofs for the following two lemmas can be found in [DGHMT18] (respectively Lemma 5.1 and Theorem 2.3). In Lemma 10, our notation $H_{N}$ corresponds to their notation H for $\Delta =0$ , and $V_{N} (\sqrt {2})$ corresponds to V for $\Delta =0$ . In Lemma 11, the equations $(E_{j})[\sqrt {2},n,N]$ correspond to their $(BE)$ , $\psi $ to $\psi $ for $\Delta =0$ .

Lemma 10. For all $N \ge 1$ , the Hamiltonian $H_{N}$ and $V_{N} (\sqrt {2})$ commute

$$ \begin{align*}H_{N} \cdot V_{N} (\sqrt{2}) = V_{N} (\sqrt{2}) \cdot H_{N}.\end{align*} $$

Lemma 11. For all N and $n\le N$ , let us denote by $({\kern1pt}\textbf{p}_{j})_{j}$ the solution of the system of equations $(E_{j})[\sqrt {2},n,N]$ , then denoting $\psi \equiv \psi _{\sqrt {2},n,N} ({\kern1pt}\textbf{p}_{1}, \ldots , \textbf {p}_{n})$ ,

$$ \begin{align*}H_{N} \cdot \psi = \bigg( 2 \sum_{k=1}^{n} \cos({\kern1pt}\textbf{p}_{k})\bigg)\cdot \psi. \end{align*} $$

Theorem 6. For all N and $2n+1 \le N/2$ , and $t \in (0,\sqrt {2})$ ,

$$ \begin{align*}\lambda_{2n+1,N} (t) = \Lambda_{2n+1,N} (t)[{\kern1pt}\textbf{p}_{1}(t) , \ldots , \textbf{p}_{2n+1} (t)].\end{align*} $$

Proof. (1) The Bethe vector is ${\neq 0}$ for ${t}$ in a neighborhood of ${\sqrt {2}}$ :

• • Limit of the Bethe vector in $\boldsymbol {\sqrt {2}}$ : Let us denote by $({\kern1pt}\textbf{p}_{j} (t))_{j}$ the solution of the system of equations $(E_{j})[t,2n+1,N]$ .

  Let us recall [Theorem 3] that for all t, and $\boldsymbol {\epsilon }$ in the canonical basis of $\Omega _{N}$ ,

  $$ \begin{align*}\psi_{t,2n+1,N} ({\kern1pt}\textbf{p}_{1} (t) , \ldots , \textbf{p}_{2n+1} (t)) [\boldsymbol{\epsilon}] = \sum_{\sigma \in \Sigma_{2n+1}} C_{\sigma}(t)[{\kern1pt}\textbf{p} (t)] \prod_{k=1}^{2n+1} e^{i\textbf{p}_{\sigma(k) (t)} \cdot q_{k} [\boldsymbol{\epsilon}]}.\end{align*} $$
  This expression admits a limit when $t \rightarrow \sqrt {2}$ , given by
  $$ \begin{align*}\sum_{\sigma \in \Sigma_{2n+1}} C_{\sigma}(\sqrt{2})[{\kern1pt}\textbf{p}(\sqrt{2})] \prod_{k=1}^{2n+1} e^{i\textbf{p}_{\sigma(k) (\sqrt{2})} \cdot q_{k} [\boldsymbol{\epsilon}]},\end{align*} $$
  where $({\kern1pt}\textbf{p}_{k} (\sqrt {2}))_{k}$ is solution of the system of equations $(E_{k})[\sqrt {2},2n+1,N]$ .

• • The expression ${\epsilon (\sigma ) C_{\sigma } (\sqrt {2})} {[}\textbf {p}{(\sqrt {2})]}$ is independent from ${\sigma }$ : Indeed, from the definition of $C_{\sigma }(t)$ we have

  $$ \begin{align*} &\prod_{1\le k < l \le 2n+1} (1 + e^{i ({\kern1pt}\textbf{p}_{\sigma(k)} (\sqrt{2})+\textbf{p}_{\sigma(l)} (\sqrt{2}))})\\[6pt] &\ \qquad = \prod_{1\le \sigma^{-1}(k) < \sigma^{-1}(l) \le 2n+1} (1 + e^{i ({\kern1pt}\textbf{p}_{k} (\sqrt{2})+\textbf{p}_{l} (\sqrt{2}))}) \\[6pt] &\ \qquad = \prod_{1\le k < l \le 2n+1} (1 + e^{i ({\kern1pt}\textbf{p}_{k} (\sqrt{2})+\textbf{p}_{l} (\sqrt{2}))}). \end{align*} $$

  Indeed, for all $l \neq k$ , one of the conditions $\sigma ^{-1} (k) < \sigma ^{-1} (l)$ or $\sigma ^{-1} (l) < \sigma ^{-1} (k)$ is verified, exclusively. This means that $(1 + e^{i ({\kern1pt}\textbf{p}_{k} (\sqrt {2})+\textbf {p}_{l} (\sqrt {2}))})$ appears exactly once in the product for each $l,k$ such that $l \neq k$ .

• • The terms ${(}{1 + e}^{{i} {(}\textbf {p}_{{k}} {(\sqrt {2})+}\textbf {p}_{{l}} {(\sqrt {2}))}}{)}$ , ${k \neq l}$ , are all non-zero: Indeed, none of the $\textbf {p}_{k} (\sqrt {2}) + \textbf {p}_{l} (\sqrt {2})$ can be equal to $\pm \pi $ . This comes from the fact that the system of Bethe equations $(E_{k})[\sqrt {2},2n+1,N]$ has a unique simple solution given by

  $$ \begin{align*}\textbf{p}_{k} (\sqrt{2}) = \frac{\pi}{N} \bigg( 2k - \frac{(2n+1+1)}{2}\bigg) = \frac{2\pi}{N} ( k - (n+1) ).\end{align*} $$
  These numbers are bounded respectively above and below by
  $$ \begin{align*}\textbf{p}_{1} (\sqrt{2})= - 2\pi \frac{n-1}{N}, \quad \textbf{p}_{n} (\sqrt{2}) = 2\pi \frac{n-1}{N}.\end{align*} $$
  Since $2n+1 \le N/2$ , these numbers are in $[-\pi /2,\pi /2]$ , and the possible sums of two different values of these numbers is in $]{-}\pi ,\pi [$ .

• • The limit of Bethe vectors is non-zero: As a consequence of the last points, we have that the $\boldsymbol {\epsilon }$ coordinate of the limit of Bethe vectors when $t \rightarrow \sqrt {2}$ is, up to a non-zero constant,

  $$ \begin{align*}\sum_{\sigma \in \Sigma_{2n+1}} \epsilon(\sigma)\cdot \prod_{k=1}^{2n+1} e^{i\textbf{p}_{\sigma(k) (\sqrt{2})} \cdot q_{k} [\boldsymbol{\epsilon}]},\end{align*} $$
  which is the determinant of the matrix $(e^{i\textbf {p}_{\sigma (k) (\sqrt {2})}. Here, q_{l} [\boldsymbol {\epsilon }]})_{k,l}$ , which is a submatrix of the matrix , where $(s_{k})$ is a sequence of distinct numbers in $]{-}\pi /2,\pi /2[$ such that for all $k \le 2n+1$ ,
  $$ \begin{align*}s_{k} = \textbf{p}_{\sigma(k) (\sqrt{2})},\end{align*} $$
  and $(s^{\prime }_{l})_{l}$ is a sequence of distinct integers such that for all $l \le n$ ,
  $$ \begin{align*}s^{\prime}_{l} = q_{l} [\boldsymbol{\epsilon}].\end{align*} $$
  If the determinant is non-zero, then the sum above is non-zero. This is the case since this last matrix is obtained from the Vandermonde matrix , whose determinant is
  $$ \begin{align*}\prod_{k<l} ( e^{is_{l}} - e^{is_{k}}) \neq 0,\end{align*} $$
  by a permutation of the columns.

(2) From the Hamiltonian to the transfer matrix:

• • Eigenvector of ${V_{N} (\sqrt {2})}$ and ${H_{N}}$ : Since the limit of Bethe vectors is not equal to zero, and it satisfies an equation which is the ‘limit’ of equations which make the Bethe vectors candidate eigenvectors, it is an eigenvector of the matrix $V_{N} (\sqrt {2})$ . It is also an eigenvector of the Hamiltonian $H_{N}$ , for the eigenvalue

  (17) $$ \begin{align} 2\bigg(\displaystyle{\sum_{k=1}^{n-1}} \cos(\frac{2\pi k}{N}) + \displaystyle{\sum_{k=N-n+1}^{N}} \cos\bigg(\frac{2\pi k}{N}\bigg)\bigg). \end{align} $$
  This is a consequence of Lemma 11, since for all j, $N\textbf {p}_{j} (\sqrt {2}) = 2\pi (j-(n+1)),$ the eigenvalue is
  $$ \begin{align*} 2\sum_{k=1}^{2n+1} \cos{( \textbf{p}_{k} (\sqrt{2}))} & = 2 \sum_{k=1}^{n} \cos{( \textbf{p}_{k} (\sqrt{2}))}+ 2 \sum_{k=n+1}^{2n+1} \cos{( N - \textbf{p}_{k} (\sqrt{2}))}\\[6pt] & = 2\bigg(\displaystyle{\sum_{k=1}^{n-1}} \cos\bigg(\frac{2\pi k}{N}\bigg) + \displaystyle{\sum_{k=N-n+1}^{N}} \cos\bigg(\frac{2\pi k}{N}\bigg)\bigg). \end{align*} $$

• • Comparison with the other eigenvalues of ${H}$ : From Theorem 5, we know that the number given by the expression in equation (17) is the largest eigenvalue of $H_{N}$ on $\Omega _{N}^{(2n+1)}$ . Indeed, it is straightforward that $\psi _{\alpha }$ is in $\Omega _{N}^{(2n+1)}$ if and only if the number of k such that $\alpha _{k} = 1$ is $2n+1$ . The sum in the statement of Theorem 5 is maximal among these sequences when

  $$ \begin{align*}\alpha_{1} = \cdots = \alpha_{n-1}=1 = \alpha_{N-n+1} = \cdots = \alpha_{N}\end{align*} $$
  and the other $\alpha _{k}$ are equal to $0$ .

• • Identification: As a consequence, from Perron–Frobenius theorem, the limit of Bethe vectors in $\sqrt {2}$ is positive, thus this is also true for t sufficiently close to $\sqrt {2}$ . From the same theorem, the Bethe vector is associated to the maximal eigenvalue of $V_{N} (t)$ . As a consequence, the Bethe value $\Lambda _{2n+1,N} (t) [{\kern1pt}\textbf{p}_{1} (t), \cdots \textbf {p}_{2n+1} (t)]$ is equal to the largest eigenvalue $\lambda _{2n+1,N} (t)$ of $V_{N} (t)$ on $\Omega _{N}^{(2n+1)}$ for these values of t. Since these two functions are analytic in t (by the implicit functions theorem on the characteristic polynomial, using the fact that the largest eigenvalue is simple), one can identify these two functions on the interval $(0,\sqrt {2})$ .

6 Asymptotic properties of Bethe roots

$\triangleright $ At this point, we have an expression of the largest eigenvalue of $V_{N}(1)$ on each of the sub-spaces $\Omega _{N}^{(2n+1)}$ with $2n+1 \le N/2$ . To obtain the entropy of $X^{s}$ , we need to understand how these expressions behave asymptotically, when n and N tend towards infinity—we can in fact assume that $n/N$ tends towards some d. For this, we need to understand how Bethe roots behave asymptotically. This is what we will do in this section.

Let us fix some $d \in [0,1/2]$ , and $(N_{k})_{k}$ and $(n_{k})_{k}$ some sequences of integers such that for all k, $n_{k} \le N_{k} / 2 +1$ and $n_{k} / N_{k} \rightarrow d$ . In this section, we study the asymptotic behavior of the sequences $(\boldsymbol {\alpha }^{(k)}_{j} (t))_{j}$ , where $t \in (0,\sqrt {2})$ ,

$$ \begin{align*}({\kern1pt}\textbf{p}^{(k)}_{j} (t))_{j} \equiv (\kappa_{t} ({\boldsymbol{\alpha}}^{(k)}_{j}(t)))_{j}\end{align*} $$

is solution of the system of Bethe equations $(E_{j})[t,n_{k},N_{k}]$ , $j \le n_{k}$ , when k tends towards $+\infty $ . For this purpose, we introduce in §6.1 the counting functions $\xi _{t}^{(k)}$ associated to the corresponding Bethe roots. The term ‘counting function’ refers to the fact that between two Bethe roots, the function increases by a constant, and thus ‘counts’ Bethe roots. In other words, these functions represent the distribution of Bethe roots in the real line. In §6.2, we prove that the sequence of functions $(\xi _{t}^{(k)})_{k}$ converges uniformly on any compact to a function $\boldsymbol {\xi }_{t,d}$ . In §6.3, we then prove the following, which will be used in §7 to compute the entropy of square ice: for all function $f: (0,+\infty ) \rightarrow (0,+\infty )$ which is continuous, decreasing and integrable,

$$ \begin{align*}\frac{1}{N_{k}} \sum_{j=\lceil n_{k} /2 \rceil +1}^{n_{k}} f(\boldsymbol{\alpha}^{(k)}_{j} (t)) \rightarrow \int_{0}^{\boldsymbol{\xi}_{t,d}^{-1} (d)} f(\alpha) \boldsymbol{\xi}_{t,d} (\alpha) \,d\alpha.\end{align*} $$

6.1 The counting functions associated to Bethe roots

In this section, we define the counting functions and prove some additional preliminary facts on the auxiliary functions $\theta _{t}$ and $\kappa _{t}$ that we will use in the following [§6.1.1]. We prove also that the number of Bethe roots vanishes as one get close to $\pm \infty $ , with a speed that does not depend on k [§6.1.2].

6.1.1 Definition

Notation 15. For all $t \in (0,\sqrt {2})$ and all integer k, let us denote by $\xi ^{(k)}_{t}: \mathbb {R} \rightarrow \mathbb {R} $ the counting function defined as follows:

$$ \begin{align*}\xi^{(k)}_{t}: \alpha \mapsto \bigg( \frac{1}{2\pi} \kappa_{t} (\alpha) + \frac{n_{k}+1}{2N_{k}} + \frac{1}{2\pi N_{k}} \sum_{j} \theta_{t} (\alpha,{\boldsymbol{\alpha}}^{(k)}_{j}(t))\bigg).\end{align*} $$

Fact 1. Let us notice some properties of these functions, that we will use in the following.

1. (1) By Bethe equations, for all j and k,

   $$ \begin{align*}\xi^{(k)}_{t} (\boldsymbol{\alpha}^{(k)}_{j} (t)) =\frac{j}{N_{k}} \equiv \rho_{j}^{(k)}.\end{align*} $$

2. (2) For all $k,t$ , the derivative of $\xi ^{(k)}_{t}$ is the function

   $$ \begin{align*}\alpha \mapsto \frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha) + \frac{1}{2\pi N_{k}} \sum_{j} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha,\boldsymbol{\alpha}_{j} (t))> 0.\end{align*} $$
   Indeed, this comes directly from the fact that $\mu _{t} \in ( {\pi }/{2}, \pi )$ . As a consequence, the counting functions are increasing.

We will use also the following proposition.

Proposition 8. We have the following limits for the functions $\kappa _{t}$ and $\theta _{t}$ on the border of their domains:

$$ \begin{align*}\displaystyle{\lim_{+\infty} \ \kappa_{t} = -\lim_{-\infty} \ \kappa_{t}} = \pi-\mu_{t}\end{align*} $$

and that for all $\beta \in \mathbb {R}$ ,

$$ \begin{align*}\lim_{+\infty} \ \theta_{t} (\alpha,y) = - \lim_{-\infty} \ \theta_{t} (\alpha,y) = 2\mu_{t} - \pi.\end{align*} $$

Proof. Let us prove this property for $\kappa _{t}$ , where the limits for $\theta _{t}$ are obtained applying the same reasoning. Let us recall that for all $\alpha \in \mathbb {R}$ ,

$$ \begin{align*}\kappa^{\prime}_{t} (\alpha) = \frac{\sin(\mu_{t})}{\cosh(\alpha)-\cos(\mu_{t})}.\end{align*} $$

Since this function is positive, $\kappa _{t}$ is increasing, and thus admits a limit in $\pm \infty $ . Since $\kappa ^{\prime }_{t}$ is integrable, these limits are finite. Since for all $\alpha $ ,

$$ \begin{align*}e^{i\kappa_{t} (\alpha)} = \frac{e^{i\mu_{t}} - e^{\alpha}}{e^{i\mu_{t} + \alpha}-1},\end{align*} $$

and the limit of this expression when $\alpha $ tends to $+\infty $ is $-e^{-i\mu _{t}}$ , then there exists some $k \in \mathbb {Z}$ such that

$$ \begin{align*}\displaystyle{\lim_{+\infty}} \kappa_{t} = 2k\pi + \pi-\mu_{t}\end{align*} $$

Since $\kappa _{t}$ is a bijective map from $\mathbb {R}$ to $I_{t}$ [Proposition 7], then $k=0$ . Thus we have

$$ \begin{align*}\displaystyle{\lim_{+\infty}} \kappa_{t} = \pi-\mu_{t}.\end{align*} $$

The limit in $-\infty $ is obtained by symmetry.

Notation 16. For any compact interval $I \subset \mathbb {R}$ , we set

$$ \begin{align*}\mathcal{V}_{I} (\epsilon,\eta) = \{z \in \mathbb{C}: |\text{Im}(z)|<\eta, d(\text{Re}(z),I)<\epsilon\}.\end{align*} $$

6.1.2 Rarefaction of Bethe roots near infinities

For all k, t and $M>0$ , we set

Theorem 7. For all $t \in (0, \sqrt {2})$ , $\epsilon>0$ , there exists some $M>0$ and $k_{0}$ such that for all $k \ge k_{0}$ ,

$$ \begin{align*}\frac{1}{N_{k}} |P_{t}^{(k)}(M)| \le \epsilon.\end{align*} $$

Idea of the proof: To prove this statement, we introduce a quantity $q_{t}$ which represents roughly the density of Bethe roots near infinities, defined as a $\limsup $ on pairs of integer and interval. It is sufficient to prove that $q_{t}=0$ to prove the statement. We extract a sequence of integers $(\nu (k_{l}))_{l}$ and $(I_{l})_{l} = ([-M_{l},M_{l}])_{l}$ that realizes this $\limsup $ . For these sequences, we bind from above and below the smallest (respectively, greatest) integer such that the corresponding Bethe root is greater than $M_{l}$ (respectively, smaller than $-M_{l}$ ). Using Bethe equations and properties of $\kappa _{t}$ and $\theta _{t}$ (boundedness and monotonicity), we prove a inequality relating these two bounds. Taking the limit $ l \rightarrow + \infty $ , we obtain an inequality that forces $q_{t}=0$ .

Proof. In this proof, we assume, to simplify the computations, that for all k, $n_{k}$ is even, and we set $n_{k} = 2m_{k}$ . However, similar arguments are valid for any sequence $(n_{k})_{k}$ . Moreover, if $d =0$ , the statement is trivial, and as a consequence, we assume in the remainder of the proof that $d>0$ . It is sufficient to prove then that for all $\epsilon>0$ , there exists some M and $k_{0}$ such that for all $k \ge k_{0}$ ,

$$ \begin{align*}\frac{1}{n_{k}} |P_{t}^{(k)}(M)| \le \epsilon.\end{align*} $$

Formulation with superior limits: If $\limsup _{m} \boldsymbol {\alpha }_{n_{k}}^{(k)}$ is finite, then the Bethe roots are bounded independently from k (from below this comes from the asymmetry of $\boldsymbol {\alpha }^{(k)}$ ), and thus the statement is verified.

Let us thus assume that $\limsup _{k} \boldsymbol {\alpha }_{n_{k}}^{(k)} = +\infty ,$ meaning that there exists some $\nu : \mathbb {N} \rightarrow \mathbb {N}$ such that

$$ \begin{align*}\boldsymbol{\alpha}_{n_{\nu(k)}}^{(\nu(k))} \rightarrow +\infty. \end{align*} $$

Let us denote, for all $k,t$ and $M>0$ , by $q_{t}^{(k)} (M)$ the proportion of positive Bethe roots $\boldsymbol {\alpha }_{j}^{(k)}$ that are greater than M. Since for all k, $\boldsymbol {\alpha }^{(k)}$ is an anti-symmetric and increasing sequence, $\boldsymbol {\alpha }_{j}^{(k)}>0$ implies that $j \ge m_{k} +1$ , and we define this proportion as

(18)

We also denote by $q_{t} (M) = \limsup _{k} q_{t}^{(\nu (k))} (M)$ and

$$ \begin{align*}q_{t} = \limsup_{M} q_{t} (M) \le 1.\end{align*} $$

By construction, there exists an increasing sequence $(M_{l})_{l}$ of real numbers and a sequence $(k_{l})_{l}$ of integers such that for all $\epsilon>0$ , there exists some $l_{0}$ and for all $l \ge l_{0}$ ,

(19) $$ \begin{align} q_{t} - \epsilon < q_{t} (M_{l}) - \frac{\epsilon}{2} < q_{t}^{(\nu(k_{l}))} (M_{l}) < q_{t}(M_{l}) + \frac{\epsilon}{2} < q_{t} + \epsilon. \end{align} $$

The proof of the statement reduces to prove that $q_{t} = 0$ .

Bounds for the cutting integers sequence:

1. (1) Lower bound: As a consequence of equation (18) and inequalities in equation (19), for $\epsilon $ and $l_{0}$ as in the previous point,

   

   Moreover,

   

   Thus the ‘cutting integer’, denoted by $\sigma _{l}$ , defined as the greatest j such that the associated Bethe root satisfies the inequality $\boldsymbol {\alpha }_{j}^{(\nu (k_{l}))} < M_{l}$ , is bounded from below by

   $$ \begin{align*}m_{\nu(k_{l})} + m_{\nu(k_{l})} \cdot \max ( 0, 1-\epsilon-q_{t}) \ge \max (0, 2 m_{\nu(k_{l})} (1-\epsilon-q_{t})).\end{align*} $$
   Since it is an integer, it is also greater than the integer $\underline {a}_{l}$ defined by
   $$ \begin{align*}\underline{a}_{l} = \max (0, \lfloor 2 m_{\nu(k_{l})} .(1-\epsilon -q_{t}) \rfloor ).\end{align*} $$

2. (2) Upper bound: Let us also set $\overline {a}_{l} = \lfloor 2 m_{\nu (k_{l})} .(1+\epsilon -q_{t}) \rfloor +1$ . For a similar reason, the cutting integer $\sigma _{l}$ is smaller than $\overline {a}_{l}$ . See a schema in Figure 9.

3. (3) Another similar bound: Moreover, since $l \ge l_{0}$ , by definition of the sequence $(q_{t}^{(k)})$ and by the inequalities in equation (19),

   $$ \begin{align*}q_{t} {}^{(\nu(k_{l}))} (M_{l_{0}}) \ge q_{t} {}^{(\nu(k_{l}))} (M_{l})> q_{t} (M_{l}) - \frac{\epsilon}{2}.\end{align*} $$

   As a consequence of a reasoning similar to the first point,

   
   and thus for all $j \le \underline {a}_{l}$ , $\boldsymbol {\alpha }_{j}^{\nu (k_{l})} < M_{l_{0}}$ .
   

   Figure 9 Illustration of the definition and lower bound of the cutting integer.

Inequality involving $\underline {{a}}_{{l}}$ and ${\overline {a}}_{{l}}$ through Bethe equations: By summing values of the counting function,

$$ \begin{align*} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \xi_{t}^{(\nu(k_{l}))} (\boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}) & = \frac{1}{2\pi} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \kappa_{t} (\boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}) + \frac{2 m_{\nu(k_{l})}+1}{2 N_{\nu(k_{l})}} (2 m_{\nu(k_{l})} + 1 - \overline{a}_{l}) \\ & \quad + \frac{1}{2\pi N_{\nu(k_{l})}} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \sum_{k^{\prime}=1}^{2 m_{\nu(k_{l})}} \theta_{t} ( \boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}, \boldsymbol{\alpha}_{k^{\prime}}^{(\nu(k_{l}))}). \end{align*} $$

By Bethe equations, we also have

$$ \begin{align*}\sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \xi_{t}^{(\nu(k_{l}))} (\boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}) = \frac{1}{N_{\nu(k_{l})}} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} k = \frac{ (2 m_{\nu(k_{l})}+\overline{a}_{l})(2 m_{\nu(k_{l})} - \overline{a}_{l} +1)}{2 N_{\nu(k_{l})}}.\end{align*} $$

As a direct consequence, and since $\theta _{t}$ is increasing in its first variable and $\theta _{t} (\alpha ,\alpha ) = 0$ for all $\alpha $ ,

$$ \begin{align*} &\frac{(2 m_{\nu(k_{l})}-\overline{a}_{l} +1)(\overline{a}_{l}-1)}{2 N_{\nu(k_{l})}}\\ &\quad= \frac{1}{2\pi} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \kappa_{t} (\boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}) + \frac{1}{2\pi N_{\nu(k_{l})}} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \sum_{k^{\prime}=1}^{2 m_{\nu(k_{l})}} \theta_{t} ( \boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}, \boldsymbol{\alpha}_{k^{\prime}}^{(\nu(k_{l}))})\\ &\quad \ge \frac{1}{2\pi} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \kappa_{t} (\boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}) + \frac{1}{2\pi N_{\nu(k_{l})}} \sum_{k=\overline{a}_{l}}^{2 m_{\nu(k_{l})}} \sum_{k^{\prime}<k} \theta_{t} ( \boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}, \boldsymbol{\alpha}_{k^{\prime}}^{(\nu(k_{l}))}). \end{align*} $$

Using again the fact that $\theta _{t}$ is increasing in its first variable, we have

$$ \begin{align*}\theta_{t} ( \boldsymbol{\alpha}_{k}^{(\nu(k_{l}))}, \boldsymbol{\alpha}_{k^{\prime}}^{(\nu(k_{l}))}) \ge \theta_{t} (M_{l}, M_{l_{0}})\end{align*} $$

when $k \ge \overline {a}_{l}$ and $k^{\prime } \le \overline {a}_{l}$ (this is a consequence of the third bound proved in the last point). The terms corresponding to other pairs $(k,k^{\prime })$ are bounded from below by $0$ . Using these facts and the fact that $\kappa _{t}$ is increasing,

$$ \begin{align*}\frac{(2 m_{\nu(k_{l})}-\overline{a}_{l} +1)(\overline{a}_{l}-1)}{2 N_{\nu(k_{l})}} &\ge (2 m_{\nu(k_{l})}-\overline{a}_{l} +1) \frac{1}{2\pi} \kappa_{t} (M_{l})\\ &\quad+ (2 m_{\nu(k_{l})}-\overline{a}_{l} +1) \frac{\underline{a}_{l}}{2\pi N_{\nu(k_{l})}} \theta_{t} (M_{l}, M_{l_{0}}).\end{align*} $$

Simplifying by $(2 m_{\nu (k_{l})}-\overline {a}_{l} +1)$ (which is possible because it is positive),

$$ \begin{align*}\frac{(\overline{a}_{l}-1)}{2 N_{\nu(k_{l})}} \ge \frac{1}{2\pi} \kappa_{t} (M_{l}) + \frac{\underline{a}_{l}}{2\pi N_{\nu(k_{l})}} \theta_{t} (M_{l}, M_{l_{0}}).\end{align*} $$

We take the limit when $l \rightarrow +\infty $ , and obtain, using the definitions of $\overline {a}_{l}$ and $\underline {a}_{l}$ ,

$$ \begin{align*}\frac{d}{2} (1-\epsilon-q_{t}) \ge \frac{\pi-\mu_{t}}{2\pi} + \frac{d}{2} \frac{2\mu_{t} - \pi}{\pi} (1-q_{t}).\end{align*} $$

Taking the limit when $\epsilon \rightarrow 0$ ,

$$ \begin{align*}\frac{d}{2} (1-q_{t}) \ge \frac{\pi-\mu_{t}}{2\pi} + \frac{d}{2} \frac{2\mu_{t} - \pi}{\pi} (1-q_{t}).\end{align*} $$

This inequality can be rewritten as

$$ \begin{align*} (1-q_{t}) \bigg( \frac{d}{2} - \frac{d}{2} \frac{2\mu_{t} -\pi}{\pi}\bigg) \ge \frac{\pi-\mu_{t}}{2\pi}.\end{align*} $$

Finally, $1-q_{t} \ge {1}/{2d} \ge 1$ , and thus since by definition $q_{t}$ is non-negative, $q_{t} = 0$ .

6.2 Convergence of the sequence of counting functions $(\xi _{t}^{(k)})_{k}$

$\triangleright $ In this section, we prove that the sequence of functions $(\xi _{t}^{(k)})_{k}$ converges uniformly on any compact to a function $\boldsymbol {\xi }_{t,d}$ . After some recalls on complex analysis [§6.2.1], we prove that if a subsequence of this sequence of functions converges on any compact of their domain towards a function, then this function verifies a Fredholm integral equation [§6.2.2], which is solved through Fourier analysis, and the solution is proved to be unique, in §6.2.3, by solving a similar equation verified by the derivative of this function. We prove in §6.2.4 that this fact implies that the sequence of counting functions converges to $\boldsymbol {\xi }_{t,d}$ .

For all t, there exists $\tau _{t}> 0$ such that for all k, the functions $\kappa _{t}$ , $\Theta _{t}$ and $\xi ^{(k)}_{t}$ can be extended analytically on the set $\mathcal {I}_{\tau _{t}} := \{z \in \mathbb {C}: |\text {Im}(z)| < \tau _{t} \} \subset \mathbb {C}$ . For the purpose of notation, the extended functions are denoted by the same symbols as their restriction on $\mathbb {R}$ .

6.2.1 Some complex analysis background

Let us recall some results of complex analysis that we will use in the remainder of this section. Let U be an open subset of $\mathbb {C}$ .

Definition 8. We say that a sequence $(f_{m})_{m}$ of functions $U \rightarrow \mathbb {C}$ is locally bounded when for all $z \in U$ , the sequence $(|f_{m} (z)|)_{m}$ is bounded.

Theorem 8. (Montel)

Let $(f_{m})_{m}$ be a locally bounded sequence of holomorphic functions $U \rightarrow \mathbb {C}$ . There exists a subsequence of $(f_{m})_{m}$ which converges uniformly on any compact subset of U.

Lemma 12. Let $(f_{m})_{m}$ be a locally bounded sequence of continuous functions $U \rightarrow \mathbb {C}$ and $f : U \rightarrow \mathbb {C}$ such that any subsequence of $(f_{m})_{m}$ which converges uniformly on any compact subset of U converges towards f. Then $(f_{m})_{m}$ converges uniformly on any compact towards f.

Proof. Let us assume that $(f_{m})_{m}$ does not converge towards f. Then there exists some $\epsilon>0$ , compact $K \subset U$ and a non-decreasing function $\nu : \mathbb {N} \rightarrow \mathbb {N}$ such that for all m,

$$ \begin{align*}\|(f_{\nu(m)}- f)_{K}\|_{\infty} \ge \epsilon.\end{align*} $$

From Montel theorem, one can extract a subsequence of $(f_{\nu (m)})_{m}$ which converges towards f uniformly on any compact of U, and in particular on the compact K. This is in contradiction to the above inequality, and we deduce that $(f_{m})_{m}$ converges towards f.

Theorem 9. (Cauchy formula)

Let us assume that U is simply connected and let $f: U \rightarrow \mathbb {C}$ be a holomorphic function and $\gamma $ a loop included in U that is homeomorphic to a circle positively oriented. Then for all z in the interior domain of the loop,

$$ \begin{align*}f(z) = \frac{1}{2\pi i} \oint_{\gamma} \frac{f(s)}{s-z}\,ds.\end{align*} $$

Let us also recall a sufficient condition for a holomorphic function to be biholomorphic.

Theorem 10. Let U be an open and simply connected set and $f : U \rightarrow \mathbb {C}$ be a holomorphic function. Let $V \subset U$ be an open set and $\gamma $ a loop included in U that is homeomorphic to a positively oriented circle, and such that V is included in the interior domain of $\gamma $ . We assume that:

1. (1) for all $z \in V$ and $s \in \gamma $ , $f(z) \neq f(s)$ ;

2. (2) and for all $z \in V$ , $f^{\prime }(z) \neq 0$ .

Then f is a biholomorphism from V onto its image, meaning that there exists some holomorphic function $g : f(V) \rightarrow U$ such that for all $z \in f(V)$ , $f(g(z)) = z$ and for all $z \in U$ , $g(f(z))= z$ . Moreover, for all $z \in f(V)$ ,

$$ \begin{align*}g(z) = \frac{1}{2\pi i} \int_{\gamma} s \frac{f^{\prime}(s)}{f(s)-z}ds.\end{align*} $$

6.2.2 The limits of subsequences of $(\xi _{t}^{(k)})_{k}$ satisfy a Fredholm integral equation

In this section, we prove the following theorem.

Theorem 11. Let $\nu : \mathbb {N} \rightarrow \mathbb N$ be a non-decreasing function, and assume that $( \xi _{t}^{(\nu (m))})_{m}$ converges uniformly on any compact of $\mathcal {I}_{\tau _{t}}$ towards a function $\xi _{t}$ . Then this function satisfies the following equation for all $\alpha \in \mathcal {I}_{\tau }$ :

$$ \begin{align*}\xi^{\prime}_{t} (\alpha) = \frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha) + \int_{\mathbb{R}} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha,\beta) \xi^{\prime}_{t} (\beta) d\beta.\end{align*} $$

Moreover, $\xi _{t} (0) = d/2$ .

Proof. Convergence of the derivative of the counting functions: Since any compact of $\mathcal {I}_{\tau _{t}}$ can be included in the interior domain of a rectangle loop, through derivation of the Cauchy formula, the derivative of $\xi _{t}^{(\nu (m))}$ converges also uniformly on any compact, towards $\xi ^{\prime }_{t}$ . Since $|(\xi _{t}^{(m)})^{\prime }|$ is bounded by a constant that does not depend on m, and that $s \mapsto |\theta _{t} (\alpha ,s)|$ is integrable on $\mathbb {R}$ for all $\alpha $ , then $s \mapsto \theta _{t} (\alpha ,s) \xi ^{\prime }_{t} (s)$ is integrable on $\mathbb {R}$ .

Some notation: Let us fix some $\epsilon>0$ , and $\alpha _{0} \in \mathbb {R}$ . In the following, we consider some irrational number (and as a consequence, not the image of a Bethe root) $M>1$ such that:

1. (1) $M \in \overset {\circ }{\xi _{t}(\mathbb {R})}$ ;

2. (2) $|P_{t}^{(k)} (M)| \le {\epsilon }/{2(2\mu _{t}-\pi )}$ for all k greater than some $k_{0}$ (this is possible to impose in virtue of Theorem 7);

3. (3) and $\alpha _{0} \in \xi _{t}^{-1} ([-M,M])$ .

Since $\xi _{t} (\mathbb {R})$ is an interval (this function is increasing on $\mathbb {R}$ ), one can take M arbitrarily close to the supremum of this interval. When M tends towards this supremum, $\xi _{t}^{-1} (M)$ tends to $+\infty $ : if it did not, then this would contradict the fact that this is the supremum (again by monotonicity). One can assume that M is such that

(20) $$ \begin{align} \frac{1}{2\pi}\bigg|\int_{(\xi_{t}^{-1}([-M,M]))^{c}} \theta_{t} (\alpha,\beta) \xi^{\prime}_{t} (\beta) \,d\beta \bigg| \le \frac{\epsilon}{4}. \end{align} $$

Let us also set $J_{t} = \xi _{t}^{-1} ([-M,M])$ .

The derivative of ${\xi _{t}}$ relative to the axis ${i\mathbb {R}}$ is non-zero when close enough to ${\mathbb {R}}$ : Indeed, for all $\alpha ,\lambda \in \mathbb {R}$ ,

$$ \begin{align*}\xi_{t}^{(k)} (\alpha+i \lambda) = \frac{1}{2\pi} \kappa_{t} (\alpha+i\lambda) + \frac{n_{k}+1}{2N_{k}} + \frac{1}{2\pi N_{k}} \sum_{j} \theta_{t} (\alpha+i\lambda, \boldsymbol{\alpha}_{j}^{(k)} (t)).\end{align*} $$

As a direct consequence, the derivative of the function $\lambda \mapsto -i \xi _{t}^{(k)} (\alpha +i \lambda )$ in $0$ is

(21) $$ \begin{align} \frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha) + \frac{1}{2 \pi N_{k} } \sum_{j} \theta_{t} (\alpha,\boldsymbol{\alpha}_{j}^{(k)} (t)) = (\xi_{t}^{(k)})^{\prime} (\alpha) \ge \frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha)> 0. \end{align} $$

Thus for all $\alpha $ , the derivative of the function $\lambda \mapsto - i \xi _{t} (\alpha +i\lambda )$ in $0$ is greater than

$$ \begin{align*}\frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha).\end{align*} $$

Moreover, since the second derivative of $\lambda \mapsto -i \xi _{t}^{(k)} (\alpha +i \lambda )$ is a bounded function of $\alpha $ , with a bound that is independent from k, through Taylor integral formula, there exists a constant $p_{t}>0$ such that for all $\lambda \in \mathbb {R}$ and $\alpha \in \mathbb {R}$ ,

$$ \begin{align*}|\xi_{t}(\alpha+i\lambda) - i \xi^{\prime}_{t} (\alpha). \lambda - \xi_{t} (\alpha)| \le p_{t} \lambda^{2},\end{align*} $$

which implies

$$ \begin{align*}|\text{Im}(\xi_{t}(\alpha+i\lambda)) - \xi^{\prime}_{t} (\alpha). \lambda |\le p_{t} \lambda^{2}.\end{align*} $$

By virtue of equation (21),

$$ \begin{align*}\text{Im}(\xi_{t}(\alpha+i\lambda)) \ge \xi^{\prime}_{t} (\alpha) \lambda - p_{t} \lambda^{2} \ge \frac{1}{2\pi} \kappa^{\prime}_{t}(\alpha)\lambda -p_{t} \lambda^{2}.\end{align*} $$

The derivative of $\xi _{t}$ relative to the axis $i\mathbb {R}$ in $\alpha \in \mathbb {R}$ is greater than $({1}/{2\pi }) \kappa ^{\prime }_{t}(\alpha )$ .

The restriction of ${\xi }_{{t}}$ on some ${\mathcal {V}}_{{J}_{{t}}} {(}{\eta }_{{t}},{\epsilon }_{{t}}{)}$ is a biholomorphism onto its image: Since M is defined so that

$$ \begin{align*}M \in \overset{\circ}{\xi_{t}(\mathbb{R})},\end{align*} $$

then $J_{t} = \xi _{t}^{-1} ([-M,M])$ is compact. This means, as a consequence of the last point, that there exists some positive number $\sigma _{t} < \tau _{t}$ such that for all $z \in \mathcal {V}_{J_{t}}(\sigma _{t},1) \backslash \mathbb {R}$ , then $\xi _{t} (z) \notin \mathbb {R}$ .

Let us consider the loop $\gamma _{t}$ given by $\partial \mathcal {V}_{J_{t}} (\sigma _{t},1)$ (see the illustration in Figure 10).

Figure 10 Illustration of the proof that $\xi _{t}$ is a biholomorphism on a neighborhood of $J_{t}$ .

Let us prove that there exist some $\epsilon _{t}>0$ and $\eta _{t}>0$ such that the values taken by the function $\xi _{t}$ on $\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})$ are distinct from any value taken by the same function on the loop $\gamma _{t}$ . This is done in two steps, as follows.

1. (1) First, we consider open neighborhoods (illustrated by dashed squares in Figure 10) for the two points of $\gamma _{t} \cap \mathbb {R}$ such that the values taken by $\xi _{t}$ on these sets are distant by more than a positive constant from the values taken on $J_{t}$ . This is possible since $\xi _{t}$ is strictly increasing on $\mathbb {R}$ .

2. (2) On the part of $\gamma _{t}$ that is not included in these two open sets, the function $\xi _{t}$ takes non-real values, and the set of values taken is compact, by continuity. As a consequence, the set of values taken on the loop $\gamma _{t}$ is included into a compact that does not intersect the set of values taken on $J_{t}$ . Thus one can separate these two sets of values with open sets, meaning that there exist some $\epsilon _{t}>0$ and $\eta _{t}>0$ such that the set of values taken by $\xi _{t}$ on $\mathcal {V}_{J_{t}} (\eta _{t} ,\epsilon _{t})$ does not intersect the set of values taken by this function on $\gamma _{t}$ .

By virtue of Theorem 10, this means that $\xi _{t}$ is a biholomorphism from $\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})$ onto its image on this set. As a consequence, it is also an open function, and its image on $\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})$ contains the image of $J_{t}$ , where $[-M,M]$ by definition.

Asymptotic biholomorphism property for ${\xi }_{{t}}^{{(\nu (k))}}$ : It can be derived from the last point that there exists some $k_{1} \ge k_{0} $ such that for all $k \ge k_{1}$ , the values of $\xi _{t}^{(\nu (k))}$ on $\gamma _{t}$ are distinct from the values of $\xi _{t}^{(k)}$ on $\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})$ , and as a consequence, for the same reason as the last point, $\xi _{t}^{(\nu (k))}$ is a biholomorphism from $\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})$ onto its image on this set. Moreover, since $\xi _{t}^{(\nu (k))}$ converges uniformly to $\xi _{t}$ on $\overline {\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})}$ , it converges also uniformly on $\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})$ . Furthermore, $\xi _{t} (\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t})) $ contains $\mathcal {V}_{[-M,M]}(\eta ^{\prime }_{t},\epsilon ^{\prime }_{t})$ , and thus there exists some $\eta ^{\prime }_{t}, \epsilon ^{\prime }_{t}>0$ and some $k_{2} \ge k_{1}$ such that for all $k \ge k_{2}$ , $\xi _{t}^{(\nu (k))} (\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t}))$ contains $\mathcal {V}_{[-M,M]}(\eta ^{\prime }_{t},\epsilon ^{\prime }_{t})$ .

Loop integral expression of the counting functions and approximation of ${\xi }_{{t}}^{{(\nu (k))}}$ : We deduce that for all $k \ge k_{2}$ and $\sigma < \eta ^{\prime }_{t}$ positive, the loop

is included into $\xi _{t}^{(\nu (k))} (\mathcal {V}_{J_{t}} (\eta _{t},\epsilon _{t}))$ . See Figure 11 for an illustration.

Figure 11 Illustration for the definition of the loop $\Gamma ^{\sigma }_{t}$ .

We then have, since $\alpha _{0} \in J_{t}$ , the following equation for all k, $t,\sigma $ :

Indeed, there are no poles for $\xi _{t}^{(\nu (k))}$ on $\Gamma _{t}^{\sigma }$ since M is irrational. The poles of the function inside the domain delimited by $\Gamma _{t}^{\sigma }$ are exactly the numbers $\rho _{j}^{(\nu (k))}$ . By the residues theorem, and since for all j, $\xi _{t}^{(\nu (k))} (\boldsymbol {\alpha }_{j} (t)) = \rho _{j}^{(\nu (k))}$ ,

(22)

Triangular inequality: We have the following triangular inequality:

(23)

We deduce from the last point (equation (22)) that for all $k \ge k_{2}$ and all $\sigma < \eta ^{\prime }_{t}$ ,

(24)

using the notation from the second point of this proof. Let us also note $k_{3} \ge k_{2}$ some integer such that for all $k \ge k_{3}$ ,

(25) $$ \begin{align} \bigg|\frac{n_{\nu(k)}+ 1}{2N_{\nu(k)}} - \frac{d}{2} \bigg|\le \frac{\epsilon}{8}. \end{align} $$

We then evaluate convergence of the various other terms involved in the triangular inequality above.

1. (1) Convergence of the bottom part of the loop integral to an integral on a real segment when ${\sigma \rightarrow 0}$ : By continuity of $\xi _{t}^{-1}$ , there exists some $\sigma _{0}>0$ such that for all $k \ge k_{3}$ , $\sigma \le \sigma _{0}$ ,

   (26) $$ \begin{align} \bigg|\int_{[-M,M]} \theta_{t} (\alpha_{0}, \xi_{t}^{-1} (\beta - i \sigma)) \,d \beta - \int_{[-M,M]} \theta_{t}(\alpha_{0},\xi_{t}^{-1} (\beta)) d \beta \bigg| \le \frac{\epsilon}{64}. \end{align} $$
   By change of variable in the second integral,
   (27) $$ \begin{align} \hspace{-10pt} \bigg|\int_{[-M,M]} \theta_{t} (\alpha_{0},\xi_{t}^{-1} (\beta - i \sigma)) \,d \beta - \int_{\xi_{t}^{-1}([-M,M])} \theta_{t}(\alpha_{0},\beta) \xi^{\prime}_{t} (\beta) \,d \beta \bigg| \le \frac{\epsilon}{64}.\quad \end{align} $$

2. (2) Bounding the lateral parts of the loop integral for ${\sigma \rightarrow 0}$ : There exists some $\sigma _{1}> 0$ such that $\sigma _{1} \le \sigma _{0}$ such that for all $\sigma \le \sigma _{1}$ , $k \ge k_{3}$ ,

   (28) $$ \begin{align} \bigg|\frac{1}{2\pi} \int_{-\sigma}^{\sigma} \theta_{t}(\alpha_{0},(\xi_{t}^{(\nu(k))})^{-1} (\pm M+i\lambda))) \frac{e^{2i\pi N_{\nu(k)} (\pm M+i\lambda) }}{(e^{2i\pi N_{\nu(k)} (\pm M+i\lambda)}-1)} \,d \lambda \bigg| \le \frac{\epsilon}{64}. \end{align} $$

3. (3) Convergence of the top and bottom parts of the loop integral when ${k \rightarrow +\infty }$ : Then there exists some $k_{4} \ge k_{3}$ such that for all $k \ge k_{4}$ ,

   (29) $$ \begin{align} \bigg|\frac{1}{2\pi} \int_{-M}^{M} \theta_{t}(\alpha_{0},(\xi_{t}^{(\nu(k))})^{-1} (\beta + i \sigma_{1} )) \frac{e^{2i\pi N_{\nu(k)}(\beta + i \sigma_{1}) }}{(e^{2i\pi N_{\nu(k)} (\pm (\beta + i \sigma_{1})}-1)} \,d \beta \bigg| \le \frac{\epsilon}{64}. \end{align} $$
   (30) $$ \begin{align} \bigg|\frac{1}{2\pi} \int_{-M}^{M} \theta_{t}(\alpha_{0},(\xi_{t}^{(\nu(k))})^{-1} (\beta - i \sigma_{1} )) \bigg( \frac{e^{2i\pi N_{\nu(k)} (\beta - i \sigma_{1}) }}{(e^{2i\pi N_{\nu(k)} (\pm (\beta - i \sigma_{1})}-1)} - 1 \bigg) \,d\beta \bigg|\le \frac{\epsilon}{64}. \end{align} $$

Using equations 23–30 together with equation (20), we have that for all $k \ge k_{4}$ ,

$$ \begin{align*}\bigg| \xi_{t}^{(\nu(k))} (\alpha_{0}) - \frac{1}{2\pi} \kappa_{t} (\alpha_{0}) - \frac{d}{2} - \frac{1}{2\pi} \int_{-\infty}^{\infty} \theta_{t} (\alpha_{0}, \beta) \xi^{\prime}_{t}(\beta) \,d\beta \bigg| \le \frac{\epsilon}{2} + \frac{\epsilon}{4}+ \frac{\epsilon}{8} + 5\frac{\epsilon}{64} \le \epsilon.\end{align*} $$

Integral equations: As a consequence, since this is true for all $\epsilon>0$ and $\alpha _{0}$ , we have the following equality for all $\alpha \in \mathbb {R}$ :

$$ \begin{align*}\xi_{t} (\alpha) = \frac{1}{2\pi} \kappa_{t} (\alpha) + \frac{d}{2} + \frac{1}{2\pi} \int_{-\infty}^{\infty} \theta_{t} (\alpha, \beta) \xi^{\prime}_{t}(\beta) \,d\beta.\end{align*} $$

Moreover, this equality is verified for any $\alpha _{0}$ , and differentiating it relatively to $\alpha $ :

$$ \begin{align*}\xi^{\prime}_{t} (\alpha) = \frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha) + \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha, \beta) \xi^{\prime}_{t}(\beta) \,d\beta.\end{align*} $$

Value of ${\xi }_{{t}} {(0)}$ : Since $\xi _{t}^{(k)}$ is increasing for all k, we have directly

$$ \begin{align*}\frac{\lfloor n_{k} /2 \rfloor}{N_{k}} = \xi_{t}^{(k)} (\boldsymbol{\alpha}_{\lfloor n_{k} /2 \rfloor}^{(k)} (t)) \le \xi_{t}^{(k)} (0) \le \xi_{t}^{(k)} (\boldsymbol{\alpha}_{\lceil n_{k} /2 \rceil+1}^{(k)} (t))= \frac{\lceil n_{k} /2 \rceil+2}{N_{k}}.\end{align*} $$

As a consequence, since we assumed at the very beginning of §6 that $n_{k}/N_{k} \rightarrow d$ , $\xi _{t} (0) = d/2$ .

6.2.3 Solution of the Fredholm equation

In this section, we prove that the integral equation on $\xi _{t}$ in the statement of Theorem 11 is unique and compute its solution.

Proposition 9. Let $t \in (0,\sqrt {2})$ and $\rho $ a continuous function in $L^{1}(\mathbb {R}, \mathbb {R})$ such that for all $\alpha \in \mathbb {R}$ ,

$$ \begin{align*}\rho(\alpha) = \frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha) + \frac{1}{2\pi} \int_{-\infty}^{+\infty} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha,\beta) \rho(\beta) \,d\beta.\end{align*} $$

Then for all $\alpha $ ,

$$ \begin{align*}\rho(\alpha) =\frac{1}{4\mu_{t} \cosh( \pi \alpha / 2\mu_{t})}.\end{align*} $$

Proof. The proof consists essentially in the application of Fourier transform techniques. We will set, for convenience, for all $\alpha $ and $\mu $ ,

$$ \begin{align*}\Xi_{\mu} (\alpha) = \frac{\sin(\mu)}{\cosh(\alpha)-\cos(\mu)}.\end{align*} $$

Application of Fourier transform: Let us denote by $\hat {\rho }$ the Fourier transform of $\rho $ : for all $\omega $ ,

$$ \begin{align*}\hat{\rho} (\omega) = \int_{-\infty}^{+\infty} \rho(\alpha) e^{i\omega \alpha} \,d \alpha,\end{align*} $$

which exists since $\rho $ is $L^{1}(\mathbb {R})$ . Additionally, we denote by ${\hat {\Xi }}_{\mu }$ the Fourier transform of $\Xi _{\mu }$ . Thus, since

$$ \begin{align*}\int_{-\infty}^{+\infty} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha,\beta) \rho(\beta) \,d \beta = -\int_{-\infty}^{+\infty} \Xi_{\mu} (\alpha-\beta) \rho(\beta) \,d \beta ,\end{align*} $$

this defines a convolution product, which is transformed into a simple product through the Fourier transform, so that for all $\omega $ ,

$$ \begin{align*}\hat{\rho } (\omega) = \frac{1}{2\pi} \hat{\Xi}_{\mu_{t}} (\omega) - \frac{1}{2\pi} \hat{\Xi}_{2\mu_{t}} (\omega) \hat{\rho} (\omega).\end{align*} $$

(31) $$ \begin{align} 2\pi \hat{\rho} (\omega) = \frac{\hat{\Xi}_{\mu_{t}} (\omega)}{1+ ({1}/{2\pi}) \hat{\Xi}_{2\mu_{t}} (\omega)}. \end{align} $$

Computation of ${\hat {\Xi }}_{{\mu }}$ :

• • Singularities of this function: The singularities of the function $\Xi _{\mu }$ are exactly the numbers $i(\mu +2k\pi )$ for $k \ge 0$ and $i(-\mu +2k\pi )$ for $k \ge 1$ , since for $\alpha \in \mathbb {C}$ , $\cosh (\alpha )=\cos (\mu )$ if and only if

  $$ \begin{align*}\cos(i\alpha) = \cos(\mu),\end{align*} $$
  and this implies that $\alpha = i(\pm \mu + 2k\pi )$ for some k.

• • Computation of the residues: For all k, the residue of $\Xi _{\mu }$ in $i(\mu +2k\pi )$ is

  $$ \begin{align*}\text{Res}(\Xi_{\mu},i\mu+2k\pi)= \frac{e^{i\gamma.i(\mu+2k\pi)}}{i} = \frac{1}{i} e^{-\gamma (\mu+2k\pi)}.\end{align*} $$
  As well,
  $$ \begin{align*}\text{Res}(\Xi_{\mu},-i\mu+2k\pi)= \frac{e^{i\gamma.i(-\mu+2k\pi)}}{i} = -\frac{1}{i} e^{-\gamma (-\mu+2k\pi)}.\end{align*} $$

  We have, for all $\gamma $ ,

  $$ \begin{align*}\int_{-\infty}^{+\infty} \Xi_{\mu} (\alpha) e^{i\alpha\gamma} \,d\alpha = 2\pi \frac{\sinh[(\pi-\mu)\gamma]}{\sinh(\pi\gamma)}.\end{align*} $$

• • Residue theorem: Let us set, for all integer n, the loop $\Gamma _{n} = [-n,n] + i[0,n]$ . The residues $\Xi _{\mu }$ inside the domain delimited by this loop are the $i(\mu + 2k\pi )$ with $k \ge 0$ , and the $i(-\mu + 2k\pi )$ with $k\ge 1$ . For all n,

  $$ \begin{align*}\int_{\Gamma_{n}} \Xi_{\mu} (\alpha) e^{i\alpha\gamma} \,d\alpha = \int_{\Gamma_{n}} \frac{\sinh(i\mu)}{i( \cosh(\alpha)-\cosh(i\mu))} e^{i\alpha\gamma} \,d\alpha. \end{align*} $$

  By the residue theorem,

  $$ \begin{align*}\int_{\Gamma_{N}} \! \Xi_{\mu} (\alpha) e^{i\alpha\gamma} \,d\alpha = 2\pi i \bigg(\!\sum_{k \ge 0} \text{Res}(\Xi_{\mu},i(\mu+2k\pi))- \!\sum_{k\ge 1} \text{Res}(\Xi_{\mu},i(-\mu+2k\pi))\bigg).\end{align*} $$

• • Asymptotic behavior: Since only the contribution on $[-n,n]$ of the integral is non-zero asymptotically, and by convergence of the integral and the sums,

  (32) $$ \begin{align} \int_{-\infty}^{+\infty} \Xi_{\mu} (\alpha) e^{i\alpha\gamma} \,d\alpha & = 2\pi e^{-\gamma \mu}+ 2\pi \sum_{k=1}^{+\infty} (-e^{\gamma \mu} + e^{-\gamma \mu}) e^{-2 \gamma k \pi} \nonumber\\ & = 2\pi e^{-\gamma \mu}+ 2\pi (-e^{\gamma \mu} + e^{-\gamma \mu})\bigg(\frac{1}{1-e^{-2\gamma\pi}}-1\bigg) \nonumber\\ & = 2\pi e^{-\gamma \mu} + 2\pi (-e^{\gamma \mu} + e^{-\gamma \mu}) \frac{e^{-\gamma \pi}}{e^{\gamma \pi} - e^{-\gamma \pi}} \nonumber\\ & = 2\pi \frac{e^{-\gamma (-\pi+\mu)} - e^{\gamma(-\pi-\mu)} - e^{\gamma (\mu-\pi)} + e^{\gamma (-\pi-\mu)}}{e^{\gamma \pi} - e^{-\gamma \pi}} \nonumber\\ \hat{\Xi}_{\mu} (\gamma) & = 2\pi \frac{\sinh(\gamma(\pi-\mu))}{\sinh(\gamma \pi)}. \end{align} $$

Computation of ${\hat {\rho }}$ : Using equations (31) and (32) with $\mu =\mu _{t}$ , for all $\omega $ ,

$$ \begin{align*} 2\pi \hat{\rho}(\omega) & = \frac{2\pi\sinh(\omega(\pi-\mu_{t}))}{\sinh(\pi\omega)+\sinh(\omega(\pi-2\mu_{t}))}\\ & = \frac{4\pi\sinh(\omega(\pi-\mu_{t}))}{e^{\omega\pi}.(1+ e^{-2\mu_{t} \omega}) - e^{-\omega\pi}.(1+ e^{2\mu_{t} \omega})}\\ & = \frac{4\pi\sinh(\omega(\pi-\mu_{t}))}{e^{\omega(\pi-\mu_{t})}.(e^{\mu_{t} \omega}+ e^{-\mu_{t} \omega}) - e^{-\omega(\pi-\mu_{t})}.(e^{-\mu_{t} \omega}+ e^{\mu_{t} \omega})}\\ & = \frac{\pi}{\cosh(\mu_{t} \omega)}. \end{align*} $$

Inverse transform: We thus have for all $\alpha $ ,

$$ \begin{align*}2\pi \rho(\alpha) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{\pi}{\cosh(\mu_t \omega)} e^{-i\omega \alpha} \,d\omega = \frac{1}{\mu_t}\int_{-\infty}^{\infty} \frac{1}{2\cosh(u)} e^{-i\frac{u}{\mu_t} \alpha} \,du,\end{align*} $$

where we used the variable change $u=\mu _{t} \omega $ . Using equation (32) for $\mu =\pi /2$ ,

$$ \begin{align*}\int_{-\infty}^{+\infty} \frac{1}{\cosh(\alpha)} e^{i\alpha\gamma} \,d\alpha = 2\pi \frac{\sinh(\pi\gamma/2)}{\sinh(\pi\gamma)} = \frac{\pi}{\cosh(\pi\gamma/2)}.\end{align*} $$

Thus we have

$$ \begin{align*}2\pi \rho(\alpha) = \frac{1}{2\mu_t} \frac{\pi}{\cosh(\pi\alpha /2\mu_t)} = \frac{\pi}{2\mu_t} \frac{1}{\cosh(\pi\alpha /2\mu_t)}\end{align*} $$

Finally,

$$ \begin{align*}\rho(\alpha) = \frac{1}{4\mu_{t}} \frac{1}{\cosh(\pi\alpha /2\mu_{t})}.\\[-40pt]\end{align*} $$

6.2.4 Convergence of $\xi _{t}^{(k)}$

Theorem 12. There exists a function $\boldsymbol {\xi }_{t,d} : \mathbb {R} \rightarrow \mathbb {R}$ such that $\xi _{t}^{(k)}$ converges uniformly on any compact towards $\boldsymbol {\xi }_{t,d}$ . Moreover, this function satisfies the following equation for all $\alpha $ :

$$ \begin{align*}\boldsymbol{\xi}^{\prime}_{t,d} (\alpha) = \frac{1}{2\pi} \kappa^{\prime}_{t} (\alpha) + \frac{1}{2\pi} \int_{\mathbb{R}} \frac{\partial \theta_{t}}{\partial \alpha} (\alpha,\beta) \boldsymbol{\xi}^{\prime}_{t,d} (\beta) \,d\beta,\end{align*} $$

and $\boldsymbol {\xi }_{t,d} (0) = d/2$ .

Proof. Consider any subsequence of $(\xi _{t}^{(k)})_{k}$ which converges uniformly on any compact of $\mathcal {I}_{\tau _{t}}$ to a function $\xi _{t}$ . Using the Cauchy formula, the derivative of $(\xi _{t}^{(k)})$ converges uniformly on any compact to $\xi ^{\prime }_{t}$ . Since the functions $\xi _{t}^{(k)}$ are uniformly bounded by a constant which is independent from k, and that for all k, $(\xi _{t}^{(k)})$ , $\xi ^{\prime }_{t}$ is positive and $\xi _{t}$ is bounded, and thus $\xi _{t}$ is in $L^{1}(\mathbb {R},\mathbb {R})$ . From Theorem 11, we get that $\xi ^{\prime }_{t}$ verifies a Fredholm equation, which has a unique solution in $L^{1} (\mathbb {R},\mathbb {R})$ [Proposition 9]. From Theorem 11, $\xi _{t}$ , as a function on $\mathbb {R}$ , is the unique primitive function of this one which has value $d/4$ on $0$ . Since this function is analytic, it determines its values on the whole stripe $\mathcal {I}_{\tau _{t}}$ . By virtue of Lemma 12, $(\xi _{t}^{(k)})_{k}$ converge towards this function.

Proposition 10. The limit of the function $\boldsymbol {\xi }_{t,d}$ in $+\infty $ is ${d}/{2}+\tfrac 14$ , and the limit in $-\infty $ is $d/2-1/4$ .

Proof. For all $\alpha $ ,

$$ \begin{align*}\boldsymbol{\xi}_{t,d} (\alpha) = \frac{d}{2} + \frac{1}{4 \mu_{t}} \int_{0}^{\alpha} \frac{1}{\cosh(\pi x /2\mu_{t})} \,dx = \frac{d}{2} + \frac{1}{2\pi} \int_{0}^{2\mu_{t} \alpha / \pi} \frac{1}{\cosh(x)} \,dx. \end{align*} $$

This converges in $+\infty $ to

$$ \begin{align*}\frac{d}{2} + \frac{1}{\pi} \int_{0}^{+\infty} \frac{e^{x}}{e^{2x}+1} \,dx &= \frac{d}{2} + \frac{1}{\pi} \int_{0}^{+\infty} (\operatorname{\mathrm{arc}}\!\tan (\exp))^{\prime}(x)\\ dx &= \frac{d}{2} + \frac{1}{2} - \frac{1}{\pi} \frac{\pi}{4} = \frac{d}{2} + \frac{1}{4}.\end{align*} $$

For the same reason, the limit in $-\infty $ is $d/2-1/4$ .

Remark 6. As a consequence, this limit is $>d$ when $d<1/2$ and equal to d when $d=1/2$ .

6.3 Condensation of Bethe roots relative to some functions

In this section, we prove that if f is a continuous function $(0,+\infty ) \rightarrow (0,+\infty )$ , decreasing and integrable, then the scaled sum of the values of f on the Bethe roots converges to an integral involving f and $\boldsymbol {\xi }_{t,d}$ [Theorem 13]. Let us set, for all $t,m$ and $M>0$ ,

and for two finite sets $S,T$ , we set $S \Delta T = S \backslash T \cup T \backslash S$ . For a compact set $K \subset \mathbb {R}$ , we denote by $\delta (K) \equiv \max _{x,y \in K} |x-y|$ its diameter. For I a bounded interval of $\mathbb {R}$ , we denote by $\mathit {l} (I)$ its length. When

$$ \begin{align*}J= \displaystyle{\bigcup_{j} I_{j}}\end{align*} $$

with $(I_{j})$ a sequence of bounded and disjoint intervals, the length of J is

$$ \begin{align*}\mathit{l} (J) = \sum_{j} \mathit{l} (I_{j}).\end{align*} $$

Theorem 13. Let $f: (0,+\infty ) \rightarrow (0,+\infty )$ be a continuous, decreasing and integrable function. Then,

$$ \begin{align*}\frac{1}{N_{k}} \sum_{j=\lceil n_{k} /2 \rceil+1}^{n_{k}} f(\boldsymbol{\alpha}^{(k)}_{j} (t)) \rightarrow \int_{0}^{\boldsymbol{\xi}_{t,d}^{-1} (d)} f(\alpha) \boldsymbol{\xi}^{\prime}_{t,d} (\alpha) \,d\alpha,\end{align*} $$

where we set $\boldsymbol {\xi }_{t,1/2}^{-1}(1/2) = +\infty $ .

Remark 7. This is another version of a statement proved in [K18] for bounded continuous and Lipschitz functions, which is not sufficient for the proof of Theorem 2.

Proof. In all the proof, the indexes j in the sums are in .

Setting: Let $\epsilon>0$ and $t \in (0,\sqrt {2})$ . Let us fix some M such that the following conditions are satisfied:

1. (1) for all k greater than some $k_{0}$ ,

   (33) $$ \begin{align}\frac{1}{N_{k}} |P_{t}^{(k)}(M)|\le \frac{\epsilon}{2\|f_{[M,+\infty)}\|_{\infty}+1}; \end{align} $$

2. (2) the following equation is satisfied:

   (34) $$ \begin{align}\bigg|\int_{[M,+\infty)} f(\alpha) \boldsymbol{\xi}^{\prime}_{t,d} (\alpha) \,d\alpha \bigg| \le \frac{\epsilon}{2}; \end{align} $$

3. (3) and if $d<1/2$ ,

   (35) $$ \begin{align} M>\boldsymbol{\xi}_{t,d}^{-1}(d), \end{align} $$
   which is possible to impose by virtue of Proposition 10.

Using the rarefaction of Bethe roots: We have the following, by definition:

(36) $$ \begin{align} \frac{1}{N_{k}} \sum_{j= \lceil n_{k} /2 \rceil+1}^{n_{k}} f(\boldsymbol{\alpha}^{(m)}_{j} (t)) & = \frac{1}{N_{k}} \sum_{j= \lceil n_{k} /2 \rceil+1}^{n_{k}} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg)\nonumber\\ & = \frac{1}{N_{k}} \sum_{j \notin P_{t}^{(k)}(M)} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) \nonumber\\ & \quad + \frac{1}{N_{k}} \sum_{j \in P_{t}^{(k)}(M)} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg). \end{align} $$

As a consequence of the inequality of equation (33) and then equation (34),

(37) $$ \begin{align} &\bigg| \frac{1}{N_{k}} \sum_{j=\lceil n_{k} /2 \rceil+1}^{n_{k}} f(\boldsymbol{\alpha}^{(k)}_{j}) - \frac{1}{N_{k}} \sum_{j \notin P_{t}^{(k)}(M)} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg)\bigg| \nonumber\\ & \quad \le \frac{1}{N_{k}}|P_{t}^{(k)}(M)|.\|f_{[M,+\infty)}\|_{\infty} \nonumber\\ & \quad \le \frac{\epsilon}{2\|f_{[M,+\infty)}\|_{\infty}+1} \|f_{[M,+\infty)}\|_{\infty}\nonumber\\ & \quad \le \frac{\epsilon}{2}, \end{align} $$

since by definition, if $j \in P_{t}^{(k)}(M)$ and $j \ge \lceil n_{k} /2 \rceil +1$ , then

$$ \begin{align*}(\xi_{t}^{(k)})^{-1} \bigg( \frac{j}{N_{k}}\bigg) \ge M.\end{align*} $$

On the asymptotic cardinality of ${(}{P}_{{t}}^{{(k)}}{(M)}{)}^{{c}} {\Delta } {(}{Q}_{{t}}^{{(k)}}{(M)}{)}^{{c}}$ :

$$ \begin{align*}\frac{1}{N_{k}} |(P_{t}^{(k)}(M))^{c} \Delta (Q_{t}^{(k)}(M))^{c}| \underset{k \rightarrow +\infty}{\rightarrow} 0.\end{align*} $$

Indeed, $(P_{t}^{(k)}(M))^{c} \Delta (Q_{t}^{(k)}(M))^{c}$ is equal to the set

thus its cardinality is smaller than

$$ \begin{align*}\delta ( N_{k} ( (\xi_{t} {}^{(k)} ([-M,M])) \Delta (\boldsymbol{\xi}_{t,d} ([-M,M]))) ) +1,\end{align*} $$

which is equal to

$$ \begin{align*}N_{k} \delta ( (\xi_{t} {}^{(k)} ([-M,M])) \Delta (\boldsymbol{\xi}_{t,d} ([-M,M])) )+1.\end{align*} $$

As a consequence,

$$ \begin{align*}\frac{1}{N_{k}} | (P_{t}^{(k)}(M))^{c} \Delta (Q_{t}^{(k)}(M))^{c}| \le \delta ( (\xi_{t} {}^{(k)} ([-M,M])) \Delta (\boldsymbol{\xi}_{t,d} ([-M,M])) ) + \frac{1}{N_{k}}.\end{align*} $$

Since $\xi _{t}^{(k)}$ converges to $\boldsymbol {\xi }_{t,d}$ on any compact, and in particular $[-M,M]$ , the diameter on the right of this inequality converges to $0$ when k tends towards $+\infty $ .

Replacing ${P}_{{t}}^{{(k)}}{(M)}$ by ${Q}_{{t}}^{{(k)}}{(M)}$ in the sums: Since f is decreasing and positive, for all ,

$$ \begin{align*}\frac{1}{N_{k}} \bigg| f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) \bigg| \le \int_{[({j-1})/{N_{k}},{j}/{N_{k}}]} f((\xi_{t}^{(k)})^{-1} (x) ) \,dx.\end{align*} $$

As a consequence, the difference

$$ \begin{align*}\frac{1}{N_{k}} \bigg| \sum_{j \notin P_{t}^{(k)}(M)} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) - \sum_{j \notin Q_{t}^{(k)}(M)} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) \bigg|\end{align*} $$

is smaller than

$$ \begin{align*}\int_{J_{k}} |f( (\xi_{t}^{(k)})^{-1}(x))| \,dx = \int_{\xi_{t}^{(k)} (I_{k})} f(x) (\xi_{t}^{(k)})^{\prime} (x) \,dx,\end{align*} $$

where $J_{k}$ is the union of the intervals

$$ \begin{align*} \bigg[\frac{j-1}{N_{k}}, \frac{j}{N_{k}}\bigg],\end{align*} $$

for $j \in (P_{t}^{(k)}(M))^{c} \Delta (Q_{t}^{(k)}(M))^{c}$ . We also used the fact that f is a positive function. Since the functions $\xi _{t}^{(k)}$ are uniformly bounded independently of k, there exists a constant $C_{t}>0$ such that for all k,

$$ \begin{align*}\int_{\xi_{t}^{(k)} (J_{k})} f(x) (\xi_{t}^{(k)})^{\prime} (x) \,dx \le C_{t} \int_{\xi_{t}^{(k)} (J_{k})} f(x) \,dx. \end{align*} $$

Since f is decreasing,

$$ \begin{align*}\int_{\xi_{t}^{(k)} (J_{k})} f(x) \le \int_{[0,\mathit{l}(\xi_{t}^{(k)} (J_{k}))]} f(x).\end{align*} $$

From the fact that $\xi _{t}^{(k)}$ is increasing,

$$ \begin{align*}\mathit{l} (\xi_{t}^{(k)} (J_{k})) = \int_{J_{k}} (\xi_{t}^{(k)})^{\prime}(\alpha) \,d\alpha.\end{align*} $$

Since the derivative of $\xi _{t}^{(k)}$ is bounded uniformly and independent of k, and that the length of $J_{k}$ is smaller than ${1}/{N_{k}} | (P_{t}^{(k)}(M))^{c} \Delta (Q_{t}^{(k)}(M))^{c}|$ ,

$$ \begin{align*}\mathit{l}(\xi_{t}^{(k)} (J_{k})) \rightarrow 0.\end{align*} $$

From the integrability of f on $(0,+\infty )$ ,

$$ \begin{align*}\int_{[0,\mathit{l}(\xi_{t}^{(k)} (J_{k}))]} f(x) \rightarrow 0.\end{align*} $$

As a consequence, there exists exists some $k_{1} \ge k_{0}$ such that for all $k \ge k_{1}$ ,

(38) $$ \begin{align} \frac{1}{N_{k}} \bigg| \sum_{j \notin P_{t}^{(k)}(M)} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) - \sum_{j \notin Q_{t}^{(k)}(M)} f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) \bigg| \le \frac{\epsilon}{4}. \end{align} $$

Approximating ${\xi }_{{t}}^{{(k)}}$ by ${\xi }_{{t,d}}$ in the sum:

1. (1) Bounding the contribution in a neighborhood of ${0}$ : With an argument similar to that used in the last point (bounding with integrals), there exists $\sigma>0$ smaller than M such that for all k,

   (39) $$ \begin{align} \frac{1}{N_{k}} \sum_{j \in (Q_{t}^{(k)} (\sigma))^{c} \cap (Q_{t}^{(k)}(M))^{c}} \bigg| f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) \bigg| \le \frac{\epsilon}{8}. \end{align} $$

2. (2) Using the convergence of ${\xi }_{{t}}^{{(k)}}$ on a compact away from ${0}$ : There exists some $k_{2} \ge k_{1}$ such that for all $k \ge k_{2}$ ,

   (40) $$ \begin{align}\frac{1}{N_{k}} \sum_{j \in Q_{t}^{(k)} (\sigma) \cap (Q_{t}^{(k)}(M))^{c}} \bigg| f\bigg((\xi_{t}^{(k)})^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) - f\bigg(\boldsymbol{\xi}_{t,d}^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) \bigg| \le \frac{\epsilon}{16}. \end{align} $$
   Indeed, for all the integers j in the sum, $\boldsymbol {\xi }_{t,d}^{-1}({j}/{N_{k}}) \in [\sigma ,M]$ , and by uniform convergence of $(\xi _{t}^{(k)})^{-1}$ on the compact $\boldsymbol {\xi }_{t,d} ([\sigma ,M])$ , for k great enough, the real numbers $(\xi _{t}^{(k)})^{-1} ({j}/{N_{k}})$ and $\boldsymbol {\xi }_{t,d}^{-1} ({j}/{N_{k}})$ for these integers k and these indexes j all lie in the same compact interval. Since f is continuous, there exists some $\eta>0$ such that whenever $x,y$ lie in this compact interval and $|x-y| \le \eta $ , then $|f(x)-f(y)|\le {\epsilon }/{8}$ . Since $(\xi _{t}^{(k)})^{-1}$ converges uniformly towards $\boldsymbol {\xi }_{t,d}^{-1}$ on the compact $\boldsymbol {\xi }_{t,d} ([\sigma ,M])$ , there exists some $k_{3} \ge k_{2}$ such that for all $k \ge k_{3}$ , and for all j such that $j \in Q_{t}^{(k)} (\sigma \sigma )$ and $j \notin Q_{t}^{(k)} (M)$ ,
   $$ \begin{align*}\bigg| (\xi_{t}^{(k)})^{-1} \bigg( \frac{j}{N_{k}}\bigg) - \boldsymbol{\xi}_{t,d}^{-1} \bigg( \frac{j}{N_{k}}\bigg)\bigg| \le \eta.\end{align*} $$
   As a consequence, we obtain the announced inequality.

Convergence of the remaining sum: The following sum is a Riemmann sum:

$$ \begin{align*}\frac{1}{N_{k}} \sum_{j \notin Q_{t}^{(k)}(M)} f\bigg(\boldsymbol{\xi}_{t,d}^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg).\end{align*} $$

Indeed,

Let us also remember that we imposed also that the indexes in the sums of the proof are all in . As a consequence, since $\boldsymbol {\xi }_{t,d}$ is increasing, the indexes are consecutive integers, from one that is at distance less than some constant from $N_{k} \boldsymbol {\xi }_{t,d} (0)$ and the last one is at distance less than this constant from $N_{k} \boldsymbol {\xi }_{t,d}(M)$ .

As a consequence, if $d=1/2$ , this sum converges towards

$$ \begin{align*}\int_{\boldsymbol{\xi}_{t,d} (0)}^{\boldsymbol{\xi}_{t,d}(M)} f (\boldsymbol{\xi}_{t,d}^{-1} (\alpha)) d \alpha= \int_{0}^{M} f (\alpha) \boldsymbol{\xi}^{\prime}_{t,d} (\alpha) \,d\alpha\end{align*} $$

by a change of variable. If $d<1/2$ , it converges towards

$$ \begin{align*}\int_{\boldsymbol{\xi}_{t,d} (0)}^{d} f (\boldsymbol{\xi}_{t,d}^{-1} (\alpha)) d \alpha= \int_{0}^{d} f (\alpha) \boldsymbol{\xi}^{\prime}_{t,d} (\alpha) \,d\alpha,\end{align*} $$

since in this case, M was chosen to satisfy the inequality in equation (35).

As a consequence, there exists some $k_{4} \ge k_{3}$ such that for all $ k \ge k_{4}$ , if $d=1/2$ ,

(41) $$ \begin{align} \bigg| \sum_{j \notin Q_{t}^{(k)}(M)} f\bigg(\boldsymbol{\xi}_{t,d}^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) - \int_{0}^{M} f (\alpha) \boldsymbol{\xi}^{\prime}_{t,d} (\alpha) \,d\alpha\bigg| \le \frac{\epsilon}{16}. \end{align} $$

If $d<1/2$ ,

(41)′ $$\begin{align} \bigg| \sum_{j \notin Q_{t}^{(k)}(M)} f\bigg(\boldsymbol{\xi}_{t,d}^{-1}\bigg(\frac{j}{N_{k}}\bigg)\bigg) - \int_{0}^{d} f (\alpha) \boldsymbol{\xi}^{\prime}_{t,d} (\alpha) \,d\alpha\bigg| \le \frac{\epsilon}{16}. \end{align}$$

Assembling the inequalities: Putting together equations 36–41, if $d=1/2$ (equation (41)^′ if $d<1/2$ ), we have for all $k \ge k_{4}$ ,

$$ \begin{align*}\bigg| \frac{1}{N_{k}} \sum_{j=\lceil n_{k} /2 \rceil+1}^{n_{k}} f(\boldsymbol{\alpha}_{j}^{(k)} (t))- \int_{0}^{\boldsymbol{\xi}^{-1}_{t} (d)} f (\alpha) \boldsymbol{\xi}^{\prime}_{t,d} (\alpha) \,d\alpha\bigg| \le \frac{\epsilon}{2} + \frac{\epsilon}{4} + \frac{\epsilon}{8} +\frac{\epsilon}{16} +\frac{\epsilon}{16} = \epsilon. \end{align*} $$

Since for all $\epsilon>0$ there exists such an integer $k_{4}$ , this proves the statement.

7 Computation of square ice entropy

$\triangleright $ Let us remember that the purpose of the paper is to compute the entropy of square ice, which is the entropy of the subshift $X_{s}$ . In §5, we have expressed the entropy of the stripes subshifts $\overline {X}_{N}^{s}$ as a sum involving Bethe roots. To compute $h(X^{s})$ , we can use the following formula:

$$ \begin{align*}h(X^{s}) = \lim_{N} \frac{h(\overline{X}_{N}^{s})}{N}.\end{align*} $$

In §6, we have dealt with the asymptotics of sums involving a positive decreasing integrable function and Bethe roots. We will thus combine the results of these two parts here.

Notation 17. For all $d \in [0,1/2]$ , we set

$$ \begin{align*}F(d) = - 2 \int_{0}^{\boldsymbol{\xi}_{t,d}^{-1} (d)} \log_{2} ( 2 |\sin(\kappa_{t} (\alpha)/2)|) \rho_{t} (\alpha)\,d\alpha.\end{align*} $$

Lemma 13. Let us consider $(N_{k})$ some sequence of integers, and $(n_{k})$ another sequence such that for all k, $2n_{k}+1 \le N_{k}/2 $ and $(2n_{k}+1)/ N_{k} \rightarrow d \in [0,1/2]$ . Then

$$ \begin{align*}\log_{2} (\lambda_{2n_{k}+1,N_{k}} (1)) \rightarrow F(d). \end{align*} $$

Proof. In this proof, for all k we set

$$ \begin{align*}({\kern1pt}\textbf{p}_{j}^{(k)})_{j} = (\kappa_{t} (\boldsymbol{\alpha}_{j}^{(k)}))_{j},\end{align*} $$

the solution of the system of Bethe equations $(E_{k})[1,2n_{k}+1,N_{k}]$ . Then for all k (we use first Theorem 6 and then Theorem 3),

$$ \begin{align*}\lambda_{2n_{k}+1,N_{k}} (1) = \Lambda_{2n_{k}+1,N_{k}} [{\kern1pt}\textbf{p}^{(k)}] = \bigg( 2 + (N_{k}-1) +\! \sum_{j \neq (n_{k}+1)} \frac{\partial \Theta_{1}}{\partial x} (0,\textbf{p}_{j}^{(k)})\bigg)\prod_{j=1}^{n_{k}} M_{1}(e^{i\textbf{p}_{j}^{(k)}}),\end{align*} $$

since by anti-symmetry of $\textbf {p}^{(k)}$ (Theorem 4), and that the length $2n_{k} +1$ of this tuple is odd, $\textbf {p}^{(k)}_{n_{k}+1}=0$ (the second case in Theorem 3 applies).

For all z such that $|z|=1$ ,

$$ \begin{align*}M_{1}(z) = \frac{z}{z-1}.\end{align*} $$

By anti-symmetry of the sequences $\textbf {p}^{(k)}$ , for all k,

$$ \begin{align*}\displaystyle{\prod_{j=1}^{n_{k}} e^{i\textbf{p}_{j}^{(k)}} = \prod_{j=1}^{n_{k}} e^{i\textbf{p}_{j}^{(k)}/2}= 1}.\end{align*} $$

As a consequence,

$$ \begin{align*} \Lambda_{2n_{k}+1,N_{k}} [{\kern1pt}\textbf{p}^{(k)}] & = \bigg( 2 + (N_{k}-1) + \sum_{j \neq (n_{k}+1)} \frac{\partial \Theta_{1}}{\partial x} (0,\textbf{p}_{j}^{(k)})\bigg) \prod_{j=1}^{n_{k}} \frac{1}{e^{i\textbf{p}_{j}^{(k)}}-1} \\ & = \bigg( 2 + (N_{k}-1) + \sum_{j \neq (n_{k}+1)} \frac{\partial \Theta_{1}}{\partial x} (0,\textbf{p}_{j}^{(k)}) \bigg) \prod_{j=1}^{n_{k}} \frac{e^{-i\textbf{p}_{j}^{(k)}/2}}{e^{i\textbf{p}_{j}^{(k)}/2}-e^{-i\textbf{p}_{j}^{(k)}/2}}. \end{align*} $$

Since this number is positive (by Perron–Frobenius theorem),

$$ \begin{align*}\Lambda_{2n_{k}+1,N_{k}} [{\kern1pt}\textbf{p}^{(k)}] &= |\Lambda_{2n_{k}+1,N_{k}} [{\kern1pt}\textbf{p}^{(k)}]|\\ &= \bigg|\,2 + (N_{k}-1) + \sum_{j \neq (n_{k}+1)} \frac{\partial \Theta_{1}}{\partial x} (0,\textbf{p}_{j}^{(k)}) \bigg|\prod_{j=1}^{n_{k}} \frac{1}{2|\sin{({\kern1pt}\textbf{p}_{j}^{(k)}/2)|}}.\end{align*} $$

As a consequence, since $\partial \Theta _{1} / \partial x$ is a bounded function,

$$ \begin{align*} \lim_{k} \log_{2} (\lambda_{2n_{k}+1,N_{k}} (1)) & = - \lim_{k} \bigg(\frac{1}{N_{k}} \sum_{j=1}^{n_{k}} \log_{2} (2|\sin{({\kern1pt}\textbf{p}_{j}^{(k)}/2)|)} + O\bigg( \frac{\log_{2} (N_{k})}{N_{k}}\bigg)\bigg) \\ & = - 2\lim_{k} \frac{1}{N_{k}} \sum_{j=\lceil n_{k} /2\rceil+1}^{n_{k}} \log_{2} (2|\sin{(\kappa_{t}(\boldsymbol{\alpha}_{k}^{(k)})/2)}|)\\ & = - 2\int_{0}^{\boldsymbol{\xi}^{-1}_{t,\textbf{d}} (\textbf{d})} \log_{2} (2|\sin(\kappa_{t} (\alpha)/2)|)\rho_{t}(\alpha)\,d\alpha\\ & = F(\textbf{d}), \end{align*} $$

where $\rho _{t} = \boldsymbol {\xi }^{\prime }_{t,d}$ , and we used the anti-symmetry of the Bethe roots vectors in the second equality. For the other equalities, they are a consequence of Theorem 13, since the function defined as $\alpha \mapsto -\log _{2} (2|\sin (\kappa _{t} (\alpha )/2)|)$ on $(0,+\infty )$ is continuous, integrable, decreasing and positive:

1. (1) Positive: For all $\alpha>0$ , $\kappa _{t} (\alpha )$ is in

   $$ \begin{align*}(0,\pi-\mu_{t}) = \bigg(0, \frac{\pi}{3} \bigg).\end{align*} $$
   As a consequence, $2\sin (\kappa _{t} (\alpha )/2)$ is in $(0,1)$ , and this implies that for all $\alpha>0$ ,
   $$ \begin{align*}-\log_2 (2|\sin(\kappa_t (\alpha)/2)|)> 0.\end{align*} $$

2. (2) Decreasing: This comes from the fact that $-\log _{2}$ is decreasing, and $\kappa _{t}$ is increasing, and the sine is increasing on $(0,\pi /6)$ .

3. (3) Integrable: Since $\kappa _{t} (0) = 0$ and $\kappa ^{\prime }_{t}(0)>0$ , for $\alpha $ positive sufficiently close to $0$ , $2\sin (\kappa _{t} (\alpha )/2) \le 2\kappa ^{\prime }_{t} (0) \alpha $ . As a consequence,

   $$ \begin{align*}-\log_2 (2|\sin(\kappa_t (\alpha)/2)|) \le - \log_2 ( 2 \kappa'_t (0) \alpha).\end{align*} $$
   Since the logarithm is integrable on any bounded neighborhood of $0$ , the function $\alpha \mapsto -\log _{2} (2|\sin (\kappa _{t} (\alpha )/2)|) $ is integrable.

The other limit is obtained by anti-symmetry of $\kappa _{t}$ .

Theorem 1. The entropy of square ice is

$$ \begin{align*}h(X^{s}) = \tfrac{3}{2} \log_{2} \big( \tfrac{4}{3} \big).\end{align*} $$

Remark 8. This value corresponds to $\log _{2} (W)$ in [L67].

Proof. Here we fix $t=1 \in (0,\sqrt {2})$ . As a consequence, $\mu _{t} = 2\pi /3$ .

Entropy of ${X}^{{s}}$ and asymptotics of the maximal eigenvalue: Let us recall that the entropy of $X^{s}$ is given by

$$ \begin{align*}h(X^{s}) = \lim_{N} \frac{1}{N} \max_{2n+1 \le N/2} \log_{2}(\lambda_{2n+1,N}(1)).\end{align*} $$

For all N, we denote by $\nu (N)$ the smallest j such that $2j+1 \le N/2$ and that for all n with $2n+1 \le N/2$ ,

$$ \begin{align*}\lambda_{2j+1,N}(1) \ge \lambda_{2n+1,N}(1).\end{align*} $$

By compactness, there exists an increasing sequence $(N_{k})$ such that $(2\nu (N_{k})+1)/N_{k}$ converges towards some non-negative real number $\textbf {d}$ . Since for all k, $2\nu (N_{k})+1 \le N_{k}/2$ , then $\textit {d} \le 1/2$ . By virtue of Lemma 13, $h(X^{s}) = F(\textbf {d})$ .

Comparison with the asymptotics of other eigenvalues: Moreover, if d is another number in $[0,1/2]$ , there exists $\nu ^{\prime } : \mathbb {N} \rightarrow \mathbb {N}$ such that

$$ \begin{align*}(2\nu^{\prime}(N)+1) / N \rightarrow d.\end{align*} $$

For all k,

$$ \begin{align*}\lambda_{2\nu^{\prime}(N_{k})+1,N_{k}} (1) \le \lambda_{2\nu(N_{k})+1,N_{k}} (1).\end{align*} $$

Also by virtue of Lemma 13, $h(X^{s}) \ge F(d)$ , and thus

$$ \begin{align*}F(\textbf{d}) = \max_{d \in [0,1/2]} F(d).\end{align*} $$

This maximum is realized only for $d=1/2$ . As a consequence $\textit {d}=1/2$ .

Rewritings: As a consequence,

$$ \begin{align*}h(X^{s}) = - 2 \int_{0}^{+\infty} \log_{2} (2|\sin(\kappa_{t} (\alpha) /2 |) \rho_{t} (\alpha) \,d\alpha.\end{align*} $$

Let us rewrite this expression of $h(X^{s})$ using

$$ \begin{align*}|\!\sin(x/2)| = \sqrt{\frac{1-\cos(x)}{2}}.\end{align*} $$

This leads to

$$ \begin{align*}h(X^{s}) = - \frac{\log_{2}(2)}{2} \int_{-\infty}^{+\infty} \rho_{t} (\alpha)\,d\alpha - \frac{1}{2} \int_{-\infty}^{+\infty} \log_{2} (1-\cos(\kappa_{t} (\alpha))).\rho_{t} (\alpha)\,d\alpha.\end{align*} $$

Thus,

$$ \begin{align*}h(X^{s}) = -\frac{1}{2}\int_{-\infty}^{+\infty} \log_{2} (2-2\cos(\kappa_{t}(\alpha))). \rho_{t} (\alpha)\,d\alpha.\end{align*} $$

Let us recall that for all $\alpha $ ,

$$ \begin{align*}\rho(\alpha) = \frac{1}{4\mu_{t} \cosh(\pi\alpha/2\mu_{t})} = \frac{3}{8 \pi \cosh(3\alpha/4)} \end{align*} $$

$$ \begin{align*}\cos(\kappa_{t} (\alpha))= \frac{\sin^{2}(\mu_{t})}{\cosh(\alpha)-\cos(\mu_{t})} - \cos(\mu_{t}) = \frac{3}{4(\cosh(\alpha)+1/2)} + \frac{1}{2}.\end{align*} $$

We thus have that

$$ \begin{align*}h(X^{s}) = -\frac{3}{16\pi} \int_{-\infty}^{+\infty} \log_{2} \bigg(1-\frac{3}{2\cosh(\alpha)+1}\bigg) \frac{1}{\cosh(3\alpha/4)}\,d\alpha.\end{align*} $$

Using the variable change $e^{\alpha } = x^{4}$ , $d\alpha .x = 4\,dx$ ,

$$ \begin{align*}h(X^{s}) = -\frac{3}{16\pi} \int_{0}^{+\infty} \log_{2} \bigg(1-\frac{3}{x^{4}+1/x^{4}+1}\bigg) \frac{2}{(x^{3} + 1/x^{3})}\frac{4}{x} \,dx.\end{align*} $$

By symmetry of the integrand,

$$ \begin{align*}h(X^{s}) = -\frac{3}{4\pi} \int_{-\infty}^{+\infty} \frac{x^{2}\,dx}{x^{6}+1} \log_{2} \bigg( \frac{(2x^{4} - 1-x^{8}) }{1+x^{4}+x^{8}}\bigg)\,dx\end{align*} $$

$$ \begin{align*}h(X^{s}) = -\frac{3}{4\pi} \int_{-\infty}^{+\infty} \frac{x^{2}\,dx}{x^{6}+1} \log_{2} \bigg( \frac{(x^{2}-1)^{2} (x^{2}+1)^{2}}{1+x^{4}+x^{8}}\bigg)\,dx.\end{align*} $$

Application of the residues theorem: In the following, we use the standard determination of the logarithm on $\mathbb {C} \backslash \mathbb {R}_{-}$ .

We apply the residue theorem to obtain (the poles of the integrand are $e^{i\pi /6}, e^{i\pi /2}, e^{i5\pi /6})$

$$ \begin{align*}\int_{-\infty}^{+\infty} \frac{x^{2}\log_{2} (x+i)}{x^{6}+1} \,dx= 2\pi i \bigg(\sum_{k=1,3,5} \frac{e^{ik\pi/3} \log_{2} (e^{ik\pi/6}+i)}{6 e^{i5k\pi/6}}\bigg),\end{align*} $$

$$ \begin{align*}\int_{-\infty}^{+\infty} \frac{x^{2}\log_{2} (x-i)}{x^{6}+1} \,dx = - 2\pi i \bigg(\sum_{k=7,9,11} \frac{e^{ik\pi/3} \log_{2} (e^{ik\pi/6}-i)}{6 e^{i5k\pi/6}}\bigg).\end{align*} $$

By summing these two equations, we obtain that $\int _{-\infty }^{+\infty } ({x^{2} \log _{2} (x^{2}+1)}/({x^{6}+1})) \,dx$ is equal to

$$ \begin{align*} \dfrac{\pi}{3} [\log_{2} (e^{i\pi/6}+i) &- \log_{2} (e^{i\pi/2}+i) + \log_{2} (e^{i5\pi/6}+i) \\[3pt] &+\log_{2} (e^{i7\pi/6} -i) - \log_{2} (e^{i9\pi/6} -i)+\log_{2} (e^{i11\pi/6} -i)].\end{align*} $$

This is equal to

$$ \begin{align*}\frac{\pi}{3} (\log_{2} (|e^{i\pi/6}+i|^{2}))-\log_{2} (|e^{i\pi/2}+i|) + \log_{2} (|e^{i5\pi/6}+i|^{2}) = \frac{2\pi}{3}\log_{2}\bigg(\frac{3}{2}\bigg).\end{align*} $$

Other computations: We do not include the following computation, since it is very similar to the previous one:

$$ \begin{align*}\int_{-\infty}^{+\infty} \frac{x^{2}}{x^{6}+1} \log_{2} (1+x^{4}x^{8})\,dx = \frac{2\pi}{3} \log_{2} \bigg( \frac{8}{3}\bigg).\end{align*} $$

For the last integral, we write $\log _{2} ((x^{2}-1)^{2}) = 2 \text {Re}(\log _{2} (x-1)+\log _{2} (x+1))$ and obtain

$$ \begin{align*} \int_{-\infty}^{+\infty} \frac{x^{2}}{x^{6}+1} \log_{2} ((x^{2}-1)^{2}) & = \text{Re}\bigg( \int_{-\infty}^{+\infty} \frac{x^{2}}{x^{6}+1} \log_{2} (x-1)\\[6pt] &\quad+ \int_{-\infty}^{+\infty} \frac{x^{2}}{x^{6}+1} \log_{2} (x+1)\bigg) \\[6pt] & = \frac{2\pi}{3} \log_{2} \bigg(\frac{1}{2}\bigg).\end{align*} $$

Summing these integrals: As a consequence,

$$ \begin{align*}h(X^{s}) &=-\frac{3}{4\pi} \frac{2\pi}{3} \bigg(\log_{2} \bigg(\frac{1}{2}\bigg)+ 2 \log_{2} \bigg(\frac{3}{2}\bigg)- \log_{2} \bigg(\frac{8}{3}\bigg)\bigg)\\[3pt] &=\frac{1}{2}\log_{2} \bigg(\frac{4^{3}}{3^{3}}\bigg)= \frac{3}{2} \log_{2} \bigg( \frac{4}{3} \bigg).\\[-36pt]\end{align*} $$

8 Comments

This text is meant as a basis for further research that would aim at extending the computation method that we exposed to a broader set of multidimensional SFT, including, for instance, Kari–Culik tilings [C96], the monomer–dimer model [see, for instance, [FP05]], subshifts of square ice [GS17], the hard square shift [P12] or a three-dimensional version of the six-vertex model. Adaptations for these models may be possible, but would not be immediate at all. We explain here at which points the method has limitations, each of them coinciding with a specific property of square ice.

Let us recall that we called the Lieb path an analytic function of transfer matrices $t \mapsto V_{N} (t)$ such that for all t, $V_{N} (t)$ is an irreducible non-negative and symmetric matrix on $\Omega _{N}$ . Although the definition of transfer matrices admits straightforward generalization to multidimensional SFT and their non-negativity does not seem difficult to achieve, the property of symmetry of the matrices $V_{N} (t)$ relies on symmetries of the alphabet and local rules of the SFT. Friedland [F97] proved that under these symmetry constraints (which are verified, for instance, by the monomer–dimer and hard square models, but a priori not by Kari–Culik tilings), entropy is algorithmically computable, through a generalization of the gluing argument exposed in Lemma 1. Outside of the class of SFT defined by these symmetry restrictions, as far as we know, only strong mixing or measure theoretic conditions ensure algorithmic computability of entropy, leading, for instance, to relatively efficient algorithms approximating the hard square shift entropy [P12]. However, the irreducibility of the matrices $V_{N} (t)$ derives from the irreducibility property of the stripes subshifts $X^{s}_{N}$ [Definition 2], that can be derived from the linear block gluing property of $X^{s}$ [GS17]. This property consists in the possibility for any pair of patterns on $\mathbb {U}^{(2)}_{N}$ to be glued in any relative positions, provided that the distance between the two patterns is greater than a minimal distance, which is $O(N)$ .

Furthermore, Lemma 1, which relies on a horizontal symmetry of the model, is a simplification in the proof of Theorem 2, whose implication is that the entropy of $X^{s}$ can be computed through entropies of subshifts $\overline {X}^{s}_{N}$ , and thus simplifies the algebraic Bethe ansatz, that we will expose in another text. One can see in [VL19] that it is possible to use the ansatz without Lemma 1. However, this application of the ansatz would lead to different Bethe equations, and it is not clear if these equations admit solutions, and if we can evaluate their asymptotic behavior. The symmetry is also involved in the equality of the entropy of $\overline {X}^{s}_{n,N}$ and the entropy of $\overline {X}^{s}_{N-n,N}$ . Without this equality, we do not know how to identify the greatest eigenvalue of $V_{N} (t)$ with the candidate eigenvalue obtained via the ansatz.