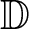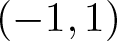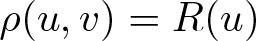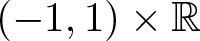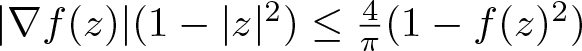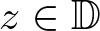1. Introduction
1.1. Schwarz lemma
The standard Schwarz lemma states that if f is a holomorphic mapping of the unit disk ![]() $\mathbb{D}$ into itself such that
$\mathbb{D}$ into itself such that ![]() $f(0)=0$, then
$f(0)=0$, then ![]() $|f(z)|\le |z|$.
$|f(z)|\le |z|$.
Its counterpart for harmonic mappings states the following ([Reference Duren8, Section 4.6]). Let f be a complex-valued function harmonic in the unit disk ![]() $\mathbb{D}$ into itself, with
$\mathbb{D}$ into itself, with ![]() $f (0) = 0$. Then
$f (0) = 0$. Then
 \begin{equation*}| f (z)| \le \frac{4}{\pi}\tan^{-1} |z|,\end{equation*}
\begin{equation*}| f (z)| \le \frac{4}{\pi}\tan^{-1} |z|,\end{equation*}and this inequality is sharp for each point ![]() $z \in \mathbb{D}$. Furthermore, the bound is sharp everywhere (but is attained only at the origin) for univalent harmonic mappings f of
$z \in \mathbb{D}$. Furthermore, the bound is sharp everywhere (but is attained only at the origin) for univalent harmonic mappings f of ![]() $\mathbb{D}$ onto itself with
$\mathbb{D}$ onto itself with ![]() $f (0) = 0.$
$f (0) = 0.$
The standard Schwarz lemma (also called Schwarz–Pick lemma) for holomorphic mappings states that every holomorphic mapping f of the unit disk onto itself satisfies the inequality
 \begin{equation}
|f^\prime(z)|\le \frac{1-|f(z)|^2}{1-|z|^2}.
\end{equation}
\begin{equation}
|f^\prime(z)|\le \frac{1-|f(z)|^2}{1-|z|^2}.
\end{equation} A very important version of the Schwarz lemma for holomorphic functions has been obtained by Ahlfors [Reference Ahlfors1], who proved the following: Let f be a holomorphic map of the unit disk ![]() $\mathbb{D}$ into a Riemann surface S endowed with a Riemannian metric ρ with Gaussian curvature
$\mathbb{D}$ into a Riemann surface S endowed with a Riemannian metric ρ with Gaussian curvature ![]() $\mathcal{K} \le -1$. Then the hyperbolic length of any curve in
$\mathcal{K} \le -1$. Then the hyperbolic length of any curve in ![]() $\mathbb{D}$ is no less than the length of its image. Equivalently,
$\mathbb{D}$ is no less than the length of its image. Equivalently,
or ![]() $ \|df(z)\|\le 1$ everywhere, where the norms are taken with respect to the hyperbolic metric on
$ \|df(z)\|\le 1$ everywhere, where the norms are taken with respect to the hyperbolic metric on ![]() $\mathbb{D}$ and the given metric on the image. For some other generalizations of the Schwarz lemma, we refer to the papers of Yau [Reference Yau23, Reference Yau24], Osserman [Reference Osserman20], Yang and Zheng [Reference Yang and Zheng22], Royden [Reference Royden21], Ni [Reference Ni18, Reference Ni19] and Broder [Reference Broder4]. The recent survey by Broder [Reference Broder3] also provides references to the Schwarz lemma in other contexts. Most of mentioned papers deal with Schwarz lemma for holomorphic functions, and the target space has a non-positive curvature.
$\mathbb{D}$ and the given metric on the image. For some other generalizations of the Schwarz lemma, we refer to the papers of Yau [Reference Yau23, Reference Yau24], Osserman [Reference Osserman20], Yang and Zheng [Reference Yang and Zheng22], Royden [Reference Royden21], Ni [Reference Ni18, Reference Ni19] and Broder [Reference Broder4]. The recent survey by Broder [Reference Broder3] also provides references to the Schwarz lemma in other contexts. Most of mentioned papers deal with Schwarz lemma for holomorphic functions, and the target space has a non-positive curvature.
We refer as well to some generalizations of Schwarz lemma for harmonic functions in the papers [Reference Burgeth5, Reference Colonna7, Reference Forstneric and Kalaj9, Reference Kalaj12–Reference Melentijevic17].
In particular, the following result was proved in [Reference Kalaj and Vuorinen13]. If ![]() $f\colon\mathbb{D}\to (-1,1)$ is a real harmonic mapping, then it satisfies the inequality
$f\colon\mathbb{D}\to (-1,1)$ is a real harmonic mapping, then it satisfies the inequality
 \begin{equation*}|\nabla f(z)|\le \frac{4}{\pi}\frac{1-f(z)^2}{1-|z|^2}\quad \text{for all}\ z\in\mathbb{D}.\end{equation*}
\begin{equation*}|\nabla f(z)|\le \frac{4}{\pi}\frac{1-f(z)^2}{1-|z|^2}\quad \text{for all}\ z\in\mathbb{D}.\end{equation*}Later, by using the same approach as that in [Reference Kalaj and Vuorinen13], Chen [Reference Chen6] improved the latter inequality by showing that
 \begin{equation*}|\nabla f(z)|\le \frac{\cos(\frac{\pi}{2}f(z))}{1-|z|^2}\quad \text{for all}\ z\in\mathbb{D}.\end{equation*}
\begin{equation*}|\nabla f(z)|\le \frac{\cos(\frac{\pi}{2}f(z))}{1-|z|^2}\quad \text{for all}\ z\in\mathbb{D}.\end{equation*}In order to state our main result, let us introduce the class of ϱ-harmonic mappings.
1.2. ϱ-Harmonic mappings
Assume that Ω is a connected open set in the complex plane. Assume that ϱ is a positive continuous function in Ω. Then (by abusing the notation), it defines a conformal metric ![]() $\varrho(z)= \varrho(z) \,{\rm d}z\otimes \overline{{\rm d}z}$ in Ω. Then ϱ defines a Riemann surface
$\varrho(z)= \varrho(z) \,{\rm d}z\otimes \overline{{\rm d}z}$ in Ω. Then ϱ defines a Riemann surface ![]() $(\Omega, \varrho)$. Moreover, assume that ϱ is a smooth function in Ω with Gaussian curvature
$(\Omega, \varrho)$. Moreover, assume that ϱ is a smooth function in Ω with Gaussian curvature ![]() $\mathcal{K}_\varrho$, where
$\mathcal{K}_\varrho$, where
 \begin{equation}
\mathcal{K}_\varrho(z):=-\frac{\Delta \log \varrho(z)}{\varrho^2(z)}.\end{equation}
\begin{equation}
\mathcal{K}_\varrho(z):=-\frac{\Delta \log \varrho(z)}{\varrho^2(z)}.\end{equation}Here Δ denote the usual Laplacian:
We assume ![]() $\sup_{z\in \Omega} |\mathcal{K}_\varrho(z)| \lt \infty$ and ϱ has a finite area defined by
$\sup_{z\in \Omega} |\mathcal{K}_\varrho(z)| \lt \infty$ and ϱ has a finite area defined by
 \begin{equation*}\mathcal{A}(\varrho)=\int_{\Omega}\varrho^2(u+{\rm i}v)\, {\rm d}u\, {\rm d}v.\end{equation*}
\begin{equation*}\mathcal{A}(\varrho)=\int_{\Omega}\varrho^2(u+{\rm i}v)\, {\rm d}u\, {\rm d}v.\end{equation*} Let ![]() $f : (D, \delta) \to (\Omega, \varrho)$ be a
$f : (D, \delta) \to (\Omega, \varrho)$ be a ![]() $\mathcal{C}^2$ map of two Riemann surfaces, where δ is the (pullback to D via the inclusion of the) Euclidean metric. We say that f is harmonic if
$\mathcal{C}^2$ map of two Riemann surfaces, where δ is the (pullback to D via the inclusion of the) Euclidean metric. We say that f is harmonic if
 \begin{equation}
f_{z\overline z}+({(\log \varrho^2)}_w\circ f) \cdot f_z\,f_{\bar z}=0,
\end{equation}
\begin{equation}
f_{z\overline z}+({(\log \varrho^2)}_w\circ f) \cdot f_z\,f_{\bar z}=0,
\end{equation}where z and w are holomorphic coordinates on D and Ω, respectively. Recall that a Euclidean harmonic function f is a solution of the Laplace equation ![]() $\Delta f=0$, and in this case
$\Delta f=0$, and in this case ![]() $\varrho\equiv 1$. Also, f satisfies Equation (1.3) if and only if its Hopf differential
$\varrho\equiv 1$. Also, f satisfies Equation (1.3) if and only if its Hopf differential
is a holomorphic quadratic differential on D.
Assume ![]() $f : \mathbb{D} \to (-1, 1)$ is a real ρ-harmonic function. Vuorinen and the first named author in [Reference Kalaj and Vuorinen13] introduced the quantity
$f : \mathbb{D} \to (-1, 1)$ is a real ρ-harmonic function. Vuorinen and the first named author in [Reference Kalaj and Vuorinen13] introduced the quantity
 \begin{equation}
S(f):=|\nabla f(z)| \frac{1-|z|^2}{1-|f(z)|^2}\end{equation}
\begin{equation}
S(f):=|\nabla f(z)| \frac{1-|z|^2}{1-|f(z)|^2}\end{equation}and showed that  $S(f) \le \frac{4}{\pi}$ for Euclidean harmonic functions. In order to extend the results in [Reference Kalaj and Vuorinen13], the first named author in [Reference Kalaj11] defined the class of admissible metrics. We say that a metric ϱ is admissible if
$S(f) \le \frac{4}{\pi}$ for Euclidean harmonic functions. In order to extend the results in [Reference Kalaj and Vuorinen13], the first named author in [Reference Kalaj11] defined the class of admissible metrics. We say that a metric ϱ is admissible if ![]() $\varrho(z)=\varphi(|z|)$, where
$\varrho(z)=\varphi(|z|)$, where ![]() $\varphi: \mathbb{D} \to \mathbb{C}\setminus (-\infty,0]$ is an analytic function defined in the unit disk satisfying the following properties:
$\varphi: \mathbb{D} \to \mathbb{C}\setminus (-\infty,0]$ is an analytic function defined in the unit disk satisfying the following properties:
(1)
 $\varphi(|z|) \le |\varphi(z)|$ and φ is nonincreasing in
$\varphi(|z|) \le |\varphi(z)|$ and φ is nonincreasing in  $[0, 1]$,
$[0, 1]$,(2)
 $\varphi(-1,1)\subset \mathbb{R}$ and
$\varphi(-1,1)\subset \mathbb{R}$ and  $\int_0^1(\sqrt{\varphi(x)}-\sqrt{\varphi(-x)})\, {\rm d}x=0$.
$\int_0^1(\sqrt{\varphi(x)}-\sqrt{\varphi(-x)})\, {\rm d}x=0$.
Then inequality (1.5) was extended by the first named author [Reference Kalaj11] to ϱ-harmonic functions, where ϱ is an admissible metric. The following question was posed in [Reference Kalaj11].
Problem 1.1.
Let ![]() $f : \mathbb{D}\to (-1, 1)$ be a real ϱ-harmonic function. Suppose ϱ has non-negative Gaussian curvature. Does the bound S
$f : \mathbb{D}\to (-1, 1)$ be a real ϱ-harmonic function. Suppose ϱ has non-negative Gaussian curvature. Does the bound S $(f) \le\frac{4}{\pi}$ hold?
$(f) \le\frac{4}{\pi}$ hold?
Remark 1.2. The assumption that the target domain has a non-negative Gaussian curvature is crucial, and this is shown in Example 2.3. This problem is somehow complementary to the already mentioned Scharz lemma-type result of Ahlfors for holomorphic functions of the unit disk onto a surface with a non-positive Gaussian curvature.
We will see in Example 3.1 that the answer to the question posed in Problem 1.1 is no. However, it will be shown in this paper that a real ϱ-harmonic function is also harmonic with respect to the modified metric ![]() $\rho(u,v)=\varrho(u,0)$, and the positiveness of the Gaussian curvature of ρ will be crucial.
$\rho(u,v)=\varrho(u,0)$, and the positiveness of the Gaussian curvature of ρ will be crucial.
Indeed, we shall prove the following theorem, which is the main content of this paper.
Theorem 1.3. Assume that f is a real ϱ-harmonic function of the unit disk onto the interval ![]() $(-1,1)$. If
$(-1,1)$. If ![]() $\rho(u,v)=\varrho(u,0)$, then f is ρ-harmonic. Assume further that the Gaussian curvature of ρ is non-negative. Then we have the sharp inequality
$\rho(u,v)=\varrho(u,0)$, then f is ρ-harmonic. Assume further that the Gaussian curvature of ρ is non-negative. Then we have the sharp inequality
 \begin{equation}S\left( f \right) = \left| {\nabla f\left( z \right)} \right|\frac{{1 - |z{|^2}}}{{1 - |f\left( z \right){|^2}}} \leqslant \frac{4}{\pi }{\text{ for all }}z \in \mathbb{D}.\end{equation}
\begin{equation}S\left( f \right) = \left| {\nabla f\left( z \right)} \right|\frac{{1 - |z{|^2}}}{{1 - |f\left( z \right){|^2}}} \leqslant \frac{4}{\pi }{\text{ for all }}z \in \mathbb{D}.\end{equation}Corollary 1.4. Assume that Ω is a hyperbolic domain in the complex plane, and let ![]() $\lambda=\lambda_\Omega$ be its hyperbolic metric of constant Gaussian curvature equal to −4. Let
$\lambda=\lambda_\Omega$ be its hyperbolic metric of constant Gaussian curvature equal to −4. Let ![]() $f:\Omega\to (-1,1)$ be a ρ-harmonic function, where
$f:\Omega\to (-1,1)$ be a ρ-harmonic function, where ![]() $\rho(u,v)=R(u)$ has a non-negative Gaussian curvature. Then we have the following sharp inequality:
$\rho(u,v)=R(u)$ has a non-negative Gaussian curvature. Then we have the following sharp inequality:
 \begin{equation}
d_h(f(z),f(w))\le \frac{4}{\pi}d_\lambda(z,w){\text{ for all }} z,w\in\Omega.
\end{equation}
\begin{equation}
d_h(f(z),f(w))\le \frac{4}{\pi}d_\lambda(z,w){\text{ for all }} z,w\in\Omega.
\end{equation}Here dh is the hyperbolic metric in the unit disk defined by
 \begin{equation*}d_h(z,w) =\tanh^{-1}\frac{|z-w|}{|1-z\bar w|}.\end{equation*}
\begin{equation*}d_h(z,w) =\tanh^{-1}\frac{|z-w|}{|1-z\bar w|}.\end{equation*} The proof of the first part of Theorem 1.3 is an easy matter, and it is presented in ![]() $\S$ 1.3, while the second part is the content of Theorem 2.1. Corollary 1.4 is a straightforward application of the definition of the hyperbolic metric. We only need to notice the following. If
$\S$ 1.3, while the second part is the content of Theorem 2.1. Corollary 1.4 is a straightforward application of the definition of the hyperbolic metric. We only need to notice the following. If ![]() $g\colon \mathbb{D}\to \Omega$ is a covering map, then
$g\colon \mathbb{D}\to \Omega$ is a covering map, then ![]() $h(z) = f(g(z))$ is a real ρ-harmonic mapping of the unit disk onto
$h(z) = f(g(z))$ is a real ρ-harmonic mapping of the unit disk onto ![]() $(-1,1)$. Moreover,
$(-1,1)$. Moreover,
So, for ![]() $w=g(z)$, in view of Equation (1.6), we have
$w=g(z)$, in view of Equation (1.6), we have
 \begin{equation*}\frac{|\nabla f(w)|}{\lambda_\Omega(w)}={|\nabla h(z)|}(1-|z|^2)\le \frac{4}{\pi}(1-h(z)^2)=\frac{4}{\pi}{(1-|f(w)|^2)}.\end{equation*}
\begin{equation*}\frac{|\nabla f(w)|}{\lambda_\Omega(w)}={|\nabla h(z)|}(1-|z|^2)\le \frac{4}{\pi}(1-h(z)^2)=\frac{4}{\pi}{(1-|f(w)|^2)}.\end{equation*}Thus,
 \begin{equation*}\frac{|\nabla f(w)|}{(1-|f(w)|^2)}\le\frac{4}{\pi}\lambda_\Omega(w).\end{equation*}
\begin{equation*}\frac{|\nabla f(w)|}{(1-|f(w)|^2)}\le\frac{4}{\pi}\lambda_\Omega(w).\end{equation*}By integrating the previous inequality throughout the family of paths joining z 1 and z 2 (as at the end of the proof of Theorem 2.1), we get
 \begin{equation}
d_h(f(z_1),f(z_2))\le \frac{4}{\pi}d_\lambda(z_1,z_2)\quad \text{for all } z_1,z_2\in\Omega.
\end{equation}
\begin{equation}
d_h(f(z_1),f(z_2))\le \frac{4}{\pi}d_\lambda(z_1,z_2)\quad \text{for all } z_1,z_2\in\Omega.
\end{equation}1.3. Real ϱ-harmonic mappings and our setting (real R-harmonic mappings)
If f is real, then Equation (1.3) can be re-stated as follows:
 \begin{equation}
\Delta f +\frac{\varrho_u(f(z),0)-{\rm i} \varrho_v(f(z),0)}{\varrho(f(z),0)}(f_x^2+f_y^2)=0.\end{equation}
\begin{equation}
\Delta f +\frac{\varrho_u(f(z),0)-{\rm i} \varrho_v(f(z),0)}{\varrho(f(z),0)}(f_x^2+f_y^2)=0.\end{equation} In particular, we see that ![]() $\varrho_v(u,0)\equiv 0$ or f is a constant function.
$\varrho_v(u,0)\equiv 0$ or f is a constant function.
Let ![]() $R(u) = \varrho(u,0)$. If f is a real harmonic function of the unit disk onto the interval
$R(u) = \varrho(u,0)$. If f is a real harmonic function of the unit disk onto the interval ![]() $(\alpha,\beta)$, then
$(\alpha,\beta)$, then
 \begin{equation}
\Delta f +\frac{R^\prime(f)}{R(f)}(|\nabla f|^2) =0,\end{equation}
\begin{equation}
\Delta f +\frac{R^\prime(f)}{R(f)}(|\nabla f|^2) =0,\end{equation}where R is a metric defined in the interval ![]() $(\alpha,\beta)$. Observe that R can be extended to the infinite strip-domain
$(\alpha,\beta)$. Observe that R can be extended to the infinite strip-domain ![]() $S(\alpha, \beta):=\{x+{\rm i} y, x\in (\alpha,\beta), y\in\mathbb{R}\}$ by setting
$S(\alpha, \beta):=\{x+{\rm i} y, x\in (\alpha,\beta), y\in\mathbb{R}\}$ by setting ![]() $\rho(u,v)=R(u)=\varrho(u,0)$.
$\rho(u,v)=R(u)=\varrho(u,0)$.
Moreover, we have this important fact: f is real ϱ-harmonic if and only if f is real ρ-harmonic. This is why we will consider the Gaussian curvature of ρ instead of ϱ. We will refer to such real harmonic mappings as real R-harmonic mappings.
The Gaussian curvature of ρ is given by
 \begin{equation}
\mathcal{K}_\rho(u,v) = -\frac{1}{R(u)^2}\left(\frac{R^\prime(u)}{R(u)}\right)^\prime.\end{equation}
\begin{equation}
\mathcal{K}_\rho(u,v) = -\frac{1}{R(u)^2}\left(\frac{R^\prime(u)}{R(u)}\right)^\prime.\end{equation}In fact, Equation (1.10) is equivalent to the Laplace equation
where
 \begin{equation}
g:=\frac{H(f)}{H(1)}:{\mathbb{D}}\to (-1,1),\end{equation}
\begin{equation}
g:=\frac{H(f)}{H(1)}:{\mathbb{D}}\to (-1,1),\end{equation}while
 \begin{equation}
H(u):=-\frac{1}{2}\left(\int_0^1 R(u)\,{\rm d}u+\int_0^{-1}R(u)\,{\rm d}u\right)+\int_0^u R(u)\,{\rm d}u,\end{equation}
\begin{equation}
H(u):=-\frac{1}{2}\left(\int_0^1 R(u)\,{\rm d}u+\int_0^{-1}R(u)\,{\rm d}u\right)+\int_0^u R(u)\,{\rm d}u,\end{equation}and
 \begin{equation*}H(1) = \frac{1}{2}\int_{-1}^1 R(u)\, {\rm d}u \lt \infty,\end{equation*}
\begin{equation*}H(1) = \frac{1}{2}\int_{-1}^1 R(u)\, {\rm d}u \lt \infty,\end{equation*}provided that R belongs to the Lebesgue space ![]() $\mathcal{L}^1(-1,1)$. We will, however, prove that this condition
$\mathcal{L}^1(-1,1)$. We will, however, prove that this condition ![]() $R\in \mathcal{L}^1(-1,1)$ is a priori satisfied for metrics of non-negative Gaussian curvature, with which we deal in our main result.
$R\in \mathcal{L}^1(-1,1)$ is a priori satisfied for metrics of non-negative Gaussian curvature, with which we deal in our main result.
The following theorem contains some results for metrics, which are not necessarily positively curved.
Theorem 1.5. Assume that f is a real R-harmonic mapping of the unit disk into the interval ![]() $(-1,1)$, and assume that R is an increasing function in
$(-1,1)$, and assume that R is an increasing function in ![]() $(-1,0)$ and decreasing in
$(-1,0)$ and decreasing in ![]() $(0,1)$. Then we have the following sharp inequality
$(0,1)$. Then we have the following sharp inequality
 \begin{equation}
|\nabla f(z)|\le 2\frac{1-|f(z)|}{1-|z|^2} {\text{ for all }} z\in\mathbb{D}.\end{equation}
\begin{equation}
|\nabla f(z)|\le 2\frac{1-|f(z)|}{1-|z|^2} {\text{ for all }} z\in\mathbb{D}.\end{equation} If ![]() $f(0)=0$ and
$f(0)=0$ and  $\int_{-1}^0R(t)\,{\rm d}t =\int_0^1R(t)\,{\rm d}t$, then we have the sharp inequality
$\int_{-1}^0R(t)\,{\rm d}t =\int_0^1R(t)\,{\rm d}t$, then we have the sharp inequality
 \begin{equation}
|f(z)|\le \frac{4}{\pi}\tan^{-1} |z|, \quad z\in\mathbb{D}.\end{equation}
\begin{equation}
|f(z)|\le \frac{4}{\pi}\tan^{-1} |z|, \quad z\in\mathbb{D}.\end{equation} The proof of Theorem 1.5 is presented in ![]() $\S$ 2.1. We also have the following straightforward corollary of Theorem 1.5.
$\S$ 2.1. We also have the following straightforward corollary of Theorem 1.5.
Corollary 1.6. If R is even in ![]() $(-1,1)$ and decreasing in
$(-1,1)$ and decreasing in ![]() $[0,1)$, then
$[0,1)$, then
 \begin{equation*}\left| {\nabla f\left( z \right)} \right| \leqslant 2\frac{{1 - f{{(z)}^2}}}{{1 - |z{|^2}}}{\text{ for all }}z \in \mathbb{D},\end{equation*}
\begin{equation*}\left| {\nabla f\left( z \right)} \right| \leqslant 2\frac{{1 - f{{(z)}^2}}}{{1 - |z{|^2}}}{\text{ for all }}z \in \mathbb{D},\end{equation*}
so that
Further, if ![]() $f(0)=0$, then
$f(0)=0$, then
 \begin{equation*}\left| {f\left( z \right)} \right| \leqslant \frac{4}{\pi }{\tan ^{ - 1}}\left| z \right|{\text{ for all }}z \in \mathbb{D}.\end{equation*}
\begin{equation*}\left| {f\left( z \right)} \right| \leqslant \frac{4}{\pi }{\tan ^{ - 1}}\left| z \right|{\text{ for all }}z \in \mathbb{D}.\end{equation*}
2. Proof of main results
Theorem 2.1 is the main part of Theorem 1.3, and it solves Problem 1.1 for the modified metrics.
Theorem 2.1. Assume that R is a metric of non-negative Gaussian curvature in ![]() $(-1,1)$. If f is an R-harmonic function of the unit disk into
$(-1,1)$. If f is an R-harmonic function of the unit disk into ![]() $(-1,1)$, then it satisfies the sharp inequalities
$(-1,1)$, then it satisfies the sharp inequalities
 \begin{equation}
|\nabla f(z)|\le \frac{4}{\pi}\frac{1-f(z)^2}{1-|z|^2}
\end{equation}
\begin{equation}
|\nabla f(z)|\le \frac{4}{\pi}\frac{1-f(z)^2}{1-|z|^2}
\end{equation}and
 \begin{equation}
d_h(f(z), f(w))\le \frac{4}{\pi} d_h(z,w)\end{equation}
\begin{equation}
d_h(f(z), f(w))\le \frac{4}{\pi} d_h(z,w)\end{equation}for ![]() $z,w\in\mathbb{D}$, where dh is the hyperbolic metric.
$z,w\in\mathbb{D}$, where dh is the hyperbolic metric.
To prove Theorem 2.1, we need the following lemma, which is of interest in its own right.
Lemma 2.2. Assume that f is an increasing ![]() $\mathcal{C}^1$ diffeomorphism of
$\mathcal{C}^1$ diffeomorphism of ![]() $[-1,1]$ onto itself such that f ʹ is log-concave. Then for all
$[-1,1]$ onto itself such that f ʹ is log-concave. Then for all ![]() $x\in[-1,1]$, we have the inequality
$x\in[-1,1]$, we have the inequality
Proof of Lemma 2.2
Let ![]() $h:=\log (f^\prime)$. Take any
$h:=\log (f^\prime)$. Take any ![]() $x\in(-1,1)$. Since h is concave, for some real k and all
$x\in(-1,1)$. Since h is concave, for some real k and all ![]() $t\in(-1,1)$, we have
$t\in(-1,1)$, we have
by approximation, without loss of generality ![]() $k\ne0$. Also, the condition that f is an increasing diffeomorphism of
$k\ne0$. Also, the condition that f is an increasing diffeomorphism of ![]() $[-1,1]$ onto itself implies that
$[-1,1]$ onto itself implies that ![]() $f(-1)=-1$ and
$f(-1)=-1$ and ![]() $f(1)=1$. So,
$f(1)=1$. So,
 \begin{equation*}
\begin{aligned}
f(x)&=1-\int_x^1 f^\prime(t)\,{\rm d}t \\
&=1-\int_x^1 {\rm e}^{h(t)}\, {\rm d}t \\
&\geqslant1-\int_x^1 {\rm e}^{h_x(t)}\, {\rm d}t \\
& =g^+(U,x):=1-U\frac{1-{\rm e}^{k(1-x)}}{-k},
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
f(x)&=1-\int_x^1 f^\prime(t)\,{\rm d}t \\
&=1-\int_x^1 {\rm e}^{h(t)}\, {\rm d}t \\
&\geqslant1-\int_x^1 {\rm e}^{h_x(t)}\, {\rm d}t \\
& =g^+(U,x):=1-U\frac{1-{\rm e}^{k(1-x)}}{-k},
\end{aligned}
\end{equation*}where
 \begin{equation}
U:={\rm e}^{h(x)}=f^\prime(x) \gt 0.
\end{equation}
\begin{equation}
U:={\rm e}^{h(x)}=f^\prime(x) \gt 0.
\end{equation}Similarly,
 \begin{equation*}
\begin{aligned}
f(x)&=-1+\int_{-1}^x {\rm e}^{h(t)}\, {\rm d}t \\
&\le-1+\int_{-1}^x {\rm e}^{h_x(t)}\, {\rm d}t \\
& =-g^-(U,x):=-1+U\frac{{\rm e}^{-k(1+x)}-1}{-k}.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
f(x)&=-1+\int_{-1}^x {\rm e}^{h(t)}\, {\rm d}t \\
&\le-1+\int_{-1}^x {\rm e}^{h_x(t)}\, {\rm d}t \\
& =-g^-(U,x):=-1+U\frac{{\rm e}^{-k(1+x)}-1}{-k}.
\end{aligned}
\end{equation*}So,
 \begin{equation}
f(x)^2\geqslant g_2(U,k,x):=\max[g^+(U,x)_+^2,g^-(U,x)_+^2],
\end{equation}
\begin{equation}
f(x)^2\geqslant g_2(U,k,x):=\max[g^+(U,x)_+^2,g^-(U,x)_+^2],
\end{equation}where ![]() $z_+:=\max(0,z)$.
$z_+:=\max(0,z)$.
We also have
 \begin{equation*}
2=\int_{-1}^1 f^\prime =\int_{-1}^1 {\rm e}^h\le \int_{-1}^1 {\rm e}^{h_x(t)}\,{\rm d}t
=U \,{\rm e}^{-k x}\,\frac{2\,\sinh k}k,
\end{equation*}
\begin{equation*}
2=\int_{-1}^1 f^\prime =\int_{-1}^1 {\rm e}^h\le \int_{-1}^1 {\rm e}^{h_x(t)}\,{\rm d}t
=U \,{\rm e}^{-k x}\,\frac{2\,\sinh k}k,
\end{equation*}so that
 \begin{equation}
U\geqslant U_{k,x}:={\rm e}^{k x}\frac k{\sinh k}.
\end{equation}
\begin{equation}
U\geqslant U_{k,x}:={\rm e}^{k x}\frac k{\sinh k}.
\end{equation}Thus, it is enough to show that
 \begin{equation}
\rho(U,k,x):=\frac{1-g_2(U,k,x)}{U(1-x^2)}\le1
\end{equation}
\begin{equation}
\rho(U,k,x):=\frac{1-g_2(U,k,x)}{U(1-x^2)}\le1
\end{equation}for ![]() $U\geqslant U_{k,x}$. Note that
$U\geqslant U_{k,x}$. Note that ![]() $\rho(U,k,x)(1-x^2)$ is a continuous piecewise-rational function of U such that
$\rho(U,k,x)(1-x^2)$ is a continuous piecewise-rational function of U such that ![]() $\mathbb{R}$ can be partitioned into several intervals such that on each of the intervals of the partition, the expression
$\mathbb{R}$ can be partitioned into several intervals such that on each of the intervals of the partition, the expression ![]() $\rho(U,k,x)(1-x^2)$ coincides with one of the following three expressions:
$\rho(U,k,x)(1-x^2)$ coincides with one of the following three expressions:
 \begin{equation}
\rho_+(U):=\frac{1-g^+(U,x)^2}U,\quad
\rho_-(U):=\frac{1-g^-(U,x)^2}U,\quad
\rho_0(U):=\frac{1-0}U.
\end{equation}
\begin{equation}
\rho_+(U):=\frac{1-g^+(U,x)^2}U,\quad
\rho_-(U):=\frac{1-g^-(U,x)^2}U,\quad
\rho_0(U):=\frac{1-0}U.
\end{equation}We have
 \begin{equation}
\rho^\prime_+(U)=-\frac{\left({\rm e}^{k-k x}-1\right)^2}{k^2}\le0,\quad
\rho^\prime_-(U)=-\frac{e^{-2 k (x+1)} \left({\rm e}^{k (x+1)}-1\right)^2}{k^2}\le0\quad
\end{equation}
\begin{equation}
\rho^\prime_+(U)=-\frac{\left({\rm e}^{k-k x}-1\right)^2}{k^2}\le0,\quad
\rho^\prime_-(U)=-\frac{e^{-2 k (x+1)} \left({\rm e}^{k (x+1)}-1\right)^2}{k^2}\le0\quad
\end{equation}and ![]() $\rho^\prime_0(U) \lt 0$.
$\rho^\prime_0(U) \lt 0$.
So, ![]() $\rho(U,k,x)$ is nonincreasing in U. It remains to show that
$\rho(U,k,x)$ is nonincreasing in U. It remains to show that
Note that ![]() $g^+(U_{k,x},x)=-g^-(U_{k,x},x)=\left({\rm e}^{k x}-{\rm e}^k\right) \operatorname{csch} k+1$. So,
$g^+(U_{k,x},x)=-g^-(U_{k,x},x)=\left({\rm e}^{k x}-{\rm e}^k\right) \operatorname{csch} k+1$. So,
 \begin{equation}
r(k,x)=\frac{1-g^+(U_{k,x},x)^2}{U_{k,x}(1-x^2)}
= \frac{2 (\cosh k-\cosh k x)\operatorname{csch} k}{k \left(1-x^2\right)}.
\end{equation}
\begin{equation}
r(k,x)=\frac{1-g^+(U_{k,x},x)^2}{U_{k,x}(1-x^2)}
= \frac{2 (\cosh k-\cosh k x)\operatorname{csch} k}{k \left(1-x^2\right)}.
\end{equation}Inequality (2.11) can be rewritten as
for real k > 0 and ![]() $x\in[0,1]$ because
$x\in[0,1]$ because ![]() $\text{dif}(-k,x)=\text{dif}(k,x)=\text{dif}(k,-x)$.
$\text{dif}(-k,x)=\text{dif}(k,x)=\text{dif}(k,-x)$.
We have ![]() $\text{dif}^{\prime\prime\prime}(x)=-2 k^2\, \operatorname{csch} k\, \sinh k x\le0$. So,
$\text{dif}^{\prime\prime\prime}(x)=-2 k^2\, \operatorname{csch} k\, \sinh k x\le0$. So, ![]() $\text{dif}^{\prime\prime}$ is non-increasing. Hence, there is some
$\text{dif}^{\prime\prime}$ is non-increasing. Hence, there is some ![]() $c\in[0,1]$ such that dif is convex on
$c\in[0,1]$ such that dif is convex on ![]() $[0,c]$ and concave on
$[0,c]$ and concave on ![]() $[c,1]$. Also,
$[c,1]$. Also, ![]() $\text{dif}^\prime(0)=\text{dif}^\prime(1)=\text{dif}(1)=0$. Thus, (2.13) follows.
$\text{dif}^\prime(0)=\text{dif}^\prime(1)=\text{dif}(1)=0$. Thus, (2.13) follows.
Proof of Theorem 2.1
Let us show that ![]() $R\in\mathcal{L}^1(-1,1).$ In view of Equation (1.11),
$R\in\mathcal{L}^1(-1,1).$ In view of Equation (1.11), ![]() $\log R$ is concave. Therefore,
$\log R$ is concave. Therefore,
 \begin{equation*}\log R(t)\leq\log R(0)+\frac{R^{\prime}(0)}{R(0)}t\;\;\;\text{ for all}\ t\in(-1,1),\end{equation*}
\begin{equation*}\log R(t)\leq\log R(0)+\frac{R^{\prime}(0)}{R(0)}t\;\;\;\text{ for all}\ t\in(-1,1),\end{equation*}and thus
 \begin{equation*}R(t)\le R(0) {\rm e}^{\frac{R^\prime(0)}{R(0)} t}.\end{equation*}
\begin{equation*}R(t)\le R(0) {\rm e}^{\frac{R^\prime(0)}{R(0)} t}.\end{equation*}Hence,
 \begin{equation*}\int_{-1}^1 R(t)\,{\rm d}t \lt \infty.\end{equation*}
\begin{equation*}\int_{-1}^1 R(t)\,{\rm d}t \lt \infty.\end{equation*}Now we put
 \begin{equation*}r:=H(1) = \frac{1}{2}\int_{-1}^1 R(u)\,{\rm d}u.\end{equation*}
\begin{equation*}r:=H(1) = \frac{1}{2}\int_{-1}^1 R(u)\,{\rm d}u.\end{equation*}Recall the Euclidean harmonic function g defined in Equation (1.12). It comes down to estimating the gradient of the derivative of the function g, which is equal to
For the real Euclidean harmonic function ![]() $g:\mathbb{D}\to (-1,1)$, we have [Reference Chen6, Reference Kalaj and Vuorinen13]
$g:\mathbb{D}\to (-1,1)$, we have [Reference Chen6, Reference Kalaj and Vuorinen13]
 \begin{equation}|\nabla g(z)|=\frac{R(f(z)) |\nabla f(z)|}{r}\le \frac{4}{\pi}\frac{\cos \frac{\pi}{2}g(z)}{1-|z|^2},\end{equation}
\begin{equation}|\nabla g(z)|=\frac{R(f(z)) |\nabla f(z)|}{r}\le \frac{4}{\pi}\frac{\cos \frac{\pi}{2}g(z)}{1-|z|^2},\end{equation}where
 \begin{equation*}g(z):=\frac{1}{r}\left(H(0)+ \int_0^{f(z)}R(u)\,{\rm d}u\right).\end{equation*}
\begin{equation*}g(z):=\frac{1}{r}\left(H(0)+ \int_0^{f(z)}R(u)\,{\rm d}u\right).\end{equation*}Let
 \begin{equation}\mathcal{R}:=\frac{4}{\pi}\,\frac{\cos\left(\frac{\pi}{2r}\left(H(0)+ \int_0^{f(z)}R(u)\,{\rm d}u\right)\right)}{1-|z|^2}.\end{equation}
\begin{equation}\mathcal{R}:=\frac{4}{\pi}\,\frac{\cos\left(\frac{\pi}{2r}\left(H(0)+ \int_0^{f(z)}R(u)\,{\rm d}u\right)\right)}{1-|z|^2}.\end{equation}Note that
 \begin{equation*}\cos\frac{\pi}{2} b\le
1-b^2\end{equation*}
\begin{equation*}\cos\frac{\pi}{2} b\le
1-b^2\end{equation*}for ![]() $b\in[0,1]$.
$b\in[0,1]$.
Let
 \begin{equation*}
\psi(v):=\frac{\pi}{2r}\left(H(0)+ \int_0^{v}R(u)\,{\rm d}u\right)\end{equation*}
\begin{equation*}
\psi(v):=\frac{\pi}{2r}\left(H(0)+ \int_0^{v}R(u)\,{\rm d}u\right)\end{equation*}and apply Lemma 2.2. We get
 \begin{equation}\mathcal{R}\le
\frac4\pi\,\frac{1-\psi(v)^2}{\psi^\prime(v)}
\le\frac4\pi\,(1-v^2).\end{equation}
\begin{equation}\mathcal{R}\le
\frac4\pi\,\frac{1-\psi(v)^2}{\psi^\prime(v)}
\le\frac4\pi\,(1-v^2).\end{equation}Combining Equations (2.15), (2.14) and (2.16), we obtain Equation (2.1). Concerning Equation (2.2), notice that the proof of [Reference Kalaj and Vuorinen13, Theorem 1.2] can be applied in this case because the ρ-harmonicity is invariant under precomposition by Möbius transformations.
The following example shows that one cannot omit the condition of positive Gaussian curvature. In fact, we cannot prove a weaker estimate with a constant larger than ![]() $4/\pi
$.
$4/\pi
$.
Example 2.3. Assume that  $\varrho(w):=\frac{1}{1-|w|^2}$ and let
$\varrho(w):=\frac{1}{1-|w|^2}$ and let  $\rho(w):=\varrho(u,0)=\frac{1}{1-u^2}$. Then
$\rho(w):=\varrho(u,0)=\frac{1}{1-u^2}$. Then ![]() $f: \mathbb{D}\to (-1,1)$ is ρ-harmonic (and ϱ-harmonic) if and only if
$f: \mathbb{D}\to (-1,1)$ is ρ-harmonic (and ϱ-harmonic) if and only if
for a Euclidean harmonic mapping g of the unit disk in the real line ![]() $\mathbb{R}$. In particular, the functions
$\mathbb{R}$. In particular, the functions
are ρ-harmonic. Then ![]() $|\nabla f(z)|=n\, \mathrm{sech}\,^2(n x),$ and so,
$|\nabla f(z)|=n\, \mathrm{sech}\,^2(n x),$ and so,
 \begin{equation*}\frac{|\nabla f(z)|}{1-|f(z)|^2}(1-|z|^2)\bigg|_{z=0}=n,\end{equation*}
\begin{equation*}\frac{|\nabla f(z)|}{1-|f(z)|^2}(1-|z|^2)\bigg|_{z=0}=n,\end{equation*}so that in Theorem 2.1, we cannot omit the condition of the positiveness of Gaussian curvature, nor can we even prove a weaker statement with a larger constant factor instead of ![]() $4/\pi$. Observe that in this case
$4/\pi$. Observe that in this case
 \begin{equation*}\mathcal{K}_\rho(z) =-2(1+x^2) \lt 0. \end{equation*}
\begin{equation*}\mathcal{K}_\rho(z) =-2(1+x^2) \lt 0. \end{equation*} Of course, the curvature of the hyperbolic (Poincar![]() $\grave{\mathrm{e}}$) metric is
$\grave{\mathrm{e}}$) metric is ![]() $\mathcal{K}_\varrho(z)=-4$, and it is not equal to the curvature of ρ, even though both curvatures are negative.
$\mathcal{K}_\varrho(z)=-4$, and it is not equal to the curvature of ρ, even though both curvatures are negative.
In the following example, a result for a metric R of zero Gaussian curvature is given.
Example 2.4. Assume that the Gaussian curvature of R is zero. Then ![]() $R(x)={\rm e}^{cx}$. Moreover, by Equation (2.14),
$R(x)={\rm e}^{cx}$. Moreover, by Equation (2.14),
 \begin{equation*}|\nabla f(z)|\le A:=\frac{4 {\rm e}^{-c f(z)}\, \sin\left[\frac{\pi}{2 \,\sinh(c)} \left({\rm e}^c-{\rm e}^{c f(z)}\right) \right] \sinh(c)}{c \pi \left(1-|z|^2\right)}.\end{equation*}
\begin{equation*}|\nabla f(z)|\le A:=\frac{4 {\rm e}^{-c f(z)}\, \sin\left[\frac{\pi}{2 \,\sinh(c)} \left({\rm e}^c-{\rm e}^{c f(z)}\right) \right] \sinh(c)}{c \pi \left(1-|z|^2\right)}.\end{equation*}Further, by the proof of Theorem 2.1,
 \begin{equation*}|\nabla f(z)|\le A\le \frac{4}{\pi}\frac{1-f(z)^2}{1-|z|^2}.\end{equation*}
\begin{equation*}|\nabla f(z)|\le A\le \frac{4}{\pi}\frac{1-f(z)^2}{1-|z|^2}.\end{equation*}2.1. Proof of Theorem 1.5
We need the following lemma.
Lemma 2.5. If ![]() $R\colon(-1,1)\to (0,+\infty)$ is positive, increasing in
$R\colon(-1,1)\to (0,+\infty)$ is positive, increasing in ![]() $(-1,0)$ and decreasing in
$(-1,0)$ and decreasing in ![]() $(0,1)$, if
$(0,1)$, if ![]() $v\in(-1,1)$, and if
$v\in(-1,1)$, and if
 \begin{equation*}r=\frac{1}{2}\int_{-1}^1 R(u) \, {\rm d}u,\end{equation*}
\begin{equation*}r=\frac{1}{2}\int_{-1}^1 R(u) \, {\rm d}u,\end{equation*}then we have the sharp inequality
 \begin{equation}\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\right]\le \frac{\pi}{2r}{\left(1-|v|\right) R(v)},\end{equation}
\begin{equation}\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\right]\le \frac{\pi}{2r}{\left(1-|v|\right) R(v)},\end{equation}and in particular
 \begin{equation*}\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2 r}\right]\le \frac{\pi}{2r} {\left(1-v^2\right) R(v)}.\end{equation*}
\begin{equation*}\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2 r}\right]\le \frac{\pi}{2r} {\left(1-v^2\right) R(v)}.\end{equation*} The constant ![]() $\pi/2$ is sharp even if we restrict the consideration to
$\pi/2$ is sharp even if we restrict the consideration to ![]() $\mathcal{C}^2$ diffeomorphisms
$\mathcal{C}^2$ diffeomorphisms ![]() $R\colon(-1,1)\to (0,\infty)$.
$R\colon(-1,1)\to (0,\infty)$.
Proof of Lemma 2.5
The proof of inequality (2.17) is easy. We use here the fact that R is decreasing in ![]() $[0,1)$ and the elementary inequality
$[0,1)$ and the elementary inequality ![]() $\sin x\le x$ for
$\sin x\le x$ for ![]() $x\in[0,\pi/2]$. Then for
$x\in[0,\pi/2]$. Then for ![]() $v\in[0,1]$, we have
$v\in[0,1]$, we have
 \begin{equation*}
\begin{split}
\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\right]&\le \frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\\
&\le \pi \frac{\left(1-v\right) R(v)}{2r}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\right]&\le \frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\\
&\le \pi \frac{\left(1-v\right) R(v)}{2r}.
\end{split}
\end{equation*} If v < 0, then we use the fact that R is increasing in ![]() $(-1,0)$. We come to the desired inequality as follows:
$(-1,0)$. We come to the desired inequality as follows:
 \begin{equation*}\sin\left(\frac{\pi}{2r} \int_v^{1}R(u)\,{\rm d}u\right)=\sin\left(\frac{\pi}{2r} \int_{-1}^{v}R(u)\,{\rm d}u\right)\le \pi \frac{\left(1+v\right) R(v)}{2r}.\end{equation*}
\begin{equation*}\sin\left(\frac{\pi}{2r} \int_v^{1}R(u)\,{\rm d}u\right)=\sin\left(\frac{\pi}{2r} \int_{-1}^{v}R(u)\,{\rm d}u\right)\le \pi \frac{\left(1+v\right) R(v)}{2r}.\end{equation*}To prove the sharpness part, observe that inequality (2.17) is equivalent to
where
 \begin{equation*} \phi(v)=\frac{\pi}{2}-\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2 \int_0^1 R(u) \, {\rm d}u}=\frac{\pi \int_0^v R(u) \, {\rm d}u}{2 \int_0^1 R(u) \, {\rm d}u}.\end{equation*}
\begin{equation*} \phi(v)=\frac{\pi}{2}-\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2 \int_0^1 R(u) \, {\rm d}u}=\frac{\pi \int_0^v R(u) \, {\rm d}u}{2 \int_0^1 R(u) \, {\rm d}u}.\end{equation*} For ![]() $s, as^2\in(0,1)$, we define the concave diffeomorphism
$s, as^2\in(0,1)$, we define the concave diffeomorphism ![]() $\psi\colon[0,1]\to[0,1]$ by the formula
$\psi\colon[0,1]\to[0,1]$ by the formula
 \begin{equation}\psi(x):= \left\{
\begin{array}{ll}
\left(1+2 a s-a s^2\right) x-a x^2 & \text{if } x \gt 0\wedge x \lt s, \\
1+\left(1-a s^2\right) (-1+x) & \text{if } x\geq s\wedge x\leq 1.
\end{array}
\right.\end{equation}
\begin{equation}\psi(x):= \left\{
\begin{array}{ll}
\left(1+2 a s-a s^2\right) x-a x^2 & \text{if } x \gt 0\wedge x \lt s, \\
1+\left(1-a s^2\right) (-1+x) & \text{if } x\geq s\wedge x\leq 1.
\end{array}
\right.\end{equation} Now we define ![]() $\phi(x) = \frac{\pi}{2}\psi(x)$.
$\phi(x) = \frac{\pi}{2}\psi(x)$.
Then for ![]() $u=as^2$, we have
$u=as^2$, we have
 \begin{equation*}\frac{\cos \phi(s)}{(1-s^2)\phi^\prime(s)}=\frac{2\,\sin\left[\frac{1}{2} \pi (1-s) (1-u)\right]}{\pi \left(1-s^2\right) (1-u)}.\end{equation*}
\begin{equation*}\frac{\cos \phi(s)}{(1-s^2)\phi^\prime(s)}=\frac{2\,\sin\left[\frac{1}{2} \pi (1-s) (1-u)\right]}{\pi \left(1-s^2\right) (1-u)}.\end{equation*} The supremum of the latter expression is equal to 1. It is ‘attained in the limit’, for instance, if ![]() $s=1/n\to 0$ and
$s=1/n\to 0$ and ![]() $u = (n-1)^2/n^2=as^2\to 1$, with
$u = (n-1)^2/n^2=as^2\to 1$, with ![]() $n\to \infty$.
$n\to \infty$.
To prove the last statement, extend ψ in ![]() $[-1,1]$ by
$[-1,1]$ by ![]() $\psi(x)= -\psi(-x)$ and define
$\psi(x)= -\psi(-x)$ and define ![]() $R(x)=\psi^\prime(x)$, for
$R(x)=\psi^\prime(x)$, for ![]() $x\in[-1,1]$. Then R is not smooth, but it is continuous on
$x\in[-1,1]$. Then R is not smooth, but it is continuous on ![]() $[-1,1]$.
$[-1,1]$.
We introduce appropriate mollifiers: Fix a smooth even function ![]() $\sigma:\mathbb{R}\to[0,1]$, which is compactly supported in the interval
$\sigma:\mathbb{R}\to[0,1]$, which is compactly supported in the interval ![]() $(-1,1)$ and satisfies
$(-1,1)$ and satisfies  $\int_{\mathbb{R}}\sigma=1$. For ɛ > 0, consider the mollifier
$\int_{\mathbb{R}}\sigma=1$. For ɛ > 0, consider the mollifier
 \begin{equation}
\sigma_\varepsilon(t):=\frac{1}{\varepsilon}\,
\sigma\left(\frac{t}{\varepsilon}\right).
\end{equation}
\begin{equation}
\sigma_\varepsilon(t):=\frac{1}{\varepsilon}\,
\sigma\left(\frac{t}{\varepsilon}\right).
\end{equation} It is compactly supported in the interval ![]() $(-\varepsilon,\varepsilon)$ and satisfies
$(-\varepsilon,\varepsilon)$ and satisfies  $\int_{\mathbb{R}}\sigma_\varepsilon=1$. For ɛ > 0, define
$\int_{\mathbb{R}}\sigma_\varepsilon=1$. For ɛ > 0, define
 \begin{equation*}\varphi_\varepsilon(x): = \int_{\mathbb{R}} \psi(y)
\frac{1}{\varepsilon}\sigma\left(\frac{x-y}{\varepsilon}\right)\,{\rm d}y=\int_{\mathbb{R}}
\psi(x-\varepsilon z)\sigma(z)\,{\rm d}z.\end{equation*}
\begin{equation*}\varphi_\varepsilon(x): = \int_{\mathbb{R}} \psi(y)
\frac{1}{\varepsilon}\sigma\left(\frac{x-y}{\varepsilon}\right)\,{\rm d}y=\int_{\mathbb{R}}
\psi(x-\varepsilon z)\sigma(z)\,{\rm d}z.\end{equation*}Because σ is even, we have
 \begin{align*}\begin{split}\varphi_\varepsilon(-x) & = \int_{\mathbb{R}}
\psi(-x-\varepsilon z)\sigma(z)\,{\rm d}z \nonumber \\
& =\int_{\mathbb{R}} \psi(x+\varepsilon z)\sigma(z)\,{\rm d}z \nonumber \\
& =-\int_{\mathbb{R}} \psi(x-\varepsilon z)\sigma(z)\,{\rm d}z \nonumber \\
& =-\varphi_\varepsilon(x),\end{split}\end{align*}
\begin{align*}\begin{split}\varphi_\varepsilon(-x) & = \int_{\mathbb{R}}
\psi(-x-\varepsilon z)\sigma(z)\,{\rm d}z \nonumber \\
& =\int_{\mathbb{R}} \psi(x+\varepsilon z)\sigma(z)\,{\rm d}z \nonumber \\
& =-\int_{\mathbb{R}} \psi(x-\varepsilon z)\sigma(z)\,{\rm d}z \nonumber \\
& =-\varphi_\varepsilon(x),\end{split}\end{align*}and
 \begin{equation*}\varphi^\prime_\varepsilon(x) =\int_{\mathbb{R}} \psi^\prime(x-\varepsilon
z)\sigma(z)\,{\rm d}z.\end{equation*}
\begin{equation*}\varphi^\prime_\varepsilon(x) =\int_{\mathbb{R}} \psi^\prime(x-\varepsilon
z)\sigma(z)\,{\rm d}z.\end{equation*} So φɛ is an increasing and odd function. Further, we define  $\psi_\varepsilon(x):=\frac{1}{\varphi_\varepsilon(1)}\varphi_\varepsilon(x)$. Then
$\psi_\varepsilon(x):=\frac{1}{\varphi_\varepsilon(1)}\varphi_\varepsilon(x)$. Then ![]() $\psi_\varepsilon(x):[-1,1]\to [-1,1]$ is a
$\psi_\varepsilon(x):[-1,1]\to [-1,1]$ is a ![]() $\mathcal{C}^\infty$ increasing odd diffeomorphism. Then
$\mathcal{C}^\infty$ increasing odd diffeomorphism. Then ![]() $\psi_\varepsilon(x)$ converges uniformly to ψ and
$\psi_\varepsilon(x)$ converges uniformly to ψ and ![]() $\psi^\prime_\varepsilon(x)$ converges uniformly to
$\psi^\prime_\varepsilon(x)$ converges uniformly to ![]() $\psi^\prime(x)$ as ɛ → 0. Thus, the function
$\psi^\prime(x)$ as ɛ → 0. Thus, the function ![]() $R_\varepsilon(x) =\psi^\prime_\varepsilon(x)$ is an even function, increasing in
$R_\varepsilon(x) =\psi^\prime_\varepsilon(x)$ is an even function, increasing in ![]() $[-1,0]$ and decreasing in
$[-1,0]$ and decreasing in ![]() $[0,1]$ that converges uniformly to R.
$[0,1]$ that converges uniformly to R.
This implies that the constant ![]() $\pi/2$ is sharp even if we restrict the consideration to
$\pi/2$ is sharp even if we restrict the consideration to ![]() $\mathcal{C}^\infty$ diffeomorphisms.
$\mathcal{C}^\infty$ diffeomorphisms.
Proof of Theorem 1.5
Since R is positive, increasing in ![]() $(-1,0)$ and decreasing in
$(-1,0)$ and decreasing in ![]() $(0,1)$, it is clear that
$(0,1)$, it is clear that ![]() $R\in\mathcal{L}(-1,1)$. From Equation (2.14), we have
$R\in\mathcal{L}(-1,1)$. From Equation (2.14), we have
 \begin{equation}|\nabla g(z)|=\frac{R(f(z)) |\nabla f(z)|}{r}\le \frac{4}{\pi}\frac{\cos \frac{\pi}{2}g(z)}{1-|z|^2},\end{equation}
\begin{equation}|\nabla g(z)|=\frac{R(f(z)) |\nabla f(z)|}{r}\le \frac{4}{\pi}\frac{\cos \frac{\pi}{2}g(z)}{1-|z|^2},\end{equation}where
 \begin{equation*}g(z):=\frac{H(0)}{2r}+\frac{1}{r}\left( \int_0^{f(z)}R(u)\,{\rm d}u\right),\end{equation*}
\begin{equation*}g(z):=\frac{H(0)}{2r}+\frac{1}{r}\left( \int_0^{f(z)}R(u)\,{\rm d}u\right),\end{equation*}with H(0) defined in Equation (1.13).
Further,
 \begin{equation*}\cos \frac{\pi}{2}g(z)=\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\right].\end{equation*}
\begin{equation*}\cos \frac{\pi}{2}g(z)=\sin\left[\frac{\pi \int_v^1 R(u) \, {\rm d}u}{2r}\right].\end{equation*} In view Lemma 2.5, the inequality (1.14) is proved. To prove Equation (1.15), in view of the assumption, we observe first that ![]() $H(0)=0$. Since the function
$H(0)=0$. Since the function  $\psi(u) =\int_0^u R(t)\frac{{\rm d}t}{r}$ is concave on
$\psi(u) =\int_0^u R(t)\frac{{\rm d}t}{r}$ is concave on ![]() $[0,1]$ with
$[0,1]$ with ![]() $\psi(0)=\psi(1)-1=0$, it satisfies the inequality
$\psi(0)=\psi(1)-1=0$, it satisfies the inequality ![]() $\psi(u)\geqslant u$. Therefore,
$\psi(u)\geqslant u$. Therefore,
 \begin{equation*}|f(z)|\le \frac{1}{r}\left| \int_0^{f(z)}R(u)\,{\rm d}u\right|=|g(z)|.\end{equation*}
\begin{equation*}|f(z)|\le \frac{1}{r}\left| \int_0^{f(z)}R(u)\,{\rm d}u\right|=|g(z)|.\end{equation*}Now we use the Schwarz lemma for Euclidean harmonic functions ([Reference Duren8, Reference Heinz10]), which implies that
 \begin{equation*}|g(z)|\le \frac{4}{\pi}\tan^{-1} |z|.\end{equation*}
\begin{equation*}|g(z)|\le \frac{4}{\pi}\tan^{-1} |z|.\end{equation*} Inequality (1.14) is sharp because of Lemma 2.5. Inequality (1.15) is sharp, since it coincides with the corresponding inequality [Reference Axler, Bourdon and Ramey2, p. 124] for Euclidean harmonic mappings (planar case), where the sharpness part is established. Observe that, if ![]() $R\equiv 1$, then R defines the Euclidean metric and satisfies the conditions of our theorem. This finishes the proof of the theorem.
$R\equiv 1$, then R defines the Euclidean metric and satisfies the conditions of our theorem. This finishes the proof of the theorem.
3. Concluding remarks
The answer to the general question posed in Problem 1.1 is negative. In the following example, it is shown that for metrics of zero Gaussian curvature, the quantity S(f) defined in Equation (1.5) can be arbitrary big.
Example 3.1. For ![]() $z=x+{\rm i} y$, let
$z=x+{\rm i} y$, let ![]() $g(z)={\rm i} k y$, where k > 0, and assume that ϕ is a conformal automorphism of
$g(z)={\rm i} k y$, where k > 0, and assume that ϕ is a conformal automorphism of ![]() $\mathcal{S}=\{x+{\rm i} y: x\in(-1,1), y\in\mathbb{R}\}$, which maps y-axis onto
$\mathcal{S}=\{x+{\rm i} y: x\in(-1,1), y\in\mathbb{R}\}$, which maps y-axis onto ![]() $(-1,1)$. Let
$(-1,1)$. Let ![]() $g_1=\phi \circ g$. For instance, one may define a conformal automorphism ϕ as follows:
$g_1=\phi \circ g$. For instance, one may define a conformal automorphism ϕ as follows:
 \begin{equation*}\phi(z) := -\frac{2 {\rm i}\, \log\left[-{\rm i}+\frac{2}{-{\rm i}+{\rm e}^{\frac{{\rm i} \pi z}{2}}}\right]}{\pi }.\end{equation*}
\begin{equation*}\phi(z) := -\frac{2 {\rm i}\, \log\left[-{\rm i}+\frac{2}{-{\rm i}+{\rm e}^{\frac{{\rm i} \pi z}{2}}}\right]}{\pi }.\end{equation*} Next let ![]() $\varrho(w)=|\zeta^\prime(w)|$, where we use notation
$\varrho(w)=|\zeta^\prime(w)|$, where we use notation ![]() $w=\phi(\zeta)$ and
$w=\phi(\zeta)$ and ![]() $w\mapsto \zeta(w)$ denotes the inverse function to ϕ. Then g 1 is ϱ-harmonic,
$w\mapsto \zeta(w)$ denotes the inverse function to ϕ. Then g 1 is ϱ-harmonic, ![]() $\lambda_0(i y)=\pi/2$ and
$\lambda_0(i y)=\pi/2$ and ![]() $|\nabla g_1(i y)|=k|\phi^\prime(i y)$. Also,
$|\nabla g_1(i y)|=k|\phi^\prime(i y)$. Also, ![]() $|\nabla g_1(0)|=2k$. Here
$|\nabla g_1(0)|=2k$. Here ![]() $\lambda_0(z)$ is the hyperbolic metric of the strip. Since the expression (1.5) is invariant with respect to conformal maps and hyperbolic metrics, by taking a conformal mapping a of the unit disk onto the strip
$\lambda_0(z)$ is the hyperbolic metric of the strip. Since the expression (1.5) is invariant with respect to conformal maps and hyperbolic metrics, by taking a conformal mapping a of the unit disk onto the strip ![]() $\mathcal{S}$ satisfying
$\mathcal{S}$ satisfying ![]() $a(0)=0$ and defining
$a(0)=0$ and defining ![]() $f(z)=g_1(a(z))$, we see that
$f(z)=g_1(a(z))$, we see that
 \begin{equation*}S(f(z))=\frac{|\nabla f(z)|(1-|z|^2)}{1-|f(z)|^2}=\frac{|\nabla g_1(a(z))|}{(1-g_1(a(z))^2)\lambda_0(a(z))}\end{equation*}
\begin{equation*}S(f(z))=\frac{|\nabla f(z)|(1-|z|^2)}{1-|f(z)|^2}=\frac{|\nabla g_1(a(z))|}{(1-g_1(a(z))^2)\lambda_0(a(z))}\end{equation*}can be arbitrary big for z = 0, namely ![]() $S(f(0))=4k/\pi$. We remark that in this case
$S(f(0))=4k/\pi$. We remark that in this case
 \begin{equation*}\varrho^2 (u,v)=\frac{2}{\cos [\pi u]+\cosh[\pi v]},\end{equation*}
\begin{equation*}\varrho^2 (u,v)=\frac{2}{\cos [\pi u]+\cosh[\pi v]},\end{equation*}so that ![]() $\mathcal{K}_\varrho=0,$ but
$\mathcal{K}_\varrho=0,$ but ![]() $\mathcal{K}_\rho=- \pi ^2 /4$, where
$\mathcal{K}_\rho=- \pi ^2 /4$, where ![]() $\rho(u,v)=\varrho(u,0)$.
$\rho(u,v)=\varrho(u,0)$.
The following example raises a similar question for positive harmonic functions.
Example 3.2. It is well known that a positive harmonic function defined in the half-plane is a contraction with respect to hyperbolic metric (see e.g. [Reference Marković14]). So, it is natural to ask whether such a result is true for positive R-harmonic functions defined in the half-plane, where R is a metric of non-negative Gaussian curvature. The following example shows that this is not true. Let ![]() $R(x)=1-{\rm e}^{-x}$ and define the positive R-harmonic function on
$R(x)=1-{\rm e}^{-x}$ and define the positive R-harmonic function on ![]() $S(0,\infty):=\{x+{\rm{i}} y: x \gt 0, y\in\mathbb{R}\}$ by
$S(0,\infty):=\{x+{\rm{i}} y: x \gt 0, y\in\mathbb{R}\}$ by
 \begin{equation*}f(x,y) := \log\left[\frac{\pi }{\frac{\pi }{2}-\tan^{-1}\left[\frac{y}{x}\right]}\right]=R\left(\Re \left[-{\rm i}/\pi\, \log({\rm i} z)\right]\right).\end{equation*}
\begin{equation*}f(x,y) := \log\left[\frac{\pi }{\frac{\pi }{2}-\tan^{-1}\left[\frac{y}{x}\right]}\right]=R\left(\Re \left[-{\rm i}/\pi\, \log({\rm i} z)\right]\right).\end{equation*} Observe that  $-\log (R(x))^{\prime\prime}=\frac{1}{4}\, \operatorname{csch}\left[\frac{x}{2}\right]^2$. So, R has a non-negative curvature.
$-\log (R(x))^{\prime\prime}=\frac{1}{4}\, \operatorname{csch}\left[\frac{x}{2}\right]^2$. So, R has a non-negative curvature.
On the other hand,
 \begin{equation*}x\frac{|\nabla f(x,y)|}{{f(x,y)}}=\frac{2 x \sqrt{\frac{1}{\left(x^2+y^2\right) \left(\pi -2 \tan^{-1}\left[\frac{y}{x}\right]\right)^2}}}{\log\left[\frac{2 \pi }{\pi -2 \tan^{-1}\left[\frac{y}{x}\right]}\right]}=\frac{2 \sqrt{\frac{1}{\left(1+t^2\right) (\pi -2 \tan^{-1}[t])^2}}}{\log\left[\frac{2 \pi }{\pi -2 \tan^{-1}[t]}\right]}\end{equation*}
\begin{equation*}x\frac{|\nabla f(x,y)|}{{f(x,y)}}=\frac{2 x \sqrt{\frac{1}{\left(x^2+y^2\right) \left(\pi -2 \tan^{-1}\left[\frac{y}{x}\right]\right)^2}}}{\log\left[\frac{2 \pi }{\pi -2 \tan^{-1}\left[\frac{y}{x}\right]}\right]}=\frac{2 \sqrt{\frac{1}{\left(1+t^2\right) (\pi -2 \tan^{-1}[t])^2}}}{\log\left[\frac{2 \pi }{\pi -2 \tan^{-1}[t]}\right]}\end{equation*}for ![]() $y=t x$. The last expression has its maximum at
$y=t x$. The last expression has its maximum at ![]() $t=-1.4771\dots$, and it is equal to
$t=-1.4771\dots$, and it is equal to ![]() $1.0482\dots$. This implies, in particular, that
$1.0482\dots$. This implies, in particular, that ![]() $f\colon S(0,\infty)\to (0,+\infty)$ is not a contraction with respect to corresponding hyperbolic metrics. It would be of interest to find the best Lipschitz constant in this context.
$f\colon S(0,\infty)\to (0,+\infty)$ is not a contraction with respect to corresponding hyperbolic metrics. It would be of interest to find the best Lipschitz constant in this context.
Acknowledgements
We would like to thank the anonymous referee for very helpful comments that had a significant impact on this paper.
Competing interests
The authors declare none.