Globally F-regular type of the moduli spaces of parabolic symplectic/orthogonal bundles on curves

Abstract

We prove that the moduli spaces of parabolic symplectic/orthogonal bundles on a smooth curve are globally F-regular type. As a consequence, all higher cohomologies of the theta line bundle vanish. During the proof, we develop a method to estimate codimension.

1 Introduction

Let X be a variety over an algebraically closed field of positive characteristic and $F_X: X\rightarrow X$ be the absolute Frobenius map. In [17], Mehta and Ramanathan introduced the notion ‘F-split’: X is said to be F-split if the natural morphism $F_X^{\#}: \mathcal {O}_X\rightarrow F_{X*}\mathcal {O}_X$ splits as an $\mathcal {O}_X$ module homomorphism. Later in [25], Smith studied a special kind of F-split varieties: globally F-regular varieties (see Section 6 for details). F-split varieties and globally F-regular varieties have many nice properties, for example, the higher cohomologies of ample line bundles(nef line bundles in the case of globally F-regular varieties) vanish.

Examples of F-split varieties include flag varieties, toric varieties and many other important varieties in algebraic geometry. In [16], Mehta and Ramadas proved that the moduli space of semistable parabolic rank two vector bundles with fixed determinant on a generic nonsingular projective curve is F-split. They conjectured that the ‘generic’ condition can be removed. Very recently, Sun and Zhou [30] show that the moduli space of semistable parabolic vector bundles with rank smaller than $\dfrac {p}{3}$ for a generic nonsingular projective curve and a generic choice of the divisor D is F-split. On the other hand, as mentioned in [29], this conjecture should be extended into the following: the moduli spaces of semistable parabolic bundles with fixed determinant on any nonsingular projective curve are globally F-regular.

In [29], Sun and Zhou studied the characteristic zero analogy of this extended conjecture. A variety over a field of characteristic zero is said to be of globally F-regular type if its modulo p reduction is globally F-regular for all $p\gg 0$ . They proved that the moduli spaces of semistable parabolic vector bundles on a smooth projective curve over an algebraically closed field of characteristic zero are of globally F-regular type. As an application, they can give a finite-dimensional proof of the so-called Verlinde formula in $\operatorname {GL_n}$ and $\operatorname {SL_n}$ case ([28]).

Globally F-regular type varieties have similar vanishing properties, namely all the higher cohomologies of nef line bundles are vanishing. Unlike the positive characteristic case, in characteristic zero, all Fano varieties with rational singularities are globally F-regular type varieties ([25]). So globally F-regular type varieties can be regarded as a generalization of Fano varieties in characteristic zero, with the vanishing properties retained, and hence it would be both interesting and important to find examples of globally F-regular type varieties.

On the other hand, properties of moduli spaces are central topics in the study of moduli problems. We already know that, for a simple simply connected algebraic group G, the moduli space of semistable G-bundles on a smooth curve is a Fano variety ([13]). However, if one considers the moduli space of semistable G-bundles with parabolic structure on a smooth curve, then one may not get a Fano variety. As mentioned before, in the case of $G=\operatorname {SL_n}$ , Sun and Zhou proved that the moduli spaces of semistable parabolic vector bundles with fixed determinant are globally F-regular type varieties ([29]). So it encourages us to consider globally F-regularity as a reasonable property of moduli spaces of G-bundles with parabolic structure on curves.

In this paper, we consider parabolic symplectic and orthogonal bundles over smooth curves. Our main theorem is the following:

Theorem 1.1 (Main theorem, see Theorem 6.5).

The moduli spaces of semistable parabolic symplectic/orthogonal bundles over any smooth projective curve are globally F-regular type varieties. As a consequence, any higher cohomologies of nef line bundles on these moduli spaces vanish.

We now describe how this paper is organized:

In Section 2, we recall some basics about parabolic vector bundles, parabolic symplectic/orthogonal bundles and the equivalence between parabolic bundles and orbifold bundles.

In Section 3, we construct the moduli space of semistable parabolic symplectic/orthogonal bundles explicitly, using geometric invariant theory. Although the moduli spaces of parabolic G-bundles have been constructed by Bhosle and Ramanathan in [2], here we give an explicit reconstruction using properties of symplectic/orthogonal groups. Our construction enables us to write down the theta line bundle and canonical line bundle explicitly and to do some codimension estimating.

In Section 4, we generalise the methods in [11] to estimate the codimension of an unsemistable locus in a given family, not only for parabolic symplectic/orthogonal bundles but also G-bundles and parabolic vector bundles. Moreover, we also construct a parabolic version for the Quot scheme, a scheme parametrizing all quotients of a given parabolic bundle with fixed parabolic type on a smooth projective curve.

In Section 5, we will firstly define theta line bundles for any family of symplectic/orthogonal bundle then prove that the theta line bundle descends to an ample line bundle on the moduli space under some numerical condition. Moreover, if we require more numerical conditions, we can prove that the theta line bundle admits a square root on the moduli space. Then we evaluate the canonical sheaf on the moduli spaces and show that, under the numerical conditions before, the canonical sheaf is a line bundle and its inverse is isomorphic to the square root of the theta line bundle, hence the moduli spaces are Fano under the numerical conditions.

In Section 6, we recall the definition and properties of globally F-regular type varieties; with the help of key Proposition 6.9, we can prove our main theorem.

2 Basics of parabolic principal bundle over curve

2.1 Parabolic vector bundles and parabolic symplectic/orthogonal bundles

Let C be a smooth projective curve of genus $g\geq 0$ over an algebraically closed field $\mathbb {K}$ of characteristic $0$ . We fix a reduced effective divisor D of C and an integer $K>0$ .

E is a vector bundle of rank r and degree d over C. By a parabolic structure on E, we mean the following:

1. (1) At each $x\in D$ , we have a choice of flag of $E_x$ :

   $$ \begin{align*} 0=F_{l_x}(E_x)\subseteq F_{l_{x}-1}(E_x)\subseteq \cdots \subseteq F_0(E_x)=E_x. \end{align*} $$
   Let $n_i(x)=\operatorname {dim}F_{i-1}(E_x)/F_i(E_x)$ and $\overrightarrow {n}(x)=\big (n_1(x),n_2(x),\cdots ,n_{l_x}(x)\big )$ . Notice that all these filtrations together are equivalent to a filtration:
   $$ \begin{align*} E(-D)=F_l(E)\subseteq F_{l-1}(E)\subseteq \cdots \subseteq F_0(E)=E. \end{align*} $$

2. (2) At each $x\in D$ , we fix a choice of sequence of integers, which are called weights:

   $$ \begin{align*}0\leq a_1(x)<a_2(x)\cdots <a_{l_x}(x) <K.\end{align*} $$
   Put $\overrightarrow {a}(x)=\big (a_1(x),a_2(x),\cdots , a_{l_x}(x)\big )$ .

We say that $\big (E, D, K, \{\overrightarrow {n}(x)\}_{x\in D}, \{\overrightarrow {a}(x)\}_{x\in D}\big )$ , or simply E, is a parabolic vector bundle, and $\sigma =\big (\{\overrightarrow {n}(x)\}_{x\in D}, \{\overrightarrow {a}(x)\}_{x\in D}\big )$ is the parabolic type of E.

For any subbundle F of the vector bundle E, it is clearly that there is an induced parabolic structure on F, with induced flags structures and same weights; similarly, there is an induced parabolic structure on $E/F$ .

Let $E_1$ and $E_2$ be two parabolic vector bundles with same weights, the space of parabolic homomorphisms $\operatorname {Hom}_{par}(E_1,E_2)$ given by $\mathcal {O}_C$ -homomorphisms between $E_1$ and $E_2$ preserving filtrations at each $x\in D$ . We can also define the parabolic sheaf of parabolic homomorphisms $\mathcal {H}om_{par}(E_1,E_2)$ in a similar way, which inherits a parabolic structure naturally. In fact, in [31] Proposition 1.1, it is shown that the category of parabolic bundles is contained in an abelian category with enough injectives. So we have the derived functors of parabolic homomorphism. We use $\operatorname {Ext}^1_{par}(E_1,E_2)$ to denote the space of parabolic extensions.

Definition 2.1. The parabolic degree of E is defined by

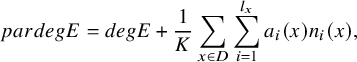$$ \begin{align*}pardegE=degE+\dfrac{1}{K}\sum_{x\in D}\sum_{i=1}^{l_x}a_i(x)n_i(x),\end{align*} $$

and E is said to be stable (resp. semistable) if for all nontrivial subbundle $F\subset E$ , concerning the induced parabolic structure, we have:

$$ \begin{align*}\dfrac{pardegF}{rankF}<\dfrac{pardegE}{rankE}\ \ \ \ \ \ (\text{resp.}\ \leq).\end{align*} $$

Now, let us talk about a family of parabolic vector bundles. Let S be a scheme of finite type over k. A family of parabolic vector bundle with type $\sigma $ over C parametrized by S is a vector bundle $\mathcal {E}$ over $S\times C$ , together with filtrations of vector bundles on $\mathcal {E}_x$ of type $\overrightarrow {n}(x)$ and weights $\overrightarrow {a}(x)$ for each $x\in D$ . As before, such filtrations are equivalent to the following:

$$ \begin{align*}\mathcal{E}\big(-(S\times D)\big)=F_l(\mathcal{E})\subseteq F_{l-1}(\mathcal{E})\subseteq \cdots \subseteq F_0(\mathcal{E})=\mathcal{E}, \end{align*} $$

where $S\times D$ is considered as an effective divisor of $S\times C$ . Following [31], we say $\mathcal {E}$ is a flat family if all $F_i(\mathcal {E})$ are flat families over S.

Definition 2.2. E is a vector bundle of rank r degree d over C. By a symplectic/orthogonal parabolic structure on E, we mean the following:

1. (1) A nondegenerated antisymmetric/symmetric two-form

   $$ \begin{align*}\omega: E\otimes E\longrightarrow \mathcal{O}_C(-D).\end{align*} $$

2. (2) At each $x\in D$ , a choice of flag:

   $$ \begin{align*}0=F_{2l_x+1}(E_x)\subseteq F_{2l_x}(E_x)\subseteq \cdots F_{l_x+1}(E_x)\subseteq F_{l_x}(E_x)\subseteq \cdots \subseteq F_0(E_x)=E_x,\end{align*} $$
   where $F_i(E_x)$ are isotropic subspaces of $E_x$ respect to the form $\omega $ and $F_{2l_x+1-i}(E_x)=F_i(E_x)^{\perp }$ for $l_x+1\leq i \leq 2l_x+1$ .

3. (3) At each $x\in D$ , we fix a choice of weights:

   $$ \begin{align*}0\leq a_1(x)<a_2(x)\cdots <a_{l_x}(x)<a_{l_x+1}(x) <\cdots <a_{2l_x+1}(x) \leq K \end{align*} $$
   satisfying $a_{i}(x)+a_{2l_x+2-i}(x)=K$ , $1\leq i \leq l_x+1$ .

As before, we put $n_i(x)=\operatorname {dim}\big (F_{i-1}(E_x)/F_i(E_x)\big )$ , and

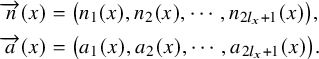$$ \begin{align*} \overrightarrow{n}(x)&=\big(n_1(x),n_2(x),\cdots,n_{2l_x+1}(x)\big),\\ \overrightarrow{a}(x)&=\big(a_1(x),a_2(x),\cdots,a_{2l_x+1}(x)\big). \end{align*} $$

We say that $\big (E, \omega , D, K, \{\overrightarrow {n}(x)\}_{x\in D}, \{\overrightarrow {a}(x)\}_{x\in D}\big )$ , or simply E, is a parabolic symplectic/orthogonal bundle and $\sigma =\big (\{\overrightarrow {n}(x)\}_{x\in D}, \{\overrightarrow {a}(x)\}_{x\in D}\big )$ is the parabolic type of E.

Convention: When talking about parabolic symplectic/orthogonal bundles, we always assume that degD is even.

Remark 2.3.

1. 1. The original definition of parabolic principal bundles is just a principal bundle together with additional structures [22]. Later in [1], Balaji, Biswas and Nagaraj establish a different definition, which shares some nice properties as in the case of parabolic vector bundles, for example, a parabolic symplectic/orthogonal bundle admits an Einstein–Hermitian connection if and only if it is polystable ([4]).

2. 2. The weights satisfy $a_{i}(x)+a_{2l_x+2-i}(x)=K$ because the isomorphism

   $$ \begin{align*}E\longrightarrow E^{\vee}\otimes\mathcal{O}_C(-D)\end{align*} $$
   should be an isomorphism of parabolic bundles.

The parabolic degree of E is given by

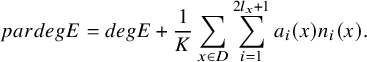$$ \begin{align*} pardegE=degE+\dfrac{1}{K}\sum_{x\in D}\sum_{i=1}^{2l_x+1}a_i(x)n_i(x). \end{align*} $$

By relations between $\overrightarrow {n}(x)$ and $\overrightarrow {a}(x)$ , we see that $pardegE=degE+\frac {r}{2}degD$ , noticing that $\omega : E\otimes E\rightarrow \mathcal {O}_X(-D)$ is nondegenerated, so $E\simeq E^{\vee }(D)$ . Thus, $degE+ \dfrac {r}{2}degD=0$ and then $pardegE=0$ .

For any subbundle F of E, we can define the parabolic degree of F by

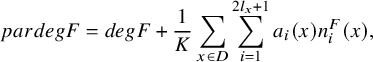$$ \begin{align*}pardegF=degF+\dfrac{1}{K}\sum_{x\in D}\sum_{i=1}^{2l_x+1}a_i(x)n_i^F(x),\end{align*} $$

where $n_i^F(x)=\operatorname {dim}\big (F_{i-1}(E_x)\cap F_x/F_i(E_x)\cap F_x\big )$ .

Definition 2.4. A parabolic symplectic/orthogonal bundle E is said to be stable(resp. semistable) if for all nontrivial isotropic subbundle $F\subset E$ (by isotropic we mean $\omega (F\otimes F)=0$ ), we have

$$ \begin{align*} pardegF<0 \ \ \ \ (\text{resp.}\ \leq). \end{align*} $$

Lemma 2.5. A parabolic symplectic/orthogonal bundle is semistable if and only if for any subbundle F, not necessarily isotropic, we have $pardegF\leq 0$ , that is, semistable as a parabolic vector bundle.

Proof. If E is semistable as a parabolic vector bundle, then it is a semistable parabolic symplectic/orthogonal bundle by definition.

Conversely, let E be a unstable parabolic vector bundle. Let

$$ \begin{align*}\mathrm{HN}:0=E_0\subset E_1\subset\cdots\subset E_t=E \end{align*} $$

be the parabolic $\mu $ -Harder–Narasimhan filtration of the parabolic bundle $E.$ Then the dual filtration

$$ \begin{align*} \mathrm{HN}^{\perp}:0=E_t^{\perp}\subset E_{t-1}^{\perp}\subset\cdots\subset E_0^{\perp}=E \end{align*} $$

is again the $\mu $ -Harder–Narasimhan filtration. So we must have $E_{t-i}=E_i^{\perp }$ by the uniqueness of the $\mu $ -Harder–Narasimhan filtration of a parabolic vector bundle. This implies that the maximal destabilizer $E_1$ is isotropic, that is, E is an unstable parabolic symplectic/orthogonal bundle.

In positive characterictic case, the Harder–Narasimhan filtration of a bundle E satisfies the following stationary property: Each quotient $E_i/E_{i-1}$ of Harder–Narasimhan filtration of $(F_C^{*})^k(E)$ is strongly semistable for $k\gg 0.$ Please refer to [7] and [8] for the applications of this property to the study of surface in positive characteristic.

2.2 Equivalence between parabolic bundles and orbifold bundles

There is an interesting and useful correspondence between parabolic bundles and orbifold bundles, which is developed in [18] and [3] for the general case. We will recall the correspondence briefly as follows:

Given $C, D, K$ as before, by Kawamata covering, there is a smooth projective curve Y and a morphism $p: Y\rightarrow C$ such that p is only ramified over D with $p^{*}D=K\sum _{x\in D}p^{-1}(x)$ ; moreover, if we put $\Gamma =\operatorname {Gal}\big (Rat(Y)/Rat(C)\big )$ to be the Galois group, then p is exactly the quotient map of Y by $\Gamma $ .

Definition 2.6. An orbifold bundle over Y is a vector bundle W over Y such that the action of $\Gamma $ lifts to W.

And an orbifold symplectic/orthogonal bundle is an orbifold bundle such that the correspondence two-form $\omega $ is a morphism of orbifold bundles.

Given an orbifold bundle W, for any $y=p^{-1}(x)\in p^{*}D$ , the stabilizer $\Gamma _y$ , which is a cyclic group of order K, acts on the fiber $W_y$ by some representation (after choosing suitable basis):

$$ \begin{align*}\xi_K\longmapsto \operatorname{diag}\{\xi_K^{a_1(x)},\cdots,\xi_K^{a_1(x)},\xi_K^{a_2(x)},\cdots,\xi_K^{a_{l_x}(x)}\},\end{align*} $$

where $0\leq a_1(x)< a_2(x)<\cdots <a_{l_x}(x)< K$ are integers, $\xi _K$ is the K-th root of unity and the multiplicity of $\xi _K^{a_i(x)}$ is given by $n_i(x)$ . Similarly in the definition of parabolic bundle, we use $\sigma =\big (\{\overrightarrow {n}(x)\}_{x\in D}, \{\overrightarrow {a}(x)\}_{x\in D}\big )$ to denote the type of an orbifold bundle W.

Proposition 2.7 ([18],[3]).

There is an equivalence between the category of orbifold bundles over Y with type $\sigma $ and the category of parabolic vector bundles over C with type $\sigma $ .

Roughly speaking, given an orbifold bundle W, then $(p_*W)^{\Gamma }$ is a parabolic vector bundle over C, with parabolic structures given by the action of stabilizers. Conversely, E is a parabolic vector bundle. We put $W_1=p^{*}E$ . After some elementary transformations of $W_1$ , we would have an orbifold bundle of type $\sigma $ . Moreover, we have

$$ \begin{align*} \#\Gamma\cdot pardegE=degW \end{align*} $$

and E is semistable as a parabolic bundle if and only if W is semistable as an orbifold bundle.

Now, we will talk about orbifold symplectic/orthogonal bundles over Y: An orbifold symplectic/orthogonal bundles is a/an symplectic/orthogonal bundle W over Y such that the action of $\Gamma $ lifts to W compatible with the symplectic/orthogonal structure. For any $y=p^{-1}(x)\in p*(D)$ , the action of stabilizer is given by:

$$ \begin{align*}\xi_K\longmapsto \operatorname{diag}\{\xi_K^{a_1(x)},\cdots,\xi_K^{a_1(x)},\xi_K^{a_2(x)},\cdots,\xi_K^{a_{l_x}(x)},\xi_K^{-a_{l_x}(x)},\cdots, \xi_K^{-a_1(x)} \}. \end{align*} $$

As before, we use $\sigma $ to denote the type of this orbifold symplectic/orthogonal bundle. Similarly, we have:

Proposition 2.8. There is an equivalence between the category of orbifold symplectic/orthogonal bundles over Y with type $\sigma $ and the category of parabolic symplectic/orthogonal bundles over C with type $\sigma $ . Moreover, this equivalence induces an equivalence between orbifold isotropic subbundles and isotropic subbundles.

Proof. See [4] Subsection 2.4.

Remark 2.9. Note that $(p_*\mathcal {O}_Y)^{\Gamma }=\mathcal {O}_C(-D),$ so a $\Gamma $ -equivariant two-form $\omega : W\otimes W\longrightarrow \mathcal {O}_Y$ over Y descends to a two-form $(p_*\omega )^{\Gamma }: (p_*W)^{\Gamma }\otimes (p_*W)^{\Gamma }\longrightarrow \mathcal {O}_C(-D).$ That’s why, when defining parabolic symplectic/orthogonal bundles, we require the two form to take value in $\mathcal {O}_C(-D)$ .

On the other hand, let $\omega :E\otimes E\longrightarrow L$ be a two form taking value in a line bundle L of even degree. We can take a line bundle N such that $N^{\otimes 2}\cong L^{\vee },$ then we have a two form takes value in $\mathcal {O}_C$ on $E\otimes N.$ So two forms taking value in different line bundles are equivalent in this sense.

3 Moduli space of semistable parabolic symplectic/orthogonal bundles

In this section, we construct the moduli space of semistable parabolic symplectic/orthogonal bundles with fixed parabolic type $\sigma $ over C. Although the moduli space is already constructed in [2] for general algebraic groups, for our purpose, we will construct the moduli spaces explicitly using Geometric Invariant Theory (GIT) constructions. The construction was based on the work of [9] which constructs the moduli space of symplectic/orthogonal bundles.

We will use E to denote a parabolic symplectic/orthogonal bundle of rank r, degree d and parabolic type $\sigma $ . We will fix an ample line bundle $\mathcal O(1)$ on C with degree c, then the Hilbert polynomial of E is $P_{E}(m)=crm+\chi (E).$ We fix an polynomial $P.$

Firstly, we notice that by Lemma 2.3 of [9], the class of semistable parabolic symplectic/orthogonal bundles with fixed rank, degree and parabolic type are bounded. So we may choose an integer $N_0$ large enough so that $E(N)$ is globally generated for all semistable parabolic bundle E with fixed Hilbert polynomial P and all integers $N\geq N_0$ ; which means, we have a quotient

$$\begin{align*}q:V\otimes \mathcal O_X(-N) \twoheadrightarrow E,\end{align*}$$

where V is the vector space $\mathbb {K}^{P(N)}$ .

Let Q be the Quot scheme of quotients of $V\otimes \mathcal O_X(-N)$ with Hilbert polynomial P.

The symplectic/orthogonal structure on E will induce a morphism:

$$\begin{align*}(V\otimes \mathcal{O}_C)\otimes (V\otimes \mathcal{O}_C) \longrightarrow E(N)\otimes E(N) \longrightarrow \mathcal O_C(2N-D),\end{align*}$$

which is equivalent to a bilinear map on V:

$$ \begin{align*}\phi: V\otimes V\longrightarrow \mathrm{ H}^0(C, \mathcal{O}_C(2N-D)),\end{align*} $$

here $\mathcal {O}_C(2N-D)=\mathcal {O}_C(2N)\otimes \mathcal {O}_C(-D)$ and we use H to denote the space $\mathrm {H}^0(C, \mathcal {O}_C(2N-D))$ .

Now, we let $Z\subset Q\times \mathbb {P}Hom(V\otimes V,H)$ be the closed subscheme such that every closed point ( $q:V\otimes \mathcal O_X(-N) \twoheadrightarrow E,\phi :V\otimes V\rightarrow H$ ) of Z represents a twisted symplectic/orthogonal bundle E.

So over $Z\times C$ , we have a universal quotient $q:V\otimes p_C^{*}\mathcal {O}_C(-N)\rightarrow \mathcal {E}\rightarrow 0$ and a nondegenerated antisymmetric/symmetric two-form $\omega : \mathcal {E}\otimes \mathcal {E}\rightarrow p_C^{*}\mathcal {O}_C(-D),$ where $p_C: Z\times C\rightarrow C$ is the projection. For any $x\in D$ , let $\mathcal E_x$ be the restriction of $\mathcal E$ on $Z\times \{x\}\cong Z$ and we put $Flag_{\vec n(x)}(\mathcal E_x)\rightarrow Z$ be the relative isotropic flag scheme of type $\vec n(x)$ .

Let $\mathcal R:= \underset {x\in D}{\times _Z}Flag_{\vec n(x)}(\mathcal E_x)\rightarrow Z,$ then a closed point of $\mathcal R$ is represented by

$$ \begin{align*}((q,\phi),(q_1(x),q_2(x),\dots,q_{2l_x}(x))_{x\in D}),\end{align*} $$

where $(q,\phi )$ is a point of Z, and $q_i(x)$ is the composition $q_i(x):V \otimes \mathcal O_X(-N) \rightarrow E \rightarrow E_x\twoheadrightarrow Q_i(x)$ . We denote by $Q_i(x)$ the quotients ${E_x}/{F_i(E)_x}$ , and let $r_i(x)=dimQ_i(x).$

For m large enough, let $\mathcal {G}=Grass_{P(m)}(V\otimes W_m)\times \mathbb {P}Hom(V\otimes V,H)\times \textbf {Flag}$ , where $W_m= H^0(V\otimes \mathcal {O}(m-N))$ , and $\textbf {Flag}$ is defined as:

$$\begin{align*}\textbf{Flag}=\prod_{x\in D}\big(Grass_{r_1(x)}(V) \times \dots \times Grass_{r_{2l_x}(x)}(V)\big).\end{align*}$$

Now, consider the $SL(V)-$ equivariant embedding

$$\begin{align*}\mathcal R \hookrightarrow \mathcal G=Grass_{P(m)}(V\otimes W_m)\times \mathbb P Hom(V\otimes V,H)\times \textbf{Flag},\end{align*}$$

which maps the point $((q,\phi ),(q_1(x),q_2(x),\dots ,q_{2l_x}(x))_{x\in D})$ of $\mathcal R$ to the point

$$ \begin{align*}(g,\phi,(g_1(x),g_2(x),\dots,g_{2l_x}(x))_{x\in D})\end{align*} $$

of $\mathcal G$ , where $g: V\otimes W_m\twoheadrightarrow H^0(E(m-N))$ and $ g_i(x): V\twoheadrightarrow Q_i(x)$ .

We give the polarisation on $\mathcal G$ by:

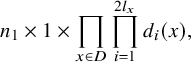$$\begin{align*}n_1 \times 1 \times \prod_{x\in D} \prod_{i=1}^{ 2l_x}d_i(x),\end{align*}$$

where $n_1= {\frac {l+KcN}{c(m-N)}} , d_i(x)=a_{i+1}(x)-a_i(x)$ and $l$ is the number satisfying

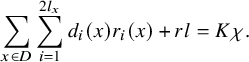$$\begin{align*}{\sum_{x\in D}\sum_{i=1}^{2l_x}d_i(x)r_i(x)+rl=K\chi}.\end{align*}$$

We will analyse the action of $SL(V)$ on $\mathcal {R}$ using a method in [9]. Let $\mathcal {R}^{s}$ (resp. $\mathcal {R}^{ss}$ ) to denote the sublocus of $\mathcal {R}$ where the corresponding parabolic symplectic/orthogonal bundles are stable(resp. semistable) and the map $\mathrm {H}^0(q):V\rightarrow \mathrm {H}^0(C, E(m))$ is an isomorphism. We are going to show $\mathcal {R}^{s}$ (respectively, $\mathcal {R}^{ss}$ ) is the stable (respectively, semistable) locus of the action in the sense of GIT. Firstly, let us recall a definition in [9]:

Definition 3.1. A weighted filtration $(E_{\bullet}, m_{\bullet})$ of a parabolic symplectic/orthogonal bundle E consists of

1. (1) a filtration of subsheaves

   $$\begin{align*}0\subset E_1 \subset E_2 \subset \dots \subset E_t \subset E_{t+1}=E. \end{align*}$$
   We denote $rk(E_i)$ by $s_i$ ;

2. (2) a sequence of positive numbers $m_1,m_2 \dots ,m_t$ , called the weights of this filtration.

Let $\Gamma =\sum _{i=1}^{t}m_i \Gamma ^{s_i}\in \mathbb C^r$ , where

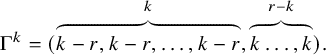$$\begin{align*}\Gamma^k=( \overbrace{k-r,k-r,\dots ,k-r}^{k},\overbrace{k\dots ,k}^{r-k}).\end{align*}$$

Now, given a weighted filtration $(E_{\bullet}, m_{\bullet})$ of a parabolic symplectic/orthogonal bundle E, let $\Gamma _{j}$ be the j-th component of $\Gamma $ , and we define

$$\begin{align*}\mu(\omega,E_{\bullet}, m_{\bullet}):=min \{ \Gamma_{s_{i_1}}+\Gamma_{s_{i_2}} : \omega \vert_{E_{i_1} \otimes E_{i_2}} \neq 0\}. \end{align*}$$

We have the following result:

Lemma 3.2 ([9], Lemma 5.6).

If $\omega $ is nondegenerate, then $\mu (\omega ,E_{\bullet}, m_{\bullet})\leq 0$ .

In the following, we use Hilbert–Mumford criterion ([20, Theorem 2.1]) to determine the (semi)stable locus for the action of $SL(V)$ of $\mathcal {R}$ .

Proposition 3.3. A point $((q,\phi ),(q_1(x),q_2(x),\dots ,q_{2l_x}(x))_{x\in D})$ of $\mathcal R$ is GIT stable (resp. GIT semistable) for the action of $SL(V)$ , with respect to the polarisation defined in Definition 2.1, if and only if for all weighted filtration $(E_{\bullet}, m_{\bullet})$ , we have

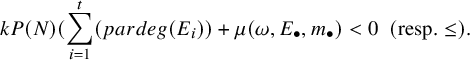$$\begin{align*}kP(N)(\sum_{i=1}^{t}(pardeg(E_i))+\mu(\omega,E_{\bullet}, m_{\bullet})<0\ \ (\text{resp.} \leq).\end{align*}$$

Proof. By the Hilbert–Mumford criterion, a point $((q,\phi ),(q_1(x),q_2(x),\dots ,q_{2l_x}(x))_{x\in D})$ is GIT semistable if and only if for any one parameter subgroup $\lambda : \mathbb {G}_m \rightarrow SL(V)$ , the corresponding Hilbert–Mumford weight is greater or equal than zero. But a one parameter subgroup of $SL(V)$ is equivalent to a weighted filtration of V and hence gives a weighted filtration $(E_{\bullet}, m_{\bullet})$ for the corresponding bundle E. Then a similar computation as in [9, Proposition 3.5] and [27, Proposition 2.9] shows that the corresponding Hilbert–Mumford weight of the weighted filtration is given by

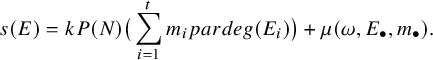$$\begin{align*}s(E)=kP(N) \big(\sum_{i=1}^{t}m_i pardeg(E_i)\big)+\mu(\omega, E_{\bullet}, m_{\bullet} ).\end{align*}$$

Hence, the point is GIT stable (resp. GIT semistable) if and only if $s(E)<(\text {resp.}\leq )\ 0 $ .

Proposition 3.4. A parabolic symplectic/orthogonal bundle E is stable(resp. semistable) if and only if the correspondence point $((q,\phi ),(q_1(x),q_2(x),\dots ,q_{2l_x}(x))_{x\in D})$ of $\mathcal R$ is GIT stable(resp. semistable) for the action of $SL(V)$ .

Proof. Let E be a stable(resp. semistable) bundle. For any weighted filtration $(E_{\bullet}, m_{\bullet})$ , we have $pardeg(E_i)<0\ (\text { resp.}\ \leq )$ by Lemma 2.5. Furthermore,by Lemma 3.2, $\mu (\omega , E_{\bullet}, m_{\bullet})\leq 0$ , hence

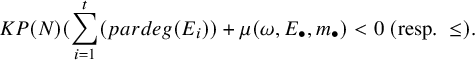$$\begin{align*}KP(N)(\sum_{i=1}^{t}(pardeg(E_i))+\mu(\omega,E_{\bullet},m_{\bullet})<0\ (\text{resp.}\ \leq).\end{align*}$$

By Proposition 3.3, this tells that the corresponding point $((q,\phi ),(q_1(x),q_2(x),\dots ,q_{2l_x}(x))_{x\in D})$ of $\mathcal R$ is GIT stable(resp. semistable).

Conversely, let E be a parabolic symplectic/orthogonal bundle such that the corresponding point $((q,\phi ),(q_1(x),q_2(x),\dots ,q_{2l_x}(x))_{x\in D})$ is GIT stable(resp. GIT semistable). We want to show that E is a stable (resp. semistable). That is, for any isotropic subbundle F of E, we have $pardeg(F)<0\ (\text {resp.}\ \leq )$ .

Since E is stable(resp. semistable), the inequality in Proposition 3.3 must hold for all weighted filtrations $(E_{\bullet}, m_{\bullet})$ . In particular, if we take the weighted filtration as: $0 \subset F \subset F^{\perp } \subset E $ and weights $m_1=m_2=1$ , then the inequality becomes

$$\begin{align*}KP(N)((pardeg(F)+pardeg(F^{\perp}))+\mu(\omega, E_{\bullet}, m_{\bullet})<0\ (\text{ resp.}\ \leq).\end{align*}$$

However, in this case we have $\mu (\omega ,E_{\bullet},m_{\bullet})=0$ and $pardeg(F)=pardeg(F^{\perp })$ , hence we have $pardeg(F)<0\ (\text {resp.}\ \leq ).$

Now, let $\mathcal {R}^{ss}\subset \mathcal R$ be the open set of $\mathcal R$ which consists of semistable parabolic orthogonal(symplectic,resp) sheaves. Let $ M_{G,P}=\mathcal R^{ss}//SL(V)$ be the GIT quotient, then we have:

Theorem 3.5. $M_{G,P}$ is the coarse moduli space of semistable parabolic symplectic/orthogonal sheaves of rank r and degree d with fixed parabolic type $\sigma $ . Moreover, $M_{G,P}$ is a normal Cohen–Macaulay projective variety, with only rational singularities.

Proof. First of all, we can show that $\mathcal {R}^{ss}$ is smooth. In fact, let $Q_F$ be the open subscheme of Q consisting of quotients $[q:V\otimes \mathcal O_X(-N) \twoheadrightarrow E]\in Q$ such that $H^1(E(N))=0$ . Let $Z_F$ be the inverse image of $Q_F$ under the projection $Z \rightarrow Q$ and $R_F$ be the inverse image of $Z_F$ under the projection $R \rightarrow Z$ . Then $Z_F$ is smooth by [22, Lemma 4.13.3]. Therefore, $\mathcal {R}_F$ is smooth because it is a flag bundle over $Z_F$ . Thus, $\mathcal {R}^{ss}$ is smooth as it is an open subscheme of $\mathcal {R}_F$ .

Since $\mathcal {R}^{ss}$ is smooth, especially $\mathcal {R}^{ss}$ is normal with only rational singularities so is its GIT quotient $M_{G,P}$ . Finally, the fact that $\mathcal {R}^{ss}$ is regular implies that $M_{G,P}$ is Cohen–Macaulay (see [19]).

4 Codimention estimate

In this section, we fix S to be a scheme of finite type over k. Let $\mathcal {E}$ be a flat family of vector bundle, principal G-bundle, parabolic vector bundle or parabolic symplectic/orthogonal bundle over C parametrized by S. Under certain conditions, we want to estimate the codimension of the unstable (unsemistable) locus, that is, the locally closed subscheme $S^{us}\subset S$ ( $S^{uss}\subset S$ ) parametrizing all $\mathcal {E}_t$ which is not stable (semistable). Our main method is a generalization of [11].

4.1 The case of vector bundle and principal G-bundle

In fact, the cases of vector bundle and principal G-bundle have been already done in [11] and [13]. For later use, we reformulate the results and give a short proof if necessary.

We begin with the following proposition:

Proposition 4.1. $\mathcal {E}$ is a flat family of vector bundles over $S\times C$ . Let $\phi : Q\rightarrow S$ be the relative Quot-scheme parametrizing all flat quotients of $\mathcal {E}$ with certain fixed rank and degree. For any $s\in S$ and $q\in \phi ^{-1}(s)$ , corresponding to exact sequence:

$$ \begin{align*}0\longrightarrow F\longrightarrow \mathcal{E}_s\longrightarrow G\longrightarrow 0,\end{align*} $$

we have the following exact sequence:

(4.1) $$ \begin{align} 0\longrightarrow \operatorname{Hom}(F,G)\longrightarrow T_qQ\longrightarrow T_sS\longrightarrow \operatorname{Ext}^1(F,G). \end{align} $$

Proof. See [10] Proposition 2.2.7.

Let E be a vector bundle over C, the classical Harder–Narasimhan filtration and Jordan–Holder filtration show that if E is not stable(resp. semistable), then there is a maximal stable subbundle $F_0\subset E$ with the property $\operatorname {deg}\mathcal {H}om(F_0,E/F_0)\leq 0$ (resp. $< 0$ ). $F_0$ is taken to be the first term of the Jordan–Holder filtration of the maximal destabilizing subbundle of E (so different choice of $F_0$ have the same slope). Moreover, if we say $F_0$ is of type $\mu =(r',d')$ , that is, F is of rank $r'$ and degree $d'$ , Then for a flat family of vector bundle $\mathcal {E}$ over $S\times C$ , the locus $S^{\mu }\subset S$ parametrizing $\mathcal {E}_t$ having a subbundle described above with type $\mu $ is locally closed and nonempty for finitely many $\mu $ .

Similarly, properties hold for principal G-bundles. Let E be a principal G-bundle, then there is a unique standard parabolic subgroup P and a unique reduction $E_P$ so that if we denote $E_{\mathsf {s}}$ to be the vector bundle associated to $E_P$ by the natural representation of P on the vector space $\mathsf {s}:=\mathsf {g}/ \mathsf {p}$ , where $\mathsf {g}$ and $\mathsf {p}$ are Lie algebras of G and P, then $\operatorname {deg}E_{\mathsf {s}}<0$ . Moreover, we have similar concept of $S^{\mu }$ . For details, please refer to [13] Proposition 3.7.

Proposition 4.2. Let $\mathcal {E}$ be a flat family of vector bundles or principal G-bundles over $S\times C$ . Assume that for each closed point $t\in S$ , the Kodaira–Spencer maps

$$ \begin{align*}T_tS\rightarrow \operatorname{Ext}^1(\mathcal{E}_t, \mathcal{E}_t)\ \ \ \ \text{or}\ \ \ \ T_tS\rightarrow H^1(C, \mathcal{E}_t(Ad))\end{align*} $$

are surjective. Then:

1. (1) In the vector bundle case, for any $s\in S^{\mu }$ , the normal space $N_sS^{\mu }$ is isomorphic to $\operatorname {Ext}^1(F_0,\mathcal {E}_s/F_0)$ , where $F_0$ is a maximal stable bundle described above.

2. (2) In the principal G-bundles case, for any $s\in S^{\mu }$ , the normal space $N_sS^{\mu }$ is isomorphic to $H^1(C, \mathcal {E}_{s,\mathsf {s}})$ where $\mathcal {E}_{s,\mathsf {s}}$ is described above.

Proof. For the vector bundle case, we first consider the Quot-scheme $\phi :Q\rightarrow S$ parametrizing all subbundles of type $\mu $ , then analyse the exact sequence 4.1. Firstly, the image of $\phi $ covers $S^{\mu }$ ; we see that the map $T_qQ\rightarrow T_sS$ factors as $T_qQ\twoheadrightarrow T_sS^{\mu } \hookrightarrow T_sS$ . Secondly, by the proof of exactness of 4.1, we see that the map $T_sS\rightarrow \operatorname {Ext}^1(F_0,\mathcal {E}_s/F_0)$ indeed factors as

$$ \begin{align*}T_sS\rightarrow\operatorname{Ext}^1(\mathcal{E}_s, \mathcal{E}_s) \rightarrow \operatorname{Ext}^1(F_0,\mathcal{E}_s/F_0).\end{align*} $$

The first map is Kodaira–Spencer map which is surjective by assumption; the second map is induced by the exact sequence:

$$ \begin{align*}0\longrightarrow F_0\longrightarrow \mathcal{E}_s \longrightarrow \mathcal{E}_s/F_0 \longrightarrow0,\end{align*} $$

which is surjective naturally. Thus, we see that $\operatorname {Ext}^1(F_0,\mathcal {E}_s/F_0)$ is isomorphic to the cokernel of $T_qQ\rightarrow T_sS$ , that is, the normal space $N_sS^{\mu }$ .

The principal bundle case is similar, except we need a variety to parametrize all reductions to P. But this is already done in [22] Lemma 4.8.1. It is an open subscheme $\mathcal {U}$ of $\operatorname {Hilb}_{(\mathcal {E}/P)_{/S}}$ , parametrizing all sections of $\mathcal {E}/P\rightarrow S$ . Now, we apply Proposition 4.1 to this $\mathcal {U}$ . With similar method above, we have our proposition.

Corollary 4.3. With the same notation and assumptions as above, if we assume S is smooth, we have:

1. (1) In the vector bundle case, the rank of $\mathcal {E}$ is assumed to be r, then we have

   $$ \begin{align*} \operatorname{codim}(S^{us})&\geq (r-1)(g-1),\\ \operatorname{codim}(S^{uss})&> (r-1)(g-1). \end{align*} $$

2. (2) In the principal bundle case, we have

   $$ \begin{align*} \operatorname{codim}(S^{us})&\geq \operatorname{rank}(\mathcal{E}_{t,\mathsf{s}})(g-1),\\ \operatorname{codim}(S^{uss})&> \operatorname{rank}(\mathcal{E}_{t,\mathsf{s}})(g-1). \end{align*} $$

Proof. Since $S^{\mu }$ is nonempty for only finitely many $\mu $ , by proposition above, we only need to calculate $\operatorname {dim}\operatorname {Ext}^1(F_0,\mathcal {E}_t/F_0)$ and $\operatorname {dim}H^1(C, \mathcal {E}_{t,\mathsf {s}})$ . Using Riemann–Roch, we have

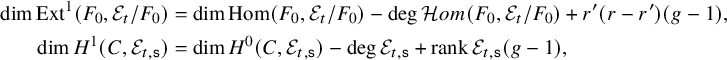$$ \begin{align*} \operatorname{dim}\operatorname{Ext}^1(F_0,\mathcal{E}_t/F_0)&=\operatorname{dim}\operatorname{Hom}(F_0,\mathcal{E}_t/F_0)-\operatorname{deg}\mathcal{H} om(F_0,\mathcal{E}_t/F_0)+r'(r-r')(g-1),\\ \operatorname{dim}H^1(C, \mathcal{E}_{t,\mathsf{s}})&=\operatorname{dim}H^0(C, \mathcal{E}_{t,\mathsf{s}})-\operatorname{deg}\mathcal{E}_{t,\mathsf{s}}+\operatorname{rank}\mathcal{E}_{t,\mathsf{s}}(g-1), \end{align*} $$

where $r'$ is the rank of F. Thus, our corollary holds by analyse of degrees of $\mathcal {H} om(F_0,\mathcal {E}_t/F_0)$ and $\mathcal {E}_{t,\mathsf {s}}$ before.

4.2 The case of parabolic vector bundle

We fix $\mathcal {E}$ to be a flat family of parabolic vector bundles of type $\sigma $ over $S\times C$ . To apply our method to the parabolic vector bundle case, we need to construct an S-scheme parametrizing all flat quotients of $\mathcal {E}$ , with fixed parabolic type $\sigma '$ .

We begin with a functor

$$ \begin{align*}\mathsf{F}:(Sch/S)^{op}\longrightarrow (Set)\end{align*} $$

as follows: For any $f:T\rightarrow S$ , $\mathsf {F}(f:T\rightarrow S)$ is the set of isomorphism classes of all quotients $f^{*}_C\mathcal {E}\rightarrow \mathcal {G}\rightarrow 0$ such that the induced parabolic structure on $\mathcal {G}$ makes $\mathcal {G}$ a flat family of parabolic vector bundle of rank $r'$ and degree $d'$ with fixed type $\sigma '$ .

Proposition 4.4. $\mathsf {F}$ is represented by a finite type scheme $\phi _P: Q_P\rightarrow S$ .

Proof. Using Proposition 2.7, we will translate parabolic bundle and orbifold bundle interchangeably.

$\mathcal {E}$ gives a flat family of orbifold bundle $\mathcal {W}$ over $S\times Y$ . Firstly, we consider the Quot-scheme $Q\rightarrow S$ , parametrizing all flat quotients of $\mathcal {W}$ with certain fixed rank and degree. Secondly, since $\mathcal {W}$ is an orbifold bundle, we see that $\Gamma $ acts on Q, and the closed subscheme $Q^{\Gamma }$ of $\Gamma $ -invariant points parametrizes all the orbifold quotients of $\mathcal {W}$ ([24] Chapter 2 Section 2). At last, by [24] again, there is an open subscheme $Q_P\subset Q^{\Gamma }$ , parametrizing all locally free orbifold quotients with fixed type $\sigma '$ . We claim that $Q_P$ represents $\mathsf {F}$ .

For any $f: T\rightarrow S$ , and any quotient $f^{*}_C\mathcal {E}\rightarrow \mathcal {G}\rightarrow 0$ , using the correspondence in Proposition 2.7, we see easily that there is an S-morphism: $T\rightarrow Q_P$ . Conversely, Given an S-morphism $\varphi : T\rightarrow Q_P$ , this would give a flat orbifold bundle quotient $f_Y^{*}\mathcal {W}\rightarrow \tilde {\mathcal {G}}\rightarrow 0$ . By our correspondence, we have a quotient

$$ \begin{align*}f^{*}_C\mathcal{E}\rightarrow \mathcal{G}\rightarrow 0,\end{align*} $$

where $\mathcal {G}$ is a flat family of parabolic vector bundles with type $\sigma '$ . Notice that this is a quotient since taking $\Gamma $ invariant sections of $\mathbb {C}$ -modules is an exact functor.

Remark 4.5. In [6] Section 3, a similar scheme is constructed in a different way.

Corollary 4.6. For any $s\in S$ and $q\in \phi _P^{-1}(s)$ , corresponding to exact sequence:

$$ \begin{align*}0\longrightarrow F\longrightarrow \mathcal{E}_s\longrightarrow G\longrightarrow 0,\end{align*} $$

then we have an exact sequence:

$$ \begin{align*}0\longrightarrow \operatorname{Hom}_{par}(F,G)\longrightarrow T_qQ_P\longrightarrow T_sS\longrightarrow \operatorname{Ext}^1_{par}(F, G).\end{align*} $$

Proof. Let $0\rightarrow \tilde {F} \rightarrow \mathcal {W}_s\rightarrow \tilde {G} \rightarrow 0$ be the corresponding exact sequence of orbifold bundles over Y. When we regard q as a point of Q, apply the exact sequence 4.1, we have an exact sequence:

$$ \begin{align*}0\longrightarrow \operatorname{Hom}(\tilde{F},\tilde{G})\longrightarrow T_qQ\longrightarrow T_sS\longrightarrow \operatorname{Ext}^1(\tilde{F},\tilde{G}).\end{align*} $$

However, this sequence is in fact a $\Gamma $ -exact sequence, Thus, we have:

$$ \begin{align*}0\longrightarrow \operatorname{Hom}(\tilde{F},\tilde{G})^{\Gamma}\longrightarrow (T_qQ)^{\Gamma}\longrightarrow T_sS\longrightarrow \operatorname{Ext}^1(\tilde{F},\tilde{G})^{\Gamma},\end{align*} $$

which is exact since taking $\Gamma $ -invariant sections of k-modules is an exact functor since the characteristic of k is $0$ . Now, it is known that $\operatorname {Hom}(\tilde {F},\tilde {G})^{\Gamma }=\operatorname {Hom}_{par}(F,G)$ and $(T_qQ)^{\Gamma }=T_qQ_P$ . Finally, spectral sequence argument tells $\operatorname {Ext}^1(\tilde {F},\tilde {G})^{\Gamma }=\operatorname {Ext}^1_{par}(F, G)$ , and we are done.

Before going further, we mention that there are Harder–Narasimhan filtration and Jordan–Holder filtration for parabolic bundles. So similarly to the previous subsection, for a parabolic bundle which is not stable (resp. semistable), there is a maximal stable subbundle $F_0$ such that $pardeg\mathcal {H}om_{par}(F_0,E/F_0)\leq 0$ (resp. $<0$ ). Moreover, for a family of parabolic vector bundle as above, $S^{\mu }$ defined as before, is locally closed and nonempty for finitely many $\mu $ .

Proposition 4.7. Assume that for any $t\in S$ , the Kodaira–Spencer map

$$ \begin{align*}T_tS\longrightarrow \operatorname{Ext}^1_{par}(\mathcal{E}_t,\mathcal{E}_t)\end{align*} $$

is surjective. Let $S^{\mu }\subset S$ be the locally closed described before. Then for any $s\in S^{\mu }$ , we have $N_sS^{\mu }\cong \operatorname {Ext}^1_{par}(F_0,\mathcal {E}_s/F_0)$ .

Proof. Similar as Proposition 4.2.

Corollary 4.8. With same assumption as above, assuming that S is smooth and $\operatorname {rank}\ \mathcal {E}=r$ , we have

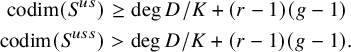$$ \begin{align*} \operatorname{codim}(S^{us})&\geq \operatorname{deg}D/K+(r-1)(g-1)\\ \operatorname{codim}(S^{uss})&> \operatorname{deg}D/K+(r-1)(g-1). \end{align*} $$

Proof. As before, it suffice to estimate $\operatorname {dim}\operatorname {Ext}^1_{par}(F_0,\mathcal {E}_s/F_0)$ . By [31], we have $\operatorname {Ext}^1_{par}(F_0,\mathcal {E}_s/F_0 )=H^1(C, \mathcal {H}om_{par}(F_0,\mathcal {E}_s/F_0))$ , so

$$ \begin{align*}\operatorname{dim}\operatorname{Ext}^1_{par}(F_0,\mathcal{E}_s/F_0)=\operatorname{dim}\operatorname{Hom}_{par}(F_0,\mathcal{E}_s/F_0)-\operatorname{deg}\mathcal{H}om_{par}(F_0,\mathcal{E}_s/F_0)+r'(r-r')(g-1).\end{align*} $$

Since $\operatorname {pardeg}\mathcal {H}om_{par}(F_0,\mathcal {E}_s/F_0)\leq 0$ . We see that $-\operatorname {deg}\mathcal {H}om_{par}(F_0,\mathcal {E}_s/F_0)\geq \operatorname {deg}D/K$ . This would give our results.

Remark 4.9. Similar results have been given in [26] Proposition 5.1 by a different method.

4.3 The case of parabolic symplectic/orthogonal bundle

The case of parabolic symplectic/orthogonal bundles is similar to those in former two sections, but we need define some notions first.

Let E be a parabolic symplectic bundle over C and W be the corresponding orbifold symplectic bundle over Y. By the constructions before, we have $W(Ad)$ and $W_{\mathsf {s}}$ for $\mathsf {s}=\mathsf {g}/\mathsf {p}$ . W is an orbifold symplectic bundle, so $W(Ad)$ and $W_{\mathsf {s}}$ are both orbifold vector bundles over Y. We use $E(Ad)$ and $E_{\mathsf {s}}$ to denote corresponding parabolic vector bundles over C.

For any family of parabolic symplectic bundle $\mathcal {E}$ over C parametrized by a scheme S, let $\mathcal {W}$ be the corresponding orbifold symplectic bundle on $S\times Y$ . For any $t\in S$ , we have the Kodaira–Spencer map

$$ \begin{align*}T_tS\longrightarrow \mathrm{H}^1(Y, \mathcal{W}_t(Ad))\end{align*} $$

for $\mathcal {W}$ . This map is obviously $\Gamma $ -invariant, so we have

$$ \begin{align*}T_tS\longrightarrow \mathrm{H}^1(Y, \mathcal{W}_t(Ad))^{\Gamma}=\mathrm{H}^1(C, \mathcal{E}_t(Ad)).\end{align*} $$

Definition 4.10. The Kodaira–Spencer map for $\mathcal {E}$ at $t\in S$ is given by

$$ \begin{align*}T_tS\longrightarrow \mathrm{ H}^1(C, \mathcal{E}_t(Ad)).\end{align*} $$

Proposition 4.11. Let S and $\mathcal {E}$ be as before. Then there is a scheme $\phi _{PS}: Q_{PS}\rightarrow S$ parametrizing all isotropic subbundles of $\mathcal {E}$ , flat over S with same fixed type $\tau '$ .

Moreover, for any $s\in S$ and $q\in \phi _{PS}^{-1}(s)$ , corresponding to an isotropic subbundle $F\subset \mathcal {E}_s$ , which corresponds to a reduction to a parabolic subgroup P of $\mathcal {W}_s$ , we have an exact sequence:

$$ \begin{align*}0\longrightarrow \mathrm{ H}^0(C,\mathcal{E}_{s,\mathsf{s}})\longrightarrow T_qQ_{PS}\longrightarrow T_sS\longrightarrow \mathrm{ H}^1(C,\mathcal{E}_{s,\mathsf{s}}).\end{align*} $$

Proof. Similar to Corollary 4.6.

With similar method, we can show that:

Corollary 4.12. With notations as before, assume that the Kodaira–Spencer map is surjective for any $s\in S$ , then we have

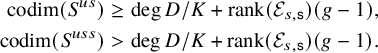$$ \begin{align*} \operatorname{codim}(S^{us})&\geq \operatorname{deg}D/K+\operatorname{rank}(\mathcal{E}_{s,\mathsf{s}})(g-1),\\ \operatorname{codim}(S^{uss})&> \operatorname{deg}D/K+\operatorname{rank}(\mathcal{E}_{s,\mathsf{s}})(g-1). \end{align*} $$

5 The theta line bundle and the canonical line bundle of $M_{G,P}$

In this subsection, we fix

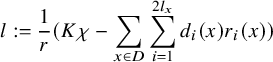$$ \begin{align*}l:=\dfrac{1}{r}(K \chi -\sum_{x\in D}\sum_{i=1}^{2l_x}d_i(x)r_i(x)) \end{align*} $$

to be an integer, and $D_l:=\sum _ql_qz_q$ to be a divisor of degree l on C. Given a scheme S and a flat family of parabolic principal G-bundle $\mathcal {F}$ over $S\times C$ with parabolic type $\big (\{\overrightarrow {n}(x)\}_{x\in D}, \{\overrightarrow {a}(x)\}_{x\in D}\big )$ , assuming that for each $x\in D$ , the filtration is given by

$$ \begin{align*}0=F_{2l_x+1}(\mathcal{F}_{S\times \{x\}})\subseteq \cdots F_{l_x+1}(\mathcal{F}_{S\times \{x\}})\subseteq F_{l_x}(\mathcal{F}_{S\times \{x\}})\subseteq \cdots \subseteq F_0(\mathcal{F}_{S\times \{x\}})=\mathcal{F}_{S\times \{x\}}, \end{align*} $$

which is equivalent to

$$ \begin{align*}\mathcal{F}_{S\times \{x\}}=Q_{2l_x+1}(\mathcal{F}_{S\times \{x\}})\twoheadrightarrow \cdots \twoheadrightarrow Q_{l_x+1}(\mathcal{F}_{S\times \{x\}})\twoheadrightarrow Q_{l_x}(\mathcal{F}_{S\times \{x\}})\twoheadrightarrow \cdots \twoheadrightarrow Q_0(\mathcal{F}_{S\times \{x\}})=0,\end{align*} $$

then we can define a line bundle $\Theta _{\mathcal {F},D_l}$ on S by

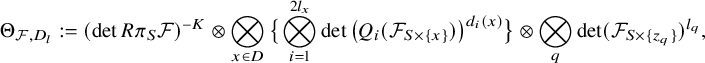$$ \begin{align*}\Theta_{\mathcal{F},D_l}:=(\operatorname{det}R\pi_S\mathcal{F})^{-K}\otimes \bigotimes_{x\in D}\big\{\bigotimes_{i=1}^{2l_x}\operatorname{det}\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big)^{d_{i}(x)}\big\}\otimes \bigotimes_{q}\operatorname{det}(\mathcal{F}_{S\times \{z_q\}})^{l_q},\end{align*} $$

where $\pi _S: S\times C\rightarrow S$ is the projection and $\operatorname {det}R_{\pi _S}\mathcal {F}$ is the determinant of cohomology: $\{\operatorname {det}R_{\pi _S}\mathcal {F}\}_t=\operatorname {det}\mathrm {H}^0(C,\mathcal {F}_t)\otimes \operatorname {det}\mathrm {H}^1(C,\mathcal {F}_t)^{-1}$ . Notice that $\operatorname {det}(\mathcal {F}_{S\times \{z_q\}})$ is trivial since $\mathcal {F}_{S\times \{z_q\}}$ is a/an symplectic/orthogonal bundle over S. So actually we have

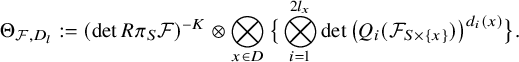$$ \begin{align*}\Theta_{\mathcal{F},D_l}:=(\operatorname{det}R\pi_S\mathcal{F})^{-K}\otimes \bigotimes_{x\in D}\big\{\bigotimes_{i=1}^{2l_x}\operatorname{det}\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big)^{d_{i}(x)}\big\}.\end{align*} $$

Lemma 5.1. The isomorphism

$$ \begin{align*} \operatorname{det}\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big)\cong \operatorname{det}\big(Q_{2l_x+1-i}(\mathcal{F}_{S\times \{x\}})\big) \end{align*} $$

holds for any $1\leq i \leq l_x$ .

Proof. Let $\omega : \mathcal {F}\otimes \mathcal {F}\rightarrow p_C^{*}\mathcal {O}_C(-D)$ be the given nondegenerated antisymmetric/symmetric two form where $p_C: S\times C\rightarrow C$ is the projection. Then we get a nondegenerated antisymmetric/symmetric two-form $\omega _s:\mathcal {F}_{S\times \{x\}}\otimes \mathcal {F}_{S\times \{x\}}\rightarrow \mathcal {O}_S$ over S by pulling pack. Then we have

$$ \begin{align*} Q_{2l_x+1-i}(\mathcal{F}_{S\times \{x\}})=\mathcal{F}_{S\times \{x\}}/F_{2l_x+1-i}(\mathcal{F}_{S\times \{x\}})= \mathcal{F}_{S\times \{x\}}/F_{i}^{\perp}(\mathcal{F}_{S\times \{x\}})\cong F_i^{\vee}(\mathcal{F}_{S\times \{x\}}). \end{align*} $$

So

$$ \begin{align*}\det\big(Q_{2l_x+1-i}(\mathcal{F}_{S\times \{x\}})\big)\cong \det(F_i(\mathcal{F}_{S\times \{x\}}))^{-1}\cong \det\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big).\\[-37pt]\end{align*} $$

From Lemma 5.1, we know that

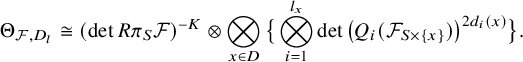$$ \begin{align*}\Theta_{\mathcal{F},D_l}\cong(\operatorname{det}R\pi_S\mathcal{F})^{-K}\otimes \bigotimes_{x\in D}\big\{\bigotimes_{i=1}^{l_x}\operatorname{det}\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big)^{2d_{i}(x)}\big\}.\end{align*} $$

So $\Theta _{\mathcal {F},D_l}$ admits a square root defined by

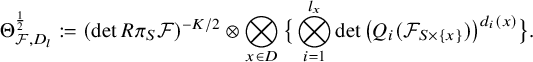$$ \begin{align*}\Theta_{\mathcal{F},D_l}^{\frac{1}{2}}:=(\operatorname{det}R\pi_S\mathcal{F})^{-K/2}\otimes \bigotimes_{x\in D}\big\{\bigotimes_{i=1}^{l_x}\operatorname{det}\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big)^{d_{i}(x)}\big\}.\end{align*} $$

$\Theta _{\mathcal {F},D_l}^{\frac {1}{2}}$ is well defined since $K=2a_{l_x+1}$ is always even.

It is clear that, for any morphism $f:T\rightarrow S$ , we have $f^{*}\Theta _{\mathcal {F},D_l}=\Theta _{f_C^{*}\mathcal {F},D_l}$ , where $f_C:T\times C\rightarrow S\times C$ is the base change of f. Moreover, we have:

Proposition 5.2. There is a unique ample line bundle $\Theta _{D_l}$ over the moduli space $M_{G,P}$ such that:

1. (1) For any scheme S and any family of semistable parabolic G-bundle $\mathcal {F}$ over $S\times C$ , let $\phi _{\mathcal {F}}:S\rightarrow M_{G,P}$ be the induced map, then we have

   $$ \begin{align*}\phi_{\mathcal{F}}^{*}\Theta_{D_l}=\Theta_{\mathcal{F},D_l}.\end{align*} $$

2. (2) Let $D_l$ and $D_l^{\prime }$ be two different effective divisor of degree l on C, then $\Theta _{D_l}$ and $\Theta _{D_l^{\prime }}$ are isomorphic. Then we denote $\Theta _{D_l}$ as $\Theta _{l}$ .

3. (3) If $r\mid \big (\frac {K}{2}\chi -\sum _{x\in D}\sum _{i=1}^{l_x}d_i(x)r_i(x)\big )$ , then $\Theta _{l}$ admits a square root $\Theta _{l}^{\frac {1}{2}}$ on $M_{G, P}$ .

Proof. $\Theta _{D_l}$ is the descend of $\Theta _{\mathcal {E},D_l}$ over $\mathcal {R}^{ss}$ for the universal parabolic symplectic/orthogonal bundle. Once we see that the pull back of polarization over $\textbf {P}Hom(V\otimes V, H)$ to $\mathcal {R}^{ss}$ is trivial, then the reason of descent of $\Theta _{\mathcal {E},D_l}$ is the same as the parabolic bundle case as in [21] Theorem 3.3. Similarly, we can show $\Theta _{D_l}$ is ample and for different choice of $D_l$ , the theta line bundles are isomorphic since $\operatorname {det}(\mathcal {F}_{S\times \{z_q\}})$ are trivial.

Finally, we define the square root $\Theta _{D_l}^{1/2}$ as follows:

Let

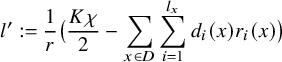$$ \begin{align*}l^\prime:=\dfrac{1}{r}\big(\frac{K\chi}{2}-\sum\limits_{x\in D}\sum\limits_{i=1}^{l_x}d_i(x)r_i(x)\big)\end{align*} $$

be the integer by assumption. Then we choose a divisor $D_{l^\prime }=\sum _{q^\prime }l_{q^\prime }z_{q^\prime }$ of degree $l^\prime $ on C. Now, consider

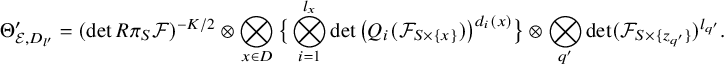$$ \begin{align*}\Theta^{\prime}_{\mathcal{E},D_{l^\prime}} =(\operatorname{det}R\pi_S\mathcal{F})^{-K/2}\otimes \bigotimes_{x\in D}\big\{\bigotimes_{i=1}^{l_x}\operatorname{det}\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big)^{d_{i}(x)}\big\}\otimes \bigotimes_{q^\prime}\operatorname{det}(\mathcal{F}_{S\times \{z_{q^\prime}\}})^{l_{q^\prime}}.\end{align*} $$

This is a square root of $\Theta _{\mathcal {E},D_l}$ since $\operatorname {det}(\mathcal {F}_{S\times \{z\}})$ is trivial for any $z\in C$ . We want to show that $\Theta ^{\prime }_{\mathcal {E},D_{l^\prime }}$ descends to a line bundle on $M_{G, P}$ .

We use a result of Kempf; see Theorem 2.3 of [5]. Then we shall check that for every $y\in \mathcal {R}^{ss}$ , if the orbit of y is closed, then the stabiliser $G_y$ acts trivially on the fiber of $\Theta ^{\prime }_{\mathcal {E},D_{l^\prime }}$ .

When y corresponds to stable parabolic symplectic/orthogonal bundles, $G_y\cong \mathbb {K}^{*}$ , then the action of $G_y$ on fiber is given by weight $(-K/2)\chi +\sum _{x\in D}\sum _{i=1}^{l_x}d_i(x)r_i(x)+rl^\prime =0$ by the definition of $l^\prime $ . We also mention that $(-K/2)\chi +\sum _{x\in D}\sum _{i=1}^{l_x}d_i(x)r_i(x)+rl^\prime =(-K/2)r(1-g)-(K/2)\operatorname {pardeg}(E)+\frac {1}{2}r\sum _{x\in D}a_{l_x+1}(x)+rl^\prime $ by a direct computation.

When y does not corresponds to stable parabolic symplectic/orthogonal bundles, it would correspond to a polystable parabolic symplectic/orthogonal bundles since the orbit of y is closed. For a polystable parabolic symplectic/orthogonal bundle E, we have the following decomposition:

$$ \begin{align*}E \cong \oplus_{s=1}^t E_s, \end{align*} $$

where $E_1$ is a stable parabolic symplectic/orthogonal bundle and $E_s\cong F_s\oplus (F^{*}\otimes L_s)$ for some stable parabolic vector bundle $F_s$ for $2\leq s \leq t$ . If we use $r_s$ to denote the rank of $E_s$ , we have equalities

$$ \begin{align*}\frac{\operatorname{pardeg}(E_s)}{r_s}=\frac{\operatorname{pardeg}(E)}{r}. \end{align*} $$

Over each $E_s$ , we have an induced parabolic structure, which reads as

$$ \begin{align*}(E_s)_x=Q_{2l_x+1}((E_s)_x)\twoheadrightarrow \cdots \twoheadrightarrow Q_{l_x+1}((E_s)_x)\twoheadrightarrow Q_{l_x}((E_s)_x) \twoheadrightarrow \cdots Q_{0}((E_s)_x)=0. \end{align*} $$

We denote $r^s_i(x)$ to denote the dimension of $Q_{i}((E_s)_x)$ , and we denote $r^s_{i}(x)-r^s_{i-1}(x)=n_i^s(x)$ . Moreover, since E is polystable, we have isomorphisms $Q_i(E_x) \cong \oplus _{s=1}^tQ_{i}((E_s)_x)$ .

As a parabolic vector bundle, the stabilizer $G_y$ is given by $\mathbb {K}^{*}\times \cdots \mathbb {K}^{*}$ ( $2t-1$ copies). But recall that we have a bilinear map $\phi $ on V as in Section 3, hence the stabiliser $G_y$ is given by $\mathbb {K}^{*}\times \cdots \mathbb {K}^{*}$ (t copies). If we use $(w_1, \cdots , w_t)$ to denote the weight of the action of $G_y$ on the fiber of $\Theta ^{\prime }_{\mathcal {E},D_{l^\prime }}$ , then

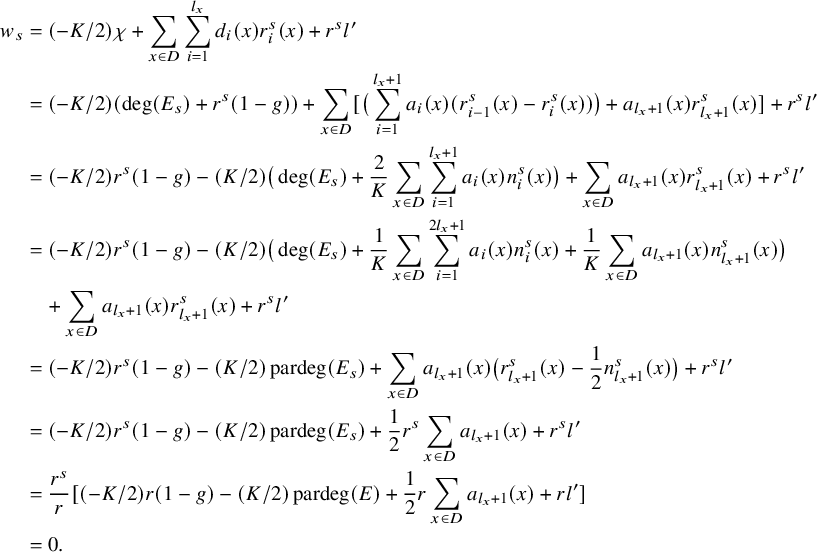$$ \begin{align*} w_s&=(-K/2)\chi+\sum_{x\in D}\sum_{i=1}^{l_x}d_i(x)r^s_i(x)+r^sl^\prime \\ &=(-K/2)(\operatorname{deg}(E_s)+r^s(1-g))+\sum_{x\in D}[\big(\sum_{i=1}^{l_x+1}a_i(x)(r^s_{i-1}(x)-r^s_i(x))\big)+a_{l_x+1}(x)r^s_{l_x+1}(x)]+r^sl^\prime \\ &=(-K/2)r^s(1-g)-(K/2)\big(\operatorname{deg}(E_s)+\frac{2}{K}\sum_{x\in D}\sum_{i=1}^{l_x+1}a_i(x)n_i^s(x)\big)+\sum_{x\in D}a_{l_x+1}(x)r_{l_x+1}^s(x)+r^sl^\prime \\ &=(-K/2)r^s(1-g)-(K/2)\big(\operatorname{deg}(E_s)+\frac{1}{K}\sum_{x\in D}\sum_{i=1}^{2l_x+1}a_i(x)n_i^s(x)+\frac{1}{K}\sum_{x\in D}a_{l_x+1}(x)n_{l_x+1}^s(x)\big)\\ &\ \ \ \ +\sum_{x\in D}a_{l_x+1}(x)r_{l_x+1}^s(x)+r^sl^\prime \\ &=(-K/2)r^s(1-g)-(K/2)\operatorname{pardeg}(E_s)+\sum_{x\in D}a_{l_x+1}(x)\big(r_{l_x+1}^s(x)-\frac{1}{2}n_{l_x+1}^s(x)\big)+r^sl^\prime \\ &=(-K/2)r^s(1-g)-(K/2)\operatorname{pardeg}(E_s)+\frac{1}{2}r^s\sum_{x\in D}a_{l_x+1}(x)+r^sl^\prime \\ &=\frac{r^s}{r}[(-K/2)r(1-g)-(K/2)\operatorname{pardeg}(E)+\frac{1}{2}r\sum_{x\in D}a_{l_x+1}(x)+rl^\prime] \\ &=0. \end{align*} $$

Hence, all the weights $w_s$ are $0$ and $\Theta ^{\prime }_{\mathcal {E},D_{l^\prime }}$ descends to a line bundle on $M_{G, P}$ . Notice that $\operatorname {Pic}M_{G,P}\rightarrow \operatorname {Pic}R^{ss}$ is injective by Proposition 4.2 of [12]. We see that $\Theta _{l}$ admits a square root $\Theta _{l}^{\frac {1}{2}}$ on $M_{G, P}$ .

For any parabolic G-bundle E, with parabolic structure $t_x\in G/P_x, \forall x \in D$ , we define $\mathbf {D}_{E}$ to be the space of infinitesimal deformation of E, that is, the space of isomorphism classes of parabolic G-bundles $\tilde {E}$ on $C[\epsilon ]$ such that $\tilde {E}|_{C}\cong E$ , where $C[\epsilon ]=C\times Spec(\mathbb {K}[\epsilon ]/(\epsilon ^2)) $ .

Proposition 5.3. There is an exact sequence:

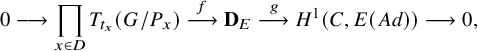$$ \begin{align*}0\longrightarrow \prod_{x\in D}T_{t_x}(G/P_x)\stackrel{f}{\longrightarrow} \mathbf{D}_{E}\stackrel{g}{\longrightarrow} H^1(C, E(Ad))\longrightarrow 0,\end{align*} $$

where $T_{t_x}(G/P_x)$ is the tangent space of $G/P_x$ at $t_x$ .

Proof. Recall that $\mathrm {H}^1(C, E(Ad))$ is the infinitesimal deformation space of E as a twisted G-bundle, so the morphism g is given by forgetting parabolic structures. Since every twisted G-bundle can be equipped with any parabolic structure, g is a surjection.

To determine the kernel of g, we need to figure out how many parabolic structures we can impose on a $\mathcal {E}$ so that the restriction to C are the parabolic structures $\{t_x\in G/P_x\}$ . The question is local, so it is equivalent to find a parabolic subgroup $\tilde {P}_x\subset G(\mathbb {K}[\epsilon ]/(\epsilon ^2))$ such that $\tilde {P}_x|_0=t_x\in G/P_x$ . The space of such groups is exactly $\prod _{x\in D}T_{t_x}(G/P_x)$ .

Lemma 5.4. Let G be $\operatorname {SO}(2n+1)$ , $\operatorname {Sp}(2n)$ or $\operatorname {SO}(2n)$ and $G/P$ be the generalized flag variety. Consider the universal quotient

$$ \begin{align*}V\otimes \mathcal{O}=\mathcal{Q}_{2l+1}\twoheadrightarrow \cdots \twoheadrightarrow \mathcal{Q}_{l+1}\twoheadrightarrow \mathcal{Q}_{l}\twoheadrightarrow \cdots \twoheadrightarrow \mathcal{Q}_0=0 \end{align*} $$

on $G/P$ , where $\operatorname {rk} \mathcal {Q}_{i}/\mathcal {Q}_{i-1}=n_i$ . Then the anticanonical line bundle can be expressed as

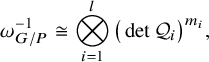$$ \begin{align*}\omega_{G/P}^{-1}\cong \bigotimes_{i=1}^{l}\big(\operatorname{det}\mathcal{Q}_{i}\big)^{m_i}, \end{align*} $$

where $m_i=n_i+n_{i+1}$ for $1\leq i \leq l-1$ ; $m_{l}=n_{l}+n_{l+1}-1$ for $G=\operatorname {SO}(2n+1)$ , $m_{l}=n_{l}+n_{l+1}+1$ for $G=\operatorname {Sp}(2n)$ and $m_{l}=n_{l}+n_{l+1}-1$ for $G=\operatorname {SO}(2n)$ .

Proof. Consider the closed embedding $i: G/P\hookrightarrow \operatorname {SL}(V)/P^\prime $ , where $\operatorname {SL}(V)/P^\prime $ parametrizes the following quotients

$$ \begin{align*}V=Q_{2l+1}\twoheadrightarrow Q_{l}\twoheadrightarrow \cdots \twoheadrightarrow Q_0=0. \end{align*} $$

Let $\mathcal {Q}_i$ be the universal quotient corresponding to $Q_i$ , and take $\mathcal {F}_i=\ker (V\otimes \mathcal {O}\twoheadrightarrow \mathcal {Q}_i)$ for $1\leq i \leq l$ . Notice that if $\mathcal {F}_l$ is isotropic, then so are $\mathcal {F}_i$ ’s. Thus, for G be $\operatorname {SO}(2n+1)$ or $\operatorname {SO}(2n)$ , $G/P$ is contained in the zero locus of a section of $\operatorname {Sym}^2\mathcal {F}_l^{\vee }$ . A direct computation shows that the codimension of $G/P$ in $\operatorname {SL}(V)/P^\prime $ equals to the rank of $\operatorname {Sym}^2\mathcal {F}_l^{\vee }$ , hence $G/P$ is the zero locus of a regular section of $\operatorname {Sym}^2\mathcal {F}_l^{\vee }$ . Now, we have the following exact sequence:

$$ \begin{align*}0\longrightarrow T_{G/P} \longrightarrow i^{*}T_{\operatorname{SL}(V)/P^\prime}\longrightarrow i^{*} \operatorname{Sym}^2\mathcal{F}_l^{\vee} \longrightarrow 0. \end{align*} $$

Thus, our formula follows from this exact sequence and Lemma 2.9 of [26]. And it is similar for the case $G=\operatorname {Sp}(2n)$ by replacing $i^{*} \operatorname {Sym}^2\mathcal {F}_l^{\vee }$ by $i^{*} \wedge ^2\mathcal {F}_l^{\vee }$ in the above exact sequence.

Corollary 5.5. For any family of stable parabolic G-bundle $\mathcal {F}$ over $S\times C$ , let $\pi _S: S\times C\longrightarrow S$ be the projection and $\varphi _S:S\longrightarrow M_{G,P}$ be the induced map, then

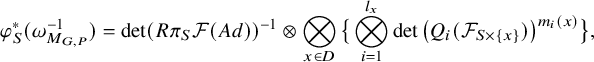$$ \begin{align*}\varphi_S^{*}(\omega_{M_{G,P}}^{-1})=\operatorname{det}(R\pi_S\mathcal{F}(Ad))^{-1}\otimes \bigotimes_{x\in D}\big\{\bigotimes_{i=1}^{l_x}\operatorname{det}\big(Q_{i}(\mathcal{F}_{S\times \{x\}})\big)^{m_i(x)} \big\},\end{align*} $$

where $m_i(x)=n_i(x)+n_{i+1}(x)$ for $1\leq i \leq l_x-1$ ; $m_{l_x}(x)=n_{l_x}(x)+n_{l_x+1}(x)-1$ for $G=\operatorname {SO}(2n+1)$ , $m_{l_x}(x)=n_{l_x}(x)+n_{l_x+1}(x)+1$ for $G=\operatorname {Sp}(2n)$ and $m_{l_x}(x)=n_{l_x}(x)+n_{l_x+1}(x)-1$ for $G=\operatorname {SO}(2n)$ .

The main results in this section is to under certain choices of weights, the moduli space of parabolic symplectic/orthogonal bundles are Fano varieties. A normal projective variety X is call Fano if $\omega _X^{-1}$ is an ample line bundle. Our method is to compare the pull back of an anticanonical line bundle over $M_{G,P}$ to $\mathcal {R}^{ss}$ with theta line bundle over $\mathcal {R}^{ss}$ . It is known that the Picard group of moduli space of symplectic/orthogonal bundles has rank one, so there exists a positive integer $\chi _G$ such that $\operatorname {det}(R\pi _S\mathcal {F}(Ad))\cong (\operatorname {det}R\pi _S\mathcal {F})^{\otimes 2\chi _G}$ . For $G=\operatorname {SO}(2n+1)$ , $\chi _G=2n-1$ , for $G=\operatorname {Sp}(2n)$ , $\chi _G=n+1$ and for $G=\operatorname {SO}(2n)$ , $\chi _G=2n-2$ (see Remark 5.3 of [14]).

Proposition 5.6. Let $G=\operatorname {SO}(2n+1), \ \operatorname {Sp}(2n) \text { or } \operatorname {SO}(2n)$ , $K=4\chi _G$ and $\overrightarrow {a}(x)$ satisfying $a_{i+1}(x)-a_{i}(x)=m_i(x)$ for $1\leq i \leq l_x$ . Then if $r\mid \big (\frac {K}{2}\chi -\sum _{x\in D}\sum _{i=1}^{l_x}d_i(x)r_i(x)\big )$ , the moduli spaces $M_{G,P}$ are Fano.

Proof. We show that under the condition in the proposition, $\Theta _{l}^{1/2}$ is equal to $\omega _{M_{G,P}}^{-1}$ . We take a similar strategy as in Theorem 2.8 of [13]. We take $M_{G,P}^{rs}$ to be the open subvariety of a regularly stable locus in $M_{G,P}$ . Then for any $E\in M_{G,P}^{rs}$ , we know that E is stable and $\mathrm {H}^0(C, E(Ad))=0$ . This implies that $\omega _{M_{G,P}}^{-1}$ is a line bundle over $M_{G,P}^{rs}$ .

We shall firstly show that $\Theta _{l}^{1/2}$ is equal to $\omega _{M_{G,P}}^{-1}$ over $M_{G,P}^{rs}$ . Since there is no universal family on $M_{G,P}^{rs}$ , we may consider the inverse image of $M_{G,P}^{rs}$ in $\mathcal {R}^{ss}$ , denoted as $\mathcal {R}^{rs}$ . Then we have a natural morphism $\nu : \mathcal {R}^{rs}\rightarrow M_{G,P}^{rs}$ so that $\nu ^{*}: \operatorname {Pic}(M_{G,P}^{rs})\rightarrow \operatorname {Pic}(\mathcal {R}^{rs})$ is injective by Proposition 4.2 of [12]. Notice that $\nu ^{*}\Theta _{l}^{1/2}=\nu ^{*}\omega _{M_{G,P}}^{-1}$ over $\mathcal {M}_{G,P}^{rs}$ , hence $\Theta _{l}^{1/2}=\omega _{M_{G,P}}^{-1}$ over $M_{G,P}^{rs}$ .

Now, we want to extend this identification over $M_{G,P}$ . Notice that $\Theta _{l}^{1/2}$ is reflexive since it is a line bundle, and $\omega _{M_{G,P}}^{-1}$ is reflexive since $M_{G,P}$ is normal by Theorem 3.5. By a similar method as in Proposition 11.6 of [15], we see that $\operatorname {Codim}(M_{G,P}\setminus M_{G,P}^{rs})\geq 2$ . Now, by Lemma 2.7 of [13] we see that $\Theta _{l}^{1/2}=\omega _{M_{G,P}}^{-1}$ over $M_{G,P}$ . Thus, $\omega _{M_{G,P}}^{-1}$ is an ample line bundle by Proposition 5.2 and $M_{G,P}$ is Fano.

6 Globally F-regular type varieties and main theorem

Let k be a perfect field of $char(k)=p>0$ and X be a normal variety over k. Consider

$$ \begin{align*} F: X\longrightarrow X\end{align*} $$

to be the absolute Frobenius map and $F^e: X\rightarrow X$ to be the e-th iteration of F.

For any Weil divisor $D\in Div(X)$ , we have a reflexive sheaf

$$ \begin{align*}\mathcal{O}_X(D)=j_*\mathcal{O}_{X^{sm}}(D),\end{align*} $$

where $j:X^{sm}\hookrightarrow X$ is the inclusion of smooth locus, and $\mathcal {O}_X(D)$ is an invertible sheaf if and only if D is a Cartier divisor.

Definition 6.1. Let X and D be as above; X is called stably Frobenius D-split if the natural homomorphism

$$ \begin{align*}\mathcal{O}_X\longrightarrow F^e_*\mathcal{O}_X(D)\end{align*} $$

is split as an $\mathcal {O}_X$ homomorphism for some $e>0$ . And X is called globally F-regular if X is stably Frobenius D-split for any effective divisor D.

We state the following lemma about globally F-regular varieties; for proof and more details, please refer to [29], [25].

Lemma 6.2 ([23] Corollary 6.4).

Let $f:X\rightarrow Y$ be a morphism of normal varieties over k. Assume that the natural map

$$ \begin{align*}f^{\#}: \mathcal{O}_Y\longrightarrow f_*\mathcal{O}_X\end{align*} $$

splits as an $\mathcal {O}_Y$ homomorphism, then if X is globally F-regular, so is Y.

Now, we let $\mathbb {K}$ be an algebraically closed field of characteristic zero.

For any scheme X over $\mathbb {K}$ , there is a finitely generated $\mathbb {Z}$ -algebra $R\subset \mathbb {K}$ such that X is ‘defined’ over R. That is, there is a flat R-scheme

$$ \begin{align*} X_R\longrightarrow S=\operatorname{Spec}R \end{align*} $$

such that $X_{\mathbb {K}}:=X_R\times _S \operatorname {Spec}\mathbb {K}\cong X$ . $X_R\longrightarrow S$ is called an integral model of $X/\mathbb {K}$ . For any closed point $s\in S$ , $X_s:=X_R\times _S \operatorname {Spec}(\overline {k(s)})$ is called the ‘modulo p reduction’ of X, where $p=char(k(s))>0$ .

Definition 6.3. A variety X over $\mathbb {K}$ is called of globally F-regular type if its ‘modulo p reduction’ of X are globally F-regular for a dense set of p for some integral model $X_R\rightarrow S$ .

Globally F-regular type varieties have many nice properties, which we will state some of them as the following theorem. Again, for proof and more details, please refer to [29] and [25].

Theorem 6.4. Let X be a projective variety over $\mathbb {K}$ if X is of globally F-regular type, then:

1. (1) X is normal, Cohen–Macaulay with rational singularities. If X is $\mathbb {Q}$ -Gorenstein, then X has log terminal singularities.

2. (2) For any nef line bundle $\mathcal {L}$ over X, we have $\mathrm {H}^i(X, \mathcal {L})=0$ , for any $i>0$ . In particular, $\mathrm {H}^i(X, \mathcal {O}_X)=0$ for any $i>0$ .

Our main theorem of this paper is:

Theorem 6.5. The moduli space of parabolic symplectic/orthogonal bundles $M_{P}$ over a smooth projective curve C over $\mathbb {C}$ is of globally F-regular type.

Corollary 6.6. Let $\Theta _{D_l}$ be the theta line bundle over $M_{G,P}$ defined before, then

$$ \begin{align*}\mathrm{ H}^i(M_P, \Theta_{D_l})=0\end{align*} $$

for any $i>0$ .

Our beginning example of globally F-regular type variety is Fano variety.

Proposition 6.7 ([25] Proposition 6.3).

A Fano variety over $\mathbb {K}$ with at most rational singularities is of globally F-regular type.

With our beginning example, the next step is to ask whether Lemma 6.2 holds in characteristic zero. To answer such question, in [29], they introduced the following:

Definition 6.8. A morphism $f: X\rightarrow Y$ of varieties over $\mathbb {K}$ is called p-compatible if there is an integral model

$$ \begin{align*} f_R: X_R\longrightarrow Y_R \end{align*} $$

such that, if for any $s\in S=\operatorname {Spec}R$ , we put $X_s=X_R\times _S\operatorname {Spec}\overline {k(s)}$ , $Y_s=Y_R\times _S\operatorname {Spec}\overline {k(s)}$ and consider

then we have that $i_s^{*}f_{R*}\mathcal {O}_{X_R}=f_{s*}j_s^{*}\mathcal {O}_{X_R}$ holds for a dense set of s.

It can be shown that if $f: X\rightarrow Y$ is a flat proper morphisms such that $\textbf {R}^if_{*}\mathcal {O}_X=0$ for all $i\geq 1$ , then f is p-compatible.

To prove our main theorem, we need to introduce a key proposition from [29].

Let $(\mathcal {R}^{\prime }, L^{\prime })$ and $(\mathcal {R},L)$ be two polarized projective varieties over $\mathbb {K}$ , with linear actions by a reductive group scheme G over K, respectively. We use $(\mathcal {R}^{\prime })^{ss}(L^{\prime })\subseteq \mathcal {R}^{\prime }$ and $\mathcal {R}^{ss}(L)\subseteq \mathcal {R}$ to denote the GIT semistable locus, then there are projective GIT quotients:

$$ \begin{align*}\psi:\mathcal{R}^{ss}(L)\rightarrow Y:=\mathcal{R}^{ss}(L)//G\ ,\ \varphi:(\mathcal{R}^{\prime})^{ss}(L^{\prime})\rightarrow Z:=(\mathcal{R}^{\prime})^{ss}(L^{\prime})//G.\end{align*} $$

Proposition 6.9 ([29] Proposition 2.10).

Let $\mathcal {R}$ , $\mathcal {R}^{\prime }$ as above. Considering the following diagram, assume

1. (1) there is a G-invariant p-compatible morphism $\hat {f}:\mathcal {R}^{\prime }\rightarrow \mathcal {R}$ such that $\hat {f}_*\mathcal {O}_{\mathcal {R^{\prime }}}=\mathcal {O}_{\mathcal {R}}$ ;

2. (2) there is a G-invariant open subset $W\subset (\mathcal {R}^{\prime })^{ss}(L^{\prime })$ such that

   $$ \begin{align*} \mathrm{Codim}(\mathcal{R}^{\prime}\setminus W)\geq 2,\ \hat{X}=\varphi^{-1}\varphi(\hat{X}), \end{align*} $$
   where $\hat {X}=W\cap \hat {f}^{-1}(\mathcal {R}^{ss}(L))$ . And we put $X=\varphi (\hat {X})$ .

Then if Z is of globally F-regular type, so is Y.

Finally, we will prove our main theorem:

Proof of Theorem 6.5.

We choose an effective divisor $D^{\prime }$ of C such that $D^{\prime }\cap D=\emptyset $ , deg $D^{\prime }$ being even and

$$ \begin{align*}\dfrac{\operatorname{deg}(D)+\operatorname{deg}(D^{\prime})}{4\chi_G}+(r-1)(g-1)\geq 2,\end{align*} $$

and for each $x\in D^{\prime }$ , we put $\overrightarrow {n}(x)=(1,\cdots , 1)$ . Let $Z^{\prime }$ be the scheme parametrizing symplectic/orthogonal bundles $(E, \omega )$ , where $\omega : E\otimes E \rightarrow \mathcal {O}_C(-D-D^{\prime })$ as we constructed in section 3. We see that $Z^{\prime }\cong Z$ . Then we let

$$ \begin{align*}\mathcal{R}^{\prime}=\underset{x\in D\cup D^{\prime}}{\times_Z}Flag_{\vec n(x)}(\mathcal F_x)=\mathcal{R}\times_Z\big(\underset{x\in D^{\prime}}{\times_Z}Flag_{\vec n(x)}(\mathcal F_x)\big)\stackrel{\hat{f}}{\longrightarrow} \mathcal{R}.\end{align*} $$

So $\hat {f}:\mathcal {R}^{\prime }\rightarrow \mathcal {R}$ is a flag bundle and hence p-compatible with $\hat {f}_*\mathcal {O}_{\mathcal {R}^{\prime }}=\mathcal {O}_{\mathcal {R}}$ . We choose polarization for $\mathcal {R}^{\prime }$ and $\mathcal {R}$ as the ones given in Section 3, say $L^{\prime }$ and L. Clearly, there are $SL(V)$ action on $\mathcal {R}^{\prime }$ and $\mathcal {R}$ and $\hat {f}$ is $SL(V)$ -invariant.

Now, we put $K=4\chi _G$ and give weights for $\mathcal {R}^{\prime }$ by $\overrightarrow {a}(x)$ satisfying $a_{i+1}(x)-a_i(x)=m_i(x),\ a_{i}(x)+a_{2l_x+2-i}(x)=K$ for $1\leq i \leq l_x$ and any $x\in D\cup D^{\prime }$ . Moreover, we choose $a_i(x)$ and $n_i(x)$ such that $r\mid \big (\frac {K}{2}\chi -\sum _{x\in D}\sum _{i=1}^{l_x}d_i(x)r_i(x)\big )$ holds. So by Proposition 5.6, we see that $Z:=(\mathcal {R}^{\prime })^{ss}(L^{\prime })//SL(V)$ is a Fano variety. We use $\varphi : (\mathcal {R}^{\prime })^{ss}\rightarrow Z$ to denote the quotient map.

Moreover, if one let $W=(\mathcal {R}^{\prime })^{s}$ , $\hat {X}=W\cap \hat {f}^{-1}(\mathcal {R}^{ss})$ and $X=\varphi (\hat {X})$ , then clearly $\hat {X}=\varphi ^{-1}(X)$ . By Corollary 4.12 and our assumption, we would have: $\operatorname {Codim}(\mathcal {R}^{\prime }\setminus W)\geq 2$ . Now, Proposition 6.9 shows that the moduli space of parabolic symplectic/orthogonal bundles $Y:=\mathcal {R}(L)^{ss}//SL(V)$ is of globally F-regular type.