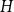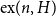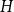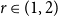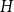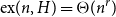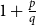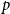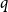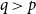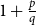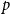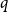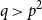1. Introduction
1.1 Rational exponent conjecture
Given a family
![]() $\mathcal{H}$
of graphs, the Turán number
$\mathcal{H}$
of graphs, the Turán number
![]() $\mathrm{ex}(n,\mathcal{H})$
is the largest number of edges in an
$\mathrm{ex}(n,\mathcal{H})$
is the largest number of edges in an
![]() $n$
-vertex graph that does not contain any member of
$n$
-vertex graph that does not contain any member of
![]() $\mathcal{H}$
as a subgraph. When
$\mathcal{H}$
as a subgraph. When
![]() $\mathcal{H}$
consists of one single graph
$\mathcal{H}$
consists of one single graph
![]() $H$
, we write
$H$
, we write
![]() $\mathrm{ex}(n,H)$
for
$\mathrm{ex}(n,H)$
for
![]() $\mathrm{ex}(n,\{H\})$
.
$\mathrm{ex}(n,\{H\})$
.
Determining Turán numbers for various graphs is one of the central problems in extremal graph theory. The celebrated Erdős-Stone-Simonovits theorem states that for any non-bipartite graph
![]() $H$
,
$H$
,
![]() $\mathrm{ex}(n,H)=\left(1-\frac{1}{\chi (H)-1}\right)\binom{n}{2}+o(n^2)$
, where
$\mathrm{ex}(n,H)=\left(1-\frac{1}{\chi (H)-1}\right)\binom{n}{2}+o(n^2)$
, where
![]() $\chi (H)$
is the chromatic number of
$\chi (H)$
is the chromatic number of
![]() $H$
. For bipartite graphs
$H$
. For bipartite graphs
![]() $H$
, it follows from the Kővári-Sós-Turán theorem that
$H$
, it follows from the Kővári-Sós-Turán theorem that
![]() $\mathrm{ex}(n,H)=O(n^{2-\alpha })$
, where
$\mathrm{ex}(n,H)=O(n^{2-\alpha })$
, where
![]() $\alpha =\alpha _H\gt 0$
is a constant. However, finding good estimates on
$\alpha =\alpha _H\gt 0$
is a constant. However, finding good estimates on
![]() $\mathrm{ex}(n,H)$
for bipartite graphs
$\mathrm{ex}(n,H)$
for bipartite graphs
![]() $H$
is difficult. Until recently, the order of magnitude of
$H$
is difficult. Until recently, the order of magnitude of
![]() $\mathrm{ex}(n,H)$
was known only for very few bipartite graphs
$\mathrm{ex}(n,H)$
was known only for very few bipartite graphs
![]() $H$
. Following [Reference Kang, Kim and Liu25], we say that a real number
$H$
. Following [Reference Kang, Kim and Liu25], we say that a real number
![]() $r\in (1,2)$
is realizable (by
$r\in (1,2)$
is realizable (by
![]() $H$
) if there exists a bipartite graph
$H$
) if there exists a bipartite graph
![]() $H$
such that
$H$
such that
![]() $\mathrm{ex}(n,H)=\Theta (n^r)$
. If
$\mathrm{ex}(n,H)=\Theta (n^r)$
. If
![]() $r$
is realizable then we also call it a Turán exponent. A well-known conjecture of Erdős and Simonovits, known as the rational exponent conjecture, asserts that every rational number
$r$
is realizable then we also call it a Turán exponent. A well-known conjecture of Erdős and Simonovits, known as the rational exponent conjecture, asserts that every rational number
![]() $r\in (1,2)$
is a Turán exponent.
$r\in (1,2)$
is a Turán exponent.
Conjecture 1.1 ([Reference Erdős8]). For all positive integers
![]() $q\gt p$
,
$q\gt p$
,
![]() $1+\frac{p}{q}$
is a Turán exponent.
$1+\frac{p}{q}$
is a Turán exponent.
Until recently, the only rationals in
![]() $(1,2)$
for which the conjecture was known to be true were rationals of the form
$(1,2)$
for which the conjecture was known to be true were rationals of the form
![]() $1+\frac{1}{q}$
and
$1+\frac{1}{q}$
and
![]() $2-\frac{1}{q}$
for positive integers
$2-\frac{1}{q}$
for positive integers
![]() $q\geq 2$
, realized by so-called theta graphs and complete bipartite graphs, respectively. In a recent breakthrough work, Bukh and Conlon [Reference Bukh and Conlon3] showed that for any rational number
$q\geq 2$
, realized by so-called theta graphs and complete bipartite graphs, respectively. In a recent breakthrough work, Bukh and Conlon [Reference Bukh and Conlon3] showed that for any rational number
![]() $r\in (1,2)$
, there exists a finite family
$r\in (1,2)$
, there exists a finite family
![]() $\mathcal{H}_r$
of graphs such that
$\mathcal{H}_r$
of graphs such that
![]() $\mathrm{ex}(n,\mathcal{H}_r)=\Theta (n^r)$
. Bukh and Conlon’s work has, to a large extent, rejuvenated people’s interest on Conjecture 1.1. In the last year or so, several new infinite sequences of new Turán exponents have been obtained by various groups. First, Jiang, Ma, and Yepremyan [Reference Jiang, Ma and Yepremyan21] showed that
$\mathrm{ex}(n,\mathcal{H}_r)=\Theta (n^r)$
. Bukh and Conlon’s work has, to a large extent, rejuvenated people’s interest on Conjecture 1.1. In the last year or so, several new infinite sequences of new Turán exponents have been obtained by various groups. First, Jiang, Ma, and Yepremyan [Reference Jiang, Ma and Yepremyan21] showed that
![]() $2-\frac{2}{2m+1}$
is realizable by generalized cubes and that
$2-\frac{2}{2m+1}$
is realizable by generalized cubes and that
![]() $\frac{7}{5}$
is realizable by the so-called
$\frac{7}{5}$
is realizable by the so-called
![]() $3$
-comb-pasting graph. A few months later, Kang, Kim, and Liu [Reference Kang, Kim and Liu25] showed that for all positive integers
$3$
-comb-pasting graph. A few months later, Kang, Kim, and Liu [Reference Kang, Kim and Liu25] showed that for all positive integers
![]() $p\lt q$
, where
$p\lt q$
, where
![]() $q\equiv \pm 1 \pmod{p}$
,
$q\equiv \pm 1 \pmod{p}$
,
![]() $2-\frac{p}{q}$
is realizable. More specifically, rationals of the form
$2-\frac{p}{q}$
is realizable. More specifically, rationals of the form
![]() $2-\frac{t}{st-1}$
, where
$2-\frac{t}{st-1}$
, where
![]() $s,t\geq 2$
, are realized by the so-called blowups of certain height
$s,t\geq 2$
, are realized by the so-called blowups of certain height
![]() $2$
trees. (We will define blowups precisely in subsection 1.2.) Rationals of the form
$2$
trees. (We will define blowups precisely in subsection 1.2.) Rationals of the form
![]() $2-\frac{t}{st+1}$
are realized by graphs obtained from theta graphs via some iterative operations. More recently, some new sequences of Turán exponents were obtained along the study of Turán numbers of subdivisions. For any integers
$2-\frac{t}{st+1}$
are realized by graphs obtained from theta graphs via some iterative operations. More recently, some new sequences of Turán exponents were obtained along the study of Turán numbers of subdivisions. For any integers
![]() $s,t\geq 1, k\geq 2$
, let
$s,t\geq 1, k\geq 2$
, let
![]() $K_{s,t}^k$
denote the graph obtained from the complete bipartite graph
$K_{s,t}^k$
denote the graph obtained from the complete bipartite graph
![]() $K_{s,t}$
by subdividing each edge
$K_{s,t}$
by subdividing each edge
![]() $k-1$
times. Let
$k-1$
times. Let
![]() $L_{s,t}(k)$
be obtained from
$L_{s,t}(k)$
be obtained from
![]() $K_{s,t}^k$
by adding an extra vertex joined to all vertices in the part of
$K_{s,t}^k$
by adding an extra vertex joined to all vertices in the part of
![]() $K_{s,t}$
of size
$K_{s,t}$
of size
![]() $t$
. Confirming a conjecture of Kang, Kim, and Liu [Reference Kang, Kim and Liu25], Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7] showed that there exists
$t$
. Confirming a conjecture of Kang, Kim, and Liu [Reference Kang, Kim and Liu25], Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7] showed that there exists
![]() $t_0$
such that for all integers
$t_0$
such that for all integers
![]() $s,k\geq 1, t\geq t_0$
,
$s,k\geq 1, t\geq t_0$
,
![]() $\mathrm{ex}\!\left(n,L_{s,t}(k)\right)=\Theta \!\left(n^{1+\frac{s}{sk+1}}\right)$
, and thus establishing
$\mathrm{ex}\!\left(n,L_{s,t}(k)\right)=\Theta \!\left(n^{1+\frac{s}{sk+1}}\right)$
, and thus establishing
![]() $1+\frac{s}{sk+1}$
as Turán exponents. Subsequently, in verifying a conjecture of Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7], Janzer [Reference Janzer18] proved that there exists a
$1+\frac{s}{sk+1}$
as Turán exponents. Subsequently, in verifying a conjecture of Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7], Janzer [Reference Janzer18] proved that there exists a
![]() $t_0$
such that for all integers
$t_0$
such that for all integers
![]() $s,k\geq 2, t\geq t_0$
,
$s,k\geq 2, t\geq t_0$
,
![]() $\mathrm{ex}\!\left(n,K_{s,t}^k\right)=\Theta \!\left(n^{1+\frac{s-1}{sk}}\right)$
, thus establishing
$\mathrm{ex}\!\left(n,K_{s,t}^k\right)=\Theta \!\left(n^{1+\frac{s-1}{sk}}\right)$
, thus establishing
![]() $1+\frac{s-1}{sk}$
as Turán exponents. Earlier, Conlon, Janzer, Lee [Reference Conlon, Janzer and Lee7] had proven the conjecture for
$1+\frac{s-1}{sk}$
as Turán exponents. Earlier, Conlon, Janzer, Lee [Reference Conlon, Janzer and Lee7] had proven the conjecture for
![]() $k=2$
, while Jiang and Qiu [Reference Jiang and Qiu22] proved the conjecture for
$k=2$
, while Jiang and Qiu [Reference Jiang and Qiu22] proved the conjecture for
![]() $k=3,4$
.
$k=3,4$
.
1.2 Our results
In this paper, we build on the recent work on subdivisions to establish the following large three-parameter family of Turán exponents, which includes all the ones obtained by Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7] and by Janzer [Reference Janzer18].
Theorem 1.2.
For any positive integers
![]() $p,k,b$
with
$p,k,b$
with
![]() $k\ge b$
,
$k\ge b$
,
![]() $1+\frac{p}{kp+b}$
is a Turán exponent.
$1+\frac{p}{kp+b}$
is a Turán exponent.
As an immediate corollary, we get the following easily stated result.
Theorem 1.3.
For any positive integers
![]() $p$
and
$p$
and
![]() $q$
with
$q$
with
![]() $q\gt p^2$
,
$q\gt p^2$
,
![]() $1+\frac{p}{q}$
is a Turán exponent.
$1+\frac{p}{q}$
is a Turán exponent.
Using a reduction lemma of Kang, Kim, and Liu [Reference Kang, Kim and Liu25], Theorem 1.2 also yields
Corollary 1.4.
For any integers
![]() $b,p,s\ge 1$
and
$b,p,s\ge 1$
and
![]() $k\ge 0$
, if
$k\ge 0$
, if
![]() $k\ge b-1$
, then
$k\ge b-1$
, then
![]() $2-\frac{kp+b}{s(kp+b)+p}$
is a Turán exponent.
$2-\frac{kp+b}{s(kp+b)+p}$
is a Turán exponent.
Corollary 1.4 implies the following.
Corollary 1.5.
For any positive integers
![]() $p,q$
with
$p,q$
with
![]() $q\gt p$
, if
$q\gt p$
, if
![]() $(q\ \mathrm{ mod }\ p)\le \sqrt{p}$
, then
$(q\ \mathrm{ mod }\ p)\le \sqrt{p}$
, then
![]() $2-\frac{p}{q}$
is a Turán exponent.
$2-\frac{p}{q}$
is a Turán exponent.
Theorem 1.2 follows from a theorem (Theorem 1.15) that we prove on the Turán number of subdivisions of
![]() $K_{s,t}$
where different edges of
$K_{s,t}$
where different edges of
![]() $K_{s,t}$
may be subdivided different number of times. The theorem is interesting on its own and partially answers a conjecture of Janzer (Conjecture 1.13), which we will describe in the next subsection.
$K_{s,t}$
may be subdivided different number of times. The theorem is interesting on its own and partially answers a conjecture of Janzer (Conjecture 1.13), which we will describe in the next subsection.
1.3 The Bukh-Conlon Conjecture and Janzer’s conjecture
At the core of the work of Bukh and Conlon [Reference Bukh and Conlon3] is the study of so-called blowups of balanced rooted trees, defined as follows (also see [Reference Bukh and Conlon3]).
Definition 1.6. A rooted tree
![]() $(T,R)$
consists of a tree
$(T,R)$
consists of a tree
![]() $T$
together with an independent set
$T$
together with an independent set
![]() $R\subseteq V(T)$
, which we refer to as the roots. When the choice of
$R\subseteq V(T)$
, which we refer to as the roots. When the choice of
![]() $R$
is clear, we will simply write
$R$
is clear, we will simply write
![]() $T$
for
$T$
for
![]() $(T,R)$
.
$(T,R)$
.
Definition 1.7. Given a rooted tree
![]() $(T,R)$
and a non-empty subset
$(T,R)$
and a non-empty subset
![]() $S\subseteq V(T)\setminus R$
, let
$S\subseteq V(T)\setminus R$
, let
![]() $\rho _{T}(S)=\frac{e(S)}{|S|}$
, where
$\rho _{T}(S)=\frac{e(S)}{|S|}$
, where
![]() $e(S)$
is the number of edges in
$e(S)$
is the number of edges in
![]() $T$
that have at least one end in
$T$
that have at least one end in
![]() $S$
. Let
$S$
. Let
![]() $\rho _T=\rho _T(V(T)\setminus R)$
and call it the density of
$\rho _T=\rho _T(V(T)\setminus R)$
and call it the density of
![]() $T$
. We say
$T$
. We say
![]() $(T,R)$
is balanced if
$(T,R)$
is balanced if
![]() $\rho _{T}(S)\ge \rho (T)$
for any non-empty subset
$\rho _{T}(S)\ge \rho (T)$
for any non-empty subset
![]() $S\subseteq V(T)\setminus R$
.
$S\subseteq V(T)\setminus R$
.
Definition 1.8. The
![]() $t$
-blowup of a rooted tree
$t$
-blowup of a rooted tree
![]() $(T,R)$
, denoted by
$(T,R)$
, denoted by
![]() $t*T_{R}$
, is the union of
$t*T_{R}$
, is the union of
![]() $t$
labelled copies of
$t$
labelled copies of
![]() $T$
which agree on
$T$
which agree on
![]() $R$
but are pairwise vertex disjoint outside
$R$
but are pairwise vertex disjoint outside
![]() $R$
. If the choice of
$R$
. If the choice of
![]() $R$
is clear, then we write
$R$
is clear, then we write
![]() $t*T$
for
$t*T$
for
![]() $t*T_{R}$
.
$t*T_{R}$
.
The key result of Bukh and Conlon [Reference Bukh and Conlon3] is the following lower bound theorem, established using an innovative random algebraic approach. Interested readers can find the full statement in [Reference Bukh and Conlon3].
Theorem 1.9 ([Reference Bukh and Conlon3]). Suppose that
![]() $(T,R)$
is a balanced rooted tree with density
$(T,R)$
is a balanced rooted tree with density
![]() $\rho$
. Then there exists an integer
$\rho$
. Then there exists an integer
![]() $t_0\ge 2$
such that for all integers
$t_0\ge 2$
such that for all integers
![]() $t\geq t_0$
we have
$t\geq t_0$
we have
![]() $\mathrm{ex}(n,t*T_R) = \Omega \!\left(n^{2-\frac 1\rho }\right)$
.
$\mathrm{ex}(n,t*T_R) = \Omega \!\left(n^{2-\frac 1\rho }\right)$
.
Bukh and Conlon further made the following conjecture on a matching upper bound.
Conjecture 1.10 ([Reference Bukh and Conlon3]). Suppose that
![]() $(T,R)$
is a balanced rooted tree with density
$(T,R)$
is a balanced rooted tree with density
![]() $\rho$
. Then for all positive integers
$\rho$
. Then for all positive integers
![]() $t$
we have
$t$
we have
![]() $\mathrm{ex}(n,t*T_R) = O\!\left(n^{2-\frac 1\rho }\right)$
.
$\mathrm{ex}(n,t*T_R) = O\!\left(n^{2-\frac 1\rho }\right)$
.
Besides being interesting on its own, a significance of Conjecture 1.10 is that it implies the rational exponent conjecture. Indeed, for each rational
![]() $r\in (1,2)$
, Bukh and Conlon were able to construct a balanced rooted tree
$r\in (1,2)$
, Bukh and Conlon were able to construct a balanced rooted tree
![]() $(T,R)$
with density
$(T,R)$
with density
![]() $\rho =\frac{1}{2-r}$
. Hence Theorem 1.9 and Conjecture 1.10 together would give
$\rho =\frac{1}{2-r}$
. Hence Theorem 1.9 and Conjecture 1.10 together would give
![]() $\mathrm{ex}(n,t*T_R)=\Theta (n^r)$
for some sufficiently large positive integer
$\mathrm{ex}(n,t*T_R)=\Theta (n^r)$
for some sufficiently large positive integer
![]() $t$
. A careful reader will note that Bukh and Conlon’s conjecture is in fact much stronger than the rational exponent conjecture. Indeed, to prove the rational exponent conjecture, it suffices to find, for each
$t$
. A careful reader will note that Bukh and Conlon’s conjecture is in fact much stronger than the rational exponent conjecture. Indeed, to prove the rational exponent conjecture, it suffices to find, for each
![]() $r\in (1,2)$
, a balanced rooted tree
$r\in (1,2)$
, a balanced rooted tree
![]() $(T,R)$
with density
$(T,R)$
with density
![]() $\rho =\frac{1}{2-r}$
for which the Bukh-Conlon conjecture holds. This suggests that one way to make further progress on the rational exponent conjecture is to find suitable balanced rooted trees to explore Conjecture 1.10 with. One family of trees whose exploration has brought some success are the so-called spiders.
$\rho =\frac{1}{2-r}$
for which the Bukh-Conlon conjecture holds. This suggests that one way to make further progress on the rational exponent conjecture is to find suitable balanced rooted trees to explore Conjecture 1.10 with. One family of trees whose exploration has brought some success are the so-called spiders.
Definition 1.11. Let
![]() $s\geq 2$
be an integer. An
$s\geq 2$
be an integer. An
![]() $s$
-legged spider
$s$
-legged spider
![]() $S$
with centre
$S$
with centre
![]() $u$
is a tree consisting of
$u$
is a tree consisting of
![]() $s$
paths (called the legs of
$s$
paths (called the legs of
![]() $S$
) that share one common end
$S$
) that share one common end
![]() $u$
but are vertex disjoint outside
$u$
but are vertex disjoint outside
![]() $u$
. Moreover, we say
$u$
. Moreover, we say
![]() $S$
has length vector
$S$
has length vector
![]() $(\,j_1,\ldots,j_s)$
and leaf vector
$(\,j_1,\ldots,j_s)$
and leaf vector
![]() $(x_1,\ldots,x_s)$
if for every
$(x_1,\ldots,x_s)$
if for every
![]() $1\le i\le s$
, its
$1\le i\le s$
, its
![]() $i$
-th leg has length
$i$
-th leg has length
![]() $j_i$
and has ends
$j_i$
and has ends
![]() $u$
and
$u$
and
![]() $x_i$
.
$x_i$
.
For spiders with roots being all of its leaves, checking balancedness is simple.
Proposition 1.12.
Let
![]() $s, k$
be integers where
$s, k$
be integers where
![]() $s\geq 2, k\geq 1$
. Let
$s\geq 2, k\geq 1$
. Let
![]() $S$
be an
$S$
be an
![]() $s$
-legged spider and
$s$
-legged spider and
![]() $R$
the set of its leaves. Suppose the longest leg of
$R$
the set of its leaves. Suppose the longest leg of
![]() $S$
has length
$S$
has length
![]() $k$
. Then
$k$
. Then
![]() $(S,R)$
is a balanced rooted tree if and only if
$(S,R)$
is a balanced rooted tree if and only if
![]() $e(S)\geq (s-1)k$
.
$e(S)\geq (s-1)k$
.
When
![]() $S$
is an
$S$
is an
![]() $s$
-legged spider with length vector
$s$
-legged spider with length vector
![]() $(k,\ldots,k)$
and
$(k,\ldots,k)$
and
![]() $R$
is the set of its leaves,
$R$
is the set of its leaves,
![]() $t*S_R$
is the subdivision
$t*S_R$
is the subdivision
![]() $K_{s,t}^k$
of
$K_{s,t}^k$
of
![]() $K_{s,t}$
, considered by Janzer [Reference Janzer18]. When
$K_{s,t}$
, considered by Janzer [Reference Janzer18]. When
![]() $S$
is an
$S$
is an
![]() $(s+1)$
-legged spider with length vector
$(s+1)$
-legged spider with length vector
![]() $(1,k,\ldots, k)$
and
$(1,k,\ldots, k)$
and
![]() $R$
is the set of its leaves,
$R$
is the set of its leaves,
![]() $t*S_R$
is the graph
$t*S_R$
is the graph
![]() $L_{s,t}(k)$
, considered by Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7]. Motivated by the earlier mentioned results on
$L_{s,t}(k)$
, considered by Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7]. Motivated by the earlier mentioned results on
![]() $\mathrm{ex}\left(n,L_{s,t}(k)\right)$
and
$\mathrm{ex}\left(n,L_{s,t}(k)\right)$
and
![]() $\mathrm{ex}\left(n,K_{s,t}^k\right)$
, Janzer [Reference Janzer18] made the following conjecture.
$\mathrm{ex}\left(n,K_{s,t}^k\right)$
, Janzer [Reference Janzer18] made the following conjecture.
Conjecture 1.13 ([Reference Janzer18]). Let
![]() $s\geq 2, k,b,t\geq 1$
be integers. Let
$s\geq 2, k,b,t\geq 1$
be integers. Let
![]() $S$
be an
$S$
be an
![]() $s$
-legged spider where the longest leg has length
$s$
-legged spider where the longest leg has length
![]() $k$
. Suppose that
$k$
. Suppose that
![]() $e(S)=(s-1)k+b$
, where
$e(S)=(s-1)k+b$
, where
![]() $0\leq b \leq k$
. Then
$0\leq b \leq k$
. Then
![]() $\mathrm{ex}(n, t*S)= O\!\left(n^{1+\frac{s-1}{(s-1)k+b}}\right)$
.
$\mathrm{ex}(n, t*S)= O\!\left(n^{1+\frac{s-1}{(s-1)k+b}}\right)$
.
Even though Janzer’s conjecture is a special case of the Bukh-Conlon conjecture, it is also interesting on its own due to its connection to the study of subdivisions. Let
![]() $S$
be as specified in Conjecture 1.13. It follows from Theorem 1.9 that there exists a
$S$
be as specified in Conjecture 1.13. It follows from Theorem 1.9 that there exists a
![]() $t_0$
such that for all
$t_0$
such that for all
![]() $t\geq t_0$
,
$t\geq t_0$
,
![]() $\mathrm{ex}(n,t*S)=\Omega \!\left(n^{1+\frac{s-1}{(s-1)k+b}}\right)$
. Hence, if Conjecture 1.13 is true, it will establish all rationals of the form
$\mathrm{ex}(n,t*S)=\Omega \!\left(n^{1+\frac{s-1}{(s-1)k+b}}\right)$
. Hence, if Conjecture 1.13 is true, it will establish all rationals of the form
![]() $1+\frac{p}{pk+b}$
as Turán exponents, where
$1+\frac{p}{pk+b}$
as Turán exponents, where
![]() $p,k$
are positive integers and
$p,k$
are positive integers and
![]() $b$
is an integer with
$b$
is an integer with
![]() $0\leq b \leq k$
. Here, we settle an important case of Conjecture 1.13 that allows us to obtain all the Turán exponents that Conjecture 1.13 would give.
$0\leq b \leq k$
. Here, we settle an important case of Conjecture 1.13 that allows us to obtain all the Turán exponents that Conjecture 1.13 would give.
Definition 1.14. For positive integers
![]() $k,b$
and
$k,b$
and
![]() $s$
, let
$s$
, let
![]() $S^s_{b,k}$
denote the
$S^s_{b,k}$
denote the
![]() $s$
-legged spider with length vector
$s$
-legged spider with length vector
![]() $(b,k,\ldots,k)$
.
$(b,k,\ldots,k)$
.
Using this notation, we have
![]() $K_{s,t}^k=t*S^s_{k,k}$
and
$K_{s,t}^k=t*S^s_{k,k}$
and
![]() $L_{s,t}(k)=t*S^{s+1}_{1,k}$
. In this paper, we will prove the following common generalization of the result of Conlon, Janzer, and Lee on
$L_{s,t}(k)=t*S^{s+1}_{1,k}$
. In this paper, we will prove the following common generalization of the result of Conlon, Janzer, and Lee on
![]() $\mathrm{ex}(n, L_{s,t}(k))$
and the result of Janzer on
$\mathrm{ex}(n, L_{s,t}(k))$
and the result of Janzer on
![]() $\mathrm{ex}\!\left(n,K_{s,t}^k\right)$
, from which our main theorem, Theorem 1.2, follows.
$\mathrm{ex}\!\left(n,K_{s,t}^k\right)$
, from which our main theorem, Theorem 1.2, follows.
Theorem 1.15.
For any
![]() $s,t\ge 2$
and
$s,t\ge 2$
and
![]() $k\ge b\ge 1$
,
$k\ge b\ge 1$
,
![]() $\mathrm{ex}\Big(n,t*S^s_{b,k}\Big)= O\!\left(n^{1+\frac{s-1}{(s-1)k+b}}\right)$
.
$\mathrm{ex}\Big(n,t*S^s_{b,k}\Big)= O\!\left(n^{1+\frac{s-1}{(s-1)k+b}}\right)$
.
As in [Reference Conlon and Lee6, Reference Conlon, Janzer and Lee7, Reference Jiang and Qiu22, Reference Janzer18], we will use the following variant of the regularization lemma of Erdős and Simonovits [Reference Erdős and Simonovits11], as given in [Reference Jiang and Seiver24]. Given a positive constant
![]() $K$
, a graph
$K$
, a graph
![]() $G$
is
$G$
is
![]() $K$
-almost-regular if
$K$
-almost-regular if
![]() $\Delta (G)\leq K\delta (G)$
.
$\Delta (G)\leq K\delta (G)$
.
Lemma 1.16 ([Reference Jiang and Seiver24]). Let
![]() $0\lt \epsilon \lt 1$
and
$0\lt \epsilon \lt 1$
and
![]() $c\ge 1$
. There exists
$c\ge 1$
. There exists
![]() $n_0=n_0(\epsilon )\gt 0$
such that the following holds for all
$n_0=n_0(\epsilon )\gt 0$
such that the following holds for all
![]() $n\ge n_0$
. If
$n\ge n_0$
. If
![]() $G$
is a graph on
$G$
is a graph on
![]() $n$
vertices with
$n$
vertices with
![]() $e(G)\ge cn^{1+\epsilon }$
, then
$e(G)\ge cn^{1+\epsilon }$
, then
![]() $G$
contains a
$G$
contains a
![]() $K$
-almost-regular subgraph
$K$
-almost-regular subgraph
![]() $G^{\prime}$
on
$G^{\prime}$
on
![]() $m\ge n^{\frac{\epsilon -\epsilon ^2}{2+2\epsilon }}$
vertices such that
$m\ge n^{\frac{\epsilon -\epsilon ^2}{2+2\epsilon }}$
vertices such that
![]() $e(G^{\prime})\ge \frac{2c}5m^{1+\epsilon }$
and
$e(G^{\prime})\ge \frac{2c}5m^{1+\epsilon }$
and
![]() $K=\Big\lceil 20\cdot 2^{\frac 1{\epsilon ^2}+1}\Big\rceil $
.
$K=\Big\lceil 20\cdot 2^{\frac 1{\epsilon ^2}+1}\Big\rceil $
.
By Lemma 1.16, in order to prove Theorem 1.15, it suffices to prove the following.
Theorem 1.17.
Let
![]() $s,t\ge 2$
and
$s,t\ge 2$
and
![]() $k\ge b\ge 1$
. Let
$k\ge b\ge 1$
. Let
![]() $K=K(s,b,k)$
be obtained by Lemma 1.16 with
$K=K(s,b,k)$
be obtained by Lemma 1.16 with
![]() $\epsilon \,:\!=\,\frac{s-1}{(s-1)k+b}$
. There exist positive constants
$\epsilon \,:\!=\,\frac{s-1}{(s-1)k+b}$
. There exist positive constants
![]() $n_0$
and
$n_0$
and
![]() $C$
depending only on
$C$
depending only on
![]() $s,t,b,k$
such that for all integers
$s,t,b,k$
such that for all integers
![]() $n\geq n_0$
if
$n\geq n_0$
if
![]() $G$
is an
$G$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $t*S^s_{b,k}$
-free
$t*S^s_{b,k}$
-free
![]() $K$
-almost-regular graph then
$K$
-almost-regular graph then
![]() $\delta (G)\lt C n^{\frac{s-1}{(s-1)k+b}}$
.
$\delta (G)\lt C n^{\frac{s-1}{(s-1)k+b}}$
.
The rest of the paper is organized as follows. In Section 2, we introduce some notation and preliminary lemmas. In Section 3, we prove Theorem 1.17, from which Theorems 1.15 and 1.2 follow. In Section 4, we give a sketch of proofs of Corollaries 1.4 and 1.5 and some concluding remarks.
2. Notation and preliminaries
Given a positive integer
![]() $m$
, let
$m$
, let
![]() $[m]=\{1,\ldots, m\}$
. Given a graph
$[m]=\{1,\ldots, m\}$
. Given a graph
![]() $G$
and a vertex
$G$
and a vertex
![]() $w$
, for each
$w$
, for each
![]() $i\ge 1$
let
$i\ge 1$
let
![]() $\Gamma _i(w)$
be the set of vertices
$\Gamma _i(w)$
be the set of vertices
![]() $z$
such that there exists a path in
$z$
such that there exists a path in
![]() $G$
of length
$G$
of length
![]() $i$
with ends
$i$
with ends
![]() $w$
and
$w$
and
![]() $z$
. When
$z$
. When
![]() $i=1$
, we often write
$i=1$
, we often write
![]() $N_G(w)$
for
$N_G(w)$
for
![]() $\Gamma _1(w)$
. Let
$\Gamma _1(w)$
. Let
![]() $e(G)$
be the number of edges in
$e(G)$
be the number of edges in
![]() $G$
. We use standard asymptotic notations, that is, given two positive functions
$G$
. We use standard asymptotic notations, that is, given two positive functions
![]() $f(n)$
and
$f(n)$
and
![]() $g(n)$
, by
$g(n)$
, by
![]() $f=o_n(g),f=\omega _n(g),f=\Omega _n(g),f=O_n(g),f=\Theta _n(g)$
, we respectively mean
$f=o_n(g),f=\omega _n(g),f=\Omega _n(g),f=O_n(g),f=\Theta _n(g)$
, we respectively mean
![]() $\lim _{n\rightarrow \infty }f/g=0,\liminf _{n\rightarrow \infty }f/g=\infty,\liminf _{n\rightarrow \infty }f/g\gt 0,\limsup _{n\rightarrow \infty }f/g\lt \infty,0\lt \liminf _{n\rightarrow \infty }f/g\le \limsup _{n\rightarrow \infty }f/g\lt \infty$
. Whenever the context is clear, we drop the subscript
$\lim _{n\rightarrow \infty }f/g=0,\liminf _{n\rightarrow \infty }f/g=\infty,\liminf _{n\rightarrow \infty }f/g\gt 0,\limsup _{n\rightarrow \infty }f/g\lt \infty,0\lt \liminf _{n\rightarrow \infty }f/g\le \limsup _{n\rightarrow \infty }f/g\lt \infty$
. Whenever the context is clear, we drop the subscript
![]() $n$
. If
$n$
. If
![]() $G$
is a graph and
$G$
is a graph and
![]() $S$
is a set of vertices in it, then we define
$S$
is a set of vertices in it, then we define
and call it the common neighbourhood of
![]() $S$
in
$S$
in
![]() $G$
.
$G$
.
For the rest of the paper, we fix integers
![]() $s,t\ge 2$
and
$s,t\ge 2$
and
![]() $k\ge b\ge 1$
, and let
$k\ge b\ge 1$
, and let
![]() $K=K(s,b,k)$
be obtained by Lemma 1.16 with
$K=K(s,b,k)$
be obtained by Lemma 1.16 with
![]() $\epsilon \,:\!=\,\frac{s-1}{(s-1)k+b}$
.
$\epsilon \,:\!=\,\frac{s-1}{(s-1)k+b}$
.
Below are some key concepts introduced in [Reference Conlon, Janzer and Lee7], which we adapt for our setting.
Definition 2.1. Let
![]() $L$
be a positive integer, we define
$L$
be a positive integer, we define
![]() $f(1,L)=L$
and for
$f(1,L)=L$
and for
![]() $j\ge 2$
,
$j\ge 2$
,
We will need the following property of the function in various places of the paper.
Proposition 2.2.
For every integer
![]() $j\geq 2$
,
$j\geq 2$
,
![]() $\frac{f(j,L)}{j^2f(j-1,L)^2}\ge \max \{2L^2,f(j-1,L)\}$
holds.
$\frac{f(j,L)}{j^2f(j-1,L)^2}\ge \max \{2L^2,f(j-1,L)\}$
holds.
The next two definitions are crucial to our overall arguments.
Definition 2.3. We recursively define
![]() $j$
-admissible,
$j$
-admissible,
![]() $j$
-light paths, and
$j$
-light paths, and
![]() $j$
-heavy paths in a graph
$j$
-heavy paths in a graph
![]() $G$
. Any edge is both 1-admissible and 1-light. For
$G$
. Any edge is both 1-admissible and 1-light. For
![]() $j\ge 2$
, a path
$j\ge 2$
, a path
![]() $P$
is
$P$
is
![]() $j$
-admissible if it has length
$j$
-admissible if it has length
![]() $j$
and for each
$j$
and for each
![]() $1\leq \ell \lt j$
every subpath of length
$1\leq \ell \lt j$
every subpath of length
![]() $\ell$
in
$\ell$
in
![]() $P$
is
$P$
is
![]() $\ell$
-light.
$\ell$
-light.
Among
![]() $j$
-admissible paths
$j$
-admissible paths
![]() $P$
with ends
$P$
with ends
![]() $x$
and
$x$
and
![]() $y$
, we further say that
$y$
, we further say that
![]() $P$
is
$P$
is
![]() $j$
-light if the number of
$j$
-light if the number of
![]() $j$
-admissible paths with ends
$j$
-admissible paths with ends
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $G$
is less than
$G$
is less than
![]() $f(j,L)$
and that
$f(j,L)$
and that
![]() $P$
is
$P$
is
![]() $j$
-heavy otherwise.
$j$
-heavy otherwise.
Since the length of a path
![]() $P$
is fixed, we often drop the prefix
$P$
is fixed, we often drop the prefix
![]() $j$
and
$j$
and
![]() $\ell$
in the definitions above. Note that
$\ell$
in the definitions above. Note that
![]() $j$
-admissible and
$j$
-admissible and
![]() $j$
-light paths are defined for all
$j$
-light paths are defined for all
![]() $j\geq 1$
while
$j\geq 1$
while
![]() $j$
-heavy paths are defined only for
$j$
-heavy paths are defined only for
![]() $j\geq 2$
. In [Reference Jiang and Qiu22], the concepts of admissible, light, and heavy paths were extended for spiders. Here, we adapt the definitions from [Reference Jiang and Qiu22] further.
$j\geq 2$
. In [Reference Jiang and Qiu22], the concepts of admissible, light, and heavy paths were extended for spiders. Here, we adapt the definitions from [Reference Jiang and Qiu22] further.
Definition 2.4. We recursively define
![]() $s$
-legged admissible, light, and heavy spiders in a graph
$s$
-legged admissible, light, and heavy spiders in a graph
![]() $G$
. Any spider of height 1 is both admissible and light. Let
$G$
. Any spider of height 1 is both admissible and light. Let
![]() $S$
be an
$S$
be an
![]() $s$
-legged spider with leaf vector
$s$
-legged spider with leaf vector
![]() $(x_1,\ldots, x_s)$
and length vector
$(x_1,\ldots, x_s)$
and length vector
![]() $(j_1,\ldots, j_s)\neq (1,1,\ldots,1)$
. We say that
$(j_1,\ldots, j_s)\neq (1,1,\ldots,1)$
. We say that
![]() $S$
is admissible if every leg of it is a light path as defined in Definition 2.3 and every
$S$
is admissible if every leg of it is a light path as defined in Definition 2.3 and every
![]() $s$
-legged proper sub-spider of
$s$
-legged proper sub-spider of
![]() $S$
is light. Suppose
$S$
is light. Suppose
![]() $S$
is admissible. Then we further say that it is light if the number of admissible spiders in
$S$
is admissible. Then we further say that it is light if the number of admissible spiders in
![]() $G$
with leaf vector
$G$
with leaf vector
![]() $(x_1,\ldots,x_s)$
and length vector
$(x_1,\ldots,x_s)$
and length vector
![]() $(j_1,\ldots,j_s)$
is less than
$(j_1,\ldots,j_s)$
is less than
![]() $f(j,L)$
where
$f(j,L)$
where
![]() $j=j_1+\cdots +j_s$
. If
$j=j_1+\cdots +j_s$
. If
![]() $S$
is admissible but not light, then we say that it is heavy.
$S$
is admissible but not light, then we say that it is heavy.
At this point, let us say a few words about the function
![]() $f(j,L)$
given in Definition 2.1, as this function plays an important role in our arguments. In application we always assume that the parameter
$f(j,L)$
given in Definition 2.1, as this function plays an important role in our arguments. In application we always assume that the parameter
![]() $L$
is sufficiently larger than
$L$
is sufficiently larger than
![]() $s,t,k$
and
$s,t,k$
and
![]() $K$
and roughly speaking
$K$
and roughly speaking
![]() $f(j,L)$
is chosen so that
$f(j,L)$
is chosen so that
![]() $f(j,L)\gg f(j-1,L)$
, that is,
$f(j,L)\gg f(j-1,L)$
, that is,
![]() $\frac{f(j,L)}{f(j-1,L)}\rightarrow \infty$
as
$\frac{f(j,L)}{f(j-1,L)}\rightarrow \infty$
as
![]() $L\rightarrow \infty$
.
$L\rightarrow \infty$
.
Next, we give several lemmas. Lemma 2.6 is similar to one used in [Reference Conlon, Janzer and Lee7]. Lemma 2.7 has its analogous counterparts in [Reference Jiang and Qiu22] and [Reference Janzer18]. However, since our terminologies and choices of constants are slightly different, we include full proofs for completeness.
Lemma 2.5.
Let
![]() $G$
be a
$G$
be a
![]() $K$
-almost-regular graph. Let
$K$
-almost-regular graph. Let
![]() $1\leq i\leq j$
be integers. Let
$1\leq i\leq j$
be integers. Let
![]() $x,w,y$
be vertices in
$x,w,y$
be vertices in
![]() $G$
. Then the number of
$G$
. Then the number of
![]() $j$
-admissible paths in
$j$
-admissible paths in
![]() $G$
that have
$G$
that have
![]() $x,w,y$
as the first,
$x,w,y$
as the first,
![]() $(i+1)$
-th and last vertices, respectively is at most
$(i+1)$
-th and last vertices, respectively is at most
![]() $f(i,L)\cdot f(j-i,L)$
. Furthermore, if
$f(i,L)\cdot f(j-i,L)$
. Furthermore, if
![]() $i=1$
or
$i=1$
or
![]() $j-1$
, then there are most
$j-1$
, then there are most
![]() $f(j-1,L)$
such paths.
$f(j-1,L)$
such paths.
Proof. Let
![]() $\mathcal{P}$
be the family of
$\mathcal{P}$
be the family of
![]() $j$
-admissible paths in
$j$
-admissible paths in
![]() $G$
that have
$G$
that have
![]() $x,w,y$
as the first,
$x,w,y$
as the first,
![]() $(i+1)$
-th, and last vertices, respectively. Let
$(i+1)$
-th, and last vertices, respectively. Let
![]() $P\in \mathcal{P}$
, by definition, each proper subpath of
$P\in \mathcal{P}$
, by definition, each proper subpath of
![]() $P$
is light. So
$P$
is light. So
![]() $P$
is the union of an
$P$
is the union of an
![]() $i$
-light path from
$i$
-light path from
![]() $x$
to
$x$
to
![]() $w$
and a
$w$
and a
![]() $(j-i)$
-light path from
$(j-i)$
-light path from
![]() $w$
to
$w$
to
![]() $y$
. By definition of light paths there are at most
$y$
. By definition of light paths there are at most
![]() $f(i,L)$
$f(i,L)$
![]() $i$
-light paths in
$i$
-light paths in
![]() $G$
with ends
$G$
with ends
![]() $x,w$
and at most
$x,w$
and at most
![]() $f(j-i,L)$
$f(j-i,L)$
![]() $(j-i)$
-light paths with ends
$(j-i)$
-light paths with ends
![]() $w$
and
$w$
and
![]() $y$
. So
$y$
. So
![]() $|\mathcal{P}|\leq f(i,L)\cdot f(j-i,L)$
.
$|\mathcal{P}|\leq f(i,L)\cdot f(j-i,L)$
.
If
![]() $i=1$
then every
$i=1$
then every
![]() $P\in \mathcal{P}$
is the union of the edge
$P\in \mathcal{P}$
is the union of the edge
![]() $xw$
and a
$xw$
and a
![]() $(j-1)$
-light path with ends
$(j-1)$
-light path with ends
![]() $w$
and
$w$
and
![]() $y$
. So
$y$
. So
![]() $|\mathcal{P}|\leq f(j-1,L)$
. The case
$|\mathcal{P}|\leq f(j-1,L)$
. The case
![]() $i=j-1$
is similar.
$i=j-1$
is similar.
Lemma 2.6.
Let
![]() $x,y$
be two vertices and
$x,y$
be two vertices and
![]() $\mathcal{C}$
be a family of
$\mathcal{C}$
be a family of
![]() $j$
-admissible paths between
$j$
-admissible paths between
![]() $x$
and
$x$
and
![]() $y$
. Then there are at least
$y$
. Then there are at least
![]() $|\mathcal{C}|/[{j^2 \cdot f(j-1,L)^2}]$
members of
$|\mathcal{C}|/[{j^2 \cdot f(j-1,L)^2}]$
members of
![]() $\mathcal{C}$
that are pairwise vertex disjoint outside
$\mathcal{C}$
that are pairwise vertex disjoint outside
![]() $\{x,y\}$
.
$\{x,y\}$
.
Proof. Let
![]() $\mathcal{C}^{\prime}=\{Q_1,\ldots,Q_r\}\subseteq \mathcal{C}$
be a maximal subfamily of
$\mathcal{C}^{\prime}=\{Q_1,\ldots,Q_r\}\subseteq \mathcal{C}$
be a maximal subfamily of
![]() $\mathcal{C}$
that are pairwise vertex disjoint outside
$\mathcal{C}$
that are pairwise vertex disjoint outside
![]() $\{x,y\}$
. Let
$\{x,y\}$
. Let
![]() $W=\bigcup _{i=1}^r V(Q_i)\setminus \{x,y\}$
. Then
$W=\bigcup _{i=1}^r V(Q_i)\setminus \{x,y\}$
. Then
![]() $|W|=(j-1)r$
. By maximality, every member of
$|W|=(j-1)r$
. By maximality, every member of
![]() $\mathcal{C}$
must contain a vertex
$\mathcal{C}$
must contain a vertex
![]() $v\in W$
as an internal vertex. For each
$v\in W$
as an internal vertex. For each
![]() $v\in W$
and each
$v\in W$
and each
![]() $1\leq i\leq j-1$
let
$1\leq i\leq j-1$
let
![]() $\mathcal{C}_{v,i}$
be the subfamily of members of
$\mathcal{C}_{v,i}$
be the subfamily of members of
![]() $\mathcal{C}$
that contain
$\mathcal{C}$
that contain
![]() $v$
as its
$v$
as its
![]() $(i+1)$
-th vertex (when the member is viewed from
$(i+1)$
-th vertex (when the member is viewed from
![]() $x$
to
$x$
to
![]() $y$
). Then
$y$
). Then
![]() $\mathcal{C}=\bigcup _{v,i} \mathcal{C}_{v,i}$
. By Lemma 2.5, for any fixed
$\mathcal{C}=\bigcup _{v,i} \mathcal{C}_{v,i}$
. By Lemma 2.5, for any fixed
![]() $v,i$
, we have
$v,i$
, we have
![]() $|\mathcal{C}_{v,i}|\leq f(i,L)\cdot f(j-i,L)\le f(j-1,L)^2$
. Hence
$|\mathcal{C}_{v,i}|\leq f(i,L)\cdot f(j-i,L)\le f(j-1,L)^2$
. Hence
 \begin{equation*} |\mathcal {C}|=\left|\bigcup _{v,i}\mathcal {C}_{v,i}\right|\leq \sum _{v\in W}\sum _{i=1}^{j-1} f(j-1,L)^2 \lt rj^2 f(j-1,L)^2. \end{equation*}
\begin{equation*} |\mathcal {C}|=\left|\bigcup _{v,i}\mathcal {C}_{v,i}\right|\leq \sum _{v\in W}\sum _{i=1}^{j-1} f(j-1,L)^2 \lt rj^2 f(j-1,L)^2. \end{equation*}
Solving the inequality for
![]() $r$
, we get the desired claim.
$r$
, we get the desired claim.
For two spiders with the same leaf vector and length vector, we say they are internally disjoint if they are vertex disjoint outside their leaves.
Lemma 2.7.
Let
![]() $\mathcal{S}$
be a family of admissible spiders with leaf vector
$\mathcal{S}$
be a family of admissible spiders with leaf vector
![]() $(x_1,\ldots,x_s)$
and length vector
$(x_1,\ldots,x_s)$
and length vector
![]() $(j_1,\ldots,j_s)$
. Then there are at least
$(j_1,\ldots,j_s)$
. Then there are at least
![]() $|\mathcal{S}|/\left[j^2 \cdot f(j-1,L)^2\right]$
members of
$|\mathcal{S}|/\left[j^2 \cdot f(j-1,L)^2\right]$
members of
![]() $\mathcal{S}$
that are pairwise vertex disjoint outside
$\mathcal{S}$
that are pairwise vertex disjoint outside
![]() $\{x_1,\ldots, x_s\}$
, where
$\{x_1,\ldots, x_s\}$
, where
![]() $j=j_1+\cdots +j_s$
.
$j=j_1+\cdots +j_s$
.
Proof. Let
![]() $\mathcal{S}^{\prime}=\{S_1,\ldots,S_r\}\subseteq \mathcal{S}$
be a maximal subfamily of members of
$\mathcal{S}^{\prime}=\{S_1,\ldots,S_r\}\subseteq \mathcal{S}$
be a maximal subfamily of members of
![]() $\mathcal{S}$
that are pairwise vertex disjoint outside
$\mathcal{S}$
that are pairwise vertex disjoint outside
![]() $\{x_1,\ldots, x_s\}$
. Let
$\{x_1,\ldots, x_s\}$
. Let
![]() $W=\bigcup _{i=1}^r V(S_i)\setminus \{x_1,\ldots, x_s\}$
. Then
$W=\bigcup _{i=1}^r V(S_i)\setminus \{x_1,\ldots, x_s\}$
. Then
![]() $|W|=(j-s+1)r$
. By maximality of
$|W|=(j-s+1)r$
. By maximality of
![]() $\mathcal{S}^{\prime}$
, every member of
$\mathcal{S}^{\prime}$
, every member of
![]() $\mathcal{S}$
must contain some
$\mathcal{S}$
must contain some
![]() $v\in W$
as a non-leaf vertex. For each
$v\in W$
as a non-leaf vertex. For each
![]() $v\in W$
let
$v\in W$
let
![]() $\mathcal{D}_v$
denote the subfamily of members of
$\mathcal{D}_v$
denote the subfamily of members of
![]() $\mathcal{S}$
that contain
$\mathcal{S}$
that contain
![]() $v$
as the centre. For each
$v$
as the centre. For each
![]() $v\in W$
,
$v\in W$
,
![]() $i\in [s]$
, and
$i\in [s]$
, and
![]() $1\leq \ell \lt j_i$
, let
$1\leq \ell \lt j_i$
, let
![]() $\mathcal{S}_{v,i,\ell }$
denote the subfamily of members of
$\mathcal{S}_{v,i,\ell }$
denote the subfamily of members of
![]() $\mathcal{S}$
in which
$\mathcal{S}$
in which
![]() $v$
is on the
$v$
is on the
![]() $i$
-th leg and the distance from
$i$
-th leg and the distance from
![]() $v$
to
$v$
to
![]() $x_i$
is
$x_i$
is
![]() $\ell$
. Then
$\ell$
. Then
![]() $\mathcal{S}=\left(\bigcup _{v\in W} \mathcal{D}_v\right) \cup \left(\bigcup _{v\in W, i\in [s], 1\leq \ell \lt j_i} \mathcal{S}_{v,i,\ell }\right)$
.
$\mathcal{S}=\left(\bigcup _{v\in W} \mathcal{D}_v\right) \cup \left(\bigcup _{v\in W, i\in [s], 1\leq \ell \lt j_i} \mathcal{S}_{v,i,\ell }\right)$
.
Let
![]() $S\in \mathcal{D}_v$
. Then by definition, for each
$S\in \mathcal{D}_v$
. Then by definition, for each
![]() $i\in [s]$
, the
$i\in [s]$
, the
![]() $i$
-th leg of
$i$
-th leg of
![]() $S$
is a
$S$
is a
![]() $j_i$
-light path between
$j_i$
-light path between
![]() $v$
and
$v$
and
![]() $x_i$
. Hence, by the definition of light paths,
$x_i$
. Hence, by the definition of light paths,
where the last inequality holds because by Definition 2.1 we have that
![]() $\prod _{i=1}^s f(j_i, L)\le f(j_1+j_2-1, L)^2\prod _{i=3}^s f(j_i, L)\le f(j_1+j_2, L)\prod _{i=3}^s f(j_i, L)\le \cdots \le f(j_1+\cdots +j_{s-1},L)f(j_s,L)\le f(j-1,L)^2$
.
$\prod _{i=1}^s f(j_i, L)\le f(j_1+j_2-1, L)^2\prod _{i=3}^s f(j_i, L)\le f(j_1+j_2, L)\prod _{i=3}^s f(j_i, L)\le \cdots \le f(j_1+\cdots +j_{s-1},L)f(j_s,L)\le f(j-1,L)^2$
.
Next, fix
![]() $v\in W$
,
$v\in W$
,
![]() $i\in [s]$
, and
$i\in [s]$
, and
![]() $1\leq \ell \lt j_i$
. Let
$1\leq \ell \lt j_i$
. Let
![]() $S\in \mathcal{S}_{v,i,\ell }$
. Since
$S\in \mathcal{S}_{v,i,\ell }$
. Since
![]() $S$
is admissible, the
$S$
is admissible, the
![]() $v,x_i$
-path in
$v,x_i$
-path in
![]() $S$
is
$S$
is
![]() $\ell$
-light while the rest of
$\ell$
-light while the rest of
![]() $S$
is an
$S$
is an
![]() $s$
-legged proper sub-spider, which by definition, is light. This implies that
$s$
-legged proper sub-spider, which by definition, is light. This implies that
Putting everything together, we obtain
 \begin{equation*} |\mathcal {S}|\leq |W| f(j-1,L)^2+\sum _{v\in W}\sum _{i=1}^{s}\sum _{\ell =1}^{j_i-1} f(j-1,L)^2, \end{equation*}
\begin{equation*} |\mathcal {S}|\leq |W| f(j-1,L)^2+\sum _{v\in W}\sum _{i=1}^{s}\sum _{\ell =1}^{j_i-1} f(j-1,L)^2, \end{equation*}
which implies that
![]() $|\mathcal{S}|\leq rj^2 f(j-1,L)^2$
, from which the claim follows.
$|\mathcal{S}|\leq rj^2 f(j-1,L)^2$
, from which the claim follows.
The following lemma is proved in [Reference Jiang and Qiu22]. A spider has height
![]() $\ell$
if all of its legs have length
$\ell$
if all of its legs have length
![]() $\ell$
.
$\ell$
.
Lemma 2.8 ([Reference Jiang and Qiu22] Lemma 3.6). Let
![]() $G$
be a
$G$
be a
![]() $K$
-almost-regular graph with minimum degree
$K$
-almost-regular graph with minimum degree
![]() $\delta$
. Let
$\delta$
. Let
![]() $x$
be a vertex. Let
$x$
be a vertex. Let
![]() $\mathcal{C}$
be a family of paths of length
$\mathcal{C}$
be a family of paths of length
![]() $h$
with one end
$h$
with one end
![]() $x$
and another end in a set
$x$
and another end in a set
![]() $S$
. For each
$S$
. For each
![]() $i\in [h]$
there exists a vertex
$i\in [h]$
there exists a vertex
![]() $x_i$
and a spider of height
$x_i$
and a spider of height
![]() $i$
with centre
$i$
with centre
![]() $x_i$
and leaves in
$x_i$
and leaves in
![]() $S$
which has at least
$S$
which has at least
![]() $|\mathcal{C}|/\big[h (K\delta )^{h-1}\big]$
legs. Furthermore,
$|\mathcal{C}|/\big[h (K\delta )^{h-1}\big]$
legs. Furthermore,
![]() $x_i=x$
if and only if
$x_i=x$
if and only if
![]() $i=h$
.
$i=h$
.
We also need a standard averaging lemma as below.
Lemma 2.9.
Let
![]() $0\lt c\lt 1$
be a real and
$0\lt c\lt 1$
be a real and
![]() $m$
be a positive integer. Let
$m$
be a positive integer. Let
![]() $G$
be a bipartite graph with a bipartition
$G$
be a bipartite graph with a bipartition
![]() $(X,Y)$
. Suppose that
$(X,Y)$
. Suppose that
![]() $e(G)\geq c|X||Y|$
and that
$e(G)\geq c|X||Y|$
and that
![]() $c|X|\geq 2m$
. Then there exists an
$c|X|\geq 2m$
. Then there exists an
![]() $m$
-set
$m$
-set
![]() $S$
in
$S$
in
![]() $X$
such that
$X$
such that
![]() $|N^*_G(S)|\geq (c/2)^m |Y|$
.
$|N^*_G(S)|\geq (c/2)^m |Y|$
.
Proof. By our assumption, the average degree of vertices in
![]() $Y$
is at least
$Y$
is at least
![]() $c|X|$
. Let
$c|X|$
. Let
![]() $\mathcal{F}$
be the family of
$\mathcal{F}$
be the family of
![]() $K_{1,m}$
’s with centre in
$K_{1,m}$
’s with centre in
![]() $Y$
. Then
$Y$
. Then
![]() $|\mathcal{F}|=\sum _{y\in Y} \binom{d_G(y)}{m}\geq |Y|\binom{c|X|}{m}$
, where the last inequality uses the convexity of the function
$|\mathcal{F}|=\sum _{y\in Y} \binom{d_G(y)}{m}\geq |Y|\binom{c|X|}{m}$
, where the last inequality uses the convexity of the function
![]() $\binom{x}{m}$
. Hence, by averaging there exists an
$\binom{x}{m}$
. Hence, by averaging there exists an
![]() $m$
-set
$m$
-set
![]() $S$
in
$S$
in
![]() $X$
such that the number of members of
$X$
such that the number of members of
![]() $\mathcal{F}$
that have
$\mathcal{F}$
that have
![]() $S$
as the leaf set is at least
$S$
as the leaf set is at least
 \begin{equation*}|Y|\frac {\binom {c|X|}{m}}{\binom {|X|}{m}} \ge |Y| \left (\frac {c|X|-m}{|X|-m}\right )^m\gt (c/2)^m|Y|, \end{equation*}
\begin{equation*}|Y|\frac {\binom {c|X|}{m}}{\binom {|X|}{m}} \ge |Y| \left (\frac {c|X|-m}{|X|-m}\right )^m\gt (c/2)^m|Y|, \end{equation*}
where the last inequality uses the condition
![]() $c|X|\geq 2m$
.
$c|X|\geq 2m$
.
Finally, we need a standard cleaning lemma.
Lemma 2.10.
If
![]() $B$
is a bipartite graph with parts
$B$
is a bipartite graph with parts
![]() $X$
and
$X$
and
![]() $Y$
, then it has subgraph
$Y$
, then it has subgraph
![]() $B^{\prime}$
such that
$B^{\prime}$
such that
![]() $e(B^{\prime})\geq \frac{e(B)}{2}$
and
$e(B^{\prime})\geq \frac{e(B)}{2}$
and
![]() $\forall x\in X\cap V(B^{\prime}), d_{B^{\prime}}(x)\geq \frac{e(B)}{4|X|}$
and
$\forall x\in X\cap V(B^{\prime}), d_{B^{\prime}}(x)\geq \frac{e(B)}{4|X|}$
and
![]() $\forall y\in Y\cap V(B^{\prime}), d_{B^{\prime}}(y)\geq \frac{e(B)}{4|Y|}$
.
$\forall y\in Y\cap V(B^{\prime}), d_{B^{\prime}}(y)\geq \frac{e(B)}{4|Y|}$
.
Proof. Whenever there is a vertex in
![]() $X$
whose degree becomes less than
$X$
whose degree becomes less than
![]() $\frac{e(B)}{4|X|}$
or a vertex in
$\frac{e(B)}{4|X|}$
or a vertex in
![]() $Y$
whose degree becomes less than
$Y$
whose degree becomes less than
![]() $\frac{e(B)}{4|Y|}$
, we delete it. Let
$\frac{e(B)}{4|Y|}$
, we delete it. Let
![]() $B^{\prime}$
denote the final subgraph of
$B^{\prime}$
denote the final subgraph of
![]() $B$
. As the number of edges deleted is at most
$B$
. As the number of edges deleted is at most
![]() $|X|\cdot \frac{e(B)}{4|X|}+|Y|\cdot \frac{e(B)}{4|Y|}=\frac{e(B)}{2}$
,
$|X|\cdot \frac{e(B)}{4|X|}+|Y|\cdot \frac{e(B)}{4|Y|}=\frac{e(B)}{2}$
,
![]() $e(B^{\prime})\geq \frac{e(B)}{2}$
. By definition,
$e(B^{\prime})\geq \frac{e(B)}{2}$
. By definition,
![]() $B^{\prime}$
satisfies our requirements.
$B^{\prime}$
satisfies our requirements.
3. Proof of Theorem 1.17
3.1 Overall structure of the proof
Our overall strategy has roots in the work of Conlon and Lee [Reference Conlon and Lee6] and the work of Conlon, Janzer, and Lee [Reference Conlon, Janzer and Lee7], particularly [Reference Conlon, Janzer and Lee7]. Some of the strategies used there were later augmented (through the concepts of admissible, light, and heavy spiders) in the work of Jiang and Qiu [Reference Jiang and Qiu22] and the work of Janzer [Reference Janzer18]. In particular, Janzer [Reference Janzer18] introduced a creative way to extending spiders, an idea that we will develop further. Overall, our proof combines ideas from [Reference Conlon, Janzer and Lee7], [Reference Jiang and Qiu22], [Reference Janzer18] and some new ideas.
Let
![]() $G$
be a
$G$
be a
![]() $K$
-almost-regular
$K$
-almost-regular
![]() $t*S^s_{b,k}$
-free graph on
$t*S^s_{b,k}$
-free graph on
![]() $n$
vertices, where
$n$
vertices, where
![]() $n$
is sufficiently large. To the prove the theorem, it suffices to show that there exists a constant
$n$
is sufficiently large. To the prove the theorem, it suffices to show that there exists a constant
![]() $C$
depending on
$C$
depending on
![]() $s,b,k$
such that if
$s,b,k$
such that if
![]() $\delta (G)\geq Cn^{\frac{s-1}{(s-1)k+b}}$
, then
$\delta (G)\geq Cn^{\frac{s-1}{(s-1)k+b}}$
, then
![]() $G$
must contain a copy of
$G$
must contain a copy of
![]() $t*S^s_{b,k}$
, which would contradict
$t*S^s_{b,k}$
, which would contradict
![]() $G$
being
$G$
being
![]() $t*S^s_{b,k}$
-free and complete the proof. The general strategy is to show that (1)
$t*S^s_{b,k}$
-free and complete the proof. The general strategy is to show that (1)
![]() $G$
contains many copies of
$G$
contains many copies of
![]() $S^s_{b,k}$
and (2) most of these copies of
$S^s_{b,k}$
and (2) most of these copies of
![]() $S^s_{b,k}$
are light. Then by averaging, there exist some vector
$S^s_{b,k}$
are light. Then by averaging, there exist some vector
![]() $(x_1,\ldots, x_s)$
of
$(x_1,\ldots, x_s)$
of
![]() $s$
vertices which is the leaf vector of a large number of light copies of
$s$
vertices which is the leaf vector of a large number of light copies of
![]() $S^s_{b,k}$
. This will imply that all these spiders are heavy, giving us contradiction. More specifically, the proof of Theorem 1.17 follows readily after we establish the following two crucial lemmas.
$S^s_{b,k}$
. This will imply that all these spiders are heavy, giving us contradiction. More specifically, the proof of Theorem 1.17 follows readily after we establish the following two crucial lemmas.
Lemma 3.1.
Let
![]() $G$
be a
$G$
be a
![]() $t*S^s_{b,k}$
-free
$t*S^s_{b,k}$
-free
![]() $K$
-almost-regular graph on
$K$
-almost-regular graph on
![]() $n$
vertices with minimum degree
$n$
vertices with minimum degree
![]() $\delta =\omega (1)$
. Then provided that
$\delta =\omega (1)$
. Then provided that
![]() $L$
is sufficiently large compared to
$L$
is sufficiently large compared to
![]() $s,t,k,K$
, for any
$s,t,k,K$
, for any
![]() $2\le j\le k$
, the number of
$2\le j\le k$
, the number of
![]() $j$
-heavy paths in
$j$
-heavy paths in
![]() $G$
is at most
$G$
is at most
![]() $\frac{(j+1)^{j+1}}{L}n\delta ^{j}$
.
$\frac{(j+1)^{j+1}}{L}n\delta ^{j}$
.
Lemma 3.2.
Let
![]() $G$
be a
$G$
be a
![]() $t*S^s_{b,k}$
-free
$t*S^s_{b,k}$
-free
![]() $K$
-almost-regular graph on
$K$
-almost-regular graph on
![]() $n$
vertices with minimum degree
$n$
vertices with minimum degree
![]() $\delta =\omega (1)$
. Let
$\delta =\omega (1)$
. Let
![]() $1\le j_1\le b$
and
$1\le j_1\le b$
and
![]() $1\le j_2,\ldots, j_s\le k$
be integers. Then provided that
$1\le j_2,\ldots, j_s\le k$
be integers. Then provided that
![]() $L$
is sufficiently large compared to
$L$
is sufficiently large compared to
![]() $s,t,k,K$
, the number of heavy spiders with length vector
$s,t,k,K$
, the number of heavy spiders with length vector
![]() $(j_1,\ldots, j_s)$
is at most
$(j_1,\ldots, j_s)$
is at most
![]() $\frac{27K^{j-2}}{L}n\delta ^j$
where
$\frac{27K^{j-2}}{L}n\delta ^j$
where
![]() $j=j_1+\cdots +j_s$
.
$j=j_1+\cdots +j_s$
.
We now show how Theorem 1.17 follows from Lemma 3.1 and Lemma 3.2.
Proof of Theorem
1.17. Let
![]() $L$
be a sufficiently large constant compared to
$L$
be a sufficiently large constant compared to
![]() $s,t,k,K$
. Let
$s,t,k,K$
. Let
![]() $G$
be a
$G$
be a
![]() $K$
-almost-regular
$K$
-almost-regular
![]() $t*S^s_{b,k}$
-free graph on
$t*S^s_{b,k}$
-free graph on
![]() $n$
vertices with minimum degree
$n$
vertices with minimum degree
![]() $\delta$
. Let
$\delta$
. Let
![]() $h=e(S^s_{b,k})=(s-1)k+b$
. Suppose to the contrary that
$h=e(S^s_{b,k})=(s-1)k+b$
. Suppose to the contrary that
![]() $\delta \geq C n^{\frac{s-1}{(s-1)k+b}}$
, where
$\delta \geq C n^{\frac{s-1}{(s-1)k+b}}$
, where
![]() $C\,:\!=\,2f(h,L) (h+1)!$
. Let
$C\,:\!=\,2f(h,L) (h+1)!$
. Let
![]() $\mathcal{S}$
be the family of spiders in
$\mathcal{S}$
be the family of spiders in
![]() $G$
with length vector
$G$
with length vector
![]() $(b,k,\ldots,k)$
. By a greedy process, it is easy to see that
$(b,k,\ldots,k)$
. By a greedy process, it is easy to see that
Let
![]() $\mathcal{S}_1$
be the family of spiders in
$\mathcal{S}_1$
be the family of spiders in
![]() $\mathcal{S}$
that contain some heavy path of length
$\mathcal{S}$
that contain some heavy path of length
![]() $2\le j\le k$
. As the maximum degree of
$2\le j\le k$
. As the maximum degree of
![]() $G$
is at most
$G$
is at most
![]() $K\delta$
, by Lemma 3.1, we have
$K\delta$
, by Lemma 3.1, we have
 \begin{equation*} |\mathcal {S}_1|\le \sum _{j=2}^k \binom {h}{j}\frac {(j+1)^{j+1}}{L}n\delta ^j (K\delta )^{h-j}\le \frac {(k+1)^{k+2}K^{sk}h!}{L}n\delta ^{h}, \end{equation*}
\begin{equation*} |\mathcal {S}_1|\le \sum _{j=2}^k \binom {h}{j}\frac {(j+1)^{j+1}}{L}n\delta ^j (K\delta )^{h-j}\le \frac {(k+1)^{k+2}K^{sk}h!}{L}n\delta ^{h}, \end{equation*}
where the factor
![]() $\binom{h}{j}$
upper bounds the number of positions of a
$\binom{h}{j}$
upper bounds the number of positions of a
![]() $j$
-heavy path in
$j$
-heavy path in
![]() $S_{b,k}^s$
. Let
$S_{b,k}^s$
. Let
![]() $\mathcal{S}_2$
be the family of spiders in
$\mathcal{S}_2$
be the family of spiders in
![]() $\mathcal{S}$
that contain some
$\mathcal{S}$
that contain some
![]() $s$
-legged heavy sub-spider. As the maximum degree of
$s$
-legged heavy sub-spider. As the maximum degree of
![]() $G$
is at most
$G$
is at most
![]() $K\delta$
, by Lemma 3.2, we have
$K\delta$
, by Lemma 3.2, we have
 \begin{equation*} |\mathcal {S}_2|\le \sum _{\substack {1\le j_1\le b\\ 1\le j_2,\ldots,j_s\le k}}\frac {27K^{j_1+\cdots +j_s-2}}{L}n\delta ^{j_1+\cdots +j_s}\cdot (K\delta )^{h-(j_1+\cdots +j_s)}\le \frac {27K^{sk}k^s}{L}n\delta ^{h}. \end{equation*}
\begin{equation*} |\mathcal {S}_2|\le \sum _{\substack {1\le j_1\le b\\ 1\le j_2,\ldots,j_s\le k}}\frac {27K^{j_1+\cdots +j_s-2}}{L}n\delta ^{j_1+\cdots +j_s}\cdot (K\delta )^{h-(j_1+\cdots +j_s)}\le \frac {27K^{sk}k^s}{L}n\delta ^{h}. \end{equation*}
Let
![]() $\mathcal{S}^{\prime}=\mathcal{S}-(\mathcal{S}_1\cup \mathcal{S}_2)$
. Then it follows that
$\mathcal{S}^{\prime}=\mathcal{S}-(\mathcal{S}_1\cup \mathcal{S}_2)$
. Then it follows that
where the last inequality holds since
![]() $L$
is sufficiently large. As
$L$
is sufficiently large. As
![]() $\delta \ge Cn^{\frac{s-1}{(s-1)k+b}}$
, and
$\delta \ge Cn^{\frac{s-1}{(s-1)k+b}}$
, and
![]() $C=2(h+1)!f(h,L)$
, it follows that
$C=2(h+1)!f(h,L)$
, it follows that
![]() $|\mathcal{S}^{\prime}|\ge f(h,L)n^s$
. By averaging, there exists an
$|\mathcal{S}^{\prime}|\ge f(h,L)n^s$
. By averaging, there exists an
![]() $s$
-tuple
$s$
-tuple
![]() $(x_1,\ldots,x_s)$
of distinct vertices, such that the subfamily
$(x_1,\ldots,x_s)$
of distinct vertices, such that the subfamily
![]() $\mathcal{S}^{\prime\prime}$
which consists of all spiders in
$\mathcal{S}^{\prime\prime}$
which consists of all spiders in
![]() $\mathcal{S}^{\prime}$
with leaf vector
$\mathcal{S}^{\prime}$
with leaf vector
![]() $(x_1,\ldots,x_s)$
has size
$(x_1,\ldots,x_s)$
has size
![]() $|\mathcal{S}^{\prime\prime}|\ge f(h,L)$
. For any
$|\mathcal{S}^{\prime\prime}|\ge f(h,L)$
. For any
![]() $S\in \mathcal{S}^{\prime\prime}$
, since
$S\in \mathcal{S}^{\prime\prime}$
, since
![]() $S$
contains no heavy path of length at most
$S$
contains no heavy path of length at most
![]() $k$
, every leg of
$k$
, every leg of
![]() $S$
is light. Since
$S$
is light. Since
![]() $S$
does not contain any
$S$
does not contain any
![]() $s$
-legged heavy sub-spider,
$s$
-legged heavy sub-spider,
![]() $S$
is light. So
$S$
is light. So
![]() $\mathcal{S}^{\prime\prime}$
is a family of at least
$\mathcal{S}^{\prime\prime}$
is a family of at least
![]() $f(h,L)$
light spiders with leaf vector
$f(h,L)$
light spiders with leaf vector
![]() $(x_1,\ldots,x_s)$
and length vector
$(x_1,\ldots,x_s)$
and length vector
![]() $(b,k,\ldots,k)$
. This contradicts the definition of the light spider with length vector
$(b,k,\ldots,k)$
. This contradicts the definition of the light spider with length vector
![]() $(b,k,\ldots,k)$
.
$(b,k,\ldots,k)$
.
Thus, to complete our proof of Theorem 1.17, it remains to prove Lemma 3.1 and Lemma 3.2. Lemma 3.2 was proved by Janzer for the case
![]() $b=k$
in details in [Reference Janzer18]. An outline of the general case was given in Lemma 4.3 in the same paper. Since our Lemma 3.2 is essentially the same as Lemma 4.3 of [Reference Janzer18] apart from some technical details, we omit its proof. Readers who are interested in the details of the proof of Lemma 3.2 are referred to the arxiv version of the manuscript [Reference Jiang and Qiu23]. As the author of [Reference Janzer18] pointed out the main obstacle to proving Conjecture 1.13 is to establish analogous statements for heavy paths. Indeed, the method developed in [Reference Conlon, Janzer and Lee7] (and later used in [Reference Jiang and Qiu22] and [Reference Janzer18]) for heavy paths is not applicable in the new setting.
$b=k$
in details in [Reference Janzer18]. An outline of the general case was given in Lemma 4.3 in the same paper. Since our Lemma 3.2 is essentially the same as Lemma 4.3 of [Reference Janzer18] apart from some technical details, we omit its proof. Readers who are interested in the details of the proof of Lemma 3.2 are referred to the arxiv version of the manuscript [Reference Jiang and Qiu23]. As the author of [Reference Janzer18] pointed out the main obstacle to proving Conjecture 1.13 is to establish analogous statements for heavy paths. Indeed, the method developed in [Reference Conlon, Janzer and Lee7] (and later used in [Reference Jiang and Qiu22] and [Reference Janzer18]) for heavy paths is not applicable in the new setting.
Our main contribution in this paper is to develop a method to handle heavy paths for
![]() $t*S^s_{b,k}$
-free graphs, resulting in Lemma 3.1. We believe that some of the ideas we developed here can be further expanded to potentially yield further progress on Conjecture 1.1 and Conjecture 1.13.
$t*S^s_{b,k}$
-free graphs, resulting in Lemma 3.1. We believe that some of the ideas we developed here can be further expanded to potentially yield further progress on Conjecture 1.1 and Conjecture 1.13.
3.2 Building
 $t*S^s_{b,k}$
using heavy paths
$t*S^s_{b,k}$
using heavy paths
The rest of the section is devoted to proving Lemma 3.1. The proof consists of two parts: the case of
![]() $j\gt \frac{k+b}{2}$
(Lemma 3.3) and the case of
$j\gt \frac{k+b}{2}$
(Lemma 3.3) and the case of
![]() $2\le j\le \frac{k+b}{2}$
(Lemma 3.4). We would like to point out that it is possible to merge the two cases into one. However, we feel that each case contains useful ideas and prefer to keep them separate.
$2\le j\le \frac{k+b}{2}$
(Lemma 3.4). We would like to point out that it is possible to merge the two cases into one. However, we feel that each case contains useful ideas and prefer to keep them separate.
3.2.1 Long heavy paths: the
 $j\gt \frac{k+b}{2}$
case
$j\gt \frac{k+b}{2}$
case
Lemma 3.3.
Let
![]() $G$
be a
$G$
be a
![]() $t*S^s_{b,k}$
-free
$t*S^s_{b,k}$
-free
![]() $K$
-almost-regular graph on
$K$
-almost-regular graph on
![]() $n$
vertices with minimum degree
$n$
vertices with minimum degree
![]() $\delta =\omega (1)$
. Then provided that
$\delta =\omega (1)$
. Then provided that
![]() $L$
is sufficiently large compared to
$L$
is sufficiently large compared to
![]() $s,t,k,K$
, for any
$s,t,k,K$
, for any
![]() $\frac{k+b}{2}\lt j\le k$
, the number of
$\frac{k+b}{2}\lt j\le k$
, the number of
![]() $j$
-heavy paths in
$j$
-heavy paths in
![]() $G$
is at most
$G$
is at most
![]() $\frac{n\delta ^{j}}L$
.
$\frac{n\delta ^{j}}L$
.
Proof. We define some constants as follows. Let
Suppose to the contrary that the number of
![]() $j$
-heavy paths is at least
$j$
-heavy paths is at least
![]() $\frac{n\delta ^{j}}L$
. By averaging, there exists a vertex
$\frac{n\delta ^{j}}L$
. By averaging, there exists a vertex
![]() $w$
such that the family
$w$
such that the family
![]() $\mathcal{P}_w$
consisting of all the
$\mathcal{P}_w$
consisting of all the
![]() $j$
-heavy paths of the form
$j$
-heavy paths of the form
![]() $xx_1\cdots x_{b-1} w x_{b+1}\cdots x_{j-1}y$
has size at least
$xx_1\cdots x_{b-1} w x_{b+1}\cdots x_{j-1}y$
has size at least
![]() $\frac{\delta ^{j}}{L}$
. Let
$\frac{\delta ^{j}}{L}$
. Let
![]() $X$
be the set of vertices in
$X$
be the set of vertices in
![]() $G$
that play the role of
$G$
that play the role of
![]() $x$
in some member of
$x$
in some member of
![]() $\mathcal{P}_w$
and
$\mathcal{P}_w$
and
![]() $Y$
the set of vertices in
$Y$
the set of vertices in
![]() $G$
that play the role of
$G$
that play the role of
![]() $y$
in some member of
$y$
in some member of
![]() $\mathcal{P}_w$
. Then
$\mathcal{P}_w$
. Then
![]() $X\subseteq \Gamma _b(w)$
and
$X\subseteq \Gamma _b(w)$
and
![]() $Y\subseteq \Gamma _{j-b}(w)$
. Since
$Y\subseteq \Gamma _{j-b}(w)$
. Since
![]() $G$
is
$G$
is
![]() $K$
-almost-regular and thus has maximum degree at most
$K$
-almost-regular and thus has maximum degree at most
![]() $K\delta$
, we have
$K\delta$
, we have
Note that
![]() $X,Y$
may not be disjoint. We define an auxiliary graph
$X,Y$
may not be disjoint. We define an auxiliary graph
![]() $B$
on
$B$
on
![]() $X\cup Y$
, such that
$X\cup Y$
, such that
![]() $\forall x\in X, y\in Y$
,
$\forall x\in X, y\in Y$
,
![]() $xy\in E(B)$
if and only if some member
$xy\in E(B)$
if and only if some member
![]() $P$
of
$P$
of
![]() $\mathcal{P}_w$
have ends
$\mathcal{P}_w$
have ends
![]() $x$
and
$x$
and
![]() $y$
.
$y$
.
Claim 1.
For every
![]() $x\in X$
there is an
$x\in X$
there is an
![]() $(x,w)$
-path of length
$(x,w)$
-path of length
![]() $b$
in
$b$
in
![]() $G$
. For every
$G$
. For every
![]() $y\in Y$
there is a
$y\in Y$
there is a
![]() $(w,y$
)-path of length
$(w,y$
)-path of length
![]() $j-b$
in
$j-b$
in
![]() $G$
. For all
$G$
. For all
![]() $x\in X, y\in Y$
such that
$x\in X, y\in Y$
such that
![]() $xy\in E(B)$
there exist at least
$xy\in E(B)$
there exist at least
![]() $L$
internally disjoint
$L$
internally disjoint
![]() $(x,y)$
-paths of length
$(x,y)$
-paths of length
![]() $j$
in
$j$
in
![]() $G$
.
$G$
.
Proof of Claim 1. The first two statements follow from the definitions of
![]() $X$
and
$X$
and
![]() $Y$
. Suppose
$Y$
. Suppose
![]() $x\in X, y\in Y$
and
$x\in X, y\in Y$
and
![]() $xy\in E(B)$
. By definition, some member
$xy\in E(B)$
. By definition, some member
![]() $P\in \mathcal{P}_w$
has
$P\in \mathcal{P}_w$
has
![]() $x,y$
as ends. By the definition of
$x,y$
as ends. By the definition of
![]() $\mathcal{P}_w$
,
$\mathcal{P}_w$
,
![]() $P$
is
$P$
is
![]() $j$
-heavy and thus there exist at least
$j$
-heavy and thus there exist at least
![]() $f(j,L)$
many
$f(j,L)$
many
![]() $j$
-admissible paths with ends
$j$
-admissible paths with ends
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $G$
. By Lemma 2.6 among them we can find at least
$G$
. By Lemma 2.6 among them we can find at least
that are pairwise vertex disjoint outside
![]() $\{x,y\}$
, where the inequality holds by Proposition 2.2.
$\{x,y\}$
, where the inequality holds by Proposition 2.2.
For any fixed
![]() $x\in X$
and
$x\in X$
and
![]() $y\in Y$
, by Lemma 2.5 there are at most
$y\in Y$
, by Lemma 2.5 there are at most
![]() $f(b,L)\cdot f(j-b,L)$
members of
$f(b,L)\cdot f(j-b,L)$
members of
![]() $\mathcal{P}_w$
that have ends
$\mathcal{P}_w$
that have ends
![]() $x$
and
$x$
and
![]() $y$
. Hence
$y$
. Hence
Now, let us colour each vertex in
![]() $X\cup Y$
with colour
$X\cup Y$
with colour
![]() $1$
or
$1$
or
![]() $2$
independently at random with probability
$2$
independently at random with probability
![]() $\frac 12$
each. Let
$\frac 12$
each. Let
![]() $X_1$
denote the set of vertices in
$X_1$
denote the set of vertices in
![]() $X$
that receive colour
$X$
that receive colour
![]() $1$
and
$1$
and
![]() $Y_2$
the set of vertices in
$Y_2$
the set of vertices in
![]() $Y$
that receive colour
$Y$
that receive colour
![]() $2$
. Let
$2$
. Let
![]() $\widetilde{B}$
denote the subgraph of
$\widetilde{B}$
denote the subgraph of
![]() $B$
consisting of edges that join a vertex in
$B$
consisting of edges that join a vertex in
![]() $X_1$
to a vertex in
$X_1$
to a vertex in
![]() $Y_2$
. Each edge of
$Y_2$
. Each edge of
![]() $B$
has probability at least
$B$
has probability at least
![]() $1/4$
of being in
$1/4$
of being in
![]() $\widetilde{B}$
. Hence there exists a colouring such that the resulting
$\widetilde{B}$
. Hence there exists a colouring such that the resulting
![]() $\widetilde{B}$
has at least
$\widetilde{B}$
has at least
![]() $(1/4)e(B)$
edges. Then
$(1/4)e(B)$
edges. Then
![]() $\widetilde{B}$
is bipartite with parts
$\widetilde{B}$
is bipartite with parts
![]() $X_1$
and
$X_1$
and
![]() $Y_2$
and by our discussion
$Y_2$
and by our discussion
By Lemma 2.10,
![]() $\widetilde{B}$
contains a subgraph
$\widetilde{B}$
contains a subgraph
![]() $B^{\prime}$
with parts
$B^{\prime}$
with parts
![]() $X^{\prime}\subseteq X_1$
and
$X^{\prime}\subseteq X_1$
and
![]() $Y^{\prime}\subseteq Y_2$
such that
$Y^{\prime}\subseteq Y_2$
such that
and
Since
![]() $X^{\prime}\subseteq X$
, by Claim 1, there are at least
$X^{\prime}\subseteq X$
, by Claim 1, there are at least
![]() $|X^{\prime}|$
paths of length
$|X^{\prime}|$
paths of length
![]() $b$
with one end
$b$
with one end
![]() $w$
and another end in
$w$
and another end in
![]() $X^{\prime}$
. By Lemma 2.8, there exists a spider
$X^{\prime}$
. By Lemma 2.8, there exists a spider
![]() $T$
of height
$T$
of height
![]() $b$
with centre
$b$
with centre
![]() $w$
and leaves in
$w$
and leaves in
![]() $X^{\prime}$
whose number of legs is at least
$X^{\prime}$
whose number of legs is at least
![]() $\frac{|X^{\prime}|}{b(K\delta )^{b-1}}\geq \frac{c_3}{bK^{b-1}} \delta =c_4\delta$
.
$\frac{|X^{\prime}|}{b(K\delta )^{b-1}}\geq \frac{c_3}{bK^{b-1}} \delta =c_4\delta$
.
Let
![]() $X^{\prime\prime}\subseteq X^{\prime}$
be the leaf set of this spider. Then
$X^{\prime\prime}\subseteq X^{\prime}$
be the leaf set of this spider. Then
![]() $|X^{\prime\prime}|\ge c_4\delta$
. Let
$|X^{\prime\prime}|\ge c_4\delta$
. Let
![]() $B^{\prime\prime}$
be the subgraph of
$B^{\prime\prime}$
be the subgraph of
![]() $B^{\prime}$
induced by
$B^{\prime}$
induced by
![]() $X^{\prime\prime}\cup Y^{\prime}$
. By (1) and (3)
$X^{\prime\prime}\cup Y^{\prime}$
. By (1) and (3)
Since
![]() $|X^{\prime\prime}|\geq c_4\delta$
and
$|X^{\prime\prime}|\geq c_4\delta$
and
![]() $\delta =\omega (1)$
, for sufficiently large
$\delta =\omega (1)$
, for sufficiently large
![]() $n$
we may assume that
$n$
we may assume that
![]() $c_5 |X^{\prime\prime}|\geq 2t$
. By Lemma 2.9
$c_5 |X^{\prime\prime}|\geq 2t$
. By Lemma 2.9
Now, let us fix a
![]() $t$
-set
$t$
-set
![]() $X_0\subseteq X^{\prime\prime}$
guaranteed in (5). Let
$X_0\subseteq X^{\prime\prime}$
guaranteed in (5). Let
![]() $T_0$
be the sub-spider of
$T_0$
be the sub-spider of
![]() $T$
with leaf set
$T$
with leaf set
![]() $X_0$
. Let
$X_0$
. Let
![]() $Y^{\prime\prime}=N^*_{B^{\prime\prime}}(X_0)$
. Then
$Y^{\prime\prime}=N^*_{B^{\prime\prime}}(X_0)$
. Then
Let
![]() $\mathcal{C}$
be the family of paths of length
$\mathcal{C}$
be the family of paths of length
![]() $j-b$
with one end
$j-b$
with one end
![]() $w$
and another end in
$w$
and another end in
![]() $Y^{\prime\prime}$
. By Claim 1,
$Y^{\prime\prime}$
. By Claim 1,
![]() $|\mathcal{C}|\geq |Y^{\prime\prime}|\geq c_6 \delta ^{j-b}$
. Since
$|\mathcal{C}|\geq |Y^{\prime\prime}|\geq c_6 \delta ^{j-b}$
. Since
![]() $G$
has maximum degree at most
$G$
has maximum degree at most
![]() $K\delta$
, for any vertex
$K\delta$
, for any vertex
![]() $u\neq w$
, the number of paths in
$u\neq w$
, the number of paths in
![]() $\mathcal{C}$
that contain
$\mathcal{C}$
that contain
![]() $u$
is at most
$u$
is at most
![]() $(j-b)(K\delta )^{j-b-1}\lt j(K\delta )^{j-b-1}$
. Let
$(j-b)(K\delta )^{j-b-1}\lt j(K\delta )^{j-b-1}$
. Let
![]() $\mathcal{C}_1$
be the family of paths in
$\mathcal{C}_1$
be the family of paths in
![]() $\mathcal{C}$
that are vertex disjoint from
$\mathcal{C}$
that are vertex disjoint from
![]() $V(T_0)-\{w\}$
. Then
$V(T_0)-\{w\}$
. Then
where the last inequality holds for sufficiently large
![]() $n$
because
$n$
because
![]() $\delta =\omega (1)$
. As
$\delta =\omega (1)$
. As
![]() $j\gt \frac{k+b}{2}$
, we have
$j\gt \frac{k+b}{2}$
, we have
![]() $k-j\lt j-b$
. Applying Lemma 2.8 to
$k-j\lt j-b$
. Applying Lemma 2.8 to
![]() $\mathcal{C}_1$
, as
$\mathcal{C}_1$
, as
![]() $\delta =\omega (1)$
, there exists a
$\delta =\omega (1)$
, there exists a
![]() $t$
-legged spider
$t$
-legged spider
![]() $T_1$
of height
$T_1$
of height
![]() $k-j$
with centre
$k-j$
with centre
![]() $v_1\neq w$
and leaf set
$v_1\neq w$
and leaf set
![]() $Y_1\subseteq Y^{\prime\prime}$
. Note that
$Y_1\subseteq Y^{\prime\prime}$
. Note that
![]() $V(T_0)\cap V(T_1)=\emptyset$
. Using the same strategy, we can find
$V(T_0)\cap V(T_1)=\emptyset$
. Using the same strategy, we can find
![]() $s-1$
vertex disjoint
$s-1$
vertex disjoint
![]() $t$
-legged spiders
$t$
-legged spiders
![]() $T_1,\ldots,T_{s-1}$
of height
$T_1,\ldots,T_{s-1}$
of height
![]() $k-j$
one by one, with
$k-j$
one by one, with
![]() $T_i$
’s centre
$T_i$
’s centre
![]() $v_i\neq w$
and leaf set
$v_i\neq w$
and leaf set
![]() $Y_i\subseteq Y^{\prime\prime}$
, such that
$Y_i\subseteq Y^{\prime\prime}$
, such that
![]() $V(T_i)\cap V(T_0)=\emptyset$
.
$V(T_i)\cap V(T_0)=\emptyset$
.
Suppose
![]() $X_0=\{x_1,\ldots, x_t\}$
. For each
$X_0=\{x_1,\ldots, x_t\}$
. For each
![]() $i\in [s-1]$
, suppose
$i\in [s-1]$
, suppose
![]() $Y_i=\left\{y_i^1,\ldots, y_i^t\right\}$
. Let
$Y_i=\left\{y_i^1,\ldots, y_i^t\right\}$
. Let
![]() $Y_0=\bigcup _{i=1}^{s-1}Y_i$
. Then
$Y_0=\bigcup _{i=1}^{s-1}Y_i$
. Then
![]() $Y_0\subseteq Y^{\prime\prime}=N^*_{B^{\prime\prime}}(X_0)$
. Hence,
$Y_0\subseteq Y^{\prime\prime}=N^*_{B^{\prime\prime}}(X_0)$
. Hence,
![]() $\forall x\in X_0, y\in Y_0$
,
$\forall x\in X_0, y\in Y_0$
,
![]() $xy\in E(B^{\prime\prime})\subseteq E(B)$
and by Claim 1 there exist at least
$xy\in E(B^{\prime\prime})\subseteq E(B)$
and by Claim 1 there exist at least
![]() $L$
internally disjoint paths of length
$L$
internally disjoint paths of length
![]() $j$
joining
$j$
joining
![]() $x$
and
$x$
and
![]() $y$
. As
$y$
. As
![]() $L$
is a sufficiently large constant, we can greedily find
$L$
is a sufficiently large constant, we can greedily find
![]() $t(s-1)$
paths
$t(s-1)$
paths
![]() $P_{i,\ell }$
of length
$P_{i,\ell }$
of length
![]() $j$
, such that for any
$j$
, such that for any
![]() $i\in [t]$
and
$i\in [t]$
and
![]() $\ell \in [s-1]$
,
$\ell \in [s-1]$
,
![]() $P_{i,\ell }$
has ends
$P_{i,\ell }$
has ends
![]() $x_i$
and
$x_i$
and
![]() $y_\ell ^i$
and intersects
$y_\ell ^i$
and intersects
![]() $\bigcup _{i=0}^{s-1} V(T_i)$
only in
$\bigcup _{i=0}^{s-1} V(T_i)$
only in
![]() $x_i$
and
$x_i$
and
![]() $y_\ell ^i$
and such that the
$y_\ell ^i$
and such that the
![]() $P_{i,\ell }$
’s are pairwise vertex disjoint outside
$P_{i,\ell }$
’s are pairwise vertex disjoint outside
![]() $\bigcup _{i=0}^{s-1} V(T_i)$
. Now,
$\bigcup _{i=0}^{s-1} V(T_i)$
. Now,
![]() $(\bigcup _{i=0}^{s-1} T_i) \cup \big(\bigcup _{i\in [t], \ell \in [s-1]} P_{i,\ell }\big)$
forms a copy of
$(\bigcup _{i=0}^{s-1} T_i) \cup \big(\bigcup _{i\in [t], \ell \in [s-1]} P_{i,\ell }\big)$
forms a copy of
![]() $t*S^s_{b,k}$
in
$t*S^s_{b,k}$
in
![]() $G$
, a contradiction. This completes our proof.
$G$
, a contradiction. This completes our proof.
3.2.2 Short heavy paths: the
 $2\le j\le \frac{k+b}{2}$
case
$2\le j\le \frac{k+b}{2}$
case
This subsection handles the most difficult part of our main proof and is where most of the new ideas are used.
Lemma 3.4.
Let
![]() $G$
be a
$G$
be a
![]() $t*S^s_{b,k}$
-free
$t*S^s_{b,k}$
-free
![]() $K$
-almost-regular graph on
$K$
-almost-regular graph on
![]() $n$
vertices with minimum degree
$n$
vertices with minimum degree
![]() $\delta =\omega (1)$
. Then provided that
$\delta =\omega (1)$
. Then provided that
![]() $L$
is sufficiently large compared to
$L$
is sufficiently large compared to
![]() $s,t,k,K$
, for any
$s,t,k,K$
, for any
![]() $2\le j\le \frac{k+b}{2}$
, the number of
$2\le j\le \frac{k+b}{2}$
, the number of
![]() $j$
-heavy paths is at most
$j$
-heavy paths is at most
![]() $\frac{(j+1)^{j+1}}{L} n\delta ^{j}$
.
$\frac{(j+1)^{j+1}}{L} n\delta ^{j}$
.
We break the proof of Lemma 3.4 into several steps. The general strategy is to show that if the family
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $j$
-heavy paths is too large then we find a copy of
$j$
-heavy paths is too large then we find a copy of
![]() $t*S^s_{b,k}$
in
$t*S^s_{b,k}$
in
![]() $G$
, which is a contradiction. We start by doing some cleaning to
$G$
, which is a contradiction. We start by doing some cleaning to
![]() $\mathcal{F}$
in order to set up further arguments. Before that, let us set some constants to be used throughout the subsection.
$\mathcal{F}$
in order to set up further arguments. Before that, let us set some constants to be used throughout the subsection.
Definition 3.5. Let
![]() $D=2K^jL f(j-1,L)^2$
and
$D=2K^jL f(j-1,L)^2$
and
![]() $M=D^{s+1}$
.
$M=D^{s+1}$
.
Comparing Definition 2.1 and Definition 3.5, we see that
Now we introduce our cleaning lemma. Given a path
![]() $P=v_0v_1\cdots v_j$
and
$P=v_0v_1\cdots v_j$
and
![]() $0\leq i\lt j$
, we define the initial
$0\leq i\lt j$
, we define the initial
![]() $i$
-segment of
$i$
-segment of
![]() $P$
to be the subpath
$P$
to be the subpath
![]() $v_0v_1\cdots v_i$
.
$v_0v_1\cdots v_i$
.
Lemma 3.6.
Let
![]() $G$
be a
$G$
be a
![]() $K$
-almost-regular graph on
$K$
-almost-regular graph on
![]() $n$
vertices with minimum degree
$n$
vertices with minimum degree
![]() $\delta =\omega (1)$
. Suppose that the number of
$\delta =\omega (1)$
. Suppose that the number of
![]() $j$
-heavy paths is at least
$j$
-heavy paths is at least
![]() $\frac{(j+1)^{j+1}}{L} n\delta ^{j}$
. Then there exist a vertex
$\frac{(j+1)^{j+1}}{L} n\delta ^{j}$
. Then there exist a vertex
![]() $w$
, vertex disjoint sets
$w$
, vertex disjoint sets
![]() $A_0,\ldots, A_j$
and a family
$A_0,\ldots, A_j$
and a family
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $j$
-heavy paths with
$j$
-heavy paths with
![]() $\bigcup _{i=0}^j A_i=\bigcup _{P\in \mathcal{F}}V(P)$
satisfying
$\bigcup _{i=0}^j A_i=\bigcup _{P\in \mathcal{F}}V(P)$
satisfying
-
1.
 $A_0\subseteq \Gamma _1(w) \text{ and } A_j\subseteq \Gamma _{j-1} (w)$
.
$A_0\subseteq \Gamma _1(w) \text{ and } A_j\subseteq \Gamma _{j-1} (w)$
. -
2. Each member of
 $\mathcal{F}$
has the form
$\mathcal{F}$
has the form
 $v_0v_1\cdots v_j$
where
$v_0v_1\cdots v_j$
where
 $\forall i\in \{0,1,\ldots, j\}, v_i\in A_i$
.
$\forall i\in \{0,1,\ldots, j\}, v_i\in A_i$
. -
3. There exists a set
 $V_0$
with
$V_0$
with
 $A_0\subseteq V_0\subseteq \Gamma _1(w)\setminus A_j$
such that for every
$A_0\subseteq V_0\subseteq \Gamma _1(w)\setminus A_j$
such that for every
 $y\in A_j$
, there are at least
$y\in A_j$
, there are at least
 $\frac{|V_0|}{D}$
many
$\frac{|V_0|}{D}$
many
 $x\in V_0$
such that
$x\in V_0$
such that
 $x,y$
are ends of a heavy
$x,y$
are ends of a heavy
 $j$
-path in
$j$
-path in
 $G$
. Furthermore,
$G$
. Furthermore,
 $|V_0|\geq (2K/D)\delta$
.
$|V_0|\geq (2K/D)\delta$
. -
4. For each
 $x\in A_0$
, there are at least
$x\in A_0$
, there are at least
 $M$
vertices
$M$
vertices
 $y\in A_j$
such that
$y\in A_j$
such that
 $x,y$
are ends of at least
$x,y$
are ends of at least
 $DM$
members of
$DM$
members of
 $\mathcal{F}$
. For each
$\mathcal{F}$
. For each
 $y\in A_j$
, there are at least
$y\in A_j$
, there are at least
 $M$
vertices
$M$
vertices
 $x\in A_0$
such that
$x\in A_0$
such that
 $x,y$
are ends of at least
$x,y$
are ends of at least
 $DM$
members of
$DM$
members of
 $\mathcal{F}$
.
$\mathcal{F}$
. -
5. For each
 $P\in \mathcal{F}$
and
$P\in \mathcal{F}$
and
 $0\leq i\lt j$
, the initial
$0\leq i\lt j$
, the initial
 $i$
-segment of
$i$
-segment of
 $P$
is contained in at least
$P$
is contained in at least
 $jM(K\delta )^{j-i-1}$
members of
$jM(K\delta )^{j-i-1}$
members of
 $\mathcal{F}$
.
$\mathcal{F}$
.
Proof. Let
![]() $\mathcal{C}$
be the collection of all
$\mathcal{C}$
be the collection of all
![]() $j$
-heavy paths in
$j$
-heavy paths in
![]() $G$
. By our assumption,
$G$
. By our assumption,
![]() $|\mathcal{C}|\geq \frac{(j+1)^{j+1}}{L}n\delta ^j$
. Let us independently colour each vertex of
$|\mathcal{C}|\geq \frac{(j+1)^{j+1}}{L}n\delta ^j$
. Let us independently colour each vertex of
![]() $G$
with a colour in
$G$
with a colour in
![]() $\{0,1,\ldots, j\}$
, with each colour chosen uniformly at random. For each
$\{0,1,\ldots, j\}$
, with each colour chosen uniformly at random. For each
![]() $0\leq i\leq j$
, let
$0\leq i\leq j$
, let
![]() $V^{\prime}_i$
denote the set of vertices in
$V^{\prime}_i$
denote the set of vertices in
![]() $G$
receiving colour
$G$
receiving colour
![]() $i$
. For any
$i$
. For any
![]() $j$
-heavy path
$j$
-heavy path
![]() $P=v_0v_1\cdots v_j$
, call
$P=v_0v_1\cdots v_j$
, call
![]() $P$
good if
$P$
good if
![]() $\forall 0\leq i\leq j, v_i\in V^{\prime}_i$
. Let
$\forall 0\leq i\leq j, v_i\in V^{\prime}_i$
. Let
![]() $\mathcal{C}^{\prime}$
denote the family of all good heavy
$\mathcal{C}^{\prime}$
denote the family of all good heavy
![]() $j$
-paths. Clearly each
$j$
-paths. Clearly each
![]() $j$
-heavy path in
$j$
-heavy path in
![]() $G$
is good with probability
$G$
is good with probability
![]() $(\frac{1}{j+1})^{j+1}$
. So there exists a vertex colouring for which
$(\frac{1}{j+1})^{j+1}$
. So there exists a vertex colouring for which
Let us fix such a colouring and the corresponding
![]() $\mathcal{C}^{\prime}$
.
$\mathcal{C}^{\prime}$
.
By averaging, there exists a vertex
![]() $w$
such that the subfamily
$w$
such that the subfamily
![]() $\mathcal{P}_w$
of members of
$\mathcal{P}_w$
of members of
![]() $\mathcal{C}^{\prime}$
of the form
$\mathcal{C}^{\prime}$
of the form
![]() $v_0wv_2\cdots v_j$
has size at least
$v_0wv_2\cdots v_j$
has size at least
![]() $|\mathcal{P}_w|\ge \frac{\delta ^{j}}{L}$
. For each
$|\mathcal{P}_w|\ge \frac{\delta ^{j}}{L}$
. For each
![]() $i\in \{0,1,\ldots,j\}$
, let
$i\in \{0,1,\ldots,j\}$
, let
![]() $V_i$
be the set of vertices in
$V_i$
be the set of vertices in
![]() $V^{\prime}_i$
that are contained in members of
$V^{\prime}_i$
that are contained in members of
![]() $\mathcal{P}_w$
. By our definitions,
$\mathcal{P}_w$
. By our definitions,
![]() $V_0\subseteq \Gamma _1(w)$
and
$V_0\subseteq \Gamma _1(w)$
and
![]() $V_j\subseteq \Gamma _{j-1}(w)$
. Since
$V_j\subseteq \Gamma _{j-1}(w)$
. Since
![]() $G$
has maximum degree at most
$G$
has maximum degree at most
![]() $K\delta$
, we have
$K\delta$
, we have
Let
![]() $B$
denote the auxiliary bipartite graph with a bipartition
$B$
denote the auxiliary bipartite graph with a bipartition
![]() $(V_0,V_j)$
such that
$(V_0,V_j)$
such that
![]() $\forall x\in V_0, y\in V_j, xy\in E(B)$
if and only if
$\forall x\in V_0, y\in V_j, xy\in E(B)$
if and only if
![]() $x,y$
are ends of some member of
$x,y$
are ends of some member of
![]() $\mathcal{P}_w$
. For each
$\mathcal{P}_w$
. For each
![]() $xy\in E(B)$
with
$xy\in E(B)$
with
![]() $x\in V_0, y\in V_j$
, let
$x\in V_0, y\in V_j$
, let
![]() $\mathcal{P}_{xy}$
be the subfamily of members of
$\mathcal{P}_{xy}$
be the subfamily of members of
![]() $\mathcal{P}_w$
that cover
$\mathcal{P}_w$
that cover
![]() $x,y$
and let
$x,y$
and let
![]() $\mathcal{J}_{xy}$
be the family of
$\mathcal{J}_{xy}$
be the family of
![]() $j$
-heavy paths in
$j$
-heavy paths in
![]() $G$
that have
$G$
that have
![]() $x,y$
as ends.
$x,y$
as ends.
Claim 1.
For each
![]() $xy\in E(B)$
, we have
$xy\in E(B)$
, we have
![]() $1\leq |\mathcal{P}_{xy}|\leq f(j-1,L)$
and
$1\leq |\mathcal{P}_{xy}|\leq f(j-1,L)$
and
![]() $|\mathcal{J}_{xy}|\geq f(j,L)$
.
$|\mathcal{J}_{xy}|\geq f(j,L)$
.
Proof of Claim 1. Let
![]() $xy\in E(B)$
, with
$xy\in E(B)$
, with
![]() $x\in V_0, y\in V_j$
. That
$x\in V_0, y\in V_j$
. That
![]() $|\mathcal{P}_{xy}|\geq 1$
is clear. Let
$|\mathcal{P}_{xy}|\geq 1$
is clear. Let
![]() $P\in \mathcal{P}_{xy}$
. By definition
$P\in \mathcal{P}_{xy}$
. By definition
![]() $P$
is
$P$
is
![]() $j$
-admissible and
$j$
-admissible and
![]() $P=xw\cup Q$
, where
$P=xw\cup Q$
, where
![]() $Q$
is a
$Q$
is a
![]() $(w,y)$
-path of length
$(w,y)$
-path of length
![]() $j-1$
. Since
$j-1$
. Since
![]() $P$
is admissible,
$P$
is admissible,
![]() $Q$
is
$Q$
is
![]() $(j-1)$
-light. So the number of possible
$(j-1)$
-light. So the number of possible
![]() $Q$
in
$Q$
in
![]() $G$
is at most
$G$
is at most
![]() $f(j-1,L)$
. So,
$f(j-1,L)$
. So,
![]() $|\mathcal{P}_{xy}|\leq f(j-1,L)$
. Next, since
$|\mathcal{P}_{xy}|\leq f(j-1,L)$
. Next, since
![]() $P$
is a
$P$
is a
![]() $j$
-heavy path in
$j$
-heavy path in
![]() $G$
with ends
$G$
with ends
![]() $x,y$
, by definition,
$x,y$
, by definition,
![]() $G$
contains at least
$G$
contains at least
![]() $f(j,L)$
$f(j,L)$
![]() $j$
-heavy paths with ends
$j$
-heavy paths with ends
![]() $x,y$
. So
$x,y$
. So
![]() $|\mathcal{J}_{xy}|\geq f(j,L)$
.
$|\mathcal{J}_{xy}|\geq f(j,L)$
.
Since
![]() $|V_j|\leq (K\delta )^{j-1}$
, (8) implies
$|V_j|\leq (K\delta )^{j-1}$
, (8) implies
Let
![]() $V^*_j$
be the set of
$V^*_j$
be the set of
![]() $y\in V_j$
for which
$y\in V_j$
for which
![]() $d_B(y)\ge \frac{|V_0|}{D}$
. Let
$d_B(y)\ge \frac{|V_0|}{D}$
. Let
![]() $B^*$
denote the subgraph of
$B^*$
denote the subgraph of
![]() $B$
induced by
$B$
induced by
![]() $V_0\cup V^*_j$
. Then
$V_0\cup V^*_j$
. Then
For each
![]() $xy\in E(B^*)$
, we have
$xy\in E(B^*)$
, we have
where the last inequality holds by (6). Let
![]() $\mathcal{J}^{\prime}_{xy}$
be a subfamily of
$\mathcal{J}^{\prime}_{xy}$
be a subfamily of
![]() $\mathcal{J}_{xy}$
of size exactly
$\mathcal{J}_{xy}$
of size exactly
![]() $10j^2D^2M$
. Let
$10j^2D^2M$
. Let
Then by (10)
We next obtain
![]() $\mathcal{F}$
from
$\mathcal{F}$
from
![]() $\mathcal{F}_0$
through some further cleaning. Initially let
$\mathcal{F}_0$
through some further cleaning. Initially let
![]() $\mathcal{F}=\mathcal{F}_0$
. Throughout the process, for each
$\mathcal{F}=\mathcal{F}_0$
. Throughout the process, for each
![]() $x\in V_0, y\in V^*_j$
let
$x\in V_0, y\in V^*_j$
let
![]() $\lambda (x,y)$
denote the number of remaining members of
$\lambda (x,y)$
denote the number of remaining members of
![]() $\mathcal{F}$
that have ends
$\mathcal{F}$
that have ends
![]() $x,y$
. We update the function
$x,y$
. We update the function
![]() $\lambda (x,y)$
automatically after each removal. Whenever is a vertex
$\lambda (x,y)$
automatically after each removal. Whenever is a vertex
![]() $x\in V_0$
such that the number of
$x\in V_0$
such that the number of
![]() $y\in V^*_j$
with
$y\in V^*_j$
with
![]() $\lambda (x,y)\geq DM$
is less than
$\lambda (x,y)\geq DM$
is less than
![]() $M$
(which we refer to as
$M$
(which we refer to as
![]() $x$
becomes small), remove all the members of
$x$
becomes small), remove all the members of
![]() $\mathcal{F}$
that contain
$\mathcal{F}$
that contain
![]() $x$
. Similarly, whenever there is a vertex
$x$
. Similarly, whenever there is a vertex
![]() $y\in V^*_j$
such that the number of
$y\in V^*_j$
such that the number of
![]() $x\in X$
with
$x\in X$
with
![]() $\lambda (x,y)\geq DM$
is less than
$\lambda (x,y)\geq DM$
is less than
![]() $M$
(which we refer to as
$M$
(which we refer to as
![]() $y$
becomes small), remove all the members of
$y$
becomes small), remove all the members of
![]() $\mathcal{F}$
that contains
$\mathcal{F}$
that contains
![]() $y$
. Whenever there is a member
$y$
. Whenever there is a member
![]() $P\in \mathcal{F}$
(viewed as a path from
$P\in \mathcal{F}$
(viewed as a path from
![]() $V_0$
to
$V_0$
to
![]() $V^*_j$
) contains an initial
$V^*_j$
) contains an initial
![]() $i$
-segment
$i$
-segment
![]() $I$
, for some
$I$
, for some
![]() $0\leq i\lt j$
, that is contained is less than
$0\leq i\lt j$
, that is contained is less than
![]() $jM(K\delta )^{j-i-1}$
members of
$jM(K\delta )^{j-i-1}$
members of
![]() $\mathcal{F}$
we remove all the members of
$\mathcal{F}$
we remove all the members of
![]() $\mathcal{F}$
containing
$\mathcal{F}$
containing
![]() $I$
. We continue the process until no further removal can be performed.
$I$
. We continue the process until no further removal can be performed.
The number of members of
![]() $\mathcal{F}$
we removed for each
$\mathcal{F}$
we removed for each
![]() $x\in V_0$
that becomes small is at most
$x\in V_0$
that becomes small is at most
for sufficiently large
![]() $n$
, since
$n$
, since
![]() $\delta =\omega (1)$
. Similarly, the number of members of
$\delta =\omega (1)$
. Similarly, the number of members of
![]() $\mathcal{F}$
that we removed for each vertex
$\mathcal{F}$
that we removed for each vertex
![]() $y\in V^*_j$
that becomes small is at most
$y\in V^*_j$
that becomes small is at most
So, the total number of members of
![]() $\mathcal{F}$
we removed due to either a vertex in
$\mathcal{F}$
we removed due to either a vertex in
![]() $X$
becoming small or a vertex in
$X$
becoming small or a vertex in
![]() $Y^*$
becoming small is at most
$Y^*$
becoming small is at most
The number of members of
![]() $\mathcal{F}$
that we removed due to some initial segment is contained in too few members is at most
$\mathcal{F}$
that we removed due to some initial segment is contained in too few members is at most
 \begin{equation*} \sum _{i=0}^{j-1}|V_0|(K\delta )^i\cdot jM(K\delta )^{j-i-1}\le j^2M(K\delta )^j. \end{equation*}
\begin{equation*} \sum _{i=0}^{j-1}|V_0|(K\delta )^i\cdot jM(K\delta )^{j-i-1}\le j^2M(K\delta )^j. \end{equation*}
Combining the above two inequalities, the total number of members of
![]() $\mathcal{F}$
that we removed is at most
$\mathcal{F}$
that we removed is at most
So in particular, the final
![]() $\mathcal{F}$
is non-empty.
$\mathcal{F}$
is non-empty.
Now, for each
![]() $0\leq i\leq j$
, let
$0\leq i\leq j$
, let
![]() $A_i$
be the set of vertices in
$A_i$
be the set of vertices in
![]() $V_i$
that are contained in members of the final
$V_i$
that are contained in members of the final
![]() $\mathcal{F}$
. In particular, note that
$\mathcal{F}$
. In particular, note that
![]() $A_j\subseteq V^*_j$
. Let us check that
$A_j\subseteq V^*_j$
. Let us check that
![]() $w,A_0,\ldots, A_j$
and
$w,A_0,\ldots, A_j$
and
![]() $\mathcal{F}$
satisfy the five conditions of the lemma. Condition 1 and condition 2 clearly hold by our discussion so far. Condition 3 holds since
$\mathcal{F}$
satisfy the five conditions of the lemma. Condition 1 and condition 2 clearly hold by our discussion so far. Condition 3 holds since
![]() $A_j\subseteq V^*_j$
and each vertex
$A_j\subseteq V^*_j$
and each vertex
![]() $y\in V^*_j$
satisfies
$y\in V^*_j$
satisfies
![]() $d_B(y)\geq \frac{|V_0|}{D}$
and
$d_B(y)\geq \frac{|V_0|}{D}$
and
![]() $|V_0|\geq (2K/D)\delta$
by (9). Conditions 4 and 5 hold due to our cleaning rules. This completes the proof of the lemma.
$|V_0|\geq (2K/D)\delta$
by (9). Conditions 4 and 5 hold due to our cleaning rules. This completes the proof of the lemma.
Lemma 3.7.
Let
![]() $G,A_0,\ldots, A_j$
and
$G,A_0,\ldots, A_j$
and
![]() $\mathcal{F}$
be as stated in Lemma 3.6
. Then
$\mathcal{F}$
be as stated in Lemma 3.6
. Then
-
1. For any
 $0\le i\lt j$
and any
$0\le i\lt j$
and any
 $u\in A_i$
, there exists an
$u\in A_i$
, there exists an
 $M$
-legged spider of height
$M$
-legged spider of height
 $j-i$
with centre
$j-i$
with centre
 $u$
and leaves in
$u$
and leaves in
 $A_j$
.
$A_j$
. -
2. Let
 $F=\{uv\,{:}\, u\in A_{j-1}, v\in A_j \text{ and } \exists P\in \mathcal{F}, \, uv\in E(P)\}$
. Then
$F=\{uv\,{:}\, u\in A_{j-1}, v\in A_j \text{ and } \exists P\in \mathcal{F}, \, uv\in E(P)\}$
. Then
 $F$
has minimum degree at least
$F$
has minimum degree at least
 $M$
.
$M$
.
Proof. Fix any
![]() $i$
with
$i$
with
![]() $0\leq i\lt j$
and
$0\leq i\lt j$
and
![]() $u\in A_i$
. By the definition of
$u\in A_i$
. By the definition of
![]() $A_i$
there exists
$A_i$
there exists
![]() $P=v_0v_1\cdots v_j\in \mathcal{F}$
, where
$P=v_0v_1\cdots v_j\in \mathcal{F}$
, where
![]() $v_i=u$
. Let
$v_i=u$
. Let
![]() $I=v_0v_1\cdots v_i$
. By condition 5 of Lemma 3.6,
$I=v_0v_1\cdots v_i$
. By condition 5 of Lemma 3.6,
![]() $I$
is contained in at least
$I$
is contained in at least
![]() $jM(K\delta )^{j-i-1}$
members of
$jM(K\delta )^{j-i-1}$
members of
![]() $\mathcal{F}$
. In other words, the family
$\mathcal{F}$
. In other words, the family
![]() $\mathcal{Q}=\{Q\,{:}\, Q\in A_{i}\times \cdots \times A_j, I\cup Q \in \mathcal{F}\}$
has size at least
$\mathcal{Q}=\{Q\,{:}\, Q\in A_{i}\times \cdots \times A_j, I\cup Q \in \mathcal{F}\}$
has size at least
![]() $jM(K\delta )^{j-i-1}$
. Since each member of
$jM(K\delta )^{j-i-1}$
. Since each member of
![]() $\mathcal{Q}$
is a path of length
$\mathcal{Q}$
is a path of length
![]() $j-i$
from
$j-i$
from
![]() $u$
to a vertex in
$u$
to a vertex in
![]() $A_j$
, by Lemma 2.8, there exists a spider of height
$A_j$
, by Lemma 2.8, there exists a spider of height
![]() $j-i$
with centre
$j-i$
with centre
![]() $u$
and leaves in
$u$
and leaves in
![]() $A_j$
whose number of legs is at least
$A_j$
whose number of legs is at least
This proves part 1 of the lemma. Applying part 1 with
![]() $i=j-1$
, we have
$i=j-1$
, we have
![]() $\forall u\in A_{j-1}$
,
$\forall u\in A_{j-1}$
,
![]() $d_F(u)\ge M$
. Let
$d_F(u)\ge M$
. Let
![]() $y\in A_j$
. By condition 4 of Lemma 3.6, there exist a vertex
$y\in A_j$
. By condition 4 of Lemma 3.6, there exist a vertex
![]() $x\in A_0$
such that there are at least
$x\in A_0$
such that there are at least
![]() $DM$
members of
$DM$
members of
![]() $\mathcal{F}$
that have ends
$\mathcal{F}$
that have ends
![]() $x,y$
. By Lemma 2.6, among these there are at least
$x,y$
. By Lemma 2.6, among these there are at least
![]() $DM/[j^2f(j-1,L)^2]\geq M$
of them that are pairwise vertex disjoint outside
$DM/[j^2f(j-1,L)^2]\geq M$
of them that are pairwise vertex disjoint outside
![]() $\{x,y\}$
. In particular, this implies
$\{x,y\}$
. In particular, this implies
![]() $d_F(y)\ge M$
. So part 2 also holds.
$d_F(y)\ge M$
. So part 2 also holds.
Definition 3.8. For the rest of the subsection, we write
![]() $b=qj+b^{\prime}$
where
$b=qj+b^{\prime}$
where
![]() $q$
and
$q$
and
![]() $b^{\prime}$
are integers with
$b^{\prime}$
are integers with
![]() $1\le b^{\prime}\le j$
.
$1\le b^{\prime}\le j$
.
The next lemma plays an important role in our proof of Lemma 3.4. It sets up a well-placed
![]() $s$
-legged spider of height
$s$
-legged spider of height
![]() $b$
to be used in building a copy of
$b$
to be used in building a copy of
![]() $t*S^s_{b,k}$
.
$t*S^s_{b,k}$
.
Lemma 3.9.
Let
![]() $G$
,
$G$
,
![]() $w$
,
$w$
,
![]() $A_0,\ldots, A_j$
, and
$A_0,\ldots, A_j$
, and
![]() $\mathcal{F}$
be as stated in Lemma 3.6
. Let
$\mathcal{F}$
be as stated in Lemma 3.6
. Let
![]() $N=M/D$
.
$N=M/D$
.
-
1. If
 $q$
is even, then there are
$q$
is even, then there are
 $N$
-legged spiders
$N$
-legged spiders
 $T$
and
$T$
and
 $T^{\prime}$
in
$T^{\prime}$
in
 $G$
, both of height
$G$
, both of height
 $b$
such that the leaf set of
$b$
such that the leaf set of
 $T$
is contained in
$T$
is contained in
 $A_{b^{\prime}}$
and the leaf set of
$A_{b^{\prime}}$
and the leaf set of
 $T^{\prime}$
is contained in
$T^{\prime}$
is contained in
 $A_{b^{\prime}-1}$
.
$A_{b^{\prime}-1}$
. -
2. If
 $q$
is odd, then there are
$q$
is odd, then there are
 $N$
-legged spiders
$N$
-legged spiders
 $T$
and
$T$
and
 $T^{\prime}$
in
$T^{\prime}$
in
 $G$
, both of height
$G$
, both of height
 $b$
, such that the leaf set of
$b$
, such that the leaf set of
 $T$
is contained in
$T$
is contained in
 $A_{j-b^{\prime}}$
and the leaf set of
$A_{j-b^{\prime}}$
and the leaf set of
 $T^{\prime}$
is contained in
$T^{\prime}$
is contained in
 $A_{j-b^{\prime}+1}$
.
$A_{j-b^{\prime}+1}$
.
Proof. Let
![]() $B$
be a bipartite graph with parts
$B$
be a bipartite graph with parts
![]() $A_0$
and
$A_0$
and
![]() $A_j$
such that
$A_j$
such that
![]() $\forall x\in A_0, y\in A_j$
$\forall x\in A_0, y\in A_j$
![]() $xy\in E(B)$
if and only if at least
$xy\in E(B)$
if and only if at least
![]() $DM$
members of
$DM$
members of
![]() $\mathcal{F}$
have ends
$\mathcal{F}$
have ends
![]() $x,y$
. By Lemma 3.6 condition 4,
$x,y$
. By Lemma 3.6 condition 4,
![]() $B$
has minimum degree at least
$B$
has minimum degree at least
![]() $M$
. By Lemma 2.6,
$M$
. By Lemma 2.6,
![]() $\forall xy\in E(B)$
, there exist at least
$\forall xy\in E(B)$
, there exist at least
![]() $DM/[j^2f(j-1,L)^2]\geq M$
internally disjoint members of
$DM/[j^2f(j-1,L)^2]\geq M$
internally disjoint members of
![]() $\mathcal{F}$
with ends
$\mathcal{F}$
with ends
![]() $x,y$
.
$x,y$
.
Fix a vertex
![]() $u\in A_0$
. Since
$u\in A_0$
. Since
![]() $\delta (B)\geq M = DN \geq (q+1)N$
, where the last inequality follows from Definition 3.5, we can greedily grow an
$\delta (B)\geq M = DN \geq (q+1)N$
, where the last inequality follows from Definition 3.5, we can greedily grow an
![]() $N$
-legged spider
$N$
-legged spider
![]() $R$
in
$R$
in
![]() $B$
that has centre
$B$
that has centre
![]() $u$
and height
$u$
and height
![]() $q+1$
. Since
$q+1$
. Since
![]() $\forall xy\in E(B)$
there are
$\forall xy\in E(B)$
there are
![]() $M$
internally disjoint members of
$M$
internally disjoint members of
![]() $\mathcal{F}$
with ends
$\mathcal{F}$
with ends
![]() $x,y$
, we can replace each edge
$x,y$
, we can replace each edge
![]() $ab$
of
$ab$
of
![]() $R$
with a member of
$R$
with a member of
![]() $\mathcal{F}$
with ends
$\mathcal{F}$
with ends
![]() $a,b$
so that the resulting graph is an
$a,b$
so that the resulting graph is an
![]() $N$
-legged spider
$N$
-legged spider
![]() $S$
of height
$S$
of height
![]() $(q+1)j$
in
$(q+1)j$
in
![]() $G$
. Let
$G$
. Let
![]() $A$
be the set of vertices in
$A$
be the set of vertices in
![]() $S$
that are at distance
$S$
that are at distance
![]() $b=qj+b^{\prime}$
from
$b=qj+b^{\prime}$
from
![]() $u$
in
$u$
in
![]() $S$
. It is easy to see from the definition of
$S$
. It is easy to see from the definition of
![]() $S$
that if
$S$
that if
![]() $q$
is even then
$q$
is even then
![]() $A\subseteq A_{b^{\prime}}$
and that if
$A\subseteq A_{b^{\prime}}$
and that if
![]() $q$
is odd then
$q$
is odd then
![]() $A\subseteq A_{j-b^{\prime}}$
. Let
$A\subseteq A_{j-b^{\prime}}$
. Let
![]() $T$
be the sub-spider of
$T$
be the sub-spider of
![]() $S$
with centre
$S$
with centre
![]() $u$
and leaf set
$u$
and leaf set
![]() $A$
. Then
$A$
. Then
![]() $T$
satisfies the first halves of statements 1 and 2.
$T$
satisfies the first halves of statements 1 and 2.
Now, fix a subset
![]() $A^{\prime}_0\subseteq A_0$
of size
$A^{\prime}_0\subseteq A_0$
of size
![]() $N$
, Since
$N$
, Since
![]() $B$
has minimum degree at least
$B$
has minimum degree at least
![]() $M\geq (q+2)N+1$
, in
$M\geq (q+2)N+1$
, in
![]() $B$
we can find
$B$
we can find
![]() $N$
disjoint paths of length
$N$
disjoint paths of length
![]() $q+1$
,
$q+1$
,
![]() $Q_1,\ldots, Q_N$
, avoiding
$Q_1,\ldots, Q_N$
, avoiding
![]() $w$
, such that
$w$
, such that
![]() $\forall i\in [N]$
,
$\forall i\in [N]$
,
![]() $Q_i$
starts from a vertex
$Q_i$
starts from a vertex
![]() $x_i\in A^{\prime}_0$
. By a similar reason as in the previous paragraph, we can replace the edges in
$x_i\in A^{\prime}_0$
. By a similar reason as in the previous paragraph, we can replace the edges in
![]() $\bigcup _{i=1}^N Q_i$
by members of
$\bigcup _{i=1}^N Q_i$
by members of
![]() $\mathcal{F}$
that avoid
$\mathcal{F}$
that avoid
![]() $w$
such that for each
$w$
such that for each
![]() $i\in [N]$
,
$i\in [N]$
,
![]() $Q_i$
is turned into a path
$Q_i$
is turned into a path
![]() $P_i$
of length
$P_i$
of length
![]() $(q+1)j$
in
$(q+1)j$
in
![]() $G$
that still avoids
$G$
that still avoids
![]() $w$
and that
$w$
and that
![]() $P_1,\ldots, P_N$
are vertex disjoint. Let
$P_1,\ldots, P_N$
are vertex disjoint. Let
![]() $S^{\prime}=\bigcup _{i=1}^N P_i\cup \{wx_1,\ldots, wx_N\}$
. Then
$S^{\prime}=\bigcup _{i=1}^N P_i\cup \{wx_1,\ldots, wx_N\}$
. Then
![]() $S^{\prime}$
is an
$S^{\prime}$
is an
![]() $N$
-legged spider in
$N$
-legged spider in
![]() $G$
with centre
$G$
with centre
![]() $w$
and height
$w$
and height
![]() $(q+1)j+1$
. Let
$(q+1)j+1$
. Let
![]() $A^{\prime}$
be the set of vertices in
$A^{\prime}$
be the set of vertices in
![]() $S^{\prime}$
that are distance
$S^{\prime}$
that are distance
![]() $b=qj+b^{\prime}$
from
$b=qj+b^{\prime}$
from
![]() $w$
in
$w$
in
![]() $S^{\prime}$
. It is easy to see by the definition of
$S^{\prime}$
. It is easy to see by the definition of
![]() $S^{\prime}$
that if
$S^{\prime}$
that if
![]() $q$
is even then
$q$
is even then
![]() $A^{\prime}\subseteq A_{b^{\prime}-1}$
and that if
$A^{\prime}\subseteq A_{b^{\prime}-1}$
and that if
![]() $q$
is odd then
$q$
is odd then
![]() $A^{\prime}\subseteq A_{j-b^{\prime}+1}$
. Let
$A^{\prime}\subseteq A_{j-b^{\prime}+1}$
. Let
![]() $T^{\prime}$
be the sub-spider of
$T^{\prime}$
be the sub-spider of
![]() $S^{\prime}$
with centre
$S^{\prime}$
with centre
![]() $w$
and leaf set
$w$
and leaf set
![]() $A^{\prime}$
. Then
$A^{\prime}$
. Then
![]() $T^{\prime}$
satisfies the second halves of statement 1 and 2.
$T^{\prime}$
satisfies the second halves of statement 1 and 2.
Lemma 3.10.
Let
![]() $G$
,
$G$
,
![]() $w$
,
$w$
,
![]() $A_0,\ldots, A_j$
and
$A_0,\ldots, A_j$
and
![]() $\mathcal{F}$
be as stated in Lemma 3.6
. Let
$\mathcal{F}$
be as stated in Lemma 3.6
. Let
![]() $m,m^{\prime}$
be positive integers such that
$m,m^{\prime}$
be positive integers such that
![]() $m^{\prime}\leq \frac{m}{2D}$
and
$m^{\prime}\leq \frac{m}{2D}$
and
![]() $m\leq \frac{M}{2k}$
. Let
$m\leq \frac{M}{2k}$
. Let
![]() $0\leq r\le j$
and
$0\leq r\le j$
and
![]() $U \subseteq A_r$
be a subset of size
$U \subseteq A_r$
be a subset of size
![]() $m$
. Let
$m$
. Let
![]() $W$
be a vertex set such that
$W$
be a vertex set such that
![]() $W\cap U=\emptyset$
and
$W\cap U=\emptyset$
and
![]() $|W|\leq M/2$
. If
$|W|\leq M/2$
. If
![]() $p\,:\!=\,k+r-2j$
is non-negative and even, then there exists an
$p\,:\!=\,k+r-2j$
is non-negative and even, then there exists an
![]() $m^{\prime}$
-legged spider
$m^{\prime}$
-legged spider
![]() $T^{\prime}$
with height
$T^{\prime}$
with height
![]() $k$
and leaf set
$k$
and leaf set
![]() $U^{\prime}\subseteq U$
such that
$U^{\prime}\subseteq U$
such that
![]() $V(T^{\prime})\setminus U^{\prime}$
is disjoint from
$V(T^{\prime})\setminus U^{\prime}$
is disjoint from
![]() $W\cup U$
.
$W\cup U$
.
Proof. Suppose
![]() $U=\{u_1,\ldots, u_m\}$
. Since
$U=\{u_1,\ldots, u_m\}$
. Since
![]() $U\subseteq A_r$
, by Lemma 3.7 statement 1, for each
$U\subseteq A_r$
, by Lemma 3.7 statement 1, for each
![]() $i\in [m]$
, there exists an
$i\in [m]$
, there exists an
![]() $M$
-legged spider of height
$M$
-legged spider of height
![]() $j-r$
with centre
$j-r$
with centre
![]() $u_i$
and leaves in
$u_i$
and leaves in
![]() $A_j$
. Since
$A_j$
. Since
![]() $M\geq km+|W|\geq (j-r+1)m+|W|$
, by a greedy process, we can find a collection of vertex disjoint paths
$M\geq km+|W|\geq (j-r+1)m+|W|$
, by a greedy process, we can find a collection of vertex disjoint paths
![]() $Q_1,\ldots, Q_m$
, where for each
$Q_1,\ldots, Q_m$
, where for each
![]() $i\in [m]$
,
$i\in [m]$
,
![]() $Q_i$
is a path of length
$Q_i$
is a path of length
![]() $j-r$
joining
$j-r$
joining
![]() $u_i$
to a vertex
$u_i$
to a vertex
![]() $y_i$
in
$y_i$
in
![]() $A_j$
that avoids the set
$A_j$
that avoids the set
![]() $W$
. Let
$W$
. Let
By Lemma 3.7 statement 2, the graph
has minimum degree at least
![]() $M$
. Using a greedy process we can find in
$M$
. Using a greedy process we can find in
![]() $F$
a collection of vertex disjoint paths
$F$
a collection of vertex disjoint paths
![]() $R_1,\ldots, R_m$
, where for each
$R_1,\ldots, R_m$
, where for each
![]() $i\in [m]$
,
$i\in [m]$
,
![]() $R_i$
is a path in
$R_i$
is a path in
![]() $F$
of length
$F$
of length
![]() $p$
that joins
$p$
that joins
![]() $y_i$
to some vertex
$y_i$
to some vertex
![]() $z_i$
and avoids the set
$z_i$
and avoids the set
![]() $(W\cup \bigcup _{\ell =1}^m V(Q_\ell ) )\setminus \{y_i\}$
. For each
$(W\cup \bigcup _{\ell =1}^m V(Q_\ell ) )\setminus \{y_i\}$
. For each
![]() $i\in [m]$
, since
$i\in [m]$
, since
![]() $y_i\in A_j$
and
$y_i\in A_j$
and
![]() $p$
is even,
$p$
is even,
![]() $z_i\in A_j$
as well. Now
$z_i\in A_j$
as well. Now
![]() $\{Q_i\cup R_i\,{:}\, i\in [m] \}$
is family of
$\{Q_i\cup R_i\,{:}\, i\in [m] \}$
is family of
![]() $m$
disjoint paths of length
$m$
disjoint paths of length
![]() $j-r+p$
that avoid
$j-r+p$
that avoid
![]() $W$
.
$W$
.
Let
![]() $Z=\{z_1,\ldots, z_m\}$
. Since
$Z=\{z_1,\ldots, z_m\}$
. Since
![]() $Z\subseteq A_j$
, by Lemma 3.6 condition 3, there exists a set
$Z\subseteq A_j$
, by Lemma 3.6 condition 3, there exists a set
![]() $V_0$
with
$V_0$
with
![]() $A_0\subseteq V_0\subseteq \Gamma _1(w)\setminus A_j$
such that
$A_0\subseteq V_0\subseteq \Gamma _1(w)\setminus A_j$
such that
![]() $|V_0|\geq (2K/D)\delta$
and for each
$|V_0|\geq (2K/D)\delta$
and for each
![]() $i\in [m]$
, there are at least
$i\in [m]$
, there are at least
![]() $|V_0|/D$
many
$|V_0|/D$
many
![]() $x\in V_0$
such that
$x\in V_0$
such that
![]() $x,z_i$
are the ends of a
$x,z_i$
are the ends of a
![]() $j$
-heavy path in
$j$
-heavy path in
![]() $G$
. Let
$G$
. Let
![]() $B$
be a bipartite graph with parts
$B$
be a bipartite graph with parts
![]() $V_0$
and
$V_0$
and
![]() $Z$
such that
$Z$
such that
![]() $\forall x\in V_0, z\in Z$
,
$\forall x\in V_0, z\in Z$
,
![]() $xz\in E(B)$
if and only if
$xz\in E(B)$
if and only if
![]() $x,z$
are the ends of a
$x,z$
are the ends of a
![]() $j$
-heavy path in
$j$
-heavy path in
![]() $G$
. Then
$G$
. Then
![]() $e(B)\geq |V_0||Z|/D$
. Since
$e(B)\geq |V_0||Z|/D$
. Since
![]() $|Z|/D=m/D\geq 2m^{\prime}$
, by Lemma 2.9 there exists an
$|Z|/D=m/D\geq 2m^{\prime}$
, by Lemma 2.9 there exists an
![]() $m^{\prime}$
-set
$m^{\prime}$
-set
![]() $Z^{\prime}\subseteq Z$
such that
$Z^{\prime}\subseteq Z$
such that
Since
![]() $|V_0|\geq (K/2D)\delta$
, while
$|V_0|\geq (K/2D)\delta$
, while
![]() $\delta =\omega (1)$
, for sufficiently large
$\delta =\omega (1)$
, for sufficiently large
![]() $n$
, we have
$n$
, we have
![]() $|N^*_B(Z^{\prime})|\gt |\bigcup _{i=1}^m V(Q_i\cup R_i) \cup W|$
. So, there exists a vertex
$|N^*_B(Z^{\prime})|\gt |\bigcup _{i=1}^m V(Q_i\cup R_i) \cup W|$
. So, there exists a vertex
![]() $x\in V_0\setminus (\bigcup _{i=1}^m V(Q_i\cup R_i) \cup W)$
that is joined to all of
$x\in V_0\setminus (\bigcup _{i=1}^m V(Q_i\cup R_i) \cup W)$
that is joined to all of
![]() $Z^{\prime}$
in
$Z^{\prime}$
in
![]() $B$
. Without loss of generality, suppose
$B$
. Without loss of generality, suppose
![]() $Z^{\prime}=\{z_1,\ldots, z_{m^{\prime}}\}$
. For each
$Z^{\prime}=\{z_1,\ldots, z_{m^{\prime}}\}$
. For each
![]() $i\in [m^{\prime}]$
, there exists a
$i\in [m^{\prime}]$
, there exists a
![]() $j$
-heavy path with ends
$j$
-heavy path with ends
![]() $x$
and
$x$
and
![]() $z_i$
. In particular, by Lemma 2.6, there are at least
$z_i$
. In particular, by Lemma 2.6, there are at least
![]() $\frac{f(j,L)}{j^2f(j-1,L)^2}\ge \frac{10j^4D^2 M}{j^2D}\ge M$
internally disjoint paths of length
$\frac{f(j,L)}{j^2f(j-1,L)^2}\ge \frac{10j^4D^2 M}{j^2D}\ge M$
internally disjoint paths of length
![]() $j$
between
$j$
between
![]() $x$
and
$x$
and
![]() $z_i$
, where the first inequality follows by Definition 3.5 and (6). As
$z_i$
, where the first inequality follows by Definition 3.5 and (6). As
![]() $M\gt m^{\prime}k+|W|$
, we can find paths
$M\gt m^{\prime}k+|W|$
, we can find paths
![]() $P_1,\ldots, P_{m^{\prime}}$
, where
$P_1,\ldots, P_{m^{\prime}}$
, where
![]() $\forall i\in [m^{\prime}]$
,
$\forall i\in [m^{\prime}]$
,
![]() $P_i$
is a path of length
$P_i$
is a path of length
![]() $j$
joining
$j$
joining
![]() $x$
to
$x$
to
![]() $z_i$
such that
$z_i$
such that
![]() $T^{\prime}\,:\!=\,\bigcup _{i=1}^{m^{\prime}} (P_i\cup Q_i\cup R_i)$
is an
$T^{\prime}\,:\!=\,\bigcup _{i=1}^{m^{\prime}} (P_i\cup Q_i\cup R_i)$
is an
![]() $m^{\prime}$
-legged spider of height
$m^{\prime}$
-legged spider of height
![]() $k$
with centre
$k$
with centre
![]() $x$
and leaf set
$x$
and leaf set
![]() $\{u_1,\ldots, u_{m^{\prime}}\}$
and such that
$\{u_1,\ldots, u_{m^{\prime}}\}$
and such that
![]() $T^{\prime}$
avoids
$T^{\prime}$
avoids
![]() $(U\setminus \{u_1,\ldots, u_{m^{\prime}}\})\cup W$
. The lemma holds for the above-defined
$(U\setminus \{u_1,\ldots, u_{m^{\prime}}\})\cup W$
. The lemma holds for the above-defined
![]() $T^{\prime}$
and
$T^{\prime}$
and
![]() $U^{\prime}=\{u_1,\ldots, u_{m^{\prime}}\}$
.
$U^{\prime}=\{u_1,\ldots, u_{m^{\prime}}\}$
.
Now, we are ready to prove Lemma 3.4.
Proof of Lemma 3.4. Suppose that the number of
![]() $j$
-heavy paths in
$j$
-heavy paths in
![]() $G$
is at least
$G$
is at least
![]() $\frac{(j+1)^{j+1}}{L}n\delta ^j$
. Let
$\frac{(j+1)^{j+1}}{L}n\delta ^j$
. Let
![]() $w$
,
$w$
,
![]() $A_0,\ldots, A_j$
and
$A_0,\ldots, A_j$
and
![]() $\mathcal{F}$
be obtained by Lemma 3.6. Our first step is to find an appropriate value of
$\mathcal{F}$
be obtained by Lemma 3.6. Our first step is to find an appropriate value of
![]() $r$
to apply Lemma 3.10 to. Recall that
$r$
to apply Lemma 3.10 to. Recall that
![]() $b=qj+b^{\prime}$
. Let
$b=qj+b^{\prime}$
. Let
 \begin{equation*} r\,:\!=\,\left \{ \begin {array}{lr} b^{\prime}, &\text { if } q \text { is even and } k+b^{\prime}-2j \text { is even} \\ b^{\prime}-1, & \text { if } q \text { is even and } k+b^{\prime}-2j \text { is odd}\\ j-b^{\prime}, & \text { if } q \text { is odd and } k+(j-b^{\prime})-2j \text { is even} \\ j-b^{\prime}+1,& \text { if } q \text { is odd and } k+(j-b^{\prime})-2j \text { is odd} \end {array} \right . \end{equation*}
\begin{equation*} r\,:\!=\,\left \{ \begin {array}{lr} b^{\prime}, &\text { if } q \text { is even and } k+b^{\prime}-2j \text { is even} \\ b^{\prime}-1, & \text { if } q \text { is even and } k+b^{\prime}-2j \text { is odd}\\ j-b^{\prime}, & \text { if } q \text { is odd and } k+(j-b^{\prime})-2j \text { is even} \\ j-b^{\prime}+1,& \text { if } q \text { is odd and } k+(j-b^{\prime})-2j \text { is odd} \end {array} \right . \end{equation*}
As
![]() $1\le b^{\prime}\le j$
, we have
$1\le b^{\prime}\le j$
, we have
![]() $0\le r\le j$
.
$0\le r\le j$
.
Let
![]() $p=k+r-2j$
. By the definitions of
$p=k+r-2j$
. By the definitions of
![]() $p$
and
$p$
and
![]() $r$
, it is easy to see
$r$
, it is easy to see
![]() $p$
is even. We claim that
$p$
is even. We claim that
![]() $p$
is non-negative. To prove this, it is enough to show that
$p$
is non-negative. To prove this, it is enough to show that
![]() $k+b^{\prime}-2j\ge 0$
when
$k+b^{\prime}-2j\ge 0$
when
![]() $q$
is even, and that
$q$
is even, and that
![]() $k+(j-b^{\prime})-2j\ge 0$
when
$k+(j-b^{\prime})-2j\ge 0$
when
![]() $q$
is odd. First assume that
$q$
is odd. First assume that
![]() $q$
is even. If
$q$
is even. If
![]() $q=0$
, then
$q=0$
, then
![]() $b=b^{\prime}$
and
$b=b^{\prime}$
and
![]() $k+b^{\prime}-2j=k+b-2j\ge 0$
where the inequality holds by our assumption
$k+b^{\prime}-2j=k+b-2j\ge 0$
where the inequality holds by our assumption
![]() $j\le \frac{k+b}{2}$
; if
$j\le \frac{k+b}{2}$
; if
![]() $q\ge 2$
, then
$q\ge 2$
, then
![]() $b\ge 2j+b^{\prime}$
and thus
$b\ge 2j+b^{\prime}$
and thus
![]() $k+b^{\prime}-2j\ge b+b^{\prime}-2j\ge 2b^{\prime}\gt 0$
. Now assume
$k+b^{\prime}-2j\ge b+b^{\prime}-2j\ge 2b^{\prime}\gt 0$
. Now assume
![]() $q$
is odd. Then we have that
$q$
is odd. Then we have that
![]() $q\ge 1$
and thus
$q\ge 1$
and thus
![]() $b\ge j+b^{\prime}$
. It follows that
$b\ge j+b^{\prime}$
. It follows that
![]() $k+(j-b^{\prime})-2j=k-(j+b^{\prime})\ge b-(j+b^{\prime})\ge 0$
. Hence
$k+(j-b^{\prime})-2j=k-(j+b^{\prime})\ge b-(j+b^{\prime})\ge 0$
. Hence
![]() $p$
is non-negative.
$p$
is non-negative.
Now, let
![]() $m_1=M/D$
and for
$m_1=M/D$
and for
![]() $i=2,\ldots, s$
, let
$i=2,\ldots, s$
, let
![]() $m_i=m_{i-1}/(2D)$
. Using the definition of
$m_i=m_{i-1}/(2D)$
. Using the definition of
![]() $D$
, it is easy to check that
$D$
, it is easy to check that
![]() $\forall i\in [s], m_i\leq M/(2sk)$
. By Lemma 3.9, there exists an
$\forall i\in [s], m_i\leq M/(2sk)$
. By Lemma 3.9, there exists an
![]() $m_1$
-legged spider
$m_1$
-legged spider
![]() $T_1$
with height
$T_1$
with height
![]() $b$
and leaf set
$b$
and leaf set
![]() $U_1\subseteq A_{r}$
. The idea of the rest of the proof is to apply Lemma 3.10
$U_1\subseteq A_{r}$
. The idea of the rest of the proof is to apply Lemma 3.10
![]() $s-1$
times. Initially let
$s-1$
times. Initially let
![]() $W=V(T_1)\setminus U_1$
. Since
$W=V(T_1)\setminus U_1$
. Since
![]() $p=k+r-2j$
is non-negative and even, applying Lemma 3.10 with
$p=k+r-2j$
is non-negative and even, applying Lemma 3.10 with
![]() $m_1$
and
$m_1$
and
![]() $m_2$
playing the roles of
$m_2$
playing the roles of
![]() $m$
and
$m$
and
![]() $m^{\prime}$
respectively and
$m^{\prime}$
respectively and
![]() $U_1$
playing the role of
$U_1$
playing the role of
![]() $U$
, we can find an
$U$
, we can find an
![]() $m_2$
-legged spider
$m_2$
-legged spider
![]() $T_2$
with height
$T_2$
with height
![]() $k$
and leaf set
$k$
and leaf set
![]() $U_2\subseteq U_1$
such that
$U_2\subseteq U_1$
such that
![]() $V(T_2)\setminus U_2$
is disjoint from
$V(T_2)\setminus U_2$
is disjoint from
![]() $W\cup U_1$
. Now, we add
$W\cup U_1$
. Now, we add
![]() $V(T_2) \setminus U_2$
to
$V(T_2) \setminus U_2$
to
![]() $W$
. Next, applying Lemma 3.10 with
$W$
. Next, applying Lemma 3.10 with
![]() $m_2,m_3$
playing the roles of
$m_2,m_3$
playing the roles of
![]() $m$
and
$m$
and
![]() $m^{\prime}$
respectively and
$m^{\prime}$
respectively and
![]() $U_2$
playing the role of
$U_2$
playing the role of
![]() $U$
, we can find an
$U$
, we can find an
![]() $m_3$
-legged spider
$m_3$
-legged spider
![]() $T_3$
with height
$T_3$
with height
![]() $k$
and leaf set
$k$
and leaf set
![]() $U_3\subseteq U_2$
, such that
$U_3\subseteq U_2$
, such that
![]() $V(T_3)\setminus U_3$
is disjoint from
$V(T_3)\setminus U_3$
is disjoint from
![]() $W\cup U_2$
. Now, we add
$W\cup U_2$
. Now, we add
![]() $V(T_3)\setminus U_3$
to
$V(T_3)\setminus U_3$
to
![]() $W$
. We continue like this. It is easy to check that we can carry out the process for at least
$W$
. We continue like this. It is easy to check that we can carry out the process for at least
![]() $s-1$
steps to find
$s-1$
steps to find
![]() $T_2,\ldots, T_s$
. Indeed, within the first
$T_2,\ldots, T_s$
. Indeed, within the first
![]() $s-1$
steps
$s-1$
steps
![]() $W$
has size at most
$W$
has size at most
![]() $km_1+km_2+\cdots +km_{s-1}\lt 2km_1=2kM/D\lt M/2$
. This together with the definitions of
$km_1+km_2+\cdots +km_{s-1}\lt 2km_1=2kM/D\lt M/2$
. This together with the definitions of
![]() $m_1,\ldots, m_s$
ensures that the conditions of Lemma 3.10 are satisfied. But now
$m_1,\ldots, m_s$
ensures that the conditions of Lemma 3.10 are satisfied. But now
![]() $\bigcup _{i=1}^s T_i$
forms a copy of
$\bigcup _{i=1}^s T_i$
forms a copy of
![]() $t*S^s_{b,k}$
in
$t*S^s_{b,k}$
in
![]() $G$
, a contradiction. This completes our proof of Lemma 3.4.
$G$
, a contradiction. This completes our proof of Lemma 3.4.
4. Concluding remarks
In [Reference Kang, Kim and Liu25], Kang, Kim and Liu extended the definition of balanced rooted trees to that of balanced rooted bipartite graphs as follows. Let
![]() $F$
be a bipartite graph and
$F$
be a bipartite graph and
![]() $R$
a proper subset of
$R$
a proper subset of
![]() $V(F)$
called the set of roots. For each non-empty set
$V(F)$
called the set of roots. For each non-empty set
![]() $S\subseteq V(F)$
, let
$S\subseteq V(F)$
, let
![]() $\rho _F(S)=\frac{e_S}{|S|}$
, where
$\rho _F(S)=\frac{e_S}{|S|}$
, where
![]() $e_S$
is the number of edges in
$e_S$
is the number of edges in
![]() $G$
with at least one end in
$G$
with at least one end in
![]() $S$
. Let
$S$
. Let
![]() $\rho (F)=\rho _F(V(F)\setminus R)$
. We say that
$\rho (F)=\rho _F(V(F)\setminus R)$
. We say that
![]() $(F,R)$
is balanced if
$(F,R)$
is balanced if
![]() $\rho _F(S)\geq \rho (F)$
for every non-empty subset
$\rho _F(S)\geq \rho (F)$
for every non-empty subset
![]() $S\subseteq V(F)\setminus R$
. A real number
$S\subseteq V(F)\setminus R$
. A real number
![]() $r\in (1, 2)$
is called balancedly realizable if there is a connected bipartite graph
$r\in (1, 2)$
is called balancedly realizable if there is a connected bipartite graph
![]() $F$
and a set
$F$
and a set
![]() $R\subseteq V(F)$
such that
$R\subseteq V(F)$
such that
![]() $(F,R)$
is balanced with
$(F,R)$
is balanced with
![]() $\rho _F= \frac{1}{2-r}$
and that there is a positive integer
$\rho _F= \frac{1}{2-r}$
and that there is a positive integer
![]() $t_0$
such that for all integers
$t_0$
such that for all integers
![]() $t\ge t_0$
,
$t\ge t_0$
,
![]() $\mathrm{ex}(n,t*F)=\Theta (n^r)$
holds. By definition, a balancedly realizable number is a Turán exponent. Using a result of Erdős and Simonovits [Reference Erdős and Simonovits11], Kang, Kim and Liu [Reference Kang, Kim and Liu25] proved the following.
$\mathrm{ex}(n,t*F)=\Theta (n^r)$
holds. By definition, a balancedly realizable number is a Turán exponent. Using a result of Erdős and Simonovits [Reference Erdős and Simonovits11], Kang, Kim and Liu [Reference Kang, Kim and Liu25] proved the following.
Lemma 4.1 ([Reference Kang, Kim and Liu25]). Let
![]() $a\lt b$
be two integers. If
$a\lt b$
be two integers. If
![]() $2-\frac{a}{b}$
is balancedly realizable, then
$2-\frac{a}{b}$
is balancedly realizable, then
![]() $2-\frac{a}{a+b}$
is also balancedly realizable.
$2-\frac{a}{a+b}$
is also balancedly realizable.
Proof of Corollary 1.4 and Corollary 1.5. By Theorem 1.9 and Theorem 1.15, for any positive integers
![]() $p,k,b$
with
$p,k,b$
with
![]() $k\ge b$
,
$k\ge b$
,
![]() $1+\frac{p}{kp+b}$
is balancedly realizable. Corollary 1.4 follows by applying Lemma 4.1 repeatedly.
$1+\frac{p}{kp+b}$
is balancedly realizable. Corollary 1.4 follows by applying Lemma 4.1 repeatedly.
Now, suppose that
![]() $q=sp+p^{\prime}$
where
$q=sp+p^{\prime}$
where
![]() $s$
is a positive integer and
$s$
is a positive integer and
![]() $0\le p^{\prime}\le \sqrt{p}$
. Since it is known that
$0\le p^{\prime}\le \sqrt{p}$
. Since it is known that
![]() $2-\frac{1}{s}$
is a Turán exponent for all any integer
$2-\frac{1}{s}$
is a Turán exponent for all any integer
![]() $s\ge 2$
, we may assume
$s\ge 2$
, we may assume
![]() $p^{\prime}\gt 0$
. Now, as
$p^{\prime}\gt 0$
. Now, as
![]() $0\lt p^{\prime}\le \sqrt{p}$
, there exists integers
$0\lt p^{\prime}\le \sqrt{p}$
, there exists integers
![]() $k$
and
$k$
and
![]() $b$
such that
$b$
such that
![]() $p=kp^{\prime}+b$
and
$p=kp^{\prime}+b$
and
![]() $k\ge p^{\prime}-1$
and
$k\ge p^{\prime}-1$
and
![]() $p^{\prime}\ge b\ge 1$
. Then
$p^{\prime}\ge b\ge 1$
. Then
![]() $2-\frac{p}{q}=2-\frac{kp^{\prime}+b}{s(kp^{\prime}+b)+p^{\prime}}$
. By Corollary 1.4, it follows that
$2-\frac{p}{q}=2-\frac{kp^{\prime}+b}{s(kp^{\prime}+b)+p^{\prime}}$
. By Corollary 1.4, it follows that
![]() $2-\frac{p}{q}$
is a Turán exponent.
$2-\frac{p}{q}$
is a Turán exponent.
Finally, even though we obtained all the Turán exponents that Janzer’s conjecture would give, it would still be very interesting to resolve his conjecture in the full. For the general bipartite Turán problem, while tools such as dependent random choice have found success in the denser end of the spectrum for bipartite graphs, it would be very interesting to develop more tools for the sparser end of the spectrum. The recent active study of the Turán problem for subdivisions is a step in that direction. It will be very interesting to continue explore problems of such nature.