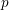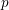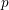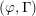1 Introduction
Let
![]() $p$
be a prime number. Results, and questions, in the
$p$
be a prime number. Results, and questions, in the
![]() $p$
-adic Langlands program may be naturally phrased, or asked, by studying
$p$
-adic Langlands program may be naturally phrased, or asked, by studying
![]() $p$
-adic families of automorphic forms [Reference EmertonEme, Reference BreuilBre15]. Regarding
$p$
-adic families of automorphic forms [Reference EmertonEme, Reference BreuilBre15]. Regarding
![]() $p$
-adic automorphic forms in their own right, the variation of the associated
$p$
-adic automorphic forms in their own right, the variation of the associated
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules is a central tool [Reference Bellaïche and ChenevierBC09]. One recent result, see [Reference Kedlaya, Pottharst and XiaoKPX14, Reference LiuLiu15], is that if a
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules is a central tool [Reference Bellaïche and ChenevierBC09]. One recent result, see [Reference Kedlaya, Pottharst and XiaoKPX14, Reference LiuLiu15], is that if a
![]() $p$
-adic family of
$p$
-adic family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules is pointwise completely reducible, i.e. a successive extension of rank-one objects, then it is also completely reducible in the family, at least generically. In language perhaps known to the reader, and used in this paper, pointwise triangulations in
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules is pointwise completely reducible, i.e. a successive extension of rank-one objects, then it is also completely reducible in the family, at least generically. In language perhaps known to the reader, and used in this paper, pointwise triangulations in
![]() $p$
-adic families extend to triangulations over open dense loci. This follows in the tradition of the famous reducibility of local Galois representations over Hida families [Reference Mazur and WilesMW86].
$p$
-adic families extend to triangulations over open dense loci. This follows in the tradition of the famous reducibility of local Galois representations over Hida families [Reference Mazur and WilesMW86].
However, there are arithmetically interesting points which fail to lie in global triangulation loci. The most concrete example is a point on the Coleman and Mazur eigencurve [Reference Coleman and MazurCM98] corresponding to the non-unit
![]() $p$
-stabilization of a
$p$
-stabilization of a
![]() $p$
-ordinary CM form. Such points lie in the image of one of Coleman’s
$p$
-ordinary CM form. Such points lie in the image of one of Coleman’s
![]() $\unicode[STIX]{x1D703}$
-maps [Reference BergdallBer14] and the associated
$\unicode[STIX]{x1D703}$
-maps [Reference BergdallBer14] and the associated
![]() $p$
-adic
$p$
-adic
![]() $L$
-function exhibits curious behavior [Reference BellaïcheBel12].
$L$
-function exhibits curious behavior [Reference BellaïcheBel12].
The aim of this article is to give a detailed account of the variation of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules near classical points in
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules near classical points in
![]() $p$
-adic families of automorphic forms, especially those which are known not to lie in a global triangulation locus. Note that we will be concerned with
$p$
-adic families of automorphic forms, especially those which are known not to lie in a global triangulation locus. Note that we will be concerned with
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules for
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules for
![]() $K/\mathbf{Q}_{p}$
a finite extension, but for the purposes of the introduction we will assume
$K/\mathbf{Q}_{p}$
a finite extension, but for the purposes of the introduction we will assume
 $K=\mathbf{Q}_{p}$
. There is no loss of content, only notation.
$K=\mathbf{Q}_{p}$
. There is no loss of content, only notation.
1.1 Trianguline
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules
We use
![]() ${\mathcal{R}}$
to denote the Robba ring over
${\mathcal{R}}$
to denote the Robba ring over
![]() $\mathbf{Q}_{p}$
. It is the ring consisting of analytic functions
$\mathbf{Q}_{p}$
. It is the ring consisting of analytic functions
![]() $f$
converging on a
$f$
converging on a
![]() $p$
-adic half-open annulus
$p$
-adic half-open annulus
 $r(f)\leqslant |T|<1$
, for some radius
$r(f)\leqslant |T|<1$
, for some radius
![]() $r(f)$
depending on
$r(f)$
depending on
![]() $f$
. There are continuous commuting actions of a Frobenius operator
$f$
. There are continuous commuting actions of a Frobenius operator
![]() $\unicode[STIX]{x1D711}$
and the group
$\unicode[STIX]{x1D711}$
and the group
![]() $\unicode[STIX]{x1D6E4}\simeq \mathbf{Z}_{p}^{\times }$
.
$\unicode[STIX]{x1D6E4}\simeq \mathbf{Z}_{p}^{\times }$
.
A
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
![]() $D$
is a finite free
$D$
is a finite free
![]() ${\mathcal{R}}$
-module equipped with commuting,
${\mathcal{R}}$
-module equipped with commuting,
![]() ${\mathcal{R}}$
-semilinear actions of
${\mathcal{R}}$
-semilinear actions of
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D6E4}$
, such that
$\unicode[STIX]{x1D6E4}$
, such that
![]() $\unicode[STIX]{x1D711}(D)$
generates
$\unicode[STIX]{x1D711}(D)$
generates
![]() $D$
as a
$D$
as a
![]() ${\mathcal{R}}$
-module (see [Reference BergerBer02]). The rank-one
${\mathcal{R}}$
-module (see [Reference BergerBer02]). The rank-one
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules are parameterized by continuous characters
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules are parameterized by continuous characters
![]() $\unicode[STIX]{x1D6FF}$
of
$\unicode[STIX]{x1D6FF}$
of
![]() $\mathbf{Q}_{p}^{\times }$
. If
$\mathbf{Q}_{p}^{\times }$
. If
![]() $\unicode[STIX]{x1D6FF}$
is such a character we denote the corresponding
$\unicode[STIX]{x1D6FF}$
is such a character we denote the corresponding
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module by
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module by
![]() ${\mathcal{R}}(\unicode[STIX]{x1D6FF})$
.
${\mathcal{R}}(\unicode[STIX]{x1D6FF})$
.
A triangulation of a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
![]() $D$
is a filtration
$D$
is a filtration
![]() $P_{\bullet }$
$P_{\bullet }$
 $$\begin{eqnarray}\displaystyle 0=P_{0}\subsetneq P_{1}\subsetneq \cdots \subsetneq P_{d-1}\subsetneq P_{d}=D & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=P_{0}\subsetneq P_{1}\subsetneq \cdots \subsetneq P_{d-1}\subsetneq P_{d}=D & & \displaystyle \nonumber\end{eqnarray}$$
by
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-submodules, such that each successive quotient
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-submodules, such that each successive quotient
 $P_{i}/P_{i-1}\simeq {\mathcal{R}}(\unicode[STIX]{x1D6FF}_{i})$
is a rank-one
$P_{i}/P_{i-1}\simeq {\mathcal{R}}(\unicode[STIX]{x1D6FF}_{i})$
is a rank-one
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module. The ordered tuple
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module. The ordered tuple
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
is called the parameter of
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
is called the parameter of
![]() $P_{\bullet }$
. We say
$P_{\bullet }$
. We say
![]() $D$
is trianguline if it may be equipped with a triangulation. Examples coming from Galois representations show there may be many ways to triangulate a given
$D$
is trianguline if it may be equipped with a triangulation. Examples coming from Galois representations show there may be many ways to triangulate a given
![]() $D$
.
$D$
.
By the work of Fontaine, Cherbonnier–Colmez, Kedlaya and Berger, see [Reference BergerBer02], there is a fully faithful embedding
 $V\mapsto D_{\operatorname{rig}}(V)$
which associates a
$V\mapsto D_{\operatorname{rig}}(V)$
which associates a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module to each continuous, finite-dimensional representation
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module to each continuous, finite-dimensional representation
![]() $V$
of
$V$
of
![]() $G_{\mathbf{Q}_{p}}$
. If
$G_{\mathbf{Q}_{p}}$
. If
![]() $V$
is crystalline, then
$V$
is crystalline, then
 $D_{\operatorname{rig}}(V)$
is trianguline and, generically, the triangulations of
$D_{\operatorname{rig}}(V)$
is trianguline and, generically, the triangulations of
 $D_{\operatorname{rig}}(V)$
are in bijection with the orderings of eigenvalues for the crystalline Frobenius acting on
$D_{\operatorname{rig}}(V)$
are in bijection with the orderings of eigenvalues for the crystalline Frobenius acting on
 $D_{\operatorname{cris}}(V)$
.
$D_{\operatorname{cris}}(V)$
.
The global context of trianguline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules, and thus this article, is spaces of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules, and thus this article, is spaces of
![]() $p$
-adic automorphic forms. It is a folklore conjecture, generalizing a conjecture of Fontaine and Mazur [Reference Fontaine and MazurFM95], that an irreducible
$p$
-adic automorphic forms. It is a folklore conjecture, generalizing a conjecture of Fontaine and Mazur [Reference Fontaine and MazurFM95], that an irreducible
![]() $\mathbf{Q}_{p}$
-linear, finite-dimensional representation of the global Galois group
$\mathbf{Q}_{p}$
-linear, finite-dimensional representation of the global Galois group
![]() $G_{\mathbf{Q}}$
which is:
$G_{\mathbf{Q}}$
which is:
-
– unramified at all but a finite set of primes; and
-
– trianguline at
 $p$
;
$p$
;
should (essentially) appear in a space of finite slope
![]() $p$
-adic automorphic forms. A precise statement was written down by Hansen recently, see [Reference HansenHan14, Conjecture 1.2.3]. The only known result is due to Emerton and settles the question in dimension two, via local–global compatibility in the
$p$
-adic automorphic forms. A precise statement was written down by Hansen recently, see [Reference HansenHan14, Conjecture 1.2.3]. The only known result is due to Emerton and settles the question in dimension two, via local–global compatibility in the
![]() $p$
-adic Langlands program for
$p$
-adic Langlands program for
![]() ${\operatorname{GL}_{2}}_{/\mathbf{Q}}$
(see [Reference EmertonEme, Theorem 1.2.4(1)]). The converse, that global representations attached to
${\operatorname{GL}_{2}}_{/\mathbf{Q}}$
(see [Reference EmertonEme, Theorem 1.2.4(1)]). The converse, that global representations attached to
![]() $p$
-adic automorphic forms are trianguline at
$p$
-adic automorphic forms are trianguline at
![]() $p$
, is known in many situations by [Reference Kedlaya, Pottharst and XiaoKPX14, Reference LiuLiu15], including eigenvarieties attached to definite unitary groups. This plays a role in recent conjectures of Breuil [Reference BreuilBre15] regarding aspects of the
$p$
, is known in many situations by [Reference Kedlaya, Pottharst and XiaoKPX14, Reference LiuLiu15], including eigenvarieties attached to definite unitary groups. This plays a role in recent conjectures of Breuil [Reference BreuilBre15] regarding aspects of the
![]() $p$
-adic local Langlands program for
$p$
-adic local Langlands program for
 $\operatorname{GL}_{n}(\mathbf{Q}_{p})$
with
$\operatorname{GL}_{n}(\mathbf{Q}_{p})$
with
![]() $n>2$
.
$n>2$
.
1.2 Critical triangulations
The basic notions of
![]() $p$
-adic Hodge theory (for example, Hodge–Tate–Sen weights and crystalline objects) extend to the category of
$p$
-adic Hodge theory (for example, Hodge–Tate–Sen weights and crystalline objects) extend to the category of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. If
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. If
 $D={\mathcal{R}}(\unicode[STIX]{x1D6FF})$
, then the Hodge–Tate–Sen weight is
$D={\mathcal{R}}(\unicode[STIX]{x1D6FF})$
, then the Hodge–Tate–Sen weight is
 $$\begin{eqnarray}\displaystyle \operatorname{wt}(\unicode[STIX]{x1D6FF})=-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FE}}\!\biggm\vert_{\unicode[STIX]{x1D6FE}=1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FE}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{wt}(\unicode[STIX]{x1D6FF})=-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FE}}\!\biggm\vert_{\unicode[STIX]{x1D6FE}=1}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FE}). & & \displaystyle \nonumber\end{eqnarray}$$
If
![]() $D$
is triangulated with parameter
$D$
is triangulated with parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
then the Hodge–Tate–Sen weights of
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
then the Hodge–Tate–Sen weights of
![]() $D$
are
$D$
are
 $\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i})\}_{i=1,\ldots ,d}$
. The following definition is key for the statement of our theorem. A more general definition will be given in the text (see § 3.2).
$\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i})\}_{i=1,\ldots ,d}$
. The following definition is key for the statement of our theorem. A more general definition will be given in the text (see § 3.2).
Definition 1.1. Let
![]() $D$
be a crystalline
$D$
be a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module with distinct Hodge–Tate weights
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module with distinct Hodge–Tate weights
 $k_{1}<\cdots <k_{d}$
. If
$k_{1}<\cdots <k_{d}$
. If
![]() $P\subset D$
is a saturated
$P\subset D$
is a saturated
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-submodule of rank
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-submodule of rank
![]() $i$
, then
$i$
, then
![]() $P$
is called non-critical if the lowest
$P$
is called non-critical if the lowest
![]() $i$
weights
$i$
weights
 $\{k_{1},\ldots ,k_{i}\}$
are the Hodge–Tate weights of
$\{k_{1},\ldots ,k_{i}\}$
are the Hodge–Tate weights of
![]() $P$
.
$P$
.
Note that
![]() $D$
is always a non-critical
$D$
is always a non-critical
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-submodule of itself. We extend the notion of non-critical to a triangulation
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-submodule of itself. We extend the notion of non-critical to a triangulation
![]() $P_{\bullet }$
by declaring a triangulation
$P_{\bullet }$
by declaring a triangulation
![]() $P_{\bullet }$
to be non-critical if
$P_{\bullet }$
to be non-critical if
![]() $P_{i}$
is non-critical for each
$P_{i}$
is non-critical for each
![]() $i$
. This agrees with the original definition of Bellaïche and Chenevier [Reference Bellaïche and ChenevierBC09]. More generally, we have the following construction. If
$i$
. This agrees with the original definition of Bellaïche and Chenevier [Reference Bellaïche and ChenevierBC09]. More generally, we have the following construction. If
![]() $D$
is a crystalline
$D$
is a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module and
![]() $P_{\bullet }$
is a triangulation, then we define the non-critical indices
$P_{\bullet }$
is a triangulation, then we define the non-critical indices
 $$\begin{eqnarray}\displaystyle I^{\operatorname{nc}}=\{i:P_{i}\text{ is non-critical}\}=\{0=i_{0}<i_{1}<i_{2}<\cdots <i_{s}=d\} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I^{\operatorname{nc}}=\{i:P_{i}\text{ is non-critical}\}=\{0=i_{0}<i_{1}<i_{2}<\cdots <i_{s}=d\} & & \displaystyle \nonumber\end{eqnarray}$$
and a filtration (called a parabolization, rather than a triangulation, following Chenevier [Reference ChenevierChe11])
 $$\begin{eqnarray}\displaystyle P_{\bullet }^{\operatorname{nc}}:0=P_{0}^{\operatorname{nc}}\subsetneq P_{1}^{\operatorname{nc}}\subsetneq \cdots \subsetneq P_{s}^{\operatorname{nc}}=D & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{\bullet }^{\operatorname{nc}}:0=P_{0}^{\operatorname{nc}}\subsetneq P_{1}^{\operatorname{nc}}\subsetneq \cdots \subsetneq P_{s}^{\operatorname{nc}}=D & & \displaystyle \nonumber\end{eqnarray}$$
by declaring that
 $P_{j}^{\operatorname{nc}}=P_{i_{j}}$
for
$P_{j}^{\operatorname{nc}}=P_{i_{j}}$
for
 $j=0,1,\ldots ,s$
. In short,
$j=0,1,\ldots ,s$
. In short,
![]() $P_{\bullet }^{\operatorname{nc}}$
only knows the non-critical steps in the triangulation
$P_{\bullet }^{\operatorname{nc}}$
only knows the non-critical steps in the triangulation
![]() $P_{\bullet }$
; it is called the maximal non-critical parabolization of
$P_{\bullet }$
; it is called the maximal non-critical parabolization of
![]() $P_{\bullet }$
.
$P_{\bullet }$
.
1.3 Refined families and
 $p$
-adic variation
$p$
-adic variation
Now suppose that
![]() $X$
is a reduced rigid analytic space over
$X$
is a reduced rigid analytic space over
![]() $\mathbf{Q}_{p}$
. In § 6.1 we will define and consider so-called refined families
$\mathbf{Q}_{p}$
. In § 6.1 we will define and consider so-called refined families
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over
![]() $X$
. For now it suffices to know that a refined family
$X$
. For now it suffices to know that a refined family
 $D_{X}=\{D_{x}\}_{x}$
is a family of
$D_{X}=\{D_{x}\}_{x}$
is a family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over a relative Robba ring
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over a relative Robba ring
![]() ${\mathcal{R}}_{X}$
with the following properties:
${\mathcal{R}}_{X}$
with the following properties:
-
– there exists continuous characters
 $\unicode[STIX]{x1D6FF}_{i}:\mathbf{Q}_{p}^{\times }\rightarrow \unicode[STIX]{x1D6E4}(X,{\mathcal{O}})^{\times }$
; and
$\unicode[STIX]{x1D6FF}_{i}:\mathbf{Q}_{p}^{\times }\rightarrow \unicode[STIX]{x1D6E4}(X,{\mathcal{O}})^{\times }$
; and -
– Zariski-dense sets of points
 $X_{\operatorname{cl}}^{\operatorname{nc}}\subset X_{\operatorname{cl}}\subset X(\overline{\mathbf{Q}}_{p})$
;
$X_{\operatorname{cl}}^{\operatorname{nc}}\subset X_{\operatorname{cl}}\subset X(\overline{\mathbf{Q}}_{p})$
;
such that:
-
– if
 $x\in X_{\operatorname{cl}}$
, then
$x\in X_{\operatorname{cl}}$
, then
 $D_{x}$
is crystalline with distinct Hodge–Tate weights; and
$D_{x}$
is crystalline with distinct Hodge–Tate weights; and -
– if
 $x\in X_{\operatorname{cl}}^{\operatorname{nc}}$
, then
$x\in X_{\operatorname{cl}}^{\operatorname{nc}}$
, then
 $D_{x}$
is triangulated by a non-critical triangulation
$D_{x}$
is triangulated by a non-critical triangulation
 $P_{\bullet ,x}$
whose parameter is
$P_{\bullet ,x}$
whose parameter is
 $(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
.
$(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
.
Here,
 $\unicode[STIX]{x1D6FF}_{i,x}:\mathbf{Q}_{p}^{\times }\rightarrow L(x)^{\times }$
is the character with values in the residue field
$\unicode[STIX]{x1D6FF}_{i,x}:\mathbf{Q}_{p}^{\times }\rightarrow L(x)^{\times }$
is the character with values in the residue field
![]() $L(x)$
obtained by post-composing with the evaluation map at
$L(x)$
obtained by post-composing with the evaluation map at
![]() $x$
. It follows from [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.13] or [Reference LiuLiu15, Theorem 5.45] that in a neighborhood of a point
$x$
. It follows from [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.13] or [Reference LiuLiu15, Theorem 5.45] that in a neighborhood of a point
 $x_{0}\in X_{\operatorname{cl}}$
, each
$x_{0}\in X_{\operatorname{cl}}$
, each
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
![]() $D_{x}$
is triangulated by a triangulation
$D_{x}$
is triangulated by a triangulation
![]() $P_{\bullet ,x}$
, which is essentially canonical as long as
$P_{\bullet ,x}$
, which is essentially canonical as long as
![]() $x_{0}$
is sufficiently generic (see Proposition 6.5). But note that the parameter of
$x_{0}$
is sufficiently generic (see Proposition 6.5). But note that the parameter of
![]() $P_{\bullet ,x}$
may (and will in critical cases) differ from the natural choice
$P_{\bullet ,x}$
may (and will in critical cases) differ from the natural choice
 $(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
.
$(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
.
Our main result shows that despite the possible non-variation of the pointwise parameters, the maximal non-critical parabolization of
![]() $P_{\bullet ,x_{0}}$
varies analytically. Strictly speaking, we only defined
$P_{\bullet ,x_{0}}$
varies analytically. Strictly speaking, we only defined
![]() $P_{\bullet ,x}^{\operatorname{nc}}$
for certain points
$P_{\bullet ,x}^{\operatorname{nc}}$
for certain points
![]() $x\in X_{\operatorname{cl}}$
but there is a way of extending the definition to every point (which requires reference to the family).
$x\in X_{\operatorname{cl}}$
but there is a way of extending the definition to every point (which requires reference to the family).
Theorem A (Theorem 6.8).
If
![]() $D_{X}$
is a refined family of
$D_{X}$
is a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules and
 $x_{0}\in X_{\operatorname{cl}}$
is very
$x_{0}\in X_{\operatorname{cl}}$
is very
![]() $\unicode[STIX]{x1D711}$
-regular,Footnote
1
then there exists an open affinoid neighborhood
$\unicode[STIX]{x1D711}$
-regular,Footnote
1
then there exists an open affinoid neighborhood
 $x_{0}\in U\subset X$
and a filtration
$x_{0}\in U\subset X$
and a filtration
 $$\begin{eqnarray}\displaystyle 0=P_{0}^{\operatorname{nc}}\subsetneq P_{1}^{\operatorname{nc}}\subsetneq \cdots \subsetneq P_{s-1}^{\operatorname{nc}}\subsetneq P_{s}^{\operatorname{nc}}=D|_{U} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=P_{0}^{\operatorname{nc}}\subsetneq P_{1}^{\operatorname{nc}}\subsetneq \cdots \subsetneq P_{s-1}^{\operatorname{nc}}\subsetneq P_{s}^{\operatorname{nc}}=D|_{U} & & \displaystyle \nonumber\end{eqnarray}$$
where each
![]() $P_{i}^{\operatorname{nc}}$
is a refined family of
$P_{i}^{\operatorname{nc}}$
is a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over
![]() $U$
, such that
$U$
, such that
 $P_{i,x}^{\operatorname{nc}}=P_{i,U}^{\operatorname{nc}}\otimes _{{\mathcal{O}}(U)}L(x)$
for all
$P_{i,x}^{\operatorname{nc}}=P_{i,U}^{\operatorname{nc}}\otimes _{{\mathcal{O}}(U)}L(x)$
for all
![]() $x\in U$
.
$x\in U$
.
The result is optimal in the following sense. If
![]() $x\in X_{\operatorname{cl}}$
is non-critical, then the Hodge–Tate weights of
$x\in X_{\operatorname{cl}}$
is non-critical, then the Hodge–Tate weights of
![]() $P_{i,x}$
are
$P_{i,x}$
are
 $\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{1,x}),\operatorname{wt}(\unicode[STIX]{x1D6FF}_{2,x}),\ldots ,\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,x})\}$
. Thus, for general
$\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{1,x}),\operatorname{wt}(\unicode[STIX]{x1D6FF}_{2,x}),\ldots ,\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,x})\}$
. Thus, for general
![]() $x\in X_{\operatorname{cl}}$
Sen’s theory of Hodge–Tate weights in families [Reference SenSen88] implies one can only hope that
$x\in X_{\operatorname{cl}}$
Sen’s theory of Hodge–Tate weights in families [Reference SenSen88] implies one can only hope that
![]() $P_{i,x}$
extends to an affinoid neighborhood of
$P_{i,x}$
extends to an affinoid neighborhood of
![]() $x$
provided that the Hodge–Tate weights of
$x$
provided that the Hodge–Tate weights of
![]() $P_{i,x}$
are
$P_{i,x}$
are
 $\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{1,x}),\ldots ,\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,x})\}$
, i.e.
$\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{1,x}),\ldots ,\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,x})\}$
, i.e.
![]() $P_{i,x}$
can only vary well in a family if it is a non-critical step in the triangulation at
$P_{i,x}$
can only vary well in a family if it is a non-critical step in the triangulation at
![]() $x$
.
$x$
.
The history of our result is relatively short. In the case where
![]() $x_{0}$
is non-critical, so an entire triangulation extends to affinoid neighborhoods, Theorem A has two independent proofs, given essentially at the same time. One proof was given by Liu [Reference LiuLiu15] using a generalization of Kisin’s interpolation of crystalline periods [Reference KisinKis03, Reference Bellaïche and ChenevierBC09] over general affinoid bases. The other proof was given by Kedlaya et al. [Reference Kedlaya, Pottharst and XiaoKPX14] and relied explicitlyFootnote
2
on the finiteness of Galois cohomology for families of
$x_{0}$
is non-critical, so an entire triangulation extends to affinoid neighborhoods, Theorem A has two independent proofs, given essentially at the same time. One proof was given by Liu [Reference LiuLiu15] using a generalization of Kisin’s interpolation of crystalline periods [Reference KisinKis03, Reference Bellaïche and ChenevierBC09] over general affinoid bases. The other proof was given by Kedlaya et al. [Reference Kedlaya, Pottharst and XiaoKPX14] and relied explicitlyFootnote
2
on the finiteness of Galois cohomology for families of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules (also proven in [Reference Kedlaya, Pottharst and XiaoKPX14]). Neither work makes any general comment on what to expect at a general classical point, especially in the critically triangulated case.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules (also proven in [Reference Kedlaya, Pottharst and XiaoKPX14]). Neither work makes any general comment on what to expect at a general classical point, especially in the critically triangulated case.
Our technique is inspired by the latter proof [Reference Kedlaya, Pottharst and XiaoKPX14] and separate work of Liu emphasizing the utility of torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules [Reference LiuLiu07]. To explain this, let us recall the Kedlaya–Pottharst–Xiao proof of Theorem A in the non-critical case.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules [Reference LiuLiu07]. To explain this, let us recall the Kedlaya–Pottharst–Xiao proof of Theorem A in the non-critical case.
Under mild regularity assumptions one can check, using the finiteness of Galois cohomology in families, that
 $\operatorname{Hom}_{(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})}({\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1}),D_{X})$
is locally free of rank one near
$\operatorname{Hom}_{(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})}({\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1}),D_{X})$
is locally free of rank one near
![]() $x_{0}$
. Indeed, it may be checked point-by-point, and essentially just at the point
$x_{0}$
. Indeed, it may be checked point-by-point, and essentially just at the point
![]() $x_{0}$
and the points in
$x_{0}$
and the points in
![]() $X_{\operatorname{cl}}^{\operatorname{nc}}$
. Choose an everywhere non-vanishing morphism
$X_{\operatorname{cl}}^{\operatorname{nc}}$
. Choose an everywhere non-vanishing morphism
 $\mathbf{e}:{\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1})\rightarrow D_{X}$
. The non-critical hypothesis on
$\mathbf{e}:{\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1})\rightarrow D_{X}$
. The non-critical hypothesis on
![]() $x_{0}$
means that the specialized morphism
$x_{0}$
means that the specialized morphism
 $\mathbf{e}_{x_{0}}:{\mathcal{R}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})\rightarrow D_{x_{0}}$
has saturated image and, thus,
$\mathbf{e}_{x_{0}}:{\mathcal{R}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})\rightarrow D_{x_{0}}$
has saturated image and, thus,
 $\operatorname{coker}(\mathbf{e}_{x_{0}})$
is free. An easy argument shows that one can shrink
$\operatorname{coker}(\mathbf{e}_{x_{0}})$
is free. An easy argument shows that one can shrink
![]() $X$
so that
$X$
so that
 $\operatorname{coker}(\mathbf{e})$
is a
$\operatorname{coker}(\mathbf{e})$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module over
![]() $X$
. The rest of the proof of Theorem A is carried about by induction from this case.
$X$
. The rest of the proof of Theorem A is carried about by induction from this case.
A generalization of this strategy, to critical points, requires us to define an a priori candidate for the first step
![]() $P_{1}^{\operatorname{nc}}$
of the sought after parabolization. In the non-critical case
$P_{1}^{\operatorname{nc}}$
of the sought after parabolization. In the non-critical case
![]() $P_{1}^{\operatorname{nc}}$
is handed to us on a platter as
$P_{1}^{\operatorname{nc}}$
is handed to us on a platter as
![]() ${\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1})$
. However, there seems to be no easy way to guess
${\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1})$
. However, there seems to be no easy way to guess
![]() $P_{1}^{\operatorname{nc}}$
ahead of time.Footnote
3
$P_{1}^{\operatorname{nc}}$
ahead of time.Footnote
3
The key feature of our proof is to embrace the non-saturatedness of the morphism
![]() $\mathbf{e}_{x_{0}}$
in the critical case. Thus, we proceed by studying more general families of
$\mathbf{e}_{x_{0}}$
in the critical case. Thus, we proceed by studying more general families of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules whose fibers have
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules whose fibers have
![]() ${\mathcal{R}}$
-torsion in them. We call such modules generalized
${\mathcal{R}}$
-torsion in them. We call such modules generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules following Liu [Reference LiuLiu07]. In § 3, we give a generalization of the notion of a triangulation of a generalized
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules following Liu [Reference LiuLiu07]. In § 3, we give a generalization of the notion of a triangulation of a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules which is well-adapted to attacking Theorem A. The novelty of our proof is the introduction of torsion into the fibers at every point in order to canonically describe a candidate for
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules which is well-adapted to attacking Theorem A. The novelty of our proof is the introduction of torsion into the fibers at every point in order to canonically describe a candidate for
 $\operatorname{coker}(P_{1}^{\operatorname{nc}}\rightarrow D)$
, thus producing
$\operatorname{coker}(P_{1}^{\operatorname{nc}}\rightarrow D)$
, thus producing
![]() $P_{1}^{\operatorname{nc}}$
as needed for Theorem A.
$P_{1}^{\operatorname{nc}}$
as needed for Theorem A.
1.4 Ramification of weights
Let us finish by mentioning an auxiliary result we prove here on the ramification of weights in refined families. Let
![]() $D_{X}$
be a refined family and
$D_{X}$
be a refined family and
 $x_{0}\in X_{\operatorname{cl}}$
. Consider the triangulation
$x_{0}\in X_{\operatorname{cl}}$
. Consider the triangulation
![]() $P_{\bullet ,x_{0}}$
and denote its parameter by
$P_{\bullet ,x_{0}}$
and denote its parameter by
 $(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
. As shown in the text, the lists of distinct weights
$(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
. As shown in the text, the lists of distinct weights
 $\{\operatorname{wt}(\widetilde{\unicode[STIX]{x1D6FF}}_{i,x_{0}})\}$
and
$\{\operatorname{wt}(\widetilde{\unicode[STIX]{x1D6FF}}_{i,x_{0}})\}$
and
 $\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,x_{0}})\}$
are the same. Thus, we may define a permutation
$\{\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,x_{0}})\}$
are the same. Thus, we may define a permutation
![]() $\unicode[STIX]{x1D70B}_{x_{0}}$
by the formula
$\unicode[STIX]{x1D70B}_{x_{0}}$
by the formula
 $\operatorname{wt}(\widetilde{\unicode[STIX]{x1D6FF}}_{i,x_{0}})=\operatorname{wt}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}_{x_{0}}(i),x_{0}})$
. We remark that
$\operatorname{wt}(\widetilde{\unicode[STIX]{x1D6FF}}_{i,x_{0}})=\operatorname{wt}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}_{x_{0}}(i),x_{0}})$
. We remark that
 $\unicode[STIX]{x1D70B}_{x_{0}}=\operatorname{id}$
if and only if
$\unicode[STIX]{x1D70B}_{x_{0}}=\operatorname{id}$
if and only if
![]() $x_{0}$
is non-critical.
$x_{0}$
is non-critical.
We now let
![]() $T_{x_{0}}X$
be the Zariski tangent space to
$T_{x_{0}}X$
be the Zariski tangent space to
![]() $X$
at
$X$
at
![]() $x_{0}$
. If
$x_{0}$
. If
![]() $f$
is the germ of a function at
$f$
is the germ of a function at
![]() $x_{0}$
and
$x_{0}$
and
![]() $v$
is a tangent vector, we let
$v$
is a tangent vector, we let
![]() $\unicode[STIX]{x1D6FB}_{v}(f)$
denote the directional derivative of
$\unicode[STIX]{x1D6FB}_{v}(f)$
denote the directional derivative of
![]() $f$
with respect to
$f$
with respect to
![]() $v$
. Our second theorem is that certain differences of weights are constant in every tangent direction.
$v$
. Our second theorem is that certain differences of weights are constant in every tangent direction.
Theorem B (Theorem 7.1).
If
![]() $D_{X}$
is a refined family over
$D_{X}$
is a refined family over
![]() $X$
and
$X$
and
 $x_{0}\in X_{\operatorname{cl}}$
is very
$x_{0}\in X_{\operatorname{cl}}$
is very
![]() $\unicode[STIX]{x1D711}$
-regular, then
$\unicode[STIX]{x1D711}$
-regular, then
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}_{v}(\operatorname{wt}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}_{x_{0}}(i),u})-\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,u}))=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}_{v}(\operatorname{wt}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70B}_{x_{0}}(i),u})-\operatorname{wt}(\unicode[STIX]{x1D6FF}_{i,u}))=0 & & \displaystyle \nonumber\end{eqnarray}$$
for all
 $i=1,\ldots ,d$
and
$i=1,\ldots ,d$
and
 $v\in T_{x_{0}}X$
. In particular, if
$v\in T_{x_{0}}X$
. In particular, if
![]() $x_{0}$
is critical, then the weight map ramifies.
$x_{0}$
is critical, then the weight map ramifies.
Theorem B was noticed independently by the author and Breuil. We reproduce an argument similar to [Reference BreuilBre15, Théorème 9.7] in § 7. Our proof will make use Liu’s results on crystalline periods [Reference LiuLiu15]. But we note that such a theorem could have been proven using only the (infinitesimal) study of crystalline periods in the weakly refined families
![]() $\wedge ^{i}D$
(as in [Reference Bellaïche and ChenevierBC09, § 4.3], for example) combined with deformation calculations similar to [Reference BergdallBer14, Proposition 2.4].
$\wedge ^{i}D$
(as in [Reference Bellaïche and ChenevierBC09, § 4.3], for example) combined with deformation calculations similar to [Reference BergdallBer14, Proposition 2.4].
1.5 Organization
Section 2 briefly recalls the theory of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules and the important theorems. Section 3 introduces triangulations and parabolizations, including a definition for torsion
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules and the important theorems. Section 3 introduces triangulations and parabolizations, including a definition for torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. Section 4 is a digression into the theorems of [Reference Kedlaya, Pottharst and XiaoKPX14] and applications. Section 6 contains our result on the variation of parabolizations in
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. Section 4 is a digression into the theorems of [Reference Kedlaya, Pottharst and XiaoKPX14] and applications. Section 6 contains our result on the variation of parabolizations in
![]() $p$
-adic families, and § 5 plays a supporting role. Finally we study the ramification of the weight parameters in § 7. A short appendix is included to deal with a ‘relative’ version of Nakayama’s lemma.
$p$
-adic families, and § 5 plays a supporting role. Finally we study the ramification of the weight parameters in § 7. A short appendix is included to deal with a ‘relative’ version of Nakayama’s lemma.
1.6 Notation and conventions
Throughout the text we will make the following conventions. They will follow [Reference Kedlaya, Pottharst and XiaoKPX14] closely.
We fix an algebraic closure
![]() $\overline{\mathbf{Q}}_{p}$
and a
$\overline{\mathbf{Q}}_{p}$
and a
![]() $p$
-adic valuation on
$p$
-adic valuation on
![]() $\overline{\mathbf{Q}}_{p}$
so that
$\overline{\mathbf{Q}}_{p}$
so that
 $|p|=p^{-1}$
.
$|p|=p^{-1}$
.
Here
![]() $K$
will always denote a finite extension
$K$
will always denote a finite extension
![]() $\mathbf{Q}_{p}$
. We let
$\mathbf{Q}_{p}$
. We let
![]() $F$
be the maximal subfield of
$F$
be the maximal subfield of
![]() $K$
unramified over
$K$
unramified over
![]() $\mathbf{Q}_{p}$
,
$\mathbf{Q}_{p}$
,
 $f_{K}=(F:\mathbf{Q}_{p})$
the inertial degree of
$f_{K}=(F:\mathbf{Q}_{p})$
the inertial degree of
![]() $K$
and
$K$
and
![]() $e_{K}$
the ramification index of
$e_{K}$
the ramification index of
![]() $K$
.
$K$
.
We will let
 $K_{\infty }=\mathop{\varinjlim }\nolimits_{n}K(\unicode[STIX]{x1D701}_{p^{n}})$
be the extension obtained by adjoining to
$K_{\infty }=\mathop{\varinjlim }\nolimits_{n}K(\unicode[STIX]{x1D701}_{p^{n}})$
be the extension obtained by adjoining to
![]() $K$
all the
$K$
all the
![]() $p$
-power roots of unity. The maximal absolutely unramified subextension of
$p$
-power roots of unity. The maximal absolutely unramified subextension of
![]() $K_{\infty }$
is denoted by
$K_{\infty }$
is denoted by
![]() $F^{\prime }$
. If
$F^{\prime }$
. If
 $H_{K}=\operatorname{Gal}(\overline{\mathbf{Q}}_{p}/K_{\infty })$
, then we define
$H_{K}=\operatorname{Gal}(\overline{\mathbf{Q}}_{p}/K_{\infty })$
, then we define
 $\unicode[STIX]{x1D6E4}_{K}=G_{K}/H_{K}$
. The cyclotomic character
$\unicode[STIX]{x1D6E4}_{K}=G_{K}/H_{K}$
. The cyclotomic character
 $\unicode[STIX]{x1D6E4}_{\mathbf{Q}_{p}}\rightarrow \mathbf{Z}_{p}^{\times }$
identifies
$\unicode[STIX]{x1D6E4}_{\mathbf{Q}_{p}}\rightarrow \mathbf{Z}_{p}^{\times }$
identifies
![]() $\unicode[STIX]{x1D6E4}_{K}$
with an open subgroup of
$\unicode[STIX]{x1D6E4}_{K}$
with an open subgroup of
![]() $\mathbf{Z}_{p}^{\times }$
.
$\mathbf{Z}_{p}^{\times }$
.
Write
![]() $\unicode[STIX]{x1D6F4}_{K}$
for the set of all of the embeddings
$\unicode[STIX]{x1D6F4}_{K}$
for the set of all of the embeddings
 $K{\hookrightarrow}\overline{\mathbf{Q}}_{p}$
. Then
$K{\hookrightarrow}\overline{\mathbf{Q}}_{p}$
. Then
![]() $L$
will always denote a finite extension of
$L$
will always denote a finite extension of
![]() $\mathbf{Q}_{p}$
contained in
$\mathbf{Q}_{p}$
contained in
![]() $\overline{\mathbf{Q}}_{p}$
such that
$\overline{\mathbf{Q}}_{p}$
such that
 $\unicode[STIX]{x1D70F}(K)\subset L$
for each
$\unicode[STIX]{x1D70F}(K)\subset L$
for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. We allow
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. We allow
![]() $L$
to change at will. Note that
$L$
to change at will. Note that
 $L\otimes _{\mathbf{Q}_{p}}K\simeq \prod _{\unicode[STIX]{x1D70F}}L$
and we denote by
$L\otimes _{\mathbf{Q}_{p}}K\simeq \prod _{\unicode[STIX]{x1D70F}}L$
and we denote by
![]() $e_{\unicode[STIX]{x1D70F}}$
the idempotent in
$e_{\unicode[STIX]{x1D70F}}$
the idempotent in
 $L\otimes _{\mathbf{Q}_{p}}K$
which projects onto the
$L\otimes _{\mathbf{Q}_{p}}K$
which projects onto the
![]() $\unicode[STIX]{x1D70F}$
-component.
$\unicode[STIX]{x1D70F}$
-component.
2 Review of
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
We give a short review of (generalized)
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, their relationship with Galois representations and the
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, their relationship with Galois representations and the
![]() $p$
-adic arithmetic theory (cohomology,
$p$
-adic arithmetic theory (cohomology,
![]() $p$
-adic Hodge theory, etc.). All of the notation from § 1.6 are enforced, including the choice of
$p$
-adic Hodge theory, etc.). All of the notation from § 1.6 are enforced, including the choice of
![]() $L$
for a generic coefficient field containing the image of each embedding of
$L$
for a generic coefficient field containing the image of each embedding of
![]() $K$
into
$K$
into
![]() $\overline{\mathbf{Q}}_{p}$
.
$\overline{\mathbf{Q}}_{p}$
.
2.1 The Robba ring
We quickly remind the reader of the definition of the Robba ring
![]() ${\mathcal{R}}$
, setting notation for the most part. We note that
${\mathcal{R}}$
, setting notation for the most part. We note that
![]() $K$
is fixed throughout, but that the definition of
$K$
is fixed throughout, but that the definition of
![]() ${\mathcal{R}}$
depends on
${\mathcal{R}}$
depends on
![]() $K$
(we simply suppress it from the notation).
$K$
(we simply suppress it from the notation).
For each pair of rational numbers
 $0<s\leqslant r\leqslant \infty$
we define a
$0<s\leqslant r\leqslant \infty$
we define a
![]() $p$
-adic annulus
$p$
-adic annulus
 $$\begin{eqnarray}\displaystyle \mathbf{A}_{/F^{\prime }}^{1}[s,r]=\{T:p^{-r/(p-1)}\leqslant |T|\leqslant p^{-s/(p-1)}\} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{A}_{/F^{\prime }}^{1}[s,r]=\{T:p^{-r/(p-1)}\leqslant |T|\leqslant p^{-s/(p-1)}\} & & \displaystyle \nonumber\end{eqnarray}$$
over
![]() $F^{\prime }$
. When
$F^{\prime }$
. When
![]() $r=\infty$
this is a
$r=\infty$
this is a
![]() $p$
-adic disc. We also let
$p$
-adic disc. We also let
 $$\begin{eqnarray}\displaystyle \mathbf{A}_{/F^{\prime }}^{1}(0,r]=\{T:p^{-r/(p-1)}\leqslant |T|<1\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{A}_{/F^{\prime }}^{1}(0,r]=\{T:p^{-r/(p-1)}\leqslant |T|<1\}. & & \displaystyle \nonumber\end{eqnarray}$$
be the half-open annulus. We denote by
![]() ${\mathcal{R}}^{[s,r]}$
the formal substitution of a certain indeterminate
${\mathcal{R}}^{[s,r]}$
the formal substitution of a certain indeterminate
![]() $\unicode[STIX]{x1D70B}_{K}$
, arising from the field of norms, for the variable
$\unicode[STIX]{x1D70B}_{K}$
, arising from the field of norms, for the variable
![]() $T$
in the ring of functions on
$T$
in the ring of functions on
 $\mathbf{A}_{/F^{\prime }}^{1}[s,r]$
. This is the ring denoted by
$\mathbf{A}_{/F^{\prime }}^{1}[s,r]$
. This is the ring denoted by
 ${\mathcal{R}}^{[s,r]}(\unicode[STIX]{x1D70B}_{K})$
in [Reference Kedlaya, Pottharst and XiaoKPX14].
${\mathcal{R}}^{[s,r]}(\unicode[STIX]{x1D70B}_{K})$
in [Reference Kedlaya, Pottharst and XiaoKPX14].
If
![]() $A$
is a
$A$
is a
![]() $\mathbf{Q}_{p}$
-affinoid algebra, then we denote
$\mathbf{Q}_{p}$
-affinoid algebra, then we denote
 ${\mathcal{R}}_{A}^{[s,r]}={\mathcal{R}}^{[s,r]}\widehat{\otimes }_{\mathbf{Q}_{p}}A$
. Let
${\mathcal{R}}_{A}^{[s,r]}={\mathcal{R}}^{[s,r]}\widehat{\otimes }_{\mathbf{Q}_{p}}A$
. Let
 $X=\operatorname{Sp}(A)$
be the associated affinoid space to
$X=\operatorname{Sp}(A)$
be the associated affinoid space to
![]() $A$
. Then
$A$
. Then
![]() ${\mathcal{R}}_{A}^{[s,r]}$
is abstractly isomorphic to the ring of rigid analytic functions on
${\mathcal{R}}_{A}^{[s,r]}$
is abstractly isomorphic to the ring of rigid analytic functions on
 $X^{[s,r]}:=\mathbf{A}^{1}[s,r]_{/F^{\prime }}\times _{\operatorname{Sp}\mathbf{Q}_{p}}\operatorname{Sp}A$
. Thus, it is a noetherian Banach algebra when equipped with the usual Gauss norm.
$X^{[s,r]}:=\mathbf{A}^{1}[s,r]_{/F^{\prime }}\times _{\operatorname{Sp}\mathbf{Q}_{p}}\operatorname{Sp}A$
. Thus, it is a noetherian Banach algebra when equipped with the usual Gauss norm.
If
 $0<s<s^{\prime }\leqslant r\leqslant \infty$
, then there is an injective restriction morphism
$0<s<s^{\prime }\leqslant r\leqslant \infty$
, then there is an injective restriction morphism
 ${\mathcal{R}}_{A}^{[s,r]}\rightarrow {\mathcal{R}}_{A}^{[s^{\prime },r]}$
which is flat and has dense image. We then define
${\mathcal{R}}_{A}^{[s,r]}\rightarrow {\mathcal{R}}_{A}^{[s^{\prime },r]}$
which is flat and has dense image. We then define
 ${\mathcal{R}}_{A}^{r}:=\bigcap _{0<s\leqslant r}{\mathcal{R}}_{A}^{[s,r]}$
and the relative Robba ring over
${\mathcal{R}}_{A}^{r}:=\bigcap _{0<s\leqslant r}{\mathcal{R}}_{A}^{[s,r]}$
and the relative Robba ring over
![]() $A$
is
$A$
is
 $$\begin{eqnarray}\displaystyle {\mathcal{R}}_{A}=\mathop{\bigcup }_{0<r}{\mathcal{R}}_{A}^{r}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}_{A}=\mathop{\bigcup }_{0<r}{\mathcal{R}}_{A}^{r}. & & \displaystyle \nonumber\end{eqnarray}$$
The ring
![]() ${\mathcal{R}}_{A}^{r}$
is the global sections on the rigid space
${\mathcal{R}}_{A}^{r}$
is the global sections on the rigid space
 $X^{r}:=\mathbf{A}_{/F^{\prime }}^{1}(0,r]\times _{\operatorname{Sp}\mathbf{Q}_{p}}X$
, the relative half open annulus. We will also use the notation
$X^{r}:=\mathbf{A}_{/F^{\prime }}^{1}(0,r]\times _{\operatorname{Sp}\mathbf{Q}_{p}}X$
, the relative half open annulus. We will also use the notation
![]() ${\mathcal{R}}_{X}^{r}$
and
${\mathcal{R}}_{X}^{r}$
and
![]() ${\mathcal{R}}_{X}$
with the obvious meaning.
${\mathcal{R}}_{X}$
with the obvious meaning.
Returning to the closed annuli, for any
 $0<s\leqslant r$
there is a continuous action of the group
$0<s\leqslant r$
there is a continuous action of the group
 $\unicode[STIX]{x1D6E4}_{K}{\twoheadrightarrow}\operatorname{Gal}(F^{\prime }/F)$
on the
$\unicode[STIX]{x1D6E4}_{K}{\twoheadrightarrow}\operatorname{Gal}(F^{\prime }/F)$
on the
![]() $F^{\prime }$
coefficients in
$F^{\prime }$
coefficients in
![]() ${\mathcal{R}}^{[s,r]}$
; we can extend this canonically, up to the choice of
${\mathcal{R}}^{[s,r]}$
; we can extend this canonically, up to the choice of
![]() $\unicode[STIX]{x1D70B}_{K}$
, to the ring
$\unicode[STIX]{x1D70B}_{K}$
, to the ring
![]() ${\mathcal{R}}^{[s,r]}$
. When
${\mathcal{R}}^{[s,r]}$
. When
![]() $r$
is sufficiently small there is also an operator
$r$
is sufficiently small there is also an operator
 $\unicode[STIX]{x1D711}:{\mathcal{R}}^{[s,r]}\rightarrow {\mathcal{R}}^{[s/p,r/p]}$
called Frobenius which acts on the coefficients in
$\unicode[STIX]{x1D711}:{\mathcal{R}}^{[s,r]}\rightarrow {\mathcal{R}}^{[s/p,r/p]}$
called Frobenius which acts on the coefficients in
![]() $F^{\prime }$
via the usual Frobenius action and acts on
$F^{\prime }$
via the usual Frobenius action and acts on
![]() $\unicode[STIX]{x1D70B}_{K}$
by a choice,Footnote
4
again, canonically up to
$\unicode[STIX]{x1D70B}_{K}$
by a choice,Footnote
4
again, canonically up to
![]() $\unicode[STIX]{x1D70B}_{K}$
. The operator
$\unicode[STIX]{x1D70B}_{K}$
. The operator
![]() $\unicode[STIX]{x1D711}$
turns
$\unicode[STIX]{x1D711}$
turns
 ${\mathcal{R}}^{[s/p,r/p]}$
into a finite free
${\mathcal{R}}^{[s/p,r/p]}$
into a finite free
![]() ${\mathcal{R}}^{[s,r]}$
-module of rank
${\mathcal{R}}^{[s,r]}$
-module of rank
![]() $p$
. Furthermore,
$p$
. Furthermore,
![]() $\unicode[STIX]{x1D711}$
extends to an operator
$\unicode[STIX]{x1D711}$
extends to an operator
 $\unicode[STIX]{x1D711}:{\mathcal{R}}^{r}\rightarrow {\mathcal{R}}^{r/p}$
and thus also extends to an operator on
$\unicode[STIX]{x1D711}:{\mathcal{R}}^{r}\rightarrow {\mathcal{R}}^{r/p}$
and thus also extends to an operator on
![]() ${\mathcal{R}}$
. When
${\mathcal{R}}$
. When
![]() $X$
is an affinoid space we extend the actions of
$X$
is an affinoid space we extend the actions of
![]() $\unicode[STIX]{x1D6E4}_{K}$
and
$\unicode[STIX]{x1D6E4}_{K}$
and
![]() $\unicode[STIX]{x1D711}$
to the relative Robba rings by acting trivially on the coefficients
$\unicode[STIX]{x1D711}$
to the relative Robba rings by acting trivially on the coefficients
![]() $A$
.
$A$
.
There are two ways to view
![]() ${\mathcal{R}}_{X}^{r/p}$
as a module over
${\mathcal{R}}_{X}^{r/p}$
as a module over
![]() ${\mathcal{R}}_{X}^{r}$
, either by the restriction map or the operator
${\mathcal{R}}_{X}^{r}$
, either by the restriction map or the operator
![]() $\unicode[STIX]{x1D711}$
. If
$\unicode[STIX]{x1D711}$
. If
![]() $Q$
is a module over
$Q$
is a module over
![]() ${\mathcal{R}}_{X}^{r}$
, then we denote by
${\mathcal{R}}_{X}^{r}$
, then we denote by
![]() $\unicode[STIX]{x1D711}^{\ast }Q$
the extension of scalars
$\unicode[STIX]{x1D711}^{\ast }Q$
the extension of scalars
 $\unicode[STIX]{x1D711}^{\ast }Q:=Q\otimes _{{\mathcal{R}}_{X}^{r},\unicode[STIX]{x1D711}}{\mathcal{R}}_{X}^{r/p}$
and
$\unicode[STIX]{x1D711}^{\ast }Q:=Q\otimes _{{\mathcal{R}}_{X}^{r},\unicode[STIX]{x1D711}}{\mathcal{R}}_{X}^{r/p}$
and
 $Q|_{(0,r/p]}$
the
$Q|_{(0,r/p]}$
the
![]() ${\mathcal{R}}_{X}^{r/p}$
-module obtained by using the restriction map.
${\mathcal{R}}_{X}^{r/p}$
-module obtained by using the restriction map.
Definition 2.1. A generalized
![]() $\unicode[STIX]{x1D711}$
-module over
$\unicode[STIX]{x1D711}$
-module over
![]() $X^{r}$
is a finitely presented
$X^{r}$
is a finitely presented
![]() ${\mathcal{R}}_{X}^{r}$
-module
${\mathcal{R}}_{X}^{r}$
-module
![]() $Q$
together with an isomorphism
$Q$
together with an isomorphism
 $\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r/p]}$
of
$\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r/p]}$
of
![]() ${\mathcal{R}}_{X}^{r/p}$
-modules. We say that
${\mathcal{R}}_{X}^{r/p}$
-modules. We say that
![]() $Q$
is a
$Q$
is a
![]() $\unicode[STIX]{x1D711}$
-module if
$\unicode[STIX]{x1D711}$
-module if
![]() $Q$
is also projective.
$Q$
is also projective.
We now fix
![]() $r_{0}>0$
. Since
$r_{0}>0$
. Since
![]() $X$
is affinoid, so is
$X$
is affinoid, so is
![]() $X^{[s,r]}$
. Thus, by Kiehl’s theorem [Reference Bosch, Güntzer and RemmertBGR84, Theorem 9.4.3/3], global sections give an equivalence of categories
$X^{[s,r]}$
. Thus, by Kiehl’s theorem [Reference Bosch, Güntzer and RemmertBGR84, Theorem 9.4.3/3], global sections give an equivalence of categories
 $$\begin{eqnarray}\displaystyle \{\text{finite }{\mathcal{R}}_{X}^{[s,r]}\text{-modules}\}\longleftrightarrow \{\text{coherent sheaves on }X^{[s,r]}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{\text{finite }{\mathcal{R}}_{X}^{[s,r]}\text{-modules}\}\longleftrightarrow \{\text{coherent sheaves on }X^{[s,r]}\}. & & \displaystyle \nonumber\end{eqnarray}$$
Since
![]() $X^{r_{0}}$
is admissibly covered by affinoid opens
$X^{r_{0}}$
is admissibly covered by affinoid opens
 $\{X^{[s,r]}\}_{0<s\leqslant r\leqslant r_{0}}$
, a coherent sheaf
$\{X^{[s,r]}\}_{0<s\leqslant r\leqslant r_{0}}$
, a coherent sheaf
![]() ${\mathcal{Q}}$
on
${\mathcal{Q}}$
on
![]() $X^{r_{0}}$
is the same as a system
$X^{r_{0}}$
is the same as a system
 ${\mathcal{Q}}=(Q^{[s,r]})_{0<s\leqslant r\leqslant r_{0}}$
of finite
${\mathcal{Q}}=(Q^{[s,r]})_{0<s\leqslant r\leqslant r_{0}}$
of finite
![]() ${\mathcal{R}}_{X}^{[s,r]}$
-modules satisfying the obvious compatibilities. The global sections of a sheaf
${\mathcal{R}}_{X}^{[s,r]}$
-modules satisfying the obvious compatibilities. The global sections of a sheaf
![]() ${\mathcal{Q}}$
may be calculated by
${\mathcal{Q}}$
may be calculated by
 $$\begin{eqnarray}\displaystyle Q=\unicode[STIX]{x1D6E4}(X^{r_{0}},{\mathcal{Q}})=\mathop{\varprojlim }\nolimits_{0<s}Q^{[s,r_{0}]}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q=\unicode[STIX]{x1D6E4}(X^{r_{0}},{\mathcal{Q}})=\mathop{\varprojlim }\nolimits_{0<s}Q^{[s,r_{0}]}. & & \displaystyle \nonumber\end{eqnarray}$$
If
![]() $Q$
is a finitely presented module over
$Q$
is a finitely presented module over
![]() $X^{r_{0}}$
, then there is a coherent sheaf defined by the compatible family
$X^{r_{0}}$
, then there is a coherent sheaf defined by the compatible family
 $Q^{[s,r]}:=Q\otimes _{{\mathcal{R}}_{X}^{r_{0}}}{\mathcal{R}}_{X}^{[s,r]}$
. We pause to include an auxiliary result on finitely presented modules over
$Q^{[s,r]}:=Q\otimes _{{\mathcal{R}}_{X}^{r_{0}}}{\mathcal{R}}_{X}^{[s,r]}$
. We pause to include an auxiliary result on finitely presented modules over
![]() $X^{r}$
. It applies, in particular, to all generalized
$X^{r}$
. It applies, in particular, to all generalized
![]() $\unicode[STIX]{x1D711}$
-modules.
$\unicode[STIX]{x1D711}$
-modules.
Lemma 2.2. Suppose that
![]() $Q$
is a finitely presented
$Q$
is a finitely presented
![]() ${\mathcal{R}}_{X}^{r}$
-module and
${\mathcal{R}}_{X}^{r}$
-module and
![]() $f\in {\mathcal{R}}^{r}$
. Then
$f\in {\mathcal{R}}^{r}$
. Then
![]() $Q/f$
is finite projective over
$Q/f$
is finite projective over
![]() ${\mathcal{R}}_{X}^{r}/f$
if and only if
${\mathcal{R}}_{X}^{r}/f$
if and only if
 $Q^{[s,r]}/f$
is finite projective over
$Q^{[s,r]}/f$
is finite projective over
 ${\mathcal{R}}^{[s,r]}/f$
for each
${\mathcal{R}}^{[s,r]}/f$
for each
 $0<s\leqslant r$
.
$0<s\leqslant r$
.
Proof. Since
![]() $Q$
is assumed to be finitely presented over
$Q$
is assumed to be finitely presented over
![]() ${\mathcal{R}}_{X}^{r}$
, the same is true for
${\mathcal{R}}_{X}^{r}$
, the same is true for
![]() $Q/f$
over
$Q/f$
over
![]() ${\mathcal{R}}_{X}^{r}/f$
and thus by [Reference MatsumuraMat89, Corollary 7.12] it suffices to replace ‘projective’ with ‘flat’ in the statement of the lemma.
${\mathcal{R}}_{X}^{r}/f$
and thus by [Reference MatsumuraMat89, Corollary 7.12] it suffices to replace ‘projective’ with ‘flat’ in the statement of the lemma.
Even without that, one direction is clear: if
![]() $Q/f$
is finite projective over
$Q/f$
is finite projective over
![]() ${\mathcal{R}}_{X}^{r}/f$
, then
${\mathcal{R}}_{X}^{r}/f$
, then
 $Q^{[s,r]}/f=Q/f\otimes _{{\mathcal{R}}_{X}^{r}/f}{\mathcal{R}}^{[s,r]}/f$
is finite projective over
$Q^{[s,r]}/f=Q/f\otimes _{{\mathcal{R}}_{X}^{r}/f}{\mathcal{R}}^{[s,r]}/f$
is finite projective over
 ${\mathcal{R}}^{[s,r]}/f$
for each
${\mathcal{R}}^{[s,r]}/f$
for each
 $0<s\leqslant r$
.
$0<s\leqslant r$
.
We will now prove the reverse direction, so assume that
 $Q^{[s,r]}/f$
is flat over
$Q^{[s,r]}/f$
is flat over
 ${\mathcal{R}}_{X}^{[s,r]}/f$
for each
${\mathcal{R}}_{X}^{[s,r]}/f$
for each
 $0<s\leqslant r$
. By [Reference MatsumuraMat89, Theorem 7.7] it suffices to show that
$0<s\leqslant r$
. By [Reference MatsumuraMat89, Theorem 7.7] it suffices to show that
 $$\begin{eqnarray}I\otimes _{{\mathcal{R}}_{X}^{r}/f}Q/f\rightarrow Q/f\end{eqnarray}$$
$$\begin{eqnarray}I\otimes _{{\mathcal{R}}_{X}^{r}/f}Q/f\rightarrow Q/f\end{eqnarray}$$
is injective for every finitely generated ideal
 $I\subset {\mathcal{R}}_{X}^{r}/f$
. Now we use the language of ‘co-admissible’ modules originally due to Schneider and Teitelbaum [Reference Schneider and TeitelbaumST03], and we will reference [Reference Kedlaya, Pottharst and XiaoKPX14, § 2.1]. By [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.4(7)] the
$I\subset {\mathcal{R}}_{X}^{r}/f$
. Now we use the language of ‘co-admissible’ modules originally due to Schneider and Teitelbaum [Reference Schneider and TeitelbaumST03], and we will reference [Reference Kedlaya, Pottharst and XiaoKPX14, § 2.1]. By [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.4(7)] the
![]() ${\mathcal{R}}_{X}^{r}$
-module
${\mathcal{R}}_{X}^{r}$
-module
![]() ${\mathcal{R}}_{X}^{r}/f$
is co-admissible, and thus so is
${\mathcal{R}}_{X}^{r}/f$
is co-admissible, and thus so is
 $I\subset {\mathcal{R}}_{X}^{r}/f$
by [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.4(6)]. Since
$I\subset {\mathcal{R}}_{X}^{r}/f$
by [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.4(6)]. Since
![]() $Q$
is co-admissible so is
$Q$
is co-admissible so is
 $Q/f=\operatorname{coker}(Q\overset{f}{\longrightarrow }Q)$
by [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.4(5)]. Thus, (1) is a morphism of co-admissible
$Q/f=\operatorname{coker}(Q\overset{f}{\longrightarrow }Q)$
by [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.4(5)]. Thus, (1) is a morphism of co-admissible
![]() ${\mathcal{R}}_{X}^{r}$
-modules and hence is injective if and only if
${\mathcal{R}}_{X}^{r}$
-modules and hence is injective if and only if
 $$\begin{eqnarray}(I\otimes _{{\mathcal{R}}_{X}^{r}/f}Q/f)^{[s,r]}\rightarrow Q^{[s,r]}/f\end{eqnarray}$$
$$\begin{eqnarray}(I\otimes _{{\mathcal{R}}_{X}^{r}/f}Q/f)^{[s,r]}\rightarrow Q^{[s,r]}/f\end{eqnarray}$$
is injective for each
 $0<s\leqslant r$
. But we see
$0<s\leqslant r$
. But we see
 $$\begin{eqnarray}\displaystyle (I\otimes _{{\mathcal{R}}_{X}^{r}/f}Q/f)^{[s,r]}\simeq (I\otimes _{{\mathcal{R}}_{X}^{r}/f}{\mathcal{R}}_{X}^{[s,r]}/f)\otimes _{{\mathcal{R}}_{X}^{[s,r]}/f}Q^{[s,r]}/f & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (I\otimes _{{\mathcal{R}}_{X}^{r}/f}Q/f)^{[s,r]}\simeq (I\otimes _{{\mathcal{R}}_{X}^{r}/f}{\mathcal{R}}_{X}^{[s,r]}/f)\otimes _{{\mathcal{R}}_{X}^{[s,r]}/f}Q^{[s,r]}/f & & \displaystyle \nonumber\end{eqnarray}$$
and then since
 ${\mathcal{R}}_{X}^{r}/f\rightarrow {\mathcal{R}}_{X}^{[s,r]}/f$
is flat we see that
${\mathcal{R}}_{X}^{r}/f\rightarrow {\mathcal{R}}_{X}^{[s,r]}/f$
is flat we see that
 $I\otimes _{{\mathcal{R}}_{X}^{r}/f}{\mathcal{R}}_{X}^{[s,r]}/f=I\cdot {\mathcal{R}}_{X}^{[s,r]}/f$
is an ideal in
$I\otimes _{{\mathcal{R}}_{X}^{r}/f}{\mathcal{R}}_{X}^{[s,r]}/f=I\cdot {\mathcal{R}}_{X}^{[s,r]}/f$
is an ideal in
 ${\mathcal{R}}_{X}^{[s,r]}/f$
. In particular, this shows that the map (2) may be identified with the natural map
${\mathcal{R}}_{X}^{[s,r]}/f$
. In particular, this shows that the map (2) may be identified with the natural map
 $$\begin{eqnarray}\displaystyle I\cdot {\mathcal{R}}_{X}^{[s,r]}/f\otimes _{{\mathcal{R}}_{X}^{[s,r]}/f}Q^{[s,r]}/f\rightarrow Q^{[s,r]}/f, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I\cdot {\mathcal{R}}_{X}^{[s,r]}/f\otimes _{{\mathcal{R}}_{X}^{[s,r]}/f}Q^{[s,r]}/f\rightarrow Q^{[s,r]}/f, & & \displaystyle \nonumber\end{eqnarray}$$
which is injective because
 $Q^{[s,r]}/f$
is flat over
$Q^{[s,r]}/f$
is flat over
 ${\mathcal{R}}_{X}^{[s,r]}/f$
by assumption. This completes the proof.◻
${\mathcal{R}}_{X}^{[s,r]}/f$
by assumption. This completes the proof.◻
Returning to
![]() $\unicode[STIX]{x1D711}$
-modules, if
$\unicode[STIX]{x1D711}$
-modules, if
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $\unicode[STIX]{x1D711}$
-module, then the isomorphism
$\unicode[STIX]{x1D711}$
-module, then the isomorphism
 $\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r_{0}/p]}$
translates into the choice of a compatible system of isomorphisms
$\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r_{0}/p]}$
translates into the choice of a compatible system of isomorphisms
 $\unicode[STIX]{x1D711}^{\ast }Q^{[s,r]}\simeq Q^{[s/p,r/p]}$
. In fact, all generalized
$\unicode[STIX]{x1D711}^{\ast }Q^{[s,r]}\simeq Q^{[s/p,r/p]}$
. In fact, all generalized
![]() $\unicode[STIX]{x1D711}$
-modules arise this way.
$\unicode[STIX]{x1D711}$
-modules arise this way.
Proposition 2.3. There is an equivalence of categories
 $$\begin{eqnarray}\displaystyle \biggl\{\begin{array}{@{}c@{}}\text{generalized }\unicode[STIX]{x1D711}\text{-modules}\\ \text{over }X^{r_{0}}\end{array}\biggr\}\longleftrightarrow \left\{\begin{array}{@{}c@{}}\text{coherent sheaves }{\mathcal{Q}}=(Q^{[s,r]})\text{ on }X^{r_{0}}\text{ equipped}\\ \text{with naturally compatible isomorphisms}\\ \unicode[STIX]{x1D711}^{\ast }Q^{[s,r]}\cong Q^{[s/p,r/p]}\end{array}\right\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl\{\begin{array}{@{}c@{}}\text{generalized }\unicode[STIX]{x1D711}\text{-modules}\\ \text{over }X^{r_{0}}\end{array}\biggr\}\longleftrightarrow \left\{\begin{array}{@{}c@{}}\text{coherent sheaves }{\mathcal{Q}}=(Q^{[s,r]})\text{ on }X^{r_{0}}\text{ equipped}\\ \text{with naturally compatible isomorphisms}\\ \unicode[STIX]{x1D711}^{\ast }Q^{[s,r]}\cong Q^{[s/p,r/p]}\end{array}\right\}. & & \displaystyle \nonumber\end{eqnarray}$$
Moreover, the
![]() $\unicode[STIX]{x1D711}$
-modules on the left-hand side correspond to sheaves on the right-hand side for which each
$\unicode[STIX]{x1D711}$
-modules on the left-hand side correspond to sheaves on the right-hand side for which each
![]() $Q^{[s,r]}$
is projective.
$Q^{[s,r]}$
is projective.
Proof. We have just explained how to go from the left-hand side to the right-hand side. Suppose we start on the right-hand side with a coherent sheaf
 ${\mathcal{Q}}=(Q^{[s,r]})$
. It is clear that all we need to do is show that its global sections are finitely presented. Choose a finite presentation for
${\mathcal{Q}}=(Q^{[s,r]})$
. It is clear that all we need to do is show that its global sections are finitely presented. Choose a finite presentation for
 $Q^{[r_{0}/p,r_{0}]}$
. By assumption this uniformly (in terms of generators and relations) gives a finite presentation for
$Q^{[r_{0}/p,r_{0}]}$
. By assumption this uniformly (in terms of generators and relations) gives a finite presentation for
 $(\unicode[STIX]{x1D711}^{\ast })^{n}Q^{[r_{0}/p,r_{0}]}\simeq Q^{[r_{0}/p^{n+1},r_{0}/p^{n}]}$
. Thus
$(\unicode[STIX]{x1D711}^{\ast })^{n}Q^{[r_{0}/p,r_{0}]}\simeq Q^{[r_{0}/p^{n+1},r_{0}/p^{n}]}$
. Thus
![]() ${\mathcal{Q}}$
is uniformly finitely presented in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, § 2.1]. By [Reference Kedlaya, Pottharst and XiaoKPX14, Proposition 2.1.13], the global sections of
${\mathcal{Q}}$
is uniformly finitely presented in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, § 2.1]. By [Reference Kedlaya, Pottharst and XiaoKPX14, Proposition 2.1.13], the global sections of
![]() ${\mathcal{Q}}$
are finitely presented.◻
${\mathcal{Q}}$
are finitely presented.◻
Remark.
The global sections of a coherent sheaf on
![]() $X^{r_{0}}$
need not have any finiteness properties (see the example in [Reference BellovinBel15, § 2.1.2, p. 380]). The key for the previous proposition is that the presence of the
$X^{r_{0}}$
need not have any finiteness properties (see the example in [Reference BellovinBel15, § 2.1.2, p. 380]). The key for the previous proposition is that the presence of the
![]() $\unicode[STIX]{x1D711}$
-operator imposes a uniformly finitely presented condition over the closed annuli.
$\unicode[STIX]{x1D711}$
-operator imposes a uniformly finitely presented condition over the closed annuli.
Corollary 2.4. The category of generalized
![]() $\unicode[STIX]{x1D711}$
-modules over
$\unicode[STIX]{x1D711}$
-modules over
![]() $X^{r_{0}}$
is abelian.
$X^{r_{0}}$
is abelian.
Proof. The category of coherent sheaves on
![]() $X^{r_{0}}$
is abelian by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 9.4.3/2]. Thus we just need to show that if
$X^{r_{0}}$
is abelian by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 9.4.3/2]. Thus we just need to show that if
 $f:{\mathcal{Q}}\rightarrow {\mathcal{P}}$
is a morphism of the corresponding sheaves, then
$f:{\mathcal{Q}}\rightarrow {\mathcal{P}}$
is a morphism of the corresponding sheaves, then
![]() $\ker (f)$
and
$\ker (f)$
and
 $\operatorname{coker}(f)$
satisfy the obvious compatibilities. But
$\operatorname{coker}(f)$
satisfy the obvious compatibilities. But
![]() $\unicode[STIX]{x1D711}^{\ast }$
is exact because
$\unicode[STIX]{x1D711}^{\ast }$
is exact because
![]() $\unicode[STIX]{x1D711}$
presents
$\unicode[STIX]{x1D711}$
presents
 ${\mathcal{R}}_{X}^{[s/p,r/p]}$
as free over
${\mathcal{R}}_{X}^{[s/p,r/p]}$
as free over
![]() ${\mathcal{R}}_{X}^{[s,r]}$
, so this is immediate.◻
${\mathcal{R}}_{X}^{[s,r]}$
, so this is immediate.◻
There is another way one might think about the
![]() $\unicode[STIX]{x1D711}$
-pullback condition on generalized
$\unicode[STIX]{x1D711}$
-pullback condition on generalized
![]() $\unicode[STIX]{x1D711}$
-modules. If
$\unicode[STIX]{x1D711}$
-modules. If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $\unicode[STIX]{x1D711}$
-module over
$\unicode[STIX]{x1D711}$
-module over
![]() $X^{r_{0}}$
then the choice of isomorphism
$X^{r_{0}}$
then the choice of isomorphism
 $\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r_{0}/p]}$
defines an operator, by
$\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r_{0}/p]}$
defines an operator, by
 $Q{\hookrightarrow}\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r_{0}/p]}$
which we also denote by
$Q{\hookrightarrow}\unicode[STIX]{x1D711}^{\ast }Q\simeq Q|_{(0,r_{0}/p]}$
which we also denote by
![]() $\unicode[STIX]{x1D711}$
. If
$\unicode[STIX]{x1D711}$
. If
 $f\in {\mathcal{R}}_{X}^{r_{0}}$
and
$f\in {\mathcal{R}}_{X}^{r_{0}}$
and
![]() $x\in Q$
, then
$x\in Q$
, then
 $\unicode[STIX]{x1D711}(fx)=\unicode[STIX]{x1D711}(f)\unicode[STIX]{x1D711}(x)$
and so this version of
$\unicode[STIX]{x1D711}(fx)=\unicode[STIX]{x1D711}(f)\unicode[STIX]{x1D711}(x)$
and so this version of
![]() $\unicode[STIX]{x1D711}$
is naturally a semilinear operator (albeit with a different source than target).
$\unicode[STIX]{x1D711}$
is naturally a semilinear operator (albeit with a different source than target).
Definition 2.5. A generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q$
over
$Q$
over
![]() $X^{r_{0}}$
is a generalized
$X^{r_{0}}$
is a generalized
![]() $\unicode[STIX]{x1D711}$
-module over
$\unicode[STIX]{x1D711}$
-module over
![]() $X^{r_{0}}$
equipped with a continuous
$X^{r_{0}}$
equipped with a continuous
![]() ${\mathcal{R}}_{X}^{r_{0}}$
-semilinear action of
${\mathcal{R}}_{X}^{r_{0}}$
-semilinear action of
![]() $\unicode[STIX]{x1D6E4}_{K}$
which commutes with
$\unicode[STIX]{x1D6E4}_{K}$
which commutes with
![]() $\unicode[STIX]{x1D711}$
. If we drop the word generalized, we insist that
$\unicode[STIX]{x1D711}$
. If we drop the word generalized, we insist that
![]() $Q$
be a
$Q$
be a
![]() $\unicode[STIX]{x1D711}$
-module.
$\unicode[STIX]{x1D711}$
-module.
Note that we insist that
![]() $\unicode[STIX]{x1D6E4}_{K}$
preserve the radius
$\unicode[STIX]{x1D6E4}_{K}$
preserve the radius
![]() $r_{0}$
of the generalized
$r_{0}$
of the generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. We are now ready to remove the finite radius assumption.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. We are now ready to remove the finite radius assumption.
Definition 2.6. A generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q$
over
$Q$
over
![]() $X$
is the base change of a generalized
$X$
is the base change of a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
 $Q=Q^{r_{0}}\otimes _{{\mathcal{R}}_{X}^{r_{0}}}{\mathcal{R}}_{X}$
over
$Q=Q^{r_{0}}\otimes _{{\mathcal{R}}_{X}^{r_{0}}}{\mathcal{R}}_{X}$
over
![]() $X^{r_{0}}$
for some
$X^{r_{0}}$
for some
![]() $r_{0}>0$
. If we drop the word generalized, we insist that
$r_{0}>0$
. If we drop the word generalized, we insist that
![]() $Q$
be a
$Q$
be a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module.
If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module, then there exists an
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module, then there exists an
![]() $r_{0}>0$
such that
$r_{0}>0$
such that
![]() $Q$
arises via base change from a generalized
$Q$
arises via base change from a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q^{r_{0}}$
over
$Q^{r_{0}}$
over
![]() $X^{r_{0}}$
. Thus, for any
$X^{r_{0}}$
. Thus, for any
![]() $r_{0}>r_{0}^{\prime }$
,
$r_{0}>r_{0}^{\prime }$
,
![]() $Q$
also arises geometrically from
$Q$
also arises geometrically from
 $Q^{r_{0}^{\prime }}:=Q|_{(0,r_{0}^{\prime }]}$
. In particular, if
$Q^{r_{0}^{\prime }}:=Q|_{(0,r_{0}^{\prime }]}$
. In particular, if
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then we may always take a radius sufficiently small to make sense of the notation
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then we may always take a radius sufficiently small to make sense of the notation
![]() $Q^{r_{0}}$
.
$Q^{r_{0}}$
.
By a morphism
 $f:Q\rightarrow Q^{\prime }$
of generalized
$f:Q\rightarrow Q^{\prime }$
of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules we mean a continuous
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules we mean a continuous
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant morphism of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant morphism of
![]() ${\mathcal{R}}_{X}$
-modules. By definition, there must exist an
${\mathcal{R}}_{X}$
-modules. By definition, there must exist an
![]() $r_{0}>0$
so that
$r_{0}>0$
so that
![]() $f$
arises from base change of a map
$f$
arises from base change of a map
 $f^{r_{0}}:Q^{r_{0}}\rightarrow (Q^{\prime })^{r_{0}}$
for
$f^{r_{0}}:Q^{r_{0}}\rightarrow (Q^{\prime })^{r_{0}}$
for
![]() $r_{0}$
sufficiently small. The space of all morphisms will be denoted by
$r_{0}$
sufficiently small. The space of all morphisms will be denoted by
 $\operatorname{Hom}(Q,Q^{\prime })$
. This is also a generalized
$\operatorname{Hom}(Q,Q^{\prime })$
. This is also a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module in the natural way. Taking
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module in the natural way. Taking
 $Q^{\prime }={\mathcal{R}}_{X}$
we obtain the dual module
$Q^{\prime }={\mathcal{R}}_{X}$
we obtain the dual module
![]() $Q^{\vee }$
, which we will only use if
$Q^{\vee }$
, which we will only use if
![]() $Q$
is a
$Q$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module.
At various points in §§ 5 and 6 we will need to shrink an affinoid space
![]() $X$
to an affinoid subdomain
$X$
to an affinoid subdomain
 $U=\operatorname{Sp}B\subset X$
. Given such a
$U=\operatorname{Sp}B\subset X$
. Given such a
![]() $U$
and a generalized
$U$
and a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q$
over
$Q$
over
![]() $X$
we denote by
$X$
we denote by
![]() $Q|_{U}$
the
$Q|_{U}$
the
![]() ${\mathcal{R}}_{U}$
-module defined by
${\mathcal{R}}_{U}$
-module defined by
 $$\begin{eqnarray}\displaystyle Q|_{U}:=Q\widehat{\otimes }_{{\mathcal{R}}_{X}}{\mathcal{R}}_{U}=Q\widehat{\otimes }_{A}B. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q|_{U}:=Q\widehat{\otimes }_{{\mathcal{R}}_{X}}{\mathcal{R}}_{U}=Q\widehat{\otimes }_{A}B. & & \displaystyle \nonumber\end{eqnarray}$$
Note since
![]() $Q$
is finitely presented over
$Q$
is finitely presented over
![]() ${\mathcal{R}}_{A}$
, the first part of the definition could equivalently be taken to be
${\mathcal{R}}_{A}$
, the first part of the definition could equivalently be taken to be
 $Q|_{U}=Q\otimes _{{\mathcal{R}}_{X}}{\mathcal{R}}_{U}$
. We record the following result for later use.
$Q|_{U}=Q\otimes _{{\mathcal{R}}_{X}}{\mathcal{R}}_{U}$
. We record the following result for later use.
Proposition 2.7. If
![]() $U\subset X$
is an affinoid subdomain, then the association
$U\subset X$
is an affinoid subdomain, then the association
 $Q\mapsto Q|_{U}$
defines an exact functor from the category of generalized
$Q\mapsto Q|_{U}$
defines an exact functor from the category of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X$
to the category of generalized
$X$
to the category of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $U$
.
$U$
.
Proof. The proposition reduces to the same result for generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X^{r_{0}}$
for each
$X^{r_{0}}$
for each
![]() $r_{0}>0$
(and the corresponding open affinoid subdomain
$r_{0}>0$
(and the corresponding open affinoid subdomain
 $U^{r_{0}}\subset X^{r_{0}}$
). Once that reduction has been made, we deduce our result from Proposition 2.3. The main point is that the exactness follows from the corresponding result for coherent sheaves on rigid spaces (see [Reference Bosch, Güntzer and RemmertBGR84, Proposition 9.4.1/1] for example).◻
$U^{r_{0}}\subset X^{r_{0}}$
). Once that reduction has been made, we deduce our result from Proposition 2.3. The main point is that the exactness follows from the corresponding result for coherent sheaves on rigid spaces (see [Reference Bosch, Güntzer and RemmertBGR84, Proposition 9.4.1/1] for example).◻
2.2 Galois representations
It will be useful to remind ourselves of the following connection between Galois representations and
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. If
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. If
![]() $A$
is an affinoid
$A$
is an affinoid
![]() $\mathbf{Q}_{p}$
-algebra, then by an
$\mathbf{Q}_{p}$
-algebra, then by an
![]() $A$
-linear representation of
$A$
-linear representation of
![]() $G_{K}$
we mean a finite projective
$G_{K}$
we mean a finite projective
![]() $A$
-module
$A$
-module
![]() $V$
together with a continuous
$V$
together with a continuous
![]() $A$
-linear action of the Galois group
$A$
-linear action of the Galois group
![]() $G_{K}$
.
$G_{K}$
.
Theorem 2.8. Let
 $X=\operatorname{Sp}(A)$
. There is a fully faithful, exact embedding
$X=\operatorname{Sp}(A)$
. There is a fully faithful, exact embedding
 $$\begin{eqnarray}\displaystyle D_{\operatorname{rig}}:\{A\text{-linear representations }V\text{ of }G_{K}\}{\hookrightarrow}\{(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})\text{-modules over }{\mathcal{R}}_{X}\} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{\operatorname{rig}}:\{A\text{-linear representations }V\text{ of }G_{K}\}{\hookrightarrow}\{(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})\text{-modules over }{\mathcal{R}}_{X}\} & & \displaystyle \nonumber\end{eqnarray}$$
such that:
-
(a)
 $D_{\operatorname{rig}}$
commutes with base change
$D_{\operatorname{rig}}$
commutes with base change
 $A\rightarrow A^{\prime }$
; and
$A\rightarrow A^{\prime }$
; and -
(b) when
 $A$
is finite over
$A$
is finite over
 $\mathbf{Q}_{p}$
,
$\mathbf{Q}_{p}$
,
 $D_{\operatorname{rig}}$
is essentially surjective onto the category of étale
$D_{\operatorname{rig}}$
is essentially surjective onto the category of étale
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules.
The theorem as we have stated it can be read off from [Reference Kedlaya and LiuKL10, Theorems 3.11 and 0.2]. The earliest results were proven when
![]() $A$
is a field. For that, Fontaine and separately, Cherbonnier and Colmez, gave proofs with the caveat that the Robba ring is replaced with a different ring of analytic functions on affinoid subdomains of discs (see [Reference FontaineFon90] and [Reference Cherbonnier and ColmezCC98]). The key step in extending the theorem to the Robba ring as we have discussed it was Kedlaya’s theorem on slope filtrations [Reference KedlayaKed04]. The family results are more recent and one does not in general have a description of the essential image.
$A$
is a field. For that, Fontaine and separately, Cherbonnier and Colmez, gave proofs with the caveat that the Robba ring is replaced with a different ring of analytic functions on affinoid subdomains of discs (see [Reference FontaineFon90] and [Reference Cherbonnier and ColmezCC98]). The key step in extending the theorem to the Robba ring as we have discussed it was Kedlaya’s theorem on slope filtrations [Reference KedlayaKed04]. The family results are more recent and one does not in general have a description of the essential image.
2.3 Rank-one
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
Rank-one
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $A$
are parametrized, essentially, by continuous characters
$A$
are parametrized, essentially, by continuous characters
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow A^{\times }$
. Let us recall the construction of
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow A^{\times }$
. Let us recall the construction of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules of character type. Note that by [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.2.14] every rank-one
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules of character type. Note that by [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.2.14] every rank-one
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
arises, locally on
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
arises, locally on
![]() $A$
, from one of character type.
$A$
, from one of character type.
Choose a uniformizer
![]() $\unicode[STIX]{x1D71B}_{K}$
of
$\unicode[STIX]{x1D71B}_{K}$
of
![]() $K$
. We can write
$K$
. We can write
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\operatorname{nr}}\unicode[STIX]{x1D6FF}^{\operatorname{wt}}$
where
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\operatorname{nr}}\unicode[STIX]{x1D6FF}^{\operatorname{wt}}$
where
 $\unicode[STIX]{x1D6FF}^{\operatorname{nr}}|_{{\mathcal{O}}_{K}^{\times }}=1$
and
$\unicode[STIX]{x1D6FF}^{\operatorname{nr}}|_{{\mathcal{O}}_{K}^{\times }}=1$
and
 $\unicode[STIX]{x1D6FF}^{\operatorname{wt}}(\unicode[STIX]{x1D71B}_{K})=1$
. Then,
$\unicode[STIX]{x1D6FF}^{\operatorname{wt}}(\unicode[STIX]{x1D71B}_{K})=1$
. Then,
![]() $\unicode[STIX]{x1D6FF}^{\operatorname{wt}}$
extends in a unique manner to the abelianization of the Galois group
$\unicode[STIX]{x1D6FF}^{\operatorname{wt}}$
extends in a unique manner to the abelianization of the Galois group
![]() $G_{K}^{\operatorname{ab}}$
, using the local Artin map, and we denote
$G_{K}^{\operatorname{ab}}$
, using the local Artin map, and we denote
![]() $\widehat{\unicode[STIX]{x1D6FF}}^{\operatorname{wt}}$
the corresponding Galois character
$\widehat{\unicode[STIX]{x1D6FF}}^{\operatorname{wt}}$
the corresponding Galois character
 $\widehat{\unicode[STIX]{x1D6FF}}^{\operatorname{wt}}:G_{K}\rightarrow A^{\times }$
. On the other hand, by [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 6.2.3] there is a unique rank-one free
$\widehat{\unicode[STIX]{x1D6FF}}^{\operatorname{wt}}:G_{K}\rightarrow A^{\times }$
. On the other hand, by [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 6.2.3] there is a unique rank-one free
 $(F\otimes _{\mathbf{Q}_{p}}A)$
-module
$(F\otimes _{\mathbf{Q}_{p}}A)$
-module
 $D_{\unicode[STIX]{x1D6FF}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})}$
equipped with an operator
$D_{\unicode[STIX]{x1D6FF}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})}$
equipped with an operator
![]() $\unicode[STIX]{x1D711}$
, semilinear with respect to
$\unicode[STIX]{x1D711}$
, semilinear with respect to
![]() $\unicode[STIX]{x1D711}\otimes 1$
, such that
$\unicode[STIX]{x1D711}\otimes 1$
, such that
 $\unicode[STIX]{x1D711}^{f_{K}}=1\otimes \unicode[STIX]{x1D6FF}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})$
. We give it the trivial
$\unicode[STIX]{x1D711}^{f_{K}}=1\otimes \unicode[STIX]{x1D6FF}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})$
. We give it the trivial
![]() $\unicode[STIX]{x1D6E4}_{K}$
-action and define the rank-one
$\unicode[STIX]{x1D6E4}_{K}$
-action and define the rank-one
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
 $$\begin{eqnarray}\displaystyle {\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}):=(D_{\unicode[STIX]{x1D6FF}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})}\otimes _{F\otimes _{\mathbf{Q}_{p}}A}{\mathcal{R}}_{A})\otimes _{{\mathcal{R}}_{A}}D_{\operatorname{rig}}(\widehat{\unicode[STIX]{x1D6FF}}^{\operatorname{wt}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}):=(D_{\unicode[STIX]{x1D6FF}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})}\otimes _{F\otimes _{\mathbf{Q}_{p}}A}{\mathcal{R}}_{A})\otimes _{{\mathcal{R}}_{A}}D_{\operatorname{rig}}(\widehat{\unicode[STIX]{x1D6FF}}^{\operatorname{wt}}). & & \displaystyle \nonumber\end{eqnarray}$$
This is independent of any choices made and satisfies
 ${\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FF}^{\prime })\simeq {\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF})\otimes _{{\mathcal{R}}_{A}}{\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}^{\prime })$
. Thus, it makes sense to define
${\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FF}^{\prime })\simeq {\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF})\otimes _{{\mathcal{R}}_{A}}{\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}^{\prime })$
. Thus, it makes sense to define
 $D(\unicode[STIX]{x1D6FF}):=D\otimes _{{\mathcal{R}}_{A}}{\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF})$
for any generalized
$D(\unicode[STIX]{x1D6FF}):=D\otimes _{{\mathcal{R}}_{A}}{\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF})$
for any generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
.
$A$
.
Assume now that
![]() $A$
is an
$A$
is an
![]() $L$
-algebra for
$L$
-algebra for
![]() $L$
as in § 1.6. If
$L$
as in § 1.6. If
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow A^{\times }$
is a character, then we can define its weights as follows. The group
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow A^{\times }$
is a character, then we can define its weights as follows. The group
![]() $K^{\times }$
, as a group over
$K^{\times }$
, as a group over
![]() $\mathbf{Q}_{p}$
, has a Lie algebra of dimension
$\mathbf{Q}_{p}$
, has a Lie algebra of dimension
 $(K:\mathbf{Q}_{p})=\#\unicode[STIX]{x1D6F4}_{K}$
. The differential action gives rise to a weights
$(K:\mathbf{Q}_{p})=\#\unicode[STIX]{x1D6F4}_{K}$
. The differential action gives rise to a weights
 $(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}))_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\in K\otimes _{\mathbf{Q}_{p}}A\simeq \prod _{\unicode[STIX]{x1D70F}}A_{\unicode[STIX]{x1D70F}}$
such that
$(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}))_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\in K\otimes _{\mathbf{Q}_{p}}A\simeq \prod _{\unicode[STIX]{x1D70F}}A_{\unicode[STIX]{x1D70F}}$
such that
 $$\begin{eqnarray}\displaystyle 0=\lim _{\substack{ a\rightarrow 0 \\ a\in {\mathcal{O}}_{K}}}\frac{|\unicode[STIX]{x1D6FF}(1+a)-1+\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D70F}(a)|}{|a|_{K}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=\lim _{\substack{ a\rightarrow 0 \\ a\in {\mathcal{O}}_{K}}}\frac{|\unicode[STIX]{x1D6FF}(1+a)-1+\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D70F}(a)|}{|a|_{K}}. & & \displaystyle \nonumber\end{eqnarray}$$
It is easy to see that
 $(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}))_{\unicode[STIX]{x1D70F}}$
only depends only
$(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}))_{\unicode[STIX]{x1D70F}}$
only depends only
![]() $\unicode[STIX]{x1D6FF}^{\operatorname{wt}}$
in the decomposition of the previous paragraph (thus the notation). We have normalized the weights so that if
$\unicode[STIX]{x1D6FF}^{\operatorname{wt}}$
in the decomposition of the previous paragraph (thus the notation). We have normalized the weights so that if
 $z:K^{\times }\rightarrow K^{\times }$
is the identity character, then
$z:K^{\times }\rightarrow K^{\times }$
is the identity character, then
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(z)=-1$
for each
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(z)=-1$
for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
.
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
.
2.4
 $p$
-adic Hodge theory
$p$
-adic Hodge theory
The definition of weight given above is a special case of extending the usual Fontaine functors
 $D_{\operatorname{Sen}},D_{\operatorname{dR}},D_{\operatorname{cris}}$
, etc. from
$D_{\operatorname{Sen}},D_{\operatorname{dR}},D_{\operatorname{cris}}$
, etc. from
![]() $p$
-adic Hodge theory to the category of
$p$
-adic Hodge theory to the category of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
modules. In particular, we have the notions of Hodge–Tate–Sen weights, crystalline
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
modules. In particular, we have the notions of Hodge–Tate–Sen weights, crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, etc. We will not recall the definitions and will refer to [Reference BergerBer02, Reference BergerBer08] as needed.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, etc. We will not recall the definitions and will refer to [Reference BergerBer02, Reference BergerBer08] as needed.
One of Berger’s main results [Reference BergerBer08, Théorème A] is that the functor
 $D_{\operatorname{pst}}(-)$
induces an equivalence
$D_{\operatorname{pst}}(-)$
induces an equivalence
 $$\begin{eqnarray}\displaystyle \{\text{potentially semistable }(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})\text{-modules over }L\}\overset{D_{\operatorname{pst}}}{\longrightarrow }\{\text{filtered }(\unicode[STIX]{x1D711},N,G_{K})\text{-modules over }L\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{\text{potentially semistable }(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})\text{-modules over }L\}\overset{D_{\operatorname{pst}}}{\longrightarrow }\{\text{filtered }(\unicode[STIX]{x1D711},N,G_{K})\text{-modules over }L\}. & & \displaystyle \nonumber\end{eqnarray}$$
The subcategory of crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules is equivalent to the full subcategory of filtered
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules is equivalent to the full subcategory of filtered
![]() $\unicode[STIX]{x1D711}$
-modules over
$\unicode[STIX]{x1D711}$
-modules over
![]() $L$
. The étale
$L$
. The étale
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules (the Galois representations, following Theorem 2.8) correspond to the weakly admissible modules on the right-hand side.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules (the Galois representations, following Theorem 2.8) correspond to the weakly admissible modules on the right-hand side.
Suppose that
![]() $D$
is crystalline. The
$D$
is crystalline. The
 $L\otimes _{\mathbf{Q}_{p}}K$
-module
$L\otimes _{\mathbf{Q}_{p}}K$
-module
 $D_{\operatorname{cris}}(D)_{K}:=D_{\operatorname{cris}}(D)\otimes _{F}K$
is equipped with an exhaustive and separated decreasing filtration
$D_{\operatorname{cris}}(D)_{K}:=D_{\operatorname{cris}}(D)\otimes _{F}K$
is equipped with an exhaustive and separated decreasing filtration
 $\operatorname{Fil}^{\bullet }D_{\operatorname{cris}}(D)_{K}$
. We denote by
$\operatorname{Fil}^{\bullet }D_{\operatorname{cris}}(D)_{K}$
. We denote by
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(D)$
the multi-set of integers such that the induced filtration on the
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(D)$
the multi-set of integers such that the induced filtration on the
![]() $L$
-vector space
$L$
-vector space
 $D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=e_{\unicode[STIX]{x1D70F}}D_{\operatorname{cris}}(D)_{K}$
has jumps given with multiplicity by
$D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=e_{\unicode[STIX]{x1D70F}}D_{\operatorname{cris}}(D)_{K}$
has jumps given with multiplicity by
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(D)$
. It is easy to see that if
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(D)$
. It is easy to see that if
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
is a character such that
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
is a character such that
![]() ${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
is crystalline then
${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
is crystalline then
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}))=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})$
. For example,
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}))=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})$
. For example,
 $D_{\operatorname{cris}}({\mathcal{R}}_{L})=F\otimes _{\mathbf{Q}_{p}}L$
with the trivial
$D_{\operatorname{cris}}({\mathcal{R}}_{L})=F\otimes _{\mathbf{Q}_{p}}L$
with the trivial
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
-action and for all
$\unicode[STIX]{x1D711}^{f_{K}}$
-action and for all
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
we have
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
we have
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}({\mathcal{R}}_{L})=0$
.
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}({\mathcal{R}}_{L})=0$
.
If
 $\unicode[STIX]{x1D70F}:K{\hookrightarrow}L$
is an embedding then we denote the corresponding character
$\unicode[STIX]{x1D70F}:K{\hookrightarrow}L$
is an embedding then we denote the corresponding character
 $K^{\times }\rightarrow L^{\times }$
by
$K^{\times }\rightarrow L^{\times }$
by
![]() $z_{\unicode[STIX]{x1D70F}}$
. It happens that
$z_{\unicode[STIX]{x1D70F}}$
. It happens that
 $D_{\operatorname{cris}}({\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}}))$
is a filtered
$D_{\operatorname{cris}}({\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}}))$
is a filtered
![]() $\unicode[STIX]{x1D711}$
-module with trivial
$\unicode[STIX]{x1D711}$
-module with trivial
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
-action and the Hodge–Tate filtration has weights
$\unicode[STIX]{x1D711}^{f_{K}}$
-action and the Hodge–Tate filtration has weights
 $$\begin{eqnarray}\displaystyle \operatorname{HT}_{\unicode[STIX]{x1D70E}}({\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}}))=\left\{\begin{array}{@{}ll@{}}-1\quad & \text{if }\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F},\\ 0\quad & \text{if }\unicode[STIX]{x1D70E}\neq \unicode[STIX]{x1D70F}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{HT}_{\unicode[STIX]{x1D70E}}({\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}}))=\left\{\begin{array}{@{}ll@{}}-1\quad & \text{if }\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F},\\ 0\quad & \text{if }\unicode[STIX]{x1D70E}\neq \unicode[STIX]{x1D70F}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
In particular,
 $D_{\operatorname{cris}}({\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}}))\subset D_{\operatorname{cris}}({\mathcal{R}}_{L})$
as filtered
$D_{\operatorname{cris}}({\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}}))\subset D_{\operatorname{cris}}({\mathcal{R}}_{L})$
as filtered
![]() $\unicode[STIX]{x1D711}$
-modules. Thus,
$\unicode[STIX]{x1D711}$
-modules. Thus,
 ${\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}})=t_{\unicode[STIX]{x1D70F}}{\mathcal{R}}_{L}$
for some
${\mathcal{R}}_{L}(z_{\unicode[STIX]{x1D70F}})=t_{\unicode[STIX]{x1D70F}}{\mathcal{R}}_{L}$
for some
![]() $t_{\unicode[STIX]{x1D70F}}$
, uniquely determined up to unit in
$t_{\unicode[STIX]{x1D70F}}$
, uniquely determined up to unit in
![]() ${\mathcal{R}}_{L}$
.
${\mathcal{R}}_{L}$
.
Proposition 2.9. Every
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
![]() ${\mathcal{R}}_{L}$
is of the form
${\mathcal{R}}_{L}$
is of the form
 $(\prod _{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}){\mathcal{R}}_{L}$
for some collection of non-negative integers
$(\prod _{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}){\mathcal{R}}_{L}$
for some collection of non-negative integers
![]() $r_{\unicode[STIX]{x1D70F}}\geqslant 0$
.
$r_{\unicode[STIX]{x1D70F}}\geqslant 0$
.
Proof. See [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 6.2.9]. ◻
It is easy to see
![]() $t_{\unicode[STIX]{x1D70F}}{\mathcal{R}}_{L}$
and
$t_{\unicode[STIX]{x1D70F}}{\mathcal{R}}_{L}$
and
![]() $t_{\unicode[STIX]{x1D70E}}{\mathcal{R}}_{L}$
are maximally coprime if
$t_{\unicode[STIX]{x1D70E}}{\mathcal{R}}_{L}$
are maximally coprime if
![]() $\unicode[STIX]{x1D70E}\neq \unicode[STIX]{x1D70F}$
. Indeed,
$\unicode[STIX]{x1D70E}\neq \unicode[STIX]{x1D70F}$
. Indeed,
 $D=t_{\unicode[STIX]{x1D70F}}{\mathcal{R}}_{L}+t_{\unicode[STIX]{x1D70E}}{\mathcal{R}}_{L}$
is
$D=t_{\unicode[STIX]{x1D70F}}{\mathcal{R}}_{L}+t_{\unicode[STIX]{x1D70E}}{\mathcal{R}}_{L}$
is
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
![]() ${\mathcal{R}}_{L}$
whose Hodge–Tate weights, computed by passing to
${\mathcal{R}}_{L}$
whose Hodge–Tate weights, computed by passing to
 $D_{\operatorname{pst}}(D)$
, are zero (for each
$D_{\operatorname{pst}}(D)$
, are zero (for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
). The element
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
). The element
 $t=\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}$
is, up to a unit, the ubiquitous
$t=\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}$
is, up to a unit, the ubiquitous
![]() $t$
which plays the role of the
$t$
which plays the role of the
![]() $p$
-adic
$p$
-adic
![]() $2\unicode[STIX]{x1D70B}i$
in all of
$2\unicode[STIX]{x1D70B}i$
in all of
![]() $p$
-adic Hodge theory. The
$p$
-adic Hodge theory. The
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule
![]() $t{\mathcal{R}}_{L}$
is crystalline, its
$t{\mathcal{R}}_{L}$
is crystalline, its
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weight is
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weight is
![]() $-1$
for each
$-1$
for each
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
 $\unicode[STIX]{x1D711}(t)=pt$
.
$\unicode[STIX]{x1D711}(t)=pt$
.
2.5 Galois cohomology
Suppose that
![]() $A$
is an affinoid algebra and that
$A$
is an affinoid algebra and that
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
. Let
$A$
. Let
 $\unicode[STIX]{x1D6E5}_{K}\subset \unicode[STIX]{x1D6E4}_{K}$
be the
$\unicode[STIX]{x1D6E5}_{K}\subset \unicode[STIX]{x1D6E4}_{K}$
be the
![]() $p$
-torsion subgroup (which only exists if
$p$
-torsion subgroup (which only exists if
![]() $p=2$
) and choose a topological generator
$p=2$
) and choose a topological generator
 $\unicode[STIX]{x1D6FE}_{0}\in \unicode[STIX]{x1D6E4}_{K}/\unicode[STIX]{x1D6E5}_{K}$
. One then defines the Herr complex [Reference HerrHer98] as the three-term complex
$\unicode[STIX]{x1D6FE}_{0}\in \unicode[STIX]{x1D6E4}_{K}/\unicode[STIX]{x1D6E5}_{K}$
. One then defines the Herr complex [Reference HerrHer98] as the three-term complex
![]() $C_{\unicode[STIX]{x1D6FE}_{0}}^{\bullet }(D)$
$C_{\unicode[STIX]{x1D6FE}_{0}}^{\bullet }(D)$

The Galois cohomology groups
![]() $H^{\bullet }(Q)$
of
$H^{\bullet }(Q)$
of
![]() $Q$
are defined to be the cohomology groups of the complex
$Q$
are defined to be the cohomology groups of the complex
![]() $C_{\unicode[STIX]{x1D6FE}_{0}}^{\bullet }(Q)$
. The complexes depend on the choice of
$C_{\unicode[STIX]{x1D6FE}_{0}}^{\bullet }(Q)$
. The complexes depend on the choice of
![]() $\unicode[STIX]{x1D6FE}_{0}$
up to canonical quasi-isomorphism, so the cohomology is well-defined.
$\unicode[STIX]{x1D6FE}_{0}$
up to canonical quasi-isomorphism, so the cohomology is well-defined.
When
![]() $A$
is finite over
$A$
is finite over
![]() $L$
, the Galois cohomology is finite-dimensional and satisfies an Euler–Poincaré formula [Reference LiuLiu07]
$L$
, the Galois cohomology is finite-dimensional and satisfies an Euler–Poincaré formula [Reference LiuLiu07]
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=0}^{2}(-1)\dim _{L}H^{i}(Q)=-(K:\mathbf{Q}_{p})\operatorname{rank}_{{\mathcal{R}}_{L}}Q, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=0}^{2}(-1)\dim _{L}H^{i}(Q)=-(K:\mathbf{Q}_{p})\operatorname{rank}_{{\mathcal{R}}_{L}}Q, & & \displaystyle \nonumber\end{eqnarray}$$
where the rank of a torsion module must be suitably interpreted (see § 2.6). The finiteness is true over general affinoid
![]() $L$
-algebras
$L$
-algebras
![]() $A$
in the case of
$A$
in the case of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules by [Reference Kedlaya, Pottharst and XiaoKPX14]. We will review that result in § 4.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules by [Reference Kedlaya, Pottharst and XiaoKPX14]. We will review that result in § 4.
But now let us review the dimensions of the cohomology of rank-one
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over a field. To shorten notation, if
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over a field. To shorten notation, if
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
is a continuous character we denote
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
is a continuous character we denote
 $H^{\bullet }(\unicode[STIX]{x1D6FF}):=H^{\bullet }({\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}))$
. We let
$H^{\bullet }(\unicode[STIX]{x1D6FF}):=H^{\bullet }({\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}))$
. We let
![]() $\widehat{T}(L)$
be the space of continuous characters
$\widehat{T}(L)$
be the space of continuous characters
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
. Define two special subsets of
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
. Define two special subsets of
![]() $\widehat{T}(L)$
by
$\widehat{T}(L)$
by
 $$\begin{eqnarray}\displaystyle \widehat{T}(L)^{+} & = & \displaystyle \biggl\{\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }:\unicode[STIX]{x1D6FF}=\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}\text{ with }r_{\unicode[STIX]{x1D70F}}\leqslant 0\text{ for each }\unicode[STIX]{x1D70F}\biggr\},\nonumber\\ \displaystyle \widehat{T}(L)^{-} & = & \displaystyle \biggl\{\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }:\unicode[STIX]{x1D6FF}=|N_{K/\mathbf{Q}_{p}}|\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}\text{ with }r_{\unicode[STIX]{x1D70F}}\geqslant 1\text{ for each }\unicode[STIX]{x1D70F}\biggr\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{T}(L)^{+} & = & \displaystyle \biggl\{\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }:\unicode[STIX]{x1D6FF}=\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}\text{ with }r_{\unicode[STIX]{x1D70F}}\leqslant 0\text{ for each }\unicode[STIX]{x1D70F}\biggr\},\nonumber\\ \displaystyle \widehat{T}(L)^{-} & = & \displaystyle \biggl\{\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }:\unicode[STIX]{x1D6FF}=|N_{K/\mathbf{Q}_{p}}|\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}\text{ with }r_{\unicode[STIX]{x1D70F}}\geqslant 1\text{ for each }\unicode[STIX]{x1D70F}\biggr\}.\nonumber\end{eqnarray}$$
The elements of
![]() $\widehat{T}(L)$
which are not in
$\widehat{T}(L)$
which are not in
![]() $\widehat{T}(L)^{+}$
or
$\widehat{T}(L)^{+}$
or
![]() $\widehat{T}(L)^{-}$
are called generic characters.
$\widehat{T}(L)^{-}$
are called generic characters.
Proposition 2.10. Let
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
be a continuous character. Then
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
be a continuous character. Then
 $$\begin{eqnarray}\displaystyle \dim _{L}H^{0}(\unicode[STIX]{x1D6FF}) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\unicode[STIX]{x1D6FF}\in \widehat{T}(L)^{+},\\ 0\quad & \text{otherwise,}\end{array}\right.\nonumber\\ \displaystyle \dim _{L}H^{1}(\unicode[STIX]{x1D6FF}) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}2\quad & \text{if }\unicode[STIX]{x1D6FF}\in \widehat{T}(L)^{+}\cup \widehat{T}(L)^{-},\\ 1\quad & \text{otherwise,}\end{array}\right.\nonumber\\ \displaystyle \dim _{L}H^{2}(\unicode[STIX]{x1D6FF}) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\unicode[STIX]{x1D6FF}\in \widehat{T}(L)^{-},\\ 0\quad & \text{otherwise.}\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim _{L}H^{0}(\unicode[STIX]{x1D6FF}) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\unicode[STIX]{x1D6FF}\in \widehat{T}(L)^{+},\\ 0\quad & \text{otherwise,}\end{array}\right.\nonumber\\ \displaystyle \dim _{L}H^{1}(\unicode[STIX]{x1D6FF}) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}2\quad & \text{if }\unicode[STIX]{x1D6FF}\in \widehat{T}(L)^{+}\cup \widehat{T}(L)^{-},\\ 1\quad & \text{otherwise,}\end{array}\right.\nonumber\\ \displaystyle \dim _{L}H^{2}(\unicode[STIX]{x1D6FF}) & = & \displaystyle \left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\unicode[STIX]{x1D6FF}\in \widehat{T}(L)^{-},\\ 0\quad & \text{otherwise.}\end{array}\right.\nonumber\end{eqnarray}$$
Proof. See [Reference Kedlaya, Pottharst and XiaoKPX14, Proposition 6.2.8]) (or [Reference NakamuraNak09, § 2.3]). ◻
Let us finish this subsection with a definition.
Definition 2.11. Suppose that
 $\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\in \widehat{T}(L)$
.
$\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\in \widehat{T}(L)$
.
-
(a) We say that
 $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
 $\unicode[STIX]{x1D6FF}^{\prime }$
are homothetic if there exists integers
$\unicode[STIX]{x1D6FF}^{\prime }$
are homothetic if there exists integers
 $(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
such that
$(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
such that
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\prime }\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}$
.
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}^{\prime }\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}$
. -
(b) We say that
 $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
 $\unicode[STIX]{x1D6FF}^{\prime }$
are generic up to homothety if
$\unicode[STIX]{x1D6FF}^{\prime }$
are generic up to homothety if
 $\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF}^{-1}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}$
is generic for every tuple
$\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF}^{-1}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}$
is generic for every tuple
 $(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
of integers.
$(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
of integers.
To put the previous definition in context, if
![]() $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
are homothetic, then following Proposition 2.10 we can find an integer
$\unicode[STIX]{x1D6FF}^{\prime }$
are homothetic, then following Proposition 2.10 we can find an integer
![]() $r$
such that
$r$
such that
 $t^{r}{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}){\hookrightarrow}{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}^{\prime })$
. Thus,
$t^{r}{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}){\hookrightarrow}{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}^{\prime })$
. Thus,
![]() ${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
and
${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
and
![]() ${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}^{\prime })$
are in a sense commensurable. If
${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}^{\prime })$
are in a sense commensurable. If
![]() $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
are generic up to homothety, then
$\unicode[STIX]{x1D6FF}^{\prime }$
are generic up to homothety, then
 $H^{2}(\unicode[STIX]{x1D702})=H^{0}(\unicode[STIX]{x1D702})=(0)$
for all characters
$H^{2}(\unicode[STIX]{x1D702})=H^{0}(\unicode[STIX]{x1D702})=(0)$
for all characters
![]() $\unicode[STIX]{x1D702}$
homothetic to
$\unicode[STIX]{x1D702}$
homothetic to
![]() $\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF}^{-1}$
.
$\unicode[STIX]{x1D6FF}^{\prime }\unicode[STIX]{x1D6FF}^{-1}$
.
2.6 Torsion
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
Note that
 $$\begin{eqnarray}\displaystyle {\mathcal{R}}_{L}={\mathcal{R}}\otimes _{\mathbf{Q}_{p}}L={\mathcal{R}}\otimes _{F}(F\otimes _{\mathbf{Q}_{p}}L)=\mathop{\prod }_{\unicode[STIX]{x1D702}\in \operatorname{Gal}(F/\mathbf{Q}_{p})}{\mathcal{R}}\otimes _{F}L. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}_{L}={\mathcal{R}}\otimes _{\mathbf{Q}_{p}}L={\mathcal{R}}\otimes _{F}(F\otimes _{\mathbf{Q}_{p}}L)=\mathop{\prod }_{\unicode[STIX]{x1D702}\in \operatorname{Gal}(F/\mathbf{Q}_{p})}{\mathcal{R}}\otimes _{F}L. & & \displaystyle \nonumber\end{eqnarray}$$
By [Reference BergerBer02, Proposition 4.12], each term in the product is an adequate Bézout domain. In particular, finitely generated
![]() ${\mathcal{R}}_{L}$
modules are free if and only if they are torsion free (with respect to the total ring of divisors) and there is a robust theory of elementary divisors over
${\mathcal{R}}_{L}$
modules are free if and only if they are torsion free (with respect to the total ring of divisors) and there is a robust theory of elementary divisors over
![]() ${\mathcal{R}}_{L}$
. As a consequence, a generalized
${\mathcal{R}}_{L}$
. As a consequence, a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $L$
is a
$L$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module if and only if it is torsion-free as an
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module if and only if it is torsion-free as an
![]() ${\mathcal{R}}_{L}$
-module.
${\mathcal{R}}_{L}$
-module.
The element
![]() $t\in {\mathcal{R}}_{L}$
is an example of a non-zero divisor. If
$t\in {\mathcal{R}}_{L}$
is an example of a non-zero divisor. If
![]() $S$
is a generalized
$S$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module we let
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module we let
![]() $S[t^{\infty }]$
denote the
$S[t^{\infty }]$
denote the
![]() $t$
-power torsion submodule. Since
$t$
-power torsion submodule. Since
![]() $t\in {\mathcal{R}}$
is an eigenvector for
$t\in {\mathcal{R}}$
is an eigenvector for
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D6E4}_{K}$
,
$\unicode[STIX]{x1D6E4}_{K}$
,
![]() $S[t^{\infty }]$
is a
$S[t^{\infty }]$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule.
Definition 2.12. Let
![]() $A$
be an
$A$
be an
![]() $L$
-affinoid algebra. A torsion
$L$
-affinoid algebra. A torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
is a generalized
$A$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $S$
over
$S$
over
![]() $A$
such that
$A$
such that
 $S[t^{\infty }]=S$
. We say that
$S[t^{\infty }]=S$
. We say that
![]() $S$
is pure if either
$S$
is pure if either
![]() $S=0$
or if
$S=0$
or if
![]() $S$
is free over
$S$
is free over
 ${\mathcal{R}}_{A}/(\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})$
for some collection of integers
${\mathcal{R}}_{A}/(\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})$
for some collection of integers
![]() $r_{\unicode[STIX]{x1D70F}}\geqslant 0$
, not all of which are zero.
$r_{\unicode[STIX]{x1D70F}}\geqslant 0$
, not all of which are zero.
The typical example of a pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module is
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module is
 ${\mathcal{R}}_{L}/(\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}){\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
for some continuous character
${\mathcal{R}}_{L}/(\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}){\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
for some continuous character
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
and non-negative integers
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
and non-negative integers
![]() $r_{\unicode[STIX]{x1D70F}}$
.
$r_{\unicode[STIX]{x1D70F}}$
.
Lemma 2.13. A generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $L$
is a
$L$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module if and only if it is
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module if and only if it is
![]() $t$
-torsion free. Any torsion
$t$
-torsion free. Any torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $L$
is a successive extension of pure torsion
$L$
is a successive extension of pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules.
Proof. The lemma is proven in the case
 $K=\mathbf{Q}_{p}$
in [Reference LiuLiu07, Proposition 4.1]. The proof in this case is the same, the main point being Proposition 2.9. We reproduce it for convenience.
$K=\mathbf{Q}_{p}$
in [Reference LiuLiu07, Proposition 4.1]. The proof in this case is the same, the main point being Proposition 2.9. We reproduce it for convenience.
Let
![]() $D$
be a generalized
$D$
be a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. If it is a bona fide
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. If it is a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then it obviously cannot have
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then it obviously cannot have
![]() $t$
-torsion. Now suppose that
$t$
-torsion. Now suppose that
![]() $D$
is
$D$
is
![]() $t$
-torsion free, and to show that
$t$
-torsion free, and to show that
![]() $D$
is a bona fide
$D$
is a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module it suffices to show that it is torsion free.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module it suffices to show that it is torsion free.
Since
![]() $D$
is finitely generated as a
$D$
is finitely generated as a
![]() ${\mathcal{R}}_{L}$
-module, and
${\mathcal{R}}_{L}$
-module, and
![]() ${\mathcal{R}}_{L}$
is a Bézout domain, we have the theory of elementary divisors. Thus, there exists a finite number of elements
${\mathcal{R}}_{L}$
is a Bézout domain, we have the theory of elementary divisors. Thus, there exists a finite number of elements
 $d_{1},\ldots ,d_{m}\in D$
which generate
$d_{1},\ldots ,d_{m}\in D$
which generate
![]() $D$
over
$D$
over
![]() ${\mathcal{R}}_{L}$
such that the ideals
${\mathcal{R}}_{L}$
such that the ideals
 $f_{i}{\mathcal{R}}_{L}:=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
are principal and
$f_{i}{\mathcal{R}}_{L}:=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
are principal and
 $f_{1}{\mathcal{R}}_{L}\supset f_{2}{\mathcal{R}}_{L}\supset \cdots \supset f_{m}{\mathcal{R}}_{L}$
. The ideals
$f_{1}{\mathcal{R}}_{L}\supset f_{2}{\mathcal{R}}_{L}\supset \cdots \supset f_{m}{\mathcal{R}}_{L}$
. The ideals
![]() $\{f_{i}{\mathcal{R}}_{L}\}$
are then uniquely determined by this property. We claim that each non-zero
$\{f_{i}{\mathcal{R}}_{L}\}$
are then uniquely determined by this property. We claim that each non-zero
![]() $f_{i}$
is a unit, which implies that
$f_{i}$
is a unit, which implies that
![]() $D$
is torsion free. Without loss of generality we can assume that
$D$
is torsion free. Without loss of generality we can assume that
![]() $f_{m}\neq 0$
and show that
$f_{m}\neq 0$
and show that
![]() $f_{m}$
is a unit.
$f_{m}$
is a unit.
We will first show that each ideal
![]() $f_{i}{\mathcal{R}}_{L}$
is a
$f_{i}{\mathcal{R}}_{L}$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
![]() ${\mathcal{R}}_{L}$
. If
${\mathcal{R}}_{L}$
. If
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{K}$
then it is easy to see that
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{K}$
then it is easy to see that
![]() $\{\unicode[STIX]{x1D6FE}(d_{i})\}$
also generates
$\{\unicode[STIX]{x1D6FE}(d_{i})\}$
also generates
![]() $D$
as a
$D$
as a
![]() ${\mathcal{R}}_{L}$
-module. Furthermore,
${\mathcal{R}}_{L}$
-module. Furthermore,
 $\operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D6FE}(d_{i}))\subset \operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D6FE}(d_{i-1}))$
for
$\operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D6FE}(d_{i}))\subset \operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D6FE}(d_{i-1}))$
for
 $1<i\leqslant m$
. Thus, by the uniqueness in the theory of elementary divisors, we have
$1<i\leqslant m$
. Thus, by the uniqueness in the theory of elementary divisors, we have
 $\unicode[STIX]{x1D6FE}(\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}))=\operatorname{Ann}_{{\mathcal{R}}_{L}}\unicode[STIX]{x1D6FE}(d_{i})=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
for each
$\unicode[STIX]{x1D6FE}(\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}))=\operatorname{Ann}_{{\mathcal{R}}_{L}}\unicode[STIX]{x1D6FE}(d_{i})=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
for each
![]() $i$
. This shows that each ideal
$i$
. This shows that each ideal
![]() $f_{i}{\mathcal{R}}_{L}$
is
$f_{i}{\mathcal{R}}_{L}$
is
![]() $\unicode[STIX]{x1D6E4}_{K}$
-stable.
$\unicode[STIX]{x1D6E4}_{K}$
-stable.
On the other hand, one may also check that the elementary divisors for
![]() $\unicode[STIX]{x1D711}^{\ast }D$
are the ideals
$\unicode[STIX]{x1D711}^{\ast }D$
are the ideals
 $\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}\otimes 1)$
(the elements
$\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}\otimes 1)$
(the elements
![]() $d_{i}\otimes 1$
written as tensors in
$d_{i}\otimes 1$
written as tensors in
 $\unicode[STIX]{x1D711}^{\ast }D=D\otimes _{{\mathcal{R}}_{L},\unicode[STIX]{x1D711}}{\mathcal{R}}_{L}$
). Since
$\unicode[STIX]{x1D711}^{\ast }D=D\otimes _{{\mathcal{R}}_{L},\unicode[STIX]{x1D711}}{\mathcal{R}}_{L}$
). Since
 $\unicode[STIX]{x1D711}^{\ast }D\simeq D$
the elementary divisors for both
$\unicode[STIX]{x1D711}^{\ast }D\simeq D$
the elementary divisors for both
![]() $\unicode[STIX]{x1D711}^{\ast }D$
and
$\unicode[STIX]{x1D711}^{\ast }D$
and
![]() $D$
are the same, hence
$D$
are the same, hence
 $\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}\otimes 1)=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
. This required only having an abstract isomorphism between
$\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}\otimes 1)=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
. This required only having an abstract isomorphism between
![]() $\unicode[STIX]{x1D711}^{\ast }D$
and
$\unicode[STIX]{x1D711}^{\ast }D$
and
![]() $D$
. On the other hand, the isomorphism
$D$
. On the other hand, the isomorphism
 $\unicode[STIX]{x1D711}^{\ast }D\rightarrow D$
is defined explicitly by sending
$\unicode[STIX]{x1D711}^{\ast }D\rightarrow D$
is defined explicitly by sending
![]() $d_{i}\otimes 1$
to
$d_{i}\otimes 1$
to
![]() $\unicode[STIX]{x1D711}(d_{i})$
, which implies that
$\unicode[STIX]{x1D711}(d_{i})$
, which implies that
 $\operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D711}(d_{i}))=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}\otimes 1)$
. Finally, we see that
$\operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D711}(d_{i}))=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}\otimes 1)$
. Finally, we see that
 $\unicode[STIX]{x1D711}(\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}))\subset \operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D711}(d_{i}))=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
. Thus, each ideal
$\unicode[STIX]{x1D711}(\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i}))\subset \operatorname{Ann}_{{\mathcal{R}}_{L}}(\unicode[STIX]{x1D711}(d_{i}))=\operatorname{Ann}_{{\mathcal{R}}_{L}}(d_{i})$
. Thus, each ideal
![]() $f_{i}{\mathcal{R}}_{L}$
is
$f_{i}{\mathcal{R}}_{L}$
is
![]() $\unicode[STIX]{x1D711}$
-stable as well.
$\unicode[STIX]{x1D711}$
-stable as well.
We now finish the proof. By Proposition 2.9, if
![]() $f_{m}$
is not unit then there exists non-negative integers
$f_{m}$
is not unit then there exists non-negative integers
![]() $r_{\unicode[STIX]{x1D70F}}\geqslant 0$
, not all zero, such that
$r_{\unicode[STIX]{x1D70F}}\geqslant 0$
, not all zero, such that
 $(\prod _{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})d_{m}=0$
. Since
$(\prod _{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})d_{m}=0$
. Since
 $(\prod _{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})$
is a divisor of
$(\prod _{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})$
is a divisor of
![]() $t^{r}$
for
$t^{r}$
for
![]() $r$
large, we conclude that
$r$
large, we conclude that
 $d_{m}\in D[t^{\infty }]$
. Since
$d_{m}\in D[t^{\infty }]$
. Since
![]() $D$
is
$D$
is
![]() $t$
-torsion free, we conclude that
$t$
-torsion free, we conclude that
![]() $d_{m}=0$
, which contradicts the choice of the elements
$d_{m}=0$
, which contradicts the choice of the elements
![]() $\{d_{i}\}$
. The calculation also clearly shows that a torsion
$\{d_{i}\}$
. The calculation also clearly shows that a torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module is a successive extension of pure torsion
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module is a successive extension of pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Indeed, if
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Indeed, if
![]() $Q$
is torsion then
$Q$
is torsion then
 $0=f_{m}Q\subset f_{m-1}Q\subset \cdots \subset f_{1}Q\subset Q$
is a filtration whose successive quotients
$0=f_{m}Q\subset f_{m-1}Q\subset \cdots \subset f_{1}Q\subset Q$
is a filtration whose successive quotients
 $f_{i}Q/f_{i+1}Q$
are pure torsion, since they are free over
$f_{i}Q/f_{i+1}Q$
are pure torsion, since they are free over
 $f_{i}{\mathcal{R}}_{L}/f_{i+1}{\mathcal{R}}_{L}$
(compare with [Reference LiuLiu07, Proposition 4.1]).◻
$f_{i}{\mathcal{R}}_{L}/f_{i+1}{\mathcal{R}}_{L}$
(compare with [Reference LiuLiu07, Proposition 4.1]).◻
If
![]() $S$
is a torsion module, then the Euler–Poincaré formula [Reference LiuLiu07, Theorem 4.7] says
$S$
is a torsion module, then the Euler–Poincaré formula [Reference LiuLiu07, Theorem 4.7] says
 $$\begin{eqnarray}\displaystyle \dim _{L}H^{0}(S)=\dim _{L}H^{1}(S)\quad \text{and}\quad \dim _{L}H^{2}(S)=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim _{L}H^{0}(S)=\dim _{L}H^{1}(S)\quad \text{and}\quad \dim _{L}H^{2}(S)=0. & & \displaystyle \nonumber\end{eqnarray}$$
By Lemma 2.13, the cohomology of torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules reduces to the cohomology of pure torsion
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules reduces to the cohomology of pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules and that is explained by the following calculation.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules and that is explained by the following calculation.
Proposition 2.14. Let
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Then for each
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Then for each
![]() $i=0,1$
we have
$i=0,1$
we have
 $$\begin{eqnarray}\displaystyle \dim _{L}H^{i}(({\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})(\unicode[STIX]{x1D6FF}))=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})\in \{0,1,\ldots ,r_{\unicode[STIX]{x1D70F}}-1\},\\ 0\quad & \text{otherwise.}\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim _{L}H^{i}(({\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}})(\unicode[STIX]{x1D6FF}))=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})\in \{0,1,\ldots ,r_{\unicode[STIX]{x1D70F}}-1\},\\ 0\quad & \text{otherwise.}\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. The case of
![]() $i=1$
and
$i=1$
and
![]() $i=0$
are equivalent by the Euler–Poincaré formula for torsion modules. The computation of the cohomology for
$i=0$
are equivalent by the Euler–Poincaré formula for torsion modules. The computation of the cohomology for
![]() $i=0$
is given by [Reference NakamuraNak09, Lemma 2.16]. For a proof in the language of
$i=0$
is given by [Reference NakamuraNak09, Lemma 2.16]. For a proof in the language of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, at least when
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, at least when
 $K=\mathbf{Q}_{p}$
, see [Reference ColmezCol08, Proposition 2.18] (warning: Colmez uses a different convention for weights).◻
$K=\mathbf{Q}_{p}$
, see [Reference ColmezCol08, Proposition 2.18] (warning: Colmez uses a different convention for weights).◻
3 Parabolizations and triangulations
Triangulations of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules arose following Colmez’s work on the
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules arose following Colmez’s work on the
![]() $p$
-adic local Langlands for
$p$
-adic local Langlands for
 $\operatorname{GL}_{2}(\mathbf{Q}_{p})$
(see [Reference ColmezCol08]). In this section we have two goals. First, we will recall parabolizations of
$\operatorname{GL}_{2}(\mathbf{Q}_{p})$
(see [Reference ColmezCol08]). In this section we have two goals. First, we will recall parabolizations of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, a more general notion due to Chenevier [Reference ChenevierChe11], and the definition of critical and non-critical triangulations. Our second goal is to extend the definition of triangulation in a reasonable way to the category of generalized
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules, a more general notion due to Chenevier [Reference ChenevierChe11], and the definition of critical and non-critical triangulations. Our second goal is to extend the definition of triangulation in a reasonable way to the category of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. We discuss the latter notion only in the case where the coefficients are a field.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. We discuss the latter notion only in the case where the coefficients are a field.
3.1 Parabolizations of
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules
Let
![]() $A$
be an affinoid
$A$
be an affinoid
![]() $L$
-algebra.
$L$
-algebra.
Definition 3.1. If
![]() $D$
is a
$D$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
, then a parabolization
$A$
, then a parabolization
![]() $P_{\bullet }$
of
$P_{\bullet }$
of
![]() $D$
(of length
$D$
(of length
![]() $s$
) is a filtration
$s$
) is a filtration
 $$\begin{eqnarray}\displaystyle 0=P_{0}\subsetneq P_{1}\subsetneq \cdots \subsetneq P_{s-1}\subsetneq P_{s}=D & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=P_{0}\subsetneq P_{1}\subsetneq \cdots \subsetneq P_{s-1}\subsetneq P_{s}=D & & \displaystyle \nonumber\end{eqnarray}$$
such that each:
-
–
 $P_{i}$
is a
$P_{i}$
is a
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module; and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module; and -
– for each
 $i=1,\ldots ,s$
we have that
$i=1,\ldots ,s$
we have that
 $P_{i}/P_{i-1}$
is a
$P_{i}/P_{i-1}$
is a
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
 $A$
which is a
$A$
which is a
 ${\mathcal{R}}_{A}$
-module direct summand of
${\mathcal{R}}_{A}$
-module direct summand of
 $P_{i}$
.
$P_{i}$
.
If
![]() $P_{\bullet }$
is a parabolization of the maximal length
$P_{\bullet }$
is a parabolization of the maximal length
 $s=\operatorname{rank}_{{\mathcal{R}}_{A}}D$
, then we say that
$s=\operatorname{rank}_{{\mathcal{R}}_{A}}D$
, then we say that
![]() $P_{\bullet }$
is a triangulation. We say
$P_{\bullet }$
is a triangulation. We say
![]() $D$
is trianguline if, after possibly extending the coefficient field
$D$
is trianguline if, after possibly extending the coefficient field
![]() $L$
, there exists a triangulation of
$L$
, there exists a triangulation of
![]() $D$
.
$D$
.
If
![]() $P_{\bullet }$
is a triangulation of a
$P_{\bullet }$
is a triangulation of a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D$
of rank
$D$
of rank
![]() $d$
, then each quotient
$d$
, then each quotient
 $P_{i}/P_{i-1}$
is of the form
$P_{i}/P_{i-1}$
is of the form
![]() ${\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}_{i})$
for some continuous character
${\mathcal{R}}_{A}(\unicode[STIX]{x1D6FF}_{i})$
for some continuous character
 $\unicode[STIX]{x1D6FF}_{i}:K^{\times }\rightarrow A^{\times }$
, at least locally on
$\unicode[STIX]{x1D6FF}_{i}:K^{\times }\rightarrow A^{\times }$
, at least locally on
 $X=\operatorname{Sp}(A)$
[Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.2.14]. We call the
$X=\operatorname{Sp}(A)$
[Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.2.14]. We call the
![]() $d$
-tuple
$d$
-tuple
![]() $(\unicode[STIX]{x1D6FF}_{i})_{i=1}^{d}$
the ordered parameter of the triangulation
$(\unicode[STIX]{x1D6FF}_{i})_{i=1}^{d}$
the ordered parameter of the triangulation
![]() $P_{\bullet }$
and we say that
$P_{\bullet }$
and we say that
![]() $D$
is trianguline with ordered parameter
$D$
is trianguline with ordered parameter
![]() $(\unicode[STIX]{x1D6FF}_{i})_{i=1}^{d}$
. If
$(\unicode[STIX]{x1D6FF}_{i})_{i=1}^{d}$
. If
![]() $D$
is trianguline with an ordered parameter
$D$
is trianguline with an ordered parameter
![]() $(\unicode[STIX]{x1D6FF}_{i})_{i=1}^{d}$
, then
$(\unicode[STIX]{x1D6FF}_{i})_{i=1}^{d}$
, then
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(D)=\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i})\}_{i=1}^{d}$
.
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(D)=\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i})\}_{i=1}^{d}$
.
For the rest of this section we will take
![]() $A$
to be the field
$A$
to be the field
![]() $L$
itself. Crystalline
$L$
itself. Crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() ${\mathcal{R}}_{L}$
provide examples of triangulations. For that we have the notion of a refinement, following [Reference LiuLiu15, Definition 5.29].
${\mathcal{R}}_{L}$
provide examples of triangulations. For that we have the notion of a refinement, following [Reference LiuLiu15, Definition 5.29].
Definition 3.2. If
![]() $D$
is a crystalline
$D$
is a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of rank
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of rank
![]() $d$
over
$d$
over
![]() $L$
, then a partial refinement
$L$
, then a partial refinement
![]() $R_{\bullet }$
of
$R_{\bullet }$
of
![]() $D$
is the choice of a
$D$
is the choice of a
![]() $\unicode[STIX]{x1D711}$
-stable
$\unicode[STIX]{x1D711}$
-stable
 $L\otimes _{\mathbf{Q}_{p}}F$
-linear filtration
$L\otimes _{\mathbf{Q}_{p}}F$
-linear filtration
 $$\begin{eqnarray}\displaystyle 0=R_{0}\subsetneq R_{1}\subsetneq \cdots \subsetneq R_{s}=D_{\operatorname{cris}}(D), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=R_{0}\subsetneq R_{1}\subsetneq \cdots \subsetneq R_{s}=D_{\operatorname{cris}}(D), & & \displaystyle \nonumber\end{eqnarray}$$
whose successive quotients are free
 $L\otimes _{\mathbf{Q}_{p}}F$
-modules. In the case that
$L\otimes _{\mathbf{Q}_{p}}F$
-modules. In the case that
![]() $s=d$
we call
$s=d$
we call
![]() $R_{\bullet }$
a refinement.
$R_{\bullet }$
a refinement.
Suppose that
![]() $R_{\bullet }$
is a refinement of a crystalline
$R_{\bullet }$
is a refinement of a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. Then each of the quotients
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. Then each of the quotients
 $R_{i}/R_{i-1}$
is a rank-one
$R_{i}/R_{i-1}$
is a rank-one
 $L\otimes _{\mathbf{Q}_{p}}F$
-module equipped with a linear operator
$L\otimes _{\mathbf{Q}_{p}}F$
-module equipped with a linear operator
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
. We denote by
$\unicode[STIX]{x1D711}^{f_{K}}$
. We denote by
 $\unicode[STIX]{x1D719}_{i}\in L^{\times }$
the eigenvalue of
$\unicode[STIX]{x1D719}_{i}\in L^{\times }$
the eigenvalue of
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
appearing in
$\unicode[STIX]{x1D711}^{f_{K}}$
appearing in
 $R_{i}/R_{i-1}$
. Furthermore,
$R_{i}/R_{i-1}$
. Furthermore,
 $D_{\operatorname{cris}}(D)_{K}$
is an
$D_{\operatorname{cris}}(D)_{K}$
is an
 $L\otimes _{\mathbf{Q}_{p}}K$
-vector space equipped with its Hodge filtration
$L\otimes _{\mathbf{Q}_{p}}K$
-vector space equipped with its Hodge filtration
 $\operatorname{Fil}^{\bullet }D_{\operatorname{cris}}(D)_{K}$
. Each of the
$\operatorname{Fil}^{\bullet }D_{\operatorname{cris}}(D)_{K}$
. Each of the
![]() $\unicode[STIX]{x1D711}$
-stable subspaces
$\unicode[STIX]{x1D711}$
-stable subspaces
![]() $(R_{i})_{K}$
has an induced Hodge filtration. We define, for each
$(R_{i})_{K}$
has an induced Hodge filtration. We define, for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and
 $i=1,\ldots ,d$
an integer
$i=1,\ldots ,d$
an integer
![]() $s_{i,\unicode[STIX]{x1D70F}}$
so that
$s_{i,\unicode[STIX]{x1D70F}}$
so that
 $\{s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{i,\unicode[STIX]{x1D70F}}\}$
are the
$\{s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{i,\unicode[STIX]{x1D70F}}\}$
are the
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights appearing in
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights appearing in
![]() $(R_{i})_{K,\unicode[STIX]{x1D70F}}$
. In summary, triangulations and refinements have the following invariants:
$(R_{i})_{K,\unicode[STIX]{x1D70F}}$
. In summary, triangulations and refinements have the following invariants:
 $$\begin{eqnarray}\displaystyle \text{a triangulation }P_{\bullet } & {\rightsquigarrow} & \displaystyle \text{the ordered parameter }(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n});\nonumber\\ \displaystyle \text{a refinement }R_{\bullet } & {\rightsquigarrow} & \displaystyle \text{the ordering of }\unicode[STIX]{x1D711}^{f_{K}}\text{-eigenvalues }(\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})\nonumber\\ \displaystyle & & \displaystyle \quad \text{and the }\unicode[STIX]{x1D70F}\text{-}\text{Hodge}{-}\text{Tate weights }(s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{d,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{a triangulation }P_{\bullet } & {\rightsquigarrow} & \displaystyle \text{the ordered parameter }(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n});\nonumber\\ \displaystyle \text{a refinement }R_{\bullet } & {\rightsquigarrow} & \displaystyle \text{the ordering of }\unicode[STIX]{x1D711}^{f_{K}}\text{-eigenvalues }(\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})\nonumber\\ \displaystyle & & \displaystyle \quad \text{and the }\unicode[STIX]{x1D70F}\text{-}\text{Hodge}{-}\text{Tate weights }(s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{d,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}.\nonumber\end{eqnarray}$$
Note that if
![]() $P_{\bullet }$
is a triangulation of a crystalline
$P_{\bullet }$
is a triangulation of a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D$
, then each step
$D$
, then each step
![]() $P_{i}$
is a crystalline
$P_{i}$
is a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module as well.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module as well.
Proposition 3.3. Let
![]() $D$
be a crystalline
$D$
be a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $L$
all of whose
$L$
all of whose
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
-eigenvalues lie in
$\unicode[STIX]{x1D711}^{f_{K}}$
-eigenvalues lie in
![]() $L^{\times }$
.
$L^{\times }$
.
-
(a) Then
 $P\mapsto D_{\operatorname{cris}}(P)$
induces bijections
$P\mapsto D_{\operatorname{cris}}(P)$
induces bijections  $$\begin{eqnarray}\displaystyle \{\text{parabolizations of }D\} & \longleftrightarrow & \displaystyle \{\text{partial refinements of }D\},\nonumber\\ \displaystyle \{\text{triangulations of }D\} & \longleftrightarrow & \displaystyle \{\text{refinements of }D\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{\text{parabolizations of }D\} & \longleftrightarrow & \displaystyle \{\text{partial refinements of }D\},\nonumber\\ \displaystyle \{\text{triangulations of }D\} & \longleftrightarrow & \displaystyle \{\text{refinements of }D\}.\nonumber\end{eqnarray}$$
-
(b) If
 $P_{\bullet }$
is a triangulation with ordered parameter
$P_{\bullet }$
is a triangulation with ordered parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n})$
, then the orderings associated to
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n})$
, then the orderings associated to
 $D_{\operatorname{cris}}(P_{\bullet })$
are given by for some (or, any) choice of uniformizer
$D_{\operatorname{cris}}(P_{\bullet })$
are given by for some (or, any) choice of uniformizer $$\begin{eqnarray}\displaystyle & (s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{d,\unicode[STIX]{x1D70F}})=(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{n})), & \displaystyle \nonumber\\ \displaystyle & (\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})=\biggl(\unicode[STIX]{x1D6FF}_{1}(\unicode[STIX]{x1D71B}_{K})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1})},\ldots ,\unicode[STIX]{x1D6FF}_{d}(\unicode[STIX]{x1D71B}_{K})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{d})}\biggr), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{d,\unicode[STIX]{x1D70F}})=(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{n})), & \displaystyle \nonumber\\ \displaystyle & (\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})=\biggl(\unicode[STIX]{x1D6FF}_{1}(\unicode[STIX]{x1D71B}_{K})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1})},\ldots ,\unicode[STIX]{x1D6FF}_{d}(\unicode[STIX]{x1D71B}_{K})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{d})}\biggr), & \displaystyle \nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
.
$\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
.
-
(c) If
 $R_{\bullet }$
is a refinement with orderings
$R_{\bullet }$
is a refinement with orderings
 $(\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
and
$(\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
and
 $(s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{d,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
then the parameter
$(s_{1,\unicode[STIX]{x1D70F}},\ldots ,s_{d,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
then the parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n})$
of the corresponding triangulation
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n})$
of the corresponding triangulation
 $P_{\bullet }$
is given by for some (or any) choice of uniformizer
$P_{\bullet }$
is given by for some (or any) choice of uniformizer $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i}(z)=\biggl(\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{-s_{i,\unicode[STIX]{x1D70F}}}\biggr)\operatorname{unr}_{\unicode[STIX]{x1D71B}_{K}}(\unicode[STIX]{x1D719}_{i})(z) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i}(z)=\biggl(\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{-s_{i,\unicode[STIX]{x1D70F}}}\biggr)\operatorname{unr}_{\unicode[STIX]{x1D71B}_{K}}(\unicode[STIX]{x1D719}_{i})(z) & & \displaystyle \nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
.
$\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
.
Proof. The first part follows from Berger’s dictionary [Reference BergerBer08] between potentially semistable
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules and filtered
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules and filtered
 $(\unicode[STIX]{x1D711},N,G_{K})$
-modules. The second two parts are easy inductions from the rank-one case. In the case that
$(\unicode[STIX]{x1D711},N,G_{K})$
-modules. The second two parts are easy inductions from the rank-one case. In the case that
 $K=\mathbf{Q}_{p}$
a longer discussion can be found in [Reference Bellaïche and ChenevierBC09, Proposition 2.4.1].◻
$K=\mathbf{Q}_{p}$
a longer discussion can be found in [Reference Bellaïche and ChenevierBC09, Proposition 2.4.1].◻
3.2 Critical and non-critical triangulations
For this subsection we work with a fixed crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D$
over the field
$D$
over the field
![]() $L$
.
$L$
.
Definition 3.4. Suppose that
![]() $P\subset D$
is a saturated
$P\subset D$
is a saturated
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule. If
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule. If
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then we say that
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then we say that
![]() $P$
is
$P$
is
![]() $\unicode[STIX]{x1D70F}$
-non-critical if there exist an integer
$\unicode[STIX]{x1D70F}$
-non-critical if there exist an integer
![]() $k_{\unicode[STIX]{x1D70F}}$
such that
$k_{\unicode[STIX]{x1D70F}}$
such that
 $$\begin{eqnarray}\displaystyle D_{\operatorname{cris}}(P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{\operatorname{cris}}(P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
We say
![]() $P$
is
$P$
is
![]() $\unicode[STIX]{x1D70F}$
-critical otherwise. Finally,
$\unicode[STIX]{x1D70F}$
-critical otherwise. Finally,
![]() $P$
is called non-critical if
$P$
is called non-critical if
![]() $P$
is
$P$
is
![]() $\unicode[STIX]{x1D70F}$
-non-critical for each
$\unicode[STIX]{x1D70F}$
-non-critical for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and
![]() $P$
is critical if there exists a
$P$
is critical if there exists a
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
such that
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
such that
![]() $P$
is
$P$
is
![]() $\unicode[STIX]{x1D70F}$
-critical.
$\unicode[STIX]{x1D70F}$
-critical.
The definition is only given for crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules as it relies on the correspondence Proposition 3.3. A more general definition will be given later which applies to certain
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules as it relies on the correspondence Proposition 3.3. A more general definition will be given later which applies to certain
![]() $p$
-adic limits of crystalline
$p$
-adic limits of crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules (see Definition 6.7).
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules (see Definition 6.7).
In the case of regular Hodge–Tate weights, we have a convenient way to check whether or not a saturated
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule is critical.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule is critical.
Lemma 3.5. Let
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Suppose that
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Suppose that
![]() $D$
is a crystalline
$D$
is a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with regular
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with regular
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
 $k_{1,\unicode[STIX]{x1D70F}}<\cdots <k_{d,\unicode[STIX]{x1D70F}}$
. Let
$k_{1,\unicode[STIX]{x1D70F}}<\cdots <k_{d,\unicode[STIX]{x1D70F}}$
. Let
![]() $P\subset D$
be a saturated
$P\subset D$
be a saturated
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of rank
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of rank
![]() $i\leqslant d$
. The following are equivalent:
$i\leqslant d$
. The following are equivalent:
-
(a)
 $P$
is
$P$
is
 $\unicode[STIX]{x1D70F}$
-non-critical;
$\unicode[STIX]{x1D70F}$
-non-critical; -
(b)
 $D_{\operatorname{cris}}(P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{i+1,\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
;
$D_{\operatorname{cris}}(P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{i+1,\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
; -
(c)
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(P)=\{k_{1,\unicode[STIX]{x1D70F}},\ldots ,k_{i,\unicode[STIX]{x1D70F}}\}$
;
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(P)=\{k_{1,\unicode[STIX]{x1D70F}},\ldots ,k_{i,\unicode[STIX]{x1D70F}}\}$
; -
(d)
 $\det P\subset \wedge ^{i}D$
is
$\det P\subset \wedge ^{i}D$
is
 $\unicode[STIX]{x1D70F}$
-non-critical.
$\unicode[STIX]{x1D70F}$
-non-critical.
Proof. First, part (b) implies part (a) by definition. Second, parts (b) and (c) are easily equivalent. Now suppose that
![]() $P$
is non-critical and choose an integer
$P$
is non-critical and choose an integer
![]() $k_{\unicode[STIX]{x1D70F}}$
such that
$k_{\unicode[STIX]{x1D70F}}$
such that
 $D_{\operatorname{cris}}(P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
. Since
$D_{\operatorname{cris}}(P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
. Since
![]() $P$
is crystalline,
$P$
is crystalline,
 $d-i=\dim _{L_{\unicode[STIX]{x1D70F}}}\operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
. Since the Hodge–Tate weights are all distinct we conclude
$d-i=\dim _{L_{\unicode[STIX]{x1D70F}}}\operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
. Since the Hodge–Tate weights are all distinct we conclude
 $\operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=\operatorname{Fil}^{k_{i+1,\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
. This shows that part (a) implies part (b).
$\operatorname{Fil}^{k_{\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}=\operatorname{Fil}^{k_{i+1,\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(D)_{K,\unicode[STIX]{x1D70F}}$
. This shows that part (a) implies part (b).
It remains to show that parts (c) and (d) are equivalent. Since
![]() $D$
has distinct Hodge–Tate weights, the unique lowest weight of
$D$
has distinct Hodge–Tate weights, the unique lowest weight of
![]() $\wedge ^{i}D$
is
$\wedge ^{i}D$
is
 $k_{1,\unicode[STIX]{x1D70F}}+\cdots +k_{i,\unicode[STIX]{x1D70F}}$
. The next highest weight is
$k_{1,\unicode[STIX]{x1D70F}}+\cdots +k_{i,\unicode[STIX]{x1D70F}}$
. The next highest weight is
 $k_{1,\unicode[STIX]{x1D70F}}+\cdots +k_{i-1,\unicode[STIX]{x1D70F}}+k_{i+1,\unicode[STIX]{x1D70F}}$
. Thus, part (c) is true if and only if
$k_{1,\unicode[STIX]{x1D70F}}+\cdots +k_{i-1,\unicode[STIX]{x1D70F}}+k_{i+1,\unicode[STIX]{x1D70F}}$
. Thus, part (c) is true if and only if
 $$\begin{eqnarray}\displaystyle D_{\operatorname{cris}}(\det P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{1,\unicode[STIX]{x1D70F}}+\cdots +k_{i-1,\unicode[STIX]{x1D70F}}+k_{i+1,\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(\wedge ^{i}D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(\wedge ^{i}D)_{K,\unicode[STIX]{x1D70F}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{\operatorname{cris}}(\det P)_{K,\unicode[STIX]{x1D70F}}\oplus \operatorname{Fil}^{k_{1,\unicode[STIX]{x1D70F}}+\cdots +k_{i-1,\unicode[STIX]{x1D70F}}+k_{i+1,\unicode[STIX]{x1D70F}}}D_{\operatorname{cris}}(\wedge ^{i}D)_{K,\unicode[STIX]{x1D70F}}=D_{\operatorname{cris}}(\wedge ^{i}D)_{K,\unicode[STIX]{x1D70F}}, & & \displaystyle \nonumber\end{eqnarray}$$
which is part (d). ◻
At this point, one could define what it means for a triangulation to be non-critical. More generally, for each parabolization
![]() $P_{\bullet }$
of a crystalline
$P_{\bullet }$
of a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module we define a subparabolization
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module we define a subparabolization
 $P_{\bullet }^{\operatorname{nc}}\subset P_{\bullet }$
for which every step is non-critical.
$P_{\bullet }^{\operatorname{nc}}\subset P_{\bullet }$
for which every step is non-critical.
Definition 3.6. Let
![]() $P_{\bullet }$
be a parabolization of a crystalline
$P_{\bullet }$
be a parabolization of a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D$
of rank
$D$
of rank
![]() $d$
. Let
$d$
. Let
 $$\begin{eqnarray}\displaystyle I^{\operatorname{nc}}=\{i:P_{i}\text{ is non-critical}\}=\{0=i_{0}<i_{1}<\cdots <i_{r}=d\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I^{\operatorname{nc}}=\{i:P_{i}\text{ is non-critical}\}=\{0=i_{0}<i_{1}<\cdots <i_{r}=d\}. & & \displaystyle \nonumber\end{eqnarray}$$
The maximal non-critical parabolization
![]() $P_{\bullet }^{\operatorname{nc}}$
is the filtration
$P_{\bullet }^{\operatorname{nc}}$
is the filtration
 $$\begin{eqnarray}\displaystyle P_{\bullet }^{\operatorname{nc}}:0=P_{i_{0}}\subsetneq P_{i_{1}}\subsetneq \cdots \subsetneq P_{i_{r}}=D. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{\bullet }^{\operatorname{nc}}:0=P_{i_{0}}\subsetneq P_{i_{1}}\subsetneq \cdots \subsetneq P_{i_{r}}=D. & & \displaystyle \nonumber\end{eqnarray}$$
We say that
![]() $P_{\bullet }$
is non-critical if
$P_{\bullet }$
is non-critical if
 $P_{\bullet }^{\operatorname{nc}}=P^{\operatorname{nc}}$
, and critical otherwise.
$P_{\bullet }^{\operatorname{nc}}=P^{\operatorname{nc}}$
, and critical otherwise.
Note that, as suggested by our notation,
![]() $I^{\operatorname{nc}}\neq \varnothing$
and
$I^{\operatorname{nc}}\neq \varnothing$
and
![]() $i_{r}=d$
, since
$i_{r}=d$
, since
![]() $D$
itself is always a non-critical
$D$
itself is always a non-critical
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of itself. In the case where
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of itself. In the case where
![]() $D$
has regular weights, Lemma 3.5 shows that
$D$
has regular weights, Lemma 3.5 shows that
![]() $P_{\bullet }^{\operatorname{nc}}$
is the unique subparabolization of
$P_{\bullet }^{\operatorname{nc}}$
is the unique subparabolization of
![]() $P_{\bullet }$
consisting of the steps whose Hodge–Tate weights are as low as possible. Furthermore, it is easy to check that
$P_{\bullet }$
consisting of the steps whose Hodge–Tate weights are as low as possible. Furthermore, it is easy to check that
 $(P_{\bullet }^{\operatorname{nc}})^{\operatorname{nc}}=P_{\bullet }^{\operatorname{nc}}$
, hence the use of the word ‘maximal’. Let us end this subsection with a brief example.
$(P_{\bullet }^{\operatorname{nc}})^{\operatorname{nc}}=P_{\bullet }^{\operatorname{nc}}$
, hence the use of the word ‘maximal’. Let us end this subsection with a brief example.
Example 3.7. Suppose now that
 $K=\mathbf{Q}_{p}$
and that
$K=\mathbf{Q}_{p}$
and that
![]() $D$
is a rank-two crystalline
$D$
is a rank-two crystalline
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{\mathbf{Q}_{p}})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{\mathbf{Q}_{p}})$
-module over
![]() $L$
, with Hodge–Tate weights
$L$
, with Hodge–Tate weights
![]() $k_{1}<k_{2}$
and distinct crystalline eigenvalues
$k_{1}<k_{2}$
and distinct crystalline eigenvalues
 $\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }\in L^{\times }$
. Since
$\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }\in L^{\times }$
. Since
![]() $\unicode[STIX]{x1D719}\neq \unicode[STIX]{x1D719}^{\prime }$
we assume without loss of generality that
$\unicode[STIX]{x1D719}\neq \unicode[STIX]{x1D719}^{\prime }$
we assume without loss of generality that
 $D_{\operatorname{cris}}(D)^{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D719}}\cap \operatorname{Fil}^{k_{2}}D_{\operatorname{cris}}(D)=(0)$
. Thus, there is always a non-critical triangulation
$D_{\operatorname{cris}}(D)^{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D719}}\cap \operatorname{Fil}^{k_{2}}D_{\operatorname{cris}}(D)=(0)$
. Thus, there is always a non-critical triangulation
 ${\mathcal{R}}_{L}(z^{-k_{1}}\operatorname{unr}(\unicode[STIX]{x1D719}))\subset D$
. The ordered parameter is
${\mathcal{R}}_{L}(z^{-k_{1}}\operatorname{unr}(\unicode[STIX]{x1D719}))\subset D$
. The ordered parameter is
 $(z^{-k_{1}}\operatorname{unr}(\unicode[STIX]{x1D719}),z^{-k_{2}}\operatorname{unr}(\unicode[STIX]{x1D719}^{\prime }))$
.
$(z^{-k_{1}}\operatorname{unr}(\unicode[STIX]{x1D719}),z^{-k_{2}}\operatorname{unr}(\unicode[STIX]{x1D719}^{\prime }))$
.
On the other hand, one can use Propositions 3.3 and 2.10 to show that
![]() $D$
is split if and only if
$D$
is split if and only if
 $D_{\operatorname{cris}}(D)^{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D719}^{\prime }}=\operatorname{Fil}^{k_{2}}D_{\operatorname{cris}}(D)$
(if
$D_{\operatorname{cris}}(D)^{\unicode[STIX]{x1D711}=\unicode[STIX]{x1D719}^{\prime }}=\operatorname{Fil}^{k_{2}}D_{\operatorname{cris}}(D)$
(if
![]() $D$
is étale, the same statement follows from the weak admissibility of the filtered
$D$
is étale, the same statement follows from the weak admissibility of the filtered
![]() $\unicode[STIX]{x1D711}$
-module
$\unicode[STIX]{x1D711}$
-module
 $D_{\operatorname{cris}}(D)$
). Thus, the triangulation corresponding to the ordering
$D_{\operatorname{cris}}(D)$
). Thus, the triangulation corresponding to the ordering
![]() $(\unicode[STIX]{x1D719}^{\prime },\unicode[STIX]{x1D719})$
is given by
$(\unicode[STIX]{x1D719}^{\prime },\unicode[STIX]{x1D719})$
is given by
 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}ll@{}}{\mathcal{R}}_{L}(z^{-k_{1}}\operatorname{unr}(\unicode[STIX]{x1D719}^{\prime }))\subset D\quad & \text{if }D\text{ is non-split,}\\ {\mathcal{R}}_{L}(z^{-k_{2}}\operatorname{unr}(\unicode[STIX]{x1D719}^{\prime }))\subset D\quad & \text{if }D\text{ is split.}\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}ll@{}}{\mathcal{R}}_{L}(z^{-k_{1}}\operatorname{unr}(\unicode[STIX]{x1D719}^{\prime }))\subset D\quad & \text{if }D\text{ is non-split,}\\ {\mathcal{R}}_{L}(z^{-k_{2}}\operatorname{unr}(\unicode[STIX]{x1D719}^{\prime }))\subset D\quad & \text{if }D\text{ is split.}\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
This triangulation is critical if and only if
![]() $D$
is split.
$D$
is split.
3.3 Generalized triangulations
Recall that a pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $L$
is a generalized
$L$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module that is either zero or free over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module that is either zero or free over
 ${\mathcal{R}}_{L}/\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}$
for some collection
${\mathcal{R}}_{L}/\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}$
for some collection
![]() $(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
of non-negative integers, not all zero.
$(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
of non-negative integers, not all zero.
Definition 3.8. We say a pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q$
is of character type if either
$Q$
is of character type if either
![]() $Q=0$
or there exists a continuous character
$Q=0$
or there exists a continuous character
 $\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
and a collection of non-negative integers
$\unicode[STIX]{x1D6FF}:K^{\times }\rightarrow L^{\times }$
and a collection of non-negative integers
![]() $(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
, not all zero, such that
$(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
, not all zero, such that
 $Q\simeq \operatorname{coker}((\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}){\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}))$
.
$Q\simeq \operatorname{coker}((\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{\unicode[STIX]{x1D70F}}}){\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}))$
.
If
![]() $Q$
is non-zero and pure torsion of character type, then we refer to the
$Q$
is non-zero and pure torsion of character type, then we refer to the
![]() $\unicode[STIX]{x1D6F4}_{K}$
-tuple
$\unicode[STIX]{x1D6F4}_{K}$
-tuple
 $(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
as the torsion exponents of
$(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
as the torsion exponents of
![]() $Q$
and
$Q$
and
 $(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}))_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
as the torsion weights of
$(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}))_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
as the torsion weights of
![]() $Q$
. The zero module
$Q$
. The zero module
![]() $(0)$
has, by definition, torsion exponents
$(0)$
has, by definition, torsion exponents
 $(0,\ldots ,0)$
and torsion weights
$(0,\ldots ,0)$
and torsion weights
 $(w_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
for any collection of integers
$(w_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}$
for any collection of integers
![]() $w_{\unicode[STIX]{x1D70F}}$
. By Proposition 2.14, these invariants, taken together, completely classify
$w_{\unicode[STIX]{x1D70F}}$
. By Proposition 2.14, these invariants, taken together, completely classify
![]() $Q$
among pure torsion
$Q$
among pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules of character type.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules of character type.
Definition 3.9. Let
![]() $Q$
be a generalized
$Q$
be a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() ${\mathcal{R}}_{L}$
. A generalized triangulation of
${\mathcal{R}}_{L}$
. A generalized triangulation of
![]() $Q$
is a filtration
$Q$
is a filtration
![]() $Q_{\bullet }$
$Q_{\bullet }$
 $$\begin{eqnarray}\displaystyle Q_{\bullet }:0=Q_{0}\subset Q_{1}\subset Q_{2}\subset \cdots \subset Q_{d-1}\subset Q_{d}=Q & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{\bullet }:0=Q_{0}\subset Q_{1}\subset Q_{2}\subset \cdots \subset Q_{d-1}\subset Q_{d}=Q & & \displaystyle \nonumber\end{eqnarray}$$
such that for
 $1\leqslant i\leqslant d$
,
$1\leqslant i\leqslant d$
,
 $Q_{i}/Q_{i-1}$
is either a rank-one
$Q_{i}/Q_{i-1}$
is either a rank-one
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module or a pure torsion
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module or a pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of character type and in either case
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of character type and in either case
 $Q_{i}/Q_{i-1}$
is a direct summand of
$Q_{i}/Q_{i-1}$
is a direct summand of
![]() $Q_{i}$
as a
$Q_{i}$
as a
![]() ${\mathcal{R}}_{L}$
-module. We say that
${\mathcal{R}}_{L}$
-module. We say that
![]() $Q$
is triangulated if it is equipped with a triangulation and trianguline if it may be triangulated, after possibly extending scalars.
$Q$
is triangulated if it is equipped with a triangulation and trianguline if it may be triangulated, after possibly extending scalars.
Note that we allow for consecutive steps
 $Q_{i}\subset Q_{i+1}$
to be equal, since
$Q_{i}\subset Q_{i+1}$
to be equal, since
![]() $(0)$
is a pure torsion
$(0)$
is a pure torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of character type under our definition. This has two consequences. First, even if
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of character type under our definition. This has two consequences. First, even if
![]() $Q$
is a bona fide
$Q$
is a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then a generalized triangulation is not a triangulation in the sense of § 3.1. We will deal with this ambiguity in the definition of standard triangulation below. Second, since we can always repeat steps in a generalized triangulation, the length of a generalized triangulation
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then a generalized triangulation is not a triangulation in the sense of § 3.1. We will deal with this ambiguity in the definition of standard triangulation below. Second, since we can always repeat steps in a generalized triangulation, the length of a generalized triangulation
![]() $Q_{\bullet }$
depends on
$Q_{\bullet }$
depends on
![]() $Q_{\bullet }$
; it is not intrinsic to
$Q_{\bullet }$
; it is not intrinsic to
![]() $Q$
, unlike lengths of triangulations of bona fide
$Q$
, unlike lengths of triangulations of bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. This remains true even if a generalized triangulation
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. This remains true even if a generalized triangulation
![]() $Q_{\bullet }$
is strictly increasing: the length still cannot be read off from
$Q_{\bullet }$
is strictly increasing: the length still cannot be read off from
![]() $Q$
since
$Q$
since
 ${\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70E}}\simeq {\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}\oplus {\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70E}}$
if
${\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70E}}\simeq {\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}\oplus {\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70E}}$
if
![]() $\unicode[STIX]{x1D70E}\neq \unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70E}\neq \unicode[STIX]{x1D70F}$
.
Note that if
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then the torsion submodule
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then the torsion submodule
 $Q_{\operatorname{tor}}=Q[t^{\infty }]\subset Q$
is
$Q_{\operatorname{tor}}=Q[t^{\infty }]\subset Q$
is
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-stable and an
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-stable and an
![]() ${\mathcal{R}}_{L}$
-module summand. The quotient
${\mathcal{R}}_{L}$
-module summand. The quotient
![]() $Q/Q_{\operatorname{tor}}$
is a bona fide
$Q/Q_{\operatorname{tor}}$
is a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module whose rank depends only on
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module whose rank depends only on
![]() $Q$
. We isolate those generalized triangulations which appear in practice.
$Q$
. We isolate those generalized triangulations which appear in practice.
Definition 3.10. If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module and
![]() $Q_{\bullet }$
is a generalized triangulation of
$Q_{\bullet }$
is a generalized triangulation of
![]() $Q$
, then
$Q$
, then
![]() $Q_{\bullet }$
is called a standard triangulation if there exists a
$Q_{\bullet }$
is called a standard triangulation if there exists a
 $0\leqslant i\leqslant d$
such that
$0\leqslant i\leqslant d$
such that
 $Q_{i}=Q_{\operatorname{tor}}$
. The integer
$Q_{i}=Q_{\operatorname{tor}}$
. The integer
![]() $i$
is called the torsion length of
$i$
is called the torsion length of
![]() $Q_{\bullet }$
and the integer
$Q_{\bullet }$
and the integer
![]() $d-i$
is called the free length of
$d-i$
is called the free length of
![]() $Q$
.
$Q$
.
In the definition, the torsion length
![]() $i$
depends on
$i$
depends on
![]() $Q_{\bullet }$
whereas the free length
$Q_{\bullet }$
whereas the free length
![]() $d-i$
depends only on
$d-i$
depends only on
![]() $Q$
(since it is equal to
$Q$
(since it is equal to
 $\operatorname{rank}_{{\mathcal{R}}_{L}}Q/Q_{\operatorname{tor}}$
). And now a standard triangulation is closer to a triangulation in the case where
$\operatorname{rank}_{{\mathcal{R}}_{L}}Q/Q_{\operatorname{tor}}$
). And now a standard triangulation is closer to a triangulation in the case where
![]() $Q$
is a bona fide
$Q$
is a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. Indeed, in that case
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. Indeed, in that case
 $Q_{\operatorname{tor}}=(0)$
and so a standard triangulation is of the form
$Q_{\operatorname{tor}}=(0)$
and so a standard triangulation is of the form
 $$\begin{eqnarray}\displaystyle 0=0=\cdots =0=Q_{i}\subsetneq Q_{i+1}\subsetneq \cdots \subsetneq Q_{d}=Q & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=0=\cdots =0=Q_{i}\subsetneq Q_{i+1}\subsetneq \cdots \subsetneq Q_{d}=Q & & \displaystyle \nonumber\end{eqnarray}$$
where
 $P_{j}:=Q_{i+j}$
defines a triangulation of
$P_{j}:=Q_{i+j}$
defines a triangulation of
![]() $Q$
as in Definition 3.1.
$Q$
as in Definition 3.1.
A standard triangulation of a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module has a number of invariants which we now detail. Suppose that
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module has a number of invariants which we now detail. Suppose that
![]() $Q_{\bullet }$
is a standard triangulation.
$Q_{\bullet }$
is a standard triangulation.
-
∙ The induced generalized triangulation on
 $Q/Q_{\operatorname{tor}}$
is an actual triangulation with ordered parameter
$Q/Q_{\operatorname{tor}}$
is an actual triangulation with ordered parameter
 $(\unicode[STIX]{x1D6FF}_{i+1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
whose length is the free length of
$(\unicode[STIX]{x1D6FF}_{i+1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
whose length is the free length of
 $Q$
.
$Q$
. -
∙ The induced generalized triangulation on
 $Q_{\operatorname{tor}}$
also has invariants. For one, it has its length
$Q_{\operatorname{tor}}$
also has invariants. For one, it has its length
 $i$
. Second, if
$i$
. Second, if
 $1\leqslant j\leqslant i$
then
$1\leqslant j\leqslant i$
then
 $Q_{j}/Q_{j-1}$
is pure torsion of character type and thus has exponents
$Q_{j}/Q_{j-1}$
is pure torsion of character type and thus has exponents
 $(r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
and weights
$(r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
and weights
 $(w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
.
$(w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
.
Note that it may happen that for some
![]() $\unicode[STIX]{x1D70F}$
,
$\unicode[STIX]{x1D70F}$
,
 $r_{j,\unicode[STIX]{x1D70F}}=0$
. For example, if there is an integer
$r_{j,\unicode[STIX]{x1D70F}}=0$
. For example, if there is an integer
![]() $j$
such that
$j$
such that
 $Q_{j}=Q_{j-1}$
, then the corresponding torsion exponents are
$Q_{j}=Q_{j-1}$
, then the corresponding torsion exponents are
![]() $r_{j,\unicode[STIX]{x1D70F}}=0$
for all
$r_{j,\unicode[STIX]{x1D70F}}=0$
for all
![]() $\unicode[STIX]{x1D70F}$
. However, ranging over
$\unicode[STIX]{x1D70F}$
. However, ranging over
![]() $j$
we can a priori predict the frequency at which this happens.
$j$
we can a priori predict the frequency at which this happens.
Definition 3.11. If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then its
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, then its
![]() $\unicode[STIX]{x1D70F}$
-torsion length is defined by
$\unicode[STIX]{x1D70F}$
-torsion length is defined by
 $$\begin{eqnarray}\displaystyle \ell _{\unicode[STIX]{x1D70F}}(Q)=\operatorname{rank}_{{\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}}Q_{\operatorname{tor}}/t_{\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{\unicode[STIX]{x1D70F}}(Q)=\operatorname{rank}_{{\mathcal{R}}_{L}/t_{\unicode[STIX]{x1D70F}}}Q_{\operatorname{tor}}/t_{\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
Fix a
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and a standard triangulation
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and a standard triangulation
![]() $Q_{\bullet }$
of a generalized
$Q_{\bullet }$
of a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with torsion length
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with torsion length
![]() $i$
and exponents
$i$
and exponents
 $((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
. Since the successive quotients of a generalized triangulation are direct summands as
$((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
. Since the successive quotients of a generalized triangulation are direct summands as
![]() ${\mathcal{R}}_{L}$
-modules, it is easy to see that
${\mathcal{R}}_{L}$
-modules, it is easy to see that
 $\ell _{\unicode[STIX]{x1D70F}}(Q)=\#\{j:r_{j,\unicode[STIX]{x1D70F}}\neq 0\}$
and that
$\ell _{\unicode[STIX]{x1D70F}}(Q)=\#\{j:r_{j,\unicode[STIX]{x1D70F}}\neq 0\}$
and that
 $\ell _{\unicode[STIX]{x1D70F}}(Q)\leqslant i$
for all
$\ell _{\unicode[STIX]{x1D70F}}(Q)\leqslant i$
for all
![]() $\unicode[STIX]{x1D70F}$
. To summarize the previous discussion we separate out the following definition.
$\unicode[STIX]{x1D70F}$
. To summarize the previous discussion we separate out the following definition.
Definition 3.12. If
![]() $Q_{\bullet }$
is a standard triangulation of a generalized
$Q_{\bullet }$
is a standard triangulation of a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q$
, then, in the notation above:
$Q$
, then, in the notation above:
-
– the torsion length is the unique integer
 $i\geqslant 1$
such that
$i\geqslant 1$
such that
 $Q_{\operatorname{tor}}=Q_{i}$
;
$Q_{\operatorname{tor}}=Q_{i}$
; -
– the torsion exponents are
 $((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
;
$((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
; -
– the torsion weights are
 $((w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
; and
$((w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
; and -
– the free parameter is the ordered parameter
 $(\unicode[STIX]{x1D6FF}_{j})_{j>i}$
.
$(\unicode[STIX]{x1D6FF}_{j})_{j>i}$
.
If we specify an element
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then we refer to
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then we refer to
 $(r_{j,\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
and
$(r_{j,\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
and
 $(w_{j,\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
as the
$(w_{j,\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
as the
![]() $\unicode[STIX]{x1D70F}$
-torsion exponents and
$\unicode[STIX]{x1D70F}$
-torsion exponents and
![]() $\unicode[STIX]{x1D70F}$
-torsion weights.
$\unicode[STIX]{x1D70F}$
-torsion weights.
Finally, we finish this section with a result that explains how standard triangulations of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules are inherently more flexible than triangulations of bona fide
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules are inherently more flexible than triangulations of bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Recall that we defined the notion of homothety among continuous characters of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Recall that we defined the notion of homothety among continuous characters of
![]() $K^{\times }$
at the end of § 2.5.
$K^{\times }$
at the end of § 2.5.
Proposition 3.13. Suppose that
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module,
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module,
![]() $Q_{\bullet }$
is a standard triangulation of torsion length
$Q_{\bullet }$
is a standard triangulation of torsion length
![]() $i$
with torsion exponents
$i$
with torsion exponents
 $((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
, torsion weights
$((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
, torsion weights
 $((w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
and free parameter
$((w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i}$
and free parameter
![]() $(\unicode[STIX]{x1D6FF}_{j})_{j>i}$
. Assume furthermore that
$(\unicode[STIX]{x1D6FF}_{j})_{j>i}$
. Assume furthermore that
![]() $\unicode[STIX]{x1D6FF}_{i+1}$
is not homothetic to
$\unicode[STIX]{x1D6FF}_{i+1}$
is not homothetic to
![]() $\unicode[STIX]{x1D6FF}_{j}$
for
$\unicode[STIX]{x1D6FF}_{j}$
for
 $j>i+1$
.
$j>i+1$
.
Then, for every
![]() $\unicode[STIX]{x1D6F4}_{K}$
-tuple
$\unicode[STIX]{x1D6F4}_{K}$
-tuple
 $(r_{i+1,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
of non-negative integers such that
$(r_{i+1,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
of non-negative integers such that
 $$\begin{eqnarray}\displaystyle j\leqslant i\;\Longrightarrow \;w_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i+1})\notin \{-r_{i+1,\unicode[STIX]{x1D70F}},\ldots ,r_{j,\unicode[STIX]{x1D70F}}-r_{i+1,\unicode[STIX]{x1D70F}}-1\}=\{-r_{i+1,\unicode[STIX]{x1D70F}}+m:0\leqslant m<r_{j,\unicode[STIX]{x1D70F}}\}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle j\leqslant i\;\Longrightarrow \;w_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i+1})\notin \{-r_{i+1,\unicode[STIX]{x1D70F}},\ldots ,r_{j,\unicode[STIX]{x1D70F}}-r_{i+1,\unicode[STIX]{x1D70F}}-1\}=\{-r_{i+1,\unicode[STIX]{x1D70F}}+m:0\leqslant m<r_{j,\unicode[STIX]{x1D70F}}\}, & & \displaystyle \nonumber\end{eqnarray}$$
there exists a unique (up to scalar) inclusion
 $\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1}){\hookrightarrow}Q$
. Its cokernel is a generalized
$\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1}){\hookrightarrow}Q$
. Its cokernel is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module which is naturally equipped with a standard triangulation having invariants:
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module which is naturally equipped with a standard triangulation having invariants:
-
– torsion length
 $i+1$
;
$i+1$
; -
– torsion exponents
 $((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{j\leqslant i+1}$
;
$((r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{j\leqslant i+1}$
; -
– torsion weights
 $((w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{j\leqslant i}\cup (\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i+1}))_{\unicode[STIX]{x1D70F}}$
; and
$((w_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{j\leqslant i}\cup (\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i+1}))_{\unicode[STIX]{x1D70F}}$
; and -
– free parameter
 $(\unicode[STIX]{x1D6FF}_{j})_{j>i+1}$
.
$(\unicode[STIX]{x1D6FF}_{j})_{j>i+1}$
.
Proof. Let
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{i+1}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}$
. For each
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{i+1}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}$
. For each
![]() $j\leqslant i$
we choose a character
$j\leqslant i$
we choose a character
![]() $\unicode[STIX]{x1D6FF}_{j}$
whose
$\unicode[STIX]{x1D6FF}_{j}$
whose
![]() $\unicode[STIX]{x1D70F}$
-weight is
$\unicode[STIX]{x1D70F}$
-weight is
![]() $w_{j,\unicode[STIX]{x1D70F}}$
and so that
$w_{j,\unicode[STIX]{x1D70F}}$
and so that
 $Q_{j}/Q_{j-1}\simeq {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{j})/\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{j,\unicode[STIX]{x1D70F}}}$
. We quickly calculate
$Q_{j}/Q_{j-1}\simeq {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{j})/\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{j,\unicode[STIX]{x1D70F}}}$
. We quickly calculate
 $$\begin{eqnarray}\displaystyle \operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j}\unicode[STIX]{x1D6FF}^{-1})=w_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i+1})+r_{i+1,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j}\unicode[STIX]{x1D6FF}^{-1})=w_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i+1})+r_{i+1,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
By our assumptions,
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j}\unicode[STIX]{x1D6FF}^{-1})\notin \{0,1,\ldots ,r_{j,\unicode[STIX]{x1D70F}}-1\}$
for each
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j}\unicode[STIX]{x1D6FF}^{-1})\notin \{0,1,\ldots ,r_{j,\unicode[STIX]{x1D70F}}-1\}$
for each
![]() $\unicode[STIX]{x1D70F}$
. Using Proposition 2.14 we see that
$\unicode[STIX]{x1D70F}$
. Using Proposition 2.14 we see that
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q_{j}/Q_{j-1})=H^{0}\biggl(\biggl({\mathcal{R}}_{L}/\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{j,\unicode[STIX]{x1D70F}}}\biggr)(\unicode[STIX]{x1D6FF}_{j}\unicode[STIX]{x1D6FF}^{-1})\biggr)=(0). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q_{j}/Q_{j-1})=H^{0}\biggl(\biggl({\mathcal{R}}_{L}/\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{j,\unicode[STIX]{x1D70F}}}\biggr)(\unicode[STIX]{x1D6FF}_{j}\unicode[STIX]{x1D6FF}^{-1})\biggr)=(0). & & \displaystyle \nonumber\end{eqnarray}$$
By induction on
 $1\leqslant j\leqslant i$
we see that
$1\leqslant j\leqslant i$
we see that
 $\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q_{i})=(0)$
. Since
$\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q_{i})=(0)$
. Since
![]() $Q_{i}$
is torsion, the Euler–Poincaré formula for torsion modules implies
$Q_{i}$
is torsion, the Euler–Poincaré formula for torsion modules implies
 $H^{1}(Q_{i}(\unicode[STIX]{x1D6FF}^{-1}))=(0)$
as well. We deduce from the long exact sequence in cohomology that the natural map
$H^{1}(Q_{i}(\unicode[STIX]{x1D6FF}^{-1}))=(0)$
as well. We deduce from the long exact sequence in cohomology that the natural map
 $\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q)\rightarrow \operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q/Q_{i})$
is an isomorphism.
$\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q)\rightarrow \operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q/Q_{i})$
is an isomorphism.
On the other hand,
![]() $Q/Q_{i}$
is triangulated by a parameter
$Q/Q_{i}$
is triangulated by a parameter
 $(\unicode[STIX]{x1D6FF}_{i+1},\ldots )$
whose higher terms are not homothetic to
$(\unicode[STIX]{x1D6FF}_{i+1},\ldots )$
whose higher terms are not homothetic to
![]() $\unicode[STIX]{x1D6FF}_{i+1}$
. From that we deduce that the inclusion
$\unicode[STIX]{x1D6FF}_{i+1}$
. From that we deduce that the inclusion
 $\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})){\hookrightarrow}\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q/Q_{i})$
is an isomorphism also. Putting the two calculations together, we see that
$\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})){\hookrightarrow}\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q/Q_{i})$
is an isomorphism also. Putting the two calculations together, we see that
 $$\begin{eqnarray}\displaystyle \dim _{L}\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q)=\dim _{L}\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1}))=1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim _{L}\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),Q)=\dim _{L}\operatorname{Hom}({\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}),{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1}))=1. & & \displaystyle \nonumber\end{eqnarray}$$
This shows that the morphism in the lemma exists and is unique up to a scalar.
But, the calculation shows more. We have shown in fact that any non-zero morphism
 $e:{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow Q$
factors through
$e:{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow Q$
factors through
![]() $Q_{i+1}$
and that
$Q_{i+1}$
and that
![]() $e$
remains non-zero when mapped into the quotient
$e$
remains non-zero when mapped into the quotient
 ${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})$
of
${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})$
of
![]() $Q_{i+1}$
. Since both
$Q_{i+1}$
. Since both
![]() ${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
and
${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
and
 ${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})$
are rank one,
${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})$
are rank one,
![]() $e$
must be injective and it induces an exact sequence
$e$
must be injective and it induces an exact sequence
 $$\begin{eqnarray}0\rightarrow Q_{i}\rightarrow Q_{i+1}/{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})/{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Q_{i}\rightarrow Q_{i+1}/{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})/{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})\rightarrow 0.\end{eqnarray}$$
Since
 ${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})$
is a direct summand of
${\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})$
is a direct summand of
![]() $Q_{i+1}$
as a
$Q_{i+1}$
as a
![]() ${\mathcal{R}}_{L}$
-module, the sequence (3) is also split as a sequence of
${\mathcal{R}}_{L}$
-module, the sequence (3) is also split as a sequence of
![]() ${\mathcal{R}}_{L}$
-modules. This means that the standard triangulation
${\mathcal{R}}_{L}$
-modules. This means that the standard triangulation
![]() $Q_{\bullet }$
on
$Q_{\bullet }$
on
![]() $Q$
induces a standard triangulation
$Q$
induces a standard triangulation
![]() $Q_{\bullet }^{\prime }$
on
$Q_{\bullet }^{\prime }$
on
 $Q/{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
whose successive quotients are given by
$Q/{\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF})$
whose successive quotients are given by
 $$\begin{eqnarray}\displaystyle Q_{j}^{\prime }/Q_{j-1}^{\prime }=\left\{\begin{array}{@{}ll@{}}Q_{j}/Q_{j-1}\quad & \text{if }j\neq i+1,\\ {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})/\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}\quad & \text{if }j=i+1.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{j}^{\prime }/Q_{j-1}^{\prime }=\left\{\begin{array}{@{}ll@{}}Q_{j}/Q_{j-1}\quad & \text{if }j\neq i+1,\\ {\mathcal{R}}_{L}(\unicode[STIX]{x1D6FF}_{i+1})/\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}\quad & \text{if }j=i+1.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
The invariants are of the new standard triangulation are easily calculated from this. ◻
Note that one can always find infinitely many such integers
![]() $r_{i+1,\unicode[STIX]{x1D70F}}$
which satisfy the hypotheses of the proposition. Also note that if
$r_{i+1,\unicode[STIX]{x1D70F}}$
which satisfy the hypotheses of the proposition. Also note that if
 $r_{i+1,\unicode[STIX]{x1D70F}}=0$
for all
$r_{i+1,\unicode[STIX]{x1D70F}}=0$
for all
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then the standard triangulation we just produced will have two consecutive steps which are equal.
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then the standard triangulation we just produced will have two consecutive steps which are equal.
4 Galois cohomology in families
In this short section we expand on § 2.5. In particular, we recall the main results of [Reference Kedlaya, Pottharst and XiaoKPX14] and develop a simple cohomology and base change framework for generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. The framework will be applied in §§ 5 and 6. Throughout this section we will let
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. The framework will be applied in §§ 5 and 6. Throughout this section we will let
![]() $A$
be a reduced affinoid
$A$
be a reduced affinoid
![]() $L$
-algebra and
$L$
-algebra and
 $X=\operatorname{Sp}(A)$
.
$X=\operatorname{Sp}(A)$
.
Suppose that
 $N_{\bullet }=[\cdots \rightarrow N_{1}\rightarrow N_{0}]$
is a complex of
$N_{\bullet }=[\cdots \rightarrow N_{1}\rightarrow N_{0}]$
is a complex of
![]() $A$
-modules and
$A$
-modules and
![]() $M$
is an
$M$
is an
![]() $A$
-module such that
$A$
-module such that
 $\operatorname{Tor}_{j}^{A}(N_{p},M)=(0)$
for each
$\operatorname{Tor}_{j}^{A}(N_{p},M)=(0)$
for each
![]() $j\geqslant 1$
and
$j\geqslant 1$
and
![]() $p\geqslant 0$
. Then the Künneth spectral sequence, see [Reference WeibelWei94, Theorem 5.6.4], is a first quadrant spectral sequence
$p\geqslant 0$
. Then the Künneth spectral sequence, see [Reference WeibelWei94, Theorem 5.6.4], is a first quadrant spectral sequence
 $$\begin{eqnarray}\displaystyle E_{pq}^{2}=\operatorname{Tor}_{p}^{A}(H_{q}(N_{\bullet }),M)\Rightarrow H_{p+q}(N_{\bullet }\otimes _{A}M). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{pq}^{2}=\operatorname{Tor}_{p}^{A}(H_{q}(N_{\bullet }),M)\Rightarrow H_{p+q}(N_{\bullet }\otimes _{A}M). & & \displaystyle \nonumber\end{eqnarray}$$
Definition 4.1. An
![]() $A$
-module
$A$
-module
![]() $Q$
is called nearly flat if
$Q$
is called nearly flat if
 $\operatorname{Tor}_{j}^{A}(Q,L(x))=(0)$
for all
$\operatorname{Tor}_{j}^{A}(Q,L(x))=(0)$
for all
![]() $j\geqslant 1$
and
$j\geqslant 1$
and
 $x\in \operatorname{Sp}(A)$
.
$x\in \operatorname{Sp}(A)$
.
Recall that if
 $x\in X(\overline{\mathbf{Q}}_{p})$
and
$x\in X(\overline{\mathbf{Q}}_{p})$
and
![]() $Q$
is an
$Q$
is an
![]() $A$
-module, then
$A$
-module, then
![]() $Q_{x}$
denotes the fiber
$Q_{x}$
denotes the fiber
 $Q\otimes _{A}L(x)$
.
$Q\otimes _{A}L(x)$
.
Proposition 4.2. If
![]() $Q$
is a nearly flat generalized
$Q$
is a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
, then there is a first quadrant spectral sequence
$A$
, then there is a first quadrant spectral sequence
 $$\begin{eqnarray}\displaystyle \operatorname{Tor}_{p}^{A}(H^{2-q}(Q),L(x))\Rightarrow H^{2-(p+q)}(Q_{x}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Tor}_{p}^{A}(H^{2-q}(Q),L(x))\Rightarrow H^{2-(p+q)}(Q_{x}) & & \displaystyle \nonumber\end{eqnarray}$$
which degenerates on the
![]() $E^{3}$
-page.
$E^{3}$
-page.
Proof. We apply the Künneth spectral sequence to
 $M=L(x)$
and the three-term Herr complex
$M=L(x)$
and the three-term Herr complex
 $C_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FE}_{K}}^{\bullet }(Q)$
, after making the obvious shift between homology and cohomology. The hypothesis in the Künneth spectral sequence is valid since
$C_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FE}_{K}}^{\bullet }(Q)$
, after making the obvious shift between homology and cohomology. The hypothesis in the Künneth spectral sequence is valid since
![]() $Q$
is nearly flat and each term of
$Q$
is nearly flat and each term of
 $C_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FE}_{K}}^{\bullet }(Q)$
is a direct sum of finitely many copies of
$C_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FE}_{K}}^{\bullet }(Q)$
is a direct sum of finitely many copies of
![]() $Q$
, if
$Q$
, if
![]() $p$
is odd. If
$p$
is odd. If
![]() $p=2$
, then each term of
$p=2$
, then each term of
 $C_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FE}_{K}}^{\bullet }(Q)$
is actually a direct sum of finitely many copies of
$C_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FE}_{K}}^{\bullet }(Q)$
is actually a direct sum of finitely many copies of
![]() $Q^{\unicode[STIX]{x1D6E5}_{K}}$
, itself a direct summand of
$Q^{\unicode[STIX]{x1D6E5}_{K}}$
, itself a direct summand of
![]() $Q$
(we thank the anonymous referee for this precision).
$Q$
(we thank the anonymous referee for this precision).
As an aid to the reader, let us explicitly write out the
![]() $E^{2}$
-page of the spectral sequence.
$E^{2}$
-page of the spectral sequence.

The arrows drawn are the differentials. Now it is clear that the spectral sequence stabilizes on the
![]() $E^{3}$
-page since the differentials there and afterwards are all zero.◻
$E^{3}$
-page since the differentials there and afterwards are all zero.◻
Proposition 4.3. Suppose
![]() $f\in {\mathcal{R}}_{L}$
is not a zero divisor. If
$f\in {\mathcal{R}}_{L}$
is not a zero divisor. If
![]() $Q$
is a nearly flat generalized
$Q$
is a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
, then for each
$A$
, then for each
![]() $x\in X$
:
$x\in X$
:
-
(a) there is a four term exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow \operatorname{Tor}_{2}^{A}(Q/f,L(x))\rightarrow Q[f]\otimes _{A}L(x)\rightarrow Q_{x}[f]\rightarrow \operatorname{Tor}_{1}^{A}(Q/f,L(x))\rightarrow 0; & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow \operatorname{Tor}_{2}^{A}(Q/f,L(x))\rightarrow Q[f]\otimes _{A}L(x)\rightarrow Q_{x}[f]\rightarrow \operatorname{Tor}_{1}^{A}(Q/f,L(x))\rightarrow 0; & & \displaystyle \nonumber\end{eqnarray}$$
-
(b) if
 $i\geqslant 1$
, then
$i\geqslant 1$
, then
 $\operatorname{Tor}_{i+2}^{A}(Q/f,L(x))\simeq \operatorname{Tor}_{i}^{A}(Q[f],L(x))$
.
$\operatorname{Tor}_{i+2}^{A}(Q/f,L(x))\simeq \operatorname{Tor}_{i}^{A}(Q[f],L(x))$
.
Proof. Consider the complex
![]() $N_{\bullet }$
of
$N_{\bullet }$
of
![]() ${\mathcal{R}}_{A}$
-modules given by
${\mathcal{R}}_{A}$
-modules given by
 $N_{\bullet }=[Q\overset{f}{\longrightarrow }Q]$
and its base change
$N_{\bullet }=[Q\overset{f}{\longrightarrow }Q]$
and its base change
 $N_{\bullet ,x}=[Q_{x}\overset{f}{\longrightarrow }Q_{x}]$
to
$N_{\bullet ,x}=[Q_{x}\overset{f}{\longrightarrow }Q_{x}]$
to
![]() $x\in X$
. Apply the Künneth spectral sequence again with
$x\in X$
. Apply the Künneth spectral sequence again with
 $M=L(x)$
. The homology groups are
$M=L(x)$
. The homology groups are
 $H_{0}(N_{\bullet })=Q/fQ$
and
$H_{0}(N_{\bullet })=Q/fQ$
and
 $H_{1}(N_{\bullet })=Q[f]$
and vanish in degree
$H_{1}(N_{\bullet })=Q[f]$
and vanish in degree
![]() $i\geqslant 2$
(the same for
$i\geqslant 2$
(the same for
![]() $N_{\bullet ,x}$
). From the spectral sequence we get for all
$N_{\bullet ,x}$
). From the spectral sequence we get for all
![]() $i\geqslant 2$
a short exact sequence
$i\geqslant 2$
a short exact sequence
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle \operatorname{coker}(\operatorname{Tor}_{i+1}^{A}(Q/f,L(x))\rightarrow \operatorname{Tor}_{i-1}^{A}(Q[f],L(x)))\rightarrow H_{i}(N_{\bullet ,x})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \ker (\operatorname{Tor}_{i}^{A}(Q/f,L(x))\rightarrow \operatorname{Tor}_{i-2}^{A}(Q[f],L(x)))\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle \operatorname{coker}(\operatorname{Tor}_{i+1}^{A}(Q/f,L(x))\rightarrow \operatorname{Tor}_{i-1}^{A}(Q[f],L(x)))\rightarrow H_{i}(N_{\bullet ,x})\nonumber\\ \displaystyle & \rightarrow & \displaystyle \ker (\operatorname{Tor}_{i}^{A}(Q/f,L(x))\rightarrow \operatorname{Tor}_{i-2}^{A}(Q[f],L(x)))\rightarrow 0.\nonumber\end{eqnarray}$$
The middle term vanishes since
![]() $i\geqslant 2$
and thus by induction we see part (b) is true and that
$i\geqslant 2$
and thus by induction we see part (b) is true and that
 $\operatorname{Tor}_{2}^{A}(Q/f,L(x)){\hookrightarrow}Q[f]\otimes _{A}L(x)$
, making the sequence in part (a) exact on the left. The spectral sequence taken when
$\operatorname{Tor}_{2}^{A}(Q/f,L(x)){\hookrightarrow}Q[f]\otimes _{A}L(x)$
, making the sequence in part (a) exact on the left. The spectral sequence taken when
 $p+q=1$
gives a short exact sequence
$p+q=1$
gives a short exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow \operatorname{coker}(\operatorname{Tor}_{2}^{A}(Q/f,L(x))\rightarrow Q[f]\otimes _{A}L(x))\rightarrow Q_{x}[f]\rightarrow \operatorname{Tor}_{1}^{A}(Q/f,L(x))\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow \operatorname{coker}(\operatorname{Tor}_{2}^{A}(Q/f,L(x))\rightarrow Q[f]\otimes _{A}L(x))\rightarrow Q_{x}[f]\rightarrow \operatorname{Tor}_{1}^{A}(Q/f,L(x))\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
which shows the rest of part (a). ◻
Following these two general base change theorems we can begin to set up a cohomology and base change framework. Recall from the end of § 2.1 that if
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $X$
and
$X$
and
 $U=\operatorname{Sp}(B)\subset X$
is an admissible open affinoid subdomain, then
$U=\operatorname{Sp}(B)\subset X$
is an admissible open affinoid subdomain, then
 $Q|_{U}:=Q\otimes _{{\mathcal{R}}_{X}}{\mathcal{R}}_{U}$
.
$Q|_{U}:=Q\otimes _{{\mathcal{R}}_{X}}{\mathcal{R}}_{U}$
.
Definition 4.4. If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
, then we say
$A$
, then we say
![]() $Q$
has finite cohomology if for every affinoid subdomain
$Q$
has finite cohomology if for every affinoid subdomain
 $U=\operatorname{Sp}(B)\subset X$
,
$U=\operatorname{Sp}(B)\subset X$
,
 $H^{i}(Q|_{U})$
is a finite
$H^{i}(Q|_{U})$
is a finite
![]() $B$
-module for
$B$
-module for
 $i=0,1,2$
.
$i=0,1,2$
.
Remark.
If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
with finite cohomology, then
$A$
with finite cohomology, then
![]() $Q|_{U}$
is a generalized
$Q|_{U}$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $B$
with finite cohomology for all affinoid subdomains
$B$
with finite cohomology for all affinoid subdomains
 $U=\operatorname{Sp}(B)\subset X$
.
$U=\operatorname{Sp}(B)\subset X$
.
Theorem 4.5 (Kedlaya–Pottharst–Xiao).
If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
, then
$A$
, then
![]() $Q$
has finite cohomology in the following situations:
$Q$
has finite cohomology in the following situations:
-
(a)
 $Q$
is a
$Q$
is a
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module;
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module; -
(b)
 $Q$
is of the form
$Q$
is of the form
 $\operatorname{coker}(Q_{1}\overset{e}{{\hookrightarrow}}Q_{2})$
where both
$\operatorname{coker}(Q_{1}\overset{e}{{\hookrightarrow}}Q_{2})$
where both
 $Q_{1}$
and
$Q_{1}$
and
 $Q_{2}$
have finite cohomology and
$Q_{2}$
have finite cohomology and
 $e$
is
$e$
is
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant.
Proof. If
![]() $Q$
is a bona fide
$Q$
is a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $X$
, then it is also a bona fide
$X$
, then it is also a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $U$
and thus each cohomology group
$U$
and thus each cohomology group
 $H^{i}(Q|_{U})$
is a finite
$H^{i}(Q|_{U})$
is a finite
![]() $B$
-module by the main theorem of [Reference Kedlaya, Pottharst and XiaoKPX14].
$B$
-module by the main theorem of [Reference Kedlaya, Pottharst and XiaoKPX14].
Now suppose that
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
have finite cohomology and that
$Q_{2}$
have finite cohomology and that
 $e:Q_{1}\rightarrow Q_{2}$
is an injective
$e:Q_{1}\rightarrow Q_{2}$
is an injective
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant map. Since
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant map. Since
![]() $U\subset X$
is an affinoid subdomain, Proposition 2.7 implies that we have a short exact sequence of generalized
$U\subset X$
is an affinoid subdomain, Proposition 2.7 implies that we have a short exact sequence of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $U$
$U$
 $$\begin{eqnarray}0\rightarrow Q_{1}|_{U}\rightarrow Q_{2}|_{U}\rightarrow Q|_{U}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Q_{1}|_{U}\rightarrow Q_{2}|_{U}\rightarrow Q|_{U}\rightarrow 0.\end{eqnarray}$$
The finiteness of each
 $H^{i}(Q|_{U})$
as a
$H^{i}(Q|_{U})$
as a
![]() $B$
-module now follows from the finiteness each
$B$
-module now follows from the finiteness each
 $H^{i}(Q_{j}|_{U})$
(
$H^{i}(Q_{j}|_{U})$
(
 $i=0,1,2$
and
$i=0,1,2$
and
 $j=1,2$
) and the long exact sequence in cohomology associated to the sequence (5). ◻
$j=1,2$
) and the long exact sequence in cohomology associated to the sequence (5). ◻
If
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $A$
, then we define functions on
$A$
, then we define functions on
![]() $X$
by the formula
$X$
by the formula
 $$\begin{eqnarray}\displaystyle d_{Q}^{i}(x):=\dim _{L(x)}H^{i}(Q_{x}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{Q}^{i}(x):=\dim _{L(x)}H^{i}(Q_{x}). & & \displaystyle \nonumber\end{eqnarray}$$
Note that the fiber is taken prior to taking cohomology.
If
![]() $Q$
has finite cohomology, then Nakayama’s lemma, together with the fact that affinoid algebras are Jacobson [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.1.1/3], implies that
$Q$
has finite cohomology, then Nakayama’s lemma, together with the fact that affinoid algebras are Jacobson [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.1.1/3], implies that
 $x\mapsto \dim _{L(x)}H^{i}(Q)\otimes _{A}L(x)$
is upper semi-continuous on
$x\mapsto \dim _{L(x)}H^{i}(Q)\otimes _{A}L(x)$
is upper semi-continuous on
![]() $X$
and, since
$X$
and, since
![]() $X$
is reduced, locally constant if and only if
$X$
is reduced, locally constant if and only if
![]() $H^{i}(Q)$
is flat. For
$H^{i}(Q)$
is flat. For
![]() $i$
fixed, we will say that
$i$
fixed, we will say that
![]() $H^{i}(Q)$
satisfies base change if the natural map
$H^{i}(Q)$
satisfies base change if the natural map
 $H^{i}(Q)\otimes _{A}L(x)\rightarrow H^{i}(Q_{x})$
is an isomorphism for all
$H^{i}(Q)\otimes _{A}L(x)\rightarrow H^{i}(Q_{x})$
is an isomorphism for all
![]() $x\in X$
.
$x\in X$
.
Proposition 4.6. If
![]() $Q$
is a nearly flat generalized
$Q$
is a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with finite cohomology and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with finite cohomology and
 $x\mapsto d_{Q}^{i}(x)$
is locally constant for
$x\mapsto d_{Q}^{i}(x)$
is locally constant for
![]() $i\geqslant k$
, then
$i\geqslant k$
, then
![]() $H^{i}(Q)$
is flat over
$H^{i}(Q)$
is flat over
![]() $X$
for
$X$
for
![]() $i\geqslant k$
and satisfies base change for
$i\geqslant k$
and satisfies base change for
 $i\geqslant k-1$
.
$i\geqslant k-1$
.
Proof. One argues by descending induction on
![]() $k$
. Since the cohomology vanishes in degrees
$k$
. Since the cohomology vanishes in degrees
![]() $k\geqslant 3$
, the proposition is vacuous for
$k\geqslant 3$
, the proposition is vacuous for
![]() $k\geqslant 4$
. When
$k\geqslant 4$
. When
![]() $k=3$
,
$k=3$
,
![]() $H^{2}(Q)$
is a cokernel, by definition, and thus always satisfies base change.
$H^{2}(Q)$
is a cokernel, by definition, and thus always satisfies base change.
Fix
![]() $k\leqslant 2$
and assume the result is true for
$k\leqslant 2$
and assume the result is true for
![]() $k+1$
. Since the hypotheses for
$k+1$
. Since the hypotheses for
![]() $k$
imply those of
$k$
imply those of
![]() $k+1$
, the induction hypothesis implies that
$k+1$
, the induction hypothesis implies that
![]() $H^{k}(Q)$
satisfies base change. By assumption,
$H^{k}(Q)$
satisfies base change. By assumption,
![]() $d_{Q}^{k}(x)$
is locally constant. Since
$d_{Q}^{k}(x)$
is locally constant. Since
![]() $X$
is reduced, Nakayama’s lemma implies that
$X$
is reduced, Nakayama’s lemma implies that
![]() $H^{k}(Q)$
is flat over
$H^{k}(Q)$
is flat over
![]() $X$
. The fact that
$X$
. The fact that
 $H^{k-1}(Q)$
satisfies base change now follows from Proposition 4.2.◻
$H^{k-1}(Q)$
satisfies base change now follows from Proposition 4.2.◻
Recall that if
![]() $X$
is a reduced rigid space and
$X$
is a reduced rigid space and
 $x_{0}\in X(\overline{\mathbf{Q}}_{p})$
then a subset
$x_{0}\in X(\overline{\mathbf{Q}}_{p})$
then a subset
 $Z\subset X(\overline{\mathbf{Q}}_{p})$
is said to accumulate at
$Z\subset X(\overline{\mathbf{Q}}_{p})$
is said to accumulate at
![]() $x_{0}$
if there exists a neighborhood basis of affinoid neighborhoods
$x_{0}$
if there exists a neighborhood basis of affinoid neighborhoods
![]() $U$
of
$U$
of
![]() $x_{0}$
such that
$x_{0}$
such that
![]() $Z\cap U$
is Zariski-dense in
$Z\cap U$
is Zariski-dense in
![]() $U$
for all
$U$
for all
![]() $U$
.
$U$
.
Corollary 4.7. Let
![]() $Q$
be a nearly flat generalized
$Q$
be a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with finite cohomology. If
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module with finite cohomology. If
![]() $x\in X$
and there exists a Zariski-dense subset
$x\in X$
and there exists a Zariski-dense subset
 $Z\subset X(\overline{\mathbf{Q}}_{p})$
accumulating at
$Z\subset X(\overline{\mathbf{Q}}_{p})$
accumulating at
![]() $x$
such that, for each
$x$
such that, for each
 $0\leqslant i\leqslant 2$
,
$0\leqslant i\leqslant 2$
,
 $d_{Q}^{i}(x)=d_{Q}^{i}(u)$
for all
$d_{Q}^{i}(x)=d_{Q}^{i}(u)$
for all
![]() $u\in Z$
, then
$u\in Z$
, then
 $H^{i}(Q|_{U})$
is flat and satisfies base change for
$H^{i}(Q|_{U})$
is flat and satisfies base change for
 $0\leqslant i\leqslant 2$
for all sufficiently small affinoid subdomains
$0\leqslant i\leqslant 2$
for all sufficiently small affinoid subdomains
 $x\in U\subset X$
.
$x\in U\subset X$
.
Proof. We have that
![]() $H^{2}(Q)$
always satisfies base change, whence
$H^{2}(Q)$
always satisfies base change, whence
 $u\mapsto d_{Q}^{2}(u)$
is upper semi-continuous on
$u\mapsto d_{Q}^{2}(u)$
is upper semi-continuous on
![]() $X$
. Since
$X$
. Since
![]() $Z$
is Zariski-dense, and
$Z$
is Zariski-dense, and
 $d_{Q}^{2}(x)=d_{Q}^{2}(u)$
for
$d_{Q}^{2}(x)=d_{Q}^{2}(u)$
for
![]() $u\in Z$
, we may shrink
$u\in Z$
, we may shrink
![]() $X$
and assume that
$X$
and assume that
![]() $d_{Q}^{2}(-)$
is constant on
$d_{Q}^{2}(-)$
is constant on
![]() $X$
. It follows from Proposition 4.6 that
$X$
. It follows from Proposition 4.6 that
![]() $H^{2}(Q)$
is flat and
$H^{2}(Q)$
is flat and
![]() $H^{1}(Q)$
satisfies base change. By assumption on
$H^{1}(Q)$
satisfies base change. By assumption on
![]() $Z$
accumulating at
$Z$
accumulating at
![]() $X$
, the hypotheses of the proposition remain true after we have shrunk
$X$
, the hypotheses of the proposition remain true after we have shrunk
![]() $X$
. Thus, we may re-do the same proof to show the result for
$X$
. Thus, we may re-do the same proof to show the result for
![]() $i=1$
and then
$i=1$
and then
![]() $i=0$
.◻
$i=0$
.◻
5 Triangulated families
Here we introduce triangulated families: families of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules which point-by-point have a triangulation. They are not the most natural families to consider, as the data are given pointwise, but they will be a useful intermediary for Theorem 6.8. Throughout this section we write
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules which point-by-point have a triangulation. They are not the most natural families to consider, as the data are given pointwise, but they will be a useful intermediary for Theorem 6.8. Throughout this section we write
 $X=\operatorname{Sp}(A)$
for a reduced rigid analytic affinoid space over
$X=\operatorname{Sp}(A)$
for a reduced rigid analytic affinoid space over
![]() $L$
.
$L$
.
5.1 Triangulated families
Definition 5.1. A pointwise triangulated family of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules with torsion centered at
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules with torsion centered at
![]() $x_{0}\in X$
is:
$x_{0}\in X$
is:
-
– a generalized
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
 $Q$
over
$Q$
over
 $X$
;
$X$
; -
– an ordered tuple
 $((s_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant d}$
of integers (called the torsion weights);
$((s_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant d}$
of integers (called the torsion weights); -
– an ordered tuple
 $(\unicode[STIX]{x1D6FF}_{j})_{1\leqslant j\leqslant d}$
of continuous characters
$(\unicode[STIX]{x1D6FF}_{j})_{1\leqslant j\leqslant d}$
of continuous characters
 $\unicode[STIX]{x1D6FF}_{j}:K^{\times }\rightarrow \unicode[STIX]{x1D6E4}(X,{\mathcal{O}})^{\times }$
(called the parameter);
$\unicode[STIX]{x1D6FF}_{j}:K^{\times }\rightarrow \unicode[STIX]{x1D6E4}(X,{\mathcal{O}})^{\times }$
(called the parameter); -
– a Zariski-dense set of points
 $X^{\operatorname{nc}}\subset X(\overline{\mathbf{Q}}_{p})$
(called the non-critical points);
$X^{\operatorname{nc}}\subset X(\overline{\mathbf{Q}}_{p})$
(called the non-critical points); -
– a point
 $x_{0}\in X(\overline{\mathbf{Q}}_{p})$
(called the center);
$x_{0}\in X(\overline{\mathbf{Q}}_{p})$
(called the center);
subject to the following.
-
(TF1) If
 $y\in X^{\operatorname{nc}}\cup \{x_{0}\}$
, then
$y\in X^{\operatorname{nc}}\cup \{x_{0}\}$
, then
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,y})<\cdots <\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{d,y})$
are distinct integers and
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,y})<\cdots <\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{d,y})$
are distinct integers and
 $\{s_{j,\unicode[STIX]{x1D70F}}\}_{j}=\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})\}_{j}$
(as sets) for all
$\{s_{j,\unicode[STIX]{x1D70F}}\}_{j}=\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})\}_{j}$
(as sets) for all
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
.
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. -
(TF2) If
 $i<j$
and
$i<j$
and
 $x\in X(\overline{\mathbf{Q}}_{p})$
, then
$x\in X(\overline{\mathbf{Q}}_{p})$
, then
 $\unicode[STIX]{x1D6FF}_{i,x}^{-1}\unicode[STIX]{x1D6FF}_{j,x}$
is generic up to homothety.
$\unicode[STIX]{x1D6FF}_{i,x}^{-1}\unicode[STIX]{x1D6FF}_{j,x}$
is generic up to homothety. -
(TF3) For each
 $x\in X(\overline{\mathbf{Q}}_{p})$
, there exists on
$x\in X(\overline{\mathbf{Q}}_{p})$
, there exists on
 $Q_{x}$
a standard triangulation of torsion length
$Q_{x}$
a standard triangulation of torsion length
 $i(x_{0})$
and free length
$i(x_{0})$
and free length
 $d-i(x_{0})$
, with
$d-i(x_{0})$
, with
 $0\leqslant i(x_{0})\leqslant d$
, independent of
$0\leqslant i(x_{0})\leqslant d$
, independent of
 $x$
, whose free parameter is term-by-term homothetic to
$x$
, whose free parameter is term-by-term homothetic to
 $(\unicode[STIX]{x1D6FF}_{j,x})_{i(x_{0})<j\leqslant d}$
.
$(\unicode[STIX]{x1D6FF}_{j,x})_{i(x_{0})<j\leqslant d}$
. -
(TF4) The standard triangulation
 $Q_{x_{0},\bullet }$
has invariants:
$Q_{x_{0},\bullet }$
has invariants:-
– torsion exponents
 $((s_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
;
$((s_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
; -
– torsion weights
 $((s_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
;
$((s_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
; -
– free parameter
 $(\unicode[STIX]{x1D6FF}_{j,x_{0}}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})-s_{j,\unicode[STIX]{x1D70F}}})_{i(x_{0})<j\leqslant d}$
.
$(\unicode[STIX]{x1D6FF}_{j,x_{0}}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})-s_{j,\unicode[STIX]{x1D70F}}})_{i(x_{0})<j\leqslant d}$
.
-
-
(TF5) If
 $y\in X^{\operatorname{nc}}$
, then the triangulation
$y\in X^{\operatorname{nc}}$
, then the triangulation
 $Q_{y,\bullet }$
has invariants:
$Q_{y,\bullet }$
has invariants:-
– torsion exponents
 $((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
;
$((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
; -
– torsion weights
 $((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
;
$((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant i(x_{0})}$
; -
– free parameter
 $(\unicode[STIX]{x1D6FF}_{j,y})_{i(x_{0})<j\leqslant d}$
.
$(\unicode[STIX]{x1D6FF}_{j,y})_{i(x_{0})<j\leqslant d}$
.
-
-
(TF6) For each
 $C>0$
the set of points accumulates at
$C>0$
the set of points accumulates at $$\begin{eqnarray}\displaystyle X_{C}^{\operatorname{nc}}=\{y\in X^{\operatorname{nc}}:\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j-1,y})>C\text{ for all }2\leqslant j\leqslant d\} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{C}^{\operatorname{nc}}=\{y\in X^{\operatorname{nc}}:\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j-1,y})>C\text{ for all }2\leqslant j\leqslant d\} & & \displaystyle \nonumber\end{eqnarray}$$
 $x_{0}$
.
$x_{0}$
.
Remark.
The axiom (TF5) does not have a typo. The torsion exponents are given in terms of weights of characters at the point
![]() $x_{0}$
and are independent of
$x_{0}$
and are independent of
 $y\in X^{\operatorname{nc}}$
. This is why
$y\in X^{\operatorname{nc}}$
. This is why
![]() $x_{0}$
is called the ‘center’ of the torsion.
$x_{0}$
is called the ‘center’ of the torsion.
Remark.
We stress that if
![]() $Q$
is a pointwise triangulated family of generalized
$Q$
is a pointwise triangulated family of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X$
, then there is no reason to believe that
$X$
, then there is no reason to believe that
 $x\mapsto Q_{x,j}$
defines a generalized
$x\mapsto Q_{x,j}$
defines a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q_{j}$
over
$Q_{j}$
over
![]() $X$
; the datum of the standard triangulations is really given only point-by-point.
$X$
; the datum of the standard triangulations is really given only point-by-point.
We will dwell further beyond these remarks. First,
![]() $i(x_{0})$
is the torsion length of the standard triangulation
$i(x_{0})$
is the torsion length of the standard triangulation
![]() $Q_{x_{0},\bullet }$
but beware that
$Q_{x_{0},\bullet }$
but beware that
![]() $Q_{x_{0}}$
may actually be torsion free, even if
$Q_{x_{0}}$
may actually be torsion free, even if
 $i(x_{0})>0$
. Indeed, our definitions allow for successive quotients in
$i(x_{0})>0$
. Indeed, our definitions allow for successive quotients in
![]() $Q_{x_{0},\bullet }$
to be zero. In particular, if
$Q_{x_{0},\bullet }$
to be zero. In particular, if
 $i(x_{0})=1$
and
$i(x_{0})=1$
and
 $s_{1,\unicode[STIX]{x1D70F}}=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
for all
$s_{1,\unicode[STIX]{x1D70F}}=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
for all
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, then
![]() $Q_{x_{0}}$
is torsion free. This situation does not arise in our applications, but we mention it because the remark applies equally well to
$Q_{x_{0}}$
is torsion free. This situation does not arise in our applications, but we mention it because the remark applies equally well to
 $y\in X^{\operatorname{nc}}$
. Indeed, if
$y\in X^{\operatorname{nc}}$
. Indeed, if
 $y\in X^{\operatorname{nc}}$
, then axiom (TF4) says that the torsion exponents of
$y\in X^{\operatorname{nc}}$
, then axiom (TF4) says that the torsion exponents of
![]() $Q_{y,1}$
are given by
$Q_{y,1}$
are given by
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})=0$
for all
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})=0$
for all
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and thus
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
and thus
 $Q_{1,y}=(0)$
.
$Q_{1,y}=(0)$
.
More generally, when
 $i(x_{0})>0$
and
$i(x_{0})>0$
and
 $y\in X^{\operatorname{nc}}$
there will be
$y\in X^{\operatorname{nc}}$
there will be
 $i(x_{0})-1$
distinct torsion steps in the standard triangulation
$i(x_{0})-1$
distinct torsion steps in the standard triangulation
![]() $Q_{y,\bullet }$
. On the other hand, in practice,
$Q_{y,\bullet }$
. On the other hand, in practice,
![]() $Q_{x_{0},\bullet }$
will have
$Q_{x_{0},\bullet }$
will have
![]() $i(x_{0})$
torsion steps. However, consider the situation where for all
$i(x_{0})$
torsion steps. However, consider the situation where for all
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
there exists a
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
there exists a
![]() $j$
such that
$j$
such that
 $j\leqslant i(x_{0})$
and
$j\leqslant i(x_{0})$
and
 $s_{j,\unicode[STIX]{x1D70F}}=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
. Then, for each
$s_{j,\unicode[STIX]{x1D70F}}=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
. Then, for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
we have an equality of
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
we have an equality of
![]() $\unicode[STIX]{x1D70F}$
-torsion lengths
$\unicode[STIX]{x1D70F}$
-torsion lengths
 $\ell _{\unicode[STIX]{x1D70F}}(Q_{y})=\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0}})$
at
$\ell _{\unicode[STIX]{x1D70F}}(Q_{y})=\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0}})$
at
![]() $x_{0}$
versus
$x_{0}$
versus
 $y\in X^{\operatorname{nc}}$
. Thus, the discrepancy in the number of torsion steps is really an artifact of how we are doing the bookkeeping. We will see in the course of proving Theorem 6.8 that it can even happen that the
$y\in X^{\operatorname{nc}}$
. Thus, the discrepancy in the number of torsion steps is really an artifact of how we are doing the bookkeeping. We will see in the course of proving Theorem 6.8 that it can even happen that the
![]() $t_{\unicode[STIX]{x1D70F}}$
-torsion submodule of
$t_{\unicode[STIX]{x1D70F}}$
-torsion submodule of
![]() $Q_{x_{0}}$
is isomorphic, as an
$Q_{x_{0}}$
is isomorphic, as an
![]() ${\mathcal{R}}_{L}$
-module, to the
${\mathcal{R}}_{L}$
-module, to the
![]() $t_{\unicode[STIX]{x1D70F}}$
-torsion submodule of
$t_{\unicode[STIX]{x1D70F}}$
-torsion submodule of
![]() $Q_{y}$
for one (and thus all)
$Q_{y}$
for one (and thus all)
 $y\in X^{\operatorname{nc}}$
.
$y\in X^{\operatorname{nc}}$
.
Example 5.2. Theorem 5.3 below will explain how to build new pointwise triangulated families out of old ones. But let us motivate the definition of pointwise triangulated families, and the need for Theorem 5.3, with an example previewing the applications in § 6.
Consider a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D$
of rank
$D$
of rank
![]() $d$
over
$d$
over
![]() $X$
and assume that it is actually a pointwise triangulated family
$X$
and assume that it is actually a pointwise triangulated family
![]() $D$
centered at
$D$
centered at
![]() $x_{0}\in X$
with
$x_{0}\in X$
with
 $i(x_{0})=0$
. For example, you could start with a densely pointwise strictly trianguline
$i(x_{0})=0$
. For example, you could start with a densely pointwise strictly trianguline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, § 6.3] (
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, § 6.3] (
![]() $D$
is triangulated at every point following [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.13]).
$D$
is triangulated at every point following [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.13]).
Starting from
![]() $D$
(with the given parameter
$D$
(with the given parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
) one can construct locally on
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
) one can construct locally on
![]() $X$
, near
$X$
, near
![]() $x_{0}$
, a
$x_{0}$
, a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant morphism
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant morphism
 ${\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1})\overset{\mathbf{e}}{{\hookrightarrow}}D$
using [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.9]. Moreover, we can assume that the base change
${\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF}_{1})\overset{\mathbf{e}}{{\hookrightarrow}}D$
using [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.9]. Moreover, we can assume that the base change
![]() $\mathbf{e}_{x}$
to any point
$\mathbf{e}_{x}$
to any point
![]() $x$
is still injective. If we set
$x$
is still injective. If we set
 $Q=\operatorname{coker}(\mathbf{e})$
then
$Q=\operatorname{coker}(\mathbf{e})$
then
![]() $Q$
provides an example of a pointwise triangulated family of generalized
$Q$
provides an example of a pointwise triangulated family of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules which is not necessarily a
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules which is not necessarily a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. It is even nearly flat.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. It is even nearly flat.
At the points
 $y\in X^{\operatorname{nc}}$
, the fiber
$y\in X^{\operatorname{nc}}$
, the fiber
![]() $Q_{y}$
will be a bona fide
$Q_{y}$
will be a bona fide
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of rank
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of rank
![]() $d-1$
. At
$d-1$
. At
![]() $x_{0}$
, however, this may not be the case. The
$x_{0}$
, however, this may not be the case. The
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D_{x_{0}}$
is triangulated by a triangulation whose first step is
$D_{x_{0}}$
is triangulated by a triangulation whose first step is
 $t^{-s}{\mathcal{R}}_{L(x_{0})}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
for some integer
$t^{-s}{\mathcal{R}}_{L(x_{0})}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
for some integer
![]() $s\geqslant 0$
. When
$s\geqslant 0$
. When
![]() $s>0$
, which is the case when the triangulation of
$s>0$
, which is the case when the triangulation of
![]() $D_{x_{0}}$
is critical, we see that the fiber
$D_{x_{0}}$
is critical, we see that the fiber
![]() $Q_{x_{0}}$
has a non-trivial torsion submodule which is killed by
$Q_{x_{0}}$
has a non-trivial torsion submodule which is killed by
![]() $t^{s}$
. Nevertheless, the generalized
$t^{s}$
. Nevertheless, the generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q$
is still a pointwise triangulated family of
$Q$
is still a pointwise triangulated family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X$
with torsion centered at
$X$
with torsion centered at
![]() $x_{0}$
, and
$x_{0}$
, and
 $i(x_{0})=1$
. One can then hope to iterate this process, in the style of [Reference Kedlaya, Pottharst and XiaoKPX14], using these more general families.
$i(x_{0})=1$
. One can then hope to iterate this process, in the style of [Reference Kedlaya, Pottharst and XiaoKPX14], using these more general families.
Let us continue now with constructing new pointwise triangulated families out of old ones in general.
Theorem 5.3. If
![]() $Q$
is a nearly flat pointwise triangulated family with torsion centered at
$Q$
is a nearly flat pointwise triangulated family with torsion centered at
 $x_{0}\in X(\overline{\mathbf{Q}}_{p})$
, free length
$x_{0}\in X(\overline{\mathbf{Q}}_{p})$
, free length
 $d-i(x_{0})>0$
and finite cohomology, then there exists an affinoid neighborhood
$d-i(x_{0})>0$
and finite cohomology, then there exists an affinoid neighborhood
 $x_{0}\in U\subset X$
and a short exact sequence
$x_{0}\in U\subset X$
and a short exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}{\mathcal{R}}_{U}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1})\rightarrow Q|_{U}\rightarrow Q^{\prime }\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}{\mathcal{R}}_{U}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1})\rightarrow Q|_{U}\rightarrow Q^{\prime }\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $U$
. Moreover,
$U$
. Moreover,
![]() $Q^{\prime }$
is a nearly flat pointwise triangulated family with torsion centered at
$Q^{\prime }$
is a nearly flat pointwise triangulated family with torsion centered at
![]() $x_{0}$
, free length
$x_{0}$
, free length
 $d-i(x_{0})-1$
and finite cohomology whose given data is the same as
$d-i(x_{0})-1$
and finite cohomology whose given data is the same as
![]() $Q$
. Thus
$Q$
. Thus
![]() $Q^{\prime }$
as in Theorem 5.3 satisfies axioms (TF1)–(TF6) with
$Q^{\prime }$
as in Theorem 5.3 satisfies axioms (TF1)–(TF6) with
![]() $i(x_{0})$
replaced by
$i(x_{0})$
replaced by
 $i(x_{0})+1$
.
$i(x_{0})+1$
.
Proof. This is an application of our cohomology and base change framework. To shorten notation, let
 $k_{j,\unicode[STIX]{x1D70F}}=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})$
and
$k_{j,\unicode[STIX]{x1D70F}}=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,x_{0}})$
and
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{i(x_{0})+1}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{k_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}}$
. Note that
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{i(x_{0})+1}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{k_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}}$
. Note that
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})=k_{1,\unicode[STIX]{x1D70F}}$
for each
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF})=k_{1,\unicode[STIX]{x1D70F}}$
for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. We are going to compute the cohomology
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. We are going to compute the cohomology
 $H^{\bullet }(Q(\unicode[STIX]{x1D6FF}^{-1}))$
.
$H^{\bullet }(Q(\unicode[STIX]{x1D6FF}^{-1}))$
.
We begin by computing the cohomology at
![]() $x_{0}$
. First,
$x_{0}$
. First,
 $H^{2}(Q_{x_{0}}(\unicode[STIX]{x1D6FF}_{x_{0}}^{-1}))=(0)$
by axiom (TF2) and the vanishing of cohomology in degree two for torsion
$H^{2}(Q_{x_{0}}(\unicode[STIX]{x1D6FF}_{x_{0}}^{-1}))=(0)$
by axiom (TF2) and the vanishing of cohomology in degree two for torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. By the Euler–Poincaré formula it remains to compute the cohomology in degree zero. Let
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. By the Euler–Poincaré formula it remains to compute the cohomology in degree zero. Let
![]() $\widetilde{\unicode[STIX]{x1D6FF}}$
be the character
$\widetilde{\unicode[STIX]{x1D6FF}}$
be the character
 $$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D6FF}_{i(x_{0})+1}\mathop{\prod }_{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{k_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-s_{i(x_{0})+1,\unicode[STIX]{x1D70F}}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D6FF}_{i(x_{0})+1}\mathop{\prod }_{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{k_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-s_{i(x_{0})+1,\unicode[STIX]{x1D70F}}}. & & \displaystyle \nonumber\end{eqnarray}$$
By axiom (TF4),
![]() $\widetilde{\unicode[STIX]{x1D6FF}}$
is the first character in the free parameter of the standard triangulation
$\widetilde{\unicode[STIX]{x1D6FF}}$
is the first character in the free parameter of the standard triangulation
![]() $Q_{x_{0},\bullet }$
and we see easily that
$Q_{x_{0},\bullet }$
and we see easily that
 $\unicode[STIX]{x1D6FF}=(\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{s_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}})\widetilde{\unicode[STIX]{x1D6FF}}$
. For each
$\unicode[STIX]{x1D6FF}=(\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{s_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}})\widetilde{\unicode[STIX]{x1D6FF}}$
. For each
 $j\leqslant i(x_{0})+1$
set
$j\leqslant i(x_{0})+1$
set
 $r_{j,\unicode[STIX]{x1D70F}}=s_{j,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}$
. According to axiom (TF4), for
$r_{j,\unicode[STIX]{x1D70F}}=s_{j,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}$
. According to axiom (TF4), for
 $j\leqslant i(x_{0})$
, these are the torsion exponents of the standard triangulation
$j\leqslant i(x_{0})$
, these are the torsion exponents of the standard triangulation
![]() $Q_{x_{0},\bullet }$
. Moreover, if
$Q_{x_{0},\bullet }$
. Moreover, if
 $j\leqslant i(x_{0})$
, then
$j\leqslant i(x_{0})$
, then
 $$\begin{eqnarray}\displaystyle s_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}})=-r_{i(x_{0})+1,\unicode[STIX]{x1D70F}}+r_{j,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}})=-r_{i(x_{0})+1,\unicode[STIX]{x1D70F}}+r_{j,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
Thus Proposition 3.13, whose non-homothetic hypothesis is valid by axiom (TF2), implies that there exists a unique, up to scalar,
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant inclusion
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant inclusion
 $$\begin{eqnarray}\displaystyle {\mathcal{R}}_{L(x_{0})}(\unicode[STIX]{x1D6FF}_{x_{0}})=\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L(x_{0})}(\widetilde{\unicode[STIX]{x1D6FF}}){\hookrightarrow}Q_{x_{0}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}_{L(x_{0})}(\unicode[STIX]{x1D6FF}_{x_{0}})=\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{r_{i+1,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L(x_{0})}(\widetilde{\unicode[STIX]{x1D6FF}}){\hookrightarrow}Q_{x_{0}}, & & \displaystyle \nonumber\end{eqnarray}$$
so
 $\dim _{L(x_{0})}H^{0}(Q_{x_{0}}(\unicode[STIX]{x1D6FF}_{x_{0}}^{-1}))=1$
. Moreover, Proposition 3.13 also explicitly describes the induced standard triangulation on the quotient
$\dim _{L(x_{0})}H^{0}(Q_{x_{0}}(\unicode[STIX]{x1D6FF}_{x_{0}}^{-1}))=1$
. Moreover, Proposition 3.13 also explicitly describes the induced standard triangulation on the quotient
 $Q_{x_{0}}/{\mathcal{R}}_{L(x_{0})}(\unicode[STIX]{x1D6FF}_{x_{0}})$
.
$Q_{x_{0}}/{\mathcal{R}}_{L(x_{0})}(\unicode[STIX]{x1D6FF}_{x_{0}})$
.
We now compute the cohomology at (some) points
 $y\in X^{\operatorname{nc}}$
. As above,
$y\in X^{\operatorname{nc}}$
. As above,
 $H^{2}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))=(0)$
by axiom (TF2) and the vanishing of cohomology in degree two for torsion
$H^{2}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))=(0)$
by axiom (TF2) and the vanishing of cohomology in degree two for torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Reset the definitions from the previous paragraph and make
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Reset the definitions from the previous paragraph and make
 $r_{j,\unicode[STIX]{x1D70F}}:=k_{j,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}$
for all
$r_{j,\unicode[STIX]{x1D70F}}:=k_{j,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}$
for all
 $j\leqslant i(x_{0})+1$
. Once again, if
$j\leqslant i(x_{0})+1$
. Once again, if
 $j\leqslant i(x_{0})$
, then
$j\leqslant i(x_{0})$
, then
![]() $(r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
gives the torsion exponents of the standard triangulation
$(r_{j,\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
gives the torsion exponents of the standard triangulation
![]() $Q_{y,\bullet }$
. For all
$Q_{y,\bullet }$
. For all
 $j\leqslant i(x_{0})$
, we easily compute
$j\leqslant i(x_{0})$
, we easily compute
 $$\begin{eqnarray}\displaystyle \operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{y})=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})+r_{i(x_{0})+1,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{y})=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})+r_{i(x_{0})+1,\unicode[STIX]{x1D70F}}. & & \displaystyle \nonumber\end{eqnarray}$$
Choose a
![]() $C$
so large that if
$C$
so large that if
 $y\in X_{C}^{\operatorname{nc}}$
, then for all
$y\in X_{C}^{\operatorname{nc}}$
, then for all
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
 $1\leqslant j\leqslant i(x_{0})$
, the negative integer
$1\leqslant j\leqslant i(x_{0})$
, the negative integer
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})$
is not among the finitely many values
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{j,y})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})$
is not among the finitely many values
 $\{-r_{i+1,\unicode[STIX]{x1D70F}},\ldots ,r_{j,\unicode[STIX]{x1D70F}}-r_{i+1,\unicode[STIX]{x1D70F}}-1\}$
. Then by axiom (TF2), we can apply Proposition 3.13 and conclude that if
$\{-r_{i+1,\unicode[STIX]{x1D70F}},\ldots ,r_{j,\unicode[STIX]{x1D70F}}-r_{i+1,\unicode[STIX]{x1D70F}}-1\}$
. Then by axiom (TF2), we can apply Proposition 3.13 and conclude that if
 $y\in X_{C}^{\operatorname{nc}}$
, then
$y\in X_{C}^{\operatorname{nc}}$
, then
 $H^{0}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))$
is one-dimensional over
$H^{0}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))$
is one-dimensional over
![]() $L(y)$
. Again, Proposition 3.13 also explains how a non-zero morphism
$L(y)$
. Again, Proposition 3.13 also explains how a non-zero morphism
 ${\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{y}){\hookrightarrow}Q_{y}$
will induce a standard triangulation on
${\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{y}){\hookrightarrow}Q_{y}$
will induce a standard triangulation on
![]() $Q_{y}$
by replacing the subquotient
$Q_{y}$
by replacing the subquotient
 ${\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})$
of
${\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})$
of
![]() $Q_{y}$
by
$Q_{y}$
by
 $$\begin{eqnarray}\displaystyle {\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})/{\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF})={\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})/\biggl(\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{k_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})/{\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF})={\mathcal{R}}_{L(y)}(\unicode[STIX]{x1D6FF}_{i(x_{0})+1,y})/\biggl(\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{k_{i(x_{0})+1,\unicode[STIX]{x1D70F}}-k_{1,\unicode[STIX]{x1D70F}}}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
By axiom (TF6) we can replace
![]() $X^{\operatorname{nc}}$
by
$X^{\operatorname{nc}}$
by
![]() $X_{C}^{\operatorname{nc}}$
and assume that
$X_{C}^{\operatorname{nc}}$
and assume that
 $H^{0}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))$
has constant dimension over all of
$H^{0}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))$
has constant dimension over all of
![]() $X^{\operatorname{nc}}$
.
$X^{\operatorname{nc}}$
.
We now go back to the entire family. By the Euler–Poincaré formula the function
 $y\mapsto \dim _{L(y)}H^{1}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))$
is constant on
$y\mapsto \dim _{L(y)}H^{1}(Q_{y}(\unicode[STIX]{x1D6FF}_{y}^{-1}))$
is constant on
![]() $X^{\operatorname{nc}}$
and agrees with
$X^{\operatorname{nc}}$
and agrees with
 $\dim _{L(x_{0})}H^{1}(Q_{x_{0}}(\unicode[STIX]{x1D6FF}_{x_{0}}^{-1}))$
. Since
$\dim _{L(x_{0})}H^{1}(Q_{x_{0}}(\unicode[STIX]{x1D6FF}_{x_{0}}^{-1}))$
. Since
![]() $Q$
is nearly flat and has finite cohomology, Corollary 4.7 implies we can choose an open neighborhood
$Q$
is nearly flat and has finite cohomology, Corollary 4.7 implies we can choose an open neighborhood
 $x_{0}\in U\subset X$
so that each
$x_{0}\in U\subset X$
so that each
 $H^{i}(Q(\unicode[STIX]{x1D6FF}^{-1})|_{U})$
is free over
$H^{i}(Q(\unicode[STIX]{x1D6FF}^{-1})|_{U})$
is free over
![]() $U$
and satisfies base change for each
$U$
and satisfies base change for each
![]() $i$
. We now replace
$i$
. We now replace
![]() $X$
by such a
$X$
by such a
![]() $U$
.
$U$
.
Choose a basis vector
 $\mathbf{e}\in H^{0}(Q(\unicode[STIX]{x1D6FF}^{-1}))$
. Since
$\mathbf{e}\in H^{0}(Q(\unicode[STIX]{x1D6FF}^{-1}))$
. Since
 $H^{0}(Q(\unicode[STIX]{x1D6FF}^{-1}))$
satisfies base change, if we specialize
$H^{0}(Q(\unicode[STIX]{x1D6FF}^{-1}))$
satisfies base change, if we specialize
![]() $\mathbf{e}$
to either
$\mathbf{e}$
to either
![]() $x=x_{0}$
or
$x=x_{0}$
or
 $x=y\in X^{\operatorname{nc}}$
, we get an injective morphism
$x=y\in X^{\operatorname{nc}}$
, we get an injective morphism
 $\mathbf{e}_{x}:{\mathcal{R}}_{L(x)}(\unicode[STIX]{x1D6FF}_{x}){\hookrightarrow}Q_{x}$
by the previous two paragraphs. By Lemma 5.4(a) below we conclude that
$\mathbf{e}_{x}:{\mathcal{R}}_{L(x)}(\unicode[STIX]{x1D6FF}_{x}){\hookrightarrow}Q_{x}$
by the previous two paragraphs. By Lemma 5.4(a) below we conclude that
![]() $\mathbf{e}$
is also injective. Let
$\mathbf{e}$
is also injective. Let
 $Q^{\prime }=\operatorname{coker}(\mathbf{e})$
so that there is a short exact sequence
$Q^{\prime }=\operatorname{coker}(\mathbf{e})$
so that there is a short exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF})\overset{\mathbf{e}}{\longrightarrow }Q\rightarrow Q^{\prime }\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF})\overset{\mathbf{e}}{\longrightarrow }Q\rightarrow Q^{\prime }\rightarrow 0.\end{eqnarray}$$
Since
![]() $Q$
has finite cohomology, by assumption, and
$Q$
has finite cohomology, by assumption, and
![]() ${\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF})$
has finite cohomology by Theorem 4.5(a),
${\mathcal{R}}_{X}(\unicode[STIX]{x1D6FF})$
has finite cohomology by Theorem 4.5(a),
![]() $Q^{\prime }$
has finite cohomology by Theorem 4.5(b).
$Q^{\prime }$
has finite cohomology by Theorem 4.5(b).
We also have to show that
![]() $Q^{\prime }$
is nearly flat (after possibly shrinking
$Q^{\prime }$
is nearly flat (after possibly shrinking
![]() $X$
more). Since
$X$
more). Since
![]() $Q$
is nearly flat over
$Q$
is nearly flat over
![]() $X$
and
$X$
and
![]() ${\mathcal{R}}_{X}$
is flat over
${\mathcal{R}}_{X}$
is flat over
![]() $X$
, it suffices to show that we can shrink
$X$
, it suffices to show that we can shrink
![]() $X$
around
$X$
around
![]() $x_{0}$
so that
$x_{0}$
so that
![]() $\mathbf{e}_{x}$
is injective for all
$\mathbf{e}_{x}$
is injective for all
![]() $x$
. Since
$x$
. Since
![]() $\mathbf{e}_{x_{0}}$
is injective it suffices by Lemma 5.4(b) to show that
$\mathbf{e}_{x_{0}}$
is injective it suffices by Lemma 5.4(b) to show that
 $x\mapsto \operatorname{rank}_{{\mathcal{R}}_{x}[1/t]}Q_{x}[1/t]$
is constant on
$x\mapsto \operatorname{rank}_{{\mathcal{R}}_{x}[1/t]}Q_{x}[1/t]$
is constant on
![]() $X$
. But this follows from axiom (TF3), which implies that
$X$
. But this follows from axiom (TF3), which implies that
![]() $Q_{x}[1/t]$
is finite free over
$Q_{x}[1/t]$
is finite free over
 ${\mathcal{R}}_{L(x)}[1/t]$
of rank
${\mathcal{R}}_{L(x)}[1/t]$
of rank
 $d-(i(x_{0})+1)$
independent of
$d-(i(x_{0})+1)$
independent of
![]() $x$
.
$x$
.
Finally, we need to check that
![]() $Q^{\prime }$
is a triangulated family with the same data as
$Q^{\prime }$
is a triangulated family with the same data as
![]() $Q$
, except
$Q$
, except
![]() $i(x_{0})$
replaced by
$i(x_{0})$
replaced by
 $i(x_{0})+1$
. The three axioms (TF1), (TF2) and (TF6) do not depend on
$i(x_{0})+1$
. The three axioms (TF1), (TF2) and (TF6) do not depend on
![]() $Q$
, so those are still true. Axiom (TF3) is true because of (6) and the fact that
$Q$
, so those are still true. Axiom (TF3) is true because of (6) and the fact that
![]() $Q^{\prime }$
is nearly flat, so that all the base changes
$Q^{\prime }$
is nearly flat, so that all the base changes
![]() $\mathbf{e}_{x}$
are injective. Checking either axiom (TF4) or (TF5) follows from our use of Proposition 3.13 at the points
$\mathbf{e}_{x}$
are injective. Checking either axiom (TF4) or (TF5) follows from our use of Proposition 3.13 at the points
![]() $x=x_{0}$
and
$x=x_{0}$
and
![]() $x=y$
.◻
$x=y$
.◻
There were two points unresolved in the previous theorem, both of which we resolve with the following lemma. For the second part, and more in the following results, we will make use of the appendix on Nakayama’s lemma.
Lemma 5.4. Let
![]() $X$
be a reduced affinoid space,
$X$
be a reduced affinoid space,
![]() $Q$
a generalized
$Q$
a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $X$
and
$X$
and
 $f:{\mathcal{R}}_{X}\rightarrow Q$
a
$f:{\mathcal{R}}_{X}\rightarrow Q$
a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant map.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant map.
-
(a) If
 $X^{\prime }\subset X(\overline{\mathbf{Q}}_{p})$
is Zariski-dense in
$X^{\prime }\subset X(\overline{\mathbf{Q}}_{p})$
is Zariski-dense in
 $X$
and the specialization
$X$
and the specialization
 $f_{u}:{\mathcal{R}}_{L(u)}\rightarrow Q_{u}$
is injective for all
$f_{u}:{\mathcal{R}}_{L(u)}\rightarrow Q_{u}$
is injective for all
 $u\in X^{\prime }$
, then
$u\in X^{\prime }$
, then
 $f$
is injective.
$f$
is injective. -
(b) If
 $x\mapsto \operatorname{rank}_{{\mathcal{R}}_{x}[1/t]}Q_{x}[1/t]$
is constant on
$x\mapsto \operatorname{rank}_{{\mathcal{R}}_{x}[1/t]}Q_{x}[1/t]$
is constant on
 $X$
,
$X$
,
 $x_{0}\in X$
and
$x_{0}\in X$
and
 $f_{x_{0}}$
is injective, then there exists an affinoid neighborhood
$f_{x_{0}}$
is injective, then there exists an affinoid neighborhood
 $x_{0}\in U\subset X$
such that
$x_{0}\in U\subset X$
such that
 $f_{u}$
is injective for all
$f_{u}$
is injective for all
 $u\in U$
.
$u\in U$
.
Remark.
In part (b),
![]() $Q_{x}[1/t]$
is automatically free over
$Q_{x}[1/t]$
is automatically free over
![]() ${\mathcal{R}}_{x}[1/t]$
for each
${\mathcal{R}}_{x}[1/t]$
for each
![]() $x$
by Lemma 2.13.
$x$
by Lemma 2.13.
Proof. We need to make use of the recollection given in § 2.1. Choose an
![]() $r_{0}$
so that
$r_{0}$
so that
![]() $Q$
arises via base change from
$Q$
arises via base change from
![]() $X^{r_{0}}$
and
$X^{r_{0}}$
and
![]() $f$
arises from a
$f$
arises from a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant map
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant map
 $f^{r_{0}}:{\mathcal{R}}_{X}^{r_{0}}\rightarrow Q^{r_{0}}$
as well.
$f^{r_{0}}:{\mathcal{R}}_{X}^{r_{0}}\rightarrow Q^{r_{0}}$
as well.
We first prove part (a). It suffices to show that
![]() $f^{r_{0}}$
is injective. If
$f^{r_{0}}$
is injective. If
 $0<s<r_{0}$
, then let
$0<s<r_{0}$
, then let
![]() $f^{[s,r_{0}]}$
denote the induced map
$f^{[s,r_{0}]}$
denote the induced map
 $$\begin{eqnarray}\displaystyle {\mathcal{R}}_{X}^{[s,r_{0}]}\overset{f^{[s,r_{0}]}}{\longrightarrow }Q^{[s,r_{0}]}:=Q^{r_{0}}\otimes _{{\mathcal{R}}_{X}^{r_{0}}}{\mathcal{R}}_{X}^{[s,r_{0}]}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}_{X}^{[s,r_{0}]}\overset{f^{[s,r_{0}]}}{\longrightarrow }Q^{[s,r_{0}]}:=Q^{r_{0}}\otimes _{{\mathcal{R}}_{X}^{r_{0}}}{\mathcal{R}}_{X}^{[s,r_{0}]}. & & \displaystyle \nonumber\end{eqnarray}$$
By [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.4(2)] it suffices to show that
![]() $f^{[s,r_{0}]}$
is injective.
$f^{[s,r_{0}]}$
is injective.
We have now reduced to working over a closed relative annulus
![]() $X^{[s,r_{0}]}$
whose rigid functions
$X^{[s,r_{0}]}$
whose rigid functions
![]() ${\mathcal{R}}_{X}^{[s,r_{0}]}$
are, in particular, noetherian. Write
${\mathcal{R}}_{X}^{[s,r_{0}]}$
are, in particular, noetherian. Write
![]() $I$
for the image of
$I$
for the image of
![]() $f^{[s,r_{0}]}$
in
$f^{[s,r_{0}]}$
in
![]() $Q^{[s,r_{0}]}$
. If
$Q^{[s,r_{0}]}$
. If
![]() $u\in X^{\prime }$
, then
$u\in X^{\prime }$
, then
 ${\mathcal{R}}_{L(u)}^{[s,r]}\rightarrow I\otimes _{A}L(u)$
is injective, as it factors
${\mathcal{R}}_{L(u)}^{[s,r]}\rightarrow I\otimes _{A}L(u)$
is injective, as it factors
![]() $f_{u}$
and we have assumed that
$f_{u}$
and we have assumed that
![]() $f_{u}$
is injective. It is also surjective since tensor product is right exact. Thus, it is an isomorphism.
$f_{u}$
is injective. It is also surjective since tensor product is right exact. Thus, it is an isomorphism.
We deduce from Nakayama’s lemma, applied to the finite module
![]() $I$
over the noetherian ring
$I$
over the noetherian ring
![]() ${\mathcal{R}}_{X}^{[s,r_{0}]}$
that
${\mathcal{R}}_{X}^{[s,r_{0}]}$
that
 $\dim _{L(v)}I_{v}\geqslant 1$
for all
$\dim _{L(v)}I_{v}\geqslant 1$
for all
 $v\in X^{[s,r_{0}]}$
(note that
$v\in X^{[s,r_{0}]}$
(note that
![]() $v$
is in the relative annulus, not just
$v$
is in the relative annulus, not just
![]() $X$
, and
$X$
, and
 $I_{v}:=I\otimes _{{\mathcal{R}}_{X}^{[s,r_{0}]}}L(v)$
). But
$I_{v}:=I\otimes _{{\mathcal{R}}_{X}^{[s,r_{0}]}}L(v)$
). But
 $\dim _{L(v)}I_{v}\leqslant 1$
for all
$\dim _{L(v)}I_{v}\leqslant 1$
for all
 $v\in X^{[s,r_{0}]}$
since
$v\in X^{[s,r_{0}]}$
since
![]() $I_{v}$
is a quotient of something free of rank one over
$I_{v}$
is a quotient of something free of rank one over
![]() $X^{[s,r_{0}]}$
. Since
$X^{[s,r_{0}]}$
. Since
![]() $X$
is reduced, so is
$X$
is reduced, so is
![]() $X^{[s,r_{0}]}$
and we just showed that
$X^{[s,r_{0}]}$
and we just showed that
 $v\mapsto \dim _{L(v)}I_{v}$
is constant on the relative annulus
$v\mapsto \dim _{L(v)}I_{v}$
is constant on the relative annulus
![]() $X^{[s,r_{0}]}$
. Thus,
$X^{[s,r_{0}]}$
. Thus,
![]() $I$
must be flat over
$I$
must be flat over
![]() $X^{[s,r_{0}]}$
by Nakayama’s lemma again. In particular,
$X^{[s,r_{0}]}$
by Nakayama’s lemma again. In particular,
 ${\mathcal{R}}_{X}^{[s,r_{0}]}\rightarrow I$
is an isomorphism, as was to be shown.
${\mathcal{R}}_{X}^{[s,r_{0}]}\rightarrow I$
is an isomorphism, as was to be shown.
Let us now prove part (b). We note that the proof of part (a) did not use that
![]() $f$
was
$f$
was
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant. Consider
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-equivariant. Consider
 $C^{r_{0}}=\operatorname{coker}({\mathcal{R}}_{X}^{r_{0}}\overset{f^{r_{0}}}{\longrightarrow }Q^{r_{0}})$
. By Corollary 2.4,
$C^{r_{0}}=\operatorname{coker}({\mathcal{R}}_{X}^{r_{0}}\overset{f^{r_{0}}}{\longrightarrow }Q^{r_{0}})$
. By Corollary 2.4,
![]() $C^{r_{0}}$
is a generalized
$C^{r_{0}}$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. If
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. If
![]() $u\in X$
then
$u\in X$
then
 $C_{u}^{r_{0}}[1/t]$
is free over
$C_{u}^{r_{0}}[1/t]$
is free over
 ${\mathcal{R}}_{L(u)}^{r_{0}}[1/t]$
by Lemma 2.13, so it makes sense to consider the function
${\mathcal{R}}_{L(u)}^{r_{0}}[1/t]$
by Lemma 2.13, so it makes sense to consider the function
 $\operatorname{rank}(u):=\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}[1/t]}(C_{u}^{r_{0}}[1/t])$
. Moreover, if we choose any
$\operatorname{rank}(u):=\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}[1/t]}(C_{u}^{r_{0}}[1/t])$
. Moreover, if we choose any
 $0<s<r_{0}$
then we also haveFootnote
5
$0<s<r_{0}$
then we also haveFootnote
5
 $$\begin{eqnarray}\operatorname{rank}(u)=\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{[s,r_{0}]}[1/t]}C_{u}^{[s,r_{0}]}[1/t].\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rank}(u)=\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{[s,r_{0}]}[1/t]}C_{u}^{[s,r_{0}]}[1/t].\end{eqnarray}$$
Consider such a choice of
![]() $s$
made now.
$s$
made now.
Since
 $\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}[1/t]}Q_{u}^{r_{0}}[1/t]=:q$
is constant on
$\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}[1/t]}Q_{u}^{r_{0}}[1/t]=:q$
is constant on
![]() $X$
, we know that
$X$
, we know that
 $\operatorname{rank}(u)$
is either
$\operatorname{rank}(u)$
is either
![]() $q$
or
$q$
or
![]() $q-1$
. Since
$q-1$
. Since
![]() $f_{x_{0}}^{r_{0}}$
is injective, so is
$f_{x_{0}}^{r_{0}}$
is injective, so is
![]() $f_{x_{0}}^{r_{0}}[1/t]$
and thus
$f_{x_{0}}^{r_{0}}[1/t]$
and thus
 $\operatorname{rank}(x_{0})=q-1$
is the minimal possible value. Since
$\operatorname{rank}(x_{0})=q-1$
is the minimal possible value. Since
![]() ${\mathcal{R}}_{X}^{[s,r_{0}]}$
is affinoid, the expression (7) and Proposition A.4(a) together imply that we may replace
${\mathcal{R}}_{X}^{[s,r_{0}]}$
is affinoid, the expression (7) and Proposition A.4(a) together imply that we may replace
![]() $X$
by an affinoid subdomain containing
$X$
by an affinoid subdomain containing
![]() $x_{0}$
so that
$x_{0}$
so that
 $\operatorname{rank}(u)=q-1$
for all
$\operatorname{rank}(u)=q-1$
for all
![]() $u\in X$
. But that clearly is equivalent to
$u\in X$
. But that clearly is equivalent to
 $\ker f_{u}^{r_{0}}[1/t]=(0)$
for all
$\ker f_{u}^{r_{0}}[1/t]=(0)$
for all
![]() $u\in X$
. Since
$u\in X$
. Since
 $f_{u}^{r_{0}}:{\mathcal{R}}_{L(u)}^{r_{0}}\rightarrow Q_{u}^{r_{0}}$
has source
$f_{u}^{r_{0}}:{\mathcal{R}}_{L(u)}^{r_{0}}\rightarrow Q_{u}^{r_{0}}$
has source
![]() ${\mathcal{R}}_{L(u)}$
, Proposition 2.9 and the fact that
${\mathcal{R}}_{L(u)}$
, Proposition 2.9 and the fact that
![]() $f_{u}^{r_{0}}[1/t]$
is injective for all
$f_{u}^{r_{0}}[1/t]$
is injective for all
![]() $u\in X$
implies that
$u\in X$
implies that
 $\ker f_{u}^{r_{0}}=(0)$
for all
$\ker f_{u}^{r_{0}}=(0)$
for all
![]() $u\in X$
(and thus
$u\in X$
(and thus
![]() $f_{u}$
is injective also).◻
$f_{u}$
is injective also).◻
5.2 Killing torsion
Note that Theorem 5.3 possibly introduces torsion
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules into the picture. Thus, its utility rests on being able to kill torsion in certain pointwise triangulated families. This is achieved in Corollary 5.8. First we need preparation. The following is an application of Nakayama’s lemma in the appendix.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules into the picture. Thus, its utility rests on being able to kill torsion in certain pointwise triangulated families. This is achieved in Corollary 5.8. First we need preparation. The following is an application of Nakayama’s lemma in the appendix.
Lemma 5.5. Let
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Suppose that
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Suppose that
![]() $Q$
is a generalized
$Q$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module such that for each
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module such that for each
![]() $x\in X$
,
$x\in X$
,
![]() $Q_{x}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
$Q_{x}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
 ${\mathcal{R}}_{L(x)}/t_{\unicode[STIX]{x1D70F}}$
. Suppose that
${\mathcal{R}}_{L(x)}/t_{\unicode[STIX]{x1D70F}}$
. Suppose that
 $x_{0}\in X(\overline{\mathbf{Q}}_{p})$
and
$x_{0}\in X(\overline{\mathbf{Q}}_{p})$
and
 $Z\subset X(\overline{\mathbf{Q}}_{p})$
is a set of points accumulating at
$Z\subset X(\overline{\mathbf{Q}}_{p})$
is a set of points accumulating at
![]() $x_{0}$
and
$x_{0}$
and
 $\operatorname{rank}_{{\mathcal{R}}_{x_{0}}/t_{\unicode[STIX]{x1D70F}}}Q_{x_{0}}/t_{\unicode[STIX]{x1D70F}}=\operatorname{rank}_{{\mathcal{R}}_{z}/t_{\unicode[STIX]{x1D70F}}}Q_{z}/t_{\unicode[STIX]{x1D70F}}$
for each
$\operatorname{rank}_{{\mathcal{R}}_{x_{0}}/t_{\unicode[STIX]{x1D70F}}}Q_{x_{0}}/t_{\unicode[STIX]{x1D70F}}=\operatorname{rank}_{{\mathcal{R}}_{z}/t_{\unicode[STIX]{x1D70F}}}Q_{z}/t_{\unicode[STIX]{x1D70F}}$
for each
![]() $z\in Z$
. Then there exists an affinoid subdomain
$z\in Z$
. Then there exists an affinoid subdomain
 $x_{0}\in U\subset X$
such that
$x_{0}\in U\subset X$
such that
 $u\mapsto \operatorname{rank}_{{\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}}Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is constant on
$u\mapsto \operatorname{rank}_{{\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}}Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is constant on
![]() $U$
.
$U$
.
Proof. First, if necessary, replace
![]() $X$
by an affinoid subdomain
$X$
by an affinoid subdomain
 $x_{0}\in U\subset X$
so that
$x_{0}\in U\subset X$
so that
![]() $Z$
is Zariski-dense in
$Z$
is Zariski-dense in
![]() $U$
. Then, we find an
$U$
. Then, we find an
![]() $r_{0}$
so that
$r_{0}$
so that
![]() $Q$
arises from a
$Q$
arises from a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $Q^{r_{0}}$
over
$Q^{r_{0}}$
over
![]() $X^{r_{0}}$
. Since
$X^{r_{0}}$
. Since
![]() $Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
$Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
 ${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
for each
${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
for each
![]() $u\in X$
, the same is true for
$u\in X$
, the same is true for
![]() $Q_{u}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}$
over
$Q_{u}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}$
over
 ${\mathcal{R}}_{L(u)}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}$
. (Since the Frobenius
${\mathcal{R}}_{L(u)}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}$
. (Since the Frobenius
 ${\mathcal{R}}_{L(u)}^{r_{0}}\rightarrow {\mathcal{R}}_{L(u)}^{r_{0}/p}$
is faithfully flat and
${\mathcal{R}}_{L(u)}^{r_{0}}\rightarrow {\mathcal{R}}_{L(u)}^{r_{0}/p}$
is faithfully flat and
![]() $Q^{r_{0}}$
is a generalized
$Q^{r_{0}}$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, it is enough to check
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module, it is enough to check
![]() $Q_{u}^{r}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
$Q_{u}^{r}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
 ${\mathcal{R}}_{L(u)}^{r}/t_{\unicode[STIX]{x1D70F}}$
for some
${\mathcal{R}}_{L(u)}^{r}/t_{\unicode[STIX]{x1D70F}}$
for some
 $0<r\leqslant r_{0}$
(possibly depending on
$0<r\leqslant r_{0}$
(possibly depending on
![]() $u$
); this follows from knowing
$u$
); this follows from knowing
![]() $Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
$Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is finite free over
 ${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
and
${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
and
![]() $Q_{u}^{r}/t$
is finitely presented over
$Q_{u}^{r}/t$
is finitely presented over
 ${\mathcal{R}}_{L(u)}^{r}/t$
for each
${\mathcal{R}}_{L(u)}^{r}/t$
for each
![]() $r$
; compare with [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.16].)
$r$
; compare with [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.16].)
Fix any
 $0<s<r_{0}$
. Then
$0<s<r_{0}$
. Then
 $$\begin{eqnarray}\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}}Q_{u}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}=\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}}Q_{u}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}}Q_{u}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}=\operatorname{rank}_{{\mathcal{R}}_{L(u)}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}}Q_{u}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}\end{eqnarray}$$
for each
![]() $u\in X$
. The ring
$u\in X$
. The ring
 ${\mathcal{R}}^{[s,r_{0}]}/t$
is reduced since
${\mathcal{R}}^{[s,r_{0}]}/t$
is reduced since
![]() $t$
is well known to be a uniformizer at the at the points of the form
$t$
is well known to be a uniformizer at the at the points of the form
 $\unicode[STIX]{x1D701}-1\in \mathbf{A}^{1}[s,r_{0}]$
where
$\unicode[STIX]{x1D701}-1\in \mathbf{A}^{1}[s,r_{0}]$
where
![]() $\unicode[STIX]{x1D701}$
is a
$\unicode[STIX]{x1D701}$
is a
![]() $p$
-power root of unity. Thus, so is the factor ring
$p$
-power root of unity. Thus, so is the factor ring
 ${\mathcal{R}}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}$
. In particular,
${\mathcal{R}}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}$
. In particular,
 ${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}={\mathcal{R}}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}\widehat{\otimes }_{\mathbf{Q}_{p}}A$
is the completed tensor product of reduced affinoid
${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}={\mathcal{R}}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}\widehat{\otimes }_{\mathbf{Q}_{p}}A$
is the completed tensor product of reduced affinoid
![]() $\mathbf{Q}_{p}$
-algebras. It follows from Proposition A.4(b) that the right-hand side of (8) has a minimum achieved on the Zariski-dense subset
$\mathbf{Q}_{p}$
-algebras. It follows from Proposition A.4(b) that the right-hand side of (8) has a minimum achieved on the Zariski-dense subset
![]() $Z\subset X$
. Since that minimum is achieved also at
$Z\subset X$
. Since that minimum is achieved also at
![]() $x_{0}$
, by assumption, Proposition A.4(a) allows us to find an affinoid subdomain
$x_{0}$
, by assumption, Proposition A.4(a) allows us to find an affinoid subdomain
 $x_{0}\in U\subset X$
on which
$x_{0}\in U\subset X$
on which
 $u\mapsto \operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}}Q_{u}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}$
is constant.◻
$u\mapsto \operatorname{rank}_{{\mathcal{R}}_{L(u)}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}}Q_{u}^{r_{0}}/t_{\unicode[STIX]{x1D70F}}$
is constant.◻
Lemma 5.6. Let
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Suppose that
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
. Suppose that
![]() $Q$
is a nearly flat generalized
$Q$
is a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module,
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module,
 $x_{0}\in X(\overline{\mathbf{Q}}_{p})$
and
$x_{0}\in X(\overline{\mathbf{Q}}_{p})$
and
 $Z\subset X(\overline{\mathbf{Q}}_{p})$
is a set of points accumulating at
$Z\subset X(\overline{\mathbf{Q}}_{p})$
is a set of points accumulating at
![]() $x_{0}$
such that:
$x_{0}$
such that:
-
(a) there exists non-negative integers
 $s,r$
such that for all
$s,r$
such that for all
 $u\in X(\overline{\mathbf{Q}}_{p})$
,
$u\in X(\overline{\mathbf{Q}}_{p})$
,
 $Q_{u}$
is triangulated by a standard triangulation with non-zero
$Q_{u}$
is triangulated by a standard triangulation with non-zero
 $\unicode[STIX]{x1D70F}$
-torsion exponents
$\unicode[STIX]{x1D70F}$
-torsion exponents
 $(m_{i,\unicode[STIX]{x1D70F}}(u))_{1\leqslant i\leqslant s}$
and free parameter of length
$(m_{i,\unicode[STIX]{x1D70F}}(u))_{1\leqslant i\leqslant s}$
and free parameter of length
 $r$
;
$r$
; -
(b)
 $z\mapsto \min _{i=1}^{s}m_{i,\unicode[STIX]{x1D70F}}(z)$
is a constant
$z\mapsto \min _{i=1}^{s}m_{i,\unicode[STIX]{x1D70F}}(z)$
is a constant
 $m$
on
$m$
on
 $Z$
; and
$Z$
; and -
(c)
 $m\leqslant \min _{i=1}^{s}m_{i,\unicode[STIX]{x1D70F}}(x_{0})$
as well.
$m\leqslant \min _{i=1}^{s}m_{i,\unicode[STIX]{x1D70F}}(x_{0})$
as well.
Then there exists an open affinoid
 $x_{0}\in U\subset X$
such that
$x_{0}\in U\subset X$
such that
 $(Q/t_{\unicode[STIX]{x1D70F}}^{m})|_{U}$
is flat over
$(Q/t_{\unicode[STIX]{x1D70F}}^{m})|_{U}$
is flat over
![]() ${\mathcal{R}}_{U}/t_{\unicode[STIX]{x1D70F}}^{m}$
.
${\mathcal{R}}_{U}/t_{\unicode[STIX]{x1D70F}}^{m}$
.
Proof. Let us begin by elucidating the first assumption. Since
![]() $t_{\unicode[STIX]{x1D70F}}$
and
$t_{\unicode[STIX]{x1D70F}}$
and
![]() $t_{\unicode[STIX]{x1D70E}}$
are maximally coprime if
$t_{\unicode[STIX]{x1D70E}}$
are maximally coprime if
![]() $\unicode[STIX]{x1D70F}\neq \unicode[STIX]{x1D70E}$
, the first assumption implies that
$\unicode[STIX]{x1D70F}\neq \unicode[STIX]{x1D70E}$
, the first assumption implies that
 $$\begin{eqnarray}\displaystyle Q_{u}\simeq \biggl(\bigoplus _{i=1}^{s}{\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{m_{i,\unicode[STIX]{x1D70F}}(u)}\biggr)\oplus {\mathcal{R}}_{L(u)}^{\oplus r}\oplus S_{u} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{u}\simeq \biggl(\bigoplus _{i=1}^{s}{\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{m_{i,\unicode[STIX]{x1D70F}}(u)}\biggr)\oplus {\mathcal{R}}_{L(u)}^{\oplus r}\oplus S_{u} & & \displaystyle \nonumber\end{eqnarray}$$
as an
![]() ${\mathcal{R}}_{L(u)}$
-module, where
${\mathcal{R}}_{L(u)}$
-module, where
 $S_{u}[t_{\unicode[STIX]{x1D70F}}]=S_{u}/t_{\unicode[STIX]{x1D70F}}=(0)$
and each
$S_{u}[t_{\unicode[STIX]{x1D70F}}]=S_{u}/t_{\unicode[STIX]{x1D70F}}=(0)$
and each
![]() $m_{i,\unicode[STIX]{x1D70F}}(u)$
is non-zero.
$m_{i,\unicode[STIX]{x1D70F}}(u)$
is non-zero.
Claim.
For each
 $1\leqslant j\leqslant m$
we may replace
$1\leqslant j\leqslant m$
we may replace
![]() $X$
by an affinoid neighborhood
$X$
by an affinoid neighborhood
 $x_{0}\in U\subset X$
such that
$x_{0}\in U\subset X$
such that
![]() $Q_{u}/t_{\unicode[STIX]{x1D70F}}^{j}$
is free of rank
$Q_{u}/t_{\unicode[STIX]{x1D70F}}^{j}$
is free of rank
![]() $r+s$
over
$r+s$
over
 ${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{j}$
.
${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{j}$
.
The proof will be given by induction in the next paragraph. Assuming the claim for the moment, let us finish the lemma. Fix
 $1\leqslant j\leqslant m$
. By the claim we may assume that
$1\leqslant j\leqslant m$
. By the claim we may assume that
![]() $Q_{u}/t_{\unicode[STIX]{x1D70F}}^{j}$
is free over
$Q_{u}/t_{\unicode[STIX]{x1D70F}}^{j}$
is free over
 ${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{j}$
with rank independent of
${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{j}$
with rank independent of
![]() $u$
. We want to show that this implies
$u$
. We want to show that this implies
![]() $Q/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
$Q/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
![]() ${\mathcal{R}}_{X}/t_{\unicode[STIX]{x1D70F}}^{j}$
. This will follow from Lemma 2.2 and [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.8(2)]. Indeed, we may first spread out
${\mathcal{R}}_{X}/t_{\unicode[STIX]{x1D70F}}^{j}$
. This will follow from Lemma 2.2 and [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.8(2)]. Indeed, we may first spread out
![]() $Q$
to a finitely presented module
$Q$
to a finitely presented module
![]() $Q^{r_{0}}$
on a half-open annulus
$Q^{r_{0}}$
on a half-open annulus
![]() $X^{r_{0}}$
. Having done that, Lemma 2.2 shows that it suffices to check that
$X^{r_{0}}$
. Having done that, Lemma 2.2 shows that it suffices to check that
 $Q^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
is finite flat over
$Q^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
is finite flat over
 ${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
for each
${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
for each
 $0<s<r_{0}$
. To check that, we observe that
$0<s<r_{0}$
. To check that, we observe that
 ${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
is the completed tensor product of an affinoid algebra
${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
is the completed tensor product of an affinoid algebra
 ${\mathcal{R}}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
with a reduced affinoid algebra
${\mathcal{R}}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
with a reduced affinoid algebra
![]() $A$
(where
$A$
(where
 $X=\operatorname{Sp}(A)$
). In particular, [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.8(2)] (which only requires one of the tensor-ands to be reduced) and the constancy
$X=\operatorname{Sp}(A)$
). In particular, [Reference Kedlaya, Pottharst and XiaoKPX14, Lemma 2.1.8(2)] (which only requires one of the tensor-ands to be reduced) and the constancy
 $u\mapsto \operatorname{rank}_{{\mathcal{R}}_{L(u)}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}}Q_{u}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
(our assumption in the claim) implies that
$u\mapsto \operatorname{rank}_{{\mathcal{R}}_{L(u)}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}}Q_{u}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
(our assumption in the claim) implies that
 $Q^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
is finite flat over
$Q^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
is finite flat over
 ${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
.
${\mathcal{R}}_{X}^{[s,r_{0}]}/t_{\unicode[STIX]{x1D70F}}^{j}$
.
Proof of claim.
We now prove the claim by induction on
 $1\leqslant j\leqslant m$
starting with
$1\leqslant j\leqslant m$
starting with
![]() $j=1$
. Since
$j=1$
. Since
 $m_{i,\unicode[STIX]{x1D70F}}(u)\geqslant 1$
for all
$m_{i,\unicode[STIX]{x1D70F}}(u)\geqslant 1$
for all
![]() $i$
and
$i$
and
![]() $u$
, we see visibly that
$u$
, we see visibly that
![]() $Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is free over
$Q_{u}/t_{\unicode[STIX]{x1D70F}}$
is free over
 ${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
of rank
${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
of rank
![]() $r+s$
for each
$r+s$
for each
![]() $u\in X$
. Let
$u\in X$
. Let
 $1\leqslant j<m$
and assume
$1\leqslant j<m$
and assume
![]() $Q_{u}/t_{\unicode[STIX]{x1D70F}}^{j}$
is free over
$Q_{u}/t_{\unicode[STIX]{x1D70F}}^{j}$
is free over
 ${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{j}$
for all
${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{j}$
for all
![]() $u\in X$
. If we show that we may shrink
$u\in X$
. If we show that we may shrink
![]() $X$
so that
$X$
so that
 $j<m_{i,\unicode[STIX]{x1D70F}}(u)$
for each
$j<m_{i,\unicode[STIX]{x1D70F}}(u)$
for each
![]() $i$
and
$i$
and
![]() $u\in X$
, then the same freeness will be true for
$u\in X$
, then the same freeness will be true for
![]() $j+1$
and we will be done.
$j+1$
and we will be done.
First,
![]() $Q/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
$Q/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
![]() ${\mathcal{R}}_{X}/t_{\unicode[STIX]{x1D70F}}^{j}$
by induction and the proof in the paragraph following the claim. Since
${\mathcal{R}}_{X}/t_{\unicode[STIX]{x1D70F}}^{j}$
by induction and the proof in the paragraph following the claim. Since
![]() ${\mathcal{R}}_{X}/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
${\mathcal{R}}_{X}/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
![]() $X$
, see [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 2.1.5], we get that
$X$
, see [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 2.1.5], we get that
![]() $Q/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
$Q/t_{\unicode[STIX]{x1D70F}}^{j}$
is flat over
![]() $X$
. Second,
$X$
. Second,
![]() $Q$
is nearly flat over
$Q$
is nearly flat over
![]() $X$
and thus Proposition 4.3 implies that the
$X$
and thus Proposition 4.3 implies that the
![]() $t_{\unicode[STIX]{x1D70F}}^{j}$
-torsion satisfies base change: for each
$t_{\unicode[STIX]{x1D70F}}^{j}$
-torsion satisfies base change: for each
 $u\in X(\overline{\mathbf{Q}}_{p})$
,
$u\in X(\overline{\mathbf{Q}}_{p})$
,
 $$\begin{eqnarray}\displaystyle Q[t_{\unicode[STIX]{x1D70F}}^{j}]_{u}=Q_{u}[t_{\unicode[STIX]{x1D70F}}^{j}]\simeq \bigoplus _{i=1}^{s}t_{\unicode[STIX]{x1D70F}}^{\max (0,m_{i,\unicode[STIX]{x1D70F}}(u)-j)}{\mathcal{R}}_{L(u)}/t^{m_{i,\unicode[STIX]{x1D70F}}(u)}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q[t_{\unicode[STIX]{x1D70F}}^{j}]_{u}=Q_{u}[t_{\unicode[STIX]{x1D70F}}^{j}]\simeq \bigoplus _{i=1}^{s}t_{\unicode[STIX]{x1D70F}}^{\max (0,m_{i,\unicode[STIX]{x1D70F}}(u)-j)}{\mathcal{R}}_{L(u)}/t^{m_{i,\unicode[STIX]{x1D70F}}(u)}. & & \displaystyle \nonumber\end{eqnarray}$$
If we define
 $Q^{\prime }:=Q/Q[t_{\unicode[STIX]{x1D70F}}^{j}]$
, then
$Q^{\prime }:=Q/Q[t_{\unicode[STIX]{x1D70F}}^{j}]$
, then
![]() $Q^{\prime }$
is a generalized
$Q^{\prime }$
is a generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $X$
and we see
$X$
and we see
 $$\begin{eqnarray}Q_{u}^{\prime }\simeq \biggl(\bigoplus _{i=1}^{s}{\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{\max (0,m_{i}(u)-j)}\biggr)\oplus {\mathcal{R}}_{L(u)}^{\oplus r}\oplus S_{u}\end{eqnarray}$$
$$\begin{eqnarray}Q_{u}^{\prime }\simeq \biggl(\bigoplus _{i=1}^{s}{\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}^{\max (0,m_{i}(u)-j)}\biggr)\oplus {\mathcal{R}}_{L(u)}^{\oplus r}\oplus S_{u}\end{eqnarray}$$
as a
![]() ${\mathcal{R}}_{L(u)}$
-module. Note immediately that
${\mathcal{R}}_{L(u)}$
-module. Note immediately that
![]() $Q_{u}^{\prime }/t_{\unicode[STIX]{x1D70F}}$
is free over
$Q_{u}^{\prime }/t_{\unicode[STIX]{x1D70F}}$
is free over
 ${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
for any
${\mathcal{R}}_{L(u)}/t_{\unicode[STIX]{x1D70F}}$
for any
![]() $u$
. Now specialize to
$u$
. Now specialize to
![]() $u=x_{0}$
or
$u=x_{0}$
or
![]() $u\in Z$
. From the assumptions (b) and (c) we have that
$u\in Z$
. From the assumptions (b) and (c) we have that
![]() $Q_{u}^{\prime }/t_{\unicode[STIX]{x1D70F}}$
has rank
$Q_{u}^{\prime }/t_{\unicode[STIX]{x1D70F}}$
has rank
![]() $r+s$
at
$r+s$
at
![]() $u=x_{0}$
and at
$u=x_{0}$
and at
![]() $u\in Z$
. By Lemma 5.5, we may replace
$u\in Z$
. By Lemma 5.5, we may replace
![]() $X$
by an affinoid subdomain so that
$X$
by an affinoid subdomain so that
![]() $Q_{u}^{\prime }/t_{\unicode[STIX]{x1D70F}}$
has precisely rank
$Q_{u}^{\prime }/t_{\unicode[STIX]{x1D70F}}$
has precisely rank
![]() $r+s$
everywhere on
$r+s$
everywhere on
![]() $X$
. The formula (9) for the fiber
$X$
. The formula (9) for the fiber
![]() $Q_{u}^{\prime }$
easily implies that
$Q_{u}^{\prime }$
easily implies that
 $m_{i}(u)-j>0$
, which is what we wanted to show.◻
$m_{i}(u)-j>0$
, which is what we wanted to show.◻
With the inductive step complete, the proof is finished. ◻
Recall we defined the
![]() $\unicode[STIX]{x1D70F}$
-torsion length
$\unicode[STIX]{x1D70F}$
-torsion length
![]() $\ell _{\unicode[STIX]{x1D70F}}(Q)$
of generalized
$\ell _{\unicode[STIX]{x1D70F}}(Q)$
of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules in § 3.3. If we know that
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules in § 3.3. If we know that
![]() $Q$
has a standard triangulation
$Q$
has a standard triangulation
![]() $Q_{\bullet }$
, then its
$Q_{\bullet }$
, then its
![]() $\unicode[STIX]{x1D70F}$
-torsion length is the number terms in the associated graded with non-zero
$\unicode[STIX]{x1D70F}$
-torsion length is the number terms in the associated graded with non-zero
![]() $\unicode[STIX]{x1D70F}$
-torsion exponent.
$\unicode[STIX]{x1D70F}$
-torsion exponent.
Proposition 5.7. Suppose that
![]() $Q$
is a nearly flat pointwise triangulated family with torsion centered at
$Q$
is a nearly flat pointwise triangulated family with torsion centered at
 $x_{0}\in X(\overline{\mathbf{Q}}_{p})$
and non-critical points
$x_{0}\in X(\overline{\mathbf{Q}}_{p})$
and non-critical points
![]() $X^{\operatorname{nc}}$
. If
$X^{\operatorname{nc}}$
. If
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
such that
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
such that
 $\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0}})=\ell _{\unicode[STIX]{x1D70F}}(Q_{y})$
at one (and, hence, all)
$\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0}})=\ell _{\unicode[STIX]{x1D70F}}(Q_{y})$
at one (and, hence, all)
 $y\in X^{\operatorname{nc}}$
, then there exists an affinoid neighborhood
$y\in X^{\operatorname{nc}}$
, then there exists an affinoid neighborhood
 $x_{0}\in U\subset X$
such that
$x_{0}\in U\subset X$
such that
 $Q[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]_{x}\simeq Q_{x}[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
for all
$Q[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]_{x}\simeq Q_{x}[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
for all
 $x\in U(\overline{\mathbf{Q}}_{p})$
and
$x\in U(\overline{\mathbf{Q}}_{p})$
and
 $Q|_{U}[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
is a nearly flat generalized
$Q|_{U}[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
is a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $U$
.
$U$
.
Proof. We are going to apply Lemma 5.6. Note that
![]() $Q_{x}/t_{\unicode[STIX]{x1D70F}}$
is free over
$Q_{x}/t_{\unicode[STIX]{x1D70F}}$
is free over
 ${\mathcal{R}}_{L(x)}/t_{\unicode[STIX]{x1D70F}}$
for all
${\mathcal{R}}_{L(x)}/t_{\unicode[STIX]{x1D70F}}$
for all
 $x\in X(\overline{\mathbf{Q}}_{p})$
. Moreover, the rank at
$x\in X(\overline{\mathbf{Q}}_{p})$
. Moreover, the rank at
![]() $x=x_{0}$
agrees with the rank over the Zariski-dense set
$x=x_{0}$
agrees with the rank over the Zariski-dense set
![]() $X^{\operatorname{nc}}$
. By axiom (TF3), the free parameters of the family
$X^{\operatorname{nc}}$
. By axiom (TF3), the free parameters of the family
![]() $Q$
have constant length
$Q$
have constant length
 $d-i(x_{0})$
on all of
$d-i(x_{0})$
on all of
![]() $X$
. Since
$X$
. Since
 $\operatorname{rank}_{{\mathcal{R}}_{L(x)}/t_{\unicode[STIX]{x1D70F}}}Q_{x}/t_{\unicode[STIX]{x1D70F}}=\ell _{\unicode[STIX]{x1D70F}}(Q_{x})+d-i(x_{0})$
, Lemma 5.5 implies that we may shrink
$\operatorname{rank}_{{\mathcal{R}}_{L(x)}/t_{\unicode[STIX]{x1D70F}}}Q_{x}/t_{\unicode[STIX]{x1D70F}}=\ell _{\unicode[STIX]{x1D70F}}(Q_{x})+d-i(x_{0})$
, Lemma 5.5 implies that we may shrink
![]() $X$
and assume that the
$X$
and assume that the
![]() $\unicode[STIX]{x1D70F}$
-torsion lengths are also constant on the entire family. In particular, the first hypothesis of Lemma 5.6 is verified. By axiom (TF5), the minimal torsion exponent at
$\unicode[STIX]{x1D70F}$
-torsion lengths are also constant on the entire family. In particular, the first hypothesis of Lemma 5.6 is verified. By axiom (TF5), the minimal torsion exponent at
 $y\in X_{\operatorname{nc}}$
is given by
$y\in X_{\operatorname{nc}}$
is given by
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
, independent of
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
, independent of
![]() $y$
. Thus the second hypothesis of Lemma 5.6 is verified. On the other hand, by axiom (TF1),
$y$
. Thus the second hypothesis of Lemma 5.6 is verified. On the other hand, by axiom (TF1),
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
is also the smallest possible value for elements in the set
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})$
is also the smallest possible value for elements in the set
 $\{s_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}}):2\leqslant j\leqslant d\}$
, which are the possible non-zero
$\{s_{j,\unicode[STIX]{x1D70F}}-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}}):2\leqslant j\leqslant d\}$
, which are the possible non-zero
![]() $\unicode[STIX]{x1D70F}$
-torsion exponents of the standard triangulation on
$\unicode[STIX]{x1D70F}$
-torsion exponents of the standard triangulation on
![]() $Q_{x_{0}}$
. Thus, the third hypothesis of Lemma 5.6 is satisfied. We conclude by Lemma 5.6 that
$Q_{x_{0}}$
. Thus, the third hypothesis of Lemma 5.6 is satisfied. We conclude by Lemma 5.6 that
 $Q|_{U}/t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}$
is flat over
$Q|_{U}/t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}$
is flat over
 ${\mathcal{R}}_{U}/t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}$
for some affinoid neighborhood
${\mathcal{R}}_{U}/t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}$
for some affinoid neighborhood
![]() $U$
of
$U$
of
![]() $x_{0}$
. Replacing
$x_{0}$
. Replacing
![]() $X$
by
$X$
by
![]() $U$
we are done by Proposition 4.3.◻
$U$
we are done by Proposition 4.3.◻
Corollary 5.8. Suppose
![]() $Q$
is a nearly flat pointwise triangulated family with torsion centered at
$Q$
is a nearly flat pointwise triangulated family with torsion centered at
 $x_{0}\in X(\overline{\mathbf{Q}}_{p})$
, non-critical points
$x_{0}\in X(\overline{\mathbf{Q}}_{p})$
, non-critical points
![]() $X^{\operatorname{nc}}$
and for each
$X^{\operatorname{nc}}$
and for each
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, we have
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, we have
 $\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0}})=\ell _{\unicode[STIX]{x1D70F}}(Q_{y})$
for one (and hence all) points
$\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0}})=\ell _{\unicode[STIX]{x1D70F}}(Q_{y})$
for one (and hence all) points
 $y\in X^{\operatorname{nc}}$
. Then we have the following.
$y\in X^{\operatorname{nc}}$
. Then we have the following.
-
(a) For each
 $\unicode[STIX]{x1D70F}$
there exists a unique
$\unicode[STIX]{x1D70F}$
there exists a unique
 $1\leqslant j_{\unicode[STIX]{x1D70F}}\leqslant i(x_{0})$
such that
$1\leqslant j_{\unicode[STIX]{x1D70F}}\leqslant i(x_{0})$
such that
 $s_{j_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D70F}}=k_{1,\unicode[STIX]{x1D70F}}$
.
$s_{j_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D70F}}=k_{1,\unicode[STIX]{x1D70F}}$
. -
(b) There exists an affinoid neighborhood
 $x_{0}\in U\subset X$
such that the quotient is a nearly flat pointwise and triangulated family of
$x_{0}\in U\subset X$
such that the quotient is a nearly flat pointwise and triangulated family of $$\begin{eqnarray}\displaystyle Q^{\prime }:=Q|_{U}/Q|_{U}\biggl[\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}\biggr] & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q^{\prime }:=Q|_{U}/Q|_{U}\biggl[\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}\biggr] & & \displaystyle \nonumber\end{eqnarray}$$
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
 $U$
with torsion centered at
$U$
with torsion centered at
 $x_{0}$
and modified data:
$x_{0}$
and modified data:-
– torsion weights
 $(s_{j,\unicode[STIX]{x1D70F}})_{j\neq j_{\unicode[STIX]{x1D70F}}}$
;
$(s_{j,\unicode[STIX]{x1D70F}})_{j\neq j_{\unicode[STIX]{x1D70F}}}$
; -
– parameter
 $(\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
;
$(\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
; -
–
 $X^{\operatorname{nc}}$
replaced by
$X^{\operatorname{nc}}$
replaced by
 $U\cap X^{\operatorname{nc}}$
.
$U\cap X^{\operatorname{nc}}$
.
In particular, the free length of
 $Q^{\prime }$
is the same as the free length of
$Q^{\prime }$
is the same as the free length of
 $Q$
.
$Q$
. -
Proof. The fact that the
![]() $j_{\unicode[STIX]{x1D70F}}$
exists is clear since the
$j_{\unicode[STIX]{x1D70F}}$
exists is clear since the
![]() $\unicode[STIX]{x1D70F}$
-torsion lengths are constant on
$\unicode[STIX]{x1D70F}$
-torsion lengths are constant on
![]() $X^{\operatorname{nc}}$
and concur with the lengths at
$X^{\operatorname{nc}}$
and concur with the lengths at
![]() $x_{0}$
. Choose, by Proposition 5.7, an affinoid neighborhood
$x_{0}$
. Choose, by Proposition 5.7, an affinoid neighborhood
 $x_{0}\in U\subset X$
over which each torsion
$x_{0}\in U\subset X$
over which each torsion
 $Q|_{U}[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
satisfies base change and is a nearly flat generalized
$Q|_{U}[t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
satisfies base change and is a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $U$
. Since the
$U$
. Since the
![]() $t_{\unicode[STIX]{x1D70F}}$
are maximally coprime within
$t_{\unicode[STIX]{x1D70F}}$
are maximally coprime within
![]() ${\mathcal{R}}$
, the torsion
${\mathcal{R}}$
, the torsion
 $Q|_{U}[\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
is also a nearly flat generalized
$Q|_{U}[\prod _{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}]$
is also a nearly flat generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module and satisfies base change over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module and satisfies base change over
![]() $U$
. Let
$U$
. Let
![]() $Q^{\prime }$
be as in the statement of part (b). Then we see that
$Q^{\prime }$
be as in the statement of part (b). Then we see that
![]() $Q^{\prime }$
is nearly flat over
$Q^{\prime }$
is nearly flat over
![]() $U$
, proving the first half of part (b). If
$U$
, proving the first half of part (b). If
![]() $x\in U$
, then the fiber of
$x\in U$
, then the fiber of
![]() $Q^{\prime }$
at
$Q^{\prime }$
at
![]() $x$
is computed as
$x$
is computed as
 $$\begin{eqnarray}\displaystyle Q_{x}^{\prime }=\operatorname{coker}\biggl(Q_{x}\biggl[\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}\biggr]{\hookrightarrow}Q_{x}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{x}^{\prime }=\operatorname{coker}\biggl(Q_{x}\biggl[\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{2,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x_{0}})}\biggr]{\hookrightarrow}Q_{x}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
The image, by definition, lands in the torsion part of
![]() $Q_{x}$
and, hence, can only effect the torsion exponents of the standard triangulation on
$Q_{x}$
and, hence, can only effect the torsion exponents of the standard triangulation on
![]() $Q_{x}^{\prime }$
. Thus the rest of part (b) follows easily follows from the observation that
$Q_{x}^{\prime }$
. Thus the rest of part (b) follows easily follows from the observation that
 $$\begin{eqnarray}\displaystyle \operatorname{coker}(t^{s-k_{2,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L}/t^{s-k_{1,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L}\rightarrow {\mathcal{R}}_{L}/t^{s-k_{1,\unicode[STIX]{x1D70F}}}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{coker}(t^{s-k_{2,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L}/t^{s-k_{1,\unicode[STIX]{x1D70F}}}{\mathcal{R}}_{L}\rightarrow {\mathcal{R}}_{L}/t^{s-k_{1,\unicode[STIX]{x1D70F}}}) & & \displaystyle \nonumber\end{eqnarray}$$
has torsion exponent
 $s-k_{2,\unicode[STIX]{x1D70F}}$
for any
$s-k_{2,\unicode[STIX]{x1D70F}}$
for any
 $s\geqslant k_{2,\unicode[STIX]{x1D70F}}>k_{1,\unicode[STIX]{x1D70F}}$
.◻
$s\geqslant k_{2,\unicode[STIX]{x1D70F}}>k_{1,\unicode[STIX]{x1D70F}}$
.◻
6
 $p$
-adic variation in refined families
$p$
-adic variation in refined families
We are now ready to state and prove the main theorem of this article. The notion of refined families given below is inspired by [Reference Bellaïche and ChenevierBC09, ch. 4] (see also [Reference LiuLiu15, § 5]). They arise naturally as arithmetic families of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over rigid spaces, for example eigenvarieties.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over rigid spaces, for example eigenvarieties.
6.1 Refined families
Let
 $X=\operatorname{Sp}(A)$
be a reduced
$X=\operatorname{Sp}(A)$
be a reduced
![]() $L$
-affinoid space.
$L$
-affinoid space.
Definition 6.1. A refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules of rank
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules of rank
![]() $d$
is:
$d$
is:
-
– a
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
 $D$
of rank
$D$
of rank
 $d$
over
$d$
over
 $X$
;
$X$
; -
– an ordered tuple
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}):K^{\times }\rightarrow A^{\times }$
of continuous characters; and
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d}):K^{\times }\rightarrow A^{\times }$
of continuous characters; and -
– a Zariski-dense subset
 $X_{\operatorname{cl}}\subset X(\overline{\mathbf{Q}}_{p})$
;
$X_{\operatorname{cl}}\subset X(\overline{\mathbf{Q}}_{p})$
;
such that the following axioms hold.
-
(RF1) For each
 $x\in X(\overline{\mathbf{Q}}_{p})$
and
$x\in X(\overline{\mathbf{Q}}_{p})$
and
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, We now label the Hodge–Tate–Sen weights by
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, We now label the Hodge–Tate–Sen weights by $$\begin{eqnarray}\displaystyle \operatorname{HT}_{\unicode[STIX]{x1D70F}}(D_{x})=\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{d,x})\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{HT}_{\unicode[STIX]{x1D70F}}(D_{x})=\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{1,x}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{d,x})\}. & & \displaystyle \nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x):=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x})$
.
$\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x):=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x})$
.
-
(RF2) For each
 $x\in X_{\operatorname{cl}}$
and
$x\in X_{\operatorname{cl}}$
and
 $i=1,\ldots ,d$
, the character
$i=1,\ldots ,d$
, the character
 $\unicode[STIX]{x1D6FF}_{i,x}$
is crystalline.
$\unicode[STIX]{x1D6FF}_{i,x}$
is crystalline. -
(RF3) If
 $x\in X_{\operatorname{cl}}$
, then
$x\in X_{\operatorname{cl}}$
, then
 $D_{x}$
is crystalline, the Hodge–Tate weights satisfy for each
$D_{x}$
is crystalline, the Hodge–Tate weights satisfy for each $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x)<\cdots <\unicode[STIX]{x1D705}_{d,\unicode[STIX]{x1D70F}}(x), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x)<\cdots <\unicode[STIX]{x1D705}_{d,\unicode[STIX]{x1D70F}}(x), & & \displaystyle \nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, and the
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, and the
 $\unicode[STIX]{x1D711}^{f_{K}}$
eigenvalues
$\unicode[STIX]{x1D711}^{f_{K}}$
eigenvalues
 $\{\unicode[STIX]{x1D719}_{1}(x),\ldots ,\unicode[STIX]{x1D719}_{d}(x)\}$
all live in
$\{\unicode[STIX]{x1D719}_{1}(x),\ldots ,\unicode[STIX]{x1D719}_{d}(x)\}$
all live in
 $L(x)^{\times }$
, are distinct, and given by for some (any) uniformizer
$L(x)^{\times }$
, are distinct, and given by for some (any) uniformizer $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{i}(x)=\unicode[STIX]{x1D6FF}_{i,x}(\unicode[STIX]{x1D71B}_{K})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{i}(x)=\unicode[STIX]{x1D6FF}_{i,x}(\unicode[STIX]{x1D71B}_{K})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)} & & \displaystyle \nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
.
$\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
.
-
(RF4) By axiom (RF3) and Proposition 3.3, every point
 $x\in X_{\operatorname{cl}}$
has a unique triangulation
$x\in X_{\operatorname{cl}}$
has a unique triangulation
 $P_{x,\bullet }$
corresponding to the ordering
$P_{x,\bullet }$
corresponding to the ordering
 $(\unicode[STIX]{x1D719}_{1}(x),\ldots ,\unicode[STIX]{x1D719}_{n}(x))$
of (distinct) crystalline eigenvalues. Let Then, for all
$(\unicode[STIX]{x1D719}_{1}(x),\ldots ,\unicode[STIX]{x1D719}_{n}(x))$
of (distinct) crystalline eigenvalues. Let Then, for all $$\begin{eqnarray}\displaystyle X_{\operatorname{cl}}^{\operatorname{nc}}:=\{x\in X_{\operatorname{cl}}:P_{x,\bullet }\text{ is a non-critical triangulation}\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{\operatorname{cl}}^{\operatorname{nc}}:=\{x\in X_{\operatorname{cl}}:P_{x,\bullet }\text{ is a non-critical triangulation}\}. & & \displaystyle \nonumber\end{eqnarray}$$
 $C>0$
, the set is Zariski-dense in
$C>0$
, the set is Zariski-dense in $$\begin{eqnarray}\displaystyle X_{\operatorname{cl},C}^{\operatorname{nc}}:=\biggl\{x\in X_{\operatorname{cl}}^{\operatorname{nc}}:C<\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D705}_{i+1,\unicode[STIX]{x1D70F}}(x)-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)\text{ for }i=1,\ldots ,n-1\biggr\} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{\operatorname{cl},C}^{\operatorname{nc}}:=\biggl\{x\in X_{\operatorname{cl}}^{\operatorname{nc}}:C<\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D705}_{i+1,\unicode[STIX]{x1D70F}}(x)-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)\text{ for }i=1,\ldots ,n-1\biggr\} & & \displaystyle \nonumber\end{eqnarray}$$
 $X$
and accumulates at every point in
$X$
and accumulates at every point in
 $X_{\operatorname{cl}}$
.
$X_{\operatorname{cl}}$
.
We will often abuse language and call
![]() $D$
the refined family, with the ordered parameter
$D$
the refined family, with the ordered parameter
 $(\unicode[STIX]{x1D6FF}_{i})_{i=1,\ldots ,d}$
and the subset
$(\unicode[STIX]{x1D6FF}_{i})_{i=1,\ldots ,d}$
and the subset
![]() $X_{\operatorname{cl}}$
understood. The subscript ‘
$X_{\operatorname{cl}}$
understood. The subscript ‘
![]() $\operatorname{cl}$
’ is meant to mean classical, but note that there are slight restrictions. Indeed, a refined family for us has a distinctness hypothesis on not only the Hodge–Tate weights over
$\operatorname{cl}$
’ is meant to mean classical, but note that there are slight restrictions. Indeed, a refined family for us has a distinctness hypothesis on not only the Hodge–Tate weights over
![]() $X_{\operatorname{cl}}$
but also the crystalline eigenvalues. In applications we will work with a slightly stronger condition.
$X_{\operatorname{cl}}$
but also the crystalline eigenvalues. In applications we will work with a slightly stronger condition.
Definition 6.2. Suppose that
![]() $D$
is a refined family of
$D$
is a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X$
. We say that
$X$
. We say that
![]() $x\in X_{\operatorname{cl}}$
is very
$x\in X_{\operatorname{cl}}$
is very
![]() $\unicode[STIX]{x1D711}$
-regular if:
$\unicode[STIX]{x1D711}$
-regular if:
-
(a)
 $\unicode[STIX]{x1D719}_{i}(x)\neq p^{f_{K}}\unicode[STIX]{x1D719}_{j}(x)$
for each
$\unicode[STIX]{x1D719}_{i}(x)\neq p^{f_{K}}\unicode[STIX]{x1D719}_{j}(x)$
for each
 $1\leqslant i<j\leqslant d$
; and
$1\leqslant i<j\leqslant d$
; and -
(b)
 $\unicode[STIX]{x1D719}_{1}(x)\cdots \unicode[STIX]{x1D719}_{i}(x)$
is a simple eigenvalue of
$\unicode[STIX]{x1D719}_{1}(x)\cdots \unicode[STIX]{x1D719}_{i}(x)$
is a simple eigenvalue of
 $\unicode[STIX]{x1D711}^{f_{K}}$
acting on
$\unicode[STIX]{x1D711}^{f_{K}}$
acting on
 $D_{\operatorname{cris}}(\wedge ^{i}D_{x})$
for each
$D_{\operatorname{cris}}(\wedge ^{i}D_{x})$
for each
 $1\leqslant i\leqslant d$
.
$1\leqslant i\leqslant d$
.
The set of all very
![]() $\unicode[STIX]{x1D711}$
-regular points is denoted by
$\unicode[STIX]{x1D711}$
-regular points is denoted by
![]() $X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
.
$X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
.
Just as axiom (RF4) says that classical points are well-approximated by points whose Hodge–Tate weights are extremely regular (i.e. far apart), the following proposition shows that we can, moreover, make such approximations by very
![]() $\unicode[STIX]{x1D711}$
-regular points as well. We let
$\unicode[STIX]{x1D711}$
-regular points as well. We let
 $X_{\operatorname{cl},C}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}=X_{\operatorname{cl},C}^{\operatorname{nc}}\cap X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
.
$X_{\operatorname{cl},C}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}=X_{\operatorname{cl},C}^{\operatorname{nc}}\cap X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
.
Proposition 6.3. If
![]() $C>0$
, then
$C>0$
, then
 $X_{\operatorname{cl},C}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
accumulates each every point in
$X_{\operatorname{cl},C}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
accumulates each every point in
![]() $X_{\operatorname{cl}}$
.
$X_{\operatorname{cl}}$
.
Proof. Let
![]() $x\in X_{\operatorname{cl}}$
. Since each character
$x\in X_{\operatorname{cl}}$
. Since each character
 $\unicode[STIX]{x1D6FF}_{i}:K^{\times }\rightarrow A^{\times }$
is continuous we may choose a neighborhood
$\unicode[STIX]{x1D6FF}_{i}:K^{\times }\rightarrow A^{\times }$
is continuous we may choose a neighborhood
![]() $U$
of
$U$
of
![]() $x$
so that the slopes
$x$
so that the slopes
 $v_{p}(\unicode[STIX]{x1D6FF}_{i,u}(\unicode[STIX]{x1D71B}_{K}))=:\unicode[STIX]{x1D708}_{i}$
are constant on
$v_{p}(\unicode[STIX]{x1D6FF}_{i,u}(\unicode[STIX]{x1D71B}_{K}))=:\unicode[STIX]{x1D708}_{i}$
are constant on
![]() $U$
for some (and, hence, any) uniformizer
$U$
for some (and, hence, any) uniformizer
![]() $\unicode[STIX]{x1D71B}_{K}$
. Let
$\unicode[STIX]{x1D71B}_{K}$
. Let
 $$\begin{eqnarray}\displaystyle C^{\prime }=\max \{C,1+e_{K}(\unicode[STIX]{x1D708}_{i}-\unicode[STIX]{x1D708}_{j}):1\leqslant i,j\leqslant d\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C^{\prime }=\max \{C,1+e_{K}(\unicode[STIX]{x1D708}_{i}-\unicode[STIX]{x1D708}_{j}):1\leqslant i,j\leqslant d\}. & & \displaystyle \nonumber\end{eqnarray}$$
Since
![]() $C\leqslant C^{\prime }$
,
$C\leqslant C^{\prime }$
,
 $X_{\operatorname{cl},C}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}\supset X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
. Thus, it suffices to show, by axiom (RF4), that
$X_{\operatorname{cl},C}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}\supset X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
. Thus, it suffices to show, by axiom (RF4), that
 $X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc}}\cap U\subset X_{\operatorname{ cl},C^{\prime }}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
. Let
$X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc}}\cap U\subset X_{\operatorname{ cl},C^{\prime }}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
. Let
 $u\in X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc}}\cap U$
and we will show
$u\in X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc}}\cap U$
and we will show
![]() $u$
is very
$u$
is very
![]() $\unicode[STIX]{x1D711}$
-regular.
$\unicode[STIX]{x1D711}$
-regular.
-
∙ Suppose
 $i<j$
and
$i<j$
and
 $\unicode[STIX]{x1D719}_{i}(u)=p^{f_{K}}\unicode[STIX]{x1D719}_{j}(u)$
. Since
$\unicode[STIX]{x1D719}_{i}(u)=p^{f_{K}}\unicode[STIX]{x1D719}_{j}(u)$
. Since
 $\unicode[STIX]{x1D719}_{i}(u)=\unicode[STIX]{x1D6FF}_{i,u}(\unicode[STIX]{x1D71B}_{K})\prod _{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(u)}$
we can take
$\unicode[STIX]{x1D719}_{i}(u)=\unicode[STIX]{x1D6FF}_{i,u}(\unicode[STIX]{x1D71B}_{K})\prod _{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D71B}_{K})^{\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(u)}$
we can take
 $p$
-adic valuations and get, since
$p$
-adic valuations and get, since
 $u\in U$
, that Thus,
$u\in U$
, that Thus, $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(u)-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(u)=e_{K}(\unicode[STIX]{x1D708}_{i}-\unicode[STIX]{x1D708}_{j}-f_{K})<C^{\prime }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(u)-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(u)=e_{K}(\unicode[STIX]{x1D708}_{i}-\unicode[STIX]{x1D708}_{j}-f_{K})<C^{\prime }. & & \displaystyle \nonumber\end{eqnarray}$$
 $u\notin X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc}}$
, a contradiction.
$u\notin X_{\operatorname{cl},C^{\prime }}^{\operatorname{nc}}$
, a contradiction.
-
∙ If
 $\unicode[STIX]{x1D719}_{1}(u)\cdots \unicode[STIX]{x1D719}_{i}(u)$
is not a simple eigenvalue on
$\unicode[STIX]{x1D719}_{1}(u)\cdots \unicode[STIX]{x1D719}_{i}(u)$
is not a simple eigenvalue on
 $D_{\operatorname{cris}}(\wedge ^{i}D_{u})$
, then one may construct a list of pairs of integers
$D_{\operatorname{cris}}(\wedge ^{i}D_{u})$
, then one may construct a list of pairs of integers
 $i_{1}<j_{1},\ldots ,i_{s}<j_{s}$
such that
$i_{1}<j_{1},\ldots ,i_{s}<j_{s}$
such that
 $\unicode[STIX]{x1D719}_{i_{1}}(u)\cdots \unicode[STIX]{x1D719}_{i_{s}}(u)=\unicode[STIX]{x1D719}_{j_{1}}(u)\cdots \unicode[STIX]{x1D719}_{j_{s}}(u)$
for some
$\unicode[STIX]{x1D719}_{i_{1}}(u)\cdots \unicode[STIX]{x1D719}_{i_{s}}(u)=\unicode[STIX]{x1D719}_{j_{1}}(u)\cdots \unicode[STIX]{x1D719}_{j_{s}}(u)$
for some
 $s\geqslant 1$
. Once again, taking slopes we get a contradiction.
$s\geqslant 1$
. Once again, taking slopes we get a contradiction. $$\begin{eqnarray}\displaystyle sC^{\prime }<\mathop{\sum }_{b=1}^{s}\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D705}_{j_{b},\unicode[STIX]{x1D70F}}(u)-\unicode[STIX]{x1D705}_{i_{b},\unicode[STIX]{x1D70F}}(u)=\mathop{\sum }_{b=1}^{s}(e_{K}(\unicode[STIX]{x1D708}_{i_{b}}-\unicode[STIX]{x1D708}_{j_{b}}))\leqslant sC^{\prime }, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle sC^{\prime }<\mathop{\sum }_{b=1}^{s}\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}\unicode[STIX]{x1D705}_{j_{b},\unicode[STIX]{x1D70F}}(u)-\unicode[STIX]{x1D705}_{i_{b},\unicode[STIX]{x1D70F}}(u)=\mathop{\sum }_{b=1}^{s}(e_{K}(\unicode[STIX]{x1D708}_{i_{b}}-\unicode[STIX]{x1D708}_{j_{b}}))\leqslant sC^{\prime }, & & \displaystyle \nonumber\end{eqnarray}$$
This concludes the proof. ◻
In the remainder of this subsection we show that point-by-point, a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules may be triangulated (in an essentially unique way depending on the ordered parameter
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules may be triangulated (in an essentially unique way depending on the ordered parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n})$
). In particular, we show that a refined family is naturally a pointwise triangulated family (with no torsion). We begin by dealing with the axiom (TF2).
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n})$
). In particular, we show that a refined family is naturally a pointwise triangulated family (with no torsion). We begin by dealing with the axiom (TF2).
Lemma 6.4. If
 $x\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then there exists an open affinoid neighborhood
$x\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then there exists an open affinoid neighborhood
 $x\in U\subset X$
such that
$x\in U\subset X$
such that
![]() $\unicode[STIX]{x1D6FF}_{i,u}^{-1}\unicode[STIX]{x1D6FF}_{j,u}$
is generic up to homothety for all
$\unicode[STIX]{x1D6FF}_{i,u}^{-1}\unicode[STIX]{x1D6FF}_{j,u}$
is generic up to homothety for all
 $u\in U(\overline{\mathbf{Q}}_{p})$
and
$u\in U(\overline{\mathbf{Q}}_{p})$
and
![]() $i<j$
.
$i<j$
.
Proof. Let
![]() $(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
be any tuple of integers and set
$(r_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}}$
be any tuple of integers and set
 $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FF}_{i}^{-1}\unicode[STIX]{x1D6FF}_{j}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{-r_{\unicode[STIX]{x1D70F}}}$
. We have to show
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FF}_{i}^{-1}\unicode[STIX]{x1D6FF}_{j}\prod _{\unicode[STIX]{x1D70F}}z_{\unicode[STIX]{x1D70F}}^{-r_{\unicode[STIX]{x1D70F}}}$
. We have to show
![]() $\unicode[STIX]{x1D702}_{u}$
is generic for
$\unicode[STIX]{x1D702}_{u}$
is generic for
![]() $u$
near
$u$
near
![]() $x$
. Choose a uniformizer
$x$
. Choose a uniformizer
![]() $\unicode[STIX]{x1D71B}_{K}$
of
$\unicode[STIX]{x1D71B}_{K}$
of
![]() $K^{\times }$
. Then by axiom (RF3),
$K^{\times }$
. Then by axiom (RF3),
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{x}=\operatorname{unr}_{\unicode[STIX]{x1D71B}_{K}}(\unicode[STIX]{x1D719}_{j}(x)\unicode[STIX]{x1D719}_{i}(x)^{-1})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x)-r_{\unicode[STIX]{x1D70F}}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{x}=\operatorname{unr}_{\unicode[STIX]{x1D71B}_{K}}(\unicode[STIX]{x1D719}_{j}(x)\unicode[STIX]{x1D719}_{i}(x)^{-1})\mathop{\prod }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}}z_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x)-r_{\unicode[STIX]{x1D70F}}}. & & \displaystyle \nonumber\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D702}_{x}$
is not generic, then a comparison of weights shows that
$\unicode[STIX]{x1D702}_{x}$
is not generic, then a comparison of weights shows that
 $$\begin{eqnarray}\displaystyle \operatorname{unr}_{\unicode[STIX]{x1D71B}_{K}}(\unicode[STIX]{x1D719}_{j}(x)\unicode[STIX]{x1D719}_{i}(x)^{-1})\in \{1,|N_{K/\mathbf{Q}_{p}}(\unicode[STIX]{x1D71B}_{K})|\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{unr}_{\unicode[STIX]{x1D71B}_{K}}(\unicode[STIX]{x1D719}_{j}(x)\unicode[STIX]{x1D719}_{i}(x)^{-1})\in \{1,|N_{K/\mathbf{Q}_{p}}(\unicode[STIX]{x1D71B}_{K})|\}. & & \displaystyle \nonumber\end{eqnarray}$$
However, since
![]() $x$
is very
$x$
is very
![]() $\unicode[STIX]{x1D711}$
-regular and
$\unicode[STIX]{x1D711}$
-regular and
![]() $i<j$
this is explicitly ruled out. Thus,
$i<j$
this is explicitly ruled out. Thus,
![]() $\unicode[STIX]{x1D702}_{x}$
is generic.
$\unicode[STIX]{x1D702}_{x}$
is generic.
To conclude over an affinoid neighborhood we make use of cohomology and base change arguments. Consider the functions
 $d_{\unicode[STIX]{x1D702}}^{i}(u):=\dim _{L(u)}H^{i}(\unicode[STIX]{x1D702}_{u})$
. Since
$d_{\unicode[STIX]{x1D702}}^{i}(u):=\dim _{L(u)}H^{i}(\unicode[STIX]{x1D702}_{u})$
. Since
![]() $H^{2}(\unicode[STIX]{x1D702})$
satisfies base change,
$H^{2}(\unicode[STIX]{x1D702})$
satisfies base change,
 $u\mapsto d_{\unicode[STIX]{x1D702}}^{2}(u)$
is upper semi-continuous on
$u\mapsto d_{\unicode[STIX]{x1D702}}^{2}(u)$
is upper semi-continuous on
![]() $X$
. Since
$X$
. Since
![]() $d_{\unicode[STIX]{x1D702}}^{2}(u)$
vanishes at
$d_{\unicode[STIX]{x1D702}}^{2}(u)$
vanishes at
![]() $u=x$
, as we showed in the previous paragraph, we may shrink
$u=x$
, as we showed in the previous paragraph, we may shrink
![]() $X$
and assume that
$X$
and assume that
 $H^{2}(\unicode[STIX]{x1D702})=(0)$
. By Proposition 4.6,
$H^{2}(\unicode[STIX]{x1D702})=(0)$
. By Proposition 4.6,
![]() $H^{1}(\unicode[STIX]{x1D702})$
satisfies base change and
$H^{1}(\unicode[STIX]{x1D702})$
satisfies base change and
 $u\mapsto d_{\unicode[STIX]{x1D702}}^{1}(u)$
is upper semi-continuous. But
$u\mapsto d_{\unicode[STIX]{x1D702}}^{1}(u)$
is upper semi-continuous. But
![]() $d_{\unicode[STIX]{x1D702}}^{0}(u)$
has a local minimum at
$d_{\unicode[STIX]{x1D702}}^{0}(u)$
has a local minimum at
![]() $u=x$
and thus so does
$u=x$
and thus so does
 $d_{\unicode[STIX]{x1D702}}^{1}(u)=1+d_{\unicode[STIX]{x1D702}}^{0}(u)$
. Thus, after shrinking
$d_{\unicode[STIX]{x1D702}}^{1}(u)=1+d_{\unicode[STIX]{x1D702}}^{0}(u)$
. Thus, after shrinking
![]() $X$
further (so that
$X$
further (so that
 $d_{\unicode[STIX]{x1D702}}^{1}(u)\equiv 1$
) we may assume that
$d_{\unicode[STIX]{x1D702}}^{1}(u)\equiv 1$
) we may assume that
![]() $H^{1}(\unicode[STIX]{x1D702})$
is flat, and
$H^{1}(\unicode[STIX]{x1D702})$
is flat, and
![]() $H^{0}(\unicode[STIX]{x1D702})$
satisfies base change. Finally, this implies that
$H^{0}(\unicode[STIX]{x1D702})$
satisfies base change. Finally, this implies that
 $H^{0}(\unicode[STIX]{x1D702})=(0)$
.◻
$H^{0}(\unicode[STIX]{x1D702})=(0)$
.◻
As noted in axiom (RF4), axiom (RF3) and Proposition 3.3 imply that for each
 $x_{0}\in X_{\operatorname{cl}}$
there exists a triangulation
$x_{0}\in X_{\operatorname{cl}}$
there exists a triangulation
![]() $P_{x_{0},\bullet }$
of
$P_{x_{0},\bullet }$
of
![]() $D_{x_{0}}$
whose parameter
$D_{x_{0}}$
whose parameter
 $(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
is homothetic to
$(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
is homothetic to
 $(\unicode[STIX]{x1D6FF}_{1,x_{0}},\ldots ,\unicode[STIX]{x1D6FF}_{d,x_{0}})$
. Moreover, if
$(\unicode[STIX]{x1D6FF}_{1,x_{0}},\ldots ,\unicode[STIX]{x1D6FF}_{d,x_{0}})$
. Moreover, if
 $x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then Lemma 6.4 implies that
$x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then Lemma 6.4 implies that
![]() $P_{x_{0},\bullet }$
is the unique such triangulation of
$P_{x_{0},\bullet }$
is the unique such triangulation of
![]() $D_{x_{0}}$
. Thus, we may unambiguously refer to the parameter
$D_{x_{0}}$
. Thus, we may unambiguously refer to the parameter
 $(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
for
$(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
for
 $x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
.
$x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
.
Proposition 6.5. If
 $x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then there exists an open affinoid neighborhood
$x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then there exists an open affinoid neighborhood
 $x_{0}\in U\subset X$
such that
$x_{0}\in U\subset X$
such that
![]() $D|_{U}$
is a pointwise triangulated family with torsion center
$D|_{U}$
is a pointwise triangulated family with torsion center
![]() $x_{0}$
(but without actual torsion) and given data:
$x_{0}$
(but without actual torsion) and given data:
-
– torsion weights
 $(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}}))_{\unicode[STIX]{x1D70F}}$
;
$(\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}}))_{\unicode[STIX]{x1D70F}}$
; -
– parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
;
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
; -
– non-critical points
 $X_{\operatorname{cl}}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
; and
$X_{\operatorname{cl}}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
; and -
– center
 $x_{0}$
.
$x_{0}$
.
Proof. We have been given the data in the statement of the proposition and so our task is to verify axioms (TF1)–(TF6). Axiom (TF1) is clear by axiom (RF3) and the definition of the parameter
 $(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
. Next, we may shrink
$(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
. Next, we may shrink
![]() $X$
so that if
$X$
so that if
![]() $i<j$
then
$i<j$
then
![]() $\unicode[STIX]{x1D6FF}_{i}^{-1}\unicode[STIX]{x1D6FF}_{j}$
is everywhere generic up to homothety by Lemma 6.4, giving axiom (TF2).
$\unicode[STIX]{x1D6FF}_{i}^{-1}\unicode[STIX]{x1D6FF}_{j}$
is everywhere generic up to homothety by Lemma 6.4, giving axiom (TF2).
Axioms (TF4)–(TF6) are easily verified by the remarks preceding the theorem, and axiom (RF4). Thus, it remains to check axiom (TF3), i.e. that each point
![]() $x$
is triangulated by a triangulation whose parameter is homothetic to
$x$
is triangulated by a triangulation whose parameter is homothetic to
 $(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
. But if
$(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
. But if
 $u\in X_{\operatorname{cl}}^{\operatorname{nc}}$
then this is true at
$u\in X_{\operatorname{cl}}^{\operatorname{nc}}$
then this is true at
![]() $u$
and, moreover, by the definition of non-critical we have that
$u$
and, moreover, by the definition of non-critical we have that
![]() $D_{u}$
has ordered parameter
$D_{u}$
has ordered parameter
 $(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
on the nose. As we have already verified, there is a unique triangulation of
$(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
on the nose. As we have already verified, there is a unique triangulation of
![]() $D_{u}$
whose parameter is homothetic to
$D_{u}$
whose parameter is homothetic to
 $(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
up to homothety. Thus, the
$(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
up to homothety. Thus, the
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D$
over
$D$
over
![]() $X$
is densely pointwise strictly trianguline with ordered parameter
$X$
is densely pointwise strictly trianguline with ordered parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, Definition 6.3.2]. The existence of the triangulation demanded by axiom (TF3) is deduced from [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.13].◻
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, Definition 6.3.2]. The existence of the triangulation demanded by axiom (TF3) is deduced from [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.13].◻
Continue to let
![]() $D$
be a refined family of
$D$
be a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules and let
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules and let
 $x\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
. Using Proposition 6.5 we assume, by shrinking
$x\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
. Using Proposition 6.5 we assume, by shrinking
![]() $X$
, that for all
$X$
, that for all
![]() $u\in X$
, the
$u\in X$
, the
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
![]() $D_{u}$
has a unique triangulation whose parameter
$D_{u}$
has a unique triangulation whose parameter
 $(\widetilde{\unicode[STIX]{x1D6FF}}_{1,u},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,u})$
is homothetic to
$(\widetilde{\unicode[STIX]{x1D6FF}}_{1,u},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,u})$
is homothetic to
 $(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
.
$(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
.
Definition 6.6. Let
 $u\in X(\overline{\mathbf{Q}}_{p})$
. The canonical (with respect to the refined family
$u\in X(\overline{\mathbf{Q}}_{p})$
. The canonical (with respect to the refined family
![]() $D$
) triangulation is the unique triangulation of
$D$
) triangulation is the unique triangulation of
![]() $D_{u}$
whose parameter is homothetic to
$D_{u}$
whose parameter is homothetic to
 $(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
.
$(\unicode[STIX]{x1D6FF}_{1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
.
Note that
 $u\mapsto \widetilde{\unicode[STIX]{x1D6FF}}_{i,u}$
does not, in the cases of interest, glue to define a continuous character
$u\mapsto \widetilde{\unicode[STIX]{x1D6FF}}_{i,u}$
does not, in the cases of interest, glue to define a continuous character
 $\widetilde{\unicode[STIX]{x1D6FF}}_{i}:K^{\times }\rightarrow A^{\times }$
. In fact, that will essentially only happen at points
$\widetilde{\unicode[STIX]{x1D6FF}}_{i}:K^{\times }\rightarrow A^{\times }$
. In fact, that will essentially only happen at points
![]() $u$
where
$u$
where
 $\widetilde{\unicode[STIX]{x1D6FF}}_{i,u}=\unicode[STIX]{x1D6FF}_{i,u}$
. The best one can hope for is that a certain subparabolization of the canonical triangulation does analytically vary over
$\widetilde{\unicode[STIX]{x1D6FF}}_{i,u}=\unicode[STIX]{x1D6FF}_{i,u}$
. The best one can hope for is that a certain subparabolization of the canonical triangulation does analytically vary over
![]() $X$
.
$X$
.
Definition 6.7. Let
 $x\in X(\overline{\mathbf{Q}}_{p})$
and
$x\in X(\overline{\mathbf{Q}}_{p})$
and
 $P_{x,\bullet }=(P_{x,i})$
be the canonical triangulation. We say that
$P_{x,\bullet }=(P_{x,i})$
be the canonical triangulation. We say that
![]() $P_{x,i}$
is non-critical if
$P_{x,i}$
is non-critical if
 $\unicode[STIX]{x1D6FF}_{1,x}\cdots \unicode[STIX]{x1D6FF}_{i,x}=\widetilde{\unicode[STIX]{x1D6FF}}_{1,x}\cdots \widetilde{\unicode[STIX]{x1D6FF}}_{i,x}$
. If
$\unicode[STIX]{x1D6FF}_{1,x}\cdots \unicode[STIX]{x1D6FF}_{i,x}=\widetilde{\unicode[STIX]{x1D6FF}}_{1,x}\cdots \widetilde{\unicode[STIX]{x1D6FF}}_{i,x}$
. If
 $$\begin{eqnarray}\displaystyle I_{x}^{\operatorname{nc}}:=\{i:P_{x,i}\text{ is non-critical}\}=\{0=i_{0}<i_{1}<i_{2}<\cdots <i_{s}=d\} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{x}^{\operatorname{nc}}:=\{i:P_{x,i}\text{ is non-critical}\}=\{0=i_{0}<i_{1}<i_{2}<\cdots <i_{s}=d\} & & \displaystyle \nonumber\end{eqnarray}$$
is the set of non-critical indices, then we define the maximal non-critical parabolization
![]() $P_{x,\bullet }^{\operatorname{nc}}$
of
$P_{x,\bullet }^{\operatorname{nc}}$
of
![]() $D_{x}$
by
$D_{x}$
by
 $$\begin{eqnarray}\displaystyle P_{x,j}^{\operatorname{nc}}:0\subsetneq P_{x,i_{0}}\subsetneq P_{x,i_{1}}\subsetneq \cdots \subsetneq P_{x,i_{s}}=D_{x}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{x,j}^{\operatorname{nc}}:0\subsetneq P_{x,i_{0}}\subsetneq P_{x,i_{1}}\subsetneq \cdots \subsetneq P_{x,i_{s}}=D_{x}. & & \displaystyle \nonumber\end{eqnarray}$$
If
![]() $x\in X_{\operatorname{cl}}$
, then a comparison of Hodge–Tate weights implies that the previous definition agrees with those given in § 3.2.
$x\in X_{\operatorname{cl}}$
, then a comparison of Hodge–Tate weights implies that the previous definition agrees with those given in § 3.2.
Suppose that
![]() $x\in X_{\operatorname{cl}}$
. If
$x\in X_{\operatorname{cl}}$
. If
![]() $x$
is non-critical, then one knows that the
$x$
is non-critical, then one knows that the
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
![]() $P_{x,i}$
are
$P_{x,i}$
are
 $\{\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x),\ldots ,\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)\}$
by Lemma 3.5 and the definition of non-critical. Thus, for general
$\{\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x),\ldots ,\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)\}$
by Lemma 3.5 and the definition of non-critical. Thus, for general
![]() $x\in X_{\operatorname{cl}}$
, Sen’s theory of Hodge–Tate weights in families [Reference SenSen88] implies that one can only hope for
$x\in X_{\operatorname{cl}}$
, Sen’s theory of Hodge–Tate weights in families [Reference SenSen88] implies that one can only hope for
![]() $P_{x,i}$
to extend to an affinoid neighborhood provided
$P_{x,i}$
to extend to an affinoid neighborhood provided
 $\operatorname{HT}_{\unicode[STIX]{x1D70F}}(P_{x,i})=\{\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x),\ldots ,\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)\}$
for each
$\operatorname{HT}_{\unicode[STIX]{x1D70F}}(P_{x,i})=\{\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x),\ldots ,\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x)\}$
for each
![]() $\unicode[STIX]{x1D70F}$
. That is, if we hope to spread
$\unicode[STIX]{x1D70F}$
. That is, if we hope to spread
![]() $P_{x,i}$
out over a neighborhood, then we need to know a priori that
$P_{x,i}$
out over a neighborhood, then we need to know a priori that
![]() $i\in I_{x}^{\operatorname{nc}}$
. Our main theorem is that the converse is true.
$i\in I_{x}^{\operatorname{nc}}$
. Our main theorem is that the converse is true.
Theorem 6.8. If
![]() $D$
is a refined family of
$D$
is a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X$
and
$X$
and
 $x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then there exists an affinoid neighborhood
$x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, then there exists an affinoid neighborhood
 $x_{0}\in U\subset X$
and a parabolization
$x_{0}\in U\subset X$
and a parabolization
![]() $P^{\operatorname{nc}}$
of
$P^{\operatorname{nc}}$
of
![]() $D|_{U}$
such that for each
$D|_{U}$
such that for each
 $u\in U=\operatorname{Sp}(B)$
, the parabolization
$u\in U=\operatorname{Sp}(B)$
, the parabolization
 $P_{\bullet }^{\operatorname{nc}}\otimes _{B}L(u)$
of
$P_{\bullet }^{\operatorname{nc}}\otimes _{B}L(u)$
of
![]() $D_{u}$
is a subparabolization of
$D_{u}$
is a subparabolization of
![]() $P_{u,\bullet }^{\operatorname{nc}}$
, with equality if
$P_{u,\bullet }^{\operatorname{nc}}$
, with equality if
![]() $u=x_{0}$
.
$u=x_{0}$
.
See the introduction for a history of this result.
Proof of Theorem 6.8.
First, assume that
![]() $X$
is sufficiently small so that the conclusion of Proposition 6.5 holds. In particular, there is a canonical triangulation
$X$
is sufficiently small so that the conclusion of Proposition 6.5 holds. In particular, there is a canonical triangulation
![]() $P_{x,\bullet }$
at each point
$P_{x,\bullet }$
at each point
![]() $x\in X$
.
$x\in X$
.
The proof will happen in three steps. By Proposition 6.5,
![]() $D$
is a pointwise triangulated family with center
$D$
is a pointwise triangulated family with center
![]() $x_{0}$
but without torsion. Fix the unique
$x_{0}$
but without torsion. Fix the unique
 $1\leqslant n\leqslant d$
such that
$1\leqslant n\leqslant d$
such that
 $P_{x_{0},1}^{\operatorname{nc}}=P_{x_{0},n}$
. We assume that
$P_{x_{0},1}^{\operatorname{nc}}=P_{x_{0},n}$
. We assume that
![]() $n<d$
, or else the theorem is proven already. It suffices to construct
$n<d$
, or else the theorem is proven already. It suffices to construct
![]() $P_{1}^{\operatorname{nc}}$
over an affinoid subdomain
$P_{1}^{\operatorname{nc}}$
over an affinoid subdomain
![]() $U$
as in the statement of the theorem. Indeed, granting its existence,
$U$
as in the statement of the theorem. Indeed, granting its existence,
![]() $P_{1}^{\operatorname{nc}}$
is a
$P_{1}^{\operatorname{nc}}$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of rank
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module of rank
![]() $n$
(since it has rank
$n$
(since it has rank
![]() $n$
at
$n$
at
![]() $x_{0}$
) and thus after replacing
$x_{0}$
) and thus after replacing
![]() $X$
by
$X$
by
![]() $U$
we have
$U$
we have
 $P_{1}^{\operatorname{nc}}\otimes _{A}L(x)=P_{x,n}$
for all
$P_{1}^{\operatorname{nc}}\otimes _{A}L(x)=P_{x,n}$
for all
![]() $x\in X$
. But then the quotient
$x\in X$
. But then the quotient
![]() $D/P_{1}^{\operatorname{nc}}$
is a refined family of
$D/P_{1}^{\operatorname{nc}}$
is a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X$
whose global parameter is
$X$
whose global parameter is
 $(\unicode[STIX]{x1D6FF}_{n+1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
. And so inductively we can apply the construction of
$(\unicode[STIX]{x1D6FF}_{n+1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
. And so inductively we can apply the construction of
![]() $P_{1}^{\operatorname{nc}}$
we are about to give, if necessary.
$P_{1}^{\operatorname{nc}}$
we are about to give, if necessary.
Now we focus on constructing
![]() $P_{1}^{\operatorname{nc}}$
. For each
$P_{1}^{\operatorname{nc}}$
. For each
![]() $\unicode[STIX]{x1D70F}$
, fix the unique integer
$\unicode[STIX]{x1D70F}$
, fix the unique integer
![]() $n_{\unicode[STIX]{x1D70F}}$
such that
$n_{\unicode[STIX]{x1D70F}}$
such that
![]() $n_{\unicode[STIX]{x1D70F}}$
such that
$n_{\unicode[STIX]{x1D70F}}$
such that
 $\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x_{0})=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{n_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D70F}})$
. Note
$\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x_{0})=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{n_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D70F}})$
. Note
![]() $n_{\unicode[STIX]{x1D70F}}\leqslant n$
because
$n_{\unicode[STIX]{x1D70F}}\leqslant n$
because
 $P_{x_{0},1}^{\operatorname{nc}}=P_{x_{0},n}$
is non-critical. Let
$P_{x_{0},1}^{\operatorname{nc}}=P_{x_{0},n}$
is non-critical. Let
 $Q_{0}=D$
and
$Q_{0}=D$
and
 $X_{0}=X$
.
$X_{0}=X$
.
Claim (Step 1).
There exists a sequence of affinoid subdomains
 $X=X_{0}\supset X_{1}\supset \cdots \supset X_{n}$
and nearly flat pointwise triangulated families
$X=X_{0}\supset X_{1}\supset \cdots \supset X_{n}$
and nearly flat pointwise triangulated families
![]() $Q_{i}$
over
$Q_{i}$
over
![]() $X_{i}$
with finite cohomology and torsion center
$X_{i}$
with finite cohomology and torsion center
![]() $x_{0}$
such that there is an exact sequence
$x_{0}$
such that there is an exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D705}_{i+1,\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x_{0})}{\mathcal{R}}_{X_{i+1}}(\unicode[STIX]{x1D6FF}_{i+1})\rightarrow Q_{i}|_{X_{i+1}}\rightarrow Q_{i+1}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D705}_{i+1,\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x_{0})}{\mathcal{R}}_{X_{i+1}}(\unicode[STIX]{x1D6FF}_{i+1})\rightarrow Q_{i}|_{X_{i+1}}\rightarrow Q_{i+1}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$
of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X_{i+1}$
and the invariants of
$X_{i+1}$
and the invariants of
![]() $Q_{i}$
are given by:
$Q_{i}$
are given by:
-
– torsion weights
 $((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant d}$
;
$((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant d}$
; -
– parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
; and
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
; and -
– non-critical points
 $X_{i}^{\operatorname{nc}}=X_{i}\cap X_{\operatorname{cl}}^{\operatorname{nc}}$
.
$X_{i}^{\operatorname{nc}}=X_{i}\cap X_{\operatorname{cl}}^{\operatorname{nc}}$
.
Moreover,
![]() $Q_{i,x}$
has free length
$Q_{i,x}$
has free length
 $d-i\geqslant d-n>0$
.
$d-i\geqslant d-n>0$
.
Proof of Step 1.
To prove the claim, one easily argues by induction on
![]() $i$
using Theorem 5.3.◻
$i$
using Theorem 5.3.◻
Since
![]() $n_{\unicode[STIX]{x1D70F}}\leqslant n$
for each
$n_{\unicode[STIX]{x1D70F}}\leqslant n$
for each
![]() $\unicode[STIX]{x1D70F}$
we see from the choice of torsion weights and the definition of
$\unicode[STIX]{x1D70F}$
we see from the choice of torsion weights and the definition of
![]() $n_{\unicode[STIX]{x1D70F}}$
that
$n_{\unicode[STIX]{x1D70F}}$
that
![]() $Q_{x_{0},n}$
has
$Q_{x_{0},n}$
has
![]() $\unicode[STIX]{x1D70F}$
-torsion length
$\unicode[STIX]{x1D70F}$
-torsion length
 $\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0},n})=n-1$
. On the other hand, if
$\ell _{\unicode[STIX]{x1D70F}}(Q_{x_{0},n})=n-1$
. On the other hand, if
 $u\in X_{n}^{\operatorname{nc}}$
then
$u\in X_{n}^{\operatorname{nc}}$
then
 $\ell _{\unicode[STIX]{x1D70F}}(Q_{u,n})=n-1$
as well. Thus, the
$\ell _{\unicode[STIX]{x1D70F}}(Q_{u,n})=n-1$
as well. Thus, the
![]() $\unicode[STIX]{x1D70F}$
-torsion lengths at
$\unicode[STIX]{x1D70F}$
-torsion lengths at
![]() $x_{0}$
agree with the
$x_{0}$
agree with the
![]() $\unicode[STIX]{x1D70F}$
-torsion lengths on a set of accumulating at
$\unicode[STIX]{x1D70F}$
-torsion lengths on a set of accumulating at
![]() $x_{0}$
. We will now kill the torsion. Let
$x_{0}$
. We will now kill the torsion. Let
 $Q_{0}^{\prime }=Q_{n}$
and
$Q_{0}^{\prime }=Q_{n}$
and
 $X_{0}^{\prime }=X_{n}$
as in step 1.
$X_{0}^{\prime }=X_{n}$
as in step 1.
Claim (Step 2).
There exists a nested sequence of affinoid subdomains
 $X_{n}=X_{1}^{\prime }\supset \cdots \supset X_{n}^{\prime }$
and nearly flat pointwise triangulated families
$X_{n}=X_{1}^{\prime }\supset \cdots \supset X_{n}^{\prime }$
and nearly flat pointwise triangulated families
![]() $Q_{i}^{\prime }$
over
$Q_{i}^{\prime }$
over
![]() $X_{i}^{\prime }$
with torsion center
$X_{i}^{\prime }$
with torsion center
![]() $x_{0}$
such that, for
$x_{0}$
such that, for
 $2\leqslant i<n$
, there is a short exact sequence
$2\leqslant i<n$
, there is a short exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow Q_{i}^{\prime }|_{X_{i+1}^{\prime }}\biggl[\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D705}_{i+1,\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x_{0})}\biggr]\rightarrow Q_{i}^{\prime }|_{X_{i+1}^{\prime }}\rightarrow Q_{i+1}^{\prime }\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow Q_{i}^{\prime }|_{X_{i+1}^{\prime }}\biggl[\mathop{\prod }_{\unicode[STIX]{x1D70F}}t_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D705}_{i+1,\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x_{0})}\biggr]\rightarrow Q_{i}^{\prime }|_{X_{i+1}^{\prime }}\rightarrow Q_{i+1}^{\prime }\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
of generalized
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() $X_{i+1}^{\prime }$
and we have the following.
$X_{i+1}^{\prime }$
and we have the following.
-
– The invariants of
 $Q_{i}^{\prime }$
are:
$Q_{i}^{\prime }$
are:-
∗ torsion weights
 $((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant d:\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}})\geqslant \unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x_{0})}$
;
$((\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}}))_{\unicode[STIX]{x1D70F}})_{1\leqslant j\leqslant d:\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}})\geqslant \unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x_{0})}$
; -
∗ parameter
 $(\unicode[STIX]{x1D6FF}_{i},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
; and
$(\unicode[STIX]{x1D6FF}_{i},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
; and -
∗ non-critical points
 $(X_{i}^{\prime })^{\operatorname{nc}}=X_{n}^{\operatorname{nc}}\cap X_{i}^{\prime }$
.
$(X_{i}^{\prime })^{\operatorname{nc}}=X_{n}^{\operatorname{nc}}\cap X_{i}^{\prime }$
.
-
-
– We have that
 $Q_{i}^{\prime }$
has free length
$Q_{i}^{\prime }$
has free length
 $d-n$
, independent of
$d-n$
, independent of
 $i$
; and
$i$
; and -
– For each
 $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
 $u\in (X_{i}^{\prime })_{\operatorname{cl}}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, the
$u\in (X_{i}^{\prime })_{\operatorname{cl}}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
, the
 $\unicode[STIX]{x1D70F}$
-torsion lengths
$\unicode[STIX]{x1D70F}$
-torsion lengths
 $\ell _{\unicode[STIX]{x1D70F}}(x_{0})$
and
$\ell _{\unicode[STIX]{x1D70F}}(x_{0})$
and
 $\ell _{\unicode[STIX]{x1D70F}}(u)$
are equal (both) to
$\ell _{\unicode[STIX]{x1D70F}}(u)$
are equal (both) to
 $n-i$
.
$n-i$
.
Proof of Step 2.
The claimed properties for
 $Q_{1}^{\prime }=Q_{n}$
follow from the conclusion of step 1. If
$Q_{1}^{\prime }=Q_{n}$
follow from the conclusion of step 1. If
 $1<i\leqslant n$
, then the existence of
$1<i\leqslant n$
, then the existence of
![]() $Q_{i}^{\prime }$
over
$Q_{i}^{\prime }$
over
![]() $X_{i}^{\prime }$
, with the given invariants, is proved by Corollary 5.8. The
$X_{i}^{\prime }$
, with the given invariants, is proved by Corollary 5.8. The
![]() $\unicode[STIX]{x1D70F}$
-torsion lengths at
$\unicode[STIX]{x1D70F}$
-torsion lengths at
 $u\in (X_{i}^{\prime })_{\operatorname{cl}}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
are easily seen to be
$u\in (X_{i}^{\prime })_{\operatorname{cl}}^{\operatorname{nc},\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
are easily seen to be
![]() $n-i$
, so to finish this step we just need to compute the
$n-i$
, so to finish this step we just need to compute the
![]() $\unicode[STIX]{x1D70F}$
-torsion length at
$\unicode[STIX]{x1D70F}$
-torsion length at
![]() $x_{0}$
. To do that we look at the non-zero
$x_{0}$
. To do that we look at the non-zero
![]() $\unicode[STIX]{x1D70F}$
-torsion exponents in the standard triangulation of
$\unicode[STIX]{x1D70F}$
-torsion exponents in the standard triangulation of
![]() $Q_{i}^{\prime }$
. The torsion exponents, are by definition, given by
$Q_{i}^{\prime }$
. The torsion exponents, are by definition, given by
 $$\begin{eqnarray}\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x_{0}}):1\leqslant j\leqslant n\text{ and }\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}})\geqslant \operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x_{0}})\}.\end{eqnarray}$$
$$\begin{eqnarray}\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}})-\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x_{0}}):1\leqslant j\leqslant n\text{ and }\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{j,x_{0}})\geqslant \operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x_{0}})\}.\end{eqnarray}$$
Since
![]() $P_{x_{0},n}$
is a non-critical step in the canonical triangulation at
$P_{x_{0},n}$
is a non-critical step in the canonical triangulation at
![]() $x_{0}$
, we see that the set of weights
$x_{0}$
, we see that the set of weights
 $\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{n,x_{0}})\}$
are the lowest
$\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{n,x_{0}})\}$
are the lowest
![]() $n$
weights and so we see immediately that there are
$n$
weights and so we see immediately that there are
 $\ell _{\unicode[STIX]{x1D70F}}(x_{0})=n-i$
non-zero elements in the set (10).◻
$\ell _{\unicode[STIX]{x1D70F}}(x_{0})=n-i$
non-zero elements in the set (10).◻
Claim (Step 3).
Finally we set
 $C_{n}=Q_{n}^{\prime }$
and
$C_{n}=Q_{n}^{\prime }$
and
 $U=X_{n}^{\prime }=\operatorname{Sp}(B)$
as in step 2. We claim that we can shrink
$U=X_{n}^{\prime }=\operatorname{Sp}(B)$
as in step 2. We claim that we can shrink
![]() $U$
so that
$U$
so that
 $P_{1}^{\operatorname{nc}}:=\ker (D{\twoheadrightarrow}C_{n})$
is a
$P_{1}^{\operatorname{nc}}:=\ker (D{\twoheadrightarrow}C_{n})$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $U$
and for all
$U$
and for all
![]() $u\in U$
,
$u\in U$
,
 $P_{1}^{\operatorname{nc}}\otimes _{B}L(u)=P_{u,n}$
.
$P_{1}^{\operatorname{nc}}\otimes _{B}L(u)=P_{u,n}$
.
Proof of Step 3.
Consider the pointwise triangulated family
 $C_{n}=Q_{n}^{\prime }$
over
$C_{n}=Q_{n}^{\prime }$
over
 $U=X_{n}^{\prime }$
. By step 2,
$U=X_{n}^{\prime }$
. By step 2,
![]() $C_{n}$
is torsion free at
$C_{n}$
is torsion free at
![]() $x=x_{0}$
or
$x=x_{0}$
or
 $x=u\in U^{\operatorname{nc}}$
. Thus, after shrinking
$x=u\in U^{\operatorname{nc}}$
. Thus, after shrinking
![]() $U$
, applying Lemma 5.5, we can assume that each fiber
$U$
, applying Lemma 5.5, we can assume that each fiber
![]() $C_{n,u}$
is finite free over
$C_{n,u}$
is finite free over
![]() ${\mathcal{R}}_{L(u)}$
of rank
${\mathcal{R}}_{L(u)}$
of rank
![]() $d-n$
, independent of
$d-n$
, independent of
![]() $u$
. Thus,
$u$
. Thus,
![]() $C_{n}$
is a
$C_{n}$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $U$
(spread
$U$
(spread
![]() $C_{n}$
out to an open annulus and use [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 2.1.7]). Defining
$C_{n}$
out to an open annulus and use [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 2.1.7]). Defining
![]() $P_{1}^{\operatorname{nc}}$
as the kernel of the natural surjection
$P_{1}^{\operatorname{nc}}$
as the kernel of the natural surjection
 $D{\twoheadrightarrow}C_{n}$
(note that all of the constructions in steps 1 and 2 were quotients), we get a
$D{\twoheadrightarrow}C_{n}$
(note that all of the constructions in steps 1 and 2 were quotients), we get a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module and thus our candidate
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module and thus our candidate
![]() $P_{1}^{\operatorname{nc}}$
.
$P_{1}^{\operatorname{nc}}$
.
It remains to compute
 $P_{1}^{\operatorname{nc}}\otimes _{B}L(u)$
as a
$P_{1}^{\operatorname{nc}}\otimes _{B}L(u)$
as a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-submodule of
![]() $D_{u}$
for each
$D_{u}$
for each
![]() $u$
. But we have assumed throughout that
$u$
. But we have assumed throughout that
![]() $X$
was sufficiently small so that for all
$X$
was sufficiently small so that for all
![]() $x\in X$
there was a unique triangulation with parameter
$x\in X$
there was a unique triangulation with parameter
 $(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
up to homothety. So, in order to check
$(\unicode[STIX]{x1D6FF}_{1,x},\ldots ,\unicode[STIX]{x1D6FF}_{d,x})$
up to homothety. So, in order to check
 $P_{1}^{\operatorname{nc}}\otimes _{B}L(u)=P_{u,n}$
it is enough to show that
$P_{1}^{\operatorname{nc}}\otimes _{B}L(u)=P_{u,n}$
it is enough to show that
![]() $C_{n,u}$
can be triangulated by a parameter homothetic to
$C_{n,u}$
can be triangulated by a parameter homothetic to
 $(\unicode[STIX]{x1D6FF}_{n+1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
for all
$(\unicode[STIX]{x1D6FF}_{n+1,u},\ldots ,\unicode[STIX]{x1D6FF}_{d,u})$
for all
![]() $u\in U$
. But that latter claim follows from applying the information from Step 2 to
$u\in U$
. But that latter claim follows from applying the information from Step 2 to
 $C_{n}=Q_{n}^{\prime }$
and using axiom (TF2).◻
$C_{n}=Q_{n}^{\prime }$
and using axiom (TF2).◻
This completes the proof. ◻
7 Ramification of weights
Let
![]() $D$
be a refined family of
$D$
be a refined family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over a reduced
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over a reduced
![]() $L$
-affinoid space
$L$
-affinoid space
 $X=\operatorname{Sp}(A)$
with parameter
$X=\operatorname{Sp}(A)$
with parameter
 $(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
and classical points
$(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{d})$
and classical points
![]() $X_{\operatorname{cl}}$
. For each
$X_{\operatorname{cl}}$
. For each
 $i=1,\ldots ,d$
and
$i=1,\ldots ,d$
and
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, we consider the analytic functions
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
, we consider the analytic functions
 $\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x):=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x})\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}})$
. The goal of this section is to study the infinitesimal differences
$\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x):=\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}_{i,x})\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}})$
. The goal of this section is to study the infinitesimal differences
 $\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}$
at classical points.
$\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}$
at classical points.
Suppose that
 $x_{0}\in X_{\operatorname{cl}}$
, write
$x_{0}\in X_{\operatorname{cl}}$
, write
![]() $P_{x_{0},\bullet }$
for its triangulation defined by axiom (RF3) and
$P_{x_{0},\bullet }$
for its triangulation defined by axiom (RF3) and
 $(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
for the corresponding parameter. For each
$(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}},\ldots ,\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})$
for the corresponding parameter. For each
![]() $\unicode[STIX]{x1D70F}$
, the set
$\unicode[STIX]{x1D70F}$
, the set
 $\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})\}$
must be the same as the set of integers
$\{\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{1,x_{0}}),\ldots ,\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{d,x_{0}})\}$
must be the same as the set of integers
 $\{\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x_{0}),\ldots ,\unicode[STIX]{x1D705}_{d,\unicode[STIX]{x1D70F}}(x_{0})\}$
. In particular, for each
$\{\unicode[STIX]{x1D705}_{1,\unicode[STIX]{x1D70F}}(x_{0}),\ldots ,\unicode[STIX]{x1D705}_{d,\unicode[STIX]{x1D70F}}(x_{0})\}$
. In particular, for each
![]() $\unicode[STIX]{x1D70F}$
there is a permutation
$\unicode[STIX]{x1D70F}$
there is a permutation
![]() $\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}$
on
$\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}$
on
![]() $d$
letters such that
$d$
letters such that
 $\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i),x_{0}})=\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x_{0})$
. To connect this with the non-critical jumps, the
$\operatorname{wt}_{\unicode[STIX]{x1D70F}}(\widetilde{\unicode[STIX]{x1D6FF}}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i),x_{0}})=\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}}(x_{0})$
. To connect this with the non-critical jumps, the
![]() $\unicode[STIX]{x1D70F}$
-non-critical indices of
$\unicode[STIX]{x1D70F}$
-non-critical indices of
![]() $P_{x_{0},\bullet }$
are exactly the integers
$P_{x_{0},\bullet }$
are exactly the integers
![]() $i$
such that
$i$
such that
![]() $\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}$
restricts to a permutation on the set
$\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}$
restricts to a permutation on the set
 $\{1,\ldots ,i\}$
. In particular,
$\{1,\ldots ,i\}$
. In particular,
![]() $\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}$
induces a permutation on the set of weights appearing in each non-critical step
$\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}$
induces a permutation on the set of weights appearing in each non-critical step
![]() $P_{x_{0},j}^{\operatorname{nc}}$
and thus permutes the set of weights appearing in each quotient
$P_{x_{0},j}^{\operatorname{nc}}$
and thus permutes the set of weights appearing in each quotient
 $P_{x_{0},j}^{\operatorname{nc}}/P_{x_{0},j-1}^{\operatorname{nc}}$
as well.
$P_{x_{0},j}^{\operatorname{nc}}/P_{x_{0},j-1}^{\operatorname{nc}}$
as well.
If
![]() $B$
is a ring, let
$B$
is a ring, let
 $B[\unicode[STIX]{x1D700}]=B[T]/(T^{2})$
be the ring of dual numbers. If
$B[\unicode[STIX]{x1D700}]=B[T]/(T^{2})$
be the ring of dual numbers. If
![]() $x_{0}\in X$
then
$x_{0}\in X$
then
![]() ${\mathcal{O}}_{X,x_{0}}^{\operatorname{rig}}$
denotes its local ring (in the rigid topology). Since
${\mathcal{O}}_{X,x_{0}}^{\operatorname{rig}}$
denotes its local ring (in the rigid topology). Since
![]() ${\mathcal{O}}_{X,x_{0}}^{\operatorname{rig}}$
is Henselian, it contains a section of its residue field. We write
${\mathcal{O}}_{X,x_{0}}^{\operatorname{rig}}$
is Henselian, it contains a section of its residue field. We write
 $T_{x_{0}}X=\operatorname{Hom}_{L(x_{0})}({\mathcal{O}}_{X,x_{0}}^{\operatorname{rig}},L(x_{0})[\unicode[STIX]{x1D700}])$
for the Zariski tangent space at
$T_{x_{0}}X=\operatorname{Hom}_{L(x_{0})}({\mathcal{O}}_{X,x_{0}}^{\operatorname{rig}},L(x_{0})[\unicode[STIX]{x1D700}])$
for the Zariski tangent space at
![]() $x_{0}$
. If
$x_{0}$
. If
![]() $f\in A$
is a function on
$f\in A$
is a function on
![]() $X$
and
$X$
and
 $v\in T_{x_{0}}X$
is a tangent vector we write
$v\in T_{x_{0}}X$
is a tangent vector we write
 $\unicode[STIX]{x1D6FB}_{v}(f)\in L(x_{0})$
for the directional derivative of
$\unicode[STIX]{x1D6FB}_{v}(f)\in L(x_{0})$
for the directional derivative of
![]() $f$
with respect to
$f$
with respect to
![]() $v$
. Explicitly it is given by
$v$
. Explicitly it is given by
 $v(f)=f(x_{0})+\unicode[STIX]{x1D6FB}_{v}(f)\unicode[STIX]{x1D700}$
.
$v(f)=f(x_{0})+\unicode[STIX]{x1D6FB}_{v}(f)\unicode[STIX]{x1D700}$
.
Theorem 7.1. If
 $x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
and
$x_{0}\in X_{\operatorname{cl}}^{\unicode[STIX]{x1D711}_{\operatorname{reg}}}$
and
 $v\in T_{x_{0}}X$
, then
$v\in T_{x_{0}}X$
, then
 $\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i),\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}})=0$
for each
$\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i),\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{i,\unicode[STIX]{x1D70F}})=0$
for each
 $1\leqslant i\leqslant d$
and
$1\leqslant i\leqslant d$
and
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
.
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{K}$
.
As mentioned in the introduction, the theorem was discovered independently by the author and Breuil. A proof, similar to the one we are about to give, is given in [Reference BreuilBre15, Lemme 9.6 and Théorème 9.7]. We’ve taken an extra effort to state a more precise result, dealing with all of the weights and over a finite extension
![]() $K/\mathbf{Q}_{p}$
.
$K/\mathbf{Q}_{p}$
.
Proof of Theorem 7.1.
Choose a uniformizer
 $\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
and write, for
$\unicode[STIX]{x1D71B}_{K}\in K^{\times }$
and write, for
 $i=1,\ldots ,d$
, the character
$i=1,\ldots ,d$
, the character
 $\unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x1D6FF}_{i}^{\operatorname{wt}}\unicode[STIX]{x1D6FF}_{i}^{\operatorname{nr}}$
as in § 2.3. Furthermore, write
$\unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x1D6FF}_{i}^{\operatorname{wt}}\unicode[STIX]{x1D6FF}_{i}^{\operatorname{nr}}$
as in § 2.3. Furthermore, write
 $\unicode[STIX]{x1D702}_{i}=\unicode[STIX]{x1D6FF}_{1}^{\operatorname{wt}}\cdots \unicode[STIX]{x1D6FF}_{i}^{\operatorname{wt}}$
and
$\unicode[STIX]{x1D702}_{i}=\unicode[STIX]{x1D6FF}_{1}^{\operatorname{wt}}\cdots \unicode[STIX]{x1D6FF}_{i}^{\operatorname{wt}}$
and
 $D_{i}:=(\wedge ^{i}D)(\unicode[STIX]{x1D702}_{i}^{-1})$
. Then
$D_{i}:=(\wedge ^{i}D)(\unicode[STIX]{x1D702}_{i}^{-1})$
. Then
![]() $D_{i}$
is a
$D_{i}$
is a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() $X$
and it has distinct lowest Hodge–Tate weight
$X$
and it has distinct lowest Hodge–Tate weight
![]() $0$
over
$0$
over
![]() $X_{\operatorname{cl}}$
. Let
$X_{\operatorname{cl}}$
. Let
 $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6FF}_{1}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})\cdots \unicode[STIX]{x1D6FF}_{i}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})^{\times }$
. Then by [Reference LiuLiu15, Theorem 4.13] the
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6FF}_{1}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})\cdots \unicode[STIX]{x1D6FF}_{i}^{\operatorname{nr}}(\unicode[STIX]{x1D71B}_{K})\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})^{\times }$
. Then by [Reference LiuLiu15, Theorem 4.13] the
 $({\mathcal{O}}_{X}\otimes _{\mathbf{Q}_{p}}F)$
-module
$({\mathcal{O}}_{X}\otimes _{\mathbf{Q}_{p}}F)$
-module
 $D_{\operatorname{cris}}(D_{i})^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D6F7}}$
is locally free of rank one and satisfies base change.
$D_{\operatorname{cris}}(D_{i})^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D6F7}}$
is locally free of rank one and satisfies base change.
Now let
 $v\in T_{x_{0}}X$
. Write
$v\in T_{x_{0}}X$
. Write
 $\widetilde{D}_{i,v}:=\unicode[STIX]{x1D6FB}_{v}(D_{i})$
for the deformation
$\widetilde{D}_{i,v}:=\unicode[STIX]{x1D6FB}_{v}(D_{i})$
for the deformation
 $D_{i}\otimes _{{\mathcal{O}}_{X,x_{0}},v}L(x_{0})[\unicode[STIX]{x1D700}]$
of
$D_{i}\otimes _{{\mathcal{O}}_{X,x_{0}},v}L(x_{0})[\unicode[STIX]{x1D700}]$
of
![]() $D_{i,x_{0}}$
in the tangent direction of
$D_{i,x_{0}}$
in the tangent direction of
![]() $v$
. By the result just mentioned,
$v$
. By the result just mentioned,
 $D_{\operatorname{cris}}(\widetilde{D}_{i,v})^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D6F7}}$
is free of rank one over
$D_{\operatorname{cris}}(\widetilde{D}_{i,v})^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D6F7}}$
is free of rank one over
 $(L(x_{0})\otimes _{\mathbf{Q}_{p}}F)[\unicode[STIX]{x1D700}]$
. Let
$(L(x_{0})\otimes _{\mathbf{Q}_{p}}F)[\unicode[STIX]{x1D700}]$
. Let
 $E=\ker (\widetilde{D}_{i,v}\rightarrow D_{i,x_{0}}\rightarrow D_{i,x_{0}}/\unicode[STIX]{x1D702}_{i,x_{0}}^{-1}\det P_{x_{0},i})$
. By the lemma below we have that
$E=\ker (\widetilde{D}_{i,v}\rightarrow D_{i,x_{0}}\rightarrow D_{i,x_{0}}/\unicode[STIX]{x1D702}_{i,x_{0}}^{-1}\det P_{x_{0},i})$
. By the lemma below we have that
![]() $E$
is a crystalline
$E$
is a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. In particular, it is Hodge–Tate.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module. In particular, it is Hodge–Tate.
But what are the Hodge–Tate weights of
![]() $E$
? The
$E$
? The
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
![]() $D_{i,x_{0}}$
are given by
$D_{i,x_{0}}$
are given by
 $$\begin{eqnarray}\displaystyle \operatorname{HT}_{\unicode[STIX]{x1D70F}}(D_{i,x_{0}})=\biggl\{\mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0}):J\subset \{1,\ldots ,d\}\text{and }\#J=i\biggr\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{HT}_{\unicode[STIX]{x1D70F}}(D_{i,x_{0}})=\biggl\{\mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0}):J\subset \{1,\ldots ,d\}\text{and }\#J=i\biggr\}. & & \displaystyle \nonumber\end{eqnarray}$$
And, the
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate–Sen weights of
$\unicode[STIX]{x1D70F}$
-Hodge–Tate–Sen weights of
 $\widetilde{D}_{i,v}=\wedge ^{i}(\widetilde{D}_{1,v})$
(which are elements of
$\widetilde{D}_{i,v}=\wedge ^{i}(\widetilde{D}_{1,v})$
(which are elements of
![]() $L(x)[\unicode[STIX]{x1D700}]$
) are then given by
$L(x)[\unicode[STIX]{x1D700}]$
) are then given by
 $$\begin{eqnarray}\displaystyle \biggl\{\biggl(\mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})+\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\unicode[STIX]{x1D700}\biggr)-\biggl(\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})+\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\unicode[STIX]{x1D700}\biggr):J\subset \{1,\ldots ,d\}\text{and }\#J=i\biggr\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl\{\biggl(\mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})+\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\unicode[STIX]{x1D700}\biggr)-\biggl(\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})+\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\unicode[STIX]{x1D700}\biggr):J\subset \{1,\ldots ,d\}\text{and }\#J=i\biggr\}. & & \displaystyle \nonumber\end{eqnarray}$$
We can reinterpret this by viewing
![]() $\widetilde{D}_{i,v}$
as a
$\widetilde{D}_{i,v}$
as a
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() ${\mathcal{R}}_{L(x_{0})}$
of twice the rank. We see that the Sen operator
${\mathcal{R}}_{L(x_{0})}$
of twice the rank. We see that the Sen operator
![]() $\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}$
acting on
$\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}$
acting on
 $D_{\operatorname{Sen}}(\widetilde{D}_{i,v})$
has a matrix built out of the blocks of the form
$D_{\operatorname{Sen}}(\widetilde{D}_{i,v})$
has a matrix built out of the blocks of the form
 $$\begin{eqnarray}\displaystyle M_{J}:=\left(\begin{array}{@{}cc@{}}\displaystyle \mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0}) & \displaystyle \mathop{\sum }_{j\in J}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\\ \displaystyle 0 & \displaystyle \mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})\end{array}\right)\in \operatorname{Mat}_{2\times 2}(L(x_{0})). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{J}:=\left(\begin{array}{@{}cc@{}}\displaystyle \mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0}) & \displaystyle \mathop{\sum }_{j\in J}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\\ \displaystyle 0 & \displaystyle \mathop{\sum }_{j\in J}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})-\mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})\end{array}\right)\in \operatorname{Mat}_{2\times 2}(L(x_{0})). & & \displaystyle \nonumber\end{eqnarray}$$
Note that
 $\det P_{x_{0},i}$
has Hodge–Tate weight
$\det P_{x_{0},i}$
has Hodge–Tate weight
 $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(1)}(x_{0})+\cdots +\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i)}(x_{0})$
and so
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(1)}(x_{0})+\cdots +\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i)}(x_{0})$
and so
 $\unicode[STIX]{x1D702}_{i,x_{0}}^{-1}\det P_{x_{0},i}$
has Hodge–Tate weight
$\unicode[STIX]{x1D702}_{i,x_{0}}^{-1}\det P_{x_{0},i}$
has Hodge–Tate weight
 $\sum _{j=1}^{i}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})$
. By the short exact sequence
$\sum _{j=1}^{i}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})$
. By the short exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow E\rightarrow \widetilde{D}_{i,v}\rightarrow D_{i,v}/\unicode[STIX]{x1D702}_{i,x_{0}}^{-1}\det P_{x_{0},i}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow E\rightarrow \widetilde{D}_{i,v}\rightarrow D_{i,v}/\unicode[STIX]{x1D702}_{i,x_{0}}^{-1}\det P_{x_{0},i}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$
of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules over
![]() ${\mathcal{R}}_{L(x_{0})}$
, the only
${\mathcal{R}}_{L(x_{0})}$
, the only
![]() $2\times 2$
block of
$2\times 2$
block of
 $\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}|_{D_{\operatorname{Sen}}(\widetilde{D}_{i,v})}$
appearing in
$\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}|_{D_{\operatorname{Sen}}(\widetilde{D}_{i,v})}$
appearing in
 $\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}|_{D_{\operatorname{Sen}}(E)}$
is the block
$\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}|_{D_{\operatorname{Sen}}(E)}$
is the block
 $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}cc@{}}\displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0}) & \displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\\ 0 & \displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}cc@{}}\displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0}) & \displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})\\ 0 & \displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}(x_{0})-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}}(x_{0})\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
corresponding to
 $J=\{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(1),\ldots ,\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i)\}$
. Finally since
$J=\{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(1),\ldots ,\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(i)\}$
. Finally since
![]() $E$
is crystalline, it is Hodge–Tate and thus
$E$
is crystalline, it is Hodge–Tate and thus
![]() $\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}$
acts semi-simply. In particular, we conclude that
$\unicode[STIX]{x1D6E9}_{\operatorname{Sen}}$
acts semi-simply. In particular, we conclude that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=1}^{i}\unicode[STIX]{x1D6FB}_{v}(\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70B}_{x_{0},\unicode[STIX]{x1D70F}}(j),\unicode[STIX]{x1D70F}}-\unicode[STIX]{x1D705}_{j,\unicode[STIX]{x1D70F}})=0. & & \displaystyle \nonumber\end{eqnarray}$$
Since this is for any
![]() $i$
, we conclude the theorem by induction on
$i$
, we conclude the theorem by induction on
![]() $i$
.◻
$i$
.◻
It remains to give the computation left unresolved in the previous proof.
Lemma 7.2. Suppose that
![]() $D$
is a crystalline
$D$
is a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() ${\mathcal{R}}_{L}$
,
${\mathcal{R}}_{L}$
,
![]() $\unicode[STIX]{x1D719}\in L^{\times }$
and
$\unicode[STIX]{x1D719}\in L^{\times }$
and
![]() $P_{1}\subset D$
is a rank-one saturated submodule such that
$P_{1}\subset D$
is a rank-one saturated submodule such that
 $D_{\operatorname{cris}}(D)^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719}}=D_{\operatorname{cris}}(P_{1})^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719}}$
is free of rank one over
$D_{\operatorname{cris}}(D)^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719}}=D_{\operatorname{cris}}(P_{1})^{\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719}}$
is free of rank one over
 $L\otimes _{\mathbf{Q}_{p}}F$
. If
$L\otimes _{\mathbf{Q}_{p}}F$
. If
 $\widetilde{D}\in \operatorname{Ext}^{1}(D,D)$
is an extension such that
$\widetilde{D}\in \operatorname{Ext}^{1}(D,D)$
is an extension such that
 $D_{\operatorname{cris}}(\widetilde{D})^{\unicode[STIX]{x1D711}^{f_{K}}=\widetilde{\unicode[STIX]{x1D719}}}$
is free of rank one over
$D_{\operatorname{cris}}(\widetilde{D})^{\unicode[STIX]{x1D711}^{f_{K}}=\widetilde{\unicode[STIX]{x1D719}}}$
is free of rank one over
 $(L\otimes _{\mathbf{Q}_{p}}F)[\unicode[STIX]{x1D700}]$
for some
$(L\otimes _{\mathbf{Q}_{p}}F)[\unicode[STIX]{x1D700}]$
for some
 $\widetilde{\unicode[STIX]{x1D719}}\equiv \unicode[STIX]{x1D719}~\mod ~\unicode[STIX]{x1D700}$
, then the image of
$\widetilde{\unicode[STIX]{x1D719}}\equiv \unicode[STIX]{x1D719}~\mod ~\unicode[STIX]{x1D700}$
, then the image of
![]() $\widetilde{D}$
under the natural map
$\widetilde{D}$
under the natural map
 $\operatorname{Ext}^{1}(D,D)\rightarrow \operatorname{Ext}^{1}(P_{1},D)$
is a crystalline
$\operatorname{Ext}^{1}(D,D)\rightarrow \operatorname{Ext}^{1}(P_{1},D)$
is a crystalline
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module over
![]() ${\mathcal{R}}_{L}$
.
${\mathcal{R}}_{L}$
.
Note that the image of
![]() $\widetilde{D}$
is given by the
$\widetilde{D}$
is given by the
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-module
 $E=\ker (\widetilde{D}\rightarrow D/P_{1})$
. Thus, the lemma actually fills the gap left in the previous proof.
$E=\ker (\widetilde{D}\rightarrow D/P_{1})$
. Thus, the lemma actually fills the gap left in the previous proof.
Proof. If
![]() $T$
is a
$T$
is a
![]() $B$
-linear operator on a
$B$
-linear operator on a
![]() $B$
-module
$B$
-module
![]() $M$
and
$M$
and
![]() $b\in B$
, then we let
$b\in B$
, then we let
![]() $M^{(T=b)}$
denote the submodule of elements
$M^{(T=b)}$
denote the submodule of elements
![]() $m\in M$
such that
$m\in M$
such that
 $(T-b)^{n}m=0$
for some
$(T-b)^{n}m=0$
for some
![]() $n\geqslant 0$
. The functor
$n\geqslant 0$
. The functor
 $M\mapsto M^{(T=b)}$
is exact.
$M\mapsto M^{(T=b)}$
is exact.
Since
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
is linear,
$\unicode[STIX]{x1D711}^{f_{K}}$
is linear,
![]() $\unicode[STIX]{x1D719}$
is a simple eigenvalue for
$\unicode[STIX]{x1D719}$
is a simple eigenvalue for
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
and
$\unicode[STIX]{x1D711}^{f_{K}}$
and
 $D_{\operatorname{cris}}(-)$
is left exact, we see that
$D_{\operatorname{cris}}(-)$
is left exact, we see that
 $D_{\operatorname{cris}}(E)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}=D_{\operatorname{cris}}(\widetilde{D})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}$
. In particular, since
$D_{\operatorname{cris}}(E)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}=D_{\operatorname{cris}}(\widetilde{D})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}$
. In particular, since
 $D_{\operatorname{cris}}(\widetilde{D})^{\unicode[STIX]{x1D711}^{f_{K}}=\widetilde{\unicode[STIX]{x1D719}}}=D_{\operatorname{cris}}(\widetilde{D})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}$
we see that
$D_{\operatorname{cris}}(\widetilde{D})^{\unicode[STIX]{x1D711}^{f_{K}}=\widetilde{\unicode[STIX]{x1D719}}}=D_{\operatorname{cris}}(\widetilde{D})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}$
we see that
 $\dim _{L}D_{\operatorname{cris}}(E)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}\geqslant 2\dim _{\mathbf{Q}_{p}}F$
. Now consider the exact sequence
$\dim _{L}D_{\operatorname{cris}}(E)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}\geqslant 2\dim _{\mathbf{Q}_{p}}F$
. Now consider the exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow D_{\operatorname{cris}}(D)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}\rightarrow D_{\operatorname{cris}}(E)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}\rightarrow D_{\operatorname{cris}}(P_{1})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow D_{\operatorname{cris}}(D)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}\rightarrow D_{\operatorname{cris}}(E)^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}\rightarrow D_{\operatorname{cris}}(P_{1})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}. & & \displaystyle \nonumber\end{eqnarray}$$
By counting dimensions we see the final map is surjective. Since
![]() $P_{1}$
is rank one,
$P_{1}$
is rank one,
 $D_{\operatorname{cris}}(P_{1})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}=D_{\operatorname{cris}}(P_{1})$
. In particular,
$D_{\operatorname{cris}}(P_{1})^{(\unicode[STIX]{x1D711}^{f_{K}}=\unicode[STIX]{x1D719})}=D_{\operatorname{cris}}(P_{1})$
. In particular,
 $D_{\operatorname{cris}}(E)\rightarrow D_{\operatorname{cris}}(P_{1})\rightarrow 0$
is exact as well, meaning that
$D_{\operatorname{cris}}(E)\rightarrow D_{\operatorname{cris}}(P_{1})\rightarrow 0$
is exact as well, meaning that
![]() $E$
is crystalline (again by dimension counts).◻
$E$
is crystalline (again by dimension counts).◻
Remark.
One can interpret Theorem 7.1, and Lemma 7.2, as making a statement about a certain deformation ring of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Indeed, let
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4}_{K})$
-modules. Indeed, let
![]() $\mathfrak{X}_{D_{x_{0}}}$
denote the functor of formal deformations of
$\mathfrak{X}_{D_{x_{0}}}$
denote the functor of formal deformations of
![]() $D_{x_{0}}$
. Let
$D_{x_{0}}$
. Let
 $R_{x_{0},\bullet }=(\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{d})$
be the refinement corresponding to the triangulation
$R_{x_{0},\bullet }=(\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{d})$
be the refinement corresponding to the triangulation
![]() $P_{x_{0},\bullet }$
by Proposition 3.3. One may define a relatively representable subfunctor
$P_{x_{0},\bullet }$
by Proposition 3.3. One may define a relatively representable subfunctor
 $\mathfrak{X}_{D_{x_{0}}}\supset \mathfrak{X}_{D_{x_{0}},R_{x_{0},\bullet }}^{h}$
consisting of deformations
$\mathfrak{X}_{D_{x_{0}}}\supset \mathfrak{X}_{D_{x_{0}},R_{x_{0},\bullet }}^{h}$
consisting of deformations
![]() $\widetilde{D}$
whose successive exterior powers
$\widetilde{D}$
whose successive exterior powers
![]() $\wedge ^{i}\widetilde{D}$
contain a free rank-one submodule on which
$\wedge ^{i}\widetilde{D}$
contain a free rank-one submodule on which
![]() $\unicode[STIX]{x1D711}^{f_{K}}$
acts by
$\unicode[STIX]{x1D711}^{f_{K}}$
acts by
 $\unicode[STIX]{x1D719}_{1}\ldots \unicode[STIX]{x1D719}_{i}$
. Neither functor
$\unicode[STIX]{x1D719}_{1}\ldots \unicode[STIX]{x1D719}_{i}$
. Neither functor
![]() $\mathfrak{X}_{?}$
is in general representable but both satisfy the natural Mayer–Vietoris condition on
$\mathfrak{X}_{?}$
is in general representable but both satisfy the natural Mayer–Vietoris condition on
 $L(x_{0})[\unicode[STIX]{x1D700}]$
-points in order to have reasonable Zariski tangent spaces
$L(x_{0})[\unicode[STIX]{x1D700}]$
-points in order to have reasonable Zariski tangent spaces
 $\mathfrak{X}_{?}(L(x_{0})[\unicode[STIX]{x1D700}])$
(see [Reference KisinKis03, Reference TanTan11]). In that case
$\mathfrak{X}_{?}(L(x_{0})[\unicode[STIX]{x1D700}])$
(see [Reference KisinKis03, Reference TanTan11]). In that case
 $\mathfrak{X}_{D_{x_{0}}}(L(x_{0})[\unicode[STIX]{x1D700}])\simeq \operatorname{Ext}^{1}(D_{x_{0}},D_{x_{0}})$
. What we just showed is that the obvious differences of Hodge–Tate weights are constant over the tangent space to
$\mathfrak{X}_{D_{x_{0}}}(L(x_{0})[\unicode[STIX]{x1D700}])\simeq \operatorname{Ext}^{1}(D_{x_{0}},D_{x_{0}})$
. What we just showed is that the obvious differences of Hodge–Tate weights are constant over the tangent space to
 $\mathfrak{X}_{D_{x_{0}},R_{x_{0},\bullet }}^{h}$
.
$\mathfrak{X}_{D_{x_{0}},R_{x_{0},\bullet }}^{h}$
.
Remark.
One might also ask whether Theorem 7.1 provides a tight bound for the rank of the weight map in a refined family. The answer is no. For example, let
 $K=\mathbf{Q}_{p}$
and consider any refined family
$K=\mathbf{Q}_{p}$
and consider any refined family
![]() $D$
of rank two with global parameter
$D$
of rank two with global parameter
![]() $(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})$
. Then one can take its symmetric square
$(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})$
. Then one can take its symmetric square
 $\operatorname{Sym}^{2}D$
equipped with the structure of a refined family of rank three, naturally having global parameter
$\operatorname{Sym}^{2}D$
equipped with the structure of a refined family of rank three, naturally having global parameter
 $(\unicode[STIX]{x1D6FF}_{1}^{2},\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2},\unicode[STIX]{x1D6FF}_{2}^{2})$
. If
$(\unicode[STIX]{x1D6FF}_{1}^{2},\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2},\unicode[STIX]{x1D6FF}_{2}^{2})$
. If
![]() $x_{0}$
defines a critically triangulated classical point for
$x_{0}$
defines a critically triangulated classical point for
![]() $D$
, then its critical type is the permutation
$D$
, then its critical type is the permutation
![]() $(12)$
, and
$(12)$
, and
![]() $x_{0}$
is also critically triangulated in the family
$x_{0}$
is also critically triangulated in the family
 $\operatorname{Sym}^{2}D$
with critical type
$\operatorname{Sym}^{2}D$
with critical type
![]() $(13)$
. Theorem 7.1 only implies that the difference of the first weight (i.e.
$(13)$
. Theorem 7.1 only implies that the difference of the first weight (i.e.
![]() $2\unicode[STIX]{x1D705}_{1}$
) and the third weight (i.e.
$2\unicode[STIX]{x1D705}_{1}$
) and the third weight (i.e.
![]() $2\unicode[STIX]{x1D705}_{2}$
) ramifies. However, the middle weight is
$2\unicode[STIX]{x1D705}_{2}$
) ramifies. However, the middle weight is
![]() $\unicode[STIX]{x1D705}_{1}+\unicode[STIX]{x1D705}_{2}$
and so the difference between the first two weights is
$\unicode[STIX]{x1D705}_{1}+\unicode[STIX]{x1D705}_{2}$
and so the difference between the first two weights is
 $2\unicode[STIX]{x1D705}_{1}-(\unicode[STIX]{x1D705}_{1}+\unicode[STIX]{x1D705}_{2})=\unicode[STIX]{x1D705}_{1}-\unicode[STIX]{x1D705}_{2}$
. This also ramifies in the family by Theorem 7.1 applied to
$2\unicode[STIX]{x1D705}_{1}-(\unicode[STIX]{x1D705}_{1}+\unicode[STIX]{x1D705}_{2})=\unicode[STIX]{x1D705}_{1}-\unicode[STIX]{x1D705}_{2}$
. This also ramifies in the family by Theorem 7.1 applied to
![]() $D$
itself, but is not detected by Theorem 7.1 applied to just
$D$
itself, but is not detected by Theorem 7.1 applied to just
 $\operatorname{Sym}^{2}D$
.
$\operatorname{Sym}^{2}D$
.
Acknowledgements
The author heartily thanks Rebecca Bellovin, Christophe Breuil, Kiran Kedlaya, Ruochuan Liu, Rob Pollack and Liang Xiao for helpful discussions and questions regarding this work. A special thanks goes to Jay Pottharst for being readily available to discuss his joint work with Kedlaya and Xiao prior to its written debut. We also thank an anonymous referee for many helpful suggestions and corrections. In particular, we owe the crucial flexibility in the definition of finite cohomology in § 4 to the referee’s suggestion. Finally, the bulk of this work was completed as a component of the author’s doctoral thesis and it is his pleasure to thank Joël Bellaïche for five years of insightful discussions and support. The author was partially supported by NSF award DMS-1402005 during the writing of this article.
Appendix Nakayama’s lemma
This brief appendix is to create a reference for a relative form of Nakayama’s lemma we used in the main text. Throughout we let
![]() $K$
be a non-Archimedean field of characteristic zero which is complete with respect to a non-trivial absolute value. If
$K$
be a non-Archimedean field of characteristic zero which is complete with respect to a non-trivial absolute value. If
![]() $X$
and
$X$
and
![]() $Y$
are
$Y$
are
![]() $K$
-rigid spaces we denote by
$K$
-rigid spaces we denote by
 $\operatorname{pr}_{X}:X\times _{K}Y\rightarrow X$
the projection map, which we note is obtained by base-changing the structure morphism
$\operatorname{pr}_{X}:X\times _{K}Y\rightarrow X$
the projection map, which we note is obtained by base-changing the structure morphism
 $Y\rightarrow \operatorname{Sp}(K)$
. We begin with two lemmas on products of
$Y\rightarrow \operatorname{Sp}(K)$
. We begin with two lemmas on products of
![]() $K$
-affinoid spaces.
$K$
-affinoid spaces.
Lemma A.1. Suppose that
![]() $X$
and
$X$
and
![]() $Y$
are
$Y$
are
![]() $K$
-affinoid spaces.
$K$
-affinoid spaces.
-
(a) If
 $U\subset X\times _{K}Y$
is an affinoid open subdomain, then the image
$U\subset X\times _{K}Y$
is an affinoid open subdomain, then the image
 $\operatorname{pr}_{X}(U)\subset X$
is a finite union of affinoid subdomains of
$\operatorname{pr}_{X}(U)\subset X$
is a finite union of affinoid subdomains of
 $X$
.
$X$
. -
(b) If
 $U\subset X\times _{K}Y$
is an admissible open, then the image
$U\subset X\times _{K}Y$
is an admissible open, then the image
 $\operatorname{pr}_{X}(U)\subset X$
is a union of affinoid open subdomains of
$\operatorname{pr}_{X}(U)\subset X$
is a union of affinoid open subdomains of
 $X$
.
$X$
.
Proof. We begin with part (a). The structure morphism
 $Y\rightarrow \operatorname{Sp}(K)$
is flat and thus
$Y\rightarrow \operatorname{Sp}(K)$
is flat and thus
![]() $\operatorname{pr}_{X}$
is also flat. Let
$\operatorname{pr}_{X}$
is also flat. Let
 $U\subset X\times _{K}Y$
be an affinoid open subdomain. The inclusion
$U\subset X\times _{K}Y$
be an affinoid open subdomain. The inclusion
 $U\subset X\times _{K}Y$
is also flat and thus the composition
$U\subset X\times _{K}Y$
is also flat and thus the composition
 $U\rightarrow X\times _{K}Y\rightarrow X$
is a flat map between
$U\rightarrow X\times _{K}Y\rightarrow X$
is a flat map between
![]() $K$
-affinoid spaces. Part (a) then follows from [Reference Bosch and LütkebohmertBL93, Corollary 5.11] because
$K$
-affinoid spaces. Part (a) then follows from [Reference Bosch and LütkebohmertBL93, Corollary 5.11] because
![]() $K$
-affinoids are quasi-compact and quasi-separated rigid spaces. To prove part (b) we write
$K$
-affinoids are quasi-compact and quasi-separated rigid spaces. To prove part (b) we write
 $U=\bigcup U_{i}$
where each
$U=\bigcup U_{i}$
where each
![]() $U_{i}$
is an affinoid open subdomain. By part (a) the image
$U_{i}$
is an affinoid open subdomain. By part (a) the image
 $\operatorname{pr}_{X}(U_{i})$
is covered by affinoid subdomains and thus so is
$\operatorname{pr}_{X}(U_{i})$
is covered by affinoid subdomains and thus so is
 $\operatorname{pr}_{X}(U)=\bigcup \operatorname{pr}_{X}(U_{i})$
.◻
$\operatorname{pr}_{X}(U)=\bigcup \operatorname{pr}_{X}(U_{i})$
.◻
Remark.
We are unable to determine whether
![]() $\operatorname{pr}_{X}$
should be open in the sense that
$\operatorname{pr}_{X}$
should be open in the sense that
![]() $\operatorname{pr}_{X}(U)$
is admissible open for each admissible open
$\operatorname{pr}_{X}(U)$
is admissible open for each admissible open
 $U\subset X\times _{K}Y$
. This contrasts with the algebraic analog of Lemma A.1, where part (b) really becomes that
$U\subset X\times _{K}Y$
. This contrasts with the algebraic analog of Lemma A.1, where part (b) really becomes that
![]() $f$
is ‘open’ because ‘covered by opens’ is synonymous with ‘open’ in the Zariski topology (see [SPA15, Tag 037G]).
$f$
is ‘open’ because ‘covered by opens’ is synonymous with ‘open’ in the Zariski topology (see [SPA15, Tag 037G]).
If
 $X=\operatorname{Sp}(A)$
is a
$X=\operatorname{Sp}(A)$
is a
![]() $K$
-affinoid space and
$K$
-affinoid space and
![]() $x\in X$
we write
$x\in X$
we write
![]() $\mathfrak{m}_{x}$
for the corresponding maximal ideal of
$\mathfrak{m}_{x}$
for the corresponding maximal ideal of
![]() $A$
. We write
$A$
. We write
![]() $\unicode[STIX]{x1D705}(x)$
for the residue field
$\unicode[STIX]{x1D705}(x)$
for the residue field
![]() $A/\mathfrak{m}_{x}$
. If
$A/\mathfrak{m}_{x}$
. If
![]() $F\in A$
and
$F\in A$
and
![]() $x\in X$
, then we use the standard notation
$x\in X$
, then we use the standard notation
![]() $F(x)$
to denote the image of
$F(x)$
to denote the image of
![]() $F$
in
$F$
in
![]() $\unicode[STIX]{x1D705}(x)$
. If
$\unicode[STIX]{x1D705}(x)$
. If
![]() $A$
and
$A$
and
![]() $B$
are two
$B$
are two
![]() $K$
-affinoid algebras,
$K$
-affinoid algebras,
 $F\in A\widehat{\otimes }_{K}B$
and
$F\in A\widehat{\otimes }_{K}B$
and
 $y\in \operatorname{Sp}(B)$
, then we use
$y\in \operatorname{Sp}(B)$
, then we use
![]() $F_{y}$
to denote the element
$F_{y}$
to denote the element
 $F_{y}\in A\otimes _{K}\unicode[STIX]{x1D705}(y)$
which is the image of
$F_{y}\in A\otimes _{K}\unicode[STIX]{x1D705}(y)$
which is the image of
![]() $F$
under the canonical map
$F$
under the canonical map
 $A\widehat{\otimes }_{K}B\rightarrow (A\widehat{\otimes }_{K}B)/\mathfrak{m}_{y}(A\widehat{\otimes }_{K}B)=A\otimes _{K}\unicode[STIX]{x1D705}(y)$
.
$A\widehat{\otimes }_{K}B\rightarrow (A\widehat{\otimes }_{K}B)/\mathfrak{m}_{y}(A\widehat{\otimes }_{K}B)=A\otimes _{K}\unicode[STIX]{x1D705}(y)$
.
Lemma A.2. Suppose that
![]() $A$
and
$A$
and
![]() $B$
are reduced affinoid
$B$
are reduced affinoid
![]() $K$
-algebras. Then:
$K$
-algebras. Then:
-
(a) the completed tensor product
 $A\widehat{\otimes }_{K}B$
is reduced;
$A\widehat{\otimes }_{K}B$
is reduced; -
(b) if
 $F\in A\widehat{\otimes }_{K}B$
, then
$F\in A\widehat{\otimes }_{K}B$
, then
 $F=0$
if and only if
$F=0$
if and only if
 $F_{y}=0$
for all
$F_{y}=0$
for all
 $y\in \operatorname{Sp}(B)$
.
$y\in \operatorname{Sp}(B)$
.
Proof. A noetherian ring
![]() $R$
is reduced if and only if satisfies the two properties
$R$
is reduced if and only if satisfies the two properties
![]() $(R_{0})$
and
$(R_{0})$
and
![]() $(S_{1})$
(see [SPA15, Tag 031R]), and being geometrically reduced is equivalent to being reduced for affinoid algebras over perfect fields [Reference ConradCon99, Lemma 3.3.1]. In particular, since
$(S_{1})$
(see [SPA15, Tag 031R]), and being geometrically reduced is equivalent to being reduced for affinoid algebras over perfect fields [Reference ConradCon99, Lemma 3.3.1]. In particular, since
![]() $K$
has characteristic zero we deduce part (a) from [Reference DucrosDuc09, Théorème 8.1].Footnote
6
$K$
has characteristic zero we deduce part (a) from [Reference DucrosDuc09, Théorème 8.1].Footnote
6
To prove part (b) we let
 $y\in \operatorname{Sp}(B)$
and note that if
$y\in \operatorname{Sp}(B)$
and note that if
 $w\in X\times _{K}Y$
lies above
$w\in X\times _{K}Y$
lies above
![]() $y$
, then we have a natural map
$y$
, then we have a natural map
 $A\otimes _{K}\unicode[STIX]{x1D705}(y)\rightarrow (A\widehat{\otimes }_{K}B)/\mathfrak{m}_{w}$
. Ranging over all
$A\otimes _{K}\unicode[STIX]{x1D705}(y)\rightarrow (A\widehat{\otimes }_{K}B)/\mathfrak{m}_{w}$
. Ranging over all
![]() $y$
we get the following commutative diagram.
$y$
we get the following commutative diagram.

By part (a) the vertical arrow of (A.1) is injective. Thus we deduce the horizontal arrow of (A.1) is injective as well, proving part (b). ◻
Lemma A.3. If
 $X=\operatorname{Sp}(A)$
and
$X=\operatorname{Sp}(A)$
and
 $Y=\operatorname{Sp}(B)$
are reduced affinoid
$Y=\operatorname{Sp}(B)$
are reduced affinoid
![]() $K$
-spaces and
$K$
-spaces and
![]() $Z\subset X$
is a Zariski-dense subset of points, then
$Z\subset X$
is a Zariski-dense subset of points, then
 $\operatorname{pr}_{X}^{-1}(Z)\subset X\times _{K}Y$
is also Zariski-dense.
$\operatorname{pr}_{X}^{-1}(Z)\subset X\times _{K}Y$
is also Zariski-dense.
Proof. Suppose that
![]() $Z\subset X$
is Zariski-dense. Let
$Z\subset X$
is Zariski-dense. Let
 $F\in A\widehat{\otimes }_{K}B$
. We need to show that if
$F\in A\widehat{\otimes }_{K}B$
. We need to show that if
 $F(z^{\prime })=0$
for all
$F(z^{\prime })=0$
for all
 $z^{\prime }\in \operatorname{pr}_{X}^{-1}(Z)$
then
$z^{\prime }\in \operatorname{pr}_{X}^{-1}(Z)$
then
![]() $F=0$
. It suffices by Lemma A.2(b) to show that
$F=0$
. It suffices by Lemma A.2(b) to show that
![]() $F_{y}=0$
for each
$F_{y}=0$
for each
![]() $y\in Y$
.
$y\in Y$
.
Let
![]() $y\in Y$
. The field
$y\in Y$
. The field
![]() $\unicode[STIX]{x1D705}(y)$
is a finite extension of
$\unicode[STIX]{x1D705}(y)$
is a finite extension of
![]() $K$
. In particular, if we fix a basis of
$K$
. In particular, if we fix a basis of
![]() $\unicode[STIX]{x1D705}(y)$
over
$\unicode[STIX]{x1D705}(y)$
over
![]() $K$
, then for any
$K$
, then for any
![]() $K$
-vector space
$K$
-vector space
![]() $C$
we get an identification of
$C$
we get an identification of
 $C\otimes _{K}\unicode[STIX]{x1D705}(y)$
with
$C\otimes _{K}\unicode[STIX]{x1D705}(y)$
with
![]() $C^{\oplus n}$
(where
$C^{\oplus n}$
(where
 $n=\dim _{K}\unicode[STIX]{x1D705}(y)$
) which is functorial in
$n=\dim _{K}\unicode[STIX]{x1D705}(y)$
) which is functorial in
![]() $C$
(but depending on the choice of basis). Applying this to
$C$
(but depending on the choice of basis). Applying this to
![]() $C=A$
and
$C=A$
and
 $C=\unicode[STIX]{x1D705}(z)$
with
$C=\unicode[STIX]{x1D705}(z)$
with
![]() $z\in Z$
we get the following commuting diagram whose vertical arrows are isomorphisms.
$z\in Z$
we get the following commuting diagram whose vertical arrows are isomorphisms.

Since
![]() $Z$
is Zariski-dense in
$Z$
is Zariski-dense in
![]() $X$
, the bottom arrow is injective. Thus, to show
$X$
, the bottom arrow is injective. Thus, to show
![]() $F_{y}=0$
it suffices to check that its image in
$F_{y}=0$
it suffices to check that its image in
 $\unicode[STIX]{x1D705}(z)\otimes _{K}\unicode[STIX]{x1D705}(y)$
is zero for each
$\unicode[STIX]{x1D705}(z)\otimes _{K}\unicode[STIX]{x1D705}(y)$
is zero for each
![]() $z\in Z$
. But that follows easily from the assumption that
$z\in Z$
. But that follows easily from the assumption that
 $F(z^{\prime })=0$
for all
$F(z^{\prime })=0$
for all
 $z^{\prime }\in \operatorname{pr}_{X}^{-1}(Z)$
. Since
$z^{\prime }\in \operatorname{pr}_{X}^{-1}(Z)$
. Since
![]() $y$
was arbitrary, we are done.◻
$y$
was arbitrary, we are done.◻
If
![]() $B$
is a ring and
$B$
is a ring and
![]() $f\in B$
is non-nilpotent, then we write
$f\in B$
is non-nilpotent, then we write
![]() $B[1/f]$
for the localization of
$B[1/f]$
for the localization of
![]() $B$
at
$B$
at
![]() $f$
. If
$f$
. If
![]() $M$
is a
$M$
is a
![]() $B$
-module we write
$B$
-module we write
 $M[1/f]=B[1/f]\otimes _{B}M$
for the localization of
$M[1/f]=B[1/f]\otimes _{B}M$
for the localization of
![]() $M$
. If
$M$
. If
![]() $A$
is a
$A$
is a
![]() $K$
-affinoid algebra,
$K$
-affinoid algebra,
![]() $M$
is a module over
$M$
is a module over
![]() $A$
and
$A$
and
![]() $x\in X$
corresponds to the maximal ideal
$x\in X$
corresponds to the maximal ideal
![]() $\mathfrak{m}_{x}$
, then we write
$\mathfrak{m}_{x}$
, then we write
![]() $M_{x}$
for
$M_{x}$
for
 $M\otimes _{A}A/\mathfrak{m}_{x}$
. Note that these two operations commute in the sense that
$M\otimes _{A}A/\mathfrak{m}_{x}$
. Note that these two operations commute in the sense that
 $M_{x}[1/f]\simeq M[1/f]_{x}$
.
$M_{x}[1/f]\simeq M[1/f]_{x}$
.
Now suppose that
![]() $A$
and
$A$
and
![]() $B$
are affinoid
$B$
are affinoid
![]() $K$
-algebras and
$K$
-algebras and
 $R=A\widehat{\otimes }_{K}B$
. If
$R=A\widehat{\otimes }_{K}B$
. If
![]() $M$
is a module over
$M$
is a module over
![]() $R$
, then
$R$
, then
 $M_{x}[1/f]$
is a module over
$M_{x}[1/f]$
is a module over
 $\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]$
for each
$\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]$
for each
![]() $x\in X$
and
$x\in X$
and
![]() $f\in B$
. Indeed, one just has to check that
$f\in B$
. Indeed, one just has to check that
 $$\begin{eqnarray}\displaystyle R_{x}[1/f] & \simeq & \displaystyle ((B\widehat{\otimes }_{K}A)\otimes _{A}A/\mathfrak{m}_{x})\otimes _{B}B[1/f]\nonumber\\ \displaystyle & \simeq & \displaystyle (B\otimes _{K}\unicode[STIX]{x1D705}(x))\otimes _{B}B[1/f]\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{x}[1/f] & \simeq & \displaystyle ((B\widehat{\otimes }_{K}A)\otimes _{A}A/\mathfrak{m}_{x})\otimes _{B}B[1/f]\nonumber\\ \displaystyle & \simeq & \displaystyle (B\otimes _{K}\unicode[STIX]{x1D705}(x))\otimes _{B}B[1/f]\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f].\end{eqnarray}$$
We now arrive at the subject of this appendix.
Proposition A.4 (Nakayama’s lemma).
Suppose that
 $X=\operatorname{Sp}(A)$
and
$X=\operatorname{Sp}(A)$
and
 $Y=\operatorname{Sp}(B)$
are reduced affinoid
$Y=\operatorname{Sp}(B)$
are reduced affinoid
![]() $K$
-spaces and that
$K$
-spaces and that
![]() $M$
is a finite module over
$M$
is a finite module over
![]() $A\widehat{\otimes }_{K}B$
. Let
$A\widehat{\otimes }_{K}B$
. Let
![]() $f\in B$
be non-zero and assume that for each
$f\in B$
be non-zero and assume that for each
![]() $x\in X$
the
$x\in X$
the
 $\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]$
-module
$\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]$
-module
 $M_{x}[1/f]$
is (finite) free. Then:
$M_{x}[1/f]$
is (finite) free. Then:
-
(a) for each
 $m\geqslant 0$
the subset is a union of affinoid subdomains of
$m\geqslant 0$
the subset is a union of affinoid subdomains of $$\begin{eqnarray}\displaystyle X_{m}=\{x\in X:\operatorname{rank}_{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}M_{x}[1/f]\leqslant m\}\subset X & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{m}=\{x\in X:\operatorname{rank}_{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}M_{x}[1/f]\leqslant m\}\subset X & & \displaystyle \nonumber\end{eqnarray}$$
 $X$
;
$X$
;
-
(b) if
 $Z\subset X$
is Zariski-dense, then
$Z\subset X$
is Zariski-dense, then
 $X_{m}\neq \varnothing \;\Longrightarrow \;Z\cap X_{m}\neq \varnothing$
; in particular, the minimum rank of
$X_{m}\neq \varnothing \;\Longrightarrow \;Z\cap X_{m}\neq \varnothing$
; in particular, the minimum rank of
 $M_{x}[1/f]$
is achieved on
$M_{x}[1/f]$
is achieved on
 $Z$
.
$Z$
.
Proof. Let
 $R=A\widehat{\otimes }_{K}B$
and consider the (non-empty, because
$R=A\widehat{\otimes }_{K}B$
and consider the (non-empty, because
![]() $f$
is not nilpotent) affine scheme
$f$
is not nilpotent) affine scheme
 $\operatorname{Spec}(R[1/f])\subset \operatorname{Spec}(R)$
. If
$\operatorname{Spec}(R[1/f])\subset \operatorname{Spec}(R)$
. If
 $\mathfrak{q}\in \operatorname{Spec}(R)$
write
$\mathfrak{q}\in \operatorname{Spec}(R)$
write
![]() $\unicode[STIX]{x1D705}(\mathfrak{q})$
for its residue field (generalizing our previous notation). Since
$\unicode[STIX]{x1D705}(\mathfrak{q})$
for its residue field (generalizing our previous notation). Since
![]() $M$
is finite over
$M$
is finite over
![]() $R$
,
$R$
,
![]() $M[1/f]$
is finite over
$M[1/f]$
is finite over
![]() $R[1/f]$
and so by the usual Nakayama’s lemma (see [Reference MatsumuraMat89, Theorem 4.10]) the set
$R[1/f]$
and so by the usual Nakayama’s lemma (see [Reference MatsumuraMat89, Theorem 4.10]) the set
 $$\begin{eqnarray}\displaystyle V_{m}=\{\mathfrak{q}\in \operatorname{Spec}(R[1/f]):\dim _{\unicode[STIX]{x1D705}(\mathfrak{q})}M[1/f]\otimes _{R[1/f]}\unicode[STIX]{x1D705}(\mathfrak{q})\leqslant m\} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{m}=\{\mathfrak{q}\in \operatorname{Spec}(R[1/f]):\dim _{\unicode[STIX]{x1D705}(\mathfrak{q})}M[1/f]\otimes _{R[1/f]}\unicode[STIX]{x1D705}(\mathfrak{q})\leqslant m\} & & \displaystyle \nonumber\end{eqnarray}$$
is Zariski-open in
 $\operatorname{Spec}(R[1/f])$
for each
$\operatorname{Spec}(R[1/f])$
for each
![]() $m\geqslant 0$
. In particular,
$m\geqslant 0$
. In particular,
 $U_{m}:=V_{m}\cap \operatorname{Sp}(R)$
is Zariski-open in
$U_{m}:=V_{m}\cap \operatorname{Sp}(R)$
is Zariski-open in
 $\operatorname{Sp}(R)=X\times _{K}Y$
. Since Zariski opens are admissible opens,
$\operatorname{Sp}(R)=X\times _{K}Y$
. Since Zariski opens are admissible opens,
![]() $U_{m}$
is admissible open in
$U_{m}$
is admissible open in
![]() $\operatorname{Sp}(R)$
. By Lemma A.1(b),
$\operatorname{Sp}(R)$
. By Lemma A.1(b),
 $\operatorname{pr}_{X}(U_{m})$
is a union of affinoid subdomains and thus it suffices to show that
$\operatorname{pr}_{X}(U_{m})$
is a union of affinoid subdomains and thus it suffices to show that
 $\operatorname{pr}_{X}(U_{m})=X_{m}$
.
$\operatorname{pr}_{X}(U_{m})=X_{m}$
.
Write
![]() $\operatorname{Sp}(R)_{f}$
for
$\operatorname{Sp}(R)_{f}$
for
 $\operatorname{Sp}(R)\cap \operatorname{Spec}(R[1/f])$
. Since
$\operatorname{Sp}(R)\cap \operatorname{Spec}(R[1/f])$
. Since
![]() $f\in B$
, the projection map
$f\in B$
, the projection map
 $\operatorname{Sp}(R)_{f}\rightarrow X$
is still surjective. Thus, if
$\operatorname{Sp}(R)_{f}\rightarrow X$
is still surjective. Thus, if
![]() $x\in X$
we may choose
$x\in X$
we may choose
 $u\in \operatorname{Sp}(R)_{f}$
lying above
$u\in \operatorname{Sp}(R)_{f}$
lying above
![]() $x$
. Then (A. 2) shows that
$x$
. Then (A. 2) shows that
 $R_{x}[1/f]\otimes _{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}\unicode[STIX]{x1D705}(u)=\unicode[STIX]{x1D705}(u)$
. We are assuming
$R_{x}[1/f]\otimes _{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}\unicode[STIX]{x1D705}(u)=\unicode[STIX]{x1D705}(u)$
. We are assuming
 $M_{x}[1/f]\simeq (R_{x}[1/f])^{\oplus n_{x}}$
for an integer
$M_{x}[1/f]\simeq (R_{x}[1/f])^{\oplus n_{x}}$
for an integer
![]() $n_{x}$
depending on
$n_{x}$
depending on
![]() $x$
. Reducing the residue field at
$x$
. Reducing the residue field at
![]() $u$
, we see that
$u$
, we see that
 $$\begin{eqnarray}\displaystyle M_{x}[1/f]\otimes _{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}\unicode[STIX]{x1D705}(u)\simeq \unicode[STIX]{x1D705}(u)^{\oplus n_{x}}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{x}[1/f]\otimes _{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}\unicode[STIX]{x1D705}(u)\simeq \unicode[STIX]{x1D705}(u)^{\oplus n_{x}}. & & \displaystyle \nonumber\end{eqnarray}$$
On the other hand, since
 $$\begin{eqnarray}\displaystyle M_{x}[1/f]\otimes _{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}\unicode[STIX]{x1D705}(u)\simeq M[1/f]\otimes _{R[1/f]}\unicode[STIX]{x1D705}(u) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{x}[1/f]\otimes _{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}\unicode[STIX]{x1D705}(u)\simeq M[1/f]\otimes _{R[1/f]}\unicode[STIX]{x1D705}(u) & & \displaystyle \nonumber\end{eqnarray}$$
this shows that
 $$\begin{eqnarray}\displaystyle \dim _{\unicode[STIX]{x1D705}(u)}M[1/f]\otimes _{R[1/f]}\unicode[STIX]{x1D705}(u)=\operatorname{rank}_{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}M_{x}[1/f] & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim _{\unicode[STIX]{x1D705}(u)}M[1/f]\otimes _{R[1/f]}\unicode[STIX]{x1D705}(u)=\operatorname{rank}_{\unicode[STIX]{x1D705}(x)\otimes _{K}B[1/f]}M_{x}[1/f] & & \displaystyle \nonumber\end{eqnarray}$$
depends only on
![]() $x$
. Now it is clear that
$x$
. Now it is clear that
 $\operatorname{pr}(U_{m})\subset X_{m}$
. The reverse inclusion follows from the surjectivity of
$\operatorname{pr}(U_{m})\subset X_{m}$
. The reverse inclusion follows from the surjectivity of
 $\operatorname{Sp}(R)_{f}\rightarrow X$
. This shows
$\operatorname{Sp}(R)_{f}\rightarrow X$
. This shows
 $\operatorname{pr}_{X}(U_{m})=X_{m}$
and we have finished the proof of part (a).
$\operatorname{pr}_{X}(U_{m})=X_{m}$
and we have finished the proof of part (a).
The proof of part (b) is nearly complete as well. The only point is that if
![]() $Z$
is Zariski-dense then Lemma A.3 guarantees that the pre-image
$Z$
is Zariski-dense then Lemma A.3 guarantees that the pre-image
 $\operatorname{pr}_{X}^{-1}(Z)\subset \operatorname{Sp}(R)$
is Zariski-dense as well. In particular, since
$\operatorname{pr}_{X}^{-1}(Z)\subset \operatorname{Sp}(R)$
is Zariski-dense as well. In particular, since
![]() $U_{m}$
is Zariski-open in
$U_{m}$
is Zariski-open in
![]() $\operatorname{Sp}(R)$
,
$\operatorname{Sp}(R)$
,
![]() $U_{m}$
is non-empty if and only if
$U_{m}$
is non-empty if and only if
 $\operatorname{pr}_{X}^{-1}(Z)\cap U_{m}$
is non-empty. Part (b) follows immediately now.◻
$\operatorname{pr}_{X}^{-1}(Z)\cap U_{m}$
is non-empty. Part (b) follows immediately now.◻