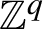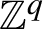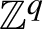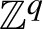1 Introduction
Let
![]() $q\in \mathbb {N}$
. Throughout this paper, by a
$q\in \mathbb {N}$
. Throughout this paper, by a
![]() $\mathbb {Z}^q$
-measure preserving dynamical system (
$\mathbb {Z}^q$
-measure preserving dynamical system (
![]() $\mathbb {Z}^q$
-MPS for short) we mean a quadruple
$\mathbb {Z}^q$
-MPS for short) we mean a quadruple
![]() $(X,\mathcal {B}_X,\mu , T)$
, where X is a compact metric space, the
$(X,\mathcal {B}_X,\mu , T)$
, where X is a compact metric space, the
![]() $\mathbb {Z}^q$
-action T is a homeomorphism from the additive group
$\mathbb {Z}^q$
-action T is a homeomorphism from the additive group
![]() $\mathbb {Z}^q$
to the group of homeomorphisms of X,
$\mathbb {Z}^q$
to the group of homeomorphisms of X,
![]() $\mathcal {B}_X$
is the Borel
$\mathcal {B}_X$
is the Borel
![]() $\sigma $
-algebra of X and
$\sigma $
-algebra of X and
![]() $\mu $
is an invariant Borel probability measure. We denote the corresponding homeomorphism of X by
$\mu $
is an invariant Borel probability measure. We denote the corresponding homeomorphism of X by
![]() $T^{\vec {v}}$
for any
$T^{\vec {v}}$
for any
![]() $\vec {v}\in \mathbb {Z}^q$
, so that
$\vec {v}\in \mathbb {Z}^q$
, so that
![]() $T^{\vec {v}}\circ T^{\vec {w}}=T^{\vec {v}+\vec {w}}$
and
$T^{\vec {v}}\circ T^{\vec {w}}=T^{\vec {v}+\vec {w}}$
and
![]() $T^{\vec {0}} $
is the identity on X.
$T^{\vec {0}} $
is the identity on X.
Kolmogorov [Reference Kolmogorov14] introduced the notion of entropy to dynamical systems, which played an important role in the study of ergodic theory and topological dynamics to measure the chaoticity or unpredictability of a system. To investigate the complexity of entropy zero systems, many invariants were introduced. Kušhnirenko [Reference Kušhnirenko16] developed an invariant, sequence entropy, to distinguish non-isomorphic entropy zero systems. We refer to [Reference Hulse11, Reference Saleski21] for further study on sequence entropy. Katok and Thouvenot [Reference Katok and Thouvenot12] introduced the notion of slow entropy for measure-preserving actions of discrete amenable groups to measure the complexity of entropy zero systems. Recently, Dou, Huang and Park [Reference Dou, Huang and Park4] introduced the notion of entropy dimension to classify the growth rate of the orbits of entropy zero systems. To investigate the Cellular Automaton map together with the Bernoulli shift, Milnor [Reference Milnor17] defined directional entropy. Many of its properties were further studied in [Reference Akin1–Reference Courbage and Kaminski3, Reference Park19, Reference Park20, Reference Zhu24].
In this paper, we introduce a new invariant, directional sequence entropy, for
![]() $\mathbb {Z}^q$
-actions based on classical sequence entropy and directional entropy. We investigate some properties of directional sequence entropy analogously to classical sequence entropy. Moreover, we discuss the relation between the directional discrete spectrum and directional sequence entropy. One of our main results is to show the directional version of Kušhnirenko theorem, which tells us that a
$\mathbb {Z}^q$
-actions based on classical sequence entropy and directional entropy. We investigate some properties of directional sequence entropy analogously to classical sequence entropy. Moreover, we discuss the relation between the directional discrete spectrum and directional sequence entropy. One of our main results is to show the directional version of Kušhnirenko theorem, which tells us that a
![]() $\mathbb {Z}^q$
-MPS has directional discrete spectrum if and only if its directional sequence entropy is always zero for any sequence along a corresponding direction. In the proof of this result, our main difficulty is that many theories of classical sequence entropy can not be directly applied to our proof such as spectral mixing theorem of Koopman–von Neumann [Reference Koopman and von Neumann15], because these results are only available for the case of group actions. Motivated by a
$\mathbb {Z}^q$
-MPS has directional discrete spectrum if and only if its directional sequence entropy is always zero for any sequence along a corresponding direction. In the proof of this result, our main difficulty is that many theories of classical sequence entropy can not be directly applied to our proof such as spectral mixing theorem of Koopman–von Neumann [Reference Koopman and von Neumann15], because these results are only available for the case of group actions. Motivated by a
![]() $\mathbb {Z}$
-MPS, which was introduced by Park [Reference Park20], we overcome this difficulty by establishing the relation between directional Kronecker algebra and classical Kronecker algebra. Taking advantage of the relation between the two, we can show our results by some classical consequences for the case of
$\mathbb {Z}$
-MPS, which was introduced by Park [Reference Park20], we overcome this difficulty by establishing the relation between directional Kronecker algebra and classical Kronecker algebra. Taking advantage of the relation between the two, we can show our results by some classical consequences for the case of
![]() $\mathbb {Z}$
-actions. Meanwhile, we show that directional sequence entropy is closely relevant to classical sequence entropy and a
$\mathbb {Z}$
-actions. Meanwhile, we show that directional sequence entropy is closely relevant to classical sequence entropy and a
![]() $\mathbb {Z}^q$
-MPS has directional discrete spectrum along q linearly independent directions if and only if it has discrete spectrum.
$\mathbb {Z}^q$
-MPS has directional discrete spectrum along q linearly independent directions if and only if it has discrete spectrum.
For convenience, we focus on
![]() $\mathbb {Z}^2$
-MPS. Using exactly the same methods, we can obtain corresponding results of
$\mathbb {Z}^2$
-MPS. Using exactly the same methods, we can obtain corresponding results of
![]() $\mathbb {Z}^q$
-MPS for any integer
$\mathbb {Z}^q$
-MPS for any integer
![]() $q\geq 2$
, which are introduced in Appendix B. To be precise, let
$q\geq 2$
, which are introduced in Appendix B. To be precise, let
![]() $(X ,\mathcal {B}_X, \mu , T)$
be a
$(X ,\mathcal {B}_X, \mu , T)$
be a
![]() $\mathbb {Z}^2$
-MPS and
$\mathbb {Z}^2$
-MPS and
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector. (For simplicity, we write
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector. (For simplicity, we write
![]() $\vec {v}$
as
$\vec {v}$
as
![]() $(1,\beta )$
. In fact all results in this paper are true when
$(1,\beta )$
. In fact all results in this paper are true when
![]() $\vec {v}=(0,1)$
because this case is the same as the case of
$\vec {v}=(0,1)$
because this case is the same as the case of
![]() $\mathbb {Z}$
-actions.) For a finite measurable partition
$\mathbb {Z}$
-actions.) For a finite measurable partition
![]() $\alpha $
of X, let
$\alpha $
of X, let
 $$ \begin{align*}H_{\mu}(\alpha)=-\sum_{A\in \alpha}\mu(A)\log{\mu(A)}.\end{align*} $$
$$ \begin{align*}H_{\mu}(\alpha)=-\sum_{A\in \alpha}\mu(A)\log{\mu(A)}.\end{align*} $$
We put
 $$ \begin{align*}\Lambda^{\vec{v}}(b)=\{(m,n)\in\mathbb{Z}^2:\beta m-b/2\leq n\leq \beta m+b/2\}.\end{align*} $$
$$ \begin{align*}\Lambda^{\vec{v}}(b)=\{(m,n)\in\mathbb{Z}^2:\beta m-b/2\leq n\leq \beta m+b/2\}.\end{align*} $$
For any infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $\Lambda ^{\vec {v}}(b)$
that
$\Lambda ^{\vec {v}}(b)$
that
![]() $\{m_i\}_{i=1}^{\infty }$
is strictly monotone, we put
$\{m_i\}_{i=1}^{\infty }$
is strictly monotone, we put
 $$ \begin{align*}h^S_{\mu}(T,\alpha)= \limsup_{k\to \infty} \frac{1}{k}H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha\bigg).\end{align*} $$
$$ \begin{align*}h^S_{\mu}(T,\alpha)= \limsup_{k\to \infty} \frac{1}{k}H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha\bigg).\end{align*} $$
Then we can define the directional sequence entropy of T for the infinite subset S by
 $$ \begin{align*}h^S_{\mu}(T)=\sup_{\alpha}h^S_{\mu}(T,\alpha),\end{align*} $$
$$ \begin{align*}h^S_{\mu}(T)=\sup_{\alpha}h^S_{\mu}(T,\alpha),\end{align*} $$
where the supremum is taken over all finite measurable partitions of X.
Define the
![]() $\vec {v}$
-directional Kronecker algebra by
$\vec {v}$
-directional Kronecker algebra by
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b)=\{B\in\mathcal{B}_X: \overline{\{U_T^{(m,n)}1_B :(m,n)\in \Lambda^{\vec{v}}(b) \}}\text{ is compact in } L^2(X,\mathcal{B}_X,\mu) \},\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b)=\{B\in\mathcal{B}_X: \overline{\{U_T^{(m,n)}1_B :(m,n)\in \Lambda^{\vec{v}}(b) \}}\text{ is compact in } L^2(X,\mathcal{B}_X,\mu) \},\end{align*} $$
where
 $U_T^{(m,n)}:L^2(X,\mathcal {B}_X,\mu )\to L^2(X,\mathcal {B}_X,\mu )$
is the unitary operator such that
$U_T^{(m,n)}:L^2(X,\mathcal {B}_X,\mu )\to L^2(X,\mathcal {B}_X,\mu )$
is the unitary operator such that
 $$ \begin{align*}U_T^{(m,n)}f=f\circ T^{(m,n)}\quad\text{for all } f\in L^2(X,\mathcal{B}_X,\mu)\end{align*} $$
$$ \begin{align*}U_T^{(m,n)}f=f\circ T^{(m,n)}\quad\text{for all } f\in L^2(X,\mathcal{B}_X,\mu)\end{align*} $$
and
![]() $1_B$
is the indicator function of
$1_B$
is the indicator function of
![]() $B\in \mathcal {B}_X$
, that is,
$B\in \mathcal {B}_X$
, that is,
 $$ \begin{align*}1_B(x)=\left\{ \begin{array}{@{}lr} 1, & x\in B,\\ 0, & x\notin B.\\ \end{array} \right.\end{align*} $$
$$ \begin{align*}1_B(x)=\left\{ \begin{array}{@{}lr} 1, & x\in B,\\ 0, & x\notin B.\\ \end{array} \right.\end{align*} $$
In §3, we prove that
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
is a
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
is a
![]() $\sigma $
-algebra and the definition of
$\sigma $
-algebra and the definition of
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
is independent of the selection of
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
is independent of the selection of
![]() $b\in (0,\infty )$
. So we omit b in
$b\in (0,\infty )$
. So we omit b in
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
and write it as
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
and write it as
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}$
.
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}$
.
Motivated by the work in [Reference Huang, Maass and Ye10], we can show the following consequence.
Theorem 1.1. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. Let
$b\in (0,\infty )$
. Let
![]() $\alpha $
be a finite measurable partition of X. For any infinite subset
$\alpha $
be a finite measurable partition of X. For any infinite subset
![]() $S'$
of
$S'$
of
![]() $\Lambda ^{\vec {v}}(b)$
,
$\Lambda ^{\vec {v}}(b)$
,
 $$ \begin{align*}h^{S'}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
Moreover, there exists an infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $ \Lambda ^{\vec {v}}(b)$
such that
$ \Lambda ^{\vec {v}}(b)$
such that
![]() $\{m_i\}_{i=1}^{\infty }$
is strictly monotone and
$\{m_i\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align*}h^{S}_{\mu}(T,\alpha)=H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\alpha)=H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
Remark 1.2. Let
![]() $\alpha $
be a finite measurable partition of X. We define
$\alpha $
be a finite measurable partition of X. We define
 $$ \begin{align}h_\mu^{\vec{v},*}(\alpha)=\sup\limits_{S\subset \Lambda^{\vec{v}}(b)}\{h^{S}_{\mu}(T,\alpha)\}, \end{align} $$
$$ \begin{align}h_\mu^{\vec{v},*}(\alpha)=\sup\limits_{S\subset \Lambda^{\vec{v}}(b)}\{h^{S}_{\mu}(T,\alpha)\}, \end{align} $$
where the supremum is taken over all infinite subsets
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $ \Lambda ^{\vec {v}}(b)$
. By Theorem 1.1,
$ \Lambda ^{\vec {v}}(b)$
. By Theorem 1.1,
 $h_\mu ^{\vec {v},*}(\alpha )=H_\mu (\alpha |\mathcal {K}_\mu ^{\kern2pt\vec {v}})$
and then (1.1) is well defined because it is independent of the selection of b.
$h_\mu ^{\vec {v},*}(\alpha )=H_\mu (\alpha |\mathcal {K}_\mu ^{\kern2pt\vec {v}})$
and then (1.1) is well defined because it is independent of the selection of b.
To investigate entropy zero systems, Kušhnirenko [Reference Kušhnirenko16] introduced the notion of sequence entropy and studied spectral theory via sequence entropy. He obtained a classical consequence, that is, a
![]() $\mathbb {Z}$
-MPS is a discrete spectrum system if and only if it is a null system. Motivated by his work, we define directional discrete spectrum systems and directional null systems as follows.
$\mathbb {Z}$
-MPS is a discrete spectrum system if and only if it is a null system. Motivated by his work, we define directional discrete spectrum systems and directional null systems as follows.
Definition 1.3. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS and
$\mathbb {Z}^2$
-MPS and
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector.
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector.
-
(a) We say
 $\mu $
has
$\mu $
has
 $\vec {v}$
-discrete spectrum if
$\vec {v}$
-discrete spectrum if
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}=\mathcal {B}_X$
.
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}=\mathcal {B}_X$
. -
(b) We say
 $(X,\mathcal {B}_X,\mu ,T)$
is
$(X,\mathcal {B}_X,\mu ,T)$
is
 $\vec {v}$
-null if for any
$\vec {v}$
-null if for any
 $b\in (0,\infty )$
and infinite subset
$b\in (0,\infty )$
and infinite subset
 $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
 $ \Lambda ^{\vec {v}}(b)$
,
$ \Lambda ^{\vec {v}}(b)$
,
 $h^{S}_{\mu }(T)=0$
.
$h^{S}_{\mu }(T)=0$
.
We obtain one of our main results which is a directional version of Kušhnirenko theorem.
Theorem 1.4. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS and
$\mathbb {Z}^2$
-MPS and
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector. Then the following two conditions are equivalent:
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector. Then the following two conditions are equivalent:
-
(a)
 $\mu $
has
$\mu $
has
 $\vec {v}$
-discrete spectrum;
$\vec {v}$
-discrete spectrum; -
(b)
 $(X,\mathcal {B}_X,\mu ,T)$
is
$(X,\mathcal {B}_X,\mu ,T)$
is
 $\vec {v}$
-null.
$\vec {v}$
-null.
Meanwhile, we establish the relation between sequence entropy (respectively discrete spectrum) and directional sequence entropy (respectively directional discrete spectrum) as follows.
Theorem 1.5. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS and
$\mathbb {Z}^2$
-MPS and
![]() $\alpha $
be a given finite measurable partition of X. If there exists an infinite subset S of
$\alpha $
be a given finite measurable partition of X. If there exists an infinite subset S of
![]() $\mathbb {Z}^2$
such that
$\mathbb {Z}^2$
such that
 $h^S_{\mu }(T,\alpha )>0$
, then there is at most one direction
$h^S_{\mu }(T,\alpha )>0$
, then there is at most one direction
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
such that
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
such that
 $h_\mu ^{\vec {v},*}(\alpha )=0$
.
$h_\mu ^{\vec {v},*}(\alpha )=0$
.
Theorem 1.6. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS. Then the following statements are equivalent:
$\mathbb {Z}^2$
-MPS. Then the following statements are equivalent:
-
(a) there exist two directions
 $\vec {v}=(1,\beta _1),\vec {w}=(1,\beta _2)\in \mathbb {R}^2$
with
$\vec {v}=(1,\beta _1),\vec {w}=(1,\beta _2)\in \mathbb {R}^2$
with
 $\beta _1\neq \beta _2$
such that
$\beta _1\neq \beta _2$
such that
 $\mu $
has
$\mu $
has
 $\vec {v}$
-discrete spectrum and
$\vec {v}$
-discrete spectrum and
 $\vec {w}$
-discrete spectrum;
$\vec {w}$
-discrete spectrum; -
(b)
 $\mu $
has discrete spectrum.
$\mu $
has discrete spectrum.
This paper is organized as follows. In §2, we recall some basic notions that we use in this paper. In §3, we introduce the directional Kronecker algebra and study many properties of directional sequence entropy to describe it. In §4, we prove Theorems 1.1 and 1.4. In §5, we prove Theorems 1.5 and 1.6. In Appendix A, we prove some consequences that are not directly relevant to the main purpose of this paper. In Appendix B, we introduce the corresponding results of
![]() $\mathbb {Z}^q$
-MPS.
$\mathbb {Z}^q$
-MPS.
2 Preliminaries
In this section, we recall some notions of measure preserving systems that are used later (see [Reference Downarowicz5–Reference Einsiedler and Ward7, Reference Walters23]).
2.1 General notions
In this article, the sets of real numbers, rational numbers, integers, non-negative integers and natural numbers are denoted by
![]() $\mathbb {R}$
,
$\mathbb {R}$
,
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
![]() $\mathbb {Z}_+$
and
$\mathbb {Z}_+$
and
![]() $\mathbb {N}$
, respectively. We use
$\mathbb {N}$
, respectively. We use
![]() $\|f\|_p$
to denote the
$\|f\|_p$
to denote the
![]() $L^p$
-norm of a function f defined in a Borel probability measure space
$L^p$
-norm of a function f defined in a Borel probability measure space
![]() $(X,\mathcal {B}_X,\mu )$
, that is,
$(X,\mathcal {B}_X,\mu )$
, that is,
 $$ \begin{align*}\|f\|_p= \bigg(\int_{X}|f|^pd\mu\bigg)^{{1}/{p}}\quad \text{if } 1\leq p<\infty\end{align*} $$
$$ \begin{align*}\|f\|_p= \bigg(\int_{X}|f|^pd\mu\bigg)^{{1}/{p}}\quad \text{if } 1\leq p<\infty\end{align*} $$
and
2.2 Conditional expectation
Let
![]() $\mathcal {X}$
be a sub-
$\mathcal {X}$
be a sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {B}_X$
. Then
$\mathcal {B}_X$
. Then
![]() $L^2(X,\mathcal {X},\mu )$
is contained as a subspace in
$L^2(X,\mathcal {X},\mu )$
is contained as a subspace in
![]() $L^2(X,\mathcal {B}_X,\mu )$
and the conditional expectation is given as the orthogonal projection map:
$L^2(X,\mathcal {B}_X,\mu )$
and the conditional expectation is given as the orthogonal projection map:
It is known that the conditional expectation is uniquely determined by the following statements (see [Reference Durrett6]):
-
(a)
 $\mathbb {E}(f|\mathcal {X})$
is
$\mathbb {E}(f|\mathcal {X})$
is
 $\mathcal {X}$
-measurable for all
$\mathcal {X}$
-measurable for all
 $f\in L^2(X,\mathcal {B}_X,\mu )$
;
$f\in L^2(X,\mathcal {B}_X,\mu )$
; -
(b) for all
 $A\in \mathcal {X}$
,
$A\in \mathcal {X}$
,
 $\int _A f d\mu =\int _A \mathbb {E}(f|\mathcal {X})\,d\mu. $
$\int _A f d\mu =\int _A \mathbb {E}(f|\mathcal {X})\,d\mu. $
Therefore, we have the following result of conditional expectation.
Proposition 2.1. Let
![]() $(X,\mathcal {B}_X,\mu )$
and
$(X,\mathcal {B}_X,\mu )$
and
![]() $(Y,\mathcal {B}_Y,\nu )$
be two Borel probability spaces. Let
$(Y,\mathcal {B}_Y,\nu )$
be two Borel probability spaces. Let
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
be sub-
$\mathcal {Y}$
be sub-
![]() $\sigma $
-algebras of
$\sigma $
-algebras of
![]() $\mathcal {B}_X$
and
$\mathcal {B}_X$
and
![]() $\mathcal {B}_Y$
, respectively. Then for any
$\mathcal {B}_Y$
, respectively. Then for any
![]() $f\in L^2(X,\mathcal {B}_X,\mu )$
and
$f\in L^2(X,\mathcal {B}_X,\mu )$
and
![]() $g\in L^2(Y,\mathcal {B}_Y,\nu )$
,
$g\in L^2(Y,\mathcal {B}_Y,\nu )$
,
for
![]() $\mu \times \nu $
-almost everywhere (a.e.)
$\mu \times \nu $
-almost everywhere (a.e.)
![]() $(x,y)\in X\times Y$
, where
$(x,y)\in X\times Y$
, where
![]() $\mathcal {X}\times \mathcal {Y}$
is the product
$\mathcal {X}\times \mathcal {Y}$
is the product
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
.
$\mathcal {Y}$
.
2.3 Classical Kronecker algebra and discrete spectrum
Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}$
-MPS and
$\mathbb {Z}$
-MPS and
![]() $\mathcal {H}=L^2(X,\mathcal {B}_X,\mu )$
. In complex Hilbert space
$\mathcal {H}=L^2(X,\mathcal {B}_X,\mu )$
. In complex Hilbert space
![]() $\mathcal {H}$
, we define a unitary operator
$\mathcal {H}$
, we define a unitary operator
![]() $U_T:\mathcal {H}\rightarrow \mathcal {H}$
by
$U_T:\mathcal {H}\rightarrow \mathcal {H}$
by
for all
![]() $f\in \mathcal {H}.$
We say that f is an almost periodic function if
$f\in \mathcal {H}.$
We say that f is an almost periodic function if
 $\overline {\{U_T^n f:n\in \mathbb {Z}\}}$
is a compact subset of
$\overline {\{U_T^n f:n\in \mathbb {Z}\}}$
is a compact subset of
![]() $\mathcal {H}$
. It is well known that the set of all bounded almost periodic functions forms a
$\mathcal {H}$
. It is well known that the set of all bounded almost periodic functions forms a
![]() $U_T$
-invariant and conjugation-invariant subalgebra of
$U_T$
-invariant and conjugation-invariant subalgebra of
![]() $\mathcal {H}$
(denoted by
$\mathcal {H}$
(denoted by
![]() $\mathcal {A}_c$
). The set of almost periodic functions is just the closure of
$\mathcal {A}_c$
). The set of almost periodic functions is just the closure of
![]() $\mathcal {A}_c$
(denoted by
$\mathcal {A}_c$
(denoted by
![]() $\mathcal {H}_c$
). It is known that (see [Reference Zimmer25, Theorem 1.2]) there exists a T-invariant sub-
$\mathcal {H}_c$
). It is known that (see [Reference Zimmer25, Theorem 1.2]) there exists a T-invariant sub-
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {K}_{\mu }$
of
$\mathcal {K}_{\mu }$
of
![]() $\mathcal {B}_X$
such that
$\mathcal {B}_X$
such that
 $$ \begin{align*}\mathcal{H}_c=L^2(X,\mathcal{K}_{\mu},\mu).\end{align*} $$
$$ \begin{align*}\mathcal{H}_c=L^2(X,\mathcal{K}_{\mu},\mu).\end{align*} $$
The sub-
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {K}_{\mu }$
is called the Kronecker algebra of
$\mathcal {K}_{\mu }$
is called the Kronecker algebra of
![]() $(X,\mathcal {B}_X,\mu ,T)$
. It is easy to know that
$(X,\mathcal {B}_X,\mu ,T)$
. It is easy to know that
![]() $\mathcal {K}_\mu $
consists of all
$\mathcal {K}_\mu $
consists of all
![]() $B\in \mathcal {B}_X$
such that
$B\in \mathcal {B}_X$
such that
 $$ \begin{align*}\overline{\{ U_T^n1_B:n\in \mathbb{Z} \}} \text{ is compact in }\mathcal{H}.\end{align*} $$
$$ \begin{align*}\overline{\{ U_T^n1_B:n\in \mathbb{Z} \}} \text{ is compact in }\mathcal{H}.\end{align*} $$
We say
![]() $\mu $
has discrete spectrum if
$\mu $
has discrete spectrum if
![]() $\mathcal {B}_X=\mathcal {K}_{\mu }$
. Similarly, the Kronecker algebra and discrete spectrum for the case of
$\mathcal {B}_X=\mathcal {K}_{\mu }$
. Similarly, the Kronecker algebra and discrete spectrum for the case of
![]() $\mathbb {Z}^q$
-actions can be defined (see [Reference Glasner9]).
$\mathbb {Z}^q$
-actions can be defined (see [Reference Glasner9]).
Let
![]() $S\subset \mathbb {Z}_+$
be an infinite sequence. We define the upper density and lower density by
$S\subset \mathbb {Z}_+$
be an infinite sequence. We define the upper density and lower density by
 $$ \begin{align*}\overline{d}(S)=\limsup\limits_{n\to \infty}\frac{1}{n}|S\cap\{0,1,\ldots, n-1\}|\end{align*} $$
$$ \begin{align*}\overline{d}(S)=\limsup\limits_{n\to \infty}\frac{1}{n}|S\cap\{0,1,\ldots, n-1\}|\end{align*} $$
and
 $$ \begin{align*}\underline{d}(S)=\liminf\limits_{n\to \infty}\frac{1}{n}|S\cap\{0,1,\ldots, n-1\}|\end{align*} $$
$$ \begin{align*}\underline{d}(S)=\liminf\limits_{n\to \infty}\frac{1}{n}|S\cap\{0,1,\ldots, n-1\}|\end{align*} $$
where
![]() $|A|$
is the number of elements of a finite set A. If
$|A|$
is the number of elements of a finite set A. If
![]() $\overline {d}(S)=\underline {d}(S)=d$
, we say S has the density d.
$\overline {d}(S)=\underline {d}(S)=d$
, we say S has the density d.
We recall the spectral mixing theorem of Koopman–von Neumann [Reference Koopman and von Neumann15].
Theorem 2.2. The Hilbert space
![]() $\mathcal {H}$
can be decomposed as
$\mathcal {H}$
can be decomposed as
 $\mathcal {H}=\mathcal {H}_c\oplus \mathcal {H}_c^{\perp }$
, where
$\mathcal {H}=\mathcal {H}_c\oplus \mathcal {H}_c^{\perp }$
, where
and
 $$ \begin{align*}\mathcal{H}_c^{\perp}&=\{f\in \mathcal{H}:\text{ there exists } S\subset \mathbb{N},\text{ }d(S)=1,\\&\quad\text{ such that } \text{for all } g\in \mathcal{H},\lim\limits_{n\to \infty\atop n\in S}\langle U_T^nf,g\rangle=0\}\end{align*} $$
$$ \begin{align*}\mathcal{H}_c^{\perp}&=\{f\in \mathcal{H}:\text{ there exists } S\subset \mathbb{N},\text{ }d(S)=1,\\&\quad\text{ such that } \text{for all } g\in \mathcal{H},\lim\limits_{n\to \infty\atop n\in S}\langle U_T^nf,g\rangle=0\}\end{align*} $$
where
![]() $d(S)$
is the density of S and
$d(S)$
is the density of S and
 $ \langle f,g\rangle =\int _X f(x)\overline {g(x)}\,dx $
is an inner product on
$ \langle f,g\rangle =\int _X f(x)\overline {g(x)}\,dx $
is an inner product on
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
2.4 Sequence entropy
Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS. Given a finite measurable partition
$\mathbb {Z}^2$
-MPS. Given a finite measurable partition
![]() $\alpha $
of X, let
$\alpha $
of X, let
 $$ \begin{align*}H_{\mu}(\alpha)=-\sum_{A\in \alpha}\mu(A)\log{\mu(A)}.\end{align*} $$
$$ \begin{align*}H_{\mu}(\alpha)=-\sum_{A\in \alpha}\mu(A)\log{\mu(A)}.\end{align*} $$
For any infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $\mathbb {Z}^2$
, we put
$\mathbb {Z}^2$
, we put
 $$ \begin{align*}h^S_{\mu}(T,\alpha)= \limsup_{k\to \infty} \frac{1}{k}H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha\bigg).\end{align*} $$
$$ \begin{align*}h^S_{\mu}(T,\alpha)= \limsup_{k\to \infty} \frac{1}{k}H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha\bigg).\end{align*} $$
Then we define the sequence entropy of T for the infinite subset S by
 $$ \begin{align*}h^S_{\mu}(T)=\sup_{\alpha}h^S_{\mu}(T,\alpha),\end{align*} $$
$$ \begin{align*}h^S_{\mu}(T)=\sup_{\alpha}h^S_{\mu}(T,\alpha),\end{align*} $$
where the supremum is taken over all finite measurable partitions of X.
2.5
 $\epsilon $
-net
$\epsilon $
-net
Let A be a subset of a normed linear space
![]() $(X,\|\cdot \|)$
and
$(X,\|\cdot \|)$
and
![]() $\epsilon>0$
. A subset
$\epsilon>0$
. A subset
![]() $A_{\epsilon }\subset X$
is called an
$A_{\epsilon }\subset X$
is called an
![]() $\epsilon $
-net for A if for each
$\epsilon $
-net for A if for each
![]() $x\in A$
, there is an element of A within an
$x\in A$
, there is an element of A within an
![]() $\epsilon $
distance to some element of
$\epsilon $
distance to some element of
![]() $A_{\epsilon }$
.
$A_{\epsilon }$
.
It is known that (see [Reference Muscat18, p. 76, Corollary 6.20]) a closed subset A of a Banach space
![]() $(X,\|\cdot \|)$
is compact if and only if for any
$(X,\|\cdot \|)$
is compact if and only if for any
![]() $\epsilon>0$
, there is a finite
$\epsilon>0$
, there is a finite
![]() $\epsilon $
-net
$\epsilon $
-net
![]() $F_{\epsilon }\subset X$
for A. That is, there is a finite set
$F_{\epsilon }\subset X$
for A. That is, there is a finite set
![]() $F_{\epsilon }\subset X$
such that
$F_{\epsilon }\subset X$
such that
 $$ \begin{align*}A\subset \bigcup_{x\in F_{\epsilon}}B(x,\epsilon).\end{align*} $$
$$ \begin{align*}A\subset \bigcup_{x\in F_{\epsilon}}B(x,\epsilon).\end{align*} $$
Note that the
![]() $\epsilon $
-net mentioned in this paper is relative to
$\epsilon $
-net mentioned in this paper is relative to
![]() $L^2$
-norm unless we explicitly indicate otherwise.
$L^2$
-norm unless we explicitly indicate otherwise.
3 Directional Kronecker algebra
In this section, we introduce the directional Kronecker algebra and describe it via directional sequence entropy.
Let
![]() $(X ,\mathcal {B}_X, \mu , T)$
be a
$(X ,\mathcal {B}_X, \mu , T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. We put
$b\in (0,\infty )$
. We put
 $$ \begin{align*}\Lambda^{\vec{v}}(b)=\{(m,n)\in\mathbb{Z}^2:\beta m-b/2\leq n\leq \beta m+b/2\}.\end{align*} $$
$$ \begin{align*}\Lambda^{\vec{v}}(b)=\{(m,n)\in\mathbb{Z}^2:\beta m-b/2\leq n\leq \beta m+b/2\}.\end{align*} $$
Let
 $\mathcal {A}_c^{\vec {v}}(b)$
be the collection of
$\mathcal {A}_c^{\vec {v}}(b)$
be the collection of
![]() $f\in L^2(X,\mathcal {B}_X,\mu )$
such that
$f\in L^2(X,\mathcal {B}_X,\mu )$
such that
 $$ \begin{align*}\overline{\{U_T^{(m,n)}f:(m,n)\in \Lambda^{\vec{v}}(b) \}}\end{align*} $$
$$ \begin{align*}\overline{\{U_T^{(m,n)}f:(m,n)\in \Lambda^{\vec{v}}(b) \}}\end{align*} $$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu ).$
It is easy to see that
$L^2(X,\mathcal {B}_X,\mu ).$
It is easy to see that
 $\mathcal {A}_c^{\vec {v}}(b)$
is a
$\mathcal {A}_c^{\vec {v}}(b)$
is a
![]() $U_{T^{\vec {w}}}$
-invariant for all
$U_{T^{\vec {w}}}$
-invariant for all
![]() $\vec {w}$
in
$\vec {w}$
in
![]() $\mathbb {Z}^2$
and conjugation-invariant subalgebra of
$\mathbb {Z}^2$
and conjugation-invariant subalgebra of
![]() $L^2(X,\mathcal {B}_X,\mu )$
. It is known that (see [Reference Zimmer25, Theorem 1.2]) there exists a T-invariant sub-
$L^2(X,\mathcal {B}_X,\mu )$
. It is known that (see [Reference Zimmer25, Theorem 1.2]) there exists a T-invariant sub-
![]() $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
of
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
of
![]() $\mathcal {B}_X$
such that
$\mathcal {B}_X$
such that
 $$ \begin{align} \mathcal{A}_c^{\vec{v}}(b)=L^2(X,\mathcal{K}_\mu^{\kern2pt\vec{v}}(b),\mu). \end{align} $$
$$ \begin{align} \mathcal{A}_c^{\vec{v}}(b)=L^2(X,\mathcal{K}_\mu^{\kern2pt\vec{v}}(b),\mu). \end{align} $$
By (3.1), the
![]() $\vec {v}$
-directional Kronecker algebra of
$\vec {v}$
-directional Kronecker algebra of
![]() $(X ,\mathcal {B}_X, \mu , T)$
can be defined by
$(X ,\mathcal {B}_X, \mu , T)$
can be defined by
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b)=\{B\in\mathcal{B}_X: \overline{\{U_T^{(m,n)}1_B :(m,n)\in \Lambda^{\vec{v}}(b) \}}\text{ is compact in } L^2(X,\mathcal{B}_X,\mu) \}.\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b)=\{B\in\mathcal{B}_X: \overline{\{U_T^{(m,n)}1_B :(m,n)\in \Lambda^{\vec{v}}(b) \}}\text{ is compact in } L^2(X,\mathcal{B}_X,\mu) \}.\end{align*} $$
The following result shows that the definition of
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
is independent of the selection of
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b)$
is independent of the selection of
![]() $b\in (0,\infty )$
.
$b\in (0,\infty )$
.
Proposition 3.1. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS and
$\mathbb {Z}^2$
-MPS and
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector. Then
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector. Then
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1)=\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2)$
for any
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1)=\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2)$
for any
![]() $b_1,b_2\in (0,\infty )$
.
$b_1,b_2\in (0,\infty )$
.
Proof. We put
 $$ \begin{align*}U(B,b)=\overline{\{U_T^{(m,n)}1_B :(m,n)\in \Lambda^{\vec{v}}(b) \}}\end{align*} $$
$$ \begin{align*}U(B,b)=\overline{\{U_T^{(m,n)}1_B :(m,n)\in \Lambda^{\vec{v}}(b) \}}\end{align*} $$
for
![]() $b\in (0,\infty )$
and
$b\in (0,\infty )$
and
![]() $B\in \mathcal {B}_X$
. Fix
$B\in \mathcal {B}_X$
. Fix
![]() $b_1,b_2\in (0,\infty )$
. Without loss of generality, we assume that
$b_1,b_2\in (0,\infty )$
. Without loss of generality, we assume that
![]() $b_1>b_2$
.
$b_1>b_2$
.
We first prove that
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1)\subset \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2).$
For a fixed
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1)\subset \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2).$
For a fixed
 $B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1)$
,
$B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1)$
,
![]() $U(B,b_1)$
is compact in
$U(B,b_1)$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu )$
and hence
$L^2(X,\mathcal {B}_X,\mu )$
and hence
![]() $U(B,b_2)$
is compact in
$U(B,b_2)$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu )$
because
$L^2(X,\mathcal {B}_X,\mu )$
because
![]() $U(B,b_2)$
is closed in
$U(B,b_2)$
is closed in
![]() $L^2(X,\mathcal {B}_X,\mu )$
and
$L^2(X,\mathcal {B}_X,\mu )$
and
![]() $U(B,b_2)\subset U(B,b_1).$
It follows that
$U(B,b_2)\subset U(B,b_1).$
It follows that
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b_1)\subset \mathcal{K}_\mu^{\kern2pt\vec{v}}(b_2).\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b_1)\subset \mathcal{K}_\mu^{\kern2pt\vec{v}}(b_2).\end{align*} $$
Next we show that
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2)\subset \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1).$
Given
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2)\subset \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1).$
Given
 $B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2), U(B,b_2)$
is compact in
$B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_2), U(B,b_2)$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu ). $
Note that we can find a finite subset C of
$L^2(X,\mathcal {B}_X,\mu ). $
Note that we can find a finite subset C of
![]() $\mathbb {Z}^2$
such that
$\mathbb {Z}^2$
such that
 $$ \begin{align} U(B,b_1)\subset \bigcup_{(m',n')\in C}\overline{\{U_T^{(m+m',n+n')}1_B :(m,n)\in \Lambda^{\vec{v}}(b_2) \}}. \end{align} $$
$$ \begin{align} U(B,b_1)\subset \bigcup_{(m',n')\in C}\overline{\{U_T^{(m+m',n+n')}1_B :(m,n)\in \Lambda^{\vec{v}}(b_2) \}}. \end{align} $$
For each
![]() $(m',n')\in C$
, one has
$(m',n')\in C$
, one has
 $$ \begin{align*}\overline{\{U_T^{(m+m',n+n')}1_B :(m,n)\in \Lambda^{\vec{v}}(b_2) \}}\end{align*} $$
$$ \begin{align*}\overline{\{U_T^{(m+m',n+n')}1_B :(m,n)\in \Lambda^{\vec{v}}(b_2) \}}\end{align*} $$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu )$
, which is from the fact that
$L^2(X,\mathcal {B}_X,\mu )$
, which is from the fact that
 $\overline {\{U_T^{(m,n)}1_B :(m,n)\in \Lambda ^{\vec {v}}(b_2) \}}$
is compact in
$\overline {\{U_T^{(m,n)}1_B :(m,n)\in \Lambda ^{\vec {v}}(b_2) \}}$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu )$
. Moreover by (3.2),
$L^2(X,\mathcal {B}_X,\mu )$
. Moreover by (3.2),
![]() $U(B,b_1)$
is compact in
$U(B,b_1)$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu )$
, because it is closed in
$L^2(X,\mathcal {B}_X,\mu )$
, because it is closed in
![]() $L^2(X,\mathcal {B}_X,\mu )$
. This implies that
$L^2(X,\mathcal {B}_X,\mu )$
. This implies that
 $B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1).$
Therefore,
$B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}}(b_1).$
Therefore,
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b_2)\subset\mathcal{K}_\mu^{\kern2pt\vec{v}}(b_1).\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(b_2)\subset\mathcal{K}_\mu^{\kern2pt\vec{v}}(b_1).\end{align*} $$
This ends the proof of Proposition 3.1.
Now we establish the relation between directional Kronecker algebra and directional sequence entropy. Let us begin with some notation. Because complex Hilbert space
![]() $\mathcal {H}=L^2(X,\mathcal {B}_X,\mu )$
is separable, there exists an infinite subset
$\mathcal {H}=L^2(X,\mathcal {B}_X,\mu )$
is separable, there exists an infinite subset
of
![]() $\Lambda ^{\vec {v}}(b)$
such that
$\Lambda ^{\vec {v}}(b)$
such that
 $\lim \limits _{i\to \infty }\langle g,U_T^{(m_i,n_i)}f\rangle $
exists for any
$\lim \limits _{i\to \infty }\langle g,U_T^{(m_i,n_i)}f\rangle $
exists for any
![]() $f,g \in \mathcal {H}$
. Now for a fixed
$f,g \in \mathcal {H}$
. Now for a fixed
![]() $f\in \mathcal {H}$
, we define
$f\in \mathcal {H}$
, we define
![]() $J:\mathcal {H}\to \mathbb {C}$
by
$J:\mathcal {H}\to \mathbb {C}$
by
 $$ \begin{align*}J(g)=\lim\limits_{i\to \infty}\langle g,U_T^{(m_i,n_i)}f\rangle.\end{align*} $$
$$ \begin{align*}J(g)=\lim\limits_{i\to \infty}\langle g,U_T^{(m_i,n_i)}f\rangle.\end{align*} $$
Obviously, J is a continuous linear functional on
![]() $\mathcal {H}$
. By Riesz representation theorem, there exists
$\mathcal {H}$
. By Riesz representation theorem, there exists
![]() $S(f)\in \mathcal {H}$
such that
$S(f)\in \mathcal {H}$
such that
for all
![]() $g\in \mathcal {H}$
.
$g\in \mathcal {H}$
.
With the help of the above analysis, we obtain the following lemma.
Lemma 3.2. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. Then for any finite measurable partition
$b\in (0,\infty )$
. Then for any finite measurable partition
![]() $\alpha $
of X, there exists an infinite subset
$\alpha $
of X, there exists an infinite subset
![]() $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
![]() $ S$
such that
$ S$
such that
![]() $\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
$\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align*}h^{S'}_{\mu}(T)\geq \sum_{B\in\hspace{0.6pt}\alpha}\int_X-S(1_B)\log{S(1_B)}\,{d\hspace{-1pt}\mu},\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T)\geq \sum_{B\in\hspace{0.6pt}\alpha}\int_X-S(1_B)\log{S(1_B)}\,{d\hspace{-1pt}\mu},\end{align*} $$
where S and
![]() $S(\cdot )$
are defined by (3.3) and (3.4), respectively.
$S(\cdot )$
are defined by (3.3) and (3.4), respectively.
Proof. Enumerate
![]() $\alpha $
as
$\alpha $
as
![]() $\{B_1,\ldots ,B_k\}$
. Fix a finite measurable partition
$\{B_1,\ldots ,B_k\}$
. Fix a finite measurable partition
![]() $\eta =\{D_1,\ldots , D_l\}$
of X. Let
$\eta =\{D_1,\ldots , D_l\}$
of X. Let
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty } $
be the subset defined in (3.3). Then
$S=\{(m_i,n_i)\}_{i=1}^{\infty } $
be the subset defined in (3.3). Then
 $$ \begin{align} \lim\limits_{i\to \infty}\langle U_T^{(m_i,n_i)}1_{B_s},1_{D_t}\rangle=\langle S(1_{B_s}),1_{D_t}\rangle \end{align} $$
$$ \begin{align} \lim\limits_{i\to \infty}\langle U_T^{(m_i,n_i)}1_{B_s},1_{D_t}\rangle=\langle S(1_{B_s}),1_{D_t}\rangle \end{align} $$
for any
![]() $s\in \{1,2,\ldots ,k\}$
and
$s\in \{1,2,\ldots ,k\}$
and
![]() $t\in \{1,2,\ldots ,l\}$
. Let
$t\in \{1,2,\ldots ,l\}$
. Let
 $$ \begin{align*}f(x)=\left\{ \begin{array}{@{}lr} -x\log x, & x>0,\\ 0, & x=0,\\ \end{array} \right.\end{align*} $$
$$ \begin{align*}f(x)=\left\{ \begin{array}{@{}lr} -x\log x, & x>0,\\ 0, & x=0,\\ \end{array} \right.\end{align*} $$
and
for each
![]() $t\in \{1,2,\ldots ,l\}$
. Then by the concavity of
$t\in \{1,2,\ldots ,l\}$
. Then by the concavity of
![]() $f(x)$
, one has
$f(x)$
, one has
 $$ \begin{align} &-\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)\log{\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)}\nonumber\\ &\quad=f\bigg(\int_{D_t}S(1_{B_s})\,{d\hspace{-1pt}\mu}_{D_t}\bigg) \geq \int_{D_t}f(S(1_{B_s}))\,{d\hspace{-1pt}\mu}_{D_t}\\ &\quad=-\int_{D_t}{S(1_{B_s})}\log{(S(1_{B_s}))}\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}.\nonumber \end{align} $$
$$ \begin{align} &-\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)\log{\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)}\nonumber\\ &\quad=f\bigg(\int_{D_t}S(1_{B_s})\,{d\hspace{-1pt}\mu}_{D_t}\bigg) \geq \int_{D_t}f(S(1_{B_s}))\,{d\hspace{-1pt}\mu}_{D_t}\\ &\quad=-\int_{D_t}{S(1_{B_s})}\log{(S(1_{B_s}))}\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}.\nonumber \end{align} $$
Therefore, we deduce
 $$ \begin{align} &\liminf_{i\to \infty}H_{\mu}(T^{-(m_i,n_i)}\alpha|\eta)\nonumber\\ &\quad=\liminf_{i\to \infty}\sum_{s,t}-\mu(T^{-(m_i,n_i)}B_s\cap D_t)\log{\bigg(\frac{\mu(T^{-(m_i,n_i)}B_s\cap D_t)}{\mu(D_t)}\bigg)}\nonumber\\ &\quad=\lim\limits_{i\to \infty}\sum_{s,t}-\langle U_T^{(m_i,n_i)}1_{B_s},1_{D_t}\rangle\log{\bigg(\frac{\langle U_T^{(m_i,n_i)}1_{B_s},1_{D_t}\rangle}{\mu(D_t)}\bigg)}\nonumber\\ &\quad \overset{(3.5)}=\sum_{s,t}-\langle S(1_{B_s}),1_{D_t}\rangle\log{\bigg(\frac{\langle S(1_{B_s}),1_{D_t}\rangle}{\mu(D_t)}\bigg)}\nonumber\\ &\quad=\sum_{s,t}\mu(D_t)\bigg(-\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)\log{\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)}\bigg)\nonumber\\ &\quad\overset{(3.6)}\geq \sum_{s,t}-\int_{D_t}{S(1_{B_s})}\log{(S(1_{B_s}))}\,{d\hspace{-1pt}\mu}\nonumber\\ &\quad=\sum_{s}-\int_XS(1_{B_s})\log{(S(1_{B_s}))}\,{d\hspace{-1pt}\mu}\nonumber\\ &\quad=\sum_{B\in\hspace{0.6pt} \alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}. \end{align} $$
$$ \begin{align} &\liminf_{i\to \infty}H_{\mu}(T^{-(m_i,n_i)}\alpha|\eta)\nonumber\\ &\quad=\liminf_{i\to \infty}\sum_{s,t}-\mu(T^{-(m_i,n_i)}B_s\cap D_t)\log{\bigg(\frac{\mu(T^{-(m_i,n_i)}B_s\cap D_t)}{\mu(D_t)}\bigg)}\nonumber\\ &\quad=\lim\limits_{i\to \infty}\sum_{s,t}-\langle U_T^{(m_i,n_i)}1_{B_s},1_{D_t}\rangle\log{\bigg(\frac{\langle U_T^{(m_i,n_i)}1_{B_s},1_{D_t}\rangle}{\mu(D_t)}\bigg)}\nonumber\\ &\quad \overset{(3.5)}=\sum_{s,t}-\langle S(1_{B_s}),1_{D_t}\rangle\log{\bigg(\frac{\langle S(1_{B_s}),1_{D_t}\rangle}{\mu(D_t)}\bigg)}\nonumber\\ &\quad=\sum_{s,t}\mu(D_t)\bigg(-\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)\log{\bigg(\int_{D_t}S(1_{B_s})\frac{{d\hspace{-1pt}\mu}}{\mu(D_t)}\bigg)}\bigg)\nonumber\\ &\quad\overset{(3.6)}\geq \sum_{s,t}-\int_{D_t}{S(1_{B_s})}\log{(S(1_{B_s}))}\,{d\hspace{-1pt}\mu}\nonumber\\ &\quad=\sum_{s}-\int_XS(1_{B_s})\log{(S(1_{B_s}))}\,{d\hspace{-1pt}\mu}\nonumber\\ &\quad=\sum_{B\in\hspace{0.6pt} \alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}. \end{align} $$
Now we can define inductively an infinite subset
![]() $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
![]() $ S$
by using (3.7) repeatedly such that
$ S$
by using (3.7) repeatedly such that
![]() $\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and for any
$\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and for any
![]() $i\in \mathbb {N}$
,
$i\in \mathbb {N}$
,
 $$ \begin{align*}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m^{\prime}_j,n^{\prime}_j)}\alpha\bigg)\geq \sum_{B\in\hspace{0.6pt}\alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}-\frac{1}{2^i}.\end{align*} $$
$$ \begin{align*}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m^{\prime}_j,n^{\prime}_j)}\alpha\bigg)\geq \sum_{B\in\hspace{0.6pt}\alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}-\frac{1}{2^i}.\end{align*} $$
As
 $H_{\mu }(\bigvee _{i=1}^k\! T^{-(m_i,n_i)}\alpha )=H_{\mu }(\bigvee _{i=1}^{k-1}\! T^{-(m_i,n_i)}\alpha )+H_{\mu }(T^{-(m_k,n_k)}\alpha |\! \bigvee _{i=1}^{k-1}\! T^{-(m_i,n_i)}\alpha )$
, therefore,
$H_{\mu }(\bigvee _{i=1}^k\! T^{-(m_i,n_i)}\alpha )=H_{\mu }(\bigvee _{i=1}^{k-1}\! T^{-(m_i,n_i)}\alpha )+H_{\mu }(T^{-(m_k,n_k)}\alpha |\! \bigvee _{i=1}^{k-1}\! T^{-(m_i,n_i)}\alpha )$
, therefore,
 $$ \begin{align*} \begin{split} h^{S'}_{\mu}(T) &=\limsup\limits_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m^{\prime}_j,n^{\prime}_j)}\alpha\bigg)}\\ &\geq \limsup\limits_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}\bigg(\sum_{B\in\hspace{0.6pt}\alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}-\frac{1}{2^i}\bigg)}\\ &=\sum_{B\in\hspace{0.6pt}\alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} h^{S'}_{\mu}(T) &=\limsup\limits_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m^{\prime}_j,n^{\prime}_j)}\alpha\bigg)}\\ &\geq \limsup\limits_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}\bigg(\sum_{B\in\hspace{0.6pt}\alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}-\frac{1}{2^i}\bigg)}\\ &=\sum_{B\in\hspace{0.6pt}\alpha}-\int_XS(1_B)\log{(S(1_B))}\,{d\hspace{-1pt}\mu}. \end{split} \end{align*} $$
Now we finish the proof of Lemma 3.2.
For further discussion, we need a classcial consequence [Reference Walters23, p. 94].
Lemma 3.3. Let
![]() $(X,\mathcal {B}_X,\mu )$
be a Borel probability space and
$(X,\mathcal {B}_X,\mu )$
be a Borel probability space and
![]() $r\geq 1$
be a fixed integer. For each
$r\geq 1$
be a fixed integer. For each
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta =\delta (\epsilon ,r)>0$
such that if
$\delta =\delta (\epsilon ,r)>0$
such that if
![]() $\alpha =\{A_1,A_2,\ldots ,A_r\}$
and
$\alpha =\{A_1,A_2,\ldots ,A_r\}$
and
![]() $\eta =\{B_1,B_2,\ldots ,B_r\}$
are any two finite measurable partitions of
$\eta =\{B_1,B_2,\ldots ,B_r\}$
are any two finite measurable partitions of
![]() $(X,\mathcal {B}_X,\mu )$
with
$(X,\mathcal {B}_X,\mu )$
with
 $\sum _{j=1}^r\mu (A_j\Delta B_j)< \delta $
, then
$\sum _{j=1}^r\mu (A_j\Delta B_j)< \delta $
, then
![]() $H_\mu (\alpha |\eta )+H_\mu (\eta |\alpha )<\epsilon $
.
$H_\mu (\alpha |\eta )+H_\mu (\eta |\alpha )<\epsilon $
.
By Lemmas 3.2 and 3.3, we can get the following result.
Theorem 3.4. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. Let
$b\in (0,\infty )$
. Let
![]() $B\in \mathcal {B}_X$
and P be an infinite subset of
$B\in \mathcal {B}_X$
and P be an infinite subset of
![]() $\Lambda ^{\vec {v}}(b)$
. Then the following conditions are equivalent:
$\Lambda ^{\vec {v}}(b)$
. Then the following conditions are equivalent:
-
(a)
 $\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is a compact subset of
$\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is a compact subset of
 $L^2(X,\mathcal {B}_X,\mu )$
;
$L^2(X,\mathcal {B}_X,\mu )$
; -
(b) for any infinite subset
 $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of P,
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of P,  $$ \begin{align*}h^{S'}_{\mu}(T,\{B,B^c\})=0;\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T,\{B,B^c\})=0;\end{align*} $$
-
(c) for any infinite subset
 $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of P that
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of P that
 $\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone,
$\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone,  $$ \begin{align*}h^{S'}_{\mu}(T,\{B,B^c\})=0.\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T,\{B,B^c\})=0.\end{align*} $$
Proof. (a)
![]() $\Rightarrow $
(b). Let
$\Rightarrow $
(b). Let
![]() $\eta =\{B,B^c\}$
. If
$\eta =\{B,B^c\}$
. If
 $\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is a compact subset of
$\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
, then for any infinite subset
$L^2(X,\mathcal {B}_X,\mu )$
, then for any infinite subset
![]() $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of P,
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of P,
 $$ \begin{align*}\overline{\{U_T^{(m',n')}1_B:(m',n')\in S'\}}\end{align*} $$
$$ \begin{align*}\overline{\{U_T^{(m',n')}1_B:(m',n')\in S'\}}\end{align*} $$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
. So for any
$L^2(X,\mathcal {B}_X,\mu )$
. So for any
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $s\in \mathbb {N}$
such that for any
$s\in \mathbb {N}$
such that for any
![]() $(m^{\prime }_i,n^{\prime }_i)\in S'$
,
$(m^{\prime }_i,n^{\prime }_i)\in S'$
,
 $$ \begin{align*}\mu(T^{-(m^{\prime}_i,n^{\prime}_i)}B\Delta T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}B)=\|U_T^{(m^{\prime}_i,n^{\prime}_i)}1_B-U_T^{(m^{\prime}_{j_i},n^{\prime}_{j_i})}1_B\|_2<\delta\end{align*} $$
$$ \begin{align*}\mu(T^{-(m^{\prime}_i,n^{\prime}_i)}B\Delta T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}B)=\|U_T^{(m^{\prime}_i,n^{\prime}_i)}1_B-U_T^{(m^{\prime}_{j_i},n^{\prime}_{j_i})}1_B\|_2<\delta\end{align*} $$
for some
![]() $j_i\in \{1,2,\ldots ,s\}$
. It follows from Lemma 3.3 that for any
$j_i\in \{1,2,\ldots ,s\}$
. It follows from Lemma 3.3 that for any
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $ (m^{\prime }_i,n^{\prime }_i)\in S'$
, there exists
$ (m^{\prime }_i,n^{\prime }_i)\in S'$
, there exists
![]() $ j_i\in \{1,2,\ldots ,s\}$
such that
$ j_i\in \{1,2,\ldots ,s\}$
such that
 $$ \begin{align*}H_\mu(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}\eta)+H_\mu(T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}\eta|T^{-(m^{\prime}_i,n^{\prime}_i)}\eta)<\epsilon.\end{align*} $$
$$ \begin{align*}H_\mu(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}\eta)+H_\mu(T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}\eta|T^{-(m^{\prime}_i,n^{\prime}_i)}\eta)<\epsilon.\end{align*} $$
Thus for any
![]() $ i>s$
,
$ i>s$
,
 $$ \begin{align*}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|\bigvee_{j=1}^{i-1}T^{-(m^{\prime}_{j},n^{\prime}_{j})}\eta\bigg)\leq H_\mu(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}\eta)<\epsilon.\end{align*} $$
$$ \begin{align*}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|\bigvee_{j=1}^{i-1}T^{-(m^{\prime}_{j},n^{\prime}_{j})}\eta\bigg)\leq H_\mu(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|T^{-(m^{\prime}_{j_i},n^{\prime}_{j_i})}\eta)<\epsilon.\end{align*} $$
We conclude that
 $$ \begin{align*}h^{S'}_{\mu}(T,\eta)=\limsup\limits_{n\to \infty}\frac{1}{n}\sum_{i=2}^{n}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|\bigvee_{j=1}^{i-1}T^{-(m^{\prime}_{j},n^{\prime}_{j})}\eta\bigg)\leq\epsilon.\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T,\eta)=\limsup\limits_{n\to \infty}\frac{1}{n}\sum_{i=2}^{n}H_\mu\bigg(T^{-(m^{\prime}_i,n^{\prime}_i)}\eta|\bigvee_{j=1}^{i-1}T^{-(m^{\prime}_{j},n^{\prime}_{j})}\eta\bigg)\leq\epsilon.\end{align*} $$
Let
![]() $\epsilon \rightarrow 0.$
We obtain that
$\epsilon \rightarrow 0.$
We obtain that
 $h^{S'}_{\mu }(T,\eta )=0.$
$h^{S'}_{\mu }(T,\eta )=0.$
(b)
![]() $\Rightarrow $
(c). This is obvious.
$\Rightarrow $
(c). This is obvious.
(c)
![]() $\Rightarrow $
(a). If
$\Rightarrow $
(a). If
 $\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is not a compact subset of
$\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is not a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
, then there exists
$L^2(X,\mathcal {B}_X,\mu )$
, then there exists
![]() $\epsilon>0$
and an infinite subset F of P such that for all
$\epsilon>0$
and an infinite subset F of P such that for all
![]() $ (m,n),(s,t)\in F$
with
$ (m,n),(s,t)\in F$
with
![]() $ (m,n)\neq (s,t)$
,
$ (m,n)\neq (s,t)$
,
 $$ \begin{align} \mu(T^{-(m,n)}B\Delta T^{-(s,t)}B)=\|U_T^{(m,n)}1_B-U_T^{(s,t)}1_B\|_2\geq \epsilon. \end{align} $$
$$ \begin{align} \mu(T^{-(m,n)}B\Delta T^{-(s,t)}B)=\|U_T^{(m,n)}1_B-U_T^{(s,t)}1_B\|_2\geq \epsilon. \end{align} $$
Similar to (3.3), we obtain an infinite subset
![]() $S_F=\{(m_i,n_i)\}_{i=1}^{\infty }$
of F such that
$S_F=\{(m_i,n_i)\}_{i=1}^{\infty }$
of F such that
 $$ \begin{align*}\lim\limits_{i\to \infty}\langle g,U_T^{(m_i,n_i)}f\rangle =\langle g,S_F(f)\rangle\end{align*} $$
$$ \begin{align*}\lim\limits_{i\to \infty}\langle g,U_T^{(m_i,n_i)}f\rangle =\langle g,S_F(f)\rangle\end{align*} $$
for any
![]() $f,g\in \mathcal {H}.$
It follows from Lemma 3.2 that there exists an infinite subset
$f,g\in \mathcal {H}.$
It follows from Lemma 3.2 that there exists an infinite subset
![]() $S^{\prime }_F=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
$S^{\prime }_F=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
![]() $S_F$
such that
$S_F$
such that
![]() $\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
$\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align*}h^{S^{\prime}_F}_{\mu}(T,\{B,B^c\})\geq \int_X-S_F(1_B)\log{(S_F(1_B))}-S_F(1_{B^c})\log{(S_F(1_{B^c}))}\,{d\hspace{-1pt}\mu}.\end{align*} $$
$$ \begin{align*}h^{S^{\prime}_F}_{\mu}(T,\{B,B^c\})\geq \int_X-S_F(1_B)\log{(S_F(1_B))}-S_F(1_{B^c})\log{(S_F(1_{B^c}))}\,{d\hspace{-1pt}\mu}.\end{align*} $$
As
 $h_{\mu }^{S^{\prime }_F}(T,\{B,B^c\})=0$
, it follows that
$h_{\mu }^{S^{\prime }_F}(T,\{B,B^c\})=0$
, it follows that
![]() $-S_F(1_B)\log {S_F(1_B)}=0$
for
$-S_F(1_B)\log {S_F(1_B)}=0$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
. So
$x\in X$
. So
![]() $S_F(1_B)$
is an indicator function and hence
$S_F(1_B)$
is an indicator function and hence
Because
 $$ \begin{align*}\langle 1_X,1_B\rangle=\lim\limits_{i\to \infty}\langle 1_X,U_T^{(m_i,n_i)}1_B\rangle=\langle 1_X,S_F(1_B)\rangle,\end{align*} $$
$$ \begin{align*}\langle 1_X,1_B\rangle=\lim\limits_{i\to \infty}\langle 1_X,U_T^{(m_i,n_i)}1_B\rangle=\langle 1_X,S_F(1_B)\rangle,\end{align*} $$
it follows that
Hence,
 $$ \begin{align*}\lim\limits_{i\to \infty}\|U_T^{(m_i,n_i)}1_B-S_F(1_B)\|_{2}= 0.\end{align*} $$
$$ \begin{align*}\lim\limits_{i\to \infty}\|U_T^{(m_i,n_i)}1_B-S_F(1_B)\|_{2}= 0.\end{align*} $$
This implies that for sufficiently large i and j,
 $$ \begin{align*}\mu(T^{-(m_i,n_i)}B\Delta T^{-(m_j,n_j)}B)< \frac{\epsilon}{2},\end{align*} $$
$$ \begin{align*}\mu(T^{-(m_i,n_i)}B\Delta T^{-(m_j,n_j)}B)< \frac{\epsilon}{2},\end{align*} $$
which contradicts (3.8). Therefore,
 $\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is a compact subset of
$\overline {\{U_T^{(m,n)}1_B:(m,n)\in P\}}$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
.
$L^2(X,\mathcal {B}_X,\mu )$
.
The following description of directional Kronecker algebra is obtained immediately from Theorem 3.4.
Corollary 3.5. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. Then for any
$b\in (0,\infty )$
. Then for any
![]() $B\in \mathcal {B}_X$
. the following statements are equivalent:
$B\in \mathcal {B}_X$
. the following statements are equivalent:
-
(a)
 $B\in \mathcal {K}^{\kern2pt\vec {v}}_\mu $
;
$B\in \mathcal {K}^{\kern2pt\vec {v}}_\mu $
; -
(b) for any infinite subset
 $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
 $\Lambda ^{\vec {v}}(b)$
,
$\Lambda ^{\vec {v}}(b)$
,  $$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0;\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0;\end{align*} $$
-
(c) for any infinite subset
 $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
 $\Lambda ^{\vec {v}}(b)$
that
$\Lambda ^{\vec {v}}(b)$
that
 $\{m_i\}_{i=1}^{\infty }$
is strictly monotone,
$\{m_i\}_{i=1}^{\infty }$
is strictly monotone,  $$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0.\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0.\end{align*} $$
Moreover, for any finite measurable partition
 $\alpha \subset \mathcal {K}^{\kern2pt\vec {v}}_{\mu }$
of X and any infinite subset
$\alpha \subset \mathcal {K}^{\kern2pt\vec {v}}_{\mu }$
of X and any infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $ \Lambda ^{\vec {v}}(b),$
$ \Lambda ^{\vec {v}}(b),$
 $$ \begin{align*}h^{S}_{\mu}(T,\alpha)=0.\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\alpha)=0.\end{align*} $$
Remark 3.6. By Corollary 3.5, we immediately obtain
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}=\{B\in\mathcal{B}_X: \text{for any infinite subset }S\text{ of } \Lambda^{\vec{v}}(b),\text{ } h^{S}_{\mu}(T,\{B,B^c\})=0 \}.\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}=\{B\in\mathcal{B}_X: \text{for any infinite subset }S\text{ of } \Lambda^{\vec{v}}(b),\text{ } h^{S}_{\mu}(T,\{B,B^c\})=0 \}.\end{align*} $$
4 Directional discrete spectrum systems and null systems
In this section, we prove Theorem 1.1, which is divided into two lemmas. Moreover, we prove the directional version of Kušhnirenko theorem, that is, Theorem 1.4. For this purpose, we begin with the following property of directional sequence entropy.
Theorem 4.1. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. Suppose that
$b\in (0,\infty )$
. Suppose that
![]() $\{\alpha _n\}_{n=1}^{\infty }$
, satisfying
$\{\alpha _n\}_{n=1}^{\infty }$
, satisfying
![]() $\alpha _n\nearrow \mathcal {B}_X$
, is a family of finite measurable partitions of X. Then for any infinite subset
$\alpha _n\nearrow \mathcal {B}_X$
, is a family of finite measurable partitions of X. Then for any infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty } $
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty } $
of
![]() $ \Lambda ^{\vec {v}}(b),$
$ \Lambda ^{\vec {v}}(b),$
 $$ \begin{align*}\lim\limits_{n\to \infty}h^{S}_{\mu}(T,\alpha_n)=h^{S}_{\mu}(T).\end{align*} $$
$$ \begin{align*}\lim\limits_{n\to \infty}h^{S}_{\mu}(T,\alpha_n)=h^{S}_{\mu}(T).\end{align*} $$
Proof. For any finite measurable partition
![]() $\eta $
of X and
$\eta $
of X and
![]() $k,n \in \mathbb {N}$
,
$k,n \in \mathbb {N}$
,
 $$ \begin{align*} H_\mu \bigg(\bigvee_{i=1}^k T ^{-(m_i,n_i)} \eta\bigg) &\leq H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} (\eta \vee \alpha_n)\bigg)\\ &= H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg) + H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \eta|\bigvee_{i=1}^k T ^{-(m_i,n_i)} \alpha_n\bigg)\\ &\leq H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg) + \sum_{i=1}^k H_\mu \bigg(T^{-(m_i,n_i)} \eta|\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg)\\ &\leq H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg)+ kH_\mu\bigg(\eta | \alpha_n\bigg). \end{align*} $$
$$ \begin{align*} H_\mu \bigg(\bigvee_{i=1}^k T ^{-(m_i,n_i)} \eta\bigg) &\leq H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} (\eta \vee \alpha_n)\bigg)\\ &= H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg) + H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \eta|\bigvee_{i=1}^k T ^{-(m_i,n_i)} \alpha_n\bigg)\\ &\leq H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg) + \sum_{i=1}^k H_\mu \bigg(T^{-(m_i,n_i)} \eta|\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg)\\ &\leq H_\mu \bigg(\bigvee_{i=1}^k T^{-(m_i,n_i)} \alpha_n\bigg)+ kH_\mu\bigg(\eta | \alpha_n\bigg). \end{align*} $$
Dividing by k from both sides and taking the upper limits when
![]() $k\to \infty $
, we can get
$k\to \infty $
, we can get
 $$ \begin{align*}h^{S}_{\mu}(T,\eta)\leq h^{S}_{\mu}(T,\alpha_n)+H_\mu(\eta|\alpha_n).\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\eta)\leq h^{S}_{\mu}(T,\alpha_n)+H_\mu(\eta|\alpha_n).\end{align*} $$
By Martingale convergence theorem [Reference Glasner9],
 $$ \begin{align*}\lim\limits_{n\to \infty} H_\mu(\eta|\alpha_n)= H_\mu(\eta|\mathcal{B}_X)=0.\end{align*} $$
$$ \begin{align*}\lim\limits_{n\to \infty} H_\mu(\eta|\alpha_n)= H_\mu(\eta|\mathcal{B}_X)=0.\end{align*} $$
It follows that
 $$ \begin{align*}h^{S}_{\mu}(T,\eta)\leq \liminf\limits_{n\to \infty} h^{S}_{\mu}(T,\alpha_n)\leq \limsup\limits_{n\to \infty} h^{S}_{\mu}(T,\alpha_n) \leq h^{S}_{\mu}(T).\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\eta)\leq \liminf\limits_{n\to \infty} h^{S}_{\mu}(T,\alpha_n)\leq \limsup\limits_{n\to \infty} h^{S}_{\mu}(T,\alpha_n) \leq h^{S}_{\mu}(T).\end{align*} $$
Therefore,
 $$ \begin{align*} h^{S}_{\mu}(T) =\sup\limits_\eta h^{S}_{\mu}(T,\eta)=\lim\limits_{n\to \infty}h^{S}_{\mu}(T,\alpha_n), \end{align*} $$
$$ \begin{align*} h^{S}_{\mu}(T) =\sup\limits_\eta h^{S}_{\mu}(T,\eta)=\lim\limits_{n\to \infty}h^{S}_{\mu}(T,\alpha_n), \end{align*} $$
where the supremum is taken over all finite measurable partitions of X.
Now we are able to prove Theorem 1.1. For clarity, let us divide the proof into two lemmas.
Lemma 4.2. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. For any finite measurable partition
$b\in (0,\infty )$
. For any finite measurable partition
![]() $\alpha $
of X and infinite subset
$\alpha $
of X and infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $\Lambda ^{\vec {v}}(b)$
,
$\Lambda ^{\vec {v}}(b)$
,
 $$ \begin{align*}h^{S}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
Proof. Because
![]() $(X,\mathcal {B}_X)$
is separable, there exist countably many finite measurable partitions
$(X,\mathcal {B}_X)$
is separable, there exist countably many finite measurable partitions
 $\{\eta _k\}_{k\in \mathbb {N}}\subset \mathcal {K}^{\kern2pt\vec {v}}_\mu $
such that
$\{\eta _k\}_{k\in \mathbb {N}}\subset \mathcal {K}^{\kern2pt\vec {v}}_\mu $
such that
 $$ \begin{align*}\lim\limits_{k \rightarrow \infty }H_{\mu}(\alpha|\eta_k)=H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
$$ \begin{align*}\lim\limits_{k \rightarrow \infty }H_{\mu}(\alpha|\eta_k)=H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
For a fixed
![]() $k\in \mathbb {N}$
and an infinite subset
$k\in \mathbb {N}$
and an infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $\Lambda ^{\vec {v}}(b)$
, one has
$\Lambda ^{\vec {v}}(b)$
, one has
 $$ \begin{align} \lim\limits_{l\to \infty}\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\eta_k\bigg)=0 \end{align} $$
$$ \begin{align} \lim\limits_{l\to \infty}\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\eta_k\bigg)=0 \end{align} $$
by Corollary 3.5. Therefore, we conclude
 $$ \begin{align*} h^{S}_{\mu}(T,\alpha) &=\limsup\limits_{l\to \infty}\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\alpha\bigg)\\ &\leq \limsup\limits_{l\to \infty}{\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}(\alpha \vee \eta_k)\bigg)}\\ &\overset{(4.1)}= \limsup\limits_{l\to \infty}{\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}(\alpha \vee \eta_k)\bigg)}-\lim\limits_{l\to \infty}\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\eta_k\bigg)\\ &=\limsup\limits_{l\to \infty}{\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\alpha|\bigvee_{i=1}^lT^{-(m_i,n_i)}\eta_k\bigg)}\\ &\leq \limsup\limits_{l\to \infty}{\frac{1}{l}\sum_{i=1}^lH_\mu(T^{-(m_i,n_i)}\alpha|T^{-(m_i,n_i)}\eta_k)}\\ &=H_\mu(\alpha|\eta_k). \end{align*} $$
$$ \begin{align*} h^{S}_{\mu}(T,\alpha) &=\limsup\limits_{l\to \infty}\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\alpha\bigg)\\ &\leq \limsup\limits_{l\to \infty}{\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}(\alpha \vee \eta_k)\bigg)}\\ &\overset{(4.1)}= \limsup\limits_{l\to \infty}{\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}(\alpha \vee \eta_k)\bigg)}-\lim\limits_{l\to \infty}\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\eta_k\bigg)\\ &=\limsup\limits_{l\to \infty}{\frac{1}{l}H_\mu\bigg(\bigvee_{i=1}^lT^{-(m_i,n_i)}\alpha|\bigvee_{i=1}^lT^{-(m_i,n_i)}\eta_k\bigg)}\\ &\leq \limsup\limits_{l\to \infty}{\frac{1}{l}\sum_{i=1}^lH_\mu(T^{-(m_i,n_i)}\alpha|T^{-(m_i,n_i)}\eta_k)}\\ &=H_\mu(\alpha|\eta_k). \end{align*} $$
We finish the proof by letting
![]() $k\to \infty $
.
$k\to \infty $
.
For further proof, we need the following result [Reference Folland8, p. 69].
Lemma 4.3. Let
![]() $(X,\mathcal {B}_X,\mu )$
and
$(X,\mathcal {B}_X,\mu )$
and
![]() $(Y,\mathcal {B}_Y,\nu )$
be two Borel probability spaces and
$(Y,\mathcal {B}_Y,\nu )$
be two Borel probability spaces and
![]() $(X\times Y,\mathcal {B}_{X\times Y},\mu \times \nu )$
be their product Borel probability space. Then for any
$(X\times Y,\mathcal {B}_{X\times Y},\mu \times \nu )$
be their product Borel probability space. Then for any
![]() $B\subset X\times Y$
, the following two statements are equivalent:
$B\subset X\times Y$
, the following two statements are equivalent:
-
(a)
 $B_x:=\{y\in Y:(x,y)\in B\}\in \mathcal {B}_Y$
for
$B_x:=\{y\in Y:(x,y)\in B\}\in \mathcal {B}_Y$
for
 $\mu $
-a.e.
$\mu $
-a.e.
 $x\in X$
,
$x\in X$
,
 $B^y:=\{x\in X|(x,y)\in B\}\in \mathcal {B}_X$
for
$B^y:=\{x\in X|(x,y)\in B\}\in \mathcal {B}_X$
for
 $\nu $
-a.e.
$\nu $
-a.e.
 $y\in Y$
;
$y\in Y$
; -
(b)
 $B\in \mathcal {B}_{X\times Y}$
.
$B\in \mathcal {B}_{X\times Y}$
.
Lemma 4.4. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS,
$\mathbb {Z}^2$
-MPS,
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector and
![]() $b\in (0,\infty )$
. Then for any finite measurable partition
$b\in (0,\infty )$
. Then for any finite measurable partition
![]() $\alpha $
of X, there is an infinite subset
$\alpha $
of X, there is an infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $ \Lambda ^{\vec {v}}(b)$
such that
$ \Lambda ^{\vec {v}}(b)$
such that
![]() $\{m_i\}_{i=1}^{\infty }$
is strictly monotone and
$\{m_i\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align*}h^{S}_{\mu}(T,\alpha)\geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\alpha)\geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
Proof. To prove our result, we need a
![]() $\mathbb {Z}$
-MPS in the direction of
$\mathbb {Z}$
-MPS in the direction of
![]() $\vec {v}$
, which was introduced by Park [Reference Park20]. Let
$\vec {v}$
, which was introduced by Park [Reference Park20]. Let
where
![]() $\mathcal {C}$
is the Borel
$\mathcal {C}$
is the Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $[0,1)^2$
and m is the Lebesgue measure on
$[0,1)^2$
and m is the Lebesgue measure on
![]() $[0,1)^2$
. Let
$[0,1)^2$
. Let
 $$ \begin{align*}\phi_{s,t}(x,u,v)=(T^{([s+u],[t+v])}x,s+u-[s+u],t+v-[t+v]),\end{align*} $$
$$ \begin{align*}\phi_{s,t}(x,u,v)=(T^{([s+u],[t+v])}x,s+u-[s+u],t+v-[t+v]),\end{align*} $$
where
![]() $[a]$
is the integer part of a. Write
$[a]$
is the integer part of a. Write
![]() $\phi _{n,n\beta }$
as
$\phi _{n,n\beta }$
as
![]() $W^n$
for any
$W^n$
for any
![]() $n\in \mathbb {N}$
. Then we get the
$n\in \mathbb {N}$
. Then we get the
![]() $\mathbb {Z}$
-MPS
$\mathbb {Z}$
-MPS
![]() $(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu },W).$
Let
$(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu },W).$
Let
![]() $\mathcal{K}_{\widetilde {\mu }}$
be the Kronecker algebra of
$\mathcal{K}_{\widetilde {\mu }}$
be the Kronecker algebra of
![]() $(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu },W).$
We divide the proof into four steps.
$(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu },W).$
We divide the proof into four steps.
Step 1.
 $\mathcal {K}_{\widetilde {\mu }}=\mathcal {K}^{\kern2pt\vec {v}}_{\mu }\times \mathcal {C}$
.
$\mathcal {K}_{\widetilde {\mu }}=\mathcal {K}^{\kern2pt\vec {v}}_{\mu }\times \mathcal {C}$
.
Proof of Step 1
It is enough to show that
 $ \mathcal {K}_{\widetilde {\mu }}\subset \mathcal {K}^{\kern2pt\vec {v}}_{\mu }\times \mathcal {C}$
because the opposite side is obviously true. We fix
$ \mathcal {K}_{\widetilde {\mu }}\subset \mathcal {K}^{\kern2pt\vec {v}}_{\mu }\times \mathcal {C}$
because the opposite side is obviously true. We fix
![]() $B\in \mathcal {K}_{\widetilde {\mu }}$
and put
$B\in \mathcal {K}_{\widetilde {\mu }}$
and put
for
![]() $(s,t)\in [0,1)^2$
. We are going to show that
$(s,t)\in [0,1)^2$
. We are going to show that
 $B\in \mathcal {K}^{\kern2pt\vec {v}}_{\mu }\times \mathcal {C}$
. By Lemma 4.3, it is enough to show that
$B\in \mathcal {K}^{\kern2pt\vec {v}}_{\mu }\times \mathcal {C}$
. By Lemma 4.3, it is enough to show that
 $B^{(s,t)}\in \mathcal {K}^{\kern2pt\vec {v}}_{\mu }$
for m-a.e.
$B^{(s,t)}\in \mathcal {K}^{\kern2pt\vec {v}}_{\mu }$
for m-a.e.
![]() $(s,t)\in [0,1)^2$
. By the definition of
$(s,t)\in [0,1)^2$
. By the definition of
 $ \mathcal {K}^{\kern2pt\vec {v}}_{\mu }$
, it is sufficient to show that
$ \mathcal {K}^{\kern2pt\vec {v}}_{\mu }$
, it is sufficient to show that
 $$ \begin{align*}\overline{\{{U_T^{(m,n)}1_{B^{(s,t)}}:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}}}\end{align*} $$
$$ \begin{align*}\overline{\{{U_T^{(m,n)}1_{B^{(s,t)}}:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}}}\end{align*} $$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
for m-a.e.
$L^2(X,\mathcal {B}_X,\mu )$
for m-a.e.
![]() $(s,t)\in [0,1)^2$
. To do this, we let
$(s,t)\in [0,1)^2$
. To do this, we let
 $$ \begin{align*}f_u(x,s,t)=2^{2u}\int_{\eta^u_{k,l}}1_B(x,\xi,\zeta)\,d\xi \,d\zeta,\text{ if }(s,t)\in \eta^u_{k,l},\end{align*} $$
$$ \begin{align*}f_u(x,s,t)=2^{2u}\int_{\eta^u_{k,l}}1_B(x,\xi,\zeta)\,d\xi \,d\zeta,\text{ if }(s,t)\in \eta^u_{k,l},\end{align*} $$
where
![]() $u\in \mathbb {N}$
and
$u\in \mathbb {N}$
and
![]() $\eta ^u_{k,l}= [k2^{-u},(k+1)2^{-u})\times [l2^{-u},(l+1)2^{-u})$
,
$\eta ^u_{k,l}= [k2^{-u},(k+1)2^{-u})\times [l2^{-u},(l+1)2^{-u})$
,
![]() $k,l\in \{0,\ldots , 2^u-1\}$
.
$k,l\in \{0,\ldots , 2^u-1\}$
.
We have the following claim.
Claim 1. The following statements are true:
-
(1) for each
 $u\in \mathbb {N}$
and
$u\in \mathbb {N}$
and
 $(s,t)\in [0,1)^2$
, is a compact subset of
$(s,t)\in [0,1)^2$
, is a compact subset of $$ \begin{align*}\overline{\{{U_{T}^{(m,n)}f_u(x,s,t):|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}}}\end{align*} $$
$$ \begin{align*}\overline{\{{U_{T}^{(m,n)}f_u(x,s,t):|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}}}\end{align*} $$
 $L^2(X,\mathcal {B}_X,\mu )$
;
$L^2(X,\mathcal {B}_X,\mu )$
;
-
(2) for m-a.e.
 $(s,t)\in [0,1)^2$
,
$(s,t)\in [0,1)^2$
,  $$ \begin{align*}\lim_{u\to\infty}\|f_u(\cdot,s,t)-1_{B^{(s,t)}}\|_{2}=0.\end{align*} $$
$$ \begin{align*}\lim_{u\to\infty}\|f_u(\cdot,s,t)-1_{B^{(s,t)}}\|_{2}=0.\end{align*} $$
Because the proof of Claim 1 is somewhat long and complicated, we move it to Appendix A. Now let us assume that Claim 1 holds. Then we deduce that
 $$ \begin{align*}\overline{\{{U_{T}^{(m,n)}1_{B^{(s,t)}}:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2}\}}\end{align*} $$
$$ \begin{align*}\overline{\{{U_{T}^{(m,n)}1_{B^{(s,t)}}:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2}\}}\end{align*} $$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
for m-a.e.
$L^2(X,\mathcal {B}_X,\mu )$
for m-a.e.
![]() $(s,t)\in [0,1)^2$
, because
$(s,t)\in [0,1)^2$
, because
![]() $1_{B^{(s,t)}}\in L^2(X,\mathcal {B}_X,\mu )$
for m-a.e.
$1_{B^{(s,t)}}\in L^2(X,\mathcal {B}_X,\mu )$
for m-a.e.
![]() $(s,t)\in [0,1)^2$
. By the arguments at the beginning, we finish the proof of Step 1.□
$(s,t)\in [0,1)^2$
. By the arguments at the beginning, we finish the proof of Step 1.□
Step 2. For a given measurable partition
![]() $\mathfrak {C}=\{D_1,D_2,\ldots , D_r\}$
, there exists an infinite subset
$\mathfrak {C}=\{D_1,D_2,\ldots , D_r\}$
, there exists an infinite subset
![]() $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
![]() $ \Lambda ^{\vec {v}}(b)$
depending on
$ \Lambda ^{\vec {v}}(b)$
depending on
![]() $\mathfrak {C}$
such that
$\mathfrak {C}$
such that
![]() $\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
$\{m^{\prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align} \lim\limits_{i\to\infty}\langle U_T^{(m^{\prime}_i,n^{\prime}_i)}(1_{D_j}-\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)),1_B\rangle=0 \end{align} $$
$$ \begin{align} \lim\limits_{i\to\infty}\langle U_T^{(m^{\prime}_i,n^{\prime}_i)}(1_{D_j}-\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)),1_B\rangle=0 \end{align} $$
for any
![]() $B\in \mathcal {B}_X$
and
$B\in \mathcal {B}_X$
and
![]() $j\in \{1,2,\ldots ,r\}.$
$j\in \{1,2,\ldots ,r\}.$
Proof of Step 2
By Theorem 2.2, there exists a sequence
 $\widetilde {S} \subset \mathbb {Z}_+$
with
$\widetilde {S} \subset \mathbb {Z}_+$
with
![]() $d(\widetilde {S})=1$
such that
$d(\widetilde {S})=1$
such that
 $$ \begin{align} &\lim\limits_{n\to \infty,n\in \widetilde{S}}\langle U_{W}^n (1_{D_j}\times 1_{[0,1)^2}-\mathbb{E}(1_{D_j}\times 1_{[0,1)^2}|\mathcal{K}_{\widetilde{\mu}})),1_B\times1_{[0,1)^2}\rangle=0 \end{align} $$
$$ \begin{align} &\lim\limits_{n\to \infty,n\in \widetilde{S}}\langle U_{W}^n (1_{D_j}\times 1_{[0,1)^2}-\mathbb{E}(1_{D_j}\times 1_{[0,1)^2}|\mathcal{K}_{\widetilde{\mu}})),1_B\times1_{[0,1)^2}\rangle=0 \end{align} $$
for any
![]() $B\in \mathcal {B}_X$
and
$B\in \mathcal {B}_X$
and
![]() $j\in \{1,2,\ldots ,r\}$
, where
$j\in \{1,2,\ldots ,r\}$
, where
![]() $1_{D_j}\times 1_{[0,1)^2}=1_{D_j}(x)\cdot 1_{[0,1)^2}(s,t)$
is defined on
$1_{D_j}\times 1_{[0,1)^2}=1_{D_j}(x)\cdot 1_{[0,1)^2}(s,t)$
is defined on
![]() $\widetilde {X}$
. We omit the independent variable for convenience. By Step 1 and Proposition 2.1, we have
$\widetilde {X}$
. We omit the independent variable for convenience. By Step 1 and Proposition 2.1, we have
 $$ \begin{align*} &\mathbb{E}(1_{D_j}\times 1_{[0,1)^2}|\mathcal{K}_{\widetilde{\mu}})=\mathbb{E}(1_{D_j}\times 1_{[0,1)^2}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}\times \mathcal{C})\\ &\quad=\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)\times \mathbb{E}(1_{[0,1)^2}|\mathcal{C})=\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)\times 1_{[0,1)^2}. \end{align*} $$
$$ \begin{align*} &\mathbb{E}(1_{D_j}\times 1_{[0,1)^2}|\mathcal{K}_{\widetilde{\mu}})=\mathbb{E}(1_{D_j}\times 1_{[0,1)^2}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}\times \mathcal{C})\\ &\quad=\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)\times \mathbb{E}(1_{[0,1)^2}|\mathcal{C})=\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)\times 1_{[0,1)^2}. \end{align*} $$
Let
 $f_j=1_{D_j}-\mathbb {E}(1_{D_j}|\mathcal {K}^{\kern2pt\vec {v}}_\mu )$
,
$f_j=1_{D_j}-\mathbb {E}(1_{D_j}|\mathcal {K}^{\kern2pt\vec {v}}_\mu )$
,
![]() $j\in \{1,2,\ldots ,r\}.$
Then we conclude
$j\in \{1,2,\ldots ,r\}.$
Then we conclude
By Fubini’s theorem,
 $$ \begin{align} &|\langle U_{W}^n (f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle-\langle U_T^{(n,[n\beta])}(f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle|\nonumber\\ &\quad=\bigg|\int_{[0,1)^2}\int_{B}(f_j(T^{([n+s],[n\beta+t])}x)-f_j(T^{(n,[n\beta])}x))\,{d\hspace{-1pt}\mu}(x) \,dt \,ds\bigg|\nonumber\\ &\quad=\bigg|\int_{[0,1)}\int_{B}(f_j(T^{(n,[n\beta+t])}x)-f_j(T^{(n,[n\beta])}x))\,{d\hspace{-1pt}\mu}(x) \,dt \bigg|\nonumber\\ &\quad=\bigg|\int_{B}\int_{1-\{n\beta\}}^{1}(f_j(T^{(n,[n\beta+t])}x)-f_j(T^{(n,[n\beta])}x)) \,dt\,{d\hspace{-1pt}\mu}(x) \bigg|\nonumber\\ &\quad\leq \{n\beta\}\int_{B}|f_j(T^{(n,[n\beta]+1)}x)|+|f_j(T^{(n,[n\beta])}x)|\,{d\hspace{-1pt}\mu}(x)\nonumber\\ &\quad\leq 2\|f_j\|_{1}\{n\beta\}, \end{align} $$
$$ \begin{align} &|\langle U_{W}^n (f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle-\langle U_T^{(n,[n\beta])}(f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle|\nonumber\\ &\quad=\bigg|\int_{[0,1)^2}\int_{B}(f_j(T^{([n+s],[n\beta+t])}x)-f_j(T^{(n,[n\beta])}x))\,{d\hspace{-1pt}\mu}(x) \,dt \,ds\bigg|\nonumber\\ &\quad=\bigg|\int_{[0,1)}\int_{B}(f_j(T^{(n,[n\beta+t])}x)-f_j(T^{(n,[n\beta])}x))\,{d\hspace{-1pt}\mu}(x) \,dt \bigg|\nonumber\\ &\quad=\bigg|\int_{B}\int_{1-\{n\beta\}}^{1}(f_j(T^{(n,[n\beta+t])}x)-f_j(T^{(n,[n\beta])}x)) \,dt\,{d\hspace{-1pt}\mu}(x) \bigg|\nonumber\\ &\quad\leq \{n\beta\}\int_{B}|f_j(T^{(n,[n\beta]+1)}x)|+|f_j(T^{(n,[n\beta])}x)|\,{d\hspace{-1pt}\mu}(x)\nonumber\\ &\quad\leq 2\|f_j\|_{1}\{n\beta\}, \end{align} $$
where
![]() $\{n\beta \}$
is the decimal part of
$\{n\beta \}$
is the decimal part of
![]() $n\beta $
. Let
$n\beta $
. Let
![]() $M=2\max _{1\leq j\leq r}\{\|f_j\|_{1}\}$
and
$M=2\max _{1\leq j\leq r}\{\|f_j\|_{1}\}$
and
![]() $\Theta _\gamma =\{n\in \mathbb {Z}_+:\{n\beta \}\leq {\epsilon }/{2^{\gamma }M}\}$
for all
$\Theta _\gamma =\{n\in \mathbb {Z}_+:\{n\beta \}\leq {\epsilon }/{2^{\gamma }M}\}$
for all
![]() $\gamma \in \mathbb {N}$
. Because
$\gamma \in \mathbb {N}$
. Because
![]() $\Theta _\gamma $
is a syndetic set (a subset S of
$\Theta _\gamma $
is a syndetic set (a subset S of
![]() $\mathbb {Z}_+$
is syndetic if it has bounded gaps, that is, there is a number
$\mathbb {Z}_+$
is syndetic if it has bounded gaps, that is, there is a number
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $\{i,i+1,\ldots ,i+N\}\cap S\neq \emptyset $
for every
$\{i,i+1,\ldots ,i+N\}\cap S\neq \emptyset $
for every
![]() $i\in \mathbb {Z}_+$
), it follows that
$i\in \mathbb {Z}_+$
), it follows that
 $d(\Theta _\gamma \cap \widetilde {S})>0$
for all
$d(\Theta _\gamma \cap \widetilde {S})>0$
for all
![]() $\gamma \in \mathbb {N}$
. Take
$\gamma \in \mathbb {N}$
. Take
 $n_\gamma \in \Theta _\gamma \cap \widetilde {S}$
for each
$n_\gamma \in \Theta _\gamma \cap \widetilde {S}$
for each
![]() $\gamma \in \mathbb {N}$
. By (4.4), we obtain that
$\gamma \in \mathbb {N}$
. By (4.4), we obtain that
 $$ \begin{align} \lim\limits_{\gamma\to\infty}|\langle U_{W}^{n_\gamma} (f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle-\langle U_T^{(n_\gamma,[n_\gamma\beta])}(f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle|=0 \end{align} $$
$$ \begin{align} \lim\limits_{\gamma\to\infty}|\langle U_{W}^{n_\gamma} (f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle-\langle U_T^{(n_\gamma,[n_\gamma\beta])}(f_j\times 1_{[0,1)^2}),1_B\times1_{[0,1)^2}\rangle|=0 \end{align} $$
for all
![]() $j\in \{1,2,\ldots , r\}.$
By the construction of
$j\in \{1,2,\ldots , r\}.$
By the construction of
![]() $\Theta _\gamma $
, there exists
$\Theta _\gamma $
, there exists
![]() $\gamma _0\in \mathbb {N}$
such that for any
$\gamma _0\in \mathbb {N}$
such that for any
![]() $\gamma>\gamma _0$
, we have
$\gamma>\gamma _0$
, we have
 $(n_\gamma ,[n_\gamma \beta ])\in \Lambda ^{\vec {v}}(b)$
. It follows that there exists an infinite subsequence
$(n_\gamma ,[n_\gamma \beta ])\in \Lambda ^{\vec {v}}(b)$
. It follows that there exists an infinite subsequence
 $\{n_\gamma \}_{\gamma =\gamma _0+1}^{\infty } $
of
$\{n_\gamma \}_{\gamma =\gamma _0+1}^{\infty } $
of
![]() $ \widetilde {S}$
such that
$ \widetilde {S}$
such that
 $(n_\gamma ,[n_\gamma \beta ])\in \Lambda ^{\vec {v}}(b)$
and
$(n_\gamma ,[n_\gamma \beta ])\in \Lambda ^{\vec {v}}(b)$
and
 $$ \begin{align*} &\lim\limits_{\gamma\to \infty}\langle U_T^{(n_\gamma,[n_\gamma\beta])} (1_{D_j}-\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)),1_B\rangle\\ &\quad=\lim\limits_{\gamma\to \infty}|\langle U_T^{(n_\gamma,[n_\gamma\beta])}(f_j\times 1_{[0,1)^2}),1_B\times 1_{[0,1)^2}\rangle|\overset{(4.3)(4.5)}=0 \end{align*} $$
$$ \begin{align*} &\lim\limits_{\gamma\to \infty}\langle U_T^{(n_\gamma,[n_\gamma\beta])} (1_{D_j}-\mathbb{E}(1_{D_j}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)),1_B\rangle\\ &\quad=\lim\limits_{\gamma\to \infty}|\langle U_T^{(n_\gamma,[n_\gamma\beta])}(f_j\times 1_{[0,1)^2}),1_B\times 1_{[0,1)^2}\rangle|\overset{(4.3)(4.5)}=0 \end{align*} $$
for all
![]() $j\in \{1,2,\ldots ,r\}.$
Let
$j\in \{1,2,\ldots ,r\}.$
Let
which is the infinite subset we want.
Step 3. Let
![]() $\eta $
be a finite measurable partition of X. Then there exists an infinite subset
$\eta $
be a finite measurable partition of X. Then there exists an infinite subset
![]() $S''=\{(m^{\prime \prime }_i,n^{\prime \prime }_i)\}_{i=1}^{\infty } $
of
$S''=\{(m^{\prime \prime }_i,n^{\prime \prime }_i)\}_{i=1}^{\infty } $
of
![]() $ \Lambda ^{\vec {v}}(b)$
such that
$ \Lambda ^{\vec {v}}(b)$
such that
![]() $\{m^{\prime \prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
$\{m^{\prime \prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align*}\liminf_{i\to\infty}H_\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}\alpha|\eta)\geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
$$ \begin{align*}\liminf_{i\to\infty}H_\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}\alpha|\eta)\geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\end{align*} $$
Proof of Step 3
Let
![]() $\alpha =\{A_1,A_2,\ldots ,A_k\}$
and
$\alpha =\{A_1,A_2,\ldots ,A_k\}$
and
![]() $\eta =\{B_1,B_2,\ldots ,B_l\}$
. By Step 2, there exists an infinite subset
$\eta =\{B_1,B_2,\ldots ,B_l\}$
. By Step 2, there exists an infinite subset
![]() $S''=\{(m^{\prime \prime }_i,n^{\prime \prime }_i)\}_{i=1}^{\infty } $
of
$S''=\{(m^{\prime \prime }_i,n^{\prime \prime }_i)\}_{i=1}^{\infty } $
of
![]() $ \Lambda ^{\vec {v}}(b)$
such that
$ \Lambda ^{\vec {v}}(b)$
such that
![]() $\{m^{\prime \prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
$\{m^{\prime \prime }_i\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align}\lim\limits_{i\to\infty}\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}(1_{A_p}-\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)),1_{B_q}\rangle=0 \end{align} $$
$$ \begin{align}\lim\limits_{i\to\infty}\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}(1_{A_p}-\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_\mu)),1_{B_q}\rangle=0 \end{align} $$
for all
![]() $p\in \{1,2,\ldots ,k\}$
and
$p\in \{1,2,\ldots ,k\}$
and
![]() $q\in \{1,2,\ldots ,l\}$
. Hence,
$q\in \{1,2,\ldots ,l\}$
. Hence,
 $$ \begin{align*} &\liminf\limits_{i\to \infty}{H_\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}\alpha|\eta)}\\ &\quad=\liminf\limits_{i\to \infty}{\sum_{p,q}-\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}A_p\cap B_q)}\log{\bigg(\frac{\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}A_p\cap B_q)}{\mu(B_q)}\bigg)}\\ &\quad=\liminf\limits_{i\to \infty}{\sum_{p,q}-\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}1_{A_p},1_{B_q}\rangle\log{\bigg(\frac{\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}1_{A_p},1_{B_q}\rangle}{\mu(B_q)}\bigg)}}\\ &\quad\overset{(4.6)}=\liminf\limits_{i\to \infty}{\sum_{p,q}-\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}),1_{B_q}\rangle\log{\bigg(\frac{\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}),1_{B_q}\rangle}{\mu(B_q)}\bigg)}}. \end{align*} $$
$$ \begin{align*} &\liminf\limits_{i\to \infty}{H_\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}\alpha|\eta)}\\ &\quad=\liminf\limits_{i\to \infty}{\sum_{p,q}-\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}A_p\cap B_q)}\log{\bigg(\frac{\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}A_p\cap B_q)}{\mu(B_q)}\bigg)}\\ &\quad=\liminf\limits_{i\to \infty}{\sum_{p,q}-\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}1_{A_p},1_{B_q}\rangle\log{\bigg(\frac{\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}1_{A_p},1_{B_q}\rangle}{\mu(B_q)}\bigg)}}\\ &\quad\overset{(4.6)}=\liminf\limits_{i\to \infty}{\sum_{p,q}-\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}),1_{B_q}\rangle\log{\bigg(\frac{\langle U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}),1_{B_q}\rangle}{\mu(B_q)}\bigg)}}. \end{align*} $$
Let
 $a_{pq}^i=-\langle U_T^{(m^{\prime \prime }_i,n^{\prime \prime }_i)}\mathbb {E}(1_{A_p}|\mathcal {K}^{\kern2pt\vec {v}}_{\mu }),1_{B_q}\rangle \log {({\langle U_T^{(m^{\prime \prime }_i,n^{\prime \prime }_i)}\mathbb {E}(1_{A_p}|\mathcal {K}^{\kern2pt\vec {v}}_{\mu }),1_{B_q}\rangle }/{\mu (B_q)})}$
and
$a_{pq}^i=-\langle U_T^{(m^{\prime \prime }_i,n^{\prime \prime }_i)}\mathbb {E}(1_{A_p}|\mathcal {K}^{\kern2pt\vec {v}}_{\mu }),1_{B_q}\rangle \log {({\langle U_T^{(m^{\prime \prime }_i,n^{\prime \prime }_i)}\mathbb {E}(1_{A_p}|\mathcal {K}^{\kern2pt\vec {v}}_{\mu }),1_{B_q}\rangle }/{\mu (B_q)})}$
and
![]() $\mu _{B_q}(\cdot )=\mu (\cdot \cap B_q)/\mu (B_q)$
. Similar to (3.6), we deduce from concavity of
$\mu _{B_q}(\cdot )=\mu (\cdot \cap B_q)/\mu (B_q)$
. Similar to (3.6), we deduce from concavity of
![]() $-x\log {x}$
that
$-x\log {x}$
that
 $$ \begin{align*} \frac{a_{pq}^i}{\mu(B_q)} &=-\bigg(\int_{B_q}{\frac{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}{\mu(B_q)}}\,{d\hspace{-1pt}\mu}\bigg)\log{\bigg(\int_{B_q}{\frac{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}{\mu(B_q)}}\,{d\hspace{-1pt}\mu}\bigg)}\\ &=-\bigg(\int_{B_q}{{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}}\,{d\hspace{-1pt}\mu}_{B_q}\bigg)\log{\bigg(\int_{B_q}{{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}}\,{d\hspace{-1pt}\mu}_{B_q}\bigg)}\\ &\geq -\int_{B_q}{{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}}\log{(U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}_{B_q}\\ &=-\int_{B_q}{\frac{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}{\mu(B_q)}}\log{(U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}. \end{align*} $$
$$ \begin{align*} \frac{a_{pq}^i}{\mu(B_q)} &=-\bigg(\int_{B_q}{\frac{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}{\mu(B_q)}}\,{d\hspace{-1pt}\mu}\bigg)\log{\bigg(\int_{B_q}{\frac{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}{\mu(B_q)}}\,{d\hspace{-1pt}\mu}\bigg)}\\ &=-\bigg(\int_{B_q}{{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}}\,{d\hspace{-1pt}\mu}_{B_q}\bigg)\log{\bigg(\int_{B_q}{{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}}\,{d\hspace{-1pt}\mu}_{B_q}\bigg)}\\ &\geq -\int_{B_q}{{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}}\log{(U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}_{B_q}\\ &=-\int_{B_q}{\frac{U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}{\mu(B_q)}}\log{(U_{T}^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}. \end{align*} $$
We conclude that
 $$ \begin{align*} \sum_{p,q}a_{pq}^i &\geq \sum_{p,q}-\int_{B_q}{U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}\log{(U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}\\ &=\sum_p -\int_X{U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}\log{(U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}\\ &=\sum_p -\int_X{\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}\log{(\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}. \end{align*} $$
$$ \begin{align*} \sum_{p,q}a_{pq}^i &\geq \sum_{p,q}-\int_{B_q}{U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}\log{(U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}\\ &=\sum_p -\int_X{U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}\log{(U_T^{(m^{\prime\prime}_i,n^{\prime\prime}_i)}\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}\\ &=\sum_p -\int_X{\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu})}\log{(\mathbb{E}(1_{A_p}|\mathcal{K}^{\kern2pt\vec{v}}_{\mu}))}\,{d\hspace{-1pt}\mu}. \end{align*} $$
Therefore,
 $$ \begin{align*}\liminf\limits_{i\to \infty}{H_\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}\alpha|\eta)} \geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\\[-1.3pc]\end{align*} $$
$$ \begin{align*}\liminf\limits_{i\to \infty}{H_\mu(T^{-(m^{\prime\prime}_i,n^{\prime\prime}_i)}\alpha|\eta)} \geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu).\\[-1.3pc]\end{align*} $$
Step 4. In this step, we finish the proof of Lemma 4.4.
We can define inductively an infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $\Lambda ^{\vec {v}}(b)$
by using Step 3 repeatedly such that
$\Lambda ^{\vec {v}}(b)$
by using Step 3 repeatedly such that
![]() $\{m_i\}_{i=1}^{\infty }$
is strictly monotone and for any
$\{m_i\}_{i=1}^{\infty }$
is strictly monotone and for any
![]() $i\in \mathbb {N}$
,
$i\in \mathbb {N}$
,
 $$ \begin{align*}H_\mu\bigg(T^{-(m_i,n_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m_j,n_j)}\alpha\bigg)\geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu)-\frac{1}{2^i}.\end{align*} $$
$$ \begin{align*}H_\mu\bigg(T^{-(m_i,n_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m_j,n_j)}\alpha\bigg)\geq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu)-\frac{1}{2^i}.\end{align*} $$
Therefore, one has
 $$ \begin{align*} h^{S}_{\mu}(T, \alpha) &=\limsup_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}H_\mu\bigg(T^{-(m_i,n_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m_j,n_j)}\alpha\bigg)}\\ &\geq\limsup_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}\bigg(H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu)-\frac{1}{2^i}\bigg)}\\ &=H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu). \end{align*} $$
$$ \begin{align*} h^{S}_{\mu}(T, \alpha) &=\limsup_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}H_\mu\bigg(T^{-(m_i,n_i)}\alpha|\bigvee_{j=1}^{i-1} T^{-(m_j,n_j)}\alpha\bigg)}\\ &\geq\limsup_{k\to \infty}{\frac{1}{k}\sum_{i=1}^{k}\bigg(H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu)-\frac{1}{2^i}\bigg)}\\ &=H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu). \end{align*} $$
This finishes the proof of Lemma 4.4.□
By Lemmas 4.2 and 4.4, one of our main results, the directional version of Kušhnirenko theorem, is proved as follows.
Proof of Theorem 1.4
Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS and
$\mathbb {Z}^2$
-MPS and
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector.
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
be a direction vector.
(a)
![]() $\Rightarrow $
(b). Assume that
$\Rightarrow $
(b). Assume that
![]() $\mu $
has a
$\mu $
has a
![]() $\vec {v}$
-discrete spectrum system. Then
$\vec {v}$
-discrete spectrum system. Then
 $\mathcal {K}^{\kern2pt\vec {v}}_\mu =\mathcal {B}_X$
. Fix
$\mathcal {K}^{\kern2pt\vec {v}}_\mu =\mathcal {B}_X$
. Fix
![]() $b\in (0,\infty )$
. By Lemma 4.2,
$b\in (0,\infty )$
. By Lemma 4.2,
 $$ \begin{align*}h^{S}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu)=0\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}^{\kern2pt\vec{v}}_\mu)=0\end{align*} $$
for any infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $\Lambda ^{\vec {v}}(b)$
, which implies
$\Lambda ^{\vec {v}}(b)$
, which implies
![]() $(X,\mathcal {B}_X,\mu ,T)$
is
$(X,\mathcal {B}_X,\mu ,T)$
is
![]() $\vec {v}$
-null.
$\vec {v}$
-null.
(b)
![]() $\Rightarrow $
(a). Assume that
$\Rightarrow $
(a). Assume that
![]() $(X,\mathcal {B}_X,\mu ,T)$
is
$(X,\mathcal {B}_X,\mu ,T)$
is
![]() $\vec {v}$
-null. Then for any
$\vec {v}$
-null. Then for any
![]() $b\in (0,\infty )$
and infinite subset
$b\in (0,\infty )$
and infinite subset
![]() $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
![]() $\Lambda ^{\vec {v}}(b)$
,
$\Lambda ^{\vec {v}}(b)$
,
 $$ \begin{align*}h^{S}_{\mu}(T)=0.\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T)=0.\end{align*} $$
Hence,
 $$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0\end{align*} $$
for any
![]() $B\in \mathcal {B}_X$
, which implies
$B\in \mathcal {B}_X$
, which implies
 $B\in \mathcal {K}^{\kern2pt\vec {v}}_\mu $
by Corollary 3.5. Therefore,
$B\in \mathcal {K}^{\kern2pt\vec {v}}_\mu $
by Corollary 3.5. Therefore,
 $\mathcal {K}^{\kern2pt\vec {v}}_\mu =\mathcal {B}_X$
, that is,
$\mathcal {K}^{\kern2pt\vec {v}}_\mu =\mathcal {B}_X$
, that is,
![]() $\mu $
has
$\mu $
has
![]() $\vec {v}$
-discrete spectrum. This completes the proof of Theorem 1.4.
$\vec {v}$
-discrete spectrum. This completes the proof of Theorem 1.4.
5 Sequence entropy and directional sequence entropy
In this section, we recall and prove Theorems 1.4 and 1.5, which establish the relation between sequence entropy (respectively discrete spectrum) and directional sequence entropy (respectively directional discrete spectrum). For these purposes, we recall a result in [Reference Kerr and Li13, Lemma 5.1], which is restated as follows.
Lemma 5.1. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS. Then the following conditions are equivalent:
$\mathbb {Z}^2$
-MPS. Then the following conditions are equivalent:
-
(a)
 $\overline {\{U_T^{(m,n)}1_B:(m,n)\in \mathbb {Z}^2\}}$
is a compact subset of
$\overline {\{U_T^{(m,n)}1_B:(m,n)\in \mathbb {Z}^2\}}$
is a compact subset of
 $L^2(X,\mathcal {B}_X,\mu )$
;
$L^2(X,\mathcal {B}_X,\mu )$
; -
(b) for any infinite subset
 $S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
$S=\{(m_i,n_i)\}_{i=1}^{\infty }$
of
 $\mathbb {Z}^2$
,
$\mathbb {Z}^2$
,  $$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0.\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\{B,B^c\})=0.\end{align*} $$
Next we prove a combinatorial result as follows.
Lemma 5.2. Let
![]() $\vec {v}=(1,\beta _1), \vec {w}=(1,\beta _2)\in \mathbb {R}^2$
be two directions with
$\vec {v}=(1,\beta _1), \vec {w}=(1,\beta _2)\in \mathbb {R}^2$
be two directions with
![]() $\beta _1\neq \beta _2$
. Then
$\beta _1\neq \beta _2$
. Then
 $$ \begin{align*}\mathbb{Z}^2=\Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)\end{align*} $$
$$ \begin{align*}\mathbb{Z}^2=\Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)\end{align*} $$
for any
![]() $b> 4([|\beta _1-\beta _2|]+1)$
, where
$b> 4([|\beta _1-\beta _2|]+1)$
, where
 $$ \begin{align*}\Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)=\{(m_1+m_2,n_1+n_2):(m_1,n_1)\in \Lambda^{\vec{v}}(b)\text{ and } (m_2,n_2)\in \Lambda^{\vec{w}}(b)\}.\end{align*} $$
$$ \begin{align*}\Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)=\{(m_1+m_2,n_1+n_2):(m_1,n_1)\in \Lambda^{\vec{v}}(b)\text{ and } (m_2,n_2)\in \Lambda^{\vec{w}}(b)\}.\end{align*} $$
Proof. Given
![]() $(m,n)\in \mathbb {Z}^2$
. By division algorithm, we can choose
$(m,n)\in \mathbb {Z}^2$
. By division algorithm, we can choose
![]() $m_1\in \mathbb {Z}$
such that
$m_1\in \mathbb {Z}$
such that
Because
![]() $b/4>[|\beta _1-\beta _2|]+1$
, we can choose
$b/4>[|\beta _1-\beta _2|]+1$
, we can choose
![]() $n_1\in \mathbb {Z}$
such that:
$n_1\in \mathbb {Z}$
such that:
-
(a)
 $\beta _1m_1-b/2\leq n_1\leq \beta _1m_1+b/2$
;
$\beta _1m_1-b/2\leq n_1\leq \beta _1m_1+b/2$
; -
(b)
 $n_1=\beta _1m_1+r$
with
$n_1=\beta _1m_1+r$
with
 $|r|\leq b/4$
.
$|r|\leq b/4$
.
Let
![]() $n_2=n-n_1$
and
$n_2=n-n_1$
and
![]() $m_2=m-m_1$
. Then it is sufficient to prove that
$m_2=m-m_1$
. Then it is sufficient to prove that
 $$ \begin{align*}(m_2,n_2)\in \Lambda^{\vec{w}}(b).\end{align*} $$
$$ \begin{align*}(m_2,n_2)\in \Lambda^{\vec{w}}(b).\end{align*} $$
Note that
 $$ \begin{align*} |n_2-\beta_2m_2|&=|n-\beta_2m+n_1-\beta_2m_1|=|n-\beta_2m+\beta_1m_1+r-\beta_2m_1|\\ &=|n-\beta_2m+(\beta_1-\beta_1)m_1+r|\overset{(5.1)}\leq|\beta_1-\beta_2|+|r|\\ &\leq ([|\beta_1-\beta_2|]+1)+b/4\leq b/2, \end{align*} $$
$$ \begin{align*} |n_2-\beta_2m_2|&=|n-\beta_2m+n_1-\beta_2m_1|=|n-\beta_2m+\beta_1m_1+r-\beta_2m_1|\\ &=|n-\beta_2m+(\beta_1-\beta_1)m_1+r|\overset{(5.1)}\leq|\beta_1-\beta_2|+|r|\\ &\leq ([|\beta_1-\beta_2|]+1)+b/4\leq b/2, \end{align*} $$
which implies
![]() $(m_2,n_2)\in \Lambda ^{\vec {w}}(b)$
. This finishes the proof of Lemma 5.2.
$(m_2,n_2)\in \Lambda ^{\vec {w}}(b)$
. This finishes the proof of Lemma 5.2.
With the help of the above lemma, we are able to prove Theorems 1.4 and 1.5, which are recalled and proved as follows.
Theorem 5.3. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS and
$\mathbb {Z}^2$
-MPS and
![]() $\alpha $
be a finite measurable partition of X. If there exists an infinite subset S of
$\alpha $
be a finite measurable partition of X. If there exists an infinite subset S of
![]() $\mathbb {Z}^2$
such that
$\mathbb {Z}^2$
such that
 $h^S_{\mu }(T,\alpha )>0$
, then there is at most one direction
$h^S_{\mu }(T,\alpha )>0$
, then there is at most one direction
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
such that
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
such that
 $$ \begin{align*}h_\mu^{\vec{v},*}(\alpha)=0,\end{align*} $$
$$ \begin{align*}h_\mu^{\vec{v},*}(\alpha)=0,\end{align*} $$
where
 $h_\mu ^{\vec {v},*}(\alpha )$
is defined by (1.1).
$h_\mu ^{\vec {v},*}(\alpha )$
is defined by (1.1).
Proof. Let
![]() $\alpha $
be a finite measurable partition of X. Assume that there exists an infinite subset S of
$\alpha $
be a finite measurable partition of X. Assume that there exists an infinite subset S of
![]() $\mathbb {Z}^2$
such that
$\mathbb {Z}^2$
such that
 $$ \begin{align*}h^S_{\mu}(T,\alpha)>0.\end{align*} $$
$$ \begin{align*}h^S_{\mu}(T,\alpha)>0.\end{align*} $$
In the following, we show that there is at most one direction
![]() $\vec {\tau }=(1,\beta )\in \mathbb {R}^2$
such that
$\vec {\tau }=(1,\beta )\in \mathbb {R}^2$
such that
 $h_\mu ^{\vec {\tau },*}(\alpha )=0.$
If this is not true, then there exist two directions
$h_\mu ^{\vec {\tau },*}(\alpha )=0.$
If this is not true, then there exist two directions
![]() $\vec {v}=(1,\beta _1), \vec {w}=(1,\beta _2)\in \mathbb {R}^2$
with
$\vec {v}=(1,\beta _1), \vec {w}=(1,\beta _2)\in \mathbb {R}^2$
with
![]() $\beta _1\neq \beta _2$
such that
$\beta _1\neq \beta _2$
such that
 $$ \begin{align*}h_\mu^{\vec{v},*}(\alpha)=0\quad\text{and}\quad h_\mu^{\vec{w},*}(\alpha)=0.\end{align*} $$
$$ \begin{align*}h_\mu^{\vec{v},*}(\alpha)=0\quad\text{and}\quad h_\mu^{\vec{w},*}(\alpha)=0.\end{align*} $$
By Lemma 4.4 and (1.1), we obtain that
 $$ \begin{align*}H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}})=H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{w}})=0,\end{align*} $$
$$ \begin{align*}H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}})=H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{w}})=0,\end{align*} $$
which implies that
 $\alpha \subset \mathcal {K}_\mu ^{\kern2pt\vec {v}} \bigcap \mathcal {K}_\mu ^{\kern2pt\vec {w}}$
. Fix
$\alpha \subset \mathcal {K}_\mu ^{\kern2pt\vec {v}} \bigcap \mathcal {K}_\mu ^{\kern2pt\vec {w}}$
. Fix
![]() $B\in\hspace{0.6pt}\alpha $
. In the following, we show that
$B\in\hspace{0.6pt}\alpha $
. In the following, we show that
 $$ \begin{align*}\overline{\{U_T^{(m,n)}1_B:(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
$$ \begin{align*}\overline{\{U_T^{(m,n)}1_B:(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
, which implies that
$L^2(X,\mathcal {B}_X,\mu )$
, which implies that
 $h^{S'}_{\mu }(T,\{B,B^c\})=0$
for any infinite subset
$h^{S'}_{\mu }(T,\{B,B^c\})=0$
for any infinite subset
![]() $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
![]() $\mathbb {Z}^2$
by Lemma 5.1. In fact, by Lemma 5.2, taking
$\mathbb {Z}^2$
by Lemma 5.1. In fact, by Lemma 5.2, taking
![]() $b=([|\beta _1-\beta _2|]+2)$
, we have
$b=([|\beta _1-\beta _2|]+2)$
, we have
 $$ \begin{align*}\Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)=\mathbb{Z}^2\end{align*} $$
$$ \begin{align*}\Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)=\mathbb{Z}^2\end{align*} $$
and hence it suffices to prove that
 $$ \begin{align*}\mathcal{R}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)\}}\end{align*} $$
$$ \begin{align*}\mathcal{R}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{v}}(b)+\Lambda^{\vec{w}}(b)\}}\end{align*} $$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
. Note that
$L^2(X,\mathcal {B}_X,\mu )$
. Note that
 $B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}} \bigcap \mathcal {K}_\mu ^{\kern2pt\vec {w}}$
. So
$B\in \mathcal {K}_\mu ^{\kern2pt\vec {v}} \bigcap \mathcal {K}_\mu ^{\kern2pt\vec {w}}$
. So
 $$ \begin{align*}\mathcal{P}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{v}}(b)\}} \quad\text{and}\quad \mathcal{Q}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{w}}(b)\}}\end{align*} $$
$$ \begin{align*}\mathcal{P}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{v}}(b)\}} \quad\text{and}\quad \mathcal{Q}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{w}}(b)\}}\end{align*} $$
are compact subsets of
![]() $L^2(X,\mathcal {B}_X,\mu )$
. For any
$L^2(X,\mathcal {B}_X,\mu )$
. For any
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
 $$ \begin{align*}\{(m_i,n_i)\}_{i=1}^s\subset \Lambda^{\vec{v}}(b)\quad\text{and}\quad \{(u_j,v_j)\}_{j=1}^s\subset \Lambda^{\vec{w}}(b)\end{align*} $$
$$ \begin{align*}\{(m_i,n_i)\}_{i=1}^s\subset \Lambda^{\vec{v}}(b)\quad\text{and}\quad \{(u_j,v_j)\}_{j=1}^s\subset \Lambda^{\vec{w}}(b)\end{align*} $$
be
![]() $\epsilon /2$
-nets of
$\epsilon /2$
-nets of
![]() $\mathcal {P}_b$
and
$\mathcal {P}_b$
and
![]() $\mathcal {Q}_b$
in
$\mathcal {Q}_b$
in
![]() $L^2(X,\mathcal {B}_X,\mu )$
, respectively. Hence for any
$L^2(X,\mathcal {B}_X,\mu )$
, respectively. Hence for any
 $(p_1,q_1)\in \Lambda ^{\vec {v}}(b)$
and
$(p_1,q_1)\in \Lambda ^{\vec {v}}(b)$
and
 $(p_2,q_2)\in \Lambda ^{\vec {w}}(b)$
, we conclude
$(p_2,q_2)\in \Lambda ^{\vec {w}}(b)$
, we conclude
 $$ \begin{align*}\|U_T^{(p_1,q_1)}1_{B}-U_T^{(m_i,n_i)}1_{B}\|_2<\epsilon/2 \quad\text{and}\quad \|U_T^{(p_2,q_2)}1_{B}-U_T^{(u_j,v_j)}1_{B}\|_2<\epsilon/2\end{align*} $$
$$ \begin{align*}\|U_T^{(p_1,q_1)}1_{B}-U_T^{(m_i,n_i)}1_{B}\|_2<\epsilon/2 \quad\text{and}\quad \|U_T^{(p_2,q_2)}1_{B}-U_T^{(u_j,v_j)}1_{B}\|_2<\epsilon/2\end{align*} $$
for some
![]() $i,j\in \{1,\ldots ,s\}$
. Moreover, we deduce
$i,j\in \{1,\ldots ,s\}$
. Moreover, we deduce
 $$ \begin{align} &\|U_T^{(p_1+p_2,q_1+q_2)}1_{B}-U_T^{(m_i+u_j,n_i+v_j)}1_{B}\|_2\nonumber\\ &\quad\leq \|U_T^{(p_1,q_1)}1_{T^{-(p_2,q_2)}B}-U_T^{(m_i,n_i)}1_{T^{-(p_2,q_2)}B}\|_2\nonumber\\ &\qquad+\|U_T^{(p_2,q_2)}1_{T^{-(m_i,n_i)}B}-U_T^{(u_j,v_j)}1_{T^{-(m_i,n_i)}B}\|_2\leq \epsilon. \end{align} $$
$$ \begin{align} &\|U_T^{(p_1+p_2,q_1+q_2)}1_{B}-U_T^{(m_i+u_j,n_i+v_j)}1_{B}\|_2\nonumber\\ &\quad\leq \|U_T^{(p_1,q_1)}1_{T^{-(p_2,q_2)}B}-U_T^{(m_i,n_i)}1_{T^{-(p_2,q_2)}B}\|_2\nonumber\\ &\qquad+\|U_T^{(p_2,q_2)}1_{T^{-(m_i,n_i)}B}-U_T^{(u_j,v_j)}1_{T^{-(m_i,n_i)}B}\|_2\leq \epsilon. \end{align} $$
It follows from (5.2) that
is a finite
![]() $\epsilon $
-net of
$\epsilon $
-net of
![]() $\mathcal {R}_b$
in
$\mathcal {R}_b$
in
![]() $L^2(X,\mathcal {B}_X,\mu )$
, which implies that
$L^2(X,\mathcal {B}_X,\mu )$
, which implies that
![]() $\mathcal {R}_b$
is a compact subset of
$\mathcal {R}_b$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
. By the arguments at the beginning of this proof, we obtain
$L^2(X,\mathcal {B}_X,\mu )$
. By the arguments at the beginning of this proof, we obtain
 $$ \begin{align*}h^{S'}_{\mu}(T,\{B,B^c\})=0\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T,\{B,B^c\})=0\end{align*} $$
for any infinite subset
![]() $S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
$S'=\{(m^{\prime }_i,n^{\prime }_i)\}_{i=1}^{\infty }$
of
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Because
![]() $\bigvee _{B\in\hspace{0.6pt}\alpha }\{B,B^c\}$
is finer than
$\bigvee _{B\in\hspace{0.6pt}\alpha }\{B,B^c\}$
is finer than
![]() $\alpha $
, it follows that
$\alpha $
, it follows that
 $$ \begin{align*}h^{S'}_{\mu}(T,\alpha)=0\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T,\alpha)=0\end{align*} $$
for any infinite subset
![]() $S'$
of
$S'$
of
![]() $\mathbb {Z}^2$
, which contradicts the fact that there exists an infinite subset S of
$\mathbb {Z}^2$
, which contradicts the fact that there exists an infinite subset S of
![]() $\mathbb {Z}^2$
such that
$\mathbb {Z}^2$
such that
 $h^S_{\mu }(T,\alpha )>0$
. This completes the proof of Theorem 5.3.
$h^S_{\mu }(T,\alpha )>0$
. This completes the proof of Theorem 5.3.
The following example shows that they could both hold at the same time that there is an infinite subset S of
![]() $\mathbb {Z}^2$
such that
$\mathbb {Z}^2$
such that
 $h^S_{\mu }(T,\alpha )>0$
and there is a direction vector
$h^S_{\mu }(T,\alpha )>0$
and there is a direction vector
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
such that
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
such that
 $h_\mu ^{\vec {v},*}(\alpha )=0$
.
$h_\mu ^{\vec {v},*}(\alpha )=0$
.
Example 5.4. Let
![]() $(Y,2^Y,\mu )$
denote the measure space, where
$(Y,2^Y,\mu )$
denote the measure space, where
![]() $Y=\{0,1\}$
,
$Y=\{0,1\}$
,
![]() $2^Y$
is the collection consisting of all subsets of Y and the points
$2^Y$
is the collection consisting of all subsets of Y and the points
![]() $0,1$
have measure
$0,1$
have measure
![]() $1/2$
. Let
$1/2$
. Let
 $$ \begin{align*}(X,\mathcal{B}_X,m)=\prod_{-\infty}^{\infty}(Y,2^Y,\mu).\end{align*} $$
$$ \begin{align*}(X,\mathcal{B}_X,m)=\prod_{-\infty}^{\infty}(Y,2^Y,\mu).\end{align*} $$
Define
![]() $T_1=Id_X:X\to X$
by
$T_1=Id_X:X\to X$
by
for any
![]() $\{x_n\}\in X$
. Define
$\{x_n\}\in X$
. Define
![]() $T_2:X\to X$
by
$T_2:X\to X$
by
where
![]() $y_n=x_{n+1}$
for all
$y_n=x_{n+1}$
for all
![]() $n\in \mathbb {Z}$
, that is,
$n\in \mathbb {Z}$
, that is,
![]() $T_2$
is the two-sided
$T_2$
is the two-sided
 $(\tfrac 12,\tfrac 12)$
-shift. Define the
$(\tfrac 12,\tfrac 12)$
-shift. Define the
![]() $\mathbb {Z}^2$
-action T by
$\mathbb {Z}^2$
-action T by
 $$ \begin{align*}T^{(m,n)}=T_1^mT_2^n.\end{align*} $$
$$ \begin{align*}T^{(m,n)}=T_1^mT_2^n.\end{align*} $$
Then we obtain a
![]() $\mathbb {Z}^2$
-MPS
$\mathbb {Z}^2$
-MPS
![]() $(X,\mathcal {B}_X,m,T).$
$(X,\mathcal {B}_X,m,T).$
Let
be a finite measurable partition of X, where
![]() $_0[j]_0=\{x=\{x_n\}:x_0=j\}.$
On the one hand, take
$_0[j]_0=\{x=\{x_n\}:x_0=j\}.$
On the one hand, take
![]() $S=\{(0,n)\}_{n=1}^{\infty }$
. It is known that (see [Reference Walters23, p. 102, Theorem 4.26])
$S=\{(0,n)\}_{n=1}^{\infty }$
. It is known that (see [Reference Walters23, p. 102, Theorem 4.26])
 $$ \begin{align} h_{\mu}^S(T,\alpha)=\limsup_{n\to \infty}\frac{1}{n}H_{\mu}\bigg(\bigvee_{i=1}^{n}T^{-(0,i)}\alpha\bigg)=\log{2}>0. \end{align} $$
$$ \begin{align} h_{\mu}^S(T,\alpha)=\limsup_{n\to \infty}\frac{1}{n}H_{\mu}\bigg(\bigvee_{i=1}^{n}T^{-(0,i)}\alpha\bigg)=\log{2}>0. \end{align} $$
On the other hand, let
![]() $\vec {v}=(1,0)$
. Because
$\vec {v}=(1,0)$
. Because
![]() $T_1=Id_X$
, it is easy to see that
$T_1=Id_X$
, it is easy to see that
 $$ \begin{align*}h_\mu^{\vec{v},*}(\alpha)=0.\end{align*} $$
$$ \begin{align*}h_\mu^{\vec{v},*}(\alpha)=0.\end{align*} $$
It is known that for a
![]() $\mathbb {Z}^q$
-MPS
$\mathbb {Z}^q$
-MPS
![]() $(X,\mathcal {B}_X,\mu ,T)$
,
$(X,\mathcal {B}_X,\mu ,T)$
,
![]() $\mu $
has discrete spectrum if and only if
$\mu $
has discrete spectrum if and only if
![]() $\mathcal {B}_X=\mathcal {K}_\mu $
, where
$\mathcal {B}_X=\mathcal {K}_\mu $
, where
![]() $\mathcal {K}_\mu $
is the Kronecker algebra of
$\mathcal {K}_\mu $
is the Kronecker algebra of
![]() $(X,\mathcal {B}_X,\mu ,T)$
(see [Reference Glasner9]). Following the proof of Theorem 5.3, we can immediately obtain the relation between classical discrete spectrum and directional discrete spectrum.
$(X,\mathcal {B}_X,\mu ,T)$
(see [Reference Glasner9]). Following the proof of Theorem 5.3, we can immediately obtain the relation between classical discrete spectrum and directional discrete spectrum.
Theorem 5.5. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^2$
-MPS. Then the following statements are equivalent:
$\mathbb {Z}^2$
-MPS. Then the following statements are equivalent:
-
(a) there exist two directions
 $\vec {v}=(1,\beta _1),\vec {w}=(1,\beta _2)\in \mathbb {R}^2$
with
$\vec {v}=(1,\beta _1),\vec {w}=(1,\beta _2)\in \mathbb {R}^2$
with
 $\beta _1\neq \beta _2$
such that
$\beta _1\neq \beta _2$
such that
 $\mu $
has
$\mu $
has
 $\vec {v}$
-discrete spectrum and
$\vec {v}$
-discrete spectrum and
 $\vec {w}$
-discrete spectrum;
$\vec {w}$
-discrete spectrum; -
(b)
 $\mu $
has discrete spectrum.
$\mu $
has discrete spectrum.
Proof. (a)
![]() $\Rightarrow $
(b). If there exist two directions
$\Rightarrow $
(b). If there exist two directions
![]() $\vec {v}=(1,\beta _1)$
and
$\vec {v}=(1,\beta _1)$
and
![]() $\vec {w}=(1,\beta _2)$
with
$\vec {w}=(1,\beta _2)$
with
![]() $\beta _1\neq \beta _2$
such that
$\beta _1\neq \beta _2$
such that
![]() $\mu $
has
$\mu $
has
![]() $\vec {v}$
-discrete spectrum and
$\vec {v}$
-discrete spectrum and
![]() $\vec {w}$
-discrete spectrum, that is,
$\vec {w}$
-discrete spectrum, that is,
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}=\mathcal{B}_X=\mathcal{K}_\mu^{\kern2pt\vec{w}}.\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}=\mathcal{B}_X=\mathcal{K}_\mu^{\kern2pt\vec{w}}.\end{align*} $$
Fix
![]() $b\in (0,\infty )$
large enough. For any
$b\in (0,\infty )$
large enough. For any
![]() $B\in \mathcal {B}_X$
,
$B\in \mathcal {B}_X$
,
 $$ \begin{align*}\mathcal{P}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{v}}(b)\}}\quad \text{ and }\quad \mathcal{Q}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{w}}(b)\}}\end{align*} $$
$$ \begin{align*}\mathcal{P}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{v}}(b)\}}\quad \text{ and }\quad \mathcal{Q}_b:=\overline{\{U_T^{(m,n)}1_B:(m,n)\in \Lambda^{\vec{w}}(b)\}}\end{align*} $$
are compact subsets of
![]() $L^2(X,\mathcal {B}_X,\mu )$
. By the proof of Theorem 5.3, we deduce
$L^2(X,\mathcal {B}_X,\mu )$
. By the proof of Theorem 5.3, we deduce
 $$ \begin{align*}\overline{\{U_T^{(m,n)}1_B:(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
$$ \begin{align*}\overline{\{U_T^{(m,n)}1_B:(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
, which implies
$L^2(X,\mathcal {B}_X,\mu )$
, which implies
![]() $\mathcal {K}_\mu =\mathcal {B}_X$
. That is
$\mathcal {K}_\mu =\mathcal {B}_X$
. That is
![]() $\mu $
has discrete spectrum.
$\mu $
has discrete spectrum.
(b)
![]() $\Rightarrow $
(a). If
$\Rightarrow $
(a). If
![]() $\mu $
has discrete spectrum, then
$\mu $
has discrete spectrum, then
![]() $\mathcal {K}_\mu =\mathcal {B}_X$
, that is,
$\mathcal {K}_\mu =\mathcal {B}_X$
, that is,
 $$ \begin{align*}\overline{\{U_T^{(m,n)}1_B:(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
$$ \begin{align*}\overline{\{U_T^{(m,n)}1_B:(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
is a compact subset of
![]() $L^2(X,\mathcal {B}_X,\mu )$
for any
$L^2(X,\mathcal {B}_X,\mu )$
for any
![]() $B\in \mathcal {B}_X$
. Because for any
$B\in \mathcal {B}_X$
. Because for any
![]() $b\in (0,\infty )$
,
$b\in (0,\infty )$
,
![]() $\mathcal {P}_b$
and
$\mathcal {P}_b$
and
![]() $\mathcal {Q}_b$
are closed subsets of
$\mathcal {Q}_b$
are closed subsets of
 $\overline {\{U_T^{(m,n)}1_B:(m,n)\in \mathbb {Z}^2\}}$
, it follows that
$\overline {\{U_T^{(m,n)}1_B:(m,n)\in \mathbb {Z}^2\}}$
, it follows that
![]() $\mathcal {P}_b$
and
$\mathcal {P}_b$
and
![]() $\mathcal {Q}_b$
are compact subsets of
$\mathcal {Q}_b$
are compact subsets of
![]() $L^2(X,\mathcal {B}_X,\mu )$
, which implies that
$L^2(X,\mathcal {B}_X,\mu )$
, which implies that
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}=\mathcal{B}_X=\mathcal{K}_\mu^{\kern2pt\vec{w}}.\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}=\mathcal{B}_X=\mathcal{K}_\mu^{\kern2pt\vec{w}}.\end{align*} $$
Therefore,
![]() $\mu $
has
$\mu $
has
![]() $\vec {v}$
-discrete spectrum and
$\vec {v}$
-discrete spectrum and
![]() $\vec {w}$
-discrete spectrum.
$\vec {w}$
-discrete spectrum.
Remark 5.6. By the proof of Theorem 5.5, it is clear that if
![]() $\mu $
has discrete spectrum, then
$\mu $
has discrete spectrum, then
![]() $\mu $
has
$\mu $
has
![]() $\vec {v}$
-discrete spectrum for any direction
$\vec {v}$
-discrete spectrum for any direction
![]() $\vec {v}=(1,\beta )\in \mathbb {R}^2$
.
$\vec {v}=(1,\beta )\in \mathbb {R}^2$
.
Acknowledgements
The authors would like to thank Wen Huang and Xiangdong Ye for making many valuable suggestions. C. Liu was partially supported by NNSF of China (12090012, 12031019, 11731003), L. Xu was partially supported by NNSF of China (11801538, 11871188, 12031019) and the USTC Research Funds of the Double First-Class Initiative.
A Appendix. Proof of Claim 1
In this section, we complete the proof of Claim 1.
It follows from Lebesgue differentiation theorem (see [Reference Stein and Shakarchi22, p. 106, Corollary 1.5]) that we obtain the following result.
Lemma A.1. For any
![]() $E\in \mathcal {C}$
with
$E\in \mathcal {C}$
with
![]() $m(E)>0$
, we deduce
$m(E)>0$
, we deduce
 $$ \begin{align} \lim\limits_{u\to \infty}\frac{m(\eta^u(s,t)\bigcap E)}{m(\eta^u(s,t))}=1 \end{align} $$
$$ \begin{align} \lim\limits_{u\to \infty}\frac{m(\eta^u(s,t)\bigcap E)}{m(\eta^u(s,t))}=1 \end{align} $$
for m-a.e.
![]() $(s,t)\in E$
, where
$(s,t)\in E$
, where
![]() $\eta ^u(s,t)$
is the cube
$\eta ^u(s,t)$
is the cube
![]() $\eta ^u_{k,l}$
containing
$\eta ^u_{k,l}$
containing
![]() $(s,t)$
.
$(s,t)$
.
By Lemma A.1, we can prove the following consequence.
Lemma A.2. For
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
,
$x\in X$
,
 $$ \begin{align*}\lim\limits_{u\to\infty}f_u(x,s,t)=1_B(x,s,t)\end{align*} $$
$$ \begin{align*}\lim\limits_{u\to\infty}f_u(x,s,t)=1_B(x,s,t)\end{align*} $$
for m-a.e.
![]() $(s,t)\in [0,1)^2$
.
$(s,t)\in [0,1)^2$
.
Proof. It is clear that
![]() $f_u(x,s,t)$
is measurable on
$f_u(x,s,t)$
is measurable on
![]() $[0,1)^2$
for
$[0,1)^2$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
. For a given
$x\in X$
. For a given
![]() $g(s,t)\in L^{\infty }([0,1)^2,\mathcal {C},m)$
, we let
$g(s,t)\in L^{\infty }([0,1)^2,\mathcal {C},m)$
, we let
 $$ \begin{align*}g_u(s,t)=2^{2u}\int_{\eta^u_{k,l}}g(\xi,\zeta)\,d\xi \,d\zeta \quad\text{if }(s,t)\in \eta^u_{k,l},\end{align*} $$
$$ \begin{align*}g_u(s,t)=2^{2u}\int_{\eta^u_{k,l}}g(\xi,\zeta)\,d\xi \,d\zeta \quad\text{if }(s,t)\in \eta^u_{k,l},\end{align*} $$
where
![]() $u\in \mathbb {N}$
and
$u\in \mathbb {N}$
and
![]() $\eta ^u_{k,l}= [k2^{-u},(k+1)2^{-u})\times [l2^{-u},(l+1)2^{-u})$
for all
$\eta ^u_{k,l}= [k2^{-u},(k+1)2^{-u})\times [l2^{-u},(l+1)2^{-u})$
for all
 $k,l\in \{0,\ldots , 2^u-1\}$
. To prove this result, we prove a stronger result, that is, for any
$k,l\in \{0,\ldots , 2^u-1\}$
. To prove this result, we prove a stronger result, that is, for any
![]() $g(s,t)\in L^{\infty }([0,1)^2,\mathcal {C},m)$
, we have
$g(s,t)\in L^{\infty }([0,1)^2,\mathcal {C},m)$
, we have
 $\lim \limits _{u\to \infty } g_u(s,t)=g(s,t)$
for m-a.e.
$\lim \limits _{u\to \infty } g_u(s,t)=g(s,t)$
for m-a.e.
![]() $(s,t)\in [0,1)^2$
.
$(s,t)\in [0,1)^2$
.
First, we assume that
![]() $g(s,t)\in C([0,1)^2)$
, where
$g(s,t)\in C([0,1)^2)$
, where
![]() $C([0,1)^2)$
represents the set of all continuous functions defined on
$C([0,1)^2)$
represents the set of all continuous functions defined on
![]() $[0,1)^2$
. For any
$[0,1)^2$
. For any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta>0$
such that for any
$\delta>0$
such that for any
![]() $(s,t),(s',t')\in [0,1)^2$
with
$(s,t),(s',t')\in [0,1)^2$
with
![]() $|(s,t)-(s',t')|<\delta $
,
$|(s,t)-(s',t')|<\delta $
,
So for any u large enough, we obtain that
 $$ \begin{align*} |g_u(s,t)-g(s,t)|&=\bigg|2^{2u}\int_{\eta^u(s,t)}g(\xi,\zeta)-g(s,t)\,d\xi \,d\zeta\bigg|\\ &\leq 2^{2u}\int_{\eta^u(s,t)}|g(\xi,\zeta)-g(s,t)|\,d\xi \,d\zeta \leq \epsilon, \end{align*} $$
$$ \begin{align*} |g_u(s,t)-g(s,t)|&=\bigg|2^{2u}\int_{\eta^u(s,t)}g(\xi,\zeta)-g(s,t)\,d\xi \,d\zeta\bigg|\\ &\leq 2^{2u}\int_{\eta^u(s,t)}|g(\xi,\zeta)-g(s,t)|\,d\xi \,d\zeta \leq \epsilon, \end{align*} $$
where
![]() $I_u(s,t)$
is the one that contains
$I_u(s,t)$
is the one that contains
![]() $(s,t)$
in
$(s,t)$
in
![]() $\{\eta ^u_{k,l}:k,l\in \{0,\ldots , 2^u-1\}\}$
. It follows that
$\{\eta ^u_{k,l}:k,l\in \{0,\ldots , 2^u-1\}\}$
. It follows that
 $\lim \limits _{u\to \infty }g_u(s,t)= g(s,t)$
pointwise.
$\lim \limits _{u\to \infty }g_u(s,t)= g(s,t)$
pointwise.
Now we prove the general case. Fix a
![]() $g(s,t)\in L^{\infty }([0,1)^2,\mathcal {C},m)$
. For any
$g(s,t)\in L^{\infty }([0,1)^2,\mathcal {C},m)$
. For any
![]() $q\in \mathbb {N}$
, taking
$q\in \mathbb {N}$
, taking
![]() $\epsilon _q={1}/{q}$
, by Lusin theorem, there exists a measurable closed set
$\epsilon _q={1}/{q}$
, by Lusin theorem, there exists a measurable closed set
 $E_q\subset [0,1)^2$
such that
$E_q\subset [0,1)^2$
such that
![]() $E_q\subset E_{q+1}$
,
$E_q\subset E_{q+1}$
,
![]() $m(E_q)>1-\epsilon _q$
and
$m(E_q)>1-\epsilon _q$
and
![]() $g|_{E_q}$
is continuous. Then
$g|_{E_q}$
is continuous. Then
 $m(\bigcup _{q=1}^{\infty }E_q)=1$
. For each
$m(\bigcup _{q=1}^{\infty }E_q)=1$
. For each
![]() $q\in ~\mathbb {N}$
, we conclude
$q\in ~\mathbb {N}$
, we conclude
 $$ \begin{align*} \lim_{u\to\infty}|g_u(s,t)-g(s,t)|&\leq \lim_{u\to\infty}\bigg(2^{2u}\int_{\eta^u(s,t)\bigcap E_q}|g(\xi,\zeta)-g(s,t)|\,d\xi \,d\zeta\\ &\quad+2^{2u}\int_{\eta^u(s,t)\bigcap E_q^c}|g(\xi,\zeta)-g(s,t)|\,d\xi \,d\zeta\bigg)\\ &\leq 0+\lim_{u\to\infty}2^{2u}\bigg(m\bigg(E_q^c \bigcap \eta^u(s,t)\bigg)\bigg)M\overset{(A.1)}=0, \end{align*} $$
$$ \begin{align*} \lim_{u\to\infty}|g_u(s,t)-g(s,t)|&\leq \lim_{u\to\infty}\bigg(2^{2u}\int_{\eta^u(s,t)\bigcap E_q}|g(\xi,\zeta)-g(s,t)|\,d\xi \,d\zeta\\ &\quad+2^{2u}\int_{\eta^u(s,t)\bigcap E_q^c}|g(\xi,\zeta)-g(s,t)|\,d\xi \,d\zeta\bigg)\\ &\leq 0+\lim_{u\to\infty}2^{2u}\bigg(m\bigg(E_q^c \bigcap \eta^u(s,t)\bigg)\bigg)M\overset{(A.1)}=0, \end{align*} $$
for m-a.e.
![]() $(s,t)\in E_q$
, where
$(s,t)\in E_q$
, where
![]() $M=\max _{(s,t)\in [0,1)^2}\{|g(s,t)|\}$
. It follows from
$M=\max _{(s,t)\in [0,1)^2}\{|g(s,t)|\}$
. It follows from
 $m(\bigcup _{q=1}^{\infty } E_q)=1$
that
$m(\bigcup _{q=1}^{\infty } E_q)=1$
that
![]() $g_u(s,t)$
converges to
$g_u(s,t)$
converges to
![]() $g(s,t)$
for m-a.e.
$g(s,t)$
for m-a.e.
![]() $(s,t)\in [0,1)^2$
as
$(s,t)\in [0,1)^2$
as
![]() $u\to \infty $
.
$u\to \infty $
.
Now we are able to prove Claim 1.
Proof of Claim 1
Before proving it, we introduce a notation, that is,
![]() $U_{\phi _{m,n}} h=h\circ \phi _{m,n}$
for all
$U_{\phi _{m,n}} h=h\circ \phi _{m,n}$
for all
![]() $h\in L^2(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu })$
. Because
$h\in L^2(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu })$
. Because
![]() $B\in \mathcal {K}_{\widetilde {\mu }}$
, it follows that
$B\in \mathcal {K}_{\widetilde {\mu }}$
, it follows that
 $$ \begin{align*}\overline{\{W^n1_B:n\in\mathbb{Z}\}}\text{ is compact in }L^2(\widetilde{X},\widetilde{\mathcal{B}},\widetilde{\mu}),\end{align*} $$
$$ \begin{align*}\overline{\{W^n1_B:n\in\mathbb{Z}\}}\text{ is compact in }L^2(\widetilde{X},\widetilde{\mathcal{B}},\widetilde{\mu}),\end{align*} $$
which implies that
 $$ \begin{align} \overline{\{U_{\phi_{m,n}}1_B:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}} \text{ is compact in } L^2(\widetilde{X},\widetilde{\mathcal{B}},\widetilde{\mu}). \end{align} $$
$$ \begin{align} \overline{\{U_{\phi_{m,n}}1_B:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}} \text{ is compact in } L^2(\widetilde{X},\widetilde{\mathcal{B}},\widetilde{\mu}). \end{align} $$
It follows from (A.2) that for any
![]() $\epsilon>0$
, there exists a finite
$\epsilon>0$
, there exists a finite
![]() $\epsilon $
-net
$\epsilon $
-net
 $\{U_{\phi _{m_i,n_i}}1_B\}_{i=1}^p$
with
$\{U_{\phi _{m_i,n_i}}1_B\}_{i=1}^p$
with
![]() $(m_i,n_i)\in \mathbb {Z}^2$
and
$(m_i,n_i)\in \mathbb {Z}^2$
and
![]() $|\beta m_i-n_i|<1$
. That is, for any
$|\beta m_i-n_i|<1$
. That is, for any
![]() $(m,n)\in \mathbb {Z}^2$
with
$(m,n)\in \mathbb {Z}^2$
with
![]() $|\beta m-n|<1$
, there exists
$|\beta m-n|<1$
, there exists
![]() $i\in \{1,2,\ldots ,p\}$
such that
$i\in \{1,2,\ldots ,p\}$
such that
 $$ \begin{align*}\bigg(\int|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,d(\mu\times m)\bigg)^{{1}/{2}}=\|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B\|_{2}<\epsilon.\end{align*} $$
$$ \begin{align*}\bigg(\int|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,d(\mu\times m)\bigg)^{{1}/{2}}=\|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B\|_{2}<\epsilon.\end{align*} $$
For a fixed u, we consider
 $\{U_{\phi _{m_i,n_i}}f_u\}_{i=1}^p$
. By Minkowski’s inequality for integrals (see [Reference Folland8, p. 194]), we conclude
$\{U_{\phi _{m_i,n_i}}f_u\}_{i=1}^p$
. By Minkowski’s inequality for integrals (see [Reference Folland8, p. 194]), we conclude
 $$ \begin{align*} &\|U_{\phi_{m_i,n_i}}f_u-U_{\phi_{m,n}}f_u\|_{2}\\&\quad=\bigg(\int_{X}\int_{[0,1)^2}|U_{\phi_{m_i,n_i}}f_u-U_{\phi_{m,n}}f_u|^2\,dm \,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}\sum_{k,l}\int_{\eta^u_{k,l}}|U_{\phi_{m_i,n_i}}f_u-U_{\phi_{m,n}}f_u|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}\sum_{k,l}\int_{\eta^u_{k,l}}|U_{T}^{(m_i,n_i)}\int_{\eta^u_{k,l}}1_Bdm-U_{T}^{(m,n)}\int_{\eta^u_{k,l}}1_Bdm|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}\sum_{k,l}m(\eta^u_{k,l})|\int_{\eta^u_{k,l}}(U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B)\,dm|^2\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad\le\bigg(\int_{X}\sum_{k,l}m(\eta^u_{k,l})\int_{\eta^u_{k,l}}|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\frac{1}{2^u}\bigg(\int_{X}\int_{[0,1)^2}|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\frac{1}{2^u}\bigg(\int_{X\times [0,1)^2}|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,d(\mu\times m)\bigg)^{{1}/{2}}\\ &\quad<\frac{1}{2^u}\epsilon. \end{align*} $$
$$ \begin{align*} &\|U_{\phi_{m_i,n_i}}f_u-U_{\phi_{m,n}}f_u\|_{2}\\&\quad=\bigg(\int_{X}\int_{[0,1)^2}|U_{\phi_{m_i,n_i}}f_u-U_{\phi_{m,n}}f_u|^2\,dm \,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}\sum_{k,l}\int_{\eta^u_{k,l}}|U_{\phi_{m_i,n_i}}f_u-U_{\phi_{m,n}}f_u|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}\sum_{k,l}\int_{\eta^u_{k,l}}|U_{T}^{(m_i,n_i)}\int_{\eta^u_{k,l}}1_Bdm-U_{T}^{(m,n)}\int_{\eta^u_{k,l}}1_Bdm|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}\sum_{k,l}m(\eta^u_{k,l})|\int_{\eta^u_{k,l}}(U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B)\,dm|^2\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad\le\bigg(\int_{X}\sum_{k,l}m(\eta^u_{k,l})\int_{\eta^u_{k,l}}|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\frac{1}{2^u}\bigg(\int_{X}\int_{[0,1)^2}|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\frac{1}{2^u}\bigg(\int_{X\times [0,1)^2}|U_{\phi_{m_i,n_i}}1_B-U_{\phi_{m,n}}1_B|^2\,d(\mu\times m)\bigg)^{{1}/{2}}\\ &\quad<\frac{1}{2^u}\epsilon. \end{align*} $$
Hence,
 $\{U_{\phi _{m_i,n_i}}f_u\}_{i=1}^p$
is a finite
$\{U_{\phi _{m_i,n_i}}f_u\}_{i=1}^p$
is a finite
![]() $\epsilon /2^u$
-net of
$\epsilon /2^u$
-net of
 $\overline {\{U_{\phi _{m,n}}f_u:|\beta m- n|<1,(m,n)\in \mathbb {Z}^2\}}$
, which implies that
$\overline {\{U_{\phi _{m,n}}f_u:|\beta m- n|<1,(m,n)\in \mathbb {Z}^2\}}$
, which implies that
 $$ \begin{align*}\overline{\{U_{\phi_{m,n}}f_u:|\beta m-n|<1,(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
$$ \begin{align*}\overline{\{U_{\phi_{m,n}}f_u:|\beta m-n|<1,(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
is compact in
![]() $L^2(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu })$
for all
$L^2(\widetilde {X},\widetilde {\mathcal {B}},\widetilde {\mu })$
for all
![]() $u\in \mathbb {N}.$
For a fixed
$u\in \mathbb {N}.$
For a fixed
![]() $u\in \mathbb {N}$
, we take a finite
$u\in \mathbb {N}$
, we take a finite
![]() $\epsilon /2^{u}$
-net
$\epsilon /2^{u}$
-net
 $\{U_{\phi _{m_i,n_i}}f_u\}_{i=1}^p.$
Note that
$\{U_{\phi _{m_i,n_i}}f_u\}_{i=1}^p.$
Note that
 $$ \begin{align*}U_{\phi_{m,n}}f_u(x,s,t)=f_u(T^{(m,n)}x,s,t).\end{align*} $$
$$ \begin{align*}U_{\phi_{m,n}}f_u(x,s,t)=f_u(T^{(m,n)}x,s,t).\end{align*} $$
So for any
![]() $(m,n)\in \mathbb {Z}^2$
with
$(m,n)\in \mathbb {Z}^2$
with
![]() $|\beta m_i-n_i|<1$
, there exists
$|\beta m_i-n_i|<1$
, there exists
![]() $i\in \{1,2,\ldots ,p\}$
such that
$i\in \{1,2,\ldots ,p\}$
such that
 $$ \begin{align} \frac{\epsilon}{2^{u}}&>\|U_{\phi_{m,n}}f_u-U_{\phi_{m_i,n_i}}f_u\|_{2}\nonumber\\ &=\bigg(\int_{X}\int_{[0,1)^2}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}. \end{align} $$
$$ \begin{align} \frac{\epsilon}{2^{u}}&>\|U_{\phi_{m,n}}f_u-U_{\phi_{m_i,n_i}}f_u\|_{2}\nonumber\\ &=\bigg(\int_{X}\int_{[0,1)^2}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}. \end{align} $$
For any
![]() $(s,t)\in [0,1)^2$
, there exist
$(s,t)\in [0,1)^2$
, there exist
![]() $k,l\in \{0,\ldots , 2^u-1\}$
such that
$k,l\in \{0,\ldots , 2^u-1\}$
such that
![]() $(s,t)\in \eta _{k,l}^u$
. Hence,
$(s,t)\in \eta _{k,l}^u$
. Hence,
 $$ \begin{align*} &\|U_T^{(m,n)}f_u(\cdot,s,t)-U_T^{(m_i,n_i)}f_u(\cdot,s,t)\|_{2}\\ &\quad=\bigg(\int_{X}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}2^{2u}\int_{\eta^u_{k,l}}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad\leq2^u\bigg(\int_{X}\int_{[0,1)^2}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad\overset{(A.3)}\leq 2^{u}\cdot\frac{\epsilon}{2^{u}}=\epsilon. \end{align*} $$
$$ \begin{align*} &\|U_T^{(m,n)}f_u(\cdot,s,t)-U_T^{(m_i,n_i)}f_u(\cdot,s,t)\|_{2}\\ &\quad=\bigg(\int_{X}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad=\bigg(\int_{X}2^{2u}\int_{\eta^u_{k,l}}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad\leq2^u\bigg(\int_{X}\int_{[0,1)^2}|f_u(T^{(m,n)}x,s,t)-f_u(T^{(m_i,n_i)}x,s,t)|^2\,dm\,{d\hspace{-1pt}\mu}\bigg)^{{1}/{2}}\\ &\quad\overset{(A.3)}\leq 2^{u}\cdot\frac{\epsilon}{2^{u}}=\epsilon. \end{align*} $$
Hence for a fixed
![]() $(s,t)\in [0,1)^2$
,
$(s,t)\in [0,1)^2$
,
 $\overline {\{U_{T}^{(m,m)}f_u:|\beta m- n|<1,(m,n)\in \mathbb {Z}^2\}}$
has a finite
$\overline {\{U_{T}^{(m,m)}f_u:|\beta m- n|<1,(m,n)\in \mathbb {Z}^2\}}$
has a finite
![]() $\epsilon $
-net
$\epsilon $
-net
 $\{U_{T}^{(m_i,n_i)}f_u(x,s,t)\}_{i=1}^p$
. It follows that
$\{U_{T}^{(m_i,n_i)}f_u(x,s,t)\}_{i=1}^p$
. It follows that
 $$ \begin{align*}\overline{\{U_{T}^{(m,m)}f_u:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
$$ \begin{align*}\overline{\{U_{T}^{(m,m)}f_u:|\beta m- n|<1,(m,n)\in \mathbb{Z}^2\}}\end{align*} $$
is compact in
![]() $L^2(X,\mathcal {B}_X,\mu )$
for each
$L^2(X,\mathcal {B}_X,\mu )$
for each
![]() $(s,t)\in [0,1)^2$
. This ends the proof of the first statement in Claim 1.
$(s,t)\in [0,1)^2$
. This ends the proof of the first statement in Claim 1.
By Lemma A.1, we deduce that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
$x\in X$
 $$ \begin{align*}\lim_{u\to\infty}f_u(x,s,t)=1_B(x,s,t)\end{align*} $$
$$ \begin{align*}\lim_{u\to\infty}f_u(x,s,t)=1_B(x,s,t)\end{align*} $$
for m-a.e.
![]() $(s,t)\in [0,1)^2.$
By dominated convergence theorem, we conclude that
$(s,t)\in [0,1)^2.$
By dominated convergence theorem, we conclude that
 $$ \begin{align*}\lim_{u\to\infty}\|f(\cdot,s,t)-1_{B^{(s,t)}}\|_{2}=0\end{align*} $$
$$ \begin{align*}\lim_{u\to\infty}\|f(\cdot,s,t)-1_{B^{(s,t)}}\|_{2}=0\end{align*} $$
for m-a.e.
![]() $(s,t)\in [0,1)^2.$
Now we finish the proof of Claim 1.
$(s,t)\in [0,1)^2.$
Now we finish the proof of Claim 1.
B Appendix. Results for
 $\mathbb {Z}^q$
-MPS
$\mathbb {Z}^q$
-MPS
In this section, we introduce the corresponding results of
![]() $\mathbb {Z}^q$
-MPS, which are proved by exactly the same methods for the case of
$\mathbb {Z}^q$
-MPS, which are proved by exactly the same methods for the case of
![]() $\mathbb {Z}^2$
-MPS. Let
$\mathbb {Z}^2$
-MPS. Let
![]() $(X ,\mathcal {B}_X, \mu , T)$
be a
$(X ,\mathcal {B}_X, \mu , T)$
be a
![]() $\mathbb {Z}^q$
-MPS. For a fixed finite measurable partition
$\mathbb {Z}^q$
-MPS. For a fixed finite measurable partition
![]() $\alpha $
of X and an infinite subset
$\alpha $
of X and an infinite subset
![]() $S=\{\vec {w}_i\}_{i=1}^{\infty }$
of
$S=\{\vec {w}_i\}_{i=1}^{\infty }$
of
![]() $\mathbb {Z}^q$
, we put
$\mathbb {Z}^q$
, we put
 $$ \begin{align*}h^S_{\mu}(T,\alpha)= \limsup_{k\to \infty} \frac{1}{k}H_\mu \bigg(\bigvee_{i=1}^k T^{-\vec{w}_i} \alpha\bigg).\end{align*} $$
$$ \begin{align*}h^S_{\mu}(T,\alpha)= \limsup_{k\to \infty} \frac{1}{k}H_\mu \bigg(\bigvee_{i=1}^k T^{-\vec{w}_i} \alpha\bigg).\end{align*} $$
Then we can define the sequence entropy of T for the infinite subset S by
 $$ \begin{align*}h^S_{\mu}(T)=\sup_{\alpha}h^S_{\mu}(T,\alpha),\end{align*} $$
$$ \begin{align*}h^S_{\mu}(T)=\sup_{\alpha}h^S_{\mu}(T,\alpha),\end{align*} $$
where the supremum is taken over all finite measurable partitions of X.
Now we define directional sequence entropy for the case of
![]() $\mathbb {Z}^q$
-actions. Let
$\mathbb {Z}^q$
-actions. Let
![]() $\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector and
$\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector and
 $\textbf {b}=(b_2,\ldots ,b_q)\in \mathbb {R}^{q-1}_+:=\{\textbf {u}=(u_1,\ldots ,u_{q-1})\in \mathbb {R}^{q-1}:u_i>0\}$
. We put
$\textbf {b}=(b_2,\ldots ,b_q)\in \mathbb {R}^{q-1}_+:=\{\textbf {u}=(u_1,\ldots ,u_{q-1})\in \mathbb {R}^{q-1}:u_i>0\}$
. We put
 $$ \begin{align*}\Lambda^{\vec{v}}(\textbf{b})&=\{\vec{w}=(m_1,\ldots,m_q)\in\mathbb{Z}^q:\beta_i m_1-b_i/2\leq m_i\\ &\leq \beta_i m_1+b_i/2,\quad i\in\{2,\ldots,q\}\}.\end{align*} $$
$$ \begin{align*}\Lambda^{\vec{v}}(\textbf{b})&=\{\vec{w}=(m_1,\ldots,m_q)\in\mathbb{Z}^q:\beta_i m_1-b_i/2\leq m_i\\ &\leq \beta_i m_1+b_i/2,\quad i\in\{2,\ldots,q\}\}.\end{align*} $$
Define the
![]() $\vec {v}$
-directional Kronecker algebra by
$\vec {v}$
-directional Kronecker algebra by
 $$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(\textbf{b})=\{B\in\mathcal{B}_X: \overline{\{U_T^{\vec{w}}1_B :\vec{w}\in \Lambda^{\vec{v}}(\textbf{b}) \}}\text{ is compact in } L^2(X,\mathcal{B}_X,\mu) \},\end{align*} $$
$$ \begin{align*}\mathcal{K}_\mu^{\kern2pt\vec{v}}(\textbf{b})=\{B\in\mathcal{B}_X: \overline{\{U_T^{\vec{w}}1_B :\vec{w}\in \Lambda^{\vec{v}}(\textbf{b}) \}}\text{ is compact in } L^2(X,\mathcal{B}_X,\mu) \},\end{align*} $$
where
 $U_T^{\vec {w}}:L^2(X,\mathcal {B}_X,\mu )\to L^2(X,\mathcal {B}_X,\mu )$
is the unitary operator such that
$U_T^{\vec {w}}:L^2(X,\mathcal {B}_X,\mu )\to L^2(X,\mathcal {B}_X,\mu )$
is the unitary operator such that
 $$ \begin{align*}U_T^{\vec{w}}f=f\circ T^{\vec{w}}\quad \text{ for all }f\in L^2(X,\mathcal{B}_X,\mu).\end{align*} $$
$$ \begin{align*}U_T^{\vec{w}}f=f\circ T^{\vec{w}}\quad \text{ for all }f\in L^2(X,\mathcal{B}_X,\mu).\end{align*} $$
Similarly, we can prove that
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(\textbf {b})$
is a
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(\textbf {b})$
is a
![]() $\sigma $
-algebra and the definition of
$\sigma $
-algebra and the definition of
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(\textbf {b})$
is independent of the selection of
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(\textbf {b})$
is independent of the selection of
![]() $\textbf {b}$
. So we omit
$\textbf {b}$
. So we omit
![]() $\textbf {b}$
in
$\textbf {b}$
in
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}(\textbf {b})$
and write it as
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}(\textbf {b})$
and write it as
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}$
.
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}$
.
Theorem B.1. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^q$
-MPS,
$\mathbb {Z}^q$
-MPS,
![]() $\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector and
$\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector and
 $\textbf {b}=(b_2,\ldots ,b_q)\in \mathbb {R}^{q-1}_+$
. Let
$\textbf {b}=(b_2,\ldots ,b_q)\in \mathbb {R}^{q-1}_+$
. Let
![]() $\alpha $
be a finite measurable partition of X. For any infinite subset
$\alpha $
be a finite measurable partition of X. For any infinite subset
![]() $S'$
of
$S'$
of
![]() $\Lambda ^{\vec {v}}(\textbf {b})$
,
$\Lambda ^{\vec {v}}(\textbf {b})$
,
 $$ \begin{align*}h^{S'}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
$$ \begin{align*}h^{S'}_{\mu}(T,\alpha)\leq H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
Moreover, there exists an infinite subset
 $S=\{\vec {w}_i=(m_1^{(i)},\ldots ,m_q^{(i)})\}_{i=1}^{\infty }$
of
$S=\{\vec {w}_i=(m_1^{(i)},\ldots ,m_q^{(i)})\}_{i=1}^{\infty }$
of
![]() $\Lambda ^{\vec {v}}(\textbf {b})$
such that
$\Lambda ^{\vec {v}}(\textbf {b})$
such that
 $\{m_1^{(i)}\}_{i=1}^{\infty }$
is strictly monotone and
$\{m_1^{(i)}\}_{i=1}^{\infty }$
is strictly monotone and
 $$ \begin{align*}h^{S}_{\mu}(T,\alpha)=H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
$$ \begin{align*}h^{S}_{\mu}(T,\alpha)=H_\mu(\alpha|\mathcal{K}_\mu^{\kern2pt\vec{v}}).\end{align*} $$
Remark B.2. Let
![]() $\alpha $
be a finite measurable partition of X. We define
$\alpha $
be a finite measurable partition of X. We define
 $$ \begin{align}h_\mu^{\vec{v},*}(\alpha)=\max\limits_{S\subset \Lambda^{\vec{v}}(\textbf{b})}\{h^{S}_{\mu}(T,\alpha)\}.\end{align} $$
$$ \begin{align}h_\mu^{\vec{v},*}(\alpha)=\max\limits_{S\subset \Lambda^{\vec{v}}(\textbf{b})}\{h^{S}_{\mu}(T,\alpha)\}.\end{align} $$
By Theorem B.1,
 $h_\mu ^{\vec {v},*}(\alpha )=H_\mu (\alpha |\mathcal {K}_\mu ^{\kern2pt\vec {v}})$
and then (B.1) is well defined because it is independent of the selection of
$h_\mu ^{\vec {v},*}(\alpha )=H_\mu (\alpha |\mathcal {K}_\mu ^{\kern2pt\vec {v}})$
and then (B.1) is well defined because it is independent of the selection of
![]() $\textbf {b}$
.
$\textbf {b}$
.
Corresponding to the case of
![]() $\mathbb {Z}^2$
-MPS, we have the following definitions.
$\mathbb {Z}^2$
-MPS, we have the following definitions.
Definition B.3. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^q$
-MPS and
$\mathbb {Z}^q$
-MPS and
![]() $\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector.
$\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector.
-
(a) We say
 $\mu $
has
$\mu $
has
 $\vec {v}$
-discrete spectrum if
$\vec {v}$
-discrete spectrum if
 $\mathcal {K}_\mu ^{\kern2pt\vec {v}}=\mathcal {B}_X$
;
$\mathcal {K}_\mu ^{\kern2pt\vec {v}}=\mathcal {B}_X$
; -
(b) we say
 $(X,\mathcal {B}_X,\mu ,T)$
is
$(X,\mathcal {B}_X,\mu ,T)$
is
 $\vec {v}$
-null if for any
$\vec {v}$
-null if for any
 $\textbf {b}=(b_2,\ldots ,b_q)\in \mathbb {R}_+^{q-1}$
and infinite subset
$\textbf {b}=(b_2,\ldots ,b_q)\in \mathbb {R}_+^{q-1}$
and infinite subset
 $S=\{\vec {w}_i=(m_1^{(i)},\ldots ,m_q^{(i)})\}_{i=1}^{\infty }$
of
$S=\{\vec {w}_i=(m_1^{(i)},\ldots ,m_q^{(i)})\}_{i=1}^{\infty }$
of
 $\Lambda ^{\vec {v}}(\textbf {b}) $
,
$\Lambda ^{\vec {v}}(\textbf {b}) $
,
 $h^{S}_{\mu }(T)=0$
.
$h^{S}_{\mu }(T)=0$
.
Now we state main conclusions for the case of
![]() $\mathbb {Z}^q$
-actions corresponding to
$\mathbb {Z}^q$
-actions corresponding to
![]() $\mathbb {Z}^2$
-actions, which are proved by exactly the same methods for the case of
$\mathbb {Z}^2$
-actions, which are proved by exactly the same methods for the case of
![]() $\mathbb {Z}^2$
-MPS as follows.
$\mathbb {Z}^2$
-MPS as follows.
Theorem B.4. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^q$
-MPS and
$\mathbb {Z}^q$
-MPS and
![]() $\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector. Then the following two conditions are equivalent:
$\vec {v}=(1,\beta _2,\ldots ,\beta _q)\in \mathbb {R}^q$
be a direction vector. Then the following two conditions are equivalent:
-
(a)
 $\mu $
has
$\mu $
has
 $\vec {v}$
-discrete spectrum;
$\vec {v}$
-discrete spectrum; -
(b)
 $(X,\mathcal {B}_X,\mu ,T)$
is
$(X,\mathcal {B}_X,\mu ,T)$
is
 $\vec {v}$
-null.
$\vec {v}$
-null.
Theorem B.5. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^q$
-MPS and
$\mathbb {Z}^q$
-MPS and
![]() $\alpha $
be a finite measurable partition of X. If there exists an infinite subset S of
$\alpha $
be a finite measurable partition of X. If there exists an infinite subset S of
![]() $\mathbb {Z}^q$
such that
$\mathbb {Z}^q$
such that
 $h^S_{\mu }(T,\alpha )>0$
, then there are at most
$h^S_{\mu }(T,\alpha )>0$
, then there are at most
![]() $q-1$
linearly independent directions
$q-1$
linearly independent directions
 $\{\vec {v_i}=(1,\beta ^i_2,\ldots ,\beta ^i_q)\}_{i=1}^{q-1}\subset \mathbb {R}^q$
such that
$\{\vec {v_i}=(1,\beta ^i_2,\ldots ,\beta ^i_q)\}_{i=1}^{q-1}\subset \mathbb {R}^q$
such that
 $$ \begin{align*}h_\mu^{\vec{v_i},*}(\alpha)=0,\quad i=1,2,\ldots,q-1.\end{align*} $$
$$ \begin{align*}h_\mu^{\vec{v_i},*}(\alpha)=0,\quad i=1,2,\ldots,q-1.\end{align*} $$
Theorem B.6. Let
![]() $(X,\mathcal {B}_X,\mu ,T)$
be a
$(X,\mathcal {B}_X,\mu ,T)$
be a
![]() $\mathbb {Z}^q$
-MPS. Then the following statements are equivalent:
$\mathbb {Z}^q$
-MPS. Then the following statements are equivalent:
-
(a) there exist q linearly independent directions
 $\{\vec {v_i}=(1,\beta ^i_2,\ldots ,\beta ^i_q)\}_{i=1}^{q}\subset \mathbb {R}^q$
such that
$\{\vec {v_i}=(1,\beta ^i_2,\ldots ,\beta ^i_q)\}_{i=1}^{q}\subset \mathbb {R}^q$
such that
 $\mu $
has
$\mu $
has
 $\vec {v_i}$
-discrete spectrum for all
$\vec {v_i}$
-discrete spectrum for all
 $i=1,\ldots ,q$
;
$i=1,\ldots ,q$
; -
(b)
 $\mu $
has discrete spectrum.
$\mu $
has discrete spectrum.