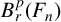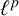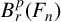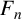1 Introduction
For a unital Banach algebra A, an idempotent in A is an element a with
![]() $a^2=a$
. Obviously, both the zero element
$a^2=a$
. Obviously, both the zero element
![]() $0$
and the unit element I are idempotents in A. An idempotent a in A is a
$0$
and the unit element I are idempotents in A. An idempotent a in A is a
![]() $\textit {nontrivial idempotent}$
if a is neither
$\textit {nontrivial idempotent}$
if a is neither
![]() $0$
nor I. In 1949, Kadison and Kaplansky conjectured that if
$0$
nor I. In 1949, Kadison and Kaplansky conjectured that if
![]() $\Gamma $
is a torsion-free discrete group, then the reduced group
$\Gamma $
is a torsion-free discrete group, then the reduced group
![]() $C^{\ast }$
-algebra
$C^{\ast }$
-algebra
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents (or, equivalently, projections). Since then, there have been many achievements around the conjecture, but whether it is true is still unknown.
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents (or, equivalently, projections). Since then, there have been many achievements around the conjecture, but whether it is true is still unknown.
An important approach to the Kadison–Kaplansky conjecture is through the Baum–Connes conjecture, namely, if
![]() $\Gamma $
is a torsion-free discrete group that satisfies the Baum–Connes conjecture (actually, surjectivity of the assembly map is sufficient), then
$\Gamma $
is a torsion-free discrete group that satisfies the Baum–Connes conjecture (actually, surjectivity of the assembly map is sufficient), then
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents (see [Reference Baum, Connes, Higson and Doran1]). This includes a large class of groups. For example, Higson and Kasparov [Reference Higson and Kasparov10] showed that the Baum–Connes conjecture is true for T-amenable groups, which include amenable groups and free groups, Lafforgue [Reference Lafforgue13] and Mineyev and Yu [Reference Mineyev and Yu15] proved that the Baum–Connes conjecture holds for hyperbolic groups. Hence, if
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents (see [Reference Baum, Connes, Higson and Doran1]). This includes a large class of groups. For example, Higson and Kasparov [Reference Higson and Kasparov10] showed that the Baum–Connes conjecture is true for T-amenable groups, which include amenable groups and free groups, Lafforgue [Reference Lafforgue13] and Mineyev and Yu [Reference Mineyev and Yu15] proved that the Baum–Connes conjecture holds for hyperbolic groups. Hence, if
![]() $\Gamma $
is a torsion-free discrete T-amenable group or hyperbolic group, then
$\Gamma $
is a torsion-free discrete T-amenable group or hyperbolic group, then
![]() $C^{\ast }_r(\Gamma )$
contains no nontrivial idempotents. For hyperbolic groups, there is another way to study the Kadison–Kaplansky conjecture, which is due to Puschnigg [Reference Puschnigg20] by using local cyclic homology.
$C^{\ast }_r(\Gamma )$
contains no nontrivial idempotents. For hyperbolic groups, there is another way to study the Kadison–Kaplansky conjecture, which is due to Puschnigg [Reference Puschnigg20] by using local cyclic homology.
There are many more results when
![]() $\Gamma $
is a free group
$\Gamma $
is a free group
![]() $F_n$
. It was first shown by Pimsner and Voiculescu [Reference Pimsner and Voiculescu19] that
$F_n$
. It was first shown by Pimsner and Voiculescu [Reference Pimsner and Voiculescu19] that
![]() $C^{\ast }_r(F_n)$
has no nontrivial idempotents (see also [Reference Cohen and Figà-Talamanca2, Reference Connes3]).
$C^{\ast }_r(F_n)$
has no nontrivial idempotents (see also [Reference Cohen and Figà-Talamanca2, Reference Connes3]).
For a discrete group
![]() $\Gamma $
, if we consider the left regular representation of
$\Gamma $
, if we consider the left regular representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\ell ^p$
-space
$\ell ^p$
-space
![]() $\ell ^p(\Gamma )$
, then we can define the reduced group
$\ell ^p(\Gamma )$
, then we can define the reduced group
![]() $\ell ^p$
-operator algebra
$\ell ^p$
-operator algebra
![]() $B^p_r(\Gamma )$
of
$B^p_r(\Gamma )$
of
![]() $\Gamma $
for
$\Gamma $
for
![]() ${p\in [1,\infty ]}$
(see Definition 2.1). These
${p\in [1,\infty ]}$
(see Definition 2.1). These
![]() $\ell ^p$
-operator algebras have been studied intensively; for example, the K-theory of some reduced group
$\ell ^p$
-operator algebras have been studied intensively; for example, the K-theory of some reduced group
![]() $\ell ^p$
-operator algebras [Reference Liao and Yu14, Reference Phillips16], the rigidity results of reduced group
$\ell ^p$
-operator algebras [Reference Liao and Yu14, Reference Phillips16], the rigidity results of reduced group
![]() $\ell ^p$
-operator algebras for
$\ell ^p$
-operator algebras for
![]() $p\neq 2$
[Reference Gardella and Thiel7], and the simplicity and tracial state of some reduced group
$p\neq 2$
[Reference Gardella and Thiel7], and the simplicity and tracial state of some reduced group
![]() $\ell ^p$
-operator algebras [Reference Gardella and Thiel7, Reference Hejazian and Pooya9, Reference Phillips17]. Phillips also posed a question concerning the existence of nontrivial idempotents in
$\ell ^p$
-operator algebras [Reference Gardella and Thiel7, Reference Hejazian and Pooya9, Reference Phillips17]. Phillips also posed a question concerning the existence of nontrivial idempotents in
![]() $B^p_r(F_n)$
[Reference Phillips18].
$B^p_r(F_n)$
[Reference Phillips18].
Question 1.1 [Reference Phillips18, part of Problem 9.3]
For
![]() $n\in \{2,3,\ldots \}$
and
$n\in \{2,3,\ldots \}$
and
![]() $p\in [1,\infty )$
, does
$p\in [1,\infty )$
, does
![]() $B^p_r(F_n)$
have nontrivial idempotents?
$B^p_r(F_n)$
have nontrivial idempotents?
We answer this question (see Example 3.10) by using property
![]() $(RD)_q$
of groups (see Definition 3.2) introduced by Liao and Yu [Reference Liao and Yu14]. The main result of this paper is the following theorem.
$(RD)_q$
of groups (see Definition 3.2) introduced by Liao and Yu [Reference Liao and Yu14]. The main result of this paper is the following theorem.
Theorem 1.2 (Theorem 3.8)
Let
![]() $p\in [1,\infty ]$
, q be its dual number and
$p\in [1,\infty ]$
, q be its dual number and
![]() $\Gamma $
be a discrete group. Assume
$\Gamma $
be a discrete group. Assume
![]() $\Gamma $
has property
$\Gamma $
has property
![]() $(RD)_q$
. If
$(RD)_q$
. If
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then both
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then both
![]() $B^p_r(\Gamma )$
and
$B^p_r(\Gamma )$
and
![]() $B^q_r(\Gamma )$
also have no nontrivial idempotents.
$B^q_r(\Gamma )$
also have no nontrivial idempotents.
Since the groups with property
![]() $(RD)$
have property
$(RD)$
have property
![]() $(RD)_q$
for any
$(RD)_q$
for any
![]() $q\in [1,2]$
, we have the following corollary.
$q\in [1,2]$
, we have the following corollary.
Corollary 1.3 (Corollary 3.9)
Let
![]() $\Gamma $
be a discrete group. Assume
$\Gamma $
be a discrete group. Assume
![]() $\Gamma $
has property
$\Gamma $
has property
![]() $(RD)$
. If
$(RD)$
. If
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then for any
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then for any
![]() $p\in [1,\infty ]$
,
$p\in [1,\infty ]$
,
![]() $B^p_r(\Gamma )$
also has no nontrivial idempotents.
$B^p_r(\Gamma )$
also has no nontrivial idempotents.
Haagerup [Reference Haagerup8] proved that the free group
![]() $F_n$
has property
$F_n$
has property
![]() $(RD)$
. Then combining the result of Pimsner and Voiculescu in [Reference Pimsner and Voiculescu19] stating that
$(RD)$
. Then combining the result of Pimsner and Voiculescu in [Reference Pimsner and Voiculescu19] stating that
![]() $C^{\ast }_r(F_n)$
has no nontrivial idempotents with the above corollary, shows that
$C^{\ast }_r(F_n)$
has no nontrivial idempotents with the above corollary, shows that
![]() $B^p_r(F_n)$
has no nontrivial idempotents for any
$B^p_r(F_n)$
has no nontrivial idempotents for any
![]() $p\in [1,\infty ]$
. This answers Question 1.1 of Phillips.
$p\in [1,\infty ]$
. This answers Question 1.1 of Phillips.
Apart from free groups, these results can also be applied to torsion-free hyperbolic groups (see Example 3.11), torsion-free groups with polynomial growth and torsion-free cocompact lattices of
![]() $\mbox {SL}(3,\mathbb {R})$
(see Example 3.12).
$\mbox {SL}(3,\mathbb {R})$
(see Example 3.12).
2 Preliminaries
In this section, we will recall some relevant concepts. Let
![]() $p\in [1,\infty ]$
and let
$p\in [1,\infty ]$
and let
![]() $\Gamma $
be a discrete group. The group algebra
$\Gamma $
be a discrete group. The group algebra
![]() $\mathbb {C}\Gamma $
is the algebra of all finitely supported functions
$\mathbb {C}\Gamma $
is the algebra of all finitely supported functions
![]() $f:\Gamma \rightarrow \mathbb {C}$
equipped with the multiplication
$f:\Gamma \rightarrow \mathbb {C}$
equipped with the multiplication
 $$ \begin{align*}f\ast g :=\sum_{\alpha,\gamma\in\Gamma}(f_{\alpha}g_{\gamma})(\alpha\gamma),\end{align*} $$
$$ \begin{align*}f\ast g :=\sum_{\alpha,\gamma\in\Gamma}(f_{\alpha}g_{\gamma})(\alpha\gamma),\end{align*} $$
for any two elements
![]() $f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
and
$f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
and
![]() $g=\sum _{\gamma \in \Gamma }g_{\gamma }\gamma $
in
$g=\sum _{\gamma \in \Gamma }g_{\gamma }\gamma $
in
![]() $\mathbb {C}\Gamma $
. The left regular representation of
$\mathbb {C}\Gamma $
. The left regular representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\ell ^p(\Gamma )$
, denoted by
$\ell ^p(\Gamma )$
, denoted by
![]() $\lambda :\Gamma \rightarrow \mathcal {B}(\ell ^p(\Gamma ))$
, is defined by
$\lambda :\Gamma \rightarrow \mathcal {B}(\ell ^p(\Gamma ))$
, is defined by
for any
![]() $\gamma ,\alpha \in \Gamma $
and
$\gamma ,\alpha \in \Gamma $
and
![]() $\xi \in \ell ^p(\Gamma )$
. For any
$\xi \in \ell ^p(\Gamma )$
. For any
![]() $f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
in
$f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
in
![]() $\mathbb {C}\Gamma $
, the reduced norm of f, denoted by
$\mathbb {C}\Gamma $
, the reduced norm of f, denoted by
![]() $\|f\|_{\mathcal {B}(\ell ^p(\Gamma ))}$
, is defined to be
$\|f\|_{\mathcal {B}(\ell ^p(\Gamma ))}$
, is defined to be
 $$ \begin{align*}\|f\|_{\mathcal{B}(\ell^p(\Gamma))}:= \bigg\|\sum_{\alpha \in \Gamma}f_{\alpha}\lambda(\alpha)\bigg\|.\end{align*} $$
$$ \begin{align*}\|f\|_{\mathcal{B}(\ell^p(\Gamma))}:= \bigg\|\sum_{\alpha \in \Gamma}f_{\alpha}\lambda(\alpha)\bigg\|.\end{align*} $$
Definition 2.1. Let
![]() $p\in [1,\infty ]$
and let
$p\in [1,\infty ]$
and let
![]() $\Gamma $
be a discrete group.
$\Gamma $
be a discrete group.
-
(1) The reduced group
 $\ell ^p$
-operator algebra of
$\ell ^p$
-operator algebra of
 $\Gamma $
, denoted by
$\Gamma $
, denoted by
 $B^p_r(\Gamma )$
, is the reduced norm closure of the group algebra
$B^p_r(\Gamma )$
, is the reduced norm closure of the group algebra
 $\mathbb {C}\Gamma $
.
$\mathbb {C}\Gamma $
. -
(2) For any
 $f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
in
$f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
in
 $\mathbb {C}\Gamma $
, let
$\mathbb {C}\Gamma $
, let
 $f^{\ast }=\sum _{\alpha \in \Gamma }\overline {f_{\alpha }}\alpha ^{-1}$
. The reduced group involution
$f^{\ast }=\sum _{\alpha \in \Gamma }\overline {f_{\alpha }}\alpha ^{-1}$
. The reduced group involution
 $\ell ^p$
-operator algebra of
$\ell ^p$
-operator algebra of
 $\Gamma $
, denoted by
$\Gamma $
, denoted by
 $B^{p,\ast }_r(\Gamma )$
, is the completion of
$B^{p,\ast }_r(\Gamma )$
, is the completion of
 $\mathbb {C}\Gamma $
with respect to the norm
$\mathbb {C}\Gamma $
with respect to the norm  $$ \begin{align*}\|f\|_{B^{p,\ast}_r(\Gamma)}:=\max\{\|f\|_{\mathcal{B}(\ell^p(\Gamma))}, \|f^{\ast}\|_{\mathcal{B}(\ell^p(\Gamma))}\}.\end{align*} $$
$$ \begin{align*}\|f\|_{B^{p,\ast}_r(\Gamma)}:=\max\{\|f\|_{\mathcal{B}(\ell^p(\Gamma))}, \|f^{\ast}\|_{\mathcal{B}(\ell^p(\Gamma))}\}.\end{align*} $$
Remark 2.2. The reduced group
![]() $\ell ^p$
-operator algebra
$\ell ^p$
-operator algebra
![]() $B^p_r(\Gamma )$
is a Banach algebra. Generally, these algebras are not the same for different p (see [Reference Gardella and Thiel6, Reference Liao and Yu14]). The reduced group involution
$B^p_r(\Gamma )$
is a Banach algebra. Generally, these algebras are not the same for different p (see [Reference Gardella and Thiel6, Reference Liao and Yu14]). The reduced group involution
![]() $\ell ^p$
-operator algebra
$\ell ^p$
-operator algebra
![]() $B^{p,\ast }_r(\Gamma )$
, defined by Liao and Yu in [Reference Liao and Yu14], is a Banach
$B^{p,\ast }_r(\Gamma )$
, defined by Liao and Yu in [Reference Liao and Yu14], is a Banach
![]() $\ast $
-algebra and there exist some groups G such that
$\ast $
-algebra and there exist some groups G such that
![]() $B^{p,\ast }_r(G) \neq B^p_r(G)$
for
$B^{p,\ast }_r(G) \neq B^p_r(G)$
for
![]() $p\neq 2$
(see [Reference Liao and Yu14]).
$p\neq 2$
(see [Reference Liao and Yu14]).
Remark 2.3. For
![]() $p\in (1,\infty )$
, let q be its dual number (that is,
$p\in (1,\infty )$
, let q be its dual number (that is,
![]() $1/p+1/q=1$
). The dual space of
$1/p+1/q=1$
). The dual space of
![]() $\ell ^p(\Gamma )$
is
$\ell ^p(\Gamma )$
is
![]() $\ell ^q(\Gamma )$
. If
$\ell ^q(\Gamma )$
. If
![]() $f^{\ast }$
is a bounded operator on
$f^{\ast }$
is a bounded operator on
![]() $\ell ^p(\Gamma )$
, then f is a bounded operator on
$\ell ^p(\Gamma )$
, then f is a bounded operator on
![]() $\ell ^q(\Gamma )$
and
$\ell ^q(\Gamma )$
and
![]() $\|f^{\ast }\|_{\mathcal {B}(\ell ^p(\Gamma ))}=\|f\|_{\mathcal {B}(\ell ^q(\Gamma ))}$
for any
$\|f^{\ast }\|_{\mathcal {B}(\ell ^p(\Gamma ))}=\|f\|_{\mathcal {B}(\ell ^q(\Gamma ))}$
for any
![]() $f\in \mathbb {C}\Gamma $
. As a consequence,
$f\in \mathbb {C}\Gamma $
. As a consequence,
![]() $B^{p,\ast }_r(\Gamma )=B^{q,\ast }_r(\Gamma )$
. Obviously,
$B^{p,\ast }_r(\Gamma )=B^{q,\ast }_r(\Gamma )$
. Obviously,
![]() $B^{1,\ast }_r(\Gamma )= B^1_r(\Gamma )=\ell ^1(\Gamma )$
and
$B^{1,\ast }_r(\Gamma )= B^1_r(\Gamma )=\ell ^1(\Gamma )$
and
![]() $B^{\infty ,\ast }_r(\Gamma )= B^{\infty }_r(\Gamma )=\ell ^1(\Gamma )$
. In addition, when
$B^{\infty ,\ast }_r(\Gamma )= B^{\infty }_r(\Gamma )=\ell ^1(\Gamma )$
. In addition, when
![]() $p=2$
, then
$p=2$
, then
![]() $B^{2,\ast }_r(\Gamma )= B^2_r(\Gamma )$
is a
$B^{2,\ast }_r(\Gamma )= B^2_r(\Gamma )$
is a
![]() $C^{\ast }$
-algebra, called the reduced group
$C^{\ast }$
-algebra, called the reduced group
![]() $C^{\ast }$
-algebra of
$C^{\ast }$
-algebra of
![]() $\Gamma $
, which we shall denote by
$\Gamma $
, which we shall denote by
![]() $C^{\ast }_r(\Gamma )$
.
$C^{\ast }_r(\Gamma )$
.
For any discrete group
![]() $\Gamma $
, we have the following relation between
$\Gamma $
, we have the following relation between
![]() $B^{p,\ast }_r(\Gamma )$
and
$B^{p,\ast }_r(\Gamma )$
and
![]() $B^p_r(\Gamma )$
.
$B^p_r(\Gamma )$
.
Lemma 2.4. Let
![]() $p\in [1,\infty ]$
, then the identity map on
$p\in [1,\infty ]$
, then the identity map on
![]() $\mathbb {C}\Gamma $
extends to a contractive, injective homomorphism of Banach algebras,
$\mathbb {C}\Gamma $
extends to a contractive, injective homomorphism of Banach algebras,
so that
![]() $B^{p,\ast }_r(\Gamma )$
is contained in
$B^{p,\ast }_r(\Gamma )$
is contained in
![]() $B^p_r(\Gamma )$
. Similarly,
$B^p_r(\Gamma )$
. Similarly,
![]() $B^{p,\ast }_r(\Gamma )$
is contained in
$B^{p,\ast }_r(\Gamma )$
is contained in
![]() $B^q_r(\Gamma )$
, where q is the dual number of p.
$B^q_r(\Gamma )$
, where q is the dual number of p.
Proof. Obviously,
![]() $\iota _{\ast ,p}$
is a contractive homomorphism and we prove that it is injective. Assume
$\iota _{\ast ,p}$
is a contractive homomorphism and we prove that it is injective. Assume
![]() $\iota _{\ast ,p}(T)=0$
and choose a family of elements
$\iota _{\ast ,p}(T)=0$
and choose a family of elements
![]() $\{f_i\}_{i\in I}$
in
$\{f_i\}_{i\in I}$
in
![]() $\mathbb {C}\Gamma $
which converges to T in
$\mathbb {C}\Gamma $
which converges to T in
![]() $B^{p,\ast }_r(\Gamma )$
. Since
$B^{p,\ast }_r(\Gamma )$
. Since
![]() $\max \{\|f_i\|_{\ell ^p(\Gamma )}, \|f_i\|_{\ell ^q(\Gamma )}\}\leq \|f_i\|_{B^{p,\ast }_r(\Gamma )}$
, it follows that
$\max \{\|f_i\|_{\ell ^p(\Gamma )}, \|f_i\|_{\ell ^q(\Gamma )}\}\leq \|f_i\|_{B^{p,\ast }_r(\Gamma )}$
, it follows that
![]() $\{f_i\}_{i\in I}$
converges to an element f in
$\{f_i\}_{i\in I}$
converges to an element f in
![]() $\ell ^p(\Gamma )\cap \ell ^q(\Gamma )$
(where q is the dual number of p) and
$\ell ^p(\Gamma )\cap \ell ^q(\Gamma )$
(where q is the dual number of p) and
![]() $T=\lambda (f)$
in
$T=\lambda (f)$
in
![]() $B^{p,\ast }_r(\Gamma )$
, which means
$B^{p,\ast }_r(\Gamma )$
, which means
as operators on
![]() $\ell ^p(\Gamma )$
and
$\ell ^p(\Gamma )$
and
![]() $\ell ^q(\Gamma )$
, where
$\ell ^q(\Gamma )$
, where
![]() $f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
(which may be an infinite sum) and
$f=\sum _{\alpha \in \Gamma }f_{\alpha }\alpha $
(which may be an infinite sum) and
![]() $\lambda $
is the left regular representation of
$\lambda $
is the left regular representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\ell ^p(\Gamma )$
and
$\ell ^p(\Gamma )$
and
![]() $\ell ^q(\Gamma )$
. By the assumption,
$\ell ^q(\Gamma )$
. By the assumption,
![]() $T=0$
as an operator on
$T=0$
as an operator on
![]() $\ell ^p(\Gamma )$
. Thus,
$\ell ^p(\Gamma )$
. Thus,
![]() $f=0$
as a vector in
$f=0$
as a vector in
![]() $\ell ^p(\Gamma )\cap \ell ^q(\Gamma )$
which implies
$\ell ^p(\Gamma )\cap \ell ^q(\Gamma )$
which implies
![]() $f_{\alpha }=0$
for any
$f_{\alpha }=0$
for any
![]() $\alpha \in \Gamma $
. Then by (2.1),
$\alpha \in \Gamma $
. Then by (2.1),
![]() $T=0$
in
$T=0$
in
![]() $B^{p,\ast }_r(\Gamma )$
, which implies that
$B^{p,\ast }_r(\Gamma )$
, which implies that
![]() $\iota _{\ast ,p}$
is an injective homomorphism.
$\iota _{\ast ,p}$
is an injective homomorphism.
By a similar argument,
![]() $B^{p,\ast }_r(\Gamma )$
is contained in
$B^{p,\ast }_r(\Gamma )$
is contained in
![]() $B^q_r(\Gamma )$
.
$B^q_r(\Gamma )$
.
The following proposition is due to Liao and Yu. For the convenience of the reader, we include its proof.
Proposition 2.5 [Reference Liao and Yu14, Proposition 2.4]
Let
![]() $p\in [1,\infty ]$
and let
$p\in [1,\infty ]$
and let
![]() $\Gamma $
be a discrete group. Then the identity map on
$\Gamma $
be a discrete group. Then the identity map on
![]() $\mathbb {C}\Gamma $
extends to a contractive, injective homomorphism of Banach algebras,
$\mathbb {C}\Gamma $
extends to a contractive, injective homomorphism of Banach algebras,
Proof. By Remark 2.3, any element
![]() $T\in B^{p,\ast }_r(\Gamma )$
is not only a bounded operator on
$T\in B^{p,\ast }_r(\Gamma )$
is not only a bounded operator on
![]() $\ell ^p(\Gamma )$
with norm less than
$\ell ^p(\Gamma )$
with norm less than
![]() $\|T\|_{B^{p,\ast }_r(\Gamma )}$
, but also a bounded operator on
$\|T\|_{B^{p,\ast }_r(\Gamma )}$
, but also a bounded operator on
![]() $\ell ^q(\Gamma )$
with norm less than
$\ell ^q(\Gamma )$
with norm less than
![]() $\|T\|_{B^{p,\ast }_r(\Gamma )}$
, where q is the dual number of p. By the Riesz–Thorin interpolation theorem, T is a bounded operator on
$\|T\|_{B^{p,\ast }_r(\Gamma )}$
, where q is the dual number of p. By the Riesz–Thorin interpolation theorem, T is a bounded operator on
![]() $\ell ^2(\Gamma )$
with norm less than
$\ell ^2(\Gamma )$
with norm less than
![]() $\|T\|_{B^{p,\ast }_r(\Gamma )}$
, which implies that
$\|T\|_{B^{p,\ast }_r(\Gamma )}$
, which implies that
![]() $\iota _{p,2}$
is a contractive homomorphism.
$\iota _{p,2}$
is a contractive homomorphism.
Now we show that
![]() $\iota _{p,2}$
is injective. Assume
$\iota _{p,2}$
is injective. Assume
![]() $\iota _{p,2}(T)=0$
. As in the proof of Lemma 2.4, there exists a vector
$\iota _{p,2}(T)=0$
. As in the proof of Lemma 2.4, there exists a vector
![]() $f\in \ell ^p(\Gamma )\cap \ell ^q(\Gamma )$
such that
$f\in \ell ^p(\Gamma )\cap \ell ^q(\Gamma )$
such that
![]() $T=\lambda (f)$
as operators on
$T=\lambda (f)$
as operators on
![]() $\ell ^p(\Gamma )$
and
$\ell ^p(\Gamma )$
and
![]() $\ell ^q(\Gamma )$
. By the Riesz–Thorin interpolation theorem again,
$\ell ^q(\Gamma )$
. By the Riesz–Thorin interpolation theorem again,
![]() $T=\lambda (f)$
as operators on
$T=\lambda (f)$
as operators on
![]() $\ell ^2(\Gamma )$
. By the assumption,
$\ell ^2(\Gamma )$
. By the assumption,
![]() $T=0$
in
$T=0$
in
![]() $C^{\ast }_r(\Gamma )$
which implies that
$C^{\ast }_r(\Gamma )$
which implies that
![]() $f=0$
, and thus
$f=0$
, and thus
![]() $T=0$
in
$T=0$
in
![]() $B^{p,\ast }_r(\Gamma )$
which implies that
$B^{p,\ast }_r(\Gamma )$
which implies that
![]() $\iota _{p,2}$
is an injective homomorphism.
$\iota _{p,2}$
is an injective homomorphism.
Recall that an idempotent in a unital Banach space is called nontrivial if it is neither the zero element
![]() $0$
nor the unit element I.
$0$
nor the unit element I.
Corollary 2.6. Let
![]() $p\in [1,\infty ]$
and
$p\in [1,\infty ]$
and
![]() $\Gamma $
be a discrete group. If
$\Gamma $
be a discrete group. If
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then
![]() $B^{p,\ast }_r(\Gamma )$
also has no nontrivial idempotents.
$B^{p,\ast }_r(\Gamma )$
also has no nontrivial idempotents.
Proof. If e is a nontrivial idempotent in
![]() $B^{p,\ast }_r(\Gamma )$
, then
$B^{p,\ast }_r(\Gamma )$
, then
![]() $\iota _{p,2}(e)$
is a nontrivial idempotent in
$\iota _{p,2}(e)$
is a nontrivial idempotent in
![]() $C^{\ast }_r(\Gamma )$
. Since
$C^{\ast }_r(\Gamma )$
. Since
![]() $\iota _{p,2}$
is an injective homomorphism, we get a contradiction.
$\iota _{p,2}$
is an injective homomorphism, we get a contradiction.
3 Idempotents and property
 $(RD)_q$
$(RD)_q$
In this section, we will explore nontrivial idempotents in
![]() $B^p_r(\Gamma )$
and in
$B^p_r(\Gamma )$
and in
![]() $B^q_r(\Gamma )$
from nontrivial idempotents in
$B^q_r(\Gamma )$
from nontrivial idempotents in
![]() $C^{\ast }_r(\Gamma )$
by using property
$C^{\ast }_r(\Gamma )$
by using property
![]() $(RD)_q$
of the group
$(RD)_q$
of the group
![]() $\Gamma $
, where
$\Gamma $
, where
![]() ${q\in [1,2]}$
and p is the dual number of q. First, we give the following key lemma.
${q\in [1,2]}$
and p is the dual number of q. First, we give the following key lemma.
Lemma 3.1. Let A be a Banach algebra. Then A has no nontrivial idempotents if and only if for some (any) dense subset
![]() $F\subseteq A$
, the spectrum
$F\subseteq A$
, the spectrum
![]() $\mathit {sp}(a)$
of a in A is connected for any
$\mathit {sp}(a)$
of a in A is connected for any
![]() $a\in F$
.
$a\in F$
.
Proof. First, if A has no nontrivial idempotents, we want to show that the spectrum of any element in A is connected. Assume it is not true, namely, there exists an element
![]() $a\in A$
, such that
$a\in A$
, such that
![]() $\mathit {sp}(a)$
is disconnected. Then there exist two disjoint open subsets
$\mathit {sp}(a)$
is disconnected. Then there exist two disjoint open subsets
![]() $U,V\subseteq \mathbb {C}$
such that
$U,V\subseteq \mathbb {C}$
such that
![]() $\mathit {sp}(a)\subseteq U\cup V$
,
$\mathit {sp}(a)\subseteq U\cup V$
,
![]() $\mathit {sp}(a)\cap U\neq \emptyset $
and
$\mathit {sp}(a)\cap U\neq \emptyset $
and
![]() $\mathit {sp}(a)\cap V\neq \emptyset $
. Let f be a function on
$\mathit {sp}(a)\cap V\neq \emptyset $
. Let f be a function on
![]() $U\cup V$
such that
$U\cup V$
such that
![]() $f|_U=0$
and
$f|_U=0$
and
![]() $f|_V=1$
. Then f is a holomorphic function on the neighbourhood of
$f|_V=1$
. Then f is a holomorphic function on the neighbourhood of
![]() $\mathit {sp}(a)$
and
$\mathit {sp}(a)$
and
![]() $f^2=f$
. Applying holomorphic functional calculus, we obtain an idempotent
$f^2=f$
. Applying holomorphic functional calculus, we obtain an idempotent
![]() $f(a)$
in A and by the spectral mapping theorem,
$f(a)$
in A and by the spectral mapping theorem,
![]() $\mathit {sp}(f(a))=\{0,1\}$
, which implies that
$\mathit {sp}(f(a))=\{0,1\}$
, which implies that
![]() $f(a)$
is a nontrivial idempotent. Thus, we get a contradiction.
$f(a)$
is a nontrivial idempotent. Thus, we get a contradiction.
For the other direction, assume A has a nontrivial idempotent a. Then
![]() $1-a$
is also a nontrivial idempotent and
$1-a$
is also a nontrivial idempotent and
![]() $\mathit {sp}(a)=\mathit {sp}(1-a)=\{0,1\}$
. Since F is dense in A, there exists an element
$\mathit {sp}(a)=\mathit {sp}(1-a)=\{0,1\}$
. Since F is dense in A, there exists an element
![]() $b\in F$
such that
$b\in F$
such that
![]() $\|b-a\|<\min \{1/(4(2\|a\|+1)), \|a\| \}$
, which implies
$\|b-a\|<\min \{1/(4(2\|a\|+1)), \|a\| \}$
, which implies
![]() $\|b^2-b\|<1/4$
. Thus,
$\|b^2-b\|<1/4$
. Thus,
![]() $\mathit {sp}(b)\subset \{x\in \mathbb {C}: \mathrm {Re}(x)\neq 1/2\}$
. Let
$\mathit {sp}(b)\subset \{x\in \mathbb {C}: \mathrm {Re}(x)\neq 1/2\}$
. Let
![]() $\chi $
be a function such that
$\chi $
be a function such that
![]() $\chi (x)=1$
for
$\chi (x)=1$
for
![]() $\mathrm { Re}(x)>1/2$
and
$\mathrm { Re}(x)>1/2$
and
![]() $\chi (x)=0$
for
$\chi (x)=0$
for
![]() $\mathrm {Re}(x)<1/2$
. Since the holomorphic functional calculus by
$\mathrm {Re}(x)<1/2$
. Since the holomorphic functional calculus by
![]() $\chi $
is norm continuous in the neighbourhood of a, there exists
$\chi $
is norm continuous in the neighbourhood of a, there exists
![]() $\delta <\min \{1/(4(2\|a\|+1)), \|a\| \}$
such that
$\delta <\min \{1/(4(2\|a\|+1)), \|a\| \}$
such that
for some
![]() $b'\in F$
with
$b'\in F$
with
![]() $\|b'-a\|<\delta $
. Thus,
$\|b'-a\|<\delta $
. Thus,
![]() $\mathit {sp}(b')\cap \{x\in \mathbb {C}: \mathrm {Re}(x)<1/2\} \neq \emptyset $
, as otherwise,
$\mathit {sp}(b')\cap \{x\in \mathbb {C}: \mathrm {Re}(x)<1/2\} \neq \emptyset $
, as otherwise,
![]() $\chi (b')=1$
, which implies that a is invertible. By a similar argument for
$\chi (b')=1$
, which implies that a is invertible. By a similar argument for
![]() $1-a$
, we see that
$1-a$
, we see that
![]() $\mathit {sp}(b')\cap \{x\in \mathbb {C}: \mathrm {Re}(x)>1/2\} \neq \emptyset $
. In conclusion,
$\mathit {sp}(b')\cap \{x\in \mathbb {C}: \mathrm {Re}(x)>1/2\} \neq \emptyset $
. In conclusion,
![]() $\mathit {sp}(b')$
is disconnected, contradicting the assumption that the spectrum of any element in F is connected.
$\mathit {sp}(b')$
is disconnected, contradicting the assumption that the spectrum of any element in F is connected.
For a discrete group
![]() $\Gamma $
, a length function on
$\Gamma $
, a length function on
![]() $\Gamma $
is a function
$\Gamma $
is a function
![]() $l:\Gamma \rightarrow [0,\infty )$
such that:
$l:\Gamma \rightarrow [0,\infty )$
such that:
-
(1)
 $l(\gamma )=0$
if and only if
$l(\gamma )=0$
if and only if
 $\gamma $
is the identity element;
$\gamma $
is the identity element; -
(2)
 $l(\gamma ^{-1})=l(\gamma )$
for any
$l(\gamma ^{-1})=l(\gamma )$
for any
 $\gamma \in \Gamma $
;
$\gamma \in \Gamma $
; -
(3)
 $l(\gamma _1+\gamma _2)\leq l(\gamma _1)+l(\gamma _2)$
for any
$l(\gamma _1+\gamma _2)\leq l(\gamma _1)+l(\gamma _2)$
for any
 $\gamma _1, \gamma _2 \in \Gamma $
.
$\gamma _1, \gamma _2 \in \Gamma $
.
Let e be the identity element of
![]() $\Gamma $
. For any
$\Gamma $
. For any
![]() $n\geq 0$
, denote by
$n\geq 0$
, denote by
![]() $B_n(e)$
the set of all elements
$B_n(e)$
the set of all elements
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma $
with
$\Gamma $
with
![]() $l(\gamma )\leq n$
.
$l(\gamma )\leq n$
.
Definition 3.2. Let
![]() $q\in [1,\infty ]$
and let
$q\in [1,\infty ]$
and let
![]() $\Gamma $
be a discrete group. We say that
$\Gamma $
be a discrete group. We say that
![]() $\Gamma $
has property
$\Gamma $
has property
![]() $(RD)_q$
(with respect to a length function l) if there exists a polynomial
$(RD)_q$
(with respect to a length function l) if there exists a polynomial
![]() $\mathcal {P}$
such that for any function
$\mathcal {P}$
such that for any function
![]() $f\in \mathbb {C}\Gamma $
with support in
$f\in \mathbb {C}\Gamma $
with support in
![]() $B_n(e)$
, we have
$B_n(e)$
, we have
Remark 3.3. The property
![]() $(RD)_q$
(more generally, defined for locally compact groups) was introduced by Liao and Yu (see [Reference Liao and Yu14, Section 4]) to compute the K-theory of
$(RD)_q$
(more generally, defined for locally compact groups) was introduced by Liao and Yu (see [Reference Liao and Yu14, Section 4]) to compute the K-theory of
![]() $B^{q}_r(\Gamma )$
and
$B^{q}_r(\Gamma )$
and
![]() $B^{q,\ast }_r(\Gamma )$
. It is obvious that every group has property
$B^{q,\ast }_r(\Gamma )$
. It is obvious that every group has property
![]() $(RD)_1$
. When
$(RD)_1$
. When
![]() $q\in (2,\infty ]$
, Liao and Yu proved that a countable discrete group has property
$q\in (2,\infty ]$
, Liao and Yu proved that a countable discrete group has property
![]() $(RD)_q$
with respect to a length function l if and only if it has polynomial growth in l (see [Reference Liao and Yu14, Section 4]). When
$(RD)_q$
with respect to a length function l if and only if it has polynomial growth in l (see [Reference Liao and Yu14, Section 4]). When
![]() $p=2$
, the property
$p=2$
, the property
![]() $(RD)_2$
, called property
$(RD)_2$
, called property
![]() $(RD)$
, was introduced by Jolissaint [Reference Jolissaint11] and has important applications to the Novikov conjecture (see [Reference Connes and Moscovici4]) and the Baum–Connes conjecture (see [Reference Lafforgue13]).
$(RD)$
, was introduced by Jolissaint [Reference Jolissaint11] and has important applications to the Novikov conjecture (see [Reference Connes and Moscovici4]) and the Baum–Connes conjecture (see [Reference Lafforgue13]).
The following theorem is due to Lafforgue. Two different proofs given by Liao and Yu and Pisier can be found in [Reference Liao and Yu14, Theorem 4.4].
Theorem 3.4 (V. Lafforgue)
If
![]() $\Gamma $
is a discrete group with property
$\Gamma $
is a discrete group with property
![]() $(RD)_q$
for some
$(RD)_q$
for some
![]() $q>1$
, then it has property
$q>1$
, then it has property
![]() $(RD)_{q^{\prime }}$
for any
$(RD)_{q^{\prime }}$
for any
![]() $q^{\prime }\in (1,q)$
. In particular, property
$q^{\prime }\in (1,q)$
. In particular, property
![]() $(RD)$
implies property
$(RD)$
implies property
![]() $(RD)_q$
for any
$(RD)_q$
for any
![]() $q\in (1,2)$
.
$q\in (1,2)$
.
Let B be a unital Banach algebra and A a subalgebra of B containing the unit element of B. We say that A is stable under the holomorphic functional calculus in B if for every
![]() $a\in A$
and f holomorphic in a neighbourhood of
$a\in A$
and f holomorphic in a neighbourhood of
![]() $\mathit {sp}_{B}(a)$
, the element
$\mathit {sp}_{B}(a)$
, the element
![]() $f(a)$
of B lies in A, where
$f(a)$
of B lies in A, where
![]() $\mathit {sp}_{B}(a)$
is the spectrum of a in B. We say that A is a spectral invariant subalgebra of B if
$\mathit {sp}_{B}(a)$
is the spectrum of a in B. We say that A is a spectral invariant subalgebra of B if
![]() $\mathit {sp}_{A}(a)=\mathit {sp}_{B}(a)$
for any element
$\mathit {sp}_{A}(a)=\mathit {sp}_{B}(a)$
for any element
![]() $a\in A$
.
$a\in A$
.
Schweitzer showed that these two notions are equivalent.
Lemma 3.5 [Reference Schweitzer21, Lemma 1.2]
Let B be a unital Banach algebra and A a Fréchet subalgebra of B containing the unit element of B. Then A is stable under the holomorphic functional calculus in B if and only if A is spectral invariant in B.
The significance of property
![]() $(RD)_q$
for groups is the following proposition proved by Liao and Yu.
$(RD)_q$
for groups is the following proposition proved by Liao and Yu.
Proposition 3.6 [Reference Liao and Yu14, Proposition 4.6]
Let
![]() $p\in [1,\infty ]$
and q be its dual number. Let
$p\in [1,\infty ]$
and q be its dual number. Let
![]() $\Gamma $
be a discrete group with property
$\Gamma $
be a discrete group with property
![]() $(RD)_q$
with respect to a length function l. Then for sufficiently large
$(RD)_q$
with respect to a length function l. Then for sufficiently large
![]() $t>0$
, the space
$t>0$
, the space
![]() $S^t_q(\Gamma )$
of elements
$S^t_q(\Gamma )$
of elements
![]() $f\in \ell ^q(\Gamma )$
such that
$f\in \ell ^q(\Gamma )$
such that
is a Banach algebra for the norm
![]() $\|\cdot \|_{S^t_q}$
. It is contained in
$\|\cdot \|_{S^t_q}$
. It is contained in
![]() $B^{p,*}_r(\Gamma )$
,
$B^{p,*}_r(\Gamma )$
,
![]() $B^p_r(\Gamma )$
and
$B^p_r(\Gamma )$
and
![]() $B^q_r(\Gamma )$
, and stable under holomorphic functional calculus in each of these three algebras.
$B^q_r(\Gamma )$
, and stable under holomorphic functional calculus in each of these three algebras.
Combining this proposition with Lemma 3.5 gives the following corollary.
Corollary 3.7. Let
![]() $p,q$
be as above and let
$p,q$
be as above and let
![]() $\Gamma $
be a discrete group with property
$\Gamma $
be a discrete group with property
![]() $(RD)_q$
. Then for any
$(RD)_q$
. Then for any
![]() $f\in \mathbb {C}\Gamma $
,
$f\in \mathbb {C}\Gamma $
,
Now, we are ready to state and prove our main theorem.
Theorem 3.8. Let
![]() $p\in [1,\infty ]$
, q be its dual number and
$p\in [1,\infty ]$
, q be its dual number and
![]() $\Gamma $
be a discrete group. Assume
$\Gamma $
be a discrete group. Assume
![]() $\Gamma $
has property
$\Gamma $
has property
![]() $(RD)_q$
. If
$(RD)_q$
. If
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then both
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then both
![]() $B^p_r(\Gamma )$
and
$B^p_r(\Gamma )$
and
![]() $B^q_r(\Gamma )$
also have no nontrivial idempotents.
$B^q_r(\Gamma )$
also have no nontrivial idempotents.
Proof. By Corollary 2.6,
![]() $B^{p,\ast }_r(\Gamma )$
has no nontrivial idempotents. Thus by Lemma 3.1, the spectrum
$B^{p,\ast }_r(\Gamma )$
has no nontrivial idempotents. Thus by Lemma 3.1, the spectrum
![]() $\mathit {sp}_{B^{p,\ast }_r(\Gamma )}(f)$
is connected for any
$\mathit {sp}_{B^{p,\ast }_r(\Gamma )}(f)$
is connected for any
![]() $f\in \mathbb {C}\Gamma $
. If
$f\in \mathbb {C}\Gamma $
. If
![]() $\Gamma $
has property
$\Gamma $
has property
![]() $(RD)_q$
, then by Corollary 3.7,
$(RD)_q$
, then by Corollary 3.7,
![]() $\mathit {sp}_{B^{p}_r(\Gamma )}(f)=\mathit {sp}_{B^{q}_r(\Gamma )}(f)=\mathit {sp}_{B^{p,\ast }_r(\Gamma )}(f)$
are all connected for any
$\mathit {sp}_{B^{p}_r(\Gamma )}(f)=\mathit {sp}_{B^{q}_r(\Gamma )}(f)=\mathit {sp}_{B^{p,\ast }_r(\Gamma )}(f)$
are all connected for any
![]() $f\in \mathbb {C}\Gamma $
. Thus, by Lemma 3.1 again, both
$f\in \mathbb {C}\Gamma $
. Thus, by Lemma 3.1 again, both
![]() $B^p_r(\Gamma )$
and
$B^p_r(\Gamma )$
and
![]() $B^q_r(\Gamma )$
have no nontrivial idempotents.
$B^q_r(\Gamma )$
have no nontrivial idempotents.
Combining this theorem with Theorem 3.4 and the fact that every group has property
![]() $(RD)_1$
gives the following corollary.
$(RD)_1$
gives the following corollary.
Corollary 3.9. Let
![]() $\Gamma $
be a discrete group with property
$\Gamma $
be a discrete group with property
![]() $(RD)$
. If
$(RD)$
. If
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then for any
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents, then for any
![]() $p\in [1,\infty ]$
,
$p\in [1,\infty ]$
,
![]() $B^p_r(\Gamma )$
also has no nontrivial idempotents.
$B^p_r(\Gamma )$
also has no nontrivial idempotents.
Example 3.10. We apply the main theorem to free groups
![]() $F_n$
for any positive integer n. Haagerup [Reference Haagerup8] proved that the free group
$F_n$
for any positive integer n. Haagerup [Reference Haagerup8] proved that the free group
![]() $F_n$
has property
$F_n$
has property
![]() $(RD)$
and Pimsner and Voiculescu [Reference Pimsner and Voiculescu19] proved that the reduced group
$(RD)$
and Pimsner and Voiculescu [Reference Pimsner and Voiculescu19] proved that the reduced group
![]() $C^{\ast }$
-algebra
$C^{\ast }$
-algebra
![]() $C^{\ast }_r(F_n)$
has no nontrivial idempotents. Thus by Corollary 3.9,
$C^{\ast }_r(F_n)$
has no nontrivial idempotents. Thus by Corollary 3.9,
![]() $B^p_r(F_n)$
has no nontrivial idempotents for any
$B^p_r(F_n)$
has no nontrivial idempotents for any
![]() $p\in [1,\infty ]$
. This answers Question 1.1 raised by Phillips.
$p\in [1,\infty ]$
. This answers Question 1.1 raised by Phillips.
Example 3.11. In this example, we consider a torsion-free hyperbolic group
![]() $\Gamma $
. Jolissaint [Reference Jolissaint11] and de la Harpe [Reference de la Harpe5] proved that hyperbolic groups have property
$\Gamma $
. Jolissaint [Reference Jolissaint11] and de la Harpe [Reference de la Harpe5] proved that hyperbolic groups have property
![]() $(RD)$
. There are at least two different ways to prove that
$(RD)$
. There are at least two different ways to prove that
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents. One is as a corollary of the Baum–Connes conjecture for hyperbolic groups (see Lafforgue [Reference Lafforgue13] and Mineyev and Yu [Reference Mineyev and Yu15]). Another, due to Puschnigg, uses local cyclic homology (see [Reference Puschnigg20]). Thus by Corollary 3.9,
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents. One is as a corollary of the Baum–Connes conjecture for hyperbolic groups (see Lafforgue [Reference Lafforgue13] and Mineyev and Yu [Reference Mineyev and Yu15]). Another, due to Puschnigg, uses local cyclic homology (see [Reference Puschnigg20]). Thus by Corollary 3.9,
![]() $B^p_r(\Gamma )$
has no nontrivial idempotents for any
$B^p_r(\Gamma )$
has no nontrivial idempotents for any
![]() $p\in [1,\infty ]$
.
$p\in [1,\infty ]$
.
Example 3.12. For a torsion-free discrete group
![]() $\Gamma $
, if
$\Gamma $
, if
![]() $\Gamma $
satisfies the Baum–Connes conjecture (actually, surjectivity of the assembly map is sufficient), then the reduced group
$\Gamma $
satisfies the Baum–Connes conjecture (actually, surjectivity of the assembly map is sufficient), then the reduced group
![]() $C^{\ast }$
-algebra
$C^{\ast }$
-algebra
![]() $C^{\ast }_r(\Gamma )$
has no nontrivial idempotents (see [Reference Baum, Connes, Higson and Doran1]). Thus by Corollary 3.9, for any
$C^{\ast }_r(\Gamma )$
has no nontrivial idempotents (see [Reference Baum, Connes, Higson and Doran1]). Thus by Corollary 3.9, for any
![]() $p\in [1,\infty ]$
,
$p\in [1,\infty ]$
,
![]() $B^p_r(\Gamma )$
has no nontrivial idempotents for every torsion-free discrete group
$B^p_r(\Gamma )$
has no nontrivial idempotents for every torsion-free discrete group
![]() $\Gamma $
which has property
$\Gamma $
which has property
![]() $(RD)$
and satisfies the Baum–Connes conjecture. Apart from hyperbolic groups, such groups
$(RD)$
and satisfies the Baum–Connes conjecture. Apart from hyperbolic groups, such groups
![]() $\Gamma $
can also be finitely generated, torsion-free groups with polynomial growth (see [Reference Higson and Kasparov10, Reference Jolissaint11]) and torsion-free cocompact lattices of
$\Gamma $
can also be finitely generated, torsion-free groups with polynomial growth (see [Reference Higson and Kasparov10, Reference Jolissaint11]) and torsion-free cocompact lattices of
![]() $\mbox {SL}(3,\mathbb {R})$
(see [Reference Lafforgue12, Reference Lafforgue13]).
$\mbox {SL}(3,\mathbb {R})$
(see [Reference Lafforgue12, Reference Lafforgue13]).