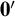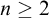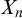1 Introduction
How difficult is it to describe an explicit presentation of an abstract mathematical structure? For a particular structure S, what is the degree spectrum of its isomorphism type, i.e., what are the Turing degrees that compute a presentation of a structure that is isomorphic to S? For a class of structures, what are the possible degree spectra of their isomorphism types? These have long been the fundamental questions in computable structure theory, and researchers in this area have obtained a huge number of interesting results on Turing degrees of presentations of isomorphism types of groups, rings, fields, linear orders, lattices, Boolean algebras, and so on [Reference Ash and Knight2, Reference Ershov, Goncharov, Nerode, Remmel and Marek12, Reference Fokina, Harizanov and Melnikov14, Reference Hirschfeldt, Khoussainov, Shore and Slinko20].
In this article we focus on presentations of compact Polish spaces. The notion of a presentation plays a central role, not only in computable structure theory, but also in computable analysis [Reference Brattka and Hertling4, Reference Brattka, Hertling and Weihrauch5, Reference Weihrauch43]. In this area, one of the most crucial problems was how to present large mathematical objects (which possibly have the cardinality of the continuum) such as metric spaces and topological spaces, and then researchers have obtained a number of answers to this question. In particular, the notion of a computable presentation of a Polish space can be traced back to the 1960s; e.g., [Reference Moschovakis34]. Computable Polish spaces have been extensively studied in computable analysis [Reference Brattka and Hertling4, Reference Pour-El and Ian Richards38, Reference Weihrauch43] and descriptive set theory [Reference Moschovakis35].
In recent years, several researchers have succeeded in obtaining various results on Turing degrees of isometric isomorphism types of Polish spaces, separable Banach spaces, and Polish groups; see [Reference Clanin, McNicholl and Stull8, Reference Lupini, Melnikov and Nies28, Reference McNicholl and Stull29, Reference Melnikov31]. All these works are devoted to metric structures. Results on Turing degrees of homeomorphism types of Polish spaces have been obtained only very recently, and independently of the present article, in [Reference Downey and Melnikov9, Reference Harrison-Trainor, Melnikov and Ng18, Reference Lupini, Melnikov and Nies28, Reference Melnikov32]. Computable Polish groups were investigated in [Reference Greenberg, Melnikov, Nies and Turetsky15, Reference Melnikov30], and general topological spaces were studied in [Reference Selivanov40] in analogy with the earlier investigation of degrees of isomorphism types of algebraic structures. Some results were also obtained for domains.
In this article, a Polish presentation of a Polish space X is a dense sequence
![]() $(s_i)_{i\in \mathbb {N}}$
in X and a complete metric d inducing the topology; for a Turing degree
$(s_i)_{i\in \mathbb {N}}$
in X and a complete metric d inducing the topology; for a Turing degree
![]() ${\mathbf {d}}$
, such a presentation is
${\mathbf {d}}$
, such a presentation is
![]() ${\mathbf {d}}$
-computable if the real numbers
${\mathbf {d}}$
-computable if the real numbers
![]() $d(s_i,s_j)$
are uniformly
$d(s_i,s_j)$
are uniformly
![]() ${\mathbf {d}}$
-computable. The Polish degree spectrum of X is then the set of Turing degrees that compute a Polish presentation of X. We will also be interested in compact presentations of a compact Polish space X, that carry a Polish presentation together with an enumeration of the finite open covers of X. The compact degree spectrum of X is the set of Turing degrees that compute a compact presentation of X.
${\mathbf {d}}$
-computable. The Polish degree spectrum of X is then the set of Turing degrees that compute a Polish presentation of X. We will also be interested in compact presentations of a compact Polish space X, that carry a Polish presentation together with an enumeration of the finite open covers of X. The compact degree spectrum of X is the set of Turing degrees that compute a compact presentation of X.
One of the first questions to be asked about presentations of Polish spaces is:
Question 1. Does there exist a Polish space with a
![]() $\mathbf {0}'$
-computable Polish presentation but not computable one?
$\mathbf {0}'$
-computable Polish presentation but not computable one?
Observe that there are continuum many homeomorphism types of Polish spaces, but there exist only countably many computable presentations of Polish spaces, so there is a Polish space which is not homeomorphic to any computably presented Polish space.
Countable spaces cannot be used to solve this problem because of the “hyperarithmetic-is-recursive” phenomenon, see [Reference Greenberg and Montalbán16]; see also Section 3. In this article we answer Question 1 in the affirmative. We note that Harrison-Trainor, Melnikov, and Ng [Reference Harrison-Trainor, Melnikov and Ng18] have recently obtained an independent solution, and via a different proof. One possible approach to solve this problem is using Stone duality between countable Boolean algebras and zero-dimensional compact Polish spaces; see also Section 3.1. Combining this idea with classical results on isomorphism types of Boolean algebras [Reference Knight and Stob27], one can conclude that every low
![]() $_4$
-presented zero-dimensional compact Polish space is homeomorphic to a computable one. This was also independently noticed by Harrison-Trainor, Melnikov, and Ng [Reference Harrison-Trainor, Melnikov and Ng18].
$_4$
-presented zero-dimensional compact Polish space is homeomorphic to a computable one. This was also independently noticed by Harrison-Trainor, Melnikov, and Ng [Reference Harrison-Trainor, Melnikov and Ng18].
Our next step is to develop new techniques beyond Stone duality. More specifically, the next question is whether there exists a Polish space whose Polish degree spectrum is different from that of a zero-dimensional compact space. In particular, it is natural to ask the following:
Question 2. Does there exist a Polish space with a low
![]() $_4$
Polish presentation but no computable one?
$_4$
Polish presentation but no computable one?
One of the main results of this article is that for every Turing degree
![]() ${\mathbf {d}}$
and every
${\mathbf {d}}$
and every
![]() $n\geq 1$
, there exists a compact Polish space
$n\geq 1$
, there exists a compact Polish space
![]() $\mathcal {X}_{{\mathbf {d}},n}$
whose compact degree spectrum is
$\mathcal {X}_{{\mathbf {d}},n}$
whose compact degree spectrum is
![]() $\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}^{(n)}\}$
and Polish degree spectrum is
$\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}^{(n)}\}$
and Polish degree spectrum is
![]() $\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}^{(n+1)}\}$
(Corollaries 5.2 and 5.12). This result was independently obtained by Melnikov [Reference Melnikov32], Lupini, Melnikov, and Nies [Reference Lupini, Melnikov and Nies28], and Downey and Melnikov [Reference Downey and Melnikov9] using different arguments, namely by proving that Čech cohomology groups of a compact space are computable. For
$\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}^{(n+1)}\}$
(Corollaries 5.2 and 5.12). This result was independently obtained by Melnikov [Reference Melnikov32], Lupini, Melnikov, and Nies [Reference Lupini, Melnikov and Nies28], and Downey and Melnikov [Reference Downey and Melnikov9] using different arguments, namely by proving that Čech cohomology groups of a compact space are computable. For
![]() $n=1$
the result presented here is obtained by investigating the computable aspects of Čech homology groups. A part of the analysis of homology groups is a direct adaptation of the analysis of cohomology groups from [Reference Downey and Melnikov9, Reference Lupini, Melnikov and Nies28], then the arguments diverge: Čech homology groups are not computable in general, but they are sufficiently effective for our purpose. More precisely, we show that the non-triviality of Čech homology groups with coefficients in
$n=1$
the result presented here is obtained by investigating the computable aspects of Čech homology groups. A part of the analysis of homology groups is a direct adaptation of the analysis of cohomology groups from [Reference Downey and Melnikov9, Reference Lupini, Melnikov and Nies28], then the arguments diverge: Čech homology groups are not computable in general, but they are sufficiently effective for our purpose. More precisely, we show that the non-triviality of Čech homology groups with coefficients in
![]() $\mathbb{Z}/2\mathbb{Z}$
is
$\mathbb{Z}/2\mathbb{Z}$
is
![]() $\Sigma^0_2$
; along the way, we also show that it is
$\Sigma^0_2$
; along the way, we also show that it is
![]() $\Sigma^1_1$
-complete when taking coefficients in
$\Sigma^1_1$
-complete when taking coefficients in
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
The result gives a solution to Questions 1 and 2: there is a space with a
![]() $\mathbf {0}'$
-computable low
$\mathbf {0}'$
-computable low
![]() $_3$
Polish presentation but no computable Polish presentation, namely the space
$_3$
Polish presentation but no computable Polish presentation, namely the space
![]() $\mathcal {X}_{{\mathbf {d}}",1}$
for any
$\mathcal {X}_{{\mathbf {d}}",1}$
for any
![]() ${\mathbf {d}}\leq \mathbf {0}'$
which is low
${\mathbf {d}}\leq \mathbf {0}'$
which is low
![]() $_3$
. It also implies the existence of a compact Polish space having a computable Polish presentation but no computable compact presentation (Corollary 5.3).
$_3$
. It also implies the existence of a compact Polish space having a computable Polish presentation but no computable compact presentation (Corollary 5.3).
Another consequence is that for
![]() $n\geq 2$
there is a space whose Polish degree spectrum is the set of high
$n\geq 2$
there is a space whose Polish degree spectrum is the set of high
![]() $_n$
degrees, namely
$_n$
degrees, namely
![]() $\mathcal {X}_{{\mathbf {d}},n-1}$
where
$\mathcal {X}_{{\mathbf {d}},n-1}$
where
![]() ${\mathbf {d}}=\mathbf {0}^{(n+1)}$
. This also clarifies substantial differences between zero-dimensional compact Polish spaces and infinite-dimensional ones since the class of high
${\mathbf {d}}=\mathbf {0}^{(n+1)}$
. This also clarifies substantial differences between zero-dimensional compact Polish spaces and infinite-dimensional ones since the class of high
![]() $_n$
-degrees is never the degree spectrum of a Boolean algebra [Reference Jockusch and Soare24].
$_n$
-degrees is never the degree spectrum of a Boolean algebra [Reference Jockusch and Soare24].
Another important question is whether a given Polish space has a least Turing degree in its Polish degree spectrum. For instance, it is known that the isomorphism types of linear orders, trees, abelian p-groups, etc. have no least presentation whenever they are not computably presentable, see [Reference Fokina, Harizanov and Melnikov14].
Question 3. Does there exist a compact Polish space with no computable Polish presentation, but whose Polish degree spectrum contains a least Turing degree?
We answer Question 3 in the negative. More precisely, we show the cone-avoidance theorem for compact Polish spaces, which states that, for any non-c.e. set
![]() $A\subseteq \mathbb {N}$
, every compact Polish space has a Polish presentation that does not enumerate A (Theorem 6.1).
$A\subseteq \mathbb {N}$
, every compact Polish space has a Polish presentation that does not enumerate A (Theorem 6.1).
It contrasts with a result proved in [Reference Lupini, Melnikov and Nies28] that for each set
![]() $A\subseteq {\mathbb {N}}$
, there exists a compact Polish space whose compact degree spectrum is
$A\subseteq {\mathbb {N}}$
, there exists a compact Polish space whose compact degree spectrum is
![]() $\{\textbf {x}:A\text { is} $
x
$\{\textbf {x}:A\text { is} $
x
![]() $\text {-c.e.}\}$
. If
$\text {-c.e.}\}$
. If
![]() $(p_i)_{i\in \mathbb {N}}$
is the increasing enumeration of the prime numbers, this space is defined as the Pontryagin dual
$(p_i)_{i\in \mathbb {N}}$
is the increasing enumeration of the prime numbers, this space is defined as the Pontryagin dual
![]() $\hat {G}$
of the subgroup G of
$\hat {G}$
of the subgroup G of
![]() $\mathbb {Q}$
generated by the elements
$\mathbb {Q}$
generated by the elements
![]() $\frac {1}{p_i}$
with
$\frac {1}{p_i}$
with
![]() $i\in A$
.
$i\in A$
.
We finally prove a precise relationship between the Polish degree spectrum and the compact degree spectrum of compact Polish spaces that are perfect (Corollary 7.2), and show that it fails for some non-perfect space (Proposition 7.5).
The article is organized as follows. In Section 2 we present the necessary background and develop the technical tools that will be used throughout the article. In Section 3 we briefly discuss the effective aspects of the Cantor–Bendixson derivative and of Stone duality. In Section 4 we investigate the computable aspects of the Čech homology groups, which will be used in Section 5, where we show how to realize certain sets of Turing degrees as degree spectra of compact Polish spaces. In Section 5 we show the cone-avoidance theorem. In Section 6 we compare degree spectra and compact degree spectra.
2 Preliminaries
Basic terminology and results of computability theory and computable structure theory are summarized in [Reference Ash and Knight2]. For basics of computable analysis, we refer the reader to [Reference Avigad and Brattka3–Reference Brattka, Hertling and Weihrauch5, Reference Weihrauch43]. For the basic definitions and facts of general topology and dimension theory, see [Reference Hurewicz and Wallman22, Reference van Mill33].
2.1 Presentations of Polish spaces
If X is a Polish space, then a Polish presentation (or simply a presentation) of X is
![]() $(X,d,S)$
where
$(X,d,S)$
where
![]() $S=(s_n)_{n\in \mathbb {N}}$
is a dense sequence in X and d is a complete metric which is compatible with the topology. For a discussion of presentations of Polish spaces, see also [Reference Gregoriades, Kispéter and Pauly17].
$S=(s_n)_{n\in \mathbb {N}}$
is a dense sequence in X and d is a complete metric which is compatible with the topology. For a discussion of presentations of Polish spaces, see also [Reference Gregoriades, Kispéter and Pauly17].
For a Turing degree
![]() ${\mathbf {d}}$
, a presentation
${\mathbf {d}}$
, a presentation
![]() $(X,d,S)$
of X is
$(X,d,S)$
of X is
![]() ${\mathbf {d}}$
-computable if the real numbers
${\mathbf {d}}$
-computable if the real numbers
![]() $d(s_i,s_j)$
are uniformly
$d(s_i,s_j)$
are uniformly
![]() ${\mathbf {d}}$
-computable. A
${\mathbf {d}}$
-computable. A
![]() $\mathbf {d}$
-computable Polish space is a Polish space which has a
$\mathbf {d}$
-computable Polish space is a Polish space which has a
![]() $\mathbf {d}$
-computable presentation. For a Polish space X, its Polish degree spectrum
$\mathbf {d}$
-computable presentation. For a Polish space X, its Polish degree spectrum
![]() $\mathrm {Sp}(X)$
is the set of all Turing degrees
$\mathrm {Sp}(X)$
is the set of all Turing degrees
![]() $\mathbf {d}$
such that X has a
$\mathbf {d}$
such that X has a
![]() $\mathbf {d}$
-computable Polish presentation.
$\mathbf {d}$
-computable Polish presentation.
Let
![]() $(X,d,S)$
be a presentation of a Polish space X. A rational open ball is
$(X,d,S)$
be a presentation of a Polish space X. A rational open ball is
![]() $B(s_i,r)=\{x\in X:d(s_i,x)<r\}$
where
$B(s_i,r)=\{x\in X:d(s_i,x)<r\}$
where
![]() $r>0$
is rational. A rational open set is a finite union of rational open balls. A code of a finite rational open cover of X is a finite set
$r>0$
is rational. A rational open set is a finite union of rational open balls. A code of a finite rational open cover of X is a finite set
![]() $E\subseteq \mathbb {N}\times \mathbb {Q}_{>0}$
such that
$E\subseteq \mathbb {N}\times \mathbb {Q}_{>0}$
such that
![]() $X=\bigcup _{(i,r)\in E}B(s_i,r)$
. If X is compact, then a compact presentation of X is a presentation of X equipped with an enumeration of the codes of all finite rational open covers of X. In particular, a compact presentation contains an information of total boundedness; that is, a function
$X=\bigcup _{(i,r)\in E}B(s_i,r)$
. If X is compact, then a compact presentation of X is a presentation of X equipped with an enumeration of the codes of all finite rational open covers of X. In particular, a compact presentation contains an information of total boundedness; that is, a function
![]() $\ell :\mathbb {N}\to \mathbb {N}$
such that for all n,
$\ell :\mathbb {N}\to \mathbb {N}$
such that for all n,
![]() $\{B(a_i,2^{-n}):i<\ell (n)\}$
covers the whole space X.
$\{B(a_i,2^{-n}):i<\ell (n)\}$
covers the whole space X.
A compact Polish space X is
![]() $\mathbf {d}$
-computably compact if it has a
$\mathbf {d}$
-computably compact if it has a
![]() $\mathbf {d}$
-computable compact presentation. Its compact degree spectrum
$\mathbf {d}$
-computable compact presentation. Its compact degree spectrum
![]() $\mathrm {Sp}_c(X)$
is the set of all Turing degrees
$\mathrm {Sp}_c(X)$
is the set of all Turing degrees
![]() $\mathbf {d}$
such that X has a
$\mathbf {d}$
such that X has a
![]() $\mathbf {d}$
-computable compact presentation.
$\mathbf {d}$
-computable compact presentation.
We will often use the next elementary result.
Lemma 2.1. Let
![]() ${X}$
be a compact Polish space. If
${X}$
be a compact Polish space. If
![]() ${X}$
has a
${X}$
has a
![]() $\mathbf {d}$
-computable Polish presentation, then
$\mathbf {d}$
-computable Polish presentation, then
![]() ${X}$
has a
${X}$
has a
![]() $\mathbf {d}'$
-computable compact presentation.
$\mathbf {d}'$
-computable compact presentation.
Proof Assume that X has a
![]() ${\mathbf {d}}$
-computable Polish presentation
${\mathbf {d}}$
-computable Polish presentation
![]() $(X,d,S)$
. By compactness of X, one can observe that E is a code of a finite rational open cover of X if and only if there exists
$(X,d,S)$
. By compactness of X, one can observe that E is a code of a finite rational open cover of X if and only if there exists
![]() $s\in {\mathbb {N}}$
such that for all
$s\in {\mathbb {N}}$
such that for all
![]() $x\in X$
we have
$x\in X$
we have
![]() $d(x,s_i)\leq r-2^{-s}$
for some
$d(x,s_i)\leq r-2^{-s}$
for some
![]() $(i,r)\in E$
. The latter is equivalent to the existence of
$(i,r)\in E$
. The latter is equivalent to the existence of
![]() $s\in {\mathbb {N}}$
such that for all
$s\in {\mathbb {N}}$
such that for all
![]() $j\in {\mathbb {N}}$
we have
$j\in {\mathbb {N}}$
we have
![]() $d(s_j,s_i)\leq r-2^{-s}$
for some
$d(s_j,s_i)\leq r-2^{-s}$
for some
![]() $(i,r)\in E$
. As E is finite, this is a
$(i,r)\in E$
. As E is finite, this is a
![]() $\Sigma ^0_2$
condition relative to
$\Sigma ^0_2$
condition relative to
![]() ${\mathbf {d}}$
, so it is
${\mathbf {d}}$
, so it is
![]() ${\mathbf {d}}'$
-c.e. In other words, X has a
${\mathbf {d}}'$
-c.e. In other words, X has a
![]() $\mathbf {d}'$
-computable compact presentation.
$\mathbf {d}'$
-computable compact presentation.
In Section 6, we will present a sharp analysis of this relationship between Polish and compact presentations.
2.1.1 Hyperspaces.
Every Polish space embeds in the Hilbert cube, and this fact induces an equivalent definition of Polish and compact presentations. The Hilbert cube
![]() $Q=[0,1]^{\mathbb {N}}$
is endowed with the complete metric
$Q=[0,1]^{\mathbb {N}}$
is endowed with the complete metric
![]() $d_Q(x,y)=\sum _i2^{-i}|x_i-y_i|$
. A point of Q is rational if its coordinates are rational and only finitely many of them are non-zero. The rational points of Q, enumerated in a canonical way, make Q a computable Polish space which is computably compact.
$d_Q(x,y)=\sum _i2^{-i}|x_i-y_i|$
. A point of Q is rational if its coordinates are rational and only finitely many of them are non-zero. The rational points of Q, enumerated in a canonical way, make Q a computable Polish space which is computably compact.
Let
![]() $\mathcal {V}(Q)$
be the hyperspace of compact subsets of Q endowed with the lower Vietoris topology. A subbasis is given by
$\mathcal {V}(Q)$
be the hyperspace of compact subsets of Q endowed with the lower Vietoris topology. A subbasis is given by
![]() $\{K\subseteq Q:K\cap B\neq \emptyset \}$
, where B is a rational ball in Q (technically, we need to add
$\{K\subseteq Q:K\cap B\neq \emptyset \}$
, where B is a rational ball in Q (technically, we need to add
![]() $\{\emptyset \}$
, which is the singleton containing the empty compact set, to make it a subbasis).
$\{\emptyset \}$
, which is the singleton containing the empty compact set, to make it a subbasis).
Let
![]() $\mathcal {K}(Q)$
be the hyperspace of compact subsets of Q endowed with the Vietoris topology. A subbasis is given by a subbasis for the lower Vietoris topology, together with
$\mathcal {K}(Q)$
be the hyperspace of compact subsets of Q endowed with the Vietoris topology. A subbasis is given by a subbasis for the lower Vietoris topology, together with
![]() $\{K\subseteq Q:K\subseteq U\}$
, where U is a rational open set in Q. The Hausdorff metric
$\{K\subseteq Q:K\subseteq U\}$
, where U is a rational open set in Q. The Hausdorff metric
![]() $d_H$
is a complete metric generating the Vietoris topology, and the dense sequence of finite sets of rational points of Q makes
$d_H$
is a complete metric generating the Vietoris topology, and the dense sequence of finite sets of rational points of Q makes
![]() $\mathcal {K}(Q)$
a computable Polish space which is computably compact.
$\mathcal {K}(Q)$
a computable Polish space which is computably compact.
We say that a compact set
![]() $K\subseteq Q$
is
$K\subseteq Q$
is
![]() ${\mathbf {d}}$
-computably overt if
${\mathbf {d}}$
-computably overt if
![]() ${\mathbf {d}}$
computes an enumeration of the basic neighborhoods of K in the lower Vietoris topology. Equivalently, K is
${\mathbf {d}}$
computes an enumeration of the basic neighborhoods of K in the lower Vietoris topology. Equivalently, K is
![]() ${\mathbf {d}}$
-computably overt if it contains a dense computable sequence. We say that K is
${\mathbf {d}}$
-computably overt if it contains a dense computable sequence. We say that K is
![]() ${\mathbf {d}}$
-computably compact if
${\mathbf {d}}$
-computably compact if
![]() ${\mathbf {d}}$
computes an enumeration of the basic neighborhoods of K in the Vietoris topology. Equivalently, K is
${\mathbf {d}}$
computes an enumeration of the basic neighborhoods of K in the Vietoris topology. Equivalently, K is
![]() ${\mathbf {d}}$
-computably compact if K is
${\mathbf {d}}$
-computably compact if K is
![]() ${\mathbf {d}}$
-computably overt and
${\mathbf {d}}$
-computably overt and
![]() $K\in \Pi ^0_1({\mathbf {d}})$
, or if
$K\in \Pi ^0_1({\mathbf {d}})$
, or if
![]() ${\mathbf {d}}$
computes a sequence of finite sets
${\mathbf {d}}$
computes a sequence of finite sets
![]() $K_n\subseteq Q$
of rationals points such that
$K_n\subseteq Q$
of rationals points such that
![]() $d_H(K_n,K)<2^{-n}$
.
$d_H(K_n,K)<2^{-n}$
.
The next result is folklore. The two parts appear in [Reference Amir and Hoyrup1, Fact 2.11] and [Reference Downey and Melnikov9, Theorem 3.36], respectively.
Proposition 2.2. A compact Polish space
![]() ${X}$
has a
${X}$
has a
![]() $\mathbf {d}$
-computable Polish presentation if and only if it has a
$\mathbf {d}$
-computable Polish presentation if and only if it has a
![]() ${\mathbf {d}}$
-computably overt copy in Q.
${\mathbf {d}}$
-computably overt copy in Q.
A compact Polish space
![]() ${X}$
has a
${X}$
has a
![]() $\mathbf {d}$
-computable compact presentation if and only if it has a
$\mathbf {d}$
-computable compact presentation if and only if it has a
![]() ${\mathbf {d}}$
-computably compact copy in Q.
${\mathbf {d}}$
-computably compact copy in Q.
Proof It is essentially an effective version of the fact that every Polish space embeds in Q.
Let
![]() $(X,d,S)$
be a
$(X,d,S)$
be a
![]() ${\mathbf {d}}$
-computable Polish presentation of X. Consider the function
${\mathbf {d}}$
-computable Polish presentation of X. Consider the function
![]() $f:X\to Q$
mapping
$f:X\to Q$
mapping
![]() $x\in X$
to
$x\in X$
to
![]() $(x_i)_{i\in \mathbb {N}}\in Q$
defined by
$(x_i)_{i\in \mathbb {N}}\in Q$
defined by
![]() $x_i=d(x,s_i)/(1+d(x,s_i))$
. It is computable and one-to-one, so it is a homeomorphism as X is compact. Its image is
$x_i=d(x,s_i)/(1+d(x,s_i))$
. It is computable and one-to-one, so it is a homeomorphism as X is compact. Its image is
![]() ${\mathbf {d}}$
-computably overt, because it contains the dense
${\mathbf {d}}$
-computably overt, because it contains the dense
![]() ${\mathbf {d}}$
-computable sequence
${\mathbf {d}}$
-computable sequence
![]() $(f(s_n))_{n\in \mathbb {N}}$
.
$(f(s_n))_{n\in \mathbb {N}}$
.
If
![]() $(X,d,S)$
is moreover
$(X,d,S)$
is moreover
![]() ${\mathbf {d}}$
-computably compact, then so is
${\mathbf {d}}$
-computably compact, then so is
![]() $f(X)$
, because the image of a
$f(X)$
, because the image of a
![]() ${\mathbf {d}}$
-computably compact set by a computable function is
${\mathbf {d}}$
-computably compact set by a computable function is
![]() ${\mathbf {d}}$
-computably compact.
${\mathbf {d}}$
-computably compact.
Conversely, if a compact set
![]() $K\subseteq Q$
is
$K\subseteq Q$
is
![]() ${\mathbf {d}}$
-computably overt, then it has a
${\mathbf {d}}$
-computably overt, then it has a
![]() ${\mathbf {d}}$
-computable Polish presentation, using the metric
${\mathbf {d}}$
-computable Polish presentation, using the metric
![]() $d_Q$
and a dense
$d_Q$
and a dense
![]() ${\mathbf {d}}$
-computable sequence in K. If K is moreover
${\mathbf {d}}$
-computable sequence in K. If K is moreover
![]() ${\mathbf {d}}$
-computably compact, then this presentation is
${\mathbf {d}}$
-computably compact, then this presentation is
![]() ${\mathbf {d}}$
-computably compact.
${\mathbf {d}}$
-computably compact.
2.2 Realizations
We recall usual operations on spaces, such as disjoint unions and wedge sum, and show that they preserve computability notions.
We will implicitly use the fact that
![]() $[0,1]^n\times Q$
and
$[0,1]^n\times Q$
and
![]() $Q\times Q$
are computably homeomorphic to Q, so the results of the next constructions are subsets of Q.
$Q\times Q$
are computably homeomorphic to Q, so the results of the next constructions are subsets of Q.
-
• If
 $X,Y\subseteq Q$
, then their disjoint union is
$X,Y\subseteq Q$
, then their disjoint union is
 $X\amalg Y=(\{0\}\times X)\cup (\{1\}\times Y)$
.
$X\amalg Y=(\{0\}\times X)\cup (\{1\}\times Y)$
. -
• If
 $X,Y\subseteq Q$
both contain
$X,Y\subseteq Q$
both contain
 $\overline {0}$
, then their wedge sum is
$\overline {0}$
, then their wedge sum is
 $X\vee Y=(X\times \{\overline {0}\})\cup (\{\overline {0}\}\times Y)$
.
$X\vee Y=(X\times \{\overline {0}\})\cup (\{\overline {0}\}\times Y)$
. -
• If
 $X_n\subseteq Q$
for all
$X_n\subseteq Q$
for all
 $n\in \mathbb {N}$
, then their disjoint union is
$n\in \mathbb {N}$
, then their disjoint union is
 $\coprod _nX_n=\bigcup _n \{0\}^n\times \{1\}\times X_n$
, and its one-point compactification is
$\coprod _nX_n=\bigcup _n \{0\}^n\times \{1\}\times X_n$
, and its one-point compactification is
 $\alpha _0(\coprod _nX_n)=\{\overline {0}\}\cup \coprod _nX_n$
, where
$\alpha _0(\coprod _nX_n)=\{\overline {0}\}\cup \coprod _nX_n$
, where
 $\overline {0}=(0,0,0,\ldots )\in Q$
.
$\overline {0}=(0,0,0,\ldots )\in Q$
.
When
![]() $X,Y$
are Polish spaces, their disjoint union
$X,Y$
are Polish spaces, their disjoint union
![]() $X\amalg Y$
is implicitly defined as the Polish space obtained by embedding X and Y in Q and applying the previous definition, and similarly for the wedge sum and the one-point compactification of the disjoint union.
$X\amalg Y$
is implicitly defined as the Polish space obtained by embedding X and Y in Q and applying the previous definition, and similarly for the wedge sum and the one-point compactification of the disjoint union.
Proposition 2.3. If
![]() $X,Y,X_n$
are uniformly
$X,Y,X_n$
are uniformly
![]() ${\mathbf {d}}$
-computably overt
${\mathbf {d}}$
-computably overt
![]() $($
resp. compact
$($
resp. compact
![]() $)$
, then
$)$
, then
![]() $X\amalg Y,X\vee Y$
and
$X\amalg Y,X\vee Y$
and
![]() $\alpha _0(\coprod _n X_n)$
are
$\alpha _0(\coprod _n X_n)$
are
![]() ${\mathbf {d}}$
-computably overt
${\mathbf {d}}$
-computably overt
![]() $($
resp. compact
$($
resp. compact
![]() $)$
.
$)$
.
Proof The result is straightforward for finite disjoint unions and wedge sums, because the sets
![]() $\{0\}\times X$
,
$\{0\}\times X$
,
![]() $\{1\}\times Y$
,
$\{1\}\times Y$
,
![]() $X\times \{\overline {0}\}$
and
$X\times \{\overline {0}\}$
and
![]() $\{\overline {0}\}\times Y$
easily inherit the computability properties of X and Y, and so do their unions.
$\{\overline {0}\}\times Y$
easily inherit the computability properties of X and Y, and so do their unions.
Let us consider the one-point compactification of the disjoint union. The function
![]() $f_n:Q\to Q$
sending
$f_n:Q\to Q$
sending
![]() $x=(x_0,x_1,\ldots )$
to
$x=(x_0,x_1,\ldots )$
to
![]() $(0,\ldots ,0,1,x_0,x_1,\ldots )$
, starting with n occurrences of
$(0,\ldots ,0,1,x_0,x_1,\ldots )$
, starting with n occurrences of
![]() $0$
, is computable uniformly in n. Equivalently, the preimages of rational balls by
$0$
, is computable uniformly in n. Equivalently, the preimages of rational balls by
![]() $f_n$
are effectively open, uniformly in n.
$f_n$
are effectively open, uniformly in n.
Assume that
![]() $X_n$
are uniformly
$X_n$
are uniformly
![]() ${\mathbf {d}}$
-computably overt. A rational open ball B intersects the set
${\mathbf {d}}$
-computably overt. A rational open ball B intersects the set
![]() $\alpha _0(\coprod _n X_n)$
iff
$\alpha _0(\coprod _n X_n)$
iff
![]() $f_n^{-1}(B)$
intersects
$f_n^{-1}(B)$
intersects
![]() $X_n$
for some n, which is
$X_n$
for some n, which is
![]() ${\mathbf {d}}$
-c.e.
${\mathbf {d}}$
-c.e.
Now assume that
![]() $X_n$
are uniformly
$X_n$
are uniformly
![]() ${\mathbf {d}}$
-computably compact. A rational open set U contains
${\mathbf {d}}$
-computably compact. A rational open set U contains
![]() $\alpha _0(\coprod _nX_n)$
iff there exists n such that
$\alpha _0(\coprod _nX_n)$
iff there exists n such that
![]() $\{0\}^n\times Q\subseteq U$
and
$\{0\}^n\times Q\subseteq U$
and
![]() $X_i\subseteq f_i^{-1}(U)$
for all
$X_i\subseteq f_i^{-1}(U)$
for all
![]() $i<n$
, which is
$i<n$
, which is
![]() ${\mathbf {d}}$
-c.e.
${\mathbf {d}}$
-c.e.
The next result will be a building block for constructing spaces that encode information about a set of natural numbers.
Proposition 2.4. Let
![]() $X_\infty $
and
$X_\infty $
and
![]() $(X_n)_{n\in \mathbb {N}}$
be uniformly computably compact subsets of Q satisfying the following conditions
$(X_n)_{n\in \mathbb {N}}$
be uniformly computably compact subsets of Q satisfying the following conditions
![]() $:$
$:$
-
• For all
 $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $X_n\subseteq X_{n+1}\subseteq X_\infty $
.
$X_n\subseteq X_{n+1}\subseteq X_\infty $
. -
•
 $d_H(X_n,X_\infty )<2^{-n}$
.
$d_H(X_n,X_\infty )<2^{-n}$
.
To a set
![]() $A\subseteq \mathbb {N}$
we associate the compact set
$A\subseteq \mathbb {N}$
we associate the compact set
 $$ \begin{align*} X_A=\begin{cases} X_{\min A},&{if~A\neq\emptyset},\\ X_\infty,&{if~A=\emptyset}. \end{cases} \end{align*} $$
$$ \begin{align*} X_A=\begin{cases} X_{\min A},&{if~A\neq\emptyset},\\ X_\infty,&{if~A=\emptyset}. \end{cases} \end{align*} $$
The set
![]() $X_A$
is uniformly computably compact relative to A and uniformly computably overt relative to any enumeration of
$X_A$
is uniformly computably compact relative to A and uniformly computably overt relative to any enumeration of
![]() $\mathbb {N}\setminus A$
.
$\mathbb {N}\setminus A$
.
Proof For
![]() $s\in \mathbb {N}$
let
$s\in \mathbb {N}$
let
![]() $X_A[s]=X_s$
if
$X_A[s]=X_s$
if
![]() $A\cap [0,s]$
is empty, and
$A\cap [0,s]$
is empty, and
![]() $X_A[s]=X_n$
where
$X_A[s]=X_n$
where
![]() $n=\min (A\cap [0,s])$
otherwise. The sequence
$n=\min (A\cap [0,s])$
otherwise. The sequence
![]() $(X_A[s])_{s\in \mathbb {N}}$
can be computed from A and satisfies
$(X_A[s])_{s\in \mathbb {N}}$
can be computed from A and satisfies
![]() $d_H(X_A[s],X_A)<2^{-s+1}$
, so
$d_H(X_A[s],X_A)<2^{-s+1}$
, so
![]() $X_A$
is computably compact relative to A.
$X_A$
is computably compact relative to A.
We show that a rational ball B intersects
![]() $X_A$
if and only if there exists
$X_A$
if and only if there exists
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $[0,n-1]\cap A=\emptyset $
and B intersects
$[0,n-1]\cap A=\emptyset $
and B intersects
![]() $X_n$
. This condition is c.e. relative to any enumeration of
$X_n$
. This condition is c.e. relative to any enumeration of
![]() $\mathbb {N}\setminus A$
. If
$\mathbb {N}\setminus A$
. If
![]() $[0,n-1]\cap A=\emptyset $
and B intersects
$[0,n-1]\cap A=\emptyset $
and B intersects
![]() $X_n$
, then
$X_n$
, then
![]() $X_A$
contains
$X_A$
contains
![]() $X_n$
, so B intersects
$X_n$
, so B intersects
![]() $X_A$
. Conversely, if B intersects
$X_A$
. Conversely, if B intersects
![]() $X_A$
, then either
$X_A$
, then either
![]() $A=\emptyset $
and any sufficiently large n satisfies the conditions, or
$A=\emptyset $
and any sufficiently large n satisfies the conditions, or
![]() $A\neq \emptyset $
and
$A\neq \emptyset $
and
![]() $n=\min A$
satisfies the conditions.
$n=\min A$
satisfies the conditions.
2.3 Good covers
We will often extract information about a compact Polish space from its finite open covers. In order for this extraction to be computable, we need to decide which open sets of such a cover intersect, which is made possible by considering good covers only. The content of this section is essentially folklore. Closely related results have appeared in [Reference Brattka and Presser6, Reference Downey and Melnikov9, Reference Iljazovic23, Reference Kamo25, Reference Pauly, Seon, Ziegler, Fernández and Muscholl37, Reference Yasugi, Mori and Tsujii44].
Let
![]() $(X,d,S)$
be a Polish presentation of X. To a rational open ball
$(X,d,S)$
be a Polish presentation of X. To a rational open ball
![]() $B(s_i,r)$
we associate the corresponding rational closed ball
$B(s_i,r)$
we associate the corresponding rational closed ball
![]() $\overline {B}(s_i,r)=\{x\in X:d(s_i,x)\leq r\}$
, and to a rational open set U we associate the corresponding union
$\overline {B}(s_i,r)=\{x\in X:d(s_i,x)\leq r\}$
, and to a rational open set U we associate the corresponding union
![]() $\overline {U}$
of rational closed balls. The closed ball always contains the closure of the open ball and is a
$\overline {U}$
of rational closed balls. The closed ball always contains the closure of the open ball and is a
![]() $\Pi ^0_1$
-subset of X, relative to the presentation of X.
$\Pi ^0_1$
-subset of X, relative to the presentation of X.
A good open cover of X is a family of rational open sets
![]() $\kern1pt\mathcal {U}=(U_i)_{i\in I}$
where
$\kern1pt\mathcal {U}=(U_i)_{i\in I}$
where
![]() $I\subseteq \mathbb {N}$
is finite, such that
$I\subseteq \mathbb {N}$
is finite, such that
![]() $X=\bigcup _{i\in I}U_i$
and for every
$X=\bigcup _{i\in I}U_i$
and for every
![]() $J\subseteq I$
, if
$J\subseteq I$
, if
![]() $\bigcap _{i\in J}U_i=\emptyset $
then
$\bigcap _{i\in J}U_i=\emptyset $
then
![]() $\bigcap _{i\in J}\overline {U}_i=\emptyset $
. An open cover
$\bigcap _{i\in J}\overline {U}_i=\emptyset $
. An open cover
![]() $(U_i)_{i\in I}$
is a strong refinement of an open cover
$(U_i)_{i\in I}$
is a strong refinement of an open cover
![]() $(V_j)_{j\in J}$
if for every
$(V_j)_{j\in J}$
if for every
![]() $i\in I$
, there exists
$i\in I$
, there exists
![]() $j\in J$
such that
$j\in J$
such that
![]() $\overline {U}_i\subseteq V_j$
.
$\overline {U}_i\subseteq V_j$
.
The next result can be found in [Reference Downey and Melnikov9, Theorems 1.1 and 3.16].
Lemma 2.5. Given a compact presentation of X, one can compute a strong refining sequence of good open covers, i.e., a sequence
![]() $(\mathcal {U}_s)_{s\in \mathbb {N}}$
of good open covers such that
$(\mathcal {U}_s)_{s\in \mathbb {N}}$
of good open covers such that
![]() $\kern1pt\mathcal {U}_{s+1}$
strongly refines
$\kern1pt\mathcal {U}_{s+1}$
strongly refines
![]() $\kern1pt\mathcal {U}_s$
.
$\kern1pt\mathcal {U}_s$
.
Proof The mesh of a finite open cover
![]() $\kern1pt\mathcal {U}=(U_i)_{i\in I}$
is the maximal diameter of the
$\kern1pt\mathcal {U}=(U_i)_{i\in I}$
is the maximal diameter of the
![]() $U_i$
’s. We first show that there are good open covers of arbitrarily small meshes, and that if
$U_i$
’s. We first show that there are good open covers of arbitrarily small meshes, and that if
![]() $\kern1pt\mathcal {U}$
is a finite open cover of X then there exists
$\kern1pt\mathcal {U}$
is a finite open cover of X then there exists
![]() $\epsilon>0$
such that every finite cover of mesh
$\epsilon>0$
such that every finite cover of mesh
![]() $<\epsilon $
strongly refines
$<\epsilon $
strongly refines
![]() $\kern1pt\mathcal {U}$
.
$\kern1pt\mathcal {U}$
.
Let
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $(B(s,\epsilon ))_{s\in I}$
be a rational open cover of X, where I is finite. By compactness, let
$(B(s,\epsilon ))_{s\in I}$
be a rational open cover of X, where I is finite. By compactness, let
![]() $\delta <\epsilon $
be such that
$\delta <\epsilon $
be such that
![]() $(B(s,\delta ))_{s\in I}$
is still a cover of X. There are only finitely many values of
$(B(s,\delta ))_{s\in I}$
is still a cover of X. There are only finitely many values of
![]() $r\in [\delta ,\epsilon ]$
such that
$r\in [\delta ,\epsilon ]$
such that
![]() $(B(s,r))_{r\in I}$
is not a good cover; indeed, these values are
$(B(s,r))_{r\in I}$
is not a good cover; indeed, these values are
![]() $\min _{x\in X}\max _{s\in J}d(x,s)$
, for
$\min _{x\in X}\max _{s\in J}d(x,s)$
, for
![]() $J\subseteq I$
; indeed, when the cover is not good there exists
$J\subseteq I$
; indeed, when the cover is not good there exists
![]() $J\subseteq I$
and a point x at distance
$J\subseteq I$
and a point x at distance
![]() $\leq r$
from every
$\leq r$
from every
![]() $s\in J$
, but no point y at distance
$s\in J$
, but no point y at distance
![]() $<r$
from every
$<r$
from every
![]() $s\in J$
, so
$s\in J$
, so
![]() $\max _{s\in J}d(x,s)=r$
and x minimizes this quantity. Therefore, there exists a rational number
$\max _{s\in J}d(x,s)=r$
and x minimizes this quantity. Therefore, there exists a rational number
![]() $r\in [\delta ,\epsilon ]$
avoiding this finite set of values, providing a good open cover of mesh
$r\in [\delta ,\epsilon ]$
avoiding this finite set of values, providing a good open cover of mesh
![]() $<2\epsilon $
.
$<2\epsilon $
.
Let
![]() $\kern1pt\mathcal {U}$
be a finite open cover of X. By compactness,
$\kern1pt\mathcal {U}$
be a finite open cover of X. By compactness,
![]() $\kern1pt\mathcal {U}$
has a Lebesgue number
$\kern1pt\mathcal {U}$
has a Lebesgue number
![]() $\delta>0$
, which means that any set of diameter
$\delta>0$
, which means that any set of diameter
![]() ${\leq} \delta $
is contained in some member of U. If
${\leq} \delta $
is contained in some member of U. If
![]() $\mathcal {V}=(V_i)_{i\in J}$
is a good cover of mesh
$\mathcal {V}=(V_i)_{i\in J}$
is a good cover of mesh
![]() ${\leq} \delta $
, then each
${\leq} \delta $
, then each
![]() $\overline {V_i}$
has diameter
$\overline {V_i}$
has diameter
![]() ${\leq} \delta $
, so
${\leq} \delta $
, so
![]() $\mathcal {V}$
strongly refines
$\mathcal {V}$
strongly refines
![]() $\kern1pt\mathcal {U}$
.
$\kern1pt\mathcal {U}$
.
Now we are given a compact presentation of X as oracle. Whether a finite rational cover is good is
![]() $\Sigma ^0_1$
, and whether it strongly refines another rational cover is
$\Sigma ^0_1$
, and whether it strongly refines another rational cover is
![]() $\Sigma ^0_1$
, and whether its mesh is
$\Sigma ^0_1$
, and whether its mesh is
![]() ${<}q$
is
${<}q$
is
![]() $\Sigma ^0_1$
. Therefore, we start with searching for some good open cover
$\Sigma ^0_1$
. Therefore, we start with searching for some good open cover
![]() $\kern1pt\mathcal {U}_0$
of mesh
$\kern1pt\mathcal {U}_0$
of mesh
![]() ${<}1$
and inductively look for a good open cover
${<}1$
and inductively look for a good open cover
![]() $\kern1pt\mathcal {U}_{s+1}$
of mesh
$\kern1pt\mathcal {U}_{s+1}$
of mesh
![]() ${<}2^{-s}$
strongly refining
${<}2^{-s}$
strongly refining
![]() $\kern1pt\mathcal {U}_s$
. These objects exist as proved above, and can be effectively found by exhaustive search.
$\kern1pt\mathcal {U}_s$
. These objects exist as proved above, and can be effectively found by exhaustive search.
2.4 Clopen subsets
We show that from a compact presentation of X, one can compute a presentation of the Boolean algebra of clopen subsets.
Proposition 2.6. Given a compact presentation of X, one can compute an enumeration
![]() $(C_i)_{i\in \mathbb {N}}$
of the clopen subsets of X, such that equality, inclusion, and the finite Boolean operations are computable.
$(C_i)_{i\in \mathbb {N}}$
of the clopen subsets of X, such that equality, inclusion, and the finite Boolean operations are computable.
Proof Assume that a compact presentation is given as oracle. One can compute an enumeration
![]() $(U_i,V_i)_{i\in \mathbb {N}}$
of all the pairs of rational open sets satisfying
$(U_i,V_i)_{i\in \mathbb {N}}$
of all the pairs of rational open sets satisfying
![]() $X=U_i\cup V_i=X$
and
$X=U_i\cup V_i=X$
and
![]() $\overline {U}_i\cap \overline {V}_i=\emptyset $
, because these conditions are c.e. relative to a compact presentation of X. Let then
$\overline {U}_i\cap \overline {V}_i=\emptyset $
, because these conditions are c.e. relative to a compact presentation of X. Let then
![]() $C_i=U_i$
for each i. One can then easily compute the Boolean operations: given i, one can compute j such that
$C_i=U_i$
for each i. One can then easily compute the Boolean operations: given i, one can compute j such that
![]() $(U_j,V_j)=(V_i,U_i)$
, so
$(U_j,V_j)=(V_i,U_i)$
, so
![]() $C_j=X\setminus C_i$
; given
$C_j=X\setminus C_i$
; given
![]() $i,j$
, one can compute k such that
$i,j$
, one can compute k such that
![]() $(U_k,V_k)=(U_i\cap U_j,V_i\cup V_j)$
, so that
$(U_k,V_k)=(U_i\cap U_j,V_i\cup V_j)$
, so that
![]() $C_k=C_i\cap C_j$
, and symmetrically for the union. The set
$C_k=C_i\cap C_j$
, and symmetrically for the union. The set
![]() $\{i\in \mathbb {N}:C_i=\emptyset \}$
can be computed, because
$\{i\in \mathbb {N}:C_i=\emptyset \}$
can be computed, because
![]() $C_i=\emptyset \iff X\subseteq V_i\iff U_i=\emptyset $
, which is both c.e. and co-c.e. relative to a compact presentation. Therefore, equality and inclusion are decidable because they reduce to emptiness of some Boolean combination.
$C_i=\emptyset \iff X\subseteq V_i\iff U_i=\emptyset $
, which is both c.e. and co-c.e. relative to a compact presentation. Therefore, equality and inclusion are decidable because they reduce to emptiness of some Boolean combination.
In particular, whether X is connected is
![]() $\Pi ^0_1$
relative to a compact presentation of X.
$\Pi ^0_1$
relative to a compact presentation of X.
2.5 Covering dimension
Let us briefly recall the covering dimension of a topological space X. If
![]() $\kern1pt\mathcal {U},\mathcal {V}$
are two open covers of X, we say that
$\kern1pt\mathcal {U},\mathcal {V}$
are two open covers of X, we say that
![]() $\mathcal {V}$
is a refinement of
$\mathcal {V}$
is a refinement of
![]() $\kern1pt\mathcal {U}$
if every
$\kern1pt\mathcal {U}$
if every
![]() $V\in \mathcal {V}$
is contained in some
$V\in \mathcal {V}$
is contained in some
![]() $U\in \mathcal {U}$
. An open cover
$U\in \mathcal {U}$
. An open cover
![]() $\kern1pt\mathcal {U}$
has order n if the intersection of any n elements of
$\kern1pt\mathcal {U}$
has order n if the intersection of any n elements of
![]() $\kern1pt\mathcal {U}$
is empty. The covering dimension of X, written
$\kern1pt\mathcal {U}$
is empty. The covering dimension of X, written
![]() $\dim (X)$
, is the least number n such that every open cover
$\dim (X)$
, is the least number n such that every open cover
![]() $\kern1pt\mathcal {U}$
of X has a refinement
$\kern1pt\mathcal {U}$
of X has a refinement
![]() $\mathcal {V}$
of order
$\mathcal {V}$
of order
![]() $n+1$
, if it exists.
$n+1$
, if it exists.
Proposition 2.7. Let
![]() $n\in \mathbb {N}$
. Given a compact presentation of X, the predicate
$n\in \mathbb {N}$
. Given a compact presentation of X, the predicate
![]() $\dim X\leq n$
is
$\dim X\leq n$
is
![]() $\Pi ^0_2$
, uniformly in n.
$\Pi ^0_2$
, uniformly in n.
Proof We are given a compact presentation of X as oracle. As X is compact, it is routine to check that in the definition of dimension, one can assume that
![]() $\kern1pt\mathcal {U}$
and
$\kern1pt\mathcal {U}$
and
![]() $\mathcal {V}$
are good covers and that
$\mathcal {V}$
are good covers and that
![]() $\mathcal {V}$
strictly refines
$\mathcal {V}$
strictly refines
![]() $\kern1pt\mathcal {U}$
. Therefore,
$\kern1pt\mathcal {U}$
. Therefore,
![]() $\dim X\leq n$
iff for every good cover
$\dim X\leq n$
iff for every good cover
![]() $\kern1pt\mathcal {U}$
, there exists a good cover
$\kern1pt\mathcal {U}$
, there exists a good cover
![]() $\mathcal {V}$
that strongly refines
$\mathcal {V}$
that strongly refines
![]() $\kern1pt\mathcal {U}$
, and such that for all
$\kern1pt\mathcal {U}$
, and such that for all
![]() $V_0,\ldots ,V_n\in \mathcal {V}$
, one has
$V_0,\ldots ,V_n\in \mathcal {V}$
, one has
![]() $\overline {V}_0\cap \cdots \cap \overline {V}_n=\emptyset $
. This is a
$\overline {V}_0\cap \cdots \cap \overline {V}_n=\emptyset $
. This is a
![]() $\Pi ^0_2$
predicate, because one can computable enumerate the good covers of X, and the strong refinements of a given good cover.
$\Pi ^0_2$
predicate, because one can computable enumerate the good covers of X, and the strong refinements of a given good cover.
Proposition 2.8. If
![]() $\dim (X)\leq n$
, then given a compact presentation of X, one can compute a strong refining sequence of good open covers
$\dim (X)\leq n$
, then given a compact presentation of X, one can compute a strong refining sequence of good open covers
![]() $(\mathcal {U}_s)_{s\in \mathbb {N}}$
of order
$(\mathcal {U}_s)_{s\in \mathbb {N}}$
of order
![]() $n+1$
.
$n+1$
.
Proof We proceed as in the proof of Lemma 2.5, but when searching for a good cover
![]() $\kern1pt\mathcal {U}_{s+1}$
that strongly refines
$\kern1pt\mathcal {U}_{s+1}$
that strongly refines
![]() $\kern1pt\mathcal {U}_s$
, we additionally test whether
$\kern1pt\mathcal {U}_s$
, we additionally test whether
![]() $\kern1pt\mathcal {U}_{s+1}$
has order
$\kern1pt\mathcal {U}_{s+1}$
has order
![]() $n+1$
, which is also a
$n+1$
, which is also a
![]() $\Sigma ^0_1$
predicate. As
$\Sigma ^0_1$
predicate. As
![]() $\dim (X)\leq n$
, it always exists so it can be effectively found.
$\dim (X)\leq n$
, it always exists so it can be effectively found.
Corollary 2.9. If X is zero-dimensional, then from any compact presentation of X, one can compute a pruned tree
![]() $T\subseteq 2^{<\omega }$
such that X is homeomorphic to
$T\subseteq 2^{<\omega }$
such that X is homeomorphic to
![]() $[T]$
.
$[T]$
.
Proof As X is zero-dimensional, one can compute by Proposition 2.8 a strongly refining sequence of good open covers
![]() $(\mathcal {U}_s)_{s\in \mathbb {N}}$
of order
$(\mathcal {U}_s)_{s\in \mathbb {N}}$
of order
![]() $1$
. Each
$1$
. Each
![]() $\kern1pt\mathcal {U}_s$
is therefore made of clopen sets. All these clopen sets ordered by inclusion form a finitely branching pruned tree, in which the number of nodes at each level can be computed. By standard arguments, it can be effectively converted into a binary tree.
$\kern1pt\mathcal {U}_s$
is therefore made of clopen sets. All these clopen sets ordered by inclusion form a finitely branching pruned tree, in which the number of nodes at each level can be computed. By standard arguments, it can be effectively converted into a binary tree.
3 Cantor–Bendixson derivative
Let X be a topological space. The Cantor–Bendixson derivative of X is the subspace
![]() $X'$
of all non-isolated points of X. We discuss the computability of
$X'$
of all non-isolated points of X. We discuss the computability of
![]() $X'$
in comparison with the computability of X. This problem has been investigated in the context of reverse mathematics in [Reference Greenberg and Montalbán16].
$X'$
in comparison with the computability of X. This problem has been investigated in the context of reverse mathematics in [Reference Greenberg and Montalbán16].
In the next result, it is important to note that in order to produce a compact presentation of
![]() $X'$
, we only use a Polish presentation of X.
$X'$
, we only use a Polish presentation of X.
Lemma 3.1. Let
![]() ${X}$
be a compact Polish space.
${X}$
be a compact Polish space.
If
![]() $X\subseteq Q$
is
$X\subseteq Q$
is
![]() ${\mathbf {d}}$
-computably overt, then
${\mathbf {d}}$
-computably overt, then
![]() $X'$
is
$X'$
is
![]() $\Pi ^0_1({\mathbf {d}}')$
and
$\Pi ^0_1({\mathbf {d}}')$
and
![]() ${\mathbf {d}}"$
-computably overt.
${\mathbf {d}}"$
-computably overt.
Therefore, if X has a
![]() ${\mathbf {d}}$
-computable Polish presentation, then its Cantor-Bendixson derivative
${\mathbf {d}}$
-computable Polish presentation, then its Cantor-Bendixson derivative
![]() $X'$
has a
$X'$
has a
![]() ${\mathbf {d}}"$
-computable compact presentation.
${\mathbf {d}}"$
-computable compact presentation.
Proof Assume that
![]() $X\subseteq Q$
is
$X\subseteq Q$
is
![]() ${\mathbf {d}}$
-computably overt, and let
${\mathbf {d}}$
-computably overt, and let
![]() $(x_i)_{i\in \mathbb {N}}$
be a
$(x_i)_{i\in \mathbb {N}}$
be a
![]() ${\mathbf {d}}$
-computable dense sequence in X.
${\mathbf {d}}$
-computable dense sequence in X.
Let
![]() $B=B(s,r)$
be a rational open ball in Q, and for
$B=B(s,r)$
be a rational open ball in Q, and for
![]() $k\in \mathbb {N}$
let
$k\in \mathbb {N}$
let
![]() $B^k=B(s,r-2^{-k})$
. We claim that B intersects
$B^k=B(s,r-2^{-k})$
. We claim that B intersects
![]() $X'$
if and only if there is k such that
$X'$
if and only if there is k such that
![]() $B^k\cap X$
contains infinitely many points. For the forward direction, choose
$B^k\cap X$
contains infinitely many points. For the forward direction, choose
![]() $x\in B\cap X'$
. One has
$x\in B\cap X'$
. One has
![]() $x\in B^k$
for sufficiently large k. Since
$x\in B^k$
for sufficiently large k. Since
![]() $B^k$
is open and x is not isolated in X,
$B^k$
is open and x is not isolated in X,
![]() $B^k$
contains infinitely many points. For the backward direction, if
$B^k$
contains infinitely many points. For the backward direction, if
![]() $B^k\cap X$
contains infinitely many points, then its closure, which is contained in
$B^k\cap X$
contains infinitely many points, then its closure, which is contained in
![]() $B\cap X$
, contains a non-isolated point; therefore, B intersects
$B\cap X$
, contains a non-isolated point; therefore, B intersects
![]() $X'$
. By this claim, the property
$X'$
. By this claim, the property
![]() $B\cap {X}'\not =\emptyset $
is equivalent to
$B\cap {X}'\not =\emptyset $
is equivalent to
which is
![]() $\Sigma ^0_3$
relative to
$\Sigma ^0_3$
relative to
![]() ${\mathbf {d}}$
, or equivalently
${\mathbf {d}}$
, or equivalently
![]() $\Sigma ^0_1$
relative to
$\Sigma ^0_1$
relative to
![]() ${\mathbf {d}}"$
. This means that
${\mathbf {d}}"$
. This means that
![]() $X'$
is
$X'$
is
![]() ${\mathbf {d}}"$
-computably overt.
${\mathbf {d}}"$
-computably overt.
Next, let
![]() $A=\{(i,k):\forall j,x_j=x_i\text { or }d_Q(x_i,x_j)\geq 2^{-k}\}$
. The set A is
$A=\{(i,k):\forall j,x_j=x_i\text { or }d_Q(x_i,x_j)\geq 2^{-k}\}$
. The set A is
![]() $\Pi ^0_1$
relative to
$\Pi ^0_1$
relative to
![]() ${\mathbf {d}}$
, hence
${\mathbf {d}}$
, hence
![]() ${\mathbf {d}}'$
-computable. One can easily see that x is isolated in
${\mathbf {d}}'$
-computable. One can easily see that x is isolated in
![]() ${X}$
if and only if
${X}$
if and only if
![]() $x\in B(x_i,2^{-k})$
for some
$x\in B(x_i,2^{-k})$
for some
![]() $(i,k)\in A$
. Thus, the set of isolated points is a
$(i,k)\in A$
. Thus, the set of isolated points is a
![]() $\Sigma ^0_1({\mathbf {d}}')$
subset of
$\Sigma ^0_1({\mathbf {d}}')$
subset of
![]() ${X}$
; hence
${X}$
; hence
![]() ${X}'$
is a
${X}'$
is a
![]() $\Pi ^0_1({\mathbf {d}}')$
subset of
$\Pi ^0_1({\mathbf {d}}')$
subset of
![]() ${X}$
, which is itself
${X}$
, which is itself
![]() $\Pi ^0_1({\mathbf {d}}')$
, so
$\Pi ^0_1({\mathbf {d}}')$
, so
![]() $X'$
is
$X'$
is
![]() $\Pi ^0_1({\mathbf {d}}')$
.
$\Pi ^0_1({\mathbf {d}}')$
.
Therefore,
![]() $X'$
is
$X'$
is
![]() ${\mathbf {d}}"$
-computably compact.
${\mathbf {d}}"$
-computably compact.
3.1 Stone duality
Here we show that spectra of compact zero-dimensional spaces are closely related to spectra of Boolean algebras. This follows from an effectivization of Stone duality in [Reference Odintsov and Selivanov36].
Let
![]() $\mathbf {B}$
be the category formed by the Boolean algebras as objects and the
$\mathbf {B}$
be the category formed by the Boolean algebras as objects and the
![]() $\{\vee ,\wedge ,\bar {}\;,0,1\}$
-homomorphisms as morphisms. Recall that a Stone space is a compact topological space X such that for any distinct
$\{\vee ,\wedge ,\bar {}\;,0,1\}$
-homomorphisms as morphisms. Recall that a Stone space is a compact topological space X such that for any distinct
![]() $x,y\in X$
there is a clopen set U with
$x,y\in X$
there is a clopen set U with
![]() $x\in U\not \ni y$
(i.e., zero-dimensional and
$x\in U\not \ni y$
(i.e., zero-dimensional and
![]() $T_1$
). Let
$T_1$
). Let
![]() $\mathbf {S}$
be the category formed by the Stone spaces as objects and the continuous mappings as morphisms.
$\mathbf {S}$
be the category formed by the Stone spaces as objects and the continuous mappings as morphisms.
The Stone duality states the dual equivalence between the categories
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {S}$
. More explicitly, the Stone space
$\mathbf {S}$
. More explicitly, the Stone space
![]() $s(B)$
corresponding to a given Boolean algebra B is formed by the set of prime filters of B with the base of open (in fact, clopen) sets consisting of the sets
$s(B)$
corresponding to a given Boolean algebra B is formed by the set of prime filters of B with the base of open (in fact, clopen) sets consisting of the sets
![]() $\{F\in s(B)\mid a\in F\}$
,
$\{F\in s(B)\mid a\in F\}$
,
![]() $a\in B$
. (Note that one could equivalently take ideals in place of filters.) Conversely, the Boolean algebra
$a\in B$
. (Note that one could equivalently take ideals in place of filters.) Conversely, the Boolean algebra
![]() $b(X)$
corresponding to a given Stone space X is formed by the set of clopen sets (with the usual set-theoretic operations). By Stone duality, any Boolean algebra B is canonically isomorphic to the Boolean algebra
$b(X)$
corresponding to a given Stone space X is formed by the set of clopen sets (with the usual set-theoretic operations). By Stone duality, any Boolean algebra B is canonically isomorphic to the Boolean algebra
![]() $b(s(B))$
(the isomorphism
$b(s(B))$
(the isomorphism
![]() $f:B\rightarrow b(s(B))$
is defined by
$f:B\rightarrow b(s(B))$
is defined by
![]() $f(a)=\{F\in s(B)\mid a\in F\}$
), and any Stone space X is canonically homeomorphic to the space
$f(a)=\{F\in s(B)\mid a\in F\}$
), and any Stone space X is canonically homeomorphic to the space
![]() $s(b(X))$
.
$s(b(X))$
.
Restricting the Stone duality to the countable Boolean algebras, we obtain their duality with the class
![]() $\mathbf {CP}_0$
of compact zero-dimensional countably based spaces, and in fact with the compact subspaces of the Cantor space
$\mathbf {CP}_0$
of compact zero-dimensional countably based spaces, and in fact with the compact subspaces of the Cantor space
![]() $2^\omega $
. As the nonempty closed subsets of
$2^\omega $
. As the nonempty closed subsets of
![]() $2^\omega $
coincide with the sets
$2^\omega $
coincide with the sets
![]() $[T]$
of infinite paths through a pruned tree
$[T]$
of infinite paths through a pruned tree
![]() $T\subseteq 2^\omega $
, we obtain a close relation between such subspaces and countable Boolean algebras.
$T\subseteq 2^\omega $
, we obtain a close relation between such subspaces and countable Boolean algebras.
Fact 3.2.
-
(1) A Boolean algebra has a
 ${\mathbf {d}}$
-c.e.
${\mathbf {d}}$
-c.e.
 $($
resp.
$($
resp.
 ${\mathbf {d}}$
-co-c.e.,
${\mathbf {d}}$
-co-c.e.,
 ${\mathbf {d}}$
-computable
${\mathbf {d}}$
-computable
 $)$
copy if and only if it is isomorphic to the Boolean algebra of clopen subsets of
$)$
copy if and only if it is isomorphic to the Boolean algebra of clopen subsets of
 $[T]$
for some
$[T]$
for some
 ${\mathbf {d}}$
-co-c.e.
${\mathbf {d}}$
-co-c.e.
 $($
resp.
$($
resp.
 ${\mathbf {d}}$
-c.e.,
${\mathbf {d}}$
-c.e.,
 ${\mathbf {d}}$
-computable
${\mathbf {d}}$
-computable
 $)$
pruned tree T.
$)$
pruned tree T. -
(2) Every
 ${\mathbf {d}}$
-co-c.e. Boolean algebra is isomorphic to a
${\mathbf {d}}$
-co-c.e. Boolean algebra is isomorphic to a
 ${\mathbf {d}}$
-computable Boolean algebra.
${\mathbf {d}}$
-computable Boolean algebra. -
(3) There is a
 ${\mathbf {d}}$
-c.e. Boolean algebra which is not isomorphic to a
${\mathbf {d}}$
-c.e. Boolean algebra which is not isomorphic to a
 ${\mathbf {d}}$
-computable Boolean algebra.
${\mathbf {d}}$
-computable Boolean algebra.
Proof The first item follows from [Reference Odintsov and Selivanov36, Lemma 3]; see also [Reference Selivanov41]. The second item follows from [Reference Odintsov and Selivanov36]. The third item follows from [Reference Feiner13].
As already noticed by Harrison-Trainer, Melnikov, and Ng [Reference Harrison-Trainor, Melnikov and Ng18], one can use Stone duality to show several results on degree spectra of zero-dimensional compacta. For instance, Stone duality can be used to show the following:
Fact 3.3 (see [Reference Harrison-Trainor, Melnikov and Ng18]).
-
(1) There exists
 $X\in \mathbf {CP}_0$
which has a
$X\in \mathbf {CP}_0$
which has a
 $\mathbf {0}'$
-computable Polish presentation, but no computable Polish presentation,
$\mathbf {0}'$
-computable Polish presentation, but no computable Polish presentation, -
(2) If
 $X\in \mathbf {CP}_0$
has a low
$X\in \mathbf {CP}_0$
has a low
 $_4$
Polish presentation, then it has a computable Polish presentation.
$_4$
Polish presentation, then it has a computable Polish presentation.
For
![]() $X\in \mathbf {CP}_0$
, Corollary 2.9 implies that X has a
$X\in \mathbf {CP}_0$
, Corollary 2.9 implies that X has a
![]() ${\mathbf {d}}$
-computable compact presentation if and only if there exists a
${\mathbf {d}}$
-computable compact presentation if and only if there exists a
![]() ${\mathbf {d}}$
-computable pruned tree
${\mathbf {d}}$
-computable pruned tree
![]() $T\subseteq 2^{<\omega }$
such that X is homeomorphic to
$T\subseteq 2^{<\omega }$
such that X is homeomorphic to
![]() $[T]$
. Therefore, we obtain the following result.
$[T]$
. Therefore, we obtain the following result.
Corollary 3.4. The degree spectra of countable Boolean algebras coincide with the compact degree spectra of zero-dimensional compact Polish spaces.
The Stone dual of the Cantor–Bendixson derivative is known as the Fréchet derivative
![]() $B'$
of a Boolean algebra B which is the quotient of B by the ideal generated by atoms (minimal non-zero elements). Since the isolated points x of the space
$B'$
of a Boolean algebra B which is the quotient of B by the ideal generated by atoms (minimal non-zero elements). Since the isolated points x of the space
![]() $s(B)$
(realized as
$s(B)$
(realized as
![]() $[F]$
above) are precisely the atoms
$[F]$
above) are precisely the atoms
![]() $[\tau ]\cap [F]$
for suitable prefix
$[\tau ]\cap [F]$
for suitable prefix
![]() $\tau \sqsubseteq x$
, we obtain the following.
$\tau \sqsubseteq x$
, we obtain the following.
Proposition 3.5. For any countable Boolean algebra B,
![]() $s(B')$
is homeomorphic to
$s(B')$
is homeomorphic to
![]() $s(B)'$
.
$s(B)'$
.
Precise complexity estimations for the Fréchet derivative were obtained in [Reference Odintsov and Selivanov36]: for any Turing degree
![]() ${\mathbf {d}}$
, a countable Boolean algebra C is
${\mathbf {d}}$
, a countable Boolean algebra C is
![]() ${\mathbf {d}}"$
-computably presentable iff C is isomorphic to
${\mathbf {d}}"$
-computably presentable iff C is isomorphic to
![]() $B'$
for some
$B'$
for some
![]() ${\mathbf {d}}$
-computable Boolean algebra B, and there is a
${\mathbf {d}}$
-computable Boolean algebra B, and there is a
![]() ${\mathbf {d}}$
-computable Boolean algebra B such that
${\mathbf {d}}$
-computable Boolean algebra B such that
![]() $B'$
is not
$B'$
is not
![]() ${\mathbf {d}}'$
-computably presentable. The iterated version is also known for any
${\mathbf {d}}'$
-computably presentable. The iterated version is also known for any
![]() $n>0$
: a countable Boolean algebra C is
$n>0$
: a countable Boolean algebra C is
![]() ${\mathbf {d}}^{(2n)}$
-computably presentable iff C is isomorphic to the nth derivative
${\mathbf {d}}^{(2n)}$
-computably presentable iff C is isomorphic to the nth derivative
![]() $B^{(n)}$
for some
$B^{(n)}$
for some
![]() ${\mathbf {d}}$
-computable Boolean algebra B, and there is a
${\mathbf {d}}$
-computable Boolean algebra B, and there is a
![]() ${\mathbf {d}}$
-computable Boolean algebra B such that the nth derivative
${\mathbf {d}}$
-computable Boolean algebra B such that the nth derivative
![]() $B^{(n)}$
is not
$B^{(n)}$
is not
![]() ${\mathbf {d}}^{(2n-1)}$
-computably presentable.
${\mathbf {d}}^{(2n-1)}$
-computably presentable.
These results have an immediate consequence in terms of compact degree spectra of spaces in
![]() $\mathbf {CP}_0$
, by Corollary 3.4 and Proposition 3.5.
$\mathbf {CP}_0$
, by Corollary 3.4 and Proposition 3.5.
Theorem 3.6. Let
![]() ${\mathbf {d}}$
be any Turing degree. For any
${\mathbf {d}}$
be any Turing degree. For any
![]() $n\geq 1$
, a space
$n\geq 1$
, a space
![]() $Y\in \mathbf {CP}_0$
has a
$Y\in \mathbf {CP}_0$
has a
![]() ${\mathbf {d}}^{(2n)}$
-computable compact presentation if and only if Y is homeomorphic to the nth derivative
${\mathbf {d}}^{(2n)}$
-computable compact presentation if and only if Y is homeomorphic to the nth derivative
![]() $X^{(n)}$
for some
$X^{(n)}$
for some
![]() ${\mathbf {d}}$
-computable compact
${\mathbf {d}}$
-computable compact
![]() $X\in \mathbf {CP}_0$
, and there is a
$X\in \mathbf {CP}_0$
, and there is a
![]() ${\mathbf {d}}$
-computable compact
${\mathbf {d}}$
-computable compact
![]() $X\in \mathbf {CP}_0$
such that the nth derivative
$X\in \mathbf {CP}_0$
such that the nth derivative
![]() $X^{(n)}$
does not have a
$X^{(n)}$
does not have a
![]() ${\mathbf {d}}^{(2n-1)}$
-computable compact presentation.
${\mathbf {d}}^{(2n-1)}$
-computable compact presentation.
It implies in particular that Lemma 3.1 is almost optimal.
3.2 Countable spaces
We next note that countable topological spaces cannot be used to construct nontrivial degree spectra inside the hyperarithmetical hierarchy.
Mazurkiewicz–Sierpiński’s theorem states that every countable compact Polish space is homeomorphic to the ordinal space
![]() $\omega ^\alpha \cdot n+1$
for some
$\omega ^\alpha \cdot n+1$
for some
![]() $\alpha <\omega _1$
and
$\alpha <\omega _1$
and
![]() $n\in \omega $
, endowed with the order topology.
$n\in \omega $
, endowed with the order topology.
Let
![]() $\omega _1^x$
be the least ordinal which is not computable in x.
$\omega _1^x$
be the least ordinal which is not computable in x.
Proposition 3.7. For any countable ordinal
![]() $\alpha $
, the compact and Polish degree spectrum of the space
$\alpha $
, the compact and Polish degree spectrum of the space
![]() $\omega ^\alpha +1$
are both
$\omega ^\alpha +1$
are both
![]() $\{x:\alpha <\omega _1^x\}$
.
$\{x:\alpha <\omega _1^x\}$
.
Proof We first show that if
![]() $\alpha $
is
$\alpha $
is
![]() $\mathbf {x}$
-computable, then
$\mathbf {x}$
-computable, then
![]() $\omega ^\alpha +1$
has an
$\omega ^\alpha +1$
has an
![]() $\mathbf {x}$
-computable compact presentation.
$\mathbf {x}$
-computable compact presentation.
Given an
![]() $\mathbf {x}$
-computable well-ordering
$\mathbf {x}$
-computable well-ordering
![]() $\preceq $
of
$\preceq $
of
![]() $\mathbb {N}$
of order type
$\mathbb {N}$
of order type
![]() $\omega ^\alpha +1$
, we build a copy X of
$\omega ^\alpha +1$
, we build a copy X of
![]() $\omega ^\alpha +1$
in
$\omega ^\alpha +1$
in
![]() $[0,1]$
as follows. We can assume w.l.o.g. that
$[0,1]$
as follows. We can assume w.l.o.g. that
![]() $0$
is minimal and
$0$
is minimal and
![]() $1$
is maximal for
$1$
is maximal for
![]() $\preceq $
. We embed
$\preceq $
. We embed
![]() $(\mathbb {N},\preceq )$
in
$(\mathbb {N},\preceq )$
in
![]() $([0,1],\leq )$
by inductively defining a rational number
$([0,1],\leq )$
by inductively defining a rational number
![]() $x_n\in [0,1]$
for each
$x_n\in [0,1]$
for each
![]() $n\in \mathbb {N}$
. We need some care to make sure that we will obtain a topological embedding, and that the copy X will be
$n\in \mathbb {N}$
. We need some care to make sure that we will obtain a topological embedding, and that the copy X will be
![]() $\mathbf {x}$
-computably compact. We start with
$\mathbf {x}$
-computably compact. We start with
![]() $x_0=0$
and
$x_0=0$
and
![]() $x_1=1$
. Let
$x_1=1$
. Let
![]() $n\geq 2$
and assume that
$n\geq 2$
and assume that
![]() $x_0,\ldots ,x_{n-1}$
have been defined. Let i and j be, respectively, the predecessor and the successor of n in
$x_0,\ldots ,x_{n-1}$
have been defined. Let i and j be, respectively, the predecessor and the successor of n in
![]() $(\{0,\ldots ,n\},\preceq )$
, and define
$(\{0,\ldots ,n\},\preceq )$
, and define
![]() $x_{n}=2^{-n}x_i+(1-2^{-n})x_j$
. Note that
$x_{n}=2^{-n}x_i+(1-2^{-n})x_j$
. Note that
![]() $x_j-x_n\leq 2^{-n}$
. Let
$x_j-x_n\leq 2^{-n}$
. Let
![]() $X=\{x_n:n\in \mathbb {N}\}$
with the topology inherited from
$X=\{x_n:n\in \mathbb {N}\}$
with the topology inherited from
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
The function
![]() $n\mapsto x_n$
is by construction an order embedding of
$n\mapsto x_n$
is by construction an order embedding of
![]() $(\mathbb {N},\preceq )$
in
$(\mathbb {N},\preceq )$
in
![]() $([0,1], \leq)$
. We need to show that it is a topological embedding, i.e., that it is continuous. It is sufficient to check that if
$([0,1], \leq)$
. We need to show that it is a topological embedding, i.e., that it is continuous. It is sufficient to check that if
![]() $n=\sup _\preceq \{m:m\prec n\}$
, then
$n=\sup _\preceq \{m:m\prec n\}$
, then
![]() $x_n=\sup _\leq \{x_m:m\prec n\}$
. There exist infinitely many m’s such that
$x_n=\sup _\leq \{x_m:m\prec n\}$
. There exist infinitely many m’s such that
![]() $m\geq n$
,
$m\geq n$
,
![]() $m\prec n$
and m is the predecessor of n in
$m\prec n$
and m is the predecessor of n in
![]() $(\{0,\ldots ,m\},\preceq )$
. When defining
$(\{0,\ldots ,m\},\preceq )$
. When defining
![]() $x_m$
for any such m, the successor of m is
$x_m$
for any such m, the successor of m is
![]() $j=n$
, so
$j=n$
, so
![]() $x_n-x_m\leq 2^{-m}$
, which is arbitrarily small, so
$x_n-x_m\leq 2^{-m}$
, which is arbitrarily small, so
![]() $x_n=\sup _\leq \{m:m\prec n\}$
as wanted.
$x_n=\sup _\leq \{m:m\prec n\}$
as wanted.
Therefore, the set
![]() $X=\{x_n:n\in \mathbb {N}\}$
is a copy of
$X=\{x_n:n\in \mathbb {N}\}$
is a copy of
![]() $\omega ^\alpha +1$
. The sequence
$\omega ^\alpha +1$
. The sequence
![]() $(x_n)_{n\in \mathbb {N}}$
is an
$(x_n)_{n\in \mathbb {N}}$
is an
![]() $\mathbf {x}$
-computable sequence of rational numbers. Let
$\mathbf {x}$
-computable sequence of rational numbers. Let
![]() $X_n=\{x_0,\ldots ,x_n\}\subseteq X$
and observe by construction that
$X_n=\{x_0,\ldots ,x_n\}\subseteq X$
and observe by construction that
![]() $d_H(X_n,X_{n-1})\leq 2^{-n}$
, so
$d_H(X_n,X_{n-1})\leq 2^{-n}$
, so
![]() $d_H(X_n,X)\leq 2^{-n}$
. As the compact sets
$d_H(X_n,X)\leq 2^{-n}$
. As the compact sets
![]() $X_n$
are uniformly
$X_n$
are uniformly
![]() $\mathbf {x}$
-computable and converge fast to X, X is
$\mathbf {x}$
-computable and converge fast to X, X is
![]() $\mathbf {x}$
-computable as well.
$\mathbf {x}$
-computable as well.
Conversely, if
![]() $\omega ^\alpha +1$
has an
$\omega ^\alpha +1$
has an
![]() $\mathbf {x}$
-computable Polish presentation, then by Lemma 2.1, it has an
$\mathbf {x}$
-computable Polish presentation, then by Lemma 2.1, it has an
![]() $\mathbf {x}'$
-computable compact presentation. In particular, there is a countable
$\mathbf {x}'$
-computable compact presentation. In particular, there is a countable
![]() $\Pi ^0_1(\mathbf {x}')$
class
$\Pi ^0_1(\mathbf {x}')$
class
![]() $P\subseteq 2^\omega $
which is homeomorphic to
$P\subseteq 2^\omega $
which is homeomorphic to
![]() $\omega ^\alpha +1$
. Since the Cantor–Bendixson rank of
$\omega ^\alpha +1$
. Since the Cantor–Bendixson rank of
![]() $\omega ^\alpha +1$
is
$\omega ^\alpha +1$
is
![]() $\alpha $
, and the Cantor–Bendixson rank is a topological invariant, the rank of P is also
$\alpha $
, and the Cantor–Bendixson rank is a topological invariant, the rank of P is also
![]() $\alpha $
. However, as noted by Kreisel, the Spector boundedness principle implies that the rank of a countable
$\alpha $
. However, as noted by Kreisel, the Spector boundedness principle implies that the rank of a countable
![]() $\Pi ^0_1(\mathbf {x}')$
class must be
$\Pi ^0_1(\mathbf {x}')$
class must be
![]() $\mathbf {x}'$
-computable; see also [Reference Cenzer7, Section 4]. As an
$\mathbf {x}'$
-computable; see also [Reference Cenzer7, Section 4]. As an
![]() $\mathbf {x}$
-hyperarithmetic ordinal is always
$\mathbf {x}$
-hyperarithmetic ordinal is always
![]() $\mathbf {x}$
-computable, this implies that
$\mathbf {x}$
-computable, this implies that
![]() $\alpha <\omega _1^{\mathbf {x}}$
.
$\alpha <\omega _1^{\mathbf {x}}$
.
The same arguments show that the compact and Polish degree spectra of
![]() $\omega ^\alpha \cdot n+1$
are both
$\omega ^\alpha \cdot n+1$
are both
![]() $\{x:\alpha <\omega _1^x\}$
. Therefore, if a countable Polish space has an hyperarithmetical compact (or even Polish) presentation, then it has a computable compact presentation.
$\{x:\alpha <\omega _1^x\}$
. Therefore, if a countable Polish space has an hyperarithmetical compact (or even Polish) presentation, then it has a computable compact presentation.
For more details, see also [Reference Ash and Knight2, Reference Greenberg and Montalbán16].
4 Computable aspects of Čech homology groups
4.1 Background on Čech homology groups
All the details about the definitions and results mentioned in this section can be found in the textbook of Hurewicz and Wallman [Reference Hurewicz and Wallman22]. We will refer to the corresponding sections in that reference.
Simplicial complexes. We refer to [Reference Hurewicz and Wallman22, Section V.9]. Let V be a finite set, whose elements are called the vertices. A simplicial complex
K on V is a collection of subsets of V such that if
![]() $A\subseteq B\subseteq V$
and
$A\subseteq B\subseteq V$
and
![]() $B\in K$
, then
$B\in K$
, then
![]() $A\in K$
. An element
$A\in K$
. An element
![]() $A\in K$
is called a simplex, and an n-simplex if the cardinality of A is
$A\in K$
is called a simplex, and an n-simplex if the cardinality of A is
![]() $n+1$
.
$n+1$
.
To a simplicial complex K corresponds a topological space
![]() $X_K$
, called its geometric realization. Assuming that
$X_K$
, called its geometric realization. Assuming that
![]() $V=\{0,\ldots ,k\}$
, let
$V=\{0,\ldots ,k\}$
, let
![]() $\Delta _V=\{(x_0,\ldots ,x_k):\forall i, x_i\in [0,1]\text { and }\sum _i x_i=1\}$
. For
$\Delta _V=\{(x_0,\ldots ,x_k):\forall i, x_i\in [0,1]\text { and }\sum _i x_i=1\}$
. For
![]() $x=(x_0,\ldots ,x_k)\in \Delta _V$
, let
$x=(x_0,\ldots ,x_k)\in \Delta _V$
, let
![]() $\mathrm {supp}(x)=\{i:x_i>0\}$
. The geometric realization of K is the subset of
$\mathrm {supp}(x)=\{i:x_i>0\}$
. The geometric realization of K is the subset of
![]() $\Delta _V$
defined by
$\Delta _V$
defined by
Let
![]() $K,L$
be simplicial complexes on vertices
$K,L$
be simplicial complexes on vertices
![]() $V_K$
and
$V_K$
and
![]() $V_L$
respectively. A simplicial map, written
$V_L$
respectively. A simplicial map, written
![]() $f:K\to L$
, is a map
$f:K\to L$
, is a map
![]() $f:V_K\to V_L$
such that if
$f:V_K\to V_L$
such that if
![]() $A\in K$
then
$A\in K$
then
![]() $f(A)=\{f(v):v\in A\}\in L$
. In other words, a simplicial map sends each simplex of K to a simplex of L. Note that if A is an n-simplex of K, then
$f(A)=\{f(v):v\in A\}\in L$
. In other words, a simplicial map sends each simplex of K to a simplex of L. Note that if A is an n-simplex of K, then
![]() $f(A)$
is a p-simplex of L for some
$f(A)$
is a p-simplex of L for some
![]() $p\leq n$
, and
$p\leq n$
, and
![]() $f(A)$
is an n-simplex if and only if the images of the vertices of A under f are pairwise distinct.
$f(A)$
is an n-simplex if and only if the images of the vertices of A under f are pairwise distinct.
Simplicial homology groups. We refer to [Reference Hurewicz and Wallman22, Sections VIII.1, VIII.3]. To a simplicial complex K are associated its homology groups
![]() $H_n(K;G)$
where G is an abelian group, called the coefficient group. Here we will only consider the coefficient group
$H_n(K;G)$
where G is an abelian group, called the coefficient group. Here we will only consider the coefficient group
![]() $G={{\mathbb {Z}}_2}:={\mathbb {Z}}/2{\mathbb {Z}}$
.
$G={{\mathbb {Z}}_2}:={\mathbb {Z}}/2{\mathbb {Z}}$
.
Let K be a simplicial complex on a finite set V of vertices. An n-chain of K is a set of n-simplices of K, orequivalently a formal sum of n-simplices with coefficients in
![]() ${{\mathbb {Z}}_2}$
. Let
${{\mathbb {Z}}_2}$
. Let
![]() $C_n(K)$
be the finite abelian group of n-chains, endowed with the sum operation. The boundary operator is the group homomorphism
$C_n(K)$
be the finite abelian group of n-chains, endowed with the sum operation. The boundary operator is the group homomorphism
![]() $\partial _n:C_{n}(K)\to C_{n-1}(K)$
that sends an n-simplex
$\partial _n:C_{n}(K)\to C_{n-1}(K)$
that sends an n-simplex
![]() $\Delta =\{v_0,\ldots ,v_{n}\}$
to
$\Delta =\{v_0,\ldots ,v_{n}\}$
to
![]() $\sum _{i=0}^{n}\Delta \setminus \{v_i\}$
.
$\sum _{i=0}^{n}\Delta \setminus \{v_i\}$
.
An n-cycle is an n-chain whose boundary is
![]() $0$
, i.e. is an element of
$0$
, i.e. is an element of
![]() $\ker \partial _{n}$
. An n-boundary is an n-chain which is the boundary of some
$\ker \partial _{n}$
. An n-boundary is an n-chain which is the boundary of some
![]() $(n+1)$
-chain, i.e. is an element of
$(n+1)$
-chain, i.e. is an element of
![]() ${\mathrm {im}} \partial _{n+1}$
. One has
${\mathrm {im}} \partial _{n+1}$
. One has
![]() $\partial _{n}\circ \partial _{n+1}=0$
, in other words
$\partial _{n}\circ \partial _{n+1}=0$
, in other words
![]() ${\mathrm {im}}\partial _{n+1}\subseteq \ker \partial _{n}$
, i.e. every n-boundary is an n-cycle. The nth homology group of K is the finite abelian group
${\mathrm {im}}\partial _{n+1}\subseteq \ker \partial _{n}$
, i.e. every n-boundary is an n-cycle. The nth homology group of K is the finite abelian group
![]() $H_n(K;{{\mathbb {Z}}_2})=\ker \partial _{n}/{\mathrm {im}} \partial _{n+1}$
.
$H_n(K;{{\mathbb {Z}}_2})=\ker \partial _{n}/{\mathrm {im}} \partial _{n+1}$
.
Let
![]() $K,L$
be simplicial complexes and
$K,L$
be simplicial complexes and
![]() $f:K\to L$
a simplicial map. For each
$f:K\to L$
a simplicial map. For each
![]() $n\in {\mathbb {N}}$
, f induces group homomorphisms
$n\in {\mathbb {N}}$
, f induces group homomorphisms
![]() $f_\#:C_n(K)\to C_n(L)$
defined as follows. If
$f_\#:C_n(K)\to C_n(L)$
defined as follows. If
![]() $A\in K$
is an n-simplex, then
$A\in K$
is an n-simplex, then
 $$ \begin{align*} f_\#(A)=\begin{cases} f(A)&\text{if }f(A)\text{ is an }n\text{-simplex,}\\ 0&\text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} f_\#(A)=\begin{cases} f(A)&\text{if }f(A)\text{ is an }n\text{-simplex,}\\ 0&\text{otherwise.} \end{cases} \end{align*} $$
Said differently,
![]() $f_\#(A)=f(A)$
if the images of the vertices of A are pairwise distinct. The homomorphism
$f_\#(A)=f(A)$
if the images of the vertices of A are pairwise distinct. The homomorphism
![]() $f_\#$
commutes with
$f_\#$
commutes with
![]() $\partial _{n+1}$
, i.e.
$\partial _{n+1}$
, i.e.
![]() $f_\#\circ \partial _{n+1}=\partial _{n+1}\circ f_\#$
, which implies that
$f_\#\circ \partial _{n+1}=\partial _{n+1}\circ f_\#$
, which implies that
![]() $f_\#$
induces a group homomorphism
$f_\#$
induces a group homomorphism
![]() $f_*:H_n(K;{{\mathbb {Z}}_2})\to H_n(L;{{\mathbb {Z}}_2})$
.
$f_*:H_n(K;{{\mathbb {Z}}_2})\to H_n(L;{{\mathbb {Z}}_2})$
.
Čech homology groups. We refer to [Reference Hurewicz and Wallman22, Section VIII.4]. There are several ways to define homology groups of more general topological spaces. We will use the Čech definition, whichapproximates the space by simplicial complexes.
Let X be a compact Polish space. To a finite open cover
![]() ${\mathcal {U}}=(U_0,\ldots ,U_k)$
of X is associated its nerve
${\mathcal {U}}=(U_0,\ldots ,U_k)$
of X is associated its nerve
![]() $K_{\mathcal {U}}$
, which is a simplicial complex. Its set of vertices is
$K_{\mathcal {U}}$
, which is a simplicial complex. Its set of vertices is
![]() $V_{\mathcal {U}}=\{0,\ldots ,k\}$
, and a simplex
$V_{\mathcal {U}}=\{0,\ldots ,k\}$
, and a simplex
![]() $A\subseteq V_{\mathcal {U}}$
belongs to
$A\subseteq V_{\mathcal {U}}$
belongs to
![]() $K_{\mathcal {U}}$
if and only if
$K_{\mathcal {U}}$
if and only if
![]() $\bigcap _{i\in A}U_i\neq \emptyset $
.
$\bigcap _{i\in A}U_i\neq \emptyset $
.
Let
![]() $({\mathcal {U}}_s)_{s\in {\mathbb {N}}}$
be a sequence of finite open covers of X such that
$({\mathcal {U}}_s)_{s\in {\mathbb {N}}}$
be a sequence of finite open covers of X such that
![]() ${\mathcal {U}}_{s+1}$
refines
${\mathcal {U}}_{s+1}$
refines
![]() ${\mathcal {U}}_s$
, i.e. each open set of
${\mathcal {U}}_s$
, i.e. each open set of
![]() ${\mathcal {U}}_{s+1}$
is contained in some open set of
${\mathcal {U}}_{s+1}$
is contained in some open set of
![]() ${\mathcal {U}}_s$
, and such that the maximal diameter of elements of
${\mathcal {U}}_s$
, and such that the maximal diameter of elements of
![]() ${\mathcal {U}}_s$
tends to
${\mathcal {U}}_s$
tends to
![]() $0$
as s grows.
$0$
as s grows.
Let
![]() $K_s$
be the nerve of
$K_s$
be the nerve of
![]() ${\mathcal {U}}_s$
. As
${\mathcal {U}}_s$
. As
![]() ${\mathcal {U}}_{s+1}$
refines
${\mathcal {U}}_{s+1}$
refines
![]() ${\mathcal {U}}_s$
, one can define a simplicial map
${\mathcal {U}}_s$
, one can define a simplicial map
![]() $f_{s}:K_{s+1}\to K_s$
by sending a vertex corresponding to
$f_{s}:K_{s+1}\to K_s$
by sending a vertex corresponding to
![]() $U\in {\mathcal {U}}_{s+1}$
to a vertex corresponding to some
$U\in {\mathcal {U}}_{s+1}$
to a vertex corresponding to some
![]() $V\in {\mathcal {U}}_s$
containing U. There are several possible choices for
$V\in {\mathcal {U}}_s$
containing U. There are several possible choices for
![]() $f_s$
, but in the end they will lead to the same result.
$f_s$
, but in the end they will lead to the same result.
The nth Čech homology group
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
of X is defined as the inverse limit of the inverse system
$\check {H}_n(X;{{\mathbb {Z}}_2})$
of X is defined as the inverse limit of the inverse system
![]() $f_{s,*}:H_n(K_{s+1};{{\mathbb {Z}}_2})\to H_n(K_{s};{{\mathbb {Z}}_2})$
. In other words,
$f_{s,*}:H_n(K_{s+1};{{\mathbb {Z}}_2})\to H_n(K_{s};{{\mathbb {Z}}_2})$
. In other words,
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
is the set of sequences
$\check {H}_n(X;{{\mathbb {Z}}_2})$
is the set of sequences
![]() $(c_s)_{s\in {\mathbb {N}}}$
with
$(c_s)_{s\in {\mathbb {N}}}$
with
![]() $c_s\in H_n(K_s;{{\mathbb {Z}}_2})$
and
$c_s\in H_n(K_s;{{\mathbb {Z}}_2})$
and
![]() $c_s=f_{s,*}(c_{s+1})$
, with component-wise addition. This group does not depend on the choice of open covers and simplicial maps.
$c_s=f_{s,*}(c_{s+1})$
, with component-wise addition. This group does not depend on the choice of open covers and simplicial maps.
If X is itself homeomorphic to the geometric realization of a simplicial complex, then the Čech homology group
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
is isomorphic to the simplicial homology group
$\check {H}_n(X;{{\mathbb {Z}}_2})$
is isomorphic to the simplicial homology group
![]() $H_n(X;{{\mathbb {Z}}_2})$
[Reference Hurewicz and Wallman22, Theorem VIII.4.E].
$H_n(X;{{\mathbb {Z}}_2})$
[Reference Hurewicz and Wallman22, Theorem VIII.4.E].
4.2 Computable aspects
Lupini, Melnikov, Nies [Reference McNicholl and Stull29] and Downey, Melnikov [Reference Downey and Melnikov9] proved that the Čech cohomology groups
![]() $\check {H}^n(X)$
of a compact Polish space X are computable, i.e. can be presented as a computable set of relations over a countable set of generators, relative to any compact presentation ofX. We will use part of their argument to investigate the computability of the Čech homology groups
$\check {H}^n(X)$
of a compact Polish space X are computable, i.e. can be presented as a computable set of relations over a countable set of generators, relative to any compact presentation ofX. We will use part of their argument to investigate the computability of the Čech homology groups
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
. However, these groups do not behave so well in terms of computability. First, they are not countable in general, so they have no countable set of generators and their computability does make immediatesense. Second, as we will show, their non-triviality is
$\check {H}_n(X;{{\mathbb {Z}}_2})$
. However, these groups do not behave so well in terms of computability. First, they are not countable in general, so they have no countable set of generators and their computability does make immediatesense. Second, as we will show, their non-triviality is
![]() $\Sigma ^1_1$
-complete when taking coefficients in
$\Sigma ^1_1$
-complete when taking coefficients in
![]() ${\mathbb {Z}}$
, which contrasts with the non-triviality of the Čech cohomology groups with coefficients in
${\mathbb {Z}}$
, which contrasts with the non-triviality of the Čech cohomology groups with coefficients in
![]() ${\mathbb {Z}}$
, which is
${\mathbb {Z}}$
, which is
![]() $\Sigma ^0_2$
. However, we now show that when taking coefficients in a finite group such as
$\Sigma ^0_2$
. However, we now show that when taking coefficients in a finite group such as
![]() ${{\mathbb {Z}}_2}$
, the non-triviality of the Čech homology groups is
${{\mathbb {Z}}_2}$
, the non-triviality of the Čech homology groups is
![]() $\Sigma ^0_2$
.
$\Sigma ^0_2$
.
Given a combinatorial description of a finite simplicial complex K, each group
![]() $H_n(K;{{\mathbb {Z}}_2})$
can be fully computed: it is a finite group whose cardinality and operation can be computed, for instance under the form of a Cayley table. Given a combinatorial description of
$H_n(K;{{\mathbb {Z}}_2})$
can be fully computed: it is a finite group whose cardinality and operation can be computed, for instance under the form of a Cayley table. Given a combinatorial description of
![]() $K,L$
and of a simplicial map
$K,L$
and of a simplicial map
![]() $f:K\to L$
, the group homomorphisms
$f:K\to L$
, the group homomorphisms
![]() $f^*_n:H_n(K;{{\mathbb {Z}}_2})\to H_n(L;{{\mathbb {Z}}_2})$
can be computed, as functions between finite sets. It makes the inverse limit
$f^*_n:H_n(K;{{\mathbb {Z}}_2})\to H_n(L;{{\mathbb {Z}}_2})$
can be computed, as functions between finite sets. It makes the inverse limit
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
a co-c.e. profinite group, in the sense of La Roche [Reference Lupini, Melnikov and Nies28] and Smith [Reference Selivanov41], i.e. the inverse limit of a computable inverse system of finite groups.
$\check {H}_n(X;{{\mathbb {Z}}_2})$
a co-c.e. profinite group, in the sense of La Roche [Reference Lupini, Melnikov and Nies28] and Smith [Reference Selivanov41], i.e. the inverse limit of a computable inverse system of finite groups.
In the next statement, a finite group is represented in the strongest possible way by a Cayley table, which encodes the cardinality of the group and the group operation. A group homomorphism is also represented in thestrongest possible way by arranging its graph in a finite list.
Proposition 4.1. Given an inverse system of finite groups
![]() $f_n:G_{n+1}\to G_{n}$
, whether their inverse limit is non-trivial is
$f_n:G_{n+1}\to G_{n}$
, whether their inverse limit is non-trivial is
![]() $\Sigma ^0_2$
.
$\Sigma ^0_2$
.
Proof Let G be the inverse limit. We claim that G is non-trivial if and only if there exist
![]() $n\in {\mathbb {N}}$
and
$n\in {\mathbb {N}}$
and
![]() $g\in G_n$
such that
$g\in G_n$
such that
![]() $g\neq 0$
and
$g\neq 0$
and
![]() $g\in {\mathrm {im}}(f_n\circ \ldots \circ f_p)$
for all
$g\in {\mathrm {im}}(f_n\circ \ldots \circ f_p)$
for all
![]() $p\geq n$
. This predicate is
$p\geq n$
. This predicate is
![]() $\Sigma ^0_2$
, because the groups are finite. In particular, the predicate
$\Sigma ^0_2$
, because the groups are finite. In particular, the predicate
![]() $g\in {\mathrm {im}}(f_n\circ \ldots \circ f_p)$
can be decided in finite time, by testing
$g\in {\mathrm {im}}(f_n\circ \ldots \circ f_p)$
can be decided in finite time, by testing
![]() $f_n\circ \ldots \circ f_p(g')=g$
for each
$f_n\circ \ldots \circ f_p(g')=g$
for each
![]() $g'$
in the finite set
$g'$
in the finite set
![]() $G_{p+1}$
.
$G_{p+1}$
.
If G is non-trivial, then let
![]() $(g_n)_{n\in {\mathbb {N}}}$
be a non-zero element of G. As it is non-zero, there exists n such that
$(g_n)_{n\in {\mathbb {N}}}$
be a non-zero element of G. As it is non-zero, there exists n such that
![]() $g_n\neq 0$
. Moreover, for every
$g_n\neq 0$
. Moreover, for every
![]() $p\geq n$
,
$p\geq n$
,
![]() $g_n=f_n\circ \ldots \circ f_p(g_{p+1})$
belongs to
$g_n=f_n\circ \ldots \circ f_p(g_{p+1})$
belongs to
![]() ${\mathrm {im}}(f_n\circ \ldots \circ f_p)$
.
${\mathrm {im}}(f_n\circ \ldots \circ f_p)$
.
Conversely, assume the existence of n and g satisfying the conditions. As the groups are finite, by König’s lemma, there exists a sequence
![]() $(g_p)_{p\geq n}$
such that
$(g_p)_{p\geq n}$
such that
![]() $g_n=g$
and
$g_n=g$
and
![]() $g_p=f_p(g_{p+1})$
for all
$g_p=f_p(g_{p+1})$
for all
![]() $p\geq n$
. For
$p\geq n$
. For
![]() $m<n$
, let
$m<n$
, let
![]() $g_m=f_m\circ \ldots \circ f_{n-1}(g)$
. The sequence
$g_m=f_m\circ \ldots \circ f_{n-1}(g)$
. The sequence
![]() $(g_n)_{n\in {\mathbb {N}}}$
is an element of G, and is non-zero as its nth coordinate is
$(g_n)_{n\in {\mathbb {N}}}$
is an element of G, and is non-zero as its nth coordinate is
![]() $g\neq 0$
.
$g\neq 0$
.
We now have all the ingredients to show that the non-triviality of Čech homology groups with coefficients in
![]() ${{\mathbb {Z}}_2}$
has limited complexity.
${{\mathbb {Z}}_2}$
has limited complexity.
Corollary 4.2. Whether the nth Čech homology group
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
of a compact Polish space X is non-trivial is
$\check {H}_n(X;{{\mathbb {Z}}_2})$
of a compact Polish space X is non-trivial is
![]() $\Sigma ^0_2$
, uniformly in n and a compact presentation of X.
$\Sigma ^0_2$
, uniformly in n and a compact presentation of X.
Proof Given a compact presentation of X and a good open cover
![]() ${\mathcal {U}}=(U_0,\ldots ,U_k)$
of X, its nerve
${\mathcal {U}}=(U_0,\ldots ,U_k)$
of X, its nerve
![]() $K_{\mathcal {U}}$
on the vertices
$K_{\mathcal {U}}$
on the vertices
![]() $V=\{0,\ldots ,k\}$
can be computed, in the sense that one can decide whether a set
$V=\{0,\ldots ,k\}$
can be computed, in the sense that one can decide whether a set
![]() $J\subseteq V$
belongs to
$J\subseteq V$
belongs to
![]() $K_{\mathcal {U}}$
. Indeed,
$K_{\mathcal {U}}$
. Indeed,
![]() $J\in K_{\mathcal {U}}$
iff
$J\in K_{\mathcal {U}}$
iff
![]() $\bigcap _{j\in J}U_j\neq \emptyset $
iff
$\bigcap _{j\in J}U_j\neq \emptyset $
iff
![]() $\bigcap _{j\in J}\overline {U}_j\neq \emptyset $
. The first inequality is
$\bigcap _{j\in J}\overline {U}_j\neq \emptyset $
. The first inequality is
![]() $\Sigma ^0_1$
and the second inequality is
$\Sigma ^0_1$
and the second inequality is
![]() $\Pi ^0_1$
, so it is decidable.
$\Pi ^0_1$
, so it is decidable.
If
![]() ${\mathcal {U}}=(U_0,\ldots ,U_k)$
and
${\mathcal {U}}=(U_0,\ldots ,U_k)$
and
![]() ${\mathcal {V}}=(V_0,\ldots ,V_l)$
are good open covers of X and
${\mathcal {V}}=(V_0,\ldots ,V_l)$
are good open covers of X and
![]() ${\mathcal {U}}$
strongly refines
${\mathcal {U}}$
strongly refines
![]() ${\mathcal {V}}$
, then one can compute a simplicial map
${\mathcal {V}}$
, then one can compute a simplicial map
![]() $f:K_{\mathcal {U}}\to K_{\mathcal {V}}$
sending each vertex
$f:K_{\mathcal {U}}\to K_{\mathcal {V}}$
sending each vertex
![]() $u_i$
for
$u_i$
for
![]() $K_{\mathcal {U}}$
to a vertex
$K_{\mathcal {U}}$
to a vertex
![]() $v_j$
of
$v_j$
of
![]() $K_{\mathcal {V}}$
such that
$K_{\mathcal {V}}$
such that
![]() $\overline {U}_i\subseteq V_j$
. Indeed, the latter inclusion is
$\overline {U}_i\subseteq V_j$
. Indeed, the latter inclusion is
![]() $\Sigma ^0_1$
, so for each i one can effectively find a suitable j.
$\Sigma ^0_1$
, so for each i one can effectively find a suitable j.
Now, from a compact presentation of X, one can compute a strong refining sequence of good open covers
![]() $({\mathcal {U}}_s)_{s\in {\mathbb {N}}}$
by Lemma 2.5. One can then compute the nerves
$({\mathcal {U}}_s)_{s\in {\mathbb {N}}}$
by Lemma 2.5. One can then compute the nerves
![]() $K_s$
of
$K_s$
of
![]() ${\mathcal {U}}_s$
as well as simplicial maps
${\mathcal {U}}_s$
as well as simplicial maps
![]() $f_s:K_{s+1}\to K_s$
. One can compute the simplicial homology groups
$f_s:K_{s+1}\to K_s$
. One can compute the simplicial homology groups
![]() $H_n(K_s)$
and the homomorphisms
$H_n(K_s)$
and the homomorphisms
![]() $f_{s,*}:H_n(K_{s+1};{{\mathbb {Z}}_2})\to H_n(K_s;{{\mathbb {Z}}_2})$
. Their inverse limit is
$f_{s,*}:H_n(K_{s+1};{{\mathbb {Z}}_2})\to H_n(K_s;{{\mathbb {Z}}_2})$
. Their inverse limit is
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
, and whether it is non-trivial is
$\check {H}_n(X;{{\mathbb {Z}}_2})$
, and whether it is non-trivial is
![]() $\Sigma ^0_2$
by Proposition 4.6.
$\Sigma ^0_2$
by Proposition 4.6.
Comparison between Čech homology and Čech cohomology. Lupini, Melnikov and Nies [Reference McNicholl and Stull29] and Downey and Melnikov [Reference Downey and Melnikov9] proved that the Čech cohomology groups
![]() $\check {H}^n(X)$
of a compact Polish space X can be computed from a compact presentation of X (we do not write the coefficient group, which is
$\check {H}^n(X)$
of a compact Polish space X can be computed from a compact presentation of X (we do not write the coefficient group, which is
![]() ${\mathbb {Z}}$
). We will neither define nor use cohomology groups, but let us mention the important fact that for each n, the simplicial cohomology groups
${\mathbb {Z}}$
). We will neither define nor use cohomology groups, but let us mention the important fact that for each n, the simplicial cohomology groups
![]() $H^n(K_s)$
and the induced homomorphisms
$H^n(K_s)$
and the induced homomorphisms
![]() $f_s^*:H^n(K_{s})\to H^{n}(K_{s+1})$
form a direct system, which is essential to show that their direct limits, the Čech cohomology groups
$f_s^*:H^n(K_{s})\to H^{n}(K_{s+1})$
form a direct system, which is essential to show that their direct limits, the Čech cohomology groups
![]() $\check {H}^n(X)$
, are computable. As we saw, the simplicial homology groups
$\check {H}^n(X)$
, are computable. As we saw, the simplicial homology groups
![]() $H_n(K_s;{{\mathbb {Z}}_2})$
form an inverse system, which makes the computation of their inverse limits, the Čech homology groups
$H_n(K_s;{{\mathbb {Z}}_2})$
form an inverse system, which makes the computation of their inverse limits, the Čech homology groups
![]() $\check {H}_n(X;{{\mathbb {Z}}_2})$
, much more difficult.
$\check {H}_n(X;{{\mathbb {Z}}_2})$
, much more difficult.
4.3 Influence of the coefficient group
Let us finally discuss the role of the coefficient group in Corollary 5.7. The same proof holds for any finite coefficient group G. Moreover, thecomputability of the Čech cohomology groups proven in [Reference McNicholl and Stull29, Reference Downey and Melnikov9] implies that Corollary 5.7 holds for the circle group
![]() $G={\mathbb {R}}/{\mathbb {Z}}$
. Indeed, there is a duality between Čech cohomology groups and Čech homology groups:
$G={\mathbb {R}}/{\mathbb {Z}}$
. Indeed, there is a duality between Čech cohomology groups and Čech homology groups:
![]() $\check {H}_n(X;{\mathbb {R}}/{\mathbb {Z}})$
is the character group of
$\check {H}_n(X;{\mathbb {R}}/{\mathbb {Z}})$
is the character group of
![]() $\check {H}^n(X)$
, i.e. is the group of homomorphisms from
$\check {H}^n(X)$
, i.e. is the group of homomorphisms from
![]() $\check {H}^n(X)$
to the circle group
$\check {H}^n(X)$
to the circle group
![]() ${\mathbb {R}}/{\mathbb {Z}}$
([Reference Hurewicz and Wallman22, Theorem VIII.4.G, p. 137]). Therefore, the non-triviality of
${\mathbb {R}}/{\mathbb {Z}}$
([Reference Hurewicz and Wallman22, Theorem VIII.4.G, p. 137]). Therefore, the non-triviality of
![]() $\check {H}_n(X;{\mathbb {R}}/{\mathbb {Z}})$
is equivalent to the non-triviality of
$\check {H}_n(X;{\mathbb {R}}/{\mathbb {Z}})$
is equivalent to the non-triviality of
![]() $\check {H}^n(X)$
, which is
$\check {H}^n(X)$
, which is
![]() $\Sigma ^0_2$
in X, as
$\Sigma ^0_2$
in X, as
![]() $\check {H}^n(X)$
is computable in X.
$\check {H}^n(X)$
is computable in X.
We now show that Corollary 5.7 does not hold for
![]() $G={\mathbb {Z}}$
, in which case the non-triviality of
$G={\mathbb {Z}}$
, in which case the non-triviality of
![]() $\check {H}_n(X;{\mathbb {Z}})$
is
$\check {H}_n(X;{\mathbb {Z}})$
is
![]() $\Sigma ^1_1$
-complete. The reason is that the groups of the inverse system are no more finite, so the existence of a path in the inverse system is similar to the existence of an infinite path in a tree.
$\Sigma ^1_1$
-complete. The reason is that the groups of the inverse system are no more finite, so the existence of a path in the inverse system is similar to the existence of an infinite path in a tree.
Theorem 4.3. Let
![]() $n\geq 1$
. Given a compact presentation of a compact Polish space X, the non-triviality of
$n\geq 1$
. Given a compact presentation of a compact Polish space X, the non-triviality of
![]() $\check {H}_n(X;{\mathbb {Z}})$
is
$\check {H}_n(X;{\mathbb {Z}})$
is
![]() $\Sigma ^1_1$
-complete.
$\Sigma ^1_1$
-complete.
Proof The arguments in [Reference Melnikov32, Reference McNicholl and Stull29, Reference Downey and Melnikov9] imply the computability of the inverse system of simplicial groups
![]() $(H_n(K_s;{\mathbb {Z}}),f_{s,*})$
: these groups are strongly completely decomposable (strictly speaking, their results are about cohomology groups
$(H_n(K_s;{\mathbb {Z}}),f_{s,*})$
: these groups are strongly completely decomposable (strictly speaking, their results are about cohomology groups
![]() $H^n(K_s)$
but apply equally to the homology groups
$H^n(K_s)$
but apply equally to the homology groups
![]() $H_n(K_s;{\mathbb {Z}})$
). Therefore, their inverse limit is non-trivial if and only if there exists a sequence
$H_n(K_s;{\mathbb {Z}})$
). Therefore, their inverse limit is non-trivial if and only if there exists a sequence
![]() $(x_s)_{s\in {\mathbb {N}}}$
with
$(x_s)_{s\in {\mathbb {N}}}$
with
![]() $x_s\in H_n(K_s;{\mathbb {Z}})$
,
$x_s\in H_n(K_s;{\mathbb {Z}})$
,
![]() $x_{s}=f_{s,*}(x_{s+1})$
for all s and
$x_{s}=f_{s,*}(x_{s+1})$
for all s and
![]() $x_s\neq 0$
for some s. This condition is
$x_s\neq 0$
for some s. This condition is
![]() $\Sigma ^1_1$
. We now show the completeness of the problem.
$\Sigma ^1_1$
. We now show the completeness of the problem.
The set of trees
![]() $T\subseteq 2^{<\omega }$
containing an infinite path with infinitely many
$T\subseteq 2^{<\omega }$
containing an infinite path with infinitely many
![]() $1$
’s is
$1$
’s is
![]() $\Sigma ^1_1$
-complete [Reference Kechris26, Proposition 25.2]. We will reduce this problem to the non-triviliaty of
$\Sigma ^1_1$
-complete [Reference Kechris26, Proposition 25.2]. We will reduce this problem to the non-triviliaty of
![]() $\check {H}_1(X;{\mathbb {Z}})$
, and explain the changes to be made for higher-dimensional homology groups. We will build an inverse system of groups and then build an inverse limit of compact spaces whose Čech homology group isthe inverse limit of the groups. Note the similarity of this strategy with [Reference Melnikov32] which builds an inverse limit of compact spaces whose first Čech cohomology group is a given direct limit ofgroups.
$\check {H}_1(X;{\mathbb {Z}})$
, and explain the changes to be made for higher-dimensional homology groups. We will build an inverse system of groups and then build an inverse limit of compact spaces whose Čech homology group isthe inverse limit of the groups. Note the similarity of this strategy with [Reference Melnikov32] which builds an inverse limit of compact spaces whose first Čech cohomology group is a given direct limit ofgroups.
We first define an inverse system of groups
![]() $(G_n,f_n)$
, i.e. a sequence
$(G_n,f_n)$
, i.e. a sequence
![]() $(G_n)_{n\in {\mathbb {N}}}$
of groups together with homomorphisms
$(G_n)_{n\in {\mathbb {N}}}$
of groups together with homomorphisms
![]() $f_n:G_{n+1}\to G_n$
. We will then associate to each tree T a subsystem
$f_n:G_{n+1}\to G_n$
. We will then associate to each tree T a subsystem
![]() $(L_n,f_n)$
, i.e. a sequence of subgroups
$(L_n,f_n)$
, i.e. a sequence of subgroups
![]() $L_n\subseteq G_n$
satisfying
$L_n\subseteq G_n$
satisfying
![]() $f_n(L_{n+1})\subseteq L_n$
.
$f_n(L_{n+1})\subseteq L_n$
.
Let
![]() $\epsilon \in 2^{<\omega }$
be the empty string,
$\epsilon \in 2^{<\omega }$
be the empty string,
![]() $S=\{\epsilon \}\cup \{1w:w\in 2^{<\omega }\}$
be the set of strings that do not start with
$S=\{\epsilon \}\cup \{1w:w\in 2^{<\omega }\}$
be the set of strings that do not start with
![]() $0$
and
$0$
and
![]() $S_n=\{w\in S:|w|=n\}$
. For each
$S_n=\{w\in S:|w|=n\}$
. For each
![]() $w\in S$
, let
$w\in S$
, let
![]() $k(w)=2^{|w|_1}$
where
$k(w)=2^{|w|_1}$
where
![]() $|w|_1$
is the number of occurrences of
$|w|_1$
is the number of occurrences of
![]() $1$
in w. Note that
$1$
in w. Note that
![]() $k(\epsilon )=1$
.
$k(\epsilon )=1$
.
For
![]() $n\in {\mathbb {N}}$
, we define
$n\in {\mathbb {N}}$
, we define
Note that
![]() $G_0={\mathbb {Z}}$
and
$G_0={\mathbb {Z}}$
and
![]() $G_1={\mathbb {Z}}^2$
. We call each
$G_1={\mathbb {Z}}^2$
. We call each
![]() ${\mathbb {Z}}^{k(w)}$
a component of
${\mathbb {Z}}^{k(w)}$
a component of
![]() $G_n$
. If
$G_n$
. If
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $w\in S_n$
, then
$w\in S_n$
, then
![]() $|w|_1\geq 1$
so
$|w|_1\geq 1$
so
![]() $k(w)$
is even: we will implicitly split each component
$k(w)$
is even: we will implicitly split each component
![]() ${\mathbb {Z}}^{k(w)}$
into
${\mathbb {Z}}^{k(w)}$
into
![]() ${\mathbb {Z}}^{k(w)/2}\oplus {\mathbb {Z}}^{k(w)/2}$
, expressing an element of
${\mathbb {Z}}^{k(w)/2}\oplus {\mathbb {Z}}^{k(w)/2}$
, expressing an element of
![]() ${\mathbb {Z}}^{k(w)}$
as a pair.
${\mathbb {Z}}^{k(w)}$
as a pair.
We define
![]() $f_n:G_{n+1}\to G_n$
on each component of
$f_n:G_{n+1}\to G_n$
on each component of
![]() $G_{n+1}$
. For each
$G_{n+1}$
. For each
![]() $w\in S_n$
, one has
$w\in S_n$
, one has
![]() $k(w0)=k(w)$
and
$k(w0)=k(w)$
and
![]() $k(w1)=2k(w)$
and we let
$k(w1)=2k(w)$
and we let
 $$ \begin{align*} f_n:{\mathbb{Z}}^{k(w0)}&\to {\mathbb{Z}}^{k(w)}\\ (x,y)&\mapsto (2x,3y) \end{align*} $$
$$ \begin{align*} f_n:{\mathbb{Z}}^{k(w0)}&\to {\mathbb{Z}}^{k(w)}\\ (x,y)&\mapsto (2x,3y) \end{align*} $$
and
 $$ \begin{align*} f_n:{\mathbb{Z}}^{k(w1)}&\to{\mathbb{Z}}^{k(w)}\\ (x,y)&\mapsto x+y. \end{align*} $$
$$ \begin{align*} f_n:{\mathbb{Z}}^{k(w1)}&\to{\mathbb{Z}}^{k(w)}\\ (x,y)&\mapsto x+y. \end{align*} $$
An element
![]() $x\in \varprojlim (G_n,f_n)$
is described as a family
$x\in \varprojlim (G_n,f_n)$
is described as a family
![]() $(x(w))_{w\in S}$
where
$(x(w))_{w\in S}$
where
![]() $x(w)\in {\mathbb {Z}}^{k(w)}$
for each
$x(w)\in {\mathbb {Z}}^{k(w)}$
for each
![]() $w\in S$
, such that
$w\in S$
, such that
![]() $x(w)=f_{|w|}(x(w0))+f_{|w|}(x(w1))$
. We define the support of x as
$x(w)=f_{|w|}(x(w0))+f_{|w|}(x(w1))$
. We define the support of x as
![]() $\mathrm {supp}(x)=\{w\in S:x(w)\neq 0\}$
. Note that
$\mathrm {supp}(x)=\{w\in S:x(w)\neq 0\}$
. Note that
![]() $x=0$
if and only if
$x=0$
if and only if
![]() $\mathrm {supp}(x)=S$
.
$\mathrm {supp}(x)=S$
.
We relate the supports of non-zero elements with the infinite binary sequences containing infinitely many
![]() $1$
’s. For an infinite sequence
$1$
’s. For an infinite sequence
![]() $q\in 2^\omega $
, let
$q\in 2^\omega $
, let
![]() $q\upharpoonright_{n}$
be the prefix of q of length n.
$q\upharpoonright_{n}$
be the prefix of q of length n.
Claim 1. Let
![]() $x\in \varprojlim (G_n,f_n)$
. One has
$x\in \varprojlim (G_n,f_n)$
. One has
![]() $x\neq 0$
iff there exists
$x\neq 0$
iff there exists
![]() $q\in 2^\omega $
starting with
$q\in 2^\omega $
starting with
![]() $1$
and containing infinitely many
$1$
and containing infinitely many
![]() $1$
’s, and such that
$1$
’s, and such that
![]() $x(q\upharpoonright_{n})\neq 0$
for all sufficiently large n.
$x(q\upharpoonright_{n})\neq 0$
for all sufficiently large n.
Proof Of course if such a q exists, then
![]() $x\neq 0$
. Assume that
$x\neq 0$
. Assume that
![]() $x\neq 0$
and let
$x\neq 0$
and let
![]() $w\in S$
be such that
$w\in S$
be such that
![]() $x(w)\neq 0$
. We build q extending w. Let
$x(w)\neq 0$
. We build q extending w. Let
![]() $n\geq |w|$
and assume by induction that
$n\geq |w|$
and assume by induction that
![]() $v:=q\upharpoonright_{n}$
has been already defined. As
$v:=q\upharpoonright_{n}$
has been already defined. As
![]() $x(v)=f_{n}(x(v0))+f_{n}(x(v1))$
, one has
$x(v)=f_{n}(x(v0))+f_{n}(x(v1))$
, one has
![]() $x(v0)\neq 0$
or
$x(v0)\neq 0$
or
![]() $x(v1)\neq 0$
. We choose the next bit of q so that
$x(v1)\neq 0$
. We choose the next bit of q so that
![]() $x(q\upharpoonright_{n+1})\neq 0$
: let
$x(q\upharpoonright_{n+1})\neq 0$
: let
![]() $q(n)=1$
if
$q(n)=1$
if
![]() $x(v1)\neq 0$
, and
$x(v1)\neq 0$
, and
![]() $q(n)=0$
otherwise. One has
$q(n)=0$
otherwise. One has
![]() $x(q\upharpoonright_{n})\neq 0$
for all
$x(q\upharpoonright_{n})\neq 0$
for all
![]() $n\geq |w|$
by construction. Assume for a contradiction that q contains only finitely many
$n\geq |w|$
by construction. Assume for a contradiction that q contains only finitely many
![]() $1$
’s. Let v be a prefix of q extending w and such that
$1$
’s. Let v be a prefix of q extending w and such that
![]() $q=v0^\omega $
. Note that for
$q=v0^\omega $
. Note that for
![]() $n\geq |v|$
,
$n\geq |v|$
,
![]() $k(q\upharpoonright_{n})$
is constantly
$k(q\upharpoonright_{n})$
is constantly
![]() $k(v)$
and
$k(v)$
and
![]() $x(q\upharpoonright_{n})\in {\mathbb {Z}}^{k(v)}$
. For such n, one must have
$x(q\upharpoonright_{n})\in {\mathbb {Z}}^{k(v)}$
. For such n, one must have
![]() $x(q\upharpoonright_{n}1)=0$
because otherwise we would have chosen
$x(q\upharpoonright_{n}1)=0$
because otherwise we would have chosen
![]() $q(n)=1$
in the construction of q. As a result, one has
$q(n)=1$
in the construction of q. As a result, one has
![]() $x(q\upharpoonright_{n})=f_n(x(q\upharpoonright_{n}0))=f_n(x(q\upharpoonright_{n+1}))$
for all
$x(q\upharpoonright_{n})=f_n(x(q\upharpoonright_{n}0))=f_n(x(q\upharpoonright_{n+1}))$
for all
![]() $n\geq |v|$
. It means that each coordinate of
$n\geq |v|$
. It means that each coordinate of
![]() $x(q\upharpoonright_{v})\in {\mathbb {Z}}^{k(v)}$
is a multiple of all
$x(q\upharpoonright_{v})\in {\mathbb {Z}}^{k(v)}$
is a multiple of all
![]() $2^i$
for all
$2^i$
for all
![]() $i\geq 0$
, or a multiple of
$i\geq 0$
, or a multiple of
![]() $3^i$
for all
$3^i$
for all
![]() $i\geq 0$
, which implies that
$i\geq 0$
, which implies that
![]() $x(q\upharpoonright_{v})=0$
. It is a contradiction because v extends w. Therefore, we have proved that q contains infinitely many
$x(q\upharpoonright_{v})=0$
. It is a contradiction because v extends w. Therefore, we have proved that q contains infinitely many
![]() $1$
’s.
$1$
’s.
Conversely,
Claim 2. If
![]() $q\in 2^{\mathbb {N}}$
starts with
$q\in 2^{\mathbb {N}}$
starts with
![]() $1$
and contains infinitely many
$1$
and contains infinitely many
![]() $1$
’s, then there exists
$1$
’s, then there exists
![]() $x\in \varprojlim (G_n,f_n)$
such that
$x\in \varprojlim (G_n,f_n)$
such that
![]() $\mathrm {supp}(x)$
is the set of prefixes of q.
$\mathrm {supp}(x)$
is the set of prefixes of q.
Proof Let
![]() $(n_i)_{i\in {\mathbb {N}}}$
be the increasing enumeration of the positions n such that
$(n_i)_{i\in {\mathbb {N}}}$
be the increasing enumeration of the positions n such that
![]() $q(n)=1$
, and observe that
$q(n)=1$
, and observe that
![]() $n_0=0$
. We build
$n_0=0$
. We build
![]() $x=(x(w))_{w\in S}$
. Let
$x=(x(w))_{w\in S}$
. Let
![]() $x(\epsilon )=1\in {\mathbb {Z}}$
. Let
$x(\epsilon )=1\in {\mathbb {Z}}$
. Let
![]() $i\in {\mathbb {N}}$
and assume by induction that
$i\in {\mathbb {N}}$
and assume by induction that
![]() $x(q\upharpoonright_{n_i})$
has been defined. The function
$x(q\upharpoonright_{n_i})$
has been defined. The function
![]() $f_{n_i}\circ \ldots \circ f_{n_{i+1}-1}:{\mathbb {Z}}^{k(q\upharpoonright_{n_{i+1}})}\to {\mathbb {Z}}^{k(q\upharpoonright_{n_i})}$
maps
$f_{n_i}\circ \ldots \circ f_{n_{i+1}-1}:{\mathbb {Z}}^{k(q\upharpoonright_{n_{i+1}})}\to {\mathbb {Z}}^{k(q\upharpoonright_{n_i})}$
maps
![]() $(a,b)$
to
$(a,b)$
to
![]() $2^ja+3^jb$
, where
$2^ja+3^jb$
, where
![]() $j=n_{i+1}-n_i-1$
. As
$j=n_{i+1}-n_i-1$
. As
![]() $2^j$
and
$2^j$
and
![]() $3^j$
are coprime, there exists
$3^j$
are coprime, there exists
![]() $(a,b)$
such that
$(a,b)$
such that
![]() $2^ja+3^jb=x(q\upharpoonright_{n_i})$
, let
$2^ja+3^jb=x(q\upharpoonright_{n_i})$
, let
![]() $x(q\upharpoonright_{n_{i+1}})=(a,b)$
. For
$x(q\upharpoonright_{n_{i+1}})=(a,b)$
. For
![]() $n_i<n<n_{i+1}$
, naturally define
$n_i<n<n_{i+1}$
, naturally define
![]() $x(q\upharpoonright_{n})=f_n\circ \ldots f_{n_{i+1}-1}(a,b)$
. Finally, let
$x(q\upharpoonright_{n})=f_n\circ \ldots f_{n_{i+1}-1}(a,b)$
. Finally, let
![]() $x(w)=0$
if w is not a prefix of q. By construction, x belongs to
$x(w)=0$
if w is not a prefix of q. By construction, x belongs to
![]() $\varprojlim (G_n,f_n)$
and
$\varprojlim (G_n,f_n)$
and
![]() $\mathrm {supp}(x)$
is the set of prefixes of q.
$\mathrm {supp}(x)$
is the set of prefixes of q.
Let
![]() $T\subseteq 2^{<\omega }$
be a tree. We can assume w.l.o.g. that
$T\subseteq 2^{<\omega }$
be a tree. We can assume w.l.o.g. that
![]() $T\subseteq S$
, replacing T with
$T\subseteq S$
, replacing T with
![]() $\{\epsilon \}\cup \{1w:x\in T\}$
if necessary. We define an inverse subsystem
$\{\epsilon \}\cup \{1w:x\in T\}$
if necessary. We define an inverse subsystem
![]() $(L_n,f_n)$
of
$(L_n,f_n)$
of
![]() $(G_n,f_n)$
. Let
$(G_n,f_n)$
. Let
![]() $T_n=\{w\in T:|w|=n\}$
and
$T_n=\{w\in T:|w|=n\}$
and
![]() $L_n=\bigoplus _{w\in T_n}{\mathbb {Z}}^{k(w)}$
. As T is a tree, one has
$L_n=\bigoplus _{w\in T_n}{\mathbb {Z}}^{k(w)}$
. As T is a tree, one has
![]() $f_n(L_{n+1})\subseteq L_n$
so
$f_n(L_{n+1})\subseteq L_n$
so
![]() $(L_n,f_n)$
is an inverse system which is a subsystem of
$(L_n,f_n)$
is an inverse system which is a subsystem of
![]() $(G_n,f_n)$
. Its inverse limit consists of the elements of the inverse limit of
$(G_n,f_n)$
. Its inverse limit consists of the elements of the inverse limit of
![]() $(G_n,f_n)$
whose support is contained in T.
$(G_n,f_n)$
whose support is contained in T.
Therefore,
![]() $\varprojlim (L_n,f_n)$
contains a non-zero element iff
$\varprojlim (L_n,f_n)$
contains a non-zero element iff
![]() $\varprojlim (G_n,f_n)$
contains a non-zero element whose support is contained in T iff T contains an infinite path with infinitely many
$\varprojlim (G_n,f_n)$
contains a non-zero element whose support is contained in T iff T contains an infinite path with infinitely many
![]() $1$
’s by Claims 4 and 5.
$1$
’s by Claims 4 and 5.
We now define a compact space
![]() $X_T$
such that
$X_T$
such that
![]() $\check {H}_1(X_T;{\mathbb {Z}})$
is isomorphic to
$\check {H}_1(X_T;{\mathbb {Z}})$
is isomorphic to
![]() $\varprojlim (L_n,f_n)$
. Let
$\varprojlim (L_n,f_n)$
. Let
![]() ${\mathbb {T}}_n={\mathbf {S}}_1^n$
be the n-dimensional torus, which is the product of n circles.
${\mathbb {T}}_n={\mathbf {S}}_1^n$
be the n-dimensional torus, which is the product of n circles.
Observe that
![]() $L_n={\mathbb {Z}}^{l_n}$
for some
$L_n={\mathbb {Z}}^{l_n}$
for some
![]() $l_n$
. We then define a space
$l_n$
. We then define a space
![]() $X_T$
as the inverse limit of
$X_T$
as the inverse limit of
![]() $X_n={\mathbb {T}}_{l_n}$
, with continuous surjective functions
$X_n={\mathbb {T}}_{l_n}$
, with continuous surjective functions
![]() $F_n:X_{n+1}\to X_n$
defined as follows. Each homomorphism
$F_n:X_{n+1}\to X_n$
defined as follows. Each homomorphism
![]() $f_n:{\mathbb {Z}}^{l_{n+1}}\to {\mathbb {Z}}^{l_n}$
can be decomposed as a direct sum of the homomorphisms
$f_n:{\mathbb {Z}}^{l_{n+1}}\to {\mathbb {Z}}^{l_n}$
can be decomposed as a direct sum of the homomorphisms
 $$ \begin{align*} g_2:{\mathbb{Z}}&\to {\mathbb{Z}}&g_3:{\mathbb{Z}}&\to{\mathbb{Z}}&g_+:{\mathbb{Z}}^2&\to{\mathbb{Z}}\\ x&\mapsto 2x&x&\mapsto 3x&(x,y)&\mapsto x+y. \end{align*} $$
$$ \begin{align*} g_2:{\mathbb{Z}}&\to {\mathbb{Z}}&g_3:{\mathbb{Z}}&\to{\mathbb{Z}}&g_+:{\mathbb{Z}}^2&\to{\mathbb{Z}}\\ x&\mapsto 2x&x&\mapsto 3x&(x,y)&\mapsto x+y. \end{align*} $$
We define
![]() $F_n$
as the corresponding product of
$F_n$
as the corresponding product of
 $$ \begin{align*} G_2:{\mathbf{S}}_1&\to{\mathbf{S}}_1&G_3:{\mathbf{S}}_1&\to{\mathbf{S}}_1&G_+:{\mathbf{S}}_1\times{\mathbf{S}}_1&\to{\mathbf{S}}_1\\ x&\mapsto 2x&x&\mapsto3x&(x,y)&\mapsto x+y, \end{align*} $$
$$ \begin{align*} G_2:{\mathbf{S}}_1&\to{\mathbf{S}}_1&G_3:{\mathbf{S}}_1&\to{\mathbf{S}}_1&G_+:{\mathbf{S}}_1\times{\mathbf{S}}_1&\to{\mathbf{S}}_1\\ x&\mapsto 2x&x&\mapsto3x&(x,y)&\mapsto x+y, \end{align*} $$
where the circle
![]() ${\mathbf {S}}_1$
is seen as an additive group. Let then
${\mathbf {S}}_1$
is seen as an additive group. Let then
![]() $X_T=\varprojlim (X_n,F_n)$
.
$X_T=\varprojlim (X_n,F_n)$
.
The homology group of
![]() $X_n={\mathbb {T}}_{l_n}$
is
$X_n={\mathbb {T}}_{l_n}$
is
![]() $H_1(X_n;{\mathbb {Z}})={\mathbb {Z}}^{l_n}=L_n$
and the homomorphism
$H_1(X_n;{\mathbb {Z}})={\mathbb {Z}}^{l_n}=L_n$
and the homomorphism
![]() $F_{n,*}:H_1(X_{n+1};{\mathbb {Z}})\to H_1(X_n;{\mathbb {Z}})$
induced by
$F_{n,*}:H_1(X_{n+1};{\mathbb {Z}})\to H_1(X_n;{\mathbb {Z}})$
induced by
![]() $F_n$
is
$F_n$
is
![]() $f_n$
. It is a classical result that the construction of Čech homology groups of compact spaces with coefficients in
$f_n$
. It is a classical result that the construction of Čech homology groups of compact spaces with coefficients in
![]() ${\mathbb {Z}}$
is continuous, i.e. commutes with inverse limits:
${\mathbb {Z}}$
is continuous, i.e. commutes with inverse limits:
This result can be found in [Reference Eilenberg and Steenrod10, Theorem X.3.1, p.261], where the statement holds for coefficient groups in the class
![]() $\mathcal {G}_R$
of modules over a ring R, and
$\mathcal {G}_R$
of modules over a ring R, and
![]() ${\mathbb {Z}}$
is indeed a module over the ring
${\mathbb {Z}}$
is indeed a module over the ring
![]() ${\mathbb {Z}}$
. Therefore,
${\mathbb {Z}}$
. Therefore,
![]() $\check {H}_1(X_T;{\mathbb {Z}})=\varprojlim (L_n,f_n)$
is non-trivial if and only if T contains a path with infinitely many
$\check {H}_1(X_T;{\mathbb {Z}})=\varprojlim (L_n,f_n)$
is non-trivial if and only if T contains a path with infinitely many
![]() $1$
’s.
$1$
’s.
We finally need to check that the construction of
![]() $X_T$
is effective in T.
$X_T$
is effective in T.
Claim 3. A compact presentation of the space
![]() $X_T$
can be uniformly computed from T.
$X_T$
can be uniformly computed from T.
Proof It is essentially the same argument as [Reference Melnikov32, Remark 2.8]. For simplicity, we assume that T is computable, the general case holds relative to and uniformly in T. First, the spaces
![]() $X_n={\mathbb {T}}_{l_n}$
have uniformly computable compact presentations, and so does their product
$X_n={\mathbb {T}}_{l_n}$
have uniformly computable compact presentations, and so does their product
![]() $P=\prod _n X_n$
. The functions
$P=\prod _n X_n$
. The functions
![]() $F_n:X_{n+1}\to X_n$
are uniformly computable so
$F_n:X_{n+1}\to X_n$
are uniformly computable so
![]() $X_T$
is a
$X_T$
is a
![]() $\Pi ^0_1$
-subspace of P. We need to show that
$\Pi ^0_1$
-subspace of P. We need to show that
![]() $X_T$
is computably overt in P. It is important to note that the functions
$X_T$
is computably overt in P. It is important to note that the functions
![]() $F_n:X_{n+1}\to X_n$
are surjective. For
$F_n:X_{n+1}\to X_n$
are surjective. For
![]() $n\leq p$
, let
$n\leq p$
, let
![]() $F_{n,p}=F_n\circ F_{n+1}\circ \ldots \circ F_{p-1}:X_p\to X_n$
, with
$F_{n,p}=F_n\circ F_{n+1}\circ \ldots \circ F_{p-1}:X_p\to X_n$
, with
![]() $F_{p,p}=\mathrm {id}$
. Let
$F_{p,p}=\mathrm {id}$
. Let
![]() $B=B_0\times \ldots \times B_p\times \prod _{q>p}X_q$
be a basic ball of P. The open set B intersects X iff the set
$B=B_0\times \ldots \times B_p\times \prod _{q>p}X_q$
be a basic ball of P. The open set B intersects X iff the set
![]() $\bigcap _{n\leq p}F_{n,p}^{-1}(B_n)$
is non-empty, which is a c.e condition. Indeed, if that set contains an element
$\bigcap _{n\leq p}F_{n,p}^{-1}(B_n)$
is non-empty, which is a c.e condition. Indeed, if that set contains an element
![]() $x_p$
, then let
$x_p$
, then let
![]() $x_n=F_{n,p}(x_p)$
for
$x_n=F_{n,p}(x_p)$
for
![]() $n<p$
and inductively choose for each
$n<p$
and inductively choose for each
![]() $q>p$
some
$q>p$
some
![]() $x_q\in X_q$
such that
$x_q\in X_q$
such that
![]() $F_{q-1}(x_q)=x_{q-1}$
, which is possible as each
$F_{q-1}(x_q)=x_{q-1}$
, which is possible as each
![]() $F_{q-1}$
is surjective. The sequence
$F_{q-1}$
is surjective. The sequence
![]() $(x_n)_{n\in {\mathbb {N}}}$
belongs to
$(x_n)_{n\in {\mathbb {N}}}$
belongs to
![]() $X\cap B$
.
$X\cap B$
.
Therefore, we have proved that the non-triviality of
![]() $\check {H}_1(X;{\mathbb {Z}})$
is
$\check {H}_1(X;{\mathbb {Z}})$
is
![]() $\Sigma ^1_1$
-complete. We can achieve the same result for
$\Sigma ^1_1$
-complete. We can achieve the same result for
![]() $\check {H}_k(X;{\mathbb {Z}})$
for any
$\check {H}_k(X;{\mathbb {Z}})$
for any
![]() $k\geq 1$
. Given a binary tree T, we build the same inverse system of groups
$k\geq 1$
. Given a binary tree T, we build the same inverse system of groups
![]() $(L_n,f_n)$
, with
$(L_n,f_n)$
, with
![]() $L_n={\mathbb {Z}}^{l_n}$
. Let
$L_n={\mathbb {Z}}^{l_n}$
. Let
![]() ${\mathbf {S}}_k$
be the k-dimensional sphere and note that
${\mathbf {S}}_k$
be the k-dimensional sphere and note that
![]() $H_k({\mathbf {S}}_k;{\mathbb {Z}})\cong {\mathbb {Z}}$
. In the previous construction, we replace the circle by
$H_k({\mathbf {S}}_k;{\mathbb {Z}})\cong {\mathbb {Z}}$
. In the previous construction, we replace the circle by
![]() ${\mathbf {S}}_k$
. However, the equality
${\mathbf {S}}_k$
. However, the equality
![]() $H_k({\mathbf {S}}_k^{l_n};{\mathbb {Z}})\cong {\mathbb {Z}}^{l_n}$
only holds for
$H_k({\mathbf {S}}_k^{l_n};{\mathbb {Z}})\cong {\mathbb {Z}}^{l_n}$
only holds for
![]() $k=1$
, so we need to replace the product by the wedge sum (the previous argument would also work with the wedge sum). Let
$k=1$
, so we need to replace the product by the wedge sum (the previous argument would also work with the wedge sum). Let
![]() $s\in {\mathbf {S}}_k$
be a distinguished point, making
$s\in {\mathbf {S}}_k$
be a distinguished point, making
![]() $({\mathbf {S}}_k,s)$
a pointed space, and let
$({\mathbf {S}}_k,s)$
a pointed space, and let
![]() $X_n=\bigvee _{i<l_n} ({\mathbf {S}}_k,s)$
. One has
$X_n=\bigvee _{i<l_n} ({\mathbf {S}}_k,s)$
. One has
![]() $H_k(X_n;{\mathbb {Z}})={\mathbb {Z}}^{l_n}$
[Reference Hatcher19, Corollary 2.25].
$H_k(X_n;{\mathbb {Z}})={\mathbb {Z}}^{l_n}$
[Reference Hatcher19, Corollary 2.25].
We define continuous surjective functions
![]() $F_n:X_{n+1}\to X_n$
in a similar way, by combining the following functions. Let
$F_n:X_{n+1}\to X_n$
in a similar way, by combining the following functions. Let
![]() $G_2,G_3:({\mathbf {S}}_k,s)\to ({\mathbf {S}}_k,s)$
be continuous functions of degrees
$G_2,G_3:({\mathbf {S}}_k,s)\to ({\mathbf {S}}_k,s)$
be continuous functions of degrees
![]() $2$
and
$2$
and
![]() $3$
respectively, i.e. inducing the maps
$3$
respectively, i.e. inducing the maps
![]() $g_2,g_3:H_k({\mathbf {S}}_k;{\mathbb {Z}})\to H_k({\mathbf {S}}_k;{\mathbb {Z}})$
respectively. Let
$g_2,g_3:H_k({\mathbf {S}}_k;{\mathbb {Z}})\to H_k({\mathbf {S}}_k;{\mathbb {Z}})$
respectively. Let
![]() $G_+:({\mathbf {S}}_k,s)\vee ({\mathbf {S}}_k,s)\to ({\mathbf {S}}_k,s)$
be defined as the identity on each copy of
$G_+:({\mathbf {S}}_k,s)\vee ({\mathbf {S}}_k,s)\to ({\mathbf {S}}_k,s)$
be defined as the identity on each copy of
![]() ${\mathbf {S}}_k$
. One has
${\mathbf {S}}_k$
. One has
![]() $H_k({\mathbf {S}}_k\vee {\mathbf {S}}_k)\cong H_k({\mathbf {S}}_k)\oplus H_k({\mathbf {S}}_k)\cong {\mathbb {Z}}^2$
and
$H_k({\mathbf {S}}_k\vee {\mathbf {S}}_k)\cong H_k({\mathbf {S}}_k)\oplus H_k({\mathbf {S}}_k)\cong {\mathbb {Z}}^2$
and
![]() $G_+$
induces
$G_+$
induces
![]() $g_+:{\mathbb {Z}}^2\to {\mathbb {Z}}$
. We finally define
$g_+:{\mathbb {Z}}^2\to {\mathbb {Z}}$
. We finally define
![]() $X=\varprojlim (X_n,F_n)$
. Again by continuity of Čech homology groups, one has
$X=\varprojlim (X_n,F_n)$
. Again by continuity of Čech homology groups, one has
![]() $\check {H}_k(X;{\mathbb {Z}})=\varprojlim (H_k(X_n;{\mathbb {Z}}),f_n)=\varprojlim (L_n,f_n)$
, which is non-trivial iff T contains a path with infinitely many
$\check {H}_k(X;{\mathbb {Z}})=\varprojlim (H_k(X_n;{\mathbb {Z}}),f_n)=\varprojlim (L_n,f_n)$
, which is non-trivial iff T contains a path with infinitely many
![]() $1$
’s.
$1$
’s.
5 Degree spectra of compact Polish spaces
In this section, we realize certain sets of degrees as spectra of compact Polish spaces. We encode a set of natural numbers into the dimensions of spheres of a space. For each
![]() $n\in \mathbb {N}$
, the n-dimensional sphere can be realized as
$n\in \mathbb {N}$
, the n-dimensional sphere can be realized as
![]() $\mathbf {S}^n=\{(x_0,\ldots ,x_n)\in \mathbb {R}^{n+1}:x_0^2+\ldots +x_d^2=1\}$
. To a set
$\mathbf {S}^n=\{(x_0,\ldots ,x_n)\in \mathbb {R}^{n+1}:x_0^2+\ldots +x_d^2=1\}$
. To a set
![]() $A\subseteq \mathbb {N}$
we associate the space
$A\subseteq \mathbb {N}$
we associate the space
![]() $\mathcal {X}_A$
, which is the one-point compactification of the locally compact space
$\mathcal {X}_A$
, which is the one-point compactification of the locally compact space
We then identify the compact and Polish degree spectra of
![]() $\mathcal {X}_A$
as follows.
$\mathcal {X}_A$
as follows.
Theorem 5.1. For all
![]() $A\subseteq \mathbb {N}$
and Turing degree
$A\subseteq \mathbb {N}$
and Turing degree
![]() ${\mathbf {d}}$
,
${\mathbf {d}}$
,
 $$ \begin{align*} {A\ is\ \Sigma^0_2\ relative\ to~{\mathbf{d}}}&\iff{\mathcal{X}_A\ has\ a\ {\mathbf{d}}-computable\ compact\ presentation,}\\ {A\ is\ \Sigma^0_3\ relative\ to~{\mathbf{d}}}&\iff{\mathcal{X}_A\ has\ a\ {\mathbf{d}}-computable\ Polish\ presentation.} \end{align*} $$
$$ \begin{align*} {A\ is\ \Sigma^0_2\ relative\ to~{\mathbf{d}}}&\iff{\mathcal{X}_A\ has\ a\ {\mathbf{d}}-computable\ compact\ presentation,}\\ {A\ is\ \Sigma^0_3\ relative\ to~{\mathbf{d}}}&\iff{\mathcal{X}_A\ has\ a\ {\mathbf{d}}-computable\ Polish\ presentation.} \end{align*} $$
Before proving this result, let us give its main consequences.
Corollary 5.2. For every Turing degree
![]() ${\mathbf {d}}$
, there exists a space
${\mathbf {d}}$
, there exists a space
![]() $\mathcal {X}_d$
whose compact degree spectrum is
$\mathcal {X}_d$
whose compact degree spectrum is
![]() $\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}'\}$
and Polish degree spectrum is
$\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}'\}$
and Polish degree spectrum is
![]() $\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}"\}$
.
$\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}"\}$
.
Proof Given the Turing degree
![]() ${\mathbf {d}}$
of a set
${\mathbf {d}}$
of a set
![]() $D\subseteq \mathbb {N}$
, let
$D\subseteq \mathbb {N}$
, let
![]() $A=\{2n:n\in D\}\cup \{2n+1:n\notin D\}$
and
$A=\{2n:n\in D\}\cup \{2n+1:n\notin D\}$
and
![]() $\mathcal {X}_{\mathbf {d}}=\mathcal {X}_A$
.
$\mathcal {X}_{\mathbf {d}}=\mathcal {X}_A$
.
Corollary 5.3. There is a compact perfect Polish space which has a computable Polish presentation, but no computable compact presentation.
Proof Let
![]() $\mathcal {X}=\mathcal {X}_{\mathbf {0}"}$
from Corollary 5.2. Its Polish degree spectrum is
$\mathcal {X}=\mathcal {X}_{\mathbf {0}"}$
from Corollary 5.2. Its Polish degree spectrum is
![]() $\{\mathbf {x}:\mathbf {0}"\leq \mathbf {x}"\}$
, while its compact degree spectrum is
$\{\mathbf {x}:\mathbf {0}"\leq \mathbf {x}"\}$
, while its compact degree spectrum is
![]() $\{\mathbf {x}:\mathbf {0}"\leq \mathbf {x}'\}$
. The former contains
$\{\mathbf {x}:\mathbf {0}"\leq \mathbf {x}'\}$
. The former contains
![]() $\mathbf {0}$
but not the latter.
$\mathbf {0}$
but not the latter.
We can solve Question 2 affirmatively.
Corollary 5.4. There is a perfect compact Polish space which is
![]() $\mathbf {0}'$
-computably presentable but not computably presentable. Its Polish degree spectrum is the set of high
$\mathbf {0}'$
-computably presentable but not computably presentable. Its Polish degree spectrum is the set of high
![]() $_2$
degrees.
$_2$
degrees.
Proof Let
![]() $X=\mathcal {X}_{\mathbf {0}"'}$
from Corollary 5.2. Its Polish degree spectrum is
$X=\mathcal {X}_{\mathbf {0}"'}$
from Corollary 5.2. Its Polish degree spectrum is
![]() $\{\mathbf {x}:\mathbf {0}"'\leq \mathbf {x}"\}$
, i.e., the high
$\{\mathbf {x}:\mathbf {0}"'\leq \mathbf {x}"\}$
, i.e., the high
![]() $_2$
degrees. It contains
$_2$
degrees. It contains
![]() $\mathbf {0}'$
but not
$\mathbf {0}'$
but not
![]() $\mathbf {0}$
.
$\mathbf {0}$
.
One can improve the degree of non-computably presentable spaces.
Corollary 5.5. For any non-low
![]() $_2$
degree
$_2$
degree
![]() ${\mathbf {d}}$
, there exists a perfect Polish space which is
${\mathbf {d}}$
, there exists a perfect Polish space which is
![]() ${\mathbf {d}}$
-computably presentable, but not computably presentable.
${\mathbf {d}}$
-computably presentable, but not computably presentable.
Proof The Polish degree spectrum of the space
![]() $\mathcal {X}_{{\mathbf {d}}"}$
is
$\mathcal {X}_{{\mathbf {d}}"}$
is
![]() $\{\mathbf {x}:{\mathbf {d}}"\leq \mathbf {x}"\}$
, so it contains
$\{\mathbf {x}:{\mathbf {d}}"\leq \mathbf {x}"\}$
, so it contains
![]() ${\mathbf {d}}$
but not
${\mathbf {d}}$
but not
![]() $\mathbf {0}$
when
$\mathbf {0}$
when
![]() ${\mathbf {d}}$
is not low
${\mathbf {d}}$
is not low
![]() $_2$
.
$_2$
.
In particular, one can take
![]() ${\mathbf {d}}\leq \mathbf {0}'$
which is low
${\mathbf {d}}\leq \mathbf {0}'$
which is low
![]() $_3$
but not low
$_3$
but not low
![]() $_2$
.
$_2$
.
We now give the proof of Theorem 5.1. We need to measure the complexity of finding the dimension of the sphere. It turns out that the descriptive complexity of measuring its covering dimension is too large, as will be made precise later; the way we detect an n-dimensional sphere is by finding a homology cycle of dimension n. Although conceptually more complicated, it results in an algorithm of lower complexity.
5.1 Learning the dimension of a sphere
Given a compact presentation of space X which is homeomorphic to the d-dimensional sphere
![]() $\mathbf {S}^d$
for some d, how difficult is it to find d?
$\mathbf {S}^d$
for some d, how difficult is it to find d?
We are going to show that d can be computed in the limit, i.e., one can compute a sequence
![]() $(d_s)_{s\in \mathbb {N}}$
such that
$(d_s)_{s\in \mathbb {N}}$
such that
![]() $d=\lim _s d_s$
.
$d=\lim _s d_s$
.
The first idea would be to detect the covering dimension of X, but it only enables to compute a sequence
![]() $(d_s)_{s\in \mathbb {N}}$
such that
$(d_s)_{s\in \mathbb {N}}$
such that
![]() $d=\liminf _sd_s$
, because the predicate
$d=\liminf _sd_s$
, because the predicate
![]() $\dim (X)\leq n$
is
$\dim (X)\leq n$
is
![]() $\Pi ^0_2$
(Proposition 2.7). This strategy cannot work, because it can be proved that if X is homeomorphic to the d-dimensional cube
$\Pi ^0_2$
(Proposition 2.7). This strategy cannot work, because it can be proved that if X is homeomorphic to the d-dimensional cube
![]() $[0,1]^d$
, then one cannot compute d in the limit. Therefore, we need to use a way of distinguishing between spheres other than the dimension, and this is given by the homology of the spheres.
$[0,1]^d$
, then one cannot compute d in the limit. Therefore, we need to use a way of distinguishing between spheres other than the dimension, and this is given by the homology of the spheres.
Lemma 5.6. There is an algorithm that, given a compact presentation of a sphere
![]() $\mathbf {S}^d$
,
$\mathbf {S}^d$
,
![]() $d\geq 1$
, computes d in the limit.
$d\geq 1$
, computes d in the limit.
Proof We show that relative to a compact presentation of
![]() $X\cong \mathbf {S}^d$
, the predicate
$X\cong \mathbf {S}^d$
, the predicate
![]() $X\cong \mathbf {S}^n$
is
$X\cong \mathbf {S}^n$
is
![]() $\Sigma ^0_2$
. It implies that it is
$\Sigma ^0_2$
. It implies that it is
![]() $\Delta ^0_2$
, because
$\Delta ^0_2$
, because
![]() $X\cong \mathbf {S}^n\iff \forall m\neq n,X\ncong \mathbf {S}^m$
is
$X\cong \mathbf {S}^n\iff \forall m\neq n,X\ncong \mathbf {S}^m$
is
![]() $\Pi ^0_2$
, therefore
$\Pi ^0_2$
, therefore
![]() $\{d\}$
is
$\{d\}$
is
![]() $\Delta ^0_2$
, and d can be computed in the limit.
$\Delta ^0_2$
, and d can be computed in the limit.
The Čech homology groups of
![]() $\mathbf {S}^d$
(with coefficients in
$\mathbf {S}^d$
(with coefficients in
![]() $\mathbb {Z}_2$
) are
$\mathbb {Z}_2$
) are
 $$ \begin{align*} \check{H}_n(\mathbf{S}^d)=\begin{cases} \mathbb{Z}_2,&\text{ if}~n=d \text{or}~n=0,\\ 0,&\text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \check{H}_n(\mathbf{S}^d)=\begin{cases} \mathbb{Z}_2,&\text{ if}~n=d \text{or}~n=0,\\ 0,&\text{otherwise.} \end{cases} \end{align*} $$
Therefore, for
![]() $n\geq 1$
, X is homeomorphic to
$n\geq 1$
, X is homeomorphic to
![]() $\mathbf {S}^n$
iff
$\mathbf {S}^n$
iff
![]() $\check {H}_n(X)$
is non-trivial, which is
$\check {H}_n(X)$
is non-trivial, which is
![]() $\Sigma ^0_2$
by Corollary 4.7.
$\Sigma ^0_2$
by Corollary 4.7.
One could adapt the argument to include the case
![]() $d=0$
in the previous lemma, but we will not need it.
$d=0$
in the previous lemma, but we will not need it.
Let us explain more concretely how the algorithm works. It searches for an approximation of X by a simplicial complex
![]() $K_s$
that contains an n-cycle c which is not a boundary, and which “survives” in each further approximation
$K_s$
that contains an n-cycle c which is not a boundary, and which “survives” in each further approximation
![]() $K_t$
,
$K_t$
,
![]() $t\geq s$
. The right way of expressing that c survives in
$t\geq s$
. The right way of expressing that c survives in
![]() $K_t$
is that there exists an n-cycle d in
$K_t$
is that there exists an n-cycle d in
![]() $K_t$
which “refines” c, in the sense that it is sent to c by the simplicial map
$K_t$
which “refines” c, in the sense that it is sent to c by the simplicial map
![]() ${f=f_{t-1}\circ \cdots \circ f_s:K_t\to K_s}$
, modulo a boundary:
${f=f_{t-1}\circ \cdots \circ f_s:K_t\to K_s}$
, modulo a boundary:
![]() $c=f(d)+\partial e$
, for some n-chain e of
$c=f(d)+\partial e$
, for some n-chain e of
![]() $K_s$
.
$K_s$
.
Note that whether a cycle c of
![]() $K_s$
survives at stage t is decidable, because it is expressed by quantification over objects
$K_s$
survives at stage t is decidable, because it is expressed by quantification over objects
![]() $d,e$
in a finite set, and the maps f and
$d,e$
in a finite set, and the maps f and
![]() $\partial $
are computable.
$\partial $
are computable.
At any stage t, there are finitely many pairs
![]() $(n,s)$
with
$(n,s)$
with
![]() $s\leq t$
such that some n-cycle in
$s\leq t$
such that some n-cycle in
![]() $K_s$
’s survives in
$K_s$
’s survives in
![]() $K_t$
. The algorithm outputs the number n for which the associated s is minimal, i.e., n is the dimension the cycle that has survived for the longest period of time.
$K_t$
. The algorithm outputs the number n for which the associated s is minimal, i.e., n is the dimension the cycle that has survived for the longest period of time.
Remark 5.7. Lemma 5.6 can be alternatively proved by using the computability of Čech cohomology groups proved in [Reference Downey and Melnikov9, Reference Lupini, Melnikov and Nies28]. Indeed,
![]() $\check {H}^n(\mathbf {S}^m)$
is non-trivial exactly when
$\check {H}^n(\mathbf {S}^m)$
is non-trivial exactly when
![]() $m=n$
(assuming
$m=n$
(assuming
![]() $m,n\geq 1$
), and non-triviality of a
$m,n\geq 1$
), and non-triviality of a
![]() $\check {H}(\mathbf {S}^m)$
is
$\check {H}(\mathbf {S}^m)$
is
![]() $\Sigma ^0_2$
.
$\Sigma ^0_2$
.
We can at last prove the main result of this section.
Proof of Theorem 5.1
Assume that
![]() ${\mathbf {d}}$
computes a compact presentation of
${\mathbf {d}}$
computes a compact presentation of
![]() $\mathcal {X}_A$
. Relative to
$\mathcal {X}_A$
. Relative to
![]() ${\mathbf {d}}$
, we compute an enumeration
${\mathbf {d}}$
, we compute an enumeration
![]() $(C_i)_{i\in \mathbb {N}}$
of the clopen subsets of
$(C_i)_{i\in \mathbb {N}}$
of the clopen subsets of
![]() $\mathcal {X}_A$
, by Proposition 2.6. One has
$\mathcal {X}_A$
, by Proposition 2.6. One has
![]() $n\in A\iff \exists i,C_i$
is connected, is not a singleton, and is homeomorphic to
$n\in A\iff \exists i,C_i$
is connected, is not a singleton, and is homeomorphic to
![]() $\mathbf {S}_{n+1}$
. When
$\mathbf {S}_{n+1}$
. When
![]() $C_i$
is connected and is not a singleton,
$C_i$
is connected and is not a singleton,
![]() $C_i$
is a sphere, so by Lemma 5.6 its dimension is limit-computable relative to
$C_i$
is a sphere, so by Lemma 5.6 its dimension is limit-computable relative to
![]() ${\mathbf {d}}$
. Therefore, A is
${\mathbf {d}}$
. Therefore, A is
![]() $\Sigma ^0_2$
relative to
$\Sigma ^0_2$
relative to
![]() ${\mathbf {d}}$
. If
${\mathbf {d}}$
. If
![]() ${\mathbf {d}}$
computes a Polish presentation of
${\mathbf {d}}$
computes a Polish presentation of
![]() $\mathcal {X}_A$
, then
$\mathcal {X}_A$
, then
![]() ${\mathbf {d}}'$
computes a compact presentation of
${\mathbf {d}}'$
computes a compact presentation of
![]() $\mathcal {X}_A$
, so A is
$\mathcal {X}_A$
, so A is
![]() $\Sigma ^0_2$
relative to
$\Sigma ^0_2$
relative to
![]() ${\mathbf {d}}'$
, hence
${\mathbf {d}}'$
, hence
![]() $\Sigma ^0_3$
relative to
$\Sigma ^0_3$
relative to
![]() ${\mathbf {d}}$
.
${\mathbf {d}}$
.
We now prove the other direction. If A is
![]() $\Sigma ^0_2$
relative to
$\Sigma ^0_2$
relative to
![]() ${\mathbf {d}}$
, then there is a
${\mathbf {d}}$
, then there is a
![]() ${\mathbf {d}}$
-computable set
${\mathbf {d}}$
-computable set
![]() $B\subseteq \mathbb {N}^3$
such that
$B\subseteq \mathbb {N}^3$
such that
![]() $n\in A\iff \exists i\forall j,(n,i,j)\in B$
, and such that when
$n\in A\iff \exists i\forall j,(n,i,j)\in B$
, and such that when
![]() $n\in A$
, there exists a unique i satisfying
$n\in A$
, there exists a unique i satisfying
![]() $(n,i,j)\in B$
for all j.
$(n,i,j)\in B$
for all j.
For each n, let
![]() $X^n_\infty $
be a canonical
$X^n_\infty $
be a canonical
![]() $(n+1)$
-sphere in Q and
$(n+1)$
-sphere in Q and
![]() $X^n_j\subseteq X^n_\infty $
be an increasing sequence of finite sets at Hausdorff distance
$X^n_j\subseteq X^n_\infty $
be an increasing sequence of finite sets at Hausdorff distance
![]() $<2^{-j}$
from
$<2^{-j}$
from
![]() $X^n_\infty $
. We can take all these sets uniformly computably compact. Let
$X^n_\infty $
. We can take all these sets uniformly computably compact. Let
 $$ \begin{align*} Y^n_i=\begin{cases} X^n_\infty,&\text{if}~\forall j,(n,i,j)\in B,\\ X^n_j,&\text{if}~j\ \text{is minimal such that}~(n,i,j)\notin B. \end{cases} \end{align*} $$
$$ \begin{align*} Y^n_i=\begin{cases} X^n_\infty,&\text{if}~\forall j,(n,i,j)\in B,\\ X^n_j,&\text{if}~j\ \text{is minimal such that}~(n,i,j)\notin B. \end{cases} \end{align*} $$
We apply Proposition 2.4, implying that the sets
![]() $Y^n_i$
are uniformly
$Y^n_i$
are uniformly
![]() ${\mathbf {d}}$
-computably compact. Therefore, the set
${\mathbf {d}}$
-computably compact. Therefore, the set
![]() $\alpha _0(\coprod _{n,i}Y^n_i\amalg \omega )$
is
$\alpha _0(\coprod _{n,i}Y^n_i\amalg \omega )$
is
![]() ${\mathbf {d}}$
-computably compact by Proposition 2.3. This set is homeomorphic to
${\mathbf {d}}$
-computably compact by Proposition 2.3. This set is homeomorphic to
![]() $\mathcal {X}_A$
, because all the finite sets
$\mathcal {X}_A$
, because all the finite sets
![]() $X^n_j$
can be seen as subsets of
$X^n_j$
can be seen as subsets of
![]() $\omega $
.
$\omega $
.
If A is
![]() $\Sigma ^0_3$
relative to
$\Sigma ^0_3$
relative to
![]() ${\mathbf {d}}$
, then A can be presented in the same way for some
${\mathbf {d}}$
, then A can be presented in the same way for some
![]() ${\mathbf {d}}$
-c.e. set B, and we consider the same realization of
${\mathbf {d}}$
-c.e. set B, and we consider the same realization of
![]() $\mathcal {X}_A$
. Again by Proposition 2.4, the sets
$\mathcal {X}_A$
. Again by Proposition 2.4, the sets
![]() $Y^n_i$
are uniformly
$Y^n_i$
are uniformly
![]() ${\mathbf {d}}$
-computably overt, and so is
${\mathbf {d}}$
-computably overt, and so is
![]() $\alpha _0(\coprod _{n,i}Y^n_i\amalg \omega )$
.
$\alpha _0(\coprod _{n,i}Y^n_i\amalg \omega )$
.
Remark 5.8 (Cycles vs dimension).
This result cannot be proved by simply using the dimension of the spheres, because detecting the dimension of a space is more complex in general. Whether a space has dimension n is not
![]() $\Delta ^0_2$
; it is complete for the descriptive complexity class consisting of differences of two
$\Delta ^0_2$
; it is complete for the descriptive complexity class consisting of differences of two
![]() $\Sigma ^0_2$
sets. In particular, given a compact presentation of
$\Sigma ^0_2$
sets. In particular, given a compact presentation of
![]() $\mathbf {I}^n$
, one cannot compute a sequence converging to n. However, one can compute a sequence
$\mathbf {I}^n$
, one cannot compute a sequence converging to n. However, one can compute a sequence
![]() $n_i$
such that
$n_i$
such that
![]() $n=\liminf _i n_i$
, and this is optimal. It implies that if the space
$n=\liminf _i n_i$
, and this is optimal. It implies that if the space
![]() $\mathcal {X}^{\prime }_A:=\alpha _0(\coprod _{n\in A}\mathbf {I}^{n+1}\amalg \omega )$
has a computable compact presentation, then A is
$\mathcal {X}^{\prime }_A:=\alpha _0(\coprod _{n\in A}\mathbf {I}^{n+1}\amalg \omega )$
has a computable compact presentation, then A is
![]() $\Sigma ^0_3$
, and it is possible to find a
$\Sigma ^0_3$
, and it is possible to find a
![]() $\Sigma ^0_3$
-complete set A such that
$\Sigma ^0_3$
-complete set A such that
![]() $\mathcal {X}^{\prime }_A$
has a computable compact presentation. However, it does not seem to be true that
$\mathcal {X}^{\prime }_A$
has a computable compact presentation. However, it does not seem to be true that
![]() $\mathcal {X}^{\prime }_A$
has a computable compact presentation for any
$\mathcal {X}^{\prime }_A$
has a computable compact presentation for any
![]() $\Sigma ^0_3$
set A.
$\Sigma ^0_3$
set A.
Remark 5.9. We do not know whether adding extra points outside the spheres is really needed. One can show that if
![]() $Y_A$
is the one-point compactification of
$Y_A$
is the one-point compactification of
![]() $\coprod _{n\in A}\mathbf {S}^{n+1}$
, then Z computes a compact presentation of
$\coprod _{n\in A}\mathbf {S}^{n+1}$
, then Z computes a compact presentation of
![]() $Y_A$
if and only if A is
$Y_A$
if and only if A is
![]() $\Sigma ^0_2$
relative to Z. It implies that if Z computes a Polish presentation of
$\Sigma ^0_2$
relative to Z. It implies that if Z computes a Polish presentation of
![]() $Y_A$
, then A is
$Y_A$
, then A is
![]() $\Sigma ^0_3$
relative to Z, but we do not know whether the other implication holds.
$\Sigma ^0_3$
relative to Z, but we do not know whether the other implication holds.
Remark 5.10. One can modify the proof of Theorem 5.1 to ensure that
![]() $\mathcal {X}_A$
is perfect, by using the one-point compactification of the following:
$\mathcal {X}_A$
is perfect, by using the one-point compactification of the following:
where
![]() $\mathbf {I}$
is the line segment. As
$\mathbf {I}$
is the line segment. As
![]() $\mathbf {I}$
has trivial homology groups, the algorithm that decodes A from
$\mathbf {I}$
has trivial homology groups, the algorithm that decodes A from
![]() $X_A$
still works. In the construction of
$X_A$
still works. In the construction of
![]() $X_A$
from A, one can replace the finite set of isolated points
$X_A$
from A, one can replace the finite set of isolated points
![]() $X^n_j$
with a finite disjoint union of line segments contained in
$X^n_j$
with a finite disjoint union of line segments contained in
![]() $\mathbf {S}^{n+1}$
, and add countably many copies of
$\mathbf {S}^{n+1}$
, and add countably many copies of
![]() $\mathbf {I}$
.
$\mathbf {I}$
.
5.2 Iterations of the Turing jump
We now prove a result similar to Theorem 5.1 for higher levels of the arithmetical hierarchy. This theorem also follows from the results independently obtained by Melnikov [Reference Melnikov32] and Lupini, Melnikov, and Nies [Reference Lupini, Melnikov and Nies28], although with a different proof.
Theorem 5.11. Let
![]() $k\geq 3$
. To a set
$k\geq 3$
. To a set
![]() $A\subseteq \mathbb {N}$
one can associate a compact Polish space
$A\subseteq \mathbb {N}$
one can associate a compact Polish space
![]() $\mathcal {X}_{A,k}$
such that for any Turing degree
$\mathcal {X}_{A,k}$
such that for any Turing degree
![]() ${\mathbf {d}}$
,
${\mathbf {d}}$
,
 $$ \begin{align*} {A\ is\ \Sigma^0_k\ relative\ to\ {\mathbf{d}}}&\iff{\mathcal{X}_{A,k}\ has\ a~{\mathbf{d}}-computable\ compact\ presentation},\\ {A\ is\ \Sigma^0_{k+1}\ relative\ to\ {\mathbf{d}}}&\iff{\mathcal{X}_{A,k}\ has\ a~{\mathbf{d}}-computable\ Polish\ presentation}. \end{align*} $$
$$ \begin{align*} {A\ is\ \Sigma^0_k\ relative\ to\ {\mathbf{d}}}&\iff{\mathcal{X}_{A,k}\ has\ a~{\mathbf{d}}-computable\ compact\ presentation},\\ {A\ is\ \Sigma^0_{k+1}\ relative\ to\ {\mathbf{d}}}&\iff{\mathcal{X}_{A,k}\ has\ a~{\mathbf{d}}-computable\ Polish\ presentation}. \end{align*} $$
Corollary 5.12. For every Turing degree
![]() ${\mathbf {d}}$
and every
${\mathbf {d}}$
and every
![]() $k\geq 2$
, there exists a space
$k\geq 2$
, there exists a space
![]() $\mathcal {X}_{{\mathbf {d}},k}$
whose compact degree spectrum is
$\mathcal {X}_{{\mathbf {d}},k}$
whose compact degree spectrum is
![]() $\{\mathbf {x}:{\mathbf {d}}\leq _T \mathbf {x}^{(k)}\}$
and Polish degree spectrum is
$\{\mathbf {x}:{\mathbf {d}}\leq _T \mathbf {x}^{(k)}\}$
and Polish degree spectrum is
![]() $\{\mathbf {x}:{\mathbf {d}}\leq _T \mathbf {x}^{(k+1)}\}$
.
$\{\mathbf {x}:{\mathbf {d}}\leq _T \mathbf {x}^{(k+1)}\}$
.
Proof Given the Turing degree
![]() ${\mathbf {d}}$
of a set
${\mathbf {d}}$
of a set
![]() $D\subseteq \mathbb {N}$
, let
$D\subseteq \mathbb {N}$
, let
![]() $A=\{2n:n\in D\}\cup \{2n+1:n\notin D\}$
and
$A=\{2n:n\in D\}\cup \{2n+1:n\notin D\}$
and
![]() $\mathcal {X}_{{\mathbf {d}},k}=\mathcal {X}_{A,k+1}$
, and note that for
$\mathcal {X}_{{\mathbf {d}},k}=\mathcal {X}_{A,k+1}$
, and note that for
![]() $j\in \{k,k+1\}$
, A is
$j\in \{k,k+1\}$
, A is
![]() $\Sigma ^0_{j+1}$
relative to
$\Sigma ^0_{j+1}$
relative to
![]() $\mathbf {x}$
iff
$\mathbf {x}$
iff
![]() ${\mathbf {d}}\leq \mathbf {x}^{(j)}$
.
${\mathbf {d}}\leq \mathbf {x}^{(j)}$
.
We recall that a degree
![]() $\mathbf {x}$
is high
$\mathbf {x}$
is high
![]() $_n$
iff
$_n$
iff
![]() $\mathbf {0}^{(n+1)}\leq \mathbf {x}^{(n)}$
. The class of high
$\mathbf {0}^{(n+1)}\leq \mathbf {x}^{(n)}$
. The class of high
![]() $_n$
degrees is the compact degree spectrum of the computable Polish space
$_n$
degrees is the compact degree spectrum of the computable Polish space
![]() $\mathcal {X}_{\mathbf {0}^{(n+1)},n}$
and is the Polish degree spectrum of the space
$\mathcal {X}_{\mathbf {0}^{(n+1)},n}$
and is the Polish degree spectrum of the space
![]() $\mathcal {X}_{\mathbf {0}^{(n+1)},n-1}$
.
$\mathcal {X}_{\mathbf {0}^{(n+1)},n-1}$
.
We now proceed with the proof of Theorem 5.11. We restrict our attention to compact Polish spaces that have countably many connected components. For such spaces, the dimension is the supremum of the dimensions of the connected components (sum theorem 1.5.3 in [Reference Engelking11]).
5.2.1 Widgets.
For
![]() $k\in \mathbb {N}$
, we inductively define spaces
$k\in \mathbb {N}$
, we inductively define spaces
![]() $S_k$
and
$S_k$
and
![]() $P_k$
.
$P_k$
.
For a space X, let
![]() $\alpha _0(X)$
be the one-point compactification of the disjoint union of countably many copies of X. It will be thought as a pointed space, with the point at infinity as basepoint. For
$\alpha _0(X)$
be the one-point compactification of the disjoint union of countably many copies of X. It will be thought as a pointed space, with the point at infinity as basepoint. For
![]() $k\geq 1$
and a compact space X, let
$k\geq 1$
and a compact space X, let
![]() $\alpha _k(X)$
be the wedge sum of the pointed space
$\alpha _k(X)$
be the wedge sum of the pointed space
![]() $(\mathbf {I}^k,(0,\ldots ,0))$
with
$(\mathbf {I}^k,(0,\ldots ,0))$
with
![]() $\alpha _0(X)$
.
$\alpha _0(X)$
.
Let
![]() $S_0=\emptyset $
and
$S_0=\emptyset $
and
![]() $P_0=\{0\}$
. For
$P_0=\{0\}$
. For
![]() $k\geq 1$
, let
$k\geq 1$
, let
 $$ \begin{align*} S_k&=\alpha_k(S_{k-1}\amalg P_{k-1}),\\ P_k&=\alpha_k(S_{k-1}). \end{align*} $$
$$ \begin{align*} S_k&=\alpha_k(S_{k-1}\amalg P_{k-1}),\\ P_k&=\alpha_k(S_{k-1}). \end{align*} $$
In particular,
 $$ \begin{align*} S_1&=\mathbf{I}\vee (\omega+1),\\ P_1&=\mathbf{I}. \end{align*} $$
$$ \begin{align*} S_1&=\mathbf{I}\vee (\omega+1),\\ P_1&=\mathbf{I}. \end{align*} $$
For
![]() $k\geq 1$
, these spaces have several properties:
$k\geq 1$
, these spaces have several properties:
-
•
 $\dim (S_k)=\dim (P_k)=k$
.
$\dim (S_k)=\dim (P_k)=k$
. -
• If C is a clopen subset of
 $S_k$
(respectively
$S_k$
(respectively
 $P_k$
) of dimension k, then C contains a clopen set that is homeomorphic to
$P_k$
) of dimension k, then C contains a clopen set that is homeomorphic to
 $S_k$
(respectively
$S_k$
(respectively
 $P_k$
).
$P_k$
).
5.2.2 A family of topological invariants.
For
![]() $k\geq 1$
, we define a topological invariant that distinguishes
$k\geq 1$
, we define a topological invariant that distinguishes
![]() $S_k$
from
$S_k$
from
![]() $P_k$
and whose complexity in the Vietoris topology is
$P_k$
and whose complexity in the Vietoris topology is
![]() $\Sigma ^0_k$
, in the sense that the collection of compact subsets of Q satisfying this invariant is
$\Sigma ^0_k$
, in the sense that the collection of compact subsets of Q satisfying this invariant is
![]() $\Sigma ^0_k$
in the hyperspace
$\Sigma ^0_k$
in the hyperspace
![]() $\mathcal {K}(Q)$
endowed with the Vietoris topology. More generally, we define a
$\mathcal {K}(Q)$
endowed with the Vietoris topology. More generally, we define a
![]() $\Sigma ^0_k$
invariant
$\Sigma ^0_k$
invariant
![]() $\mathcal {J}_{a,k}$
that distinguishes
$\mathcal {J}_{a,k}$
that distinguishes
![]() $\mathbf {I}^a\times S_k$
from
$\mathbf {I}^a\times S_k$
from
![]() $\mathbf {I}^a\times P_k$
.
$\mathbf {I}^a\times P_k$
.
Definition 5.13. For
![]() $a\in \mathbb {N}$
and
$a\in \mathbb {N}$
and
![]() $k\geq 1$
, we inductively define a topological invariant
$k\geq 1$
, we inductively define a topological invariant
![]() $\mathcal {J}_{a,k}$
as follows:
$\mathcal {J}_{a,k}$
as follows:
-
(1)
 $X\in \mathcal {J}_{a,1}\iff X$
is disconnected.
$X\in \mathcal {J}_{a,1}\iff X$
is disconnected. -
(2) For
 $k\geq 2$
,
$k\geq 2$
,
 $X\in \mathcal {J}_{a,k}\iff X$
contains a clopen set of dimension
$X\in \mathcal {J}_{a,k}\iff X$
contains a clopen set of dimension
 $\geq a+k-1$
that does not satisfy
$\geq a+k-1$
that does not satisfy
 $\mathcal {J}_{a,k-1}$
.
$\mathcal {J}_{a,k-1}$
.
Remark 5.14.
![]() $\mathcal {J}_{a,k}$
enjoys some form of heredity: X satisfies
$\mathcal {J}_{a,k}$
enjoys some form of heredity: X satisfies
![]() $\mathcal {J}_{a,k}$
iff X contains a clopen set satisfying
$\mathcal {J}_{a,k}$
iff X contains a clopen set satisfying
![]() $\mathcal {J}_{a,k}$
.
$\mathcal {J}_{a,k}$
.
Lemma 5.15. Let
![]() $k\geq 1$
.
$k\geq 1$
.
![]() $\mathcal {J}_{a,k}$
is satisfied by
$\mathcal {J}_{a,k}$
is satisfied by
![]() $\mathbf {I}^a\times S_k$
but not by
$\mathbf {I}^a\times S_k$
but not by
![]() $\mathbf {I}^a\times P_k$
.
$\mathbf {I}^a\times P_k$
.
Proof For
![]() $k=1$
, it is straightforward:
$k=1$
, it is straightforward:
![]() $\mathbf {I}^a\times S_1=\mathbf {I}^a\times (\mathbf {I}\vee (\omega +1))$
is disconnected, but
$\mathbf {I}^a\times S_1=\mathbf {I}^a\times (\mathbf {I}\vee (\omega +1))$
is disconnected, but
![]() $\mathbf {I}^a\times P_1=\mathbf {I}^{a+1}$
is connected.
$\mathbf {I}^a\times P_1=\mathbf {I}^{a+1}$
is connected.
Let
![]() $k\geq 2$
. We assume the result for
$k\geq 2$
. We assume the result for
![]() $k-1$
, and prove it for k.
$k-1$
, and prove it for k.
![]() $\mathbf {I}^a\times S_k$
contains a clopen set C which is a copy of
$\mathbf {I}^a\times S_k$
contains a clopen set C which is a copy of
![]() $\mathbf {I}^a\times P_{k-1}$
. One has
$\mathbf {I}^a\times P_{k-1}$
. One has
![]() $\dim (C)=a+k-1$
and by induction hypothesis, this set does not satisfy
$\dim (C)=a+k-1$
and by induction hypothesis, this set does not satisfy
![]() $\mathcal {J}_{a,k-1}$
.
$\mathcal {J}_{a,k-1}$
.
Let C be a clopen subset of
![]() $I^a\times P_k$
of dimension
$I^a\times P_k$
of dimension
![]() $\geq a+k-1$
. We show that C satisfies
$\geq a+k-1$
. We show that C satisfies
![]() $\mathcal {J}_{a,k-1}$
. We claim that C contains a clopen set D which is a copy of
$\mathcal {J}_{a,k-1}$
. We claim that C contains a clopen set D which is a copy of
![]() $\mathbf {I}^a\times S_{k-1}$
, which implies that C satisfies
$\mathbf {I}^a\times S_{k-1}$
, which implies that C satisfies
![]() $\mathcal {J}_{a,k-1}$
by heredity.
$\mathcal {J}_{a,k-1}$
by heredity.
If
![]() $\dim (C)=a+k$
, then C contains a clopen set which is a copy of
$\dim (C)=a+k$
, then C contains a clopen set which is a copy of
![]() $\mathbf {I}^a\times P_k$
, which in turns contains a clopen copy of
$\mathbf {I}^a\times P_k$
, which in turns contains a clopen copy of
![]() $\mathbf {I}^a\times S_{k-1}$
. If
$\mathbf {I}^a\times S_{k-1}$
. If
![]() $\dim (C)=a+k-1$
, then C is disjoint from
$\dim (C)=a+k-1$
, then C is disjoint from
![]() $\mathbf {I}^a\times \mathbf {I}^k$
, so it is a disjoint union of clopen subsets of
$\mathbf {I}^a\times \mathbf {I}^k$
, so it is a disjoint union of clopen subsets of
![]() $\mathbf {I}^a\times S_{k-1}$
. One of them, call it E, must have dimension
$\mathbf {I}^a\times S_{k-1}$
. One of them, call it E, must have dimension
![]() $a+k-1$
. Being a clopen subset of
$a+k-1$
. Being a clopen subset of
![]() $\mathbf {I}^a\times S_{k-1}$
of dimension
$\mathbf {I}^a\times S_{k-1}$
of dimension
![]() $a+k-1$
, E contains a clopen set D which is a copy of
$a+k-1$
, E contains a clopen set D which is a copy of
![]() $\mathbf {I}^a\times S_{k-1}$
. D is a clopen subset of C as wanted.
$\mathbf {I}^a\times S_{k-1}$
. D is a clopen subset of C as wanted.
Therefore, we have proved that C satisfies
![]() $\mathcal {J}_{a,k-1}$
for every clopen subset of
$\mathcal {J}_{a,k-1}$
for every clopen subset of
![]() $\mathbf {I}^a\times P_k$
of dimension
$\mathbf {I}^a\times P_k$
of dimension
![]() $\geq a-k-1$
, so
$\geq a-k-1$
, so
![]() $\mathbf {I}^a\times P_k$
does not satisfy
$\mathbf {I}^a\times P_k$
does not satisfy
![]() $\mathcal {J}_{a,k}$
.
$\mathcal {J}_{a,k}$
.
Lemma 5.16. For
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $\mathcal {J}_{a,k}$
has complexity
$\mathcal {J}_{a,k}$
has complexity
![]() $\Sigma ^0_k$
in the Vietoris topology.
$\Sigma ^0_k$
in the Vietoris topology.
Proof We prove the result by induction. For
![]() $k=1$
, being disconnected is
$k=1$
, being disconnected is
![]() $\Sigma ^0_1$
.
$\Sigma ^0_1$
.
Let
![]() $k\geq 2$
and assume that
$k\geq 2$
and assume that
![]() $\mathcal {J}_{a,k-1}$
is
$\mathcal {J}_{a,k-1}$
is
![]() $\Sigma ^0_{k-1}$
. Having dimension
$\Sigma ^0_{k-1}$
. Having dimension
![]() $\geq a+k-1$
is
$\geq a+k-1$
is
![]() $\Sigma ^0_2$
(Proposition 2.7), hence
$\Sigma ^0_2$
(Proposition 2.7), hence
![]() $\Sigma ^0_k$
, the complement of
$\Sigma ^0_k$
, the complement of
![]() $\mathcal {J}_{a,k-1}$
is
$\mathcal {J}_{a,k-1}$
is
![]() $\Pi ^0_{k-1}$
by induction hypothesis. Therefore, containing a clopen set of dimension
$\Pi ^0_{k-1}$
by induction hypothesis. Therefore, containing a clopen set of dimension
![]() $\geq a+k-1$
that does not satisfy
$\geq a+k-1$
that does not satisfy
![]() $\mathcal {J}_{a,k-1}$
is
$\mathcal {J}_{a,k-1}$
is
![]() $\Sigma ^0_k$
.
$\Sigma ^0_k$
.
5.2.3 Encoding a set in a space.
Let
![]() $k\geq 3$
be fixed. We define
$k\geq 3$
be fixed. We define
![]() $a_n=(k+1)n$
for all
$a_n=(k+1)n$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Let
![]() $A\subseteq \mathbb {N}$
. We define the space
$A\subseteq \mathbb {N}$
. We define the space
![]() $\mathcal {X}_{A,k}$
as the one-point compactification of the disjoint union of the spaces
$\mathcal {X}_{A,k}$
as the one-point compactification of the disjoint union of the spaces
![]() $\mathbf {I}^{a_n}\times S_k$
for
$\mathbf {I}^{a_n}\times S_k$
for
![]() $n\in A$
and
$n\in A$
and
![]() $\mathbf {I}^{a_n}\times P_k$
for
$\mathbf {I}^{a_n}\times P_k$
for
![]() $n\notin A$
.
$n\notin A$
.
The role of
![]() $a_n$
is to use the dimension to distinguish between the difference pieces. In particular, if a clopen subset of
$a_n$
is to use the dimension to distinguish between the difference pieces. In particular, if a clopen subset of
![]() $\mathcal {X}_{A,k}$
has dimension
$\mathcal {X}_{A,k}$
has dimension
![]() $< a_n$
, then C does not intersect
$< a_n$
, then C does not intersect
![]() $\mathbf {I}^{a_n}\times S_k$
or
$\mathbf {I}^{a_n}\times S_k$
or
![]() $\mathbf {I}^{a_n}\times P_k$
.
$\mathbf {I}^{a_n}\times P_k$
.
Lemma 5.17. One has
![]() $n\in A$
iff
$n\in A$
iff
![]() $\mathcal {X}_{A,k}$
contains a clopen set of dimension
$\mathcal {X}_{A,k}$
contains a clopen set of dimension
![]() $\leq a_n+k$
satisfying
$\leq a_n+k$
satisfying
![]() $\mathcal {J}_{a_n,k}$
.
$\mathcal {J}_{a_n,k}$
.
Proof Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $a=a_n$
.
$a=a_n$
.
First assume that
![]() $n\in A$
.
$n\in A$
.
![]() $\mathcal {X}_{A,k}$
contains
$\mathcal {X}_{A,k}$
contains
![]() $\mathbf {I}^{a}\times S_k$
as a clopen set, which has dimension
$\mathbf {I}^{a}\times S_k$
as a clopen set, which has dimension
![]() $a+k$
and satisfies
$a+k$
and satisfies
![]() $\mathcal {J}_{a,k}$
.
$\mathcal {J}_{a,k}$
.
Now let
![]() $n\notin A$
and assume for a contradiction that
$n\notin A$
and assume for a contradiction that
![]() $\mathcal {X}_{A,k}$
contains a clopen set C of dimension
$\mathcal {X}_{A,k}$
contains a clopen set C of dimension
![]() $\leq a+k$
satisfying
$\leq a+k$
satisfying
![]() $\mathcal {J}_{a,k}$
. First, C is contained in the union of the sets
$\mathcal {J}_{a,k}$
. First, C is contained in the union of the sets
![]() $\mathbf {I}^{a_m}\times S_k$
or
$\mathbf {I}^{a_m}\times S_k$
or
![]() $\mathbf {I}^{a_m}\times P_k$
for
$\mathbf {I}^{a_m}\times P_k$
for
![]() $m\leq n$
. As C satisfies
$m\leq n$
. As C satisfies
![]() $\mathcal {J}_{a,k}$
, C contains a clopen set D of dimension
$\mathcal {J}_{a,k}$
, C contains a clopen set D of dimension
![]() $\geq a+k-1$
that does not satisfy
$\geq a+k-1$
that does not satisfy
![]() $\mathcal {J}_{a,k-1}$
. Therefore, the intersection
$\mathcal {J}_{a,k-1}$
. Therefore, the intersection
![]() $E=D\cap (\mathbf {I}^a\times P_k)$
does not satisfy
$E=D\cap (\mathbf {I}^a\times P_k)$
does not satisfy
![]() $\mathcal {J}_{a,k-1}$
by heredity. One has
$\mathcal {J}_{a,k-1}$
by heredity. One has
![]() $\dim (E)\geq a+k-1$
, because the part of D which is outside
$\dim (E)\geq a+k-1$
, because the part of D which is outside
![]() $\mathbf {I}^a\times P_k$
has dimension
$\mathbf {I}^a\times P_k$
has dimension
![]() ${<}a$
. As a result,
${<}a$
. As a result,
![]() $\mathbf {I}^a\times P_k$
satisfies
$\mathbf {I}^a\times P_k$
satisfies
![]() $\mathbf {I}^a\times P_k$
, which is a contradiction.
$\mathbf {I}^a\times P_k$
, which is a contradiction.
Note that the property expressed in the lemma is
![]() $\Sigma ^0_k$
in the Vietoris topology, when
$\Sigma ^0_k$
in the Vietoris topology, when
![]() $k\geq 3$
(however, it is not
$k\geq 3$
(however, it is not
![]() $\Sigma ^0_2$
when
$\Sigma ^0_2$
when
![]() $k=2$
, so Theorem 5.1 cannot be proved in this way). Therefore, for any Turing degree
$k=2$
, so Theorem 5.1 cannot be proved in this way). Therefore, for any Turing degree
![]() ${\mathbf {d}}$
computing a compact presentation of
${\mathbf {d}}$
computing a compact presentation of
![]() $\mathcal {X}_{A,k}$
, A is
$\mathcal {X}_{A,k}$
, A is
![]() $\Sigma ^0_k$
relative to
$\Sigma ^0_k$
relative to
![]() ${\mathbf {d}}$
; hence for any Turing degree
${\mathbf {d}}$
; hence for any Turing degree
![]() ${\mathbf {d}}$
computing a Polish presentation of
${\mathbf {d}}$
computing a Polish presentation of
![]() $\mathcal {X}_{A,k}$
,
$\mathcal {X}_{A,k}$
,
![]() ${\mathbf {d}}'$
computes a compact presentation of
${\mathbf {d}}'$
computes a compact presentation of
![]() $\mathcal {X}_{A,k}$
(Lemma 2.1) and therefore A is
$\mathcal {X}_{A,k}$
(Lemma 2.1) and therefore A is
![]() $\Sigma ^0_{k+1}$
relative to
$\Sigma ^0_{k+1}$
relative to
![]() ${\mathbf {d}}$
.
${\mathbf {d}}$
.
We now show that if A is
![]() $\Sigma ^0_k$
relative to
$\Sigma ^0_k$
relative to
![]() ${\mathbf {d}}$
, then
${\mathbf {d}}$
, then
![]() ${\mathbf {d}}$
computes a compact presentation of
${\mathbf {d}}$
computes a compact presentation of
![]() $\mathcal {X}_{A,k}$
, and if A is
$\mathcal {X}_{A,k}$
, and if A is
![]() $\Sigma ^0_{k+1}$
relative to
$\Sigma ^0_{k+1}$
relative to
![]() ${\mathbf {d}}$
, then
${\mathbf {d}}$
, then
![]() ${\mathbf {d}}$
computes a Polish presentation of
${\mathbf {d}}$
computes a Polish presentation of
![]() $\mathcal {X}_{A,k}$
. Thanks to Proposition 2.4, the two results can be proved with a single argument. We prove it by induction on k, the next result is the case
$\mathcal {X}_{A,k}$
. Thanks to Proposition 2.4, the two results can be proved with a single argument. We prove it by induction on k, the next result is the case
![]() $k=1$
.
$k=1$
.
Lemma 5.18. For a set A, let
 $$ \begin{align*} Y_n=\begin{cases} S_1,&\text{if }n\in A,\\ P_1,&\text{if }n\notin A. \end{cases} \end{align*} $$
$$ \begin{align*} Y_n=\begin{cases} S_1,&\text{if }n\in A,\\ P_1,&\text{if }n\notin A. \end{cases} \end{align*} $$
If A is
![]() $\Sigma ^0_1\ (resp.~\Sigma ^0_2)$
relative to
$\Sigma ^0_1\ (resp.~\Sigma ^0_2)$
relative to
![]() ${\mathbf {d}}$
, then there exist copies of
${\mathbf {d}}$
, then there exist copies of
![]() $Y_n$
that are uniformly
$Y_n$
that are uniformly
![]() ${\mathbf {d}}$
-computably compact
${\mathbf {d}}$
-computably compact
![]() $($
resp. overt
$($
resp. overt
![]() $)$
.
$)$
.
Proof For
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
 $$ \begin{align*} X_k&=[2^{-k},1]\cup\{2^{-k}-2^{-n}:n\geq k\},\\ X_\infty&=[0,1]. \end{align*} $$
$$ \begin{align*} X_k&=[2^{-k},1]\cup\{2^{-k}-2^{-n}:n\geq k\},\\ X_\infty&=[0,1]. \end{align*} $$
Observe that
![]() $X_k\cong S_1$
,
$X_k\cong S_1$
,
![]() $X_\infty \cong P_1$
,
$X_\infty \cong P_1$
,
![]() $X_k\subseteq X_{k+1}\subseteq \cdots \subseteq X_\infty $
, and
$X_k\subseteq X_{k+1}\subseteq \cdots \subseteq X_\infty $
, and
![]() $d_H(X_k,X_\infty )<2^{-k-1}$
.
$d_H(X_k,X_\infty )<2^{-k-1}$
.
Let A be given by a predicate
![]() $n\in A\iff \exists k,(n,k)\in B$
. To n we associate
$n\in A\iff \exists k,(n,k)\in B$
. To n we associate
![]() $Y_n=X_k$
if k is minimal such that
$Y_n=X_k$
if k is minimal such that
![]() $(n,k)\in B$
, and
$(n,k)\in B$
, and
![]() $Y_n=X_\infty $
if there is no such k, i.e.,
$Y_n=X_\infty $
if there is no such k, i.e.,
![]() $n\notin A$
.
$n\notin A$
.
We apply Proposition 2.4. If B is computable relative to
![]() ${\mathbf {d}}$
, then
${\mathbf {d}}$
, then
![]() $Y_n$
is uniformly
$Y_n$
is uniformly
![]() ${\mathbf {d}}$
-computably compact. If B is
${\mathbf {d}}$
-computably compact. If B is
![]() $\Pi ^0_1$
relative to
$\Pi ^0_1$
relative to
![]() ${\mathbf {d}}$
, then
${\mathbf {d}}$
, then
![]() $Y_n$
is uniformly
$Y_n$
is uniformly
![]() ${\mathbf {d}}$
-computably overt.
${\mathbf {d}}$
-computably overt.
Lemma 5.19. Let
![]() $k\geq 1$
. For a set A, let
$k\geq 1$
. For a set A, let
 $$ \begin{align*} Y_n=\begin{cases} S_k,&\text{if }n\in A,\\ P_k,&\text{if }n\notin A. \end{cases} \end{align*} $$
$$ \begin{align*} Y_n=\begin{cases} S_k,&\text{if }n\in A,\\ P_k,&\text{if }n\notin A. \end{cases} \end{align*} $$
If A is
![]() $\Sigma ^0_k\ (resp.~\Sigma ^0_{k+1})$
relative to
$\Sigma ^0_k\ (resp.~\Sigma ^0_{k+1})$
relative to
![]() ${\mathbf {d}}$
, then there exist copies of
${\mathbf {d}}$
, then there exist copies of
![]() $Y_n$
that are uniformly
$Y_n$
that are uniformly
![]() ${\mathbf {d}}$
-computably compact
${\mathbf {d}}$
-computably compact
![]() $($
resp. overt
$($
resp. overt
![]() $)$
.
$)$
.
Proof The case
![]() $k=1$
is Lemma 5.18. Let
$k=1$
is Lemma 5.18. Let
![]() $k\geq 2$
and assume the result for
$k\geq 2$
and assume the result for
![]() $k-1$
.
$k-1$
.
Let A be given by a predicate
![]() $n\in A\iff \exists i,(n,i)\in B$
where B is
$n\in A\iff \exists i,(n,i)\in B$
where B is
![]() $\Pi ^0_{k-1}$
relative to
$\Pi ^0_{k-1}$
relative to
![]() ${\mathbf {d}}$
. We can assume that if
${\mathbf {d}}$
. We can assume that if
![]() $\exists i,(n,i)\in B$
, then there exist infinitely many i’s such that
$\exists i,(n,i)\in B$
, then there exist infinitely many i’s such that
![]() $(n,i)\in B$
and infinitely many i’s such that
$(n,i)\in B$
and infinitely many i’s such that
![]() $(n,i)\notin B$
. Indeed, define
$(n,i)\notin B$
. Indeed, define
![]() $B'$
as follows:
$B'$
as follows:
![]() $(n,2i)\in B'$
if there exists
$(n,2i)\in B'$
if there exists
![]() $j\leq i$
such that
$j\leq i$
such that
![]() $(n,j)\in B$
, and
$(n,j)\in B$
, and
![]() $(n,2i+1)\notin B'$
.
$(n,2i+1)\notin B'$
.
![]() $B'$
is
$B'$
is
![]() $\Pi ^0_{k-1}$
and
$\Pi ^0_{k-1}$
and
![]() $n\in A\iff \exists i,(n,i)\in B'$
.
$n\in A\iff \exists i,(n,i)\in B'$
.
Let
![]() $X_{n,i}=S_{k-1}$
if
$X_{n,i}=S_{k-1}$
if
![]() $(n,i)\notin B$
and
$(n,i)\notin B$
and
![]() $X_{n,i}=P_{k-1}$
if
$X_{n,i}=P_{k-1}$
if
![]() $(n,i)\in B$
. By induction hypothesis, given
$(n,i)\in B$
. By induction hypothesis, given
![]() $(n,i)$
one can produce a copy of
$(n,i)$
one can produce a copy of
![]() $X_{n,i}$
which is uniformly
$X_{n,i}$
which is uniformly
![]() ${\mathbf {d}}$
-computable compact. Build the space
${\mathbf {d}}$
-computable compact. Build the space
![]() $X_n$
which is the wedge sum of
$X_n$
which is the wedge sum of
![]() $I^k$
and the one-point compactification of
$I^k$
and the one-point compactification of
![]() $\coprod _{n,i}X_{n,i}$
. If
$\coprod _{n,i}X_{n,i}$
. If
![]() $n\in A$
, then
$n\in A$
, then
![]() $X_n=S_k$
; if
$X_n=S_k$
; if
![]() $n\notin A$
, then
$n\notin A$
, then
![]() $X_n=P_k$
.
$X_n=P_k$
.
If B is
![]() $\Pi ^0_k$
relative to
$\Pi ^0_k$
relative to
![]() ${\mathbf {d}}$
, then the very same argument gives uniformly
${\mathbf {d}}$
, then the very same argument gives uniformly
![]() ${\mathbf {d}}$
-computably overt copies of
${\mathbf {d}}$
-computably overt copies of
![]() $Y_n$
by induction.
$Y_n$
by induction.
Finally, a presentation of
![]() $\mathcal {X}_{A,k}$
from A is then achieved by building products of
$\mathcal {X}_{A,k}$
from A is then achieved by building products of
![]() $\mathbf {I}^{a_n}$
with copies of
$\mathbf {I}^{a_n}$
with copies of
![]() $S_k$
or
$S_k$
or
![]() $P_k$
as above, using Proposition 2.3. The proof of Theorem 5.11 is complete.
$P_k$
as above, using Proposition 2.3. The proof of Theorem 5.11 is complete.
6 Cone-avoidance
In this section, we solve Question 3 by showing the following:
Theorem 6.1. Let
![]() $A\subseteq \mathbb {N}$
be a non-c.e. set. Every compact Polish space has a Polish presentation that does not enumerate A.
$A\subseteq \mathbb {N}$
be a non-c.e. set. Every compact Polish space has a Polish presentation that does not enumerate A.
In particular,
Corollary 6.2. The degree spectrum of a compact Polish space cannot be the upper cone
![]() $\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}\}$
for any non-computable degree
$\{\mathbf {x}:{\mathbf {d}}\leq \mathbf {x}\}$
for any non-computable degree
![]() ${\mathbf {d}}$
.
${\mathbf {d}}$
.
Actually the proof also shows that if for each i we choose a non-c.e. set
![]() $A_i$
, then every compact Polish space has a presentation that does not enumerate any
$A_i$
, then every compact Polish space has a presentation that does not enumerate any
![]() $A_i$
. It implies that the degree spectrum of a compact Polish space cannot be a countable union of non-trivial upper cones
$A_i$
. It implies that the degree spectrum of a compact Polish space cannot be a countable union of non-trivial upper cones
![]() $\bigcup _{i\in \omega }\{\mathbf {x}:{\mathbf {d}}_i\leq \mathbf {x}\}$
.
$\bigcup _{i\in \omega }\{\mathbf {x}:{\mathbf {d}}_i\leq \mathbf {x}\}$
.
In order to prove the result, we need ideas from computability theory and ideas from topology.
6.1 Overtness argument
Overtness captures a familiar argument in computably theory, which we describe now.
We will apply the technique to the space
![]() $X=\mathcal {V}(Q)$
; however, it is easier to state the result for an abstract space X.
$X=\mathcal {V}(Q)$
; however, it is easier to state the result for an abstract space X.
Let X be a countably based space with a fixed indexed basis
![]() $(B_i)_{i\in \mathbb {N}}$
that is closed under finite intersections. We say that
$(B_i)_{i\in \mathbb {N}}$
that is closed under finite intersections. We say that
![]() $A\subseteq \mathbb {N}$
is reducible to
$A\subseteq \mathbb {N}$
is reducible to
![]() $x\in X$
, written
$x\in X$
, written
![]() $A\leq _e x$
, if A is enumeration reducible to
$A\leq _e x$
, if A is enumeration reducible to
![]() $N_x=\{i\in \mathbb {N}:x\in B_i\}$
. We write
$N_x=\{i\in \mathbb {N}:x\in B_i\}$
. We write
![]() $M(x)=A$
if M enumerates A from any enumeration of
$M(x)=A$
if M enumerates A from any enumeration of
![]() $N_x$
. We say that a set
$N_x$
. We say that a set
![]() $S\subseteq X$
is computably overt if the set
$S\subseteq X$
is computably overt if the set
![]() $\{i\in \mathbb {N}:S\cap B_i\neq \emptyset \}$
is c.e.
$\{i\in \mathbb {N}:S\cap B_i\neq \emptyset \}$
is c.e.
For a Turing machine M and a set
![]() $A\subseteq \mathbb {N}$
, we say that M fails to enumerate A from x if M outputs some
$A\subseteq \mathbb {N}$
, we say that M fails to enumerate A from x if M outputs some
![]() $n\notin A$
on some enumeration of
$n\notin A$
on some enumeration of
![]() $N_x$
. We denote by
$N_x$
. We denote by
![]() $F_{M,A}$
the set of x’s on which M fails to enumerate A. That set is open, because when M outputs some
$F_{M,A}$
the set of x’s on which M fails to enumerate A. That set is open, because when M outputs some
![]() $n\notin A$
, it has only read a finite part of
$n\notin A$
, it has only read a finite part of
![]() $N_x$
, which can be extended to an enumeration of
$N_x$
, which can be extended to an enumeration of
![]() $N_y$
for any y in some neighborhood of x, so each such y also belongs to
$N_y$
for any y in some neighborhood of x, so each such y also belongs to
![]() $F_{M,A}$
.
$F_{M,A}$
.
Lemma 6.3. Let X be a countably based space. Let
![]() $x\in X$
,
$x\in X$
,
![]() $A\subseteq \mathbb {N}$
be a non-c.e. set, and M a Turing machine. If
$A\subseteq \mathbb {N}$
be a non-c.e. set, and M a Turing machine. If
![]() $M(x)=A$
, then
$M(x)=A$
, then
![]() $F_{M,A}$
intersects every computably overt subset of X containing x.
$F_{M,A}$
intersects every computably overt subset of X containing x.
Proof Assume that
![]() $M(x)=A$
and let V be a computably overt set containing x. If
$M(x)=A$
and let V be a computably overt set containing x. If
![]() $F_{M,A}$
does not intersect V, then we describe an effective procedure that enumerates A, contradicting the assumption that A is not c.e. The procedure is as follows: enumerate all the prefixes of names of elements of V (which is possible because V is computably overt), simulate M on them, and collect all the outputs. As
$F_{M,A}$
does not intersect V, then we describe an effective procedure that enumerates A, contradicting the assumption that A is not c.e. The procedure is as follows: enumerate all the prefixes of names of elements of V (which is possible because V is computably overt), simulate M on them, and collect all the outputs. As
![]() $F_{M,A}$
does not intersect V, all the outputs are correct, i.e., belong to A, and every element of A appears because M enumerates A on each name of
$F_{M,A}$
does not intersect V, all the outputs are correct, i.e., belong to A, and every element of A appears because M enumerates A on each name of
![]() $x\in V$
. As a result, this procedure enumerates A, which is then c.e. The contradiction implies that
$x\in V$
. As a result, this procedure enumerates A, which is then c.e. The contradiction implies that
![]() $F_{M,A}$
intersects V.
$F_{M,A}$
intersects V.
6.2 Perturbations
We now come to the topological ingredient of the proof, based on the notion of
![]() $\epsilon $
-perturbation. The proof is a Baire category argument: if
$\epsilon $
-perturbation. The proof is a Baire category argument: if
![]() $A\subseteq \mathbb {N}$
is not c.e., then one can perturb any compact set
$A\subseteq \mathbb {N}$
is not c.e., then one can perturb any compact set
![]() $K\subseteq Q$
so that its perturbed copy
$K\subseteq Q$
so that its perturbed copy
![]() $K'$
does not enumerate A, when seeing
$K'$
does not enumerate A, when seeing
![]() $K'$
as an element of the space
$K'$
as an element of the space
![]() $\mathcal {V}(Q)$
.
$\mathcal {V}(Q)$
.
Definition 6.4. An
![]() $\epsilon $
-perturbation is a one-to-one continuous function
$\epsilon $
-perturbation is a one-to-one continuous function
![]() $f:Q\to Q$
such that
$f:Q\to Q$
such that
![]() $d(f(x),x)<\epsilon $
for all
$d(f(x),x)<\epsilon $
for all
![]() $x\in Q$
.
$x\in Q$
.
Lemma 6.5. Let
![]() $S=\{s_0,\ldots ,s_n\}$
and
$S=\{s_0,\ldots ,s_n\}$
and
![]() $T=\{t_0,\ldots ,t_n\}$
be finite subsets of Q such that
$T=\{t_0,\ldots ,t_n\}$
be finite subsets of Q such that
![]() $d(s_i,t_i)<\epsilon $
for
$d(s_i,t_i)<\epsilon $
for
![]() $i=0,\ldots ,n$
. There exists an
$i=0,\ldots ,n$
. There exists an
![]() $\epsilon $
-perturbation f such that
$\epsilon $
-perturbation f such that
![]() $f(s_i)=t_i$
for
$f(s_i)=t_i$
for
![]() $i=0,\ldots ,n$
.
$i=0,\ldots ,n$
.
Proof It is a direct application of the homeomorphism extension theorem from [Reference van Mill33]. It relies on the notion of Z-set, which we recall for completeness; however, it is not important to understand this notion, we will only use the fact that finite subsets of Q are Z-sets.
The following definition and results are taken from [Reference van Mill33]. A closed set
![]() $A\subseteq Q$
is a Z-set if for every continuous function
$A\subseteq Q$
is a Z-set if for every continuous function
![]() $f:Q\to Q$
and every
$f:Q\to Q$
and every
![]() $\epsilon>0$
, there exists a continuous function
$\epsilon>0$
, there exists a continuous function
![]() $g:Q\to Q$
such that
$g:Q\to Q$
such that
![]() $d(f(x),g(x))<\epsilon $
for all
$d(f(x),g(x))<\epsilon $
for all
![]() $x\in Q$
, and
$x\in Q$
, and
![]() $g(Q)\cap A=\emptyset $
(see Section 5.1 in [Reference van Mill33]). By Remark 5.1.4 in [Reference van Mill33], every singleton is a Z-set. Lemma 5.1.2(3) in [Reference van Mill33] states that any finite union of Z-sets is a Z-set; therefore, every finite set is a Z-set.
$g(Q)\cap A=\emptyset $
(see Section 5.1 in [Reference van Mill33]). By Remark 5.1.4 in [Reference van Mill33], every singleton is a Z-set. Lemma 5.1.2(3) in [Reference van Mill33] states that any finite union of Z-sets is a Z-set; therefore, every finite set is a Z-set.
The homeomorphism extension theorem (Theorem 5.3.7 in [Reference van Mill33]) states that if
![]() $S,T\subseteq Q$
are Z-sets and
$S,T\subseteq Q$
are Z-sets and
![]() $f:S\to T$
is a homeomorphism satisfying
$f:S\to T$
is a homeomorphism satisfying
![]() $d(f(x),x)<\epsilon $
for all
$d(f(x),x)<\epsilon $
for all
![]() $x\in S$
, then f can be extended to a homeomorphism
$x\in S$
, then f can be extended to a homeomorphism
![]() $\overline {f}:Q\to Q$
satisfying
$\overline {f}:Q\to Q$
satisfying
![]() $d(\overline {f}(x),x)<\epsilon $
for all
$d(\overline {f}(x),x)<\epsilon $
for all
![]() $x\in Q$
. Therefore, the statement is just an application of the homeomorphism extension theorem to finite sets.
$x\in Q$
. Therefore, the statement is just an application of the homeomorphism extension theorem to finite sets.
We remind the reader that
![]() $\mathcal {V}(Q)$
is a countably based topological space endowed with the lower Vietoris topology. In the next statement, the notions of computable overtness and closure are meant in that topology.
$\mathcal {V}(Q)$
is a countably based topological space endowed with the lower Vietoris topology. In the next statement, the notions of computable overtness and closure are meant in that topology.
Lemma 6.6. Let
![]() $K\subseteq Q$
be a compact set and
$K\subseteq Q$
be a compact set and
![]() $\epsilon>0$
. There exists a computably overt set
$\epsilon>0$
. There exists a computably overt set
![]() $\mathcal {A}\subseteq \mathcal {V}(Q)$
with
$\mathcal {A}\subseteq \mathcal {V}(Q)$
with
![]() $K\in \mathcal {A}$
, such that
$K\in \mathcal {A}$
, such that
![]() $\mathcal {A}$
is contained in the closure of the set of
$\mathcal {A}$
is contained in the closure of the set of
![]() $\epsilon $
-deformations of K.
$\epsilon $
-deformations of K.
Proof Let
![]() $\mathcal {F}\subseteq \mathcal {V}(Q)$
be the family of finite sets of rational points, which can be computably indexed in an obvious way. We are going to define
$\mathcal {F}\subseteq \mathcal {V}(Q)$
be the family of finite sets of rational points, which can be computably indexed in an obvious way. We are going to define
![]() $\mathcal {A}$
in such a way that:
$\mathcal {A}$
in such a way that:
-
(1)
 $\mathcal {F}\cap \mathcal {A}$
is dense in
$\mathcal {F}\cap \mathcal {A}$
is dense in
 $\mathcal {A}$
(w.r.t. the lower Vietoris topology).
$\mathcal {A}$
(w.r.t. the lower Vietoris topology). -
(2)
 $\mathcal {F}\cap \mathcal {A}$
is computably enumerable.
$\mathcal {F}\cap \mathcal {A}$
is computably enumerable. -
(3) Every element of
 $\mathcal {F}\cap \mathcal {A}$
is contained in some
$\mathcal {F}\cap \mathcal {A}$
is contained in some
 $\epsilon $
-deformation of K.
$\epsilon $
-deformation of K.
The first two conditions imply that
![]() $\mathcal {A}$
is computably overt, because it is the closure of a computable sequence listing the elements of
$\mathcal {A}$
is computably overt, because it is the closure of a computable sequence listing the elements of
![]() $\mathcal {F}\cap \mathcal {A}$
.
$\mathcal {F}\cap \mathcal {A}$
.
The first and third conditions imply that
![]() $\mathcal {A}$
is contained in the closure of the set of
$\mathcal {A}$
is contained in the closure of the set of
![]() $\epsilon $
-deformations of K:
$\epsilon $
-deformations of K:
![]() $\mathcal {A}$
is the closure of
$\mathcal {A}$
is the closure of
![]() $\mathcal {F}\cap \mathcal {A}$
, and each element of
$\mathcal {F}\cap \mathcal {A}$
, and each element of
![]() $\mathcal {F}\cap \mathcal {A}$
is a subset of an
$\mathcal {F}\cap \mathcal {A}$
is a subset of an
![]() $\epsilon $
-deformation
$\epsilon $
-deformation
![]() $K'$
of K, so belongs to the closure of
$K'$
of K, so belongs to the closure of
![]() $\{K'\}$
(the lower Vietoris closed open sets are upwards closed, equivalently the lower Vietoris closed sets are downwards closed).
$\{K'\}$
(the lower Vietoris closed open sets are upwards closed, equivalently the lower Vietoris closed sets are downwards closed).
We now define
![]() $\mathcal {A}$
satisfying these conditions. If K was perfect, then we could just take some small rational ball in the Hausdorff metric containing K. However we need a bit more work in the general case.
$\mathcal {A}$
satisfying these conditions. If K was perfect, then we could just take some small rational ball in the Hausdorff metric containing K. However we need a bit more work in the general case.
We first show that there exist open sets
![]() $U_0,\ldots ,U_n\subseteq Q$
that cover K, such that for every
$U_0,\ldots ,U_n\subseteq Q$
that cover K, such that for every
![]() $x\in U_0$
,
$x\in U_0$
,
![]() $K\cap B(x,\epsilon )$
is infinite and
$K\cap B(x,\epsilon )$
is infinite and
![]() $K\cap U_i$
is a singleton for each
$K\cap U_i$
is a singleton for each
![]() $i\geq 1$
. Let
$i\geq 1$
. Let
![]() $K_N$
be the set of non-isolated points of K and let
$K_N$
be the set of non-isolated points of K and let
![]() $U_0=\{x\in Q:d(x,K_N)<\epsilon \}$
. The set
$U_0=\{x\in Q:d(x,K_N)<\epsilon \}$
. The set
![]() $K\setminus U_0$
is finite, because it is compact and all its points are isolated. Therefore, there exist basic balls
$K\setminus U_0$
is finite, because it is compact and all its points are isolated. Therefore, there exist basic balls
![]() $U_1,\ldots ,U_n$
isolating the points of
$U_1,\ldots ,U_n$
isolating the points of
![]() $K\setminus U_0$
. We can make sure that all the open sets
$K\setminus U_0$
. We can make sure that all the open sets
![]() $U_i$
are pairwise disjoint. By compactness of K, we can assume that
$U_i$
are pairwise disjoint. By compactness of K, we can assume that
![]() $U_0$
is a finite union of basic balls. We can now define our computably overt subset of
$U_0$
is a finite union of basic balls. We can now define our computably overt subset of
![]() $\mathcal {V}(Q)$
: let
$\mathcal {V}(Q)$
: let
 $$ \begin{align*} \mathcal{A}=\left\{C\in\mathcal{V}(Q):C\subseteq \bigcup_{0\leq i\leq n} U_i\text{ and }|C\cap U_i|=1\text{ for all }i\geq 1\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{A}=\left\{C\in\mathcal{V}(Q):C\subseteq \bigcup_{0\leq i\leq n} U_i\text{ and }|C\cap U_i|=1\text{ for all }i\geq 1\right\}. \end{align*} $$
We check condition 1. Let
![]() $C\in \mathcal {A}$
. C is a limit in the Vietoris topology of finite sets
$C\in \mathcal {A}$
. C is a limit in the Vietoris topology of finite sets
![]() $C_k$
of rational points (note that here we use the Vietoris rather than the lower Vietoris topology). As
$C_k$
of rational points (note that here we use the Vietoris rather than the lower Vietoris topology). As
![]() $C\in \mathcal {A}$
, for sufficiently large k,
$C\in \mathcal {A}$
, for sufficiently large k,
![]() $C_k$
is contained in
$C_k$
is contained in
![]() $\bigcup _i U_i$
and intersects
$\bigcup _i U_i$
and intersects
![]() $U_1,\ldots ,U_n$
. For
$U_1,\ldots ,U_n$
. For
![]() $i\geq 1$
, if
$i\geq 1$
, if
![]() $C_k\cap U_i$
contains more than one point, then keep only one of them. Let
$C_k\cap U_i$
contains more than one point, then keep only one of them. Let
![]() $C^{\prime }_k\subseteq C_k$
be obtained this way. One has
$C^{\prime }_k\subseteq C_k$
be obtained this way. One has
![]() $C^{\prime }_k\in \mathcal {F}\cap \mathcal {A}$
by construction, and
$C^{\prime }_k\in \mathcal {F}\cap \mathcal {A}$
by construction, and
![]() $C^{\prime }_k$
converges to C in the Vietoris (hence lower Vietoris) topology.
$C^{\prime }_k$
converges to C in the Vietoris (hence lower Vietoris) topology.
Condition 2 is easily checked: the conditions defining
![]() $C\in \mathcal {A}$
are c.e., when C is a finite set of rational points.
$C\in \mathcal {A}$
are c.e., when C is a finite set of rational points.
We now prove condition 3. We show that for every finite set
![]() $T\in \mathcal {A}$
, there exists an
$T\in \mathcal {A}$
, there exists an
![]() $\epsilon $
-deformation of K containing T.
$\epsilon $
-deformation of K containing T.
Let
![]() $T=\{t_0,\ldots ,t_n\}$
belong to
$T=\{t_0,\ldots ,t_n\}$
belong to
![]() $\mathcal {A}$
. We build a finite set
$\mathcal {A}$
. We build a finite set
![]() $S=\{s_0,\ldots ,s_n\}\subseteq K$
with
$S=\{s_0,\ldots ,s_n\}\subseteq K$
with
![]() $d(s_i,t_i)<\epsilon $
. For each i, if
$d(s_i,t_i)<\epsilon $
. For each i, if
![]() $t_i\in U_0$
, then the intersection of
$t_i\in U_0$
, then the intersection of
![]() $B(t_i,\epsilon )$
with K is infinite, so we can choose a point
$B(t_i,\epsilon )$
with K is infinite, so we can choose a point
![]() $s_i$
in the intersection, so that
$s_i$
in the intersection, so that
![]() $s_i\neq s_j$
for
$s_i\neq s_j$
for
![]() $i\neq j$
. If
$i\neq j$
. If
![]() $t_i\in U_k$
with
$t_i\in U_k$
with
![]() $k\geq 1$
, then we define
$k\geq 1$
, then we define
![]() $s_i$
as the unique point of K in
$s_i$
as the unique point of K in
![]() $U_k$
. The points
$U_k$
. The points
![]() $s_i$
are pairwise distinct, because if
$s_i$
are pairwise distinct, because if
![]() $i\neq j$
, then
$i\neq j$
, then
![]() $s_i$
and
$s_i$
and
![]() $s_j$
cannot both belong to a common
$s_j$
cannot both belong to a common
![]() $U_k$
,
$U_k$
,
![]() $k\geq 1$
, as
$k\geq 1$
, as
![]() $K\in \mathcal {A}$
.
$K\in \mathcal {A}$
.
One has
![]() $d(s_i,t_i)<\epsilon $
for each i, so we can apply Lemma 6.5 to obtain an
$d(s_i,t_i)<\epsilon $
for each i, so we can apply Lemma 6.5 to obtain an
![]() $\epsilon $
-perturbation f mapping each
$\epsilon $
-perturbation f mapping each
![]() $s_i$
to
$s_i$
to
![]() $t_i$
. One has
$t_i$
. One has
![]() $T=f(S)\subseteq f(K)$
, so the proof is complete.
$T=f(S)\subseteq f(K)$
, so the proof is complete.
We now have all the ingredients needed to prove the result.
Proof of Theorem 6.1
Let X be a compact Polish space. We prove that some copy of X in
![]() $\mathcal {V}(Q)$
does not enumerate A. It implies the result, because any name of a copy of X in
$\mathcal {V}(Q)$
does not enumerate A. It implies the result, because any name of a copy of X in
![]() $\mathcal {V}(Q)$
computes a presentation of X.
$\mathcal {V}(Q)$
computes a presentation of X.
The space
![]() $\mathcal {I}(Q)=\{\phi :Q\to Q\text { continuous one-to-one}\}$
, with the topology induced by the metric
$\mathcal {I}(Q)=\{\phi :Q\to Q\text { continuous one-to-one}\}$
, with the topology induced by the metric
![]() $\rho (\phi ,\psi )=\sup _x d(\phi (x),\psi (x))$
is Polish (Corollary 1.3.11 in [Reference van Mill33]). For any compact set
$\rho (\phi ,\psi )=\sup _x d(\phi (x),\psi (x))$
is Polish (Corollary 1.3.11 in [Reference van Mill33]). For any compact set
![]() $K\subseteq Q$
and any non-c.e. set
$K\subseteq Q$
and any non-c.e. set
![]() $A\subseteq \mathbb {N}$
, we prove that the set
$A\subseteq \mathbb {N}$
, we prove that the set
![]() $\{\phi \in \mathcal {I}(Q):A\leq _e \phi (K)\}$
is meager in
$\{\phi \in \mathcal {I}(Q):A\leq _e \phi (K)\}$
is meager in
![]() $\mathcal {I}(Q)$
, which implies the existence of a copy
$\mathcal {I}(Q)$
, which implies the existence of a copy
![]() $K'$
of K such that
$K'$
of K such that
![]() $A\nleq _e K'$
(
$A\nleq _e K'$
(
![]() $K'$
is seen as an element of the space
$K'$
is seen as an element of the space
![]() $\mathcal {V}(Q)$
). It is done by showing that for each Turing machine M, the set
$\mathcal {V}(Q)$
). It is done by showing that for each Turing machine M, the set
![]() $\{\phi \in \mathcal {I}(Q):M(\phi (K))=A\}$
is nowhere dense in
$\{\phi \in \mathcal {I}(Q):M(\phi (K))=A\}$
is nowhere dense in
![]() $\mathcal {I}(Q)$
.
$\mathcal {I}(Q)$
.
Let
![]() $\phi \in \mathcal {I}(Q)$
be such that
$\phi \in \mathcal {I}(Q)$
be such that
![]() $M(\phi (K))=A$
. For
$M(\phi (K))=A$
. For
![]() $\epsilon>0$
, we prove that there exists
$\epsilon>0$
, we prove that there exists
![]() $\psi \in \mathcal {I}(Q)$
such that
$\psi \in \mathcal {I}(Q)$
such that
![]() $\rho (\phi ,\psi )<\epsilon $
and such that
$\rho (\phi ,\psi )<\epsilon $
and such that
![]() $\psi (K)\in F_{M,A}$
(the set
$\psi (K)\in F_{M,A}$
(the set
![]() $F_{M,A}$
was defined before Lemma 6.3). It implies the result, because for every
$F_{M,A}$
was defined before Lemma 6.3). It implies the result, because for every
![]() $\psi '$
sufficiently close to
$\psi '$
sufficiently close to
![]() $\psi $
, one also has
$\psi $
, one also has
![]() $\psi '\in F_{M,A}$
as
$\psi '\in F_{M,A}$
as
![]() $F_{M,A}$
is open.
$F_{M,A}$
is open.
Lemma 6.6 provides a computably overt set
![]() $\mathcal {A}$
containing
$\mathcal {A}$
containing
![]() $\phi (K)$
, in which the set of
$\phi (K)$
, in which the set of
![]() $\epsilon $
-deformations of
$\epsilon $
-deformations of
![]() $\phi (K)$
is dense. By Lemma 6.3,
$\phi (K)$
is dense. By Lemma 6.3,
![]() $F_{M,A}$
intersects
$F_{M,A}$
intersects
![]() $\mathcal {A}$
. As
$\mathcal {A}$
. As
![]() $F_{M,A}$
is open, there exists an
$F_{M,A}$
is open, there exists an
![]() $\epsilon $
-deformation of
$\epsilon $
-deformation of
![]() $\phi (K)$
in
$\phi (K)$
in
![]() $F_{M,A}$
. Let f be the corresponding
$F_{M,A}$
. Let f be the corresponding
![]() $\epsilon $
-perturbation, and
$\epsilon $
-perturbation, and
![]() $\psi =f\circ \phi $
. One has
$\psi =f\circ \phi $
. One has
![]() $\rho (\psi ,\phi )<\epsilon $
and
$\rho (\psi ,\phi )<\epsilon $
and
![]() $\psi (K)\in F_{M,A}$
.
$\psi (K)\in F_{M,A}$
.
7 Comparing compact and Polish presentations
Let X be a compact Polish space. In the proofs we frequently used the fact that the jump of any Polish presentation of X computes a compact presentation of X, which is stated precisely in Lemma 2.1. Here we investigate whether it can compute more. Of course, it always computes
![]() $\mathbf {0}'$
, and we show that if X is perfect, then it does not compute more in general: every compact presentation of X, paired with
$\mathbf {0}'$
, and we show that if X is perfect, then it does not compute more in general: every compact presentation of X, paired with
![]() $\mathbf {0}'$
, computes the jump of a Polish presentation of X. However, we will see after that it is no more true for non-perfect spaces and we give a counter-example.
$\mathbf {0}'$
, computes the jump of a Polish presentation of X. However, we will see after that it is no more true for non-perfect spaces and we give a counter-example.
Theorem 7.1. Let X be a compact perfect Polish space. If X has a
![]() ${\mathbf {d}}$
-computable compact presentation, then there exists
${\mathbf {d}}$
-computable compact presentation, then there exists
![]() $\mathbf {e}$
such that X has an
$\mathbf {e}$
such that X has an
![]() $\mathbf {e}$
-computable Polish presentation and
$\mathbf {e}$
-computable Polish presentation and
![]() $\mathbf {e}'\leq {\mathbf {d}}\oplus \mathbf {0}'$
.
$\mathbf {e}'\leq {\mathbf {d}}\oplus \mathbf {0}'$
.
Corollary 7.2. Let X be a compact perfect Polish space. One has
Proof If
![]() $\mathbf {e}\in \mathrm {Sp}(X)$
, then let
$\mathbf {e}\in \mathrm {Sp}(X)$
, then let
![]() ${\mathbf {d}}=\mathbf {e}'$
. One has
${\mathbf {d}}=\mathbf {e}'$
. One has
![]() ${\mathbf {d}}\in \mathrm {Sp}_c(X)$
by Lemma 2.1, and
${\mathbf {d}}\in \mathrm {Sp}_c(X)$
by Lemma 2.1, and
![]() $\mathbf {e}'={\mathbf {d}}\oplus \mathbf {0}'$
.
$\mathbf {e}'={\mathbf {d}}\oplus \mathbf {0}'$
.
If
![]() ${\mathbf {d}}\in \mathrm {Sp}_c(X)$
, then there exists
${\mathbf {d}}\in \mathrm {Sp}_c(X)$
, then there exists
![]() $\mathbf {e}_0\in \mathrm {Sp}(X)$
such that
$\mathbf {e}_0\in \mathrm {Sp}(X)$
such that
![]() $\mathbf {e}_0'\leq {\mathbf {d}}\oplus \mathbf {0}'$
by Theorem 7.1. Friedberg’s jump inversion theorem relative to
$\mathbf {e}_0'\leq {\mathbf {d}}\oplus \mathbf {0}'$
by Theorem 7.1. Friedberg’s jump inversion theorem relative to
![]() $\mathbf {e}_0$
states that if
$\mathbf {e}_0$
states that if
![]() $\mathbf {a}\geq \mathbf {e}_0'$
, then there exists
$\mathbf {a}\geq \mathbf {e}_0'$
, then there exists
![]() $\mathbf {f}$
such that
$\mathbf {f}$
such that
![]() $\mathbf {a}=(\mathbf {e}_0\oplus \mathbf {f})'$
. We apply it to
$\mathbf {a}=(\mathbf {e}_0\oplus \mathbf {f})'$
. We apply it to
![]() $\mathbf {a}={\mathbf {d}}\oplus \mathbf {0}'$
, and let
$\mathbf {a}={\mathbf {d}}\oplus \mathbf {0}'$
, and let
![]() $\mathbf {e}=\mathbf {e}_0\oplus \mathbf {f}$
. One has
$\mathbf {e}=\mathbf {e}_0\oplus \mathbf {f}$
. One has
![]() ${\mathbf {d}} \oplus \mathbf {0}'=\mathbf {e}'$
and
${\mathbf {d}} \oplus \mathbf {0}'=\mathbf {e}'$
and
![]() $\mathbf {e}\in \mathrm {Sp}(X)$
as
$\mathbf {e}\in \mathrm {Sp}(X)$
as
![]() $\mathbf {e}\geq \mathbf {e}_0\in \mathrm {Sp}(X)$
.
$\mathbf {e}\geq \mathbf {e}_0\in \mathrm {Sp}(X)$
.
7.1 Reformulation
Again, we use an overtness argument to reformulate the problem.
As we have already seen, the degrees of Polish presentations of X coincide with the degrees of copies of X as elements of
![]() $\mathcal {V}(Q)$
. In the same way, we show that the jumps of these degrees are exactly the jumps of the copies of X in
$\mathcal {V}(Q)$
. In the same way, we show that the jumps of these degrees are exactly the jumps of the copies of X in
![]() $\mathcal {V}(Q)$
.
$\mathcal {V}(Q)$
.
Again, we abstract away from
![]() $\mathcal {V}(Q)$
to make the results easier to read. Let S be a countably based space with a fixed index basis
$\mathcal {V}(Q)$
to make the results easier to read. Let S be a countably based space with a fixed index basis
![]() $(B_i)_{i\in \mathbb {N}}$
that is closed under finite intersections. Let
$(B_i)_{i\in \mathbb {N}}$
that is closed under finite intersections. Let
![]() $(U_i)_{i\in \mathbb {N}}$
be the canonical enumeration of the effective open subsets of S defined by
$(U_i)_{i\in \mathbb {N}}$
be the canonical enumeration of the effective open subsets of S defined by
![]() $U_i=\bigcup _{j\in W_i}B_j$
, where
$U_i=\bigcup _{j\in W_i}B_j$
, where
![]() $W_i$
is the ith c.e. subset of
$W_i$
is the ith c.e. subset of
![]() $\mathbb {N}$
. We will apply the next result to
$\mathbb {N}$
. We will apply the next result to
![]() $S=\mathcal {V}(Q)$
.
$S=\mathcal {V}(Q)$
.
Definition 7.3. The jump of
![]() $x\in S$
is the set
$x\in S$
is the set
![]() $J(x)=\{i\in \mathbb {N}:x\in U_i\}$
.
$J(x)=\{i\in \mathbb {N}:x\in U_i\}$
.
Lemma 7.4. If x is a point of an effective countably based space S, the Turing degree of
![]() $J(x)$
is the least element of
$J(x)$
is the least element of
![]() $\{{\mathbf {d}}':{\mathbf {d}}\text { computes }x\}$
.
$\{{\mathbf {d}}':{\mathbf {d}}\text { computes }x\}$
.
Proof Let
![]() $\delta _S:\subseteq \mathbb {N}^{\mathbb {N}}\to S$
be the standard representation of S, mapping p to x if
$\delta _S:\subseteq \mathbb {N}^{\mathbb {N}}\to S$
be the standard representation of S, mapping p to x if
![]() $\{i:\exists n,p(n)=i+1\}=\{i:x\in B_i\}$
, in which case we say that p is a name of x. The function
$\{i:\exists n,p(n)=i+1\}=\{i:x\in B_i\}$
, in which case we say that p is a name of x. The function
![]() $\delta _S$
is computable and effectively open: the image of an effective open set is an effective open set, uniformly. Observe that
$\delta _S$
is computable and effectively open: the image of an effective open set is an effective open set, uniformly. Observe that
![]() ${\mathbf {d}}$
computes x if and only if
${\mathbf {d}}$
computes x if and only if
![]() ${\mathbf {d}}$
computes some name of x.
${\mathbf {d}}$
computes some name of x.
As
![]() $\delta _S$
is computable, the preimages of effective open sets are effectively open, so if p is a name of x, then
$\delta _S$
is computable, the preimages of effective open sets are effectively open, so if p is a name of x, then
![]() $p'$
computes
$p'$
computes
![]() $J(x)$
.
$J(x)$
.
Conversely, we show that
![]() $J(x)$
computes
$J(x)$
computes
![]() $p'$
for some name p of x. Let
$p'$
for some name p of x. Let
![]() $(U_n)_{n\in \mathbb {N}}$
be the canonical enumeration of the effective open subsets of
$(U_n)_{n\in \mathbb {N}}$
be the canonical enumeration of the effective open subsets of
![]() $\mathbb {N}^{\mathbb {N}}$
. The set
$\mathbb {N}^{\mathbb {N}}$
. The set
![]() $\delta _S^{-1}(x)$
is
$\delta _S^{-1}(x)$
is
![]() $\Pi ^0_2$
relative to
$\Pi ^0_2$
relative to
![]() $J(x)$
: indeed, one has
$J(x)$
: indeed, one has
![]() $p\in \delta _S^{-1}(x)$
iff
$p\in \delta _S^{-1}(x)$
iff
![]() $\forall i,[x\in B_i\iff \exists n,p(n)=i+1]$
, which is a
$\forall i,[x\in B_i\iff \exists n,p(n)=i+1]$
, which is a
![]() $\Pi ^0_2$
formula relative to
$\Pi ^0_2$
formula relative to
![]() $J(x)$
. Let then
$J(x)$
. Let then
![]() $V_n$
be uniformly
$V_n$
be uniformly
![]() $J(x)$
-effective open sets such that
$J(x)$
-effective open sets such that
![]() $\delta _S^{-1}(x)=\bigcap _nV_n$
. Moreover, if
$\delta _S^{-1}(x)=\bigcap _nV_n$
. Moreover, if
![]() $W\subseteq \mathbb {N}^{\mathbb {N}}$
is an effective open set, given by an index, then we can decide using
$W\subseteq \mathbb {N}^{\mathbb {N}}$
is an effective open set, given by an index, then we can decide using
![]() $J(x)$
whether W intersects
$J(x)$
whether W intersects
![]() $\delta _S^{-1}(x)$
, because it is equivalent to
$\delta _S^{-1}(x)$
, because it is equivalent to
![]() $x\in \delta _S(W)$
, which is an effective open set for which we have an index.
$x\in \delta _S(W)$
, which is an effective open set for which we have an index.
At stage s, we have produced a finite prefix
![]() $p_s$
of p, such that
$p_s$
of p, such that
![]() $[p_s]$
is contained in
$[p_s]$
is contained in
![]() $V_{s-1}$
and intersects
$V_{s-1}$
and intersects
![]() $\delta ^{-1}_S(x)$
. Using
$\delta ^{-1}_S(x)$
. Using
![]() $J(x)$
, we can decide whether
$J(x)$
, we can decide whether
![]() $[p_s]\cap U_s$
intersects
$[p_s]\cap U_s$
intersects
![]() $\delta _S^{-1}(x)$
. If it does, then we extend
$\delta _S^{-1}(x)$
. If it does, then we extend
![]() $p_s$
to
$p_s$
to
![]() $p_{s+1}$
so that
$p_{s+1}$
so that
![]() $[p_{s+1}]$
is contained in
$[p_{s+1}]$
is contained in
![]() $U_s\cap V_s$
and intersects
$U_s\cap V_s$
and intersects
![]() $\delta _S^{-1}(x)$
, and we declare that
$\delta _S^{-1}(x)$
, and we declare that
![]() $p\in U_s$
. If it does not, then we simply extend
$p\in U_s$
. If it does not, then we simply extend
![]() $p_s$
to
$p_s$
to
![]() $p_{s+1}$
so that
$p_{s+1}$
so that
![]() $[p_{s+1}]$
is contained in
$[p_{s+1}]$
is contained in
![]() $V_s$
and intersects
$V_s$
and intersects
![]() $\delta _S^{-1}(x)$
, and we declare that
$\delta _S^{-1}(x)$
, and we declare that
![]() $p\notin U_s$
.
$p\notin U_s$
.
In the limit, we obtain some
![]() $p\in \bigcap _s V_s$
, so p is a name of x. For each s, we have decided along the construction whether
$p\in \bigcap _s V_s$
, so p is a name of x. For each s, we have decided along the construction whether
![]() $p\in U_s$
, so we have computed
$p\in U_s$
, so we have computed
![]() $p'$
.
$p'$
.
Proof of Theorem 7.1
Let
![]() $X\in \mathcal {K}(Q)$
be
$X\in \mathcal {K}(Q)$
be
![]() ${\mathbf {d}}$
-computably compact and perfect. Using
${\mathbf {d}}$
-computably compact and perfect. Using
![]() ${\mathbf {d}}$
and
${\mathbf {d}}$
and
![]() $\mathbf {0}'$
as oracles, we progressively compute a copy K of X, together with its jump
$\mathbf {0}'$
as oracles, we progressively compute a copy K of X, together with its jump
![]() $J(K)$
, seeing K as a point of
$J(K)$
, seeing K as a point of
![]() $\mathcal {V}(Q)$
. Let
$\mathcal {V}(Q)$
. Let
![]() $(\mathcal {U}_n)_{n\in \mathbb {N}}$
be an effective enumeration of the effective open subsets of
$(\mathcal {U}_n)_{n\in \mathbb {N}}$
be an effective enumeration of the effective open subsets of
![]() $\mathcal {V}(Q)$
. For each n, we need to decide as long as we build K, whether
$\mathcal {V}(Q)$
. For each n, we need to decide as long as we build K, whether
![]() $K\in \mathcal {U}_n$
.
$K\in \mathcal {U}_n$
.
We start from some
![]() $\epsilon _0>0$
and some basic
$\epsilon _0>0$
and some basic
![]() $\epsilon _0/2$
-ball
$\epsilon _0/2$
-ball
![]() $\mathcal {B}_0$
in the Hausdorff metric, containing X.
$\mathcal {B}_0$
in the Hausdorff metric, containing X.
![]() $\mathcal {B}_0$
is a computably overt set in
$\mathcal {B}_0$
is a computably overt set in
![]() $\mathcal {V}(Q)$
, so we can decide using
$\mathcal {V}(Q)$
, so we can decide using
![]() $\mathbf {0}'$
whether it intersects
$\mathbf {0}'$
whether it intersects
![]() $\kern1pt\mathcal {U}_0$
. There are two cases:
$\kern1pt\mathcal {U}_0$
. There are two cases:
-
(1) Assume that
 $\mathcal {B}_0$
intersects
$\mathcal {B}_0$
intersects
 $\kern1pt\mathcal {U}_0$
. As in Lemma 6.6 there exists an
$\kern1pt\mathcal {U}_0$
. As in Lemma 6.6 there exists an
 $\epsilon _0$
-perturbation
$\epsilon _0$
-perturbation
 $f_0$
mapping X to
$f_0$
mapping X to
 $X_0\in \mathcal {U}_0$
(as X is perfect, the computably overt set given by Lemma 6.6 can be replaced by the
$X_0\in \mathcal {U}_0$
(as X is perfect, the computably overt set given by Lemma 6.6 can be replaced by the
 $\epsilon _0/2$
-ball
$\epsilon _0/2$
-ball
 $\mathcal {B}_0$
).
$\mathcal {B}_0$
).We now show that one can compute such an
 $f_0$
. The space
$f_0$
. The space
 $\mathcal {P}_{\epsilon _0}$
of
$\mathcal {P}_{\epsilon _0}$
of
 $\epsilon _0$
-perturbations is a computable Polish space, the function
$\epsilon _0$
-perturbations is a computable Polish space, the function
 $\Phi :\mathcal {P}_{\epsilon _0}\to \mathcal {V}(Q)$
mapping f to
$\Phi :\mathcal {P}_{\epsilon _0}\to \mathcal {V}(Q)$
mapping f to
 $f(X)$
is
$f(X)$
is
 ${\mathbf {d}}$
-computable, so
${\mathbf {d}}$
-computable, so
 $\Phi ^{-1}(\mathcal {U}_0)$
is a
$\Phi ^{-1}(\mathcal {U}_0)$
is a
 ${\mathbf {d}}$
-effective open set; therefore, one can
${\mathbf {d}}$
-effective open set; therefore, one can
 ${\mathbf {d}}$
-computably find some
${\mathbf {d}}$
-computably find some
 $f_0$
there.
$f_0$
there.We now pick a ball
 $\mathcal {B}_1$
of some radius
$\mathcal {B}_1$
of some radius
 $\epsilon _1$
(to be chosen, see below) around
$\epsilon _1$
(to be chosen, see below) around
 $X_0$
, whose closure is contained in
$X_0$
, whose closure is contained in
 $\mathcal {B}_0\cap \mathcal {U}_0$
and in which we are going to stay forever, so that in the limit, the copy K of X belongs to
$\mathcal {B}_0\cap \mathcal {U}_0$
and in which we are going to stay forever, so that in the limit, the copy K of X belongs to
 $\kern1pt\mathcal {U}_0$
. We declare that
$\kern1pt\mathcal {U}_0$
. We declare that
 $K\in \mathcal {U}_0$
.
$K\in \mathcal {U}_0$
. -
(2) Now assume that
 $\mathcal {B}_0$
does not intersect
$\mathcal {B}_0$
does not intersect
 $\kern1pt\mathcal {U}_0$
. We do nothing and proceed by picking a ball
$\kern1pt\mathcal {U}_0$
. We do nothing and proceed by picking a ball
 $\mathcal {B}_1$
of some radius
$\mathcal {B}_1$
of some radius
 $\epsilon _1$
around X whose closure is contained in
$\epsilon _1$
around X whose closure is contained in
 $\mathcal {B}_0$
. In the sequel, we stay forever in this ball, so in the limit,
$\mathcal {B}_0$
. In the sequel, we stay forever in this ball, so in the limit,
 $K\in \mathcal {B}_0$
; hence, K does not belong to
$K\in \mathcal {B}_0$
; hence, K does not belong to
 $\kern1pt\mathcal {U}_0$
. We declare that
$\kern1pt\mathcal {U}_0$
. We declare that
 $K\notin \mathcal {U}_0$
.
$K\notin \mathcal {U}_0$
.
In both cases, we have decided whether the set K belongs to
![]() $\kern1pt\mathcal {U}_0$
. We now iterate this process with
$\kern1pt\mathcal {U}_0$
. We now iterate this process with
![]() $\kern1pt\mathcal {U}_1,\mathcal {U}_2$
, etc., choosing
$\kern1pt\mathcal {U}_1,\mathcal {U}_2$
, etc., choosing
![]() $\epsilon _1,\epsilon _2,\ldots $
smaller and smaller so that the composition of the
$\epsilon _1,\epsilon _2,\ldots $
smaller and smaller so that the composition of the
![]() $\epsilon _i$
-perturbations converges to an injective function (the Inductive Convergence Criterion [Reference van Mill33, Theorem 1.6.2] tells us that we can always choose the next
$\epsilon _i$
-perturbations converges to an injective function (the Inductive Convergence Criterion [Reference van Mill33, Theorem 1.6.2] tells us that we can always choose the next
![]() $\epsilon _i$
sufficiently small to ensure that the limit is a injective, and moreover
$\epsilon _i$
sufficiently small to ensure that the limit is a injective, and moreover
![]() $\epsilon _i$
can be chosen in a computable way), and taking the closure of
$\epsilon _i$
can be chosen in a computable way), and taking the closure of
![]() $\mathcal {B}_{n+1}$
contained in
$\mathcal {B}_{n+1}$
contained in
![]() $\mathcal {B}_n$
. In the limit, we have built a copy K of X and computed its jump, using
$\mathcal {B}_n$
. In the limit, we have built a copy K of X and computed its jump, using
![]() ${\mathbf {d}}$
and
${\mathbf {d}}$
and
![]() $\mathbf {0}'$
as oracles.
$\mathbf {0}'$
as oracles.
The argument is uniform: there is a uniform procedure relative to
![]() $\mathbf {0}'$
that, given a compact presentation of any compact perfect Polish space
$\mathbf {0}'$
that, given a compact presentation of any compact perfect Polish space
![]() $\mathcal {X}$
, computes the jump of some Polish presentation of
$\mathcal {X}$
, computes the jump of some Polish presentation of
![]() $\mathcal {X}$
. We now observe that there cannot exist a uniform argument including non-perfect Polish spaces. Indeed, whether X is not perfect is
$\mathcal {X}$
. We now observe that there cannot exist a uniform argument including non-perfect Polish spaces. Indeed, whether X is not perfect is
![]() $\Sigma ^0_2$
for a Polish presentation, so it is
$\Sigma ^0_2$
for a Polish presentation, so it is
![]() $\Sigma ^0_1$
in its jump. If there was a uniform argument relative
$\Sigma ^0_1$
in its jump. If there was a uniform argument relative
![]() $\mathbf {0}'$
, then being non-perfect would be
$\mathbf {0}'$
, then being non-perfect would be
![]() $\Sigma ^0_1(\mathbf {0}')$
for compact presentations, in particular it would be open in
$\Sigma ^0_1(\mathbf {0}')$
for compact presentations, in particular it would be open in
![]() $\mathcal {K}(Q)$
endowed with the Hausdorff metric. However, the set of non-perfect compact sets is not open, as witnessed for instance by a sequence of segments shrinking to a singleton.
$\mathcal {K}(Q)$
endowed with the Hausdorff metric. However, the set of non-perfect compact sets is not open, as witnessed for instance by a sequence of segments shrinking to a singleton.
We actually show that Theorem 7.1 simply does not extend to non-perfect Polish spaces. Observe that a consequence of Theorem 7.1 is that if X is a perfect Polish space with a
![]() $\mathbf {0}'$
-computable compact presentation, then it has a low Polish presentation. We show that it fails for some non-perfect Polish space.
$\mathbf {0}'$
-computable compact presentation, then it has a low Polish presentation. We show that it fails for some non-perfect Polish space.
Proposition 7.5. There exists a
![]() $($
non-perfect
$($
non-perfect
![]() $)$
compact Polish space
$)$
compact Polish space
![]() $\mathcal {X}$
with a
$\mathcal {X}$
with a
![]() $\mathbf {0}'$
-computable compact presentation, but no low Polish presentation.
$\mathbf {0}'$
-computable compact presentation, but no low Polish presentation.
Proof By Theorem 3.6 applied to
![]() ${\mathbf {d}}=\mathbf {0}'$
, there is a space
${\mathbf {d}}=\mathbf {0}'$
, there is a space
![]() $\mathcal {X}$
having a
$\mathcal {X}$
having a
![]() $\mathbf {0}'$
-computable compact presentation, but such that its Cantor–Bendixson derivative
$\mathbf {0}'$
-computable compact presentation, but such that its Cantor–Bendixson derivative
![]() $\mathcal {X}'$
does not have a
$\mathcal {X}'$
does not have a
![]() $\mathbf {0}"$
-computable compact presentation. If
$\mathbf {0}"$
-computable compact presentation. If
![]() $\mathcal {X}$
had a low Polish presentation, then by Lemma 3.1,
$\mathcal {X}$
had a low Polish presentation, then by Lemma 3.1,
![]() $\mathcal {X}'$
would have a
$\mathcal {X}'$
would have a
![]() $\mathbf {0}"$
-computable compact presentation.
$\mathbf {0}"$
-computable compact presentation.
Therefore, for
![]() ${\mathbf {d}}=\mathbf {0}'$
, this space
${\mathbf {d}}=\mathbf {0}'$
, this space
![]() $\mathcal {X}$
has a
$\mathcal {X}$
has a
![]() ${\mathbf {d}}$
-computable compact presentation, but there is no
${\mathbf {d}}$
-computable compact presentation, but there is no
![]() $\mathbf {e}$
such that X has an
$\mathbf {e}$
such that X has an
![]() $\mathbf {e}$
-computable Polish presentation and
$\mathbf {e}$
-computable Polish presentation and
![]() $\mathbf {e}'\leq {\mathbf {d}}\oplus\mathbf {0}'=\mathbf {0}'$
.
$\mathbf {e}'\leq {\mathbf {d}}\oplus\mathbf {0}'=\mathbf {0}'$
.
Funding
This work benefited of Inria’s program Chercheur Invité. Kihara’s research was partially supported by JSPS KAKENHI Grant 19K03602, 15H03634, and the JSPS Core-to-Core Program (A. Advanced Research Networks). Selivanov’s contributions to most of the results of this paper, in particular to those in Section 3, were supported by the Russian Science Foundation, project 19-71-30002.