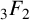OHNO–ZAGIER TYPE RELATIONS FOR MULTIPLE t-VALUES

Abstract

We study Ohno–Zagier type relations for multiple t-values and multiple t-star values. We represent the generating function of sums of multiple t-(star) values with fixed weight, depth and height in terms of the generalised hypergeometric function $\,_3F_2$ . As applications, we get a formula for the generating function of sums of multiple t-(star) values of maximal height and a weighted sum formula for sums of multiple t-(star) values with fixed weight and depth.

1 Introduction

A finite sequence $\mathbf {k}=(k_1,\ldots ,k_n)$ of positive integers is called an index. The weight, depth and height of the index $\mathbf {k}$ are defined respectively by $k_1{\kern-1.5pt}+\cdots +k_n$ , n and the cardinality $|\{\,j\mid 1\leq j\leq n, k_j\geq 2\}|$ . If $k_1>1$ , the index $\mathbf {k}$ is called admissible. For an admissible index $\mathbf {k}=(k_1,\ldots ,k_n)$ , the multiple zeta value $\zeta (\mathbf {k})$ and the multiple zeta-star value $\zeta ^{\star }(\mathbf {k})$ are defined respectively by

$$ \begin{align*} \zeta(\mathbf{k})=\zeta(k_1,\ldots,k_n) & =\sum\limits_{m_1>\cdots>m_n>0}\frac{1}{m_1^{k_1}\cdots m_n^{k_n}},\\ \zeta^{\star}(\mathbf{k})=\zeta^{\star}(k_1,\ldots,k_n) & =\sum\limits_{m_1\geq\cdots\geq m_n>0}\frac{1}{m_1^{k_1}\cdots m_n^{k_n}}. \end{align*} $$

A systematic study of multiple zeta values was carried out by Hoffman [2] and Zagier [10]. More results of multiple zeta values can be found in the book [11] of Zhao.

We focus on Ohno–Zagier type relations. For nonnegative integers $k,n,s$ , denote by $I_0(k,n,s)$ the set of admissible indices of weight k, depth n and height s. It is easy to see that $I_0(k,n,s)$ is nonempty if and only if $k\geq n+s$ and $n\geq s\geq 1$ . Using the Gaussian hypergeometric function, Ohno and Zagier proved in [7] that

$$ \begin{align*} \sum\limits_{k\geq n+s,n\geq s\geq 1} & \bigg(\sum\limits_{\mathbf{k}\in I_0(k,n,s)}\zeta(\mathbf{k})\bigg)\,u^{k-n-s}v^{n-s}w^{s-1}\\ &=\frac{1}{uv-w}\bigg\{1-\exp\bigg(\sum\limits_{n=2}^\infty\frac{\zeta(n)}{n}(u^n+v^n-\alpha^n-\beta^n)\bigg)\bigg\}, \end{align*} $$

where $\alpha $ and $\beta $ are determined by $\alpha +\beta =u+v$ and $\alpha \beta =w$ . Similar studies were carried out on various generalisations of multiple zeta values. For example, Aoki et al. [1] gave a similar formula for the sums of multiple zeta-star values involving the generalised hypergeometric function ${}_3F_2$ :

$$ \begin{align*} \sum\limits_{k\geq n+s,n\geq s\geq 1} & \bigg(\sum\limits_{\mathbf{k}\in I_0(k,n,s)}\zeta^{\star}(\mathbf{k})\bigg)\,u^{k-n-s}v^{n-s}w^{2s-2}\\ &=\frac{1}{(1-v)(1-\beta)}\,_3F_2\bigg({1-\beta,1-\beta+u,1\atop 2-v,2-\beta};1\bigg) \end{align*} $$

with $\alpha $ and $\beta $ determined by $\alpha +\beta =u+v$ and $\alpha \beta =uv-w^2$ . Here, for a positive integer m and complex numbers $a_1,\ldots ,a_{m+1},b_1,\ldots ,b_m$ with $b_1,\ldots ,b_m\neq 0,-1,-2,\ldots ,$ the generalised hypergeometric function ${}_{m+1}F_m$ is defined by

$$ \begin{align*} \,_{m+1}F_m\bigg({a_1,\ldots,a_{m+1}\atop b_1,\ldots,b_m};z\bigg)=&\sum\limits_{n=0}^\infty\frac{(a_1)_n\cdots(a_{m+1})_n}{n!(b_1)_n\cdots(b_m)_n}z^n, \end{align*} $$

with the Pochhammer symbol $(a)_n$ defined by

$$ \begin{align*}(a)_n=\frac{\Gamma(a+n)}{\Gamma(a)}=\begin{cases} 1 & \text{if } n=0,\\ a(a+1)\cdots (a+n-1) & \text{if } n>0. \end{cases}\end{align*} $$

It is known that this formal power series converges absolutely for $|z|<1$ , and it also converges absolutely for $|z|=1$ if $\Re (\sum b_i-\sum a_i)>0$ . If $m=1$ , we get the Gaussian hypergeometric function.

In [9], Takeyama studied the Ohno–Zagier type relation for a level two variant of multiple zeta values, called multiple T-values, introduced by Kaneko and Tsumura [6]. As a consequence, a weighted sum formula of multiple T-values with fixed weight and depth was given in [9]. We consider another level two variant of multiple zeta values, called multiple t-values, introduced by Hoffman in [3].

For an admissible index $\mathbf {k}=(k_1,\ldots ,k_n)$ , the multiple t-value $t(\mathbf {k})$ and the multiple t-star value $t^{\star }(\mathbf {k})$ are defined respectively by

$$ \begin{align*} t(\mathbf{k})=t(k_1,\ldots,k_n) & =\sum\limits_{\substack{m_1>\cdots>m_n>0\\ m_i\,\text{odd}}}\frac{1}{m_1^{k_1}\cdots m_n^{k_n}},\\ t^{\star}(\mathbf{k})=t^{\star}(k_1,\ldots,k_n) & =\sum\limits_{\substack{m_1\geq \cdots\geq m_n>0\\ m_i\,\text{odd}}}\frac{1}{m_1^{k_1}\cdots m_n^{k_n}}. \end{align*} $$

It is easy to obtain the following iterated integral representations:

$$ \begin{align*} t(\mathbf{k}) & =\int_0^1\bigg(\frac{dt}{t}\bigg)^{k_1-1}\frac{t\,dt}{1-t^2}\cdots \bigg(\frac{dt}{t}\bigg)^{k_{n-1}-1}\frac{t\,dt}{1-t^2}\bigg(\frac{dt}{t}\bigg)^{k_n-1}\frac{dt}{1-t^2},\\ t^{\star}(\mathbf{k}) & =\int_0^1\bigg(\frac{dt}{t}\bigg)^{k_1-1}\frac{dt}{t(1-t^2)}\cdots\bigg(\frac{dt}{t}\bigg)^{k_{n-1}-1}\frac{dt}{t(1-t^2)}\bigg(\frac{dt}{t}\bigg)^{k_n-1}\frac{dt}{1-t^2}, \end{align*} $$

where $({dt}/{t})^{k_i-1}={{dt}/{t}\cdots {dt}/{t}}\ (k_i-1 \mbox { factors})$ , and for one-forms $\omega _i(t)=f_i(t)dt$ , $i=1,2,\ldots ,k$ , we define the iterated integral

$$ \begin{align*}\int_0^z\omega_1(t)\cdots\omega_k(t)=\int_{z>t_1>\cdots>t_k>0}f_1(t_1)\cdots f_k(t_k)\,dt_1\cdots dt_k.\end{align*} $$

We want to study the sum of multiple t-(star) values with fixed weight, depth and height. For nonnegative integers $k,n,s$ , define

$$ \begin{align*}G_0(k,n,s)=\sum\limits_{\mathbf{k}\in I_0(k,n,s)}t(\mathbf{k}),\quad G_0^{\star}(k,n,s)=\sum\limits_{\mathbf{k}\in I_0(k,n,s)}t^{\star}(\mathbf{k}).\end{align*} $$

Then we obtain Ohno–Zagier type relations which represent the generating functions of $G_0(k,n,s)$ and $G_0^{\star }(k,n,s)$ by the generalised hypergeometric function ${}_3F_2$ .

Theorem 1.1. For formal variables $u,v,w$ ,

$$ \begin{align*}\sum\limits_{k\geq n+s,n\geq s\geq 1}G_0(k,n,s)u^{k-n-s}v^{n-s}w^{s-1}=\frac{1}{1-u}\,_3F_2\bigg({\alpha,\beta,1\atop \frac{3-u}{2},\frac{3}{2}};1\bigg),\end{align*} $$

where $\alpha $ and $\beta $ are determined by $\alpha +\beta {\kern-1pt}={\kern-1pt}1-\frac{1}{2}u+\frac{1}{2}v$ and $\alpha \beta {\kern-1pt}={\kern-1pt}\tfrac 14(1{\kern-1pt}-{\kern-1pt}u+v- uv+w)$ .

Theorem 1.2. For formal variables $u,v,w$ ,

$$ \begin{align*} \sum\limits_{k\geq n+s,n\geq s\geq 1}G_0^{\star}(k,n,s)u^{k-n-s}v^{n-s}w^{s-1}=\frac{1}{1-u-v+uv-w}\,_3F_2 \bigg({\frac{1-u}{2},\frac{1}{2},1\atop \alpha^{\star},\beta^{\star}};1\bigg), \end{align*} $$

where $\alpha ^{\star }$ and $\beta ^{\star }$ are determined by $\alpha ^{\star }+\beta ^{\star }=3-\frac{1}{2}u-\frac{1}{2}v$ and $\alpha \beta =\tfrac 14(9-3u-3v+uv-w)$ .

From these theorems and using summation formulae for $\,_3F_2$ , we obtain several corollaries in Section 2. For example, we give a formula for the generating function of sums of multiple t-(star) values of maximal height and a weighted sum formula of sums of multiple t-(star) values with fixed weight and depth. Finally, we prove Theorems 1.1 and 1.2 in Section 3.

2 Applications

2.1 Sums of height one

To save space, we denote a sequence of k repeated n times by $\{k\}^n$ .

Setting $w=0$ in Theorem 1.1,

$$ \begin{align*}\alpha,\beta=\frac{1-u}{2},\frac{1+v}{2}.\end{align*} $$

Hence, we get the following result, which gives the generating function of height one multiple t-values.

Corollary 2.1 [3, Theorem 5.1]

We have

$$ \begin{align*}\sum\limits_{k\geq n+1,n\geq 1}t(k-n+1,\{1\}^{n-1})u^{k-n-1}v^{n-1}=\frac{1}{1-u}\,_3F_2\bigg({\frac{1-u}{2},\frac{1+v}{2},1\atop \frac{3-u}{2},\frac{3}{2}};1\bigg).\end{align*} $$

Similarly, setting $w=0$ in Theorem 1.2,

$$ \begin{align*}\alpha^{\star},\beta^{\star}=\frac{3-u}{2},\frac{3-v}{2}.\end{align*} $$

Therefore, we obtain the generating function of height one multiple t-star values.

Corollary 2.2. We have

$$ \begin{align*}\sum\limits_{k\geq n+1,n\geq 1}t^{\star}(k-n+1,\{1\}^{n-1})u^{k-n-1}v^{n-1}=\frac{1}{(1-u)(1-v)}\,_3F_2\bigg({\frac{1-u}{2},\frac{1}{2},1\atop \frac{3-u}{2},\frac{3-v}{2}};1\bigg).\end{align*} $$

Note that using [3, Lemma 5.2], for any integer $m\geq 2$ ,

$$ \begin{align*} \sum\limits_{n=1}^\infty t(m,\{1\}^{n-1})v^{n-1}=\,_{m+1}F_{m}\bigg({\frac{1+v}{2},1,\{\frac{1}{2}\}^{m-1}\atop \{\frac{3}{2}\}^m};1\bigg),\\ \sum\limits_{n=1}^\infty t^{\star}(m,\{1\}^{n-1})v^{n-1}=\frac{1}{1-v}\,_{m+1}F_{m}\bigg({1,\{\frac{1}{2}\}^{m}\atop \frac{3-v}{2},\{\frac{3}{2}\}^{m-1}};1\bigg). \end{align*} $$

2.2 Sums of maximal height

Setting $v=0$ in Theorem 1.1, we get the generating function of sums of multiple t-values of maximal height. By the symmetric sum formula [3, Theorem 3.2], the sum of multiple t-values with fixed weight, depth and maximal height can be represented by t-values. Here we give a closed formula for the generating function of the sums of maximal height.

Corollary 2.3. For formal variables $u,w$ ,

(2.1) $$ \begin{align} 1+\sum\limits_{k\geq 2n,n\geq 1}G_0(k,n,n)u^{k-2n}w^n=\exp\bigg\{\sum\limits_{n=2}^\infty\frac{t(n)}{n}(u^n-x^n-y^n)\bigg\}, \end{align} $$

where x and y are determined by $x+y=u$ and $xy=w$ .

Proof. Setting $v=0$ in Theorem 1.1, we get $\alpha +\beta =1-\frac{1}{2}u$ and $\alpha \beta =\tfrac 14(1-u+w)$ . Let $x=1-2\alpha $ and $y=1-2\beta $ , then $x+y=u$ and $xy=w$ . Using the summation formula [8, 7.4.4.28],

(2.2) $$ \begin{align} \,_3F_2\bigg({a,b,1\atop c,2+a+b-c};1\bigg) =\frac{1+a+b-c}{(1+a-c)(1+b-c)}\bigg(1-c+\frac{\Gamma(c)\Gamma(1+a+b-c)}{\Gamma(a)\Gamma(b)}\bigg). \end{align} $$

With $a=\alpha $ , $b=\beta $ and $c=\tfrac 32$ ,

$$ \begin{align*} \frac{1}{1-u}\,_3F_2\bigg({\alpha,\beta,1\atop \frac{3-u}{2},\frac{3}{2}};1\bigg) &=\frac{1}{1-u}\frac{\frac{1-u}{2}}{(\alpha-\frac{1}{2})(\,\beta-\frac{1}{2})}\bigg(-\frac{1}{2}+\frac{\Gamma(\frac{3}{2})\Gamma(\frac{1-u}{2})}{\Gamma(\alpha)\Gamma(\,\beta)}\bigg)\\ &=-\frac{1}{w}+\frac{\sqrt{\pi}}{w}\frac{\Gamma(\frac{1-u}{2})}{\Gamma(\frac{1-x}{2})\Gamma(\frac{1-y}{2})}. \end{align*} $$

Using the duplication formula

$$ \begin{align*}\Gamma\bigg(\frac{1}{2}-\frac{z}{2}\bigg)=\frac{\sqrt{\pi}2^{z}\Gamma(1-z)}{\Gamma(1-\frac{z}{2})}\end{align*} $$

and the expansion

(2.3) $$ \begin{align} \Gamma(1-z)=\exp\bigg(\gamma z+\sum\limits_{n=2}^\infty\frac{\zeta(n)}{n}z^n\bigg), \end{align} $$

where $\gamma $ is Euler’s constant,

$$ \begin{align*}\Gamma\bigg(\frac{1-z}{2}\bigg)=\sqrt{\pi}2^z\exp\bigg\{\frac{\gamma z}{2}+\sum\limits_{n=2}^\infty \frac{\zeta(n)}{n}(1-2^{-n})z^n\bigg\}.\end{align*} $$

Since $t(n)=(1-2^{-n})\zeta (n)$ , we find that (see also [3, Theorem 3.3])

(2.4) $$ \begin{align} \Gamma\bigg(\frac{1-z}{2}\bigg)=\sqrt{\pi}2^z\exp\bigg\{\frac{\gamma z}{2}+\sum\limits_{n=2}^\infty \frac{t(n)}{n}z^n\bigg\}. \end{align} $$

Now it is easy to finish the proof.

Similarly, we have a formula for the generating function of the sums of multiple t-star values of maximal height.

Corollary 2.4. For formal variables $u,w$ ,

(2.5) $$ \begin{align} 1+\sum\limits_{k\geq 2n,n\geq 1}G_0^{\star}(k,n,n)u^{k-2n}w^n=\exp\bigg\{\sum\limits_{n=2}^\infty\frac{t(n)}{n}((x^\star)^n+(y^{\star})^n-u^n)\bigg\}, \end{align} $$

where $x^{\star }$ and $y^{\star }$ are determined by $x^{\star }+y^{\star }=u$ and $x^{\star }y^{\star }=-w$ .

Proof. Setting $v=0$ in Theorem 1.2, we obtain $\alpha ^{\star }+\beta ^{\star }=3-\frac{1}{2}u$ and $\alpha ^{\star }\beta ^{\star }=\tfrac 14 (9-3u-w)$ . Let $x^{\star }=3-2\alpha ^{\star }$ and $y^{\star }=3-2\beta ^{\star }$ , so that $x^{\star }+y^{\star }=u$ and $x^{\star }y^{\star }=-w$ . Using the summation formula (2.2) with $a=\frac{1}{2}(1-u)$ , $b=\tfrac 12$ and $c=\alpha ^{\star }$ ,

$$ \begin{align*} \frac{1}{1-u-w}\,_3F_2\bigg({\frac{1-u}{2},\frac{1}{2},1\atop \alpha^{\star},\beta^{\star}};1\bigg) &=\frac{1}{1-u-w}\frac{-(\,\beta^{\star}-1)}{(\alpha^{\star}-\frac{3}{2})(\,\beta^{\star}-\frac{3}{2})}\bigg(1-\alpha^{\star}+\frac{\Gamma(\alpha^{\star})\Gamma(\,\beta^{\star}-1)}{\Gamma(\frac{1-u}{2})\Gamma(\frac{1}{2})}\bigg)\\ &=-\frac{1}{w}+\frac{1}{w\sqrt{\pi}}\frac{\Gamma(\frac{1-x^{\star}}{2})\Gamma(\frac{1-y^{\star}}{2})}{\Gamma(\frac{1-u}{2})}. \end{align*} $$

Now the result follows from (2.4).

From (2.1) and (2.5),

$$ \begin{align*}\bigg(1+\sum\limits_{k\geq 2n,n\geq 1}G_0(k,n,n)u^{k-2n}w^n\bigg)\bigg(1+\sum\limits_{k\geq 2n,n\geq 1}(-1)^nG_0^{\star}(k,n,n)u^{k-2n}w^n\bigg)=1.\end{align*} $$

Also, setting $u=0$ in (2.1) and (2.5),

$$ \begin{align*} 1+\sum\limits_{n=1}^{\infty}t(\{2\}^n)w^n & =\exp\bigg\{\sum\limits_{n=1}^\infty\frac{(-1)^{n-1}}{n}t(2n)w^n\bigg\},\\ 1+\sum\limits_{n=1}^{\infty}t^{\star}(\{2\}^n)w^n & =\exp\bigg\{\sum\limits_{n=1}^\infty\frac{1}{n}t(2n)w^n\bigg\}. \end{align*} $$

These formulae can also be deduced from the identities [4, 5]

$$ \begin{align*} \frac{1}{1-z_kw}=\exp_{\ast}\bigg(\sum\limits_{n=1}^\infty \frac{(-1)^{n-1}}{n}z_{nk}w^n\bigg), \quad \bigg(\frac{1}{1+z_kt}\bigg)\ast S\bigg(\frac{1}{1-z_kt}\bigg)=1, \end{align*} $$

in the harmonic shuffle algebra.

2.3 A weighted sum formula

Let $I_0(k,n)$ be the set of admissible indices of weight k and depth n, and define

$$ \begin{align*}G_0(k,n)=\sum\limits_{\mathbf{k}\in I_0(k,n)}t(\mathbf{k}),\quad G_0^{\star}(k,n)=\sum\limits_{\mathbf{k}\in I_0(k,n)}t^{\star}(\mathbf{k}),\end{align*} $$

which are the sums of multiple t-values and multiple t-star values with fixed weight k and depth n, respectively. By setting $w=uv$ and then $v=2u$ or $v=-2u$ in Theorems 1.1 and 1.2, we obtain the following results.

Proposition 2.5. For a formal variable u,

(2.6) $$ \begin{align} \sum\limits_{k=2}^\infty\bigg(\sum\limits_{n=1}^{k-1}2^{n-1}G_0(k,n)\bigg)u^{k-2} & =\sum\limits_{k=2}^\infty\bigg(\sum\limits_{n=1}^{k-1}(-1)^{k-n-1}2^{n-1}G_0^{\star}(k,n)\bigg)u^{k-2}\nonumber\\ & = 2^{2u}t(2)\exp\bigg(\sum\limits_{n=2}^\infty\frac{4(2^{n-1}-1)}{n(2^n-1)}t(n)u^n\bigg). \end{align} $$

Proof. If $w=uv$ in Theorem 1.1,

$$ \begin{align*}\alpha,\beta=\frac{1-u+v}{2},\frac{1}{2}.\end{align*} $$

Hence, we get the expression for the generating function of sums of multiple t-values with fixed weight and depth:

$$ \begin{align*}\sum\limits_{k>n\geq 1}G_0(k,n)u^{k-n-1}v^{n-1}=\frac{1}{1-u}\,_3F_2\bigg({\frac{1-u+v}{2},\frac{1}{2},1\atop \frac{3-u}{2},\frac{3}{2}};1\bigg).\end{align*} $$

Setting $v=2u$ ,

$$ \begin{align*}\sum\limits_{k>n\geq 1}2^{n-1}G_0(k,n)u^{k-2}=\frac{1}{1-u}\,_3F_2\bigg({\frac{1+u}{2},\frac{1}{2},1\atop \frac{3-u}{2},\frac{3}{2}};1\bigg).\end{align*} $$

Using Dixon’s summation formula [8, 7.4.4.21]: for $\Re (a-2b-2c)>-2$ ,

$$ \begin{align*} \,_3F_2\bigg({a,b,c\atop 1+a-b,1+a-c};1\bigg) =\frac{\sqrt{\pi}}{2^a}\frac{\Gamma(1+a-b)\Gamma(1+a-c)\Gamma(1+\frac{a}{2}-b-c)}{\Gamma(\frac{1+a}{2})\Gamma(1+\frac{a}{2}-b)\Gamma(1+\frac{a}{2}-c)\Gamma(1+a-b-c)}, \end{align*} $$

with $a=1$ , $b=\tfrac 12$ and $c=\frac{1}{2}(1+u)$ , we get

$$ \begin{align*} \frac{1}{1-u}\,_3F_2\bigg({\frac{1+u}{2},\frac{1}{2},1\atop \frac{3-u}{2},\frac{3}{2}};1\bigg) =\frac{1}{1-u} \frac{\sqrt{\pi}}{2}\frac{\Gamma(\frac{3}{2})\Gamma(\frac{3-u}{2})\Gamma(\frac{1-u}{2})}{\Gamma(1-\frac{u}{2})\Gamma(1-\frac{u}{2})} =\frac{\pi}{8}\frac{\Gamma(\frac{1-u}{2})^2}{\Gamma(1-\frac{u}{2})^2}. \end{align*} $$

Then using (2.3), (2.4), the relation $\zeta (n)=(1-2^{-n})^{-1}t(n)$ and $t(2)={\pi ^2}/{8}$ , we get

$$ \begin{align*}\sum\limits_{k=2}^\infty\bigg(\sum\limits_{n=1}^{k-1}2^{n-1}G_0(k,n)\bigg)u^{k-2}=2^{2u}t(2)\exp\bigg(\sum\limits_{n=2}^\infty\frac{4(2^{n-1}-1)}{n(2^n-1)}t(n)u^n\bigg).\end{align*} $$

Similarly, setting $w=uv$ in Theorem 1.2,

$$ \begin{align*}\alpha^{\star},\beta^{\star}=\frac{3-u-v}{2},\frac{3}{2}.\end{align*} $$

Hence,

$$ \begin{align*}\sum\limits_{k>n\geq 1}G_0^{\star}(k,n)u^{k-n-1}v^{n-1}=\frac{1}{1-u-v}\,_3F_2\bigg({\frac{1-u}{2},\frac{1}{2},1\atop \frac{3-u-v}{2},\frac{3}{2}};1\bigg).\end{align*} $$

Let $v=-2u$ . Then

$$ \begin{align*}\sum\limits_{k>n\geq 1}(-2)^{n-1}G_0^{\star}(k,n)u^{k-2}=\frac{1}{1+u}\,_3F_2\bigg({\frac{1-u}{2},\frac{1}{2},1\atop \frac{3+u}{2},\frac{3}{2}};1\bigg).\end{align*} $$

Now it is easy to finish the proof.

Expanding the right-hand side of (2.6) gives the following weighted sum formula.

Corollary 2.6. For any integer $k\geq 2$ ,

$$ \begin{align*} \sum\limits_{n=1}^{k-1} & 2^{n-1}G_0(k,n) =\sum\limits_{n=1}^{k-1}(-1)^{k-n-1}2^{n-1}G_0^{\star}(k,n)\\ & =\sum\limits_{\substack{n+n_1+\cdots+n_m=k-2\\ n,m\geq 0,n_1,\ldots,n_m\geq 2}}\frac{2^{n+2m}(2^{n_1-1}-1)\cdots(2^{n_m-1}-1)}{n!m!n_1\cdots n_m(2^{n_1}-1)\cdots(2^{n_m}-1)}t(2)t(n_1)\cdots t(n_m)\log^n 2. \end{align*} $$

3 Proofs of Theorems 1.1 and 1.2

The proofs of Theorems 1.1 and 1.2 are similar to that of the Ohno–Zagier relation for multiple zeta values in [7].

As in [3], for an index $\mathbf {k}=(k_1,\ldots ,k_n)$ , define

$$ \begin{align*} &\mathcal{L}_{\mathbf{k}}(z)=\mathcal{L}_{k_1,\ldots,k_n}(z)=\sum\limits_{\substack{m_1>\cdots>m_n>0\\ m_i\,\text{odd}}}\frac{z^{m_1}}{m_1^{k_1}\cdots m_n^{k_n}},\\ &\mathcal{L}_{\mathbf{k}}^{\star}(z)=\mathcal{L}_{k_1,\ldots,k_n}^{\star}(z)=\sum\limits_{\substack{m_1\geq\cdots\geq m_n>0\\ m_i\,\text{odd}}}\frac{z^{m_1}}{m_1^{k_1}\cdots m_n^{k_n}}. \end{align*} $$

Then $\mathcal {L}_{\mathbf {k}}(z)$ and $\mathcal {L}_{\mathbf {k}}^{\star }(z)$ converge absolutely for $|z|<1$ . If $k_1>1$ , $\mathcal {L}_{\mathbf {k}}(1)=t(\mathbf {k})$ and $\mathcal {L}_{\mathbf {k}}^{\star }(1)=t^{\star }(\mathbf {k})$ . From [3, Lemma 5.1],

(3.1) $$ \begin{align} \frac{d}{dz}\mathcal{L}_{k_1,\ldots,k_n}(z)=\begin{cases} \displaystyle\frac{1}{z}\mathcal{L}_{k_1-1,k_2,\ldots,k_n}(z) & \text{if } k_1>1,\\ \displaystyle\frac{z}{1-z^2}\mathcal{L}_{k_2,\ldots,k_n}(z) & \text{if } n\geq 2, k_1=1,\\ \displaystyle\frac{1}{1-z^2} & \text{if } n=k_1=1. \end{cases} \end{align} $$

Similarly,

(3.2) $$ \begin{align} \frac{d}{dz}\mathcal{L}_{k_1,\ldots,k_n}^{\star}(z)=\begin{cases} \displaystyle\frac{1}{z}\mathcal{L}_{k_1-1,k_2,\ldots,k_n}^{\star}(z) & \text{if } k_1>1,\\ \displaystyle\frac{1}{z(1-z^2)}\mathcal{L}_{k_2,\ldots,k_n}^{\star}(z) & \text{if } n\geq 2, k_1=1,\\ \displaystyle\frac{1}{1-z^2} & \text{if } n=k_1=1. \end{cases} \end{align} $$

One can also obtain (3.1) and (3.2) from the following iterated integral representations:

$$ \begin{align*} &\mathcal{L}_{k_1,\ldots,k_n}(z)=\int_0^z\bigg(\frac{dt}{t}\bigg)^{k_1-1}\frac{t\,dt}{1-t^2}\cdots\bigg(\frac{dt}{t}\bigg)^{k_{n-1}-1}\frac{t\,dt}{1-t^2}\bigg(\frac{dt}{t}\bigg)^{k_n-1}\frac{dt}{1-t^2},\\ &\mathcal{L}_{k_1,\ldots,k_n}^{\star}(z)=\int_0^z\bigg(\frac{dt}{t}\bigg)^{k_1-1}\frac{dt}{t(1-t^2)}\cdots\bigg(\frac{dt}{t}\bigg)^{k_{n-1}-1}\frac{dt}{t(1-t^2)}\bigg(\frac{dt}{t}\bigg)^{k_n-1}\frac{dt}{1-t^2}. \end{align*} $$

3.1 Proof of Theorem 1.1

For nonnegative integers $k,n,s$ , denote by $I(k,n,s)$ the set of indices of weight k, depth n and height s, and define the sums

$$ \begin{align*}G(k,n,s;z)=\sum\limits_{\mathbf{k}\in I(k,n,s)}\mathcal{L}_{\mathbf{k}}(z),\quad G_0(k,n,s;z)=\sum\limits_{\mathbf{k}\in I_0(k,n,s)}\mathcal{L}_{\mathbf{k}}(z).\end{align*} $$

If the index set is empty, the sum is treated as zero. We also set $G(0,0,0;z)=1$ . Note that if $k\geq n+s$ and $n\geq s\geq 1$ ,

$$ \begin{align*}G_0(k,n,s;1)=G_0(k,n,s).\end{align*} $$

For integers $k,n,s$ , using (3.1), we have the following identities:

1. (1) if $k\geq n+s$ and $n\geq s\geq 1$ ,

   (3.3) $$ \begin{align} \frac{d}{dz} & G_0(k,n,s;z) \nonumber\\ & =\frac{1}{z}[G(k-1,n,s-1;z)+G_0(k-1,n,s;z)-G_0(k-1,n,s-1;z)]; \end{align} $$

2. (2) if $k\geq n+s$ , $n\geq s\geq 0$ and $n\geq 2$ ,

   (3.4) $$ \begin{align} \frac{d}{dz}[G(k,n,s;z)-G_0(k,n,s;z)]=\frac{z}{1-z^2}G(k-1,n-1,s;z). \end{align} $$

We define the generating functions

$$ \begin{align*} \Phi(z)&=\Phi(u,v,w;z)=\sum\limits_{k,n,s\geq 0}G(k,n,s;z)u^{k-n-s}v^{n-s}w^{s},\\ &=1+\mathcal{L}_1(z)v+\sum\limits_{k\geq 2}\mathcal{L}_k(z)u^{k-2}w+\sum\limits_{\substack{k\geq n+s\\ n\geq s\geq 0,n\geq 2}}G(k,n,s;z)u^{k-n-s}v^{n-s}w^{s},\\ \Phi_0(z)&=\Phi_0(u,v,w;z)=\sum\limits_{k,n,s\geq 0}G_0(k,n,s;z)u^{k-n-s}v^{n-s}w^{s-1}\\ &=\sum\limits_{\substack{k\geq n+s\\ n\geq s\geq 1}}G_0(k,n,s;z)u^{k-n-s}v^{n-s}w^{s-1}. \end{align*} $$

Using (3.1), (3.3) and (3.4),

$$ \begin{align*} &\frac{d}{dz}\Phi_0(z)=\frac{1}{vz}(\Phi(z)-1-w\Phi_0(z))+\frac{u}{z}\Phi_0(z),\\ &\frac{d}{dz}(\Phi(z)-w\Phi_0(z))=\frac{vz}{1-z^2}\Phi(z)+\frac{v}{1+z}. \end{align*} $$

Eliminating $\Phi (z)$ , we obtain the differential equation satisfied by $\Phi _0(z)$ .

Proposition 3.1. $\Phi _0=\Phi _0(z)$ satisfies the following differential equation:

(3.5) $$ \begin{align} z(1-z^2)\Phi_0"+[(1-u)(1-z^2)-vz^2]\Phi_0'+(uv-w)z\Phi_0=1. \end{align} $$

We want to find the unique power series solution $\Phi _0(z)=\sum _{n=1}^\infty a_nz^n$ . From (3.5), we see that $a_1={1}/({1-u})$ , $a_2=0$ and

$$ \begin{align*}a_{n+1}=\frac{(n-1)(n-2)+(1-u+v)(n-1)-(uv-w)}{(n+1-u)(n+1)}a_{n-1},\quad n\geq 2.\end{align*} $$

Hence, for any $n\geq 1$ , we have $a_{2n}=0$ and

$$ \begin{align*} a_{2n+1}=\frac{(n-\frac{1}{2})(n-1)+(\frac{1}{2}-\frac{u}{2}+\frac{v}{2})(n-\frac{1}{2})-\frac{1}{4}(uv-w)}{(n+\frac{1}{2}-\frac{u}{2})(n+\frac{1}{2})}a_{2n-1}.\end{align*} $$

Since $(\alpha -1)+(\,\beta -1)=-1-\frac{1}{2}u+\frac{1}{2}v$ and $(\alpha -1)(\,\beta -1)=\tfrac 14(1+u-v-uv+w)$ ,

$$ \begin{align*} a_{2n+1}=\frac{(n+\alpha-1)(n+\beta-1)}{(n+\frac{1}{2}-\frac{u}{2})(n+\frac{1}{2})}a_{2n-1}=\frac{(\alpha)_n(\,\beta)_n}{(\frac{3-u}{2})_n(\frac{3}{2})_n}\frac{1}{1-u}. \end{align*} $$

Therefore, we can represent $\Phi _0(z)$ by the generalised hypergeometric function $\,_3F_2$ as displayed in the following theorem.

Theorem 3.2. We have

$$ \begin{align*}\Phi_0(k,n,s;z)=\frac{z}{1-u}\,_3F_2\bigg({\alpha,\beta,1\atop \frac{3-u}{2},\frac{3}{2}};z^2\bigg).\end{align*} $$

Finally, setting $z=1$ in Theorem 3.2, we get Theorem 1.1.

3.2 Proof of Theorem 1.2

Similarly, for nonnegative integers $k,n,s$ , we define the sums

$$ \begin{align*}G^{\star}(k,n,s;z)=\sum\limits_{\mathbf{k}\in I(k,n,s)}\mathcal{L}_{\mathbf{k}}^{\star}(z),\quad G_0^{\star}(k,n,s;z)=\sum\limits_{\mathbf{k}\in I_0(k,n,s)}\mathcal{L}_{\mathbf{k}}^{\star}(z)\end{align*} $$

with $G^{\star }(0,0,0;z)=1$ . Using (3.2), we have the following identities:

1. (1) if $k\geq n+s$ and $n\geq s\geq 1$ ,

   (3.6) $$ \begin{align} &\frac{d}{dz} G_0^{\star}(k,n,s;z)\nonumber\\ &\quad =\frac{1}{z}[G^{\star}(k-1,n,s-1;z)+G_0^{\star}(k-1,n,s;z)-G_0^{\star}(k-1,n,s-1;z)]; \end{align} $$

2. (2) if $k\geq n+s$ , $n\geq s\geq 0$ and $n\geq 2$ ,

   (3.7) $$ \begin{align} \frac{d}{dz}[G^{\star}(k,n,s;z)-G_0^{\star}(k,n,s;z)]=\frac{1}{z(1-z^2)}G^{\star}(k-1,n-1,s;z). \end{align} $$

We define the generating functions

$$ \begin{align*} \Phi^{\star}(z) & =\Phi^{\star}(u,v,w;z)=\sum\limits_{k,n,s\geq 0}G^{\star}(k,n,s;z)u^{k-n-s}v^{n-s}w^{s},\\ \Phi_0^{\star}(z) & =\Phi_0^{\star}(u,v,w;z)=\sum\limits_{k,n,s\geq 0}G_0^{\star}(k,n,s;z)u^{k-n-s}v^{n-s}w^{s-1}. \end{align*} $$

Then using (3.2), (3.6) and (3.7),

$$ \begin{align*} &\frac{d}{dz}\Phi_0^{\star}(z)=\frac{1}{vz}(\Phi^{\star}(z)-1-w\Phi_0^{\star}(z))+\frac{u}{z}\Phi_0^{\star}(z),\\ &\frac{d}{dz}(\Phi^{\star}(z)-w\Phi_0^{\star}(z))=\frac{v}{z(1-z^2)}\Phi^{\star}(z)-\frac{v}{z(1+z)}. \end{align*} $$

Eliminating $\Phi ^{\star }(z)$ , we get the differential equation satisfied by $\Phi _0^{\star }(z)$ .

Proposition 3.3. $\Phi _0^{\star }=\Phi _0^{\star }(z)$ satisfies the following differential equation:

(3.8) $$ \begin{align} z^2(1-z^2)(\Phi_0^{\star})"+[(1-u)z(1-z^2)-vz](\Phi_0^{\star})'+(uv-w)\Phi_0^{\star}=z. \end{align} $$

Assume that $\Phi _0^{\star }(z){\kern-1pt}={\kern-2pt}\sum _{n=1}^\infty{\kern-1pt} a_n^{\star }z^n$ . Using (3.8), we find that $a_1^{\star }{\kern-1pt}={\kern-1pt}{1}/({1{\kern-1pt}-{\kern-1pt}u{\kern-1pt}-{\kern-1pt}v+uv{\kern-1pt}-{\kern-1pt}w})$ , $a_2^{\star }=0$ and

$$ \begin{align*}a_{n}^{\star}=\frac{(n-2)(n-2-u)}{n(n-1)+n(1-u-v)+uv-w}a_{n-2}^{\star},\quad n\geq 3.\end{align*} $$

Hence, for any $n\geq 1$ , we have $a_{2n}^{\star }=0$ and

$$ \begin{align*} a_{2n+1}^{\star}=\frac{(n-\frac{1}{2}-\frac{u}{2})(n-\frac{1}{2})}{(n+\alpha^{\star}-1)(n+\beta^{\star}-1)}a_{2n-1}^{\star}=\frac{(\frac{1-u}{2})_n(\frac{1}{2})_n}{(\alpha^{\star})_n(\,\beta^{\star})_n} \frac{1}{1-u-v+uv-w}.\end{align*} $$

Therefore, we have the following theorem.

Theorem 3.4. We have

$$ \begin{align*}\Phi_0^{\star}(k,n,s;z)=\frac{z}{1-u-v+uv-w}\,_3F_2\bigg({\frac{1-u}{2},\frac{1}{2},1\atop \alpha^{\star},\beta^{\star}};z^2\bigg).\end{align*} $$

Finally, setting $z=1$ in Theorem 3.4, we get Theorem 1.2.