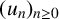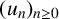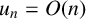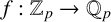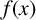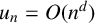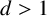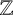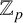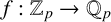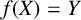1 Introduction
In what follows, p is a prime number,
![]() $\mathbb {Q}_p$
is the field of p-adic numbers and
$\mathbb {Q}_p$
is the field of p-adic numbers and
![]() $\mathbb {Z}_p$
is the ring of p-adic integers. Let
$\mathbb {Z}_p$
is the ring of p-adic integers. Let
![]() $(u_n)_{n\geq 0}$
be a sequence of integers. If there exists a continuous function
$(u_n)_{n\geq 0}$
be a sequence of integers. If there exists a continuous function
![]() $f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
such that
$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
such that
![]() $f(n)=u_n$
for all nonnegative integers n, we say that f is a p-adic interpolation of
$f(n)=u_n$
for all nonnegative integers n, we say that f is a p-adic interpolation of
![]() $(u_n)_{n\geq 0}$
. In addition, if f is analytic, we say that it is a p-adic analytic interpolation of this sequence. Since the set of nonnegative integers is a dense subset of
$(u_n)_{n\geq 0}$
. In addition, if f is analytic, we say that it is a p-adic analytic interpolation of this sequence. Since the set of nonnegative integers is a dense subset of
![]() $\mathbb {Z}_p$
, any given sequence of integers admits at most one such interpolation, which will only exist under certain strong conditions on the sequence (for more details, see [Reference Schikhof17]).
$\mathbb {Z}_p$
, any given sequence of integers admits at most one such interpolation, which will only exist under certain strong conditions on the sequence (for more details, see [Reference Schikhof17]).
Many authors have studied the problem of p-adic interpolation. Bihani et al. [Reference Bihani, Sheppard and Young2] considered the problem of p-adic interpolation of the Fibonacci sequence, they proved that the sequence
![]() $(2^nF_n)_{n\geq 0}$
can be interpolated by a p-adic hypergeometric function on
$(2^nF_n)_{n\geq 0}$
can be interpolated by a p-adic hypergeometric function on
![]() $\mathbb {Z}_5$
. Rowland and Yassawi in [Reference Rowland and Yassawi16] studied p-adic properties of sequences of integers (or p-adic integers) that satisfy a linear recurrence with constant coefficients. For such a sequence, they obtained an explicit approximate twisted interpolation to
$\mathbb {Z}_5$
. Rowland and Yassawi in [Reference Rowland and Yassawi16] studied p-adic properties of sequences of integers (or p-adic integers) that satisfy a linear recurrence with constant coefficients. For such a sequence, they obtained an explicit approximate twisted interpolation to
![]() $\mathbb {Z}_p$
. In particular, they proved that for any prime
$\mathbb {Z}_p$
. In particular, they proved that for any prime
![]() $p\neq 2$
, there is a twisted interpolation of the Fibonacci sequence by a finite family of p-adic analytic functions with coefficients in some finite extension of
$p\neq 2$
, there is a twisted interpolation of the Fibonacci sequence by a finite family of p-adic analytic functions with coefficients in some finite extension of
![]() $\mathbb {Q}_p$
. Inspired by the Skolem–Mahler–Lech theorem on linear recurrent sequences, Bell [Reference Bell1] proved that for a suitable choice of a p-adic analytic function f and a starting point
$\mathbb {Q}_p$
. Inspired by the Skolem–Mahler–Lech theorem on linear recurrent sequences, Bell [Reference Bell1] proved that for a suitable choice of a p-adic analytic function f and a starting point
![]() $\overline {x}$
, the iterate-computing map
$\overline {x}$
, the iterate-computing map
![]() $n\mapsto f^n(\overline {x})$
extends to a p-adic analytic function g defined for all
$n\mapsto f^n(\overline {x})$
extends to a p-adic analytic function g defined for all
![]() $x\in \mathbb {Z}_p$
. That is, the sequence
$x\in \mathbb {Z}_p$
. That is, the sequence
![]() $f^n(\overline {x})$
can be interpolated by the p-adic analytic function g.
$f^n(\overline {x})$
can be interpolated by the p-adic analytic function g.
Mahler [Reference Mahler7] states that the polynomial functions

with
![]() $n\geq 0$
integer, form an orthonormal basis, called the Mahler basis, for the space of p-adic continuous functions
$n\geq 0$
integer, form an orthonormal basis, called the Mahler basis, for the space of p-adic continuous functions
![]() $\mathcal {C}(\mathbb {Z}_p\rightarrow \mathbb {Q}_p)$
. More precisely, he showed that every continuous function
$\mathcal {C}(\mathbb {Z}_p\rightarrow \mathbb {Q}_p)$
. More precisely, he showed that every continuous function
![]() $f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
has a unique uniformly convergent expansion
$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
has a unique uniformly convergent expansion
 $$ \begin{align} f(x)=\sum_{n=0}^{\infty}a_n\binom{x}{n}, \end{align} $$
$$ \begin{align} f(x)=\sum_{n=0}^{\infty}a_n\binom{x}{n}, \end{align} $$
where
![]() $a_n\rightarrow 0$
and
$a_n\rightarrow 0$
and
![]() $\|f\|_{\scriptsize \mbox {sup}}=\max _{n\geq 0}\|a_n\|_p$
. Conversely, every such expansion defines a continuous function. Furthermore, if
$\|f\|_{\scriptsize \mbox {sup}}=\max _{n\geq 0}\|a_n\|_p$
. Conversely, every such expansion defines a continuous function. Furthermore, if
![]() $f\in \mathcal {C}(\mathbb {Z}_p\rightarrow \mathbb {Q}_p)$
has a Mahler expansion given by (1.1), then the Mahler coefficients
$f\in \mathcal {C}(\mathbb {Z}_p\rightarrow \mathbb {Q}_p)$
has a Mahler expansion given by (1.1), then the Mahler coefficients
![]() $a_n$
can be reconstructed from f by the inversion formula
$a_n$
can be reconstructed from f by the inversion formula
 $$ \begin{align} a_n=\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}f(\,j) \quad(n=0,1,2,\ldots). \end{align} $$
$$ \begin{align} a_n=\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}f(\,j) \quad(n=0,1,2,\ldots). \end{align} $$
Using the Mahler expansion (1.1) and the inversion formula (1.2), we conclude that the sequence
![]() $(u_n)_{n\geq 0}$
of integers can be p-adically interpolated if and only if
$(u_n)_{n\geq 0}$
of integers can be p-adically interpolated if and only if
 $$ \begin{align*} \bigg\|\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}u_j\bigg\|_p\rightarrow0\quad\mbox{as}\ n\rightarrow\infty. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}u_j\bigg\|_p\rightarrow0\quad\mbox{as}\ n\rightarrow\infty. \end{align*} $$
We became interested in studying the p-adic analytic interpolation of sequences of integers with polynomial growth while studying a problem about p-adic Liouville numbers. Based on the classic definition of complex Liouville numbers, Clark [Reference Clark3] called a p-adic integer
![]() $\lambda $
a p-adic Liouville number if
$\lambda $
a p-adic Liouville number if
It is easily seen that all p-adic Liouville numbers are transcendental p-adic numbers. Moreover, if
![]() $\lambda $
is a p-adic Liouville number and
$\lambda $
is a p-adic Liouville number and
![]() $a,b$
are integers, with
$a,b$
are integers, with
![]() $a>0$
, then
$a>0$
, then
![]() $a\lambda +b$
is also a p-adic Liouville number.
$a\lambda +b$
is also a p-adic Liouville number.
In his book, Maillet [Reference Maillet10, Ch. III] discusses some arithmetic properties of complex Liouville numbers. One of them states that given a nonconstant rational function f with rational coefficients, if
![]() $\xi $
is a Liouville number, then so is
$\xi $
is a Liouville number, then so is
![]() $f(\xi )$
. Motivated by this fact, Mahler [Reference Mahler9] posed the following question.
$f(\xi )$
. Motivated by this fact, Mahler [Reference Mahler9] posed the following question.
Question 1.1 (Mahler [Reference Mahler9])
Are there transcendental entire functions
![]() $f:\mathbb {C}\rightarrow \mathbb {C}$
such that if
$f:\mathbb {C}\rightarrow \mathbb {C}$
such that if
![]() $\xi $
is any Liouville number, then
$\xi $
is any Liouville number, then
![]() $f(\xi )$
is also a Liouville number?
$f(\xi )$
is also a Liouville number?
He pointed out: ‘The difficulty of this problem lies of course in the fact that the set of all Liouville numbers is nonenumerable.’ We are interested in studying the analogous question for p-adic Liouville numbers.
Question 1.2. Are there p-adic transcendental analytic functions
![]() $f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
such that if
$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
such that if
![]() $\lambda $
is a p-adic Liouville number, then so is
$\lambda $
is a p-adic Liouville number, then so is
![]() $f(\lambda )$
?
$f(\lambda )$
?
It is important to note that the analogue of Maillet’s result is not true for p-adic Liouville numbers. In fact, Lelis and Marques [Reference Lelis and Marques5] proved that the analogue of Maillet’s result is true for a class of p-adic numbers called weak p-adic Liouville numbers, but not for all p-adic Liouville numbers.
Inspired by an argument presented by Marques and Moreira in [Reference Marques and Moreira11] and discussed by Lelis and Marques in [Reference Lelis and Marques6], we approached Question 1.2 as follows. If there were a positive integer sequence
![]() $(u_n)_{n\geq 0}$
satisfying
$(u_n)_{n\geq 0}$
satisfying
![]() $u_n\rightarrow \infty $
and
$u_n\rightarrow \infty $
and
![]() $u_n=O(n)$
that could be interpolated by a p-adic transcendental analytic function
$u_n=O(n)$
that could be interpolated by a p-adic transcendental analytic function
![]() $f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
, then f would answer Question 1.2 affirmatively. Indeed, assuming all that is true, if we get any p-adic Liouville number
$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
, then f would answer Question 1.2 affirmatively. Indeed, assuming all that is true, if we get any p-adic Liouville number
![]() $\lambda \in \mathbb {Z}_p$
, by definition there would be a sequence of integers
$\lambda \in \mathbb {Z}_p$
, by definition there would be a sequence of integers
![]() $(n_{k})_{k\geq 0}$
such that
$(n_{k})_{k\geq 0}$
such that
The function f being analytic would satisfy a Lipschitz condition (see [Reference Robert15, Ch. 5, Section 3]). Thus, there would be a constant
![]() $c>0$
such that
$c>0$
such that
and so
where
![]() $u_{n_k}\rightarrow \infty $
and
$u_{n_k}\rightarrow \infty $
and
![]() $u_{n_k}=O(n_k)$
. So
$u_{n_k}=O(n_k)$
. So
![]() $f(\lambda )$
would also be a p-adic Liouville number.
$f(\lambda )$
would also be a p-adic Liouville number.
In light of this, it is natural to try to characterise the p-adic analytic functions which interpolate sequences of integers
![]() $(u_n)_{n \geq 0}$
of linear growth. There are other reasons for seeking such characterisations. Indeed, one may ask whether there exists a p-adic interpolation of some arithmetic function (many of which have linear growth) or, more generally, if polynomials with integer coefficients are the only p-adic analytic functions that take positive integers into positive integers with polynomial order.
$(u_n)_{n \geq 0}$
of linear growth. There are other reasons for seeking such characterisations. Indeed, one may ask whether there exists a p-adic interpolation of some arithmetic function (many of which have linear growth) or, more generally, if polynomials with integer coefficients are the only p-adic analytic functions that take positive integers into positive integers with polynomial order.
Theorem 1.3. Let
![]() $(u_n)_{n\geq 0}$
be a sequence of positive integers such that
$(u_n)_{n\geq 0}$
be a sequence of positive integers such that
![]() $u_n=O(n^d)$
for some fixed
$u_n=O(n^d)$
for some fixed
![]() $d\geq 0 \ (d\in \mathbb {R})$
. Assume there exists a p-adic analytic function
$d\geq 0 \ (d\in \mathbb {R})$
. Assume there exists a p-adic analytic function
![]() $f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
which interpolates the sequence
$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
which interpolates the sequence
![]() $(u_n)_{n\geq 0}$
.
$(u_n)_{n\geq 0}$
.
-
(i) If
 $d\leq 1$
, then f is a polynomial function of degree at most one.
$d\leq 1$
, then f is a polynomial function of degree at most one. -
(ii) If
 $d>1$
and the Mahler expansion of f converges for all
$d>1$
and the Mahler expansion of f converges for all
 $x\in \mathbb {Q}_p$
, then f is a polynomial function of degree at most
$x\in \mathbb {Q}_p$
, then f is a polynomial function of degree at most
 $\lfloor d\rfloor $
.
$\lfloor d\rfloor $
.
We remark that the condition ‘f is a p-adic analytic function on
![]() $\mathbb {Z}_p$
’ is fundamental in the result above. Indeed, if we write
$\mathbb {Z}_p$
’ is fundamental in the result above. Indeed, if we write
![]() $n=\sum _{i=0}^{k}a_ip^i$
in base p, then the function
$n=\sum _{i=0}^{k}a_ip^i$
in base p, then the function
![]() $f:\{0\}\cup \mathbb {N}\to \mathbb {Q}_p$
given by
$f:\{0\}\cup \mathbb {N}\to \mathbb {Q}_p$
given by
 $$ \begin{align*} f(n)=\begin{cases} \displaystyle\sum_{i=0}^{k-1}a_ip^i&\mbox{if}\ n\geq p,\\ n&\mbox{if}\ 0\leq n\leq p-1, \end{cases} \end{align*} $$
$$ \begin{align*} f(n)=\begin{cases} \displaystyle\sum_{i=0}^{k-1}a_ip^i&\mbox{if}\ n\geq p,\\ n&\mbox{if}\ 0\leq n\leq p-1, \end{cases} \end{align*} $$
clearly can be extended in a unique way to a continuous function
![]() $\overline {f}:\mathbb {Z}_p\to \mathbb {Q}_p$
such that
$\overline {f}:\mathbb {Z}_p\to \mathbb {Q}_p$
such that
![]() $\overline {f}(n)=O(n)$
. However,
$\overline {f}(n)=O(n)$
. However,
![]() $\overline {f}$
is nonanalytic and it is clearly not a polynomial function.
$\overline {f}$
is nonanalytic and it is clearly not a polynomial function.
Moreover, consider the p-adic function
![]() $f_d:\mathbb {Z}_p\to \mathbb {Q}_p$
defined by
$f_d:\mathbb {Z}_p\to \mathbb {Q}_p$
defined by
 $$ \begin{align*} f_d(z)=\sum_{k=0}^{\infty}a_kp^{dk}, \end{align*} $$
$$ \begin{align*} f_d(z)=\sum_{k=0}^{\infty}a_kp^{dk}, \end{align*} $$
where
![]() $z=\sum _{k=0}^{\infty }a_kp^k$
is the p-adic expansion of
$z=\sum _{k=0}^{\infty }a_kp^k$
is the p-adic expansion of
![]() $z\in \mathbb {Z}_p$
. Then it is well known that
$z\in \mathbb {Z}_p$
. Then it is well known that
![]() $f_d$
is a continuous function for all integers
$f_d$
is a continuous function for all integers
![]() $d\geq 2$
. In fact, if
$d\geq 2$
. In fact, if
![]() $d\geq 2$
is an integer, then
$d\geq 2$
is an integer, then
In particular, we have
![]() $f^{\prime }_d(x)=0$
for all
$f^{\prime }_d(x)=0$
for all
![]() $x\in \mathbb {Q}_p$
and
$x\in \mathbb {Q}_p$
and
![]() $f_d\in \mathcal {C}^1(\mathbb {Z}_p\to \mathbb {Q}_p)\subset \mathcal {C}(\mathbb {Z}_p\to \mathbb {Q}_p)$
. Note that
$f_d\in \mathcal {C}^1(\mathbb {Z}_p\to \mathbb {Q}_p)\subset \mathcal {C}(\mathbb {Z}_p\to \mathbb {Q}_p)$
. Note that
![]() $f_d(n)=O(n^d)$
, but
$f_d(n)=O(n^d)$
, but
![]() $f_d$
is not a polynomial function. However, since
$f_d$
is not a polynomial function. However, since
![]() $f_d$
is not a p-adic analytic function, its Mahler expansion does not converge for all
$f_d$
is not a p-adic analytic function, its Mahler expansion does not converge for all
![]() $x\in \mathbb {Q}_p$
.
$x\in \mathbb {Q}_p$
.
Very strict conditions must be satisfied for a sequence
![]() $(u_n)_{n\geq 0}$
to be interpolated by a p-adic analytic function. However, if the set
$(u_n)_{n\geq 0}$
to be interpolated by a p-adic analytic function. However, if the set
![]() $A=\{u_0,u_1,\ldots \}\subseteq \mathbb {Z}$
is a dense subset of
$A=\{u_0,u_1,\ldots \}\subseteq \mathbb {Z}$
is a dense subset of
![]() $\mathbb {Z}_p$
, one may ask whether there is some re-enumeration
$\mathbb {Z}_p$
, one may ask whether there is some re-enumeration
![]() $\sigma :\{0\}\cup \mathbb {N}\rightarrow \{0\}\cup \mathbb {N}$
such that
$\sigma :\{0\}\cup \mathbb {N}\rightarrow \{0\}\cup \mathbb {N}$
such that
![]() $(u_{\sigma (n)})_{n\geq 0}$
can be interpolated by a p-adic analytic function.
$(u_{\sigma (n)})_{n\geq 0}$
can be interpolated by a p-adic analytic function.
In the complex case, Georg [Reference Georg4] established that for each countable subset
![]() $X\subset \mathbb {C}$
and each dense subset
$X\subset \mathbb {C}$
and each dense subset
![]() $Y\subseteq \mathbb {C}$
, there exists a transcendental entire function f such that
$Y\subseteq \mathbb {C}$
, there exists a transcendental entire function f such that
![]() $f(X)\subset Y$
. In 1902, Stäckel [Reference Stäckel18] used another construction to show that there is a function
$f(X)\subset Y$
. In 1902, Stäckel [Reference Stäckel18] used another construction to show that there is a function
![]() $f(z)$
, analytic in a neighbourhood of the origin and with the property that both
$f(z)$
, analytic in a neighbourhood of the origin and with the property that both
![]() $f(z)$
and its inverse function assume, in this neighbourhood, algebraic values at all algebraic points. Based on these results, Mahler [Reference Mahler8] suggested the following question about the set of algebraic numbers
$f(z)$
and its inverse function assume, in this neighbourhood, algebraic values at all algebraic points. Based on these results, Mahler [Reference Mahler8] suggested the following question about the set of algebraic numbers
![]() $\overline {\mathbb {Q}}$
.
$\overline {\mathbb {Q}}$
.
Question 1.4 (Mahler, [Reference Mahler8])
Are there transcendental entire functions
![]() $f(z)=\sum c_nz^n$
with rational coefficients
$f(z)=\sum c_nz^n$
with rational coefficients
![]() $c_n$
and such that
$c_n$
and such that
![]() $f(\overline {\mathbb {Q}})\subset \overline {\mathbb {Q}}$
and
$f(\overline {\mathbb {Q}})\subset \overline {\mathbb {Q}}$
and
![]() $f^{-1}(\overline {\mathbb {Q}})\subset \overline {\mathbb {Q}}$
?
$f^{-1}(\overline {\mathbb {Q}})\subset \overline {\mathbb {Q}}$
?
This question was answered positively by Marques and Moreira [Reference Marques and Moreira12]. Moreover, in a more recent paper [Reference Marques and Moreira13], they proved that if X and Y are countable subsets of
![]() $\mathbb {C}$
satisfying some conditions necessary for analyticity, then there are uncountably many transcendental entire functions
$\mathbb {C}$
satisfying some conditions necessary for analyticity, then there are uncountably many transcendental entire functions
![]() $f(z)=\sum a_nz^n$
with rational coefficients such that
$f(z)=\sum a_nz^n$
with rational coefficients such that
![]() $f(X)\subset Y$
and
$f(X)\subset Y$
and
![]() $f^{-1}(Y)\subset X$
. Keeping these results in mind, we prove the following theorem.
$f^{-1}(Y)\subset X$
. Keeping these results in mind, we prove the following theorem.
Theorem 1.5. Let X and Y be subsets of
![]() $\mathbb {Z}$
dense in
$\mathbb {Z}$
dense in
![]() $\mathbb {Z}_p$
. Then there are uncountably many p-adic analytic injective functions
$\mathbb {Z}_p$
. Then there are uncountably many p-adic analytic injective functions
![]() $f:\mathbb {Z}_p\to \mathbb {Q}_p$
with
$f:\mathbb {Z}_p\to \mathbb {Q}_p$
with
 $$ \begin{align*} f(x)=\sum_{n=0}^{\infty} c_nx^n\in\mathbb{Q}[[x]] \end{align*} $$
$$ \begin{align*} f(x)=\sum_{n=0}^{\infty} c_nx^n\in\mathbb{Q}[[x]] \end{align*} $$
such that
![]() $f(X)=Y$
.
$f(X)=Y$
.
Note that by Theorem 1.5, if
![]() $Y=\{y_0,y_1,y_2,\ldots \}\subset \mathbb {Z}$
is a dense subset of
$Y=\{y_0,y_1,y_2,\ldots \}\subset \mathbb {Z}$
is a dense subset of
![]() $\mathbb {Z}_p$
, that is, if Y contains a complete system of residues modulo any power of p, then there is a p-adic analytic function
$\mathbb {Z}_p$
, that is, if Y contains a complete system of residues modulo any power of p, then there is a p-adic analytic function
 $$ \begin{align*} f(x)=\sum_{n=0}^{\infty}c_nx^n,\quad c_n\in\mathbb{Q} \mbox{ for all}\ n\geq0, \end{align*} $$
$$ \begin{align*} f(x)=\sum_{n=0}^{\infty}c_nx^n,\quad c_n\in\mathbb{Q} \mbox{ for all}\ n\geq0, \end{align*} $$
and a bijection
![]() $\sigma :\{0\}\cup \mathbb {N}\rightarrow \{0\}\cup \mathbb {N}$
such that
$\sigma :\{0\}\cup \mathbb {N}\rightarrow \{0\}\cup \mathbb {N}$
such that
![]() $f(n)=u_{\sigma (n)}$
, where we take
$f(n)=u_{\sigma (n)}$
, where we take
![]() $X=\{0\}\cup \mathbb {N}$
. Moreover, the series above converges for all
$X=\{0\}\cup \mathbb {N}$
. Moreover, the series above converges for all
![]() $x\in \mathbb {Z}_p$
. Thus, if we consider the Mahler expansion, then we immediately obtain the following result.
$x\in \mathbb {Z}_p$
. Thus, if we consider the Mahler expansion, then we immediately obtain the following result.
Corollary 1.6. Let
![]() $Y=\{y_0,y_1,y_2,\ldots \}$
be a subset of
$Y=\{y_0,y_1,y_2,\ldots \}$
be a subset of
![]() $\mathbb {Z}$
dense in
$\mathbb {Z}$
dense in
![]() $\mathbb {Z}_p$
. Then there are
$\mathbb {Z}_p$
. Then there are
![]() $a_0,a_1,a_2,\ldots \in \mathbb {Z}$
and a bijection
$a_0,a_1,a_2,\ldots \in \mathbb {Z}$
and a bijection
![]() $\sigma :\{0\}\cup \mathbb {N}\rightarrow \{0\}\cup \mathbb {N}$
such that
$\sigma :\{0\}\cup \mathbb {N}\rightarrow \{0\}\cup \mathbb {N}$
such that
 $$ \begin{align*} \sum_{i=0}^{n}a_i\binom{i}{n}=y_{\sigma(n)}, \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{n}a_i\binom{i}{n}=y_{\sigma(n)}, \end{align*} $$
for all integers
![]() $n\geq 0$
, where
$n\geq 0$
, where
![]() $v_p(a_n/n!)\to \infty $
as
$v_p(a_n/n!)\to \infty $
as
![]() $n\to \infty $
.
$n\to \infty $
.
We end this section by presenting some questions which we are still unable to answer. One may ask whether Theorem 1.5 is still true if X and Y are free to contain elements outside
![]() $\mathbb {Z}$
. What could one do to guarantee rational coefficients in f in a situation like that? Moreover, if we consider the algebraic closure of
$\mathbb {Z}$
. What could one do to guarantee rational coefficients in f in a situation like that? Moreover, if we consider the algebraic closure of
![]() $\mathbb {Q}_p$
, denoted by
$\mathbb {Q}_p$
, denoted by
![]() $\overline {\mathbb {Q}}_p$
, and its completion
$\overline {\mathbb {Q}}_p$
, and its completion
![]() $\mathbb {C}_p$
, we may ask a probably more difficult question.
$\mathbb {C}_p$
, we may ask a probably more difficult question.
Question 1.7. Are there p-adic transcendental entire functions
![]() $f:\mathbb {C}_p\to \mathbb {C}_p$
given by
$f:\mathbb {C}_p\to \mathbb {C}_p$
given by
 $$ \begin{align*} f(z)=\sum_{n=0}^{\infty} c_nz^n,\quad c_n\in\mathbb{Q} \mbox{ for all}\ n\geq0, \end{align*} $$
$$ \begin{align*} f(z)=\sum_{n=0}^{\infty} c_nz^n,\quad c_n\in\mathbb{Q} \mbox{ for all}\ n\geq0, \end{align*} $$
such that
![]() $f(\overline {\mathbb {Q}}_p)\subset \overline {\mathbb {Q}}_p$
and
$f(\overline {\mathbb {Q}}_p)\subset \overline {\mathbb {Q}}_p$
and
![]() $f^{-1}(\overline {\mathbb {Q}}_p)\subset \overline {\mathbb {Q}}_p$
?
$f^{-1}(\overline {\mathbb {Q}}_p)\subset \overline {\mathbb {Q}}_p$
?
Naturally, the main difficulty of this problem lies again in the fact that the set
![]() $\overline {\mathbb {Q}}_p$
is uncountable.
$\overline {\mathbb {Q}}_p$
is uncountable.
2 Proof of Theorem 1.3
We start by introducing the classic Strassmann’s theorem about zeros of p-adic power series. This result says that a p-adic analytic function with coefficients in
![]() $\mathbb {Q}_p$
has finitely many zeros in
$\mathbb {Q}_p$
has finitely many zeros in
![]() $\mathbb {Z}_p$
and provides a bound for the number of zeros.
$\mathbb {Z}_p$
and provides a bound for the number of zeros.
Theorem 2.1 (Strassmann, [Reference Murty14])
Let
![]() $f(x)=\sum _{n=0}^{\infty }c_nx^n$
be a nonzero power series with coefficients in
$f(x)=\sum _{n=0}^{\infty }c_nx^n$
be a nonzero power series with coefficients in
![]() $\mathbb {Q}_p$
and suppose that
$\mathbb {Q}_p$
and suppose that
![]() $\lim _{n\rightarrow \infty }c_n=0$
so that
$\lim _{n\rightarrow \infty }c_n=0$
so that
![]() $f(x)$
converges for all x in
$f(x)$
converges for all x in
![]() $\mathbb {Z}_p$
. Let N be the integer defined by conditions
$\mathbb {Z}_p$
. Let N be the integer defined by conditions
Then the function
![]() $f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
defined by
$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
defined by
![]() $x\mapsto f(x)$
has at most N zeros.
$x\mapsto f(x)$
has at most N zeros.
Proof of Theorem 1.3
Let
![]() $(u_n)_{n\geq 0}$
be a sequence of integers of linear or sublinear growth, that is,
$(u_n)_{n\geq 0}$
be a sequence of integers of linear or sublinear growth, that is,
![]() $u_n=O(n)$
. Suppose that
$u_n=O(n)$
. Suppose that
![]() $(u_n)_{n\geq 0}$
can be interpolated by some p-adic analytic function
$(u_n)_{n\geq 0}$
can be interpolated by some p-adic analytic function
 $$ \begin{align*} f(x)=\sum_{n=0}^{\infty}c_nx^n\in\mathbb{Q}_p[[x]]. \end{align*} $$
$$ \begin{align*} f(x)=\sum_{n=0}^{\infty}c_nx^n\in\mathbb{Q}_p[[x]]. \end{align*} $$
Since
![]() $f(x)$
is a p-adic analytic function,
$f(x)$
is a p-adic analytic function,
![]() $\lim _{n\rightarrow \infty }\|c_n\|_p=0$
. Thus, there exists an integer N defined by the conditions
$\lim _{n\rightarrow \infty }\|c_n\|_p=0$
. Thus, there exists an integer N defined by the conditions
and Strassman’s theorem guarantees that the function
![]() $f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
has at most N zeros.
$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$
has at most N zeros.
By hypothesis,
![]() $u_n=O(n)$
, so there is a
$u_n=O(n)$
, so there is a
![]() $C>0$
such that
$C>0$
such that
![]() $0 < u_n\leq Cn$
for all
$0 < u_n\leq Cn$
for all
![]() $n\geq 0$
. Taking the subsequence
$n\geq 0$
. Taking the subsequence
![]() $(u_{p^k})_{k\geq 0}$
,
$(u_{p^k})_{k\geq 0}$
,
Since f is an analytic function, it is easily seen that it satisfies the Lipschitz condition
for all
![]() $x,y \in \mathbb {Z}_p$
. In particular,
$x,y \in \mathbb {Z}_p$
. In particular,
and it follows that
with
![]() $t_k\in \mathbb {Z}_+$
, because
$t_k\in \mathbb {Z}_+$
, because
![]() $u_{p^k}$
is a positive integer. By (2.1) and (2.2), we conclude that
$u_{p^k}$
is a positive integer. By (2.1) and (2.2), we conclude that
![]() $0\leq t_k\leq C$
. Hence, by the pigeonhole principle, there exists an integer t with
$0\leq t_k\leq C$
. Hence, by the pigeonhole principle, there exists an integer t with
![]() $0\leq t\leq C$
such that
$0\leq t\leq C$
such that
for infinitely many
![]() $j\geq 0$
. Thus, the function
$j\geq 0$
. Thus, the function
 $$ \begin{align*} f(x)-u_0-tx=(c_1-t)x+\sum_{n=2}^{\infty}c_nx^n \end{align*} $$
$$ \begin{align*} f(x)-u_0-tx=(c_1-t)x+\sum_{n=2}^{\infty}c_nx^n \end{align*} $$
has infinitely many roots and by Strassman’s theorem, we conclude that
![]() $f(x)=u_0+tx$
.
$f(x)=u_0+tx$
.
Now suppose that
![]() $u_n=O(n^d)$
for some fixed positive real number
$u_n=O(n^d)$
for some fixed positive real number
![]() $d>1$
. Let
$d>1$
. Let
 $$ \begin{align*} f(x)=\sum_{n=0}^{\infty}a_n\binom{x}{n} \end{align*} $$
$$ \begin{align*} f(x)=\sum_{n=0}^{\infty}a_n\binom{x}{n} \end{align*} $$
be the Mahler expansion of f. By hypothesis, the Mahler expansion of f converges for all
![]() $x\in \mathbb {Q}_p$
, so the function
$x\in \mathbb {Q}_p$
, so the function
![]() $x\mapsto \sum _{n=0}^{\infty }a_n\binom {x}{n}$
is analytic on
$x\mapsto \sum _{n=0}^{\infty }a_n\binom {x}{n}$
is analytic on
![]() $\mathbb {C}_p$
and
$\mathbb {C}_p$
and
for all real numbers
![]() $r>0$
(see [Reference Schikhof17, Ch. 3]). Taking
$r>0$
(see [Reference Schikhof17, Ch. 3]). Taking
![]() $r=p^2$
, we find
$r=p^2$
, we find
![]() $v_p(a_n)\geq 2n$
for all n sufficiently large. Moreover,
$v_p(a_n)\geq 2n$
for all n sufficiently large. Moreover,
![]() $a_n$
is an integer for all
$a_n$
is an integer for all
![]() $n\geq 0$
. In fact, by the Mahler expansion,
$n\geq 0$
. In fact, by the Mahler expansion,
 $$ \begin{align*} a_n=\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}f(\kern2pt j)=\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}u_j\quad(n=0,1,2,\ldots), \end{align*} $$
$$ \begin{align*} a_n=\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}f(\kern2pt j)=\sum_{j=0}^{n}(-1)^{n-j}\binom{n}{j}u_j\quad(n=0,1,2,\ldots), \end{align*} $$
where
![]() $u_j\in \mathbb {Z}_+$
for all
$u_j\in \mathbb {Z}_+$
for all
![]() $j\geq 0$
. Hence, either
$j\geq 0$
. Hence, either
![]() $a_n=0$
or
$a_n=0$
or
However,
 $$ \begin{align*} \|a_n\|_{\infty}=\bigg\|\sum_{j=0}^{n}(-1)^{n-j\,}\binom{n}{j}u_j\bigg\|_{\infty} \quad(n=0,1,2,\ldots). \end{align*} $$
$$ \begin{align*} \|a_n\|_{\infty}=\bigg\|\sum_{j=0}^{n}(-1)^{n-j\,}\binom{n}{j}u_j\bigg\|_{\infty} \quad(n=0,1,2,\ldots). \end{align*} $$
Since
![]() $\|u_j\|_{\infty }\leq j^d\leq n^d$
for all
$\|u_j\|_{\infty }\leq j^d\leq n^d$
for all
![]() $j\leq n$
, it follows that
$j\leq n$
, it follows that
where
![]() $D>0$
is a fixed constant. It is easily seen that (2.3) and (2.4) cannot both be true for n sufficiently large. Hence, there exists an
$D>0$
is a fixed constant. It is easily seen that (2.3) and (2.4) cannot both be true for n sufficiently large. Hence, there exists an
![]() $N>0$
such that
$N>0$
such that
![]() $a_n=0$
for all
$a_n=0$
for all
![]() $n>N$
. Consequently, f is a polynomial function. Furthermore,
$n>N$
. Consequently, f is a polynomial function. Furthermore,
![]() $f(n)=O(n^d)$
, so its degree must be at most
$f(n)=O(n^d)$
, so its degree must be at most
![]() $\lfloor d\rfloor $
.
$\lfloor d\rfloor $
.
3 Proof of Theorem 1.5
Suppose that
![]() $X=\{x_0,x_1,x_2,\ldots \}$
and
$X=\{x_0,x_1,x_2,\ldots \}$
and
![]() $Y=\{y_0,y_1,y_2,\ldots \}$
are subsets of
$Y=\{y_0,y_1,y_2,\ldots \}$
are subsets of
![]() $\mathbb {Z}$
dense in
$\mathbb {Z}$
dense in
![]() $\mathbb {Z}_p$
. Our proof consists in determining a sequence of polynomial functions
$\mathbb {Z}_p$
. Our proof consists in determining a sequence of polynomial functions
![]() $f_0,f_1,\ldots $
such that
$f_0,f_1,\ldots $
such that
![]() $f_n\to f$
as
$f_n\to f$
as
![]() $n\to \infty $
, where f is a p-adic analytic injective function on
$n\to \infty $
, where f is a p-adic analytic injective function on
![]() $\mathbb {Z}_p$
with rational coefficients satisfying
$\mathbb {Z}_p$
with rational coefficients satisfying
![]() $f(X)=Y$
. In addition, we will show that there are uncountably many such functions.
$f(X)=Y$
. In addition, we will show that there are uncountably many such functions.
To be more precise, we will construct a sequence of polynomial functions
![]() $f_0,f_1,f_2,\ldots \in \mathbb {Q}[x]$
of degrees
$f_0,f_1,f_2,\ldots \in \mathbb {Q}[x]$
of degrees
![]() $t_0,t_1,t_2,\ldots \in \mathbb {Z}$
, respectively, such that for all
$t_0,t_1,t_2,\ldots \in \mathbb {Z}$
, respectively, such that for all
![]() $m\geq 0$
,
$m\geq 0$
,
 $$ \begin{align} f_m(x)=\sum_{i=0}^{t_m}c_ix^i, \end{align} $$
$$ \begin{align} f_m(x)=\sum_{i=0}^{t_m}c_ix^i, \end{align} $$
where
![]() $c_0=y_0-x_0$
,
$c_0=y_0-x_0$
,
![]() $c_1=1$
and
$c_1=1$
and
![]() $\|c_i\|_p\leq p^{-1}$
for all
$\|c_i\|_p\leq p^{-1}$
for all
![]() $2\leq i\leq t_m$
. Furthermore, our sequence will obey the recurrence relation
$2\leq i\leq t_m$
. Furthermore, our sequence will obey the recurrence relation
where the polynomial functions
![]() $P_m\in \mathbb {Z}[x]$
are given by
$P_m\in \mathbb {Z}[x]$
are given by
 $$ \begin{align} P_m(x)=\prod_{k\in X_m\cup Y^{-1}_m}(x-k), \end{align} $$
$$ \begin{align} P_m(x)=\prod_{k\in X_m\cup Y^{-1}_m}(x-k), \end{align} $$
with
![]() $X_m=\{x_0,\ldots ,x_m\}$
and
$X_m=\{x_0,\ldots ,x_m\}$
and
![]() $Y^{-1}_m=f_m^{-1}(\{y_0,\ldots ,y_m\})$
, and
$Y^{-1}_m=f_m^{-1}(\{y_0,\ldots ,y_m\})$
, and
![]() $\delta _m$
and
$\delta _m$
and
![]() $\epsilon _m$
are rational numbers such that
$\epsilon _m$
are rational numbers such that
Finally, our sequence will also satisfy
![]() $f_m(x_k)\in Y$
and
$f_m(x_k)\in Y$
and
![]() $f_m^{-1}(\{y_k\})\cap X \neq \emptyset $
for all
$f_m^{-1}(\{y_k\})\cap X \neq \emptyset $
for all
![]() ${0\leq k\leq m}$
.
${0\leq k\leq m}$
.
We make some remarks regarding such a sequence of polynomials. First, since
![]() $f_m$
is a polynomial,
$f_m$
is a polynomial,
![]() $Y^{-1}_m$
must be a finite subset of
$Y^{-1}_m$
must be a finite subset of
![]() $\mathbb {Z}_p$
for each m, so the polynomials
$\mathbb {Z}_p$
for each m, so the polynomials
![]() $P_m$
are well defined. Second, by (3.1),
$P_m$
are well defined. Second, by (3.1),
![]() $\|c_1\|_p> \|c_i\|_p$
for all
$\|c_1\|_p> \|c_i\|_p$
for all
![]() $i \geq 2$
, so each
$i \geq 2$
, so each
![]() $f_m$
is necessarily injective on
$f_m$
is necessarily injective on
![]() $\mathbb {Z}_p$
by Strassmann’s theorem. Lastly, since
$\mathbb {Z}_p$
by Strassmann’s theorem. Lastly, since
![]() $f_m$
is injective, there is only one
$f_m$
is injective, there is only one
![]() $x_s \in X \cap f_m^{-1}(\{y_k\})$
. The existence of such a sequence is guaranteed by the following lemma.
$x_s \in X \cap f_m^{-1}(\{y_k\})$
. The existence of such a sequence is guaranteed by the following lemma.
Lemma 3.1. Suppose that
![]() $ f_m(x)=c_0+c_1x+\cdots +c_{t_m}x^{t_m}\in \mathbb {Q}[x] $
is a polynomial with
$ f_m(x)=c_0+c_1x+\cdots +c_{t_m}x^{t_m}\in \mathbb {Q}[x] $
is a polynomial with
such that
![]() $f_m(X_m)\subset Y$
and
$f_m(X_m)\subset Y$
and
![]() $Y_m^{-1}\subset X$
. Then there exist rational numbers
$Y_m^{-1}\subset X$
. Then there exist rational numbers
![]() $\delta _m$
and
$\delta _m$
and
![]() $\epsilon _m$
with
$\epsilon _m$
with
such that the function
is a polynomial given by
satisfying
![]() $f_{m+1}(X_{m+1})\subset X$
and
$f_{m+1}(X_{m+1})\subset X$
and
![]() $Y_{m+1}^{-1}\subset X$
and, moreover,
$Y_{m+1}^{-1}\subset X$
and, moreover,
![]() $\|c_i\|_p<\|c_1\|_p$
for all integers i with
$\|c_i\|_p<\|c_1\|_p$
for all integers i with
![]() $2\leq i\leq t_{m+1}$
.
$2\leq i\leq t_{m+1}$
.
Proof. Suppose that for some
![]() $m\geq 0$
, there is a function
$m\geq 0$
, there is a function
![]() $f_m$
satisfying the hypotheses of the lemma. We will show that we can choose rational numbers
$f_m$
satisfying the hypotheses of the lemma. We will show that we can choose rational numbers
![]() $\delta _m$
and
$\delta _m$
and
![]() $\epsilon _m$
such that
$\epsilon _m$
such that
in such a way that the polynomial
![]() $f_{m+1}$
in (3.2) has the desired properties.
$f_{m+1}$
in (3.2) has the desired properties.
First, we will determine
![]() $\delta _m\in \mathbb {Q}$
such that
$\delta _m\in \mathbb {Q}$
such that
![]() $f_{m+1}(x_{m+1})\in Y$
. Suppose that
$f_{m+1}(x_{m+1})\in Y$
. Suppose that
![]() $ f_m(x_{m+1}) \in \{y_0,y_1,\ldots ,y_m\}$
. Since
$ f_m(x_{m+1}) \in \{y_0,y_1,\ldots ,y_m\}$
. Since
![]() $P_m(x_{m+1})=0$
, we have
$P_m(x_{m+1})=0$
, we have
![]() $f_{m+1}(x_{m+1}) = f_{m}(x_{m+1})\in Y$
. Note that here we did not make direct use of
$f_{m+1}(x_{m+1}) = f_{m}(x_{m+1})\in Y$
. Note that here we did not make direct use of
![]() $\delta _m$
to get
$\delta _m$
to get
![]() $f_{m+1}(x_{m+1}) \in Y$
. So we are free to choose any
$f_{m+1}(x_{m+1}) \in Y$
. So we are free to choose any
![]() $\delta _m \in \mathbb {Q}$
and we do so by setting
$\delta _m \in \mathbb {Q}$
and we do so by setting
![]() $\delta _m = p^m$
. Now, suppose that
$\delta _m = p^m$
. Now, suppose that
![]() $f_m(x_{m+1})\notin \{y_0,y_1,\ldots ,y_m\}$
, which implies that
$f_m(x_{m+1})\notin \{y_0,y_1,\ldots ,y_m\}$
, which implies that
![]() $P_m(x_{m+1})\neq 0$
. Since Y is a dense subset of
$P_m(x_{m+1})\neq 0$
. Since Y is a dense subset of
![]() $\mathbb {Z}_p$
, there exists
$\mathbb {Z}_p$
, there exists
![]() $\hat {y}\in Y$
such that
$\hat {y}\in Y$
such that
 $$ \begin{align*} 0<\bigg\|\frac{\hat{y}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}\bigg\|_p\leq p^{-m}. \end{align*} $$
$$ \begin{align*} 0<\bigg\|\frac{\hat{y}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}\bigg\|_p\leq p^{-m}. \end{align*} $$
Then, taking
 $$ \begin{align*} \delta_m=\frac{\hat{y}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}, \end{align*} $$
$$ \begin{align*} \delta_m=\frac{\hat{y}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}, \end{align*} $$
we obtain
![]() $f_{m+1}(x_{m+1})=\hat {y}\in Y$
independently of
$f_{m+1}(x_{m+1})=\hat {y}\in Y$
independently of
![]() $\epsilon _m$
. Observe that in both cases just analysed,
$\epsilon _m$
. Observe that in both cases just analysed,
![]() $\|\delta _m\|_p \leq p^{-m}$
.
$\|\delta _m\|_p \leq p^{-m}$
.
Now we will choose
![]() $\epsilon _m \in \mathbb {Q}$
to get
$\epsilon _m \in \mathbb {Q}$
to get
![]() $f_{m+1}(\hat {x})=y_{m+1}$
for some
$f_{m+1}(\hat {x})=y_{m+1}$
for some
![]() $\hat {x}\in X$
. Since
$\hat {x}\in X$
. Since
![]() $f_m$
is injective on
$f_m$
is injective on
![]() $\mathbb {Z}_p$
, there is at most one
$\mathbb {Z}_p$
, there is at most one
![]() $\hat {x}\in X$
such that
$\hat {x}\in X$
such that
![]() $f_m(\hat {x})=y_{m+1}$
. If there exists
$f_m(\hat {x})=y_{m+1}$
. If there exists
![]() $\hat {x}\in X_m$
such that
$\hat {x}\in X_m$
such that
![]() $f_m(\hat {x})=y_{m+1}$
, then
$f_m(\hat {x})=y_{m+1}$
, then
![]() $P_m(\hat {x})=0$
and we obtain
$P_m(\hat {x})=0$
and we obtain
![]() $f_{m+1}(\hat {x})=y_{m+1}$
. In this case,
$f_{m+1}(\hat {x})=y_{m+1}$
. In this case,
![]() $\epsilon _m$
does not play a role and we are free to set
$\epsilon _m$
does not play a role and we are free to set
![]() $\epsilon _m=p^m$
. It remains to consider the case where there is no
$\epsilon _m=p^m$
. It remains to consider the case where there is no
![]() $\hat {x} \in X_m$
with
$\hat {x} \in X_m$
with
![]() $f_m(\hat {x})=y_{m+1}$
. Note that if we choose
$f_m(\hat {x})=y_{m+1}$
. Note that if we choose
 $$ \begin{align*} \delta_m=\frac{y_{m+1}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}, \end{align*} $$
$$ \begin{align*} \delta_m=\frac{y_{m+1}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}, \end{align*} $$
then
![]() $f_{m+1}(x_{m+1})=y_{m+1}$
and we have
$f_{m+1}(x_{m+1})=y_{m+1}$
and we have
![]() $\hat {x} = x_{m+1}$
. Since we again did not use
$\hat {x} = x_{m+1}$
. Since we again did not use
![]() $\epsilon _m$
to ensure that
$\epsilon _m$
to ensure that
![]() $f_{m+1}(x_{m+1})=y_{m+1}$
, we are free to take
$f_{m+1}(x_{m+1})=y_{m+1}$
, we are free to take
![]() $\epsilon _m=p^m$
. However, if
$\epsilon _m=p^m$
. However, if
 $$ \begin{align*} \delta_m\neq\frac{y_{m+1}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}, \end{align*} $$
$$ \begin{align*} \delta_m\neq\frac{y_{m+1}-f_m(x_{m+1})}{(x_{m+1})^{t_m+1}P_m(x_{m+1})}, \end{align*} $$
we consider the polynomial equation
Since
![]() $\|\delta _m\|_p\leq p^{-m}$
and
$\|\delta _m\|_p\leq p^{-m}$
and
![]() $\|c_i\|_p<p^{-1}$
for
$\|c_i\|_p<p^{-1}$
for
![]() $i\geq 2$
,
$i\geq 2$
,
for all
![]() $m\geq 2$
. Thus, the congruence
$m\geq 2$
. Thus, the congruence
has a solution
![]() $\overline {x} \equiv y_{m+1}-y_0 \pmod {p\mathbb {Z}_p}$
. Moreover, taking the formal derivative,
$\overline {x} \equiv y_{m+1}-y_0 \pmod {p\mathbb {Z}_p}$
. Moreover, taking the formal derivative,
Hence, by Hensel’s lemma [Reference Murty14], there exists
![]() $b\in \mathbb {Z}_p$
such that
$b\in \mathbb {Z}_p$
such that
Let
![]() $v_p(x)$
be the p-adic valuation of
$v_p(x)$
be the p-adic valuation of
![]() $x\in \mathbb {Z}_p$
and take
$x\in \mathbb {Z}_p$
and take
Note that
![]() $s<+\infty $
, since
$s<+\infty $
, since
![]() $P_m(b)(b-x_{m+1})\neq 0$
. Thus, we have a Lipschitz condition on
$P_m(b)(b-x_{m+1})\neq 0$
. Thus, we have a Lipschitz condition on
![]() $\mathbb {Z}_p$
, namely
$\mathbb {Z}_p$
, namely
for all
![]() $x,y\in \mathbb {Z}_p$
. Since X is a dense subset of
$x,y\in \mathbb {Z}_p$
. Since X is a dense subset of
![]() $\mathbb {Z}_p$
, there is an integer
$\mathbb {Z}_p$
, there is an integer
![]() $\hat {x}\in X$
such that
$\hat {x}\in X$
such that
 $$ \begin{align*} \|\hat{x}-b\|_p\leq\frac{1}{p^{s+m}} \end{align*} $$
$$ \begin{align*} \|\hat{x}-b\|_p\leq\frac{1}{p^{s+m}} \end{align*} $$
and
![]() $v_p(\hat {x}^{t_m+1}P_m(\hat {x})(\hat {x}-x_{m+1}))=s$
. So,
$v_p(\hat {x}^{t_m+1}P_m(\hat {x})(\hat {x}-x_{m+1}))=s$
. So,
 $$ \begin{align*} \|f_m(\hat{x})+\delta_m\hat{x}^{t_m+1}P_m(\hat{x})-y_{m+1}\|_p\leq \frac{1}{p^{s+m}}. \end{align*} $$
$$ \begin{align*} \|f_m(\hat{x})+\delta_m\hat{x}^{t_m+1}P_m(\hat{x})-y_{m+1}\|_p\leq \frac{1}{p^{s+m}}. \end{align*} $$
Taking
 $$ \begin{align*} \epsilon_m=\frac{y_{m+1}-f_m(\hat{x})-\delta_m\hat{x}^{t_m+1}P_m(\hat{x})}{\hat{x}^{t_m+1}P_m(\hat{x})(\hat{x}-x_{m+1})}, \end{align*} $$
$$ \begin{align*} \epsilon_m=\frac{y_{m+1}-f_m(\hat{x})-\delta_m\hat{x}^{t_m+1}P_m(\hat{x})}{\hat{x}^{t_m+1}P_m(\hat{x})(\hat{x}-x_{m+1})}, \end{align*} $$
we get
![]() $\epsilon _m\in \mathbb {Q}$
,
$\epsilon _m\in \mathbb {Q}$
,
![]() $\|\epsilon _m\|_p<p^{-m}$
and
$\|\epsilon _m\|_p<p^{-m}$
and
![]() $f_{m+1}(\hat {x})=y_{m+1}$
. This completes the proof of the lemma.
$f_{m+1}(\hat {x})=y_{m+1}$
. This completes the proof of the lemma.
Proof of Theorem 1.5
If in Lemma 3.1 we start with
![]() $f_0(x)=(x-x_0)+y_0$
, we get a sequence of polynomials as described in the beginning of this section. Furthermore, in each step, we have at least two options for the choice of
$f_0(x)=(x-x_0)+y_0$
, we get a sequence of polynomials as described in the beginning of this section. Furthermore, in each step, we have at least two options for the choice of
![]() $\delta _m$
and
$\delta _m$
and
![]() $\epsilon _m$
so we get uncountably many sequences. We will fix one of these sequences and prove that
$\epsilon _m$
so we get uncountably many sequences. We will fix one of these sequences and prove that
![]() $f(x)=\lim _{m\rightarrow \infty }f_m(x)$
solves Theorem 1.5. Indeed,
$f(x)=\lim _{m\rightarrow \infty }f_m(x)$
solves Theorem 1.5. Indeed,
 $$ \begin{align*} f_m(x)=y_0+(x-x_0)+\sum_{j=1}^{m-1}x^{t_j+1}P_j(x)[\delta_j+\epsilon_j(x-x_{j+1})]=\sum_{j=0}^{t_m}c_jx^j, \end{align*} $$
$$ \begin{align*} f_m(x)=y_0+(x-x_0)+\sum_{j=1}^{m-1}x^{t_j+1}P_j(x)[\delta_j+\epsilon_j(x-x_{j+1})]=\sum_{j=0}^{t_m}c_jx^j, \end{align*} $$
where
![]() $\|c_i\|_p\leq p^{-j}$
for
$\|c_i\|_p\leq p^{-j}$
for
![]() $t_{j-1}<i\leq t_j$
and
$t_{j-1}<i\leq t_j$
and
![]() $1\leq j\leq m$
(since
$1\leq j\leq m$
(since
![]() $\max \{\|\delta _j\|_p,\|\epsilon _j\|_p\}\leq p^{-j}$
). Therefore,
$\max \{\|\delta _j\|_p,\|\epsilon _j\|_p\}\leq p^{-j}$
). Therefore,
![]() $\lim _{i\rightarrow \infty }\|c_i\|_p=0$
and
$\lim _{i\rightarrow \infty }\|c_i\|_p=0$
and
is a p-adic analytic function on
![]() $\mathbb {Z}_p$
.
$\mathbb {Z}_p$
.
Moreover,
![]() $f(X)= Y$
. Indeed, we are assuming that
$f(X)= Y$
. Indeed, we are assuming that
![]() $f_k(x_k)\in Y$
. By (3.3),
$f_k(x_k)\in Y$
. By (3.3),
![]() ${P_m(x_k)=0}$
for all
${P_m(x_k)=0}$
for all
![]() $m \geq k \geq 0$
and, consequently,
$m \geq k \geq 0$
and, consequently,
![]() $f_m(x_k)=f_{m-1}(x_k)=\cdots =f_k(x_k)$
. Thus, we conclude that
$f_m(x_k)=f_{m-1}(x_k)=\cdots =f_k(x_k)$
. Thus, we conclude that
However, by hypothesis, given an integer
![]() $j\geq 0$
, there exists an integer
$j\geq 0$
, there exists an integer
![]() $s\geq 0$
such that
$s\geq 0$
such that
![]() $f_j(x_s)=y_j$
. Similarly,
$f_j(x_s)=y_j$
. Similarly,
and we conclude
![]() $f(X)= Y$
.
$f(X)= Y$
.
It remains to prove that f is injective. For this, suppose that there are
![]() $a_1$
and
$a_1$
and
![]() $a_2$
in
$a_2$
in
![]() $\mathbb {Z}_p$
such that
$\mathbb {Z}_p$
such that
![]() $f(a_1)=f(a_2)=b\in \mathbb {Z}_p$
and note that by (3.1),
$f(a_1)=f(a_2)=b\in \mathbb {Z}_p$
and note that by (3.1),
![]() $c_1=1$
satisfies
$c_1=1$
satisfies
Now, consider the function
 $$ \begin{align*} f(x)-b=(y_0-x_0-b)+x+\sum_{n=2}^{\infty}c_nx^n. \end{align*} $$
$$ \begin{align*} f(x)-b=(y_0-x_0-b)+x+\sum_{n=2}^{\infty}c_nx^n. \end{align*} $$
Note that in the equation above,
![]() $c_1=1$
still satisfies the conditions in (3.4). Hence,
$c_1=1$
still satisfies the conditions in (3.4). Hence,
![]() $f(x)-b$
has at most one zero (by Strassman’s theorem), so we have
$f(x)-b$
has at most one zero (by Strassman’s theorem), so we have
![]() $a_1=a_2$
.
$a_1=a_2$
.