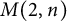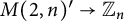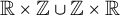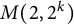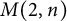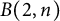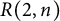1 Content
In this paper, we study the free metabelian group
![]() $M(2,n)$
of prime power exponent n in two generators, that is, the quotient of the Burnside group
$M(2,n)$
of prime power exponent n in two generators, that is, the quotient of the Burnside group
![]() $B(2,n)$
by its second derived subgroup. Contrary to Burnside groups, the groups
$B(2,n)$
by its second derived subgroup. Contrary to Burnside groups, the groups
![]() $M(2,n)$
are known to be finite for every n. However, their order has been determined in very few cases if n is not prime. We define invariants (group homomorphisms)
$M(2,n)$
are known to be finite for every n. However, their order has been determined in very few cases if n is not prime. We define invariants (group homomorphisms)
![]() $\Lambda : M(2,n)'\to \mathbb {Z}_n$
and use them to prove that certain identities do not hold in
$\Lambda : M(2,n)'\to \mathbb {Z}_n$
and use them to prove that certain identities do not hold in
![]() $M(2,n)$
and to improve bounds for its order obtained by Newman in [Reference Newman38]. Note that the abelianization of
$M(2,n)$
and to improve bounds for its order obtained by Newman in [Reference Newman38]. Note that the abelianization of
![]() $M(2,n)$
has order
$M(2,n)$
has order
![]() $n^2$
, and since
$n^2$
, and since
![]() $M(2,n)'$
is finite abelian of exponent n, there is a monomorphism
$M(2,n)'$
is finite abelian of exponent n, there is a monomorphism
![]() $M(2,n)'\to (\mathbb {Z}_n)^r$
(a product of invariants
$M(2,n)'\to (\mathbb {Z}_n)^r$
(a product of invariants
![]() $\Lambda $
as above) for r big enough, and the order of
$\Lambda $
as above) for r big enough, and the order of
![]() $M(2,n)'$
is then the order of the image of that map.
$M(2,n)'$
is then the order of the image of that map.
Algebraic tools have been used to study Engel identities and the nilpotence class of
![]() $M(2,n)$
in works by Bachmuth et al. [Reference Bachmuth, Heilbronn and Mochizuki6] and Dark–Newell [Reference Dark and Newell13]. Here, we use instead combinatorial ideas based on a construction introduced in [Reference Barmak8], called the winding invariant. To each word w in the derived subgroup
$M(2,n)$
in works by Bachmuth et al. [Reference Bachmuth, Heilbronn and Mochizuki6] and Dark–Newell [Reference Dark and Newell13]. Here, we use instead combinatorial ideas based on a construction introduced in [Reference Barmak8], called the winding invariant. To each word w in the derived subgroup
![]() $F_2'$
of the free group
$F_2'$
of the free group
![]() $F_2=F(x,y)$
of rank
$F_2=F(x,y)$
of rank
![]() $2$
, we associate a Laurent polynomial
$2$
, we associate a Laurent polynomial
![]() $P_w\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. This can be seen as a labeling of finitely many squares in the grid
$P_w\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. This can be seen as a labeling of finitely many squares in the grid
![]() $\mathbb {R} \times \mathbb {Z} \cup \mathbb {Z} \times \mathbb {R}$
by nonzero integer numbers. We use different colorings of the squares in the grid to define the invariants
$\mathbb {R} \times \mathbb {Z} \cup \mathbb {Z} \times \mathbb {R}$
by nonzero integer numbers. We use different colorings of the squares in the grid to define the invariants
![]() $M(2,n)'\to \mathbb {Z}_n$
.
$M(2,n)'\to \mathbb {Z}_n$
.
Some results that we prove are:
![]() $[x,y]^{\frac {n}{2}}$
is not a product of nth powers in
$[x,y]^{\frac {n}{2}}$
is not a product of nth powers in
![]() $F_2$
if
$F_2$
if
![]() $4|n$
(Proposition 7),
$4|n$
(Proposition 7),
![]() $M(2,2^k)$
satisfies the so-called
$M(2,2^k)$
satisfies the so-called
![]() $(k+3)$
th Morse identity but not the
$(k+3)$
th Morse identity but not the
![]() $(k+1)$
th (Proposition 15), and
$(k+1)$
th (Proposition 15), and
![]() $n^22^{\frac {5n^2}{16}-1}\le |M(2,n)|\le n^{(n-1)^2}$
if
$n^22^{\frac {5n^2}{16}-1}\le |M(2,n)|\le n^{(n-1)^2}$
if
![]() $n \ge 8$
is a power of
$n \ge 8$
is a power of
![]() $2$
(Theorem 18 and Proposition 22). We also give a lower bound for the order of the restricted Burnside group
$2$
(Theorem 18 and Proposition 22). We also give a lower bound for the order of the restricted Burnside group
![]() $R(2,8)$
in Proposition 23 and obtain a complete invariant for
$R(2,8)$
in Proposition 23 and obtain a complete invariant for
![]() $M(2,4)$
in Examples 17 and 21.
$M(2,4)$
in Examples 17 and 21.
This paper is the third in the winding invariant series, after [Reference Barmak7, Reference Barmak8], and it is a continuation of the results obtained in [Reference Barmak8, Section 6.3]. The combinatorial techniques introduced in this article can be used to study different equations over the group
![]() $F_2$
in the directions described in [Reference Barmak8].
$F_2$
in the directions described in [Reference Barmak8].
2 Background on the restricted Burnside problem and metabelian Burnside groups
In 1902, Burnside asked whether a finitely generated group of exponent n is necessarily finite [Reference Bruck12]. Any such group G generated by d elements is a quotient of the free group of exponent n,
![]() $B(d,n)=\langle x_1,x_2, \ldots , x_d| w^n, w\in F(x_1,x_2, \ldots , x_d)\rangle $
, also called the Burnside group of exponent n and d generators. Thus, Burnside question is about finiteness of Burnside groups. Burnside proved that
$B(d,n)=\langle x_1,x_2, \ldots , x_d| w^n, w\in F(x_1,x_2, \ldots , x_d)\rangle $
, also called the Burnside group of exponent n and d generators. Thus, Burnside question is about finiteness of Burnside groups. Burnside proved that
![]() $B(d,n)$
is finite for
$B(d,n)$
is finite for
![]() $n= 3$
and arbitrary d. Sanov proved in [Reference Sanov42] the finiteness of
$n= 3$
and arbitrary d. Sanov proved in [Reference Sanov42] the finiteness of
![]() $B(d,4)$
, and Hall [Reference Hall21] did it for
$B(d,4)$
, and Hall [Reference Hall21] did it for
![]() $B(d,6)$
. In 1968, Adian and Novikov proved that not all Burnside groups are finite. Indeed, they proved in [Reference Adian and Novikov3] that for
$B(d,6)$
. In 1968, Adian and Novikov proved that not all Burnside groups are finite. Indeed, they proved in [Reference Adian and Novikov3] that for
![]() $d\ge 2$
and n odd greater than or equal to
$d\ge 2$
and n odd greater than or equal to
![]() $4381$
,
$4381$
,
![]() $B(d,n)$
is infinite. Later, Adian [Reference Adian1] was able to replace the number
$B(d,n)$
is infinite. Later, Adian [Reference Adian1] was able to replace the number
![]() $4381$
by
$4381$
by
![]() $665$
. Ivanov proved in [Reference Ivanov27] that for
$665$
. Ivanov proved in [Reference Ivanov27] that for
![]() $n\ge 2^{48}$
divisible by
$n\ge 2^{48}$
divisible by
![]() $2^9$
,
$2^9$
,
![]() $B(d,n)$
is infinite. Later, Lysënok improved this result. In particular, there exist only finitely many exponents n for which
$B(d,n)$
is infinite. Later, Lysënok improved this result. In particular, there exist only finitely many exponents n for which
![]() $B(d,n)$
can be finite. The complete answer to Burnside’s problem is still unknown. For instance, it has not been decided yet whether
$B(d,n)$
can be finite. The complete answer to Burnside’s problem is still unknown. For instance, it has not been decided yet whether
![]() $B(2,5)$
and
$B(2,5)$
and
![]() $B(2,8)$
are finite.
$B(2,8)$
are finite.
In 1950, Magnus [Reference Magnus36] formulated a variant of Burnside’s problem, known as the restricted Burnside problem: Given
![]() $d,n\ge 1$
, is there a largest finite quotient
$d,n\ge 1$
, is there a largest finite quotient
![]() $R(d,n)$
of
$R(d,n)$
of
![]() $B(d,n)$
? This is equivalent to the following question: are there only finitely many finite groups (up to isomorphism) generated by d elements and with exponent n? Indeed, if we define N to be the intersection of all the finite-index subgroups of
$B(d,n)$
? This is equivalent to the following question: are there only finitely many finite groups (up to isomorphism) generated by d elements and with exponent n? Indeed, if we define N to be the intersection of all the finite-index subgroups of
![]() $B(d,n)$
, then N is normal and every d-generator finite group of exponent n is a homomorphic image of
$B(d,n)$
, then N is normal and every d-generator finite group of exponent n is a homomorphic image of
![]() $B(d,n)/N$
. The restricted Burnside problem asks whether
$B(d,n)/N$
. The restricted Burnside problem asks whether
![]() $B(d,n)/N$
is finite. In that case,
$B(d,n)/N$
is finite. In that case,
![]() $R(d,n)=B(d,n)/N$
is called the restricted Burnside group or universal finite d-generator group of exponent n. In 1958, Kostrikin [Reference Kostrikin29, Reference Kostrikin30, Reference Khukhro and Mazurov33] proved that
$R(d,n)=B(d,n)/N$
is called the restricted Burnside group or universal finite d-generator group of exponent n. In 1958, Kostrikin [Reference Kostrikin29, Reference Kostrikin30, Reference Khukhro and Mazurov33] proved that
![]() $R(d,p)$
exists for every prime p. This was previous to Adian–Novikov’s proof of the existence of infinite Burnside groups and was key in the development of their result (see [Reference Adian2]). Hall and Higman [Reference Hall and Higman23] had already reduced the proof of the restricted Burnside problem to the proof of the prime power exponent case under the assumption that there are only finitely many finite simple groups of a given exponent and that the outer automorphism group of any finite simple group is solvable. In 1990, Zel’manov [Reference Zel’manov53, Reference Zel’manov54] gave a positive answer to the restricted Burnside problem for prime power exponent, and this, together with Hall–Higman’s reduction and the classification of finite simple groups, provided a positive answer to the restricted Burnside problem for arbitrary exponent. One of the key elements in Kostrikin and Zel’manov’s work is the relationship with Engel identities in Lie algebras. In fact, for prime exponent p, the restricted Burnside problem can be reduced to the proof that every Lie algebra over
$R(d,p)$
exists for every prime p. This was previous to Adian–Novikov’s proof of the existence of infinite Burnside groups and was key in the development of their result (see [Reference Adian2]). Hall and Higman [Reference Hall and Higman23] had already reduced the proof of the restricted Burnside problem to the proof of the prime power exponent case under the assumption that there are only finitely many finite simple groups of a given exponent and that the outer automorphism group of any finite simple group is solvable. In 1990, Zel’manov [Reference Zel’manov53, Reference Zel’manov54] gave a positive answer to the restricted Burnside problem for prime power exponent, and this, together with Hall–Higman’s reduction and the classification of finite simple groups, provided a positive answer to the restricted Burnside problem for arbitrary exponent. One of the key elements in Kostrikin and Zel’manov’s work is the relationship with Engel identities in Lie algebras. In fact, for prime exponent p, the restricted Burnside problem can be reduced to the proof that every Lie algebra over
![]() $\mathbb {Z}_p$
which satisfies the so-called Engel identity
$\mathbb {Z}_p$
which satisfies the so-called Engel identity
![]() $E_{p-1}$
is locally nilpotent.
$E_{p-1}$
is locally nilpotent.
Although
![]() $R(d,n)$
is known to exist for each
$R(d,n)$
is known to exist for each
![]() $d,n$
, little is known about its structure, in general. In particular, the order of
$d,n$
, little is known about its structure, in general. In particular, the order of
![]() $R(d,n)$
is known in very few cases. For each d and each prime power n, the p-quotient algorithm can be used to obtain a consistent polycyclic/power-commutator presentation of
$R(d,n)$
is known in very few cases. For each d and each prime power n, the p-quotient algorithm can be used to obtain a consistent polycyclic/power-commutator presentation of
![]() $R(d,n)$
and then to compute its order (see [Reference Sims45, Section 11.7], [Reference O’Brien and Vaughan-Lee41, Reference Vaughan-Lee49]); however, a direct implementation of this algorithm takes in general too much time. Havas et al. [Reference Havas, Wall and Wamsley25] proved that
$R(d,n)$
and then to compute its order (see [Reference Sims45, Section 11.7], [Reference O’Brien and Vaughan-Lee41, Reference Vaughan-Lee49]); however, a direct implementation of this algorithm takes in general too much time. Havas et al. [Reference Havas, Wall and Wamsley25] proved that
![]() $|R(2,5)|=5^{34}$
, O’Brien and Vaughan-Lee [Reference O’Brien and Vaughan-Lee41] proved that
$|R(2,5)|=5^{34}$
, O’Brien and Vaughan-Lee [Reference O’Brien and Vaughan-Lee41] proved that
![]() $|R(2,7)|=7^{20416}$
, and Newman and O’Brien [Reference Nickel39] proved that
$|R(2,7)|=7^{20416}$
, and Newman and O’Brien [Reference Nickel39] proved that
![]() $|B(5,4)|=2^{2728}$
and
$|B(5,4)|=2^{2728}$
and
![]() $|R(3,5)|=5^{2282}$
. Furthermore,
$|R(3,5)|=5^{2282}$
. Furthermore,
![]() $|B(3,4)|=2^{69}$
[Reference Bayes, Kautsky and Wamsley9] and
$|B(3,4)|=2^{69}$
[Reference Bayes, Kautsky and Wamsley9] and
![]() $|B(4,4)|=2^{422}$
[Reference Alford, Havas and Newman4]. The order of
$|B(4,4)|=2^{422}$
[Reference Alford, Havas and Newman4]. The order of
![]() $B(d,4)$
for arbitrary d is still unknown. Upper and lower bounds for
$B(d,4)$
for arbitrary d is still unknown. Upper and lower bounds for
![]() $|R(d,n)|$
have been given by Vaughan-Lee and Zel’manov [Reference Vaughan-Lee and Zelmanov50–Reference Vaughan-Lee and Zelmanov52] and by Groves and Vaughan-Lee [Reference Groves and Vaughan-Lee16].
$|R(d,n)|$
have been given by Vaughan-Lee and Zel’manov [Reference Vaughan-Lee and Zelmanov50–Reference Vaughan-Lee and Zelmanov52] and by Groves and Vaughan-Lee [Reference Groves and Vaughan-Lee16].
It has long been known that there are connections between groups of prime power exponent and Engel conditions. The first Engel word is
![]() $e_1=[y,x]=yxy^{-1}x^{-1}\in F_2$
. The mth Engel word is defined by
$e_1=[y,x]=yxy^{-1}x^{-1}\in F_2$
. The mth Engel word is defined by
![]() $e_m=[y,e_{m-1}]\in F_2$
. A group G is said to be m-Engel if
$e_m=[y,e_{m-1}]\in F_2$
. A group G is said to be m-Engel if
![]() $e_m(a,b)=1\in G$
for every
$e_m(a,b)=1\in G$
for every
![]() $a,b\in G$
.Footnote
1
Every group of exponent
$a,b\in G$
.Footnote
1
Every group of exponent
![]() $3$
is
$3$
is
![]() $2$
-Engel. This appears in [Reference Levi35] but is already implicit in Burnside’s paper [Reference Bruck12]. It is equivalent to saying that
$2$
-Engel. This appears in [Reference Levi35] but is already implicit in Burnside’s paper [Reference Bruck12]. It is equivalent to saying that
![]() $e_2\in F_2$
is a product of cubes. Every group of exponent
$e_2\in F_2$
is a product of cubes. Every group of exponent
![]() $4$
is
$4$
is
![]() $5$
-Engel (
$5$
-Engel (
![]() $e_5$
is a product of fourth powers). Kostrikin observed [Reference Kostrikin31, Reference Kostrikin32] that if the sixth Engel word
$e_5$
is a product of fourth powers). Kostrikin observed [Reference Kostrikin31, Reference Kostrikin32] that if the sixth Engel word
![]() $e_6$
is not a product of fifth powers in
$e_6$
is not a product of fifth powers in
![]() $F_2$
, then
$F_2$
, then
![]() $B(2,5)$
is infinite.
$B(2,5)$
is infinite.
In the quest for finding a solution to the restricted Burnside problem, before Zel’manov’s proof, other relations apart from Engel conditions had been searched among groups of prime power exponent. Some papers have explored this path by imposing extra relations to the groups, in particular, the metabelian law. Recall that a group G is termed metabelian if
![]() $G''=1$
. Every d-generated metabelian group of exponent n is a quotient of the free metabelian group
$G''=1$
. Every d-generated metabelian group of exponent n is a quotient of the free metabelian group
![]() $M(d,n)$
of exponent n. If G is a group and
$M(d,n)$
of exponent n. If G is a group and
![]() $n\ge 1$
, we denote by
$n\ge 1$
, we denote by
![]() $G^n$
the subgroup of G generated by the nth powers. If
$G^n$
the subgroup of G generated by the nth powers. If
![]() $F_d$
denotes the free group of rank d, then
$F_d$
denotes the free group of rank d, then
![]() $M(d,n)=\frac {F_d}{F_d^nF_d''}$
. As explained by Newman in [Reference Newman38], one advantage of these groups is that they are always finite. Indeed, if we define
$M(d,n)=\frac {F_d}{F_d^nF_d''}$
. As explained by Newman in [Reference Newman38], one advantage of these groups is that they are always finite. Indeed, if we define
![]() $R=F_d^n F_d'$
and
$R=F_d^n F_d'$
and
![]() $S=R^nR'$
, then
$S=R^nR'$
, then
![]() $|F_d:R|=n^d$
, so by the Schreier formula,
$|F_d:R|=n^d$
, so by the Schreier formula,
![]() $\textrm {rk}(R)=1+(d-1)n^d$
. Similarly,
$\textrm {rk}(R)=1+(d-1)n^d$
. Similarly,
![]() $|R:S|=n^{\textrm {rk}(R)}=n^{1+(d-1)n^d}$
, so
$|R:S|=n^{\textrm {rk}(R)}=n^{1+(d-1)n^d}$
, so
![]() $|F_d/S|=n^{1+d+(d-1)n^d}$
. On the other hand, it is easy to see that
$|F_d/S|=n^{1+d+(d-1)n^d}$
. On the other hand, it is easy to see that
![]() $S\leqslant F_d^n F_d''$
. Thus,
$S\leqslant F_d^n F_d''$
. Thus,
![]() $|M(d,n)|\leq n^{1+d+(d-1)n^d}$
. If
$|M(d,n)|\leq n^{1+d+(d-1)n^d}$
. If
![]() $n=p^k$
for p a prime, Newman computes also a lower bound for
$n=p^k$
for p a prime, Newman computes also a lower bound for
![]() $|M(d,n)|$
, which is
$|M(d,n)|$
, which is
![]() $p^{1+d(k-1)+(d-1)p^{(k-1)d}}$
. This is explained later in this article. Since
$p^{1+d(k-1)+(d-1)p^{(k-1)d}}$
. This is explained later in this article. Since
![]() $M(d,n)$
is finite, its order gives a lower bound for
$M(d,n)$
is finite, its order gives a lower bound for
![]() $|R(d,n)|$
. Moreover, if we know that a certain identity does not hold in
$|R(d,n)|$
. Moreover, if we know that a certain identity does not hold in
![]() $M(d,n)$
then it will not hold in
$M(d,n)$
then it will not hold in
![]() $R(d,n)$
nor in
$R(d,n)$
nor in
![]() $B(d,n)$
. Recall that for a group G, the lower central series is defined by
$B(d,n)$
. Recall that for a group G, the lower central series is defined by
![]() $\gamma _1(G)=G$
and
$\gamma _1(G)=G$
and
![]() $\gamma _{l+1}(G)=[G, \gamma _l(G)]$
for
$\gamma _{l+1}(G)=[G, \gamma _l(G)]$
for
![]() $l\ge 1$
. A group G is nilpotent if there exists
$l\ge 1$
. A group G is nilpotent if there exists
![]() $l\ge 0$
such that
$l\ge 0$
such that
![]() $\gamma _{l+1}(G)=1$
, and the smallest l with this property is the nilpotency class of G. If n is a prime power,
$\gamma _{l+1}(G)=1$
, and the smallest l with this property is the nilpotency class of G. If n is a prime power,
![]() $M(d,n)$
is nilpotent, and its class is known in many cases by results of Meier-Wunderli [Reference Meier-Wunderli37], Bachmuth et al. [Reference Bachmuth, Heilbronn and Mochizuki6], Dark–Newell [Reference Dark and Newell13], Gupta et al. [Reference Gupta and Tobin19], and Newman [Reference Newman38]. In particular, the class of
$M(d,n)$
is nilpotent, and its class is known in many cases by results of Meier-Wunderli [Reference Meier-Wunderli37], Bachmuth et al. [Reference Bachmuth, Heilbronn and Mochizuki6], Dark–Newell [Reference Dark and Newell13], Gupta et al. [Reference Gupta and Tobin19], and Newman [Reference Newman38]. In particular, the class of
![]() $M(2,p^k)$
is
$M(2,p^k)$
is
![]() $k(p-1)p^{k-1}$
. The order of
$k(p-1)p^{k-1}$
. The order of
![]() $M(d,n)$
is known when n is prime (see [Reference Meier-Wunderli37, Reference Newman38]), but the general case is open. Even for
$M(d,n)$
is known when n is prime (see [Reference Meier-Wunderli37, Reference Newman38]), but the general case is open. Even for
![]() $d=p=2$
, Newman’s bounds only give
$d=p=2$
, Newman’s bounds only give
![]() $n^22^{\frac {n^2}{4}-1} \le |M(2,n)|\le n^{n^2+3}$
, and it is not known, asymptotically, which of the two bounds is closer to reality. Given a positive integer d and a prime power n, we can compute
$n^22^{\frac {n^2}{4}-1} \le |M(2,n)|\le n^{n^2+3}$
, and it is not known, asymptotically, which of the two bounds is closer to reality. Given a positive integer d and a prime power n, we can compute
![]() $|M(d,n)|$
from any finite presentation using coset enumeration. Moreover, the nilpotent quotient algorithm computes a consistent power-commutator presentation (see [Reference Havas and Newman24, Reference Newman38, Reference Vaughan-Lee49]) for
$|M(d,n)|$
from any finite presentation using coset enumeration. Moreover, the nilpotent quotient algorithm computes a consistent power-commutator presentation (see [Reference Havas and Newman24, Reference Newman38, Reference Vaughan-Lee49]) for
![]() $M(d,n)$
from which its order can be directly read off. However, the number of operations needed to complete this task is unknown, and
$M(d,n)$
from which its order can be directly read off. However, the number of operations needed to complete this task is unknown, and
![]() $|M(d,n)|$
has been computed in very few cases. Once we have such a presentation, it can be decided whether an arbitrary word
$|M(d,n)|$
has been computed in very few cases. Once we have such a presentation, it can be decided whether an arbitrary word
![]() $w\in F(x_1,x_2, \ldots , x_d)$
is trivial in
$w\in F(x_1,x_2, \ldots , x_d)$
is trivial in
![]() $M(d,n)$
, but again, there is no general method known to do this for arbitrary
$M(d,n)$
, but again, there is no general method known to do this for arbitrary
![]() $w,d,n$
without implementation of this algorithm or other variants. For example, apart from the cases in which n is prime, the order of
$w,d,n$
without implementation of this algorithm or other variants. For example, apart from the cases in which n is prime, the order of
![]() $M(d,n)$
is known in the following cases:
$M(d,n)$
is known in the following cases:
![]() $(d,n)\in \{(2,4),(3,4),(4,4),(5,4),(2,8),(3,8),(4,8),(2,9),(3,9)\}$
(computed by Gupta–Tobin [Reference Gupta, Newman and Tobin20], Hermanns [Reference Hermanns26], and Newman [Reference Newman38]). The order of
$(d,n)\in \{(2,4),(3,4),(4,4),(5,4),(2,8),(3,8),(4,8),(2,9),(3,9)\}$
(computed by Gupta–Tobin [Reference Gupta, Newman and Tobin20], Hermanns [Reference Hermanns26], and Newman [Reference Newman38]). The order of
![]() $M(2,16)$
is known to be smaller than or equal to
$M(2,16)$
is known to be smaller than or equal to
![]() $2^{376}$
[Reference Newman38]. For p prime and
$2^{376}$
[Reference Newman38]. For p prime and
![]() $n=p^2$
, Skopin [Reference Skopin46] has shown that
$n=p^2$
, Skopin [Reference Skopin46] has shown that
![]() $|M(2,n)|\le p^{\frac {3}{2}p^4-\frac {3}{2}p^3-2p^2+p+5}$
, which improves Newman’s general bound that gives here
$|M(2,n)|\le p^{\frac {3}{2}p^4-\frac {3}{2}p^3-2p^2+p+5}$
, which improves Newman’s general bound that gives here
![]() $|M(2,n)|\le p^{2p^4+6}$
. In [Reference Skopin47], Skopin proves that the largest class
$|M(2,n)|\le p^{2p^4+6}$
. In [Reference Skopin47], Skopin proves that the largest class
![]() $36$
quotient
$36$
quotient
![]() $M(2,27)/\gamma _{37}(M(2,27))$
of
$M(2,27)/\gamma _{37}(M(2,27))$
of
![]() $M(2,27)$
has order less than or equal to
$M(2,27)$
has order less than or equal to
![]() $3^{648}$
.
$3^{648}$
.
3 Horizontal invariants
We start by recalling the constructions and results of [Reference Barmak8] that we will need. We will also recall some of the proofs for the sake of completeness and in order to make clear subsequent ideas.
An element
![]() $z\in F_2'$
in the derived subgroup of the free group
$z\in F_2'$
in the derived subgroup of the free group
![]() $F_2$
generated by
$F_2$
generated by
![]() $x,y$
is a word
$x,y$
is a word
![]() $x_1^{\epsilon _1}x_2^{\epsilon _2}\ldots x_l^{\epsilon _l}$
in the letters
$x_1^{\epsilon _1}x_2^{\epsilon _2}\ldots x_l^{\epsilon _l}$
in the letters
![]() $x,y$
with total exponents
$x,y$
with total exponents
![]() $\exp (x,z)=\exp (y,z) =0$
. One such word has an associated closed curve
$\exp (x,z)=\exp (y,z) =0$
. One such word has an associated closed curve
![]() $\gamma _z$
in the integer grid
$\gamma _z$
in the integer grid
![]() $\mathbb {R} \times \mathbb {Z} \cup \mathbb {Z} \times \mathbb {R} \subseteq \mathbb {R}^2$
which begins in the origin and is a concatenation of curves
$\mathbb {R} \times \mathbb {Z} \cup \mathbb {Z} \times \mathbb {R} \subseteq \mathbb {R}^2$
which begins in the origin and is a concatenation of curves
![]() $\gamma _1, \gamma _2, \ldots , \gamma _l$
. The curve
$\gamma _1, \gamma _2, \ldots , \gamma _l$
. The curve
![]() $\gamma _i$
moves one unit horizontally if
$\gamma _i$
moves one unit horizontally if
![]() $x_i=x$
and vertically if
$x_i=x$
and vertically if
![]() $x_i=y$
, to the right or upward if
$x_i=y$
, to the right or upward if
![]() $\epsilon _i=1$
and to the left or downward if
$\epsilon _i=1$
and to the left or downward if
![]() $\epsilon _i=-1$
. The winding invariant of z is the Laurent polynomial
$\epsilon _i=-1$
. The winding invariant of z is the Laurent polynomial
![]() $P_z=\sum \limits _{i,j\in \mathbb {Z}} a_{i,j}X^iY^j \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, where
$P_z=\sum \limits _{i,j\in \mathbb {Z}} a_{i,j}X^iY^j \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, where
![]() $a_{i,j}$
is the winding number of
$a_{i,j}$
is the winding number of
![]() $\gamma _z$
around
$\gamma _z$
around
![]() $(i+\frac {1}{2}, j+\frac {1}{2})\in \mathbb {R}^2$
. For instance, if
$(i+\frac {1}{2}, j+\frac {1}{2})\in \mathbb {R}^2$
. For instance, if
![]() $z=[x,y]=xyx^{-1}y^{-1}$
, the curve
$z=[x,y]=xyx^{-1}y^{-1}$
, the curve
![]() $\gamma _z$
traverses the boundary of the square with vertices
$\gamma _z$
traverses the boundary of the square with vertices
![]() $(0,0), (1,0), (1,1), (0,1)$
once counterclockwise, so
$(0,0), (1,0), (1,1), (0,1)$
once counterclockwise, so
![]() $P_z=1 \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. The winding invariant map
$P_z=1 \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. The winding invariant map
![]() $W:F_2'\to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
which maps z to
$W:F_2'\to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
which maps z to
![]() $P_z$
has many different interpretations [Reference Barmak8]. Clearly, W is a group homomorphism. It is surjective, and its kernel is
$P_z$
has many different interpretations [Reference Barmak8]. Clearly, W is a group homomorphism. It is surjective, and its kernel is
![]() $F_2''$
[Reference Barmak8, Theorem 14], and thus, it induces an isomorphism
$F_2''$
[Reference Barmak8, Theorem 14], and thus, it induces an isomorphism
![]() $M_2' \to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
from the derived subgroup of the free metabelian group
$M_2' \to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
from the derived subgroup of the free metabelian group
![]() $M_2=F_2/F_2''$
of rank
$M_2=F_2/F_2''$
of rank
![]() $2$
. This map will also be denoted by W.
$2$
. This map will also be denoted by W.
An elementary property which follows easily from the definition is the following result.
Remark 1 If
![]() $z\in F_2'$
and
$z\in F_2'$
and
![]() $u\in F_2$
, then
$u\in F_2$
, then
![]() $P_{uzu^{-1}}=X^iY^jP_z$
where
$P_{uzu^{-1}}=X^iY^jP_z$
where
![]() $(i,j)=(\exp (x,u),\exp (y,u))$
. Therefore,
$(i,j)=(\exp (x,u),\exp (y,u))$
. Therefore,
![]() $P_{[u,z]}=(X^iY^j-1)P_z$
.
$P_{[u,z]}=(X^iY^j-1)P_z$
.
We recall the following result from [Reference Barmak8].
Proposition 2 [Reference Barmak8, Proposition 8]
Let
![]() $n\ge 1$
. If
$n\ge 1$
. If
![]() $z\in F_2'$
is a product of two nth powers, then
$z\in F_2'$
is a product of two nth powers, then
![]() $P_z$
is a multiple of
$P_z$
is a multiple of
![]() $1+m+m^2+\cdots +m^{n-1}$
for some monomial
$1+m+m^2+\cdots +m^{n-1}$
for some monomial
![]() $m=X^iY^j$
.
$m=X^iY^j$
.
Proof If
![]() $z=a^nb^n=(ab)b^{-1}(ab)bb^{-2}(ab)b^2\ldots b^{1-n}(ab)b^{n-1}$
, then
$z=a^nb^n=(ab)b^{-1}(ab)bb^{-2}(ab)b^2\ldots b^{1-n}(ab)b^{n-1}$
, then
![]() $ab\in F_2'$
, and by Remark 1,
$ab\in F_2'$
, and by Remark 1,
![]() $P_{z}=P_{ab}(1+m+m^2+\cdots +m^{n-1})$
, for
$P_{z}=P_{ab}(1+m+m^2+\cdots +m^{n-1})$
, for
![]() $m=X^{\exp (x,b^{-1})}Y^{\exp (y,b^{-1})}$
.▪
$m=X^{\exp (x,b^{-1})}Y^{\exp (y,b^{-1})}$
.▪
In [Reference Barmak8], we proved that the area invariant
![]() $A:F_2' \to \mathbb {Z}$
defined by
$A:F_2' \to \mathbb {Z}$
defined by
![]() $A(z)=P_z(1,1)$
maps a product of nth powers in
$A(z)=P_z(1,1)$
maps a product of nth powers in
![]() $F_2$
to a multiple of
$F_2$
to a multiple of
![]() $\frac {n}{2}$
when n is even and to a multiple of n when n is odd. In particular, a product of fourth powers has even area. This is not a sufficient condition for an element
$\frac {n}{2}$
when n is even and to a multiple of n when n is odd. In particular, a product of fourth powers has even area. This is not a sufficient condition for an element
![]() $z\in M_2'$
to be a product of fourth powers in
$z\in M_2'$
to be a product of fourth powers in
![]() $M_2$
. There is another invariant
$M_2$
. There is another invariant
![]() $\kappa :F_2' \to \mathbb {Z}$
which, instead of adding all the coefficients of
$\kappa :F_2' \to \mathbb {Z}$
which, instead of adding all the coefficients of
![]() $P_z$
, adds some of them and subtracts others. A product of fourth powers must have
$P_z$
, adds some of them and subtracts others. A product of fourth powers must have
![]() $\kappa (z)$
divisible by
$\kappa (z)$
divisible by
![]() $4$
. The main tools that we develop in this article are different generalizations of the invariant
$4$
. The main tools that we develop in this article are different generalizations of the invariant
![]() $\kappa $
, which take into account higher powers of
$\kappa $
, which take into account higher powers of
![]() $2$
.
$2$
.
In Section 9, we give an example in which the invariant technique successfully describes a variety of groups. We will see that the area invariant completely characterizes the free nilpotent group
![]() $N(2,n)$
of class
$N(2,n)$
of class
![]() $2$
, rank
$2$
, rank
![]() $2$
, and exponent n for any
$2$
, and exponent n for any
![]() $n\ge 1$
, determining an isomorphism
$n\ge 1$
, determining an isomorphism
![]() $\overline {A}:N(2,n)' \to \mathbb {Z}_l$
, where
$\overline {A}:N(2,n)' \to \mathbb {Z}_l$
, where
![]() $l=\frac {n}{2}$
if n is even and
$l=\frac {n}{2}$
if n is even and
![]() $l=n$
if n is odd. In particular, the order
$l=n$
if n is odd. In particular, the order
![]() $|N(2,n)|$
is
$|N(2,n)|$
is
![]() $\frac {n^3}{2}$
or
$\frac {n^3}{2}$
or
![]() $n^3$
. For the free metabelian group
$n^3$
. For the free metabelian group
![]() $M(2,n)$
of exponent n, the problem is much harder, and other invariants will be introduced.
$M(2,n)$
of exponent n, the problem is much harder, and other invariants will be introduced.
Let
![]() $k\ge 1, n=2^k$
. A good coloring of
$k\ge 1, n=2^k$
. A good coloring of
![]() $\mathbb {Z}_n$
is a function
$\mathbb {Z}_n$
is a function
![]() $c:\mathbb {Z}_n\to \{ \textrm {black}, \textrm {white}\}$
, which satisfies that for every
$c:\mathbb {Z}_n\to \{ \textrm {black}, \textrm {white}\}$
, which satisfies that for every
![]() $a\in \mathbb {Z}_n$
, the color
$a\in \mathbb {Z}_n$
, the color
![]() $c(a)$
of a is different from the color
$c(a)$
of a is different from the color
![]() $c(a+\frac {n}{2})$
of
$c(a+\frac {n}{2})$
of
![]() $a+\frac {n}{2}$
. A function
$a+\frac {n}{2}$
. A function
![]() $\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
together with a good coloring c induces a coloring of the squares in the grid
$\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
together with a good coloring c induces a coloring of the squares in the grid
![]() $\mathbb {R} \times \mathbb {Z} \cup \mathbb {Z} \times \mathbb {R}$
: the square (whose lower left corner is)
$\mathbb {R} \times \mathbb {Z} \cup \mathbb {Z} \times \mathbb {R}$
: the square (whose lower left corner is)
![]() $(i,j)$
is painted with color
$(i,j)$
is painted with color
![]() $c\varphi (i,j)$
. The invariant
$c\varphi (i,j)$
. The invariant
![]() $\Lambda =\Lambda _{\varphi , c}:\mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n$
associated with
$\Lambda =\Lambda _{\varphi , c}:\mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n$
associated with
![]() $\varphi $
and c is defined as follows. Given
$\varphi $
and c is defined as follows. Given
![]() $P \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, define
$P \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, define
Here,
![]() $P\{(i,j)\}$
denotes the coefficient of the monomial
$P\{(i,j)\}$
denotes the coefficient of the monomial
![]() $X^iY^j$
. The composition
$X^iY^j$
. The composition
![]() $\Lambda W:F_2'\to \mathbb {Z}_n$
will also be denoted by
$\Lambda W:F_2'\to \mathbb {Z}_n$
will also be denoted by
![]() $\Lambda =\Lambda _{\varphi , c}$
. That is, for
$\Lambda =\Lambda _{\varphi , c}$
. That is, for
![]() $z\in F_2'$
,
$z\in F_2'$
,
![]() $\Lambda (z)=\Lambda (P_z)$
. Of course,
$\Lambda (z)=\Lambda (P_z)$
. Of course,
![]() $\Lambda : F_2'\to \mathbb {Z}_n$
is a group homomorphism. Since
$\Lambda : F_2'\to \mathbb {Z}_n$
is a group homomorphism. Since
![]() $\textrm {ker}(W)=F_2''$
,
$\textrm {ker}(W)=F_2''$
,
![]() $\Lambda $
induces a map
$\Lambda $
induces a map
![]() $M_2'=F_2' /F_2''\to \mathbb {Z}_n$
, which is denoted
$M_2'=F_2' /F_2''\to \mathbb {Z}_n$
, which is denoted
![]() $\Lambda $
as well. Given a region A of the plane, which is a union of squares in the grid, we define the invariant
$\Lambda $
as well. Given a region A of the plane, which is a union of squares in the grid, we define the invariant
![]() $\Lambda (A)$
of A as the number of black squares in A minus the number of white squares, modulo n.
$\Lambda (A)$
of A as the number of black squares in A minus the number of white squares, modulo n.
Example 3 Let
![]() $k=2$
, so
$k=2$
, so
![]() $n=4$
, and let
$n=4$
, and let
![]() $c:\mathbb {Z}_4 \to \{\textrm {black, white}\}$
be the coloring that paints
$c:\mathbb {Z}_4 \to \{\textrm {black, white}\}$
be the coloring that paints
![]() $0,1$
with black and
$0,1$
with black and
![]() $2,3$
with white. Let
$2,3$
with white. Let
![]() $\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_4$
be defined by
$\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_4$
be defined by
![]() $\varphi (a,b)=b \in \mathbb {Z}_4$
. The coloring associated to
$\varphi (a,b)=b \in \mathbb {Z}_4$
. The coloring associated to
![]() $\varphi $
and c is illustrated in Figure 1, at the left. All the rows congruent with
$\varphi $
and c is illustrated in Figure 1, at the left. All the rows congruent with
![]() $0$
or
$0$
or
![]() $1$
modulo
$1$
modulo
![]() $4$
are painted with black, whereas the remaining rows are painted with white.
$4$
are painted with black, whereas the remaining rows are painted with white.

Figure 1: The coloring associated to
![]() $\varphi $
and c, the curve
$\varphi $
and c, the curve
![]() $\gamma _z$
with the winding numbers, and the superposition which computes
$\gamma _z$
with the winding numbers, and the superposition which computes
![]() $\Lambda (z)$
.
$\Lambda (z)$
.
Let
![]() $z=x^2yx^{-1}y^{-1}xy^3x^{-3}yxy^{-4}\in F_2'$
. The curve
$z=x^2yx^{-1}y^{-1}xy^3x^{-3}yxy^{-4}\in F_2'$
. The curve
![]() $\gamma _z$
is depicted in the center of Figure 1, together with the (nonzero) winding numbers of the curve around the squares. The winding invariant of z is thus
$\gamma _z$
is depicted in the center of Figure 1, together with the (nonzero) winding numbers of the curve around the squares. The winding invariant of z is thus
![]() $P_z=1+2X+Y+XY+Y^2+XY^2-X^{-1}Y^3\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. The invariant
$P_z=1+2X+Y+XY+Y^2+XY^2-X^{-1}Y^3\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. The invariant
![]() $\Lambda _{\varphi ,c}(z)$
is just the sum of the coefficients in black squares minus the sum of the coefficients in white squares. That is,
$\Lambda _{\varphi ,c}(z)$
is just the sum of the coefficients in black squares minus the sum of the coefficients in white squares. That is,
![]() $\Lambda (z)=1+2+1+1-(1+1-1)=0\in \mathbb {Z}_4$
.
$\Lambda (z)=1+2+1+1-(1+1-1)=0\in \mathbb {Z}_4$
.
Lemma 4 Let
![]() $n,d$
be positive integers such that
$n,d$
be positive integers such that
![]() $2d$
divides n. Then, the elements of the integer interval
$2d$
divides n. Then, the elements of the integer interval
![]() $[n]=\{0,1,2,\ldots , n-1\}$
can be matched in such a way that matched elements differ in d.
$[n]=\{0,1,2,\ldots , n-1\}$
can be matched in such a way that matched elements differ in d.
Proof For
![]() $0\le i \le d-1$
, match i with
$0\le i \le d-1$
, match i with
![]() $i+d$
. These pairs cover the set
$i+d$
. These pairs cover the set
![]() $[2d]$
, and translations of them cover the whole set
$[2d]$
, and translations of them cover the whole set
![]() $[n]$
.▪
$[n]$
.▪
Lemma 5 Let
![]() $k\ge 1$
,
$k\ge 1$
,
![]() $n=2^k$
. Let
$n=2^k$
. Let
![]() $c:\mathbb {Z}_n \to \{ \textrm {black, white} \}$
be a good coloring.
$c:\mathbb {Z}_n \to \{ \textrm {black, white} \}$
be a good coloring.
![]() $\mathrm{(i)}$
Let
$\mathrm{(i)}$
Let
![]() $a, a+b, a+2b, \ldots , a+(n-1)b$
be an arithmetic progression of length n in
$a, a+b, a+2b, \ldots , a+(n-1)b$
be an arithmetic progression of length n in
![]() $\mathbb {Z}$
. When we see this progression in
$\mathbb {Z}$
. When we see this progression in
![]() $\mathbb {Z}_n$
, the number of black terms minus the number of white terms is a multiple of n.
$\mathbb {Z}_n$
, the number of black terms minus the number of white terms is a multiple of n.
![]() $\mathrm{(ii)}$
Let
$\mathrm{(ii)}$
Let
![]() $a, a+b, a+2b, \ldots , a+(\frac {n}{2}-1)b$
be an arithmetic progression of length
$a, a+b, a+2b, \ldots , a+(\frac {n}{2}-1)b$
be an arithmetic progression of length
![]() $\frac {n}{2}$
in
$\frac {n}{2}$
in
![]() $\mathbb {Z}$
with b even. When we see this progression in
$\mathbb {Z}$
with b even. When we see this progression in
![]() $\mathbb {Z}_n$
, the number of black terms minus the number of white terms is a multiple of
$\mathbb {Z}_n$
, the number of black terms minus the number of white terms is a multiple of
![]() $\frac {n}{2}$
. Moreover, if n divides b, this number is
$\frac {n}{2}$
. Moreover, if n divides b, this number is
![]() $\frac {n}{2}$
modulo n, and if n does not divide b, this number is
$\frac {n}{2}$
modulo n, and if n does not divide b, this number is
![]() $0$
modulo n.
$0$
modulo n.
Proof We prove first part (i). If n divides b, the n numbers in the progression have the same color. Suppose then that
![]() $n \nmid b$
. Let
$n \nmid b$
. Let
![]() $d\in \mathbb {Z}$
be the greatest common divisor of n and b. By assumption
$d\in \mathbb {Z}$
be the greatest common divisor of n and b. By assumption
![]() $d<n$
, so
$d<n$
, so
![]() $\frac {n}{2d} \in \mathbb {Z}$
and
$\frac {n}{2d} \in \mathbb {Z}$
and
![]() $2 \frac {n}{2d}$
divides n. By Lemma 4,
$2 \frac {n}{2d}$
divides n. By Lemma 4,
![]() $[n]$
admits a matching with matched elements of difference
$[n]$
admits a matching with matched elements of difference
![]() $\frac {n}{2d}$
. Thus, the set
$\frac {n}{2d}$
. Thus, the set
![]() $a+b[n]=\{a,a+b, a+2b, \ldots , a+(n-1)b\}$
admits a matching with matched elements of difference
$a+b[n]=\{a,a+b, a+2b, \ldots , a+(n-1)b\}$
admits a matching with matched elements of difference
![]() $b\frac {n}{2d}$
. But
$b\frac {n}{2d}$
. But
![]() $b\frac {n}{2d}=\frac {b}{d}\frac {n}{2}$
is an odd multiple of
$b\frac {n}{2d}=\frac {b}{d}\frac {n}{2}$
is an odd multiple of
![]() $\frac {n}{2}$
. Since c is good, matched elements have different colors, so the sequence has the same number of black terms and white terms.
$\frac {n}{2}$
. Since c is good, matched elements have different colors, so the sequence has the same number of black terms and white terms.
For part (ii), if
![]() $n | b$
, the
$n | b$
, the
![]() $\frac {n}{2}$
terms of the progression have the same color. Otherwise,
$\frac {n}{2}$
terms of the progression have the same color. Otherwise,
![]() $d=\mathrm {gcd}(n,b)<n$
, and d is even by hypothesis. Then,
$d=\mathrm {gcd}(n,b)<n$
, and d is even by hypothesis. Then,
![]() $2 \frac {n}{2d}$
divides
$2 \frac {n}{2d}$
divides
![]() $\frac {n}{2}$
, and by Lemma 4,
$\frac {n}{2}$
, and by Lemma 4,
![]() $[\frac {n}{2}]$
can by matched with difference
$[\frac {n}{2}]$
can by matched with difference
![]() $\frac {n}{2d}$
, so
$\frac {n}{2d}$
, so
![]() $a+b[\frac {n}{2}]$
admits a matching with difference
$a+b[\frac {n}{2}]$
admits a matching with difference
![]() $b\frac {n}{2d}$
, and as in the first case matched elements receive opposite colors.▪
$b\frac {n}{2d}$
, and as in the first case matched elements receive opposite colors.▪
Let
![]() $n=2^k$
for some
$n=2^k$
for some
![]() $k\ge 2$
. Let
$k\ge 2$
. Let
![]() $c:\mathbb {Z}_n \to \{\textrm {black, white}\}$
be a good coloring. Define a group homomorphism
$c:\mathbb {Z}_n \to \{\textrm {black, white}\}$
be a good coloring. Define a group homomorphism
![]() $\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
by
$\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
by
![]() $\varphi (1,0)=0$
,
$\varphi (1,0)=0$
,
![]() $\varphi (0,1)=1$
. Let
$\varphi (0,1)=1$
. Let
![]() $\textbf {h}=\Lambda _{\varphi , c}:F_2' \to \mathbb {Z}_n$
be the associated invariant. It is called the horizontal invariant associated to c. In this case, all the squares in a row are painted with the same color. If two rows are
$\textbf {h}=\Lambda _{\varphi , c}:F_2' \to \mathbb {Z}_n$
be the associated invariant. It is called the horizontal invariant associated to c. In this case, all the squares in a row are painted with the same color. If two rows are
![]() $\frac {n}{2}$
units away one from the other, then they are painted with opposite colors. This says in particular that among n consecutive squares in a column, half of them are black and the other half are white. If the distance between two rows is a multiple of n, they have the same color. The invariant in Example 3 is of this kind.
$\frac {n}{2}$
units away one from the other, then they are painted with opposite colors. This says in particular that among n consecutive squares in a column, half of them are black and the other half are white. If the distance between two rows is a multiple of n, they have the same color. The invariant in Example 3 is of this kind.
Theorem 6 Let
![]() $n=2^k$
for some
$n=2^k$
for some
![]() $k\ge 2$
. Let c be a good coloring of
$k\ge 2$
. Let c be a good coloring of
![]() $\mathbb {Z}_n$
. If
$\mathbb {Z}_n$
. If
![]() $z\in F_2'$
lies in
$z\in F_2'$
lies in
![]() $F_2^nF_2''$
, then
$F_2^nF_2''$
, then
![]() $\textbf {h} (z)=0 \in \mathbb {Z}_n$
. In particular, any element in
$\textbf {h} (z)=0 \in \mathbb {Z}_n$
. In particular, any element in
![]() $F_2'$
which is a product of nth powers of elements in
$F_2'$
which is a product of nth powers of elements in
![]() $F_2$
has trivial
$F_2$
has trivial
![]() $\textbf {h}$
-invariant.
$\textbf {h}$
-invariant.
Proof The proof is similar to that of Theorem 59 in [Reference Barmak8]. Let
![]() $z\in F_2' \cap F_2^n F_2''$
. Since
$z\in F_2' \cap F_2^n F_2''$
. Since
![]() $F_2'' =\ker W \leqslant \ker \textbf {h}$
, we may assume
$F_2'' =\ker W \leqslant \ker \textbf {h}$
, we may assume
![]() $z\in F_2' \cap F_2^n$
. Suppose then
$z\in F_2' \cap F_2^n$
. Suppose then
![]() $z=u_1^nu_2^n\ldots u_r^n$
for some
$z=u_1^nu_2^n\ldots u_r^n$
for some
![]() $u_i\in F_2$
.
$u_i\in F_2$
.
Step 1: We may assume
![]() $r=3$
. Indeed, we can find
$r=3$
. Indeed, we can find
![]() $v_2,v_3, \ldots , v_{r-2}\in F_2$
such that
$v_2,v_3, \ldots , v_{r-2}\in F_2$
such that
![]() $u_1^nu_2^nv_2^n$
,
$u_1^nu_2^nv_2^n$
,
![]() $v_2^{-n}u_3^nv_3^n$
,
$v_2^{-n}u_3^nv_3^n$
,
![]() $v_3^{-n}u_4^nv_4^n, \ldots , v_{r-3}^{-n}u_{r-2}^nv_{r-2}^n$
,
$v_3^{-n}u_4^nv_4^n, \ldots , v_{r-3}^{-n}u_{r-2}^nv_{r-2}^n$
,
![]() $v_{r-2}^{-n}u_{r-1}^nu_{r}^n$
are all in
$v_{r-2}^{-n}u_{r-1}^nu_{r}^n$
are all in
![]() $F_2'$
. Since
$F_2'$
. Since
![]() $\textbf {h}: F_2'\to \mathbb {Z}_n$
is a group homomorphism, we may then assume that
$\textbf {h}: F_2'\to \mathbb {Z}_n$
is a group homomorphism, we may then assume that
![]() $r=3$
. Suppose then that
$r=3$
. Suppose then that
![]() $z=u^nv^nw^n$
for certain
$z=u^nv^nw^n$
for certain
![]() $u,v,w\in F_2$
.
$u,v,w\in F_2$
.
Step 2: We prove that
![]() $\textbf {h} (z)$
depends only on the exponents of
$\textbf {h} (z)$
depends only on the exponents of
![]() $x,y$
in
$x,y$
in
![]() $u,v,w$
. If we replace u by another element
$u,v,w$
. If we replace u by another element
![]() $\widetilde {u}\in F_2$
with same exponents in x and y, then
$\widetilde {u}\in F_2$
with same exponents in x and y, then
![]() $\widetilde {z}=\widetilde {u}^nv^nw^n$
satisfies that
$\widetilde {z}=\widetilde {u}^nv^nw^n$
satisfies that
![]() $z^{-1}\widetilde {z}$
is a conjugate of an element in
$z^{-1}\widetilde {z}$
is a conjugate of an element in
![]() $F_2'$
which is product of two nth powers. Then, by Proposition 2,
$F_2'$
which is product of two nth powers. Then, by Proposition 2,
![]() $P_{z^{-1}\widetilde {z}}$
is a multiple of
$P_{z^{-1}\widetilde {z}}$
is a multiple of
![]() $1+m+m^2+\cdots +m^{n-1}$
for some monomial m. The same happens if we replace v or w by other elements with the same exponents. So, it suffices to check that for monomials
$1+m+m^2+\cdots +m^{n-1}$
for some monomial m. The same happens if we replace v or w by other elements with the same exponents. So, it suffices to check that for monomials
![]() $m=X^iY^j,m'=X^{i'}Y^{j'}$
, the polynomial
$m=X^iY^j,m'=X^{i'}Y^{j'}$
, the polynomial
![]() $P=m'(1+m+m^2+\cdots +m^{n-1})$
has invariant
$P=m'(1+m+m^2+\cdots +m^{n-1})$
has invariant
![]() $\textbf {h}(P)=0$
. By definition,
$\textbf {h}(P)=0$
. By definition,
![]() $\textbf {h}(P)$
is (modulo n) the number of black elements minus the number of white elements in the sequence
$\textbf {h}(P)$
is (modulo n) the number of black elements minus the number of white elements in the sequence
![]() $j', j'+j, j'+2j, \ldots , j'+(n-1)j \in \mathbb {Z}_n$
. By Lemma 5, this is
$j', j'+j, j'+2j, \ldots , j'+(n-1)j \in \mathbb {Z}_n$
. By Lemma 5, this is
![]() $0$
.
$0$
.
Step 3: The stairs. Let
![]() $(a,b)=(\exp (x,u),\exp (y,u))$
,
$(a,b)=(\exp (x,u),\exp (y,u))$
,
![]() $(c,d)=(\exp (x,uv),\exp (y,uv)) \in \mathbb {Z}^2$
. Let R be the rectangle circumscribed about the triangle T with vertices
$(c,d)=(\exp (x,uv),\exp (y,uv)) \in \mathbb {Z}^2$
. Let R be the rectangle circumscribed about the triangle T with vertices
![]() $(0,0),(a,b), (c,d)$
. By the previous step, we can assume
$(0,0),(a,b), (c,d)$
. By the previous step, we can assume
![]() $u=x^ay^b$
or
$u=x^ay^b$
or
![]() $u=y^bx^a$
,
$u=y^bx^a$
,
![]() $v=x^{c-a}y^{d-b}$
or
$v=x^{c-a}y^{d-b}$
or
![]() $v=y^{d-b}x^{c-a}$
, and
$v=y^{d-b}x^{c-a}$
, and
![]() $w=x^{-c}y^{-d}$
or
$w=x^{-c}y^{-d}$
or
![]() $w=y^{-d}x^{-c}$
. We choose
$w=y^{-d}x^{-c}$
. We choose
![]() $u,v,w$
in such a way that the curve
$u,v,w$
in such a way that the curve
![]() $\gamma _{z}$
associated to
$\gamma _{z}$
associated to
![]() $z=u^nv^nw^n$
lies outside T (see Figure 2). We must show that the bounded region
$z=u^nv^nw^n$
lies outside T (see Figure 2). We must show that the bounded region
![]() $T'$
determined by
$T'$
determined by
![]() $\gamma _z$
has trivial horizontal invariant, because up to sign, this is
$\gamma _z$
has trivial horizontal invariant, because up to sign, this is
![]() $\textbf {h}(z)$
. Since the height of R is a multiple of n,
$\textbf {h}(z)$
. Since the height of R is a multiple of n,
![]() $\textbf {h}(R)=0\in \mathbb {Z}_n$
. Therefore, it suffices to prove that the region
$\textbf {h}(R)=0\in \mathbb {Z}_n$
. Therefore, it suffices to prove that the region
![]() $R-T'$
has trivial invariant. Now,
$R-T'$
has trivial invariant. Now,
![]() $R-T'$
consists of three stair-like regions and possibly a rectangular region.
$R-T'$
consists of three stair-like regions and possibly a rectangular region.

Figure 2: The rectangle R circumscribed about T. In this picture,
![]() $n=4$
. The curve
$n=4$
. The curve
![]() $\gamma _z$
appears with orange, and the region
$\gamma _z$
appears with orange, and the region
![]() $R-T'$
is shaded.
$R-T'$
is shaded.
Therefore, the proof reduces to showing that in any rectangular region with sides divisible by n and in stair-like regions with
![]() $n-1$
steps, the number of black squares minus the number of white squares is a multiple of n. For a rectangle, we have the same argument we used for R.
$n-1$
steps, the number of black squares minus the number of white squares is a multiple of n. For a rectangle, we have the same argument we used for R.
Consider a stair-like region with
![]() $n-1$
steps as in Figure 3. We must prove that the number of black squares minus the number of white squares is a multiple of n, independently of the position of the stair in the integer lattice, the height and the length of the steps.
$n-1$
steps as in Figure 3. We must prove that the number of black squares minus the number of white squares is a multiple of n, independently of the position of the stair in the integer lattice, the height and the length of the steps.

Figure 3: A seven-step stair. Here,
![]() $k=3$
. The rectangle of type
$k=3$
. The rectangle of type
![]() $0$
appears with red in the picture, those of type
$0$
appears with red in the picture, those of type
![]() $1$
are blue, and those of type
$1$
are blue, and those of type
![]() $2$
are green.
$2$
are green.
Let
![]() $h,l \ge 1$
be the height and the length of the steps in the stair. We divide the stairs in rectangles as shown in Figure 3. There are
$h,l \ge 1$
be the height and the length of the steps in the stair. We divide the stairs in rectangles as shown in Figure 3. There are
![]() $2^i$
rectangles of size
$2^i$
rectangles of size
![]() $2^{k-i-1}l \times 2^{k-i-1}h$
for every
$2^{k-i-1}l \times 2^{k-i-1}h$
for every
![]() $0\le i\le k-1$
. We call the
$0\le i\le k-1$
. We call the
![]() $2^{k-i-1}l \times 2^{k-i-1}h$
rectangles, rectangles of type i. We prove that for each i, among all the rectangles of type i, the number of black squares minus the number of white squares is a multiple of
$2^{k-i-1}l \times 2^{k-i-1}h$
rectangles, rectangles of type i. We prove that for each i, among all the rectangles of type i, the number of black squares minus the number of white squares is a multiple of
![]() $2^k$
. The first row of one rectangle of type i and the first row of the next rectangle of that type are
$2^k$
. The first row of one rectangle of type i and the first row of the next rectangle of that type are
![]() $2^{k-i}h$
rows apart. Therefore, if
$2^{k-i}h$
rows apart. Therefore, if
![]() $2^i| h$
, all the rectangles of type i are painted exactly in the same way. Moreover, in this case, each of the columns in these rectangles has height
$2^i| h$
, all the rectangles of type i are painted exactly in the same way. Moreover, in this case, each of the columns in these rectangles has height
![]() $2^{k-i-1}h$
, which is a multiple of
$2^{k-i-1}h$
, which is a multiple of
![]() $2^{k-1}$
, so in particular it is even. It is easy to see, then, that in each column, the number of black squares minus the number of white squares is even. But there are
$2^{k-1}$
, so in particular it is even. It is easy to see, then, that in each column, the number of black squares minus the number of white squares is even. But there are
![]() $2^{k-1}l$
of these columns, so the number of black squares minus the number of white squares among all the rectangles of type i is a multiple of
$2^{k-1}l$
of these columns, so the number of black squares minus the number of white squares among all the rectangles of type i is a multiple of
![]() $2^k$
. It remains to analyze the case that
$2^k$
. It remains to analyze the case that
![]() $2^i$
does not divide h. In this case, not all the rectangles of type i are painted in the same way. In fact, if
$2^i$
does not divide h. In this case, not all the rectangles of type i are painted in the same way. In fact, if
![]() $2^r$
is the maximum power of
$2^r$
is the maximum power of
![]() $2$
dividing h (so in particular
$2$
dividing h (so in particular
![]() $r\le i-1$
), then the jth rectangle and the
$r\le i-1$
), then the jth rectangle and the
![]() $(j+2^{i-r-1})$
th rectangle of type i are
$(j+2^{i-r-1})$
th rectangle of type i are
![]() $2^{i-r-1}2^{k-i}h=2^{k-r-1}h$
rows apart. But
$2^{i-r-1}2^{k-i}h=2^{k-r-1}h$
rows apart. But
![]() $2^{k-r-1}h$
is a multiple of
$2^{k-r-1}h$
is a multiple of
![]() $2^{k-1}$
and not a multiple of
$2^{k-1}$
and not a multiple of
![]() $2^k$
. This implies that the two rectangles are painted exactly with opposite colors. Thus, the rectangles of type i can be paired in such a way that paired rectangles are painted with opposite colors (
$2^k$
. This implies that the two rectangles are painted exactly with opposite colors. Thus, the rectangles of type i can be paired in such a way that paired rectangles are painted with opposite colors (
![]() $[2^i]$
can be matched with matched elements of difference
$[2^i]$
can be matched with matched elements of difference
![]() $2^{i-r-1}$
by Lemma 4). Therefore, among rectangles of type i, there is the same number of black and white squares.▪
$2^{i-r-1}$
by Lemma 4). Therefore, among rectangles of type i, there is the same number of black and white squares.▪
In [Reference Struik48], Struik proves that for any even positive integer n,
![]() $[x,y]^{\frac {n}{2}}\in \gamma _3(F_2)F_2^n$
. This is not hard to prove using the area invariant (see Section 9 below). This result is closely related to a result of Sanov [Reference Sanov43] and a conjecture by Bruck [Reference Burnside11].
$[x,y]^{\frac {n}{2}}\in \gamma _3(F_2)F_2^n$
. This is not hard to prove using the area invariant (see Section 9 below). This result is closely related to a result of Sanov [Reference Sanov43] and a conjecture by Bruck [Reference Burnside11].
Our horizontal invariants can be used to prove that the result is false when we replace
![]() $\gamma _3(F_2)$
by the smaller subgroup
$\gamma _3(F_2)$
by the smaller subgroup
![]() $F_2''$
.
$F_2''$
.
Proposition 7 Let n be a positive integer divisible by
![]() $4$
. Then,
$4$
. Then,
![]() $[x,y]^{\frac {n}{2}} \notin F_2'' F_2^n$
. In particular,
$[x,y]^{\frac {n}{2}} \notin F_2'' F_2^n$
. In particular,
![]() $[x,y]^{\frac {n}{2}}$
is not a product of nth powers in
$[x,y]^{\frac {n}{2}}$
is not a product of nth powers in
![]() $F_2$
.
$F_2$
.
Proof Suppose
![]() $n=2^kq$
for q odd,
$n=2^kq$
for q odd,
![]() $k\ge 2$
. Let
$k\ge 2$
. Let
![]() $c:\mathbb {Z}_{2^k} \to \{\textrm {black, white}\}$
be any good coloring of
$c:\mathbb {Z}_{2^k} \to \{\textrm {black, white}\}$
be any good coloring of
![]() $\mathbb {Z}_{2^k}$
. Let
$\mathbb {Z}_{2^k}$
. Let
![]() $\textbf {h} :F_2' \to \mathbb {Z}_{2^k}$
be the horizontal invariant associated with c. Then,
$\textbf {h} :F_2' \to \mathbb {Z}_{2^k}$
be the horizontal invariant associated with c. Then,
![]() $P_ {[x,y]^{\frac {n}{2}}}=\frac {n}{2} \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, so
$P_ {[x,y]^{\frac {n}{2}}}=\frac {n}{2} \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, so
![]() $\textbf {h}([x,y]^{\frac {n}{2}})=\frac {n}{2}=2^{k-1} \in \mathbb {Z}_{2^k}$
. Since
$\textbf {h}([x,y]^{\frac {n}{2}})=\frac {n}{2}=2^{k-1} \in \mathbb {Z}_{2^k}$
. Since
![]() $\textbf {h} ([x,y]^{\frac {n}{2}})$
is nontrivial, then by Theorem 6,
$\textbf {h} ([x,y]^{\frac {n}{2}})$
is nontrivial, then by Theorem 6,
![]() $[x,y]^{\frac {n}{2}}$
is not in
$[x,y]^{\frac {n}{2}}$
is not in
![]() $F_2''F_2^{2^k}$
, and then not in
$F_2''F_2^{2^k}$
, and then not in
![]() $F_2''F_2^n$
.▪
$F_2''F_2^n$
.▪
From the previous result, we deduce that if n is divisible by
![]() $4$
, the exponent of
$4$
, the exponent of
![]() $M(2,n)'$
is n, and not less. Indeed, if l is the order of
$M(2,n)'$
is n, and not less. Indeed, if l is the order of
![]() $[x,y]$
in
$[x,y]$
in
![]() $M(2,n)'$
,
$M(2,n)'$
,
![]() $[x,y]^{l}\in F_2''F_2^n$
, so the area
$[x,y]^{l}\in F_2''F_2^n$
, so the area
![]() $l=A([x,y]^l)$
is a multiple of
$l=A([x,y]^l)$
is a multiple of
![]() $\frac {n}{2}$
. By Proposition 7,
$\frac {n}{2}$
. By Proposition 7,
![]() $l\neq \frac {n}{2}$
, so
$l\neq \frac {n}{2}$
, so
![]() $l=n$
.
$l=n$
.
4 Engel and Morse identities
Given a word w in the free group
![]() $F=F(x_1,x_2,\ldots , x_s)$
and a group G, we say that G satisfies the identity w if for every homomorphism
$F=F(x_1,x_2,\ldots , x_s)$
and a group G, we say that G satisfies the identity w if for every homomorphism
![]() $\phi :F\to G$
we have
$\phi :F\to G$
we have
![]() $\phi (w)=1$
. If G is a quotient of a group H and G does not satisfy identity w, then neither does H. For instance, from Proposition 7, we deduce that the restricted Burnside group
$\phi (w)=1$
. If G is a quotient of a group H and G does not satisfy identity w, then neither does H. For instance, from Proposition 7, we deduce that the restricted Burnside group
![]() $R(2,n)$
does not satisfy the identity
$R(2,n)$
does not satisfy the identity
![]() $[x,y]^{\frac {n}{2}}$
for any n divisible by
$[x,y]^{\frac {n}{2}}$
for any n divisible by
![]() $4$
. A group is m-Engel if it satisfies the identity
$4$
. A group is m-Engel if it satisfies the identity
![]() $e_m$
(defined in Section 2). Note that
$e_m$
(defined in Section 2). Note that
![]() $B(2,n)$
is m-Engel if and only if
$B(2,n)$
is m-Engel if and only if
![]() $e_m\in F_2$
is a product of nth powers. It is known that
$e_m\in F_2$
is a product of nth powers. It is known that
![]() $R(2,5)$
is
$R(2,5)$
is
![]() $6$
-Engel, so if
$6$
-Engel, so if
![]() $e_6$
is not a product of fifth powers,
$e_6$
is not a product of fifth powers,
![]() $B(2,5)$
is not finite. Of course, a nilpotent group of class m is m-Engel. Conversely, Zorn’s theorem establishes that a finite m-Engel group is nilpotent. Not every Burnside group satisfies an Engel identity:
$B(2,5)$
is not finite. Of course, a nilpotent group of class m is m-Engel. Conversely, Zorn’s theorem establishes that a finite m-Engel group is nilpotent. Not every Burnside group satisfies an Engel identity:
![]() $B(2,6)$
is not nilpotent and finite. It is an open problem whether every finitely generated m-Engel group is nilpotent (see [Reference Kostrikin28, 14.70]). Metabelian groups of prime power exponent are (finite and) nilpotent, but if n is not a prime power and
$B(2,6)$
is not nilpotent and finite. It is an open problem whether every finitely generated m-Engel group is nilpotent (see [Reference Kostrikin28, 14.70]). Metabelian groups of prime power exponent are (finite and) nilpotent, but if n is not a prime power and
![]() $d \ge 2$
,
$d \ge 2$
,
![]() $M(d,n)$
is (finite and) not nilpotent [Reference Bachmuth, Heilbronn and Mochizuki6]. By results of Bachmuth et al. [Reference Bachmuth, Heilbronn and Mochizuki6] and of Dark–Newell [Reference Dark and Newell13], it is known that the class of
$M(d,n)$
is (finite and) not nilpotent [Reference Bachmuth, Heilbronn and Mochizuki6]. By results of Bachmuth et al. [Reference Bachmuth, Heilbronn and Mochizuki6] and of Dark–Newell [Reference Dark and Newell13], it is known that the class of
![]() $M(2,p^k)$
is
$M(2,p^k)$
is
![]() $m=k(p-1)p^{k-1}$
and
$m=k(p-1)p^{k-1}$
and
![]() $M(2,p^k)$
does not satisfy the
$M(2,p^k)$
does not satisfy the
![]() $(m-1)$
-Engel identity. In order to prove that
$(m-1)$
-Engel identity. In order to prove that
![]() $e_{m-1}\neq 1 \in M(2,p^k)$
, Bachmuth et al. find a representation of
$e_{m-1}\neq 1 \in M(2,p^k)$
, Bachmuth et al. find a representation of
![]() $M(2,p^k)$
by
$M(2,p^k)$
by
![]() $2\times 2$
matrices using the Magnus embedding. Since Engel identities are completely understood for metabelian groups of prime power exponent, our results are not new, and we only exhibit examples that illustrate how to use the invariants introduced in the previous section. In the next section, however, we will study basic commutator identities, which generalize Engel identities.
$2\times 2$
matrices using the Magnus embedding. Since Engel identities are completely understood for metabelian groups of prime power exponent, our results are not new, and we only exhibit examples that illustrate how to use the invariants introduced in the previous section. In the next section, however, we will study basic commutator identities, which generalize Engel identities.
Engel identities (or congruences which are a variant for nonnilpotent groups) have been studied for Burnside (nonmetabelian) groups. Here, the problem becomes harder, and there is a still open conjecture by Bruck (see [Reference Burnside11, Reference Glauberman, Krause and Struik15, Reference Grunewald, Havas, Mennicke and Newman17, Reference Gupta and Newman18, Reference Krause34, Reference Sanov43]).
Since our invariant
![]() $\textbf {h}$
is trivial in
$\textbf {h}$
is trivial in
![]() $F_2''F_2^n$
, it can be used to detect nontrivial elements in
$F_2''F_2^n$
, it can be used to detect nontrivial elements in
![]() $M(2,n)$
and to prove that certain identities do not hold in that group. Using Remark 1, it is easy to prove that the winding invariant of
$M(2,n)$
and to prove that certain identities do not hold in that group. Using Remark 1, it is easy to prove that the winding invariant of
![]() $e_m$
is
$e_m$
is
![]() $P_{e_m}= -(Y-1)^{m-1}$
.
$P_{e_m}= -(Y-1)^{m-1}$
.
Lemma 8 Let
![]() $k\ge 2$
. Then,
$k\ge 2$
. Then,
![]() $\binom {2^k}{2^{k-1}}-2$
is not a multiple of
$\binom {2^k}{2^{k-1}}-2$
is not a multiple of
![]() $8$
.
$8$
.
Proof There is an action of the cyclic group
![]() $\mathbb {Z}_{2^k}$
on the set
$\mathbb {Z}_{2^k}$
on the set
![]() $\binom {\mathbb {Z}_{2^k}}{2^{k-1}}$
of subsets of
$\binom {\mathbb {Z}_{2^k}}{2^{k-1}}$
of subsets of
![]() $\mathbb {Z}_{2^k}$
of cardinality
$\mathbb {Z}_{2^k}$
of cardinality
![]() $2^{k-1}$
, induced by the natural action of
$2^{k-1}$
, induced by the natural action of
![]() $\mathbb {Z}_{2^k}$
on itself. The orbits of this action have order a power of
$\mathbb {Z}_{2^k}$
on itself. The orbits of this action have order a power of
![]() $2$
. There is no orbit of cardinality
$2$
. There is no orbit of cardinality
![]() $1$
. There is exactly one orbit of cardinality
$1$
. There is exactly one orbit of cardinality
![]() $2$
, given by the subset of even numbers in
$2$
, given by the subset of even numbers in
![]() $\mathbb {Z}_{2^k}$
and the subset of odd numbers. There is exactly one orbit of cardinality
$\mathbb {Z}_{2^k}$
and the subset of odd numbers. There is exactly one orbit of cardinality
![]() $4$
, and it is the orbit of the subset of numbers congruent to
$4$
, and it is the orbit of the subset of numbers congruent to
![]() $0$
and
$0$
and
![]() $1$
modulo
$1$
modulo
![]() $4$
in
$4$
in
![]() $\mathbb {Z}_{2^k}$
. All the other orbits have cardinality divisible by
$\mathbb {Z}_{2^k}$
. All the other orbits have cardinality divisible by
![]() $8$
. Thus,
$8$
. Thus,
![]() $\binom {2^k}{2^{k-1}}\equiv 6\ \ \mod 8$
.▪
$\binom {2^k}{2^{k-1}}\equiv 6\ \ \mod 8$
.▪
Example 9 Let
![]() $n=2^k$
for some
$n=2^k$
for some
![]() $k\ge 3$
. Then, the
$k\ge 3$
. Then, the
![]() $(n+1)$
-Engel word
$(n+1)$
-Engel word
![]() $e_{n+1}$
is not a product of nth powers. Moreover,
$e_{n+1}$
is not a product of nth powers. Moreover,
![]() $M(2,n)$
is not
$M(2,n)$
is not
![]() $(n+1)$
-Engel. This follows immediately from Bachmuth et al. results:
$(n+1)$
-Engel. This follows immediately from Bachmuth et al. results:
![]() $M(2,n)$
is not
$M(2,n)$
is not
![]() $(m-1)$
-Engel for
$(m-1)$
-Engel for
![]() $m=k2^{k-1}$
, and
$m=k2^{k-1}$
, and
![]() $m-1\ge n+1$
. However, we give a short proof of this using our invariant
$m-1\ge n+1$
. However, we give a short proof of this using our invariant
![]() $\textbf {h}$
. Moreover, the advantage of our approach is that in Proposition 19, we will be able to extend this example to all the basic commutators of weight
$\textbf {h}$
. Moreover, the advantage of our approach is that in Proposition 19, we will be able to extend this example to all the basic commutators of weight
![]() $\le n+2$
, using the notion of diagonal invariant.
$\le n+2$
, using the notion of diagonal invariant.
The winding invariant of
![]() $e_{n+1}$
is
$e_{n+1}$
is
![]() $-(Y-1)^n$
. Take the coloring
$-(Y-1)^n$
. Take the coloring
![]() $\mathbb {Z}_n\to \{\textrm {black,white}\}$
which paints
$\mathbb {Z}_n\to \{\textrm {black,white}\}$
which paints
![]() $0,1, \ldots , n/2-1$
with black and
$0,1, \ldots , n/2-1$
with black and
![]() $n/2, n/2+1, \ldots , n-1$
with white. We will prove that
$n/2, n/2+1, \ldots , n-1$
with white. We will prove that
![]() $\textbf {h}(e_{n+1}) \in \mathbb {Z}_n$
is not a multiple of
$\textbf {h}(e_{n+1}) \in \mathbb {Z}_n$
is not a multiple of
![]() $8$
. By definition,
$8$
. By definition,
 $\textbf {h}(e_{n+1})=\sum \limits _{i=0}^{n/2-1} (-1)^{i+1}\binom {n}{i}-\sum \limits _{i=n/2}^{n-1} (-1)^{i+1}\binom {n}{i}-1$
. Since
$\textbf {h}(e_{n+1})=\sum \limits _{i=0}^{n/2-1} (-1)^{i+1}\binom {n}{i}-\sum \limits _{i=n/2}^{n-1} (-1)^{i+1}\binom {n}{i}-1$
. Since
![]() $\binom {n}{i}=\binom {n}{n-i}$
for every i, most of the terms in this expression cancel out, and we obtain
$\binom {n}{i}=\binom {n}{n-i}$
for every i, most of the terms in this expression cancel out, and we obtain
![]() $\textbf {h}(e_{n+1})=\binom {n}{n/2}-2$
. The result follows then from Lemma 8 and Theorem 6.
$\textbf {h}(e_{n+1})=\binom {n}{n/2}-2$
. The result follows then from Lemma 8 and Theorem 6.
Example 10
![]() $M(2,16)$
is not a
$M(2,16)$
is not a
![]() $25$
-Engel group. In fact, Bachmuth–Heilbronn–Mochizuki’s result says that it is not
$25$
-Engel group. In fact, Bachmuth–Heilbronn–Mochizuki’s result says that it is not
![]() $31$
-Engel. Our proof is easy by considering the invariant
$31$
-Engel. Our proof is easy by considering the invariant
![]() $\textbf {h}$
as above. We only have to check that
$\textbf {h}$
as above. We only have to check that
![]() $\textbf {h}(e_{25})\neq 0$
. The winding invariant of
$\textbf {h}(e_{25})\neq 0$
. The winding invariant of
![]() $e_{25}$
is
$e_{25}$
is
![]() $-(Y-1)^{24}=\sum \limits _{i=0}^{24} (-1)^{i+1}\binom {24}{i}Y^i$
. Modulo
$-(Y-1)^{24}=\sum \limits _{i=0}^{24} (-1)^{i+1}\binom {24}{i}Y^i$
. Modulo
![]() $16$
, the coefficients of this polynomial are:
$16$
, the coefficients of this polynomial are:
![]() $-1,8,-4,8, -2,8, -4,8, 1,0, 8,0, 4,0,8,0,1,8,-4,8,-2,8,-4,8,-1$
. Thus,
$-1,8,-4,8, -2,8, -4,8, 1,0, 8,0, 4,0,8,0,1,8,-4,8,-2,8,-4,8,-1$
. Thus,
![]() $\textbf {h}(e_{25})=(-1+8-4+8-2+8-4+8)-(1+0+8+0+4+0+8+0)+(1+8-4+8-2+8-4+8)-(-1)=5-5+7+1=8\in \mathbb {Z}_{16}$
.
$\textbf {h}(e_{25})=(-1+8-4+8-2+8-4+8)-(1+0+8+0+4+0+8+0)+(1+8-4+8-2+8-4+8)-(-1)=5-5+7+1=8\in \mathbb {Z}_{16}$
.
We define the following
![]() $n/2$
colorings of
$n/2$
colorings of
![]() $\mathbb {Z}_n$
,
$\mathbb {Z}_n$
,
![]() $c_0,c_1,\ldots , c_{n/2-1}:\mathbb {Z}_n \to \{\textrm {black, white}\}$
. The coloring
$c_0,c_1,\ldots , c_{n/2-1}:\mathbb {Z}_n \to \{\textrm {black, white}\}$
. The coloring
![]() $c_i$
paints
$c_i$
paints
![]() $i,i+1,\ldots , i+n/2-1$
with black and the remaining elements with white. The associated horizontal invariants are
$i,i+1,\ldots , i+n/2-1$
with black and the remaining elements with white. The associated horizontal invariants are
![]() $\textbf {h}^0$
,
$\textbf {h}^0$
,
![]() $\textbf {h}^1, \ldots , \textbf {h}^{n/2-1}$
. Similarly, we have the vertical invariants
$\textbf {h}^1, \ldots , \textbf {h}^{n/2-1}$
. Similarly, we have the vertical invariants
![]() $\textbf {v}^0$
,
$\textbf {v}^0$
,
![]() $\textbf {v}^1,\ldots , \textbf {v}^{n/2-1}$
. The invariant
$\textbf {v}^1,\ldots , \textbf {v}^{n/2-1}$
. The invariant
![]() $\textbf {v}^i$
is associated to the coloring of the squares in the grid which paints the columns congruent to
$\textbf {v}^i$
is associated to the coloring of the squares in the grid which paints the columns congruent to
![]() $i,i+1,\ldots , i+n/2-1$
with black and the remaining columns with white. That is,
$i,i+1,\ldots , i+n/2-1$
with black and the remaining columns with white. That is,
![]() $\textbf {v}^i(z)=\textbf {h}^i(P_z(Y,X))$
. By Theorem 6, the map
$\textbf {v}^i(z)=\textbf {h}^i(P_z(Y,X))$
. By Theorem 6, the map
![]() $\Omega : F_2' \to (\mathbb {Z}_n)^n=\mathbb {Z}_n \times \cdots \times \mathbb {Z}_n$
defined by
$\Omega : F_2' \to (\mathbb {Z}_n)^n=\mathbb {Z}_n \times \cdots \times \mathbb {Z}_n$
defined by
is trivial in
![]() $F_2''F_2^n$
, so it induces a well-defined homomorphism
$F_2''F_2^n$
, so it induces a well-defined homomorphism
![]() $\Omega : M(2,n)' \to (\mathbb {Z}_n)^n$
.
$\Omega : M(2,n)' \to (\mathbb {Z}_n)^n$
.
Lemma 11
![]() $\Omega $
is trivial in
$\Omega $
is trivial in
![]() $\gamma _{j+1}(F_2)$
if and only if
$\gamma _{j+1}(F_2)$
if and only if
![]() $\Omega (e_j)=0$
.
$\Omega (e_j)=0$
.
Proof Since
![]() $e_j\in \gamma _{j+1}(F_2)$
, one implication is trivial. Suppose now that
$e_j\in \gamma _{j+1}(F_2)$
, one implication is trivial. Suppose now that
![]() $\Omega (e_j)=0$
. Then, by symmetry,
$\Omega (e_j)=0$
. Then, by symmetry,
![]() $\Omega (e_j(y,x))=0$
. Let
$\Omega (e_j(y,x))=0$
. Let
![]() $z\in \gamma _{j+1}(F_2)$
. Using Remark 1, it is easy to see that
$z\in \gamma _{j+1}(F_2)$
. Using Remark 1, it is easy to see that
![]() $P_z$
is a sum of multiples of polynomials of the form
$P_z$
is a sum of multiples of polynomials of the form
![]() $(m_1-1)(m_2-1)\ldots (m_{j-1}-1)$
, where the
$(m_1-1)(m_2-1)\ldots (m_{j-1}-1)$
, where the
![]() $m_i$
are monomials (see also [Reference Barmak8, Proposition 23]). If
$m_i$
are monomials (see also [Reference Barmak8, Proposition 23]). If
![]() $P \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
and m is a monomial,
$P \in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
and m is a monomial,
![]() $\Omega (P)$
and
$\Omega (P)$
and
![]() $\Omega (m P)$
have the same coordinates up to a shift and change of sign. It suffices to prove then that for a polynomial
$\Omega (m P)$
have the same coordinates up to a shift and change of sign. It suffices to prove then that for a polynomial
![]() $P=(m_1-1)(m_2-1)\ldots (m_{j-1}-1)$
, where the
$P=(m_1-1)(m_2-1)\ldots (m_{j-1}-1)$
, where the
![]() $m_i$
are monomials,
$m_i$
are monomials,
![]() $\Omega $
vanishes. Now, we can consider only the invariants
$\Omega $
vanishes. Now, we can consider only the invariants
![]() $\textbf {h}^0, \textbf {h}^1, \ldots , \textbf {h}^{n/2-1}$
, since for the
$\textbf {h}^0, \textbf {h}^1, \ldots , \textbf {h}^{n/2-1}$
, since for the
![]() $\textbf {v}^i$
, the proof is symmetrical. Since the colors of the squares in the integer lattice used to compute
$\textbf {v}^i$
, the proof is symmetrical. Since the colors of the squares in the integer lattice used to compute
![]() $\textbf {h}^i$
depend only on the row, we may also assume that each monomial
$\textbf {h}^i$
depend only on the row, we may also assume that each monomial
![]() $m_i$
is a power of Y. Furthermore, since
$m_i$
is a power of Y. Furthermore, since
![]() $Y-1$
divides
$Y-1$
divides
![]() $Y^l-1$
for every
$Y^l-1$
for every
![]() $l\in \mathbb {Z}$
, P is a multiple of
$l\in \mathbb {Z}$
, P is a multiple of
![]() $(Y-1)^{j-1}=-P_{e_j}$
, so as
$(Y-1)^{j-1}=-P_{e_j}$
, so as
![]() $\Omega $
vanishes at
$\Omega $
vanishes at
![]() $e_j$
, it also vanishes at z.▪
$e_j$
, it also vanishes at z.▪
We consider the map
![]() $\overline {\Omega }:F_2'\to \mathbb {Z}_{n/2} \times (\mathbb {Z}_n)^n$
defined by
$\overline {\Omega }:F_2'\to \mathbb {Z}_{n/2} \times (\mathbb {Z}_n)^n$
defined by
![]() $\overline {\Omega }(z)=(A(z), \Omega (z))$
. Recall that A denotes the area invariant
$\overline {\Omega }(z)=(A(z), \Omega (z))$
. Recall that A denotes the area invariant
![]() $A:F_2' \to \mathbb {Z}_{n/2}$
defined by
$A:F_2' \to \mathbb {Z}_{n/2}$
defined by
![]() $A(z)=P_z(1,1)$
, which is trivial in
$A(z)=P_z(1,1)$
, which is trivial in
![]() $F_2''F_2^n$
by Theorem 59 of [Reference Barmak8].
$F_2''F_2^n$
by Theorem 59 of [Reference Barmak8].
Proposition 12 The image
![]() $\textrm {Im}(\Omega )$
of
$\textrm {Im}(\Omega )$
of
![]() $\Omega :F_2' \to (\mathbb {Z}_n)^n$
is a subgroup of order
$\Omega :F_2' \to (\mathbb {Z}_n)^n$
is a subgroup of order
![]() $2(n/2)^n$
, and
$2(n/2)^n$
, and
![]() $\textrm {Im}(\overline {\Omega })$
has order
$\textrm {Im}(\overline {\Omega })$
has order
![]() $(n/2)^{n+1}$
.
$(n/2)^{n+1}$
.
Proof Let
![]() $z\in F_2'$
be an element with winding invariant
$z\in F_2'$
be an element with winding invariant
![]() $P_z=1-Y^{-1}$
. It is easy to see that
$P_z=1-Y^{-1}$
. It is easy to see that
![]() $\Omega (z)=(2,0,0, \ldots , 0) \in \textrm {Im}(\Omega )$
. For
$\Omega (z)=(2,0,0, \ldots , 0) \in \textrm {Im}(\Omega )$
. For
![]() $1\le i\le n/2-1$
, the elements
$1\le i\le n/2-1$
, the elements
![]() $y^{i}zy^{-i}$
give permutations of the coordinates of this vector with the nontrivial coordinate in any of the first
$y^{i}zy^{-i}$
give permutations of the coordinates of this vector with the nontrivial coordinate in any of the first
![]() $n/2$
positions. Changing Y by X, we obtain the remaining permutations of the coordinates. This already proves that
$n/2$
positions. Changing Y by X, we obtain the remaining permutations of the coordinates. This already proves that
![]() $\textrm {Im}(\Omega )$
contains a subgroup D of order
$\textrm {Im}(\Omega )$
contains a subgroup D of order
![]() $(n/2)^n$
. The element
$(n/2)^n$
. The element
![]() $z=1$
has
$z=1$
has
![]() $\Omega (z) \notin D$
. On the other hand, it is easy to see that for any
$\Omega (z) \notin D$
. On the other hand, it is easy to see that for any
![]() $z\in F_2'$
, all the coordinates of
$z\in F_2'$
, all the coordinates of
![]() $\Omega (z)$
have the same parity, so
$\Omega (z)$
have the same parity, so
![]() $|D|<|\textrm {Im}(\Omega )|\le 2(n/2)^n$
, and the result follows.
$|D|<|\textrm {Im}(\Omega )|\le 2(n/2)^n$
, and the result follows.
The area of an element
![]() $z\in F_2'$
with winding invariant
$z\in F_2'$
with winding invariant
![]() $P_z=1+X^{n/2}Y^{n/2}$
is
$P_z=1+X^{n/2}Y^{n/2}$
is
![]() $2$
, while
$2$
, while
![]() $\Omega (z)=0$
. Thus,
$\Omega (z)=0$
. Thus,
![]() $|\textrm {Im}(\overline {\Omega })|\ge 2(n/2)^{n}n/4=(n/2)^{n+1}$
. The parity of the area is also determined by the value of
$|\textrm {Im}(\overline {\Omega })|\ge 2(n/2)^{n}n/4=(n/2)^{n+1}$
. The parity of the area is also determined by the value of
![]() $\Omega $
, so the other inequality holds as well.▪
$\Omega $
, so the other inequality holds as well.▪
Recall that
![]() $M(2,16)$
is nilpotent of class
$M(2,16)$
is nilpotent of class
![]() $m=32$
. In Example 10, we proved that
$m=32$
. In Example 10, we proved that
![]() $\textbf {h}^0(e_{25})\neq 0 \in \mathbb {Z}_{16}$
. It is easy to prove that
$\textbf {h}^0(e_{25})\neq 0 \in \mathbb {Z}_{16}$
. It is easy to prove that
![]() $\textbf {h}^0(e_{26})=0$
and moreover that in fact
$\textbf {h}^0(e_{26})=0$
and moreover that in fact
![]() $\Omega (e_{26})=0$
. By Lemma 11,
$\Omega (e_{26})=0$
. By Lemma 11,
![]() $\Omega $
is trivial in
$\Omega $
is trivial in
![]() $\gamma _{27}(F_2)$
. The area invariant is already trivial in
$\gamma _{27}(F_2)$
. The area invariant is already trivial in
![]() $\gamma _3(F_2)$
. Thus,
$\gamma _3(F_2)$
. Thus,
![]() $\overline {\Omega }$
induces a map
$\overline {\Omega }$
induces a map
![]() $\overline {\Omega }: M(2,16)'/\gamma _{27}(M(2,16))\to \mathbb {Z}_{8} \times (\mathbb {Z}_{16})^{16}$
, and from Proposition 12, we deduce that
$\overline {\Omega }: M(2,16)'/\gamma _{27}(M(2,16))\to \mathbb {Z}_{8} \times (\mathbb {Z}_{16})^{16}$
, and from Proposition 12, we deduce that
![]() $|\frac {M(2,16)'}{\gamma _{27}(M(2,16))}|\ge 2^{51}$
. On the other hand,
$|\frac {M(2,16)'}{\gamma _{27}(M(2,16))}|\ge 2^{51}$
. On the other hand,
![]() $|\frac {M(2,16)}{M(2,16)'}|=16^2=2^8$
. Therefore, we deduce the following result.
$|\frac {M(2,16)}{M(2,16)'}|=16^2=2^8$
. Therefore, we deduce the following result.
Proposition 13 The order
![]() $|M(2,16)/\gamma _{27}(M(2,16))|$
of the largest class
$|M(2,16)/\gamma _{27}(M(2,16))|$
of the largest class
![]() $26$
quotient of
$26$
quotient of
![]() $M(2,16)$
is greater than or equal to
$M(2,16)$
is greater than or equal to
![]() $2^{59}$
.
$2^{59}$
.
A similar result can be obtained for
![]() $n=8$
. Here,
$n=8$
. Here,
![]() $\Omega (e_{10})=0\in \mathbb {Z}_8$
, so
$\Omega (e_{10})=0\in \mathbb {Z}_8$
, so
![]() $\overline {\Omega }$
is trivial in
$\overline {\Omega }$
is trivial in
![]() $\gamma _{11}(F_2)$
, and we deduce from Proposition 12.
$\gamma _{11}(F_2)$
, and we deduce from Proposition 12.
Remark 14 The order of
![]() $M(2,8)/\gamma _{11}(M(2,8))$
is greater than or equal to
$M(2,8)/\gamma _{11}(M(2,8))$
is greater than or equal to
![]() $2^{24}$
.
$2^{24}$
.
In fact, something stronger is already known.
![]() $M(2,8)$
has nilpotency class
$M(2,8)$
has nilpotency class
![]() $12$
, and its order has been computed by Hermanns [Reference Hermanns26]:
$12$
, and its order has been computed by Hermanns [Reference Hermanns26]:
![]() $|M(2,8)|=2^{63}$
. Skopin computed in [Reference Skopin46] the orders of all the factors
$|M(2,8)|=2^{63}$
. Skopin computed in [Reference Skopin46] the orders of all the factors
![]() $\gamma _l(M(2,8))/\gamma _{l+1}(M(2,8))$
, from which it can be seen that
$\gamma _l(M(2,8))/\gamma _{l+1}(M(2,8))$
, from which it can be seen that
![]() $M(2,8)/ \gamma _{11}(M(2,8))$
has order
$M(2,8)/ \gamma _{11}(M(2,8))$
has order
![]() $2^{54}$
. As far as we know, the order of
$2^{54}$
. As far as we know, the order of
![]() $M(2,16)$
has not been determined, but
$M(2,16)$
has not been determined, but
![]() $2^{87} \le |M(2,16)|\le 2^{376}$
(see [Reference Newman38] and the next section). A GAP [14] program using the package NQ [Reference Newman and O’Brien40] returns after 120 hours that
$2^{87} \le |M(2,16)|\le 2^{376}$
(see [Reference Newman38] and the next section). A GAP [14] program using the package NQ [Reference Newman and O’Brien40] returns after 120 hours that
![]() $|M(2,16)/\gamma _{17} (M(2,16))|=2^{185}$
, which is of course much better than our result in Proposition 13, and improves the lower bound given above. The computation that
$|M(2,16)/\gamma _{17} (M(2,16))|=2^{185}$
, which is of course much better than our result in Proposition 13, and improves the lower bound given above. The computation that
![]() $|M(2,16)/\gamma _{9}(M(2,16))|=2^{70}$
takes seconds.
$|M(2,16)/\gamma _{9}(M(2,16))|=2^{70}$
takes seconds.
For
![]() $n=4$
, Proposition 12 implies that
$n=4$
, Proposition 12 implies that
![]() $|M(2,4)|\ge 2^9$
. In fact,
$|M(2,4)|\ge 2^9$
. In fact,
![]() $|M(2,4)|=2^{10}$
, so
$|M(2,4)|=2^{10}$
, so
![]() $\Omega $
(and
$\Omega $
(and
![]() $\overline {\Omega }$
) is very close to a complete invariant that could be used to solve the word problem in
$\overline {\Omega }$
) is very close to a complete invariant that could be used to solve the word problem in
![]() $M(2,4)$
in an explicit way. In the next section, we will introduce invariants more general that the horizontal and vertical invariants, though based on the same coloring ideas, and we will use them to obtain a complete invariant for
$M(2,4)$
in an explicit way. In the next section, we will introduce invariants more general that the horizontal and vertical invariants, though based on the same coloring ideas, and we will use them to obtain a complete invariant for
![]() $M(2,4)$
.
$M(2,4)$
.
A semigroup identity is an identity of the form
![]() $uv^{-1}$
, where
$uv^{-1}$
, where
![]() $u,v\in F(x_1,x_2,\ldots , x_s)$
are positive words (no letter appears with negative exponent). The Burnside identity
$u,v\in F(x_1,x_2,\ldots , x_s)$
are positive words (no letter appears with negative exponent). The Burnside identity
![]() $x^n$
is an example of this type. Another is the (mth) Morse identity
$x^n$
is an example of this type. Another is the (mth) Morse identity
![]() $u_mv_m^{-1}\in F_2$
, where
$u_mv_m^{-1}\in F_2$
, where
![]() $u_1=x$
,
$u_1=x$
,
![]() $v_1=y$
, and
$v_1=y$
, and
![]() $u_{i+1}=u_iv_i$
,
$u_{i+1}=u_iv_i$
,
![]() $v_{i+1}=v_iu_i$
for every
$v_{i+1}=v_iu_i$
for every
![]() $i\ge 1$
. In some sense Burnside identities and Morse identities generate all the semigroup identities (see [Reference Shalev, Hartley, Seitz, Borovik and Bryant44, Theorem 5.7]). Finite groups satisfying a Morse identity are completely characterized by a theorem of Boffa and Point [Reference Boffa and Point10, Corollarie]: they are the extensions of a nilpotent group by a 2-group. The Morse identities are related to the original proof of Novikov and Adian that there are infinite Burnside groups (see [Reference Allouche and Shallit5, Section 6]).
$i\ge 1$
. In some sense Burnside identities and Morse identities generate all the semigroup identities (see [Reference Shalev, Hartley, Seitz, Borovik and Bryant44, Theorem 5.7]). Finite groups satisfying a Morse identity are completely characterized by a theorem of Boffa and Point [Reference Boffa and Point10, Corollarie]: they are the extensions of a nilpotent group by a 2-group. The Morse identities are related to the original proof of Novikov and Adian that there are infinite Burnside groups (see [Reference Allouche and Shallit5, Section 6]).
It is easy to see that the total exponents of x and of y in both
![]() $u_m$
and
$u_m$
and
![]() $v_m$
is
$v_m$
is
![]() $2^{m-2}$
if
$2^{m-2}$
if
![]() $m\ge 2$
. Let
$m\ge 2$
. Let
![]() $m\ge 3$
. Since
$m\ge 3$
. Since
![]() $u_{m}v_{m}^{-1}=u_{m-1}v_{m-1}u_{m-1}^{-1}v_{m-1}^{-1}$
and
$u_{m}v_{m}^{-1}=u_{m-1}v_{m-1}u_{m-1}^{-1}v_{m-1}^{-1}$
and
![]() $v_{m-1}u_{m-1}^{-1}\in F_2'$
, then the winding invariant
$v_{m-1}u_{m-1}^{-1}\in F_2'$
, then the winding invariant
![]() $P_{u_{m}v_{m}^{-1}}=P_{u_{m-1}v_{m-1}^{-1}}+X^{2^{m-3}}Y^{2^{m-3}}P_{v_{m-1}u_{m-1}^{-1}}=(1-X^{2^{m-3}}Y^{2^{m-3}}) P_{u_{m-1}v_{m-1}^{-1}}$
. By induction, we obtain then
$P_{u_{m}v_{m}^{-1}}=P_{u_{m-1}v_{m-1}^{-1}}+X^{2^{m-3}}Y^{2^{m-3}}P_{v_{m-1}u_{m-1}^{-1}}=(1-X^{2^{m-3}}Y^{2^{m-3}}) P_{u_{m-1}v_{m-1}^{-1}}$
. By induction, we obtain then
Proposition 15 Let
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $n=2^k$
. Then,
$n=2^k$
. Then,
![]() $M(2,n)$
satisfies the
$M(2,n)$
satisfies the
![]() $(k+3)$
th Morse identity, but it does not satisfy the
$(k+3)$
th Morse identity, but it does not satisfy the
![]() $(k+1)$
th Morse identity. In particular, the restricted Burnside group
$(k+1)$
th Morse identity. In particular, the restricted Burnside group
![]() $R(2,n)$
does not satisfy the
$R(2,n)$
does not satisfy the
![]() $(k+1)$
th Morse identity, and neither does
$(k+1)$
th Morse identity, and neither does
![]() $B(2,n)$
.
$B(2,n)$
.
Proof In order to check that
![]() $M(2,n)$
satisfies the
$M(2,n)$
satisfies the
![]() $(k+3)$
th Morse identity, we only have to show that
$(k+3)$
th Morse identity, we only have to show that
![]() $u_{k+3}v_{k+3}^{-1}=1\in M(2,n)$
. The winding invariant of
$u_{k+3}v_{k+3}^{-1}=1\in M(2,n)$
. The winding invariant of
![]() $u_{k+3}v_{k+3}^{-1}$
is
$u_{k+3}v_{k+3}^{-1}$
is
![]() $P_{u_{k+3}v_{k+3}^{-1}}=(1-X^nY^n)Q$
for some polynomial Q. Let
$P_{u_{k+3}v_{k+3}^{-1}}=(1-X^nY^n)Q$
for some polynomial Q. Let
![]() $w\in F_2'$
be such that
$w\in F_2'$
be such that
![]() $P_w=Q$
. Then,
$P_w=Q$
. Then,
![]() $P_{[w,(xy)^n]}=(1-X^nY^n)Q$
. Thus,
$P_{[w,(xy)^n]}=(1-X^nY^n)Q$
. Thus,
![]() $u_{k+3}v_{k+3}^{-1}=[w,(xy)^{n}] \ \ \mod \ker (W)=F_2''$
, and since
$u_{k+3}v_{k+3}^{-1}=[w,(xy)^{n}] \ \ \mod \ker (W)=F_2''$
, and since
![]() $[w,(xy)^n]$
is a product of nth powers,
$[w,(xy)^n]$
is a product of nth powers,
![]() $u_{k+3}v_{k+3}^{-1}\in F_2''F_2^n$
, as we wanted to show.
$u_{k+3}v_{k+3}^{-1}\in F_2''F_2^n$
, as we wanted to show.
To prove that
![]() $M(2,n)$
does not satisfy the
$M(2,n)$
does not satisfy the
![]() $(k+1)$
th Morse identity, it suffices to prove that
$(k+1)$
th Morse identity, it suffices to prove that
![]() $\Omega (u_{k+1}v_{k+1}^{-1})\neq 1$
, where
$\Omega (u_{k+1}v_{k+1}^{-1})\neq 1$
, where
![]() $\Omega : F_2' \to (\mathbb {Z}_{n})^{n}$
is the invariant defined above. Now,
$\Omega : F_2' \to (\mathbb {Z}_{n})^{n}$
is the invariant defined above. Now,
![]() $P_{u_{k+1}v_{k+1}^{-1}}=1+R$
, where R is a polynomial with monomials
$P_{u_{k+1}v_{k+1}^{-1}}=1+R$
, where R is a polynomial with monomials
![]() $X^lY^l$
for
$X^lY^l$
for
![]() $1\le l\le 2^{k-1}-1=n/2-1$
. Thus, the difference between
$1\le l\le 2^{k-1}-1=n/2-1$
. Thus, the difference between
![]() $\textbf {h}^0(u_{k+1}v_{k+1}^{-1})$
and
$\textbf {h}^0(u_{k+1}v_{k+1}^{-1})$
and
![]() $\textbf {h}^1(u_{k+1}v_{k+1}^{-1})$
is
$\textbf {h}^1(u_{k+1}v_{k+1}^{-1})$
is
![]() $2\in \mathbb {Z}_n$
. In particular, one of them has to be nonzero, so
$2\in \mathbb {Z}_n$
. In particular, one of them has to be nonzero, so
![]() $u_{k+1}v_{k+1}^{-1}$
is nontrivial in
$u_{k+1}v_{k+1}^{-1}$
is nontrivial in
![]() $M(2,n)$
.▪
$M(2,n)$
.▪
5 More invariants
In the previous section, we have deduced some lower bounds for the order of
![]() $M(2,n)$
via the invariant
$M(2,n)$
via the invariant
![]() $\overline {\Omega }$
which is composed by n invariants
$\overline {\Omega }$
which is composed by n invariants
![]() $M(2,n)'\to \mathbb {Z}_n$
and the area invariant
$M(2,n)'\to \mathbb {Z}_n$
and the area invariant
![]() $M(2,n)'\to \mathbb {Z}_{\frac {n}{2}}$
. We proved (a refinement of) the inequality
$M(2,n)'\to \mathbb {Z}_{\frac {n}{2}}$
. We proved (a refinement of) the inequality
![]() $|M(2,n)|\ge n^2 (\frac {n}{2})^{n+1}$
. On the other hand, Newman’s remarks in [Reference Newman38] show that
$|M(2,n)|\ge n^2 (\frac {n}{2})^{n+1}$
. On the other hand, Newman’s remarks in [Reference Newman38] show that
![]() $n^22^{\frac {n^2}{4}-1}\le |M(2,n)|\le n^{n^2+3}$
. This suggests that we should be able to find quadratically many invariants
$n^22^{\frac {n^2}{4}-1}\le |M(2,n)|\le n^{n^2+3}$
. This suggests that we should be able to find quadratically many invariants
![]() $M(2,n)'\to \mathbb {Z}_n$
and not just linearly many. As explained in Section 1, there exists a monomorphism
$M(2,n)'\to \mathbb {Z}_n$
and not just linearly many. As explained in Section 1, there exists a monomorphism
![]() $M(2,n)'\to (\mathbb {Z}_n)^r$
for r big enough, so it makes sense to look for more invariants of this type. The aim of this section is to find and make explicit some of those maps.
$M(2,n)'\to (\mathbb {Z}_n)^r$
for r big enough, so it makes sense to look for more invariants of this type. The aim of this section is to find and make explicit some of those maps.
Theorem 16 Let
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $n=2^k$
. Let c be a good coloring of
$n=2^k$
. Let c be a good coloring of
![]() $\mathbb {Z}_n$
, and let
$\mathbb {Z}_n$
, and let
![]() $\varphi :\mathbb {Z} \times \mathbb {Z}\to \mathbb {Z}_n$
be a homomorphism such that
$\varphi :\mathbb {Z} \times \mathbb {Z}\to \mathbb {Z}_n$
be a homomorphism such that
![]() $\varphi (1,0)$
and
$\varphi (1,0)$
and
![]() $\varphi (0,1) \in \mathbb {Z}_n$
are odd. Let
$\varphi (0,1) \in \mathbb {Z}_n$
are odd. Let
![]() $t:\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z} \times \mathbb {Z}$
be a translation by any vector
$t:\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z} \times \mathbb {Z}$
be a translation by any vector
![]() $(i_0,j_0)\in \mathbb {Z} \times \mathbb {Z}$
. Let
$(i_0,j_0)\in \mathbb {Z} \times \mathbb {Z}$
. Let
![]() $\Lambda =\Lambda _{\varphi t, c}$
be the associated invariant. Then, for any
$\Lambda =\Lambda _{\varphi t, c}$
be the associated invariant. Then, for any
![]() $z\in F_2'$
which is a product of nth powers in
$z\in F_2'$
which is a product of nth powers in
![]() $F_2$
,
$F_2$
,
![]() $\Lambda (z)=0\in \mathbb {Z}_n$
.
$\Lambda (z)=0\in \mathbb {Z}_n$
.
Proof Note that
![]() $\Lambda _{\varphi t,c}(z)=\Lambda _{\varphi t,c}(P_z)=\Lambda _{\varphi ,c}(X^{i_0}Y^{j_0}P_z)=\Lambda _{\varphi , c}(x^{i_0}y^{j_0}zy^{-j_0}x^{-i_0})$
. Thus, we may assume
$\Lambda _{\varphi t,c}(z)=\Lambda _{\varphi t,c}(P_z)=\Lambda _{\varphi ,c}(X^{i_0}Y^{j_0}P_z)=\Lambda _{\varphi , c}(x^{i_0}y^{j_0}zy^{-j_0}x^{-i_0})$
. Thus, we may assume
![]() $i_0=j_0=0$
.
$i_0=j_0=0$
.
Just as in Theorem 6, we can assume z is a product of three nth powers. Then, we must show that for any polynomial of the form
![]() $P=m'(1+m+m^2+\cdots +m^{n-1})$
, the invariant
$P=m'(1+m+m^2+\cdots +m^{n-1})$
, the invariant
![]() $\Lambda $
is trivial. But if
$\Lambda $
is trivial. But if
![]() $m'=X^{i'}Y^{j'}$
and
$m'=X^{i'}Y^{j'}$
and
![]() $m=X^iY^j$
, then
$m=X^iY^j$
, then
![]() $\Lambda (P)$
is the number of black terms minus the number of white terms in the progression
$\Lambda (P)$
is the number of black terms minus the number of white terms in the progression
![]() $\varphi (i',j'), \varphi (i',j')+\varphi (i,j), \varphi (i',j')+2\varphi (i,j), \ldots , \varphi (i',j')+(n-1)\varphi (i,j)$
, which is
$\varphi (i',j'), \varphi (i',j')+\varphi (i,j), \varphi (i',j')+2\varphi (i,j), \ldots , \varphi (i',j')+(n-1)\varphi (i,j)$
, which is
![]() $0$
modulo n by Lemma 5.
$0$
modulo n by Lemma 5.
We move to Step 3 in the proof of Theorem 6. Note that in any n consecutive squares in a row or a column, there are exactly
![]() $\frac {n}{2}$
which are black and
$\frac {n}{2}$
which are black and
![]() $\frac {n}{2}$
which are white. This is because
$\frac {n}{2}$
which are white. This is because
![]() $\varphi (1,0)$
and
$\varphi (1,0)$
and
![]() $\varphi (0,1)$
are odd. Thus, for any rectangle with side lengths multiple of n, the number of black squares is the same as white squares. So we consider once again the stair-like regions.
$\varphi (0,1)$
are odd. Thus, for any rectangle with side lengths multiple of n, the number of black squares is the same as white squares. So we consider once again the stair-like regions.
Because this coloring is not symmetric with respect to horizontal and vertical reflections, we need to consider in principle four types of stairs: one that we walk up from right to left and the three rotations of these, by
![]() $\pi /2, \pi $
and
$\pi /2, \pi $
and
![]() $3\pi /2$
. Again, we must show that the number of black squares minus the number of white squares is a multiple of n. The proof will be by induction on the length l and the height h of the steps.
$3\pi /2$
. Again, we must show that the number of black squares minus the number of white squares is a multiple of n. The proof will be by induction on the length l and the height h of the steps.
Case 1: h is odd and l is even. Assume first that the stair is in the position of Figure 4, so one climbs up from right to left. We divide the stair in four regions,
![]() $A,-A,B,C$
. Region A consists of the top
$A,-A,B,C$
. Region A consists of the top
![]() $n/2-1$
levels of the stair, while
$n/2-1$
levels of the stair, while
![]() $-A$
is region A translated downward
$-A$
is region A translated downward
![]() $\frac {n}{2}h$
units. Since h is odd,
$\frac {n}{2}h$
units. Since h is odd,
![]() $\varphi (0,1)$
is odd and c is good, then A and
$\varphi (0,1)$
is odd and c is good, then A and
![]() $-A$
are painted with opposite colors. Region B consists of the squares below A which are not in
$-A$
are painted with opposite colors. Region B consists of the squares below A which are not in
![]() $-A$
. Region
$-A$
. Region
![]() $B'$
is outside the stairs and is the translation of B by
$B'$
is outside the stairs and is the translation of B by
![]() $\frac {n}{2}l$
units to the right. Since l is even, B and
$\frac {n}{2}l$
units to the right. Since l is even, B and
![]() $B'$
are painted identically, so the invariant
$B'$
are painted identically, so the invariant
![]() $\Lambda $
of the stair is the invariant of the rectangle
$\Lambda $
of the stair is the invariant of the rectangle
![]() $C\cup B'$
, where C are the squares of the stair which are not in
$C\cup B'$
, where C are the squares of the stair which are not in
![]() $A,-A,B$
. But this rectangle has one side of length
$A,-A,B$
. But this rectangle has one side of length
![]() $\frac {n}{2}l$
, which is a multiple of n, so its invariant
$\frac {n}{2}l$
, which is a multiple of n, so its invariant
![]() $\Lambda (C\cup B')$
is trivial.
$\Lambda (C\cup B')$
is trivial.

Figure 4: An
![]() $(n-1)$
-step stair for
$(n-1)$
-step stair for
![]() $n=8$
, h odd, l even.
$n=8$
, h odd, l even.
If the stair is in a different position (climbing from left to right, or the corresponding upside-down stairs), the same proof works. We have not used an induction argument for this case.
Case 2: h even, l odd, is symmetric to Case 1.
Case 3: h and l even. In this case, we consider four
![]() $(n-1)$
-step stairs contained in our big stair (see Figure 5). The height of the steps in these four small stairs is
$(n-1)$
-step stairs contained in our big stair (see Figure 5). The height of the steps in these four small stairs is
![]() $h/2$
, and the length is
$h/2$
, and the length is
![]() $l/2$
. Region A is disjoint from
$l/2$
. Region A is disjoint from
![]() $B,C,D$
, and D is also disjoint from B and C. But B and C overlap in
$B,C,D$
, and D is also disjoint from B and C. But B and C overlap in
![]() $n-1$
steps of size
$n-1$
steps of size
![]() $l/2\times h/2$
. They are marked with the sign
$l/2\times h/2$
. They are marked with the sign
![]() $-$
in the figure. There are
$-$
in the figure. There are
![]() $n-1$
rectangles of size
$n-1$
rectangles of size
![]() $l/2\times h/2$
in the big stair which are not in
$l/2\times h/2$
in the big stair which are not in
![]() $A\cup B\cup C\cup D$
. They are marked with sign
$A\cup B\cup C\cup D$
. They are marked with sign
![]() $+$
.
$+$
.

Figure 5: An
![]() $(n-1)$
-step stair for
$(n-1)$
-step stair for
![]() $n=8$
, h and l even.
$n=8$
, h and l even.
By induction, the invariants
![]() $\Lambda (A), \Lambda (B), \Lambda (C)$
, and
$\Lambda (A), \Lambda (B), \Lambda (C)$
, and
![]() $\Lambda (D)$
are zero, so the invariant in the big stair is the invariant in the union of the
$\Lambda (D)$
are zero, so the invariant in the big stair is the invariant in the union of the
![]() $+$
regions minus the invariant in the
$+$
regions minus the invariant in the
![]() $-$
regions. We add two
$-$
regions. We add two
![]() $l/2\times h/2$
rectangles to the picture, those marked with
$l/2\times h/2$
rectangles to the picture, those marked with
![]() $+'$
and
$+'$
and
![]() $-'$
. Since they are
$-'$
. Since they are
![]() $\frac {n}{2}h$
squares apart and h is even, they are painted with the same color. Now, the
$\frac {n}{2}h$
squares apart and h is even, they are painted with the same color. Now, the
![]() $+$
rectangles together with the
$+$
rectangles together with the
![]() $+'$
rectangle are n rectangles which are aligned, and the distance between two consecutive is constant. Thus, the characteristic polynomial of this region (the sum of the monomials
$+'$
rectangle are n rectangles which are aligned, and the distance between two consecutive is constant. Thus, the characteristic polynomial of this region (the sum of the monomials
![]() $X^iY^j$
for squares
$X^iY^j$
for squares
![]() $(i,j)$
of the region) is a multiple of a polynomial of the form
$(i,j)$
of the region) is a multiple of a polynomial of the form
![]() $1+m+m^2+\cdots +m^{n-1}$
, so we already know that the invariant is trivial. The same happens with the region formed by the
$1+m+m^2+\cdots +m^{n-1}$
, so we already know that the invariant is trivial. The same happens with the region formed by the
![]() $-$
rectangles together with the
$-$
rectangles together with the
![]() $-'$
rectangle. Thus, the invariant of the big stair is also trivial.
$-'$
rectangle. Thus, the invariant of the big stair is also trivial.
Case 4: h and l odd. Just as in Case 1, we consider regions A and
![]() $-A$
inside the stair (see Figure 6). Since h is odd, they are painted with opposite colors, and we only care about region B, which consists of the squares which are not in A nor in
$-A$
inside the stair (see Figure 6). Since h is odd, they are painted with opposite colors, and we only care about region B, which consists of the squares which are not in A nor in
![]() $-A$
.
$-A$
.

Figure 6: An
![]() $(n-1)$
-step stair for
$(n-1)$
-step stair for
![]() $n=8$
, h and l odd.
$n=8$
, h and l odd.
Consider region C formed by the squares of B which satisfy that the neighboring squares to the left and below are not in B (they appear with gray in Figure 6). The characteristic polynomial of C is
![]() $P=m'(1+m+m^2+\cdots +m^{\frac {n}{2}-1})$
for
$P=m'(1+m+m^2+\cdots +m^{\frac {n}{2}-1})$
for
![]() $m=X^lY^{-h}$
and some monomial
$m=X^lY^{-h}$
and some monomial
![]() $m'$
. In order to understand the invariant
$m'$
. In order to understand the invariant
![]() $\Lambda (P)$
, we should analyze the colors of the numbers
$\Lambda (P)$
, we should analyze the colors of the numbers
![]() $a,a+b,a+2b,\ldots , a+(\frac {n}{2}-1)b \in \mathbb {Z}_n$
, where a depends on
$a,a+b,a+2b,\ldots , a+(\frac {n}{2}-1)b \in \mathbb {Z}_n$
, where a depends on
![]() $m'$
and
$m'$
and
![]() $b=\varphi (l,-h)$
. By assumption, b is even, so Lemma 5 says that
$b=\varphi (l,-h)$
. By assumption, b is even, so Lemma 5 says that
![]() $\Lambda (C)$
is a multiple of
$\Lambda (C)$
is a multiple of
![]() $\frac {n}{2}$
. Moreover,
$\frac {n}{2}$
. Moreover,
![]() $\Lambda (C)=\frac {n}{2}\in \mathbb {Z}_n$
if
$\Lambda (C)=\frac {n}{2}\in \mathbb {Z}_n$
if
![]() $n|b$
and
$n|b$
and
![]() $\Lambda (C)=0$
if
$\Lambda (C)=0$
if
![]() $n\nmid b$
. Region B can be covered by
$n\nmid b$
. Region B can be covered by
![]() $hl\frac {n}{2}$
translates of region C. Each of them has the same invariant as C. Since
$hl\frac {n}{2}$
translates of region C. Each of them has the same invariant as C. Since
![]() $k\ge 2$
,
$k\ge 2$
,
![]() $hl\frac {n}{2}$
is even, and
$hl\frac {n}{2}$
is even, and
![]() $\Lambda (B)=hl\frac {n}{2}\Lambda (C)=0\in \mathbb {Z}_n$
.▪
$\Lambda (B)=hl\frac {n}{2}\Lambda (C)=0\in \mathbb {Z}_n$
.▪
If
![]() $\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
, c and
$\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
, c and
![]() $(i_0,j_0)$
are in the hypotheses of Theorem 16, then
$(i_0,j_0)$
are in the hypotheses of Theorem 16, then
![]() $\Lambda _{\varphi t,c}:F_2' \to \mathbb {Z}_n$
induces a well-defined group homomorphism
$\Lambda _{\varphi t,c}:F_2' \to \mathbb {Z}_n$
induces a well-defined group homomorphism
![]() $\Lambda _{\varphi t,c}: M(2,n)' \to \mathbb {Z}_n$
.
$\Lambda _{\varphi t,c}: M(2,n)' \to \mathbb {Z}_n$
.
Example 17 In this example, we exhibit a complete invariant for
![]() $M(2,4)$
, that is, a concrete solution to the word problem. We describe a method which decides for any
$M(2,4)$
, that is, a concrete solution to the word problem. We describe a method which decides for any
![]() $u\in F_2$
, whether u is trivial in
$u\in F_2$
, whether u is trivial in
![]() $M(2,4)$
. Of course, this can be obtained from any finite presentation and coset enumeration or a consistent power-commutator presentation, but our methods are elementary and very easy to carry out by hand in short time.
$M(2,4)$
. Of course, this can be obtained from any finite presentation and coset enumeration or a consistent power-commutator presentation, but our methods are elementary and very easy to carry out by hand in short time.
Remember that we constructed the map
![]() $\Omega :M(2,4)'\to (\mathbb {Z}_4)^4$
whose image has order
$\Omega :M(2,4)'\to (\mathbb {Z}_4)^4$
whose image has order
![]() $2^5$
. Consider the map
$2^5$
. Consider the map
![]() $\widetilde {\Omega }:M(2,4)' \to (\mathbb {Z}_4)^5$
defined by
$\widetilde {\Omega }:M(2,4)' \to (\mathbb {Z}_4)^5$
defined by
![]() $\widetilde {\Omega }(w)=(\Omega (w), \Lambda (w))$
, where
$\widetilde {\Omega }(w)=(\Omega (w), \Lambda (w))$
, where
![]() $\Lambda :M(2,4)'\to \mathbb {Z}_4$
is the diagonal invariant defined as in the statement of Theorem 16 for
$\Lambda :M(2,4)'\to \mathbb {Z}_4$
is the diagonal invariant defined as in the statement of Theorem 16 for
![]() $\varphi (1,0)=\varphi (0,1)=1$
,
$\varphi (1,0)=\varphi (0,1)=1$
,
![]() $(i_0,j_0)=(0,0)$
, and
$(i_0,j_0)=(0,0)$
, and
![]() $c:\mathbb {Z}_4\to \{\textrm {black, white}\}$
the coloring that paints
$c:\mathbb {Z}_4\to \{\textrm {black, white}\}$
the coloring that paints
![]() $0,1$
with black and
$0,1$
with black and
![]() $2,3$
with white. Figure 7 shows the five invariants that compose
$2,3$
with white. Figure 7 shows the five invariants that compose
![]() $\widetilde {\Omega }$
. If
$\widetilde {\Omega }$
. If
![]() $w\in F_2'$
is such that
$w\in F_2'$
is such that
![]() $P_w=1+X^2Y^2$
, then
$P_w=1+X^2Y^2$
, then
![]() $\widetilde {\Omega }(w)=(0,0,0,0,2)$
. This already implies that the order
$\widetilde {\Omega }(w)=(0,0,0,0,2)$
. This already implies that the order
![]() $|\textrm {Im} (\widetilde {\Omega })|\ge 2 |\textrm {Im} (\Omega )|=2^6$
. On the other hand, since
$|\textrm {Im} (\widetilde {\Omega })|\ge 2 |\textrm {Im} (\Omega )|=2^6$
. On the other hand, since
![]() $|M(2,4)|=2^{10}$
, then
$|M(2,4)|=2^{10}$
, then
![]() $|M(2,4)'|=2^6$
, so
$|M(2,4)'|=2^6$
, so
![]() $\widetilde {\Omega }$
is a monomorphism.
$\widetilde {\Omega }$
is a monomorphism.

Figure 7: The five colorings that form a complete invariant for
![]() $M(2,4)$
: two horizontal invariants, two vertical invariants, and a diagonal invariant.
$M(2,4)$
: two horizontal invariants, two vertical invariants, and a diagonal invariant.
The algorithm to decide whether a given element
![]() $u\in F_2$
is trivial in
$u\in F_2$
is trivial in
![]() $M(2,4)$
is the following: compute the total exponents
$M(2,4)$
is the following: compute the total exponents
![]() $a=\exp (x,u)$
and
$a=\exp (x,u)$
and
![]() $b=\exp (y,u)$
. If any of them is not divisible by
$b=\exp (y,u)$
. If any of them is not divisible by
![]() $4$
, u is nontrivial in
$4$
, u is nontrivial in
![]() $M(2,4)$
. Otherwise, let
$M(2,4)$
. Otherwise, let
![]() $v=x^{-a}y^{-b}u\in F_2'$
. Compute
$v=x^{-a}y^{-b}u\in F_2'$
. Compute
![]() $\widetilde {\Omega }(v)$
. If this is nontrivial, v and then u are nontrivial in
$\widetilde {\Omega }(v)$
. If this is nontrivial, v and then u are nontrivial in
![]() $M(2,4)$
. If it is trivial, then
$M(2,4)$
. If it is trivial, then
![]() $u=v=1\in M(2,4)$
.
$u=v=1\in M(2,4)$
.
In the previous example, we have used that
![]() $|M(2,4)|=2^{10}$
. In fact, the inequality
$|M(2,4)|=2^{10}$
. In fact, the inequality
![]() $|M(2,4)|\ge 2^{10}$
follows from the fact that
$|M(2,4)|\ge 2^{10}$
follows from the fact that
![]() $|\textrm {Im}(\widetilde {\Omega })|\ge 2^6$
. In Example 21, we will prove the inequality
$|\textrm {Im}(\widetilde {\Omega })|\ge 2^6$
. In Example 21, we will prove the inequality
![]() $|M(2,4)|\le 2^{10}$
by different methods, thus providing an alternative proof that
$|M(2,4)|\le 2^{10}$
by different methods, thus providing an alternative proof that
![]() $|M(2,4)|=2^{10}$
.
$|M(2,4)|=2^{10}$
.
Let
![]() $n=2^k$
. As we recalled in Section 2 and the beginning of this section, Newman proves in [Reference Newman38] that
$n=2^k$
. As we recalled in Section 2 and the beginning of this section, Newman proves in [Reference Newman38] that
![]() $|M(2,n)|\ge n^22^{\frac {n^2}{4}-1}$
. His short argument is as follows. Take
$|M(2,n)|\ge n^22^{\frac {n^2}{4}-1}$
. His short argument is as follows. Take
![]() $R=F_2^{\frac {n}{2}}F_2'\leqslant F_2$
and
$R=F_2^{\frac {n}{2}}F_2'\leqslant F_2$
and
![]() $S=R^2R'\leqslant F_2$
. Then,
$S=R^2R'\leqslant F_2$
. Then,
![]() $F_2'\leqslant R$
, so
$F_2'\leqslant R$
, so
![]() $F_2''\leqslant R'\leqslant S$
and
$F_2''\leqslant R'\leqslant S$
and
![]() $F_2^n\leqslant R^2 \leqslant S$
. Thus,
$F_2^n\leqslant R^2 \leqslant S$
. Thus,
![]() $F_2^n F_2'' \leqslant S$
, which shows that the order of
$F_2^n F_2'' \leqslant S$
, which shows that the order of
![]() $M(2,n)=F_2/F_2^nF_2''$
is greater than or equal to the order of
$M(2,n)=F_2/F_2^nF_2''$
is greater than or equal to the order of
![]() $F_2/S$
. But the latter is easy to compute. Note that
$F_2/S$
. But the latter is easy to compute. Note that
![]() $F_2/R$
is an abelian group of order
$F_2/R$
is an abelian group of order
![]() $(\frac {n}{2})^2$
, so by the Schreier formula, R is a free group of rank
$(\frac {n}{2})^2$
, so by the Schreier formula, R is a free group of rank
![]() $1+(\frac {n}{2})^2$
. Once again,
$1+(\frac {n}{2})^2$
. Once again,
![]() $R/S$
is abelian of order
$R/S$
is abelian of order
![]() $2^{\textrm {rk}(R)}=2^{1+(\frac {n}{2})^2}$
, and the order of
$2^{\textrm {rk}(R)}=2^{1+(\frac {n}{2})^2}$
, and the order of
![]() $F_2/S$
is
$F_2/S$
is
![]() $|F_2/R||R/S|=(\frac {n}{2})^22^{\frac {n^2}{4}+1}$
.
$|F_2/R||R/S|=(\frac {n}{2})^22^{\frac {n^2}{4}+1}$
.
Our next result improves Newman’s lower bound just a little bit.
Theorem 18 Let
![]() $k\ge 3$
and
$k\ge 3$
and
![]() $n=2^k$
. Then,
$n=2^k$
. Then,
![]() $|M(2,n)|\ge n^2 2^{\frac {5n^2}{16}-1}$
.
$|M(2,n)|\ge n^2 2^{\frac {5n^2}{16}-1}$
.
Proof Let
![]() $S=R^2R'$
be as above. It suffices to prove then that
$S=R^2R'$
be as above. It suffices to prove then that
![]() $|S/F_2^nF_2''|\ge 2^{\frac {n^2}{16}}$
. We will show that
$|S/F_2^nF_2''|\ge 2^{\frac {n^2}{16}}$
. We will show that
![]() $|\frac {S\cap F_2'}{F_2^nF_2'' \cap F_2'}|\ge 2^{\frac {n^2}{16}}$
. Given any Laurent polynomial
$|\frac {S\cap F_2'}{F_2^nF_2'' \cap F_2'}|\ge 2^{\frac {n^2}{16}}$
. Given any Laurent polynomial
![]() $P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, there exists
$P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, there exists
![]() $z\in F_2'$
with
$z\in F_2'$
with
![]() $P_z=P$
. Thus,
$P_z=P$
. Thus,
![]() $z^2\in S\cap F_2'$
and
$z^2\in S\cap F_2'$
and
![]() $2P\in W(S\cap F_2') \leqslant \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
.
$2P\in W(S\cap F_2') \leqslant \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
.
Let
![]() $O=\{1,9,17,\ldots , n-7\}$
be the set of integers congruent to
$O=\{1,9,17,\ldots , n-7\}$
be the set of integers congruent to
![]() $1$
modulo
$1$
modulo
![]() $8$
between
$8$
between
![]() $0$
and
$0$
and
![]() $n-1$
. Let
$n-1$
. Let
![]() $c_0,c_1:\mathbb {Z}_n\to \{\textrm {black, white}\}$
be two good colorings which differ only in
$c_0,c_1:\mathbb {Z}_n\to \{\textrm {black, white}\}$
be two good colorings which differ only in
![]() $0$
and
$0$
and
![]() $n/2$
.
$n/2$
.
Consider the action of
![]() $\Gamma =\mathbb {Z}_8 \times \mathbb {Z}_2$
on
$\Gamma =\mathbb {Z}_8 \times \mathbb {Z}_2$
on
![]() $\mathbb {Z}_n \times \mathbb {Z}_n$
where the generator of
$\mathbb {Z}_n \times \mathbb {Z}_n$
where the generator of
![]() $\mathbb {Z}_8$
maps a pair
$\mathbb {Z}_8$
maps a pair
![]() $(i,j)\in \mathbb {Z}_n\times \mathbb {Z}_n$
to
$(i,j)\in \mathbb {Z}_n\times \mathbb {Z}_n$
to
![]() $(i-n/8, j+n/8)$
and the generator of
$(i-n/8, j+n/8)$
and the generator of
![]() $\mathbb {Z}_2$
maps
$\mathbb {Z}_2$
maps
![]() $(i,j)$
to
$(i,j)$
to
![]() $(i+n/2,j)$
. Let
$(i+n/2,j)$
. Let
![]() $\Xi $
be a set of representatives of the orbits of this action. This set has
$\Xi $
be a set of representatives of the orbits of this action. This set has
![]() $n^2/16$
elements.
$n^2/16$
elements.
Let
![]() $\phi : M(2,n)' \to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
be the group homomorphism defined by
$\phi : M(2,n)' \to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
be the group homomorphism defined by
![]() $\phi (z)_{b,c,(i_0,j_0)}=\Lambda _{\varphi _{1,b}t_{-(i_0,j_0)},c}(z)$
, where
$\phi (z)_{b,c,(i_0,j_0)}=\Lambda _{\varphi _{1,b}t_{-(i_0,j_0)},c}(z)$
, where
![]() $\varphi _{1,b}:\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
is the homomorphism determined by
$\varphi _{1,b}:\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
is the homomorphism determined by
![]() $\varphi _{1,b}(i,j)=i+bj$
and
$\varphi _{1,b}(i,j)=i+bj$
and
![]() $t_{-(i_0,j_0)}$
is the translation by the vector
$t_{-(i_0,j_0)}$
is the translation by the vector
![]() $-(i_0,j_0)$
(any vector in the fiber of
$-(i_0,j_0)$
(any vector in the fiber of
![]() $\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n \times \mathbb {Z}_n$
over
$\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n \times \mathbb {Z}_n$
over
![]() $-(i_0,j_0)$
). By Theorem 16,
$-(i_0,j_0)$
). By Theorem 16,
![]() $\phi $
is a well-defined group homomorphism. To prove the result, it suffices to show that the order of
$\phi $
is a well-defined group homomorphism. To prove the result, it suffices to show that the order of
![]() $\phi (S\cap F_2'/F_2^nF_2''\cap F_2')$
is greater than or equal to
$\phi (S\cap F_2'/F_2^nF_2''\cap F_2')$
is greater than or equal to
![]() $2^{\frac {n^2}{16}}$
. Let
$2^{\frac {n^2}{16}}$
. Let
![]() $\overline {\phi }: \mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
be defined by
$\overline {\phi }: \mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
be defined by
![]() $\overline {\phi }(P)_{b,c,(i_0,j_0)}=\Lambda _{\varphi _{1,b}t_{-(i_0,j_0)},c}(P)$
, so we have
$\overline {\phi }(P)_{b,c,(i_0,j_0)}=\Lambda _{\varphi _{1,b}t_{-(i_0,j_0)},c}(P)$
, so we have
![]() $\overline {\phi }W=\phi q$
, where
$\overline {\phi }W=\phi q$
, where
![]() $q:F_2'\to M(2,n)'$
is the projection. Then,
$q:F_2'\to M(2,n)'$
is the projection. Then,
![]() $\phi (S\cap F_2'/F_2^nF_2'' \cap F_2')=\overline {\phi }W(S\cap F_2')\geqslant \overline {\phi }(2\mathbb {Z}[X^{\pm 1},Y^{\pm 1}])$
. The map
$\phi (S\cap F_2'/F_2^nF_2'' \cap F_2')=\overline {\phi }W(S\cap F_2')\geqslant \overline {\phi }(2\mathbb {Z}[X^{\pm 1},Y^{\pm 1}])$
. The map
![]() $\overline {\phi }$
factorizes as
$\overline {\phi }$
factorizes as
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \twoheadrightarrow \mathbb {Z}_n[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
, and we are going to study the restriction
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \twoheadrightarrow \mathbb {Z}_n[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
, and we are going to study the restriction
![]() $\psi $
of the map
$\psi $
of the map
![]() $\mathbb {Z}_n[X^{\pm 1},Y^{\pm 1}]\to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
to the subgroup H of Laurent polynomials with coefficients in
$\mathbb {Z}_n[X^{\pm 1},Y^{\pm 1}]\to \mathbb {Z}_n^{O\times \{c_0,c_1\} \times \Xi }$
to the subgroup H of Laurent polynomials with coefficients in
![]() $\mathbb {Z}_n$
supported in the square
$\mathbb {Z}_n$
supported in the square
![]() $[n]^2$
and with all coefficients even, i.e.,
$[n]^2$
and with all coefficients even, i.e.,
![]() $P\{(i,j)\}$
is even for every
$P\{(i,j)\}$
is even for every
![]() $i,j\in \mathbb {Z}$
and
$i,j\in \mathbb {Z}$
and
![]() $P\{(i,j)\}\neq 0$
implies that
$P\{(i,j)\}\neq 0$
implies that
![]() $0\le i,j \le n-1$
. Note that the order of H is
$0\le i,j \le n-1$
. Note that the order of H is
![]() $\left (\frac {n}{2} \right )^{n^2}$
. We want to prove that
$\left (\frac {n}{2} \right )^{n^2}$
. We want to prove that
![]() $|\textrm {Im}(\psi )|\ge 2^{\frac {n^2}{16}}$
.
$|\textrm {Im}(\psi )|\ge 2^{\frac {n^2}{16}}$
.
We have a sequence
Let
![]() $P \in \textrm {ker}(\psi )$
. This means that for every
$P \in \textrm {ker}(\psi )$
. This means that for every
![]() $b\in O$
,
$b\in O$
,
![]() $c=c_0,c_1$
and
$c=c_0,c_1$
and
![]() $(i_0,j_0)\in \Xi $
,
$(i_0,j_0)\in \Xi $
,
If we subtract the equations corresponding to
![]() $c_0$
and to
$c_0$
and to
![]() $c_1$
, we obtain
$c_1$
, we obtain
Here, the equalities
![]() $i-i_0+b(j-j_0)=0$
and
$i-i_0+b(j-j_0)=0$
and
![]() $i-i_0+b(j-j_0)=n/2$
are considered modulo n.
$i-i_0+b(j-j_0)=n/2$
are considered modulo n.
We make b vary among all the elements in O and add all these equations to obtain
Given
![]() $0\le i,j\le n-1$
, the coefficient
$0\le i,j\le n-1$
, the coefficient
![]() $P\{(i,j)\}$
appears in the left term of equation (1) if and only if
$P\{(i,j)\}$
appears in the left term of equation (1) if and only if
![]() $i-i_0+b(j-j_0) \equiv 0 \ \ \mod n$
for some
$i-i_0+b(j-j_0) \equiv 0 \ \ \mod n$
for some
![]() $b \equiv 1 \ \ \mod 8$
. This is equivalent to
$b \equiv 1 \ \ \mod 8$
. This is equivalent to
![]() $d=\gcd (8(j-j_0),n) | \ i-i_0+j-j_0$
. In this case, the number of times that
$d=\gcd (8(j-j_0),n) | \ i-i_0+j-j_0$
. In this case, the number of times that
![]() $P\{(i,j)\}$
appears in the left term is
$P\{(i,j)\}$
appears in the left term is
![]() $d/8$
(multiplied by the coefficient
$d/8$
(multiplied by the coefficient
![]() $2$
). On the other hand,
$2$
). On the other hand,
![]() $P\{(i,j)\}$
appears in the right term of equation (1) if and only if
$P\{(i,j)\}$
appears in the right term of equation (1) if and only if
![]() $i-i_0+b(j-j_0) \equiv n/2 \ \ \mod n$
for some
$i-i_0+b(j-j_0) \equiv n/2 \ \ \mod n$
for some
![]() $b\in O$
. This is equivalent to
$b\in O$
. This is equivalent to
![]() $d | \ i-i_0+j-j_0-n/2$
, and the number of times
$d | \ i-i_0+j-j_0-n/2$
, and the number of times
![]() $P\{(i,j)\}$
appears is also
$P\{(i,j)\}$
appears is also
![]() $d/8$
. Therefore, if
$d/8$
. Therefore, if
![]() $n/8$
does not divide
$n/8$
does not divide
![]() $j-j_0$
, the coefficient
$j-j_0$
, the coefficient
![]() $P\{(i,j)\}$
in equation (1) cancels out. The unique coefficients that survive in the equation are those
$P\{(i,j)\}$
in equation (1) cancels out. The unique coefficients that survive in the equation are those
![]() $P\{(i,j)\}$
in the left term with
$P\{(i,j)\}$
in the left term with
![]() $j\equiv j_0 \ \ \mod n/8$
and
$j\equiv j_0 \ \ \mod n/8$
and
![]() $i\equiv i_0+j_0-j \ \ \mod n$
, and those
$i\equiv i_0+j_0-j \ \ \mod n$
, and those
![]() $P\{(i,j)\}$
in the right with
$P\{(i,j)\}$
in the right with
![]() $j\equiv j_0 \ \ \mod n/8$
and
$j\equiv j_0 \ \ \mod n/8$
and
![]() $i\equiv i_0+j_0-j +n/2 \ \ \mod n$
. Each of them appears
$i\equiv i_0+j_0-j +n/2 \ \ \mod n$
. Each of them appears
![]() $d/8=n/8$
times, multiplied by the coefficient
$d/8=n/8$
times, multiplied by the coefficient
![]() $2$
. The coefficients in the left have positive sign, and those in the right negative. But since
$2$
. The coefficients in the left have positive sign, and those in the right negative. But since
![]() $P\in H$
,
$P\in H$
,
![]() $P\{(i,j)\}$
is even for all
$P\{(i,j)\}$
is even for all
![]() $(i,j)$
, so
$(i,j)$
, so
![]() $\frac {n}{4}P\{(i,j)\}=-\frac {n}{4}P\{(i,j)\} \in \mathbb {Z}_n$
. In conclusion,
$\frac {n}{4}P\{(i,j)\}=-\frac {n}{4}P\{(i,j)\} \in \mathbb {Z}_n$
. In conclusion,
 $$ \begin{align*}\frac{n}{4} \sum\limits_{(i,j)\in \Gamma \cdot (i_0,j_0)} P\{(i,j)\}= 0\in \mathbb{Z}_n,\end{align*} $$
$$ \begin{align*}\frac{n}{4} \sum\limits_{(i,j)\in \Gamma \cdot (i_0,j_0)} P\{(i,j)\}= 0\in \mathbb{Z}_n,\end{align*} $$
where
![]() $\Gamma \cdot (i_0,j_0)$
is the orbit of
$\Gamma \cdot (i_0,j_0)$
is the orbit of
![]() $(i_0,j_0)$
under
$(i_0,j_0)$
under
![]() $\Gamma =\mathbb {Z}_8 \times \mathbb {Z}_2$
. In other words,
$\Gamma =\mathbb {Z}_8 \times \mathbb {Z}_2$
. In other words,
This means that if
![]() $P\in \ker (\psi )$
, the congruence of
$P\in \ker (\psi )$
, the congruence of
![]() $P\{(i_0,j_0)\}$
modulo
$P\{(i_0,j_0)\}$
modulo
![]() $4$
is determined by the other coefficients
$4$
is determined by the other coefficients
![]() $P\{(i,j)\}$
with
$P\{(i,j)\}$
with
![]() $(i,j)$
in the orbit of
$(i,j)$
in the orbit of
![]() $(i_0,j_0)$
. Thus, the order of
$(i_0,j_0)$
. Thus, the order of
![]() $\ker (\psi )$
is smaller than or equal to
$\ker (\psi )$
is smaller than or equal to
![]() $\left ( \left (\frac {n}{2} \right )^{15} \frac {n}{4} \right )^{\frac {n^2}{16}}$
(there are
$\left ( \left (\frac {n}{2} \right )^{15} \frac {n}{4} \right )^{\frac {n^2}{16}}$
(there are
![]() $\frac {n^2}{16}$
orbits and there are only
$\frac {n^2}{16}$
orbits and there are only
![]() $\frac {n}{4}$
choices for
$\frac {n}{4}$
choices for
![]() $P\{(i_0,j_0)\}$
once we have chosen the other
$P\{(i_0,j_0)\}$
once we have chosen the other
![]() $15$
values of
$15$
values of
![]() $P\{(i,j)\}$
in the same orbit). Finally,
$P\{(i,j)\}$
in the same orbit). Finally,
 $$ \begin{align*}|\textrm{Im}(\psi)|=\frac{|H|}{|\ker (\psi)|}\ge \frac{\left(\frac{n}{2} \right)^{n^2}}{\left(\frac{n}{2} \right)^{n^2} \frac{1}{2^{\frac{n^2}{16}}}}=2^{\frac{n^2}{16}}.\\[-45pt]\end{align*} $$
$$ \begin{align*}|\textrm{Im}(\psi)|=\frac{|H|}{|\ker (\psi)|}\ge \frac{\left(\frac{n}{2} \right)^{n^2}}{\left(\frac{n}{2} \right)^{n^2} \frac{1}{2^{\frac{n^2}{16}}}}=2^{\frac{n^2}{16}}.\\[-45pt]\end{align*} $$
▪
Recall that for every
![]() $m\ge 1$
,
$m\ge 1$
,
![]() $\gamma _m(F_2)/ \gamma _{m+1} (F_2)$
is a free abelian group of finite rank, and a basis is given by the basic commutators of weight m. The basic commutators of weight
$\gamma _m(F_2)/ \gamma _{m+1} (F_2)$
is a free abelian group of finite rank, and a basis is given by the basic commutators of weight m. The basic commutators of weight
![]() $1$
are y and x. We set
$1$
are y and x. We set
![]() $y<x$
. Once we have defined the basic commutators of weight smaller than m and we have ordered them, we define those basic commutators of weight m: they are commutators
$y<x$
. Once we have defined the basic commutators of weight smaller than m and we have ordered them, we define those basic commutators of weight m: they are commutators
![]() $[c_j,c_i]$
where
$[c_j,c_i]$
where
![]() $c_j$
and
$c_j$
and
![]() $c_i$
are basic commutators of weights j and i,
$c_i$
are basic commutators of weights j and i,
![]() $j+i=m$
,
$j+i=m$
,
![]() $c_j<c_i$
, and if
$c_j<c_i$
, and if
![]() $i\ge 2$
and
$i\ge 2$
and
![]() $c_i=[c_t,c_s]$
, then
$c_i=[c_t,c_s]$
, then
![]() $c_t\le c_j$
. We set an arbitrary order among the basic commutators of weight m. Each of them is greater than any commutator of weight
$c_t\le c_j$
. We set an arbitrary order among the basic commutators of weight m. Each of them is greater than any commutator of weight
![]() $<m$
. Our basic commutators are the inverses of the classical ones, which are defined using the other convention for commutators
$<m$
. Our basic commutators are the inverses of the classical ones, which are defined using the other convention for commutators
![]() $(a,b)=a^{-1}b^{-1}ab$
(see [Reference Hall22, Chapter 11]). If
$(a,b)=a^{-1}b^{-1}ab$
(see [Reference Hall22, Chapter 11]). If
![]() $[c_j,c_i]$
is a basic commutator constructed as above, which is nontrivial in the free metabelian group
$[c_j,c_i]$
is a basic commutator constructed as above, which is nontrivial in the free metabelian group
![]() $M_2=F_2/F_2''$
of rank
$M_2=F_2/F_2''$
of rank
![]() $2$
, then
$2$
, then
![]() $c_j$
has to be a basic commutator of weight
$c_j$
has to be a basic commutator of weight
![]() $1$
(i.e., x or y), and
$1$
(i.e., x or y), and
![]() $c_i$
has to be nontrivial in
$c_i$
has to be nontrivial in
![]() $M_2$
. If
$M_2$
. If
![]() $c_i=[c_t,c_s]$
, then
$c_i=[c_t,c_s]$
, then
![]() $c_t$
is also of weight
$c_t$
is also of weight
![]() $1$
and
$1$
and
![]() $c_t\le c_j$
. Thus, for
$c_t\le c_j$
. Thus, for
![]() $m\ge 2$
,
$m\ge 2$
,
![]() $\gamma _m(M_2)/\gamma _{m+1}(M_2)$
is generated by the basic commutators
$\gamma _m(M_2)/\gamma _{m+1}(M_2)$
is generated by the basic commutators
 $e_{i,m-i-1}=[\underbrace {x,x,\ldots , x}_{i},\underbrace {y,y, \ldots , y}_{m-i-1},x]=[x,[x, \ldots , [x, [y,[y, \ldots , [y,x]]\ldots ]$
, where
$e_{i,m-i-1}=[\underbrace {x,x,\ldots , x}_{i},\underbrace {y,y, \ldots , y}_{m-i-1},x]=[x,[x, \ldots , [x, [y,[y, \ldots , [y,x]]\ldots ]$
, where
![]() $0\le i\le m-2$
. For
$0\le i\le m-2$
. For
![]() $i=0$
,
$i=0$
,
![]() $e_{0,m-1}$
this is just the
$e_{0,m-1}$
this is just the
![]() $(m-1)$
-Engel word
$(m-1)$
-Engel word
![]() $e_{m-1}$
.
$e_{m-1}$
.
Proposition 19 Let
![]() $n=2^k$
for some
$n=2^k$
for some
![]() $k\ge 3$
. Then,
$k\ge 3$
. Then,
![]() $e_{i,m-i-1}$
is nontrivial in the class m factor
$e_{i,m-i-1}$
is nontrivial in the class m factor
![]() $\gamma _{m}(M(2,n)) /\gamma _{m+1}(M(2,n))$
for every
$\gamma _{m}(M(2,n)) /\gamma _{m+1}(M(2,n))$
for every
![]() $2\le m\le n+2$
and every
$2\le m\le n+2$
and every
![]() $0\le i\le m-2$
.
$0\le i\le m-2$
.
Proof It suffices to prove the statement for
![]() $m=n+2$
. The winding invariant of
$m=n+2$
. The winding invariant of
![]() $e_{i,n-i+1}$
is
$e_{i,n-i+1}$
is
![]() $-(X-1)^i(Y-1)^{n-i}$
. Let
$-(X-1)^i(Y-1)^{n-i}$
. Let
![]() $\Lambda :M(2,n)' \to \mathbb {Z}_n$
be the diagonal invariant associated to
$\Lambda :M(2,n)' \to \mathbb {Z}_n$
be the diagonal invariant associated to
![]() $\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
, where
$\varphi :\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
, where
![]() $\varphi (1,0)=\varphi (0,1)=1$
, t the identity of
$\varphi (1,0)=\varphi (0,1)=1$
, t the identity of
![]() $\mathbb {Z} \times \mathbb {Z}$
, and
$\mathbb {Z} \times \mathbb {Z}$
, and
![]() $c:\mathbb {Z}_n \to \{\textrm {black, white}\}$
the good coloring which paints
$c:\mathbb {Z}_n \to \{\textrm {black, white}\}$
the good coloring which paints
![]() $0,1,\ldots , \frac {n}{2}-1$
with black. Since
$0,1,\ldots , \frac {n}{2}-1$
with black. Since
![]() $\Lambda (X^rY^s)=\Lambda (Y^{r+s})=\textbf {h}^0(Y^{r+s})$
, then
$\Lambda (X^rY^s)=\Lambda (Y^{r+s})=\textbf {h}^0(Y^{r+s})$
, then
![]() $\Lambda (e_{i,n-i+1})=\textbf {h}^0 (-(Y-1)^{n})=\textbf {h}^0 (e_{n+1})=\binom {n}{n/2}-2 \in \mathbb {Z}_n$
is not a multiple of
$\Lambda (e_{i,n-i+1})=\textbf {h}^0 (-(Y-1)^{n})=\textbf {h}^0 (e_{n+1})=\binom {n}{n/2}-2 \in \mathbb {Z}_n$
is not a multiple of
![]() $8$
by Example 9 and Lemma 8. On the other hand, we will see that
$8$
by Example 9 and Lemma 8. On the other hand, we will see that
![]() $\Lambda (z)$
is a multiple of
$\Lambda (z)$
is a multiple of
![]() $8$
for every
$8$
for every
![]() $z\in \gamma _{n+3}(F_2)$
. The proof is similar to that of Lemma 11. If
$z\in \gamma _{n+3}(F_2)$
. The proof is similar to that of Lemma 11. If
![]() $z\in \gamma _{n+3}(F_2)$
, then
$z\in \gamma _{n+3}(F_2)$
, then
![]() $P_z$
is a sum of multiples of polynomials of the form
$P_z$
is a sum of multiples of polynomials of the form
![]() $P=(m_1-1)(m_2-1)\ldots (m_{n+1}-1)$
, where the
$P=(m_1-1)(m_2-1)\ldots (m_{n+1}-1)$
, where the
![]() $m_i$
are monomials. Thus, it suffices to prove that for any good coloring
$m_i$
are monomials. Thus, it suffices to prove that for any good coloring
![]() $c':\mathbb {Z}_n \to \{\textrm {black, white}\}$
, the diagonal invariant
$c':\mathbb {Z}_n \to \{\textrm {black, white}\}$
, the diagonal invariant
![]() $\Lambda ': F_2' \to \mathbb {Z}_n$
associated to
$\Lambda ': F_2' \to \mathbb {Z}_n$
associated to
![]() $\varphi $
, t, and
$\varphi $
, t, and
![]() $c'$
, satisfies that
$c'$
, satisfies that
![]() $\Lambda '(P)$
is a multiple of
$\Lambda '(P)$
is a multiple of
![]() $8$
. Now,
$8$
. Now,
![]() $\Lambda '(P(X,Y))=\Lambda '(P(Y,Y))$
, and
$\Lambda '(P(X,Y))=\Lambda '(P(Y,Y))$
, and
![]() $P(Y,Y)$
is a multiple of
$P(Y,Y)$
is a multiple of
![]() $Q=(Y-1)^{n+1}$
. Therefore, it suffices to prove that
$Q=(Y-1)^{n+1}$
. Therefore, it suffices to prove that
![]() $\Lambda ' (Q)$
is a multiple of
$\Lambda ' (Q)$
is a multiple of
![]() $8$
for each good coloring
$8$
for each good coloring
![]() $c'$
.
$c'$
.
Suppose first that
![]() $c'=c$
, so
$c'=c$
, so
![]() $\Lambda '=\Lambda $
. Then,
$\Lambda '=\Lambda $
. Then,
 $$ \begin{align*}\Lambda (Q)=\sum\limits_{i=0}^{\frac{n}{2}-1} (-1)^{i+1} \binom{n+1}{i}-\sum\limits_{i=\frac{n}{2}}^{n-1} (-1)^{i+1} \binom{n+1}{i}+\sum\limits_{i=n}^{n+1} (-1)^{i+1} \binom{n+1}{i}.\end{align*} $$
$$ \begin{align*}\Lambda (Q)=\sum\limits_{i=0}^{\frac{n}{2}-1} (-1)^{i+1} \binom{n+1}{i}-\sum\limits_{i=\frac{n}{2}}^{n-1} (-1)^{i+1} \binom{n+1}{i}+\sum\limits_{i=n}^{n+1} (-1)^{i+1} \binom{n+1}{i}.\end{align*} $$
Using that
![]() $\binom {n+1}{i}=\binom {n}{i-1}+\binom {n}{i}$
for
$\binom {n+1}{i}=\binom {n}{i-1}+\binom {n}{i}$
for
![]() $i\ge 1$
, we obtain that
$i\ge 1$
, we obtain that
![]() $\Lambda (Q)=2\binom {n}{n/2-1}-2n$
. Now, the action of
$\Lambda (Q)=2\binom {n}{n/2-1}-2n$
. Now, the action of
![]() $\mathbb {Z}_n$
on the set
$\mathbb {Z}_n$
on the set
![]() $\binom {\mathbb {Z}_n}{n/2-1}$
is free: if
$\binom {\mathbb {Z}_n}{n/2-1}$
is free: if
![]() $S\subseteq \mathbb {Z}_n$
is a subset of cardinality
$S\subseteq \mathbb {Z}_n$
is a subset of cardinality
![]() $n/2-1$
and
$n/2-1$
and
![]() $\frac {n}{2} \cdot S=S$
, then
$\frac {n}{2} \cdot S=S$
, then
![]() $|S|=2|S\cap [n/2]|$
is even, a contradiction. Thus, every orbit has cardinality n, and then
$|S|=2|S\cap [n/2]|$
is even, a contradiction. Thus, every orbit has cardinality n, and then
![]() $\binom {n}{n/2-1}$
is a multiple of n. This proves that
$\binom {n}{n/2-1}$
is a multiple of n. This proves that
![]() $\Lambda (Q)=0\in \mathbb {Z}_n$
, so in particular, it is a multiple of
$\Lambda (Q)=0\in \mathbb {Z}_n$
, so in particular, it is a multiple of
![]() $8$
.
$8$
.
Suppose now that
![]() $c':\mathbb {Z}_n\to \{\textrm {black, white}\}$
is any good coloring. Then,
$c':\mathbb {Z}_n\to \{\textrm {black, white}\}$
is any good coloring. Then,
![]() $c'$
can be obtained from c by a sequence of changes of colors of pairs
$c'$
can be obtained from c by a sequence of changes of colors of pairs
![]() $j, j+\frac {n}{2}$
for
$j, j+\frac {n}{2}$
for
![]() $0\le j\le \frac {n}{2}-1$
. Thus, it suffices to prove that if two good colorings
$0\le j\le \frac {n}{2}-1$
. Thus, it suffices to prove that if two good colorings
![]() $c', c''$
of
$c', c''$
of
![]() $\mathbb {Z}_n$
differ only in j and
$\mathbb {Z}_n$
differ only in j and
![]() $j+\frac {n}{2}$
, then
$j+\frac {n}{2}$
, then
![]() $\Lambda ''(Q)-\Lambda '(Q)$
is a multiple of
$\Lambda ''(Q)-\Lambda '(Q)$
is a multiple of
![]() $8$
for the invariants
$8$
for the invariants
![]() $\Lambda ', \Lambda ''$
associated to
$\Lambda ', \Lambda ''$
associated to
![]() $c',c''$
.
$c',c''$
.
If
![]() $j=0$
, then
$j=0$
, then
![]() $\Lambda ''(Q)-\Lambda '(Q)=2(\binom {n+1}{0}-\binom {n+1}{n/2}+\binom {n+1}{n}) \equiv 2(2-\binom {n+1}{n/2}) \ \ \mod 8$
. Again,
$\Lambda ''(Q)-\Lambda '(Q)=2(\binom {n+1}{0}-\binom {n+1}{n/2}+\binom {n+1}{n}) \equiv 2(2-\binom {n+1}{n/2}) \ \ \mod 8$
. Again,
![]() $\binom {n+1}{n/2}=\binom {n}{n/2-1}+\binom {n}{n/2}$
, and the first term is a multiple of n. By the argument in Lemma 8,
$\binom {n+1}{n/2}=\binom {n}{n/2-1}+\binom {n}{n/2}$
, and the first term is a multiple of n. By the argument in Lemma 8,
![]() $\binom {n}{n/2} \equiv 2 \ \ \mod 4$
, so
$\binom {n}{n/2} \equiv 2 \ \ \mod 4$
, so
![]() $\Lambda ''(Q)-\Lambda '(Q)$
is a multiple of
$\Lambda ''(Q)-\Lambda '(Q)$
is a multiple of
![]() $8$
.
$8$
.
If
![]() $j=1$
,
$j=1$
,
![]() $\Lambda ''(Q)-\Lambda '(Q)=2(-\binom {n+1}{1}+\binom {n+1}{n/2+1}-\binom {n+1}{n+1})\equiv 2(\binom {n+1}{n/2}-2) \equiv 0 \ \ \mod 8$
by the previous paragraph.
$\Lambda ''(Q)-\Lambda '(Q)=2(-\binom {n+1}{1}+\binom {n+1}{n/2+1}-\binom {n+1}{n+1})\equiv 2(\binom {n+1}{n/2}-2) \equiv 0 \ \ \mod 8$
by the previous paragraph.
Suppose now that
![]() $2\le j \le \frac {n}{2}-1$
. Then,
$2\le j \le \frac {n}{2}-1$
. Then,
 $\Lambda ''(Q)-\Lambda '(Q)= (-1)^j2\big(\binom {n+1}{j}-\binom {n+1}{n/2+j}\big)=(-1)^j2\big(\binom {n}{j-1}+\binom {n}{j}-\binom {n}{n/2+j-1}-\binom {n}{n/2+j}\big)$
. If
$\Lambda ''(Q)-\Lambda '(Q)= (-1)^j2\big(\binom {n+1}{j}-\binom {n+1}{n/2+j}\big)=(-1)^j2\big(\binom {n}{j-1}+\binom {n}{j}-\binom {n}{n/2+j-1}-\binom {n}{n/2+j}\big)$
. If
![]() $0\le r \le n$
is different from
$0\le r \le n$
is different from
![]() $0, \frac {n}{2}, n$
, then the action of
$0, \frac {n}{2}, n$
, then the action of
![]() $\mathbb {Z}_n$
on
$\mathbb {Z}_n$
on
![]() $\binom {\mathbb {Z}_n}{r}$
has no orbits of cardinality
$\binom {\mathbb {Z}_n}{r}$
has no orbits of cardinality
![]() $1$
or
$1$
or
![]() $2$
. In this case,
$2$
. In this case,
![]() $4|\binom {n}{r}$
. Since
$4|\binom {n}{r}$
. Since
![]() $j-1,j,\frac {n}{2}+j-1$
and
$j-1,j,\frac {n}{2}+j-1$
and
![]() $\frac {n}{2}+j$
are different from
$\frac {n}{2}+j$
are different from
![]() $0, \frac {n}{2}, n$
, then
$0, \frac {n}{2}, n$
, then
![]() $\Lambda ''(Q)-\Lambda '(Q)$
is a multiple of
$\Lambda ''(Q)-\Lambda '(Q)$
is a multiple of
![]() $8$
.▪
$8$
.▪
Proposition 19 shows that the order of each of the
![]() $m-1$
generators
$m-1$
generators
![]() $e_{i,m-i-1}$
of the class m factor
$e_{i,m-i-1}$
of the class m factor
![]() $\gamma _{m}(M(2,n)) /\gamma _{m+1}(M(2,n))$
is at least
$\gamma _{m}(M(2,n)) /\gamma _{m+1}(M(2,n))$
is at least
![]() $2$
. If moreover one could prove that the order of this factor is greater than or equal to
$2$
. If moreover one could prove that the order of this factor is greater than or equal to
![]() $2^{m-1}$
, for
$2^{m-1}$
, for
![]() $2\le m\le n+2$
, then
$2\le m\le n+2$
, then
![]() $|M(2,n)'|\ge 2^{\frac {(n+1)(n+2)}{2}}$
, and this would provide a better bound than that given in Theorem 18.
$|M(2,n)'|\ge 2^{\frac {(n+1)(n+2)}{2}}$
, and this would provide a better bound than that given in Theorem 18.
6 Upper bounds for
 $|M(2,2^k)|$
$|M(2,2^k)|$
As explained in Section 2, Newman proved [Reference Newman38] that
![]() $|M(2,2^k)|\le 2^{3k+k2^{2k}}$
. In general, this bound is far from optimal. In this section, we use the winding invariant map to find better upper bounds. We will focus on the special case
$|M(2,2^k)|\le 2^{3k+k2^{2k}}$
. In general, this bound is far from optimal. In this section, we use the winding invariant map to find better upper bounds. We will focus on the special case
![]() $k=2$
, where the bounds found are sharp.
$k=2$
, where the bounds found are sharp.
We recall from [Reference Barmak8] the construction of the winding invariant map associated to a group with a cocommutative presentation. A Laurent polynomial
![]() $P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
can be represented graphically by writing each nonzero coefficient
$P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
can be represented graphically by writing each nonzero coefficient
![]() $P\{(i,j)\}$
in the square
$P\{(i,j)\}$
in the square
![]() $(i,j)$
of the grid. The graphical representation of a polynomial is called a piece, so we will also say that a polynomial is a piece. The piece
$(i,j)$
of the grid. The graphical representation of a polynomial is called a piece, so we will also say that a polynomial is a piece. The piece
![]() $P_w=W(w)$
associated to an element
$P_w=W(w)$
associated to an element
![]() $w\in F_2'$
has, inside each square, the winding number of the curve
$w\in F_2'$
has, inside each square, the winding number of the curve
![]() $\gamma _w$
around the center of that square.
$\gamma _w$
around the center of that square.
In [Reference Barmak8, Proposition 18], it is proved that for a group G presented by
![]() $\langle x,y| S\rangle $
where S is a subset of
$\langle x,y| S\rangle $
where S is a subset of
![]() $F_2'$
,
$F_2'$
,
![]() $W:F_2' \to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
induces an epimorphism
$W:F_2' \to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
induces an epimorphism
![]() $\overline {W}:G' \to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
, where I is the ideal of
$\overline {W}:G' \to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
, where I is the ideal of
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
generated by the polynomials
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
generated by the polynomials
![]() $P_s$
with
$P_s$
with
![]() $s\in S$
. Moreover,
$s\in S$
. Moreover,
![]() $\textrm {ker}(\overline {W})=G''$
, so there is an induced isomorphism
$\textrm {ker}(\overline {W})=G''$
, so there is an induced isomorphism
![]() $G'/G''\to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
, which we also denote by
$G'/G''\to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
, which we also denote by
![]() $\overline {W}$
. We apply this to the group G presented by
$\overline {W}$
. We apply this to the group G presented by
![]() $\langle x,y| \ F_2' \cap F_2^n\rangle $
. We have then that
$\langle x,y| \ F_2' \cap F_2^n\rangle $
. We have then that
![]() $G'/G''$
is isomorphic to
$G'/G''$
is isomorphic to
![]() $M(2,n)'$
, so there is an isomorphism
$M(2,n)'$
, so there is an isomorphism
![]() $\overline {W}:M(2,n)'\to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
, where I is the ideal generated by (consisting of) the polynomials
$\overline {W}:M(2,n)'\to \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
, where I is the ideal generated by (consisting of) the polynomials
![]() $P_s$
with
$P_s$
with
![]() $s\in S= F_2' \cap F_2^n$
. The obvious observation is then the following result.
$s\in S= F_2' \cap F_2^n$
. The obvious observation is then the following result.
Remark 20 The order of
![]() $M(2,n)'$
is smaller than or equal to the cardinality of any set
$M(2,n)'$
is smaller than or equal to the cardinality of any set
![]() $A\subseteq \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
which contains a representative of each equivalence class of
$A\subseteq \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
which contains a representative of each equivalence class of
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
.
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
.
We will understand the quotient
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
graphically. The sum of two pieces
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
graphically. The sum of two pieces
![]() $P,Q\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
is the piece which is obtained by adding the two numbers of each square. The product of a piece P by a monomial
$P,Q\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
is the piece which is obtained by adding the two numbers of each square. The product of a piece P by a monomial
![]() $X^iY^j$
is the translation of the piece by the vector
$X^iY^j$
is the translation of the piece by the vector
![]() $(i,j)\in \mathbb {Z} \times \mathbb {Z}$
. All the computations that follow can be done algebraically, but we believe the graphical representation makes proofs simpler.
$(i,j)\in \mathbb {Z} \times \mathbb {Z}$
. All the computations that follow can be done algebraically, but we believe the graphical representation makes proofs simpler.
Example 21 Gupta and Tobin [Reference Gupta, Newman and Tobin20] proved that
![]() $|M(2,4)|=2^{10}$
. Because
$|M(2,4)|=2^{10}$
. Because
![]() $M(2,4)/M(2,4)'=\mathbb {Z}_4\times \mathbb {Z}_4$
, this is equivalent to proving that
$M(2,4)/M(2,4)'=\mathbb {Z}_4\times \mathbb {Z}_4$
, this is equivalent to proving that
![]() $|M(2,4)'|=2^6$
. In Example 17, we gave an alternative proof that
$|M(2,4)'|=2^6$
. In Example 17, we gave an alternative proof that
![]() $|M(2,4)'|\ge 2^6$
. We will use the representation by pieces together with Remark 20 to give an alternative proof that
$|M(2,4)'|\ge 2^6$
. We will use the representation by pieces together with Remark 20 to give an alternative proof that
![]() $|M(2,4)'|\le 2^6$
, thus providing a different proof of Gupta and Tobin’s result. In turn, this will give a new algorithm to decide whether an element in
$|M(2,4)'|\le 2^6$
, thus providing a different proof of Gupta and Tobin’s result. In turn, this will give a new algorithm to decide whether an element in
![]() $M(2,4)$
is trivial (different from the one given in Example 17).
$M(2,4)$
is trivial (different from the one given in Example 17).
Step 1. Suppose first that k is an arbitrary positive integer and
![]() $n=2^k$
. Let
$n=2^k$
. Let
![]() $[x,y]=xyx^{-1}y^{-1}\in F_2$
. Then,
$[x,y]=xyx^{-1}y^{-1}\in F_2$
. Then,
![]() $w=[x,y]^n\in S= F_2' \cap F_2^n$
and
$w=[x,y]^n\in S= F_2' \cap F_2^n$
and
![]() $W(w)=n\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. Therefore, the piece that has the number n in the square
$W(w)=n\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
. Therefore, the piece that has the number n in the square
![]() $(0,0)$
and all the other numbers equal to zero is in I. Hence, all the pieces whose coefficients are divisible by n are also in I. This proves that any element in
$(0,0)$
and all the other numbers equal to zero is in I. Hence, all the pieces whose coefficients are divisible by n are also in I. This proves that any element in
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
has a representative with all the coefficients in the interval
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
has a representative with all the coefficients in the interval
![]() $\{0,1,2,\ldots , n-1\}$
.
$\{0,1,2,\ldots , n-1\}$
.
Step 2. Let
![]() $u=([x,y]y[y,x])^ny^{-n}\in S$
. Then,
$u=([x,y]y[y,x])^ny^{-n}\in S$
. Then,
![]() $W(u)=1-Y^n\in I$
. Thus, the second piece in Figure 8 lies in I. For any piece in
$W(u)=1-Y^n\in I$
. Thus, the second piece in Figure 8 lies in I. For any piece in
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, we can add and subtract translates of u to obtain a representative whose only nonzero coefficients lie in the rows
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, we can add and subtract translates of u to obtain a representative whose only nonzero coefficients lie in the rows
![]() $0,1,\ldots , n-1$
. A symmetric argument shows that, in fact, there is a representative with all the nonzero coefficients in the square
$0,1,\ldots , n-1$
. A symmetric argument shows that, in fact, there is a representative with all the nonzero coefficients in the square
![]() $[0,n]\times [0,n]$
of rows
$[0,n]\times [0,n]$
of rows
![]() $0$
to
$0$
to
![]() $n-1$
and columns
$n-1$
and columns
![]() $0$
to
$0$
to
![]() $n-1$
. We say that the representative is concentrated in the square
$n-1$
. We say that the representative is concentrated in the square
![]() $[0,n]\times [0,n]$
.
$[0,n]\times [0,n]$
.

Figure 8: The pieces associated to
![]() $w=[x,y]^n$
,
$w=[x,y]^n$
,
![]() $u=([x,y]y[y,x])^ny^{-n}$
, and
$u=([x,y]y[y,x])^ny^{-n}$
, and
![]() $([x,y]x[y,x])^nx^{-n}$
turn any element of
$([x,y]x[y,x])^nx^{-n}$
turn any element of
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
to a representative concentrated in
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
to a representative concentrated in
![]() $[0,n]\times [0,n]$
with all the coefficients in the interval
$[0,n]\times [0,n]$
with all the coefficients in the interval
![]() $[0,n-1]$
. In this picture,
$[0,n-1]$
. In this picture,
![]() $n=4$
.
$n=4$
.
This argument shows that
![]() $|M(2,n)'|$
is smaller than or equal to
$|M(2,n)'|$
is smaller than or equal to
![]() $n^{n^2}=2^{k2^{2k}}$
, so
$n^{n^2}=2^{k2^{2k}}$
, so
![]() $|M(2,n)|\le n^{n^2+2}$
.
$|M(2,n)|\le n^{n^2+2}$
.
Step 3. Let
![]() $v=(xyx^{-1})^ny^{-n}\in S$
, so
$v=(xyx^{-1})^ny^{-n}\in S$
, so
![]() $W(v)=1+Y+Y^2+\cdots + Y^{n-1}\in I$
is the piece which appears in Figure 9. Adding multiples of horizontal translates of this piece, we can turn any piece concentrated in the square
$W(v)=1+Y+Y^2+\cdots + Y^{n-1}\in I$
is the piece which appears in Figure 9. Adding multiples of horizontal translates of this piece, we can turn any piece concentrated in the square
![]() $[0,n]\times [0,n]$
to another piece concentrated in the rectangle
$[0,n]\times [0,n]$
to another piece concentrated in the rectangle
![]() $[0,n]\times [0,n-1]$
. And by a symmetric argument, for any element in
$[0,n]\times [0,n-1]$
. And by a symmetric argument, for any element in
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, there is a representative concentrated in the square
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
, there is a representative concentrated in the square
![]() $[0,n-1]\times [0,n-1]$
with all the coefficients between
$[0,n-1]\times [0,n-1]$
with all the coefficients between
![]() $0$
and
$0$
and
![]() $n-1$
. Therefore,
$n-1$
. Therefore,
![]() $|M(2,n)'|\le n^{(n-1)^2}$
(so
$|M(2,n)'|\le n^{(n-1)^2}$
(so
![]() $|M(2,n)|\le n^{(n-1)^2+2}$
).
$|M(2,n)|\le n^{(n-1)^2+2}$
).

Figure 9: The pieces associated to
![]() $v=(xyx^{-1})^ny^{-n}$
and
$v=(xyx^{-1})^ny^{-n}$
and
![]() $x^n(yx^{-1}y^{-1})^n$
turn any element of
$x^n(yx^{-1}y^{-1})^n$
turn any element of
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
concentrated in
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
concentrated in
![]() $[0,n]\times [0,n]$
to a representative concentrated in
$[0,n]\times [0,n]$
to a representative concentrated in
![]() $[0,n-1]\times [0,n-1]$
. Together with piece w, we can assume each coefficient is in the interval
$[0,n-1]\times [0,n-1]$
. Together with piece w, we can assume each coefficient is in the interval
![]() $[0,n-1]$
.
$[0,n-1]$
.
Before going further, let us summarize some simple yet useful remarks. If
![]() $Q\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
is a piece in I, then any translate of Q is in I and any multiple as well. In particular,
$Q\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
is a piece in I, then any translate of Q is in I and any multiple as well. In particular,
![]() $-Q\in I$
, which is the piece that contains in each square of the grid the opposite of the coefficient Q has. Furthermore, if
$-Q\in I$
, which is the piece that contains in each square of the grid the opposite of the coefficient Q has. Furthermore, if
![]() $s=s(x,y)\in S=F_2'\cap F_2^n$
, then
$s=s(x,y)\in S=F_2'\cap F_2^n$
, then
![]() $s(x^{-1},y)$
also lies in S. Thus, if
$s(x^{-1},y)$
also lies in S. Thus, if
![]() $Q=Q(X,Y)$
is a piece in I, the symmetric piece
$Q=Q(X,Y)$
is a piece in I, the symmetric piece
![]() $Q(X^{-1},Y)$
with respect to the y-axis also lies in I. A similar argument shows that rotations of Q by
$Q(X^{-1},Y)$
with respect to the y-axis also lies in I. A similar argument shows that rotations of Q by
![]() $\pi /2, \pi $
, and
$\pi /2, \pi $
, and
![]() $3\pi /2$
are also in I. Therefore, I is invariant by translations, rotations of angle multiple of
$3\pi /2$
are also in I. Therefore, I is invariant by translations, rotations of angle multiple of
![]() $\pi /2$
, and symmetries about the axes and the lines
$\pi /2$
, and symmetries about the axes and the lines
![]() $y=x$
and
$y=x$
and
![]() $y=-x$
.
$y=-x$
.
Remark. Suppose A is a region (a union of squares of the grid), and that a piece
![]() $P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
is concentrated in A. That is, all the coefficients of P out of A are zero. If Q is a piece in I which is also concentrated in A, and if
$P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
is concentrated in A. That is, all the coefficients of P out of A are zero. If Q is a piece in I which is also concentrated in A, and if
![]() $(i,j)$
is a square of Q with coefficient
$(i,j)$
is a square of Q with coefficient
![]() $1$
or
$1$
or
![]() $-1$
, then there is a representative of P in
$-1$
, then there is a representative of P in
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
concentrated in region B, obtained from A by removing the square
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
concentrated in region B, obtained from A by removing the square
![]() $(i,j)$
. This representative is just P plus a multiple of Q. This is the idea we already used in Step 3 (and Step 2 as well).
$(i,j)$
. This representative is just P plus a multiple of Q. This is the idea we already used in Step 3 (and Step 2 as well).
Step 4. The first three steps worked for arbitrary k. From now on, we will assume
![]() $k=2$
and
$k=2$
and
![]() $n=4$
. Let
$n=4$
. Let
![]() $t=x^4(x^{-1}y)^4y^{-4}\in S$
. The piece corresponding to t appears in Figure 10, together with a translate T of a symmetric. The difference between the two pieces is
$t=x^4(x^{-1}y)^4y^{-4}\in S$
. The piece corresponding to t appears in Figure 10, together with a translate T of a symmetric. The difference between the two pieces is
![]() $Q_1\in I$
. Subtracting a translate of
$Q_1\in I$
. Subtracting a translate of
![]() $Q_1$
to itself, we obtain the piece
$Q_1$
to itself, we obtain the piece
![]() $Q_2\in I$
.
$Q_2\in I$
.

Figure 10: The piece associated to
![]() $t=x^4(x^{-1}y)^4y^{-4}$
and a symmetric T. At the right, the pieces
$t=x^4(x^{-1}y)^4y^{-4}$
and a symmetric T. At the right, the pieces
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
.
$Q_2$
.
We apply the idea of the Remark to the piece
![]() $Q_1\in I$
. This can be used to transform an element
$Q_1\in I$
. This can be used to transform an element
![]() $P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
concentrated in the square
$P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
concentrated in the square
![]() $[0,3]\times [0,3]$
into a representative concentrated in a region with one square less (see Figure 11). We do this two more times with
$[0,3]\times [0,3]$
into a representative concentrated in a region with one square less (see Figure 11). We do this two more times with
![]() $Q_1$
and a rotation of
$Q_1$
and a rotation of
![]() $Q_1$
to find a representative concentrated in the stair of three steps.
$Q_1$
to find a representative concentrated in the stair of three steps.

Figure 11: An element concentrated in
![]() $[0,3]\times [0,3]$
has a representative concentrated in the region of five squares.
$[0,3]\times [0,3]$
has a representative concentrated in the region of five squares.
We then use the piece T in Figure 10 to obtain a representative concentrated in the last region of Figure 11, which consists of just five squares.
Step 5. Let
![]() $t'=x^8(x^{-2}y)^4y^{-4}\in S$
. The piece associated to
$t'=x^8(x^{-2}y)^4y^{-4}\in S$
. The piece associated to
![]() $t'$
appears in Figure 12. If we subtract the piece associated to t, then we subtract (a translate of) the horizontal piece in Figure 9, then piece
$t'$
appears in Figure 12. If we subtract the piece associated to t, then we subtract (a translate of) the horizontal piece in Figure 9, then piece
![]() $Q_2$
, and, finally piece T, we obtain a piece with only two nonzero coefficients, both equal to
$Q_2$
, and, finally piece T, we obtain a piece with only two nonzero coefficients, both equal to
![]() $-2$
. This is piece
$-2$
. This is piece
![]() $D\in I$
.
$D\in I$
.

Figure 12: Using pieces from I, we obtain piece
![]() $D\in I$
.
$D\in I$
.
Step 6. From previous steps, we know that any element
![]() $P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
has a representative in
$P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
has a representative in
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
concentrated in the region of five squares in Figure 11. Adding multiples of piece D and of its vertical version, we can find a representative of P concentrated in the same five-square region, and where four of the five coefficients inside are
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
concentrated in the region of five squares in Figure 11. Adding multiples of piece D and of its vertical version, we can find a representative of P concentrated in the same five-square region, and where four of the five coefficients inside are
![]() $0$
or
$0$
or
![]() $1$
. Finally, we can use the piece associated with w (Step 1), to make the last coefficient lie in the interval
$1$
. Finally, we can use the piece associated with w (Step 1), to make the last coefficient lie in the interval
![]() $\{0,1,2,3\}$
. There are only
$\{0,1,2,3\}$
. There are only
![]() $2^6$
pieces satisfying these conditions, so the order of
$2^6$
pieces satisfying these conditions, so the order of
![]() $\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
is at most this number (Figure 13).
$\mathbb {Z}[X^{\pm 1},Y^{\pm 1}]/I$
is at most this number (Figure 13).

Figure 13: The representative of P is one among
![]() $64$
pieces.
$64$
pieces.
This finishes the proof that
![]() $|M(2,4)|\le 2^{10}$
.
$|M(2,4)|\le 2^{10}$
.
In the previous example, we have proved the following bound for arbitrary
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $n=2^k$
:
$n=2^k$
:
![]() $|M(2,n)|\le n^{(n-1)^2+2}$
. In fact, using the piece corresponding to
$|M(2,n)|\le n^{(n-1)^2+2}$
. In fact, using the piece corresponding to
![]() $t=x^n(x^{-1}y)^ny^{-n}$
twice, we can obtain a representative concentrated in the region
$t=x^n(x^{-1}y)^ny^{-n}$
twice, we can obtain a representative concentrated in the region
![]() $[0,n-1]\times [0,n-1]$
with two squares removed. Note that this part of the proof does not use the fact that n is a power of
$[0,n-1]\times [0,n-1]$
with two squares removed. Note that this part of the proof does not use the fact that n is a power of
![]() $2$
. It works for an arbitrary integer
$2$
. It works for an arbitrary integer
![]() $n\ge 3$
. Thus, we have proved the following proposition.
$n\ge 3$
. Thus, we have proved the following proposition.
Proposition 22 Let
![]() $n\ge 3$
be an integer. Then,
$n\ge 3$
be an integer. Then,
![]() $|M(2,n)|\le n^{(n-1)^2}$
.
$|M(2,n)|\le n^{(n-1)^2}$
.
7 A lower bound for the order of the restricted Burnside group
 $R(2,8)$
$R(2,8)$
Although Zel’manov [Reference Zel’manov53, Reference Zel’manov54] proved that the restricted Burnside group
![]() $R(d,m)$
exists for all
$R(d,m)$
exists for all
![]() $d,m$
, its order is known in very few cases (see Section 2 above). As far as we know, the best lower bound for
$d,m$
, its order is known in very few cases (see Section 2 above). As far as we know, the best lower bound for
![]() $|R(2,8)|$
available in the literature is given in [Reference Grunewald, Havas, Mennicke and Newman17]:
$|R(2,8)|$
available in the literature is given in [Reference Grunewald, Havas, Mennicke and Newman17]:
![]() $2^{4109}$
. In fact, this is the order of the group
$2^{4109}$
. In fact, this is the order of the group
![]() $F_2/(F_2^4)^2$
. Indeed,
$F_2/(F_2^4)^2$
. Indeed,
![]() $|F_2/F_2^4|=|B(2,4)|=2^{12}$
, so by Schreier’s formula,
$|F_2/F_2^4|=|B(2,4)|=2^{12}$
, so by Schreier’s formula,
![]() $\textrm {rk} (F_2^4)=1+2^{12}=4097$
. Now,
$\textrm {rk} (F_2^4)=1+2^{12}=4097$
. Now,
![]() $(F_2^4)' \leqslant (F_2^4)^2$
, so
$(F_2^4)' \leqslant (F_2^4)^2$
, so
![]() $F_2^4/(F_2^4)^2$
is abelian of order
$F_2^4/(F_2^4)^2$
is abelian of order
![]() $2^{\textrm {rk} F_2^4}$
. Thus,
$2^{\textrm {rk} F_2^4}$
. Thus,
![]() $|F_2/(F_2^4)^2|=|F_2/F_2^4||F_2^4/(F_2^4)^2|=2^{4109}$
. We will use our invariants to show that this bound is not sharp. Moreover, we will prove the following proposition.
$|F_2/(F_2^4)^2|=|F_2/F_2^4||F_2^4/(F_2^4)^2|=2^{4109}$
. We will use our invariants to show that this bound is not sharp. Moreover, we will prove the following proposition.
Proposition 23
![]() $|R(2,8)|\ge 2^{4115}$
.
$|R(2,8)|\ge 2^{4115}$
.
It is not hard to see that
![]() $F_2^8F_2'''$
is a finite-index subgroup of
$F_2^8F_2'''$
is a finite-index subgroup of
![]() $F_2$
. To prove this, we define
$F_2$
. To prove this, we define
![]() $R=F_2^8F_2'\leqslant F_2$
,
$R=F_2^8F_2'\leqslant F_2$
,
![]() $S=R^8R'\leqslant F_2$
, and
$S=R^8R'\leqslant F_2$
, and
![]() $T=S^8S'\leqslant F_2$
. Then,
$T=S^8S'\leqslant F_2$
. Then,
![]() $|F_2:R|$
is finite, so R has finite rank. Similarly,
$|F_2:R|$
is finite, so R has finite rank. Similarly,
![]() $|R:S|$
is finite and
$|R:S|$
is finite and
![]() $|S:T|$
is finite. Then,
$|S:T|$
is finite. Then,
![]() $F_2/T$
is finite. In fact, we can compute its order explicitly, but we will not need that. Furthermore, it is easy to prove that
$F_2/T$
is finite. In fact, we can compute its order explicitly, but we will not need that. Furthermore, it is easy to prove that
![]() $T\leqslant F_2^8F_2'''$
. It suffices to show that
$T\leqslant F_2^8F_2'''$
. It suffices to show that
![]() $S \leqslant F_2^8F_2''$
, and similarly, this follows from
$S \leqslant F_2^8F_2''$
, and similarly, this follows from
![]() $R\leqslant F_2^8F_2'$
. Thus,
$R\leqslant F_2^8F_2'$
. Thus,
![]() $F_2^8F_2'''$
is a finite-index subgroup of
$F_2^8F_2'''$
is a finite-index subgroup of
![]() $F_2$
.
$F_2$
.
Since both
![]() $F_2^8F_2'''$
and
$F_2^8F_2'''$
and
![]() $(F_2^4)^2$
are finite-index subgroups of
$(F_2^4)^2$
are finite-index subgroups of
![]() $F_2$
,
$F_2$
,
![]() $\frac {F_2}{(F_2^8F_2''')\cap (F_2^4)^2}$
is a finite group of exponent
$\frac {F_2}{(F_2^8F_2''')\cap (F_2^4)^2}$
is a finite group of exponent
![]() $8$
, and its order gives a lower bound for
$8$
, and its order gives a lower bound for
![]() $|R(2,8)|$
.
$|R(2,8)|$
.
 $$ \begin{align*}\left|\frac{F_2}{(F_2^8F_2''')\cap (F_2^4)^2}\right|=\left|\frac{F_2}{(F_2^4)^2} \right| \left|\frac{(F_2^4)^2}{(F_2^8F_2''')\cap (F_2^4)^2} \right|.\end{align*} $$
$$ \begin{align*}\left|\frac{F_2}{(F_2^8F_2''')\cap (F_2^4)^2}\right|=\left|\frac{F_2}{(F_2^4)^2} \right| \left|\frac{(F_2^4)^2}{(F_2^8F_2''')\cap (F_2^4)^2} \right|.\end{align*} $$
Let
![]() $\phi : \frac {(F_2^4)^2\cap F_2'}{(F_2^8F_2''')\cap (F_2^4)^2 \cap F_2'} \to (\mathbb {Z}_8)^8$
be the map induced by the restriction of
$\phi : \frac {(F_2^4)^2\cap F_2'}{(F_2^8F_2''')\cap (F_2^4)^2 \cap F_2'} \to (\mathbb {Z}_8)^8$
be the map induced by the restriction of
![]() $\Omega : F_2' \to (\mathbb {Z}_8)^8$
. Note that
$\Omega : F_2' \to (\mathbb {Z}_8)^8$
. Note that
![]() $\phi $
is well defined, since
$\phi $
is well defined, since
![]() $F_2^8F_2''' \cap F_2' \leqslant F_2^8F_2'' \cap F_2'$
. Let
$F_2^8F_2''' \cap F_2' \leqslant F_2^8F_2'' \cap F_2'$
. Let
![]() $z=(x^4(x^{-1}y)^4y^{-4})^2 \in (F_2^4)^2\cap F_2'$
. It is easy to see that
$z=(x^4(x^{-1}y)^4y^{-4})^2 \in (F_2^4)^2\cap F_2'$
. It is easy to see that
![]() $\phi (z)=(4,0,0,4,4,0,0,4)$
. Moreover, considering the conjugates
$\phi (z)=(4,0,0,4,4,0,0,4)$
. Moreover, considering the conjugates
![]() $x^iy^jzy^{-j}x^{-i}$
with
$x^iy^jzy^{-j}x^{-i}$
with
![]() $i,j=0,1,2$
, we obtain the nine
$i,j=0,1,2$
, we obtain the nine
![]() $8$
-tuples
$8$
-tuples
![]() $(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)$
where
$(a_0,a_1,a_2,a_3,b_0,b_1,b_2,b_3)$
where
![]() $(a_0,a_1,a_2,a_3), (b_0,b_1,b_2,b_3)\in \{(4,0,0,4), (4,4,0,0), (0,4,4,0)\}$
. These
$(a_0,a_1,a_2,a_3), (b_0,b_1,b_2,b_3)\in \{(4,0,0,4), (4,4,0,0), (0,4,4,0)\}$
. These
![]() $8$
-tuples generate a subgroup of
$8$
-tuples generate a subgroup of
![]() $(\mathbb {Z}_8)^8$
of order
$(\mathbb {Z}_8)^8$
of order
![]() $2^6$
. Thus,
$2^6$
. Thus,
![]() $|\frac {(F_2^4)^2\cap F_2'}{(F_2^8F_2''')\cap (F_2^4)^2 \cap F_2'}|\ge 2^6$
. In particular,
$|\frac {(F_2^4)^2\cap F_2'}{(F_2^8F_2''')\cap (F_2^4)^2 \cap F_2'}|\ge 2^6$
. In particular,
![]() $|R(2,8)|\ge 2^{4109}2^6=2^{4115}$
.
$|R(2,8)|\ge 2^{4109}2^6=2^{4115}$
.
8 Other primes, other colors
Up to this point, we have only studied the case that the exponent n is a power of
![]() $2$
. Many of the techniques we developed naturally extend to powers of different primes. In this section, we will generalize the notion of good coloring. In fact, this is a generalization of a variant of the notion we know already. For the case
$2$
. Many of the techniques we developed naturally extend to powers of different primes. In this section, we will generalize the notion of good coloring. In fact, this is a generalization of a variant of the notion we know already. For the case
![]() $p=2$
, this new notion would have led to the same results already proved.
$p=2$
, this new notion would have led to the same results already proved.
Let p be a positive prime number. Given a subset S of the integers and d a positive integer, a p-matching of S of difference d is a partition of S in which every part is an arithmetic progression of p terms and common difference d. We have the following version of Lemma 4.
Lemma 24 Let n, d be positive integers. If
![]() $pd$
divides n, then there is a p-matching of
$pd$
divides n, then there is a p-matching of
![]() $[n]=\{0,1,\ldots , n-1\}$
of difference d.
$[n]=\{0,1,\ldots , n-1\}$
of difference d.
Let k be a positive integer, and let
![]() $n=p^k$
. A p-good coloring of
$n=p^k$
. A p-good coloring of
![]() $\mathbb {Z}_n$
is a function
$\mathbb {Z}_n$
is a function
![]() $c:\mathbb {Z}_n\to \mathbb {Z}_n$
such that for every arithmetic progression
$c:\mathbb {Z}_n\to \mathbb {Z}_n$
such that for every arithmetic progression
![]() $a,a+\frac {n}{p},a+2\frac {n}{p},\ldots ,a+(p-1)\frac {n}{p}$
of p terms and difference
$a,a+\frac {n}{p},a+2\frac {n}{p},\ldots ,a+(p-1)\frac {n}{p}$
of p terms and difference
![]() $\frac {n}{p}$
, we have that the sum
$\frac {n}{p}$
, we have that the sum
![]() $c(a)+c(a+\frac {n}{p})+c(a+2\frac {n}{p})+c(a+(p-1)\frac {n}{p})$
of its colors is zero in
$c(a)+c(a+\frac {n}{p})+c(a+2\frac {n}{p})+c(a+(p-1)\frac {n}{p})$
of its colors is zero in
![]() $\mathbb {Z}_n$
. Note that a
$\mathbb {Z}_n$
. Note that a
![]() $2$
-good coloring is not exactly the same as a good coloring in the sense of previous sections. We have the following lemma.
$2$
-good coloring is not exactly the same as a good coloring in the sense of previous sections. We have the following lemma.
Lemma 25 Let
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $n=p^k$
. Let
$n=p^k$
. Let
![]() $c:\mathbb {Z}_n \to \mathbb {Z}_n$
be a p-good coloring.
$c:\mathbb {Z}_n \to \mathbb {Z}_n$
be a p-good coloring.
![]() $\mathrm{(i)}$
Let
$\mathrm{(i)}$
Let
![]() $a, a+b, a+2b, \ldots , a+(n-1)b$
be an arithmetic progression of length n in
$a, a+b, a+2b, \ldots , a+(n-1)b$
be an arithmetic progression of length n in
![]() $\mathbb {Z}$
. Then, we have
$\mathbb {Z}$
. Then, we have
![]() $c(a)+c(a+b)+c(a+2b)+ \cdots +c(a+(n-1)b)=0\in \mathbb {Z}_n$
.
$c(a)+c(a+b)+c(a+2b)+ \cdots +c(a+(n-1)b)=0\in \mathbb {Z}_n$
.
![]() $\mathrm{(ii)}$
Let
$\mathrm{(ii)}$
Let
![]() $a, a+b, a+2b, \ldots , a+(\frac {n}{p}-1)b$
be an arithmetic progression of length
$a, a+b, a+2b, \ldots , a+(\frac {n}{p}-1)b$
be an arithmetic progression of length
![]() $\frac {n}{p}$
in
$\frac {n}{p}$
in
![]() $\mathbb {Z}$
with b a multiple of p. Then, the sum of the colors of its terms is a multiple of
$\mathbb {Z}$
with b a multiple of p. Then, the sum of the colors of its terms is a multiple of
![]() $\frac {n}{p}$
.
$\frac {n}{p}$
.
The proofs of these lemmas are similar to the proofs of Lemmas 4 and 5, so we omit them.
Given a function
![]() $\varphi : \mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
and a p-good coloring c of
$\varphi : \mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
and a p-good coloring c of
![]() $\mathbb {Z}_n$
, define the associated invariant
$\mathbb {Z}_n$
, define the associated invariant
![]() $\Lambda =\Lambda _{\varphi , c} :\mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n$
by
$\Lambda =\Lambda _{\varphi , c} :\mathbb {Z}[X^{\pm 1},Y^{\pm 1}] \to \mathbb {Z}_n$
by
For
![]() $z\in F_2'$
, we define
$z\in F_2'$
, we define
![]() $\Lambda (z)=\Lambda (P_z)$
.
$\Lambda (z)=\Lambda (P_z)$
.
Theorem 26 Let p be a positive prime,
![]() $k\ge 2$
, and
$k\ge 2$
, and
![]() $n=p^k$
. Let c be a p-good coloring of
$n=p^k$
. Let c be a p-good coloring of
![]() $\mathbb {Z}_n$
, and let
$\mathbb {Z}_n$
, and let
![]() $\varphi :\mathbb {Z} \times \mathbb {Z}\to \mathbb {Z}_n$
be a homomorphism such that
$\varphi :\mathbb {Z} \times \mathbb {Z}\to \mathbb {Z}_n$
be a homomorphism such that
![]() $\varphi (1,0)$
,
$\varphi (1,0)$
,
![]() $\varphi (0,1) \in \mathbb {Z}_n$
are invertible. Let
$\varphi (0,1) \in \mathbb {Z}_n$
are invertible. Let
![]() $t:\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z} \times \mathbb {Z}$
be a translation by any vector
$t:\mathbb {Z} \times \mathbb {Z} \to \mathbb {Z} \times \mathbb {Z}$
be a translation by any vector
![]() $(i_0,j_0)\in \mathbb {Z} \times \mathbb {Z}$
. Let
$(i_0,j_0)\in \mathbb {Z} \times \mathbb {Z}$
. Let
![]() $\Lambda =\Lambda _{\varphi t, c}$
be the associated invariant. Then, for any
$\Lambda =\Lambda _{\varphi t, c}$
be the associated invariant. Then, for any
![]() $z\in F_2'$
which is a product of nth powers in
$z\in F_2'$
which is a product of nth powers in
![]() $F_2$
,
$F_2$
,
![]() $\Lambda (z) \in \mathbb {Z}_{n}$
is trivial in
$\Lambda (z) \in \mathbb {Z}_{n}$
is trivial in
![]() $\mathbb {Z}_{\frac {n}{p}}$
.
$\mathbb {Z}_{\frac {n}{p}}$
.
Proof The proof is almost identical to the proof of Theorem 16. The difference is perhaps in Case 4. The cost that we pay for using
![]() $p\neq 2$
and the general notion of p-good coloring is that
$p\neq 2$
and the general notion of p-good coloring is that
![]() $\Lambda (z)$
may be nontrivial in
$\Lambda (z)$
may be nontrivial in
![]() $\mathbb {Z}_n$
, so we have to descend to
$\mathbb {Z}_n$
, so we have to descend to
![]() $\mathbb {Z}_{\frac {n}{p}}$
.
$\mathbb {Z}_{\frac {n}{p}}$
.
We may assume
![]() $(i_0,j_0)=(0,0)$
and that z is a product of three nth powers. By Lemma 25, we only have to study the invariant for stair-like regions.
$(i_0,j_0)=(0,0)$
and that z is a product of three nth powers. By Lemma 25, we only have to study the invariant for stair-like regions.
Case 1:
![]() $p \nmid h$
,
$p \nmid h$
,
![]() $p| l$
. Inside the stair of
$p| l$
. Inside the stair of
![]() $n-1$
steps, consider region
$n-1$
steps, consider region
![]() $A_0$
formed by the top
$A_0$
formed by the top
![]() $\frac {n}{p}-1$
levels (see Figure 14). We define regions
$\frac {n}{p}-1$
levels (see Figure 14). We define regions
![]() $A_1, A_2, \ldots , A_{p-1}$
, where
$A_1, A_2, \ldots , A_{p-1}$
, where
![]() $A_{i+1}$
is the translation of
$A_{i+1}$
is the translation of
![]() $A_i$
by
$A_i$
by
![]() $\frac {hn}{p}$
units downward.
$\frac {hn}{p}$
units downward.

Figure 14: Here,
![]() $p=5$
,
$p=5$
,
![]() $n=5^2$
,
$n=5^2$
,
![]() $p \nmid h$
, and
$p \nmid h$
, and
![]() $p | l$
.
$p | l$
.
Since
![]() $p \nmid \varphi (0,1)$
and c is p-good, the sum of the invariants of regions
$p \nmid \varphi (0,1)$
and c is p-good, the sum of the invariants of regions
![]() $A_i$
is trivial in
$A_i$
is trivial in
![]() $\mathbb {Z}_n$
. For
$\mathbb {Z}_n$
. For
![]() $0\le i \le p-2$
, we define
$0\le i \le p-2$
, we define
![]() $B_i$
as the region between
$B_i$
as the region between
![]() $A_i$
and
$A_i$
and
![]() $A_{i+1}$
.
$A_{i+1}$
.
![]() $B_i'$
is the translation of
$B_i'$
is the translation of
![]() $B_i$
by
$B_i$
by
![]() $(i+1)\frac {ln}{p}$
units to the right, so it is outside the original stairs. Since
$(i+1)\frac {ln}{p}$
units to the right, so it is outside the original stairs. Since
![]() $n| \frac {(i+1)ln}{p}$
,
$n| \frac {(i+1)ln}{p}$
,
![]() $B_i'$
and
$B_i'$
and
![]() $B_i$
are painted in the same way. Therefore, the invariant
$B_i$
are painted in the same way. Therefore, the invariant
![]() $\Lambda $
of the original stairs is a sum of invariants of rectangles with one side of length divisible by n and, thus, trivial in
$\Lambda $
of the original stairs is a sum of invariants of rectangles with one side of length divisible by n and, thus, trivial in
![]() $\mathbb {Z}_n$
.
$\mathbb {Z}_n$
.
Case 2:
![]() $p | h$
,
$p | h$
,
![]() $p \nmid l$
, is symmetric to Case 1.
$p \nmid l$
, is symmetric to Case 1.
Case 3:
![]() $p| h$
,
$p| h$
,
![]() $p | l$
. We must show that the stairs with
$p | l$
. We must show that the stairs with
![]() $n-1$
steps have trivial invariant. We will change here the proof we did in Theorem 16 just a bit to make the argument simpler. We can add one more step to the stairs without changing the value of
$n-1$
steps have trivial invariant. We will change here the proof we did in Theorem 16 just a bit to make the argument simpler. We can add one more step to the stairs without changing the value of
![]() $\Lambda $
, since the l new columns that we added have height
$\Lambda $
, since the l new columns that we added have height
![]() $hn$
, a multiple of n.
$hn$
, a multiple of n.
The n-step stair appears in Figure 15. We consider region
![]() $A_0$
inside the top
$A_0$
inside the top
![]() $n/p$
levels of the stairs.
$n/p$
levels of the stairs.
![]() $A_0$
is an n-step stair itself but with height
$A_0$
is an n-step stair itself but with height
![]() $h/p$
and length
$h/p$
and length
![]() $l/p$
. We define
$l/p$
. We define
![]() $A_1,A_2, \ldots , A_{p-1}$
where
$A_1,A_2, \ldots , A_{p-1}$
where
![]() $A_{i+1}$
is obtained from
$A_{i+1}$
is obtained from
![]() $A_i$
by a translation of
$A_i$
by a translation of
![]() $\frac {n}{p}(l,-h)$
. By induction, each stair
$\frac {n}{p}(l,-h)$
. By induction, each stair
![]() $A_i$
has invariant
$A_i$
has invariant
![]() $\Lambda $
trivial in
$\Lambda $
trivial in
![]() $\mathbb {Z}_{\frac {n}{p}}$
. In fact, this holds when we remove one step from
$\mathbb {Z}_{\frac {n}{p}}$
. In fact, this holds when we remove one step from
![]() $A_i$
, but again, removing columns of height
$A_i$
, but again, removing columns of height
![]() $\frac {hn}{p}$
does not change
$\frac {hn}{p}$
does not change
![]() $\Lambda $
, since this is a multiple of n. The region below the
$\Lambda $
, since this is a multiple of n. The region below the
![]() $A_i$
’s is a union of rectangles of size
$A_i$
’s is a union of rectangles of size
![]() $\frac {ln}{p} \times \frac {hn}{p}$
, so its invariant is trivial in
$\frac {ln}{p} \times \frac {hn}{p}$
, so its invariant is trivial in
![]() $\mathbb {Z}_n$
. The region above the
$\mathbb {Z}_n$
. The region above the
![]() $A_i$
’s appears in Figure 15 with the sign
$A_i$
’s appears in Figure 15 with the sign
![]() $+$
. This region is a union of n regions of the form C,
$+$
. This region is a union of n regions of the form C,
![]() $C+v$
,
$C+v$
,
![]() $C+2v$
,
$C+2v$
,
![]() $\ldots $
,
$\ldots $
,
![]() $C+(n-1)v$
for certain vector v and certain region C. By Lemma 25, its invariant is trivial in
$C+(n-1)v$
for certain vector v and certain region C. By Lemma 25, its invariant is trivial in
![]() $\mathbb {Z}_n$
.
$\mathbb {Z}_n$
.

Figure 15: Here,
![]() $p=3$
,
$p=3$
,
![]() $n=3^2$
,
$n=3^2$
,
![]() $p | h$
, and
$p | h$
, and
![]() $p | l$
.
$p | l$
.
Case 4:
![]() $p \nmid h$
,
$p \nmid h$
,
![]() $p \nmid l$
. We have arrived to the crux of the proof, where we have to pay the price that
$p \nmid l$
. We have arrived to the crux of the proof, where we have to pay the price that
![]() $\Lambda $
is trivial in
$\Lambda $
is trivial in
![]() $\mathbb {Z}_{\frac {n}{p}}$
and maybe not in
$\mathbb {Z}_{\frac {n}{p}}$
and maybe not in
![]() $\mathbb {Z}_n$
. Consider regions
$\mathbb {Z}_n$
. Consider regions
![]() $A_0, A_1, \ldots , A_{p-1}$
defined as in Case 1 (see Figure 16).
$A_0, A_1, \ldots , A_{p-1}$
defined as in Case 1 (see Figure 16).

Figure 16: Here
![]() $p=5$
,
$p=5$
,
![]() $n=5^2$
,
$n=5^2$
,
![]() $p \nmid h$
, and
$p \nmid h$
, and
![]() $p \nmid l$
.
$p \nmid l$
.
Let B be the region inside the stairs which is at the right of
![]() $A_1$
. The complement C of the region formed by the
$A_1$
. The complement C of the region formed by the
![]() $A_i$
’s is a union of
$A_i$
’s is a union of
![]() $\frac {p(p-1)}{2}$
translates of B. Take the square Q in B which is a neighbor of
$\frac {p(p-1)}{2}$
translates of B. Take the square Q in B which is a neighbor of
![]() $A_1$
and is in the left margin of the stairs. Let
$A_1$
and is in the left margin of the stairs. Let
![]() $v=(l,-h)$
and
$v=(l,-h)$
and
![]() $v'=(0,-h)$
. Consider the
$v'=(0,-h)$
. Consider the
![]() $\frac {(p-1)n}{2}$
translates of Q which appear with gray in Figure 16. They are
$\frac {(p-1)n}{2}$
translates of Q which appear with gray in Figure 16. They are
![]() $(\text{Line}\ 0)$
$(\text{Line}\ 0)$
![]() $Q,Q+v,Q+2v, \ldots , Q+(\frac {(p-1)n}{p}-1)v,$
$Q,Q+v,Q+2v, \ldots , Q+(\frac {(p-1)n}{p}-1)v,$
![]() $(\text{Line}\ 1)$
$(\text{Line}\ 1)$
![]() $Q+\frac {n}{p}v', Q+\frac {n}{p}v'+v, Q+\frac {n}{p}v'+2v, \ldots , Q+\frac {n}{p}v'+(\frac {(p-2)n}{p}-1)v,$
$Q+\frac {n}{p}v', Q+\frac {n}{p}v'+v, Q+\frac {n}{p}v'+2v, \ldots , Q+\frac {n}{p}v'+(\frac {(p-2)n}{p}-1)v,$
![]() $(\text{Line}\ 2)$
$(\text{Line}\ 2)$
![]() $Q+\frac {2n}{p}v', Q+\frac {2n}{p}v'+v, Q+\frac {2n}{p}v'+2v, \ldots , Q+\frac {2n}{p}v'+(\frac {(p-3)n}{p}-1)v,$
$Q+\frac {2n}{p}v', Q+\frac {2n}{p}v'+v, Q+\frac {2n}{p}v'+2v, \ldots , Q+\frac {2n}{p}v'+(\frac {(p-3)n}{p}-1)v,$
![]() $\ldots $
$\ldots $
![]() $(\text{Line}\ p-2)$
$(\text{Line}\ p-2)$
![]() $Q+\frac {(p-2)n}{p}v', Q+\frac {(p-2)n}{p}v'+v, Q+\frac {(p-2)n}{p}v'+2v, \ldots , Q+\frac {(p-2)n}{p}v'+(\frac {n}{p}-1)v$
.
$Q+\frac {(p-2)n}{p}v', Q+\frac {(p-2)n}{p}v'+v, Q+\frac {(p-2)n}{p}v'+2v, \ldots , Q+\frac {(p-2)n}{p}v'+(\frac {n}{p}-1)v$
.
If
![]() $b=\varphi (v) \in \mathbb {Z}_n$
is not invertible, then by Lemma 25(ii), the sum of the invariants of the translates in each of these lines is trivial in
$b=\varphi (v) \in \mathbb {Z}_n$
is not invertible, then by Lemma 25(ii), the sum of the invariants of the translates in each of these lines is trivial in
![]() $\mathbb {Z}_{\frac {n}{p}}$
, so the invariant of the gray region is trivial in
$\mathbb {Z}_{\frac {n}{p}}$
, so the invariant of the gray region is trivial in
![]() $\mathbb {Z}_{\frac {n}{p}}$
.
$\mathbb {Z}_{\frac {n}{p}}$
.
If
![]() $b=\varphi (v)$
is invertible in
$b=\varphi (v)$
is invertible in
![]() $\mathbb {Z}_n$
, then we claim that we can divide the
$\mathbb {Z}_n$
, then we claim that we can divide the
![]() $p-1$
lines above in groups, in such a way that for each group, the sequences obtained after applying
$p-1$
lines above in groups, in such a way that for each group, the sequences obtained after applying
![]() $\varphi $
can be concatenated to form an arithmetic progression in
$\varphi $
can be concatenated to form an arithmetic progression in
![]() $\mathbb {Z}_n$
of length divisible by n.
$\mathbb {Z}_n$
of length divisible by n.
Let
![]() $a=\varphi (Q)$
and
$a=\varphi (Q)$
and
![]() $b'=\varphi (v')$
. When we apply
$b'=\varphi (v')$
. When we apply
![]() $\varphi $
to Line 0 above, we obtain an arithmetic progression of difference b which begins in a and finishes in
$\varphi $
to Line 0 above, we obtain an arithmetic progression of difference b which begins in a and finishes in
![]() $a+(\frac {(p-1)n}{p}-1)b$
. So, the next term of this sequence should be
$a+(\frac {(p-1)n}{p}-1)b$
. So, the next term of this sequence should be
![]() $a+\frac {(p-1)n}{p}b$
.
$a+\frac {(p-1)n}{p}b$
.
After applying
![]() $\varphi $
, Line 1 begins with
$\varphi $
, Line 1 begins with
![]() $a+\frac {n}{p}b'$
and finishes with
$a+\frac {n}{p}b'$
and finishes with
![]() $a+\frac {n}{p}b'+ (\frac {(p-2)n}{p}-1)b$
, so the next term should be
$a+\frac {n}{p}b'+ (\frac {(p-2)n}{p}-1)b$
, so the next term should be
![]() $a+\frac {n}{p}b'+\frac {(p-2)n}{p}b$
.
$a+\frac {n}{p}b'+\frac {(p-2)n}{p}b$
.
We do this for each line. Line i begins with
![]() $a+i\frac {n}{p}b'$
, and the next term after the last one should be
$a+i\frac {n}{p}b'$
, and the next term after the last one should be
![]() $a+i\frac {n}{p}b'+\frac {(p-(i+1))n}{p}b$
. In order to prove that these lines can be glued to form longer arithmetic progressions, we will prove the following Claim: the subsets
$a+i\frac {n}{p}b'+\frac {(p-(i+1))n}{p}b$
. In order to prove that these lines can be glued to form longer arithmetic progressions, we will prove the following Claim: the subsets
![]() $\{a+i\frac {n}{p}b'\}_{0\le i\le p-2}$
and
$\{a+i\frac {n}{p}b'\}_{0\le i\le p-2}$
and
![]() $\{a+i\frac {n}{p}b'+\frac {(p-(i+1))n}{p}b\}_{0\le i\le p-2}$
of
$\{a+i\frac {n}{p}b'+\frac {(p-(i+1))n}{p}b\}_{0\le i\le p-2}$
of
![]() $\mathbb {Z}_n$
are equal, and each of them has
$\mathbb {Z}_n$
are equal, and each of them has
![]() $p-1$
elements.
$p-1$
elements.
This is equivalent to proving that the subsets
![]() $\{ib'\}_{0\le i\le p-2}$
and
$\{ib'\}_{0\le i\le p-2}$
and
![]() $\{ib'-(i+1)b\}_{0\le i\le p-2}$
of
$\{ib'-(i+1)b\}_{0\le i\le p-2}$
of
![]() $\mathbb {Z}_p$
are equal, and that each has
$\mathbb {Z}_p$
are equal, and that each has
![]() $p-1$
elements. That their cardinality is
$p-1$
elements. That their cardinality is
![]() $p-1$
follows from the fact that
$p-1$
follows from the fact that
![]() $b'$
and
$b'$
and
![]() $b'-b$
are invertible in
$b'-b$
are invertible in
![]() $\mathbb {Z}_p$
, and this, in turn, follows from the hypothesis that
$\mathbb {Z}_p$
, and this, in turn, follows from the hypothesis that
![]() $\varphi (1,0)$
and
$\varphi (1,0)$
and
![]() $\varphi (0,1)$
are invertible, and that
$\varphi (0,1)$
are invertible, and that
![]() $p\nmid hl$
. In order to see that both sets are equal, it suffices to observe that the missing element
$p\nmid hl$
. In order to see that both sets are equal, it suffices to observe that the missing element
![]() $(p-1)b'$
of the first set is equal to the missing element
$(p-1)b'$
of the first set is equal to the missing element
![]() $(p-1)b'-pb$
in the second.
$(p-1)b'-pb$
in the second.
The Claim says that we can glue the
![]() $p-1$
arithmetic progressions to form arithmetic cycles in
$p-1$
arithmetic progressions to form arithmetic cycles in
![]() $\mathbb {Z}_n$
of difference b. By arithmetic cycle of difference b, we mean an arithmetic progression
$\mathbb {Z}_n$
of difference b. By arithmetic cycle of difference b, we mean an arithmetic progression
![]() $e,e+b, e+2b, \ldots , e+(t-1)b \in \mathbb {Z}_n$
such that
$e,e+b, e+2b, \ldots , e+(t-1)b \in \mathbb {Z}_n$
such that
![]() $e+tb=e\in \mathbb {Z}_n$
. Since
$e+tb=e\in \mathbb {Z}_n$
. Since
![]() $b\in \mathbb {Z}_n$
is invertible, the length t of one such cycle must be a multiple of n. Thus, the invariant
$b\in \mathbb {Z}_n$
is invertible, the length t of one such cycle must be a multiple of n. Thus, the invariant
![]() $\Lambda $
of the gray region is the sum of the colors of arithmetic progressions of lengths divisible by n. By Lemma 25(i), the invariant of the gray region is trivial in
$\Lambda $
of the gray region is the sum of the colors of arithmetic progressions of lengths divisible by n. By Lemma 25(i), the invariant of the gray region is trivial in
![]() $\mathbb {Z}_{\frac {n}{p}}$
.
$\mathbb {Z}_{\frac {n}{p}}$
.
Now, region C is a union of translates of the gray region, so we have that
![]() $\Lambda (C)=0\in \mathbb {Z}_{\frac {n}{p}}$
, and then the invariant of the stairs is also trivial in
$\Lambda (C)=0\in \mathbb {Z}_{\frac {n}{p}}$
, and then the invariant of the stairs is also trivial in
![]() $\mathbb {Z}_{\frac {n}{p}}$
.▪
$\mathbb {Z}_{\frac {n}{p}}$
.▪
In the hypotheses of Theorem 26,
![]() $\Lambda (z)$
need not be trivial in
$\Lambda (z)$
need not be trivial in
![]() $\mathbb {Z}_n$
. This fails even for
$\mathbb {Z}_n$
. This fails even for
![]() $p=2$
. Let
$p=2$
. Let
![]() $n=4$
. Consider the
$n=4$
. Consider the
![]() $2$
-good coloring
$2$
-good coloring
![]() $c:\mathbb {Z}_4 \to \mathbb {Z}_4$
defined by
$c:\mathbb {Z}_4 \to \mathbb {Z}_4$
defined by
![]() $c(0)=c(2)=0$
,
$c(0)=c(2)=0$
,
![]() $c(1)=1$
, and
$c(1)=1$
, and
![]() $c(3)=3$
. Let
$c(3)=3$
. Let
![]() $\varphi : \mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
be defined by
$\varphi : \mathbb {Z} \times \mathbb {Z} \to \mathbb {Z}_n$
be defined by
![]() $\varphi (1,0)=\varphi (0,1)=1$
. Then,
$\varphi (1,0)=\varphi (0,1)=1$
. Then,
![]() $\Lambda _{\varphi , c}(x^4(x^{-1}y)^4y^{-4})=2\neq 0\in \mathbb {Z}_4$
.
$\Lambda _{\varphi , c}(x^4(x^{-1}y)^4y^{-4})=2\neq 0\in \mathbb {Z}_4$
.
9 The free nilpotent group of class
 $2$
and exponent n
$2$
and exponent n
In the previous sections, we tried to understand some features of the free metabelian group
![]() $M(2,n)$
of rank
$M(2,n)$
of rank
![]() $2$
and exponent n. The free nilpotent group of class
$2$
and exponent n. The free nilpotent group of class
![]() $2$
, rank
$2$
, rank
![]() $2$
, and exponent n is the group
$2$
, and exponent n is the group
![]() $N(2,n)=\frac {F_2}{\gamma _3(F_2) F_2^n}$
, where
$N(2,n)=\frac {F_2}{\gamma _3(F_2) F_2^n}$
, where
![]() $\gamma _3(F_2)=[F_2,F_2']$
denotes the third term in the lower central series of
$\gamma _3(F_2)=[F_2,F_2']$
denotes the third term in the lower central series of
![]() $F_2$
. Since
$F_2$
. Since
![]() $F_2'' \leqslant \gamma _3(F_2)$
,
$F_2'' \leqslant \gamma _3(F_2)$
,
![]() $N(2,n)$
is a quotient of
$N(2,n)$
is a quotient of
![]() $M(2,n)$
. This group is much easier to understand, even for arbitrary
$M(2,n)$
. This group is much easier to understand, even for arbitrary
![]() $n\ge 1$
, using invariants. In fact, the area invariant
$n\ge 1$
, using invariants. In fact, the area invariant
![]() $A:F_2' \to \mathbb {Z}$
,
$A:F_2' \to \mathbb {Z}$
,
![]() $A(z)=P_z(1,1)$
describes
$A(z)=P_z(1,1)$
describes
![]() $N(2,n)$
completely in the following sense.
$N(2,n)$
completely in the following sense.
We already know by Remark 1 that if
![]() $z \in \gamma _3(F_2)$
, then
$z \in \gamma _3(F_2)$
, then
![]() $P_z$
is a sum of multiples of polynomials of the form
$P_z$
is a sum of multiples of polynomials of the form
![]() $m-1$
where m is a monomial, so the area
$m-1$
where m is a monomial, so the area
![]() $A(z)=0$
. Conversely, each
$A(z)=0$
. Conversely, each
![]() $P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
with
$P\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$
with
![]() $P(1,1)=0$
is a linear combination of
$P(1,1)=0$
is a linear combination of
![]() $(X-1)$
and
$(X-1)$
and
![]() $(Y-1)$
, so
$(Y-1)$
, so
![]() $A(z)=0$
implies that
$A(z)=0$
implies that
![]() $z\in \gamma _3(F_2)$
. If n is even, denote by
$z\in \gamma _3(F_2)$
. If n is even, denote by
![]() $\overline {A}:F_2' \to \mathbb {Z}_{\frac {n}{2}}$
the composition of A with the projection. If n is odd, take
$\overline {A}:F_2' \to \mathbb {Z}_{\frac {n}{2}}$
the composition of A with the projection. If n is odd, take
![]() $\overline {A}: F_2' \to \mathbb {Z}_n$
, instead. Theorem 59 in [Reference Barmak8] implies that
$\overline {A}: F_2' \to \mathbb {Z}_n$
, instead. Theorem 59 in [Reference Barmak8] implies that
![]() $\gamma _3(F_2)F_2^n \cap F_2' \leqslant \ker (\overline {A})$
. Conversely, if
$\gamma _3(F_2)F_2^n \cap F_2' \leqslant \ker (\overline {A})$
. Conversely, if
![]() $z \in \ker (\overline {A})$
, there exists
$z \in \ker (\overline {A})$
, there exists
![]() $w\in F_2^n$
with the same area: indeed,
$w\in F_2^n$
with the same area: indeed,
![]() $A(x^n(x^{-1}y)^ny^{-n})=\frac {n(n-1)}{2}$
and
$A(x^n(x^{-1}y)^ny^{-n})=\frac {n(n-1)}{2}$
and
![]() $A([x,y]^n)=n$
, so a product of powers of those two elements has area
$A([x,y]^n)=n$
, so a product of powers of those two elements has area
![]() $\gcd (\frac {n(n-1)}{2}, n)$
, which is
$\gcd (\frac {n(n-1)}{2}, n)$
, which is
![]() $\frac {n}{2}$
or n, depending on the parity of n. Thus,
$\frac {n}{2}$
or n, depending on the parity of n. Thus,
![]() $A(w^{-1}z)=0$
, which shows that
$A(w^{-1}z)=0$
, which shows that
![]() $w^{-1}z\in \gamma _3(F_2)$
, so
$w^{-1}z\in \gamma _3(F_2)$
, so
![]() $z\in \gamma _3(F_2)F_2^n \cap F_2'$
. Since
$z\in \gamma _3(F_2)F_2^n \cap F_2'$
. Since
![]() $\overline {A}$
is surjective, we deduce that
$\overline {A}$
is surjective, we deduce that
![]() $N(2,n)'$
is isomorphic to
$N(2,n)'$
is isomorphic to
![]() $\mathbb {Z}_{\frac {n}{2}}$
for even n and to
$\mathbb {Z}_{\frac {n}{2}}$
for even n and to
![]() $\mathbb {Z}_n$
for odd n. Since the abelianization of
$\mathbb {Z}_n$
for odd n. Since the abelianization of
![]() $N(2,n)$
has order
$N(2,n)$
has order
![]() $n^2$
, we conclude that
$n^2$
, we conclude that
![]() $|N(2,n)|=\frac {n^3}{2}$
for even n and
$|N(2,n)|=\frac {n^3}{2}$
for even n and
![]() $|N(2,n)|=n^3$
for odd n.
$|N(2,n)|=n^3$
for odd n.
So, this is a case where the idea of invariants works pretty well. This case is of course much simpler than the metabelian.
In [Reference Sanov43], Sanov proved that for any prime p and
![]() $1\le i \le k$
, the Engel congruence
$1\le i \le k$
, the Engel congruence
![]() $e_{ip^i-1} (x,y)^{p^{k-i}} \in \gamma _{ip^i+1}(F_2)F_2^{p^k}$
holds. When
$e_{ip^i-1} (x,y)^{p^{k-i}} \in \gamma _{ip^i+1}(F_2)F_2^{p^k}$
holds. When
![]() $p=2$
and
$p=2$
and
![]() $i=1$
, this reduces to
$i=1$
, this reduces to
![]() $[x,y]^{2^{k-1}} \in \gamma _3(F_2) F_2^{2^k}$
. An alternative proof of this particular case has been given by Struik in [Reference Struik48, Theorem 1] in which she proves that
$[x,y]^{2^{k-1}} \in \gamma _3(F_2) F_2^{2^k}$
. An alternative proof of this particular case has been given by Struik in [Reference Struik48, Theorem 1] in which she proves that
![]() $[x,y]^{\frac {n}{2}}\in \gamma _3(F_2)F_2^{n}$
for each even positive integer n. Note that this follows immediately from the exposition above:
$[x,y]^{\frac {n}{2}}\in \gamma _3(F_2)F_2^{n}$
for each even positive integer n. Note that this follows immediately from the exposition above:
![]() $A([x,y]^{\frac {n}{2}})=\frac {n}{2}$
, so
$A([x,y]^{\frac {n}{2}})=\frac {n}{2}$
, so
![]() $[x,y]^{\frac {n}{2}} \in \ker (\overline {A})=\gamma _3(F_2)F_2^n \cap F_2'$
. In fact, the area invariant gives a complete description of all the elements in
$[x,y]^{\frac {n}{2}} \in \ker (\overline {A})=\gamma _3(F_2)F_2^n \cap F_2'$
. In fact, the area invariant gives a complete description of all the elements in
![]() $\gamma _3(F_2)F_2^n$
.
$\gamma _3(F_2)F_2^n$
.
Acknowledgment
I would like to thank Iván Sadofschi Costa for useful discussions.