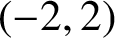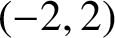1 Introduction
The work of Montgomery on the pair-correlation of zeros of
![]() $\zeta (s)$
in [Reference Montgomery and Diamond32] revealed, for the first time, the ties between zeros of L-functions and eigenvalues of random matrices. In more recent years, there has been growing interest in the study of low-lying zeros of L-functions due to the important roles they play in problems such as determining the rank of the Mordell–Weil groups of elliptic curves and the size of class numbers of imaginary quadratic number fields. The relation between these low-lying zeros and the random matrices is predicted by the density conjecture of Katz and Sarnak [Reference Katz and Sarnak24, Reference Katz and Sarnak25], which asserts that the distribution of zeros near the central point of a family of L-functions is the same as that of the eigenvalues near
$\zeta (s)$
in [Reference Montgomery and Diamond32] revealed, for the first time, the ties between zeros of L-functions and eigenvalues of random matrices. In more recent years, there has been growing interest in the study of low-lying zeros of L-functions due to the important roles they play in problems such as determining the rank of the Mordell–Weil groups of elliptic curves and the size of class numbers of imaginary quadratic number fields. The relation between these low-lying zeros and the random matrices is predicted by the density conjecture of Katz and Sarnak [Reference Katz and Sarnak24, Reference Katz and Sarnak25], which asserts that the distribution of zeros near the central point of a family of L-functions is the same as that of the eigenvalues near
![]() $1$
of a corresponding classical compact group.
$1$
of a corresponding classical compact group.
A rich literature exists on the density conjecture for various families of L-functions. Some examples include results for Dirichlet [Reference Hughes and Rudnick21, Reference Özlük and Snyder34],Hecke [Reference Fouvry and Iwaniec12, Reference Miller and Peckner31], automorphic [Reference Gao and Zhao14, Reference Hughes and Miller20, Reference Iwaniec, Luo and Sarnak23], elliptic curve [Reference Baier and Zhao1, Reference Heath-Brown19, Reference Young44], Dedekind [Reference Shankar, Södergren and Templier39, Reference Yang43], Artin [Reference Cho and Kim3] and symmetric power L-functions [Reference Dueñez and Miller7, Reference Güloğlu18]. Among these various families, the investigation of the families of quadratic Dirichlet L-functions has a relatively long history. They were first examined by Özlük and Snyder in [Reference Özlük and Snyder34] on the one-level density of low-lying zeros of the family, under the assumption of the generalized Riemann hypothesis (GRH). Further work in this direction can be found in [Reference Gao13, Reference Miller29, Reference Rubinstein38].
The density conjecture predicts the main term behavior of the n-level density of low-lying zeros of families of L-functions for all n. One can actually do more on the number theory side by computing the lower-order terms of these n-level densities. These lower-order terms serve to provide a better understanding of the n-level densities. Examples of such computations can be found in [Reference Miller30, Reference Ricotta and Royer35, Reference Young45].
For the family of quadratic Dirichlet L-functions, the lower-order terms of one-level density were first analyzed by Miller in [Reference Miller29] for test functions whose Fourier transforms are supported in
![]() $(-1, 1)$
. On the other hand, we note that the above-mentioned result of Özlük and Snyder [Reference Özlük and Snyder34] on the one-level density is valid with the assumption of the GRH as long as the Fourier transforms of test functions are supported in
$(-1, 1)$
. On the other hand, we note that the above-mentioned result of Özlük and Snyder [Reference Özlük and Snyder34] on the one-level density is valid with the assumption of the GRH as long as the Fourier transforms of test functions are supported in
![]() $(-2, 2)$
. Thus, one expects that the computation of the corresponding lower-order terms for all such functions should be possible. This was indeed achieved by a recent result of Fiorilli et al. in [Reference Fiorilli, Parks and Södergren10] which assumes the GRH.
$(-2, 2)$
. Thus, one expects that the computation of the corresponding lower-order terms for all such functions should be possible. This was indeed achieved by a recent result of Fiorilli et al. in [Reference Fiorilli, Parks and Södergren10] which assumes the GRH.
In [Reference Gao and Zhao15], we studied the one-level density of low-lying zeros of quadratic Hecke L-functions in the Gaussian field. Assuming the GRH, we showed that our result confirms the density conjecture when the Fourier transforms of test functions are supported in
![]() $(-2, 2)$
, a result analogous to that of the family of quadratic Dirichlet L-functions. In view of this, it is natural to ask whether one can compute the lower-order terms as well, as in [Reference Fiorilli, Parks and Södergren10]. We also point out here that in [Reference Waxman42], Waxman computed low-order terms of the one-level density for a symplectic family of L-functions attached to Hecke characters of infinite order in the Gaussian field. It is our goal in this paper to continue our work in this direction.
$(-2, 2)$
, a result analogous to that of the family of quadratic Dirichlet L-functions. In view of this, it is natural to ask whether one can compute the lower-order terms as well, as in [Reference Fiorilli, Parks and Södergren10]. We also point out here that in [Reference Waxman42], Waxman computed low-order terms of the one-level density for a symplectic family of L-functions attached to Hecke characters of infinite order in the Gaussian field. It is our goal in this paper to continue our work in this direction.
We write
![]() $K=\mathbb Q(i)$
for the Gaussian field and
$K=\mathbb Q(i)$
for the Gaussian field and
![]() $\mathcal {O}_{K}=\mathbb Z[i]$
for the ring of integers in K. We write
$\mathcal {O}_{K}=\mathbb Z[i]$
for the ring of integers in K. We write
![]() $N(n)$
for the norm of an element
$N(n)$
for the norm of an element
![]() $n \in \mathcal {O}_{K}$
and we reserve the symbol
$n \in \mathcal {O}_{K}$
and we reserve the symbol
![]() $\chi _{n}$
for the quadratic Hecke character
$\chi _{n}$
for the quadratic Hecke character
![]() $({n}/{\cdot })$
defined in Section 2.1. We denote by
$({n}/{\cdot })$
defined in Section 2.1. We denote by
![]() $\zeta _{K}(s)$
the Dedekind zeta function of K. We assume the GRH throughout this paper and we are concerned with the following family of L-functions:
$\zeta _{K}(s)$
the Dedekind zeta function of K. We assume the GRH throughout this paper and we are concerned with the following family of L-functions:
Let
![]() $L(s, \chi )$
be one of the L-functions in
$L(s, \chi )$
be one of the L-functions in
![]() $\mathcal F$
, and write
$\mathcal F$
, and write
![]() $\chi $
here for the corresponding Hecke character. We denote the nontrivial zeros of
$\chi $
here for the corresponding Hecke character. We denote the nontrivial zeros of
![]() $L(s, \chi )$
by
$L(s, \chi )$
by
![]() $1/2+i \gamma _{\chi , j}$
so that
$1/2+i \gamma _{\chi , j}$
so that
![]() $\gamma _{\chi , j} \in \mathbb R$
under the GRH. We order them as
$\gamma _{\chi , j} \in \mathbb R$
under the GRH. We order them as
Let X be a large real number. We set
![]() $\mathcal {L}=\log X$
throughout the paper, and we normalize the zeros by defining
$\mathcal {L}=\log X$
throughout the paper, and we normalize the zeros by defining
 $$ \begin{align*} \tilde{\gamma}_{\chi, j}= \frac{\gamma_{\chi, j}}{2 \pi} \mathcal{L}. \end{align*} $$
$$ \begin{align*} \tilde{\gamma}_{\chi, j}= \frac{\gamma_{\chi, j}}{2 \pi} \mathcal{L}. \end{align*} $$
Fix two even Schwartz class functions
![]() $\phi , w$
such that w is nonzero and nonnegative. We regard
$\phi , w$
such that w is nonzero and nonnegative. We regard
![]() $\phi $
as a test function and w as a weight function. We define the one-level density for the single L-function
$\phi $
as a test function and w as a weight function. We define the one-level density for the single L-function
![]() $L(s, \chi )$
with respect to
$L(s, \chi )$
with respect to
![]() $\phi $
by the sum
$\phi $
by the sum
 $$ \begin{align*} S(\kern1.5pt\chi, \phi)=\sum_{j} \phi(\tilde{\gamma}_{\chi, j}). \end{align*} $$
$$ \begin{align*} S(\kern1.5pt\chi, \phi)=\sum_{j} \phi(\tilde{\gamma}_{\chi, j}). \end{align*} $$
The one-level density of the family
![]() $\mathcal F $
with respect to w is then defined as the weighted sum
$\mathcal F $
with respect to w is then defined as the weighted sum
 $$ \begin{align} D(\phi;w, X) =\frac 1{W(X)}\sideset{}{^{*}}\sum_{c} w\bigg( \frac {N(c)}X \bigg) S(\kern1.5pt\chi_{i(1+i)^{5}c}, \phi), \end{align} $$
$$ \begin{align} D(\phi;w, X) =\frac 1{W(X)}\sideset{}{^{*}}\sum_{c} w\bigg( \frac {N(c)}X \bigg) S(\kern1.5pt\chi_{i(1+i)^{5}c}, \phi), \end{align} $$
where we use
![]() $\sum ^{*}$
to denote a sum over square-free elements in
$\sum ^{*}$
to denote a sum over square-free elements in
![]() $\mathcal {O}_{K}$
throughout the paper, and
$\mathcal {O}_{K}$
throughout the paper, and
![]() $W(X)$
here is the total weight given by
$W(X)$
here is the total weight given by
 $$ \begin{align*} W(X)=\sideset{}{^{*}}\sum_{c} w\bigg( \frac {N(c)}X \bigg). \end{align*} $$
$$ \begin{align*} W(X)=\sideset{}{^{*}}\sum_{c} w\bigg( \frac {N(c)}X \bigg). \end{align*} $$
Our first result in this paper is an asymptotic expansion of
![]() $D(\phi ;w, X)$
in descending powers of
$D(\phi ;w, X)$
in descending powers of
![]() $\log X$
.
$\log X$
.
Theorem 1.1. Suppose that the GRH holds for the family of L-functions in
![]() $\mathcal F $
as well as for
$\mathcal F $
as well as for
![]() $\zeta _{K}(s)$
. Let
$\zeta _{K}(s)$
. Let
![]() $\phi (x)$
be an even Schwartz function whose Fourier transform
$\phi (x)$
be an even Schwartz function whose Fourier transform
![]() $\hat {\phi }(u)$
has compact support in
$\hat {\phi }(u)$
has compact support in
![]() $(-2,2)$
, and let w be an even nonzero and nonnegative Schwartz function. Let
$(-2,2)$
, and let w be an even nonzero and nonnegative Schwartz function. Let
![]() $D(\phi ;w, X)$
be defined as in (1-1). Then, for any integer
$D(\phi ;w, X)$
be defined as in (1-1). Then, for any integer
![]() $M \geq 1$
,
$M \geq 1$
,
 $$ \begin{align} D(\phi;w, X) = \widehat{\phi}(0)-\frac{1}2\int_{-1}^{1} \widehat{\phi}(u)\, {d} u +\sum_{m=1}^{M} \frac {R_{w,m}(\phi)}{\mathcal{L}^{m}} +O\bigg( \frac 1{\mathcal{L}^{M+1}}\bigg), \end{align} $$
$$ \begin{align} D(\phi;w, X) = \widehat{\phi}(0)-\frac{1}2\int_{-1}^{1} \widehat{\phi}(u)\, {d} u +\sum_{m=1}^{M} \frac {R_{w,m}(\phi)}{\mathcal{L}^{m}} +O\bigg( \frac 1{\mathcal{L}^{M+1}}\bigg), \end{align} $$
where the coefficients
![]() $R_{w,m}(\phi )$
are linear functionals in
$R_{w,m}(\phi )$
are linear functionals in
![]() $\phi $
that can be given explicitly in terms of w, and the derivatives of
$\phi $
that can be given explicitly in terms of w, and the derivatives of
![]() $\widehat \phi $
at the points
$\widehat \phi $
at the points
![]() $0$
and
$0$
and
![]() $1$
(see (4-4)).
$1$
(see (4-4)).
We note that Theorem 1.1 gives a refinement of [Reference Gao and Zhao15, Theorem 1.1], which can be regarded as computing only the main term of the expansion for
![]() $\phi $
given in (1-2). Our result is similar to [Reference Fiorilli, Parks and Södergren10, Theorem 1.1], and we follow closely many of the steps in [Reference Fiorilli, Parks and Södergren10] in the proof of Theorem 1.1. Additionally, our proof of Theorem 1.1 proceeds along the same lines as that of [Reference Gao and Zhao15, Theorem 1.1] with extra efforts to keep track of all the lower-order terms.
$\phi $
given in (1-2). Our result is similar to [Reference Fiorilli, Parks and Södergren10, Theorem 1.1], and we follow closely many of the steps in [Reference Fiorilli, Parks and Södergren10] in the proof of Theorem 1.1. Additionally, our proof of Theorem 1.1 proceeds along the same lines as that of [Reference Gao and Zhao15, Theorem 1.1] with extra efforts to keep track of all the lower-order terms.
When deriving these lower-order terms, a powerful tool to deploy is the L-functions ratios conjecture of Conrey et al. in [Reference Conrey, Farmer and Zirnbauer4, Section 5]. This approach was applied by Conrey and Snaith in [Reference Conrey and Snaith5] to study the one-level density function for zeros of quadratic Dirichlet L-functions. The general n-level density of the same family was examined by Mason and Snaith in [Reference Mason and Snaith27], and further enabled them to show in [Reference Mason and Snaith26] that the result agrees with the density conjecture when the Fourier transforms of test functions are supported in
![]() $(-2, 2)$
.
$(-2, 2)$
.
It is then highly desirable and interesting to compare the expressions for the n-level density functions conditional on the ratios conjecture to those obtained without the conjecture. For the family of quadratic Dirichlet L-functions, a result of Miller [Reference Miller29] matches the lower-order terms of the one-level density function obtained with or without the assumption of the ratios conjecture, when the Fourier transforms of test functions are supported in
![]() $(-1, 1)$
. When the support is enlarged to
$(-1, 1)$
. When the support is enlarged to
![]() $(-2,2)$
, Fiorilli et al. obtained the lower-order terms of the one-level density function in [Reference Fiorilli, Parks and Södergren10, Reference Fiorilli, Parks and Södergren11] by applying either the ratios conjecture or otherwise. Their work assumes the GRH, and the results obtained are further shown to match up to the first lower-order term in [Reference Fiorilli, Parks and Södergren11].
$(-2,2)$
, Fiorilli et al. obtained the lower-order terms of the one-level density function in [Reference Fiorilli, Parks and Södergren10, Reference Fiorilli, Parks and Södergren11] by applying either the ratios conjecture or otherwise. Their work assumes the GRH, and the results obtained are further shown to match up to the first lower-order term in [Reference Fiorilli, Parks and Södergren11].
Motivated by the above works, our next objective in the paper is to evaluate
![]() $D(\phi ;w, X)$
using the ratios conjecture. We formulate the appropriate version of the ratios conjecture concerning our family
$D(\phi ;w, X)$
using the ratios conjecture. We formulate the appropriate version of the ratios conjecture concerning our family
![]() $\mathcal F$
in Conjecture 5.1, and use it to prove in Section 5 the following asymptotic expression of
$\mathcal F$
in Conjecture 5.1, and use it to prove in Section 5 the following asymptotic expression of
![]() $D(\phi ;w, X)$
.
$D(\phi ;w, X)$
.
Theorem 1.2. Assume the truth of the GRH for the family of L-functions in
![]() $\mathcal F $
as well as for
$\mathcal F $
as well as for
![]() $\zeta _{K}(s)$
and Conjecture 5.1. Let
$\zeta _{K}(s)$
and Conjecture 5.1. Let
![]() $w(t)$
be an even, nonzero and nonnegative Schwartz function and
$w(t)$
be an even, nonzero and nonnegative Schwartz function and
![]() $\phi (x)$
an even Schwartz function whose Fourier transform
$\phi (x)$
an even Schwartz function whose Fourier transform
 $\widehat {\phi }(u)$
has compact support. Then, for any
$\widehat {\phi }(u)$
has compact support. Then, for any
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
 $$ \begin{align} D(\phi;w, X)&=\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2it)}{\zeta_{K}(1+2it)} + 2A_{\alpha}(it,it) \nonumber\\[3pt] &\quad +\log \bigg(\frac {32N(c)}{\pi^{2}}\bigg) +\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12-it\bigg) + \frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12+it \bigg) \nonumber\\[3pt] &\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+it\bigg)\zeta_{K}(1-2it)A(-it,it) \bigg) \, \phi\bigg(\frac{t\mathcal{L}}{2\pi}\bigg) \, {d} t \nonumber\\[3pt] &\quad + O_{\varepsilon}(X^{-1/2+\varepsilon}), \end{align} $$
$$ \begin{align} D(\phi;w, X)&=\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2it)}{\zeta_{K}(1+2it)} + 2A_{\alpha}(it,it) \nonumber\\[3pt] &\quad +\log \bigg(\frac {32N(c)}{\pi^{2}}\bigg) +\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12-it\bigg) + \frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12+it \bigg) \nonumber\\[3pt] &\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+it\bigg)\zeta_{K}(1-2it)A(-it,it) \bigg) \, \phi\bigg(\frac{t\mathcal{L}}{2\pi}\bigg) \, {d} t \nonumber\\[3pt] &\quad + O_{\varepsilon}(X^{-1/2+\varepsilon}), \end{align} $$
where the functions
![]() $X_{c}$
, A and
$X_{c}$
, A and
![]() $A_{\alpha }$
are given in (5-3), (5-7) and Lemma 5.1, respectively.
$A_{\alpha }$
are given in (5-3), (5-7) and Lemma 5.1, respectively.
Our next goal is to compare the expression given for
![]() $D(\phi ;w, X)$
in Theorem 1.2 with the one obtained in Theorem 1.1. To this end, we prove (see Lemma 2.6) the following expression for
$D(\phi ;w, X)$
in Theorem 1.2 with the one obtained in Theorem 1.1. To this end, we prove (see Lemma 2.6) the following expression for
![]() $D(\phi ;w, X)$
when
$D(\phi ;w, X)$
when
![]() $\phi $
is an even Schwartz test function with compactly supported Fourier transform:
$\phi $
is an even Schwartz test function with compactly supported Fourier transform:
 $$ \begin{align} D(\phi;w, X) &= \frac {\widehat{\phi}(0)}{ \mathcal{L} W(X)}\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \log N(c) \nonumber\\[1pt] &\quad +\frac {\widehat\phi(0)}{\mathcal{L}} \bigg( \log\frac {32}{\pi^{2}}+ 2\frac{\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg ) \nonumber\\[1pt] &\quad -\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L}; \hat{\phi}) \nonumber\\[1pt] &\quad +\frac{2}{\mathcal{L}}\int_{0}^{\infty}\frac{e^{-x/2}}{1-e^{-x}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{x}{\mathcal{L}}\bigg)\bigg)\, {d} x, \end{align} $$
$$ \begin{align} D(\phi;w, X) &= \frac {\widehat{\phi}(0)}{ \mathcal{L} W(X)}\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \log N(c) \nonumber\\[1pt] &\quad +\frac {\widehat\phi(0)}{\mathcal{L}} \bigg( \log\frac {32}{\pi^{2}}+ 2\frac{\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg ) \nonumber\\[1pt] &\quad -\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L}; \hat{\phi}) \nonumber\\[1pt] &\quad +\frac{2}{\mathcal{L}}\int_{0}^{\infty}\frac{e^{-x/2}}{1-e^{-x}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{x}{\mathcal{L}}\bigg)\bigg)\, {d} x, \end{align} $$
where
 $$ \begin{align*} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L} ;\hat{\phi})=\sum_{\varpi\,\equiv 1 \bmod {(1+i)^{3}}}\frac { \log N(\varpi)}{\sqrt{N(\varpi^{\kern1.8pt j})}}\chi_{i(1+i)^{5}c} ( \varpi^{\kern1.8pt j} ) \, \hat{\phi} \bigg( \frac {\log N(\varpi^{\kern1.8pt j})}{\mathcal{L}} \bigg), \end{align*} $$
$$ \begin{align*} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L} ;\hat{\phi})=\sum_{\varpi\,\equiv 1 \bmod {(1+i)^{3}}}\frac { \log N(\varpi)}{\sqrt{N(\varpi^{\kern1.8pt j})}}\chi_{i(1+i)^{5}c} ( \varpi^{\kern1.8pt j} ) \, \hat{\phi} \bigg( \frac {\log N(\varpi^{\kern1.8pt j})}{\mathcal{L}} \bigg), \end{align*} $$
with the sum over
![]() $\varpi $
running over primes in
$\varpi $
running over primes in
![]() $\mathcal {O}_{K}$
. Here we note that in
$\mathcal {O}_{K}$
. Here we note that in
![]() $\mathcal {O}_{K}$
, every ideal coprime to
$\mathcal {O}_{K}$
, every ideal coprime to
![]() $(1+i)$
has a unique generator congruent to
$(1+i)$
has a unique generator congruent to
![]() $1$
modulo
$1$
modulo
![]() $(1+i)^{3}$
, and such a generator is called primary. We use
$(1+i)^{3}$
, and such a generator is called primary. We use
![]() $\sum _{\varpi \equiv 1 \bmod {(1+i)^{3}}}$
(or sum over other variables) to indicate a sum over primary elements in
$\sum _{\varpi \equiv 1 \bmod {(1+i)^{3}}}$
(or sum over other variables) to indicate a sum over primary elements in
![]() $\mathcal {O}_{K}$
.
$\mathcal {O}_{K}$
.
For any function W, we denote its Mellin transform by
![]() $ \mathcal M W$
, so that
$ \mathcal M W$
, so that
 $$ \begin{align} \mathcal M W(s) =\int^{\infty}_{0}W(t)t^{s}\frac {{d} t}{t}. \end{align} $$
$$ \begin{align} \mathcal M W(s) =\int^{\infty}_{0}W(t)t^{s}\frac {{d} t}{t}. \end{align} $$
We further note that around
![]() $s=1$
,
$s=1$
,
 $$ \begin{align} \zeta_{K}(s)=\frac {\pi}{4}\cdot \frac 1{s-1}+\gamma_{K}+O(|s-1|), \end{align} $$
$$ \begin{align} \zeta_{K}(s)=\frac {\pi}{4}\cdot \frac 1{s-1}+\gamma_{K}+O(|s-1|), \end{align} $$
where
![]() $\gamma _{K}$
is a constant. We write
$\gamma _{K}$
is a constant. We write
![]() $\gamma =0.57\cdots $
for the Euler constant.
$\gamma =0.57\cdots $
for the Euler constant.
The following result shows the agreement of the two expressions for
![]() $D(\phi ;w, X)$
given in (1-3) and (1-4) up to the first lower-order term.
$D(\phi ;w, X)$
given in (1-3) and (1-4) up to the first lower-order term.
Theorem 1.3. Assume the truth of the GRH for the family of L-functions in
![]() $\mathcal F $
as well as for
$\mathcal F $
as well as for
![]() $\zeta _{K}(s)$
and Conjecture 5.1. Let
$\zeta _{K}(s)$
and Conjecture 5.1. Let
![]() $w(t)$
be an even, nonzero and nonnegative Schwartz function and
$w(t)$
be an even, nonzero and nonnegative Schwartz function and
![]() $\phi (x)$
an even Schwartz function whose Fourier transform
$\phi (x)$
an even Schwartz function whose Fourier transform
 $\widehat {\phi }(u)$
has compact support. Then expression (1-3) gives that
$\widehat {\phi }(u)$
has compact support. Then expression (1-3) gives that
 $$ \begin{align} &D (\phi;w, X) \nonumber\\[1pt] &\quad =\widehat{\phi}(0) + \int^{\infty}_{1} \widehat{\phi}(\tau) \, {d} \tau+ \frac{\widehat{\phi}(0)}{\mathcal{L}}\bigg( \log \frac{32}{\pi^{2}} +2\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12\bigg) + \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x \, {d} x \bigg) \nonumber\\[1pt] &\qquad+\frac{2}{\mathcal{L}} \int_{0}^{\infty}\frac{e^{-t/2}}{1-e^{-t}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{t}{\mathcal{L}}\bigg)\bigg)\, {d} t \nonumber \\ &\qquad - \frac{2}{\mathcal{L}} \sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 1}} \frac{\log N(\varpi)}{N(\varpi)^{j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\bigg( \frac{2j \log N(\varpi)}{\mathcal{L}} \bigg) \nonumber\\[3pt] &\qquad +\frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma+ \log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O( \mathcal{L}^{-2} ). \end{align} $$
$$ \begin{align} &D (\phi;w, X) \nonumber\\[1pt] &\quad =\widehat{\phi}(0) + \int^{\infty}_{1} \widehat{\phi}(\tau) \, {d} \tau+ \frac{\widehat{\phi}(0)}{\mathcal{L}}\bigg( \log \frac{32}{\pi^{2}} +2\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12\bigg) + \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x \, {d} x \bigg) \nonumber\\[1pt] &\qquad+\frac{2}{\mathcal{L}} \int_{0}^{\infty}\frac{e^{-t/2}}{1-e^{-t}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{t}{\mathcal{L}}\bigg)\bigg)\, {d} t \nonumber \\ &\qquad - \frac{2}{\mathcal{L}} \sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 1}} \frac{\log N(\varpi)}{N(\varpi)^{j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\bigg( \frac{2j \log N(\varpi)}{\mathcal{L}} \bigg) \nonumber\\[3pt] &\qquad +\frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma+ \log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O( \mathcal{L}^{-2} ). \end{align} $$
Also, when
![]() $\sup (\mathrm {supp}(\hat {\phi }(u)))<2$
, the above expression agrees with that given in (1-4).
$\sup (\mathrm {supp}(\hat {\phi }(u)))<2$
, the above expression agrees with that given in (1-4).
We give the proof of Theorem 1.3 in Section 6. Our approach is inspired by the proof of [Reference Fiorilli, Parks and Södergren11, Theorems 1.1 and 1.4], although the computation in our situation is more involved.
2 Preliminaries
2.1 Number fields background
Recall that in this paper,
![]() $K=\mathbb Q(i)$
is the Gaussian field. We denote by
$K=\mathbb Q(i)$
is the Gaussian field. We denote by
![]() $U_{K}$
the group of units in
$U_{K}$
the group of units in
![]() ${\mathcal O}_{K}$
, so that
${\mathcal O}_{K}$
, so that
![]() $U_{K}=\{ \pm 1, \pm i\}$
. As it is well known that K has class number one, we do not distinguish n and
$U_{K}=\{ \pm 1, \pm i\}$
. As it is well known that K has class number one, we do not distinguish n and
![]() $(n)$
when this causes no confusion from the context. We therefore write
$(n)$
when this causes no confusion from the context. We therefore write
![]() $\mu _{[i]}(n)$
to mean the Möbius function
$\mu _{[i]}(n)$
to mean the Möbius function
![]() $\mu _{[i]}((n))$
. We use
$\mu _{[i]}((n))$
. We use
![]() $\varpi $
to denote a prime (or prime ideal) in K and write
$\varpi $
to denote a prime (or prime ideal) in K and write
![]() $\Lambda (n)$
for the von Mangoldt function on
$\Lambda (n)$
for the von Mangoldt function on
![]() $\mathcal {O}_{K}$
so that
$\mathcal {O}_{K}$
so that
 $$ \begin{align*} \Lambda(n)=\begin{cases} \log N(\varpi) & n=\varpi^{k}, \; \varpi\text{ prime}, \; k \geq 1, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \Lambda(n)=\begin{cases} \log N(\varpi) & n=\varpi^{k}, \; \varpi\text{ prime}, \; k \geq 1, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
Let
![]() $({\cdot }/{n})_{4}$
stand for the quartic residue symbol on
$({\cdot }/{n})_{4}$
stand for the quartic residue symbol on
![]() $\mathcal {O}_{K}$
. For a prime
$\mathcal {O}_{K}$
. For a prime
![]() $\varpi \in \mathcal {O}_{K}$
with
$\varpi \in \mathcal {O}_{K}$
with
![]() $N(\varpi ) \neq 2$
, the quartic symbol is defined for
$N(\varpi ) \neq 2$
, the quartic symbol is defined for
![]() $a \in \mathcal {O}_{K}$
,
$a \in \mathcal {O}_{K}$
,
![]() $(a, \varpi )=1$
by
$(a, \varpi )=1$
by
![]() $({a}/{\varpi })_{4} \equiv a^{(N(\varpi )-1)/4} ({\operatorname {mod}}\,\,\varpi )$
, with
$({a}/{\varpi })_{4} \equiv a^{(N(\varpi )-1)/4} ({\operatorname {mod}}\,\,\varpi )$
, with
![]() $({a}/{\varpi })_{4} \in \{ \pm 1, \pm i \}$
. When
$({a}/{\varpi })_{4} \in \{ \pm 1, \pm i \}$
. When
![]() $\varpi | a$
, we define
$\varpi | a$
, we define
![]() $({a}/{\varpi })_{4} =0$
. Then the quartic symbol can be extended to any composite n with
$({a}/{\varpi })_{4} =0$
. Then the quartic symbol can be extended to any composite n with
![]() $(N(n), 2)=1$
multiplicatively. We further define
$(N(n), 2)=1$
multiplicatively. We further define
 $({\cdot }/{n})=({\cdot }/{n})^{2}_{4}$
to be the quadratic residue symbol for these n.
$({\cdot }/{n})=({\cdot }/{n})^{2}_{4}$
to be the quadratic residue symbol for these n.
We say that an element
![]() $c \in \mathcal {O}_{K}$
(or the ideal
$c \in \mathcal {O}_{K}$
(or the ideal
![]() $(c)$
) is odd if
$(c)$
) is odd if
![]() $(c, 1+i)=1$
. Note that in
$(c, 1+i)=1$
. Note that in
![]() $\mathcal {O}_{K}$
, every odd ideal has a unique generator congruent to
$\mathcal {O}_{K}$
, every odd ideal has a unique generator congruent to
![]() $1$
modulo
$1$
modulo
![]() $(1+i)^{3}$
. Such a generator is called primary. For two primary integers
$(1+i)^{3}$
. Such a generator is called primary. For two primary integers
![]() $m, n \in \mathcal {O}_{K}$
, we note that the quadratic reciprocity law (see [Reference Gao and Zhao15, formula (2.1)]) gives
$m, n \in \mathcal {O}_{K}$
, we note that the quadratic reciprocity law (see [Reference Gao and Zhao15, formula (2.1)]) gives
 $$ \begin{align} \bigg(\frac{m}{n}\bigg) = \bigg(\frac{n}{m}\bigg). \end{align} $$
$$ \begin{align} \bigg(\frac{m}{n}\bigg) = \bigg(\frac{n}{m}\bigg). \end{align} $$
Let
![]() $\chi $
denote a Hecke character of K. We say that
$\chi $
denote a Hecke character of K. We say that
![]() $\chi $
is of trivial infinite type if its component at the infinite place of K is trivial. In particular,
$\chi $
is of trivial infinite type if its component at the infinite place of K is trivial. In particular,
![]() $\chi _{c}$
defined earlier is a Hecke character of trivial infinite type. It is further shown in [Reference Gao and Zhao15, Section 2.1] that when c is square-free and coprime to
$\chi _{c}$
defined earlier is a Hecke character of trivial infinite type. It is further shown in [Reference Gao and Zhao15, Section 2.1] that when c is square-free and coprime to
![]() $1+i$
,
$1+i$
,
![]() $\chi _{i(1+i)^{5}c}$
defines a primitive Hecke character
$\chi _{i(1+i)^{5}c}$
defines a primitive Hecke character
![]() $\text {mod} ((1+i)^{5}c)$
of trivial infinite type.
$\text {mod} ((1+i)^{5}c)$
of trivial infinite type.
For any primitive Hecke character
![]() $\chi ({\operatorname {mod}}\,\,m)$
of trivial infinite type, let
$\chi ({\operatorname {mod}}\,\,m)$
of trivial infinite type, let
where
![]() $L(s, \chi )$
is the L-function attached to
$L(s, \chi )$
is the L-function attached to
![]() $\chi $
and
$\chi $
and
![]() $D_{K}=-4$
is the discriminant of K. In particular, we use
$D_{K}=-4$
is the discriminant of K. In particular, we use
![]() $\zeta _{K}(s)$
to denote the Dedekind zeta function of K.
$\zeta _{K}(s)$
to denote the Dedekind zeta function of K.
It was shown by Hecke that
![]() $\Lambda (s, \chi )$
is an entire function and satisfies the functional equation [Reference Iwaniec and Kowalski22, Theorem 3.8]
$\Lambda (s, \chi )$
is an entire function and satisfies the functional equation [Reference Iwaniec and Kowalski22, Theorem 3.8]
where
![]() $|W(\chi )|=(N(m))^{1/2}$
.
$|W(\chi )|=(N(m))^{1/2}$
.
2.2 Poisson summation
For any
![]() $r,n \in \mathcal {O}_{K}$
with n odd, we define the Gauss sum
$r,n \in \mathcal {O}_{K}$
with n odd, we define the Gauss sum
![]() $g(r,n)$
as
$g(r,n)$
as
 $$ \begin{align*} g(r,n) = \sum_{x \bmod{n}} \bigg(\frac{x}{n}\bigg)\, \widetilde{e}\,\bigg(\frac{rx}{n}\bigg) \end{align*} $$
$$ \begin{align*} g(r,n) = \sum_{x \bmod{n}} \bigg(\frac{x}{n}\bigg)\, \widetilde{e}\,\bigg(\frac{rx}{n}\bigg) \end{align*} $$
where
![]() $ \widetilde {e}(z) =\exp ( 2\pi i (( {z}/{2i}) - ({\overline {z}}/{2i}) ))$
. It is shown in [Reference Gao and Zhao15, Lemma 2.2] that, for a primary prime
$ \widetilde {e}(z) =\exp ( 2\pi i (( {z}/{2i}) - ({\overline {z}}/{2i}) ))$
. It is shown in [Reference Gao and Zhao15, Lemma 2.2] that, for a primary prime
![]() $\varpi $
,
$\varpi $
,
 $$ \begin{align*} g(r, \varpi)=\bigg(\frac{ir}{\varpi}\bigg)N(\varpi)^{1/2}. \end{align*} $$
$$ \begin{align*} g(r, \varpi)=\bigg(\frac{ir}{\varpi}\bigg)N(\varpi)^{1/2}. \end{align*} $$
We quote the following Poisson summation formula from [Reference Gao and Zhao15, Lemma 2.7].
Lemma 2.1. Let
![]() $n \in \mathcal {O}_{K}$
be primary and
$n \in \mathcal {O}_{K}$
be primary and
![]() $\chi $
a quadratic character
$\chi $
a quadratic character
![]() $ ({\operatorname {mod}}\,\,n)$
of trivial infinite type. For any Schwartz class function W, we have
$ ({\operatorname {mod}}\,\,n)$
of trivial infinite type. For any Schwartz class function W, we have
 $$ \begin{align} \sum_{m \in \mathcal{O}_{K}}\chi(m)W\bigg(\frac {N(m)}{X}\bigg)=\frac {X}{N(n)}\sum_{k \in \mathcal{O}_{K}}g(k,n)\widetilde{W}\bigg(\sqrt{\frac {N(k)X}{N(n)}}\bigg) \end{align} $$
$$ \begin{align} \sum_{m \in \mathcal{O}_{K}}\chi(m)W\bigg(\frac {N(m)}{X}\bigg)=\frac {X}{N(n)}\sum_{k \in \mathcal{O}_{K}}g(k,n)\widetilde{W}\bigg(\sqrt{\frac {N(k)X}{N(n)}}\bigg) \end{align} $$
and
 $$ \begin{align} \sum_{m \in \mathcal{O}_{K}} W\bigg(\frac {N(m)}{X}\bigg)=X \sum_{k \in \mathcal{O}_{K}}\widetilde{W}(\sqrt{N(k)X}\,), \end{align} $$
$$ \begin{align} \sum_{m \in \mathcal{O}_{K}} W\bigg(\frac {N(m)}{X}\bigg)=X \sum_{k \in \mathcal{O}_{K}}\widetilde{W}(\sqrt{N(k)X}\,), \end{align} $$
where
 $$ \begin{align} \widetilde{W}(t) &=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}W(N(x+yi))\, \widetilde{e}\,(- t(x+yi))\,{d} x \,{d} y, \quad t \geq 0. \end{align} $$
$$ \begin{align} \widetilde{W}(t) &=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}W(N(x+yi))\, \widetilde{e}\,(- t(x+yi))\,{d} x \,{d} y, \quad t \geq 0. \end{align} $$
We include here our conventions for various transforms used in this paper. For any function W, we write
![]() $\widehat {W}$
for the Fourier transform of W and recall that its Mellin transform
$\widehat {W}$
for the Fourier transform of W and recall that its Mellin transform
![]() $ \mathcal M w$
is defined in (1-5). We note that, for any Schwartz class function W and any integer
$ \mathcal M w$
is defined in (1-5). We note that, for any Schwartz class function W and any integer
![]() $E \geq 0$
, integration by parts
$E \geq 0$
, integration by parts
![]() $E+1$
times yields that for
$E+1$
times yields that for
![]() $\mathrm {Re}(s)>0$
,
$\mathrm {Re}(s)>0$
,
 $$ \begin{align} \mathcal M {W}(s) \ll \frac{1}{|s| (1+|s|)^{E}}. \end{align} $$
$$ \begin{align} \mathcal M {W}(s) \ll \frac{1}{|s| (1+|s|)^{E}}. \end{align} $$
Furthermore, we set

When
![]() $W(t)$
is a real smooth function, one follows the arguments that lead to the bounds given in [Reference Gao and Zhao15, formula (2.12)] to get that both
$W(t)$
is a real smooth function, one follows the arguments that lead to the bounds given in [Reference Gao and Zhao15, formula (2.12)] to get that both
![]() $\widetilde {W}$
and
$\widetilde {W}$
and
![]() are real and
are real and

for all integers
![]() $\mu \geq 0$
,
$\mu \geq 0$
,
![]() $j \geq 1$
and all real t.
$j \geq 1$
and all real t.
2.3 Some consequences of the GRH
In this section we state a few results that are derived by using the GRH. The first one is for sums over primes.
Lemma 2.2. Suppose that the GRH is true. For any Hecke character
![]() $\chi ({\operatorname {mod}}\,\,m)$
of trivial infinite type, we have for
$\chi ({\operatorname {mod}}\,\,m)$
of trivial infinite type, we have for
![]() $X \geq 1$
,
$X \geq 1$
,
 $$ \begin{align} \sum_{\substack {N(\varpi) \leq X\\ \varpi \equiv 1 \bmod {(1+i)^{3}}}} \chi (\varpi) \log N(\varpi) =\delta_{\chi} X+ O( X^{1/2} \log^{2} (2X) \log N(m) ), \end{align} $$
$$ \begin{align} \sum_{\substack {N(\varpi) \leq X\\ \varpi \equiv 1 \bmod {(1+i)^{3}}}} \chi (\varpi) \log N(\varpi) =\delta_{\chi} X+ O( X^{1/2} \log^{2} (2X) \log N(m) ), \end{align} $$
where
![]() $\delta _{\chi }=1$
if
$\delta _{\chi }=1$
if
![]() $\chi $
is principal and
$\chi $
is principal and
![]() $\delta _{\chi }=0$
otherwise. Moreover, we have
$\delta _{\chi }=0$
otherwise. Moreover, we have
 $$ \begin{align} \sum_{\substack{ N(\varpi) \leq X \\ \varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac {\log N(\varpi)}{N(\varpi) }= \log X+O(1). \end{align} $$
$$ \begin{align} \sum_{\substack{ N(\varpi) \leq X \\ \varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac {\log N(\varpi)}{N(\varpi) }= \log X+O(1). \end{align} $$
Proof. The formula in (2-7) follows directly from [Reference Iwaniec and Kowalski22, Theorem 5.15] and (2-8) is derived from (2-7) by taking
![]() $\chi $
to be the principal character modulo
$\chi $
to be the principal character modulo
![]() $1$
and using partial summation.
$1$
and using partial summation.
Our next two lemmas provide estimations on certain weighted quadratic character sums. The following one is a generalization of [Reference Fiorilli, Parks and Södergren9, Lemma 2.10].
Lemma 2.3. Suppose that the GRH is true. For any even, nonzero and nonnegative Schwartz function w, we have for any primary
![]() $n \in \mathcal {O}_{K}$
and
$n \in \mathcal {O}_{K}$
and
![]() $\epsilon>0$
,
$\epsilon>0$
,
 $$ \begin{align*} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {i(1+i)^{5}c}{n} \bigg)&= \delta_{\chi_{n} } \frac{\pi X}{3\zeta_{K}(2)} \widehat w(0) \prod_{\varpi\mid n} \bigg(1+\frac 1{N(\varpi)} \bigg)^{-1} \\[3pt] &\quad +O(N(n)^{3(1-\delta_{\chi_{n} })/8 +\varepsilon}X^{1/4+\varepsilon}). \end{align*} $$
$$ \begin{align*} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {i(1+i)^{5}c}{n} \bigg)&= \delta_{\chi_{n} } \frac{\pi X}{3\zeta_{K}(2)} \widehat w(0) \prod_{\varpi\mid n} \bigg(1+\frac 1{N(\varpi)} \bigg)^{-1} \\[3pt] &\quad +O(N(n)^{3(1-\delta_{\chi_{n} })/8 +\varepsilon}X^{1/4+\varepsilon}). \end{align*} $$
Here we recall that
![]() $\sum ^{*}$
denotes the sum over square-free elements in
$\sum ^{*}$
denotes the sum over square-free elements in
![]() $\mathcal {O}_{K}$
.
$\mathcal {O}_{K}$
.
Proof. Since each c coprime to
![]() $1+i$
can be uniquely written as the product of a unit and a primary element, it follows that
$1+i$
can be uniquely written as the product of a unit and a primary element, it follows that
 $$ \begin{align*} &\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {(1+i)^{5}c}{n} \bigg) \\[1pt] &\quad= \bigg(1+ \bigg(\frac{-1}{n}\bigg)+\bigg(\frac{i}{n}\bigg)+\bigg(\frac{i^{3}}{n}\bigg) \bigg) \sideset{}{^{*}}\sum_{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} } w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {(1+i)c}{n}\bigg) \nonumber \\&\quad= 2\bigg(1+ \bigg(\frac{i}{n}\bigg) \bigg)\bigg(\frac {1+i}{n} \bigg) \sideset{}{^{*}}\sum_{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} } w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {c}{n} \bigg). \end{align*} $$
$$ \begin{align*} &\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {(1+i)^{5}c}{n} \bigg) \\[1pt] &\quad= \bigg(1+ \bigg(\frac{-1}{n}\bigg)+\bigg(\frac{i}{n}\bigg)+\bigg(\frac{i^{3}}{n}\bigg) \bigg) \sideset{}{^{*}}\sum_{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} } w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {(1+i)c}{n}\bigg) \nonumber \\&\quad= 2\bigg(1+ \bigg(\frac{i}{n}\bigg) \bigg)\bigg(\frac {1+i}{n} \bigg) \sideset{}{^{*}}\sum_{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} } w\bigg( \frac {N(c)}X \bigg) \bigg(\frac {c}{n} \bigg). \end{align*} $$
Note further that the quadratic reciprocity law (2-1) allows us to write
![]() $\chi _{n}(c)$
for
$\chi _{n}(c)$
for
![]() $({c}/{n})$
, and
$({c}/{n})$
, and
![]() $\chi _{n}$
is a Hecke character. We then apply the Mellin inversion formula and get
$\chi _{n}$
is a Hecke character. We then apply the Mellin inversion formula and get
 $$ \begin{align*} &\sideset{}{^{*}}\sum_{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} } w\bigg( \frac {N(c)}X \bigg)\,\chi_{n}(c) \\[3pt] &\qquad = \frac 1{2\pi i } \int_{(2)} \sum_{\substack{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3}}} \frac{\mu_{[i]}^{2}(c) \chi_{n}(c) }{N(c)^{s}} X^{s} \mathcal M w(s)\, {d} s \\[3pt] &\qquad= \frac 1{2\pi i } \int_{(2)} \prod_{\substack{\varpi \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} \\ (\varpi, 1+i)=1}} \bigg(1+ \frac{\chi_{n}(\varpi)}{N(\varpi)^{s}} \bigg) \mathcal M w (s)X^{s}\, {d} s \\[3pt] &\qquad = \frac 1{2\pi i } \int_{(2)} \frac{L(s, \chi_{n})}{L(2s, \chi^{2}_{n})}\bigg(1+ \frac{\chi_{n}(1+i)}{N(1+i)^{s}} \bigg)^{-1} \mathcal M w (s)X^{s}\, {d} s. \end{align*} $$
$$ \begin{align*} &\sideset{}{^{*}}\sum_{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} } w\bigg( \frac {N(c)}X \bigg)\,\chi_{n}(c) \\[3pt] &\qquad = \frac 1{2\pi i } \int_{(2)} \sum_{\substack{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3}}} \frac{\mu_{[i]}^{2}(c) \chi_{n}(c) }{N(c)^{s}} X^{s} \mathcal M w(s)\, {d} s \\[3pt] &\qquad= \frac 1{2\pi i } \int_{(2)} \prod_{\substack{\varpi \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3} \\ (\varpi, 1+i)=1}} \bigg(1+ \frac{\chi_{n}(\varpi)}{N(\varpi)^{s}} \bigg) \mathcal M w (s)X^{s}\, {d} s \\[3pt] &\qquad = \frac 1{2\pi i } \int_{(2)} \frac{L(s, \chi_{n})}{L(2s, \chi^{2}_{n})}\bigg(1+ \frac{\chi_{n}(1+i)}{N(1+i)^{s}} \bigg)^{-1} \mathcal M w (s)X^{s}\, {d} s. \end{align*} $$
Here and henceforth, we write
![]() $\int _{(c)}$
for the integral over the vertical line with
$\int _{(c)}$
for the integral over the vertical line with
![]() $\mathrm {Re}(s) = c$
.
$\mathrm {Re}(s) = c$
.
We shift the line of integration to
![]() $\mathrm {Re}(s)=1/4+\varepsilon $
and we encounter a pole at
$\mathrm {Re}(s)=1/4+\varepsilon $
and we encounter a pole at
![]() $s=1$
only when
$s=1$
only when
![]() $\chi _{n}$
is a principal character. In that case, the residue is easily seen (recall that the residue of
$\chi _{n}$
is a principal character. In that case, the residue is easily seen (recall that the residue of
![]() $\zeta _{K}(s)$
at
$\zeta _{K}(s)$
at
![]() $s = 1$
is
$s = 1$
is
![]() $\pi /4$
) to be
$\pi /4$
) to be
 $$ \begin{align*} &\frac {\pi}{6}\zeta^{-1}_{K}(2) \prod_{\varpi | n} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \mathcal M w (1) X \\[3pt] &\quad = \frac {\pi}{12}\zeta^{-1}_{K}(2) \prod_{\varpi | n} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat w (0) X, \end{align*} $$
$$ \begin{align*} &\frac {\pi}{6}\zeta^{-1}_{K}(2) \prod_{\varpi | n} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \mathcal M w (1) X \\[3pt] &\quad = \frac {\pi}{12}\zeta^{-1}_{K}(2) \prod_{\varpi | n} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat w (0) X, \end{align*} $$
by noting that
![]() $\mathcal M w (1)=\widehat w (0)/2 $
when w is even. The remaining integral over the line
$\mathcal M w (1)=\widehat w (0)/2 $
when w is even. The remaining integral over the line
![]() $\mathrm {Re}(s)=1/4+\varepsilon $
can be estimated by using (2-5) for a suitable E and the bound
$\mathrm {Re}(s)=1/4+\varepsilon $
can be estimated by using (2-5) for a suitable E and the bound
assuming the GRH, which follows from [Reference Iwaniec and Kowalski22, Theorem 5.19]. This gives the result when
![]() $\chi _{n}$
is a principal character.
$\chi _{n}$
is a principal character.
When
![]() $\chi _{n}$
is not principal, we apply the convexity bound [Reference Iwaniec and Kowalski22, formula (5.20)] for L-functions attached to nonprincipal characters, such that
$\chi _{n}$
is not principal, we apply the convexity bound [Reference Iwaniec and Kowalski22, formula (5.20)] for L-functions attached to nonprincipal characters, such that
Combining this with (2-9) allows us to readily deduce the assertion of the lemma for
![]() $\chi _{n}$
being nonprincipal. This completes the proof.
$\chi _{n}$
being nonprincipal. This completes the proof.
By taking
![]() $n=1$
in Lemma 2.3, we immediately obtain that
$n=1$
in Lemma 2.3, we immediately obtain that
 $$ \begin{align} W(X)= \frac{\pi X}{3\zeta_{K}(2)} \widehat w(0) +O ( X^{1/4+\varepsilon} ). \end{align} $$
$$ \begin{align} W(X)= \frac{\pi X}{3\zeta_{K}(2)} \widehat w(0) +O ( X^{1/4+\varepsilon} ). \end{align} $$
Lemma 2.4. Suppose that the GRH is true. For any even, nonzero and nonnegative Schwartz function w, we have
 $$ \begin{align*} &\frac {1}{ W(X)}\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \log N(c) \\[3pt] &\quad = \log X + \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x \, {d} x +O ( X^{-1/2 +\varepsilon} ). \end{align*} $$
$$ \begin{align*} &\frac {1}{ W(X)}\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \log N(c) \\[3pt] &\quad = \log X + \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x \, {d} x +O ( X^{-1/2 +\varepsilon} ). \end{align*} $$
Proof. We have
 $$ \begin{align*} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} & w\bigg( \frac {N(c)}X \bigg) \log N(c) \\[3pt] =& -\frac 4{2\pi i}\int_{(2)} \frac{{d}}{{d} s} \bigg( \sum_{ \substack{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3}}} \frac{\mu^{2}_{[i]}(c)}{N(c)^{s}} \bigg) \mathcal M w(s)X^{s} \, {d} s \\[3pt] =& -\frac 4{2\pi i}\int_{(2)} \frac{{d}}{{d} s} \bigg( \frac{\zeta_{K}(s)}{\zeta_{K}(2s) ( 1+2^{-s} )} \bigg) \mathcal M w(s)X^{s} \, {d} s. \end{align*} $$
$$ \begin{align*} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} & w\bigg( \frac {N(c)}X \bigg) \log N(c) \\[3pt] =& -\frac 4{2\pi i}\int_{(2)} \frac{{d}}{{d} s} \bigg( \sum_{ \substack{c \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3}}} \frac{\mu^{2}_{[i]}(c)}{N(c)^{s}} \bigg) \mathcal M w(s)X^{s} \, {d} s \\[3pt] =& -\frac 4{2\pi i}\int_{(2)} \frac{{d}}{{d} s} \bigg( \frac{\zeta_{K}(s)}{\zeta_{K}(2s) ( 1+2^{-s} )} \bigg) \mathcal M w(s)X^{s} \, {d} s. \end{align*} $$
We shift the contour of integration to the line
![]() $\mathrm {Re}(s)=1/4+\varepsilon $
. Note that under the GRH, the only poles of the function
$\mathrm {Re}(s)=1/4+\varepsilon $
. Note that under the GRH, the only poles of the function
 $$ \begin{align*} \frac{{d}}{{d} s} & \bigg( \frac{\zeta_{K}(s)}{\zeta_{K}(2s) ( 1+2^{-s} )} \bigg) \\[3pt] & = \frac{\zeta^{\prime}_{K}(s)}{\zeta_{K}(2s) ( 1+2^{-s} )}- \frac{2\zeta^{\prime}_{K}(2s)\zeta_{K}(s)}{\zeta^{2}_{K}(2s) ( 1+2^{-s} )}+\frac{\log 2 \cdot \zeta_{K}(s)}{2^{s} \zeta_{K}(2s) ( 1+2^{-s} )^{2} } \end{align*} $$
$$ \begin{align*} \frac{{d}}{{d} s} & \bigg( \frac{\zeta_{K}(s)}{\zeta_{K}(2s) ( 1+2^{-s} )} \bigg) \\[3pt] & = \frac{\zeta^{\prime}_{K}(s)}{\zeta_{K}(2s) ( 1+2^{-s} )}- \frac{2\zeta^{\prime}_{K}(2s)\zeta_{K}(s)}{\zeta^{2}_{K}(2s) ( 1+2^{-s} )}+\frac{\log 2 \cdot \zeta_{K}(s)}{2^{s} \zeta_{K}(2s) ( 1+2^{-s} )^{2} } \end{align*} $$
in the region
![]() $1/4+\varepsilon \leq \mathrm {Re}(s)\leq 2$
are at
$1/4+\varepsilon \leq \mathrm {Re}(s)\leq 2$
are at
![]() $s=1$
and
$s=1$
and
![]() $s=1/2$
. Only the contribution of the residue at
$s=1/2$
. Only the contribution of the residue at
![]() $s=1$
is much greater than X. It is then easy to compute the contribution of the residues to be
$s=1$
is much greater than X. It is then easy to compute the contribution of the residues to be
 $$ \begin{align*} \frac{2\pi }{3\zeta_{K}(2)} \mathcal M w(1)X \log X+\frac{2\pi }{3\zeta_{K}(2)} (\mathcal M w)^{\prime}(1)X+O(X^{1/2+\varepsilon}). \end{align*} $$
$$ \begin{align*} \frac{2\pi }{3\zeta_{K}(2)} \mathcal M w(1)X \log X+\frac{2\pi }{3\zeta_{K}(2)} (\mathcal M w)^{\prime}(1)X+O(X^{1/2+\varepsilon}). \end{align*} $$
The assertion of the lemma follows from this and (2-10), by noting that
![]() $\mathcal M w(1)=\widehat {w}(0)/2$
.
$\mathcal M w(1)=\widehat {w}(0)/2$
.
2.4 The explicit formula
Let f be an even, positive Schwartz function whose Fourier transform
![]() $\hat {f}$
is a smooth function with compact support. Let
$\hat {f}$
is a smooth function with compact support. Let
![]() $\chi $
be a primitive Hecke character
$\chi $
be a primitive Hecke character
![]() $\chi ({\operatorname {mod}}\,\,m)$
of trivial infinite type. In this section we derive an explicit formula which allows us to convert the evaluation of f at the nontrivial zeros of
$\chi ({\operatorname {mod}}\,\,m)$
of trivial infinite type. In this section we derive an explicit formula which allows us to convert the evaluation of f at the nontrivial zeros of
![]() $L(s,\chi )$
to a sum over powers of prime ideals. Note that the nontrivial zeros of
$L(s,\chi )$
to a sum over powers of prime ideals. Note that the nontrivial zeros of
![]() $L(s,\chi )$
are precisely those of the corresponding
$L(s,\chi )$
are precisely those of the corresponding
![]() $\Lambda (s, \chi )$
. For some
$\Lambda (s, \chi )$
. For some
![]() $c>1$
, consider the integral
$c>1$
, consider the integral
 $$ \begin{align*} \frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s. \end{align*} $$
$$ \begin{align*} \frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s. \end{align*} $$
By moving the line of integration to
![]() $1-c$
, we obtain
$1-c$
, we obtain
 $$ \begin{align*} &\frac 1{2 \pi i}\int_{(c)} \frac {\Lambda^{\prime}}{\Lambda}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s \\[3pt] &\quad = \sum_{j}f \bigg( \frac {\gamma_{\chi,j}}{2 \pi} \bigg)+ \frac 1{2 \pi i}\int_{(1-c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s. \end{align*} $$
$$ \begin{align*} &\frac 1{2 \pi i}\int_{(c)} \frac {\Lambda^{\prime}}{\Lambda}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s \\[3pt] &\quad = \sum_{j}f \bigg( \frac {\gamma_{\chi,j}}{2 \pi} \bigg)+ \frac 1{2 \pi i}\int_{(1-c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s. \end{align*} $$
Now the functional equation
![]() $\Lambda (s, \chi )=W(\chi )(N(m))^{-1/2}\Lambda (1-s, \overline {\chi })$
implies
$\Lambda (s, \chi )=W(\chi )(N(m))^{-1/2}\Lambda (1-s, \overline {\chi })$
implies
 $$ \begin{align*} \frac {\Lambda^{\prime}}{\Lambda}(s, \chi)=-\frac {\Lambda^{\prime}}{\Lambda}(1-s, \overline{\chi}). \end{align*} $$
$$ \begin{align*} \frac {\Lambda^{\prime}}{\Lambda}(s, \chi)=-\frac {\Lambda^{\prime}}{\Lambda}(1-s, \overline{\chi}). \end{align*} $$
It follows that
 $$ \begin{align*} \sum_{j}f \bigg( \frac {\gamma_{\chi,j}}{2 \pi} \bigg)&=\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda} (s, \chi) f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s \\[3pt] &\quad +\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \overline{\chi}) f\bigg( \frac {1/2-s}{2 \pi i} \bigg)\, {d} s. \end{align*} $$
$$ \begin{align*} \sum_{j}f \bigg( \frac {\gamma_{\chi,j}}{2 \pi} \bigg)&=\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda} (s, \chi) f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s \\[3pt] &\quad +\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \overline{\chi}) f\bigg( \frac {1/2-s}{2 \pi i} \bigg)\, {d} s. \end{align*} $$
Using
 $$ \begin{align*} \frac {\Lambda^{\prime}}{\Lambda}(s, \chi)=\frac 1{2}\log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+\frac {\Gamma^{\prime}}{\Gamma}(s)+\frac {L^{\prime}}{L}(s, \chi), \end{align*} $$
$$ \begin{align*} \frac {\Lambda^{\prime}}{\Lambda}(s, \chi)=\frac 1{2}\log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+\frac {\Gamma^{\prime}}{\Gamma}(s)+\frac {L^{\prime}}{L}(s, \chi), \end{align*} $$
we obtain that
 $$ \begin{align*} &\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \chi) f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s +\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \overline{\chi}) f\bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s =T_{1}+T_{2}, \end{align*} $$
$$ \begin{align*} &\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \chi) f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\, {d} s +\frac 1{2 \pi i}\int_{(c)}\frac {\Lambda^{\prime}}{\Lambda}(s, \overline{\chi}) f\bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s =T_{1}+T_{2}, \end{align*} $$
where
 $$ \begin{align*} T_{1} &= \frac 1{2 \pi i}\int_{(c)} \bigg( \frac 1{2}\log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+\frac {\Gamma^{\prime}}{\Gamma}(s)\bigg) f \bigg( \frac {s-1/2}{2 \pi i} \bigg) \,{d} s \\[3pt] &\quad +\frac 1{2 \pi i}\int_{(c)}\bigg( \frac 1{2}\log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+\frac {\Gamma^{\prime}}{\Gamma}(s)\bigg) f \bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s \end{align*} $$
$$ \begin{align*} T_{1} &= \frac 1{2 \pi i}\int_{(c)} \bigg( \frac 1{2}\log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+\frac {\Gamma^{\prime}}{\Gamma}(s)\bigg) f \bigg( \frac {s-1/2}{2 \pi i} \bigg) \,{d} s \\[3pt] &\quad +\frac 1{2 \pi i}\int_{(c)}\bigg( \frac 1{2}\log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+\frac {\Gamma^{\prime}}{\Gamma}(s)\bigg) f \bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s \end{align*} $$
and
 $$ \begin{align*} T_{2} = \frac 1{2 \pi i}\int_{(c)}\frac {L^{\prime}}{L}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg) \,{d} s+\frac 1{2 \pi i}\int_{(c)}\frac {L^{\prime}}{L}(s, \overline{\chi})f \bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s. \end{align*} $$
$$ \begin{align*} T_{2} = \frac 1{2 \pi i}\int_{(c)}\frac {L^{\prime}}{L}(s, \chi)f \bigg( \frac {s-1/2}{2 \pi i} \bigg) \,{d} s+\frac 1{2 \pi i}\int_{(c)}\frac {L^{\prime}}{L}(s, \overline{\chi})f \bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s. \end{align*} $$
For
![]() $T_{1}$
, we move the line of integration to
$T_{1}$
, we move the line of integration to
![]() $1/2$
and apply the change of variables
$1/2$
and apply the change of variables
![]() $s=1/2+2\pi i t$
. In so doing, we obtain
$s=1/2+2\pi i t$
. In so doing, we obtain
 $$ \begin{align} T_{1} &=\int^{\infty}_{-\infty}\bigg( \log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+ \frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac{1}{2}+2\pi i t \bigg)+ \frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac{1}{2}-2\pi i t \bigg) \bigg) f(t) \,{d} t \nonumber\\[3pt] &=\int^{\infty}_{-\infty}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg )f(t) \,{d} t \nonumber\\[3pt] & \quad+\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}} ( 2\hat{f}(0)-\hat{f}(t)-\hat{f}(-t) ) \,{d} t, \end{align} $$
$$ \begin{align} T_{1} &=\int^{\infty}_{-\infty}\bigg( \log \frac {|D_{K}|N(m)}{(2\pi)^{2}}+ \frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac{1}{2}+2\pi i t \bigg)+ \frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac{1}{2}-2\pi i t \bigg) \bigg) f(t) \,{d} t \nonumber\\[3pt] &=\int^{\infty}_{-\infty}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg )f(t) \,{d} t \nonumber\\[3pt] & \quad+\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}} ( 2\hat{f}(0)-\hat{f}(t)-\hat{f}(-t) ) \,{d} t, \end{align} $$
where the second equality above follows from [Reference Montgomery and Vaughan33, Lemma 12.14].
We express
![]() $T_{2}$
as
$T_{2}$
as
 $$ \begin{align*} T_{2}&=-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \chi(n)\Lambda(n) \frac 1{2 \pi i}\int_{(c)}\frac 1{N(n)^{s}}f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\,{d} s \\[3pt] &\quad -\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \overline{\chi}(n) \Lambda(n)\frac 1{2 \pi i}\int_{(c)}\frac 1{N(n)^{s}}f \bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s. \end{align*} $$
$$ \begin{align*} T_{2}&=-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \chi(n)\Lambda(n) \frac 1{2 \pi i}\int_{(c)}\frac 1{N(n)^{s}}f \bigg( \frac {s-1/2}{2 \pi i} \bigg)\,{d} s \\[3pt] &\quad -\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \overline{\chi}(n) \Lambda(n)\frac 1{2 \pi i}\int_{(c)}\frac 1{N(n)^{s}}f \bigg( \frac {1/2-s}{2 \pi i} \bigg) \,{d} s. \end{align*} $$
Moving the lines of integration for
![]() $I_{2}$
to
$I_{2}$
to
![]() $\mathrm {Re}(s)=1/2$
and setting
$\mathrm {Re}(s)=1/2$
and setting
![]() $s=1/2+2\pi i t$
, the integrations become
$s=1/2+2\pi i t$
, the integrations become
 $$ \begin{align*} \int^{\infty}_{-\infty}\frac 1{N(n)^{1/2 \pm 2 \pi i t}}f(t)\,dt=\frac 1{\sqrt{N(n)}}\hat{f}(\mp \log N(n)). \end{align*} $$
$$ \begin{align*} \int^{\infty}_{-\infty}\frac 1{N(n)^{1/2 \pm 2 \pi i t}}f(t)\,dt=\frac 1{\sqrt{N(n)}}\hat{f}(\mp \log N(n)). \end{align*} $$
Thus,
 $$ \begin{align} T_{2}=-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}(-\log N(n))-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\overline{\chi}(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}( \log N(n)). \end{align} $$
$$ \begin{align} T_{2}=-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}(-\log N(n))-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\overline{\chi}(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}( \log N(n)). \end{align} $$
We then derive from (2-11) and (2-12) that
 $$ \begin{align*} \sum_{j}f \bigg( \frac {\gamma_{\chi,j}}{2 \pi} \bigg) &= \int^{\infty}_{-\infty}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma}\bigg( \frac 12 \bigg) \bigg)f(t) \,{d} t \\[3pt] &\quad +\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}} ( 2\hat{f}(0)-\hat{f}(t)-\hat{f}(- t) ) \,{d} t \\[3pt] &\quad -\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}(-\log N(n))-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\overline{\chi}(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}( \log N(n)). \end{align*} $$
$$ \begin{align*} \sum_{j}f \bigg( \frac {\gamma_{\chi,j}}{2 \pi} \bigg) &= \int^{\infty}_{-\infty}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma}\bigg( \frac 12 \bigg) \bigg)f(t) \,{d} t \\[3pt] &\quad +\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}} ( 2\hat{f}(0)-\hat{f}(t)-\hat{f}(- t) ) \,{d} t \\[3pt] &\quad -\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}(-\log N(n))-\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\overline{\chi}(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f}( \log N(n)). \end{align*} $$
Now an easy computation in Fourier transforms gives
 $$ \begin{align*} \sum_{j}f \bigg( \frac {\log X \gamma_{\chi,j}}{2 \pi} \bigg) &= \frac 1{\log X} \int^{\infty}_{-\infty}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg )f(t) \,{d} t \\[1pt] &\quad +\frac 1{\log X}\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}} \bigg( 2\hat{f}(0)-\hat{f} \bigg( \frac {t}{\log X} \bigg)-\hat{f}\bigg( -\frac {t}{\log X} \bigg) \bigg) \,{d} t \\[1pt] &\quad -\frac 1{\log X}\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f} \bigg( -\frac {\log N(n)}{\log X} \bigg) \\[1pt] &\quad -\frac 1{\log X}\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\overline{\chi}(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f} \bigg( \frac {\log N(n)}{\log X} \bigg). \end{align*} $$
$$ \begin{align*} \sum_{j}f \bigg( \frac {\log X \gamma_{\chi,j}}{2 \pi} \bigg) &= \frac 1{\log X} \int^{\infty}_{-\infty}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg )f(t) \,{d} t \\[1pt] &\quad +\frac 1{\log X}\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}} \bigg( 2\hat{f}(0)-\hat{f} \bigg( \frac {t}{\log X} \bigg)-\hat{f}\bigg( -\frac {t}{\log X} \bigg) \bigg) \,{d} t \\[1pt] &\quad -\frac 1{\log X}\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f} \bigg( -\frac {\log N(n)}{\log X} \bigg) \\[1pt] &\quad -\frac 1{\log X}\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\overline{\chi}(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f} \bigg( \frac {\log N(n)}{\log X} \bigg). \end{align*} $$
Recall that
![]() $\mathcal {L}=\log X$
and note that as f is even, so is
$\mathcal {L}=\log X$
and note that as f is even, so is
![]() $\hat {f}$
. Thus, when
$\hat {f}$
. Thus, when
![]() $\chi $
is a quadratic Hecke character, we can simplify the above expression as
$\chi $
is a quadratic Hecke character, we can simplify the above expression as
 $$ \begin{align} \sum_{j}f\bigg( \frac {\mathcal{L} \gamma_{\chi,j}}{2 \pi} \bigg) &= \frac 1{\mathcal{L}}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma}\bigg( \frac 12 \bigg) \bigg )\hat{f}(0) \nonumber\\[1pt] &\quad +\frac 2{\mathcal{L}}\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}}\bigg( \hat{f}(0)-\hat{f}\bigg(\frac {t}{\mathcal{L}}\bigg) \bigg) \,{d} t \nonumber\\[1pt] &\quad -\frac 2{\mathcal{L}}\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f} \bigg( \frac {\log N(n)}{\mathcal{L}} \bigg). \end{align} $$
$$ \begin{align} \sum_{j}f\bigg( \frac {\mathcal{L} \gamma_{\chi,j}}{2 \pi} \bigg) &= \frac 1{\mathcal{L}}\bigg( \log\frac {|D_{K}|N(m)}{(2\pi)^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma}\bigg( \frac 12 \bigg) \bigg )\hat{f}(0) \nonumber\\[1pt] &\quad +\frac 2{\mathcal{L}}\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}}\bigg( \hat{f}(0)-\hat{f}\bigg(\frac {t}{\mathcal{L}}\bigg) \bigg) \,{d} t \nonumber\\[1pt] &\quad -\frac 2{\mathcal{L}}\sum_{\substack{(n) \\ n \in \mathcal{O}_{K}}} \frac {\chi(n)\Lambda(n)}{\sqrt{N(n)}}\hat{f} \bigg( \frac {\log N(n)}{\mathcal{L}} \bigg). \end{align} $$
Recall that every odd prime
![]() $\varpi \in \mathcal {O}_{K}$
has a primary generator. In our paper, we work explicitly with the Hecke characters
$\varpi \in \mathcal {O}_{K}$
has a primary generator. In our paper, we work explicitly with the Hecke characters
![]() $\chi _{i(1+i)^{5}c}$
for odd, square-free c. Our choice for such characters is inspired by the Dirichlet characters
$\chi _{i(1+i)^{5}c}$
for odd, square-free c. Our choice for such characters is inspired by the Dirichlet characters
![]() $\chi _{8d}$
for odd, square-free rational integers d considered by Soundararajan [Reference Soundararajan40] in his work on nonvanishing of quadratic Dirichlet L-functions at the central value. The advantage of using the characters
$\chi _{8d}$
for odd, square-free rational integers d considered by Soundararajan [Reference Soundararajan40] in his work on nonvanishing of quadratic Dirichlet L-functions at the central value. The advantage of using the characters
![]() $\chi _{i(1+i)^{5}c}$
is that, besides their primitivity, the presence of the factors
$\chi _{i(1+i)^{5}c}$
is that, besides their primitivity, the presence of the factors
![]() $i(1+i)^{3}$
makes the resulting expression much neater after applying the Poisson summation formula given in Lemma 2.1. We now apply the formula given in (2-13) to the special case
$i(1+i)^{3}$
makes the resulting expression much neater after applying the Poisson summation formula given in Lemma 2.1. We now apply the formula given in (2-13) to the special case
![]() $\chi _{i(1+i)^{5}c}$
for odd, square-free c to arrive at the following lemma.
$\chi _{i(1+i)^{5}c}$
for odd, square-free c to arrive at the following lemma.
Lemma 2.5 (Explicit formula)
Let
![]() $\phi (x)$
be an even Schwartz function whose Fourier transform
$\phi (x)$
be an even Schwartz function whose Fourier transform
![]() $\hat {\phi }(u)$
has compact support. Let c be an odd and square-free element of
$\hat {\phi }(u)$
has compact support. Let c be an odd and square-free element of
![]() $\mathcal{O}_K$
satisfying
$\mathcal{O}_K$
satisfying
![]() $(c, 1+i)=1$
.We have
$(c, 1+i)=1$
.We have
 $$ \begin{align*} S(\kern1.5pt\chi_{i(1+i)^{5}c}, \phi) &= \frac 1{\mathcal{L}} \bigg( \log\frac {32N(c)}{\pi^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg )\hat{\phi}(0) \\[1pt] &\quad +\frac 2{\mathcal{\mathcal{L}}}\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}}\bigg( \hat{\phi}(0)-\hat{\phi}\bigg( \frac {t}{\mathcal{\mathcal{L}}} \bigg) \bigg) \,{d} t -\frac 2{\mathcal{L}}\sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L} ;\hat{\phi}), \end{align*} $$
$$ \begin{align*} S(\kern1.5pt\chi_{i(1+i)^{5}c}, \phi) &= \frac 1{\mathcal{L}} \bigg( \log\frac {32N(c)}{\pi^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg )\hat{\phi}(0) \\[1pt] &\quad +\frac 2{\mathcal{\mathcal{L}}}\int^{\infty}_{0}\frac {e^{-t/2}}{1-e^{-t}}\bigg( \hat{\phi}(0)-\hat{\phi}\bigg( \frac {t}{\mathcal{\mathcal{L}}} \bigg) \bigg) \,{d} t -\frac 2{\mathcal{L}}\sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L} ;\hat{\phi}), \end{align*} $$
where
 $$ \begin{align*} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L};\hat{\phi})=\sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}}\frac { \log N(\varpi)}{\sqrt{N(\varpi^{\kern1.8pt j})}}\chi_{i(1+i)^{5}c} ( \varpi^{\kern1.8pt j} ) \hat{\phi}\bigg( \frac {\log N(\varpi^{\kern1.8pt j})}{\mathcal{L}} \bigg), \end{align*} $$
$$ \begin{align*} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L};\hat{\phi})=\sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}}\frac { \log N(\varpi)}{\sqrt{N(\varpi^{\kern1.8pt j})}}\chi_{i(1+i)^{5}c} ( \varpi^{\kern1.8pt j} ) \hat{\phi}\bigg( \frac {\log N(\varpi^{\kern1.8pt j})}{\mathcal{L}} \bigg), \end{align*} $$
with the sum over
![]() $\varpi $
running over primes in
$\varpi $
running over primes in
![]() $\mathcal {O}_{K}$
.
$\mathcal {O}_{K}$
.
Using Lemma 2.5, upon summing over c against the weight function w, we obtain the following result (the formula in (1-4)) for
![]() $D(\phi ;w, X)$
.
$D(\phi ;w, X)$
.
Lemma 2.6. Assume that
![]() $\phi $
is an even Schwartz test function whose Fourier transform has compact support. Then we have
$\phi $
is an even Schwartz test function whose Fourier transform has compact support. Then we have
 $$ \begin{align*} D (\phi;w, X) &= \frac {\widehat{\phi}(0)}{ \mathcal{L} W(X)}\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \log N(c) +\frac {\widehat\phi(0)}{\mathcal{L}} \bigg( \log\frac {32}{\pi^{2}}+ 2\frac{\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg ) \\[3pt] &\quad -\frac 2{\mathcal{L}W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L};\hat{\phi}) \\[3pt] &\quad +\frac{2}{\mathcal{L}}\int_{0}^{\infty}\frac{e^{-x/2}}{1-e^{-x}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{x}{\mathcal{L}}\bigg)\bigg) \,{d} x. \end{align*} $$
$$ \begin{align*} D (\phi;w, X) &= \frac {\widehat{\phi}(0)}{ \mathcal{L} W(X)}\underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \log N(c) +\frac {\widehat\phi(0)}{\mathcal{L}} \bigg( \log\frac {32}{\pi^{2}}+ 2\frac{\Gamma^{\prime}}{\Gamma} \bigg( \frac 12 \bigg) \bigg ) \\[3pt] &\quad -\frac 2{\mathcal{L}W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c}, \mathcal{L};\hat{\phi}) \\[3pt] &\quad +\frac{2}{\mathcal{L}}\int_{0}^{\infty}\frac{e^{-x/2}}{1-e^{-x}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{x}{\mathcal{L}}\bigg)\bigg) \,{d} x. \end{align*} $$
Now let
![]() $w(t)$
be an even, nonzero and nonnegative Schwartz function as in the theorems. We define
$w(t)$
be an even, nonzero and nonnegative Schwartz function as in the theorems. We define
 $$ \begin{align} g(y)=\widetilde{w}(\sqrt{2 }y ), \quad g_{1}(y)=\tilde{g}( \sqrt{y} ), \end{align} $$
$$ \begin{align} g(y)=\widetilde{w}(\sqrt{2 }y ), \quad g_{1}(y)=\tilde{g}( \sqrt{y} ), \end{align} $$
where we recall that for any function W, the definition of
![]() $\widetilde {W}$
is given in (2-4).
$\widetilde {W}$
is given in (2-4).
Our next lemma establishes a relation between the Mellin transforms of g and
![]() $g_{2}$
. This is a generalization of [Reference Fiorilli, Parks and Södergren11, formula (2.3)].
$g_{2}$
. This is a generalization of [Reference Fiorilli, Parks and Södergren11, formula (2.3)].
Lemma 2.7. For any
![]() $z \in \mathbb C, z \neq 0, -1$
, we have
$z \in \mathbb C, z \neq 0, -1$
, we have
Proof. Our proof of this lemma is motivated by Riemann’s proof of the functional equation of the Riemann zeta function
![]() $\zeta (s)$
(see [Reference Davenport6, Section 8]). We first note that, for
$\zeta (s)$
(see [Reference Davenport6, Section 8]). We first note that, for
![]() $\mathrm {Re}(z)>1$
,
$\mathrm {Re}(z)>1$
,
 $$ \begin{align*} \zeta_{K}(z) \mathcal M g(z) &= \frac 14\sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\int^{\infty}_{0}g(t)\bigg( \frac {t}{N(k)} \bigg)^{z} \frac {{d} t}{t} = \frac 14\sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\int^{\infty}_{0}g(N(k) t)t^{z} \frac {{d} t}{t} \\[3pt] &= -\frac 14\frac {g(0)}z+ \frac 14 \int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}} g(N(k) t) t^{z} \frac {{d} t}{t}+ \frac 14\int^{1}_{0} \sum_{\substack{ k \in \mathcal O_{K} }}g(N(k) t) t^{z} \frac {{d} t}{t}. \end{align*} $$
$$ \begin{align*} \zeta_{K}(z) \mathcal M g(z) &= \frac 14\sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\int^{\infty}_{0}g(t)\bigg( \frac {t}{N(k)} \bigg)^{z} \frac {{d} t}{t} = \frac 14\sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\int^{\infty}_{0}g(N(k) t)t^{z} \frac {{d} t}{t} \\[3pt] &= -\frac 14\frac {g(0)}z+ \frac 14 \int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}} g(N(k) t) t^{z} \frac {{d} t}{t}+ \frac 14\int^{1}_{0} \sum_{\substack{ k \in \mathcal O_{K} }}g(N(k) t) t^{z} \frac {{d} t}{t}. \end{align*} $$
Now applying (2-3) to the second of the above sums and another change of variables, we get
 $$ \begin{align*} \zeta_{K}(z) \mathcal M g(z) &= -\frac 14\frac {g(0)}z +\frac 14\frac {\widetilde g(0)}{z-1}+ \frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}g(N(k) t) t^{z} \frac {{d} t}{t} \\[3pt] &\quad + \frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\widetilde g(\sqrt{N(k) t}) t^{-z+1} \frac {{d} t}{t}. \end{align*} $$
$$ \begin{align*} \zeta_{K}(z) \mathcal M g(z) &= -\frac 14\frac {g(0)}z +\frac 14\frac {\widetilde g(0)}{z-1}+ \frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}g(N(k) t) t^{z} \frac {{d} t}{t} \\[3pt] &\quad + \frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\widetilde g(\sqrt{N(k) t}) t^{-z+1} \frac {{d} t}{t}. \end{align*} $$
Note that the last two integrals converge absolutely for all
![]() $z \in \mathbb C$
, by applying estimate (2-6) to both g and
$z \in \mathbb C$
, by applying estimate (2-6) to both g and
![]() $\widetilde g$
. The last expression above thus gives an analytical extension of
$\widetilde g$
. The last expression above thus gives an analytical extension of
![]() $\zeta _{K}(z) \mathcal M g(z)$
to all
$\zeta _{K}(z) \mathcal M g(z)$
to all
![]() $z \in \mathbb C, z \neq 0$
, 1.
$z \in \mathbb C, z \neq 0$
, 1.
Similarly, we also deduce from (2-3) that for
![]() $\mathrm {Re}(z)>0$
,
$\mathrm {Re}(z)>0$
,
 $$ \begin{align*} \zeta_{K}(z+1) \mathcal M g_{1}(z+1)&= \frac 14\sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\int^{\infty}_{0} \widetilde g (\sqrt{t}) \bigg( \frac {t}{N(k)} \bigg)^{z+1} \frac {{d} t}{t} \\[3pt] &= \frac 14\frac {g(0)}z-\frac 14\frac {\widetilde g(0)}{z+1}+\frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\widetilde g (\sqrt{N(k)t}) t^{z+1} \frac {{d} t}{t} \\[3pt] &\quad +\frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}} g(N(k)t) t^{-z} \frac {{d} t}{t}. \end{align*} $$
$$ \begin{align*} \zeta_{K}(z+1) \mathcal M g_{1}(z+1)&= \frac 14\sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\int^{\infty}_{0} \widetilde g (\sqrt{t}) \bigg( \frac {t}{N(k)} \bigg)^{z+1} \frac {{d} t}{t} \\[3pt] &= \frac 14\frac {g(0)}z-\frac 14\frac {\widetilde g(0)}{z+1}+\frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}}\widetilde g (\sqrt{N(k)t}) t^{z+1} \frac {{d} t}{t} \\[3pt] &\quad +\frac 14\int^{\infty}_{1} \sum_{\substack{ k \in \mathcal O_{K} \\ k \neq 0}} g(N(k)t) t^{-z} \frac {{d} t}{t}. \end{align*} $$
Once again by applying estimate (2-6) to both g and
![]() $\widetilde g$
, we see that the last two integrals above converge absolutely for all
$\widetilde g$
, we see that the last two integrals above converge absolutely for all
![]() $z \in \mathbb C$
, so the last expression above gives an analytical extension of
$z \in \mathbb C$
, so the last expression above gives an analytical extension of
![]() $\zeta _{K}(z+1) \mathcal M g_{1}(z+1)$
to all
$\zeta _{K}(z+1) \mathcal M g_{1}(z+1)$
to all
![]() $z \in \mathbb C, z \neq 0$
, 1. Now, by comparing the above expressions for
$z \in \mathbb C, z \neq 0$
, 1. Now, by comparing the above expressions for
![]() $\zeta _{K}(z) \mathcal M g(z)$
and
$\zeta _{K}(z) \mathcal M g(z)$
and
![]() $\zeta _{K}(z+1) \mathcal M g_{1}(z+1)$
, we readily deduce the assertion of the lemma.
$\zeta _{K}(z+1) \mathcal M g_{1}(z+1)$
, we readily deduce the assertion of the lemma.
3 Analyzing sums over primes
We devote this section to the analysis of the sum over primes in (1-4). We first separate the odd and the even prime powers by writing
 $$ \begin{align} S_{\mathrm{odd}}= -\frac 2{\mathcal{L}W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{\substack{j \geq 1 \\ j \equiv 1 ({\operatorname{mod}}\,\,2)}} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L};\hat{\phi}), \end{align} $$
$$ \begin{align} S_{\mathrm{odd}}= -\frac 2{\mathcal{L}W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{\substack{j \geq 1 \\ j \equiv 1 ({\operatorname{mod}}\,\,2)}} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L};\hat{\phi}), \end{align} $$
and similarly for
![]() $S_{\mathrm {even}}$
. Moreover, it follows from Lemma 2.3, (2-8) and (2-10) that
$S_{\mathrm {even}}$
. Moreover, it follows from Lemma 2.3, (2-8) and (2-10) that
 $$ \begin{align} S_{\mathrm{even}} &= - \frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 1}} \frac{\log N(\varpi)}{N(\varpi)^{j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\bigg( \frac{2j \log N(\varpi)}{\mathcal{L}} \bigg) +O (X^{-3/4+\varepsilon }). \end{align} $$
$$ \begin{align} S_{\mathrm{even}} &= - \frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 1}} \frac{\log N(\varpi)}{N(\varpi)^{j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\bigg( \frac{2j \log N(\varpi)}{\mathcal{L}} \bigg) +O (X^{-3/4+\varepsilon }). \end{align} $$
3.1 Estimation of
 $S_{\text {even}}$
$S_{\text {even}}$
We first expand
![]() $S_{\mathrm {even}}$
into descending powers of
$S_{\mathrm {even}}$
into descending powers of
![]() $\mathcal {L}$
. We generalize [Reference Fiorilli, Parks and Södergren10, Lemma 3.7] to obtain the following result.
$\mathcal {L}$
. We generalize [Reference Fiorilli, Parks and Södergren10, Lemma 3.7] to obtain the following result.
Lemma 3.1. Suppose that
 $\sigma =\sup (\mathrm {supp }\,\widehat {\phi } )<\infty $
. Then, for any integer
$\sigma =\sup (\mathrm {supp }\,\widehat {\phi } )<\infty $
. Then, for any integer
![]() $M \geq 1$
, we have the expansion
$M \geq 1$
, we have the expansion
 $$ \begin{align} S_{\mathrm{even}} =-\frac{\phi(0)}2 + \sum_{m=1}^{M} \frac{d_{m} \widehat{\phi}^{(m-1)}(0)}{\mathcal{L}^{m}} +O\bigg( \frac 1{\mathcal{L}^{M+1}} \bigg), \end{align} $$
$$ \begin{align} S_{\mathrm{even}} =-\frac{\phi(0)}2 + \sum_{m=1}^{M} \frac{d_{m} \widehat{\phi}^{(m-1)}(0)}{\mathcal{L}^{m}} +O\bigg( \frac 1{\mathcal{L}^{M+1}} \bigg), \end{align} $$
where the coefficients
![]() $d_{m}$
are real numbers that can be given explicitly.
$d_{m}$
are real numbers that can be given explicitly.
Proof. It suffices to show that the expansion given in (3-3) is valid if we ignore the
![]() $O (X^{-3/4+\varepsilon } )$
term in (3-2). As
$O (X^{-3/4+\varepsilon } )$
term in (3-2). As
![]() $\sigma $
is finite, the sum in (3-2) is finite as we must have
$\sigma $
is finite, the sum in (3-2) is finite as we must have
![]() $N(\varpi )^{2j} \leq X^{\sigma }$
. It follows that the sum of the terms with
$N(\varpi )^{2j} \leq X^{\sigma }$
. It follows that the sum of the terms with
![]() $ j \geq 2$
can be expanded as follows:
$ j \geq 2$
can be expanded as follows:
 $$ \begin{align} &-\frac 2{\mathcal{L}} \sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 2 , \ N(\varpi)^{2j} \leq X^{\sigma}}} \frac{\log N(\varpi)}{N(\varpi)^{j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \nonumber\\[6pt] &\quad\quad \times \bigg(\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!} \bigg(\frac{2j \log N(\varpi)}{\mathcal{L}} \bigg)^{m}+O\bigg( \bigg(\frac{ 2j\log N(\varpi)}{\mathcal{L}}\bigg)^{M+1} \bigg) \bigg) \nonumber\\[6pt] &\quad= - \frac {2 }{\mathcal{L}} \sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!\mathcal{L}^{m}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 2 , \ N(\varpi)^{2j} \leq X^{\sigma}}} \frac{\log N(\varpi)(2j \log N(\varpi))^{m}}{N(\varpi)^{j}} \nonumber\\[6pt] &\quad\quad \times \bigg( 1+\frac 1{N(\varpi)}\bigg)^{-1} +O( \mathcal{L}^{-M-2} ) \nonumber\\[6pt] &\quad= - \frac {2 }{\mathcal{L}} \sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!\mathcal{L}^{m}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 2 }} \frac{\log N(\varpi)(2j \log N(\varpi))^{m}}{N(\varpi)^{j}} \nonumber\\[6pt] &\quad\quad \times \bigg( 1+\frac 1{N(\varpi)}\bigg)^{-1} +O( \mathcal{L}^{-M-2} ), \end{align} $$
$$ \begin{align} &-\frac 2{\mathcal{L}} \sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 2 , \ N(\varpi)^{2j} \leq X^{\sigma}}} \frac{\log N(\varpi)}{N(\varpi)^{j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \nonumber\\[6pt] &\quad\quad \times \bigg(\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!} \bigg(\frac{2j \log N(\varpi)}{\mathcal{L}} \bigg)^{m}+O\bigg( \bigg(\frac{ 2j\log N(\varpi)}{\mathcal{L}}\bigg)^{M+1} \bigg) \bigg) \nonumber\\[6pt] &\quad= - \frac {2 }{\mathcal{L}} \sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!\mathcal{L}^{m}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 2 , \ N(\varpi)^{2j} \leq X^{\sigma}}} \frac{\log N(\varpi)(2j \log N(\varpi))^{m}}{N(\varpi)^{j}} \nonumber\\[6pt] &\quad\quad \times \bigg( 1+\frac 1{N(\varpi)}\bigg)^{-1} +O( \mathcal{L}^{-M-2} ) \nonumber\\[6pt] &\quad= - \frac {2 }{\mathcal{L}} \sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!\mathcal{L}^{m}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 2 }} \frac{\log N(\varpi)(2j \log N(\varpi))^{m}}{N(\varpi)^{j}} \nonumber\\[6pt] &\quad\quad \times \bigg( 1+\frac 1{N(\varpi)}\bigg)^{-1} +O( \mathcal{L}^{-M-2} ), \end{align} $$
by noting that the inner sum of the last expression above converges.
It remains to expand the terms with
![]() $j=1$
. For this, we first note that, using the Taylor expansion of
$j=1$
. For this, we first note that, using the Taylor expansion of
![]() $\hat {\phi }$
around the origin and rewriting
$\hat {\phi }$
around the origin and rewriting
![]() $(1+N(\varpi )^{-1})^{-1}$
as a geometric series,
$(1+N(\varpi )^{-1})^{-1}$
as a geometric series,
 $$ \begin{align} & -\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\,\bigg( \frac{2 \log N(\varpi)}{\mathcal{L}} \bigg) \nonumber\\[3pt] &\quad=-\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \nonumber\\[3pt] &\quad\quad \times \bigg(\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!} \bigg(\frac{2 \log N(\varpi)}{\mathcal{L}} \bigg)^{m}+O\bigg( \bigg(\frac{ \log N(\varpi)}{\mathcal{L}}\bigg)^{M+1} \bigg) \bigg) \nonumber\\[3pt] &\quad=-\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)} \bigg(\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!} \bigg(\frac{2 \log N(\varpi)}{\mathcal{L}} \bigg)^{m} \nonumber\\[3pt] &\quad\quad +O\bigg( \bigg(\frac{ \log N(\varpi)}{\mathcal{L}}\bigg)^{M+1} \bigg) \bigg) -\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)C_{1}(m)}{m!\mathcal{L}^{m+1}}+O(\mathcal{L}^{-M-1} ) \nonumber\\[3pt] &\quad=-\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)}\widehat{\phi}\bigg( \frac{2 \log N(\varpi)}{\mathcal{L}} \bigg) -\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)C_{1}(m)}{m!\mathcal{L}^{m+1}} +O_{K}(\mathcal{L}^{-M-1}) \end{align} $$
$$ \begin{align} & -\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\,\bigg( \frac{2 \log N(\varpi)}{\mathcal{L}} \bigg) \nonumber\\[3pt] &\quad=-\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \nonumber\\[3pt] &\quad\quad \times \bigg(\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!} \bigg(\frac{2 \log N(\varpi)}{\mathcal{L}} \bigg)^{m}+O\bigg( \bigg(\frac{ \log N(\varpi)}{\mathcal{L}}\bigg)^{M+1} \bigg) \bigg) \nonumber\\[3pt] &\quad=-\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)} \bigg(\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)}{m!} \bigg(\frac{2 \log N(\varpi)}{\mathcal{L}} \bigg)^{m} \nonumber\\[3pt] &\quad\quad +O\bigg( \bigg(\frac{ \log N(\varpi)}{\mathcal{L}}\bigg)^{M+1} \bigg) \bigg) -\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)C_{1}(m)}{m!\mathcal{L}^{m+1}}+O(\mathcal{L}^{-M-1} ) \nonumber\\[3pt] &\quad=-\frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)}\widehat{\phi}\bigg( \frac{2 \log N(\varpi)}{\mathcal{L}} \bigg) -\sum_{m=0}^{M} \frac{\widehat{\phi}^{(m)}(0)C_{1}(m)}{m!\mathcal{L}^{m+1}} +O_{K}(\mathcal{L}^{-M-1}) \end{align} $$
where
 $$ \begin{align*} & C_{1}(m) =\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \sum_{l\geq 1} (-1)^{l} \frac{(2\log N(\varpi))^{m+1}}{N(\varpi)^{l+1}} < \infty. \end{align*} $$
$$ \begin{align*} & C_{1}(m) =\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \sum_{l\geq 1} (-1)^{l} \frac{(2\log N(\varpi))^{m+1}}{N(\varpi)^{l+1}} < \infty. \end{align*} $$
Next, we note that
 $$ \begin{align} E(t) := \sum_{\substack{ N(\varpi) \leq t \\ \varpi \equiv 1 \bmod {(1+i)^{3}}}} \log N(\varpi)- t \ll t^{1/2+\varepsilon} \end{align} $$
$$ \begin{align} E(t) := \sum_{\substack{ N(\varpi) \leq t \\ \varpi \equiv 1 \bmod {(1+i)^{3}}}} \log N(\varpi)- t \ll t^{1/2+\varepsilon} \end{align} $$
from (2-7).
We then apply partial summation to arrive at
 $$ \begin{align} &-\frac 2{\mathcal{L}} \sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)}\widehat{\phi}\bigg( \frac{2 \log N(\varpi)}{\mathcal{L}} \bigg) \nonumber\\[3pt] &\quad= -\frac 2{\mathcal{L}}\int_{1}^{\infty} \frac 1t \widehat{\phi}\bigg( \frac{2 \log t}{\mathcal{L}} \bigg) \,{d} ( t+E(t)) \nonumber\\[3pt] &\quad= -\int_{0}^{\infty} \widehat{\phi}(u)\, {d} u +\frac 2{\mathcal{L}}\int_{1}^{\infty} E(t) \frac{{d}}{{d} t} \bigg(\frac{1}{t} \widehat{\phi}\bigg( \frac{2 \log t}{\mathcal{L}} \bigg) \bigg) \, {d} t \nonumber\\[3pt] &\quad= -\frac 12 \phi(0)+\frac 2{\mathcal{L}}\int_{1}^{\infty} E(t) \frac{{d}}{{d} t} \bigg( \frac{1}{t} \widehat{\phi}\bigg( \frac{2 \log t}{\mathcal{L}} \bigg) \bigg) \, {d} t , \end{align} $$
$$ \begin{align} &-\frac 2{\mathcal{L}} \sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}}}} \frac{\log N(\varpi)}{N(\varpi)}\widehat{\phi}\bigg( \frac{2 \log N(\varpi)}{\mathcal{L}} \bigg) \nonumber\\[3pt] &\quad= -\frac 2{\mathcal{L}}\int_{1}^{\infty} \frac 1t \widehat{\phi}\bigg( \frac{2 \log t}{\mathcal{L}} \bigg) \,{d} ( t+E(t)) \nonumber\\[3pt] &\quad= -\int_{0}^{\infty} \widehat{\phi}(u)\, {d} u +\frac 2{\mathcal{L}}\int_{1}^{\infty} E(t) \frac{{d}}{{d} t} \bigg(\frac{1}{t} \widehat{\phi}\bigg( \frac{2 \log t}{\mathcal{L}} \bigg) \bigg) \, {d} t \nonumber\\[3pt] &\quad= -\frac 12 \phi(0)+\frac 2{\mathcal{L}}\int_{1}^{\infty} E(t) \frac{{d}}{{d} t} \bigg( \frac{1}{t} \widehat{\phi}\bigg( \frac{2 \log t}{\mathcal{L}} \bigg) \bigg) \, {d} t , \end{align} $$
with
![]() $E(t)$
defined in (3-6). We can now expand the derivative in the last integrand in (3-7) into Taylor expansions involving powers of
$E(t)$
defined in (3-6). We can now expand the derivative in the last integrand in (3-7) into Taylor expansions involving powers of
![]() $2\log t/\mathcal {L}$
and use the corresponding series to calculate the last integral above. Note that the new integrals emerging from this process are all convergent because of the bound (3-6). The assertion of the lemma now follows by combining (3-4), (3-5) and (3-7).
$2\log t/\mathcal {L}$
and use the corresponding series to calculate the last integral above. Note that the new integrals emerging from this process are all convergent because of the bound (3-6). The assertion of the lemma now follows by combining (3-4), (3-5) and (3-7).
3.2 Estimation of
 $S_{\text {odd}}$
: Poisson summation
$S_{\text {odd}}$
: Poisson summation
Starting from this section, we concentrate on the estimation of
![]() $S_{\mathrm {odd}}$
. First note that the contribution from the terms with
$S_{\mathrm {odd}}$
. First note that the contribution from the terms with
![]() $j\geq 3$
in (3-1) is
$j\geq 3$
in (3-1) is
![]() $O(X^{-3/4+\varepsilon })$
by Lemma 2.3. It thus remains to treat the case for
$O(X^{-3/4+\varepsilon })$
by Lemma 2.3. It thus remains to treat the case for
![]() $j=1$
. For this case, we use the Möbius function to detect the condition that c is square-free to get
$j=1$
. For this case, we use the Möbius function to detect the condition that c is square-free to get
 $$ \begin{align*} S_{\mathrm{odd}}&= -\frac 2{\mathcal{L} W(X) }\sum_{\substack {l \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3}}}\mu_{[i]}(l) \sum_{\substack{ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{\sqrt{N(\varpi)}} \hat{\phi} \bigg( \frac {\log N( \varpi)}{\log X} \bigg) \\[3pt] &\quad\times \sum_{(c, 1+i)=1} \bigg(\frac{i(1+i)cl^{2}}{\varpi}\bigg) w \bigg( \frac {N(cl^{2})}{X} \bigg) +O(X^{-3/4+\varepsilon}). \end{align*} $$
$$ \begin{align*} S_{\mathrm{odd}}&= -\frac 2{\mathcal{L} W(X) }\sum_{\substack {l \equiv 1 \ {\operatorname{mod}}\ (1+i)^{3}}}\mu_{[i]}(l) \sum_{\substack{ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{\sqrt{N(\varpi)}} \hat{\phi} \bigg( \frac {\log N( \varpi)}{\log X} \bigg) \\[3pt] &\quad\times \sum_{(c, 1+i)=1} \bigg(\frac{i(1+i)cl^{2}}{\varpi}\bigg) w \bigg( \frac {N(cl^{2})}{X} \bigg) +O(X^{-3/4+\varepsilon}). \end{align*} $$
We divide the sum over l above into two parts, one over
![]() $l \leq Z$
and the other over
$l \leq Z$
and the other over
![]() $l>Z$
, with Z to be chosen optimally later. Note that if c is odd, then
$l>Z$
, with Z to be chosen optimally later. Note that if c is odd, then
![]() $i(1+i)^{5}cl^{2}$
is never a square. Similarly to the treatment of
$i(1+i)^{5}cl^{2}$
is never a square. Similarly to the treatment of
![]() $S_{R}(X,Y; \hat {\phi }, \Phi )$
in [Reference Gao and Zhao15, Section 3.3] (except that we use Lemma 2.2 here instead of [Reference Gao and Zhao15, Lemma 2.5]), we get that the terms with
$S_{R}(X,Y; \hat {\phi }, \Phi )$
in [Reference Gao and Zhao15, Section 3.3] (except that we use Lemma 2.2 here instead of [Reference Gao and Zhao15, Lemma 2.5]), we get that the terms with
![]() $l> Z$
are
$l> Z$
are
For the terms with
![]() $l \leq Z$
, we apply the Poisson summation (2-2) given in Lemma 2.1 and argue as in [Reference Gao and Zhao15] (the treatment here is essentially the same as that of
$l \leq Z$
, we apply the Poisson summation (2-2) given in Lemma 2.1 and argue as in [Reference Gao and Zhao15] (the treatment here is essentially the same as that of
![]() $S_{M}(X,Y; \hat {\phi }, \Phi )$
in [Reference Gao and Zhao15, Section 3.2]) to arrive at the following lemma.
$S_{M}(X,Y; \hat {\phi }, \Phi )$
in [Reference Gao and Zhao15, Section 3.2]) to arrive at the following lemma.
Lemma 3.2. Suppose that the GRH is true. We have for any
![]() $Z \geq 1$
and any
$Z \geq 1$
and any
![]() $\epsilon>0$
,
$\epsilon>0$
,
 $$ \begin{align} S_{\mathrm{odd}} &= -\frac X{\mathcal{L} W(X)} \sum_{\substack {N(l) \leq Z\\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{k \in \mathbb Z[i]}(-1)^{N(k)} \nonumber\\[3pt] &\quad \times \sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}} \frac {\log N(\varpi)}{N(\varpi)}\bigg(\frac{kl^{2}}{\varpi}\bigg)\hat{\phi}\bigg( \frac {\log N( \varpi)}{\log X} \bigg) \widetilde{w}\bigg(\sqrt{\frac {N(k)X}{2N(l^{2}\varpi)}}\bigg) \nonumber\\[3pt] &\quad +O( X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1} ). \end{align} $$
$$ \begin{align} S_{\mathrm{odd}} &= -\frac X{\mathcal{L} W(X)} \sum_{\substack {N(l) \leq Z\\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{k \in \mathbb Z[i]}(-1)^{N(k)} \nonumber\\[3pt] &\quad \times \sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}} \frac {\log N(\varpi)}{N(\varpi)}\bigg(\frac{kl^{2}}{\varpi}\bigg)\hat{\phi}\bigg( \frac {\log N( \varpi)}{\log X} \bigg) \widetilde{w}\bigg(\sqrt{\frac {N(k)X}{2N(l^{2}\varpi)}}\bigg) \nonumber\\[3pt] &\quad +O( X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1} ). \end{align} $$
We now generalize [Reference Fiorilli, Parks and Södergren10, Lemma 2.7] to further analyze the sums in (3-8), obtaining the following result.
Lemma 3.3. Suppose that the GRH is true and that
 $\sigma =\sup (\mathrm {supp }\,\widehat {\phi })<\infty $
. Then, we have for any
$\sigma =\sup (\mathrm {supp }\,\widehat {\phi })<\infty $
. Then, we have for any
![]() $1 \leq Z \leq X^{2}$
and any
$1 \leq Z \leq X^{2}$
and any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 $$ \begin{align} S_{\mathrm{odd}} &= \frac X{ W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \bigg (\frac 12 I_{(1+i)l}(X)-I_{l}(X) \bigg ) \nonumber\\[3pt] &\quad+O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ), \end{align} $$
$$ \begin{align} S_{\mathrm{odd}} &= \frac X{ W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \bigg (\frac 12 I_{(1+i)l}(X)-I_{l}(X) \bigg ) \nonumber\\[3pt] &\quad+O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ), \end{align} $$
where
 $$ \begin{align} I_{l}(X) = \int_{0}^{\infty} \widehat{\phi}( u ) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} \widetilde{w}\bigg(2N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \,{d} u. \end{align} $$
$$ \begin{align} I_{l}(X) = \int_{0}^{\infty} \widehat{\phi}( u ) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} \widetilde{w}\bigg(2N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \,{d} u. \end{align} $$
Proof. Note that as in [Reference Gao and Zhao15, Section 3.4] the inner sum in (3-8) corresponding to
![]() $k=0$
is zero. It also follows from the treatment of [Reference Gao and Zhao15, Section 3.5] by setting
$k=0$
is zero. It also follows from the treatment of [Reference Gao and Zhao15, Section 3.5] by setting
![]() $U=1$
and dividing the estimation obtained in [Reference Gao and Zhao15, formula (3.9)] by X (since our definition of
$U=1$
and dividing the estimation obtained in [Reference Gao and Zhao15, formula (3.9)] by X (since our definition of
![]() $S_{\mathrm {odd}}$
differs from
$S_{\mathrm {odd}}$
differs from
![]() $S_{M}(X,Y; \hat {\phi }, \Phi )$
defined in [Reference Gao and Zhao15] by an extra factor
$S_{M}(X,Y; \hat {\phi }, \Phi )$
defined in [Reference Gao and Zhao15] by an extra factor
![]() $W^{-1}(X)$
) that the contribution of
$W^{-1}(X)$
) that the contribution of
![]() $k \neq \square $
(k is not a square) to the expression for
$k \neq \square $
(k is not a square) to the expression for
![]() $S_{\mathrm {odd}}$
given in (3-8) is
$S_{\mathrm {odd}}$
given in (3-8) is
We are left to consider the contribution from
![]() $k=\square $
(k is a square),
$k=\square $
(k is a square),
![]() $k \neq 0$
, to the expression for
$k \neq 0$
, to the expression for
![]() $S_{\mathrm {odd}}$
given in (3-8). For this, we make a change of variables
$S_{\mathrm {odd}}$
given in (3-8). For this, we make a change of variables
![]() $k \mapsto k^{2}$
, while noting that
$k \mapsto k^{2}$
, while noting that
 $k^{2}_{1}=k^{2}_{2}$
if and only if
$k^{2}_{1}=k^{2}_{2}$
if and only if
![]() $k_{1} = \pm k_{2}$
, and deduce that
$k_{1} = \pm k_{2}$
, and deduce that
 $$ \begin{align*} S_{\mathrm{odd}} & = -\frac X{2 \mathcal{L} W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {(\varpi , l )=1 \\ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{N(\varpi)}\hat{\phi} \bigg( \frac {\log N( \varpi)}{\log X} \bigg) \\[3pt] & \quad \times \sum_{\substack {k \in \mathbb Z[i] , k \neq 0 \\ (k, \varpi)=1}}(-1)^{N(k)}\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2}\varpi)}}\bigg) \\[3pt] &\quad +O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon} ). \end{align*} $$
$$ \begin{align*} S_{\mathrm{odd}} & = -\frac X{2 \mathcal{L} W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {(\varpi , l )=1 \\ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{N(\varpi)}\hat{\phi} \bigg( \frac {\log N( \varpi)}{\log X} \bigg) \\[3pt] & \quad \times \sum_{\substack {k \in \mathbb Z[i] , k \neq 0 \\ (k, \varpi)=1}}(-1)^{N(k)}\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2}\varpi)}}\bigg) \\[3pt] &\quad +O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon} ). \end{align*} $$
In view of the rapid decay property of
![]() $\widetilde {w}$
implied by (2-6), we now remove the condition that
$\widetilde {w}$
implied by (2-6), we now remove the condition that
![]() $(\varpi , l)=1$
at the cost of an error
$(\varpi , l)=1$
at the cost of an error
 $$ \begin{align*} & \ll \frac 1{\mathcal{L}}\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \sum_{\substack {\varpi | l \\ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{N(\varpi)}\sum_{\substack {k \in \mathbb Z[i] ,\ k \neq 0 \\ N(k) \leq \sqrt{2N(l^{2}\varpi)/X}}}1 \\[3pt] & \ll X^{-1/2}\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l)} \sum_{\substack {\varpi | l \\ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{\sqrt{N(\varpi)}} \ll X^{-1/2}Z^{\varepsilon}, \end{align*} $$
$$ \begin{align*} & \ll \frac 1{\mathcal{L}}\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \sum_{\substack {\varpi | l \\ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{N(\varpi)}\sum_{\substack {k \in \mathbb Z[i] ,\ k \neq 0 \\ N(k) \leq \sqrt{2N(l^{2}\varpi)/X}}}1 \\[3pt] & \ll X^{-1/2}\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l)} \sum_{\substack {\varpi | l \\ \varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{\sqrt{N(\varpi)}} \ll X^{-1/2}Z^{\varepsilon}, \end{align*} $$
where we use the well-known fact that for
![]() $N(l) \geq 3$
, the number,
$N(l) \geq 3$
, the number,
![]() $\omega (l)$
, of distinct primes in
$\omega (l)$
, of distinct primes in
![]() $\mathbb Z[i]$
dividing l can be bounded as
$\mathbb Z[i]$
dividing l can be bounded as
 $$ \begin{align*} \omega(l) \ll \frac {\log N(l)}{\log \log N(l)}. \end{align*} $$
$$ \begin{align*} \omega(l) \ll \frac {\log N(l)}{\log \log N(l)}. \end{align*} $$
One can show similarly that removing the condition
![]() $(k,\varpi )=1$
introduces an error of size much less than
$(k,\varpi )=1$
introduces an error of size much less than
![]() $ X^{-1/2}Z^{\varepsilon }$
. We thus derive, using (2-7), that
$ X^{-1/2}Z^{\varepsilon }$
. We thus derive, using (2-7), that
 $$ \begin{align*} S_{\mathrm{odd}} &= -\frac X{2 \mathcal{L} W(X)}\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {\varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{N(\varpi)} \\[3pt] & \quad \times \hat{\phi} \bigg( \frac {\log N( \varpi)}{\log X} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)}\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2}\varpi)}}\bigg)\\[3pt] &\quad +O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ) \\[3pt] &= -\frac {X}{2 \mathcal{L} W(X) }\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \\[3pt] & \quad \times \int^{\infty}_{1}\frac 1y \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\,{d} (y+ h(y) ) \\[3pt] & \quad +O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ) \\[3pt] &= S_{1}+S_{2}+O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ), \end{align*} $$
$$ \begin{align*} S_{\mathrm{odd}} &= -\frac X{2 \mathcal{L} W(X)}\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {\varpi \equiv 1 \bmod {(1+i)^{3}} }} \frac {\log N(\varpi)}{N(\varpi)} \\[3pt] & \quad \times \hat{\phi} \bigg( \frac {\log N( \varpi)}{\log X} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)}\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2}\varpi)}}\bigg)\\[3pt] &\quad +O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ) \\[3pt] &= -\frac {X}{2 \mathcal{L} W(X) }\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \\[3pt] & \quad \times \int^{\infty}_{1}\frac 1y \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\,{d} (y+ h(y) ) \\[3pt] & \quad +O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ) \\[3pt] &= S_{1}+S_{2}+O(X^{-3/4+\varepsilon}+X^{\varepsilon}(\log Z)^{3}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ), \end{align*} $$
where h is a function satisfying
![]() $h(y) = O( y^{1/2} \log ^{2} (2y) )$
,
$h(y) = O( y^{1/2} \log ^{2} (2y) )$
,
 $$ \begin{align*} S_{1}&= -\frac{X}{2 \mathcal{L}W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \\[3pt] &\quad \times \int^{\infty}_{1}\frac 1y \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\,{d} y \end{align*} $$
$$ \begin{align*} S_{1}&= -\frac{X}{2 \mathcal{L}W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \\[3pt] &\quad \times \int^{\infty}_{1}\frac 1y \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\,{d} y \end{align*} $$
and
 $$ \begin{align*} S_{2} &= -\frac{X}{2 \mathcal{L}W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \\[3pt] &\quad \times \int^{\infty}_{1} \frac 1y \hat{\phi}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\,{d} h(y). \end{align*} $$
$$ \begin{align*} S_{2} &= -\frac{X}{2 \mathcal{L}W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \\[3pt] &\quad \times \int^{\infty}_{1} \frac 1y \hat{\phi}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\,{d} h(y). \end{align*} $$
Note that
 $$ \begin{align*} S_{2} &\ll \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \\[3pt] &\quad \times \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\int^{\infty}_{1} y^{1/2} \log^{2} (2y) \frac{{d}}{{d} y} \bigg(\frac 1y \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg) \bigg ) \,{d} y \\[3pt] & \ll S_{2,1}+S_{2,2}, \end{align*} $$
$$ \begin{align*} S_{2} &\ll \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \\[3pt] &\quad \times \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\int^{\infty}_{1} y^{1/2} \log^{2} (2y) \frac{{d}}{{d} y} \bigg(\frac 1y \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg) \bigg ) \,{d} y \\[3pt] & \ll S_{2,1}+S_{2,2}, \end{align*} $$
where
 $$ \begin{align*} S_{2,1} = \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\bigg | \widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})}}\bigg)\bigg | \end{align*} $$
$$ \begin{align*} S_{2,1} = \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\bigg | \widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})}}\bigg)\bigg | \end{align*} $$
and
 $$ \begin{align*} S_{2,2} &= \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \int^{\infty}_{1} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} y^{1/2} \log^{2} (2y) \\[3pt] &\quad \times \bigg( \bigg |\bigg( \frac 1{y^{2}\mathcal{L}}\hat{\phi}^{\prime} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | +\bigg |\frac 1{y^{2}} \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \\[3pt] &\quad +\bigg | \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)N(k)\sqrt{\frac {X}{8N(l^{2})}}y^{-5/2}\widetilde{w}^{\prime}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \bigg ) \,{d} y. \end{align*} $$
$$ \begin{align*} S_{2,2} &= \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})} \int^{\infty}_{1} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} y^{1/2} \log^{2} (2y) \\[3pt] &\quad \times \bigg( \bigg |\bigg( \frac 1{y^{2}\mathcal{L}}\hat{\phi}^{\prime} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | +\bigg |\frac 1{y^{2}} \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \\[3pt] &\quad +\bigg | \hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)N(k)\sqrt{\frac {X}{8N(l^{2})}}y^{-5/2}\widetilde{w}^{\prime}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \bigg ) \,{d} y. \end{align*} $$
Using (2-6), we deduce that
 $$ \begin{align*} \sum_{\substack {k \in\mathbb Z[i] \\ k \neq 0}}\bigg |\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \ll \sqrt {\frac {N(l^{2})y}{X}} \end{align*} $$
$$ \begin{align*} \sum_{\substack {k \in\mathbb Z[i] \\ k \neq 0}}\bigg |\widetilde{w}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \ll \sqrt {\frac {N(l^{2})y}{X}} \end{align*} $$
and
 $$ \begin{align*} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\bigg | N(k)\widetilde{w}^{\prime}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \ll \frac {N(l^{2})y}{X}. \end{align*} $$
$$ \begin{align*} \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\bigg | N(k)\widetilde{w}^{\prime}\bigg(N(k)\sqrt{\frac {X}{2N(l^{2})y}}\bigg)\bigg | \ll \frac {N(l^{2})y}{X}. \end{align*} $$
Thus, it follows that
 $$ \begin{align*} S_{2,2} &\ll \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})}\int^{\infty}_{1} y^{1/2} \log^{2} (2y) \\[3pt] & \quad \times \bigg( \frac 1{y^{2}\mathcal{L}}\bigg |\hat{\phi} ^{\prime}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg |\sqrt {\frac {N(l^{2})y}{X}}+\frac 1{y^{2}}\bigg | \hat{\phi}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\sqrt {\frac {N(l^{2})y}{X}}\bigg | \\[3pt] & \quad + \bigg |\hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg | \sqrt{\frac {X}{8N(l^{2})}}y^{-5/2}\frac {N(l^{2})y}{X}\bigg )\,{d} y \\[3pt] & \ll X^{-1/2}Z^{\varepsilon}\int^{\infty}_{1} \log^{2} (2y)\bigg ( \bigg | \hat{\phi}^{\prime}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg |+ \bigg |\hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg | \bigg) \,{d} \bigg( \frac {\log y}{\mathcal{L}} \bigg) \\[3pt] & \ll X^{-1/2+\varepsilon}Z^{\varepsilon}, \end{align*} $$
$$ \begin{align*} S_{2,2} &\ll \frac 1{\mathcal{L}} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {1}{N(l^{2})}\int^{\infty}_{1} y^{1/2} \log^{2} (2y) \\[3pt] & \quad \times \bigg( \frac 1{y^{2}\mathcal{L}}\bigg |\hat{\phi} ^{\prime}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg |\sqrt {\frac {N(l^{2})y}{X}}+\frac 1{y^{2}}\bigg | \hat{\phi}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\sqrt {\frac {N(l^{2})y}{X}}\bigg | \\[3pt] & \quad + \bigg |\hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg | \sqrt{\frac {X}{8N(l^{2})}}y^{-5/2}\frac {N(l^{2})y}{X}\bigg )\,{d} y \\[3pt] & \ll X^{-1/2}Z^{\varepsilon}\int^{\infty}_{1} \log^{2} (2y)\bigg ( \bigg | \hat{\phi}^{\prime}\bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg |+ \bigg |\hat{\phi} \bigg( \frac {\log y}{\mathcal{L}} \bigg)\bigg | \bigg) \,{d} \bigg( \frac {\log y}{\mathcal{L}} \bigg) \\[3pt] & \ll X^{-1/2+\varepsilon}Z^{\varepsilon}, \end{align*} $$
where the last estimation above follows by using a change of variable
![]() $u = \log y/\mathcal {L}$
to evaluate the proceeding integral and noting that the integrand has compact support. Similarly, we have that
$u = \log y/\mathcal {L}$
to evaluate the proceeding integral and noting that the integrand has compact support. Similarly, we have that
![]() $S_{2,1} \ll X^{-1/2+\varepsilon }Z^{\varepsilon }$
so that
$S_{2,1} \ll X^{-1/2+\varepsilon }Z^{\varepsilon }$
so that
It follows from the above bound that
![]() $S_{2}$
can be absorbed into the O-term in (3-9).It remains to evaluate
$S_{2}$
can be absorbed into the O-term in (3-9).It remains to evaluate
![]() $S_{1}$
, and applying exactly the same change of variable as above now leads to
$S_{1}$
, and applying exactly the same change of variable as above now leads to
 $$ \begin{align} S_{1} &= -\frac X{ 2W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \nonumber\\[3pt] &\quad \times \int_{0}^{\infty} \widehat{\phi}( u ) \sum_{\substack {k \in \mathbb Z[i] , k \neq 0}}(-1)^{N(k)} \widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \,{d} u. \end{align} $$
$$ \begin{align} S_{1} &= -\frac X{ 2W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \nonumber\\[3pt] &\quad \times \int_{0}^{\infty} \widehat{\phi}( u ) \sum_{\substack {k \in \mathbb Z[i] , k \neq 0}}(-1)^{N(k)} \widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \,{d} u. \end{align} $$
We note that, for any
![]() $l \in \mathcal O_{K}$
, we have
$l \in \mathcal O_{K}$
, we have
 $$ \begin{align*} &\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \\[3pt] &\quad= \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 \\ 1+i|k}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg)-\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 \\ (1+i,k)=1}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \nonumber \\&\quad= 2\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 \\ 1+i|k}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg)-\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \\[3pt] &\quad= 2\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 }}\widetilde{w}\bigg(2 N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg)-\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg). \end{align*} $$
$$ \begin{align*} &\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}(-1)^{N(k)} \widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \\[3pt] &\quad= \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 \\ 1+i|k}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg)-\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 \\ (1+i,k)=1}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \nonumber \\&\quad= 2\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 \\ 1+i|k}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg)-\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \\[3pt] &\quad= 2\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0 }}\widetilde{w}\bigg(2 N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg)-\sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg). \end{align*} $$
Applying the above in (3-11), we derive that
 $$ \begin{align*} S_{1} = \frac X{ W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \bigg (\frac 12 I_{(1+i)l}(X)-I_{l}(X) \bigg ). \end{align*} $$
$$ \begin{align*} S_{1} = \frac X{ W(X) } \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \bigg (\frac 12 I_{(1+i)l}(X)-I_{l}(X) \bigg ). \end{align*} $$
The above gives precisely the main term in (3-9) for
![]() $S_{\mathrm {odd}}$
, and this completes the proof.
$S_{\mathrm {odd}}$
, and this completes the proof.
3.3 Estimation of
 $S_{\text {odd}}$
: small support
$S_{\text {odd}}$
: small support
In this section, we apply Lemma 3.3 to show that there are no new lower-order terms in powers of
![]() $\mathcal {L}^{-1}$
when
$\mathcal {L}^{-1}$
when
 $\sigma =\sup (\mathrm {supp }\,\widehat {\phi })\,{<}\,1$
. We generalize [Reference Fiorilli, Parks and Södergren10, Proposition 3.1] and state our result in the following proposition.
$\sigma =\sup (\mathrm {supp }\,\widehat {\phi })\,{<}\,1$
. We generalize [Reference Fiorilli, Parks and Södergren10, Proposition 3.1] and state our result in the following proposition.
Proposition 3.4. Suppose that the GRH is true and that
 $\sigma =\sup (\mathrm {supp }\,\widehat {\phi })<1$
. Then, we have for any
$\sigma =\sup (\mathrm {supp }\,\widehat {\phi })<1$
. Then, we have for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
Proof. We let
 $$ \begin{align} \Phi(X)= \sum_{\substack{N(l) \leq X \\ l \equiv 1 \bmod {(1+i)^{3}} }} \frac{\mu_{[i]}(l)}{N(l)^{2}}= \frac 4{3\zeta_{K}(2)} +O(X^{-3/2 + \varepsilon}), \end{align} $$
$$ \begin{align} \Phi(X)= \sum_{\substack{N(l) \leq X \\ l \equiv 1 \bmod {(1+i)^{3}} }} \frac{\mu_{[i]}(l)}{N(l)^{2}}= \frac 4{3\zeta_{K}(2)} +O(X^{-3/2 + \varepsilon}), \end{align} $$
where the last equality above follows from the observation that under the GRH we have
 $$ \begin{align*}\sum_{\substack{N(l) \leq X \\ (l, 1+i)=1 }} \mu_{[i]}(l) \ll X^{1/2+\varepsilon}.\end{align*} $$
$$ \begin{align*}\sum_{\substack{N(l) \leq X \\ (l, 1+i)=1 }} \mu_{[i]}(l) \ll X^{1/2+\varepsilon}.\end{align*} $$
We then deduce that for
![]() $0\leq u \leq 1$
,
$0\leq u \leq 1$
,
 $$ \begin{align*} &\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) = \int_{0^{+}}^{Z} \widetilde{w}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \,{d} \Phi(t) \\[3pt] &\qquad =\int_{0^{+}}^{Z} \widetilde{w}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \,{d} \bigg(\frac 4{3\zeta_{K}(2)}+O(t^{-3/2 + \epsilon})\bigg ) \nonumber \\&\qquad = \widetilde{w}\bigg(\frac {N(k)}{Z}\sqrt{\frac {X^{1-u}}{2}}\bigg) O(Z^{-3/2 + \varepsilon})+ N(k)\sqrt{\frac {X^{1-u}}{2}}\int_{0^{+}}^{Z} \widetilde{w}^{\prime}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) O (t^{-3/2 + \varepsilon})\frac{ {d} t}{t^{2}} \\[3pt] & \qquad\ll Z^{-3/2 +\varepsilon} \bigg|\widetilde{w}\bigg(\frac {N(k)}{Z}\sqrt{\frac {X^{1-u}}{2}}\bigg)\bigg| +N(k)X^{(1-u)/2}\int_{0^{+}}^{Z} \bigg|\widetilde{w}^{\prime}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \bigg| \frac{{d} t}{t^{7/2-\varepsilon}}. \end{align*} $$
$$ \begin{align*} &\sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})}\widetilde{w}\bigg(N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) = \int_{0^{+}}^{Z} \widetilde{w}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \,{d} \Phi(t) \\[3pt] &\qquad =\int_{0^{+}}^{Z} \widetilde{w}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \,{d} \bigg(\frac 4{3\zeta_{K}(2)}+O(t^{-3/2 + \epsilon})\bigg ) \nonumber \\&\qquad = \widetilde{w}\bigg(\frac {N(k)}{Z}\sqrt{\frac {X^{1-u}}{2}}\bigg) O(Z^{-3/2 + \varepsilon})+ N(k)\sqrt{\frac {X^{1-u}}{2}}\int_{0^{+}}^{Z} \widetilde{w}^{\prime}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) O (t^{-3/2 + \varepsilon})\frac{ {d} t}{t^{2}} \\[3pt] & \qquad\ll Z^{-3/2 +\varepsilon} \bigg|\widetilde{w}\bigg(\frac {N(k)}{Z}\sqrt{\frac {X^{1-u}}{2}}\bigg)\bigg| +N(k)X^{(1-u)/2}\int_{0^{+}}^{Z} \bigg|\widetilde{w}^{\prime}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \bigg| \frac{{d} t}{t^{7/2-\varepsilon}}. \end{align*} $$
Note that the part of the last integral for
![]() $ t \in (0,X^{(1-u)/2-\varepsilon }]$
is
$ t \in (0,X^{(1-u)/2-\varepsilon }]$
is
![]() $O((N(k)X)^{-A})$
for any
$O((N(k)X)^{-A})$
for any
![]() $A\geq 1$
, by the rapid decay of
$A\geq 1$
, by the rapid decay of
![]() $\widetilde w^{\prime }$
. Summing over k and integrating over u, we obtain that
$\widetilde w^{\prime }$
. Summing over k and integrating over u, we obtain that
 $$ \begin{align*} & \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})}I_{l}(X) \\[3pt] &\qquad \ll \int_{0}^{\infty} |\widehat{\phi}( u )| \sum_{\substack{k \in \mathbb Z[i] \\ k \neq 0}} \bigg(Z^{-3/2 +\varepsilon} \bigg|\widetilde{w}\bigg(\frac {N(k)}{Z}\sqrt{\frac {X^{1-u}}{2}}\bigg)\bigg|\\[3pt] &\qquad \quad+N(k)X^{(1-u)/2}\int_{0^{+}}^{Z} \bigg|\widetilde{w}^{\prime}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \bigg| \frac{{d} t}{t^{7/2-\varepsilon}} \bigg)\,{d} u +X^{-1} \\[3pt] &\qquad \ll \int_{0}^{\infty} |\widehat{\phi}( u )| \bigg(Z^{-3/2 +\varepsilon} \frac{Z}{X^{(1-u)/2}}+\frac 1{X^{(1-u)/2}}\int_{X^{(1-u)/2-\varepsilon}}^{Z} \frac{{d} t}{t^{3/2-\varepsilon}} \bigg)\, {d} u + X^{-1}\\[3pt] &\qquad \ll \frac{X^{(\sigma-1)/2}}{Z^{1/2 -\varepsilon}} + X^{3\sigma/4 -3/4+\varepsilon}. \end{align*} $$
$$ \begin{align*} & \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})}I_{l}(X) \\[3pt] &\qquad \ll \int_{0}^{\infty} |\widehat{\phi}( u )| \sum_{\substack{k \in \mathbb Z[i] \\ k \neq 0}} \bigg(Z^{-3/2 +\varepsilon} \bigg|\widetilde{w}\bigg(\frac {N(k)}{Z}\sqrt{\frac {X^{1-u}}{2}}\bigg)\bigg|\\[3pt] &\qquad \quad+N(k)X^{(1-u)/2}\int_{0^{+}}^{Z} \bigg|\widetilde{w}^{\prime}\bigg(\frac {N(k)}{t}\sqrt{\frac {X^{1-u}}{2}}\bigg) \bigg| \frac{{d} t}{t^{7/2-\varepsilon}} \bigg)\,{d} u +X^{-1} \\[3pt] &\qquad \ll \int_{0}^{\infty} |\widehat{\phi}( u )| \bigg(Z^{-3/2 +\varepsilon} \frac{Z}{X^{(1-u)/2}}+\frac 1{X^{(1-u)/2}}\int_{X^{(1-u)/2-\varepsilon}}^{Z} \frac{{d} t}{t^{3/2-\varepsilon}} \bigg)\, {d} u + X^{-1}\\[3pt] &\qquad \ll \frac{X^{(\sigma-1)/2}}{Z^{1/2 -\varepsilon}} + X^{3\sigma/4 -3/4+\varepsilon}. \end{align*} $$
Similarly, we have
 $$ \begin{align*} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})}I_{(1+i)l}(X) \ll \frac{X^{(\sigma-1)/2}}{Z^{1/2 -\varepsilon}} + X^{3\sigma/4 -3/4+\varepsilon}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})}I_{(1+i)l}(X) \ll \frac{X^{(\sigma-1)/2}}{Z^{1/2 -\varepsilon}} + X^{3\sigma/4 -3/4+\varepsilon}. \end{align*} $$
Hence, it follows from Lemma 3.3 that for
![]() $Z\leq X^{2}$
,
$Z\leq X^{2}$
,
 $$ \begin{align*} S_{\mathrm{odd}} &\ll \frac{X^{(\sigma-1)/2}}{Z^{1/2 -\varepsilon}} +X^{3\sigma/4 -3/4+\varepsilon} +X^{-3/4+\varepsilon}+X^{\varepsilon}Z^{-1} +ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon}. \end{align*} $$
$$ \begin{align*} S_{\mathrm{odd}} &\ll \frac{X^{(\sigma-1)/2}}{Z^{1/2 -\varepsilon}} +X^{3\sigma/4 -3/4+\varepsilon} +X^{-3/4+\varepsilon}+X^{\varepsilon}Z^{-1} +ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon}. \end{align*} $$
The result follows by taking
![]() $Z=X^{1/2-\sigma /4}$
.
$Z=X^{1/2-\sigma /4}$
.
3.5 Estimation of
 $S_{\text {odd}}$
: extended support
$S_{\text {odd}}$
: extended support
In this section, we analyze the lower-order terms of
![]() $S_{\mathrm {odd}}$
when
$S_{\mathrm {odd}}$
when
 $\sigma =\sup (\mathrm {supp }\,\widehat {\phi }) \geq 1$
.
$\sigma =\sup (\mathrm {supp }\,\widehat {\phi }) \geq 1$
.
Lemma 3.5. Suppose that
 $\sigma =\sup (\mathrm {supp }\,\widehat {\phi })<\infty $
. Then, concerning the function
$\sigma =\sup (\mathrm {supp }\,\widehat {\phi })<\infty $
. Then, concerning the function
![]() $I_{l}(X)$
defined in (3-10), we have
$I_{l}(X)$
defined in (3-10), we have
 $$ \begin{align} I_{l}(X)&= -\widetilde w (0)\int_{1}^{\infty} \widehat{\phi}(u)\,du +\frac {\tilde{g}(0)}{\mathcal{L}} \int^{\infty}_{0}\phi( 1+\tau/\mathcal{L} ) e^{\tau/2}N(l) \, {d} \tau \nonumber\\[3pt] &\quad +\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}}\tilde{g}(\lower 2pt\sqrt {N(j) e^{\tau/2}N(l)}) \, {d} \tau \nonumber\\[3pt] &\quad +\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi} \bigg( 1-\frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}}g\bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) \,{d} \tau+O(N(l)X^{-1/2}) \end{align} $$
$$ \begin{align} I_{l}(X)&= -\widetilde w (0)\int_{1}^{\infty} \widehat{\phi}(u)\,du +\frac {\tilde{g}(0)}{\mathcal{L}} \int^{\infty}_{0}\phi( 1+\tau/\mathcal{L} ) e^{\tau/2}N(l) \, {d} \tau \nonumber\\[3pt] &\quad +\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}}\tilde{g}(\lower 2pt\sqrt {N(j) e^{\tau/2}N(l)}) \, {d} \tau \nonumber\\[3pt] &\quad +\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi} \bigg( 1-\frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}}g\bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) \,{d} \tau+O(N(l)X^{-1/2}) \end{align} $$
and
 $$ \begin{align} I_{(1+i)l}(X)&= -\widetilde w (0)\int_{1}^{\infty} \widehat{\phi}(u)\,du +\frac {2\tilde{g}(0)}{\mathcal{L}} \int^{\infty}_{0}\phi\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg)e^{\tau/2}N(l) \, {d} \tau \nonumber\\[3pt] & \quad+\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) 2e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}}\tilde{g}(2\lower 2pt\sqrt {N(j) e^{\tau/2}N(l)}) \, {d} \tau \nonumber\\[3pt] &\quad +\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 - \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}}g\bigg(\frac {N(k)}{2}\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) \,{d} \tau, \end{align} $$
$$ \begin{align} I_{(1+i)l}(X)&= -\widetilde w (0)\int_{1}^{\infty} \widehat{\phi}(u)\,du +\frac {2\tilde{g}(0)}{\mathcal{L}} \int^{\infty}_{0}\phi\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg)e^{\tau/2}N(l) \, {d} \tau \nonumber\\[3pt] & \quad+\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) 2e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}}\tilde{g}(2\lower 2pt\sqrt {N(j) e^{\tau/2}N(l)}) \, {d} \tau \nonumber\\[3pt] &\quad +\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 - \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}}g\bigg(\frac {N(k)}{2}\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) \,{d} \tau, \end{align} $$
where
![]() $g(y)$
is given as in (2-14).
$g(y)$
is given as in (2-14).
Proof. We first extend the integral in (3-10) to
![]() $\mathbb R$
and make the substitution
$\mathbb R$
and make the substitution
![]() $\tau ~=~\mathcal {L}(u-~1)$
to obtain that
$\tau ~=~\mathcal {L}(u-~1)$
to obtain that
 $$ \begin{align} I_{l}(X)&=\frac 1{\mathcal{L}} \int_{-\infty}^{\infty} \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}} \widetilde{w}\bigg(2N(k)\sqrt{\frac {e^{-\tau}}{2N(l^{2})}}\bigg) \,{d} \tau \nonumber\\[3pt] &\quad +O(N(l)X^{-1/2}), \end{align} $$
$$ \begin{align} I_{l}(X)&=\frac 1{\mathcal{L}} \int_{-\infty}^{\infty} \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}} \widetilde{w}\bigg(2N(k)\sqrt{\frac {e^{-\tau}}{2N(l^{2})}}\bigg) \,{d} \tau \nonumber\\[3pt] &\quad +O(N(l)X^{-1/2}), \end{align} $$
since for
![]() $u \leq 0$
, we have
$u \leq 0$
, we have
 $$ \begin{align*} &\int^{0}_{-\infty} \widehat{\phi}( u ) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} \widetilde{w}\bigg(2N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \,{d} u \\[3pt] &\quad \ll \int^{0}_{-\infty} \widehat{\phi}( u ) \sqrt{\frac {N(l^{2})}{X^{1-u}}} \,{d} u \ll N(l)X^{-1/2}. \end{align*} $$
$$ \begin{align*} &\int^{0}_{-\infty} \widehat{\phi}( u ) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} \widetilde{w}\bigg(2N(k)\sqrt{\frac {X^{1-u}}{2N(l^{2})}}\bigg) \,{d} u \\[3pt] &\quad \ll \int^{0}_{-\infty} \widehat{\phi}( u ) \sqrt{\frac {N(l^{2})}{X^{1-u}}} \,{d} u \ll N(l)X^{-1/2}. \end{align*} $$
We then break the integral in (3-15) into integrals over
![]() $(-\infty ,0]$
and
$(-\infty ,0]$
and
![]() $[0,\infty )$
and denote them, respectively, by
$[0,\infty )$
and denote them, respectively, by
![]() $I_{l}^{-}(X)$
and
$I_{l}^{-}(X)$
and
![]() $I_{l}^{+}(X)$
. By applying the Poisson summation formula (2-3) given in Lemma 2.1, we see that
$I_{l}^{+}(X)$
. By applying the Poisson summation formula (2-3) given in Lemma 2.1, we see that
 $$ \begin{align*} I_{l}^{+}(X)&= \frac 1{\mathcal{L}}\int_{0}^{\infty} \widehat{\phi}\bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \bigg(-\widetilde{w}(0) + \sum_{k \in \mathbb Z[i]} g\bigg(N(k)\sqrt{\frac {e^{-\tau}}{N(l^{2})}}\bigg) \bigg)\, {d} \tau \\[3pt] &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) \bigg(-\widetilde{w}(0) + e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] }}\tilde{g}(\lower 2pt\sqrt{N(j) e^{\tau/2}N(l)})\bigg) \, {d} \tau \\[3pt] &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) \bigg(-\widetilde{w}(0) + e^{\tau/2}N(l)\tilde{g}(0)+ e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}}\tilde{g}(\lower 2pt\sqrt{N(j) e^{\tau/2}N(l)})\bigg) \, {d} \tau. \end{align*} $$
$$ \begin{align*} I_{l}^{+}(X)&= \frac 1{\mathcal{L}}\int_{0}^{\infty} \widehat{\phi}\bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \bigg(-\widetilde{w}(0) + \sum_{k \in \mathbb Z[i]} g\bigg(N(k)\sqrt{\frac {e^{-\tau}}{N(l^{2})}}\bigg) \bigg)\, {d} \tau \\[3pt] &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) \bigg(-\widetilde{w}(0) + e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] }}\tilde{g}(\lower 2pt\sqrt{N(j) e^{\tau/2}N(l)})\bigg) \, {d} \tau \\[3pt] &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) \bigg(-\widetilde{w}(0) + e^{\tau/2}N(l)\tilde{g}(0)+ e^{\tau/2}N(l)\sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}}\tilde{g}(\lower 2pt\sqrt{N(j) e^{\tau/2}N(l)})\bigg) \, {d} \tau. \end{align*} $$
Moreover, substituting
![]() $\tau $
by
$\tau $
by
![]() $-\tau $
in
$-\tau $
in
![]() $I_{l}^{-}(X)$
, we obtain that
$I_{l}^{-}(X)$
, we obtain that
 $$ \begin{align*}I^{-}_{l}(X)=\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}g \bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) \,{d} \tau. \end{align*} $$
$$ \begin{align*}I^{-}_{l}(X)=\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1 + \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}g \bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) \,{d} \tau. \end{align*} $$
Combining the above expressions for
![]() $I_{l}^{-}(X)$
and
$I_{l}^{-}(X)$
and
![]() $I_{l}^{+}(X)$
, we readily derive the expression for
$I_{l}^{+}(X)$
, we readily derive the expression for
![]() $I_{l}(X)$
in (3-13). The expression for
$I_{l}(X)$
in (3-13). The expression for
![]() $I_{(1+i)l}(X)$
in (3-14) can be similarly obtained via the expression for
$I_{(1+i)l}(X)$
in (3-14) can be similarly obtained via the expression for
![]() $I_{l}(X)$
with the function
$I_{l}(X)$
with the function
![]() $g(y)$
replaced by
$g(y)$
replaced by
![]() $g(y/2)$
, and this completes the proof.
$g(y/2)$
, and this completes the proof.
We define the functions
 $$ \begin{align*} h_{1}(x) = \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\sum_{\substack{l \equiv 1 \bmod {(1+i)^{3}}}}\frac {\mu_{[i]}(l)}{N(l)} ( \tilde{g}(\!\sqrt{2 N(l)x } )- \tilde{g}(\!\sqrt{ N(l)x } ) ) \end{align*} $$
$$ \begin{align*} h_{1}(x) = \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\sum_{\substack{l \equiv 1 \bmod {(1+i)^{3}}}}\frac {\mu_{[i]}(l)}{N(l)} ( \tilde{g}(\!\sqrt{2 N(l)x } )- \tilde{g}(\!\sqrt{ N(l)x } ) ) \end{align*} $$
and
 $$ \begin{align*} h_{2}(x)= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\sum_{\substack{ l \equiv 1 \bmod {(1+i)^{3}}}}\frac {\mu_{[i]}(l)}{N(l^{2})}\bigg (\frac 12 g\bigg(\frac {x}{2N(l)}\bigg)- g\bigg(\frac {x}{N(l)}\bigg)\bigg). \end{align*} $$
$$ \begin{align*} h_{2}(x)= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\sum_{\substack{ l \equiv 1 \bmod {(1+i)^{3}}}}\frac {\mu_{[i]}(l)}{N(l^{2})}\bigg (\frac 12 g\bigg(\frac {x}{2N(l)}\bigg)- g\bigg(\frac {x}{N(l)}\bigg)\bigg). \end{align*} $$
It is easy to see that
![]() $h_{1}(x)$
and
$h_{1}(x)$
and
![]() $h_{2}(x)$
are smooth on
$h_{2}(x)$
are smooth on
![]() $(0, \infty )$
and
$(0, \infty )$
and
![]() $[0, \infty )$
, respectively. Moreover, we have the bounds
$[0, \infty )$
, respectively. Moreover, we have the bounds
![]() $h_{1}(x)\ll x^{-A}$
for any
$h_{1}(x)\ll x^{-A}$
for any
![]() $A\geq 1$
and
$A\geq 1$
and
![]() $h_{2}(x)\ll x^{-3/2+\varepsilon }$
for any
$h_{2}(x)\ll x^{-3/2+\varepsilon }$
for any
![]() $\varepsilon>0$
under the GRH. We point out here that the above notation and bounds are inspired by the corresponding notation introduced on page 1206 of [Reference Fiorilli, Parks and Södergren10].
$\varepsilon>0$
under the GRH. We point out here that the above notation and bounds are inspired by the corresponding notation introduced on page 1206 of [Reference Fiorilli, Parks and Södergren10].
We now apply Lemma 3.4 to derive the following generalization of [Reference Fiorilli, Parks and Södergren10, Corollary 3.4].
Lemma 3.6. Suppose that the GRH is true. Then, we have for
![]() $\sigma <2$
,
$\sigma <2$
,
 $$ \begin{align*} S_{\mathrm{odd}} = \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u+ J(X)+O(X^{\sigma/6-1/3+\varepsilon}), \end{align*} $$
$$ \begin{align*} S_{\mathrm{odd}} = \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u+ J(X)+O(X^{\sigma/6-1/3+\varepsilon}), \end{align*} $$
where
 $$ \begin{align} J(X) &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \bigg( \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) +\widehat{\phi} \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau. \end{align} $$
$$ \begin{align} J(X) &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \bigg( \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) +\widehat{\phi} \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau. \end{align} $$
Proof. First note that by following the arguments that lead to [Reference Gao and Zhao15, formula (2.13)], we have
 $$ \begin{align} \widetilde{w}(0) = \frac {\pi }{2}\widehat{w}(0). \end{align} $$
$$ \begin{align} \widetilde{w}(0) = \frac {\pi }{2}\widehat{w}(0). \end{align} $$
It follows from (2-10), (3-12) and (3-17) that
 $$ \begin{align} \frac{X}{W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}}\frac {\mu_{[i]}(l)}{N(l^{2})} \widetilde{w}(0) \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u = 2 \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u +O(Z^{-3/2+\varepsilon}). \end{align} $$
$$ \begin{align} \frac{X}{W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}}\frac {\mu_{[i]}(l)}{N(l^{2})} \widetilde{w}(0) \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u = 2 \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u +O(Z^{-3/2+\varepsilon}). \end{align} $$
We now combine Lemmas 3.3, 3.4 and (3-18) to obtain that if
![]() $Z \leq X^{2}$
, then
$Z \leq X^{2}$
, then
 $$ \begin{align} S_{\mathrm{odd}} &= \frac{X}{W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \bigg( \int_{0}^{\infty} \widehat \phi \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2}N(l)\ \nonumber\\[3pt] &\quad \times \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} ( \tilde{g}(2\lower 2pt\sqrt{N(\,j) e^{\tau/2}N(l)} )-\tilde{g}(\lower 2pt\sqrt {N(\,j) e^{\tau/2}N(l)}) ) \, {d} \tau\nonumber\\[3pt] &\quad +\int_{0}^{\infty} \widehat{\phi}\, \bigg( 1 -\frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}}\bigg ( \frac 12 g\bigg(\frac {N(k)}{2}\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) -g\bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg)\bigg ) \,{d} \tau \bigg ) \nonumber\\[3pt] &\quad +\int_{1}^{\infty} \widehat{\phi}(u)\, {d} u +O(X^{-3/4+\varepsilon}+X^{\varepsilon}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ). \end{align} $$
$$ \begin{align} S_{\mathrm{odd}} &= \frac{X}{W(X)} \sum_{\substack{N(l) \leq Z \\ l \equiv 1 \bmod {(1+i)^{3}}}} \frac {\mu_{[i]}(l)}{N(l^{2})} \bigg( \int_{0}^{\infty} \widehat \phi \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2}N(l)\ \nonumber\\[3pt] &\quad \times \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} ( \tilde{g}(2\lower 2pt\sqrt{N(\,j) e^{\tau/2}N(l)} )-\tilde{g}(\lower 2pt\sqrt {N(\,j) e^{\tau/2}N(l)}) ) \, {d} \tau\nonumber\\[3pt] &\quad +\int_{0}^{\infty} \widehat{\phi}\, \bigg( 1 -\frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}}\bigg ( \frac 12 g\bigg(\frac {N(k)}{2}\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg) -g\bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg)\bigg ) \,{d} \tau \bigg ) \nonumber\\[3pt] &\quad +\int_{1}^{\infty} \widehat{\phi}(u)\, {d} u +O(X^{-3/4+\varepsilon}+X^{\varepsilon}Z^{-1}+ZX^{\sigma/2-1+\varepsilon}+X^{-1/2+\varepsilon}Z^{\varepsilon} ). \end{align} $$
Note that for the first two integrals in the above expression, we have
 $$ \begin{align*} &\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2}N(l) \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} ( \tilde{g}(2\lower 2pt\sqrt {N(\,j) e^{\tau/2}N(l)}) -\tilde{g}(\lower 2pt\sqrt {N(\,j) e^{\tau/2}N(l)}\,))\, {d} \tau \\[3pt] &\quad \ll \frac {1}{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\, \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \, {d} \tau \ll 1 \end{align*} $$
$$ \begin{align*} &\frac 1{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2}N(l) \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} ( \tilde{g}(2\lower 2pt\sqrt {N(\,j) e^{\tau/2}N(l)}) -\tilde{g}(\lower 2pt\sqrt {N(\,j) e^{\tau/2}N(l)}\,))\, {d} \tau \\[3pt] &\quad \ll \frac {1}{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi}\, \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \, {d} \tau \ll 1 \end{align*} $$
and
 $$ \begin{align*} &\frac {1}{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi} \bigg( 1 - \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\bigg ( \frac 12 g\bigg(\frac {N(k)}{2}\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg)-g\bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg)\bigg) \,{d} \tau \\[3pt] &\quad \ll \frac {1}{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi} \bigg( 1 - \frac{\tau}{\mathcal{L}} \bigg) N(l) e^{-\tau/2} \,{d} \tau \ll N(l). \end{align*} $$
$$ \begin{align*} &\frac {1}{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi} \bigg( 1 - \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}}\bigg ( \frac 12 g\bigg(\frac {N(k)}{2}\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg)-g\bigg(N(k)\sqrt{\frac {e^{\tau}}{N(l^{2})}}\bigg)\bigg) \,{d} \tau \\[3pt] &\quad \ll \frac {1}{\mathcal{L}} \int_{0}^{\infty} \widehat{\phi} \bigg( 1 - \frac{\tau}{\mathcal{L}} \bigg) N(l) e^{-\tau/2} \,{d} \tau \ll N(l). \end{align*} $$
We can therefore use
![]() $\Phi (X)$
defined in (3-12) and partial summation to extend the sum over l to all odd elements in
$\Phi (X)$
defined in (3-12) and partial summation to extend the sum over l to all odd elements in
![]() $\mathcal {O}_{K}$
by introducing an extra error term of size
$\mathcal {O}_{K}$
by introducing an extra error term of size
![]() $O(X^{\varepsilon }Z^{-3/2})$
. We now set
$O(X^{\varepsilon }Z^{-3/2})$
. We now set
![]() $Z=X^{2/3 - \sigma /3}$
, change the order of summation in (3-19) and apply (2-10) to derive the desired result.
$Z=X^{2/3 - \sigma /3}$
, change the order of summation in (3-19) and apply (2-10) to derive the desired result.
4 Proof of Theorem 1.1
We combine Lemmas 2.4, 2.6, 3.1 and 3.5 to arrive at the following result.
Lemma 4.1. Suppose that the GRH is true. Let
![]() $\phi (x)$
be an even Schwartz function whose Fourier transform
$\phi (x)$
be an even Schwartz function whose Fourier transform
![]() $\hat {\phi }(u)$
has compact support in
$\hat {\phi }(u)$
has compact support in
![]() $(-2,2)$
and let w be an even nonzero and nonnegative Schwartz function. For any integer
$(-2,2)$
and let w be an even nonzero and nonnegative Schwartz function. For any integer
![]() $M \geq 1$
, the one-level density of low-lying zeros in the family
$M \geq 1$
, the one-level density of low-lying zeros in the family
![]() $\mathcal F$
of quadratic Hecke L-functions is given by
$\mathcal F$
of quadratic Hecke L-functions is given by
 $$ \begin{align} \mathcal D(\phi;w, X) &= \widehat{\phi} (0)-\frac{1}2\int_{-1}^{1} \widehat{\phi}(u)\, {d} u \nonumber\\[3pt] &\quad +\frac{\widehat{\phi}(0)}{\mathcal{L}} \bigg( \log\frac {32}{\pi^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma}\bigg( \frac 12 \bigg) + \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x\, {d} x \bigg) \nonumber\\[3pt] &\quad +J(X) +\frac{2}{\mathcal{L} }\int_{0}^{\infty}\frac{e^{-x/2}}{1-e^{-x}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{x}{\mathcal{L} }\bigg)\bigg) \,{d} x \nonumber\\[3pt] &\quad + \sum_{m=1}^{M} \frac{d_{m} \widehat{\phi}^{(m-1)}(0)}{\mathcal{L} {}^{m}} +O\bigg( \frac 1{\mathcal{L} {}^{M+1}} \bigg), \end{align} $$
$$ \begin{align} \mathcal D(\phi;w, X) &= \widehat{\phi} (0)-\frac{1}2\int_{-1}^{1} \widehat{\phi}(u)\, {d} u \nonumber\\[3pt] &\quad +\frac{\widehat{\phi}(0)}{\mathcal{L}} \bigg( \log\frac {32}{\pi^{2}}+ 2\frac {\Gamma^{\prime}}{\Gamma}\bigg( \frac 12 \bigg) + \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x\, {d} x \bigg) \nonumber\\[3pt] &\quad +J(X) +\frac{2}{\mathcal{L} }\int_{0}^{\infty}\frac{e^{-x/2}}{1-e^{-x}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{x}{\mathcal{L} }\bigg)\bigg) \,{d} x \nonumber\\[3pt] &\quad + \sum_{m=1}^{M} \frac{d_{m} \widehat{\phi}^{(m-1)}(0)}{\mathcal{L} {}^{m}} +O\bigg( \frac 1{\mathcal{L} {}^{M+1}} \bigg), \end{align} $$
where
![]() $J(X)$
is given as in Lemma 3.5 and the coefficients
$J(X)$
is given as in Lemma 3.5 and the coefficients
![]() $d_{k}$
are explicitly computable numbers given in Lemma 3.1.
$d_{k}$
are explicitly computable numbers given in Lemma 3.1.
The next lemma allows us to expand
![]() $J(X)$
in descending powers of
$J(X)$
in descending powers of
![]() $\mathcal {L} = \log X$
. This is a generalization of [Reference Fiorilli, Parks and Södergren10, Lemma 3.6].
$\mathcal {L} = \log X$
. This is a generalization of [Reference Fiorilli, Parks and Södergren10, Lemma 3.6].
Lemma 4.2. Suppose that the GRH is true and suppose that
 $$ \begin{align*} \sigma=\sup(\mathrm{supp }\,\widehat{\phi})< 2. \end{align*} $$
$$ \begin{align*} \sigma=\sup(\mathrm{supp }\,\widehat{\phi})< 2. \end{align*} $$
Then, for any integer
![]() $M\geq 1$
, we have the expansion
$M\geq 1$
, we have the expansion
 $$ \begin{align} J(X)=\sum_{m=1}^{M} \frac{c_{w,m} \widehat{\phi}^{(m-1)}(1)}{\mathcal{L}^{m}}+ O\bigg( \frac 1{\mathcal{L} {}^{M+1}} \bigg), \end{align} $$
$$ \begin{align} J(X)=\sum_{m=1}^{M} \frac{c_{w,m} \widehat{\phi}^{(m-1)}(1)}{\mathcal{L}^{m}}+ O\bigg( \frac 1{\mathcal{L} {}^{M+1}} \bigg), \end{align} $$
where the constants
![]() $c_{w,m}$
can be given explicitly.
$c_{w,m}$
can be given explicitly.
Proof. Note that as
 $\sigma =\sup (\mathrm {supp }\,\widehat {\phi })< 2$
, we have
$\sigma =\sup (\mathrm {supp }\,\widehat {\phi })< 2$
, we have
 $$ \begin{align*} & J(X)\\[3pt] &\quad= \frac 1{\mathcal{L}} \int_{0}^{\mathcal{L} } \bigg( \widehat{\phi} ( 1+ \tau/\mathcal{L} ) \sqrt{2}e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) +\widehat{\phi} ( 1-\tau/\mathcal{L} ) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau. \end{align*} $$
$$ \begin{align*} & J(X)\\[3pt] &\quad= \frac 1{\mathcal{L}} \int_{0}^{\mathcal{L} } \bigg( \widehat{\phi} ( 1+ \tau/\mathcal{L} ) \sqrt{2}e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) +\widehat{\phi} ( 1-\tau/\mathcal{L} ) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau. \end{align*} $$
Recall that we have the bounds
![]() $h_{1}(x)\ll x^{-N}$
for any
$h_{1}(x)\ll x^{-N}$
for any
![]() $N\geq 1$
and
$N\geq 1$
and
![]() $h_{2}(x)\ll x^{-3/2+\varepsilon }$
for any
$h_{2}(x)\ll x^{-3/2+\varepsilon }$
for any
![]() $\varepsilon>0$
under the GRH. It follows from this that we can expand
$\varepsilon>0$
under the GRH. It follows from this that we can expand
![]() $\widehat {\phi }$
in Taylor series to obtain that
$\widehat {\phi }$
in Taylor series to obtain that
 $$ \begin{align} J(X)&= \sum_{m=1}^{M} \frac {\widehat{\phi}^{(m-1)}(1)}{(m-1)!\mathcal{L} {}^{m}} \int_{0}^{\mathcal{L} } \bigg( \tau^{m-1} e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) \nonumber\\[3pt] &\quad + (-\tau)^{m-1} \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau +O(\mathcal{L} {}^{-M-1}), \end{align} $$
$$ \begin{align} J(X)&= \sum_{m=1}^{M} \frac {\widehat{\phi}^{(m-1)}(1)}{(m-1)!\mathcal{L} {}^{m}} \int_{0}^{\mathcal{L} } \bigg( \tau^{m-1} e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) \nonumber\\[3pt] &\quad + (-\tau)^{m-1} \sum_{\substack {k \in \mathbb Z[i]\\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau +O(\mathcal{L} {}^{-M-1}), \end{align} $$
since here the error term introduced can be estimated as
 $$ \begin{align*} & \ll \mathcal{L} {}^{-M-1} \int_{0}^{\mathcal{L} } ( \tau^{M}e^{-\tau/2} + (-\tau)^{M}e^{-(3/4+\varepsilon)\tau} )\, {d} \tau \\[3pt] & \ll \mathcal{L} {}^{-M-1} \int_{0}^{\infty} ( \tau^{M}e^{-\tau/2} + (-\tau)^{M}e^{-(3/4+\varepsilon)\tau} )\, {d} \tau \ll \mathcal{L} {}^{-M-1}. \end{align*} $$
$$ \begin{align*} & \ll \mathcal{L} {}^{-M-1} \int_{0}^{\mathcal{L} } ( \tau^{M}e^{-\tau/2} + (-\tau)^{M}e^{-(3/4+\varepsilon)\tau} )\, {d} \tau \\[3pt] & \ll \mathcal{L} {}^{-M-1} \int_{0}^{\infty} ( \tau^{M}e^{-\tau/2} + (-\tau)^{M}e^{-(3/4+\varepsilon)\tau} )\, {d} \tau \ll \mathcal{L} {}^{-M-1}. \end{align*} $$
We now extend the integral in (4-3) to infinity and note that the error introduced by this extension can be easily shown to be
 $$ \begin{align*} \ll \sum_{m=1}^{M} \frac {\widehat{\phi}^{(m-1)}(1)}{(m-1)!\mathcal{L} {}^{m}} \int^{\infty}_{\mathcal{L}} ( \tau^{m-1}e^{-\tau}+ (-\tau)^{m-1} e^{-(3/4+\epsilon)\tau})\, {d} \tau \ll \mathcal{L} {}^{-M-1}. \end{align*} $$
$$ \begin{align*} \ll \sum_{m=1}^{M} \frac {\widehat{\phi}^{(m-1)}(1)}{(m-1)!\mathcal{L} {}^{m}} \int^{\infty}_{\mathcal{L}} ( \tau^{m-1}e^{-\tau}+ (-\tau)^{m-1} e^{-(3/4+\epsilon)\tau})\, {d} \tau \ll \mathcal{L} {}^{-M-1}. \end{align*} $$
We then deduce from this and (4-3) that
 $$ \begin{align*} J(X)&= \sum_{m=1}^{M} \frac {\widehat{\phi}^{(m-1)}(1)}{(m-1)!\mathcal{L} {}^{m}} \int_{0}^{\infty} \bigg( \tau^{m-1}\sqrt{2}e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ (j, 1+i)\,=1}} h_{1}(N(j)e^{\tau/2}) \\[3pt] &\quad + (-\tau)^{m-1} \sum_{\substack {k \in \mathbb Z[i] , k \neq 0}}(-1)^{N(k)} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau +O(\mathcal{L} {}^{-M-1}). \end{align*} $$
$$ \begin{align*} J(X)&= \sum_{m=1}^{M} \frac {\widehat{\phi}^{(m-1)}(1)}{(m-1)!\mathcal{L} {}^{m}} \int_{0}^{\infty} \bigg( \tau^{m-1}\sqrt{2}e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ (j, 1+i)\,=1}} h_{1}(N(j)e^{\tau/2}) \\[3pt] &\quad + (-\tau)^{m-1} \sum_{\substack {k \in \mathbb Z[i] , k \neq 0}}(-1)^{N(k)} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau +O(\mathcal{L} {}^{-M-1}). \end{align*} $$
As the integral in the above expression converges, the assertion of the lemma now follows from this.
We now substitute (4-2) into (4-1) and expand
 $\widehat {\phi }(x/\mathcal {L} )$
into its Taylor series around
$\widehat {\phi }(x/\mathcal {L} )$
into its Taylor series around
![]() $0$
so that
$0$
so that
 $$ \begin{align*} \widehat{\phi}(x/\mathcal{L} )=& \sum_{m=0}^{M} \frac {\widehat{\phi}^{(m)}(0)}{(m)!\mathcal{L} {}^{m}} \int_{0}^{\infty} \bigg( \tau^{m-1}\sqrt{2}e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ (j, 1+i)=1}} h_{1}(N(j)e^{\tau/2}) \\[3pt] & + (-\tau)^{m-1} \sum_{\substack {k \in \mathbb Z[i] , k \neq 0}}(-1)^{N(k)} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau +O(\mathcal{L} {}^{-M-1}), \end{align*} $$
$$ \begin{align*} \widehat{\phi}(x/\mathcal{L} )=& \sum_{m=0}^{M} \frac {\widehat{\phi}^{(m)}(0)}{(m)!\mathcal{L} {}^{m}} \int_{0}^{\infty} \bigg( \tau^{m-1}\sqrt{2}e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ (j, 1+i)=1}} h_{1}(N(j)e^{\tau/2}) \\[3pt] & + (-\tau)^{m-1} \sum_{\substack {k \in \mathbb Z[i] , k \neq 0}}(-1)^{N(k)} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau +O(\mathcal{L} {}^{-M-1}), \end{align*} $$
and an interchange of the series and the integral allow us to deduce (1-2). In particular, we see that we have for
![]() $m \geq 2$
,
$m \geq 2$
,
 $$ \begin{align} R_{w,m}(\phi)=c_{w,m} \widehat{\phi}^{(m-1)}(1)+d_{m}\widehat{\phi}^{(m-1)}(0)-\frac {2\widehat{\phi}^{(m-1)}(0)}{(m-1)!}\int_{0}^{\infty}\frac{e^{-x/2}x^{m-1}}{1-e^{-x}}\,{d} x. \end{align} $$
$$ \begin{align} R_{w,m}(\phi)=c_{w,m} \widehat{\phi}^{(m-1)}(1)+d_{m}\widehat{\phi}^{(m-1)}(0)-\frac {2\widehat{\phi}^{(m-1)}(0)}{(m-1)!}\int_{0}^{\infty}\frac{e^{-x/2}x^{m-1}}{1-e^{-x}}\,{d} x. \end{align} $$
This completes the proof of Theorem 1.1.
5 Proof of Theorem 1.2
We first follow the recipe given in [Reference Conrey, Farmer and Zirnbauer4] to derive a suitable version of the ratios conjecture for the family
![]() $\mathcal F$
. We start by considering the expression
$\mathcal F$
. We start by considering the expression
 $$ \begin{align} R(\alpha,\beta)=\frac1{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{L(1/2+\alpha,\chi_{i(1+i)^{5}c})}{L(1/2+\beta,\chi_{i(1+i)^{5}c})}. \end{align} $$
$$ \begin{align} R(\alpha,\beta)=\frac1{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{L(1/2+\alpha,\chi_{i(1+i)^{5}c})}{L(1/2+\beta,\chi_{i(1+i)^{5}c})}. \end{align} $$
Similarly to the treatment in [Reference Gao and Zhao16, Section 4.1], we use the approximation
 $$ \begin{align} L(s, \chi_{i(1+i)^{5}c})\approx \sum_{\mathfrak{n} \neq 0} \frac{\chi_{i(1+i)^{5}c}(\mathfrak{n})}{N(\mathfrak{n})^{s}}+X_{c}(s)\sum_{\mathfrak{n} \neq 0} \frac{\chi_{i(1+i)^{5}c}(\mathfrak{n} )}{N(\mathfrak{n})^{1-s}}, \end{align} $$
$$ \begin{align} L(s, \chi_{i(1+i)^{5}c})\approx \sum_{\mathfrak{n} \neq 0} \frac{\chi_{i(1+i)^{5}c}(\mathfrak{n})}{N(\mathfrak{n})^{s}}+X_{c}(s)\sum_{\mathfrak{n} \neq 0} \frac{\chi_{i(1+i)^{5}c}(\mathfrak{n} )}{N(\mathfrak{n})^{1-s}}, \end{align} $$
where
![]() $\sum _{\mathfrak {n} \neq 0}$
denotes a sum over nonzero integral ideals in
$\sum _{\mathfrak {n} \neq 0}$
denotes a sum over nonzero integral ideals in
![]() $\mathcal {O}_{K}$
and
$\mathcal {O}_{K}$
and
 $$ \begin{align} X_{c}(s)=\frac{\Gamma(1-s)}{\Gamma(s )}\bigg(\frac{\pi^{2}}{32N(c)}\bigg)^{s-1/2}. \end{align} $$
$$ \begin{align} X_{c}(s)=\frac{\Gamma(1-s)}{\Gamma(s )}\bigg(\frac{\pi^{2}}{32N(c)}\bigg)^{s-1/2}. \end{align} $$
Writing
![]() $\mu _{[i]}$
for the Möbius function on K, we obtain that for
$\mu _{[i]}$
for the Möbius function on K, we obtain that for
![]() $\mathrm {Re}(s)>1$
,
$\mathrm {Re}(s)>1$
,
 $$ \begin{align} \frac{1}{L(s,\chi_{i(1+i)^{5}c})} = \sum_{\mathfrak{m} \neq 0} \frac{\mu_{[i]}(\mathfrak{m})\chi_{i(1+i)^{5}c}(\mathfrak{m})}{N(\mathfrak{m})^{s}}. \end{align} $$
$$ \begin{align} \frac{1}{L(s,\chi_{i(1+i)^{5}c})} = \sum_{\mathfrak{m} \neq 0} \frac{\mu_{[i]}(\mathfrak{m})\chi_{i(1+i)^{5}c}(\mathfrak{m})}{N(\mathfrak{m})^{s}}. \end{align} $$
Applying (5-2) and (5-4) to (5-1), we see that
where
 $$ \begin{align*} R_{1}(\alpha, \beta) = \frac1{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \sum_{\mathfrak{m},\mathfrak{n}\neq 0} \frac{\mu_{[i]}(\mathfrak{m})\chi_{i(1+i)^{5}c}(\mathfrak{nm})}{N(\mathfrak{m})^{1/2+\beta}N(\mathfrak{n})^{1/2 +\alpha}} \end{align*} $$
$$ \begin{align*} R_{1}(\alpha, \beta) = \frac1{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \sum_{\mathfrak{m},\mathfrak{n}\neq 0} \frac{\mu_{[i]}(\mathfrak{m})\chi_{i(1+i)^{5}c}(\mathfrak{nm})}{N(\mathfrak{m})^{1/2+\beta}N(\mathfrak{n})^{1/2 +\alpha}} \end{align*} $$
and
 $$ \begin{align*} R_{2}(\alpha, \beta)= \frac1{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) X_{c}\bigg(\frac{1}{2} + \alpha\bigg) \sum_{\mathfrak{m},\mathfrak{n}\neq 0} \frac{\mu_{[i]}(\mathfrak{m})\chi_{i(1+i)^{5}c}(\mathfrak{nm})}{N(\mathfrak{m})^{1/2+\beta}N(\mathfrak{n})^{1/2 -\alpha}}. \end{align*} $$
$$ \begin{align*} R_{2}(\alpha, \beta)= \frac1{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) X_{c}\bigg(\frac{1}{2} + \alpha\bigg) \sum_{\mathfrak{m},\mathfrak{n}\neq 0} \frac{\mu_{[i]}(\mathfrak{m})\chi_{i(1+i)^{5}c}(\mathfrak{nm})}{N(\mathfrak{m})^{1/2+\beta}N(\mathfrak{n})^{1/2 -\alpha}}. \end{align*} $$
When
![]() $\mathfrak {nm}$
is an odd square, we expect to gain a main contribution to both
$\mathfrak {nm}$
is an odd square, we expect to gain a main contribution to both
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
. Applying Lemma 2.3, we have in this case
$R_{2}$
. Applying Lemma 2.3, we have in this case
 $$ \begin{align*} \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg)\,\chi_{i(1+i)^{5}c}(\mathfrak{nm})\approx \prod_{\substack{ \varpi \equiv 1 \bmod {(1+i)^{3}} \\ \varpi\mid \mathfrak{nm}}} \bigg(1+\frac 1{N(\varpi)} \bigg)^{-1}. \end{align*} $$
$$ \begin{align*} \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg)\,\chi_{i(1+i)^{5}c}(\mathfrak{nm})\approx \prod_{\substack{ \varpi \equiv 1 \bmod {(1+i)^{3}} \\ \varpi\mid \mathfrak{nm}}} \bigg(1+\frac 1{N(\varpi)} \bigg)^{-1}. \end{align*} $$
We then deduce that, upon writing
![]() $\square $
for a perfect square,
$\square $
for a perfect square,
 $$ \begin{align*} R_{1}(\alpha, \beta) \sim \widetilde R_{1}(\alpha, \beta)&= \sum_{\mathfrak{nm} = \text{odd } \square} \frac{\mu_{[i]}(\mathfrak{m})}{N(\mathfrak{m})^{1/2+\beta}N(\mathfrak{n})^{1/2 + \alpha}} \\[3pt] &\quad \times \prod_{\substack{ \varpi \equiv 1 \bmod {(1+i)^{3}} \\ \varpi\mid \mathfrak{nm}}} \bigg(1+\frac 1{N(\varpi)} \bigg)^{-1}. \end{align*} $$
$$ \begin{align*} R_{1}(\alpha, \beta) \sim \widetilde R_{1}(\alpha, \beta)&= \sum_{\mathfrak{nm} = \text{odd } \square} \frac{\mu_{[i]}(\mathfrak{m})}{N(\mathfrak{m})^{1/2+\beta}N(\mathfrak{n})^{1/2 + \alpha}} \\[3pt] &\quad \times \prod_{\substack{ \varpi \equiv 1 \bmod {(1+i)^{3}} \\ \varpi\mid \mathfrak{nm}}} \bigg(1+\frac 1{N(\varpi)} \bigg)^{-1}. \end{align*} $$
A computation using the Euler product of
![]() $\zeta_K$
shows that
$\zeta_K$
shows that
 $$ \begin{align} \widetilde R_{1}(\alpha,\beta)= \frac{\zeta_{K}(1+2\alpha)}{\zeta_{K}(1+\alpha+\beta)}A(\alpha,\beta), \end{align} $$
$$ \begin{align} \widetilde R_{1}(\alpha,\beta)= \frac{\zeta_{K}(1+2\alpha)}{\zeta_{K}(1+\alpha+\beta)}A(\alpha,\beta), \end{align} $$
where
 $$ \begin{align} A(\alpha,\beta) &= \bigg(\frac{2^{1+\alpha+\beta}-2^{\beta-\alpha}}{2^{1+\alpha+\beta}-1}\bigg) \prod_{\varpi\, \equiv 1 \bmod {(1+i)^{3}}} \bigg(1 -\frac{1}{N(\varpi)^{1+\alpha+\beta}}\bigg)^{-1} \nonumber\\[3pt] &\quad \times \bigg(1-\frac{1}{(N(\varpi)+1)N(\varpi)^{1+2\alpha}} -\frac{1}{(N(\varpi)+1)N(\varpi)^{\alpha+\beta}}\bigg). \end{align} $$
$$ \begin{align} A(\alpha,\beta) &= \bigg(\frac{2^{1+\alpha+\beta}-2^{\beta-\alpha}}{2^{1+\alpha+\beta}-1}\bigg) \prod_{\varpi\, \equiv 1 \bmod {(1+i)^{3}}} \bigg(1 -\frac{1}{N(\varpi)^{1+\alpha+\beta}}\bigg)^{-1} \nonumber\\[3pt] &\quad \times \bigg(1-\frac{1}{(N(\varpi)+1)N(\varpi)^{1+2\alpha}} -\frac{1}{(N(\varpi)+1)N(\varpi)^{\alpha+\beta}}\bigg). \end{align} $$
Note that the product
![]() $A(\alpha ,\beta )$
is absolutely convergent for
$A(\alpha ,\beta )$
is absolutely convergent for
![]() $\mathrm {Re}(\alpha )$
,
$\mathrm {Re}(\alpha )$
,
![]() $\mathrm {Re}(\beta )> -1/4$
.
$\mathrm {Re}(\beta )> -1/4$
.
Similarly, we obtain
 $$ \begin{align} R_{2}(\alpha, \beta) \approx \widetilde R_{2}(\alpha, \beta)=\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) X_{c}\bigg(\frac{1}{2} + \alpha\bigg)\widetilde R_{1}(-\alpha,\beta). \end{align} $$
$$ \begin{align} R_{2}(\alpha, \beta) \approx \widetilde R_{2}(\alpha, \beta)=\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) X_{c}\bigg(\frac{1}{2} + \alpha\bigg)\widetilde R_{1}(-\alpha,\beta). \end{align} $$
Combining (5-5) with (5-6) and (5-8), we deduce the following appropriate version of the ratios conjecture for our family
![]() $\mathcal F$
.
$\mathcal F$
.
Conjecture 5.1. Let
![]() $\varepsilon>0$
and let w be an even and nonnegative Schwartz test function on
$\varepsilon>0$
and let w be an even and nonnegative Schwartz test function on
![]() $\mathbb {R}$
which is not identically zero. For complex numbers
$\mathbb {R}$
which is not identically zero. For complex numbers
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
satisfying
$\beta $
satisfying
![]() $|\mathrm {Re}(\alpha )|< 1/4$
,
$|\mathrm {Re}(\alpha )|< 1/4$
,
![]() $(\log X)^{-1} \ll \mathrm {Re}(\,\beta ) < 1/4$
and
$(\log X)^{-1} \ll \mathrm {Re}(\,\beta ) < 1/4$
and
![]() $\mathrm {Im}(\alpha ), \mathrm {Im}(\beta ) \ll X^{1-\varepsilon }$
, we have that
$\mathrm {Im}(\alpha ), \mathrm {Im}(\beta ) \ll X^{1-\varepsilon }$
, we have that
 $$ \begin{align*} &\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{L( 1/2 +\alpha,\chi_{i(1+i)^{5}c} )}{L( 1/2 + \beta,\chi_{i(1+i)^{5}c} )} \\[3pt] &\quad= \frac{\zeta_{K}(1+2\alpha)}{\zeta_{K}(1+\alpha+\beta)}A(\alpha,\beta) \\[3pt] &\qquad+\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) X_{c}\bigg(\frac{1}{2}+\alpha\bigg) \frac{\zeta_{K}(1-2\alpha)}{\zeta_{K}(1-\alpha+\beta)}A(-\alpha,\beta) \\[3pt] &\qquad+ O_{\varepsilon}(X^{-1/2+\varepsilon}), \end{align*} $$
$$ \begin{align*} &\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{L( 1/2 +\alpha,\chi_{i(1+i)^{5}c} )}{L( 1/2 + \beta,\chi_{i(1+i)^{5}c} )} \\[3pt] &\quad= \frac{\zeta_{K}(1+2\alpha)}{\zeta_{K}(1+\alpha+\beta)}A(\alpha,\beta) \\[3pt] &\qquad+\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) X_{c}\bigg(\frac{1}{2}+\alpha\bigg) \frac{\zeta_{K}(1-2\alpha)}{\zeta_{K}(1-\alpha+\beta)}A(-\alpha,\beta) \\[3pt] &\qquad+ O_{\varepsilon}(X^{-1/2+\varepsilon}), \end{align*} $$
where
![]() $A(\alpha ,\beta )$
is defined in (5-7) and
$A(\alpha ,\beta )$
is defined in (5-7) and
![]() $X_{c}(s)$
is defined in (5-3).
$X_{c}(s)$
is defined in (5-3).
Similarly to the derivation of [Reference Gao and Zhao16, Lemma 4.3], we deduce from Conjecture 5.1 the following result needed in the calculation of the one-level density.
Lemma 5.2. Assuming the truth of the GRH and Conjecture 5.1, we have for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $(\log X)^{-1} \ll \mathrm {Re}(r)<1/4$
and
$(\log X)^{-1} \ll \mathrm {Re}(r)<1/4$
and
![]() $\mathrm {Im}(r)\ll X^{1-\varepsilon }$
,
$\mathrm {Im}(r)\ll X^{1-\varepsilon }$
,
 $$ \begin{align*} &\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{L^{\prime} ( 1/2 + r,\chi_{i(1+i)^{5}c} )}{L ( 1/2 + r,\chi_{i(1+i)^{5}c} )} \\[3pt] &\quad= \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+A_{\alpha}(r,r) -\frac 4{\pi}\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \\[3pt] & \qquad \times X_{c}\bigg(\frac{1}{2}+r\bigg) \zeta_{K}(1-2r)A(-r,r)+ O_{\varepsilon}(X^{-1/2+\varepsilon}), \end{align*} $$
$$ \begin{align*} &\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{L^{\prime} ( 1/2 + r,\chi_{i(1+i)^{5}c} )}{L ( 1/2 + r,\chi_{i(1+i)^{5}c} )} \\[3pt] &\quad= \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+A_{\alpha}(r,r) -\frac 4{\pi}\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \\[3pt] & \qquad \times X_{c}\bigg(\frac{1}{2}+r\bigg) \zeta_{K}(1-2r)A(-r,r)+ O_{\varepsilon}(X^{-1/2+\varepsilon}), \end{align*} $$
where
 $$ \begin{align*} A_{\alpha}(r,r) = \frac{\partial}{\partial \alpha}A(\alpha,\beta)\bigg|_{\alpha=\beta=r}. \end{align*} $$
$$ \begin{align*} A_{\alpha}(r,r) = \frac{\partial}{\partial \alpha}A(\alpha,\beta)\bigg|_{\alpha=\beta=r}. \end{align*} $$
We now proceed as in [Reference Gao and Zhao16, Section 4.4]. Assuming the truth of the GRH, it follows from Lemma 5.1 that
 $$ \begin{align} D(\phi;w, X)&= \frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i}\int_{(a-1/2)} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)} \nonumber\\[3pt] &\quad +2A_{\alpha}(r,r) -\frac{X_{c}^{\prime}(1/2+r)}{X_{c}(1/2+r)} \nonumber\\[3pt] &\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i \mathcal{L} r}{2\pi}\bigg) \,{d} r \nonumber\\[3pt] &\quad + O_{\varepsilon} ( X^{-1/2+\varepsilon} ), \end{align} $$
$$ \begin{align} D(\phi;w, X)&= \frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i}\int_{(a-1/2)} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)} \nonumber\\[3pt] &\quad +2A_{\alpha}(r,r) -\frac{X_{c}^{\prime}(1/2+r)}{X_{c}(1/2+r)} \nonumber\\[3pt] &\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i \mathcal{L} r}{2\pi}\bigg) \,{d} r \nonumber\\[3pt] &\quad + O_{\varepsilon} ( X^{-1/2+\varepsilon} ), \end{align} $$
where
![]() $D(\phi ;w, X)$
is defined in (1-1). Note that the integrand in (5-9) is analytic in the region
$D(\phi ;w, X)$
is defined in (1-1). Note that the integrand in (5-9) is analytic in the region
![]() $\mathrm {Re}(r) \geq 0$
(in particular, it is analytic at
$\mathrm {Re}(r) \geq 0$
(in particular, it is analytic at
![]() $r = 0$
). The assertion of Theorem 1.2 now follows by moving the contour of integration from
$r = 0$
). The assertion of Theorem 1.2 now follows by moving the contour of integration from
![]() $\mathrm {Re}(r)=a-1/2$
to
$\mathrm {Re}(r)=a-1/2$
to
![]() $\mathrm {Re}(r)=0$
.
$\mathrm {Re}(r)=0$
.
6 Proof of Theorem 1.3
6.1 Initial treatment
In this section, we consider the expansions of the
![]() $D(\phi ;w, X)$
given in (1-3) as powers of
$D(\phi ;w, X)$
given in (1-3) as powers of
![]() $1/\mathcal {L}$
with
$1/\mathcal {L}$
with
![]() $\mathcal {L}=\log X$
. Recall from (5-9) that, up to an error term of size
$\mathcal {L}=\log X$
. Recall from (5-9) that, up to an error term of size
![]() $O(\mathcal {L}^{-2})$
, we have
$O(\mathcal {L}^{-2})$
, we have
 $$ \begin{align} D (\phi;w, X) &=\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \dfrac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r) \nonumber\\[3pt] & \quad -\frac{X_{c}^{\prime}(1/2+r)}{X_{c}(1/2+r)} -\frac {8}{\pi} X_{c}\bigg(\dfrac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i \mathcal{L} r}{2\pi}\bigg) \,{d} r , \end{align} $$
$$ \begin{align} D (\phi;w, X) &=\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \dfrac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r) \nonumber\\[3pt] & \quad -\frac{X_{c}^{\prime}(1/2+r)}{X_{c}(1/2+r)} -\frac {8}{\pi} X_{c}\bigg(\dfrac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i \mathcal{L} r}{2\pi}\bigg) \,{d} r , \end{align} $$
where
![]() $\mathcal {L}^{-1}<a^{\prime }< 1/4$
.
$\mathcal {L}^{-1}<a^{\prime }< 1/4$
.
We set
 $$ \begin{align} &I=-\frac {8}{\pi} \frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i} \nonumber\\[3pt] &\quad \int_{(a^{\prime})} \bigg( X_{c}\bigg(\frac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i \mathcal{L} r}{2\pi}\bigg) \,{d} r. \end{align} $$
$$ \begin{align} &I=-\frac {8}{\pi} \frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i} \nonumber\\[3pt] &\quad \int_{(a^{\prime})} \bigg( X_{c}\bigg(\frac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i \mathcal{L} r}{2\pi}\bigg) \,{d} r. \end{align} $$
We postpone the evaluation of I to the next section and proceed here with the treatment of the other terms on the right-hand side of (6-1).
We deduce first from Lemma 2.3 and (2-10), after partial summation, that
 $$ \begin{align} &\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R} \log\bigg(\frac{32N(c)}{\pi^{2}}\bigg) \phi\bigg(\frac{t \mathcal{L}}{2\pi}\bigg) \, {d} t \nonumber\\[3pt] &\quad= \frac{\widehat{\phi}(0)}{\mathcal{L}}\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \log\bigg(\frac{32N(c)}{\pi^{2}}\bigg) \nonumber\\[3pt] &\quad= \frac{\widehat{\phi}(0)}{\mathcal{L}}\bigg ( \log \frac{32}{\pi^{2}}+\mathcal{L}+ \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x \, {d} x \bigg )+O ( \mathcal{L}^{-2} ). \end{align} $$
$$ \begin{align} &\frac{1}{W(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R} \log\bigg(\frac{32N(c)}{\pi^{2}}\bigg) \phi\bigg(\frac{t \mathcal{L}}{2\pi}\bigg) \, {d} t \nonumber\\[3pt] &\quad= \frac{\widehat{\phi}(0)}{\mathcal{L}}\frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \log\bigg(\frac{32N(c)}{\pi^{2}}\bigg) \nonumber\\[3pt] &\quad= \frac{\widehat{\phi}(0)}{\mathcal{L}}\bigg ( \log \frac{32}{\pi^{2}}+\mathcal{L}+ \frac 2{\widehat w(0)}\int_{0}^{\infty} w(x) \log x \, {d} x \bigg )+O ( \mathcal{L}^{-2} ). \end{align} $$
Next note that, similarly to [Reference Gao and Zhao16, formula (4.33)], we have
 $$ \begin{align} &\frac{1}{{W}(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R}\bigg( \frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12-it\bigg) +\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12+it \bigg)\bigg) \phi\bigg(\frac{t\mathcal{L} }{2\pi}\bigg) \, {d} t\nonumber\\[3pt] &\quad= 2\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12\bigg)\frac{\widehat{\phi}(0)}{\mathcal{L}} +\frac{2}{\mathcal{L}} \int_{0}^{\infty}\frac{e^{-t/2}}{1-e^{-t}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{t}{\mathcal{L}}\bigg)\bigg) \,{d} t. \end{align} $$
$$ \begin{align} &\frac{1}{{W}(X)} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R}\bigg( \frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12-it\bigg) +\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12+it \bigg)\bigg) \phi\bigg(\frac{t\mathcal{L} }{2\pi}\bigg) \, {d} t\nonumber\\[3pt] &\quad= 2\frac{\Gamma^{\prime}}{\Gamma}\bigg(\frac 12\bigg)\frac{\widehat{\phi}(0)}{\mathcal{L}} +\frac{2}{\mathcal{L}} \int_{0}^{\infty}\frac{e^{-t/2}}{1-e^{-t}}\bigg(\widehat{\phi}(0)-\widehat{\phi}\bigg(\frac{t}{\mathcal{L}}\bigg)\bigg) \,{d} t. \end{align} $$
Furthermore, we follow the treatment of [Reference Fiorilli, Parks and Södergren11, Lemma 4.1] to obtain via a direct calculation (noting that
![]() $A(r,r)=1$
) that
$A(r,r)=1$
) that
 $$ \begin{align*} A_{\alpha}(r,r)+\frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}=\frac{-1}{N(\varpi) +1} \sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}} \frac{N(\varpi)\log N(\varpi)}{N(\varpi)^{1+2r}-1}. \end{align*} $$
$$ \begin{align*} A_{\alpha}(r,r)+\frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}=\frac{-1}{N(\varpi) +1} \sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}} \frac{N(\varpi)\log N(\varpi)}{N(\varpi)^{1+2r}-1}. \end{align*} $$
It follows from this, after the substitution
![]() $u=-i\mathcal {L} r/(2\pi )$
and interchanging the summations and the integral, that
$u=-i\mathcal {L} r/(2\pi )$
and interchanging the summations and the integral, that
 $$ \begin{align} &\frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r) \bigg) \phi\bigg(\frac{i\mathcal{L} r}{2\pi}\bigg) \,{d} r \nonumber\\[3pt] &\quad= -\frac{2}{\mathcal{L}}\sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}} \frac{N(\varpi)\log N(\varpi)}{N(\varpi)+1} \nonumber\\[3pt] & \qquad \times \sum_{j=1}^{\infty} \frac{1}{N(\varpi)^{\,j}}\int_{\mathcal C^{\prime}}\phi(u)\exp \bigg( -2\pi i u\bigg(\frac{2j\log N(\varpi)}{\mathcal{L}}\bigg) \bigg) \,{d} u, \end{align} $$
$$ \begin{align} &\frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r) \bigg) \phi\bigg(\frac{i\mathcal{L} r}{2\pi}\bigg) \,{d} r \nonumber\\[3pt] &\quad= -\frac{2}{\mathcal{L}}\sum_{\varpi \equiv 1 \bmod {(1+i)^{3}}} \frac{N(\varpi)\log N(\varpi)}{N(\varpi)+1} \nonumber\\[3pt] & \qquad \times \sum_{j=1}^{\infty} \frac{1}{N(\varpi)^{\,j}}\int_{\mathcal C^{\prime}}\phi(u)\exp \bigg( -2\pi i u\bigg(\frac{2j\log N(\varpi)}{\mathcal{L}}\bigg) \bigg) \,{d} u, \end{align} $$
where
![]() $\mathcal C^{\prime }$
denotes the horizontal line
$\mathcal C^{\prime }$
denotes the horizontal line
![]() $\mathrm {Im}(u)=-\mathcal {L} a^{\prime }/(2\pi )$
.
$\mathrm {Im}(u)=-\mathcal {L} a^{\prime }/(2\pi )$
.
As
![]() $\widehat {\phi }$
is compactly supported and
$\widehat {\phi }$
is compactly supported and
 $\phi (z)=\int _{\mathbb {R}}\widehat \phi (x)e^{2\pi ixz}\, {d} x$
, it follows from integration by parts that uniformly for
$\phi (z)=\int _{\mathbb {R}}\widehat \phi (x)e^{2\pi ixz}\, {d} x$
, it follows from integration by parts that uniformly for
![]() $-\mathcal {L} c^{\prime }/(2\pi ) \leq t\leq 0$
,
$-\mathcal {L} c^{\prime }/(2\pi ) \leq t\leq 0$
,
 $$ \begin{align*} |\phi(T+it)| \ll \frac1{|T|+1}. \end{align*} $$
$$ \begin{align*} |\phi(T+it)| \ll \frac1{|T|+1}. \end{align*} $$
In view of this, we can shift the contour of the last integration in (6-5) from
![]() $\mathcal C^{\prime }$
to
$\mathcal C^{\prime }$
to
![]() $\mathrm {Im}(u) =0$
to deduce that
$\mathrm {Im}(u) =0$
to deduce that
 $$ \begin{align} &\frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r)\bigg) \phi\bigg(\frac{i\mathcal{L} r}{2\pi}\bigg) \,{d} r \nonumber\\[3pt] &\quad =- \frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 1}} \frac{\log N(\varpi)}{N(\varpi)^{\,j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\bigg( \frac{2j \log N(\varpi)}{\mathcal{L}} \bigg). \end{align} $$
$$ \begin{align} &\frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r)\bigg) \phi\bigg(\frac{i\mathcal{L} r}{2\pi}\bigg) \,{d} r \nonumber\\[3pt] &\quad =- \frac 2{\mathcal{L}}\sum_{\substack{\varpi \equiv 1 \bmod {(1+i)^{3}} \\ j\geq 1}} \frac{\log N(\varpi)}{N(\varpi)^{\,j}} \bigg( 1+\frac 1{N(\varpi)} \bigg)^{-1} \widehat{\phi}\bigg( \frac{2j \log N(\varpi)}{\mathcal{L}} \bigg). \end{align} $$
6.2 Evaluation of I
In this section, we evaluate I, defined in (6-2). Our treatment here follows from the proof of [Reference Fiorilli, Parks and Södergren11, Lemma 4.6]. We deduce from (5-7) that
 $$ \begin{align*} A(-\gamma,\gamma)=\frac {3(2-2^{2r})}{4-2^{2r}}\frac {\zeta_{K}(2)}{\zeta_{K}(2-2r)}. \end{align*} $$
$$ \begin{align*} A(-\gamma,\gamma)=\frac {3(2-2^{2r})}{4-2^{2r}}\frac {\zeta_{K}(2)}{\zeta_{K}(2-2r)}. \end{align*} $$
Substituting the above in the right-hand side of (6-2), we deduce from the definitions of
![]() $X_{c}$
given in (5-3) and a change of variable
$X_{c}$
given in (5-3) and a change of variable
![]() $r=2\pi i \tau / \mathcal {L}$
that
$r=2\pi i \tau / \mathcal {L}$
that
 $$ \begin{align} I&= - \frac {8}{\pi} \frac{\zeta_{K}(2)}{\mathcal{L}}\int_{\mathcal C^{\prime}} \bigg(\frac{\Gamma(1/2 - 2\pi i \tau/\mathcal{L})}{\Gamma(1/2 +2\pi i \tau/\mathcal{L} )} \bigg)\bigg(\frac{\pi^{2}}{32}\bigg)^{2 \pi i \tau/\mathcal{L}}\bigg(1+\frac{2-2^{4\pi i \tau/\mathcal{L} +1}}{4-2^{4\pi i \tau/\mathcal{L}}}\bigg) \nonumber\\[3pt] &\quad\times \frac{\zeta_{K}(1-4\pi i \tau/\mathcal{L} )}{\zeta_{K}(2- 4\pi i \tau/\mathcal{L})} \phi(\tau) \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{- 2\pi i \tau/\mathcal{L}} \,{d} \tau, \end{align} $$
$$ \begin{align} I&= - \frac {8}{\pi} \frac{\zeta_{K}(2)}{\mathcal{L}}\int_{\mathcal C^{\prime}} \bigg(\frac{\Gamma(1/2 - 2\pi i \tau/\mathcal{L})}{\Gamma(1/2 +2\pi i \tau/\mathcal{L} )} \bigg)\bigg(\frac{\pi^{2}}{32}\bigg)^{2 \pi i \tau/\mathcal{L}}\bigg(1+\frac{2-2^{4\pi i \tau/\mathcal{L} +1}}{4-2^{4\pi i \tau/\mathcal{L}}}\bigg) \nonumber\\[3pt] &\quad\times \frac{\zeta_{K}(1-4\pi i \tau/\mathcal{L} )}{\zeta_{K}(2- 4\pi i \tau/\mathcal{L})} \phi(\tau) \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{- 2\pi i \tau/\mathcal{L}} \,{d} \tau, \end{align} $$
where we also use
![]() $\mathcal C^{\prime }$
to denote the horizontal line
$\mathcal C^{\prime }$
to denote the horizontal line
![]() $\mathrm {Im}(\tau )=- \mathcal {L} a^{\prime }/(2\pi )$
.
$\mathrm {Im}(\tau )=- \mathcal {L} a^{\prime }/(2\pi )$
.
Applying Mellin inversion to the last sum in (6-7), we obtain for
![]() ${0\leq \mathrm{Re}(r) \leq 1/2}$
,
${0\leq \mathrm{Re}(r) \leq 1/2}$
,
 $$ \begin{align*} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-r}= \frac 4{2\pi i} \int_{(2)}\frac{2^{s+r}}{2^{s+r}+1} \frac{\zeta_{K}(s+r)}{\zeta_{K}(2(s+r))} X^{s} \mathcal M w(s) \, {d} s. \end{align*} $$
$$ \begin{align*} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-r}= \frac 4{2\pi i} \int_{(2)}\frac{2^{s+r}}{2^{s+r}+1} \frac{\zeta_{K}(s+r)}{\zeta_{K}(2(s+r))} X^{s} \mathcal M w(s) \, {d} s. \end{align*} $$
We shift the contour of integration to the line
![]() $\mathrm {Re}(s)=1/2 -\mathrm {Re}(r)+\varepsilon $
to encounter a simple pole at
$\mathrm {Re}(s)=1/2 -\mathrm {Re}(r)+\varepsilon $
to encounter a simple pole at
![]() $s=1-r$
. On the new line of integration, the convexity bound (see [Reference Iwaniec and Kowalski22, Exercise 3, page 100]), together with the rapid decay of
$s=1-r$
. On the new line of integration, the convexity bound (see [Reference Iwaniec and Kowalski22, Exercise 3, page 100]), together with the rapid decay of
![]() $\mathcal M w$
, gives
$\mathcal M w$
, gives
With this and recalling that the residue of
![]() $\zeta _{K}(s)$
at
$\zeta _{K}(s)$
at
![]() $s=1$
is
$s=1$
is
![]() $\pi /4$
, we get
$\pi /4$
, we get
 $$ \begin{align*} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-r} = \frac{2\pi}{3\zeta_{K}(2)}X^{1-r}\mathcal M w(1-r) +O_{\varepsilon,w}((|\mathrm{Im}(r)|+1)^{1/2+\varepsilon}X^{1/2-\mathrm{Re}(r)+\varepsilon}). \end{align*} $$
$$ \begin{align*} \sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-r} = \frac{2\pi}{3\zeta_{K}(2)}X^{1-r}\mathcal M w(1-r) +O_{\varepsilon,w}((|\mathrm{Im}(r)|+1)^{1/2+\varepsilon}X^{1/2-\mathrm{Re}(r)+\varepsilon}). \end{align*} $$
Combining the above with (2-10), we deduce that for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $0\leq \mathrm {Re}(r) \leq 1/2$
,
$0\leq \mathrm {Re}(r) \leq 1/2$
,
 $$ \begin{align*} \begin{split} & \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-r} \\[3pt] & \quad= \frac{2}{\widehat{w}(0)}X^{-r}\mathcal M w(1-r) +O_{\varepsilon,w}((|\mathrm{Im}(r)|+1)^{1/2+\varepsilon}X^{-1/2-\mathrm{Re} (r)+\varepsilon}). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} & \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-r} \\[3pt] & \quad= \frac{2}{\widehat{w}(0)}X^{-r}\mathcal M w(1-r) +O_{\varepsilon,w}((|\mathrm{Im}(r)|+1)^{1/2+\varepsilon}X^{-1/2-\mathrm{Re} (r)+\varepsilon}). \end{split} \end{align*} $$
For small
![]() $\varepsilon , \eta>0$
, we change the contour
$\varepsilon , \eta>0$
, we change the contour
![]() $\mathcal C^{\prime }$
in (6-7) to the path
$\mathcal C^{\prime }$
in (6-7) to the path
where
and
As
![]() $\phi $
decays rapidly, the integration of I over
$\phi $
decays rapidly, the integration of I over
![]() $C_{0}$
can be shown to be negligible. We now apply the Taylor expansion to treat the integration of I over
$C_{0}$
can be shown to be negligible. We now apply the Taylor expansion to treat the integration of I over
![]() $C_{1}\cup C_{2}$
by noting that
$C_{1}\cup C_{2}$
by noting that
 $$ \begin{align*} \frac{\Gamma(1/2 - 2\pi i \tau/\mathcal{L} )}{\Gamma(1/2 + 2\pi i \tau/\mathcal{L} )} =1-2\frac {\Gamma^{\prime}(1/2)}{\Gamma(1/2)} \frac{2\pi i \tau}{\mathcal{L}} +O\bigg( \frac{|\tau|^{2}}{\mathcal{L}^{2}}\bigg), \end{align*} $$
$$ \begin{align*} \frac{\Gamma(1/2 - 2\pi i \tau/\mathcal{L} )}{\Gamma(1/2 + 2\pi i \tau/\mathcal{L} )} =1-2\frac {\Gamma^{\prime}(1/2)}{\Gamma(1/2)} \frac{2\pi i \tau}{\mathcal{L}} +O\bigg( \frac{|\tau|^{2}}{\mathcal{L}^{2}}\bigg), \end{align*} $$
and that (see [Reference Gradshteyn and Ryzhik17, Formula 2, Section 8.366])
 $$ \begin{align*} -\frac {\Gamma^{\prime}(1/2)}{\Gamma(1/2)}=2\log 2+\gamma. \end{align*} $$
$$ \begin{align*} -\frac {\Gamma^{\prime}(1/2)}{\Gamma(1/2)}=2\log 2+\gamma. \end{align*} $$
Using Taylor expansion and (1-6), we get
 $$ \begin{align*} & \bigg(1+\frac{2-2^{4\pi i \tau/\mathcal{L}+1}}{4-2^{4\pi i \tau/\mathcal{L}}}\bigg)\frac{1}{\zeta_{K}(2- 4\pi i \tau/\mathcal{L})} \\[3pt] &\quad = \frac {1}{\zeta_{K}(2)}+\bigg ( \frac {1}{\zeta_{K}(2)} \bigg(-\frac {2\log 2}{3} \bigg) +\frac {\zeta^{\prime}_{K}(2)}{\zeta_{K}^{2}(2)} \bigg)\frac{4\pi i \tau}{\mathcal{L}}+O\bigg( \frac{|\tau|^{2}}{\mathcal{L}^{2}}\bigg) \end{align*} $$
$$ \begin{align*} & \bigg(1+\frac{2-2^{4\pi i \tau/\mathcal{L}+1}}{4-2^{4\pi i \tau/\mathcal{L}}}\bigg)\frac{1}{\zeta_{K}(2- 4\pi i \tau/\mathcal{L})} \\[3pt] &\quad = \frac {1}{\zeta_{K}(2)}+\bigg ( \frac {1}{\zeta_{K}(2)} \bigg(-\frac {2\log 2}{3} \bigg) +\frac {\zeta^{\prime}_{K}(2)}{\zeta_{K}^{2}(2)} \bigg)\frac{4\pi i \tau}{\mathcal{L}}+O\bigg( \frac{|\tau|^{2}}{\mathcal{L}^{2}}\bigg) \end{align*} $$
and
 $$ \begin{align*} \zeta_{K}\bigg(1-\frac{4\pi i \tau}{\mathcal{L}}\bigg)= -\frac {\pi}{4}\cdot \frac{\mathcal{L}}{4\pi i \tau}+\gamma_{K} +O\bigg( \frac{|\tau|}{\mathcal{L}}\bigg). \end{align*} $$
$$ \begin{align*} \zeta_{K}\bigg(1-\frac{4\pi i \tau}{\mathcal{L}}\bigg)= -\frac {\pi}{4}\cdot \frac{\mathcal{L}}{4\pi i \tau}+\gamma_{K} +O\bigg( \frac{|\tau|}{\mathcal{L}}\bigg). \end{align*} $$
Using the above formulas, we get, after a short computation,
 $$ \begin{align*} & -\dfrac {8}{\pi} \dfrac{\zeta_{K}(2)}{\mathcal{L}} \dfrac{\Gamma ( 1/2 -2\pi i \tau/\mathcal{L} )}{\Gamma(1/2 + 2\pi i \tau/\mathcal{L})} \bigg(\dfrac{\pi^{2}}{32}\bigg)^{{2 \pi i \tau}/{\mathcal{L}}}\bigg(1+\dfrac{2-2^{({4\pi i \tau}/\mathcal{L})+1}}{4-2^{{4\pi i \tau}/\mathcal{L}}}\bigg) \\[3pt] &\qquad \times \dfrac{\zeta_{K}(1-4\pi i \tau/\mathcal{L})}{\zeta_{K}(2-4\pi i \tau/\mathcal{L})} \phi(\tau)\dfrac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-2\pi i \tau/\mathcal{L}} \\[3pt] &\quad= \dfrac 1{2\pi i\tau} \bigg( 1+ \dfrac{2\pi i \tau }{\mathcal{L}}\bigg( 2\gamma +2 \log 4 + \log \bigg( \dfrac {\pi^{2}}{32} \bigg)+2\dfrac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\dfrac{4}{3} \log 2 -\dfrac {8}{\pi} \gamma_{K} \\[3pt] &\qquad -\dfrac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O\bigg( \dfrac{|\tau|^{2}}{\mathcal{L}^{2}}\bigg)\bigg)\phi(\tau) e^{-2\pi i \tau} +O_{\varepsilon,w}(X^{-1/2+\varepsilon}). \end{align*} $$
$$ \begin{align*} & -\dfrac {8}{\pi} \dfrac{\zeta_{K}(2)}{\mathcal{L}} \dfrac{\Gamma ( 1/2 -2\pi i \tau/\mathcal{L} )}{\Gamma(1/2 + 2\pi i \tau/\mathcal{L})} \bigg(\dfrac{\pi^{2}}{32}\bigg)^{{2 \pi i \tau}/{\mathcal{L}}}\bigg(1+\dfrac{2-2^{({4\pi i \tau}/\mathcal{L})+1}}{4-2^{{4\pi i \tau}/\mathcal{L}}}\bigg) \\[3pt] &\qquad \times \dfrac{\zeta_{K}(1-4\pi i \tau/\mathcal{L})}{\zeta_{K}(2-4\pi i \tau/\mathcal{L})} \phi(\tau)\dfrac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) N(c)^{-2\pi i \tau/\mathcal{L}} \\[3pt] &\quad= \dfrac 1{2\pi i\tau} \bigg( 1+ \dfrac{2\pi i \tau }{\mathcal{L}}\bigg( 2\gamma +2 \log 4 + \log \bigg( \dfrac {\pi^{2}}{32} \bigg)+2\dfrac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\dfrac{4}{3} \log 2 -\dfrac {8}{\pi} \gamma_{K} \\[3pt] &\qquad -\dfrac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O\bigg( \dfrac{|\tau|^{2}}{\mathcal{L}^{2}}\bigg)\bigg)\phi(\tau) e^{-2\pi i \tau} +O_{\varepsilon,w}(X^{-1/2+\varepsilon}). \end{align*} $$
We then deduce that
 $$ \begin{align*} I = \frac{1}{2\pi i} \int_{C_{1}\cup C_{2}} \frac {\phi(\tau)}{\tau} e^{-2\pi i \tau} \,{d} \tau+I^{\prime}+ O_{w}(\mathcal{L}^{-2}),\end{align*} $$
$$ \begin{align*} I = \frac{1}{2\pi i} \int_{C_{1}\cup C_{2}} \frac {\phi(\tau)}{\tau} e^{-2\pi i \tau} \,{d} \tau+I^{\prime}+ O_{w}(\mathcal{L}^{-2}),\end{align*} $$
where, combining the logarithm terms,
 $$ \begin{align*} I^{\prime} =&\frac 1{\mathcal{L}} \bigg( 2\gamma+ \log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)}-\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) \int_{C_{1}\cup C_{2}}\phi(\tau) e^{-2\pi i \tau} \,{d} \tau \\[3pt] =& \frac 1{\mathcal{L}} \bigg( 2\gamma+\log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) \nonumber \\& \times \int_{\mathbb R}\phi(\tau) e^{-2\pi i \tau} \,{d} \tau+O(\mathcal{L}^{-2}) \\[3pt] =& \frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma+\log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg) +2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O(\mathcal{L}^{-2}). \end{align*} $$
$$ \begin{align*} I^{\prime} =&\frac 1{\mathcal{L}} \bigg( 2\gamma+ \log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)}-\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) \int_{C_{1}\cup C_{2}}\phi(\tau) e^{-2\pi i \tau} \,{d} \tau \\[3pt] =& \frac 1{\mathcal{L}} \bigg( 2\gamma+\log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) \nonumber \\& \times \int_{\mathbb R}\phi(\tau) e^{-2\pi i \tau} \,{d} \tau+O(\mathcal{L}^{-2}) \\[3pt] =& \frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma+\log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg) +2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O(\mathcal{L}^{-2}). \end{align*} $$
Similarly to the treatment of
![]() $I_{1}$
in the proof of [Reference Fiorilli, Parks and Södergren11, Lemma 4.6], we have
$I_{1}$
in the proof of [Reference Fiorilli, Parks and Södergren11, Lemma 4.6], we have
 $$ \begin{align*} \int_{C_{1}\cup C_{2}} \frac 1{2\pi i\tau} \phi(\tau) e^{-2\pi i \tau} \,{d} \tau & =\int^{\infty}_{1} \widehat{\phi}(\tau) \,{d} \tau +O(\mathcal{L}^{-2}). \end{align*} $$
$$ \begin{align*} \int_{C_{1}\cup C_{2}} \frac 1{2\pi i\tau} \phi(\tau) e^{-2\pi i \tau} \,{d} \tau & =\int^{\infty}_{1} \widehat{\phi}(\tau) \,{d} \tau +O(\mathcal{L}^{-2}). \end{align*} $$
Thus, we conclude that
 $$ \begin{align*} I &= \int^{\infty}_{1} \widehat{\phi}(\tau) \,{d} \tau +\frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma+\log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) \\[3pt] &\quad +O(\mathcal{L}^{-2}). \end{align*} $$
$$ \begin{align*} I &= \int^{\infty}_{1} \widehat{\phi}(\tau) \,{d} \tau +\frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma+\log \bigg( \frac {\pi^{2}}{2^{7/3}} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) \\[3pt] &\quad +O(\mathcal{L}^{-2}). \end{align*} $$
Combining the above expression for I with (6-1)–(6-4) and (6-6), we deduce that expression (1-7) is valid.
6.3 Comparing terms
In this section we show that the expression given in (1-7) is in agreement with that given in (1-4) when
 $\sigma =\mathrm {sup}(\mathrm {supp }\,\widehat {\phi })<2$
. In fact, applying (6-3) and (6-4) in (1-3) and comparing it with (1-4), we see that, with the help of Lemma 2.3, it suffices to show that
$\sigma =\mathrm {sup}(\mathrm {supp }\,\widehat {\phi })<2$
. In fact, applying (6-3) and (6-4) in (1-3) and comparing it with (1-4), we see that, with the help of Lemma 2.3, it suffices to show that
 $$ \begin{align} &-\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L};\hat{\phi}) \nonumber\\[3pt] &\quad= \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2it)}{\zeta_{K}(1+2it)} + 2A_{\alpha}(it,it) \nonumber\\[3pt] &\quad\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+it\bigg)\zeta_{K}(1-2it)A(-it,it) \bigg) \, \phi\bigg(\frac{t\mathcal{L}}{2\pi}\bigg) \, {d} t \nonumber\\[3pt] &\quad= \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r) \nonumber\\[3pt] &\quad\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i\mathcal{L} r}{2\pi}\bigg) \,{d} r, \end{align} $$
$$ \begin{align} &-\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L};\hat{\phi}) \nonumber\\[3pt] &\quad= \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi} \int_{\mathbb R} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2it)}{\zeta_{K}(1+2it)} + 2A_{\alpha}(it,it) \nonumber\\[3pt] &\quad\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+it\bigg)\zeta_{K}(1-2it)A(-it,it) \bigg) \, \phi\bigg(\frac{t\mathcal{L}}{2\pi}\bigg) \, {d} t \nonumber\\[3pt] &\quad= \frac{1}{W(X)}\sideset{}{^{*}}\sum_{(c,1+i)=1} w\bigg( \frac {N(c)}X \bigg) \frac{1}{2\pi i}\int_{(a^{\prime})} \bigg(2 \frac{\zeta^{\prime}_{K}(1+2r)}{\zeta_{K}(1+2r)}+2A_{\alpha}(r,r) \nonumber\\[3pt] &\quad\quad -\frac {8}{\pi} X_{c}\bigg(\frac{1}{2}+r\bigg)\zeta_{K}(1-2r)A(-r,r)\bigg) \phi\bigg(\frac{i\mathcal{L} r}{2\pi}\bigg) \,{d} r, \end{align} $$
where
![]() $(\log X)^{-1}<a^{\prime }< 1/4$
.
$(\log X)^{-1}<a^{\prime }< 1/4$
.
Now, similarly to the treatment in Section 3, we write
 $$ \begin{align} -\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1}S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L};\hat{\phi}) = S_{\mathrm{odd}}+S_{\mathrm{even}}, \end{align} $$
$$ \begin{align} -\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{j \geq 1}S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L};\hat{\phi}) = S_{\mathrm{odd}}+S_{\mathrm{even}}, \end{align} $$
where
 $$ \begin{align*} S_{\mathrm{odd}}=-\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{\substack{j \geq 1 \\ j \,\equiv 1 ({\operatorname{mod}}\,\,2)}} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L} ;\hat{\phi}) \end{align*} $$
$$ \begin{align*} S_{\mathrm{odd}}=-\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{\substack{j \geq 1 \\ j \,\equiv 1 ({\operatorname{mod}}\,\,2)}} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L} ;\hat{\phi}) \end{align*} $$
and
 $$ \begin{align*} S_{\mathrm{even}}= -\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{\substack{j \geq 1 \\ j \,\equiv 0 ({\operatorname{mod}}\,\,2)}} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L} ;\hat{\phi}). \end{align*} $$
$$ \begin{align*} S_{\mathrm{even}}= -\frac 2{\mathcal{L} W(X)} \underset{(c, 1+i) =1 }{\sum \nolimits^{*}} w\bigg( \frac {N(c)}X \bigg) \sum_{\substack{j \geq 1 \\ j \,\equiv 0 ({\operatorname{mod}}\,\,2)}} S_{j}(\chi_{i(1+i)^{5}c},\mathcal{L} ;\hat{\phi}). \end{align*} $$
We then deduce from (6-6), (6-8), (6-9) and (3-2) that it remains to show that
where I is defined in (6-2).
6.4 Evaluation of
 $S_{{\bf odd}}$
, first order term
$S_{{\bf odd}}$
, first order term
In this section we evaluate
![]() $S_{\mathrm {odd}}$
to the first lower-order term. Our treatment here largely follows the approach in the proof of [Reference Fiorilli, Parks and Södergren11, Theorem 1.1]. We recall from (3.5) that
$S_{\mathrm {odd}}$
to the first lower-order term. Our treatment here largely follows the approach in the proof of [Reference Fiorilli, Parks and Södergren11, Theorem 1.1]. We recall from (3.5) that
 $$ \begin{align} S_{\mathrm{odd}} = \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u+ J(X)+O(\mathcal{L}^{-2} ), \end{align} $$
$$ \begin{align} S_{\mathrm{odd}} = \int_{1}^{\infty} \widehat{\phi}(u)\, {d} u+ J(X)+O(\mathcal{L}^{-2} ), \end{align} $$
where
 $$ \begin{align*} J(X) &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \bigg( \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) \\[3pt] &\quad +\widehat{\phi} \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau. \end{align*} $$
$$ \begin{align*} J(X) &= \frac 1{\mathcal{L}} \int_{0}^{\infty} \bigg( \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) e^{\tau/2} \sum_{\substack{ j \in \mathbb Z[i] \\ j \neq 0}} h_{1}(N(j)e^{\tau/2}) \\[3pt] &\quad +\widehat{\phi} \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) \sum_{\substack {k \in \mathbb Z[i] \\ k \neq 0}} h_{2}(N(k)e^{\tau/2})\bigg)\, {d} \tau. \end{align*} $$
We now evaluate
![]() $h_{1}(x)$
by applying the Mellin inversion to recast it as
$h_{1}(x)$
by applying the Mellin inversion to recast it as
 $$ \begin{align*} h_{1}(x) &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(5/2)}\sum_{\substack{ l \,\equiv 1 \bmod {(1+i)^{3}}}}(2^{-z}-1)\frac {\mu_{[i]}(l)}{N(l)^{1+z}} \mathcal M g_{1}(z)\frac{{d} z}{x^{z}} \\[3pt] &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(5/2)} \frac{2^{-z}-1}{( 1- 2^{-1-z})\zeta_{K}(1+z)} \mathcal M g_{1}(z)\frac{{d} z}{x^{z}}. \end{align*} $$
$$ \begin{align*} h_{1}(x) &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(5/2)}\sum_{\substack{ l \,\equiv 1 \bmod {(1+i)^{3}}}}(2^{-z}-1)\frac {\mu_{[i]}(l)}{N(l)^{1+z}} \mathcal M g_{1}(z)\frac{{d} z}{x^{z}} \\[3pt] &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(5/2)} \frac{2^{-z}-1}{( 1- 2^{-1-z})\zeta_{K}(1+z)} \mathcal M g_{1}(z)\frac{{d} z}{x^{z}}. \end{align*} $$
Similarly, we have, with a change of variables
![]() $z \to -z$
,
$z \to -z$
,
 $$ \begin{align*} h_{2} (x) &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(1/2)}\sum_{\substack{l \equiv 1 \bmod {(1+i)^{3}}}}(2^{z-1}-1)\frac {\mu_{[i]}(l)}{N(l)^{2-z}} \mathcal M g(z)\frac{{d} z}{x^{z}} \\[3pt] &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(-1/2)} \frac{2^{-z-1}-1}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z)x^{z} \,{d} z \\[3pt] &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(-5/4)} \frac{2^{-z-1}-1}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z)x^{z} \,{d} z. \end{align*} $$
$$ \begin{align*} h_{2} (x) &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(1/2)}\sum_{\substack{l \equiv 1 \bmod {(1+i)^{3}}}}(2^{z-1}-1)\frac {\mu_{[i]}(l)}{N(l)^{2-z}} \mathcal M g(z)\frac{{d} z}{x^{z}} \\[3pt] &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(-1/2)} \frac{2^{-z-1}-1}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z)x^{z} \,{d} z \\[3pt] &= \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i} \int_{(-5/4)} \frac{2^{-z-1}-1}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z)x^{z} \,{d} z. \end{align*} $$
With the above expressions for
![]() $h_{1}(x)$
and
$h_{1}(x)$
and
![]() $h_{2}(x)$
, we can write
$h_{2}(x)$
, we can write
![]() $J(x)$
given in (3-16) as
$J(x)$
given in (3-16) as
 $$ \begin{align} J(X) &= \frac{Y}{\mathcal{L}}\int_{0}^{\infty} \bigg( \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \int_{(5/2)} \frac{4(2^{-z}-1)\zeta_{K}(z)}{( 1- 2^{-1-z})\zeta_{K}(1+z)} \mathcal Mg_{1}(z)\frac{{d} z}{e^{(z-1)\tau/2}} \nonumber\\[3pt] &\quad +\widehat{\phi} \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) \int_{(-5/4)} \frac{ 4(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z)e^{z\tau/2} \,{d} z \bigg) \, {d} \tau \nonumber\\[3pt] &= \frac{Y}{\mathcal{L}}\bigg( \int_{(3/2)} \frac{4(2^{-z}-1)\zeta_{K}(z)}{( 1- 2^{-1-z})\zeta_{K}(1+z)} \mathcal M g_{1} (z) \int_{0}^{\infty} \widehat{\phi} \bigg( 1+\frac{\tau}{\mathcal{L}} \bigg)e^{-(z-1)\tau/2} \,{d} \tau \,{d} z \nonumber\\[3pt] &\quad + \int_{(-5/4)} \frac{4(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z) \int_{0}^{\infty}\widehat\phi \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) e^{z\tau/2} \,{d} \tau \,{d} z \bigg)\, , \end{align} $$
$$ \begin{align} J(X) &= \frac{Y}{\mathcal{L}}\int_{0}^{\infty} \bigg( \widehat{\phi} \bigg( 1+ \frac{\tau}{\mathcal{L}} \bigg) \int_{(5/2)} \frac{4(2^{-z}-1)\zeta_{K}(z)}{( 1- 2^{-1-z})\zeta_{K}(1+z)} \mathcal Mg_{1}(z)\frac{{d} z}{e^{(z-1)\tau/2}} \nonumber\\[3pt] &\quad +\widehat{\phi} \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) \int_{(-5/4)} \frac{ 4(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z)e^{z\tau/2} \,{d} z \bigg) \, {d} \tau \nonumber\\[3pt] &= \frac{Y}{\mathcal{L}}\bigg( \int_{(3/2)} \frac{4(2^{-z}-1)\zeta_{K}(z)}{( 1- 2^{-1-z})\zeta_{K}(1+z)} \mathcal M g_{1} (z) \int_{0}^{\infty} \widehat{\phi} \bigg( 1+\frac{\tau}{\mathcal{L}} \bigg)e^{-(z-1)\tau/2} \,{d} \tau \,{d} z \nonumber\\[3pt] &\quad + \int_{(-5/4)} \frac{4(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z) \int_{0}^{\infty}\widehat\phi \bigg( 1- \frac{\tau}{\mathcal{L}} \bigg) e^{z\tau/2} \,{d} \tau \,{d} z \bigg)\, , \end{align} $$
where
 $$ \begin{align*} Y = \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i}. \end{align*} $$
$$ \begin{align*} Y = \frac{3\zeta_{K}(2)}{\pi \widehat w(0)}\frac 1{2 \pi i}. \end{align*} $$
Now we consider the Taylor expansions, centered at
![]() $1$
, of the terms
$1$
, of the terms
 $\widehat \phi ( 1+ \tau /\mathcal {L} )$
and
$\widehat \phi ( 1+ \tau /\mathcal {L} )$
and
 ${\widehat \phi ( 1- \tau /\mathcal {L} )}$
in (6-12). By keeping only the constant terms, we see that their contribution to
${\widehat \phi ( 1- \tau /\mathcal {L} )}$
in (6-12). By keeping only the constant terms, we see that their contribution to
![]() $J(X)$
equals, with another change of variables
$J(X)$
equals, with another change of variables
![]() $z \to z+1$
in the first integral,
$z \to z+1$
in the first integral,
 $$ \begin{align} &\frac{3\zeta_{K}(2)}{\mathcal{L} \pi \widehat w(0)} \frac{ 8\widehat{\phi}( 1)}{2 \pi i}\bigg( \int_{(1/2)} \frac{(2^{-z-1}-1)\zeta_{K}(z+1)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g_{1}(z+1) \frac{ {d} z}{z} \nonumber\\[3pt] &\quad - \int_{(-5/4)} \frac{(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z) \frac{{d} z}z \bigg). \end{align} $$
$$ \begin{align} &\frac{3\zeta_{K}(2)}{\mathcal{L} \pi \widehat w(0)} \frac{ 8\widehat{\phi}( 1)}{2 \pi i}\bigg( \int_{(1/2)} \frac{(2^{-z-1}-1)\zeta_{K}(z+1)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g_{1}(z+1) \frac{ {d} z}{z} \nonumber\\[3pt] &\quad - \int_{(-5/4)} \frac{(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \mathcal M g(-z) \frac{{d} z}z \bigg). \end{align} $$
We now shift the contour of the last integration to the line
![]() $\mathrm {Re}(z) = 1/2$
. We apply Lemma 2.7 to see that the quantity in (6-13) equals
$\mathrm {Re}(z) = 1/2$
. We apply Lemma 2.7 to see that the quantity in (6-13) equals
 $$ \begin{align*} \frac{3\zeta_{K}(2)}{\mathcal{L} \pi \widehat w(0)}\frac{ 8\widehat{\phi}( 1)}{2 \pi i}R, \end{align*} $$
$$ \begin{align*} \frac{3\zeta_{K}(2)}{\mathcal{L} \pi \widehat w(0)}\frac{ 8\widehat{\phi}( 1)}{2 \pi i}R, \end{align*} $$
where R is the residue of the function
 $$ \begin{align*} \frac{(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \frac{\mathcal M g(-z)}z \end{align*} $$
$$ \begin{align*} \frac{(2^{-z-1}-1)\zeta_{K}(-z)}{( 1- 2^{-2-z})\zeta_{K}(2+z)} \frac{\mathcal M g(-z)}z \end{align*} $$
at
![]() $z=0$
. We observe via integration by parts that
$z=0$
. We observe via integration by parts that
 $$ \begin{align*} \mathcal M g(-z) =\int^{\infty}_{0} g(t)t^{-z}\frac {{d} t}{t}=\int^{\infty}_{0} g(t) \,{d} \bigg ( \frac {t^{-z}}{-z} \bigg )=\frac 1{z}\int^{\infty}_{0}t^{-z} g^{\prime}(t) \,{d} t. \end{align*} $$
$$ \begin{align*} \mathcal M g(-z) =\int^{\infty}_{0} g(t)t^{-z}\frac {{d} t}{t}=\int^{\infty}_{0} g(t) \,{d} \bigg ( \frac {t^{-z}}{-z} \bigg )=\frac 1{z}\int^{\infty}_{0}t^{-z} g^{\prime}(t) \,{d} t. \end{align*} $$
As
 $$ \begin{align*} \lim_{z \rightarrow 0}\int^{\infty}_{0}t^{-z} g^{\prime}(t) \,{d} t=g(0)=\widehat{w}(0)>0, \end{align*} $$
$$ \begin{align*} \lim_{z \rightarrow 0}\int^{\infty}_{0}t^{-z} g^{\prime}(t) \,{d} t=g(0)=\widehat{w}(0)>0, \end{align*} $$
it follows that
![]() $\mathcal M g(-z)$
has a pole at
$\mathcal M g(-z)$
has a pole at
![]() $z=0$
. We apply (3-17) and get that around
$z=0$
. We apply (3-17) and get that around
![]() $z=0$
,
$z=0$
,
 $$ \begin{align} \mathcal M g(-z) &= \frac {-g(0)}{z}-\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t+O(z^{2}) \nonumber\\[3pt] &= \frac {-\widetilde{w}(0)}{z}-\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t+O(z^{2}) \nonumber\\[3pt] &= -\frac {\pi}{2}\frac {\widehat{w}(0)}{z}-\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t+O(z^{2}). \end{align} $$
$$ \begin{align} \mathcal M g(-z) &= \frac {-g(0)}{z}-\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t+O(z^{2}) \nonumber\\[3pt] &= \frac {-\widetilde{w}(0)}{z}-\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t+O(z^{2}) \nonumber\\[3pt] &= -\frac {\pi}{2}\frac {\widehat{w}(0)}{z}-\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t+O(z^{2}). \end{align} $$
Moreover, we have around
![]() $z=0$
,
$z=0$
,
 $$ \begin{align} \frac{2^{-z-1}-1}{1- 2^{-2-z}}= -\frac 23+\frac{-\log 2 \big(\tfrac 38\big)+\tfrac 12 (\log 2) \tfrac 14}{(1- 2^{-2})^{2}}z=-\frac 23-\frac 49 (\log 2)z \end{align} $$
$$ \begin{align} \frac{2^{-z-1}-1}{1- 2^{-2-z}}= -\frac 23+\frac{-\log 2 \big(\tfrac 38\big)+\tfrac 12 (\log 2) \tfrac 14}{(1- 2^{-2})^{2}}z=-\frac 23-\frac 49 (\log 2)z \end{align} $$
and
 $$ \begin{align} \frac{\zeta_{K}(-z)}{\zeta_{K}(2+z)}= \frac{\zeta_{K}(0)}{\zeta_{K}(2)}+\frac{-\zeta^{\prime}_{K}(0)\zeta_{K}(2)-\zeta_{K}(0)\zeta^{\prime}_{K}(2)}{\zeta^{2}_{K}(2)}z+O(z^{2}). \end{align} $$
$$ \begin{align} \frac{\zeta_{K}(-z)}{\zeta_{K}(2+z)}= \frac{\zeta_{K}(0)}{\zeta_{K}(2)}+\frac{-\zeta^{\prime}_{K}(0)\zeta_{K}(2)-\zeta_{K}(0)\zeta^{\prime}_{K}(2)}{\zeta^{2}_{K}(2)}z+O(z^{2}). \end{align} $$
Using (6-14), (6-15) and (6-16), we get
 $$ \begin{align} R&=-\frac {\pi}{2} \widehat{w}(0) \bigg( -\frac 23 \bigg) \frac{-\zeta^{\prime}_{K}(0)\zeta_{K}(2)-\zeta_{K}(0)\zeta^{\prime}_{K}(2)}{\zeta^{2}_{K}(2)} \nonumber\\[3pt] &\quad - \frac {\pi}{2}\widehat{w}(0) \bigg( -\frac 49 \log 2 \bigg) \frac{\zeta_{K}(0)}{\zeta_{K}(2)} -\frac 23\frac{\zeta_{K}(0)}{\zeta_{K}(2)} \bigg( -\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t \bigg). \end{align} $$
$$ \begin{align} R&=-\frac {\pi}{2} \widehat{w}(0) \bigg( -\frac 23 \bigg) \frac{-\zeta^{\prime}_{K}(0)\zeta_{K}(2)-\zeta_{K}(0)\zeta^{\prime}_{K}(2)}{\zeta^{2}_{K}(2)} \nonumber\\[3pt] &\quad - \frac {\pi}{2}\widehat{w}(0) \bigg( -\frac 49 \log 2 \bigg) \frac{\zeta_{K}(0)}{\zeta_{K}(2)} -\frac 23\frac{\zeta_{K}(0)}{\zeta_{K}(2)} \bigg( -\int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t \bigg). \end{align} $$
To further simplify R, we use the fact that
![]() $s\Gamma (s) = 1$
(see [Reference Davenport6, Section 10]) when
$s\Gamma (s) = 1$
(see [Reference Davenport6, Section 10]) when
![]() $s = 0$
and the functional equation for
$s = 0$
and the functional equation for
![]() $\zeta _{K}(s)$
(see [Reference Iwaniec and Kowalski22, Theorem 3.8]),
$\zeta _{K}(s)$
(see [Reference Iwaniec and Kowalski22, Theorem 3.8]),
to obtain that
![]() $\zeta _{K}(0) = -1/4$
.
$\zeta _{K}(0) = -1/4$
.
We further use the relation (see [Reference Davenport6, Section 10])
 $$ \begin{align*} \Gamma(s)\Gamma(1-s)=\frac {\pi}{\sin (\pi s)} \end{align*} $$
$$ \begin{align*} \Gamma(s)\Gamma(1-s)=\frac {\pi}{\sin (\pi s)} \end{align*} $$
to derive that
Applying (1-6), we see that around
![]() $s=1$
, we have
$s=1$
, we have
 $$ \begin{align*} \zeta_{K}(s)\sin (\pi s)=-\frac {\pi^{2}}{4}-\pi \gamma_{K}(s-1)+O((s-1)^{2}). \end{align*} $$
$$ \begin{align*} \zeta_{K}(s)\sin (\pi s)=-\frac {\pi^{2}}{4}-\pi \gamma_{K}(s-1)+O((s-1)^{2}). \end{align*} $$
Using the above expansion and the fact that
![]() $\Gamma ^{\prime }(1)=-\gamma $
(see [Reference Gradshteyn and Ryzhik17, Formula 1, Section 8.366] by noting also that
$\Gamma ^{\prime }(1)=-\gamma $
(see [Reference Gradshteyn and Ryzhik17, Formula 1, Section 8.366] by noting also that
![]() $\Gamma (1)=1$
), we take the derivative on both sides of (6-18) to see that
$\Gamma (1)=1$
), we take the derivative on both sides of (6-18) to see that
 $$ \begin{align*} -\zeta^{\prime}_{K}(0)=-\frac {1}{\pi}\gamma_{K}+\frac {\gamma}{2}+\frac {\log \pi}{2}. \end{align*} $$
$$ \begin{align*} -\zeta^{\prime}_{K}(0)=-\frac {1}{\pi}\gamma_{K}+\frac {\gamma}{2}+\frac {\log \pi}{2}. \end{align*} $$
Now, inserting the values of
![]() $\zeta _{K}(0), -\zeta ^{\prime }_{K}(0)$
into (6-17), together with a short calculation, we obtain that
$\zeta _{K}(0), -\zeta ^{\prime }_{K}(0)$
into (6-17), together with a short calculation, we obtain that
 $$ \begin{align} J(X)&= \frac{3\zeta_{K}(2)}{\mathcal{L} \pi \widehat w(0)}\frac{ 8\widehat{\phi}( 1)}{2 \pi i}R+O(\mathcal{L}^{-2}) \nonumber\\[3pt] &= \frac{8\widehat{\phi}( 1)}{\mathcal{L}}\bigg(-\frac {\gamma_{K}}{\pi}+\frac {\gamma}{2}+\frac {\log \pi}{2}+\frac 14\frac {\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)}\nonumber\\[3pt] &\quad+ \bigg( \frac 23 \log 2 \bigg)\zeta_{K}(0) -\frac {1}{2\pi \widehat{w}(0)} \bigg( \int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t \bigg) \bigg)+O(\mathcal{L}^{-2}). \end{align} $$
$$ \begin{align} J(X)&= \frac{3\zeta_{K}(2)}{\mathcal{L} \pi \widehat w(0)}\frac{ 8\widehat{\phi}( 1)}{2 \pi i}R+O(\mathcal{L}^{-2}) \nonumber\\[3pt] &= \frac{8\widehat{\phi}( 1)}{\mathcal{L}}\bigg(-\frac {\gamma_{K}}{\pi}+\frac {\gamma}{2}+\frac {\log \pi}{2}+\frac 14\frac {\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)}\nonumber\\[3pt] &\quad+ \bigg( \frac 23 \log 2 \bigg)\zeta_{K}(0) -\frac {1}{2\pi \widehat{w}(0)} \bigg( \int^{\infty}_{0}(\log t) g^{\prime}(t) \,{d} t \bigg) \bigg)+O(\mathcal{L}^{-2}). \end{align} $$
We evaluate the last integral above by noticing that for small
![]() $\eta>0$
, we have
$\eta>0$
, we have
 $$ \begin{align*} \int_{0}^{\infty} (\log x) g^{\prime}(x) \,{d} x &=\int_{0}^{\infty} \sqrt{2} \log x \widetilde w^{\prime}(\sqrt{2}x) \,{d} x = \int_{0}^{\infty} \log \bigg(\frac x{\sqrt{2}}\bigg) \widetilde w^{\prime}(x) \,{d} x \\[3pt] &= \widetilde w(0) \log (\sqrt{2}) +\int_{\eta}^{\infty} (\log x) \widetilde w^{\prime}(x) \,{d} x +O(\eta \log (\eta^{-1})). \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty} (\log x) g^{\prime}(x) \,{d} x &=\int_{0}^{\infty} \sqrt{2} \log x \widetilde w^{\prime}(\sqrt{2}x) \,{d} x = \int_{0}^{\infty} \log \bigg(\frac x{\sqrt{2}}\bigg) \widetilde w^{\prime}(x) \,{d} x \\[3pt] &= \widetilde w(0) \log (\sqrt{2}) +\int_{\eta}^{\infty} (\log x) \widetilde w^{\prime}(x) \,{d} x +O(\eta \log (\eta^{-1})). \end{align*} $$
Now the above expression becomes, after integration by parts,
 $$ \begin{align*} \widetilde w(0) \log (\sqrt{2}) -\int_{\eta}^{\infty} \frac{\widetilde w(x)-\widetilde w(0)I_{[0,1]}(x)}x \,{d} x +O(\eta \log (\eta^{-1})), \end{align*} $$
$$ \begin{align*} \widetilde w(0) \log (\sqrt{2}) -\int_{\eta}^{\infty} \frac{\widetilde w(x)-\widetilde w(0)I_{[0,1]}(x)}x \,{d} x +O(\eta \log (\eta^{-1})), \end{align*} $$
where
![]() $I_{[0,1]}$
is the characteristic function of the interval
$I_{[0,1]}$
is the characteristic function of the interval
![]() $[0,1]$
.
$[0,1]$
.
By evaluating
![]() $\widetilde {w}(x)$
in polar coordinates, we see that
$\widetilde {w}(x)$
in polar coordinates, we see that
 $$ \begin{align*} \widetilde{w}(x) =& 4\int^{\pi/2}_{0}\int^{\infty}_{0}\cos (2\pi r x \sin \theta)w(r^{2}) \ r \,{d} r \,{d} \theta. \end{align*} $$
$$ \begin{align*} \widetilde{w}(x) =& 4\int^{\pi/2}_{0}\int^{\infty}_{0}\cos (2\pi r x \sin \theta)w(r^{2}) \ r \,{d} r \,{d} \theta. \end{align*} $$
It follows from this, and by letting
![]() $\eta \rightarrow 0^{+}$
and using [Reference Vladimirov and Jeffrey41, Example (e) on page 132], that
$\eta \rightarrow 0^{+}$
and using [Reference Vladimirov and Jeffrey41, Example (e) on page 132], that
 $$ \begin{align} \int_{0}^{\infty} (\log x )g^{\prime}(x) \,{d} x &= \widetilde w(0) \log (\!\sqrt{2}) -\int_{0}^{\infty} \frac{\widetilde w(x)-\widetilde w(0)I_{[0,1]}(x)}x \,{d} x \nonumber\\[3pt] &= \widetilde w(0) \log (\sqrt{2}) -4\int^{\infty}_{0}w(r^{2})r\int^{\pi/2}_{0} \mathcal{I}(\theta) \,{d} \theta \,{d} r , \end{align} $$
$$ \begin{align} \int_{0}^{\infty} (\log x )g^{\prime}(x) \,{d} x &= \widetilde w(0) \log (\!\sqrt{2}) -\int_{0}^{\infty} \frac{\widetilde w(x)-\widetilde w(0)I_{[0,1]}(x)}x \,{d} x \nonumber\\[3pt] &= \widetilde w(0) \log (\sqrt{2}) -4\int^{\infty}_{0}w(r^{2})r\int^{\pi/2}_{0} \mathcal{I}(\theta) \,{d} \theta \,{d} r , \end{align} $$
where
 $$ \begin{align*} \mathcal{I} (\theta) = \int^{1}_{0} \frac {\cos (2\pi r x \sin \theta )-1}{x} \,{d} x + \int^{\infty}_{1} \frac {\cos (2\pi r x \sin \theta )}{x} \,{d} x. \end{align*} $$
$$ \begin{align*} \mathcal{I} (\theta) = \int^{1}_{0} \frac {\cos (2\pi r x \sin \theta )-1}{x} \,{d} x + \int^{\infty}_{1} \frac {\cos (2\pi r x \sin \theta )}{x} \,{d} x. \end{align*} $$
Now, with some changes of variables,
 $$ \begin{align*} \mathcal{I}(\theta) = \int^{2\pi r \sin \theta }_{0} \frac {\cos (u)-1}{u} \,{d} u + \int^{\infty}_{2\pi r \sin \theta} \frac {\cos (u)}{u} \,{d} u = \gamma +\log ( 2\pi r \sin \theta ). \end{align*} $$
$$ \begin{align*} \mathcal{I}(\theta) = \int^{2\pi r \sin \theta }_{0} \frac {\cos (u)-1}{u} \,{d} u + \int^{\infty}_{2\pi r \sin \theta} \frac {\cos (u)}{u} \,{d} u = \gamma +\log ( 2\pi r \sin \theta ). \end{align*} $$
Hence, the expression in (6-20) is
 $$ \begin{align*} \widetilde w(0) \log (\sqrt{2}) & +\frac {\pi \gamma \widehat{w}(0)}{2} +\frac {\pi \log \pi \widehat{w}(0)}{2}+\frac {\pi \log 2 \widehat{w}(0)}{2} \\[3pt] & +\frac {\pi}{2} \int^{\infty}_{0}w(r)\log r \,{d} r+ 2\int^{\infty}_{0}w(r) \,{d} r\int^{\pi/2}_{0} \log ( \sin \theta ) \,{d} \theta. \end{align*} $$
$$ \begin{align*} \widetilde w(0) \log (\sqrt{2}) & +\frac {\pi \gamma \widehat{w}(0)}{2} +\frac {\pi \log \pi \widehat{w}(0)}{2}+\frac {\pi \log 2 \widehat{w}(0)}{2} \\[3pt] & +\frac {\pi}{2} \int^{\infty}_{0}w(r)\log r \,{d} r+ 2\int^{\infty}_{0}w(r) \,{d} r\int^{\pi/2}_{0} \log ( \sin \theta ) \,{d} \theta. \end{align*} $$
As we have (see [Reference Gradshteyn and Ryzhik17, Formula 3, Section 4.224])
 $$ \begin{align*} \int^{\pi/2}_{0} \log ( \sin \theta ) \,{d} \theta=-\frac {\pi}{2}\log 2. \end{align*} $$
$$ \begin{align*} \int^{\pi/2}_{0} \log ( \sin \theta ) \,{d} \theta=-\frac {\pi}{2}\log 2. \end{align*} $$
We thus conclude that
 $$ \begin{align*} \int_{0}^{\infty} (\log x )g^{\prime}(x) \,{d} x &= \frac {\pi \widehat{w}(0)}{4} \log 2 +\frac {\pi \gamma \widehat{w}(0)}{2} +\frac {\pi \log \pi \widehat{w}(0)}{2}+ \frac {\pi}{2} \mathcal M w^{\prime}(1). \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty} (\log x )g^{\prime}(x) \,{d} x &= \frac {\pi \widehat{w}(0)}{4} \log 2 +\frac {\pi \gamma \widehat{w}(0)}{2} +\frac {\pi \log \pi \widehat{w}(0)}{2}+ \frac {\pi}{2} \mathcal M w^{\prime}(1). \end{align*} $$
Applying this to (6-19), we see that
 $$ \begin{align*} J(X)&=\frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma +2\log 4+\log \bigg( \frac {\pi^{2}}{32} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} \\[3pt] &\quad - \frac 43 \log 2 -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O(\mathcal{L}^{-2}). \end{align*} $$
$$ \begin{align*} J(X)&=\frac {\widehat{\phi}(1)}{\mathcal{L}} \bigg( 2\gamma +2\log 4+\log \bigg( \frac {\pi^{2}}{32} \bigg)+2\frac{\zeta^{\prime}_{K}(2)}{\zeta_{K}(2)} \\[3pt] &\quad - \frac 43 \log 2 -\frac {8}{\pi} \gamma_{K} -\frac{\mathcal M w^{\prime}(1)}{\mathcal Mw(1)} \bigg) +O(\mathcal{L}^{-2}). \end{align*} $$
With the above expression for
![]() $J(X)$
and (6-11), we conclude that the expression given in (6-10) is valid, and this completes the proof of Theorem 1.3.
$J(X)$
and (6-11), we conclude that the expression given in (6-10) is valid, and this completes the proof of Theorem 1.3.