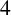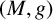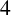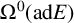1 Introduction
Let
![]() $(M,g)$
be a closed Riemannian manifold of real dimension
$(M,g)$
be a closed Riemannian manifold of real dimension
![]() $4$
and let E be a vector bundle over M with structure group G, where G is a compact Lie group. The Yang–Mills functional, defined on the space of connections of E, is given by
$4$
and let E be a vector bundle over M with structure group G, where G is a compact Lie group. The Yang–Mills functional, defined on the space of connections of E, is given by
where
![]() $\nabla $
is a metric compatible connection,
$\nabla $
is a metric compatible connection,
![]() $F_{\nabla }$
denotes the curvature, and the pointwise norm
$F_{\nabla }$
denotes the curvature, and the pointwise norm
![]() $|\cdot |$
is given by g and the Killing form of
$|\cdot |$
is given by g and the Killing form of
![]() $\mathrm {Lie}(G)$
. The connection
$\mathrm {Lie}(G)$
. The connection
![]() $\nabla $
is called a Yang–Mills connection of E if it satisfies the Yang–Mills equation:
$\nabla $
is called a Yang–Mills connection of E if it satisfies the Yang–Mills equation:
A solution of the Yang–Mills flow is given by a family of connections
![]() $\nabla _t:=\nabla (x,t)$
such that
$\nabla _t:=\nabla (x,t)$
such that
The Yang–Mills flow was initially studied by Atiyah–Bott [Reference Atiyah and Bott2] to understand the topology of the space of connections by infinite dimensional Morse theory.
We consider the Yang–Mills–Higgs k-functional (or Yang–Mills–Higgs k-energy):
where
![]() $k\in \mathbb {N}\cup \{0\}$
,
$k\in \mathbb {N}\cup \{0\}$
,
![]() $\nabla $
is a connection on E and u is a section of
$\nabla $
is a connection on E and u is a section of
![]() $\Omega ^0(\text {ad}E)$
. In [Reference Zhang13], we considered the case when u is a section of
$\Omega ^0(\text {ad}E)$
. In [Reference Zhang13], we considered the case when u is a section of
![]() $\Omega ^0(E)$
. When
$\Omega ^0(E)$
. When
![]() $k=0$
, (1.1) is the Yang–Mills–Higgs functional studied in [Reference Hassell4, Reference Hong and Tian5]. In [Reference Hassell4], Hassell proved the global existence of the Yang–Mills–Higgs flow in 3-dimensional Euclidean space. In [Reference Hong and Tian5], Hong–Tian studied the global existence of the Yang–Mills–Higgs flow in 3-dimensional hyperbolic space. Their results yield non-self-dual Yang–Mills connections on
$k=0$
, (1.1) is the Yang–Mills–Higgs functional studied in [Reference Hassell4, Reference Hong and Tian5]. In [Reference Hassell4], Hassell proved the global existence of the Yang–Mills–Higgs flow in 3-dimensional Euclidean space. In [Reference Hong and Tian5], Hong–Tian studied the global existence of the Yang–Mills–Higgs flow in 3-dimensional hyperbolic space. Their results yield non-self-dual Yang–Mills connections on
![]() $S^4$
. The Yang–Mills–Higgs flow has aroused much attention. For example, Li–Zhang [Reference Li and Zhang8] and Song–Wang [Reference Song and Wang10] studied the asymptotic behaviour at time infinity of some Yang–Mills–Higgs flows.
$S^4$
. The Yang–Mills–Higgs flow has aroused much attention. For example, Li–Zhang [Reference Li and Zhang8] and Song–Wang [Reference Song and Wang10] studied the asymptotic behaviour at time infinity of some Yang–Mills–Higgs flows.
The Yang–Mills–Higgs k-system, that is, the corresponding Euler–Lagrange equations of (1.1), is
 $$ \begin{align*} \begin{cases} \displaystyle(-1)^kD^*_{\nabla}\Delta_{\nabla}^{(k)}F_{\nabla}+\sum_{v=0}^{2k-1}P_1^{(v)}[F_{\nabla}]+P_2^{(2k-1)}[F_{\nabla}] +\sum_{i=0}^k\nabla^{*(i)}(\nabla^{(k+1)}u\ast \nabla^{(k-i)}u)=0,\\ \nabla^{*(k+1)}\nabla^{(k+1)}u=0, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \displaystyle(-1)^kD^*_{\nabla}\Delta_{\nabla}^{(k)}F_{\nabla}+\sum_{v=0}^{2k-1}P_1^{(v)}[F_{\nabla}]+P_2^{(2k-1)}[F_{\nabla}] +\sum_{i=0}^k\nabla^{*(i)}(\nabla^{(k+1)}u\ast \nabla^{(k-i)}u)=0,\\ \nabla^{*(k+1)}\nabla^{(k+1)}u=0, \end{cases} \end{align*} $$
where
![]() $\Delta _{\nabla }^{(k)}$
denotes k iterations of the Bochner Laplacian
$\Delta _{\nabla }^{(k)}$
denotes k iterations of the Bochner Laplacian
![]() $-\nabla ^*\nabla $
and the notation P is defined in (2.1). A solution of the Yang–Mills–Higgs k-flow is given by a family of pairs
$-\nabla ^*\nabla $
and the notation P is defined in (2.1). A solution of the Yang–Mills–Higgs k-flow is given by a family of pairs
![]() $(\nabla (x,t),u(x,t)):=(\nabla _t,u_t)$
such that
$(\nabla (x,t),u(x,t)):=(\nabla _t,u_t)$
such that
 $$ \begin{align} \begin{cases} \displaystyle\dfrac{\partial \nabla_t}{\partial t}&\hspace{-9pt}\displaystyle=(-1)^{(k+1)}D^*_{\nabla_t}\Delta_{\nabla_t}^{(k)}F_{\nabla_t}+\sum\limits_{v=0}^{2k-1}P_1^{(v)}[F_{\nabla_t}] \\ &\displaystyle +\ P_2^{(2k-1)}[F_{\nabla_t}]+\sum\limits_{i=0}^k\nabla_t^{*(i)}(\nabla_t^{(k+1)}u_t\ast \nabla_t^{(k-i)}u_t), \\ \dfrac{\partial u_t}{\partial t}&\hspace{-9pt}=-\ \nabla^{*(k+1)}_t\nabla_t^{(k+1)}u_t, \quad \mbox{in } M\times [0,T). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \displaystyle\dfrac{\partial \nabla_t}{\partial t}&\hspace{-9pt}\displaystyle=(-1)^{(k+1)}D^*_{\nabla_t}\Delta_{\nabla_t}^{(k)}F_{\nabla_t}+\sum\limits_{v=0}^{2k-1}P_1^{(v)}[F_{\nabla_t}] \\ &\displaystyle +\ P_2^{(2k-1)}[F_{\nabla_t}]+\sum\limits_{i=0}^k\nabla_t^{*(i)}(\nabla_t^{(k+1)}u_t\ast \nabla_t^{(k-i)}u_t), \\ \dfrac{\partial u_t}{\partial t}&\hspace{-9pt}=-\ \nabla^{*(k+1)}_t\nabla_t^{(k+1)}u_t, \quad \mbox{in } M\times [0,T). \end{cases} \end{align} $$
When
![]() $k=0$
, the flow (1.2) is a Yang–Mills–Higgs flow [Reference Hong and Tian5].
$k=0$
, the flow (1.2) is a Yang–Mills–Higgs flow [Reference Hong and Tian5].
From an analytic point of view, the Yang–Mills–Higgs k-flow (1.2) admits similar properties to the case in which the Higgs field takes values in
![]() $\Omega ^0(E)$
. In fact, by the approach in [Reference Zhang13], we can prove the following theorem.
$\Omega ^0(E)$
. In fact, by the approach in [Reference Zhang13], we can prove the following theorem.
Theorem 1.1. Let E be a vector bundle over a closed Riemannian
![]() $4$
-manifold
$4$
-manifold
![]() $(M,g)$
and k be an integer with
$(M,g)$
and k be an integer with
![]() $k> 1$
. For every smooth initial data
$k> 1$
. For every smooth initial data
![]() $(\nabla _0,u_0)$
, there exists a unique smooth solution
$(\nabla _0,u_0)$
, there exists a unique smooth solution
![]() $(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
$(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
![]() $M\times [0,+\infty )$
.
$M\times [0,+\infty )$
.
Our motivation for considering such flows comes from recent work of Waldron who proved long-time existence for the Yang–Mills flow [Reference Waldron12], thereby settling a long standing conjecture. In the context of the Yang–Mills–Higgs flow, it is still unknown whether the flow exists for all times on a Riemannian 4-manifold. The above theorem shows that provided
![]() $k> 1$
, the Yang–Mills–Higgs k flow does obey long time existence on a 4-manifold. A question that arises at this point is to understand what is the optimum value for k. By assuming our bundle E is a line bundle, we are able to make progress on this question and show that long-time existence holds for all positive k.
$k> 1$
, the Yang–Mills–Higgs k flow does obey long time existence on a 4-manifold. A question that arises at this point is to understand what is the optimum value for k. By assuming our bundle E is a line bundle, we are able to make progress on this question and show that long-time existence holds for all positive k.
Theorem 1.2. Let E be a line bundle over a closed Riemannian
![]() $4$
-manifold
$4$
-manifold
![]() $(M,g)$
and k be an integer with
$(M,g)$
and k be an integer with
![]() $k>0$
. For every smooth initial data
$k>0$
. For every smooth initial data
![]() $(\nabla _0,u_0)$
, there exists a unique smooth solution
$(\nabla _0,u_0)$
, there exists a unique smooth solution
![]() $(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
$(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
![]() $M\times [0,+\infty )$
.
$M\times [0,+\infty )$
.
At present, we do not know if this theorem is optimal, meaning that we cannot rule out long-time existence occurring for
![]() $k=0$
.
$k=0$
.
The proof of Theorem 1.1 involves local
![]() $L^2$
derivative estimates, energy estimates and blow-up analysis. An interesting aspect of this work is that by using a different blow-up procedure, we are able to obtain a proof of Theorem 1.2, which may be of independent interest. Another interesting aspect is that the proof of long-time existence obstruction (see Theorem 3.7) relies on properties of the Green function, which is very different from the previous techniques in [Reference Kelleher6, Reference Saratchandran9, Reference Zhang13].
$L^2$
derivative estimates, energy estimates and blow-up analysis. An interesting aspect of this work is that by using a different blow-up procedure, we are able to obtain a proof of Theorem 1.2, which may be of independent interest. Another interesting aspect is that the proof of long-time existence obstruction (see Theorem 3.7) relies on properties of the Green function, which is very different from the previous techniques in [Reference Kelleher6, Reference Saratchandran9, Reference Zhang13].
2 Preliminaries
In this section, we introduce the basic setup and notation that will be used throughout the paper. We follow the notation of [Reference Kelleher6, Reference Saratchandran9, Reference Zhang13].
Let E be a vector bundle over a smooth closed manifold
![]() $(M,g)$
of real dimension n. The set of all smooth unitary connections on E will be denoted by
$(M,g)$
of real dimension n. The set of all smooth unitary connections on E will be denoted by
![]() $\mathcal {A}_E$
. A given connection
$\mathcal {A}_E$
. A given connection
![]() $\nabla \in \mathcal {A}_E$
can be extended to other tensor bundles by coupling with the corresponding Levi–Civita connection
$\nabla \in \mathcal {A}_E$
can be extended to other tensor bundles by coupling with the corresponding Levi–Civita connection
![]() $\nabla _M$
on
$\nabla _M$
on
![]() $(M,g)$
.
$(M,g)$
.
Let
![]() $D_{\nabla }$
be the exterior derivative, or skew symmetrisation of
$D_{\nabla }$
be the exterior derivative, or skew symmetrisation of
![]() $\nabla $
. The curvature tensor of E is denoted by
$\nabla $
. The curvature tensor of E is denoted by
We set
![]() $\nabla ^{*},D_{\nabla }^{*}$
to be the formal
$\nabla ^{*},D_{\nabla }^{*}$
to be the formal
![]() $L^2$
-adjoints of
$L^2$
-adjoints of
![]() $\nabla ,D_{\nabla }$
, respectively. The Bochner and Hodge Laplacians are given respectively by
$\nabla ,D_{\nabla }$
, respectively. The Bochner and Hodge Laplacians are given respectively by
Let
![]() $\xi ,\eta $
be p-forms valued in E or
$\xi ,\eta $
be p-forms valued in E or
![]() $\mathrm {End}(E)$
. Let
$\mathrm {End}(E)$
. Let
![]() $\xi \ast \eta $
denote any multilinear form obtained from a tensor product
$\xi \ast \eta $
denote any multilinear form obtained from a tensor product
![]() $\xi \otimes \eta $
in a universal way. That is to say,
$\xi \otimes \eta $
in a universal way. That is to say,
![]() $\xi \ast \eta $
is obtained by starting with
$\xi \ast \eta $
is obtained by starting with
![]() $\xi \otimes \eta $
, taking any linear combination of this tensor, taking any number of metric contractions and switching any number of factors in the product. We then have
$\xi \otimes \eta $
, taking any linear combination of this tensor, taking any number of metric contractions and switching any number of factors in the product. We then have
Denote
We will also use the P notation, as introduced in [Reference Kuwert and Schätzle7]. Given a tensor
![]() $\xi $
, we denote
$\xi $
, we denote
 $$ \begin{align} P_v^{(k)}[\xi]:=\sum_{w_1+\cdots+w_v=k}(\nabla^{(w_1)}\xi)\ast\cdots\ast(\nabla^{(w_v)}\xi)\ast T, \end{align} $$
$$ \begin{align} P_v^{(k)}[\xi]:=\sum_{w_1+\cdots+w_v=k}(\nabla^{(w_1)}\xi)\ast\cdots\ast(\nabla^{(w_v)}\xi)\ast T, \end{align} $$
where
![]() $k,v\in \mathbb {N}$
and T is a generic background tensor dependent only on g.
$k,v\in \mathbb {N}$
and T is a generic background tensor dependent only on g.
3 Long-time existence obstruction
We can use De Turck’s trick to establish the local existence of the Yang–Mills–Higgs k-flow. We refer to [Reference Kelleher6, Reference Saratchandran9, Reference Zhang13] for more details. As the proof is standard, we will omit the details.
Theorem 3.1 (Local existence)
Let E be a vector bundle over a closed Riemannian manifold
![]() $(M,g)$
. There exists a unique smooth solution
$(M,g)$
. There exists a unique smooth solution
![]() $(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
$(\nabla _t,u_t)$
to the Yang–Mills–Higgs k-flow (1.2) in
![]() $M\times [0,\epsilon )$
with smooth initial value
$M\times [0,\epsilon )$
with smooth initial value
![]() $(\nabla _0,u_0)$
.
$(\nabla _0,u_0)$
.
Following [Reference Kelleher6, Reference Saratchandran9], we can derive estimates of Bernstein–Bando–Shi type, similar to [Reference Zhang13, Proposition 4.10].
Proposition 3.2. Let
![]() $q\in \mathbb {N}$
,
$q\in \mathbb {N}$
,
![]() $\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
and
$\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
and
![]() $(\nabla _t,u_t)$
be a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
be a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M\times I$
. Suppose
$M\times I$
. Suppose
![]() $Q=\max \{1,\sup _{t\in I} |F_{\nabla _t}|\}$
,
$Q=\max \{1,\sup _{t\in I} |F_{\nabla _t}|\}$
,
![]() $K=\max \{1,\sup _{t\in I}|u_t|\}$
and
$K=\max \{1,\sup _{t\in I}|u_t|\}$
and
![]() $s\geq (k+1)(q+1)$
. For
$s\geq (k+1)(q+1)$
. For
![]() $t\in [0,T)\subset I$
with
$t\in [0,T)\subset I$
with
![]() $T<{1}/{(QK)^{4}}$
, there exists a positive constant
$T<{1}/{(QK)^{4}}$
, there exists a positive constant
![]() $C_q:=C_q(\mathrm {dim} (M),\mathrm {rk} (E),G,q,k,s,g,\gamma )\in \mathbb {R}_{>0}$
such that
$C_q:=C_q(\mathrm {dim} (M),\mathrm {rk} (E),G,q,k,s,g,\gamma )\in \mathbb {R}_{>0}$
such that
The following corollary is a direct consequence of the above proposition and will be used in the blow-up analysis. The proof relies on the Sobolev embedding,
![]() $W^{p,2}\subset C^0$
provided
$W^{p,2}\subset C^0$
provided
![]() $p>{n}{/2}$
, and Kato’s inequality
$p>{n}{/2}$
, and Kato’s inequality
![]() $|d|u_t||\leq |\nabla _tu_t|$
. More details can be found in Kelleher’s paper [Reference Kelleher6, Corollary 3.14].
$|d|u_t||\leq |\nabla _tu_t|$
. More details can be found in Kelleher’s paper [Reference Kelleher6, Corollary 3.14].
Corollary 3.3. Suppose
![]() $(\nabla _t,u_t)$
solves the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
solves the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M\times [0,\tau ]$
. Set
$M\times [0,\tau ]$
. Set
![]() $\bar {\tau }:=\min \{\tau ,1\}$
. Suppose
$\bar {\tau }:=\min \{\tau ,1\}$
. Suppose
![]() $Q=\max \{1,\sup _{t\in [0,\bar {\tau }]} |F_{\nabla _t}|\}$
,
$Q=\max \{1,\sup _{t\in [0,\bar {\tau }]} |F_{\nabla _t}|\}$
,
![]() $K\,{=}\,\max \{1,\sup _{t\in [0,\bar {\tau }]}|u_t|\}$
. Assume
$K\,{=}\,\max \{1,\sup _{t\in [0,\bar {\tau }]}|u_t|\}$
. Assume
![]() $\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
. For
$\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
. For
![]() $s,l\in \mathbb {N}$
with
$s,l\in \mathbb {N}$
with
![]() $s\geq (k+1)(l+1)$
, there exists
$s\geq (k+1)(l+1)$
, there exists
![]() $C_l:=C_l(\dim (M),\mathrm {rk}(E),K,Q,G,s,k,l,\tau ,g,\gamma )\in \mathbb {R}_{>0}$
such that
$C_l:=C_l(\dim (M),\mathrm {rk}(E),K,Q,G,s,k,l,\tau ,g,\gamma )\in \mathbb {R}_{>0}$
such that
From Corollary 3.3, we deduce the following corollary, which can be used for finding obstructions to long-time existence.
Corollary 3.4. Suppose
![]() $(\nabla _t,u_t)$
solves the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
solves the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M\times [0,T)$
for
$M\times [0,T)$
for
![]() $T\in [0,+\infty )$
. Suppose
$T\in [0,+\infty )$
. Suppose
and
are finite. Assume
![]() $\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
. Then, for
$\gamma \in C^{\infty }_c(M)\ (0\leq \gamma \leq 1)$
. Then, for
![]() $t\in [0,T)$
and
$t\in [0,T)$
and
![]() $s,l\in \mathbb {N}$
with
$s,l\in \mathbb {N}$
with
![]() ${s\geq (k+1)(l+1)}$
, there exists
${s\geq (k+1)(l+1)}$
, there exists
![]() $C_l:=C_l(\nabla _0,u_0,\dim (M),\mathrm {rk}(E),K,Q,G,s,k,l,g,\gamma )\in \mathbb {R}_{>0}$
such that
$C_l:=C_l(\nabla _0,u_0,\dim (M),\mathrm {rk}(E),K,Q,G,s,k,l,g,\gamma )\in \mathbb {R}_{>0}$
such that
We will use Corollary 3.4 to show that the only obstruction to long-time existence of the Yang–Mills–Higgs k-flow (1.2) is a lack of a supremal bound on
![]() $|F_{\nabla _t}|+|\nabla _tu_t|$
. Before doing so, we need the following proposition, which is similar to [Reference Zhang13, Proposition 4.15].
$|F_{\nabla _t}|+|\nabla _tu_t|$
. Before doing so, we need the following proposition, which is similar to [Reference Zhang13, Proposition 4.15].
Proposition 3.5. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M\times [0,T)$
for
$M\times [0,T)$
for
![]() $T\in [0,+\infty )$
. Suppose that for all
$T\in [0,+\infty )$
. Suppose that for all
![]() $l\in \mathbb {N}\cup \{0\}$
, there exists
$l\in \mathbb {N}\cup \{0\}$
, there exists
![]() $C_l\in \mathbb {R}_{>0}$
such that
$C_l\in \mathbb {R}_{>0}$
such that
 $$ \begin{align*}\max\bigg\{\sup_{M\times[0,T)}\bigg|\nabla_t^{(l)}\bigg[\frac{\partial \nabla_t}{\partial t}\bigg]\bigg|, \sup_{M\times[0,T)}\bigg|\nabla_t^{(l)}\bigg[\frac{\partial u_t}{\partial t}\bigg]\bigg|\bigg\}\leq C_l.\end{align*} $$
$$ \begin{align*}\max\bigg\{\sup_{M\times[0,T)}\bigg|\nabla_t^{(l)}\bigg[\frac{\partial \nabla_t}{\partial t}\bigg]\bigg|, \sup_{M\times[0,T)}\bigg|\nabla_t^{(l)}\bigg[\frac{\partial u_t}{\partial t}\bigg]\bigg|\bigg\}\leq C_l.\end{align*} $$
Then
![]() $\lim _{t\rightarrow T}(\nabla _t,u_t)=(\nabla _T,u_T)$
exists and is smooth.
$\lim _{t\rightarrow T}(\nabla _t,u_t)=(\nabla _T,u_T)$
exists and is smooth.
The following proposition is straightforward.
Proposition 3.6. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M\times [0,T)$
. We have
$M\times [0,T)$
. We have
Using Propositions 3.5 and 3.6, we are ready to prove the main result in this section.
Theorem 3.7. Assume E is a line bundle. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) for some maximal
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) for some maximal
![]() $T<+\infty $
. Then,
$T<+\infty $
. Then,
Proof. Suppose to the contrary that
which means that
Denote by
![]() $G_t(x,y)$
the Green function associated to the operator
$G_t(x,y)$
the Green function associated to the operator
![]() $\Delta _{\nabla _t}$
. Then for any fixed
$\Delta _{\nabla _t}$
. Then for any fixed
![]() $x\in M$
,
$x\in M$
,
![]() $\|\nabla _0 G_t(x,\cdot )\|_{L^{\infty }(M)}\leq C_G$
for a constant
$\|\nabla _0 G_t(x,\cdot )\|_{L^{\infty }(M)}\leq C_G$
for a constant
![]() $C_G$
from [Reference Alesker and Shelukhin1, Appendix A]. Note that
$C_G$
from [Reference Alesker and Shelukhin1, Appendix A]. Note that
![]() $\nabla _tG_t-\nabla _0 G_t=[\nabla _t-\nabla _0,G_t]=0$
. We conclude that
$\nabla _tG_t-\nabla _0 G_t=[\nabla _t-\nabla _0,G_t]=0$
. We conclude that
![]() $\|\nabla _t G_t\|_{L^{\infty }(M)}$
is also uniformly bounded. Therefore, using the properties of the Green function in [Reference Alesker and Shelukhin1, Appendix A],
$\|\nabla _t G_t\|_{L^{\infty }(M)}$
is also uniformly bounded. Therefore, using the properties of the Green function in [Reference Alesker and Shelukhin1, Appendix A],
 $$ \begin{align*} \begin{split} \bigg|u_t(x)-\frac{1}{\text{Vol}(M)}\int_M u_t(y)\,{d}y\bigg|&=\bigg|\int_M \Delta_{\nabla_t} G_t(x,y) u_t(y)\,{d}y\bigg|\\ &=\bigg|\int_M \nabla_t G_t(x,y)\nabla_tu_t(y)\,{d}y\bigg|\\ &< +\infty, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \bigg|u_t(x)-\frac{1}{\text{Vol}(M)}\int_M u_t(y)\,{d}y\bigg|&=\bigg|\int_M \Delta_{\nabla_t} G_t(x,y) u_t(y)\,{d}y\bigg|\\ &=\bigg|\int_M \nabla_t G_t(x,y)\nabla_tu_t(y)\,{d}y\bigg|\\ &< +\infty, \end{split} \end{align*} $$
which together with Proposition 3.6 implies
For all
![]() $t\in [0,T)$
and
$t\in [0,T)$
and
![]() $l\in \mathbb {N}\cup \{0\}$
, by Corollary 3.4,
$l\in \mathbb {N}\cup \{0\}$
, by Corollary 3.4,
![]() $\sup _{M}(|\nabla _t^{(l)}F_{\nabla _{t}}|^2+|\nabla _t^{(l)}u_t|^2)$
is uniformly bounded and so by Proposition 3.5,
$\sup _{M}(|\nabla _t^{(l)}F_{\nabla _{t}}|^2+|\nabla _t^{(l)}u_t|^2)$
is uniformly bounded and so by Proposition 3.5,
![]() $\lim _{t\rightarrow T}(\nabla _t,u_t)=(\nabla _T,u_T)$
exists and is smooth. However, by local existence (Theorem 3.1), there exists
$\lim _{t\rightarrow T}(\nabla _t,u_t)=(\nabla _T,u_T)$
exists and is smooth. However, by local existence (Theorem 3.1), there exists
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
![]() $(\nabla _t,u_t)$
exists over the extended domain
$(\nabla _t,u_t)$
exists over the extended domain
![]() $[0,T+\epsilon )$
, which contradicts the assumption that T is maximal. Thus, we prove the theorem.
$[0,T+\epsilon )$
, which contradicts the assumption that T is maximal. Thus, we prove the theorem.
4 Blow-up analysis
In this section, we will address the possibility that the Yang–Mills–Higgs k-flow admits a singularity given no bound on
![]() $|F_{\nabla _t}|+|\nabla _tu_t|$
. To begin with, we first establish some preliminary scaling laws for the Yang–Mills–Higgs k-flow.
$|F_{\nabla _t}|+|\nabla _tu_t|$
. To begin with, we first establish some preliminary scaling laws for the Yang–Mills–Higgs k-flow.
Proposition 4.1. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M\times [0,T)$
. Define the 1-parameter family
$M\times [0,T)$
. Define the 1-parameter family
![]() $\nabla _t^{\rho }$
with local coefficient matrices given by
$\nabla _t^{\rho }$
with local coefficient matrices given by
where
![]() $\Gamma _t(x)$
is the local coefficient matrix of
$\Gamma _t(x)$
is the local coefficient matrix of
![]() $\nabla _t$
. Define the
$\nabla _t$
. Define the
![]() $\rho $
-scaled Higgs field
$\rho $
-scaled Higgs field
![]() $u_t^{\rho }$
by
$u_t^{\rho }$
by
Then
![]() $(\nabla _t^{\rho },u_t^{\rho })$
is also a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t^{\rho },u_t^{\rho })$
is also a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $[0,{T}/{\rho ^{2(k+1)}})$
.
$[0,{T}/{\rho ^{2(k+1)}})$
.
Next we will show that if the curvature coupled with a Higgs field is blowing up as one approaches the maximal time, then one can extract a blow-up limit. The proof will closely follow the arguments in [Reference Kelleher6, Proposition 3.25] and [Reference Zhang13, Theorem 5.2].
Theorem 4.2. Assume E is a line bundle. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on some maximal time interval
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on some maximal time interval
![]() $[0,T)$
with
$[0,T)$
with
![]() $T< +\infty $
. Then there exists a blow-up sequence
$T< +\infty $
. Then there exists a blow-up sequence
![]() $(\nabla ^i_t,u^i_t)$
which converges pointwise to a smooth solution
$(\nabla ^i_t,u^i_t)$
which converges pointwise to a smooth solution
![]() $(\nabla ^{\infty }_t,u^{\infty }_t)$
to the Yang–Mills–Higgs k-flow (1.2) defined on the domain
$(\nabla ^{\infty }_t,u^{\infty }_t)$
to the Yang–Mills–Higgs k-flow (1.2) defined on the domain
![]() $\mathbb {R}^n\times \mathbb {R}_{<0}$
.
$\mathbb {R}^n\times \mathbb {R}_{<0}$
.
Proof. From Theorem 3.7,
Therefore, we can choose a sequence of times
![]() $t_i\nearrow T$
within
$t_i\nearrow T$
within
![]() $[0,T)$
and a sequence of points
$[0,T)$
and a sequence of points
![]() $x_i$
, such that
$x_i$
, such that
Let
![]() $\{\rho _i\}\subset \mathbb {R}_{>0}$
be constants to be determined. Define
$\{\rho _i\}\subset \mathbb {R}_{>0}$
be constants to be determined. Define
![]() $\nabla _t^i(x)$
by
$\nabla _t^i(x)$
by
and
By Proposition 4.1,
![]() $(\nabla ^i_t,u^i_t)$
are also solutions to the Yang–Mills–Higgs k-flow (1.2) and the domain for each
$(\nabla ^i_t,u^i_t)$
are also solutions to the Yang–Mills–Higgs k-flow (1.2) and the domain for each
![]() $(\nabla ^i_t,u^i_t)$
is
$(\nabla ^i_t,u^i_t)$
is
![]() $B_0(\,\rho _i^{-{1}/{2(k+1)}})\times [-{t_i}/{\rho _i},{(T-t_i)}/{\rho _i})$
. We observe that
$B_0(\,\rho _i^{-{1}/{2(k+1)}})\times [-{t_i}/{\rho _i},{(T-t_i)}/{\rho _i})$
. We observe that
which means that
 $$ \begin{align*} \begin{split} &\sup_{t\in[-{t_i}/{\rho_i},{T-t_i}/{\rho_i})} (|F_t^i(x)|+|\nabla_{t}^iu_t^i(x)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}\sup_{t\in[-{t_i}/{\rho_i},{T-t_i}/{\rho_i})}(|F_{\nabla_{\rho_i t+t_i}}(\,\rho_i^{{1}/{2(k+1)}} x+x_i)|+|\nabla_{\rho_i t+t_i} u_{\rho_i t+t_i}(\,\rho_i^{{1}/{2(k+1)}} x+x_i)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}\sup_{t\in[0,t_i]}(|F_{\nabla_t}(x)|+|\nabla_tu_t(x)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}(|F_{\nabla_{t_i}}(x_i)|+|\nabla_{t_i}u_{t_i}(x_i)|). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} &\sup_{t\in[-{t_i}/{\rho_i},{T-t_i}/{\rho_i})} (|F_t^i(x)|+|\nabla_{t}^iu_t^i(x)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}\sup_{t\in[-{t_i}/{\rho_i},{T-t_i}/{\rho_i})}(|F_{\nabla_{\rho_i t+t_i}}(\,\rho_i^{{1}/{2(k+1)}} x+x_i)|+|\nabla_{\rho_i t+t_i} u_{\rho_i t+t_i}(\,\rho_i^{{1}/{2(k+1)}} x+x_i)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}\sup_{t\in[0,t_i]}(|F_{\nabla_t}(x)|+|\nabla_tu_t(x)|)\\ &\qquad =\rho_i^{{1}/{(k+1)}}(|F_{\nabla_{t_i}}(x_i)|+|\nabla_{t_i}u_{t_i}(x_i)|). \end{split} \end{align*} $$
Therefore, setting
gives
Now, we are ready to construct smoothing estimates for the sequence
![]() $(\nabla ^i_t,u^i_t)$
. Let
$(\nabla ^i_t,u^i_t)$
. Let
![]() $y\in \mathbb {R}^n$
,
$y\in \mathbb {R}^n$
,
![]() $\tau \in \mathbb {R}_{\leq 0}$
. For any
$\tau \in \mathbb {R}_{\leq 0}$
. For any
![]() $s\in \mathbb {N}$
,
$s\in \mathbb {N}$
,
Note that E is a line bundle and, similar to the proof of Theorem 3.7, it suffices to use Corollary 3.3. Then for all
![]() $q\in \mathbb {N}$
, one may choose
$q\in \mathbb {N}$
, one may choose
![]() $s\geq (k+1)(q+1)$
so that there exists a positive constant
$s\geq (k+1)(q+1)$
so that there exists a positive constant
![]() $C_q$
such that
$C_q$
such that
 $$ \begin{align*} \begin{split} &\sup_{x\in B_y({1}/{2})}(|(\nabla^i_{\tau})^{(q)} F^i_{\tau}(x)|+|(\nabla^i_{\tau})^{(q)} u^i_{\tau}(x)|)\\ &\quad \leq\sup_{x\in B_y(1)}(|\gamma^s_y(\nabla^i_{\tau})^{(q)} F^i_{\tau}(x)|+|\gamma^s_y(\nabla^i_{\tau})^{(q)} u^i_{\tau}(x)|) \leq C_q. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} &\sup_{x\in B_y({1}/{2})}(|(\nabla^i_{\tau})^{(q)} F^i_{\tau}(x)|+|(\nabla^i_{\tau})^{(q)} u^i_{\tau}(x)|)\\ &\quad \leq\sup_{x\in B_y(1)}(|\gamma^s_y(\nabla^i_{\tau})^{(q)} F^i_{\tau}(x)|+|\gamma^s_y(\nabla^i_{\tau})^{(q)} u^i_{\tau}(x)|) \leq C_q. \end{split} \end{align*} $$
Then by the Coulomb gauge theorem of Uhlenbeck [Reference Uhlenbeck11, Theorem 1.3] (see also [Reference Hong and Tian5]) and the gauge patching theorem [Reference Donaldson and Kronheimer3, Corollary 4.4.8], passing to a subsequence (without changing notation) and in an appropriate gauge,
![]() $(\nabla ^i_t,u^i_t)\rightarrow (\nabla ^{\infty }_t,u^{\infty }_t)$
in
$(\nabla ^i_t,u^i_t)\rightarrow (\nabla ^{\infty }_t,u^{\infty }_t)$
in
![]() $C^{\infty }$
.
$C^{\infty }$
.
5 Proof of Theorem 1.2
The following energy estimates are similar to the ones in [Reference Zhang13, Section 6].
Proposition 5.1. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M\times [0,T)$
. Then the Yang–Mills–Higgs k-energy (1.1) is decreasing along the flow (1.2).
$M\times [0,T)$
. Then the Yang–Mills–Higgs k-energy (1.1) is decreasing along the flow (1.2).
Proposition 5.2. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M^4\times [0,T)$
with
$M^4\times [0,T)$
with
![]() $T< +\infty $
. Then the Yang–Mills–Higgs energy
$T< +\infty $
. Then the Yang–Mills–Higgs energy
is bounded along the flow (1.2).
Next, we will complete the proof of Theorem 1.2. To accomplish this, we first show that the
![]() $L^p$
-norm controls the
$L^p$
-norm controls the
![]() $L^{\infty }$
-norm by blow-up analysis.
$L^{\infty }$
-norm by blow-up analysis.
Proposition 5.3. Assume E is a line bundle. Suppose
![]() $(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
$(\nabla _t,u_t)$
is a solution to the Yang–Mills–Higgs k-flow (1.2) defined on
![]() $M^4\times [0,T)$
and
$M^4\times [0,T)$
and
If
![]() $p>2$
, then
$p>2$
, then
Proof. To obtain a contradiction, assume
As we did in Theorem 4.2, we can construct a blow-up sequence
![]() $(\nabla ^i_t,u^i_t)$
, with blow-up limit
$(\nabla ^i_t,u^i_t)$
, with blow-up limit
![]() $(\nabla ^{\infty }_t,u^{\infty }_t)$
. Noting (4.1), by Fatou’s lemma and the natural scaling law,
$(\nabla ^{\infty }_t,u^{\infty }_t)$
. Noting (4.1), by Fatou’s lemma and the natural scaling law,
 $$ \begin{align*} \begin{split} \|F_{\nabla^{\infty}_t}\|^p_{L^p}+\|\nabla_t^{\infty} u^{\infty}_t \|^p_{L^p} &\leq \lim_{i\rightarrow +\infty}\inf(\|F_{\nabla^{i}_t}\|^p_{L^p}+\|\nabla_t^i u^{i}_t \|^p_{L^p})\\ &\leq \lim_{i\rightarrow +\infty}\rho_i^{{(2p-4)}/{(2k+2)}}(\|F_{\nabla_t}\|^p_{L^p}+\|\nabla_t u_t\|^p_{L^p}). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \|F_{\nabla^{\infty}_t}\|^p_{L^p}+\|\nabla_t^{\infty} u^{\infty}_t \|^p_{L^p} &\leq \lim_{i\rightarrow +\infty}\inf(\|F_{\nabla^{i}_t}\|^p_{L^p}+\|\nabla_t^i u^{i}_t \|^p_{L^p})\\ &\leq \lim_{i\rightarrow +\infty}\rho_i^{{(2p-4)}/{(2k+2)}}(\|F_{\nabla_t}\|^p_{L^p}+\|\nabla_t u_t\|^p_{L^p}). \end{split} \end{align*} $$
Since
![]() $\lim _{i\rightarrow +\infty }\rho _i^{{(2p-4)}/{(2k+2)}}=0$
when
$\lim _{i\rightarrow +\infty }\rho _i^{{(2p-4)}/{(2k+2)}}=0$
when
![]() $p>2$
, the right-hand side of the above inequality tends to zero, which is a contradiction since the blow-up limit has nonvanishing curvature.
$p>2$
, the right-hand side of the above inequality tends to zero, which is a contradiction since the blow-up limit has nonvanishing curvature.
Now we are ready to give the proof of Theorem 1.2.
Proof of Theorem 1.2
By the Sobolev embedding theorem, we can solve for p such that
![]() $W^{k,2}\subset L^{p}$
, when
$W^{k,2}\subset L^{p}$
, when
![]() $k>0$
. Using the interpolation inequalities [Reference Kuwert and Schätzle7, Corollary 5.5]:
$k>0$
. Using the interpolation inequalities [Reference Kuwert and Schätzle7, Corollary 5.5]:
 $$ \begin{align*} \begin{split} \|F_{\nabla_t}\|_{L^{p}}+\|\nabla_t u_t\|_{L^{p}} & \leq CS_{k,p}\sum_{j=0}^k(\|\nabla_t^{(j)}F_{\nabla_t}\|^2_{L^2}+\|\nabla_t^{(j)}u_t\|^2_{L^2}+1)\\ & \leq CS_{k,p}(\|\nabla_t^{(k)}F_{\nabla_t}\|^2_{L^2}+\|F_{\nabla_t}\|^2_{L^2}+\|\nabla_t^{(k+1)}u_t\|^2_{L^2}+\|u_t\|^2_{L^2}+1)\\ & \leq CS_{k,p}(\mathcal{YMH}_k(\nabla_t,u_t)+\mathcal{YMH}(\nabla_t,u_t)+\|u_t\|^2_{L^2}+1), \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \|F_{\nabla_t}\|_{L^{p}}+\|\nabla_t u_t\|_{L^{p}} & \leq CS_{k,p}\sum_{j=0}^k(\|\nabla_t^{(j)}F_{\nabla_t}\|^2_{L^2}+\|\nabla_t^{(j)}u_t\|^2_{L^2}+1)\\ & \leq CS_{k,p}(\|\nabla_t^{(k)}F_{\nabla_t}\|^2_{L^2}+\|F_{\nabla_t}\|^2_{L^2}+\|\nabla_t^{(k+1)}u_t\|^2_{L^2}+\|u_t\|^2_{L^2}+1)\\ & \leq CS_{k,p}(\mathcal{YMH}_k(\nabla_t,u_t)+\mathcal{YMH}(\nabla_t,u_t)+\|u_t\|^2_{L^2}+1), \end{split} \end{align*} $$
then using Propositions 5.1, 3.6 and 5.2, we conclude that the flow exists smoothly for all time.