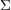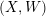1 Introduction
The Fukaya category is an intricate invariant of symplectic manifolds. One of the many subtleties of the theory is that pseudo-holomorphic discs, which control compositions of morphisms in the Fukaya category, are global in nature. As a consequence, there is no way to calculate the Fukaya category of a general symplectic manifold by breaking it down into local pieces.Footnote
1
In the case of exact symplectic manifolds, however, the Fukaya category is expected to have good local-to-global properties. For instance, if
![]() $S=T^{\ast }M$
is the cotangent bundle of an analytic variety, this follows from work of Nadler and Zaslow. They prove in [Reference Nadler and ZaslowNZ09, Reference NadlerNad09] that the (infinitesimal) Fukaya category of
$S=T^{\ast }M$
is the cotangent bundle of an analytic variety, this follows from work of Nadler and Zaslow. They prove in [Reference Nadler and ZaslowNZ09, Reference NadlerNad09] that the (infinitesimal) Fukaya category of
![]() $S$
is equivalent to the category of constructible sheaves on the base manifold
$S$
is equivalent to the category of constructible sheaves on the base manifold
![]() $M$
. This implies in particular that the Fukaya category of
$M$
. This implies in particular that the Fukaya category of
![]() $S$
localizes as a sheaf of categories over
$S$
localizes as a sheaf of categories over
![]() $M$
.
$M$
.
Recently Kontsevich [Reference KontsevichKon09] has proposed that the Fukaya category of a Stein manifold
![]() $S$
can be described in terms of a (co)sheaf of categories on a skeleton of
$S$
can be described in terms of a (co)sheaf of categories on a skeleton of
![]() $S$
. A skeleton is, roughly, a half-dimensional CW complex
$S$
. A skeleton is, roughly, a half-dimensional CW complex
![]() $X$
embedded in
$X$
embedded in
![]() $S$
as a Lagrangian deformation retract. According to Kontsevich,
$S$
as a Lagrangian deformation retract. According to Kontsevich,
![]() $X$
should carry a cosheaf of categories, which we will denote
$X$
should carry a cosheaf of categories, which we will denote
![]() ${\mathcal{F}}^{\text{top}}$
, that encodes in a universal way the local geometry of the singularities of
${\mathcal{F}}^{\text{top}}$
, that encodes in a universal way the local geometry of the singularities of
![]() $X$
. He conjectures that the global sections of
$X$
. He conjectures that the global sections of
![]() ${\mathcal{F}}^{\text{top}}$
on
${\mathcal{F}}^{\text{top}}$
on
![]() $X$
should be equivalent to the wrapped Fukaya category of
$X$
should be equivalent to the wrapped Fukaya category of
![]() $S$
.
$S$
.
Giving a rigorous definition of the cosheaf
![]() ${\mathcal{F}}^{\text{top}}$
is subtle. Work of several authors has clarified the case of punctured Riemann surfaces [Reference Dyckerhoff and KapranovDK18, Reference NadlerNad15, Reference Sibilla, Treumann and ZaslowSTZ14], while generalizations to higher dimensions have been pursued in [Reference NadlerNad16a, Reference NadlerNad16b]. The theory is considerably easier in complex dimension one because skeleta of punctured Riemann surfaces, also known as ribbon graphs or spines, have a simple and well studied combinatorics and geometry, while the higher-dimensional picture is only beginning to emerge [Reference Ruddat, Sibilla, Treumann and ZaslowRSTZ14, Reference NadlerNad17b]. Implementing Kontsevich’s ideas, the formalism developed in [Reference Dyckerhoff and KapranovDK18, Reference NadlerNad15, Reference Sibilla, Treumann and ZaslowSTZ14] defines a covariant functor
${\mathcal{F}}^{\text{top}}$
is subtle. Work of several authors has clarified the case of punctured Riemann surfaces [Reference Dyckerhoff and KapranovDK18, Reference NadlerNad15, Reference Sibilla, Treumann and ZaslowSTZ14], while generalizations to higher dimensions have been pursued in [Reference NadlerNad16a, Reference NadlerNad16b]. The theory is considerably easier in complex dimension one because skeleta of punctured Riemann surfaces, also known as ribbon graphs or spines, have a simple and well studied combinatorics and geometry, while the higher-dimensional picture is only beginning to emerge [Reference Ruddat, Sibilla, Treumann and ZaslowRSTZ14, Reference NadlerNad17b]. Implementing Kontsevich’s ideas, the formalism developed in [Reference Dyckerhoff and KapranovDK18, Reference NadlerNad15, Reference Sibilla, Treumann and ZaslowSTZ14] defines a covariant functor
![]() ${\mathcal{F}}^{\text{top}}(-)$
from a category of ribbon graphs and open inclusions to triangulated dg categories.
${\mathcal{F}}^{\text{top}}(-)$
from a category of ribbon graphs and open inclusions to triangulated dg categories.
An important feature of the theory is that, if
![]() $X$
and
$X$
and
![]() $X^{\prime }$
are two distinct compact skeleta of a punctured surface
$X^{\prime }$
are two distinct compact skeleta of a punctured surface
![]() $\unicode[STIX]{x1D6F4}$
, there is an equivalence
$\unicode[STIX]{x1D6F4}$
, there is an equivalence
We will refer to
![]() ${\mathcal{F}}^{\text{top}}(X)$
as the topological Fukaya category of
${\mathcal{F}}^{\text{top}}(X)$
as the topological Fukaya category of
![]() $\unicode[STIX]{x1D6F4}$
, and we denote it
$\unicode[STIX]{x1D6F4}$
, and we denote it
![]() $\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
. In this paper we take
$\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
. In this paper we take
![]() $\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
as a model for the category of A-branes on
$\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
as a model for the category of A-branes on
![]() $\unicode[STIX]{x1D6F4}$
. We prove homological mirror symmetry for punctured Riemann surfaces by showing that
$\unicode[STIX]{x1D6F4}$
. We prove homological mirror symmetry for punctured Riemann surfaces by showing that
![]() $\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
is equivalent to the category of B-branes on a mirror geometry LG model.
$\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
is equivalent to the category of B-branes on a mirror geometry LG model.
1.1 Hori–Vafa homological mirror symmetry
Let us review the setting of Hori–Vafa mirror symmetry for LG models [Reference Hori and VafaHV15, Reference Gross, Katzarkov and RuddatGKR17]. Let
![]() $X$
be a toric threefold with trivial canonical bundle. The fan of
$X$
be a toric threefold with trivial canonical bundle. The fan of
![]() $X$
can be realized as a smooth subdivision of the cone over a two-dimensional lattice polytope, see § 3.1.1 for more details. The height function on the fan of
$X$
can be realized as a smooth subdivision of the cone over a two-dimensional lattice polytope, see § 3.1.1 for more details. The height function on the fan of
![]() $X$
gives rise to a regular map
$X$
gives rise to a regular map
which is called the superpotential. The category of B-branes for the LG model
![]() $(X,W)$
is the
$(X,W)$
is the
![]() $\mathbb{Z}_{2}$
-graded category of matrix factorizations
$\mathbb{Z}_{2}$
-graded category of matrix factorizations
![]() $MF(X,W)$
. The mirror of the LG model
$MF(X,W)$
. The mirror of the LG model
![]() $(X,W)$
is a smooth algebraic curve
$(X,W)$
is a smooth algebraic curve
![]() $\unicode[STIX]{x1D6F4}_{W}$
in
$\unicode[STIX]{x1D6F4}_{W}$
in
![]() $\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
, called the mirror curve (see § 3). The following is our main result.
$\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
, called the mirror curve (see § 3). The following is our main result.
Theorem 1.1 (Hori–Vafa homological mirror symmetry).
There is an equivalence
Theorem 1.1 provides a proof of homological mirror symmetry for punctured surfaces, provided that we model the category of A-branes via the topological Fukaya category. This extends to all genera earlier results for curves of genus zero and one which were obtained in [Reference Sibilla, Treumann and ZaslowSTZ14] and [Reference Dyckerhoff and KapranovDK18]. We also mention work of Nadler, who studies both directions of Hori–Vafa mirror symmetry for higher-dimensional pairs of pants [Reference NadlerNad17a, Reference NadlerNad16a, Reference NadlerNad16b].
We learnt the statement of Hori–Vafa homological mirror symmetry for punctured surfaces from the inspiring paper [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13]. In [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] the authors prove homological mirror symmetry for punctured spheres. Their main theorem is parallel to our own (in genus zero) with the important difference that they work with the wrapped Fukaya category, rather than with its topological model. See also related work of Bocklandt [Reference BocklandtBoc16]. Mirror symmetry for higher-dimensional pairs of pants was studied by Sheridan in [Reference SheridanShe11].
Denote by
![]() $\text{Fuk}^{\text{wr}}(\unicode[STIX]{x1D6F4})$
the wrapped Fukaya category of a punctured surface
$\text{Fuk}^{\text{wr}}(\unicode[STIX]{x1D6F4})$
the wrapped Fukaya category of a punctured surface
![]() $\unicode[STIX]{x1D6F4}$
. Our main result combined with the main result of [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] gives equivalences
$\unicode[STIX]{x1D6F4}$
. Our main result combined with the main result of [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] gives equivalences
for all Riemann surfaces
![]() $\unicode[STIX]{x1D6F4}_{W}$
which can be realized as unramified cyclic covers of punctured spheres. Thus, for this class of examples, the topological Fukaya category captures the wrapped Fukaya category, corroborating Kontsevich’s proposal. We also remark that a proof of the equivalence between topological and wrapped Fukaya category, with different methods, appeared recently in [Reference Haiden, Katzarkov and KontsevichHKK17].
$\unicode[STIX]{x1D6F4}_{W}$
which can be realized as unramified cyclic covers of punctured spheres. Thus, for this class of examples, the topological Fukaya category captures the wrapped Fukaya category, corroborating Kontsevich’s proposal. We also remark that a proof of the equivalence between topological and wrapped Fukaya category, with different methods, appeared recently in [Reference Haiden, Katzarkov and KontsevichHKK17].
Remark 1.2. When we were close to completing the project we learnt that Lee, in her thesis [Reference LeeLe15], extends the results of [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] to all genera. Although our techniques are very different, conceptually the approach pursued in this work and in Lee’s are closely related. The results of this paper are logically independent of those of [Reference LeeLe15], since we use the topological version of the Fukaya category instead of the version defined in terms of pseudo-holomorphic curves.
Remark 1.3. Theorem 1.1 gives a homological mirror symmetry picture for the wrapped Fukaya category of punctured Riemann surfaces. Our techniques can also be used to obtain more general mirror symmetry statements for partially wrapped Fukaya categories: this corresponds to considering noncompact skeleta having semi-infinite edges that approach the punctures of the Riemann surface. In the parlance of partially wrapped Fukaya categories, the noncompact ends of the skeleton are called stops: they encode the directions along which wrapping is not allowed.
For brevity, we limit ourselves to a sketch of the theory in this more general setting. Let
![]() $S\subset \unicode[STIX]{x1D6F4}_{W}$
be such a skeleton with noncompact edges. Then
$S\subset \unicode[STIX]{x1D6F4}_{W}$
be such a skeleton with noncompact edges. Then
![]() $S$
determines a (nonunique) stacky partial compactification
$S$
determines a (nonunique) stacky partial compactification
![]() $\widetilde{X}$
of
$\widetilde{X}$
of
![]() $X$
, which is no longer Calabi–Yau. The punctures of
$X$
, which is no longer Calabi–Yau. The punctures of
![]() $\unicode[STIX]{x1D6F4}_{W}$
are in bijection with the nonproper irreducible components of the singular locus of
$\unicode[STIX]{x1D6F4}_{W}$
are in bijection with the nonproper irreducible components of the singular locus of
![]() $W$
. These are all isomorphic to
$W$
. These are all isomorphic to
![]() $\mathbb{A}^{1}$
: considering a skeleton
$\mathbb{A}^{1}$
: considering a skeleton
![]() $S$
with
$S$
with
![]() $n$
noncompact edges approaching a given puncture corresponds to compactifying that copy of
$n$
noncompact edges approaching a given puncture corresponds to compactifying that copy of
![]() $\mathbb{A}^{1}$
to a stacky rational curve
$\mathbb{A}^{1}$
to a stacky rational curve
![]() $\mathbb{P}^{1}(1,n)$
.
$\mathbb{P}^{1}(1,n)$
.
The superpotential in general will not extend to
![]() $\widetilde{X}$
, and thus we cannot work with categories of matrix factorizations. We can however formulate our theory in terms of the more flexible formalism of the derived category of singularities. Recall that if
$\widetilde{X}$
, and thus we cannot work with categories of matrix factorizations. We can however formulate our theory in terms of the more flexible formalism of the derived category of singularities. Recall that if
![]() $X_{0}=W^{-1}(0)\subset X$
is the fiber at
$X_{0}=W^{-1}(0)\subset X$
is the fiber at
![]() $0\in \mathbb{A}^{1}$
of the superpotential, by Orlov’s Theorem [Reference OrlovOrl04], there is an equivalence
$0\in \mathbb{A}^{1}$
of the superpotential, by Orlov’s Theorem [Reference OrlovOrl04], there is an equivalence
where
![]() $D_{\text{sg}}(X_{0})$
denotes the derived category of singularities of
$D_{\text{sg}}(X_{0})$
denotes the derived category of singularities of
![]() $X_{0}$
. Although the category of matrix factorizations might not be well defined after compactifying to
$X_{0}$
. Although the category of matrix factorizations might not be well defined after compactifying to
![]() $\widetilde{X}$
, we can still make sense of the derived category of singularities. Namely, denote by
$\widetilde{X}$
, we can still make sense of the derived category of singularities. Namely, denote by
![]() $\widetilde{X}_{0}\subset \widetilde{X}$
the compactification of the zero fiber
$\widetilde{X}_{0}\subset \widetilde{X}$
the compactification of the zero fiber
![]() $X_{0}$
. The claim is that there is an equivalence of categories
$X_{0}$
. The claim is that there is an equivalence of categories
We expect that we could prove the homological mirror symmetry equivalence (1) exactly in the same way as we prove Theorem 1.1. We refer the reader to Remark 8.6 in the main text for additional details. Let us also mention recent work of Lekili–Polishchuk who give a different picture of homological mirror symmetry for partially wrapped Fukaya categories of punctured surfaces in terms of Auslander orders [Reference Lekili and PolishchuckLP18].
1.2 The topological Fukaya category and pants decompositions
The technical core of the paper is a study of the way in which the topological Fukaya category interacts with pants decompositions. By construction
![]() ${\mathcal{F}}^{\text{top}}(-)$
is a cosheaf of categories on the spine of a punctured surface. So locality is built into the definition of the topological Fukaya category. From a geometric perspective, this locality corresponds to cutting up the surface into flat polygons having their vertices at the punctures.
${\mathcal{F}}^{\text{top}}(-)$
is a cosheaf of categories on the spine of a punctured surface. So locality is built into the definition of the topological Fukaya category. From a geometric perspective, this locality corresponds to cutting up the surface into flat polygons having their vertices at the punctures.
In this paper we prove that the topological Fukaya category of a punctured surface satisfies also a different kind of local-to-global behavior: it can be glued together from the Fukaya categories of the pairs of pants making up a pants decomposition of it. We believe that this result is of independent interest. We expect this to be a feature of the topological Fukaya category in all dimensions, and we will return to this in future work. Based on recent parallel advances in the theory of the wrapped Fukaya category [Reference LeeLe15], this seems to be a promising avenue to compare the wrapped and the topological pictures of the category of A-branes on Stein manifolds. In order to explain the gluing formula for pants decompositions we need to sketch first a construction that attaches to a tropical curve
![]() $G$
a category
$G$
a category
![]() ${\mathcal{B}}(G)$
; full details can be found in § 3.1.3.
${\mathcal{B}}(G)$
; full details can be found in § 3.1.3.
Let
![]() $\unicode[STIX]{x1D705}$
be the ground field. We denote by
$\unicode[STIX]{x1D705}$
be the ground field. We denote by
![]() $MF(X,f)$
the category of matrix factorizations of the function
$MF(X,f)$
the category of matrix factorizations of the function
![]() $f:X\rightarrow \mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
and by
$f:X\rightarrow \mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
and by
![]() $\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
the topological Fukaya category of
$\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4})$
the topological Fukaya category of
![]() $\unicode[STIX]{x1D6F4}$
. We denote by
$\unicode[STIX]{x1D6F4}$
. We denote by
![]() $MF^{\infty }(X,f)$
and
$MF^{\infty }(X,f)$
and
![]() $\text{Fuk}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6F4})$
the Ind completions of these categories. We attach to a vertex
$\text{Fuk}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6F4})$
the Ind completions of these categories. We attach to a vertex
![]() $v$
of
$v$
of
![]() $G$
the category
$G$
the category
and to an edge
![]() $e$
of
$e$
of
![]() $G$
the category
$G$
the category
where
![]() $y$
and
$y$
and
![]() $z$
are coordinates on
$z$
are coordinates on
![]() $\mathbb{A}_{\unicode[STIX]{x1D705}}^{2}$
. If a vertex
$\mathbb{A}_{\unicode[STIX]{x1D705}}^{2}$
. If a vertex
![]() $v$
is incident to an edge
$v$
is incident to an edge
![]() $e$
there is a restriction functor
$e$
there is a restriction functor
![]() ${\mathcal{B}}(v)\rightarrow {\mathcal{B}}(e)$
. We define
${\mathcal{B}}(v)\rightarrow {\mathcal{B}}(e)$
. We define
![]() ${\mathcal{B}}(G)$
as the (homotopy) limit of these restriction functors.
${\mathcal{B}}(G)$
as the (homotopy) limit of these restriction functors.
Theorem 1.4. Let
![]() $\unicode[STIX]{x1D6F4}$
be an algebraic curve in
$\unicode[STIX]{x1D6F4}$
be an algebraic curve in
![]() $\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
and let
$\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
and let
![]() $G$
be its tropicalization. Then there is an equivalence
$G$
be its tropicalization. Then there is an equivalence
As proved in [Reference PreygelPre12],
![]() $MF^{\infty }(X,f)$
is a sheaf of categories for the étale topology on
$MF^{\infty }(X,f)$
is a sheaf of categories for the étale topology on
![]() $X$
. This gives rise to an expression for
$X$
. This gives rise to an expression for
![]() $MF^{\infty }(X,f)$
which is exactly parallel to (2). Our main theorem follows easily from here.
$MF^{\infty }(X,f)$
which is exactly parallel to (2). Our main theorem follows easily from here.
1.3 The topological Fukaya category and closed covers
The proof of Theorem 1.4 hinges on the key observation that the cosheaf
![]() ${\mathcal{F}}^{\text{top}}(-)$
behaves like a sheaf with respect to a certain type of closed cover. This somewhat surprising property of
${\mathcal{F}}^{\text{top}}(-)$
behaves like a sheaf with respect to a certain type of closed cover. This somewhat surprising property of
![]() ${\mathcal{F}}^{\text{top}}(-)$
is very natural from the viewpoint of mirror symmetry, because it is mirror to Zariski descent of quasi-coherent sheaves and matrix factorizations.
${\mathcal{F}}^{\text{top}}(-)$
is very natural from the viewpoint of mirror symmetry, because it is mirror to Zariski descent of quasi-coherent sheaves and matrix factorizations.
We formulate our gluing result in terms of the Ind-completion
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(-)$
of
${\mathcal{F}}_{\infty }^{\text{top}}(-)$
of
![]() ${\mathcal{F}}^{\text{top}}(-)$
. In order to simplify the exposition, in the statement below we do not specify all our assumptions on the closed cover. We refer the reader to the main text for the precise statement of our main gluing result, Theorem 6.6.
${\mathcal{F}}^{\text{top}}(-)$
. In order to simplify the exposition, in the statement below we do not specify all our assumptions on the closed cover. We refer the reader to the main text for the precise statement of our main gluing result, Theorem 6.6.
Theorem 1.5. Let
![]() $X$
be a ribbon graph.
$X$
be a ribbon graph.
– If
 $Z$
is a closed subgraph of
$Z$
is a closed subgraph of
 $X$
there are restriction functors
$X$
there are restriction functors  $$\begin{eqnarray}R:{\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(Z),\quad R_{\infty }:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(Z).\end{eqnarray}$$
$$\begin{eqnarray}R:{\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(Z),\quad R_{\infty }:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(Z).\end{eqnarray}$$
– Let
 $Z_{1}$
and
$Z_{1}$
and
 $Z_{2}$
be closed subgraphs of
$Z_{2}$
be closed subgraphs of
 $X$
, such that
$X$
, such that
 $Z_{1}\cup Z_{2}=Z$
. Assume that the underlying topological space of the intersection
$Z_{1}\cup Z_{2}=Z$
. Assume that the underlying topological space of the intersection
 $Z_{12}=Z_{1}\cap Z_{2}$
is a disjoint union of copies of
$Z_{12}=Z_{1}\cap Z_{2}$
is a disjoint union of copies of
 $S^{1}$
. Then, under suitable assumptions on
$S^{1}$
. Then, under suitable assumptions on
 $Z_{1}$
and
$Z_{1}$
and
 $Z_{2}$
, the diagramis a homotopy fiber product of dg categories.
$Z_{2}$
, the diagramis a homotopy fiber product of dg categories.
Restrictions to closed subgraphs for the topological Fukaya category have also been considered by Dyckerhoff in [Reference DyckerhoffDyc17]. From the perspective of the wrapped Fukaya category, they are closely related to the stop removal functors appearing in recent work of Sylvan [Reference SylvanSyl15]. The technique of gluing the topological Fukaya category across a decomposition of skeleta into closed pieces also plays a central role in [Reference KuwagakiKuw16]. Theorem 1.5 is a key ingredient in the proof of Theorem 1.4, which also depends on a careful study of the geometry of skeleta under pants attachments. Indeed, our proof of Theorem 1.4 hinges on a recursion where, at each step, we are simultaneously gluing in a pair of pants and deforming the skeleton on the surface to make it compatible with this gluing. The topological analysis required for the argument is carried out in § 7.
1.4 The structure of the paper
In § 2 we fix notation on dg categories and ribbon graphs. In § 3 we explain the set-up of Hori–Vafa mirror symmetry and prove a key decomposition of the category of matrix factorizations, which is a simple consequence of its sheaf properties. Section 4 contains a summary of the theory of the topological Fukaya category based mostly on [Reference Dyckerhoff and KapranovDK18], while in § 5 we study restriction functors to open and closed subgraphs, and their compatibilities. In § 6 we prove that the topological Fukaya category can be glued from a special kind of cover by closed subgraphs. Section 7 is devoted to a careful examination of the interactions between ribbon graphs and pants decompositions. This plays a key role in the proof of the main theorem, which is contained in § 8.
2 Notation and conventions
– We fix throughout a ground field
 $\unicode[STIX]{x1D705}$
of characteristic
$\unicode[STIX]{x1D705}$
of characteristic
 $0$
.
$0$
.– Throughout the paper we will work with small and large categories, and the categories that they form. We will ignore set-theoretic issues, and limit ourselves to mention that they can be formally obviated by placing oneself in appropriate Grothendieck universes, see for instance § 2 of [Reference ToënToe07].
2.1 Categories
In this paper we will work in the setting of dg categories. The theory of ordinary triangulated categories suffers from limitations which make it unsuitable to many applications in modern geometry. These limitations are essentially of two kinds. First, there are issues arising when working within a given triangulated category, and that originate from the lack of functorial universal constructions, such as cones. Additionally, triangulated categories do not themselves form a well-behaved category. Among other things, this implies that we have no workable notion of limits and colimits of triangulated categories, which are essential to perform gluing of categories.
The theory of dg categories gives us means to overcome both kinds of limitations. As opposed to ordinary triangulated categories, dg categories fit inside homotopically enriched categories and this allows us to perform operations such as taking limits and colimits. There are two main ways to define dg categories and to understand the structure of the category that they form.
(i) Dg categories can be defined as ordinary categories strictly enriched over chain complexes. Dg categories then form an ordinary category equipped with a model structure. In fact, there are several meaningful options for the model structure: the one that is most relevant for us is the Morita model structure considered in [Reference TabuadaTab05] and [Reference ToënToe07].
(ii) Dg categories can also be defined as
 $\unicode[STIX]{x1D705}$
-linear
$\unicode[STIX]{x1D705}$
-linear
 $\infty$
-categories: that is, as
$\infty$
-categories: that is, as
 $\infty$
-categories that carry an action of the symmetric monoidal
$\infty$
-categories that carry an action of the symmetric monoidal
 $\infty$
-category of chain complexes. Following this definition, dg categories form naturally an
$\infty$
-category of chain complexes. Following this definition, dg categories form naturally an
 $\infty$
-category. This approach is taken up for instance in the important recent reference [Reference Gaitsgory and RozenblyumGR17].
$\infty$
-category. This approach is taken up for instance in the important recent reference [Reference Gaitsgory and RozenblyumGR17].
Approaches (i) and (ii) each have several distinct advantages. It is often useful to have recourse to both viewpoints simultaneously, and this is what we shall do in the present paper. Categories strictly enriched over chain complexes are much more concrete objects, and their homotopy limits in the model category of dg categories can be calculated explicitly. On the other hand, perspective (ii) gives rise to more natural definitions and constructions and puts at our disposal the comprehensive foundations on
![]() $\infty$
-categories provided by the work of Lurie [Reference LurieLur09] and Gaitsgory–Rozenblyum [Reference Gaitsgory and RozenblyumGR17].
$\infty$
-categories provided by the work of Lurie [Reference LurieLur09] and Gaitsgory–Rozenblyum [Reference Gaitsgory and RozenblyumGR17].
In fact, there is a well-understood dictionary between these two viewpoints. Inverting weak equivalences in the model structure of dg categories (i) yields an
![]() $\infty$
-category which is equivalent to the
$\infty$
-category which is equivalent to the
![]() $\infty$
-category of dg categories (ii). As a consequence homotopy limits and colimits match, via this correspondence, their
$\infty$
-category of dg categories (ii). As a consequence homotopy limits and colimits match, via this correspondence, their
![]() $\infty$
-categorical counterparts. A proof of this equivalence was given by Cohn [Reference CohnCoh13] and then in a more general context by Haugseng [Reference HaugsengHau15] (see § 2.1.1 below). Throughout the paper we adopt the flexible
$\infty$
-categorical counterparts. A proof of this equivalence was given by Cohn [Reference CohnCoh13] and then in a more general context by Haugseng [Reference HaugsengHau15] (see § 2.1.1 below). Throughout the paper we adopt the flexible
![]() $\infty$
-categorical formalism coming from viewpoint (ii) while performing all actual calculations (e.g. of limits) in the model category of dg categories made available by viewpoint (i). We shall give more precise pointers to the literature below.
$\infty$
-categorical formalism coming from viewpoint (ii) while performing all actual calculations (e.g. of limits) in the model category of dg categories made available by viewpoint (i). We shall give more precise pointers to the literature below.
Before proceeding, however, we remark that we will be mostly interested in
![]() $\mathbb{Z}_{2}$
-graded, rather than
$\mathbb{Z}_{2}$
-graded, rather than
![]() $\mathbb{Z}$
-graded, dg categories. Some of the results which we will recall in the following have not been stated explicitly in the literature in the
$\mathbb{Z}$
-graded, dg categories. Some of the results which we will recall in the following have not been stated explicitly in the literature in the
![]() $\mathbb{Z}_{2}$
-graded setting. However, they can all be transported to the
$\mathbb{Z}_{2}$
-graded setting. However, they can all be transported to the
![]() $\mathbb{Z}_{2}$
-graded setting without variations. We refer to Section 1 of [Reference Dyckerhoff and KapranovDK18] and Section 2 of [Reference DyckerhoffDyc17] for a detailed summary of the Morita homotopy theory of
$\mathbb{Z}_{2}$
-graded setting without variations. We refer to Section 1 of [Reference Dyckerhoff and KapranovDK18] and Section 2 of [Reference DyckerhoffDyc17] for a detailed summary of the Morita homotopy theory of
![]() $\mathbb{Z}_{2}$
-graded dg categories, which is closely patterned on the
$\mathbb{Z}_{2}$
-graded dg categories, which is closely patterned on the
![]() $\mathbb{Z}$
-graded theory developed in [Reference ToënToe07].
$\mathbb{Z}$
-graded theory developed in [Reference ToënToe07].
The standard reference for
![]() $\infty$
-categories is [Reference LurieLur09]. We will follow closely the treatment of dg categories given in [Reference Drinfeld and GaitsgoryDG15] and [Reference Gaitsgory and RozenblyumGR17, I.1.10.3], to which we refer the reader for additional details. In particular, the notation and basic facts below are all taken from these two references. The only difference is that we will systematically place ourselves in the
$\infty$
-categories is [Reference LurieLur09]. We will follow closely the treatment of dg categories given in [Reference Drinfeld and GaitsgoryDG15] and [Reference Gaitsgory and RozenblyumGR17, I.1.10.3], to which we refer the reader for additional details. In particular, the notation and basic facts below are all taken from these two references. The only difference is that we will systematically place ourselves in the
![]() $\mathbb{Z}_{2}$
-graded setting.
$\mathbb{Z}_{2}$
-graded setting.
We denote by
![]() $\text{Vect}^{(2)}$
the presentable, stable and symmetric monoidal
$\text{Vect}^{(2)}$
the presentable, stable and symmetric monoidal
![]() $\infty$
-category of
$\infty$
-category of
![]() $\mathbb{Z}_{2}$
-periodic chain complexes of
$\mathbb{Z}_{2}$
-periodic chain complexes of
![]() $\unicode[STIX]{x1D705}$
-vector spaces. We denote by
$\unicode[STIX]{x1D705}$
-vector spaces. We denote by
![]() $\text{Vect}^{(2),\text{fd}}$
its full subcategory of compact objects. For the rest of this section we will call:
$\text{Vect}^{(2),\text{fd}}$
its full subcategory of compact objects. For the rest of this section we will call:
–
 $\infty$
-categories tensored over
$\infty$
-categories tensored over
 $\text{Vect}^{(2),\text{fd}},$
$\text{Vect}^{(2),\text{fd}},$
 $\unicode[STIX]{x1D705}$
-linear
$\unicode[STIX]{x1D705}$
-linear
 $\infty$
-categories;
$\infty$
-categories;– cocomplete
 $\infty$
-categories tensored over
$\infty$
-categories tensored over
 $\text{Vect}^{(2)},$
cocomplete
$\text{Vect}^{(2)},$
cocomplete
 $\unicode[STIX]{x1D705}$
-linear
$\unicode[STIX]{x1D705}$
-linear
 $\infty$
-categories.
$\infty$
-categories.
These are dg categories in the sense of viewpoint (ii). We introduce the following notation.
– We denote by
 $\text{DGCat}^{(2),\text{non\text{-}cocmpl}}$
the
$\text{DGCat}^{(2),\text{non\text{-}cocmpl}}$
the
 $\infty$
-category of (not necessarily small)
$\infty$
-category of (not necessarily small)
 $\unicode[STIX]{x1D705}$
-linear
$\unicode[STIX]{x1D705}$
-linear
 $\infty$
-categories.
$\infty$
-categories.– We denote by
 $\text{DGCat}_{\text{cont}}^{(2)}$
the
$\text{DGCat}_{\text{cont}}^{(2)}$
the
 $\infty$
-category of cocomplete
$\infty$
-category of cocomplete
 $\unicode[STIX]{x1D705}$
-linear graded dg categories, and continuous functors between them;
$\unicode[STIX]{x1D705}$
-linear graded dg categories, and continuous functors between them;
 $\text{DGCat}_{\text{cont}}^{(2)}$
carries a symmetric monoidal structure, and we denote its internal Hom by
$\text{DGCat}_{\text{cont}}^{(2)}$
carries a symmetric monoidal structure, and we denote its internal Hom by
 $\text{Fun}_{\text{cont}}(-,-)$
.
$\text{Fun}_{\text{cont}}(-,-)$
.– We denote by
 $\text{DGCat}_{\text{small}}^{(2)}$
the
$\text{DGCat}_{\text{small}}^{(2)}$
the
 $\infty$
-category of small
$\infty$
-category of small
 $\unicode[STIX]{x1D705}$
-linear
$\unicode[STIX]{x1D705}$
-linear
 $\infty$
-categories;
$\infty$
-categories;
 $\text{DGCat}_{\text{small}}^{(2)}$
also carries a natural symmetric monoidal structure and we denote its internal Hom by
$\text{DGCat}_{\text{small}}^{(2)}$
also carries a natural symmetric monoidal structure and we denote its internal Hom by
 $\text{Fun}(-,-)$
.
$\text{Fun}(-,-)$
.– If
 $\text{C}$
is an object in
$\text{C}$
is an object in
 $\text{DGCat}_{\text{cont}}^{(2)}$
, we denote by
$\text{DGCat}_{\text{cont}}^{(2)}$
, we denote by
 $\text{C}^{\unicode[STIX]{x1D714}}$
its subcategory of compact objects,
$\text{C}^{\unicode[STIX]{x1D714}}$
its subcategory of compact objects,  $$\begin{eqnarray}\text{C}^{\unicode[STIX]{x1D714}}\in \text{DGCat}_{\text{small}}^{(2)}.\end{eqnarray}$$
$$\begin{eqnarray}\text{C}^{\unicode[STIX]{x1D714}}\in \text{DGCat}_{\text{small}}^{(2)}.\end{eqnarray}$$
We have the forgetful and the Ind-completion functors
The Ind-completion functor can be defined, on objects, via the formula (see [Reference Gaitsgory and RozenblyumGR17, I.1], Lemma 10.5.6)
where
![]() $\text{Fun}_{k}(-,-)$
denotes the
$\text{Fun}_{k}(-,-)$
denotes the
![]() $\infty$
-category of
$\infty$
-category of
![]() $\text{Vect}^{(2),\text{fd}}$
-linear functors.
$\text{Vect}^{(2),\text{fd}}$
-linear functors.
Remark 2.1. In the main text we will apply the Ind-completion functor only to small
![]() $\unicode[STIX]{x1D705}$
-linear
$\unicode[STIX]{x1D705}$
-linear
![]() $\infty$
-categories: that is, to objects in the full subcategory
$\infty$
-categories: that is, to objects in the full subcategory
Lemma 2.2. The functor
![]() $\text{Ind}$
preserves small colimits of small categories.
$\text{Ind}$
preserves small colimits of small categories.
Proof. In the general setting of
![]() $\infty$
-categories, this is proved as [Reference Gaitsgory and RozenblyumGR17, I.7], Corollary 7.2.7. The proof carries over to the
$\infty$
-categories, this is proved as [Reference Gaitsgory and RozenblyumGR17, I.7], Corollary 7.2.7. The proof carries over to the
![]() $\unicode[STIX]{x1D705}$
-linear setting without variations.◻
$\unicode[STIX]{x1D705}$
-linear setting without variations.◻
2.1.1 Rigid models
As we have already mentioned, the two viewpoints (i) and (ii) on foundations of dg categories which we discussed in § 2.1 can be fully mapped onto each other. This will allow us to leverage the computational power of model structures, while retaining at the same time the flexibility of the
![]() $\infty$
-categorical formalism. A precise formulation of the equivalence between perspectives (i) and (ii) was given in work of Cohn [Reference CohnCoh13]. We recall this below with the usual proviso that we will state it in the
$\infty$
-categorical formalism. A precise formulation of the equivalence between perspectives (i) and (ii) was given in work of Cohn [Reference CohnCoh13]. We recall this below with the usual proviso that we will state it in the
![]() $\mathbb{Z}_{2}$
-graded setting.
$\mathbb{Z}_{2}$
-graded setting.
We will sometimes refer to categories strictly enriched over chain complexes as (ordinary) dg categories in order to differentiate them from
![]() $\unicode[STIX]{x1D705}$
-linear
$\unicode[STIX]{x1D705}$
-linear
![]() $\infty$
-categories. Let
$\infty$
-categories. Let
![]() $\text{dgCat}_{\unicode[STIX]{x1D705}}^{(2)}$
be the model category of small categories strictly enriched over chain complexes equipped with the Morita model structure [Reference ToënToe07]. Let
$\text{dgCat}_{\unicode[STIX]{x1D705}}^{(2)}$
be the model category of small categories strictly enriched over chain complexes equipped with the Morita model structure [Reference ToënToe07]. Let
![]() ${\mathcal{W}}$
be the set of weak equivalences for the Morita model structure: these are dg functors which induce quasi-equivalences at the level of (
${\mathcal{W}}$
be the set of weak equivalences for the Morita model structure: these are dg functors which induce quasi-equivalences at the level of (
![]() $\mathbb{Z}_{2}$
-graded) module categories.
$\mathbb{Z}_{2}$
-graded) module categories.
Proposition 2.3 [Reference CohnCoh13, Corollary 5.5].
There is an equivalence of
![]() $\infty$
-categories
$\infty$
-categories
where
![]() $N(-)$
is the nerve.
$N(-)$
is the nerve.
We will also need an analogue of Cohn’s result in the setting of large categories, that is for
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
. Let us denote by
$\text{DGCat}_{\text{cont}}^{(2)}$
. Let us denote by
![]() $\text{dgCat}_{\unicode[STIX]{x1D705},\text{cont}}^{(2)}$
the strictly enriched analogue of
$\text{dgCat}_{\unicode[STIX]{x1D705},\text{cont}}^{(2)}$
the strictly enriched analogue of
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
. This is the Morita model category of cocomplete categories strictly enriched over
$\text{DGCat}_{\text{cont}}^{(2)}$
. This is the Morita model category of cocomplete categories strictly enriched over
![]() $\unicode[STIX]{x1D705}-\text{mod}^{(2)}$
. Then the analogue of Proposition 2.3 is discussed as Example 5.11 of [Reference HaugsengHau15]. In many situations having recourse to the model category of dg categories has great computational advantages. In particular, we will be able to compute
$\unicode[STIX]{x1D705}-\text{mod}^{(2)}$
. Then the analogue of Proposition 2.3 is discussed as Example 5.11 of [Reference HaugsengHau15]. In many situations having recourse to the model category of dg categories has great computational advantages. In particular, we will be able to compute
![]() $\infty$
-categorical (co)limits in
$\infty$
-categorical (co)limits in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
and
$\text{DGCat}_{\text{cont}}^{(2)}$
and
![]() $\text{DGCat}_{\text{small}}^{(2)}$
by calculating the respective homotopy (co)limits of the strict models in
$\text{DGCat}_{\text{small}}^{(2)}$
by calculating the respective homotopy (co)limits of the strict models in
![]() $\text{dgCat}_{\unicode[STIX]{x1D705},\text{cont}}^{(2)}$
.
$\text{dgCat}_{\unicode[STIX]{x1D705},\text{cont}}^{(2)}$
.
Working with rigid models is often also helpful when considering commutative diagrams, as it allows us to sidestep issues of homotopy coherence in
![]() $\infty$
-categories. Recall that a diagram of ordinary dg categories
$\infty$
-categories. Recall that a diagram of ordinary dg categories

commutes if there is a natural transformation
![]() $\unicode[STIX]{x1D6FC}:H\circ F\Rightarrow K\circ G$
, which becomes a natural equivalence when passing to homotopy categories. All commutative diagrams of dg categories in this paper will be understood as coming from commutative diagrams of ordinary dg categories as above.
$\unicode[STIX]{x1D6FC}:H\circ F\Rightarrow K\circ G$
, which becomes a natural equivalence when passing to homotopy categories. All commutative diagrams of dg categories in this paper will be understood as coming from commutative diagrams of ordinary dg categories as above.
2.1.2 Limits of dg categories
Homotopy limits of dg categories can be calculated explicitly. Colimits of dg categories are, on the other hand, quite subtle. It is therefore an important observation that, under suitable assumptions, colimits can actually be turned into limits. This key fact can be formulated in various settings. For instance, in the context of colimits of presentable
![]() $\infty$
-categories such a result follows from Propositions 5.5.3.13 and 5.5.3.18 of [Reference LurieLur09]. We will recall a formulation of this fact in the setting of dg categories due to Drinfeld and Gaitsgory. We follow closely § 1.7.2 of [Reference Drinfeld and GaitsgoryDG15], with the usual difference that we adapt every statement to the
$\infty$
-categories such a result follows from Propositions 5.5.3.13 and 5.5.3.18 of [Reference LurieLur09]. We will recall a formulation of this fact in the setting of dg categories due to Drinfeld and Gaitsgory. We follow closely § 1.7.2 of [Reference Drinfeld and GaitsgoryDG15], with the usual difference that we adapt every statement to the
![]() $\mathbb{Z}_{2}$
-graded setting.
$\mathbb{Z}_{2}$
-graded setting.
Let
![]() $I$
be a small
$I$
be a small
![]() $\infty$
-category, and let
$\infty$
-category, and let
![]() $\unicode[STIX]{x1D6F9}:I\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
be a functor. For every pair of objects
$\unicode[STIX]{x1D6F9}:I\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
be a functor. For every pair of objects
![]() $i,j\in I$
and morphism
$i,j\in I$
and morphism
![]() $i\rightarrow j,$
we set
$i\rightarrow j,$
we set
Assume that each functor
![]() $\unicode[STIX]{x1D713}_{i,j}$
admits a continuous right adjoint
$\unicode[STIX]{x1D713}_{i,j}$
admits a continuous right adjoint
![]() $\unicode[STIX]{x1D719}_{j,i}$
. Then there is a functor
$\unicode[STIX]{x1D719}_{j,i}$
. Then there is a functor
![]() $\unicode[STIX]{x1D6F7}:I^{\text{op}}\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
such that
$\unicode[STIX]{x1D6F7}:I^{\text{op}}\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
such that
Proposition 2.4 [Reference Drinfeld and GaitsgoryDG15, Proposition 1.7.5].
The colimit
is canonically equivalent to the limit
2.1.3 Sheaves of dg categories
We will make frequent recourse to the concept of sheaf of dg categories either on graphs, or on schemes equipped with the Zariski topology. For our purposes it will be enough to use a rather weak notion of sheaf, which does not take into consideration hypercovers. Let
![]() ${\mathcal{F}}$
be a presheaf of dg categories over a topological space
${\mathcal{F}}$
be a presheaf of dg categories over a topological space
![]() $X$
. We say that
$X$
. We say that
![]() ${\mathcal{F}}$
satisfies Čech descent if, for all open subsets
${\mathcal{F}}$
satisfies Čech descent if, for all open subsets
![]() $U\subset X$
and covers
$U\subset X$
and covers
![]() ${\mathcal{U}}=\{{U_{i}\}}_{i\in I}$
of
${\mathcal{U}}=\{{U_{i}\}}_{i\in I}$
of
![]() $U$
, the restriction functor
$U$
, the restriction functor
realizes
![]() ${\mathcal{F}}(U)$
as the limit of the semi-cosimplicial object obtained by evaluating
${\mathcal{F}}(U)$
as the limit of the semi-cosimplicial object obtained by evaluating
![]() ${\mathcal{F}}$
on the Čech nerve of
${\mathcal{F}}$
on the Čech nerve of
![]() ${\mathcal{U}}$
. If
${\mathcal{U}}$
. If
![]() ${\mathcal{F}}$
satisfies Čech descent, we say that
${\mathcal{F}}$
satisfies Čech descent, we say that
![]() ${\mathcal{F}}$
is a sheaf of dg categories. The dual notion of cosheaf of dg categories is defined by reversing all the arrows in (3).
${\mathcal{F}}$
is a sheaf of dg categories. The dual notion of cosheaf of dg categories is defined by reversing all the arrows in (3).
There are two conditions under which (3) can be simplified, and that will occur in the examples we will be considering in the rest of the paper:
(a) when triple and higher intersections of the cover
 ${\mathcal{U}}$
are empty;
${\mathcal{U}}$
are empty;(b) when
 ${\mathcal{F}}$
evaluated on the triple and higher intersection of the cover
${\mathcal{F}}$
evaluated on the triple and higher intersection of the cover
 ${\mathcal{U}}$
is equivalent to the zero category.
${\mathcal{U}}$
is equivalent to the zero category.
We remark that condition (a) is in fact a special case of condition (b), but it is useful to keep them distinct. In this paper we will consider (co)sheaves of categories on graphs, which have covering dimension one and where therefore condition (a) is automatically satisfied. Also, we will consider sheaves of matrix factorizations on three-dimensional toric varieties equipped with the Zariski topology: there, although triple overlaps will not be empty, condition (b) will apply.
Let
![]() ${\mathcal{U}}=\{U_{1},\ldots ,U_{n}\}$
be an open cover of
${\mathcal{U}}=\{U_{1},\ldots ,U_{n}\}$
be an open cover of
![]() $U$
and assume that either condition (a) or (b) are satisfied. Then the sheaf axiom (3) is equivalent to requiring that
$U$
and assume that either condition (a) or (b) are satisfied. Then the sheaf axiom (3) is equivalent to requiring that
![]() ${\mathcal{F}}(U)$
is the limit of the following much smaller diagram, which coincides with the truncation of the Čech nerve encoding the sheaf axiom in the classical setting of sheaves of sets
${\mathcal{F}}(U)$
is the limit of the following much smaller diagram, which coincides with the truncation of the Čech nerve encoding the sheaf axiom in the classical setting of sheaves of sets
The same reasoning applies to cosheaves of categories, with the only difference that the arrows in (4) have to be reversed.
We will always work in settings where either (a) (in the case of the topological Fukaya category) or (b) (in the case of matrix factorizations) are satisfied, and therefore we always implicitly reduce to (4).
2.1.4 Schemes and stacks
If
![]() $X$
is a scheme or stack we denote by
$X$
is a scheme or stack we denote by
the
![]() $\mathbb{Z}_{2}$
-periodization of the dg categories of perfect complexes and of quasi-coherent sheaves on
$\mathbb{Z}_{2}$
-periodization of the dg categories of perfect complexes and of quasi-coherent sheaves on
![]() $X$
. We refer the reader to § 1.2 of [Reference Dyckerhoff and KapranovDK18] for the definition of
$X$
. We refer the reader to § 1.2 of [Reference Dyckerhoff and KapranovDK18] for the definition of
![]() $\mathbb{Z}_{2}$
-periodization. All schemes appearing in this paper will be quasi-compact and with affine diagonal. All DM stacks will be global quotients of such schemes by affine groups. Using the terminology introduced in [Reference Ben-Zvi, Francis and NadlerBFN10], these are all examples perfect stacks. This implies in particular that, if
$\mathbb{Z}_{2}$
-periodization. All schemes appearing in this paper will be quasi-compact and with affine diagonal. All DM stacks will be global quotients of such schemes by affine groups. Using the terminology introduced in [Reference Ben-Zvi, Francis and NadlerBFN10], these are all examples perfect stacks. This implies in particular that, if
![]() $X$
is such a scheme or stack, the category of quasi-coherent sheaves over
$X$
is such a scheme or stack, the category of quasi-coherent sheaves over
![]() $X$
is equivalent to the Ind-completion of its category of perfect complexes
$X$
is equivalent to the Ind-completion of its category of perfect complexes
2.2 Ribbon graphs
For a survey of the theory of ribbon graphs see [Reference Mulase and PenkavaMP98], and § 3.3 of [Reference Dyckerhoff and KapranovDK18]. We will just review some standard terminology. A graph
![]() $X$
is a pair
$X$
is a pair
![]() $(V,H)$
of finite sets equipped with the following extra data:
$(V,H)$
of finite sets equipped with the following extra data:
– an involution
 $\unicode[STIX]{x1D70E}:H\rightarrow H$
;
$\unicode[STIX]{x1D70E}:H\rightarrow H$
;– a map
 $I:H\rightarrow V$
.
$I:H\rightarrow V$
.
We call
![]() $V$
the set of vertices, and
$V$
the set of vertices, and
![]() $H$
the set of half-edges. Let
$H$
the set of half-edges. Let
![]() $v$
be a vertex. We say that the half-edges in
$v$
be a vertex. We say that the half-edges in
![]() $I^{-1}(v)$
are incident to
$I^{-1}(v)$
are incident to
![]() $v$
. The cardinality of
$v$
. The cardinality of
![]() $I^{-1}(v)$
is called the valency of the vertex
$I^{-1}(v)$
is called the valency of the vertex
![]() $v$
. The edges of
$v$
. The edges of
![]() $X$
are the equivalence classes of half-edges under the action of
$X$
are the equivalence classes of half-edges under the action of
![]() $\unicode[STIX]{x1D70E}$
. We denote by
$\unicode[STIX]{x1D70E}$
. We denote by
![]() $E$
the set of edges of
$E$
the set of edges of
![]() $\unicode[STIX]{x1D70E}$
. The set of external edges of
$\unicode[STIX]{x1D70E}$
. The set of external edges of
![]() $X$
is the subset
$X$
is the subset
![]() $E^{o}\subset E$
of equivalence classes of cardinality one, which correspond to the fixed points of
$E^{o}\subset E$
of equivalence classes of cardinality one, which correspond to the fixed points of
![]() $\unicode[STIX]{x1D70E}$
. The internal edges of
$\unicode[STIX]{x1D70E}$
. The internal edges of
![]() $X$
are the elements of
$X$
are the elements of
![]() $E-E^{o}$
. Subdividing an edge
$E-E^{o}$
. Subdividing an edge
![]() $e$
of
$e$
of
![]() $X$
means adding to
$X$
means adding to
![]() $X$
a two-valent vertex lying on
$X$
a two-valent vertex lying on
![]() $e$
. More formally, let
$e$
. More formally, let
![]() $e$
be equal to
$e$
be equal to
![]() $\{h_{1},h_{2}\}\subset H$
. We add a new vertex
$\{h_{1},h_{2}\}\subset H$
. We add a new vertex
![]() $v_{e}$
to
$v_{e}$
to
![]() $V$
, and two new half-edges
$V$
, and two new half-edges
![]() $h_{1}^{\prime }$
and
$h_{1}^{\prime }$
and
![]() $h_{2}^{\prime }$
to
$h_{2}^{\prime }$
to
![]() $H$
. We modify the maps
$H$
. We modify the maps
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $I$
by setting
$I$
by setting
It is often useful to view a graph as a topological space. This is done by modeling the external and the internal edges of
![]() $G$
, respectively, as semiclosed and closed intervals, and gluing them according to the incidence relations. We refer to this topological model as the underlying topological space of
$G$
, respectively, as semiclosed and closed intervals, and gluing them according to the incidence relations. We refer to this topological model as the underlying topological space of
![]() $X$
. When talking about the embedding of a graph
$X$
. When talking about the embedding of a graph
![]() $X$
into a topological space, we always mean the embedding of its underlying topological space.
$X$
into a topological space, we always mean the embedding of its underlying topological space.
Definition 2.5. A ribbon graph is a graph
![]() $X=(V,H)$
together with the datum of a cyclic ordering of the set
$X=(V,H)$
together with the datum of a cyclic ordering of the set
![]() $I^{-1}(v)$
, for all vertices
$I^{-1}(v)$
, for all vertices
![]() $v$
of
$v$
of
![]() $X$
.
$X$
.
If a graph
![]() $X$
is embedded in an oriented surface it acquires a canonical ribbon graph structure by ordering the edges at each vertex counter-clockwise with respect to the orientation. Conversely, it is possible to attach to any ribbon graph
$X$
is embedded in an oriented surface it acquires a canonical ribbon graph structure by ordering the edges at each vertex counter-clockwise with respect to the orientation. Conversely, it is possible to attach to any ribbon graph
![]() $X$
a noncompact oriented surface inside which
$X$
a noncompact oriented surface inside which
![]() $X$
is embedded as a strong deformation retract. See [Reference Mulase and PenkavaMP98] for additional details on these constructions. If
$X$
is embedded as a strong deformation retract. See [Reference Mulase and PenkavaMP98] for additional details on these constructions. If
![]() $\unicode[STIX]{x1D6F4}$
is a Riemann surface, a skeleton or spine of
$\unicode[STIX]{x1D6F4}$
is a Riemann surface, a skeleton or spine of
![]() $\unicode[STIX]{x1D6F4}$
is a ribbon graph
$\unicode[STIX]{x1D6F4}$
is a ribbon graph
![]() $X$
together with an embedding
$X$
together with an embedding
![]() $X\rightarrow \unicode[STIX]{x1D6F4}$
as a strong deformation retract.
$X\rightarrow \unicode[STIX]{x1D6F4}$
as a strong deformation retract.
3 Hori–Vafa mirror symmetry
In this section we review the setting of mirror symmetry for toric Calabi–Yau LG models in dimension three. Mirror symmetry for LG models was first proposed by Hori and Vafa [Reference Hori and VafaHV15], and is the subject of a vast literature in string theory and mathematics, see [Reference Gross, Katzarkov and RuddatGKR17] and references therein. In this paper we compare the category of B-branes on toric Calabi–Yau LG models and the category of A-branes on the mirror.
3.1 B-branes
3.1.1 Toric Calabi–Yau threefolds
Let
![]() $\widetilde{N}$
be a
$\widetilde{N}$
be a
![]() $(n-1)$
-dimensional lattice, and let
$(n-1)$
-dimensional lattice, and let
![]() $P$
be a lattice polytope in
$P$
be a lattice polytope in
![]() $\widetilde{N}_{\mathbb{R}}=\widetilde{N}\otimes \mathbb{R}$
. Set
$\widetilde{N}_{\mathbb{R}}=\widetilde{N}\otimes \mathbb{R}$
. Set
![]() $N:=\widetilde{N}\oplus \mathbb{Z}$
, and
$N:=\widetilde{N}\oplus \mathbb{Z}$
, and
![]() $N_{\mathbb{R}}:=N\otimes \mathbb{R}$
. Denote by
$N_{\mathbb{R}}:=N\otimes \mathbb{R}$
. Denote by
![]() $C(P)\subset N_{\mathbb{R}}$
the cone over the polytope
$C(P)\subset N_{\mathbb{R}}$
the cone over the polytope
![]() $P$
placed at height one in
$P$
placed at height one in
![]() $N_{\mathbb{R}}$
. More formally, consider
$N_{\mathbb{R}}$
. More formally, consider
and let
![]() $C(P)$
be the cone generated by
$C(P)$
be the cone generated by
![]() $\{1\}\times P$
inside
$\{1\}\times P$
inside
![]() $N_{\mathbb{R}}$
. Let
$N_{\mathbb{R}}$
. Let
![]() $F(P)$
be the fan consisting of
$F(P)$
be the fan consisting of
![]() $C(P)$
and all its faces. The affine toric variety
$C(P)$
and all its faces. The affine toric variety
![]() $X_{P}$
corresponding to
$X_{P}$
corresponding to
![]() $F(P)$
has an isolated Gorenstein singularity. The toric resolutions of
$F(P)$
has an isolated Gorenstein singularity. The toric resolutions of
![]() $X_{P}$
are in bijection with smooth subdivisions of the cone
$X_{P}$
are in bijection with smooth subdivisions of the cone
![]() $C(P)$
. We will be interested in toric crepant resolutions, that is, resolutions with trivial canonical bundle.
$C(P)$
. We will be interested in toric crepant resolutions, that is, resolutions with trivial canonical bundle.
Toric crepant resolutions of
![]() $X_{P}$
are given by unimodular triangulations of
$X_{P}$
are given by unimodular triangulations of
![]() $P$
, i.e. triangulations of
$P$
, i.e. triangulations of
![]() $P$
by elementary lattice simplices. Any such triangulation
$P$
by elementary lattice simplices. Any such triangulation
![]() ${\mathcal{T}}$
gives rise to a smooth subdivision of the cone
${\mathcal{T}}$
gives rise to a smooth subdivision of the cone
![]() $C(P)$
. We denote by
$C(P)$
. We denote by
![]() $C({\mathcal{T}})$
the set of cones on the simplices
$C({\mathcal{T}})$
the set of cones on the simplices
![]() $T\in {\mathcal{T}}$
placed at height one in
$T\in {\mathcal{T}}$
placed at height one in
![]() $N_{\mathbb{R}}$
. Let
$N_{\mathbb{R}}$
. Let
![]() $F({\mathcal{T}})$
be the corresponding fan, and let
$F({\mathcal{T}})$
be the corresponding fan, and let
![]() $X_{{\mathcal{T}}}$
be the toric variety with fan
$X_{{\mathcal{T}}}$
be the toric variety with fan
![]() $F({\mathcal{T}})$
. The variety
$F({\mathcal{T}})$
. The variety
![]() $X_{{\mathcal{T}}}$
is smooth and Calabi–Yau. All toric crepant resolutions of
$X_{{\mathcal{T}}}$
is smooth and Calabi–Yau. All toric crepant resolutions of
![]() $X_{P}$
are isomorphic to
$X_{P}$
are isomorphic to
![]() $X_{{\mathcal{T}}}$
for some unimodular triangulation
$X_{{\mathcal{T}}}$
for some unimodular triangulation
![]() ${\mathcal{T}}$
of
${\mathcal{T}}$
of
![]() $P$
.
$P$
.
The following definition will be useful later on, see for instance [Reference Brodsky, Joswig, Morrison and SturmfelsBJMS15] for additional details on this construction.
Definition 3.1. Assume that
![]() $n=3$
. We denote by
$n=3$
. We denote by
![]() $G_{{\mathcal{T}}}$
the tropical curve dual to the triangulation
$G_{{\mathcal{T}}}$
the tropical curve dual to the triangulation
![]() ${\mathcal{T}}$
of
${\mathcal{T}}$
of
![]() $P$
.
$P$
.
Let
![]() $\widetilde{M}=\text{Hom}(\widetilde{N},\mathbb{Z})$
and
$\widetilde{M}=\text{Hom}(\widetilde{N},\mathbb{Z})$
and
![]() $M=\text{Hom}(N,\mathbb{Z})$
. The height function on
$M=\text{Hom}(N,\mathbb{Z})$
. The height function on
![]() $N$
is by definition the projection
$N$
is by definition the projection
The height function corresponds to the lattice point
![]() $(1,0)\in M\cong \mathbb{Z}\times \widetilde{M},$
which determines a monomial function
$(1,0)\in M\cong \mathbb{Z}\times \widetilde{M},$
which determines a monomial function
The category of B-branes on the Landau–Ginzburg model
![]() $(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
is the category of matrix factorizations for
$(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
is the category of matrix factorizations for
![]() $W_{{\mathcal{T}}}$
,
$W_{{\mathcal{T}}}$
,
![]() $MF(W_{{\mathcal{T}}})$
. We review the theory of matrix factorizations next.
$MF(W_{{\mathcal{T}}})$
. We review the theory of matrix factorizations next.
3.1.2 Matrix factorizations
Let
![]() $X$
be a scheme or a smooth DM stack and let
$X$
be a scheme or a smooth DM stack and let
![]() $f:X\rightarrow \mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
be a regular function. The category of matrix factorizations for the pair
$f:X\rightarrow \mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
be a regular function. The category of matrix factorizations for the pair
![]() $(X,f)$
was defined in [Reference Lin and PomerleanoLP13] and [Reference OrlovOrl12], extending the theory of matrix factorizations for algebras that goes back to classical work of Eisenbud [Reference EisenbudEis80]. These references make various assumptions on
$(X,f)$
was defined in [Reference Lin and PomerleanoLP13] and [Reference OrlovOrl12], extending the theory of matrix factorizations for algebras that goes back to classical work of Eisenbud [Reference EisenbudEis80]. These references make various assumptions on
![]() $f$
and
$f$
and
![]() $X$
, which are always satisfied in the cases we are interested in. In the following
$X$
, which are always satisfied in the cases we are interested in. In the following
![]() $X$
will always be smooth of finite type, and
$X$
will always be smooth of finite type, and
![]() $f$
will be flat. We will work with a dg enhancement of the category of matrix factorizations, which has been studied for instance in [Reference Lunts and SchnürerLS16] and [Reference PreygelPre12]. We refer to these papers for additional details. We denote by
$f$
will be flat. We will work with a dg enhancement of the category of matrix factorizations, which has been studied for instance in [Reference Lunts and SchnürerLS16] and [Reference PreygelPre12]. We refer to these papers for additional details. We denote by
![]() $MF(X,f)$
the
$MF(X,f)$
the
![]() $\mathbb{Z}_{2}$
-periodic dg category of matrix factorizations of the pair
$\mathbb{Z}_{2}$
-periodic dg category of matrix factorizations of the pair
![]() $(X,f)$
. It will often be useful to work with Ind-completed categories of matrix factorization.
$(X,f)$
. It will often be useful to work with Ind-completed categories of matrix factorization.
Definition 3.2. We denote by
![]() $MF^{\infty }(X,f)$
the Ind-completion of
$MF^{\infty }(X,f)$
the Ind-completion of
![]() $MF(X,f)$
,
$MF(X,f)$
,
The category
![]() $MF^{\infty }(X,f)$
has the following important descent property.
$MF^{\infty }(X,f)$
has the following important descent property.
Proposition 3.3 [Reference PreygelPre12, Proposition A.3.1].
Let
![]() $f:X\rightarrow \mathbb{A}^{1}$
be a morphism. Then the assignment
$f:X\rightarrow \mathbb{A}^{1}$
be a morphism. Then the assignment
determines a sheaf for the étale topology.
Using Proposition 3.3 we can give a very concrete description of
![]() $MF^{\infty }(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
, where
$MF^{\infty }(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
, where
![]() $X_{{\mathcal{T}}}$
and
$X_{{\mathcal{T}}}$
and
![]() $W_{{\mathcal{T}}}$
are as in § 3.1.1. In order to do so, we need to explain how to attach a matrix factorizations-type category to a certain class of planar graphs. This will require setting up some notation and preliminaries.
$W_{{\mathcal{T}}}$
are as in § 3.1.1. In order to do so, we need to explain how to attach a matrix factorizations-type category to a certain class of planar graphs. This will require setting up some notation and preliminaries.
Let
![]() $I$
be a set of cardinality three, say
$I$
be a set of cardinality three, say
![]() $I=\{a,b,c\}$
. Denote
$I=\{a,b,c\}$
. Denote
and let
![]() $f$
be the regular function
$f$
be the regular function
For all
![]() $j\in I$
, let
$j\in I$
, let
![]() $I_{j}$
be the subset
$I_{j}$
be the subset
![]() $I-\{j\}\subset I$
. Let
$I-\{j\}\subset I$
. Let
![]() $U_{j}$
be the open subscheme
$U_{j}$
be the open subscheme
![]() $X-\{t_{j}=0\}$
, and let
$X-\{t_{j}=0\}$
, and let
![]() $\unicode[STIX]{x1D704}_{j}$
be the inclusion
$\unicode[STIX]{x1D704}_{j}$
be the inclusion
![]() $U_{j}\subset X$
. Denote by
$U_{j}\subset X$
. Denote by
the restriction functor. Let
![]() $f_{j}$
be the regular function
$f_{j}$
be the regular function
Note that
![]() $f|_{U_{j}}$
is given by
$f|_{U_{j}}$
is given by
![]() $t_{j}f_{j}$
.
$t_{j}f_{j}$
.
Proposition 3.4. There are equivalences of dg categories
Proof. Recall that objects of
![]() $MF(U_{j},f_{j})$
are pairs of free finite rank vector bundles on
$MF(U_{j},f_{j})$
are pairs of free finite rank vector bundles on
![]() $U_{j}$
, and maps between them
$U_{j}$
, and maps between them
having the property that
Thus the assignment
determines an equivalence
The first equivalence is obtained by Ind-completion.
The second equivalence follows from Knörrer periodicity. For a very general formulation of Knörrer periodicity see Theorem 9.1.7(ii) of [Reference PreygelPre12]. Let us assume for convenience that
![]() $I=\{1,2,3\}$
, and that
$I=\{1,2,3\}$
, and that
![]() $j=1$
. Then
$j=1$
. Then
![]() $U_{j}=\mathbb{G}_{m}\times \mathbb{A}_{\unicode[STIX]{x1D705}}^{2}$
, and
$U_{j}=\mathbb{G}_{m}\times \mathbb{A}_{\unicode[STIX]{x1D705}}^{2}$
, and
![]() $f_{j}=t_{2}\cdot t_{3}$
, where
$f_{j}=t_{2}\cdot t_{3}$
, where
![]() $t_{2}$
and
$t_{2}$
and
![]() $t_{3}$
are coordinate on the factor
$t_{3}$
are coordinate on the factor
![]() $\mathbb{A}_{\unicode[STIX]{x1D705}}^{2}$
. By Knörrer periodicity
$\mathbb{A}_{\unicode[STIX]{x1D705}}^{2}$
. By Knörrer periodicity
![]() $MF(U_{j},f_{j})$
is equivalent to the
$MF(U_{j},f_{j})$
is equivalent to the
![]() $\mathbb{Z}_{2}$
-periodic category of perfect complexes on the first factor,
$\mathbb{Z}_{2}$
-periodic category of perfect complexes on the first factor,
![]() $\mathbb{G}_{m}$
. This concludes the proof.◻
$\mathbb{G}_{m}$
. This concludes the proof.◻
Remark 3.5. The equivalences constructed in Proposition 3.4 are given by explicit functors, and do not rely on further choices. For the second equivalence, this follows from the proof of Knörrer periodicity in [Reference PreygelPre12]. Abusing notation we sometimes denote by
![]() $\unicode[STIX]{x1D704}_{j}^{\ast }$
also the composition of the pullback with the equivalences from Proposition 3.4. Thus we may write
$\unicode[STIX]{x1D704}_{j}^{\ast }$
also the composition of the pullback with the equivalences from Proposition 3.4. Thus we may write
We can abstract from Remark 3.5 a formalism of restriction functors which will be useful in the next section. If
![]() $L$
is a set of cardinality two, denote
$L$
is a set of cardinality two, denote
and let
![]() $f$
be the morphism
$f$
be the morphism
Definition 3.6. Let
![]() $I$
and
$I$
and
![]() $L$
be sets of cardinality three and two respectively, and assume that we are given an embedding
$L$
be sets of cardinality three and two respectively, and assume that we are given an embedding
![]() $L\subset I$
. We denote by
$L\subset I$
. We denote by
![]() $R_{\infty }^{MF}$
the composite
$R_{\infty }^{MF}$
the composite
where:
(i)
 $\{j\}=I-L$
, and
$\{j\}=I-L$
, and
 $\unicode[STIX]{x1D704}_{j}^{\ast }$
is defined as in Remark 3.5;
$\unicode[STIX]{x1D704}_{j}^{\ast }$
is defined as in Remark 3.5;(ii) the equivalence
 $MF^{\infty }(U_{j},f_{j})\simeq MF^{\infty }(X_{L},f)$
is determined by the isomorphism of
$MF^{\infty }(U_{j},f_{j})\simeq MF^{\infty }(X_{L},f)$
is determined by the isomorphism of
 $\unicode[STIX]{x1D705}$
-algebras that sends
$\unicode[STIX]{x1D705}$
-algebras that sends $$\begin{eqnarray}\unicode[STIX]{x1D705}[t_{i},i\in I][t_{j}^{-1}]=\unicode[STIX]{x1D705}[t_{l},l\in L][t_{j},t_{j}^{-1}]\stackrel{\cong }{\longrightarrow }\unicode[STIX]{x1D705}[t_{l},l\in L][u,u^{-1}]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}[t_{i},i\in I][t_{j}^{-1}]=\unicode[STIX]{x1D705}[t_{l},l\in L][t_{j},t_{j}^{-1}]\stackrel{\cong }{\longrightarrow }\unicode[STIX]{x1D705}[t_{l},l\in L][u,u^{-1}]\end{eqnarray}$$
 $t_{l}$
to
$t_{l}$
to
 $t_{l}$
, and
$t_{l}$
, and
 $t_{j}$
to
$t_{j}$
to
 $t_{u}$
.
$t_{u}$
.
3.1.3 Planar graphs and matrix factorizations
Let
![]() $G$
be a trivalent, planar graph. Assume for simplicity that
$G$
be a trivalent, planar graph. Assume for simplicity that
![]() $G$
does not contain any loop. We will explain how to attach to
$G$
does not contain any loop. We will explain how to attach to
![]() $G$
a matrix factorization-type category. We denote by
$G$
a matrix factorization-type category. We denote by
![]() $V_{G}$
the set of vertices of
$V_{G}$
the set of vertices of
![]() $G$
, and by
$G$
, and by
![]() $E_{G}$
the set of edges.
$E_{G}$
the set of edges.
– Let
 $v\in V_{G}$
, and take a sufficiently small ball
$v\in V_{G}$
, and take a sufficiently small ball
 $B_{v}$
in
$B_{v}$
in
 $\mathbb{R}^{2}$
centered at
$\mathbb{R}^{2}$
centered at
 $v$
. Then the set of connected components of
$v$
. Then the set of connected components of
 $B_{v}-G$
has cardinality three, and we denote it
$B_{v}-G$
has cardinality three, and we denote it
 $I_{v}$
.
$I_{v}$
.– Let
 $e\in V_{G}$
, and take a sufficiently small ball
$e\in V_{G}$
, and take a sufficiently small ball
 $B_{e}$
centered at any point in the relative interior of
$B_{e}$
centered at any point in the relative interior of
 $e$
. The set of connected components of
$e$
. The set of connected components of
 $B_{v}-G$
has cardinality two, and we denote it
$B_{v}-G$
has cardinality two, and we denote it
 $L_{e}$
.
$L_{e}$
.
Remark 3.7. Note that the sets
![]() $I_{v}$
and
$I_{v}$
and
![]() $L_{e}$
do not depend (up to canonical identifications) on
$L_{e}$
do not depend (up to canonical identifications) on
![]() $B_{e}$
and
$B_{e}$
and
![]() $B_{v}$
. Further, if a vertex
$B_{v}$
. Further, if a vertex
![]() $v$
is incident to an edge
$v$
is incident to an edge
![]() $e$
, there is a canonical embedding:
$e$
, there is a canonical embedding:
![]() $L_{e}\subset I_{v}$
.
$L_{e}\subset I_{v}$
.
We attach to each vertex and edge of
![]() $G$
a category of matrix factorizations in the following way.
$G$
a category of matrix factorizations in the following way.
– We assign to
 $v\in V_{G}$
the category
$v\in V_{G}$
the category  $$\begin{eqnarray}{\mathcal{B}}(v):=MF^{\infty }(X_{I_{v}},f).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}(v):=MF^{\infty }(X_{I_{v}},f).\end{eqnarray}$$
– We assign to
 $e\in E_{G}$
the category
$e\in E_{G}$
the category  $$\begin{eqnarray}{\mathcal{B}}(e):=MF^{\infty }(X_{L_{e}},f).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}(e):=MF^{\infty }(X_{L_{e}},f).\end{eqnarray}$$
By Remark 3.7, and Definition 3.6, if a vertex
![]() $v$
is incident to an edge
$v$
is incident to an edge
![]() $e$
we have a restriction functor
$e$
we have a restriction functor
If two vertices
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
are incident to an edge
$v_{2}$
are incident to an edge
![]() $e$
, we obtain a diagram of restriction functors
$e$
, we obtain a diagram of restriction functors
Running over the vertices and edges of
![]() $G$
, we obtain a Čech-type diagram in
$G$
, we obtain a Čech-type diagram in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
$\text{DGCat}_{\text{cont}}^{(2)}$
Definition 3.8. We denote by
![]() ${\mathcal{B}}(G)$
the equalizer of diagram (6) in
${\mathcal{B}}(G)$
the equalizer of diagram (6) in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
.
$\text{DGCat}_{\text{cont}}^{(2)}$
.
We say that a subset
![]() $T\subset G$
is a subgraph of
$T\subset G$
is a subgraph of
![]() $G$
if:
$G$
if:
–
 $T$
is a trivalent graph;
$T$
is a trivalent graph;– if
 $e$
is an edge of
$e$
is an edge of
 $G$
such that
$G$
such that
 $T\cap e$
is nonempty, then
$T\cap e$
is nonempty, then
 $e$
is contained in
$e$
is contained in
 $T$
.
$T$
.
Note that if
![]() $T$
is a subgraph of
$T$
is a subgraph of
![]() $G$
we have inclusions
$G$
we have inclusions
![]() $V_{T}\subset V_{G}$
and
$V_{T}\subset V_{G}$
and
![]() $E_{T}\subset E_{G}$
. We can define a restriction functor
$E_{T}\subset E_{G}$
. We can define a restriction functor
This is obtained by considering the natural map between Čech-type diagrams given by the obvious projections shown in the following diagram.

It is useful to extend to a general pair of graphs
![]() $T\subset G$
the notation for restriction functors that we introduced in (5) in the case of a vertex and a neighboring edge.
$T\subset G$
the notation for restriction functors that we introduced in (5) in the case of a vertex and a neighboring edge.
Definition 3.9. If
![]() $T$
is a subgraph of
$T$
is a subgraph of
![]() $G$
, we denote the restriction functor
$G$
, we denote the restriction functor
The definition of
![]() ${\mathcal{B}}(G)$
allows us to encode the category of matrix factorizations of a toric Calabi–Yau LG model in a simple combinatorial package. We use the notation of § 3.1.1.
${\mathcal{B}}(G)$
allows us to encode the category of matrix factorizations of a toric Calabi–Yau LG model in a simple combinatorial package. We use the notation of § 3.1.1.
Theorem 3.10. Let
![]() $P$
be a planar lattice polytope, equipped with a unimodular triangulation
$P$
be a planar lattice polytope, equipped with a unimodular triangulation
![]() ${\mathcal{T}}$
. Let
${\mathcal{T}}$
. Let
![]() $G_{{\mathcal{T}}}$
be the dual graph of
$G_{{\mathcal{T}}}$
be the dual graph of
![]() ${\mathcal{T}}$
. Then there is an equivalence of dg categories
${\mathcal{T}}$
. Then there is an equivalence of dg categories
Proof. Let
![]() $C$
be the set of maximal cones in the fan of
$C$
be the set of maximal cones in the fan of
![]() $X_{{\mathcal{T}}}$
. Consider the standard open cover of
$X_{{\mathcal{T}}}$
. Consider the standard open cover of
![]() $X_{{\mathcal{T}}}$
by toric affine patches:
$X_{{\mathcal{T}}}$
by toric affine patches:
![]() $\{{U_{\unicode[STIX]{x1D70E}}\}}_{\unicode[STIX]{x1D70E}\in C},$
$\{{U_{\unicode[STIX]{x1D70E}}\}}_{\unicode[STIX]{x1D70E}\in C},$
![]() $U_{\unicode[STIX]{x1D70E}}\cong \mathbb{A}_{\unicode[STIX]{x1D705}}^{3}$
. By Proposition 3.3 the category
$U_{\unicode[STIX]{x1D70E}}\cong \mathbb{A}_{\unicode[STIX]{x1D705}}^{3}$
. By Proposition 3.3 the category
![]() $MF^{\infty }(X_{{\mathcal{T}}},f_{{\mathcal{T}}})$
can be expressed as the limit of the Čech diagram for the open cover
$MF^{\infty }(X_{{\mathcal{T}}},f_{{\mathcal{T}}})$
can be expressed as the limit of the Čech diagram for the open cover
![]() $\{{U_{\unicode[STIX]{x1D70E}}\}}_{\unicode[STIX]{x1D70E}\in C}$
: the vertices of this diagram are products of the categories
$\{{U_{\unicode[STIX]{x1D70E}}\}}_{\unicode[STIX]{x1D70E}\in C}$
: the vertices of this diagram are products of the categories
and the arrows are products of pullback functors.
Note that there is a natural bijection
![]() $\unicode[STIX]{x1D719}$
between the set
$\unicode[STIX]{x1D719}$
between the set
![]() $V_{{\mathcal{T}}}$
of vertices of
$V_{{\mathcal{T}}}$
of vertices of
![]() $G_{{\mathcal{T}}}$
and
$G_{{\mathcal{T}}}$
and
![]() $C$
. Moreover the definition of
$C$
. Moreover the definition of
![]() $I_{v}$
gives an identification
$I_{v}$
gives an identification
![]() $X_{I_{v}}\cong U_{\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70E})}$
, and thus a canonical equivalence
$X_{I_{v}}\cong U_{\unicode[STIX]{x1D719}(\unicode[STIX]{x1D70E})}$
, and thus a canonical equivalence
Similarly, by Remark 3.5, if
![]() $v$
and
$v$
and
![]() $v^{\prime }$
are two vertices of
$v^{\prime }$
are two vertices of
![]() $G_{{\mathcal{T}}}$
and
$G_{{\mathcal{T}}}$
and
![]() $e$
is the edge connecting them, we obtain a commutative diagram
$e$
is the edge connecting them, we obtain a commutative diagram

where the horizontal arrows are canonical equivalences, and
![]() $\unicode[STIX]{x1D704}^{\ast }$
is the restriction of matrix factorizations along the embedding
$\unicode[STIX]{x1D704}^{\ast }$
is the restriction of matrix factorizations along the embedding
Thus the diagrams computing
![]() ${\mathcal{B}}(G_{{\mathcal{T}}})$
and
${\mathcal{B}}(G_{{\mathcal{T}}})$
and
![]() $MF^{\infty }(X_{{\mathcal{T}}},f_{{\mathcal{T}}})$
are equivalent, and this concludes the proof.◻
$MF^{\infty }(X_{{\mathcal{T}}},f_{{\mathcal{T}}})$
are equivalent, and this concludes the proof.◻
3.2 A-branes
As explained in [Reference Hori and VafaHV15], the mirror of a toric Calabi–Yau LG model
![]() $(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
is a punctured Riemann surface
$(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
is a punctured Riemann surface
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
embedded as an algebraic curve in
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
embedded as an algebraic curve in
![]() $\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
. The graph
$\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
. The graph
![]() $G_{{\mathcal{T}}}$
is the tropicalization of
$G_{{\mathcal{T}}}$
is the tropicalization of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
. Since we are interested in studying the A-model on
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
. Since we are interested in studying the A-model on
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
we can disregard its complex structure and focus on its topology, which is captured by the genus and the number of punctures (see for instance [Reference Bouchard and SułkowskiBS12] for an explicit algebraic equation of
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
we can disregard its complex structure and focus on its topology, which is captured by the genus and the number of punctures (see for instance [Reference Bouchard and SułkowskiBS12] for an explicit algebraic equation of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
). These can be read off from
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
). These can be read off from
![]() $G_{{\mathcal{T}}}$
. The genus of
$G_{{\mathcal{T}}}$
. The genus of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
is equal to the number of relatively compact connected components in
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
is equal to the number of relatively compact connected components in
![]() $\mathbb{R}^{2}-G_{{\mathcal{T}}}$
. The number of punctures of
$\mathbb{R}^{2}-G_{{\mathcal{T}}}$
. The number of punctures of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
is equal to the number of unbounded edges of
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
is equal to the number of unbounded edges of
![]() $G_{{\mathcal{T}}}$
. See Figure 1.
$G_{{\mathcal{T}}}$
. See Figure 1.

Figure 1. The picture shows an example of the relationship between the triangulation
![]() ${\mathcal{T}}$
, the tropical curve
${\mathcal{T}}$
, the tropical curve
![]() $G_{{\mathcal{T}}}$
, and the mirror curve
$G_{{\mathcal{T}}}$
, and the mirror curve
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
.
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
.
When
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
has genus
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
has genus
![]() $0$
, the authors of [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] consider the wrapped Fukaya category of
$0$
, the authors of [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] consider the wrapped Fukaya category of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
, and prove that it is equivalent to the category of matrix factorizations of the mirror toric LG model. In this paper we will consider an alternative model for the category of A-branes on a punctured Riemann surface, called the topological Fukaya category. The construction of the topological Fukaya category was first suggested by Kontsevich [Reference KontsevichKon09] and was studied in [Reference Dyckerhoff and KapranovDK18, Reference NadlerNad15, Reference Sibilla, Treumann and ZaslowSTZ14] and elsewhere in the case of punctured Riemann surfaces. We summarize the theory of the topological Fukaya category in § 4 below.
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
, and prove that it is equivalent to the category of matrix factorizations of the mirror toric LG model. In this paper we will consider an alternative model for the category of A-branes on a punctured Riemann surface, called the topological Fukaya category. The construction of the topological Fukaya category was first suggested by Kontsevich [Reference KontsevichKon09] and was studied in [Reference Dyckerhoff and KapranovDK18, Reference NadlerNad15, Reference Sibilla, Treumann and ZaslowSTZ14] and elsewhere in the case of punctured Riemann surfaces. We summarize the theory of the topological Fukaya category in § 4 below.
4 The topological Fukaya category
In this section we recall the definition of the topological Fukaya for punctured Riemann surfaces. We will mostly follow the approach of [Reference Dyckerhoff and KapranovDK18], see also [Reference NadlerNad15, Reference Sibilla, Treumann and ZaslowSTZ14, Reference Haiden, Katzarkov and KontsevichHKK17] for related alternative formulations of this theory. It will be important to consider the Ind-completion of the topological Fukaya category. We discuss this in § 4.2.
4.1 The cyclic category and the topological Fukaya category
We briefly review the setting of [Reference Dyckerhoff and KapranovDK18]. We refer for more details to the original paper and to [Reference DyckerhoffDyc17].
Definition 4.1 [Reference ConnesCon94].
Let
![]() $\unicode[STIX]{x1D6EC}$
be the category defined as follows.
$\unicode[STIX]{x1D6EC}$
be the category defined as follows.
– The set of objects of
 $\unicode[STIX]{x1D6EC}$
is in bijection with the set of natural numbers. For all
$\unicode[STIX]{x1D6EC}$
is in bijection with the set of natural numbers. For all
 $n\in N$
,
$n\in N$
,
 $\langle n\rangle \in \unicode[STIX]{x1D6EC}$
is a copy of
$\langle n\rangle \in \unicode[STIX]{x1D6EC}$
is a copy of
 $S^{1}$
with
$S^{1}$
with
 $n+1$
marked points given by the
$n+1$
marked points given by the
 $(n+1)$
th roots of unity.
$(n+1)$
th roots of unity.– A morphism
 $\langle m\rangle \rightarrow \langle n\rangle$
is represented by a monotone degree one continuous map
$\langle m\rangle \rightarrow \langle n\rangle$
is represented by a monotone degree one continuous map
 $S^{1}\rightarrow S^{1}$
taking the
$S^{1}\rightarrow S^{1}$
taking the
 $m+1$
marked points in the domain to the
$m+1$
marked points in the domain to the
 $n+1$
marked points in the range; such maps are considered up to homotopy relative to the marked points.
$n+1$
marked points in the range; such maps are considered up to homotopy relative to the marked points.
Proposition 4.2. There is a natural equivalence of categories
![]() $(-)^{\ast }:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}^{\text{op}}$
.
$(-)^{\ast }:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}^{\text{op}}$
.
Proof. This equivalence is called interstice duality. See [Reference Dyckerhoff and KapranovDK18] § 2.5.◻
Definition 4.3. Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category.
$\infty$
-category.
– A cyclic object in
 $C$
is a functor
$C$
is a functor
 $N(\unicode[STIX]{x1D6EC}^{\text{op}})\rightarrow C$
. We denote by
$N(\unicode[STIX]{x1D6EC}^{\text{op}})\rightarrow C$
. We denote by
 $C_{\unicode[STIX]{x1D6EC}}$
the
$C_{\unicode[STIX]{x1D6EC}}$
the
 $\infty$
-category of cyclic objects in
$\infty$
-category of cyclic objects in
 $C$
. If
$C$
. If
 $C={\mathcal{S}}$
is the
$C={\mathcal{S}}$
is the
 $\infty$
-category of spaces we denote by the Yoneda functor.
$\infty$
-category of spaces we denote by the Yoneda functor. $$\begin{eqnarray}L:N(\unicode[STIX]{x1D6EC})\rightarrow {\mathcal{S}}_{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
$$\begin{eqnarray}L:N(\unicode[STIX]{x1D6EC})\rightarrow {\mathcal{S}}_{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
– A cocyclic object in
 $C$
is a functor
$C$
is a functor
 $N(\unicode[STIX]{x1D6EC})\rightarrow C$
. We denote by
$N(\unicode[STIX]{x1D6EC})\rightarrow C$
. We denote by
 $C^{\unicode[STIX]{x1D6EC}}$
the
$C^{\unicode[STIX]{x1D6EC}}$
the
 $\infty$
-category of cocyclic objects in
$\infty$
-category of cocyclic objects in
 $C$
.
$C$
.
Consider the map
![]() $\mathbb{A}_{\unicode[STIX]{x1D705}}^{1}\stackrel{z^{n}}{\longrightarrow }\mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
. We denote by
$\mathbb{A}_{\unicode[STIX]{x1D705}}^{1}\stackrel{z^{n}}{\longrightarrow }\mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
. We denote by
![]() ${\mathcal{E}}^{n}$
the (
${\mathcal{E}}^{n}$
the (
![]() $\mathbb{Z}_{n+1}$
-graded category) of matrix factorizations
$\mathbb{Z}_{n+1}$
-graded category) of matrix factorizations
![]() $MF(\mathbb{A}_{\unicode[STIX]{x1D705}}^{1},z^{n+1})\in \text{DGCat}_{\text{small}}^{(2)}$
, see § 2.3.5 of [Reference Dyckerhoff and KapranovDK18] for additional details. The categories
$MF(\mathbb{A}_{\unicode[STIX]{x1D705}}^{1},z^{n+1})\in \text{DGCat}_{\text{small}}^{(2)}$
, see § 2.3.5 of [Reference Dyckerhoff and KapranovDK18] for additional details. The categories
![]() ${\mathcal{E}}^{n}$
assemble to a cyclic object in
${\mathcal{E}}^{n}$
assemble to a cyclic object in
![]() $\text{DGCat}_{\text{small}}^{(2)}$
. We state the precise result below.
$\text{DGCat}_{\text{small}}^{(2)}$
. We state the precise result below.
Proposition 4.4 [Reference Dyckerhoff and KapranovDK18, Proposition 2.4.1], [Reference DyckerhoffDyc17, Theorem 3.2].
There is a cocyclic object
that is defined on objects by the assignment
Lemma 4.5. The structure maps of the cocyclic object
![]() ${\mathcal{E}}^{\bullet }$
admit a left and a right adjoint.
${\mathcal{E}}^{\bullet }$
admit a left and a right adjoint.
Proof. For all
![]() $n\in \mathbb{N}$
the category
$n\in \mathbb{N}$
the category
![]() ${\mathcal{E}}^{n}$
is the
${\mathcal{E}}^{n}$
is the
![]() $\mathbb{Z}_{2}$
-periodization of a smooth and proper dg category, namely the dg category of representations of the
$\mathbb{Z}_{2}$
-periodization of a smooth and proper dg category, namely the dg category of representations of the
![]() $A_{n-1}$
-quiver (see [Reference Dyckerhoff and KapranovDK18], Theorem 2.3.6). Now, functors between smooth and proper dg categories always admit both a right and a left adjoint. In the
$A_{n-1}$
-quiver (see [Reference Dyckerhoff and KapranovDK18], Theorem 2.3.6). Now, functors between smooth and proper dg categories always admit both a right and a left adjoint. In the
![]() $\mathbb{Z}$
-graded setting a convenient recent reference for this fact is Theorem 7.4 [Reference GenoveseGen17], and the proof carries over to the
$\mathbb{Z}$
-graded setting a convenient recent reference for this fact is Theorem 7.4 [Reference GenoveseGen17], and the proof carries over to the
![]() $\mathbb{Z}_{2}$
-graded setting.◻
$\mathbb{Z}_{2}$
-graded setting.◻
Let
be the auto-equivalence of
![]() $\text{DGCat}_{\text{small}}^{(2)}$
sending a category to its opposite category.
$\text{DGCat}_{\text{small}}^{(2)}$
sending a category to its opposite category.
Definition 4.6. Denote by
![]() ${\mathcal{E}}_{\bullet }:\unicode[STIX]{x1D6EC}^{\text{op}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the cyclic object defined as the composite
${\mathcal{E}}_{\bullet }:\unicode[STIX]{x1D6EC}^{\text{op}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the cyclic object defined as the composite
Remark 4.7. There are several equivalent ways to define
![]() ${\mathcal{E}}_{\bullet }$
. We list them below.
${\mathcal{E}}_{\bullet }$
. We list them below.
(i) Denote by
 $(-)^{\vee }:(\text{DGCat}_{\text{small}}^{(2)})^{\text{op}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the functor mapping a category
$(-)^{\vee }:(\text{DGCat}_{\text{small}}^{(2)})^{\text{op}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the functor mapping a category
 $D$
in
$D$
in
 $\text{DGCat}_{\text{small}}^{(2)}$
to
$\text{DGCat}_{\text{small}}^{(2)}$
to
 $\text{Fun}(D,\text{Vect}^{(2),\text{fd}})$
. Then
$\text{Fun}(D,\text{Vect}^{(2),\text{fd}})$
. Then
 ${\mathcal{E}}_{\bullet }$
is equivalent to the cyclic object given by the compositionSee [Reference Dyckerhoff and KapranovDK18] § 3.2 for a discussion of this fact.
${\mathcal{E}}_{\bullet }$
is equivalent to the cyclic object given by the compositionSee [Reference Dyckerhoff and KapranovDK18] § 3.2 for a discussion of this fact.
(ii) By Lemma 4.5 all the structure maps of
 ${\mathcal{E}}^{\bullet }$
admit right adjoints. Passing to right adjoints yields a contravariant functor out of
${\mathcal{E}}^{\bullet }$
admit right adjoints. Passing to right adjoints yields a contravariant functor out of
 $N(\unicode[STIX]{x1D6EC}),$
which we denote
$N(\unicode[STIX]{x1D6EC}),$
which we denote
 $({\mathcal{E}}^{\bullet })^{R}$
,and which is also equivalent to the cyclic object
$({\mathcal{E}}^{\bullet })^{R}$
,and which is also equivalent to the cyclic object
 ${\mathcal{E}}_{\bullet }$
.
${\mathcal{E}}_{\bullet }$
.
To any ribbon graph
![]() $X$
, we may associate a cyclic set
$X$
, we may associate a cyclic set
![]() ${\mathcal{L}}(X)\in {\mathcal{S}}et_{\unicode[STIX]{x1D6EC}}$
(called the cyclic membrane in [Reference Dyckerhoff and KapranovDK18]) as follows. Given a vertex
${\mathcal{L}}(X)\in {\mathcal{S}}et_{\unicode[STIX]{x1D6EC}}$
(called the cyclic membrane in [Reference Dyckerhoff and KapranovDK18]) as follows. Given a vertex
![]() $v$
of
$v$
of
![]() $X$
, denote by
$X$
, denote by
![]() $E(v)$
the set of edges at
$E(v)$
the set of edges at
![]() $v$
, and set
$v$
, and set
![]() $B(v)=E(v)^{\ast }$
. Let
$B(v)=E(v)^{\ast }$
. Let
![]() $\unicode[STIX]{x1D6EC}^{B(v)}$
be the cyclic simplex corresponding to the cyclically ordered set
$\unicode[STIX]{x1D6EC}^{B(v)}$
be the cyclic simplex corresponding to the cyclically ordered set
![]() $B(v)$
. For an edge
$B(v)$
. For an edge
![]() $e$
of
$e$
of
![]() $X$
, we have a two element set
$X$
, we have a two element set
![]() $B(e)=V(e)^{\ast }$
, where
$B(e)=V(e)^{\ast }$
, where
![]() $V(e)$
is the set of vertices that
$V(e)$
is the set of vertices that
![]() $e$
joins. Let
$e$
joins. Let
![]() $\unicode[STIX]{x1D6EC}^{B(e)}$
be the corresponding cyclic 1-simplex. Next, define the incidence category
$\unicode[STIX]{x1D6EC}^{B(e)}$
be the corresponding cyclic 1-simplex. Next, define the incidence category
![]() $X_{[0,1]}$
of
$X_{[0,1]}$
of
![]() $X$
: the set of objects of
$X$
: the set of objects of
![]() $X_{[0,1]}$
is the disjoint union of the set of vertices and the set of edges of
$X_{[0,1]}$
is the disjoint union of the set of vertices and the set of edges of
![]() $X$
, and there is a unique morphism
$X$
, and there is a unique morphism
![]() $v\rightarrow e$
for each flag
$v\rightarrow e$
for each flag
![]() $(v,e)$
in
$(v,e)$
in
![]() $X$
(consisting of a pair of a vertex
$X$
(consisting of a pair of a vertex
![]() $v$
and an edge
$v$
and an edge
![]() $e$
incident to
$e$
incident to
![]() $v$
). The cyclic simplices
$v$
). The cyclic simplices
![]() $\unicode[STIX]{x1D6EC}^{B(v)}$
and
$\unicode[STIX]{x1D6EC}^{B(v)}$
and
![]() $\unicode[STIX]{x1D6EC}^{B(e)}$
assemble into a functor
$\unicode[STIX]{x1D6EC}^{B(e)}$
assemble into a functor
![]() $U_{X}:X_{[0,1]}^{\text{op}}\rightarrow {\mathcal{S}}et_{\unicode[STIX]{x1D6EC}}$
, and we define
$U_{X}:X_{[0,1]}^{\text{op}}\rightarrow {\mathcal{S}}et_{\unicode[STIX]{x1D6EC}}$
, and we define
Proposition 4.8 [Reference Dyckerhoff and KapranovDK18, Proposition 3.4.4].
The cyclic membrane construction
extends to a functor from the category
![]() ${\mathcal{R}}ib$
of ribbon graphs and contractions between them to the category of cyclic sets.
${\mathcal{R}}ib$
of ribbon graphs and contractions between them to the category of cyclic sets.
If
![]() $X$
and
$X$
and
![]() $X^{\prime }$
are ribbon graphs, a contraction
$X^{\prime }$
are ribbon graphs, a contraction
![]() $X\rightarrow X^{\prime }$
is a map between the underlying topological spaces having the property that the preimage of each point in
$X\rightarrow X^{\prime }$
is a map between the underlying topological spaces having the property that the preimage of each point in
![]() $X^{\prime }$
is either a point, or a sub-tree of
$X^{\prime }$
is either a point, or a sub-tree of
![]() $X$
. We refer the reader to [Reference Dyckerhoff and KapranovDK18] for additional details on the definition of
$X$
. We refer the reader to [Reference Dyckerhoff and KapranovDK18] for additional details on the definition of
![]() ${\mathcal{R}}ib$
and a proof of the proposition.
${\mathcal{R}}ib$
and a proof of the proposition.
As explained in [Reference DyckerhoffDyc17] the functor constructed in Proposition 4.8 can be enhanced to a functor of
![]() $\infty$
-categories
$\infty$
-categories
where
![]() ${\mathcal{S}}$
is the
${\mathcal{S}}$
is the
![]() $\infty$
-category of spaces.
$\infty$
-category of spaces.
Definition 4.9.
– Denote by
 ${\mathcal{F}}^{{\mathcal{E}}}:{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the
${\mathcal{F}}^{{\mathcal{E}}}:{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the
 $\infty$
-categorical left Kan extension of along
$\infty$
-categorical left Kan extension of along $$\begin{eqnarray}N(\unicode[STIX]{x1D6EC})\stackrel{{\mathcal{E}}^{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\end{eqnarray}$$
$$\begin{eqnarray}N(\unicode[STIX]{x1D6EC})\stackrel{{\mathcal{E}}^{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\end{eqnarray}$$
 $N(\unicode[STIX]{x1D6EC})\xrightarrow[{}]{L}{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
.
$N(\unicode[STIX]{x1D6EC})\xrightarrow[{}]{L}{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
.– Denote by
 ${\mathcal{F}}_{{\mathcal{E}}}:({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the
${\mathcal{F}}_{{\mathcal{E}}}:({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}\rightarrow \text{DGCat}_{\text{small}}^{(2)}$
the
 $\infty$
-categorical right Kan extension of along
$\infty$
-categorical right Kan extension of along $$\begin{eqnarray}N(\unicode[STIX]{x1D6EC}^{\text{op}})\stackrel{{\mathcal{E}}_{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\end{eqnarray}$$
$$\begin{eqnarray}N(\unicode[STIX]{x1D6EC}^{\text{op}})\stackrel{{\mathcal{E}}_{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\end{eqnarray}$$
 $N(\unicode[STIX]{x1D6EC})^{\text{op}}\xrightarrow[{}]{(L)^{\text{op}}}({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}$
.
$N(\unicode[STIX]{x1D6EC})^{\text{op}}\xrightarrow[{}]{(L)^{\text{op}}}({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}$
.
Let
![]() $\unicode[STIX]{x1D6F4}$
be a Riemann surface with boundary and let
$\unicode[STIX]{x1D6F4}$
be a Riemann surface with boundary and let
![]() $X\subset \unicode[STIX]{x1D6F4}$
be a spanning ribbon graph. The implementation of Kontsevich’s ideas due to Dyckerhoff and Kapranov [Reference Dyckerhoff and KapranovDK18] (see also [Reference NadlerNad15] and [Reference Sibilla, Treumann and ZaslowSTZ14]) gives ways to compute a model for the Fukaya category of
$X\subset \unicode[STIX]{x1D6F4}$
be a spanning ribbon graph. The implementation of Kontsevich’s ideas due to Dyckerhoff and Kapranov [Reference Dyckerhoff and KapranovDK18] (see also [Reference NadlerNad15] and [Reference Sibilla, Treumann and ZaslowSTZ14]) gives ways to compute a model for the Fukaya category of
![]() $\unicode[STIX]{x1D6F4}$
from the combinatorics of
$\unicode[STIX]{x1D6F4}$
from the combinatorics of
![]() $X$
. We will refer to it as the topological (compact) Fukaya category of
$X$
. We will refer to it as the topological (compact) Fukaya category of
![]() $X$
or sometimes as the topological (compact) Fukaya category of the pair
$X$
or sometimes as the topological (compact) Fukaya category of the pair
![]() $(\unicode[STIX]{x1D6F4},X)$
. The next definition gives the construction of the topological (compact) Fukaya category, see Definition 4.1.1 of [Reference Dyckerhoff and KapranovDK18].
$(\unicode[STIX]{x1D6F4},X)$
. The next definition gives the construction of the topological (compact) Fukaya category, see Definition 4.1.1 of [Reference Dyckerhoff and KapranovDK18].
Definition 4.10. Let
![]() $(\unicode[STIX]{x1D6F4},X)$
be a punctured Riemann surface.
$(\unicode[STIX]{x1D6F4},X)$
be a punctured Riemann surface.
– The topological Fukaya category of
 $X$
is given by
$X$
is given by  $$\begin{eqnarray}{\mathcal{F}}^{\text{top}}(X):={\mathcal{F}}^{{\mathcal{E}}}({\mathcal{L}}(X)).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}^{\text{top}}(X):={\mathcal{F}}^{{\mathcal{E}}}({\mathcal{L}}(X)).\end{eqnarray}$$
– The topological compact Fukaya category of
 $X$
is given by
$X$
is given by  $$\begin{eqnarray}{\mathcal{F}}_{\text{top}}(X):={\mathcal{F}}_{{\mathcal{E}}}({\mathcal{L}}(X)).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\text{top}}(X):={\mathcal{F}}_{{\mathcal{E}}}({\mathcal{L}}(X)).\end{eqnarray}$$
Remark 4.11. The terminology we use in this paper differs slightly from the one introduced in [Reference Dyckerhoff and KapranovDK18]. Namely:
–
 ${\mathcal{F}}^{\text{top}}(X)$
in [Reference Dyckerhoff and KapranovDK18] is called the topological coFukaya category;
${\mathcal{F}}^{\text{top}}(X)$
in [Reference Dyckerhoff and KapranovDK18] is called the topological coFukaya category;–
 ${\mathcal{F}}_{\text{top}}(X)$
in [Reference Dyckerhoff and KapranovDK18] is called the topological Fukaya category.
${\mathcal{F}}_{\text{top}}(X)$
in [Reference Dyckerhoff and KapranovDK18] is called the topological Fukaya category.
Proposition 4.12. There is a natural equivalence
Proof. See the discussion after Definition 4.1.1 of [Reference Dyckerhoff and KapranovDK18]. ◻
4.2 The Ind-completion of the topological Fukaya category
In this section we introduce the Ind-completed version of the topological (compact) Fukaya category. This plays an important role in proving that
![]() ${\mathcal{F}}^{\text{top}}(-)$
exhibits an interesting sheaf-like behavior with respect to closed coverings of ribbon graphs that we study in § 5.2. We remark that Definitions 4.13 and 4.15 mirror exactly Proposition 4.4 and Definitions 4.6 and 4.9 from the previous section, the only difference being that we are now working with cocomplete dg categories.
${\mathcal{F}}^{\text{top}}(-)$
exhibits an interesting sheaf-like behavior with respect to closed coverings of ribbon graphs that we study in § 5.2. We remark that Definitions 4.13 and 4.15 mirror exactly Proposition 4.4 and Definitions 4.6 and 4.9 from the previous section, the only difference being that we are now working with cocomplete dg categories.
Definition 4.13.
– Denote by
 ${\mathcal{I}}{\mathcal{E}}^{\bullet }:N(\unicode[STIX]{x1D6EC})\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the cocylic object defined by the composition
${\mathcal{I}}{\mathcal{E}}^{\bullet }:N(\unicode[STIX]{x1D6EC})\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the cocylic object defined by the composition  $$\begin{eqnarray}N(\unicode[STIX]{x1D6EC})\stackrel{{\mathcal{E}}^{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\stackrel{\text{Ind}}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}.\end{eqnarray}$$
$$\begin{eqnarray}N(\unicode[STIX]{x1D6EC})\stackrel{{\mathcal{E}}^{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\stackrel{\text{Ind}}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}.\end{eqnarray}$$
– Denote by
 ${\mathcal{I}}{\mathcal{E}}_{\bullet }:N(\unicode[STIX]{x1D6EC}^{\text{op}})\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the cyclic object defined by the composition
${\mathcal{I}}{\mathcal{E}}_{\bullet }:N(\unicode[STIX]{x1D6EC}^{\text{op}})\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the cyclic object defined by the composition  $$\begin{eqnarray}N(\unicode[STIX]{x1D6EC}^{\text{op}})\stackrel{{\mathcal{E}}_{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\stackrel{\text{Ind}}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}.\end{eqnarray}$$
$$\begin{eqnarray}N(\unicode[STIX]{x1D6EC}^{\text{op}})\stackrel{{\mathcal{E}}_{\bullet }}{\longrightarrow }\text{DGCat}_{\text{small}}^{(2)}\stackrel{\text{Ind}}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}.\end{eqnarray}$$
Remark 4.14. The same consideration of Remark 4.7 applies to the Ind-completed setting. In particular, the structure maps of
![]() ${\mathcal{I}}{\mathcal{E}}^{\bullet }$
admit right and left adjoints, which are the Ind-completions of the right and left adjoints given by Lemma 4.5. Then the cyclic object
${\mathcal{I}}{\mathcal{E}}^{\bullet }$
admit right and left adjoints, which are the Ind-completions of the right and left adjoints given by Lemma 4.5. Then the cyclic object
![]() ${\mathcal{I}}{\mathcal{E}}_{\bullet }$
is equivalent to
${\mathcal{I}}{\mathcal{E}}_{\bullet }$
is equivalent to
![]() $({\mathcal{I}}{\mathcal{E}}^{\bullet })^{R}$
, which is defined exactly in the same way as in Remark 4.7.
$({\mathcal{I}}{\mathcal{E}}^{\bullet })^{R}$
, which is defined exactly in the same way as in Remark 4.7.
Definition 4.15.
– Denote by
 ${\mathcal{I}}{\mathcal{F}}^{{\mathcal{E}}}:{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the
${\mathcal{I}}{\mathcal{F}}^{{\mathcal{E}}}:{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the
 $\infty$
-categorical left Kan extension of along
$\infty$
-categorical left Kan extension of along $$\begin{eqnarray}N(\unicode[STIX]{x1D6EC})\stackrel{{\mathcal{I}}{\mathcal{E}}^{\bullet }}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}\end{eqnarray}$$
$$\begin{eqnarray}N(\unicode[STIX]{x1D6EC})\stackrel{{\mathcal{I}}{\mathcal{E}}^{\bullet }}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}\end{eqnarray}$$
 $N(\unicode[STIX]{x1D6EC})\xrightarrow[{}]{L}{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
.
$N(\unicode[STIX]{x1D6EC})\xrightarrow[{}]{L}{\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
.– Denote by
 ${\mathcal{I}}{\mathcal{F}}_{{\mathcal{E}}}:({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the
${\mathcal{I}}{\mathcal{F}}_{{\mathcal{E}}}:({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}\rightarrow \text{DGCat}_{\text{cont}}^{(2)}$
the
 $\infty$
-categorical right Kan extension of along
$\infty$
-categorical right Kan extension of along $$\begin{eqnarray}N(\unicode[STIX]{x1D6EC}^{\text{op}})\stackrel{{\mathcal{I}}{\mathcal{E}}_{\bullet }}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}\end{eqnarray}$$
$$\begin{eqnarray}N(\unicode[STIX]{x1D6EC}^{\text{op}})\stackrel{{\mathcal{I}}{\mathcal{E}}_{\bullet }}{\longrightarrow }\text{DGCat}_{\text{cont}}^{(2)}\end{eqnarray}$$
 $N(\unicode[STIX]{x1D6EC}^{\text{op}})\xrightarrow[{}]{(L)^{\text{op}}}({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}$
.
$N(\unicode[STIX]{x1D6EC}^{\text{op}})\xrightarrow[{}]{(L)^{\text{op}}}({\mathcal{S}}_{\unicode[STIX]{x1D6EC}})^{\text{op}}$
.
Proposition 4.16. For all
![]() $X\in {\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
there is an equivalence
$X\in {\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
there is an equivalence
Proof. This is a formal consequence of Proposition 2.4. By Remark 4.14,
![]() ${\mathcal{I}}{\mathcal{E}}_{\bullet }$
can be realized by taking right adjoints of the structure morphisms of
${\mathcal{I}}{\mathcal{E}}_{\bullet }$
can be realized by taking right adjoints of the structure morphisms of
![]() ${\mathcal{I}}{\mathcal{E}}^{\bullet }$
. If
${\mathcal{I}}{\mathcal{E}}^{\bullet }$
. If
![]() ${\mathcal{L}}$
is in
${\mathcal{L}}$
is in
![]() ${\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
, by the general formula for pointwise Kan extensions we have
${\mathcal{S}}_{\unicode[STIX]{x1D6EC}}$
, by the general formula for pointwise Kan extensions we have
Definition 4.17. If
![]() $X$
is a ribbon graph, we set
$X$
is a ribbon graph, we set
We call
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
the Ind-completed topological Fukaya category of X.
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
the Ind-completed topological Fukaya category of X.
By Lemma 2.2 Ind-completion preserves colimits, and this immediately implies the following statement.
Proposition 4.18. If
![]() $X$
is a ribbon graph there is an equivalence
$X$
is a ribbon graph there is an equivalence
Proposition 4.16 and Definition 4.17 indicate a key difference with the setting of small categories considered in § 4.1: if we work with the Ind-completed (co)cyclic objects
![]() ${\mathcal{I}}{\mathcal{E}}^{\bullet }$
and
${\mathcal{I}}{\mathcal{E}}^{\bullet }$
and
![]() ${\mathcal{I}}{\mathcal{E}}_{\bullet },$
there is no difference between Fukaya and compact Fukaya category. However, it is important to remark that
${\mathcal{I}}{\mathcal{E}}_{\bullet },$
there is no difference between Fukaya and compact Fukaya category. However, it is important to remark that
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is not equivalent in general to the Ind-completion of
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is not equivalent in general to the Ind-completion of
![]() ${\mathcal{F}}_{\text{top}}(X)$
. Instead
${\mathcal{F}}_{\text{top}}(X)$
. Instead
![]() $\text{Ind}({\mathcal{F}}_{\text{top}}(X))$
is a full subcategory of
$\text{Ind}({\mathcal{F}}_{\text{top}}(X))$
is a full subcategory of
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
. We clarify the relationship between these two categories in Example 4.19 below.
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
. We clarify the relationship between these two categories in Example 4.19 below.
Example 4.19. Consider the ribbon graph
![]() $X$
given by a loop with no vertices. We can tabulate the value of the topological (compact) Fukaya category of
$X$
given by a loop with no vertices. We can tabulate the value of the topological (compact) Fukaya category of
![]() $X$
and of its Ind-completed version as follows.
$X$
and of its Ind-completed version as follows.
– The category
 ${\mathcal{F}}^{\text{top}}(X)$
is equivalent to
${\mathcal{F}}^{\text{top}}(X)$
is equivalent to
 ${\mathcal{P}}\text{erf}^{(2)}(\mathbb{G}_{m})$
.
${\mathcal{P}}\text{erf}^{(2)}(\mathbb{G}_{m})$
.– The category
 ${\mathcal{F}}_{\text{top}}(X)$
is equivalent to the full subcategory of
${\mathcal{F}}_{\text{top}}(X)$
is equivalent to the full subcategory of
 ${\mathcal{P}}\text{erf}^{(2)}(\mathbb{G}_{m})$
given by complexes with compact support,
${\mathcal{P}}\text{erf}^{(2)}(\mathbb{G}_{m})$
given by complexes with compact support,
 ${\mathcal{P}}\text{erf}_{cs}^{(2)}(\mathbb{G}_{m})$
.
${\mathcal{P}}\text{erf}_{cs}^{(2)}(\mathbb{G}_{m})$
.– By Proposition 4.18 the category
 ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is equivalent to
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is equivalent to
 ${\mathcal{Q}}\text{Coh}^{(2)}(\mathbb{G}_{m})$
.
${\mathcal{Q}}\text{Coh}^{(2)}(\mathbb{G}_{m})$
.
Note that
![]() $\text{Ind}({\mathcal{F}}_{\text{top}}(X))\simeq \text{Ind}({\mathcal{P}}\text{erf}_{cs}^{(2)}(\mathbb{G}_{m}))$
is a strict subcategory of
$\text{Ind}({\mathcal{F}}_{\text{top}}(X))\simeq \text{Ind}({\mathcal{P}}\text{erf}_{cs}^{(2)}(\mathbb{G}_{m}))$
is a strict subcategory of
5 The topological Fukaya category and restrictions
In this section we explore various naturality properties of
![]() ${\mathcal{F}}_{\infty }^{\text{top}}$
with respect to open and closed embeddings of ribbon graphs. As first suggested by Kontsevich [Reference KontsevichKon09], the topological Fukaya category behaves like a (co)sheaf with respect to open covers. This aspect was investigated for instance in [Reference Sibilla, Treumann and ZaslowSTZ14, Reference DyckerhoffDyc17]. In § 6 we will prove that, additionally, the topological Fukaya category behaves like a sheaf also with respect to certain closed covers.
${\mathcal{F}}_{\infty }^{\text{top}}$
with respect to open and closed embeddings of ribbon graphs. As first suggested by Kontsevich [Reference KontsevichKon09], the topological Fukaya category behaves like a (co)sheaf with respect to open covers. This aspect was investigated for instance in [Reference Sibilla, Treumann and ZaslowSTZ14, Reference DyckerhoffDyc17]. In § 6 we will prove that, additionally, the topological Fukaya category behaves like a sheaf also with respect to certain closed covers.
5.1 Restriction to open subgraphs
Let
![]() $X$
be a ribbon graph. With a small abuse of notation we denote by
$X$
be a ribbon graph. With a small abuse of notation we denote by
![]() $X$
also its underlying topological space. We say that
$X$
also its underlying topological space. We say that
![]() $Y\subset X$
is a subgraph if it is a subspace having the property that, if the intersection of
$Y\subset X$
is a subgraph if it is a subspace having the property that, if the intersection of
![]() $Y$
with an edge
$Y$
with an edge
![]() $e$
of
$e$
of
![]() $X$
is not empty or a vertex, then
$X$
is not empty or a vertex, then
![]() $e$
is contained in
$e$
is contained in
![]() $Y$
. If
$Y$
. If
![]() $Y$
is a subgraph of
$Y$
is a subgraph of
![]() $X$
, then it is canonically the underlying topological space of a ribbon graph, which we also denote
$X$
, then it is canonically the underlying topological space of a ribbon graph, which we also denote
![]() $Y$
. Note that if
$Y$
. Note that if
![]() $U$
and
$U$
and
![]() $V$
are open subgraphs of
$V$
are open subgraphs of
![]() $X$
, then their intersection
$X$
, then their intersection
![]() $U\cap V$
is also an open subgraph of
$U\cap V$
is also an open subgraph of
![]() $X$
.
$X$
.
Proposition 5.1. Let
![]() $X$
be a ribbon graph and let
$X$
be a ribbon graph and let
![]() $U\subset X$
be an open subgraph. Then there are corestriction functors:
$U\subset X$
be an open subgraph. Then there are corestriction functors:
–
 $C_{U}:{\mathcal{F}}^{\text{top}}(U)\rightarrow {\mathcal{F}}^{\text{top}}(X)$
;
$C_{U}:{\mathcal{F}}^{\text{top}}(U)\rightarrow {\mathcal{F}}^{\text{top}}(X)$
;–
 $C_{\infty ,U}:{\mathcal{F}}_{\infty }^{\text{top}}(U)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(X)$
.
$C_{\infty ,U}:{\mathcal{F}}_{\infty }^{\text{top}}(U)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(X)$
.
When the target of the corestriction functors is not clear from the context we will use the notation
![]() $C_{U}^{X}$
and
$C_{U}^{X}$
and
![]() $C_{\infty ,U}^{X}$
.
$C_{\infty ,U}^{X}$
.
Proof. The construction of the functor
![]() $C_{U}$
is a formal consequence of the definition of
$C_{U}$
is a formal consequence of the definition of
![]() ${\mathcal{F}}^{\text{top}}(X)$
as a colimit. The definition
${\mathcal{F}}^{\text{top}}(X)$
as a colimit. The definition
![]() ${\mathcal{F}}^{\text{top}}(X)={\mathcal{F}}^{{\mathcal{E}}}({\mathcal{L}}(X))$
expresses
${\mathcal{F}}^{\text{top}}(X)={\mathcal{F}}^{{\mathcal{E}}}({\mathcal{L}}(X))$
expresses
![]() ${\mathcal{F}}^{\text{top}}(X)$
as a colimit of dg categories indexed by the vertices and edges of
${\mathcal{F}}^{\text{top}}(X)$
as a colimit of dg categories indexed by the vertices and edges of
![]() $X$
. In the same way,
$X$
. In the same way,
![]() ${\mathcal{F}}^{\text{top}}(U)$
is defined as a colimit of dg categories indexed by the vertices and edges of
${\mathcal{F}}^{\text{top}}(U)$
is defined as a colimit of dg categories indexed by the vertices and edges of
![]() $U$
, which are a subset of those of
$U$
, which are a subset of those of
![]() $X$
. Thus the colimit diagram defining
$X$
. Thus the colimit diagram defining
![]() ${\mathcal{F}}^{\text{top}}(U)$
is a subdiagram of the one defining
${\mathcal{F}}^{\text{top}}(U)$
is a subdiagram of the one defining
![]() ${\mathcal{F}}^{\text{top}}(X)$
, and
${\mathcal{F}}^{\text{top}}(X)$
, and
![]() $C_{U}$
is the resulting map between the colimits. The functor
$C_{U}$
is the resulting map between the colimits. The functor
![]() $C_{\infty ,U}$
is obtained by Ind-completion. See also [Reference DyckerhoffDyc17] § 4 for a treatment of these corestriction functors.◻
$C_{\infty ,U}$
is obtained by Ind-completion. See also [Reference DyckerhoffDyc17] § 4 for a treatment of these corestriction functors.◻
Remark 5.2. By Proposition 4.18
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(U)$
and
${\mathcal{F}}_{\infty }^{\text{top}}(U)$
and
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
are equivalent to the Ind-completions of
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
are equivalent to the Ind-completions of
![]() ${\mathcal{F}}^{\text{top}}(U)$
and
${\mathcal{F}}^{\text{top}}(U)$
and
![]() ${\mathcal{F}}^{\text{top}}(X)$
. There is a natural equivalence
${\mathcal{F}}^{\text{top}}(X)$
. There is a natural equivalence
In particular the corestriction
![]() $C_{\infty ,U}$
is a morphism in
$C_{\infty ,U}$
is a morphism in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
.
$\text{DGCat}_{\text{cont}}^{(2)}$
.
Definition 5.3. Let
![]() $X$
be a ribbon graph and let
$X$
be a ribbon graph and let
![]() $U\subset X$
be an open subgraph. Then we define restriction functors as follows.
$U\subset X$
be an open subgraph. Then we define restriction functors as follows.
– By Proposition 4.12 there is a natural equivalence between
 ${\mathcal{F}}_{\text{top}}(-)$
and the dual of
${\mathcal{F}}_{\text{top}}(-)$
and the dual of
 ${\mathcal{F}}^{\text{top}}(-)$
. The restriction
${\mathcal{F}}^{\text{top}}(-)$
. The restriction
 $R^{U}:{\mathcal{F}}_{\text{top}}(X)\rightarrow {\mathcal{F}}_{\text{top}}(U)$
is obtained by dualizing
$R^{U}:{\mathcal{F}}_{\text{top}}(X)\rightarrow {\mathcal{F}}_{\text{top}}(U)$
is obtained by dualizing
 $C_{U}$
.
$C_{U}$
.– The restriction
 $R_{\infty }^{U}:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(U)$
is the right adjoint of the corestriction
$R_{\infty }^{U}:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(U)$
is the right adjoint of the corestriction
 $C_{\infty ,U}$
.
$C_{\infty ,U}$
.
When the target of the restriction functors is not clear from the context we will use the notation
![]() $R_{X}^{U}$
and
$R_{X}^{U}$
and
![]() $R_{\infty ,X}^{U}$
.
$R_{\infty ,X}^{U}$
.
Remark 5.4. Note that the functor
![]() $R_{\infty }^{U}$
cannot be realized as
$R_{\infty }^{U}$
cannot be realized as
![]() $\text{Ind}(R^{U})$
. In fact, as shown by Example 4.19, in general the functors
$\text{Ind}(R^{U})$
. In fact, as shown by Example 4.19, in general the functors
![]() $R_{\infty }^{U}$
and
$R_{\infty }^{U}$
and
![]() $\text{Ind}(R^{U})$
are going to have different source and target.
$\text{Ind}(R^{U})$
are going to have different source and target.
Remark 5.5. Let
![]() $X$
be a ribbon graph. Let
$X$
be a ribbon graph. Let
![]() $V\subset U\subset X$
be open subgraphs. Then the following diagram commutes.
$V\subset U\subset X$
be open subgraphs. Then the following diagram commutes.

Proposition 5.6. Let
![]() $X$
be a ribbon graph and let
$X$
be a ribbon graph and let
![]() $U$
and
$U$
and
![]() $V$
be open subgraphs such that
$V$
be open subgraphs such that
![]() $X=U\cup V$
.
$X=U\cup V$
.
– The following is a push-out in
 $\text{DGCat}_{\text{small}}^{(2)}$
.
$\text{DGCat}_{\text{small}}^{(2)}$
. 
– The following is a push-out in
 $\text{DGCat}_{\text{cont}}^{(2)}$
.
$\text{DGCat}_{\text{cont}}^{(2)}$
.
Proof. The first part of the claim can be proved in the same way as Proposition 4.2 of [Reference DyckerhoffDyc17]. The second part follows because, by Lemma 2.2, the Ind-completion commutes with colimits.◻
Proposition 5.7. Let
![]() $X$
be a ribbon graph and let
$X$
be a ribbon graph and let
![]() $U$
and
$U$
and
![]() $V$
be open subgraphs such that
$V$
be open subgraphs such that
![]() $X=U\cup V$
.
$X=U\cup V$
.
– The following is a fiber product in
 $\text{DGCat}_{\text{small}}^{(2)}$
.
$\text{DGCat}_{\text{small}}^{(2)}$
. 
– The following is a fiber product in
 $\text{DGCat}_{\text{cont}}^{(2)}$
.
$\text{DGCat}_{\text{cont}}^{(2)}$
.
Proof. The claim follows by dualizing the push-outs in Proposition 5.6.◻
Remark 5.8. The second diagram of Proposition 5.7 has very different formal properties from the second diagram of Proposition 5.6. If
![]() $U\subset X$
is an open subgraph the corestriction
$U\subset X$
is an open subgraph the corestriction
![]() $C_{\infty ,X}$
preserves compact objects, but in general this is not the case for the restriction
$C_{\infty ,X}$
preserves compact objects, but in general this is not the case for the restriction
![]() $R_{\infty }^{U}$
(see Remark 5.4). Thus (in general) we cannot apply
$R_{\infty }^{U}$
(see Remark 5.4). Thus (in general) we cannot apply
![]() $(-)^{\unicode[STIX]{x1D714}}$
to the second diagram of Proposition 5.7 and obtain a diagram of small categories.
$(-)^{\unicode[STIX]{x1D714}}$
to the second diagram of Proposition 5.7 and obtain a diagram of small categories.
Propositions 5.6 and 5.7 can be extended in the usual way to account for arbitrary open covers of
![]() $X$
: given any open cover of
$X$
: given any open cover of
![]() $X$
, the (Ind-completed) (compact) Fukaya category can be realized as the homotopy (co)limit of the appropriate Čech diagram of local sections. This clarifies that this formalism is indeed an implementation of the idea that the Fukaya category of a punctured surface should define either a sheaf or a cosheaf of categories on its spine.
$X$
, the (Ind-completed) (compact) Fukaya category can be realized as the homotopy (co)limit of the appropriate Čech diagram of local sections. This clarifies that this formalism is indeed an implementation of the idea that the Fukaya category of a punctured surface should define either a sheaf or a cosheaf of categories on its spine.
5.2 Restriction to closed subgraphs
In this section we turn our attention to closed subgraphs and closed covers of ribbon graphs. In the context of the topological Fukaya category, restrictions to closed subgraphs have also been investigated by Dyckerhoff [Reference DyckerhoffDyc17]. To avoid producing parallel arguments here we will refer to the lucid treatment contained in § 4 of [Reference DyckerhoffDyc17].
Definition 5.9. Let
![]() $X$
be a ribbon graph.
$X$
be a ribbon graph.
– An open subgraph
 $U$
of
$U$
of
 $X$
is good if its complement
$X$
is good if its complement
 $X-U$
does not have vertices of valency one.
$X-U$
does not have vertices of valency one.– A closed subgraph
 $Z$
of
$Z$
of
 $X$
is good if it is the complement in
$X$
is good if it is the complement in
 $X$
of a good open subgraph.
$X$
of a good open subgraph.
We introduce next restriction functors of
![]() ${\mathcal{F}}^{\text{top}}$
and
${\mathcal{F}}^{\text{top}}$
and
![]() ${\mathcal{F}}_{\infty }^{\text{top}}$
to good closed subgraphs: we will sometimes refer to these as exceptional restrictions, in order to mark their difference from the (co)restrictions to open subgraphs that were discussed in the previous section.
${\mathcal{F}}_{\infty }^{\text{top}}$
to good closed subgraphs: we will sometimes refer to these as exceptional restrictions, in order to mark their difference from the (co)restrictions to open subgraphs that were discussed in the previous section.
Proposition 5.10. Let
![]() $X$
be a ribbon graph and let
$X$
be a ribbon graph and let
![]() $Z\subset X$
be a good closed subgraph. Then there are exceptional restriction functors:
$Z\subset X$
be a good closed subgraph. Then there are exceptional restriction functors:
–
 $S^{Z}:{\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(Z)$
;
$S^{Z}:{\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(Z)$
;–
 $S_{\infty }^{Z}:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(Z)$
.
$S_{\infty }^{Z}:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(Z)$
.
When the source of the exceptional restriction functors is not clear from the context we will use the notation
![]() $S_{X}^{Z}$
and
$S_{X}^{Z}$
and
![]() $S_{\infty ,X}^{Z}$
.
$S_{\infty ,X}^{Z}$
.
Proof. Our definition of
![]() $S^{Z}$
follows § 4 of [Reference DyckerhoffDyc17]. Let
$S^{Z}$
follows § 4 of [Reference DyckerhoffDyc17]. Let
![]() $Z$
be a closed subgraph,
$Z$
be a closed subgraph,
![]() $U=X-Z$
, and consider the open subgraph
$U=X-Z$
, and consider the open subgraph
![]() $V$
consisting of
$V$
consisting of
![]() $Z$
together with all half-edges of
$Z$
together with all half-edges of
![]() $X$
that touch
$X$
that touch
![]() $Z$
. Then
$Z$
. Then
![]() $X=U\cup V$
is an open covering, and by Proposition 5.6 we have the following push-out square.
$X=U\cup V$
is an open covering, and by Proposition 5.6 we have the following push-out square.

Next, we may consider another graph
![]() $\overline{V}$
that is obtained from
$\overline{V}$
that is obtained from
![]() $V$
by adding a 1-valent vertex to each edge of
$V$
by adding a 1-valent vertex to each edge of
![]() $V$
that does not belong to
$V$
that does not belong to
![]() $Z$
. There is a covering
$Z$
. There is a covering
![]() $\overline{V}=V\cup \unicode[STIX]{x1D6F9}$
, where
$\overline{V}=V\cup \unicode[STIX]{x1D6F9}$
, where
![]() $\unicode[STIX]{x1D6F9}$
is the disjoint union of several copies of the graph with one vertex and one half-open edge. Another application of Proposition 5.6 yields the following push-out square.
$\unicode[STIX]{x1D6F9}$
is the disjoint union of several copies of the graph with one vertex and one half-open edge. Another application of Proposition 5.6 yields the following push-out square.

Next, we make two observations: one is that
![]() $\unicode[STIX]{x1D6F9}\cap V$
naturally contains
$\unicode[STIX]{x1D6F9}\cap V$
naturally contains
![]() $U\cap V$
, the second is that
$U\cap V$
, the second is that
![]() ${\mathcal{F}}^{\text{top}}(\unicode[STIX]{x1D6F9})\simeq 0$
. This implies that the first push-out diagram maps to the second, and so there is a map
${\mathcal{F}}^{\text{top}}(\unicode[STIX]{x1D6F9})\simeq 0$
. This implies that the first push-out diagram maps to the second, and so there is a map
![]() ${\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(\overline{V})$
. Lastly we use the fact that
${\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(\overline{V})$
. Lastly we use the fact that
![]() ${\mathcal{F}}^{\text{top}}(\overline{V})\simeq {\mathcal{F}}^{\text{top}}(Z)$
, since
${\mathcal{F}}^{\text{top}}(\overline{V})\simeq {\mathcal{F}}^{\text{top}}(Z)$
, since
![]() $Z$
is obtained from
$Z$
is obtained from
![]() $\overline{V}$
by contracting edges. The resulting functor is
$\overline{V}$
by contracting edges. The resulting functor is
![]() $S^{Z}:{\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(Z)$
. The functor
$S^{Z}:{\mathcal{F}}^{\text{top}}(X)\rightarrow {\mathcal{F}}^{\text{top}}(Z)$
. The functor
![]() $S_{\infty }^{Z}$
is the Ind-completion of
$S_{\infty }^{Z}$
is the Ind-completion of
![]() $S^{Z}$
.◻
$S^{Z}$
.◻
Remark 5.11. The property that the closed subgraph
![]() $Z$
is good is not strictly necessary to define exceptional restrictions. However this assumption allows for a somewhat simpler exposition, and it is essential in Theorem 6.6 in the next section. We refer the reader to [Reference DyckerhoffDyc17] for a treatment of exceptional restrictions which does not impose additional requirements on the closed subgraphs.
$Z$
is good is not strictly necessary to define exceptional restrictions. However this assumption allows for a somewhat simpler exposition, and it is essential in Theorem 6.6 in the next section. We refer the reader to [Reference DyckerhoffDyc17] for a treatment of exceptional restrictions which does not impose additional requirements on the closed subgraphs.
Proposition 5.12. Let
![]() $X$
be a ribbon graph, let
$X$
be a ribbon graph, let
![]() $U\subset X$
be a good open subset and let
$U\subset X$
be a good open subset and let
![]() $Z=X-U$
. The following are cofiber sequences in
$Z=X-U$
. The following are cofiber sequences in
![]() $\text{DGCat}_{\text{small}}^{(2)}$
and in
$\text{DGCat}_{\text{small}}^{(2)}$
and in
![]() $\text{DGCat}_{\text{cont}}^{(2)},$
respectively
$\text{DGCat}_{\text{cont}}^{(2)},$
respectively
Proof. This is Proposition 4.9 of [Reference DyckerhoffDyc17].◻
Definition 5.13. Let
![]() $X$
be a ribbon graph and let
$X$
be a ribbon graph and let
![]() $Z\subset X$
be a good closed subgraph. Then we denote by
$Z\subset X$
be a good closed subgraph. Then we denote by
the right adjoint of the exceptional restriction functor. We will call it the exceptional corestriction functor. When the source of the exceptional corestriction functor is not clear from the context we will use the notation
![]() $T_{\infty ,Z}^{X}$
.
$T_{\infty ,Z}^{X}$
.
Proposition 5.14 is a compatibility statement that relates the various restrictions that we have introduced so far, and it will be useful in the next section.
Proposition 5.14. Let
![]() $X$
be a ribbon graph. Let
$X$
be a ribbon graph. Let
![]() $U\subset X$
be an open subgraph and let
$U\subset X$
be an open subgraph and let
![]() $Z\subset X$
be a good closed subgraph. If
$Z\subset X$
be a good closed subgraph. If
![]() $Z$
is contained in
$Z$
is contained in
![]() $U$
then the following diagram commutes.
$U$
then the following diagram commutes.

Before proving Proposition 5.14 we introduce some preliminary notation and results.
Definition 5.15. Let
![]() $x$
be a vertex of
$x$
be a vertex of
![]() $X$
. We denote:
$X$
. We denote:
–
 $U_{x}$
, the smallest open subgraph of
$U_{x}$
, the smallest open subgraph of
 $X$
containing the vertex
$X$
containing the vertex
 $x$
;
$x$
;–
 $K_{x}$
, the open subgraph of
$K_{x}$
, the open subgraph of
 $X$
given by
$X$
given by
 $X-x$
;
$X-x$
;–
 $U_{x}^{p}$
, the intersection
$U_{x}^{p}$
, the intersection
 $U_{x}\cap K_{x}$
(the superscript
$U_{x}\cap K_{x}$
(the superscript
 $p$
stands for punctured neighborhood).
$p$
stands for punctured neighborhood).
Definition 5.16. Let
![]() $F:A\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
be a functor. We say that
$F:A\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
be a functor. We say that
![]() $A$
is not supported on
$A$
is not supported on
![]() $x$
if the composite
$x$
if the composite
is equivalent to the zero functor.
Lemma 5.17. Let
![]() $x$
be a vertex of
$x$
be a vertex of
![]() $X$
, and let
$X$
, and let
![]() $F:A\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
be a functor. If
$F:A\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
be a functor. If
![]() $A$
is not supported on
$A$
is not supported on
![]() $x$
, then there is a natural equivalence
$x$
, then there is a natural equivalence
Proof. We fix first some notation. If
![]() $\unicode[STIX]{x1D6E4}$
is a ribbon graph, and
$\unicode[STIX]{x1D6E4}$
is a ribbon graph, and
![]() $W$
is a subset of the vertices of
$W$
is a subset of the vertices of
![]() $\unicode[STIX]{x1D6E4}$
we set
$\unicode[STIX]{x1D6E4}$
we set
Also if
![]() $L$
and
$L$
and
![]() $L^{\prime }$
are objects in
$L^{\prime }$
are objects in
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6E4})$
, we denote their Hom-complex
${\mathcal{F}}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6E4})$
, we denote their Hom-complex
![]() $\text{Hom}_{\unicode[STIX]{x1D6E4}}(L,L^{\prime })$
.
$\text{Hom}_{\unicode[STIX]{x1D6E4}}(L,L^{\prime })$
.
Let us now return to the statement of the lemma. Let
![]() $V$
be the set of vertices of
$V$
be the set of vertices of
![]() $X$
. By Proposition 5.7 the Ind-complete topological Fukaya category
$X$
. By Proposition 5.7 the Ind-complete topological Fukaya category
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is naturally equivalent to the equalizerFootnote
2
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is naturally equivalent to the equalizerFootnote
2
in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
, where
$\text{DGCat}_{\text{cont}}^{(2)}$
, where
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{2}$
are products of restriction functors. Using the notation introduced in (8), we can rewrite this equalizer as
$r_{2}$
are products of restriction functors. Using the notation introduced in (8), we can rewrite this equalizer as
Similarly if
![]() $W=V-\{x\}$
is the set of vertices of
$W=V-\{x\}$
is the set of vertices of
![]() $K_{x}$
, we obtain an equalizer diagram.
$K_{x}$
, we obtain an equalizer diagram.
The inclusion
![]() $W\subset V$
gives projections
$W\subset V$
gives projections
![]() $P$
and
$P$
and
![]() $Q$
that fit in a morphism of diagrams.
$Q$
that fit in a morphism of diagrams.

Further, the restriction
![]() $R_{\infty ,X}^{K_{x}}$
coincides with the morphism between the equalizers
$R_{\infty ,X}^{K_{x}}$
coincides with the morphism between the equalizers
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
and
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
and
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
induced by (11). Denote by
${\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
induced by (11). Denote by
![]() $(P)^{L}$
and
$(P)^{L}$
and
![]() $(Q)^{L}$
the left adjoints of
$(Q)^{L}$
the left adjoints of
![]() $P$
and
$P$
and
![]() $Q$
. The functor
$Q$
. The functor
![]() $(P)^{L}$
is given by the obvious quasi-fully faithful embedding
$(P)^{L}$
is given by the obvious quasi-fully faithful embedding
and similarly for
![]() $(Q)^{L}$
.
$(Q)^{L}$
.
We will prove the lemma in two steps. First, we show that the diagram

is commutative, that is, there are natural equivalences
We remark that the commutativity does not hold if we do not precompose with
![]() $F$
. It is sufficient to prove that, for all
$F$
. It is sufficient to prove that, for all
![]() $v$
and
$v$
and
![]() $v^{\prime }$
in
$v^{\prime }$
in
![]() $V$
, the diagram commutes after composing on the left with the restriction
$V$
, the diagram commutes after composing on the left with the restriction
If both
![]() $v$
and
$v$
and
![]() $v^{\prime }$
are different from
$v^{\prime }$
are different from
![]() $x$
, then
$x$
, then
and so commutativity holds also when precomposing with
![]() $F$
. Assume on the other hand that
$F$
. Assume on the other hand that
![]() $v=x$
. Then
$v=x$
. Then
The first equivalence follows from the support assumption on
![]() $A$
, and the second one is a consequence of the fact that
$A$
, and the second one is a consequence of the fact that
![]() $R_{\infty }^{U_{x}\cap U_{v^{\prime }}}\circ (Q)^{L}=0$
. Thus diagram (12) commutes as claimed.
$R_{\infty }^{U_{x}\cap U_{v^{\prime }}}\circ (Q)^{L}=0$
. Thus diagram (12) commutes as claimed.
The commutativity of (12) and the universal property of the equalizer give us a functor
Note that both
![]() $P\circ (P)^{L}$
and
$P\circ (P)^{L}$
and
![]() $Q\circ (Q)^{L}$
are naturally equivalent to the identity functor, and thus
$Q\circ (Q)^{L}$
are naturally equivalent to the identity functor, and thus
The second and final step in the proof consists in noticing that
![]() $\tilde{F}$
is equivalent to
$\tilde{F}$
is equivalent to
![]() $C_{\infty ,K_{x}}^{X}\circ F$
. That is, for all
$C_{\infty ,K_{x}}^{X}\circ F$
. That is, for all
![]() $L_{A}$
in the image of
$L_{A}$
in the image of
![]() $F$
, and
$F$
, and
![]() $L_{X}$
in
$L_{X}$
in
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
, there is a natural equivalence
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
, there is a natural equivalence
where
![]() $\text{Hom}_{X}(-,-)$
and
$\text{Hom}_{X}(-,-)$
and
![]() $\text{Hom}_{K_{x}}(-,-)$
denote respectively the hom spaces in
$\text{Hom}_{K_{x}}(-,-)$
denote respectively the hom spaces in
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
and in
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
and in
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
. This can be checked by computing explicitly the Hom-complexes on both sides in terms of the equalizers (9) and (10), see Proposition 2.2 of [Reference Sibilla, Treumann and ZaslowSTZ14] for a similar calculation. As a consequence there is a chain of equivalences
${\mathcal{F}}_{\infty }^{\text{top}}(K_{x})$
. This can be checked by computing explicitly the Hom-complexes on both sides in terms of the equalizers (9) and (10), see Proposition 2.2 of [Reference Sibilla, Treumann and ZaslowSTZ14] for a similar calculation. As a consequence there is a chain of equivalences
and this concludes the proof. ◻
Let
![]() $Z$
be a good closed subgraph of
$Z$
be a good closed subgraph of
![]() $X$
. Recall that
$X$
. Recall that
is the right adjoint of
![]() $S_{\infty ,Z}^{X}$
.
$S_{\infty ,Z}^{X}$
.
Proposition 5.18. Let
![]() $x$
be a vertex of
$x$
be a vertex of
![]() $X$
which does not belong to
$X$
which does not belong to
![]() $Z$
. Then we have the following.
$Z$
. Then we have the following.
(i) The functor
is not supported on $$\begin{eqnarray}{\mathcal{F}}_{\infty }^{\text{top}}(Z)\stackrel{T_{\infty ,Z}^{K_{x}}}{\longrightarrow }{\mathcal{F}}_{\infty }^{\text{top}}(K_{x})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\infty }^{\text{top}}(Z)\stackrel{T_{\infty ,Z}^{K_{x}}}{\longrightarrow }{\mathcal{F}}_{\infty }^{\text{top}}(K_{x})\end{eqnarray}$$
 $x$
.
$x$
.(ii) The diagram
is commutative.
Proof. It follows from Proposition 5.12 that
is a fiber sequence, and thus the composite is the zero functor. Since
![]() $U_{x}^{p}$
is contained in
$U_{x}^{p}$
is contained in
![]() $K_{x}-Z$
, the restriction
$K_{x}-Z$
, the restriction
![]() $R_{\infty ,K_{x}}^{U_{x}^{p}}$
factors through
$R_{\infty ,K_{x}}^{U_{x}^{p}}$
factors through
![]() $R_{\infty ,K_{x}}^{K_{x}-Z}$
. This implies the first claim. As for the second claim, let us show first that there is a natural equivalence
$R_{\infty ,K_{x}}^{K_{x}-Z}$
. This implies the first claim. As for the second claim, let us show first that there is a natural equivalence
Consider the commutative square on the right-hand side of the following diagram.

The functor induced between the fibers, which is denoted by the dashed arrow, is equivalent to the identity. This gives equivalence (13). As a consequence we obtain
Indeed, the first equivalence follows from (13) and the second one from Lemma 5.17. This concludes the proof.◻
The proof of Proposition 5.14.
Let
![]() $W$
be the set of vertices of
$W$
be the set of vertices of
![]() $X$
that do not belong to
$X$
that do not belong to
![]() $U$
. Note that
$U$
. Note that
![]() $U$
is a connected component of the open subgraph
$U$
is a connected component of the open subgraph
![]() $(X-W)\subset X$
. By induction it is sufficient to prove the claim in the following two cases:
$(X-W)\subset X$
. By induction it is sufficient to prove the claim in the following two cases:
(i) when
 $U$
is equal to
$U$
is equal to
 $K_{x}$
for some vertex
$K_{x}$
for some vertex
 $x$
of
$x$
of
 $X$
;
$X$
;(ii) when
 $U$
is a connected component of
$U$
is a connected component of
 $X$
.
$X$
.
Proposition 5.18 gives a proof in the first case. Indeed, it is sufficient to take right adjoints in claim (ii) of Proposition 5.18 to recover the commutativity statement from Proposition 5.14 for this class of open subgraphs. The second case is easier. The complement
![]() $X-U$
is open and we have a splitting
$X-U$
is open and we have a splitting
and the claim follows immediately from here.◻
6 The topological Fukaya category and closed covers
In this section we prove a key gluing statement which is one of the main inputs in our proof of mirror symmetry for three-dimensional LG models.
Let
![]() $X$
be a connected ribbon graph whose underlying topological space is homeomorphic to a copy of
$X$
be a connected ribbon graph whose underlying topological space is homeomorphic to a copy of
![]() $S^{1}$
together with a finite number of open edges attached to it. We call such a ribbon graph a wheel. Any choice of orientation on
$S^{1}$
together with a finite number of open edges attached to it. We call such a ribbon graph a wheel. Any choice of orientation on
![]() $S^{1}$
partitions the sets of open edges of
$S^{1}$
partitions the sets of open edges of
![]() $X$
into two subsets, which we call upward and downward edges respectively. An upward or downward edge is also called a spoke. For our purposes it will not be important to label either of these two sets as the set of upward or downward edges, but only to distinguish between the two. Thus we do not need to impose on
$X$
into two subsets, which we call upward and downward edges respectively. An upward or downward edge is also called a spoke. For our purposes it will not be important to label either of these two sets as the set of upward or downward edges, but only to distinguish between the two. Thus we do not need to impose on
![]() $X$
any additional structure beyond the ribbon structure (such as a choice of orientation).
$X$
any additional structure beyond the ribbon structure (such as a choice of orientation).
Definition 6.1. Let
![]() $n_{1}$
and
$n_{1}$
and
![]() $n_{2}$
be in
$n_{2}$
be in
![]() $\mathbb{Z}_{{\geqslant}0}$
. We denote by
$\mathbb{Z}_{{\geqslant}0}$
. We denote by
![]() $\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
a wheel with
$\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
a wheel with
![]() $n_{1}$
upward and
$n_{1}$
upward and
![]() $n_{2}$
downward edges. With small abuse of notation, we sometimes denote
$n_{2}$
downward edges. With small abuse of notation, we sometimes denote
![]() $\unicode[STIX]{x1D6EC}(0,0)$
simply by
$\unicode[STIX]{x1D6EC}(0,0)$
simply by
![]() $S^{1}$
.
$S^{1}$
.
We denote by
![]() $E(+)$
and
$E(+)$
and
![]() $E(-)$
the open subgraphs of
$E(-)$
the open subgraphs of
![]() $\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
given by the collection of the
$\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
given by the collection of the
![]() $n_{1}$
upward edges, and of the
$n_{1}$
upward edges, and of the
![]() $n_{2}$
downward edges respectively.
$n_{2}$
downward edges respectively.
Remark 6.2. The notation
![]() $\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
does not pick out a single ribbon graph, but rather a class of ribbon graphs. Indeed specifying the number of upward and downward edges does not suffice to pin down a homeomorphism type, or even the number of vertices. However all graphs of type
$\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
does not pick out a single ribbon graph, but rather a class of ribbon graphs. Indeed specifying the number of upward and downward edges does not suffice to pin down a homeomorphism type, or even the number of vertices. However all graphs of type
![]() $\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
deform into one another in a way that does not affect the sections of
$\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
deform into one another in a way that does not affect the sections of
![]() ${\mathcal{F}}^{\text{top}}$
and
${\mathcal{F}}^{\text{top}}$
and
![]() ${\mathcal{F}}_{\infty }^{\text{top}}$
(see [Reference Dyckerhoff and KapranovDK18]). We use
${\mathcal{F}}_{\infty }^{\text{top}}$
(see [Reference Dyckerhoff and KapranovDK18]). We use
![]() $\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
to refer to any ribbon graph having the properties listed in the definition.
$\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
to refer to any ribbon graph having the properties listed in the definition.
The category
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6EC}(n_{1},n_{2}))$
can be described explicitly in terms of quiver representations. Consider the closed subgraph
${\mathcal{F}}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6EC}(n_{1},n_{2}))$
can be described explicitly in terms of quiver representations. Consider the closed subgraph
where
![]() $S$
is the central circle of the wheel. The graph
$S$
is the central circle of the wheel. The graph
![]() $S$
has
$S$
has
![]() $n_{1}+n_{2}$
bivalent vertices, which are in canonical bijection with the spokes of
$n_{1}+n_{2}$
bivalent vertices, which are in canonical bijection with the spokes of
![]() $\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
, and its underlying topological space is
$\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
, and its underlying topological space is
![]() $S^{1}$
. Label the vertices of
$S^{1}$
. Label the vertices of
![]() $S$
with
$S$
with
![]() $+$
or
$+$
or
![]() $-$
depending on whether the corresponding spoke is upward or downward. We choose an orientation on
$-$
depending on whether the corresponding spoke is upward or downward. We choose an orientation on
![]() $S$
. An orientation determines a cyclic order on the edges of
$S$
. An orientation determines a cyclic order on the edges of
![]() $S$
. If
$S$
. If
![]() $e$
is an edge we denote by
$e$
is an edge we denote by
![]() $\unicode[STIX]{x1D70F}(e)$
the edge that follows it in the cyclic order. There is a (unique) vertex of
$\unicode[STIX]{x1D70F}(e)$
the edge that follows it in the cyclic order. There is a (unique) vertex of
![]() $S$
incident to both
$S$
incident to both
![]() $e$
and
$e$
and
![]() $\unicode[STIX]{x1D70F}(e)$
: we say that the pair
$\unicode[STIX]{x1D70F}(e)$
: we say that the pair
![]() $e,\unicode[STIX]{x1D70F}(e)$
is right-handed if this vertex is labeled by a
$e,\unicode[STIX]{x1D70F}(e)$
is right-handed if this vertex is labeled by a
![]() $+$
, and left-handed if it is labeled by a
$+$
, and left-handed if it is labeled by a
![]() $-$
.
$-$
.
Let
![]() $Q(n_{1},n_{2})$
be the quiver defined as follows.
$Q(n_{1},n_{2})$
be the quiver defined as follows.
– The set of vertices of
 $Q(n_{1},n_{2})$
is the set the edges of
$Q(n_{1},n_{2})$
is the set the edges of
 $S$
. If
$S$
. If
 $e$
is an edge of
$e$
is an edge of
 $S$
, we denote by
$S$
, we denote by
 $v_{e}$
the corresponding vertex of
$v_{e}$
the corresponding vertex of
 $Q(n_{1},n_{2})$
.
$Q(n_{1},n_{2})$
.– There is an arrow joining
 $v_{e}$
and
$v_{e}$
and
 $v_{\unicode[STIX]{x1D70F}(e)}$
. It is oriented from
$v_{\unicode[STIX]{x1D70F}(e)}$
. It is oriented from
 $v_{e}$
to
$v_{e}$
to
 $v_{\unicode[STIX]{x1D70F}(e)}$
if the pair
$v_{\unicode[STIX]{x1D70F}(e)}$
if the pair
 $e,\unicode[STIX]{x1D70F}(e)$
is right-handed, and from
$e,\unicode[STIX]{x1D70F}(e)$
is right-handed, and from
 $v_{\unicode[STIX]{x1D70F}(e)}$
to
$v_{\unicode[STIX]{x1D70F}(e)}$
to
 $v_{e}$
otherwise.
$v_{e}$
otherwise.
Recall that we can attach to a
![]() $\mathbb{Z}$
-graded dg category a
$\mathbb{Z}$
-graded dg category a
![]() $\mathbb{Z}_{2}$
-graded category by
$\mathbb{Z}_{2}$
-graded category by
![]() $\mathbb{Z}_{2}$
-periodization, see Section 1.2 of [Reference Dyckerhoff and KapranovDK18] for more details. Denote by
$\mathbb{Z}_{2}$
-periodization, see Section 1.2 of [Reference Dyckerhoff and KapranovDK18] for more details. Denote by
![]() $Rep^{\infty }(Q(n_{1},n_{2}))$
the
$Rep^{\infty }(Q(n_{1},n_{2}))$
the
![]() $\mathbb{Z}_{2}$
-periodization of the triangulated dg category of (non-necessarily finite dimensional) representations of
$\mathbb{Z}_{2}$
-periodization of the triangulated dg category of (non-necessarily finite dimensional) representations of
![]() $Q(n_{1},n_{2})$
,
$Q(n_{1},n_{2})$
,
![]() $Rep^{\infty }(Q(n_{1},n_{2}))\in \text{DGCat}_{\text{cont}}^{(2)}$
.
$Rep^{\infty }(Q(n_{1},n_{2}))\in \text{DGCat}_{\text{cont}}^{(2)}$
.
Lemma 6.3. There is an equivalence
Proof. This can be seen by appealing to the description of the Fukaya category of a surface provided by [Reference Haiden, Katzarkov and KontsevichHKK17], which involves giving explicit presentations of the category as representations of quivers associated to certain collections of arcs on the surface. In [Reference Haiden, Katzarkov and KontsevichHKK17, § 3.6], it is shown that this definition of the category coincides with the cosheaf-of-categories approach used in this paper. The desired quiver description corresponds to choosing a certain collection of arcs as follows. The graph
![]() $\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
embeds in to a cylinder
$\unicode[STIX]{x1D6EC}(n_{1},n_{2})$
embeds in to a cylinder
![]() $[0,1]\times S^{1}$
, in such a way that the upward edges end on
$[0,1]\times S^{1}$
, in such a way that the upward edges end on
![]() $\{1\}\times S^{1}$
and the downward edges end on
$\{1\}\times S^{1}$
and the downward edges end on
![]() $\{0\}\times S^{1}$
. The dual family of arcs is obtained by choosing one arc connecting the two boundary components
$\{0\}\times S^{1}$
. The dual family of arcs is obtained by choosing one arc connecting the two boundary components
![]() $\{0\}\times S^{1}$
to
$\{0\}\times S^{1}$
to
![]() $\{1\}\times S^{1}$
passing between each consecutive pair of edges. A representative example is depicted in Figure 2. The solid lines are the ribbon graph, while the dashed lines are the dual collection of arcs. Each arc corresponds to a vertex of the quiver, and the arrows in the quiver correspond to the arrows shown in the figure. The quiver corresponding to this collection of arcs is then nothing but
$\{1\}\times S^{1}$
passing between each consecutive pair of edges. A representative example is depicted in Figure 2. The solid lines are the ribbon graph, while the dashed lines are the dual collection of arcs. Each arc corresponds to a vertex of the quiver, and the arrows in the quiver correspond to the arrows shown in the figure. The quiver corresponding to this collection of arcs is then nothing but
![]() $Q(n_{1},n_{2})$
.◻
$Q(n_{1},n_{2})$
.◻

Figure 2. A ribbon graph of class
![]() $\unicode[STIX]{x1D6EC}(3,3)$
(solid), and the dual collection of arcs (dashed). The corresponding quiver has one vertex for each arc, and arrows that correspond to those shown.
$\unicode[STIX]{x1D6EC}(3,3)$
(solid), and the dual collection of arcs (dashed). The corresponding quiver has one vertex for each arc, and arrows that correspond to those shown.
Remark 6.4. In the preceding proof, we have used an equivalence between the model of the Fukaya category used in [Reference Haiden, Katzarkov and KontsevichHKK17] and the one used in the present paper. One may ask how this comparison is justified technically, since [Reference Haiden, Katzarkov and KontsevichHKK17] is written in terms of the model category of
![]() $A_{\infty }$
categories and the present paper uses an
$A_{\infty }$
categories and the present paper uses an
![]() $\infty$
-category of dg categories (a dg category being the special case of an
$\infty$
-category of dg categories (a dg category being the special case of an
![]() $A_{\infty }$
category with vanishing higher products). Fortunately, the statement of [Reference Haiden, Katzarkov and KontsevichHKK17, Theorem 3.1] asserts that the Fukaya category as defined in [Reference Haiden, Katzarkov and KontsevichHKK17], which is an
$A_{\infty }$
category with vanishing higher products). Fortunately, the statement of [Reference Haiden, Katzarkov and KontsevichHKK17, Theorem 3.1] asserts that the Fukaya category as defined in [Reference Haiden, Katzarkov and KontsevichHKK17], which is an
![]() $A_{\infty }$
category, is Morita equivalent to a homotopy colimit of a diagram of dg categories (not
$A_{\infty }$
category, is Morita equivalent to a homotopy colimit of a diagram of dg categories (not
![]() $A_{\infty }$
categories). Further, homotopy colimits in the model category of dg categories compute
$A_{\infty }$
categories). Further, homotopy colimits in the model category of dg categories compute
![]() $\infty$
-categorical colimits in the
$\infty$
-categorical colimits in the
![]() $\infty$
-category obtained by localizing at weak equivalences; see [Reference LurieLur09, § 4.2.4] where such a comparison is made.
$\infty$
-category obtained by localizing at weak equivalences; see [Reference LurieLur09, § 4.2.4] where such a comparison is made.
Lemma 6.5. The following is a fiber product in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
.
$\text{DGCat}_{\text{cont}}^{(2)}$
.

Proof. The claim could be proved directly, but it is instructive to give a proof based on mirror symmetry. Indeed, this clarifies the connection between gluing along closed subskeleta and Zariski descent. Let
![]() $\mathbb{P}^{1}(n_{1},n_{2})$
be the projective line with two stacky points at
$\mathbb{P}^{1}(n_{1},n_{2})$
be the projective line with two stacky points at
![]() $0$
and
$0$
and
![]() $\infty$
having isotropy isomorphic to the groups of roots of unity
$\infty$
having isotropy isomorphic to the groups of roots of unity
![]() $\unicode[STIX]{x1D707}_{n_{1}}$
and
$\unicode[STIX]{x1D707}_{n_{1}}$
and
![]() $\unicode[STIX]{x1D707}_{n_{2}}$
. More formally,
$\unicode[STIX]{x1D707}_{n_{2}}$
. More formally,
![]() $\mathbb{P}^{1}(n_{1},n_{2})$
is the push-out of the following diagram in the category of DM stacks,
$\mathbb{P}^{1}(n_{1},n_{2})$
is the push-out of the following diagram in the category of DM stacks,

where
![]() $[\mathbb{A}^{1}/\unicode[STIX]{x1D707}_{n_{1}}]$
and
$[\mathbb{A}^{1}/\unicode[STIX]{x1D707}_{n_{1}}]$
and
![]() $[\mathbb{A}^{2}/\unicode[STIX]{x1D707}_{n_{2}}]$
are the quotient stacks of
$[\mathbb{A}^{2}/\unicode[STIX]{x1D707}_{n_{2}}]$
are the quotient stacks of
![]() $\mathbb{A}^{1}$
under the canonical action of
$\mathbb{A}^{1}$
under the canonical action of
![]() $\unicode[STIX]{x1D707}_{n_{1}}$
and
$\unicode[STIX]{x1D707}_{n_{1}}$
and
![]() $\unicode[STIX]{x1D707}_{n_{2}}$
. Zariski descent implies that the diagram
$\unicode[STIX]{x1D707}_{n_{2}}$
. Zariski descent implies that the diagram

where all the arrows are pullbacks, is a fiber product. It follows from [Reference Sibilla, Treumann and ZaslowSTZ14] and [Reference Dyckerhoff and KapranovDK18] that diagram (14) is in fact equivalent to the diagram in the statement of the lemma. More precisely, there are commutative diagrams

and

such that all vertical arrows are equivalences. Since diagram (14) is a fiber product we conclude that also the diagram in the statement of the lemma is a fiber product.◻
The following is the main result of this section. In order to avoid cluttering the diagrams, we denote restrictions and exotic restrictions simply by
![]() $R_{\infty }$
and
$R_{\infty }$
and
![]() $S_{\infty }$
.
$S_{\infty }$
.
Let
![]() $X$
be a ribbon graph, and let
$X$
be a ribbon graph, and let
![]() $Z$
be a closed subgraph. It is useful to consider a combinatorial analogue of a tubular neighborhood of
$Z$
be a closed subgraph. It is useful to consider a combinatorial analogue of a tubular neighborhood of
![]() $Z$
inside
$Z$
inside
![]() $X$
, which we denote
$X$
, which we denote
![]() $N_{Z}X$
: the graph
$N_{Z}X$
: the graph
![]() $N_{Z}X$
is given by
$N_{Z}X$
is given by
![]() $Z$
plus additional open edges for each edge in
$Z$
plus additional open edges for each edge in
![]() $X$
that does not lie in
$X$
that does not lie in
![]() $Z$
, but is incident to a vertex in
$Z$
, but is incident to a vertex in
![]() $Z$
. Here is a formal definition. We subdivide all the edges of
$Z$
. Here is a formal definition. We subdivide all the edges of
![]() $X$
which do not lie in
$X$
which do not lie in
![]() $Z$
, but whose endpoints lie in
$Z$
, but whose endpoints lie in
![]() $Z$
. We denote the resulting graph again
$Z$
. We denote the resulting graph again
![]() $X$
: from now on, every time we will consider the object
$X$
: from now on, every time we will consider the object
![]() $N_{Z}X$
, we will assume implicitly that the edges of
$N_{Z}X$
, we will assume implicitly that the edges of
![]() $X$
are sufficiently subdivided. Let
$X$
are sufficiently subdivided. Let
![]() $\overline{Z}^{c}$
be the maximal (non-necessarily good) closed subgraph of
$\overline{Z}^{c}$
be the maximal (non-necessarily good) closed subgraph of
![]() $X$
such that
$X$
such that
We denote by
![]() $N_{Z}X$
the open subgraph
$N_{Z}X$
the open subgraph
Theorem 6.6. Let
![]() $X$
be a ribbon graph. Let
$X$
be a ribbon graph. Let
![]() $Z_{1}$
and
$Z_{1}$
and
![]() $Z_{2}$
be good closed subgraphs such that:
$Z_{2}$
be good closed subgraphs such that:
–
 $Z_{1}\cup Z_{2}=X$
;
$Z_{1}\cup Z_{2}=X$
;– the underlying topological space of
 $Z_{1,2}:=Z_{1}\cap Z_{2}$
is a disjoint union of circles;
$Z_{1,2}:=Z_{1}\cap Z_{2}$
is a disjoint union of circles;– for every connected component
 $C$
of
$C$
of
 $Z_{1,2}$
the triple of ribbon graphs is isomorphic to
$Z_{1,2}$
the triple of ribbon graphs is isomorphic to $$\begin{eqnarray}N_{C}X\cap Z_{1}\,\subset \,N_{C}X\,\supset \,N_{C}X\cap Z_{2}\end{eqnarray}$$
for some
$$\begin{eqnarray}N_{C}X\cap Z_{1}\,\subset \,N_{C}X\,\supset \,N_{C}X\cap Z_{2}\end{eqnarray}$$
for some $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(n_{1},0)\subset \unicode[STIX]{x1D6EC}(n_{1},n_{2})\supset \unicode[STIX]{x1D6EC}(0,n_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(n_{1},0)\subset \unicode[STIX]{x1D6EC}(n_{1},n_{2})\supset \unicode[STIX]{x1D6EC}(0,n_{2})\end{eqnarray}$$
 $n_{1},n_{2}\in \mathbb{N}$
.
$n_{1},n_{2}\in \mathbb{N}$
.
Then the commutative diagram

is a fiber product in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
.
$\text{DGCat}_{\text{cont}}^{(2)}$
.
We will assume for simplicity that
![]() $Z_{1,2}$
has only one connected component: the general case is proved in the same way.
$Z_{1,2}$
has only one connected component: the general case is proved in the same way.
Proving Theorem 6.6 will require some preparation. Let
![]() $X$
,
$X$
,
![]() $Z_{1}$
and
$Z_{1}$
and
![]() $Z_{2}$
be as in Theorem 6.6, and assume that
$Z_{2}$
be as in Theorem 6.6, and assume that
![]() $Z_{1,2}$
has only one connected component. By assumption
$Z_{1,2}$
has only one connected component. By assumption
![]() $N_{Z_{1,2}}X$
,
$N_{Z_{1,2}}X$
,
![]() $N_{Z_{1,2}}Z_{1}$
and
$N_{Z_{1,2}}Z_{1}$
and
![]() $N_{Z_{1,2}}Z_{2}$
are all wheel-type graphs. We make the following notation:
$N_{Z_{1,2}}Z_{2}$
are all wheel-type graphs. We make the following notation:
–
 $U_{1}=Z_{1}\cup N_{Z_{1,2}}X$
, the graph
$U_{1}=Z_{1}\cup N_{Z_{1,2}}X$
, the graph
 $U_{1}$
is an open subgraph of
$U_{1}$
is an open subgraph of
 $X$
and
$X$
and
 $Z_{1}$
is a good closed subgraph of
$Z_{1}$
is a good closed subgraph of
 $U_{1}$
;
$U_{1}$
;–
 $U_{2}=Z_{2}\cup N_{Z_{1,2}}X$
, the graph
$U_{2}=Z_{2}\cup N_{Z_{1,2}}X$
, the graph
 $U_{2}$
is an open subgraph of
$U_{2}$
is an open subgraph of
 $X$
and
$X$
and
 $Z_{2}$
is a good closed subgraph of
$Z_{2}$
is a good closed subgraph of
 $U_{2}$
;
$U_{2}$
;–
 $U_{1,2}=U_{1}\cap U_{2}$
;
$U_{1,2}=U_{1}\cap U_{2}$
;–
 $U_{1}^{\text{o}}=Z_{1}-Z_{1,2},$
and
$U_{1}^{\text{o}}=Z_{1}-Z_{1,2},$
and
 $U_{2}^{\text{o}}=Z_{2}-Z_{1,2}$
, where the superscript ‘o’ stands for open; the graphs
$U_{2}^{\text{o}}=Z_{2}-Z_{1,2}$
, where the superscript ‘o’ stands for open; the graphs
 $U_{1}^{\text{o}}$
and
$U_{1}^{\text{o}}$
and
 $U_{2}^{\text{o}}$
are open subgraphs of
$U_{2}^{\text{o}}$
are open subgraphs of
 $X$
;
$X$
;–
 $U_{1}^{\text{e}}=U_{1,2}\cap U_{1}^{\text{o}}$
and
$U_{1}^{\text{e}}=U_{1,2}\cap U_{1}^{\text{o}}$
and
 $U_{2}^{\text{e}}=U_{1,2}\cap U_{2}^{\text{o}}$
, where the superscript ‘e’ stands for edges.
$U_{2}^{\text{e}}=U_{1,2}\cap U_{2}^{\text{o}}$
, where the superscript ‘e’ stands for edges.
Note that
![]() $U_{1,2}$
is equal to
$U_{1,2}$
is equal to
![]() $N_{Z_{1,2}}X\cong \unicode[STIX]{x1D6EC}(n_{1},n_{2})$
, and that the embeddings
$N_{Z_{1,2}}X\cong \unicode[STIX]{x1D6EC}(n_{1},n_{2})$
, and that the embeddings
are isomorphic to the embeddings of the spokes
Also, we have identifications
![]() $N_{Z_{1,2}}Z_{1}=Z_{1}\cap U_{12}$
, and
$N_{Z_{1,2}}Z_{1}=Z_{1}\cap U_{12}$
, and
![]() $N_{Z_{1,2}}Z_{2}=Z_{2}\cap U_{12}$
.
$N_{Z_{1,2}}Z_{2}=Z_{2}\cap U_{12}$
.
The key ingredient in the proof of Theorem 6.6 is the following lemma.
Lemma 6.7. All the interior squares in the commutative diagram

are fiber products.
Proof. Number clockwise the interior squares from one to four, starting with the top left one. Square
![]() $1$
is a fiber product by Proposition 5.7. Square
$1$
is a fiber product by Proposition 5.7. Square
![]() $3$
is a fiber product by Lemma 6.5. Up to swapping
$3$
is a fiber product by Lemma 6.5. Up to swapping
![]() $U_{1}$
with
$U_{1}$
with
![]() $U_{2}$
, squares
$U_{2}$
, squares
![]() $2$
and
$2$
and
![]() $4$
are identical. So it is enough to prove that square
$4$
are identical. So it is enough to prove that square
![]() $2$
is a fiber product. The proof consists of three steps.
$2$
is a fiber product. The proof consists of three steps.
Step one. We express all the vertices of square
![]() $2$
as fiber products. We start with the top vertices. Each of the following two diagrams
$2$
as fiber products. We start with the top vertices. Each of the following two diagrams

is a fiber product in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
by Proposition 5.7. Let us consider the bottom vertices next. The diagrams
$\text{DGCat}_{\text{cont}}^{(2)}$
by Proposition 5.7. Let us consider the bottom vertices next. The diagrams

are trivially fiber products in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
since the horizontal arrows are identities, and any two parallel arrows are equal to each other.
$\text{DGCat}_{\text{cont}}^{(2)}$
since the horizontal arrows are identities, and any two parallel arrows are equal to each other.
Step two. The arrows in square 2 can be written in terms of morphisms between the fiber product diagrams constructed in step one. Let us focus, for instance, on the bottom horizontal map in square 2
This map, which is indicated in the diagram below by a dashed arrow, is induced by the map of diagrams in
![]() $\text{DGCat}_{\text{cont}}^{(2)}$
given by the three arrows in the middle:
$\text{DGCat}_{\text{cont}}^{(2)}$
given by the three arrows in the middle:
![]() $S_{\infty }$
,
$S_{\infty }$
,
![]() $Id$
and
$Id$
and
![]() $Id$
.
$Id$
.

A similar reasoning holds also for the other arrows in square
![]() $2$
.
$2$
.
Step three. We complete the proof by using the fact that limits commute with limits. We have to show that square 2, which we reproduce as diagram (17), is a fiber product.

We can commute (17) and the fiber products constructed in step one past each other: thus, in order to show that (17) is a fiber product, we can prove instead that the following are fiber products.

These diagrams have the property that the horizontal arrows are identities, and any two parallel arrows are equal to each other, so they are fiber products. This concludes the proof.◻
The proof of Theorem 6.6.
Note first that the diagram from the statement of Theorem 6.6 is the exterior square of the diagram from Lemma 6.7. Indeed by Proposition 5.14
By general properties of fiber products, since all the interior squares are fiber products, the exterior one is a fiber product as well. This concludes the proof.◻
Remark 6.8. Although Theorem 6.6 is sufficient for our purposes, we expect that gluing formulas under closed covers hold more generally. The importance of this kind of gluing formula lies in the fact that they are powerful computational tools, and that they often correspond via mirror symmetry to Zariski descent statement for quasi-coherent sheaves and matrix factorizations (see, for instance, the proof of Lemma 6.5). We will return to the problem of developing a comprehensive formalism of gluing formulas along closed subskeleta for
![]() ${\mathcal{F}}^{\text{top}}$
, in dimension two and higher, in future work.
${\mathcal{F}}^{\text{top}}$
, in dimension two and higher, in future work.
7 Tropical and surface topology
7.1 Surface topology
This section contains some remarks on surface topology that will be useful in later constructions.
Denote by
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
an oriented surface of genus
$\unicode[STIX]{x1D6F4}_{g,n}$
an oriented surface of genus
![]() $g$
with
$g$
with
![]() $n$
punctures. Since the topology of these surfaces enters our discussion in a relatively coarse way, we will often draw the punctures as if they were boundaries, but strictly speaking
$n$
punctures. Since the topology of these surfaces enters our discussion in a relatively coarse way, we will often draw the punctures as if they were boundaries, but strictly speaking
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
is a noncompact (if
$\unicode[STIX]{x1D6F4}_{g,n}$
is a noncompact (if
![]() $n>0$
) manifold without boundary. The surface
$n>0$
) manifold without boundary. The surface
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
has
$\unicode[STIX]{x1D6F4}_{g,n}$
has
![]() $n$
ends corresponding to the punctures.Footnote
3
$n$
ends corresponding to the punctures.Footnote
3
If
![]() $\unicode[STIX]{x1D6F4}_{1}$
and
$\unicode[STIX]{x1D6F4}_{1}$
and
![]() $\unicode[STIX]{x1D6F4}_{2}$
are two oriented punctured surfaces, we may form a new surface by the well-known end connect sum operation.
$\unicode[STIX]{x1D6F4}_{2}$
are two oriented punctured surfaces, we may form a new surface by the well-known end connect sum operation.
Definition 7.1. Choose a puncture
![]() $p_{1}$
on
$p_{1}$
on
![]() $\unicode[STIX]{x1D6F4}_{1}$
and a puncture
$\unicode[STIX]{x1D6F4}_{1}$
and a puncture
![]() $p_{2}$
on
$p_{2}$
on
![]() $\unicode[STIX]{x1D6F4}_{2}$
. Identify a neighborhood of
$\unicode[STIX]{x1D6F4}_{2}$
. Identify a neighborhood of
![]() $p_{1}$
with
$p_{1}$
with
![]() $S^{1}\times (-1,-1/2)$
and a neighborhood of
$S^{1}\times (-1,-1/2)$
and a neighborhood of
![]() $p_{2}$
with
$p_{2}$
with
![]() $S^{1}\times (1/2,1)$
, and replace the union of these neighborhoods by a single punctured cylinder
$S^{1}\times (1/2,1)$
, and replace the union of these neighborhoods by a single punctured cylinder
![]() $S^{1}\times (-1,1)\setminus (1,0)$
. The result
$S^{1}\times (-1,1)\setminus (1,0)$
. The result
![]() ${\unicode[STIX]{x1D6F4}_{1}\#}_{p_{1},p_{2}}\unicode[STIX]{x1D6F4}_{2}$
is called the end connect sum of
${\unicode[STIX]{x1D6F4}_{1}\#}_{p_{1},p_{2}}\unicode[STIX]{x1D6F4}_{2}$
is called the end connect sum of
![]() $\unicode[STIX]{x1D6F4}_{1}$
and
$\unicode[STIX]{x1D6F4}_{1}$
and
![]() $\unicode[STIX]{x1D6F4}_{2}$
at the punctures
$\unicode[STIX]{x1D6F4}_{2}$
at the punctures
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
.
$p_{2}$
.
The end connect sum can also be described as attaching a one-handle to
![]() $\unicode[STIX]{x1D6F4}_{1}\coprod \unicode[STIX]{x1D6F4}_{2}$
. If alternatively we think in terms of bordered surfaces, the operation consists of adding a strip connecting two boundary components. If
$\unicode[STIX]{x1D6F4}_{1}\coprod \unicode[STIX]{x1D6F4}_{2}$
. If alternatively we think in terms of bordered surfaces, the operation consists of adding a strip connecting two boundary components. If
![]() $\unicode[STIX]{x1D6F4}_{i}$
has genus
$\unicode[STIX]{x1D6F4}_{i}$
has genus
![]() $g_{i}$
and
$g_{i}$
and
![]() $n_{i}$
punctures (
$n_{i}$
punctures (
![]() $i=1,2$
), then
$i=1,2$
), then
![]() $\unicode[STIX]{x1D6F4}\#_{p_{1},p_{2}}\unicode[STIX]{x1D6F4}_{2}$
has genus
$\unicode[STIX]{x1D6F4}\#_{p_{1},p_{2}}\unicode[STIX]{x1D6F4}_{2}$
has genus
![]() $g_{1}+g_{2}$
and
$g_{1}+g_{2}$
and
![]() $n_{1}+n_{2}-1$
punctures.
$n_{1}+n_{2}-1$
punctures.
The effect of end connect sum on skeleta is straightforward.
Lemma 7.2. Let
![]() $X_{i}$
be a skeleton for
$X_{i}$
be a skeleton for
![]() $\unicode[STIX]{x1D6F4}_{i}~(i=1,2)$
. Produce from
$\unicode[STIX]{x1D6F4}_{i}~(i=1,2)$
. Produce from
![]() $X_{i}$
a ribbon graph with a noncompact edge connecting
$X_{i}$
a ribbon graph with a noncompact edge connecting
![]() $X_{i}$
to the puncture
$X_{i}$
to the puncture
![]() $p_{i}$
; call the result
$p_{i}$
; call the result
![]() $X_{i}^{\prime }$
. Then a skeleton for
$X_{i}^{\prime }$
. Then a skeleton for
![]() ${\unicode[STIX]{x1D6F4}_{1}\#}_{p_{1},p_{2}}\unicode[STIX]{x1D6F4}_{2}$
is obtained by connecting the noncompact edges of
${\unicode[STIX]{x1D6F4}_{1}\#}_{p_{1},p_{2}}\unicode[STIX]{x1D6F4}_{2}$
is obtained by connecting the noncompact edges of
![]() $X_{1}^{\prime }$
and
$X_{1}^{\prime }$
and
![]() $X_{2}^{\prime }$
inside the attaching region.
$X_{2}^{\prime }$
inside the attaching region.
Example 7.3. We can decompose
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
(
$\unicode[STIX]{x1D6F4}_{g,n}$
(
![]() $n>0$
) into an iterated end connect sum of
$n>0$
) into an iterated end connect sum of
![]() $\unicode[STIX]{x1D6F4}_{1,1}$
and
$\unicode[STIX]{x1D6F4}_{1,1}$
and
![]() $\unicode[STIX]{x1D6F4}_{0,2}$
. Indeed, taking end connect sum of
$\unicode[STIX]{x1D6F4}_{0,2}$
. Indeed, taking end connect sum of
![]() $g$
copies of
$g$
copies of
![]() $\unicode[STIX]{x1D6F4}_{1,1}$
(always summing at the unique punctures) yields a surface of type
$\unicode[STIX]{x1D6F4}_{1,1}$
(always summing at the unique punctures) yields a surface of type
![]() $\unicode[STIX]{x1D6F4}_{g,1}$
. Taking end connect sum of
$\unicode[STIX]{x1D6F4}_{g,1}$
. Taking end connect sum of
![]() $n-1$
copies of
$n-1$
copies of
![]() $\unicode[STIX]{x1D6F4}_{0,2}$
(summing at a single puncture of each) yields a surface of type
$\unicode[STIX]{x1D6F4}_{0,2}$
(summing at a single puncture of each) yields a surface of type
![]() $\unicode[STIX]{x1D6F4}_{0,n}$
. Then end connect summing
$\unicode[STIX]{x1D6F4}_{0,n}$
. Then end connect summing
![]() $\unicode[STIX]{x1D6F4}_{g,1}$
and
$\unicode[STIX]{x1D6F4}_{g,1}$
and
![]() $\unicode[STIX]{x1D6F4}_{0,n}$
yields
$\unicode[STIX]{x1D6F4}_{0,n}$
yields
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
. By choosing skeleta for
$\unicode[STIX]{x1D6F4}_{g,n}$
. By choosing skeleta for
![]() $\unicode[STIX]{x1D6F4}_{1,1}$
(consisting, say, of two loops on the torus) and for
$\unicode[STIX]{x1D6F4}_{1,1}$
(consisting, say, of two loops on the torus) and for
![]() $\unicode[STIX]{x1D6F4}_{0,2}$
(say a single circle), we thus obtain a skeleton for
$\unicode[STIX]{x1D6F4}_{0,2}$
(say a single circle), we thus obtain a skeleton for
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
. This is pictured in Figure 3.
$\unicode[STIX]{x1D6F4}_{g,n}$
. This is pictured in Figure 3.

Figure 3. Decomposition of
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
into end connect sum of
$\unicode[STIX]{x1D6F4}_{g,n}$
into end connect sum of
![]() $g$
copies of
$g$
copies of
![]() $\unicode[STIX]{x1D6F4}_{1,1}$
and
$\unicode[STIX]{x1D6F4}_{1,1}$
and
![]() $n-1$
copies of
$n-1$
copies of
![]() $\unicode[STIX]{x1D6F4}_{0,2}$
.
$\unicode[STIX]{x1D6F4}_{0,2}$
.
In this paper, we are interested in skeleta with a certain shape near the punctures.
Definition 7.4. Let
![]() $\unicode[STIX]{x1D6F4}$
be a punctured surface,
$\unicode[STIX]{x1D6F4}$
be a punctured surface,
![]() $p$
a puncture of
$p$
a puncture of
![]() $\unicode[STIX]{x1D6F4}$
, and
$\unicode[STIX]{x1D6F4}$
, and
![]() $X\subset \unicode[STIX]{x1D6F4}$
a skeleton for
$X\subset \unicode[STIX]{x1D6F4}$
a skeleton for
![]() $\unicode[STIX]{x1D6F4}$
. The component of
$\unicode[STIX]{x1D6F4}$
. The component of
![]() $\unicode[STIX]{x1D6F4}\setminus X$
containing the puncture
$\unicode[STIX]{x1D6F4}\setminus X$
containing the puncture
![]() $p$
is topologically a punctured disk, and its boundary is a subgraph of
$p$
is topologically a punctured disk, and its boundary is a subgraph of
![]() $X$
. We say that
$X$
. We say that
![]() $X$
has a cycle at the puncture
$X$
has a cycle at the puncture
![]() $p$
if this subgraph is a cycle.
$p$
if this subgraph is a cycle.
If
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
are distinct punctures, we say that
$p_{2}$
are distinct punctures, we say that
![]() $X$
has disjoint cycles at
$X$
has disjoint cycles at
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
if it has cycles at
$p_{2}$
if it has cycles at
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
and these cycles are disjoint in
$p_{2}$
and these cycles are disjoint in
![]() $X$
.
$X$
.
Model the pair of pants as
![]() $\mathbb{C}-\{-2,2\}$
. If
$\mathbb{C}-\{-2,2\}$
. If
![]() $x$
and
$x$
and
![]() $y$
are in
$y$
are in
![]() $\mathbb{C}$
, and
$\mathbb{C}$
, and
![]() $\unicode[STIX]{x1D716}$
is a positive real number, we denote by
$\unicode[STIX]{x1D716}$
is a positive real number, we denote by
![]() $S(x,\unicode[STIX]{x1D716})\subset \mathbb{C}$
the circle of center
$S(x,\unicode[STIX]{x1D716})\subset \mathbb{C}$
the circle of center
![]() $x$
and radius
$x$
and radius
![]() $\unicode[STIX]{x1D716}$
, and by
$\unicode[STIX]{x1D716}$
, and by
![]() $I(x,y)\subset \mathbb{C}$
the straight segment joining
$I(x,y)\subset \mathbb{C}$
the straight segment joining
![]() $x$
and
$x$
and
![]() $y$
. We call
$y$
. We call
![]() $\unicode[STIX]{x1D6E9}$
graph the skeleton of the pair of pants given by
$\unicode[STIX]{x1D6E9}$
graph the skeleton of the pair of pants given by
We call dumbell graph the skeleton given by
The
![]() $\unicode[STIX]{x1D6E9}$
graph has a cycle at each of the three punctures, whereas the dumbbell graph has a cycle at only two: for the third puncture, the boundary of the corresponding component of
$\unicode[STIX]{x1D6E9}$
graph has a cycle at each of the three punctures, whereas the dumbbell graph has a cycle at only two: for the third puncture, the boundary of the corresponding component of
![]() $\unicode[STIX]{x1D6F4}\setminus X$
consists of the entire skeleton. On the other hand, in the
$\unicode[STIX]{x1D6F4}\setminus X$
consists of the entire skeleton. On the other hand, in the
![]() $\unicode[STIX]{x1D6E9}$
graph the cycles for any two punctures are not disjoint, whereas in the dumbbell graph they are disjoint. These graphs are shown in Figure 4.
$\unicode[STIX]{x1D6E9}$
graph the cycles for any two punctures are not disjoint, whereas in the dumbbell graph they are disjoint. These graphs are shown in Figure 4.

Figure 4. Two skeleta for the pair of pants. (a)
![]() $\unicode[STIX]{x1D6E9}$
graph. (b) Dumbbell graph.
$\unicode[STIX]{x1D6E9}$
graph. (b) Dumbbell graph.
Lemma 7.5. The surface
![]() $\unicode[STIX]{x1D6F4}_{g,n}$
admits a skeleton that has a cycle at every puncture but one.
$\unicode[STIX]{x1D6F4}_{g,n}$
admits a skeleton that has a cycle at every puncture but one.
Proof. This is furnished by Example 7.3.◻
In fact, whenever
![]() $X$
is a skeleton with a cycle at a particular puncture,
$X$
is a skeleton with a cycle at a particular puncture,
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $X$
can be decomposed into an end connect sum in a manner similar to that of Example 7.3.
$X$
can be decomposed into an end connect sum in a manner similar to that of Example 7.3.
Lemma 7.6. Let
![]() $X$
be a ribbon graph for
$X$
be a ribbon graph for
![]() $\unicode[STIX]{x1D6F4}$
that has a cycle at the puncture
$\unicode[STIX]{x1D6F4}$
that has a cycle at the puncture
![]() $p$
. Suppose that
$p$
. Suppose that
![]() $r$
other edges are incident to the cycle at
$r$
other edges are incident to the cycle at
![]() $p$
. Then
$p$
. Then
![]() $\unicode[STIX]{x1D6F4}$
can be decomposed into an end connect sum of
$\unicode[STIX]{x1D6F4}$
can be decomposed into an end connect sum of
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
and
$\unicode[STIX]{x1D6F4}^{\prime }$
and
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
, where
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
, where
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }\cong \unicode[STIX]{x1D6F4}_{0,2}$
, and
$\unicode[STIX]{x1D6F4}^{\prime \prime }\cong \unicode[STIX]{x1D6F4}_{0,2}$
, and
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
has one fewer puncture than
$\unicode[STIX]{x1D6F4}^{\prime }$
has one fewer puncture than
![]() $\unicode[STIX]{x1D6F4}$
, and
$\unicode[STIX]{x1D6F4}$
, and
![]() $X$
can be decomposed into the sum of
$X$
can be decomposed into the sum of
![]() $X^{\prime }$
and
$X^{\prime }$
and
![]() $X^{\prime \prime }$
, where
$X^{\prime \prime }$
, where
![]() $X^{\prime }$
and
$X^{\prime }$
and
![]() $X^{\prime \prime }$
are ribbon graphs embedded in
$X^{\prime \prime }$
are ribbon graphs embedded in
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
and
$\unicode[STIX]{x1D6F4}^{\prime }$
and
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
respectively, each with
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
respectively, each with
![]() $r$
noncompact edges approaching the punctures where the connect sum is taken, and
$r$
noncompact edges approaching the punctures where the connect sum is taken, and
![]() $X$
is obtained by connecting the noncompact edges of
$X$
is obtained by connecting the noncompact edges of
![]() $X^{\prime }$
to those of
$X^{\prime }$
to those of
![]() $X^{\prime \prime }$
. See Figure 5.
$X^{\prime \prime }$
. See Figure 5.

Figure 5. Decomposition of
![]() $\unicode[STIX]{x1D6F4}$
into an end connect sum, depending on a choice of path
$\unicode[STIX]{x1D6F4}$
into an end connect sum, depending on a choice of path
![]() $\unicode[STIX]{x1D6FE}$
between two punctures. The dashed line is for visual reference.
$\unicode[STIX]{x1D6FE}$
between two punctures. The dashed line is for visual reference.
Proof. The idea is to deform our picture of
![]() $\unicode[STIX]{x1D6F4}$
so that the cycle at
$\unicode[STIX]{x1D6F4}$
so that the cycle at
![]() $p$
is pulled out at another puncture
$p$
is pulled out at another puncture
![]() $q$
of
$q$
of
![]() $\unicode[STIX]{x1D6F4}$
. To do this, what is needed is a path
$\unicode[STIX]{x1D6F4}$
. To do this, what is needed is a path
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\unicode[STIX]{x1D6F4}$
from
$\unicode[STIX]{x1D6F4}$
from
![]() $p$
to
$p$
to
![]() $q$
that does not cross any other points of the skeleton
$q$
that does not cross any other points of the skeleton
![]() $X$
. But this is always possible, since every component of
$X$
. But this is always possible, since every component of
![]() $\unicode[STIX]{x1D6F4}\setminus X$
is homeomorphic to a punctured disk.◻
$\unicode[STIX]{x1D6F4}\setminus X$
is homeomorphic to a punctured disk.◻
We remark that the proof shows that if
![]() $r$
edges are incident to the cycle at
$r$
edges are incident to the cycle at
![]() $p$
, then there are essentially
$p$
, then there are essentially
![]() $r$
choices for how to decompose
$r$
choices for how to decompose
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $X$
as in the lemma.
$X$
as in the lemma.
Lemma 7.7.
(i) Let
 $X_{1}$
and
$X_{1}$
and
 $X_{2}$
be two ribbon graphs for
$X_{2}$
be two ribbon graphs for
 $\unicode[STIX]{x1D6F4}$
that both have cycles at the puncture
$\unicode[STIX]{x1D6F4}$
that both have cycles at the puncture
 $p$
. Then it is possible to connect
$p$
. Then it is possible to connect
 $X_{1}$
to
$X_{1}$
to
 $X_{2}$
by a sequence of contractions and expansions so that every intermediate graph also has a cycle at
$X_{2}$
by a sequence of contractions and expansions so that every intermediate graph also has a cycle at
 $p$
.
$p$
.(ii) Let
 $\unicode[STIX]{x1D6F4}$
be a surface with at least three punctures. Let
$\unicode[STIX]{x1D6F4}$
be a surface with at least three punctures. Let
 $p$
be a puncture of
$p$
be a puncture of
 $\unicode[STIX]{x1D6F4}$
, and let
$\unicode[STIX]{x1D6F4}$
, and let
 $X$
be a skeleton for
$X$
be a skeleton for
 $\unicode[STIX]{x1D6F4}$
that has a cycle at
$\unicode[STIX]{x1D6F4}$
that has a cycle at
 $p$
. Let
$p$
. Let
 $p^{\prime }$
be another puncture of
$p^{\prime }$
be another puncture of
 $X$
. It is possible to modify
$X$
. It is possible to modify
 $X$
to
$X$
to
 $X^{\prime }$
so that
$X^{\prime }$
so that
 $X^{\prime }$
also has cycles at
$X^{\prime }$
also has cycles at
 $p$
and
$p$
and
 $p^{\prime }$
, and so that every intermediate graph also has a cycle at
$p^{\prime }$
, and so that every intermediate graph also has a cycle at
 $p$
.
$p$
.
Proof. (i) First, if there is more than one edge incident to the cycle at
![]() $p$
in
$p$
in
![]() $X_{1}$
or
$X_{1}$
or
![]() $X_{2}$
, we can apply contractions to gather together all of these edges into a single vertex of valence
$X_{2}$
, we can apply contractions to gather together all of these edges into a single vertex of valence
![]() $r+2$
, and then apply a single expansion to ensure that in both
$r+2$
, and then apply a single expansion to ensure that in both
![]() $X_{1}$
and
$X_{1}$
and
![]() $X_{2}$
only a single edge is incident to the cycle at
$X_{2}$
only a single edge is incident to the cycle at
![]() $p$
. None of these moves destroy the cycle at
$p$
. None of these moves destroy the cycle at
![]() $p$
in
$p$
in
![]() $X_{1}$
or
$X_{1}$
or
![]() $X_{2}$
.
$X_{2}$
.
Let
![]() $p^{\prime }\neq p$
be another puncture. Choose a path
$p^{\prime }\neq p$
be another puncture. Choose a path
![]() $\unicode[STIX]{x1D6FE}$
from
$\unicode[STIX]{x1D6FE}$
from
![]() $p$
to
$p$
to
![]() $p^{\prime }$
. As in Lemma 7.6, we may assume that
$p^{\prime }$
. As in Lemma 7.6, we may assume that
![]() $\unicode[STIX]{x1D6FE}$
only crosses
$\unicode[STIX]{x1D6FE}$
only crosses
![]() $X_{1}$
at the cycle at
$X_{1}$
at the cycle at
![]() $p$
. Once this choice is made, we cannot assume the same holds true for
$p$
. Once this choice is made, we cannot assume the same holds true for
![]() $X_{2}$
, so
$X_{2}$
, so
![]() $\unicode[STIX]{x1D6FE}$
will cross
$\unicode[STIX]{x1D6FE}$
will cross
![]() $X_{2}$
at some number of edges not contained in the cycle at
$X_{2}$
at some number of edges not contained in the cycle at
![]() $p$
; let
$p$
; let
![]() $k$
be this number. Now we apply the idea of stretching the surface from Lemma 7.6, using the chosen path
$k$
be this number. Now we apply the idea of stretching the surface from Lemma 7.6, using the chosen path
![]() $\unicode[STIX]{x1D6FE}$
. This decomposes
$\unicode[STIX]{x1D6FE}$
. This decomposes
![]() $\unicode[STIX]{x1D6F4}$
into an end connect sum of
$\unicode[STIX]{x1D6F4}$
into an end connect sum of
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
and
$\unicode[STIX]{x1D6F4}^{\prime }$
and
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
, where
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
, where
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
has genus 0 and 2 punctures in such a way that the cycle at
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
has genus 0 and 2 punctures in such a way that the cycle at
![]() $p$
ends up in the
$p$
ends up in the
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
factor. See Figure 6(a).
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
factor. See Figure 6(a).
Now we consider how
![]() $X_{1}$
and
$X_{1}$
and
![]() $X_{2}$
look with respect to this decomposition. Since the path
$X_{2}$
look with respect to this decomposition. Since the path
![]() $\unicode[STIX]{x1D6FE}$
only intersects
$\unicode[STIX]{x1D6FE}$
only intersects
![]() $X_{1}$
at the cycle at
$X_{1}$
at the cycle at
![]() $p$
,
$p$
,
![]() $X_{1}$
decomposes just as in Lemma 7.6. On the other hand,
$X_{1}$
decomposes just as in Lemma 7.6. On the other hand,
![]() $X_{2}$
is as shown in Figure 6(a). The part of
$X_{2}$
is as shown in Figure 6(a). The part of
![]() $X_{2}$
that ends up in
$X_{2}$
that ends up in
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
consists of a cycle at
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
consists of a cycle at
![]() $p$
together with
$p$
together with
![]() $k$
parallel arcs. This is connected to the rest of
$k$
parallel arcs. This is connected to the rest of
![]() $X_{2}$
via
$X_{2}$
via
![]() $2k+1$
noncompact edges.
$2k+1$
noncompact edges.
The next step is to apply moves to
![]() $X_{2}$
that move the
$X_{2}$
that move the
![]() $k$
arcs out of
$k$
arcs out of
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
and into
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
and into
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
. Observe that the space between two neighboring arcs corresponds, in the summed surface
$\unicode[STIX]{x1D6F4}^{\prime }$
. Observe that the space between two neighboring arcs corresponds, in the summed surface
![]() $\unicode[STIX]{x1D6F4}$
, to a component of
$\unicode[STIX]{x1D6F4}$
, to a component of
![]() $\unicode[STIX]{x1D6F4}\setminus X_{2}$
, which is a punctured disk. Start with the outermost arc, call it
$\unicode[STIX]{x1D6F4}\setminus X_{2}$
, which is a punctured disk. Start with the outermost arc, call it
![]() $a$
. Let
$a$
. Let
![]() $D$
denote the punctured disk corresponding to the region just inside
$D$
denote the punctured disk corresponding to the region just inside
![]() $a$
, so
$a$
, so
![]() $D$
is a punctured disk. The arc
$D$
is a punctured disk. The arc
![]() $a$
ends at two vertices in
$a$
ends at two vertices in
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
. By a sequence of contractions and expansions, we may move one of the ends along the boundary of
$\unicode[STIX]{x1D6F4}^{\prime }$
. By a sequence of contractions and expansions, we may move one of the ends along the boundary of
![]() $D$
, through
$D$
, through
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
, and back into
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
, and back into
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
. We can also follow the disk
$\unicode[STIX]{x1D6F4}^{\prime }$
. We can also follow the disk
![]() $D$
throughout this process. (Depending on how it is done, the puncture of
$D$
throughout this process. (Depending on how it is done, the puncture of
![]() $D$
may also move through
$D$
may also move through
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
.) This is depicted in Figure 6(b). Since none of these moves destroy the cycle at
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
.) This is depicted in Figure 6(b). Since none of these moves destroy the cycle at
![]() $p$
, this reduces us to the situation where
$p$
, this reduces us to the situation where
![]() $k=0$
.
$k=0$
.
In the case
![]() $k=0$
, we have decompositions of
$k=0$
, we have decompositions of
![]() $X_{1}$
and
$X_{1}$
and
![]() $X_{2}$
into end connect sums of
$X_{2}$
into end connect sums of
![]() $X_{1}^{\prime }$
and
$X_{1}^{\prime }$
and
![]() $X_{2}^{\prime }$
in
$X_{2}^{\prime }$
in
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
, each having a single noncompact edge, and
$\unicode[STIX]{x1D6F4}^{\prime }$
, each having a single noncompact edge, and
![]() $X^{\prime \prime }$
in
$X^{\prime \prime }$
in
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
consisting of a single cycle with a single noncompact edge. Now we apply the fact that any two ribbon graphs for
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
consisting of a single cycle with a single noncompact edge. Now we apply the fact that any two ribbon graphs for
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
with a single noncompact edge asymptotic to a puncture can be connected by a sequence of moves, by a result of Harer [Reference Dyckerhoff and KapranovDK18, Proposition 3.3.9]. Evidently, such moves do not destroy the cycle at the puncture in
$\unicode[STIX]{x1D6F4}^{\prime }$
with a single noncompact edge asymptotic to a puncture can be connected by a sequence of moves, by a result of Harer [Reference Dyckerhoff and KapranovDK18, Proposition 3.3.9]. Evidently, such moves do not destroy the cycle at the puncture in
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
, so we are done.
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
, so we are done.
(ii) Since the surface
![]() $\unicode[STIX]{x1D6F4}$
has at least three punctures, there is a ribbon graph
$\unicode[STIX]{x1D6F4}$
has at least three punctures, there is a ribbon graph
![]() $X^{\prime }$
that has cycles at both
$X^{\prime }$
that has cycles at both
![]() $p$
and
$p$
and
![]() $p^{\prime }$
. Now apply the first part of the lemma.◻
$p^{\prime }$
. Now apply the first part of the lemma.◻

Figure 6. (a) Decomposition of surface into end connect sum, and corresponding decomposition of ribbon graph. (b) Moving an arc through
![]() $\unicode[STIX]{x1D6F4}^{\prime \prime }$
. The point marked
$\unicode[STIX]{x1D6F4}^{\prime \prime }$
. The point marked
![]() $a$
is the end of the arc that is being moved.
$a$
is the end of the arc that is being moved.
7.2 Tropical topology
Since our strategy is to prove homological mirror symmetry (HMS) inductively by gluing together pairs of pants, and the gluings are controlled by a balanced tropical graph
![]() $G_{{\mathcal{T}}}$
associated to the given toric Calabi–Yau Landau-Ginzburg model
$G_{{\mathcal{T}}}$
associated to the given toric Calabi–Yau Landau-Ginzburg model
![]() $(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
, we collect here some elementary remarks about the topology of such graphs that will be useful. The main point is to keep track of the noncompact edges of
$(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
, we collect here some elementary remarks about the topology of such graphs that will be useful. The main point is to keep track of the noncompact edges of
![]() $G$
, since these are edges where we never need to glue in our induction; we also point out that
$G$
, since these are edges where we never need to glue in our induction; we also point out that
![]() $G$
can be built up in such a way that we never need to glue along all the edges incident to a single vertex.
$G$
can be built up in such a way that we never need to glue along all the edges incident to a single vertex.
Let
![]() $G$
be trivalent graph with both finite and infinite edges. For each edge
$G$
be trivalent graph with both finite and infinite edges. For each edge
![]() $e$
, we have an orientation line
$e$
, we have an orientation line
![]() $\det (e)$
that is the
$\det (e)$
that is the
![]() $\mathbb{Z}$
-module generated by the two orientations of
$\mathbb{Z}$
-module generated by the two orientations of
![]() $e$
modulo the relation that their sum is zero. A (planar integral) momentum vector
$e$
modulo the relation that their sum is zero. A (planar integral) momentum vector
![]() $p_{e}$
on the edge
$p_{e}$
on the edge
![]() $e$
is a linear map
$e$
is a linear map
![]() $p_{e}:\det (e)\rightarrow \mathbb{Z}^{2}$
.
$p_{e}:\det (e)\rightarrow \mathbb{Z}^{2}$
.
Definition 7.8. A pair
![]() $(G,\{{p_{e}\}}_{e\in \operatorname{Edge}(G)})$
consisting of a graph and a set of momenta is a balanced tropical graph if momentum is conserved at each vertex. Namely, for each vertex
$(G,\{{p_{e}\}}_{e\in \operatorname{Edge}(G)})$
consisting of a graph and a set of momenta is a balanced tropical graph if momentum is conserved at each vertex. Namely, for each vertex
![]() $v$
of
$v$
of
![]() $G$
,
$G$
,
where the sum is over all edges
![]() $e$
incident to
$e$
incident to
![]() $v$
, and the inward orientation is the one pointing toward
$v$
, and the inward orientation is the one pointing toward
![]() $v$
.
$v$
.
Such a graph is additionally called nondegenerate if the values of the momenta at each vertex span
![]() $\mathbb{Z}^{2}$
, or equivalently if not all momenta at a given vertex are proportional.
$\mathbb{Z}^{2}$
, or equivalently if not all momenta at a given vertex are proportional.
Definition 7.9. A planar immersion of
![]() $(G,\{{p_{e}\}}_{e\in \operatorname{Edge}(G)})$
is a continuous map
$(G,\{{p_{e}\}}_{e\in \operatorname{Edge}(G)})$
is a continuous map
![]() $i:G\rightarrow \mathbb{R}^{2}$
, such that the derivative of
$i:G\rightarrow \mathbb{R}^{2}$
, such that the derivative of
![]() $i$
along an edge
$i$
along an edge
![]() $e$
in the direction
$e$
in the direction
![]() $o$
is positively proportional to the momentum
$o$
is positively proportional to the momentum
![]() $p_{e}(o)$
. Note that we do not require
$p_{e}(o)$
. Note that we do not require
![]() $i$
to be proper on infinite edges.
$i$
to be proper on infinite edges.
From now on we will consider nondegenerate balanced tropical graphs
![]() $(G,\{{p_{e}\}}_{e\in \operatorname{Edge}(G)})$
with planar immersion
$(G,\{{p_{e}\}}_{e\in \operatorname{Edge}(G)})$
with planar immersion
![]() $i$
. Planar immersions of balanced tropical graphs are in some sense ‘harmonic’, so it is not surprising that they satisfy a version of the maximum principle.
$i$
. Planar immersions of balanced tropical graphs are in some sense ‘harmonic’, so it is not surprising that they satisfy a version of the maximum principle.
Lemma 7.10. The graph
![]() $G$
has at least two infinite edges.
$G$
has at least two infinite edges.
Proof. Let
![]() $i:G\rightarrow \mathbb{R}^{2}$
be a planar immersion, and let
$i:G\rightarrow \mathbb{R}^{2}$
be a planar immersion, and let
![]() $\unicode[STIX]{x1D70B}:\mathbb{R}^{2}\rightarrow \mathbb{R}$
be the orthogonal projection onto any given line of irrational slope. Then consider the function
$\unicode[STIX]{x1D70B}:\mathbb{R}^{2}\rightarrow \mathbb{R}$
be the orthogonal projection onto any given line of irrational slope. Then consider the function
![]() $\unicode[STIX]{x1D70B}\circ i:G\rightarrow \mathbb{R}$
. Nondegeneracy implies that
$\unicode[STIX]{x1D70B}\circ i:G\rightarrow \mathbb{R}$
. Nondegeneracy implies that
![]() $p_{e}\neq 0$
for any
$p_{e}\neq 0$
for any
![]() $e$
, so
$e$
, so
![]() $\unicode[STIX]{x1D70B}\circ i$
is not constant on any edge.
$\unicode[STIX]{x1D70B}\circ i$
is not constant on any edge.
We claim that
![]() $\unicode[STIX]{x1D70B}\circ i$
does not achieve its supremum. For if it did, this would necessarily occur at a vertex, as
$\unicode[STIX]{x1D70B}\circ i$
does not achieve its supremum. For if it did, this would necessarily occur at a vertex, as
![]() $\unicode[STIX]{x1D70B}\circ i$
is linear and nonconstant on all edges. At the vertex, the images under
$\unicode[STIX]{x1D70B}\circ i$
is linear and nonconstant on all edges. At the vertex, the images under
![]() $i$
of all incident edges lie in the same half-plane determined by the linear function
$i$
of all incident edges lie in the same half-plane determined by the linear function
![]() $\unicode[STIX]{x1D70B}$
. This is not compatible with the balancing condition, since three nonzero vectors in the same half-plane cannot sum to zero.
$\unicode[STIX]{x1D70B}$
. This is not compatible with the balancing condition, since three nonzero vectors in the same half-plane cannot sum to zero.
The same reasoning applied to
![]() $-\unicode[STIX]{x1D70B}\circ i$
shows that
$-\unicode[STIX]{x1D70B}\circ i$
shows that
![]() $\unicode[STIX]{x1D70B}\circ i$
does not achieve its infimum. Therefore there must be two infinite edges on which the supremum and infinimum are approached but not obtained.◻
$\unicode[STIX]{x1D70B}\circ i$
does not achieve its infimum. Therefore there must be two infinite edges on which the supremum and infinimum are approached but not obtained.◻
Now let
![]() $e_{0}$
be an infinite edge of
$e_{0}$
be an infinite edge of
![]() $G$
; it is incident to a vertex
$G$
; it is incident to a vertex
![]() $v_{0}$
, and there are three possibilities for the local structure of
$v_{0}$
, and there are three possibilities for the local structure of
![]() $G$
at
$G$
at
![]() $v_{0}$
:
$v_{0}$
:
(i)
 $v_{0}$
is incident to one infinite edge, namely
$v_{0}$
is incident to one infinite edge, namely
 $e_{0}$
;
$e_{0}$
;(ii)
 $v_{0}$
is incident to two infinite edges, namely
$v_{0}$
is incident to two infinite edges, namely
 $e_{0}$
and one other
$e_{0}$
and one other
 $e_{1}$
;
$e_{1}$
;(iii)
 $v_{0}$
is incident to three infinite edges, then
$v_{0}$
is incident to three infinite edges, then
 $v_{0}$
and these three edges comprise a connected component of
$v_{0}$
and these three edges comprise a connected component of
 $G$
.
$G$
.
See Figure 7.

Figure 7. Cases at a vertex.
Lemma 7.11. In case (i), let
![]() $G^{\prime }$
be the graph obtained from
$G^{\prime }$
be the graph obtained from
![]() $G$
by deleting
$G$
by deleting
![]() $e_{0}$
and
$e_{0}$
and
![]() $v_{0}$
. In case (ii), let
$v_{0}$
. In case (ii), let
![]() $G^{\prime }$
be the graph obtained from
$G^{\prime }$
be the graph obtained from
![]() $G$
by deleting
$G$
by deleting
![]() $e_{0},e_{1}$
and
$e_{0},e_{1}$
and
![]() $v_{0}$
. Then
$v_{0}$
. Then
![]() $G^{\prime }$
has an infinite edge not originally incident to
$G^{\prime }$
has an infinite edge not originally incident to
![]() $v_{0}$
(in
$v_{0}$
(in
![]() $G$
).
$G$
).
Proof. In case (ii), this follows from Lemma 7.10, as
![]() $G^{\prime }$
must have two infinite edges, and only one is incident to
$G^{\prime }$
must have two infinite edges, and only one is incident to
![]() $v_{0}$
.
$v_{0}$
.
In case (i), let
![]() $e_{1}$
and
$e_{1}$
and
![]() $e_{2}$
be the other edges incident to
$e_{2}$
be the other edges incident to
![]() $v_{0}$
; these become infinite edges in
$v_{0}$
; these become infinite edges in
![]() $G^{\prime }$
. Let
$G^{\prime }$
. Let
![]() $\unicode[STIX]{x1D70B}:\mathbb{R}^{2}\rightarrow \mathbb{R}$
be an orthogonal projection onto an irrational line chosen so that both
$\unicode[STIX]{x1D70B}:\mathbb{R}^{2}\rightarrow \mathbb{R}$
be an orthogonal projection onto an irrational line chosen so that both
![]() $i(e_{1})$
and
$i(e_{1})$
and
![]() $i(e_{2})$
lie in the half-plane defined by the inequality
$i(e_{2})$
lie in the half-plane defined by the inequality
![]() $\unicode[STIX]{x1D70B}(x)\geqslant \unicode[STIX]{x1D70B}(i(v_{0}))$
. The argument from the proof of Lemma 7.10 shows that
$\unicode[STIX]{x1D70B}(x)\geqslant \unicode[STIX]{x1D70B}(i(v_{0}))$
. The argument from the proof of Lemma 7.10 shows that
![]() $\unicode[STIX]{x1D70B}\circ i$
approaches its supremum along some infinite edge. This edge cannot be
$\unicode[STIX]{x1D70B}\circ i$
approaches its supremum along some infinite edge. This edge cannot be
![]() $e_{1}$
or
$e_{1}$
or
![]() $e_{2}$
, as
$e_{2}$
, as
![]() $\unicode[STIX]{x1D70B}\circ i$
is decreasing in the noncompact direction on these edges.◻
$\unicode[STIX]{x1D70B}\circ i$
is decreasing in the noncompact direction on these edges.◻
Lemma 7.12. Given
![]() $i:G\rightarrow \mathbb{R}^{2}$
a planar immersion, there exists a sequence
$i:G\rightarrow \mathbb{R}^{2}$
a planar immersion, there exists a sequence
![]() $i_{j}:G_{j}\rightarrow \mathbb{R}^{2}$
,
$i_{j}:G_{j}\rightarrow \mathbb{R}^{2}$
,
![]() $j=1,\ldots ,N$
with the following properties:
$j=1,\ldots ,N$
with the following properties:
(i)
 $i_{j}:G_{j}\rightarrow \mathbb{R}^{2}$
is a planar immersion of the tropical graph
$i_{j}:G_{j}\rightarrow \mathbb{R}^{2}$
is a planar immersion of the tropical graph
 $G_{j}$
;
$G_{j}$
;(ii)
 $i_{N}:G_{N}\rightarrow \mathbb{R}^{2}$
equals
$i_{N}:G_{N}\rightarrow \mathbb{R}^{2}$
equals
 $i:G\rightarrow \mathbb{R}^{2}$
;
$i:G\rightarrow \mathbb{R}^{2}$
;(iii) there is a continuous embedding
 $G_{j}\rightarrow G_{j+1}$
such that
$G_{j}\rightarrow G_{j+1}$
such that
 $i_{j}=i_{j+1}|G_{j}$
, and such that
$i_{j}=i_{j+1}|G_{j}$
, and such that
 $G_{j+1}$
is obtained from
$G_{j+1}$
is obtained from
 $G_{j}$
by gluing a single trivalent vertex to
$G_{j}$
by gluing a single trivalent vertex to
 $G_{j}$
along either one or two of the noncompact edges of
$G_{j}$
along either one or two of the noncompact edges of
 $G_{j}$
, and also extending some other noncompact edges of
$G_{j}$
, and also extending some other noncompact edges of
 $G_{j}$
.
$G_{j}$
.
Proof. Begin with
![]() $i:G\rightarrow \mathbb{R}^{2}$
, and once again choose a projection
$i:G\rightarrow \mathbb{R}^{2}$
, and once again choose a projection
![]() $\unicode[STIX]{x1D70B}:\mathbb{R}^{2}\rightarrow \mathbb{R}$
. If
$\unicode[STIX]{x1D70B}:\mathbb{R}^{2}\rightarrow \mathbb{R}$
. If
![]() $\unicode[STIX]{x1D70B}$
is chosen generically, each fiber of
$\unicode[STIX]{x1D70B}$
is chosen generically, each fiber of
![]() $\unicode[STIX]{x1D70B}\circ i$
will contain at most one vertex of
$\unicode[STIX]{x1D70B}\circ i$
will contain at most one vertex of
![]() $G$
. Let the values of
$G$
. Let the values of
![]() $\unicode[STIX]{x1D70B}\circ i$
on the vertices be
$\unicode[STIX]{x1D70B}\circ i$
on the vertices be
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{n}\in \mathbb{R}$
. Then take
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{n}\in \mathbb{R}$
. Then take
![]() $G_{i}=(\unicode[STIX]{x1D70B}\circ i)^{-1}(-\infty ,\unicode[STIX]{x1D706}_{i})$
.◻
$G_{i}=(\unicode[STIX]{x1D70B}\circ i)^{-1}(-\infty ,\unicode[STIX]{x1D706}_{i})$
.◻
8 The induction
This section contains the main induction that proves HMS.
For any oriented punctured surface
![]() $\unicode[STIX]{x1D6F4}$
equipped with a skeleton
$\unicode[STIX]{x1D6F4}$
equipped with a skeleton
![]() $X$
, we associate the topological Fukaya category
$X$
, we associate the topological Fukaya category
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
. Recall that we denote by
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
. Recall that we denote by
![]() $S^{1}$
a ribbon graph consisting of type
$S^{1}$
a ribbon graph consisting of type
![]() $\unicode[STIX]{x1D6EC}(0,0)$
. For each puncture
$\unicode[STIX]{x1D6EC}(0,0)$
. For each puncture
![]() $p$
of
$p$
of
![]() $\unicode[STIX]{x1D6F4}$
, we can define a restriction functor
$\unicode[STIX]{x1D6F4}$
, we can define a restriction functor
as follows. If the graph
![]() $X$
contains a cycle corresponding to the puncture
$X$
contains a cycle corresponding to the puncture
![]() $p$
, then
$p$
, then
![]() $R$
is defined directly as an exceptional restriction functor. If not, then
$R$
is defined directly as an exceptional restriction functor. If not, then
![]() $R$
is defined by first choosing another skeleton
$R$
is defined by first choosing another skeleton
![]() $X^{\prime }$
that does have a cycle corresponding to the puncture
$X^{\prime }$
that does have a cycle corresponding to the puncture
![]() $p$
, and that is obtained from
$p$
, and that is obtained from
![]() $X$
by a sequence of contractions and expansions. By Proposition 4.8, there is an equivalence
$X$
by a sequence of contractions and expansions. By Proposition 4.8, there is an equivalence
which is canonically associated with such a sequence of contractions and expansions. Composing
![]() $\unicode[STIX]{x1D6F7}$
with the closed restriction functor
$\unicode[STIX]{x1D6F7}$
with the closed restriction functor
![]() $S_{\infty }^{S^{1}}:{\mathcal{F}}_{\infty }^{\text{top}}(X^{\prime })\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(S^{1})$
gives the desired restriction functor. We first show that this functor does not depend on the choice of skeleton used to define it.
$S_{\infty }^{S^{1}}:{\mathcal{F}}_{\infty }^{\text{top}}(X^{\prime })\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(S^{1})$
gives the desired restriction functor. We first show that this functor does not depend on the choice of skeleton used to define it.
Lemma 8.1. Let
![]() $X_{1}$
and
$X_{1}$
and
![]() $X_{2}$
be two skeleta for
$X_{2}$
be two skeleta for
![]() $\unicode[STIX]{x1D6F4}$
that both have cycles corresponding to the puncture
$\unicode[STIX]{x1D6F4}$
that both have cycles corresponding to the puncture
![]() $p$
, and that are obtained from each other via a sequence of contractions and expansions. Then there is a commutative diagram
$p$
, and that are obtained from each other via a sequence of contractions and expansions. Then there is a commutative diagram

where
![]() $\unicode[STIX]{x1D6F7}$
denotes the canonical equivalence, and
$\unicode[STIX]{x1D6F7}$
denotes the canonical equivalence, and
![]() $R$
denotes closed restriction maps.
$R$
denotes closed restriction maps.
Proof. This is an application of Lemma 7.7. Since we an arrange that the contractions and expansions that implement
![]() $\unicode[STIX]{x1D6F7}$
do not destroy the cycle at
$\unicode[STIX]{x1D6F7}$
do not destroy the cycle at
![]() $p$
, at every step the desired commutative diagram both makes sense and holds true.◻
$p$
, at every step the desired commutative diagram both makes sense and holds true.◻
Definition 8.2. Let
![]() $p$
be a puncture of
$p$
be a puncture of
![]() $\unicode[STIX]{x1D6F4}$
. We denote by
$\unicode[STIX]{x1D6F4}$
. We denote by
the corresponding restriction functor.
By Definition 3.8, for any nondegenerate balanced graph with planar immersion
![]() $G$
, we have a matrix-factorization-type category
$G$
, we have a matrix-factorization-type category
![]() ${\mathcal{B}}(G)$
. For each external edge of
${\mathcal{B}}(G)$
. For each external edge of
![]() $G$
, there is a restriction functor
$G$
, there is a restriction functor
![]() ${\mathcal{B}}(G)\rightarrow {\mathcal{B}}(E)$
, where
${\mathcal{B}}(G)\rightarrow {\mathcal{B}}(E)$
, where
![]() $E$
is the graph consisting of a single bi-infinite edge. We can associate to the graph
$E$
is the graph consisting of a single bi-infinite edge. We can associate to the graph
![]() $G$
a punctured Riemann surface
$G$
a punctured Riemann surface
![]() $\unicode[STIX]{x1D6F4}(G)$
in a way that generalizes the familiar correspondence between an algebraic curve and its tropicalization. Namely, each vertex of
$\unicode[STIX]{x1D6F4}(G)$
in a way that generalizes the familiar correspondence between an algebraic curve and its tropicalization. Namely, each vertex of
![]() $G$
corresponds to a pair of pants, while the edges correspond to cylinders: the graph
$G$
corresponds to a pair of pants, while the edges correspond to cylinders: the graph
![]() $G$
encodes the way in which the pairs of pants are glued along cylinders. Then the genus of
$G$
encodes the way in which the pairs of pants are glued along cylinders. Then the genus of
![]() $\unicode[STIX]{x1D6F4}(G)$
is equal to the number of relatively compact connected components in
$\unicode[STIX]{x1D6F4}(G)$
is equal to the number of relatively compact connected components in
![]() $\mathbb{R}^{2}-G$
, and the number of punctures is given by the number of infinite edges of
$\mathbb{R}^{2}-G$
, and the number of punctures is given by the number of infinite edges of
![]() $G$
.
$G$
.
Now we come to the main result, that category
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is equivalent to the category
${\mathcal{F}}_{\infty }^{\text{top}}(X)$
is equivalent to the category
![]() ${\mathcal{B}}(G)$
(see Definition 3.8), where
${\mathcal{B}}(G)$
(see Definition 3.8), where
![]() $X$
is a skeleton for
$X$
is a skeleton for
![]() $\unicode[STIX]{x1D6F4}(G)$
. Since our method involves successively gluing pairs of pants inductively, we must include in the induction a statement on the restriction maps at the punctures.
$\unicode[STIX]{x1D6F4}(G)$
. Since our method involves successively gluing pairs of pants inductively, we must include in the induction a statement on the restriction maps at the punctures.
Theorem 8.3. If
![]() $X$
is a skeleton for
$X$
is a skeleton for
![]() $\unicode[STIX]{x1D6F4}(G)$
, then there is an equivalence of categories
$\unicode[STIX]{x1D6F4}(G)$
, then there is an equivalence of categories
![]() $\unicode[STIX]{x1D6F9}:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{B}}(G)$
with the property that for each infinite edge
$\unicode[STIX]{x1D6F9}:{\mathcal{F}}_{\infty }^{\text{top}}(X)\rightarrow {\mathcal{B}}(G)$
with the property that for each infinite edge
![]() $e$
of
$e$
of
![]() $G$
, and corresponding puncture
$G$
, and corresponding puncture
![]() $p(e)$
, there is a commutative diagram
$p(e)$
, there is a commutative diagram

where the vertical arrows are restriction functors.
Proof. We may regard the graph
![]() $G$
as being constructed from a collection of trivalent vertices by gluing infinite edges to each other. By Lemma 7.12, there is a collection of graphs
$G$
as being constructed from a collection of trivalent vertices by gluing infinite edges to each other. By Lemma 7.12, there is a collection of graphs
![]() $G_{i}$
,
$G_{i}$
,
![]() $i=1,\ldots ,N$
such that
$i=1,\ldots ,N$
such that
![]() $G_{N}=G$
, and
$G_{N}=G$
, and
![]() $G_{i+1}$
is obtained from
$G_{i+1}$
is obtained from
![]() $G_{i}$
by gluing a single trivalent vertex to either one or two infinite edges of
$G_{i}$
by gluing a single trivalent vertex to either one or two infinite edges of
![]() $G_{i}$
(but not at all three edges simultaneously).
$G_{i}$
(but not at all three edges simultaneously).
We shall prove the assertions in the theorem by induction on
![]() $i$
. In the base case
$i$
. In the base case
![]() $i=1$
, we are simply considering the pair of pants, for which the result is known. See for instance Theorem 1.13 of [Reference NadlerNad16b].
$i=1$
, we are simply considering the pair of pants, for which the result is known. See for instance Theorem 1.13 of [Reference NadlerNad16b].
For the induction step, the induction hypothesis is the statement of the theorem for
![]() $G_{i}$
. In passing from
$G_{i}$
. In passing from
![]() $G_{i}$
to
$G_{i}$
to
![]() $G_{i+1}$
, we attach a trivalent vertex
$G_{i+1}$
, we attach a trivalent vertex
![]() $T$
; correspondingly,
$T$
; correspondingly,
![]() $\unicode[STIX]{x1D6F4}(G_{i+1})$
is obtained from
$\unicode[STIX]{x1D6F4}(G_{i+1})$
is obtained from
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
by attaching a pair of pants
$\unicode[STIX]{x1D6F4}(G_{i})$
by attaching a pair of pants
![]() $\unicode[STIX]{x1D6F4}(T)$
. Now there are two cases, depending on whether the gluing involves one edge or two.
$\unicode[STIX]{x1D6F4}(T)$
. Now there are two cases, depending on whether the gluing involves one edge or two.
Case of one edge. Denote by
![]() $e$
the edge along which
$e$
the edge along which
![]() $G_{i}$
is glued to
$G_{i}$
is glued to
![]() $T$
. Then both
$T$
. Then both
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
and
$\unicode[STIX]{x1D6F4}(G_{i})$
and
![]() $\unicode[STIX]{x1D6F4}(T)$
have a puncture corresponding to
$\unicode[STIX]{x1D6F4}(T)$
have a puncture corresponding to
![]() $e$
: we denote in the same way, namely by
$e$
: we denote in the same way, namely by
![]() $p(e)$
, the corresponding puncture on
$p(e)$
, the corresponding puncture on
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
and the puncture on
$\unicode[STIX]{x1D6F4}(G_{i})$
and the puncture on
![]() $\unicode[STIX]{x1D6F4}(T)$
. We may choose skeleta
$\unicode[STIX]{x1D6F4}(T)$
. We may choose skeleta
![]() $X$
for
$X$
for
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
and
$\unicode[STIX]{x1D6F4}(G_{i})$
and
![]() $Y$
for
$Y$
for
![]() $\unicode[STIX]{x1D6F4}(T)$
such that both
$\unicode[STIX]{x1D6F4}(T)$
such that both
![]() $X$
and
$X$
and
![]() $Y$
have a cycle, respectively, at the puncture
$Y$
have a cycle, respectively, at the puncture
![]() $p(e)$
of
$p(e)$
of
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
and at the puncture
$\unicode[STIX]{x1D6F4}(G_{i})$
and at the puncture
![]() $p(e)$
of
$p(e)$
of
![]() $\unicode[STIX]{x1D6F4}(T)$
. We then have a diagram
$\unicode[STIX]{x1D6F4}(T)$
. We then have a diagram

where the horizontal arrows are restriction functors, and the vertical arrows are the equivalences given by the induction hypothesis. The fact that both squares commute is also part of the induction hypothesis. This equivalence of diagrams implies the equivalence of fiber products shown in the following diagram.

In the diagram above, the squares are fiber products, and the curved arrows are equivalences of categories. In particular, since
![]() ${G_{i+1}\coprod }_{E}T=G_{i}$
, and
${G_{i+1}\coprod }_{E}T=G_{i}$
, and
![]() $X\coprod _{S_{1}}Y$
is a skeleton for
$X\coprod _{S_{1}}Y$
is a skeleton for
![]() $\unicode[STIX]{x1D6F4}(G_{i+1})$
, we have an equivalence
$\unicode[STIX]{x1D6F4}(G_{i+1})$
, we have an equivalence
To complete the proof of the induction step, we must also consider the restriction functors to the punctures of
![]() $\unicode[STIX]{x1D6F4}(G_{i+1})$
. On the
$\unicode[STIX]{x1D6F4}(G_{i+1})$
. On the
![]() ${\mathcal{B}}$
-side, the infinite edges
${\mathcal{B}}$
-side, the infinite edges
![]() $G_{i+1}$
correspond to infinite edges of
$G_{i+1}$
correspond to infinite edges of
![]() $G_{i}$
and
$G_{i}$
and
![]() $T$
, minus the edge
$T$
, minus the edge
![]() $e$
that we glue along. For each infinite edge
$e$
that we glue along. For each infinite edge
![]() $e^{\prime }$
of
$e^{\prime }$
of
![]() $G_{i+1}$
, we have a restriction functor
$G_{i+1}$
, we have a restriction functor
![]() $R_{\infty }^{{\mathcal{B}}}:{\mathcal{B}}(G_{i+1})\rightarrow {\mathcal{B}}(e^{\prime })$
. This functor factors through either
$R_{\infty }^{{\mathcal{B}}}:{\mathcal{B}}(G_{i+1})\rightarrow {\mathcal{B}}(e^{\prime })$
. This functor factors through either
![]() ${\mathcal{B}}(G_{i})$
or
${\mathcal{B}}(G_{i})$
or
![]() ${\mathcal{B}}(T)$
, according to whether
${\mathcal{B}}(T)$
, according to whether
![]() $e^{\prime }$
comes from
$e^{\prime }$
comes from
![]() $G_{i}$
or
$G_{i}$
or
![]() $T$
. On the
$T$
. On the
![]() ${\mathcal{F}}$
-side, we have a corresponding restriction functor
${\mathcal{F}}$
-side, we have a corresponding restriction functor
![]() $R_{p(e^{\prime })}:{\mathcal{F}}_{\infty }^{\text{top}}(X\coprod _{S^{1}}Y)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(S^{1})$
. Strictly speaking, the definition of this functor requires choosing a skeleton for
$R_{p(e^{\prime })}:{\mathcal{F}}_{\infty }^{\text{top}}(X\coprod _{S^{1}}Y)\rightarrow {\mathcal{F}}_{\infty }^{\text{top}}(S^{1})$
. Strictly speaking, the definition of this functor requires choosing a skeleton for
![]() $\unicode[STIX]{x1D6F4}(G_{i+1})$
that has a cycle at the puncture
$\unicode[STIX]{x1D6F4}(G_{i+1})$
that has a cycle at the puncture
![]() $p(e^{\prime })$
, and
$p(e^{\prime })$
, and
![]() $X\coprod _{S^{1}}Y$
may not have this property (and furthermore it is impossible for it to have this property with respect to every puncture simultaneously). The solution is Lemma 7.7, which says that we can modify either
$X\coprod _{S^{1}}Y$
may not have this property (and furthermore it is impossible for it to have this property with respect to every puncture simultaneously). The solution is Lemma 7.7, which says that we can modify either
![]() $X$
or
$X$
or
![]() $Y$
only in order to achieve that
$Y$
only in order to achieve that
![]() $X\coprod _{S^{1}}Y$
also has a cycle at
$X\coprod _{S^{1}}Y$
also has a cycle at
![]() $p(e^{\prime })$
. Since this modification can be implemented on
$p(e^{\prime })$
. Since this modification can be implemented on
![]() $X\coprod _{S^{1}}Y$
simultaneously, we find that the restriction to
$X\coprod _{S^{1}}Y$
simultaneously, we find that the restriction to
![]() $p(e^{\prime })$
factors through the closed restriction to either
$p(e^{\prime })$
factors through the closed restriction to either
![]() $X$
or
$X$
or
![]() $Y$
. If the puncture
$Y$
. If the puncture
![]() $p(e^{\prime })$
comes from
$p(e^{\prime })$
comes from
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
, there is therefore a commutative diagram of closed restriction functors.
$\unicode[STIX]{x1D6F4}(G_{i})$
, there is therefore a commutative diagram of closed restriction functors.

In the case that
![]() $p(e^{\prime })$
comes from
$p(e^{\prime })$
comes from
![]() $T$
, the same diagram holds with
$T$
, the same diagram holds with
![]() $Y$
in place of
$Y$
in place of
![]() $X$
in the upper-right node. Comparing the two sides, we have the following diagram.
$X$
in the upper-right node. Comparing the two sides, we have the following diagram.

In this diagram, the curved
![]() $\unicode[STIX]{x1D6F9}$
arrows (which are equivalences) form commutative squares with the horizontal and vertical arrows, and therefore they also form a commutative square with the diagonal arrows. This establishes the desired compatibility between restriction functors to infinite edges of
$\unicode[STIX]{x1D6F9}$
arrows (which are equivalences) form commutative squares with the horizontal and vertical arrows, and therefore they also form a commutative square with the diagonal arrows. This establishes the desired compatibility between restriction functors to infinite edges of
![]() $G_{i+1}$
with restrictions to punctures of
$G_{i+1}$
with restrictions to punctures of
![]() $\unicode[STIX]{x1D6F4}(G_{i+1})$
.
$\unicode[STIX]{x1D6F4}(G_{i+1})$
.
Case of two edges. Let
![]() $e_{1}$
and
$e_{1}$
and
![]() $e_{2}$
be the two edges along which
$e_{2}$
be the two edges along which
![]() $G_{i}$
and
$G_{i}$
and
![]() $T$
are glued. As before, we denote by
$T$
are glued. As before, we denote by
![]() $p(e_{1})$
and
$p(e_{1})$
and
![]() $p(e_{2})$
both the two punctures on
$p(e_{2})$
both the two punctures on
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
, and the two punctures on
$\unicode[STIX]{x1D6F4}(G_{i})$
, and the two punctures on
![]() $\unicode[STIX]{x1D6F4}(T)$
, that correspond to
$\unicode[STIX]{x1D6F4}(T)$
, that correspond to
![]() $e_{1}$
and
$e_{1}$
and
![]() $e_{2}$
. Choose a skeleton
$e_{2}$
. Choose a skeleton
![]() $X$
for
$X$
for
![]() $\unicode[STIX]{x1D6F4}(G_{i})$
that has disjoint cycles at the punctures
$\unicode[STIX]{x1D6F4}(G_{i})$
that has disjoint cycles at the punctures
![]() $p(e_{1})$
and
$p(e_{1})$
and
![]() $p(e_{2})$
. Choose a skeleton
$p(e_{2})$
. Choose a skeleton
![]() $Y$
for
$Y$
for
![]() $T$
that has disjoint cycles at the punctures
$T$
that has disjoint cycles at the punctures
![]() $p(e_{1})$
and
$p(e_{1})$
and
![]() $p(e_{2})$
(this
$p(e_{2})$
(this
![]() $Y$
is necessarily a dumbbell graph). The argument proceeds as before, but we glue
$Y$
is necessarily a dumbbell graph). The argument proceeds as before, but we glue
![]() $X$
to
$X$
to
![]() $Y$
along
$Y$
along
![]() $S^{1}\coprod S^{1}$
, and
$S^{1}\coprod S^{1}$
, and
![]() $G_{i}$
to
$G_{i}$
to
![]() $T$
along
$T$
along
![]() $e_{1}\coprod e_{2}$
. Thus we have a diagram
$e_{1}\coprod e_{2}$
. Thus we have a diagram

where the two squares are fiber products and the curved arrows are equivalences.
It remains to analyze the restriction functors. If
![]() $e^{\prime }$
is an infinite edge of
$e^{\prime }$
is an infinite edge of
![]() $G_{i+1}={G_{i}\coprod }_{E\coprod E}T$
, then the restriction to
$G_{i+1}={G_{i}\coprod }_{E\coprod E}T$
, then the restriction to
![]() $e^{\prime }$
factors through restriction either to
$e^{\prime }$
factors through restriction either to
![]() $G_{i}$
or
$G_{i}$
or
![]() $T$
. Similarly, we claim that the restriction from
$T$
. Similarly, we claim that the restriction from
![]() ${\mathcal{F}}_{\infty }^{\text{top}}(X\coprod _{S^{1}\coprod S^{1}}Y)$
factors through restriction either to
${\mathcal{F}}_{\infty }^{\text{top}}(X\coprod _{S^{1}\coprod S^{1}}Y)$
factors through restriction either to
![]() $X$
or
$X$
or
![]() $Y$
. The only issue here is that we may not be able to choose a skeleton that has disjoint cycles at three punctures simultaneously. This occurs when we consider the third puncture of
$Y$
. The only issue here is that we may not be able to choose a skeleton that has disjoint cycles at three punctures simultaneously. This occurs when we consider the third puncture of
![]() $\unicode[STIX]{x1D6F4}(T)$
, since
$\unicode[STIX]{x1D6F4}(T)$
, since
![]() $Y$
is a dumbbell graph, or if
$Y$
is a dumbbell graph, or if
![]() $X$
has only three punctures. On the other hand, the modification we need to do in order to produce a puncture at
$X$
has only three punctures. On the other hand, the modification we need to do in order to produce a puncture at
![]() $p(e^{\prime })$
can be localized in a neighborhood of either
$p(e^{\prime })$
can be localized in a neighborhood of either
![]() $X$
or
$X$
or
![]() $Y$
inside
$Y$
inside
![]() $X\coprod _{S^{1}\coprod S^{1}}Y$
. Since an open restriction followed by a closed restriction is a closed restriction (see Proposition 5.14), it suffices to understand the closed restriction functor from a neighborhood of
$X\coprod _{S^{1}\coprod S^{1}}Y$
. Since an open restriction followed by a closed restriction is a closed restriction (see Proposition 5.14), it suffices to understand the closed restriction functor from a neighborhood of
![]() $X$
or
$X$
or
![]() $Y$
to the puncture. After restricting to a small enough neighborhood of
$Y$
to the puncture. After restricting to a small enough neighborhood of
![]() $X$
or
$X$
or
![]() $Y$
, the closed restriction to
$Y$
, the closed restriction to
![]() $X$
or
$X$
or
![]() $Y$
consists then of merely removing some noncompact edges of the skeleton, and it makes no difference whether we do this before or after modifying the skeleton. Thus the restriction to the puncture
$Y$
consists then of merely removing some noncompact edges of the skeleton, and it makes no difference whether we do this before or after modifying the skeleton. Thus the restriction to the puncture
![]() $p(e^{\prime })$
factors through restriction first to
$p(e^{\prime })$
factors through restriction first to
![]() $X$
or
$X$
or
![]() $Y$
. The rest of the argument is the same as in the previous case.◻
$Y$
. The rest of the argument is the same as in the previous case.◻
We are now ready to prove our main theorem. We use the notation of § 3.1.1. Let
![]() $(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
be a toric Calabi–Yau LG model, and let
$(X_{{\mathcal{T}}},W_{{\mathcal{T}}})$
be a toric Calabi–Yau LG model, and let
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
be the mirror curve.
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
be the mirror curve.
Theorem 8.4. There is an equivalence of categories
Proof. Let
![]() $G_{{\mathcal{T}}}$
be the tropical curve dual to the triangulation
$G_{{\mathcal{T}}}$
be the tropical curve dual to the triangulation
![]() ${\mathcal{T}}$
. Recall that
${\mathcal{T}}$
. Recall that
![]() $\text{Fuk}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
denotes the Ind-completion of
$\text{Fuk}_{\infty }^{\text{top}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
denotes the Ind-completion of
![]() $\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
. By Theorem 3.10 and Theorem 8.3 there are equivalences
$\text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
. By Theorem 3.10 and Theorem 8.3 there are equivalences
They restrict to an equivalence between the categories of compact objects inside
![]() $MF^{\infty }(X,W)$
and
$MF^{\infty }(X,W)$
and
![]() $\text{Fuk}_{\text{top}}^{\infty }(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
$\text{Fuk}_{\text{top}}^{\infty }(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
and this concludes the proof.◻
Remark 8.5. Let
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
be an unramified cyclic cover of a punctured surface and let
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
be an unramified cyclic cover of a punctured surface and let
![]() $\text{Fuk}^{\text{wr}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
be the wrapped Fukaya category. By [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] there is an equivalence
$\text{Fuk}^{\text{wr}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
be the wrapped Fukaya category. By [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] there is an equivalence
Together with Theorem 8.4, this yields an equivalence
This establishes Kontsevich’s claim [Reference KontsevichKon09], according to which the topological Fukaya category is equivalent to the wrapped Fukaya category, for a large class of punctured Riemann surfaces. In her thesis Lee [Reference LeeLe15] extends the results of [Reference Abouzaid, Auroux, Efimov, Katzarkov and OrlovAAEKO13] to all genera. This, combined with Theorem 8.4, gives a complete proof of Kontsevich’s claim for punctured surfaces. A different proof of this result, with different methods, was given in [Reference Haiden, Katzarkov and KontsevichHKK17].
Remark 8.6. Let us return to the picture of HMS for partially wrapped Fukaya categories delineated in Remark 1.3. As we explained there, the semi-infinite edges of a noncompact skeleton
![]() $\widetilde{S}$
of
$\widetilde{S}$
of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
correspond to a smooth stacky partial compactification
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
correspond to a smooth stacky partial compactification
![]() $\widetilde{X}_{{\mathcal{T}}}$
of
$\widetilde{X}_{{\mathcal{T}}}$
of
![]() $X_{{\mathcal{T}}}$
with the following property: each puncture
$X_{{\mathcal{T}}}$
with the following property: each puncture
![]() $p$
of
$p$
of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
corresponds to an irreducible component
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
corresponds to an irreducible component
![]() $\mathbb{A}^{1}$
of the singular locus of
$\mathbb{A}^{1}$
of the singular locus of
![]() $W_{{\mathcal{T}}}$
.Footnote
4
If
$W_{{\mathcal{T}}}$
.Footnote
4
If
![]() $S$
has
$S$
has
![]() $n$
noncompact edges approaching the puncture
$n$
noncompact edges approaching the puncture
![]() $p$
, then we compactify that copy of
$p$
, then we compactify that copy of
![]() $\mathbb{A}^{1}$
to a stacky rational curve
$\mathbb{A}^{1}$
to a stacky rational curve
![]() $\mathbb{P}^{1}(1,n)$
. That is, we cap the
$\mathbb{P}^{1}(1,n)$
. That is, we cap the
![]() $\mathbb{A}^{1}$
with a copy of
$\mathbb{A}^{1}$
with a copy of
![]() $[\mathbb{A}^{1}/\unicode[STIX]{x1D707}_{n}]$
.
$[\mathbb{A}^{1}/\unicode[STIX]{x1D707}_{n}]$
.
Let
![]() $(X_{{\mathcal{T}}})_{0}$
be the zero fiber of
$(X_{{\mathcal{T}}})_{0}$
be the zero fiber of
![]() $X_{{\mathcal{T}}}$
, and denote by
$X_{{\mathcal{T}}}$
, and denote by
![]() $(\widetilde{X}_{{\mathcal{T}}})_{0}$
its compactification inside
$(\widetilde{X}_{{\mathcal{T}}})_{0}$
its compactification inside
![]() $\widetilde{X}_{{\mathcal{T}}}$
. As we explained in Remark 1.3, we expect that the general statement of HMS for the partially wrapped category
$\widetilde{X}_{{\mathcal{T}}}$
. As we explained in Remark 1.3, we expect that the general statement of HMS for the partially wrapped category
![]() ${\mathcal{F}}(\widetilde{S})$
can be formulated as an equivalence
${\mathcal{F}}(\widetilde{S})$
can be formulated as an equivalence
Equivalence (28) should follow from our Theorem 8.4 and exotic gluing (Theorem 6.6). Assume for simplicity that the noncompact edges of
![]() $\widetilde{S}$
approach a unique puncture
$\widetilde{S}$
approach a unique puncture
![]() $p$
of
$p$
of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
: the general case is proved via an iteration of the argument. Removing the noncompact edges from
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
: the general case is proved via an iteration of the argument. Removing the noncompact edges from
![]() $\widetilde{S}$
yields a compact skeleton
$\widetilde{S}$
yields a compact skeleton
![]() $S$
of
$S$
of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
. By modifying
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
. By modifying
![]() $\widetilde{S}$
, and hence
$\widetilde{S}$
, and hence
![]() $S$
, in the interior of
$S$
, in the interior of
![]() $\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
, it is possible to arrange that
$\unicode[STIX]{x1D6F4}_{{\mathcal{T}}}$
, it is possible to arrange that
![]() $S$
has a cycle at
$S$
has a cycle at
![]() $p$
, and that
$p$
, and that
![]() $\widetilde{S}$
consists of
$\widetilde{S}$
consists of
![]() $S$
with several noncompact edges approaching
$S$
with several noncompact edges approaching
![]() $p$
. The derived category of singularities should enjoy the same descent properties as the category of matrix factorizations: although this result as such does not seem to appear in the literature, it should follow from the techniques of [Reference PreygelPre12, Appendix A]. Then Zariski descent for
$p$
. The derived category of singularities should enjoy the same descent properties as the category of matrix factorizations: although this result as such does not seem to appear in the literature, it should follow from the techniques of [Reference PreygelPre12, Appendix A]. Then Zariski descent for
![]() $D_{\text{sg}}^{b}(-)$
and Theorem 6.6 give, respectively, the following two equivalences
$D_{\text{sg}}^{b}(-)$
and Theorem 6.6 give, respectively, the following two equivalences
By Theorem 8.4 we have that
![]() $D_{\text{sg}}^{b}((X_{{\mathcal{T}}})_{0})\simeq MF(X_{{\mathcal{T}}},W_{{\mathcal{T}}})\simeq \text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
. Additionally there is an equivalence
$D_{\text{sg}}^{b}((X_{{\mathcal{T}}})_{0})\simeq MF(X_{{\mathcal{T}}},W_{{\mathcal{T}}})\simeq \text{Fuk}^{\text{top}}(\unicode[STIX]{x1D6F4}_{{\mathcal{T}}})$
. Additionally there is an equivalence
![]() ${\mathcal{P}}\text{erf}([\mathbb{A}^{1}/\unicode[STIX]{x1D707}_{n}])\simeq {\mathcal{F}}(\unicode[STIX]{x1D6EC}(0,n))$
. Thus we can deduce equivalence (28) exactly as in the proof of Theorem 8.4.
${\mathcal{P}}\text{erf}([\mathbb{A}^{1}/\unicode[STIX]{x1D707}_{n}])\simeq {\mathcal{F}}(\unicode[STIX]{x1D6EC}(0,n))$
. Thus we can deduce equivalence (28) exactly as in the proof of Theorem 8.4.
Acknowledgements
We thank David Ben-Zvi, Dario Beraldo, Gaëtan Borot, Tobias Dyckerhoff, Mikhail Kapranov, Gabriel Kerr, Charles Rezk, Sarah Scherotzke, Paul Seidel, and Eric Zaslow for useful discussions and for their interest in this project. Yankı Lekili helped us with Remarks 1.3 and 8.6. We also thank the anonymous referee for comments that significantly improved the exposition. This project started when both authors were visiting the Max Planck Institute for Mathematics in Bonn in the Summer of 2014, and they thank the institute for its hospitality and support. JP was partially supported by NSF Grant DMS-1522670. NS thanks the University of Oxford and Wadham College, where part of this work was carried out, for excellent working conditions.