No CrossRef data available.
Published online by Cambridge University Press: 20 May 2022
In this paper, we treat a nonlinear and unbalanced 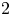 $2$-color urn scheme, subjected to two different nonlinear drawing rules, depending on the color withdrawn. We prove a central limit theorem as well as a law of large numbers for the urn composition. We also give an estimate of the mean and variance of both types of balls.
$2$-color urn scheme, subjected to two different nonlinear drawing rules, depending on the color withdrawn. We prove a central limit theorem as well as a law of large numbers for the urn composition. We also give an estimate of the mean and variance of both types of balls.