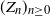1. Introduction
A Galton–Watson process can be described as follows:
 \begin{equation*} Z_0=1,\quad Z_{n+1}= \sum_{i=1}^{Z_n} X_{n,i} \quad \text{for $ n \geq 0$,} \end{equation*}
\begin{equation*} Z_0=1,\quad Z_{n+1}= \sum_{i=1}^{Z_n} X_{n,i} \quad \text{for $ n \geq 0$,} \end{equation*}
where
![]() $X_{n,i}$
is the offspring number of the ith individual of the generation n. Moreover, the random variables
$X_{n,i}$
is the offspring number of the ith individual of the generation n. Moreover, the random variables
![]() $ (X_{n,i})_{i\geq 1} $
are independent of each other with common distribution law
$ (X_{n,i})_{i\geq 1} $
are independent of each other with common distribution law
and are also independent of
![]() $Z_n$
.
$Z_n$
.
An important task in statistical inference for Galton–Watson processes is to estimate the average offspring number of an individual m, usually termed the offspring mean. Clearly we have
Let v denote the standard variance of
![]() $Z_1$
, that is,
$Z_1$
, that is,
To avoid triviality, assume that
![]() $v> 0$
. For estimation of the offspring mean m, the Lotka–Nagaev [Reference Lotka12, Reference Nagaev14] estimator
$v> 0$
. For estimation of the offspring mean m, the Lotka–Nagaev [Reference Lotka12, Reference Nagaev14] estimator
![]() $Z_{n+1}/Z_{n}$
plays an important role. Throughout the paper we assume that
$Z_{n+1}/Z_{n}$
plays an important role. Throughout the paper we assume that
Then the Lotka–Nagaev estimator is well-defined
![]() $\mathbb{P}$
-a.s. For the Galton–Watson processes, Athreya [Reference Athreya1] has established large deviations for the normalized Lotka–Nagaev estimator (see also Chu [Reference Chu3] for self-normalized large deviations); Ney and Vidyashankar [Reference Ney and Vidyashankar15, Reference Ney and Vidyashankar16] and He [Reference He9] obtained sharp rate estimates for the large deviation behavior of the Lotka–Nagaev estimator; Maaouia and Touati [Reference Maaouia and Touati13] established a self-normalized central limit theorem (CLT) for the maximum likelihood estimator of m; Bercu and Touati [Reference Bercu and Touati2] proved an exponential inequality for the Lotka–Nagaev estimator via self-normalized martingale methods. Alternative approaches for obtaining self-normalized exponential inequalities can be found in de la Peña, Lai, and Shao [Reference De la Peña, Lai and Shao4]. Despite the fact that the Lotka–Nagaev estimator is well studied, there is no result for self-normalized Cramér moderate deviations for the Lotka–Nagaev estimator. The main purpose of this paper is to fill this gap.
$\mathbb{P}$
-a.s. For the Galton–Watson processes, Athreya [Reference Athreya1] has established large deviations for the normalized Lotka–Nagaev estimator (see also Chu [Reference Chu3] for self-normalized large deviations); Ney and Vidyashankar [Reference Ney and Vidyashankar15, Reference Ney and Vidyashankar16] and He [Reference He9] obtained sharp rate estimates for the large deviation behavior of the Lotka–Nagaev estimator; Maaouia and Touati [Reference Maaouia and Touati13] established a self-normalized central limit theorem (CLT) for the maximum likelihood estimator of m; Bercu and Touati [Reference Bercu and Touati2] proved an exponential inequality for the Lotka–Nagaev estimator via self-normalized martingale methods. Alternative approaches for obtaining self-normalized exponential inequalities can be found in de la Peña, Lai, and Shao [Reference De la Peña, Lai and Shao4]. Despite the fact that the Lotka–Nagaev estimator is well studied, there is no result for self-normalized Cramér moderate deviations for the Lotka–Nagaev estimator. The main purpose of this paper is to fill this gap.
Let us briefly introduce our main result. Assume that
![]() $n_0, n \in \mathbb{N}$
. Notice that, by the classical CLT for independent and identically distributed (i.i.d.) random variables,
$n_0, n \in \mathbb{N}$
. Notice that, by the classical CLT for independent and identically distributed (i.i.d.) random variables,
asymptotically behaves like a vector of i.i.d. Gaussian random variables with mean 0 and variance
![]() $v^2$
(even if
$v^2$
(even if
![]() $n_0$
depends on n) and the convergence rate to Gaussian distribution is exponential; see Kuelbs and Vidyashankar [Reference Kuelbs and Vidyashankar11]. Because
$n_0$
depends on n) and the convergence rate to Gaussian distribution is exponential; see Kuelbs and Vidyashankar [Reference Kuelbs and Vidyashankar11]. Because
 \[\dfrac1n \sum_{k=n_0}^{n_0+n-1} Z_{ k} \biggl( \dfrac{Z_{ k+1}}{Z_{ k}} - m \biggr)^2\]
\[\dfrac1n \sum_{k=n_0}^{n_0+n-1} Z_{ k} \biggl( \dfrac{Z_{ k+1}}{Z_{ k}} - m \biggr)^2\]
is an estimator of the offspring variance
![]() $v^2$
, it is natural to compare the self-normalized sum
$v^2$
, it is natural to compare the self-normalized sum
 \[M_{n_0,n}\,{:\!=}\, \dfrac{ {(n v^2)^{-1/2}} \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( {{Z_{ k+1}}/{Z_{ k}}} -m )}{\sqrt{ {(n v^2)^{-1}} \sum_{k=n_0}^{n_0+n-1} Z_{ k} ( {{Z_{ k+1}}/{Z_{ k}}} - m )^2 } }=\dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( {{Z_{ k+1}}/{Z_{ k}}} -m )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} Z_{ k} ( {{Z_{ k+1}}/{Z_{ k}}} - m )^2 } }\]
\[M_{n_0,n}\,{:\!=}\, \dfrac{ {(n v^2)^{-1/2}} \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( {{Z_{ k+1}}/{Z_{ k}}} -m )}{\sqrt{ {(n v^2)^{-1}} \sum_{k=n_0}^{n_0+n-1} Z_{ k} ( {{Z_{ k+1}}/{Z_{ k}}} - m )^2 } }=\dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( {{Z_{ k+1}}/{Z_{ k}}} -m )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} Z_{ k} ( {{Z_{ k+1}}/{Z_{ k}}} - m )^2 } }\]
to the tail of the Gaussian distribution. This is the main purpose of the paper. Assume that
![]() $ \mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
$ \mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
![]() $ \rho \in (0, 1]$
. We prove the following self-normalized Cramér moderate deviations for the Lotka–Nagaev estimator. It holds that
$ \rho \in (0, 1]$
. We prove the following self-normalized Cramér moderate deviations for the Lotka–Nagaev estimator. It holds that
uniformly for
![]() $x \in [0, \, {\textrm{o}}( n^{\rho/(4+2\rho)} ))$
as
$x \in [0, \, {\textrm{o}}( n^{\rho/(4+2\rho)} ))$
as
![]() $n\rightarrow \infty$
; see Theorem 2.1. This type of result is user-friendly in the statistical inference of m, since in practice we usually do not know the variance
$n\rightarrow \infty$
; see Theorem 2.1. This type of result is user-friendly in the statistical inference of m, since in practice we usually do not know the variance
![]() $v^2$
or the distribution of
$v^2$
or the distribution of
![]() $Z_1$
. Let
$Z_1$
. Let
![]() $\kappa_n \in (0, 1)$
. Assume that
$\kappa_n \in (0, 1)$
. Assume that
From (1) we can easily obtain a
![]() $1-\kappa_n$
confidence interval for m, for n large enough. Clearly, the right-hand side of (1) and
$1-\kappa_n$
confidence interval for m, for n large enough. Clearly, the right-hand side of (1) and
![]() $M_{n_0,n}$
do not depend on
$M_{n_0,n}$
do not depend on
![]() $v^2$
, so the confidence interval of m does not depend on
$v^2$
, so the confidence interval of m does not depend on
![]() $v^2$
; see Proposition 3.1. Due to these significant advantages, the limit theory for self-normalized processes is attracting more and more attention. We refer to Jing, Shao, and Wang [Reference Jing, Shao and Wang10] and Fan et al. [Reference Fan, Grama, Liu and Shao8] for closely related results.
$v^2$
; see Proposition 3.1. Due to these significant advantages, the limit theory for self-normalized processes is attracting more and more attention. We refer to Jing, Shao, and Wang [Reference Jing, Shao and Wang10] and Fan et al. [Reference Fan, Grama, Liu and Shao8] for closely related results.
The paper is organized as follows. In Section 2 we present Cramér moderate deviations for the self-normalized Lotka–Nagaev estimator, provided that
![]() $(Z_n)_{n\geq0}$
can be observed. In Section 3 we present some applications of our results in statistics. The remaining sections are devoted to the proofs of theorems.
$(Z_n)_{n\geq0}$
can be observed. In Section 3 we present some applications of our results in statistics. The remaining sections are devoted to the proofs of theorems.
2. Main results
Assume that the total populations
![]() $(Z_{k})_{k\geq 0}$
of all generations can be observed. For
$(Z_{k})_{k\geq 0}$
of all generations can be observed. For
![]() $n_0, n \in \mathbb{N}$
, recall the definition of
$n_0, n \in \mathbb{N}$
, recall the definition of
![]() $M_{n_0,n}$
:
$M_{n_0,n}$
:
 \begin{equation*}M_{n_0,n}= \dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( {{Z_{ k+1}}/{Z_{ k}}} -m )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} Z_{ k} ( {{Z_{ k+1}}/{Z_{ k}}} - m )^2 } }.\end{equation*}
\begin{equation*}M_{n_0,n}= \dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( {{Z_{ k+1}}/{Z_{ k}}} -m )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} Z_{ k} ( {{Z_{ k+1}}/{Z_{ k}}} - m )^2 } }.\end{equation*}
Here
![]() $n_0$
may depend on n. For instance, we can take
$n_0$
may depend on n. For instance, we can take
![]() $n_0$
as a function of n. We may take
$n_0$
as a function of n. We may take
![]() $n_0=0$
. However, in real-world applications it may happen that we know historical data
$n_0=0$
. However, in real-world applications it may happen that we know historical data
![]() $(Z_{k})_{ n_0 \leq k \leq n_0+n}$
for some
$(Z_{k})_{ n_0 \leq k \leq n_0+n}$
for some
![]() $n_0\geq2$
, as well as the increment n of generation numbers, but do not know the data
$n_0\geq2$
, as well as the increment n of generation numbers, but do not know the data
![]() $(Z_{k})_{ 0 \leq k \leq n_0-1}$
. In such a case
$(Z_{k})_{ 0 \leq k \leq n_0-1}$
. In such a case
![]() $M_{0,n}$
is no longer applicable to estimating m, whereas
$M_{0,n}$
is no longer applicable to estimating m, whereas
![]() $M_{n_0,n}$
is suitable. Motivated by this problem, it would be better to consider the more general case
$M_{n_0,n}$
is suitable. Motivated by this problem, it would be better to consider the more general case
![]() $n_0\geq0$
instead of taking
$n_0\geq0$
instead of taking
![]() $n_0=0$
. As
$n_0=0$
. As
![]() $(Z_k)_{k=n_0,\ldots,n_0+n}$
can be observed,
$(Z_k)_{k=n_0,\ldots,n_0+n}$
can be observed,
![]() $M_{n_0,n}$
can be regarded as a time-type self-normalized process for the Lotka–Nagaev estimator
$M_{n_0,n}$
can be regarded as a time-type self-normalized process for the Lotka–Nagaev estimator
![]() $Z_{k+1}/Z_{k}$
. The following theorem gives a self-normalized Cramér moderate deviation result for the Galton–Watson processes.
$Z_{k+1}/Z_{k}$
. The following theorem gives a self-normalized Cramér moderate deviation result for the Galton–Watson processes.
Theorem 2.1.
Assume that
![]() $ \mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
$ \mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
![]() $ \rho \in (0, 1]$
.
$ \rho \in (0, 1]$
.
-
(i) If
 $\rho \in (0, 1)$
, then for all
$\rho \in (0, 1)$
, then for all
 $x \in [0,\, {\textrm{o}}( \sqrt{n} ))$
,(2)where
$x \in [0,\, {\textrm{o}}( \sqrt{n} ))$
,(2)where \begin{equation}\biggl|\ln\dfrac{\mathbb{P}(M_{n_0,n} \geq x)}{1-\Phi(x)} \biggr| \leq C_\rho \biggl( \dfrac{ x^{2+\rho} }{n^{\rho/2}} + \dfrac{ (1+x)^{1-\rho(2+\rho)/4} }{n^{\rho(2-\rho)/8}} \biggr) ,\end{equation}
\begin{equation}\biggl|\ln\dfrac{\mathbb{P}(M_{n_0,n} \geq x)}{1-\Phi(x)} \biggr| \leq C_\rho \biggl( \dfrac{ x^{2+\rho} }{n^{\rho/2}} + \dfrac{ (1+x)^{1-\rho(2+\rho)/4} }{n^{\rho(2-\rho)/8}} \biggr) ,\end{equation}
 $C_\rho$
depends only on the constants
$C_\rho$
depends only on the constants
 $\rho, v$
and
$\rho, v$
and
 $ \mathbb{E} Z_1 ^{2+\rho}$
.
$ \mathbb{E} Z_1 ^{2+\rho}$
.
-
(ii) If
 $\rho =1$
, then for all
$\rho =1$
, then for all
 $x \in [0,\, {\textrm{o}}( \sqrt{n} ))$
,(3)where C depends only on the constants v and
$x \in [0,\, {\textrm{o}}( \sqrt{n} ))$
,(3)where C depends only on the constants v and \begin{equation}\biggl|\ln\dfrac{\mathbb{P}(M_{n_0,n} \geq x)}{1-\Phi(x)} \biggr| \leq C \biggl( \dfrac{ x^{3} }{\sqrt{n} } + \dfrac{ \ln n }{\sqrt{n} } + \dfrac{ (1+x)^{1/4} }{n^{1/8}} \biggr) ,\end{equation}
\begin{equation}\biggl|\ln\dfrac{\mathbb{P}(M_{n_0,n} \geq x)}{1-\Phi(x)} \biggr| \leq C \biggl( \dfrac{ x^{3} }{\sqrt{n} } + \dfrac{ \ln n }{\sqrt{n} } + \dfrac{ (1+x)^{1/4} }{n^{1/8}} \biggr) ,\end{equation}
 $ \mathbb{E} Z_1 ^{3}$
.
$ \mathbb{E} Z_1 ^{3}$
.
In particular, inequalities (2) and (3) together imply that
uniformly for
![]() $ x \in [0, \, {\textrm{o}}(n^{\rho/(4+2\rho)}))$
as
$ x \in [0, \, {\textrm{o}}(n^{\rho/(4+2\rho)}))$
as
![]() $n\rightarrow \infty$
. Moreover, the same inequalities remain valid when
$n\rightarrow \infty$
. Moreover, the same inequalities remain valid when
is replaced by
Notice that the mean of a standard normal random variable is 0. By the maximum likelihood method, it is natural to let
![]() $M_{n_0,n}=0$
; then we have
$M_{n_0,n}=0$
; then we have
 \[\sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} \biggl( \frac{Z_{ k+1}}{Z_{ k}} -m \biggr)=0,\]
\[\sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} \biggl( \frac{Z_{ k+1}}{Z_{ k}} -m \biggr)=0,\]
which implies that
 \[\overline{m}_n \,{:\!=}\, \dfrac{1}{\sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} } \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} \biggl( \dfrac{Z_{ k+1}}{Z_{ k}} \biggr)\]
\[\overline{m}_n \,{:\!=}\, \dfrac{1}{\sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} } \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} \biggl( \dfrac{Z_{ k+1}}{Z_{ k}} \biggr)\]
can be regarded as a random weighted Lotka–Nagaev estimator for m.
Equality (4) implies that
![]() $\mathbb{P}(M_{n_0,n} \leq x) \rightarrow \Phi(x)$
as n tends to
$\mathbb{P}(M_{n_0,n} \leq x) \rightarrow \Phi(x)$
as n tends to
![]() $\infty$
. Thus Theorem 2.1 implies the central limit theory for
$\infty$
. Thus Theorem 2.1 implies the central limit theory for
![]() $M_{n_0,n}$
. Moreover, equality (4) states that the relative error of normal approximation for
$M_{n_0,n}$
. Moreover, equality (4) states that the relative error of normal approximation for
![]() $M_{n_0,n}$
tends to zero uniformly for
$M_{n_0,n}$
tends to zero uniformly for
![]() $ x \in [0, \, {\textrm{o}}(n^{\rho/(4+2\rho)})) $
as
$ x \in [0, \, {\textrm{o}}(n^{\rho/(4+2\rho)})) $
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
Theorem 2.1 implies the following moderate deviation principle (MDP) result for the time-type self-normalized Lotka–Nagaev estimator.
Corollary 2.1.
Assume the conditions of Theorem 2.1. Let
![]() $(a_n)_{n\geq1}$
be any sequence of real numbers satisfying
$(a_n)_{n\geq1}$
be any sequence of real numbers satisfying
![]() $a_n \rightarrow \infty$
and
$a_n \rightarrow \infty$
and
![]() $a_n/ \sqrt{n} \rightarrow 0$
as
$a_n/ \sqrt{n} \rightarrow 0$
as
![]() $n\rightarrow \infty$
. Then, for each Borel set B,
$n\rightarrow \infty$
. Then, for each Borel set B,
where
![]() $B^o$
and
$B^o$
and
![]() $\overline{B}$
denote the interior and the closure of B, respectively.
$\overline{B}$
denote the interior and the closure of B, respectively.
Remark 2.1. From (2) and (3), it is easy to derive the following Berry–Esseen bound for the self-normalized Lotka–Nagaev estimator:
where
![]() $C_\rho$
depends only on the constants
$C_\rho$
depends only on the constants
![]() $\rho, v$
and
$\rho, v$
and
![]() $ \mathbb{E} Z_1 ^{2+\rho}$
. When
$ \mathbb{E} Z_1 ^{2+\rho}$
. When
![]() $\rho> 1$
, by the self-normalized Berry–Esseen bound for martingales in Fan and Shao [Reference Fan and Shao6], we can get a Berry–Esseen bound of order
$\rho> 1$
, by the self-normalized Berry–Esseen bound for martingales in Fan and Shao [Reference Fan and Shao6], we can get a Berry–Esseen bound of order
![]() $n^{- \rho/(6+2\rho) }$
.
$n^{- \rho/(6+2\rho) }$
.
The last remark gives a self-normalized Berry–Esseen bound for the Lotka–Nagaev estimator, while the next theorem presents a normalized Berry–Esseen bound for the Lotka–Nagaev estimator. Denote
 \[H_{n_0, n}= \dfrac{1}{ \sqrt{n } v }\sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} \biggl( \dfrac{Z_{k+1}}{Z_{k}} -m \biggr).\]
\[H_{n_0, n}= \dfrac{1}{ \sqrt{n } v }\sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} \biggl( \dfrac{Z_{k+1}}{Z_{k}} -m \biggr).\]
Notice that the random variables
![]() $(X_{k,i})_{1\leq i\leq Z_k}$
have the same distribution as
$(X_{k,i})_{1\leq i\leq Z_k}$
have the same distribution as
![]() $Z_1$
, and that
$Z_1$
, and that
![]() $(X_{k,i})_{1\leq i\leq Z_k}$
are independent of
$(X_{k,i})_{1\leq i\leq Z_k}$
are independent of
![]() $Z_k$
. Then, for the Galton–Watson processes, it holds that
$Z_k$
. Then, for the Galton–Watson processes, it holds that
 \[\mathbb{E} [ (Z_{k+1} -m Z_{k})^2 \mid Z_k] = \mathbb{E} \Biggl[ \Biggl( \sum_{i=1}^{Z_k} (X_{k,i} -m) \Biggr)^2 \biggm| Z_k \Biggr] = Z_{k} v^2.\]
\[\mathbb{E} [ (Z_{k+1} -m Z_{k})^2 \mid Z_k] = \mathbb{E} \Biggl[ \Biggl( \sum_{i=1}^{Z_k} (X_{k,i} -m) \Biggr)^2 \biggm| Z_k \Biggr] = Z_{k} v^2.\]
It is easy to see that
 \[H_{n_0, n}= \sum_{k=n_0}^{n_0+n-1} \frac{1}{ \sqrt{\, n v^2 / Z_{ k} }} \biggl( \frac{Z_{k+1}}{Z_{k}} -m \biggr) .\]
\[H_{n_0, n}= \sum_{k=n_0}^{n_0+n-1} \frac{1}{ \sqrt{\, n v^2 / Z_{ k} }} \biggl( \frac{Z_{k+1}}{Z_{k}} -m \biggr) .\]
Thus
![]() $H_{n_0,n}$
can be regarded as a normalized process for the Lotka–Nagaev estimator
$H_{n_0,n}$
can be regarded as a normalized process for the Lotka–Nagaev estimator
![]() $Z_{k+1}/Z_{k}$
. We have the following normalized Berry–Esseen bounds for the Galton–Watson processes.
$Z_{k+1}/Z_{k}$
. We have the following normalized Berry–Esseen bounds for the Galton–Watson processes.
Theorem 2.2. Assume the conditions of Theorem 2.1.
-
(i) If
 $\rho \in (0, 1)$
, then
(5)where
$\rho \in (0, 1)$
, then
(5)where \begin{equation} \sup_{x \in \mathbb{R}}|\mathbb{P}( H_{n_0,n} \leq x) - \Phi(x) | \leq \dfrac{ C_\rho }{ n^{\rho/2}},\end{equation}
\begin{equation} \sup_{x \in \mathbb{R}}|\mathbb{P}( H_{n_0,n} \leq x) - \Phi(x) | \leq \dfrac{ C_\rho }{ n^{\rho/2}},\end{equation}
 $C_\rho$
depends only on
$C_\rho$
depends only on
 $\rho, v$
and
$\rho, v$
and
 $ \mathbb{E} Z_1 ^{2+\rho}$
.
$ \mathbb{E} Z_1 ^{2+\rho}$
.
-
(ii) If
 $\rho =1$
, then
(6)where C depends only on v and
$\rho =1$
, then
(6)where C depends only on v and \begin{equation}\sup_{x \in \mathbb{R}}|\mathbb{P}( H_{n_0,n} \leq x) - \Phi(x) | \leq C \dfrac{ \ln n }{ \sqrt{n} },\end{equation}
\begin{equation}\sup_{x \in \mathbb{R}}|\mathbb{P}( H_{n_0,n} \leq x) - \Phi(x) | \leq C \dfrac{ \ln n }{ \sqrt{n} },\end{equation}
 $ \mathbb{E} Z_1 ^{3}$
.
$ \mathbb{E} Z_1 ^{3}$
.
Moreover, the same inequalities remain valid when
![]() $H_{n_0,n}$
is replaced by
$H_{n_0,n}$
is replaced by
![]() $-H_{n_0,n}$
.
$-H_{n_0,n}$
.
The convergence rates of (5) and (6) are identical to the best possible convergence rates of the Berry–Esseen bounds for martingales; see Theorem 2.1 of Fan [Reference Fan5] and the associated comment. Notice that
![]() $H_{n_0,n}$
is a martingale with respect to the natural filtration.
$H_{n_0,n}$
is a martingale with respect to the natural filtration.
3. Applications
Cramér moderate deviations certainly have many applications in statistics.
3.1. p-value for hypothesis testing
Self-normalized Cramér moderate deviations can be applied to hypothesis testing of m for the Galton–Watson processes. When
![]() $(Z_{k})_{k=n_0,\ldots,n_0+n}$
can be observed, we can use Theorem 2.1 to estimate the p-value. Assume that
$(Z_{k})_{k=n_0,\ldots,n_0+n}$
can be observed, we can use Theorem 2.1 to estimate the p-value. Assume that
![]() $ \mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
$ \mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
![]() $0 < \rho \leq 1$
, and that
$0 < \rho \leq 1$
, and that
![]() $m> 1$
. Let
$m> 1$
. Let
![]() $(z_{k})_{k=n_0,\ldots,n_0+n}$
be the observed value of the
$(z_{k})_{k=n_0,\ldots,n_0+n}$
be the observed value of the
![]() $(Z_{k})_{k=n_0,\ldots,n_0+n}$
. In order to estimate the offspring mean m, we can make use of the Harris estimator [Reference Bercu and Touati2] given by
$(Z_{k})_{k=n_0,\ldots,n_0+n}$
. In order to estimate the offspring mean m, we can make use of the Harris estimator [Reference Bercu and Touati2] given by
 \[\widehat{m}_n=\dfrac{\sum_{k=n_0}^{n_0+n-1} Z_{ k+1}}{\sum_{k=n_0}^{n_0+n-1}Z_{ k}}.\]
\[\widehat{m}_n=\dfrac{\sum_{k=n_0}^{n_0+n-1} Z_{ k+1}}{\sum_{k=n_0}^{n_0+n-1}Z_{ k}}.\]
Then the observation for the Harris estimator is
 \[\widehat{m}_n=\dfrac{\sum_{k=n_0}^{n_0+n-1} z_{ k+1}}{\sum_{k=n_0}^{n_0+n-1}z_{ k}}.\]
\[\widehat{m}_n=\dfrac{\sum_{k=n_0}^{n_0+n-1} z_{ k+1}}{\sum_{k=n_0}^{n_0+n-1}z_{ k}}.\]
By Theorem 2.1, it is easy to see that
uniformly for
![]() $ x \in [0, {\textrm{o}}( n^{\rho/(4+2\rho)} ))$
. Notice that
$ x \in [0, {\textrm{o}}( n^{\rho/(4+2\rho)} ))$
. Notice that
![]() $ 1-\Phi(x) = \Phi (\!-x). $
Thus, when
$ 1-\Phi(x) = \Phi (\!-x). $
Thus, when
![]() $|\widetilde{m}_n|={\textrm{o}}( n^{\rho/(4+2\rho)} )$
, by (7), the probability
$|\widetilde{m}_n|={\textrm{o}}( n^{\rho/(4+2\rho)} )$
, by (7), the probability
![]() $\mathbb{P}(M_{n_0,n} > |\widetilde{m}_n|)$
is almost equal to
$\mathbb{P}(M_{n_0,n} > |\widetilde{m}_n|)$
is almost equal to
![]() $2 \Phi (\!-|\widetilde{m}_n|) $
, where
$2 \Phi (\!-|\widetilde{m}_n|) $
, where
 \[ \widetilde{m}_n= \dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{z_{ k}} ( z_{ k+1}/z_{ k} -\widehat{m}_n )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} z_{ k} ( z_{ k+1}/z_{ k} - \widehat{m}_n )^2 } }. \]
\[ \widetilde{m}_n= \dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{z_{ k}} ( z_{ k+1}/z_{ k} -\widehat{m}_n )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} z_{ k} ( z_{ k+1}/z_{ k} - \widehat{m}_n )^2 } }. \]
3.2. Construction of confidence intervals
Assume the data
![]() $(Z_{k})_{k\geq 0}$
can be observed. Cramér moderate deviations can also be applied to the construction of confidence intervals of m. We use Theorem 2.1 to construct confidence intervals.
$(Z_{k})_{k\geq 0}$
can be observed. Cramér moderate deviations can also be applied to the construction of confidence intervals of m. We use Theorem 2.1 to construct confidence intervals.
Proposition 3.1.
Assume that
![]() $\mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
$\mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
![]() $ \rho \in (0, 1]$
. Let
$ \rho \in (0, 1]$
. Let
![]() $\kappa_n \in (0, 1)$
. Assume that
$\kappa_n \in (0, 1)$
. Assume that
Let
 \begin{align*}a_{n_0, n}&= \Biggl( \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{k}} \Biggr)^2- (\Phi^{-1}(1-\kappa_n /2) )^2 \sum_{k=n_0}^{n_0+n-1} Z_{k}, \\b_{n_0, n}&= 2 (\Phi^{-1}(1-\kappa_n /2) )^2 \sum_{k=n_0}^{n_0+n-1} Z_{k+1} - 2 \Biggl( \sum_{k=n_0}^{n_0+n-1} \dfrac{Z_{k+1}}{\sqrt{Z_{k }}} \Biggr)\Biggl( \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{k}} \Biggr), \\c_{n_0, n}&= \Biggl( \sum_{k=n_0}^{n_0+n-1} \dfrac{Z_{k+1}}{\sqrt{Z_{k }}} \Biggr)^2 - (\Phi^{-1}(1-\kappa_n /2) )^2 \sum_{k=n_0}^{n_0+n-1} \dfrac{Z_{k+1}^2}{Z_{k}}.\end{align*}
\begin{align*}a_{n_0, n}&= \Biggl( \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{k}} \Biggr)^2- (\Phi^{-1}(1-\kappa_n /2) )^2 \sum_{k=n_0}^{n_0+n-1} Z_{k}, \\b_{n_0, n}&= 2 (\Phi^{-1}(1-\kappa_n /2) )^2 \sum_{k=n_0}^{n_0+n-1} Z_{k+1} - 2 \Biggl( \sum_{k=n_0}^{n_0+n-1} \dfrac{Z_{k+1}}{\sqrt{Z_{k }}} \Biggr)\Biggl( \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{k}} \Biggr), \\c_{n_0, n}&= \Biggl( \sum_{k=n_0}^{n_0+n-1} \dfrac{Z_{k+1}}{\sqrt{Z_{k }}} \Biggr)^2 - (\Phi^{-1}(1-\kappa_n /2) )^2 \sum_{k=n_0}^{n_0+n-1} \dfrac{Z_{k+1}^2}{Z_{k}}.\end{align*}
Then
![]() $[A_{n_0, n},B_{n_0, n}]$
, with
$[A_{n_0, n},B_{n_0, n}]$
, with
 \begin{equation*}A_{n_0, n}=\dfrac{- b_{n_0, n} - \sqrt{b_{n_0, n}^2-4 a_{n_0, n}c_{n_0, n} }}{ 2 a_{n_0, n} }\end{equation*}
\begin{equation*}A_{n_0, n}=\dfrac{- b_{n_0, n} - \sqrt{b_{n_0, n}^2-4 a_{n_0, n}c_{n_0, n} }}{ 2 a_{n_0, n} }\end{equation*}
and
 \begin{equation*}B_{n_0, n}=\dfrac{ -b_{n_0, n} + \sqrt{b_{n_0, n}^2-4 a_{n_0, n}c_{n_0, n} }}{ 2 a_{n_0, n} },\end{equation*}
\begin{equation*}B_{n_0, n}=\dfrac{ -b_{n_0, n} + \sqrt{b_{n_0, n}^2-4 a_{n_0, n}c_{n_0, n} }}{ 2 a_{n_0, n} },\end{equation*}
is a
![]() $1-\kappa_n$
confidence interval for m, for n large enough.
$1-\kappa_n$
confidence interval for m, for n large enough.
Proof. Notice that
![]() $ 1-\Phi(x) = \Phi (\!-x). $
Theorem 2.1 implies that
$ 1-\Phi(x) = \Phi (\!-x). $
Theorem 2.1 implies that
uniformly for
![]() $0\leq x={\textrm{o}}( n^ {\rho/(4+2\rho)} )$
; see (4). Notice that the inverse function
$0\leq x={\textrm{o}}( n^ {\rho/(4+2\rho)} )$
; see (4). Notice that the inverse function
![]() $\Phi^{-1}$
of a standard normal distribution function
$\Phi^{-1}$
of a standard normal distribution function
![]() $\Phi$
has the following asymptotic expansion:
$\Phi$
has the following asymptotic expansion:
In particular, this says that for any positive sequence
![]() $(\kappa_n)_{n\geq1} $
that converges to zero, as
$(\kappa_n)_{n\geq1} $
that converges to zero, as
![]() $n\rightarrow \infty$
, we have
$n\rightarrow \infty$
, we have
Thus, when
![]() $\kappa_n$
satisfies the condition (8), the upper
$\kappa_n$
satisfies the condition (8), the upper
![]() $(\kappa_n/2)$
th quantile of a standard normal distribution is of order
$(\kappa_n/2)$
th quantile of a standard normal distribution is of order
![]() ${\textrm{o}}( n^ {\rho/(4+2\rho)} )$
. Then, applying (9) to the last equality, we complete the proof of Proposition 3.1. Notice that
${\textrm{o}}( n^ {\rho/(4+2\rho)} )$
. Then, applying (9) to the last equality, we complete the proof of Proposition 3.1. Notice that
![]() $A_{n_0, n}$
and
$A_{n_0, n}$
and
![]() $B_{n_0, n}$
are solutions of the following equation:
$B_{n_0, n}$
are solutions of the following equation:
 \[\dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( Z_{ k+1}/Z_{ k} -x )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} Z_{ k} ( Z_{ k+1}/Z_{ k} - x )^2 } }=\Phi^{-1}(1-\kappa_n /2).\]
\[\dfrac{ \sum_{k=n_0}^{n_0+n-1} \sqrt{Z_{ k}} ( Z_{ k+1}/Z_{ k} -x )}{\sqrt{\sum_{k=n_0}^{n_0+n-1} Z_{ k} ( Z_{ k+1}/Z_{ k} - x )^2 } }=\Phi^{-1}(1-\kappa_n /2).\]
This completes the proof of Proposition 3.1.
Assume the parameter
![]() $v^2$
is known. When
$v^2$
is known. When
![]() $v^2$
is known, we can apply normalized Berry–Esseen bounds (see Theorem 2.2) to construct confidence intervals.
$v^2$
is known, we can apply normalized Berry–Esseen bounds (see Theorem 2.2) to construct confidence intervals.
Proposition 3.2.
Assume that
![]() $\mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
$\mathbb{E} Z_1 ^{2+\rho}< \infty$
for some
![]() $ \rho \in (0, 1]$
. Let
$ \rho \in (0, 1]$
. Let
![]() $\kappa_n \in (0, 1)$
. Assume that
$\kappa_n \in (0, 1)$
. Assume that
Then
![]() $[A_n,B_n]$
, with
$[A_n,B_n]$
, with
 \begin{equation*}A_n=\dfrac{ \sum_{k=n_0}^{n_0+n } Z_{k+1}/\sqrt{Z_k}-\sqrt{n } v \Phi^{-1}(1-\kappa_n/2) }{ \sum_{k=n_0}^{n_0+n } \sqrt{Z_{k}}}\end{equation*}
\begin{equation*}A_n=\dfrac{ \sum_{k=n_0}^{n_0+n } Z_{k+1}/\sqrt{Z_k}-\sqrt{n } v \Phi^{-1}(1-\kappa_n/2) }{ \sum_{k=n_0}^{n_0+n } \sqrt{Z_{k}}}\end{equation*}
and
 \begin{equation*}B_n=\dfrac{ \sum_{k=n_0}^{n_0+n } Z_{k+1}/\sqrt{Z_k}+\sqrt{n } v \Phi^{-1}(1-\kappa_n/2) }{ \sum_{k=n_0}^{n_0+n } \sqrt{Z_{k}}} ,\end{equation*}
\begin{equation*}B_n=\dfrac{ \sum_{k=n_0}^{n_0+n } Z_{k+1}/\sqrt{Z_k}+\sqrt{n } v \Phi^{-1}(1-\kappa_n/2) }{ \sum_{k=n_0}^{n_0+n } \sqrt{Z_{k}}} ,\end{equation*}
is a
![]() $1-\kappa_n$
confidence interval for m, for n large enough.
$1-\kappa_n$
confidence interval for m, for n large enough.
Proof. Theorem 2.2 implies that
uniformly for
![]() $0\leq x={\textrm{o}}( \sqrt{\ln n} )$
. The upper
$0\leq x={\textrm{o}}( \sqrt{\ln n} )$
. The upper
![]() $(\kappa_n/2)$
th quantile of a standard normal distribution satisfies
$(\kappa_n/2)$
th quantile of a standard normal distribution satisfies
which, by (10), is of order
![]() $ {\textrm{o}}( \sqrt{\ln n} )$
. Proposition 3.2 follows from applying (11) to
$ {\textrm{o}}( \sqrt{\ln n} )$
. Proposition 3.2 follows from applying (11) to
![]() $H_{n_0,n}$
.
$H_{n_0,n}$
.
4. Proof of Theorem 2.1
In the proof of Theorem 2.1 we will use the following lemma (see Corollary 2.3 of Fan et al. [Reference Fan, Grama, Liu and Shao7]), which gives self-normalized Cramér moderate deviations for martingales.
Lemma 4.1.
Let
![]() $(\eta_k, \mathcal{F}_k)_{k=1,\ldots,n}$
be a finite sequence of martingale differences. Assume that there exist a constant
$(\eta_k, \mathcal{F}_k)_{k=1,\ldots,n}$
be a finite sequence of martingale differences. Assume that there exist a constant
![]() $\rho \in (0, 1]$
and numbers
$\rho \in (0, 1]$
and numbers
![]() $\gamma_n>0$
and
$\gamma_n>0$
and
![]() $\delta_n\geq 0$
satisfying
$\delta_n\geq 0$
satisfying
![]() $\gamma_n, \delta_n \rightarrow 0$
such that for all
$\gamma_n, \delta_n \rightarrow 0$
such that for all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
and
 \begin{equation} \Biggl| \sum_{k=1}^n \mathbb{E}[ \eta_{k} ^2 \mid \mathcal{F}_{k-1 } ]-1\Biggr| \leq \delta_n^2 \quad {a.s.}\end{equation}
\begin{equation} \Biggl| \sum_{k=1}^n \mathbb{E}[ \eta_{k} ^2 \mid \mathcal{F}_{k-1 } ]-1\Biggr| \leq \delta_n^2 \quad {a.s.}\end{equation}
Denote
 \[V_n= \dfrac{\sum_{k=1}^n \eta_{k} }{ \sqrt{\sum_{k=1}^n \eta_{k}^2} }\]
\[V_n= \dfrac{\sum_{k=1}^n \eta_{k} }{ \sqrt{\sum_{k=1}^n \eta_{k}^2} }\]
and
-
(i) If
 $\rho \in (0, 1)$
, then for all
$\rho \in (0, 1)$
, then for all
 $0\leq x = {\textrm{o}}( \gamma_n^{-1} )$
,
$0\leq x = {\textrm{o}}( \gamma_n^{-1} )$
, \begin{equation*}\biggl|\ln \dfrac{\mathbb{P}(V_n \geq x)}{1-\Phi(x)} \biggr| \leq C_{\rho} \bigl( x^{2+\rho} \gamma_n^\rho+ x^2 \delta_n^2 +(1+x)( \delta_n + \widehat{\gamma}_n(x, \rho) ) \bigr) .\end{equation*}
\begin{equation*}\biggl|\ln \dfrac{\mathbb{P}(V_n \geq x)}{1-\Phi(x)} \biggr| \leq C_{\rho} \bigl( x^{2+\rho} \gamma_n^\rho+ x^2 \delta_n^2 +(1+x)( \delta_n + \widehat{\gamma}_n(x, \rho) ) \bigr) .\end{equation*}
-
(ii) If
 $\rho =1$
, then for all
$\rho =1$
, then for all
 $0\leq x = {\textrm{o}}( \gamma_n^{-1} )$
,
$0\leq x = {\textrm{o}}( \gamma_n^{-1} )$
, \begin{equation*}\biggl|\ln \dfrac{\mathbb{P}(V_n \geq x)}{1-\Phi(x)} \biggr| \leq C \bigl( x^{3} \gamma_n + x^2 \delta_n^2+(1+x)( \delta_n+ \gamma_n |\!\ln \gamma_n| +\widehat{\gamma}_n(x, 1) ) \bigr) .\end{equation*}
\begin{equation*}\biggl|\ln \dfrac{\mathbb{P}(V_n \geq x)}{1-\Phi(x)} \biggr| \leq C \bigl( x^{3} \gamma_n + x^2 \delta_n^2+(1+x)( \delta_n+ \gamma_n |\!\ln \gamma_n| +\widehat{\gamma}_n(x, 1) ) \bigr) .\end{equation*}
Now we are in a position to prove Theorem 2.1. Denote
![]() $\mathcal{F}_{n_0} =\{ \emptyset, \Omega \} $
and
$\mathcal{F}_{n_0} =\{ \emptyset, \Omega \} $
and
![]() $\mathcal{F}_{k+1}=\sigma \{ Z_{i}\colon n_0\leq i\leq k+1 \}$
for all
$\mathcal{F}_{k+1}=\sigma \{ Z_{i}\colon n_0\leq i\leq k+1 \}$
for all
![]() $k\geq n_0$
. Notice that
$k\geq n_0$
. Notice that
![]() $X_{k,i}$
is independent of
$X_{k,i}$
is independent of
![]() $Z_k$
. Then it is easy to verify that
$Z_k$
. Then it is easy to verify that
 \begin{align*} \mathbb{E}[ \hat{\xi}_{k+1} \mid \mathcal{F}_{k } ] &= Z_{ k} ^{-1/2} \mathbb{E}[ Z_{ k+1} -mZ_{ k} \mid \mathcal{F}_{k } ]\notag \\ &= Z_{ k} ^{-1/2} \sum_{i=1}^{Z_k} \mathbb{E}[ X_{ k, i} -m \mid \mathcal{F}_{k } ] \notag \\& = Z_{ k} ^{-1/2} \sum_{i=1}^{Z_k} \mathbb{E}[ X_{ k, i} -m ] \notag \\& =0.\end{align*}
\begin{align*} \mathbb{E}[ \hat{\xi}_{k+1} \mid \mathcal{F}_{k } ] &= Z_{ k} ^{-1/2} \mathbb{E}[ Z_{ k+1} -mZ_{ k} \mid \mathcal{F}_{k } ]\notag \\ &= Z_{ k} ^{-1/2} \sum_{i=1}^{Z_k} \mathbb{E}[ X_{ k, i} -m \mid \mathcal{F}_{k } ] \notag \\& = Z_{ k} ^{-1/2} \sum_{i=1}^{Z_k} \mathbb{E}[ X_{ k, i} -m ] \notag \\& =0.\end{align*}
Thus
![]() $(\hat{\xi}_k, \mathcal{F}_k)_{k=n_0+1,\ldots,n_0+n}$
is a finite sequence of martingale differences. Notice that
$(\hat{\xi}_k, \mathcal{F}_k)_{k=n_0+1,\ldots,n_0+n}$
is a finite sequence of martingale differences. Notice that
![]() $X_{ k, i}-m$
,
$X_{ k, i}-m$
,
![]() $i\geq 1$
, are centered and independent random variables. Thus the following equalities hold:
$i\geq 1$
, are centered and independent random variables. Thus the following equalities hold:
 \begin{align*} \sum_{k=n_0}^{n_0+n-1} \mathbb{E}[ \hat{\xi}_{k+1}^2 \mid \mathcal{F}_{k } ] &=\sum_{k=n_0}^{n_0+n-1} Z_{k}^{-1} \mathbb{E}[ ( Z_{ k+1} -mZ_{ k} )^2 \mid \mathcal{F}_{k } ]\notag \\& = \sum_{k=n_0}^{n_0+n-1} Z_{k}^{-1} \mathbb{E}\Biggl[ \Biggl( \sum_{i=1}^{Z_k} (X_{ k, i} -m) \Biggr)^2 \biggm|\mathcal{F}_{k } \Biggr] \notag \\&=\sum_{k=n_0}^{n_0+n-1} Z_{k}^{-1} Z_k \mathbb{E}[ (X_{ k, i} -m)^2 ] \notag \\&= n v^2. \end{align*}
\begin{align*} \sum_{k=n_0}^{n_0+n-1} \mathbb{E}[ \hat{\xi}_{k+1}^2 \mid \mathcal{F}_{k } ] &=\sum_{k=n_0}^{n_0+n-1} Z_{k}^{-1} \mathbb{E}[ ( Z_{ k+1} -mZ_{ k} )^2 \mid \mathcal{F}_{k } ]\notag \\& = \sum_{k=n_0}^{n_0+n-1} Z_{k}^{-1} \mathbb{E}\Biggl[ \Biggl( \sum_{i=1}^{Z_k} (X_{ k, i} -m) \Biggr)^2 \biggm|\mathcal{F}_{k } \Biggr] \notag \\&=\sum_{k=n_0}^{n_0+n-1} Z_{k}^{-1} Z_k \mathbb{E}[ (X_{ k, i} -m)^2 ] \notag \\&= n v^2. \end{align*}
Moreover, it is easy to see that
 \begin{align} \mathbb{E}[ |\hat{\xi}_{k+1}|^{2+\rho} \mid \mathcal{F}_{k } ] &= Z_{k}^{-1-\rho/2} \mathbb{E}[ | Z_{ k+1} -mZ_{ k} |^{2+\rho } \mid \mathcal{F}_{k } ] \notag \\[3pt] & = Z_{k}^{-1-\rho/2} \mathbb{E}\Biggl[ \Biggl| \sum_{i=1}^{Z_k} (X_{ k, i} -m) \Biggr|^{2+\rho } \biggm| \mathcal{F}_{k } \Biggr] . \end{align}
\begin{align} \mathbb{E}[ |\hat{\xi}_{k+1}|^{2+\rho} \mid \mathcal{F}_{k } ] &= Z_{k}^{-1-\rho/2} \mathbb{E}[ | Z_{ k+1} -mZ_{ k} |^{2+\rho } \mid \mathcal{F}_{k } ] \notag \\[3pt] & = Z_{k}^{-1-\rho/2} \mathbb{E}\Biggl[ \Biggl| \sum_{i=1}^{Z_k} (X_{ k, i} -m) \Biggr|^{2+\rho } \biggm| \mathcal{F}_{k } \Biggr] . \end{align}
By Rosenthal’s inequality, we have
 \begin{align*} \mathbb{E}\Biggl[ \Biggl| \sum_{i=1}^{Z_k} (X_{ k, i} -m) \Biggr|^{2+\rho } \biggm|\mathcal{F}_{k } \Biggr]&\leq C^{\prime}_\rho \Biggl(\Biggl( \sum_{i=1}^{Z_k}\mathbb{E}( X_{ k, i} -m )^2 \Biggr)^{1+\rho/2} + \sum_{i=1}^{Z_k}\mathbb{E}| X_{ k, i} -m |^{2+\rho } \Biggr) \\[3pt] & \leq C^{\prime}_\rho \bigl( Z_k^{1+\rho/2} v^{2+\rho} + Z_k \mathbb{E}| Z_1 -m |^{2+\rho } \bigr).\end{align*}
\begin{align*} \mathbb{E}\Biggl[ \Biggl| \sum_{i=1}^{Z_k} (X_{ k, i} -m) \Biggr|^{2+\rho } \biggm|\mathcal{F}_{k } \Biggr]&\leq C^{\prime}_\rho \Biggl(\Biggl( \sum_{i=1}^{Z_k}\mathbb{E}( X_{ k, i} -m )^2 \Biggr)^{1+\rho/2} + \sum_{i=1}^{Z_k}\mathbb{E}| X_{ k, i} -m |^{2+\rho } \Biggr) \\[3pt] & \leq C^{\prime}_\rho \bigl( Z_k^{1+\rho/2} v^{2+\rho} + Z_k \mathbb{E}| Z_1 -m |^{2+\rho } \bigr).\end{align*}
Since the set of extinction of the process
![]() $(Z_{k})_{k\geq 0}$
is negligible with respect to the annealed law
$(Z_{k})_{k\geq 0}$
is negligible with respect to the annealed law
![]() $\mathbb{P}$
, we have
$\mathbb{P}$
, we have
![]() $Z_k\geq 1$
for any k. From (14), by the last inequality and the fact
$Z_k\geq 1$
for any k. From (14), by the last inequality and the fact
![]() $Z_k\geq 1$
, we deduce that
$Z_k\geq 1$
, we deduce that
 \begin{align} \mathbb{E}[ |\hat{\xi}_{k+1}|^{2+\rho} \mid \mathcal{F}_{k } ] &\leq C^{\prime}_\rho \bigl( v^{ \rho} + \mathbb{E}| Z_1 -m |^{2+\rho }/v^2 \bigr) v^2 \notag \\[3pt] & = C^{\prime}_\rho \bigl( v^{ \rho} + \mathbb{E}| Z_1 -m |^{2+\rho }/v^2 \bigr) \mathbb{E}[ \hat{\xi}_{k+1}^{2} \mid \mathcal{F}_{k } ]\notag \\[3pt] &\leq C^{\prime}_\rho \bigl( v^{ \rho} + 2^{1+\rho} \bigl(\mathbb{E} Z_1 ^{2+\rho } + m ^{2+\rho }\bigr)/v^2 \bigr) \mathbb{E}[ \hat{\xi}_{k+1}^{2} \mid \mathcal{F}_{k } ] . \notag\end{align}
\begin{align} \mathbb{E}[ |\hat{\xi}_{k+1}|^{2+\rho} \mid \mathcal{F}_{k } ] &\leq C^{\prime}_\rho \bigl( v^{ \rho} + \mathbb{E}| Z_1 -m |^{2+\rho }/v^2 \bigr) v^2 \notag \\[3pt] & = C^{\prime}_\rho \bigl( v^{ \rho} + \mathbb{E}| Z_1 -m |^{2+\rho }/v^2 \bigr) \mathbb{E}[ \hat{\xi}_{k+1}^{2} \mid \mathcal{F}_{k } ]\notag \\[3pt] &\leq C^{\prime}_\rho \bigl( v^{ \rho} + 2^{1+\rho} \bigl(\mathbb{E} Z_1 ^{2+\rho } + m ^{2+\rho }\bigr)/v^2 \bigr) \mathbb{E}[ \hat{\xi}_{k+1}^{2} \mid \mathcal{F}_{k } ] . \notag\end{align}
By Jensen’s inequality, we have
![]() $ m ^{2+\rho } = (\mathbb{E} Z_1) ^{2+\rho } \leq \mathbb{E} Z_1 ^{2+\rho }. $
Thus we have
$ m ^{2+\rho } = (\mathbb{E} Z_1) ^{2+\rho } \leq \mathbb{E} Z_1 ^{2+\rho }. $
Thus we have
Let
![]() $\eta_k =\hat{\xi}_{n_0+k}/(\sqrt{n} v)$
and
$\eta_k =\hat{\xi}_{n_0+k}/(\sqrt{n} v)$
and
![]() $\mathcal{F}_{k}=\mathcal{F}_{n_0+k}$
. Then
$\mathcal{F}_{k}=\mathcal{F}_{n_0+k}$
. Then
![]() $(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n}$
is a martingale difference sequence and satisfies conditions (12) and (13) with
$(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n}$
is a martingale difference sequence and satisfies conditions (12) and (13) with
![]() $ \delta_n=0$
and
$ \delta_n=0$
and
Clearly,
 \[M_{n_0,n}= \dfrac{ \sum_{k=1}^{n} \eta_{k } }{\sqrt{\sum_{k=1}^{n} \eta_{k }^2 } }.\]
\[M_{n_0,n}= \dfrac{ \sum_{k=1}^{n} \eta_{k } }{\sqrt{\sum_{k=1}^{n} \eta_{k }^2 } }.\]
Applying Lemma 4.1 to
![]() $(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n}$
, we obtain the desired inequalities. Notice that for any
$(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n}$
, we obtain the desired inequalities. Notice that for any
![]() $\rho \in (0, 1]$
and all
$\rho \in (0, 1]$
and all
![]() $x\geq 0$
, the following inequality holds:
$x\geq 0$
, the following inequality holds:
5. Proof of Corollary 2.1
We only give a proof of Corollary 2.1 for
![]() $\rho \in (0, 1)$
. The proof for
$\rho \in (0, 1)$
. The proof for
![]() $\rho=1$
is similar. We first show that for any Borel set
$\rho=1$
is similar. We first show that for any Borel set
![]() $B\subset \mathbb{R}$
,
$B\subset \mathbb{R}$
,
When
![]() $B =\emptyset$
, the last inequality is obvious, with
$B =\emptyset$
, the last inequality is obvious, with
![]() $-\inf_{x \in \emptyset}{{x^2}/{2}}=-\infty$
. Thus we may assume that
$-\inf_{x \in \emptyset}{{x^2}/{2}}=-\infty$
. Thus we may assume that
![]() $B \neq \emptyset$
. Let
$B \neq \emptyset$
. Let
![]() $x_0=\inf_{x\in B} |x|$
. Clearly, we have
$x_0=\inf_{x\in B} |x|$
. Clearly, we have
![]() $x_0\geq\inf_{x\in \overline{B}} |x|$
. Then, by Theorem 2.1, it follows that for
$x_0\geq\inf_{x\in \overline{B}} |x|$
. Then, by Theorem 2.1, it follows that for
![]() $\rho \in (0, 1)$
and
$\rho \in (0, 1)$
and
![]() $a_n ={\textrm{o}}(\sqrt{n})$
,
$a_n ={\textrm{o}}(\sqrt{n})$
,
 \begin{align*} \mathbb{P}\biggl(\dfrac{ M_{n_0,n} }{ a_n } \in B \biggr) &\leq \mathbb{P}( | M_{n_0,n}| \geq a_n x_0)\\ & \leq 2( 1-\Phi ( a_nx_0)) \exp\biggl\{ C_\rho \biggl( \dfrac{ ( a_nx_0)^{2+\rho} }{n^{\rho/2}} + \dfrac{ (1+a_nx_0)^{1-\rho(2+\rho)/4} }{n^{\rho(2-\rho)/8}} \biggr) \biggr\}.\end{align*}
\begin{align*} \mathbb{P}\biggl(\dfrac{ M_{n_0,n} }{ a_n } \in B \biggr) &\leq \mathbb{P}( | M_{n_0,n}| \geq a_n x_0)\\ & \leq 2( 1-\Phi ( a_nx_0)) \exp\biggl\{ C_\rho \biggl( \dfrac{ ( a_nx_0)^{2+\rho} }{n^{\rho/2}} + \dfrac{ (1+a_nx_0)^{1-\rho(2+\rho)/4} }{n^{\rho(2-\rho)/8}} \biggr) \biggr\}.\end{align*}
Using the inequalities
and the fact that
![]() $a_n \rightarrow \infty$
and
$a_n \rightarrow \infty$
and
![]() $a_n/\sqrt{n}\rightarrow 0$
, we obtain
$a_n/\sqrt{n}\rightarrow 0$
, we obtain
which gives (15).
Next we prove that
When
![]() $B^o =\emptyset$
, the last inequality is obvious, with
$B^o =\emptyset$
, the last inequality is obvious, with
![]() $ -\inf_{x \in \emptyset}{{x^2}/{2}}=-\infty$
. Thus we may assume that
$ -\inf_{x \in \emptyset}{{x^2}/{2}}=-\infty$
. Thus we may assume that
![]() $B^o \neq \emptyset$
. Since
$B^o \neq \emptyset$
. Since
![]() $B^o$
is an open set, for any given small
$B^o$
is an open set, for any given small
![]() $\varepsilon_1>0$
there exists an
$\varepsilon_1>0$
there exists an
![]() $x_0 \in B^o$
such that
$x_0 \in B^o$
such that
Again by the fact that
![]() $B^o$
is an open set, for
$B^o$
is an open set, for
![]() $x_0 \in B^o$
and all sufficiently small
$x_0 \in B^o$
and all sufficiently small
![]() $\varepsilon_2 \in (0, |x_0|] $
, we have
$\varepsilon_2 \in (0, |x_0|] $
, we have
![]() $(x_0-\varepsilon_2, x_0+\varepsilon_2] \subset B^o$
. Without loss of generality, we may assume that
$(x_0-\varepsilon_2, x_0+\varepsilon_2] \subset B^o$
. Without loss of generality, we may assume that
![]() $x_0>0$
. Clearly, we have
$x_0>0$
. Clearly, we have
 \begin{align}\mathbb{P}\biggl(\dfrac{M_{n_0,n} }{ a_n } \in B \biggr) &\geq \mathbb{P}( M_{n_0,n} \in (a_n ( x_0-\varepsilon_2), a_n( x_0+\varepsilon_2)] ) \notag \\&= \mathbb{P}( M_{n_0,n} \geq a_n ( x_0-\varepsilon_2) )-\mathbb{P}( M_{n_0,n} \geq a_n( x_0+\varepsilon_2) x). \end{align}
\begin{align}\mathbb{P}\biggl(\dfrac{M_{n_0,n} }{ a_n } \in B \biggr) &\geq \mathbb{P}( M_{n_0,n} \in (a_n ( x_0-\varepsilon_2), a_n( x_0+\varepsilon_2)] ) \notag \\&= \mathbb{P}( M_{n_0,n} \geq a_n ( x_0-\varepsilon_2) )-\mathbb{P}( M_{n_0,n} \geq a_n( x_0+\varepsilon_2) x). \end{align}
Again by Theorem 2.1, it is easy to see that for
![]() $a_n \rightarrow \infty$
and
$a_n \rightarrow \infty$
and
![]() $ a_n ={\textrm{o}}(\sqrt{n} )$
,
$ a_n ={\textrm{o}}(\sqrt{n} )$
,
From (18), by the last line and Theorem 2.1, for all n large enough and
![]() $a_n ={\textrm{o}}(\sqrt{n} )$
it holds that
$a_n ={\textrm{o}}(\sqrt{n} )$
it holds that
 \begin{align*}\mathbb{P}\biggl(\dfrac{M_{n_0,n} }{ a_n } \in B \biggr) & \geq \dfrac12 \mathbb{P}( M_{n_0,n} \geq a_n ( x_0-\varepsilon_2) ) \\& \geq \dfrac12 ( 1-\Phi ( a_n( x_0-\varepsilon_2))) \exp\biggl\{ -C_\rho \biggl( \dfrac{ ( a_nx_0)^{2+\rho} }{n^{\rho/2}} + \dfrac{ (1+a_nx_0)^{1-\rho(2+\rho)/4} }{n^{\rho(2-\rho)/8}} \biggr) \biggr\}.\end{align*}
\begin{align*}\mathbb{P}\biggl(\dfrac{M_{n_0,n} }{ a_n } \in B \biggr) & \geq \dfrac12 \mathbb{P}( M_{n_0,n} \geq a_n ( x_0-\varepsilon_2) ) \\& \geq \dfrac12 ( 1-\Phi ( a_n( x_0-\varepsilon_2))) \exp\biggl\{ -C_\rho \biggl( \dfrac{ ( a_nx_0)^{2+\rho} }{n^{\rho/2}} + \dfrac{ (1+a_nx_0)^{1-\rho(2+\rho)/4} }{n^{\rho(2-\rho)/8}} \biggr) \biggr\}.\end{align*}
Using (16) and the fact that
![]() $a_n \rightarrow \infty$
and
$a_n \rightarrow \infty$
and
![]() $a_n/\sqrt{n}\rightarrow 0$
, after some calculations we get
$a_n/\sqrt{n}\rightarrow 0$
, after some calculations we get
Letting
![]() $\varepsilon_2\rightarrow 0$
, we deduce that
$\varepsilon_2\rightarrow 0$
, we deduce that
Since
![]() $\varepsilon_1$
can be arbitrarily small, we get (17). Combining (15) and (17), we complete the proof of Corollary 2.1.
$\varepsilon_1$
can be arbitrarily small, we get (17). Combining (15) and (17), we complete the proof of Corollary 2.1.
6. Proof of Theorem 2.2
Recall the martingale differences
![]() $(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n }$
defined in the proof of Theorem 2.1. Then
$(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n }$
defined in the proof of Theorem 2.1. Then
![]() $\eta_k$
satisfies conditions (12) and (13) with
$\eta_k$
satisfies conditions (12) and (13) with
![]() $\delta_n=0$
and
$\delta_n=0$
and
Clearly, we have
![]() $H_{n_0,n}= \sum_{k=1}^{n} \eta_k$
. Applying Theorem 2.1 of Fan [Reference Fan5] to
$H_{n_0,n}= \sum_{k=1}^{n} \eta_k$
. Applying Theorem 2.1 of Fan [Reference Fan5] to
![]() $(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n}$
, we obtain the desired inequalities.
$(\eta_k, \mathcal{F}_{k})_{k=1,\ldots,n}$
, we obtain the desired inequalities.
Acknowledgements
The authors would like to thank the two referees for their helpful remarks and suggestions.
Funding information
The research is partially supported by the National Nature Science Foundation of China NSFC (grants 12031005 and 11971063) and Shenzhen Outstanding Talents Training Fund, China.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.