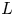1. Introduction
The investigation of relations between periods of automorphic forms and special values of ![]() $L$-functions is a main focus of research in number theory. The central special values are of keen interest in light of the Birch and Swinnerton-Dyer conjecture and its generalizations.
$L$-functions is a main focus of research in number theory. The central special values are of keen interest in light of the Birch and Swinnerton-Dyer conjecture and its generalizations.
Gross and Prasad [Reference Gross and PrasadGP92, Reference Gross and PrasadGP94] proclaimed a global conjecture relating non-vanishing of certain period integrals on special orthogonal groups to non-vanishing of central special values of certain tensor product ![]() $L$-functions, together with the local counterpart conjecture in the early 1990s. Later with Gan [Reference Gan, Gross and PrasadGGP12], they extended the conjecture to classical groups and metaplectic groups. Meanwhile a refinement of the Gross–Prasad conjecture, which is a precise formula for the central special values of the tensor product
$L$-functions, together with the local counterpart conjecture in the early 1990s. Later with Gan [Reference Gan, Gross and PrasadGGP12], they extended the conjecture to classical groups and metaplectic groups. Meanwhile a refinement of the Gross–Prasad conjecture, which is a precise formula for the central special values of the tensor product ![]() $L$-functions for tempered cuspidal automorphic representations, was formulated by Ichino and Ikeda [Reference Ichino and IkedaII10] in the co-dimension-one special orthogonal case. Subsequently Harris [Reference HarrisHar14] formulated a refinement of the Gan–Gross–Prasad conjecture in the co-dimension-one unitary case. Later an extension of the work of Ichino–Ikeda and Harris to the general Bessel period case was formulated by Liu [Reference LiuLiu16] and to the general Fourier–Jacobi period case for symplectic–metaplectic groups was formulated by Xue [Reference XueXue17].
$L$-functions for tempered cuspidal automorphic representations, was formulated by Ichino and Ikeda [Reference Ichino and IkedaII10] in the co-dimension-one special orthogonal case. Subsequently Harris [Reference HarrisHar14] formulated a refinement of the Gan–Gross–Prasad conjecture in the co-dimension-one unitary case. Later an extension of the work of Ichino–Ikeda and Harris to the general Bessel period case was formulated by Liu [Reference LiuLiu16] and to the general Fourier–Jacobi period case for symplectic–metaplectic groups was formulated by Xue [Reference XueXue17].
In [Reference Furusawa and MorimotoFM17] we investigated the Gross–Prasad conjecture for Bessel periods for ![]() $\mathrm {SO}(2n+1)\times \mathrm {SO}(2)$ when the character on
$\mathrm {SO}(2n+1)\times \mathrm {SO}(2)$ when the character on ![]() $\mathrm {SO}(2)$ is trivial, i.e. the special Bessel periods case and then, in the sequel [Reference Furusawa and MorimotoFM21], we proved its refinement, i.e. the Ichino–Ikeda-type precise
$\mathrm {SO}(2)$ is trivial, i.e. the special Bessel periods case and then, in the sequel [Reference Furusawa and MorimotoFM21], we proved its refinement, i.e. the Ichino–Ikeda-type precise ![]() $L$-value formula under the condition that the base field is totally real and all components at archimedean places are discrete series representations. As a corollary of our special value formula in [Reference Furusawa and MorimotoFM21], we obtained a proof of the long-standing conjecture by Böcherer in [Reference BöchererBöc86], concerning central critical values of imaginary quadratic twists of spinor
$L$-value formula under the condition that the base field is totally real and all components at archimedean places are discrete series representations. As a corollary of our special value formula in [Reference Furusawa and MorimotoFM21], we obtained a proof of the long-standing conjecture by Böcherer in [Reference BöchererBöc86], concerning central critical values of imaginary quadratic twists of spinor ![]() $L$-functions for holomorphic Siegel cusp forms of degree two which are Hecke eigenforms, thanks to the explicit calculations of the local integrals by Dickson, Pitale, Saha and Schmidt [Reference Dickson, Pitale, Saha and SchmidtDPSS20].
$L$-functions for holomorphic Siegel cusp forms of degree two which are Hecke eigenforms, thanks to the explicit calculations of the local integrals by Dickson, Pitale, Saha and Schmidt [Reference Dickson, Pitale, Saha and SchmidtDPSS20].
In this paper, for ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$, we vastly generalize the main results in [Reference Furusawa and MorimotoFM17, Reference Furusawa and MorimotoFM21]. Namely we prove the Gross–Prasad conjecture and its refinement for any Bessel period in the case of
$(\mathrm {SO}(5), \mathrm {SO}(2))$, we vastly generalize the main results in [Reference Furusawa and MorimotoFM17, Reference Furusawa and MorimotoFM21]. Namely we prove the Gross–Prasad conjecture and its refinement for any Bessel period in the case of ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$. As a corollary, we prove the generalized Böcherer conjecture in the square-free case formulated in [Reference Dickson, Pitale, Saha and SchmidtDPSS20].
$(\mathrm {SO}(5), \mathrm {SO}(2))$. As a corollary, we prove the generalized Böcherer conjecture in the square-free case formulated in [Reference Dickson, Pitale, Saha and SchmidtDPSS20].
Let us introduce some notation and then state our main results precisely.
1.1 Notation
Let ![]() $F$ be a number field. We denote its ring of adeles by
$F$ be a number field. We denote its ring of adeles by ![]() $\mathbb {A}_F$, which is mostly abbreviated as
$\mathbb {A}_F$, which is mostly abbreviated as ![]() $\mathbb {A}$ for simplicity. Let
$\mathbb {A}$ for simplicity. Let ![]() $\psi$ be a non-trivial character of
$\psi$ be a non-trivial character of ![]() $\mathbb {A} / F$. For
$\mathbb {A} / F$. For ![]() $a \in F^\times$, we denote by
$a \in F^\times$, we denote by ![]() $\psi ^a$ the character of
$\psi ^a$ the character of ![]() $\mathbb {A} / F$ defined by
$\mathbb {A} / F$ defined by ![]() $\psi ^a(x) = \psi (ax)$. For a place
$\psi ^a(x) = \psi (ax)$. For a place ![]() $v$ of
$v$ of ![]() $F$, we denote by
$F$, we denote by ![]() $F_v$ the completion of
$F_v$ the completion of ![]() $F$ at
$F$ at ![]() $v$. When
$v$. When ![]() $v$ is non-archimedean, we denote by
$v$ is non-archimedean, we denote by ![]() $\varpi _v$ and
$\varpi _v$ and ![]() $q_v$ a uniformizer of
$q_v$ a uniformizer of ![]() $F_v$ and the cardinality of the residue field of
$F_v$ and the cardinality of the residue field of ![]() $F_v$, respectively.
$F_v$, respectively.
Let ![]() $E$ be a quadratic extension of
$E$ be a quadratic extension of ![]() $F$ and
$F$ and ![]() $\mathbb {A}_E$ be its ring of adeles. We denote by
$\mathbb {A}_E$ be its ring of adeles. We denote by ![]() $x\mapsto x^\sigma$ the unique non-trivial automorphism of
$x\mapsto x^\sigma$ the unique non-trivial automorphism of ![]() $E$ over
$E$ over ![]() $F$. Let us denote by
$F$. Let us denote by ![]() $\mathrm {N}_{E / F}$ the norm map from
$\mathrm {N}_{E / F}$ the norm map from ![]() $E$ to
$E$ to ![]() $F$. We choose
$F$. We choose ![]() $\eta \in E^\times$ such that
$\eta \in E^\times$ such that ![]() $\eta ^\sigma =-\eta$ and fix. Let
$\eta ^\sigma =-\eta$ and fix. Let ![]() $d=\eta ^2$. We denote by
$d=\eta ^2$. We denote by ![]() $\chi _E$ the quadratic character of
$\chi _E$ the quadratic character of ![]() $\mathbb {A}^\times$ corresponding to the quadratic extension
$\mathbb {A}^\times$ corresponding to the quadratic extension ![]() $E / F$. We fix a character
$E / F$. We fix a character ![]() $\Lambda$ of
$\Lambda$ of ![]() $\mathbb {A}_E^\times / E^\times$ whose restriction to
$\mathbb {A}_E^\times / E^\times$ whose restriction to ![]() $\mathbb {A}^\times$ is trivial once and for all.
$\mathbb {A}^\times$ is trivial once and for all.
1.2 Measures
Throughout the paper, for an algebraic group ![]() $\mathbf {G}$ defined over
$\mathbf {G}$ defined over ![]() $F$, we let
$F$, we let ![]() $\mathbf {G}_v$ denote
$\mathbf {G}_v$ denote ![]() $\mathbf {G}(F_v)$, the group of rational points of
$\mathbf {G}(F_v)$, the group of rational points of ![]() $\mathbf {G}$ over
$\mathbf {G}$ over ![]() $F_v$, and we always take the measure
$F_v$, and we always take the measure ![]() $dg$ on
$dg$ on ![]() $\mathbf {G}(\mathbb {A})$ to be the Tamagawa measure unless specified otherwise. For each
$\mathbf {G}(\mathbb {A})$ to be the Tamagawa measure unless specified otherwise. For each ![]() $v$, we take the self-dual measure with respect to
$v$, we take the self-dual measure with respect to ![]() $\psi _v$ on
$\psi _v$ on ![]() $F_v$. Then recall that the product measure on
$F_v$. Then recall that the product measure on ![]() $\mathbb {A}$ is the self-dual measure with respect to
$\mathbb {A}$ is the self-dual measure with respect to ![]() $\psi$ and is also the Tamagawa measure since
$\psi$ and is also the Tamagawa measure since ![]() $\mathrm {Vol}(\mathbb {A}/ F)=1$. For a unipotent algebraic group
$\mathrm {Vol}(\mathbb {A}/ F)=1$. For a unipotent algebraic group ![]() $\mathbf {U}$ defined over
$\mathbf {U}$ defined over ![]() $F$, we also specify the local measure
$F$, we also specify the local measure ![]() $du_v$ on
$du_v$ on ![]() $\mathbf {U}(F_v)$ to be the measure corresponding to the gauge form defined over
$\mathbf {U}(F_v)$ to be the measure corresponding to the gauge form defined over ![]() $F$, together with our choice of the measure on
$F$, together with our choice of the measure on ![]() $F_v$, at each place
$F_v$, at each place ![]() $v$ of
$v$ of ![]() $F$. Thus, in particular, we have
$F$. Thus, in particular, we have
1.3 Similitudes
Various similitude groups appear in this article. Where there is no risk of confusion, we denote by ![]() $\lambda (g)$ the similitude of an element
$\lambda (g)$ the similitude of an element ![]() $g$ of a similitude group for simplicity.
$g$ of a similitude group for simplicity.
1.4 Bessel periods
First we recall that when ![]() $V$ is a five-dimensional vector space over
$V$ is a five-dimensional vector space over ![]() $F$ equipped with a non-degenerate symmetric bilinear form whose Witt index is at least one, there exists a quaternion algebra
$F$ equipped with a non-degenerate symmetric bilinear form whose Witt index is at least one, there exists a quaternion algebra ![]() $D$ over
$D$ over ![]() $F$ such that
$F$ such that
where ![]() $\mathbb {G}_D=G_D/ Z_D$,
$\mathbb {G}_D=G_D/ Z_D$, ![]() $G_D$ is a similitude quaternionic unitary group over
$G_D$ is a similitude quaternionic unitary group over ![]() $F$ defined by
$F$ defined by
and ![]() $Z_D$ is the center of
$Z_D$ is the center of ![]() $G_D$. Here
$G_D$. Here
where denoted by ![]() $x\mapsto \overline {x}$ for
$x\mapsto \overline {x}$ for ![]() $x\in D$ is the canonical involution of
$x\in D$ is the canonical involution of ![]() $D$. In addition, we define a quaternionic unitary group
$D$. In addition, we define a quaternionic unitary group ![]() $G_D^1$ over
$G_D^1$ over ![]() $F$ by
$F$ by
Let
where ![]() $\mathrm {tr}_D$ denotes the reduced trace of
$\mathrm {tr}_D$ denotes the reduced trace of ![]() $D$ over
$D$ over ![]() $F$. We recall that when
$F$. We recall that when ![]() $D\simeq \mathrm {Mat}_{2\times 2}(F)$,
$D\simeq \mathrm {Mat}_{2\times 2}(F)$, ![]() $G_D$ is isomorphic to the similitude symplectic group
$G_D$ is isomorphic to the similitude symplectic group ![]() $\mathrm {GSp}_2$ which we denote by
$\mathrm {GSp}_2$ which we denote by ![]() $G$, i.e.
$G$, i.e.
In addition, we define the symplectic group ![]() $\mathrm {Sp}_2$, which we denote by
$\mathrm {Sp}_2$, which we denote by ![]() $G^1$, as
$G^1$, as
We let ![]() $\mathrm {PGSp}_2 = G / Z_G$ by
$\mathrm {PGSp}_2 = G / Z_G$ by ![]() $\mathbb {G}$, where
$\mathbb {G}$, where ![]() $Z_G$ denotes the center of
$Z_G$ denotes the center of ![]() $G$. Thus, when
$G$. Thus, when ![]() $D$ is split,
$D$ is split, ![]() $G_D\simeq G=\mathrm {GSp}_2$,
$G_D\simeq G=\mathrm {GSp}_2$, ![]() $G_D^1 \simeq G^1 = \mathrm {Sp}_2$ and
$G_D^1 \simeq G^1 = \mathrm {Sp}_2$ and ![]() $\mathbb {G}_D\simeq \mathbb {G}=\mathrm {PGSp}_2$.
$\mathbb {G}_D\simeq \mathbb {G}=\mathrm {PGSp}_2$.
The Siegel parabolic subgroup ![]() $P_D$ of
$P_D$ of ![]() $G_D$ has the Levi decomposition
$G_D$ has the Levi decomposition ![]() $P_D = M_{D} N_{D}$ where
$P_D = M_{D} N_{D}$ where
For ![]() $\xi \in D^-(F)$, let us define a character
$\xi \in D^-(F)$, let us define a character ![]() $\psi _\xi$ on
$\psi _\xi$ on ![]() $N_D(\mathbb {A})$ by
$N_D(\mathbb {A})$ by
We note that for ![]() $\big (\begin{smallmatrix}x & 0\\0 & \mu \cdot x\end{smallmatrix}\big )\in M_D(F)$, we have
$\big (\begin{smallmatrix}x & 0\\0 & \mu \cdot x\end{smallmatrix}\big )\in M_D(F)$, we have
Suppose that ![]() $F(\xi )\simeq E$. Let us define a subgroup
$F(\xi )\simeq E$. Let us define a subgroup ![]() $T_\xi$ of
$T_\xi$ of ![]() $D^\times$ by
$D^\times$ by
Then since ![]() $F(\xi )$ is a maximal commutative subfield of
$F(\xi )$ is a maximal commutative subfield of ![]() $D$, we have
$D$, we have
We identify ![]() $T_\xi$ with the subgroup of
$T_\xi$ with the subgroup of ![]() $M_D$ given by
$M_D$ given by
We note that by (1.4.5), we have
We define the Bessel subgroup ![]() $R_{\xi }$ of
$R_{\xi }$ of ![]() $G_D$ by
$G_D$ by
Then the Bessel periods defined below are indeed the periods in question in the Gross–Prasad conjecture for ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$.
$(\mathrm {SO}(5), \mathrm {SO}(2))$.
Definition 1.1 Let ![]() $\pi$ be an irreducible cuspidal automorphic representation of
$\pi$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ whose central character is trivial and
$G_D(\mathbb {A})$ whose central character is trivial and ![]() $V_\pi$ its space of automorphic forms. Let
$V_\pi$ its space of automorphic forms. Let ![]() $\Lambda$ be a character of
$\Lambda$ be a character of ![]() $\mathbb {A}_E^\times / E^\times$ whose restriction to
$\mathbb {A}_E^\times / E^\times$ whose restriction to ![]() $\mathbb {A}^\times$ is trivial. Let
$\mathbb {A}^\times$ is trivial. Let ![]() $\xi \in D^-(F)$ such that
$\xi \in D^-(F)$ such that ![]() $F(\xi )\simeq E$. Fix an
$F(\xi )\simeq E$. Fix an ![]() $F$-isomorphism
$F$-isomorphism ![]() $T_\xi \simeq E^\times$ and regard
$T_\xi \simeq E^\times$ and regard ![]() $\Lambda$ as a character of
$\Lambda$ as a character of ![]() $T_\xi (\mathbb {A}) / T_\xi (F)$. We define a character
$T_\xi (\mathbb {A}) / T_\xi (F)$. We define a character ![]() $\chi ^{\xi,\Lambda }$ on
$\chi ^{\xi,\Lambda }$ on ![]() $R_\xi (\mathbb {A})$ by
$R_\xi (\mathbb {A})$ by
Then for ![]() $f\in V_\pi$, we define
$f\in V_\pi$, we define ![]() $B_{\xi, \Lambda,\psi }(f)$, the
$B_{\xi, \Lambda,\psi }(f)$, the ![]() $(\xi, \Lambda,\psi )$-Bessel period of
$(\xi, \Lambda,\psi )$-Bessel period of ![]() $f$, by
$f$, by
We say that ![]() $\pi$ has the
$\pi$ has the ![]() $(\xi, \Lambda, \psi )$-Bessel period when the linear form
$(\xi, \Lambda, \psi )$-Bessel period when the linear form ![]() $B_{\xi,\Lambda, \psi }$ is not identically zero on
$B_{\xi,\Lambda, \psi }$ is not identically zero on ![]() $V_\pi$.
$V_\pi$.
Remark 1.1 Here we record the dependency of ![]() $B_{\xi,\Lambda,\psi }$ on the choices of
$B_{\xi,\Lambda,\psi }$ on the choices of ![]() $\xi$ and
$\xi$ and ![]() $\psi$. First we note that for
$\psi$. First we note that for ![]() $\xi ^\prime \in D^-(F)$, we have
$\xi ^\prime \in D^-(F)$, we have ![]() $F(\xi ^\prime )\simeq E$ if and only if
$F(\xi ^\prime )\simeq E$ if and only if
by the Skolem–Noether theorem. Suppose that ![]() $\xi ^\prime \in D^-(F)$ satisfies (1.4.12) and
$\xi ^\prime \in D^-(F)$ satisfies (1.4.12) and ![]() $\psi ^\prime =\psi ^a$ where
$\psi ^\prime =\psi ^a$ where ![]() $a\in F^\times$. Let
$a\in F^\times$. Let ![]() $m_0=\big (\begin{smallmatrix}\alpha & 0\\ 0 & a^{-1}\mu \cdot \alpha \end{smallmatrix}\big ) \in M_D(F)$. Then by (1.4.5), we have
$m_0=\big (\begin{smallmatrix}\alpha & 0\\ 0 & a^{-1}\mu \cdot \alpha \end{smallmatrix}\big ) \in M_D(F)$. Then by (1.4.5), we have
 \begin{align} B_{\xi, \Lambda, \psi}(\pi(m_0)f) &= \int_{\mathbb{A}^\times T_{\xi^\prime}(F) \backslash T_{\xi^\prime}(\mathbb{A})}\int_{N_D(F)\backslash N_D(\mathbb{A})} f(t^\prime n^\prime)\Lambda(t^{\prime})^{-1} \psi^\prime_{\xi^\prime}(n^\prime)\, dt^\prime\, dn^\prime \nonumber\\ &= B_{\xi^\prime,\Lambda, \psi^\prime}(f) , \end{align}
\begin{align} B_{\xi, \Lambda, \psi}(\pi(m_0)f) &= \int_{\mathbb{A}^\times T_{\xi^\prime}(F) \backslash T_{\xi^\prime}(\mathbb{A})}\int_{N_D(F)\backslash N_D(\mathbb{A})} f(t^\prime n^\prime)\Lambda(t^{\prime})^{-1} \psi^\prime_{\xi^\prime}(n^\prime)\, dt^\prime\, dn^\prime \nonumber\\ &= B_{\xi^\prime,\Lambda, \psi^\prime}(f) , \end{align}
where we identify ![]() $T_{\xi ^\prime }(F)$ with
$T_{\xi ^\prime }(F)$ with ![]() $E^\times$ via the
$E^\times$ via the ![]() $F$-isomorphism
$F$-isomorphism ![]() $F(\xi ^\prime )\ni x\mapsto \alpha x\alpha ^{-1}\in F(\xi ) \simeq E$.
$F(\xi ^\prime )\ni x\mapsto \alpha x\alpha ^{-1}\in F(\xi ) \simeq E$.
Definition 1.2 Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ whose central character is trivial. Let
$G_D(\mathbb {A})$ whose central character is trivial. Let ![]() $\Lambda$ be a character of
$\Lambda$ be a character of ![]() $\mathbb {A}_E^\times / E^\times$ whose restriction to
$\mathbb {A}_E^\times / E^\times$ whose restriction to ![]() $\mathbb {A}^\times$ is trivial. Then we say that
$\mathbb {A}^\times$ is trivial. Then we say that ![]() $\pi$ has the
$\pi$ has the ![]() $(E,\Lambda )$-Bessel period if there exist
$(E,\Lambda )$-Bessel period if there exist ![]() $\xi \in D^-(F)$ such that
$\xi \in D^-(F)$ such that ![]() $F(\xi )\simeq E$ and a non-trivial character
$F(\xi )\simeq E$ and a non-trivial character ![]() $\psi$ of
$\psi$ of ![]() $\mathbb {A}/ F$ so that
$\mathbb {A}/ F$ so that ![]() $\pi$ has the
$\pi$ has the ![]() $(\xi,\Lambda,\psi )$-Bessel period. This terminology is well-defined because of the relation (1.4.13).
$(\xi,\Lambda,\psi )$-Bessel period. This terminology is well-defined because of the relation (1.4.13).
1.5 Gross–Prasad conjecture
First we introduce the following definition which is inspired by the notion of local ![]() $G$-equivalence in Hiraga and Saito [Reference Hiraga and SaitoHS12, p. 23].
$G$-equivalence in Hiraga and Saito [Reference Hiraga and SaitoHS12, p. 23].
Definition 1.3 Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ whose central character is trivial. Let
$G_D(\mathbb {A})$ whose central character is trivial. Let ![]() $D^\prime$ be a quaternion algebra over
$D^\prime$ be a quaternion algebra over ![]() $F$ and
$F$ and ![]() $(\pi ^\prime, V_{\pi ^\prime })$ an irreducible cuspidal automorphic representation of
$(\pi ^\prime, V_{\pi ^\prime })$ an irreducible cuspidal automorphic representation of ![]() $G_{D^\prime }(\mathbb {A})$. Then we say that
$G_{D^\prime }(\mathbb {A})$. Then we say that ![]() $\pi$ is locally
$\pi$ is locally ![]() $G^+$-equivalent to
$G^+$-equivalent to ![]() $\pi ^\prime$ if at almost all places
$\pi ^\prime$ if at almost all places ![]() $v$ of
$v$ of ![]() $F$ where
$F$ where ![]() $D(F_v)\simeq D^\prime (F_v)$, there exists a character
$D(F_v)\simeq D^\prime (F_v)$, there exists a character ![]() $\chi _v$ of
$\chi _v$ of ![]() $G_D(F_v) / G_D(F_v)^+$ such that
$G_D(F_v) / G_D(F_v)^+$ such that ![]() $\pi _v \otimes \chi _v \simeq \pi _v^\prime$. Here
$\pi _v \otimes \chi _v \simeq \pi _v^\prime$. Here
Remark 1.2 When ![]() $\pi$ and
$\pi$ and ![]() $\pi ^\prime$ have weak functorial lifts to
$\pi ^\prime$ have weak functorial lifts to ![]() $\mathrm {GL}_4(\mathbb {A})$, say
$\mathrm {GL}_4(\mathbb {A})$, say ![]() $\Pi$ and
$\Pi$ and ![]() $\Pi ^\prime$, respectively, the notion of local
$\Pi ^\prime$, respectively, the notion of local ![]() $G^+$-equivalence is described simply as the following. Suppose that
$G^+$-equivalence is described simply as the following. Suppose that ![]() $\pi$ and
$\pi$ and ![]() $\pi ^\prime$ are locally
$\pi ^\prime$ are locally ![]() $G^+$-equivalent. Then there exists a character
$G^+$-equivalent. Then there exists a character ![]() $\omega$ of
$\omega$ of ![]() $G_D(\mathbb {A})$ such that
$G_D(\mathbb {A})$ such that ![]() $\pi \otimes \omega$ is nearly equivalent to
$\pi \otimes \omega$ is nearly equivalent to ![]() $\pi ^\prime$, where
$\pi ^\prime$, where ![]() $\omega$ may not be automorphic. Since
$\omega$ may not be automorphic. Since ![]() $\omega _v$ is either
$\omega _v$ is either ![]() $\chi _{E_v}$ or trivial at almost all places
$\chi _{E_v}$ or trivial at almost all places ![]() $v$ of
$v$ of ![]() $F$, we have
$F$, we have ![]() $\mathrm {BC}_{E/ F}(\Pi )\simeq \mathrm {BC}_{E/ F}(\Pi ^\prime )$ where
$\mathrm {BC}_{E/ F}(\Pi )\simeq \mathrm {BC}_{E/ F}(\Pi ^\prime )$ where ![]() $\mathrm {BC}_{E/ F}$ denotes the base change lift to
$\mathrm {BC}_{E/ F}$ denotes the base change lift to ![]() $\mathrm {GL}_4(\mathbb {A}_E)$. Then by a result of Arthur and Clozel [Reference Arthur and ClozelAC89, Theorem 3.1], we have
$\mathrm {GL}_4(\mathbb {A}_E)$. Then by a result of Arthur and Clozel [Reference Arthur and ClozelAC89, Theorem 3.1], we have ![]() $\Pi \simeq \Pi ^\prime$ or
$\Pi \simeq \Pi ^\prime$ or ![]() $\Pi ^\prime \otimes \chi _E$. Hence,
$\Pi ^\prime \otimes \chi _E$. Hence, ![]() $\pi$ is nearly equivalent to either
$\pi$ is nearly equivalent to either ![]() $\pi ^\prime$ or
$\pi ^\prime$ or ![]() $\pi ^\prime \otimes \chi _E$. The converse is clear.
$\pi ^\prime \otimes \chi _E$. The converse is clear.
Then our first main result is on the Gross–Prasad conjecture for ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$.
$(\mathrm {SO}(5), \mathrm {SO}(2))$.
Theorem 1.1 Let ![]() $E$ be a quadratic extension of
$E$ be a quadratic extension of ![]() $F$. Let
$F$. Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character and
$G_D(\mathbb {A})$ with a trivial central character and ![]() $\Lambda$ a character of
$\Lambda$ a character of ![]() $\mathbb {A}_E^\times / E^\times$ whose restriction to
$\mathbb {A}_E^\times / E^\times$ whose restriction to ![]() $\mathbb {A}^\times$ is trivial.
$\mathbb {A}^\times$ is trivial.
(i) Suppose that
 $\pi$ has the
$\pi$ has the  $(E,\Lambda )$-Bessel period. Moreover, assume that:
(1.5.2)Here
$(E,\Lambda )$-Bessel period. Moreover, assume that:
(1.5.2)Here \begin{align} & \text{there exists a finite place $w$ of $F$ such that} \nonumber\\ &\qquad\qquad\qquad\qquad \text{$\pi_w$ and its local theta lift to $\mathrm{GSO}_{4,2}(F_w)$ are generic.} \end{align}
\begin{align} & \text{there exists a finite place $w$ of $F$ such that} \nonumber\\ &\qquad\qquad\qquad\qquad \text{$\pi_w$ and its local theta lift to $\mathrm{GSO}_{4,2}(F_w)$ are generic.} \end{align} $\mathrm {GSO}_{4,2}$ denotes the identity component of
$\mathrm {GSO}_{4,2}$ denotes the identity component of  $\mathrm {GO}_{4,2}$, the similitude orthogonal group associated to the six-dimensional orthogonal space
$\mathrm {GO}_{4,2}$, the similitude orthogonal group associated to the six-dimensional orthogonal space  $(E, \mathrm {N}_{E / F}) \oplus \mathbb {H}^2$ over
$(E, \mathrm {N}_{E / F}) \oplus \mathbb {H}^2$ over  $F$ where
$F$ where  $\mathbb {H}$ denotes the hyperbolic plane over
$\mathbb {H}$ denotes the hyperbolic plane over  $F$.
$F$.
Then there exists a finite set
 $S_0$ of places of
$S_0$ of places of  $F$ containing all archimedean places of
$F$ containing all archimedean places of  $F$ such that the partial
$F$ such that the partial  $L$-function
(1.5.3)for any finite set
$L$-function
(1.5.3)for any finite set \begin{equation} L^S \big(\tfrac{1}{2}, \pi \times \mathcal{AI} (\Lambda)\big) \ne 0 \end{equation}
\begin{equation} L^S \big(\tfrac{1}{2}, \pi \times \mathcal{AI} (\Lambda)\big) \ne 0 \end{equation} $S$ of places of
$S$ of places of  $F$ with
$F$ with  $S\supset S_0$. Here,
$S\supset S_0$. Here,  $\mathcal {AI}(\Lambda )$ denotes the automorphic induction of
$\mathcal {AI}(\Lambda )$ denotes the automorphic induction of  $\Lambda$ from
$\Lambda$ from  $\mathrm {GL}_1(\mathbb {A}_E)$ to
$\mathrm {GL}_1(\mathbb {A}_E)$ to  $\mathrm {GL}_2(\mathbb {A})$. Moreover, there exists a globally generic irreducible cuspidal automorphic representation
$\mathrm {GL}_2(\mathbb {A})$. Moreover, there exists a globally generic irreducible cuspidal automorphic representation  $\pi ^\circ$ of
$\pi ^\circ$ of  $G(\mathbb {A})$ which is locally
$G(\mathbb {A})$ which is locally  $G^+$-equivalent to
$G^+$-equivalent to  $\pi$.
$\pi$.(ii) Assume that:
(1.5.4)Here \begin{align} & \text{the endoscopic classification of Arthur,} \nonumber\\ &\qquad\qquad\quad \text{i.e. [Art13, Conjectures~9.4.2, 9.5.4] holds for $\mathbb{G}_{D_\circ}$.} \end{align}
\begin{align} & \text{the endoscopic classification of Arthur,} \nonumber\\ &\qquad\qquad\quad \text{i.e. [Art13, Conjectures~9.4.2, 9.5.4] holds for $\mathbb{G}_{D_\circ}$.} \end{align} $D_\circ$ denotes an arbitrary quaternion algebra over
$D_\circ$ denotes an arbitrary quaternion algebra over  $F$.
$F$.
Suppose that
 $\pi$ has a generic Arthur parameter, namely the parameter is of the form
$\pi$ has a generic Arthur parameter, namely the parameter is of the form  $\Pi _0$ or
$\Pi _0$ or  $\Pi _1 \boxplus \Pi _2$ where
$\Pi _1 \boxplus \Pi _2$ where  $\Pi _i$ is an irreducible cuspidal automorphic representation of
$\Pi _i$ is an irreducible cuspidal automorphic representation of  $\mathrm {GL}_4(\mathbb {A})$ for
$\mathrm {GL}_4(\mathbb {A})$ for  $i=0$ and of
$i=0$ and of  $\mathrm {GL}_2(\mathbb {A})$ for
$\mathrm {GL}_2(\mathbb {A})$ for  $i=1,2$, respectively, such that
$i=1,2$, respectively, such that  $L(s, \Pi _i, \wedge ^2)$ has a pole at
$L(s, \Pi _i, \wedge ^2)$ has a pole at  $s=1$.
$s=1$.Then we have
(1.5.5)if and only if there exists a pair \begin{equation} L \big(\tfrac{1}{2}, \pi \times \mathcal{AI} (\Lambda)\big) \ne 0 \end{equation}
\begin{equation} L \big(\tfrac{1}{2}, \pi \times \mathcal{AI} (\Lambda)\big) \ne 0 \end{equation} $(D^\prime, \pi ^\prime )$ where
$(D^\prime, \pi ^\prime )$ where  $D^\prime$ is a quaternion algebra over
$D^\prime$ is a quaternion algebra over  $F$ containing
$F$ containing  $E$ and
$E$ and  $\pi ^\prime$ an irreducible cuspidal automorphic representation of
$\pi ^\prime$ an irreducible cuspidal automorphic representation of  $G_{D^\prime }$ which is nearly equivalent to
$G_{D^\prime }$ which is nearly equivalent to  $\pi$ such that
$\pi$ such that  $\pi ^\prime$ has the
$\pi ^\prime$ has the  $(E,\Lambda )$-Bessel period.
$(E,\Lambda )$-Bessel period.
Moreover, when
 $\pi$ is tempered, the pair
$\pi$ is tempered, the pair  $(D^\prime, \pi ^\prime )$ is uniquely determined.
$(D^\prime, \pi ^\prime )$ is uniquely determined.
Remark 1.3 In (1.5.5), ![]() $L (s, \pi \times \mathcal {AI} (\Lambda ))$ denotes the complete
$L (s, \pi \times \mathcal {AI} (\Lambda ))$ denotes the complete ![]() $L$-function defined as the following.
$L$-function defined as the following.
When ![]() $\mathcal {AI} (\Lambda )$ is not cuspidal, i.e.
$\mathcal {AI} (\Lambda )$ is not cuspidal, i.e. ![]() $\Lambda =\Lambda _0 \circ \mathrm {N}_{E / F}$ for a character
$\Lambda =\Lambda _0 \circ \mathrm {N}_{E / F}$ for a character ![]() $\Lambda _0$ of
$\Lambda _0$ of ![]() $\mathbb {A}^\times / F^\times$, we define
$\mathbb {A}^\times / F^\times$, we define
where each factor on the right-hand side is defined by the doubling method as in Lapid and Rallis [Reference Lapid and RallisLR05] or Yamana [Reference YamanaYam14].
When ![]() $\mathcal {AI} (\Lambda )$ is cuspidal, the partial
$\mathcal {AI} (\Lambda )$ is cuspidal, the partial ![]() $L$-function
$L$-function ![]() $L^S(s,\pi \times \mathcal {AI}(\Lambda ))$ may be defined by Theorem C.1 in Appendix C for a finite set
$L^S(s,\pi \times \mathcal {AI}(\Lambda ))$ may be defined by Theorem C.1 in Appendix C for a finite set ![]() $S$ of places of
$S$ of places of ![]() $F$ such that
$F$ such that ![]() $\pi _v$ and
$\pi _v$ and ![]() $\Pi (\Lambda )_v$ are unramified at
$\Pi (\Lambda )_v$ are unramified at ![]() $v \not \in S$. Further, we define the local
$v \not \in S$. Further, we define the local ![]() $L$-factor at each place
$L$-factor at each place ![]() $v \in S$ by the local Langlands parameters for
$v \in S$ by the local Langlands parameters for ![]() $\pi _v$ and
$\pi _v$ and ![]() $\Pi (\Lambda )_v$, where the local Langlands parameters are given by Gan and Takeda [Reference Gan and TakedaGT11a] for
$\Pi (\Lambda )_v$, where the local Langlands parameters are given by Gan and Takeda [Reference Gan and TakedaGT11a] for ![]() $\mathbb {G}(F_v)$ (also Arthur [Reference ArthurArt13]), Gan and Tantono [Reference Gan and TantonoGT14] for
$\mathbb {G}(F_v)$ (also Arthur [Reference ArthurArt13]), Gan and Tantono [Reference Gan and TantonoGT14] for ![]() $\mathbb {G}_D(F_v)$, Kutzko [Reference KutzkoKut80] for
$\mathbb {G}_D(F_v)$, Kutzko [Reference KutzkoKut80] for ![]() $\mathrm {GL}_2(F_v)$ at finite places and by Langlands [Reference LanglandsLan89] at archimedean places.
$\mathrm {GL}_2(F_v)$ at finite places and by Langlands [Reference LanglandsLan89] at archimedean places.
We note that the condition (1.5.3) and the condition (1.5.5) are equivalent from the definition of local ![]() $L$-factors when
$L$-factors when ![]() $\pi$ is tempered.
$\pi$ is tempered.
Remark 1.4 Suppose that at a finite place ![]() $w$ of
$w$ of ![]() $F$, the group
$F$, the group ![]() $G_D(F_w)$ is split and the representation
$G_D(F_w)$ is split and the representation ![]() $\pi _w$ is generic and tempered. Then by Gan and Ichino [Reference Gan and IchinoGI14, Proposition C.4], the big theta lift of
$\pi _w$ is generic and tempered. Then by Gan and Ichino [Reference Gan and IchinoGI14, Proposition C.4], the big theta lift of ![]() $\pi _w$ and the local theta lift of
$\pi _w$ and the local theta lift of ![]() $\pi _w$ coincide. Thus, the genericity of the local theta lift of
$\pi _w$ coincide. Thus, the genericity of the local theta lift of ![]() $\pi _w$ follows from Gan and Takeda [Reference Gan and TakedaGT11b, Corollary 4.4] for the dual pair
$\pi _w$ follows from Gan and Takeda [Reference Gan and TakedaGT11b, Corollary 4.4] for the dual pair ![]() $(G, \mathrm {GSO}_{3,3})$ and from a local analogue of the computations in [Reference MorimotoMor14a, § 3.1] for the dual pair
$(G, \mathrm {GSO}_{3,3})$ and from a local analogue of the computations in [Reference MorimotoMor14a, § 3.1] for the dual pair ![]() $(G^+,\mathrm {GSO}_{4,2})$, respectively. Here
$(G^+,\mathrm {GSO}_{4,2})$, respectively. Here
When a local representation ![]() $\pi _w$ is unramified and tempered,
$\pi _w$ is unramified and tempered, ![]() $\pi _w$ is generic as remarked in [Reference Furusawa and MorimotoFM17, Remark 2]. Hence, the assumption (1.5.2) is fulfilled when
$\pi _w$ is generic as remarked in [Reference Furusawa and MorimotoFM17, Remark 2]. Hence, the assumption (1.5.2) is fulfilled when ![]() $\pi$ is tempered.
$\pi$ is tempered.
In our previous paper [Reference Furusawa and MorimotoFM17], Theorem 1.1 for the pair ![]() $(\mathrm {SO}(2n+1),\mathrm {SO}(2))$ was proved when
$(\mathrm {SO}(2n+1),\mathrm {SO}(2))$ was proved when ![]() $\Lambda$ is trivial. Meanwhile Jiang and Zhang [Reference Jiang and ZhangJZ20] studied the Gross–Prasad conjecture in a very general setting assuming the endoscopic classification of Arthur, in general, by using the twisted automorphic descent. Though Theorem 1.1 is subsumed in [Reference Jiang and ZhangJZ20] as a special case, we believe that our method, which is different from theirs, has its own merits because of its concreteness. We also note that because of the temperedness of
$\Lambda$ is trivial. Meanwhile Jiang and Zhang [Reference Jiang and ZhangJZ20] studied the Gross–Prasad conjecture in a very general setting assuming the endoscopic classification of Arthur, in general, by using the twisted automorphic descent. Though Theorem 1.1 is subsumed in [Reference Jiang and ZhangJZ20] as a special case, we believe that our method, which is different from theirs, has its own merits because of its concreteness. We also note that because of the temperedness of ![]() $\pi$, the uniqueness of the pair
$\pi$, the uniqueness of the pair ![]() $(D^\prime,\pi ^\prime )$ in Theorem 1.1(ii) follows from the local Gan–Gross–Prasad conjecture for
$(D^\prime,\pi ^\prime )$ in Theorem 1.1(ii) follows from the local Gan–Gross–Prasad conjecture for ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$ by Prasad and Takloo-Bighash [Reference Prasad and Takloo-BighashPT11, Theorem 2] (see also Waldspurger [Reference WaldspurgerWal85] in the general case) at finite places and by Luo [Reference LuoLuo20] at archimedean places. We shall give another proof of this uniqueness by reducing it to a similar assertion in the unitary group case.
$(\mathrm {SO}(5), \mathrm {SO}(2))$ by Prasad and Takloo-Bighash [Reference Prasad and Takloo-BighashPT11, Theorem 2] (see also Waldspurger [Reference WaldspurgerWal85] in the general case) at finite places and by Luo [Reference LuoLuo20] at archimedean places. We shall give another proof of this uniqueness by reducing it to a similar assertion in the unitary group case.
1.6 Refined Gross–Prasad conjecture
Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of ![]() $G_D(\mathbb {A})$ with trivial central character. For
$G_D(\mathbb {A})$ with trivial central character. For ![]() $\phi _1, \phi _2 \in V_{\pi }$, we define the Petersson inner product
$\phi _1, \phi _2 \in V_{\pi }$, we define the Petersson inner product ![]() $(\phi _1,\phi _2)_{\pi }$ on
$(\phi _1,\phi _2)_{\pi }$ on ![]() $V_\pi$ by
$V_\pi$ by
where ![]() $dg$ denotes the Tamagawa measure. Then at each place
$dg$ denotes the Tamagawa measure. Then at each place ![]() $v$ of
$v$ of ![]() $F$, we take a
$F$, we take a ![]() $G_D(F_v)$-invariant hermitian inner product on
$G_D(F_v)$-invariant hermitian inner product on ![]() $V_{\pi _v}$ so that we have a decomposition
$V_{\pi _v}$ so that we have a decomposition ![]() $(\,{,}\,)_\pi =\prod _v(\,{,}\,)_{\pi _v}$. In the definition of the Bessel period (1.4.11), we take
$(\,{,}\,)_\pi =\prod _v(\,{,}\,)_{\pi _v}$. In the definition of the Bessel period (1.4.11), we take ![]() $dr=dt\,du$ where
$dr=dt\,du$ where ![]() $dt$ and
$dt$ and ![]() $du$ are the Tamagawa measures on
$du$ are the Tamagawa measures on ![]() $T_\xi (\mathbb {A})$ and
$T_\xi (\mathbb {A})$ and ![]() $N_D(\mathbb {Z})$, respectively. We take and fix the local measures
$N_D(\mathbb {Z})$, respectively. We take and fix the local measures ![]() $du_v$ and
$du_v$ and ![]() $dt_v$ so that
$dt_v$ so that ![]() $du=\prod _v du_v$ and
$du=\prod _v du_v$ and
where ![]() $C_\xi$ is a constant called the Haar measure constant in [Reference Ichino and IkedaII10]. Then the local Bessel period
$C_\xi$ is a constant called the Haar measure constant in [Reference Ichino and IkedaII10]. Then the local Bessel period ![]() $\alpha ^{\xi,\Lambda }_v:V_{\pi _v}\times V_{\pi _v}\to \mathbb {C}$ and the local hermitian inner product
$\alpha ^{\xi,\Lambda }_v:V_{\pi _v}\times V_{\pi _v}\to \mathbb {C}$ and the local hermitian inner product ![]() $(\,{,}\,)_{\pi _v}$ are defined as in § 2.4.
$(\,{,}\,)_{\pi _v}$ are defined as in § 2.4.
Suppose that ![]() $D$ is not split. Then by Li [Reference LiLi92], there exists a pair
$D$ is not split. Then by Li [Reference LiLi92], there exists a pair ![]() $(\xi ^\prime, \Lambda ^\prime )$ such that
$(\xi ^\prime, \Lambda ^\prime )$ such that ![]() $\pi$ has the
$\pi$ has the ![]() $(\xi ^\prime,\Lambda ^\prime, \psi )$-Bessel period. Here
$(\xi ^\prime,\Lambda ^\prime, \psi )$-Bessel period. Here ![]() $\xi ^\prime \in D^-(F)$ such that
$\xi ^\prime \in D^-(F)$ such that ![]() $E^\prime :=F(\xi ^\prime )$ is a quadratic extension of
$E^\prime :=F(\xi ^\prime )$ is a quadratic extension of ![]() $F$ and
$F$ and ![]() $\Lambda ^\prime$ is a character on
$\Lambda ^\prime$ is a character on ![]() $\mathbb {A}_{E^\prime }^\times / \mathbb {A}^\times {E^\prime }^\times$. Then by Proposition 4.1, which is a consequence of the proof of Theorem 1.1(i), there exists an irreducible cuspidal automorphic representation
$\mathbb {A}_{E^\prime }^\times / \mathbb {A}^\times {E^\prime }^\times$. Then by Proposition 4.1, which is a consequence of the proof of Theorem 1.1(i), there exists an irreducible cuspidal automorphic representation ![]() $\pi ^\circ$ of
$\pi ^\circ$ of ![]() $G(\mathbb {A})$ which is generic and locally
$G(\mathbb {A})$ which is generic and locally ![]() $G^+$-equivalent to
$G^+$-equivalent to ![]() $\pi$. We take the functorial lift of
$\pi$. We take the functorial lift of ![]() $\pi ^\circ$ to
$\pi ^\circ$ to ![]() $\mathrm {GL}_4 (\mathbb {A})$ by Cogdell, Kim, Piatetski-Shapiro and Shahidi [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04], which is of the form
$\mathrm {GL}_4 (\mathbb {A})$ by Cogdell, Kim, Piatetski-Shapiro and Shahidi [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04], which is of the form ![]() $\Pi _1 \boxplus \cdots \boxplus \Pi _{\ell _0}$ with
$\Pi _1 \boxplus \cdots \boxplus \Pi _{\ell _0}$ with ![]() $\Pi _i$ an irreducible cuspidal automorphic representation of
$\Pi _i$ an irreducible cuspidal automorphic representation of ![]() $\mathrm {GL}_{m_i}(\mathbb {A})$ for each
$\mathrm {GL}_{m_i}(\mathbb {A})$ for each ![]() $i$. Then we define an integer
$i$. Then we define an integer ![]() $\ell (\pi )$ by
$\ell (\pi )$ by ![]() $\ell (\pi )=\ell _0$. We note that
$\ell (\pi )=\ell _0$. We note that ![]() $\pi ^\circ$ may not be unique, but
$\pi ^\circ$ may not be unique, but ![]() $\ell (\pi )$ does not depend on the choice of the pair
$\ell (\pi )$ does not depend on the choice of the pair ![]() $(\xi ^\prime,\Lambda ^\prime )$ by Proposition 4.1 and Lemmas 4.2 and 4.3, and thus it depends only on
$(\xi ^\prime,\Lambda ^\prime )$ by Proposition 4.1 and Lemmas 4.2 and 4.3, and thus it depends only on ![]() $(\pi, V_\pi )$. When
$(\pi, V_\pi )$. When ![]() $D$ is split, then
$D$ is split, then ![]() $\pi$ has the functorial lift to
$\pi$ has the functorial lift to ![]() $\mathrm {GL}_4(\mathbb {A})$ by Arthur [Reference ArthurArt13] (see also Cai, Friedberg and Kaplan [Reference Cai, Friedberg and KaplanCFK18]) and we define
$\mathrm {GL}_4(\mathbb {A})$ by Arthur [Reference ArthurArt13] (see also Cai, Friedberg and Kaplan [Reference Cai, Friedberg and KaplanCFK18]) and we define ![]() $\ell (\pi )$ in a similar way.
$\ell (\pi )$ in a similar way.
Our second main result is the refined Gross–Prasad conjecture formulated by Liu [Reference LiuLiu16], i.e. the Ichino–Ikeda-type explicit central value formula, in the case of ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$.
$(\mathrm {SO}(5), \mathrm {SO}(2))$.
Theorem 1.2 Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character.
$G_D(\mathbb {A})$ with a trivial central character.
Then for any non-zero decomposable cusp form ![]() $\phi =\otimes _v\phi _v\in V_\pi$, we have
$\phi =\otimes _v\phi _v\in V_\pi$, we have
 \begin{equation} \frac{|B_{\xi, \Lambda,\psi}(\phi)|^2}{( \phi,\phi )_\pi} =2^{-\ell(\pi)}\,C_{\xi}\cdot \bigg(\prod_{j=1}^2\zeta_F(2j)\bigg) \frac{L\big(\frac{1}{2},\pi \times \mathcal{AI} (\Lambda)\big)}{L(1,\pi,\mathrm{Ad})L(1,\chi_E)} \cdot\prod_v\frac{\alpha_v^\natural(\phi_v)}{ (\phi_v,\phi_v)_{\pi_v}}. \end{equation}
\begin{equation} \frac{|B_{\xi, \Lambda,\psi}(\phi)|^2}{( \phi,\phi )_\pi} =2^{-\ell(\pi)}\,C_{\xi}\cdot \bigg(\prod_{j=1}^2\zeta_F(2j)\bigg) \frac{L\big(\frac{1}{2},\pi \times \mathcal{AI} (\Lambda)\big)}{L(1,\pi,\mathrm{Ad})L(1,\chi_E)} \cdot\prod_v\frac{\alpha_v^\natural(\phi_v)}{ (\phi_v,\phi_v)_{\pi_v}}. \end{equation}
Here ![]() $\zeta _F(s)$ denotes the complete zeta function of
$\zeta _F(s)$ denotes the complete zeta function of ![]() $F$ and
$F$ and ![]() $\alpha _v^\natural (\phi _v)$ is defined by
$\alpha _v^\natural (\phi _v)$ is defined by
 \[ \alpha_v^\natural(\phi_v) =\frac{L(1,\pi_v,\mathrm{Ad}) L(1,\chi_{E,v})}{L(1/2,\pi_v \times \Pi (\Lambda)_v) \prod_{j=1}^2\zeta_{F_v}(2j)}\cdot \alpha_{\Lambda_v, \psi_{\xi, v}}(\phi_v,\phi_v). \]
\[ \alpha_v^\natural(\phi_v) =\frac{L(1,\pi_v,\mathrm{Ad}) L(1,\chi_{E,v})}{L(1/2,\pi_v \times \Pi (\Lambda)_v) \prod_{j=1}^2\zeta_{F_v}(2j)}\cdot \alpha_{\Lambda_v, \psi_{\xi, v}}(\phi_v,\phi_v). \]
We note that ![]() ${\alpha _v^\natural (\phi _v)}/{(\phi _v,\phi _v)_{\pi _v}}=1$ for almost all places
${\alpha _v^\natural (\phi _v)}/{(\phi _v,\phi _v)_{\pi _v}}=1$ for almost all places ![]() $v$ of
$v$ of ![]() $F$ by [Reference LiuLiu16].
$F$ by [Reference LiuLiu16].
Remark 1.5 Under the assumption (1.5.4), we have ![]() $|\mathcal {S}(\phi _\pi )| =2^{\ell (\pi )}$, where
$|\mathcal {S}(\phi _\pi )| =2^{\ell (\pi )}$, where ![]() $\phi _\pi$ denotes the Arthur parameter of
$\phi _\pi$ denotes the Arthur parameter of ![]() $\pi$ and
$\pi$ and ![]() $\mathcal {S}(\phi _\pi )$ the centralizer of
$\mathcal {S}(\phi _\pi )$ the centralizer of ![]() $\phi _\pi$ in the complex dual group
$\phi _\pi$ in the complex dual group ![]() $\hat {G}$. Hence, (1.6.2) coincides with the conjectural formula in Liu [Reference LiuLiu16, Conjecture 2.5 (3)]. Thus, when
$\hat {G}$. Hence, (1.6.2) coincides with the conjectural formula in Liu [Reference LiuLiu16, Conjecture 2.5 (3)]. Thus, when ![]() $D$ is split, i.e.
$D$ is split, i.e. ![]() $G_D\simeq G$, our theorem proves Liu's conjecture since the assumption (1.5.4) is indeed fulfilled. After submitting this paper, Ishimoto posted a preprint [Reference IshimotoIsh24] on arXiv, in which he gives the endoscopic classification of representations of non-quasi-split orthogonal groups for generic Arthur parameters. Hence, our theorem proves [Reference LiuLiu16, Conjecture 2.5 (3)] completely in the case of
$G_D\simeq G$, our theorem proves Liu's conjecture since the assumption (1.5.4) is indeed fulfilled. After submitting this paper, Ishimoto posted a preprint [Reference IshimotoIsh24] on arXiv, in which he gives the endoscopic classification of representations of non-quasi-split orthogonal groups for generic Arthur parameters. Hence, our theorem proves [Reference LiuLiu16, Conjecture 2.5 (3)] completely in the case of ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$.
$(\mathrm {SO}(5), \mathrm {SO}(2))$.
Remark 1.6 Let ![]() $\pi _{\rm gen}$ denote the irreducible cuspidal globally generic automorphic representation of
$\pi _{\rm gen}$ denote the irreducible cuspidal globally generic automorphic representation of ![]() $G(\mathbb {A})$ which has the same
$G(\mathbb {A})$ which has the same ![]() $L$-parameter as
$L$-parameter as ![]() $\pi$. When
$\pi$. When ![]() $\pi _v$ is unramified at any finite place
$\pi _v$ is unramified at any finite place ![]() $v$ of
$v$ of ![]() $F$, Chen and Ichino [Reference Chen and IchinoCI23] proved an explicit formula of the ratio
$F$, Chen and Ichino [Reference Chen and IchinoCI23] proved an explicit formula of the ratio ![]() $L(1,\pi,\mathrm {Ad})/ (\Phi _{\rm gen}, \Phi _{\rm gen})$ for a suitably normalized cusp form
$L(1,\pi,\mathrm {Ad})/ (\Phi _{\rm gen}, \Phi _{\rm gen})$ for a suitably normalized cusp form ![]() $\Phi _{\rm gen}$ in the space of
$\Phi _{\rm gen}$ in the space of ![]() $\pi _{\rm gen}$.
$\pi _{\rm gen}$.
Remark 1.7 In the unitary case, remarkable progress has been made in the Gan–Gross–Prasad conjecture and its refinement for Bessel periods, by studying the Jacquet–Rallis relative trace formula. In the striking paper [Reference Beuzart-Plessis, Liu, Zhang and ZhuBLZZ21] by Beuzart-Plessis, Liu, Zhang and Zhu, a proof in the co-dimension-one case for irreducible cuspidal tempered automorphic representations of unitary groups such that their base change lifts are cuspidal was given by establishing an ingenious method to isolate the cuspidal spectrum. In yet another striking paper by Beuzart-Plessis, Chaudouard and Zydor [Reference Beuzart-Plessis, Chaudouard and ZydorBCZ22], a proof for all endoscopic cases in the co-dimension one setting was given by a precise study of the relative trace formula. Very recently, in a remarkable preprint by Beuzart-Plessis and Chaudouard [Reference Beuzart-Plessis and ChaudouardBC23], the above results are extended to arbitrary co-dimension cases. Thus the Gan–Gross–Prasad conjecture and its refinement for Bessel periods on unitary groups are now proved in general.
In contrast, the orthogonal case in general is still open. We note that, in the ![]() $(\mathrm {SO}(5),\mathrm {SO}(2))$ case, the first author has formulated relative trace formulas to approach the formula (1.6.2) and proved the fundamental lemmas in his joint work with Shalika [Reference Furusawa and ShalikaFS03], Martin [Reference Furusawa and MartinFM11] and Martin and Shalika [Reference Furusawa and MartinFM13a]. In order to deduce the
$(\mathrm {SO}(5),\mathrm {SO}(2))$ case, the first author has formulated relative trace formulas to approach the formula (1.6.2) and proved the fundamental lemmas in his joint work with Shalika [Reference Furusawa and ShalikaFS03], Martin [Reference Furusawa and MartinFM11] and Martin and Shalika [Reference Furusawa and MartinFM13a]. In order to deduce the ![]() $L$-value formula from these relative trace formulas, several issues such as smooth transfer of test functions must be overcome. In the above-mentioned co-dimension-one unitary group case, reductions to Lie algebras played crucial roles to solve similar issues. However Bessel periods in our case involves integration over unipotent subgroups and it is not clear, at least to the first author, how to make the reduction to Lie algebras work.
$L$-value formula from these relative trace formulas, several issues such as smooth transfer of test functions must be overcome. In the above-mentioned co-dimension-one unitary group case, reductions to Lie algebras played crucial roles to solve similar issues. However Bessel periods in our case involves integration over unipotent subgroups and it is not clear, at least to the first author, how to make the reduction to Lie algebras work.
Remark 1.8 In the co-dimension-one orthogonal group case, the refined Gross–Prasad conjecture has been deduced from the Waldspurger formula [Reference WaldspurgerWal85] in the ![]() $(\mathrm {SO}(3), \mathrm {SO}(2))$ case and from the Ichino formula [Reference IchinoIch08] in the
$(\mathrm {SO}(3), \mathrm {SO}(2))$ case and from the Ichino formula [Reference IchinoIch08] in the ![]() $(\mathrm {SO}(4), \mathrm {SO}(3))$ case, respectively. Gan and Ichino [Reference Gan and IchinoGI11] studied the
$(\mathrm {SO}(4), \mathrm {SO}(3))$ case, respectively. Gan and Ichino [Reference Gan and IchinoGI11] studied the ![]() $(\mathrm {SO}(5), \mathrm {SO}(4))$-case when the representation of
$(\mathrm {SO}(5), \mathrm {SO}(4))$-case when the representation of ![]() $\mathrm {SO}(5)$ is a theta lift from
$\mathrm {SO}(5)$ is a theta lift from ![]() $\mathrm {GSO}(4)$ by reduction to the
$\mathrm {GSO}(4)$ by reduction to the ![]() $(\mathrm {SO}(4), \mathrm {SO}(3))$ case.
$(\mathrm {SO}(4), \mathrm {SO}(3))$ case.
Liu [Reference LiuLiu16] proved Theorem 1.2 when ![]() $D$ is split and
$D$ is split and ![]() $\pi$ is an endoscopic lift, i.e. a Yoshida lift, by reducing it to the Waldspurger formula [Reference WaldspurgerWal85]. The case when
$\pi$ is an endoscopic lift, i.e. a Yoshida lift, by reducing it to the Waldspurger formula [Reference WaldspurgerWal85]. The case when ![]() $\pi$ is a non-endoscopic Yoshida lift was proved later by Corbett [Reference CorbettCor17] in a similar manner.
$\pi$ is a non-endoscopic Yoshida lift was proved later by Corbett [Reference CorbettCor17] in a similar manner.
As a corollary of Theorem 1.2, we prove the ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$ case of the Gan–Gross–Prasad conjecture in the form as stated in [Reference Gan, Gross and PrasadGGP12, Conjecture 24.1].
$(\mathrm {SO}(5), \mathrm {SO}(2))$ case of the Gan–Gross–Prasad conjecture in the form as stated in [Reference Gan, Gross and PrasadGGP12, Conjecture 24.1].
Corollary 1.1 Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character. Then the following three conditions are equivalent:
$G_D(\mathbb {A})$ with a trivial central character. Then the following three conditions are equivalent:
(i) the
 $(\xi,\Lambda, \psi )$-Bessel period does not vanish on
$(\xi,\Lambda, \psi )$-Bessel period does not vanish on  $\pi$;
$\pi$;(ii)
 $L (\frac {1}{2}, \pi \times \mathcal {AI}(\Lambda )) \ne 0$ and the local Bessel period
$L (\frac {1}{2}, \pi \times \mathcal {AI}(\Lambda )) \ne 0$ and the local Bessel period  $\alpha _{\Lambda _v, \psi _{\xi, v}}\not \equiv 0$ on
$\alpha _{\Lambda _v, \psi _{\xi, v}}\not \equiv 0$ on  $\pi _v$ at any place
$\pi _v$ at any place  $v$ of
$v$ of  $F$;
$F$;(iii)
 $L (\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$ and
$L (\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$ and  $\mathrm {Hom}_{R_{\xi,v}}(\pi _v,\chi ^{\xi,\Lambda }_v) \ne \{0\}$ at any place
$\mathrm {Hom}_{R_{\xi,v}}(\pi _v,\chi ^{\xi,\Lambda }_v) \ne \{0\}$ at any place  $v$ of
$v$ of  $F$.
$F$.
Remark 1.9 The equivalence between conditions (i) and (ii) is immediate from Theorem 1.2. The equivalence
is proved by Waldspurger [Reference WaldspurgerWal12b] at any non-archimedean place ![]() $v$ and by Luo [Reference LuoLuo20] recently at any archimedean place
$v$ and by Luo [Reference LuoLuo20] recently at any archimedean place ![]() $v$, respectively.
$v$, respectively.
1.7 Method
In [Reference Furusawa and MorimotoFM17, Reference Furusawa and MorimotoFM21] we used the theta correspondence for the dual pair ![]() $(\mathrm {SO}(2n+1), \mathrm {Mp}_n)$.
$(\mathrm {SO}(2n+1), \mathrm {Mp}_n)$.
The main tool in [Reference Furusawa and MorimotoFM17] was the pull-back formula by the first author [Reference FurusawaFur95] for the Whittaker period on ![]() $\mathrm {Mp}_n$, which is expressed by a certain integral involving the Special Bessel period on
$\mathrm {Mp}_n$, which is expressed by a certain integral involving the Special Bessel period on ![]() $\mathrm {SO}(2n+1)$. This forced us the restriction that the character
$\mathrm {SO}(2n+1)$. This forced us the restriction that the character ![]() $\Lambda$ on
$\Lambda$ on ![]() $\mathrm {SO}(2)$ is trivial.
$\mathrm {SO}(2)$ is trivial.
In [Reference Furusawa and MorimotoFM21], to prove the refined Gross–Prasad conjecture for ![]() $(\mathrm {SO}(2n+1),\mathrm {SO}(2))$ when
$(\mathrm {SO}(2n+1),\mathrm {SO}(2))$ when ![]() $\Lambda$ is trivial, the following additional restrictions were necessary.
$\Lambda$ is trivial, the following additional restrictions were necessary.
(i) The base field
 $F$ is totally real and at every archimedean place
$F$ is totally real and at every archimedean place  $v$ of
$v$ of  $F$, the representation
$F$, the representation  $\pi _v$ is a discrete series representation.
$\pi _v$ is a discrete series representation.(ii) The assumption (1.5.4).
An additional main tool needed in [Reference Furusawa and MorimotoFM21] was the Ichino–Ikeda-type formula for the Whittaker periods on ![]() $\mathrm {Mp}_n$ by Lapid and Mao [Reference Lapid and MaoLM17], which imposed on us condition (i). In fact, their proof was to reduce the global identity to certain local identities. They proved the local identities in general at non-archimedean places. On the other hand, at archimedean places, their proof was to note the equivalence between their local identities and the formal degree conjecture by Hiraga, Ichino and Ikeda [Reference Hiraga, Ichino and IkedaHII08a, Reference Hiraga, Ichino and IkedaHII08b] and then to prove the latter when
$\mathrm {Mp}_n$ by Lapid and Mao [Reference Lapid and MaoLM17], which imposed on us condition (i). In fact, their proof was to reduce the global identity to certain local identities. They proved the local identities in general at non-archimedean places. On the other hand, at archimedean places, their proof was to note the equivalence between their local identities and the formal degree conjecture by Hiraga, Ichino and Ikeda [Reference Hiraga, Ichino and IkedaHII08a, Reference Hiraga, Ichino and IkedaHII08b] and then to prove the latter when ![]() $\pi$ is a discrete series representation. Our proof in [Reference Furusawa and MorimotoFM21] was to reduce to the case when
$\pi$ is a discrete series representation. Our proof in [Reference Furusawa and MorimotoFM21] was to reduce to the case when ![]() $\pi$ has the special Bessel period by the assumption (1.5.4) and to combine these two main tools with the Siegel–Weil formula.
$\pi$ has the special Bessel period by the assumption (1.5.4) and to combine these two main tools with the Siegel–Weil formula.
It does not seem plausible that a straightforward generalization of the method of [Reference Furusawa and MorimotoFM17, Reference Furusawa and MorimotoFM21] would allow us to remove these restrictions. Thus, we need to adopt a new strategy in this paper.
Our main method here is again theta correspondence but we use it differently and in a more intricate way. First we consider the quaternionic dual pair ![]() $(G^+_D,\mathrm {GSU}_{3,D})$ where
$(G^+_D,\mathrm {GSU}_{3,D})$ where ![]() $\mathrm {GSU}_{3,D}$ denotes the identity component of the similitude quaternion unitary group
$\mathrm {GSU}_{3,D}$ denotes the identity component of the similitude quaternion unitary group ![]() $\mathrm {GU}_{3,D}$ defined by (2.1.9) and
$\mathrm {GU}_{3,D}$ defined by (2.1.9) and ![]() $G^+_D$ defined by (1.5.1). Then we recall the accidental isomorphism
$G^+_D$ defined by (1.5.1). Then we recall the accidental isomorphism
when ![]() $D\simeq D_\varepsilon$ given by (2.1.1) and
$D\simeq D_\varepsilon$ given by (2.1.1) and ![]() $\mathrm {GU}_{4,\varepsilon }$ is the similitude unitary group defined by (2.1.14). Hence, we have
$\mathrm {GU}_{4,\varepsilon }$ is the similitude unitary group defined by (2.1.14). Hence, we have
 \begin{equation} \mathrm{GU}_{4,\varepsilon}\simeq \begin{cases} \mathrm{GU}_{2,2}, & \text{when $D$ is split, i.e. $\varepsilon\in\mathrm{N}_{E/ F} (E^\times)$};\\ \mathrm{GU}_{3,1}, & \text{when $D$ is non-split, i.e. $\varepsilon\notin\mathrm{N}_{E/ F} (E^\times)$}. \end{cases} \end{equation}
\begin{equation} \mathrm{GU}_{4,\varepsilon}\simeq \begin{cases} \mathrm{GU}_{2,2}, & \text{when $D$ is split, i.e. $\varepsilon\in\mathrm{N}_{E/ F} (E^\times)$};\\ \mathrm{GU}_{3,1}, & \text{when $D$ is non-split, i.e. $\varepsilon\notin\mathrm{N}_{E/ F} (E^\times)$}. \end{cases} \end{equation}
Thus, our theta correspondence for ![]() $(G^+_D,\mathrm {GSU}_{3,D})$ induces a correspondence for the pair
$(G^+_D,\mathrm {GSU}_{3,D})$ induces a correspondence for the pair ![]() $(\mathbb {G}_D,\mathrm {PGU}_{4,\varepsilon })$. Then we note that the pull-back of a certain Bessel period on
$(\mathbb {G}_D,\mathrm {PGU}_{4,\varepsilon })$. Then we note that the pull-back of a certain Bessel period on ![]() $\mathrm {PGU}_{4,\varepsilon }$ is an integral involving the
$\mathrm {PGU}_{4,\varepsilon }$ is an integral involving the ![]() $(\xi,\Lambda, \psi )$-Bessel period on
$(\xi,\Lambda, \psi )$-Bessel period on ![]() $G_D$.
$G_D$.
Theorem 1.1 is reduced essentially to the Gan–Gross–Prasad conjecture for the Bessel periods on ![]() $\mathrm {GU}_{4,\varepsilon }$, which we proved in [Reference Furusawa and MorimotoFM22] using the theta correspondence for the pair
$\mathrm {GU}_{4,\varepsilon }$, which we proved in [Reference Furusawa and MorimotoFM22] using the theta correspondence for the pair ![]() $(\mathrm {GU}_{4,\varepsilon },\mathrm {GU}_{2,2})$.
$(\mathrm {GU}_{4,\varepsilon },\mathrm {GU}_{2,2})$.
Similarly Theorem 1.2 is reduced to the refined Gan–Gross–Prasad conjecture for the Bessel periods on ![]() $\mathrm {GU}_{4,\varepsilon }$. For the reader's sake, here we present an outline of the proof when the
$\mathrm {GU}_{4,\varepsilon }$. For the reader's sake, here we present an outline of the proof when the ![]() $(\xi,\Lambda,\psi )$-Bessel period does not vanish. Note that in the following paragraph the notation used is provisional and the argument is not rigorous since our intention here is to present a rough sketch of the main idea.
$(\xi,\Lambda,\psi )$-Bessel period does not vanish. Note that in the following paragraph the notation used is provisional and the argument is not rigorous since our intention here is to present a rough sketch of the main idea.
Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character. Suppose that the
$G_D(\mathbb {A})$ with a trivial central character. Suppose that the ![]() $(\xi,\Lambda,\psi )$-Bessel period, which we denote by
$(\xi,\Lambda,\psi )$-Bessel period, which we denote by ![]() $B$, does not vanish on
$B$, does not vanish on ![]() $\pi$. Let
$\pi$. Let ![]() $\theta (\pi )$ be the theta lift of
$\theta (\pi )$ be the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSU}_{3,D}$. When
$\mathrm {GSU}_{3,D}$. When ![]() $G_D=G$ and the theta lift of
$G_D=G$ and the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{3,1}$ is non-zero,
$\mathrm {GSO}_{3,1}$ is non-zero, ![]() $\theta (\pi )$ is not cuspidal but the explicit formula (1.6.2) has been already proved by Corbett [Reference CorbettCor17]. Thus, suppose otherwise. Then
$\theta (\pi )$ is not cuspidal but the explicit formula (1.6.2) has been already proved by Corbett [Reference CorbettCor17]. Thus, suppose otherwise. Then ![]() $\theta (\pi )$ is a non-zero irreducible cuspidal tempered automorphic representation. The pull-back of a certain Bessel period, which we denote by
$\theta (\pi )$ is a non-zero irreducible cuspidal tempered automorphic representation. The pull-back of a certain Bessel period, which we denote by ![]() $\mathcal {B}$ on
$\mathcal {B}$ on ![]() $\mathrm {GSU}_{3,D}$ is written as an integral involving
$\mathrm {GSU}_{3,D}$ is written as an integral involving ![]() $B$. As in our previous paper [Reference Furusawa and MorimotoFM21], the explicit formula for
$B$. As in our previous paper [Reference Furusawa and MorimotoFM21], the explicit formula for ![]() $B$ is reduced to that for
$B$ is reduced to that for ![]() $\mathcal {B}$, which we obtain in the following steps.
$\mathcal {B}$, which we obtain in the following steps.
(1) Via the isomorphism (1.7.1), regard
 $\theta (\pi )$ as an automorphic representation of
$\theta (\pi )$ as an automorphic representation of  $\mathrm {GU}_{4,\varepsilon }$ and then consider its theta lift
$\mathrm {GU}_{4,\varepsilon }$ and then consider its theta lift  $\theta _\Lambda (\theta (\pi ))$, which depends on
$\theta _\Lambda (\theta (\pi ))$, which depends on  $\Lambda$, to
$\Lambda$, to  $\mathrm {GU}_{2,2}$. The temperedness of
$\mathrm {GU}_{2,2}$. The temperedness of  $\pi$ implies that
$\pi$ implies that  $\theta _\Lambda (\theta (\pi ))$ is an irreducible cuspidal automorphic representation of
$\theta _\Lambda (\theta (\pi ))$ is an irreducible cuspidal automorphic representation of  $\mathrm {GU}_{2,2}$. Then the pull-back of a certain Whittaker period
$\mathrm {GU}_{2,2}$. Then the pull-back of a certain Whittaker period  $\mathcal {W}$ on
$\mathcal {W}$ on  $\mathrm {GU}_{2,2}$ is written as an integral involving the Bessel period
$\mathrm {GU}_{2,2}$ is written as an integral involving the Bessel period  $\mathcal {B}$. Then in [Reference Furusawa and MorimotoFM22], it is shown that the explicit formula for
$\mathcal {B}$. Then in [Reference Furusawa and MorimotoFM22], it is shown that the explicit formula for  $\mathcal {B}$ follows from that for
$\mathcal {B}$ follows from that for  $\mathcal {W}$. Thus, we are reduced to show the explicit formula for
$\mathcal {W}$. Thus, we are reduced to show the explicit formula for  $\mathcal {W}$.
$\mathcal {W}$.(2) Via the isomorphism
 $\mathrm {PGU}_{2,2}\simeq \mathrm {PGSO}_{4,2}$, regard
$\mathrm {PGU}_{2,2}\simeq \mathrm {PGSO}_{4,2}$, regard  $\theta _\Lambda (\theta (\pi ))$ as an automorphic representation of
$\theta _\Lambda (\theta (\pi ))$ as an automorphic representation of  $\mathrm {GSO}_{4,2}$. Let
$\mathrm {GSO}_{4,2}$. Let  $\pi ^\prime$ be the theta lift of
$\pi ^\prime$ be the theta lift of  $\theta _\Lambda (\theta (\pi ))$ to
$\theta _\Lambda (\theta (\pi ))$ to  $G=\mathrm {GSp}_2$. Then it is shown that
$G=\mathrm {GSp}_2$. Then it is shown that  $\pi ^\prime$ is a globally generic cuspidal automorphic representation of
$\pi ^\prime$ is a globally generic cuspidal automorphic representation of  $G$ and indeed the pull-back of the Whittaker period
$G$ and indeed the pull-back of the Whittaker period  $W$ on
$W$ on  $G$ is expressed as an integral involving
$G$ is expressed as an integral involving  $\mathcal {W}$. Hence, we are reduced to the explicit formula for
$\mathcal {W}$. Hence, we are reduced to the explicit formula for  $W$.
$W$.(3) Since the theta lift of the globally generic cuspidal automorphic representation
 $\pi ^\prime$ of
$\pi ^\prime$ of  $G$ to either
$G$ to either  $\mathrm {GSO}_{2,2}$ or
$\mathrm {GSO}_{2,2}$ or  $\mathrm {GSO}_{3,3}$ is non-zero and cuspidal, we are further reduced to the explicit formulas for the Whittaker periods on
$\mathrm {GSO}_{3,3}$ is non-zero and cuspidal, we are further reduced to the explicit formulas for the Whittaker periods on  $\mathrm {PGSO}_{2,2}$ and
$\mathrm {PGSO}_{2,2}$ and  $\mathrm {PGSO}_{3,3}$ by the pull-back computation.
$\mathrm {PGSO}_{3,3}$ by the pull-back computation.(4) Recall the accidental isomorphisms
 $\mathrm {PGSO}_{2,2}\simeq \mathrm {PGL}_2\times \mathrm {PGL}_2$,
$\mathrm {PGSO}_{2,2}\simeq \mathrm {PGL}_2\times \mathrm {PGL}_2$,  $\mathrm {PGSO}_{3,3}\simeq \mathrm {PGL}_4$. Since the explicit formula for the Whittaker period on
$\mathrm {PGSO}_{3,3}\simeq \mathrm {PGL}_4$. Since the explicit formula for the Whittaker period on  $\mathrm {PGL}_n$ is already proved by Lapid and Mao [Reference Lapid and MaoLM15], we are done.
$\mathrm {PGL}_n$ is already proved by Lapid and Mao [Reference Lapid and MaoLM15], we are done.
Remark 1.10 Though we only consider the case when ![]() $\mathrm {SO}(2)$ is non-split in this paper, the split case is proved by a similar argument as follows. First we note that
$\mathrm {SO}(2)$ is non-split in this paper, the split case is proved by a similar argument as follows. First we note that ![]() $D$ is necessarily split when
$D$ is necessarily split when ![]() $\mathrm {SO}(2)$ is split and, hence,
$\mathrm {SO}(2)$ is split and, hence, ![]() $G_D\simeq G$. If the theta lift to
$G_D\simeq G$. If the theta lift to ![]() $\mathrm {GSO}_{2,2}$ is non-zero, it is a Yoshida lift and Liu [Reference LiuLiu16] proved the explicit formula. Suppose otherwise. Then the theta lift to
$\mathrm {GSO}_{2,2}$ is non-zero, it is a Yoshida lift and Liu [Reference LiuLiu16] proved the explicit formula. Suppose otherwise. Then the theta lift to ![]() $\mathrm {GSO}_{3,3}$ is non-zero and cuspidal. The pull-back of a certain Bessel period on
$\mathrm {GSO}_{3,3}$ is non-zero and cuspidal. The pull-back of a certain Bessel period on ![]() $\mathrm {GSO}_{3,3}$ is an integral involving the split Bessel period on
$\mathrm {GSO}_{3,3}$ is an integral involving the split Bessel period on ![]() $G$ (see § 3.1.2). We recall the accidental isomorphism
$G$ (see § 3.1.2). We recall the accidental isomorphism ![]() $\mathrm {PGSO}_{3,3} \simeq \mathrm {PGL}_4$. We consider the theta correspondence for the pair
$\mathrm {PGSO}_{3,3} \simeq \mathrm {PGL}_4$. We consider the theta correspondence for the pair ![]() $(\mathrm {GL}_4,\mathrm {GL}_4)$ instead of
$(\mathrm {GL}_4,\mathrm {GL}_4)$ instead of ![]() $(\mathrm {GU}_{4,\varepsilon },\mathrm {GU}_{4,\varepsilon })$ in the non-split case. Then the pull-back computation may be interpreted as expressing the pull-back of the Whittaker period on
$(\mathrm {GU}_{4,\varepsilon },\mathrm {GU}_{4,\varepsilon })$ in the non-split case. Then the pull-back computation may be interpreted as expressing the pull-back of the Whittaker period on ![]() $\mathrm {GL}_4$ as an integral involving the Bessel period on
$\mathrm {GL}_4$ as an integral involving the Bessel period on ![]() $\mathrm {GSO}_{3,3}$, which is given in [Reference Furusawa and MorimotoFM22]. Thus, as in the non-split case, we are reduced to the Ichino–Ikeda-type explicit formula for the Whittaker period on
$\mathrm {GSO}_{3,3}$, which is given in [Reference Furusawa and MorimotoFM22]. Thus, as in the non-split case, we are reduced to the Ichino–Ikeda-type explicit formula for the Whittaker period on ![]() $\mathrm {GL}_4$.
$\mathrm {GL}_4$.
We now give the statement of the theorem in the split case.
Theorem 1.3 Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A})$ with trivial central character. Suppose that
$G(\mathbb {A})$ with trivial central character. Suppose that ![]() $D$ is split and the Arthur parameter of
$D$ is split and the Arthur parameter of ![]() $\pi$ is generic.
$\pi$ is generic.
Let ![]() $\xi \in D^-(F)$ such that
$\xi \in D^-(F)$ such that ![]() $F(\xi )\simeq F\oplus F$ and fix an
$F(\xi )\simeq F\oplus F$ and fix an ![]() $F$-isomorphism
$F$-isomorphism ![]() $T_\xi \simeq F^\times \times F^\times$. For a character
$T_\xi \simeq F^\times \times F^\times$. For a character ![]() $\Lambda$ of
$\Lambda$ of ![]() $\mathbb {A}^\times / F^\times$, we also denote by
$\mathbb {A}^\times / F^\times$, we also denote by ![]() $\Lambda$ the character of
$\Lambda$ the character of ![]() $T_\xi (\mathbb {A})$ defined by
$T_\xi (\mathbb {A})$ defined by ![]() $\Lambda (a,b):=\Lambda (ab^{-1})$.
$\Lambda (a,b):=\Lambda (ab^{-1})$.
The following assertions hold.
(1) The
 $(\xi, \Lambda,\psi )$-Bessel period does not vanish on
$(\xi, \Lambda,\psi )$-Bessel period does not vanish on  $V_\pi$ if and only if
$V_\pi$ if and only if  $\pi$ is generic and
$\pi$ is generic and  $L(\frac {1}{2},\pi \times \Lambda )\ne 0$. Here we note that
$L(\frac {1}{2},\pi \times \Lambda )\ne 0$. Here we note that  $L(\frac {1}{2},\pi \times \Lambda ^{-1})$ is the complex conjugate of
$L(\frac {1}{2},\pi \times \Lambda ^{-1})$ is the complex conjugate of  $L(\frac {1}{2},\pi \times \Lambda )$ since
$L(\frac {1}{2},\pi \times \Lambda )$ since  $\pi$ is self-dual.
$\pi$ is self-dual.(2) Further assume that
 $\pi$ is tempered. Then for any non-zero decomposable cusp form
$\pi$ is tempered. Then for any non-zero decomposable cusp form  $\phi =\otimes _v\,\phi _v\in V_\pi$, we have
where
$\phi =\otimes _v\,\phi _v\in V_\pi$, we have
where \begin{align*} \frac{|B_{\xi,
\Lambda,\psi}(\phi)|^2}{( \phi,\phi )_\pi} &=
2^{-\ell(\pi)}\,C_{\xi} \cdot
\bigg(\prod_{j=1}^2\zeta_F(2j)\bigg)\frac{L(\frac{1}{2},\pi \times \Lambda)L(\frac{1}{2},
\pi \times \Lambda^{-1})}{L(1,\pi,\mathrm{Ad})\zeta_F(1)}
\cdot\prod_v\frac{\alpha_v^\natural(\phi_v)}{(\phi_v,\phi_v)_{\pi_v}}
\end{align*}
\begin{align*} \frac{|B_{\xi,
\Lambda,\psi}(\phi)|^2}{( \phi,\phi )_\pi} &=
2^{-\ell(\pi)}\,C_{\xi} \cdot
\bigg(\prod_{j=1}^2\zeta_F(2j)\bigg)\frac{L(\frac{1}{2},\pi \times \Lambda)L(\frac{1}{2},
\pi \times \Lambda^{-1})}{L(1,\pi,\mathrm{Ad})\zeta_F(1)}
\cdot\prod_v\frac{\alpha_v^\natural(\phi_v)}{(\phi_v,\phi_v)_{\pi_v}}
\end{align*}
 $\zeta _F(1)$ stands for
$\zeta _F(1)$ stands for  $\mathrm {Res}_{s=1}\, \zeta _F(s)$.
$\mathrm {Res}_{s=1}\, \zeta _F(s)$.
1.8 Generalized Böcherer conjecture
Thanks to the meticulous local computation by Dickson, Pitale, Saha and Schmidt [Reference Dickson, Pitale, Saha and SchmidtDPSS20], Theorem 1.2 implies the generalized Böcherer conjecture. For brevity, we only state the scalar-valued full modular case here in the introduction. Indeed, a more general version shall be proved in § 8.3 as Theorem 8.1.
Theorem 1.4 Let ![]() $\Phi$ be a holomorphic Siegel cusp form of degree two and weight
$\Phi$ be a holomorphic Siegel cusp form of degree two and weight ![]() $k$ with respect to
$k$ with respect to ![]() $\mathrm {Sp}_2(\mathbb {Z})$ which is a Hecke eigenform and
$\mathrm {Sp}_2(\mathbb {Z})$ which is a Hecke eigenform and ![]() $\pi (\Phi )$ the associated automorphic representation of
$\pi (\Phi )$ the associated automorphic representation of ![]() $\mathbb {G}(\mathbb {A}_\mathbb {Q})$. Let
$\mathbb {G}(\mathbb {A}_\mathbb {Q})$. Let
be the Fourier expansion of ![]() $\Phi$ where
$\Phi$ where ![]() $T$ runs over semi-integral positive-definite two-by-two symmetric matrices and
$T$ runs over semi-integral positive-definite two-by-two symmetric matrices and ![]() $\mathfrak H_2$ denotes the Siegel upper half-space of degree two.
$\mathfrak H_2$ denotes the Siegel upper half-space of degree two.
Let ![]() $E$ be an imaginary quadratic extension of
$E$ be an imaginary quadratic extension of ![]() $\mathbb {Q}$. We denote by
$\mathbb {Q}$. We denote by ![]() $-D_E$ its discriminant,
$-D_E$ its discriminant, ![]() $\mathrm {Cl}_E$ its ideal class group and
$\mathrm {Cl}_E$ its ideal class group and ![]() $w(E)$ the number of distinct roots of unity in
$w(E)$ the number of distinct roots of unity in ![]() $E$. In (1.8.1), when
$E$. In (1.8.1), when ![]() $T^\prime ={}^t\gamma T\gamma$ for some
$T^\prime ={}^t\gamma T\gamma$ for some ![]() $\gamma \in \mathrm {SL}_2(\mathbb {Z})$, we have
$\gamma \in \mathrm {SL}_2(\mathbb {Z})$, we have ![]() $a(\Phi, T^\prime )=a(\Phi,T)$. By the Gauss composition law, we may naturally identify the
$a(\Phi, T^\prime )=a(\Phi,T)$. By the Gauss composition law, we may naturally identify the ![]() $\mathrm {SL}_2(\mathbb {Z})$-equivalence classes of binary quadratic forms of discriminant
$\mathrm {SL}_2(\mathbb {Z})$-equivalence classes of binary quadratic forms of discriminant ![]() $-D_E$ with the elements of
$-D_E$ with the elements of ![]() $\mathrm {Cl}_E$. Thus, the notation
$\mathrm {Cl}_E$. Thus, the notation ![]() $a(\Phi, c)$ for
$a(\Phi, c)$ for ![]() $c \in \mathrm {Cl}_E$ makes sense. For a character
$c \in \mathrm {Cl}_E$ makes sense. For a character ![]() $\Lambda$ of
$\Lambda$ of ![]() $\mathrm {Cl}_E$, we define
$\mathrm {Cl}_E$, we define ![]() $\mathcal {B}_\Lambda (\Phi,E)$ by
$\mathcal {B}_\Lambda (\Phi,E)$ by
Suppose that ![]() $\Phi$ is not a Saito–Kurokawa lift. Then we have
$\Phi$ is not a Saito–Kurokawa lift. Then we have
Here
Remark 1.11 In Theorem 8.1, we prove (1.8.2) allowing ![]() $\Phi$ to have a square-free level and to be vector-valued. Moreover, assuming the temperedness of
$\Phi$ to have a square-free level and to be vector-valued. Moreover, assuming the temperedness of ![]() $\pi (\Phi )$, the weight
$\pi (\Phi )$, the weight ![]() $2$ case, which is of significant interest because of the modularity conjecture for abelian surfaces, is also included.
$2$ case, which is of significant interest because of the modularity conjecture for abelian surfaces, is also included.
Formula (1.8.2) and its generalization (8.3.1) are expected to have a broad spectrum of interesting applications both arithmetic and analytic. Some of the examples are [Reference BlomerBlo19], [Reference Dickson, Pitale, Saha and SchmidtDPSS20, § 3], [Reference DummiganDum22], [Reference Hsieh and YamanaHY24], [Reference SahaSah14] and [Reference WaibelWai19].
1.9 Organization of the paper
This paper is organized as follows. In § 2, we introduce some more notation and define local and global Bessel periods. In § 3, we carry out the pull-back computation of Bessel periods. In § 4, we shall prove Theorem 1.1 using the results in § 3. We also note some consequences of our proof of Theorem 1.1(i), which will be used in the proof of Theorem 1.2 later. In § 5, we recall the Rallis inner product formula for similitude groups. In § 6, we will give an explicit formula for Bessel periods on ![]() $\mathrm {GU}_{4,\varepsilon }$ in certain cases as explained in our strategy for the proof of Theorem 1.2. In § 7, we complete our proof of Theorem 1.2. In § 8, we prove the generalized Böcherer conjecture, including the vector valued case. In Appendix A, we will give an explicit formula of Whittaker periods for irreducible cuspidal tempered automorphic representations of
$\mathrm {GU}_{4,\varepsilon }$ in certain cases as explained in our strategy for the proof of Theorem 1.2. In § 7, we complete our proof of Theorem 1.2. In § 8, we prove the generalized Böcherer conjecture, including the vector valued case. In Appendix A, we will give an explicit formula of Whittaker periods for irreducible cuspidal tempered automorphic representations of ![]() $G$. In Appendix B, we compute the local Bessel periods explicitly for representation of
$G$. In Appendix B, we compute the local Bessel periods explicitly for representation of ![]() $G(\mathbb {R})$ corresponding to vector-valued holomorphic Siegel modular forms. This result is used in § 8. In Appendix C, we consider the meromorphic continuation of the
$G(\mathbb {R})$ corresponding to vector-valued holomorphic Siegel modular forms. This result is used in § 8. In Appendix C, we consider the meromorphic continuation of the ![]() $L$-function for
$L$-function for ![]() $\mathrm {SO}(5) \times \mathrm {SO}(2)$.
$\mathrm {SO}(5) \times \mathrm {SO}(2)$.
1.10 Index of notation
 $M_D, N_D$, 2117
$M_D, N_D$, 2117 $G_D$, 2116
$G_D$, 2116 $G$, 2117
$G$, 2117 $G_D^1$, 2117
$G_D^1$, 2117 $G^1$, 2117
$G^1$, 2117 $T_{\xi }$, 2117
$T_{\xi }$, 2117 $G_D^+$, 2118
$G_D^+$, 2118 $B_{\xi, \Lambda, \psi }$, 2118
$B_{\xi, \Lambda, \psi }$, 2118 $\mathcal {AI}(\Lambda )$, 2119
$\mathcal {AI}(\Lambda )$, 2119 $\mathcal {B}_\Lambda (\Phi, E)$, 2125
$\mathcal {B}_\Lambda (\Phi, E)$, 2125 $J_m$, 2126
$J_m$, 2126 $\mathrm {GO}_{n+2, n}, \mathrm {GSO}_{n+2, n}$, 2126
$\mathrm {GO}_{n+2, n}, \mathrm {GSO}_{n+2, n}$, 2126 $\mathrm {GU}_{3, D}, \mathrm {GSU}_{3, D}$, 2127
$\mathrm {GU}_{3, D}, \mathrm {GSU}_{3, D}$, 2127 $\mathrm {GU}_{4, \varepsilon }$, 2127
$\mathrm {GU}_{4, \varepsilon }$, 2127 $\Phi _D$, 2129
$\Phi _D$, 2129 $\Phi$, 2130
$\Phi$, 2130 $M$,
$M$,  $N$, 2130
$N$, 2130 $T_S$, 2130
$T_S$, 2130 $B_{S, \Lambda, \psi }$, 2131
$B_{S, \Lambda, \psi }$, 2131 $M_{3, D}$
$M_{3, D}$  $N_{3, D}$, 2131
$N_{3, D}$, 2131 $M_{X, D}$, 2131
$M_{X, D}$, 2131 $\mathcal {B}_{X, \chi, \psi }$, 2131
$\mathcal {B}_{X, \chi, \psi }$, 2131 $\mathcal {B}_{X, \chi, \psi }^D$, 2131
$\mathcal {B}_{X, \chi, \psi }^D$, 2131 $M_{4,2}$
$M_{4,2}$  $N_{4,2}$, 2132
$N_{4,2}$, 2132 $M_{X}$, 2133
$M_{X}$, 2133 $\alpha _{\chi, \psi _N}(\phi, \phi ^\prime )$, 2133
$\alpha _{\chi, \psi _N}(\phi, \phi ^\prime )$, 2133Type I-A, Type I-B, 2152
 $W^{\psi _U}$, 2161
$W^{\psi _U}$, 2161 $\mathcal {W}^{\psi _U}$, 2165
$\mathcal {W}^{\psi _U}$, 2165 $\mathcal {W}^\circ _{G, v}, \mathcal {W}_{G, v}$, 2163
$\mathcal {W}^\circ _{G, v}, \mathcal {W}_{G, v}$, 2163 $\mathcal {L}_v^\circ (\phi _v, f_v), \mathcal {L}_v(\phi _v, f_v)$, 2164
$\mathcal {L}_v^\circ (\phi _v, f_v), \mathcal {L}_v(\phi _v, f_v)$, 2164 $W_{\psi _{U_G}}$, 2163
$W_{\psi _{U_G}}$, 2163 $\phi _{\Phi, S}$, 2193
$\phi _{\Phi, S}$, 2193
2. Preliminaries
2.1 Groups
2.1.1 Quaternion algebras
Let ![]() $X(E : F)$ denote the set of
$X(E : F)$ denote the set of ![]() $F$-isomorphism classes of central simple algebras over
$F$-isomorphism classes of central simple algebras over ![]() $F$ containing
$F$ containing ![]() $E$. Then we recall that the map
$E$. Then we recall that the map ![]() $\varepsilon \mapsto D_{\varepsilon }$ gives a bijection between
$\varepsilon \mapsto D_{\varepsilon }$ gives a bijection between ![]() $F^\times / \mathrm {N}_{E / F}(E^\times )$ and
$F^\times / \mathrm {N}_{E / F}(E^\times )$ and ![]() $X(E : F)$ (see [Reference Furusawa and ShalikaFS03, Lemma 1.3]) where
$X(E : F)$ (see [Reference Furusawa and ShalikaFS03, Lemma 1.3]) where
Here we regard ![]() $E$ as a subalgebra of
$E$ as a subalgebra of ![]() $D_\varepsilon$ by
$D_\varepsilon$ by
We also note that ![]() $D_\varepsilon \simeq \mathrm {Mat}_{2 \times 2}(F)$ when
$D_\varepsilon \simeq \mathrm {Mat}_{2 \times 2}(F)$ when ![]() $\varepsilon \in \mathrm {N}_{E/ F}(E^\times )$. The canonical involution
$\varepsilon \in \mathrm {N}_{E/ F}(E^\times )$. The canonical involution ![]() $D_\varepsilon \ni x\mapsto \bar {x}\in D_\varepsilon$ is given by
$D_\varepsilon \ni x\mapsto \bar {x}\in D_\varepsilon$ is given by
We denote the reduced trace of ![]() $D$ by
$D$ by ![]() $\mathrm {tr}_D$.
$\mathrm {tr}_D$.
2.1.2 Orthogonal groups
For a non-negative integer ![]() $n$, a symmetric matrix
$n$, a symmetric matrix ![]() $S_n\in \mathrm {Mat}_{(2n+2) \times (2n+2)}(F)$ is defined inductively by
$S_n\in \mathrm {Mat}_{(2n+2) \times (2n+2)}(F)$ is defined inductively by
 \begin{equation} S_0: = \begin{pmatrix}2 & 0\\ 0 & -2d \end{pmatrix}\quad \text{and} \quad S_n: = \begin{pmatrix}0 & 0 & 1\\ 0 & S_{n-1} & 0\\ 1 & 0 & 0\end{pmatrix}\quad \text{for $n\ge 1$}. \end{equation}
\begin{equation} S_0: = \begin{pmatrix}2 & 0\\ 0 & -2d \end{pmatrix}\quad \text{and} \quad S_n: = \begin{pmatrix}0 & 0 & 1\\ 0 & S_{n-1} & 0\\ 1 & 0 & 0\end{pmatrix}\quad \text{for $n\ge 1$}. \end{equation}
We recall that ![]() $E=F(\eta )$ where
$E=F(\eta )$ where ![]() $\eta ^2=d$. Then we denote the corresponding orthogonal group, the special orthogonal group and the similitude orthogonal group by
$\eta ^2=d$. Then we denote the corresponding orthogonal group, the special orthogonal group and the similitude orthogonal group by
respectively. Let ![]() $\mathrm {GSO}_{n+2,n}$ denote the identity component of
$\mathrm {GSO}_{n+2,n}$ denote the identity component of ![]() $\mathrm {GO}_{n+2,n}$. Thus,
$\mathrm {GO}_{n+2,n}$. Thus,
where
For a positive integer ![]() $n$, we denote by
$n$, we denote by ![]() $J_{2n}$ the
$J_{2n}$ the ![]() $2n\times 2n$ symmetric matrix with ones on the non-principal diagonal and zeros elsewhere, i.e.
$2n\times 2n$ symmetric matrix with ones on the non-principal diagonal and zeros elsewhere, i.e.
 \begin{equation} J_2=\begin{pmatrix}0 & 1\\1 & 0\end{pmatrix}\quad\text{and}\quad J_{2(n+1)}=\begin{pmatrix}0 & 0 & 1\\0 & J_{2n} & 0\\1 & 0 & 0\end{pmatrix}\quad\text{for $n\ge 1$}. \end{equation}
\begin{equation} J_2=\begin{pmatrix}0 & 1\\1 & 0\end{pmatrix}\quad\text{and}\quad J_{2(n+1)}=\begin{pmatrix}0 & 0 & 1\\0 & J_{2n} & 0\\1 & 0 & 0\end{pmatrix}\quad\text{for $n\ge 1$}. \end{equation}
Then the similitude orthogonal group ![]() $\mathrm {GO}_{n,n}$ is defined by
$\mathrm {GO}_{n,n}$ is defined by
and we denote by ![]() $\mathrm {GSO}_{n,n}$ its identity component, which is given by
$\mathrm {GSO}_{n,n}$ its identity component, which is given by
2.1.3 Quaternionic unitary groups
Let ![]() $D$ be a quaternion algebra over
$D$ be a quaternion algebra over ![]() $F$ containing
$F$ containing ![]() $E$. Recall that
$E$. Recall that ![]() $G_D$ denotes the similitude quaternionic unitary group of degree
$G_D$ denotes the similitude quaternionic unitary group of degree ![]() $2$ defined by (1.4.2).
$2$ defined by (1.4.2).
We define a similitude quaternionic unitary group ![]() $\mathrm {GU}_{3,D}$ of degree
$\mathrm {GU}_{3,D}$ of degree ![]() $3$ by
$3$ by
where we define a skew-hermitian matrix ![]() ${\bf J}_\eta$ by
${\bf J}_\eta$ by
 \begin{equation} {\bf J}_\eta := \begin{pmatrix} 0 & 0 & \eta\\0 & \eta & 0\\ \eta & 0 & 0\end{pmatrix}. \end{equation}
\begin{equation} {\bf J}_\eta := \begin{pmatrix} 0 & 0 & \eta\\0 & \eta & 0\\ \eta & 0 & 0\end{pmatrix}. \end{equation}
Here ![]() $\bar {A}=(\bar {a}_{ij})$ for
$\bar {A}=(\bar {a}_{ij})$ for ![]() $A=(a_{ij})\in \mathrm {Mat}_{m \times n}(D)$. Let us denote by
$A=(a_{ij})\in \mathrm {Mat}_{m \times n}(D)$. Let us denote by ![]() $\mathrm {GSU}_{3,D}$ the identity component of
$\mathrm {GSU}_{3,D}$ the identity component of ![]() $\mathrm {GU}_{3,D}$. Then unlike the orthogonal case, as noted in [Reference Mœglin, Vigneras and WaldspurgerMVW87, p. 21–22], we have
$\mathrm {GU}_{3,D}$. Then unlike the orthogonal case, as noted in [Reference Mœglin, Vigneras and WaldspurgerMVW87, p. 21–22], we have
and
Moreover, when ![]() $D\otimes _F F_v$ is split at a place
$D\otimes _F F_v$ is split at a place ![]() $v$ of
$v$ of ![]() $F$, we have
$F$, we have
 \begin{equation} \mathrm{GU}_{3, D}(F_v)\simeq \begin{cases} \mathrm{GO}_{4,2}(F_v) & \text{if $E\otimes F_v$ is a quadratic extension of $F_v$};\\ \mathrm{GO}_{3,3}(F_v) & \text{if $E\otimes F_v\simeq F_v\oplus F_v$.} \end{cases} \end{equation}
\begin{equation} \mathrm{GU}_{3, D}(F_v)\simeq \begin{cases} \mathrm{GO}_{4,2}(F_v) & \text{if $E\otimes F_v$ is a quadratic extension of $F_v$};\\ \mathrm{GO}_{3,3}(F_v) & \text{if $E\otimes F_v\simeq F_v\oplus F_v$.} \end{cases} \end{equation} We also define ![]() $\mathrm {GU}_{1,D}$ by
$\mathrm {GU}_{1,D}$ by
and denote its identity component by ![]() $\mathrm {GSU}_{1,D}$. Then we note that
$\mathrm {GSU}_{1,D}$. Then we note that
 \begin{align} \mathrm{GSU}_{1,D}(F)&=\{\alpha\in D^\times:\bar{\alpha} \eta \alpha = \mathrm{n}_D(\alpha) \eta\} \nonumber\\ &=\{x\in D^\times\mid x\eta=\eta x\}=T_\eta , \end{align}
\begin{align} \mathrm{GSU}_{1,D}(F)&=\{\alpha\in D^\times:\bar{\alpha} \eta \alpha = \mathrm{n}_D(\alpha) \eta\} \nonumber\\ &=\{x\in D^\times\mid x\eta=\eta x\}=T_\eta , \end{align}
where ![]() $T_\eta$ is defined by (1.4.6) with
$T_\eta$ is defined by (1.4.6) with ![]() $\xi =\eta$ and
$\xi =\eta$ and ![]() $\mathrm {n}_D$ denotes the reduced norm of
$\mathrm {n}_D$ denotes the reduced norm of ![]() $D$.
$D$.
2.1.4 Unitary groups
Suppose that ![]() $D=D_\varepsilon$ defined by (2.1.1). Then we define
$D=D_\varepsilon$ defined by (2.1.1). Then we define ![]() $\mathrm {GU}_{4,\varepsilon }$ a similitude unitary group of degree
$\mathrm {GU}_{4,\varepsilon }$ a similitude unitary group of degree ![]() $4$ by
$4$ by
where we define a hermitian matrix ![]() $\mathcal {J}_\varepsilon$ by
$\mathcal {J}_\varepsilon$ by
 \[ \mathcal{J}_\varepsilon := \begin{pmatrix} 0 & 0 & 0 & 1\\ 0 & -1 & 0 & 0\\ 0 & 0 & \varepsilon & 0\\ 1 & 0 & 0 & 0\end{pmatrix}. \]
\[ \mathcal{J}_\varepsilon := \begin{pmatrix} 0 & 0 & 0 & 1\\ 0 & -1 & 0 & 0\\ 0 & 0 & \varepsilon & 0\\ 1 & 0 & 0 & 0\end{pmatrix}. \]
Here ![]() $A^\sigma =(a_{ij}^\sigma )$ for
$A^\sigma =(a_{ij}^\sigma )$ for ![]() $A=(a_{ij})\in \mathrm {Mat}_{m \times n}(E)$. Then we have
$A=(a_{ij})\in \mathrm {Mat}_{m \times n}(E)$. Then we have
 \begin{equation} \mathrm{GU}_{4,\varepsilon}\simeq \begin{cases} \mathrm{GU}_{2,2}, & \text{when $D$ is split, i.e. $\varepsilon\in \mathrm{N}_{E/ F}(E^\times)$};\\ \mathrm{GU}_{3,1}, & \text{when $D$ is non-split, i.e. $\varepsilon\notin \mathrm{N}_{E/ F}(E^\times)$}. \end{cases} \end{equation}
\begin{equation} \mathrm{GU}_{4,\varepsilon}\simeq \begin{cases} \mathrm{GU}_{2,2}, & \text{when $D$ is split, i.e. $\varepsilon\in \mathrm{N}_{E/ F}(E^\times)$};\\ \mathrm{GU}_{3,1}, & \text{when $D$ is non-split, i.e. $\varepsilon\notin \mathrm{N}_{E/ F}(E^\times)$}. \end{cases} \end{equation} We also define ![]() $\mathrm {GU}_{2,\varepsilon }$ a similitude unitary group of degree
$\mathrm {GU}_{2,\varepsilon }$ a similitude unitary group of degree ![]() $2$ by
$2$ by
2.2 Accidental isomorphisms
We need to explicate the accidental isomorphisms of our concern, since we use them in a crucial way to transfer an automorphic period on one group to the one on the other group. The reader may consult, for example, Satake [Reference SatakeSat61] and Tsukamoto [Reference TsukamotoTsu61] about the details of the material here.
2.2.1  $\mathrm {PGSU}_{3,D}\simeq \mathrm {PGU}_{4,\varepsilon }$
$\mathrm {PGSU}_{3,D}\simeq \mathrm {PGU}_{4,\varepsilon }$
Suppose that ![]() $D=D_\varepsilon$. Then we may naturally realize
$D=D_\varepsilon$. Then we may naturally realize ![]() $\mathrm {GSU}_{3,D}(F)$ as a subgroup of
$\mathrm {GSU}_{3,D}(F)$ as a subgroup of ![]() $\mathrm {GL}_6(E)$. We note that
$\mathrm {GL}_6(E)$. We note that
 \[ \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & -\varepsilon & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -\varepsilon & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & -\varepsilon \end{pmatrix}\,{}^{t}\bar{g}\, \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & -\varepsilon & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -\varepsilon & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & -\varepsilon \end{pmatrix}^{-1}= {}^{t}g^\sigma \]
\[ \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & -\varepsilon & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -\varepsilon & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & -\varepsilon \end{pmatrix}\,{}^{t}\bar{g}\, \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & -\varepsilon & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -\varepsilon & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & -\varepsilon \end{pmatrix}^{-1}= {}^{t}g^\sigma \]
and
 \[ \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & -1 & 0 \end{pmatrix}\,{}^{t}\bar{g}\, \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & -1 & 0 \end{pmatrix}^{-1}= {}^{t}g. \]
\[ \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & -1 & 0 \end{pmatrix}\,{}^{t}\bar{g}\, \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & -1 & 0 \end{pmatrix}^{-1}= {}^{t}g. \]
Thus, in this realization, we have
where
 \[ \mathcal{J}_{\varepsilon}^\circ =- \begin{pmatrix} 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & \varepsilon\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & \varepsilon & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 0 & \varepsilon & 0 & 0 & 0 & 0 \end{pmatrix}. \]
\[ \mathcal{J}_{\varepsilon}^\circ =- \begin{pmatrix} 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & \varepsilon\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & \varepsilon & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 0 & \varepsilon & 0 & 0 & 0 & 0 \end{pmatrix}. \]
Here we recall that
In fact, the isomorphism (2.2.2) is realized as follows. Let us take the standard basis
of ![]() $E^4$. Then we may consider
$E^4$. Then we may consider ![]() $V:=\wedge ^2 E^4$ as an orthogonal space over
$V:=\wedge ^2 E^4$ as an orthogonal space over ![]() $E$ with a quadratic form
$E$ with a quadratic form ![]() $(\,{,}\,)_V$ defined by
$(\,{,}\,)_V$ defined by
for ![]() $v_1, v_2 \in V$. As a basis of
$v_1, v_2 \in V$. As a basis of ![]() $V$ over
$V$ over ![]() $E$, we take
$E$, we take ![]() $\{ \varepsilon _i: 1\le i\le 6 \}$ given by
$\{ \varepsilon _i: 1\le i\le 6 \}$ given by
Let the group ![]() $\mathrm {GL}_4(E) \times \mathrm {GL}_1(E)$ act on
$\mathrm {GL}_4(E) \times \mathrm {GL}_1(E)$ act on ![]() $V$ by
$V$ by ![]() $(g, a)(w_1 \wedge w_2) = a \cdot (gw_1 \wedge gw_2)$ where
$(g, a)(w_1 \wedge w_2) = a \cdot (gw_1 \wedge gw_2)$ where ![]() $w_1,w_2\in E^4$. This action defines a homomorphism
$w_1,w_2\in E^4$. This action defines a homomorphism
where we take ![]() $\{\varepsilon _i: 1\le i\le 6\}$ as a basis of
$\{\varepsilon _i: 1\le i\le 6\}$ as a basis of ![]() $V$ and the homomorphism (2.2.3) induces the isomorphism (2.2.2). By a direct computation we observe that
$V$ and the homomorphism (2.2.3) induces the isomorphism (2.2.2). By a direct computation we observe that ![]() $(-\mathcal {J}_\varepsilon, 1)$ is mapped to
$(-\mathcal {J}_\varepsilon, 1)$ is mapped to ![]() $\mathcal {J}_\varepsilon ^\circ$ under (2.2.3) and the restriction of the homomorphism (2.2.3) gives a homomorphism
$\mathcal {J}_\varepsilon ^\circ$ under (2.2.3) and the restriction of the homomorphism (2.2.3) gives a homomorphism
Then it is easily seen that the isomorphism
is induced.
2.2.2  $\mathrm {PGU}_{2,2} \simeq \mathrm {PGSO}_{4,2}$
$\mathrm {PGU}_{2,2} \simeq \mathrm {PGSO}_{4,2}$
When ![]() $\varepsilon \in \mathrm {N}_{E / F}(E^\times )$, the quaternion algebra
$\varepsilon \in \mathrm {N}_{E / F}(E^\times )$, the quaternion algebra ![]() $D=D_\varepsilon$ is split and the isomorphism (2.2.5) gives an isomorphism
$D=D_\varepsilon$ is split and the isomorphism (2.2.5) gives an isomorphism ![]() $\mathrm {PGU}_{2,2}\simeq \mathrm {PGSO}_{4,2}$. We recall the concrete realization of this isomorphism. First we define
$\mathrm {PGU}_{2,2}\simeq \mathrm {PGSO}_{4,2}$. We recall the concrete realization of this isomorphism. First we define ![]() $\mathrm {GU}_{2,2}$ by
$\mathrm {GU}_{2,2}$ by
 \begin{align*} \mathrm{GU}_{2,2} &:=
\{g\in\mathrm{GL}_4(E): {}^tg^\sigma\, J_4\,g
=\lambda(g)J_4, \lambda(g)\in F^\times\}, \quad \text{where $J_4=\begin{pmatrix} 0 & 0 &
0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0
\end{pmatrix}$} \end{align*}
\begin{align*} \mathrm{GU}_{2,2} &:=
\{g\in\mathrm{GL}_4(E): {}^tg^\sigma\, J_4\,g
=\lambda(g)J_4, \lambda(g)\in F^\times\}, \quad \text{where $J_4=\begin{pmatrix} 0 & 0 &
0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0
\end{pmatrix}$} \end{align*}
as (2.1.6). Let
 \[ {\mathcal{V}}: = \left\{B((x_i)_{1\le i\le 6}):= \left(\begin{matrix} 0 & \eta x_1 & x_3 + \eta x_4 & x_2\\ -\eta x_1 & 0 & x_5 & -x_3 +\eta x_4\\ -x_3 -\eta x_4 & -x_5 & 0 & \eta^{-1} x_6\\ -x_2 & x_3 -\eta x_4 & -\eta^{-1} x_6 & 0\\ \end{matrix}\right): x_i \in F (1\le i\le6)\right\}. \]
\[ {\mathcal{V}}: = \left\{B((x_i)_{1\le i\le 6}):= \left(\begin{matrix} 0 & \eta x_1 & x_3 + \eta x_4 & x_2\\ -\eta x_1 & 0 & x_5 & -x_3 +\eta x_4\\ -x_3 -\eta x_4 & -x_5 & 0 & \eta^{-1} x_6\\ -x_2 & x_3 -\eta x_4 & -\eta^{-1} x_6 & 0\\ \end{matrix}\right): x_i \in F (1\le i\le6)\right\}. \]
We define ![]() $\Psi : {\mathcal {V}} \rightarrow F$ by
$\Psi : {\mathcal {V}} \rightarrow F$ by
Then we have
Let ![]() $\mathrm {GSU}_{2,2}$ denote the identity component of
$\mathrm {GSU}_{2,2}$ denote the identity component of ![]() $\mathrm {GU}_{2,2}$, i.e.
$\mathrm {GU}_{2,2}$, i.e.
We let ![]() $\mathrm {GSU}_{2,2}$ act on
$\mathrm {GSU}_{2,2}$ act on ![]() $\mathcal {V}$ by
$\mathcal {V}$ by
 \[ \mathrm{GSU}_{2,2}\times \mathcal{V}\ni (g,B)\mapsto (wg w)B(w\,{}^tg w)\in\mathcal{V}, \quad\text{where $w=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\end{pmatrix}$.} \]
\[ \mathrm{GSU}_{2,2}\times \mathcal{V}\ni (g,B)\mapsto (wg w)B(w\,{}^tg w)\in\mathcal{V}, \quad\text{where $w=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\end{pmatrix}$.} \]
Then this action induces a homomorphism ![]() $\phi : \mathrm {GSU}_{2,2} \rightarrow \mathrm {GO}({\mathcal {V}})$. We note that
$\phi : \mathrm {GSU}_{2,2} \rightarrow \mathrm {GO}({\mathcal {V}})$. We note that
and this implies that the image of ![]() $\phi$ is contained in
$\phi$ is contained in ![]() $\mathrm {GSO}(\mathcal {V})$. As a basis of
$\mathrm {GSO}(\mathcal {V})$. As a basis of ![]() ${\mathcal {V}}$, we may take
${\mathcal {V}}$, we may take
 \begin{gather*} f_1=\begin{pmatrix} 0 &
\eta & 0 & 0\\ -\eta & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 &
0 & 0\\ \end{pmatrix},\quad f_2=\begin{pmatrix} 0 & 0 & 0 &
1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0\\
\end{pmatrix},\quad f_3=\begin{pmatrix} 0 & 0 & 1 & 0\\ 0 &
0 & 0 & -1\\ -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\
\end{pmatrix},\\ f_4= \begin{pmatrix} 0 & 0 & \eta & 0\\ 0
& 0 & 0 & \eta\\ -\eta & 0 & 0 & 0\\ 0 & -\eta & 0 & 0\\
\end{pmatrix},\quad f_5=\begin{pmatrix} 0 & 0 & 0 & 0\\ 0 &
0 & 1 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 0\\
\end{pmatrix},\quad f_6=\begin{pmatrix} 0 & 0 & 0 & 0\\ 0 &
0 & 0 & 0\\ 0 & 0 & 0 & \eta^{-1}\\ 0 & 0 & -\eta^{-1} &
0\\ \end{pmatrix}. \end{gather*}
\begin{gather*} f_1=\begin{pmatrix} 0 &
\eta & 0 & 0\\ -\eta & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 &
0 & 0\\ \end{pmatrix},\quad f_2=\begin{pmatrix} 0 & 0 & 0 &
1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0\\
\end{pmatrix},\quad f_3=\begin{pmatrix} 0 & 0 & 1 & 0\\ 0 &
0 & 0 & -1\\ -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\
\end{pmatrix},\\ f_4= \begin{pmatrix} 0 & 0 & \eta & 0\\ 0
& 0 & 0 & \eta\\ -\eta & 0 & 0 & 0\\ 0 & -\eta & 0 & 0\\
\end{pmatrix},\quad f_5=\begin{pmatrix} 0 & 0 & 0 & 0\\ 0 &
0 & 1 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 0\\
\end{pmatrix},\quad f_6=\begin{pmatrix} 0 & 0 & 0 & 0\\ 0 &
0 & 0 & 0\\ 0 & 0 & 0 & \eta^{-1}\\ 0 & 0 & -\eta^{-1} &
0\\ \end{pmatrix}. \end{gather*}
With respect to this basis, we may regard ![]() $\phi$ as a homomorphism from
$\phi$ as a homomorphism from ![]() $\mathrm {GSU}_{2,2}$ to
$\mathrm {GSU}_{2,2}$ to ![]() $\mathrm {GO}_{4,2}$, where the group
$\mathrm {GO}_{4,2}$, where the group ![]() $\mathrm {GO}_{4,2}$ is given by (2.1.5) for
$\mathrm {GO}_{4,2}$ is given by (2.1.5) for ![]() $n=2$. Let us consider
$n=2$. Let us consider ![]() $\mathrm {GSU}_{2,2}\rtimes E^\times$ where the action of
$\mathrm {GSU}_{2,2}\rtimes E^\times$ where the action of ![]() $\alpha \in E^\times$ on
$\alpha \in E^\times$ on ![]() $g\in \mathrm {GSU}_{2,2}$ is given by
$g\in \mathrm {GSU}_{2,2}$ is given by
 \[ \alpha \cdot g = \begin{pmatrix} \alpha & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & (\alpha^{\sigma})^{-1} \end{pmatrix}\,g \,\begin{pmatrix} \alpha & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & (\alpha^{\sigma})^{-1} \end{pmatrix}^{-1}. \]
\[ \alpha \cdot g = \begin{pmatrix} \alpha & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & (\alpha^{\sigma})^{-1} \end{pmatrix}\,g \,\begin{pmatrix} \alpha & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & (\alpha^{\sigma})^{-1} \end{pmatrix}^{-1}. \]
Then as in [Reference MorimotoMor14a, p. 32–34], ![]() $\phi$ may be extended to
$\phi$ may be extended to ![]() $\mathrm {GSU}_{2,2}\rtimes E^\times$ and we have a homomorphism
$\mathrm {GSU}_{2,2}\rtimes E^\times$ and we have a homomorphism ![]() $\mathrm {GSU}_{2,2}\rtimes E^\times \to \mathrm {PGSO}_{4,2}$ which induces the isomorphism
$\mathrm {GSU}_{2,2}\rtimes E^\times \to \mathrm {PGSO}_{4,2}$ which induces the isomorphism
2.3 Bessel periods
Let us introduce Bessel periods on various groups.
2.3.1 Bessel periods on  $G=\mathrm {GSp}_2$
$G=\mathrm {GSp}_2$
Though we already introduced Bessel periods on ![]() $G_D$ in general as (1.4.11), we would like to describe them concretely in the case of
$G_D$ in general as (1.4.11), we would like to describe them concretely in the case of ![]() $G$ here for our explicit pull-back computations in the next section.
$G$ here for our explicit pull-back computations in the next section.
Let ![]() $P$ be the Siegel parabolic subgroup of
$P$ be the Siegel parabolic subgroup of ![]() $G$ with the Levi decomposition
$G$ with the Levi decomposition ![]() $P = MN$ where
$P = MN$ where
Here ![]() $\mathrm {Sym}_n(F)$ denotes the set of
$\mathrm {Sym}_n(F)$ denotes the set of ![]() $n$ by
$n$ by ![]() $n$ symmetric matrices with entries in
$n$ symmetric matrices with entries in ![]() $F$ for a positive integer
$F$ for a positive integer ![]() $n$. For
$n$. For ![]() $S \in \mathrm {Sym}_2(F)$, let us define a character
$S \in \mathrm {Sym}_2(F)$, let us define a character ![]() $\psi _{S}$ of
$\psi _{S}$ of ![]() $N(\mathbb {A})$ by
$N(\mathbb {A})$ by
For ![]() $S\in \mathrm {Sym}_2(F)$ such that
$S\in \mathrm {Sym}_2(F)$ such that ![]() $\det S\ne 0$, let
$\det S\ne 0$, let
We identify ![]() $T_S$ with the subgroup of
$T_S$ with the subgroup of ![]() $G$ given by
$G$ given by
Definition 2.1 Let us take ![]() $S\in \mathrm {Sym}_2(F)$ such that
$S\in \mathrm {Sym}_2(F)$ such that ![]() $T_S(F)$ is isomorphic to
$T_S(F)$ is isomorphic to ![]() $E^\times$. Let
$E^\times$. Let ![]() $\pi$ be an irreducible cuspidal automorphic representation of
$\pi$ be an irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A})$ whose central character is trivial and
$G(\mathbb {A})$ whose central character is trivial and ![]() $V_\pi$ its space of automorphic forms. Fix an
$V_\pi$ its space of automorphic forms. Fix an ![]() $F$-isomorphism
$F$-isomorphism ![]() $T_S(F)\simeq E^\times$. Let
$T_S(F)\simeq E^\times$. Let ![]() $\Lambda$ be a character of
$\Lambda$ be a character of ![]() $\mathbb {A}_E^\times / E^\times$ such that
$\mathbb {A}_E^\times / E^\times$ such that ![]() $\Lambda \mid _{\mathbb {A}^\times }$ is trivial. We regard
$\Lambda \mid _{\mathbb {A}^\times }$ is trivial. We regard ![]() $\Lambda$ as a character of
$\Lambda$ as a character of ![]() $T_S(\mathbb {A}) / \mathbb {A}^\times \, T_S(F)$.
$T_S(\mathbb {A}) / \mathbb {A}^\times \, T_S(F)$.
Then for ![]() $\varphi \in V_\pi$, we define
$\varphi \in V_\pi$, we define ![]() $B_{S,\Lambda,\psi }(\varphi )$, the
$B_{S,\Lambda,\psi }(\varphi )$, the ![]() $(S,\Lambda,\psi )$-Bessel period of
$(S,\Lambda,\psi )$-Bessel period of ![]() $\varphi$ by
$\varphi$ by
We say that ![]() $\pi$ has the
$\pi$ has the ![]() $(S,\Lambda,\psi )$-Bessel period when
$(S,\Lambda,\psi )$-Bessel period when ![]() $B_{S, \Lambda,\psi }\not \equiv 0$ on
$B_{S, \Lambda,\psi }\not \equiv 0$ on ![]() $V_\pi$. Then we also say that
$V_\pi$. Then we also say that ![]() $\pi$ has the
$\pi$ has the ![]() $(E,\Lambda )$-Bessel period as in Definition 1.2.
$(E,\Lambda )$-Bessel period as in Definition 1.2.
2.3.2 Bessel periods on  $\mathrm {GSU}_{3,D}$
$\mathrm {GSU}_{3,D}$
Let us introduce Bessel periods on the group ![]() $\mathrm {GSU}_{3,D}$ defined in § 2.1.3. Let
$\mathrm {GSU}_{3,D}$ defined in § 2.1.3. Let ![]() $P_{3,D}$ be a maximal parabolic subgroup of
$P_{3,D}$ be a maximal parabolic subgroup of ![]() $\mathrm {GSU}_{3,D}$ with the Levi decomposition
$\mathrm {GSU}_{3,D}$ with the Levi decomposition ![]() $P_{3,D}=M_{3,D}N_{3,D}$ where
$P_{3,D}=M_{3,D}N_{3,D}$ where
 \[ M_{3,D} = \left\{\begin{pmatrix} g & 0 & 0\\ 0 & h & 0\\ 0 & 0 & g \end{pmatrix}:\begin{aligned} & g\in D^\times,\\ & h \in T_\eta,\\ & \mathrm{n}_D(g)=\mathrm{n}_D(h) \end{aligned}\right\},\quad N_{3,D} = \left\{\begin{pmatrix} 1 & A^\prime & B\\ 0 & 1 & A\\ 0 & 0 & 1 \end{pmatrix} \in \mathrm{GSU}_{3,D}\right\}.\label{d:N3,D} \]
\[ M_{3,D} = \left\{\begin{pmatrix} g & 0 & 0\\ 0 & h & 0\\ 0 & 0 & g \end{pmatrix}:\begin{aligned} & g\in D^\times,\\ & h \in T_\eta,\\ & \mathrm{n}_D(g)=\mathrm{n}_D(h) \end{aligned}\right\},\quad N_{3,D} = \left\{\begin{pmatrix} 1 & A^\prime & B\\ 0 & 1 & A\\ 0 & 0 & 1 \end{pmatrix} \in \mathrm{GSU}_{3,D}\right\}.\label{d:N3,D} \]
As for ![]() $T_\eta$, we recall (2.1.13) and
$T_\eta$, we recall (2.1.13) and ![]() $T_\eta \simeq E^\times$. For
$T_\eta \simeq E^\times$. For ![]() $X \in D^\times$, we define a character
$X \in D^\times$, we define a character ![]() $\psi _{X, D}$ of
$\psi _{X, D}$ of ![]() $N_{3, D}(\mathbb {A})$ by
$N_{3, D}(\mathbb {A})$ by
 \[ \psi_{X, D} \begin{pmatrix} 1 & A^\prime & B\\ 0 & 1 & A\\ 0 & 0 & 1 \end{pmatrix} = \psi [\mathrm{tr}_D(XA)]. \]
\[ \psi_{X, D} \begin{pmatrix} 1 & A^\prime & B\\ 0 & 1 & A\\ 0 & 0 & 1 \end{pmatrix} = \psi [\mathrm{tr}_D(XA)]. \]
Then the identity component of the stabilizer of ![]() $\psi _{X, D}$ in
$\psi _{X, D}$ in ![]() $M_{3,D}$ is
$M_{3,D}$ is
 \[ M_{X, D} = \left\{\!\begin{pmatrix} h^{X} & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^{X} \end{pmatrix}: h \in T_\eta \right\},\quad \text{where}\ h^X = XhX^{-1}.\label{M_X D} \]
\[ M_{X, D} = \left\{\!\begin{pmatrix} h^{X} & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^{X} \end{pmatrix}: h \in T_\eta \right\},\quad \text{where}\ h^X = XhX^{-1}.\label{M_X D} \]
We identify ![]() $M_X$ with
$M_X$ with ![]() $T_\eta$ by
$T_\eta$ by
 \begin{equation} M_{X, D}\ni \begin{pmatrix} h^{X} & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^{X}\end{pmatrix} \mapsto h\in T_\eta \end{equation}
\begin{equation} M_{X, D}\ni \begin{pmatrix} h^{X} & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^{X}\end{pmatrix} \mapsto h\in T_\eta \end{equation}
and we fix an ![]() $F$-isomorphism
$F$-isomorphism ![]() $T_\eta \simeq E^\times$.
$T_\eta \simeq E^\times$.
Definition 2.2 Let ![]() $\sigma _D$ be an irreducible cuspidal automorphic representation of
$\sigma _D$ be an irreducible cuspidal automorphic representation of ![]() $\mathrm {GSU}_{3,D}(\mathbb {A})$ and
$\mathrm {GSU}_{3,D}(\mathbb {A})$ and ![]() $V_{\sigma _D}$ its space of automorphic forms. Let
$V_{\sigma _D}$ its space of automorphic forms. Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $\mathbb {A}_E^\times / E^\times$ and we regard
$\mathbb {A}_E^\times / E^\times$ and we regard ![]() $\chi$ as a character of
$\chi$ as a character of ![]() $M_{X,D}(\mathbb {A}) / M_{X,D}(F)$. Suppose that
$M_{X,D}(\mathbb {A}) / M_{X,D}(F)$. Suppose that ![]() $\chi |_{\mathbb {A}^\times } = \omega _{\sigma _D}$, the central character of
$\chi |_{\mathbb {A}^\times } = \omega _{\sigma _D}$, the central character of ![]() $\sigma _D$.
$\sigma _D$.
Then for ![]() $\varphi \in V_{\sigma _D}$, we define
$\varphi \in V_{\sigma _D}$, we define ![]() $\mathcal {B}^D_{X, \chi, \psi } (\varphi )$, the
$\mathcal {B}^D_{X, \chi, \psi } (\varphi )$, the ![]() $(X,\chi, \psi )$-Bessel period of
$(X,\chi, \psi )$-Bessel period of ![]() $\varphi$ by
$\varphi$ by
2.3.3 Bessel periods on  $\mathrm {GU}_{4,\varepsilon }$
$\mathrm {GU}_{4,\varepsilon }$
In light of the accidental isomorphism (2.2.5), Bessel periods on the group ![]() $\mathrm {GU}_{4,\varepsilon }$ is defined as follows.
$\mathrm {GU}_{4,\varepsilon }$ is defined as follows.
Let ![]() $P_{4,\varepsilon }$ be a maximal parabolic subgroup of
$P_{4,\varepsilon }$ be a maximal parabolic subgroup of ![]() $\mathrm {GU}_{4,\varepsilon }$ with the Levi decomposition
$\mathrm {GU}_{4,\varepsilon }$ with the Levi decomposition ![]() $M_{4,\varepsilon }N_{4,\varepsilon }$ where
$M_{4,\varepsilon }N_{4,\varepsilon }$ where
 \begin{align*} M_{4,\varepsilon}(F) &= \left\{\!\begin{pmatrix} a & 0 & 0\\ 0 & g & 0\\ 0 & 0 & \lambda(g) (a^\sigma)^{-1} \end{pmatrix}: a \in E^\times, g \in \mathrm{GU}_{2,\varepsilon}(F) \right\},\\ N_{4,\varepsilon}(F) &= \left\{\!\begin{pmatrix} 1 & A & B\\ 0 & 1_2 & A^\prime\\ 0 & 0 & 1 \end{pmatrix} \in \mathrm{GU}_{4,\varepsilon}(F) \right\}. \end{align*}
\begin{align*} M_{4,\varepsilon}(F) &= \left\{\!\begin{pmatrix} a & 0 & 0\\ 0 & g & 0\\ 0 & 0 & \lambda(g) (a^\sigma)^{-1} \end{pmatrix}: a \in E^\times, g \in \mathrm{GU}_{2,\varepsilon}(F) \right\},\\ N_{4,\varepsilon}(F) &= \left\{\!\begin{pmatrix} 1 & A & B\\ 0 & 1_2 & A^\prime\\ 0 & 0 & 1 \end{pmatrix} \in \mathrm{GU}_{4,\varepsilon}(F) \right\}. \end{align*}
Let us take an anisotropic vector ![]() $e\in E^4$ of the form
$e\in E^4$ of the form ![]() ${}^{t}(0, \ast, \ast, 0)$. Then we define a character
${}^{t}(0, \ast, \ast, 0)$. Then we define a character ![]() $\chi _e$ of
$\chi _e$ of ![]() $N_{4,\varepsilon }(\mathbb {A})$ by
$N_{4,\varepsilon }(\mathbb {A})$ by
Here we recall that ![]() $J_\varepsilon$ is as given in (2.1.16) and
$J_\varepsilon$ is as given in (2.1.16) and ![]() $b_1={}^t(1,0,0,0)$. Let
$b_1={}^t(1,0,0,0)$. Let ![]() $D_e$ denote the subgroup of
$D_e$ denote the subgroup of ![]() $M_{4,\varepsilon }$ given by
$M_{4,\varepsilon }$ given by
 \[ D_{e} := \left\{\!\begin{pmatrix}1 & 0 & 0\\ 0 & h & 0\\ 0 & 0 & 1\end{pmatrix}: h \in \mathrm{U}_{2,\varepsilon},\ h e = e \right\}. \]
\[ D_{e} := \left\{\!\begin{pmatrix}1 & 0 & 0\\ 0 & h & 0\\ 0 & 0 & 1\end{pmatrix}: h \in \mathrm{U}_{2,\varepsilon},\ h e = e \right\}. \]
Then the group ![]() $D_e(\mathbb {A})$ stabilizes the character
$D_e(\mathbb {A})$ stabilizes the character ![]() $\chi _e$ by conjugation. We note that
$\chi _e$ by conjugation. We note that
Hence, for a character ![]() $\Lambda$ of
$\Lambda$ of ![]() $\mathbb {A}_E^\times$ which is trivial on
$\mathbb {A}_E^\times$ which is trivial on ![]() $\mathbb {A}^\times$, we may regard
$\mathbb {A}^\times$, we may regard ![]() $\Lambda$ as a character of
$\Lambda$ as a character of ![]() $D_e(\mathbb {A})$ by
$D_e(\mathbb {A})$ by ![]() $d \mapsto \Lambda (\det d)$. Then we define a character
$d \mapsto \Lambda (\det d)$. Then we define a character ![]() $\chi _{e, \Lambda }$ of
$\chi _{e, \Lambda }$ of ![]() $R_e(\mathbb {A})$ where
$R_e(\mathbb {A})$ where ![]() $R_e:=D_eN_{4,\varepsilon }$ by
$R_e:=D_eN_{4,\varepsilon }$ by
Definition 2.3 For a cusp form ![]() $\varphi$ on
$\varphi$ on ![]() $\mathrm {GU}_{4,\varepsilon }(\mathbb {A}_F)$ with a trivial central character, we define
$\mathrm {GU}_{4,\varepsilon }(\mathbb {A}_F)$ with a trivial central character, we define ![]() $B_{e, \Lambda,\psi }(\varphi )$, the
$B_{e, \Lambda,\psi }(\varphi )$, the ![]() $(e, \Lambda,\psi )$-Bessel period of
$(e, \Lambda,\psi )$-Bessel period of ![]() $\varphi$, by
$\varphi$, by
2.3.4 Bessel periods on  $\mathrm {GSO}_{4,2}$ and
$\mathrm {GSO}_{4,2}$ and  $\mathrm {GSO}_{3,3}$
$\mathrm {GSO}_{3,3}$
By combining the accidental isomorphisms (2.2.5) and (2.2.6) in the split case, we shall define Bessel periods on ![]() $\mathrm {GSO}_{4,2}$ and
$\mathrm {GSO}_{4,2}$ and ![]() $\mathrm {GSO}_{3,3}$ as the following.
$\mathrm {GSO}_{3,3}$ as the following.
Let ![]() $P_{4,2}$ denote a maximal parabolic subgroup of
$P_{4,2}$ denote a maximal parabolic subgroup of ![]() $\mathrm {GSO}_{4,2}$ with the Levi decomposition
$\mathrm {GSO}_{4,2}$ with the Levi decomposition ![]() $P_{4,2}= M_{4,2}N_{4,2}$ where
$P_{4,2}= M_{4,2}N_{4,2}$ where
 \[ M_{4,2} = \left\{\!\begin{pmatrix} g & 0 & 0\\0 & h & 0\\0 & 0 & g^\ast\cdot \det h\end{pmatrix} : \begin{aligned} & g \in \mathrm{GL}_2,\\ & h \in \mathrm{GSO}_{2 ,0} \end{aligned}\right\},\quad N_{4,2}= \left\{\!\begin{pmatrix} 1_2 & A^\prime & B\\ 0 & 1_2 & A\\ 0 & 0 & 1_2 \end{pmatrix} \in \mathrm{GSO}_{4,2}\right\}.\label{d:N4,2} \]
\[ M_{4,2} = \left\{\!\begin{pmatrix} g & 0 & 0\\0 & h & 0\\0 & 0 & g^\ast\cdot \det h\end{pmatrix} : \begin{aligned} & g \in \mathrm{GL}_2,\\ & h \in \mathrm{GSO}_{2 ,0} \end{aligned}\right\},\quad N_{4,2}= \left\{\!\begin{pmatrix} 1_2 & A^\prime & B\\ 0 & 1_2 & A\\ 0 & 0 & 1_2 \end{pmatrix} \in \mathrm{GSO}_{4,2}\right\}.\label{d:N4,2} \]
Here
Then for ![]() $X\in \mathrm {Mat}_{2\times 2}(F)$, we define a character
$X\in \mathrm {Mat}_{2\times 2}(F)$, we define a character ![]() $\psi _X$ of
$\psi _X$ of ![]() $N_{4,2}(\mathbb {A})$ by
$N_{4,2}(\mathbb {A})$ by
 \[ \psi_{X} \begin{pmatrix}1_2 & A^\prime & B\\ 0 & 1_2 & A\\0 & 0 & 1_2 \end{pmatrix}= \psi [\mathrm{tr}(XA)]. \]
\[ \psi_{X} \begin{pmatrix}1_2 & A^\prime & B\\ 0 & 1_2 & A\\0 & 0 & 1_2 \end{pmatrix}= \psi [\mathrm{tr}(XA)]. \]
Suppose that ![]() $\det X \ne 0$ and let
$\det X \ne 0$ and let
 \[ M_{X} := \left\{\!\begin{pmatrix} (\det h) \cdot (h^X)^\ast & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^X \end{pmatrix} : h \in \mathrm{GSO}_{2,0} \right\},\label{M_X} \]
\[ M_{X} := \left\{\!\begin{pmatrix} (\det h) \cdot (h^X)^\ast & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^X \end{pmatrix} : h \in \mathrm{GSO}_{2,0} \right\},\label{M_X} \]
where ![]() $h^X = XhX^{-1}$ . Then
$h^X = XhX^{-1}$ . Then ![]() $M_X(\mathbb {A})$ stabilizes the character
$M_X(\mathbb {A})$ stabilizes the character ![]() $\psi _X$ and
$\psi _X$ and ![]() $M_X$ is isomorphic to
$M_X$ is isomorphic to ![]() $\mathrm {GSO}_{2,0}$. We fix an isomorphism
$\mathrm {GSO}_{2,0}$. We fix an isomorphism ![]() $\mathrm {GSO}_{2,0}(F)\simeq E^\times$ and we regard a character of
$\mathrm {GSO}_{2,0}(F)\simeq E^\times$ and we regard a character of ![]() $\mathbb {A}_E^\times$ as a character of
$\mathbb {A}_E^\times$ as a character of ![]() $M_X(\mathbb {A})$.
$M_X(\mathbb {A})$.
Definition 2.4 Let ![]() $\sigma$ be an irreducible cuspidal automorphic representation of
$\sigma$ be an irreducible cuspidal automorphic representation of ![]() $\mathrm {GSO}_{4,2}(\mathbb {A})$ with its space of automorphic forms
$\mathrm {GSO}_{4,2}(\mathbb {A})$ with its space of automorphic forms ![]() $V_\sigma$ and the central character
$V_\sigma$ and the central character ![]() $\omega _\sigma$. For a character
$\omega _\sigma$. For a character ![]() $\chi$ of
$\chi$ of ![]() $\mathbb {A}_E^\times$ such that
$\mathbb {A}_E^\times$ such that ![]() $\chi |_{\mathbb {A}^\times } = \omega _{\sigma }$, we define
$\chi |_{\mathbb {A}^\times } = \omega _{\sigma }$, we define ![]() $\mathcal {B}_{X,\chi, \psi }(\varphi )$, the
$\mathcal {B}_{X,\chi, \psi }(\varphi )$, the ![]() $(X, \chi, \psi )$-Bessel period of
$(X, \chi, \psi )$-Bessel period of ![]() $\varphi \in V_\sigma$ by
$\varphi \in V_\sigma$ by
When ![]() $d \in (F^\times )^2$, we know that
$d \in (F^\times )^2$, we know that ![]() $\mathrm {GSO}(S_2) \simeq \mathrm {GSO}_{3,3}$. Hence, as above, for a cusp form
$\mathrm {GSO}(S_2) \simeq \mathrm {GSO}_{3,3}$. Hence, as above, for a cusp form ![]() $\varphi$ on
$\varphi$ on ![]() $\mathrm {GSO}_{3,3}$ with central character
$\mathrm {GSO}_{3,3}$ with central character ![]() $\omega$ and characters
$\omega$ and characters ![]() $\Lambda _1, \Lambda _2$ of
$\Lambda _1, \Lambda _2$ of ![]() $\mathbb {A}^\times / F^\times$ such that
$\mathbb {A}^\times / F^\times$ such that ![]() $\Lambda _1 \Lambda _2=\omega$, we define
$\Lambda _1 \Lambda _2=\omega$, we define ![]() $(X, \Lambda _1, \Lambda _2, \psi )$-Bessel period by
$(X, \Lambda _1, \Lambda _2, \psi )$-Bessel period by
Here, since ![]() $M_{4,2} \simeq \mathrm {GL}_2 \times \mathrm {GSO}_{1,1}$ and
$M_{4,2} \simeq \mathrm {GL}_2 \times \mathrm {GSO}_{1,1}$ and ![]() $\mathrm {GSO}_{1,1}(F) = \big \{\big (\begin{smallmatrix} a & \\ & b\end{smallmatrix}\big ) : a, b \in F^\times \big \}$, we define a character
$\mathrm {GSO}_{1,1}(F) = \big \{\big (\begin{smallmatrix} a & \\ & b\end{smallmatrix}\big ) : a, b \in F^\times \big \}$, we define a character ![]() $\chi _{\Lambda _1, \Lambda _2}$ of
$\chi _{\Lambda _1, \Lambda _2}$ of ![]() $\mathrm {GSO}_{1,1}(\mathbb {A})$ by
$\mathrm {GSO}_{1,1}(\mathbb {A})$ by
When ![]() $\omega$ is trivial, we have
$\omega$ is trivial, we have ![]() $\Lambda _2 = \Lambda _1^{-1}$. In this case, we simply call
$\Lambda _2 = \Lambda _1^{-1}$. In this case, we simply call ![]() $(X, \Lambda _1, \Lambda _1^{-1}, \psi )$-Bessel period as
$(X, \Lambda _1, \Lambda _1^{-1}, \psi )$-Bessel period as ![]() $(X, \Lambda _1, \psi )$-Bessel period and simply write
$(X, \Lambda _1, \psi )$-Bessel period and simply write ![]() $\chi _{\Lambda _1, \Lambda _1^{-1}} = \Lambda _1$.
$\chi _{\Lambda _1, \Lambda _1^{-1}} = \Lambda _1$.
2.4 Local Bessel periods
Let us introduce local counterparts to the global Bessel periods. Let ![]() $k$ be a local field of characteristic zero and
$k$ be a local field of characteristic zero and ![]() $D$ a quaternion algebra over
$D$ a quaternion algebra over ![]() $k$.
$k$.
Since the local Bessel periods are deduced from the global ones in a uniform way, by abuse of notation, let a quintuple ![]() $(H, T, N,\chi,\psi _N)$ stand for one of
$(H, T, N,\chi,\psi _N)$ stand for one of
 \begin{align*} &\text{$(G_D, T_\xi, N_D,
\Lambda,\psi_\xi)$ in (1.4.11),} \\
&\text{$(\mathrm{GSp}_2, T_S, N, \Lambda,\psi_S)$ in
(2.3.1) or} \\
&\text{$(\mathrm{GSU}_{3,D}, M_X, N_{4,2},\chi,\psi_{X})$
in (2.3.3).} \end{align*}
\begin{align*} &\text{$(G_D, T_\xi, N_D,
\Lambda,\psi_\xi)$ in (1.4.11),} \\
&\text{$(\mathrm{GSp}_2, T_S, N, \Lambda,\psi_S)$ in
(2.3.1) or} \\
&\text{$(\mathrm{GSU}_{3,D}, M_X, N_{4,2},\chi,\psi_{X})$
in (2.3.3).} \end{align*}
Let ![]() $(\pi, V_\pi )$ be an irreducible tempered representation of
$(\pi, V_\pi )$ be an irreducible tempered representation of ![]() $H=H(k)$ with trivial central character and
$H=H(k)$ with trivial central character and ![]() $[\,,\,]$ a
$[\,,\,]$ a ![]() $H$-invariant hermitian pairing on
$H$-invariant hermitian pairing on ![]() $V_\pi$, the space of
$V_\pi$, the space of ![]() $\pi$. Let us denote by
$\pi$. Let us denote by ![]() $V_\pi ^\infty$ the space of smooth vectors in
$V_\pi ^\infty$ the space of smooth vectors in ![]() $V_\pi$. When
$V_\pi$. When ![]() $k$ is non-archimedean, clearly
$k$ is non-archimedean, clearly ![]() $V_\pi ^\infty = V_\pi$. Let
$V_\pi ^\infty = V_\pi$. Let ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $T=T(k)$ which is trivial on
$T=T(k)$ which is trivial on ![]() $Z_H=Z_H(k)$, where
$Z_H=Z_H(k)$, where ![]() $Z_H$ denotes the center of
$Z_H$ denotes the center of ![]() $H$.
$H$.
Suppose that ![]() $k$ is non-archimedean. Then for
$k$ is non-archimedean. Then for ![]() $\phi,\phi ^\prime \in V_\pi$, we define the local Bessel period
$\phi,\phi ^\prime \in V_\pi$, we define the local Bessel period ![]() $\alpha _{\chi, \psi _N}^H(\phi, \phi ^\prime ) = \alpha _{\chi, \psi _N}(\phi, \phi ^\prime ) = \alpha (\phi,\phi ^\prime )$ by
$\alpha _{\chi, \psi _N}^H(\phi, \phi ^\prime ) = \alpha _{\chi, \psi _N}(\phi, \phi ^\prime ) = \alpha (\phi,\phi ^\prime )$ by
Here the inner integral of (2.4.1) is the stable integral in the sense of Lapid and Mao [Reference Lapid and MaoLM15, Definition 2.1, Remark 2.2]. Indeed it is shown that for any ![]() $t\in T$ the inner integral stabilizes at a certain compact open subgroup of
$t\in T$ the inner integral stabilizes at a certain compact open subgroup of ![]() $N=N(k)$ and the outer integral converges by Liu [Reference LiuLiu16, Proposition 3.1, Theorem 2.1]. We note that it is also shown in Waldspurger [Reference WaldspurgerWal12a, § 5.1, Lemme] that (2.4.1) is well-defined. We often simply write
$N=N(k)$ and the outer integral converges by Liu [Reference LiuLiu16, Proposition 3.1, Theorem 2.1]. We note that it is also shown in Waldspurger [Reference WaldspurgerWal12a, § 5.1, Lemme] that (2.4.1) is well-defined. We often simply write ![]() $\alpha (\phi ) = \alpha (\phi, \phi )$.
$\alpha (\phi ) = \alpha (\phi, \phi )$.
Now suppose that ![]() $k$ is archimedean. Then the local Bessel period is defined as a regularized integral whose regularization is achieved by the Fourier transform as in Liu [Reference LiuLiu16, 3.4]. Let us briefly recall the definition. We define a subgroup
$k$ is archimedean. Then the local Bessel period is defined as a regularized integral whose regularization is achieved by the Fourier transform as in Liu [Reference LiuLiu16, 3.4]. Let us briefly recall the definition. We define a subgroup ![]() $N_{-\infty }$ of
$N_{-\infty }$ of ![]() $N=N(k)$ by
$N=N(k)$ by
 \begin{align*}
N_{-\infty}&:= \bigg\{\!\begin{pmatrix}1 & u\\0 & 1\end{pmatrix}\in N_D:
\mathrm{tr}_D(\xi u)=0\bigg\}\quad\text{in the
$G_D$-case}, \\ N_{-\infty}&:=
\bigg\{\!\begin{pmatrix}1 & Y\\0 & 1\end{pmatrix}\in N:
\mathrm{tr}(SY)=0\bigg\}\quad\text{in the
$\mathrm{GSp}_2$-case},\\ N_{-\infty}&:=
\left\{\!\begin{pmatrix}1 & A^\prime & B\\0 & 1 & A\\0 & 0 &
1\end{pmatrix}\in N_{3,D}:
\mathrm{tr}_D(XA)=0\right\}\quad\text{in the
$\mathrm{GSU}_{3,D}$-case}, \end{align*}
\begin{align*}
N_{-\infty}&:= \bigg\{\!\begin{pmatrix}1 & u\\0 & 1\end{pmatrix}\in N_D:
\mathrm{tr}_D(\xi u)=0\bigg\}\quad\text{in the
$G_D$-case}, \\ N_{-\infty}&:=
\bigg\{\!\begin{pmatrix}1 & Y\\0 & 1\end{pmatrix}\in N:
\mathrm{tr}(SY)=0\bigg\}\quad\text{in the
$\mathrm{GSp}_2$-case},\\ N_{-\infty}&:=
\left\{\!\begin{pmatrix}1 & A^\prime & B\\0 & 1 & A\\0 & 0 &
1\end{pmatrix}\in N_{3,D}:
\mathrm{tr}_D(XA)=0\right\}\quad\text{in the
$\mathrm{GSU}_{3,D}$-case}, \end{align*}
respectively. Then it is shown in Liu [Reference LiuLiu16, Corollary 3.13] that for ![]() $u \in N$,
$u \in N$,
converges absolutely for ![]() $\varphi,\varphi ^\prime \in V_\pi ^\infty$ and it gives a tempered distribution on
$\varphi,\varphi ^\prime \in V_\pi ^\infty$ and it gives a tempered distribution on ![]() $N / N_{-\infty }$.
$N / N_{-\infty }$.
For an abelian Lie group ![]() $\mathcal {N}$, we denote by
$\mathcal {N}$, we denote by ![]() $\mathcal {D}(\mathcal {N})$ (respectively,
$\mathcal {D}(\mathcal {N})$ (respectively, ![]() $\mathcal {S}(\mathcal {N})$) the space of tempered distributions (respectively, Schwartz functions) on
$\mathcal {S}(\mathcal {N})$) the space of tempered distributions (respectively, Schwartz functions) on ![]() $\mathcal {N}$. Then we recall that the Fourier transform
$\mathcal {N}$. Then we recall that the Fourier transform ![]() $\hat {}: \mathcal {D}(\mathcal {N}) \rightarrow \mathcal {D}(\mathcal {N})$ is defined by the formula
$\hat {}: \mathcal {D}(\mathcal {N}) \rightarrow \mathcal {D}(\mathcal {N})$ is defined by the formula
where ![]() $(\,{,}\,)$ denotes the natural pairing
$(\,{,}\,)$ denotes the natural pairing ![]() $\mathcal {D}(\mathcal {N}) \times \mathcal {S}(\mathcal {N}) \rightarrow \mathbb {C}$ and
$\mathcal {D}(\mathcal {N}) \times \mathcal {S}(\mathcal {N}) \rightarrow \mathbb {C}$ and ![]() $\hat {\phi }$ is the Fourier transform of
$\hat {\phi }$ is the Fourier transform of ![]() $\phi \in \mathcal {S}(\mathcal {N})$.
$\phi \in \mathcal {S}(\mathcal {N})$.
Then by Liu [Reference LiuLiu16, Proposition 3.14], the Fourier transform ![]() $\widehat {\alpha _{\phi, \phi ^\prime }}$ is smooth on the regular locus
$\widehat {\alpha _{\phi, \phi ^\prime }}$ is smooth on the regular locus ![]() $(\widehat {N / N_{-\infty }})^{\rm reg}$ of the Pontryagin dual
$(\widehat {N / N_{-\infty }})^{\rm reg}$ of the Pontryagin dual ![]() $\widehat {N / N_{-\infty }}$ and we define the local Bessel period
$\widehat {N / N_{-\infty }}$ and we define the local Bessel period ![]() $\alpha (\phi,\phi ^\prime )$ by
$\alpha (\phi,\phi ^\prime )$ by
As in the non-archimedean case, we often simply write ![]() $\alpha (\phi ) = \alpha (\phi, \phi )$.
$\alpha (\phi ) = \alpha (\phi, \phi )$.
3. Pull-back of Bessel periods
In this section, we establish the pull-back formulas of the global Bessel periods with respect to the dual pairs, ![]() $(\mathrm {GSp}_2,\mathrm {GSO}_{4,2})$,
$(\mathrm {GSp}_2,\mathrm {GSO}_{4,2})$, ![]() $(\mathrm {GSp}_2,\mathrm {GSO}_{3,3})$ and
$(\mathrm {GSp}_2,\mathrm {GSO}_{3,3})$ and ![]() $(G_D,\mathrm {GSU}_{3,D})$. We recall that the first two cases may be regarded as the special case when
$(G_D,\mathrm {GSU}_{3,D})$. We recall that the first two cases may be regarded as the special case when ![]() $D$ is split of the last one, by the accidental isomorphisms explained in § 2.2.
$D$ is split of the last one, by the accidental isomorphisms explained in § 2.2.
3.1  $(\mathrm {GSp}_2,\mathrm {GSO}_{4,2})$ and
$(\mathrm {GSp}_2,\mathrm {GSO}_{4,2})$ and  $(\mathrm {GSp}_2,\mathrm {GSO}_{3,3})$ case
$(\mathrm {GSp}_2,\mathrm {GSO}_{3,3})$ case
3.1.1 Symplectic-orthogonal theta correspondence with similitudes
Let ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) be a finite-dimensional vector space over
$Y$) be a finite-dimensional vector space over ![]() $F$ equipped with a non-degenerate alternating (respectively, symmetric) bilinear form. Assume that
$F$ equipped with a non-degenerate alternating (respectively, symmetric) bilinear form. Assume that ![]() $\dim _F Y$ is even. We denote their similitude groups by
$\dim _F Y$ is even. We denote their similitude groups by ![]() $\mathrm {GSp}(X)$ and
$\mathrm {GSp}(X)$ and ![]() $\mathrm {GO}(Y)$, and, their isometry groups by
$\mathrm {GO}(Y)$, and, their isometry groups by ![]() $\mathrm {Sp}(X)$ and
$\mathrm {Sp}(X)$ and ![]() $\mathrm {O}(Y)$, respectively. We denote the identity component of
$\mathrm {O}(Y)$, respectively. We denote the identity component of ![]() $\mathrm {GO}(Y)$ and
$\mathrm {GO}(Y)$ and ![]() $\mathrm {O}(Y)$ by
$\mathrm {O}(Y)$ by ![]() $\mathrm {GSO}(Y)$ and
$\mathrm {GSO}(Y)$ and ![]() $\mathrm {SO}(Y)$, respectively. We let
$\mathrm {SO}(Y)$, respectively. We let ![]() $\mathrm {GSp}(X)$ (respectively,
$\mathrm {GSp}(X)$ (respectively, ![]() $\mathrm {GO}(Y)$) act on
$\mathrm {GO}(Y)$) act on ![]() $X$ from right (respectively, left). The space
$X$ from right (respectively, left). The space ![]() $Z = X \otimes Y$ has a natural non-degenerate alternating form
$Z = X \otimes Y$ has a natural non-degenerate alternating form ![]() $\langle \,{,} \, \rangle$, and we have an embedding
$\langle \,{,} \, \rangle$, and we have an embedding ![]() $\mathrm {Sp}(X) \times \mathrm {O}(Y) \rightarrow \mathrm {Sp}(Z)$ defined by
$\mathrm {Sp}(X) \times \mathrm {O}(Y) \rightarrow \mathrm {Sp}(Z)$ defined by
Fix a polarization ![]() $Z = Z_{+} \oplus Z_{-}$. Let us denote by
$Z = Z_{+} \oplus Z_{-}$. Let us denote by ![]() $(\omega _{\psi }, \mathcal {S}(Z_{+}(\mathbb {A})))$ the Schrödinger model of the Weil representation of
$(\omega _{\psi }, \mathcal {S}(Z_{+}(\mathbb {A})))$ the Schrödinger model of the Weil representation of ![]() $\widetilde {\mathrm {Sp}}(Z)$ corresponding to this polarization with the Schwartz–Bruhat space
$\widetilde {\mathrm {Sp}}(Z)$ corresponding to this polarization with the Schwartz–Bruhat space ![]() $\mathcal {S}(Z_{+})$ on
$\mathcal {S}(Z_{+})$ on ![]() $Z_{+}$. We denote a typical element of
$Z_{+}$. We denote a typical element of ![]() $\mathrm {Sp}(Z)$ by
$\mathrm {Sp}(Z)$ by
 \[ \begin{pmatrix} A & B\\ C & D\\ \end{pmatrix},\quad\text{where}\ \begin{cases} A \in {\rm Hom}(Z_{+} , Z_{+}), & B \in {\rm Hom}(Z_{+} , Z_{-}),\\ C \in {\rm Hom}(Z_{-} , Z_{+}), & D \in {\rm Hom}(Z_{-} , Z_{-}). \end{cases} \]
\[ \begin{pmatrix} A & B\\ C & D\\ \end{pmatrix},\quad\text{where}\ \begin{cases} A \in {\rm Hom}(Z_{+} , Z_{+}), & B \in {\rm Hom}(Z_{+} , Z_{-}),\\ C \in {\rm Hom}(Z_{-} , Z_{+}), & D \in {\rm Hom}(Z_{-} , Z_{-}). \end{cases} \]
Then the action of ![]() $\omega _{\psi }$ on
$\omega _{\psi }$ on ![]() $\phi \in \mathcal {S}(Z_+)$ is given by the following formulas:
$\phi \in \mathcal {S}(Z_+)$ is given by the following formulas:
where ![]() $\gamma _{\psi }(t)$ is a certain eighth root of unity called the Weil factor. Moreover, since the embedding given by (3.1.1) splits in the metaplectic group
$\gamma _{\psi }(t)$ is a certain eighth root of unity called the Weil factor. Moreover, since the embedding given by (3.1.1) splits in the metaplectic group ![]() $\mathrm {Mp}(Z)$, we obtain the Weil representation of
$\mathrm {Mp}(Z)$, we obtain the Weil representation of ![]() $\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y, \mathbb {A})$ by restriction. We also denote this representation by
$\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y, \mathbb {A})$ by restriction. We also denote this representation by ![]() $\omega _\psi$.
$\omega _\psi$.
We have a natural homomorphism
given by the action (3.1.1). Then we note that ![]() $\lambda (i(g,h)) = \lambda (g)\lambda (h)^{-1}$. Let
$\lambda (i(g,h)) = \lambda (g)\lambda (h)^{-1}$. Let
We may define an extension of the Weil representation of ![]() $\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y, \mathbb {A})$ to
$\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y, \mathbb {A})$ to ![]() $R(\mathbb {A})$ as follows. Let
$R(\mathbb {A})$ as follows. Let ![]() $X= X_+ \oplus X_-$ be a polarization of
$X= X_+ \oplus X_-$ be a polarization of ![]() $X$ and use the polarization
$X$ and use the polarization ![]() $Z_{\pm } = X_{\pm } \otimes Y$ of
$Z_{\pm } = X_{\pm } \otimes Y$ of ![]() $Z$ to realize the Weil representation
$Z$ to realize the Weil representation ![]() $\omega _\psi$. Then we note that
$\omega _\psi$. Then we note that
Thus, we define an action ![]() $L$ of
$L$ of ![]() $\mathrm {GO}(Y,\mathbb {A})$ on
$\mathrm {GO}(Y,\mathbb {A})$ on ![]() $\mathcal {S}(Z_+(\mathbb {A}))$ by
$\mathcal {S}(Z_+(\mathbb {A}))$ by
Then we may extend the Weil representation ![]() $\omega _\psi$ of
$\omega _\psi$ of ![]() $\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y, \mathbb {A})$ to
$\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y, \mathbb {A})$ to ![]() $R(\mathbb {A})$ by
$R(\mathbb {A})$ by
where
In general, for any polarization ![]() $Z= Z_+^\prime \oplus Z_-^\prime$, there exists an
$Z= Z_+^\prime \oplus Z_-^\prime$, there exists an ![]() $\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y)(\mathbb {A})$-isomorphism
$\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y)(\mathbb {A})$-isomorphism ![]() $p : \mathcal {S}(Z_+(\mathbb {A})) \to \mathcal {S}(Z_+^\prime (\mathbb {A}))$ given by an integral transform (see Ichino and Prasanna [Reference Ichino and PrasannaIP21, Lemma 3.3]). Let us denote the realization of the Weil representation of
$p : \mathcal {S}(Z_+(\mathbb {A})) \to \mathcal {S}(Z_+^\prime (\mathbb {A}))$ given by an integral transform (see Ichino and Prasanna [Reference Ichino and PrasannaIP21, Lemma 3.3]). Let us denote the realization of the Weil representation of ![]() ${\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y)(\mathbb {A})}$ on
${\mathrm {Sp}(X, \mathbb {A}) \times \mathrm {O}(Y)(\mathbb {A})}$ on ![]() $\mathcal {S}(Z_+^\prime (\mathbb {A}))$ by
$\mathcal {S}(Z_+^\prime (\mathbb {A}))$ by ![]() $\omega _\psi ^\prime$. Then we may extend
$\omega _\psi ^\prime$. Then we may extend ![]() $\omega _\psi ^\prime$ to
$\omega _\psi ^\prime$ to ![]() $R(\mathbb {A})$ by
$R(\mathbb {A})$ by
For ![]() $\phi \in \mathcal {S}(Z_{+}(\mathbb {A}))$, we define the theta kernel
$\phi \in \mathcal {S}(Z_{+}(\mathbb {A}))$, we define the theta kernel ![]() $\theta ^\phi$ by
$\theta ^\phi$ by
Let
and ![]() $\mathrm {GSp}(X, F)^{+} = \mathrm {GSp}(X, \mathbb {A})^{+} \cap \mathrm {GSp}(X, F)$.
$\mathrm {GSp}(X, F)^{+} = \mathrm {GSp}(X, \mathbb {A})^{+} \cap \mathrm {GSp}(X, F)$.
As in [Reference Harris and KudlaHK92, § 5.1], for a cusp form ![]() $f$ on
$f$ on ![]() $\mathrm {GSp}(X, \mathbb {A})^{+}$, we define its theta lift to
$\mathrm {GSp}(X, \mathbb {A})^{+}$, we define its theta lift to ![]() $\mathrm {GO}(Y, \mathbb {A})$ by
$\mathrm {GO}(Y, \mathbb {A})$ by
for ![]() $h \in \mathrm {GO}(Y, \mathbb {A})$, where
$h \in \mathrm {GO}(Y, \mathbb {A})$, where ![]() $g \in \mathrm {GSp}(X, \mathbb {A})^+$ is chosen so that
$g \in \mathrm {GSp}(X, \mathbb {A})^+$ is chosen so that ![]() $\lambda (g) = \lambda (h)$. It defines an automorphic form on
$\lambda (g) = \lambda (h)$. It defines an automorphic form on ![]() $\mathrm {GO}(Y, \mathbb {A})$. For a cuspidal automorphic representation
$\mathrm {GO}(Y, \mathbb {A})$. For a cuspidal automorphic representation ![]() $(\pi _+, V_{\pi _+})$ of
$(\pi _+, V_{\pi _+})$ of ![]() $\mathrm {GSp}(X, \mathbb {A})^+$, we denote by
$\mathrm {GSp}(X, \mathbb {A})^+$, we denote by ![]() $\Theta _\psi (\pi _+)$ the theta lift of
$\Theta _\psi (\pi _+)$ the theta lift of ![]() $\pi _+$ to
$\pi _+$ to ![]() $\mathrm {GO}(Y, \mathbb {A})$. Namely,
$\mathrm {GO}(Y, \mathbb {A})$. Namely,
Furthermore, for an irreducible cuspidal automorphic representation ![]() $(\pi, V_\pi )$ of
$(\pi, V_\pi )$ of ![]() $\mathrm {GSp}(X, \mathbb {A})$, we define
$\mathrm {GSp}(X, \mathbb {A})$, we define
where ![]() $\pi |_{\mathrm {GSp}(X, \mathbb {A})^+}$ denotes the automorphic representation of
$\pi |_{\mathrm {GSp}(X, \mathbb {A})^+}$ denotes the automorphic representation of ![]() $\mathrm {GSp}(X, \mathbb {A})^+$ with its space of automorphic forms
$\mathrm {GSp}(X, \mathbb {A})^+$ with its space of automorphic forms ![]() $\{\varphi |_{\mathrm {GSp}(X, \mathbb {A})^+} : \varphi \in V_\pi \}$.
$\{\varphi |_{\mathrm {GSp}(X, \mathbb {A})^+} : \varphi \in V_\pi \}$.
As for the opposite direction, for a cusp form ![]() $f^\prime$ on
$f^\prime$ on ![]() $\mathrm {GO}(Y, \mathbb {A})$, we define its theta lift
$\mathrm {GO}(Y, \mathbb {A})$, we define its theta lift ![]() $\Theta (f^\prime, \phi )$ to
$\Theta (f^\prime, \phi )$ to ![]() $\mathrm {GSp}(X, \mathbb {A})^+$ by
$\mathrm {GSp}(X, \mathbb {A})^+$ by
where ![]() $h \in \mathrm {GO}(Y,\mathbb {A})$ is chosen so that
$h \in \mathrm {GO}(Y,\mathbb {A})$ is chosen so that ![]() $\lambda (g) = \lambda (h)$. For an irreducible cuspidal automorphic representation
$\lambda (g) = \lambda (h)$. For an irreducible cuspidal automorphic representation ![]() $(\sigma, V_\sigma )$ of
$(\sigma, V_\sigma )$ of ![]() $\mathrm {GO}(Y, \mathbb {A})$, we define the theta lift
$\mathrm {GO}(Y, \mathbb {A})$, we define the theta lift ![]() $\Theta _\psi (\sigma )$ of
$\Theta _\psi (\sigma )$ of ![]() $\sigma$ to
$\sigma$ to ![]() $\mathrm {GSp}(X, \mathbb {A})^+$ by
$\mathrm {GSp}(X, \mathbb {A})^+$ by
Moreover, we extend ![]() $\theta (f^\prime, \phi )$ to an automorphic form on
$\theta (f^\prime, \phi )$ to an automorphic form on ![]() $\mathrm {GSp}(X, \mathbb {A})$ by the natural embedding
$\mathrm {GSp}(X, \mathbb {A})$ by the natural embedding
and extension by zero. Then we define the theta lift ![]() $\Theta _\psi (\sigma )$ of
$\Theta _\psi (\sigma )$ of ![]() $\sigma$ to
$\sigma$ to ![]() $\mathrm {GSp}(X, \mathbb {A})$ as the
$\mathrm {GSp}(X, \mathbb {A})$ as the ![]() $\mathrm {GSp}(X,\mathbb {A})$ representation generated by such
$\mathrm {GSp}(X,\mathbb {A})$ representation generated by such ![]() $\theta (f^\prime,\phi )$ for
$\theta (f^\prime,\phi )$ for ![]() $f^\prime \in V_\sigma$ and
$f^\prime \in V_\sigma$ and ![]() $\phi \in \mathcal {S}(Z_+(\mathbb {A}))$.
$\phi \in \mathcal {S}(Z_+(\mathbb {A}))$.
For some ![]() $X$ and
$X$ and ![]() $Y$, theta correspondence for the dual pair
$Y$, theta correspondence for the dual pair ![]() $(\mathrm {GSp}(X)^+, \mathrm {GO}(Y))$ gives theta correspondence between
$(\mathrm {GSp}(X)^+, \mathrm {GO}(Y))$ gives theta correspondence between ![]() $\mathrm {GSp}(X)^+$ and
$\mathrm {GSp}(X)^+$ and ![]() $\mathrm {GSO}(Y)$ by the restriction of representations of
$\mathrm {GSO}(Y)$ by the restriction of representations of ![]() $\mathrm {GO}(Y)$ to
$\mathrm {GO}(Y)$ to ![]() $\mathrm {GSO}(Y)$. Indeed, when
$\mathrm {GSO}(Y)$. Indeed, when ![]() $\dim X=4$ and
$\dim X=4$ and ![]() $\dim Y = 6$, we may consider theta correspondence for the pair
$\dim Y = 6$, we may consider theta correspondence for the pair ![]() $(\mathrm {GSp}(X)^+, \mathrm {GSO}(Y))$. In Gan and Takeda [Reference Gan and TakedaGT10, Reference Gan and TakedaGT11b], they study the case when
$(\mathrm {GSp}(X)^+, \mathrm {GSO}(Y))$. In Gan and Takeda [Reference Gan and TakedaGT10, Reference Gan and TakedaGT11b], they study the case when ![]() $\mathrm {GSO}(Y) \simeq \mathrm {GSO_{3,3}}$ or
$\mathrm {GSO}(Y) \simeq \mathrm {GSO_{3,3}}$ or ![]() $\mathrm {GSO}_{5,1}$, and, in [Reference MorimotoMor14a], the case when
$\mathrm {GSO}_{5,1}$, and, in [Reference MorimotoMor14a], the case when ![]() $\mathrm {GSO}(Y) \simeq \mathrm {GSO_{4,2}}$ is studied. In these cases, for a cusp form
$\mathrm {GSO}(Y) \simeq \mathrm {GSO_{4,2}}$ is studied. In these cases, for a cusp form ![]() $f$ on
$f$ on ![]() $\mathrm {GSp}(X, \mathbb {A})^{+}$, we denote by
$\mathrm {GSp}(X, \mathbb {A})^{+}$, we denote by ![]() $\theta (f, \phi )$ the restriction of
$\theta (f, \phi )$ the restriction of ![]() $\Theta (f, \phi )$ to
$\Theta (f, \phi )$ to ![]() $\mathrm {GSO}(Y, \mathbb {A})$. Moreover, for a cuspidal automorphic representation
$\mathrm {GSO}(Y, \mathbb {A})$. Moreover, for a cuspidal automorphic representation ![]() $(\pi _+, V_{\pi _+})$ of
$(\pi _+, V_{\pi _+})$ of ![]() $\mathrm {GSp}(X, \mathbb {A})^+$, we define the theta lift
$\mathrm {GSp}(X, \mathbb {A})^+$, we define the theta lift ![]() $\theta _\psi (\pi _+)$ of
$\theta _\psi (\pi _+)$ of ![]() $\pi _+$ to
$\pi _+$ to ![]() $\mathrm {GSO}(Y, \mathbb {A})$ by
$\mathrm {GSO}(Y, \mathbb {A})$ by
Similarly, for a cusp form ![]() $f^\prime$ on
$f^\prime$ on ![]() $\mathrm {GSO}(Y, \mathbb {A})$, we define its theta lift
$\mathrm {GSO}(Y, \mathbb {A})$, we define its theta lift ![]() $\theta (f^\prime, \phi )$ to
$\theta (f^\prime, \phi )$ to ![]() $\mathrm {GSp}(X, \mathbb {A})^+$ by
$\mathrm {GSp}(X, \mathbb {A})^+$ by
where ![]() $h \in \mathrm {GSO}(Y,\mathbb {A})$ is chosen so that
$h \in \mathrm {GSO}(Y,\mathbb {A})$ is chosen so that ![]() $\lambda (g) = \lambda (h)$. We extend it to an automorphic from on
$\lambda (g) = \lambda (h)$. We extend it to an automorphic from on ![]() $\mathrm {GSp}(X, \mathbb {A})$ as above. For a cuspidal automorphic representation
$\mathrm {GSp}(X, \mathbb {A})$ as above. For a cuspidal automorphic representation ![]() $(\sigma, V_\sigma )$ of
$(\sigma, V_\sigma )$ of ![]() $\mathrm {GSO}(Y, \mathbb {A})$, we define the theta lift
$\mathrm {GSO}(Y, \mathbb {A})$, we define the theta lift ![]() $\theta _\psi (\sigma )$ of
$\theta _\psi (\sigma )$ of ![]() $\sigma$ to
$\sigma$ to ![]() $\mathrm {GSp}(X, \mathbb {A})^+$ by
$\mathrm {GSp}(X, \mathbb {A})^+$ by
Remark 3.1 Suppose that ![]() $\Theta _\psi (\pi _+)$ (respectively,
$\Theta _\psi (\pi _+)$ (respectively, ![]() $\theta _\psi (\sigma )$) is non-zero and cuspidal where
$\theta _\psi (\sigma )$) is non-zero and cuspidal where ![]() $(\pi _+, V_{\pi _+})$ (respectively,
$(\pi _+, V_{\pi _+})$ (respectively, ![]() $(\sigma, V_\sigma )$) is an irreducible cuspidal automorphic representation of
$(\sigma, V_\sigma )$) is an irreducible cuspidal automorphic representation of ![]() $\mathrm {GSp}(X, \mathbb {A})^+$ (respectively,
$\mathrm {GSp}(X, \mathbb {A})^+$ (respectively, ![]() $\mathrm {GO}(Y, \mathbb {A})$). Then Gan [Reference GanGan08, Proposition 2.12] has shown that the Howe duality, which was proved by Howe [Reference HoweHow89] at archimedean places, by Waldspurger [Reference WaldspurgerWal90] at odd finite places and finally by Gan and Takeda [Reference Gan and TakedaGT16] at all finite places, implies that
$\mathrm {GO}(Y, \mathbb {A})$). Then Gan [Reference GanGan08, Proposition 2.12] has shown that the Howe duality, which was proved by Howe [Reference HoweHow89] at archimedean places, by Waldspurger [Reference WaldspurgerWal90] at odd finite places and finally by Gan and Takeda [Reference Gan and TakedaGT16] at all finite places, implies that ![]() $\Theta _\psi (\pi _+)$ (respectively,
$\Theta _\psi (\pi _+)$ (respectively, ![]() $\theta _\psi (\sigma )$) is irreducible and cuspidal. Moreover, in the case of our concern, namely when
$\theta _\psi (\sigma )$) is irreducible and cuspidal. Moreover, in the case of our concern, namely when ![]() $\dim _FX=4$ and
$\dim _FX=4$ and ![]() $\dim _FY=6$, the irreducibility of
$\dim _FY=6$, the irreducibility of ![]() $\Theta _\psi (\pi _+)$ implies that of
$\Theta _\psi (\pi _+)$ implies that of ![]() $\theta _\psi (\pi _+)$ by the conservation relation due to Sun and Zhu [Reference Sun and ZhuSZ15].
$\theta _\psi (\pi _+)$ by the conservation relation due to Sun and Zhu [Reference Sun and ZhuSZ15].
3.1.2 Pull-back of the global Bessel periods for the dual pairs  $(\mathrm {GSp}_2,\mathrm {GSO}_{4,2})$ and
$(\mathrm {GSp}_2,\mathrm {GSO}_{4,2})$ and  $(\mathrm {GSp}_2,\mathrm {GSO}_{3,3})$
$(\mathrm {GSp}_2,\mathrm {GSO}_{3,3})$
Our goal here is to prove the pull-back formula (3.1.6).
First we introduce the set-up. Let ![]() $X$ be the space of four-dimensional row vectors over
$X$ be the space of four-dimensional row vectors over ![]() $F$ equipped with the symplectic form
$F$ equipped with the symplectic form
Let us take the standard basis of ![]() $X$ and name the basis vectors as
$X$ and name the basis vectors as
Then the matrix representation of ![]() $\mathrm {GSp}(X)$ with respect to the standard basis is
$\mathrm {GSp}(X)$ with respect to the standard basis is ![]() $G=\mathrm {GSp}_2$ defined by (1.4.3). We let
$G=\mathrm {GSp}_2$ defined by (1.4.3). We let ![]() $G$ act on
$G$ act on ![]() $X$ from the right.
$X$ from the right.
Let ![]() $Y$ be the space of six-dimensional column vectors over
$Y$ be the space of six-dimensional column vectors over ![]() $F$ equipped with the non-degenerate symmetric bilinear form
$F$ equipped with the non-degenerate symmetric bilinear form
where the symmetric matrix ![]() $S_2$ is given by (2.1.2). Let us take the standard basis of
$S_2$ is given by (2.1.2). Let us take the standard basis of ![]() $Y$ and name the basis vectors as
$Y$ and name the basis vectors as
 \begin{align*} y_{-2} &= {}^{t}(1, 0, 0, 0, 0, 0),\quad y_{-1} = {}^{t}(0, 1, 0, 0, 0, 0),\\ e_1&= {}^{t}(0, 0, 1, 0, 0, 0),\quad e_2 = {}^{t}(0, 0, 0, 1, 0, 0),\\ y_{1} &= {}^{t}(0, 0, 0, 0, 1, 0),\quad y_{2} = {}^{t}(0, 0, 0, 0, 0, 1). \end{align*}
\begin{align*} y_{-2} &= {}^{t}(1, 0, 0, 0, 0, 0),\quad y_{-1} = {}^{t}(0, 1, 0, 0, 0, 0),\\ e_1&= {}^{t}(0, 0, 1, 0, 0, 0),\quad e_2 = {}^{t}(0, 0, 0, 1, 0, 0),\\ y_{1} &= {}^{t}(0, 0, 0, 0, 1, 0),\quad y_{2} = {}^{t}(0, 0, 0, 0, 0, 1). \end{align*}
We note that ![]() $( y_i , y_j )=\delta _{ij}, ( e_1 , e_1)=2$ and
$( y_i , y_j )=\delta _{ij}, ( e_1 , e_1)=2$ and ![]() $( e_2 , e_2) =-2d$. Since
$( e_2 , e_2) =-2d$. Since ![]() $d \in F^\times \setminus (F^\times )^2$, with respect to the standard basis, the matrix representations of
$d \in F^\times \setminus (F^\times )^2$, with respect to the standard basis, the matrix representations of ![]() $\mathrm {GO}(Y)$ and
$\mathrm {GO}(Y)$ and ![]() $\mathrm {GSO}(Y)$ are
$\mathrm {GSO}(Y)$ are ![]() $\mathrm {GO}_{4,2}$ defined by (2.1.5) and
$\mathrm {GO}_{4,2}$ defined by (2.1.5) and ![]() $\mathrm {GSO}_{4,2}$ defined by (2.1.4), respectively. In this section, we also study the theta correspondence for the dual pair
$\mathrm {GSO}_{4,2}$ defined by (2.1.4), respectively. In this section, we also study the theta correspondence for the dual pair ![]() $(\mathrm {GSp}(X), \mathrm {GSO}_{3,3})$, for which, we may use the above matrix representation with
$(\mathrm {GSp}(X), \mathrm {GSO}_{3,3})$, for which, we may use the above matrix representation with ![]() $d \in (F^\times )^2$. Hence, in the remaining of this section, we study theta correspondence for
$d \in (F^\times )^2$. Hence, in the remaining of this section, we study theta correspondence for ![]() $(\mathrm {GSp}(X), \mathrm {GSO}(Y))$ for an arbitrary
$(\mathrm {GSp}(X), \mathrm {GSO}(Y))$ for an arbitrary ![]() $d \in F^\times$.
$d \in F^\times$.
We shall denote ![]() $\mathrm {GSp}(X, \mathbb {A})^+$ by
$\mathrm {GSp}(X, \mathbb {A})^+$ by ![]() $G(\mathbb {A})^+$ and also
$G(\mathbb {A})^+$ and also ![]() $\mathrm {GSp}(X, F)^+$ by
$\mathrm {GSp}(X, F)^+$ by ![]() $G(F)^+$. We note that when
$G(F)^+$. We note that when ![]() $d \in (F^\times )^2$,
$d \in (F^\times )^2$, ![]() $\mathrm {GSp}(X)^+ = \mathrm {GSp}(X)$.
$\mathrm {GSp}(X)^+ = \mathrm {GSp}(X)$.
Let ![]() $Z=X\otimes Y$ and we take a polarization
$Z=X\otimes Y$ and we take a polarization ![]() $Z=Z_+\oplus Z_-$ as follows. First we take
$Z=Z_+\oplus Z_-$ as follows. First we take ![]() $X=X_+\oplus X_-$ where
$X=X_+\oplus X_-$ where
as the polarization of ![]() $X$. Then we decompose
$X$. Then we decompose ![]() $Y$ as
$Y$ as ![]() $Y=Y_+\oplus Y_0\oplus Y_-$ where
$Y=Y_+\oplus Y_0\oplus Y_-$ where
Then let
where the double sign corresponds. To simplify the notation, we sometimes write ![]() $z_+\in Z_+$ as
$z_+\in Z_+$ as ![]() $z_+=(a_1,a_2;b_1,b_2)$ when
$z_+=(a_1,a_2;b_1,b_2)$ when
Let us compute the pull-back of ![]() $(X, \chi, \psi )$-Bessel periods on
$(X, \chi, \psi )$-Bessel periods on ![]() $\mathrm {GSO}(Y)$ defined by (2.3.6) with respect to the theta lift from
$\mathrm {GSO}(Y)$ defined by (2.3.6) with respect to the theta lift from ![]() $G$.
$G$.
Proposition 3.1 Let ![]() $(\pi,V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi,V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A})$ whose central character is
$G(\mathbb {A})$ whose central character is ![]() $\omega _\pi$ and
$\omega _\pi$ and ![]() $\chi$ a character of
$\chi$ a character of ![]() $\mathbb {A}_E^\times$ such that
$\mathbb {A}_E^\times$ such that ![]() $\chi \mid _{\mathbb {A}^\times }=\omega _\pi ^{-1}$. Let
$\chi \mid _{\mathbb {A}^\times }=\omega _\pi ^{-1}$. Let ![]() $X\in \mathrm {Mat}_{2\times 2}(F)$ such that
$X\in \mathrm {Mat}_{2\times 2}(F)$ such that ![]() $\det X\ne 0$.
$\det X\ne 0$.
Then for ![]() $f \in V_\pi$ and
$f \in V_\pi$ and ![]() $\phi \in \mathcal {S}(Z_+(\mathbb {A}))$, we have
$\phi \in \mathcal {S}(Z_+(\mathbb {A}))$, we have
where ![]() $B_{S_X, \chi ^{-1},\psi }$ is the
$B_{S_X, \chi ^{-1},\psi }$ is the ![]() $(S_X,\chi ^{-1},\psi )$-Bessel period on
$(S_X,\chi ^{-1},\psi )$-Bessel period on ![]() $G$ defined by (2.3.1).
$G$ defined by (2.3.1).
Here, for ![]() $X= \big (\begin{smallmatrix}x_{11} & x_{12}\\x_{21} & x_{22} \end{smallmatrix}\big )$, we define a vector
$X= \big (\begin{smallmatrix}x_{11} & x_{12}\\x_{21} & x_{22} \end{smallmatrix}\big )$, we define a vector ![]() $v_X\in Z_+$ by
$v_X\in Z_+$ by
and a ![]() $2$-by-
$2$-by-![]() $2$ symmetric matrix
$2$ symmetric matrix ![]() $S_X$ by
$S_X$ by
We regard ![]() $\chi$ as a character of
$\chi$ as a character of ![]() $\mathrm {GSO}(S_X)(\mathbb {A})$ by
$\mathrm {GSO}(S_X)(\mathbb {A})$ by
In particular, the ![]() $(S_X, \chi ^{-1},\psi )$-Bessel period does not vanish on
$(S_X, \chi ^{-1},\psi )$-Bessel period does not vanish on ![]() $V_\pi$ if and only if the
$V_\pi$ if and only if the ![]() $(X,\chi, \psi )$-Bessel period does not vanish on
$(X,\chi, \psi )$-Bessel period does not vanish on ![]() $\theta _\psi (\pi )$.
$\theta _\psi (\pi )$.
Proof. We compute the ![]() $(X,\chi, \psi )$-Bessel period defined by (2.3.6) in stages. We consider subgroups of
$(X,\chi, \psi )$-Bessel period defined by (2.3.6) in stages. We consider subgroups of ![]() $N_{4,2}$ given by
$N_{4,2}$ given by
 \begin{align} N_0(F) &= \left\{u_0(x) :=\left.\begin{pmatrix} 1 & -{}^{t}X_0 S_1 & 0\\ 0 & 1_4 & X_0\\ 0 & 0 & 1 \end{pmatrix}\right| X_0 = \begin{pmatrix} x\\0\\0\\0\end{pmatrix}\right\}; \end{align}
\begin{align} N_0(F) &= \left\{u_0(x) :=\left.\begin{pmatrix} 1 & -{}^{t}X_0 S_1 & 0\\ 0 & 1_4 & X_0\\ 0 & 0 & 1 \end{pmatrix}\right| X_0 = \begin{pmatrix} x\\0\\0\\0\end{pmatrix}\right\}; \end{align} \begin{align} N_1(F) &= \left\{u_1(s_1, t_1) :=\left.\begin{pmatrix} 1 & -{}^{t}X_1 S_1 & -\dfrac{1}{2}{}^{t}X_1 S_1 X_1\\ 0 & 1_4 & X_1\\ 0 & 0 & 1 \end{pmatrix}\right| X_1 = \begin{pmatrix} 0\\s_1\\t_1\\0 \end{pmatrix}\right\}; \end{align}
\begin{align} N_1(F) &= \left\{u_1(s_1, t_1) :=\left.\begin{pmatrix} 1 & -{}^{t}X_1 S_1 & -\dfrac{1}{2}{}^{t}X_1 S_1 X_1\\ 0 & 1_4 & X_1\\ 0 & 0 & 1 \end{pmatrix}\right| X_1 = \begin{pmatrix} 0\\s_1\\t_1\\0 \end{pmatrix}\right\}; \end{align} \begin{align} N_2(F) &= \left\{u_2(s_2, t_2) := \left.\begin{pmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 1 & -{}^{t}X_2 S_0 & -\dfrac{1}{2}{}^{t}X_2 S_0 X_2 & 0\\ 0 & 0 & 1_2 & X_2 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}\right| X_2 = \begin{pmatrix} s_2\\ t_2 \end{pmatrix}\right\}, \end{align}
\begin{align} N_2(F) &= \left\{u_2(s_2, t_2) := \left.\begin{pmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 1 & -{}^{t}X_2 S_0 & -\dfrac{1}{2}{}^{t}X_2 S_0 X_2 & 0\\ 0 & 0 & 1_2 & X_2 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}\right| X_2 = \begin{pmatrix} s_2\\ t_2 \end{pmatrix}\right\}, \end{align}
where ![]() $S_0$ and
$S_0$ and ![]() $S_1$ are given by (2.1.2). Then we have
$S_1$ are given by (2.1.2). Then we have
Thus, we may write
 \begin{align} \mathcal{B}_{X, \chi, \psi}(\theta(f: \phi)) &= \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{(F \backslash \mathbb{A}_{F})^2} \int_{(F \backslash \mathbb{A}_{F})^2} \int_{F \backslash \mathbb{A}_{F}} \theta(f, \phi)(u_0(x) u_1(s_1, t_1) u_2(s_2, t_2) h) \nonumber\\ &\quad \times \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1}\chi (h)^{-1} \, {dx} \,ds_1 \,dt_1 \,ds_2 \,dt_2 \,dh. \end{align}
\begin{align} \mathcal{B}_{X, \chi, \psi}(\theta(f: \phi)) &= \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{(F \backslash \mathbb{A}_{F})^2} \int_{(F \backslash \mathbb{A}_{F})^2} \int_{F \backslash \mathbb{A}_{F}} \theta(f, \phi)(u_0(x) u_1(s_1, t_1) u_2(s_2, t_2) h) \nonumber\\ &\quad \times \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1}\chi (h)^{-1} \, {dx} \,ds_1 \,dt_1 \,ds_2 \,dt_2 \,dh. \end{align}
For ![]() $h \in \mathrm {GSO}(Y, \mathbb {A})$, let us define
$h \in \mathrm {GSO}(Y, \mathbb {A})$, let us define
From the definition of the theta lift, we have
 \begin{align} & W_0(\theta(f, \phi))(h) \nonumber\\ &\quad =\int_{F \backslash \mathbb{A}_F} \int_{G^1(F) \backslash G^1(\mathbb{A}_F)} \sum_{a_i \in X, b_i \in X_{+}} (\omega_\psi(g_1 \lambda_s(\nu(h)), u_0(x) h) \phi)(a_1, a_2; b_1, b_2) \nonumber\\ &\qquad \times f(g_1 \lambda_s(\lambda(h)))\, dg_1 \, {dx}. \end{align}
\begin{align} & W_0(\theta(f, \phi))(h) \nonumber\\ &\quad =\int_{F \backslash \mathbb{A}_F} \int_{G^1(F) \backslash G^1(\mathbb{A}_F)} \sum_{a_i \in X, b_i \in X_{+}} (\omega_\psi(g_1 \lambda_s(\nu(h)), u_0(x) h) \phi)(a_1, a_2; b_1, b_2) \nonumber\\ &\qquad \times f(g_1 \lambda_s(\lambda(h)))\, dg_1 \, {dx}. \end{align}
Here, for ![]() $a \in \mathbb {A}^\times$, we let
$a \in \mathbb {A}^\times$, we let
Since ![]() $Z_{-}(1, u_0(x))= Z_{-}$ and we have
$Z_{-}(1, u_0(x))= Z_{-}$ and we have
we observe that
Thus, in the summation of the right-hand side of (3.1.14), only ![]() $a_i$ such that
$a_i$ such that ![]() $\langle a_1, a_2 \rangle = 0$ contributes to the integral
$\langle a_1, a_2 \rangle = 0$ contributes to the integral ![]() $W_0(\theta (f, \phi ))$, and we obtain
$W_0(\theta (f, \phi ))$, and we obtain
 \begin{align*} W_0(\theta(f, \phi))(h) &= \int_{G^1(F) \backslash G^1(\mathbb{A}_F)}\\ &\quad \times\sum_{\substack{a_i \in X, \langle a_1, a_2 \rangle =0,\\ b_i \in X_{+}}} (\omega_\psi(g_1 \lambda_s(\lambda(h)), h) \phi) (a_1, a_2; b_1, b_2) f(g_1 \lambda_s(\lambda(h)))\,dg_1. \end{align*}
\begin{align*} W_0(\theta(f, \phi))(h) &= \int_{G^1(F) \backslash G^1(\mathbb{A}_F)}\\ &\quad \times\sum_{\substack{a_i \in X, \langle a_1, a_2 \rangle =0,\\ b_i \in X_{+}}} (\omega_\psi(g_1 \lambda_s(\lambda(h)), h) \phi) (a_1, a_2; b_1, b_2) f(g_1 \lambda_s(\lambda(h)))\,dg_1. \end{align*}
Since the space spanned by ![]() $a_1$ and
$a_1$ and ![]() $a_2$ is isotropic, there exists
$a_2$ is isotropic, there exists ![]() $\gamma \in G^1(F)$ such that
$\gamma \in G^1(F)$ such that ![]() $a_1 \gamma ^{-1}, a_2 \gamma ^{-1} \in X_{-}$. Let us define an equivalence relation
$a_1 \gamma ^{-1}, a_2 \gamma ^{-1} \in X_{-}$. Let us define an equivalence relation ![]() $\sim$ on
$\sim$ on ![]() $(X_{-})^{2}$ by
$(X_{-})^{2}$ by
Let us denote by ![]() $\mathcal {X}_{-}$ the set of equivalence classes
$\mathcal {X}_{-}$ the set of equivalence classes ![]() $(X_{-})^2 / \sim$ and by
$(X_{-})^2 / \sim$ and by ![]() $\overline {(a_1, a_2)}$ the equivalence class containing
$\overline {(a_1, a_2)}$ the equivalence class containing ![]() $(a_1,a_2)\in (X_{-})^2$. Then we may write
$(a_1,a_2)\in (X_{-})^2$. Then we may write ![]() $W_0 (\theta (f, \phi )) (h)$ as
$W_0 (\theta (f, \phi )) (h)$ as
 \begin{align*}
& \int_{G^1(F) \backslash
G^1(\mathbb{A}_F)} \sum_{\overline{(a_1 ,
a_2)} \in \mathcal{X}_{-}}\ \sum_{\gamma \in V(a_1 , a_2)
\backslash G^1(F)}\ \sum_{b_i \in X_{+}} (\omega_\psi (g_1
\lambda_s(\lambda(h)) , h) \phi)(a_1\gamma, a_2 \gamma;
b_1, b_2)\\ &\quad \times f(g_1 \lambda_s(\lambda(h))) \,
dg_1. \end{align*}
\begin{align*}
& \int_{G^1(F) \backslash
G^1(\mathbb{A}_F)} \sum_{\overline{(a_1 ,
a_2)} \in \mathcal{X}_{-}}\ \sum_{\gamma \in V(a_1 , a_2)
\backslash G^1(F)}\ \sum_{b_i \in X_{+}} (\omega_\psi (g_1
\lambda_s(\lambda(h)) , h) \phi)(a_1\gamma, a_2 \gamma;
b_1, b_2)\\ &\quad \times f(g_1 \lambda_s(\lambda(h))) \,
dg_1. \end{align*}
Here
Lemma 3.1 For any ![]() $g \in G(\mathbb {A})^+$ and
$g \in G(\mathbb {A})^+$ and ![]() $h \in \mathrm {GSO}(Y, \mathbb {A})$ such that
$h \in \mathrm {GSO}(Y, \mathbb {A})$ such that ![]() $\lambda (g) = \lambda (h)$,
$\lambda (g) = \lambda (h)$,
Proof. This is proved by an argument similar to that for [Reference FurusawaFur95, Lemma 2].
Further, by an argument similar to the one for ![]() $W_0 (\theta (f, \phi )) (h)$, we shall prove the following lemma.
$W_0 (\theta (f, \phi )) (h)$, we shall prove the following lemma.
Lemma 3.2 For any ![]() $g \in G(\mathbb {A})^+$ and
$g \in G(\mathbb {A})^+$ and ![]() $h \in \mathrm {GSO}(Y, \mathbb {A})$ such that
$h \in \mathrm {GSO}(Y, \mathbb {A})$ such that ![]() $\lambda (g) = \lambda (h)$,
$\lambda (g) = \lambda (h)$,
 \begin{align*} & \int_{(F \backslash \mathbb{A}_F)^{2}} \psi^{-1}(x_{21}s_1+x_{22}t_1) (\omega_\psi (g , u_{1}(s_1, t_1) h) \phi)(a_1 , a_2 , b_1, b_2)\,ds_1\,dt_1\\ &\quad = \left\{\begin{array}{@{}ll} (\omega_\psi (g , h)\phi)(a_1 , a_2 , b_1, b_2) & \text{if $ \langle a_2, b_1 \rangle =-\dfrac{x_{21}}{2}$ and $\langle a_2, b_2 \rangle= \dfrac{x_{22}}{2d}$};\\ & \\ 0 & \text{otherwise}\\ \end{array}\right. \end{align*}
\begin{align*} & \int_{(F \backslash \mathbb{A}_F)^{2}} \psi^{-1}(x_{21}s_1+x_{22}t_1) (\omega_\psi (g , u_{1}(s_1, t_1) h) \phi)(a_1 , a_2 , b_1, b_2)\,ds_1\,dt_1\\ &\quad = \left\{\begin{array}{@{}ll} (\omega_\psi (g , h)\phi)(a_1 , a_2 , b_1, b_2) & \text{if $ \langle a_2, b_1 \rangle =-\dfrac{x_{21}}{2}$ and $\langle a_2, b_2 \rangle= \dfrac{x_{22}}{2d}$};\\ & \\ 0 & \text{otherwise}\\ \end{array}\right. \end{align*}
and
 \begin{align*} & \int_{(F \backslash \mathbb{A}_F)^{2}} \psi^{-1}(x_{11} s_2+x_{12}t_2) (\omega_\psi(g , u_{2}(s_2, t_2) h) \phi)(a_1 , a_2 , b_1, b_2)\, ds_2\, dt_2\\ &\quad =\left\{\begin{array}{@{}ll} (\omega_\psi (g , h)\phi)(a_1 , a_2 , b_1, b_2) & \text{if $ \langle a_1 , b_1 \rangle =-\dfrac{x_{11}}{2}$ and $\langle a_1, b_2 \rangle =\dfrac{x_{12}}{2d}$};\\ & \\ 0 & \text{otherwise}.\\ \end{array}\right. \end{align*}
\begin{align*} & \int_{(F \backslash \mathbb{A}_F)^{2}} \psi^{-1}(x_{11} s_2+x_{12}t_2) (\omega_\psi(g , u_{2}(s_2, t_2) h) \phi)(a_1 , a_2 , b_1, b_2)\, ds_2\, dt_2\\ &\quad =\left\{\begin{array}{@{}ll} (\omega_\psi (g , h)\phi)(a_1 , a_2 , b_1, b_2) & \text{if $ \langle a_1 , b_1 \rangle =-\dfrac{x_{11}}{2}$ and $\langle a_1, b_2 \rangle =\dfrac{x_{12}}{2d}$};\\ & \\ 0 & \text{otherwise}.\\ \end{array}\right. \end{align*}
Proof. Since ![]() $Z_-\, (1, u_1(s_1, t_1)) = Z_-$ and we have
$Z_-\, (1, u_1(s_1, t_1)) = Z_-$ and we have
 \begin{align*} z_+(1, u_1(s_1, t_1)) &= z_{+} +2s_1 (b_1 \otimes y_{-2}) - 2dt_1(b_2 \otimes y_{-2})\\ &\quad +(-s_1^2+2dt_1^2)a_2 \otimes y_{-2}-s_1a_2 \otimes e_1-t_1 a_2 \otimes e_2, \end{align*}
\begin{align*} z_+(1, u_1(s_1, t_1)) &= z_{+} +2s_1 (b_1 \otimes y_{-2}) - 2dt_1(b_2 \otimes y_{-2})\\ &\quad +(-s_1^2+2dt_1^2)a_2 \otimes y_{-2}-s_1a_2 \otimes e_1-t_1 a_2 \otimes e_2, \end{align*}
we obtain
 \begin{align*} & (\omega_\psi(1, u_1(s_1, t_1)) \phi)(z_+) = \psi \big(\tfrac{1}{2} (2s_1\langle a_2, b_1 \rangle -2dt_1 \langle a_2, b_2 \rangle)\big)\\ &\qquad \times\psi \big(\tfrac{1}{2} ((-s_1^2+2dt_1^2) \langle a_2, a_2 \rangle -2s_1 \langle b_1, a_2 \rangle +2dt_1 \langle b_2, a_2 \rangle)\big)\phi(z_+)\\ &\quad =\psi (2s_1\langle a_2, b_1 \rangle -2dt_1 \langle a_2, b_2 \rangle)\phi(z_+). \end{align*}
\begin{align*} & (\omega_\psi(1, u_1(s_1, t_1)) \phi)(z_+) = \psi \big(\tfrac{1}{2} (2s_1\langle a_2, b_1 \rangle -2dt_1 \langle a_2, b_2 \rangle)\big)\\ &\qquad \times\psi \big(\tfrac{1}{2} ((-s_1^2+2dt_1^2) \langle a_2, a_2 \rangle -2s_1 \langle b_1, a_2 \rangle +2dt_1 \langle b_2, a_2 \rangle)\big)\phi(z_+)\\ &\quad =\psi (2s_1\langle a_2, b_1 \rangle -2dt_1 \langle a_2, b_2 \rangle)\phi(z_+). \end{align*}
Then the first assertion readily follows.
Similarly, since ![]() $Z_- \,(1, u_2(s_2, t_2)) = Z_-$ and we have
$Z_- \,(1, u_2(s_2, t_2)) = Z_-$ and we have
we obtain
 \begin{align*} & \omega(1, u_2(s_2, t_2)) \phi(z_+)= \psi \big(\tfrac{1}{2} (-2s_2 \langle b_1, a_1 \rangle +2dt_2 \langle b_2, a_1 \rangle)\big)\\ &\qquad \times\psi \big(\tfrac{1}{2}(2s_2 \langle a_1, b_1 \rangle -2dt_2 \langle a_1, b_2 \rangle)\big)\phi(z_+)\\ &\quad =\psi (2s_2 \langle a_1, b_1 \rangle -2dt_2 \langle a_1, b_2 \rangle) \phi(z_+) \end{align*}
\begin{align*} & \omega(1, u_2(s_2, t_2)) \phi(z_+)= \psi \big(\tfrac{1}{2} (-2s_2 \langle b_1, a_1 \rangle +2dt_2 \langle b_2, a_1 \rangle)\big)\\ &\qquad \times\psi \big(\tfrac{1}{2}(2s_2 \langle a_1, b_1 \rangle -2dt_2 \langle a_1, b_2 \rangle)\big)\phi(z_+)\\ &\quad =\psi (2s_2 \langle a_1, b_1 \rangle -2dt_2 \langle a_1, b_2 \rangle) \phi(z_+) \end{align*}
and the second assertion follows.
Lemma 3.2 implies that
 \begin{align*} \mathcal{B}_{X, \chi, \psi}(\theta(f: \phi)) &= \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{G^1(F) \backslash G^1(\mathbb{A}_F)} \chi (h)^{-1}\\ &\quad \times\sum _{ \overline{(a_1 , a_2)} \in \mathcal{X}_{-}} \sum_{\gamma \in V(a_1 , a_2) \backslash G^1(F)} \sum_{\substack{ b_i \in X_{+}, \langle a_i, b_1 \rangle = {{x_{i1}}/{2}},\\ \langle a_i, b_2 \rangle =- ({x_{i2}}/{2d}) }}\\ &\quad \times(\omega_\psi (\gamma g_1 \lambda_s(\lambda(h)) , h) \phi) (a_1, a_2, b_1, b_2) f(g_1 \lambda_s(\lambda(h))) \, dg_1\,dh. \end{align*}
\begin{align*} \mathcal{B}_{X, \chi, \psi}(\theta(f: \phi)) &= \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{G^1(F) \backslash G^1(\mathbb{A}_F)} \chi (h)^{-1}\\ &\quad \times\sum _{ \overline{(a_1 , a_2)} \in \mathcal{X}_{-}} \sum_{\gamma \in V(a_1 , a_2) \backslash G^1(F)} \sum_{\substack{ b_i \in X_{+}, \langle a_i, b_1 \rangle = {{x_{i1}}/{2}},\\ \langle a_i, b_2 \rangle =- ({x_{i2}}/{2d}) }}\\ &\quad \times(\omega_\psi (\gamma g_1 \lambda_s(\lambda(h)) , h) \phi) (a_1, a_2, b_1, b_2) f(g_1 \lambda_s(\lambda(h))) \, dg_1\,dh. \end{align*}
We note that ![]() $a_1$ and
$a_1$ and ![]() $a_2$ are linearly independent from the conditions on
$a_2$ are linearly independent from the conditions on ![]() $a_i$ and
$a_i$ and ![]() $\det (X) \ne 0$. Since
$\det (X) \ne 0$. Since ![]() $a_i \in X_-$ and
$a_i \in X_-$ and ![]() $\dim X_- =2$, we may take
$\dim X_- =2$, we may take ![]() $(a_1,a_2)=(x_{-2},x_{-1})$ as a representative. Then we should have
$(a_1,a_2)=(x_{-2},x_{-1})$ as a representative. Then we should have
Hence, we get
 \begin{align} \mathcal{B}_{X, \chi, \psi}(\theta(f: \phi)) &= \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{G^1(F) \backslash G^1(\mathbb{A}_F)}\chi(h)^{-1} \nonumber\\ &\quad \times \sum_{\gamma \in N(F) \backslash G^1(F)} (\omega_\psi (\gamma g_1 \lambda_s(\lambda(h)), h) \phi)(v_X) f(g_1 \lambda_s(\lambda(h))) \, dg_1\,dh \nonumber\\ &= \int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \nonumber\\ &\quad \times\chi(h)^{-1}\omega (v g_1 \lambda_s(\lambda(h)), h) \phi(v_X) f(v g_1 \lambda_s(\lambda(h))) \, dv\,dg_1\,dh , \end{align}
\begin{align} \mathcal{B}_{X, \chi, \psi}(\theta(f: \phi)) &= \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{G^1(F) \backslash G^1(\mathbb{A}_F)}\chi(h)^{-1} \nonumber\\ &\quad \times \sum_{\gamma \in N(F) \backslash G^1(F)} (\omega_\psi (\gamma g_1 \lambda_s(\lambda(h)), h) \phi)(v_X) f(g_1 \lambda_s(\lambda(h))) \, dg_1\,dh \nonumber\\ &= \int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \nonumber\\ &\quad \times\chi(h)^{-1}\omega (v g_1 \lambda_s(\lambda(h)), h) \phi(v_X) f(v g_1 \lambda_s(\lambda(h))) \, dv\,dg_1\,dh , \end{align}
where we put ![]() $v_X = (x_{-2}, x_{-1}; ( {x_{21}}/{2})x_1+{{x_{11}}/{2}} x_2, -({x_{22}}/{2d})x_1-({x_{12}}/{2d}) x_2)$.
$v_X = (x_{-2}, x_{-1}; ( {x_{21}}/{2})x_1+{{x_{11}}/{2}} x_2, -({x_{22}}/{2d})x_1-({x_{12}}/{2d}) x_2)$.
For ![]() $u=\big (\begin{smallmatrix}1_2 & A\\0 & 1_2\end{smallmatrix}\big )$ where
$u=\big (\begin{smallmatrix}1_2 & A\\0 & 1_2\end{smallmatrix}\big )$ where ![]() $A= \big (\begin{smallmatrix}a & b\\ b & c\end{smallmatrix}\big ) \in \mathrm {Sym}^2$, we have
$A= \big (\begin{smallmatrix}a & b\\ b & c\end{smallmatrix}\big ) \in \mathrm {Sym}^2$, we have
 \begin{align*} & \bigg( x_{-2} \otimes y_1 + x_{-1} \otimes y_2+ \bigg(\frac{x_{21}}{2}x_1+\frac{x_{11}}{2} x_2 \bigg) \otimes e_1 + \bigg( -\frac{x_{22}}{2d}x_1-\frac{x_{12}}{2d} x_2 \bigg)\otimes e_2 \bigg)(u,1) \\ &\quad = x_{-2} \otimes y_1 + x_{-1} \otimes y_2+ \bigg(\frac{x_{21}}{2}(x_1 +a x_{-1}+b x_{-2} )+ \frac{x_{11}}{2} (x_2+bx_{-1} +c x_{-2})\bigg) \otimes e_1 \\ &\qquad +\bigg(-\frac{x_{22}}{2d}(x_1 +a x_{-1}+b x_{-2} )- \frac{x_{12}}{2d} (x_2+bx_{-1} +c x_{-2})\bigg)\otimes e_2. \end{align*}
\begin{align*} & \bigg( x_{-2} \otimes y_1 + x_{-1} \otimes y_2+ \bigg(\frac{x_{21}}{2}x_1+\frac{x_{11}}{2} x_2 \bigg) \otimes e_1 + \bigg( -\frac{x_{22}}{2d}x_1-\frac{x_{12}}{2d} x_2 \bigg)\otimes e_2 \bigg)(u,1) \\ &\quad = x_{-2} \otimes y_1 + x_{-1} \otimes y_2+ \bigg(\frac{x_{21}}{2}(x_1 +a x_{-1}+b x_{-2} )+ \frac{x_{11}}{2} (x_2+bx_{-1} +c x_{-2})\bigg) \otimes e_1 \\ &\qquad +\bigg(-\frac{x_{22}}{2d}(x_1 +a x_{-1}+b x_{-2} )- \frac{x_{12}}{2d} (x_2+bx_{-1} +c x_{-2})\bigg)\otimes e_2. \end{align*}
Hence, when we put
 \begin{align*} S_X &= \frac{1}{4d}{}^{t}(J_2{}^{t}XJ_2)S_0 (J_2{}^{t}XJ_2)\\ &= \frac{1}{2d} \begin{pmatrix} x_{22}^2-dx_{21}^2 & x_{22}x_{12}-dx_{21}x_{11} \\ x_{22}x_{12}-dx_{21}x_{11} & x_{12}^2-dx_{11}^2 \end{pmatrix}\in \mathrm{Sym}^2(F), \end{align*}
\begin{align*} S_X &= \frac{1}{4d}{}^{t}(J_2{}^{t}XJ_2)S_0 (J_2{}^{t}XJ_2)\\ &= \frac{1}{2d} \begin{pmatrix} x_{22}^2-dx_{21}^2 & x_{22}x_{12}-dx_{21}x_{11} \\ x_{22}x_{12}-dx_{21}x_{11} & x_{12}^2-dx_{11}^2 \end{pmatrix}\in \mathrm{Sym}^2(F), \end{align*}
for ![]() $u\in N(\mathbb {A})$, we have
$u\in N(\mathbb {A})$, we have
Therefore, we get
 \begin{align*} & \int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \chi(h)^{-1} \\ &\qquad \times (\omega_\psi (g_1 \lambda_s(\lambda(h)), h) \phi)(v_X) f(u g_1 \lambda_s(\lambda(h))) \psi_{S_X}(u)^{-1} \, du \, dh\, dg_1 \\ &\quad =\int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \chi (h)^{-1} \\ &\qquad \times\omega_\psi (\lambda_s(\lambda(h)) g_1, h) \phi(v_X) |\lambda(h)|^3 f(u \lambda_s(\lambda(h)) g_1)\psi_{S_X}(u)^{-1}\, du \, dh\, dg_1. \end{align*}
\begin{align*} & \int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \chi(h)^{-1} \\ &\qquad \times (\omega_\psi (g_1 \lambda_s(\lambda(h)), h) \phi)(v_X) f(u g_1 \lambda_s(\lambda(h))) \psi_{S_X}(u)^{-1} \, du \, dh\, dg_1 \\ &\quad =\int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times M_{X}(F) \backslash M_X(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \chi (h)^{-1} \\ &\qquad \times\omega_\psi (\lambda_s(\lambda(h)) g_1, h) \phi(v_X) |\lambda(h)|^3 f(u \lambda_s(\lambda(h)) g_1)\psi_{S_X}(u)^{-1}\, du \, dh\, dg_1. \end{align*}
By a direct computation, we see that
when we let
 \[ h = \begin{pmatrix} (\det h) (h^X)^\ast & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^X \end{pmatrix},\quad h_0 = \begin{pmatrix} ({}^{t}XJ_2)^{-1} {}^{t}h ({}^{t}XJ_2) & 0\\ 0 & (J_2X) h^{-1} (J_2X)^{-1} \end{pmatrix}. \]
\[ h = \begin{pmatrix} (\det h) (h^X)^\ast & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^X \end{pmatrix},\quad h_0 = \begin{pmatrix} ({}^{t}XJ_2)^{-1} {}^{t}h ({}^{t}XJ_2) & 0\\ 0 & (J_2X) h^{-1} (J_2X)^{-1} \end{pmatrix}. \]
For ![]() $g \in \mathrm {GSO}(S_0)$, we have
$g \in \mathrm {GSO}(S_0)$, we have ![]() ${}^{t}g = wgw$ and we may write
${}^{t}g = wgw$ and we may write
Since we have
we get
 \begin{align} & \int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times T_{S_X}(F) \backslash T_{S_X}(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \chi(h) \nonumber\\ &\qquad \times(\omega_\psi (g_1, 1) \phi)(v_X) f(u h g_1) \psi_{S_X}(u)^{-1} \, du \, dh\, dg_1 \nonumber\\ &\quad =\int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} B_{S_X, \chi^{-1}}(\pi(g_1)f) (\omega_\psi (g_1, 1) \phi)(v_X) \,dg_1 , \end{align}
\begin{align} & \int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} \int_{\mathbb{A}^\times T_{S_X}(F) \backslash T_{S_X}(\mathbb{A})} \int_{N(F) \backslash N(\mathbb{A})} \chi(h) \nonumber\\ &\qquad \times(\omega_\psi (g_1, 1) \phi)(v_X) f(u h g_1) \psi_{S_X}(u)^{-1} \, du \, dh\, dg_1 \nonumber\\ &\quad =\int_{N(\mathbb{A}) \backslash G^1(\mathbb{A}_F)} B_{S_X, \chi^{-1}}(\pi(g_1)f) (\omega_\psi (g_1, 1) \phi)(v_X) \,dg_1 , \end{align}
where we regard ![]() $\chi$ as a character of
$\chi$ as a character of ![]() $\mathrm {GSO}(S_X)(\mathbb {A})$ by (3.1.9).
$\mathrm {GSO}(S_X)(\mathbb {A})$ by (3.1.9).
Finally, the last statement concerning the equivalence of the non-vanishing conditions on the ![]() $(S_X,\chi ^{-1},\psi )$-Bessel period and the
$(S_X,\chi ^{-1},\psi )$-Bessel period and the ![]() $(X,\chi )$-Bessel period follows from the pull-back formula (3.1.6) by an argument similar to that in the proof of Proposition 2 in [Reference Furusawa and MorimotoFM17].
$(X,\chi )$-Bessel period follows from the pull-back formula (3.1.6) by an argument similar to that in the proof of Proposition 2 in [Reference Furusawa and MorimotoFM17].
3.2  $(G_D, \mathrm {GSU}_{3,D})$ case
$(G_D, \mathrm {GSU}_{3,D})$ case
3.2.1 Theta correspondence for quaternionic dual pair with similitudes
Let ![]() $D$ be a quaternion division algebra over
$D$ be a quaternion division algebra over ![]() $F$. Let
$F$. Let ![]() $X_D$ (respectively,
$X_D$ (respectively, ![]() $Y_D$) be a right (respectively, left)
$Y_D$) be a right (respectively, left) ![]() $D$-vector space of finite rank equipped with a non-degenerate hermitian bilinear form
$D$-vector space of finite rank equipped with a non-degenerate hermitian bilinear form ![]() $(\,{,}\,)_{X_D}$ (respectively, non-degenerate skew-hermitian bilinear form
$(\,{,}\,)_{X_D}$ (respectively, non-degenerate skew-hermitian bilinear form ![]() $\langle \, {,} \, \rangle _{Y_D}$). Hence
$\langle \, {,} \, \rangle _{Y_D}$). Hence ![]() $(\,{,}\,)_{X_D}$ and
$(\,{,}\,)_{X_D}$ and ![]() $\langle \, {,} \,\rangle _{Y_D}$ are
$\langle \, {,} \,\rangle _{Y_D}$ are ![]() $D$-valued
$D$-valued ![]() $F$-bilinear form on
$F$-bilinear form on ![]() $X_D$ and
$X_D$ and ![]() $Y_D$ satisfying
$Y_D$ satisfying
 \begin{gather*} \overline{(x ,x^\prime)_{X_D}} = (x^\prime,x)_{X_D},\quad (xa,x^\prime b)_{X_D} = \bar{a}(x,x^\prime)_{X_D} b, \\ \overline{\langle y,y^\prime \rangle_{Y_D}} = -\langle y^\prime,y\rangle_{Y_D}, \quad \langle ay,y^\prime b \rangle_{Y_D} = a \langle y,y^\prime \rangle_{Y_D} \bar{b}, \end{gather*}
\begin{gather*} \overline{(x ,x^\prime)_{X_D}} = (x^\prime,x)_{X_D},\quad (xa,x^\prime b)_{X_D} = \bar{a}(x,x^\prime)_{X_D} b, \\ \overline{\langle y,y^\prime \rangle_{Y_D}} = -\langle y^\prime,y\rangle_{Y_D}, \quad \langle ay,y^\prime b \rangle_{Y_D} = a \langle y,y^\prime \rangle_{Y_D} \bar{b}, \end{gather*}
for ![]() $x, x^\prime \in X_D$,
$x, x^\prime \in X_D$, ![]() $y, y^\prime \in Y_D$ and
$y, y^\prime \in Y_D$ and ![]() $a,b\in D$. We denote the isometry group of
$a,b\in D$. We denote the isometry group of ![]() $X_D$ and
$X_D$ and ![]() $Y_D$ by
$Y_D$ by ![]() $\mathrm {U}(X_D)$ and
$\mathrm {U}(X_D)$ and ![]() $\mathrm {U}(Y_D)$, respectively. Then the space
$\mathrm {U}(Y_D)$, respectively. Then the space ![]() $Z_D = X_D \otimes _D Y_D$ is regarded as a symplectic space over
$Z_D = X_D \otimes _D Y_D$ is regarded as a symplectic space over ![]() $F$ with the non-degenerate alternating form
$F$ with the non-degenerate alternating form ![]() $\langle \,{,} \, \rangle$ defined by
$\langle \,{,} \, \rangle$ defined by
and we have a homomorphism ![]() $\mathrm {U}(X_D) \times \mathrm {U}(Y_D) \rightarrow \mathrm {Sp}(Z_D)$ defined by
$\mathrm {U}(X_D) \times \mathrm {U}(Y_D) \rightarrow \mathrm {Sp}(Z_D)$ defined by
As in the case when ![]() $D \simeq \mathrm {Mat}_{2 \times 2}$, this mapping splits in the metaplectic group
$D \simeq \mathrm {Mat}_{2 \times 2}$, this mapping splits in the metaplectic group ![]() $\mathrm {Mp}(Z_D)$. Hence we have the Weil representation
$\mathrm {Mp}(Z_D)$. Hence we have the Weil representation ![]() $\omega _\psi$ of
$\omega _\psi$ of ![]() $\mathrm {U}(X_D, \mathbb {A}) \times \mathrm {U}(Y_D, \mathbb {A})$ by restriction.
$\mathrm {U}(X_D, \mathbb {A}) \times \mathrm {U}(Y_D, \mathbb {A})$ by restriction.
From now on, we suppose that the rank of ![]() $X_D$ is
$X_D$ is ![]() $2k$ and
$2k$ and ![]() $X_D$ is maximally split, in the sense that its maximal isotropic subspace has rank
$X_D$ is maximally split, in the sense that its maximal isotropic subspace has rank ![]() $k$.
$k$.
Let us denote by ![]() $\mathrm {GU}(X_D)$ (respectively,
$\mathrm {GU}(X_D)$ (respectively, ![]() $\mathrm {GU}(Y_D)$) the similitude unitary group of
$\mathrm {GU}(Y_D)$) the similitude unitary group of ![]() $X_D$ (respectively,
$X_D$ (respectively, ![]() $Y_D$) with the similitude character
$Y_D$) with the similitude character ![]() $\lambda _D$ (respectively,
$\lambda _D$ (respectively, ![]() $\nu _D$). In addition, we denote the identity component of
$\nu _D$). In addition, we denote the identity component of ![]() $\mathrm {GU}(Y_D)$ by
$\mathrm {GU}(Y_D)$ by ![]() $\mathrm {GSU}(Y_D)$. Then the action (3.2.2) extends to a homomorphism
$\mathrm {GSU}(Y_D)$. Then the action (3.2.2) extends to a homomorphism
with the property ![]() $\lambda (i_D(g, h)) = \lambda _D(g) \nu _D(h)^{-1}$. Let
$\lambda (i_D(g, h)) = \lambda _D(g) \nu _D(h)^{-1}$. Let
Since ![]() $X_D$ is maximally split, we have a Witt decomposition
$X_D$ is maximally split, we have a Witt decomposition ![]() $X_D = X_D^+ \oplus X_D^-$ with maximal isotropic subspaces
$X_D = X_D^+ \oplus X_D^-$ with maximal isotropic subspaces ![]() $X_{D}^{\pm }$. Then as in § 3.1.1, we may realize the Weil representation
$X_{D}^{\pm }$. Then as in § 3.1.1, we may realize the Weil representation ![]() $\omega _\psi$ of
$\omega _\psi$ of ![]() $\mathrm {U}(X_D) \times \mathrm {U}(Y_D)$ on
$\mathrm {U}(X_D) \times \mathrm {U}(Y_D)$ on ![]() $\mathcal {S}((X_D^+ \otimes Y_D)(\mathbb {A}))$. In this realization, for
$\mathcal {S}((X_D^+ \otimes Y_D)(\mathbb {A}))$. In this realization, for ![]() $h \in \mathrm {U}(Y_D)$ and
$h \in \mathrm {U}(Y_D)$ and ![]() $\phi \in \mathcal {S}((X_D^+ \otimes Y_D)(\mathbb {A}))$, we have
$\phi \in \mathcal {S}((X_D^+ \otimes Y_D)(\mathbb {A}))$, we have
Hence, as in § 3.1.1, we may extend ![]() $\omega _\psi$ to
$\omega _\psi$ to ![]() $R_D(\mathbb {A})$ by
$R_D(\mathbb {A})$ by
for ![]() $(g,h)\in R_D(\mathbb {A})$, where
$(g,h)\in R_D(\mathbb {A})$, where
Then as in § 3.1.1, we may extend the Weil representation ![]() $\omega _\psi$ of
$\omega _\psi$ of ![]() $\mathrm {U}(X_D) \times \mathrm {U}(Y_D)$ on
$\mathrm {U}(X_D) \times \mathrm {U}(Y_D)$ on ![]() $\mathcal {S}(Z_+(\mathbb {A}_F))$, where
$\mathcal {S}(Z_+(\mathbb {A}_F))$, where ![]() $Z_D = Z_D^+ \oplus Z_D^-$ is an arbitrary polarization, to
$Z_D = Z_D^+ \oplus Z_D^-$ is an arbitrary polarization, to ![]() $R_D(\mathbb {A})$, by using the
$R_D(\mathbb {A})$, by using the ![]() $\mathrm {U}(X_D) \times \mathrm {U}(Y_D)$-isomorphism
$\mathrm {U}(X_D) \times \mathrm {U}(Y_D)$-isomorphism ![]() $p:\mathcal {S}((X_D^+ \otimes Y_D)(\mathbb {A}))\to \mathcal {S}(Z_+(\mathbb {A}_F))$. Thus for
$p:\mathcal {S}((X_D^+ \otimes Y_D)(\mathbb {A}))\to \mathcal {S}(Z_+(\mathbb {A}_F))$. Thus for ![]() $\phi \in \mathcal {S}(Z_+(\mathbb {A}_F))$, the theta kernel
$\phi \in \mathcal {S}(Z_+(\mathbb {A}_F))$, the theta kernel ![]() $\theta ^\phi _\psi =\theta ^\phi$ on
$\theta ^\phi _\psi =\theta ^\phi$ on ![]() $R_D(\mathbb {A})$ is defined by
$R_D(\mathbb {A})$ is defined by
Let us define
and
We note that ![]() $\nu _D (\mathrm {GU}(Y_D, F_v))$ contains
$\nu _D (\mathrm {GU}(Y_D, F_v))$ contains ![]() $N_D(D(F_v)^\times )$ for any place
$N_D(D(F_v)^\times )$ for any place ![]() $v$. Thus, if
$v$. Thus, if ![]() $v$ is non-archimedean or complex, we have
$v$ is non-archimedean or complex, we have ![]() $\mathrm {GU}(X_D, F_v)^+ = \mathrm {GU}(X_D, F_v)$, and if
$\mathrm {GU}(X_D, F_v)^+ = \mathrm {GU}(X_D, F_v)$, and if ![]() $v$ is real,
$v$ is real, ![]() $|\mathrm {GU}(X_D, F_v) / \mathrm {GU}(X_D, F_v)^+| \leq 2$.
$|\mathrm {GU}(X_D, F_v) / \mathrm {GU}(X_D, F_v)^+| \leq 2$.
For a cusp form ![]() $f$ on
$f$ on ![]() $\mathrm {GU}(X_D, \mathbb {A})^+$, as in § 3.1.1, we define the theta lift of
$\mathrm {GU}(X_D, \mathbb {A})^+$, as in § 3.1.1, we define the theta lift of ![]() $f$ to
$f$ to ![]() $\mathrm {GU}(Y_D, \mathbb {A})$ by
$\mathrm {GU}(Y_D, \mathbb {A})$ by
where ![]() $g \in \mathrm {GU}(X_D, \mathbb {A})^+$ is chosen so that
$g \in \mathrm {GU}(X_D, \mathbb {A})^+$ is chosen so that ![]() $\lambda _D(g) = \nu _D(h)$. It defines an automorphic form on
$\lambda _D(g) = \nu _D(h)$. It defines an automorphic form on ![]() $\mathrm {GU}(Y_D, \mathbb {A})$. When we regard
$\mathrm {GU}(Y_D, \mathbb {A})$. When we regard ![]() $\Theta (f, \phi )(h)$ as an automorphic form on
$\Theta (f, \phi )(h)$ as an automorphic form on ![]() $\mathrm {GSU}(Y_D, \mathbb {A})$ by the restriction, we denote it as
$\mathrm {GSU}(Y_D, \mathbb {A})$ by the restriction, we denote it as ![]() $\theta (f, \phi )(h)$. For an irreducible cuspidal automorphic representation
$\theta (f, \phi )(h)$. For an irreducible cuspidal automorphic representation ![]() $(\pi _+, V_{\pi _+})$ of
$(\pi _+, V_{\pi _+})$ of ![]() $\mathrm {GU}(X_D, \mathbb {A})^+$, we denote by
$\mathrm {GU}(X_D, \mathbb {A})^+$, we denote by ![]() $\Theta _\psi (\pi _+)$ (respectively,
$\Theta _\psi (\pi _+)$ (respectively, ![]() $\theta _\psi (\pi _+)$) the theta lift of
$\theta _\psi (\pi _+)$) the theta lift of ![]() $\pi _+$ to
$\pi _+$ to ![]() $\mathrm {GU}(Y_D, \mathbb {A})$ (respectively,
$\mathrm {GU}(Y_D, \mathbb {A})$ (respectively, ![]() $\mathrm {GSU}(Y_D, \mathbb {A})$), namely
$\mathrm {GSU}(Y_D, \mathbb {A})$), namely
 \begin{align*} \Theta_\psi(\pi) &:= \{\Theta (f, \phi) : f \in V_{\pi_+}, \phi \in \mathcal{S}(Z_D^+(\mathbb{A}))\},\\ \theta_\psi(\pi) &:= \{\theta (f, \phi) : f \in V_{\pi_+}, \phi \in \mathcal{S}(Z_D^+(\mathbb{A}))\}, \end{align*}
\begin{align*} \Theta_\psi(\pi) &:= \{\Theta (f, \phi) : f \in V_{\pi_+}, \phi \in \mathcal{S}(Z_D^+(\mathbb{A}))\},\\ \theta_\psi(\pi) &:= \{\theta (f, \phi) : f \in V_{\pi_+}, \phi \in \mathcal{S}(Z_D^+(\mathbb{A}))\}, \end{align*}
respectively. Moreover, for an irreducible cuspidal automorphic representation ![]() $(\pi, V_\pi )$ of
$(\pi, V_\pi )$ of ![]() $\mathrm {GU}(X_D, \mathbb {A})$, we define the theta lift
$\mathrm {GU}(X_D, \mathbb {A})$, we define the theta lift ![]() $\Theta _\psi (\pi )$ (respectively,
$\Theta _\psi (\pi )$ (respectively, ![]() $\theta _\psi (\pi )$) of
$\theta _\psi (\pi )$) of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GU}(Y_D, \mathbb {A})$ (respectively,
$\mathrm {GU}(Y_D, \mathbb {A})$ (respectively, ![]() $\mathrm {GSU}(Y_D, \mathbb {A})$) by
$\mathrm {GSU}(Y_D, \mathbb {A})$) by ![]() $\Theta _\psi (\pi ) := \Theta _\psi (\pi |_{\mathrm {GU}(X_D, \mathbb {A})^+}\!)$ (respectively,
$\Theta _\psi (\pi ) := \Theta _\psi (\pi |_{\mathrm {GU}(X_D, \mathbb {A})^+}\!)$ (respectively, ![]() $\theta _\psi (\pi ) := \theta _\psi (\pi |_{\mathrm {GU}(X_D, \mathbb {A})^+}\!)$).
$\theta _\psi (\pi ) := \theta _\psi (\pi |_{\mathrm {GU}(X_D, \mathbb {A})^+}\!)$).
As for the opposite direction, as in § 3.1.1, for a cusp form ![]() $f^\prime$ on
$f^\prime$ on ![]() $\mathrm {GSU}(Y_D, \mathbb {A})$, we define the theta lift of
$\mathrm {GSU}(Y_D, \mathbb {A})$, we define the theta lift of ![]() $f^\prime$ to
$f^\prime$ to ![]() $\mathrm {GU}(X_D, \mathbb {A})^+$ by
$\mathrm {GU}(X_D, \mathbb {A})^+$ by
where ![]() $h \in \mathrm {GSU}(Y_D, \mathbb {A})$ is chosen so that
$h \in \mathrm {GSU}(Y_D, \mathbb {A})$ is chosen so that ![]() $\lambda _D(g) = \nu _D(h)$. For an irreducible cuspidal automorphic representation
$\lambda _D(g) = \nu _D(h)$. For an irreducible cuspidal automorphic representation ![]() $(\sigma, V_\sigma )$ of
$(\sigma, V_\sigma )$ of ![]() $\mathrm {GSU}(Y_D, \mathbb {A})$, we denote by
$\mathrm {GSU}(Y_D, \mathbb {A})$, we denote by ![]() $\theta _\psi (\sigma )$ the theta lift of
$\theta _\psi (\sigma )$ the theta lift of ![]() $\sigma$ to
$\sigma$ to ![]() $\mathrm {GU}(X_D, \mathbb {A})^+$. Moreover, we extend
$\mathrm {GU}(X_D, \mathbb {A})^+$. Moreover, we extend ![]() $\theta (f^\prime, \phi )$ to an automorphic form on
$\theta (f^\prime, \phi )$ to an automorphic form on ![]() $\mathrm {GU}(X_D, \mathbb {A})$ by the natural embedding
$\mathrm {GU}(X_D, \mathbb {A})$ by the natural embedding
and extension by zero. Then we define the theta lift ![]() $\Theta _\psi (\sigma )$ of
$\Theta _\psi (\sigma )$ of ![]() $\sigma$ to
$\sigma$ to ![]() $\mathrm {GU}(X_D, \mathbb {A})$ as the
$\mathrm {GU}(X_D, \mathbb {A})$ as the ![]() $\mathrm {GU}(X_D, \mathbb {A})$ representation generated by such
$\mathrm {GU}(X_D, \mathbb {A})$ representation generated by such ![]() $\theta (f^\prime,\phi )$ for
$\theta (f^\prime,\phi )$ for ![]() $f^\prime \in V_\sigma$ and
$f^\prime \in V_\sigma$ and ![]() $\phi \in \mathcal {S} (Z_+(\mathbb {A}))$.
$\phi \in \mathcal {S} (Z_+(\mathbb {A}))$.
Remark 3.2 Suppose that ![]() $(\pi _+, V_{\pi _+})$ (respectively,
$(\pi _+, V_{\pi _+})$ (respectively, ![]() $(\sigma, V_\sigma )$) is an irreducible cuspidal automorphic representation of
$(\sigma, V_\sigma )$) is an irreducible cuspidal automorphic representation of ![]() $\mathrm {GU}(X_D, \mathbb {A})^+$ (respectively,
$\mathrm {GU}(X_D, \mathbb {A})^+$ (respectively, ![]() $\mathrm {GSU}(Y_D, \mathbb {A})$). Suppose moreover that the theta lift
$\mathrm {GSU}(Y_D, \mathbb {A})$). Suppose moreover that the theta lift ![]() $\Theta _\psi (\pi _+)$ (respectively,
$\Theta _\psi (\pi _+)$ (respectively, ![]() $\theta _\psi (\sigma )$) is non-zero and cuspidal. Then by Gan [Reference GanGan08, Proposition 2.12],
$\theta _\psi (\sigma )$) is non-zero and cuspidal. Then by Gan [Reference GanGan08, Proposition 2.12], ![]() $\Theta _\psi (\pi _+)$ (respectively,
$\Theta _\psi (\pi _+)$ (respectively, ![]() $\theta _\psi (\sigma )$) is an irreducible cuspidal automorphic representation because of the Howe duality for quaternionic dual pairs proved by Gan and Sun [Reference Gan and SunGS17] and Gan and Takeda [Reference Gan and TakedaGT16]. We shall study the case
$\theta _\psi (\sigma )$) is an irreducible cuspidal automorphic representation because of the Howe duality for quaternionic dual pairs proved by Gan and Sun [Reference Gan and SunGS17] and Gan and Takeda [Reference Gan and TakedaGT16]. We shall study the case ![]() $\dim _D~X_D=2$ and
$\dim _D~X_D=2$ and ![]() $\dim _D~Y_D=3$. In this case, by the conservation relation proved by Sun and Zhu [Reference Sun and ZhuSZ15], the irreducibility of
$\dim _D~Y_D=3$. In this case, by the conservation relation proved by Sun and Zhu [Reference Sun and ZhuSZ15], the irreducibility of ![]() $\Theta _\psi (\pi _+)$ implies that of
$\Theta _\psi (\pi _+)$ implies that of ![]() $\theta _\psi (\pi _+)$.
$\theta _\psi (\pi _+)$.
3.2.2 Pull-back of the global Bessel periods for the dual pair  $(\mathrm {G}_D,\mathrm {GSU}_{3,D})$
$(\mathrm {G}_D,\mathrm {GSU}_{3,D})$
The set-up is as follows.
Let ![]() $X_D$ be the space of two-dimensional row vectors over
$X_D$ be the space of two-dimensional row vectors over ![]() $D$ equipped with the hermitian form
$D$ equipped with the hermitian form
Let us take the standard basis of ![]() $X_D$ and name the basis vectors as
$X_D$ and name the basis vectors as
Then ![]() $G_D$ defined by (1.4.2) is the matrix representation of the similitude unitary group
$G_D$ defined by (1.4.2) is the matrix representation of the similitude unitary group ![]() $\mathrm {GU}(X_D)$ for
$\mathrm {GU}(X_D)$ for ![]() $X_D$ with respect to the standard basis.
$X_D$ with respect to the standard basis.
Let ![]() $Y_D$ be the space of three-dimensional column vectors over
$Y_D$ be the space of three-dimensional column vectors over ![]() $D$ equipped with the skew-hermitian form
$D$ equipped with the skew-hermitian form
 \[ \langle y, y^\prime \rangle_{Y_D} = {}^{t} y\, \begin{pmatrix} 0 & 0 & \eta\\ 0 & \eta & 0 \\ \eta & 0 & 0 \end{pmatrix}\overline{y^\prime}. \]
\[ \langle y, y^\prime \rangle_{Y_D} = {}^{t} y\, \begin{pmatrix} 0 & 0 & \eta\\ 0 & \eta & 0 \\ \eta & 0 & 0 \end{pmatrix}\overline{y^\prime}. \]
Let us take the standard basis of ![]() $Y_D$ and name the basis vectors as
$Y_D$ and name the basis vectors as
Then ![]() $\mathrm {GSU}_{3,D}$ defined in § 2.1.3 is the matrix representation of the group
$\mathrm {GSU}_{3,D}$ defined in § 2.1.3 is the matrix representation of the group ![]() $\mathrm {GSU}(Y_D)$ for
$\mathrm {GSU}(Y_D)$ for ![]() $Y_D$ with respect to the standard basis.
$Y_D$ with respect to the standard basis.
We take a polarization ![]() $Z_D=Z_{D,+}\oplus Z_{D,-}$ of
$Z_D=Z_{D,+}\oplus Z_{D,-}$ of ![]() $Z_D=X_D\otimes _D Y_D$ defined as follows. Let
$Z_D=X_D\otimes _D Y_D$ defined as follows. Let
where the double sign corresponds. We decompose ![]() $Y_D$ as
$Y_D$ as ![]() $Y_D=Y_{D,+}\oplus Y_{D,0}\oplus Y_{D,-}$ where
$Y_D=Y_{D,+}\oplus Y_{D,0}\oplus Y_{D,-}$ where
Then let
where the double sign corresponds. To simplify the notation, we denote ![]() $z_+ \in Z_{D,+}(\mathbb {A})$ as
$z_+ \in Z_{D,+}(\mathbb {A})$ as ![]() $z_+=(a,b)$ when
$z_+=(a,b)$ when
and ![]() $\phi (z_+)$ as
$\phi (z_+)$ as ![]() $\phi (a,b)$ for
$\phi (a,b)$ for ![]() $\phi \in \mathcal {S}(Z_{D,+}(\mathbb {A}))$.
$\phi \in \mathcal {S}(Z_{D,+}(\mathbb {A}))$.
Let us compute the pull-back of the ![]() $(X,\chi, \psi )$-Bessel periods on
$(X,\chi, \psi )$-Bessel periods on ![]() $\mathrm {GSU}_{3,D}$ defined by (2.3.3) with respect to the theta lift from
$\mathrm {GSU}_{3,D}$ defined by (2.3.3) with respect to the theta lift from ![]() $G_D$.
$G_D$.
Proposition 3.2 Let ![]() $(\pi _D, V_{\pi _D})$ be an irreducible cuspidal automorphic representation of
$(\pi _D, V_{\pi _D})$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ whose central character is
$G_D(\mathbb {A})$ whose central character is ![]() $\omega _\pi$ and
$\omega _\pi$ and ![]() $\chi$ a character of
$\chi$ a character of ![]() $\mathbb {A}_E^\times$ such that
$\mathbb {A}_E^\times$ such that ![]() $\chi \mid _{\mathbb {A}^\times }=\omega _\pi ^{-1}$. Let
$\chi \mid _{\mathbb {A}^\times }=\omega _\pi ^{-1}$. Let ![]() $X\in D^\times$.
$X\in D^\times$.
Then for ![]() $f \in V_{\pi _D}$ and
$f \in V_{\pi _D}$ and ![]() $\phi \in \mathcal {S}(Z_{D, +}(\mathbb {A}))$, we have
$\phi \in \mathcal {S}(Z_{D, +}(\mathbb {A}))$, we have
where
and ![]() $B_{\xi _X, \chi ^{-1},\psi }$ denotes the
$B_{\xi _X, \chi ^{-1},\psi }$ denotes the ![]() $(\xi _X, \chi ^{-1},\psi )$-Bessel period on
$(\xi _X, \chi ^{-1},\psi )$-Bessel period on ![]() $G_D$ defined by (1.4.11).
$G_D$ defined by (1.4.11).
In particular, the ![]() $(\xi _X, \chi ^{-1},\psi )$-Bessel period does not vanish on
$(\xi _X, \chi ^{-1},\psi )$-Bessel period does not vanish on ![]() $V_{\pi _D}$ if and only if the
$V_{\pi _D}$ if and only if the ![]() $(X,\chi, \psi )$-Bessel period does not vanish on
$(X,\chi, \psi )$-Bessel period does not vanish on ![]() $\theta _\psi (\pi _D)$.
$\theta _\psi (\pi _D)$.
Proof. The proof of this proposition is similar to that for Proposition 3.1.
Let ![]() $N_{0,D}$ be a subgroup of
$N_{0,D}$ be a subgroup of ![]() $N_{3,D}$ given by
$N_{3,D}$ given by
 \[ N_{0, D}(F) = \left\{ u_D(x):=\begin{pmatrix} 1 & 0 & \eta x\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} : x \in F\right\}. \]
\[ N_{0, D}(F) = \left\{ u_D(x):=\begin{pmatrix} 1 & 0 & \eta x\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} : x \in F\right\}. \]
Then we note that ![]() $N_{0, D}$ is a normal subgroup of
$N_{0, D}$ is a normal subgroup of ![]() $N_{3,D}$ and
$N_{3,D}$ and ![]() $\psi _{X, D}$ is trivial on
$\psi _{X, D}$ is trivial on ![]() $N_{0, D}(\mathbb {A})$. Since
$N_{0, D}(\mathbb {A})$. Since
we have
Thus, by an argument similar to that in the proof of Proposition 3.1, one may show that
 \begin{align} & \int_{N_{3,D}(F)
\backslash N_{3,D}(\mathbb{A})} \theta(f; \phi)(hu)
\psi^{-1}_{X, D}(u) \, du \nonumber\\ &\quad
=\int_{N_{3,D}(F) \backslash
N_{3,D}(\mathbb{A})}\int_{G_D^1(F) \backslash
G_D^1(\mathbb{A})} \sum _{ \overline{a} \in
\mathcal{X}_{D,-}}\ \sum_{\gamma \in V_D(a) \backslash
G_D^1(F)}\ \sum_{b \in X_{D,+}} \nonumber\\ &\qquad \times
(\omega (\gamma g_1 \lambda_s^D(\nu(h)) , uh) \phi)(a, b)
f(g_1 \lambda_s(\nu(h))) \, dg_1 \, du.
\end{align}
\begin{align} & \int_{N_{3,D}(F)
\backslash N_{3,D}(\mathbb{A})} \theta(f; \phi)(hu)
\psi^{-1}_{X, D}(u) \, du \nonumber\\ &\quad
=\int_{N_{3,D}(F) \backslash
N_{3,D}(\mathbb{A})}\int_{G_D^1(F) \backslash
G_D^1(\mathbb{A})} \sum _{ \overline{a} \in
\mathcal{X}_{D,-}}\ \sum_{\gamma \in V_D(a) \backslash
G_D^1(F)}\ \sum_{b \in X_{D,+}} \nonumber\\ &\qquad \times
(\omega (\gamma g_1 \lambda_s^D(\nu(h)) , uh) \phi)(a, b)
f(g_1 \lambda_s(\nu(h))) \, dg_1 \, du.
\end{align}
Here ![]() $\mathcal {X}_{D,-}$ is the set of equivalence classes
$\mathcal {X}_{D,-}$ is the set of equivalence classes ![]() $X_{D,-}/ \sim$ where
$X_{D,-}/ \sim$ where ![]() $a\sim a^\prime$ if and only if there exists a
$a\sim a^\prime$ if and only if there exists a ![]() $\gamma \in G_D^1(F)$ such that
$\gamma \in G_D^1(F)$ such that ![]() $a^\prime =a\gamma$,
$a^\prime =a\gamma$, ![]() $\bar {a}$ denotes the equivalence class of
$\bar {a}$ denotes the equivalence class of ![]() $\mathcal {X}_{D,-}$ containing
$\mathcal {X}_{D,-}$ containing ![]() $a\in X_{D,-}$, and,
$a\in X_{D,-}$, and, ![]() $V(a)=\{\gamma \in G_D^1(F)\mid a\gamma =a\}$. Then we may rewrite (3.2.6) as
$V(a)=\{\gamma \in G_D^1(F)\mid a\gamma =a\}$. Then we may rewrite (3.2.6) as
 \begin{align} & \int_{N_{3,D}(F)
\backslash N_{3,D}(\mathbb{A})} \theta(f; \phi)(hu)
\psi^{-1}_{X, D}(u) \, du\nonumber\\ &\quad =\int_{N_{3,D}(F) \backslash
N_{3,D}(\mathbb{A})}\int_{G_D^1(F) \backslash
G_D^1(\mathbb{A})} \nonumber\\ &\quad\quad \times \sum_{N_D(F)
\backslash G_D^1(F)}\ \sum_{b \in X_{D,+}} (\omega (\gamma
g_1 \lambda_s^D(\nu(h)), uh) \phi)(x_{-}, b) f(g_1
\lambda_s(\nu(h))) \, dg_1 \, du.
\end{align}
\begin{align} & \int_{N_{3,D}(F)
\backslash N_{3,D}(\mathbb{A})} \theta(f; \phi)(hu)
\psi^{-1}_{X, D}(u) \, du\nonumber\\ &\quad =\int_{N_{3,D}(F) \backslash
N_{3,D}(\mathbb{A})}\int_{G_D^1(F) \backslash
G_D^1(\mathbb{A})} \nonumber\\ &\quad\quad \times \sum_{N_D(F)
\backslash G_D^1(F)}\ \sum_{b \in X_{D,+}} (\omega (\gamma
g_1 \lambda_s^D(\nu(h)), uh) \phi)(x_{-}, b) f(g_1
\lambda_s(\nu(h))) \, dg_1 \, du.
\end{align}
Since, for ![]() $u = \bigg (\begin{smallmatrix} 1 & -\eta ^{-1} \bar {A} \eta & B\\ 0 & 1 & A\\ 0 & 0 & 1 \end{smallmatrix}\bigg ) \in N_{3,D}(\mathbb {A})$, we have
$u = \bigg (\begin{smallmatrix} 1 & -\eta ^{-1} \bar {A} \eta & B\\ 0 & 1 & A\\ 0 & 0 & 1 \end{smallmatrix}\bigg ) \in N_{3,D}(\mathbb {A})$, we have ![]() $Z_{D,-}(\mathbb {A})(1, u) = Z_{D,-}(\mathbb {A})$ and
$Z_{D,-}(\mathbb {A})(1, u) = Z_{D,-}(\mathbb {A})$ and
 \begin{align*} z_+ (1, u) &= z_++ x_- \otimes (B^\prime y_- - A e +y_+) +b \otimes (\eta^{-1} \bar{A} \eta y_- + e)\\ &= z_+ + x_- \otimes (B^\prime y_- - A e) +b \otimes (\eta^{-1} \bar{A} \eta y_-) , \end{align*}
\begin{align*} z_+ (1, u) &= z_++ x_- \otimes (B^\prime y_- - A e +y_+) +b \otimes (\eta^{-1} \bar{A} \eta y_- + e)\\ &= z_+ + x_- \otimes (B^\prime y_- - A e) +b \otimes (\eta^{-1} \bar{A} \eta y_-) , \end{align*}
we obtain
Hence, in (3.2.7), only ![]() $b\in X_{D,-}$ satisfying
$b\in X_{D,-}$ satisfying ![]() $\eta \langle b, x_- \rangle = X$, i.e.
$\eta \langle b, x_- \rangle = X$, i.e. ![]() $b=x_+(-\overline {X}\eta ^{-1} )$ contributes. Thus, our integral is equal to
$b=x_+(-\overline {X}\eta ^{-1} )$ contributes. Thus, our integral is equal to
 \begin{align*} & \int_{N_{D}(F) \backslash G_D^1(\mathbb{A})} (\omega (g_1 \lambda_s^D(\nu(h)) , uh) \phi)(v_{D, X}) f(g_1 \lambda_s^D(\nu(h))) \, dg_1 \, du \\ &\quad =\int_{N_{D}(\mathbb{A}) \backslash G_D^1(\mathbb{A})} \int_{N_{D}(F) \backslash N_{D}(\mathbb{A})} \omega (u g_1 \lambda_s^D(\nu(h)) , uh) \phi(v_{D, X})\\ &\qquad \times f( u g_1 \lambda_s^D(\nu(h))) \, dg_1 \, du, \end{align*}
\begin{align*} & \int_{N_{D}(F) \backslash G_D^1(\mathbb{A})} (\omega (g_1 \lambda_s^D(\nu(h)) , uh) \phi)(v_{D, X}) f(g_1 \lambda_s^D(\nu(h))) \, dg_1 \, du \\ &\quad =\int_{N_{D}(\mathbb{A}) \backslash G_D^1(\mathbb{A})} \int_{N_{D}(F) \backslash N_{D}(\mathbb{A})} \omega (u g_1 \lambda_s^D(\nu(h)) , uh) \phi(v_{D, X})\\ &\qquad \times f( u g_1 \lambda_s^D(\nu(h))) \, dg_1 \, du, \end{align*}
where ![]() $v_{D, X} =( x_-, x_+(-\overline {X}\eta ^{-1} ))$. Further, for
$v_{D, X} =( x_-, x_+(-\overline {X}\eta ^{-1} ))$. Further, for ![]() $u=\big (\begin{smallmatrix}1 & a\\0 & 1\end{smallmatrix}\big ) \in N_D(\mathbb {A})$, we have
$u=\big (\begin{smallmatrix}1 & a\\0 & 1\end{smallmatrix}\big ) \in N_D(\mathbb {A})$, we have
where we put ![]() $\xi _{X} = X \eta \overline {X}$. Thus, our integral becomes
$\xi _{X} = X \eta \overline {X}$. Thus, our integral becomes
As for the integration over ![]() $\mathbb {A}^\times M_{X, D}(F) \backslash M_{X, D}(\mathbb {A})$ in (2.3.3), by a direct computation, we see that
$\mathbb {A}^\times M_{X, D}(F) \backslash M_{X, D}(\mathbb {A})$ in (2.3.3), by a direct computation, we see that
where
 \[ h = \begin{pmatrix} n_D(h) \cdot (h^X)^\ast & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^X\end{pmatrix}\quad \text{and} \quad h_0 = \begin{pmatrix} \overline{h^X} & 0\\ 0 & (h^X)^{-1} \end{pmatrix}. \]
\[ h = \begin{pmatrix} n_D(h) \cdot (h^X)^\ast & 0 & 0\\ 0 & h & 0\\ 0 & 0 & h^X\end{pmatrix}\quad \text{and} \quad h_0 = \begin{pmatrix} \overline{h^X} & 0\\ 0 & (h^X)^{-1} \end{pmatrix}. \]
Therefore, as in the previous case, we obtain
The equivalence of the non-vanishing conditions follows from the pull-back formula (3.2.4) as Proposition 3.1.
3.3 Theta correspondence for similitude unitary groups
In our proof of Theorems 1.1 and 1.2, we shall use theta correspondence for similitude unitary groups in addition to theta correspondences for dual pairs ![]() $(\mathrm {GSp}_2, \mathrm {GSO}_{4,2})$ and
$(\mathrm {GSp}_2, \mathrm {GSO}_{4,2})$ and ![]() $(G_D, \mathrm {GSU}_{3,D})$. Let us recall the definition of the theta lifts in this case.
$(G_D, \mathrm {GSU}_{3,D})$. Let us recall the definition of the theta lifts in this case.
Let ![]() $(X, (\,{,}\,)_X)$ be an
$(X, (\,{,}\,)_X)$ be an ![]() $m$-dimensional hermitian space over
$m$-dimensional hermitian space over ![]() $E$, and let
$E$, and let ![]() $(Y, (\,{,} \,)_Y)$ be an
$(Y, (\,{,} \,)_Y)$ be an ![]() $n$-dimensional skew-hermitian space over
$n$-dimensional skew-hermitian space over ![]() $E$. Then we may define the quadratic space
$E$. Then we may define the quadratic space
This is a ![]() $2mn$-dimensional symplectic space over
$2mn$-dimensional symplectic space over ![]() $F$. Then we denote its isometry group by
$F$. Then we denote its isometry group by ![]() $\mathrm {Sp}(W_{X, Y})$. For each place
$\mathrm {Sp}(W_{X, Y})$. For each place ![]() $v$ of
$v$ of ![]() $F$, we denote the metaplectic extension of
$F$, we denote the metaplectic extension of ![]() $\mathrm {Sp}(W_{X, Y})(F_v)$ by
$\mathrm {Sp}(W_{X, Y})(F_v)$ by ![]() $\mathrm {Mp}(W_{X, Y})(F_v)$. In addition,
$\mathrm {Mp}(W_{X, Y})(F_v)$. In addition, ![]() $\mathrm {Mp}(W_{X, Y})(\mathbb {A})$ denotes the metaplectic extension of
$\mathrm {Mp}(W_{X, Y})(\mathbb {A})$ denotes the metaplectic extension of ![]() $\mathrm {Sp}(W_{X, Y})(\mathbb {A})$.
$\mathrm {Sp}(W_{X, Y})(\mathbb {A})$.
Let ![]() $\chi _X$ and
$\chi _X$ and ![]() $\chi _Y$ be characters of
$\chi _Y$ be characters of ![]() $\mathbb {A}_E^\times / E^\times$ such that
$\mathbb {A}_E^\times / E^\times$ such that ![]() $\chi _{X}|_{\mathbb {A}^\times } = \chi _E^m$ and
$\chi _{X}|_{\mathbb {A}^\times } = \chi _E^m$ and ![]() $\chi _{Y}|_{\mathbb {A}^\times } = \chi _E^n$. For each place
$\chi _{Y}|_{\mathbb {A}^\times } = \chi _E^n$. For each place ![]() $v$ of
$v$ of ![]() $F$, let
$F$, let
be the local splitting given by Kudla [Reference KudlaKud94] depending on the choice of a pair of characters ![]() $\chi _v =(\chi _{X,v}, \chi _{Y,v})$. Using this local splitting, we get a splitting
$\chi _v =(\chi _{X,v}, \chi _{Y,v})$. Using this local splitting, we get a splitting
depending on ![]() $\chi = (\chi _X, \chi _Y)$. Then by the pull-back, we obtain the Weil representation
$\chi = (\chi _X, \chi _Y)$. Then by the pull-back, we obtain the Weil representation ![]() $\omega _{\psi, \chi }$ of
$\omega _{\psi, \chi }$ of ![]() $\mathrm {U}(X)(\mathbb {A}) \times \mathrm {U}(Y)(\mathbb {A})$. When we fix a polarization
$\mathrm {U}(X)(\mathbb {A}) \times \mathrm {U}(Y)(\mathbb {A})$. When we fix a polarization ![]() $W_{X, Y} = W_{X, Y}^+ \oplus W_{X, Y}^-$, we may realize
$W_{X, Y} = W_{X, Y}^+ \oplus W_{X, Y}^-$, we may realize ![]() $\omega _{\psi, \chi }$ so that its space of smooth vectors is given by
$\omega _{\psi, \chi }$ so that its space of smooth vectors is given by ![]() $\mathcal {S}(W_{X, Y}^+(\mathbb {A}))$, the space of Schwartz–Bruhat functions on
$\mathcal {S}(W_{X, Y}^+(\mathbb {A}))$, the space of Schwartz–Bruhat functions on ![]() $W_{X, Y}^+(\mathbb {A})$. We define
$W_{X, Y}^+(\mathbb {A})$. We define
Suppose that ![]() $\dim Y$ is even and
$\dim Y$ is even and ![]() $Y$ is maximally split, in the sense that
$Y$ is maximally split, in the sense that ![]() $Y$ has a maximal isotropic subspace of dimension
$Y$ has a maximal isotropic subspace of dimension ![]() $\frac {1}{2} \dim Y$. In this case, as in §§ 3.1.1 and 3.2.1, we may extend
$\frac {1}{2} \dim Y$. In this case, as in §§ 3.1.1 and 3.2.1, we may extend ![]() $\omega _{\psi,\chi }$ to
$\omega _{\psi,\chi }$ to ![]() $R(\mathbb {A})$. On the other hand, in this case, we have an explicit local splitting of
$R(\mathbb {A})$. On the other hand, in this case, we have an explicit local splitting of ![]() $R(F_v) \rightarrow \mathrm {Sp}(W_{X, Y})(F_v)$ by Zhang [Reference ZhangZha13] and we may extend
$R(F_v) \rightarrow \mathrm {Sp}(W_{X, Y})(F_v)$ by Zhang [Reference ZhangZha13] and we may extend ![]() $\omega _{\psi,\chi }$ to
$\omega _{\psi,\chi }$ to ![]() $R(\mathbb {A})$ using this splitting. These two extensions of
$R(\mathbb {A})$ using this splitting. These two extensions of ![]() $\omega _{\psi,\chi }$ to
$\omega _{\psi,\chi }$ to ![]() $R(\mathbb {A})$ coincide.
$R(\mathbb {A})$ coincide.
Then for ![]() $\phi \in \mathcal {S}(W_{X, Y}^+(\mathbb {A}))$, we define the theta function
$\phi \in \mathcal {S}(W_{X, Y}^+(\mathbb {A}))$, we define the theta function ![]() $\theta _{\psi, \chi }^\phi$ on
$\theta _{\psi, \chi }^\phi$ on ![]() $R(\mathbb {A})$ by
$R(\mathbb {A})$ by
 \begin{equation} \theta_{\psi, \chi}^\phi(g, h) = \sum_{w \in W_{X, Y}^+(F)} \omega_{\psi, \chi}(g, h)\phi(w). \end{equation}
\begin{equation} \theta_{\psi, \chi}^\phi(g, h) = \sum_{w \in W_{X, Y}^+(F)} \omega_{\psi, \chi}(g, h)\phi(w). \end{equation}Let us define
 \begin{align*} \mathrm{GU}(X)(\mathbb{A})^{+}&:= \{g \in \mathrm{GU}(X)(\mathbb{A}) : \lambda(g) \in \lambda(\mathrm{GU}(Y)(\mathbb{A}))\},\\ \mathrm{GU}(X)(F)^{+} &:= \mathrm{GU}(X)(\mathbb{A})^{+} \cap \mathrm{GU}(X)(F). \end{align*}
\begin{align*} \mathrm{GU}(X)(\mathbb{A})^{+}&:= \{g \in \mathrm{GU}(X)(\mathbb{A}) : \lambda(g) \in \lambda(\mathrm{GU}(Y)(\mathbb{A}))\},\\ \mathrm{GU}(X)(F)^{+} &:= \mathrm{GU}(X)(\mathbb{A})^{+} \cap \mathrm{GU}(X)(F). \end{align*}
We define ![]() $\mathrm {GU}(Y)(\mathbb {A})^{+}$ and
$\mathrm {GU}(Y)(\mathbb {A})^{+}$ and ![]() $\mathrm {GU}(Y)(F)^{+}$ in a similar manner. Let
$\mathrm {GU}(Y)(F)^{+}$ in a similar manner. Let ![]() $(\sigma, V_\sigma )$ be an irreducible cuspidal automorphic representation of
$(\sigma, V_\sigma )$ be an irreducible cuspidal automorphic representation of ![]() $\mathrm {GU}(X)(\mathbb {A})^{+}$. Then for
$\mathrm {GU}(X)(\mathbb {A})^{+}$. Then for ![]() $\varphi \in V_\sigma$ and
$\varphi \in V_\sigma$ and ![]() $\phi \in \mathcal {S}(W_{X, Y}^+(\mathbb {A}))$, we define the theta lift of
$\phi \in \mathcal {S}(W_{X, Y}^+(\mathbb {A}))$, we define the theta lift of ![]() $\varphi$ by
$\varphi$ by
where ![]() $g_1 \in \mathrm {GU}(X)(\mathbb {A})^+$ is chosen so that
$g_1 \in \mathrm {GU}(X)(\mathbb {A})^+$ is chosen so that ![]() $\lambda (g) = \lambda (h)$. Further, we define the theta lift of
$\lambda (g) = \lambda (h)$. Further, we define the theta lift of ![]() $\sigma$ by
$\sigma$ by
When the space we consider is clear, we simply write ![]() $\Theta ^{X, Y}_{\psi, \chi }(\sigma ) = \Theta _{\psi, \chi }(\sigma )$. Similarly, for an irreducible cuspidal automorphic representation
$\Theta ^{X, Y}_{\psi, \chi }(\sigma ) = \Theta _{\psi, \chi }(\sigma )$. Similarly, for an irreducible cuspidal automorphic representation ![]() $\tau$ of
$\tau$ of ![]() $\mathrm {U}(Y)(\mathbb {A})$, we define
$\mathrm {U}(Y)(\mathbb {A})$, we define ![]() $\Theta _{\psi, \chi }^{Y, X}(\tau )$ and we simply write it by
$\Theta _{\psi, \chi }^{Y, X}(\tau )$ and we simply write it by ![]() $\Theta _{\psi, \chi }(\tau )$.
$\Theta _{\psi, \chi }(\tau )$.
4. Proof of the Gross–Prasad conjecture for  $(\mathrm {SO}(5),\mathrm {SO}(2))$
$(\mathrm {SO}(5),\mathrm {SO}(2))$
In this section we prove Theorem 1.1, i.e. the Gross–Prasad conjecture for ![]() $(\mathrm {SO}(5),\mathrm {SO}(2))$, based on the pull-back formulas obtained in the previous section.
$(\mathrm {SO}(5),\mathrm {SO}(2))$, based on the pull-back formulas obtained in the previous section.
4.1 Proof of statement (i) in Theorem 1.1
Let ![]() $(\pi, V_\pi )$ be as in Theorem 1.1(i). By the uniqueness of the Bessel model due to Gan, Gross and Prasad [Reference Gan, Gross and PrasadGGP12, Corollary 15.3] at finite places and to Jiang, Sun and Zhu [Reference Jiang, Sun and ZhuJSZ10, Theorem A] at archimedean places, there exists uniquely an irreducible constituent
$(\pi, V_\pi )$ be as in Theorem 1.1(i). By the uniqueness of the Bessel model due to Gan, Gross and Prasad [Reference Gan, Gross and PrasadGGP12, Corollary 15.3] at finite places and to Jiang, Sun and Zhu [Reference Jiang, Sun and ZhuJSZ10, Theorem A] at archimedean places, there exists uniquely an irreducible constituent ![]() $\pi _+^B$ of
$\pi _+^B$ of ![]() $\pi \mid _{G_D(\mathbb {A})^+}$ that has the
$\pi \mid _{G_D(\mathbb {A})^+}$ that has the ![]() $(\xi, \Lambda, \psi )$-Bessel period.
$(\xi, \Lambda, \psi )$-Bessel period.
When ![]() $D$ is split and
$D$ is split and ![]() $\pi _+^B$ is a theta lift from an irreducible cuspidal automorphic representation of
$\pi _+^B$ is a theta lift from an irreducible cuspidal automorphic representation of ![]() $\mathrm {GSO}_{3,1}(\mathbb {A})$, our assertion has been proved by Corbett [Reference CorbettCor17]. Hence in the remainder of this subsection, we assume that:
$\mathrm {GSO}_{3,1}(\mathbb {A})$, our assertion has been proved by Corbett [Reference CorbettCor17]. Hence in the remainder of this subsection, we assume that:
Let us proceed under the assumption (4.1.1). By Propositions 3.1 and 3.2, the theta lift ![]() $\theta _\psi (\pi _+^B)$ of
$\theta _\psi (\pi _+^B)$ of ![]() $\pi _+^B$ to
$\pi _+^B$ to ![]() $\mathrm {GSU}_{3,D}(\mathbb {A})$ has the
$\mathrm {GSU}_{3,D}(\mathbb {A})$ has the ![]() $(X_\xi, \Lambda ^{-1}, \psi )$-Bessel period and, in particular,
$(X_\xi, \Lambda ^{-1}, \psi )$-Bessel period and, in particular, ![]() $\theta _\psi (\pi _+^B) \ne 0$ where we take
$\theta _\psi (\pi _+^B) \ne 0$ where we take ![]() $X_\xi \in D^-(F)$ so that
$X_\xi \in D^-(F)$ so that ![]() $\xi _{X_\xi } = \xi$. For example, when we take
$\xi _{X_\xi } = \xi$. For example, when we take ![]() $\xi =\eta$, we may take
$\xi =\eta$, we may take ![]() $X_\xi =1$.
$X_\xi =1$.
Lemma 4.1 The theta lift ![]() $\theta _\psi (\pi _+^B)$ is an irreducible cuspidal automorphic representation of
$\theta _\psi (\pi _+^B)$ is an irreducible cuspidal automorphic representation of ![]() $\mathrm {GSU}_{3,D}(\mathbb {A})$.
$\mathrm {GSU}_{3,D}(\mathbb {A})$.
Proof. First we note that the irreducibility follows from the cuspidality by Remarks 3.1 and 3.2.
Let us show the cuspidality. Suppose in contrast that ![]() $\theta _\psi (\pi _+^B)$ is not cuspidal.
$\theta _\psi (\pi _+^B)$ is not cuspidal.
When ![]() $D$ is not split, the Rallis tower property implies that the theta lift
$D$ is not split, the Rallis tower property implies that the theta lift ![]() $\theta _{D, \psi }(\pi _+^B)$ of
$\theta _{D, \psi }(\pi _+^B)$ of ![]() $\pi _+^B$ to
$\pi _+^B$ to ![]() $\mathrm {GSU}_{1,D}( \mathbb {A})$ is non-zero and cuspidal. Let
$\mathrm {GSU}_{1,D}( \mathbb {A})$ is non-zero and cuspidal. Let ![]() $w$ be a finite place of
$w$ be a finite place of ![]() $F$ such that
$F$ such that ![]() $D(F_w)$ is split and
$D(F_w)$ is split and ![]() $\pi _{+,w}^B$ is a generic representation of
$\pi _{+,w}^B$ is a generic representation of ![]() $G(F_w)^+$. Since
$G(F_w)^+$. Since ![]() $\pi _{+,w}^B$ is generic, the theta lift of
$\pi _{+,w}^B$ is generic, the theta lift of ![]() $\pi _{+, w}^B$ to
$\pi _{+, w}^B$ to ![]() $\mathrm {GSO}_2(F_w)$ vanishes by the same argument as for [Reference Ginzburg, Rallis and SoudryGRS97, Proposition 2.4]. We note that
$\mathrm {GSO}_2(F_w)$ vanishes by the same argument as for [Reference Ginzburg, Rallis and SoudryGRS97, Proposition 2.4]. We note that ![]() $\mathrm {GSU}_{1,D}( F_w) \simeq \mathrm {GSO}_2(F_w)$ and, hence, the theta lift of
$\mathrm {GSU}_{1,D}( F_w) \simeq \mathrm {GSO}_2(F_w)$ and, hence, the theta lift of ![]() $\pi _+^B$ to
$\pi _+^B$ to ![]() $\mathrm {GSU}_{1,D}( \mathbb {A})$ must vanish. This is a contradiction.
$\mathrm {GSU}_{1,D}( \mathbb {A})$ must vanish. This is a contradiction.
Suppose that ![]() $D$ is split. Then the theta lift of
$D$ is split. Then the theta lift of ![]() $\pi _+^B$ to
$\pi _+^B$ to ![]() $\mathrm {GSO}_{3,1}$ is non-zero by the Rallis tower property. Moreover, it is not cuspidal by our assumption on
$\mathrm {GSO}_{3,1}$ is non-zero by the Rallis tower property. Moreover, it is not cuspidal by our assumption on ![]() $\pi$. Thus, the theta lift of
$\pi$. Thus, the theta lift of ![]() $\pi _+^B$ to
$\pi _+^B$ to ![]() $\mathrm {GSO}_{2,0}$ is non-zero, again by the Rallis tower property. Then we reach a contradiction by the same argument as in the non-split case.
$\mathrm {GSO}_{2,0}$ is non-zero, again by the Rallis tower property. Then we reach a contradiction by the same argument as in the non-split case.
We may regard ![]() $\theta _\psi (\pi _+^B)$ as an irreducible cuspidal automorphic representation of
$\theta _\psi (\pi _+^B)$ as an irreducible cuspidal automorphic representation of ![]() $\mathrm {PGU}_{2,2}$ or
$\mathrm {PGU}_{2,2}$ or ![]() $\mathrm {PGU}_{3,1}$ according to whether
$\mathrm {PGU}_{3,1}$ according to whether ![]() $D$ is split or not, under the isomorphism
$D$ is split or not, under the isomorphism ![]() $\Phi$ in (2.2.6) or
$\Phi$ in (2.2.6) or ![]() $\Phi _D$ in (2.2.5). Recall our assumption that
$\Phi _D$ in (2.2.5). Recall our assumption that ![]() $\theta _{\psi _{w}}(\pi _{+,w}^B)$ is generic at a finite place
$\theta _{\psi _{w}}(\pi _{+,w}^B)$ is generic at a finite place ![]() $w$. Then the non-vanishing of
$w$. Then the non-vanishing of ![]() $(X_\xi, \Lambda ^{-1}, \psi )$-Bessel period on
$(X_\xi, \Lambda ^{-1}, \psi )$-Bessel period on ![]() $\theta _\psi (\pi _+^B)$ implies the non-vanishing of the central value of the standard
$\theta _\psi (\pi _+^B)$ implies the non-vanishing of the central value of the standard ![]() $L$-function for
$L$-function for ![]() $\theta _\psi (\pi _+^B)$ of
$\theta _\psi (\pi _+^B)$ of ![]() $\mathrm {PGU}_4$ twisted by
$\mathrm {PGU}_4$ twisted by ![]() $\Lambda ^{-1}$, namely
$\Lambda ^{-1}$, namely
for any finite set ![]() $S$ of places of
$S$ of places of ![]() $F$ containing all archimedean places because of the unitary group case of the Gan–Gross–Prasad conjecture for
$F$ containing all archimedean places because of the unitary group case of the Gan–Gross–Prasad conjecture for ![]() $\theta _\psi (\pi _+^B)$ proved by Proposition A.2 and Remark A.1 in [Reference Furusawa and MorimotoFM22]. Moreover, from the explicit computation of local theta correspondence in [Reference Gan and TakedaGT11b, Reference MorimotoMor14a], we see that
$\theta _\psi (\pi _+^B)$ proved by Proposition A.2 and Remark A.1 in [Reference Furusawa and MorimotoFM22]. Moreover, from the explicit computation of local theta correspondence in [Reference Gan and TakedaGT11b, Reference MorimotoMor14a], we see that
at a finite place ![]() $v$ where all data are unramified. Thus, when we take
$v$ where all data are unramified. Thus, when we take ![]() $S_0$, a finite set of places of
$S_0$, a finite set of places of ![]() $F$ containing all archimedean places, so that all data are unramified at
$F$ containing all archimedean places, so that all data are unramified at ![]() $v\notin S_0$, we have
$v\notin S_0$, we have
for any finite set ![]() $S$ of places of
$S$ of places of ![]() $F$ with
$F$ with ![]() $S\supset S_0$.
$S\supset S_0$.
Let us show an existence of ![]() $\pi ^\circ$. We denote
$\pi ^\circ$. We denote ![]() $\theta _\psi (\pi _+^B)$ by
$\theta _\psi (\pi _+^B)$ by ![]() $\sigma$. Then the theta lift
$\sigma$. Then the theta lift ![]() $\Sigma : = \Theta _{\psi, (\Lambda ^{-1}, \Lambda ^{-1})}(\sigma )$ of
$\Sigma : = \Theta _{\psi, (\Lambda ^{-1}, \Lambda ^{-1})}(\sigma )$ of ![]() $\sigma$ to
$\sigma$ to ![]() $\mathrm {GU}_{2,2}$ which we may regard as an automorphic representation of
$\mathrm {GU}_{2,2}$ which we may regard as an automorphic representation of ![]() $\mathrm {GSO}_{4,2}$ by the accidental isomorphism (2.2.6), is an irreducible cuspidal globally generic automorphic representation with trivial central character by the proof of [Reference Furusawa and MorimotoFM22, Proposition A.2] since
$\mathrm {GSO}_{4,2}$ by the accidental isomorphism (2.2.6), is an irreducible cuspidal globally generic automorphic representation with trivial central character by the proof of [Reference Furusawa and MorimotoFM22, Proposition A.2] since ![]() $\theta _\psi (\pi _+^B)$ has the
$\theta _\psi (\pi _+^B)$ has the ![]() $(X_\xi, \Lambda ^{-1}, \psi )$-Bessel period.
$(X_\xi, \Lambda ^{-1}, \psi )$-Bessel period.
Here we recall that, by the conservation relation due to Sun and Zhu [Reference Sun and ZhuSZ15, Theorems 1.10, 7.6], for any irreducible admissible representations ![]() $\tau$ of
$\tau$ of ![]() $\mathrm {GO}_{4,2}(k)$ (respectively,
$\mathrm {GO}_{4,2}(k)$ (respectively, ![]() $\mathrm {GO}_{3,3}(k)$) over a local field
$\mathrm {GO}_{3,3}(k)$) over a local field ![]() $k$ of characteristic zero, theta lifts of either
$k$ of characteristic zero, theta lifts of either ![]() $\tau$ or
$\tau$ or ![]() $\tau \otimes \det$ to
$\tau \otimes \det$ to ![]() $\mathrm {GSp}_3(k)^+$ (respectively,
$\mathrm {GSp}_3(k)^+$ (respectively, ![]() $\mathrm {GSp}_3(k)$) is non-zero. Thus, we may extend
$\mathrm {GSp}_3(k)$) is non-zero. Thus, we may extend ![]() $\Sigma$ to an automorphic representation of
$\Sigma$ to an automorphic representation of ![]() $\mathrm {GO}_{4,2}(\mathbb {A})$ as in Harris, Soudry and Taylor [Reference Harris, Soudry and TaylorHST93, Proposition 2] so that its local theta lift to
$\mathrm {GO}_{4,2}(\mathbb {A})$ as in Harris, Soudry and Taylor [Reference Harris, Soudry and TaylorHST93, Proposition 2] so that its local theta lift to ![]() $\mathrm {GSp}_3(F_v)^+$ is non-zero at every place
$\mathrm {GSp}_3(F_v)^+$ is non-zero at every place ![]() $v$.
$v$.
On the other hand, since ![]() $\Sigma$ is nearly equivalent to
$\Sigma$ is nearly equivalent to ![]() $\sigma$, we have
$\sigma$, we have
for a sufficiently large finite set ![]() $S$ of places of
$S$ of places of ![]() $F$ containing all archimedean places by the explicit computation of local theta correspondences in [Reference Gan and TakedaGT11b, Reference MorimotoMor14a]. Here
$F$ containing all archimedean places by the explicit computation of local theta correspondences in [Reference Gan and TakedaGT11b, Reference MorimotoMor14a]. Here
by Yamana [Reference YamanaYam14, Proof of Theorems 10.2, 10.3], since the theta lift ![]() $\theta _\psi (\pi _+^B)$ of
$\theta _\psi (\pi _+^B)$ of ![]() $\pi _+^B$ to
$\pi _+^B$ to ![]() $\mathrm {GSU}_{3,D}( \mathbb {A})$ is non-zero and cuspidal. Hence, the left-hand side of (4.1.2) has a pole at
$\mathrm {GSU}_{3,D}( \mathbb {A})$ is non-zero and cuspidal. Hence, the left-hand side of (4.1.2) has a pole at ![]() $s=1$. In particular, it is non-zero and the theta lift of
$s=1$. In particular, it is non-zero and the theta lift of ![]() $\Sigma$ to
$\Sigma$ to ![]() $\mathrm {GSp}_3(\mathbb {A})^+$ is non-zero by Takeda [Reference TakedaTak11, Theorem 1.1 (1)]. Further, again by Takeda [Reference TakedaTak11, Theorem 1.1 (1)], this theta lift actually descends to
$\mathrm {GSp}_3(\mathbb {A})^+$ is non-zero by Takeda [Reference TakedaTak11, Theorem 1.1 (1)]. Further, again by Takeda [Reference TakedaTak11, Theorem 1.1 (1)], this theta lift actually descends to ![]() $\mathrm {GSp}_2(\mathbb {A})^+ =G(\mathbb {A})^+$. Namely, the theta lift
$\mathrm {GSp}_2(\mathbb {A})^+ =G(\mathbb {A})^+$. Namely, the theta lift ![]() $\pi ^\prime _+ := \theta _{\psi ^{-1}}(\Sigma )$ of
$\pi ^\prime _+ := \theta _{\psi ^{-1}}(\Sigma )$ of ![]() $\Sigma$ to
$\Sigma$ to ![]() $G(\mathbb {A})^+$ is non-zero since
$G(\mathbb {A})^+$ is non-zero since ![]() $L^S(s, \Sigma, \mathrm {std})$ actually has a pole at
$L^S(s, \Sigma, \mathrm {std})$ actually has a pole at ![]() $s=1$.
$s=1$.
Suppose that ![]() $\pi ^\prime _+$ is not cuspidal. Then by the Rallis tower property, the theta lift of
$\pi ^\prime _+$ is not cuspidal. Then by the Rallis tower property, the theta lift of ![]() $\Sigma$ to
$\Sigma$ to ![]() $\mathrm {GL}_2(\mathbb {A})^+$ is non-zero and cuspidal. Meanwhile, the local theta lift of
$\mathrm {GL}_2(\mathbb {A})^+$ is non-zero and cuspidal. Meanwhile, the local theta lift of ![]() $\Sigma _v$ to
$\Sigma _v$ to ![]() $\mathrm {GL}_2(F_v)^+$ vanishes by a computation similar to that for [Reference Ginzburg, Rallis and SoudryGRS97, Proposition 3.3] since
$\mathrm {GL}_2(F_v)^+$ vanishes by a computation similar to that for [Reference Ginzburg, Rallis and SoudryGRS97, Proposition 3.3] since ![]() $\Sigma _v$ is generic. This is a contradiction and, hence,
$\Sigma _v$ is generic. This is a contradiction and, hence, ![]() $\pi ^\prime _+$ is cuspidal.
$\pi ^\prime _+$ is cuspidal.
Since ![]() $\Sigma$ is generic, so is
$\Sigma$ is generic, so is ![]() $\pi ^\prime _+$ by [Reference MorimotoMor14a, Proposition 3.3]. Let us take an extension
$\pi ^\prime _+$ by [Reference MorimotoMor14a, Proposition 3.3]. Let us take an extension ![]() $\pi ^\circ$ of
$\pi ^\circ$ of ![]() $\pi _+^\prime$ to
$\pi _+^\prime$ to ![]() $G(\mathbb {A})$. Since
$G(\mathbb {A})$. Since ![]() $|G(F_v) / G(F_v)^+|=2$, we have
$|G(F_v) / G(F_v)^+|=2$, we have ![]() $\pi ^\prime _{v} \simeq \pi _v$ or
$\pi ^\prime _{v} \simeq \pi _v$ or ![]() $\pi ^\prime _{v} \simeq \pi _v \otimes \chi _{E_v}$ at almost all places
$\pi ^\prime _{v} \simeq \pi _v \otimes \chi _{E_v}$ at almost all places ![]() $v$ such that
$v$ such that ![]() $\pi _{+,v}^\prime \simeq \pi _{+, v}^B$. Hence,
$\pi _{+,v}^\prime \simeq \pi _{+, v}^B$. Hence, ![]() $\pi$ is locally
$\pi$ is locally ![]() $G^+$-nearly equivalent to
$G^+$-nearly equivalent to ![]() $\pi ^\circ$.
$\pi ^\circ$.
4.2 Some consequences of the proof of Theorem 1.1(i)
As preliminaries for our further considerations, we would like to discuss some consequence of the proof of Theorem 1.1(i) and related results.
First we note the following result concerning the functorial transfer.
Proposition 4.1 Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character. Assume that there exists a finite place
$G_D(\mathbb {A})$ with a trivial central character. Assume that there exists a finite place ![]() $w$ at which
$w$ at which ![]() $\pi _w$ is generic and tempered.
$\pi _w$ is generic and tempered.
Then there exists a globally generic irreducible cuspidal automorphic representation ![]() $\pi ^\circ$ of
$\pi ^\circ$ of ![]() $G(\mathbb {A})$ and an étale quadratic extension
$G(\mathbb {A})$ and an étale quadratic extension ![]() $E^\circ$ of
$E^\circ$ of ![]() $F$ such that
$F$ such that ![]() $\pi ^\circ$ is
$\pi ^\circ$ is ![]() $G^{+, E^\circ }$-nearly equivalent to
$G^{+, E^\circ }$-nearly equivalent to ![]() $\pi$. In particular, we have a weak functorial lift of
$\pi$. In particular, we have a weak functorial lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GL}_4(\mathbb {A}_{E^\circ })$ with respect to
$\mathrm {GL}_4(\mathbb {A}_{E^\circ })$ with respect to ![]() $\mathrm {BC} \circ \mathrm {spin}$.
$\mathrm {BC} \circ \mathrm {spin}$.
Moreover, ![]() $\pi$ is tempered if and only if
$\pi$ is tempered if and only if ![]() $\pi ^\circ$ is tempered.
$\pi ^\circ$ is tempered.
Remark 4.1 When ![]() $D$ is split, our assumption implies that
$D$ is split, our assumption implies that ![]() $\pi$ has a generic Arthur parameter. Though our assertion thus follows from the global descent method by Ginzburg, Rallis and Soudry [Reference Ginzburg, Rallis and SoudryGRS11] and Arthur [Reference ArthurArt13], we shall present another proof which does not refer to these papers.
$\pi$ has a generic Arthur parameter. Though our assertion thus follows from the global descent method by Ginzburg, Rallis and Soudry [Reference Ginzburg, Rallis and SoudryGRS11] and Arthur [Reference ArthurArt13], we shall present another proof which does not refer to these papers.
Proof. Suppose that ![]() $D$ is split. When
$D$ is split. When ![]() $\pi$ participates in the theta correspondence with
$\pi$ participates in the theta correspondence with ![]() $\mathrm {GSO}_{3,1}$, our assertion follows from [Reference RobertsRob01]. Thus, we now assume that the theta lift of
$\mathrm {GSO}_{3,1}$, our assertion follows from [Reference RobertsRob01]. Thus, we now assume that the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{3,1}$ is zero. By [Reference LiLi92],
$\mathrm {GSO}_{3,1}$ is zero. By [Reference LiLi92], ![]() $\pi$ has
$\pi$ has ![]() $(S_\circ, \Lambda _\circ, \psi )$-Bessel period for some
$(S_\circ, \Lambda _\circ, \psi )$-Bessel period for some ![]() $S_\circ$ and
$S_\circ$ and ![]() $\Lambda _\circ$. When
$\Lambda _\circ$. When ![]() $\mathrm {GSO}(S_\circ )$ is not split, the existence of a globally generic irreducible cuspidal automorphic representation follows from Theorem 1.1(i). Suppose that
$\mathrm {GSO}(S_\circ )$ is not split, the existence of a globally generic irreducible cuspidal automorphic representation follows from Theorem 1.1(i). Suppose that ![]() $\mathrm {GSO}(S_\circ )$ is split. Then by Proposition 3.1, the theta lift of
$\mathrm {GSO}(S_\circ )$ is split. Then by Proposition 3.1, the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{3,3}$ is non-zero. Since
$\mathrm {GSO}_{3,3}$ is non-zero. Since ![]() $\pi _w$ is generic, the local theta lift of
$\pi _w$ is generic, the local theta lift of ![]() $\pi _w$ to
$\pi _w$ to ![]() $\mathrm {GSO}_{1,1}$ is zero as in the proof of Theorem 1.1(i) and, hence, the theta lift of
$\mathrm {GSO}_{1,1}$ is zero as in the proof of Theorem 1.1(i) and, hence, the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{1,1}$ is zero. Hence, by the Rallis tower property, either the theta lift of
$\mathrm {GSO}_{1,1}$ is zero. Hence, by the Rallis tower property, either the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{2,2}$ or to
$\mathrm {GSO}_{2,2}$ or to ![]() $\mathrm {GSO}_{3,3}$ is non-zero and cuspidal. Then
$\mathrm {GSO}_{3,3}$ is non-zero and cuspidal. Then ![]() $\pi$ itself is globally generic by Proposition A.1 in the former case. In the latter case, the global genericity of
$\pi$ itself is globally generic by Proposition A.1 in the former case. In the latter case, the global genericity of ![]() $\pi$ readily follows from the proof of Soudry [Reference SoudrySou87, Proposition 1.1] (see also Theorem on p. 264 of [Reference SoudrySou87]).
$\pi$ readily follows from the proof of Soudry [Reference SoudrySou87, Proposition 1.1] (see also Theorem on p. 264 of [Reference SoudrySou87]).
In any case when ![]() $D$ is split, we have a globally generic irreducible cuspidal automorphic representation
$D$ is split, we have a globally generic irreducible cuspidal automorphic representation ![]() $\pi ^\circ$ of
$\pi ^\circ$ of ![]() $G(\mathbb {A})$ which is nearly equivalent to
$G(\mathbb {A})$ which is nearly equivalent to ![]() $\pi$. Thus, when we take the strong lift of
$\pi$. Thus, when we take the strong lift of ![]() $\pi ^\circ$ to
$\pi ^\circ$ to ![]() $\mathrm {GL}_4(\mathbb {A})$ by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04], it is a weak lift of
$\mathrm {GL}_4(\mathbb {A})$ by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04], it is a weak lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GL}_4(\mathbb {A})$.
$\mathrm {GL}_4(\mathbb {A})$.
Suppose that ![]() $D$ is not split. Then by Li [Reference LiLi92], there exist an
$D$ is not split. Then by Li [Reference LiLi92], there exist an ![]() $\eta _\circ \in D^-(F)$ where
$\eta _\circ \in D^-(F)$ where ![]() $E_\circ :=F(\eta _\circ )$ is a quadratic extension of
$E_\circ :=F(\eta _\circ )$ is a quadratic extension of ![]() $F$, and a character
$F$, and a character ![]() $\Lambda _\circ$ of
$\Lambda _\circ$ of ![]() $\mathbb {A}_{E_\circ }^\times / E_\circ ^\times \mathbb {A}^\times$ such that
$\mathbb {A}_{E_\circ }^\times / E_\circ ^\times \mathbb {A}^\times$ such that ![]() $\pi$ has the
$\pi$ has the ![]() $(\eta _\circ, \Lambda _\circ )$-Bessel period. Then there exists a desired automorphic representation
$(\eta _\circ, \Lambda _\circ )$-Bessel period. Then there exists a desired automorphic representation ![]() $\pi ^\circ$ of
$\pi ^\circ$ of ![]() $G(\mathbb {A})$ by Theorem 1.1(i).
$G(\mathbb {A})$ by Theorem 1.1(i).
Let us discuss the temperedness. Denote ![]() $\sigma$,
$\sigma$, ![]() $\Sigma$ and
$\Sigma$ and ![]() $\pi _+^\prime$ as in the proof of Theorem 1.1(i). Suppose that
$\pi _+^\prime$ as in the proof of Theorem 1.1(i). Suppose that ![]() $\pi$ is tempered. Then the temperedness of
$\pi$ is tempered. Then the temperedness of ![]() $\sigma$ follows from a similar argument as in Atobe and Gan [Reference Atobe and GanAG17, Proposition 5.5] (see also [Reference Gan and IchinoGI14, Proposition C.1]) at finite places, from Paul [Reference PaulPau98, Theorems 15, 30], [Reference PaulPau05, Theorems 15, 18, Corollary 24] and Li, Paul, Tan and Zhu [Reference Li, Paul, Tan and ZhuLPTZ03, Theorems 4.20, 5.1] at real places and from Adams and Barbasch [Reference Adams and BarbaschAB95, Theorem 2.7] at complex places. Then the temperedness of
$\sigma$ follows from a similar argument as in Atobe and Gan [Reference Atobe and GanAG17, Proposition 5.5] (see also [Reference Gan and IchinoGI14, Proposition C.1]) at finite places, from Paul [Reference PaulPau98, Theorems 15, 30], [Reference PaulPau05, Theorems 15, 18, Corollary 24] and Li, Paul, Tan and Zhu [Reference Li, Paul, Tan and ZhuLPTZ03, Theorems 4.20, 5.1] at real places and from Adams and Barbasch [Reference Adams and BarbaschAB95, Theorem 2.7] at complex places. Then the temperedness of ![]() $\sigma$ implies that of
$\sigma$ implies that of ![]() $\Sigma$ by Atobe and Gan [Reference Atobe and GanAG17, Proposition 5.5] at finite places, by Paul [Reference PaulPau00, Theorem 3.4] at non-split real places, by Mœglin [Reference MœglinMœg89, Proposition III.9] at split real places and by Adams and Barbasch [Reference Adams and BarbaschAB95, Theorem 2.6] at complex places. As we obtained the temperedness of
$\Sigma$ by Atobe and Gan [Reference Atobe and GanAG17, Proposition 5.5] at finite places, by Paul [Reference PaulPau00, Theorem 3.4] at non-split real places, by Mœglin [Reference MœglinMœg89, Proposition III.9] at split real places and by Adams and Barbasch [Reference Adams and BarbaschAB95, Theorem 2.6] at complex places. As we obtained the temperedness of ![]() $\sigma$ from that of
$\sigma$ from that of ![]() $\pi$, the temperedness of
$\pi$, the temperedness of ![]() $\Sigma$ implies that of
$\Sigma$ implies that of ![]() $\pi ^\prime _+$ and, hence,
$\pi ^\prime _+$ and, hence, ![]() $\pi ^\circ$ is tempered. The opposite direction, i.e. the temperedness of
$\pi ^\circ$ is tempered. The opposite direction, i.e. the temperedness of ![]() $\pi ^\circ$ implies that of
$\pi ^\circ$ implies that of ![]() $\pi$, follows by the same argument.
$\pi$, follows by the same argument.
Lemma 4.2 Let ![]() $\pi$ be as in Theorem 1.1(i). Suppose that
$\pi$ be as in Theorem 1.1(i). Suppose that ![]() $\sigma =\theta _\psi (\pi _+^B)$ is an irreducible cuspidal automorphic representation of
$\sigma =\theta _\psi (\pi _+^B)$ is an irreducible cuspidal automorphic representation of ![]() $\mathrm {GSU}_{3,D} (\mathbb {A})$. Here
$\mathrm {GSU}_{3,D} (\mathbb {A})$. Here ![]() $\pi _+^B$ denotes the unique irreducible constituent of
$\pi _+^B$ denotes the unique irreducible constituent of ![]() $\pi |_{G_D(\mathbb {A})^+}$ such that
$\pi |_{G_D(\mathbb {A})^+}$ such that ![]() $\pi _+^B$ has the
$\pi _+^B$ has the ![]() $(E, \Lambda )$-Bessel period. We regard
$(E, \Lambda )$-Bessel period. We regard ![]() $\sigma$ as an automorphic representation of
$\sigma$ as an automorphic representation of ![]() $\mathrm {GU}_{4,\varepsilon }(\mathbb {A})$ via (2.2.5) or (2.2.6) and let
$\mathrm {GU}_{4,\varepsilon }(\mathbb {A})$ via (2.2.5) or (2.2.6) and let ![]() $\Pi _\sigma$ denote the base change lift of
$\Pi _\sigma$ denote the base change lift of ![]() $\sigma |_{\mathrm {U}_{4,\varepsilon }(\mathbb {A})}$ to
$\sigma |_{\mathrm {U}_{4,\varepsilon }(\mathbb {A})}$ to ![]() $\mathrm {GL}_4(\mathbb {A}_E)$. Let
$\mathrm {GL}_4(\mathbb {A}_E)$. Let ![]() $\pi ^\circ$ be a globally generic irreducible cuspidal automorphic representation of
$\pi ^\circ$ be a globally generic irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A})$ whose existence is proved in Theorem 1.1(i). We denote the functorial lift of
$G(\mathbb {A})$ whose existence is proved in Theorem 1.1(i). We denote the functorial lift of ![]() $\pi ^\circ$ to
$\pi ^\circ$ to ![]() $\mathrm {GL}_4(\mathbb {A})$ by
$\mathrm {GL}_4(\mathbb {A})$ by ![]() $\Pi _{\pi ^\circ }$.
$\Pi _{\pi ^\circ }$.
Suppose that
where ![]() $\Pi _i$ are irreducible cuspidal automorphic representations of
$\Pi _i$ are irreducible cuspidal automorphic representations of ![]() $\mathrm {GL}_{n_i}(\mathbb {A})$ and
$\mathrm {GL}_{n_i}(\mathbb {A})$ and
where ![]() $\Pi _j^\prime$ are irreducible cuspidal automorphic representations of
$\Pi _j^\prime$ are irreducible cuspidal automorphic representations of ![]() $\mathrm {GL}_{m_j}(\mathbb {A}_E)$.
$\mathrm {GL}_{m_j}(\mathbb {A}_E)$.
Then we have ![]() $\Pi _\sigma =\mathrm {BC}(\Pi _{\pi ^\circ })$,
$\Pi _\sigma =\mathrm {BC}(\Pi _{\pi ^\circ })$, ![]() $\Pi _{\pi ^\circ }\not \simeq \Pi _{\pi ^\circ }\otimes \chi _E$ and
$\Pi _{\pi ^\circ }\not \simeq \Pi _{\pi ^\circ }\otimes \chi _E$ and ![]() $\mathrm {BC}(\Pi _i)$ is cuspidal for each
$\mathrm {BC}(\Pi _i)$ is cuspidal for each ![]() $i$. In particular, we have
$i$. In particular, we have ![]() $\ell =k$. Here
$\ell =k$. Here ![]() $\mathrm {BC}$ denotes the base change from
$\mathrm {BC}$ denotes the base change from ![]() $F$ to
$F$ to ![]() $E$.
$E$.
Proof. By the explicit computation of local theta correspondences in [Reference Gan and TakedaGT11b, Reference MorimotoMor14a], we see that ![]() $(\Pi _{\sigma })_v\simeq \mathrm {BC}(\Pi _{\pi ^\circ } )_v$ at almost all finite places
$(\Pi _{\sigma })_v\simeq \mathrm {BC}(\Pi _{\pi ^\circ } )_v$ at almost all finite places ![]() $v$ of
$v$ of ![]() $E$. Thus,
$E$. Thus, ![]() $\Pi _{\sigma }= \mathrm {BC}(\Pi _{\pi ^\circ } )$ by the strong multiplicity one theorem. In addition, by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04], we know that
$\Pi _{\sigma }= \mathrm {BC}(\Pi _{\pi ^\circ } )$ by the strong multiplicity one theorem. In addition, by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04], we know that ![]() $\ell = 1$ or
$\ell = 1$ or ![]() $2$.
$2$.
Suppose that ![]() $\ell =1$. We note that the cuspidality of
$\ell =1$. We note that the cuspidality of ![]() $\mathrm {BC}(\Pi _{\pi ^\circ })$ is equivalent to
$\mathrm {BC}(\Pi _{\pi ^\circ })$ is equivalent to ![]() $\Pi _{\pi ^\circ } \otimes \chi _E \not \simeq \Pi _{\pi ^\circ }$. Suppose otherwise, i.e.
$\Pi _{\pi ^\circ } \otimes \chi _E \not \simeq \Pi _{\pi ^\circ }$. Suppose otherwise, i.e. ![]() $\Pi _{\pi ^\circ } \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Then
$\Pi _{\pi ^\circ } \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Then ![]() $\Pi _{\pi ^\circ } = \mathcal {AI}(\tau )$ for some irreducible cuspidal automorphic representation
$\Pi _{\pi ^\circ } = \mathcal {AI}(\tau )$ for some irreducible cuspidal automorphic representation ![]() $\tau$ of
$\tau$ of ![]() $\mathrm {GL}_2(\mathbb {A}_E)$. Since
$\mathrm {GL}_2(\mathbb {A}_E)$. Since ![]() $\Pi _{\pi ^\circ }$ is a lift from
$\Pi _{\pi ^\circ }$ is a lift from ![]() $\mathrm {PGSp}_2$, the central character of
$\mathrm {PGSp}_2$, the central character of ![]() $\tau$ needs to be trivial and, hence,
$\tau$ needs to be trivial and, hence, ![]() $\tau \simeq \tau ^\vee$. On the other hand, we have
$\tau \simeq \tau ^\vee$. On the other hand, we have
Since this is a base change lift of ![]() $\sigma |_{\mathrm {U}_{4,\varepsilon }(\mathbb {A})}$, we have
$\sigma |_{\mathrm {U}_{4,\varepsilon }(\mathbb {A})}$, we have ![]() $\tau = (\tau ^\sigma )^\vee$ and
$\tau = (\tau ^\sigma )^\vee$ and ![]() $\tau \not \simeq \tau ^\sigma$ by [Reference Arthur and ClozelAC89] (see also [Reference Prasad and RamakrishnanPR99, Proposition 3.1]). In particular,
$\tau \not \simeq \tau ^\sigma$ by [Reference Arthur and ClozelAC89] (see also [Reference Prasad and RamakrishnanPR99, Proposition 3.1]). In particular, ![]() $\tau \not \simeq \tau ^\vee$ and we have a contradiction. Thus,
$\tau \not \simeq \tau ^\vee$ and we have a contradiction. Thus, ![]() $\mathrm {BC}(\Pi _{\pi ^\circ })$ is cuspidal and
$\mathrm {BC}(\Pi _{\pi ^\circ })$ is cuspidal and ![]() $k=1$.
$k=1$.
Suppose that ![]() $\ell =2$. First we show that
$\ell =2$. First we show that ![]() $\Pi _{\pi ^\circ } \not \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Suppose otherwise, i.e.
$\Pi _{\pi ^\circ } \not \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Suppose otherwise, i.e. ![]() $\Pi _{\pi ^\circ } \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Then either
$\Pi _{\pi ^\circ } \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Then either ![]() $\Pi _i \simeq \Pi _i \otimes \chi _E$ for
$\Pi _i \simeq \Pi _i \otimes \chi _E$ for ![]() $i=1,2$ or
$i=1,2$ or ![]() $\Pi _2 \simeq \Pi _1 \otimes \chi _E$. In the former case, we have
$\Pi _2 \simeq \Pi _1 \otimes \chi _E$. In the former case, we have ![]() $\Pi _i=\mathcal {AI}(\chi _i)$ with a character
$\Pi _i=\mathcal {AI}(\chi _i)$ with a character ![]() $\chi _i$ of
$\chi _i$ of ![]() $\mathbb {A}_E^\times / E^\times$ for
$\mathbb {A}_E^\times / E^\times$ for ![]() $i=1,2$. Then we have
$i=1,2$. Then we have ![]() $\Pi _{\pi ^\circ }=\mathcal {AI}(\chi _1)\boxplus \mathcal {AI}(\chi _2)$ and
$\Pi _{\pi ^\circ }=\mathcal {AI}(\chi _1)\boxplus \mathcal {AI}(\chi _2)$ and ![]() $\Pi _\sigma =\chi _1 \boxplus \chi _1^\sigma \boxplus \chi _2 \boxplus \chi _2^\sigma$. Since
$\Pi _\sigma =\chi _1 \boxplus \chi _1^\sigma \boxplus \chi _2 \boxplus \chi _2^\sigma$. Since ![]() $\Pi _{\pi ^\circ }$ is a lift from
$\Pi _{\pi ^\circ }$ is a lift from ![]() $\mathrm {PGSp}_2$, the central character of
$\mathrm {PGSp}_2$, the central character of ![]() $\mathcal {AI}(\chi _i)$ is trivial and, hence,
$\mathcal {AI}(\chi _i)$ is trivial and, hence, ![]() $\chi _i\mid _{\mathbb {A}^\times }=\chi _E$. On the other hand, since
$\chi _i\mid _{\mathbb {A}^\times }=\chi _E$. On the other hand, since ![]() $\Pi _\sigma$ is a base change lift of
$\Pi _\sigma$ is a base change lift of ![]() $\sigma |_{\mathrm {U}_{4,\varepsilon }(\mathbb {A})}$, we see that
$\sigma |_{\mathrm {U}_{4,\varepsilon }(\mathbb {A})}$, we see that ![]() $\chi _i\mid _{\mathbb {A}^\times }$ is trivial. This is a contradiction. In the latter case, we have
$\chi _i\mid _{\mathbb {A}^\times }$ is trivial. This is a contradiction. In the latter case, we have ![]() $\mathrm {BC}(\Pi _2)=\mathrm {BC}(\Pi _1 \otimes \chi _E) =\mathrm {BC}(\Pi _1)$ and, hence,
$\mathrm {BC}(\Pi _2)=\mathrm {BC}(\Pi _1 \otimes \chi _E) =\mathrm {BC}(\Pi _1)$ and, hence, ![]() $\Pi _\sigma =\mathrm {BC}(\Pi _1)\boxplus \mathrm {BC}(\Pi _1)$. This implies that
$\Pi _\sigma =\mathrm {BC}(\Pi _1)\boxplus \mathrm {BC}(\Pi _1)$. This implies that ![]() $\Pi _\sigma$ is not in the image of the base change lift from the unitary group and again we have a contradiction. Thus, we have
$\Pi _\sigma$ is not in the image of the base change lift from the unitary group and again we have a contradiction. Thus, we have ![]() $\Pi _{\pi ^\circ } \not \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Then
$\Pi _{\pi ^\circ } \not \simeq \Pi _{\pi ^\circ } \otimes \chi _E$. Then ![]() $\Pi _i \not \simeq \Pi _i \otimes \chi _E$ at least one of
$\Pi _i \not \simeq \Pi _i \otimes \chi _E$ at least one of ![]() $i=1,2$. Suppose that this is so only for one of the two, say
$i=1,2$. Suppose that this is so only for one of the two, say ![]() $i=2$. Then
$i=2$. Then ![]() $\Pi _1=\mathcal {AI}(\chi )$ for some character
$\Pi _1=\mathcal {AI}(\chi )$ for some character ![]() $\chi$ of
$\chi$ of ![]() $\mathbb {A}_E^\times / E^\times$ and
$\mathbb {A}_E^\times / E^\times$ and ![]() $\mathrm {BC}(\Pi _2)$ is cuspidal. We have
$\mathrm {BC}(\Pi _2)$ is cuspidal. We have ![]() $\Pi _{\pi ^\circ }=\mathcal {AI}(\chi )\boxplus \Pi _2$ and
$\Pi _{\pi ^\circ }=\mathcal {AI}(\chi )\boxplus \Pi _2$ and ![]() $\Pi _\sigma =\chi \boxplus \chi ^\sigma \boxplus \mathrm {BC}(\Pi _2)$. Then
$\Pi _\sigma =\chi \boxplus \chi ^\sigma \boxplus \mathrm {BC}(\Pi _2)$. Then ![]() $\chi \mid _{\mathbb {A}^\times }$ is trivial from the former equality and
$\chi \mid _{\mathbb {A}^\times }$ is trivial from the former equality and ![]() $\chi \mid _{\mathbb {A}^\times }=\chi _E$ from the latter equality as above. Hence, we have a contradiction. Thus,
$\chi \mid _{\mathbb {A}^\times }=\chi _E$ from the latter equality as above. Hence, we have a contradiction. Thus, ![]() $\mathrm {BC}(\Pi _i)$ for
$\mathrm {BC}(\Pi _i)$ for ![]() $i=1,2$ are both cuspidal,
$i=1,2$ are both cuspidal, ![]() $\Pi _\sigma =\mathrm {BC}(\Pi _1)\boxplus \mathrm {BC}(\Pi _2)$ and
$\Pi _\sigma =\mathrm {BC}(\Pi _1)\boxplus \mathrm {BC}(\Pi _2)$ and ![]() $k=2$.
$k=2$.
The following lemma gives the uniqueness of the constant ![]() $\ell (\pi )$ defined before Theorem 1.2.
$\ell (\pi )$ defined before Theorem 1.2.
Lemma 4.3 Let ![]() $\pi$ be as in Theorem 1.1(i). For
$\pi$ be as in Theorem 1.1(i). For ![]() $i=1,2$, let
$i=1,2$, let ![]() $E_i$ be a quadratic extension of
$E_i$ be a quadratic extension of ![]() $F$ and
$F$ and ![]() $\pi ^\circ _i$ an irreducible cuspidal automorphic representation of
$\pi ^\circ _i$ an irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A})$ which is
$G(\mathbb {A})$ which is ![]() $G^{+,E_i}$-locally near equivalent to
$G^{+,E_i}$-locally near equivalent to ![]() $\pi$. Let
$\pi$. Let ![]() $\Pi _{\pi ^\circ _i}$ be the functorial lift of
$\Pi _{\pi ^\circ _i}$ be the functorial lift of ![]() $\pi _i^\circ$ to
$\pi _i^\circ$ to ![]() $\mathrm {GL}_4(\mathbb {A})$ and consider the decomposition
$\mathrm {GL}_4(\mathbb {A})$ and consider the decomposition
as (4.2.1). Then we have ![]() $\ell _1=\ell _2$.
$\ell _1=\ell _2$.
Proof. Since the case when ![]() $E_1=E_2$ is trivial, suppose that
$E_1=E_2$ is trivial, suppose that ![]() $E_1\ne E_2$. Let
$E_1\ne E_2$. Let ![]() $K=E_1E_2$. From the definition of the base change, we have
$K=E_1E_2$. From the definition of the base change, we have
Hence,
where ![]() $\chi _{K/ E_1}$ denotes the character of
$\chi _{K/ E_1}$ denotes the character of ![]() $\mathbb {A}_E^\times$ corresponding to
$\mathbb {A}_E^\times$ corresponding to ![]() $K / E_1$. In the former case, we have
$K / E_1$. In the former case, we have
and our claim follows. In the latter case, since ![]() $\chi _{K/ E_1} = \chi _{E_2} \circ N_{E_1 / F}$, we have
$\chi _{K/ E_1} = \chi _{E_2} \circ N_{E_1 / F}$, we have
and our claim follows.
Definition 4.1 Let ![]() $\pi$ be as in Theorem 1.1(i). Then we say that
$\pi$ be as in Theorem 1.1(i). Then we say that ![]() $\pi$ is of type I if
$\pi$ is of type I if ![]() $\pi$ and
$\pi$ and ![]() $\pi \otimes \chi _E$ are nearly equivalent. Moreover, we say that
$\pi \otimes \chi _E$ are nearly equivalent. Moreover, we say that ![]() $\pi$ is of type I-A if
$\pi$ is of type I-A if ![]() $\pi$ participates in the theta correspondence with
$\pi$ participates in the theta correspondence with ![]() $\mathrm {GSO}(S_1) =\mathrm {GSO}_{3,1}$ and that
$\mathrm {GSO}(S_1) =\mathrm {GSO}_{3,1}$ and that ![]() $\pi$ is of type I-B if
$\pi$ is of type I-B if ![]() $\pi$ participates in the theta correspondence with
$\pi$ participates in the theta correspondence with ![]() $\mathrm {GSO}(X_\circ )$ for some four-dimensional anisotropic orthogonal space
$\mathrm {GSO}(X_\circ )$ for some four-dimensional anisotropic orthogonal space ![]() $X_\circ$ over
$X_\circ$ over ![]() $F$ with discriminant algebra
$F$ with discriminant algebra ![]() $E$.
$E$.
Remark 4.2 From the proof of Theorem 1.1(i), if ![]() $\pi$ is not of type I-A, then the theta lift of
$\pi$ is not of type I-A, then the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSU}_{3,D}$ is cuspidal. Further, we note that
$\mathrm {GSU}_{3,D}$ is cuspidal. Further, we note that ![]() $D$ is necessarily split when
$D$ is necessarily split when ![]() $\pi$ is of type I-A or I-B, by definition.
$\pi$ is of type I-A or I-B, by definition.
In order to study an explicit formula using theta lifts from ![]() $G_D(\mathbb {A})$, the following lemma will be important later.
$G_D(\mathbb {A})$, the following lemma will be important later.
Lemma 4.4 Let ![]() $\pi$ be as in Theorem 1.1(i). Then
$\pi$ be as in Theorem 1.1(i). Then ![]() $\pi$ is either type I-A or I-B if and only if
$\pi$ is either type I-A or I-B if and only if ![]() $\pi$ is nearly equivalent to
$\pi$ is nearly equivalent to ![]() $\pi \otimes \chi _E$. In particular, when
$\pi \otimes \chi _E$. In particular, when ![]() $\pi$ is neither of type I-A nor I-B,
$\pi$ is neither of type I-A nor I-B, ![]() $\pi |_{\mathcal {G}_D}$ is irreducible where
$\pi |_{\mathcal {G}_D}$ is irreducible where
Proof. Suppose that ![]() $\pi$ is nearly equivalent to
$\pi$ is nearly equivalent to ![]() $\pi \otimes \chi _E$. Then at almost all places
$\pi \otimes \chi _E$. Then at almost all places ![]() $v$ of
$v$ of ![]() $F$,
$F$, ![]() $\mathrm {Ind}_{G_D(F_v)^+}^{G_D(F_v)}(\pi _{+,v})$ is irreducible where
$\mathrm {Ind}_{G_D(F_v)^+}^{G_D(F_v)}(\pi _{+,v})$ is irreducible where ![]() $\pi _{+,v}$ is an irreducible constituent of
$\pi _{+,v}$ is an irreducible constituent of ![]() $\pi _v\mid _{G_D(F_v)^+}$. This implies that
$\pi _v\mid _{G_D(F_v)^+}$. This implies that ![]() $\pi$ and
$\pi$ and ![]() $\pi ^\circ$ are nearly equivalent and, hence,
$\pi ^\circ$ are nearly equivalent and, hence, ![]() $\pi ^\circ$ is nearly equivalent to
$\pi ^\circ$ is nearly equivalent to ![]() $\pi ^\circ \otimes \chi _E$. Thus,
$\pi ^\circ \otimes \chi _E$. Thus, ![]() $\Pi _{\pi ^\circ }$ is nearly equivalent to
$\Pi _{\pi ^\circ }$ is nearly equivalent to ![]() $\Pi _{\pi ^\circ } \otimes \chi _E$ and, hence,
$\Pi _{\pi ^\circ } \otimes \chi _E$ and, hence, ![]() $\Pi _{\pi ^\circ } = \Pi _{\pi ^\circ } \otimes \chi _E$ by the strong multiplicity one theorem. When
$\Pi _{\pi ^\circ } = \Pi _{\pi ^\circ } \otimes \chi _E$ by the strong multiplicity one theorem. When ![]() $\pi$ is neither of type I-A nor I-B, this does not happen by Lemmas 4.1 and 4.2.
$\pi$ is neither of type I-A nor I-B, this does not happen by Lemmas 4.1 and 4.2.
Suppose that ![]() $\pi$ is either of type I-A or I-B. Then
$\pi$ is either of type I-A or I-B. Then ![]() $D$ is split and the functorial lift
$D$ is split and the functorial lift ![]() $\Pi _\pi$ of
$\Pi _\pi$ of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GL}_4(\mathbb {A})$ is of the form
$\mathrm {GL}_4(\mathbb {A})$ is of the form ![]() $\mathcal {AI}(\tau )$ for an irreducible automorphic representation
$\mathcal {AI}(\tau )$ for an irreducible automorphic representation ![]() $\tau$ of
$\tau$ of ![]() $\mathrm {GL}_2(\mathbb {A}_E)$ by Roberts [Reference RobertsRob01]. Then we have
$\mathrm {GL}_2(\mathbb {A}_E)$ by Roberts [Reference RobertsRob01]. Then we have ![]() $\Pi _\pi =\Pi _\pi \otimes \chi _E$. Hence,
$\Pi _\pi =\Pi _\pi \otimes \chi _E$. Hence, ![]() $\pi$ is nearly equivalent to
$\pi$ is nearly equivalent to ![]() $\pi \otimes \chi _E$.
$\pi \otimes \chi _E$.
When ![]() $\pi$ is not nearly equivalent to
$\pi$ is not nearly equivalent to ![]() $\pi \otimes \chi _E$,
$\pi \otimes \chi _E$, ![]() $\pi \mid _{\mathcal {G}_D}$ is irreducible since
$\pi \mid _{\mathcal {G}_D}$ is irreducible since ![]() $\mathcal {G}_D$ is of index
$\mathcal {G}_D$ is of index ![]() $2$ in
$2$ in ![]() $G_D(\mathbb {A})$.
$G_D(\mathbb {A})$.
Remark 4.3 This lemma gives a classification of ![]() $\pi$ such that the twist
$\pi$ such that the twist ![]() $\pi \otimes \chi _E$ of
$\pi \otimes \chi _E$ of ![]() $\pi$ by
$\pi$ by ![]() $\chi _E$ has the same Arthur parameter as
$\chi _E$ has the same Arthur parameter as ![]() $\pi$. A classification of
$\pi$. A classification of ![]() $\pi$ such that
$\pi$ such that ![]() $\pi$ and
$\pi$ and ![]() $\pi \otimes \chi _E$ are isomorphic when
$\pi \otimes \chi _E$ are isomorphic when ![]() $G_D \simeq G$ is given in Chan [Reference ChanCha10].
$G_D \simeq G$ is given in Chan [Reference ChanCha10].
4.3 Proof of statement (ii) in Theorem 1.1
Suppose that ![]() $\pi$ has a generic Arthur parameter.
$\pi$ has a generic Arthur parameter.
When there exists a pair ![]() $(D^\prime,\pi ^\prime )$ as described in Theorem 1.1(ii),
$(D^\prime,\pi ^\prime )$ as described in Theorem 1.1(ii), ![]() $\pi$ and
$\pi$ and ![]() $\pi ^\prime$ share the same generic Arthur parameter since they are nearly equivalent to each other. Hence, by Theorem 1.1(i), we have
$\pi ^\prime$ share the same generic Arthur parameter since they are nearly equivalent to each other. Hence, by Theorem 1.1(i), we have
when ![]() $S$ is a sufficiently large finite set of places of
$S$ is a sufficiently large finite set of places of ![]() $F$. Then by Remark 1.3, we have
$F$. Then by Remark 1.3, we have
i.e. (1.5.5) holds.
Conversely suppose that ![]() $L (\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$. There exists an irreducible cuspidal globally generic automorphic representation
$L (\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$. There exists an irreducible cuspidal globally generic automorphic representation ![]() $\pi ^\circ$ of
$\pi ^\circ$ of ![]() $G(\mathbb {A})$ which is nearly equivalent to
$G(\mathbb {A})$ which is nearly equivalent to ![]() $\pi$ since
$\pi$ since ![]() $\pi$ has a generic Arthur parameter. Let
$\pi$ has a generic Arthur parameter. Let ![]() $U$ be a maximal unipotent subgroup of
$U$ be a maximal unipotent subgroup of ![]() $\mathrm {GSO}_{4,2}$ and
$\mathrm {GSO}_{4,2}$ and ![]() $\psi _U$ be a non-degenerate character of
$\psi _U$ be a non-degenerate character of ![]() $U(\mathbb {A})$ defined below by (6.1.2) and (6.1.3), which are the same as [Reference MorimotoMor14a, (2.4)] and [Reference MorimotoMor14a, (3.1)], respectively. Let
$U(\mathbb {A})$ defined below by (6.1.2) and (6.1.3), which are the same as [Reference MorimotoMor14a, (2.4)] and [Reference MorimotoMor14a, (3.1)], respectively. Let ![]() $U_G$ be the maximal unipotent subgroup of
$U_G$ be the maximal unipotent subgroup of ![]() $\mathrm {GSp}_{2}$ defined by (6.2.1) and
$\mathrm {GSp}_{2}$ defined by (6.2.1) and ![]() $\psi _{U_G}$ the non-degenerate character of
$\psi _{U_G}$ the non-degenerate character of ![]() $U_G(\mathbb {A})$ defined by (6.2.2) in § 6.2. Note that in [Reference MorimotoMor14a],
$U_G(\mathbb {A})$ defined by (6.2.2) in § 6.2. Note that in [Reference MorimotoMor14a], ![]() $U_G$ is denoted by
$U_G$ is denoted by ![]() $N$ and
$N$ and ![]() $\psi _{U_G}$ is denoted by
$\psi _{U_G}$ is denoted by ![]() $\psi _{N}$ in [Reference MorimotoMor14a, p. 34] and [Reference MorimotoMor14a, (3.2)], respectively. Then we note that the restriction of
$\psi _{N}$ in [Reference MorimotoMor14a, p. 34] and [Reference MorimotoMor14a, (3.2)], respectively. Then we note that the restriction of ![]() $\pi ^\circ$ to
$\pi ^\circ$ to ![]() $G(\mathbb {A})^+$ contains a unique
$G(\mathbb {A})^+$ contains a unique ![]() $\psi _{U_G}$-generic irreducible constituent and we denote it by
$\psi _{U_G}$-generic irreducible constituent and we denote it by ![]() $\pi _+^\circ$. Let us consider the theta lift
$\pi _+^\circ$. Let us consider the theta lift ![]() $\Sigma :=\theta _\psi (\pi _+^\circ )$ of
$\Sigma :=\theta _\psi (\pi _+^\circ )$ of ![]() $\pi _+^\circ$ to
$\pi _+^\circ$ to ![]() $\mathrm {GSO}_{4,2}(\mathbb {A})$. Then by [Reference MorimotoMor14a, Proposition 3.3], we know that
$\mathrm {GSO}_{4,2}(\mathbb {A})$. Then by [Reference MorimotoMor14a, Proposition 3.3], we know that ![]() $\Sigma$ is
$\Sigma$ is ![]() $\psi _U$-globally generic and, hence, non-zero. We divide into two cases according to the cuspidality of
$\psi _U$-globally generic and, hence, non-zero. We divide into two cases according to the cuspidality of ![]() $\Sigma$.
$\Sigma$.
Suppose that ![]() $\Sigma$ is not cuspidal. Then by Rallis tower property,
$\Sigma$ is not cuspidal. Then by Rallis tower property, ![]() $\pi ^\circ _+$ participates in the theta correspondence with
$\pi ^\circ _+$ participates in the theta correspondence with ![]() $\mathrm {GSO}_{3,1}$. As in the proof of Lemma 4.1, the theta lift of
$\mathrm {GSO}_{3,1}$. As in the proof of Lemma 4.1, the theta lift of ![]() $\pi ^\circ _+$ to
$\pi ^\circ _+$ to ![]() $\mathrm {GSO}_2$ is zero since
$\mathrm {GSO}_2$ is zero since ![]() $\pi ^\circ _+$ is generic. Hence, the theta lift
$\pi ^\circ _+$ is generic. Hence, the theta lift ![]() $\tau :=\theta _\psi ^{X, S_1}(\pi ^\circ _+)$ of
$\tau :=\theta _\psi ^{X, S_1}(\pi ^\circ _+)$ of ![]() $\pi ^\circ _+$ to
$\pi ^\circ _+$ to ![]() $\mathrm {GSO}_{3,1}$ is cuspidal and non-zero. By Remark 3.1,
$\mathrm {GSO}_{3,1}$ is cuspidal and non-zero. By Remark 3.1, ![]() $\tau$ is also irreducible.
$\tau$ is also irreducible.
Recall that
Then we may regard ![]() $\tau$ as an irreducible cuspidal automorphic representation of
$\tau$ as an irreducible cuspidal automorphic representation of ![]() $\mathrm {GL}_2(\mathbb {A}_E)$ with a trivial central character since the central character of
$\mathrm {GL}_2(\mathbb {A}_E)$ with a trivial central character since the central character of ![]() $\pi ^\circ _+$ is trivial.
$\pi ^\circ _+$ is trivial.
Let ![]() $\Pi$ denote the strong functorial lift of
$\Pi$ denote the strong functorial lift of ![]() $\pi ^\circ$ to
$\pi ^\circ$ to ![]() $\mathrm {GL}_4(\mathbb {A})$ by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04]. Then at almost all finite places
$\mathrm {GL}_4(\mathbb {A})$ by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04]. Then at almost all finite places ![]() $v$ of
$v$ of ![]() $F$, we have
$F$, we have ![]() $\Pi _v \simeq \mathcal {AI}(\tau )_v$, and thus by the strong multiplicity one theorem,
$\Pi _v \simeq \mathcal {AI}(\tau )_v$, and thus by the strong multiplicity one theorem, ![]() $\Pi = \mathcal {AI}(\tau )$ holds. Since
$\Pi = \mathcal {AI}(\tau )$ holds. Since ![]() $\pi$ is nearly equivalent to
$\pi$ is nearly equivalent to ![]() $\pi ^\circ$, Remark 1.3 and our assumption imply that for a sufficiently large finite set
$\pi ^\circ$, Remark 1.3 and our assumption imply that for a sufficiently large finite set ![]() $S$ of places of
$S$ of places of ![]() $F$, we have
$F$, we have
 \begin{align*} L^S \big(\tfrac{1}{2},
\tau \times \Lambda \big) L^S \big(\tfrac{1}{2}, \tau
\times \Lambda^{-1} \big) &= L^S \big(\tfrac{1}{2},
\pi^\circ \times \mathcal{AI} (\Lambda)\big)\\ & = L^S
\big(\tfrac{1}{2}, \pi \times \mathcal{AI} (\Lambda)\big)
\ne 0. \end{align*}
\begin{align*} L^S \big(\tfrac{1}{2},
\tau \times \Lambda \big) L^S \big(\tfrac{1}{2}, \tau
\times \Lambda^{-1} \big) &= L^S \big(\tfrac{1}{2},
\pi^\circ \times \mathcal{AI} (\Lambda)\big)\\ & = L^S
\big(\tfrac{1}{2}, \pi \times \mathcal{AI} (\Lambda)\big)
\ne 0. \end{align*}
Then by Waldspurger [Reference WaldspurgerWal85], ![]() $\tau$ has the split torus model with respect to the character
$\tau$ has the split torus model with respect to the character ![]() $(\Lambda, \Lambda ^{-1})$. Hence, the equation in Corbett [Reference CorbettCor17, p. 78] implies that
$(\Lambda, \Lambda ^{-1})$. Hence, the equation in Corbett [Reference CorbettCor17, p. 78] implies that ![]() $\pi ^\circ$ has the
$\pi ^\circ$ has the ![]() $(E, \Lambda )$-Bessel period. Hence, we may take
$(E, \Lambda )$-Bessel period. Hence, we may take ![]() $D^\prime = \mathrm {Mat}_{2 \times 2}$ and
$D^\prime = \mathrm {Mat}_{2 \times 2}$ and ![]() $\pi ^\prime = \pi ^\circ$. Thus, the case when
$\pi ^\prime = \pi ^\circ$. Thus, the case when ![]() $\Sigma$ is not cuspidal is settled.
$\Sigma$ is not cuspidal is settled.
Suppose that ![]() $\Sigma$ is cuspidal. We may regard
$\Sigma$ is cuspidal. We may regard ![]() $\Sigma$ as an irreducible cuspidal globally generic automorphic representation of
$\Sigma$ as an irreducible cuspidal globally generic automorphic representation of ![]() $\mathrm {GU}(2,2)$ with trivial central character because of the accidental isomorphism (2.2.6). As in the proof of Theorem 1.1(i), our assumption implies that
$\mathrm {GU}(2,2)$ with trivial central character because of the accidental isomorphism (2.2.6). As in the proof of Theorem 1.1(i), our assumption implies that ![]() $L (\frac {1}{2}, \Sigma \times \Lambda ) \ne 0$. Then by [Reference Furusawa and MorimotoFM22, Proposition A.2], there exists an irreducible cuspidal automorphic representation
$L (\frac {1}{2}, \Sigma \times \Lambda ) \ne 0$. Then by [Reference Furusawa and MorimotoFM22, Proposition A.2], there exists an irreducible cuspidal automorphic representation ![]() $\Sigma ^\prime$ of
$\Sigma ^\prime$ of ![]() $\mathrm {GU}(V)$ such that
$\mathrm {GU}(V)$ such that ![]() $\Sigma ^\prime$ is locally
$\Sigma ^\prime$ is locally ![]() $\mathrm {U}(V)$-nearly equivalent to
$\mathrm {U}(V)$-nearly equivalent to ![]() $\Sigma$ and
$\Sigma$ and ![]() $\Sigma ^\prime$ has the
$\Sigma ^\prime$ has the ![]() $(e, \Lambda, \psi )$-Bessel period where
$(e, \Lambda, \psi )$-Bessel period where ![]() $V$ is a
$V$ is a ![]() $4$-dimensional hermitian space over
$4$-dimensional hermitian space over ![]() $E$ whose Witt index is at least
$E$ whose Witt index is at least ![]() $1$. Then we note that
$1$. Then we note that ![]() $\mathrm {PGU}(V) \simeq \mathrm {PGSO}_{4,2}$ or
$\mathrm {PGU}(V) \simeq \mathrm {PGSO}_{4,2}$ or ![]() $\mathrm {P}\mathrm {GU}_{3,D^\prime }$ for some quaternion division algebra
$\mathrm {P}\mathrm {GU}_{3,D^\prime }$ for some quaternion division algebra ![]() $D^\prime$ over
$D^\prime$ over ![]() $F$.
$F$.
In the first case, we consider the theta lift ![]() $\pi ^\prime _+:=\theta _{\psi ^{-1}}(\Sigma ^\prime )$ of
$\pi ^\prime _+:=\theta _{\psi ^{-1}}(\Sigma ^\prime )$ of ![]() $\Sigma ^\prime$ to
$\Sigma ^\prime$ to ![]() $G(\mathbb {A})^+$. Then by the same argument as in the proof of Theorem 1.1(i), we see that
$G(\mathbb {A})^+$. Then by the same argument as in the proof of Theorem 1.1(i), we see that ![]() $\pi _+^\prime \ne 0$ by Takeda [Reference TakedaTak11, Theorem 1.1 (1)] and that it is an irreducible cuspidal automorphic representation of
$\pi _+^\prime \ne 0$ by Takeda [Reference TakedaTak11, Theorem 1.1 (1)] and that it is an irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A})^+$. Since
$G(\mathbb {A})^+$. Since ![]() $\Sigma ^\prime$ has the
$\Sigma ^\prime$ has the ![]() $(e, \Lambda, \psi )$-Bessel period,
$(e, \Lambda, \psi )$-Bessel period, ![]() $\pi ^\prime _+$ has the
$\pi ^\prime _+$ has the ![]() $(E, \Lambda )$-Bessel period by Proposition 3.1. From the definition,
$(E, \Lambda )$-Bessel period by Proposition 3.1. From the definition, ![]() $\pi _+^\prime$ is nearly equivalent to
$\pi _+^\prime$ is nearly equivalent to ![]() $\pi _+^\circ$. Let us take an irreducible cuspidal automorphic representation
$\pi _+^\circ$. Let us take an irreducible cuspidal automorphic representation ![]() $(\pi ^\prime, V_{\pi ^\prime })$ of
$(\pi ^\prime, V_{\pi ^\prime })$ of ![]() $G(\mathbb {A})$ such that
$G(\mathbb {A})$ such that ![]() $\pi ^\prime \mid _{G(\mathbb {A})^+} \supset \pi _+^\prime$. Then
$\pi ^\prime \mid _{G(\mathbb {A})^+} \supset \pi _+^\prime$. Then ![]() $\pi ^\prime$ is locally
$\pi ^\prime$ is locally ![]() $G^+$-nearly equivalent, and thus either
$G^+$-nearly equivalent, and thus either ![]() $\pi ^\prime$ or
$\pi ^\prime$ or ![]() $\pi ^\prime \otimes \chi _E$ is nearly equivalent to
$\pi ^\prime \otimes \chi _E$ is nearly equivalent to ![]() $\pi$ by Remark 1.2. Since both
$\pi$ by Remark 1.2. Since both ![]() $\pi ^\prime$ and
$\pi ^\prime$ and ![]() $\pi ^\prime \otimes \chi _E$ have the
$\pi ^\prime \otimes \chi _E$ have the ![]() $(E, \Lambda )$-Bessel period, our claim follows.
$(E, \Lambda )$-Bessel period, our claim follows.
In the second case, we consider the theta lift of ![]() $\Sigma ^\prime$ to
$\Sigma ^\prime$ to ![]() $G_{D^\prime }(\mathbb {A})$. Then by an argument similar to that in the first case, we may show that the theta lift of
$G_{D^\prime }(\mathbb {A})$. Then by an argument similar to that in the first case, we may show that the theta lift of ![]() $\Sigma ^\prime$ to
$\Sigma ^\prime$ to ![]() $G_{D^\prime }(\mathbb {A})$ contains an irreducible constituent which is cuspidal, locally
$G_{D^\prime }(\mathbb {A})$ contains an irreducible constituent which is cuspidal, locally ![]() $G^+$-nearly equivalent to
$G^+$-nearly equivalent to ![]() $\pi$ and has the
$\pi$ and has the ![]() $(E, \Lambda )$-Bessel period. Here we use [Reference YamanaYam14, Lemma 10.2] and its proof in the case of (
$(E, \Lambda )$-Bessel period. Here we use [Reference YamanaYam14, Lemma 10.2] and its proof in the case of (![]() ${\rm I}_1$) with
${\rm I}_1$) with ![]() $n=3, m=2$, noting Remark 4.5. This completes our proof of the existence of a pair
$n=3, m=2$, noting Remark 4.5. This completes our proof of the existence of a pair ![]() $(D^\prime,\pi ^\prime )$.
$(D^\prime,\pi ^\prime )$.
Let us show the uniqueness of a pair ![]() $(D^\prime,\pi ^\prime )$ under the assumption that
$(D^\prime,\pi ^\prime )$ under the assumption that ![]() $\pi$ is tempered. Suppose that for
$\pi$ is tempered. Suppose that for ![]() $i=1,2$ there exists a pair
$i=1,2$ there exists a pair ![]() $(D_i,\pi _i)$ where
$(D_i,\pi _i)$ where ![]() $D_i$ is a quaternion algebra over
$D_i$ is a quaternion algebra over ![]() $F$ and
$F$ and ![]() $\pi _i$ is an irreducible cuspidal automorphic representation of
$\pi _i$ is an irreducible cuspidal automorphic representation of ![]() $G_{D_i}(\mathbb {A})$ which is nearly equivalent to
$G_{D_i}(\mathbb {A})$ which is nearly equivalent to ![]() $\pi$ such that
$\pi$ such that ![]() $\pi _i$ has the
$\pi _i$ has the ![]() $(E, \Lambda )$-Bessel period.
$(E, \Lambda )$-Bessel period.
Suppose that ![]() $\pi _i$ is nearly equivalent to
$\pi _i$ is nearly equivalent to ![]() $\pi _i \otimes \chi _E$ for
$\pi _i \otimes \chi _E$ for ![]() $i=1,2$. Then by Lemma 4.4,
$i=1,2$. Then by Lemma 4.4, ![]() $\pi _1$,
$\pi _1$, ![]() $\pi _2$ are of type I-A or I-B and, in particular,
$\pi _2$ are of type I-A or I-B and, in particular, ![]() $D_1 \simeq D_2 \simeq \mathrm {Mat}_{2 \times 2}$. Hence, for
$D_1 \simeq D_2 \simeq \mathrm {Mat}_{2 \times 2}$. Hence, for ![]() $i=1,2$, there exist a four-dimensional orthogonal space
$i=1,2$, there exist a four-dimensional orthogonal space ![]() $X_i$ over
$X_i$ over ![]() $F$ with discriminant algebra
$F$ with discriminant algebra ![]() $E$ and an irreducible cuspidal automorphic representation
$E$ and an irreducible cuspidal automorphic representation ![]() $\sigma _i$ of
$\sigma _i$ of ![]() $\mathrm {GSO}(X_i, \mathbb {A})$ such that
$\mathrm {GSO}(X_i, \mathbb {A})$ such that ![]() $\pi _i= \theta _{\psi }(\sigma _i)$. Since
$\pi _i= \theta _{\psi }(\sigma _i)$. Since ![]() $\mathrm {PGSO}(X_i, F) \simeq (D_i^\prime )^\times (E)/ E^\times$ for some quaternion algebra
$\mathrm {PGSO}(X_i, F) \simeq (D_i^\prime )^\times (E)/ E^\times$ for some quaternion algebra ![]() $D_i^\prime$ over
$D_i^\prime$ over ![]() $F$, we may regard
$F$, we may regard ![]() $\sigma _i$ as an automorphic representation of
$\sigma _i$ as an automorphic representation of ![]() $(D_i^\prime )^\times (\mathbb {A}_E)$ with the trivial central character. Since
$(D_i^\prime )^\times (\mathbb {A}_E)$ with the trivial central character. Since ![]() $\pi _i$ has the
$\pi _i$ has the ![]() $(E, \Lambda )$-Bessel period,
$(E, \Lambda )$-Bessel period, ![]() $\sigma _i$ has the split torus period with respect to a character
$\sigma _i$ has the split torus period with respect to a character ![]() $(\Lambda,\Lambda ^{-1})$ by [Reference CorbettCor17, p. 78]. Hence,
$(\Lambda,\Lambda ^{-1})$ by [Reference CorbettCor17, p. 78]. Hence, ![]() $D_i^\prime (E) \simeq \mathrm {Mat}_{2 \times 2}(E)$ by [Reference WaldspurgerWal85]. Since
$D_i^\prime (E) \simeq \mathrm {Mat}_{2 \times 2}(E)$ by [Reference WaldspurgerWal85]. Since ![]() $\sigma _1$ is nearly equivalent to
$\sigma _1$ is nearly equivalent to ![]() $\sigma _2$, we have
$\sigma _2$, we have ![]() $\sigma _1=\sigma _2$ by the strong multiplicity one. Thus,
$\sigma _1=\sigma _2$ by the strong multiplicity one. Thus, ![]() $\pi _1\simeq \pi _2$.
$\pi _1\simeq \pi _2$.
Suppose that ![]() $\pi _i$ is neither type I-A nor I-B for
$\pi _i$ is neither type I-A nor I-B for ![]() $i=1,2$. For each
$i=1,2$. For each ![]() $i$, let us take a unique irreducible constituent
$i$, let us take a unique irreducible constituent ![]() $\pi _{i, +}^B$ of
$\pi _{i, +}^B$ of ![]() $\pi _{i}|_{G_{D_i}(\mathbb {A})^+}$ that has the
$\pi _{i}|_{G_{D_i}(\mathbb {A})^+}$ that has the ![]() $(\xi _i, \Lambda, \psi )$-Bessel period. Note that
$(\xi _i, \Lambda, \psi )$-Bessel period. Note that ![]() $\pi _{1, +}^B$ and
$\pi _{1, +}^B$ and ![]() $\pi _{2, +}^B$ are nearly equivalent to each other.
$\pi _{2, +}^B$ are nearly equivalent to each other.
Now let ![]() $\sigma _i$ denote the theta lift
$\sigma _i$ denote the theta lift ![]() $\theta _{\psi }(\pi _{i, +}^B)$ of
$\theta _{\psi }(\pi _{i, +}^B)$ of ![]() $\pi _{i, +}^B$ to
$\pi _{i, +}^B$ to ![]() $\mathrm {GSU}_{3,D_i}$. Then we regard
$\mathrm {GSU}_{3,D_i}$. Then we regard ![]() $\sigma _i$ as an automorphic representation of
$\sigma _i$ as an automorphic representation of ![]() $\mathrm {GU}_{4,\varepsilon }$ via (2.2.5), (2.2.6) and let
$\mathrm {GU}_{4,\varepsilon }$ via (2.2.5), (2.2.6) and let ![]() $\Sigma _i := \Theta _{\psi, (\Lambda ^{-1}, \Lambda ^{-1})}$ denote the theta lift of
$\Sigma _i := \Theta _{\psi, (\Lambda ^{-1}, \Lambda ^{-1})}$ denote the theta lift of ![]() $\sigma _i$ to
$\sigma _i$ to ![]() $\mathrm {GU}_{2,2}$. In turn, we regard
$\mathrm {GU}_{2,2}$. In turn, we regard ![]() $\Sigma _i$ as an automorphic representation of
$\Sigma _i$ as an automorphic representation of ![]() $\mathrm {GSO}_{4,2}$ via (2.2.6) and we denote by
$\mathrm {GSO}_{4,2}$ via (2.2.6) and we denote by ![]() $\pi _{i,+}^\prime$ its theta lift to
$\pi _{i,+}^\prime$ its theta lift to ![]() $G(\mathbb {A})^+$. Then from the proof of Theorem 1.1(i),
$G(\mathbb {A})^+$. Then from the proof of Theorem 1.1(i), ![]() $\sigma _i$,
$\sigma _i$, ![]() $\Sigma _i$ and
$\Sigma _i$ and ![]() $\pi _{i,+}^\prime$ are irreducible and cuspidal. Moreover,
$\pi _{i,+}^\prime$ are irreducible and cuspidal. Moreover, ![]() $\pi _{1,+}^\prime$ and
$\pi _{1,+}^\prime$ and ![]() $\pi _{2,+}^\prime$ are both globally generic and nearly equivalent to each other. Furthermore, since
$\pi _{2,+}^\prime$ are both globally generic and nearly equivalent to each other. Furthermore, since ![]() $\pi _i$ is tempered,
$\pi _i$ is tempered, ![]() $\sigma _i=\theta _{\psi }(\pi _{i, +}^B)$ is tempered at finite places by an argument similar to that in Atobe and Gan [Reference Atobe and GanAG17, Proposition 5.5] (see also [Reference Gan and IchinoGI14, Proposition C.1]) and similarly at real and complex places by Paul [Reference PaulPau98, Theorems 15, 30] and Li, Paul, Tan and Zhu [Reference Li, Paul, Tan and ZhuLPTZ03, Theorems 4.20, 5.1] and, by Adams and Barbasch [Reference Adams and BarbaschAB95, Theorem 2.7], respectively. Similarly
$\sigma _i=\theta _{\psi }(\pi _{i, +}^B)$ is tempered at finite places by an argument similar to that in Atobe and Gan [Reference Atobe and GanAG17, Proposition 5.5] (see also [Reference Gan and IchinoGI14, Proposition C.1]) and similarly at real and complex places by Paul [Reference PaulPau98, Theorems 15, 30] and Li, Paul, Tan and Zhu [Reference Li, Paul, Tan and ZhuLPTZ03, Theorems 4.20, 5.1] and, by Adams and Barbasch [Reference Adams and BarbaschAB95, Theorem 2.7], respectively. Similarly ![]() $\Sigma _i$ and
$\Sigma _i$ and ![]() $\pi _{i,+}^\prime$ are also tempered.
$\pi _{i,+}^\prime$ are also tempered.
By Propositions 3.1 and 3.2, we know that ![]() $\sigma _i$ has the
$\sigma _i$ has the ![]() $(X_{\xi _i}, \Lambda, \psi )$-Bessel period. Let
$(X_{\xi _i}, \Lambda, \psi )$-Bessel period. Let ![]() $\mathrm {GU}_i$ denote the similitude unitary group which modulo center is isomorphic to
$\mathrm {GU}_i$ denote the similitude unitary group which modulo center is isomorphic to ![]() $\mathrm {PGSU}_{3, D_i}$ by (2.2.5). Then
$\mathrm {PGSU}_{3, D_i}$ by (2.2.5). Then ![]() $\sigma _i\mid _{\mathrm {U}_i}$ has a unique irreducible constituent
$\sigma _i\mid _{\mathrm {U}_i}$ has a unique irreducible constituent ![]() $\nu _i$ which has the
$\nu _i$ which has the ![]() $(X_{\xi _i}, \Lambda, \psi )$-Bessel period. Then by Beuzart-Plessis [Reference Beuzart-PlessisBeu16, Reference Beuzart-PlessisBeu20] (also by Xue [Reference XueXue23] at the real place), we see that
$(X_{\xi _i}, \Lambda, \psi )$-Bessel period. Then by Beuzart-Plessis [Reference Beuzart-PlessisBeu16, Reference Beuzart-PlessisBeu20] (also by Xue [Reference XueXue23] at the real place), we see that ![]() $\mathrm {U}_1 \simeq \mathrm {U}_2$ since
$\mathrm {U}_1 \simeq \mathrm {U}_2$ since ![]() $\nu _1$ and
$\nu _1$ and ![]() $\nu _2$ are equivalent to each other. This implies that
$\nu _2$ are equivalent to each other. This implies that ![]() $D_1 \simeq D_2$ and, hence,
$D_1 \simeq D_2$ and, hence, ![]() $G_{D_1} \simeq G_{D_2}$. Let
$G_{D_1} \simeq G_{D_2}$. Let ![]() $D^\prime \simeq D_i$ for
$D^\prime \simeq D_i$ for ![]() $i=1,2$.
$i=1,2$.
We take an irreducible cuspidal automorphic representation ![]() $\pi _{i}^\prime$ of
$\pi _{i}^\prime$ of ![]() $G(\mathbb {A})$ such that
$G(\mathbb {A})$ such that ![]() $\pi _i^\prime |_{G(\mathbb {A})^+}$ contains
$\pi _i^\prime |_{G(\mathbb {A})^+}$ contains ![]() $\pi _{i,+}^\prime$. Then by Remark 1.2, we may suppose that
$\pi _{i,+}^\prime$. Then by Remark 1.2, we may suppose that ![]() $\pi _1^\prime$ is nearly equivalent to
$\pi _1^\prime$ is nearly equivalent to ![]() $\pi _2^\prime$ or
$\pi _2^\prime$ or ![]() $\pi _2^\prime \otimes \chi _E$. Thus replacing
$\pi _2^\prime \otimes \chi _E$. Thus replacing ![]() $\pi _2^\prime$ by
$\pi _2^\prime$ by ![]() $\pi _2^\prime \otimes \chi _E$ if necessary, we may assume that
$\pi _2^\prime \otimes \chi _E$ if necessary, we may assume that ![]() $\pi _1^\prime$ and
$\pi _1^\prime$ and ![]() $\pi _2^\prime$ are nearly equivalent to each other. Then since
$\pi _2^\prime$ are nearly equivalent to each other. Then since ![]() $\pi _1^\prime$ and
$\pi _1^\prime$ and ![]() $\pi _2^\prime$ are generic and they have the same
$\pi _2^\prime$ are generic and they have the same ![]() $L$-parameter because of the temperedness of
$L$-parameter because of the temperedness of ![]() $\pi _i^\prime$, we have
$\pi _i^\prime$, we have ![]() $\pi _1^\prime \simeq \pi _2^\prime$ by the uniqueness of the generic member in the
$\pi _1^\prime \simeq \pi _2^\prime$ by the uniqueness of the generic member in the ![]() $L$-packet by Atobe [Reference AtobeAto17] or Varma [Reference VarmaVar17] at finite places and by Vogan [Reference VoganVog78] at archimedean places. Hence, in particular,
$L$-packet by Atobe [Reference AtobeAto17] or Varma [Reference VarmaVar17] at finite places and by Vogan [Reference VoganVog78] at archimedean places. Hence, in particular, ![]() $\pi _{1,+}^\prime \simeq \pi _{2,+}^\prime$.
$\pi _{1,+}^\prime \simeq \pi _{2,+}^\prime$.
From the definition of ![]() $\pi _{+,i}^\prime$, we get
$\pi _{+,i}^\prime$, we get ![]() $\pi _{1,+}^B \simeq \pi _{2,+}^B$. Then, we see that
$\pi _{1,+}^B \simeq \pi _{2,+}^B$. Then, we see that ![]() $\pi _1 \simeq \pi _2 \otimes \omega$ for some character
$\pi _1 \simeq \pi _2 \otimes \omega$ for some character ![]() $\omega$ of
$\omega$ of ![]() $G_{D^\prime }(\mathbb {A})$ such that
$G_{D^\prime }(\mathbb {A})$ such that ![]() $\omega _v$ is trivial or
$\omega _v$ is trivial or ![]() $\chi _{E,v}$ at each place
$\chi _{E,v}$ at each place ![]() $v$ of
$v$ of ![]() $F$. Since
$F$. Since ![]() $\pi _1$ and
$\pi _1$ and ![]() $\pi _2$ have the same
$\pi _2$ have the same ![]() $L$-parameter,
$L$-parameter, ![]() $\pi _{1,v}$ and
$\pi _{1,v}$ and ![]() $\pi _{1,v}\otimes \omega _v$ are in the same
$\pi _{1,v}\otimes \omega _v$ are in the same ![]() $L$-packet for every place
$L$-packet for every place ![]() $v$ of
$v$ of ![]() $F$.
$F$.
Let us take a place ![]() $v$ of
$v$ of ![]() $F$, and write the
$F$, and write the ![]() $L$-parameter of
$L$-parameter of ![]() $\pi _{1, v}$ as
$\pi _{1, v}$ as ![]() $\phi _v : WD_{F_v} \rightarrow G^1(\mathbb {C})$. If
$\phi _v : WD_{F_v} \rightarrow G^1(\mathbb {C})$. If ![]() $\phi _v$ is an irreducible four-dimensional representation, the
$\phi _v$ is an irreducible four-dimensional representation, the ![]() $L$-packet of
$L$-packet of ![]() $\phi _v$ is singleton and, thus,
$\phi _v$ is singleton and, thus, ![]() $\pi _{1, v} \simeq \pi _{2,v}$. Thus, let us suppose that
$\pi _{1, v} \simeq \pi _{2,v}$. Thus, let us suppose that ![]() $\phi _{v} = \phi _1 \oplus \phi _2$ with two-dimensional irreducible representations
$\phi _{v} = \phi _1 \oplus \phi _2$ with two-dimensional irreducible representations ![]() $\phi _i$. Further, we may suppose that
$\phi _i$. Further, we may suppose that ![]() $\omega _v = \chi _{E,v}$ since there is nothing to prove when
$\omega _v = \chi _{E,v}$ since there is nothing to prove when ![]() $\omega _v$ is trivial. This implies that
$\omega _v$ is trivial. This implies that ![]() $\phi _v \otimes \chi _{E ,v}\simeq \phi _v$. Then, by [Reference Prasad and RamakrishnanPR99, Proposition 3.1], we have
$\phi _v \otimes \chi _{E ,v}\simeq \phi _v$. Then, by [Reference Prasad and RamakrishnanPR99, Proposition 3.1], we have ![]() $\phi _i=\pi (\chi _i)$ for some character
$\phi _i=\pi (\chi _i)$ for some character ![]() $\chi _i$ of
$\chi _i$ of ![]() $E_v^\times$ for
$E_v^\times$ for ![]() $i=1,2$. Moreover, any member of the
$i=1,2$. Moreover, any member of the ![]() $L$-packet of
$L$-packet of ![]() $\pi _1$ is given by the theta lift from an irreducible representation
$\pi _1$ is given by the theta lift from an irreducible representation ![]() $\mathrm {JL}(\pi (\chi _1)) \boxtimes \pi (\chi _2)$ of
$\mathrm {JL}(\pi (\chi _1)) \boxtimes \pi (\chi _2)$ of ![]() $D^\prime (F_v)^\times \times \mathrm {GL}_2(F_v)$ where
$D^\prime (F_v)^\times \times \mathrm {GL}_2(F_v)$ where ![]() $\mathrm {JL}$ denotes the Jacquet–Langlands transfer. Since the theta lift preserves the character twist, we see that
$\mathrm {JL}$ denotes the Jacquet–Langlands transfer. Since the theta lift preserves the character twist, we see that
by ![]() $\pi (\chi _i) \otimes \chi _{E, v} \simeq \pi (\chi _i)$. This shows that in this case, any element in the
$\pi (\chi _i) \otimes \chi _{E, v} \simeq \pi (\chi _i)$. This shows that in this case, any element in the ![]() $L$-packet is invariant under the twist by
$L$-packet is invariant under the twist by ![]() $\chi _{E,v}$. Thus
$\chi _{E,v}$. Thus ![]() $\pi _{1, v} \otimes \chi _{E, v} \simeq \pi _{2,v}$ and, hence,
$\pi _{1, v} \otimes \chi _{E, v} \simeq \pi _{2,v}$ and, hence, ![]() $\pi _{1,v} \simeq \pi _{2,v}$.
$\pi _{1,v} \simeq \pi _{2,v}$.
Remark 4.4 As we remarked in the end of § 1.5, the uniqueness of ![]() $(D^\prime, \pi ^\prime )$ follows from the local Gan–Gross–Prasad conjecture for
$(D^\prime, \pi ^\prime )$ follows from the local Gan–Gross–Prasad conjecture for ![]() $(\mathrm {SO}(5), \mathrm {SO}(2))$, which is proved by Luo [Reference LuoLuo20] at archimedean places and by Prasad and Takloo-Bighash [Reference Prasad and Takloo-BighashPT11] (see also Waldspurger [Reference WaldspurgerWal12b] in general case) at finite places. Our proof gives another proof of the uniqueness.
$(\mathrm {SO}(5), \mathrm {SO}(2))$, which is proved by Luo [Reference LuoLuo20] at archimedean places and by Prasad and Takloo-Bighash [Reference Prasad and Takloo-BighashPT11] (see also Waldspurger [Reference WaldspurgerWal12b] in general case) at finite places. Our proof gives another proof of the uniqueness.
Remark 4.5 There is a typo in the statement of [Reference YamanaYam14, Lemma 10.2]. The first condition stated there should be the holomorphy at ![]() $s=-s_m+\frac {1}{2}$.
$s=-s_m+\frac {1}{2}$.
5. Rallis inner product formula for similitude groups
In this section, as a preliminary for the proof of Theorem 1.2, we recall Rallis inner product formulas for similitude dual pairs.
5.1 For the theta lift from  $G$ to
$G$ to  $\mathrm {GSO}_{4,2}$
$\mathrm {GSO}_{4,2}$
In this section, we shall recall the Rallis inner product formula for the theta lift from ![]() $G$ to
$G$ to ![]() $\mathrm {GSO}_{4,2}$. It is derived from the isometry case in a manner similar to that in Gan and Ichino [Reference Gan and IchinoGI11, § 6], where the case of the theta lift from
$\mathrm {GSO}_{4,2}$. It is derived from the isometry case in a manner similar to that in Gan and Ichino [Reference Gan and IchinoGI11, § 6], where the case of the theta lift from ![]() $\mathrm {GL}_2$ to
$\mathrm {GL}_2$ to ![]() $\mathrm {GSO}_{3,1}$ is treated.
$\mathrm {GSO}_{3,1}$ is treated.
Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A})$ with a trivial central character. Let us define a subgroup
$G(\mathbb {A})$ with a trivial central character. Let us define a subgroup ![]() $\mathcal {G}$ of
$\mathcal {G}$ of ![]() $G(\mathbb {A})$ by
$G(\mathbb {A})$ by
and in this section we assume that:
for our later use.
Let us recall the notation in § 3.1.2. Thus ![]() $X$ denotes the four-dimensional symplectic space on which
$X$ denotes the four-dimensional symplectic space on which ![]() $G$ acts on the right and
$G$ acts on the right and ![]() $Y$ denotes the six-dimensional orthogonal space on which
$Y$ denotes the six-dimensional orthogonal space on which ![]() $\mathrm {GSO}_{4,2}$ acts on the left. Then
$\mathrm {GSO}_{4,2}$ acts on the left. Then ![]() $Z=X\otimes Y$ is a symplectic space over
$Z=X\otimes Y$ is a symplectic space over ![]() $F$. Here we take
$F$. Here we take ![]() $X_\pm \otimes Y$ as the polarization and we realize the Weil representation
$X_\pm \otimes Y$ as the polarization and we realize the Weil representation ![]() $\omega _\psi$ of
$\omega _\psi$ of ![]() $\mathrm {Mp}(Z)(\mathbb {A})$ on
$\mathrm {Mp}(Z)(\mathbb {A})$ on ![]() $V_\omega :=\mathcal {S}((X_+ \otimes Y)(\mathbb {A}))$.
$V_\omega :=\mathcal {S}((X_+ \otimes Y)(\mathbb {A}))$.
Put ![]() $X^\Box = X \oplus (-X)$. Then
$X^\Box = X \oplus (-X)$. Then ![]() $X^\Box$ is naturally a symplectic space. Let
$X^\Box$ is naturally a symplectic space. Let ![]() $\widetilde {G}:=\mathrm {GSp}(X^\Box )$ and we denote by
$\widetilde {G}:=\mathrm {GSp}(X^\Box )$ and we denote by ![]() $\mathbf {G}$ a subgroup of
$\mathbf {G}$ a subgroup of ![]() $G\times G$ given by
$G\times G$ given by
which has a natural embedding ![]() $\iota :\mathbf {G}\to \widetilde {G}$. We define the canonical pairing
$\iota :\mathbf {G}\to \widetilde {G}$. We define the canonical pairing ![]() $\mathcal {B}_\omega : V_\omega \otimes V_\omega \rightarrow \mathbb {C}$ by
$\mathcal {B}_\omega : V_\omega \otimes V_\omega \rightarrow \mathbb {C}$ by
where ![]() ${dx}$ denotes the Tamagawa measure on
${dx}$ denotes the Tamagawa measure on ![]() $(X_+ \otimes Y)(\mathbb {A})$.
$(X_+ \otimes Y)(\mathbb {A})$.
Let ![]() $\widetilde {Z} = X^\Box \otimes Y$ and we take a polarization
$\widetilde {Z} = X^\Box \otimes Y$ and we take a polarization ![]() $\widetilde {Z}=\widetilde {Z}_+\oplus \widetilde {Z}_-$ with
$\widetilde {Z}=\widetilde {Z}_+\oplus \widetilde {Z}_-$ with
where the double sign corresponds. Let us denote by ![]() $\widetilde {\omega }_\psi$ the Weil representation of
$\widetilde {\omega }_\psi$ the Weil representation of ![]() $\mathrm {Mp}(\widetilde {Z}(\mathbb {A}))$ on
$\mathrm {Mp}(\widetilde {Z}(\mathbb {A}))$ on ![]() $\mathcal {S}( \widetilde {Z}^+(\mathbb {A}))$. On the other hand, let
$\mathcal {S}( \widetilde {Z}^+(\mathbb {A}))$. On the other hand, let
Then we have a natural isomorphism
by which we regard ![]() $\mathcal {S}( \widetilde {X}^\nabla (\mathbb {A}))$ as a representation of
$\mathcal {S}( \widetilde {X}^\nabla (\mathbb {A}))$ as a representation of ![]() $\mathrm {Mp}(Z)(\mathbb {A}) \times \mathrm {Mp}(Z)(\mathbb {A})$. Meanwhile, we may realize
$\mathrm {Mp}(Z)(\mathbb {A}) \times \mathrm {Mp}(Z)(\mathbb {A})$. Meanwhile, we may realize ![]() $\widetilde {\omega }_\psi$ on
$\widetilde {\omega }_\psi$ on ![]() $\mathcal {S}(\widetilde {X}^\nabla (\mathbb {A}) )$ and indeed we have an isomorphism
$\mathcal {S}(\widetilde {X}^\nabla (\mathbb {A}) )$ and indeed we have an isomorphism
as representations of ![]() $\mathrm {Mp}(\widetilde {Z})(\mathbb {A})$ such that
$\mathrm {Mp}(\widetilde {Z})(\mathbb {A})$ such that
Let us define Petersson inner products on ![]() $G(\mathbb {A})$ and
$G(\mathbb {A})$ and ![]() $G(\mathbb {A})^+$ as follows. For
$G(\mathbb {A})^+$ as follows. For ![]() $f_1, f_2 \in V_\pi$, we define the Petersson inner product
$f_1, f_2 \in V_\pi$, we define the Petersson inner product ![]() $(\, {,}\,)_\pi$ on
$(\, {,}\,)_\pi$ on ![]() $G(\mathbb {A})$ by
$G(\mathbb {A})$ by
where ![]() $dg$ denotes the Tamagawa measure. Then regarding
$dg$ denotes the Tamagawa measure. Then regarding ![]() $f_1, f_2$ as automorphic forms on
$f_1, f_2$ as automorphic forms on ![]() $G(\mathbb {A})^+$, we define
$G(\mathbb {A})^+$, we define
where the measure ![]() $dh$ is normalized so that
$dh$ is normalized so that
Then from our assumption (5.1.2) on ![]() $\pi$, as in [Reference Gan and IchinoGI11, Lemma 6.3], we see that
$\pi$, as in [Reference Gan and IchinoGI11, Lemma 6.3], we see that
since ![]() $\mathrm {Vol}(\mathbb {A}^\times G(F) \backslash G(\mathbb {A})) =2$. For each place
$\mathrm {Vol}(\mathbb {A}^\times G(F) \backslash G(\mathbb {A})) =2$. For each place ![]() $v$ of
$v$ of ![]() $F$, we take a hermitian
$F$, we take a hermitian ![]() $G(F_v)$-invariant local pairing
$G(F_v)$-invariant local pairing ![]() $(\, {,}\,)_{\pi _v}$ of
$(\, {,}\,)_{\pi _v}$ of ![]() $\pi _v$ so that
$\pi _v$ so that
We also choose a local Haar measure ![]() $d g_v$ on
$d g_v$ on ![]() $G(F_v)$ for each place
$G(F_v)$ for each place ![]() $v$ of
$v$ of ![]() $F$ so that
$F$ so that ![]() $\mathrm {Vol}(K_{G, v}, d_{g_v})=1$ at almost all
$\mathrm {Vol}(K_{G, v}, d_{g_v})=1$ at almost all ![]() $v$, where
$v$, where ![]() $K_{G, v}$ is a maximal compact subgroup of
$K_{G, v}$ is a maximal compact subgroup of ![]() $G(F_v)$. We define positive constants
$G(F_v)$. We define positive constants ![]() $C_{G}$ by
$C_{G}$ by
Local doubling zeta integrals are defined as follows. Let ![]() $I(s)$ denote the degenerate principal series representation of
$I(s)$ denote the degenerate principal series representation of ![]() $\widetilde {G}(\mathbb {A})$ defined by
$\widetilde {G}(\mathbb {A})$ defined by
where ![]() $\widetilde {P}$ denotes the Siegel parabolic subgroup of
$\widetilde {P}$ denotes the Siegel parabolic subgroup of ![]() $\widetilde {G}$. Then for each place
$\widetilde {G}$. Then for each place ![]() $v$, we define a local zeta integral by
$v$, we define a local zeta integral by
for ![]() $\Phi _v\in I(s)$,
$\Phi _v\in I(s)$, ![]() $f_{1,v},f_{2,v}\in V_{\pi _v}$, where
$f_{1,v},f_{2,v}\in V_{\pi _v}$, where ![]() $G^1=\{g\in G:\lambda (g)=1\}$. The integral converges absolutely at
$G^1=\{g\in G:\lambda (g)=1\}$. The integral converges absolutely at ![]() $s=\frac {1}{2}$ when
$s=\frac {1}{2}$ when ![]() $\Phi _v \in I_v(s)$ is a holomorphic section by [Reference Piatetski-Shapiro and RallisPR, Proposition 6.4] (see also [Reference Gan and IchinoGI11, Lemma 6.5]). Moreover, when we define a map
$\Phi _v \in I_v(s)$ is a holomorphic section by [Reference Piatetski-Shapiro and RallisPR, Proposition 6.4] (see also [Reference Gan and IchinoGI11, Lemma 6.5]). Moreover, when we define a map ![]() $\mathcal {S}( \widetilde {X}^\nabla (\mathbb {A})) \ni \varphi \mapsto [\varphi ]\in I (\frac {1}{2})$ by
$\mathcal {S}( \widetilde {X}^\nabla (\mathbb {A})) \ni \varphi \mapsto [\varphi ]\in I (\frac {1}{2})$ by
we may naturally extend ![]() $[\varphi ]$ to a holomorphic section in
$[\varphi ]$ to a holomorphic section in ![]() $I(s)$.
$I(s)$.
By an argument similar to that in the proof of [Reference Gan and IchinoGI11, Proposition 6.10], we may derive the following Rallis inner product formula in the similitude groups case from the one [Reference Gan, Qiu and TakedaGQT14, Theorem 8.1] in the isometry groups case.
Proposition 5.1 Keep the above notation.
Then for decomposable vectors ![]() $f = \otimes f_v \in V_\pi$ and
$f = \otimes f_v \in V_\pi$ and ![]() $\phi = \otimes \phi _v\in V_\omega$, we have
$\phi = \otimes \phi _v\in V_\omega$, we have
Here we recall that ![]() $\Theta _\psi (f; \phi )$ is the theta lift of
$\Theta _\psi (f; \phi )$ is the theta lift of ![]() $f$ to
$f$ to ![]() $\mathrm {GO}_{4,2}$,
$\mathrm {GO}_{4,2}$, ![]() $\langle \, {,} \,\rangle$ denotes the Petersson inner product with respect to the Tamagawa measure and we define
$\langle \, {,} \,\rangle$ denotes the Petersson inner product with respect to the Tamagawa measure and we define
which is equal to ![]() $1$ at almost all places
$1$ at almost all places ![]() $v$ of
$v$ of ![]() $F$ by [Reference Piatetski-Shapiro and RallisPR].
$F$ by [Reference Piatetski-Shapiro and RallisPR].
Recall that ![]() $\theta (f; \phi )$ denotes the restriction of
$\theta (f; \phi )$ denotes the restriction of ![]() $\Theta _\psi (f; \phi )$ to
$\Theta _\psi (f; \phi )$ to ![]() $\mathrm {GSO}_{4,2}(\mathbb {A})$, namely the theta lift of
$\mathrm {GSO}_{4,2}(\mathbb {A})$, namely the theta lift of ![]() $f$ to
$f$ to ![]() $\mathrm {GSO}_{4,2}$. Then as in [Reference Gan and IchinoGI11, Lemma 2.1], we see that
$\mathrm {GSO}_{4,2}$. Then as in [Reference Gan and IchinoGI11, Lemma 2.1], we see that
where the right-hand side denotes the Petersson inner product on ![]() $\mathrm {GSO}_{4,2}$ with respect to the Tamagawa measure. Hence, Proposition 5.1 yields
$\mathrm {GSO}_{4,2}$ with respect to the Tamagawa measure. Hence, Proposition 5.1 yields
5.2 Theta lift from  $G_D$ to
$G_D$ to  $\mathrm {GSU}_{3,D}$
$\mathrm {GSU}_{3,D}$
In this subsection, we shall consider the Rallis inner product formula for the theta lift from ![]() $G_D$ to
$G_D$ to ![]() $\mathrm {GSU}_{3,D}$ as in the previous section. We recall that the formula in the case of isometry groups is proved by Yamana [Reference YamanaYam14, Lemma 10.1] where our case corresponds to (
$\mathrm {GSU}_{3,D}$ as in the previous section. We recall that the formula in the case of isometry groups is proved by Yamana [Reference YamanaYam14, Lemma 10.1] where our case corresponds to (![]() ${\rm I}_3$) with
${\rm I}_3$) with ![]() $m=3, n=2$.
$m=3, n=2$.
Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character. Recall that
$G_D(\mathbb {A})$ with a trivial central character. Recall that ![]() $\mathcal {G}_D$ denotes the subgroup of
$\mathcal {G}_D$ denotes the subgroup of ![]() $G_D(\mathbb {A})$ given by (4.2.3). In this section, assume that
$G_D(\mathbb {A})$ given by (4.2.3). In this section, assume that
for our later use.
Let us recall the notation in § 3.2.2. Thus, ![]() $X_D$ denotes the hermitian space of degree two over
$X_D$ denotes the hermitian space of degree two over ![]() $D$ on which
$D$ on which ![]() $G_D$ acts on the right and
$G_D$ acts on the right and ![]() $Y_D$ denotes the skew-hermitian space of degree three over
$Y_D$ denotes the skew-hermitian space of degree three over ![]() $D$ on which
$D$ on which ![]() $\mathrm {GSU}_{3,D}$ acts on the left. Then
$\mathrm {GSU}_{3,D}$ acts on the left. Then ![]() $Z_D= X_D \otimes _D Y_D$ is a symplectic space over
$Z_D= X_D \otimes _D Y_D$ is a symplectic space over ![]() $F$ by (3.2.1). Here we take
$F$ by (3.2.1). Here we take ![]() $X_{D,\pm }\otimes _D Y_D$ as the polarization and we realize the Weil representation
$X_{D,\pm }\otimes _D Y_D$ as the polarization and we realize the Weil representation ![]() $\omega _\psi$ of
$\omega _\psi$ of ![]() $\mathrm {Mp}(Z_D)(\mathbb {A})$ on
$\mathrm {Mp}(Z_D)(\mathbb {A})$ on ![]() $V_{\omega,D}:=\mathcal {S}((X_{D,+}\otimes _D Y_D)(\mathbb {A}))$.
$V_{\omega,D}:=\mathcal {S}((X_{D,+}\otimes _D Y_D)(\mathbb {A}))$.
Put ![]() $X_D^\Box = X_D \oplus \overline {X_D}$. Then
$X_D^\Box = X_D \oplus \overline {X_D}$. Then ![]() $X_D^\Box$ is naturally a hermitian space over
$X_D^\Box$ is naturally a hermitian space over ![]() $D$. Let
$D$. Let ![]() $\widetilde {G}_D:=\mathrm {GU}(X_D^\Box )$ and we denote by
$\widetilde {G}_D:=\mathrm {GU}(X_D^\Box )$ and we denote by ![]() $\mathbf {G}_D$ a subgroup of
$\mathbf {G}_D$ a subgroup of ![]() $G_D\times G_D$ given by
$G_D\times G_D$ given by
which has a natural embedding ![]() $\iota :\mathbf {G}_D\to \widetilde {G}_D$. We define the canonical pairing
$\iota :\mathbf {G}_D\to \widetilde {G}_D$. We define the canonical pairing ![]() $\mathcal {B}_\omega : V_{\omega,D} \otimes V_{\omega,D}\rightarrow \mathbb {C}$ by
$\mathcal {B}_\omega : V_{\omega,D} \otimes V_{\omega,D}\rightarrow \mathbb {C}$ by
where ![]() ${dx}$ denotes the Tamagawa measure on
${dx}$ denotes the Tamagawa measure on ![]() $(X_{D,+} \otimes Y_D)(\mathbb {A})$.
$(X_{D,+} \otimes Y_D)(\mathbb {A})$.
Let ![]() $\widetilde {Z}_D = X_D^\Box \otimes Y_D$ and we take a polarization
$\widetilde {Z}_D = X_D^\Box \otimes Y_D$ and we take a polarization ![]() $\widetilde {Z}_D=\widetilde {Z}_{D,+}\oplus \widetilde {Z}_{D,-}$ with
$\widetilde {Z}_D=\widetilde {Z}_{D,+}\oplus \widetilde {Z}_{D,-}$ with
where the double sign corresponds. Let us denote by ![]() $\widetilde {\omega }_\psi$ the Weil representation of
$\widetilde {\omega }_\psi$ the Weil representation of ![]() $\mathrm {Mp}(\widetilde {Z}_D)(\mathbb {A})$ on
$\mathrm {Mp}(\widetilde {Z}_D)(\mathbb {A})$ on ![]() $\mathcal {S}( \widetilde {Z}_{D,+}(\mathbb {A}))$. On the other hand, let
$\mathcal {S}( \widetilde {Z}_{D,+}(\mathbb {A}))$. On the other hand, let
Then we have a natural isomorphism
by which we regard ![]() $\mathcal {S}( \widetilde {X}_D^\nabla (\mathbb {A}))$ as a representation of
$\mathcal {S}( \widetilde {X}_D^\nabla (\mathbb {A}))$ as a representation of ![]() $\mathrm {Mp}(Z_D)(\mathbb {A}) \times \mathrm {Mp}(Z_D)(\mathbb {A})$. Meanwhile, we may realize
$\mathrm {Mp}(Z_D)(\mathbb {A}) \times \mathrm {Mp}(Z_D)(\mathbb {A})$. Meanwhile, we may realize ![]() $\widetilde {\omega }_\psi$ on
$\widetilde {\omega }_\psi$ on ![]() $\mathcal {S}(\widetilde {X}_D^\nabla (\mathbb {A}) )$ and indeed we have an isomorphism
$\mathcal {S}(\widetilde {X}_D^\nabla (\mathbb {A}) )$ and indeed we have an isomorphism
as representations of ![]() $\mathrm {Mp}(\widetilde {Z}_D)(\mathbb {A})$ such that
$\mathrm {Mp}(\widetilde {Z}_D)(\mathbb {A})$ such that
Let us define Petersson inner products on ![]() $G_D(\mathbb {A})$ and
$G_D(\mathbb {A})$ and ![]() $G_D(\mathbb {A})^+$ as follows. For
$G_D(\mathbb {A})^+$ as follows. For ![]() $f_1, f_2 \in V_{\pi _D}$, we define the Petersson inner product
$f_1, f_2 \in V_{\pi _D}$, we define the Petersson inner product ![]() $(\, {,}\,)_{\pi _D}$ on
$(\, {,}\,)_{\pi _D}$ on ![]() $G_D(\mathbb {A})$ by
$G_D(\mathbb {A})$ by
where ![]() $dg$ denotes the Tamagawa measure. Then regarding
$dg$ denotes the Tamagawa measure. Then regarding ![]() $f_1, f_2$ as automorphic forms on
$f_1, f_2$ as automorphic forms on ![]() $G_D(\mathbb {A})^+$, we define
$G_D(\mathbb {A})^+$, we define
where the measure ![]() $dh$ is normalized so that
$dh$ is normalized so that
Then from our assumption (5.2.1) on ![]() $\pi _D$, as in [Reference Gan and IchinoGI11, Lemma 6.3], we see that
$\pi _D$, as in [Reference Gan and IchinoGI11, Lemma 6.3], we see that
since ![]() $\mathrm {Vol}(\mathbb {A}^\times G_D(F) \backslash G_D(\mathbb {A})) =2$. For each place
$\mathrm {Vol}(\mathbb {A}^\times G_D(F) \backslash G_D(\mathbb {A})) =2$. For each place ![]() $v$ of
$v$ of ![]() $F$, we take a hermitian
$F$, we take a hermitian ![]() $G_D(F_v)$-invariant local pairing
$G_D(F_v)$-invariant local pairing ![]() $(\, {,}\,)_{\pi _{D,v}}$ of
$(\, {,}\,)_{\pi _{D,v}}$ of ![]() $\pi _{D,v}$ so that
$\pi _{D,v}$ so that
As in the previous section, we choose local Haar measures ![]() $dg_v$ on
$dg_v$ on ![]() $G_D(F_v)$ at each place
$G_D(F_v)$ at each place ![]() $v$ of
$v$ of ![]() $F$ and we have
$F$ and we have
for some positive constant ![]() $C_{G_D}$.
$C_{G_D}$.
Local doubling zeta integrals are defined as follows. Let ![]() $I_D(s)$ denote the degenerate principal series representation of
$I_D(s)$ denote the degenerate principal series representation of ![]() $\widetilde {G}_D(\mathbb {A})$ defined by
$\widetilde {G}_D(\mathbb {A})$ defined by
where ![]() $\widetilde {P}_D$ denotes the Siegel parabolic subgroup of
$\widetilde {P}_D$ denotes the Siegel parabolic subgroup of ![]() $\widetilde {G}_D$. Then for each place
$\widetilde {G}_D$. Then for each place ![]() $v$, we define a local zeta integral for
$v$, we define a local zeta integral for ![]() $\Phi _v\in I_{D,v}(s)$,
$\Phi _v\in I_{D,v}(s)$, ![]() $f_{1,v},f_{2,v}\in V_{\pi _{D,v}}$ by
$f_{1,v},f_{2,v}\in V_{\pi _{D,v}}$ by
where ![]() $G_D^1=\{g\in G_D:\lambda (g)=1\}$. The integral converges absolutely at
$G_D^1=\{g\in G_D:\lambda (g)=1\}$. The integral converges absolutely at ![]() $s=\frac {1}{2}$ when
$s=\frac {1}{2}$ when ![]() $\Phi _v \in I_{D,v}(s)$ is a holomorphic section by [Reference Piatetski-Shapiro and RallisPR, Proposition 6.4] (see also [Reference Gan and IchinoGI11, Lemma 6.5]). Moreover, when we define a map
$\Phi _v \in I_{D,v}(s)$ is a holomorphic section by [Reference Piatetski-Shapiro and RallisPR, Proposition 6.4] (see also [Reference Gan and IchinoGI11, Lemma 6.5]). Moreover, when we define a map ![]() $\mathcal {S}( \widetilde {X}_D^\nabla (\mathbb {A})) \ni \varphi \mapsto [\varphi ]\in I_D (\frac {1}{2})$ by
$\mathcal {S}( \widetilde {X}_D^\nabla (\mathbb {A})) \ni \varphi \mapsto [\varphi ]\in I_D (\frac {1}{2})$ by
we may naturally extend ![]() $[\varphi ]$ to a holomorphic section in
$[\varphi ]$ to a holomorphic section in ![]() $I_D(s)$.
$I_D(s)$.
By an argument similar to that in the proof of [Reference Gan and IchinoGI11, Proposition 6.10], we may derive the following Rallis inner product formula in the similitude groups case from that [Reference YamanaYam13, Theorem 2] in the isometry groups case.
Proposition 5.2 Keep the above notation.
Then for decomposable vectors ![]() $f = \otimes f_v \in V_{\pi _D}$ and
$f = \otimes f_v \in V_{\pi _D}$ and ![]() $\phi = \otimes \phi _v\in V_{\omega,D}$, we have
$\phi = \otimes \phi _v\in V_{\omega,D}$, we have
Here recall that ![]() $\theta _\psi (f; \phi )$ is the theta lift of
$\theta _\psi (f; \phi )$ is the theta lift of ![]() $f$ to
$f$ to ![]() $\mathrm {GSU}_{3,D}$,
$\mathrm {GSU}_{3,D}$, ![]() $\langle \, {,}\,\rangle$ denotes the Petersson inner product with respect to the Tamagawa measure and we define
$\langle \, {,}\,\rangle$ denotes the Petersson inner product with respect to the Tamagawa measure and we define
 \begin{align*} Z_v^\sharp \bigg(\frac{1}{2}, [\delta(\phi_v \otimes \phi_v)], f_v, f_v \bigg) &:= \frac{1}{(f_v, f_v)_{\pi_{D, v}}}\frac{L(3, \chi_{E_v / F_v}) L(2, \mathbf{1}_v) L(4, \mathbf{1}_v) }{L(1, \pi_v, \mathrm{std} \otimes\chi_{E_v / F_v})}\\ &\quad \times Z_v \bigg(\frac{1}{2}, [\delta(\phi_v \otimes \phi_v)], f_v, f_v \bigg), \end{align*}
\begin{align*} Z_v^\sharp \bigg(\frac{1}{2}, [\delta(\phi_v \otimes \phi_v)], f_v, f_v \bigg) &:= \frac{1}{(f_v, f_v)_{\pi_{D, v}}}\frac{L(3, \chi_{E_v / F_v}) L(2, \mathbf{1}_v) L(4, \mathbf{1}_v) }{L(1, \pi_v, \mathrm{std} \otimes\chi_{E_v / F_v})}\\ &\quad \times Z_v \bigg(\frac{1}{2}, [\delta(\phi_v \otimes \phi_v)], f_v, f_v \bigg), \end{align*}
which is equal to ![]() $1$ at almost all places
$1$ at almost all places ![]() $v$ of
$v$ of ![]() $F$ by [Reference Piatetski-Shapiro and RallisPR].
$F$ by [Reference Piatetski-Shapiro and RallisPR].
6. Explicit formula for Bessel periods on  $\mathrm {GU}(4)$
$\mathrm {GU}(4)$
Let ![]() $\mathrm {GU}(4)$ stand for one of
$\mathrm {GU}(4)$ stand for one of ![]() $\mathrm {GU}_{2,2}$ or
$\mathrm {GU}_{2,2}$ or ![]() $\mathrm {GU}_{3,1}$. In [Reference Furusawa and MorimotoFM22], the explicit formula for the Bessel periods on
$\mathrm {GU}_{3,1}$. In [Reference Furusawa and MorimotoFM22], the explicit formula for the Bessel periods on ![]() $\mathrm {GU}(4)$ is proved under the assumption that the explicit formula for the Whittaker periods on
$\mathrm {GU}(4)$ is proved under the assumption that the explicit formula for the Whittaker periods on ![]() $\mathrm {GU}_{2,2}$ holds. In this section we shall show that this assumption is indeed satisfied in the cases we need, from the explicit formula for the Whittaker periods on
$\mathrm {GU}_{2,2}$ holds. In this section we shall show that this assumption is indeed satisfied in the cases we need, from the explicit formula for the Whittaker periods on ![]() $G=\mathrm {GSp}_2$, which, in turn, will be proved in Appendix A. Thus, the explicit formula for the Bessel periods on
$G=\mathrm {GSp}_2$, which, in turn, will be proved in Appendix A. Thus, the explicit formula for the Bessel periods on ![]() $\mathrm {GU}(4)$ holds by [Reference Furusawa and MorimotoFM22], in the cases which we need for the proof of Theorem 1.2.
$\mathrm {GU}(4)$ holds by [Reference Furusawa and MorimotoFM22], in the cases which we need for the proof of Theorem 1.2.
6.1 Explicit formulas
Let ![]() $(\pi, V_{\pi })$ be an irreducible cuspidal tempered globally generic automorphic representation of
$(\pi, V_{\pi })$ be an irreducible cuspidal tempered globally generic automorphic representation of ![]() $G(\mathbb {A})$ such that
$G(\mathbb {A})$ such that ![]() $\pi |_{\mathcal {G}}$ is irreducible. We recall that the subgroup
$\pi |_{\mathcal {G}}$ is irreducible. We recall that the subgroup ![]() $\mathcal {G}$ of
$\mathcal {G}$ of ![]() $G(\mathbb {A})$ is defined by (5.1.1). Let
$G(\mathbb {A})$ is defined by (5.1.1). Let ![]() $\pi ^\circ$ denote the unique generic irreducible constituent of
$\pi ^\circ$ denote the unique generic irreducible constituent of ![]() $\pi |_{G(\mathbb {A})^+}$. Let
$\pi |_{G(\mathbb {A})^+}$. Let ![]() $(\Sigma, V_\Sigma )$ denote the theta lift of
$(\Sigma, V_\Sigma )$ denote the theta lift of ![]() $\pi ^\circ$ to
$\pi ^\circ$ to ![]() $\mathrm {GSO}_{4,2}(\mathbb {A})$. Then as in [Reference MorimotoMor14a, Proposition 3.3], we know that
$\mathrm {GSO}_{4,2}(\mathbb {A})$. Then as in [Reference MorimotoMor14a, Proposition 3.3], we know that ![]() $\Sigma$ is an irreducible globally generic cuspidal tempered automorphic representation. Here we prove the explicit formula for the Whittaker periods for
$\Sigma$ is an irreducible globally generic cuspidal tempered automorphic representation. Here we prove the explicit formula for the Whittaker periods for ![]() $\Sigma$ assuming the explicit formula for the Whittaker periods for
$\Sigma$ assuming the explicit formula for the Whittaker periods for ![]() $\pi$.
$\pi$.
Let us recall some notation. Let ![]() $X, Y, Y_0$ and
$X, Y, Y_0$ and ![]() $Z$ be as in § 3.1.2 and we use a polarization
$Z$ be as in § 3.1.2 and we use a polarization ![]() $Z = Z_+ \oplus Z_-$ with
$Z = Z_+ \oplus Z_-$ with
where the double sign corresponds. We write ![]() $z_+=(a_1, a_2; b_1, b_2)$ when
$z_+=(a_1, a_2; b_1, b_2)$ when
Recall that the unipotent subgroups ![]() $N_0$,
$N_0$, ![]() $N_1$ and
$N_1$ and ![]() $N_2$ of
$N_2$ of ![]() $\mathrm {GSO}_{4,2}$ are defined by (3.1.10), (3.1.11) and (3.1.12), respectively. Let us define an unipotent subgroup
$\mathrm {GSO}_{4,2}$ are defined by (3.1.10), (3.1.11) and (3.1.12), respectively. Let us define an unipotent subgroup ![]() $\tilde {U}$ of
$\tilde {U}$ of ![]() $\mathrm {GSO}_{4,2}$ by
$\mathrm {GSO}_{4,2}$ by
 \begin{equation} \tilde{U} := \left\{\tilde{u}(b):= \begin{pmatrix} 1 & -{}^{t}\widetilde{X} S_1 & 0\\ 0 & 1_4 & \widetilde{X}\\ 0 & 0 & 1 \end{pmatrix}: \widetilde{X} = \begin{pmatrix} 0\\0\\0\\-b\end{pmatrix}\right\}, \end{equation}
\begin{equation} \tilde{U} := \left\{\tilde{u}(b):= \begin{pmatrix} 1 & -{}^{t}\widetilde{X} S_1 & 0\\ 0 & 1_4 & \widetilde{X}\\ 0 & 0 & 1 \end{pmatrix}: \widetilde{X} = \begin{pmatrix} 0\\0\\0\\-b\end{pmatrix}\right\}, \end{equation}
where ![]() $S_1$ is given by (2.1.2). Let
$S_1$ is given by (2.1.2). Let
Then ![]() $U$ is a maximal unipotent subgroup of
$U$ is a maximal unipotent subgroup of ![]() $\mathrm {GSO}_{4,2}$ and we have
$\mathrm {GSO}_{4,2}$ and we have
Then we define a non-degenerate character ![]() $\psi _U$ of
$\psi _U$ of ![]() $U(\mathbb {A})$ by
$U(\mathbb {A})$ by
By [Reference MorimotoMor14a, Proposition 3.3], ![]() $\Sigma$ is
$\Sigma$ is ![]() $\psi _U$-generic. Namely
$\psi _U$-generic. Namely
is not identically zero on ![]() $V_\Sigma$. Now we regard
$V_\Sigma$. Now we regard ![]() $\Sigma$ as an automorphic representation of
$\Sigma$ as an automorphic representation of ![]() $\mathrm {GU}_{2,2}$ by the accidental isomorphism (2.2.6) and let
$\mathrm {GU}_{2,2}$ by the accidental isomorphism (2.2.6) and let ![]() $\Pi _{\Sigma } =\Pi _{1}^\prime \boxplus \cdots \boxplus \Pi _\ell ^\prime$ denote the base change lift of
$\Pi _{\Sigma } =\Pi _{1}^\prime \boxplus \cdots \boxplus \Pi _\ell ^\prime$ denote the base change lift of ![]() $\Sigma \mid _{\mathrm {U}_{2,2}}$ to
$\Sigma \mid _{\mathrm {U}_{2,2}}$ to ![]() $\mathrm {GL}_4(\mathbb {A}_E)$ where
$\mathrm {GL}_4(\mathbb {A}_E)$ where ![]() $\Pi _i^\prime$ is an irreducible cuspidal automorphic representations of
$\Pi _i^\prime$ is an irreducible cuspidal automorphic representations of ![]() $\mathrm {GL}_{m_i}(\mathbb {A}_E)$. Here the existence of
$\mathrm {GL}_{m_i}(\mathbb {A}_E)$. Here the existence of ![]() $\Pi _\Sigma$ follows from [Reference Kaletha, Minguez, Shin and WhiteKMSW14].
$\Pi _\Sigma$ follows from [Reference Kaletha, Minguez, Shin and WhiteKMSW14].
Recall that in § 5.1, the Petersson inner products on ![]() $G(\mathbb {A})$ and
$G(\mathbb {A})$ and ![]() $\mathrm {GSO}_{4,2}(\mathbb {A})$ using the Tamagawa measures, denoted respectively as
$\mathrm {GSO}_{4,2}(\mathbb {A})$ using the Tamagawa measures, denoted respectively as ![]() $(\, {,}\,)$ and
$(\, {,}\,)$ and ![]() $\langle \, {,}\,\rangle$, are introduced. Moreover at each place
$\langle \, {,}\,\rangle$, are introduced. Moreover at each place ![]() $v$ of
$v$ of ![]() $F$, we choose and fix an
$F$, we choose and fix an ![]() $G(F_v)$-invariant hermitian inner product
$G(F_v)$-invariant hermitian inner product ![]() $(\,{,}\,)_v$ on
$(\,{,}\,)_v$ on ![]() $V_{\pi ^\circ _v}$ so that the decomposition formula (5.1.3) holds. Similarly at each place
$V_{\pi ^\circ _v}$ so that the decomposition formula (5.1.3) holds. Similarly at each place ![]() $v$, we choose and fix a
$v$, we choose and fix a ![]() $\mathrm {GSO}_{4,2}(F_v)$-invariant hermitian inner product
$\mathrm {GSO}_{4,2}(F_v)$-invariant hermitian inner product ![]() $\langle \,{,}\,\rangle _v$ on
$\langle \,{,}\,\rangle _v$ on ![]() $V_{\Sigma _v}$ so that the decomposition formula
$V_{\Sigma _v}$ so that the decomposition formula
holds.
Then as in § 2.4, at each place ![]() $v$ of
$v$ of ![]() $F$, we may define a local period
$F$, we may define a local period ![]() $\mathcal {W}_v(\varphi _v)$ for
$\mathcal {W}_v(\varphi _v)$ for ![]() $\varphi _v \in V_{\Sigma _v}$ by the stable integral
$\varphi _v \in V_{\Sigma _v}$ by the stable integral
when ![]() $v$ is finite. When
$v$ is finite. When ![]() $v$ is archimedean, we use the Fourier transform to define
$v$ is archimedean, we use the Fourier transform to define ![]() $\mathcal {W}_v(\varphi _v)$. See [Reference LiuLiu16, Propositions 3.5, 3.15] for the details.
$\mathcal {W}_v(\varphi _v)$. See [Reference LiuLiu16, Propositions 3.5, 3.15] for the details.
We shall prove the following theorem, namely the explicit formula for the Whittaker periods on ![]() $V_\Sigma$, in § 6.2.
$V_\Sigma$, in § 6.2.
Theorem 6.1 For a non-zero decomposable vector ![]() $\varphi = \otimes \varphi _v \in V_\Sigma$, we have
$\varphi = \otimes \varphi _v \in V_\Sigma$, we have
 \begin{equation} \frac{|W^{\psi_U}(\varphi)|^2}{ \langle \varphi, \varphi \rangle} = \frac{1}{2^\ell}\cdot \frac{\prod_{j=1}^4 L (j, \chi_{E}^j)}{L (1, \Pi_{\Sigma}, \mathrm{As}^+)} \cdot \prod_v \mathcal{W}_v^\circ(\varphi_v), \end{equation}
\begin{equation} \frac{|W^{\psi_U}(\varphi)|^2}{ \langle \varphi, \varphi \rangle} = \frac{1}{2^\ell}\cdot \frac{\prod_{j=1}^4 L (j, \chi_{E}^j)}{L (1, \Pi_{\Sigma}, \mathrm{As}^+)} \cdot \prod_v \mathcal{W}_v^\circ(\varphi_v), \end{equation}where
 \[ \mathcal{W}_v^\circ(\varphi_v):=\frac{L(1,\Pi_{\Sigma_v}, \mathrm{As}^+)}{ \prod_{j=1}^4 L (j, \chi_{E_v}^j)}\cdot \mathcal{W}_v(\varphi_v). \]
\[ \mathcal{W}_v^\circ(\varphi_v):=\frac{L(1,\Pi_{\Sigma_v}, \mathrm{As}^+)}{ \prod_{j=1}^4 L (j, \chi_{E_v}^j)}\cdot \mathcal{W}_v(\varphi_v). \]
Here we note that ![]() $\mathcal {W}_v^\circ (\varphi _v) = 1$ at almost all places
$\mathcal {W}_v^\circ (\varphi _v) = 1$ at almost all places ![]() $v$ by Lapid and Mao [Reference Lapid and MaoLM15].
$v$ by Lapid and Mao [Reference Lapid and MaoLM15].
Before proceeding to the proof of Theorem 6.1, by assuming it, we prove the following theorem, namely the explicit formula for the Bessel periods on ![]() $\mathrm {GU}(4)$.
$\mathrm {GU}(4)$.
Theorem 6.2 Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of ![]() $G_D(\mathbb {A})$ with trivial central character. Suppose that
$G_D(\mathbb {A})$ with trivial central character. Suppose that ![]() $\pi$ has the
$\pi$ has the ![]() $(\xi,\Lambda,\psi )$-Bessel period and that
$(\xi,\Lambda,\psi )$-Bessel period and that ![]() $\pi$ is neither of type I-A nor type I-B. Let
$\pi$ is neither of type I-A nor type I-B. Let ![]() $\pi _+^B$ denote the unique irreducible constituent of
$\pi _+^B$ denote the unique irreducible constituent of ![]() $\pi |_{G_D(\mathbb {A})^+}$ which has the
$\pi |_{G_D(\mathbb {A})^+}$ which has the ![]() $(\xi,\Lambda,\psi )$-Bessel period. We denote by
$(\xi,\Lambda,\psi )$-Bessel period. We denote by ![]() $(\sigma, V_\sigma )$ the theta lift of
$(\sigma, V_\sigma )$ the theta lift of ![]() $\pi _+^B$ to
$\pi _+^B$ to ![]() $\mathrm {GSU}_{3,D}$, which is an irreducible cuspidal automorphic representation by Lemmas 4.1 and 4.4.
$\mathrm {GSU}_{3,D}$, which is an irreducible cuspidal automorphic representation by Lemmas 4.1 and 4.4.
Then for a non-zero decomposable vector ![]() $\varphi = \otimes \varphi _v \in V_\sigma$, we have
$\varphi = \otimes \varphi _v \in V_\sigma$, we have
 \[ \frac{|\mathcal{B}_{X, \psi. \Lambda}(\varphi)|^2}{(\varphi, \varphi)} =\frac{1}{2^\ell} \bigg(\prod_{j=1}^4 L(1, \chi_E^j)\bigg) \frac{L (\frac{1}{2}, \sigma \times \Lambda^{-1})}{L(1, \pi, \mathrm{std} \otimes \chi_E) L(1, \chi_E)} \prod_v \alpha_{\Lambda_v, \psi_{X, v}}^{\natural}(\varphi_v), \]
\[ \frac{|\mathcal{B}_{X, \psi. \Lambda}(\varphi)|^2}{(\varphi, \varphi)} =\frac{1}{2^\ell} \bigg(\prod_{j=1}^4 L(1, \chi_E^j)\bigg) \frac{L (\frac{1}{2}, \sigma \times \Lambda^{-1})}{L(1, \pi, \mathrm{std} \otimes \chi_E) L(1, \chi_E)} \prod_v \alpha_{\Lambda_v, \psi_{X, v}}^{\natural}(\varphi_v), \]
where
 \[ \alpha_{\Lambda_v, \psi_{X, v}}^{\natural}(\varphi_v) = \bigg(\prod_{j=1}^4 L(1, \chi_{E, v}^j)\bigg)^{-1} \frac{L(1, \pi_v, \mathrm{std} \otimes \chi_{E,v}) L(1, \chi_{E_v})}{L (\frac{1}{2}, \sigma_v \times \Lambda_v^{-1})}\cdot \frac{\alpha_{\Lambda_v, \psi_{X, v}}(\varphi_v)}{(\varphi_v, \varphi_v)_v} \]
\[ \alpha_{\Lambda_v, \psi_{X, v}}^{\natural}(\varphi_v) = \bigg(\prod_{j=1}^4 L(1, \chi_{E, v}^j)\bigg)^{-1} \frac{L(1, \pi_v, \mathrm{std} \otimes \chi_{E,v}) L(1, \chi_{E_v})}{L (\frac{1}{2}, \sigma_v \times \Lambda_v^{-1})}\cdot \frac{\alpha_{\Lambda_v, \psi_{X, v}}(\varphi_v)}{(\varphi_v, \varphi_v)_v} \]
and ![]() $X\in D^\times$ is taken so that
$X\in D^\times$ is taken so that ![]() $\xi =S_X$ in (3.2.5).
$\xi =S_X$ in (3.2.5).
Proof. Let us regard ![]() $\sigma$ as an automorphic representation of
$\sigma$ as an automorphic representation of ![]() $\mathrm {GU}(4)$ with trivial central character via the accidental isomorphisms
$\mathrm {GU}(4)$ with trivial central character via the accidental isomorphisms ![]() $\Phi$ (2.2.6) or
$\Phi$ (2.2.6) or ![]() $\Phi _D$ (2.2.5), depending whether
$\Phi _D$ (2.2.5), depending whether ![]() $D$ is split or not. Let
$D$ is split or not. Let ![]() $\theta (\sigma ) = \Theta _{\psi, (\Lambda ^{-1},\Lambda ^{-1})}(\sigma )$ denote the theta lift of
$\theta (\sigma ) = \Theta _{\psi, (\Lambda ^{-1},\Lambda ^{-1})}(\sigma )$ denote the theta lift of ![]() $\sigma$ to
$\sigma$ to ![]() $\mathrm {GU}_{2,2}$ with respect to
$\mathrm {GU}_{2,2}$ with respect to ![]() $\psi$ and
$\psi$ and ![]() $(\Lambda ^{-1}, \Lambda ^{-1})$. By [Reference Furusawa and MorimotoFM22, Proposition 3.1],
$(\Lambda ^{-1}, \Lambda ^{-1})$. By [Reference Furusawa and MorimotoFM22, Proposition 3.1], ![]() $\theta (\sigma )$ is globally generic and, in particular, non-zero. By the same argument as in the proof of [Reference Furusawa and MorimotoFM22, Theorem 1], we see that
$\theta (\sigma )$ is globally generic and, in particular, non-zero. By the same argument as in the proof of [Reference Furusawa and MorimotoFM22, Theorem 1], we see that ![]() $\theta (\sigma )$ is cuspidal and hence irreducible by Remarks 3.1 and 3.2. Moreover by the unramified computations in [Reference KudlaKud86] and [Reference MorimotoMor14a, (3.6)], we see that
$\theta (\sigma )$ is cuspidal and hence irreducible by Remarks 3.1 and 3.2. Moreover by the unramified computations in [Reference KudlaKud86] and [Reference MorimotoMor14a, (3.6)], we see that ![]() $L^S(s, \Sigma, \wedge _t^2)$ has a pole at
$L^S(s, \Sigma, \wedge _t^2)$ has a pole at ![]() $s=1$ when
$s=1$ when ![]() $S$ is a sufficiently large finite set of places of
$S$ is a sufficiently large finite set of places of ![]() $F$ containing all archimedean places, where
$F$ containing all archimedean places, where ![]() $L^S(s, \Sigma, \wedge _t^2)$ denotes the twisted exterior square
$L^S(s, \Sigma, \wedge _t^2)$ denotes the twisted exterior square ![]() $L$-function of
$L$-function of ![]() $\Sigma$ (see [Reference Furusawa and MorimotoFM13b, § 2.1.1] for the definition). Since
$\Sigma$ (see [Reference Furusawa and MorimotoFM13b, § 2.1.1] for the definition). Since ![]() $\theta (\sigma )$ is generic, [Reference Furusawa and MorimotoFM13b, Theorem 4.1] implies that it has the unitary Shalika period defined in [Reference Furusawa and MorimotoFM13b, (2.5)]. Then, by [Reference MorimotoMor14a, Theorem B], the theta lift of
$\theta (\sigma )$ is generic, [Reference Furusawa and MorimotoFM13b, Theorem 4.1] implies that it has the unitary Shalika period defined in [Reference Furusawa and MorimotoFM13b, (2.5)]. Then, by [Reference MorimotoMor14a, Theorem B], the theta lift of ![]() $\theta (\sigma )$ to
$\theta (\sigma )$ to ![]() $G(\mathbb {A})^+$, which we denote by
$G(\mathbb {A})^+$, which we denote by ![]() $(\pi _{+}^\prime, V_{\pi _{+}^\prime })$, is an irreducible cuspidal globally generic automorphic representation of
$(\pi _{+}^\prime, V_{\pi _{+}^\prime })$, is an irreducible cuspidal globally generic automorphic representation of ![]() $G(\mathbb {A})^+$. We note that
$G(\mathbb {A})^+$. We note that ![]() $\pi _+^B$ is nearly equivalent to
$\pi _+^B$ is nearly equivalent to ![]() $\pi _+^\prime$.
$\pi _+^\prime$.
Let us take an irreducible cuspidal automorphic representation ![]() $(\pi ^\prime, V_{\pi ^\prime })$ of
$(\pi ^\prime, V_{\pi ^\prime })$ of ![]() $G(\mathbb {A})$ such that
$G(\mathbb {A})$ such that ![]() $V_{\pi ^\prime }|_{G(\mathbb {A})^+} \supset V_{\pi _+^\prime }$. Then
$V_{\pi ^\prime }|_{G(\mathbb {A})^+} \supset V_{\pi _+^\prime }$. Then ![]() $\pi ^\prime$ is globally generic. Moreover,
$\pi ^\prime$ is globally generic. Moreover, ![]() $\pi ^\prime \otimes \chi _E$ is not nearly equivalent to
$\pi ^\prime \otimes \chi _E$ is not nearly equivalent to ![]() $\pi ^\prime$ by our assumption on
$\pi ^\prime$ by our assumption on ![]() $\pi$. Hence,
$\pi$. Hence, ![]() $\pi ^\prime |_{\mathcal {G}}$ is irreducible. Thus, we may apply Theorem 6.1, taking
$\pi ^\prime |_{\mathcal {G}}$ is irreducible. Thus, we may apply Theorem 6.1, taking ![]() $\pi ^\circ = \pi ^\prime$ and
$\pi ^\circ = \pi ^\prime$ and ![]() $\Sigma = \theta (\sigma )$, and we obtain the explicit formula for the Whittaker periods on
$\Sigma = \theta (\sigma )$, and we obtain the explicit formula for the Whittaker periods on ![]() $\theta (\sigma )$. Then by [Reference Furusawa and MorimotoFM22, Theorem A.1], the required explicit formula for the Bessel periods follows.
$\theta (\sigma )$. Then by [Reference Furusawa and MorimotoFM22, Theorem A.1], the required explicit formula for the Bessel periods follows.
6.2 Proof of Theorem 6.1
We reduce Theorem 6.1 to a certain local identity in § 6.2.2 and then prove the local identity in § 6.2.3.
As we stated in the beginning of this section, what we do essentially is to deduce the explicit formula (6.1.6) for the Whittaker periods on ![]() $\mathrm {GSO}_{4,2}$ from (6.2.3) below, the one for the Whittaker periods on
$\mathrm {GSO}_{4,2}$ from (6.2.3) below, the one for the Whittaker periods on ![]() $G$.
$G$.
6.2.1 Explicit formula for the Whittaker periods on  $G=\mathrm {GSp}_2$
$G=\mathrm {GSp}_2$
Let ![]() $U_G$ denote the maximal unipotent subgroup of
$U_G$ denote the maximal unipotent subgroup of ![]() $G$. Namely
$G$. Namely
where ![]() $m(h)=\big (\begin{smallmatrix} h & 0 \\0 & {}^{t}h^{-1}\end{smallmatrix}\big )$ for
$m(h)=\big (\begin{smallmatrix} h & 0 \\0 & {}^{t}h^{-1}\end{smallmatrix}\big )$ for ![]() $h\in \mathrm {GL}_2$ and
$h\in \mathrm {GL}_2$ and ![]() $N_2$ denotes the group of upper unipotent matrices in
$N_2$ denotes the group of upper unipotent matrices in ![]() $\mathrm {GL}_2$. Then we define a non-degenerate character
$\mathrm {GL}_2$. Then we define a non-degenerate character ![]() $\psi _{U_G}$ of
$\psi _{U_G}$ of ![]() $U_G(\mathbb {A})$ by
$U_G(\mathbb {A})$ by
Then for an automorphic form ![]() $\phi$ on
$\phi$ on ![]() $G(\mathbb {A})$, we define the Whittaker period
$G(\mathbb {A})$, we define the Whittaker period ![]() $W_{\psi _{U_G}}(\phi )$ of
$W_{\psi _{U_G}}(\phi )$ of ![]() $\phi$ by
$\phi$ by
The following theorem shall be proved in Appendix A.
Theorem 6.3 Suppose that ![]() $(\pi,V_{\pi })$ is an irreducible cuspidal tempered globally generic automorphic representation of
$(\pi,V_{\pi })$ is an irreducible cuspidal tempered globally generic automorphic representation of ![]() $G(\mathbb {A})$. Let
$G(\mathbb {A})$. Let ![]() $\Pi _{\pi } = \Pi _1 \boxplus \cdots \boxplus \Pi _k$ denote the functorial lift of
$\Pi _{\pi } = \Pi _1 \boxplus \cdots \boxplus \Pi _k$ denote the functorial lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GL}_4(\mathbb {A})$.
$\mathrm {GL}_4(\mathbb {A})$.
Then for any non-zero decomposable vector ![]() $\varphi = \otimes \varphi _v \in V_{\pi }$, we have
$\varphi = \otimes \varphi _v \in V_{\pi }$, we have
 \begin{equation} \frac{|W_{\psi_{U_G}}(\varphi)|^2}{(\varphi, \varphi)} = \frac{1}{2^k}\cdot \frac{\prod_{j=1}^2\xi_F(2j)}{L(1, \Pi_{\pi}, \mathrm{Sym}^2)} \cdot \prod_v \mathcal{W}_{G,v}^\circ(\varphi_v). \end{equation}
\begin{equation} \frac{|W_{\psi_{U_G}}(\varphi)|^2}{(\varphi, \varphi)} = \frac{1}{2^k}\cdot \frac{\prod_{j=1}^2\xi_F(2j)}{L(1, \Pi_{\pi}, \mathrm{Sym}^2)} \cdot \prod_v \mathcal{W}_{G,v}^\circ(\varphi_v). \end{equation}
Here ![]() $\mathcal {W}^\circ _{G, v}(\varphi _v)$ is defined by
$\mathcal {W}^\circ _{G, v}(\varphi _v)$ is defined by
 \[ \mathcal{W}^\circ_{G, v}(\varphi_v) =\frac{L(1, \Pi_{\pi, v}, \mathrm{Sym}^2)}{\prod_{j=1}^2 \zeta_{F_v}(2j)} \mathcal{W}_{G, v}(\varphi_v)\label{mathcal W_G} \]
\[ \mathcal{W}^\circ_{G, v}(\varphi_v) =\frac{L(1, \Pi_{\pi, v}, \mathrm{Sym}^2)}{\prod_{j=1}^2 \zeta_{F_v}(2j)} \mathcal{W}_{G, v}(\varphi_v)\label{mathcal W_G} \]
and ![]() $\mathcal {W}_{G, v}(\varphi _v)$ is defined by
$\mathcal {W}_{G, v}(\varphi _v)$ is defined by
when ![]() $v$ is finite and by the Fourier transform when
$v$ is finite and by the Fourier transform when ![]() $v$ is archimedean.
$v$ is archimedean.
6.2.2 Reduction to a local identity
Let us go back to the situation stated in the beginning of § 6.1.
First we note that the unramified computation in [Reference KudlaKud86] implies the following lemma.
Lemma 6.1 There exists a finite set ![]() $S_0$ of places of
$S_0$ of places of ![]() $F$ containing all archimedean places such that for a place
$F$ containing all archimedean places such that for a place ![]() $v\notin S_0$, we have
$v\notin S_0$, we have
Let us recall the following pull-back formula for the Whittaker period on ![]() $\Sigma = \theta _\psi (\pi ^\circ )$.
$\Sigma = \theta _\psi (\pi ^\circ )$.
Proposition 6.1 [Reference MorimotoMor14a, p. 40]
Let ![]() $f \in V_{\pi ^\circ }$ and
$f \in V_{\pi ^\circ }$ and ![]() $\phi \in \mathcal {S}(Z_+(\mathbb {A}))$. Then
$\phi \in \mathcal {S}(Z_+(\mathbb {A}))$. Then
Suppose that ![]() $f=\otimes f_v$ and
$f=\otimes f_v$ and ![]() $\phi =\otimes \phi _v$. Then by an argument similar to that in obtaining [Reference Furusawa and MorimotoFM21, (2.27)], when
$\phi =\otimes \phi _v$. Then by an argument similar to that in obtaining [Reference Furusawa and MorimotoFM21, (2.27)], when ![]() $W_{\psi _{U_G}}(f) \ne 0$, we have
$W_{\psi _{U_G}}(f) \ne 0$, we have
where
when ![]() $\phi = \otimes _v \phi _v$ and
$\phi = \otimes _v \phi _v$ and ![]() $f = \otimes _v f_v$. We also define
$f = \otimes _v f_v$. We also define
 \[ \mathcal{L}_v(\phi_v, f_v): = \frac{\prod_{j=1}^2 \xi_f(2j)}{L(1,\Pi_{\pi, v}, \mathrm{Sym}^2)} \frac{\mathcal{L}_v^\circ(\phi_v, f_v)}{ \mathcal{W}_{G, v}(f_v)}.\label{mathcal L} \]
\[ \mathcal{L}_v(\phi_v, f_v): = \frac{\prod_{j=1}^2 \xi_f(2j)}{L(1,\Pi_{\pi, v}, \mathrm{Sym}^2)} \frac{\mathcal{L}_v^\circ(\phi_v, f_v)}{ \mathcal{W}_{G, v}(f_v)}.\label{mathcal L} \]
Here the measures are taken as the following. Let ![]() $dg_v$ be the measure on
$dg_v$ be the measure on ![]() $G^1(F_v)$ defined by the gauge form and
$G^1(F_v)$ defined by the gauge form and ![]() $dn_v$ the measure on
$dn_v$ the measure on ![]() $N(F_v)$ defined in the manner stated in § 1.2. Then we take the measure
$N(F_v)$ defined in the manner stated in § 1.2. Then we take the measure ![]() $dg_{1,v}$ on
$dg_{1,v}$ on ![]() $N(F_v) \backslash G^1(F_v)$ so that
$N(F_v) \backslash G^1(F_v)$ so that ![]() $dg_v=dn_v \, dg_{1,v}$.
$dg_v=dn_v \, dg_{1,v}$.
Let ![]() $\Theta (\pi _v^\circ,\psi _v):=\operatorname {Hom}_{G(F_v)^+} (\Omega _{\psi _v},\bar {\pi }_v^\circ )$ where
$\Theta (\pi _v^\circ,\psi _v):=\operatorname {Hom}_{G(F_v)^+} (\Omega _{\psi _v},\bar {\pi }_v^\circ )$ where ![]() $\Omega _{\psi _v}$ is the extended local Weil representation of
$\Omega _{\psi _v}$ is the extended local Weil representation of ![]() $G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$ realized on
$G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$ realized on ![]() $\mathcal {S}(Z_+(F_v))$, the space of Schwartz–Bruhat functions on
$\mathcal {S}(Z_+(F_v))$, the space of Schwartz–Bruhat functions on ![]() $Z_+(F_v)$. We recall that the action of
$Z_+(F_v)$. We recall that the action of ![]() $G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$ on
$G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$ on ![]() $\mathcal {S}(Z_+(F_v))$ via
$\mathcal {S}(Z_+(F_v))$ via ![]() $\Omega _{\psi _v}$ is defined as in the global case (see, e.g., [Reference MorimotoMor14a, 2.2]). We also recall that for
$\Omega _{\psi _v}$ is defined as in the global case (see, e.g., [Reference MorimotoMor14a, 2.2]). We also recall that for ![]() $\Sigma =\theta _\psi (\pi ^\circ )$, we have
$\Sigma =\theta _\psi (\pi ^\circ )$, we have ![]() $\Sigma =\otimes _v \Sigma _v$ where
$\Sigma =\otimes _v \Sigma _v$ where ![]() $\Sigma _v=\theta _{\psi _v}(\pi _v^\circ )$ is the local theta lift of
$\Sigma _v=\theta _{\psi _v}(\pi _v^\circ )$ is the local theta lift of ![]() $\pi _v^\circ$.
$\pi _v^\circ$.
Let
be a ![]() $G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$-equivariant linear map, which is unique up to a scalar multiplication. Since the global mapping
$G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$-equivariant linear map, which is unique up to a scalar multiplication. Since the global mapping
is ![]() $G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$-equivariant at any place
$G(F_v)^+ \times \mathrm {GSO}_{4,2}(F_v)$-equivariant at any place ![]() $v$, by the uniqueness of
$v$, by the uniqueness of ![]() $\theta _v$, we may adjust
$\theta _v$, we may adjust ![]() $\{\theta _v\}_v$ so that
$\{\theta _v\}_v$ so that
Then as in [Reference Furusawa and MorimotoFM21, § 2.4], combining Theorem 6.3, the Rallis inner product formula (5.1.4), Lemmas 6.1 and 4.2 and Proposition 6.1, we see that a proof of Theorem 6.1 is reduced to a proof of the following local identity (6.2.5).
Proposition 6.2 Let ![]() $v$ be an arbitrary place of
$v$ be an arbitrary place of ![]() $F$. For a given
$F$. For a given ![]() $f_v \in V_{\pi ^\circ _v}^\infty$ satisfying
$f_v \in V_{\pi ^\circ _v}^\infty$ satisfying ![]() $\mathcal {W}_{G_,v}(f_v) \ne 0$, there exists
$\mathcal {W}_{G_,v}(f_v) \ne 0$, there exists ![]() $\phi _v \in \mathcal {S}(Z_+(F_v))$ such that the local integral
$\phi _v \in \mathcal {S}(Z_+(F_v))$ such that the local integral ![]() $\mathcal {L}_v(\phi _v, f_v)$ converges absolutely,
$\mathcal {L}_v(\phi _v, f_v)$ converges absolutely, ![]() $\mathcal {L}_v(\phi _v, f_v) \ne 0$ and the equality
$\mathcal {L}_v(\phi _v, f_v) \ne 0$ and the equality
holds with respect to the specified local measures.
Let us define a hermitian inner product ![]() $\mathcal {B}_{\omega _v}$ on
$\mathcal {B}_{\omega _v}$ on ![]() $\mathcal {S}(Z_+(F_v))$ by
$\mathcal {S}(Z_+(F_v))$ by
Here on ![]() $Z_+(F_v) \simeq (F_v)^{12}$, we take the product measure of the one on
$Z_+(F_v) \simeq (F_v)^{12}$, we take the product measure of the one on ![]() $F_v$. Then we consider the integral
$F_v$. Then we consider the integral
 \begin{align} Z^{\flat}(f, f^\prime;
\phi, \phi^\prime) &= \int_{G^1(F_v)} \langle \pi_v^\circ(g)
f, f^\prime \rangle_v
\mathcal{B}_{\omega_v}(\omega_{\psi}(g)\phi, \phi^\prime)
\, dg \nonumber\\ &=\int_{G^1(F_v)} \int_{Z_+(F_v)}
\langle \pi_v^\circ(g) f, f^\prime \rangle_v
(\omega_{\psi_v}(g,1)\phi)(z) \overline{\phi^\prime(z)} \,
{dx} \,dg \quad\text{for $f, f^\prime \in
V_{\pi_v^\circ}$}.
\end{align}
\begin{align} Z^{\flat}(f, f^\prime;
\phi, \phi^\prime) &= \int_{G^1(F_v)} \langle \pi_v^\circ(g)
f, f^\prime \rangle_v
\mathcal{B}_{\omega_v}(\omega_{\psi}(g)\phi, \phi^\prime)
\, dg \nonumber\\ &=\int_{G^1(F_v)} \int_{Z_+(F_v)}
\langle \pi_v^\circ(g) f, f^\prime \rangle_v
(\omega_{\psi_v}(g,1)\phi)(z) \overline{\phi^\prime(z)} \,
{dx} \,dg \quad\text{for $f, f^\prime \in
V_{\pi_v^\circ}$}.
\end{align}
The integral (6.2.6) converges absolutely by Yamana [Reference YamanaYam14, Lemma 7.2]. As in Gan and Ichino [Reference Gan and IchinoGI14, 16.5], we may define a ![]() $\mathrm {GSO}_{4,2}(F_v)$-invariant hermitian inner product
$\mathrm {GSO}_{4,2}(F_v)$-invariant hermitian inner product ![]() $\mathcal {B}_{\Sigma _v} : V_{\Sigma _v} \times V_{\Sigma _v} \rightarrow \mathbb {C}$ by
$\mathcal {B}_{\Sigma _v} : V_{\Sigma _v} \times V_{\Sigma _v} \rightarrow \mathbb {C}$ by
Here we note that for ![]() $h \in \mathrm {SO}_{4,2}(F_v)$, we have
$h \in \mathrm {SO}_{4,2}(F_v)$, we have
As in the definition of ![]() $W_v$, we define
$W_v$, we define
Then by an argument similar to that in [Reference Furusawa and MorimotoFM21, 3.2–3.3], indeed word for word, Proposition 6.2 is reduced to the following another local identity, which is regarded as a local pull-back computation of the Whittaker periods with respect to the theta lift.
Proposition 6.3 For any ![]() $f, f^\prime \in V_{\pi _v^\circ }$ and any
$f, f^\prime \in V_{\pi _v^\circ }$ and any ![]() $\phi,\phi ^\prime \in C_c^\infty (Z_+(F_v))$, we have
$\phi,\phi ^\prime \in C_c^\infty (Z_+(F_v))$, we have
 \begin{align} \mathcal{W}_{\psi_U}(\theta(\phi\otimes f), \theta(\phi^\prime\otimes f^\prime)) &= \int_{N(F_v)\backslash G^1(F_v)}\int_{N(F_v)\backslash G^1(F_v)} \nonumber\\ &\quad \times\mathcal{W}_{G,v}(\pi_v^\circ(g)f,\pi_v^\circ(g^\prime)f^\prime) (\omega_{\psi_v}(g,1)\phi)(x_0) \overline{(\omega_{\psi_v}(g^\prime,1)\phi^\prime)(x_0)}\, dg\, dg^\prime. \end{align}
\begin{align} \mathcal{W}_{\psi_U}(\theta(\phi\otimes f), \theta(\phi^\prime\otimes f^\prime)) &= \int_{N(F_v)\backslash G^1(F_v)}\int_{N(F_v)\backslash G^1(F_v)} \nonumber\\ &\quad \times\mathcal{W}_{G,v}(\pi_v^\circ(g)f,\pi_v^\circ(g^\prime)f^\prime) (\omega_{\psi_v}(g,1)\phi)(x_0) \overline{(\omega_{\psi_v}(g^\prime,1)\phi^\prime)(x_0)}\, dg\, dg^\prime. \end{align}Remark 6.1 Since ![]() $\{ g \cdot x_0 : g \in G^1(F_v) \}$ is locally closed in
$\{ g \cdot x_0 : g \in G^1(F_v) \}$ is locally closed in ![]() $Z_+(F_v)$, the mappings
$Z_+(F_v)$, the mappings
are compactly supported and, thus, the right-hand side of (6.2.7) converges absolutely for ![]() $\phi, \phi ^\prime \in C_c^\infty (Z_+(F_v))$.
$\phi, \phi ^\prime \in C_c^\infty (Z_+(F_v))$.
6.2.3 Local pull-back computation
Here we shall prove Proposition 6.3 and, thus, complete our proof of Theorem 6.1.
Since we work over a fixed place ![]() $v$ of
$v$ of ![]() $F$, we shall suppress
$F$, we shall suppress ![]() $v$ from the notation in this subsection, e.g.
$v$ from the notation in this subsection, e.g. ![]() $F$ means
$F$ means ![]() $F_v$. Further, for any algebraic group
$F_v$. Further, for any algebraic group ![]() $K$ over
$K$ over ![]() $F$, we denote its group of
$F$, we denote its group of ![]() $F$-rational points
$F$-rational points ![]() $K(F)$ by
$K(F)$ by ![]() $K$ for simplicity.
$K$ for simplicity.
The case when  $F$ is non-archimedean
$F$ is non-archimedean
Suppose that ![]() $F$ is non-archimedean. From the definition, the local Whittaker period is equal to
$F$ is non-archimedean. From the definition, the local Whittaker period is equal to
 \[ \int_{U}^{\rm st} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, n) \phi)(x) \overline{\phi^\prime(x)} \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}(n)^{-1} \, {dx} \, dg \, dn. \]
\[ \int_{U}^{\rm st} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, n) \phi)(x) \overline{\phi^\prime(x)} \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}(n)^{-1} \, {dx} \, dg \, dn. \]
Recall that we have defined subgroups ![]() $N_0, N_1, N_2$ and
$N_0, N_1, N_2$ and ![]() $\widetilde {U}$ of
$\widetilde {U}$ of ![]() $U$ in (3.1.10), (3.1.11), (3.1.12) and (6.1.1), respectively. Then because of the absolute convergence of the integral (6.2.6), the above local integral can be written as
$U$ in (3.1.10), (3.1.11), (3.1.12) and (6.1.1), respectively. Then because of the absolute convergence of the integral (6.2.6), the above local integral can be written as
 \begin{align} & \int_{\widetilde{U}}^{\rm st} \int_{N}^{\rm st} \int_{N_1} \int_{N_0} \int_{Z_+} \int_{G^1} (\omega_{\psi}(g, u_0 u_1 u_2 \tilde{u}) \phi)(x) \overline{ \phi^\prime(x)} \nonumber\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}(u_2 \tilde{u})^{-1} \, {dx} \, dg \, du_0\, du_1 \, du_2\, d\tilde{u}. \end{align}
\begin{align} & \int_{\widetilde{U}}^{\rm st} \int_{N}^{\rm st} \int_{N_1} \int_{N_0} \int_{Z_+} \int_{G^1} (\omega_{\psi}(g, u_0 u_1 u_2 \tilde{u}) \phi)(x) \overline{ \phi^\prime(x)} \nonumber\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}(u_2 \tilde{u})^{-1} \, {dx} \, dg \, du_0\, du_1 \, du_2\, d\tilde{u}. \end{align} Let us define ![]() $Z_{+, \circ } := \{ (a_1, a_2 ; 0,0) \in Z_+ : a_1\ {\rm and}\ a_2\ {\rm are\ linearly\ independent}\}$. Then since
$Z_{+, \circ } := \{ (a_1, a_2 ; 0,0) \in Z_+ : a_1\ {\rm and}\ a_2\ {\rm are\ linearly\ independent}\}$. Then since ![]() $Z_{+, \circ } \oplus (X_+ \otimes Y_0)$ is open and dense in
$Z_{+, \circ } \oplus (X_+ \otimes Y_0)$ is open and dense in ![]() $Z_+$, we have
$Z_+$, we have
for any ![]() $\Phi \in L^1(Z_+)$. We consider a map
$\Phi \in L^1(Z_+)$. We consider a map ![]() $p : Z_{+, \circ } \rightarrow F$ defined by
$p : Z_{+, \circ } \rightarrow F$ defined by ![]() $p((a_1, a_2; 0, 0)) = \langle a_1, a_2\rangle$. This is clearly surjective. For each
$p((a_1, a_2; 0, 0)) = \langle a_1, a_2\rangle$. This is clearly surjective. For each ![]() $t \in F$, we fix
$t \in F$, we fix ![]() $x_t \in Z_{+, \circ }$ such that
$x_t \in Z_{+, \circ }$ such that ![]() $p(x_t) = t$. Then by Witt's theorem, the fiber
$p(x_t) = t$. Then by Witt's theorem, the fiber ![]() $p^{-1}(x_t)$ of
$p^{-1}(x_t)$ of ![]() $x_t :=(a_1^t, a_2^t; 0, 0)$ is given by
$x_t :=(a_1^t, a_2^t; 0, 0)$ is given by
We may identify this space with ![]() $G^1 / R_t$ as a
$G^1 / R_t$ as a ![]() $G^1$-homogeneous space. Here
$G^1$-homogeneous space. Here ![]() $R_t$ denotes the stabilizer of
$R_t$ denotes the stabilizer of ![]() $x_t$ in
$x_t$ in ![]() $G^1$. From this observation, the following lemma readily follows (cf. [Reference Furusawa and MorimotoFM21, Lemma 3]).
$G^1$. From this observation, the following lemma readily follows (cf. [Reference Furusawa and MorimotoFM21, Lemma 3]).
Lemma 6.2 For each ![]() $x_t \in Z_{+, \circ }$, there exists a Haar measure
$x_t \in Z_{+, \circ }$, there exists a Haar measure ![]() $dr_t$ on
$dr_t$ on ![]() $R_t$ such that
$R_t$ such that
Here ![]() $dg_t$ denotes the quotient measure
$dg_t$ denotes the quotient measure ![]() $dr_t \backslash dg$ on
$dr_t \backslash dg$ on ![]() $R_t \backslash G^1$.
$R_t \backslash G^1$.
Further, we note that the following lemma, which is proved by an argument similar to that for [Reference LiuLiu16, Lemma 3.20] (cf. [Reference Furusawa and MorimotoFM21, Lemma 3]).
Lemma 6.3 For ![]() $\phi _1,\phi _2\in C_c^\infty \big (Z_+\big )$ and
$\phi _1,\phi _2\in C_c^\infty \big (Z_+\big )$ and ![]() $f_1,f_2\in V_{\pi ^\circ }$, let
$f_1,f_2\in V_{\pi ^\circ }$, let
for ![]() $t \in F$. Then the integral is absolutely convergent and is locally constant.
$t \in F$. Then the integral is absolutely convergent and is locally constant.
Remark 6.2 When ![]() $F$ is archimedean, by an argument similar to that for [Reference LiuLiu16, Proposition 3.22], we see that this integral is absolutely convergent and is a continuous function on
$F$ is archimedean, by an argument similar to that for [Reference LiuLiu16, Proposition 3.22], we see that this integral is absolutely convergent and is a continuous function on ![]() $F$ not only for
$F$ not only for ![]() $C_c^\infty (Z_+)$ but also for
$C_c^\infty (Z_+)$ but also for ![]() $\mathcal {S}(Z_+)$.
$\mathcal {S}(Z_+)$.
By Lemma 6.2, the integral (6.2.8) can be written as
 \begin{align*} & \int_{N_0} \int_{F} \int_{R_t \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(g, u_0 h) \phi)(\gamma^{-1} \cdot x_t+z) \overline{\phi^\prime(\gamma^{-1} \cdot x_t+z)} \\ &\quad \times\langle \pi^\circ(g)f, f^\prime \rangle \, dg \, dz \, d\gamma_t \, dt \, du_0. \end{align*}
\begin{align*} & \int_{N_0} \int_{F} \int_{R_t \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(g, u_0 h) \phi)(\gamma^{-1} \cdot x_t+z) \overline{\phi^\prime(\gamma^{-1} \cdot x_t+z)} \\ &\quad \times\langle \pi^\circ(g)f, f^\prime \rangle \, dg \, dz \, d\gamma_t \, dt \, du_0. \end{align*}
Moreover, by the computation in [Reference MorimotoMor14a, § 3.1], we have
Then because of Lemma 6.3, we may apply the Fourier inversion with respect to ![]() $x$ and
$x$ and ![]() $t$, and thus the above integral is equal to
$t$, and thus the above integral is equal to
 \begin{align} & \int_{R_0 \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(g, h) \phi)(\gamma^{-1} \cdot x_0+z) \overline{ \phi^\prime(\gamma^{-1} \cdot x_0+z)} \nonumber\\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle\, dg \, dz \, d\gamma_0 \, dt \, du_0 \nonumber\\ &\quad = \int_{R_0 \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(\gamma g, h) \phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \nonumber\\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle\, dg \, dz \, d\gamma_0. \end{align}
\begin{align} & \int_{R_0 \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(g, h) \phi)(\gamma^{-1} \cdot x_0+z) \overline{ \phi^\prime(\gamma^{-1} \cdot x_0+z)} \nonumber\\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle\, dg \, dz \, d\gamma_0 \, dt \, du_0 \nonumber\\ &\quad = \int_{R_0 \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(\gamma g, h) \phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \nonumber\\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle\, dg \, dz \, d\gamma_0. \end{align}
The support of ![]() $\phi ^\prime (\gamma ^{-1} \cdot x_0+z)$ as a function of
$\phi ^\prime (\gamma ^{-1} \cdot x_0+z)$ as a function of ![]() $X_+ \otimes Y_0$ is compact since
$X_+ \otimes Y_0$ is compact since ![]() $\phi ^\prime \in C_c^\infty (Z_+)$. Therefore this integral converges absolutely and is equal to
$\phi ^\prime \in C_c^\infty (Z_+)$. Therefore this integral converges absolutely and is equal to
Now, let us take ![]() $(x_{-2}, x_{-1}: 0, 0)$ as
$(x_{-2}, x_{-1}: 0, 0)$ as ![]() $x_0$. Then we have
$x_0$. Then we have
Let us define a map ![]() $q : X_+ \otimes Y_0 \rightarrow \mathrm {Mat}_{2 \times 2}$ by
$q : X_+ \otimes Y_0 \rightarrow \mathrm {Mat}_{2 \times 2}$ by
with ![]() $b_i \in X_+$. Clearly this map is bijective. Hence, there exists a measure
$b_i \in X_+$. Clearly this map is bijective. Hence, there exists a measure ![]() $dT$ on
$dT$ on ![]() $\mathrm {Mat}_{2 \times 2}$ such that we have
$\mathrm {Mat}_{2 \times 2}$ such that we have
with ![]() $x_T = q^{-1}(T)$. Here we note that the measure
$x_T = q^{-1}(T)$. Here we note that the measure ![]() $dz$ on
$dz$ on ![]() $X_+ \otimes Y_0$ is taken to be the Tamagawa measure and hence we have the Fourier inversion
$X_+ \otimes Y_0$ is taken to be the Tamagawa measure and hence we have the Fourier inversion
with the above Haar measures ![]() $dT, dT^\prime$ on
$dT, dT^\prime$ on ![]() $\mathrm {Mat}_{2 \times 2}$ if the integral converges. Thus, we have
$\mathrm {Mat}_{2 \times 2}$ if the integral converges. Thus, we have
 \begin{align*} & \int_{N_2}^{\rm st} \int_{N_1}\int_{X_+ \otimes Y_0} \int_{N \backslash G^1} \int_{G^1} (\omega_{\psi}(\gamma g, u_1 u_2 h)\phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+z)} \\ &\qquad \times\langle \pi^\circ(g)f, f^\prime \rangle \, dg \, d\gamma_0 \, dz \, du_1 \, du_2\\ &\quad =\int_{N}^{\rm st} \int_{N_1}\int_{\mathrm{Mat}_{2 \times 2}} \int_{N \backslash G^1} \int_{G^1} (\omega_{\psi}(\gamma g, u_1 u_2 h)\phi)(x_0+x_T) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_T)} \\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle\, dg \, d\gamma_0 \, dT \, du_1 \, du_2. \end{align*}
\begin{align*} & \int_{N_2}^{\rm st} \int_{N_1}\int_{X_+ \otimes Y_0} \int_{N \backslash G^1} \int_{G^1} (\omega_{\psi}(\gamma g, u_1 u_2 h)\phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+z)} \\ &\qquad \times\langle \pi^\circ(g)f, f^\prime \rangle \, dg \, d\gamma_0 \, dz \, du_1 \, du_2\\ &\quad =\int_{N}^{\rm st} \int_{N_1}\int_{\mathrm{Mat}_{2 \times 2}} \int_{N \backslash G^1} \int_{G^1} (\omega_{\psi}(\gamma g, u_1 u_2 h)\phi)(x_0+x_T) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_T)} \\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle\, dg \, d\gamma_0 \, dT \, du_1 \, du_2. \end{align*}
Moreover, similarly to the global computation in [Reference MorimotoMor14a, § 3.1], we may write this integral as
 \begin{align} & \int_{N_2}^{\rm st} \int_{N_1} \int_{\mathrm{Mat}_{2 \times 2}} \int_{N \backslash G^1} \int_{G^1} \psi \bigg(\mathrm{tr} \bigg(\begin{pmatrix}s_1 & s_2\\ t_1 & t_2 \end{pmatrix}S_0 (x_T-x_{T_0})\bigg)\bigg) \nonumber\\ &\quad \times (\omega_{\psi}(\gamma g, h)\phi)(x_0+x_T) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_T)} \langle \pi^\circ(g)f, f^\prime \rangle \, dg \, d\gamma_0 \, dT \, du_1 \, du_2 , \end{align}
\begin{align} & \int_{N_2}^{\rm st} \int_{N_1} \int_{\mathrm{Mat}_{2 \times 2}} \int_{N \backslash G^1} \int_{G^1} \psi \bigg(\mathrm{tr} \bigg(\begin{pmatrix}s_1 & s_2\\ t_1 & t_2 \end{pmatrix}S_0 (x_T-x_{T_0})\bigg)\bigg) \nonumber\\ &\quad \times (\omega_{\psi}(\gamma g, h)\phi)(x_0+x_T) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_T)} \langle \pi^\circ(g)f, f^\prime \rangle \, dg \, d\gamma_0 \, dT \, du_1 \, du_2 , \end{align}
where we let ![]() $u_1 = u_1(s_1, t_1)$ and
$u_1 = u_1(s_1, t_1)$ and ![]() $u_2 = u_2(s_2, t_2)$, and we put
$u_2 = u_2(s_2, t_2)$, and we put ![]() $T_0 = \big (\begin{smallmatrix}0 & 0\\0 & 1 \end{smallmatrix}\big )$. By an argument similar to the proof to show (6.2.9), we may apply the Fourier inversion to this integral, and we see that this is equal to
$T_0 = \big (\begin{smallmatrix}0 & 0\\0 & 1 \end{smallmatrix}\big )$. By an argument similar to the proof to show (6.2.9), we may apply the Fourier inversion to this integral, and we see that this is equal to
Now we note that from the argument to obtain (6.2.9), this integral converges absolutely. Then by telescoping the ![]() $G^1$-integration, we obtain
$G^1$-integration, we obtain
 \begin{align*} & \int_{N \backslash G^1} \int_{N \backslash G^1} \int_{N} (\omega_{\psi}( r g, h) \phi)(x_0+x_{T_0}) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_{T_0})} \\ &\quad \times \langle \pi^\circ(r g)f, \pi^\circ(\gamma)f^\prime \rangle\, dr \, dg \, d\gamma_0. \end{align*}
\begin{align*} & \int_{N \backslash G^1} \int_{N \backslash G^1} \int_{N} (\omega_{\psi}( r g, h) \phi)(x_0+x_{T_0}) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_{T_0})} \\ &\quad \times \langle \pi^\circ(r g)f, \pi^\circ(\gamma)f^\prime \rangle\, dr \, dg \, d\gamma_0. \end{align*}
Put ![]() $z_0 = x_0+x_{T_0} = (x_{-2}, x_{-1}, 0, x_2)$. Recall that from the computation in [Reference MorimotoMor14a, § 3.1], we have
$z_0 = x_0+x_{T_0} = (x_{-2}, x_{-1}, 0, x_2)$. Recall that from the computation in [Reference MorimotoMor14a, § 3.1], we have
when we let ![]() $A =\big (\begin{smallmatrix}a_{11} & a_{12}\\a_{21} & a_{22} \end{smallmatrix}\big )$, and we have
$A =\big (\begin{smallmatrix}a_{11} & a_{12}\\a_{21} & a_{22} \end{smallmatrix}\big )$, and we have
Therefore, ![]() $\mathcal {W}_{\psi _U}(\theta (\phi \otimes f), \theta (\phi ^\prime \otimes f^\prime ))$ is equal to
$\mathcal {W}_{\psi _U}(\theta (\phi \otimes f), \theta (\phi ^\prime \otimes f^\prime ))$ is equal to
 \begin{align*} & \int_{F}^{\rm st}\int_{N \backslash G^1} \int_{N \backslash G^1} \int_{N} \psi(-b) (\omega_{\psi}(r g, \tilde{u}(b)) \phi)(z_0) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(z_0)} \\ &\qquad \times \langle \pi^\circ(rg)f, \pi^\circ(\gamma)f^\prime \rangle\, dr \, dg \, d\gamma_0 \, db \\ &\quad =\int_{F}^{\rm st}\int_{N \backslash G^1} \int_{N \backslash G^1} \int_{\mathrm{Sym}^2} \psi(-b-da_{22})(\omega_{\psi}(w(b)g, 1)\phi)(z_0)\\ &\qquad \times(\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(z_0)} \langle \pi^\circ(v(A)g)f, \pi^\circ(\gamma)f^\prime \rangle \, dA \, dg \, d\gamma_0 \, db. \end{align*}
\begin{align*} & \int_{F}^{\rm st}\int_{N \backslash G^1} \int_{N \backslash G^1} \int_{N} \psi(-b) (\omega_{\psi}(r g, \tilde{u}(b)) \phi)(z_0) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(z_0)} \\ &\qquad \times \langle \pi^\circ(rg)f, \pi^\circ(\gamma)f^\prime \rangle\, dr \, dg \, d\gamma_0 \, db \\ &\quad =\int_{F}^{\rm st}\int_{N \backslash G^1} \int_{N \backslash G^1} \int_{\mathrm{Sym}^2} \psi(-b-da_{22})(\omega_{\psi}(w(b)g, 1)\phi)(z_0)\\ &\qquad \times(\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(z_0)} \langle \pi^\circ(v(A)g)f, \pi^\circ(\gamma)f^\prime \rangle \, dA \, dg \, d\gamma_0 \, db. \end{align*}
By an argument similar to that in [Reference Furusawa and MorimotoFM21] showing that [Reference Furusawa and MorimotoFM21, (3.30)] is equal to ![]() $\alpha (\pi (g) \phi, \pi (h)\phi ^\prime )$ there, indeed word for word, we see that this integral is equal to
$\alpha (\pi (g) \phi, \pi (h)\phi ^\prime )$ there, indeed word for word, we see that this integral is equal to
Thus, Proposition 6.3 in the non-archimedean case is proved.
The case when  $F$ is archimedean
$F$ is archimedean
Suppose that ![]() $F$ is archimedean. Recall that
$F$ is archimedean. Recall that
where we set
which converges absolutely and gives a tempered distribution on ![]() $U / U_{-\infty }$ by [Reference LiuLiu16, Corollary 3.13]. Let us define
$U / U_{-\infty }$ by [Reference LiuLiu16, Corollary 3.13]. Let us define ![]() $U^\prime = N_0 N_1 N_2$. Then
$U^\prime = N_0 N_1 N_2$. Then ![]() $U^\prime _{-\infty } = U_{-\infty }$. Moreover, for any
$U^\prime _{-\infty } = U_{-\infty }$. Moreover, for any ![]() $\tilde {u} \in \widetilde {U}$ and
$\tilde {u} \in \widetilde {U}$ and ![]() $u^\prime \in U^\prime$, we have
$u^\prime \in U^\prime$, we have ![]() $\tilde {u} u^\prime \tilde {u}^{-1} (u^\prime )^{-1} \in U^\prime _{-\infty }$ and we obtain
$\tilde {u} u^\prime \tilde {u}^{-1} (u^\prime )^{-1} \in U^\prime _{-\infty }$ and we obtain ![]() $\mathcal {W}_{\tilde {\phi }_1, \tilde {\phi }_2}(\tilde {u} u^\prime ) = \mathcal {W}_{\tilde {\phi }_1, \tilde {\phi }_2}(u^\prime \tilde {u})$. Hence, we may regard it as a tempered distribution on
$\mathcal {W}_{\tilde {\phi }_1, \tilde {\phi }_2}(\tilde {u} u^\prime ) = \mathcal {W}_{\tilde {\phi }_1, \tilde {\phi }_2}(u^\prime \tilde {u})$. Hence, we may regard it as a tempered distribution on ![]() $\tilde {U} \times (U^\prime / U_{-\infty }^\prime )$. Then for a tempered distribution
$\tilde {U} \times (U^\prime / U_{-\infty }^\prime )$. Then for a tempered distribution ![]() $I$ on
$I$ on ![]() $\tilde {U} \times (U^\prime / U_{-\infty }^\prime )$, we define partial Fourier transforms
$\tilde {U} \times (U^\prime / U_{-\infty }^\prime )$, we define partial Fourier transforms ![]() $\widehat {I^j}$ of
$\widehat {I^j}$ of ![]() $I$ for
$I$ for ![]() $j=1,2$ by
$j=1,2$ by
where ![]() $f_1 \in \mathcal {S} (\tilde {U})$ and
$f_1 \in \mathcal {S} (\tilde {U})$ and ![]() $f_2 \in \mathcal {S} (U^\prime / U_{-\infty }^\prime )$, respectively. Then we have
$f_2 \in \mathcal {S} (U^\prime / U_{-\infty }^\prime )$, respectively. Then we have
From the definition of ![]() $\mathcal {B}_\Sigma$, we have
$\mathcal {B}_\Sigma$, we have
 \begin{align*} \mathcal{W}_{\theta(\phi \otimes f), \theta(\phi^\prime \otimes f^\prime)}(n) &= \int_{U_{-\infty}} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, nu) \phi)(x) \overline{\phi^\prime(x)}\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}^{-1}(n u) \, {dx} \, dg \, du\\ &=\int_{U_{-\infty} / N_0} \int_{N_0} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, nu_0u) \phi)(x) \overline{ \phi^\prime(x)}\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}^{-1}(n u) \, {dx} \, dg \, du_0 \, du, \end{align*}
\begin{align*} \mathcal{W}_{\theta(\phi \otimes f), \theta(\phi^\prime \otimes f^\prime)}(n) &= \int_{U_{-\infty}} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, nu) \phi)(x) \overline{\phi^\prime(x)}\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}^{-1}(n u) \, {dx} \, dg \, du\\ &=\int_{U_{-\infty} / N_0} \int_{N_0} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, nu_0u) \phi)(x) \overline{ \phi^\prime(x)}\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \psi_{U}^{-1}(n u) \, {dx} \, dg \, du_0 \, du, \end{align*}
for ![]() $\phi, \phi ^\prime \in \mathcal {S}(Z_+)$ and
$\phi, \phi ^\prime \in \mathcal {S}(Z_+)$ and ![]() $f, f^\prime \in V_{\pi ^\circ }^\infty$. Clearly, Lemma 6.2 holds in the archimedean case also. Then as in (6.2.9), because of Remark 6.2 and the Fourier inversion, the above integral is equal to
$f, f^\prime \in V_{\pi ^\circ }^\infty$. Clearly, Lemma 6.2 holds in the archimedean case also. Then as in (6.2.9), because of Remark 6.2 and the Fourier inversion, the above integral is equal to
 \begin{align*} & \int_{U_{-\infty} / N_0} \int_{N \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(\gamma g, nu) \phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \\ &\qquad \times\langle \pi^\circ(g)f, f^\prime \rangle \, dg \, dz \, d\gamma_0 \, du. \end{align*}
\begin{align*} & \int_{U_{-\infty} / N_0} \int_{N \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1} (\omega_{\psi}(\gamma g, nu) \phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \\ &\qquad \times\langle \pi^\circ(g)f, f^\prime \rangle \, dg \, dz \, d\gamma_0 \, du. \end{align*}
As (6.2.9), this integral converges absolutely. Let us denote this integral by ![]() $J_{\phi, \phi ^\prime, f, f^\prime }(n)$. Then, from the definition,
$J_{\phi, \phi ^\prime, f, f^\prime }(n)$. Then, from the definition,
Again, from the definition, for ![]() $\varphi \in \mathcal {S}(U^\prime / U^\prime _{-\infty })$, we have
$\varphi \in \mathcal {S}(U^\prime / U^\prime _{-\infty })$, we have
 \begin{align*} (\widehat{J_{\phi,
\phi^\prime, f, f^\prime}}^2, \psi_U \cdot \varphi) =
(J_{\phi, \phi^\prime, f, f^\prime}, \widehat{\psi_U \cdot
\varphi}) &= \int_{U^\prime / U^\prime_{-\infty}}
\int_{U_{-\infty}^\prime / N_0} \int_{N \backslash
G^1} \int_{X_+ \otimes Y_0} \int_{G^1} \\ &\quad \times
(\omega_{\psi}(\gamma g, nu) \phi)(x_0+z)
(\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \\
&\quad \times\langle \pi^\circ(g)f, f^\prime \rangle
\widehat{\varphi}(n) \psi_U^{-1}(n)\, dg \, dz \, d\gamma_0
\, du \, dn. \end{align*}
\begin{align*} (\widehat{J_{\phi,
\phi^\prime, f, f^\prime}}^2, \psi_U \cdot \varphi) =
(J_{\phi, \phi^\prime, f, f^\prime}, \widehat{\psi_U \cdot
\varphi}) &= \int_{U^\prime / U^\prime_{-\infty}}
\int_{U_{-\infty}^\prime / N_0} \int_{N \backslash
G^1} \int_{X_+ \otimes Y_0} \int_{G^1} \\ &\quad \times
(\omega_{\psi}(\gamma g, nu) \phi)(x_0+z)
(\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \\
&\quad \times\langle \pi^\circ(g)f, f^\prime \rangle
\widehat{\varphi}(n) \psi_U^{-1}(n)\, dg \, dz \, d\gamma_0
\, du \, dn. \end{align*}
By a computation similar to that used to obtain (6.2.10), this integral is equal to
 \begin{align*} & \int_{N_1} \int_{N_2} \int_{N \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1}(\omega_{\psi}(\gamma g, u_1 u_2u) \phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle \widehat{\varphi}(u_1 u_2) \psi_U^{-1}(u_1 u_2)\, dg \, dz \, d\gamma_0 \, du \, du_1 \, du_2\\ &\quad =\int_{N_1} \int_{N_2}\int_{\mathrm{Mat}_{2 \times 2}} \int_{N \backslash G^1} \int_{G^1} \psi \bigg(\mathrm{tr} \bigg(\begin{pmatrix}s_1 & s_2\\ t_1 & t_2 \end{pmatrix}S_0 (x_T-x_{T_0}) \bigg) \bigg) \\ &\qquad \times (\omega_{\psi}(\gamma g, h)\phi)(x_0+x_T) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_T)} \\ &\qquad \times\langle \pi^\circ(g)f, f^\prime \rangle \widehat{\varphi}(u_1 u_2)\, dg \, d\gamma_0 \, dT \, du_1 \, du_2. \end{align*}
\begin{align*} & \int_{N_1} \int_{N_2} \int_{N \backslash G^1} \int_{X_+ \otimes Y_0} \int_{G^1}(\omega_{\psi}(\gamma g, u_1 u_2u) \phi)(x_0+z) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+z)} \\ &\qquad \times \langle \pi^\circ(g)f, f^\prime \rangle \widehat{\varphi}(u_1 u_2) \psi_U^{-1}(u_1 u_2)\, dg \, dz \, d\gamma_0 \, du \, du_1 \, du_2\\ &\quad =\int_{N_1} \int_{N_2}\int_{\mathrm{Mat}_{2 \times 2}} \int_{N \backslash G^1} \int_{G^1} \psi \bigg(\mathrm{tr} \bigg(\begin{pmatrix}s_1 & s_2\\ t_1 & t_2 \end{pmatrix}S_0 (x_T-x_{T_0}) \bigg) \bigg) \\ &\qquad \times (\omega_{\psi}(\gamma g, h)\phi)(x_0+x_T) (\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(x_0+x_T)} \\ &\qquad \times\langle \pi^\circ(g)f, f^\prime \rangle \widehat{\varphi}(u_1 u_2)\, dg \, d\gamma_0 \, dT \, du_1 \, du_2. \end{align*}
As above, we may apply the Fourier inversion and, thus, this is equal to
Hence,
Here, we note that by Remark 6.2, this integral converges absolutely. Then this identity shows that we have
 \begin{align} \widehat{\widehat{J_{\phi, \phi^\prime, f, f^\prime}}^2}^1(\varphi) &= \int_{\tilde{U}} \int_{N \backslash G^1} \int_{G^1} (\omega_{\psi}(\gamma g,b) \phi)(x_0+x_{T_0}) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+x_{T_0})} \nonumber\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \varphi(b)\, dg \, d\gamma_0 \, db \end{align}
\begin{align} \widehat{\widehat{J_{\phi, \phi^\prime, f, f^\prime}}^2}^1(\varphi) &= \int_{\tilde{U}} \int_{N \backslash G^1} \int_{G^1} (\omega_{\psi}(\gamma g,b) \phi)(x_0+x_{T_0}) (\overline{\omega_{\psi}(\gamma, 1) \phi^\prime)(x_0+x_{T_0})} \nonumber\\ &\quad \times \langle \pi^\circ(g)f, f^\prime \rangle \varphi(b)\, dg \, d\gamma_0 \, db \end{align}
for ![]() $\varphi \in \mathcal {S}(\tilde {U})$. As in the non-archimedean case, by (6.2.11) and (6.2.12), we may easily show that this is equal to
$\varphi \in \mathcal {S}(\tilde {U})$. As in the non-archimedean case, by (6.2.11) and (6.2.12), we may easily show that this is equal to
 \begin{align*} & \int_{N \backslash G^1} \int_{N \backslash G^1} \int_{N} \int_{F} \psi_{U_{G}}^{-1}(v(x) n) (\omega_{\psi}(g, 1)\phi)(z_0)(\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(z_0)} \nonumber\\ &\quad \times \langle \pi^\circ(v(x)ng)f, \pi^\circ(\gamma)f^\prime \rangle \varphi(\tilde{u}(x)) \,{dx}\, dn \, dg \, d\gamma_0 \end{align*}
\begin{align*} & \int_{N \backslash G^1} \int_{N \backslash G^1} \int_{N} \int_{F} \psi_{U_{G}}^{-1}(v(x) n) (\omega_{\psi}(g, 1)\phi)(z_0)(\overline{\omega_{\psi}(\gamma, 1)\phi^\prime)(z_0)} \nonumber\\ &\quad \times \langle \pi^\circ(v(x)ng)f, \pi^\circ(\gamma)f^\prime \rangle \varphi(\tilde{u}(x)) \,{dx}\, dn \, dg \, d\gamma_0 \end{align*}
since the integral in (6.2.13) converges absolutely. Thus, Proposition 6.3 is proved in the archimedean case also.
7. Proof of Theorem 1.2
In this section, we complete our proof of Theorem 1.2. Let ![]() $(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of
$(\pi, V_\pi )$ be an irreducible cuspidal tempered automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character. Throughout this section, we suppose that
$G_D(\mathbb {A})$ with a trivial central character. Throughout this section, we suppose that ![]() $\pi$ is neither of type I-A nor type I-B. When
$\pi$ is neither of type I-A nor type I-B. When ![]() $\pi$ is one of these types, our theorem is already proved in [Reference CorbettCor17, Theorem 7.5].
$\pi$ is one of these types, our theorem is already proved in [Reference CorbettCor17, Theorem 7.5].
The case when ![]() $B_{\xi, \Lambda,\psi } \not \equiv 0$ on
$B_{\xi, \Lambda,\psi } \not \equiv 0$ on ![]() $V_\pi$ is treated in § 7.1 and the case when
$V_\pi$ is treated in § 7.1 and the case when ![]() $B_{\xi, \Lambda, \psi } \equiv 0$ on
$B_{\xi, \Lambda, \psi } \equiv 0$ on ![]() $V_\pi$ is treated in § 7.2, respectively.
$V_\pi$ is treated in § 7.2, respectively.
7.1 Proof of Theorem 1.2 when  $B_{\xi, \Lambda,\psi } \not \equiv 0$
$B_{\xi, \Lambda,\psi } \not \equiv 0$
7.1.1 Reduction to a local identity
Suppose that ![]() $B_{\xi, \Lambda,\psi } \not \equiv 0$ on
$B_{\xi, \Lambda,\psi } \not \equiv 0$ on ![]() $V_\pi$. Let
$V_\pi$. Let ![]() $(\sigma, V_\sigma )$ denote the theta lift of
$(\sigma, V_\sigma )$ denote the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSU}_{3,D}(\mathbb {A})$, which is an irreducible cuspidal automorphic representation. As in the proof of Theorem 6.1, our theorem may be reduced to a certain local identity. Let us set some notation to explain our local identity.
$\mathrm {GSU}_{3,D}(\mathbb {A})$, which is an irreducible cuspidal automorphic representation. As in the proof of Theorem 6.1, our theorem may be reduced to a certain local identity. Let us set some notation to explain our local identity.
As in §§ 5.1 and 5.2, we fix the Petersson inner product ![]() $(\,{,}\,)$ on
$(\,{,}\,)$ on ![]() $V_{\pi }$ and the local hermitian pairing
$V_{\pi }$ and the local hermitian pairing ![]() $(\,{,}\,)_v$ on
$(\,{,}\,)_v$ on ![]() $\pi _v$. As in (3.2.3), we define the maximal isotropic subspaces
$\pi _v$. As in (3.2.3), we define the maximal isotropic subspaces ![]() $Z_{D, \pm }$. Let
$Z_{D, \pm }$. Let
be the ![]() $G_D(F_v)^+ \times \mathrm {GSU}_{3, D}(F_v)$-equivariant linear map, which is unique up to multiplication by a scalar. As in § 6.1, let us adjust
$G_D(F_v)^+ \times \mathrm {GSU}_{3, D}(F_v)$-equivariant linear map, which is unique up to multiplication by a scalar. As in § 6.1, let us adjust ![]() $\{\theta _{D, v}\}_v$ so that
$\{\theta _{D, v}\}_v$ so that
for ![]() $f^\prime =\otimes _v f_v^\prime \in V_{\pi }$ and
$f^\prime =\otimes _v f_v^\prime \in V_{\pi }$ and ![]() $\phi ^\prime =\otimes _v \phi _v^\prime \in \mathcal {S}(Z_{D, +}(\mathbb {A}))$. Let us choose
$\phi ^\prime =\otimes _v \phi _v^\prime \in \mathcal {S}(Z_{D, +}(\mathbb {A}))$. Let us choose ![]() $X \in D^\times (F)$ so that
$X \in D^\times (F)$ so that ![]() $S_{X} =\xi$. Then by Proposition 3.2, we have
$S_{X} =\xi$. Then by Proposition 3.2, we have
where ![]() $f = \otimes f_v \in V_{\pi _D}$ and
$f = \otimes f_v \in V_{\pi _D}$ and ![]() $\phi = \otimes \phi _v \in \mathcal {S}(Z_{D, +}(\mathbb {A}))$, and we define
$\phi = \otimes \phi _v \in \mathcal {S}(Z_{D, +}(\mathbb {A}))$, and we define
Here, we take the measure ![]() $dh_{v}$ on
$dh_{v}$ on ![]() $G_D^1(F_v)$ defined by the gauge form, the measure
$G_D^1(F_v)$ defined by the gauge form, the measure ![]() $dn_v$ on
$dn_v$ on ![]() $N_{G_D}(F_v)$ defined in § 1.2 under the identification
$N_{G_D}(F_v)$ defined in § 1.2 under the identification ![]() $D(F_v) \simeq F_v^4$ and the measure
$D(F_v) \simeq F_v^4$ and the measure ![]() $dg_{1,v}$ on
$dg_{1,v}$ on ![]() $N_{G_D}(F_v) \backslash G_D^1(F_v)$ such that
$N_{G_D}(F_v) \backslash G_D^1(F_v)$ such that ![]() $dh_v=dn_v \, dg_{1,v}$.
$dh_v=dn_v \, dg_{1,v}$.
Then by combining the explicit formula of the Bessel periods on ![]() $\sigma$ given in Theorem 6.2, the Rallis inner product formulas (5.1.4) and Proposition 5.2, Lemmas 6.1 and 4.2, and the above pull-back formula (7.1.1), we see that Theorem 1.2 is reduced to the following local identity.
$\sigma$ given in Theorem 6.2, the Rallis inner product formulas (5.1.4) and Proposition 5.2, Lemmas 6.1 and 4.2, and the above pull-back formula (7.1.1), we see that Theorem 1.2 is reduced to the following local identity.
Proposition 7.1 Let ![]() $v$ be an arbitrary place of
$v$ be an arbitrary place of ![]() $F$. For a given
$F$. For a given ![]() $f_v \!\in\! V_{\pi _v}$ satisfying
$f_v \!\in\! V_{\pi _v}$ satisfying ![]() $\alpha _{\xi, \Lambda, v}(f_v)\ne 0$, there exists
$\alpha _{\xi, \Lambda, v}(f_v)\ne 0$, there exists ![]() $\phi _v \in \mathcal {S}(Z_{D, +}(F_v))$ such that the local integral
$\phi _v \in \mathcal {S}(Z_{D, +}(F_v))$ such that the local integral ![]() $\mathcal {K}_v(f_v;\phi _v)$ converges absolutely,
$\mathcal {K}_v(f_v;\phi _v)$ converges absolutely, ![]() $\mathcal {K}_v(f_v;\phi _v) \ne 0$ and the equality
$\mathcal {K}_v(f_v;\phi _v) \ne 0$ and the equality
holds.
Remark 7.1 In Corollary 7.1, the existence of ![]() $f_v$ with
$f_v$ with ![]() $\alpha _{\Lambda _v, \psi _{\xi, v}}(f_v)\ne 0$ is shown.
$\alpha _{\Lambda _v, \psi _{\xi, v}}(f_v)\ne 0$ is shown.
Let us define hermitian inner product on ![]() $\mathcal {S}(Z_{D, +}(F_v))$ by
$\mathcal {S}(Z_{D, +}(F_v))$ by
Then we consider the integral
for ![]() $f, f^\prime \in \pi _v$ and
$f, f^\prime \in \pi _v$ and ![]() $\phi, \phi ^\prime \in \mathcal {S}(Z_{D, +}(F_v))$. As in § 6.2, this converges absolutely and gives a
$\phi, \phi ^\prime \in \mathcal {S}(Z_{D, +}(F_v))$. As in § 6.2, this converges absolutely and gives a ![]() $\mathrm {GSU}_{3,D}(F_v)$-invariant hermitian inner product
$\mathrm {GSU}_{3,D}(F_v)$-invariant hermitian inner product
by
By the Rallis inner product formula (5.1.4) and Proposition 5.2, at any place ![]() $v$, there exist
$v$, there exist ![]() $f_v, f_v^\prime, \phi, \phi ^\prime$ such that
$f_v, f_v^\prime, \phi, \phi ^\prime$ such that ![]() $Z^{\bullet }(f, f^\prime ; \phi, \phi ^\prime ) \ne 0$ since
$Z^{\bullet }(f, f^\prime ; \phi, \phi ^\prime ) \ne 0$ since ![]() $\theta _{\psi, D}(\pi ) \ne 0$. Thus,
$\theta _{\psi, D}(\pi ) \ne 0$. Thus, ![]() $\mathcal {B}_{\sigma _v} \not \equiv 0$.
$\mathcal {B}_{\sigma _v} \not \equiv 0$.
For ![]() $\widetilde {\phi }_i \in \sigma _v$, we define
$\widetilde {\phi }_i \in \sigma _v$, we define
 \[ \mathcal{A}(\tilde{\phi}_1, \tilde{\phi}_2):= \int_{N_{3, D}(F_v)}^{\rm st} \int_{M_{X}(F_v)} \mathcal{B}_{\sigma_v}(\sigma_v(nt)\tilde{\phi}_1, \tilde{\phi}_2) \Lambda_{D,v}(t) \psi_{X, D, v}(n)^{-1} \, dt \, dn. \]
\[ \mathcal{A}(\tilde{\phi}_1, \tilde{\phi}_2):= \int_{N_{3, D}(F_v)}^{\rm st} \int_{M_{X}(F_v)} \mathcal{B}_{\sigma_v}(\sigma_v(nt)\tilde{\phi}_1, \tilde{\phi}_2) \Lambda_{D,v}(t) \psi_{X, D, v}(n)^{-1} \, dt \, dn. \]
Here, at an archimedean place ![]() $v$, a stable integration means the Fourier transform as in the definition of
$v$, a stable integration means the Fourier transform as in the definition of ![]() $\alpha _{\chi, \psi _N}$. Then by an argument similar to that in [Reference Furusawa and MorimotoFM21, 3.2–3.3], we may reduce Proposition 7.1 to the following identity.
$\alpha _{\chi, \psi _N}$. Then by an argument similar to that in [Reference Furusawa and MorimotoFM21, 3.2–3.3], we may reduce Proposition 7.1 to the following identity.
Proposition 7.2 For any ![]() $f, f^\prime \in V_{\pi _v}$ and any
$f, f^\prime \in V_{\pi _v}$ and any ![]() $\phi,\phi ^\prime \in C_c^\infty (Z_{D, +}(F_v))$, we have
$\phi,\phi ^\prime \in C_c^\infty (Z_{D, +}(F_v))$, we have
 \begin{align}
\mathcal{A}(\theta(\phi\otimes f),\theta(\phi^\prime\otimes
f^\prime)) &=\int_{N_D(F_v)\backslash
G_D^1(F_v)}\int_{N_D(F_v)\backslash G_D^1(F_v)}
\alpha_{\Lambda_v, \psi_{\xi,
v}}(\pi_v(h)f,\pi_v(h^\prime)f^\prime) \nonumber\\ &\quad
\times (\omega_{\psi_v}(h,1)\phi)(x_0)
\overline{(\omega_{\psi_v}(h^\prime,1)\phi^\prime)(x_0)}\,
dh\, dh^\prime.
\end{align}
\begin{align}
\mathcal{A}(\theta(\phi\otimes f),\theta(\phi^\prime\otimes
f^\prime)) &=\int_{N_D(F_v)\backslash
G_D^1(F_v)}\int_{N_D(F_v)\backslash G_D^1(F_v)}
\alpha_{\Lambda_v, \psi_{\xi,
v}}(\pi_v(h)f,\pi_v(h^\prime)f^\prime) \nonumber\\ &\quad
\times (\omega_{\psi_v}(h,1)\phi)(x_0)
\overline{(\omega_{\psi_v}(h^\prime,1)\phi^\prime)(x_0)}\,
dh\, dh^\prime.
\end{align}Before proceeding to a proof of this proposition, we give some corollaries of this identity.
Corollary 7.1 For an arbitrary place ![]() $v$ of
$v$ of ![]() $F$, we have
$F$, we have ![]() $\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on
$\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on ![]() $\pi _v$.
$\pi _v$.
Proof. Since ![]() $\mathcal {B}_{\sigma _v} \not \equiv 0$, (7.1.2) implies that
$\mathcal {B}_{\sigma _v} \not \equiv 0$, (7.1.2) implies that ![]() $\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on
$\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on ![]() $\pi _v$ if and only if
$\pi _v$ if and only if ![]() $\alpha _{\Lambda _v^{-1}, \psi _{X, v}} \not \equiv 0$ on
$\alpha _{\Lambda _v^{-1}, \psi _{X, v}} \not \equiv 0$ on ![]() $\sigma _v$. Moreover, by [Reference Furusawa and MorimotoFM21, Corollary 5.1],
$\sigma _v$. Moreover, by [Reference Furusawa and MorimotoFM21, Corollary 5.1], ![]() $\alpha _{\Lambda _v^{-1}, \psi _{X, v}} \not \equiv 0$ on
$\alpha _{\Lambda _v^{-1}, \psi _{X, v}} \not \equiv 0$ on ![]() $\sigma _v$ since the theta lift of
$\sigma _v$ since the theta lift of ![]() $\sigma _v$ to
$\sigma _v$ to ![]() $\mathrm {GU}_{2,2}(F_v)$ is generic. Thus, our claim follows.
$\mathrm {GU}_{2,2}(F_v)$ is generic. Thus, our claim follows.
As another corollary, a non-vanishing of local theta lifts follows from a non-vanishing of local periods.
Corollary 7.2 Let ![]() $k$ be a local field of characteristic zero and
$k$ be a local field of characteristic zero and ![]() $\mathcal {D}$ be a quaternion algebra over
$\mathcal {D}$ be a quaternion algebra over ![]() $k$. Let
$k$. Let ![]() $\tau$ be an irreducible admissible tempered representation of
$\tau$ be an irreducible admissible tempered representation of ![]() $G_{\mathcal {D}}$ with a trivial central character. Let
$G_{\mathcal {D}}$ with a trivial central character. Let ![]() $S_{\mathcal {D}} \in \mathcal {D}^1$ and
$S_{\mathcal {D}} \in \mathcal {D}^1$ and ![]() $\chi$ be a character of
$\chi$ be a character of ![]() $T_{\mathcal {D}, S_{\mathcal {D}}}$. Suppose that
$T_{\mathcal {D}, S_{\mathcal {D}}}$. Suppose that ![]() $\alpha _{\chi, \psi _{S_{\mathcal {D}}}} \not \equiv 0$ on
$\alpha _{\chi, \psi _{S_{\mathcal {D}}}} \not \equiv 0$ on ![]() $\tau$. Then
$\tau$. Then ![]() $\mathcal {A} \not \equiv 0$ on
$\mathcal {A} \not \equiv 0$ on ![]() $\theta _{\psi, \mathcal {D}}(\tau ) \times \theta _{\psi, \mathcal {D}}(\tau )$. In particular,
$\theta _{\psi, \mathcal {D}}(\tau ) \times \theta _{\psi, \mathcal {D}}(\tau )$. In particular, ![]() $\theta _{\psi, \mathcal {D}}(\tau ) \ne 0$ and
$\theta _{\psi, \mathcal {D}}(\tau ) \ne 0$ and ![]() $Z^\bullet (\phi, \phi ^\prime, f, f^\prime ) \ne 0$ for some
$Z^\bullet (\phi, \phi ^\prime, f, f^\prime ) \ne 0$ for some ![]() $f, f^\prime \in \tau$ and
$f, f^\prime \in \tau$ and ![]() $\phi, \phi ^\prime \in \mathcal {S}(Z_{\mathcal {D}, +})$.
$\phi, \phi ^\prime \in \mathcal {S}(Z_{\mathcal {D}, +})$.
Remark 7.2 By [Reference YamanaYam14, Lemma 8.6, Remark 8.4 (1)], we know that the existence of such ![]() $f, f^\prime, \phi, \phi ^\prime$ is equivalent to the non-vanishing of the theta lift of
$f, f^\prime, \phi, \phi ^\prime$ is equivalent to the non-vanishing of the theta lift of ![]() $\tau$ to
$\tau$ to ![]() $\mathrm {GSU}_{3,\mathcal {D}}$ when
$\mathrm {GSU}_{3,\mathcal {D}}$ when ![]() $k \ne \mathbb {R}$. Though the equivalence is not clear when
$k \ne \mathbb {R}$. Though the equivalence is not clear when ![]() $k=\mathbb {R}$, we shall use Corollary 7.2 to show that the local non-vanishing of the theta lifts implies the global non-vanishing of the theta lifts in § 7.2.
$k=\mathbb {R}$, we shall use Corollary 7.2 to show that the local non-vanishing of the theta lifts implies the global non-vanishing of the theta lifts in § 7.2.
Proof. By our assumption, the right-hand side of (7.1.2) is not zero for some ![]() $f, f^\prime, \phi, \phi ^\prime$ when
$f, f^\prime, \phi, \phi ^\prime$ when ![]() $F_v \ne \mathbb {R}$. Hence, the left-hand side is not zero and, in particular,
$F_v \ne \mathbb {R}$. Hence, the left-hand side is not zero and, in particular, ![]() $Z^\bullet (\phi, \phi ^\prime, f, f^\prime ) \ne 0$.
$Z^\bullet (\phi, \phi ^\prime, f, f^\prime ) \ne 0$.
7.1.2 Local pull-back computation
Here we shall prove the identity (7.1.2) and, thus, we complete our proof of Theorem 1.2 when ![]() $B_{\xi, \psi, \Lambda } \not \equiv 0$. Here we give a proof of (7.1.2) only in the non-archimedean case since the archimedean case is similarly proved as in the proof of Proposition 6.3. Our proof is a local analogue of the proof of Propositions 3.1 and 3.2. Moreover, we will consider only the case when
$B_{\xi, \psi, \Lambda } \not \equiv 0$. Here we give a proof of (7.1.2) only in the non-archimedean case since the archimedean case is similarly proved as in the proof of Proposition 6.3. Our proof is a local analogue of the proof of Propositions 3.1 and 3.2. Moreover, we will consider only the case when ![]() $D$ is split since the proof is similar and indeed is easier in the non-split case as in the global computation. Since the argument in this subsection is purely local, in order to simplify the notation, we omit subscripts
$D$ is split since the proof is similar and indeed is easier in the non-split case as in the global computation. Since the argument in this subsection is purely local, in order to simplify the notation, we omit subscripts ![]() $v$ and we simply write
$v$ and we simply write ![]() $K(F)$ by
$K(F)$ by ![]() $K$ for any algebraic group
$K$ for any algebraic group ![]() $K$ defined over
$K$ defined over ![]() $F=F_v$.
$F=F_v$.
From the definition, we may write the left-hand side of (7.1.2) as
 \[ \int_{N_{4,2}}^{\rm st} \int_{M_{X}} \int_{G^1} \int_{Z_+} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(g, nt) \phi)(x) \overline{\phi^\prime(x)}\Lambda(t) \psi_{X}(n)^{-1} \, {dx} \, dg \, dt \, dn, \]
\[ \int_{N_{4,2}}^{\rm st} \int_{M_{X}} \int_{G^1} \int_{Z_+} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(g, nt) \phi)(x) \overline{\phi^\prime(x)}\Lambda(t) \psi_{X}(n)^{-1} \, {dx} \, dg \, dt \, dn, \]
where ![]() $X$ is chosen so that
$X$ is chosen so that ![]() $S_X =S$. Further as in (3.1.13), this is equal to
$S_X =S$. Further as in (3.1.13), this is equal to
 \begin{align*} & \int_{F}^{\rm st} \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{M_{X}} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, u_0(s) u_1(s_1, t_1) u_2(s_2, t_2) t) \phi)(x) \overline{\phi^\prime(x)} \\ &\quad \times \langle \pi(g)f, f^\prime \rangle \Lambda(t) \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1} \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 \,ds \end{align*}
\begin{align*} & \int_{F}^{\rm st} \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{M_{X}} \int_{G^1} \int_{Z_+} (\omega_{\psi}(g, u_0(s) u_1(s_1, t_1) u_2(s_2, t_2) t) \phi)(x) \overline{\phi^\prime(x)} \\ &\quad \times \langle \pi(g)f, f^\prime \rangle \Lambda(t) \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1} \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 \,ds \end{align*}
when we let ![]() $X = \big (\begin{smallmatrix} x_{11} & x_{12}\\ x_{21} & x_{22}\end{smallmatrix}\big )$. For each
$X = \big (\begin{smallmatrix} x_{11} & x_{12}\\ x_{21} & x_{22}\end{smallmatrix}\big )$. For each ![]() $r \in F$, we may take
$r \in F$, we may take ![]() $A_r =(a_1^r, a_2^r, 0, 0) \in Z_+$ such that
$A_r =(a_1^r, a_2^r, 0, 0) \in Z_+$ such that ![]() $a_1^r,a_2^r$ are linearly independent and
$a_1^r,a_2^r$ are linearly independent and ![]() $\langle a_1^r, a_2^r \rangle =r$. Let us denote by
$\langle a_1^r, a_2^r \rangle =r$. Let us denote by ![]() $Q_r$ the stabilizer of
$Q_r$ the stabilizer of ![]() $x_r$ in
$x_r$ in ![]() $G^1$. Then as in the proof of Proposition 6.3, for each
$G^1$. Then as in the proof of Proposition 6.3, for each ![]() $r \in F$, there is a Haar measure
$r \in F$, there is a Haar measure ![]() $dq_r$ of
$dq_r$ of ![]() $Q_r$ such that
$Q_r$ such that
with ![]() $dh_r=dq_r \backslash dh$, provided that the both sides converge. Then applying the Fourier inversion, because of (3.1.15), our integral becomes
$dh_r=dq_r \backslash dh$, provided that the both sides converge. Then applying the Fourier inversion, because of (3.1.15), our integral becomes
 \begin{align*} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{M_{X} }\int_{G^1}\int_{Q_0 \backslash G^1} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle\Lambda(t) \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1} \\ &\quad \times(\omega_{\psi}(hg, u_1(s_1, t_1) u_2(s_2, t_2) t) \phi)(A_0+b) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 \end{align*}
\begin{align*} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{M_{X} }\int_{G^1}\int_{Q_0 \backslash G^1} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle\Lambda(t) \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1} \\ &\quad \times(\omega_{\psi}(hg, u_1(s_1, t_1) u_2(s_2, t_2) t) \phi)(A_0+b) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 \end{align*}
with ![]() $A_0=(x_{-2}, x_{-1}, 0, 0)$. This is verified by an argument similar to that for [Reference LiuLiu16, Lemma 3.20]. We note that
$A_0=(x_{-2}, x_{-1}, 0, 0)$. This is verified by an argument similar to that for [Reference LiuLiu16, Lemma 3.20]. We note that ![]() $Q_0 = N$ from the definition. Moreover, as in [Reference LiuLiu16, Lemma 3.19], the inner integral
$Q_0 = N$ from the definition. Moreover, as in [Reference LiuLiu16, Lemma 3.19], the inner integral ![]() $\int _{M_{X}} \int _{G^1}\int _{Q_0 \backslash G^1} \int _{X_+^2}$ converges absolutely and, thus, this is equal to
$\int _{M_{X}} \int _{G^1}\int _{Q_0 \backslash G^1} \int _{X_+^2}$ converges absolutely and, thus, this is equal to
 \begin{align*} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{Q_0 \backslash G^1} \int_{G^1} \int_{M_{X}} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle \Lambda(t) \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1} \\ &\quad \times(\omega_{\psi}(hg, u_1(s_1, t_1) u_2(s_2, t_2) t) \phi)(A_0+b) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 . \end{align*}
\begin{align*} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{Q_0 \backslash G^1} \int_{G^1} \int_{M_{X}} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle \Lambda(t) \psi(x_{21}s_1+x_{22}t_1+x_{11}s_2+x_{12}t_2)^{-1} \\ &\quad \times(\omega_{\psi}(hg, u_1(s_1, t_1) u_2(s_2, t_2) t) \phi)(A_0+b) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 . \end{align*}
From the proof of Lemma 3.2, this integral is equal to
 \begin{align} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{Q_0 \backslash G^1} \int_{G^1} \int_{M_{X}} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(hg, t) \phi)(A_0+b) \nonumber\\ &\quad \times \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \Lambda(t)\psi \bigg(\mathrm{tr} \begin{pmatrix} s_2 & t_2\\ s_1 & t_1 \end{pmatrix} \bigg(S_0 \begin{pmatrix} \langle x_{-2}, b_1 \rangle & \langle x_{-2}, b_2 \rangle\\ \langle x_{-1}, b_1 \rangle & \langle x_{-1}, b_2 \rangle \end{pmatrix} -X\bigg) \bigg) \nonumber\\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 . \end{align}
\begin{align} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{Q_0 \backslash G^1} \int_{G^1} \int_{M_{X}} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(hg, t) \phi)(A_0+b) \nonumber\\ &\quad \times \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \Lambda(t)\psi \bigg(\mathrm{tr} \begin{pmatrix} s_2 & t_2\\ s_1 & t_1 \end{pmatrix} \bigg(S_0 \begin{pmatrix} \langle x_{-2}, b_1 \rangle & \langle x_{-2}, b_2 \rangle\\ \langle x_{-1}, b_1 \rangle & \langle x_{-1}, b_2 \rangle \end{pmatrix} -X\bigg) \bigg) \nonumber\\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 . \end{align}Now we claim that we may define the stable integral
 \begin{align*} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(hg, t) \phi)(A_0+b) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \\ &\quad \times\Lambda(t) \psi \bigg(\mathrm{tr} \begin{pmatrix} s_2 & t_2\\ s_1 & t_1 \end{pmatrix}\bigg(S_0 \begin{pmatrix} \langle x_{-2}, b_1 \rangle & \langle x_{-2}, b_2 \rangle\\ \langle x_{-1}, b_1 \rangle & \langle x_{-1}, b_2 \rangle \end{pmatrix} -X\bigg)\bigg) db \, ds_2 \,dt_2 \,ds_1 \, dt_1 \end{align*}
\begin{align*} & \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(hg, t) \phi)(A_0+b) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \\ &\quad \times\Lambda(t) \psi \bigg(\mathrm{tr} \begin{pmatrix} s_2 & t_2\\ s_1 & t_1 \end{pmatrix}\bigg(S_0 \begin{pmatrix} \langle x_{-2}, b_1 \rangle & \langle x_{-2}, b_2 \rangle\\ \langle x_{-1}, b_1 \rangle & \langle x_{-1}, b_2 \rangle \end{pmatrix} -X\bigg)\bigg) db \, ds_2 \,dt_2 \,ds_1 \, dt_1 \end{align*}
and we may choose a sufficiently large compact open subgroup ![]() $F_i$ of
$F_i$ of ![]() $F$ (
$F$ (![]() $1 \leq i \leq 4$) so that it depends only on
$1 \leq i \leq 4$) so that it depends only on ![]() $\psi$ and
$\psi$ and ![]() $\int _{F^2}^{\rm st} \int _{F^2}^{\rm st}\cdots = \int _{F_1} \int _{F_2}\int _{F_3}\int _{F_4}\cdots$. This claim easily follows from the following lemma in the one-dimensional case.
$\int _{F^2}^{\rm st} \int _{F^2}^{\rm st}\cdots = \int _{F_1} \int _{F_2}\int _{F_3}\int _{F_4}\cdots$. This claim easily follows from the following lemma in the one-dimensional case.
Lemma 7.1 Let ![]() $f$ be a locally constant function on
$f$ be a locally constant function on ![]() $F$ which is in
$F$ which is in ![]() $L^1(F)$. Then there exists a compact open subgroup
$L^1(F)$. Then there exists a compact open subgroup ![]() $F_0$ of
$F_0$ of ![]() $F$ such that for any compact open subgroups
$F$ such that for any compact open subgroups ![]() $F^\prime$ and
$F^\prime$ and ![]() $F^{\prime \prime }$ of
$F^{\prime \prime }$ of ![]() $F$ containing
$F$ containing ![]() $F_0$, we have
$F_0$, we have
Proof. Suppose that ![]() $\psi$ is trivial on
$\psi$ is trivial on ![]() $F_0 : =\varpi ^{m}\mathcal {O}_F$ and not trivial on
$F_0 : =\varpi ^{m}\mathcal {O}_F$ and not trivial on ![]() $\varpi ^{m-1}\mathcal {O}_F$. Put
$\varpi ^{m-1}\mathcal {O}_F$. Put ![]() $F^\prime = \varpi ^{m^\prime } \mathcal {O}_F$ with
$F^\prime = \varpi ^{m^\prime } \mathcal {O}_F$ with ![]() $m^{\prime } \leq m$. Then we may write the left-hand side of (7.1.4) as
$m^{\prime } \leq m$. Then we may write the left-hand side of (7.1.4) as
The first integral of (7.1.5) converges absolutely. Hence by interchanging the order of integration, it is equal to
since ![]() $y \mapsto \psi (xy)$ is a non-trivial character of
$y \mapsto \psi (xy)$ is a non-trivial character of ![]() $F^\prime$ for each
$F^\prime$ for each ![]() $x \in F\setminus \mathcal {O}$. As for the second integral of (7.1.5), we have
$x \in F\setminus \mathcal {O}$. As for the second integral of (7.1.5), we have
where the inner integral of the second integral vanishes as above. Thus, the left-hand side of (7.1.4) is equal to
Similarly the right-hand side of (7.1.4) becomes as above, and our claim follows.
By Lemma 7.1, we see that (7.1.3) is equal to
 \begin{align*} & \int_{N \backslash G^1} \int_{G^1} \int_{M_{X}} \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(hg, t) \phi)(A_0+b) \\ &\quad \times \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \Lambda(t) \psi \bigg(\mathrm{tr} \begin{pmatrix} s_2 & t_2\\ s_1 & t_1 \end{pmatrix}\bigg(S_0 \begin{pmatrix} \langle x_{-2}, b_1 \rangle & \langle x_{-2}, b_2 \rangle\\ \langle x_{-1}, b_1 \rangle & \langle x_{-1}, b_2 \rangle \end{pmatrix} -X\bigg)\bigg)\\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 . \end{align*}
\begin{align*} & \int_{N \backslash G^1} \int_{G^1} \int_{M_{X}} \int_{F^2}^{\rm st} \int_{F^2}^{\rm st} \int_{X_+^2} \langle \pi(g)f, f^\prime \rangle (\omega_{\psi}(hg, t) \phi)(A_0+b) \\ &\quad \times \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+b)} \Lambda(t) \psi \bigg(\mathrm{tr} \begin{pmatrix} s_2 & t_2\\ s_1 & t_1 \end{pmatrix}\bigg(S_0 \begin{pmatrix} \langle x_{-2}, b_1 \rangle & \langle x_{-2}, b_2 \rangle\\ \langle x_{-1}, b_1 \rangle & \langle x_{-1}, b_2 \rangle \end{pmatrix} -X\bigg)\bigg)\\ &\quad \times db \, dh \, {dx} \, dg \, dt \, ds_2 \,dt_2 \,ds_1 \, dt_1 . \end{align*}
Then applying the Fourier inversion, we get
where ![]() $B_0 = (0, 0,( {x_{21}}/{2})x_1+({x_{11}}/{2}) x_2, -({x_{22}}/{2d})x_1-( {x_{12}}/{2d}) x_2)$ and
$B_0 = (0, 0,( {x_{21}}/{2})x_1+({x_{11}}/{2}) x_2, -({x_{22}}/{2d})x_1-( {x_{12}}/{2d}) x_2)$ and ![]() $x_0=A_0+B_0$. By [Reference LiuLiu16, Proposition 3.1], for a sufficiently large compact open subgroup
$x_0=A_0+B_0$. By [Reference LiuLiu16, Proposition 3.1], for a sufficiently large compact open subgroup ![]() $N_0$ of
$N_0$ of ![]() $N$, we have
$N$, we have
and, thus, we may define
Further, we note a simple fact that we have
when both sides are defined. Thus, (7.1.6) is equal to
 \begin{align*} & \int_{N \backslash G^1} \int_{N \backslash G^1} \int_{M_{X}} \int_{N}^{\rm st} \langle \pi(g)f, f^\prime \rangle \\ &\quad \times (\omega_{\psi}(hg, t) \phi)(A_0+B_0) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+B_0)} \Lambda(t) \, db \, dh \, {dx} \, dg \, dt . \end{align*}
\begin{align*} & \int_{N \backslash G^1} \int_{N \backslash G^1} \int_{M_{X}} \int_{N}^{\rm st} \langle \pi(g)f, f^\prime \rangle \\ &\quad \times (\omega_{\psi}(hg, t) \phi)(A_0+B_0) \overline{(\omega_{\psi}(h,1)\phi^\prime)(A_0+B_0)} \Lambda(t) \, db \, dh \, {dx} \, dg \, dt . \end{align*}
Then the same computation as that to get (3.1.17) from (3.1.16) may be applied to the above integral, and, thus, we see that our integral is equal to
Hence, the identity (7.1.2) holds when ![]() $B_{\xi, \Lambda,\psi } \not \equiv 0$.
$B_{\xi, \Lambda,\psi } \not \equiv 0$.
7.2 Proof of Theorem 1.2 when  $B_{\xi, \Lambda,\psi } \equiv 0$
$B_{\xi, \Lambda,\psi } \equiv 0$
First we note the following proposition concerning the non-vanishing of the ![]() $L$-values.
$L$-values.
Proposition 7.3 Let ![]() $\pi$ be an irreducible cuspidal tempered automorphic representation of
$\pi$ be an irreducible cuspidal tempered automorphic representation of ![]() $G_D(\mathbb {A})$ with trivial central character. If
$G_D(\mathbb {A})$ with trivial central character. If ![]() $G_D \simeq G$ and
$G_D \simeq G$ and ![]() $\pi$ is a theta lift from
$\pi$ is a theta lift from ![]() $\mathrm {GSO}_{3,1}$, then
$\mathrm {GSO}_{3,1}$, then ![]() $L(s, \pi, \mathrm {std} \otimes \chi _E)$ has a simple pole at
$L(s, \pi, \mathrm {std} \otimes \chi _E)$ has a simple pole at ![]() $s=1$. Otherwise
$s=1$. Otherwise ![]() $L(s, \pi, \mathrm {std} \otimes \chi _E)$ is holomorphic and non-zero at
$L(s, \pi, \mathrm {std} \otimes \chi _E)$ is holomorphic and non-zero at ![]() $s=1$.
$s=1$.
Proof. Suppose that ![]() $G_D \simeq G$, i.e.
$G_D \simeq G$, i.e. ![]() $D$ is split. Then there exists an irreducible cuspidal globally generic automorphic representation
$D$ is split. Then there exists an irreducible cuspidal globally generic automorphic representation ![]() $\pi _0$ of
$\pi _0$ of ![]() $G(\mathbb {A})$ such that
$G(\mathbb {A})$ such that ![]() $\pi$ and
$\pi$ and ![]() $\pi _0$ are nearly equivalent. Then our claim follows from [Reference YamanaYam14, Lemma 10.2] and [Reference ShahidiSha81, Theorem 5.1].
$\pi _0$ are nearly equivalent. Then our claim follows from [Reference YamanaYam14, Lemma 10.2] and [Reference ShahidiSha81, Theorem 5.1].
Suppose that ![]() $D$ is not split. Let us take a quadratic extension
$D$ is not split. Let us take a quadratic extension ![]() $E_0$ of
$E_0$ of ![]() $F$ such that
$F$ such that ![]() $\pi$ has
$\pi$ has ![]() $(E_0, \Lambda _0)$-Bessel period for some character
$(E_0, \Lambda _0)$-Bessel period for some character ![]() $\Lambda _0$ of
$\Lambda _0$ of ![]() $\mathbb {A}_{E_0}^\times / E_0^\times$. Then by Theorem 1.1(i), we see that there exists an irreducible cuspidal tempered automorphic representation
$\mathbb {A}_{E_0}^\times / E_0^\times$. Then by Theorem 1.1(i), we see that there exists an irreducible cuspidal tempered automorphic representation ![]() $\pi _0$ of
$\pi _0$ of ![]() $G(\mathbb {A})$ such that for a sufficiently large finite set
$G(\mathbb {A})$ such that for a sufficiently large finite set ![]() $S$ of places of
$S$ of places of ![]() $F$ containing all archimedean places,
$F$ containing all archimedean places, ![]() $\pi _v, \pi _{0,v}$ are unramified and
$\pi _v, \pi _{0,v}$ are unramified and ![]() $\mathrm {BC}_{E_0 / F}(\pi _v) \simeq \mathrm {BC}_{E_0 / F}(\pi _{0,v})$ for
$\mathrm {BC}_{E_0 / F}(\pi _v) \simeq \mathrm {BC}_{E_0 / F}(\pi _{0,v})$ for ![]() $v\not \in S$. This implies that
$v\not \in S$. This implies that
From the case when ![]() $G_D \simeq G$, the left-hand side of this identity is not zero at
$G_D \simeq G$, the left-hand side of this identity is not zero at ![]() $s=1$, and, thus, so is the right-hand side, which possibly has a pole at
$s=1$, and, thus, so is the right-hand side, which possibly has a pole at ![]() $s=1$.
$s=1$.
Suppose that ![]() $L^S(s, \pi, \mathrm {std} \otimes \chi _{E_0 / F} \chi _E)$ has a pole at
$L^S(s, \pi, \mathrm {std} \otimes \chi _{E_0 / F} \chi _E)$ has a pole at ![]() $s=1$. We may take a quadratic extension
$s=1$. We may take a quadratic extension ![]() $E_1 \subset D$ of
$E_1 \subset D$ of ![]() $F$ such that
$F$ such that ![]() $\chi _{E_1} = \chi _{E_0} \chi _E$. Then by Yamana [Reference YamanaYam14, Lemma 10.2],
$\chi _{E_1} = \chi _{E_0} \chi _E$. Then by Yamana [Reference YamanaYam14, Lemma 10.2], ![]() $\pi$ is a theta lift from
$\pi$ is a theta lift from ![]() $\mathrm {GSU}_{1,D}$, which is a similitude quaternion unitary group of degree one defined by an element in
$\mathrm {GSU}_{1,D}$, which is a similitude quaternion unitary group of degree one defined by an element in ![]() $E_1$ as in (2.1.12). In this case,
$E_1$ as in (2.1.12). In this case, ![]() $\pi$ is not tempered and, thus, it contradicts our assumption on
$\pi$ is not tempered and, thus, it contradicts our assumption on ![]() $\pi$. Thus,
$\pi$. Thus, ![]() $L^S(s, \pi, \mathrm {std} \otimes \chi _{E_0 / F} \chi _E)$ is holomorphic at
$L^S(s, \pi, \mathrm {std} \otimes \chi _{E_0 / F} \chi _E)$ is holomorphic at ![]() $s=1$. Further, by an argument similar to that for
$s=1$. Further, by an argument similar to that for ![]() $L^S(s, \pi, \mathrm {std} \otimes \chi _{E_0 / F} \chi _E)$, we see that
$L^S(s, \pi, \mathrm {std} \otimes \chi _{E_0 / F} \chi _E)$, we see that ![]() $L^S(s, \pi, \mathrm {std} \otimes \chi _E)$ is holomorphic. Therefore, it is holomorphic and non-zero at
$L^S(s, \pi, \mathrm {std} \otimes \chi _E)$ is holomorphic. Therefore, it is holomorphic and non-zero at ![]() $s=1$.
$s=1$.
Suppose that ![]() $B_{\xi, \Lambda,\psi } \equiv 0$ on
$B_{\xi, \Lambda,\psi } \equiv 0$ on ![]() $V_\pi$. We shall show that the right-hand side of (1.6.2) is zero. If
$V_\pi$. We shall show that the right-hand side of (1.6.2) is zero. If ![]() $L(\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) = 0$, then there is nothing to prove. Hence, we may suppose that
$L(\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) = 0$, then there is nothing to prove. Hence, we may suppose that ![]() $L(\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$. Then we shall show that for some place
$L(\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$. Then we shall show that for some place ![]() $v$ of
$v$ of ![]() $F$, we have
$F$, we have ![]() $\alpha _{\Lambda _v, \psi _{\xi, v}}\equiv 0$ on
$\alpha _{\Lambda _v, \psi _{\xi, v}}\equiv 0$ on ![]() $\pi _v$.
$\pi _v$.
Assume the contrary, i.e. ![]() $\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on
$\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on ![]() $\pi _v$ for any
$\pi _v$ for any ![]() $v$. Let us denote by
$v$. Let us denote by ![]() $\pi _+^{B, {\rm loc}}$ the unique irreducible constituent of
$\pi _+^{B, {\rm loc}}$ the unique irreducible constituent of ![]() $\pi |_{G_D(\mathbb {A})^+}$ such that
$\pi |_{G_D(\mathbb {A})^+}$ such that ![]() $\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on
$\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on ![]() $\pi _{+,v}^{B, \mathrm {loc}}$ for any
$\pi _{+,v}^{B, \mathrm {loc}}$ for any ![]() $v$. From our assumption
$v$. From our assumption ![]() $\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on
$\alpha _{\Lambda _v, \psi _{\xi, v}} \not \equiv 0$ on ![]() $\pi _v$ and Corollary 7.2, we see that
$\pi _v$ and Corollary 7.2, we see that ![]() $\alpha _{\Lambda _v^{-1}, \psi _{X, v}} \not \equiv 0$ on the theta lift
$\alpha _{\Lambda _v^{-1}, \psi _{X, v}} \not \equiv 0$ on the theta lift ![]() $\theta _{\psi _v, D}(\pi _v)$ of
$\theta _{\psi _v, D}(\pi _v)$ of ![]() $\pi _v$ to
$\pi _v$ to ![]() $\mathrm {GSU}_{3,D}(F_v)$ and
$\mathrm {GSU}_{3,D}(F_v)$ and ![]() $Z_v(\phi _v, f_v, \pi ) \ne 0$ for some
$Z_v(\phi _v, f_v, \pi ) \ne 0$ for some ![]() $f_v \in \pi _v$ and
$f_v \in \pi _v$ and ![]() $\phi _v \in \mathcal {S}(Z_{D, +}(F_v))$. Since
$\phi _v \in \mathcal {S}(Z_{D, +}(F_v))$. Since ![]() $\pi ^\prime$ is nearly equivalent to
$\pi ^\prime$ is nearly equivalent to ![]() $\pi$, we have
$\pi$, we have ![]() $L(1, \pi, \mathrm {std} \otimes \chi _E) \ne 0$. Therefore, the theta lift
$L(1, \pi, \mathrm {std} \otimes \chi _E) \ne 0$. Therefore, the theta lift ![]() $\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ of
$\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ of ![]() $\pi _+^{B, \mathrm {loc}}$ to
$\pi _+^{B, \mathrm {loc}}$ to ![]() $\mathrm {GSU}_{3,D}(\mathbb {A})$ is non-zero by Yamana [Reference YamanaYam14, Theorem 10.3], which states that the non-vanishing of local theta lifts at all places together with the non-vanishing of the
$\mathrm {GSU}_{3,D}(\mathbb {A})$ is non-zero by Yamana [Reference YamanaYam14, Theorem 10.3], which states that the non-vanishing of local theta lifts at all places together with the non-vanishing of the ![]() $L$-value implies the non-vanishing of the global theta lift. We note that actually in [Reference YamanaYam14, Theorem 10.3], there is an assumption that
$L$-value implies the non-vanishing of the global theta lift. We note that actually in [Reference YamanaYam14, Theorem 10.3], there is an assumption that ![]() $D$ is not split at real places, which was necessary to ensure that the non-vanishing of the local theta lift implies
$D$ is not split at real places, which was necessary to ensure that the non-vanishing of the local theta lift implies ![]() $Z_v(\phi _v, f_v, \pi ) \ne 0$ for some
$Z_v(\phi _v, f_v, \pi ) \ne 0$ for some ![]() $f_v \in \pi _v$ and
$f_v \in \pi _v$ and ![]() $\phi _v \in \mathcal {S}(Z_{D, +}(F_v))$. Since the non-vanishing of
$\phi _v \in \mathcal {S}(Z_{D, +}(F_v))$. Since the non-vanishing of ![]() $Z_v(\phi _v, f_v, \pi )$ for some
$Z_v(\phi _v, f_v, \pi )$ for some ![]() $f_v$ and
$f_v$ and ![]() $\phi _v$ is shown in our case by the argument above, we may apply [Reference YamanaYam14, Theorem 10.3] regardless of the assumption.
$\phi _v$ is shown in our case by the argument above, we may apply [Reference YamanaYam14, Theorem 10.3] regardless of the assumption.
Recall that from the proof of Theorem 1.1(i), ![]() $\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ is tempered. Let us regard
$\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ is tempered. Let us regard ![]() $\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ as automorphic representations of
$\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ as automorphic representations of ![]() $\mathrm {GU}_{4, \varepsilon }$. By the uniqueness of the Bessel model for
$\mathrm {GU}_{4, \varepsilon }$. By the uniqueness of the Bessel model for ![]() $\mathrm {GU}_{4, \varepsilon }$ proved in [Reference Furusawa and MorimotoFM22, Proposition A.1], there uniquely exists an irreducible constituent
$\mathrm {GU}_{4, \varepsilon }$ proved in [Reference Furusawa and MorimotoFM22, Proposition A.1], there uniquely exists an irreducible constituent ![]() $\tau$ of
$\tau$ of ![]() $\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})|_{\mathrm {U}(4)}$ such that
$\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})|_{\mathrm {U}(4)}$ such that ![]() $\tau$ has the local
$\tau$ has the local ![]() $(X, \Lambda _v^{-1},\psi _v)$-Bessel model at any place
$(X, \Lambda _v^{-1},\psi _v)$-Bessel model at any place ![]() $v$.
$v$.
On the other hand, we note ![]() $L(1 / 2, \tau \times \Lambda ^{-1}) \ne 0$ since
$L(1 / 2, \tau \times \Lambda ^{-1}) \ne 0$ since ![]() $L(\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$. Then by [Reference Furusawa and MorimotoFM22, Theorem 1.2], there exists an irreducible cuspidal automorphic representation
$L(\frac {1}{2}, \pi \times \mathcal {AI} (\Lambda )) \ne 0$. Then by [Reference Furusawa and MorimotoFM22, Theorem 1.2], there exists an irreducible cuspidal automorphic representation ![]() $\tau ^\prime$ of
$\tau ^\prime$ of ![]() $\mathrm {U}(V_0)$ with four-dimensional hermitian space
$\mathrm {U}(V_0)$ with four-dimensional hermitian space ![]() $V_0$ over
$V_0$ over ![]() $E$ such that
$E$ such that ![]() $\tau ^\prime$ has
$\tau ^\prime$ has ![]() $(X, \Lambda _v,\psi _v)$-Bessel period. Then we know that
$(X, \Lambda _v,\psi _v)$-Bessel period. Then we know that ![]() $\tau$ and
$\tau$ and ![]() $\tau ^\prime$ have the same
$\tau ^\prime$ have the same ![]() $L$-parameter, in particular,
$L$-parameter, in particular, ![]() $\tau _v \simeq \tau _v^\prime$ when
$\tau _v \simeq \tau _v^\prime$ when ![]() $v$ is split. At a non-split place
$v$ is split. At a non-split place ![]() $v$, by the uniqueness of an element of the tempered
$v$, by the uniqueness of an element of the tempered ![]() $L$-packet which has the same Bessel period due to Beuzart-Plessis [Reference Beuzart-PlessisBeu16, Reference Beuzart-PlessisBeu20], we see that
$L$-packet which has the same Bessel period due to Beuzart-Plessis [Reference Beuzart-PlessisBeu16, Reference Beuzart-PlessisBeu20], we see that ![]() $\mathrm {U}(V_0) \simeq \mathrm {U}(J_D)$ and
$\mathrm {U}(V_0) \simeq \mathrm {U}(J_D)$ and ![]() $\tau \simeq \tau ^\prime$. Moreover, by Mok [Reference MokMok15], we have
$\tau \simeq \tau ^\prime$. Moreover, by Mok [Reference MokMok15], we have ![]() $\tau = \tau ^\prime$. Therefore,
$\tau = \tau ^\prime$. Therefore, ![]() $\tau = \tau ^\prime$ has
$\tau = \tau ^\prime$ has ![]() $(X, \Lambda ^{-1},\psi )$-Bessel period, and this implies that
$(X, \Lambda ^{-1},\psi )$-Bessel period, and this implies that ![]() $\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ also has
$\theta _{\psi, D}(\pi _+^{B, \mathrm {loc}})$ also has ![]() $(X, \Lambda ^{-1},\psi )$-Bessel period. Then Propositions 3.1 and 3.2 show that
$(X, \Lambda ^{-1},\psi )$-Bessel period. Then Propositions 3.1 and 3.2 show that ![]() $\pi$ has
$\pi$ has ![]() $(E,\Lambda )$-Bessel period, and this is a contradiction. Thus, (1.6.2) holds when
$(E,\Lambda )$-Bessel period, and this is a contradiction. Thus, (1.6.2) holds when ![]() $B_{\xi, \Lambda,\psi } \equiv 0$ on
$B_{\xi, \Lambda,\psi } \equiv 0$ on ![]() $V_\pi$.
$V_\pi$.
8. Generalized Böcherer conjecture
In this section we prove the generalized Böcherer conjecture. In fact, we shall prove Theorem 8.1 below, which is more general than Theorem 1.4 stated in the introduction.
8.1 Temperedness condition
In order to apply Theorem 1.2 to holomorphic Siegel cusp forms of degree two, we need to verify the temperedness for corresponding automorphic representations.
Proposition 8.1 Suppose that ![]() $F$ is totally real. Let
$F$ is totally real. Let ![]() $\tau$ be an irreducible cuspidal automorphic representation of
$\tau$ be an irreducible cuspidal automorphic representation of ![]() $G_D(\mathbb {A})$ with a trivial central character such that
$G_D(\mathbb {A})$ with a trivial central character such that ![]() $\tau _v$ is a discrete series representation for every real place
$\tau _v$ is a discrete series representation for every real place ![]() $v$ of
$v$ of ![]() $F$. Suppose moreover that
$F$. Suppose moreover that ![]() $\tau$ is not CAP (cuspidal representation associated to parabolic subgroup). Then
$\tau$ is not CAP (cuspidal representation associated to parabolic subgroup). Then ![]() $\tau$ is tempered.
$\tau$ is tempered.
Remark 8.1 When ![]() $D$ is split, i.e.
$D$ is split, i.e. ![]() $G_D \simeq G$, Weissauer [Reference WeissauerWei09] proved that
$G_D \simeq G$, Weissauer [Reference WeissauerWei09] proved that ![]() $\tau _v$ is tempered at a place
$\tau _v$ is tempered at a place ![]() $v$ when
$v$ when ![]() $\tau _v$ is unramified. Moreover, when
$\tau _v$ is unramified. Moreover, when ![]() $\tau _v$ is a holomorphic discrete series representation at each archimedean place
$\tau _v$ is a holomorphic discrete series representation at each archimedean place ![]() $v$, Jorza [Reference JorzaJor13] showed the temperedness at finite places not dividing
$v$, Jorza [Reference JorzaJor13] showed the temperedness at finite places not dividing ![]() $2$.
$2$.
Proof. First suppose that ![]() $G_D \simeq G$. Let
$G_D \simeq G$. Let ![]() $\Pi$ denote the functorial lift of
$\Pi$ denote the functorial lift of ![]() $\tau$ to
$\tau$ to ![]() $\mathrm {GL}_4(\mathbb {A})$ established by Arthur [Reference ArthurArt13] (see also Cai, Friedberg and Kaplan [Reference Cai, Friedberg and KaplanCFK18]).
$\mathrm {GL}_4(\mathbb {A})$ established by Arthur [Reference ArthurArt13] (see also Cai, Friedberg and Kaplan [Reference Cai, Friedberg and KaplanCFK18]).
When ![]() $\Pi$ is not cuspidal, since
$\Pi$ is not cuspidal, since ![]() $\tau$ is not CAP,
$\tau$ is not CAP, ![]() $\Pi$ is of the form
$\Pi$ is of the form ![]() $\Pi =\Pi _1 \boxplus \Pi _2$ with irreducible cuspidal automorphic representations
$\Pi =\Pi _1 \boxplus \Pi _2$ with irreducible cuspidal automorphic representations ![]() $\Pi _i$ of
$\Pi _i$ of ![]() $\mathrm {GL}_2(\mathbb {A})$. Since
$\mathrm {GL}_2(\mathbb {A})$. Since ![]() $\tau _v$ is a discrete series representation for any real place
$\tau _v$ is a discrete series representation for any real place ![]() $v$,
$v$, ![]() $\Pi _{i,v}$ is also a discrete series representation. Then
$\Pi _{i,v}$ is also a discrete series representation. Then ![]() $\Pi _i$ is tempered by [Reference BlasiusBla06] and, thus, the Langlands parameter of
$\Pi _i$ is tempered by [Reference BlasiusBla06] and, thus, the Langlands parameter of ![]() $\Pi _v$ is tempered at all places
$\Pi _v$ is tempered at all places ![]() $v$ of
$v$ of ![]() $F$. Hence,
$F$. Hence, ![]() $\tau$ is tempered.
$\tau$ is tempered.
Suppose that ![]() $\Pi$ is cuspidal. Then by Raghuram and Sarnobat [Reference Raghuram and SarnobatRS18, Theorem 5.6],
$\Pi$ is cuspidal. Then by Raghuram and Sarnobat [Reference Raghuram and SarnobatRS18, Theorem 5.6], ![]() $\Pi _v$ is tempered and cohomological at any real place
$\Pi _v$ is tempered and cohomological at any real place ![]() $v$. Let us take an imaginary quadratic extension
$v$. Let us take an imaginary quadratic extension ![]() $E$ of
$E$ of ![]() $F$ such that the base change lift
$F$ such that the base change lift ![]() $\mathrm {BC}(\Pi )$ of
$\mathrm {BC}(\Pi )$ of ![]() $\Pi$ to
$\Pi$ to ![]() $\mathrm {GL}_4(\mathbb {A}_E)$ is cuspidal. Note that
$\mathrm {GL}_4(\mathbb {A}_E)$ is cuspidal. Note that ![]() $\mathrm {BC}(\Pi )$ is cohomological and that
$\mathrm {BC}(\Pi )$ is cohomological and that ![]() $\mathrm {BC}(\Pi )^\vee \simeq \mathrm {BC}(\Pi ^\vee )\simeq \mathrm {BC}(\Pi ) \simeq \mathrm {BC}(\Pi )^\sigma$. Then Caraiani [Reference CaraianiCar12, Theorem 1.2] shows that
$\mathrm {BC}(\Pi )^\vee \simeq \mathrm {BC}(\Pi ^\vee )\simeq \mathrm {BC}(\Pi ) \simeq \mathrm {BC}(\Pi )^\sigma$. Then Caraiani [Reference CaraianiCar12, Theorem 1.2] shows that ![]() $\mathrm {BC}(\Pi )$ is tempered at all finite places. This implies that
$\mathrm {BC}(\Pi )$ is tempered at all finite places. This implies that ![]() $\Pi _v$ is also tempered for any finite place
$\Pi _v$ is also tempered for any finite place ![]() $v$. Thus,
$v$. Thus, ![]() $\tau$ is tempered.
$\tau$ is tempered.
Now let us consider the case when ![]() $D$ is not split. Since
$D$ is not split. Since ![]() $\tau$ is not CAP, by Proposition 4.1, there exists an irreducible cuspidal automorphic representation
$\tau$ is not CAP, by Proposition 4.1, there exists an irreducible cuspidal automorphic representation ![]() $\tau ^\prime$ of
$\tau ^\prime$ of ![]() $G(\mathbb {A})$ and a quadratic extension
$G(\mathbb {A})$ and a quadratic extension ![]() $E_0$ of
$E_0$ of ![]() $F$ such that
$F$ such that ![]() $\tau ^\prime$ is
$\tau ^\prime$ is ![]() $G^{+, E_0}$-locally equivalent to
$G^{+, E_0}$-locally equivalent to ![]() $\tau$. Moreover
$\tau$. Moreover ![]() $\tau$ is tempered if and only if
$\tau$ is tempered if and only if ![]() $\tau ^\prime$ is tempered. By [Reference Li, Paul, Tan and ZhuLPTZ03, Reference MœglinMœg89, Reference PaulPau98, Reference PaulPau00],
$\tau ^\prime$ is tempered. By [Reference Li, Paul, Tan and ZhuLPTZ03, Reference MœglinMœg89, Reference PaulPau98, Reference PaulPau00], ![]() $\tau ^\prime _v$ is a discrete series representation at any real place
$\tau ^\prime _v$ is a discrete series representation at any real place ![]() $v$. Then the temperedness of
$v$. Then the temperedness of ![]() $\tau ^\prime$ follows from the split case. Hence,
$\tau ^\prime$ follows from the split case. Hence, ![]() $\tau$ is also tempered.
$\tau$ is also tempered.
As an application of Proposition 8.1, the following corollary holds.
Corollary 8.1 Suppose that ![]() $F$ is totally real. Let
$F$ is totally real. Let ![]() $\tau$ be an irreducible cuspidal globally generic automorphic representation of
$\tau$ be an irreducible cuspidal globally generic automorphic representation of ![]() $G(\mathbb {A})$ such that
$G(\mathbb {A})$ such that ![]() $\tau _v$ is a discrete series representation at any real place
$\tau _v$ is a discrete series representation at any real place ![]() $v$. Then
$v$. Then ![]() $\tau$ is tempered and, hence, the explicit formula (6.2.3) for the Whittaker periods holds for any non-zero decomposable vector in
$\tau$ is tempered and, hence, the explicit formula (6.2.3) for the Whittaker periods holds for any non-zero decomposable vector in ![]() $V_\tau$.
$V_\tau$.
Proof. Recall that the functorial lift ![]() $\Pi$ of
$\Pi$ of ![]() $\tau$ to
$\tau$ to ![]() $\mathrm {GL}_4(\mathbb {A})$ is cuspidal or an isobaric sum of irreducible cuspidal automorphic representations of
$\mathrm {GL}_4(\mathbb {A})$ is cuspidal or an isobaric sum of irreducible cuspidal automorphic representations of ![]() $\mathrm {GL}_2$ by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04]. In particular,
$\mathrm {GL}_2$ by [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPS04]. In particular, ![]() $\tau$ is not CAP by Arthur [Reference ArthurArt13]. Then by Proposition 8.1,
$\tau$ is not CAP by Arthur [Reference ArthurArt13]. Then by Proposition 8.1, ![]() $\tau$ is tempered and our claim follows from Theorem 6.3.
$\tau$ is tempered and our claim follows from Theorem 6.3.
8.2 Vector-valued Siegel cusp forms and Bessel periods
Let ![]() $\mathfrak H_2$ be the Siegel upper half-space of degree two, i.e. the set of two-by-two symmetric complex matrices whose imaginary parts are positive definite. Then the group
$\mathfrak H_2$ be the Siegel upper half-space of degree two, i.e. the set of two-by-two symmetric complex matrices whose imaginary parts are positive definite. Then the group ![]() $G(\mathbb {R})^+=\{g\in G(\mathbb {R}):\nu (g)>0\}$ acts on
$G(\mathbb {R})^+=\{g\in G(\mathbb {R}):\nu (g)>0\}$ acts on ![]() $\mathfrak H_2$ by
$\mathfrak H_2$ by
and the factor of automorphy ![]() $J(g,Z)$ is defined by
$J(g,Z)$ is defined by
For an integer ![]() $N\ge 1$, let
$N\ge 1$, let
8.2.1 Vector-valued Siegel cusp forms
Let ![]() $(\varrho, V_\varrho )$ be an algebraic representation of
$(\varrho, V_\varrho )$ be an algebraic representation of ![]() $\mathrm {GL}_2(\mathbb {C})$. Then a holomorphic mapping
$\mathrm {GL}_2(\mathbb {C})$. Then a holomorphic mapping ![]() $\Phi :\mathfrak H_2\to V_\varrho$ is a Siegel cusp form of weight
$\Phi :\mathfrak H_2\to V_\varrho$ is a Siegel cusp form of weight ![]() $\varrho$ with respect to
$\varrho$ with respect to ![]() $\Gamma _0(N)$ when
$\Gamma _0(N)$ when ![]() $\Phi$ vanishes at the cusps and satisfies
$\Phi$ vanishes at the cusps and satisfies
We denote by ![]() $S_\varrho (\Gamma _0(N))$ the complex vector space of Siegel cusp forms of weight
$S_\varrho (\Gamma _0(N))$ the complex vector space of Siegel cusp forms of weight ![]() $\varrho$ with respect to
$\varrho$ with respect to ![]() $\Gamma _0(N)$. Then
$\Gamma _0(N)$. Then ![]() $\Phi \in S_\varrho (\Gamma _0(N))$ has a Fourier expansion
$\Phi \in S_\varrho (\Gamma _0(N))$ has a Fourier expansion
Here ![]() $T$ runs over positive-definite two-by-two symmetric matrices which are semi-integral, i.e.
$T$ runs over positive-definite two-by-two symmetric matrices which are semi-integral, i.e. ![]() $T$ is of the form
$T$ is of the form ![]() $T=\big (\begin{smallmatrix}a & b/ 2\\ b/ 2 & c\end{smallmatrix}\big )$,
$T=\big (\begin{smallmatrix}a & b/ 2\\ b/ 2 & c\end{smallmatrix}\big )$, ![]() $a,b,c\in \mathbb {Z}$. We note that (8.2.1) implies
$a,b,c\in \mathbb {Z}$. We note that (8.2.1) implies
From now until the end of this paper, we assume ![]() $\varrho$ to be irreducible. It is well known that the irreducible algebraic representations of
$\varrho$ to be irreducible. It is well known that the irreducible algebraic representations of ![]() $\mathrm {GL}_2(\mathbb {C})$ are parametrized by
$\mathrm {GL}_2(\mathbb {C})$ are parametrized by
Namely the parametrization is given by assigning
Suppose that ![]() $\varrho =\varrho _\kappa$ with
$\varrho =\varrho _\kappa$ with ![]() $\kappa =(n+k,k)\in \mathbb {L}$. Then we realize
$\kappa =(n+k,k)\in \mathbb {L}$. Then we realize ![]() $\varrho$ concretely by taking its space of representation
$\varrho$ concretely by taking its space of representation ![]() $V_{\varrho }$ to be
$V_{\varrho }$ to be ![]() $\mathbb {C}[X,Y]_{n}$, the space of degree
$\mathbb {C}[X,Y]_{n}$, the space of degree ![]() $n$ homogeneous polynomials of
$n$ homogeneous polynomials of ![]() $X$ and
$X$ and ![]() $Y$, where the action of
$Y$, where the action of ![]() $\mathrm {GL}_2(\mathbb {C})$ is given by
$\mathrm {GL}_2(\mathbb {C})$ is given by
Let us define a bilinear form
by
 \begin{equation} (X^iY^{n-i}, X^j Y^{n-j})_n= \begin{cases} \displaystyle{(-1)^i \begin{pmatrix}n\\ i\end{pmatrix}} & \text{if $i+j=n$}; \\ 0 & \text{otherwise.} \end{cases} \end{equation}
\begin{equation} (X^iY^{n-i}, X^j Y^{n-j})_n= \begin{cases} \displaystyle{(-1)^i \begin{pmatrix}n\\ i\end{pmatrix}} & \text{if $i+j=n$}; \\ 0 & \text{otherwise.} \end{cases} \end{equation}Then we have
We define a positive-definite hermitian inner product ![]() $\langle \,{,}\,\rangle _\varrho$ on
$\langle \,{,}\,\rangle _\varrho$ on ![]() $V_\varrho$ by
$V_\varrho$ by
Here ![]() $\overline {Q}$ denotes the polynomial obtained from
$\overline {Q}$ denotes the polynomial obtained from ![]() $Q$ by taking the complex conjugates of its coefficients. Then (8.2.5) implies that we have
$Q$ by taking the complex conjugates of its coefficients. Then (8.2.5) implies that we have
In particular, the hermitian inner product ![]() $\langle \,{,}\,\rangle _\varrho$ is
$\langle \,{,}\,\rangle _\varrho$ is ![]() $\mathrm {U}_2(\mathbb {R})$-invariant. Then for
$\mathrm {U}_2(\mathbb {R})$-invariant. Then for ![]() $\Phi,\Phi ^\prime \in S_{\varrho }(\Gamma _0(N))$, we define the Petersson inner product
$\Phi,\Phi ^\prime \in S_{\varrho }(\Gamma _0(N))$, we define the Petersson inner product ![]() $\langle \Phi,\Phi ^\prime \rangle _{\varrho }$ by
$\langle \Phi,\Phi ^\prime \rangle _{\varrho }$ by
where ![]() $X=\mathrm {Re}(Z)$ and
$X=\mathrm {Re}(Z)$ and ![]() $Y=\mathrm {Im}(Z)$. The space
$Y=\mathrm {Im}(Z)$. The space ![]() $S_{\varrho }(\Gamma _0(N))$ has a natural orthogonal decomposition with respect to the Petersson inner product
$S_{\varrho }(\Gamma _0(N))$ has a natural orthogonal decomposition with respect to the Petersson inner product
into the oldspace and the newspace in the sense of Schmidt [Reference SchmidtSch05, 3.3]. We note that when ![]() $n$ is odd, we have
$n$ is odd, we have ![]() $S_\varrho (\Gamma _0(N))=\{0\}$ for
$S_\varrho (\Gamma _0(N))=\{0\}$ for ![]() $\varrho$ with
$\varrho$ with ![]() $\kappa =(n+k,k)$ by (8.2.1) since
$\kappa =(n+k,k)$ by (8.2.1) since ![]() $-1_4\in \Gamma _0(N)$.
$-1_4\in \Gamma _0(N)$.
8.2.2 Adelization
Given ![]() $\Phi \in S_\varrho (\Gamma _0(N))$, its adelization
$\Phi \in S_\varrho (\Gamma _0(N))$, its adelization ![]() $\varphi _\Phi :G(\mathbb {A})\to V_\varrho$ is defined as follows (cf. [Reference SahaSah15, 3.1] and [Reference SchmidtSch05, 3.2]). For each prime number
$\varphi _\Phi :G(\mathbb {A})\to V_\varrho$ is defined as follows (cf. [Reference SahaSah15, 3.1] and [Reference SchmidtSch05, 3.2]). For each prime number ![]() $p$, let us define a compact open subgroup
$p$, let us define a compact open subgroup ![]() $P_{1,p}(N)$ of
$P_{1,p}(N)$ of ![]() $G(\mathbb {Q}_p)$ by
$G(\mathbb {Q}_p)$ by
Then we define a mapping ![]() $\varphi _{\Phi }:G(\mathbb {A}) \to V_{\varrho }$ by
$\varphi _{\Phi }:G(\mathbb {A}) \to V_{\varrho }$ by
when
Let ![]() $L$ be any non-zero linear form on
$L$ be any non-zero linear form on ![]() $V_\varrho$. Then
$V_\varrho$. Then ![]() $L(\varphi _\Phi ):G(\mathbb {A})\to \mathbb {C}$ defined by
$L(\varphi _\Phi ):G(\mathbb {A})\to \mathbb {C}$ defined by ![]() $L(\varphi _\Phi )(g)=L(\varphi _\Phi (g))$ is a scalar-valued automorphic form on
$L(\varphi _\Phi )(g)=L(\varphi _\Phi (g))$ is a scalar-valued automorphic form on ![]() $G(\mathbb {A})$. Let
$G(\mathbb {A})$. Let ![]() $V(\Phi )$ denote the space generated by right
$V(\Phi )$ denote the space generated by right ![]() $G(\mathbb {A})$-translates of
$G(\mathbb {A})$-translates of ![]() $L(\varphi _\Phi )$. Then
$L(\varphi _\Phi )$. Then ![]() $V(\Phi )$ does not depend on the choice of
$V(\Phi )$ does not depend on the choice of ![]() $L$ and we denote by
$L$ and we denote by ![]() $\pi (\Phi )$ the right regular representation of
$\pi (\Phi )$ the right regular representation of ![]() $G(\mathbb {A})$ on
$G(\mathbb {A})$ on ![]() $V(\Phi )$. Note that the central character of
$V(\Phi )$. Note that the central character of ![]() $\pi (\Phi )$ is trivial.
$\pi (\Phi )$ is trivial.
We recall that for scalar-valued automorphic forms ![]() $\phi$,
$\phi$, ![]() $\phi ^\prime$ on
$\phi ^\prime$ on ![]() $G(\mathbb {A})$ with a trivial central character, their Petersson inner product
$G(\mathbb {A})$ with a trivial central character, their Petersson inner product ![]() $\langle \phi,\phi ^\prime \rangle$ is defined by
$\langle \phi,\phi ^\prime \rangle$ is defined by
where ![]() $Z_G$ denotes the center of
$Z_G$ denotes the center of ![]() $G$ and
$G$ and ![]() $dg$ is the Tamagawa measure.
$dg$ is the Tamagawa measure.
Lemma 8.1 Let ![]() $L$ be a non-zero linear form on
$L$ be a non-zero linear form on ![]() $V_\varrho$. Take
$V_\varrho$. Take ![]() $v^\prime \in V_\varrho$ such that
$v^\prime \in V_\varrho$ such that ![]() $L(v)=\langle v,v^\prime \rangle _\varrho$ for any
$L(v)=\langle v,v^\prime \rangle _\varrho$ for any ![]() $v\in V_\varrho$.
$v\in V_\varrho$.
Then we have
where
Proof. Let ![]() $K_\infty =\mathrm {U}_2(\mathbb {R})$. We identify
$K_\infty =\mathrm {U}_2(\mathbb {R})$. We identify ![]() $K_\infty$ as a subgroup of
$K_\infty$ as a subgroup of ![]() $\mathrm {Sp}_2(\mathbb {R})$ via
$\mathrm {Sp}_2(\mathbb {R})$ via
Let ![]() $dk$ be the Haar measure on
$dk$ be the Haar measure on ![]() $K_\infty$ such that
$K_\infty$ such that ![]() $\mathrm {Vol}(K_\infty, dk)=1$. Then by the Schur orthogonality relations, we have
$\mathrm {Vol}(K_\infty, dk)=1$. Then by the Schur orthogonality relations, we have
On the other hand, it is easily seen that for ![]() $\Phi \in S_\varrho (\Gamma _0(N))$, we have
$\Phi \in S_\varrho (\Gamma _0(N))$, we have
where
Hence,
 \begin{align*} \langle\Phi,\Phi\rangle_\varrho &= C(v^\prime)^{-1} \int_{Z_G(\mathbb{A}) G(\mathbb{Q}) \backslash G(\mathbb{A})} \int_{K_\infty}| L(\varrho(k)^{-1}\varphi_\Phi(g))|^2\, dk\,dg \\ &= C(v^\prime)^{-1}\int_{K_\infty} \int_{Z_G(\mathbb{A}) G(\mathbb{Q}) \backslash G(\mathbb{A})} | L(\varphi_\Phi(gk))|^2\,dg\,dk \\ &= C(v^\prime)^{-1}\cdot\langle L(\varphi_\Phi),L(\varphi_\Phi)\rangle_\varrho. \end{align*}
\begin{align*} \langle\Phi,\Phi\rangle_\varrho &= C(v^\prime)^{-1} \int_{Z_G(\mathbb{A}) G(\mathbb{Q}) \backslash G(\mathbb{A})} \int_{K_\infty}| L(\varrho(k)^{-1}\varphi_\Phi(g))|^2\, dk\,dg \\ &= C(v^\prime)^{-1}\int_{K_\infty} \int_{Z_G(\mathbb{A}) G(\mathbb{Q}) \backslash G(\mathbb{A})} | L(\varphi_\Phi(gk))|^2\,dg\,dk \\ &= C(v^\prime)^{-1}\cdot\langle L(\varphi_\Phi),L(\varphi_\Phi)\rangle_\varrho. \end{align*}
8.2.3 Bessel periods of vector-valued Siegel cusp forms
Let ![]() $E$ be an imaginary quadratic field of
$E$ be an imaginary quadratic field of ![]() $\mathbb {Q}$ and
$\mathbb {Q}$ and ![]() $-D_E$ its discriminant. We put
$-D_E$ its discriminant. We put
 \begin{equation} S_E:=\begin{cases}
\,\begin{pmatrix} 1 & 0\\ 0 & D_E/ 4 \end{pmatrix} &
\text{when $D_E\equiv 0\pmod{4}$};\\ \begin{pmatrix} 1 &
1/ 2\\ 1/ 2 & (1+D_E)/ 4 \end{pmatrix} &
\text{when $D_E\equiv -1\pmod{4}$}. \end{cases}
\end{equation}
\begin{equation} S_E:=\begin{cases}
\,\begin{pmatrix} 1 & 0\\ 0 & D_E/ 4 \end{pmatrix} &
\text{when $D_E\equiv 0\pmod{4}$};\\ \begin{pmatrix} 1 &
1/ 2\\ 1/ 2 & (1+D_E)/ 4 \end{pmatrix} &
\text{when $D_E\equiv -1\pmod{4}$}. \end{cases}
\end{equation}
Given ![]() $S=S_E$ as above, we define
$S=S_E$ as above, we define ![]() $T_S$,
$T_S$, ![]() $N$ and
$N$ and ![]() $\psi _{S}$ as in § 2.3.1. Then
$\psi _{S}$ as in § 2.3.1. Then ![]() $T_S(\mathbb {Q})\simeq E^\times$.
$T_S(\mathbb {Q})\simeq E^\times$.
Let ![]() $\Lambda$ be a character of
$\Lambda$ be a character of ![]() $T_S(\mathbb {A})$ which is trivial on
$T_S(\mathbb {A})$ which is trivial on ![]() $\mathbb {A}^\times T_S(\mathbb {Q})$. Let
$\mathbb {A}^\times T_S(\mathbb {Q})$. Let ![]() $\psi$ be the unique character of
$\psi$ be the unique character of ![]() $\mathbb {A}/ \mathbb {Q}$ such that
$\mathbb {A}/ \mathbb {Q}$ such that ![]() $\psi _\infty (x)=e^{-2\pi \sqrt {-1}\, x}$ and the conductor of
$\psi _\infty (x)=e^{-2\pi \sqrt {-1}\, x}$ and the conductor of ![]() $\psi _\ell$ is
$\psi _\ell$ is ![]() $\mathbb {Z}_\ell$ for any prime number
$\mathbb {Z}_\ell$ for any prime number ![]() $\ell$.
$\ell$.
Then for a scalar-valued automorphic form ![]() $\phi$ on
$\phi$ on ![]() $G(\mathbb {A})$ with a trivial central character, we define its
$G(\mathbb {A})$ with a trivial central character, we define its ![]() $(S, \Lambda, \psi )$-Bessel period
$(S, \Lambda, \psi )$-Bessel period ![]() $B_{S,\Lambda, \psi }(\phi )$ by (2.3.1) with the Haar measures
$B_{S,\Lambda, \psi }(\phi )$ by (2.3.1) with the Haar measures ![]() $du$ on
$du$ on ![]() $N(\mathbb {A})$ and
$N(\mathbb {A})$ and ![]() $dt=dt_\infty \, dt_f$ on
$dt=dt_\infty \, dt_f$ on ![]() $T_S(\mathbb {A})=T_S(\mathbb {R}) \times T_S(\mathbb {A}_f)$ are taken so that
$T_S(\mathbb {A})=T_S(\mathbb {R}) \times T_S(\mathbb {A}_f)$ are taken so that ![]() $\mathrm {Vol}(N(\mathbb {Q})\backslash N(\mathbb {A}), du)=1$ and
$\mathrm {Vol}(N(\mathbb {Q})\backslash N(\mathbb {A}), du)=1$ and
Then we note that
For a ![]() $V_\varrho$-valued automorphic form
$V_\varrho$-valued automorphic form ![]() $\varphi$ with a trivial central character, it is clear that for a linear form
$\varphi$ with a trivial central character, it is clear that for a linear form ![]() $L:V_\varrho \to \mathbb {C}$ we have
$L:V_\varrho \to \mathbb {C}$ we have
Recall that we may identify the ideal class group ![]() $\mathrm {Cl}_E$ of
$\mathrm {Cl}_E$ of ![]() $E$ with the quotient group
$E$ with the quotient group
Let ![]() $\{t_c: c\in \mathrm {Cl}_E\}$ be a set of representatives of
$\{t_c: c\in \mathrm {Cl}_E\}$ be a set of representatives of ![]() $\mathrm {Cl}_E$ such that
$\mathrm {Cl}_E$ such that ![]() $t_c\in \prod _{p<\infty }T(\mathbb {Q}_p)$. We let
$t_c\in \prod _{p<\infty }T(\mathbb {Q}_p)$. We let ![]() $t_c=\gamma _c\,m_c\,\kappa _c$ with
$t_c=\gamma _c\,m_c\,\kappa _c$ with ![]() $\gamma _c\in \mathrm {GL}_2(\mathbb {Q})$,
$\gamma _c\in \mathrm {GL}_2(\mathbb {Q})$, ![]() $m_c\in \{g\in \mathrm {GL}_2(\mathbb {R}):\det g>0\}$,
$m_c\in \{g\in \mathrm {GL}_2(\mathbb {R}):\det g>0\}$, ![]() $\kappa _c\in \prod _{p<\infty }\mathrm {GL}_2(\mathbb {Z}_p)$. Let
$\kappa _c\in \prod _{p<\infty }\mathrm {GL}_2(\mathbb {Z}_p)$. Let ![]() $S_c=(\det \gamma _c)^{-1}\cdot {}^t\gamma _c S\gamma _c$. Then the set
$S_c=(\det \gamma _c)^{-1}\cdot {}^t\gamma _c S\gamma _c$. Then the set ![]() $\{S_c: c\in \mathrm {Cl}_E\}$ is a set of representatives for the
$\{S_c: c\in \mathrm {Cl}_E\}$ is a set of representatives for the ![]() $\mathrm {SL}_2(\mathbb {Z})$-equivalence classes of primitive semi-integral positive-definite two-by-two symmetric matrices of discriminant
$\mathrm {SL}_2(\mathbb {Z})$-equivalence classes of primitive semi-integral positive-definite two-by-two symmetric matrices of discriminant ![]() $D_E$.
$D_E$.
Thus, when ![]() $\varphi =\varphi _\Phi$ for
$\varphi =\varphi _\Phi$ for ![]() $\Phi \in S_\varrho (\Gamma _0(N))$ and
$\Phi \in S_\varrho (\Gamma _0(N))$ and ![]() $\Lambda$ is a character of
$\Lambda$ is a character of ![]() $\mathrm {Cl}_E$, we may write (8.2.12) as
$\mathrm {Cl}_E$, we may write (8.2.12) as
where
 \begin{equation} B_\Lambda (\Phi; E):= w(E)^{-1}\cdot \pi_\varrho\bigg(\sum_{c\in\mathrm{Cl}_E} \Lambda(c)^{-1} \cdot a(S_c,\Phi)\bigg) \end{equation}
\begin{equation} B_\Lambda (\Phi; E):= w(E)^{-1}\cdot \pi_\varrho\bigg(\sum_{c\in\mathrm{Cl}_E} \Lambda(c)^{-1} \cdot a(S_c,\Phi)\bigg) \end{equation}
is the vector-valued ![]() $(S, \Lambda, \psi )$-Bessel period where
$(S, \Lambda, \psi )$-Bessel period where
(e.g. Dickson et al. [Reference Dickson, Pitale, Saha and SchmidtDPSS20, Proposition 3.5] and Sugano [Reference SuganoSug85, (1-26)]).
Remark 8.2 (An erratum to [Reference Furusawa and MorimotoFM17])
The definition of ![]() $B(\Phi ;E)$ in the vector-valued case in [Reference Furusawa and MorimotoFM17, Theorem 5] should be replaced by (8.2.14). The statement and the proof of [Reference Furusawa and MorimotoFM17, Theorem 5] remain valid.
$B(\Phi ;E)$ in the vector-valued case in [Reference Furusawa and MorimotoFM17, Theorem 5] should be replaced by (8.2.14). The statement and the proof of [Reference Furusawa and MorimotoFM17, Theorem 5] remain valid.
Suppose that ![]() $\varrho =\varrho _\kappa$ where
$\varrho =\varrho _\kappa$ where ![]() $\kappa =(2r+k,k) \in \mathbb {L}$. We define
$\kappa =(2r+k,k) \in \mathbb {L}$. We define ![]() $Q_{S,\varrho }\in \mathbb {C}[X,Y]_{2r}$ by
$Q_{S,\varrho }\in \mathbb {C}[X,Y]_{2r}$ by
Then for ![]() $\Phi \in S_\varrho (\Gamma _0(N))$, the scalar-valued
$\Phi \in S_\varrho (\Gamma _0(N))$, the scalar-valued ![]() $(S, \Lambda, \psi )$-Bessel period
$(S, \Lambda, \psi )$-Bessel period ![]() ${\mathcal {B}}_\Lambda (\Phi ; E)$ of
${\mathcal {B}}_\Lambda (\Phi ; E)$ of ![]() $\Phi$ is defined by
$\Phi$ is defined by
8.3 Explicit  $L$-value formula in the vector-valued case
$L$-value formula in the vector-valued case
Let us state our explicit formula for holomorphic Siegel modular forms. In what follows, whenever we refer to a type of an admissible representation of ![]() $G$ over a non-archimedean local field, we use the standard classification due to Roberts and Schmidt [Reference Raghuram and SarnobatRS18].
$G$ over a non-archimedean local field, we use the standard classification due to Roberts and Schmidt [Reference Raghuram and SarnobatRS18].
Let ![]() $N$ be a squarefree integer. We say that a non-zero
$N$ be a squarefree integer. We say that a non-zero ![]() $\Phi \in S_\varrho (\Gamma _0(N))$ is a newform if:
$\Phi \in S_\varrho (\Gamma _0(N))$ is a newform if:
(1)
 $\Phi \in S_\varrho (\Gamma _0(N))^{\text {new}}$;
$\Phi \in S_\varrho (\Gamma _0(N))^{\text {new}}$;(2)
 $\Phi$ is an eigenform for the local Hecke algebras for all primes
$\Phi$ is an eigenform for the local Hecke algebras for all primes  $p$ not dividing
$p$ not dividing  $N$ and an eigenfunction of the local
$N$ and an eigenfunction of the local  $U(p)$ operator (see Saha and Schmidt [Reference Saha and SchmidtSS13, 2.3]) for all primes dividing
$U(p)$ operator (see Saha and Schmidt [Reference Saha and SchmidtSS13, 2.3]) for all primes dividing  $N$;
$N$;(3) the representation
 $\pi (\Phi )$ of
$\pi (\Phi )$ of  $G(\mathbb {A})$ is irreducible.
$G(\mathbb {A})$ is irreducible.
Then the following theorem is derived from Theorem 1.2 exactly as in Dickson, Pitale, Saha and Schmidt [Reference Dickson, Pitale, Saha and SchmidtDPSS20, Theorem 1.13] except that we need to compute local Bessel periods at the real place adapting to the vector valued case. We perform the computation of them in Appendix B.
Theorem 8.1 Let ![]() $N\ge 1$ be an odd squarefree integer. Let
$N\ge 1$ be an odd squarefree integer. Let ![]() $\varrho =\varrho _\kappa$ where
$\varrho =\varrho _\kappa$ where ![]() $\kappa =(2r+k,k)$ with
$\kappa =(2r+k,k)$ with ![]() $k\ge 2$. Let
$k\ge 2$. Let ![]() $\Phi$ be a non-CAP newform in
$\Phi$ be a non-CAP newform in ![]() $S_{\varrho }(\Gamma _0(N))$. Suppose that
$S_{\varrho }(\Gamma _0(N))$. Suppose that ![]() $({{D_E}/{p}})=-1$ for all primes
$({{D_E}/{p}})=-1$ for all primes ![]() $p$ dividing
$p$ dividing ![]() $N$. When
$N$. When ![]() $k=2$, suppose moreover that
$k=2$, suppose moreover that ![]() $\pi (\Phi )$ is tempered.
$\pi (\Phi )$ is tempered.
Then we have
 \begin{equation} \frac{|{\mathcal{B}}_\Lambda(\Phi;E)|^2}{\langle\Phi,\Phi\rangle_{\varrho}} =\frac{2^{4k+6r-c}}{D_E}\cdot \frac{L(1/ 2,\pi(\Phi) \times \mathcal{AI} (\Lambda))}{L(1,\pi(\Phi),\mathrm{Ad})}\cdot \prod_{p \,|\, N}J_p, \end{equation}
\begin{equation} \frac{|{\mathcal{B}}_\Lambda(\Phi;E)|^2}{\langle\Phi,\Phi\rangle_{\varrho}} =\frac{2^{4k+6r-c}}{D_E}\cdot \frac{L(1/ 2,\pi(\Phi) \times \mathcal{AI} (\Lambda))}{L(1,\pi(\Phi),\mathrm{Ad})}\cdot \prod_{p \,|\, N}J_p, \end{equation}
where ![]() $c=5$ if
$c=5$ if ![]() $\Phi$ is a Yoshida lift in the sense of Saha [Reference SahaSah15, § 4] and
$\Phi$ is a Yoshida lift in the sense of Saha [Reference SahaSah15, § 4] and ![]() $c=4$ otherwise. The quantities
$c=4$ otherwise. The quantities ![]() $J_p$ for
$J_p$ for ![]() $p$ dividing
$p$ dividing ![]() $N$ are given by
$N$ are given by
 \[ J_p=(1+p^{-2})(1+p^{-1})\times \begin{cases} 1 & \text{if $\pi(\Phi)_p$ is of type $\mathrm{IIIa}$}; \\ 2 & \text{if $\pi(\Phi)_p$ is of type $\mathrm{VIb}$};\\ 0 & \text{otherwise.} \end{cases} \]
\[ J_p=(1+p^{-2})(1+p^{-1})\times \begin{cases} 1 & \text{if $\pi(\Phi)_p$ is of type $\mathrm{IIIa}$}; \\ 2 & \text{if $\pi(\Phi)_p$ is of type $\mathrm{VIb}$};\\ 0 & \text{otherwise.} \end{cases} \]
Remark 8.3 When ![]() $k\ge 3$,
$k\ge 3$, ![]() $\pi (\Phi )$ is tempered by Proposition 8.1.
$\pi (\Phi )$ is tempered by Proposition 8.1.
Remark 8.4 Since ![]() $\mathcal {B}(\Phi ;E)=2^{k}D_E^{-({k}/{2})} \cdot B(\Phi ;E)$ when
$\mathcal {B}(\Phi ;E)=2^{k}D_E^{-({k}/{2})} \cdot B(\Phi ;E)$ when ![]() $r=0$, (1.8.2) follows from (8.3.1) by putting
$r=0$, (1.8.2) follows from (8.3.1) by putting ![]() $N=1$ and
$N=1$ and ![]() $r=0$.
$r=0$.
Remark 8.5 In the statement of the theorem, we used the notion of Yoshida lifts in the sense of Saha [Reference SahaSah15]. Though it is necessary to extend the arguments concerning Yoshida lifts in [Reference SahaSah15, § 4] in the scalar-valued case to the vector-valued case to be rigorous, we omit it here since it is straightforward. We also mention that the arguments in [Reference SahaSah15, 4.4] now work unconditionally since the classification theory in Arthur [Reference ArthurArt13] is complete for ![]() $\mathbb {G}=\mathrm {PGSp}_2\simeq \mathrm {SO}(3,2)$.
$\mathbb {G}=\mathrm {PGSp}_2\simeq \mathrm {SO}(3,2)$.
Remark 8.6 Recall that the ![]() $L$-functions in (8.3.1) are complete
$L$-functions in (8.3.1) are complete ![]() $L$-functions. We may rewrite the explicit formula in terms of the finite parts of the
$L$-functions. We may rewrite the explicit formula in terms of the finite parts of the ![]() $L$-functions by observing that the relevant archimedean
$L$-functions by observing that the relevant archimedean ![]() $L$-factors are given by
$L$-factors are given by
and
respectively.
Remark 8.7 Let us consider the case when ![]() $D$ is a quaternion algebra over
$D$ is a quaternion algebra over ![]() $\mathbb {Q}$ which is split at the real place, i.e.
$\mathbb {Q}$ which is split at the real place, i.e. ![]() $D(\mathbb {R}) \simeq \mathrm {Mat}_{2 \times 2}(\mathbb {R})$. Assuming that the endoscopic classification holds for
$D(\mathbb {R}) \simeq \mathrm {Mat}_{2 \times 2}(\mathbb {R})$. Assuming that the endoscopic classification holds for ![]() $\mathbb {G}_D=G_D/ Z_D$, we may apply Theorem 1.2 to holomorphic modular forms on
$\mathbb {G}_D=G_D/ Z_D$, we may apply Theorem 1.2 to holomorphic modular forms on ![]() $\mathbb {G}_D(\mathbb {A})$. In this case, Hsieh and Yamana [Reference Hsieh and YamanaHY24] compute local Bessel periods and show an explicit formula for Bessel periods such as (8.3.1) for scalar-valued holomorphic modular forms, including the case when
$\mathbb {G}_D(\mathbb {A})$. In this case, Hsieh and Yamana [Reference Hsieh and YamanaHY24] compute local Bessel periods and show an explicit formula for Bessel periods such as (8.3.1) for scalar-valued holomorphic modular forms, including the case when ![]() $G_D =G$ and
$G_D =G$ and ![]() $N$ is an even squarefree integer. Meanwhile, we shall maintain
$N$ is an even squarefree integer. Meanwhile, we shall maintain ![]() $N$ to be odd in Theorem 8.1, since our computation of the local Bessel period at the real place in the vector-valued case in Appendix B is performed under the assumption that
$N$ to be odd in Theorem 8.1, since our computation of the local Bessel period at the real place in the vector-valued case in Appendix B is performed under the assumption that ![]() $N$ is odd.
$N$ is odd.
As we noted in Remark 1.5, after the submission of this paper, Ishimoto [Reference IshimotoIsh24] showed the endoscopic classification of ![]() $\mathrm {SO}(4,1)$ for generic Arthur parameters. Therefore, we may apply our theorem to the case of
$\mathrm {SO}(4,1)$ for generic Arthur parameters. Therefore, we may apply our theorem to the case of ![]() $\Bbb G_D \simeq \mathrm {SO}(4,1)$.
$\Bbb G_D \simeq \mathrm {SO}(4,1)$.
Remark 8.8 A global explicit formula such as (8.3.1) is obtained in a certain non-squarefree level case by Pitale, Saha and Schmidt [Reference Pitale, Saha and SchmidtPSS23, Theorem 4.8].
Acknowledgements
This paper was partly written while the second author stayed at National University of Singapore (NUS). He would like to thank the people at NUS for their warm hospitality. The authors would like to thank the anonymous referee for his/her careful reading of the earlier version of the manuscript and providing many helpful comments and suggestions. The first author would like to dedicate this paper to the memory of his brother, Akira Furusawa (1952–2020).
Conflicts of interest
None.
Financial support
The research of the first author was supported in part by JSPS KAKENHI Grant Number 19K03407, 22K03235 and by Osaka Central Advanced Mathematical Institute (MEXT Promotion of Distinctive Joint Research Center Program JPMXP0723833165). The research of the second author was supported in part by JSPS KAKENHI Grant Number 17K14166, 21K03164 and by Kobe University Long Term Overseas Visiting Program for Young Researchers Fund.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.
Appendix A. Explicit formula for the Whittaker periods on  $G=\mathrm {GSp}_2$
$G=\mathrm {GSp}_2$
Here we shall prove Theorem 6.3.
Let ![]() $(\pi, V_{\pi })$ be an irreducible cuspidal globally generic automorphic representation of
$(\pi, V_{\pi })$ be an irreducible cuspidal globally generic automorphic representation of ![]() $G(\mathbb {A})$. Then Soudry [Reference SoudrySou87] has shown that the theta lift of
$G(\mathbb {A})$. Then Soudry [Reference SoudrySou87] has shown that the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{3,3}$ is non-zero and globally generic. We may divide into two cases according to whether the theta lift of
$\mathrm {GSO}_{3,3}$ is non-zero and globally generic. We may divide into two cases according to whether the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{3,3}$ is cuspidal or not.
$\mathrm {GSO}_{3,3}$ is cuspidal or not.
Suppose that the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{3,3}$ is cuspidal. Since
$\mathrm {GSO}_{3,3}$ is cuspidal. Since ![]() $\mathrm {PGSO}_{3,3}\simeq \mathrm {PGL}_4$ and the explicit formula for the Whittaker periods on
$\mathrm {PGSO}_{3,3}\simeq \mathrm {PGL}_4$ and the explicit formula for the Whittaker periods on ![]() $\mathrm {GL}_n$ is known by Lapid and Mao [Reference Lapid and MaoLM15], the arguments in § 6.2 and 6.2.3, which are used to obtain (6.1.6) in Theorem 6.1 from (6.2.3), work mutatis mutandis to obtain (6.2.3) from the Lapid–Mao formula in the case of
$\mathrm {GL}_n$ is known by Lapid and Mao [Reference Lapid and MaoLM15], the arguments in § 6.2 and 6.2.3, which are used to obtain (6.1.6) in Theorem 6.1 from (6.2.3), work mutatis mutandis to obtain (6.2.3) from the Lapid–Mao formula in the case of ![]() $\mathrm {GL}_4$.
$\mathrm {GL}_4$.
Suppose that the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{3,3}$ is not cuspidal. Then the theta lift of
$\mathrm {GSO}_{3,3}$ is not cuspidal. Then the theta lift of ![]() $\pi$ to
$\pi$ to ![]() $\mathrm {GSO}_{2,2}$ is non-zero and cuspidal.
$\mathrm {GSO}_{2,2}$ is non-zero and cuspidal.
Thus, here we give a proof of Theorem 6.3 only in the case when ![]() $\pi$ is a theta lift from
$\pi$ is a theta lift from ![]() $\mathrm {GSO}_{2,2}$. Recall that
$\mathrm {GSO}_{2,2}$. Recall that ![]() $\mathrm {PGSO}_{2,2}\simeq \mathrm {PGL}_2\times \mathrm {PGL}_2$. Our argument is similar to that for [Reference LiuLiu16, Theorem 4.3]. Indeed, we shall prove (6.2.3) by pushing forward the Lapid–Mao formula for
$\mathrm {PGSO}_{2,2}\simeq \mathrm {PGL}_2\times \mathrm {PGL}_2$. Our argument is similar to that for [Reference LiuLiu16, Theorem 4.3]. Indeed, we shall prove (6.2.3) by pushing forward the Lapid–Mao formula for ![]() $\mathrm {GSO}_{2,2}$ to
$\mathrm {GSO}_{2,2}$ to ![]() $G$.
$G$.
A.1 Global pull-back computation
Let ![]() $(X,\langle \,{,}\,\rangle )$ be the four-dimensional symplectic space as in § 3.1.2 and let
$(X,\langle \,{,}\,\rangle )$ be the four-dimensional symplectic space as in § 3.1.2 and let ![]() $\{x_1,x_2,x_{-1},x_{-2}\}$ be the standard basis of
$\{x_1,x_2,x_{-1},x_{-2}\}$ be the standard basis of ![]() $X$ given by (3.1.5).
$X$ given by (3.1.5).
Let ![]() $Y=F^4$ be an orthogonal space with a non-degenerate symmetric bilinear form defined by
$Y=F^4$ be an orthogonal space with a non-degenerate symmetric bilinear form defined by
where ![]() $J_4$ is given by (2.1.6). We take a standard basis
$J_4$ is given by (2.1.6). We take a standard basis ![]() $\{y_{-2},y_{-1},y_1,y_2\}$ of
$\{y_{-2},y_{-1},y_1,y_2\}$ of ![]() $Y = F^{4}$ given by
$Y = F^{4}$ given by
We note that ![]() $(y_i, y_{-j})=\delta _{ij}$ for
$(y_i, y_{-j})=\delta _{ij}$ for ![]() $1\le i,j\le 2$.
$1\le i,j\le 2$.
Put ![]() $Z=X \otimes Y$. Then
$Z=X \otimes Y$. Then ![]() $Z$ is naturally a symplectic space over
$Z$ is naturally a symplectic space over ![]() $F$. We take a polarization
$F$. We take a polarization ![]() $Z = Z_+ \oplus Z_-$ where
$Z = Z_+ \oplus Z_-$ where
and ![]() $X_\pm =F\cdot x_{\pm 1}+F\cdot x_{\pm 2}$. Here all the double signs correspond. When
$X_\pm =F\cdot x_{\pm 1}+F\cdot x_{\pm 2}$. Here all the double signs correspond. When ![]() $z_+=x_1\otimes a_1+x_2\otimes a_2\in Z_+(\mathbb {A})$ where
$z_+=x_1\otimes a_1+x_2\otimes a_2\in Z_+(\mathbb {A})$ where ![]() $a_1,a_2\in Y$, we let
$a_1,a_2\in Y$, we let ![]() $z_+=(a_1,a_2)$ and
$z_+=(a_1,a_2)$ and ![]() $\phi (z_+)=\phi (a_1,a_2)$ for
$\phi (z_+)=\phi (a_1,a_2)$ for ![]() $\phi \in \mathcal {S}(Z_+(\mathbb {A}))$.
$\phi \in \mathcal {S}(Z_+(\mathbb {A}))$.
Let ![]() $N_{2,2}$ denote the group of upper triangular unipotent matrices of
$N_{2,2}$ denote the group of upper triangular unipotent matrices of ![]() $\mathrm {GO}_{2,2}$, i.e.
$\mathrm {GO}_{2,2}$, i.e.
 \[ N_{2,2}(F) = \left.\left\{\begin{pmatrix} 1 & x & y & -xy\\ 0 & 1 & 0 & -y\\ 0 & 0 & 1 & -x\\ 0 & 0 & 0 & 1 \end{pmatrix}\,\right|\, x, y \in F \right\}. \]
\[ N_{2,2}(F) = \left.\left\{\begin{pmatrix} 1 & x & y & -xy\\ 0 & 1 & 0 & -y\\ 0 & 0 & 1 & -x\\ 0 & 0 & 0 & 1 \end{pmatrix}\,\right|\, x, y \in F \right\}. \]
We define a non-degenerate character ![]() $\psi _{2,2}$ of
$\psi _{2,2}$ of ![]() $N_{2,2}(\mathbb {A})$ by
$N_{2,2}(\mathbb {A})$ by
 \[ \psi_{2,2} \begin{pmatrix} 1 & x & y & -xy\\ 0 & 1 & 0 & -y\\ 0 & 0 & 1 & -x\\ 0 & 0 & 0 & 1 \end{pmatrix} = \psi(x+y). \]
\[ \psi_{2,2} \begin{pmatrix} 1 & x & y & -xy\\ 0 & 1 & 0 & -y\\ 0 & 0 & 1 & -x\\ 0 & 0 & 0 & 1 \end{pmatrix} = \psi(x+y). \]
Then for a cusp form ![]() $f$ on
$f$ on ![]() $\mathrm {GSO}_{2,2}(\mathbb {A})$, we define its Whittaker period
$\mathrm {GSO}_{2,2}(\mathbb {A})$, we define its Whittaker period ![]() $W_{2,2}(f)$ by
$W_{2,2}(f)$ by
The following identity is stated in [Reference Ginzburg, Rallis and SoudryGRS97, p. 113] but without a proof. Though it is shown by an argument similar to that for [Reference Ginzburg, Rallis and SoudryGRS97, Proposition 2.6], here we give a proof for the convenience of the reader.
Proposition A.1 Let ![]() $\varphi$ be a cusp form on
$\varphi$ be a cusp form on ![]() $\mathrm {GO}_{2,2}(\mathbb {A})$. For
$\mathrm {GO}_{2,2}(\mathbb {A})$. For ![]() $\phi \in \mathcal {S}(Z(\mathbb {A})_+)$, let
$\phi \in \mathcal {S}(Z(\mathbb {A})_+)$, let ![]() $\Theta _\psi (\varphi,\phi )$ (respectively,
$\Theta _\psi (\varphi,\phi )$ (respectively, ![]() $\theta _\psi (\varphi,\phi )$) be the theta lift of
$\theta _\psi (\varphi,\phi )$) be the theta lift of ![]() $\sigma$ (respectively, the restriction of
$\sigma$ (respectively, the restriction of ![]() $\varphi$ to
$\varphi$ to ![]() $\mathrm {GSO}_{2,2}(\mathbb {A})$) to
$\mathrm {GSO}_{2,2}(\mathbb {A})$) to ![]() $G(\mathbb {A})$.
$G(\mathbb {A})$.
Then we have
where ![]() $N_0$ denotes the unipotent subgroup
$N_0$ denotes the unipotent subgroup
 \[ N_0 = \left\{\begin{pmatrix} 1 & x & -x & x^2\\ 0 & 1 & 0 & -x\\ 0 & 0 & 1 & x\\ 0 & 0 & 0 & 1 \end{pmatrix}\right\}, \]
\[ N_0 = \left\{\begin{pmatrix} 1 & x & -x & x^2\\ 0 & 1 & 0 & -x\\ 0 & 0 & 1 & x\\ 0 & 0 & 0 & 1 \end{pmatrix}\right\}, \]
which is the stabilizer of ![]() $y_{-2}$ and
$y_{-2}$ and ![]() $y_{-1}+y_1$.
$y_{-1}+y_1$.
Similarly, we have
Proof. Since the proofs are similar, we prove only (A.1.1). From the definition of the theta lift, we may write
 \begin{align*} & \int_{N(F) \backslash N(\mathbb{A})} \Theta_\psi(\varphi, \phi)(ug) \psi_{U_G}(u)^{-1} \,du\\ &\quad =\int_{\mathrm{O}_{2,2}(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \sum_{(a_1, a_2) \in \mathcal{X}} \omega_{\psi}(g, h)\phi(a_1, a_2) \varphi(h) \, dh, \end{align*}
\begin{align*} & \int_{N(F) \backslash N(\mathbb{A})} \Theta_\psi(\varphi, \phi)(ug) \psi_{U_G}(u)^{-1} \,du\\ &\quad =\int_{\mathrm{O}_{2,2}(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \sum_{(a_1, a_2) \in \mathcal{X}} \omega_{\psi}(g, h)\phi(a_1, a_2) \varphi(h) \, dh, \end{align*}
where
Then as in [Reference FurusawaFur95, Lemma 1], only ![]() $(a_1,a_2)\in \mathcal {X}$ such that
$(a_1,a_2)\in \mathcal {X}$ such that ![]() $a_1$ and
$a_1$ and ![]() $a_2$ are linearly independent contributes in the above sum. Thus, by Witt's theorem, we may rewrite the above integral as
$a_2$ are linearly independent contributes in the above sum. Thus, by Witt's theorem, we may rewrite the above integral as
 \begin{align*} & \int_{\mathrm{O}_{2,2}(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \sum_{\gamma \in N_0(F) \backslash \mathrm{O}_{2,2}(F)} \omega_{\psi}(g, h) \phi(\gamma^{-1} y_{-2}, \gamma^{-1} (y_{-1}+y_1)) \varphi(h) \, dh\\ &\quad =\int_{\mathrm{O}_{2,2}(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \sum_{\gamma \in N_0(F) \backslash \mathrm{O}_{2,2}(F)} \omega_{\psi}(g, \gamma h) \phi(y_{-2}, y_{-1}+y_1) \varphi(h) \, dh \\ &\quad =\int_{N_0(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \omega_{\psi}(g, h) \phi( y_{-2}, y_{-1}+y_1) \varphi(h) \, dh\\ &\quad =\int_{N_0(\mathbb{A}) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \int_{N_0(F) \backslash N_0(\mathbb{A})} \omega_{\psi}(g, h) \phi( y_{-2}, y_{-1}+y_1) \varphi(n h) \, dn \, dh. \end{align*}
\begin{align*} & \int_{\mathrm{O}_{2,2}(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \sum_{\gamma \in N_0(F) \backslash \mathrm{O}_{2,2}(F)} \omega_{\psi}(g, h) \phi(\gamma^{-1} y_{-2}, \gamma^{-1} (y_{-1}+y_1)) \varphi(h) \, dh\\ &\quad =\int_{\mathrm{O}_{2,2}(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \sum_{\gamma \in N_0(F) \backslash \mathrm{O}_{2,2}(F)} \omega_{\psi}(g, \gamma h) \phi(y_{-2}, y_{-1}+y_1) \varphi(h) \, dh \\ &\quad =\int_{N_0(F) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \omega_{\psi}(g, h) \phi( y_{-2}, y_{-1}+y_1) \varphi(h) \, dh\\ &\quad =\int_{N_0(\mathbb{A}) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \int_{N_0(F) \backslash N_0(\mathbb{A})} \omega_{\psi}(g, h) \phi( y_{-2}, y_{-1}+y_1) \varphi(n h) \, dn \, dh. \end{align*}
Thus, by (6.2.1) we have
 \begin{align} W_{\psi_{U_G}}(\Theta_\psi(\varphi,\phi)) &= \int_{N_0(\mathbb{A}) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \int_{N_2(F) \backslash N_2(\mathbb{A})} \int_{N_0(F) \backslash N_0(\mathbb{A})} \nonumber\\ &\quad \times \omega_{\psi}(m(u)g, h)\phi( y_{-2}, y_{-1}+y_1) \varphi(nh) \psi_{U_G}(m(u))^{-1} \, dh \, du. \end{align}
\begin{align} W_{\psi_{U_G}}(\Theta_\psi(\varphi,\phi)) &= \int_{N_0(\mathbb{A}) \backslash \mathrm{O}_{2,2}(\mathbb{A})} \int_{N_2(F) \backslash N_2(\mathbb{A})} \int_{N_0(F) \backslash N_0(\mathbb{A})} \nonumber\\ &\quad \times \omega_{\psi}(m(u)g, h)\phi( y_{-2}, y_{-1}+y_1) \varphi(nh) \psi_{U_G}(m(u))^{-1} \, dh \, du. \end{align}Here we have
where
 \[m_0(u) =\begin{pmatrix}1 & {{a}/{2}} & {{a}/{2}} & {{a^2}/{4}}\\ 0 & 1 & 0 & -{{a}/{2}}\\ 0 & 0 & 1 & -{{a}/{2}}\\ 0 & 0 & 0 & 1 \end{pmatrix}\quad \text{for } u=\begin{pmatrix}1 & a\\0 & 1\end{pmatrix}, \]
\[m_0(u) =\begin{pmatrix}1 & {{a}/{2}} & {{a}/{2}} & {{a^2}/{4}}\\ 0 & 1 & 0 & -{{a}/{2}}\\ 0 & 0 & 1 & -{{a}/{2}}\\ 0 & 0 & 0 & 1 \end{pmatrix}\quad \text{for } u=\begin{pmatrix}1 & a\\0 & 1\end{pmatrix}, \]
since ![]() $\psi _{U_G}(m(u))^{-1} = \psi (-a)$. By noting the decomposition
$\psi _{U_G}(m(u))^{-1} = \psi (-a)$. By noting the decomposition
 \[ \begin{pmatrix} 1 & x & y & -xy\\ 0 & 1 & 0 & -y\\ 0 & 0 & 1 & -x\\ 0 & 0 & 0 & 1\end{pmatrix}=\begin{pmatrix} 1 & \dfrac{x+y}{2} & \dfrac{x+y}{2} & \dfrac{(x+y)^2}{4}\\ 0 & 1 & 0 & -\dfrac{x+y}{2}\\ 0 & 0 & 1 & -\dfrac{x+y}{2}\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & \dfrac{x-y}{2} & -\dfrac{x-y}{2} & \dfrac{(x-y)^2}{4}\\ 0 & 1 & 0 & -\dfrac{x-y}{2}\\ 0 & 0 & 1 & -\dfrac{x-y}{2}\\ 0 & 0 & 0 & 1 \end{pmatrix}, \]
\[ \begin{pmatrix} 1 & x & y & -xy\\ 0 & 1 & 0 & -y\\ 0 & 0 & 1 & -x\\ 0 & 0 & 0 & 1\end{pmatrix}=\begin{pmatrix} 1 & \dfrac{x+y}{2} & \dfrac{x+y}{2} & \dfrac{(x+y)^2}{4}\\ 0 & 1 & 0 & -\dfrac{x+y}{2}\\ 0 & 0 & 1 & -\dfrac{x+y}{2}\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & \dfrac{x-y}{2} & -\dfrac{x-y}{2} & \dfrac{(x-y)^2}{4}\\ 0 & 1 & 0 & -\dfrac{x-y}{2}\\ 0 & 0 & 1 & -\dfrac{x-y}{2}\\ 0 & 0 & 0 & 1 \end{pmatrix}, \]
Recall the exact sequence
Hence, we have
where ![]() $\varphi ^\varepsilon = \sigma (\varepsilon )\varphi$ and
$\varphi ^\varepsilon = \sigma (\varepsilon )\varphi$ and ![]() $\phi ^\varepsilon =\omega _\psi (\varepsilon ) \phi$. Thus, we have
$\phi ^\varepsilon =\omega _\psi (\varepsilon ) \phi$. Thus, we have
where
A.2 Lapid–Mao formula
Let us recall the Lapid–Mao formula in the ![]() $\mathrm {GL}_2$ case. Let
$\mathrm {GL}_2$ case. Let ![]() $(\tau, V_\tau )$ denote an irreducible cuspidal unitary automorphic representation of
$(\tau, V_\tau )$ denote an irreducible cuspidal unitary automorphic representation of ![]() $\mathrm {GL}_2(\mathbb {A})$. Then for
$\mathrm {GL}_2(\mathbb {A})$. Then for ![]() $f \in V_\tau$, its Whittaker period is defined by
$f \in V_\tau$, its Whittaker period is defined by
with the Tamagawa measure ![]() ${dx} = \prod dx_v$. Let
${dx} = \prod dx_v$. Let ![]() $v$ be a place of
$v$ be a place of ![]() $F$. For
$F$. For ![]() $f_v \in \tau _v$ and
$f_v \in \tau _v$ and ![]() $\widetilde {f}_v \in \overline {\tau }_v$, by [Reference LiuLiu16] (see also [Reference Lapid and MaoLM15, § 2]), we may define
$\widetilde {f}_v \in \overline {\tau }_v$, by [Reference LiuLiu16] (see also [Reference Lapid and MaoLM15, § 2]), we may define
Put
which is equal to ![]() $1$ at almost all places
$1$ at almost all places ![]() $v$ by [Reference Lapid and MaoLM15, Proposition 2.14]. Let us define
$v$ by [Reference Lapid and MaoLM15, Proposition 2.14]. Let us define
where ![]() $dg$ is the Tamagawa measure. We note that
$dg$ is the Tamagawa measure. We note that ![]() $\mathrm {Vol}(\mathbb {A}^\times \mathrm {GL}_2(F)\backslash \mathrm {GL}_2(\mathbb {A}), dg)=2$. Further, let us take a local
$\mathrm {Vol}(\mathbb {A}^\times \mathrm {GL}_2(F)\backslash \mathrm {GL}_2(\mathbb {A}), dg)=2$. Further, let us take a local ![]() $\mathrm {GL}_2(F_v)$-invariant pairing
$\mathrm {GL}_2(F_v)$-invariant pairing ![]() $\langle \,{,}\, \rangle _v$ on
$\langle \,{,}\, \rangle _v$ on ![]() $\tau _v \times \tau _v$ such that
$\tau _v \times \tau _v$ such that ![]() $\langle f, f \rangle =\prod \langle f_v, f_v \rangle _v$. Then by [Reference Lapid and MaoLM15, Theorem 4.1], we have
$\langle f, f \rangle =\prod \langle f_v, f_v \rangle _v$. Then by [Reference Lapid and MaoLM15, Theorem 4.1], we have
for a factorizable vector ![]() $f = \otimes f_v \in V_\tau$.
$f = \otimes f_v \in V_\tau$.
A.3 Local pull-back computation
We fix a place ![]() $v$ of
$v$ of ![]() $F$ which will be suppressed from the notation in this appendix. Further, we simply write
$F$ which will be suppressed from the notation in this appendix. Further, we simply write ![]() $X(F)$ by
$X(F)$ by ![]() $X$ for any object
$X$ for any object ![]() $X$ defined over
$X$ defined over ![]() $F$. Let
$F$. Let ![]() $\sigma$ be an irreducible tempered representation of
$\sigma$ be an irreducible tempered representation of ![]() $\mathrm {GO}_{2,2}$ such that its big theta lift
$\mathrm {GO}_{2,2}$ such that its big theta lift ![]() $\Theta (\sigma )$ to
$\Theta (\sigma )$ to ![]() $H$ is non-zero. Because of the Howe duality proved by Howe [Reference HoweHow89], Waldspurger [Reference WaldspurgerWal90] and Gan and Takeda [Reference Gan and TakedaGT16], combined with Roberts [Reference RobertsRob96],
$H$ is non-zero. Because of the Howe duality proved by Howe [Reference HoweHow89], Waldspurger [Reference WaldspurgerWal90] and Gan and Takeda [Reference Gan and TakedaGT16], combined with Roberts [Reference RobertsRob96], ![]() $\Theta (\sigma )$ has a unique irreducible quotient, which we denote by
$\Theta (\sigma )$ has a unique irreducible quotient, which we denote by ![]() $\pi$. Put
$\pi$. Put ![]() $R= \{(g, h) \in G \times \mathrm {GO}_{2,2} : \lambda (g)=\nu (h)\}.$ Then we have a unique
$R= \{(g, h) \in G \times \mathrm {GO}_{2,2} : \lambda (g)=\nu (h)\}.$ Then we have a unique ![]() $R$-equivariant map
$R$-equivariant map
Let ![]() $\mathcal {B}_\omega : \omega _\psi \otimes \overline {\omega _\psi } \rightarrow \mathbb {C}$ be the canonical bilinear pairing defined by
$\mathcal {B}_\omega : \omega _\psi \otimes \overline {\omega _\psi } \rightarrow \mathbb {C}$ be the canonical bilinear pairing defined by
By [Reference Gan and IchinoGI11, Lemma 5.6], the pairing ![]() $\mathcal {Z} : (\sigma \otimes \overline {\sigma }) \otimes (\omega _\psi \otimes \overline {\omega _\psi }) \rightarrow \mathbb {C}$, defined as
$\mathcal {Z} : (\sigma \otimes \overline {\sigma }) \otimes (\omega _\psi \otimes \overline {\omega _\psi }) \rightarrow \mathbb {C}$, defined as
which converges absolutely by [Reference LiuLiu16, Lemma 3.19], gives a pairing ![]() $\mathcal {B}_\pi : \pi \otimes \overline {\pi } \rightarrow \mathbb {C}$ by
$\mathcal {B}_\pi : \pi \otimes \overline {\pi } \rightarrow \mathbb {C}$ by
Proposition A.2 We let ![]() $y_0=(y_{-2}, y_{-1}+y_1)$. For any
$y_0=(y_{-2}, y_{-1}+y_1)$. For any ![]() $u \in N_{2}$,
$u \in N_{2}$,
 \begin{align*} & \bigg(\frac{\zeta_F(2) \zeta_F(4)}{L(1, \sigma, \mathrm{std})} \bigg)^{-1} \int_{N_H}^{\rm st} \mathcal{B}_\pi (\pi(n m(u)) \theta(\varphi, \phi), \theta(\widetilde{\varphi}, \widetilde{\phi}) ) \psi_{U_H}(n)^{-1} \, dn \\ &\quad =\int_{\mathrm{O}_{2,2}} \int_{N_0 \backslash \mathrm{SO}_{2,2}} (\omega_{\psi}(g, m(u))\phi)(y_0) \overline{\widetilde{\phi}(h^{-1} \cdot y_0)} \langle \sigma(g) \varphi, \sigma(h) \widetilde{\varphi} \rangle \, dg \, dh. \end{align*}
\begin{align*} & \bigg(\frac{\zeta_F(2) \zeta_F(4)}{L(1, \sigma, \mathrm{std})} \bigg)^{-1} \int_{N_H}^{\rm st} \mathcal{B}_\pi (\pi(n m(u)) \theta(\varphi, \phi), \theta(\widetilde{\varphi}, \widetilde{\phi}) ) \psi_{U_H}(n)^{-1} \, dn \\ &\quad =\int_{\mathrm{O}_{2,2}} \int_{N_0 \backslash \mathrm{SO}_{2,2}} (\omega_{\psi}(g, m(u))\phi)(y_0) \overline{\widetilde{\phi}(h^{-1} \cdot y_0)} \langle \sigma(g) \varphi, \sigma(h) \widetilde{\varphi} \rangle \, dg \, dh. \end{align*}
Let us define
Take the measure ![]() $dh_0 =2 dh|_{\mathrm {SO}_{2,2}}$. Then
$dh_0 =2 dh|_{\mathrm {SO}_{2,2}}$. Then
 \begin{align*} & \bigg(\frac{\zeta_F(2)
\zeta_F(4)}{L(1, \sigma, \mathrm{std})}\bigg)^{-1}
\mathcal{W}_{\psi_{U_H}}(\theta(\varphi, \phi),
\theta(\widetilde{\varphi}, \widetilde{\phi}))\\ &\quad
=\int_{N_2}^{\rm st} \int_{\mathrm{O}_{2,2}} \int_{N_0
\backslash \mathrm{SO}_{2,2}} (\omega_{\psi}(g,
m(u))\phi)(y_0) \overline{\widetilde{\phi}(h^{-1} \cdot
y_0)}\langle \sigma(g) \varphi, \sigma(h)
\widetilde{\varphi} \rangle \,dg \, dh \, du.
\end{align*}
\begin{align*} & \bigg(\frac{\zeta_F(2)
\zeta_F(4)}{L(1, \sigma, \mathrm{std})}\bigg)^{-1}
\mathcal{W}_{\psi_{U_H}}(\theta(\varphi, \phi),
\theta(\widetilde{\varphi}, \widetilde{\phi}))\\ &\quad
=\int_{N_2}^{\rm st} \int_{\mathrm{O}_{2,2}} \int_{N_0
\backslash \mathrm{SO}_{2,2}} (\omega_{\psi}(g,
m(u))\phi)(y_0) \overline{\widetilde{\phi}(h^{-1} \cdot
y_0)}\langle \sigma(g) \varphi, \sigma(h)
\widetilde{\varphi} \rangle \,dg \, dh \, du.
\end{align*}
By an argument similar to that for [Reference Furusawa and MorimotoFM21, § 3.4.2] and [Reference Furusawa and MorimotoFM22, § 5.4], we see that this is equal to
 \[ \int_{N_0 \backslash \mathrm{O}_{2,2}} \int_{N_0 \backslash \mathrm{SO}_{2,2}} \int_{N_{2,2}}^{\rm st} (\omega_{\psi}(g, m(u))\phi)(y_0) \overline{\widetilde{\phi}(h^{-1} \cdot y_0)} \langle \sigma(g) \varphi, \sigma(h) \widetilde{\varphi} \rangle \,dg \, dh \, du. \]
\[ \int_{N_0 \backslash \mathrm{O}_{2,2}} \int_{N_0 \backslash \mathrm{SO}_{2,2}} \int_{N_{2,2}}^{\rm st} (\omega_{\psi}(g, m(u))\phi)(y_0) \overline{\widetilde{\phi}(h^{-1} \cdot y_0)} \langle \sigma(g) \varphi, \sigma(h) \widetilde{\varphi} \rangle \,dg \, dh \, du. \]
Further, it is equal to
 \begin{align} & \sum_{\varepsilon=\pm1}
\int_{N_0 \backslash \mathrm{SO}_{2,2}} \int_{N_0
\backslash \mathrm{SO}_{2,2}} \int_{N_{2,2}}^{\rm st}
(\omega_{\psi}(g, m(u))\phi^\varepsilon)(y_0)
\overline{\widetilde{\phi}(h^{-1} \cdot y_0)} \langle \sigma(g) \varphi^\varepsilon,
\sigma(h) \widetilde{\varphi} \rangle \, dg \, dh \, du
\nonumber\\ &\quad =\sum_{\varepsilon=\pm1} \int_{N_0
\backslash \mathrm{SO}_{2,2}} \int_{N_0 \backslash
\mathrm{SO}_{2,2}} \phi^\varepsilon(g^{-1} \cdot y_0)
\widetilde{\phi}(h^{-1} \cdot y_0)
\mathcal{W}_{2,2}(\sigma(g)\varphi^\varepsilon,
\sigma(h)\widetilde{\varphi}) \, dg \, dh ,
\end{align}
\begin{align} & \sum_{\varepsilon=\pm1}
\int_{N_0 \backslash \mathrm{SO}_{2,2}} \int_{N_0
\backslash \mathrm{SO}_{2,2}} \int_{N_{2,2}}^{\rm st}
(\omega_{\psi}(g, m(u))\phi^\varepsilon)(y_0)
\overline{\widetilde{\phi}(h^{-1} \cdot y_0)} \langle \sigma(g) \varphi^\varepsilon,
\sigma(h) \widetilde{\varphi} \rangle \, dg \, dh \, du
\nonumber\\ &\quad =\sum_{\varepsilon=\pm1} \int_{N_0
\backslash \mathrm{SO}_{2,2}} \int_{N_0 \backslash
\mathrm{SO}_{2,2}} \phi^\varepsilon(g^{-1} \cdot y_0)
\widetilde{\phi}(h^{-1} \cdot y_0)
\mathcal{W}_{2,2}(\sigma(g)\varphi^\varepsilon,
\sigma(h)\widetilde{\varphi}) \, dg \, dh ,
\end{align}where we define
 \[ \mathcal{W}_{2,2}(\varphi_1, \varphi_2):= \int_{N_{2,2}}^{\rm st} \langle \sigma(u)\varphi_1, \varphi_2 \rangle \psi_{2,2}^{-1}(u) \,du \quad\text{for}\ \varphi_i \in V_\sigma. \]
\[ \mathcal{W}_{2,2}(\varphi_1, \varphi_2):= \int_{N_{2,2}}^{\rm st} \langle \sigma(u)\varphi_1, \varphi_2 \rangle \psi_{2,2}^{-1}(u) \,du \quad\text{for}\ \varphi_i \in V_\sigma. \]
Let us introduce a measure ![]() $d^\prime h = \zeta _F(2)^2 dh$. Then we get
$d^\prime h = \zeta _F(2)^2 dh$. Then we get
 \begin{align*} \mathcal{W}_{\psi_{U_H}}^\natural(\theta(\varphi, \phi), \theta(\widetilde{\varphi}, \widetilde{\phi})) &= \sum_{\varepsilon=\pm1} \int_{N_0 \backslash \mathrm{SO}_{2,2}} \int_{N_0 \backslash \mathrm{SO}_{2,2}} \phi^\varepsilon(g^{-1} \cdot y_0)\widetilde{\phi}(h^{-1} \cdot y_0) \\ &\quad \times\mathcal{W}_{2,2}^\natural(\sigma(g)\varphi^\varepsilon, \sigma(h)\widetilde{\varphi}) \, dg \, d^\prime h. \end{align*}
\begin{align*} \mathcal{W}_{\psi_{U_H}}^\natural(\theta(\varphi, \phi), \theta(\widetilde{\varphi}, \widetilde{\phi})) &= \sum_{\varepsilon=\pm1} \int_{N_0 \backslash \mathrm{SO}_{2,2}} \int_{N_0 \backslash \mathrm{SO}_{2,2}} \phi^\varepsilon(g^{-1} \cdot y_0)\widetilde{\phi}(h^{-1} \cdot y_0) \\ &\quad \times\mathcal{W}_{2,2}^\natural(\sigma(g)\varphi^\varepsilon, \sigma(h)\widetilde{\varphi}) \, dg \, d^\prime h. \end{align*}
Here
A.4 Proof of Theorem 6.3
Let ![]() $(\sigma, V_{\sigma })$ be an irreducible cuspidal automorphic representation of the group
$(\sigma, V_{\sigma })$ be an irreducible cuspidal automorphic representation of the group ![]() $\mathrm {GO}_{2,2}(\mathbb {A})$. Suppose that
$\mathrm {GO}_{2,2}(\mathbb {A})$. Suppose that ![]() $\sigma$ is induced by the representation
$\sigma$ is induced by the representation ![]() $\sigma _1 \boxtimes \sigma _2$ of
$\sigma _1 \boxtimes \sigma _2$ of ![]() $\mathrm {GL}_2(\mathbb {A}) \times \mathrm {GL}_2(\mathbb {A})$. For
$\mathrm {GL}_2(\mathbb {A}) \times \mathrm {GL}_2(\mathbb {A})$. For ![]() $f = f_1 \otimes f_2 \in V_{\sigma _1} \otimes V_{\sigma _2}$, we have
$f = f_1 \otimes f_2 \in V_{\sigma _1} \otimes V_{\sigma _2}$, we have
for ![]() $h=(h_1, h_2) \in \mathrm {SO}_{2,2}(\mathbb {A})$. Moreover, for any place
$h=(h_1, h_2) \in \mathrm {SO}_{2,2}(\mathbb {A})$. Moreover, for any place ![]() $v$ of
$v$ of ![]() $F$, we have
$F$, we have
with ![]() $\varphi _v = (\varphi _{1,v}, \varphi _{2,v})$ and
$\varphi _v = (\varphi _{1,v}, \varphi _{2,v})$ and ![]() $\widetilde {\varphi }_v = (\widetilde {\varphi }_{1,v}, \widetilde {\varphi }_{2,v})$. Then by (A.1.2) and the Lapid–Mao formula (A.2.1), we obtain
$\widetilde {\varphi }_v = (\widetilde {\varphi }_{1,v}, \widetilde {\varphi }_{2,v})$. Then by (A.1.2) and the Lapid–Mao formula (A.2.1), we obtain
 \begin{align*} & \mathbb{W}_{\psi_{U_H}}(\theta_\psi(\varphi^\varepsilon, \phi^\varepsilon)) = \frac{1}{4} \frac{\zeta_F(2)^2}{L(1, \sigma_1, \mathrm{Ad})L(1, \sigma_2, \mathrm{Ad})} \\ &\qquad \times\int_{\mu_2(F) \backslash \mu_2(\mathbb{A})}\prod_v \int \int_{(N_{0}(F_v) \backslash \mathrm{SO}_{2,2})^2} \bigg(\prod_{\alpha=1, 2} \mathcal{W}_2^\natural((\sigma(g_v)\varphi_{v}^\varepsilon)_\alpha, (\overline{\sigma}(h_v)\overline{\varphi}_{v})_\alpha)\bigg) \\ &\qquad \times\phi_{v}^\varepsilon (g_v^{-1} \cdot y_0)\overline{\phi}_{v} (h_v^{-1} \cdot y_0) \, dg \, dh \\ &\quad =\frac{1}{4} \frac{\zeta_F(2)^2}{L(1, \sigma_1, \mathrm{Ad})L(1, \sigma_2, \mathrm{Ad})} \int_{\mu_2(F) \backslash \mu_2(\mathbb{A})} \prod_v \int \int_{(N_{0}(F_v) \backslash \mathrm{SO}_{2,2})^2} \\ &\qquad \times\mathcal{W}_{2,2}^\natural(\sigma(g_v)\varphi_v, \overline{\sigma}_v(h_v)\overline{\varphi}_v) \phi_{v}^\varepsilon (g_v^{-1} \cdot y_0)\overline{\phi}_{v} (h_v^{-1} \cdot y_0) \, dg \, dh. \end{align*}
\begin{align*} & \mathbb{W}_{\psi_{U_H}}(\theta_\psi(\varphi^\varepsilon, \phi^\varepsilon)) = \frac{1}{4} \frac{\zeta_F(2)^2}{L(1, \sigma_1, \mathrm{Ad})L(1, \sigma_2, \mathrm{Ad})} \\ &\qquad \times\int_{\mu_2(F) \backslash \mu_2(\mathbb{A})}\prod_v \int \int_{(N_{0}(F_v) \backslash \mathrm{SO}_{2,2})^2} \bigg(\prod_{\alpha=1, 2} \mathcal{W}_2^\natural((\sigma(g_v)\varphi_{v}^\varepsilon)_\alpha, (\overline{\sigma}(h_v)\overline{\varphi}_{v})_\alpha)\bigg) \\ &\qquad \times\phi_{v}^\varepsilon (g_v^{-1} \cdot y_0)\overline{\phi}_{v} (h_v^{-1} \cdot y_0) \, dg \, dh \\ &\quad =\frac{1}{4} \frac{\zeta_F(2)^2}{L(1, \sigma_1, \mathrm{Ad})L(1, \sigma_2, \mathrm{Ad})} \int_{\mu_2(F) \backslash \mu_2(\mathbb{A})} \prod_v \int \int_{(N_{0}(F_v) \backslash \mathrm{SO}_{2,2})^2} \\ &\qquad \times\mathcal{W}_{2,2}^\natural(\sigma(g_v)\varphi_v, \overline{\sigma}_v(h_v)\overline{\varphi}_v) \phi_{v}^\varepsilon (g_v^{-1} \cdot y_0)\overline{\phi}_{v} (h_v^{-1} \cdot y_0) \, dg \, dh. \end{align*}
By (A.3.1), this is equal to
and, thus, this completes our proof of Theorem 6.3.
Appendix B. Explicit computation of local Bessel periods at the real place
The goal of this appendix is to compute explicitly the local Bessel periods at the real place and to complete our proof of Theorem 8.1. In this appendix, we use the same notation as in § 8.
For a newform ![]() $\Phi \in S_\varrho (\Gamma _0(N))$ in Theorem 8.1, we define a scalar-valued automorphic form
$\Phi \in S_\varrho (\Gamma _0(N))$ in Theorem 8.1, we define a scalar-valued automorphic form ![]() $\phi _{\Phi,S}$ on
$\phi _{\Phi,S}$ on ![]() $G(\mathbb {A})$ by
$G(\mathbb {A})$ by
where ![]() $\varphi _\Phi$ is the adelization of
$\varphi _\Phi$ is the adelization of ![]() $\Phi$ given by (8.2.9) and
$\Phi$ given by (8.2.9) and ![]() $Q_{S,\varrho }$ by (8.2.16). We note that by the argument in [Reference Dickson, Pitale, Saha and SchmidtDPSS20, 3.2],
$Q_{S,\varrho }$ by (8.2.16). We note that by the argument in [Reference Dickson, Pitale, Saha and SchmidtDPSS20, 3.2], ![]() $\phi _{\Phi,S}$ is a factorizable vector
$\phi _{\Phi,S}$ is a factorizable vector ![]() $\phi _{\Phi, S}=\otimes _v\,\phi _{\Phi, S, v}$. For a place
$\phi _{\Phi, S}=\otimes _v\,\phi _{\Phi, S, v}$. For a place ![]() $v$ of
$v$ of ![]() $\mathbb {Q}$, we define
$\mathbb {Q}$, we define ![]() $J_v$ by
$J_v$ by
It is clear that ![]() $J_v$ remains invariant under replacing
$J_v$ remains invariant under replacing ![]() $\phi _{\Phi, S,v}$ by its non-zero scalar multiple. Further, we put
$\phi _{\Phi, S,v}$ by its non-zero scalar multiple. Further, we put
with the Haar measure constant ![]() $C_\xi$ defined by (1.6.1). Then the following identity holds.
$C_\xi$ defined by (1.6.1). Then the following identity holds.
Theorem B.1 We have
Recall that ![]() $C(Q_{S,\varrho })$ is defined by (8.2.10) for
$C(Q_{S,\varrho })$ is defined by (8.2.10) for ![]() $v^\prime =Q_{S,\varrho }$.
$v^\prime =Q_{S,\varrho }$.
Remark B.1 In the scalar-valued case, i.e. ![]() $r=0$, the explicit computation of
$r=0$, the explicit computation of ![]() $J_\infty$ is done in Dickson et al. [Reference Dickson, Pitale, Saha and SchmidtDPSS20, 3.5] using the explicit formula for matrix coefficients when
$J_\infty$ is done in Dickson et al. [Reference Dickson, Pitale, Saha and SchmidtDPSS20, 3.5] using the explicit formula for matrix coefficients when ![]() $k \geq 3$. Meanwhile Hsieh and Yamana [Reference Hsieh and YamanaHY24, Proposition 5.7] compute
$k \geq 3$. Meanwhile Hsieh and Yamana [Reference Hsieh and YamanaHY24, Proposition 5.7] compute ![]() $J_ \infty$ in a different way when
$J_ \infty$ in a different way when ![]() $k \geq 2$, based on Shimura's work on confluent hypergeometric functions.
$k \geq 2$, based on Shimura's work on confluent hypergeometric functions.
We note that the left-hand side of (B.0.4) depends only on the archimedean representation ![]() $\pi (\Phi )_\infty$ and the vector
$\pi (\Phi )_\infty$ and the vector ![]() $\phi _{\Phi, S,\infty }$. Thus, our strategy is to first obtain an explicit formula (B.1.12) for the Bessel periods of vector-valued Yoshida lifts by combining the results in Hsieh and Namikawa [Reference Hsieh and NamikawaHN17, Reference Hsieh and NamikawaHN18], Chida and Hsieh [Reference Chida and HsiehCH18], Martin and Whitehouse [Reference Martin and WhitehouseMW09], and, then to evaluate
$\phi _{\Phi, S,\infty }$. Thus, our strategy is to first obtain an explicit formula (B.1.12) for the Bessel periods of vector-valued Yoshida lifts by combining the results in Hsieh and Namikawa [Reference Hsieh and NamikawaHN17, Reference Hsieh and NamikawaHN18], Chida and Hsieh [Reference Chida and HsiehCH18], Martin and Whitehouse [Reference Martin and WhitehouseMW09], and, then to evaluate ![]() $C(Q_{S,\varrho }) \mathcal {C} J_\infty$ by singling out the real place contribution, comparing (B.1.12) with (1.6.2).
$C(Q_{S,\varrho }) \mathcal {C} J_\infty$ by singling out the real place contribution, comparing (B.1.12) with (1.6.2).
B.1 Explicit formula for Bessel periods of Yoshida lifts
For a prime number ![]() $p$, let
$p$, let
and ![]() $S_k(\Gamma _0^{(1)}(p))$ the space of cusp forms of weight
$S_k(\Gamma _0^{(1)}(p))$ the space of cusp forms of weight ![]() $k$ with respect to
$k$ with respect to ![]() $\Gamma _0^{(1)}(p)$.
$\Gamma _0^{(1)}(p)$.
In order to insure what follows to be non-vacuous, first we shall prove the following technical lemma.
Lemma B.1 Let ![]() $k_1$ and
$k_1$ and ![]() $k_2$ be integers with
$k_2$ be integers with ![]() $k_1 \geq k_2\ge 0$. Then there is a constant
$k_1 \geq k_2\ge 0$. Then there is a constant ![]() $N=N(k_1, k_2, E) \in \mathbb {R}$ such that for any prime
$N=N(k_1, k_2, E) \in \mathbb {R}$ such that for any prime ![]() $p > N$, there exist distinct normalized newforms
$p > N$, there exist distinct normalized newforms ![]() $f_i\in S_{2k_i+2}(\Gamma _0^{(1)}(p))$ for
$f_i\in S_{2k_i+2}(\Gamma _0^{(1)}(p))$ for ![]() $i=1,2$ satisfying the condition:
$i=1,2$ satisfying the condition:
Proof. We divide into the following two cases:
Suppose that (B.1.2a) holds. Then by Iwaniec, Luo and Sarnak [Reference Iwaniec, Luo and SarnakILS00, Corollary 2.14], there is a constant ![]() $N(k_1, k_2)$ such that, for any prime
$N(k_1, k_2)$ such that, for any prime ![]() $p > N(k_1, k_2)$, there exist distinct normalized newforms
$p > N(k_1, k_2)$, there exist distinct normalized newforms ![]() $f_i\in S_{2k_i+2}(\Gamma _0^{(1)}(p))$ for
$f_i\in S_{2k_i+2}(\Gamma _0^{(1)}(p))$ for ![]() $i=1,2$ such that
$i=1,2$ such that
where ![]() $\pi _i$ denotes the automorphic representation of
$\pi _i$ denotes the automorphic representation of ![]() $\mathrm {GL}_2(\mathbb {A})$ corresponding to
$\mathrm {GL}_2(\mathbb {A})$ corresponding to ![]() $f_i$ for
$f_i$ for ![]() $i=1,2$. Since
$i=1,2$. Since ![]() $\pi _i$ is unramified at all prime numbers different from
$\pi _i$ is unramified at all prime numbers different from ![]() $p$, we have
$p$, we have
Hence, ![]() $\varepsilon _p(1/ 2,\pi _1)=\varepsilon _p(1/ 2,\pi _2)$ by (B.1.2a). Then by the relationship between the local
$\varepsilon _p(1/ 2,\pi _1)=\varepsilon _p(1/ 2,\pi _2)$ by (B.1.2a). Then by the relationship between the local ![]() $\varepsilon$-factor at
$\varepsilon$-factor at ![]() $p$ and the Atkin–Lehner eigenvalue at
$p$ and the Atkin–Lehner eigenvalue at ![]() $p$ (e.g. [Reference Hsieh and NamikawaHN18, 4.4]), we see that (B.1.1) holds.
$p$ (e.g. [Reference Hsieh and NamikawaHN18, 4.4]), we see that (B.1.1) holds.
Suppose that (B.1.2b) holds. Then by Michel and Ramakrishnan [Reference Michel and RamakrishnanMR12, Theorem 3] or Ramakrishnan and Rogawski [Reference Ramakrishnan and RogawskiRR05, Corollary B], there exists a constant ![]() $N_1=N_1(k_1, E)$ such that for any prime
$N_1=N_1(k_1, E)$ such that for any prime ![]() $p > N_1$, there exists a normalized newform
$p > N_1$, there exists a normalized newform ![]() $f_1\in S_{2k_1+2}(\Gamma _0^{(1)}(p))$ such that
$f_1\in S_{2k_1+2}(\Gamma _0^{(1)}(p))$ such that
In particular, ![]() $\varepsilon (1/ 2,\pi _1)=1$ and, thus, as in the previous case, we have
$\varepsilon (1/ 2,\pi _1)=1$ and, thus, as in the previous case, we have
Moreover, by [Reference Iwaniec, Luo and SarnakILS00, Corollary 2.14], there exists a constant ![]() $N_2 = N_2(k_2)$ such that for any prime
$N_2 = N_2(k_2)$ such that for any prime ![]() $p > N_2$, there exists a normalized newform
$p > N_2$, there exists a normalized newform ![]() $f_2\in S_{2k_2+2}(\Gamma _0^{(1)}(p))$ such that
$f_2\in S_{2k_2+2}(\Gamma _0^{(1)}(p))$ such that
Then by taking the constant ![]() $N$ to be
$N$ to be ![]() $\mathrm {max}(N_1, N_2)$, the condition (B.1.1) holds by the same argument as above.
$\mathrm {max}(N_1, N_2)$, the condition (B.1.1) holds by the same argument as above.
B.1.1 Vector-valued Yoshida lift
As for the Yoshida lifting, we refer the reader to our main references by Hsieh and Namikawa [Reference Hsieh and NamikawaHN17, Reference Hsieh and NamikawaHN18] for the details.
Let ![]() $k_1$ and
$k_1$ and ![]() $k_2$ be integers with
$k_2$ be integers with ![]() $k_1\ge k_2\ge 0$. Then by Lemma B.1, we may take a prime number
$k_1\ge k_2\ge 0$. Then by Lemma B.1, we may take a prime number ![]() $p$ satisfying the condition:
$p$ satisfying the condition:
and may take distinct normalized newforms ![]() $f_i\in S_{2k_i+2}(\Gamma _0^{(1)}(p))$ (
$f_i\in S_{2k_i+2}(\Gamma _0^{(1)}(p))$ (![]() $i=1,2$) satisfying the condition (B.1.1).
$i=1,2$) satisfying the condition (B.1.1).
For a non-negative integer ![]() $r$, we denote by
$r$, we denote by ![]() $(\tau _r,\mathcal {W}_r)$ the representation
$(\tau _r,\mathcal {W}_r)$ the representation ![]() $(\varrho,V_\varrho )$ of
$(\varrho,V_\varrho )$ of ![]() $\mathrm {GL}_2(\mathbb {C})$ where
$\mathrm {GL}_2(\mathbb {C})$ where ![]() $\varrho =\varrho _{(r,-r)}$, i.e.
$\varrho =\varrho _{(r,-r)}$, i.e. ![]() $\tau _r=\mathrm {Sym}^{2r}\otimes \det ^{-r}$. We note that the action of the center of
$\tau _r=\mathrm {Sym}^{2r}\otimes \det ^{-r}$. We note that the action of the center of ![]() $\mathrm {GL}_2(\mathbb {C})$ on
$\mathrm {GL}_2(\mathbb {C})$ on ![]() $\mathcal {W}_r$ by
$\mathcal {W}_r$ by ![]() $\tau _r$ is trivial and the pairing
$\tau _r$ is trivial and the pairing ![]() $(\, {,}\,)_{2r}$ is
$(\, {,}\,)_{2r}$ is ![]() $\mathrm {GL}_2(\mathbb {C})$-invariant by (8.2.5). Let
$\mathrm {GL}_2(\mathbb {C})$-invariant by (8.2.5). Let ![]() $p$ be a prime number and
$p$ be a prime number and ![]() $D=D_{p,\infty }$ the unique division quaternion algebra over
$D=D_{p,\infty }$ the unique division quaternion algebra over ![]() $\mathbb {Q}$ which ramifies precisely at
$\mathbb {Q}$ which ramifies precisely at ![]() $p$ and
$p$ and ![]() $\infty$. Let
$\infty$. Let ![]() $\mathcal {O}_D$ be the maximal order of
$\mathcal {O}_D$ be the maximal order of ![]() $D$ specified as in [Reference Hsieh and NamikawaHN17, 3.2] and we put
$D$ specified as in [Reference Hsieh and NamikawaHN17, 3.2] and we put ![]() $\hat {\mathcal {O}}_D=\mathcal {O}_D\otimes _{\mathbb {Z}} \hat {\mathbb {Z}}$.
$\hat {\mathcal {O}}_D=\mathcal {O}_D\otimes _{\mathbb {Z}} \hat {\mathbb {Z}}$.
Definition B.1 We have ![]() $\mathcal {A}_r(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)$, the space of automorphic forms of weight
$\mathcal {A}_r(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)$, the space of automorphic forms of weight ![]() $r$ and level
$r$ and level ![]() $\hat {\mathcal {O}}_D$ on
$\hat {\mathcal {O}}_D$ on ![]() $D^\times (\mathbb {A})$ is a space of functions
$D^\times (\mathbb {A})$ is a space of functions ![]() $\mathbf {g}:D^\times (\mathbb {A}) \to \mathcal {W}_r$ satisfying
$\mathbf {g}:D^\times (\mathbb {A}) \to \mathcal {W}_r$ satisfying
for ![]() $z\in \mathbb {A}^\times$,
$z\in \mathbb {A}^\times$, ![]() $\gamma \in D^\times (\mathbb {Q})$,
$\gamma \in D^\times (\mathbb {Q})$, ![]() $u\in \hat {\mathcal {O}}_D^\times$ and
$u\in \hat {\mathcal {O}}_D^\times$ and ![]() $h=(h_\infty, h_f) \in D^\times (\mathbb {R})\times D^\times (\mathbb {A}_f)$.
$h=(h_\infty, h_f) \in D^\times (\mathbb {R})\times D^\times (\mathbb {A}_f)$.
For ![]() $i=1,2$, let
$i=1,2$, let ![]() $\pi _i$ be the irreducible cuspidal automorphic representation of
$\pi _i$ be the irreducible cuspidal automorphic representation of ![]() $\mathrm {GL}_2(\mathbb {A})$ corresponding to
$\mathrm {GL}_2(\mathbb {A})$ corresponding to ![]() $f_i$. Let
$f_i$. Let ![]() $\pi ^D_i$ be the Jacquet–Langlands transfer of
$\pi ^D_i$ be the Jacquet–Langlands transfer of ![]() $\pi _i$ to
$\pi _i$ to ![]() $D^\times (\mathbb {A})$. We denote by
$D^\times (\mathbb {A})$. We denote by ![]() $\mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)[\pi _i^D]$ the
$\mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)[\pi _i^D]$ the ![]() $\pi _i^D$-isotypic subspace of
$\pi _i^D$-isotypic subspace of ![]() $\mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)$. Then
$\mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)$. Then ![]() $\mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)[\pi _i^D]$ has a subspace of newforms, which is one dimensional. Let us take newforms
$\mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)[\pi _i^D]$ has a subspace of newforms, which is one dimensional. Let us take newforms ![]() $\mathbf {f}_i\in \mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)[\pi _i^D]$ for
$\mathbf {f}_i\in \mathcal {A}_{k_i}(D^\times (\mathbb {A}), \hat {\mathcal {O}}_D)[\pi _i^D]$ for ![]() $i=1,2$ and fix. Then to the pair
$i=1,2$ and fix. Then to the pair ![]() $\mathbf {f}=(\mathbf {f}_1,\mathbf {f}_2)$, Hsieh and Namikawa [Reference Hsieh and NamikawaHN17, 3.7] associate the Yoshida lift
$\mathbf {f}=(\mathbf {f}_1,\mathbf {f}_2)$, Hsieh and Namikawa [Reference Hsieh and NamikawaHN17, 3.7] associate the Yoshida lift ![]() $\theta _{\mathbf {f}}$, a
$\theta _{\mathbf {f}}$, a ![]() $V_\varrho$-valued cuspidal automorphic form on
$V_\varrho$-valued cuspidal automorphic form on ![]() $G(\mathbb {A})$ where
$G(\mathbb {A})$ where ![]() $\varrho =\varrho _\kappa$ with
$\varrho =\varrho _\kappa$ with
The classical Yoshida lift ![]() $\theta ^\ast _{\mathbf {f}}\in S_\varrho (\Gamma _0(p))$ is also attached to
$\theta ^\ast _{\mathbf {f}}\in S_\varrho (\Gamma _0(p))$ is also attached to ![]() $\mathbf {f}$ in [Reference Hsieh and NamikawaHN17, 3.7] so that
$\mathbf {f}$ in [Reference Hsieh and NamikawaHN17, 3.7] so that ![]() $\theta _{\mathbf {f}}$ is obtained from
$\theta _{\mathbf {f}}$ is obtained from ![]() $\theta ^\ast _{\mathbf {f}}$ by the adelization procedure in (8.2.9).
$\theta ^\ast _{\mathbf {f}}$ by the adelization procedure in (8.2.9).
B.1.2 Bessel periods of Yoshida lifts
Let ![]() $\phi _{\mathbf {f},S}$ denote a scalar-valued automorphic form attached to
$\phi _{\mathbf {f},S}$ denote a scalar-valued automorphic form attached to ![]() $\theta ^\ast _{\mathbf {f}}$ as in (B.0.1). Hsieh and Namikawa evaluated the Bessel periods of
$\theta ^\ast _{\mathbf {f}}$ as in (B.0.1). Hsieh and Namikawa evaluated the Bessel periods of ![]() $\phi _{\mathbf {f},S}$ in [Reference Hsieh and NamikawaHN17].
$\phi _{\mathbf {f},S}$ in [Reference Hsieh and NamikawaHN17].
First we remark that by [Reference Hsieh and NamikawaHN17, Theorem 5.3], for any sufficiently large prime number ![]() $q$ which is different from
$q$ which is different from ![]() $p$, we may take a character
$p$, we may take a character ![]() $\Lambda _0$ of
$\Lambda _0$ of ![]() $\mathbb {A}_E^\times$ satisfying:
$\mathbb {A}_E^\times$ satisfying:
Then [Reference Hsieh and NamikawaHN17, Proposition 4.7] yields the following formula.
Lemma B.2 We have
 \begin{equation} B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f},S})= q^{2m}\cdot (-2\sqrt{-1})^{k_1+k_2}\cdot e^{-2\pi\,\mathrm{Tr}(S)}\cdot\prod_{i=1}^2 P(\mathbf{f}_i, \Lambda_0^{\alpha_i},1_2), \end{equation}
\begin{equation} B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f},S})= q^{2m}\cdot (-2\sqrt{-1})^{k_1+k_2}\cdot e^{-2\pi\,\mathrm{Tr}(S)}\cdot\prod_{i=1}^2 P(\mathbf{f}_i, \Lambda_0^{\alpha_i},1_2), \end{equation}
where ![]() $\alpha _i=(-1)^{i+1}$ and
$\alpha _i=(-1)^{i+1}$ and
From (B.1.5), we have
 \begin{equation} |B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f},S})|^2= q^{4m} \cdot 2^{2(k_1+k_2)}\cdot e^{-4\pi\,\mathrm{tr}(S)}\cdot\prod_{i=1}^2 |P(\mathbf{f}_i, \Lambda_0^{\alpha_i},1_2)|^2. \end{equation}
\begin{equation} |B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f},S})|^2= q^{4m} \cdot 2^{2(k_1+k_2)}\cdot e^{-4\pi\,\mathrm{tr}(S)}\cdot\prod_{i=1}^2 |P(\mathbf{f}_i, \Lambda_0^{\alpha_i},1_2)|^2. \end{equation}
Since ![]() $p$ is odd and inert in
$p$ is odd and inert in ![]() $E$, we may evaluate the right-hand side of (B.1.6) by Martin and Whitehouse [Reference Martin and WhitehouseMW09]. Namely the following formula holds by [Reference Martin and WhitehouseMW09, Theorem 4.1].
$E$, we may evaluate the right-hand side of (B.1.6) by Martin and Whitehouse [Reference Martin and WhitehouseMW09]. Namely the following formula holds by [Reference Martin and WhitehouseMW09, Theorem 4.1].
Lemma B.3 We have
 \begin{align} \frac{|P(\mathbf{f}_i,
\Lambda_0^{\alpha_i}, 1_2)|^2}{\|\phi_{\mathbf{f}_i}\|^2} &=
\frac{1}{4}\cdot
\frac{\xi(2)}{\zeta_{\mathbb{Q}_p}(2)}\cdot \frac{L(1
/ 2, \pi_i \otimes \mathcal{AI}
(\Lambda_0^{\alpha_i}))}{L(1, \pi_i, \mathrm{Ad})} \cdot
(1+p^{-1})^{-1} \nonumber\\ &\quad
\times\frac{\Gamma(2k_i+2)}{2q^m \pi D_E^{1/
2}\Gamma(k_i+1)^2} ,
\end{align}
\begin{align} \frac{|P(\mathbf{f}_i,
\Lambda_0^{\alpha_i}, 1_2)|^2}{\|\phi_{\mathbf{f}_i}\|^2} &=
\frac{1}{4}\cdot
\frac{\xi(2)}{\zeta_{\mathbb{Q}_p}(2)}\cdot \frac{L(1
/ 2, \pi_i \otimes \mathcal{AI}
(\Lambda_0^{\alpha_i}))}{L(1, \pi_i, \mathrm{Ad})} \cdot
(1+p^{-1})^{-1} \nonumber\\ &\quad
\times\frac{\Gamma(2k_i+2)}{2q^m \pi D_E^{1/
2}\Gamma(k_i+1)^2} ,
\end{align}
where ![]() $\xi (s)$ denotes the complete Riemann zeta function,
$\xi (s)$ denotes the complete Riemann zeta function, ![]() $\phi _{\mathbf {f}_i}$ the scalar-valued automorphic form on
$\phi _{\mathbf {f}_i}$ the scalar-valued automorphic form on ![]() $D^\times (\mathbb {A})$ defined by
$D^\times (\mathbb {A})$ defined by
and
Here ![]() $dh$ is the Tamagawa measure on
$dh$ is the Tamagawa measure on ![]() $\mathbb {A}^\times \backslash D^\times (\mathbb {A})$ and, thus,
$\mathbb {A}^\times \backslash D^\times (\mathbb {A})$ and, thus,
Remark B.2 The factor ![]() $\frac {1}{4}$ in (B.1.7) originates from the difference of measures between the one used here and the one in [Reference Martin and WhitehouseMW09].
$\frac {1}{4}$ in (B.1.7) originates from the difference of measures between the one used here and the one in [Reference Martin and WhitehouseMW09].
In order to utilize the explicit inner product formula for vector-valued Yoshida lifts in Hsieh and Namikawa [Reference Hsieh and NamikawaHN18], we need the following lemma.
Lemma B.4 Let us define an inner product ![]() $\langle \mathbf {f}_i,\mathbf {f}_i\rangle$ for
$\langle \mathbf {f}_i,\mathbf {f}_i\rangle$ for ![]() $i=1,2$ by
$i=1,2$ by
where ![]() $\langle \,{,}\,\rangle _{\tau _{k_i}}$ is defined by (8.2.6),
$\langle \,{,}\,\rangle _{\tau _{k_i}}$ is defined by (8.2.6), ![]() $a$ runs over double coset representatives of
$a$ runs over double coset representatives of ![]() $D^\times (\mathbb {Q})\backslash D^\times (\mathbb {A}_f)/ \hat {\mathcal {O}}_D^\times$ and
$D^\times (\mathbb {Q})\backslash D^\times (\mathbb {A}_f)/ \hat {\mathcal {O}}_D^\times$ and ![]() $\Gamma _a=(a \hat {\mathcal {O}}_D^\times a^{-1}\cap D^\times (\mathbb {Q}))/ \{\pm 1\}$.
$\Gamma _a=(a \hat {\mathcal {O}}_D^\times a^{-1}\cap D^\times (\mathbb {Q}))/ \{\pm 1\}$.
Then for ![]() $i=1,2$, we have
$i=1,2$, we have
Proof. Since ![]() $\|\phi _{\mathbf {f}_i}\|^2=\|\pi _i^D(h_\infty ) \phi _{\mathbf {f}_i}\|^2$ for
$\|\phi _{\mathbf {f}_i}\|^2=\|\pi _i^D(h_\infty ) \phi _{\mathbf {f}_i}\|^2$ for ![]() $h_\infty \in D^\times (\mathbb {R})$, we have
$h_\infty \in D^\times (\mathbb {R})$, we have
By interchanging the order of integration, we have
Here the Schur orthogonality implies
 \begin{align*} & \frac{1}{\mathrm{Vol}(\mathbb{R}^\times\backslash D^\times(\mathbb{R}), dh_\infty)} \int_{\mathbb{R}^\times\backslash D^\times(\mathbb{R})} |((XY)^{k_i},\mathbf{f}_i(hh_\infty))_{2k_i}|^2\,dh_\infty\\ &\quad =d_i^{-1}\cdot((XY)^{k_i},(XY)^{k_i})_{2k_i}\cdot (\mathbf{f}_i(h),\overline{\mathbf{f}_i(h)})_{2k_i}, \end{align*}
\begin{align*} & \frac{1}{\mathrm{Vol}(\mathbb{R}^\times\backslash D^\times(\mathbb{R}), dh_\infty)} \int_{\mathbb{R}^\times\backslash D^\times(\mathbb{R})} |((XY)^{k_i},\mathbf{f}_i(hh_\infty))_{2k_i}|^2\,dh_\infty\\ &\quad =d_i^{-1}\cdot((XY)^{k_i},(XY)^{k_i})_{2k_i}\cdot (\mathbf{f}_i(h),\overline{\mathbf{f}_i(h)})_{2k_i}, \end{align*}
where ![]() $d_i=\dim \mathrm {Sym}^{2k_i}=2k_i+1$ and
$d_i=\dim \mathrm {Sym}^{2k_i}=2k_i+1$ and ![]() $((XY)^{k_i},(XY)^{k_i})_{2k_i}=(-1)^{k_i} \big (\begin{smallmatrix}2k_i\\k_i\end{smallmatrix}\big )^{-1}$. Hence,
$((XY)^{k_i},(XY)^{k_i})_{2k_i}=(-1)^{k_i} \big (\begin{smallmatrix}2k_i\\k_i\end{smallmatrix}\big )^{-1}$. Hence,
 \[ \|\phi_{\mathbf{f}_i}\|^2=\begin{pmatrix}2k_i\\ k_i \end{pmatrix}^{-1} (2k_i+1)^{-1} \int_{\mathbb{A}^\times D^\times(\mathbb{Q}) \backslash D^\times(\mathbb{A})} (\mathbf{f}_i(h), \overline{\mathbf{f}_i(h)})_{2k_i}\, dh. \]
\[ \|\phi_{\mathbf{f}_i}\|^2=\begin{pmatrix}2k_i\\ k_i \end{pmatrix}^{-1} (2k_i+1)^{-1} \int_{\mathbb{A}^\times D^\times(\mathbb{Q}) \backslash D^\times(\mathbb{A})} (\mathbf{f}_i(h), \overline{\mathbf{f}_i(h)})_{2k_i}\, dh. \]
By [Reference Hsieh and NamikawaHN17, Lemma 6], we have
Finally by Chida and Hsieh [Reference Chida and HsiehCH18, (3.10)] with the following Remark B.3, we obtain (B.1.9).
Remark B.3 In [Reference Chida and HsiehCH18], the Eichler mass formula is used to express the right-hand side of (B.1.10) in terms of the inner product defined by (B.1.8). There is a typo in the Eichler mass formula in [Reference Chida and HsiehCH18, p. 103]. The right-hand side of the formula quoted there should be multiplied by ![]() $2$.
$2$.
Let us recall the inner product formula for ![]() $\theta ^\ast _{\mathbf {f}}$ by Hsieh and Namikawa [Reference Hsieh and NamikawaHN18, Theorem A].
$\theta ^\ast _{\mathbf {f}}$ by Hsieh and Namikawa [Reference Hsieh and NamikawaHN18, Theorem A].
Proposition B.1 We have
Here ![]() $\langle \theta _{\mathbf {f}}^\ast, \theta _{\mathbf {f}}^\ast \rangle _{ \varrho }$ is given by
$\langle \theta _{\mathbf {f}}^\ast, \theta _{\mathbf {f}}^\ast \rangle _{ \varrho }$ is given by
with ![]() $\varrho =\varrho _\kappa$ where
$\varrho =\varrho _\kappa$ where ![]() $\kappa =(k_1+k_2+2,k_1-k_2+2)$.
$\kappa =(k_1+k_2+2,k_1-k_2+2)$.
Thus, by combining (B.1.6), (B.1.7), (B.1.9) and (B.1.11), we have
 \begin{align} \frac{|B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f},S})|^2}{\langle \theta_{\mathbf{f}}^\ast, \theta_{\mathbf{f}}^\ast \rangle_{\varrho}} &= \frac{2^{4k_1 + 2k_2+ 5} e^{-4\pi \,\mathrm{tr}(S)}}{D_E}\cdot 2(1+p^{-1})(1+p^{-2}) \cdot q^{2m} \nonumber\\ &\quad \times \frac{L(1 / 2, \pi_1 \otimes \mathcal{AI}(\Lambda_0)) L(1 / 2,\pi_2 \otimes \mathcal{AI}(\Lambda_0^{-1}))}{L(1, \pi_1, \mathrm{Ad}) L(1, \pi_2, \mathrm{Ad}) L(1, \pi_1 \times \pi_2)}. \end{align}
\begin{align} \frac{|B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f},S})|^2}{\langle \theta_{\mathbf{f}}^\ast, \theta_{\mathbf{f}}^\ast \rangle_{\varrho}} &= \frac{2^{4k_1 + 2k_2+ 5} e^{-4\pi \,\mathrm{tr}(S)}}{D_E}\cdot 2(1+p^{-1})(1+p^{-2}) \cdot q^{2m} \nonumber\\ &\quad \times \frac{L(1 / 2, \pi_1 \otimes \mathcal{AI}(\Lambda_0)) L(1 / 2,\pi_2 \otimes \mathcal{AI}(\Lambda_0^{-1}))}{L(1, \pi_1, \mathrm{Ad}) L(1, \pi_2, \mathrm{Ad}) L(1, \pi_1 \times \pi_2)}. \end{align}Here we note that the both sides of (B.1.12) are non-zero due to the conditions (B.1.1) and (B.1.4).
B.2 Proof of Theorem B.1
Since the Ichino–Ikeda-type formula has been proved for Yoshida lifts by Liu [Reference LiuLiu16, Theorem 4.3], the computations in Dickson et al. [Reference Dickson, Pitale, Saha and SchmidtDPSS20] imply
 \begin{align} \frac{|B_{S,\Lambda_0, \psi}(\phi_{\mathbf{f},S})|^2}{\langle \phi_{\mathbf{f},S},\phi_{\mathbf{f},S}\rangle} &= \frac{\mathcal{C}J_\infty}{2^2}\cdot 2(1+p^{-1})(1+p^{-2}) \cdot J_q \nonumber\\ &\quad \times \frac{L(1 / 2, \pi_1 \otimes \mathcal{AI}(\Lambda_0)) L(1 / 2,\pi_2 \otimes \mathcal{AI}(\Lambda_0^{-1}))}{L(1, \pi_1, \mathrm{Ad}) L(1, \pi_2, \mathrm{Ad}) L(1, \pi_1 \times \pi_2)}. \end{align}
\begin{align} \frac{|B_{S,\Lambda_0, \psi}(\phi_{\mathbf{f},S})|^2}{\langle \phi_{\mathbf{f},S},\phi_{\mathbf{f},S}\rangle} &= \frac{\mathcal{C}J_\infty}{2^2}\cdot 2(1+p^{-1})(1+p^{-2}) \cdot J_q \nonumber\\ &\quad \times \frac{L(1 / 2, \pi_1 \otimes \mathcal{AI}(\Lambda_0)) L(1 / 2,\pi_2 \otimes \mathcal{AI}(\Lambda_0^{-1}))}{L(1, \pi_1, \mathrm{Ad}) L(1, \pi_2, \mathrm{Ad}) L(1, \pi_1 \times \pi_2)}. \end{align}
Thus, in order to evaluate ![]() $J_\infty$, we need to determine
$J_\infty$, we need to determine ![]() $J_q$.
$J_q$.
Here we use a scalar-valued Yoshida lift to evaluate ![]() $J_q$. First we recall that (B.0.4) holds in the scalar-valued case, i.e. when
$J_q$. First we recall that (B.0.4) holds in the scalar-valued case, i.e. when ![]() $k_2=0$, as we noted in Remark B.1. By Lemma B.1, when
$k_2=0$, as we noted in Remark B.1. By Lemma B.1, when ![]() $q$ is large enough, there also exist distinct normalized newforms
$q$ is large enough, there also exist distinct normalized newforms ![]() $f_1^\prime \in S_{2k_1+2}(\Gamma _0^{(1)}(p))$ and
$f_1^\prime \in S_{2k_1+2}(\Gamma _0^{(1)}(p))$ and ![]() $f_2^\prime \in S_{2}(\Gamma _0^{(1)}(p))$ satisfying the condition (B.1.1), and a character
$f_2^\prime \in S_{2}(\Gamma _0^{(1)}(p))$ satisfying the condition (B.1.1), and a character ![]() $\lambda _0^\prime$ of
$\lambda _0^\prime$ of ![]() $\mathbb {A}_E^\times$ satisfying the conditions (B.1.4) for
$\mathbb {A}_E^\times$ satisfying the conditions (B.1.4) for ![]() $\pi _i^\prime$
$\pi _i^\prime$ ![]() $(i=1,2)$ where
$(i=1,2)$ where ![]() $\pi _i^\prime$ is the automorphic representation of
$\pi _i^\prime$ is the automorphic representation of ![]() $\mathrm {GL}_2(\mathbb {A})$. Define
$\mathrm {GL}_2(\mathbb {A})$. Define ![]() $\mathbf {f}^\prime$ similarly for
$\mathbf {f}^\prime$ similarly for ![]() $\pi _1^\prime$ and
$\pi _1^\prime$ and ![]() $\pi _2^\prime$. Since (B.0.4) is valid in the scalar-valued case, we have
$\pi _2^\prime$. Since (B.0.4) is valid in the scalar-valued case, we have
 \begin{align*} \frac{|B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f}^\prime,S})|^2}{\langle \phi_{\mathbf{f}^\prime,S},\phi_{\mathbf{f}^\prime,S}\rangle} &= \frac{2^{4k_1+5}e^{-4\pi\,\mathrm{tr}(S)}}{D_E}\cdot C(Q_{S,\varrho_{(k_1, k_1)}})^{-1} \\ &\quad \cdot 2(1+p^{-1})(1+p^{-2}) \cdot J_q \cdot \frac{L(1 / 2, \pi_1^\prime\otimes \mathcal{AI}(\Lambda_0^\prime)) L(1 / 2, \pi_2^\prime \otimes \mathcal{AI}(\Lambda_0^{\prime\, -1}))}{L(1, \pi_1^\prime, \mathrm{Ad}) L(1, \pi_2^\prime, \mathrm{Ad}) L(1, \pi_1^\prime \times \pi_2^\prime)}. \end{align*}
\begin{align*} \frac{|B_{S, \Lambda_0, \psi}(\phi_{\mathbf{f}^\prime,S})|^2}{\langle \phi_{\mathbf{f}^\prime,S},\phi_{\mathbf{f}^\prime,S}\rangle} &= \frac{2^{4k_1+5}e^{-4\pi\,\mathrm{tr}(S)}}{D_E}\cdot C(Q_{S,\varrho_{(k_1, k_1)}})^{-1} \\ &\quad \cdot 2(1+p^{-1})(1+p^{-2}) \cdot J_q \cdot \frac{L(1 / 2, \pi_1^\prime\otimes \mathcal{AI}(\Lambda_0^\prime)) L(1 / 2, \pi_2^\prime \otimes \mathcal{AI}(\Lambda_0^{\prime\, -1}))}{L(1, \pi_1^\prime, \mathrm{Ad}) L(1, \pi_2^\prime, \mathrm{Ad}) L(1, \pi_1^\prime \times \pi_2^\prime)}. \end{align*}
We note that ![]() $J_q$ here is the same as that in (B.2.1). Then by comparing the formula above with (B.1.12) for
$J_q$ here is the same as that in (B.2.1). Then by comparing the formula above with (B.1.12) for ![]() $\mathbf {f}^\prime$ and
$\mathbf {f}^\prime$ and ![]() $\Lambda _0^\prime$, we have
$\Lambda _0^\prime$, we have ![]() $J_q=q^{2m}$.
$J_q=q^{2m}$.
Finally, by comparing (B.1.12) with (B.2.1) substituting ![]() $J_q=q^{2m}$, we have
$J_q=q^{2m}$, we have
in the general case.
For ![]() $\Phi$ in Theorem 8.1, a scalar-valued automorphic form
$\Phi$ in Theorem 8.1, a scalar-valued automorphic form ![]() $\phi _{\Phi,S}$ defined by
$\phi _{\Phi,S}$ defined by
is factorizable, i.e. ![]() $\phi _{\Phi, S}=\otimes _v \phi _{\Phi, S,v}$. Let us choose
$\phi _{\Phi, S}=\otimes _v \phi _{\Phi, S,v}$. Let us choose ![]() $k_1$ and
$k_1$ and ![]() $k_2$ so that
$k_2$ so that
Then for ![]() $\phi _{\mathbf {f},S}=\otimes _v \phi _{\mathbf {f},S,v}$ in (B.2.1), the archimedean factor
$\phi _{\mathbf {f},S}=\otimes _v \phi _{\mathbf {f},S,v}$ in (B.2.1), the archimedean factor ![]() $\phi _{\mathbf {f},S,\infty }$ is a non-zero scalar multiple of
$\phi _{\mathbf {f},S,\infty }$ is a non-zero scalar multiple of ![]() $\phi _{\Phi, S,\infty }$. Thus, (B.0.4) follows from (B.2.2).
$\phi _{\Phi, S,\infty }$. Thus, (B.0.4) follows from (B.2.2).
B.3 Proof of Theorem 8.1
Let us complete our proof of Theorem 8.1.
By Theorem 1.2, we have
 \begin{equation} \frac{|B_{S,\Lambda, \psi}(\phi_{\Phi,S})|^2}{\langle \phi_{\Phi,S},\phi_{\Phi,S}\rangle}=\frac{\mathcal{C}J_\infty}{2^{c-3}}\cdot \frac{L(1/ 2,\pi(\Phi) \times \mathcal{AI} (\Lambda))}{L(1,\pi(\Phi),\mathrm{Ad})}\cdot \prod_{p | N} J_p, \end{equation}
\begin{equation} \frac{|B_{S,\Lambda, \psi}(\phi_{\Phi,S})|^2}{\langle \phi_{\Phi,S},\phi_{\Phi,S}\rangle}=\frac{\mathcal{C}J_\infty}{2^{c-3}}\cdot \frac{L(1/ 2,\pi(\Phi) \times \mathcal{AI} (\Lambda))}{L(1,\pi(\Phi),\mathrm{Ad})}\cdot \prod_{p | N} J_p, \end{equation}
where ![]() $c$ is as stated in Theorem 8.1. By (8.2.13) and (8.2.17), we have
$c$ is as stated in Theorem 8.1. By (8.2.13) and (8.2.17), we have
Since ![]() $\langle \phi _{\Phi,S},\phi _{\Phi,S}\rangle =C(Q_{S,\varrho })\cdot \langle \Phi,\Phi \rangle _\varrho$ by Lemma 8.1, we have
$\langle \phi _{\Phi,S},\phi _{\Phi,S}\rangle =C(Q_{S,\varrho })\cdot \langle \Phi,\Phi \rangle _\varrho$ by Lemma 8.1, we have
Thus, by combining (B.3.1), (B.3.2) and (B.0.4), the identity (8.3.1) holds.
Appendix C. Meromorphic continuation of  $L$-functions for
$L$-functions for  $\mathrm {SO}(5) \times \mathrm {SO}(2)$
$\mathrm {SO}(5) \times \mathrm {SO}(2)$
As we remarked in Remark 1.3, here we show the meromorphic continuation of ![]() $L^S(s, \pi \times \mathcal {AI}(\Lambda ))$ in Theorem 1.1, when
$L^S(s, \pi \times \mathcal {AI}(\Lambda ))$ in Theorem 1.1, when ![]() $\mathcal {AI} (\Lambda )$ is cuspidal and
$\mathcal {AI} (\Lambda )$ is cuspidal and ![]() $S$ is a sufficiently large finite set of places of
$S$ is a sufficiently large finite set of places of ![]() $F$ containing all archimedean places. The following theorem clearly suffices.
$F$ containing all archimedean places. The following theorem clearly suffices.
Theorem C.1 Let ![]() $\pi$ (respectively,
$\pi$ (respectively, ![]() $\tau$) be an irreducible unitary cuspidal automorphic representation
$\tau$) be an irreducible unitary cuspidal automorphic representation ![]() $\pi$ of
$\pi$ of ![]() $G_D(\mathbb {A})$ (respectively,
$G_D(\mathbb {A})$ (respectively, ![]() $\mathrm {GL}_2(\mathbb {A})$) with a trivial central character. Then
$\mathrm {GL}_2(\mathbb {A})$) with a trivial central character. Then ![]() $L^S(s, \pi \times \tau )$ has a meromorphic continuation to
$L^S(s, \pi \times \tau )$ has a meromorphic continuation to ![]() $\mathbb {C}$ and it is holomorphic at
$\mathbb {C}$ and it is holomorphic at ![]() $s= \frac {1}{2}$ for a sufficiently large finite set
$s= \frac {1}{2}$ for a sufficiently large finite set ![]() $S$ of places of
$S$ of places of ![]() $F$ containing all archimedean places.
$F$ containing all archimedean places.
When ![]() $D$ is split, then
$D$ is split, then ![]() $G_D\simeq G$ and the theorem follows from Arthur [Reference ArthurArt13]. Hence, from now on we assume that
$G_D\simeq G$ and the theorem follows from Arthur [Reference ArthurArt13]. Hence, from now on we assume that ![]() $D$ is non-split.
$D$ is non-split.
By [Reference LiLi92], for some ![]() $\xi$ and
$\xi$ and ![]() $\Lambda$,
$\Lambda$, ![]() $\pi$ has the
$\pi$ has the ![]() $(\xi, \Lambda, \psi )$-Bessel period. Thus, we may use the integral representation of the
$(\xi, \Lambda, \psi )$-Bessel period. Thus, we may use the integral representation of the ![]() $L$-function for
$L$-function for ![]() $G_D\times \mathrm {GL}_2$ introduced in [Reference MorimotoMor14b]. Then the meromorphic continuation of the Siegel Eisenstein series on
$G_D\times \mathrm {GL}_2$ introduced in [Reference MorimotoMor14b]. Then the meromorphic continuation of the Siegel Eisenstein series on ![]() $\mathrm {GU}_{3,3}$, which is used in the integral representation is known by the main theorem of Tan [Reference TanTan99] (see also [Reference Pitale, Saha and SchmidtPSS14, Proposition 3.6.2]). Hence, by the standard argument, our theorem is reduced to the analysis of the local zeta integrals. Meanwhile the non-archimedean local integrals are already studied in [Reference MorimotoMor14b, Lemma 5.1]. Hence, it suffices for us to investigate the archimedean ones. Since the case when
$\mathrm {GU}_{3,3}$, which is used in the integral representation is known by the main theorem of Tan [Reference TanTan99] (see also [Reference Pitale, Saha and SchmidtPSS14, Proposition 3.6.2]). Hence, by the standard argument, our theorem is reduced to the analysis of the local zeta integrals. Meanwhile the non-archimedean local integrals are already studied in [Reference MorimotoMor14b, Lemma 5.1]. Hence, it suffices for us to investigate the archimedean ones. Since the case when ![]() $E_v$ is a quadratic extension field of
$E_v$ is a quadratic extension field of ![]() $F_v$ is similar to, and indeed simpler than, the split case, here we only consider the split case.
$F_v$ is similar to, and indeed simpler than, the split case, here we only consider the split case.
Let us briefly recall our local zeta integral (see [Reference MorimotoMor14b, (28)]). Let ![]() $v$ be an archimedean place of
$v$ be an archimedean place of ![]() $F$. Since we consider the split case,
$F$. Since we consider the split case, ![]() $D_v$ is split and we may assume that
$D_v$ is split and we may assume that ![]() $G_{D}(F_v)=G(F_v) =\mathrm {GSp}_2(F_v)$ and
$G_{D}(F_v)=G(F_v) =\mathrm {GSp}_2(F_v)$ and ![]() $\xi =\big (\begin{smallmatrix}1 & 0\\0 & -1\end{smallmatrix}\big )$. Then we have
$\xi =\big (\begin{smallmatrix}1 & 0\\0 & -1\end{smallmatrix}\big )$. Then we have
In what follows, we omit the subscript ![]() $v$ from any object in order to simplify the notation. Let
$v$ from any object in order to simplify the notation. Let ![]() $\Lambda$ be a unitary character of
$\Lambda$ be a unitary character of ![]() $F^\times$. Then we regard
$F^\times$. Then we regard ![]() $\Lambda$ as a character of
$\Lambda$ as a character of ![]() $T_\xi (F)$ by
$T_\xi (F)$ by
For a non-trivial character ![]() $\psi$ of
$\psi$ of ![]() $F$, let
$F$, let ![]() $\mathcal {B}_{\xi, \Lambda, \psi }(\pi )$ denote the
$\mathcal {B}_{\xi, \Lambda, \psi }(\pi )$ denote the ![]() $(\xi, \Lambda, \psi )$-Bessel model of
$(\xi, \Lambda, \psi )$-Bessel model of ![]() $\pi$, i.e. the space of functions
$\pi$, i.e. the space of functions ![]() $B:G(F)\to \mathbb {C}$ such that
$B:G(F)\to \mathbb {C}$ such that
which affords ![]() $\pi$ by the right regular representation. Let
$\pi$ by the right regular representation. Let ![]() $\mathcal {W}(\tau )$ denote the Whittaker model of
$\mathcal {W}(\tau )$ denote the Whittaker model of ![]() $\pi$, i.e. the space of functions
$\pi$, i.e. the space of functions ![]() $W:\mathrm {GL}_2(F)\to \mathbb {C}$ such that
$W:\mathrm {GL}_2(F)\to \mathbb {C}$ such that
which affords ![]() $\tau$ by the right translation. Let
$\tau$ by the right translation. Let ![]() $G_0(F)= \mathrm {GL}_2(F) \times G(F)$ and we regard
$G_0(F)= \mathrm {GL}_2(F) \times G(F)$ and we regard ![]() $G$ as a subgroup of
$G$ as a subgroup of ![]() $\mathrm {GL}_6(F)$ by the embedding
$\mathrm {GL}_6(F)$ by the embedding
 \[ \iota : G_0 \ni \bigg(\begin{pmatrix}a & b\\ c & d\end{pmatrix}, \begin{pmatrix}A & B\\ C & C\end{pmatrix}\bigg)\hookrightarrow \begin{pmatrix}a & 0 & b & 0\\ 0 & A & 0 & B\\ c & 0 & d & 0\\ 0 & C & 0 & D\end{pmatrix} \in \mathrm{GL}_6(F). \]
\[ \iota : G_0 \ni \bigg(\begin{pmatrix}a & b\\ c & d\end{pmatrix}, \begin{pmatrix}A & B\\ C & C\end{pmatrix}\bigg)\hookrightarrow \begin{pmatrix}a & 0 & b & 0\\ 0 & A & 0 & B\\ c & 0 & d & 0\\ 0 & C & 0 & D\end{pmatrix} \in \mathrm{GL}_6(F). \]
Let us define a subgroup ![]() $H_0$ of
$H_0$ of ![]() $G_0$ as
$G_0$ as
where
Let ![]() $P_3$ be the maximal parabolic subgroup of
$P_3$ be the maximal parabolic subgroup of ![]() $\mathrm {GL}_6$ defined by
$\mathrm {GL}_6$ defined by
Then we consider a principal series representation
 \[ I(\Lambda, s) =\bigg\{f_s :
\mathrm{GL}_6(F) \rightarrow \mathbb{C} \,\biggl|\, f_s
\bigg(\bigg(\begin{smallmatrix} h_1 & X\\0 &
h_2\end{smallmatrix}\bigg) h\bigg) =
\Lambda\bigg(\frac{\det h_1}{\det h_2}\bigg)
\bigg|\frac{\det h_1}{\det
h_2}\bigg|^{3s+{{3}/{2}}}f_s(h)\bigg\}. \]
\[ I(\Lambda, s) =\bigg\{f_s :
\mathrm{GL}_6(F) \rightarrow \mathbb{C} \,\biggl|\, f_s
\bigg(\bigg(\begin{smallmatrix} h_1 & X\\0 &
h_2\end{smallmatrix}\bigg) h\bigg) =
\Lambda\bigg(\frac{\det h_1}{\det h_2}\bigg)
\bigg|\frac{\det h_1}{\det
h_2}\bigg|^{3s+{{3}/{2}}}f_s(h)\bigg\}. \]
For ![]() $f_s \in I(\Lambda, s)$,
$f_s \in I(\Lambda, s)$, ![]() $B \in \mathcal {B}_{\xi, \Lambda, \psi }(\pi )$ and
$B \in \mathcal {B}_{\xi, \Lambda, \psi }(\pi )$ and ![]() $W \in \mathcal {W}(\tau )$, our local zeta integral
$W \in \mathcal {W}(\tau )$, our local zeta integral ![]() $Z(f_s, B, W)$ is given by
$Z(f_s, B, W)$ is given by
where ![]() $Z_0$ denotes the center of
$Z_0$ denotes the center of ![]() $G_0$ and
$G_0$ and
 \[ \theta_{0}=\begin{pmatrix} 0 & 0 & 0 & 0 & 0 & -1\\ 0 & 1 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 1 & -1 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & -1\\ 0 & 0 & 0 & 1 & 0 & -1 \end{pmatrix}. \]
\[ \theta_{0}=\begin{pmatrix} 0 & 0 & 0 & 0 & 0 & -1\\ 0 & 1 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 1 & -1 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & -1\\ 0 & 0 & 0 & 1 & 0 & -1 \end{pmatrix}. \]
As explained above, Theorem C.1 follows by the standard argument if we prove the following lemma.
Lemma C.1 Let ![]() $s_0$ be an arbitrary point in
$s_0$ be an arbitrary point in ![]() $\mathbb {C}$. Then we may choose
$\mathbb {C}$. Then we may choose ![]() $f_s, B$ and
$f_s, B$ and ![]() $W$ so that
$W$ so that ![]() $Z(f_s, B, W)$ has a meromorphic continuation to
$Z(f_s, B, W)$ has a meromorphic continuation to ![]() $\mathbb {C}$ and is holomorphic and non-zero at
$\mathbb {C}$ and is holomorphic and non-zero at ![]() $s=s_0$.
$s=s_0$.
Proof. For ![]() $\varphi \in C_c^\infty (\mathrm {GL}_6(F))$, we may define
$\varphi \in C_c^\infty (\mathrm {GL}_6(F))$, we may define ![]() $P_s[\varphi ] \in I(\Lambda, s)$ by
$P_s[\varphi ] \in I(\Lambda, s)$ by
 \begin{align*} P_s[\varphi](h) &= \int_{\mathrm{GL}_3(F)} \int_{\mathrm{GL}_3(F)} \int_{\mathrm{Mat}_{3 \times 3}(F)}\varphi \bigg(\begin{pmatrix}h_1 & 0\\ 0 & h_2 \end{pmatrix} \begin{pmatrix}1_3 & X\\ & 1_3 \end{pmatrix} h \bigg) \\ &\quad \times\bigg|\frac{\det h_1}{\det h_2}\bigg|^{-3s+{{3}/{2}}} \Lambda\bigg(\frac{\det h_1}{\det h_2}\bigg)^{-1}\, dh_1 \, dh_2 \, dX. \end{align*}
\begin{align*} P_s[\varphi](h) &= \int_{\mathrm{GL}_3(F)} \int_{\mathrm{GL}_3(F)} \int_{\mathrm{Mat}_{3 \times 3}(F)}\varphi \bigg(\begin{pmatrix}h_1 & 0\\ 0 & h_2 \end{pmatrix} \begin{pmatrix}1_3 & X\\ & 1_3 \end{pmatrix} h \bigg) \\ &\quad \times\bigg|\frac{\det h_1}{\det h_2}\bigg|^{-3s+{{3}/{2}}} \Lambda\bigg(\frac{\det h_1}{\det h_2}\bigg)^{-1}\, dh_1 \, dh_2 \, dX. \end{align*}
In what follows we construct ![]() $\varphi$ of a special form, whose support is contained in the open double coset
$\varphi$ of a special form, whose support is contained in the open double coset ![]() $P_3(F) \theta _0 G_0(F)$ in
$P_3(F) \theta _0 G_0(F)$ in ![]() $\mathrm {GL}_6(F)$.
$\mathrm {GL}_6(F)$.
Let ![]() $B_0$ be the group of upper triangular matrices in
$B_0$ be the group of upper triangular matrices in ![]() $\mathrm {GL}_2$ and let
$\mathrm {GL}_2$ and let ![]() $P_0$ be the mirabolic subgroup of
$P_0$ be the mirabolic subgroup of ![]() $\mathrm {GL}_2$, i.e.
$\mathrm {GL}_2$, i.e.
We define a subgroup ![]() $M_0$ of
$M_0$ of ![]() $G$ by
$G$ by
and ![]() $M = \iota (P_0, M_0)$. Then by the Iwasawa decomposition for
$M = \iota (P_0, M_0)$. Then by the Iwasawa decomposition for ![]() $G_0(F)$ and the inclusion
$G_0(F)$ and the inclusion
we have
where ![]() $K_0$ is a maximal compact subgroup of
$K_0$ is a maximal compact subgroup of ![]() $G_0(F)$. We take
$G_0(F)$. We take ![]() $K_0=\iota (K_1,K_2)$ where
$K_0=\iota (K_1,K_2)$ where ![]() $K_1$ (respectively,
$K_1$ (respectively, ![]() $K_2$) is a maximal compact subgroup of
$K_2$) is a maximal compact subgroup of ![]() $\mathrm {GL}_2(F)$ (respectively,
$\mathrm {GL}_2(F)$ (respectively, ![]() $G(F)$). By direct computations, we see that
$G(F)$). By direct computations, we see that
 \[ \begin{cases} \theta_0 \,N(F)\, \theta_0^{-1} \cap P_3(F) =\{ 1_6 \};\\ \theta_0 \,M(F)\, \theta_0^{-1} \cap P_3(F) =\theta_0 \,A(F)\, \theta_0^{-1};\\ \theta_0 \,K_0\,\theta_0^{-1} \cap P_3(F) =\{ 1_6 \}, \end{cases} \]
\[ \begin{cases} \theta_0 \,N(F)\, \theta_0^{-1} \cap P_3(F) =\{ 1_6 \};\\ \theta_0 \,M(F)\, \theta_0^{-1} \cap P_3(F) =\theta_0 \,A(F)\, \theta_0^{-1};\\ \theta_0 \,K_0\,\theta_0^{-1} \cap P_3(F) =\{ 1_6 \}, \end{cases} \]
where
Let us define subgroups ![]() $T_0$,
$T_0$, ![]() $N_0$ of
$N_0$ of ![]() $G_0$ by
$G_0$ by
 \begin{align*} T_0(F) &= \left\{\iota\left(\begin{pmatrix}a & \\ & 1 \end{pmatrix}, \begin{pmatrix}x & & & \\ & y & & \\ & & \lambda x^{-1} & \\ & & & \lambda y^{-1} \end{pmatrix}\right): x, y, \lambda \in F^\times\right\};\\ N_0(F) &= \left\{\iota \left(\begin{pmatrix}1 & x\\ & 1 \end{pmatrix}, \begin{pmatrix}1 & y & & \\ & 1 & & \\ & & 1 & \\ & & -y & 1 \end{pmatrix}\right) : x, y \in F\right\}. \end{align*}
\begin{align*} T_0(F) &= \left\{\iota\left(\begin{pmatrix}a & \\ & 1 \end{pmatrix}, \begin{pmatrix}x & & & \\ & y & & \\ & & \lambda x^{-1} & \\ & & & \lambda y^{-1} \end{pmatrix}\right): x, y, \lambda \in F^\times\right\};\\ N_0(F) &= \left\{\iota \left(\begin{pmatrix}1 & x\\ & 1 \end{pmatrix}, \begin{pmatrix}1 & y & & \\ & 1 & & \\ & & 1 & \\ & & -y & 1 \end{pmatrix}\right) : x, y \in F\right\}. \end{align*}
Then for ![]() $\varphi _1 \in C_c^\infty (N_0(F))$,
$\varphi _1 \in C_c^\infty (N_0(F))$, ![]() $\varphi _2 \in C_c^\infty (T_0(F))$,
$\varphi _2 \in C_c^\infty (T_0(F))$, ![]() $\varphi _3, \varphi _4 \in C_c^\infty (\mathrm {GL}_3(F))$,
$\varphi _3, \varphi _4 \in C_c^\infty (\mathrm {GL}_3(F))$, ![]() $\varphi _5 \in C_c^\infty (\mathrm {Mat}_{3 \times 3}(F))$ and
$\varphi _5 \in C_c^\infty (\mathrm {Mat}_{3 \times 3}(F))$ and ![]() $\varphi _6 \in C_c^\infty (K_0)$, we may construct
$\varphi _6 \in C_c^\infty (K_0)$, we may construct ![]() $\varphi ^\prime \in C_c^\infty (\mathrm {GL}_6(F))$, whose support is contained in
$\varphi ^\prime \in C_c^\infty (\mathrm {GL}_6(F))$, whose support is contained in ![]() $P_3(F) \theta _0 G_0(F)$, by
$P_3(F) \theta _0 G_0(F)$, by
 \begin{align*} & \varphi^\prime \bigg(\begin{pmatrix}h_1 & 0\\ 0 & h_2 \end{pmatrix} \begin{pmatrix}1_3 & X\\ 0 & 1_3 \end{pmatrix} \theta_0\, n_0\, t_0\, k \bigg)\\ &\quad =\varphi_6(k) \varphi_3(h_1) \varphi_4(h_2) \varphi_5(X) \varphi_1(n_0 ) \int_{A(F)} \varphi_2(t_0\, a) \, d^\times a, \end{align*}
\begin{align*} & \varphi^\prime \bigg(\begin{pmatrix}h_1 & 0\\ 0 & h_2 \end{pmatrix} \begin{pmatrix}1_3 & X\\ 0 & 1_3 \end{pmatrix} \theta_0\, n_0\, t_0\, k \bigg)\\ &\quad =\varphi_6(k) \varphi_3(h_1) \varphi_4(h_2) \varphi_5(X) \varphi_1(n_0 ) \int_{A(F)} \varphi_2(t_0\, a) \, d^\times a, \end{align*}
where ![]() $n_0 \in N_0(F)$,
$n_0 \in N_0(F)$, ![]() $t_0 \in T_0(F)$ and
$t_0 \in T_0(F)$ and ![]() $k \in K_0$.
$k \in K_0$.
Then the local zeta integral ![]() $Z(P_s[\varphi ^\prime ], B, W)$ is written as
$Z(P_s[\varphi ^\prime ], B, W)$ is written as
 \begin{align*}
& Z(P_s[\varphi^\prime], B, W)\\
&\quad = \int \varphi^\prime \bigg(\begin{pmatrix}h_1 & 0\\
0 & h_2 \end{pmatrix} \begin{pmatrix}1_3 & X\\ & 1_3
\end{pmatrix} \iota(n_{0,1}, n_{0,2})\iota(t_{0,1},
t_{0,2}) \iota(k_1, k_2) \bigg) \\ &\qquad\quad
\times\bigg|\frac{\det h_1}{\det
h_2}\bigg|^{-3s+{{3}/{2}}} \Lambda\bigg(\frac{\det
h_1}{\det h_2}\bigg)^{-1} W(n_{0,1} t_{0,1} k_1) B(n_{0,2}
t_{0, 2}k_2)\, dh_1 \, dh_2 \, dX \, dn_0 \, dt_0\, dk\\
&\quad =\int \varphi_6(\iota(k_1, k_2)) \varphi_3(h_1)
\varphi_4(h_2) \varphi_5(X) \varphi_1(n_0 ) \varphi_2(t_0a)
\bigg|\frac{\det h_1}{\det h_2}\bigg|^{-3s+{{3}/{2}}}
\Lambda\bigg(\frac{\det h_1}{\det h_2}\bigg)^{-1} \\
&\qquad\quad \times W(n_{0,1} t_{0,1} k_1) B(n_{0,2} t_{0,
2}k_2)\, d^\times a \, dh_1 \, dh_2 \, dX \, dn_0 \, dt_0\,
dk \\ &\quad =\int \varphi_6(\iota(k_1, k_2))
\varphi_3(h_1) \varphi_4(h_2) \varphi_5(X) \varphi_1(n_0 )
\varphi_2(t_0) \bigg|\frac{\det h_1}{\det
h_2}\bigg|^{-3s+{{3}/{2}}} \Lambda\bigg(\frac{\det
h_1}{\det h_2}\bigg)^{-1} \\ &\qquad\quad \times
\Lambda(\lambda)|\lambda|^{3s-{{9}/{2}}}W \bigg(n_{0,1}
\begin{pmatrix}\lambda & 0\\ 0 & 1 \end{pmatrix} t_{0,1}
k_1\bigg) B \bigg(n_{0,2} \begin{pmatrix} \lambda \cdot 1_2
& 0\\ 0 & 1_2 \end{pmatrix} t_{0, 2}k_2 \bigg)\\ &\qquad\quad
\times d^\times \lambda \, dh_1 \, dh_2 \, dX \, dn_0 \,
dt_0\, dk, \end{align*}
\begin{align*}
& Z(P_s[\varphi^\prime], B, W)\\
&\quad = \int \varphi^\prime \bigg(\begin{pmatrix}h_1 & 0\\
0 & h_2 \end{pmatrix} \begin{pmatrix}1_3 & X\\ & 1_3
\end{pmatrix} \iota(n_{0,1}, n_{0,2})\iota(t_{0,1},
t_{0,2}) \iota(k_1, k_2) \bigg) \\ &\qquad\quad
\times\bigg|\frac{\det h_1}{\det
h_2}\bigg|^{-3s+{{3}/{2}}} \Lambda\bigg(\frac{\det
h_1}{\det h_2}\bigg)^{-1} W(n_{0,1} t_{0,1} k_1) B(n_{0,2}
t_{0, 2}k_2)\, dh_1 \, dh_2 \, dX \, dn_0 \, dt_0\, dk\\
&\quad =\int \varphi_6(\iota(k_1, k_2)) \varphi_3(h_1)
\varphi_4(h_2) \varphi_5(X) \varphi_1(n_0 ) \varphi_2(t_0a)
\bigg|\frac{\det h_1}{\det h_2}\bigg|^{-3s+{{3}/{2}}}
\Lambda\bigg(\frac{\det h_1}{\det h_2}\bigg)^{-1} \\
&\qquad\quad \times W(n_{0,1} t_{0,1} k_1) B(n_{0,2} t_{0,
2}k_2)\, d^\times a \, dh_1 \, dh_2 \, dX \, dn_0 \, dt_0\,
dk \\ &\quad =\int \varphi_6(\iota(k_1, k_2))
\varphi_3(h_1) \varphi_4(h_2) \varphi_5(X) \varphi_1(n_0 )
\varphi_2(t_0) \bigg|\frac{\det h_1}{\det
h_2}\bigg|^{-3s+{{3}/{2}}} \Lambda\bigg(\frac{\det
h_1}{\det h_2}\bigg)^{-1} \\ &\qquad\quad \times
\Lambda(\lambda)|\lambda|^{3s-{{9}/{2}}}W \bigg(n_{0,1}
\begin{pmatrix}\lambda & 0\\ 0 & 1 \end{pmatrix} t_{0,1}
k_1\bigg) B \bigg(n_{0,2} \begin{pmatrix} \lambda \cdot 1_2
& 0\\ 0 & 1_2 \end{pmatrix} t_{0, 2}k_2 \bigg)\\ &\qquad\quad
\times d^\times \lambda \, dh_1 \, dh_2 \, dX \, dn_0 \,
dt_0\, dk, \end{align*}
where we let ![]() $n_0 = \iota (n_{0,1}, n_{0,2}) \in N_0(F)$,
$n_0 = \iota (n_{0,1}, n_{0,2}) \in N_0(F)$, ![]() $t_0 = \iota (t_{0,1}, t_{0,2}) \in T_0(F)$ and
$t_0 = \iota (t_{0,1}, t_{0,2}) \in T_0(F)$ and ![]() $k = \iota (k_1, k_2) \in K_0$. Since we may vary
$k = \iota (k_1, k_2) \in K_0$. Since we may vary ![]() $\varphi _i$ (
$\varphi _i$ (![]() $1\le i\le 6$), our assertion in Lemma C.1 follows from the same assertion for the integral
$1\le i\le 6$), our assertion in Lemma C.1 follows from the same assertion for the integral
For any ![]() $\phi \in C_c^\infty (F^\times )$, there exists
$\phi \in C_c^\infty (F^\times )$, there exists ![]() $W_\phi \in W(\tau )$ such that
$W_\phi \in W(\tau )$ such that ![]() $W_\phi \big (\begin{smallmatrix}a & 0\\0 & 1\end{smallmatrix}\big )= \phi (a)$ by the theory of Kirillov model for
$W_\phi \big (\begin{smallmatrix}a & 0\\0 & 1\end{smallmatrix}\big )= \phi (a)$ by the theory of Kirillov model for ![]() $\mathrm {GL}_2(\mathbb {R})$ by Jacquet [Reference JacquetJac10, Proposition 5] and for
$\mathrm {GL}_2(\mathbb {R})$ by Jacquet [Reference JacquetJac10, Proposition 5] and for ![]() $\mathrm {GL}_2(\mathbb {C})$ by Kemarsky [Reference KemarskyKem15, Theorem 1]. Thus, our assertion clearly holds for the integral (C.0.2).
$\mathrm {GL}_2(\mathbb {C})$ by Kemarsky [Reference KemarskyKem15, Theorem 1]. Thus, our assertion clearly holds for the integral (C.0.2).