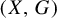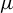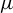1 Introduction
In 1973, in a profound and influential paper [Reference Bowen3], Bowen introduced a definition of topological entropy of subsets inspired by Hausdorff dimension, which is now known as Bowen topological entropy or dimensional entropy. For dynamical systems over compact Hausdorff spaces, Bowen showed that Bowen topological entropy on the whole space coincides with the Adler–Konheim–McAndrew topological entropy defined through open covers.
Bowen topological entropy can be viewed as dynamically analogous to Hausdorff dimension and has exhibited very deep connections with dimension theory in dynamical system and multifractal analysis ever since its appearance (see, for example, [Reference Pesin19]). It is natural to consider the analogous concepts in dynamical systems for other forms of dimensions. For pointwise dimension (of a measure), its dynamical correspondence is the Brin–Katok local entropy [Reference Brin, Katok and Palis4]. For packing dimension, its dynamical correspondence is the packing topological entropy, which was introduced by Feng and Huang [Reference Hofmann and Stoyanov9]. Applying the methods in geometric measure theory, they also provided variational principles for Bowen topological entropy and packing topological entropy. Other works on packing topological entropy can be found in [Reference Zhou, Chen and Cheng27], where the packing topological entropy for certain non-compact subsets was considered.
In this paper we focus on packing topological entropy in the framework of countable discrete amenable group actions.
1.1 Amenable packing entropy and local entropies
Let
![]() $(X,G)$
be a G-action topological dynamical system, where X is a compact metric space with metric d and G is a topological group acting continuously on X. Throughout this paper we assume that G is a countable infinite discrete amenable group unless otherwise specified. Recall that a countable discrete group G is amenable if there is a sequence of non-empty finite subsets
$(X,G)$
be a G-action topological dynamical system, where X is a compact metric space with metric d and G is a topological group acting continuously on X. Throughout this paper we assume that G is a countable infinite discrete amenable group unless otherwise specified. Recall that a countable discrete group G is amenable if there is a sequence of non-empty finite subsets
![]() $\{F_n\}$
of G which are asymptotically invariant, that is,
$\{F_n\}$
of G which are asymptotically invariant, that is,
Such sequences are called Følner sequences. One may refer to [Reference Kerr and Li14, Reference Ornstein and Weiss18] for more details on amenable groups and their actions. A Følner sequence
![]() $\{F_n\}$
in G is said to be tempered if there exists a constant
$\{F_n\}$
in G is said to be tempered if there exists a constant
![]() $C>0$
which is independent of n such that
$C>0$
which is independent of n such that
 $$ \begin{align} \bigg|\bigcup_{k<n}F_k^{-1}F_n\bigg|\le C|F_n|\quad\text{for any }n. \end{align} $$
$$ \begin{align} \bigg|\bigcup_{k<n}F_k^{-1}F_n\bigg|\le C|F_n|\quad\text{for any }n. \end{align} $$
Let
![]() $F(G)$
denote the collection of finite subsets of G. For
$F(G)$
denote the collection of finite subsets of G. For
![]() $F\in F(G)$
, let
$F\in F(G)$
, let
![]() $d_F$
be the metric defined by
$d_F$
be the metric defined by
Let
![]() $\varepsilon>0$
and x in X; we denote
$\varepsilon>0$
and x in X; we denote
and
which are respectively the open and closed (F-)Bowen balls with center x and radius
![]() $\varepsilon $
. When we want to clarify the underlying metric d, we also denote the above balls by
$\varepsilon $
. When we want to clarify the underlying metric d, we also denote the above balls by
![]() $B_{F}(x,\varepsilon ,d)$
and
$B_{F}(x,\varepsilon ,d)$
and
![]() $\overline {B}_{F}(x,\varepsilon ,d)$
. For a
$\overline {B}_{F}(x,\varepsilon ,d)$
. For a
![]() $\mathbb Z$
-action (or
$\mathbb Z$
-action (or
![]() $\mathbb N$
-action) topological dynamical system
$\mathbb N$
-action) topological dynamical system
![]() $(X,T)$
(T is the homeomorphism (or the continuous onto map) on X), let
$(X,T)$
(T is the homeomorphism (or the continuous onto map) on X), let
![]() $F=\{0,1,\ldots ,n-1\}:=[0,n-1]$
. The (F-)Bowen balls will be written as
$F=\{0,1,\ldots ,n-1\}:=[0,n-1]$
. The (F-)Bowen balls will be written as
![]() $B_n(x,\varepsilon ,T)$
or
$B_n(x,\varepsilon ,T)$
or
![]() $B_n(x,\varepsilon ,d)$
.
$B_n(x,\varepsilon ,d)$
.
Definition 1.1 Let
![]() $\{F_n\}$
be a sequence of finite subsets of G with
$\{F_n\}$
be a sequence of finite subsets of G with
![]() $|F_n|\rightarrow \infty $
(which need not be Følner). For
$|F_n|\rightarrow \infty $
(which need not be Følner). For
![]() $Z\subseteq X, s\ge 0, N\in \mathbb N$
and
$Z\subseteq X, s\ge 0, N\in \mathbb N$
and
![]() $\varepsilon> 0$
, define
$\varepsilon> 0$
, define
where the supremum is taken over all finite or countable pairwise disjoint families
![]() $\{\overline {B}_{F_{n_i}}(x_i,\varepsilon )\}$
such that
$\{\overline {B}_{F_{n_i}}(x_i,\varepsilon )\}$
such that
![]() $x_i\in Z, n_i\ge N$
for all i. The quantity
$x_i\in Z, n_i\ge N$
for all i. The quantity
![]() $P(Z,N,\varepsilon ,s,\{F_n\})$
does not increase as N increases, hence the following limit exists:
$P(Z,N,\varepsilon ,s,\{F_n\})$
does not increase as N increases, hence the following limit exists:
Define
 $$ \begin{align*} \mathcal{P}(Z,\varepsilon,s,\{F_n\})=\inf \bigg\{\sum_{i=1}^{+\infty}P(Z_i,\varepsilon,s,\{F_n\}): \bigcup_{i=1}^{+\infty}Z_i\supset Z\bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{P}(Z,\varepsilon,s,\{F_n\})=\inf \bigg\{\sum_{i=1}^{+\infty}P(Z_i,\varepsilon,s,\{F_n\}): \bigcup_{i=1}^{+\infty}Z_i\supset Z\bigg\}. \end{align*} $$
It is easy to see that if
![]() $Z\subseteq \bigcup \nolimits _{i=1}^{+\infty }Z_i$
, then
$Z\subseteq \bigcup \nolimits _{i=1}^{+\infty }Z_i$
, then
![]() $\mathcal {P}(Z,\varepsilon ,s,\{F_n\})\le \sum \nolimits _{i=1}^{+\infty }\mathcal {P}(Z_i,\varepsilon ,s,\{F_n\})$
. There exists a critical value of the parameter s, which we will denote by
$\mathcal {P}(Z,\varepsilon ,s,\{F_n\})\le \sum \nolimits _{i=1}^{+\infty }\mathcal {P}(Z_i,\varepsilon ,s,\{F_n\})$
. There exists a critical value of the parameter s, which we will denote by
![]() $h_{\mathrm {top}}^{P}(Z,\varepsilon , \{F_n\})$
, where
$h_{\mathrm {top}}^{P}(Z,\varepsilon , \{F_n\})$
, where
![]() $\mathcal {P}(Z,\varepsilon ,s,\{F_n\})$
jumps from
$\mathcal {P}(Z,\varepsilon ,s,\{F_n\})$
jumps from
![]() $+\infty $
to
$+\infty $
to
![]() $0$
, that is,
$0$
, that is,
 $$ \begin{align*} \mathcal{P}(Z,\varepsilon,s,\{F_n\})=\begin{cases} 0, \quad& s> h_{\mathrm{top}}^P(Z,\varepsilon, \{F_n\}),\\ +\infty,\quad& s < h_{\mathrm{top}}^P(Z,\varepsilon, \{F_n\}). \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{P}(Z,\varepsilon,s,\{F_n\})=\begin{cases} 0, \quad& s> h_{\mathrm{top}}^P(Z,\varepsilon, \{F_n\}),\\ +\infty,\quad& s < h_{\mathrm{top}}^P(Z,\varepsilon, \{F_n\}). \end{cases} \end{align*} $$
It is not hard to see that
![]() $h_{\mathrm {top}}^P(Z,\varepsilon , \{F_n\})$
increases when
$h_{\mathrm {top}}^P(Z,\varepsilon , \{F_n\})$
increases when
![]() $\varepsilon $
decreases. We call
$\varepsilon $
decreases. We call
the amenable packing topological entropy (amenable packing entropy or packing entropy, for short) of Z (with respect to the Følner sequence
![]() $\{F_n\}$
).
$\{F_n\}$
).
Let
![]() $M(X)$
denote the collection of Borel probability measures on X.
$M(X)$
denote the collection of Borel probability measures on X.
Definition 1.2 Let
![]() $\{F_n\}$
be a sequence of finite subsets of G with
$\{F_n\}$
be a sequence of finite subsets of G with
![]() $|F_n|\rightarrow \infty $
. For
$|F_n|\rightarrow \infty $
. For
![]() $\mu \in M(X)$
and
$\mu \in M(X)$
and
![]() $Z\in \mathcal {B}(X)$
(the Borel
$Z\in \mathcal {B}(X)$
(the Borel
![]() $\sigma $
-algebra on X), denote
$\sigma $
-algebra on X), denote
and
which are called the upper local entropy and the lower local entropy of
![]() $\mu $
over Z (with respect to
$\mu $
over Z (with respect to
![]() $\{F_n\}$
), respectively.
$\{F_n\}$
), respectively.
In the
![]() $\mathbb Z$
-action or
$\mathbb Z$
-action or
![]() $\mathbb N$
-action case, if the sequence
$\mathbb N$
-action case, if the sequence
![]() $\{F_n\}$
is chosen to be
$\{F_n\}$
is chosen to be
![]() $F_n=[0,n-1]$
(hence
$F_n=[0,n-1]$
(hence
![]() $\{F_n\}$
is naturally a Følner sequence), the local entropies of a topological dynamical system
$\{F_n\}$
is naturally a Følner sequence), the local entropies of a topological dynamical system
![]() $(X,T)$
will be denoted by
$(X,T)$
will be denoted by
![]() $\underline h_{\mu }^{\mathrm {loc}}(Z,T)$
and
$\underline h_{\mu }^{\mathrm {loc}}(Z,T)$
and
![]() $\overline h_{\mu }^{\mathrm {loc}}(Z,T)$
, respectively.
$\overline h_{\mu }^{\mathrm {loc}}(Z,T)$
, respectively.
By the Brin–Katok entropy formula for amenable group actions (see [Reference Zheng and Chen26]), if
![]() $\mu $
is in addition G-invariant and
$\mu $
is in addition G-invariant and
![]() $\{F_n\}$
is a tempered Følner sequence which satisfies the growth condition
$\{F_n\}$
is a tempered Følner sequence which satisfies the growth condition
then the values of the upper and lower local entropies over the whole space X coincide with the measure-theoretic entropy of the system
![]() $(X,G)$
.
$(X,G)$
.
We will prove the following variational principle between amenable packing entropy and upper local entropy.
Theorem 1.3 Let
![]() $(X,G)$
be a G-action topological dynamical system and G a countable infinite discrete amenable group. Let
$(X,G)$
be a G-action topological dynamical system and G a countable infinite discrete amenable group. Let
![]() $\{F_n\}$
be a sequence of finite subsets in G satisfying the growth condition (1.2). Then for any non-empty Borel subset Z of X,
$\{F_n\}$
be a sequence of finite subsets in G satisfying the growth condition (1.2). Then for any non-empty Borel subset Z of X,
1.2 Amenable packing entropy inequalities via factor maps
Let
![]() $(X,G)$
and
$(X,G)$
and
![]() $(Y,G)$
be two G-action topological dynamical systems. A continuous map
$(Y,G)$
be two G-action topological dynamical systems. A continuous map
![]() $\pi :(X,G)\to (Y,G)$
is called a homomorphism or a factor map from
$\pi :(X,G)\to (Y,G)$
is called a homomorphism or a factor map from
![]() $(X,G)$
to
$(X,G)$
to
![]() $(Y,G)$
if it is onto and
$(Y,G)$
if it is onto and
![]() $\pi \circ g=g\circ \pi $
, for all
$\pi \circ g=g\circ \pi $
, for all
![]() $g\in G$
. We also say that
$g\in G$
. We also say that
![]() $(X,G)$
is an extension of
$(X,G)$
is an extension of
![]() $(Y,G)$
or
$(Y,G)$
or
![]() $(Y,G)$
is a factor of
$(Y,G)$
is a factor of
![]() $(X,G)$
.
$(X,G)$
.
For a subset Z of X, we denote by
![]() $h_{\mathrm {top}}^{UC}(Z,\{F_n\})$
the upper capacity topological entropy of Z (defined in §2). We will show in §2 that the packing entropy can be estimated via the upper capacity topological entropy with parameters (Proposition 2.7). This is a dynamical version of the fact that the packing dimension can be defined via the upper Minkowski dimension. Applying Proposition 2.7, we can prove the following packing entropy inequalities for factor maps.
$h_{\mathrm {top}}^{UC}(Z,\{F_n\})$
the upper capacity topological entropy of Z (defined in §2). We will show in §2 that the packing entropy can be estimated via the upper capacity topological entropy with parameters (Proposition 2.7). This is a dynamical version of the fact that the packing dimension can be defined via the upper Minkowski dimension. Applying Proposition 2.7, we can prove the following packing entropy inequalities for factor maps.
Theorem 1.4 Let G be a countable infinite discrete amenable group and
![]() $\pi :(X,G)\to (Y,G)$
be a factor map between two G-action topological dynamical systems. Let
$\pi :(X,G)\to (Y,G)$
be a factor map between two G-action topological dynamical systems. Let
![]() $\{F_n\}$
be any tempered Følner sequence in G satisfying the growth condition (1.2). Then, for any Borel subset E of X,
$\{F_n\}$
be any tempered Følner sequence in G satisfying the growth condition (1.2). Then, for any Borel subset E of X,
 $$ \begin{align} h^P_{\mathrm{top}}(\pi (E),\{F_n\})&\leq h^P_{\mathrm{top}}( E,\{F_n\})\leq h^P_{\mathrm{top}}(\pi (E),\{F_n\})\nonumber\\&\quad+\mathop{\mathrm{sup}}\limits_{y\in Y}h_{\mathrm{top}}^{UC}(\pi^{-1}(y),\{F_n\}). \end{align} $$
$$ \begin{align} h^P_{\mathrm{top}}(\pi (E),\{F_n\})&\leq h^P_{\mathrm{top}}( E,\{F_n\})\leq h^P_{\mathrm{top}}(\pi (E),\{F_n\})\nonumber\\&\quad+\mathop{\mathrm{sup}}\limits_{y\in Y}h_{\mathrm{top}}^{UC}(\pi^{-1}(y),\{F_n\}). \end{align} $$
We remark here that for
![]() $\mathbb Z$
-actions, the inequalities were proved in [Reference Zhao, Chen, Hong and Zhou24]. But for amenable group actions, except employing Bowen’s idea in [Reference Bowen2] and the quasi-tiling techniques developed by Ornstein and Weiss [Reference Ornstein and Weiss18], we need a crucial covering lemma for amenable groups built by Lindenstrauss while proving pointwise theorems for amenable groups in [Reference Lindenstrauss15].
$\mathbb Z$
-actions, the inequalities were proved in [Reference Zhao, Chen, Hong and Zhou24]. But for amenable group actions, except employing Bowen’s idea in [Reference Bowen2] and the quasi-tiling techniques developed by Ornstein and Weiss [Reference Ornstein and Weiss18], we need a crucial covering lemma for amenable groups built by Lindenstrauss while proving pointwise theorems for amenable groups in [Reference Lindenstrauss15].
1.3 Amenable packing entropy for certain subsets
Let
![]() $M(X,G)$
and
$M(X,G)$
and
![]() $E(X,G)$
be the collection of G-invariant and ergodic G-invariant Borel probability measures on X, respectively. Since G is amenable,
$E(X,G)$
be the collection of G-invariant and ergodic G-invariant Borel probability measures on X, respectively. Since G is amenable,
![]() $M(X,G)$
and
$M(X,G)$
and
![]() $E(X,G)$
are both non-empty. For
$E(X,G)$
are both non-empty. For
![]() $\mu \in M(X,G)$
, let
$\mu \in M(X,G)$
, let
![]() $h_{\mu }(X,G)$
denote the measure-theoretic entropy of
$h_{\mu }(X,G)$
denote the measure-theoretic entropy of
![]() $(X,G)$
with respect to
$(X,G)$
with respect to
![]() $\mu $
.
$\mu $
.
For
![]() $\mu \in M(X,G)$
and a Følner sequence
$\mu \in M(X,G)$
and a Følner sequence
![]() $\{F_n\}$
in G, let
$\{F_n\}$
in G, let
![]() $G_{\mu ,\{F_n\}}$
be the set of generic points for
$G_{\mu ,\{F_n\}}$
be the set of generic points for
![]() $\mu $
(with respect to
$\mu $
(with respect to
![]() $\{F_n\}$
), which is defined by
$\{F_n\}$
), which is defined by
 $$ \begin{align*} G_{\mu,\{F_n\}}=\bigg\{x\in X: \lim_{n\rightarrow+\infty}\frac{1}{|F_n|}\sum_{g\in F_n}f(gx)=\int_Xf\,d{\kern-1pt}{\mu}, \text{ for any }f\in C(X)\bigg\}. \end{align*} $$
$$ \begin{align*} G_{\mu,\{F_n\}}=\bigg\{x\in X: \lim_{n\rightarrow+\infty}\frac{1}{|F_n|}\sum_{g\in F_n}f(gx)=\int_Xf\,d{\kern-1pt}{\mu}, \text{ for any }f\in C(X)\bigg\}. \end{align*} $$
For simplicity, we write
![]() $G_{\mu ,\{F_n\}}$
as
$G_{\mu ,\{F_n\}}$
as
![]() $G_{\mu }$
when there is no ambiguity over
$G_{\mu }$
when there is no ambiguity over
![]() $\{F_n\}$
. But we should note that for different Følner sequence
$\{F_n\}$
. But we should note that for different Følner sequence
![]() $\{F_n\}$
, the corresponding
$\{F_n\}$
, the corresponding
![]() $G_{\mu }$
may not coincide. When
$G_{\mu }$
may not coincide. When
![]() $\mu $
is ergodic and the Følner sequence
$\mu $
is ergodic and the Følner sequence
![]() $\{F_n\}$
is tempered,
$\{F_n\}$
is tempered,
![]() $G_{\mu }$
has full measure for
$G_{\mu }$
has full measure for
![]() $\mu $
(see Remark 5.1). But when
$\mu $
(see Remark 5.1). But when
![]() $\mu $
is not ergodic, the set
$\mu $
is not ergodic, the set
![]() $G_{\mu }$
could be empty.
$G_{\mu }$
could be empty.
For the case
![]() $G=\mathbb Z$
, Bowen [Reference Bowen3] proved that the Bowen topological entropy of
$G=\mathbb Z$
, Bowen [Reference Bowen3] proved that the Bowen topological entropy of
![]() $G_{\mu }$
equals the measure-theoretic entropy of
$G_{\mu }$
equals the measure-theoretic entropy of
![]() $\mu $
if
$\mu $
if
![]() $\mu $
is ergodic. Pfister and Sullivan [Reference Pfister and Sullivan20] extended Bowen’s result to the system with the so-called g-almost product property for invariant Borel probability measure
$\mu $
is ergodic. Pfister and Sullivan [Reference Pfister and Sullivan20] extended Bowen’s result to the system with the so-called g-almost product property for invariant Borel probability measure
![]() $\mu $
. And the results for the amenable group action version were proved by Zheng and Chen [Reference Zheng and Chen26] and Zhang [Reference Zhang23]. The g-almost product property (see [Reference Pfister and Sullivan20]) is an extension of the specification property for
$\mu $
. And the results for the amenable group action version were proved by Zheng and Chen [Reference Zheng and Chen26] and Zhang [Reference Zhang23]. The g-almost product property (see [Reference Pfister and Sullivan20]) is an extension of the specification property for
![]() $\mathbb Z$
-systems and was generalized to amenable systems in [Reference Zhang23] (called the almost specification property there). It was shown in [Reference Zhang23] that weak specification implies almost specification for amenable systems. We defer the detailed definitions of almost specification and weak specification to §5.
$\mathbb Z$
-systems and was generalized to amenable systems in [Reference Zhang23] (called the almost specification property there). It was shown in [Reference Zhang23] that weak specification implies almost specification for amenable systems. We defer the detailed definitions of almost specification and weak specification to §5.
We will prove for packing entropy the following theorem.
Theorem 1.5 Let
![]() $(X,G)$
be a G-action topological dynamical system with G a countable infinite discrete amenable group and let
$(X,G)$
be a G-action topological dynamical system with G a countable infinite discrete amenable group and let
![]() $\mu \in M(X,G)$
and
$\mu \in M(X,G)$
and
![]() $\{F_n\}$
be a Følner sequence in G satisfying the growth condition (1.2). If either
$\{F_n\}$
be a Følner sequence in G satisfying the growth condition (1.2). If either
![]() $\mu $
is ergodic and
$\mu $
is ergodic and
![]() $\{F_n\}$
is tempered or
$\{F_n\}$
is tempered or
![]() $(X,G)$
satisfies the almost specification property, then
$(X,G)$
satisfies the almost specification property, then
In geometric measure theory, a set is said to be regular (or ‘dimension-regular’) if it has equal Hausdorff and packing dimensions [Reference Tricot22]. As a counterpart in dynamical systems, we have the following definition.
Definition 1.6 A subset is said to be regular in the sense of dimensional entropy (or regular for short) if it has equal Bowen entropy and packing entropy.
An affirmative task in the study of packing entropy is to compute the dimensional entropies (including packing entropy and its dual, Bowen entropy) for various subsets and to make clear which subsets are regular. From Theorem 1.5 and results in [Reference Zhang23, Reference Zheng and Chen26] for Bowen entropy, under the conditions in Theorem 1.5, the set
![]() $G_{\mu }$
is regular since both of its dimensional entropies equal the measure-theoretic entropy for
$G_{\mu }$
is regular since both of its dimensional entropies equal the measure-theoretic entropy for
![]() $\mu $
.
$\mu $
.
1.4 Organization of the paper
In §2 we give some properties of amenable packing entropy including connections with Bowen entropy and upper capacity entropy. We devote §3 to the proof of Theorem 1.3, the variational principle between amenable packing entropy and upper local entropy. This extends Feng and Huang’s result in [Reference Hofmann and Stoyanov9] from
![]() $\mathbb Z$
-actions to amenable group actions. In §4 we prove the packing entropy inequalities for factor maps (Theorem 1.4). Finally, in §5, we give the proof of Theorem 1.5 and provide some examples to discuss the regularity for certain subsets. These examples include subsets of symbolic dynamical system and fibers of the
$\mathbb Z$
-actions to amenable group actions. In §4 we prove the packing entropy inequalities for factor maps (Theorem 1.4). Finally, in §5, we give the proof of Theorem 1.5 and provide some examples to discuss the regularity for certain subsets. These examples include subsets of symbolic dynamical system and fibers of the
![]() $(T,T^{-1})$
transformation. Some detailed computations on these examples are included in Appendix A.
$(T,T^{-1})$
transformation. Some detailed computations on these examples are included in Appendix A.
2 Properties of amenable packing entropy
Due to the definition of packing entropy in §1, it is not hard to prove that the packing entropy has the following properties.
Proposition 2.1 Let
![]() $\{F_n\}$
be a sequence of finite subsets in G with
$\{F_n\}$
be a sequence of finite subsets in G with
![]() $|F_n|\rightarrow \infty $
, and let
$|F_n|\rightarrow \infty $
, and let
![]() $Z,Z'$
and
$Z,Z'$
and
![]() $Z_i (i=1,2,\ldots )$
be subsets of X.
$Z_i (i=1,2,\ldots )$
be subsets of X.
-
(1) If
 $Z\subseteq Z'$
, then
$Z\subseteq Z'$
, then  $$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_n\})\le h_{\mathrm{top}}^P(Z',\{F_n\}).\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_n\})\le h_{\mathrm{top}}^P(Z',\{F_n\}).\end{align*} $$
-
(2) If
 $Z\subseteq \bigcup \nolimits _{i=1}^{+\infty }Z_i$
, then for any
$Z\subseteq \bigcup \nolimits _{i=1}^{+\infty }Z_i$
, then for any
 $\varepsilon>0$
, Hence
$\varepsilon>0$
, Hence $$ \begin{align*}h_{\mathrm{top}}^P(Z,\varepsilon,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{i\ge 1}h_{\mathrm{top}}^P(Z_i,\varepsilon,\{F_n\}).\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^P(Z,\varepsilon,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{i\ge 1}h_{\mathrm{top}}^P(Z_i,\varepsilon,\{F_n\}).\end{align*} $$
 $$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{i\ge 1}h_{\mathrm{top}}^P(Z_i,\{F_n\}).\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{i\ge 1}h_{\mathrm{top}}^P(Z_i,\{F_n\}).\end{align*} $$
-
(3) If
 $\{F_{n_k}\}$
is a subsequence of
$\{F_{n_k}\}$
is a subsequence of
 $\{F_n\}$
, then
$\{F_n\}$
, then  $$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_{n_k}\})\le h_{\mathrm{top}}^P(Z,\{F_n\}).\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_{n_k}\})\le h_{\mathrm{top}}^P(Z,\{F_n\}).\end{align*} $$
In the following we recall the definition of amenable Bowen topological entropy which was introduced in [Reference Zheng and Chen25].
Let
![]() $\{F_n\}$
be a sequence of finite subsets in G with
$\{F_n\}$
be a sequence of finite subsets in G with
![]() $|F_n|\rightarrow \infty $
. For
$|F_n|\rightarrow \infty $
. For
![]() $Z\subseteq X, s\ge 0, N\in \mathbb N$
and
$Z\subseteq X, s\ge 0, N\in \mathbb N$
and
![]() $\varepsilon> 0$
, define
$\varepsilon> 0$
, define
where the infimum is taken over all finite or countable families
![]() $\{B_{F_{n_i}}(x_i,\varepsilon )\}$
such that
$\{B_{F_{n_i}}(x_i,\varepsilon )\}$
such that
![]() $x_i\in X, n_i\ge N$
and
$x_i\in X, n_i\ge N$
and
![]() $\bigcup \nolimits _i B_{F_{n_i}}(x_i,\varepsilon )\supseteq Z$
. The quantity
$\bigcup \nolimits _i B_{F_{n_i}}(x_i,\varepsilon )\supseteq Z$
. The quantity
![]() $\mathcal {M}(Z,N,\varepsilon ,s,\{F_n\})$
does not decrease as N increases and
$\mathcal {M}(Z,N,\varepsilon ,s,\{F_n\})$
does not decrease as N increases and
![]() $\varepsilon $
decreases, hence the following limits exist:
$\varepsilon $
decreases, hence the following limits exist:
and
The Bowen topological entropy
![]() $h^B_{\mathrm {top}}(Z,\{F_n\})$
is then defined as the critical value of the parameter s, where
$h^B_{\mathrm {top}}(Z,\{F_n\})$
is then defined as the critical value of the parameter s, where
![]() $\mathcal {M}(Z,s,\{F_n\})$
jumps from
$\mathcal {M}(Z,s,\{F_n\})$
jumps from
![]() $+\infty $
to
$+\infty $
to
![]() $0$
, that is,
$0$
, that is,
 $$ \begin{align*} \mathcal{M}(Z,s,\{F_n\})=\begin{cases} 0, \quad& s> h^B_{\mathrm{top}}(Z,\{F_n\}),\\ +\infty,\quad& s < h^B_{\mathrm{top}}(Z,\{F_n\}). \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{M}(Z,s,\{F_n\})=\begin{cases} 0, \quad& s> h^B_{\mathrm{top}}(Z,\{F_n\}),\\ +\infty,\quad& s < h^B_{\mathrm{top}}(Z,\{F_n\}). \end{cases} \end{align*} $$
Next we will compare packing topological entropy with Bowen topological entropy.
Proposition 2.2 Let
![]() $\{F_n\}$
be a sequence of finite subsets in G with
$\{F_n\}$
be a sequence of finite subsets in G with
![]() $|F_n|\rightarrow \infty $
. For any
$|F_n|\rightarrow \infty $
. For any
![]() $Z\subseteq X$
,
$Z\subseteq X$
,
Proof. The proof for the case
![]() $h_{\mathrm {top}}^B(Z,\{F_n\})=0$
is obvious. Now assume
$h_{\mathrm {top}}^B(Z,\{F_n\})=0$
is obvious. Now assume
![]() $h^B_{\mathrm {top}} (Z,\{F_n\}){\,>\,}0$
and let
$h^B_{\mathrm {top}} (Z,\{F_n\}){\,>\,}0$
and let
![]() $0< s <h^B_{\mathrm {top}}(Z,\{F_n\})$
.
$0< s <h^B_{\mathrm {top}}(Z,\{F_n\})$
.
Let
![]() $\{Z_i\}_{i=1}^{+\infty }$
be any covering of Z. For each i, for any
$\{Z_i\}_{i=1}^{+\infty }$
be any covering of Z. For each i, for any
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $\varepsilon>0$
, let
$\varepsilon>0$
, let
![]() $\{\overline B_{F_n}(x_{i,j}, \varepsilon )\}_{j=1}^{N_i}$
be a disjoint subfamily of
$\{\overline B_{F_n}(x_{i,j}, \varepsilon )\}_{j=1}^{N_i}$
be a disjoint subfamily of
![]() $\{\overline B_{F_n}(x, \varepsilon )\}_{x\in Z_i}$
with maximal cardinality
$\{\overline B_{F_n}(x, \varepsilon )\}_{x\in Z_i}$
with maximal cardinality
![]() $N_i$
. Then
$N_i$
. Then
 $$ \begin{align*}\bigcup_{i=1}^{N_i}B_{F_n}(x_{i,j},3\varepsilon)\supseteq Z_i.\end{align*} $$
$$ \begin{align*}\bigcup_{i=1}^{N_i}B_{F_n}(x_{i,j},3\varepsilon)\supseteq Z_i.\end{align*} $$
So
and hence
Thus
 $$ \begin{align*} \mathcal M(Z,3\varepsilon,s,\{F_n\})\le \sum_{i=1}^{+\infty}M(Z_i,3\varepsilon,s,\{F_n\}) \le \sum_{i=1}^{+\infty} P(Z_i,\varepsilon,s,\{F_n\}), \end{align*} $$
$$ \begin{align*} \mathcal M(Z,3\varepsilon,s,\{F_n\})\le \sum_{i=1}^{+\infty}M(Z_i,3\varepsilon,s,\{F_n\}) \le \sum_{i=1}^{+\infty} P(Z_i,\varepsilon,s,\{F_n\}), \end{align*} $$
from which we deduce that
Since
![]() $s<h^B_{\mathrm {top}}(Z,\{F_n\})$
, we have
$s<h^B_{\mathrm {top}}(Z,\{F_n\})$
, we have
![]() $\mathcal M(Z,s,\{F_n\})=+\infty $
. So
$\mathcal M(Z,s,\{F_n\})=+\infty $
. So
whenever
![]() $\varepsilon $
is sufficiently small. This implies that
$\varepsilon $
is sufficiently small. This implies that
Letting
![]() $\varepsilon \rightarrow 0$
, we have
$\varepsilon \rightarrow 0$
, we have
![]() $h_{\mathrm {top}}^P(Z,\{F_n\})\ge s$
. Hence
$h_{\mathrm {top}}^P(Z,\{F_n\})\ge s$
. Hence
Corollary 2.3 Let
![]() $\mu \in M(X,G)$
,
$\mu \in M(X,G)$
,
![]() $Z\subseteq X$
with
$Z\subseteq X$
with
![]() $\mu (Z)=1$
and
$\mu (Z)=1$
and
![]() $\{F_n\}$
be a Følner sequence in G. Then
$\{F_n\}$
be a Følner sequence in G. Then
Proof. Let
![]() $\{F_{n_k}\}$
be a subsequence of
$\{F_{n_k}\}$
be a subsequence of
![]() $\{F_n\}$
which is tempered and satisfies the growth condition (1.2). By [Reference Zheng and Chen26],
$\{F_n\}$
which is tempered and satisfies the growth condition (1.2). By [Reference Zheng and Chen26],
![]() $h_{\mu }(X,G)\le h_{\mathrm {top}}^B(Z,\{F_{n_k}\})$
. Together with Proposition 2.2 and (3) of Proposition 2.1, we have
$h_{\mu }(X,G)\le h_{\mathrm {top}}^B(Z,\{F_{n_k}\})$
. Together with Proposition 2.2 and (3) of Proposition 2.1, we have
Let
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
![]() $Z\subseteq X$
and
$Z\subseteq X$
and
![]() $F\in F(G)$
. A subset
$F\in F(G)$
. A subset
![]() $E\subseteq Z$
is said to be an
$E\subseteq Z$
is said to be an
![]() $(F,\varepsilon )$
-separated set of Z if, for any two distinct points
$(F,\varepsilon )$
-separated set of Z if, for any two distinct points
![]() $x, y\in E$
,
$x, y\in E$
,
![]() $d_F(x, y)>\varepsilon $
. Let
$d_F(x, y)>\varepsilon $
. Let
![]() $s_F(Z, \varepsilon )$
denote the largest cardinality of
$s_F(Z, \varepsilon )$
denote the largest cardinality of
![]() $(F, \varepsilon )$
-separated sets for Z. A subset
$(F, \varepsilon )$
-separated sets for Z. A subset
![]() $E\subseteq X$
is said to be an
$E\subseteq X$
is said to be an
![]() $(F,\varepsilon )$
-spanning set of Z if, for any
$(F,\varepsilon )$
-spanning set of Z if, for any
![]() $x\in Z$
, there exists
$x\in Z$
, there exists
![]() $y\in E$
with
$y\in E$
with
![]() $d_{F}(x,y)\le \varepsilon $
. Let
$d_{F}(x,y)\le \varepsilon $
. Let
![]() $r_F(Z, \varepsilon )$
(sometimes we use
$r_F(Z, \varepsilon )$
(sometimes we use
![]() $r_F(Z, \varepsilon ,d)$
to indicate the accompanied metric d) denote the smallest cardinality of
$r_F(Z, \varepsilon ,d)$
to indicate the accompanied metric d) denote the smallest cardinality of
![]() $(F, \varepsilon )$
-spanning sets for Z. For a sequence of finite subsets
$(F, \varepsilon )$
-spanning sets for Z. For a sequence of finite subsets
![]() $\{F_n\}$
in G with
$\{F_n\}$
in G with
![]() $|F_n|\rightarrow \infty $
, the upper capacity topological entropy of Z is defined as
$|F_n|\rightarrow \infty $
, the upper capacity topological entropy of Z is defined as
The second equality comes from the following simple fact:
For convention we denote
and then
We note here that for the case
![]() $Z=X$
and where
$Z=X$
and where
![]() $\{F_n\}$
is a Følner sequence, the quantity
$\{F_n\}$
is a Følner sequence, the quantity
![]() $h_{\mathrm {top}}^{UC}(X,\{F_n\})$
coincides with
$h_{\mathrm {top}}^{UC}(X,\{F_n\})$
coincides with
![]() $h_{\mathrm {top}}(X,G)$
, the topological entropy of
$h_{\mathrm {top}}(X,G)$
, the topological entropy of
![]() $(X,G)$
.
$(X,G)$
.
Proposition 2.4 Let
![]() $\{F_n\}$
be a sequence of finite subsets in G satisfying the growth condition (1.2). Then for any subset Z of X and any
$\{F_n\}$
be a sequence of finite subsets in G satisfying the growth condition (1.2). Then for any subset Z of X and any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
Hence
Proof. Let
![]() $\varepsilon>0$
be fixed. The proposition is obvious for the case
$\varepsilon>0$
be fixed. The proposition is obvious for the case
![]() $h_{\mathrm {top}}^P(Z,\varepsilon ,\{F_n\})=0$
. Assume
$h_{\mathrm {top}}^P(Z,\varepsilon ,\{F_n\})=0$
. Assume
![]() $h_{\mathrm {top}}^P(Z,\varepsilon , \{F_n\})>0$
and let
$h_{\mathrm {top}}^P(Z,\varepsilon , \{F_n\})>0$
and let
![]() $0<t<s<h_{\mathrm {top}}^P(Z,\varepsilon ,\{F_n\})$
. Then
$0<t<s<h_{\mathrm {top}}^P(Z,\varepsilon ,\{F_n\})$
. Then
Thus for any N, there exists a countable pairwise disjoint family
![]() $\{\overline {B}_{F_{n_i}}(x_i, \varepsilon )\}$
with
$\{\overline {B}_{F_{n_i}}(x_i, \varepsilon )\}$
with
![]() $x_i\in Z$
and
$x_i\in Z$
and
![]() $n_i\ge N$
for all i such that
$n_i\ge N$
for all i such that
![]() $1< \sum \nolimits _ie^{-|F_{n_i}|s}$
. For each k, let
$1< \sum \nolimits _ie^{-|F_{n_i}|s}$
. For each k, let
![]() $m_k$
be the number of i with
$m_k$
be the number of i with
![]() $n_i=k$
. Then we have
$n_i=k$
. Then we have
Since
![]() $\{F_n\}$
satisfies the growth condition
$\{F_n\}$
satisfies the growth condition
![]() $\lim \nolimits _{n\rightarrow +\infty }({|F_n|}/{\log n})=+\infty $
,
$\lim \nolimits _{n\rightarrow +\infty }({|F_n|}/{\log n})=+\infty $
,
![]() $\sum \nolimits _{k\ge 1}e^{|F_k|(t-s)}$
converges. Let
$\sum \nolimits _{k\ge 1}e^{|F_k|(t-s)}$
converges. Let
![]() $M=\sum \nolimits _{k\ge 1}e^{|F_k|(t-s)}$
. There must be some
$M=\sum \nolimits _{k\ge 1}e^{|F_k|(t-s)}$
. There must be some
![]() $k\ge N$
such that
$k\ge N$
such that
![]() $m_k>({1}/{M})e^{|F_k|t}$
, otherwise the above sum is at most
$m_k>({1}/{M})e^{|F_k|t}$
, otherwise the above sum is at most
 $$ \begin{align*}\sum_{k\ge 1}\frac{1}{M}e^{|F_k|t}e^{-|F_k|s}=1.\end{align*} $$
$$ \begin{align*}\sum_{k\ge 1}\frac{1}{M}e^{|F_k|t}e^{-|F_k|s}=1.\end{align*} $$
So
![]() $s_{F_k}(Z, \varepsilon )\ge m_k> ({1}/{M})e^{|F_k|t}$
and hence
$s_{F_k}(Z, \varepsilon )\ge m_k> ({1}/{M})e^{|F_k|t}$
and hence
 $$ \begin{align*}h_{\mathrm{top}}^{UC}(Z,\varepsilon,\{F_n\})=\limsup_{k\rightarrow +\infty}\frac{1}{|F_k|}\log s_{F_k}(Z, \varepsilon)\ge t,\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^{UC}(Z,\varepsilon,\{F_n\})=\limsup_{k\rightarrow +\infty}\frac{1}{|F_k|}\log s_{F_k}(Z, \varepsilon)\ge t,\end{align*} $$
from which we deduce that
![]() $h_{\mathrm {top}}^P(Z,\varepsilon ,\{F_n\})\le h_{\mathrm {top}}^{UC}(Z,\varepsilon ,\{F_n\})$
.
$h_{\mathrm {top}}^P(Z,\varepsilon ,\{F_n\})\le h_{\mathrm {top}}^{UC}(Z,\varepsilon ,\{F_n\})$
.
As a corollary, we have the following result.
Corollary 2.5 If
![]() $\{F_n\}$
is a Følner sequence that satisfies the growth condition (1.2), then
$\{F_n\}$
is a Følner sequence that satisfies the growth condition (1.2), then
Proof. By Corollary 2.3, for any
![]() $\mu \in M(X,G)$
,
$\mu \in M(X,G)$
,
![]() $h_{\mu }(X,G)\le h_{\mathrm {top}}^P(X,\{F_n\})$
. Applying the variational principle for amenable topological entropy (cf. [Reference Ollagnier and Pinchon17, Reference Stepin and Tagi-Zade21]), we have
$h_{\mu }(X,G)\le h_{\mathrm {top}}^P(X,\{F_n\})$
. Applying the variational principle for amenable topological entropy (cf. [Reference Ollagnier and Pinchon17, Reference Stepin and Tagi-Zade21]), we have
![]() $h_{\mathrm {top}}^P(X,\{F_n\})\ge h_{\mathrm {top}}(X,G)$
. By Proposition 2.4, we have
$h_{\mathrm {top}}^P(X,\{F_n\})\ge h_{\mathrm {top}}(X,G)$
. By Proposition 2.4, we have
![]() $h_{\mathrm {top}}^P(X,\{F_n\})\le h_{\mathrm {top}}(X,G)$
.
$h_{\mathrm {top}}^P(X,\{F_n\})\le h_{\mathrm {top}}(X,G)$
.
Remark 2.6
-
(1) By [Reference Feng and Huang8] (see also [Reference Zheng and Chen25]), if
 $\{F_n\}$
is a tempered Følner sequence and satisfies the growth condition (1.2), then
$\{F_n\}$
is a tempered Følner sequence and satisfies the growth condition (1.2), then  $$ \begin{align*}h_{\mathrm{top}}^P(X,\{F_n\})= h_{\mathrm{top}}(X,G)=h_{\mathrm{top}}^B(X,\{F_n\}).\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^P(X,\{F_n\})= h_{\mathrm{top}}(X,G)=h_{\mathrm{top}}^B(X,\{F_n\}).\end{align*} $$
-
(2) If we replace X by a G-invariant compact subset, the above equality also holds and hence any G-invariant compact subset is regular (when the Følner sequence
 $\{F_n\}$
is tempered and satisfies the growth condition (1.2)).
$\{F_n\}$
is tempered and satisfies the growth condition (1.2)).
At the end of this section we will give further relations between packing entropy and upper capacity topological entropy.
Proposition 2.7 Let
![]() $\varepsilon>0$
, Z be a subset of X and let
$\varepsilon>0$
, Z be a subset of X and let
![]() $\{F_n\}$
be a sequence of finite subsets in G satisfying the growth condition (1.2).
$\{F_n\}$
be a sequence of finite subsets in G satisfying the growth condition (1.2).
-
(1) We have
Hence $$ \begin{align*} h^P_{\mathrm{top}}(Z,\varepsilon,\{F_n\})\le \inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\varepsilon,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}. \end{align*} $$
$$ \begin{align*} h^P_{\mathrm{top}}(Z,\varepsilon,\{F_n\})\le \inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\varepsilon,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}. \end{align*} $$
 $$ \begin{align*} h^P_{\mathrm{top}}(Z,\{F_n\})\le\inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}. \end{align*} $$
$$ \begin{align*} h^P_{\mathrm{top}}(Z,\{F_n\})\le\inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}. \end{align*} $$
-
(2) For any
 $\delta>0$
, there exists a cover
$\delta>0$
, there exists a cover
 $\bigcup _{i=1}^{\infty }Z_i=Z$
(which depends on both
$\bigcup _{i=1}^{\infty }Z_i=Z$
(which depends on both
 $\varepsilon $
and
$\varepsilon $
and
 $\delta $
) such that
$\delta $
) such that  $$ \begin{align*} h^P_{\mathrm{top}}(Z,\varepsilon,\{F_n\})+\delta\ge \mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,3\varepsilon,\{F_n\}). \end{align*} $$
$$ \begin{align*} h^P_{\mathrm{top}}(Z,\varepsilon,\{F_n\})+\delta\ge \mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,3\varepsilon,\{F_n\}). \end{align*} $$
Proof. For any
![]() $Z=\bigcup _{i=1}^{\infty }Z_i$
, by Propositions 2.1 and 2.4,
$Z=\bigcup _{i=1}^{\infty }Z_i$
, by Propositions 2.1 and 2.4,
Hence
 $$ \begin{align*}h^P_{\mathrm{top}}(Z,\varepsilon,\{F_n\})\le \inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\varepsilon,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}.\end{align*} $$
$$ \begin{align*}h^P_{\mathrm{top}}(Z,\varepsilon,\{F_n\})\le \inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\varepsilon,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}.\end{align*} $$
For the opposite direction, we may assume that
![]() $h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\})<\infty $
. Let
$h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\})<\infty $
. Let
![]() $\delta>0$
be fixed and set
$\delta>0$
be fixed and set
![]() $s=h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\})+\delta $
. By the definition of the amenable packing entropy, we have that
$s=h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\})+\delta $
. By the definition of the amenable packing entropy, we have that
![]() $\mathcal {P}(Z,\varepsilon ,s,\{F_n\})=0$
. Then there exists a cover
$\mathcal {P}(Z,\varepsilon ,s,\{F_n\})=0$
. Then there exists a cover
![]() $\bigcup _{i=1}^{\infty }Z_i\supseteq Z$
such that
$\bigcup _{i=1}^{\infty }Z_i\supseteq Z$
such that
For each
![]() $Z_i$
, when N is large enough, we have
$Z_i$
, when N is large enough, we have
![]() $P(Z_i,N,\varepsilon ,s,\{F_n\})<1$
. Let E be any
$P(Z_i,N,\varepsilon ,s,\{F_n\})<1$
. Let E be any
![]() $(F_N,3\varepsilon )$
-separated subset of
$(F_N,3\varepsilon )$
-separated subset of
![]() $Z_i$
. Noting that the closed Bowen balls
$Z_i$
. Noting that the closed Bowen balls
![]() $\overline B_{F_N}(x_i,\varepsilon )$
(
$\overline B_{F_N}(x_i,\varepsilon )$
(
![]() $x_i\in E\subset Z_i$
) are pairwise disjoint, we have
$x_i\in E\subset Z_i$
) are pairwise disjoint, we have
 $$ \begin{align*} |E|e^{-s|F_N|}=\sum_{x_i\in E}e^{-s|F_N|}\le P(Z_i,N,\varepsilon,s,\{F_n\})<1. \end{align*} $$
$$ \begin{align*} |E|e^{-s|F_N|}=\sum_{x_i\in E}e^{-s|F_N|}\le P(Z_i,N,\varepsilon,s,\{F_n\})<1. \end{align*} $$
Hence
![]() $s_{F_N}(Z_i,3\varepsilon )<e^{s|F_N|}$
, which leads to
$s_{F_N}(Z_i,3\varepsilon )<e^{s|F_N|}$
, which leads to
![]() $h^{UC}_{\mathrm {top}}(Z_i,3\varepsilon ,\{F_n\})\le s$
. Thus we have
$h^{UC}_{\mathrm {top}}(Z_i,3\varepsilon ,\{F_n\})\le s$
. Thus we have
Remark 2.8 Proposition 2.4 is motivated from the equivalent definition of packing dimension through Minkowski dimension in geometric measure theory, which was due to Tricot [Reference Tricot22] (see also [Reference Mattila16] for reference). It is unclear to us whether
 $$ \begin{align*} h^P_{\mathrm{top}}(Z,\{F_n\})= \inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}. \end{align*} $$
$$ \begin{align*} h^P_{\mathrm{top}}(Z,\{F_n\})= \inf\Big\{\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(Z_i,\{F_n\}): Z=\bigcup_{i=1}^{\infty}Z_i\Big\}. \end{align*} $$
3 A variational principle for amenable packing entropy
In this section we will give the proof of our Theorem 1.3, the variational principle for amenable packing topological entropy. We assume in this section that
![]() $\{F_n\}$
is a sequence of finite subsets in G and satisfies growth condition (1.2).
$\{F_n\}$
is a sequence of finite subsets in G and satisfies growth condition (1.2).
3.1 Lower bound
Proposition 3.1 Let
![]() $Z\subseteq X$
be a Borel set. Then
$Z\subseteq X$
be a Borel set. Then
For the proof, we need the following classical
![]() $5r$
-lemma in geometric measure theory (cf. [Reference Mattila16, Theorem 2.1]).
$5r$
-lemma in geometric measure theory (cf. [Reference Mattila16, Theorem 2.1]).
Lemma 3.2 (
 $5r$
-lemma)
$5r$
-lemma)
Let
![]() $(X, d)$
be a compact metric space and
$(X, d)$
be a compact metric space and
![]() $\mathcal B =\{B(x_i, r_i)\}_{i\in I}$
be a family of closed (or open) balls in X. Then there exists a finite or countable subfamily
$\mathcal B =\{B(x_i, r_i)\}_{i\in I}$
be a family of closed (or open) balls in X. Then there exists a finite or countable subfamily
![]() $\mathcal B'=\{B(x_i, r_i)\}_{i\in I'}$
of pairwise disjoint balls in
$\mathcal B'=\{B(x_i, r_i)\}_{i\in I'}$
of pairwise disjoint balls in
![]() $\mathcal B$
such that
$\mathcal B$
such that
We also need the following lemma, which comes directly from the definition of the packing entropy.
Lemma 3.3 Let
![]() $E\subset X$
and
$E\subset X$
and
![]() $s>0$
. Then for any
$s>0$
. Then for any
![]() $0<\varepsilon _1<\varepsilon _2$
,
$0<\varepsilon _1<\varepsilon _2$
,
Proof Proof of Proposition 3.1
Let
![]() $\mu \in M(X)$
with
$\mu \in M(X)$
with
![]() $\mu (Z)=1$
and assume
$\mu (Z)=1$
and assume
![]() $\overline h_{\mu }^{\mathrm {loc}}(Z,\{F_n\})>0$
.
$\overline h_{\mu }^{\mathrm {loc}}(Z,\{F_n\})>0$
.
Let
![]() $0<s<\overline h_{\mu }^{\mathrm {loc}}(Z,\{F_n\})$
. Then there exist
$0<s<\overline h_{\mu }^{\mathrm {loc}}(Z,\{F_n\})$
. Then there exist
![]() $\varepsilon ,\delta>0$
and a Borel set
$\varepsilon ,\delta>0$
and a Borel set
![]() $A\subset Z$
with
$A\subset Z$
with
![]() $\mu (A)>0$
such that for every
$\mu (A)>0$
such that for every
![]() $x\in A$
,
$x\in A$
,
where
![]() $\overline h_{\mu }(x,\varepsilon ,\{F_n\}):=\limsup \nolimits _{n\rightarrow +\infty }-({1}/{|F_n|})\log \mu (B_{F_n}(x,\varepsilon ))$
.
$\overline h_{\mu }(x,\varepsilon ,\{F_n\}):=\limsup \nolimits _{n\rightarrow +\infty }-({1}/{|F_n|})\log \mu (B_{F_n}(x,\varepsilon ))$
.
Let
![]() $E\subset A$
be any Borel set with
$E\subset A$
be any Borel set with
![]() $\mu (E)>0$
. Define
$\mu (E)>0$
. Define
Then
![]() $\bigcup _{n=N}^{+\infty }E_n=E$
for any
$\bigcup _{n=N}^{+\infty }E_n=E$
for any
![]() $N\in \mathbb N$
, and hence
$N\in \mathbb N$
, and hence
![]() $\mu (\bigcup _{n=N}^{+\infty }E_n)=\mu (E)$
. Fix
$\mu (\bigcup _{n=N}^{+\infty }E_n)=\mu (E)$
. Fix
![]() $N\in \mathbb N$
. There exists
$N\in \mathbb N$
. There exists
![]() $n\ge N$
such that
$n\ge N$
such that
Fix such n and consider the family of Bowen balls
![]() $\{B_{F_n}(x,{\varepsilon }/{5}):x\in E_n\}$
. By the
$\{B_{F_n}(x,{\varepsilon }/{5}):x\in E_n\}$
. By the
![]() $5r$
-lemma, Lemma 3.2 (we use metric
$5r$
-lemma, Lemma 3.2 (we use metric
![]() $d_{F_n}$
instead of d), there exists a finite pairwise disjoint family
$d_{F_n}$
instead of d), there exists a finite pairwise disjoint family
![]() $\{B_{F_n}(x_i,{\varepsilon }/{5})\}$
with
$\{B_{F_n}(x_i,{\varepsilon }/{5})\}$
with
![]() $x_i\in E_n$
such that
$x_i\in E_n$
such that
 $$ \begin{align*}\bigcup_{i}B_{F_n}(x_i,\varepsilon)\supset \bigcup_{x\in E_n}B_{F_n}\bigg(x,\frac{\varepsilon}{5}\bigg)\supset E_n.\end{align*} $$
$$ \begin{align*}\bigcup_{i}B_{F_n}(x_i,\varepsilon)\supset \bigcup_{x\in E_n}B_{F_n}\bigg(x,\frac{\varepsilon}{5}\bigg)\supset E_n.\end{align*} $$
Thus
 $$ \begin{align*} P\bigg(E,N,\frac{\varepsilon}{5},s,\{F_n\}\bigg)&\ge P\bigg(E_n,N,\frac{\varepsilon}{5},s,\{F_n\}\bigg)\ge \sum_{i}e^{-|F_n|s}=e^{|F_n|\delta}\sum_{i}e^{-|F_{n}|(s+\delta)}\\ &\ge e^{|F_n|\delta}\sum_{i}\mu(B_{F_n}(x_i,\varepsilon))\ge e^{|F_n|\delta}\mu(E_n)\ge \frac{e^{|F_n|\delta}}{n(n+1)}\mu(E). \end{align*} $$
$$ \begin{align*} P\bigg(E,N,\frac{\varepsilon}{5},s,\{F_n\}\bigg)&\ge P\bigg(E_n,N,\frac{\varepsilon}{5},s,\{F_n\}\bigg)\ge \sum_{i}e^{-|F_n|s}=e^{|F_n|\delta}\sum_{i}e^{-|F_{n}|(s+\delta)}\\ &\ge e^{|F_n|\delta}\sum_{i}\mu(B_{F_n}(x_i,\varepsilon))\ge e^{|F_n|\delta}\mu(E_n)\ge \frac{e^{|F_n|\delta}}{n(n+1)}\mu(E). \end{align*} $$
By the growth condition (1.2) of the sequence
![]() $\{F_n\}$
, we have
$\{F_n\}$
, we have
 $$ \begin{align*}\frac{e^{|F_n|\delta}}{n(n+1)}\rightarrow +\infty\quad\text{as }n\rightarrow +\infty.\end{align*} $$
$$ \begin{align*}\frac{e^{|F_n|\delta}}{n(n+1)}\rightarrow +\infty\quad\text{as }n\rightarrow +\infty.\end{align*} $$
Letting
![]() $N\rightarrow +\infty $
, we obtain that
$N\rightarrow +\infty $
, we obtain that
 $$ \begin{align*}P\bigg(E,\frac{\varepsilon}{5},s,\{F_n\}\bigg)=+\infty.\end{align*} $$
$$ \begin{align*}P\bigg(E,\frac{\varepsilon}{5},s,\{F_n\}\bigg)=+\infty.\end{align*} $$
Note that this equality holds for every Borel set
![]() $E\subset A$
with
$E\subset A$
with
![]() $\mu (E)>0$
.
$\mu (E)>0$
.
Let
![]() $\{A_i\}_{i=1}^\infty $
be any covering of A. Then by Lemma 3.3,
$\{A_i\}_{i=1}^\infty $
be any covering of A. Then by Lemma 3.3,
 $$ \begin{align*}\sum_i P\bigg(A_i,\frac{\varepsilon}{10},s,\{F_n\}\bigg)\ge \sum_i P\bigg(\overline A_i,\frac{\varepsilon}{5},s,\{F_n\}\bigg).\end{align*} $$
$$ \begin{align*}\sum_i P\bigg(A_i,\frac{\varepsilon}{10},s,\{F_n\}\bigg)\ge \sum_i P\bigg(\overline A_i,\frac{\varepsilon}{5},s,\{F_n\}\bigg).\end{align*} $$
Since there must exist some
![]() $A_i$
such that
$A_i$
such that
![]() $\overline A_i\cap A$
(which is a Borel set now) contains a Borel subset
$\overline A_i\cap A$
(which is a Borel set now) contains a Borel subset
![]() $E\subset \overline A_i\cap A$
with
$E\subset \overline A_i\cap A$
with
![]() $\mu (E)>0$
, we have
$\mu (E)>0$
, we have
 $$ \begin{align*}\sum_i P\bigg(A_i,\frac{\varepsilon}{10},s,\{F_n\}\bigg)\ge P\bigg(E,\frac{\varepsilon}{5},s,\{F_n\}\bigg)=+\infty.\end{align*} $$
$$ \begin{align*}\sum_i P\bigg(A_i,\frac{\varepsilon}{10},s,\{F_n\}\bigg)\ge P\bigg(E,\frac{\varepsilon}{5},s,\{F_n\}\bigg)=+\infty.\end{align*} $$
Thus
 $$ \begin{align*}\mathcal P \bigg(Z,\frac{\varepsilon}{10},s,\{F_n\}\bigg)\ge \mathcal P \bigg(A,\frac{\varepsilon}{10},s,\{F_n\}\bigg)=+\infty,\end{align*} $$
$$ \begin{align*}\mathcal P \bigg(Z,\frac{\varepsilon}{10},s,\{F_n\}\bigg)\ge \mathcal P \bigg(A,\frac{\varepsilon}{10},s,\{F_n\}\bigg)=+\infty,\end{align*} $$
from which we deduce that
 $$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_n\})\ge h_{\mathrm{top}}^P\bigg(Z,\frac{\varepsilon}{10},\{F_n\}\bigg)\ge s.\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^P(Z,\{F_n\})\ge h_{\mathrm{top}}^P\bigg(Z,\frac{\varepsilon}{10},\{F_n\}\bigg)\ge s.\end{align*} $$
Since s is chosen arbitrarily in
![]() $(0,\overline h_{\mu }(Z,\{F_n\}))$
, we finally show that
$(0,\overline h_{\mu }(Z,\{F_n\}))$
, we finally show that
This finishes the proof of Proposition 3.1.
3.2 Upper bound
The following proposition is the upper bound part of the variational principle. In fact it is valid for any analytic set Z. Recall that a set in a metric space is said to be analytic if it is a continuous image of the set
![]() $\mathcal N$
of infinite sequences of natural numbers. In a Polish space, the collection of analytic subsets contains Borel sets and is closed under countable unions and intersections (cf. [Reference Jech11]).
$\mathcal N$
of infinite sequences of natural numbers. In a Polish space, the collection of analytic subsets contains Borel sets and is closed under countable unions and intersections (cf. [Reference Jech11]).
Proposition 3.4 Let
![]() $Z\subseteq X$
be an analytic set with
$Z\subseteq X$
be an analytic set with
![]() $h^P_{\mathrm {top}}(Z, \{F_n\})>0$
. For any
$h^P_{\mathrm {top}}(Z, \{F_n\})>0$
. For any
![]() $0<s<h^P_{\mathrm {top}}(Z, \{F_n\})$
, there exist a compact set
$0<s<h^P_{\mathrm {top}}(Z, \{F_n\})$
, there exist a compact set
![]() $K\subseteq Z$
and
$K\subseteq Z$
and
![]() $\mu \in M(K)$
such that
$\mu \in M(K)$
such that
![]() $\overline h_{\mu }^{\mathrm {loc}}(K,\{F_n\})\ge ~s$
.
$\overline h_{\mu }^{\mathrm {loc}}(K,\{F_n\})\ge ~s$
.
The following lemma is needed.
Lemma 3.5 Let
![]() $Z\subseteq X$
and
$Z\subseteq X$
and
![]() $s,\varepsilon>0.$
Assume that
$s,\varepsilon>0.$
Assume that
![]() $\mathcal P (Z,\varepsilon ,s,\{F_n\})=+\infty $
. Then for any given finite interval
$\mathcal P (Z,\varepsilon ,s,\{F_n\})=+\infty $
. Then for any given finite interval
![]() $(a,b)\subset \mathbb R$
with
$(a,b)\subset \mathbb R$
with
![]() $a\ge 0$
and any
$a\ge 0$
and any
![]() $N\in \mathbb N$
, there exists a finite disjoint collection
$N\in \mathbb N$
, there exists a finite disjoint collection
![]() $\{\overline B_{F_{n_i}}(x_i, \varepsilon )\}$
such that
$\{\overline B_{F_{n_i}}(x_i, \varepsilon )\}$
such that
![]() $x_i\in Z, n_i\ge N$
and
$x_i\in Z, n_i\ge N$
and
![]() $\sum _i\exp (-|F_{n_i}|s)\in (a,b)$
.
$\sum _i\exp (-|F_{n_i}|s)\in (a,b)$
.
Proof. See [Reference Hofmann and Stoyanov9, Lemma 4.1].
Proof Proof of Proposition 3.4
Since Z is analytic, there exists a continuous surjective map
![]() $\phi : \mathcal {N}\rightarrow Z$
. Let
$\phi : \mathcal {N}\rightarrow Z$
. Let
![]() $\Gamma _{n_1,n_2,\ldots ,n_p}=\{(m_1,m_2, \ldots )\in \mathcal {N}: m_1\le n_1, m_2\le n_2, \ldots , m_p\le n_p\}$
and let
$\Gamma _{n_1,n_2,\ldots ,n_p}=\{(m_1,m_2, \ldots )\in \mathcal {N}: m_1\le n_1, m_2\le n_2, \ldots , m_p\le n_p\}$
and let
![]() $Z_{n_1,\ldots ,n_p}=\phi (\Gamma _{n_1,\ldots ,n_p})$
.
$Z_{n_1,\ldots ,n_p}=\phi (\Gamma _{n_1,\ldots ,n_p})$
.
For
![]() $0<s<h^P_{\mathrm {top}}(Z, \{F_n\})$
, take
$0<s<h^P_{\mathrm {top}}(Z, \{F_n\})$
, take
![]() $\varepsilon>0$
small enough to make
$\varepsilon>0$
small enough to make
![]() $0<s<h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\})$
and take
$0<s<h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\})$
and take
![]() $t\in (s, h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\}))$
. Following Feng and Huang’s steps (which are inspired by the work of Joyce and Preiss [Reference Joyce and Preiss12] on packing measures), we will construct inductively the following data:
$t\in (s, h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\}))$
. Following Feng and Huang’s steps (which are inspired by the work of Joyce and Preiss [Reference Joyce and Preiss12] on packing measures), we will construct inductively the following data:
-
(D-1) a sequence of finite sets
 $(K_i)_{i=1}^{+\infty }$
with
$(K_i)_{i=1}^{+\infty }$
with
 $K_i\subset Z$
;
$K_i\subset Z$
; -
(D-2) a sequence of finite measures
 $(\mu _i)_{i=1}^{+\infty }$
with each
$(\mu _i)_{i=1}^{+\infty }$
with each
 $\mu _i$
supported on
$\mu _i$
supported on
 $K_i$
;
$K_i$
; -
(D-3) a sequence of integers
 $(n_i)_{i=1}^{+\infty }$
and a sequence of positive numbers
$(n_i)_{i=1}^{+\infty }$
and a sequence of positive numbers
 $(\gamma _i)_{i=1}^{+\infty }$
;
$(\gamma _i)_{i=1}^{+\infty }$
; -
(D-4) a sequence of integer-valued functions
 $(m_i: K_i\rightarrow \mathbb N)_{i=1}^{+\infty }$
.
$(m_i: K_i\rightarrow \mathbb N)_{i=1}^{+\infty }$
.
Moreover, the sequences
![]() $(K_i),(\mu _i), (n_i),(\gamma _i)$
and
$(K_i),(\mu _i), (n_i),(\gamma _i)$
and
![]() $(m_i(\cdot ))$
will be constructed to satisfy the following conditions.
$(m_i(\cdot ))$
will be constructed to satisfy the following conditions.
-
(C-1) For each i, the family
 $\mathcal V_i:=\{B(x,\gamma _i)\}_{x\in K_i}$
is disjoint. Each element in
$\mathcal V_i:=\{B(x,\gamma _i)\}_{x\in K_i}$
is disjoint. Each element in
 $\mathcal V_{i+1}$
is a subset of
$\mathcal V_{i+1}$
is a subset of
 $B(x,\gamma _i/2)$
for some
$B(x,\gamma _i/2)$
for some
 $x\in K_i$
.
$x\in K_i$
. -
(C-2) For each i,
 $K_i\subset Z_{n_1,\ldots ,n_i}$
and
$K_i\subset Z_{n_1,\ldots ,n_i}$
and
 $\mu _i=\sum _{y\in K_i}e^{-|F_{m_i(y)}|s}\delta _y$
with
$\mu _i=\sum _{y\in K_i}e^{-|F_{m_i(y)}|s}\delta _y$
with
 $1<\mu _1(K_1)<2$
.
$1<\mu _1(K_1)<2$
. -
(C-3) For each
 $x\in K_i$
and
$x\in K_i$
and
 $z\in B(x,\gamma _i)$
, (3.1)and
$z\in B(x,\gamma _i)$
, (3.1)and $$ \begin{align} \overline B_{F_{m_i(x)}}(z,\varepsilon)\cap \bigcup_{y\in K_i\setminus \{x\}}B(y,\gamma_i)=\emptyset \end{align} $$
(3.2)where
$$ \begin{align} \overline B_{F_{m_i(x)}}(z,\varepsilon)\cap \bigcup_{y\in K_i\setminus \{x\}}B(y,\gamma_i)=\emptyset \end{align} $$
(3.2)where $$ \begin{align} \mu_i(B(x,\gamma_i))=e^{-|F_{m_i(x)}|s}\le \sum_{y\in E_{i+1}(x)}e^{-|F_{m_{i+1}(y)}|s}<(1+2^{-(i+1)})\mu_i(B(x,\gamma_i)), \end{align} $$
$$ \begin{align} \mu_i(B(x,\gamma_i))=e^{-|F_{m_i(x)}|s}\le \sum_{y\in E_{i+1}(x)}e^{-|F_{m_{i+1}(y)}|s}<(1+2^{-(i+1)})\mu_i(B(x,\gamma_i)), \end{align} $$
 $E_{i+1}(x)=B(x,\gamma _i)\cap K_{i+1}$
.
$E_{i+1}(x)=B(x,\gamma _i)\cap K_{i+1}$
.
We will give the construction later.
Suppose the sequences
![]() $(K_i),(\mu _i), (n_i),(\gamma _i)$
and
$(K_i),(\mu _i), (n_i),(\gamma _i)$
and
![]() $(m_i(\cdot ))$
have been constructed. By (3.2), for
$(m_i(\cdot ))$
have been constructed. By (3.2), for
![]() $V_i\in \mathcal V_i$
,
$V_i\in \mathcal V_i$
,
 $$ \begin{align*} \mu_i(V_i)\le \mu_{i+1}(V_i)=\sum_{V\in\mathcal V_{i+1},V\subset V_i}\mu_{i+1}(V)\le (1+2^{-(i+1)})\mu_i(V_i). \end{align*} $$
$$ \begin{align*} \mu_i(V_i)\le \mu_{i+1}(V_i)=\sum_{V\in\mathcal V_{i+1},V\subset V_i}\mu_{i+1}(V)\le (1+2^{-(i+1)})\mu_i(V_i). \end{align*} $$
Repeatedly using the above inequalities, we have for any
![]() $j>i$
and any
$j>i$
and any
![]() $V_i\in \mathcal V_i$
,
$V_i\in \mathcal V_i$
,
 $$ \begin{align} \mu_i(V_i)\le \mu_j(V_i)\le \prod_{n=i+1}^j(1+2^{-n})\mu_i(V_i)\le C\mu_i(V_i), \end{align} $$
$$ \begin{align} \mu_i(V_i)\le \mu_j(V_i)\le \prod_{n=i+1}^j(1+2^{-n})\mu_i(V_i)\le C\mu_i(V_i), \end{align} $$
where
![]() $C:=\prod _{n=1}^{+\infty }(1+2^{-n})<+\infty $
.
$C:=\prod _{n=1}^{+\infty }(1+2^{-n})<+\infty $
.
Let
![]() $\tilde \mu $
be a limit point of
$\tilde \mu $
be a limit point of
![]() $(\mu _i)$
in the weak
$(\mu _i)$
in the weak
![]() $^*$
topology. Let
$^*$
topology. Let
 $$ \begin{align*}K=\bigcap_{n=1}^{+\infty}\overline{\bigcup_{i\ge n}K_i}.\end{align*} $$
$$ \begin{align*}K=\bigcap_{n=1}^{+\infty}\overline{\bigcup_{i\ge n}K_i}.\end{align*} $$
Then
![]() $\tilde \mu $
is supported on K. Furthermore,
$\tilde \mu $
is supported on K. Furthermore,
 $$ \begin{align*}K\subset\bigcap_{p=1}^{+\infty}\overline{Z_{n_1,\ldots,n_p}}.\end{align*} $$
$$ \begin{align*}K\subset\bigcap_{p=1}^{+\infty}\overline{Z_{n_1,\ldots,n_p}}.\end{align*} $$
By the continuity of
![]() $\phi $
, applying Cantor’s diagonal argument, we can show that
$\phi $
, applying Cantor’s diagonal argument, we can show that
![]() $\bigcap _{p=1}^{+\infty }Z_{n_1,\ldots ,n_p}=\bigcap _{p=1}^{+\infty }\overline {Z_{n_1,\ldots ,n_p}}$
. Hence K is a compact subset of Z.
$\bigcap _{p=1}^{+\infty }Z_{n_1,\ldots ,n_p}=\bigcap _{p=1}^{+\infty }\overline {Z_{n_1,\ldots ,n_p}}$
. Hence K is a compact subset of Z.
By (3.3), for any
![]() $x\in K_i$
,
$x\in K_i$
,
In particular,
Note that
![]() $K\subset \bigcup _{x\in K_i}B(x,\gamma _i/2)$
. By (3.1), the first part of (C-3), for each
$K\subset \bigcup _{x\in K_i}B(x,\gamma _i/2)$
. By (3.1), the first part of (C-3), for each
![]() $x\in K_i$
and
$x\in K_i$
and
![]() $z\in \overline B(x,\gamma _i)$
, reads
$z\in \overline B(x,\gamma _i)$
, reads
For each
![]() $z\in K$
and
$z\in K$
and
![]() $i\in \mathbb N$
,
$i\in \mathbb N$
,
![]() $z\in \overline B(x,\gamma _i/2)$
for some
$z\in \overline B(x,\gamma _i/2)$
for some
![]() $x\in K_i$
. Hence
$x\in K_i$
. Hence
Define
![]() $\mu =\tilde \mu /\tilde \mu (K)$
. Then
$\mu =\tilde \mu /\tilde \mu (K)$
. Then
![]() $\mu \in M(K)$
. For each
$\mu \in M(K)$
. For each
![]() $z\in K$
, there exists a sequence
$z\in K$
, there exists a sequence
![]() $k_i\uparrow +\infty $
such that
$k_i\uparrow +\infty $
such that
![]() $\mu (B_{F_{k_i}}(z,\varepsilon ))\le Ce^{-|F_{k_i}|s}/\tilde \mu (K)$
. Hence
$\mu (B_{F_{k_i}}(z,\varepsilon ))\le Ce^{-|F_{k_i}|s}/\tilde \mu (K)$
. Hence
![]() $\overline h_{\mu }^{\mathrm {loc}}(K,\{F_n\})\ge s$
.
$\overline h_{\mu }^{\mathrm {loc}}(K,\{F_n\})\ge s$
.
Now the only thing left is to give the inductive construction of the data
![]() $(K_i),(\mu _i)$
,
$(K_i),(\mu _i)$
,
![]() $(n_i),(\gamma _i)$
and
$(n_i),(\gamma _i)$
and
![]() $(m_i(\cdot ))$
. The inductive steps are as follows.
$(m_i(\cdot ))$
. The inductive steps are as follows.
Step 1 Construct the data
![]() $K_1,\mu _1, n_1,\gamma _1$
and
$K_1,\mu _1, n_1,\gamma _1$
and
![]() $m_1(\cdot )$
.
$m_1(\cdot )$
.
Since
![]() $t\in (s, h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\}))$
, we have that
$t\in (s, h^P_{\mathrm {top}}(Z,\varepsilon ,\{F_n\}))$
, we have that
![]() $\mathcal P (Z,\varepsilon ,t,\{F_n\})=+\infty $
. Let
$\mathcal P (Z,\varepsilon ,t,\{F_n\})=+\infty $
. Let
Then by the separability of X, H is a countable union of the open sets U. Hence
![]() $\mathcal P (Z\cap H,\varepsilon ,t,\{F_n\})=0$
. Let
$\mathcal P (Z\cap H,\varepsilon ,t,\{F_n\})=0$
. Let
![]() $Z'=Z\setminus H=Z\cap (X\setminus H)$
. If
$Z'=Z\setminus H=Z\cap (X\setminus H)$
. If
![]() $\mathcal P (Z'\cap U,\varepsilon ,t,\{F_n\})=0$
for some open set U, then
$\mathcal P (Z'\cap U,\varepsilon ,t,\{F_n\})=0$
for some open set U, then
So
![]() $U\subset H$
and then
$U\subset H$
and then
![]() $Z' \cap U=\emptyset $
. Hence for any open set
$Z' \cap U=\emptyset $
. Hence for any open set
![]() $U\subset X$
, either
$U\subset X$
, either
![]() $Z' \cap U =\emptyset $
or
$Z' \cap U =\emptyset $
or
![]() $\mathcal P (Z' \cap U,\varepsilon ,t,\{F_n\})>0$
.
$\mathcal P (Z' \cap U,\varepsilon ,t,\{F_n\})>0$
.
Because
![]() $\mathcal P (\kern-0.5pt Z,\varepsilon ,t,\kern-0.5pt\{\kern-0.6pt F_n\})\kern-1.3pt\le\kern-0.5pt \mathcal P (\kern-0.5pt Z',\varepsilon ,t,\{\kern-1ptF_n\})\kern-1pt+\mathcal P (\kern-0.6ptZ\cap H,\varepsilon ,t,\{\kern-1pt F_n\})\kern-1pt=\mathcal P (\kern-0.5ptZ',\varepsilon ,t, \{\kern-1pt F_n\})$
, we have
$\mathcal P (\kern-0.5pt Z,\varepsilon ,t,\kern-0.5pt\{\kern-0.6pt F_n\})\kern-1.3pt\le\kern-0.5pt \mathcal P (\kern-0.5pt Z',\varepsilon ,t,\{\kern-1ptF_n\})\kern-1pt+\mathcal P (\kern-0.6ptZ\cap H,\varepsilon ,t,\{\kern-1pt F_n\})\kern-1pt=\mathcal P (\kern-0.5ptZ',\varepsilon ,t, \{\kern-1pt F_n\})$
, we have
![]() $\mathcal P (Z',\varepsilon ,t,\{F_n\})= \mathcal P (Z,\varepsilon ,t,\{F_n\})=+\infty $
. Then
$\mathcal P (Z',\varepsilon ,t,\{F_n\})= \mathcal P (Z,\varepsilon ,t,\{F_n\})=+\infty $
. Then
![]() $\mathcal P (Z',\varepsilon ,s,{\{F_n\})=+\infty }$
.
$\mathcal P (Z',\varepsilon ,s,{\{F_n\})=+\infty }$
.
By Lemma 3.5, we can find a finite set
![]() $K_1\subset Z' $
, an integer-valued function
$K_1\subset Z' $
, an integer-valued function
![]() $m_1(x)$
on
$m_1(x)$
on
![]() $K_1$
such that the collection
$K_1$
such that the collection
![]() $\{\overline B_{F_{m_1(x)}}(x,\varepsilon )\}_{x\in K_1}$
is disjoint and
$\{\overline B_{F_{m_1(x)}}(x,\varepsilon )\}_{x\in K_1}$
is disjoint and
Define
![]() $\mu _1=\sum _{x\in K_1} e^{-|F_{m_1(x)}|s}\delta _x$
, where
$\mu _1=\sum _{x\in K_1} e^{-|F_{m_1(x)}|s}\delta _x$
, where
![]() $\delta _x$
denotes the Dirac measure at x. Take
$\delta _x$
denotes the Dirac measure at x. Take
![]() $\gamma _1>0$
sufficiently small such that for any function
$\gamma _1>0$
sufficiently small such that for any function
![]() $z:K_1\rightarrow X$
with
$z:K_1\rightarrow X$
with
![]() $\max _{x\in K_1}d(x, z(x))\le \gamma _1$
, we have for each
$\max _{x\in K_1}d(x, z(x))\le \gamma _1$
, we have for each
![]() $x\in K_1$
,
$x\in K_1$
,
 $$ \begin{align} ( \overline B(z(x),\gamma_1)\cup \overline B_{F_{m_1(x)}}(z(x),\varepsilon) )\cap \bigg(\bigcup_{y\in K_1\setminus \{x\}}\overline B(z(y),\gamma_1)\cup \overline B_{F_{m_1(y)}}(z(y),\varepsilon)\bigg)=\emptyset. \end{align} $$
$$ \begin{align} ( \overline B(z(x),\gamma_1)\cup \overline B_{F_{m_1(x)}}(z(x),\varepsilon) )\cap \bigg(\bigcup_{y\in K_1\setminus \{x\}}\overline B(z(y),\gamma_1)\cup \overline B_{F_{m_1(y)}}(z(y),\varepsilon)\bigg)=\emptyset. \end{align} $$
Since
![]() $K_1\subset Z'$
, we have
$K_1\subset Z'$
, we have
![]() $\mathcal P (Z\cap B(x,\gamma _1/4),\varepsilon ,t,\{F_n\})\ge \mathcal P (Z'\cap B(x,\gamma _1/4),\varepsilon ,t, \{F_n\})>0$
for each
$\mathcal P (Z\cap B(x,\gamma _1/4),\varepsilon ,t,\{F_n\})\ge \mathcal P (Z'\cap B(x,\gamma _1/4),\varepsilon ,t, \{F_n\})>0$
for each
![]() $x\in K_1$
. Therefore we can pick a sufficiently large
$x\in K_1$
. Therefore we can pick a sufficiently large
![]() $n_1\in \mathbb N$
so that
$n_1\in \mathbb N$
so that
![]() $Z_{n_1}\supset K_1$
and
$Z_{n_1}\supset K_1$
and
![]() $\mathcal P (Z_{n_1}\cap B(x,\gamma _1/4),\varepsilon ,t,\{F_n\})>0$
for each
$\mathcal P (Z_{n_1}\cap B(x,\gamma _1/4),\varepsilon ,t,\{F_n\})>0$
for each
![]() $x\in K_1$
.
$x\in K_1$
.
Step 2 Construct the data
![]() $K_2,\mu _2, n_2,\gamma _2$
and
$K_2,\mu _2, n_2,\gamma _2$
and
![]() $m_2(\cdot )$
.
$m_2(\cdot )$
.
By (3.4), the family of balls
![]() $\{B(x,\gamma _1)\}_{x\in K_1}$
are pairwise disjoint. For each
$\{B(x,\gamma _1)\}_{x\in K_1}$
are pairwise disjoint. For each
![]() $x\in K_1$
, since
$x\in K_1$
, since
![]() $\mathcal P (Z_{n_1}\cap B(x,\gamma _1/4),\varepsilon ,t,\{F_n\})>0$
, similarly to Step 1, we can construct a finite set
$\mathcal P (Z_{n_1}\cap B(x,\gamma _1/4),\varepsilon ,t,\{F_n\})>0$
, similarly to Step 1, we can construct a finite set
![]() $E_2(x)\subset Z_{n_1}\cap B(x,\gamma _1/4)$
and an integer-valued function
$E_2(x)\subset Z_{n_1}\cap B(x,\gamma _1/4)$
and an integer-valued function
![]() $m_2:E_2(x)\rightarrow \mathbb N\cap [\max \{m_1(y):y\in K_1\},+\infty )$
such that:
$m_2:E_2(x)\rightarrow \mathbb N\cap [\max \{m_1(y):y\in K_1\},+\infty )$
such that:
-
(2-a) for each open set U with
 $U\cap E_2(x)\neq \emptyset $
,
$U\cap E_2(x)\neq \emptyset $
,
 $\mathcal P (Z_{n_1}\cap U,\varepsilon ,t,\{F_n\})>0$
;
$\mathcal P (Z_{n_1}\cap U,\varepsilon ,t,\{F_n\})>0$
; -
(2-b) the elements in the family
 $\{\overline B_{F_{m_2(y)}}(y,\varepsilon )\}_{y\in E_2(x)}$
are pairwise disjoint and
$\{\overline B_{F_{m_2(y)}}(y,\varepsilon )\}_{y\in E_2(x)}$
are pairwise disjoint and  $$ \begin{align*} \mu_1(\{x\})<\sum_{y\in E_2(x)}e^{-|F_{m_2(y)}|s}<(1+2^{-2})\mu_1(\{x\}). \end{align*} $$
$$ \begin{align*} \mu_1(\{x\})<\sum_{y\in E_2(x)}e^{-|F_{m_2(y)}|s}<(1+2^{-2})\mu_1(\{x\}). \end{align*} $$
To see this, we fix
![]() $x\in K_1$
. Denote
$x\in K_1$
. Denote
![]() $V=Z_{n_1}\cap B(x, \gamma _1/4)$
. Let
$V=Z_{n_1}\cap B(x, \gamma _1/4)$
. Let
Set
![]() $V'=V\setminus H_x$
. Then as in Step 1, we can show that
$V'=V\setminus H_x$
. Then as in Step 1, we can show that
Moreover, for any open set
![]() $U\subset X$
, either
$U\subset X$
, either
![]() $V'\cap U =\emptyset $
or
$V'\cap U =\emptyset $
or
![]() $\mathcal P (V'\cap U,\varepsilon ,t,\{F_n\})>0$
. Since
$\mathcal P (V'\cap U,\varepsilon ,t,\{F_n\})>0$
. Since
![]() $s<t$
, we have that
$s<t$
, we have that
![]() $\mathcal P (V',\varepsilon ,s,\{F_n\})=+\infty $
. By Lemma 3.5, we can find a finite set
$\mathcal P (V',\varepsilon ,s,\{F_n\})=+\infty $
. By Lemma 3.5, we can find a finite set
![]() $E_2(x)\subset V'$
and a map
$E_2(x)\subset V'$
and a map
![]() $m_2: E_2(x)\rightarrow \mathbb N\cap [\max \{m_1(y):y\in K_1\},+\infty )$
such that (2-b) holds. Notice that if an open set U satisfies
$m_2: E_2(x)\rightarrow \mathbb N\cap [\max \{m_1(y):y\in K_1\},+\infty )$
such that (2-b) holds. Notice that if an open set U satisfies
![]() $U\cap E_2(x)\neq \emptyset $
, then
$U\cap E_2(x)\neq \emptyset $
, then
![]() $U\cap V'\neq \emptyset $
. So
$U\cap V'\neq \emptyset $
. So
![]() $\mathcal P (Z_{n_1}\cap U,\varepsilon ,t,\{F_n\})\ge \mathcal P (V'\cap U,\varepsilon ,t,\{F_n\})>0$
. Hence (2-a) holds.
$\mathcal P (Z_{n_1}\cap U,\varepsilon ,t,\{F_n\})\ge \mathcal P (V'\cap U,\varepsilon ,t,\{F_n\})>0$
. Hence (2-a) holds.
Since the family
![]() $\{B(x,\gamma _1)\}_{x\in K_1}$
is disjoint, so is the family
$\{B(x,\gamma _1)\}_{x\in K_1}$
is disjoint, so is the family
![]() $\{E_2(x)\}_{x\in K_1}$
. Define
$\{E_2(x)\}_{x\in K_1}$
. Define
 $$ \begin{align*}K_2=\bigcup_{x\in K_1}E_2(x)\quad\text{and}\quad\mu_2=\sum_{y\in K_2}e^{-|F_{m_2(y)}|s}\delta_y.\end{align*} $$
$$ \begin{align*}K_2=\bigcup_{x\in K_1}E_2(x)\quad\text{and}\quad\mu_2=\sum_{y\in K_2}e^{-|F_{m_2(y)}|s}\delta_y.\end{align*} $$
By (3.4) and (2-b), the elements in
![]() $\{\overline B_{F_{m_2(y)}}(y,\varepsilon )\}_{y\in K_2}$
are pairwise disjoint. Hence we can take
$\{\overline B_{F_{m_2(y)}}(y,\varepsilon )\}_{y\in K_2}$
are pairwise disjoint. Hence we can take
![]() $0<\gamma _2<\gamma _1/4$
such that for any function
$0<\gamma _2<\gamma _1/4$
such that for any function
![]() $z:K_2\rightarrow X$
satisfying
$z:K_2\rightarrow X$
satisfying
![]() $\max _{x\in K_{2}}d(x,z(x))< \gamma _2$
, we have for
$\max _{x\in K_{2}}d(x,z(x))< \gamma _2$
, we have for
![]() $x\in K_2$
,
$x\in K_2$
,
 $$ \begin{align} ( \overline B(z(x),\gamma_2)\cup \overline B_{F_{m_2(x)}}(z(x),\varepsilon) )\cap \bigg(\bigcup_{y\in K_2\setminus \{x\}}\overline B(z(y),\gamma_2)\cup \overline B_{F_{m_2(y)}}(z(y),\varepsilon)\bigg)=\emptyset. \end{align} $$
$$ \begin{align} ( \overline B(z(x),\gamma_2)\cup \overline B_{F_{m_2(x)}}(z(x),\varepsilon) )\cap \bigg(\bigcup_{y\in K_2\setminus \{x\}}\overline B(z(y),\gamma_2)\cup \overline B_{F_{m_2(y)}}(z(y),\varepsilon)\bigg)=\emptyset. \end{align} $$
Choose a sufficiently large
![]() $n_2\in \mathbb N$
so that
$n_2\in \mathbb N$
so that
![]() $Z_{n_1,n_2}\supset K_2$
and
$Z_{n_1,n_2}\supset K_2$
and
for each
![]() $x\in K_2$
.
$x\in K_2$
.
Step 3 Next we suppose that the data
![]() $K_i,\mu _i, n_i,\gamma _i$
and
$K_i,\mu _i, n_i,\gamma _i$
and
![]() $m_i(\cdot )$
(
$m_i(\cdot )$
(
![]() $i=1,\ldots ,p$
) have been constructed. We will construct the data
$i=1,\ldots ,p$
) have been constructed. We will construct the data
![]() $K_{p+1},\mu _{p+1}, n_{p+1},\gamma _{p+1}$
and
$K_{p+1},\mu _{p+1}, n_{p+1},\gamma _{p+1}$
and
![]() $m_{p+1}(\cdot )$
.
$m_{p+1}(\cdot )$
.
Assume that we have constructed
![]() $K_i,\mu _i, n_i,\gamma _i$
and
$K_i,\mu _i, n_i,\gamma _i$
and
![]() $m_i(\cdot )$
for
$m_i(\cdot )$
for
![]() $i=1,\ldots ,p$
. And assume that for any function
$i=1,\ldots ,p$
. And assume that for any function
![]() $z:K_p\rightarrow X$
with
$z:K_p\rightarrow X$
with
![]() $d(x,z(x))<\gamma _p$
for all
$d(x,z(x))<\gamma _p$
for all
![]() $x\in K_p$
, we have
$x\in K_p$
, we have
 $$ \begin{align} ( \overline B(z(x),\gamma_p)\cup \overline B_{F_{m_p(x)}}(z(x),\varepsilon) )\cap \bigg(\bigcup_{y\in K_p\setminus \{x\}}\overline B(z(y),\gamma_p)\cup \overline B_{F_{m_p(y)}}(z(y),\varepsilon)\bigg)=\emptyset \end{align} $$
$$ \begin{align} ( \overline B(z(x),\gamma_p)\cup \overline B_{F_{m_p(x)}}(z(x),\varepsilon) )\cap \bigg(\bigcup_{y\in K_p\setminus \{x\}}\overline B(z(y),\gamma_p)\cup \overline B_{F_{m_p(y)}}(z(y),\varepsilon)\bigg)=\emptyset \end{align} $$
for each
![]() $x\in K_p$
; and
$x\in K_p$
; and
![]() $Z_{n_1,\ldots ,n_p}\supset K_p$
and
$Z_{n_1,\ldots ,n_p}\supset K_p$
and
![]() $\mathcal P (Z_{n_1,\ldots ,n_p}\cap B(x,\gamma _p/4),\varepsilon ,t,\{F_n\})>0$
for each
$\mathcal P (Z_{n_1,\ldots ,n_p}\cap B(x,\gamma _p/4),\varepsilon ,t,\{F_n\})>0$
for each
![]() $x\in K_p$
.
$x\in K_p$
.
Note that the family of balls
![]() $\{\overline B(x,\gamma _p)\}_{x\in K_p}$
are pairwise disjoint. For each
$\{\overline B(x,\gamma _p)\}_{x\in K_p}$
are pairwise disjoint. For each
![]() $x\in K_p$
, since
$x\in K_p$
, since
![]() $\mathcal P (Z_{n_1,\ldots ,n_p}\cap B(x,\gamma _p/4),\varepsilon ,t,\{F_n\})>0$
, similarly to Step 2, we can construct a finite set
$\mathcal P (Z_{n_1,\ldots ,n_p}\cap B(x,\gamma _p/4),\varepsilon ,t,\{F_n\})>0$
, similarly to Step 2, we can construct a finite set
![]() $E_{p+1}(x)\subset Z_{n_1,\ldots ,n_p}\cap B(x,\gamma _p/4)$
and an integer-valued function
$E_{p+1}(x)\subset Z_{n_1,\ldots ,n_p}\cap B(x,\gamma _p/4)$
and an integer-valued function
![]() $m_{p+1}:E_{p+1}(x)\rightarrow \mathbb N\cap [\max \{m_p(y):y\in K_p\},+\infty )$
such that:
$m_{p+1}:E_{p+1}(x)\rightarrow \mathbb N\cap [\max \{m_p(y):y\in K_p\},+\infty )$
such that:
-
(3-a) for each open set U with
 $U\cap E_{p+1}(x)\neq \emptyset $
,
$U\cap E_{p+1}(x)\neq \emptyset $
,
 $\mathcal P (Z_{n_1,\ldots ,n_p}\cap U,\varepsilon ,t,\{F_n\})>0$
;
$\mathcal P (Z_{n_1,\ldots ,n_p}\cap U,\varepsilon ,t,\{F_n\})>0$
; -
(3-b) the elements in the family
 $\{\overline B_{F_{m_{p+1}(y)}}(y,\varepsilon )\}_{y\in E_{p+1}(x)}$
are pairwise disjoint and
$\{\overline B_{F_{m_{p+1}(y)}}(y,\varepsilon )\}_{y\in E_{p+1}(x)}$
are pairwise disjoint and  $$ \begin{align*} \mu_p(\{x\})<\sum_{y\in E_{p+1}(x)}e^{-|F_{m_{p+1}(y)}|s}<(1+2^{-(p+1)})\mu_p(\{x\}). \end{align*} $$
$$ \begin{align*} \mu_p(\{x\})<\sum_{y\in E_{p+1}(x)}e^{-|F_{m_{p+1}(y)}|s}<(1+2^{-(p+1)})\mu_p(\{x\}). \end{align*} $$
By (3.6) and (3-b), the family
![]() $\{\overline B_{F_{m_{p+1}(y)}}(y,\varepsilon )\}_{y\in K_{p+1}}$
is disjoint. Hence we can take
$\{\overline B_{F_{m_{p+1}(y)}}(y,\varepsilon )\}_{y\in K_{p+1}}$
is disjoint. Hence we can take
![]() $0<\gamma _{p+1}< \gamma _p/4$
such that for any function
$0<\gamma _{p+1}< \gamma _p/4$
such that for any function
![]() $z:K_{p+1}\rightarrow X$
with
$z:K_{p+1}\rightarrow X$
with
![]() $\max _{x\in K_{p+1}}d(x,z(x))<\gamma _{p+1}$
, we have for each
$\max _{x\in K_{p+1}}d(x,z(x))<\gamma _{p+1}$
, we have for each
![]() $x\in K_{p+1}$
,
$x\in K_{p+1}$
,
 $$ \begin{align} ( \overline B(z(x),\gamma_{p+1})\cup &\overline B_{F_{m_{p+1}(x)}}(z(x),\varepsilon) )\nonumber \\ &\cap \bigg(\bigcup_{y\in K_{p+1}\setminus \{x\}}\overline B(z(y),\gamma_{p+1})\cup \overline B_{F_{m_{p+1}(y)}}(z(y),\varepsilon)\bigg)=\emptyset. \end{align} $$
$$ \begin{align} ( \overline B(z(x),\gamma_{p+1})\cup &\overline B_{F_{m_{p+1}(x)}}(z(x),\varepsilon) )\nonumber \\ &\cap \bigg(\bigcup_{y\in K_{p+1}\setminus \{x\}}\overline B(z(y),\gamma_{p+1})\cup \overline B_{F_{m_{p+1}(y)}}(z(y),\varepsilon)\bigg)=\emptyset. \end{align} $$
Choose a sufficiently large
![]() $n_{p+1}\in \mathbb N$
so that
$n_{p+1}\in \mathbb N$
so that
![]() $Z_{n_1,\ldots ,n_{p+1}}\supset K_{p+1}$
and
$Z_{n_1,\ldots ,n_{p+1}}\supset K_{p+1}$
and
![]() $\mathcal P (Z_{n_1,\ldots ,n_{p+1}}\cap B(x,\gamma _{p+1}/4),\varepsilon ,t,\{F_n\})>0$
for each
$\mathcal P (Z_{n_1,\ldots ,n_{p+1}}\cap B(x,\gamma _{p+1}/4),\varepsilon ,t,\{F_n\})>0$
for each
![]() $x\in K_{p+1}$
.
$x\in K_{p+1}$
.
Then we finish the required construction and complete the proof of the proposition.
4 Packing entropy inequalities for factor maps
In this section we will prove Theorem 1.4. The proof is a combination of Bowen’s method in [Reference Bowen2] and quasi-tiling techniques for amenable groups.
4.1 Preliminaries for amenable groups
Let G be a countable infinite discrete amenable group. Let A and K be two non-empty finite subsets of G. Recall that
![]() $B(A,K)$
, the K-boundary of A, is defined by
$B(A,K)$
, the K-boundary of A, is defined by
For
![]() $\delta>0$
, the set A is said to be
$\delta>0$
, the set A is said to be
![]() $(K, \delta )$
-invariant if
$(K, \delta )$
-invariant if
We say a sequence of non-empty finite subsets
![]() $\{F_n\}$
of G becomes more and more invariant if, for any
$\{F_n\}$
of G becomes more and more invariant if, for any
![]() $\delta>0$
and any non-empty finite subset K of G,
$\delta>0$
and any non-empty finite subset K of G,
![]() $F_n$
is
$F_n$
is
![]() $(K,\delta )$
-invariant for sufficiently large n. An equivalent condition for the sequence
$(K,\delta )$
-invariant for sufficiently large n. An equivalent condition for the sequence
![]() $\{F_n\}$
to be a Følner sequence is that
$\{F_n\}$
to be a Følner sequence is that
![]() $\{F_n\}$
becomes more and more invariant (see [Reference Ornstein and Weiss18]).
$\{F_n\}$
becomes more and more invariant (see [Reference Ornstein and Weiss18]).
Let
![]() $\tilde {\mathcal {F}}$
be a collection of finite subsets of G. It is said to be
$\tilde {\mathcal {F}}$
be a collection of finite subsets of G. It is said to be
![]() $\delta $
-disjoint if for every
$\delta $
-disjoint if for every
![]() $A\in \tilde {\mathcal {F}}$
there exists an
$A\in \tilde {\mathcal {F}}$
there exists an
![]() $A'\subset A$
such that
$A'\subset A$
such that
![]() $|A'|\ge (1-\delta )|A|$
and such that
$|A'|\ge (1-\delta )|A|$
and such that
![]() $A'\cap B'=\emptyset $
for every
$A'\cap B'=\emptyset $
for every
![]() $A\neq B\in \tilde {\mathcal {F}}$
.
$A\neq B\in \tilde {\mathcal {F}}$
.
The following is a covering lemma for amenable groups by Lindenstrauss.
Lemma 4.1 (Lindenstrauss’s covering lemma, [Reference Lindenstrauss15, Corollary 2.7])
For any
![]() $\delta \in (0,1/100), C>0$
and finite
$\delta \in (0,1/100), C>0$
and finite
![]() $D\subset G$
, let
$D\subset G$
, let
![]() $M\in \mathbb N$
be sufficiently large (depending only on
$M\in \mathbb N$
be sufficiently large (depending only on
![]() $\delta ,C$
and D). Let
$\delta ,C$
and D). Let
![]() $F_{i,j}$
be an array of finite subsets of G where
$F_{i,j}$
be an array of finite subsets of G where
![]() $i=1,\ldots ,M$
and
$i=1,\ldots ,M$
and
![]() $j=1,\ldots ,N_i$
, with the following two requirements.
$j=1,\ldots ,N_i$
, with the following two requirements.
-
(1) For every i,
 $\bar {F}_{i,*}=\{F_{i,j}\}_{j=1}^{N_i}$
satisfies
$\bar {F}_{i,*}=\{F_{i,j}\}_{j=1}^{N_i}$
satisfies  $$ \begin{align*}\bigg|\bigcup_{k'<k}F_{i,k'}^{-1}F_{i,k}\bigg|\le C|F_{i,k}|\quad \text{ for }k=2,\ldots,N_i.\end{align*} $$
$$ \begin{align*}\bigg|\bigcup_{k'<k}F_{i,k'}^{-1}F_{i,k}\bigg|\le C|F_{i,k}|\quad \text{ for }k=2,\ldots,N_i.\end{align*} $$
-
(2) Denote
 $F_{i,*}=\bigcup \bar {F}_{i,*}$
. The finite set sequences
$F_{i,*}=\bigcup \bar {F}_{i,*}$
. The finite set sequences
 $F_{i,*}$
satisfy that for every
$F_{i,*}$
satisfy that for every
 $1<i\le M$
and every
$1<i\le M$
and every
 $1\le k \le N_i$
,
$1\le k \le N_i$
,  $$ \begin{align*}\bigg|\bigcup_{i'<i}DF_{i',*}^{-1}F_{i,k}\bigg|\le (1+\delta)|F_{i,k}|.\end{align*} $$
$$ \begin{align*}\bigg|\bigcup_{i'<i}DF_{i',*}^{-1}F_{i,k}\bigg|\le (1+\delta)|F_{i,k}|.\end{align*} $$
Assume that
![]() $A_{i,j}$
is another array of finite subsets of G with
$A_{i,j}$
is another array of finite subsets of G with
![]() $F_{i,j}A_{i,j}\subset F$
for some finite subset F of G. Let
$F_{i,j}A_{i,j}\subset F$
for some finite subset F of G. Let
![]() $A_{i,*}=\bigcup _jA_{i,j}$
and
$A_{i,*}=\bigcup _jA_{i,j}$
and
Then the collection of subsets of F,
has a subcollection
![]() $\mathcal {F}$
that is
$\mathcal {F}$
that is
![]() $10\delta ^{1/4}$
-disjoint such that
$10\delta ^{1/4}$
-disjoint such that
 $$ \begin{align*}\bigg|\bigcup \mathcal{F}\bigg|\ge (\alpha-\delta^{1/4})|F|.\end{align*} $$
$$ \begin{align*}\bigg|\bigcup \mathcal{F}\bigg|\ge (\alpha-\delta^{1/4})|F|.\end{align*} $$
4.2 Proof of Theorem 1.4
Let G,
![]() $\{F_n\}$
and
$\{F_n\}$
and
![]() $\pi :(X,G)\to (Y,G)$
be as in Theorem 1.4 and
$\pi :(X,G)\to (Y,G)$
be as in Theorem 1.4 and
![]() $E\subset X$
be a Borel set. Let d and
$E\subset X$
be a Borel set. Let d and
![]() $\rho $
be the compatible metrics on X and Y, respectively.
$\rho $
be the compatible metrics on X and Y, respectively.
For any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\delta>0$
such that, for any
$\delta>0$
such that, for any
![]() $x_1,x_2\in X$
with
$x_1,x_2\in X$
with
![]() $d(x_1,x_2)\le \delta $
, one has
$d(x_1,x_2)\le \delta $
, one has
![]() $\rho (\pi (x_1),\pi (x_2))\le \varepsilon $
. Now let
$\rho (\pi (x_1),\pi (x_2))\le \varepsilon $
. Now let
![]() $\{y_i\}_{i=1}^{k}\subset \pi (E)$
be any
$\{y_i\}_{i=1}^{k}\subset \pi (E)$
be any
![]() $(F_n,\varepsilon )$
-separated set of
$(F_n,\varepsilon )$
-separated set of
![]() $\pi (E)$
and choose for each i a point
$\pi (E)$
and choose for each i a point
![]() $x_i\in \pi ^{-1}(y_i)\cap E$
. Then
$x_i\in \pi ^{-1}(y_i)\cap E$
. Then
![]() $\{x_i\}_{i=1}^k$
forms an
$\{x_i\}_{i=1}^k$
forms an
![]() $(F_n,\delta )$
-separated set of E. Hence
$(F_n,\delta )$
-separated set of E. Hence
and
By Proposition 2.7(2), for any
![]() $\eta>0$
, there exists a cover
$\eta>0$
, there exists a cover
![]() $\bigcup _{i=1}^{\infty }E_i=E$
such that
$\bigcup _{i=1}^{\infty }E_i=E$
such that
Then we have
 $$ \begin{align*} h^P_{\mathrm{top}}(\pi (E),\varepsilon,\{F_n\})&\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{P}_{\mathrm{top}}(\pi(E_i),\varepsilon,\{F_n\})\quad \text{(by Proposition 2.1(2))}\\[-2pt] &\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(\pi(E_i),\varepsilon,\{F_n\})\quad \text{(by Proposition 2.4)}\\[-2pt] &\le \mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(E_i,\delta,\{F_n\})\quad \text{(noting that 4 also holds for each}\ E_i)\\[-2pt] &\le h^P_{\mathrm{top}}(E,\delta/3,\{F_n\})+\eta, \end{align*} $$
$$ \begin{align*} h^P_{\mathrm{top}}(\pi (E),\varepsilon,\{F_n\})&\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{P}_{\mathrm{top}}(\pi(E_i),\varepsilon,\{F_n\})\quad \text{(by Proposition 2.1(2))}\\[-2pt] &\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(\pi(E_i),\varepsilon,\{F_n\})\quad \text{(by Proposition 2.4)}\\[-2pt] &\le \mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(E_i,\delta,\{F_n\})\quad \text{(noting that 4 also holds for each}\ E_i)\\[-2pt] &\le h^P_{\mathrm{top}}(E,\delta/3,\{F_n\})+\eta, \end{align*} $$
which implies that
To get the upper bound, we need to prove the following inequality for amenable upper capacity topological entropy, which extends a result by Bowen [Reference Bowen2, Theorem 17] to amenable group actions.
Theorem 4.2 Let G be a countable infinite discrete amenable group and
![]() $\pi :(X,G)\to (Y,G)$
be a factor map between two G-action topological dynamical systems. Let
$\pi :(X,G)\to (Y,G)$
be a factor map between two G-action topological dynamical systems. Let
![]() $\{F_n\}$
be any tempered Følner sequence in G satisfying growth condition (1.2). Then for any subset E of X,
$\{F_n\}$
be any tempered Følner sequence in G satisfying growth condition (1.2). Then for any subset E of X,
Proof. If
![]() $\mathop {\mathrm {sup}}\limits _{y\in Y}h_{\mathrm {top}}^{UC}(\pi ^{-1}(y),\{F_n\})=\infty $
then there is nothing to prove. So we assume that
$\mathop {\mathrm {sup}}\limits _{y\in Y}h_{\mathrm {top}}^{UC}(\pi ^{-1}(y),\{F_n\})=\infty $
then there is nothing to prove. So we assume that
To verify (4.2), we need some preparations in the following three steps.
Step 1 Construct
![]() $F_{i,j}$
, the array of subsets of G.
$F_{i,j}$
, the array of subsets of G.
Fix
![]() $\tau>0$
. For any
$\tau>0$
. For any
![]() $\varepsilon>0$
, let
$\varepsilon>0$
, let
![]() $0<\delta <\min \{\varepsilon ,1/100\}$
be small enough. Let
$0<\delta <\min \{\varepsilon ,1/100\}$
be small enough. Let
![]() $C>0$
be the constant in the tempered condition (1.1) for the Følner sequence
$C>0$
be the constant in the tempered condition (1.1) for the Følner sequence
![]() $\{F_n\}$
and let
$\{F_n\}$
and let
![]() $D=\{e_G\}\subset G$
, where
$D=\{e_G\}\subset G$
, where
![]() $e_G$
is the identity element of G. Let
$e_G$
is the identity element of G. Let
![]() $M>0$
be large enough as in Lemma 4.1 corresponding to
$M>0$
be large enough as in Lemma 4.1 corresponding to
![]() $\delta , C$
and D.
$\delta , C$
and D.
For each
![]() $y\in Y$
, choose
$y\in Y$
, choose
![]() $m(y)\in \mathbb N$
such that for any
$m(y)\in \mathbb N$
such that for any
![]() $n\ge m(y)$
,
$n\ge m(y)$
,
Here recall that
![]() $r_{F_{n}}(\pi ^{-1}(y),\varepsilon ,d)$
denotes the smallest cardinality of
$r_{F_{n}}(\pi ^{-1}(y),\varepsilon ,d)$
denotes the smallest cardinality of
![]() $(F_{n}, \varepsilon )$
-spanning sets for
$(F_{n}, \varepsilon )$
-spanning sets for
![]() $\pi ^{-1}(y)$
. Let
$\pi ^{-1}(y)$
. Let
![]() $E_y$
be an
$E_y$
be an
![]() $(F_{m(y)},\varepsilon )$
-spanning set of
$(F_{m(y)},\varepsilon )$
-spanning set of
![]() $\pi ^{-1}(y)$
with the smallest cardinality
$\pi ^{-1}(y)$
with the smallest cardinality
![]() $|E_y|=r_{F_{m(y)}}(\pi ^{-1}(y),\varepsilon ,d).$
Denote
$|E_y|=r_{F_{m(y)}}(\pi ^{-1}(y),\varepsilon ,d).$
Denote
which is an open neighborhood of
![]() $\pi ^{-1}(y)$
. Since
$\pi ^{-1}(y)$
. Since
![]() $\bigcap _{\gamma>0}\pi ^{-1}(\overline {B(y,\gamma ,\rho )})=\pi ^{-1}(y)$
, we have
$\bigcap _{\gamma>0}\pi ^{-1}(\overline {B(y,\gamma ,\rho )})=\pi ^{-1}(y)$
, we have
![]() $(X\setminus U_y)\bigcap (\bigcap _{\gamma>0}\pi ^{-1}(\overline {B(y,\gamma ,\rho )}) )=\emptyset $
. Hence by the finite intersection property of compact sets, there is a
$(X\setminus U_y)\bigcap (\bigcap _{\gamma>0}\pi ^{-1}(\overline {B(y,\gamma ,\rho )}) )=\emptyset $
. Hence by the finite intersection property of compact sets, there is a
![]() $W_y:=B(y,\gamma _y,\rho )$
for some
$W_y:=B(y,\gamma _y,\rho )$
for some
![]() $\gamma _y>0$
such that
$\gamma _y>0$
such that
![]() $U_y\supset \pi ^{-1}(W_y).$
Since Y is compact, there exist
$U_y\supset \pi ^{-1}(W_y).$
Since Y is compact, there exist
![]() $y_{1,1},\ldots , y_{1,r_1}$
such that
$y_{1,1},\ldots , y_{1,r_1}$
such that
![]() $W_{y_{1,1}},\ldots ,W_{y_{1,r_1}}$
cover Y. List the Følner sets in the collection
$W_{y_{1,1}},\ldots ,W_{y_{1,r_1}}$
cover Y. List the Følner sets in the collection
![]() $\{F_{m(y_{1,k})}: 1\le k\le r_1\}$
by
$\{F_{m(y_{1,k})}: 1\le k\le r_1\}$
by
Note that
![]() $N_1=\#\{F_{m(y_{1,k})}: 1\le k\le r_1\}\le r_1$
.
$N_1=\#\{F_{m(y_{1,k})}: 1\le k\le r_1\}\le r_1$
.
For each
![]() $y\in Y$
, choose
$y\in Y$
, choose
![]() $m(y)>n_{1,N_1}$
such that (4.3) holds for any
$m(y)>n_{1,N_1}$
such that (4.3) holds for any
![]() $n\ge m(y)$
. Repeating the above process, we can obtain
$n\ge m(y)$
. Repeating the above process, we can obtain
![]() $y_{2,1},\ldots , y_{2,r_2}\in Y$
such that
$y_{2,1},\ldots , y_{2,r_2}\in Y$
such that
![]() $W_{y_{2,1}},\ldots ,W_{y_{2,r_2}}$
cover Y. We then list the Følner sets in the collection
$W_{y_{2,1}},\ldots ,W_{y_{2,r_2}}$
cover Y. We then list the Følner sets in the collection
![]() $\{F_{m(y_{2,k})}: 1\le k\le r_2\}$
:
$\{F_{m(y_{2,k})}: 1\le k\le r_2\}$
:
Note that
![]() $N_2=\#\{F_{m(y_{2,k})}: 1\le k\le r_2\}\le r_2$
.
$N_2=\#\{F_{m(y_{2,k})}: 1\le k\le r_2\}\le r_2$
.
Repeating the above steps inductively, we can obtain, for each
![]() $1\le i\le M$
:
$1\le i\le M$
:
-
(1) a collection of points
 $y_{i,1},\ldots , y_{i,r_i}\in Y$
such that
$y_{i,1},\ldots , y_{i,r_i}\in Y$
such that
 $W_{y_{i,1}},\ldots ,W_{y_{i,r_i}}$
cover Y;
$W_{y_{i,1}},\ldots ,W_{y_{i,r_i}}$
cover Y; -
(2) a collection of Følner sets
 $\{F_{n_{i,1}}, F_{n_{2,2}},\ldots , F_{n_{i,N_i}}\}$
(
$\{F_{n_{i,1}}, F_{n_{2,2}},\ldots , F_{n_{i,N_i}}\}$
(
 $=\{F_{m(y_{i,k})}: 1\le k\le r_i\}$
) with
$=\{F_{m(y_{i,k})}: 1\le k\le r_i\}$
) with
 $n_{i,1}<n_{i,2}<\cdots <n_{i,N_i}$
and
$n_{i,1}<n_{i,2}<\cdots <n_{i,N_i}$
and
 $N_i\le r_i$
.
$N_i\le r_i$
.
From the above construction, for each
![]() $1\le i\le M-1$
, we have
$1\le i\le M-1$
, we have
![]() $n_{i,N_i}<n_{i+1,1}$
. Moreover,
$n_{i,N_i}<n_{i+1,1}$
. Moreover,
![]() $n_{i+1,1}$
can be chosen sufficiently large compared with
$n_{i+1,1}$
can be chosen sufficiently large compared with
![]() $n_{i,N_i}$
such that, for every
$n_{i,N_i}$
such that, for every
![]() $1<i\le M$
and every
$1<i\le M$
and every
![]() $1\le k \le N_i$
,
$1\le k \le N_i$
,
 $$ \begin{align} \bigg|\bigcup_{i'<i}F_{n_{i'},*}^{-1}F_{n_i,k}\bigg|\le (1+\delta)|F_{n_i,k}|. \end{align} $$
$$ \begin{align} \bigg|\bigcup_{i'<i}F_{n_{i'},*}^{-1}F_{n_i,k}\bigg|\le (1+\delta)|F_{n_i,k}|. \end{align} $$
For simplification, we denote
![]() $F_{i,j}=F_{n_{i,j}}$
for each
$F_{i,j}=F_{n_{i,j}}$
for each
![]() $1\le i\le M$
and
$1\le i\le M$
and
![]() $1\le j\le N_i$
, which is the array of G we required.
$1\le j\le N_i$
, which is the array of G we required.
Step 2 Produce quasi-tilings from
![]() $F_{i,j}$
.
$F_{i,j}$
.
Let
![]() $\eta _1$
be a common Lebesgue number of the family of open covers
$\eta _1$
be a common Lebesgue number of the family of open covers
![]() $\{W_{y_{i,1}},\ldots ,W_{y_{i,r_i}}\}$
with respect to the metric
$\{W_{y_{i,1}},\ldots ,W_{y_{i,r_i}}\}$
with respect to the metric
![]() $\rho $
. Denote
$\rho $
. Denote
![]() $\eta =({\eta _1}/{2})$
.
$\eta =({\eta _1}/{2})$
.
Let N be large enough such that, for every
![]() $n>N$
,
$n>N$
,
![]() $F_n$
is
$F_n$
is
![]() $(F_{i,*}\cup \{e_G\},\delta )$
-invariant for all
$(F_{i,*}\cup \{e_G\},\delta )$
-invariant for all
![]() $1\le i\le M$
.
$1\le i\le M$
.
For each
![]() $y\in Y$
and
$y\in Y$
and
![]() $n>N$
, let
$n>N$
, let
 $$ \begin{align*} A_{i,j}&=\{a\in F_n: F_{i,j}a\subset F_n \text{ and there exists }1\le k\le r_i \text{ such that } F_{m(y_{i,k})}=F_{i,j} \\ &\quad \ \text{ and }\overline{B}(ay,\eta,\rho)\subseteq W_{y_{i,k}} \}. \end{align*} $$
$$ \begin{align*} A_{i,j}&=\{a\in F_n: F_{i,j}a\subset F_n \text{ and there exists }1\le k\le r_i \text{ such that } F_{m(y_{i,k})}=F_{i,j} \\ &\quad \ \text{ and }\overline{B}(ay,\eta,\rho)\subseteq W_{y_{i,k}} \}. \end{align*} $$
We note here that
![]() $A_{i,j}$
depends on y.
$A_{i,j}$
depends on y.
For any
![]() $g\in F_n\setminus B(F_n,F_{i,*}\cup \{e_G\})$
, we have
$g\in F_n\setminus B(F_n,F_{i,*}\cup \{e_G\})$
, we have
![]() $F_{i,*}g\subset F_n$
. Since
$F_{i,*}g\subset F_n$
. Since
![]() $\eta _1$
(
$\eta _1$
(
![]() $=2\eta $
) is a Lebesgue number of
$=2\eta $
) is a Lebesgue number of
![]() $\{W_{y_{i,1}},\ldots ,W_{y_{i,r_i}}\}$
,
$\{W_{y_{i,1}},\ldots ,W_{y_{i,r_i}}\}$
,
![]() $\overline {B}(gy,\eta ,\rho )$
is contained in some
$\overline {B}(gy,\eta ,\rho )$
is contained in some
![]() $W_{y_{i,k}}$
and then
$W_{y_{i,k}}$
and then
![]() $g\in A_{i,*}$
. Hence
$g\in A_{i,*}$
. Hence
for each
![]() $1\le i \le M$
, and
$1\le i \le M$
, and
We are now able to apply Lemma 4.1: the temperedness assumption for
![]() $\{F_n\}$
makes requirement (1) of that lemma hold and (4.4) makes requirement (2) hold. From the collection of subsets of
$\{F_n\}$
makes requirement (1) of that lemma hold and (4.4) makes requirement (2) hold. From the collection of subsets of
![]() $F_n$
,
$F_n$
,
we can find by Lemma 4.1 a subcollection
![]() $\mathcal {F}$
which is
$\mathcal {F}$
which is
![]() $10\delta ^{1/4}$
-disjoint and
$10\delta ^{1/4}$
-disjoint and
In fact, this subcollection
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $10\delta ^{1/4}$
quasi-tiling of
$10\delta ^{1/4}$
quasi-tiling of
![]() $F_n$
subordinate to
$F_n$
subordinate to
![]() $y\in Y$
(see, for example, [Reference Kerr and Li14] for the detail definition of quasi-tiling).
$y\in Y$
(see, for example, [Reference Kerr and Li14] for the detail definition of quasi-tiling).
There may exist overlaps between elements in
![]() $\mathcal {F}$
. Since
$\mathcal {F}$
. Since
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $10\delta ^{1/4}$
-disjoint, there exits
$10\delta ^{1/4}$
-disjoint, there exits
![]() $T'\subset T$
for each
$T'\subset T$
for each
![]() $T\in \mathcal {F}$
such that
$T\in \mathcal {F}$
such that
![]() $|T'|/|T|\ge 1-10\delta ^{1/4}$
and the collection
$|T'|/|T|\ge 1-10\delta ^{1/4}$
and the collection
![]() $\{T': T\in \mathcal {F}\}$
is disjoint. Denote this new collection by
$\{T': T\in \mathcal {F}\}$
is disjoint. Denote this new collection by
![]() $\mathcal {F}'$
. By (4.5),
$\mathcal {F}'$
. By (4.5),
 $$ \begin{align} \left|\bigcup \mathcal{F}\right|\le\sum_{T\in\mathcal{F}}|T|\le \frac{1}{1-10\delta^{1/4}}\sum_{T\in\mathcal{F}}|T'|\le \frac{1}{1-10\delta^{1/4}}|F_n| \end{align} $$
$$ \begin{align} \left|\bigcup \mathcal{F}\right|\le\sum_{T\in\mathcal{F}}|T|\le \frac{1}{1-10\delta^{1/4}}\sum_{T\in\mathcal{F}}|T'|\le \frac{1}{1-10\delta^{1/4}}|F_n| \end{align} $$
and
 $$ \begin{align} \left|\bigcup\mathcal{F}'\right|= \sum_{T\in\mathcal{F}}|T'|\ge (1-10\delta^{1/4})(1-\delta-\delta^{1/4})|F_n|. \end{align} $$
$$ \begin{align} \left|\bigcup\mathcal{F}'\right|= \sum_{T\in\mathcal{F}}|T'|\ge (1-10\delta^{1/4})(1-\delta-\delta^{1/4})|F_n|. \end{align} $$
Step 3 Cover
![]() $\pi ^{-1}B_{F_n}(y,\eta ,\rho )$
through
$\pi ^{-1}B_{F_n}(y,\eta ,\rho )$
through
![]() $F_n$
-Bowen balls in
$F_n$
-Bowen balls in
![]() $(X,G)$
.
$(X,G)$
.
Claim. When
![]() $\delta $
is sufficiently small, for any
$\delta $
is sufficiently small, for any
![]() $y\in Y$
and
$y\in Y$
and
![]() $n>N$
, there exist
$n>N$
, there exist
![]() $l(y)>0$
and
$l(y)>0$
and
![]() $v_1(y),v_2(y),\ldots , v_{l(y)}(y)\in X$
such that
$v_1(y),v_2(y),\ldots , v_{l(y)}(y)\in X$
such that
 $$ \begin{align*}\bigcup_{i=1}^{l(y)}B_{F_n}(v_i(y),4\varepsilon,d)\supseteq \pi^{-1}(B_{F_n}(y,\eta,\rho))\end{align*} $$
$$ \begin{align*}\bigcup_{i=1}^{l(y)}B_{F_n}(v_i(y),4\varepsilon,d)\supseteq \pi^{-1}(B_{F_n}(y,\eta,\rho))\end{align*} $$
and
Proof Proof of the Claim
For each
![]() $T=F_{i,j}a\in \mathcal {F}$
, since
$T=F_{i,j}a\in \mathcal {F}$
, since
![]() $a\in A_{i,j}$
, by the construction of
$a\in A_{i,j}$
, by the construction of
![]() $A_{i,j}$
, there exists some point in
$A_{i,j}$
, there exists some point in
![]() $\{y_{i,1}, y_{i,2}, \ldots , y_{i,r_i}\}$
, denoted by
$\{y_{i,1}, y_{i,2}, \ldots , y_{i,r_i}\}$
, denoted by
![]() $y_T$
, such that
$y_T$
, such that
![]() $\overline {B}(ay,\eta ,\rho )\subseteq W_{y_T}$
and
$\overline {B}(ay,\eta ,\rho )\subseteq W_{y_T}$
and
![]() $F_{m(y_T)}=F_{i,j}$
.
$F_{m(y_T)}=F_{i,j}$
.
In the following we will recover the
![]() $F_n$
-orbits of
$F_n$
-orbits of
![]() $(X,G)$
from the T-orbits.
$(X,G)$
from the T-orbits.
Let
![]() $E\subset X$
be any finite
$E\subset X$
be any finite
![]() $\varepsilon $
-spanning set under the metric d. For any sequence of points
$\varepsilon $
-spanning set under the metric d. For any sequence of points
![]() $\{z_T\}_{T\in \mathcal {F}}$
with each
$\{z_T\}_{T\in \mathcal {F}}$
with each
![]() $z_T\in E_{y_{T}}$
and any sequence of points
$z_T\in E_{y_{T}}$
and any sequence of points
![]() $\{z_g\}_{g\in F_n\setminus \cup \mathcal {F}'}$
with each
$\{z_g\}_{g\in F_n\setminus \cup \mathcal {F}'}$
with each
![]() $z_g\in E$
, let
$z_g\in E$
, let
 $$ \begin{align*} V(y;\{z_T\}, \{z_g\}):=\Big\{&u\in\ X: d_{T'}(u,a^{-1}z_T)<2\varepsilon \text{ for all }T=F_{i,j}a\in \mathcal{F}, \\ &d(gu,z_g)<2\varepsilon \text{ for all }g\in F_n\setminus \bigcup\mathcal {F}'\Big\}. \end{align*} $$
$$ \begin{align*} V(y;\{z_T\}, \{z_g\}):=\Big\{&u\in\ X: d_{T'}(u,a^{-1}z_T)<2\varepsilon \text{ for all }T=F_{i,j}a\in \mathcal{F}, \\ &d(gu,z_g)<2\varepsilon \text{ for all }g\in F_n\setminus \bigcup\mathcal {F}'\Big\}. \end{align*} $$
It is not hard to verify that
 $$ \begin{align*} \bigcup_{\{z_T\}, \{z_g\}}V(y;\{z_T\}, \{z_g\})\supseteq\pi^{-1}(B_{F_n}(y,\eta,\rho)), \end{align*} $$
$$ \begin{align*} \bigcup_{\{z_T\}, \{z_g\}}V(y;\{z_T\}, \{z_g\})\supseteq\pi^{-1}(B_{F_n}(y,\eta,\rho)), \end{align*} $$
that is, the family
![]() $\{V(y;\{z_T\}, \{z_g\}):z_T\in E_{y_{T}}, T\in \mathcal {F}, z_g\in E, g\in F_n\setminus \bigcup \mathcal {F}'\}$
forms an open cover of
$\{V(y;\{z_T\}, \{z_g\}):z_T\in E_{y_{T}}, T\in \mathcal {F}, z_g\in E, g\in F_n\setminus \bigcup \mathcal {F}'\}$
forms an open cover of
![]() $\pi ^{-1}(B_{F_n}(y,\eta ,\rho )).$
We also note that some of the
$\pi ^{-1}(B_{F_n}(y,\eta ,\rho )).$
We also note that some of the
![]() $V(y;\{z_T\}, \{z_g\})$
may be empty.
$V(y;\{z_T\}, \{z_g\})$
may be empty.
We pick any point
![]() $v(\{z_T\}, \{z_g\})$
in each non-empty
$v(\{z_T\}, \{z_g\})$
in each non-empty
![]() $V(y;\{z_T\}, \{z_g\})$
. Then
$V(y;\{z_T\}, \{z_g\})$
. Then
Enumerate these
![]() $v(\{z_T\}, \{z_g\})$
by
$v(\{z_T\}, \{z_g\})$
by
![]() $y_1,y_2,\ldots ,y_{l(y)}$
. We then obtain
$y_1,y_2,\ldots ,y_{l(y)}$
. We then obtain
 $$ \begin{align} \bigcup_{i=1}^{l(y)}B_{F_n}(y_i, 4\varepsilon, d)\supseteq\pi^{-1}(B_{F_n}(y,\eta,\rho)). \end{align} $$
$$ \begin{align} \bigcup_{i=1}^{l(y)}B_{F_n}(y_i, 4\varepsilon, d)\supseteq\pi^{-1}(B_{F_n}(y,\eta,\rho)). \end{align} $$
Now the only thing left is to estimate
![]() $l(y)$
. Clearly,
$l(y)$
. Clearly,
 $$ \begin{align*} l(y)&\le \prod_{T\in\mathcal{F}}|E_{y_T}|\cdot\prod_{g\in F_n\setminus \cup\mathcal {F}'}|E| = \prod_{T\in\mathcal{F}}r_{F_{m(y_T)}}(\pi^{-1}(y),\varepsilon,d)\cdot |E|^{|F_n|-|\bigcup\mathcal {F}'|}\\ &\le \exp\bigg(\sum_{T\in\mathcal{F}}|F_{m(y_T)}|(a+\tau)+\left(|F_n|-\left|\bigcup\mathcal {F}'\right|\right)\log|E|\bigg)\\ &\le \exp\bigg( \bigg(\frac{1}{1-10\delta^{1/4}}(a+\tau)+(1-(1-10\delta^{1/4})(1-\delta-\delta^{1/4}))\log|E|\bigg)|F_n|\bigg)\\ &\qquad\qquad\qquad\qquad\,\quad\text{(by (4.6) and (4.7))}\\ &\le \exp((a+2\tau)|F_n| )\quad \text{(when }\delta \text{ is sufficiently small). }\\[-3.2pc] \end{align*} $$
$$ \begin{align*} l(y)&\le \prod_{T\in\mathcal{F}}|E_{y_T}|\cdot\prod_{g\in F_n\setminus \cup\mathcal {F}'}|E| = \prod_{T\in\mathcal{F}}r_{F_{m(y_T)}}(\pi^{-1}(y),\varepsilon,d)\cdot |E|^{|F_n|-|\bigcup\mathcal {F}'|}\\ &\le \exp\bigg(\sum_{T\in\mathcal{F}}|F_{m(y_T)}|(a+\tau)+\left(|F_n|-\left|\bigcup\mathcal {F}'\right|\right)\log|E|\bigg)\\ &\le \exp\bigg( \bigg(\frac{1}{1-10\delta^{1/4}}(a+\tau)+(1-(1-10\delta^{1/4})(1-\delta-\delta^{1/4}))\log|E|\bigg)|F_n|\bigg)\\ &\qquad\qquad\qquad\qquad\,\quad\text{(by (4.6) and (4.7))}\\ &\le \exp((a+2\tau)|F_n| )\quad \text{(when }\delta \text{ is sufficiently small). }\\[-3.2pc] \end{align*} $$
We now proceed to prove (4.2). For any subset E of X, let H be an
![]() $(F_n,\eta )$
-spanning set of
$(F_n,\eta )$
-spanning set of
![]() $\pi (E)$
with minimal cardinality
$\pi (E)$
with minimal cardinality
![]() $r_{F_n}(\pi (E),\eta ,\rho )$
. Then by the above claim, the set
$r_{F_n}(\pi (E),\eta ,\rho )$
. Then by the above claim, the set
![]() $R=\{v_i(y):1\le i\le l(y), y\in H\}$
forms an
$R=\{v_i(y):1\le i\le l(y), y\in H\}$
forms an
![]() $(F_n, 4\varepsilon )$
-spanning set of E, since
$(F_n, 4\varepsilon )$
-spanning set of E, since
 $$ \begin{align*} \bigcup_{y\in H}\bigcup_{i=1}^{l(y)}B_{F_n}(v_i(y),4\varepsilon,d)&\supseteq \bigcup_{y\in H}\pi^{-1}(B_{F_n}(y,\eta,\rho))\supseteq \pi^{-1}\pi(E)\supseteq E. \end{align*} $$
$$ \begin{align*} \bigcup_{y\in H}\bigcup_{i=1}^{l(y)}B_{F_n}(v_i(y),4\varepsilon,d)&\supseteq \bigcup_{y\in H}\pi^{-1}(B_{F_n}(y,\eta,\rho))\supseteq \pi^{-1}\pi(E)\supseteq E. \end{align*} $$
Hence
From this we deduce that
Letting
![]() $\tau $
tend to
$\tau $
tend to
![]() $0$
, (4.2) is proved.
$0$
, (4.2) is proved.
Proof Proof of the upper bound of
 $h^P_{\mathrm {top}}( E,\{F_n\})$
$h^P_{\mathrm {top}}( E,\{F_n\})$
What we need in fact is inequality (4.9) in the proof of Theorem 4.2.
From (2.1), we first convert inequality (4.9) into
This implies that
By Proposition 2.7(2) again, for any
![]() $\delta>0$
, there exists a cover
$\delta>0$
, there exists a cover
![]() $\bigcup _{i=1}^{\infty }V_i=\pi (E)$
such that
$\bigcup _{i=1}^{\infty }V_i=\pi (E)$
such that
Using an similar argument to that in the proof of the lower bound,
 $$ \begin{align*} h^P_{\mathrm{top}}(E,8\varepsilon,\{F_n\})&\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{P}_{\mathrm{top}}(\pi^{-1}(V_i),8\varepsilon,\{F_n\})\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(\pi^{-1}(V_i),8\varepsilon,\{F_n\})\\ &\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(V_i,\eta,\{F_n\})+a+2\tau\\ &\le h^P_{\mathrm{top}}(\pi(E),\eta/3,\{F_n\})+\delta+a+2\tau. \end{align*} $$
$$ \begin{align*} h^P_{\mathrm{top}}(E,8\varepsilon,\{F_n\})&\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{P}_{\mathrm{top}}(\pi^{-1}(V_i),8\varepsilon,\{F_n\})\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(\pi^{-1}(V_i),8\varepsilon,\{F_n\})\\ &\le\mathop{\mathrm{sup}}\limits_{i\ge 1} h^{UC}_{\mathrm{top}}(V_i,\eta,\{F_n\})+a+2\tau\\ &\le h^P_{\mathrm{top}}(\pi(E),\eta/3,\{F_n\})+\delta+a+2\tau. \end{align*} $$
Hence
Since
![]() $\tau>0$
is arbitrary, we finally obtain
$\tau>0$
is arbitrary, we finally obtain
5 Amenable packing entropy for certain subsets
5.1 The set of generic points
Recall that for
![]() $\mu \in M(X,G)$
and a Følner sequence
$\mu \in M(X,G)$
and a Følner sequence
![]() $\{F_n\}$
in G, the set of generic points for
$\{F_n\}$
in G, the set of generic points for
![]() $\mu $
(with respect to
$\mu $
(with respect to
![]() $\{F_n\}$
) is defined by
$\{F_n\}$
) is defined by
 $$ \begin{align*} G_{\mu}=\bigg\{x\in X: \lim_{n\rightarrow+\infty}\frac{1}{|F_n|}\sum_{g\in F_n}f(gx)=\int_Xf\, d{\kern-1pt}{\mu}, \text{ for any }f\in C(X)\bigg\}. \end{align*} $$
$$ \begin{align*} G_{\mu}=\bigg\{x\in X: \lim_{n\rightarrow+\infty}\frac{1}{|F_n|}\sum_{g\in F_n}f(gx)=\int_Xf\, d{\kern-1pt}{\mu}, \text{ for any }f\in C(X)\bigg\}. \end{align*} $$
Remark 5.1 If
![]() $\mu \in E(X,G)$
and
$\mu \in E(X,G)$
and
![]() $\{F_n\}$
is a tempered Følner sequence then
$\{F_n\}$
is a tempered Følner sequence then
![]() $\mu (G_{\mu })=1$
. To show this, let
$\mu (G_{\mu })=1$
. To show this, let
![]() $\{f_i\}_{i=1}^{\infty }$
be a countable dense subset of
$\{f_i\}_{i=1}^{\infty }$
be a countable dense subset of
![]() $C(X)$
and denote
$C(X)$
and denote
 $$ \begin{align*}X_i=\bigg\{x\in X: \lim_{n\rightarrow+\infty}\frac{1}{|F_n|}\sum_{g\in F_n}f_i(gx)=\int_Xf_i\, d{\kern-1pt}{\mu}\bigg\}.\end{align*} $$
$$ \begin{align*}X_i=\bigg\{x\in X: \lim_{n\rightarrow+\infty}\frac{1}{|F_n|}\sum_{g\in F_n}f_i(gx)=\int_Xf_i\, d{\kern-1pt}{\mu}\bigg\}.\end{align*} $$
By the pointwise ergodic theorem,
![]() $\mu (X_i)=1$
. Hence
$\mu (X_i)=1$
. Hence
![]() $G_{\mu }=\bigcap _{i=1}^\infty X_i$
has full measure.
$G_{\mu }=\bigcap _{i=1}^\infty X_i$
has full measure.
The system
![]() $(X,G)$
is said to have the almost specification property if there exists a non-decreasing function
$(X,G)$
is said to have the almost specification property if there exists a non-decreasing function
![]() $g: (0,1)\rightarrow (0,1)$
with
$g: (0,1)\rightarrow (0,1)$
with
![]() $\lim _{r\rightarrow 0}g(r)=0$
(a mistake-density function) and a map
$\lim _{r\rightarrow 0}g(r)=0$
(a mistake-density function) and a map
![]() $m: (0,1)\rightarrow F(G)\times (0,1)$
such that for any
$m: (0,1)\rightarrow F(G)\times (0,1)$
such that for any
![]() $k\in \mathbb N$
, any
$k\in \mathbb N$
, any
![]() $\varepsilon _1, \varepsilon _2,\ldots , \varepsilon _k\in (0,1)$
, and any
$\varepsilon _1, \varepsilon _2,\ldots , \varepsilon _k\in (0,1)$
, and any
![]() $x_1, x_2,\ldots ,x_k\in X$
, if
$x_1, x_2,\ldots ,x_k\in X$
, if
![]() $F_i$
is
$F_i$
is
![]() $m(\varepsilon _i)$
-invariant,
$m(\varepsilon _i)$
-invariant,
![]() $i=1, 2,\ldots , k$
, and
$i=1, 2,\ldots , k$
, and
![]() $\{F_i\}_{i=1}^k$
are pairwise disjoint, then
$\{F_i\}_{i=1}^k$
are pairwise disjoint, then
where
![]() $B(g; F,x,\varepsilon ):=\{y\in X: |\{h\in F: d(hx,hy)>\varepsilon \}|\le g(\varepsilon )|F|\}$
, the Bowen ball allowing a mistake with density
$B(g; F,x,\varepsilon ):=\{y\in X: |\{h\in F: d(hx,hy)>\varepsilon \}|\le g(\varepsilon )|F|\}$
, the Bowen ball allowing a mistake with density
![]() $g(\varepsilon )$
.
$g(\varepsilon )$
.
Remark 5.2 It was shown in [Reference Zhang23] that the weak specification implies the almost specification. Recall that in [Reference Chung and Li6] the system
![]() $(X,G)$
(the group G need not be amenable) has weak specification if for any
$(X,G)$
(the group G need not be amenable) has weak specification if for any
![]() $\varepsilon>0$
there exists a non-empty finite subset F of G with the following property: for any finite collection
$\varepsilon>0$
there exists a non-empty finite subset F of G with the following property: for any finite collection
![]() $F_1, \ldots , F_m$
of finite subsets G with
$F_1, \ldots , F_m$
of finite subsets G with
and for any collection of points
![]() $x_1,\ldots ,x_m \in X$
, there exists a point
$x_1,\ldots ,x_m \in X$
, there exists a point
![]() $y\in X$
such that
$y\in X$
such that
that is,
In this section, we will prove Theorem 1.5, that is, if
![]() $\mu \in M(X,G)$
, the Følner sequence
$\mu \in M(X,G)$
, the Følner sequence
![]() $\{F_n\}$
satisfies the growth condition (1.2) and either
$\{F_n\}$
satisfies the growth condition (1.2) and either
![]() $\mu $
is ergodic and
$\mu $
is ergodic and
![]() $\{F_n\}$
is tempered or
$\{F_n\}$
is tempered or
![]() $(X,G)$
has almost specification, then
$(X,G)$
has almost specification, then
The idea of the proof comes from Pfister and Sullivan [Reference Pfister and Sullivan20] (see also [Reference Zhang23, Reference Zheng and Chen26] for amenable group actions).
5.1.1 Upper bound for
 $h_{\mathrm {top}}^P(G_{\mu },\{F_n\})$
$h_{\mathrm {top}}^P(G_{\mu },\{F_n\})$
In the following we are going to prove
![]() $h_{\mathrm {top}}^P(G_{\mu },\{F_n\})\leq h_{\mu }(X,G)$
assuming that the Følner sequence
$h_{\mathrm {top}}^P(G_{\mu },\{F_n\})\leq h_{\mu }(X,G)$
assuming that the Følner sequence
![]() $\{F_n\}$
satisfies the growth condition (1.2).
$\{F_n\}$
satisfies the growth condition (1.2).
For
![]() $\mu \in M(X,G)$
, let
$\mu \in M(X,G)$
, let
![]() $\{K_m\}_{m\in \mathbb N}$
be a decreasing sequence of closed convex neighborhoods of
$\{K_m\}_{m\in \mathbb N}$
be a decreasing sequence of closed convex neighborhoods of
![]() $\mu $
in
$\mu $
in
![]() $M(X)$
such that
$M(X)$
such that
![]() $\bigcap _{m\in \mathbb N}K_m=\{\mu \}$
. Let
$\bigcap _{m\in \mathbb N}K_m=\{\mu \}$
. Let
 $$ \begin{align*}A_{n,m}=\bigg\{x\in X:\frac{1}{|F_n|}\sum_{g\in F_n}\delta_x\circ g^{-1}\in K_m\bigg\}\quad\text{for }m,n\in\mathbb N,\end{align*} $$
$$ \begin{align*}A_{n,m}=\bigg\{x\in X:\frac{1}{|F_n|}\sum_{g\in F_n}\delta_x\circ g^{-1}\in K_m\bigg\}\quad\text{for }m,n\in\mathbb N,\end{align*} $$
and
 $$ \begin{align*}R_{N,m}=\bigg\{x\in X:\text{ for any }n>N, \frac{1}{|F_n|}\sum_{g\in F_n}\delta_x\circ g^{-1}\in K_m\bigg\}\quad\text{for }m,N\in\mathbb N.\end{align*} $$
$$ \begin{align*}R_{N,m}=\bigg\{x\in X:\text{ for any }n>N, \frac{1}{|F_n|}\sum_{g\in F_n}\delta_x\circ g^{-1}\in K_m\bigg\}\quad\text{for }m,N\in\mathbb N.\end{align*} $$
Then for any
![]() $m,N\ge 1$
,
$m,N\ge 1$
,
For
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $Z\subseteq X$
, recall that
$Z\subseteq X$
, recall that
![]() $s_{F_n}(Z,\varepsilon )$
denotes the maximal cardinality of any
$s_{F_n}(Z,\varepsilon )$
denotes the maximal cardinality of any
![]() $(F_n,\varepsilon )$
-separated subset of Z. Then we have
$(F_n,\varepsilon )$
-separated subset of Z. Then we have
By the claim in [Reference Zheng and Chen26, p. 878] (we note that it also works for non-ergodic invariant measures),
Hence for any
![]() $\eta>0$
, there exists
$\eta>0$
, there exists
![]() $0<\varepsilon _1$
such that, for any
$0<\varepsilon _1$
such that, for any
![]() $0<\varepsilon <\varepsilon _1$
, there exists
$0<\varepsilon <\varepsilon _1$
, there exists
![]() $M=M(\varepsilon )\in \mathbb N$
such that
$M=M(\varepsilon )\in \mathbb N$
such that
whenever
![]() $m\ge M$
. Especially,
$m\ge M$
. Especially,
Taking (5.2) and (5.3) together, for any
![]() $0<\varepsilon <\varepsilon _1$
, we have that for any
$0<\varepsilon <\varepsilon _1$
, we have that for any
![]() $N\in \mathbb N$
,
$N\in \mathbb N$
,
Since for any
![]() $N'\in \mathbb N$
,
$N'\in \mathbb N$
,
![]() $G_{\mu }\subseteq \bigcup _{N\ge N'}R_{N,M}$
, by Propositions 2.1 and 2.4,
$G_{\mu }\subseteq \bigcup _{N\ge N'}R_{N,M}$
, by Propositions 2.1 and 2.4,
 $$ \begin{align*}h_{\mathrm{top}}^P(G_{\mu},\varepsilon,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{N\ge N'}h_{\mathrm{top}}^P(R_{N,M},\varepsilon,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{N\ge N'}\limsup_{n\rightarrow+\infty}\frac{1}{|F_n|}\log s_{F_n}(R_{N,M},\varepsilon),\end{align*} $$
$$ \begin{align*}h_{\mathrm{top}}^P(G_{\mu},\varepsilon,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{N\ge N'}h_{\mathrm{top}}^P(R_{N,M},\varepsilon,\{F_n\})\le \mathop{\mathrm{sup}}\limits_{N\ge N'}\limsup_{n\rightarrow+\infty}\frac{1}{|F_n|}\log s_{F_n}(R_{N,M},\varepsilon),\end{align*} $$
from which it follows that
Letting
![]() $\varepsilon \rightarrow 0$
and then
$\varepsilon \rightarrow 0$
and then
![]() $\eta \rightarrow 0$
, we obtain that
$\eta \rightarrow 0$
, we obtain that
![]() $h_{\mathrm {top}}^P(G_{\mu },\{F_n\})\le h_{\mu }(X,G)$
.
$h_{\mathrm {top}}^P(G_{\mu },\{F_n\})\le h_{\mu }(X,G)$
.
5.1.2 Lower bound for
 $h_{\mathrm {top}}^P(G_{\mu },\{F_n\})$
$h_{\mathrm {top}}^P(G_{\mu },\{F_n\})$
For the case where
![]() $\mu $
is ergodic and
$\mu $
is ergodic and
![]() $\{F_n\}$
is tempered, since
$\{F_n\}$
is tempered, since
![]() $\mu (G_{\mu })=1$
, Corollary 2.3 gives the lower bound.
$\mu (G_{\mu })=1$
, Corollary 2.3 gives the lower bound.
For the case when
![]() $\mu \in M(X,G)$
and the system
$\mu \in M(X,G)$
and the system
![]() $(X,G)$
has almost specification property, the proof of the lower bound becomes rather complicated because of the quasi-tiling techniques for amenable groups. But it was shown in [Reference Zhang23] that
$(X,G)$
has almost specification property, the proof of the lower bound becomes rather complicated because of the quasi-tiling techniques for amenable groups. But it was shown in [Reference Zhang23] that
![]() $h_{\mathrm {top}}^B(G_{\mu },\{F_n\})= h_{\mu }(X,G)$
. Hence by Proposition 2.2, we obtain
$h_{\mathrm {top}}^B(G_{\mu },\{F_n\})= h_{\mu }(X,G)$
. Hence by Proposition 2.2, we obtain
![]() $h_{\mathrm {top}}^P(G_{\mu },\{F_n\})\ge h_{\mu }(X,G)$
.
$h_{\mathrm {top}}^P(G_{\mu },\{F_n\})\ge h_{\mu }(X,G)$
.
5.2 G-symbolic dynamical system
Let A be a finite set with cardinality
![]() $|A|\ge 2$
and let
$|A|\ge 2$
and let
![]() $A^G=\{(x_g)_{g\in G}: x_g\in A\}$
be the G-symbolic space over A. Consider the left action of G on
$A^G=\{(x_g)_{g\in G}: x_g\in A\}$
be the G-symbolic space over A. Consider the left action of G on
![]() $A^G$
:
$A^G$
:
![]() $(A^G,G)$
forms a G-symbolic dynamical system or a G-acting full shift (over A). For any non-empty closed G-invariant subset X of
$(A^G,G)$
forms a G-symbolic dynamical system or a G-acting full shift (over A). For any non-empty closed G-invariant subset X of
![]() $A^G$
, the subsystem
$A^G$
, the subsystem
![]() $(X,G)$
is called a subshift. For
$(X,G)$
is called a subshift. For
![]() $x=(x_g)_{g\in G}$
and a finite subset
$x=(x_g)_{g\in G}$
and a finite subset
![]() $F\subset G$
, denote by
$F\subset G$
, denote by
![]() $x|_F=(x_g)_{g\in F}\in A^F$
the restriction of x to F and denote
$x|_F=(x_g)_{g\in F}\in A^F$
the restriction of x to F and denote
![]() $[x|_F]=\{\omega \in A^G: \omega _g=x_g \text { for all }g\in F\}$
(which is called a cylinder).
$[x|_F]=\{\omega \in A^G: \omega _g=x_g \text { for all }g\in F\}$
(which is called a cylinder).
Fix any tempered Følner sequence
![]() $\{F_n\}$
of G with
$\{F_n\}$
of G with
![]() $F_0=\{e_G\}\subsetneq F_1\subsetneq F_2\subsetneq \ldots $
and
$F_0=\{e_G\}\subsetneq F_1\subsetneq F_2\subsetneq \ldots $
and
![]() $\bigcup _{n}F_n=G$
. Note that
$\bigcup _{n}F_n=G$
. Note that
![]() $\{F_n\}$
satisfies the growth condition (1.2) automatically. We can then define a metric d on
$\{F_n\}$
satisfies the growth condition (1.2) automatically. We can then define a metric d on
![]() $A^G$
associated to
$A^G$
associated to
![]() $\{F_n\}$
as follows:
$\{F_n\}$
as follows:
 $$ \begin{align} d(x,y)=\begin{cases} 1\quad& \text{if }x \text{ and }y \text{ are not equal on } F_0,\\ e^{-|F_n|}\quad& n=\max\{k: x|_{F_k}=y|_{F_k}\}. \end{cases} \end{align} $$
$$ \begin{align} d(x,y)=\begin{cases} 1\quad& \text{if }x \text{ and }y \text{ are not equal on } F_0,\\ e^{-|F_n|}\quad& n=\max\{k: x|_{F_k}=y|_{F_k}\}. \end{cases} \end{align} $$
To discuss the regularity for subsets of
![]() $(A^G,G)$
, we need to consider the relation between Bowen entropy (packing entropy) and the corresponding Hausdorff dimension (packing dimension). Before that, we recall the definitions of Hausdorff dimension and packing dimension (cf. [Reference Mattila16]).
$(A^G,G)$
, we need to consider the relation between Bowen entropy (packing entropy) and the corresponding Hausdorff dimension (packing dimension). Before that, we recall the definitions of Hausdorff dimension and packing dimension (cf. [Reference Mattila16]).
Definition 5.3 Let
![]() $(X,d)$
be a compact metric space. Let
$(X,d)$
be a compact metric space. Let
![]() $0\le s<\infty $
. For
$0\le s<\infty $
. For
![]() $E\subset X$
and
$E\subset X$
and
![]() $\varepsilon>0$
, put
$\varepsilon>0$
, put
where the supremum is taken over all disjoint families of closed balls
![]() $\{\overline B_i\}$
such that
$\{\overline B_i\}$
such that
![]() $\text {diam} B_i \le \varepsilon $
and the centers of the
$\text {diam} B_i \le \varepsilon $
and the centers of the
![]() $B_i$
are in E.
$B_i$
are in E.
Then set
![]() $P^s(E)=\lim \nolimits _{\varepsilon \rightarrow 0}P_{\varepsilon }^s(E)$
(since
$P^s(E)=\lim \nolimits _{\varepsilon \rightarrow 0}P_{\varepsilon }^s(E)$
(since
![]() $P_{\varepsilon }^s(E)$
is non-decreasing on
$P_{\varepsilon }^s(E)$
is non-decreasing on
![]() $\varepsilon $
) and define
$\varepsilon $
) and define
 $$ \begin{align*}\mathcal P^s(E)=\inf \bigg\{\sum_{i=1}^{\infty}P^s(E_i): E=\bigcup_{i=1}^{\infty}E_i\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal P^s(E)=\inf \bigg\{\sum_{i=1}^{\infty}P^s(E_i): E=\bigcup_{i=1}^{\infty}E_i\bigg\}.\end{align*} $$
The packing dimension of E is then defined by
Let
![]() $\mathcal H^s(E)=\lim \nolimits _{\varepsilon \rightarrow 0}\mathcal H_{\varepsilon }^s(E)$
, where
$\mathcal H^s(E)=\lim \nolimits _{\varepsilon \rightarrow 0}\mathcal H_{\varepsilon }^s(E)$
, where
 $$ \begin{align*}\mathcal H_{\varepsilon}^s(E)=\inf\bigg\{\sum_{i=1}^\infty(\text{diam} E_i)^s: E\subset \bigcup_{i=1}^\infty E_i, \text{diam} E_i\le \varepsilon\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal H_{\varepsilon}^s(E)=\inf\bigg\{\sum_{i=1}^\infty(\text{diam} E_i)^s: E\subset \bigcup_{i=1}^\infty E_i, \text{diam} E_i\le \varepsilon\bigg\}.\end{align*} $$
The Hausdorff dimension of E is then defined by
Comparing with the definitions of dimensional entropies, we have the following proposition.
Proposition 5.4 Let the Følner sequence
![]() $\{F_n\}$
satisfy the following two conditions:
$\{F_n\}$
satisfy the following two conditions:
-
(1)
 $F_mF_n\subset F_{m+n}$
for each
$F_mF_n\subset F_{m+n}$
for each
 $m,n\in \mathbb N$
;
$m,n\in \mathbb N$
; -
(2)
 $\lim \nolimits _{n\rightarrow \infty } (({F_{n+1}})/{{F_n}})=1$
.
$\lim \nolimits _{n\rightarrow \infty } (({F_{n+1}})/{{F_n}})=1$
.
Then for any
![]() $E\subset A^G$
,
$E\subset A^G$
,
where the dimensions
![]() $\text {dim}_H$
and
$\text {dim}_H$
and
![]() $\text {dim}_P$
are both under the metric d defined in (5.4).
$\text {dim}_P$
are both under the metric d defined in (5.4).
Proof. See Appendix A.1.
Remark 5.5
-
(1) Due to [Reference den Hollander and Steif10], the sequence of finite subsets
 $\{F_n\}$
of G satisfying condition (1) in Proposition 5.4 is called a regular system. If G is a finitely generated group, and letting
$\{F_n\}$
of G satisfying condition (1) in Proposition 5.4 is called a regular system. If G is a finitely generated group, and letting
 $F_n$
be the collection of elements in G with word length (with respect to a finite symmetric generating subset) no more than n, then
$F_n$
be the collection of elements in G with word length (with respect to a finite symmetric generating subset) no more than n, then
 $\{F_n\}$
satisfies condition (1).
$\{F_n\}$
satisfies condition (1). -
(2) There are examples of amenable groups which admit Følner sequences satisfying the conditions in Proposition 5.4. An abelian example of the group G is
 $\mathbb Z^d$
, with
$\mathbb Z^d$
, with
 $F_n=[-n,n]^d$
. An non-abelian example of the group G is the dihedral group, with
$F_n=[-n,n]^d$
. An non-abelian example of the group G is the dihedral group, with
 $F_n$
chosen to be the collection of elements with word length no more than n (see [Reference Ceccherini-Silberstein and Coornaert5]).
$F_n$
chosen to be the collection of elements with word length no more than n (see [Reference Ceccherini-Silberstein and Coornaert5]).
By Proposition 5.4, we have the following result.
Proposition 5.6 Let the Følner sequence
![]() $\{F_n\}$
satisfy the conditions in Proposition 5.4. Then any subset
$\{F_n\}$
satisfy the conditions in Proposition 5.4. Then any subset
![]() $E\subset A^G$
is regular in the sense of dimensional entropy if and only if E is dimension-regular (under the Følner sequence
$E\subset A^G$
is regular in the sense of dimensional entropy if and only if E is dimension-regular (under the Følner sequence
![]() $\{F_n\}$
and metric d).
$\{F_n\}$
and metric d).
By Remark 2.6, any non-empty closed G-invariant subset X of
![]() $A^G$
is regular in the sense of dimensional entropy. Hence we have the following corollary.
$A^G$
is regular in the sense of dimensional entropy. Hence we have the following corollary.
Corollary 5.7 Let the Følner sequence
![]() $\{F_n\}$
satisfy the conditions in Proposition 5.4. Then any non-empty closed G-invariant subset X of
$\{F_n\}$
satisfy the conditions in Proposition 5.4. Then any non-empty closed G-invariant subset X of
![]() $A^G$
is both regular in the sense of dimensional entropy and dimension-regular (under the Følner sequence
$A^G$
is both regular in the sense of dimensional entropy and dimension-regular (under the Følner sequence
![]() $\{F_n\}$
and metric d).
$\{F_n\}$
and metric d).
Let
![]() $0\le \alpha < \beta \le 1$
and
$0\le \alpha < \beta \le 1$
and
![]() $A=\{0,1\}$
. Let
$A=\{0,1\}$
. Let
![]() $H\subset G$
such that
$H\subset G$
such that
that is H is a subset of G with lower density
![]() $\alpha $
and upper density
$\alpha $
and upper density
![]() $\beta $
with respect to
$\beta $
with respect to
![]() $\{F_n\}$
. Now we define
$\{F_n\}$
. Now we define
![]() $X_{\alpha ,\beta }\subset \{0,1\}^G$
by
$X_{\alpha ,\beta }\subset \{0,1\}^G$
by
Assume in addition that
![]() $\{F_n\}$
satisfies the conditions in Proposition 5.4. Then we have the following proposition.
$\{F_n\}$
satisfies the conditions in Proposition 5.4. Then we have the following proposition.
Proposition 5.8
![]() $h_{\mathrm {top}}^B (X_{\alpha ,\beta },\{F_n\})=\alpha \log 2$
and
$h_{\mathrm {top}}^B (X_{\alpha ,\beta },\{F_n\})=\alpha \log 2$
and
![]() $h_{\mathrm {top}}^P(X_{\alpha ,\beta },\{F_n\})=\beta \log 2$
. Hence
$h_{\mathrm {top}}^P(X_{\alpha ,\beta },\{F_n\})=\beta \log 2$
. Hence
![]() $X_{\alpha ,\beta }$
is not regular.
$X_{\alpha ,\beta }$
is not regular.
Proof. See Appendix A.2.
5.3 Fibers of
 $\{T,T^{-1}\}$
transformation
$\{T,T^{-1}\}$
transformation
Random walk in random scenery (RWRS) is a class of stationary random processes which are well studied in both probability theory and ergodic theory. RWRS provides measure-theoretic models with amazingly rich behavior (see [Reference Aaronson1, Reference Dou and Zhang7]). Among the class of RWRS,
![]() $\{T,T^{-1}\}$
transformation, although apparently simple, is possibly the best known in the history of ergodic theory since it is a natural example of a K-automorphism that is not Bernoulli [Reference Kalikow13]. In spite of its measure-theoretic aspect, we will consider the topological model of the
$\{T,T^{-1}\}$
transformation, although apparently simple, is possibly the best known in the history of ergodic theory since it is a natural example of a K-automorphism that is not Bernoulli [Reference Kalikow13]. In spite of its measure-theoretic aspect, we will consider the topological model of the
![]() $\{T,T^{-1}\}$
transformation and investigate subsets of the topological system.
$\{T,T^{-1}\}$
transformation and investigate subsets of the topological system.
Definition 5.9 (Topological
 $\{T,T^{-1}\}$
transformation)
$\{T,T^{-1}\}$
transformation)
Let
![]() $A=\{1,-1\}$
, and by convention we denote the shift map on
$A=\{1,-1\}$
, and by convention we denote the shift map on
![]() $A^{\mathbb Z}$
by T, which is defined by
$A^{\mathbb Z}$
by T, which is defined by
The
![]() $\{T,T^{-1}\}$
transformation, denoted by S, on
$\{T,T^{-1}\}$
transformation, denoted by S, on
![]() $A^{\mathbb Z}\times A^{\mathbb Z}$
is defined by
$A^{\mathbb Z}\times A^{\mathbb Z}$
is defined by
 $$ \begin{align*} S(x,y)=\begin{cases} (T(x), T(y)) \quad&\text{if }y_0=1,\\ (T^{-1}(x), T(y)) \quad&\text{if }y_0=-1. \end{cases} \end{align*} $$
$$ \begin{align*} S(x,y)=\begin{cases} (T(x), T(y)) \quad&\text{if }y_0=1,\\ (T^{-1}(x), T(y)) \quad&\text{if }y_0=-1. \end{cases} \end{align*} $$
Then
![]() $S^n(x,y)=(T^{\omega (y,n)}(x),T^ny)$
for
$S^n(x,y)=(T^{\omega (y,n)}(x),T^ny)$
for
![]() $n\in \mathbb Z$
, where
$n\in \mathbb Z$
, where
 $$ \begin{align*} \omega(y,n):=\begin{cases} \sum_{j=0}^{n-1}y_j\quad& \text{if }n>0,\\ 0\quad& \text{if }n=0,\\ -\sum_{j=n}^{-1}y_j \quad& \text{if }n<0. \end{cases} \end{align*} $$
$$ \begin{align*} \omega(y,n):=\begin{cases} \sum_{j=0}^{n-1}y_j\quad& \text{if }n>0,\\ 0\quad& \text{if }n=0,\\ -\sum_{j=n}^{-1}y_j \quad& \text{if }n<0. \end{cases} \end{align*} $$
Clearly for the system
![]() $(A^{\mathbb Z}\times A^{\mathbb Z},S)$
, the acting group G here is the integer group
$(A^{\mathbb Z}\times A^{\mathbb Z},S)$
, the acting group G here is the integer group
![]() $\mathbb Z$
. The Følner sequence
$\mathbb Z$
. The Følner sequence
![]() $\{F_n\}$
is chosen naturally to be
$\{F_n\}$
is chosen naturally to be
![]() $F_n=\{0,1,\ldots ,n-1\}:=[0,n-1]$
. Define a metric
$F_n=\{0,1,\ldots ,n-1\}:=[0,n-1]$
. Define a metric
![]() $\rho $
on
$\rho $
on
![]() $A^{\mathbb Z}\times A^{\mathbb Z}$
by
$A^{\mathbb Z}\times A^{\mathbb Z}$
by
where d is the metric on
![]() $A^{\mathbb Z}$
defined by
$A^{\mathbb Z}$
defined by
We note that the metric d here is different from (5.4).
Let
![]() $\pi : A^{\mathbb Z}\times A^{\mathbb Z}\rightarrow A^{\mathbb Z}$
be the projection to the second coordinate. Then it induces a factor map between
$\pi : A^{\mathbb Z}\times A^{\mathbb Z}\rightarrow A^{\mathbb Z}$
be the projection to the second coordinate. Then it induces a factor map between
![]() $(A^{\mathbb Z}\times A^{\mathbb Z},S)$
and
$(A^{\mathbb Z}\times A^{\mathbb Z},S)$
and
![]() $(A^{\mathbb Z},T)$
. For any
$(A^{\mathbb Z},T)$
. For any
![]() $y\in A^{\mathbb Z}$
, let
$y\in A^{\mathbb Z}$
, let
![]() $E_{y}:=A^{\mathbb Z}\times \{y\}$
denote the fiber of y under the factor map
$E_{y}:=A^{\mathbb Z}\times \{y\}$
denote the fiber of y under the factor map
![]() $\pi $
. We denote by
$\pi $
. We denote by
the packing and Bowen entropies of
![]() $E_y$
for the
$E_y$
for the
![]() $\mathbb Z$
-system
$\mathbb Z$
-system
![]() $(A^{\mathbb Z}\times A^{\mathbb Z},S)$
, respectively.
$(A^{\mathbb Z}\times A^{\mathbb Z},S)$
, respectively.
For
![]() $n>0$
, denote
$n>0$
, denote
Proposition 5.10 For the packing and Bowen entropies of
![]() $E_y$
, we have:
$E_y$
, we have:
-
(1)
 $h_{\mathrm {top}}^P(E_{y},S)=\limsup \nolimits _{n\rightarrow +\infty }(({M(y,n)-m(y,n)})/{n})h_{\mathrm {top}}(A^{\mathbb Z},T);$
$h_{\mathrm {top}}^P(E_{y},S)=\limsup \nolimits _{n\rightarrow +\infty }(({M(y,n)-m(y,n)})/{n})h_{\mathrm {top}}(A^{\mathbb Z},T);$
-
(2)
 $h_{\mathrm {top}}^B(E_{y},S)=\liminf \nolimits _{n\rightarrow +\infty }(({M(y,n)-m(y,n)})/{n})h_{\mathrm {top}}(A^{\mathbb Z},T)$
.
$h_{\mathrm {top}}^B(E_{y},S)=\liminf \nolimits _{n\rightarrow +\infty }(({M(y,n)-m(y,n)})/{n})h_{\mathrm {top}}(A^{\mathbb Z},T)$
.
Here
![]() $h_{\mathrm {top}}(A^{\mathbb Z},T)(=\log 2)$
is the topological entropy of the symbolic dynamical system
$h_{\mathrm {top}}(A^{\mathbb Z},T)(=\log 2)$
is the topological entropy of the symbolic dynamical system
![]() $(A^{\mathbb Z},T)$
. Hence
$(A^{\mathbb Z},T)$
. Hence
![]() $E_y$
is regular if and only if
$E_y$
is regular if and only if
![]() $\lim \nolimits _{n\rightarrow +\infty }({M(y,n)-m(y,n)})/{n}$
exists.
$\lim \nolimits _{n\rightarrow +\infty }({M(y,n)-m(y,n)})/{n}$
exists.
Proof. See Appendix A.3.
Acknowledgements
The authors are grateful to the referee for his/her valuable suggestions and comments. The first and the third authors also thank Prof. Wen Huang for his helpful discussions. This research is supported by NNSF of China (Grant No. 11790274, 12171233, 11701275, 12171175 and 11801193) and Tianyuan Mathematical Center in Southwest China.
A Appendix. Proofs of Propositions 5.4, 5.8 and 5.10
In this appendix we will give detailed proofs of Propositions 5.4, 5.8 and 5.10.
A.1 Proof of Proposition 5.4
Let E be a subset of the compact metric space
![]() $(A^G,d)$
as defined in §5.2. Recall that in Proposition 5.4 the Følner sequence
$(A^G,d)$
as defined in §5.2. Recall that in Proposition 5.4 the Følner sequence
![]() $\{F_n\}$
satisfies the following two conditions:
$\{F_n\}$
satisfies the following two conditions:
-
(1)
 $F_mF_n\subseteq F_{m+n}$
for each
$F_mF_n\subseteq F_{m+n}$
for each
 $m,n\in \mathbb N$
;
$m,n\in \mathbb N$
; -
(2)
 $\lim \nolimits _{n\rightarrow \infty } (({F_{n+1}})/{{F_n}})=1$
.
$\lim \nolimits _{n\rightarrow \infty } (({F_{n+1}})/{{F_n}})=1$
.
We divide the proof of Proposition 5.4 into two parts.
Part 1. Proof of
![]() $h_{\mathrm {top}}^B(E,\{F_n\})=\text {dim}_HE$
. Let
$h_{\mathrm {top}}^B(E,\{F_n\})=\text {dim}_HE$
. Let
![]() $s>h_{\mathrm {top}}^B(E,\{F_n\})$
. From the definition of Bowen entropy, we have
$s>h_{\mathrm {top}}^B(E,\{F_n\})$
. From the definition of Bowen entropy, we have
Hence for any
![]() $N>0$
,
$N>0$
,
![]() $\mathcal {M}(E,N,1,s,\{F_n\})=0$
. For any
$\mathcal {M}(E,N,1,s,\{F_n\})=0$
. For any
![]() $\delta>0$
, there exists a countable family
$\delta>0$
, there exists a countable family
![]() $\{B_{F_{n_i}}(x^i,1)\}$
with
$\{B_{F_{n_i}}(x^i,1)\}$
with
![]() $x^i\in E, n_i\ge N$
and
$x^i\in E, n_i\ge N$
and
![]() $\bigcup \nolimits _i B_{F_{n_i}}(x^i,1)\supset E$
such that
$\bigcup \nolimits _i B_{F_{n_i}}(x^i,1)\supset E$
such that
Notice that
 $$ \begin{align} B_{F_{n_i}}(x^i,1)&=\{y\in A^{G}:\rho(gx^i,gy)<1,\text{ for all } g\in F_{n_i}\}\nonumber\\[-2pt] &= \{y\in A^{G}:(gx^i)_{e_G}=(gy)_{e_G},\text{ for all } g\in F_{n_i}\}\nonumber\\[-2pt] &=[x^i|_{F_{n_i}}] \end{align} $$
$$ \begin{align} B_{F_{n_i}}(x^i,1)&=\{y\in A^{G}:\rho(gx^i,gy)<1,\text{ for all } g\in F_{n_i}\}\nonumber\\[-2pt] &= \{y\in A^{G}:(gx^i)_{e_G}=(gy)_{e_G},\text{ for all } g\in F_{n_i}\}\nonumber\\[-2pt] &=[x^i|_{F_{n_i}}] \end{align} $$
and
![]() $\text {diam}[x^i|_{F_{n_i}}]=e^{-|F_{n_i}|}\le e^{-|F_N|}$
. Since the family of cylinders
$\text {diam}[x^i|_{F_{n_i}}]=e^{-|F_{n_i}|}\le e^{-|F_N|}$
. Since the family of cylinders
![]() $\{[x^i|_{F_{n_i}}]\}$
covers E, we have
$\{[x^i|_{F_{n_i}}]\}$
covers E, we have
Therefore
![]() $\mathcal H_{e^{-|F_N|}}^s(E)=0$
and then
$\mathcal H_{e^{-|F_N|}}^s(E)=0$
and then
![]() $\mathcal H^s(E)=0$
. This means that
$\mathcal H^s(E)=0$
. This means that
![]() $\text {dim}_HE\le s$
. Since
$\text {dim}_HE\le s$
. Since
![]() $s>h_{\mathrm {top}}^B(E,\{F_n\})$
is arbitrary,
$s>h_{\mathrm {top}}^B(E,\{F_n\})$
is arbitrary,
![]() $h_{\mathrm {top}}^B(E,\{F_n\})\ge \text {dim}_HE$
.
$h_{\mathrm {top}}^B(E,\{F_n\})\ge \text {dim}_HE$
.
Now we will show
![]() $h_{\mathrm {top}}^B(E,\{F_n\})\le \text {dim}_HE$
.
$h_{\mathrm {top}}^B(E,\{F_n\})\le \text {dim}_HE$
.
If
![]() $h_{\mathrm {top}}^B(E,\{F_n\})=0$
, then there is nothing to prove. Assume
$h_{\mathrm {top}}^B(E,\{F_n\})=0$
, then there is nothing to prove. Assume
![]() $h_{\mathrm {top}}^B(E,\{F_n\})>0$
and let
$h_{\mathrm {top}}^B(E,\{F_n\})>0$
and let
![]() $0<s<h_{\mathrm {top}}^B(E,\{F_n\})$
. Then there exists
$0<s<h_{\mathrm {top}}^B(E,\{F_n\})$
. Then there exists
![]() $0<\varepsilon <1$
such that
$0<\varepsilon <1$
such that
Assume
![]() $\varepsilon \in (e^{-|F_k|},e^{-|F_{k-1}|}]$
for some
$\varepsilon \in (e^{-|F_k|},e^{-|F_{k-1}|}]$
for some
![]() $k\in \mathbb N$
and let
$k\in \mathbb N$
and let
![]() $\eta>0$
be fixed. By condition (2), there exists
$\eta>0$
be fixed. By condition (2), there exists
![]() $N'>k$
such that
$N'>k$
such that
By (A.2), there exists
![]() $N>N'$
such that
$N>N'$
such that
![]() $\mathcal M(E,N,\varepsilon ,s,\{F_n\})>1$
.
$\mathcal M(E,N,\varepsilon ,s,\{F_n\})>1$
.
Let
![]() $\{E_i\}_{i=1}^\infty $
be any countable family that covers E and
$\{E_i\}_{i=1}^\infty $
be any countable family that covers E and
![]() $\text {diam}E_i<e^{-|F_{N+k}|}$
for each i. By the definition of the metric d,
$\text {diam}E_i<e^{-|F_{N+k}|}$
for each i. By the definition of the metric d,
![]() $\text {diam}E_i=e^{-|F_{n_i}|}$
for some
$\text {diam}E_i=e^{-|F_{n_i}|}$
for some
![]() $n_i>N+k$
. Choose any point
$n_i>N+k$
. Choose any point
![]() $x^i\in E_i$
. Then
$x^i\in E_i$
. Then
![]() $E_i\subset [x^i|_{F_{n_i}}]$
.
$E_i\subset [x^i|_{F_{n_i}}]$
.
Noticing that
 $$ \begin{align} B_{F_{n_i-k}}(x^i,\varepsilon)&=\{y\in A^G: \rho(gx^i,gy)<\varepsilon, \text{ for all }g\in F_{n_i-k}\}\nonumber\\ &=\{y\in A^G: \rho(gx^i,gy)\le e^{|F_k|}, \text{ for all }g\in F_{n_i-k}\} \nonumber \\ &=\{y\in A^G: (gx^i)|_{F_k}=(gy)|_{F_k}, \text{ for all }g\in F_{n_i-k}\} \nonumber \\ &=\{y\in A^G: x^i|_{F_kF_{n_i-k}}=y|_{F_kF_{n_i-k}}\}=[x^i|_{F_kF_{n_i-k}}] \nonumber \\ &\supseteq [x^i|_{F_{n_i}}]\quad (\text{since }F_kF_{n_i-k}\subseteq F_{n_i}), \end{align} $$
$$ \begin{align} B_{F_{n_i-k}}(x^i,\varepsilon)&=\{y\in A^G: \rho(gx^i,gy)<\varepsilon, \text{ for all }g\in F_{n_i-k}\}\nonumber\\ &=\{y\in A^G: \rho(gx^i,gy)\le e^{|F_k|}, \text{ for all }g\in F_{n_i-k}\} \nonumber \\ &=\{y\in A^G: (gx^i)|_{F_k}=(gy)|_{F_k}, \text{ for all }g\in F_{n_i-k}\} \nonumber \\ &=\{y\in A^G: x^i|_{F_kF_{n_i-k}}=y|_{F_kF_{n_i-k}}\}=[x^i|_{F_kF_{n_i-k}}] \nonumber \\ &\supseteq [x^i|_{F_{n_i}}]\quad (\text{since }F_kF_{n_i-k}\subseteq F_{n_i}), \end{align} $$
the family
![]() $\{B_{F_{n_i-k}}(x^i,\varepsilon )\}_{i=1}^\infty $
also covers E (with each
$\{B_{F_{n_i-k}}(x^i,\varepsilon )\}_{i=1}^\infty $
also covers E (with each
![]() $n_i-k>N$
). So
$n_i-k>N$
). So
 $$ \begin{align*}\sum_{i=1}^\infty e^{-s|F_{n_i-k}|}\ge \mathcal M(E,N,\varepsilon,s,\{F_n\})>1.\end{align*} $$
$$ \begin{align*}\sum_{i=1}^\infty e^{-s|F_{n_i-k}|}\ge \mathcal M(E,N,\varepsilon,s,\{F_n\})>1.\end{align*} $$
Hence
 $$ \begin{align*} \sum_{i=1}^\infty e^{-({s}/({1+\eta}))|F_{n_i}|}=\sum_{i=1}^\infty e^{-({s}/({1+\eta}))({|F_{n_i}|}/{|F_{n_i-k}|})|F_{n_i-k}|}>\sum_{i=1}^\infty e^{-s|F_{n_i-k}|}>1, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^\infty e^{-({s}/({1+\eta}))|F_{n_i}|}=\sum_{i=1}^\infty e^{-({s}/({1+\eta}))({|F_{n_i}|}/{|F_{n_i-k}|})|F_{n_i-k}|}>\sum_{i=1}^\infty e^{-s|F_{n_i-k}|}>1, \end{align*} $$
which implies that
![]() $\mathcal H^{({s}/({1+\eta }))}(E)\ge \mathcal H_{e^{-|F_{N+k}|}}^{({s}/({1+\eta }))}(E)\ge 1$
. Thus
$\mathcal H^{({s}/({1+\eta }))}(E)\ge \mathcal H_{e^{-|F_{N+k}|}}^{({s}/({1+\eta }))}(E)\ge 1$
. Thus
![]() $\text {dim}_HE\ge ({s}/({1+\eta }))$
.
$\text {dim}_HE\ge ({s}/({1+\eta }))$
.
Letting
![]() $\eta \rightarrow 0$
, we have
$\eta \rightarrow 0$
, we have
![]() $\text {dim}_HE\ge s$
. Since
$\text {dim}_HE\ge s$
. Since
![]() $0<s<h_{\mathrm {top}}^B(E,\{F_n\})$
is chosen arbitrarily, we obtain that
$0<s<h_{\mathrm {top}}^B(E,\{F_n\})$
is chosen arbitrarily, we obtain that
![]() $h_{\mathrm {top}}^B(E,\{F_n\})\le \text {dim}_HE$
.
$h_{\mathrm {top}}^B(E,\{F_n\})\le \text {dim}_HE$
.
Part 2. Proof of
![]() $h_{\mathrm {top}}^P(E,\{F_n\})=\text {dim}_PE$
. We first show
$h_{\mathrm {top}}^P(E,\{F_n\})=\text {dim}_PE$
. We first show
![]() $h_{\mathrm {top}}^P(E,\{F_n\})\ge \text {dim}_PE$
.
$h_{\mathrm {top}}^P(E,\{F_n\})\ge \text {dim}_PE$
.
Let
![]() $s>h_{\mathrm {top}}^P(E,\{F_n\})$
. Then, for any
$s>h_{\mathrm {top}}^P(E,\{F_n\})$
. Then, for any
![]() $0<\varepsilon <1$
, we have that
$0<\varepsilon <1$
, we have that
![]() $h_{\mathrm {top}}^P(E,\varepsilon ,\{F_n\})<s$
and hence
$h_{\mathrm {top}}^P(E,\varepsilon ,\{F_n\})<s$
and hence
![]() $\mathcal P(E,\varepsilon , s,\{F_n\})=0$
. So for any
$\mathcal P(E,\varepsilon , s,\{F_n\})=0$
. So for any
![]() $\delta>0$
, there exists a countable covering
$\delta>0$
, there exists a countable covering
![]() $\{E_i\}_{i=1}^\infty $
of E such that
$\{E_i\}_{i=1}^\infty $
of E such that
 $$ \begin{align*}\sum_{i=1}^\infty P(E_i,\varepsilon, s,\{F_n\})<\delta.\end{align*} $$
$$ \begin{align*}\sum_{i=1}^\infty P(E_i,\varepsilon, s,\{F_n\})<\delta.\end{align*} $$
For each i, we can find
![]() $N_i\in \mathbb N$
sufficiently large such that
$N_i\in \mathbb N$
sufficiently large such that
Let
![]() $\{B_{i,j}\}_{j=1}^\infty $
be a family of disjoint closed balls in
$\{B_{i,j}\}_{j=1}^\infty $
be a family of disjoint closed balls in
![]() $A^G$
(with centers
$A^G$
(with centers
![]() $x^{i,j}\in E_i$
and
$x^{i,j}\in E_i$
and
![]() $\text {diam} B_{i,j}\le e^{-|F_{N_i}|}$
) such that
$\text {diam} B_{i,j}\le e^{-|F_{N_i}|}$
) such that
 $$ \begin{align*}P_{e^{-|F_{N_i}|}}^s(E_i)\le \sum_{j=1}^\infty (\text{diam }B_{i,j})^s+\frac{\delta}{2^i}.\end{align*} $$
$$ \begin{align*}P_{e^{-|F_{N_i}|}}^s(E_i)\le \sum_{j=1}^\infty (\text{diam }B_{i,j})^s+\frac{\delta}{2^i}.\end{align*} $$
From the definition of the metric d,
![]() $\text {diam }B_{i,j}=e^{-|F_{n_{i,j}}|}$
for some
$\text {diam }B_{i,j}=e^{-|F_{n_{i,j}}|}$
for some
![]() $n_{i,j}\ge N_i$
. Noticing that
$n_{i,j}\ge N_i$
. Noticing that
 $$ \begin{align*} B_{i,j}&=B(x^{i,j}, e^{-|F_{n_{i,j}}|})=[x^{i,j}|_{F_{n_{i,j}}}]\\ &\supseteq \overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon)\quad(\text{here we have assumed }\varepsilon<1), \end{align*} $$
$$ \begin{align*} B_{i,j}&=B(x^{i,j}, e^{-|F_{n_{i,j}}|})=[x^{i,j}|_{F_{n_{i,j}}}]\\ &\supseteq \overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon)\quad(\text{here we have assumed }\varepsilon<1), \end{align*} $$
![]() $\{\overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon )\}_{j=1}^\infty $
is also a pairwise disjoint family. Hence
$\{\overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon )\}_{j=1}^\infty $
is also a pairwise disjoint family. Hence
 $$ \begin{align*} \mathcal P^s(E)&\le \sum_{i=1}^\infty P^s(E_i)\le \sum_{i=1}^\infty P_{e^{-|F_{N_i}|}}^s(E_i) \le \sum_{i=1}^\infty \bigg(\sum_{j=1}^\infty e^{-s|F_{n_{i,j}}|}+\frac{\delta}{2^i}\bigg)\\ &\le \sum_{i=1}^\infty P(E_i, N_i, \varepsilon, s, \{F_n\}) +\delta < \sum_{i=1}^\infty \bigg (P(E_i, \varepsilon, s, \{F_n\}) +\frac{\delta}{2^i} \bigg )+\delta\\ &<3\delta. \end{align*} $$
$$ \begin{align*} \mathcal P^s(E)&\le \sum_{i=1}^\infty P^s(E_i)\le \sum_{i=1}^\infty P_{e^{-|F_{N_i}|}}^s(E_i) \le \sum_{i=1}^\infty \bigg(\sum_{j=1}^\infty e^{-s|F_{n_{i,j}}|}+\frac{\delta}{2^i}\bigg)\\ &\le \sum_{i=1}^\infty P(E_i, N_i, \varepsilon, s, \{F_n\}) +\delta < \sum_{i=1}^\infty \bigg (P(E_i, \varepsilon, s, \{F_n\}) +\frac{\delta}{2^i} \bigg )+\delta\\ &<3\delta. \end{align*} $$
Thus
![]() $\mathcal P^s(E)=0$
and
$\mathcal P^s(E)=0$
and
![]() $\text {dim}_PE\le s$
. Since
$\text {dim}_PE\le s$
. Since
![]() $s>h_{\mathrm {top}}^P(E,\{F_n\})$
is arbitrary, we obtain
$s>h_{\mathrm {top}}^P(E,\{F_n\})$
is arbitrary, we obtain
![]() $\text {dim}_PE\le h_{\mathrm {top}}^P(E,\{F_n\})$
.
$\text {dim}_PE\le h_{\mathrm {top}}^P(E,\{F_n\})$
.
Next we will show
![]() $h_{\mathrm {top}}^P(E,\{F_n\})\le \text {dim}_PE$
.
$h_{\mathrm {top}}^P(E,\{F_n\})\le \text {dim}_PE$
.
Assume
![]() $h_{\mathrm {top}}^P(E,\{F_n\})>0$
, otherwise there is nothing to prove. Let
$h_{\mathrm {top}}^P(E,\{F_n\})>0$
, otherwise there is nothing to prove. Let
![]() $0<s<h_{\mathrm {top}}^P(E,\{F_n\})$
. Then there exists
$0<s<h_{\mathrm {top}}^P(E,\{F_n\})$
. Then there exists
![]() $0<\varepsilon <1$
such that
$0<\varepsilon <1$
such that
![]() $h_{\mathrm {top}}^P(E,\varepsilon ,\{F_n\})>s$
. Assume
$h_{\mathrm {top}}^P(E,\varepsilon ,\{F_n\})>s$
. Assume
![]() $\varepsilon \in (e^{-|F_k|},e^{-|F_{k-1}|}]$
for some
$\varepsilon \in (e^{-|F_k|},e^{-|F_{k-1}|}]$
for some
![]() $k\in \mathbb N$
and let
$k\in \mathbb N$
and let
![]() $\eta>0$
be fixed. Similarly to Part 1, by condition (2), there exists
$\eta>0$
be fixed. Similarly to Part 1, by condition (2), there exists
![]() $N>k$
such that
$N>k$
such that
Let
![]() $\{E_i\}_{i=1}^\infty $
be any countable family that covers E. Then
$\{E_i\}_{i=1}^\infty $
be any countable family that covers E. Then
 $$ \begin{align*}\sum_{i=1}^\infty P(E_i,\varepsilon,s,\{F_n\})\ge \mathcal P(E,\varepsilon,s,\{F_n\})=\infty.\end{align*} $$
$$ \begin{align*}\sum_{i=1}^\infty P(E_i,\varepsilon,s,\{F_n\})\ge \mathcal P(E,\varepsilon,s,\{F_n\})=\infty.\end{align*} $$
For each i, let
![]() $N_i>N$
be sufficiently large such that
$N_i>N$
be sufficiently large such that
Let
![]() $\{\overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon )\}_{j=1}^\infty $
be a disjoint family with
$\{\overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon )\}_{j=1}^\infty $
be a disjoint family with
![]() $x^{i,j}\in E_i$
and
$x^{i,j}\in E_i$
and
![]() $n_{i,j}\ge N_i$
for each j such that
$n_{i,j}\ge N_i$
for each j such that
 $$ \begin{align*}P(E_i,N_i,\varepsilon,s, \{F_n\})<\sum_{j=1}^\infty e^{-s|F_{n_{i,j}}|}+\frac{1}{2^i}.\end{align*} $$
$$ \begin{align*}P(E_i,N_i,\varepsilon,s, \{F_n\})<\sum_{j=1}^\infty e^{-s|F_{n_{i,j}}|}+\frac{1}{2^i}.\end{align*} $$
With similar discussion to (A.3),
![]() $\overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon ){\supseteq}[x^{i,j}|_{F_{n_{i,j}+k}}]$
and hence
$\overline B_{F_{n_{i,j}}}(x^{i,j},\varepsilon ){\supseteq}[x^{i,j}|_{F_{n_{i,j}+k}}]$
and hence
![]() $\{[x^{i,j}|_{F_{n_{i,j}+k}}]\}_{j=1}^\infty $
is a disjoint family of closed balls with
$\{[x^{i,j}|_{F_{n_{i,j}+k}}]\}_{j=1}^\infty $
is a disjoint family of closed balls with
Therefore
 $$ \begin{align*}P_{e^{-|F_{N_i+k}|}}^{({s}/({1+\eta}))}(E_i)\ge \sum_{j=1}^\infty e^{-({s}/({1+\eta}))|F_{n_{i,j}+k}|}.\end{align*} $$
$$ \begin{align*}P_{e^{-|F_{N_i+k}|}}^{({s}/({1+\eta}))}(E_i)\ge \sum_{j=1}^\infty e^{-({s}/({1+\eta}))|F_{n_{i,j}+k}|}.\end{align*} $$
Thus we have
 $$ \begin{align*} \sum_{i=1}^\infty P^{({s}/({1+\eta}))}(E_i)&>\sum_{i=1}^\infty P_{e^{-|F_{N_i+k}|}}^{({s}/({1+\eta}))}(E_i)-1 \ge \sum_{i=1}^\infty \sum_{j=1}^\infty e^{-({s}/({1+\eta}))|F_{n_{i,j}+k}|} -1\\ &= \sum_{i=1}^\infty \sum_{j=1}^\infty e^{-({s}/({1+\eta}))({|F_{n_{i,j}+k}|}/{|F_{n_{i,j}}|})|F_{n_{i,j}}|} -1 \ge \sum_{i=1}^\infty \sum_{j=1}^\infty e^{-s|F_{n_{i,j}}|} -1 \\ &> \sum_{i=1}^\infty \bigg( P(E_i,N_i,\varepsilon,s, \{F_n\})-\frac{1}{2^i}\bigg )-1\\ &\ge \sum_{i=1}^\infty P(E_i,\varepsilon,s, \{F_n\})-2=\infty, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^\infty P^{({s}/({1+\eta}))}(E_i)&>\sum_{i=1}^\infty P_{e^{-|F_{N_i+k}|}}^{({s}/({1+\eta}))}(E_i)-1 \ge \sum_{i=1}^\infty \sum_{j=1}^\infty e^{-({s}/({1+\eta}))|F_{n_{i,j}+k}|} -1\\ &= \sum_{i=1}^\infty \sum_{j=1}^\infty e^{-({s}/({1+\eta}))({|F_{n_{i,j}+k}|}/{|F_{n_{i,j}}|})|F_{n_{i,j}}|} -1 \ge \sum_{i=1}^\infty \sum_{j=1}^\infty e^{-s|F_{n_{i,j}}|} -1 \\ &> \sum_{i=1}^\infty \bigg( P(E_i,N_i,\varepsilon,s, \{F_n\})-\frac{1}{2^i}\bigg )-1\\ &\ge \sum_{i=1}^\infty P(E_i,\varepsilon,s, \{F_n\})-2=\infty, \end{align*} $$
which implies that
![]() $\mathcal P^{({s}/({1+\eta }))}(E)=\infty $
and then
$\mathcal P^{({s}/({1+\eta }))}(E)=\infty $
and then
![]() $\text {dim}_P E\ge ({s}/({1+\eta }))$
.
$\text {dim}_P E\ge ({s}/({1+\eta }))$
.
Letting
![]() $\eta \rightarrow 0$
, we have
$\eta \rightarrow 0$
, we have
![]() $\text {dim}_P E\ge s$
. Since
$\text {dim}_P E\ge s$
. Since
![]() $0<s<h_{\mathrm {top}}^P(E,\{F_n\})$
is chosen arbitrarily, we obtain that
$0<s<h_{\mathrm {top}}^P(E,\{F_n\})$
is chosen arbitrarily, we obtain that
![]() $h_{\mathrm {top}}^P(E,\{F_n\})\le \text {dim}_P E$
.
$h_{\mathrm {top}}^P(E,\{F_n\})\le \text {dim}_P E$
.
A.2 Proof of Proposition 5.8
Recall that for Proposition 5.8 we let
![]() $0\le \alpha < \beta \le 1$
,
$0\le \alpha < \beta \le 1$
,
![]() $A=\{0,1\}$
and let
$A=\{0,1\}$
and let
![]() $H\subset G$
such that
$H\subset G$
such that
![]() $X_{\alpha ,\beta }\subset \{0,1\}^G$
is defined by
$X_{\alpha ,\beta }\subset \{0,1\}^G$
is defined by
Let
![]() $\mu \in M(X_{\alpha ,\beta })$
such that
$\mu \in M(X_{\alpha ,\beta })$
such that
![]() $\displaystyle \mu ([x|_{F_n}])=({1}/{2^{|H\cap F_n|}})$
for every
$\displaystyle \mu ([x|_{F_n}])=({1}/{2^{|H\cap F_n|}})$
for every
![]() $x\in X_{\alpha ,\beta }$
and
$x\in X_{\alpha ,\beta }$
and
![]() $n\in \mathbb N$
. Noticing that
$n\in \mathbb N$
. Noticing that
![]() $B_{F_n}(x,1)=[x|_{F_n}]$
(see (A.1)), we have
$B_{F_n}(x,1)=[x|_{F_n}]$
(see (A.1)), we have
 $$ \begin{align*} \underline h_{\mu}^{\mathrm{loc}}(X_{\alpha,\beta},\{F_n\})&=\int_{X_{\alpha,\beta}}\lim_{\varepsilon\rightarrow 0}\liminf_{n\rightarrow +\infty}-\frac{1}{|F_n|}\log \mu(B_{F_n}(x,\varepsilon))\,d{\kern-1pt}{\mu}\\ &\ge\int_{X_{\alpha,\beta}}\liminf_{n\rightarrow +\infty}-\frac{1}{|F_n|}\log \mu([x|_{F_n}])\,d{\kern-1pt}{\mu}\\ &=\liminf_{n\rightarrow +\infty}-\frac{1}{|F_n|}\log \frac{1}{2^{|H\cap F_n|}}=\alpha \log 2, \end{align*} $$
$$ \begin{align*} \underline h_{\mu}^{\mathrm{loc}}(X_{\alpha,\beta},\{F_n\})&=\int_{X_{\alpha,\beta}}\lim_{\varepsilon\rightarrow 0}\liminf_{n\rightarrow +\infty}-\frac{1}{|F_n|}\log \mu(B_{F_n}(x,\varepsilon))\,d{\kern-1pt}{\mu}\\ &\ge\int_{X_{\alpha,\beta}}\liminf_{n\rightarrow +\infty}-\frac{1}{|F_n|}\log \mu([x|_{F_n}])\,d{\kern-1pt}{\mu}\\ &=\liminf_{n\rightarrow +\infty}-\frac{1}{|F_n|}\log \frac{1}{2^{|H\cap F_n|}}=\alpha \log 2, \end{align*} $$
and similarly,
Applying [Reference Zheng and Chen25, Theorem 3.1] (the variational principle for amenable Bowen entropy) and Theorem 1.3 (the variational principle for amenable packing entropy) respectively, we have
To prove
![]() $h_{\mathrm {top}}^B (X_{\alpha ,\beta },\{F_n\})\le \alpha \log 2$
, by Proposition 5.4, we only need to prove that
$h_{\mathrm {top}}^B (X_{\alpha ,\beta },\{F_n\})\le \alpha \log 2$
, by Proposition 5.4, we only need to prove that
![]() $\text {dim}_H(X_{\alpha ,\beta })\le \alpha \log 2$
.
$\text {dim}_H(X_{\alpha ,\beta })\le \alpha \log 2$
.
Let
which is a subset of
![]() $X_{\alpha ,\beta }$
with cardinality
$X_{\alpha ,\beta }$
with cardinality
![]() $\# E_n=2^{|H\cap F_n|}$
. Note that
$\# E_n=2^{|H\cap F_n|}$
. Note that
![]() $\bigcup _{x\in E_n} [x|_{F_n}]\supseteq X_{\alpha ,\beta }$
and
$\bigcup _{x\in E_n} [x|_{F_n}]\supseteq X_{\alpha ,\beta }$
and
![]() $\text {diam}[x|_{F_n}]=e^{-|F_n|}$
for each
$\text {diam}[x|_{F_n}]=e^{-|F_n|}$
for each
![]() $x\in E_n$
. Let
$x\in E_n$
. Let
![]() $\delta>0$
and
$\delta>0$
and
![]() $N\in \mathbb N$
be fixed. When
$N\in \mathbb N$
be fixed. When
![]() $n>N$
,
$n>N$
,
 $$ \begin{align*}\mathcal H_{e^{-|F_N|}} ^{(\alpha+\delta)\log 2}(X_{\alpha,\beta}) \le \sum_{x\in E_n}e^{-(\alpha+\delta)\log 2 |F_n|}=e^{\log 2|F_n|(({|H\cap F_n|}/{|F_n|})-\alpha-\delta)}.\end{align*} $$
$$ \begin{align*}\mathcal H_{e^{-|F_N|}} ^{(\alpha+\delta)\log 2}(X_{\alpha,\beta}) \le \sum_{x\in E_n}e^{-(\alpha+\delta)\log 2 |F_n|}=e^{\log 2|F_n|(({|H\cap F_n|}/{|F_n|})-\alpha-\delta)}.\end{align*} $$
Since
![]() $\liminf _{n\rightarrow +\infty }({|H\cap F_n|}/{|F_n|})=\alpha $
, we have
$\liminf _{n\rightarrow +\infty }({|H\cap F_n|}/{|F_n|})=\alpha $
, we have
Thus
from which we deduce that
Finally, we will prove that
![]() $h_{\mathrm {top}}^P (X_{\alpha ,\beta },\{F_n\})\le \beta \log 2$
.
$h_{\mathrm {top}}^P (X_{\alpha ,\beta },\{F_n\})\le \beta \log 2$
.
Let
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $\varepsilon \in (e^{-|F_k|},e^{-|F_{k-1}|}]$
for some
$\varepsilon \in (e^{-|F_k|},e^{-|F_{k-1}|}]$
for some
![]() $k\in \mathbb N$
. Noticing that
$k\in \mathbb N$
. Noticing that
![]() $[x|_{F_{n+k}}]\subseteq B_{F_n}(x,\varepsilon )$
(see (A.3); here condition (1) of Proposition 5.4 is used), one can check that the set
$[x|_{F_{n+k}}]\subseteq B_{F_n}(x,\varepsilon )$
(see (A.3); here condition (1) of Proposition 5.4 is used), one can check that the set
![]() $E_{n+k}$
, defined by (A.4), is an
$E_{n+k}$
, defined by (A.4), is an
![]() $(F_n,\varepsilon )$
-spanning set of
$(F_n,\varepsilon )$
-spanning set of
![]() $X_{\alpha ,\beta }$
. Hence
$X_{\alpha ,\beta }$
. Hence
![]() $r_{F_n}(X_{\alpha ,\beta },\varepsilon )\le 2^{|H\cap F_{n+k}|}$
. Then
$r_{F_n}(X_{\alpha ,\beta },\varepsilon )\le 2^{|H\cap F_{n+k}|}$
. Then
where for the last equality we use condition (2) of Proposition 5.4. Thus
A.3 Proof of Proposition 5.10
(1) For any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $x\in A^{\mathbb Z}$
, in the system
$x\in A^{\mathbb Z}$
, in the system
![]() $(A^{\mathbb Z}\times A^{\mathbb Z},S)$
, we have
$(A^{\mathbb Z}\times A^{\mathbb Z},S)$
, we have
 $$ \begin{align} B_{n}((x,y),\varepsilon,\rho)\cap E_y&=\{(x',y):\rho(S^i(x',y),S^i(x,y))<\varepsilon,\text{ for }0\le i\le n-1\}\nonumber\\[-2pt] &=\{(x',y): d(T^{\omega(y,i)}(x'),T^{\omega(y,i)}x)<\varepsilon,\text{ for }0\le i\le n-1\}\nonumber\\[-2pt] &=B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon,d)\times\{y\}. \end{align} $$
$$ \begin{align} B_{n}((x,y),\varepsilon,\rho)\cap E_y&=\{(x',y):\rho(S^i(x',y),S^i(x,y))<\varepsilon,\text{ for }0\le i\le n-1\}\nonumber\\[-2pt] &=\{(x',y): d(T^{\omega(y,i)}(x'),T^{\omega(y,i)}x)<\varepsilon,\text{ for }0\le i\le n-1\}\nonumber\\[-2pt] &=B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon,d)\times\{y\}. \end{align} $$
Let
![]() $\mu $
be the
$\mu $
be the
![]() $\{\tfrac 12,\tfrac 12\}$
Bernoulli measure on
$\{\tfrac 12,\tfrac 12\}$
Bernoulli measure on
![]() $(A^{\mathbb Z},T)$
and
$(A^{\mathbb Z},T)$
and
![]() $\delta _y$
be the Dirac probability measure at the point y. Then
$\delta _y$
be the Dirac probability measure at the point y. Then
 $$ \begin{align} \overline h_{\mu\times \delta_y}^{\mathrm{loc}}(E_y,S)&=\int_{E_y}\lim_{\varepsilon\rightarrow 0}\limsup_{n\rightarrow +\infty}-\frac{1}{n}\log (\mu\times \delta_y)(B_{n}((x,y),\varepsilon,\rho))\,d(\mu\times \delta_y)\nonumber\\[-2pt] &=\int_{A^{\mathbb Z}}\lim_{\varepsilon\rightarrow 0}\limsup_{n\rightarrow +\infty}-\frac{1}{n}\log\mu(B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon,d))\,d{\kern-1pt}{\mu}\nonumber\\[-2pt] &=\limsup_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}(A^{\mathbb Z},T), \end{align} $$
$$ \begin{align} \overline h_{\mu\times \delta_y}^{\mathrm{loc}}(E_y,S)&=\int_{E_y}\lim_{\varepsilon\rightarrow 0}\limsup_{n\rightarrow +\infty}-\frac{1}{n}\log (\mu\times \delta_y)(B_{n}((x,y),\varepsilon,\rho))\,d(\mu\times \delta_y)\nonumber\\[-2pt] &=\int_{A^{\mathbb Z}}\lim_{\varepsilon\rightarrow 0}\limsup_{n\rightarrow +\infty}-\frac{1}{n}\log\mu(B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon,d))\,d{\kern-1pt}{\mu}\nonumber\\[-2pt] &=\limsup_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}(A^{\mathbb Z},T), \end{align} $$
where for the last inequality we use the simple facts that
![]() $M(y,n-1)\le M(y,n)\le M(y,n-1)+1$
and
$M(y,n-1)\le M(y,n)\le M(y,n-1)+1$
and
![]() $m(y,n-1)-1\le m(y,n)\le m(y,n-1)$
. Hence by Theorem 1.3, we have
$m(y,n-1)-1\le m(y,n)\le m(y,n-1)$
. Hence by Theorem 1.3, we have
Let
![]() $E\times \{y\}$
be any
$E\times \{y\}$
be any
![]() $(n,\varepsilon )$
-separated set for
$(n,\varepsilon )$
-separated set for
![]() $E_y$
. Note that, from (A.5), E must be an
$E_y$
. Note that, from (A.5), E must be an
![]() $([m(y,n-1),M(y,n-1)],\varepsilon )$
-separated set for
$([m(y,n-1),M(y,n-1)],\varepsilon )$
-separated set for
![]() $A^{\mathbb Z}$
. We have
$A^{\mathbb Z}$
. We have
 $$ \begin{align*} h_{\mathrm{top}}^{UC}(E_y,S)&\le \limsup_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}^{UC}(A^{\mathbb Z},T)\\[-2pt] &=\limsup_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}(A^{\mathbb Z},T). \end{align*} $$
$$ \begin{align*} h_{\mathrm{top}}^{UC}(E_y,S)&\le \limsup_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}^{UC}(A^{\mathbb Z},T)\\[-2pt] &=\limsup_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}(A^{\mathbb Z},T). \end{align*} $$
By Proposition 2.4,
This finishes the proof of (1).
(2) Similarly to (A.6), we have
 $$ \begin{align*} \underline h_{\mu\times \delta_y}^{\mathrm{loc}}(E_y,S)&=\int_{E_y}\lim_{\varepsilon\rightarrow 0}\liminf_{n\rightarrow +\infty}-\frac{1}{n}\log (\mu\times \delta_y)(B_{n}((x,y),\varepsilon,\rho))\,d(\mu\times \delta_y)\\[-12pt] \\ &=\int_{A^{\mathbb Z}}\lim_{\varepsilon\rightarrow 0}\liminf_{n\rightarrow +\infty}-\frac{1}{n}\log\mu(B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon,d))\,d{\kern-1pt}{\mu}\\ &=\liminf_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}(A^{\mathbb Z},T). \end{align*} $$
$$ \begin{align*} \underline h_{\mu\times \delta_y}^{\mathrm{loc}}(E_y,S)&=\int_{E_y}\lim_{\varepsilon\rightarrow 0}\liminf_{n\rightarrow +\infty}-\frac{1}{n}\log (\mu\times \delta_y)(B_{n}((x,y),\varepsilon,\rho))\,d(\mu\times \delta_y)\\[-12pt] \\ &=\int_{A^{\mathbb Z}}\lim_{\varepsilon\rightarrow 0}\liminf_{n\rightarrow +\infty}-\frac{1}{n}\log\mu(B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon,d))\,d{\kern-1pt}{\mu}\\ &=\liminf_{n\rightarrow+\infty}\frac{M(y,n)-m(y,n)}{n}h_{\mathrm{top}}(A^{\mathbb Z},T). \end{align*} $$
Hence by [Reference Zheng and Chen25], the variational principle for amenable Bowen entropy, we have
We now prove the upper bound for
![]() $h_{\mathrm {top}}^B(E_{y})$
, that is,
$h_{\mathrm {top}}^B(E_{y})$
, that is,
Let
![]() $\delta>0$
be fixed. For any
$\delta>0$
be fixed. For any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $k\in \mathbb N$
such that for any
$k\in \mathbb N$
such that for any
![]() $x,z\in A^{\mathbb Z}$
, whenever
$x,z\in A^{\mathbb Z}$
, whenever
![]() $x_i=z_i$
for every
$x_i=z_i$
for every
![]() $|i|\le k$
, we have that
$|i|\le k$
, we have that
![]() $d(x,y)<\varepsilon $
. Hence for any interval
$d(x,y)<\varepsilon $
. Hence for any interval
![]() $[m.n]$
of integers, we have
$[m.n]$
of integers, we have
where
![]() $[x|_{[-k+m,k+n]}]:=\{z\in A^{\mathbb Z}: z_i=x_i, \text { for every }-k+m\le i\le k+n\}$
is the cylinder in
$[x|_{[-k+m,k+n]}]:=\{z\in A^{\mathbb Z}: z_i=x_i, \text { for every }-k+m\le i\le k+n\}$
is the cylinder in
![]() $A^{\mathbb Z}$
.
$A^{\mathbb Z}$
.
Let
Consider the family
This evidently covers
![]() $E_y$
, since
$E_y$
, since
![]() $B_{n}((x,y),\varepsilon ,\rho )\cap E_y=B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon ,d)\times \{y\}$
(by (A.5)). Hence for any
$B_{n}((x,y),\varepsilon ,\rho )\cap E_y=B_{[m(y,n-1),M(y,n-1)]}(x,\varepsilon ,d)\times \{y\}$
(by (A.5)). Hence for any
![]() $N\in \mathbb N$
, we have for any
$N\in \mathbb N$
, we have for any
![]() $n\ge N$
,
$n\ge N$
,
 $$ \begin{align*} \mathcal M(E_y,N,\varepsilon,s,\{F_n\})&\le (\# E_n) e^{-sn}\\ &=2^{M(y,n-1)-m(y,n-1)+2k+1}e^{-sn}\\ &=e^{n ((({M(y,n-1)-m(y,n-1)+2k+1})/{n})\log 2-s)}. \end{align*} $$
$$ \begin{align*} \mathcal M(E_y,N,\varepsilon,s,\{F_n\})&\le (\# E_n) e^{-sn}\\ &=2^{M(y,n-1)-m(y,n-1)+2k+1}e^{-sn}\\ &=e^{n ((({M(y,n-1)-m(y,n-1)+2k+1})/{n})\log 2-s)}. \end{align*} $$
Note that there exist infinitely many
![]() $n\in \mathbb N$
such that
$n\in \mathbb N$
such that
Then for any
![]() $s>(\liminf \nolimits _{n\rightarrow +\infty }(({M(y,n)-m(y,n)})/{n})+\delta )\log 2$
, we can deduce that
$s>(\liminf \nolimits _{n\rightarrow +\infty }(({M(y,n)-m(y,n)})/{n})+\delta )\log 2$
, we can deduce that
Letting
![]() $N\rightarrow +\infty $
,
$N\rightarrow +\infty $
,
![]() $\varepsilon \rightarrow 0$
and then
$\varepsilon \rightarrow 0$
and then
![]() $\delta \rightarrow 0$
, from the definition of the Bowen entropy, we can conclude that
$\delta \rightarrow 0$
, from the definition of the Bowen entropy, we can conclude that
This finishes the proof of (2) of Proposition 5.10.