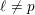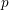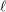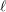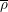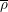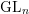1 Introduction
Let
![]() $\ell$
and
$\ell$
and
![]() $p$
be primes,
$p$
be primes,
![]() $L$
be a finite extension of
$L$
be a finite extension of
![]() $\mathbf{Q}_{\ell }$
, and
$\mathbf{Q}_{\ell }$
, and
![]() $\unicode[STIX]{x1D6E4}_{L}$
be the absolute Galois group of
$\unicode[STIX]{x1D6E4}_{L}$
be the absolute Galois group of
![]() $L$
. Suppose
$L$
. Suppose
![]() ${\mathcal{O}}$
is the ring of integers in a
${\mathcal{O}}$
is the ring of integers in a
![]() $p$
-adic field with residue field
$p$
-adic field with residue field
![]() $k$
. For a reductive group
$k$
. For a reductive group
![]() $G$
, it is important to study deformations of a continuous representation
$G$
, it is important to study deformations of a continuous representation
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
. Information about the universal deformation ring, and quotients corresponding to restricted classes of deformations, have many applications, for example to producing congruences between modular forms, proving modularity lifting theorems, and understanding generalizations of Serre’s conjecture and of the Breuil–Mézard conjecture. The case
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
. Information about the universal deformation ring, and quotients corresponding to restricted classes of deformations, have many applications, for example to producing congruences between modular forms, proving modularity lifting theorems, and understanding generalizations of Serre’s conjecture and of the Breuil–Mézard conjecture. The case
![]() $G=\operatorname{GL}_{n}$
has received the most attention. In this paper, we assume
$G=\operatorname{GL}_{n}$
has received the most attention. In this paper, we assume
![]() $\ell \neq p$
and generalize the minimally ramified deformation condition for
$\ell \neq p$
and generalize the minimally ramified deformation condition for
![]() $\operatorname{GL}_{n}$
studied by Clozel, Harris and Taylor [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] to symplectic and orthogonal groups.
$\operatorname{GL}_{n}$
studied by Clozel, Harris and Taylor [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] to symplectic and orthogonal groups.
This question was originally motivated by the problem of producing geometric deformations of representations of the absolute Galois group of a number field using a generalization of a method introduced by Ramakrishna [Reference RamakrishnaRam99, Reference RamakrishnaRam02]. For use in Ramakrishna’s method, we would like to define a deformation condition of lifts which are ‘ramified no worse than
![]() $\overline{\unicode[STIX]{x1D70C}}$
’, such that the resulting deformation condition is liftable despite the fact that the unrestricted deformation condition for
$\overline{\unicode[STIX]{x1D70C}}$
’, such that the resulting deformation condition is liftable despite the fact that the unrestricted deformation condition for
![]() $\overline{\unicode[STIX]{x1D70C}}$
may not be liftable. When
$\overline{\unicode[STIX]{x1D70C}}$
may not be liftable. When
![]() $G=\operatorname{GL}_{n}$
, the minimally ramified deformation condition defined in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] works. Attempting to generalize the argument of [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] to groups besides
$G=\operatorname{GL}_{n}$
, the minimally ramified deformation condition defined in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] works. Attempting to generalize the argument of [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] to groups besides
![]() $\operatorname{GL}_{n}$
leads to a deformation condition based on parabolics which is not liftable. Instead, inspired by the arguments of [Reference TaylorTay08, § 3] we define a deformation condition for symplectic and orthogonal groups based on deformations of a nilpotent element of
$\operatorname{GL}_{n}$
leads to a deformation condition based on parabolics which is not liftable. Instead, inspired by the arguments of [Reference TaylorTay08, § 3] we define a deformation condition for symplectic and orthogonal groups based on deformations of a nilpotent element of
![]() $\operatorname{Lie}G_{k}$
. This condition is liftable, which illustrates how genuinely new ideas are needed to study the deformation rings for representations valued in groups besides
$\operatorname{Lie}G_{k}$
. This condition is liftable, which illustrates how genuinely new ideas are needed to study the deformation rings for representations valued in groups besides
![]() $\operatorname{GL}_{n}$
.
$\operatorname{GL}_{n}$
.
In § 5.2, we define a minimally ramified deformation condition for symplectic and orthogonal groups after extending the residue field
![]() $k$
. This extension is harmless for the original application, and for that application it is also convenient to consider deformations with a fixed similitude character. Our main result is the following, which is precisely the local input needed in Ramakrishna’s method in the
$k$
. This extension is harmless for the original application, and for that application it is also convenient to consider deformations with a fixed similitude character. Our main result is the following, which is precisely the local input needed in Ramakrishna’s method in the
![]() $\ell \neq p$
case.
$\ell \neq p$
case.
Theorem 1.1. Let
![]() $G$
be
$G$
be
![]() $\operatorname{GSp}_{n}$
or
$\operatorname{GSp}_{n}$
or
![]() $\operatorname{GO}_{n}$
over
$\operatorname{GO}_{n}$
over
![]() $\mathbf{Z}_{p}$
with
$\mathbf{Z}_{p}$
with
![]() $p>n$
, and let
$p>n$
, and let
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
be a continuous representation with
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
be a continuous representation with
![]() $\ell \neq p$
. After extending
$\ell \neq p$
. After extending
![]() $k$
, the minimally ramified deformation condition with fixed similitude character is a liftable deformation condition (in the sense of Definition 2.5), and its tangent space has dimension
$k$
, the minimally ramified deformation condition with fixed similitude character is a liftable deformation condition (in the sense of Definition 2.5), and its tangent space has dimension
![]() $\dim H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
.
$\dim H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
.
This can equivalently be expressed as exhibiting a formally smooth quotient of the universal lifting ring
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\Box }$
. In this paper, we study only the local theory: the applications to producing geometric lifts are discussed in [Reference BooherBoo19]. In the remainder of the introduction, we will sketch how to correctly generalize the minimally ramified deformation condition introduced for
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\Box }$
. In this paper, we study only the local theory: the applications to producing geometric lifts are discussed in [Reference BooherBoo19]. In the remainder of the introduction, we will sketch how to correctly generalize the minimally ramified deformation condition introduced for
![]() $\operatorname{GL}_{n}$
and analyze it. The strategy could work for general
$\operatorname{GL}_{n}$
and analyze it. The strategy could work for general
![]() $G$
, but several pieces of the argument are specific to orthogonal or symplectic groups (or
$G$
, but several pieces of the argument are specific to orthogonal or symplectic groups (or
![]() $\operatorname{GL}_{n}$
), which was all that was needed for the original application.
$\operatorname{GL}_{n}$
), which was all that was needed for the original application.
The first step in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] is to reduce to studying certain tamely ramified representations. Clozel, Harris and Taylor reduce the problem to defining a nice class of deformations for representations of the group
![]() $T_{q}:=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
, where the first factor is generated by a Frobenius
$T_{q}:=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
, where the first factor is generated by a Frobenius
![]() $\unicode[STIX]{x1D719}$
and the second by an element
$\unicode[STIX]{x1D719}$
and the second by an element
![]() $\unicode[STIX]{x1D70F}$
in the inertia group. They satisfy the relation
$\unicode[STIX]{x1D70F}$
in the inertia group. They satisfy the relation
![]() $\unicode[STIX]{x1D719}\unicode[STIX]{x1D70F}\unicode[STIX]{x1D719}^{-1}=q\unicode[STIX]{x1D70F}$
for some
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D70F}\unicode[STIX]{x1D719}^{-1}=q\unicode[STIX]{x1D70F}$
for some
![]() $q$
prime to
$q$
prime to
![]() $p$
. This reduction generalizes without surprises to symplectic and orthogonal groups in § 6 (but the argument is genuinely restricted to orthogonal and symplectic groups as it relies heavily on the pairing).
$p$
. This reduction generalizes without surprises to symplectic and orthogonal groups in § 6 (but the argument is genuinely restricted to orthogonal and symplectic groups as it relies heavily on the pairing).
The second step is to specify when a lift of
![]() $\overline{\unicode[STIX]{x1D70C}}:T_{q}\rightarrow \operatorname{GL}_{n}(k)$
is ‘ramified no worse than
$\overline{\unicode[STIX]{x1D70C}}:T_{q}\rightarrow \operatorname{GL}_{n}(k)$
is ‘ramified no worse than
![]() $\overline{\unicode[STIX]{x1D70C}}$
’. For a coefficient ring
$\overline{\unicode[STIX]{x1D70C}}$
’. For a coefficient ring
![]() $R$
, a deformation
$R$
, a deformation
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow \operatorname{GL}_{n}(R)$
is minimally ramified according to [Reference Clozel, Harris and TaylorCHT08] when the natural
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow \operatorname{GL}_{n}(R)$
is minimally ramified according to [Reference Clozel, Harris and TaylorCHT08] when the natural
![]() $k$
-linear map
$k$
-linear map
is an isomorphism for all
![]() $i$
. The deformation condition is analyzed as follows.
$i$
. The deformation condition is analyzed as follows.
∙ Defining
 $V_{i}=\ker ((\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})-1_{n})^{i})$
gives a flag This flag determines a parabolic
$V_{i}=\ker ((\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})-1_{n})^{i})$
gives a flag This flag determines a parabolic $$\begin{eqnarray}0\subset V_{r}\subset V_{r-1}\subset \cdots \subset V_{1}\subset k^{n}.\end{eqnarray}$$
$$\begin{eqnarray}0\subset V_{r}\subset V_{r-1}\subset \cdots \subset V_{1}\subset k^{n}.\end{eqnarray}$$
 $k$
-subgroup
$k$
-subgroup
 $\overline{P}\subset \operatorname{GL}_{n}$
(points which preserve the flag) such that
$\overline{P}\subset \operatorname{GL}_{n}$
(points which preserve the flag) such that
 $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}\overline{P})(k)$
and
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}\overline{P})(k)$
and
 $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})\in \overline{P}(k)$
.
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})\in \overline{P}(k)$
.∙ Lift
 $\overline{P}$
to a parabolic subgroup
$\overline{P}$
to a parabolic subgroup
 $P$
of
$P$
of
 $\operatorname{GL}_{n}$
. The deformation functor of such lifts is formally smooth, and for any minimally ramified deformation
$\operatorname{GL}_{n}$
. The deformation functor of such lifts is formally smooth, and for any minimally ramified deformation
 $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
 $R$
there is a choice of such
$R$
there is a choice of such
 $P$
for which
$P$
for which
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}P)(R)$
and
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}P)(R)$
and
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})\in P(R)$
. Conversely, any
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})\in P(R)$
. Conversely, any
 $\unicode[STIX]{x1D70C}$
with this property is minimally ramified.
$\unicode[STIX]{x1D70C}$
with this property is minimally ramified.∙ Finally, for the standard block-upper-triangular choice of
 $P$
, one shows the deformation functor is formally smooth by building the universal lift over a power series ring: this uses explicit calculations with block-upper-triangular matrices.
$P$
, one shows the deformation functor is formally smooth by building the universal lift over a power series ring: this uses explicit calculations with block-upper-triangular matrices. $$\begin{eqnarray}\{(T,\unicode[STIX]{x1D6F7}):T\in {\mathcal{R}}_{u}P,\unicode[STIX]{x1D6F7}\in P,\unicode[STIX]{x1D6F7}T\unicode[STIX]{x1D6F7}^{-1}=T^{q},\overline{T}=\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F}),\overline{\unicode[STIX]{x1D6F7}}=\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})\}\end{eqnarray}$$
$$\begin{eqnarray}\{(T,\unicode[STIX]{x1D6F7}):T\in {\mathcal{R}}_{u}P,\unicode[STIX]{x1D6F7}\in P,\unicode[STIX]{x1D6F7}T\unicode[STIX]{x1D6F7}^{-1}=T^{q},\overline{T}=\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F}),\overline{\unicode[STIX]{x1D6F7}}=\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})\}\end{eqnarray}$$
To generalize beyond
![]() $\operatorname{GL}_{n}$
, we need to replace (1.1) with a more group-theoretic criterion. The naive generalization is to associate a parabolic
$\operatorname{GL}_{n}$
, we need to replace (1.1) with a more group-theoretic criterion. The naive generalization is to associate a parabolic
![]() $\overline{P}$
to
$\overline{P}$
to
![]() $\overline{\unicode[STIX]{x1D70C}}$
and then use the following definition.
$\overline{\unicode[STIX]{x1D70C}}$
and then use the following definition.
Definition 1.2. For a coefficient ring
![]() $R$
, say a lift
$R$
, say a lift
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
is ramified with respect to
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
is ramified with respect to
![]() $\overline{P}$
provided that there exists a parabolic
$\overline{P}$
provided that there exists a parabolic
![]() $R$
-subgroup
$R$
-subgroup
![]() $P\subset G_{R}$
lifting
$P\subset G_{R}$
lifting
![]() $\overline{P}$
such that
$\overline{P}$
such that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}P)(R)$
and
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}P)(R)$
and
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})\in P(R)$
.
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})\in P(R)$
.
This idea does not work. Let us focus on the symplectic case to illustrate what goes wrong.
The first problem is to associate a parabolic subgroup to
![]() $\overline{\unicode[STIX]{x1D70C}}$
. Recall that parabolic subgroups of a symplectic group correspond to isotropic flags
$\overline{\unicode[STIX]{x1D70C}}$
. Recall that parabolic subgroups of a symplectic group correspond to isotropic flags
![]() $0\subset V_{1}\subset \cdots \subset V_{r}\subset V_{r}^{\bot }\subset \cdots \subset V_{1}^{\bot }\subset k^{2n}$
. There is no reason that the flag determined by (1.1) is isotropic, so we would need some other method of producing a parabolic
$0\subset V_{1}\subset \cdots \subset V_{r}\subset V_{r}^{\bot }\subset \cdots \subset V_{1}^{\bot }\subset k^{2n}$
. There is no reason that the flag determined by (1.1) is isotropic, so we would need some other method of producing a parabolic
![]() $\overline{P}$
such that
$\overline{P}$
such that
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}\overline{P})(k)$
. In [Reference Borel and TitsBT71], Borel and Tits give a natural way to associate to the unipotent
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}\overline{P})(k)$
. In [Reference Borel and TitsBT71], Borel and Tits give a natural way to associate to the unipotent
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
a smooth connected unipotent
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
a smooth connected unipotent
![]() $k$
-subgroup of
$k$
-subgroup of
![]() $G$
. The normalizer of this subgroup is always parabolic and so gives a candidate for
$G$
. The normalizer of this subgroup is always parabolic and so gives a candidate for
![]() $\overline{P}$
. However, working out examples in
$\overline{P}$
. However, working out examples in
![]() $\operatorname{GL}_{n}$
for small
$\operatorname{GL}_{n}$
for small
![]() $n$
shows that this produces a different parabolic than the one determined by (1.1). This raises the natural question of how sensitive the smoothness of the deformation condition is to the choice of parabolic.
$n$
shows that this produces a different parabolic than the one determined by (1.1). This raises the natural question of how sensitive the smoothness of the deformation condition is to the choice of parabolic.
This leads to the second, larger problem: there are examples such that for every parabolic
![]() $\overline{P}$
satisfying
$\overline{P}$
satisfying
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}\overline{P})(k)$
, not all deformations ramified with respect to
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in ({\mathcal{R}}_{u}\overline{P})(k)$
, not all deformations ramified with respect to
![]() $\overline{P}$
are liftable.
$\overline{P}$
are liftable.
Example 1.3. Take
![]() $L=\mathbf{Q}_{29}$
and
$L=\mathbf{Q}_{29}$
and
![]() $k=\mathbf{F}_{7}$
. Consider the representation
$k=\mathbf{F}_{7}$
. Consider the representation
![]() $\overline{\unicode[STIX]{x1D70C}}:T_{29}\simeq \widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{7}\rightarrow \operatorname{GSp}_{4}(\mathbf{F}_{7})$
defined by
$\overline{\unicode[STIX]{x1D70C}}:T_{29}\simeq \widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{7}\rightarrow \operatorname{GSp}_{4}(\mathbf{F}_{7})$
defined by
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})=\left(\begin{array}{@{}cccc@{}}1 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right)\quad \text{and}\quad \overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})=\left(\begin{array}{@{}cccc@{}}1 & -1 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})=\left(\begin{array}{@{}cccc@{}}1 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right)\quad \text{and}\quad \overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})=\left(\begin{array}{@{}cccc@{}}1 & -1 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 1\end{array}\right).\end{eqnarray}$$
The deformation condition of lifts ramified relative to a parabolic
![]() $\overline{P}$
of
$\overline{P}$
of
![]() $\operatorname{GSp}_{4}$
whose unipotent radical contains
$\operatorname{GSp}_{4}$
whose unipotent radical contains
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
is not liftable for any choice of
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
is not liftable for any choice of
![]() $\overline{P}$
: there are lifts to the dual numbers that do not lift to
$\overline{P}$
: there are lifts to the dual numbers that do not lift to
![]() $\mathbf{F}_{7}[\unicode[STIX]{x1D716}]/(\unicode[STIX]{x1D716}^{3})$
. This is easy to check with a computer algebra system such as [SAGE], since the existence of lifts can be reduced to a problem in linear algebra. This is a general phenomenon, which we will explain conceptually in § 5.3.
$\mathbf{F}_{7}[\unicode[STIX]{x1D716}]/(\unicode[STIX]{x1D716}^{3})$
. This is easy to check with a computer algebra system such as [SAGE], since the existence of lifts can be reduced to a problem in linear algebra. This is a general phenomenon, which we will explain conceptually in § 5.3.
The correct approach is to define a lift
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
to be minimally ramified if
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
to be minimally ramified if
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
has ‘the same unipotent structure’ as
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
has ‘the same unipotent structure’ as
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
. It is more convenient to work with nilpotent elements, using the exponential and logarithm maps (defined for nilpotent and unipotent elements since
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
. It is more convenient to work with nilpotent elements, using the exponential and logarithm maps (defined for nilpotent and unipotent elements since
![]() $p>n$
). There are combinatorial parametrizations of nilpotent orbits of algebraic groups over an algebraically closed field, for example in terms of partitions or root data, which make precise the notion that the values of
$p>n$
). There are combinatorial parametrizations of nilpotent orbits of algebraic groups over an algebraically closed field, for example in terms of partitions or root data, which make precise the notion that the values of
![]() $N\in \mathfrak{g}_{{\mathcal{O}}}$
in the special and generic fiber lie in the same nilpotent orbit. In particular, for each nilpotent orbit
$N\in \mathfrak{g}_{{\mathcal{O}}}$
in the special and generic fiber lie in the same nilpotent orbit. In particular, for each nilpotent orbit
![]() $\unicode[STIX]{x1D70E}$
, we use the results of § 3.1 to choose particular elements
$\unicode[STIX]{x1D70E}$
, we use the results of § 3.1 to choose particular elements
![]() $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}_{{\mathcal{O}}}$
with this property lifting
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}_{{\mathcal{O}}}$
with this property lifting
![]() $\overline{N}\in \mathfrak{g}_{k}$
. In § 3.2, we define the pure nilpotents lifting
$\overline{N}\in \mathfrak{g}_{k}$
. In § 3.2, we define the pure nilpotents lifting
![]() $\overline{N}$
to be the
$\overline{N}$
to be the
![]() $\widehat{G}(R)$
-conjugates of
$\widehat{G}(R)$
-conjugates of
![]() $N_{\unicode[STIX]{x1D70E}}$
for a coefficient ring
$N_{\unicode[STIX]{x1D70E}}$
for a coefficient ring
![]() $R$
.
$R$
.
Example 1.4. For example, let
![]() $G=\operatorname{GL}_{3}$
and
$G=\operatorname{GL}_{3}$
and
 $$\begin{eqnarray}\overline{N}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\overline{N}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
Consider the lifts
 $$\begin{eqnarray}N_{1}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right)\in \mathfrak{g}\quad \text{and}\quad N_{2}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & p\\ 0 & 0 & 0\end{array}\right)\in \mathfrak{g}.\end{eqnarray}$$
$$\begin{eqnarray}N_{1}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right)\in \mathfrak{g}\quad \text{and}\quad N_{2}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & p\\ 0 & 0 & 0\end{array}\right)\in \mathfrak{g}.\end{eqnarray}$$
Both are nilpotent under the embedding of
![]() ${\mathcal{O}}$
into its fraction field
${\mathcal{O}}$
into its fraction field
![]() $K$
. The images of
$K$
. The images of
![]() $N_{1}$
in
$N_{1}$
in
![]() $\mathfrak{g}_{K}$
and
$\mathfrak{g}_{K}$
and
![]() $\mathfrak{g}_{k}$
both lie in the nilpotent orbit corresponding to the partition
$\mathfrak{g}_{k}$
both lie in the nilpotent orbit corresponding to the partition
![]() $2+1$
, so
$2+1$
, so
![]() $N_{1}$
is an example of the type of nilpotent lift we want to consider. On the other hand, the image of
$N_{1}$
is an example of the type of nilpotent lift we want to consider. On the other hand, the image of
![]() $N_{2}$
in
$N_{2}$
in
![]() $\mathfrak{g}_{K}$
lies in the nilpotent orbit corresponding to the partition
$\mathfrak{g}_{K}$
lies in the nilpotent orbit corresponding to the partition
![]() $3$
, while the image on
$3$
, while the image on
![]() $\mathfrak{g}_{k}$
lies in the orbit corresponding to
$\mathfrak{g}_{k}$
lies in the orbit corresponding to
![]() $2+1$
, so we do not want to use it. The pure nilpotents lifting
$2+1$
, so we do not want to use it. The pure nilpotents lifting
![]() $\overline{N}$
are
$\overline{N}$
are
![]() $\widehat{G}(R)$
-conjugates of
$\widehat{G}(R)$
-conjugates of
![]() $N_{1}$
.
$N_{1}$
.
We finally define a lift
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
to be minimally ramified provided
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
to be minimally ramified provided
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
is the exponential of a pure nilpotent lifting
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
is the exponential of a pure nilpotent lifting
![]() $\log \overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})=\overline{N}$
. Proposition 5.6 shows that this deformation condition is liftable. The main technical fact needed to analyze this deformation condition is that the scheme-theoretic centralizer
$\log \overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})=\overline{N}$
. Proposition 5.6 shows that this deformation condition is liftable. The main technical fact needed to analyze this deformation condition is that the scheme-theoretic centralizer
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
![]() ${\mathcal{O}}$
for
${\mathcal{O}}$
for
![]() $N_{\unicode[STIX]{x1D70E}}$
as above. The smoothness of such centralizers over algebraically closed fields is well understood, and in § 4 we study
$N_{\unicode[STIX]{x1D70E}}$
as above. The smoothness of such centralizers over algebraically closed fields is well understood, and in § 4 we study
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
and show that
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
and show that
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is flat over
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is flat over
![]() ${\mathcal{O}}$
and hence smooth. Lemma 4.4 gives a criterion for flatness that is easy to verify for classical groups, which suffices for our applications. We can reduce checking
${\mathcal{O}}$
and hence smooth. Lemma 4.4 gives a criterion for flatness that is easy to verify for classical groups, which suffices for our applications. We can reduce checking
![]() ${\mathcal{O}}$
-flatness to the problem of finding elements
${\mathcal{O}}$
-flatness to the problem of finding elements
![]() $g\in Z_{G}(N_{\unicode[STIX]{x1D70E}})({\mathcal{O}})$
such that
$g\in Z_{G}(N_{\unicode[STIX]{x1D70E}})({\mathcal{O}})$
such that
![]() $g_{k}$
lies in any specified component of
$g_{k}$
lies in any specified component of
![]() $Z_{G_{k}}(\overline{N})/Z_{G_{k}}(\overline{N})^{\circ }$
. There are difficulties beyond the classical cases due to the varied structure of
$Z_{G_{k}}(\overline{N})/Z_{G_{k}}(\overline{N})^{\circ }$
. There are difficulties beyond the classical cases due to the varied structure of
![]() $\unicode[STIX]{x1D70B}_{0}(Z_{G}(\overline{N})_{\overline{k}})$
in general.
$\unicode[STIX]{x1D70B}_{0}(Z_{G}(\overline{N})_{\overline{k}})$
in general.
Remark 1.5. It is a fortuitous coincidence (for [Reference Clozel, Harris and TaylorCHT08]) that for
![]() $\operatorname{GL}_{n}$
the lifts minimally ramified in the preceding sense are exactly the lifts ramified with respect to a parabolic subgroup of
$\operatorname{GL}_{n}$
the lifts minimally ramified in the preceding sense are exactly the lifts ramified with respect to a parabolic subgroup of
![]() $G$
. This rests on the fact that all nilpotent orbits of
$G$
. This rests on the fact that all nilpotent orbits of
![]() $\operatorname{GL}_{n}$
are Richardson orbits (see § 5.3 for details).
$\operatorname{GL}_{n}$
are Richardson orbits (see § 5.3 for details).
1.1 Structure of the paper
Section 2 discusses deformation conditions, deformation rings, and lifting rings. Section 3 constructs integral representatives for nilpotent orbits, and defines the notion of a pure nilpotent lift. This notion requires a study of the
![]() ${\mathcal{O}}$
-smoothness of
${\mathcal{O}}$
-smoothness of
![]() $Z_{G}(N)$
, which is carried out in §4. Finally §§ 5 and 6 define and study the minimally ramified deformation condition, first in a special tamely ramified case and then in general.
$Z_{G}(N)$
, which is carried out in §4. Finally §§ 5 and 6 define and study the minimally ramified deformation condition, first in a special tamely ramified case and then in general.
1.2 Notation and assumptions
Throughout the paper,
![]() $\ell$
and
$\ell$
and
![]() $p$
will be distinct primes, and
$p$
will be distinct primes, and
![]() ${\mathcal{O}}$
will be a discrete valuation ring with residue field
${\mathcal{O}}$
will be a discrete valuation ring with residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
. We will ultimately work with orthogonal or symplectic (similitude) groups, or
$p$
. We will ultimately work with orthogonal or symplectic (similitude) groups, or
![]() $\operatorname{GL}_{n}$
over
$\operatorname{GL}_{n}$
over
![]() ${\mathcal{O}}$
, although the strategy of the argument (but not the details) would work in greater generality. Since reductive group schemes have connected fibers (a restriction going back to [Reference Demazure and GrothendieckSGA3, XIX, 2.7] to avoid the component group jumping across fibers), and since
${\mathcal{O}}$
, although the strategy of the argument (but not the details) would work in greater generality. Since reductive group schemes have connected fibers (a restriction going back to [Reference Demazure and GrothendieckSGA3, XIX, 2.7] to avoid the component group jumping across fibers), and since
![]() $\operatorname{GO}_{m}$
may be disconnected, the natural class of group schemes to work with are what we call almost-reductive groups. By this we mean a smooth separated group scheme over
$\operatorname{GO}_{m}$
may be disconnected, the natural class of group schemes to work with are what we call almost-reductive groups. By this we mean a smooth separated group scheme over
![]() ${\mathcal{O}}$
such that the identity components of the fibers are reductive. Then
${\mathcal{O}}$
such that the identity components of the fibers are reductive. Then
![]() $G^{\circ }$
is a reductive
$G^{\circ }$
is a reductive
![]() ${\mathcal{O}}$
-subgroup scheme of
${\mathcal{O}}$
-subgroup scheme of
![]() $G$
and
$G$
and
![]() $G/G^{\circ }$
is a separated étale
$G/G^{\circ }$
is a separated étale
![]() ${\mathcal{O}}$
-group scheme of finite presentation [Reference ConradCon14, Proposition 3.1.3 and Theorem 5.3.5]. Furthermore, by a result of Raynaud
${\mathcal{O}}$
-group scheme of finite presentation [Reference ConradCon14, Proposition 3.1.3 and Theorem 5.3.5]. Furthermore, by a result of Raynaud
![]() $G$
is affine as it is a flat, separated, and of finite type with affine generic fiber over the discrete valuation ring
$G$
is affine as it is a flat, separated, and of finite type with affine generic fiber over the discrete valuation ring
![]() ${\mathcal{O}}$
[Reference Prasad and YuPY06, Proposition 3.1].
${\mathcal{O}}$
[Reference Prasad and YuPY06, Proposition 3.1].
We will often assume that
![]() $p$
is very good for
$p$
is very good for
![]() $G$
: in cases of interest this means that
$G$
: in cases of interest this means that
![]() $p\neq 2$
if
$p\neq 2$
if
![]() $G$
is orthogonal or symplectic, and
$G$
is orthogonal or symplectic, and
![]() $p\nmid n$
when
$p\nmid n$
when
![]() $G=\operatorname{GL}_{n}$
. To make uniform statements, we say that characteristic zero is very good for any
$G=\operatorname{GL}_{n}$
. To make uniform statements, we say that characteristic zero is very good for any
![]() $G$
.
$G$
.
We will also work with a nilpotent
![]() $\overline{N}\in \mathfrak{g}_{k}$
associated to a continuous representation
$\overline{N}\in \mathfrak{g}_{k}$
associated to a continuous representation
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
, where
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
, where
![]() $L$
is an
$L$
is an
![]() $\ell$
-adic field. We will eventually impose additional hypotheses, including the following:
$\ell$
-adic field. We will eventually impose additional hypotheses, including the following:
(A1)
 $G$
is
$G$
is
 $\operatorname{GSp}_{n}$
,
$\operatorname{GSp}_{n}$
,
 $\operatorname{GO}_{n}$
or
$\operatorname{GO}_{n}$
or
 $\operatorname{GL}_{n}$
and
$\operatorname{GL}_{n}$
and
 $p$
is very good for
$p$
is very good for
 $G$
;
$G$
;(A2)
 $p>n$
;
$p>n$
;(A3)
 $k$
and
$k$
and
 ${\mathcal{O}}$
are large enough so that
${\mathcal{O}}$
are large enough so that
 $q$
, the size of the residue field of
$q$
, the size of the residue field of
 $L$
, is a square in
$L$
, is a square in
 ${\mathcal{O}}^{\times }$
, and
${\mathcal{O}}^{\times }$
, and
 ${\mathcal{O}}^{\times }$
includes square roots of
${\mathcal{O}}^{\times }$
includes square roots of
 $-1$
and
$-1$
and
 $2$
;
$2$
;(A4)
 $k$
and
$k$
and
 ${\mathcal{O}}$
are large enough so there exists a pure nilpotent
${\mathcal{O}}$
are large enough so there exists a pure nilpotent
 $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
 $\overline{N}$
for which
$\overline{N}$
for which
 $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth.
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth.
2 Deformations of Galois representations
We recall some facts about the deformation theory for Galois representations: a basic reference is [Reference MazurMaz97], with the extension to algebraic groups beyond
![]() $\operatorname{GL}_{n}$
discussed in [Reference TilouineTil96]. While we are mainly concerned with classical groups, there are no problems with doing so for any smooth group scheme
$\operatorname{GL}_{n}$
discussed in [Reference TilouineTil96]. While we are mainly concerned with classical groups, there are no problems with doing so for any smooth group scheme
![]() $G$
over a discrete valuation ring
$G$
over a discrete valuation ring
![]() ${\mathcal{O}}$
with residue field
${\mathcal{O}}$
with residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
.
$p$
.
Let
![]() $\unicode[STIX]{x1D6E4}$
be a pro-finite group satisfying the following finiteness property: for every open subgroup
$\unicode[STIX]{x1D6E4}$
be a pro-finite group satisfying the following finiteness property: for every open subgroup
![]() $\unicode[STIX]{x1D6E4}_{0}\subset \unicode[STIX]{x1D6E4}$
, there are only finitely many continuous homomorphisms from
$\unicode[STIX]{x1D6E4}_{0}\subset \unicode[STIX]{x1D6E4}$
, there are only finitely many continuous homomorphisms from
![]() $\unicode[STIX]{x1D6E4}_{0}$
to
$\unicode[STIX]{x1D6E4}_{0}$
to
![]() $\mathbf{Z}/p\mathbf{Z}$
. This is true for the absolute Galois group of a local field and for the Galois group of the maximal extension of a number field unramified outside a finite set of places.
$\mathbf{Z}/p\mathbf{Z}$
. This is true for the absolute Galois group of a local field and for the Galois group of the maximal extension of a number field unramified outside a finite set of places.
Let
![]() $\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
be the category of coefficient
$\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
be the category of coefficient
![]() ${\mathcal{O}}$
-algebras: complete local Noetherian rings with residue field
${\mathcal{O}}$
-algebras: complete local Noetherian rings with residue field
![]() $k$
, with morphisms local homomorphisms inducing the identity map on
$k$
, with morphisms local homomorphisms inducing the identity map on
![]() $k$
and with the structure morphism a map of coefficient rings. Let
$k$
and with the structure morphism a map of coefficient rings. Let
![]() ${\mathcal{C}}_{{\mathcal{O}}}$
denote the full subcategory of Artinian coefficient
${\mathcal{C}}_{{\mathcal{O}}}$
denote the full subcategory of Artinian coefficient
![]() ${\mathcal{O}}$
-algebras. Recall that a small surjection of coefficient
${\mathcal{O}}$
-algebras. Recall that a small surjection of coefficient
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
![]() $f:A_{1}\rightarrow A_{0}$
is a surjection such that
$f:A_{1}\rightarrow A_{0}$
is a surjection such that
![]() $\ker (f)\cdot \mathfrak{m}_{A_{1}}=0$
.
$\ker (f)\cdot \mathfrak{m}_{A_{1}}=0$
.
For
![]() $A\in \widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
, define
$A\in \widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
, define
We are interested in deforming a fixed
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}\rightarrow G(k)$
. Let
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}\rightarrow G(k)$
. Let
![]() $\mathfrak{g}=\operatorname{Lie}G$
.
$\mathfrak{g}=\operatorname{Lie}G$
.
∙ Let
 $f:A_{1}\rightarrow A_{0}$
be a morphism in
$f:A_{1}\rightarrow A_{0}$
be a morphism in
 $\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
and
$\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
and
 $\unicode[STIX]{x1D70C}_{0}:\unicode[STIX]{x1D6E4}\rightarrow G(A_{0})$
a continuous homomorphism. A lift of
$\unicode[STIX]{x1D70C}_{0}:\unicode[STIX]{x1D6E4}\rightarrow G(A_{0})$
a continuous homomorphism. A lift of
 $\unicode[STIX]{x1D70C}_{0}$
to
$\unicode[STIX]{x1D70C}_{0}$
to
 $A_{1}$
is a continuous homomorphism
$A_{1}$
is a continuous homomorphism
 $\unicode[STIX]{x1D70C}_{1}:\unicode[STIX]{x1D6E4}\rightarrow G(A_{1})$
such that the following diagram commutes. Define the functor
$\unicode[STIX]{x1D70C}_{1}:\unicode[STIX]{x1D6E4}\rightarrow G(A_{1})$
such that the following diagram commutes. Define the functor
 $D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }:\widehat{{\mathcal{C}}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
by sending a coefficient
$D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }:\widehat{{\mathcal{C}}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
by sending a coefficient
 ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
 $A$
to the set of lifts of
$A$
to the set of lifts of
 $\overline{\unicode[STIX]{x1D70C}}$
to
$\overline{\unicode[STIX]{x1D70C}}$
to
 $A$
.
$A$
.∙ With the notation above, two lifts
 $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
 $\unicode[STIX]{x1D70C}^{\prime }$
of
$\unicode[STIX]{x1D70C}^{\prime }$
of
 $\overline{\unicode[STIX]{x1D70C}}$
to
$\overline{\unicode[STIX]{x1D70C}}$
to
 $A_{1}\in {\mathcal{C}}_{{\mathcal{O}}}$
are strictly equivalent if they are conjugate by an element of
$A_{1}\in {\mathcal{C}}_{{\mathcal{O}}}$
are strictly equivalent if they are conjugate by an element of
 $\widehat{G}(A_{1})$
. A deformation of
$\widehat{G}(A_{1})$
. A deformation of
 $\unicode[STIX]{x1D70C}_{0}$
to
$\unicode[STIX]{x1D70C}_{0}$
to
 $A_{1}$
is a strict equivalence class of lifts. Define the functor
$A_{1}$
is a strict equivalence class of lifts. Define the functor
 $D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}:\widehat{{\mathcal{C}}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
by sending a coefficient
$D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}:\widehat{{\mathcal{C}}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
by sending a coefficient
 ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
 $A$
to the set of deformations of
$A$
to the set of deformations of
 $\overline{\unicode[STIX]{x1D70C}}$
to
$\overline{\unicode[STIX]{x1D70C}}$
to
 $A$
.
$A$
.
We will drop the subscript
![]() ${\mathcal{O}}$
when it is clear from context.
${\mathcal{O}}$
when it is clear from context.
Fact 2.1. The functor
![]() $D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }$
is representable. When
$D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }$
is representable. When
![]() $\mathfrak{g}_{k}^{\unicode[STIX]{x1D6E4}}=\operatorname{Lie}(Z_{G})_{k}$
, the functor
$\mathfrak{g}_{k}^{\unicode[STIX]{x1D6E4}}=\operatorname{Lie}(Z_{G})_{k}$
, the functor
![]() $D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
is representable.
$D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
is representable.
The first part is simple, the second is a reformulation of [Reference TilouineTil96, Theorem 3.3].
The representing objects are denoted
![]() $R_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }$
and (when it exists)
$R_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }$
and (when it exists)
![]() $R_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
. The former is called the universal lifting ring, while the latter is the universal deformation ring. While we usually care about deformations, it is technically easier to work with lifts.
$R_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
. The former is called the universal lifting ring, while the latter is the universal deformation ring. While we usually care about deformations, it is technically easier to work with lifts.
This deformation theory is controlled by Galois cohomology. Let
![]() $\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})$
denote the representation of
$\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})$
denote the representation of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\mathfrak{g}_{k}$
via the adjoint representation. Letting
$\mathfrak{g}_{k}$
via the adjoint representation. Letting
![]() $G^{\prime }$
be the derived subgroup of
$G^{\prime }$
be the derived subgroup of
![]() $G^{\circ }$
with Lie algebra
$G^{\circ }$
with Lie algebra
![]() $\mathfrak{g}^{\prime }$
, we also consider the representation
$\mathfrak{g}^{\prime }$
, we also consider the representation
![]() $\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}})$
of
$\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}})$
of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\mathfrak{g}_{k}^{\prime }$
. As
$\mathfrak{g}_{k}^{\prime }$
. As
![]() $p$
is very good, we have
$p$
is very good, we have
![]() $\mathfrak{g}_{k}=\mathfrak{g}_{k}^{\prime }\oplus \mathfrak{z}_{\mathfrak{g}}$
where
$\mathfrak{g}_{k}=\mathfrak{g}_{k}^{\prime }\oplus \mathfrak{z}_{\mathfrak{g}}$
where
![]() $\mathfrak{z}_{\mathfrak{g}}$
is the Lie algebra of
$\mathfrak{z}_{\mathfrak{g}}$
is the Lie algebra of
![]() $Z_{G}$
. The condition in Fact 2.1 is just that
$Z_{G}$
. The condition in Fact 2.1 is just that
![]() $H^{0}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))=\mathfrak{z}_{\mathfrak{g}}$
, or equivalently that
$H^{0}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))=\mathfrak{z}_{\mathfrak{g}}$
, or equivalently that
![]() $H^{0}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))=0$
. In general, since
$H^{0}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))=0$
. In general, since
![]() $p$
is very good the natural map
$p$
is very good the natural map
![]() $H^{i}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))\rightarrow H^{i}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
is injective for all
$H^{i}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))\rightarrow H^{i}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
is injective for all
![]() $i$
; we often use this without comment.
$i$
; we often use this without comment.
We can use the first order exponential map [Reference TilouineTil96, § 3.5] to understand the tangent space. Recall that for a smooth
![]() ${\mathcal{O}}$
-group scheme
${\mathcal{O}}$
-group scheme
![]() $G$
, and a small surjection
$G$
, and a small surjection
![]() $f:A\rightarrow A/I$
of coefficient rings (
$f:A\rightarrow A/I$
of coefficient rings (
![]() $I\cdot \mathfrak{m}_{A}=0$
), smoothness gives an isomorphism
$I\cdot \mathfrak{m}_{A}=0$
), smoothness gives an isomorphism
The tangent space
![]() $D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}(k[\unicode[STIX]{x1D716}]/\unicode[STIX]{x1D716}^{2})$
is identified with
$D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}(k[\unicode[STIX]{x1D716}]/\unicode[STIX]{x1D716}^{2})$
is identified with
![]() $H^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
: Under this isomorphism, the cohomology class of a
$H^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
: Under this isomorphism, the cohomology class of a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\unicode[STIX]{x1D70F}$
corresponds to the lift
$\unicode[STIX]{x1D70F}$
corresponds to the lift
![]() $\unicode[STIX]{x1D70C}(g)=\exp (\unicode[STIX]{x1D716}\unicode[STIX]{x1D70F}(g))\overline{\unicode[STIX]{x1D70C}}(g)$
. For the universal lifting ring
$\unicode[STIX]{x1D70C}(g)=\exp (\unicode[STIX]{x1D716}\unicode[STIX]{x1D70F}(g))\overline{\unicode[STIX]{x1D70C}}(g)$
. For the universal lifting ring
![]() $R_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }$
, the tangent space is identified with the
$R_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }$
, the tangent space is identified with the
![]() $k$
-vector space
$k$
-vector space
![]() $Z^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
of (continuous)
$Z^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
of (continuous)
![]() $1$
-cocycles of
$1$
-cocycles of
![]() $\unicode[STIX]{x1D6E4}$
valued in
$\unicode[STIX]{x1D6E4}$
valued in
![]() $\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})$
.
$\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})$
.
Remark 2.2. We also observe that
since the space of coboundaries admits a surjection from
![]() $\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})$
with kernel
$\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})$
with kernel
![]() $\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})^{\unicode[STIX]{x1D6E4}}$
. This will be useful when comparing dimensions of lifting rings and deformation rings that are smooth.
$\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}})^{\unicode[STIX]{x1D6E4}}$
. This will be useful when comparing dimensions of lifting rings and deformation rings that are smooth.
We will want to study special classes of deformations.
Definition 2.3. A lifting condition is a sub-functor
![]() ${\mathcal{D}}^{\Box }\subset D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }:{\mathcal{C}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
such that we have the following.
${\mathcal{D}}^{\Box }\subset D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }:{\mathcal{C}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
such that we have the following.
(i) For any coefficient ring
 $A$
,
$A$
,
 ${\mathcal{D}}^{\Box }(A)$
is closed under strict equivalence.
${\mathcal{D}}^{\Box }(A)$
is closed under strict equivalence.(ii) Given a Cartesian diagram in
 ${\mathcal{C}}_{{\mathcal{O}}}$
and
${\mathcal{C}}_{{\mathcal{O}}}$
and
 $\unicode[STIX]{x1D70C}\in D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }(A_{1}\times _{A_{0}}A_{2})$
, we have
$\unicode[STIX]{x1D70C}\in D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}^{\Box }(A_{1}\times _{A_{0}}A_{2})$
, we have
 $\unicode[STIX]{x1D70C}\in {\mathcal{D}}^{\Box }(A_{1}\times _{A_{0}}A_{2})$
if and only if
$\unicode[STIX]{x1D70C}\in {\mathcal{D}}^{\Box }(A_{1}\times _{A_{0}}A_{2})$
if and only if
 ${\mathcal{D}}^{\Box }(\unicode[STIX]{x1D70B}_{1})\circ \unicode[STIX]{x1D70C}\in {\mathcal{D}}^{\Box }(A_{1})$
and
${\mathcal{D}}^{\Box }(\unicode[STIX]{x1D70B}_{1})\circ \unicode[STIX]{x1D70C}\in {\mathcal{D}}^{\Box }(A_{1})$
and
 ${\mathcal{D}}^{\Box }(\unicode[STIX]{x1D70B}_{2})\circ \unicode[STIX]{x1D70C}\in {\mathcal{D}}^{\Box }(A_{2})$
.
${\mathcal{D}}^{\Box }(\unicode[STIX]{x1D70B}_{2})\circ \unicode[STIX]{x1D70C}\in {\mathcal{D}}^{\Box }(A_{2})$
.
As it is closed under strict equivalence, we naturally obtain a deformation condition, a sub-functor
![]() ${\mathcal{D}}\subset D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
.
${\mathcal{D}}\subset D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
.
By Schlessinger’s criterion [Reference SchlessingerSch68, Theorem 2.11] being a lifting condition is equivalent to the functor
![]() ${\mathcal{D}}^{\Box }$
being pro-representable. Likewise, the deformation condition
${\mathcal{D}}^{\Box }$
being pro-representable. Likewise, the deformation condition
![]() ${\mathcal{D}}$
associated to a lifting condition
${\mathcal{D}}$
associated to a lifting condition
![]() ${\mathcal{D}}^{\Box }$
is pro-representable provided that
${\mathcal{D}}^{\Box }$
is pro-representable provided that
![]() $D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
is.
$D_{\overline{\unicode[STIX]{x1D70C}},{\mathcal{O}}}$
is.
The tangent space of a deformation condition
![]() ${\mathcal{D}}$
is a
${\mathcal{D}}$
is a
![]() $k$
-subspace of
$k$
-subspace of
![]() $H^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
, and will be denoted by
$H^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
, and will be denoted by
![]() $H_{{\mathcal{D}}}^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
. For a small surjection
$H_{{\mathcal{D}}}^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
. For a small surjection
![]() $A_{1}\rightarrow A_{0}$
and
$A_{1}\rightarrow A_{0}$
and
![]() $\unicode[STIX]{x1D70C}\in {\mathcal{D}}(A_{0})$
, the set of deformations of
$\unicode[STIX]{x1D70C}\in {\mathcal{D}}(A_{0})$
, the set of deformations of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $A_{1}$
subject to
$A_{1}$
subject to
![]() ${\mathcal{D}}$
is a
${\mathcal{D}}$
is a
![]() $H_{{\mathcal{D}}}^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
-torsor. This torsor-structure is compatible with the action of the unrestricted tangent space to
$H_{{\mathcal{D}}}^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
-torsor. This torsor-structure is compatible with the action of the unrestricted tangent space to
![]() $D_{\overline{\unicode[STIX]{x1D70C}}}$
on the space of all deformations of
$D_{\overline{\unicode[STIX]{x1D70C}}}$
on the space of all deformations of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $A_{1}$
.
$A_{1}$
.
Example 2.4. Suppose
![]() $G$
is almost-reductive, and let
$G$
is almost-reductive, and let
![]() $G^{\prime }$
be the derived group of
$G^{\prime }$
be the derived group of
![]() $G^{\circ }$
. The most basic examples of deformation conditions are the conditions imposed by fixing the lift of the homomorphism
$G^{\circ }$
. The most basic examples of deformation conditions are the conditions imposed by fixing the lift of the homomorphism
![]() $\unicode[STIX]{x1D6E4}\rightarrow (G/G^{\prime })(k)$
. To be precise, for the quotient map
$\unicode[STIX]{x1D6E4}\rightarrow (G/G^{\prime })(k)$
. To be precise, for the quotient map
![]() $\unicode[STIX]{x1D707}:G\rightarrow G/G^{\prime }=:S$
, a fixed
$\unicode[STIX]{x1D707}:G\rightarrow G/G^{\prime }=:S$
, a fixed
![]() $\unicode[STIX]{x1D708}:\unicode[STIX]{x1D6E4}\rightarrow S({\mathcal{O}})$
lifting
$\unicode[STIX]{x1D708}:\unicode[STIX]{x1D6E4}\rightarrow S({\mathcal{O}})$
lifting
![]() $\unicode[STIX]{x1D707}\circ \overline{\unicode[STIX]{x1D70C}}$
, and
$\unicode[STIX]{x1D707}\circ \overline{\unicode[STIX]{x1D70C}}$
, and
![]() $A\in \widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
with structure morphism
$A\in \widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
with structure morphism
![]() $\imath :{\mathcal{O}}\rightarrow A$
, we define a deformation condition
$\imath :{\mathcal{O}}\rightarrow A$
, we define a deformation condition
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D708}}\subset {\mathcal{D}}_{\overline{\unicode[STIX]{x1D70C}}}$
by
${\mathcal{D}}_{\unicode[STIX]{x1D708}}\subset {\mathcal{D}}_{\overline{\unicode[STIX]{x1D70C}}}$
by
One checks this is a deformation condition. Its tangent space is
![]() $H^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
since
$H^{1}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
since
![]() $p$
is very good. We define
$p$
is very good. We define
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D708}}^{\Box }$
similarly.
${\mathcal{D}}_{\unicode[STIX]{x1D708}}^{\Box }$
similarly.
Another important example is the unramified deformation condition for a non-archimedean place
![]() $v$
where
$v$
where
![]() $\overline{\unicode[STIX]{x1D70C}}$
is unramified: this consists of lifts that are unramified (possibly with a specified choice of
$\overline{\unicode[STIX]{x1D70C}}$
is unramified: this consists of lifts that are unramified (possibly with a specified choice of
![]() $\unicode[STIX]{x1D708}$
). The tangent space is
$\unicode[STIX]{x1D708}$
). The tangent space is
![]() $H_{\operatorname{nr}}^{1}(\unicode[STIX]{x1D6E4}_{v},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
(respectively
$H_{\operatorname{nr}}^{1}(\unicode[STIX]{x1D6E4}_{v},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))$
(respectively
![]() $H_{\operatorname{nr}}^{1}(\unicode[STIX]{x1D6E4}_{v},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
).
$H_{\operatorname{nr}}^{1}(\unicode[STIX]{x1D6E4}_{v},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
).
Definition 2.5. A deformation condition
![]() ${\mathcal{D}}$
is liftable (over
${\mathcal{D}}$
is liftable (over
![]() ${\mathcal{O}}$
) if for all small surjections
${\mathcal{O}}$
) if for all small surjections
![]() $f:A_{1}\rightarrow A_{0}$
of coefficient
$f:A_{1}\rightarrow A_{0}$
of coefficient
![]() ${\mathcal{O}}$
-algebras the natural map
${\mathcal{O}}$
-algebras the natural map
is surjective.
A geometric way to check local liftability is to show that the corresponding deformation ring (when it exists) is smooth. Obviously it suffices to check liftability for lifts instead of deformations, so we can work with the lifting deformation ring and avoid representability issues for
![]() ${\mathcal{D}}_{\overline{\unicode[STIX]{x1D70C}}}$
.
${\mathcal{D}}_{\overline{\unicode[STIX]{x1D70C}}}$
.
Example 2.6. The unramified deformation condition is liftable: an unramified lift is completely determined by the image of Frobenius in
![]() $G(A_{0})$
, and
$G(A_{0})$
, and
![]() $G$
is smooth over
$G$
is smooth over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
When attempting to lift with a fixed lift
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $\unicode[STIX]{x1D6E4}\rightarrow (G/G^{\prime })(k)$
, the obstruction to lifting is measured by a
$\unicode[STIX]{x1D6E4}\rightarrow (G/G^{\prime })(k)$
, the obstruction to lifting is measured by a
![]() $2$
-cocycle
$2$
-cocycle
![]() $\operatorname{ob}(\unicode[STIX]{x1D70C}_{0})$
that lies in
$\operatorname{ob}(\unicode[STIX]{x1D70C}_{0})$
that lies in
![]() $H^{2}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
. To see this, recall that the obstruction cocycle is defined by picking a continuous set theoretic lift
$H^{2}(\unicode[STIX]{x1D6E4},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
. To see this, recall that the obstruction cocycle is defined by picking a continuous set theoretic lift
![]() $\unicode[STIX]{x1D70C}_{1}$
of a given
$\unicode[STIX]{x1D70C}_{1}$
of a given
![]() $\unicode[STIX]{x1D70C}_{0}:\unicode[STIX]{x1D6E4}_{K}\rightarrow G(A_{0})$
: the
$\unicode[STIX]{x1D70C}_{0}:\unicode[STIX]{x1D6E4}_{K}\rightarrow G(A_{0})$
: the
![]() $2$
-cocycle records the failure of
$2$
-cocycle records the failure of
![]() $\unicode[STIX]{x1D70C}_{1}$
to be a homomorphism. By choosing the lift
$\unicode[STIX]{x1D70C}_{1}$
to be a homomorphism. By choosing the lift
![]() $\unicode[STIX]{x1D6E4}_{K}\rightarrow G(A_{1})$
so that
$\unicode[STIX]{x1D6E4}_{K}\rightarrow G(A_{1})$
so that
![]() $\unicode[STIX]{x1D6E4}_{K}\rightarrow (G/G^{\prime })(A_{0})$
agrees with
$\unicode[STIX]{x1D6E4}_{K}\rightarrow (G/G^{\prime })(A_{0})$
agrees with
![]() $\unicode[STIX]{x1D708}$
(as we may easily do since
$\unicode[STIX]{x1D708}$
(as we may easily do since
![]() $\ker \unicode[STIX]{x1D70C}_{0}$
is open in
$\ker \unicode[STIX]{x1D70C}_{0}$
is open in
![]() $\unicode[STIX]{x1D6E4}_{K}$
), the obstruction cocycle takes values in
$\unicode[STIX]{x1D6E4}_{K}$
), the obstruction cocycle takes values in
![]() $\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}})$
.
$\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}})$
.
3 Representatives for nilpotent orbits and pure nilpotents
As a first step on the road to defining the minimally ramified deformation condition, we study integral representatives of nilpotent orbits and then define pure nilpotent lifts. Useful background about nilpotent orbits is collected in [Reference JantzenJan04]. We focus on classical groups, so consider
![]() $G=\operatorname{GL}_{n}$
,
$G=\operatorname{GL}_{n}$
,
![]() $G=\operatorname{Sp}_{m}$
, or
$G=\operatorname{Sp}_{m}$
, or
![]() $G=\operatorname{O}_{m}$
over a discrete valuation ring
$G=\operatorname{O}_{m}$
over a discrete valuation ring
![]() ${\mathcal{O}}$
with residue field
${\mathcal{O}}$
with residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>0$
. Assume
$p>0$
. Assume
![]() $p$
is very good for
$p$
is very good for
![]() $G_{k}$
. Let
$G_{k}$
. Let
![]() $\mathfrak{g}=\operatorname{Lie}G$
and
$\mathfrak{g}=\operatorname{Lie}G$
and
![]() $K$
be the field of fractions of
$K$
be the field of fractions of
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
3.1 Integral representatives
The nilpotent orbits for
![]() $G$
over an algebraically closed field of good characteristic can be classified by combinatorial data
$G$
over an algebraically closed field of good characteristic can be classified by combinatorial data
![]() ${\mathcal{C}}$
that is independent of the characteristic. For classical groups, nilpotent orbits can be classified by their Jordan canonical form in terms of partitions. For a partition
${\mathcal{C}}$
that is independent of the characteristic. For classical groups, nilpotent orbits can be classified by their Jordan canonical form in terms of partitions. For a partition
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
, let
$\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
, let
![]() ${\mathcal{O}}_{F,\unicode[STIX]{x1D70E}}\subset \mathfrak{g}_{F}$
denote the corresponding orbit over the algebraically closed field
${\mathcal{O}}_{F,\unicode[STIX]{x1D70E}}\subset \mathfrak{g}_{F}$
denote the corresponding orbit over the algebraically closed field
![]() $F$
. For
$F$
. For
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
, we seek elements
$\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
, we seek elements
This makes precise the statement that
![]() $N_{K}$
and
$N_{K}$
and
![]() $N_{k}$
‘lie in the same nilpotent orbit’.
$N_{k}$
‘lie in the same nilpotent orbit’.
Remark 3.1. For a general reductive group scheme
![]() $G$
, the Bala–Carter classification can be interpreted as giving a characteristic-free classification of nilpotent orbits, allowing a generalization of the condition in (3.1). One can obtain such
$G$
, the Bala–Carter classification can be interpreted as giving a characteristic-free classification of nilpotent orbits, allowing a generalization of the condition in (3.1). One can obtain such
![]() $N_{\unicode[STIX]{x1D70E}}$
in terms of root data following [Reference Springer and SteinbergSS70, III.4.29]. We need the additional information provided by the concrete description in the symplectic and orthogonal cases to analyze the centralizer
$N_{\unicode[STIX]{x1D70E}}$
in terms of root data following [Reference Springer and SteinbergSS70, III.4.29]. We need the additional information provided by the concrete description in the symplectic and orthogonal cases to analyze the centralizer
![]() $Z_{G}(N)$
as an
$Z_{G}(N)$
as an
![]() ${\mathcal{O}}$
-scheme, so do not use this.
${\mathcal{O}}$
-scheme, so do not use this.
Example 3.2. Nilpotent orbits for
![]() $\operatorname{GL}_{n}$
correspond to partitions
$\operatorname{GL}_{n}$
correspond to partitions
![]() $n=n_{1}+n_{2}+\cdots +n_{r}$
. For a partition
$n=n_{1}+n_{2}+\cdots +n_{r}$
. For a partition
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $n$
, Let
$n$
, Let
![]() $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
be the nilpotent matrix in Jordan canonical form whose blocks (in order) are of sizes
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
be the nilpotent matrix in Jordan canonical form whose blocks (in order) are of sizes
![]() $n_{1},n_{2},\ldots ,n_{r}$
. Clearly
$n_{1},n_{2},\ldots ,n_{r}$
. Clearly
![]() $N_{\unicode[STIX]{x1D70E}}$
has entries in
$N_{\unicode[STIX]{x1D70E}}$
has entries in
![]() ${\mathcal{O}}$
and satisfies (3.1).
${\mathcal{O}}$
and satisfies (3.1).
For symplectic and orthogonal groups, we can produce the desired
![]() $N_{\unicode[STIX]{x1D70E}}$
using a minor extension of the classical results known over algebraically closed fields [Reference JantzenJan04, § 1]. Let
$N_{\unicode[STIX]{x1D70E}}$
using a minor extension of the classical results known over algebraically closed fields [Reference JantzenJan04, § 1]. Let
![]() $G=\operatorname{Sp}_{m}$
with
$G=\operatorname{Sp}_{m}$
with
![]() $m=2n$
, or
$m=2n$
, or
![]() $G=\operatorname{O}_{m}$
with
$G=\operatorname{O}_{m}$
with
![]() $m=2n$
or
$m=2n$
or
![]() $m=2n+1$
. We assume
$m=2n+1$
. We assume
![]() $n\geqslant 2$
. Recall that
$n\geqslant 2$
. Recall that
![]() $\operatorname{Sp}_{m}$
and
$\operatorname{Sp}_{m}$
and
![]() $\operatorname{O}_{m}$
are defined using standard pairings on a free
$\operatorname{O}_{m}$
are defined using standard pairings on a free
![]() ${\mathcal{O}}$
-module
${\mathcal{O}}$
-module
![]() $M$
of rank
$M$
of rank
![]() $m$
. For
$m$
. For
![]() $m=2n$
, the standard alternating pairing
$m=2n$
, the standard alternating pairing
![]() $\unicode[STIX]{x1D711}_{\text{std}}$
on
$\unicode[STIX]{x1D711}_{\text{std}}$
on
![]() ${\mathcal{O}}^{m}$
is the one given by the block matrix
${\mathcal{O}}^{m}$
is the one given by the block matrix
where
![]() $I_{n}^{\prime }$
denotes the anti-diagonal matrix with
$I_{n}^{\prime }$
denotes the anti-diagonal matrix with
![]() $1$
s on the diagonal. The standard symmetric pairing
$1$
s on the diagonal. The standard symmetric pairing
![]() $\unicode[STIX]{x1D711}_{\text{std}}$
on
$\unicode[STIX]{x1D711}_{\text{std}}$
on
![]() ${\mathcal{O}}^{m}$
is the one given by the matrix
${\mathcal{O}}^{m}$
is the one given by the matrix
![]() $I_{m}^{\prime }$
.
$I_{m}^{\prime }$
.
Remark 3.3. We chose to work with
![]() $\operatorname{O}_{m}$
instead of
$\operatorname{O}_{m}$
instead of
![]() $\operatorname{SO}_{m}$
, as the classification is cleaner for
$\operatorname{SO}_{m}$
, as the classification is cleaner for
![]() $\operatorname{O}_{m}$
. The nilpotent orbits are almost the same for
$\operatorname{O}_{m}$
. The nilpotent orbits are almost the same for
![]() $\operatorname{SO}_{m}$
, except that certain nilpotent orbits of
$\operatorname{SO}_{m}$
, except that certain nilpotent orbits of
![]() $\operatorname{O}_{m}$
(the ones where the partition contains only even parts) split into two
$\operatorname{O}_{m}$
(the ones where the partition contains only even parts) split into two
![]() $\operatorname{SO}_{m}$
-orbits [Reference JantzenJan04, Proposition 1.12] (conjugation by an element of
$\operatorname{SO}_{m}$
-orbits [Reference JantzenJan04, Proposition 1.12] (conjugation by an element of
![]() $\operatorname{O}_{m}$
with determinant
$\operatorname{O}_{m}$
with determinant
![]() $-1$
carries one such orbit into the other).
$-1$
carries one such orbit into the other).
Definition 3.4. Let
![]() $\unicode[STIX]{x1D70E}$
denote a partition
$\unicode[STIX]{x1D70E}$
denote a partition
![]() $m=m_{1}+m_{2}+\cdots +m_{r}$
of
$m=m_{1}+m_{2}+\cdots +m_{r}$
of
![]() $m$
. It is admissible if
$m$
. It is admissible if
∙ every even
 $m_{i}$
appears an even number of times when
$m_{i}$
appears an even number of times when
 $G=\operatorname{O}_{m}$
;
$G=\operatorname{O}_{m}$
;∙ every odd
 $m_{i}$
appears an even number of times when
$m_{i}$
appears an even number of times when
 $G=\operatorname{Sp}_{m}$
.
$G=\operatorname{Sp}_{m}$
.
The admissible partitions of
![]() $m$
are in bijection with nilpotent orbits of
$m$
are in bijection with nilpotent orbits of
![]() $\operatorname{Sp}_{m}$
or
$\operatorname{Sp}_{m}$
or
![]() $\operatorname{O}_{m}$
over any algebraically closed field of good characteristic [Reference JantzenJan04, Theorem 1.6]. The corresponding orbit is the intersection of
$\operatorname{O}_{m}$
over any algebraically closed field of good characteristic [Reference JantzenJan04, Theorem 1.6]. The corresponding orbit is the intersection of
![]() $\mathfrak{g}\subset \mathfrak{gl}_{m}$
with the
$\mathfrak{g}\subset \mathfrak{gl}_{m}$
with the
![]() $\operatorname{GL}_{m}$
-orbit corresponding to that partition of
$\operatorname{GL}_{m}$
-orbit corresponding to that partition of
![]() $m$
. Note that
$m$
. Note that
![]() $\operatorname{GL}_{m}$
-orbit representatives in Jordan canonical form need not lie in
$\operatorname{GL}_{m}$
-orbit representatives in Jordan canonical form need not lie in
![]() $\mathfrak{g}$
.
$\mathfrak{g}$
.
We will construct nilpotents together with a pairing, and then show how to relate the constructed pairing to the standard pairings used to define
![]() $G$
. Let
$G$
. Let
![]() $\unicode[STIX]{x1D716}=1$
in the case of
$\unicode[STIX]{x1D716}=1$
in the case of
![]() $\operatorname{O}_{m}$
, and
$\operatorname{O}_{m}$
, and
![]() $\unicode[STIX]{x1D716}=-1$
in the case of
$\unicode[STIX]{x1D716}=-1$
in the case of
![]() $\operatorname{Sp}_{m}$
.
$\operatorname{Sp}_{m}$
.
Definition 3.5. Let
![]() $d\geqslant 2$
be an integer. Define
$d\geqslant 2$
be an integer. Define
![]() $M(d)={\mathcal{O}}^{d}$
, with basis
$M(d)={\mathcal{O}}^{d}$
, with basis
![]() $v_{1},\ldots ,v_{d}$
and a perfect pairing
$v_{1},\ldots ,v_{d}$
and a perfect pairing
![]() $\unicode[STIX]{x1D711}_{d}$
such that
$\unicode[STIX]{x1D711}_{d}$
such that
(alternating for even
![]() $d$
, symmetric for odd
$d$
, symmetric for odd
![]() $d$
). Define a nilpotent
$d$
). Define a nilpotent
![]() $N_{d}\in \operatorname{End}(M(d))$
by
$N_{d}\in \operatorname{End}(M(d))$
by
![]() $N_{d}v_{i}=v_{i-1}$
for
$N_{d}v_{i}=v_{i-1}$
for
![]() $1<i\leqslant d$
and
$1<i\leqslant d$
and
![]() $N_{d}v_{1}=0$
.
$N_{d}v_{1}=0$
.
Similarly, define
![]() $M(d,d)={\mathcal{O}}^{2d}$
with basis
$M(d,d)={\mathcal{O}}^{2d}$
with basis
![]() $v_{1},\ldots ,v_{d},v_{1}^{\prime },\ldots ,v_{d}^{\prime }$
and a perfect
$v_{1},\ldots ,v_{d},v_{1}^{\prime },\ldots ,v_{d}^{\prime }$
and a perfect
![]() $\unicode[STIX]{x1D716}$
-symmetric pairing
$\unicode[STIX]{x1D716}$
-symmetric pairing
![]() $\unicode[STIX]{x1D711}_{d,d}$
by extending
$\unicode[STIX]{x1D711}_{d,d}$
by extending
Define a nilpotent
![]() $N_{d,d}\in \operatorname{End}(M(d,d))$
by
$N_{d,d}\in \operatorname{End}(M(d,d))$
by
![]() $N_{d,d}v_{i}=v_{i-1}$
and
$N_{d,d}v_{i}=v_{i-1}$
and
![]() $N_{d,d}v_{i}^{\prime }=v_{i-1}^{\prime }$
for
$N_{d,d}v_{i}^{\prime }=v_{i-1}^{\prime }$
for
![]() $1<i\leqslant d$
, and
$1<i\leqslant d$
, and
![]() $N_{d,d}v_{1}=N_{d,d}v_{1}^{\prime }=0$
.
$N_{d,d}v_{1}=N_{d,d}v_{1}^{\prime }=0$
.
Note that the pairing
![]() $\unicode[STIX]{x1D711}_{d,d}$
can be symmetric or alternating depending on the parity of
$\unicode[STIX]{x1D711}_{d,d}$
can be symmetric or alternating depending on the parity of
![]() $d$
. It is straightforward to verify the pairings are perfect and that
$d$
. It is straightforward to verify the pairings are perfect and that
![]() $N_{d}$
(respectively
$N_{d}$
(respectively
![]() $N_{d,d}$
) is skew with respect to
$N_{d,d}$
) is skew with respect to
![]() $\unicode[STIX]{x1D711}_{d}$
(respectively
$\unicode[STIX]{x1D711}_{d}$
(respectively
![]() $\unicode[STIX]{x1D711}d,d$
) in the sense that for
$\unicode[STIX]{x1D711}d,d$
) in the sense that for
![]() $v,w\in M(d)$
we have
$v,w\in M(d)$
we have
Given an admissible partition
![]() $\unicode[STIX]{x1D70E}:m=m_{1}+m_{2}+\cdots +m_{r}$
, we will construct a free
$\unicode[STIX]{x1D70E}:m=m_{1}+m_{2}+\cdots +m_{r}$
, we will construct a free
![]() ${\mathcal{O}}$
-module of rank
${\mathcal{O}}$
-module of rank
![]() $m$
with an
$m$
with an
![]() $\unicode[STIX]{x1D716}$
-symmetric perfect pairing and a nilpotent endomorphism that is skew with respect to the pairing such that the Jordan block structure of nilpotent endomorphism in geometric fibers is given by
$\unicode[STIX]{x1D716}$
-symmetric perfect pairing and a nilpotent endomorphism that is skew with respect to the pairing such that the Jordan block structure of nilpotent endomorphism in geometric fibers is given by
![]() $\unicode[STIX]{x1D70E}$
. Let
$\unicode[STIX]{x1D70E}$
. Let
![]() $n_{i}(\unicode[STIX]{x1D70E})=\text{\#}\{j:m_{j}=i\}$
.
$n_{i}(\unicode[STIX]{x1D70E})=\text{\#}\{j:m_{j}=i\}$
.
∙ If
 $G=\operatorname{O}_{m}$
, then
$G=\operatorname{O}_{m}$
, then
 $n_{i}(\unicode[STIX]{x1D70E})$
is even for even
$n_{i}(\unicode[STIX]{x1D70E})$
is even for even
 $i$
, so we can define
$i$
, so we can define  $$\begin{eqnarray}M_{\unicode[STIX]{x1D70E}}=\underset{i\,\text{odd}}{\bigoplus }M(i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})}\oplus \underset{i\,\text{even}}{\bigoplus }M(i,i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})/2}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\unicode[STIX]{x1D70E}}=\underset{i\,\text{odd}}{\bigoplus }M(i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})}\oplus \underset{i\,\text{even}}{\bigoplus }M(i,i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})/2}.\end{eqnarray}$$
∙ If
 $G=\operatorname{Sp}_{m}$
, then
$G=\operatorname{Sp}_{m}$
, then
 $n_{i}(\unicode[STIX]{x1D70E})$
is even for odd
$n_{i}(\unicode[STIX]{x1D70E})$
is even for odd
 $i$
, so we can define
$i$
, so we can define  $$\begin{eqnarray}M_{\unicode[STIX]{x1D70E}}=\underset{i\,\text{odd}}{\bigoplus }M(i,i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})/2}\oplus \underset{i\,\text{even}}{\bigoplus }M(i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\unicode[STIX]{x1D70E}}=\underset{i\,\text{odd}}{\bigoplus }M(i,i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})/2}\oplus \underset{i\,\text{even}}{\bigoplus }M(i)^{\oplus n_{i}(\unicode[STIX]{x1D70E})}.\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
and
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
and
![]() $N_{\unicode[STIX]{x1D70E}}$
denote the pairing and nilpotent endomorphism defined by the pairing and nilpotent endomorphism on each piece using Definition 3.5. In all cases,
$N_{\unicode[STIX]{x1D70E}}$
denote the pairing and nilpotent endomorphism defined by the pairing and nilpotent endomorphism on each piece using Definition 3.5. In all cases,
![]() $M_{\unicode[STIX]{x1D70E}}$
is a free
$M_{\unicode[STIX]{x1D70E}}$
is a free
![]() ${\mathcal{O}}$
-module of rank
${\mathcal{O}}$
-module of rank
![]() $m$
. For each
$m$
. For each
![]() $\unicode[STIX]{x1D70E},$
let
$\unicode[STIX]{x1D70E},$
let
![]() $G_{\unicode[STIX]{x1D70E}}$
be the automorphism scheme
$G_{\unicode[STIX]{x1D70E}}$
be the automorphism scheme
![]() $\text{}\underline{\operatorname{Aut}}(M_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}})$
, so for an algebraically closed field
$\text{}\underline{\operatorname{Aut}}(M_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}})$
, so for an algebraically closed field
![]() $F$
over
$F$
over
![]() ${\mathcal{O}}$
we have an isomorphism
${\mathcal{O}}$
we have an isomorphism
![]() $(G_{\unicode[STIX]{x1D70E}})_{F}\simeq G_{F}$
well defined up to
$(G_{\unicode[STIX]{x1D70E}})_{F}\simeq G_{F}$
well defined up to
![]() $G(F)$
-conjugation by using
$G(F)$
-conjugation by using
![]() $F$
-linear isomorphisms
$F$
-linear isomorphisms
![]() $(M_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}})_{F}\simeq (F^{m},\unicode[STIX]{x1D711}_{\text{std}})$
.
$(M_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}})_{F}\simeq (F^{m},\unicode[STIX]{x1D711}_{\text{std}})$
.
Lemma 3.6. For all admissible partitions of
![]() $m$
, the specializations of the
$m$
, the specializations of the
![]() $N_{\unicode[STIX]{x1D70E}}$
at geometric points
$N_{\unicode[STIX]{x1D70E}}$
at geometric points
![]() $\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D709}$
of
![]() $\operatorname{Spec}{\mathcal{O}}$
constitute a set of representatives for the nilpotent orbits of
$\operatorname{Spec}{\mathcal{O}}$
constitute a set of representatives for the nilpotent orbits of
![]() $G_{\unicode[STIX]{x1D709}}$
, and the specializations lie in the orbit corresponding to
$G_{\unicode[STIX]{x1D709}}$
, and the specializations lie in the orbit corresponding to
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Proof. The set of admissible partitions of
![]() $m$
is in bijection with the set of nilpotent orbits over any algebraically closed field. The
$m$
is in bijection with the set of nilpotent orbits over any algebraically closed field. The
![]() $N_{\unicode[STIX]{x1D70E}}$
we constructed are integral versions of the representatives constructed in [Reference JantzenJan04, § 1.7].◻
$N_{\unicode[STIX]{x1D70E}}$
we constructed are integral versions of the representatives constructed in [Reference JantzenJan04, § 1.7].◻
Let
![]() $e_{1},e_{2},\ldots ,e_{m}$
be the standard basis for
$e_{1},e_{2},\ldots ,e_{m}$
be the standard basis for
![]() ${\mathcal{O}}^{m}$
. The elements
${\mathcal{O}}^{m}$
. The elements
![]() $e_{i}$
and
$e_{i}$
and
![]() $e_{m+1-i}$
pair non-trivially under the standard pairing. When
$e_{m+1-i}$
pair non-trivially under the standard pairing. When
![]() $m=2n+1$
,
$m=2n+1$
,
![]() $e_{n+1}$
pairs non-trivially with itself under the standard pairing. We now relate the standard pairings to the pairings
$e_{n+1}$
pairs non-trivially with itself under the standard pairing. We now relate the standard pairings to the pairings
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
.
Proposition 3.7. Suppose that
![]() $\sqrt{-1},\sqrt{2}\in {\mathcal{O}}^{\times }$
. Then
$\sqrt{-1},\sqrt{2}\in {\mathcal{O}}^{\times }$
. Then
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
is equivalent to the standard pairing over
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
is equivalent to the standard pairing over
![]() ${\mathcal{O}}$
. There exists an
${\mathcal{O}}$
. There exists an
![]() ${\mathcal{O}}$
-basis
${\mathcal{O}}$
-basis
![]() $\{v_{i}\}$
of
$\{v_{i}\}$
of
![]() ${\mathcal{O}}^{m}$
with respect to which the pairing is given by
${\mathcal{O}}^{m}$
with respect to which the pairing is given by
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
and
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
and
![]() $N_{\unicode[STIX]{x1D70E}}$
satisfies the condition in (3.1) for
$N_{\unicode[STIX]{x1D70E}}$
satisfies the condition in (3.1) for
![]() $G=\operatorname{Sp}_{m}$
or
$G=\operatorname{Sp}_{m}$
or
![]() $G=\operatorname{O}_{m}$
.
$G=\operatorname{O}_{m}$
.
Proof. The standard pairings are very similar to
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
. In the case of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
. In the case of
![]() $\operatorname{Sp}_{m}$
, each basis vector pairs trivially against all but one other basis vector, with which it pairs as
$\operatorname{Sp}_{m}$
, each basis vector pairs trivially against all but one other basis vector, with which it pairs as
![]() $\pm 1$
. So after reordering the basis,
$\pm 1$
. So after reordering the basis,
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
is the standard pairing. The case of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
is the standard pairing. The case of
![]() $\operatorname{O}_{m}$
is slightly more complicated. Let
$\operatorname{O}_{m}$
is slightly more complicated. Let
![]() $\unicode[STIX]{x1D70E}:m=m_{1}+m_{2}+\cdots +m_{r}$
be an admissible partition. The construction of
$\unicode[STIX]{x1D70E}:m=m_{1}+m_{2}+\cdots +m_{r}$
be an admissible partition. The construction of
![]() $M_{\unicode[STIX]{x1D70E}}$
and
$M_{\unicode[STIX]{x1D70E}}$
and
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
gives a basis
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
gives a basis
![]() $\{v_{i,j}\}$
where
$\{v_{i,j}\}$
where
![]() $1\leqslant i\leqslant r$
and
$1\leqslant i\leqslant r$
and
![]() $1\leqslant j\leqslant m_{i}$
. From the construction of
$1\leqslant j\leqslant m_{i}$
. From the construction of
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
, we see that
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
, we see that
![]() $v_{i,j}$
pairs trivially against all basis vectors except for
$v_{i,j}$
pairs trivially against all basis vectors except for
![]() $v_{i,m_{i}+1-j}$
. So as long as
$v_{i,m_{i}+1-j}$
. So as long as
![]() $2j\neq m_{i}+1$
, we obtain a pair of basis vectors which are orthogonal to all others and which pair to
$2j\neq m_{i}+1$
, we obtain a pair of basis vectors which are orthogonal to all others and which pair to
![]() $\pm 1$
. For each odd
$\pm 1$
. For each odd
![]() $m_{i}$
, the vector
$m_{i}$
, the vector
![]() $v_{i,(m_{i}+1)/2}$
pairs non-trivially with itself. The standard pairing with respect to the basis
$v_{i,(m_{i}+1)/2}$
pairs non-trivially with itself. The standard pairing with respect to the basis
![]() $e_{i}$
has such a vector only when
$e_{i}$
has such a vector only when
![]() $m=2n+1$
and then only for one
$m=2n+1$
and then only for one
![]() $e_{i}$
.
$e_{i}$
.
We must change the basis over
![]() ${\mathcal{O}}$
so that
${\mathcal{O}}$
so that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
becomes the standard symmetric pairing. Let
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
becomes the standard symmetric pairing. Let
![]() $v=v_{i,(m_{i}+1)/2}$
and
$v=v_{i,(m_{i}+1)/2}$
and
![]() $v^{\prime }=v_{j,(m_{j}+1)/2}$
be two distinct vectors which pair non-trivially with themselves. In particular,
$v^{\prime }=v_{j,(m_{j}+1)/2}$
be two distinct vectors which pair non-trivially with themselves. In particular,
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v,v)=(-1)^{(m_{i}+1)/2}:=\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v,v)=(-1)^{(m_{i}+1)/2}:=\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v^{\prime },v^{\prime })=(-1)^{(m_{j}+1)/2}:=\unicode[STIX]{x1D702}^{\prime }$
. Define
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v^{\prime },v^{\prime })=(-1)^{(m_{j}+1)/2}:=\unicode[STIX]{x1D702}^{\prime }$
. Define
Then we see that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(w,w)=0=\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(w^{\prime },w^{\prime })$
and
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(w,w)=0=\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(w^{\prime },w^{\prime })$
and
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(w,w^{\prime })=1$
. Making this change of variable over
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(w,w^{\prime })=1$
. Making this change of variable over
![]() ${\mathcal{O}}$
(which requires
${\mathcal{O}}$
(which requires
![]() $\sqrt{-1},\sqrt{2}\in {\mathcal{O}}^{\times }$
), we have reduced the number of basis vectors which pair non-trivially with themselves by two, and produced a new pair of basis vectors orthogonal to the others and which pair to
$\sqrt{-1},\sqrt{2}\in {\mathcal{O}}^{\times }$
), we have reduced the number of basis vectors which pair non-trivially with themselves by two, and produced a new pair of basis vectors orthogonal to the others and which pair to
![]() $1$
. By induction, we may therefore pick a basis
$1$
. By induction, we may therefore pick a basis
![]() $v_{1}^{\prime },\ldots ,v_{m}^{\prime }$
for which at most one basis vector pairs non-trivially with itself under
$v_{1}^{\prime },\ldots ,v_{m}^{\prime }$
for which at most one basis vector pairs non-trivially with itself under
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
. After re-ordering, we may further assume that
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
. After re-ordering, we may further assume that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=0$
unless
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=0$
unless
![]() $i+j=m+1$
, in which case
$i+j=m+1$
, in which case
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=\pm 1$
. Suppose
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=\pm 1$
. Suppose
![]() $j=m+1-i$
. If
$j=m+1-i$
. If
![]() $i\neq j$
, by scaling
$i\neq j$
, by scaling
![]() $v_{i}^{\prime }$
we may assume that
$v_{i}^{\prime }$
we may assume that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=1$
. If
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=1$
. If
![]() $i=j$
, we already know that
$i=j$
, we already know that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=1$
. With respect to this basis,
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}(v_{i}^{\prime },v_{j}^{\prime })=1$
. With respect to this basis,
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
is the standard pairing.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
is the standard pairing.
The last statement immediately follows from Lemma 3.6.◻
3.2 Pure nilpotent lifts
For a nilpotent element
![]() $\overline{N}\in \mathfrak{g}_{k}$
of type
$\overline{N}\in \mathfrak{g}_{k}$
of type
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
, we will define the notion of a pure nilpotent lift of
$\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
, we will define the notion of a pure nilpotent lift of
![]() $\overline{N}$
in
$\overline{N}$
in
![]() $\mathfrak{g}_{k}$
and study the space of such lifts, assuming there exists
$\mathfrak{g}_{k}$
and study the space of such lifts, assuming there exists
![]() $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
![]() $\overline{N}$
such that
$\overline{N}$
such that
![]() $(N_{\unicode[STIX]{x1D70E}})_{\overline{K}}\in O_{\overline{K},\unicode[STIX]{x1D70E}}$
and such that
$(N_{\unicode[STIX]{x1D70E}})_{\overline{K}}\in O_{\overline{K},\unicode[STIX]{x1D70E}}$
and such that
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Remark 3.8. Section 3.1 shows that for any nilpotent
![]() $\overline{N}\in \mathfrak{g}_{k}$
, there exists
$\overline{N}\in \mathfrak{g}_{k}$
, there exists
![]() $N_{\unicode[STIX]{x1D70E}}^{\prime }\in \mathfrak{g}$
such that
$N_{\unicode[STIX]{x1D70E}}^{\prime }\in \mathfrak{g}$
such that
![]() $(N_{\unicode[STIX]{x1D70E}}^{\prime })_{\overline{k}}\in O_{\overline{k},\unicode[STIX]{x1D70E}}$
and such that
$(N_{\unicode[STIX]{x1D70E}}^{\prime })_{\overline{k}}\in O_{\overline{k},\unicode[STIX]{x1D70E}}$
and such that
![]() $(N_{\unicode[STIX]{x1D70E}}^{\prime })_{k}$
and
$(N_{\unicode[STIX]{x1D70E}}^{\prime })_{k}$
and
![]() $\overline{N}$
are
$\overline{N}$
are
![]() $G(\overline{k})$
-conjugate. We will address the
$G(\overline{k})$
-conjugate. We will address the
![]() ${\mathcal{O}}$
-smoothness of
${\mathcal{O}}$
-smoothness of
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
in § 4, especially Proposition 4.17. Then
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
in § 4, especially Proposition 4.17. Then
![]() $(N_{\unicode[STIX]{x1D70E}}^{\prime })_{k}$
and
$(N_{\unicode[STIX]{x1D70E}}^{\prime })_{k}$
and
![]() $\overline{N}$
are conjugate by
$\overline{N}$
are conjugate by
![]() $\overline{g}\in G(k^{\prime })$
for some finite extension
$\overline{g}\in G(k^{\prime })$
for some finite extension
![]() $k^{\prime }/k$
. Lift
$k^{\prime }/k$
. Lift
![]() $\overline{g}$
to an element
$\overline{g}$
to an element
![]() $g\in G({\mathcal{O}}^{\prime })$
for a Henselian discrete valuation ring local over
$g\in G({\mathcal{O}}^{\prime })$
for a Henselian discrete valuation ring local over
![]() ${\mathcal{O}}$
and having residue field
${\mathcal{O}}$
and having residue field
![]() $k^{\prime }$
. The element
$k^{\prime }$
. The element
![]() $N_{\unicode[STIX]{x1D70E}}:=gN_{\unicode[STIX]{x1D70E}}^{\prime }g^{-1}\in \mathfrak{g}_{{\mathcal{O}}^{\prime }}$
reduces to
$N_{\unicode[STIX]{x1D70E}}:=gN_{\unicode[STIX]{x1D70E}}^{\prime }g^{-1}\in \mathfrak{g}_{{\mathcal{O}}^{\prime }}$
reduces to
![]() $\overline{N}_{k^{\prime }}$
and has the required properties. So the above hypothesis is satisfied after a finite flat local extension of
$\overline{N}_{k^{\prime }}$
and has the required properties. So the above hypothesis is satisfied after a finite flat local extension of
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Definition 3.9. Fix an
![]() $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
![]() $\overline{N}$
such that
$\overline{N}$
such that
![]() $(N_{\unicode[STIX]{x1D70E}})_{\overline{K}}\in O_{\overline{K},\unicode[STIX]{x1D70E}}$
and such that
$(N_{\unicode[STIX]{x1D70E}})_{\overline{K}}\in O_{\overline{K},\unicode[STIX]{x1D70E}}$
and such that
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
![]() ${\mathcal{O}}$
. Define the functor
${\mathcal{O}}$
. Define the functor
![]() $\operatorname{Nil}_{\overline{N}}:{\mathcal{C}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
by
$\operatorname{Nil}_{\overline{N}}:{\mathcal{C}}_{{\mathcal{O}}}\rightarrow \operatorname{Sets}$
by
Call these
![]() $N\in \operatorname{Nil}_{\overline{N}}(R)$
the pure nilpotents lifting
$N\in \operatorname{Nil}_{\overline{N}}(R)$
the pure nilpotents lifting
![]() $\overline{N}$
.
$\overline{N}$
.
This is obviously a subfunctor of the formal neighborhood of
![]() $\overline{N}$
in the affine space
$\overline{N}$
in the affine space
![]() $\text{}\underline{\mathfrak{g}}$
over
$\text{}\underline{\mathfrak{g}}$
over
![]() ${\mathcal{O}}$
attached to
${\mathcal{O}}$
attached to
![]() $\mathfrak{g}$
. The key to analyzing
$\mathfrak{g}$
. The key to analyzing
![]() $\operatorname{Nil}_{\overline{N}}$
is that
$\operatorname{Nil}_{\overline{N}}$
is that
![]() $Z_{G_{R}}(N)$
is smooth over
$Z_{G_{R}}(N)$
is smooth over
![]() $R$
since
$R$
since
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
![]() ${\mathcal{O}}$
-smooth and
${\mathcal{O}}$
-smooth and
![]() $N$
is in the
$N$
is in the
![]() $G$
-orbit of
$G$
-orbit of
![]() $(N_{\unicode[STIX]{x1D70E}})_{R}$
. To ease notation below, we shall write
$(N_{\unicode[STIX]{x1D70E}})_{R}$
. To ease notation below, we shall write
![]() $gNg^{-1}$
rather than
$gNg^{-1}$
rather than
![]() $\operatorname{Ad}_{G}(g)(N)$
for
$\operatorname{Ad}_{G}(g)(N)$
for
![]() $g\in \widehat{G}(R)$
.
$g\in \widehat{G}(R)$
.
Lemma 3.10. Assuming
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
![]() ${\mathcal{O}}$
-smooth, the functor
${\mathcal{O}}$
-smooth, the functor
![]() $\operatorname{Nil}_{\overline{N}}$
is pro-representable.
$\operatorname{Nil}_{\overline{N}}$
is pro-representable.
Proof. We will use Schlessinger’s criterion to check pro-representability. As
![]() $\operatorname{Nil}_{\overline{N}}$
is a subfunctor of the formal neighborhood of the scheme
$\operatorname{Nil}_{\overline{N}}$
is a subfunctor of the formal neighborhood of the scheme
![]() $\text{}\underline{\mathfrak{g}}$
at
$\text{}\underline{\mathfrak{g}}$
at
![]() $\overline{N}$
, the only condition to check is the analogue of Definition 2.3(ii): given a Cartesian diagram in
$\overline{N}$
, the only condition to check is the analogue of Definition 2.3(ii): given a Cartesian diagram in
![]() ${\mathcal{C}}_{{\mathcal{O}}}$
${\mathcal{C}}_{{\mathcal{O}}}$

and
![]() $N_{i}\in \operatorname{Nil}_{\overline{N}}(R_{i})$
such that
$N_{i}\in \operatorname{Nil}_{\overline{N}}(R_{i})$
such that
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
reduce to
$N_{2}$
reduce to
![]() $N_{0}$
, we want to check that
$N_{0}$
, we want to check that
![]() $N_{1}\times N_{2}\in \operatorname{Nil}_{\overline{N}}(R_{1}\times _{R_{0}}R_{2})$
. By definition, there exists
$N_{1}\times N_{2}\in \operatorname{Nil}_{\overline{N}}(R_{1}\times _{R_{0}}R_{2})$
. By definition, there exists
![]() $g_{1}\in \widehat{G}(R_{1})$
and
$g_{1}\in \widehat{G}(R_{1})$
and
![]() $g_{2}\in \widehat{G}(R_{2})$
such that
$g_{2}\in \widehat{G}(R_{2})$
such that
![]() $N_{1}=g_{1}N_{\unicode[STIX]{x1D70E}}g_{1}^{-1}$
and
$N_{1}=g_{1}N_{\unicode[STIX]{x1D70E}}g_{1}^{-1}$
and
![]() $N_{2}=g_{2}N_{\unicode[STIX]{x1D70E}}g_{2}^{-1}$
. Consider the element
$N_{2}=g_{2}N_{\unicode[STIX]{x1D70E}}g_{2}^{-1}$
. Consider the element
![]() $g_{1}g_{2}^{-1}\in \widehat{G}(R_{0})$
. Observe that
$g_{1}g_{2}^{-1}\in \widehat{G}(R_{0})$
. Observe that
In particular,
![]() $g_{1}g_{2}^{-1}\in Z_{G}(N_{\unicode[STIX]{x1D70E}})(R_{0})$
. The extension
$g_{1}g_{2}^{-1}\in Z_{G}(N_{\unicode[STIX]{x1D70E}})(R_{0})$
. The extension
![]() $R_{2}\rightarrow R_{0}$
has nilpotent kernel, so as
$R_{2}\rightarrow R_{0}$
has nilpotent kernel, so as
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth over
![]() ${\mathcal{O}}$
there exists
${\mathcal{O}}$
there exists
![]() $h\in Z_{G}(N_{\unicode[STIX]{x1D70E}})(R_{2})$
lifting
$h\in Z_{G}(N_{\unicode[STIX]{x1D70E}})(R_{2})$
lifting
![]() $g_{1}g_{2}^{-1}$
. The element
$g_{1}g_{2}^{-1}$
. The element
conjugates
![]() $N_{1}\times N_{2}$
to
$N_{1}\times N_{2}$
to
![]() $N_{\unicode[STIX]{x1D70E}}$
. Hence
$N_{\unicode[STIX]{x1D70E}}$
. Hence
![]() $N_{1}\times N_{2}\in \operatorname{Nil}_{\overline{N}}(R_{1}\times _{R_{0}}R_{2})$
.◻
$N_{1}\times N_{2}\in \operatorname{Nil}_{\overline{N}}(R_{1}\times _{R_{0}}R_{2})$
.◻
Lemma 3.11. The functor
![]() $\operatorname{Nil}_{\overline{N}}$
is formally smooth, in the sense that for a small surjection
$\operatorname{Nil}_{\overline{N}}$
is formally smooth, in the sense that for a small surjection
![]() $R_{2}\rightarrow R_{1}$
of coefficient
$R_{2}\rightarrow R_{1}$
of coefficient
![]() ${\mathcal{O}}$
-algebras the map
${\mathcal{O}}$
-algebras the map
is surjective. Moreover, when
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
![]() ${\mathcal{O}}$
-smooth and
${\mathcal{O}}$
-smooth and
![]() $\operatorname{Nil}_{\overline{N}}$
is representable, it has relative dimension
$\operatorname{Nil}_{\overline{N}}$
is representable, it has relative dimension
![]() $\dim G_{k}-\dim Z_{G_{k}}(N_{k})$
over
$\dim G_{k}-\dim Z_{G_{k}}(N_{k})$
over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Proof. Given
![]() $N\in \operatorname{Nil}_{\overline{N}}(R_{1})$
, there exists
$N\in \operatorname{Nil}_{\overline{N}}(R_{1})$
, there exists
![]() $g\in \widehat{G}(R_{1})$
such that
$g\in \widehat{G}(R_{1})$
such that
![]() $gNg^{-1}=N_{\unicode[STIX]{x1D70E}}$
. As
$gNg^{-1}=N_{\unicode[STIX]{x1D70E}}$
. As
![]() $G$
is smooth over
$G$
is smooth over
![]() ${\mathcal{O}}$
, we may find
${\mathcal{O}}$
, we may find
![]() $g^{\prime }\in \widehat{G}(R_{2})$
lifting
$g^{\prime }\in \widehat{G}(R_{2})$
lifting
![]() $g$
. Then
$g$
. Then
![]() $(g^{\prime })^{-1}N_{\unicode[STIX]{x1D70E}}g^{\prime }$
is a lift of
$(g^{\prime })^{-1}N_{\unicode[STIX]{x1D70E}}g^{\prime }$
is a lift of
![]() $N$
to
$N$
to
![]() $R_{2}$
. From its definition, the tangent space to
$R_{2}$
. From its definition, the tangent space to
![]() $\operatorname{Nil}_{\overline{N}}$
is
$\operatorname{Nil}_{\overline{N}}$
is
![]() $\mathfrak{g}_{k}/\mathfrak{z}_{\mathfrak{g}}(N_{k})$
, so the formally smooth
$\mathfrak{g}_{k}/\mathfrak{z}_{\mathfrak{g}}(N_{k})$
, so the formally smooth
![]() $\operatorname{Nil}_{\overline{N}}$
has relative dimension
$\operatorname{Nil}_{\overline{N}}$
has relative dimension
![]() $\dim G_{k}-\dim Z_{G_{k}}(N_{k})$
since
$\dim G_{k}-\dim Z_{G_{k}}(N_{k})$
since
![]() $Z_{G}(N)$
is
$Z_{G}(N)$
is
![]() ${\mathcal{O}}$
-smooth.◻
${\mathcal{O}}$
-smooth.◻
Lemma 3.12. Suppose that
![]() $A$
is a complete local Noetherian
$A$
is a complete local Noetherian
![]() ${\mathcal{O}}$
-algebra with residue field
${\mathcal{O}}$
-algebra with residue field
![]() $k$
. Under the assumption that
$k$
. Under the assumption that
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
![]() ${\mathcal{O}}$
-smooth, the inverse limit
${\mathcal{O}}$
-smooth, the inverse limit
![]() $\varprojlim \operatorname{Nil}_{\overline{N}}(A/\mathfrak{m}_{A}^{n})$
equals
$\varprojlim \operatorname{Nil}_{\overline{N}}(A/\mathfrak{m}_{A}^{n})$
equals
![]() $\{N\in \mathfrak{g}_{A}:N=gN_{\unicode[STIX]{x1D70E}}g^{-1}\text{ for some }g\in G(A)\}$
.
$\{N\in \mathfrak{g}_{A}:N=gN_{\unicode[STIX]{x1D70E}}g^{-1}\text{ for some }g\in G(A)\}$
.
Proof. This is immediate since
![]() $A$
is complete and
$A$
is complete and
![]() $\operatorname{Nil}_{\overline{N}}$
is representable by an affine scheme.◻
$\operatorname{Nil}_{\overline{N}}$
is representable by an affine scheme.◻
Remark 3.13. If we had defined
![]() $\operatorname{Nil}_{\overline{N}}$
on the larger category
$\operatorname{Nil}_{\overline{N}}$
on the larger category
![]() $\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
in the obvious way, Lemma 3.12 would say that
$\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
in the obvious way, Lemma 3.12 would say that
![]() $\operatorname{Nil}_{\overline{N}}$
is continuous.
$\operatorname{Nil}_{\overline{N}}$
is continuous.
Remark 3.14. There is no problem generalizing Definition 3.9 to any almost-reductive group, using a construction of
![]() $N_{\unicode[STIX]{x1D70E}}$
using root data as discussed in Remark 3.1. However, we only establish the smoothness of
$N_{\unicode[STIX]{x1D70E}}$
using root data as discussed in Remark 3.1. However, we only establish the smoothness of
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
for classical groups.
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
for classical groups.
Remark 3.15. One can define a scheme-theoretic ‘nilpotent cone’ over
![]() ${\mathcal{O}}$
as the vanishing locus of the ideal of non-constant homogeneous
${\mathcal{O}}$
as the vanishing locus of the ideal of non-constant homogeneous
![]() $G$
-invariant polynomials on
$G$
-invariant polynomials on
![]() $\mathfrak{g}$
. The arguments in this section could be rephrased as constructing a formal scheme of pure nilpotents inside the formal neighborhood of
$\mathfrak{g}$
. The arguments in this section could be rephrased as constructing a formal scheme of pure nilpotents inside the formal neighborhood of
![]() $\overline{N}$
in
$\overline{N}$
in
![]() $\text{}\underline{\mathfrak{g}}$
. A natural question is whether there is a broader notion of pure nilpotents that gives a locally closed subscheme of the scheme-theoretic nilpotent cone. For instance, for
$\text{}\underline{\mathfrak{g}}$
. A natural question is whether there is a broader notion of pure nilpotents that gives a locally closed subscheme of the scheme-theoretic nilpotent cone. For instance, for
![]() $N,N^{\prime }\in \mathfrak{g}$
, if their images in
$N,N^{\prime }\in \mathfrak{g}$
, if their images in
![]() $\mathfrak{g}_{K}$
and
$\mathfrak{g}_{K}$
and
![]() $\mathfrak{g}_{k}$
are nilpotent in orbits with the same combinatorial parameters, are
$\mathfrak{g}_{k}$
are nilpotent in orbits with the same combinatorial parameters, are
![]() $N$
and
$N$
and
![]() $N^{\prime }$
conjugate under
$N^{\prime }$
conjugate under
![]() $G$
over a discrete valuation ring local over
$G$
over a discrete valuation ring local over
![]() ${\mathcal{O}}$
?
${\mathcal{O}}$
?
When
![]() $G=\operatorname{GL}_{n}$
, this has been explored by Taylor in the course of constructing local deformation conditions [Reference TaylorTay08, Lemma 2.5]. The method uses the explicit description of the orbit closures given by specifying the Jordan canonical form to define an analogue of the orbit closures over
$G=\operatorname{GL}_{n}$
, this has been explored by Taylor in the course of constructing local deformation conditions [Reference TaylorTay08, Lemma 2.5]. The method uses the explicit description of the orbit closures given by specifying the Jordan canonical form to define an analogue of the orbit closures over
![]() ${\mathcal{O}}$
. It would be interesting to find a way to do so more generally.
${\mathcal{O}}$
. It would be interesting to find a way to do so more generally.
4 Smoothness of centralizers of pure nilpotents
In order for the functor
![]() $\operatorname{Nil}_{\overline{N}}$
to be representable, we need that
$\operatorname{Nil}_{\overline{N}}$
to be representable, we need that
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
![]() ${\mathcal{O}}$
-smooth. Recall that for
${\mathcal{O}}$
-smooth. Recall that for
![]() $N\in \mathfrak{g}$
, the scheme-theoretic centralizer
$N\in \mathfrak{g}$
, the scheme-theoretic centralizer
![]() $Z_{G}(N)$
represents the functor
$Z_{G}(N)$
represents the functor
for
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
![]() $R$
. We will study the centralizer
$R$
. We will study the centralizer
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
in more detail where
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
in more detail where
![]() $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
is an element satisfying (3.1). In particular, this centralizer will be shown to be smooth when
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
is an element satisfying (3.1). In particular, this centralizer will be shown to be smooth when
![]() $G$
is symplectic or orthogonal. We first review the known theory over fields, and then develop and apply a technique to deduce smoothness over
$G$
is symplectic or orthogonal. We first review the known theory over fields, and then develop and apply a technique to deduce smoothness over
![]() ${\mathcal{O}}$
(i.e.
${\mathcal{O}}$
(i.e.
![]() ${\mathcal{O}}$
-flatness) from the known smoothness in the field case.
${\mathcal{O}}$
-flatness) from the known smoothness in the field case.
4.1 Centralizers over fields
In this section, let
![]() $k$
be an algebraically closed field,
$k$
be an algebraically closed field,
![]() $G$
be a connected reductive group over
$G$
be a connected reductive group over
![]() $k$
, and
$k$
, and
![]() $N$
a nilpotent element of
$N$
a nilpotent element of
![]() $\mathfrak{g}=\operatorname{Lie}G$
. As the formation of the scheme-theoretic centralizer commutes with base change, smoothness results for
$\mathfrak{g}=\operatorname{Lie}G$
. As the formation of the scheme-theoretic centralizer commutes with base change, smoothness results for
![]() $Z_{G}(N)$
over
$Z_{G}(N)$
over
![]() $k$
will imply such results over general fields (not necessarily algebraically closed).
$k$
will imply such results over general fields (not necessarily algebraically closed).
The group scheme
![]() $Z_{G}(N)$
is the fiber over
$Z_{G}(N)$
is the fiber over
![]() $0\in \mathfrak{g}$
of the composition
$0\in \mathfrak{g}$
of the composition
Hence
![]() $\operatorname{Lie}Z_{G}(N)$
is the kernel of
$\operatorname{Lie}Z_{G}(N)$
is the kernel of
which is the Lie algebra centralizer
![]() $\mathfrak{z}_{\mathfrak{g}}(N)$
.
$\mathfrak{z}_{\mathfrak{g}}(N)$
.
Remark 4.1. In references using the language of varieties rather than schemes (such as [Reference JantzenJan04]),
![]() $Z_{G}(N)$
is usually defined via its geometric points and hence is reduced and smooth, so the condition that the scheme
$Z_{G}(N)$
is usually defined via its geometric points and hence is reduced and smooth, so the condition that the scheme
![]() $Z_{G}(N)$
is smooth becomes the condition that the variety
$Z_{G}(N)$
is smooth becomes the condition that the variety
![]() $Z_{G}(N)$
has Lie algebra
$Z_{G}(N)$
has Lie algebra
![]() $\mathfrak{z}_{\mathfrak{g}}(N)$
.
$\mathfrak{z}_{\mathfrak{g}}(N)$
.
In a wide range of situations, all nilpotent centralizers are smooth. A direct calculation shows that this holds for
![]() $G=\operatorname{GL}_{n}$
(see [Reference JantzenJan04, § 2.3]), and a criterion of Richardson [Reference JantzenJan04, Theorem 2.5] can be applied to show to following.
$G=\operatorname{GL}_{n}$
(see [Reference JantzenJan04, § 2.3]), and a criterion of Richardson [Reference JantzenJan04, Theorem 2.5] can be applied to show to following.
Fact 4.2. If
![]() $G$
is an orthogonal or symplectic (similitude) group, any nilpotent centralizer is smooth over
$G$
is an orthogonal or symplectic (similitude) group, any nilpotent centralizer is smooth over
![]() $k$
.
$k$
.
Remark 4.3. Suppose
![]() $Z_{G}(N)$
is smooth over
$Z_{G}(N)$
is smooth over
![]() $k$
and
$k$
and
![]() $p$
is good for
$p$
is good for
![]() $G$
. The classification of nilpotent orbits is independent of
$G$
. The classification of nilpotent orbits is independent of
![]() $p$
, as are their dimensions, so the dimension of
$p$
, as are their dimensions, so the dimension of
![]() $Z_{G}(N)$
is independent of
$Z_{G}(N)$
is independent of
![]() $p$
as well.
$p$
as well.
4.2 Checking flatness over a Dedekind base
We want to analyze smoothness of centralizers in the relative setting (especially over
![]() $\operatorname{Spec}{\mathcal{O}}$
). If
$\operatorname{Spec}{\mathcal{O}}$
). If
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})\rightarrow \operatorname{Spec}{\mathcal{O}}$
is flat and the special and generic fibers are smooth, then
$Z_{G}(N_{\unicode[STIX]{x1D70E}})\rightarrow \operatorname{Spec}{\mathcal{O}}$
is flat and the special and generic fibers are smooth, then
![]() $Z_{G}(N)$
is smooth over
$Z_{G}(N)$
is smooth over
![]() ${\mathcal{O}}$
. The following lemma gives a way to check that a morphism to a Dedekind scheme is flat.
${\mathcal{O}}$
. The following lemma gives a way to check that a morphism to a Dedekind scheme is flat.
Lemma 4.4. Let
![]() $f:X\rightarrow S$
be finite type for a connected Dedekind scheme
$f:X\rightarrow S$
be finite type for a connected Dedekind scheme
![]() $S$
. Then
$S$
. Then
![]() $f$
is flat provided the following all hold.
$f$
is flat provided the following all hold.
(i) For each
 $s\in S$
,
$s\in S$
,
 $X_{s}$
is reduced and non-empty.
$X_{s}$
is reduced and non-empty.(ii) For each
 $s\in S$
,
$s\in S$
,
 $X_{s}$
is equidimensional with dimension independent of
$X_{s}$
is equidimensional with dimension independent of
 $s$
.
$s$
.(iii) There are sections
 $\{\unicode[STIX]{x1D70E}_{i}\in X(S)\}$
to
$\{\unicode[STIX]{x1D70E}_{i}\in X(S)\}$
to
 $f$
such that for every irreducible component of a fiber above a closed point, there is a section
$f$
such that for every irreducible component of a fiber above a closed point, there is a section
 $\unicode[STIX]{x1D70E}_{i}$
which meets the fiber only in that component.
$\unicode[STIX]{x1D70E}_{i}$
which meets the fiber only in that component.
Remark 4.5. This lemma is a modification of [Reference Gan and YuGY03, Proposition 6.1] to allow multiple irreducible components in the fibers.
Proof. It suffices to prove the result when
![]() $S=\operatorname{Spec}(A)$
for
$S=\operatorname{Spec}(A)$
for
![]() $A$
a discrete valuation ring with uniformizer
$A$
a discrete valuation ring with uniformizer
![]() $\unicode[STIX]{x1D70B}$
. Let
$\unicode[STIX]{x1D70B}$
. Let
![]() $X_{\unicode[STIX]{x1D702}}$
be the generic fiber and
$X_{\unicode[STIX]{x1D702}}$
be the generic fiber and
![]() $X_{s}$
the special fiber. Consider the schematic closure
$X_{s}$
the special fiber. Consider the schematic closure
![]() $\imath :X^{\prime }{\hookrightarrow}X$
of the generic fiber. The scheme
$\imath :X^{\prime }{\hookrightarrow}X$
of the generic fiber. The scheme
![]() $X^{\prime }$
is flat over
$X^{\prime }$
is flat over
![]() $\operatorname{Spec}(A)$
since flatness is equivalent to being torsion-free over a discrete valuation ring, and there is an exact sequence
$\operatorname{Spec}(A)$
since flatness is equivalent to being torsion-free over a discrete valuation ring, and there is an exact sequence
where
![]() $J$
is a coherent sheaf killed by a power of
$J$
is a coherent sheaf killed by a power of
![]() $\unicode[STIX]{x1D70B}$
. We will show that
$\unicode[STIX]{x1D70B}$
. We will show that
![]() $\imath$
is an isomorphism by analyzing the special fiber.
$\imath$
is an isomorphism by analyzing the special fiber.
First, we claim that the dimension of each irreducible component on the special fiber of
![]() $X^{\prime }$
is the same as the dimension of the equidimensional
$X^{\prime }$
is the same as the dimension of the equidimensional
![]() $X_{\unicode[STIX]{x1D702}}$
. We will get this from flatness of
$X_{\unicode[STIX]{x1D702}}$
. We will get this from flatness of
![]() $X^{\prime }$
. The generic fiber of
$X^{\prime }$
. The generic fiber of
![]() $X^{\prime }$
is
$X^{\prime }$
is
![]() $X_{\unicode[STIX]{x1D702}}$
, which is equidimensional and non-empty by hypothesis. Furthermore,
$X_{\unicode[STIX]{x1D702}}$
, which is equidimensional and non-empty by hypothesis. Furthermore,
![]() $X^{\prime }$
is the union of the closures
$X^{\prime }$
is the union of the closures
![]() $Z_{i}$
of the reduced irreducible components
$Z_{i}$
of the reduced irreducible components
![]() $X_{\unicode[STIX]{x1D702},i}$
of
$X_{\unicode[STIX]{x1D702},i}$
of
![]() $X_{\unicode[STIX]{x1D702}}$
, and each
$X_{\unicode[STIX]{x1D702}}$
, and each
![]() $Z_{i}$
is
$Z_{i}$
is
![]() $A$
-flat with integral
$A$
-flat with integral
![]() $\unicode[STIX]{x1D702}$
-fiber, hence integral. We just need to analyze the dimension of irreducible components of
$\unicode[STIX]{x1D702}$
-fiber, hence integral. We just need to analyze the dimension of irreducible components of
![]() $(Z_{i})_{s}$
when
$(Z_{i})_{s}$
when
![]() $(Z_{i})_{s}\neq \emptyset$
. Since
$(Z_{i})_{s}\neq \emptyset$
. Since
![]() $Z_{i}$
is integral, we can apply [Reference MatsumuraMat89, Theorem 15.1, 15.5] to such
$Z_{i}$
is integral, we can apply [Reference MatsumuraMat89, Theorem 15.1, 15.5] to such
![]() $Z_{i}$
to conclude that the dimension of each irreducible component of the special fiber of
$Z_{i}$
to conclude that the dimension of each irreducible component of the special fiber of
![]() $X^{\prime }$
is the same as the dimension of the generic fiber.
$X^{\prime }$
is the same as the dimension of the generic fiber.
Observe that the sections
![]() $\unicode[STIX]{x1D70E}_{i}$
factor through the closed subscheme
$\unicode[STIX]{x1D70E}_{i}$
factor through the closed subscheme
![]() $X^{\prime }\subset X$
, as we can check this on the generic fiber since
$X^{\prime }\subset X$
, as we can check this on the generic fiber since
![]() $X^{\prime }$
is
$X^{\prime }$
is
![]() $A$
-flat. Thus
$A$
-flat. Thus
![]() $X^{\prime }$
meets every irreducible component of
$X^{\prime }$
meets every irreducible component of
![]() $X_{s}$
away from the other irreducible components of
$X_{s}$
away from the other irreducible components of
![]() $X_{s}$
. We would have that
$X_{s}$
. We would have that
![]() $|X_{s}^{\prime }|=|X_{s}|$
if
$|X_{s}^{\prime }|=|X_{s}|$
if
![]() $X_{s}^{\prime }$
is equidimensional of the same dimension as the equidimensional
$X_{s}^{\prime }$
is equidimensional of the same dimension as the equidimensional
![]() $X_{s}$
. We have shown the dimension of any irreducible component in
$X_{s}$
. We have shown the dimension of any irreducible component in
![]() $X_{s}^{\prime }$
is the same dimension as the common dimension of irreducible components of the generic fiber
$X_{s}^{\prime }$
is the same dimension as the common dimension of irreducible components of the generic fiber
![]() $X_{\unicode[STIX]{x1D702}}$
of
$X_{\unicode[STIX]{x1D702}}$
of
![]() $X^{\prime }$
. By hypothesis, the dimension of any irreducible component of the generic fiber of
$X^{\prime }$
. By hypothesis, the dimension of any irreducible component of the generic fiber of
![]() $X$
is the same as the dimension of any irreducible component of the special fiber of
$X$
is the same as the dimension of any irreducible component of the special fiber of
![]() $X$
. Thus the dimension of any irreducible component of
$X$
. Thus the dimension of any irreducible component of
![]() $X_{s}^{\prime }$
is the same as the dimension of each irreducible component of
$X_{s}^{\prime }$
is the same as the dimension of each irreducible component of
![]() $X_{s}$
, giving that
$X_{s}$
, giving that
![]() $|X_{s}^{\prime }|=|X_{s}|$
. As
$|X_{s}^{\prime }|=|X_{s}|$
. As
![]() $X_{s}$
is reduced, this forces
$X_{s}$
is reduced, this forces
![]() $\imath _{s}:X_{s}^{\prime }{\hookrightarrow}X_{s}$
to be an isomorphism.
$\imath _{s}:X_{s}^{\prime }{\hookrightarrow}X_{s}$
to be an isomorphism.
Now tensoring (4.1) with the residue field of
![]() $A$
gives an exact sequence
$A$
gives an exact sequence
because
![]() ${\mathcal{O}}_{X^{\prime }}$
is
${\mathcal{O}}_{X^{\prime }}$
is
![]() $A$
-flat. But
$A$
-flat. But
![]() $J/\unicode[STIX]{x1D70B}J=0$
as
$J/\unicode[STIX]{x1D70B}J=0$
as
![]() $\imath _{s}$
is an isomorphism. Hence
$\imath _{s}$
is an isomorphism. Hence
![]() $J=\unicode[STIX]{x1D70B}J=\unicode[STIX]{x1D70B}^{2}J=\cdots =\unicode[STIX]{x1D70B}^{n}J=0$
for
$J=\unicode[STIX]{x1D70B}J=\unicode[STIX]{x1D70B}^{2}J=\cdots =\unicode[STIX]{x1D70B}^{n}J=0$
for
![]() $n$
large, so
$n$
large, so
![]() $X=X^{\prime }$
is flat over
$X=X^{\prime }$
is flat over
![]() $A$
.◻
$A$
.◻
Corollary 4.6. In the situation of the lemma, if the fibers are also smooth, then
![]() $X$
is smooth.
$X$
is smooth.
Proof. For a flat morphism of finite type between Noetherian schemes, smoothness of all fibers is equivalent to smoothness of the morphism.◻
4.3 Centralizers for orthogonal and symplectic groups
To apply Corollary 4.6, we need information about the component group of centralizers of nilpotents. For
![]() $\operatorname{GL}_{n}$
over a field, all such centralizers are connected. For symplectic and orthogonal groups, there is an explicit description of
$\operatorname{GL}_{n}$
over a field, all such centralizers are connected. For symplectic and orthogonal groups, there is an explicit description of
![]() $Z(N_{\unicode[STIX]{x1D70E}})$
where
$Z(N_{\unicode[STIX]{x1D70E}})$
where
![]() $N_{\unicode[STIX]{x1D70E}}$
is the nilpotent constructed in § 3. We continue the notation of that section:
$N_{\unicode[STIX]{x1D70E}}$
is the nilpotent constructed in § 3. We continue the notation of that section:
![]() $G$
is
$G$
is
![]() $\operatorname{Sp}_{m}$
or
$\operatorname{Sp}_{m}$
or
![]() $\operatorname{O}_{m}$
(with
$\operatorname{O}_{m}$
(with
![]() $m\geqslant 4$
) over a discrete valuation ring
$m\geqslant 4$
) over a discrete valuation ring
![]() ${\mathcal{O}}$
with a residue field
${\mathcal{O}}$
with a residue field
![]() $k$
of good characteristic
$k$
of good characteristic
![]() $p\neq 2$
.
$p\neq 2$
.
Let
![]() $\unicode[STIX]{x1D70E}:m_{1}+\cdots +m_{r}$
be an admissible partition of
$\unicode[STIX]{x1D70E}:m_{1}+\cdots +m_{r}$
be an admissible partition of
![]() $m$
. We assume that
$m$
. We assume that
![]() ${\mathcal{O}}$
is large enough so that Proposition 3.7 holds, and take
${\mathcal{O}}$
is large enough so that Proposition 3.7 holds, and take
![]() $N:=N_{\unicode[STIX]{x1D70E}}$
. Then there exists elements
$N:=N_{\unicode[STIX]{x1D70E}}$
. Then there exists elements
![]() $v_{1},\ldots ,v_{r}\in M:={\mathcal{O}}^{m}$
such that
$v_{1},\ldots ,v_{r}\in M:={\mathcal{O}}^{m}$
such that
is a basis for
![]() $M$
. Furthermore,
$M$
. Furthermore,
![]() $N^{m_{i}}v_{i}=0$
for
$N^{m_{i}}v_{i}=0$
for
![]() $i=1,\ldots r$
, and the pairing between basis elements is given by
$i=1,\ldots r$
, and the pairing between basis elements is given by
![]() $\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
. In particular, each
$\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
. In particular, each
![]() $v_{i}$
pairs non-trivially with only one other basis element
$v_{i}$
pairs non-trivially with only one other basis element
![]() $X^{d_{i}-1}v_{i^{\ast }}$
, for some
$X^{d_{i}-1}v_{i^{\ast }}$
, for some
![]() $i^{\ast }\in \{1,\ldots ,r\}$
.
$i^{\ast }\in \{1,\ldots ,r\}$
.
To understand the
![]() $G$
-centralizer of
$G$
-centralizer of
![]() $N$
, we construct an associated grading of
$N$
, we construct an associated grading of
![]() $M$
as in [Reference JantzenJan04, § 3.3,3.4]. This is motivated by the Jacobson–Morosov theory of
$M$
as in [Reference JantzenJan04, § 3.3,3.4]. This is motivated by the Jacobson–Morosov theory of
![]() $\mathfrak{sl}_{2}$
-triples over a field of sufficiently large characteristic, but for symplectic and orthogonal groups it is constructed by hand in characteristic
$\mathfrak{sl}_{2}$
-triples over a field of sufficiently large characteristic, but for symplectic and orthogonal groups it is constructed by hand in characteristic
![]() $p\neq 2$
below.
$p\neq 2$
below.
Remark 4.7. Let
![]() $M_{k}=M\otimes _{{\mathcal{O}}}k=k^{m}$
. Every nilpotent
$M_{k}=M\otimes _{{\mathcal{O}}}k=k^{m}$
. Every nilpotent
![]() $X\in \operatorname{End}(M_{k})$
gives a filtration (and grading) of
$X\in \operatorname{End}(M_{k})$
gives a filtration (and grading) of
![]() $M_{k}$
defined by
$M_{k}$
defined by
![]() $\operatorname{Fil}^{i}=\ker (X^{i})$
. For
$\operatorname{Fil}^{i}=\ker (X^{i})$
. For
![]() $\operatorname{GL}_{n}$
, this is a nice filtration and is used in [Reference Clozel, Harris and TaylorCHT08] to define the minimally ramified deformation condition for
$\operatorname{GL}_{n}$
, this is a nice filtration and is used in [Reference Clozel, Harris and TaylorCHT08] to define the minimally ramified deformation condition for
![]() $\operatorname{GL}_{n}$
. However, this filtration need not be isotropic with respect to the pairing, so we will construct a nicer grading associated to
$\operatorname{GL}_{n}$
. However, this filtration need not be isotropic with respect to the pairing, so we will construct a nicer grading associated to
![]() $X$
.
$X$
.
Definition 4.8. Let
![]() $M(s)$
be the span of
$M(s)$
be the span of
![]() $N^{j}v_{i}$
for all
$N^{j}v_{i}$
for all
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $s=2j+1-m_{i}$
. We set
$s=2j+1-m_{i}$
. We set
![]() $M^{(s)}=\bigoplus _{t\geqslant s}M(t)$
, and also define
$M^{(s)}=\bigoplus _{t\geqslant s}M(t)$
, and also define
![]() $L(s)$
to be the span of
$L(s)$
to be the span of
![]() $\{v_{i}:v_{i}\in M(s)\}$
.
$\{v_{i}:v_{i}\in M(s)\}$
.
We now record some elementary properties of the preceding construction; all are routine to check, and the analogous proofs over a field may be found in [Reference JantzenJan04, § 3.4]. We have that
![]() $M=\bigoplus _{s}M(s)$
, and
$M=\bigoplus _{s}M(s)$
, and
Furthermore, we know
![]() $N\cdot M(s)\subset M(s+2)$
and
$N\cdot M(s)\subset M(s+2)$
and
![]() $M(s)=N\cdot M(s-2)\oplus L(s)$
for
$M(s)=N\cdot M(s-2)\oplus L(s)$
for
![]() $s\leqslant 0$
.
$s\leqslant 0$
.
The dimension of
![]() $M(s)$
is
$M(s)$
is
![]() $m_{s}(\unicode[STIX]{x1D70E}):=\text{\#}\{j:d_{j}-1\geqslant |s|\}$
. The dimension of
$m_{s}(\unicode[STIX]{x1D70E}):=\text{\#}\{j:d_{j}-1\geqslant |s|\}$
. The dimension of
![]() $L(s)$
equals
$L(s)$
equals
![]() $l_{s}(\unicode[STIX]{x1D70E}):=m_{s+1}(\unicode[STIX]{x1D70E})-m_{s}(\unicode[STIX]{x1D70E})$
. Furthermore, the pairing
$l_{s}(\unicode[STIX]{x1D70E}):=m_{s+1}(\unicode[STIX]{x1D70E})-m_{s}(\unicode[STIX]{x1D70E})$
. Furthermore, the pairing
![]() $\unicode[STIX]{x1D711}$
interacts well with the grading: a computation with basis elements gives that
$\unicode[STIX]{x1D711}$
interacts well with the grading: a computation with basis elements gives that
![]() $\unicode[STIX]{x1D711}(M(s),M(t))\neq 0$
implies
$\unicode[STIX]{x1D711}(M(s),M(t))\neq 0$
implies
![]() $s+t=0$
.
$s+t=0$
.
The above grading on
![]() $M$
corresponds to the one-parameter subgroup
$M$
corresponds to the one-parameter subgroup
![]() $\unicode[STIX]{x1D706}:\mathbf{G}_{m}\rightarrow G$
for which the action of
$\unicode[STIX]{x1D706}:\mathbf{G}_{m}\rightarrow G$
for which the action of
![]() $t\in \mathbf{G}_{m}$
on
$t\in \mathbf{G}_{m}$
on
![]() $M(s)$
is given by scaling by
$M(s)$
is given by scaling by
![]() $t^{s}$
. The dynamic method (see [Reference Conrad, Gabber and PrasadCGP15, § 2.1]) associates to
$t^{s}$
. The dynamic method (see [Reference Conrad, Gabber and PrasadCGP15, § 2.1]) associates to
![]() $\unicode[STIX]{x1D706}$
a parabolic subgroup
$\unicode[STIX]{x1D706}$
a parabolic subgroup
![]() $P_{G}(\unicode[STIX]{x1D706})$
with Levi
$P_{G}(\unicode[STIX]{x1D706})$
with Levi
![]() $Z_{G}(\unicode[STIX]{x1D706})$
. Define
$Z_{G}(\unicode[STIX]{x1D706})$
. Define
![]() $C_{N}$
and
$C_{N}$
and
![]() $U_{N}$
to be the scheme-theoretic intersections
$U_{N}$
to be the scheme-theoretic intersections
Fact 4.9. The group-scheme
![]() $Z_{G}(N)_{k}$
is a semidirect product of
$Z_{G}(N)_{k}$
is a semidirect product of
![]() $(C_{N})_{k}$
and the smooth connected unipotent subgroup
$(C_{N})_{k}$
and the smooth connected unipotent subgroup
![]() $(U_{N})_{k}$
. In particular, the connected components of
$(U_{N})_{k}$
. In particular, the connected components of
![]() $Z_{G}(N)_{k}$
are the same as the connected components of
$Z_{G}(N)_{k}$
are the same as the connected components of
![]() $(C_{N})_{k}$
.
$(C_{N})_{k}$
.
Remark 4.10. This is [Reference JantzenJan04, Proposition 3.12]. The existence of
![]() $\unicode[STIX]{x1D706}$
and this decomposition is not specific to symplectic and orthogonal groups [Reference JantzenJan04, Proposition 5.10].
$\unicode[STIX]{x1D706}$
and this decomposition is not specific to symplectic and orthogonal groups [Reference JantzenJan04, Proposition 5.10].
We finally give a concrete description of
![]() $C_{N}$
. We first define a pairing on
$C_{N}$
. We first define a pairing on
![]() $L(s)$
. Recall that the space
$L(s)$
. Recall that the space
![]() $L(s)$
of ‘lowest weight vectors’ in
$L(s)$
of ‘lowest weight vectors’ in
![]() $M(s)$
has basis
$M(s)$
has basis
![]() $\{v_{i}:1-d_{i}=s\}$
. We define a pairing on
$\{v_{i}:1-d_{i}=s\}$
. We define a pairing on
![]() $L(s)$
by
$L(s)$
by
A direct calculation shows that
![]() $\unicode[STIX]{x1D713}_{s}$
is non-degenerate and that
$\unicode[STIX]{x1D713}_{s}$
is non-degenerate and that
![]() $\unicode[STIX]{x1D713}_{s}$
is symmetric if
$\unicode[STIX]{x1D713}_{s}$
is symmetric if
![]() $(-1)^{s}=\unicode[STIX]{x1D716}$
and is alternating if
$(-1)^{s}=\unicode[STIX]{x1D716}$
and is alternating if
![]() $(-1)^{s}=-\unicode[STIX]{x1D716}$
[Reference JantzenJan04, § 3.7].
$(-1)^{s}=-\unicode[STIX]{x1D716}$
[Reference JantzenJan04, § 3.7].
A point of
![]() $C_{N}$
preserves the grading on
$C_{N}$
preserves the grading on
![]() $M$
, and since it commutes with the ‘raising operator’
$M$
, and since it commutes with the ‘raising operator’
![]() $N$
its action on
$N$
its action on
![]() $M$
is determined by its action on the space
$M$
is determined by its action on the space
![]() $L(s)$
of ‘lowest weight vectors’ in
$L(s)$
of ‘lowest weight vectors’ in
![]() $M(s)$
. So the following fact is no surprise.
$M(s)$
. So the following fact is no surprise.
Proposition 4.11. There is an isomorphism of algebraic groups
The corresponding statement over a field is [Reference JantzenJan04, § 3.8 Propositions 2, 3]: the proof is the same.
Example 4.12. Let
![]() $G=\operatorname{Sp}_{m}$
. Unraveling when
$G=\operatorname{Sp}_{m}$
. Unraveling when
![]() $\unicode[STIX]{x1D713}_{s}$
is symmetric or alternating, we see that
$\unicode[STIX]{x1D713}_{s}$
is symmetric or alternating, we see that
The special fibers of the symplectic factors are connected, while the orthogonal factors have two connected components in the special fiber. Thus there are
![]() $2^{t}$
connected components, where
$2^{t}$
connected components, where
![]() $t$
is the number of odd
$t$
is the number of odd
![]() $s$
for which
$s$
for which
![]() $L(s)\neq 0$
. For each component, there is a section
$L(s)\neq 0$
. For each component, there is a section
![]() $g\in C_{N}({\mathcal{O}})$
meeting that component corresponding to a choice of
$g\in C_{N}({\mathcal{O}})$
meeting that component corresponding to a choice of
![]() $\pm \operatorname{Id}\in \operatorname{O}(L(s),\unicode[STIX]{x1D713}_{s})$
for each odd
$\pm \operatorname{Id}\in \operatorname{O}(L(s),\unicode[STIX]{x1D713}_{s})$
for each odd
![]() $s$
with
$s$
with
![]() $L(s)\neq 0$
. The connected components of
$L(s)\neq 0$
. The connected components of
![]() $Z_{G}(N)$
are the same as those for
$Z_{G}(N)$
are the same as those for
![]() $C_{N}$
by Fact 4.9.
$C_{N}$
by Fact 4.9.
Example 4.13. Let
![]() $G=\operatorname{O}_{m}$
. We likewise see that
$G=\operatorname{O}_{m}$
. We likewise see that
Again there are
![]() $2^{t}$
connected components of
$2^{t}$
connected components of
![]() $Z_{G}(N)$
, where
$Z_{G}(N)$
, where
![]() $t$
is the number of even
$t$
is the number of even
![]() $s$
for which
$s$
for which
![]() $L(s)\neq 0$
.
$L(s)\neq 0$
.
Now suppose that
![]() $G=\operatorname{SO}_{m}$
. The elements
$G=\operatorname{SO}_{m}$
. The elements
![]() $N$
we considered in this section are representatives for some of the nilpotent orbits of
$N$
we considered in this section are representatives for some of the nilpotent orbits of
![]() $\operatorname{SO}_{m}$
. The group
$\operatorname{SO}_{m}$
. The group
![]() $C_{N}$
has the same structure as for
$C_{N}$
has the same structure as for
![]() $G=\operatorname{O}_{m}$
, except we require that the overall determinant be
$G=\operatorname{O}_{m}$
, except we require that the overall determinant be
![]() $1$
; this has
$1$
; this has
![]() $2^{t-1}$
connected components. Though
$2^{t-1}$
connected components. Though
![]() $\operatorname{SO}_{m}$
has more nilpotent orbits than
$\operatorname{SO}_{m}$
has more nilpotent orbits than
![]() $\operatorname{O}_{m}$
, according to Remark 3.3 their representatives are conjugate by an element
$\operatorname{O}_{m}$
, according to Remark 3.3 their representatives are conjugate by an element
![]() $\operatorname{O}_{m}(k)$
with determinant
$\operatorname{O}_{m}(k)$
with determinant
![]() $-1$
to the representatives constructed in Proposition 3.7. This shows that there are sections
$-1$
to the representatives constructed in Proposition 3.7. This shows that there are sections
![]() $g\in C_{N}({\mathcal{O}})$
meeting each component.
$g\in C_{N}({\mathcal{O}})$
meeting each component.
Remark 4.14. Suppose
![]() $q$
is a square in
$q$
is a square in
![]() ${\mathcal{O}}^{\times }$
. For use in the proof of Proposition 5.6, we need the existence of an element
${\mathcal{O}}^{\times }$
. For use in the proof of Proposition 5.6, we need the existence of an element
![]() $\unicode[STIX]{x1D6F7}\in G({\mathcal{O}})$
such that
$\unicode[STIX]{x1D6F7}\in G({\mathcal{O}})$
such that
![]() $\operatorname{ad}_{G}(\unicode[STIX]{x1D6F7})N_{\unicode[STIX]{x1D70E}}=qN_{\unicode[STIX]{x1D70E}}$
. If
$\operatorname{ad}_{G}(\unicode[STIX]{x1D6F7})N_{\unicode[STIX]{x1D70E}}=qN_{\unicode[STIX]{x1D70E}}$
. If
![]() $\unicode[STIX]{x1D6FC}^{2}=q$
, taking
$\unicode[STIX]{x1D6FC}^{2}=q$
, taking
![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC})$
would work:
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC})$
would work:
![]() $\unicode[STIX]{x1D6F7}$
would scale
$\unicode[STIX]{x1D6F7}$
would scale
![]() $N_{\unicode[STIX]{x1D70E}}^{j}v_{i}\in M(s)$
by
$N_{\unicode[STIX]{x1D70E}}^{j}v_{i}\in M(s)$
by
![]() $\unicode[STIX]{x1D6FC}^{s}$
, and
$\unicode[STIX]{x1D6FC}^{s}$
, and
![]() $N_{\unicode[STIX]{x1D70E}}$
increases the degree by
$N_{\unicode[STIX]{x1D70E}}$
increases the degree by
![]() $2$
.
$2$
.
This
![]() $\unicode[STIX]{x1D6F7}$
is a version for symplectic and orthogonal groups of the diagonal matrix denoted
$\unicode[STIX]{x1D6F7}$
is a version for symplectic and orthogonal groups of the diagonal matrix denoted
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70E},a,q)$
whose diagonal entries are increasing powers of
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70E},a,q)$
whose diagonal entries are increasing powers of
![]() $q$
used in [Reference TaylorTay08, §2.3]. There it is checked that
$q$
used in [Reference TaylorTay08, §2.3]. There it is checked that
![]() $\operatorname{ad}_{G}(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70E},a,q))N_{\unicode[STIX]{x1D70E}}=qN_{\unicode[STIX]{x1D70E}}$
where
$\operatorname{ad}_{G}(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70E},a,q))N_{\unicode[STIX]{x1D70E}}=qN_{\unicode[STIX]{x1D70E}}$
where
![]() $N_{\unicode[STIX]{x1D70E}}$
is the nilpotent representative in Jordan canonical form considered in Example 3.2 for the partition
$N_{\unicode[STIX]{x1D70E}}$
is the nilpotent representative in Jordan canonical form considered in Example 3.2 for the partition
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $m$
.
$m$
.
4.4 Smoothness of centralizers
We now return the case when
![]() $G$
is an almost-reductive group over a discrete valuation ring
$G$
is an almost-reductive group over a discrete valuation ring
![]() ${\mathcal{O}}$
with residue field
${\mathcal{O}}$
with residue field
![]() $k$
of very good characteristic
$k$
of very good characteristic
![]() $p>0$
. Suppose we are given an integral representative
$p>0$
. Suppose we are given an integral representative
![]() $N=N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}:=\operatorname{Lie}G$
for the nilpotent orbit on geometric fibers corresponding to
$N=N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}:=\operatorname{Lie}G$
for the nilpotent orbit on geometric fibers corresponding to
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
as in (3.1): that is, an element such that
$\unicode[STIX]{x1D70E}\in {\mathcal{C}}$
as in (3.1): that is, an element such that
Proposition 3.7 provides such
![]() $N$
in symplectic and orthogonal cases when
$N$
in symplectic and orthogonal cases when
![]() $\sqrt{-1},\sqrt{2}\in {\mathcal{O}}^{\times }$
. We wish to check that the
$\sqrt{-1},\sqrt{2}\in {\mathcal{O}}^{\times }$
. We wish to check that the
![]() $Z_{G}(N)$
is smooth over
$Z_{G}(N)$
is smooth over
![]() ${\mathcal{O}}$
. This
${\mathcal{O}}$
. This
![]() $N$
satisfies
$N$
satisfies
Remark 4.15. Some assumption on
![]() $N$
is essential. Otherwise
$N$
is essential. Otherwise
![]() $N_{\overline{K}}$
and
$N_{\overline{K}}$
and
![]() $N_{\overline{k}}$
can lie in different nilpotent orbits (in terms of the combinatorial characteristic-free classification of geometric orbits), and so
$N_{\overline{k}}$
can lie in different nilpotent orbits (in terms of the combinatorial characteristic-free classification of geometric orbits), and so
![]() $Z_{G_{K}}(N_{K})$
and
$Z_{G_{K}}(N_{K})$
and
![]() $Z_{G_{k}}(N_{k})$
could have different dimensions, in which case
$Z_{G_{k}}(N_{k})$
could have different dimensions, in which case
![]() $Z_{G}(N)$
cannot be
$Z_{G}(N)$
cannot be
![]() ${\mathcal{O}}$
-flat. An example of this is the element
${\mathcal{O}}$
-flat. An example of this is the element
![]() $N_{2}$
in Example 1.4.
$N_{2}$
in Example 1.4.
Now we wish to check the conditions necessary to apply Corollary 4.6. We define
and study when the following holds:
Note that this checks the criterion in Corollary 4.6 as
by Lang’s theorem, and since the irreducible components of
![]() $Z_{G_{k}}(N_{K})$
are the same as connected components by smoothness.
$Z_{G_{k}}(N_{K})$
are the same as connected components by smoothness.
We are free to make a local flat extension of
![]() ${\mathcal{O}}$
, as it suffices to check flatness after such an extension. In particular, it suffices to check (4.3) when
${\mathcal{O}}$
, as it suffices to check flatness after such an extension. In particular, it suffices to check (4.3) when
![]() ${\mathcal{O}}$
is Henselian and
${\mathcal{O}}$
is Henselian and
![]() $k$
is algebraically closed, and
$k$
is algebraically closed, and
![]() $\sqrt{-1},\sqrt{2}\in {\mathcal{O}}$
. Examples 4.12 and 4.13 give such sections when
$\sqrt{-1},\sqrt{2}\in {\mathcal{O}}$
. Examples 4.12 and 4.13 give such sections when
![]() $G=\operatorname{Sp}_{m}$
or
$G=\operatorname{Sp}_{m}$
or
![]() $G=\operatorname{SO}_{m}$
. We will use these cases to get a result for similitude groups.
$G=\operatorname{SO}_{m}$
. We will use these cases to get a result for similitude groups.
Let
![]() $\unicode[STIX]{x1D70B}:\widetilde{G^{\prime }}\rightarrow G^{\prime }$
be the simply connected central cover of the derived group
$\unicode[STIX]{x1D70B}:\widetilde{G^{\prime }}\rightarrow G^{\prime }$
be the simply connected central cover of the derived group
![]() $G^{\prime }$
over
$G^{\prime }$
over
![]() ${\mathcal{O}}$
. As
${\mathcal{O}}$
. As
![]() $p$
is very good,
$p$
is very good,
![]() $\widetilde{G^{\prime }}$
and
$\widetilde{G^{\prime }}$
and
![]() $G^{\prime }$
have isomorphic Lie algebras via
$G^{\prime }$
have isomorphic Lie algebras via
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\operatorname{Lie}G^{\prime }$
is a direct factor of
$\operatorname{Lie}G^{\prime }$
is a direct factor of
![]() $\operatorname{Lie}G$
with complement
$\operatorname{Lie}G$
with complement
![]() $\operatorname{Lie}(Z_{G})$
, so we may abuse notation and view
$\operatorname{Lie}(Z_{G})$
, so we may abuse notation and view
![]() $N$
as an element of all of these Lie algebras over
$N$
as an element of all of these Lie algebras over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Let
![]() $S$
be a (split) maximal central torus in
$S$
be a (split) maximal central torus in
![]() $G$
. Consider the isogeny
$G$
. Consider the isogeny
![]() $S\times \widetilde{G^{\prime }}\rightarrow G$
. As
$S\times \widetilde{G^{\prime }}\rightarrow G$
. As
![]() $S$
acts trivially on
$S$
acts trivially on
![]() $N$
, we see that
$N$
, we see that
![]() $S\times Z_{\widetilde{G^{\prime }}}(N)$
is the preimage of
$S\times Z_{\widetilde{G^{\prime }}}(N)$
is the preimage of
![]() $Z_{G^{\prime }}(N)$
under this isogeny. As
$Z_{G^{\prime }}(N)$
under this isogeny. As
![]() $p$
is very good for
$p$
is very good for
![]() $G$
, we obtain finite étale surjections
$G$
, we obtain finite étale surjections
over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Lemma 4.16. The condition (4.3) holds for
![]() $\widetilde{G^{\prime }}$
if and only if (4.3) holds for
$\widetilde{G^{\prime }}$
if and only if (4.3) holds for
![]() $G$
.
$G$
.
Proof. Assume
![]() $\widetilde{G^{\prime }}$
satisfies (4.3). Pick a connected component
$\widetilde{G^{\prime }}$
satisfies (4.3). Pick a connected component
![]() $C$
of
$C$
of
![]() $Z_{G_{k}}(N_{k})$
. The preimage of
$Z_{G_{k}}(N_{k})$
. The preimage of
![]() $C$
under
$C$
under
![]() $S\times Z_{\widetilde{G^{\prime }}}(N)\rightarrow Z_{G}(N)$
is a union of
$S\times Z_{\widetilde{G^{\prime }}}(N)\rightarrow Z_{G}(N)$
is a union of
![]() $k$
-fiber components of the form
$k$
-fiber components of the form
![]() $S_{k}\times C^{\prime }$
where
$S_{k}\times C^{\prime }$
where
![]() $C^{\prime }$
is a connected component of
$C^{\prime }$
is a connected component of
![]() $Z_{\widetilde{G_{k}^{\prime }}}(N_{k})$
. By assumption, there exists
$Z_{\widetilde{G_{k}^{\prime }}}(N_{k})$
. By assumption, there exists
![]() $s\in Z_{\widetilde{G^{\prime }}}(N)({\mathcal{O}})$
meeting any such
$s\in Z_{\widetilde{G^{\prime }}}(N)({\mathcal{O}})$
meeting any such
![]() $C^{\prime }$
. The image of
$C^{\prime }$
. The image of
![]() $(1,s)$
is a point of
$(1,s)$
is a point of
![]() $Z_{G}(N)({\mathcal{O}})$
meeting
$Z_{G}(N)({\mathcal{O}})$
meeting
![]() $C$
.
$C$
.
Conversely, assume
![]() $G$
satisfies (4.3). Pick a connected component
$G$
satisfies (4.3). Pick a connected component
![]() $C^{\prime }$
of
$C^{\prime }$
of
![]() $Z_{\widetilde{G_{k}^{\prime }}}(N_{k})$
. Under
$Z_{\widetilde{G_{k}^{\prime }}}(N_{k})$
. Under
![]() $S\times Z_{\widetilde{G^{\prime }}}(N)\rightarrow Z_{G}(N)$
,
$S\times Z_{\widetilde{G^{\prime }}}(N)\rightarrow Z_{G}(N)$
,
![]() $S_{k}\times C^{\prime }$
maps onto a connected component
$S_{k}\times C^{\prime }$
maps onto a connected component
![]() $C$
of
$C$
of
![]() $Z_{G_{k}}(N_{k})$
. By assumption, there exists
$Z_{G_{k}}(N_{k})$
. By assumption, there exists
![]() $s\in Z_{G}(N)({\mathcal{O}})$
such that
$s\in Z_{G}(N)({\mathcal{O}})$
such that
![]() $s_{k}\in C$
. As
$s_{k}\in C$
. As
![]() $k$
is algebraically closed, there is
$k$
is algebraically closed, there is
![]() $s_{k}^{\prime }\in (S\times Z_{\widetilde{G^{\prime }}}(N))(k)$
lifting
$s_{k}^{\prime }\in (S\times Z_{\widetilde{G^{\prime }}}(N))(k)$
lifting
![]() $s_{k}$
and lying in
$s_{k}$
and lying in
![]() $C^{\prime }$
. As
$C^{\prime }$
. As
![]() $S\times Z_{\widetilde{G^{\prime }}}(N)\rightarrow Z_{G}(N)$
is a finite étale cover and
$S\times Z_{\widetilde{G^{\prime }}}(N)\rightarrow Z_{G}(N)$
is a finite étale cover and
![]() ${\mathcal{O}}$
is Henselian, there exists
${\mathcal{O}}$
is Henselian, there exists
![]() $s^{\prime }\in (S\times Z_{\widetilde{G^{\prime }}}(N))({\mathcal{O}})$
lifting
$s^{\prime }\in (S\times Z_{\widetilde{G^{\prime }}}(N))({\mathcal{O}})$
lifting
![]() $s$
and reducing to
$s$
and reducing to
![]() $s_{k}^{\prime }$
.◻
$s_{k}^{\prime }$
.◻
For example, this lets us pass between
![]() $\operatorname{Sp}_{2n}$
and
$\operatorname{Sp}_{2n}$
and
![]() $\operatorname{GSp}_{2n}$
by way of the projective symplectic group.
$\operatorname{GSp}_{2n}$
by way of the projective symplectic group.
Proposition 4.17. For
![]() $G$
a symplectic or orthogonal similitude group, and
$G$
a symplectic or orthogonal similitude group, and
![]() $N=N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
the element satisfying (3.1) given by Proposition 3.7 for an admissible partition
$N=N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
the element satisfying (3.1) given by Proposition 3.7 for an admissible partition
![]() $\unicode[STIX]{x1D70E}$
, the centralizer
$\unicode[STIX]{x1D70E}$
, the centralizer
![]() $Z_{G}(N)$
is smooth over
$Z_{G}(N)$
is smooth over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Proof. By Fact 4.2,
![]() $Z_{G_{k}}(N_{k})$
and
$Z_{G_{k}}(N_{k})$
and
![]() $Z_{G_{K}}(N_{K})$
are smooth. By the classification of nilpotent orbits over algebraically closed fields, the dimension of the orbit only depends on the combinatorial classification for the orbit in very good characteristic and in characteristic
$Z_{G_{K}}(N_{K})$
are smooth. By the classification of nilpotent orbits over algebraically closed fields, the dimension of the orbit only depends on the combinatorial classification for the orbit in very good characteristic and in characteristic
![]() $0$
, so these fibers are equidimensional of the same dimension. By Corollary 4.6, it suffices to find
$0$
, so these fibers are equidimensional of the same dimension. By Corollary 4.6, it suffices to find
![]() $s\in Z_{G}(N)({\mathcal{O}})$
meeting any connected component of
$s\in Z_{G}(N)({\mathcal{O}})$
meeting any connected component of
![]() $Z_{G_{k}}(N_{k})$
.
$Z_{G_{k}}(N_{k})$
.
Using Lemma 4.16, we reduce checking (4.3) to the cases of
![]() $\operatorname{Sp}_{m}$
and
$\operatorname{Sp}_{m}$
and
![]() $\operatorname{SO}_{m}$
, covered by Examples 4.12 and 4.13.◻
$\operatorname{SO}_{m}$
, covered by Examples 4.12 and 4.13.◻
Remark 4.18. Consider a nilpotent orbit of
![]() $\operatorname{GL}_{n}$
with representative
$\operatorname{GL}_{n}$
with representative
![]() $N$
given in Example 3.2. As
$N$
given in Example 3.2. As
![]() $Z_{G_{k}}(N_{k})$
is connected [Reference JantzenJan04, Proposition 3.10], the identity section shows (4.3) holds. This shows
$Z_{G_{k}}(N_{k})$
is connected [Reference JantzenJan04, Proposition 3.10], the identity section shows (4.3) holds. This shows
![]() $Z_{G}(N)$
is smooth.
$Z_{G}(N)$
is smooth.
Remark 4.19. It is not hard to extend the above argument to work for groups such that all the irreducible factors of the root system are of classical type. For the exceptional groups, one could find
![]() $N$
as in Remark 3.1 and attempt to check (4.3) holds by hand (there are finitely many cases). A conceptual approach would be preferable.
$N$
as in Remark 3.1 and attempt to check (4.3) holds by hand (there are finitely many cases). A conceptual approach would be preferable.
Remark 4.20. McNinch analyzes the centralizer of an ‘equidimensional nilpotent’ in [Reference McNinchMcN08]. An equidimensional nilpotent is an element
![]() $N\in \mathfrak{g}$
such that
$N\in \mathfrak{g}$
such that
![]() $N_{K}$
is nilpotent and the dimension of the special and generic fibers of
$N_{K}$
is nilpotent and the dimension of the special and generic fibers of
![]() $Z_{G}(N)$
are the same. [Reference McNinchMcN08, § 5.2] claims that such
$Z_{G}(N)$
are the same. [Reference McNinchMcN08, § 5.2] claims that such
![]() $Z_{G}(N)$
are
$Z_{G}(N)$
are
![]() ${\mathcal{O}}$
-smooth because the fibers are smooth of the same dimension. This deduction is incorrect: it relies on [Reference McNinchMcN08, 2.3.2] which uses the wrong definition of an equidimensional morphism and thereby incorrectly applies [Reference GrothendieckSGA1, Exp. II, Proposition 2.3].
${\mathcal{O}}$
-smooth because the fibers are smooth of the same dimension. This deduction is incorrect: it relies on [Reference McNinchMcN08, 2.3.2] which uses the wrong definition of an equidimensional morphism and thereby incorrectly applies [Reference GrothendieckSGA1, Exp. II, Proposition 2.3].
According to [Reference GrothendieckSGA1, Exp. II, Proposition 2.3] (or [Reference GrothendieckEGAIV3
, §§ 13.3, 14.4.6, 15.2.3]), for a Noetherian scheme
![]() $Y$
, a morphism
$Y$
, a morphism
![]() $f:X\rightarrow Y$
locally of finite type, and points
$f:X\rightarrow Y$
locally of finite type, and points
![]() $x\in X$
and
$x\in X$
and
![]() $y=f(x)$
with
$y=f(x)$
with
![]() $\mathscr{O}_{y}$
normal,
$\mathscr{O}_{y}$
normal,
![]() $f$
is smooth at
$f$
is smooth at
![]() $x$
if and only if
$x$
if and only if
![]() $f$
is equidimensional at
$f$
is equidimensional at
![]() $x$
and
$x$
and
![]() $f^{-1}(y)$
is smooth over
$f^{-1}(y)$
is smooth over
![]() $k(y)$
at
$k(y)$
at
![]() $x$
. But by definition in [Reference GrothendieckEGAIV3
, 13.3.2], an equidimensional morphism is more than just a morphism all of whose fibers are of the same dimension (the condition checked in [Reference McNinchMcN08, 2.3.2]): a locally finite type morphism
$x$
. But by definition in [Reference GrothendieckEGAIV3
, 13.3.2], an equidimensional morphism is more than just a morphism all of whose fibers are of the same dimension (the condition checked in [Reference McNinchMcN08, 2.3.2]): a locally finite type morphism
![]() $f$
is called equidimensional of dimension
$f$
is called equidimensional of dimension
![]() $d$
at
$d$
at
![]() $x\in X$
when there exists an open neighborhood
$x\in X$
when there exists an open neighborhood
![]() $U$
of
$U$
of
![]() $x$
such that for every irreducible component
$x$
such that for every irreducible component
![]() $Z$
of
$Z$
of
![]() $U$
through
$U$
through
![]() $x$
,
$x$
,
![]() $f(Z)$
is dense in some irreducible component of
$f(Z)$
is dense in some irreducible component of
![]() $Y$
containing
$Y$
containing
![]() $y$
and for all
$y$
and for all
![]() $x^{\prime }\in U$
the fiber
$x^{\prime }\in U$
the fiber
![]() $f^{-1}(f(x^{\prime }))\cap U$
has all irreducible components of dimension
$f^{-1}(f(x^{\prime }))\cap U$
has all irreducible components of dimension
![]() $d$
.
$d$
.
This is much stronger than the fibers simply being of the same dimension. To see the importance of the extra conditions, consider a discrete valuation ring
![]() ${\mathcal{O}}$
with field of fractions
${\mathcal{O}}$
with field of fractions
![]() $K$
and residue field
$K$
and residue field
![]() $k$
, and the morphism from
$k$
, and the morphism from
![]() $X$
, the disjoint union of
$X$
, the disjoint union of
![]() $\operatorname{Spec}K$
and
$\operatorname{Spec}K$
and
![]() $\operatorname{Spec}k$
, to
$\operatorname{Spec}k$
, to
![]() $Y=\operatorname{Spec}{\mathcal{O}}$
. The fibers are of the same dimension (zero) and smooth but the morphism is not flat. This morphism is also not equidimensional at
$Y=\operatorname{Spec}{\mathcal{O}}$
. The fibers are of the same dimension (zero) and smooth but the morphism is not flat. This morphism is also not equidimensional at
![]() $\operatorname{Spec}k$
: the only irreducible component of
$\operatorname{Spec}k$
: the only irreducible component of
![]() $X$
containing
$X$
containing
![]() $\operatorname{Spec}k$
is the point itself, with image the closed point of
$\operatorname{Spec}k$
is the point itself, with image the closed point of
![]() $\operatorname{Spec}{\mathcal{O}}$
. This is not dense in
$\operatorname{Spec}{\mathcal{O}}$
. This is not dense in
![]() $\operatorname{Spec}{\mathcal{O}}$
, the only irreducible component of the only open set containing the closed point of
$\operatorname{Spec}{\mathcal{O}}$
, the only irreducible component of the only open set containing the closed point of
![]() $\operatorname{Spec}{\mathcal{O}}$
.
$\operatorname{Spec}{\mathcal{O}}$
.
The smoothness of centralizers of an equidimensional pure nilpotent is important to proving the main results of [Reference McNinchMcN08]. In particular, the results in [Reference McNinchMcN08, §§ 6 and 7] crucially rely on the smoothness of the centralizers of such nilpotents, leaving a gap in the proof of Theorem B in [Reference McNinchMcN08] concerning the component group of centralizers. The method we have discussed here reverses this, understanding the geometric component group well enough to produce sufficiently many
![]() ${\mathcal{O}}$
-valued points in order to deduce smoothness of the centralizer in classical cases in very good characteristic via Lemma 4.4.
${\mathcal{O}}$
-valued points in order to deduce smoothness of the centralizer in classical cases in very good characteristic via Lemma 4.4.
5 Minimally ramified deformations: tame case
In this section, we will generalize the tamely ramified case of the minimally ramified deformation condition introduced in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] for
![]() $\operatorname{GL}_{n}$
to symplectic and orthogonal groups. We also explain why another more immediate notion based on parabolic subgroups, giving the same deformation condition for
$\operatorname{GL}_{n}$
to symplectic and orthogonal groups. We also explain why another more immediate notion based on parabolic subgroups, giving the same deformation condition for
![]() $\operatorname{GL}_{n}$
, is not liftable in general (even for
$\operatorname{GL}_{n}$
, is not liftable in general (even for
![]() $\operatorname{GSp}_{4}$
).
$\operatorname{GSp}_{4}$
).
5.1 Passing between unipotents and nilpotents
As before,
![]() $G$
is either
$G$
is either
![]() $\operatorname{GSp}_{m}$
or
$\operatorname{GSp}_{m}$
or
![]() $\operatorname{GO}_{m}$
(or
$\operatorname{GO}_{m}$
(or
![]() $\operatorname{GL}_{m}$
to recover the results of [Reference Clozel, Harris and TaylorCHT08, § 2.4.4]) over the ring of integers
$\operatorname{GL}_{m}$
to recover the results of [Reference Clozel, Harris and TaylorCHT08, § 2.4.4]) over the ring of integers
![]() ${\mathcal{O}}$
in a
${\mathcal{O}}$
in a
![]() $p$
-adic field with residue field
$p$
-adic field with residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>0$
. As always, we assume that
$p>0$
. As always, we assume that
![]() $p$
is very good for
$p$
is very good for
![]() $G_{k}$
(i.e.
$G_{k}$
(i.e.
![]() $p\neq 2$
). Let
$p\neq 2$
). Let
![]() $\mathfrak{g}=\operatorname{Lie}(G)$
.
$\mathfrak{g}=\operatorname{Lie}(G)$
.
As in § 3.2, we work with a pure nilpotent
![]() $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
for which
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
for which
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is
![]() ${\mathcal{O}}$
-smooth,
${\mathcal{O}}$
-smooth,
![]() $(N_{\unicode[STIX]{x1D70E}})_{\overline{K}}\in O_{\overline{K},\unicode[STIX]{x1D70E}}$
, and
$(N_{\unicode[STIX]{x1D70E}})_{\overline{K}}\in O_{\overline{K},\unicode[STIX]{x1D70E}}$
, and
![]() $(N_{\unicode[STIX]{x1D70E}})_{\overline{k}}\in O_{\overline{k},\unicode[STIX]{x1D70E}}$
. Define
$(N_{\unicode[STIX]{x1D70E}})_{\overline{k}}\in O_{\overline{k},\unicode[STIX]{x1D70E}}$
. Define
![]() $\overline{N}:=(N_{\unicode[STIX]{x1D70E}})_{k}$
. We studied deformations of
$\overline{N}:=(N_{\unicode[STIX]{x1D70E}})_{k}$
. We studied deformations of
![]() $\overline{N}$
in § 3.2, but will ultimately want to analyze deformations of Galois representations which take on unipotent values at certain elements of a local Galois group. Thus, we need a way to pass between unipotent and nilpotent elements. For classical groups, we can use a truncated version of the exponential and logarithm maps as follows.
$\overline{N}$
in § 3.2, but will ultimately want to analyze deformations of Galois representations which take on unipotent values at certain elements of a local Galois group. Thus, we need a way to pass between unipotent and nilpotent elements. For classical groups, we can use a truncated version of the exponential and logarithm maps as follows.
Fact 5.1. Suppose that
![]() $p\geqslant m$
and that
$p\geqslant m$
and that
![]() $R$
is an
$R$
is an
![]() ${\mathcal{O}}$
-algebra. If
${\mathcal{O}}$
-algebra. If
![]() $A\in \operatorname{Mat}_{m}(R)$
has characteristic polynomial
$A\in \operatorname{Mat}_{m}(R)$
has characteristic polynomial
![]() $x^{m}$
, then
$x^{m}$
, then
has characteristic polynomial
![]() $(x-1)^{m}$
. If
$(x-1)^{m}$
. If
![]() $B\in \operatorname{Mat}_{m}(R)$
has characteristic polynomial
$B\in \operatorname{Mat}_{m}(R)$
has characteristic polynomial
![]() $(x-1)^{m}$
, then
$(x-1)^{m}$
, then
has characteristic polynomial
![]() $x^{m}$
. Furthermore for
$x^{m}$
. Furthermore for
![]() $C\in \operatorname{GL}_{m}(R)$
and an integer
$C\in \operatorname{GL}_{m}(R)$
and an integer
![]() $q$
, we have
$q$
, we have
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\bullet ~\exp (CAC^{-1})=C\exp (A)C^{-1}\quad & \bullet ~\exp (\log (B))=B\\ \bullet ~\log (CBC^{-1})=C\log (B)C^{-1}\quad & \bullet ~\exp (qA)=\exp (A)^{q}\\ \bullet ~\log (\exp (A))=A\quad & \bullet ~\log (B^{q})=q\log (B).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\bullet ~\exp (CAC^{-1})=C\exp (A)C^{-1}\quad & \bullet ~\exp (\log (B))=B\\ \bullet ~\log (CBC^{-1})=C\log (B)C^{-1}\quad & \bullet ~\exp (qA)=\exp (A)^{q}\\ \bullet ~\log (\exp (A))=A\quad & \bullet ~\log (B^{q})=q\log (B).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
This is [Reference TaylorTay08, Lemma 2.4]. The key idea is that because all the higher powers of
![]() $A$
and
$A$
and
![]() $B-1$
vanish and all of the denominators appearing are invertible as
$B-1$
vanish and all of the denominators appearing are invertible as
![]() $p\geqslant m$
, we can deduce these facts from results about the exponential and logarithm in characteristic zero.
$p\geqslant m$
, we can deduce these facts from results about the exponential and logarithm in characteristic zero.
Suppose
![]() $J$
is the matrix for a perfect symmetric or alternating pairing over
$J$
is the matrix for a perfect symmetric or alternating pairing over
![]() $R$
.
$R$
.
Corollary 5.2. For
![]() $A$
and
$A$
and
![]() $B$
as in Fact 5.1 with
$B$
as in Fact 5.1 with
![]() $\exp (A)=B$
,
$\exp (A)=B$
,
![]() $A^{T}J+JA=0$
if and only if
$A^{T}J+JA=0$
if and only if
![]() $B^{T}JB=J$
.
$B^{T}JB=J$
.
Proof. Directly from the definitions we see that
![]() $\exp (A^{T})=\exp (A)^{T}$
. Observe that
$\exp (A^{T})=\exp (A)^{T}$
. Observe that
Thus
![]() $JAJ^{-1}=-A^{T}$
if and only if
$JAJ^{-1}=-A^{T}$
if and only if
![]() $(B^{T})^{-1}=JBJ^{-1}$
.◻
$(B^{T})^{-1}=JBJ^{-1}$
.◻
We shall use this exponential map to convert pure nilpotents into unipotent elements. Let
![]() $R$
be a coefficient ring over
$R$
be a coefficient ring over
![]() ${\mathcal{O}}$
. By Definition 3.9, any pure nilpotent
${\mathcal{O}}$
. By Definition 3.9, any pure nilpotent
![]() $N\in \operatorname{Nil}_{\overline{N}}(R)$
is
$N\in \operatorname{Nil}_{\overline{N}}(R)$
is
![]() $G(R)$
-conjugate to
$G(R)$
-conjugate to
![]() $N_{\unicode[STIX]{x1D70E}}$
, so it has characteristic polynomial
$N_{\unicode[STIX]{x1D70E}}$
, so it has characteristic polynomial
![]() $x^{m}$
. Denoting the derived group of
$x^{m}$
. Denoting the derived group of
![]() $G$
by
$G$
by
![]() $G^{\prime }$
, any nilpotent element of
$G^{\prime }$
, any nilpotent element of
![]() $\mathfrak{g}$
lies in
$\mathfrak{g}$
lies in
![]() $(\mathfrak{g}^{\prime })=(\operatorname{Lie}G^{\prime })$
, so
$(\mathfrak{g}^{\prime })=(\operatorname{Lie}G^{\prime })$
, so
![]() $NJ+JN=0$
(and not just
$NJ+JN=0$
(and not just
![]() $NJ+JN=\unicode[STIX]{x1D706}J$
for some
$NJ+JN=\unicode[STIX]{x1D706}J$
for some
![]() $\unicode[STIX]{x1D706}\in {\mathcal{O}}$
). Thus, Corollary 5.2 shows that
$\unicode[STIX]{x1D706}\in {\mathcal{O}}$
). Thus, Corollary 5.2 shows that
![]() $\exp (N)\in G(R)$
. This gives an exponential map
$\exp (N)\in G(R)$
. This gives an exponential map
such that for
![]() $g\in \widehat{G}(R)$
,
$g\in \widehat{G}(R)$
,
![]() $N\in \operatorname{Nil}_{\overline{N}}(R)$
, and
$N\in \operatorname{Nil}_{\overline{N}}(R)$
, and
![]() $q\in \mathbf{Z}$
we have
$q\in \mathbf{Z}$
we have
![]() $\exp (qN)=\exp (N)^{q}$
and
$\exp (qN)=\exp (N)^{q}$
and
![]() $g\exp (N)g^{-1}=\exp (\operatorname{Ad}_{G}(g)N)$
.
$g\exp (N)g^{-1}=\exp (\operatorname{Ad}_{G}(g)N)$
.
Remark 5.3. This is a realization over
![]() ${\mathcal{O}}$
of a special case of the Springer isomorphism identifying the nilpotent and unipotent varieties in very good characteristic. For later purposes, we will need that the identification is compatible with the multiplication in the sense that
${\mathcal{O}}$
of a special case of the Springer isomorphism identifying the nilpotent and unipotent varieties in very good characteristic. For later purposes, we will need that the identification is compatible with the multiplication in the sense that
![]() $\exp (qA)=\exp (A)^{q}$
. In the case of
$\exp (qA)=\exp (A)^{q}$
. In the case of
![]() $\operatorname{GL}_{m}$
, a Springer isomorphism that works in any characteristic is given by
$\operatorname{GL}_{m}$
, a Springer isomorphism that works in any characteristic is given by
![]() $X\rightarrow 1+X$
for nilpotent
$X\rightarrow 1+X$
for nilpotent
![]() $X$
, but this is not compatible with multiplication.
$X$
, but this is not compatible with multiplication.
5.2 Minimally ramified deformations
As before,
![]() $G$
is
$G$
is
![]() $\operatorname{GSp}_{m}$
,
$\operatorname{GSp}_{m}$
,
![]() $\operatorname{GO}_{m}$
or
$\operatorname{GO}_{m}$
or
![]() $\operatorname{GL}_{m}$
over the ring of integers
$\operatorname{GL}_{m}$
over the ring of integers
![]() ${\mathcal{O}}$
of a
${\mathcal{O}}$
of a
![]() $p$
-adic field with residue field
$p$
-adic field with residue field
![]() $k$
with
$k$
with
![]() $p>m$
. Let
$p>m$
. Let
![]() $L$
be a finite extension of
$L$
be a finite extension of
![]() $\mathbf{Q}_{\ell }$
(with
$\mathbf{Q}_{\ell }$
(with
![]() $\ell \neq p$
), and denote its absolute Galois group by
$\ell \neq p$
), and denote its absolute Galois group by
![]() $\unicode[STIX]{x1D6E4}_{L}$
. Consider a representation
$\unicode[STIX]{x1D6E4}_{L}$
. Consider a representation
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
. We wish to define a (large) smooth deformation condition for
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
. We wish to define a (large) smooth deformation condition for
![]() $\overline{\unicode[STIX]{x1D70C}}$
generalizing the minimally ramified deformation condition for
$\overline{\unicode[STIX]{x1D70C}}$
generalizing the minimally ramified deformation condition for
![]() $\operatorname{GL}_{n}$
defined in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4]. In this section we do so for a special class of tamely ramified representations. This requires making an étale local extension of
$\operatorname{GL}_{n}$
defined in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4]. In this section we do so for a special class of tamely ramified representations. This requires making an étale local extension of
![]() ${\mathcal{O}}$
, which will be harmless for our purposes.
${\mathcal{O}}$
, which will be harmless for our purposes.
Recall that
![]() $\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
, the Galois group of the maximal tamely ramified extension of
$\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
, the Galois group of the maximal tamely ramified extension of
![]() $L$
, is isomorphic to the semidirect product
$L$
, is isomorphic to the semidirect product
where
![]() $\widehat{\mathbf{Z}}$
is generated by a Frobenius
$\widehat{\mathbf{Z}}$
is generated by a Frobenius
![]() $\unicode[STIX]{x1D719}$
and the conjugation action by
$\unicode[STIX]{x1D719}$
and the conjugation action by
![]() $\unicode[STIX]{x1D719}$
on the direct product is given by the cyclotomic character. We consider representations of
$\unicode[STIX]{x1D719}$
on the direct product is given by the cyclotomic character. We consider representations of
![]() $\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
which factor through the quotient
$\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
which factor through the quotient
![]() $\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
. Picking a topological generator
$\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
. Picking a topological generator
![]() $\unicode[STIX]{x1D70F}$
for
$\unicode[STIX]{x1D70F}$
for
![]() $\mathbf{Z}_{p}$
, the action is explicitly given by
$\mathbf{Z}_{p}$
, the action is explicitly given by
where
![]() $q$
is the size of the residue field of
$q$
is the size of the residue field of
![]() $L$
. Note
$L$
. Note
![]() $q$
is a power of
$q$
is a power of
![]() $\ell$
, so it is relatively prime to
$\ell$
, so it is relatively prime to
![]() $p$
. This leads us to study representations of the group
$p$
. This leads us to study representations of the group
![]() $T_{q}:=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
.
$T_{q}:=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
.
Let
![]() $\overline{\unicode[STIX]{x1D70C}}:T_{q}\rightarrow G(k)$
be such a representation. We first claim that
$\overline{\unicode[STIX]{x1D70C}}:T_{q}\rightarrow G(k)$
be such a representation. We first claim that
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in G(k)$
is unipotent. This element decomposes as a commuting product of semisimple and unipotent elements of
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})\in G(k)$
is unipotent. This element decomposes as a commuting product of semisimple and unipotent elements of
![]() $G(k)$
. The order of a semisimple element in
$G(k)$
. The order of a semisimple element in
![]() $G(k)$
is prime to
$G(k)$
is prime to
![]() $p$
, while by continuity there is an
$p$
, while by continuity there is an
![]() $r\geqslant 0$
such that
$r\geqslant 0$
such that
![]() $\unicode[STIX]{x1D70F}^{p^{r}}\in \ker (\overline{\unicode[STIX]{x1D70C}})$
. Thus
$\unicode[STIX]{x1D70F}^{p^{r}}\in \ker (\overline{\unicode[STIX]{x1D70C}})$
. Thus
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
is unipotent.
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
is unipotent.
Informally, a deformation
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
will be minimally ramified if
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
will be minimally ramified if
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
lies in the ‘same’ unipotent orbit as
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
lies in the ‘same’ unipotent orbit as
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
. To make this meaningful over an infinitesimal thickening of
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
. To make this meaningful over an infinitesimal thickening of
![]() $k$
, we shall use the notion of pure nilpotents as in Definition 3.9 since unipotence and unipotent orbits are not good notions when not over a field. As
$k$
, we shall use the notion of pure nilpotents as in Definition 3.9 since unipotence and unipotent orbits are not good notions when not over a field. As
![]() $\overline{N}:=\log (\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F}))$
is nilpotent, by Remark 3.8 after making an étale local extension of
$\overline{N}:=\log (\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F}))$
is nilpotent, by Remark 3.8 after making an étale local extension of
![]() ${\mathcal{O}}$
we may assume that there exists a pure nilpotent
${\mathcal{O}}$
we may assume that there exists a pure nilpotent
![]() $N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
$N_{\unicode[STIX]{x1D70E}}\in \mathfrak{g}$
lifting
![]() $\overline{N}$
for which
$\overline{N}$
for which
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth. Making a further extension if necessary, we may also assume that the unit
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth. Making a further extension if necessary, we may also assume that the unit
![]() $q\in {\mathcal{O}}^{\times }$
is a square. We obtain an exponential map
$q\in {\mathcal{O}}^{\times }$
is a square. We obtain an exponential map
![]() $\exp :\operatorname{Nil}_{\overline{N}}\rightarrow G$
as in (5.1).
$\exp :\operatorname{Nil}_{\overline{N}}\rightarrow G$
as in (5.1).
Definition 5.4. Under our standing assumptions (collected as (A1)–(A4) in § 1.2), for a coefficient ring
![]() $R$
over
$R$
over
![]() ${\mathcal{O}}$
, a continuous lift
${\mathcal{O}}$
, a continuous lift
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
of
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
of
![]() $\overline{\unicode[STIX]{x1D70C}}$
is minimally ramified if
$\overline{\unicode[STIX]{x1D70C}}$
is minimally ramified if
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})=\exp (N)$
for some
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})=\exp (N)$
for some
![]() $N\in \operatorname{Nil}_{\overline{N}}(R)$
.
$N\in \operatorname{Nil}_{\overline{N}}(R)$
.
Example 5.5. Take
![]() $G=\operatorname{GL}_{m}$
. Then
$G=\operatorname{GL}_{m}$
. Then
![]() $X\mapsto 1_{m}+X$
gives an identification of nilpotents and unipotents. Up to conjugacy, over algebraically closed fields parabolic subgroups correspond to partitions of
$X\mapsto 1_{m}+X$
gives an identification of nilpotents and unipotents. Up to conjugacy, over algebraically closed fields parabolic subgroups correspond to partitions of
![]() $m$
and every nilpotent orbit is the Richardson orbit of such a parabolic. Let
$m$
and every nilpotent orbit is the Richardson orbit of such a parabolic. Let
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})-1_{m}=:\overline{N}$
correspond to the partition
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})-1_{m}=:\overline{N}$
correspond to the partition
![]() $\unicode[STIX]{x1D70E}=n_{1}+n_{2}+\cdots +n_{r}$
. By Example 3.2, the lift
$\unicode[STIX]{x1D70E}=n_{1}+n_{2}+\cdots +n_{r}$
. By Example 3.2, the lift
![]() $N_{\unicode[STIX]{x1D70E}}$
of
$N_{\unicode[STIX]{x1D70E}}$
of
![]() $\overline{N}$
is conjugate to a block nilpotent matrix with blocks of size
$\overline{N}$
is conjugate to a block nilpotent matrix with blocks of size
![]() $n_{1},n_{2},\ldots ,n_{r}$
. The points
$n_{1},n_{2},\ldots ,n_{r}$
. The points
![]() $N\in \operatorname{Nil}_{\overline{N}}(R)$
are the
$N\in \operatorname{Nil}_{\overline{N}}(R)$
are the
![]() $\widehat{G}(R)$
-conjugates of
$\widehat{G}(R)$
-conjugates of
![]() $N_{\unicode[STIX]{x1D70E}}$
. It is clear (since
$N_{\unicode[STIX]{x1D70E}}$
. It is clear (since
![]() $p>m$
) that if
$p>m$
) that if
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in \operatorname{Nil}_{\overline{N}}(R)$
, then
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in \operatorname{Nil}_{\overline{N}}(R)$
, then
is an isomorphism for all
![]() $i$
. Conversely, repeated applications of [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.15] show that any
$i$
. Conversely, repeated applications of [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.15] show that any
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
satisfying this collection of isomorphism conditions is
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})$
satisfying this collection of isomorphism conditions is
![]() $\widehat{G}(R)$
-conjugate to
$\widehat{G}(R)$
-conjugate to
![]() $N_{\unicode[STIX]{x1D70E}}$
. Thus the minimally ramified deformation condition for
$N_{\unicode[STIX]{x1D70E}}$
. Thus the minimally ramified deformation condition for
![]() $\operatorname{GL}_{m}$
defined in [Reference Clozel, Harris and TaylorCHT08] agrees with our definition. Note that the identification
$\operatorname{GL}_{m}$
defined in [Reference Clozel, Harris and TaylorCHT08] agrees with our definition. Note that the identification
![]() $X\mapsto 1_{m}+X$
does not satisfy
$X\mapsto 1_{m}+X$
does not satisfy
![]() $qX\rightarrow (1+X)^{q}$
, so it will not work in our argument. The proof of [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19] uses a different method for which this non-homomorphic identification suffices.
$qX\rightarrow (1+X)^{q}$
, so it will not work in our argument. The proof of [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19] uses a different method for which this non-homomorphic identification suffices.
The functor of minimally ramified lifts is pro-representable by a ring
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
as it suffices to specify images of
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
as it suffices to specify images of
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D719}$
subject to constraints that
$\unicode[STIX]{x1D719}$
subject to constraints that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})=\exp (N)$
and
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})=\exp (N)$
and
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})^{-1}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})^{q}$
.
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719})^{-1}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})^{q}$
.
Proposition 5.6. Under assumptions (A1)–(A4), the lifting ring
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
is formally smooth over
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
is formally smooth over
![]() ${\mathcal{O}}$
of relative dimension
${\mathcal{O}}$
of relative dimension
![]() $\dim G_{k}$
.
$\dim G_{k}$
.
Proof. Let
![]() $\overline{\unicode[STIX]{x1D6F7}}=\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})\in G(k)$
and let
$\overline{\unicode[STIX]{x1D6F7}}=\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})\in G(k)$
and let
![]() $\widehat{G}_{\overline{\unicode[STIX]{x1D6F7}}}$
be the formal completion of
$\widehat{G}_{\overline{\unicode[STIX]{x1D6F7}}}$
be the formal completion of
![]() $G$
at
$G$
at
![]() $\overline{\unicode[STIX]{x1D6F7}}$
. Using the relation
$\overline{\unicode[STIX]{x1D6F7}}$
. Using the relation
we deduce that
![]() $\overline{\unicode[STIX]{x1D6F7}}\,\overline{N}\,\overline{\unicode[STIX]{x1D6F7}}^{-1}=q\overline{N}$
. Therefore we study the functor
$\overline{\unicode[STIX]{x1D6F7}}\,\overline{N}\,\overline{\unicode[STIX]{x1D6F7}}^{-1}=q\overline{N}$
. Therefore we study the functor
![]() $M_{\overline{N}}$
on
$M_{\overline{N}}$
on
![]() $\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
defined by
$\widehat{{\mathcal{C}}}_{{\mathcal{O}}}$
defined by
Any such lift
![]() $(\unicode[STIX]{x1D6F7},N)$
to a coefficient ring
$(\unicode[STIX]{x1D6F7},N)$
to a coefficient ring
![]() $R$
determines a homomorphism
$R$
determines a homomorphism
![]() $T_{q}\rightarrow G(R)$
lifting
$T_{q}\rightarrow G(R)$
lifting
![]() $\overline{\unicode[STIX]{x1D70C}}$
via
$\overline{\unicode[STIX]{x1D70C}}$
via
![]() $\unicode[STIX]{x1D719}\mapsto \unicode[STIX]{x1D6F7}$
and
$\unicode[STIX]{x1D719}\mapsto \unicode[STIX]{x1D6F7}$
and
![]() $\unicode[STIX]{x1D70F}\mapsto \exp (N)$
: it is continuous because
$\unicode[STIX]{x1D70F}\mapsto \exp (N)$
: it is continuous because
![]() $\exp (\overline{N})$
is unipotent. We will analyze
$\exp (\overline{N})$
is unipotent. We will analyze
![]() $M_{\overline{N}}$
through the composition
$M_{\overline{N}}$
through the composition
First, observe that
![]() $M_{\overline{N}}\rightarrow \operatorname{Nil}_{\overline{N}}$
is relatively representable as ‘
$M_{\overline{N}}\rightarrow \operatorname{Nil}_{\overline{N}}$
is relatively representable as ‘
![]() $\unicode[STIX]{x1D6F7}N=qN\unicode[STIX]{x1D6F7}$
’ is a formal closed condition on points
$\unicode[STIX]{x1D6F7}N=qN\unicode[STIX]{x1D6F7}$
’ is a formal closed condition on points
![]() $\unicode[STIX]{x1D6F7}$
of
$\unicode[STIX]{x1D6F7}$
of
![]() $(\widehat{G}_{\overline{\unicode[STIX]{x1D6F7}}})_{R}$
for each
$(\widehat{G}_{\overline{\unicode[STIX]{x1D6F7}}})_{R}$
for each
![]() $N\in \operatorname{Nil}_{\overline{N}}(R)$
.
$N\in \operatorname{Nil}_{\overline{N}}(R)$
.
From Lemma 3.11, we know that
![]() $\operatorname{Nil}_{\overline{N}}$
is formally smooth over
$\operatorname{Nil}_{\overline{N}}$
is formally smooth over
![]() ${\mathcal{O}}$
, and the universal nilpotent is
${\mathcal{O}}$
, and the universal nilpotent is
![]() $gN_{\unicode[STIX]{x1D70E}}g^{-1}$
for some
$gN_{\unicode[STIX]{x1D70E}}g^{-1}$
for some
![]() $g\in \widehat{G}(\operatorname{Nil}_{\overline{N}})$
. To check formal smoothness of the map
$g\in \widehat{G}(\operatorname{Nil}_{\overline{N}})$
. To check formal smoothness of the map
![]() $M_{\overline{N}}\rightarrow \operatorname{Nil}_{\overline{N}}$
, it therefore suffices to check the formal smoothness of the fiber of
$M_{\overline{N}}\rightarrow \operatorname{Nil}_{\overline{N}}$
, it therefore suffices to check the formal smoothness of the fiber of
![]() $M_{\overline{N}}$
over the
$M_{\overline{N}}$
over the
![]() ${\mathcal{O}}$
-point
${\mathcal{O}}$
-point
![]() $N_{\unicode[STIX]{x1D70E}}$
of
$N_{\unicode[STIX]{x1D70E}}$
of
![]() $\operatorname{Nil}_{\overline{N}}$
.
$\operatorname{Nil}_{\overline{N}}$
.
We have written down
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}\in G({\mathcal{O}})$
satisfying
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}\in G({\mathcal{O}})$
satisfying
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}N_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}^{-1}=qN_{\unicode[STIX]{x1D70E}}$
in Remark 4.14. Observe that
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}N_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}^{-1}=qN_{\unicode[STIX]{x1D70E}}$
in Remark 4.14. Observe that
![]() $\overline{\unicode[STIX]{x1D6F7}}\,\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D70E}}^{-1}\in Z_{G}(N_{\unicode[STIX]{x1D70E}})(k)$
. By smoothness, we may lift
$\overline{\unicode[STIX]{x1D6F7}}\,\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D70E}}^{-1}\in Z_{G}(N_{\unicode[STIX]{x1D70E}})(k)$
. By smoothness, we may lift
![]() $\overline{\unicode[STIX]{x1D6F7}}\,\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D70E}}^{-1}$
to an element
$\overline{\unicode[STIX]{x1D6F7}}\,\overline{\unicode[STIX]{x1D6F7}}_{\unicode[STIX]{x1D70E}}^{-1}$
to an element
![]() $s\in Z_{G}(N_{\unicode[STIX]{x1D70E}})({\mathcal{O}})$
. Then
$s\in Z_{G}(N_{\unicode[STIX]{x1D70E}})({\mathcal{O}})$
. Then
![]() $s\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}$
reduces to
$s\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}}$
reduces to
![]() $\overline{\unicode[STIX]{x1D6F7}}$
and satisfies
$\overline{\unicode[STIX]{x1D6F7}}$
and satisfies
![]() $(s\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}})N_{\unicode[STIX]{x1D70E}}(s\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}})^{-1}=qN_{\unicode[STIX]{x1D70E}}$
, so the fiber of
$(s\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}})N_{\unicode[STIX]{x1D70E}}(s\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70E}})^{-1}=qN_{\unicode[STIX]{x1D70E}}$
, so the fiber of
![]() $M_{\overline{N}}$
over
$M_{\overline{N}}$
over
![]() $N_{\unicode[STIX]{x1D70E}}$
has an
$N_{\unicode[STIX]{x1D70E}}$
has an
![]() ${\mathcal{O}}$
-point. The relative dimension of the formally smooth
${\mathcal{O}}$
-point. The relative dimension of the formally smooth
![]() $\operatorname{Nil}_{\overline{N}}$
is
$\operatorname{Nil}_{\overline{N}}$
is
![]() $\dim G_{k}-\dim Z_{G_{k}}(\overline{N})$
by Lemma 3.11, and
$\dim G_{k}-\dim Z_{G_{k}}(\overline{N})$
by Lemma 3.11, and
![]() $M_{\overline{N}}\rightarrow \operatorname{Nil}_{\overline{N}}$
is a
$M_{\overline{N}}\rightarrow \operatorname{Nil}_{\overline{N}}$
is a
![]() $\widehat{Z_{G}(N_{\unicode[STIX]{x1D70E}})}$
-torsor since it has an
$\widehat{Z_{G}(N_{\unicode[STIX]{x1D70E}})}$
-torsor since it has an
![]() ${\mathcal{O}}$
-point over
${\mathcal{O}}$
-point over
![]() $N_{\unicode[STIX]{x1D70E}}$
. As
$N_{\unicode[STIX]{x1D70E}}$
. As
![]() $Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth it follows that
$Z_{G}(N_{\unicode[STIX]{x1D70E}})$
is smooth it follows that
![]() $M_{\overline{N}}$
is formally smooth over
$M_{\overline{N}}$
is formally smooth over
![]() $\operatorname{Spf}{\mathcal{O}}$
of relative dimension
$\operatorname{Spf}{\mathcal{O}}$
of relative dimension
![]() $\dim G_{k}$
.◻
$\dim G_{k}$
.◻
Example 5.7. This recovers [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19] in the case
![]() $G=\operatorname{GL}_{m}$
.
$G=\operatorname{GL}_{m}$
.
Let
![]() $S$
be the (torus) quotient of
$S$
be the (torus) quotient of
![]() $G$
by its derived group
$G$
by its derived group
![]() $G^{\prime }$
, and
$G^{\prime }$
, and
![]() $\unicode[STIX]{x1D707}:G\rightarrow S$
the quotient map. For use later, we now study a variant where we fix a lift
$\unicode[STIX]{x1D707}:G\rightarrow S$
the quotient map. For use later, we now study a variant where we fix a lift
![]() $\unicode[STIX]{x1D708}:T_{q}\rightarrow S({\mathcal{O}})$
of
$\unicode[STIX]{x1D708}:T_{q}\rightarrow S({\mathcal{O}})$
of
![]() $\unicode[STIX]{x1D707}\circ \overline{\unicode[STIX]{x1D70C}}:T_{q}\rightarrow S(k)$
, as follows.
$\unicode[STIX]{x1D707}\circ \overline{\unicode[STIX]{x1D70C}}:T_{q}\rightarrow S(k)$
, as follows.
Corollary 5.8. Under assumptions (A1)–(A4), the deformation condition of minimally ramified lifts
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
satisfying
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow G(R)$
satisfying
![]() $\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D708}$
is a liftable deformation condition. The lifting ring
$\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D708}$
is a liftable deformation condition. The lifting ring
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }$
is of relative dimension
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }$
is of relative dimension
![]() $\dim G_{k}-1$
, and the tangent space to the deformation functor has dimension
$\dim G_{k}-1$
, and the tangent space to the deformation functor has dimension
![]() $\dim _{k}H^{0}(T_{q},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))-1$
.
$\dim _{k}H^{0}(T_{q},\operatorname{ad}(\overline{\unicode[STIX]{x1D70C}}))-1$
.
Proof. The last claim about the dimension of the tangent space to the deformation functor follows from the claim about the dimension of the lifting ring and Remark 2.2.
The quotient torus
![]() $S=G/G^{\prime }$
is split of rank
$S=G/G^{\prime }$
is split of rank
![]() $1$
, so the subscheme
$1$
, so the subscheme
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }\subset R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
is the vanishing of locus of a single function. As
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }\subset R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
is the vanishing of locus of a single function. As
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
is formally smooth over
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
is formally smooth over
![]() ${\mathcal{O}}$
with relative dimension
${\mathcal{O}}$
with relative dimension
![]() $\dim G_{k}$
, it suffices to check that the tangent space of
$\dim G_{k}$
, it suffices to check that the tangent space of
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }$
over
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }$
over
![]() $k$
(in the sense of [Reference MazurMaz97, § 15]) is a proper subspace of the tangent space of
$k$
(in the sense of [Reference MazurMaz97, § 15]) is a proper subspace of the tangent space of
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
: this will establish formal smoothness and the dimension claim.
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
: this will establish formal smoothness and the dimension claim.
Let
![]() $Z$
be the maximal central torus of
$Z$
be the maximal central torus of
![]() $G$
. On the level of Lie algebras, we know that
$G$
. On the level of Lie algebras, we know that
![]() $\operatorname{Lie}G$
splits over
$\operatorname{Lie}G$
splits over
![]() ${\mathcal{O}}$
as a direct sum of
${\mathcal{O}}$
as a direct sum of
![]() $\operatorname{Lie}G^{\prime }$
and
$\operatorname{Lie}G^{\prime }$
and
![]() $\operatorname{Lie}S\simeq \operatorname{Lie}Z$
as
$\operatorname{Lie}S\simeq \operatorname{Lie}Z$
as
![]() $p$
is very good for
$p$
is very good for
![]() $G$
. We can modify a lift
$G$
. We can modify a lift
![]() $\unicode[STIX]{x1D70C}_{0}$
over
$\unicode[STIX]{x1D70C}_{0}$
over
![]() $R=k[\unicode[STIX]{x1D716}]/(\unicode[STIX]{x1D716}^{2})$
by multiplying against an unramified non-trivial character
$R=k[\unicode[STIX]{x1D716}]/(\unicode[STIX]{x1D716}^{2})$
by multiplying against an unramified non-trivial character
![]() $T_{q}\rightarrow Z(R)$
with trivial reduction, changing
$T_{q}\rightarrow Z(R)$
with trivial reduction, changing
![]() $\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70C}_{0}$
. Thus the tangent space of
$\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70C}_{0}$
. Thus the tangent space of
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }$
is a proper subspace of that of
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708},\Box }$
is a proper subspace of that of
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
.◻
$R_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.}\Box }$
.◻
5.3 Deformation conditions based on parabolic subgroups
The use of nilpotent orbits is not the only approach to defining a deformation condition at ramified places not above
![]() $p$
. As discussed in the introduction, the method used to prove [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19] suggests a generalization from
$p$
. As discussed in the introduction, the method used to prove [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19] suggests a generalization from
![]() $\operatorname{GL}_{n}$
to other groups
$\operatorname{GL}_{n}$
to other groups
![]() $G$
based on deformations lying in certain parabolic subgroups of
$G$
based on deformations lying in certain parabolic subgroups of
![]() $G$
. This deformation condition is not smooth for algebraic groups beyond
$G$
. This deformation condition is not smooth for algebraic groups beyond
![]() $\operatorname{GL}_{n}$
, so it does not work in Ramakrishna’s method. In this section we give a conceptual explanation for this phenomenon.
$\operatorname{GL}_{n}$
, so it does not work in Ramakrishna’s method. In this section we give a conceptual explanation for this phenomenon.
Let
![]() $P\subset G$
be a parabolic
$P\subset G$
be a parabolic
![]() ${\mathcal{O}}$
-subgroup. The Richardson orbit for
${\mathcal{O}}$
-subgroup. The Richardson orbit for
![]() $P_{k}$
intersects
$P_{k}$
intersects
![]() $(\operatorname{Lie}R_{u}P)_{k}$
in a dense open set which is a single geometric orbit under
$(\operatorname{Lie}R_{u}P)_{k}$
in a dense open set which is a single geometric orbit under
![]() $P_{k}$
. Suppose that
$P_{k}$
. Suppose that
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
is the exponential of a
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
is the exponential of a
![]() $k$
-point
$k$
-point
![]() $\overline{N}$
in the Richardson orbit, and consider deformations
$\overline{N}$
in the Richardson orbit, and consider deformations
![]() $\unicode[STIX]{x1D70C}:T_{q}\rightarrow G({\mathcal{O}})$
of
$\unicode[STIX]{x1D70C}:T_{q}\rightarrow G({\mathcal{O}})$
of
![]() $\overline{\unicode[STIX]{x1D70C}}$
ramified with respect to
$\overline{\unicode[STIX]{x1D70C}}$
ramified with respect to
![]() $P$
in the sense that
$P$
in the sense that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in P$
(compare with Definition 1.2). This requires specifying a lift of
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70F})\in P$
(compare with Definition 1.2). This requires specifying a lift of
![]() $\overline{N}$
that lies in
$\overline{N}$
that lies in
![]() $\operatorname{Lie}P$
. One could hope that such lifts would automatically be
$\operatorname{Lie}P$
. One could hope that such lifts would automatically be
![]() $G({\mathcal{O}})$
-conjugate to the fixed lift
$G({\mathcal{O}})$
-conjugate to the fixed lift
![]() $N_{\unicode[STIX]{x1D70E}}$
defined in Proposition 3.7, reminiscent of the definition we gave for
$N_{\unicode[STIX]{x1D70E}}$
defined in Proposition 3.7, reminiscent of the definition we gave for
![]() $\operatorname{Nil}_{\overline{N}}$
, a situation in which the associated deformation (or lifting) ring is smooth.
$\operatorname{Nil}_{\overline{N}}$
, a situation in which the associated deformation (or lifting) ring is smooth.
We now show that often smoothness fails if
![]() $\overline{N}$
does not lie in the Richardson orbit of
$\overline{N}$
does not lie in the Richardson orbit of
![]() $P_{k}$
. Lifts of
$P_{k}$
. Lifts of
![]() $\overline{N}$
can ‘change nilpotent type’ yet still lie in a parabolic lifting
$\overline{N}$
can ‘change nilpotent type’ yet still lie in a parabolic lifting
![]() $P_{k}$
, such as the example of the standard Borel subgroup in
$P_{k}$
, such as the example of the standard Borel subgroup in
![]() $\operatorname{GL}_{3}$
with
$\operatorname{GL}_{3}$
with
 $$\begin{eqnarray}N=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & p\\ 0 & 0 & 0\end{array}\right)\quad \text{lifting}\quad \overline{N}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}N=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & p\\ 0 & 0 & 0\end{array}\right)\quad \text{lifting}\quad \overline{N}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
In particular, we easily obtain non-pure nilpotents. This is very bad: the nilpotent orbits over a field are smooth but the nilpotent cone is not smooth, so the deformation problem of deforming with respect to
![]() $P$
should not be smooth because ‘it sees multiple orbits’. Furthermore, even if we could lift
$P$
should not be smooth because ‘it sees multiple orbits’. Furthermore, even if we could lift
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
appropriately, there would still be problems lifting
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F})$
appropriately, there would still be problems lifting
![]() $\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})$
because the centralizer of a non-pure nilpotent is not smooth over
$\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D719})$
because the centralizer of a non-pure nilpotent is not smooth over
![]() ${\mathcal{O}}$
(the special and generic fiber typically have different dimensions). So it is crucial to choose a parabolic such that
${\mathcal{O}}$
(the special and generic fiber typically have different dimensions). So it is crucial to choose a parabolic such that
![]() $\overline{N}$
lies in the Richardson orbit of
$\overline{N}$
lies in the Richardson orbit of
![]() $P_{k}$
.
$P_{k}$
.
For
![]() $\operatorname{GL}_{n}$
, all nilpotent orbits are Richardson orbits. This is not true in general. In particular, we should not expect the deformation condition of being ramified with respect to a parabolic to be liftable. Example 1.3 illustrates this phenomenon for
$\operatorname{GL}_{n}$
, all nilpotent orbits are Richardson orbits. This is not true in general. In particular, we should not expect the deformation condition of being ramified with respect to a parabolic to be liftable. Example 1.3 illustrates this phenomenon for
![]() $\operatorname{GSp}_{4}$
, which we now revisit in a more conceptual manner.
$\operatorname{GSp}_{4}$
, which we now revisit in a more conceptual manner.
Example 5.9. Take
![]() $G=\operatorname{GSp}_{4}$
. Parabolic subgroups correspond to isotropic flags. Up to conjugacy, these subgroups are stabilizers of the flags
$G=\operatorname{GSp}_{4}$
. Parabolic subgroups correspond to isotropic flags. Up to conjugacy, these subgroups are stabilizers of the flags
where
![]() $\{v_{1},v_{2},v_{2},v_{4}\}$
is a basis of
$\{v_{1},v_{2},v_{2},v_{4}\}$
is a basis of
![]() $k^{4}$
. Their Richardson orbits correspond to the nilpotent orbits indexed respectively by the partitions
$k^{4}$
. Their Richardson orbits correspond to the nilpotent orbits indexed respectively by the partitions
![]() $1+1+1+1$
,
$1+1+1+1$
,
![]() $4$
,
$4$
,
![]() $4$
, and
$4$
, and
![]() $2+2$
. In particular, the same nilpotent orbit is associated with two flags, and the nilpotent orbit corresponding to the partition
$2+2$
. In particular, the same nilpotent orbit is associated with two flags, and the nilpotent orbit corresponding to the partition
![]() $2+1+1$
does not appear. This corresponds to a nilpotent orbit that is not a Richardson orbit; for the representation in Example 1.3,
$2+1+1$
does not appear. This corresponds to a nilpotent orbit that is not a Richardson orbit; for the representation in Example 1.3,
![]() $\log (\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F}))$
is in this nilpotent orbit.
$\log (\overline{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70F}))$
is in this nilpotent orbit.
6 Minimally ramified deformations in general
We continue the notation of the previous section. We have defined the minimally ramified deformation condition for representations factoring through the quotient
![]() $T_{q}=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
of the tame Galois group
$T_{q}=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
of the tame Galois group
![]() $\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
at a place away from
$\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
at a place away from
![]() $p$
. In this section, we will adapt the matrix-theoretic methods in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4], making use of more conceptual module-theoretic arguments, to define the minimally ramified deformation condition for any representation when
$p$
. In this section, we will adapt the matrix-theoretic methods in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4], making use of more conceptual module-theoretic arguments, to define the minimally ramified deformation condition for any representation when
![]() $G=\operatorname{GSp}_{m}$
or
$G=\operatorname{GSp}_{m}$
or
![]() $G=\operatorname{GO}_{m}$
. (Minor variants of this method work for
$G=\operatorname{GO}_{m}$
. (Minor variants of this method work for
![]() $\operatorname{Sp}_{m}$
and
$\operatorname{Sp}_{m}$
and
![]() $\operatorname{SO}_{m}$
, and the original method of [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] works for
$\operatorname{SO}_{m}$
, and the original method of [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] works for
![]() $\operatorname{GL}_{m}$
.) We naturally embed
$\operatorname{GL}_{m}$
.) We naturally embed
![]() $G$
into
$G$
into
![]() $\operatorname{GL}(M)$
for a free
$\operatorname{GL}(M)$
for a free
![]() ${\mathcal{O}}$
-module
${\mathcal{O}}$
-module
![]() $M$
of rank
$M$
of rank
![]() $m$
, and let
$m$
, and let
![]() $V$
denote the reduction of
$V$
denote the reduction of
![]() $M$
, a vector space over the residue field
$M$
, a vector space over the residue field
![]() $k$
.
$k$
.
We consider a representation
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)\subset \operatorname{GL}(V)(k)$
which may be wildly ramified (with
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)\subset \operatorname{GL}(V)(k)$
which may be wildly ramified (with
![]() $L$
an
$L$
an
![]() $\ell$
-adic field for
$\ell$
-adic field for
![]() $\ell \neq p$
). We will define a deformation condition for
$\ell \neq p$
). We will define a deformation condition for
![]() $\overline{\unicode[STIX]{x1D70C}}$
in terms of the minimally ramified deformation condition for certain associated tamely ramified representations, after possibly extending
$\overline{\unicode[STIX]{x1D70C}}$
in terms of the minimally ramified deformation condition for certain associated tamely ramified representations, after possibly extending
![]() ${\mathcal{O}}$
. In § 6.1, we analyze
${\mathcal{O}}$
. In § 6.1, we analyze
![]() $\overline{\unicode[STIX]{x1D70C}}$
as being built out of two pieces of data: representations of a closed normal subgroup
$\overline{\unicode[STIX]{x1D70C}}$
as being built out of two pieces of data: representations of a closed normal subgroup
![]() $\unicode[STIX]{x1D6EC}_{L}$
of
$\unicode[STIX]{x1D6EC}_{L}$
of
![]() $\unicode[STIX]{x1D6E4}_{L}$
whose pro-order is prime to
$\unicode[STIX]{x1D6E4}_{L}$
whose pro-order is prime to
![]() $p$
, and tamely ramified representations of
$p$
, and tamely ramified representations of
![]() $\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
. The representation theory of
$\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
. The representation theory of
![]() $\unicode[STIX]{x1D6EC}_{L}$
is manageable since its pro-order is prime to
$\unicode[STIX]{x1D6EC}_{L}$
is manageable since its pro-order is prime to
![]() $p$
, and representations of
$p$
, and representations of
![]() $\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
can be understood using the results of the previous section.
$\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
can be understood using the results of the previous section.
6.1 Decomposing representations
We begin with a few preliminaries about representations over rings. Let
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
be a profinite group and
$\unicode[STIX]{x1D6EC}^{\prime }$
be a profinite group and
![]() $R$
be an Artinian coefficient ring with residue field
$R$
be an Artinian coefficient ring with residue field
![]() $k$
. If
$k$
. If
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
has pro-order prime to
$\unicode[STIX]{x1D6EC}^{\prime }$
has pro-order prime to
![]() $p$
, the representation theory of
$p$
, the representation theory of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
over
$\unicode[STIX]{x1D6EC}^{\prime }$
over
![]() $k$
is nice: every finite-dimensional continuous representation is a direct sum of irreducibles, and every such representation is projective over
$k$
is nice: every finite-dimensional continuous representation is a direct sum of irreducibles, and every such representation is projective over
![]() $k[\unicode[STIX]{x1D6EC}]$
for any finite discrete quotient
$k[\unicode[STIX]{x1D6EC}]$
for any finite discrete quotient
![]() $\unicode[STIX]{x1D6EC}$
of
$\unicode[STIX]{x1D6EC}$
of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
through which the representation factors. We are also interested in corresponding statements over an Artinian coefficient ring
$\unicode[STIX]{x1D6EC}^{\prime }$
through which the representation factors. We are also interested in corresponding statements over an Artinian coefficient ring
![]() $R$
.
$R$
.
Fact 6.1. Let
![]() $R$
be an Artinian coefficient ring with residue field
$R$
be an Artinian coefficient ring with residue field
![]() $k$
. Suppose the pro-order of
$k$
. Suppose the pro-order of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
is prime to
$\unicode[STIX]{x1D6EC}^{\prime }$
is prime to
![]() $p$
. Let
$p$
. Let
![]() $P$
and
$P$
and
![]() $P^{\prime }$
be
$P^{\prime }$
be
![]() $R[\unicode[STIX]{x1D6EC}^{\prime }]$
-modules that are finitely generated over
$R[\unicode[STIX]{x1D6EC}^{\prime }]$
-modules that are finitely generated over
![]() $R$
with continuous action of
$R$
with continuous action of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
, and
$\unicode[STIX]{x1D6EC}^{\prime }$
, and
![]() $F$
be a
$F$
be a
![]() $k[\unicode[STIX]{x1D6EC}^{\prime }]$
-module that is finite dimensional over
$k[\unicode[STIX]{x1D6EC}^{\prime }]$
-module that is finite dimensional over
![]() $k$
with continuous action of
$k$
with continuous action of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
. Let
$\unicode[STIX]{x1D6EC}^{\prime }$
. Let
![]() $\unicode[STIX]{x1D6EC}$
be a finite discrete quotient of
$\unicode[STIX]{x1D6EC}$
be a finite discrete quotient of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
through which the
$\unicode[STIX]{x1D6EC}^{\prime }$
through which the
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
-actions on
$\unicode[STIX]{x1D6EC}^{\prime }$
-actions on
![]() $P$
,
$P$
,
![]() $P^{\prime }$
, and
$P^{\prime }$
, and
![]() $F$
factor.
$F$
factor.
(i) If
 $P$
is free as an
$P$
is free as an
 $R$
-module, it is projective as a
$R$
-module, it is projective as a
 $R[\unicode[STIX]{x1D6EC}]$
-module.
$R[\unicode[STIX]{x1D6EC}]$
-module.(ii) If
 $P$
and
$P$
and
 $P^{\prime }$
are projective over
$P^{\prime }$
are projective over
 $R[\unicode[STIX]{x1D6EC}]$
, they are isomorphic if and only if
$R[\unicode[STIX]{x1D6EC}]$
, they are isomorphic if and only if
 $\overline{P}$
and
$\overline{P}$
and
 $\overline{P^{\prime }}$
are isomorphic.
$\overline{P^{\prime }}$
are isomorphic.(iii) There exists a projective
 $R[\unicode[STIX]{x1D6EC}]$
-module (unique up to isomorphism) whose reduction is
$R[\unicode[STIX]{x1D6EC}]$
-module (unique up to isomorphism) whose reduction is
 $F$
.
$F$
.
These statements are special cases of results in [Reference SerreSer77, § 14.4]. We now record two lemmas which do not need the assumption that the pro-order of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
is prime to
$\unicode[STIX]{x1D6EC}^{\prime }$
is prime to
![]() $p$
. Here and elsewhere, we use
$p$
. Here and elsewhere, we use
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\prime }}$
to denote homomorphisms as representations of
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\prime }}$
to denote homomorphisms as representations of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
(equivalently as
$\unicode[STIX]{x1D6EC}^{\prime }$
(equivalently as
![]() $R[\unicode[STIX]{x1D6EC}^{\prime }]$
-modules).
$R[\unicode[STIX]{x1D6EC}^{\prime }]$
-modules).
Lemma 6.2. Let
![]() $P$
and
$P$
and
![]() $P^{\prime }$
be
$P^{\prime }$
be
![]() $R[\unicode[STIX]{x1D6EC}^{\prime }]$
-modules, finitely generated over
$R[\unicode[STIX]{x1D6EC}^{\prime }]$
-modules, finitely generated over
![]() $R$
with continuous action of
$R$
with continuous action of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
factoring through a finite discrete quotient
$\unicode[STIX]{x1D6EC}^{\prime }$
factoring through a finite discrete quotient
![]() $\unicode[STIX]{x1D6EC}$
of
$\unicode[STIX]{x1D6EC}$
of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
. Assume
$\unicode[STIX]{x1D6EC}^{\prime }$
. Assume
![]() $P$
and
$P$
and
![]() $P^{\prime }$
are
$P^{\prime }$
are
![]() $R[\unicode[STIX]{x1D6EC}]$
-projective. The natural map gives an isomorphism
$R[\unicode[STIX]{x1D6EC}]$
-projective. The natural map gives an isomorphism
Proof. We may replace
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\prime }}$
with
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\prime }}$
with
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}$
. Note that
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}$
. Note that
![]() $\mathfrak{m}P^{\prime }=\mathfrak{m}\otimes _{R}P^{\prime }$
, so
$\mathfrak{m}P^{\prime }=\mathfrak{m}\otimes _{R}P^{\prime }$
, so
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P,\mathfrak{m}P^{\prime })=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P,P^{\prime })\otimes _{R}\mathfrak{m}$
as
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P,\mathfrak{m}P^{\prime })=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P,P^{\prime })\otimes _{R}\mathfrak{m}$
as
![]() $P$
and
$P$
and
![]() $P^{\prime }$
are
$P^{\prime }$
are
![]() $R[\unicode[STIX]{x1D6EC}]$
-projective. Then apply
$R[\unicode[STIX]{x1D6EC}]$
-projective. Then apply
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P,-)$
to the exact sequence
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(P,-)$
to the exact sequence
![]() $0\rightarrow \mathfrak{m}P^{\prime }\rightarrow P^{\prime }\rightarrow P^{\prime }/\mathfrak{m}P^{\prime }\rightarrow 0$
.◻
$0\rightarrow \mathfrak{m}P^{\prime }\rightarrow P^{\prime }\rightarrow P^{\prime }/\mathfrak{m}P^{\prime }\rightarrow 0$
.◻
Lemma 6.3. Let
![]() $\unicode[STIX]{x1D6EC}$
be a finite group and let
$\unicode[STIX]{x1D6EC}$
be a finite group and let
![]() $M$
and
$M$
and
![]() $M^{\prime }$
be finite
$M^{\prime }$
be finite
![]() $R[\unicode[STIX]{x1D6EC}]$
-modules whose reductions
$R[\unicode[STIX]{x1D6EC}]$
-modules whose reductions
![]() $\overline{M}$
and
$\overline{M}$
and
![]() $\overline{M}^{\prime }$
are non-isomorphic irreducible
$\overline{M}^{\prime }$
are non-isomorphic irreducible
![]() $k[\unicode[STIX]{x1D6EC}]$
-modules. Then
$k[\unicode[STIX]{x1D6EC}]$
-modules. Then
![]() $\operatorname{Hom}_{R[\unicode[STIX]{x1D6EC}]}(M,M^{\prime })=0$
.
$\operatorname{Hom}_{R[\unicode[STIX]{x1D6EC}]}(M,M^{\prime })=0$
.
Proof. Filter
![]() $M^{\prime }$
by the composition series
$M^{\prime }$
by the composition series
![]() $\{\mathfrak{m}^{i}M^{\prime }\}$
, and consider the surjection
$\{\mathfrak{m}^{i}M^{\prime }\}$
, and consider the surjection
Now
![]() $\unicode[STIX]{x1D6EC}$
acts on
$\unicode[STIX]{x1D6EC}$
acts on
![]() $\mathfrak{m}^{i}/\mathfrak{m}^{i+1}\otimes M^{\prime }$
via its action on
$\mathfrak{m}^{i}/\mathfrak{m}^{i+1}\otimes M^{\prime }$
via its action on
![]() $\overline{M}^{\prime }$
, so as a
$\overline{M}^{\prime }$
, so as a
![]() $k[\unicode[STIX]{x1D6EC}]$
-module
$k[\unicode[STIX]{x1D6EC}]$
-module
![]() $\mathfrak{m}^{i}M^{\prime }/\mathfrak{m}^{i+1}M^{\prime }$
is isomorphic to a direct sum of copies of
$\mathfrak{m}^{i}M^{\prime }/\mathfrak{m}^{i+1}M^{\prime }$
is isomorphic to a direct sum of copies of
![]() $\overline{M}^{\prime }$
. Thus
$\overline{M}^{\prime }$
. Thus
as
![]() $\overline{M}$
and
$\overline{M}$
and
![]() $\overline{M}^{\prime }$
are non-isomorphic
$\overline{M}^{\prime }$
are non-isomorphic
![]() $k[\unicode[STIX]{x1D6EC}]$
-modules.
$k[\unicode[STIX]{x1D6EC}]$
-modules.
By descending induction on
![]() $i$
, we shall show that
$i$
, we shall show that
For large
![]() $i$
,
$i$
,
![]() $\mathfrak{m}^{i}M^{\prime }=0$
. Consider the exact sequence
$\mathfrak{m}^{i}M^{\prime }=0$
. Consider the exact sequence
Applying
![]() $\operatorname{Hom}_{R[\unicode[STIX]{x1D6EC}]}(M,-)$
, we obtain a left exact sequence
$\operatorname{Hom}_{R[\unicode[STIX]{x1D6EC}]}(M,-)$
, we obtain a left exact sequence
The left term is 0 by induction, and the right term is 0 by the above calculation. This completes the induction.◻
Given
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)\subset \operatorname{GL}(V)(k)$
and a lift
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)\subset \operatorname{GL}(V)(k)$
and a lift
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(R)\subset \operatorname{GL}(M)(R)$
for some
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(R)\subset \operatorname{GL}(M)(R)$
for some
![]() $R\in {\mathcal{C}}_{{\mathcal{O}}}$
, we now turn to decomposing the
$R\in {\mathcal{C}}_{{\mathcal{O}}}$
, we now turn to decomposing the
![]() $R[\unicode[STIX]{x1D6E4}_{L}]$
-module
$R[\unicode[STIX]{x1D6E4}_{L}]$
-module
![]() $M$
. Let
$M$
. Let
![]() $I_{L}\subset \unicode[STIX]{x1D6E4}_{L}$
be the inertia group, and pick a surjection
$I_{L}\subset \unicode[STIX]{x1D6E4}_{L}$
be the inertia group, and pick a surjection
![]() $I_{L}\rightarrow \mathbf{Z}_{p}$
. Define
$I_{L}\rightarrow \mathbf{Z}_{p}$
. Define
![]() $\unicode[STIX]{x1D6EC}_{L}$
to be the kernel of this surjection (normal in
$\unicode[STIX]{x1D6EC}_{L}$
to be the kernel of this surjection (normal in
![]() $\unicode[STIX]{x1D6E4}_{L}$
). This is a pro-finite group with pro-order prime to
$\unicode[STIX]{x1D6E4}_{L}$
). This is a pro-finite group with pro-order prime to
![]() $p$
, and is independent of the choice of surjection. Define the quotient
$p$
, and is independent of the choice of surjection. Define the quotient
which is a quotient of the tamely ramified Galois group
![]() $\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
and of the form
$\unicode[STIX]{x1D6E4}_{L}^{\operatorname{t}}$
and of the form
![]() $T_{q}=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
as in § 5. We wish to compatibly decompose
$T_{q}=\widehat{\mathbf{Z}}\ltimes \mathbf{Z}_{p}$
as in § 5. We wish to compatibly decompose
![]() $V$
and
$V$
and
![]() $M$
as
$M$
as
![]() $\unicode[STIX]{x1D6EC}_{L}$
-modules and then understand the action of
$\unicode[STIX]{x1D6EC}_{L}$
-modules and then understand the action of
![]() $\unicode[STIX]{x1D6E4}_{L}$
on the decomposition.
$\unicode[STIX]{x1D6E4}_{L}$
on the decomposition.
We first make a finite extension of
![]() $k$
(and of
$k$
(and of
![]() ${\mathcal{O}}$
) so that all of the (finitely many) irreducible representations of
${\mathcal{O}}$
) so that all of the (finitely many) irreducible representations of
![]() $\unicode[STIX]{x1D6EC}_{L}$
over
$\unicode[STIX]{x1D6EC}_{L}$
over
![]() $k$
occurring in
$k$
occurring in
![]() $V$
are absolutely irreducible over
$V$
are absolutely irreducible over
![]() $k$
.
$k$
.
Because
![]() $\unicode[STIX]{x1D6EC}_{L}$
has order prime to
$\unicode[STIX]{x1D6EC}_{L}$
has order prime to
![]() $p$
,
$p$
,
![]() $\operatorname{Res}_{\unicode[STIX]{x1D6EC}_{L}}^{\unicode[STIX]{x1D6E4}_{L}}(V)$
is completely reducible and we can write
$\operatorname{Res}_{\unicode[STIX]{x1D6EC}_{L}}^{\unicode[STIX]{x1D6E4}_{L}}(V)$
is completely reducible and we can write
where
![]() $\unicode[STIX]{x1D70F}$
runs through the set of isomorphism classes of irreducible representations of
$\unicode[STIX]{x1D70F}$
runs through the set of isomorphism classes of irreducible representations of
![]() $\unicode[STIX]{x1D6EC}_{L}$
over
$\unicode[STIX]{x1D6EC}_{L}$
over
![]() $k$
occurring in
$k$
occurring in
![]() $V$
, and each
$V$
, and each
![]() $V_{\unicode[STIX]{x1D70F}}$
is the
$V_{\unicode[STIX]{x1D70F}}$
is the
![]() $\unicode[STIX]{x1D70F}$
-isotypic component. We will obtain an analogous decomposition for
$\unicode[STIX]{x1D70F}$
-isotypic component. We will obtain an analogous decomposition for
![]() $M$
.
$M$
.
Let
![]() $\unicode[STIX]{x1D6E4}$
be a finite discrete quotient of
$\unicode[STIX]{x1D6E4}$
be a finite discrete quotient of
![]() $\unicode[STIX]{x1D6E4}_{L}$
through which
$\unicode[STIX]{x1D6E4}_{L}$
through which
![]() $\unicode[STIX]{x1D70C}$
factors, and let
$\unicode[STIX]{x1D70C}$
factors, and let
![]() $\unicode[STIX]{x1D6EC}$
be the image of
$\unicode[STIX]{x1D6EC}$
be the image of
![]() $\unicode[STIX]{x1D6EC}_{L}$
in
$\unicode[STIX]{x1D6EC}_{L}$
in
![]() $\unicode[STIX]{x1D6E4}$
. Using Fact 6.1(iii) we can lift
$\unicode[STIX]{x1D6E4}$
. Using Fact 6.1(iii) we can lift
![]() $\unicode[STIX]{x1D70F}$
to a projective
$\unicode[STIX]{x1D70F}$
to a projective
![]() $R[\unicode[STIX]{x1D6EC}]$
-module
$R[\unicode[STIX]{x1D6EC}]$
-module
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
unique up to isomorphism. We will eventually want this lift to have additional properties (see § 6.2), but this is not yet necessary. We set
$\widetilde{\unicode[STIX]{x1D70F}}$
unique up to isomorphism. We will eventually want this lift to have additional properties (see § 6.2), but this is not yet necessary. We set
![]() $W_{\unicode[STIX]{x1D70F}}:=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}},M)$
and consider the natural morphism
$W_{\unicode[STIX]{x1D70F}}:=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}},M)$
and consider the natural morphism
Note that
![]() $M$
is
$M$
is
![]() $R[\unicode[STIX]{x1D6EC}]$
-projective by Fact 6.1(i).
$R[\unicode[STIX]{x1D6EC}]$
-projective by Fact 6.1(i).
Lemma 6.4. This map is an isomorphism of
![]() $R[\unicode[STIX]{x1D6EC}_{L}]$
-modules.
$R[\unicode[STIX]{x1D6EC}_{L}]$
-modules.
Proof. It suffices to check the map is an isomorphism of
![]() $R[\unicode[STIX]{x1D6EC}]$
-modules. When
$R[\unicode[STIX]{x1D6EC}]$
-modules. When
![]() $R=k$
,
$R=k$
,
![]() $\operatorname{End}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})=k$
as we extended
$\operatorname{End}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})=k$
as we extended
![]() $k$
so that all of the irreducible representations of
$k$
so that all of the irreducible representations of
![]() $\unicode[STIX]{x1D6EC}$
over
$\unicode[STIX]{x1D6EC}$
over
![]() $k$
occurring inside
$k$
occurring inside
![]() $V$
are absolutely irreducible. Splitting up
$V$
are absolutely irreducible. Splitting up
![]() $V$
as a direct sum of irreducibles, we obtain the desired isomorphism.
$V$
as a direct sum of irreducibles, we obtain the desired isomorphism.
In the general case, the map is an isomorphism after reducing modulo
![]() $\mathfrak{m}$
(use Lemma 6.2). Thus by Nakayama’s lemma it is surjective. Since
$\mathfrak{m}$
(use Lemma 6.2). Thus by Nakayama’s lemma it is surjective. Since
![]() $M$
is
$M$
is
![]() $R$
-projective, the formation of the kernel commutes with reduction modulo
$R$
-projective, the formation of the kernel commutes with reduction modulo
![]() $\mathfrak{m}$
. Thus, again using Nakayama’s lemma, the kernel is zero.◻
$\mathfrak{m}$
. Thus, again using Nakayama’s lemma, the kernel is zero.◻
We define
![]() $M_{\unicode[STIX]{x1D70F}}$
to be the image of
$M_{\unicode[STIX]{x1D70F}}$
to be the image of
![]() $\widetilde{\unicode[STIX]{x1D70F}}\otimes _{R}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}},M)$
in
$\widetilde{\unicode[STIX]{x1D70F}}\otimes _{R}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}},M)$
in
![]() $M$
. It is the largest
$M$
. It is the largest
![]() $R[\unicode[STIX]{x1D6EC}_{L}]$
-direct summand whose reduction is a direct sum of copies of
$R[\unicode[STIX]{x1D6EC}_{L}]$
-direct summand whose reduction is a direct sum of copies of
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
We next seek to understand the action of
![]() $\unicode[STIX]{x1D6E4}_{L}$
on this canonical decomposition of
$\unicode[STIX]{x1D6E4}_{L}$
on this canonical decomposition of
![]() $M$
. For
$M$
. For
![]() $g\in \unicode[STIX]{x1D6E4}_{L}$
, consider the
$g\in \unicode[STIX]{x1D6E4}_{L}$
, consider the
![]() $R[\unicode[STIX]{x1D6EC}_{L}]$
-module
$R[\unicode[STIX]{x1D6EC}_{L}]$
-module
![]() $gM_{\unicode[STIX]{x1D70F}}$
: it is a direct summand of
$gM_{\unicode[STIX]{x1D70F}}$
: it is a direct summand of
![]() $M$
over
$M$
over
![]() $R$
whose reduction is a direct sum of copies of the representation
$R$
whose reduction is a direct sum of copies of the representation
![]() $\unicode[STIX]{x1D70F}^{g}$
defined by
$\unicode[STIX]{x1D70F}^{g}$
defined by
![]() $\unicode[STIX]{x1D70F}^{g}(h)=\unicode[STIX]{x1D70F}(g^{-1}hg)$
for
$\unicode[STIX]{x1D70F}^{g}(h)=\unicode[STIX]{x1D70F}(g^{-1}hg)$
for
![]() $h\in \unicode[STIX]{x1D6EC}_{L}$
. Thus we see that
$h\in \unicode[STIX]{x1D6EC}_{L}$
. Thus we see that
![]() $gM_{\unicode[STIX]{x1D70F}}=M_{\unicode[STIX]{x1D70F}^{g}}$
inside
$gM_{\unicode[STIX]{x1D70F}}=M_{\unicode[STIX]{x1D70F}^{g}}$
inside
![]() $M$
, and
$M$
, and
![]() $\unicode[STIX]{x1D6E4}_{L}$
permutes the modules
$\unicode[STIX]{x1D6E4}_{L}$
permutes the modules
![]() $M_{\unicode[STIX]{x1D70F}}$
. The orbits corresponds to sets of conjugate representations.
$M_{\unicode[STIX]{x1D70F}}$
. The orbits corresponds to sets of conjugate representations.
Consider the stabilizer of
![]() $V_{\unicode[STIX]{x1D70F}}$
:
$V_{\unicode[STIX]{x1D70F}}$
:
with corresponding image
Then the
![]() $k$
-span of the
$k$
-span of the
![]() $\unicode[STIX]{x1D6E4}_{L}$
-orbit of
$\unicode[STIX]{x1D6E4}_{L}$
-orbit of
![]() $V_{\unicode[STIX]{x1D70F}}$
is exactly the representation
$V_{\unicode[STIX]{x1D70F}}$
is exactly the representation
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}V_{\unicode[STIX]{x1D70F}}=\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}}V_{\unicode[STIX]{x1D70F}}$
. Letting
$\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}V_{\unicode[STIX]{x1D70F}}=\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}}V_{\unicode[STIX]{x1D70F}}$
. Letting
![]() $[\unicode[STIX]{x1D70F}]$
denote the set of
$[\unicode[STIX]{x1D70F}]$
denote the set of
![]() $R[\unicode[STIX]{x1D6EC}]$
-isomorphism classes of
$R[\unicode[STIX]{x1D6EC}]$
-isomorphism classes of
![]() $\unicode[STIX]{x1D6EC}$
-representations
$\unicode[STIX]{x1D6EC}$
-representations
![]() $\unicode[STIX]{x1D6E4}$
-conjugate to
$\unicode[STIX]{x1D6E4}$
-conjugate to
![]() $\unicode[STIX]{x1D70F}$
, by taking into account the action of
$\unicode[STIX]{x1D70F}$
, by taking into account the action of
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
the isomorphism in Lemma 6.4 becomes an isomorphism of
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
the isomorphism in Lemma 6.4 becomes an isomorphism of
![]() $R[\unicode[STIX]{x1D6E4}_{L}]$
-modules
$R[\unicode[STIX]{x1D6E4}_{L}]$
-modules
using one representative
![]() $\unicode[STIX]{x1D70F}$
per
$\unicode[STIX]{x1D70F}$
per
![]() $\unicode[STIX]{x1D6E4}_{L}$
-conjugacy class
$\unicode[STIX]{x1D6E4}_{L}$
-conjugacy class
![]() $[\unicode[STIX]{x1D70F}]$
.
$[\unicode[STIX]{x1D70F}]$
.
For orthogonal or symplectic representations, we will make precise the notion that this decomposition is ‘compatible with duality’. Denote the similitude character by
![]() $\unicode[STIX]{x1D707}$
, and let
$\unicode[STIX]{x1D707}$
, and let
![]() $\overline{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D707}\circ \overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow k^{\times }$
. Let
$\overline{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D707}\circ \overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow k^{\times }$
. Let
![]() $N$
be a free
$N$
be a free
![]() ${\mathcal{O}}$
-module of rank
${\mathcal{O}}$
-module of rank
![]() $1$
on which
$1$
on which
![]() $\unicode[STIX]{x1D6E4}_{L}$
acts by a specified continuous
$\unicode[STIX]{x1D6E4}_{L}$
acts by a specified continuous
![]() ${\mathcal{O}}^{\times }$
-valued lift
${\mathcal{O}}^{\times }$
-valued lift
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $\overline{\unicode[STIX]{x1D708}}$
, and let
$\overline{\unicode[STIX]{x1D708}}$
, and let
![]() $\overline{N}$
be its reduction modulo
$\overline{N}$
be its reduction modulo
![]() $\mathfrak{m}$
. For an
$\mathfrak{m}$
. For an
![]() $R$
-module
$R$
-module
![]() $M$
, define
$M$
, define
![]() $M^{\vee }=\operatorname{Hom}_{R}(M,N_{R})$
with the evident
$M^{\vee }=\operatorname{Hom}_{R}(M,N_{R})$
with the evident
![]() $\unicode[STIX]{x1D6E4}_{L}$
-action.
$\unicode[STIX]{x1D6E4}_{L}$
-action.
Now suppose we have chosen
![]() $\unicode[STIX]{x1D708}$
so that
$\unicode[STIX]{x1D708}$
so that
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70C}$
(viewed as maps
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70C}$
(viewed as maps
![]() $\unicode[STIX]{x1D6E4}_{L}\rightarrow R^{\times }$
). The perfect pairing on the
$\unicode[STIX]{x1D6E4}_{L}\rightarrow R^{\times }$
). The perfect pairing on the
![]() $M$
corresponding to
$M$
corresponding to
![]() $\unicode[STIX]{x1D70C}$
gives an isomorphism of
$\unicode[STIX]{x1D70C}$
gives an isomorphism of
![]() $R[\unicode[STIX]{x1D6E4}_{L}]$
-modules
$R[\unicode[STIX]{x1D6E4}_{L}]$
-modules
![]() $\unicode[STIX]{x1D713}:M\simeq M^{\vee }$
. In particular, using Lemma 6.4 we see that
$\unicode[STIX]{x1D713}:M\simeq M^{\vee }$
. In particular, using Lemma 6.4 we see that
To simplify notation, we will write
![]() $M_{\unicode[STIX]{x1D70F}}^{\vee }$
for
$M_{\unicode[STIX]{x1D70F}}^{\vee }$
for
![]() $(M_{\unicode[STIX]{x1D70F}})^{\vee }$
. Note that the right side is also an isotypic decomposition, with
$(M_{\unicode[STIX]{x1D70F}})^{\vee }$
. Note that the right side is also an isotypic decomposition, with
![]() $M_{\unicode[STIX]{x1D70F}}^{\vee }$
the maximal direct whose direct sum is a direct sum of copies of
$M_{\unicode[STIX]{x1D70F}}^{\vee }$
the maximal direct whose direct sum is a direct sum of copies of
![]() $\unicode[STIX]{x1D70F}^{\vee }$
. By comparing isotypic pieces, we obtain a natural isomorphism (of
$\unicode[STIX]{x1D70F}^{\vee }$
. By comparing isotypic pieces, we obtain a natural isomorphism (of
![]() $R[\unicode[STIX]{x1D6EC}_{L}]$
-modules)
$R[\unicode[STIX]{x1D6EC}_{L}]$
-modules)
for some irreducible representation
![]() $\unicode[STIX]{x1D70F}^{\ast }$
of
$\unicode[STIX]{x1D70F}^{\ast }$
of
![]() $\unicode[STIX]{x1D6EC}_{L}$
occurring in
$\unicode[STIX]{x1D6EC}_{L}$
occurring in
![]() $V$
. Note that
$V$
. Note that
![]() $\unicode[STIX]{x1D70F}^{\ast }\simeq \unicode[STIX]{x1D70F}^{\vee }$
as
$\unicode[STIX]{x1D70F}^{\ast }\simeq \unicode[STIX]{x1D70F}^{\vee }$
as
![]() $k[\unicode[STIX]{x1D6EC}_{L}]$
-modules, but that
$k[\unicode[STIX]{x1D6EC}_{L}]$
-modules, but that
![]() $\unicode[STIX]{x1D70F}^{\ast }$
is not necessarily the dual of
$\unicode[STIX]{x1D70F}^{\ast }$
is not necessarily the dual of
![]() $\unicode[STIX]{x1D70F}$
as
$\unicode[STIX]{x1D70F}$
as
![]() $k[\unicode[STIX]{x1D6E4}_{L}]$
-modules. There are three cases.
$k[\unicode[STIX]{x1D6E4}_{L}]$
-modules. There are three cases.
∙ Case 1:
 $\unicode[STIX]{x1D70F}$
is not
$\unicode[STIX]{x1D70F}$
is not
 $\unicode[STIX]{x1D6E4}_{L}$
-conjugate to
$\unicode[STIX]{x1D6E4}_{L}$
-conjugate to
 $\unicode[STIX]{x1D70F}^{\ast }$
.
$\unicode[STIX]{x1D70F}^{\ast }$
.∙ Case 2:
 $\unicode[STIX]{x1D70F}$
is isomorphic to
$\unicode[STIX]{x1D70F}$
is isomorphic to
 $\unicode[STIX]{x1D70F}^{\ast }$
as
$\unicode[STIX]{x1D70F}^{\ast }$
as
 $\unicode[STIX]{x1D6E4}_{L}$
-modules.
$\unicode[STIX]{x1D6E4}_{L}$
-modules.∙ Case 3:
 $\unicode[STIX]{x1D70F}$
is
$\unicode[STIX]{x1D70F}$
is
 $\unicode[STIX]{x1D6E4}_{L}$
-conjugate to
$\unicode[STIX]{x1D6E4}_{L}$
-conjugate to
 $\unicode[STIX]{x1D70F}^{\ast }$
but not isomorphic.
$\unicode[STIX]{x1D70F}^{\ast }$
but not isomorphic.
In the second case, we claim that the isomorphism of
![]() $k[\unicode[STIX]{x1D6EC}_{L}]$
-modules
$k[\unicode[STIX]{x1D6EC}_{L}]$
-modules
![]() $\imath :\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\vee }$
gives a sign-symmetric (for some fixed sign
$\imath :\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\vee }$
gives a sign-symmetric (for some fixed sign
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
) perfect pairing on
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
) perfect pairing on
![]() $\unicode[STIX]{x1D70F}$
. Note that
$\unicode[STIX]{x1D70F}$
. Note that
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F},V)$
by Lemma 6.2, and that
$\overline{W}_{\unicode[STIX]{x1D70F}}=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F},V)$
by Lemma 6.2, and that
Denote this isomorphism by
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}$
: it defines a pairing
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}$
: it defines a pairing
![]() $\langle \,,\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}$
on
$\langle \,,\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}$
on
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
via
$\overline{W}_{\unicode[STIX]{x1D70F}}$
via
We can also define
![]() $\langle v_{1},v_{2}\rangle _{\unicode[STIX]{x1D70F}}:=\imath (v_{1})(v_{2})$
for
$\langle v_{1},v_{2}\rangle _{\unicode[STIX]{x1D70F}}:=\imath (v_{1})(v_{2})$
for
![]() $v_{1},v_{2}\in \unicode[STIX]{x1D70F}$
. We have a commutative diagram of isomorphisms.
$v_{1},v_{2}\in \unicode[STIX]{x1D70F}$
. We have a commutative diagram of isomorphisms.

The commutativity says that for elementary tensors
![]() $m_{i}=v_{i}\otimes w_{i}\in V_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}\otimes \overline{W}_{\unicode[STIX]{x1D70F}}$
we have
$m_{i}=v_{i}\otimes w_{i}\in V_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}\otimes \overline{W}_{\unicode[STIX]{x1D70F}}$
we have
Remember that the pairing on
![]() $V$
is
$V$
is
![]() $\unicode[STIX]{x1D716}$
-symmetric.
$\unicode[STIX]{x1D716}$
-symmetric.
Lemma 6.5. The pairing
![]() $\langle \,,\rangle _{\unicode[STIX]{x1D70F}}$
is a sign-symmetric (for fixed sign
$\langle \,,\rangle _{\unicode[STIX]{x1D70F}}$
is a sign-symmetric (for fixed sign
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
).
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
).
Proof. Suppose there exists
![]() $v\in \unicode[STIX]{x1D70F}$
such that
$v\in \unicode[STIX]{x1D70F}$
such that
![]() $\imath (v)(v)\neq 0$
. For
$\imath (v)(v)\neq 0$
. For
![]() $w_{1},w_{2}\in \overline{W}_{\unicode[STIX]{x1D70F}}$
, (6.2) gives
$w_{1},w_{2}\in \overline{W}_{\unicode[STIX]{x1D70F}}$
, (6.2) gives
Canceling
![]() $\imath (v)(v)$
, we conclude that
$\imath (v)(v)$
, we conclude that
![]() $\langle w_{1},w_{2}\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}=\unicode[STIX]{x1D716}\langle w_{2},w_{1}\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}$
. Using (6.2), we conclude that
$\langle w_{1},w_{2}\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}=\unicode[STIX]{x1D716}\langle w_{2},w_{1}\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}$
. Using (6.2), we conclude that
Choosing
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
with
$w_{2}$
with
![]() $\langle w_{2},w_{1}\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}\neq 0$
(possible as
$\langle w_{2},w_{1}\rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}\neq 0$
(possible as
![]() $\langle \,,\rangle _{V}$
is perfect), we then conclude that
$\langle \,,\rangle _{V}$
is perfect), we then conclude that
![]() $\langle v_{1},v_{2}\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}=\langle v_{2},v_{1}\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}$
.
$\langle v_{1},v_{2}\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}=\langle v_{2},v_{1}\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}$
.
Otherwise
![]() $\imath (v)(v)=0$
for all
$\imath (v)(v)=0$
for all
![]() $v\in \unicode[STIX]{x1D70F}$
, in which case
$v\in \unicode[STIX]{x1D70F}$
, in which case
![]() $\langle \,,\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}$
is alternating.◻
$\langle \,,\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}$
is alternating.◻
In § 6.2 we will see that the action of
![]() $\unicode[STIX]{x1D6EC}_{L}$
on the module underlying
$\unicode[STIX]{x1D6EC}_{L}$
on the module underlying
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
can be extended to an action of
$\widetilde{\unicode[STIX]{x1D70F}}$
can be extended to an action of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
factoring through
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
factoring through
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
. Therefore,
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
. Therefore,
![]() $W_{\unicode[STIX]{x1D70F}}=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}},M)$
is naturally a representation of
$W_{\unicode[STIX]{x1D70F}}=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}},M)$
is naturally a representation of
![]() $T_{L,\unicode[STIX]{x1D70F}}:=\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D6EC}_{L}$
, and of
$T_{L,\unicode[STIX]{x1D70F}}:=\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D6EC}_{L}$
, and of
![]() $T_{\unicode[STIX]{x1D70F}}:=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D6EC}$
(a finite quotient of
$T_{\unicode[STIX]{x1D70F}}:=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D6EC}$
(a finite quotient of
![]() $T_{L,\unicode[STIX]{x1D70F}}$
). In § 6.4, we will use the minimally ramified deformation condition of § 5 to specify which deformations
$T_{L,\unicode[STIX]{x1D70F}}$
). In § 6.4, we will use the minimally ramified deformation condition of § 5 to specify which deformations
![]() $W_{\unicode[STIX]{x1D70F}}$
are allowed. Together with the decomposition (6.1)
$W_{\unicode[STIX]{x1D70F}}$
are allowed. Together with the decomposition (6.1)
this defines a deformation condition for
![]() $\overline{\unicode[STIX]{x1D70C}}$
. Some care is needed to ensure compatibility of the lifts with the pairing on
$\overline{\unicode[STIX]{x1D70C}}$
. Some care is needed to ensure compatibility of the lifts with the pairing on
![]() $M$
, which will require breaking into cases in the next sections based on the relationship between
$M$
, which will require breaking into cases in the next sections based on the relationship between
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}^{\ast }$
.
$\unicode[STIX]{x1D70F}^{\ast }$
.
6.2 Extension of representations
We continue the notation of the previous section, where
![]() $\unicode[STIX]{x1D70F}$
is an absolutely irreducible representation of
$\unicode[STIX]{x1D70F}$
is an absolutely irreducible representation of
![]() $\unicode[STIX]{x1D6EC}_{L}$
over
$\unicode[STIX]{x1D6EC}_{L}$
over
![]() $k$
. We need to lift this to a representation over
$k$
. We need to lift this to a representation over
![]() ${\mathcal{O}}$
and extend it to a representation of
${\mathcal{O}}$
and extend it to a representation of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
. We will have to do something extra for the representation to be compatible with a pairing, depending on how
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
. We will have to do something extra for the representation to be compatible with a pairing, depending on how
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}^{\ast }$
are related.
$\unicode[STIX]{x1D70F}^{\ast }$
are related.
In Case 1, we ignore the pairing. Lemma 2.4.11 of [Reference Clozel, Harris and TaylorCHT08] lets us pick a
![]() ${\mathcal{O}}[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}]$
-module
${\mathcal{O}}[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}]$
-module
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
that is a free
$\widetilde{\unicode[STIX]{x1D70F}}$
that is a free
![]() ${\mathcal{O}}$
-module and reduces to
${\mathcal{O}}$
-module and reduces to
![]() $\unicode[STIX]{x1D70F}$
. In this case,
$\unicode[STIX]{x1D70F}$
. In this case,
![]() $\widetilde{\unicode[STIX]{x1D70F}}^{\vee }$
is a free
$\widetilde{\unicode[STIX]{x1D70F}}^{\vee }$
is a free
![]() ${\mathcal{O}}$
-module reducing to
${\mathcal{O}}$
-module reducing to
![]() $\unicode[STIX]{x1D70F}^{\ast }$
.
$\unicode[STIX]{x1D70F}^{\ast }$
.
In Case 2, from Lemma 6.5 it follows that
![]() $\unicode[STIX]{x1D70F}$
is a symplectic or orthogonal representation. We will adapt the
$\unicode[STIX]{x1D70F}$
is a symplectic or orthogonal representation. We will adapt the
![]() $\operatorname{GL}_{n}$
-technique of [Reference Clozel, Harris and TaylorCHT08] to produce a symplectic or orthogonal extension
$\operatorname{GL}_{n}$
-technique of [Reference Clozel, Harris and TaylorCHT08] to produce a symplectic or orthogonal extension
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
. Letting
$\widetilde{\unicode[STIX]{x1D70F}}$
. Letting
![]() $n=\dim \unicode[STIX]{x1D70F}$
, the representation
$n=\dim \unicode[STIX]{x1D70F}$
, the representation
![]() $\unicode[STIX]{x1D70F}$
gives a homomorphism
$\unicode[STIX]{x1D70F}$
gives a homomorphism
![]() $\unicode[STIX]{x1D70F}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G(k)$
where
$\unicode[STIX]{x1D70F}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G(k)$
where
![]() $G$
is
$G$
is
![]() $\operatorname{GSp}_{n}$
or
$\operatorname{GSp}_{n}$
or
![]() $\operatorname{GO}_{n}$
.
$\operatorname{GO}_{n}$
.
First, we claim that there is a continuous lift
![]() $\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G(W(k))$
: without the pairing, this would be Fact 6.1(iii). To also take into account the pairing, consider deformation theory for the residual representation
$\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G(W(k))$
: without the pairing, this would be Fact 6.1(iii). To also take into account the pairing, consider deformation theory for the residual representation
![]() $\unicode[STIX]{x1D70F}$
. This is a smooth deformation condition as
$\unicode[STIX]{x1D70F}$
. This is a smooth deformation condition as
![]() $H^{2}(\unicode[STIX]{x1D6EC}_{L},\operatorname{ad}\unicode[STIX]{x1D70F})=0$
:
$H^{2}(\unicode[STIX]{x1D6EC}_{L},\operatorname{ad}\unicode[STIX]{x1D70F})=0$
:
![]() $\unicode[STIX]{x1D6EC}_{L}$
has pro-order prime to
$\unicode[STIX]{x1D6EC}_{L}$
has pro-order prime to
![]() $p$
and
$p$
and
![]() $\operatorname{ad}\unicode[STIX]{x1D70F}$
has order a power of
$\operatorname{ad}\unicode[STIX]{x1D70F}$
has order a power of
![]() $p$
. Therefore the desired lift exists. It is unique (up to conjugation by an element of
$p$
. Therefore the desired lift exists. It is unique (up to conjugation by an element of
![]() $\widehat{G}({\mathcal{O}})$
) because the tangent space is zero dimensional as
$\widehat{G}({\mathcal{O}})$
) because the tangent space is zero dimensional as
![]() $H^{1}(\unicode[STIX]{x1D6EC}_{L},\operatorname{ad}\unicode[STIX]{x1D70F})=0$
. By considering representations of the group
$H^{1}(\unicode[STIX]{x1D6EC}_{L},\operatorname{ad}\unicode[STIX]{x1D70F})=0$
. By considering representations of the group
![]() $\unicode[STIX]{x1D6EC}_{L}/\text{ker}(\unicode[STIX]{x1D70F})$
, we may and do assume that
$\unicode[STIX]{x1D6EC}_{L}/\text{ker}(\unicode[STIX]{x1D70F})$
, we may and do assume that
![]() $\ker (\widetilde{\unicode[STIX]{x1D70F}})=\ker (\unicode[STIX]{x1D70F})$
as subgroups of
$\ker (\widetilde{\unicode[STIX]{x1D70F}})=\ker (\unicode[STIX]{x1D70F})$
as subgroups of
![]() $\unicode[STIX]{x1D6EC}_{L}$
.
$\unicode[STIX]{x1D6EC}_{L}$
.
Remark 6.6. For
![]() $g\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, the
$g\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, the
![]() $k[\unicode[STIX]{x1D6EC}_{L}]$
-modules
$k[\unicode[STIX]{x1D6EC}_{L}]$
-modules
![]() $\unicode[STIX]{x1D70F}^{g}\simeq \unicode[STIX]{x1D70F}$
are isomorphic. By uniqueness of the lift, this means that there is
$\unicode[STIX]{x1D70F}^{g}\simeq \unicode[STIX]{x1D70F}$
are isomorphic. By uniqueness of the lift, this means that there is
![]() $A\in G({\mathcal{O}})$
such that
$A\in G({\mathcal{O}})$
such that
![]() $\widetilde{\unicode[STIX]{x1D70F}}^{g}(\unicode[STIX]{x1D6FE})=A\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FE})A^{-1}$
for all
$\widetilde{\unicode[STIX]{x1D70F}}^{g}(\unicode[STIX]{x1D6FE})=A\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FE})A^{-1}$
for all
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{L}$
. Furthermore,
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{L}$
. Furthermore,
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}=\{g\in \unicode[STIX]{x1D6E4}_{L}:\widetilde{\unicode[STIX]{x1D70F}}^{g}\simeq \widetilde{\unicode[STIX]{x1D70F}}\}$
.
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}=\{g\in \unicode[STIX]{x1D6E4}_{L}:\widetilde{\unicode[STIX]{x1D70F}}^{g}\simeq \widetilde{\unicode[STIX]{x1D70F}}\}$
.
We will now show how to continuously extend
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
to
$\widetilde{\unicode[STIX]{x1D70F}}$
to
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
. The first step in constructing the extension is to understand the structure of
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
. The first step in constructing the extension is to understand the structure of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
and
![]() $I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, where
$I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, where
![]() $I_{L}$
is the inertia group.
$I_{L}$
is the inertia group.
Recall that
![]() $T_{L}=\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
is the semidirect product of
$T_{L}=\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
is the semidirect product of
![]() $\widehat{\mathbf{Z}}$
and
$\widehat{\mathbf{Z}}$
and
![]() $\mathbf{Z}_{p}$
, where
$\mathbf{Z}_{p}$
, where
![]() $\widehat{\mathbf{Z}}$
is generated by a lift of Frobenius
$\widehat{\mathbf{Z}}$
is generated by a lift of Frobenius
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\mathbf{Z}_{p}$
is generated by an element
$\mathbf{Z}_{p}$
is generated by an element
![]() $\unicode[STIX]{x1D70E}$
, with
$\unicode[STIX]{x1D70E}$
, with
![]() $\unicode[STIX]{x1D719}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{-1}=\unicode[STIX]{x1D70E}^{q}$
where
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{-1}=\unicode[STIX]{x1D70E}^{q}$
where
![]() $q=\ell ^{a}$
is the size of the residue field of
$q=\ell ^{a}$
is the size of the residue field of
![]() $L$
.
$L$
.
Fact 6.7. The exact sequence
is topologically split, so
![]() $\unicode[STIX]{x1D6E4}_{L}$
is a semidirect product.
$\unicode[STIX]{x1D6E4}_{L}$
is a semidirect product.
Proof. This is [Reference Clozel, Harris and TaylorCHT08, 2.4.10].◻
For
![]() $T_{L,\unicode[STIX]{x1D70F}}:=\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D6EC}_{L}$
, this gives a topological splitting of
$T_{L,\unicode[STIX]{x1D70F}}:=\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D6EC}_{L}$
, this gives a topological splitting of
As
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
is an open subgroup of
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
is an open subgroup of
![]() $\unicode[STIX]{x1D6E4}_{L}$
, we observe that
$\unicode[STIX]{x1D6E4}_{L}$
, we observe that
![]() $T_{L,\unicode[STIX]{x1D70F}}$
is an open subgroup of
$T_{L,\unicode[STIX]{x1D70F}}$
is an open subgroup of
![]() $T_{L}$
. Note that
$T_{L}$
. Note that
![]() $T_{L,\unicode[STIX]{x1D70F}}$
is normal and topologically generated by some powers of
$T_{L,\unicode[STIX]{x1D70F}}$
is normal and topologically generated by some powers of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D70E}$
which will be denoted by
$\unicode[STIX]{x1D70E}$
which will be denoted by
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
(since any open subgroup of a semidirect product
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
(since any open subgroup of a semidirect product
![]() $C\ltimes C^{\prime }$
for pro-cyclic
$C\ltimes C^{\prime }$
for pro-cyclic
![]() $C$
and
$C$
and
![]() $C^{\prime }$
is of the form
$C^{\prime }$
is of the form
![]() $C_{0}\ltimes C_{0}^{\prime }$
for open subgroups
$C_{0}\ltimes C_{0}^{\prime }$
for open subgroups
![]() $C_{0}\subset C$
and
$C_{0}\subset C$
and
![]() $C_{0}^{\prime }\subset C^{\prime }$
). In particular, using the notation of § 5.2
$C_{0}^{\prime }\subset C^{\prime }$
). In particular, using the notation of § 5.2
![]() $T_{L,\unicode[STIX]{x1D70F}}$
is itself isomorphic to
$T_{L,\unicode[STIX]{x1D70F}}$
is itself isomorphic to
![]() $T_{q^{\prime }}$
for some
$T_{q^{\prime }}$
for some
![]() $q^{\prime }$
. The element
$q^{\prime }$
. The element
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D6EC}_{L}$
together topologically generate
$\unicode[STIX]{x1D6EC}_{L}$
together topologically generate
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
.
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
.
Before extending
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
, we need several technical lemmas.
$\widetilde{\unicode[STIX]{x1D70F}}$
, we need several technical lemmas.
Lemma 6.8. We have that
![]() $\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}})={\mathcal{O}}$
.
$\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}})={\mathcal{O}}$
.
Proof. As
![]() $\unicode[STIX]{x1D70F}$
is absolutely irreducible,
$\unicode[STIX]{x1D70F}$
is absolutely irreducible,
![]() $\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\unicode[STIX]{x1D70F})=k$
. By Lemma 6.2, we see that the reduction of
$\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\unicode[STIX]{x1D70F})=k$
. By Lemma 6.2, we see that the reduction of
![]() $\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}})$
modulo the maximal ideal of
$\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}})$
modulo the maximal ideal of
![]() ${\mathcal{O}}$
is
${\mathcal{O}}$
is
![]() $k$
, so the map
$k$
, so the map
![]() ${\mathcal{O}}{\hookrightarrow}\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}})$
is surjective by Nakayama’s lemma.◻
${\mathcal{O}}{\hookrightarrow}\operatorname{End}_{\unicode[STIX]{x1D6EC}_{L}}(\widetilde{\unicode[STIX]{x1D70F}})$
is surjective by Nakayama’s lemma.◻
Lemma 6.9. The dimension of
![]() $\unicode[STIX]{x1D70F}$
is not divisible by
$\unicode[STIX]{x1D70F}$
is not divisible by
![]() $p$
.
$p$
.
Proof. As
![]() $\unicode[STIX]{x1D70F}$
is continuous and
$\unicode[STIX]{x1D70F}$
is continuous and
![]() $\unicode[STIX]{x1D6EC}_{L}$
has pro-order prime to
$\unicode[STIX]{x1D6EC}_{L}$
has pro-order prime to
![]() $p$
, the representation
$p$
, the representation
![]() $\unicode[STIX]{x1D70F}$
factors through a finite discrete quotient
$\unicode[STIX]{x1D70F}$
factors through a finite discrete quotient
![]() $\unicode[STIX]{x1D6EC}$
of
$\unicode[STIX]{x1D6EC}$
of
![]() $\unicode[STIX]{x1D6EC}_{L}$
whose order is prime to
$\unicode[STIX]{x1D6EC}_{L}$
whose order is prime to
![]() $p$
. Such a representation is the reduction of a projective
$p$
. Such a representation is the reduction of a projective
![]() ${\mathcal{O}}[\unicode[STIX]{x1D6EC}]$
-module by Fact 6.1(iii). Inverting
${\mathcal{O}}[\unicode[STIX]{x1D6EC}]$
-module by Fact 6.1(iii). Inverting
![]() $p$
, we obtain a representation of
$p$
, we obtain a representation of
![]() $\unicode[STIX]{x1D6EC}$
in characteristic zero that is absolutely irreducible since the ‘reduction’
$\unicode[STIX]{x1D6EC}$
in characteristic zero that is absolutely irreducible since the ‘reduction’
![]() $\unicode[STIX]{x1D70F}$
is absolutely irreducible over
$\unicode[STIX]{x1D70F}$
is absolutely irreducible over
![]() $k$
. By [Reference SerreSer77, § 6.5 Corollary 2], the dimension of this representation (equal to the dimension of
$k$
. By [Reference SerreSer77, § 6.5 Corollary 2], the dimension of this representation (equal to the dimension of
![]() $\unicode[STIX]{x1D70F}$
) divides the order of
$\unicode[STIX]{x1D70F}$
) divides the order of
![]() $\unicode[STIX]{x1D6EC}$
.◻
$\unicode[STIX]{x1D6EC}$
.◻
We will now extend
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
from
$\widetilde{\unicode[STIX]{x1D70F}}$
from
![]() $\unicode[STIX]{x1D6EC}_{L}\subset I_{L}$
to
$\unicode[STIX]{x1D6EC}_{L}\subset I_{L}$
to
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
by defining it on the topological generators
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
by defining it on the topological generators
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
. We say that such an extension has tame determinant if
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
. We say that such an extension has tame determinant if
![]() $\det (\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}))$
has finite order which is prime to
$\det (\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}))$
has finite order which is prime to
![]() $p$
. Lemmas 6.10 and 6.11 adapt [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.11] and fill in some details.
$p$
. Lemmas 6.10 and 6.11 adapt [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.11] and fill in some details.
Lemma 6.10. There is a unique continuous extension
![]() $\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}\rightarrow G({\mathcal{O}})$
with tame determinant.
$\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}\rightarrow G({\mathcal{O}})$
with tame determinant.
Proof. A continuous extension of
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
to
$\widetilde{\unicode[STIX]{x1D70F}}$
to
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
is determined by its value on
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
is determined by its value on
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
. As
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
. As
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, in light of Remark 6.6 there is an
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, in light of Remark 6.6 there is an
![]() $A\in G({\mathcal{O}})$
such that for
$A\in G({\mathcal{O}})$
such that for
![]() $g\in \unicode[STIX]{x1D6EC}_{L}$
we have
$g\in \unicode[STIX]{x1D6EC}_{L}$
we have
We would like to send
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
to the element
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
to the element
![]() $A$
. For an appropriate modification of
$A$
. For an appropriate modification of
![]() $A$
(still lying in
$A$
(still lying in
![]() $G({\mathcal{O}})$
), this will produce a continuous extension with tame determinant. As
$G({\mathcal{O}})$
), this will produce a continuous extension with tame determinant. As
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
is a topological generator for a group isomorphic to
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
is a topological generator for a group isomorphic to
![]() $\mathbf{Z}_{p}$
, the continuity of the extension with
$\mathbf{Z}_{p}$
, the continuity of the extension with
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\mapsto A$
is equivalent to some
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\mapsto A$
is equivalent to some
![]() $p$
-power of
$p$
-power of
![]() $A$
having trivial reduction. We wish to show that there is a unique choice of such
$A$
having trivial reduction. We wish to show that there is a unique choice of such
![]() $A$
that also makes the extension have tame determinant.
$A$
that also makes the extension have tame determinant.
We will first show that some power
![]() $A^{p^{b}}$
lies in the centralizer of the image
$A^{p^{b}}$
lies in the centralizer of the image
![]() $\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6EC}_{L})$
. Consider the conjugation action of
$\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6EC}_{L})$
. Consider the conjugation action of
![]() $\langle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\rangle$
on
$\langle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\rangle$
on
![]() $\unicode[STIX]{x1D6EC}_{L}$
. As
$\unicode[STIX]{x1D6EC}_{L}$
. As
![]() $\ker \widetilde{\unicode[STIX]{x1D70F}}=\ker \unicode[STIX]{x1D70F}$
is a normal subgroup of
$\ker \widetilde{\unicode[STIX]{x1D70F}}=\ker \unicode[STIX]{x1D70F}$
is a normal subgroup of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
(if
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
(if
![]() $g\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
and
$g\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D70F}(h)=1$
, then
$\unicode[STIX]{x1D70F}(h)=1$
, then
![]() $\unicode[STIX]{x1D70F}^{g}(h)$
is conjugate to
$\unicode[STIX]{x1D70F}^{g}(h)$
is conjugate to
![]() $\unicode[STIX]{x1D70F}(h)=1$
by Remark 6.6) we get an action of
$\unicode[STIX]{x1D70F}(h)=1$
by Remark 6.6) we get an action of
![]() $\langle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\rangle$
on
$\langle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}\rangle$
on
![]() $\unicode[STIX]{x1D6EC}_{L}/\text{ker}\,\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6EC}_{L})$
. The action is continuous, so there is a power
$\unicode[STIX]{x1D6EC}_{L}/\text{ker}\,\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6EC}_{L})$
. The action is continuous, so there is a power
![]() $p^{b}$
such that for all
$p^{b}$
such that for all
![]() $g\in \unicode[STIX]{x1D6EC}_{L}$
we have
$g\in \unicode[STIX]{x1D6EC}_{L}$
we have
As
![]() $\ker \widetilde{\unicode[STIX]{x1D70F}}=\ker \unicode[STIX]{x1D70F}$
, we see that
$\ker \widetilde{\unicode[STIX]{x1D70F}}=\ker \unicode[STIX]{x1D70F}$
, we see that
Therefore
![]() $A^{p^{b}}$
lies in the centralizer of
$A^{p^{b}}$
lies in the centralizer of
![]() $\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6EC}_{L})$
in
$\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6EC}_{L})$
in
![]() $G({\mathcal{O}})$
.
$G({\mathcal{O}})$
.
By Lemma 6.8, this centralizer is isomorphic to
![]() ${\mathcal{O}}^{\times }$
. We claim that by multiplying
${\mathcal{O}}^{\times }$
. We claim that by multiplying
![]() $A$
by some unit in
$A$
by some unit in
![]() ${\mathcal{O}}$
, we can arrange for the continuous extension
${\mathcal{O}}$
, we can arrange for the continuous extension
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
to exist and have tame determinant. We will use the fact that an element of
$\widetilde{\unicode[STIX]{x1D70F}}$
to exist and have tame determinant. We will use the fact that an element of
![]() ${\mathcal{O}}^{\times }$
is the product of a
${\mathcal{O}}^{\times }$
is the product of a
![]() $1$
-unit and a Teichmuller lift of an element of
$1$
-unit and a Teichmuller lift of an element of
![]() $k^{\times }$
. As
$k^{\times }$
. As
![]() $A^{p^{b}}\in {\mathcal{O}}^{\times }$
and the
$A^{p^{b}}\in {\mathcal{O}}^{\times }$
and the
![]() $p$
th power map is an automorphism of
$p$
th power map is an automorphism of
![]() $k^{\times }$
, we may multiply
$k^{\times }$
, we may multiply
![]() $A$
by a unit scalar so that
$A$
by a unit scalar so that
![]() $A^{p^{b}}$
reduces to the identity matrix. By Lemma 6.9, the dimension
$A^{p^{b}}$
reduces to the identity matrix. By Lemma 6.9, the dimension
![]() $n$
of
$n$
of
![]() $\unicode[STIX]{x1D70F}$
is prime to
$\unicode[STIX]{x1D70F}$
is prime to
![]() $p$
so we may multiply
$p$
so we may multiply
![]() $A$
by a
$A$
by a
![]() $1$
-unit so that
$1$
-unit so that
![]() $\det (A)$
has finite order prime to
$\det (A)$
has finite order prime to
![]() $p$
. Sending
$p$
. Sending
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
to this particular
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
to this particular
![]() $A$
gives a continuous extension with tame determinant.
$A$
gives a continuous extension with tame determinant.
Let us show this extension is unique. Any extension must send
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
to an element of the form
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
to an element of the form
![]() $wA$
for
$wA$
for
![]() $w\in {\mathcal{O}}^{\times }$
(the centralizer of the image
$w\in {\mathcal{O}}^{\times }$
(the centralizer of the image
![]() $\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6EC}_{L})$
). By continuity, there is a power
$\widetilde{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6EC}_{L})$
). By continuity, there is a power
![]() $p^{b}$
such that
$p^{b}$
such that
![]() $(wA)^{p^{b}}$
reduces to the identity. This means that
$(wA)^{p^{b}}$
reduces to the identity. This means that
![]() $w^{p^{b}}$
reduces to the identity, and hence that
$w^{p^{b}}$
reduces to the identity, and hence that
![]() $w$
reduces to the identity. On the other hand,
$w$
reduces to the identity. On the other hand,
![]() $\det (wA)\det (A)^{-1}=w^{n}$
. The left side has finite order that is relatively prime to
$\det (wA)\det (A)^{-1}=w^{n}$
. The left side has finite order that is relatively prime to
![]() $p$
, so
$p$
, so
![]() $w^{n}$
does too. This forces
$w^{n}$
does too. This forces
![]() $w^{n}=1$
since its reduction is
$w^{n}=1$
since its reduction is
![]() $1$
. But as
$1$
. But as
![]() $n$
is prime to
$n$
is prime to
![]() $p$
(Lemma 6.9), the only
$p$
(Lemma 6.9), the only
![]() $n$
th roots of unity in
$n$
th roots of unity in
![]() ${\mathcal{O}}^{\times }$
are Teichmuller lifts. Therefore
${\mathcal{O}}^{\times }$
are Teichmuller lifts. Therefore
![]() $w=1$
.◻
$w=1$
.◻
Lemma 6.11. There is a continuous extension
![]() $\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\rightarrow G({\mathcal{O}})$
.
$\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\rightarrow G({\mathcal{O}})$
.
Proof. We extend
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
in Lemma 6.10 continuously to
$\widetilde{\unicode[STIX]{x1D70F}}$
in Lemma 6.10 continuously to
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
by defining it on
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
by defining it on
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
. As
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
. As
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, by Remark 6.6 there is an element
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
, by Remark 6.6 there is an element
![]() $A\in G({\mathcal{O}})$
conjugating
$A\in G({\mathcal{O}})$
conjugating
![]() $\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G({\mathcal{O}})$
to
$\widetilde{\unicode[STIX]{x1D70F}}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G({\mathcal{O}})$
to
![]() $\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G({\mathcal{O}})$
. Each has a unique extension to a continuous morphism from
$\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}:\unicode[STIX]{x1D6EC}_{L}\rightarrow G({\mathcal{O}})$
. Each has a unique extension to a continuous morphism from
![]() $I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
to
$I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
to
![]() $G({\mathcal{O}})$
with tame determinant. Therefore for
$G({\mathcal{O}})$
with tame determinant. Therefore for
![]() $g\in I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
we have
$g\in I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
we have
since the right side has the same (tame) determinant as
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
on
$\widetilde{\unicode[STIX]{x1D70F}}$
on
![]() $I_{L}\cap \,T_{\unicode[STIX]{x1D70F}}$
. We can continuously extend
$I_{L}\cap \,T_{\unicode[STIX]{x1D70F}}$
. We can continuously extend
![]() $\widetilde{\unicode[STIX]{x1D70F}}:I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\rightarrow G({\mathcal{O}})$
by sending
$\widetilde{\unicode[STIX]{x1D70F}}:I_{L}\cap \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\rightarrow G({\mathcal{O}})$
by sending
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
to
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
to
![]() $A$
since
$A$
since
![]() $A$
has reduction with finite order.◻
$A$
has reduction with finite order.◻
This gives the desired lift and extension of
![]() $\unicode[STIX]{x1D70F}$
in the case that
$\unicode[STIX]{x1D70F}$
in the case that
![]() $\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\ast }$
.
$\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\ast }$
.
In Case 3,
![]() $\unicode[STIX]{x1D70F}$
is conjugate to
$\unicode[STIX]{x1D70F}$
is conjugate to
![]() $\unicode[STIX]{x1D70F}^{\ast }$
but not isomorphic. The argument follows the same structure as the previous case, but we make a few modifications to treat
$\unicode[STIX]{x1D70F}^{\ast }$
but not isomorphic. The argument follows the same structure as the previous case, but we make a few modifications to treat
![]() $\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
together. In particular, we can pick a copy of the
$\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
together. In particular, we can pick a copy of the
![]() $k[\unicode[STIX]{x1D6EC}_{L}]$
-module
$k[\unicode[STIX]{x1D6EC}_{L}]$
-module
![]() $\unicode[STIX]{x1D70F}$
inside
$\unicode[STIX]{x1D70F}$
inside
![]() $V$
and a copy of
$V$
and a copy of
![]() $\unicode[STIX]{x1D70F}^{\ast }\simeq \unicode[STIX]{x1D70F}^{\vee }$
inside
$\unicode[STIX]{x1D70F}^{\ast }\simeq \unicode[STIX]{x1D70F}^{\vee }$
inside
![]() $V$
such that the pairing restricted to
$V$
such that the pairing restricted to
![]() $\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
is perfect. It is sign-symmetric with sign
$\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
is perfect. It is sign-symmetric with sign
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.
Define
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}=\{g\in \unicode[STIX]{x1D6E4}_{L}:(\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast })^{g}\simeq \unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }\}$
. It contains
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}=\{g\in \unicode[STIX]{x1D6E4}_{L}:(\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast })^{g}\simeq \unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }\}$
. It contains
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
with index
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
with index
![]() $2$
, as conjugation either preserves
$2$
, as conjugation either preserves
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}^{\ast }$
or swaps them. Arguing as in the paragraph after Fact 6.7, we obtain a split exact sequence
$\unicode[STIX]{x1D70F}^{\ast }$
or swaps them. Arguing as in the paragraph after Fact 6.7, we obtain a split exact sequence
where
![]() $T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is an open normal subgroup of
$T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is an open normal subgroup of
![]() $T_{L}$
topologically generated by some powers of
$T_{L}$
topologically generated by some powers of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D70E}$
which we denote by
$\unicode[STIX]{x1D70E}$
which we denote by
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
and
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
. We may arrange that either:
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
. We may arrange that either:
∙ Case 3a:
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{2}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{2}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
and
 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
; or
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
; or∙ Case 3b:
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
and
 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{2}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
.
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{2}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
.
In Case 3a, we begin by lifting
![]() $\unicode[STIX]{x1D70F}$
to
$\unicode[STIX]{x1D70F}$
to
![]() ${\mathcal{O}}$
as a representation of
${\mathcal{O}}$
as a representation of
![]() $\unicode[STIX]{x1D6EC}_{L}$
: as before, we do this using the fact that the pro-order of
$\unicode[STIX]{x1D6EC}_{L}$
: as before, we do this using the fact that the pro-order of
![]() $\unicode[STIX]{x1D6EC}_{L}$
is prime to
$\unicode[STIX]{x1D6EC}_{L}$
is prime to
![]() $p$
, and obtain a lift
$p$
, and obtain a lift
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
unique up to isomorphism. We extend
$\widetilde{\unicode[STIX]{x1D70F}}$
unique up to isomorphism. We extend
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
to be a representation of
$\widetilde{\unicode[STIX]{x1D70F}}$
to be a representation of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
by defining it on
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
by defining it on
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
using the
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
using the
![]() $\operatorname{GL}_{n}$
-version of Lemma 6.10, [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.11]. There it is shown all such extensions are unique up to equivalence. In particular,
$\operatorname{GL}_{n}$
-version of Lemma 6.10, [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.11]. There it is shown all such extensions are unique up to equivalence. In particular,
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
and
$\widetilde{\unicode[STIX]{x1D70F}}$
and
![]() $(\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}})^{\vee }$
are isomorphic
$(\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}})^{\vee }$
are isomorphic
![]() ${\mathcal{O}}[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}]$
-modules. We can use this to define a sign-symmetric perfect pairing on
${\mathcal{O}}[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}]$
-modules. We can use this to define a sign-symmetric perfect pairing on
![]() $\widetilde{\unicode[STIX]{x1D70F}}\oplus \widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
that is compatible with the action of
$\widetilde{\unicode[STIX]{x1D70F}}\oplus \widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
that is compatible with the action of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
and
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}\cap I_{L}$
and
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
, hence of
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
, hence of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.
In Case 3b, as
![]() $\unicode[STIX]{x1D70F}^{\vee }$
and
$\unicode[STIX]{x1D70F}^{\vee }$
and
![]() $\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
are isomorphic
$\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
are isomorphic
![]() $k[\unicode[STIX]{x1D6EC}_{L}]$
-modules it follows that
$k[\unicode[STIX]{x1D6EC}_{L}]$
-modules it follows that
![]() $\widetilde{\unicode[STIX]{x1D70F}}^{\vee }$
and
$\widetilde{\unicode[STIX]{x1D70F}}^{\vee }$
and
![]() $\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
are isomorphic
$\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
are isomorphic
![]() ${\mathcal{O}}[\unicode[STIX]{x1D6EC}_{L}]$
-modules. In particular, this isomorphism gives a natural way to define a sign-symmetric perfect pairing on
${\mathcal{O}}[\unicode[STIX]{x1D6EC}_{L}]$
-modules. In particular, this isomorphism gives a natural way to define a sign-symmetric perfect pairing on
![]() $M=\widetilde{\unicode[STIX]{x1D70F}}\oplus \widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
lifting the residual one. This pairing is compatible with the action of
$M=\widetilde{\unicode[STIX]{x1D70F}}\oplus \widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
lifting the residual one. This pairing is compatible with the action of
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\cap I_{L}$
(which is generated by
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\cap I_{L}$
(which is generated by
![]() $\unicode[STIX]{x1D6EC}_{L}$
and
$\unicode[STIX]{x1D6EC}_{L}$
and
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
). Finally, we claim that
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
). Finally, we claim that
![]() $M$
and
$M$
and
![]() $M^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
are isomorphic. As
$M^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
are isomorphic. As
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
preserves
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}\in \unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
preserves
![]() $\unicode[STIX]{x1D70F}$
, acting by
$\unicode[STIX]{x1D70F}$
, acting by
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
gives an isomorphism
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
gives an isomorphism
![]() $\overline{\unicode[STIX]{x1D713}}:\overline{M}\simeq \overline{M}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
of
$\overline{\unicode[STIX]{x1D713}}:\overline{M}\simeq \overline{M}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
of
![]() $k[\unicode[STIX]{x1D6EC}_{L}]$
-modules such that
$k[\unicode[STIX]{x1D6EC}_{L}]$
-modules such that
![]() $\overline{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
. By uniqueness of the lift of
$\overline{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
. By uniqueness of the lift of
![]() $\unicode[STIX]{x1D70F}$
as a
$\unicode[STIX]{x1D70F}$
as a
![]() ${\mathcal{O}}[\unicode[STIX]{x1D6EC}_{L}]$
-module, we obtain an isomorphism
${\mathcal{O}}[\unicode[STIX]{x1D6EC}_{L}]$
-module, we obtain an isomorphism
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
of
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
of
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
and
$\widetilde{\unicode[STIX]{x1D70F}}$
and
![]() $\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
and hence an isomorphism
$\widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
and hence an isomorphism
![]() $\unicode[STIX]{x1D713}:M\simeq M^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
via the identifications
$\unicode[STIX]{x1D713}:M\simeq M^{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}}$
via the identifications
This isomorphism is compatible with the pairing. The key observation is that for
![]() $m\in \widetilde{\unicode[STIX]{x1D70F}}$
and
$m\in \widetilde{\unicode[STIX]{x1D70F}}$
and
![]() $f\in \widetilde{\unicode[STIX]{x1D70F}}^{\vee }\simeq \widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
, we have that
$f\in \widetilde{\unicode[STIX]{x1D70F}}^{\vee }\simeq \widetilde{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
, we have that
Then proceed as in the proof of Lemma 6.11, defining an image of
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
using the isomorphism
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
using the isomorphism
![]() $\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D713}$
.
In conclusion, we have shown the following.
Lemma 6.12. In Case 3, there exists an
![]() ${\mathcal{O}}[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}]$
-module
${\mathcal{O}}[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}]$
-module
![]() $\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
with pairing lifting
$\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
with pairing lifting
![]() $\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
together with its pairing.
$\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
together with its pairing.
6.3 Lifts with pairings
We continue the notation of § 6.1, and analyze how the duality pairing interacts with the decomposition (6.1). Recall that we obtained an isomorphism
![]() $M\simeq M^{\vee }$
of
$M\simeq M^{\vee }$
of
![]() $R[\unicode[STIX]{x1D6E4}_{L}]$
-modules which gave isomorphisms
$R[\unicode[STIX]{x1D6E4}_{L}]$
-modules which gave isomorphisms
![]() $M_{\unicode[STIX]{x1D70F}}\simeq M_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
of
$M_{\unicode[STIX]{x1D70F}}\simeq M_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
of
![]() $R[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}]$
-modules. The key point is that for any lift and extension
$R[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}]$
-modules. The key point is that for any lift and extension
![]() $\unicode[STIX]{x1D70F}^{\prime }$
of
$\unicode[STIX]{x1D70F}^{\prime }$
of
![]() $\unicode[STIX]{x1D70F}$
, the isomorphism of
$\unicode[STIX]{x1D70F}$
, the isomorphism of
![]() $R[\unicode[STIX]{x1D6EC}_{L}]$
-modules
$R[\unicode[STIX]{x1D6EC}_{L}]$
-modules
is compatible with the
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
-action.
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
-action.
To do this, it is convenient to break into the cases introduced at the end of § 6.1. For an irreducible
![]() $k[\unicode[STIX]{x1D6EC}]$
-module
$k[\unicode[STIX]{x1D6EC}]$
-module
![]() $\unicode[STIX]{x1D70F}$
occurring in
$\unicode[STIX]{x1D70F}$
occurring in
![]() $V$
, note that
$V$
, note that
![]() $(\unicode[STIX]{x1D70F}^{g})^{\vee }=(\unicode[STIX]{x1D70F}^{\vee })^{g}$
for any
$(\unicode[STIX]{x1D70F}^{g})^{\vee }=(\unicode[STIX]{x1D70F}^{\vee })^{g}$
for any
![]() $g\in \unicode[STIX]{x1D6E4}_{L}$
, so if
$g\in \unicode[STIX]{x1D6E4}_{L}$
, so if
![]() $\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\ast }$
then
$\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\ast }$
then
![]() $\unicode[STIX]{x1D70F}^{g}\simeq (\unicode[STIX]{x1D70F}^{g})^{\ast }$
. We let
$\unicode[STIX]{x1D70F}^{g}\simeq (\unicode[STIX]{x1D70F}^{g})^{\ast }$
. We let
∙
 $\unicode[STIX]{x1D6F4}_{n}$
denote the set of
$\unicode[STIX]{x1D6F4}_{n}$
denote the set of
 $\unicode[STIX]{x1D6E4}_{L}$
-conjugacy classes of such
$\unicode[STIX]{x1D6E4}_{L}$
-conjugacy classes of such
 $\unicode[STIX]{x1D70F}$
for which
$\unicode[STIX]{x1D70F}$
for which
 $\unicode[STIX]{x1D70F}$
is not conjugate to
$\unicode[STIX]{x1D70F}$
is not conjugate to
 $\unicode[STIX]{x1D70F}^{\ast }$
;
$\unicode[STIX]{x1D70F}^{\ast }$
;∙
 $\unicode[STIX]{x1D6F4}_{e}$
denote the set of
$\unicode[STIX]{x1D6F4}_{e}$
denote the set of
 $\unicode[STIX]{x1D6E4}_{L}$
-conjugacy classes of such
$\unicode[STIX]{x1D6E4}_{L}$
-conjugacy classes of such
 $\unicode[STIX]{x1D70F}$
for which
$\unicode[STIX]{x1D70F}$
for which
 $\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\ast }$
;
$\unicode[STIX]{x1D70F}\simeq \unicode[STIX]{x1D70F}^{\ast }$
;∙
 $\unicode[STIX]{x1D6F4}_{c}$
denote the set of
$\unicode[STIX]{x1D6F4}_{c}$
denote the set of
 $\unicode[STIX]{x1D6E4}_{L}$
-conjugacy classes of such
$\unicode[STIX]{x1D6E4}_{L}$
-conjugacy classes of such
 $\unicode[STIX]{x1D70F}$
for which
$\unicode[STIX]{x1D70F}$
for which
 $\unicode[STIX]{x1D70F}^{\ast }$
is conjugate to
$\unicode[STIX]{x1D70F}^{\ast }$
is conjugate to
 $\unicode[STIX]{x1D70F}$
but
$\unicode[STIX]{x1D70F}$
but
 $\unicode[STIX]{x1D70F}\not \simeq \unicode[STIX]{x1D70F}^{\ast }$
.
$\unicode[STIX]{x1D70F}\not \simeq \unicode[STIX]{x1D70F}^{\ast }$
.
From (6.1), we obtain a decomposition
where
![]() $\unicode[STIX]{x1D70F}^{\prime }$
is any lift and extension of
$\unicode[STIX]{x1D70F}^{\prime }$
is any lift and extension of
![]() $\unicode[STIX]{x1D70F}$
to
$\unicode[STIX]{x1D70F}$
to
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
and
![]() $W_{\unicode[STIX]{x1D70F}}=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F}^{\prime },M)$
is a representation of
$W_{\unicode[STIX]{x1D70F}}=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F}^{\prime },M)$
is a representation of
![]() $T_{L,\unicode[STIX]{x1D70F}}$
. Note that
$T_{L,\unicode[STIX]{x1D70F}}$
. Note that
![]() $W_{\unicode[STIX]{x1D70F}}$
is free as an
$W_{\unicode[STIX]{x1D70F}}$
is free as an
![]() $R$
-module (since
$R$
-module (since
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D70F}^{\prime }$
are, with
$\unicode[STIX]{x1D70F}^{\prime }$
are, with
![]() $\unicode[STIX]{x1D70F}^{\prime }\neq 0$
and
$\unicode[STIX]{x1D70F}^{\prime }\neq 0$
and
![]() $R$
local), and hence that
$R$
local), and hence that
![]() $W_{\unicode[STIX]{x1D70F}}$
is tamely ramified of the type considered in § 5.
$W_{\unicode[STIX]{x1D70F}}$
is tamely ramified of the type considered in § 5.
We may rewrite this to make use of the special extensions constructed in § 6.2. In particular, for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
we rewrite
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
we rewrite
This uses the notation and results from Case 3 in § 6.2, in particular the fact that
![]() $\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
is an irreducible representation of the group
$\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
is an irreducible representation of the group
![]() $\unicode[STIX]{x1D6EC}_{L}^{\prime }$
generated by
$\unicode[STIX]{x1D6EC}_{L}^{\prime }$
generated by
![]() $\unicode[STIX]{x1D6EC}_{L}$
and a
$\unicode[STIX]{x1D6EC}_{L}$
and a
![]() $g\in \unicode[STIX]{x1D6E4}_{L}$
with
$g\in \unicode[STIX]{x1D6E4}_{L}$
with
![]() $\unicode[STIX]{x1D70F}^{\ast }\simeq \unicode[STIX]{x1D70F}^{g}$
, and the definition
$\unicode[STIX]{x1D70F}^{\ast }\simeq \unicode[STIX]{x1D70F}^{g}$
, and the definition
![]() $W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}:=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}^{\prime }}(\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},M)$
. Note that
$W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}:=\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{L}^{\prime }}(\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},M)$
. Note that
![]() $W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is a representation of
$W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is a representation of
![]() $T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
, which is a subgroup of
$T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
, which is a subgroup of
![]() $T_{L}=\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
, hence of the form
$T_{L}=\unicode[STIX]{x1D6E4}_{L}/\unicode[STIX]{x1D6EC}_{L}$
, hence of the form
![]() $T_{q}$
as considered in § 5. Using the extensions
$T_{q}$
as considered in § 5. Using the extensions
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
and
$\widetilde{\unicode[STIX]{x1D70F}}$
and
![]() $\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
from Cases
$\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
from Cases
![]() $1$
and
$1$
and
![]() $2$
from § 6.2, we obtain a decomposition
$2$
from § 6.2, we obtain a decomposition
Now let
![]() $M^{\prime }$
be another
$M^{\prime }$
be another
![]() $R[\unicode[STIX]{x1D6E4}_{L}]$
-module that is finite free over
$R[\unicode[STIX]{x1D6E4}_{L}]$
-module that is finite free over
![]() $R$
such that the irreducible representations of
$R$
such that the irreducible representations of
![]() $\unicode[STIX]{x1D6EC}_{L}$
occurring in
$\unicode[STIX]{x1D6EC}_{L}$
occurring in
![]() $V^{\prime }:=M^{\prime }/\mathfrak{m}M^{\prime }$
are among the irreducible representations occurring in
$V^{\prime }:=M^{\prime }/\mathfrak{m}M^{\prime }$
are among the irreducible representations occurring in
![]() $V=M/\mathfrak{m}M$
, so
$V=M/\mathfrak{m}M$
, so
Lemma 6.13. The natural map
 $$\begin{eqnarray}\displaystyle & & \displaystyle \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}}}(W_{\unicode[STIX]{x1D70F}},W_{\unicode[STIX]{x1D70F}}^{\prime })\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}}}(W_{\unicode[STIX]{x1D70F}},W_{\unicode[STIX]{x1D70F}}^{\prime })\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}(W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \operatorname{Hom}_{\unicode[STIX]{x1D6E4}_{L}}(M,M^{\prime })\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}}}(W_{\unicode[STIX]{x1D70F}},W_{\unicode[STIX]{x1D70F}}^{\prime })\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}}}(W_{\unicode[STIX]{x1D70F}},W_{\unicode[STIX]{x1D70F}}^{\prime })\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}(W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \operatorname{Hom}_{\unicode[STIX]{x1D6E4}_{L}}(M,M^{\prime })\nonumber\end{eqnarray}$$
is an isomorphism.
Proof. We may immediately pass to working with representations of the finite discrete groups
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6EC}$
. Notice that
$\unicode[STIX]{x1D6EC}$
. Notice that
where the second isomorphism uses that
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}}(M_{\unicode[STIX]{x1D70F}^{g}},M_{\unicode[STIX]{x1D70F}}^{\prime })=0$
by Lemma 6.3 when
$\operatorname{Hom}_{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}}(M_{\unicode[STIX]{x1D70F}^{g}},M_{\unicode[STIX]{x1D70F}}^{\prime })=0$
by Lemma 6.3 when
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}^{g}$
are non-isomorphic. Furthermore, if
$\unicode[STIX]{x1D70F}^{g}$
are non-isomorphic. Furthermore, if
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
are not
$\unicode[STIX]{x1D70F}_{2}$
are not
![]() $\unicode[STIX]{x1D6E4}$
-conjugate, then
$\unicode[STIX]{x1D6E4}$
-conjugate, then
using Lemma 6.3 as
![]() $\unicode[STIX]{x1D70F}_{1}^{g}$
is not isomorphic to
$\unicode[STIX]{x1D70F}_{1}^{g}$
is not isomorphic to
![]() $\unicode[STIX]{x1D70F}_{2}$
for any
$\unicode[STIX]{x1D70F}_{2}$
for any
![]() $g\in \unicode[STIX]{x1D6E4}$
. Then using (6.1) we see that
$g\in \unicode[STIX]{x1D6E4}$
. Then using (6.1) we see that
All the irreducible finite-dimensional representations of
![]() $\unicode[STIX]{x1D6EC}$
occurring in
$\unicode[STIX]{x1D6EC}$
occurring in
![]() $V$
and
$V$
and
![]() $V^{\prime }$
are absolutely irreducible over
$V^{\prime }$
are absolutely irreducible over
![]() $k$
by design. For
$k$
by design. For
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}\cup \unicode[STIX]{x1D6F4}_{e}$
, consider the natural inclusion
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}\cup \unicode[STIX]{x1D6F4}_{e}$
, consider the natural inclusion
using that
![]() $W_{\unicode[STIX]{x1D70F}}$
and
$W_{\unicode[STIX]{x1D70F}}$
and
![]() $W_{\unicode[STIX]{x1D70F}}^{\prime }$
are
$W_{\unicode[STIX]{x1D70F}}^{\prime }$
are
![]() $R$
-free of finite rank and
$R$
-free of finite rank and
![]() $\unicode[STIX]{x1D6EC}$
acts trivially. But
$\unicode[STIX]{x1D6EC}$
acts trivially. But
![]() $R{\hookrightarrow}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(\widetilde{\unicode[STIX]{x1D70F}},\widetilde{\unicode[STIX]{x1D70F}})$
is an isomorphism because
$R{\hookrightarrow}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(\widetilde{\unicode[STIX]{x1D70F}},\widetilde{\unicode[STIX]{x1D70F}})$
is an isomorphism because
![]() $\operatorname{End}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})=k$
and because surjectivity can be checked modulo
$\operatorname{End}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D70F})=k$
and because surjectivity can be checked modulo
![]() $\mathfrak{m}_{R}$
using Lemma 6.2. As
$\mathfrak{m}_{R}$
using Lemma 6.2. As
![]() $M_{\unicode[STIX]{x1D70F}}\simeq \widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}}$
, this implies that
$M_{\unicode[STIX]{x1D70F}}\simeq \widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}}$
, this implies that
where
![]() $T_{\unicode[STIX]{x1D70F}}$
is the image of
$T_{\unicode[STIX]{x1D70F}}$
is the image of
![]() $T_{L,\unicode[STIX]{x1D70F}}$
in
$T_{L,\unicode[STIX]{x1D70F}}$
in
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
. An analogous computation in the case
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70F}}$
. An analogous computation in the case
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
completes the proof.◻
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
completes the proof.◻
We can now consider the duality isomorphism
![]() $M\simeq M^{\vee }$
. By Lemma 6.13, this is equivalent to a collection of isomorphisms of
$M\simeq M^{\vee }$
. By Lemma 6.13, this is equivalent to a collection of isomorphisms of
![]() $R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules
$R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
for
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{n}$
and an isomorphism of
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{n}$
and an isomorphism of
![]() $R[T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}]$
-modules
$R[T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}]$
-modules
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\simeq W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
for
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\simeq W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
. We analyze the cases separately.
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
. We analyze the cases separately.
In Case 1 (when
![]() $\unicode[STIX]{x1D70F}$
is not conjugate to
$\unicode[STIX]{x1D70F}$
is not conjugate to
![]() $\unicode[STIX]{x1D70F}^{\ast }$
), note that
$\unicode[STIX]{x1D70F}^{\ast }$
), note that
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}}$
is an isotropic subspace of
$\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}}$
is an isotropic subspace of
![]() $M$
. In particular, the perfect sign-symmetric pairing on
$M$
. In particular, the perfect sign-symmetric pairing on
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}}\oplus \operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}^{\ast }}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}^{\ast }}$
is equivalent to an isomorphism of
$\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}}\oplus \operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}^{\ast }}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}^{\ast }}$
is equivalent to an isomorphism of
![]() $R[\unicode[STIX]{x1D6E4}_{L}]$
-modules
$R[\unicode[STIX]{x1D6E4}_{L}]$
-modules
which is equivalent to the isomorphism of
![]() $R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules
$R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
. (Note that the similitude character
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
. (Note that the similitude character
![]() $\unicode[STIX]{x1D708}$
is present in the use of the dual.)
$\unicode[STIX]{x1D708}$
is present in the use of the dual.)
In Case 2 (when
![]() $\unicode[STIX]{x1D70F}$
is isomorphic to
$\unicode[STIX]{x1D70F}$
is isomorphic to
![]() $\unicode[STIX]{x1D70F}^{\ast }$
), the perfect sign-symmetric pairing on
$\unicode[STIX]{x1D70F}^{\ast }$
), the perfect sign-symmetric pairing on
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}}$
is equivalent to an isomorphism
$\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}M_{\unicode[STIX]{x1D70F}}$
is equivalent to an isomorphism
![]() $W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}}^{\vee }$
of
$W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}}^{\vee }$
of
![]() $R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules. Thus it gives a pairing
$R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules. Thus it gives a pairing
![]() $\langle \,,\rangle _{W_{\unicode[STIX]{x1D70F}}}$
on
$\langle \,,\rangle _{W_{\unicode[STIX]{x1D70F}}}$
on
![]() $W_{\unicode[STIX]{x1D70F}}$
via
$W_{\unicode[STIX]{x1D70F}}$
via
We claim this pairing is sign-symmetric.
From § 6.2 we have an isomorphism
![]() $\imath :\widetilde{\unicode[STIX]{x1D70F}}\simeq \widetilde{\unicode[STIX]{x1D70F}}^{\vee }$
of
$\imath :\widetilde{\unicode[STIX]{x1D70F}}\simeq \widetilde{\unicode[STIX]{x1D70F}}^{\vee }$
of
![]() $R[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}]$
-modules. As at the end of § 6.1, let
$R[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}]$
-modules. As at the end of § 6.1, let
![]() $\unicode[STIX]{x1D713}:M\rightarrow M^{\vee }$
be the isomorphism of
$\unicode[STIX]{x1D713}:M\rightarrow M^{\vee }$
be the isomorphism of
![]() $R[\unicode[STIX]{x1D6E4}_{L}]$
-modules given by
$R[\unicode[STIX]{x1D6E4}_{L}]$
-modules given by
![]() $m\mapsto \langle m,-\rangle _{M}$
, and define
$m\mapsto \langle m,-\rangle _{M}$
, and define
![]() $\langle v_{1},v_{2}\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}:=\imath (v_{1})(v_{2})$
. We have a commutative diagram as follows.
$\langle v_{1},v_{2}\rangle _{\widetilde{\unicode[STIX]{x1D70F}}}:=\imath (v_{1})(v_{2})$
. We have a commutative diagram as follows.

The commutativity says that for elementary tensors
![]() $m_{i}=v_{i}\otimes w_{i}\in M_{\unicode[STIX]{x1D70F}}=\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}}$
we have
$m_{i}=v_{i}\otimes w_{i}\in M_{\unicode[STIX]{x1D70F}}=\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}}$
we have
The pairings are perfect and
![]() $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F}}$
is
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F}}$
is
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
-symmetric, so the pairing on
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
-symmetric, so the pairing on
![]() $W_{\unicode[STIX]{x1D70F}}$
is
$W_{\unicode[STIX]{x1D70F}}$
is
![]() $\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}$
-symmetric if and only if the pairing on
$\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}$
-symmetric if and only if the pairing on
![]() $M_{\unicode[STIX]{x1D70F}}$
is
$M_{\unicode[STIX]{x1D70F}}$
is
![]() $\unicode[STIX]{x1D716}$
-symmetric. We have that
$\unicode[STIX]{x1D716}$
-symmetric. We have that
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
.
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}$
.
In Case 3 (
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
), an analogous argument using the isomorphism
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
), an analogous argument using the isomorphism
![]() $\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\simeq \widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
of
$\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\simeq \widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
of
![]() $R[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}]$
-modules (which define the
$R[\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}]$
-modules (which define the
![]() $\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
-symmetric pairing on
$\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
-symmetric pairing on
![]() $\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
) shows that the pairing induced by
$\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
) shows that the pairing induced by
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\simeq W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
is
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\simeq W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
is
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
-symmetric if and only if the pairing on
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
-symmetric if and only if the pairing on
induced from the pairing on
![]() $M$
is sign-symmetric with sign
$M$
is sign-symmetric with sign
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
.
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
.
6.4 Minimally ramified deformations
We can now define the minimally ramified deformation condition for
![]() $\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
, under the continuing assumption that we have extended
$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(k)$
, under the continuing assumption that we have extended
![]() $k$
so all irreducible representations of
$k$
so all irreducible representations of
![]() $\unicode[STIX]{x1D6EC}_{L}$
occurring in
$\unicode[STIX]{x1D6EC}_{L}$
occurring in
![]() $V$
are absolutely irreducible over
$V$
are absolutely irreducible over
![]() $k$
. From (6.4), we obtain a decomposition
$k$
. From (6.4), we obtain a decomposition
where
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
is a representation of
$\overline{W}_{\unicode[STIX]{x1D70F}}$
is a representation of
![]() $T_{L,\unicode[STIX]{x1D70F}}$
over
$T_{L,\unicode[STIX]{x1D70F}}$
over
![]() $k$
and
$k$
and
![]() $\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is a representation of
$\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is a representation of
![]() $T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.
$T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.
If
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
, define
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
, define
![]() $\overline{G}_{\unicode[STIX]{x1D70F}}:=\text{}\underline{\operatorname{Aut}}(\overline{W}_{\unicode[STIX]{x1D70F}})$
. If
$\overline{G}_{\unicode[STIX]{x1D70F}}:=\text{}\underline{\operatorname{Aut}}(\overline{W}_{\unicode[STIX]{x1D70F}})$
. If
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, there is a sign-symmetric perfect pairing
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, there is a sign-symmetric perfect pairing
![]() $\langle \cdot ,\cdot \rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}$
on
$\langle \cdot ,\cdot \rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}}$
on
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
; in that case define
$\overline{W}_{\unicode[STIX]{x1D70F}}$
; in that case define
![]() $\overline{G}_{\unicode[STIX]{x1D70F}}:=\text{}\underline{\operatorname{GAut}}(\overline{W}_{\unicode[STIX]{x1D70F}},\langle \cdot ,\cdot \rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}})$
. (The notation
$\overline{G}_{\unicode[STIX]{x1D70F}}:=\text{}\underline{\operatorname{GAut}}(\overline{W}_{\unicode[STIX]{x1D70F}},\langle \cdot ,\cdot \rangle _{\overline{W}_{\unicode[STIX]{x1D70F}}})$
. (The notation
![]() $\text{}\underline{\operatorname{GAut}}$
means automorphisms preserving the pairing up to scalar.) If
$\text{}\underline{\operatorname{GAut}}$
means automorphisms preserving the pairing up to scalar.) If
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
, there is a sign-symmetric perfect pairing on
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
, there is a sign-symmetric perfect pairing on
![]() $\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
; in that case define
$\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
; in that case define
![]() $\overline{G}_{\unicode[STIX]{x1D70F}}:=\text{}\underline{\operatorname{GAut}}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\langle \cdot ,\cdot \rangle _{\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}})$
. Make a finite extension of
$\overline{G}_{\unicode[STIX]{x1D70F}}:=\text{}\underline{\operatorname{GAut}}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\langle \cdot ,\cdot \rangle _{\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}})$
. Make a finite extension of
![]() $k$
so that all the pairings are split. Lift
$k$
so that all the pairings are split. Lift
![]() $\overline{G}_{\unicode[STIX]{x1D70F}}$
to a split reductive group
$\overline{G}_{\unicode[STIX]{x1D70F}}$
to a split reductive group
![]() $G_{\unicode[STIX]{x1D70F}}$
over
$G_{\unicode[STIX]{x1D70F}}$
over
![]() ${\mathcal{O}}$
by lifting the split linear algebra data.
${\mathcal{O}}$
by lifting the split linear algebra data.
Definition 6.14. Let
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(R)$
be a continuous Galois representation lifting
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(R)$
be a continuous Galois representation lifting
![]() $\overline{\unicode[STIX]{x1D70C}}$
as above, with associated
$\overline{\unicode[STIX]{x1D70C}}$
as above, with associated
![]() $R[\unicode[STIX]{x1D6E4}]$
-module
$R[\unicode[STIX]{x1D6E4}]$
-module
We say that
![]() $\unicode[STIX]{x1D70C}$
is minimally ramified with similitude character
$\unicode[STIX]{x1D70C}$
is minimally ramified with similitude character
![]() $\unicode[STIX]{x1D708}$
if each
$\unicode[STIX]{x1D708}$
if each
![]() $W_{\unicode[STIX]{x1D70F}}$
and
$W_{\unicode[STIX]{x1D70F}}$
and
![]() $W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is minimally ramified in the sense of Definition 5.4 as a representation of
$W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is minimally ramified in the sense of Definition 5.4 as a representation of
![]() $T_{L,\unicode[STIX]{x1D70F}}$
or
$T_{L,\unicode[STIX]{x1D70F}}$
or
![]() $T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
valued in the group
$T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
valued in the group
![]() $G_{\unicode[STIX]{x1D70F}}$
with specified similitude character. (Note that defining the minimally ramified deformation condition as in § 5 may require an additional étale local extension of
$G_{\unicode[STIX]{x1D70F}}$
with specified similitude character. (Note that defining the minimally ramified deformation condition as in § 5 may require an additional étale local extension of
![]() ${\mathcal{O}}$
, which as always is harmless for applications.)
${\mathcal{O}}$
, which as always is harmless for applications.)
Let
![]() $D_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}$
denote the deformation functor for
$D_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}$
denote the deformation functor for
![]() $\overline{\unicode[STIX]{x1D70C}}$
with specified similitude character
$\overline{\unicode[STIX]{x1D70C}}$
with specified similitude character
![]() $\unicode[STIX]{x1D708}$
, and
$\unicode[STIX]{x1D708}$
, and
![]() ${\mathcal{D}}_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.}}$
(respectively
${\mathcal{D}}_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.}}$
(respectively
![]() ${\mathcal{D}}_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}$
) denote the deformation functor for
${\mathcal{D}}_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}$
) denote the deformation functor for
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
or
$\overline{W}_{\unicode[STIX]{x1D70F}}$
or
![]() $\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
viewed as a representation valued in
$\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
viewed as a representation valued in
![]() $G_{\unicode[STIX]{x1D70F}}$
(respectively with specified similitude character
$G_{\unicode[STIX]{x1D70F}}$
(respectively with specified similitude character
![]() $\unicode[STIX]{x1D708}$
). In particular, letting
$\unicode[STIX]{x1D708}$
). In particular, letting
![]() $r=\dim \overline{W}_{\unicode[STIX]{x1D70F}}$
(or
$r=\dim \overline{W}_{\unicode[STIX]{x1D70F}}$
(or
![]() $\dim \overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
when
$\dim \overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
when
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
), we have that the adjoint representation
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
), we have that the adjoint representation
![]() $\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}}$
is the Lie algebra of
$\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}}$
is the Lie algebra of
![]() $\overline{G}_{\unicode[STIX]{x1D70F}}$
, which is the Lie algebra of
$\overline{G}_{\unicode[STIX]{x1D70F}}$
, which is the Lie algebra of
![]() $\operatorname{GSp}_{r}$
or
$\operatorname{GSp}_{r}$
or
![]() $\operatorname{GO}_{r}$
when
$\operatorname{GO}_{r}$
when
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
or
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
or
![]() $\unicode[STIX]{x1D6F4}_{c}$
, and the Lie algebra of
$\unicode[STIX]{x1D6F4}_{c}$
, and the Lie algebra of
![]() $\operatorname{GL}_{r}$
when
$\operatorname{GL}_{r}$
when
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
. Let
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
. Let
![]() $\unicode[STIX]{x1D6F4}_{n}^{\prime }$
consist of one representative for each pair of representations
$\unicode[STIX]{x1D6F4}_{n}^{\prime }$
consist of one representative for each pair of representations
![]() $\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70F}^{\ast }\in \unicode[STIX]{x1D6F4}_{n}$
.
$\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70F}^{\ast }\in \unicode[STIX]{x1D6F4}_{n}$
.
Proposition 6.15. There is a natural isomorphism of functors
Proof. This expresses the decomposition obtained in this section: given a lift
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\overline{\unicode[STIX]{x1D70C}}$
, we obtain a decomposition of
$\overline{\unicode[STIX]{x1D70C}}$
, we obtain a decomposition of
![]() $M$
as in Definition 6.14. Our analysis with pairings shows that when
$M$
as in Definition 6.14. Our analysis with pairings shows that when
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
,
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
,
![]() $W_{\unicode[STIX]{x1D70F}}$
is a deformation of
$W_{\unicode[STIX]{x1D70F}}$
is a deformation of
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
together with its
$\overline{W}_{\unicode[STIX]{x1D70F}}$
together with its
![]() $\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}$
-symmetric perfect pairing. Likewise, when
$\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}$
-symmetric perfect pairing. Likewise, when
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
we know that
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
we know that
![]() $W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is a deformation of
$W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
is a deformation of
![]() $\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
together with its
$\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
together with its
![]() $\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
-symmetric pairing. When
$\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}$
-symmetric pairing. When
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
, we know
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
, we know
![]() $W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
. This gives the natural map: to
$W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
. This gives the natural map: to
![]() $\unicode[STIX]{x1D70C}\in D_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}(R)$
associate the collection of the
$\unicode[STIX]{x1D70C}\in D_{\overline{\unicode[STIX]{x1D70C}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}(R)$
associate the collection of the
![]() $W_{\unicode[STIX]{x1D70F}}$
for
$W_{\unicode[STIX]{x1D70F}}$
for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{c}\cup \unicode[STIX]{x1D6F4}_{n}^{\prime }$
.
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{c}\cup \unicode[STIX]{x1D6F4}_{n}^{\prime }$
.
Conversely, given
![]() $W_{\unicode[STIX]{x1D70F}}$
for
$W_{\unicode[STIX]{x1D70F}}$
for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{c}\cup \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, and defining
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{c}\cup \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, and defining
![]() $W_{\unicode[STIX]{x1D70F}^{\ast }}:=W_{\unicode[STIX]{x1D70F}}^{\vee }$
for
$W_{\unicode[STIX]{x1D70F}^{\ast }}:=W_{\unicode[STIX]{x1D70F}}^{\vee }$
for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
we can define a lift
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
we can define a lift
as in (6.1). (Note that the groups
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
depend only on the fixed residual representation
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
depend only on the fixed residual representation
![]() $V$
.) For
$V$
.) For
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, the perfect pairing on the lift
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, the perfect pairing on the lift
![]() $W_{\unicode[STIX]{x1D70F}}$
gives an isomorphism
$W_{\unicode[STIX]{x1D70F}}$
gives an isomorphism
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}}^{\vee }$
of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}}^{\vee }$
of
![]() $R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules, which gives a sign-symmetric pairing (with sign
$R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules, which gives a sign-symmetric pairing (with sign
![]() $\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D716}$
) on
$\unicode[STIX]{x1D716}_{W_{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D716}$
) on
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}})$
(using equation (6.6)). Likewise, for
$\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}})$
(using equation (6.6)). Likewise, for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
the sign-symmetric pairing on
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
the sign-symmetric pairing on
![]() $W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
gives one on
$W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
gives one on
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\otimes W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})$
. For
$\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}\otimes W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})$
. For
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
, we obtain an isomorphism
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}$
, we obtain an isomorphism
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
of
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}:W_{\unicode[STIX]{x1D70F}}\simeq W_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
of
![]() $R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules and hence an
$R[T_{L,\unicode[STIX]{x1D70F}}]$
-modules and hence an
![]() $\unicode[STIX]{x1D716}$
-symmetric perfect pairing on
$\unicode[STIX]{x1D716}$
-symmetric perfect pairing on
![]() $(\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}})\oplus (\widetilde{\unicode[STIX]{x1D70F}}^{\vee }\otimes W_{\unicode[STIX]{x1D70F}^{\ast }})$
which gives one on
$(\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}})\oplus (\widetilde{\unicode[STIX]{x1D70F}}^{\vee }\otimes W_{\unicode[STIX]{x1D70F}^{\ast }})$
which gives one on
![]() $\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}})\oplus \operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}}^{\vee }\otimes W_{\unicode[STIX]{x1D70F}^{\ast }})$
. Putting these together, we obtain a sign-symmetric pairing on
$\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}}\otimes W_{\unicode[STIX]{x1D70F}})\oplus \operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}}^{\unicode[STIX]{x1D6E4}_{L}}(\widetilde{\unicode[STIX]{x1D70F}}^{\vee }\otimes W_{\unicode[STIX]{x1D70F}^{\ast }})$
. Putting these together, we obtain a sign-symmetric pairing on
![]() $M$
; the action of
$M$
; the action of
![]() $\unicode[STIX]{x1D6E4}_{L}$
preserves it up to scalar, giving a continuous homomorphism
$\unicode[STIX]{x1D6E4}_{L}$
preserves it up to scalar, giving a continuous homomorphism
![]() $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(R)$
.
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D6E4}_{L}\rightarrow G(R)$
.
Finally, we claim that these constructions are compatible with strict equivalence of lifts, giving an identification of the deformation functors. For
![]() $g\in \widehat{G}(R)$
, decompose the
$g\in \widehat{G}(R)$
, decompose the
![]() $g$
-conjugate
$g$
-conjugate
![]() $\unicode[STIX]{x1D6E4}_{L}$
-representation
$\unicode[STIX]{x1D6E4}_{L}$
-representation
![]() $M^{g}$
according to (6.4). As
$M^{g}$
according to (6.4). As
![]() $g$
reduces to the identity, it must respect the decomposition into
$g$
reduces to the identity, it must respect the decomposition into
![]() $\unicode[STIX]{x1D70F}$
-isotypic pieces, so gives automorphisms
$\unicode[STIX]{x1D70F}$
-isotypic pieces, so gives automorphisms
![]() $g_{\unicode[STIX]{x1D70F}}\in \operatorname{Aut}(W_{\unicode[STIX]{x1D70F}})$
and
$g_{\unicode[STIX]{x1D70F}}\in \operatorname{Aut}(W_{\unicode[STIX]{x1D70F}})$
and
![]() $g_{\unicode[STIX]{x1D70F}}\in \operatorname{Aut}(W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})$
. If
$g_{\unicode[STIX]{x1D70F}}\in \operatorname{Aut}(W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})$
. If
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
or
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
or
![]() $\unicode[STIX]{x1D6F4}_{c}$
, as
$\unicode[STIX]{x1D6F4}_{c}$
, as
![]() $g$
is compatible with the pairing on
$g$
is compatible with the pairing on
![]() $M$
we see
$M$
we see
![]() $g_{\unicode[STIX]{x1D70F}}$
is compatible with the pairing as well. For
$g_{\unicode[STIX]{x1D70F}}$
is compatible with the pairing as well. For
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, the
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, the
![]() $g_{\unicode[STIX]{x1D70F}}$
-conjugate
$g_{\unicode[STIX]{x1D70F}}$
-conjugate
![]() $T_{L,\unicode[STIX]{x1D70F}}$
-representation
$T_{L,\unicode[STIX]{x1D70F}}$
-representation
![]() $W_{\unicode[STIX]{x1D70F}}^{g_{\unicode[STIX]{x1D70F}}}$
is minimally ramified as minimally ramified lifts of
$W_{\unicode[STIX]{x1D70F}}^{g_{\unicode[STIX]{x1D70F}}}$
is minimally ramified as minimally ramified lifts of
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
for the group
$\overline{W}_{\unicode[STIX]{x1D70F}}$
for the group
![]() $T_{L,\unicode[STIX]{x1D70F}}$
are a deformation condition, and likewise for
$T_{L,\unicode[STIX]{x1D70F}}$
are a deformation condition, and likewise for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
and
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
and
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
.
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
.
Conversely, given
![]() $g_{\unicode[STIX]{x1D70F}}\in \operatorname{Aut}(W_{\unicode[STIX]{x1D70F}})$
reducing to the identity (compatible with the pairing on
$g_{\unicode[STIX]{x1D70F}}\in \operatorname{Aut}(W_{\unicode[STIX]{x1D70F}})$
reducing to the identity (compatible with the pairing on
![]() $W_{\unicode[STIX]{x1D70F}}$
or
$W_{\unicode[STIX]{x1D70F}}$
or
![]() $W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
if there is one), using (6.1) and acting on each piece we obtain a lift of the form
$W_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
if there is one), using (6.1) and acting on each piece we obtain a lift of the form
![]() $M^{g}$
for
$M^{g}$
for
![]() $g\in \widehat{G}(R)$
. Thus the identification is compatible with strict equivalence.◻
$g\in \widehat{G}(R)$
. Thus the identification is compatible with strict equivalence.◻
Corollary 6.16. Under the assumptions (A1)–(A4) needed to analyze the tame case, and our standing assumption that all the irreducible representations of
![]() $\unicode[STIX]{x1D6EC}_{L}$
appearing in
$\unicode[STIX]{x1D6EC}_{L}$
appearing in
![]() $V$
are absolutely irreducible over
$V$
are absolutely irreducible over
![]() $k$
, the minimally ramified deformation condition with fixed similitude character is liftable. The dimension of the tangent space is
$k$
, the minimally ramified deformation condition with fixed similitude character is liftable. The dimension of the tangent space is
![]() $h^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
.
$h^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
.
Proof. Liftability is a consequence of Proposition 6.15 and the smoothness of the minimally ramified lifting ring for representations of
![]() $T_{L,\unicode[STIX]{x1D70F}}$
(Proposition 5.6 and Corollary 5.8). By Corollary 5.8, for
$T_{L,\unicode[STIX]{x1D70F}}$
(Proposition 5.6 and Corollary 5.8). By Corollary 5.8, for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
the dimension of the tangent space of
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
the dimension of the tangent space of
![]() $D_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}$
is
$D_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.},\unicode[STIX]{x1D708}}$
is
![]() $h^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}})-1=h^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}})$
, and for
$h^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}})-1=h^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}})$
, and for
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
the dimension is
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
the dimension is
![]() $h^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})-1=h^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})$
. For
$h^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})-1=h^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})$
. For
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, by Proposition 5.6 the dimension of the tangent space of
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, by Proposition 5.6 the dimension of the tangent space of
![]() $D_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.}}$
is
$D_{G_{\unicode[STIX]{x1D70F}}}^{\operatorname{m.r.}}$
is
![]() $h^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}})$
. Using Proposition 6.15, we see that the dimension of the tangent space of the minimally ramified deformation condition is
$h^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{ad}\overline{W}_{\unicode[STIX]{x1D70F}})$
. Using Proposition 6.15, we see that the dimension of the tangent space of the minimally ramified deformation condition is
It remains to identify this quantity with
![]() $h^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
. Using Lemma 6.13
$h^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
. Using Lemma 6.13
 $$\begin{eqnarray}\displaystyle H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{End}(V)) & = & \displaystyle \operatorname{Hom}_{k[\unicode[STIX]{x1D6E4}_{L}]}(V,V)\nonumber\\ \displaystyle & = & \displaystyle \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{n}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}}}(\overline{W}_{\unicode[STIX]{x1D70F}},\overline{W}_{\unicode[STIX]{x1D70F}})\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})\nonumber\\ \displaystyle & = & \displaystyle \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{n}}{\bigoplus }H^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}}))\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}}{\bigoplus }H^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{End}(V)) & = & \displaystyle \operatorname{Hom}_{k[\unicode[STIX]{x1D6E4}_{L}]}(V,V)\nonumber\\ \displaystyle & = & \displaystyle \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{n}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}}}(\overline{W}_{\unicode[STIX]{x1D70F}},\overline{W}_{\unicode[STIX]{x1D70F}})\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}}{\bigoplus }\operatorname{Hom}_{T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})\nonumber\\ \displaystyle & = & \displaystyle \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}\cup \unicode[STIX]{x1D6F4}_{n}}{\bigoplus }H^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}}))\oplus \underset{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}}{\bigoplus }H^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }})).\nonumber\end{eqnarray}$$
We are interested in
![]() $H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
: the elements
$H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{ad}^{0}(\overline{\unicode[STIX]{x1D70C}}))$
: the elements
![]() $\unicode[STIX]{x1D713}\in H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{End}(V))$
compatible with the pairing on
$\unicode[STIX]{x1D713}\in H^{0}(\unicode[STIX]{x1D6E4}_{L},\operatorname{End}(V))$
compatible with the pairing on
![]() $V$
in the sense that for
$V$
in the sense that for
![]() $v,v^{\prime }\in V$
$v,v^{\prime }\in V$
The pairing on
![]() $V_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}\otimes \overline{W}_{\unicode[STIX]{x1D70F}}$
is induced by the pairings on
$V_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D70F}\otimes \overline{W}_{\unicode[STIX]{x1D70F}}$
is induced by the pairings on
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
and
$\overline{W}_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D70F}$
when
$\unicode[STIX]{x1D70F}$
when
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, and is induced by the pairings on
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, and is induced by the pairings on
![]() $\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
and
$\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
and
![]() $\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
when
$\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }$
when
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
. When
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
. When
![]() $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, the pairing on
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, the pairing on
![]() $V_{\unicode[STIX]{x1D70F}}\oplus V_{\unicode[STIX]{x1D70F}^{\ast }}$
comes from the
$V_{\unicode[STIX]{x1D70F}}\oplus V_{\unicode[STIX]{x1D70F}^{\ast }}$
comes from the
![]() $\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
-isomorphism
$\unicode[STIX]{x1D6E4}_{L,\unicode[STIX]{x1D70F}}$
-isomorphism
![]() $V_{\unicode[STIX]{x1D70F}}\simeq V_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
which in turn comes from the
$V_{\unicode[STIX]{x1D70F}}\simeq V_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
which in turn comes from the
![]() $T_{L,\unicode[STIX]{x1D70F}}$
-isomorphism
$T_{L,\unicode[STIX]{x1D70F}}$
-isomorphism
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}\simeq \overline{W}_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
. So
$\overline{W}_{\unicode[STIX]{x1D70F}}\simeq \overline{W}_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
. So
![]() $\unicode[STIX]{x1D713}$
is compatible with the pairing if and only if the following hold.
$\unicode[STIX]{x1D713}$
is compatible with the pairing if and only if the following hold.
∙ When
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, the associated
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{e}$
, the associated
 $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\in H^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}}))$
is compatible with the pairing on
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\in H^{0}(T_{L,\unicode[STIX]{x1D70F}},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}}))$
is compatible with the pairing on
 $\overline{W}_{\unicode[STIX]{x1D70F}}$
.
$\overline{W}_{\unicode[STIX]{x1D70F}}$
.∙ When
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
, the associated
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{c}$
, the associated
 $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\in H^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}))$
is compatible with the pairing on
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\in H^{0}(T_{L,\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }},\operatorname{End}(\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}))$
is compatible with the pairing on
 $\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.
$\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
.∙ When
 $\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, the associated
$\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6F4}_{n}^{\prime }$
, the associated
 $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
and
 $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}^{\ast }}$
are identified by duality and the isomorphism
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}^{\ast }}$
are identified by duality and the isomorphism
 $\overline{W}_{\unicode[STIX]{x1D70F}}\simeq \overline{W}_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
.
$\overline{W}_{\unicode[STIX]{x1D70F}}\simeq \overline{W}_{\unicode[STIX]{x1D70F}^{\ast }}^{\vee }$
.
In the first two cases,
![]() $\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}}$
and
$\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}}$
and
![]() $\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
are the symplectic or orthogonal Lie algebra, consisting exactly of endomorphisms compatible with the pairing on
$\operatorname{ad}^{0}\overline{W}_{\unicode[STIX]{x1D70F}\oplus \unicode[STIX]{x1D70F}^{\ast }}$
are the symplectic or orthogonal Lie algebra, consisting exactly of endomorphisms compatible with the pairing on
![]() $\overline{W}_{\unicode[STIX]{x1D70F}}$
. In the third, we just choose one of
$\overline{W}_{\unicode[STIX]{x1D70F}}$
. In the third, we just choose one of
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}^{\ast }}$
without restriction, which determines the other. Thus we see
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}^{\ast }}$
without restriction, which determines the other. Thus we see
◻
The Corollary is a more precise version of Theorem 1.1.
Acknowledgements
This work forms part of my thesis [Reference BooherBoo16], and I am extremely grateful for the generosity and support of my advisor Brian Conrad, and for his extensive and helpful comments on drafts of my thesis. The thesis was originally submitted as a single paper before being split into this paper and [Reference BooherBoo19]: I thank the referee for a careful reading.