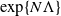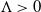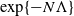Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems

Abstract

This article examines large-time behaviour of finite-state mean-field interacting particle systems. Our first main result is a sharp estimate (in the exponential scale) of the time required for convergence of the empirical measure process of the N-particle system to its invariant measure; we show that when time is of the order $\exp\{N\Lambda\}$ for a suitable constant $\Lambda > 0$ , the process has mixed well and it is close to its invariant measure. We then obtain large-N asymptotics of the second-largest eigenvalue of the generator associated with the empirical measure process when it is reversible with respect to its invariant measure. We show that its absolute value scales as $\exp\{{-}N\Lambda\}$ . The main tools used in establishing our results are the large deviation properties of the empirical measure process from its large-N limit. As an application of the study of large-time behaviour, we also show convergence of the empirical measure of the system of particles to a global minimum of a certain ‘entropy’ function when particles are added over time in a controlled fashion. The controlled addition of particles is analogous to the cooling schedule associated with the search for a global minimum of a function using the simulated annealing algorithm.

1. Introduction

In this paper, we study large-time behaviour and the second eigenvalue problem for Markovian mean-field interacting particle systems with jumps. Our motivation is to provide an understanding of metastable phenomena in engineered systems such as load balancing networks [1, 2, 37, 36, 24] and wireless local area networks [7, 6, 11, 28, 41, 8], and in natural systems involving grammar acquisition, sexual evolution [40, 39], and epidemic spread [29, 3], to name a few. These systems are briefly described in Section 1.4.

Before we discuss our main contributions, let us describe the setting of our mean-field interacting particle system.

1.1. The setting

Let there be N particles. Each particle has a state associated with it which comes from a finite set $\mathcal{Z}$ ; the state of the nth particle at time t is denoted by $X_n^N(t) \in \mathcal{Z}$ . The empirical measure of the system of particles at time t is defined by

\begin{align*} \mu_N(t) \,:\!=\, \frac{1}{N} \sum_{n=1}^N \delta_{X_n^N(t)} \in M_1(\mathcal{Z}),\end{align*}

where $\delta_{\cdot}$ denotes the Dirac measure on $\mathcal{Z}$ . Here, $M_1(\mathcal{Z})$ denotes the space of probability measures on $\mathcal{Z}$ equipped with the total variation metric (which generates the topology of weak convergence on $M_1(\mathcal{Z})$ ). Each particle has a set of allowed transitions; to define this, let $(\mathcal{Z}, \mathcal{E})$ be a directed graph with the interpretation that whenever $(z,z^\prime) \in \mathcal{E}$ , a particle in state z is allowed to move from z to $z^\prime$ . To specify the interaction among the particles and the evolution of the states of the particles over time, for each $(z,z^\prime) \in \mathcal{E}$ , we are given a function $\lambda_{z,z^\prime}\,:\, M_1(\mathcal{Z}) \to [0, \infty)$ . We consider the generator $\Psi^N$ acting on functions f on $\mathcal{Z}^N$ by

\begin{align*} \Psi^N f\big(\mathbf{z}^N\big) = \sum_{n=1}^N \sum_{z_n^\prime\,:\, \big(z_n, z_n^\prime\big) \in \mathcal{E}} \lambda_{z_n, z_n^\prime}\big(\overline{\mathbf{z}^N}\big) \Big(\,f\Big(\mathbf{z}^N_{n,z_n,z_n^\prime}\Big) - f\big(\mathbf{z}^N\big)\Big);\end{align*}

here

\begin{equation*}\overline{\mathbf{z}^N} = \frac{1}{N}\sum_{n=1}^N \delta_{z_n} \in M_1(\mathcal{Z})\end{equation*}

denotes the empirical measure associated with the configuration $\mathbf{z}^N \in \mathcal{Z}^N$ , and

\begin{equation*}\mathbf{z}^N_{n,z_n,z_n^\prime}\end{equation*}

denotes the resultant configuration of the particles when the nth particle changes its state from $z_n$ to $z_n^\prime$ .

We make the following assumptions on the model:

1. (A1) The graph $(\mathcal{Z}, \mathcal{E})$ is irreducible.

2. (A2) The functions $\lambda_{z,z^\prime}({\cdot})$ , $(z,z^\prime) \in \mathcal{E}$ , are Lipschitz continuous on $M_1(\mathcal{Z})$ , and there exist positive constants c, C such that $c \leq \lambda_{z,z^\prime}(\xi) \leq C$ for all $(z,z^\prime) \in \mathcal{E}$ and all $\xi \in M_1(\mathcal{Z})$ .

Let $D\big([0, \infty), \mathcal{Z}^N\big)$ denote the space of $\mathcal{Z}^N$ -valued functions on $[0, \infty)$ that are right-continuous with left limits (càdlàg), equipped with the Skorokhod $J_1$ topology (see [19, Chapter 3]). Since the transition rates are bounded (by Assumption (A2)), the $D\big([0, \infty), \mathcal{Z}^N\big)$ -valued martingale problem for $\Psi^N$ is well posed (see [19, Exercise 15, Section 4.1]); therefore, given an initial configuration of the particles $\big(X_n^N(0), 1 \leq n \leq N\big) \in \mathcal{Z}^N$ , we have a Markov process $\left( \big(X_n^N(t), 1 \leq n \leq N\big), t \geq 0\right)$ whose sample paths are elements of $D\big([0,\infty),\mathcal{Z}^N\big)$ . To describe the process in words, a particle in state z at time t moves to state $z^\prime$ at rate $\lambda_{z,z^\prime}(\mu_N(t))$ independent of everything else; i.e., the evolution of the state of a particle depends on the states of the other particles via the empirical measure of the states of all the particles, hence the name mean-field interaction. Note that the empirical measure process $(\mu_N(t), t \geq 0)$ is also a Markov process with state space $M_1^N(\mathcal{Z})$ , which is the set of elements of $M_1(\mathcal{Z})$ that can arise as empirical measures of N-particle configurations on $\mathcal{Z}^N$ . Its generator $L^N$ acting on functions f on $M_1^N(\mathcal{Z})$ is given by

\begin{align*} L^N f(\xi) = \sum_{(z,z^\prime) \in \mathcal{E}} N\xi(z) \lambda_{z,z^\prime}(\xi) \left[f\left( \xi + \frac{\delta_{z^\prime}}{N} - \frac{\delta_z}{N}\right) - f(\xi) \right].\end{align*}

Since $\mu_N$ is a Markov process on a finite state space, and since the graph $(\mathcal{Z},\mathcal{E})$ of allowed particle transitions is irreducible (Assumption (A1)), there exists a unique invariant probability measure for $\mu_N$ , which we denote by $\wp_N$ . Also, let $\mathbb{P}_\nu$ denote the law of $(\mu_N(t), t \geq 0)$ with initial condition $\mu_N(0) = \nu \in M_1^N(\mathcal{Z})$ (i.e., the solution to the $D([0,\infty),M_1(\mathcal{Z}))$ -valued martingale problem for $L^N$ with initial condition $\nu \in M_1^N(\mathcal{Z})$ ), and let $\mathbb{E}_\nu$ denote integration with respect to $\mathbb{P}_\nu$ ; in both $\mathbb{P}_\nu$ and $\mathbb{E}_\nu$ we suppress the dependence on N for greater readability.

1.2. Main results

Let us now discuss the main results of the paper. All our results are established under Assumptions (A1) and (A2) on the particle system, and a further assumption (B1) on the structure of the large-time behaviour of the ordinary differential equation (ODE) (1.1) (see Section 3).

1.2.1. Convergence to the invariant measure

Our first main result is on the time required for the process $\mu_N$ to equilibrate. This time grows at an exponential rate with the number of particles N, where the rate is the constant $\Lambda > 0$ which will be defined in (3.6).

Theorem 1.1. Given $\delta > 0$ there exist $\varepsilon > 0$ and $N_0 \geq 1 $ such that, with $T = \exp\{N(\Lambda+\delta)\}$ ,

\begin{align*} \sup_{\nu \in M_1^N(\mathcal{Z})} \left| \mathbb{E}_\nu (\,f(\mu_N(T) ))- \langle\, f, \wp_N \rangle \right| \leq \|\,f\|_\infty \exp\{{-}\exp\!(N\varepsilon)\} \end{align*}

for all $N \geq N_0$ and all bounded Borel-measurable functions f on $M_1(\mathcal{Z})$ .

The result says that when time is of the order $\exp\{N(\Lambda+\delta)\}$ for any $\delta > 0$ , the process has mixed well and it is close to its invariant measure. The proof of this result is based on the study of the large-time behaviour of the process $\mu_N$ . Before we describe this, let us mention a well-known law of large numbers for the process $\mu_N$ [33, 22, 44, 6]. This will not only pave the way for a suitable description of the constant $\Lambda$ but also lead us to a converse of Theorem 1.1 and the significance of $\Lambda$ .

Assume (A1) and (A2), and suppose that the initial conditions $\{\mu_N(0)\}_{N \geq 1}$ converge weakly to a deterministic measure $\nu \in M_1(\mathcal{Z})$ . Then for any fixed $T > 0$ , the empirical measure process $(\mu_N(t), 0 \leq t \leq T)$ converges in $D([0,T],M_1(\mathcal{Z}))$ , in probability, to the solution to the ODE

(1.1) \begin{align} \dot{\mu}(t) = \Lambda_{\mu(t)}^* \mu(t), \qquad 0 \leq t \leq T, \qquad \mu(0) = \nu; \end{align}

here, for any $\xi \in M_1(\mathcal{Z})$ , $\Lambda_{\xi}$ denotes the $|\mathcal{Z}|\times |\mathcal{Z}|$ rate matrix when the empirical measure is $\xi$ (i.e., $\Lambda_\xi(z,z^\prime)= \lambda_{z,z^\prime}(\xi)$ when $(z,z^\prime) \in \mathcal{E}$ , $\Lambda_{\xi}(z,z^\prime) = 0$ when $(z,z^\prime) \notin \mathcal{E}$ , and $\Lambda_{\xi}(z,z) = -\sum_{z^\prime \neq z} \lambda_{z,z^\prime}(\xi)$ for all $z \in \mathcal{Z}$ ), $\Lambda^*_\xi$ denotes its transpose, $D([0,T],M_1(\mathcal{Z}))$ denotes the space of $M_1(\mathcal{Z})$ -valued càdlàg functions on [0, T] equipped with the Skorokhod $J_1$ topology (we assume that all paths are left-continuous at T), and both $\mu(t)$ and $\dot{\mu}(t)$ are viewed as column vectors. The above ODE is referred to as the McKean–Vlasov equation. The above convergence result enables one to view the process $\mu_N$ as a small random perturbation of the ODE (1.1).

We now elaborate on the large-time behaviour of $\mu_N$ . Suppose that the limiting McKean–Vlasov equation (1.1) has multiple $\omega$ -limit sets (multiple stable equilibria and/or limit cycles). If we focus on a fixed time interval [0, T], let the number of particles $N \to \infty$ , and let the initial conditions $\mu_N(0)$ converge weakly to a deterministic limit $\nu$ , then the mean-field convergence suggests that the empirical measure process tracks the solution to the McKean–Vlasov equation (1.1) over [0, T] starting at $\nu$ . If we then let $T \to \infty$ , the solution to the McKean–Vlasov equation goes to an $\omega$ -limit set of (1.1) depending on the initial condition $\nu$ . On the other hand, for a large but fixed N, the process would track the McKean–Vlasov equation with high probability and, as time becomes large, would thus enter a neighbourhood of the $\omega$ -limit set corresponding to the initial condition $\nu$ ; however, because of the randomness in the finite-N system, the process can exit the basin of attraction of this $\omega$ -limit set. It is then likely to remain in a neighbourhood of another $\omega$ -limit set for a large amount of time before transiting to the next one, and so on. These are examples of metastable phenomena, and it turns out that the sojourn times in the basin of attraction of an $\omega$ -limit set are of the order $\exp\{O(N)\}$ , as we shall soon see. The proof of Theorem 1.1 exploits quantitative estimates of the following metastable phenomena:

1. (i) the mean time spent by the process near an $\omega$ -limit set,

2. (ii) the probability of first reaching a particular $\omega$ -limit set’s neighbourhood before reaching the neighbourhood of another one, and

3. (iii) the probability of traversing the neighbourhoods of a given set of $\omega$ -limit sets in a particular order.

These quantifications are important in their own right as they help predict the performance of engineered systems, some of which we will describe in Section 1.4. We study the aforementioned metastability questions in Section 3. Such large-time phenomena for diffusion processes with a small noise parameter have been studied in the past by Freidlin and Wentzell [20] under the ‘general position condition’ (see [20, Sections 6.4–6.6]). Hwang and Sheu [25] studied large-time behaviour for diffusion processes under a more general setup. The key in both these works is the large deviation properties of the small-noise diffusion processes over finite time durations, which have been established in [20, Chapter 5]. In this paper, we extend the analysis to Markov mean-field jump processes, specifically $(\mu_N({\cdot}))_{N \geq 1}$ .

The proof of Theorem 1.1 is carried out using lower bounds (Theorem 3.2) for the probability that, starting from any point in $M_1^N(\mathcal{Z})$ , the process $\mu_N$ is in a small neighbourhood of (one of) the most stable $\omega$ -limit set(s) (see Section 3.5 for a precise definition) of the McKean–Vlasov equation (1.1) when time is of the order $\exp\{N(\Lambda-\delta_0)\}$ , for a small $\delta_0>0$ . The constant $\Lambda$ is defined using ‘costs of passages’ between the $\omega$ -limit sets of the McKean–Vlasov equation (1.1). These costs are quantified in terms of the large deviations rate function associated with the process $\mu_N$ via certain graphs called W-graphs (see Section 3.2 for the definition of W-graphs). In particular, $\Lambda$ is positive when the limiting dynamics (1.1) has multiple stable $\omega$ -limit sets. See (3.6) for a precise definition of $\Lambda$ .

Our next result is, in a certain sense, a converse of Theorem 1.1. Let $i_0$ be (one of) the most stable $\omega$ -limit set(s) of (1.1).

Theorem 1.2. There exist $\nu_0 \in M_1(\mathcal{Z})$ , $\delta > 0$ , $\beta >0$ , $\rho_1 > 0$ , and $N_0 \geq 1$ such that, with $T = \exp\{N(\Lambda-\delta)\}$ ,

\begin{align*} \mathbb{P}_{\nu}\big(\mu_N(T) \in \big(the\ \rho_1-neighbourhood\ of\ i_0\big)\big) \leq \exp\{{-}N\beta\} \end{align*}

for all $\nu$ in the $\rho_1$ -neighbourhood of $\nu_0$ in $M_1^N(\mathcal{Z})$ and $N \geq N_0$ .

In other words, when time is of the order $\exp\{N(\Lambda - \delta) \}$ , there are initial conditions $\nu \in M_1^N(\mathcal{Z})$ such that the probability that $\mu_N(\!\exp\{N(\Lambda - \delta) \})$ is in a small neighbourhood of (one of) the most stable $\omega$ -limit set(s) is exponentially small. The process is then not likely to have equilibrated because it has not visited a set with high invariant measure. Thus, Theorem 1.1 and Theorem 1.2 together indicate that the constant $\Lambda$ is sharp (in the exponential scale) for the time required for equilibration of $\mu_N({\cdot})$ .

A convergence result similar to that of Theorem 1.1 for the mean-field discrete-time setting but without the specification of the constant $\Lambda$ was established by Panageas and Vishnoi [40]. Let us reemphasise that our setting is a continuous-time setting. To identify the constant $\Lambda$ in this setting, we must study the large deviation asymptotics in greater detail. Theorems 1.1 and 1.2 combine time and the number of particles. Additionally, Theorem 1.1 is a statement that holds uniformly over all initial conditions, unlike convergence bounds (over time) for a fixed number of particles with a given initial condition, e.g. [45]. The proof of Theorem 1.1 is inspired by that of Hwang and Sheu in [25, Theorem 2.1, Part I], where similar results are established for small-noise diffusions.

1.2.2. Asymptotics of the second-largest eigenvalue

Our second main result is on the asymptotics of the second-largest eigenvalue of the generator $L^N$ of the Markov process $\mu_N=(\mu_N(t), t \geq 0)$ when it is reversible with respect to its invariant measure $\wp_N$ . That is, the operator $L^N$ is self-adjoint in $L^2(\wp_N)$ and it admits a spectral expansion; let $0 = \lambda_1^N > -\lambda_2^N \geq - \lambda_3^N \geq \cdots$ denote its eigenvalues in decreasing order. (See Example 4.1 for a description of a reversible system that arises in statistical physics.) For a fixed N, the convergence speed of the process $\mu_N$ to its invariant measure (over time) can be understood by studying the modulus of the second-largest eigenvalue of $L^N$ . Using the results on the large-time behaviour of $\mu_N$ and the convergence result in Theorem 1.1, we show that the modulus of the second-largest eigenvalue of $L^N$ $\big($ i.e., $\lambda_2^N\big)$ scales as $\exp\{{-}N\Lambda\}$ ; here $\Lambda$ (defined in (3.6)) is the constant that appears in the statement of Theorem 1.1. More precisely, we have the following.

Theorem 1.3. Assume that $L^N$ is reversible with respect to $\wp_N$ for each $N \geq 1$ . Then

\begin{align*} \lim_{N \to \infty} \frac{1}{N} \log \lambda_2^N = -\Lambda. \end{align*}

It turns out that $\Lambda$ can be positive only when there are metastable states in the limiting dynamics (1.1) (i.e., when (1.1) possesses multiple $\omega$ -limit sets). In such situations, one expects slower convergence to the invariant measure for large values of N. On the other hand, $\Lambda$ can be 0, for example, when the limiting dynamics (1.1) has a unique globally asymptotically stable equilibrium; in this special case, convergence of $\mu_N$ to its invariant measure does not suffer from the slowing-down phenomenon associated with positive $\Lambda$ . In fact, Panageas and Vishnoi [40] and Panageas et al. [39] show that the mixing time is $O(\!\log N)$ in the discrete-time setting. Kifer [26] considers a more restrictive discrete-time model, which does not cover the mean-field model, and identifies the constant analogous to $\Lambda$ [26, Theorem 4.3]. The restriction is that the state space of $\mu_N$ is the same for each N and that a certain uniform finite-duration large deviation principle (LDP) should hold with the rate function satisfying a continuity property. One can view our result as an extension of Kifer’s [26, Theorem 4.3] to the continuous-time mean-field setting, where the state space of the Markov process $\mu_N$ changes with N. Hwang and Sheu [25] establish a result similar to ours on the scaling of the second-largest eigenvalue of a reversible small-noise diffusion process, and our method of proof is inspired by their approach.

1.2.3. Convergence to a global minimum via controlled addition of particles

Our third main result is on the convergence of the empirical measure process to a global minimum of a natural ‘entropy’ function when particles are injected over time at a specific rate reminiscent of the simulated annealing algorithm’s cooling schedule, $N(t) = \big\lfloor \frac{\log\! (2+t)}{c^* + \delta}\big\rfloor$ for a suitable $c^*$ and any $\delta > 0$ . This entropy function is the large deviations rate function associated with the sequence of invariant measures $\{\wp_N, N \geq 1\}$ , which is in turn defined in terms of the large deviations rate function associated with the process $\mu_N$ ; see (3.5) for its definition.

Fix $c>0$ . Let $N_0 = \min\{n \in \mathbb{N} \,:\, \exp\{nc\} - 2 \geq 0 \}$ , $t_{N_0} = 0$ , and for each $N > N_0$ , let $t_N = \exp\{Nc\}-2$ . We construct a process with controlled addition of particles as follows. We start with $N_0$ particles with certain initial states and let the process evolve according to the generator $L^{N_0}$ until time $t_{N_0+1}$ . For each $N > N_0$ , we add an extra particle at time $t_N$ , and for a fixed state $z_0 \in \mathcal{Z}$ , we set the state of the new particle to $z_0$ and let the process evolve according to the generator $L^{N}$ from $t_{N}$ to $t_{N+1}$ (see Section 5 for a more precise description of the process). Let $\bar{\mu}$ denote the above time-inhomogeneous Markov process and let $\mathbb{P}_{0,\nu}$ denote the law of $\bar{\mu}$ on $D([0,\infty), M_1(\mathcal{Z}))$ with initial condition $\bar{\mu}(0) = \nu$ . Also, let $\tilde{L}_0$ denote the set of all global minima of the entropy function (see Section 3.5.1 for the precise definition of $\tilde{L}_0$ ). Our convergence result is the following.

Theorem 1.4. Assume that $\tilde{L}_0 \neq L$ . There exists a constant $c^*>0$ such that for all $c > c^*$ and any $\rho_1 > 0$ ,

\begin{align*} \mathbb{P}_{0,\nu} \big(\bar{\mu}(t) \in \big(\text{the } \rho_1-neighbourhood\ of\ \tilde{L}_0\big)\big) \to 1 \end{align*}

as $t \to \infty$ , uniformly for all $\nu \in M_1^{N_0}(\mathcal{Z})$ .

Note that the convergence to a global minimum holds for all starting points. This is of use in situations where a population growth schedule is applied in order to engineer the mean-field system’s movement to a desired equilibrium point, as time $t \to \infty$ . One can also use this approach to study numerically the most likely region in which the process $\mu_N$ spends time for large values of N, under stationarity. Again, our proof is inspired by the analysis of the simulated annealing algorithm in [25, Part III]. We can also choose the transition rates of the particles so as to minimise a given ‘nice’ function on $M_1(\mathcal{Z})$ ; see Example 5.1.

1.3. Key ingredients for the proofs

The proofs of our main results follow the outlines in [25]. However, in order to make them work in our present context (which involves jump Markov processes and the mean-field setting), we make use of the following properties:

• a uniform version of the finite-duration LDP for $\{(\mu_N(t), 0 \leq t \leq T), N \geq 1\}$ , where the uniformity is over the initial condition;

• continuity of the cost function associated with movement between points on the simplex $M_1(\mathcal{Z})$ ;

• the strong Markov property of $\mu_N({\cdot})$ .

The key insight of this paper is the abstraction of these three properties and their importance in establishing the large-time behaviour and metastability properties of mean-field systems. We leverage the results of [12] to establish the above properties.

We now describe the key ideas in each of the main results.

To prove Theorem 1.1, one possible approach is to wait long enough for the process $\mu_N$ to hit a neighbourhood of (one of) the most stable $\omega$ -limit set(s) of (1.1), regardless of the initial condition, and then allow sufficient additional time for the process to mix well. We prove Theorem 1.1 using this idea; we first consider a sequence of passages of $\mu_N$ between neighbourhoods of $\omega$ -limit sets of (1.1) to reach (one of) the most stable $\omega$ -limit set(s). Each of these passages takes place between ‘stable’ subsets of $\omega$ -limit sets called cycles (see Section 3.3). The probability of each of these passages over time intervals of the form $\exp\{N\times \text{constant}\}$ for appropriate constants can be bounded below, thanks to the uniform large deviation property of $\mu_N$ (see Theorem 3.2). We then tie them up using the strong Markov property of $\mu_N$ . These steps yield a lower bound on the transition probability for $\mu_N$ (see Corollary 3.4), and Theorem 1.1 follows as a consequence of this. We can also produce an upper bound for the probability of these passages for suitable initial conditions if not enough time has elapsed (see (3.8) in Theorem 3.2). Theorem 1.2 follows as a consequence of this upper bound.

Theorem 1.3 follows from an application of Theorem 1.1. We use the spectral expansion of the generator of $\mu_N$ , when it is reversible with respect to its invariant measure $\wp_N$ , and the LDP for $\{\wp_N, N \geq 1\}$ to prove Theorem 1.3.

In Theorem 1.4, to bring the process $\mu_N$ to (one of) the most stable $\omega$ -limit set(s) of (1.1) (i.e., one of the global minima of our entropy function), regardless of the initial condition, we introduce new particles over time in a controlled fashion. Before reaching a global minimum, the system may possibly explore other local minima. Since addition of particles amounts to reduction of ‘noise’ in the process $\mu_N$ , we must make sure that particles are introduced sufficiently slowly over time so that the system does not get trapped in a local minimum. This is achieved by the choice of our particle addition schedule N(t), $t \geq 0$ , which is the analogue of the cooling schedule in simulated annealing. The schedule also enables us to apply the uniform LDP over sufficiently long time durations to $\bar{\mu}$ so as to extend the results on large-time behaviour used in the proof of Theorem 1.1 to the present situation when the number of particles changes over time (see Lemmas 5.1–5.3). These extensions, along with the method of analysing the passages of the system through cycles (the idea used in the proof of Theorem 1.1), enable us to prove a $1- o(1)$ lower bound on the probability that $\bar{\mu}(t)$ belongs to a neighbourhood of a global minimum of our entropy function as $t \to \infty$ , no matter where we start the process.

1.4. Examples

The mean-field interacting particle system that we have described can be used to model many interesting phenomena that arise in various domains, such as physics, engineering, and biology. In this section, we shall describe some applications that are relevant to communication networks and shall indicate the related literature that studies these applications via mean-field models. Naturally, the examples and the related literature that we mention below are by no means exhaustive.

The first example is load balancing in networks. We describe the simplest model, the power of two choices, studied by Mitzenmacher [36]. Here, each particle is a single-server M/M/1 queue, and the state represents the number of customers waiting in the queue. In load balancing, one is interested in routing the incoming customers to an appropriate queue so as to minimise the average delay experienced by a customer. The obvious way to do this is to route the customer to a queue with the lowest number of waiting customers. But, since there are a large number of queues, it is expensive to poll all of them and find the ones with the lowest number of customers. So a simple alternative is to pick a queue at random and route the incoming customer to that queue; this is studied in [24]. It turns out that, if we pick two queues at random and route the customer to the least loaded queue of the two (with ties broken uniformly at random), the delay decreases dramatically. This algorithm demonstrates the power of two choices, and the evolution of the state of each queue under this algorithm can be described using the mean-field model which has been used to analyse the delay performance [36]. For related problems on load balancing in networks, see Mukhopadhyay et al. [37], who study heterogeneous servers, Aghajani et al. [1, 2], who study non-Markovian queues, and the references therein. Note that one important difference from our setting is that the state space of a queue is countably infinite in this class of problems. The finite-state-space model arises in the above settings when the buffers are finite and packets arriving at a fully buffered queue are lost.

Another example arises in the modelling of a wireless local area network (WLAN). Here, each particle is a wireless node trying to access a common medium, and the state of a particle represents the aggressiveness with which a packet transmission is attempted. The nodes interact with each other via the medium access control (MAC) protocol implemented in the system. Whenever a wireless node encounters a collision due to a transmission from another node, it changes its state to a less aggressive one, and whenever it succeeds, it changes its state to a more aggressive one. Therefore, the evolution of the state of a node depends on the empirical measure of the states of all the nodes, as in our mean-field model. This model was first proposed by Bianchi [8] and has proved to be useful in analysing the performance of the MAC protocol. Other works that focus on the WLAN application include Bordenave et al. [11], who studied a two-time-scale mean-field interacting particle system with a fast-varying background process to model partial interference among nodes; Kumar et al. [28], who used the mean-field model to study the performance of WLANs using a fixed-point analysis; and Ramaiyan et al. [41] and Bhattacharya and Kumar [7], who looked at the problem of short-term unfairness using the aforementioned fixed-point analysis. Note that our model is a continuous-time modification of the discrete-time models in the above papers. Yet the continuous-time model provides accurate predictions about the discrete-time model; see [12, p. 4]. Some papers work directly with the continuous-time model; see, for example, Boorstyn et al. [10].

Other applications that use the mean-field model include analysis and control of spread of epidemics in networks [6, 3, 29], dynamic routing in circuit-switched networks [4], scheduling in cellular systems [32], and game-theoretic modelling and analysis of behaviour of agents in societal networks [42, 31].

1.5. Outline of the paper

The rest of the paper is organised as follows. In Section 2, we discuss LDPs for the empirical measure process $\mu_N$ over a finite time horizon. These play an important role in the study of the large-time behaviour of $\mu_N$ and the LDP for the invariant measure $\{\wp_N\}_{N\geq 1}$ . We then study the large-time behaviour of the process $\mu_N$ in Section 3, and prove our first main result on the proximity of the law of $\mu_N$ to its invariant measure. In Section 4, we study the asymptotics of the second-largest eigenvalue of the generator of the process $\mu_N$ in the reversible case. Finally, in Section 5, we study the convergence of the empirical measure process to a global minimum of the aforementioned entropy function when particles are injected into the system at a suitable rate.

2. Preliminaries: large deviations over finite time durations

In this section, we present a large deviation principle (LDP) for the process $\mu_N$ over finite time durations. This result will be used later to study the large-time behaviour of $\mu_N$ and the rate of convergence of $\mu_N$ to its invariant measure.

Fix $T>0$ . We introduce some notation. Let $\mathbb{P}_{\nu_N, [0,T]}^{(N)}$ denote the solution to the $D([0,T], M_1(\mathcal{Z}))$ -valued martingale problem for $L^N$ , i.e., the law of the empirical measure process $(\mu_N(t), 0 \leq t \leq T)$ , and let $\mathbb{P}_{\nu_N,T}^{(N)}$ denote the law of the terminal-time empirical measure $\mu_N(T) \in M_1(\mathcal{Z})$ , with a deterministic initial condition $ \mu_N(0) = \nu_N $ . Let $\mathcal{AC}[0,T]$ denote the space of absolutely continuous $M_1(\mathcal{Z})$ -valued paths on [0, T] (in particular they are differentiable for almost all $t \in [0,T]$ ; see [30, Definition 3.1]). Define

\begin{align*} \tau^*(u) \,:\!=\, \left\{ \begin{array}{l@{\quad}l@{\quad}l} \infty & \text{ if } u < -1, \\[3pt] 1 & \text{ if } u = -1, \\[3pt] (u+1) \log\! (u+1) - u& \text{ if } u > -1, \end{array} \right.\end{align*}

which is the Fenchel–Legendre transform of $\tau(u) = e^u-u-1$ , $u \in \mathbb{R}$ . Recall the definition of the family of rate matrices $(\Lambda_\xi, \xi \in M_1(\mathcal{Z}))$ from Section 1. We have the following LDP for the sequence $\left\{\mathbb{P}_{\nu_N, [0,T]}^{(N)}\right\}_{N \geq 1}$ on $D([0,T], M_1(\mathcal{Z}))$ (see [30, Theorem 3.1], [12, Theorem 3.2]). See [17, Section 1.2] for the definition of an LDP and a good rate function.

Theorem 2.1. Suppose that the initial conditions $\nu_N \to \nu$ in $M_1(\mathcal{Z})$ . Then the sequence of probability measures $\left\{\mathbb{P}_{\nu_N, [0,T]}^{(N)}, N\geq 1 \right\}$ on the space $D([0,T], M_1(\mathcal{Z}))$ satisfies the LDP with good rate function $S_{[0,T]}({\cdot}|\nu)$ defined as follows. If $\mu(0) = \nu$ and $\mu \in \mathcal{AC}[0,T]$ , then

\begin{align*} S_{[0,T]}(\mu|\nu) & = \int_{[0,T]} \sup_{\alpha \in \mathbb{R}^{|\mathcal{Z}|}} \Biggr\{ \sum_{z \in \mathcal{Z}} \alpha(z)(\dot{\mu}_t(z) - \Lambda_{\mu_t}^*\mu_t(z)) \\ & \qquad - \sum_{(z,z^\prime) \in \mathcal{E}} \tau(\alpha(z^\prime) - \alpha(z)) \lambda_{z,z^\prime}(\mu_t) \mu_t(z) \Biggr\} dt, \end{align*}

and $S_{[0,T]}(\mu | \nu) = +\infty$ otherwise. Moreover, if $S_{[0,T]}(\mu|\nu) < \infty$ , then there exists a unique family of rate matrices $L(t) = \big(l_{z,z^\prime}(t), z,z^\prime \in \mathcal{Z}\big)$ , $0 \leq t \leq T$ , such that $t \mapsto L(t)$ is measurable, $\mu$ is the solution to

\begin{align*} \dot{\mu}(t) = L(t)^* \mu(t), \, 0 \leq t \leq T, \, \mu(0) = \nu, \end{align*}

and

\begin{align*} & S_{[0,T]}(\mu|\nu) = \int_{[0,T]} \sum_{(z,z^\prime)\in \mathcal{E}} \mu(t)(z) \lambda_{z,z^\prime}(\mu(t)) \tau^*\left( \frac{l_{z,z^\prime}(t)}{\lambda_{z,z^\prime}(\mu(t))} -1 \right) dt, \end{align*}

where $L(t)^*$ denotes the transpose of L(t), $t \in [0,T]$ .

We can interpret the rate function $S_{[0,T]}$ as follows. Starting at $\nu_N$ , the process $\mu_N$ is likely to be in the neighbourhood of the solution to the McKean–Vlasov equation (1.1) with initial condition $\nu$ (with high probability). In order for the process $\mu_N$ to be in the neighbourhood of some other path, we need to apply a control given by the rate matrix L; $S_{[0,T]}(\mu|\nu)$ is the cost of this control. In particular, since the solution to the McKean–Vlasov equation starting at $\nu$ has zero cost (i.e., $S_{[0,T]}(\mu_{\nu}|\nu) = 0$ , where $\mu_\nu$ denotes the solution to (1.1) starting at $\nu$ ), the limiting behaviour that $\mu_N({\cdot}) \xrightarrow{\mathbb{P}} \mu_\nu({\cdot})$ in $D([0,T],M_1(\mathcal{Z}))$ as $N \to \infty$ follows. See [18] for some remarks about the form of the rate function and for another representation of the rate function in terms of a relative entropy.

Here is an outline of the proof of Theorem 2.1: one looks at a system of non-interacting particles where the transition rates of a particle do not depend on the empirical measure, and considers the corresponding empirical measure process over [0, T]. Since at most one particle can jump at a given point in time, the measure $\mathbb{P}_{\nu_N, [0,T]}^{(N)}$ is absolutely continuous with the measure corresponding to the above non-interacting system on $D([0,T],M_1(\mathcal{Z}))$ . One can then write the Radon–Nikodym derivative using the Girsanov formula and show continuity properties of the same. An application of an extension of Sanov’s theorem (see [14, Theorem 3.5]) tells us that the non-interacting particle system obeys the LDP on $D([0,T],M_1(\mathcal{Z}))$ . The above theorem then follows by an application of Varadhan’s integral lemma (see [17, Theorem 4.3.1]). This approach has been carried out for a system of interacting diffusions in [14] and for jump processes in [30, 12]. One can also prove various special cases of Theorem 2.1 via other simpler methods; for example, for fixed initial conditions, i.e., when $\nu_N = \delta_{z}$ for some $z \in \mathcal{Z}$ and for all $N \geq 1$ , one can use a modification of Varadhan’s lemma to obtain the LDP for $\mathbb{P}_{\delta_{z}, [0,T]}^{(N)}$ (see [16]). However, it is crucial to let the initial condition be arbitrary, except for the constraint that $\nu_N \to \nu$ weakly, to obtain a uniform version of Theorem 2.1 (see Corollary 2.1), which is used to prove our main results.

We now recall a theorem that gives the LDP for the sequence $\left\{\mathbb{P}_{\nu_N,T}^{(N)}\right\}_{N \geq 1}$ on $M_1(\mathcal{Z})$ . This can be obtained from the above theorem by an application of the contraction principle to the coordinate projection map $D([0,T], M_1(\mathcal{Z})) \ni \mu \mapsto \mu(T)$ (see [17, Theorem 4.2.1], [12, Theorem 3.3]).

Theorem 2.2. Suppose that the initial conditions $\nu_N \to \nu$ in $M_1(\mathcal{Z})$ . Then the sequence of probability measures $\left\{\mathbb{P}_{\nu_N,T}^{(N)}\right\}_{N \geq 1}$ on the space $M_1(\mathcal{Z})$ satisfies the LDP with the good rate function

\begin{align*} S_T(\xi|\nu) \,:\!=\, \inf \{S_{[0,T]}(\mu|\nu)\,:\, & \mu(0) = \nu, \mu(T) = \xi, \mu \in \mathcal{AC}[0,T]\}. \end{align*}

Moreover, the above infimum is attained, i.e., there exists a path $\hat{\mu} \in \mathcal{AC}[0,T] $ such that $\hat{\mu} (0)=\nu,\, \hat{\mu} (T) = \xi$ , and $S_{[0,T]}(\hat{\mu}|\nu) = S_T(\xi|\nu)$ .

Here, $S_T(\xi|\nu)$ can be interpreted as the minimum cost of passage from the profile $\nu$ to the profile $\xi$ in time T, among all paths from $\nu$ to $\xi$ in time T. It can be shown that $S_T$ is continuous on $M_1(\mathcal{Z}) \times M_1(\mathcal{Z})$ by constructing piecewise constant velocity trajectories between points on $M_1(\mathcal{Z})$ (see [12, Lemma 3.3]).

We also have the following uniform LDP for the sequence $\left\{\mathbb{P}_{\nu_N, [0,T]}^{(N)}\right\}_{ N \geq 1}$ (see [12, Corollary 3.1]) when the initial condition is allowed to lie in a compact set.

Corollary 2.1. For any compact set $K \subset M_1(\mathcal{Z})$ , any closed set $F \subset D([0,T], M_1(\mathcal{Z}))$ , and any open set $G \subset D([0,T], M_1(\mathcal{Z}))$ , we have

(2.1) \begin{align} \limsup_{N \to \infty} \frac{1}{N} \log \sup_{\nu \in K \cap M_1^N(\mathcal{Z})} \mathbb{P}_{\nu, [0,T]}^{(N)} (\mu_N \in F) \leq - \inf_{\nu \in K } \inf_{\mu \in F} S_{[0,T]} (\mu|\nu), \end{align}

and

(2.2) \begin{align} \liminf_{N \to \infty} \frac{1}{N} \log \inf_{\nu \in K \cap M_1^N(\mathcal{Z})} \mathbb{P}_{\nu, [0,T]}^{(N)} (\mu_N \in G) \geq - \sup_{\nu \in K} \inf_{\mu \in G} S_{[0,T]} (\mu|\nu). \end{align}

For a proof of the above, see [17, Corollary 5.6.15]. Note that, since the space $M_1(\mathcal{Z})$ is compact, we may take $K = M_1(\mathcal{Z})$ in the above corollary.

Remark 2.1. The version of the uniform LDP presented in Corollary 2.1 is slightly different from the definition of the uniform LDP in Freidlin and Wentzell [20, Section 3, Chapter 3]. The version presented here suffices for the proofs of our main results, since our state space $M_1(\mathcal{Z})$ is compact and the rate function $S_T$ defined in Theorem 2.2 is continuous (see [43, Theorem 2.7] and [12, Appendix A]).

3. Large-time behaviour

In the study of the large-time behaviour of $\mu_N$ , an important role is played by the Freidlin–Wentzell quasipotential $V \,:\, M_1(\mathcal{Z}) \times M_1(\mathcal{Z}) \to [0, \infty)$ , defined by

\begin{align*} V(\nu,\xi) \,:\!=\, \inf\! \big\{S_{[0,T]}(\mu|\nu)\,:\,\mu(T)= \xi, T > 0\big\};\end{align*}

i.e., $V(\nu, \xi)$ denotes the minimum cost of transport from $\nu$ to $\xi$ in an arbitrary but finite time.

We say that $\nu \sim \xi$ ( $\nu$ is equivalent to $\xi$ ) if $V(\nu, \xi) = 0$ and $V(\xi, \nu) = 0$ . It is easy to see that $\sim$ defines an equivalence relation on $M_1(\mathcal{Z})$ . To study the large-time behaviour of the process $\mu_N$ , we make the following assumptions on the McKean–Vlasov equation (1.1) (see [20, Chapter 6, Section 2, Condition A]):

1. (B1) There exist a finite number of compact sets $K_1, K_2, \ldots, K_l$ such that the following hold:

• For each $i = 1,2, \ldots, l$ , $\nu_1, \nu_2 \in K_i$ implies $\nu_1 \sim \nu_2$ .

• For each $i \neq j$ , $\nu_1 \in K_i$ and $\nu_2 \in K_j$ implies $\nu_1 \nsim \nu_2$ .

• Every $\omega$ -limit set of the dynamical system (1.1) lies completely in one of the compact sets $K_i$ .

Since $V(\nu_1, \nu_2) = 0$ whenever $\nu_1,\nu_2 \in K_i$ for any $1 \leq i \leq l$ , we can define

\begin{align*} V\big(K_i, K_j\big) \,:\!=\, \inf\!\big\{S_{[0,T]}(\mu|\nu)\,:\,\nu \in K_i, \mu(T) \in K_j, T > 0\big\},\end{align*}

which is interpreted as the minimum cost of going from $K_i$ to $K_j$ . We also define the minimum cost of going from $K_i$ to $K_j$ without touching the other compact sets $K_k$ , $k \neq i,j$ , by

(3.1) \begin{align} \tilde{V}\big(K_i, K_j\big) \,:\!=\, \inf\!\big\{S_{[0,T]}(\mu|\nu)\,:\ &\nu \in K_i, \ \mu(t) \notin \cup_{k\neq i, j} K_k \nonumber \\ & \text{for all } 0 \leq t \leq T, \ \mu(T) \in K_j, \ T>0\big\}.\end{align}

Using the definition of the rate function $S_T$ , note that

\begin{align*} V(\nu,\xi) = \inf_{T > 0} S_T(\xi|\nu) \quad \text{ and } \quad V\big(K_i, K_j\big) = \inf_{\nu \in K_i, \xi \in K_j} V(\nu, \xi). \end{align*}

Example 3.1. We provide two examples where (B1) is satisfied.

1. 1. (Wireless local area network.) Let $\mathcal{Z} = \{0,1\}$ . The edgeset $\mathcal{E}$ consists of the edges (0, 1) and (1, 0). Define the transition rates

   \begin{align*} \lambda_{z,z^\prime}(\xi) = \left\{ \begin{array}{l@{\quad}l} c_0(1-\exp\{{-}(c_0\xi(0)+c_1\xi(1))\}) & \text{ if } z=0, \ z^\prime = 1,\\[4pt] c_1 & \text{ if } z=1 , \ z^\prime = 0, \end{array} \right. \end{align*}
   where $c_0, c_1 > 0$ . The limiting dynamics (1.1) is a one-dimensional ODE, and it is given by
   \begin{align*} \dot{\mu}_t(0) &= -c_0\mu_t(0)(1-\exp\{{-}(c_0\mu_t(0)+c_1(1-\mu_t(0)))\})+ c_1 (1-\mu_t(0)), \qquad t \geq 0. \end{align*}
   Let $f(x) = -c_0x(1-\exp\{{-}(c_0x+c_1(1-x))\}) + c_1 (1-x)$ , $x \in [0,1]$ . Note that $f(0) > 0$ and $f(1) < 0$ . It is easy to check that if $c_0 > c_1$ , then $f^\prime(x) < 0$ for all $x \in (0, 1)$ . As a consequence, there exists a unique $\xi^* \in M_1(\mathcal{Z})$ such that all trajectories of the above dynamical system converge to $\xi^*(0)$ . Thus, Assumption (B1) holds with $l = 1$ , $K_1 = \{\xi^*\}$ .

2. 2. (Dynamic alternate routing in loss networks.) Fix $C \in \mathbb{Z}_+$ and let $\mathcal{Z} = \{0,1,\ldots, C\}$ . The edgeset $\mathcal{E}$ consists of the forward edges $\{(z,z+1), \ 0 \leq z \leq C-1\}$ and the backward edges $\{(z,z-1), \ 1 \leq z \leq C\}$ . For $(z,z^\prime) \in \mathcal{E}$ and $\xi \in M_1(\mathcal{Z})$ , define the transition rates

   \begin{align*} \lambda_{z,z^\prime}(\xi) = \left\{ \begin{array}{l@{\quad}l} z & \text{ if } z \neq 0, \ z^\prime = z-1,\\[4pt] \alpha + \alpha \xi(C) \times 2(1-\xi(C)) & \text{ if } z \neq C, \ z^\prime = z+1, \end{array} \right. \end{align*}
   where $\alpha > 0$ . This model arises in the context of dynamic alternate routing in loss networks. For certain values of $\alpha$ , the limiting ODE (1.1) possesses two stable equilibria $\big($ say $\xi_1^*$ and $\xi_2^*\big)$ and an unstable equilibrium $\big($ say $\xi_3^*\big)$ [23, 38]. Thus, Assumption (B1) is satisfied with $l=3$ , $K_i = \{\xi_i^*\}$ , $i=1,2,3$ .

For a model of malware propagation where a limit cycle and an unstable equilibrium arise, see Benaïm and Le Boudec [6, Section 4.1].

3.1. Preliminary results

It turns out that, under Assumption (B1), the large-time behaviour of the process $\mu_N$ can be studied via a discrete-time Markov chain whose state space is the union of small neighbourhoods of the compact sets $K_i$ , $1 \leq i \leq l$ . To study this chain, we introduce some notation. Let $L = \{1,2,\ldots, l\}$ . Given $0 < \rho_1 < \rho_0$ , let $\gamma_i$ (resp. $\Gamma_i$ ) denote the $\rho_1$ -open neighbourhood (resp. $\rho_0$ -open neighbourhood) of $K_i$ . Let $\gamma = \cup_{i=1}^l \gamma_i$ , $\Gamma = \cup_{i=1}^l \Gamma_i$ , and $C =M_1(\mathcal{Z}) \setminus \overline{\Gamma}$ . For a set $A \subset M_1(\mathcal{Z})$ and $\delta>0$ , let $[A]_\delta$ denote the $\delta$ -open neighbourhood of A, and for a subset $W \subset L$ , abusing notation, let $[W]_\delta$ denote the $\delta$ -open neighbourhood of $\cup_{i \in W} K_i$ . For each $n \geq 1$ , we define the sequence of stopping times $\tau_0\,:\!=\, 0$ , $\sigma_n \,:\!=\, \inf\{t>\tau_{n-1}\,:\, \mu_N(t) \in C\}$ , $\tau_n \,:\!=\, \inf\{t > \sigma_n \,:\, \mu_N(t) \in \gamma\}$ ; and we define $Z^N_n \,:\!=\, \mu_N(\tau_n)$ . Since $\mu_N$ is strong Markov, $Z^N$ is a discrete-time Markov chain, and $Z_n^N \in \gamma \cap M^N_1(\mathcal{Z})$ for all $n \geq 1$ . For a measurable set $A \in M_1(\mathcal{Z})$ , we define the stopping time $\tau_A \,:\!=\, \inf\{t > 0\,:\, \mu_N(t) \notin A\}$ , which denotes the time of first exit from the set A. Finally, for a subset $W \subset L$ , we define the stopping times $\hat{\tau}_W \,:\!=\, \inf\{t >0 \,:\, \mu_N(t) \in \cup_{i \in W}\gamma_i\}$ and $\bar{\tau}_W \,:\!=\, \inf \{t > 0\,:\, \mu_N(t) \in \cup_{i \in L \setminus W} \gamma_i \}$ , which denote the time of entry into the $\rho_1$ -neighbourhood of W and the time of entry into the $\rho_1$ -neighbourhood of $L \setminus W$ , respectively.

We now state some results on the behaviour of the exit time from certain sets, which will be used in the paper subsequently. These results are known in the case of both Markov jump processes and diffusion processes; see [12, Appendix], and [20, Chapter 6, Section 2]. The main ingredients that are used in proving these results are (i) the strong Markov property of the $\mu_N$ process, (ii) Theorem 2.1 and Corollary 2.1 on the LDP for finite time durations, and (iii) the joint continuity of the terminal-time rate function $S_T({\cdot}|{\cdot})$ (see [12, Lemma 3.3]). Recall that $\mathbb{P}_\nu$ denotes the law of $(\mu_N(t), t \geq 0)$ with initial condition $\mu_N(0) = \nu$ and $\mathbb{E}_\nu$ denotes the corresponding expectation.

Lemma 3.1. ([12, Lemma A.3].) Let $K \subset M_1(\mathcal{Z})$ be a compact set such that all points in K are equivalent to each other (i.e., $\nu_1 \sim \nu_2$ for all $\nu_1, \nu_2 \in K$ ), and $K \neq M_1(\mathcal{Z})$ . Then, given $\varepsilon> 0$ , there exist $\delta > 0$ and $N_0 \geq 1$ such that for all $N \geq N_0$ and $\nu \in [K]_{\delta}\cap M^N_1(\mathcal{Z})$ ,

\begin{align*} \mathbb{E}_\nu \tau_{[K]_{\delta}} \leq \exp\{N\varepsilon\}. \end{align*}

Lemma 3.2. ([12, Lemma A.4].) Let $K \subset M_1(\mathcal{Z})$ be a compact set and let G be a neighbourhood of K. Then, given $\varepsilon > 0$ , there exist $\delta>0$ and $N_0 \geq 1$ such that for all $\nu \in \overline{[K]_{\delta}} \cap M_1^N(\mathcal{Z})$ and $N \geq N_0$ ,

\begin{align*} \mathbb{E}_\nu\!\left( \int_0^{\tau_G} 1_{\{\mu_N(t) \in \overline{[K]_\delta}\}} dt \right) \geq \exp\{{-}N\varepsilon\}. \end{align*}

Lemma 3.3. ([12, Lemma A.5].) Let $K \subset M_1(\mathcal{Z})$ be a compact set that does not contain any $\omega$ -limit set of (1.1) entirely. Then, there exist positive constants $c, T_0$ and $N_0 \geq 1$ such that for all $T \geq T_0$ , $N \geq N_0$ and any $\nu \in K \cap M_1^N(\mathcal{Z})$ , we have

\begin{align*} \mathbb{P}_{\nu}( \tau_K \geq T ) \leq \exp\{{-}Nc(T-T_0)\}. \end{align*}

Corollary 3.1. Under the conditions of Lemma 3.3, there exist $ C>0$ and $N_0 \geq 1$ such that for all $\nu \in K \cap M_1^N(\mathcal{Z})$ and $N \geq N_0$ ,

\begin{align*} \mathbb{E}_\nu \tau_K \leq C. \end{align*}

Recall the definition of the discrete-time Markov chain $Z^N$ on $\gamma \cap M_1^N(\mathcal{Z})$ . The next lemma gives upper and lower bounds on the one-step transition probabilities of the chain $Z^N$ . These estimates play an important role in the study of the large-time behaviour of the process $\mu_N$ , as we shall see in the sequel.

Lemma 3.4. ([12, Lemma A.6].) Given $\varepsilon >0$ , there exist $\rho_0 >0$ and $N_0 \geq 1$ such that, for any $\rho_2 < \rho_0$ , there exists $\rho_1 < \rho_2$ such that for any $\nu \in [K_i]_{\rho_2} \cap M_1^N(\mathcal{Z})$ and $N \geq N_0$ , the one-step transition probability of the chain $Z^N$ satisfies

(3.2) \begin{align} \exp\!\big\{{-}N\big(\tilde{V}\big(K_i, K_j\big)+\varepsilon\big)\big\} \leq \mathbb{P}\big(\nu, \gamma_j\big) \leq \exp\!\big\{{-}N\big(\tilde{V}\big(K_i, K_j\big)-\varepsilon\big)\big\}. \end{align}

Remark 3.1. In the above statement, $\mathbb{P}\big(\nu, \gamma_j\big)$ is defined as $\mathbb{P}\big(\nu, \gamma_j\big) \,:\!=\, \mathbb{P}_\nu\big(Z^N_1 \in \gamma_j\big) = \mathbb{P}_\nu\big(\mu_N(\tau_1) \in \gamma_j\big)$ .

The key ingredient in the proof of the above lemma is Corollary 2.1 on the uniform LDP on bounded sets. For the lower bound, one constructs a specific trajectory from $\nu$ to $K_j$ and examines its cost. For the upper bound, one uses the strong Markov property at the hitting time of $[L]_{\rho_1}$ and the uniform LDP. For details, the reader is referred to the proof of [12, Lemma A.6] for the case of Markov jump processes, and the proof of [20, Lemma 2.1, p. 152] for the case of small-noise diffusions.

3.2. Behaviour near attractors indexed by subsets of L

We now recall some results on the behaviour of the process $\mu_N$ near a small neighbourhood of attractors indexed by a given subset of L. Let $W \subset L$ , $W \neq \emptyset$ . A W-graph is a directed graph on L such that (i) each element of $L \setminus W$ has exactly one outgoing arrow and (ii) there are no closed cycles in the graph. We denote the set of W-graphs by G(W). For each $i \in L$ , we denote $G(\{i\})$ by G(i). For a W-graph g, define

(3.3) \begin{align} \tilde{V}(g) = \sum_{(m\to n) \in g} \tilde{V}(K_m, K_n).\end{align}

If g does not have any edges (e.g., when L is a singleton), we use the convention $\tilde{V}(g) = 0$ . Note that, using the estimate (3.2), $\tilde{V}$ can be used to estimate the probability that the process $\mu_N$ traverses a sequence of neighbourhoods in the order specified by the graph g.

For $i \in L\setminus W$ and $j \in W$ , let $G_{i,j}(W)$ denote the set of W-graphs in which there is a sequence of arrows leading from i to j. Define

\begin{align*} I_{i,j}(W) \,:\!=\, \min\{\tilde{V}(g)\,:\,g \in G_{i,j}(W)\} - \min\{\tilde{V}(g)\,:\, g \in G(W)\}.\end{align*}

We recall the following result on the probability that the first entry of $\mu_N$ into a neighbourhood of a set $W \subset L$ takes place via a given compact set $K_j$ , starting from a neighbourhood of $K_i$ .

Lemma 3.5. Let $W \subset L$ , and let $i \in L \setminus W$ and $j \in W$ . Given $\varepsilon > 0$ , there exist $\rho > 0$ and $N_0 \geq 1 $ such that for any $\rho_1 \leq \rho$ , $\nu \in \gamma_i \cap M^N_1(\mathcal{Z})$ , and $N \geq N_0$ , we have

\begin{align*} \exp\!\big\{{-}N\big(I_{i,j}(W)+\varepsilon\big)\big\} \leq \mathbb{P}_\nu\big(\mu_N\big(\hat{\tau}_W\big) \in \gamma_j\big) \leq \exp\!\big\{{-}N\big(I_{i,j}(W)-\varepsilon\big)\big\}. \end{align*}

Proof. The proof of [20, Lemma 3.3, p. 159] holds verbatim, by making use of the estimates in Lemma 3.4.

Remark 3.2. While the above lemma provides an estimate of the probability $\mathbb{P}_\nu\big(\mu_N\big(\hat{\tau}_W\big) \in \gamma_j\big)$ , it does not provide any information about the sequence of states in L visited by the process $\mu_N$ while traversing from i to j. The latter can be understood via studying the minimisations in the definition of $I_{i,j}$ ; see [21].

Our next step is to understand the mean entry time $\mathbb{E}_\nu \hat{\tau}_W$ . For this, we need the following estimate on the stopping time $\tau_1$ ; see [25, Lemma 1.3, Part I] for a similar estimate for small-noise diffusion processes.

Lemma 3.6. Given $\varepsilon >0$ , there exist $\rho_1 >0$ and $N_0 \geq 1$ such that, for any $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ and $N \geq N_0$ , we have

\begin{align*} \mathbb{E}_\nu \tau_1 \leq \exp\{N\varepsilon\}. \end{align*}

Proof. With a sufficiently small $\rho_1 > 0$ to be chosen later, let $\rho_0 = 2 \rho_1$ so that $[K_i]_{\rho_0}$ does not intersect with $[K_j]_{\rho_0}$ for all $j \neq i$ . Note that, for any $\nu \in \gamma$ ,

\begin{align*} \mathbb{E}_{\nu} \tau_1 = \mathbb{E}_\nu \sigma_1 +\mathbb{E}_\nu (\tau_1 - \sigma_1). \end{align*}

Consider the first term. By Lemma 3.1, there exist $\rho > 0$ and $N_0 \geq 1$ such that for all $\rho_1 \leq \rho$ , $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ , and $N \geq N_0$ , we have

\begin{align*} \mathbb{E}_\nu \sigma_1 \leq \exp\{N\varepsilon/2\}. \end{align*}

Let $F = M_1(\mathcal{Z}) \setminus \gamma$ . By the strong Markov property, the second term is

\begin{align*} \mathbb{E}_\nu (\tau_1 - \sigma_1) = \mathbb{E}_{\mu_N(\sigma_1)} (\tau_{F}). \end{align*}

Therefore, it suffices to estimate $\mathbb{E}_{\nu^\prime} \tau_F$ for $\nu^\prime \in F$ . Since the compact set F does not contain any $\omega$ -limit set, by Corollary 3.1, there exist a constant $C >0$ and $N_1 \geq N_0$ such that for any $\nu^\prime \in F \cap M_1^N(\mathcal{Z})$

\begin{align*} \mathbb{E}_{\nu^\prime} \tau_{F} \leq C. \end{align*}

This completes the proof of the lemma.

Define

\begin{align*} I_i(W) \,:\!=\, &\min\{\tilde{V}(g)\,:\, g \in G(W)\} \\ & - \min\{\tilde{V}(g)\,:\, g \in G( W \cup \{i\}) \text{ or } g \in G_{i,j}(W \cup \{j\}), i \neq j, j \in L\setminus W\}.\end{align*}

The next lemma is about the mean entry time into a neighbourhood of a given set $W \subset L$ starting from a neighbourhood of $K_i$ ; see [25, Lemma 1.6, Part I] for a similar estimate on small-noise diffusion processes.

Lemma 3.7. Let $W \subset L$ , and let $i \in L \setminus W$ . Given $\varepsilon > 0$ , there exist $\rho > 0$ and $N_0 \geq 1 $ such that for any $\rho_1 \leq \rho$ , $\nu \in \gamma_i \cap M^N_1(\mathcal{Z})$ , and $N \geq N_0$ , we have

\begin{align*} \exp\{N(I_i(W)-\varepsilon)\} \leq \mathbb{E}_\nu \hat{\tau}_W \leq \exp\{N(I_i(W)+\varepsilon)\}. \end{align*}

Proof. We first prove the upper bound. Note that, by the strong Markov property, we have

\begin{align*} \mathbb{E}_\nu \hat{\tau}_W = \mathbb{E}_\nu \tau_v \leq \sum_{m=1}^\infty \mathbb{E}_\nu\!\left(1_{\{v = m\}} \times m \sup_{\nu^\prime \in \gamma} \mathbb{E}_{\nu^\prime} \tau_1 \right), \end{align*}

where v is the hitting time of the chain $Z_n^N$ on the set W. Using Lemma 3.6 and the upper bound on $\mathbb{E}_\nu v$ derived in [20, Lemma 3.4, p. 162], for sufficiently small $\rho_1$ and sufficiently large N, we have that

\begin{align*} \mathbb{E}_\nu \hat{\tau}_W \leq \exp\{N(I_i(W) +\varepsilon)\} \end{align*}

holds for all $\nu \in \gamma_i \cap M_1^N(\mathcal{Z})$ . For the lower bound, Lemma 3.2 implies that, for all sufficiently small $\rho_1$ and sufficiently large N, we have that

\begin{align*} \mathbb{E}_\nu \tau_1 \geq \exp\{{-}N\varepsilon\} \end{align*}

holds for all $\nu \in \gamma$ . Also,

\begin{align*} \mathbb{E}_\nu \hat{\tau}_W = \mathbb{E}_\nu \tau_v \geq \sum_{m=1}^\infty \mathbb{E}_\nu\!\left(1_{\{v = m\}} \times m \inf_{\nu^\prime \in \gamma} \mathbb{E}_{\nu^\prime} \tau_1 \right); \end{align*}

hence, using the lower bound on $\mathbb{E}_\nu v$ derived in [20, Lemma 3.4, p. 162], we get

\begin{align*} \mathbb{E}_\nu \hat{\tau}_W \geq \exp\{N(I_i(W) - \varepsilon)\} \end{align*}

for all $\nu \in \gamma_i \cap M_1^N(\mathcal{Z})$ and sufficiently large N.

3.3. Cycles

We now define the notion of cycles, which helps us to describe the most probable way in which the process $\mu_N$ , for large N, traverses neighbourhoods of various compact sets $K_i$ , and the time required to go from one to another. Recall the definition of $\tilde{V}$ from (3.1). We interpret $\tilde{V}\big(K_i, K_j\big)$ as the ‘communication cost’ from i to j. Define $\tilde{V}(K_i) \,:\!=\, \min_{j \neq i} \tilde{V}\big(K_i, K_j\big)$ . We say that $i \to j$ if $\tilde{V}(K_i) = \tilde{V}\big(K_i,K_j\big)$ . For $j \neq i$ , the probability that $\mu_N$ hits a small neighbourhood of $K_j$ upon exit from a small neighbourhood of $K_i$ is of the form $\exp\!\big\{{-}N(\tilde{V}\big(K_i, K_j\big) - \tilde{V}(K_i))\big\}$ , and the mean exit time from a small neighbourhood of $K_i$ is of the form $\exp\!\big\{N\tilde{V}(K_i)\big\}$ [20, Chapter 6, Section 5]. In particular, the indices that attain the minimum above are the sets most likely to be visited by the process $\mu_N$ , for large enough N, starting from a neighbourhood of $K_i$ . For $i, j \in L$ , we say that $i \Rightarrow j$ if there exists a sequence of arrows leading from i to j, i.e., if there exist $i_1, i_2 , \ldots, i_n$ in L such that $i \to i_1 \to i_2 \to \cdots \to i_n \to j$ . Again, the above sequence of arrows from i to j is one among the locally most likely sequences for the process to traverse from a neighbourhood of $K_i$ to a neighbourhood of $K_j$ , for large N.

Definition 3.1. A 1-cycle $\pi$ is a directed graph on a subset of elements of L satisfying the following:

1. 1. $i \in \pi$ and $i \Rightarrow j$ implies $j \in \pi$ .

2. 2. For any $i \neq j$ in $\pi$ , we have $i \Rightarrow j $ and $j \Rightarrow i$ .

That is, a 1-cycle is a subset of the elements of L along with a certain assignment of arrows among them according to the numbers $\tilde{V}(\cdot, \cdot)$ . For example, if $L = \{1,2,3\}$ , and $1 \to 2$ , $2 \to 1$ , and $3 \to 1$ are the only possible arrows (i.e., $\tilde{V}(K_1) = \tilde{V}(K_1, K_2) < \tilde{V}(K_1, K_3)$ , $\tilde{V}(K_2) = \tilde{V}(K_2, K_1) < \tilde{V}(K_2, K_3)$ , and $\tilde{V}(K_3) = \tilde{V}(K_3, K_1) < \tilde{V}(K_3, K_2)$ ), then the graph on $\{1,2\}$ consisting of the arrows $1 \to 2$ and $2 \to 1$ is a 1-cycle. The set $\{3\}$ is not part of a 1-cycle. It can be shown that a 1-cycle always exists for all L (see the proof of [25, Lemma 1.9, Part I]).

We now define cycles of 1-cycles. Let $L_0 = L$ . Define

\begin{align*} L_1 \,:\!=\, \{\pi\,:\, \pi \text{ is a 1-cycle in } L\} \cup \{i \in L\,:\, i \text{ is not in any 1-cycle}\}.\end{align*}

That is, the elements of $L_1$ are either 1-cycles in L or elements of L that do not belong to any 1-cycle. In the previous example, $L_1$ is the set $\{\{1,2\}\} \cup \{\{3\}\}$ . Ultimately, we view the elements of $L_1$ as subsets of L. If $\pi \in L_1$ , we write $K \in \pi$ to indicate that the index of the compact set K in $\{1,2,\ldots, l\}$ is an element of $\pi$ . We now proceed to define the ‘communication cost’ between the elements of $L_1$ . For $\pi_1, \pi_2 \in L_1$ , $\pi_1 \neq \pi_2$ , define

\begin{align*} \hat{V}(\pi_1) \,:\!=\, \max\! \big\{\tilde{V}(K)\,:\, K \in \pi_1\big\},\end{align*}

\begin{align*} \tilde{V}(\pi_1, \pi_2) \,:\!=\, \hat{V}(\pi_1) + \min\!\big\{\tilde{V}(K_1, K_2)-\tilde{V}(K_1)\,:\, K_1 \in \pi_1, K_2 \in \pi_2\big\},\end{align*}

and

\begin{align*} \tilde{V}(\pi_1) \,:\!=\, \min\!\big\{\tilde{V}(\pi_1, \pi_2)\,:\, \pi_2 \in L_1, \pi_2 \neq \pi_1\big\}.\end{align*}

That is, $\tilde{V}(\pi_1, \pi_2)$ is the communication cost from $\pi_1$ to $\pi_2$ , and it generalises the quantity $\tilde{V}\big(K_i, K_j\big)$ to 1-cycles. Similarly, $\tilde{V}(\pi_1)$ generalises the quantity $\tilde{V}(K_i)$ to 1-cycles. If $\pi_1, \pi_2$ are 1-cycles, $\pi_1 \neq \pi_2$ , then upon exit from a small neighbourhood of the elements of $\pi_1$ , the probability that the process $\mu_N$ enters a small neighbourhood of the elements of $\pi_2$ is of the form $\exp\!\big\{{-}N\big(\tilde{V}(\pi_1, \pi_2) - \tilde{V}(\pi_1)\big)\big\}$ , and the mean exit time from a small neighbourhood of the elements of $\pi_1$ is of the form $\exp\!\big\{N\tilde{V}(\pi_1)\big\}$ . We say that $\pi_1 \to \pi_2$ if $ \tilde{V}(\pi_1) = \tilde{V}(\pi_1, \pi_2)$ , and we say that $\pi_1 \Rightarrow \pi_2$ if there is a sequence of arrows leading from $\pi_1$ to $\pi_2$ . This gives a cycle of 1-cycles, which we call a 2-cycle.

Let us now define the hierarchy of cycles. Having defined $(m-1)$ -cycles and the sets $L_0, L_1, \ldots, L_{m-2}$ , we define m-cycles as follows. Define

\begin{align*} L_{m-1} = \, & \big\{\pi^{m-1}\,:\, \pi^{m-1} \text{ is an } (m-1)\text{-cycle}\big\} \\ & \cup \big\{\pi^{m-2} \in L_{m-2} \,:\, \pi^{m-2} \text{ is not in any } (m-1)\text{-cycle}\big\}.\end{align*}

That is, the elements of $L_{m-1}$ are either $(m-1)$ -cycles or elements of $L_{m-2}$ that are not part of any $(m-1)$ -cycle; in both cases, they are ultimately viewed as subsets of L. Given $\pi^{m-1} \in L_{m-1}$ and an $(m-2)$ -cycle $\pi^{m-2}$ , we write $\pi^{m-2} \in \pi^{m-1}$ if the elements of $\pi^{m-2}$ (when it is viewed as a subset of L) are part of $\pi^{m-1}$ . For $\pi^{m-1} \in L_{m-1}$ , define

\begin{align*} \hat{V}\big(\pi^{m-1}\big) \,:\!=\, \max\! \big\{\tilde{V}\big(\pi^{m-2}\big)\,:\, \pi^{m-2} \in \pi^{m-1}\big\},\end{align*}

\begin{align*} \tilde{V}\big(\pi_1^{m-1}, \pi_2^{m-1}\big) \,:\!=\, \, & \hat{V}\big(\pi_1^{m-1}\big) \\ & + \min\!\big\{\tilde{V}\big(\pi_1^{m-2}, \pi_2^{m-2}\big)-\tilde{V}\big(\pi_1^{m-2}\big) \,:\, \pi_1^{m-2} \in \pi_1^{m-1}, \pi_2^{m-2} \in \pi_2^{m-1}\big\},\end{align*}

and

\begin{align*} \tilde{V}\big(\pi_1^{m-1}\big) \,:\!=\, \min\!\big\{\tilde{V}\big(\pi_1^{m-1}, \pi_2^{m-1}\big)\,:\, \pi_2^{m-1} \in L_{m-1}, \pi_2^{m-1} \neq \pi_1^{m-1}\big\}.\end{align*}

We say that $\pi_1^{m-1} \to \pi_2^{m-1}$ if $\tilde{V}\big(\pi_1^{m-1}\big) = \tilde{V}\big(\pi_1^{m-1}, \pi_2^{m-1}\big) $ . We then have the following definition.

Definition 3.2. An m-cycle $\pi^m$ is a directed graph on a subset of elements of $L_{m-1}$ satisfying the following:

1. 1. For $\pi_1^{m-1}, \pi_2^{m-1} \in L_{m-1}$ , $\pi_1^{m-1} \in \pi^m$ and $\pi_1^{m-1} \Rightarrow \pi_2^{m-1}$ implies $\pi_2^{m-1} \in \pi^m$ .

2. 2. For any $\pi_1^{m-1}, \pi_2^{m-1} \in \pi^m$ , we have $\pi_1^{m-1} \Rightarrow \pi_2^{m-1}$ and $\pi_2^{m-1}\Rightarrow \pi_1^{m-1}$ .

If we continue this way, for some $m \geq 1$ , the set $L_m$ will eventually be a singleton, at which point we stop. See [46] for a numerical example that consists of three 1-cycles and a 2-cycle when L has 9 elements.

We now state some results on the mean exit time from a cycle and the most probable cycle for the process $\mu_N$ to visit upon exit from a given cycle. For convenience, the set of elements of L constituting a k-cycle $\pi^k$ (through the hierarchy of cycles) is also denoted by $\pi^k$ . Also, for $W \subset L$ , we define $\gamma_W = \cup_{i \in W} \gamma_i$ .

Corollary 3.2. Let $\pi^k$ be a k-cycle and $K_i \in \pi^k$ . Let $W = L \setminus \pi^k$ . Given $\varepsilon > 0$ , there exist $\rho >0$ and $N_0 \geq 1$ such that for all $\rho_1 \leq \rho$ , $\nu \in \gamma_i \cap M_1^N(\mathcal{Z})$ , and $N \geq N_0$ , we have

\begin{align*} \exp\! \big\{N\big(\tilde{V}\big(\pi^k\big) - \varepsilon\big)\big\} \leq \mathbb{E}_\nu \hat{\tau}_W \leq \exp\! \big\{N\big(\tilde{V}\big(\pi^k\big) + \varepsilon\big)\big\}. \end{align*}

Corollary 3.3. Let $\pi_1^k, \pi_2^k$ be k-cycles, $\pi_1^k \neq \pi_2^k$ , and $K_i \in \pi_1^k$ . Let $W = L \setminus \pi_1^k$ . Given $\varepsilon > 0$ , there exist $\rho >0$ and $N_0 \geq 1$ such that for all $\rho_1 \leq \rho$ , $\nu \in \gamma_i \cap M_1^N(\mathcal{Z})$ , and $N \geq N_0$ , we have

\begin{align*} \exp\! \big\{{-}N\big(\tilde{V}\big(\pi_1^k, \pi_2^k\big) - \tilde{V}\big(\pi_1^k\big) + \varepsilon\big)\big\} & \leq \mathbb{P}_\nu \big(\mu_N(\hat{\tau}_W) \in \gamma_{\pi_2^k}\big) \\ &\leq \exp\! \big\{{-}N\big(\tilde{V}\big(\pi_1^k, \pi_2^k\big) - \tilde{V}\big(\pi_1^k\big) - \varepsilon\big)\big\}. \end{align*}

Remark 3.3. Note that Corollary 3.2 follows from Lemma 3.7 and the fact that $I_i(W) = \tilde{V}\big(\pi^k\big)$ (which is shown in [25, Corollary A.4, Appendix]). Corollary 3.3 is a consequence of Lemma 3.5 along with the fact that $\min\!\big\{I_{i,j}(W) \,:\, i \in \hat{\pi}^k\big\} = \tilde{V}\big(\pi^k, \hat{\pi}^k\big) - \tilde{V}\big(\pi^k\big)$ (see [25, Corollary A.6, Appendix]). Similar estimates as in Corollaries 3.2 and 3.3 in the case of small-noise diffusion processes have been shown in [25, Corollary 1.10, Part I] and [25, Corollary 1.11, Part I], respectively.

We also need the following lemmas that provide estimates on the probabilities of exit within certain times from given cycles.

Lemma 3.8. Let $\pi_1^k, \pi_2^k$ be k-cycles and let $\pi_1^k \to \pi_2^k$ . Then, given $\varepsilon >0$ , there exist $\delta >0$ , $\rho >0$ , and $N_0 \geq 1$ such that for all $\rho_1 \leq \rho$ , $\nu \in \gamma_{\pi_1^k} \cap M_1^N(\mathcal{Z})$ , and $N \geq N_0$ , we have

\begin{align*} \mathbb{P}_\nu\!\left(\bar{\tau}_{\pi_1^k} \leq \exp\!\big\{N\big(\tilde{V}\big(\pi_1^k\big)-\delta\big)\big\}, \mu_N\big(\bar{\tau}_{\pi_1^k}\big) \in \gamma_{\pi_2^k} \right) \geq \exp\{{-}N\varepsilon\}. \end{align*}

Lemma 3.9. Let $\pi^k$ be a k-cycle. Then, given $\varepsilon > 0$ , there exists $\rho > 0$ such that for all $\rho_1 \leq \rho$ , we have

\begin{align*} \lim_{N \to \infty} \sup_{\nu \in \gamma_{\pi^k} \cap M_1^N(\mathcal{Z})} \mathbb{P}_\nu\Big(\!\exp\!\big\{N\big(\tilde{V}\big(\pi^k\big) - \varepsilon\big)\big\} \leq \bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\tilde{V}\big(\pi^k\big) + \varepsilon\big)\big\} \Big) =1. \end{align*}

Furthermore, given $\varepsilon > 0$ , there exist $\delta >0$ , $\rho > 0$ , and $N_0 \geq 1$ such that for all $\rho_1 \leq \rho$ , $N \geq N_0$ , and $\nu \in \gamma_{\pi^k} \cap M^N_1(\mathcal{Z})$ , we have

\begin{align*} \mathbb{P}_\nu\Big( \bar{\tau}_{\pi^k} < \exp\!\big\{N\big(\tilde{V}\big(\pi^k\big) - \delta\big)\big\} \Big) \leq \exp\{{-}N\varepsilon\},\ and \\ \mathbb{P}_\nu\Big( \bar{\tau}_{\pi^k} > \exp\!\big\{N\big(\tilde{V}\big(\pi^k\big) + \delta\big)\big\} \Big) \leq \exp\{{-}N\varepsilon\}. \end{align*}

Remark 3.4. Lemma 3.9 can be proved as follows. From Corollary 3.2, we have that the mean exit time from a small neighbourhood of the elements of $\pi_1^k$ is of the form $\exp\!\big\{N\tilde{V}\big(\pi_1^k\big)\big\}$ . From Corollary 3.3, we have that, upon exit from a small neighbourhood of the elements of $\pi_1^k$ , the probability that the process $\mu_N$ enters a small neighbourhood of the elements of $\pi_2^k$ is of the form $\exp\!\big\{{-}N\big(\tilde{V}\big(\pi_1^k, \pi_2^k\big) - \tilde{V}\big(\pi_1^k\big)\big\}$ . Using these facts, we can proceed via the proof of [20, Chapter 4, Theorem 4.2] to transfer the estimate on the mean of $\bar{\tau}_{\pi_1^k}$ to the estimates on the probability for $\bar{\tau}_{\pi_1^k}$ to lie between $\exp\!\big\{N\big(\tilde{V}\big(\pi_1^k\big) - \delta\big)\big\}$ and $\exp\!\big\{N\big(\tilde{V}\big(\pi_1^k\big) + \delta\big)\big\}$ . To prove Lemma 3.8, in addition to the above facts, we note that with high probability, the process $\mu_N$ enters a small neighbourhood of the elements of $\pi_2^k$ upon exit from a small neighbourhood of the elements of $\pi_1^k$ when $\pi_1^k \to \pi_2^k$ . Similar estimates as in Lemmas 3.8 and 3.9 in the case of small-noise diffusion processes have been shown in [25, Lemma 2.1, Part I] and [25, Lemma 2.2, Part I], respectively.

Lemma 3.10. Let $\pi^k$ be a k-cycle and assume that $\tilde{V}\big(\pi^k\big) > 0$ . Given $\varepsilon > 0$ , there exist $\delta>0$ , $\rho >0$ , and $N_0 \geq 1$ such that for all $\rho_1 \leq \rho$ , $\nu \in M_1^N(\mathcal{Z})$ , and $N \geq N_0$ , we have

\begin{align*} \mathbb{P}_{\nu}\big(\bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big\}\big) \leq \exp\!\big\{{-}N\big(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) - \varepsilon\big)\big\}. \end{align*}

Proof. We proceed via the steps in the proof of [25, Lemma 2.1, Part III]. Let $\pi^{k-1} \in \pi^k$ be a $(k-1)$ -cycle such that $\tilde{V}\big(\pi^{k-1}\big) = \hat{V}\big(\pi^k\big)$ . With $\rho_1>0$ to be chosen later, for each $n \geq 1$ , define the minimum of $\bar{\tau}_{\pi^k}$ and successive entry and exit times from a $\rho_1$ -neighbourhood of $\pi^{k-1}$ as follows:

\begin{align*} \hat{\theta}_0 & \,:\!=\, \inf\!\big\{ t >0 \,:\, \mu_N(t) \in \big[\pi^{k-1}\big]_{\rho_1}\big\} \wedge \bar{\tau}_{\pi^k}, \\ \bar{\theta}_n & \,:\!=\, \inf\!\big\{t > \hat{\theta}_{n-1}\,:\, \mu_N(t) \in \big[L \setminus \pi^{k-1}\big]_{\rho_1} \big\} \wedge \bar{\tau}_{\pi^k} , \\ \hat{\theta}_{n+1}& \,:\!=\, \inf\!\big\{t > \bar{\theta}_n \,:\, \mu_N(t) \in \big[\pi^{k-1}\big]_{\rho_1} \big\} \wedge \bar{\tau}_{\pi^k}. \end{align*}

With $\delta > 0$ to be chosen later, using the strong Markov property, for any $\nu \in \big[\pi^k\big]_{\rho_1} \cap M_1^N(\mathcal{Z})$ , we have

(3.4) \begin{align} \mathbb{P}_{\nu}&\big(\bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\}\big) \nonumber \\ & = \mathbb{P}_\nu \big(\hat{\theta}_0 = \bar{\tau}_{\pi^k}, \bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\}\big) \nonumber \\ & \qquad + \mathbb{P}_\nu\Bigg(\hat{\theta}_0 < \bar{\tau}_{\pi^k}, \bigcup_{n \geq 1} \left\{\bar{\tau}_{\pi^k} = \bar{\theta}_n, \bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\}, \bar{\tau}_{\pi^k} \geq \hat{\theta}_{n-1} \right\} \Bigg) \nonumber \\ & \qquad + \mathbb{P}_\nu\Bigg(\hat{\theta}_0 < \bar{\tau}_{\pi^k}, \bigcup_{n\geq 1} \left\{\bar{\tau}_{\pi^k} = \hat{\theta}_n, \bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\}, \bar{\tau}_{\pi^k} \geq \bar{\theta}_n \right\} \Bigg). \end{align}

We now upper-bound each of the terms in (3.4). Consider the first term. It can be shown using Corollary 3.3 and [25, Corollary A.6, Appendix] that there exist $\rho_1>0$ and $\delta > 0$ such that for any $\nu \in \big[\pi^k\big]_{\rho_1}$ and sufficiently large N, we have

\begin{align*} \mathbb{P}_\nu\big(\hat{\theta}_0 = \bar{\tau}_{\pi^k}\big) \leq \exp\!\big\{{-}N\big(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) - \varepsilon\big)\big\}. \end{align*}

Consider the second term in (3.4). For any $\nu_1 \in \big[\pi^{k-1}\big]_{\rho_1} \cap M_1^N(\mathcal{Z})$ , the probability of the unionised event can be bounded above by

\begin{align*} & \mathbb{P}_{\nu_1}\! \left(\bigcup_{n \geq 1}\left\{\bar{\tau}_{\pi^k} = \bar{\theta}_n, \bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\}, \bar{\tau}_{\pi^k} \geq \hat{\theta}_{n-1} \right\} \right)\\ & \quad\leq \mathbb{P}_{\nu_1}\! \left(\bigcup_{n=1}^M \left\{\bar{\tau}_{\pi^k} = \bar{\theta}_n, \bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\}, \bar{\tau}_{\pi^k} \geq \hat{\theta}_{n-1} \right\} \right) \\ & \qquad\! + \mathbb{P}_{\nu_1}\! \left( \bigcup_{n \geq M+1} \left\{\bar{\tau}_{\pi^k} = \bar{\theta}_n, \bar{\tau}_{\pi^k} \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\}, \bar{\tau}_{\pi^k} \geq \hat{\theta}_{n-1} \right\} \right) \\ & \quad\leq \mathbb{P}_{\nu_1} \big(\bar{\tau}_{\pi^k} = \bar{\theta}_n \text{ and } \bar{\tau}_{\pi^k} \geq \hat{\theta}_{n-1} \text{ for some } n \leq M\big) \\ & \qquad\! + \mathbb{P}_{\nu_1} \big(\hat{\theta}_M \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\} \text{ and } \hat{\theta}_M \leq \bar{\tau}_{\pi^k}\big)\\ & \quad\leq \mathbb{P}_{\nu_1}\big(\hat{\theta}_M = \bar{\tau}_{\pi^k}\big) + \mathbb{P}_{\nu_1} \big(\hat{\theta}_M \leq \exp\!\big\{N\big(\hat{V}\big(\pi^k\big)+\delta\big)\big\} \text{ and } \hat{\theta}_M \leq \bar{\tau}_{\pi^k}\big). \end{align*}

Again, the first term above can be bounded by

\begin{align*} \mathbb{P}_{\nu_1}\big(\hat{\theta}_M \leq \bar{\tau}_{\pi^k}\big) \leq \exp\!\big\{{-}N\big(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) - \varepsilon\big)\big\}, \end{align*}

for all $\nu_1 \in \big[\pi^{k-1}\big]_{\rho_1} \cap M_1^N(\mathcal{Z})$ and sufficiently large N. The second term can be bounded by $\exp\{{-}NM\}$ for large enough M, by the same argument used in the proof of [25, Lemma 1.7, Part I]. If we choose M sufficiently large, the above implies that the second term in (3.4) is bounded by $\exp\!\big\{{-}N\big(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) - \varepsilon\big)\big\}$ . A similar argument gives the same bound for the third term in (3.4).

3.4. LDP for the invariant measure

Using the estimates (3.2) of the transition probabilities of the discrete-time Markov chain $Z^N$ , we can study large deviations for the process $\mu_N$ in the stationary regime. Recall that $\wp_N$ denotes the unique invariant probability measure of the process $\mu_N$ . Also recall that G(i) is the set of all directed graphs g on L such that (a) every node other than i has exactly one outgoing arrow and (b) there are no closed cycles in g. We state the following result.

Theorem 3.1. ([12, Theorem 2.2].) Assume (A1), (A2), and (B1). Then the sequence of invariant measures $\{\wp_N\}_{N \geq 1}$ satisfies the LDP on $M_1(\mathcal{Z})$ with good rate functions given by

(3.5) \begin{align} s(\xi) = \min_{1 \leq i \leq l} \{W(i) + V(K_i, \xi)\} - \min_{1 \leq j \leq l} W(j), \end{align}

where

\begin{align*} W(i) = \min_{g \in G(i)} \sum_{(m,n) \in g} \tilde{V}(m,n). \end{align*}

The form of the rate function s in Theorem 3.1 is also related to the form of the invariant measure in the context of Markov chains on finite state spaces whose transition kernels are of the form (3.2); see, for example, [15, Section 1.1]. Also, see [9] for an analogous result in a boundary-driven symmetric simple exclusion process, which involves the study of the LDP for the invariant measure in an infinite-dimensional setting. However, our focus is on sharp estimates on the rate of convergence to the invariant measure, which is the subject of the next section.

3.5. Convergence to the invariant measure

In this section, we prove our first main result on the time required for the convergence of $\mu_N$ to its invariant measure.

Let $i_0 \in L$ be such that $ \min\!\big\{\tilde{V}(g)\,:\, g \in G(i_0)\big\} = \min\!\big\{\tilde{V}(g)\,:\, g \in G(i), i \in L \big\} $ . We anticipate that $K_{i_0}$ is one of the most stable $\omega$ -limit sets (possibly among others) for the dynamics (1.1). This is because Theorem 3.1 tells us that the rate function that governs the LDP for $\{\wp_N\}_{N \geq 1}$ vanishes on $K_{i_0}$ . Hence, for a large but fixed N, over large time intervals, one expects that there is positive probability (in the exponential scale) for the process $\mu_N$ to be in a small neighbourhood of $K_{i_0}$ .

Define

(3.6) \begin{align} \Lambda \,:\!=\, \left\{ \begin{array}{l@{\quad}l} \min\!\big\{\tilde{V}(g)\,:\, g \in G( \{ i \} ), i \in L \big\} - \min\!\big\{\tilde{V}(g)\,:\, g \in G(\{ i, j\}), i, j \in L, i \neq j\big\} & \text{ if } |L|\geq 2,\\[4pt] 0 &\text{ if } |L| = 1. \end{array} \right. \end{align}

Since we are interested in the case when (1.1) has multiple $\omega$ -limit sets, we assume throughout that $\Lambda > 0$ . The motivation to define this constant $\Lambda$ is the following. Since the process $\mu_N$ spends most of the time near one of the compact sets $K_i$ , we expect that it mixes well when the discrete-time Markov chain $Z^N$ , with transition probabilities of the form $\exp\!\big\{{-}N\tilde{V}\big(K_i, K_j\big)\big\}$ given in (3.2), mixes well. The mixing time of $Z^N$ is determined by the real part of $\big(1-\hat{\lambda}^N_2\big)$ , where $\hat{\lambda}^N_2$ is the second-largest (in absolute value) eigenvalue of an $l \times l$ transition probability matrix whose (i, j)th entry, for $i \neq j$ , is given by $\exp\!\big\{{-}N\tilde{V}\big(K_i, K_j\big)\big\}$ ; it turns out that this scales as $\exp\{{-}N\Lambda\}$ [20, Chapter 6, Theorem 7.3]. Thus, we expect that, when time is of the order $\exp\{N\Lambda\}$ , the process $\mu_N$ mixes well.

Let $\mathbb{P}_T(\nu, \cdot ) = \mathbb{P}_{\nu}(\mu_N(T) \in \cdot )$ denote the transition probability kernel associated with the process $\mu_N$ . Note that we suppress the dependence on N for greater readability. We first show a lower bound for the transition probability $\mathbb{P}_T\big(\nu_1, K_{i_0} \big) $ of reaching a small neighbourhood of $K_{i_0}$ when T is of the order $\exp\{N(\Lambda-\delta_0)\}$ for some $\delta_0>0$ .

Theorem 3.2. Given $\varepsilon >0$ , there exist $\delta_0 > 0$ , $\rho > 0$ , and $N_0 \geq 1$ such that for all $\rho_1 \leq \rho$ , $N \geq N_0$ , $\nu \in M_1^N(\mathcal{Z})$ , we have

(3.7) \begin{align} \mathbb{P}_{T_0}(\nu, \gamma_{i_0}) \geq \exp\{{-}N\varepsilon\}, \end{align}

where $T_0 =\exp\{N(\Lambda - \delta_0)\}$ . Furthermore, there exist $\nu_0 \in M_1(\mathcal{Z})$ and $\beta >0$ such that for all $N \geq N_0$ and $\nu \in [\nu_0]_{\rho_1} \cap M_1^N(\mathcal{Z})$ ,

(3.8) \begin{align} \mathbb{P}_{T_0}(\nu, \gamma_{i_0}) \leq \exp\{{-}N\beta\}. \end{align}

Proof. We follow the steps in Hwang and Sheu [25, Part I, Theorem 2.3]. With $\rho > 0$ to be chosen later, we first show that (3.7) holds for all $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ . Towards this, let m be the smallest integer such that $L_{m+1}$ is a singleton. For $0 \leq k \leq m$ , let $\pi_0^k \in L_k$ be the k-cycle containing $i_0$ . Let $V_k = \max\! \big\{\tilde{V}\big(\pi^k\big) \,:\, \pi^k \subset \pi_0^{k+1}, \pi^k \neq \pi_0^k\big\}$ . Using [25, Lemma A.10, Appendix], we have $\Lambda = \max\{V_k\,:\, 0 \leq k \leq m\}$ .

Fix $j \in L$ and consider $\nu \in [K_j]_{\rho}$ . Let $\pi_1^m \in L_m$ be such that $K_j \in \pi_1^m$ . If $\pi_1^m \neq \pi_0^m$ , then we have $\pi_1^m \Rightarrow \pi_0^m$ ; that is, there exist $\pi_2^m, \pi_3^m, \ldots, \pi_n^m =\pi_0^m$ , $n \leq l$ , such that $\pi_1^m \to \pi_2^m \to \pi_3^m \to \cdots \to \pi_n^m = \pi_0^m$ . Therefore, with $\delta$ to be chosen later, by the strong Markov property, we have

\begin{align*} \mathbb{P}_\nu \big(\hat{\tau}_{\pi^m_0} & \leq n \exp\!\big\{N(V_m - \delta)\big\}\big) \\ & \geq \mathbb{E}_\nu \bigg(1_{\big\{\bar{\tau}_{\pi^m_1} \leq \exp\!\big\{N(V_m -\delta )\big\}\big\}}\cdot 1_{\big\{ \mu_N\big(\bar{\tau}_{\pi^m_1}\big) \in \pi_2^m\big\}} \\ & \qquad \times \mathbb{E}_{\mu_N\big(\bar{\tau}_{\pi^m_1}\big)}\bigg(1_{\big\{\bar{\tau}_{\pi_2^m} \leq \exp\!\big\{N(V_m -\delta )\big\}\big\}} \cdot 1_{\big\{\mu_N\big(\bar{\tau}_{\pi^m_2}\big) \in \pi_3^m\big\}} \\ & \qquad \cdots \times \mathbb{E}_{\mu_N\big(\bar{\tau}_{\pi^m_{n-2}}\big)}\bigg( 1_{\big\{\bar{\tau}_{\pi^m_{n-1}} \leq \exp\!\big\{N(V_m -\delta )\big\}\big\}} \cdot 1_{\big\{\mu_N\big(\bar{\tau}_{\pi^m_{n-1}}\big) \in \pi_0^m\big\}}\bigg)\\ & \qquad \cdots \bigg)\bigg). \end{align*}

Since $V\big(\pi_i^m\big) \leq V_m$ for all $1 \leq i \leq n$ , the above becomes

\begin{align*} \mathbb{P}_\nu \Big(\hat{\tau}_{\pi^m_0} & \leq n \exp\{N(V_m - \delta)\}\Big) \\ & \geq \mathbb{E}_\nu \bigg(1_{\big\{\bar{\tau}_{\pi^m_1} \leq \exp\!\big\{N\big(\tilde{V}(\pi_1^m) -\delta \big)\big\}\big\}} \cdot 1_{\big\{ \mu_N\big(\bar{\tau}_{\pi^m_1}\big) \in \pi_2^m\big\}} \\ & \qquad \times \mathbb{E}_{\mu_N\big(\bar{\tau}_{\pi^m_1}\big)}\bigg(1_{\big\{\bar{\tau}_{\pi_2^m} \leq \exp\!\big\{N\big(\tilde{V}\big(\pi_2^m\big)-\delta \big)\big\}\big\}}\cdot 1_{\big\{\mu_N\big(\bar{\tau}_{\pi^m_2}\big) \in \pi_3^m\big\}} \\ & \qquad \cdots \times \mathbb{E}_{\mu_N\Big(\bar{\tau}_{\pi^m_{n-2}}\Big)}\bigg(1_{\big\{\bar{\tau}_{\pi^m_{n-1}} \leq \exp\!\big\{N\big(\tilde{V}\big(\pi_{n-1}^m\big) -\delta \big)\big\}\big\}} \cdot 1_{\big\{\mu_N\big(\bar{\tau}_{\pi^m_{n-1}}\big) \in \pi_0^m\big\}}\bigg)\\ & \qquad \cdots \bigg)\bigg). \end{align*}

By Lemma 3.8, there exist $\rho >0$ , $\delta > 0$ , and $N_0 \geq 1 $ such that each of the above probabilities is at least $\exp\{{-}N\varepsilon/l\}$ for sufficiently large N, i.e., we have

\begin{align*} \mathbb{P}_\nu \Big(\hat{\tau}_{\pi^m_0} \leq n \exp\!\big\{N(V_m - \delta))\big\}\Big) \geq \exp\{{-}N n \varepsilon/l\} \geq \exp\{{-}N\varepsilon\}, \end{align*}

On the other hand, if $K_j$ is such that $K_j \in \pi_0^m$ , the above holds trivially. Therefore, there exist $\delta_1 > 0$ and $N_1 \geq 1$ such that for all $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ and $N \geq N_1$ , we have

\begin{align*} \mathbb{P}_\nu \Big(\hat{\tau}_{\pi^m_0} \leq \exp\{N(V_m - \delta_1)\}\Big) \geq \exp\{{-}N \varepsilon\}. \end{align*}

We now use the above bound to show (3.7). Let $T = \exp\{N(\Lambda - \delta_1)\}$ , $T_m = \exp\{N(V_m - \delta_1)\}$ , and $T_{m-1} =\exp\{N(V_{m-1}-\delta_1)\}$ . Then, for any $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ and $N \geq N_1$ , we have

(3.9) \begin{align} \mathbb{P}_\nu \big(\mu_N(T) \in \gamma_{i_0}\big)& \geq \mathbb{E}_\nu \bigg(1_{\big\{\hat{\tau}_{\pi^m_0} \leq T_m\big\}} \cdot 1_{\big\{\mu_N\big(T-\hat{\tau}_{\pi^m_0}\big) \in \gamma_{i_0}\big\}}\bigg) \nonumber\\ & = \mathbb{E}_\nu \bigg(1_{\big\{\hat{\tau}_{\pi^m_0} \leq T_m\big\}} \cdot \mathbb{E}_{\mu_N\big(\hat{\tau}_{\pi_0^m}\big)} \bigg(1_{\big\{\mu_N\big(T-\hat{\tau}_{\pi^m_0}\big) \in \gamma_{i_0}\big\}}\bigg)\bigg) \nonumber \\ & \geq \inf_{\substack{\nu^\prime \in \big[\pi_0^m\big]_{\rho}\cap M_1^N\big(\mathcal{Z}\big) \\ T-T_m \leq t \leq T}} \mathbb{P}_{\nu^\prime} \big(\mu_N(t) \in \gamma_{i_0}\big) \mathbb{P}_\nu \big(\hat{\tau}_{\pi^m_0}\leq T_m\big) \nonumber \\ & \geq \inf_{\substack{ \nu^\prime \in \big[\pi_0^m\big]_{\rho}\cap M_1^N(\mathcal{Z}) \\ T-T_m \leq t \leq T}} \mathbb{P}_{\nu^\prime} \big(\mu_N(t) \in \gamma_{i_0}\big) \exp\!\big\{{-}N\varepsilon\big\}, \end{align}

where the second equality follows from the strong Markov property. To get a lower bound for the above infimum, fix $\nu \in \big[\pi_0^m\big]_\rho \cap M_1^N(\mathcal{Z})$ and $T-T_{m} \leq t \leq T$ . Define the stopping time $\theta \,:\!=\, \inf\!\big\{s> t-T_{m-1} \,:\, \mu_N(s) \in \big[\pi_0^m\big]_{\rho}\big\}$ . Then, for a large $T^*$ (not depending on N) to be chosen later, we have

(3.10) \begin{align} \mathbb{P}_\nu &\big(\mu_N(t) \in \gamma_{i_0}\big) \nonumber \\ &\geq \mathbb{E}_\nu \bigg(1_{\big\{\theta \leq t-T_{m-1}+T^* , \bar{\tau}_{\pi_0^m} > T\big\}} \cdot \mathbb{E}_{\mu_N(\theta)}\bigg( 1_{\big\{\mu_N(t-\theta) \in \gamma_{i_0}\big\}}\bigg) \nonumber \\ & \geq \mathbb{P}_\nu\Big(\theta \leq t-T_{m-1}+T^* , \bar{\tau}_{\pi_0^m} > T\Big) \inf_{\substack{\nu^\prime \in \big[\pi_0^m\big]_{\rho}\cap M_1^N\big(\mathcal{Z}\big) \\ T_{m-1}-T^*\leq t \leq T_{m-1}}} \mathbb{P}_{\nu^\prime} \big(\mu_N(t) \in \gamma_{i_0}\big). \end{align}

Note that

\begin{align*} \mathbb{P}_\nu\big(\theta \leq t-T_{m-1}+T^*, \bar{\tau}_{\pi_0^m} > T\big)= \mathbb{P}_\nu\Big(\bar{\tau}_{\pi^m_0} > T\Big) - \mathbb{P}_\nu\big(\theta > t-T_{m-1}+T^* , \bar{\tau}_{\pi_0^m} > T\big). \end{align*}

By Lemma 3.9, since $\Lambda \leq \tilde{V}\big(\pi^m_0\big)$ , we have

\begin{align*} \mathbb{P}_\nu\Big(\bar{\tau}_{\pi^m_0} > T\Big) \geq \mathbb{P}_\nu\big(\bar{\tau}_{\pi^m_0} > \exp\!\big\{N\big(\tilde{V}\big(\pi^m_0\big) - \delta\big)\big\}\big) \to 1 \end{align*}

as $N \to \infty$ . For the second term, note that

\begin{align*} \mathbb{P}_\nu& \big(\theta > t-T_{m-1}+T^* , \bar{\tau}_{\pi_0^m} > T\big) & \\ & = \mathbb{P}_\nu \big(\mu_N(s) \notin \big[\pi_0^m\big]_\rho \text{ for all } t-T_{m-1}\leq s \leq t-T_{m-1}+T^*, \bar{\tau}_{\pi_0^m} > T\big) \\ & = \mathbb{P}_\nu \big(\mu_N(s) \notin \gamma \text{ for all } t-T_{m-1}\leq s \leq t-T_{m-1}+T^*, \bar{\tau}_{\pi_0^m} > T\big) \\ & \leq \mathbb{P}_\nu \big(\mu_N(s) \notin \gamma \text{ for all } t-T_{m-1}\leq s \leq t-T_{m-1}+T^*\big). \end{align*}

The second equality follows since $\mu_N(s) \notin \big[\pi_0^m\big]_\rho$ and $\bar{\tau}_{\pi_0^m} > T$ implies that we have exited $\big[\pi_0^m\big]_\rho$ and we have not yet entered a neighbourhood of any other attractor, which is the same as saying $\mu_N(t) \notin \gamma$ and $\bar{\tau}_{\pi_0^m} >T$ . By the Markov property, the above probability equals

\begin{align*} \mathbb{E}_\nu \! \left( \mathbb{E}_{\mu_N\big(t-T_{m-1}\big)}\bigg(1_{\big\{\mu_N(s) \notin \gamma \text{ for all } s \in \big[t-T_{m-1}, t-T_{m-1}+T^*\big]\big\}}\bigg) \right) \leq \sup_{\nu^\prime \in F} \mathbb{P}_{\nu^\prime} \big(\tau_F \geq T^*\big), \end{align*}

where $F = M_1(\mathcal{Z}) \setminus \gamma$ . By Lemma 3.3, $T^*$ can be chosen large enough (not depending on N) that the above probability is at most $1/2$ . Therefore, (3.10) becomes

\begin{align*} \inf_{\substack{\nu \in \big[\pi_0^m\big]_\rho \cap M_1^N(\mathcal{Z}) \\ T-T_m \leq t \leq T}} \mathbb{P}_\nu\big(\mu_N(t) \in \gamma_{i_0}\big) \geq \frac{1}{2} \inf_{\substack{\nu^\prime \in \big[\pi_0^m\big]_{\rho} \cap M_1^N(\mathcal{Z}) \\ T_{m-1}-T^* \leq t \leq T_{m-1}}} \mathbb{P}_{\nu^\prime} \big(\mu_N(t) \in \gamma_{i_0}\big), \end{align*}

and (3.9) becomes

\begin{align*} \mathbb{P}_\nu \big(\mu_N(T) \in \gamma_{i_0}\big) \geq \frac{1}{2} \exp\{{-}N\varepsilon\} \inf_{\substack{\nu^\prime \in \big[\pi_0^m\big]_{\rho} \cap M_1^N(\mathcal{Z}) \\ T_{m-1}-T^* \leq t \leq T_{m-1}}} \mathbb{P}_{\nu^\prime} \big(\mu_N(t) \in \gamma_{i_0}\big), \end{align*}

for sufficiently large N and $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ . Repeating the above argument m times, we see that there exists $N_2 \geq 1$ such that for all $\nu \in \gamma$ and $N \geq N_2$ , we have

\begin{align*} \mathbb{P}_\nu\big(\mu_N(T) \in \gamma_{i_0}\big) & \geq \left(\frac{1}{2}\right)^m\exp\{{-}Nm\varepsilon\} \inf_{\substack{\nu^\prime \in \big[\pi_0^1\big]_{\rho}\cap M_1^N(\mathcal{Z}) \\ T_0 -T^*\leq t \leq T_0}} \mathbb{P}_{\nu^\prime} \big(\mu_N(t) \in \gamma_{i_0}\big) \\ & \geq \left(\frac{1}{2}\right)^{m}\exp\{{-}N(m+1)\varepsilon\} \inf_{\substack{\nu^\prime \in [K_0]_{\rho} \cap M_1^N(\mathcal{Z})\\ T_0 -T^*\leq t \leq T_0}} \mathbb{P}_{\nu^\prime} \big(\mu_N(t) \in \gamma_{i_0}\big) \\ & \geq \left(\frac{1}{2}\right)^{m+1}\exp\{{-}N(m+1)\varepsilon\}, \end{align*}

where $T_0 = \exp\{N(V_0 - m\delta)\}$ . Thus, we conclude that there exist $N_3 \geq 1$ , $\delta_3>0$ , and $\rho > 0$ such that for all $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ and $N \geq N_3$ , we have

\begin{align*} \mathbb{P}_\nu\big(\mu_N(T) \in \gamma_{i_0}\big) \geq \exp\{{-}N(m+3)\varepsilon\}, \end{align*}

where $T = \exp\{N(\Lambda-\delta_3)\}$ . This establishes (3.7) for all $\nu \in \gamma \cap M_1^N(\mathcal{Z})$ . For any $\nu \in M_1^N(\mathcal{Z})\setminus \gamma$ , from Lemma 3.3, there exist $T^\prime$ large enough and $N_4 \geq N_3$ such that $\mathbb{P}_\nu\big(\tau_{M_1(\mathcal{Z}) \setminus \gamma} \leq T^\prime\big) \geq \frac{1}{2}$ for all $N \geq N_4$ . Therefore, we have

\begin{align*} \mathbb{P}_\nu\big(\mu_N(T) \in \gamma_{i_0}\big) & \geq \mathbb{E}_\nu \bigg( 1_{\big\{\tau_{M_1(\mathcal{Z}) \setminus \gamma} \leq T^\prime\big\}} \cdot \mathbb{E}_{\mu_N(\tau_F)} \bigg(1_{\big\{\mu_N(T-T^\prime) \in \gamma_{i_0}\big\}}\bigg)\bigg) \\ & \geq \frac{1}{2} \inf_{\nu^\prime \in \gamma} \mathbb{P}_{\nu^\prime}\big(\mu_N(T-T^\prime) \in \gamma_{i_0}\big) \\ & \geq \frac{1}{2}\exp\{{-}N(m+3)\varepsilon\}. \end{align*}

Thus, we have established (3.7) for any $\nu \in M_1^N(\mathcal{Z})$ .

We now turn to (3.8). Since $\Lambda = \max\{V_k, 0 \leq k \leq m\}$ , there exists a k such that $V_k = \Lambda$ . From the definition of $V_k$ , we see that there exists $\pi^k \in L_k$ such that

\begin{align*} \tilde{V}\big(\pi^k\big) = \Lambda, \qquad \pi^k \subset \pi_0^{k+1}, \qquad \text{and }\pi^k \neq \pi^k_0, \end{align*}

where $\pi_0^{k+1}$ is the $(k+1)$ -cycle that contains $K_{i_0}$ . Therefore, Lemma 3.9 implies that, for some $\beta > 0$ , for some $\delta_4 < \delta_3$ and an appropriately chosen $\rho > 0$ , with $T = \exp\{N(\Lambda-\delta_3)\} = \exp\!\big\{N\big(\tilde{V}\big(\pi^k\big) - \delta_3\big)\big\}$ , we have

\begin{align*} \mathbb{P}_\nu\big(\mu_N(T) \in \gamma_{i_0}\big) \leq \mathbb{P}_\nu\big(\bar{\tau}_{\pi^k} \leq T\big) \leq \exp\{{-}N\beta\}, \end{align*}

for any $\nu \in \big[\pi^k\big]_{\rho} \cap M_1^N(\mathcal{Z})$ and sufficiently large N. This completes the proof of the theorem.

The above theorem immediately gives a lower bound on $\mathbb{P}_T(\nu, \xi)$ for any $\xi$ in a small neighbourhood of $K_{i_0}$ , over time durations of order $\exp\{N(\Lambda-\delta)\}$ for some $\delta > 0$ . Let us make this precise.

Corollary 3.4. Under the conditions of Theorem 3.2, for all $\nu \in M_1^N(\mathcal{Z})$ , $\xi \in \gamma_{i_0} \cap M_1^N(\mathcal{Z})$ , and N sufficiently large, we have

\begin{align*} \mathbb{P}_{T_0}(\nu, \xi) \geq \exp\{{-}2N\varepsilon\}. \end{align*}

Proof. Given $\varepsilon > 0$ , let $\rho$ , $N_0$ , and $T_0$ be as in the statement of Theorem 3.2. Choose t large enough (not depending on N) and $\rho^\prime < \rho$ so that for all $\rho_1 \leq \rho^\prime$ we have $S_t(\nu_1|\nu_2) \leq \varepsilon/2$ for all $\nu_1, \nu_2 \in \gamma_{i_0}$ . This is possible by the joint continuity of the rate function $S_t({\cdot}|{\cdot})$ and the fact that $V(\nu_1, \nu_2) = 0$ whenever $\nu_1, \nu_2 \in K_{i_0}$ . Therefore, using the large deviation lower bound, there exists $N_2 \geq N_1$ such that

\begin{align*} \mathbb{P}_t(\nu_1, \nu_2) \geq \exp\{{-}N(S_t(\nu_2 | \nu_1) + \varepsilon/2)\} \geq \exp\{{-}N\varepsilon\}, \end{align*}

for all $\nu_1, \nu_2 \in \gamma_{i_0} \cap M_1^N(\mathcal{Z})$ and $N \geq N_2$ . Therefore, by Theorem 3.2, for $\nu \in M_1^N(\mathcal{Z})$ , $\xi \in \gamma_{i_0} \cap M_1^N(\mathcal{Z})$ , and $N \geq N_2$ , we have

\begin{align*} \mathbb{P}_{T_0}(\nu, \xi) & = \sum_{\nu_2 \in \gamma_{i_0} \cap M_1^N(\mathcal{Z})} \mathbb{P}_{T_0-t}(\nu_1, \nu_2) \mathbb{P}_t\big(\nu_2, \xi\big) \\ & \geq \mathbb{P}_{T_0-t}\big(\nu_1, \gamma_{i_0}\big) \inf_{\nu_2 \in \gamma_{i_0} \cap M_1^N(\mathcal{Z})} \mathbb{P}_t\big(\nu_2, \xi\big) \\ & \geq \exp\{{-}2N \varepsilon\}. \end{align*}

3.5.1. Proofs of Theorem 1.1 and Theorem 1.2

We now prove our first main result (Theorem 1.1) on the convergence of $\mu_N$ to the invariant measure and its converse Theorem 1.2. Theorem 1.1 together with Theorem 1.2 shows that the constant $\Lambda$ is sharp (in the exponential scale) for the time required for $\mu_N$ to equilibrate.

Define $\tilde{L}_0 \,:\!=\, \{i \in L \,:\, s(K_i) = 0\}$ ; i.e, $\tilde{L}_0$ denotes the set of minimisers of the rate function s (see (3.5)). Let $B(M_1(\mathcal{Z}))$ denote the space of bounded Borel-measurable functions on $M_1(\mathcal{Z})$ .

Proof of Theorem 1.1.We follow the steps in Hwang and Sheu [25, Part I, Theorem 2.5]. Let $\varepsilon > 0$ , and let $T_0$ , $\delta_0$ , $\rho$ , $\rho_1$ , and $N_0 \geq1$ be as in the statement of Theorem 3.2. Note that, for any $\nu \in M_1^N(\mathcal{Z})$ , $\xi \notin \big[\tilde{L}_0\big]_{\rho_1}$ and for some fixed $t > 0$ ,

\begin{align*} \mathbb{P}_{T_0}(\nu,\xi)& = \sum_{\nu^\prime \in \big[K_{i_0}\big]} \mathbb{P}_{T_0-t}(\nu, \nu^\prime) \mathbb{P}_t(\nu^\prime, \xi)\\ & \geq \exp\{{-}2N\varepsilon\} \inf_{\nu^\prime \in \big[K_{i_0}\big]} \mathbb{P}_t(\nu^\prime, \xi) \\ & \geq \exp\{{-}2N\varepsilon\} \exp\!\Bigg\{{-}N\sup_{\nu^\prime \in \big[K_{i_0}\big]} S_t\big(\xi|\nu^\prime\big)\Bigg\}, \end{align*}

where the first inequality follows from Corollary 3.4 and the second from the uniform LDP (Corollary 2.1). Hence, we can find a function $U \,:\, M_1(\mathcal{Z}) \to [0, \infty)$ such that $U(\xi) = 0$ for $\xi \in \big[\tilde{L}_0\big]_{\rho_1}$ and

(3.11) \begin{align} \mathbb{P}_{T_0}(\nu,\xi) \geq c_N \exp\{{-}NU(\xi)\} \end{align}

holds for all $\nu \in M_1^N(\mathcal{Z})$ , $\xi \notin \big[\tilde{L}_0\big]_{\rho_1}$ and sufficiently large N; here $c_N$ is such that

\begin{align*} \pi_N(\xi) = c_N\exp\{{-}NU(\xi)\} \end{align*}

is a probability measure on $M_1^N(\mathcal{Z})$ . Define $Q_{T_0}(\nu ,\cdot) \,:\!=\, \mathbb{P}_{T_0}(\nu, \cdot)/ \pi_{N}({\cdot})$ . Note that $c_N \to 0$ exponentially fast as $N \to \infty$ . Indeed, since $U(\xi) = 0$ for all $\xi \in \big[\tilde{L}_0\big]_{\rho_1}$ , each of these points yield $\pi_N(\xi) = c_N$ . Since the number of points in $\big[\tilde{L}_0\big]_{\rho_1} \cap M_1^N(\mathcal{Z})$ is exponential in N and since $\pi_N$ is a probability measure, we see that $c_N$ must decay exponentially fast in N. We have, for any $\nu_1, \nu_2 \in M_1^N(\mathcal{Z})$ and sufficiently large N,

\begin{align*} \mathbb{E}_{\nu_1}&(\,f(\mu_N(T_0))) - \mathbb{E}_{\nu_2}(\,f(\mu_N(T_0))) \\ & = \sum_{\xi \in M_1^N(\mathcal{Z})}\mathbb{P}_{T_0}(\nu_1,\xi) f(\xi) - \sum_{\xi \in M_1^N(\mathcal{Z})}\mathbb{P}_{T_0}(\nu_2,\xi) f(\xi) \\ & = \sum_{\xi \in M_1^N(\mathcal{Z})}Q_{T_0}(\nu_1,\xi) f(\xi) \pi_N(\xi)- \sum_{\xi \in M_1^N(\mathcal{Z})}Q_{T_0}(\nu_2,\xi) f(\xi) \pi_N(\xi) \\ & = \sum_{\xi \in M_1^N(\mathcal{Z})}(Q_{T_0}(\nu_1,\xi)- \exp\{{-}2N\varepsilon\})f(\xi) \pi_N(\xi) \\ & \qquad -\sum_{\xi \in M_1^N(\mathcal{Z})}(Q_{T_0}(\nu_2,\xi) - \exp\{{-}2N\varepsilon\}) f(\xi) \pi_N(\xi) \\ & \leq (1-\exp\{{-}2N\varepsilon\}) \bigg(\sup_\xi f(\xi) - \inf_\xi f(\xi)\bigg), \end{align*}

where the last inequality follows from (3.11) and the fact that $Q_{T_0}(\cdot, \cdot) \geq 1$ . Therefore, we have that

\begin{align*} \sup_{\nu_1, \nu_2} | \mathbb{E}_{\nu_1}&(\,f(\mu_N(T_0))) - \mathbb{E}_{\nu_2}(\,f(\mu_N(T_0))) | \leq (1-\exp\{{-}2N\varepsilon\}) \| f\|_\infty. \end{align*}

Continuing this procedure k times, and by using the Markov property, we get

\begin{align*} \sup_{\nu_1, \nu_2} |\mathbb{E}_{\nu_1}&(\,f(\mu_N(kT_0))) - \mathbb{E}_{\nu_2}(\,f(\mu_N(kT_0))) | \leq (1-\exp\{{-}2N\varepsilon\})^k \| f\|_\infty, \end{align*}

and hence we have

\begin{align*} \sup_{\nu} | \mathbb{E}_{\nu}&(\,f(\mu_N(kT_0))) - \langle\, f, \wp_N \rangle | \leq (1-\exp\{{-}2N\varepsilon\})^k \| f\|_\infty. \end{align*}

Choose $k = \exp\{N(\delta_0+\delta)\}$ ; then we have $kT_0 = \exp\{N(\Lambda + \delta)\}$ , and the above becomes

\begin{align*} \sup_{\nu} | \mathbb{E}_{\nu}&(\,f(\mu_N(kT_0))) - \langle\, f, \wp_N \rangle | \leq \exp\{{-}\exp\!(N({-}2\varepsilon+\delta_0 + \delta))\}. \end{align*}

We can choose $\varepsilon$ small enough so that the quantity $-2\varepsilon+ \delta > 0$ , and hence for some $\varepsilon^\prime > 0$ , we have

\begin{align*} \sup_{\nu} | \mathbb{E}_{\nu}&(\,f(\mu_N(T))) - \langle\, f, \wp_N \rangle | \leq \exp\{{-}\exp\!(N\varepsilon^\prime)\}, \end{align*}

for sufficiently large N, where $T = \exp\{N(\Lambda+\delta)\}$ . This establishes the result.

Proof of Theorem 1.2.This is a direct consequence of (3.8), established in Theorem 3.2.

4. Asymptotics of the second-largest eigenvalue for reversible processes

In this section, our goal is to understand the rate of convergence of $\mu_N$ to its invariant measure for a fixed N. For this purpose, we shall assume that the Markov process $\mu_N$ is reversible. That is, the operator $L^N$ is self-adjoint in $L^2(\wp_N)$ and it admits a spectral expansion; let $0 =\lambda_1^N > -\lambda_2^N \geq -\lambda_3^N \ldots$ denote its eigenvalues in decreasing order, and let $u_1^N \equiv 1, u_2^N, u_3^N,\ldots$ denote their corresponding eigenfunctions. Without loss of generality, we assume that the eigenfunctions are orthonormal, i.e., $\big(u_i^N, u_i^N\big) = 1$ for each i and $\big(u_i^N, u_j^N\big) = 0$ for each $i \neq j$ , where $( \cdot, \cdot )$ denotes the inner product in $L^2(\wp_N)$ . The spectral expansion [5, Section 1.7.2] enables us to write, for any $f \in B(M_1(\mathcal{Z}))$ ,

(4.1) \begin{align} \mathbb{E}_\nu f(\mu_N(t)) = \langle\, f, \wp_N\rangle + \sum_{k \geq 2} e^{-t\lambda_k^N} \big( f, u_k^N \big) u_k^N(\nu). \end{align}

Therefore, the rate of convergence of $\mathbb{E}_\nu f(\mu_N(t))$ to its stationary value $\langle\, f, \wp_N \rangle$ is determined by the leading term in the above sum, which is the second-largest eigenvalue $-\lambda_2^N$ . Hence, to understand the convergence of $\mu_N$ to its invariant measure, we study the asymptotics of $\lambda_2^N$ .

We first need the following lemma, which estimates the probability that the process $\mu_N$ is outside a small neighbourhood of the set $\cup_{i=1}^l K_i$ .

Lemma 4.1. Fix $\rho_1 >0$ and let B be the $\rho_1$ -neighbourhood of $\cup_{i \in L} K_i$ . Given $\varepsilon > 0$ , there exist $\delta >0$ and $N_0 \geq 1$ such that for each $\nu \in M_1^N(\mathcal{Z})$ and $N \geq N_0$ , we have

\begin{align*} \mathbb{P}_\nu\!\left(\mu_N(T) \in M_1^N(\mathcal{Z}) \setminus B\right) \leq \exp\{{-}N\delta\}, \end{align*}

where $T = \exp\{N(\Lambda+ \varepsilon)\}$ .

This result can be proved using Theorem 1.1, which deals with the convergence to the invariant measure, and Theorem 3.4, which addresses large deviations of the invariant measure $\{\wp_N\}_{N \geq 1}$ . Indeed, from Theorem 3.1, since the function s in (3.5) is strictly positive outside $\cup_{i=1}^l K_i$ , the probability of the complement of a small neighbourhood of $\cup_{i=1}^l K_i$ under $\wp_N$ decays exponentially in N. But when T is of the order $\exp\{N(\Lambda+\varepsilon)\}$ , from Theorem 1.1, the law of the random variable $\mu_N(T)$ is not far from $\wp_N$ . Therefore, the probability that $\mu_N(T)$ lies outside a small neighbourhood of $\cup_{i=1}^l K_i$ decays exponentially in N.

We are now ready to prove our next main result (Theorem 1.3) on the asymptotics of the modulus of the second-largest eigenvalue $\big($ i.e., $\lambda_2^N\big)$ .

Proof of Theorem 1.3.Lower bound: Suppose that there exists a subsequence $\{N_k\}_{k \geq 1}$ such that

(4.2) \begin{align} \log \lambda_2^{N_k} < -N_k(\Lambda + \varepsilon) \end{align}

for some $\varepsilon > 0$ . We will show that this contradicts $\int\!\Big(u_2^{N_k}(\nu)\Big)^2 \wp_N(d\nu) =1 $ for sufficiently large k. Fix $\rho >0 $ and define $B \,:\!=\, \cup_{i=1}^l [K_i]_{\rho}$ . Then, using the lower semicontinuity of the rate function $S_t({\cdot}|{\cdot})$ and Corollary 2.1 on uniform LDP, we see that for sufficiently large t, there exists $\delta_1 >0$ such that $\inf\{S_t(\xi|\nu)\,:\,\xi, \nu \in B^c\} = \delta_1 > 0$ . Therefore, for any $\nu \in B^c \cap M_1^N(\mathcal{Z})$ and any $\delta_2>0$ , there exists $N_0 \geq 1$ such that for all $N \geq N_0$ ,

\begin{align*} \mathbb{P}_\nu(\mu_N(t) = \nu) \leq \exp\{{-}N(S_t(\nu|\nu) - \delta_2)\} \leq \exp\{{-}N(\delta_1 + \delta_2)\}. \end{align*}

On the other hand, (4.1) implies that

\begin{align*} \mathbb{P}_\nu(\mu_N(t) = \nu) & = \mathbb{E}_\nu(1_{\{\nu\}}(\mu_N(t))) \\ &\geq e^{-\lambda_2^Nt} \big(u_2^N(\nu)\big)^2 \wp_N(\nu), \end{align*}

so that

(4.3) \begin{align} \int_{B^c} \big|u_2^N\big|^2 \wp_N (d \nu) \leq \exp\{{-}N(\delta_1 + \delta_2)\} \end{align}

for all $N \geq N_0$ . To bound the integral over B, by Theorem 1.1, with $T = \exp\{N(\Lambda+\varepsilon/2)\}$ , there exist $\delta_3>0$ and $N_1 \geq N_0$ such that for all $N \geq N_1$ ,

\begin{align*} \left|\mathbb{E}_\nu f(\mu_N(T)) - \langle\, f, \wp_N \rangle \right| \leq \|\,f\|_\infty \exp\{{-}\exp\!(N\delta_3)\}, \end{align*}

for any $f \in B(M_1(\mathcal{Z}))$ . On the other hand, from (4.1), for any $\nu \in B \cap M_1^N(\mathcal{Z})$ , with $f = 1_{\{\nu\}}$ , we have

\begin{align*} \left| \mathbb{E}_\nu f(\mu_N(T)) - \langle\, f, \wp_N \rangle \right| & = \biggr| \sum_{i \geq 2} \exp\!\big\{{-}\lambda_i^NT\big\} \big( f, u_i^N(\nu)\big) u_i^{N}(\nu) \biggr| \\ & \geq \exp\big\{{-}\lambda_2^{N}T\big\} \big(u_2^{N}(\nu)\big)^2 \wp_N(\nu), \end{align*}

so that, by our assumption (4.2), there exists a $k_0 \geq 1$ such that

\begin{align*} u_2^{N_k}(\nu))^2 \wp_{N_k}(\nu) & \leq \exp\!\big\{\lambda_2^{N_k}T\big\} \exp\{{-}\exp\!(N_k\delta_3)\} \\ & \leq \exp\{2\exp\!({-}N_k(\Lambda+\varepsilon)) \exp\!(N_k(\Lambda+\varepsilon/2))\} \exp\{{-}N_k\delta_3\} \end{align*}

for all $k \geq k_0$ . Since $\big|M_1^{N_k}(\mathcal{Z})\big| \leq (N_k+1)^{|\mathcal{Z}|}$ for all k, the above implies that, for some $\delta_4 > 0$ ,

(4.4) \begin{align} \int_B \Big(u_2^{N_k}(\nu)\Big)^2 \wp_{N_k}(d\nu) \leq \exp\{{-}N_k\delta_4\} \end{align}

for all $k \geq k_0$ . Therefore, (4.3) and (4.4) imply that, for some $\delta > 0$ ,

\begin{align*} \int_{M_1(\mathcal{Z})} \Big(u_2^{N_k}(\nu)\Big)^2 \wp_{N_k}(d\nu) \leq \exp\{{-}N_k\delta\} \end{align*}

for all sufficiently large k, which is a contradiction to $\int\!\Big(u_2^{N_k}(\nu)\Big)^2 \wp_{N_k} (d\nu) =1$ for all sufficiently large k.

Upper bound: Suppose that there exists a subsequence $\{N_k\}_{k \geq 1}$ such that $\log \lambda_2^N > $ $N_k({-}\Lambda + \varepsilon)$ for some $\varepsilon>0$ . Let $\nu_0$ , $\delta_0<\varepsilon/2$ , $\rho$ , $N_0$ be as in Theorem 3.2. Then, with $f(\nu) =1_{\big\{\big[K_{i_0}\big]_{\rho/2}\big\}}(\nu)$ and $T = \exp\{N(\Lambda-\delta_0/2)\}$ , (3.8) implies that

\begin{align*} \mathbb{E}_\nu f(\mu_N(T)) = \mathbb{P}_\nu\big(\mu_N(T) \in \big[K_{i_0}\big]_{\rho/2}\big) \leq \exp\{{-}N\beta\} \end{align*}

for all $N \geq N_0$ and $\nu \in [\nu_0]_{\rho/2 } \cap M_1^N(\mathcal{Z})$ . Also, by Theorem 3.1, for any $\delta >0$ , there exists $N_1 \geq N_0$ such that for all $N \geq N_1$ , we have

\begin{align*} \langle\, f, \wp_N \rangle = \wp_N\big(\big[K_{i_0}\big]_{\rho/2}\big) \geq \exp\{{-}N\delta\}. \end{align*}

This is possible since $\inf_{\xi \in \big[K_{i_0}\big]_{\rho/2}}s(\xi) =0$ . Therefore, for all $N \geq N_1$ ,

\begin{align*} \int_{M_1(\mathcal{Z})} |\mathbb{E}_\nu(\,f(\mu_N(T))) & - \langle\, f, \wp_N \rangle |^2 \wp_N(d\nu) \\ &\geq \int_{[\nu_0]_{\rho/2}} \left|\mathbb{E}_\nu(\,f(\mu_N(T))) - \langle\, f, \wp_N \rangle \right|^2 \wp_N(d\nu) \\ & \geq \wp_N([\nu_0]_{\rho/2}) (\!\exp\{{-}N\beta\} - \exp\{{-}N\delta\}) \\ &\geq \wp_N([\nu_0]_{\rho/2}) \exp\{{-}N\delta_1\}, \text{ for some } \delta_1 > 0 \\ &\geq \exp\{{-}N\delta_2\}, \text{ for some } \delta_2 > 0, \end{align*}

where the last inequality follows by Theorem 3.1. On the other hand, for any function f with $\int\! |f|^2 d\wp_N \leq 1$ , we have

\begin{align*} \int_{M_1(\mathcal{Z})} |\mathbb{E}_\nu(\,f(\mu_N(T))) & - \langle\, f, \wp_N \rangle |^2 \wp_N(d\nu) \\ & = \int_{M_1(\mathcal{Z})} \sum_{k\geq 2} e^{-2\lambda_k^NT} \big( f, u_k^N\big)^2 u_k^N(\nu)^2 \wp_N(d\nu) \\ &\leq \exp\!\big\{{-}2\lambda_2^NT\big\} \int_{M_1(\mathcal{Z})} |f|^2 d\wp_N \\ &\leq \exp\!\big\{{-}2\lambda_2^NT\big\}. \end{align*}

Therefore, we have $ \exp\!\big\{{-}2\lambda_2^{N}T\big\} \geq \exp\{{-}N\delta_2\}$ whenever $N \geq N_1$ . By our assumption, we see that

\begin{align*} \exp\{{-}2\exp\!({-}N_k(\Lambda-\varepsilon)) \exp\!(N_k(\Lambda-\delta_0))\} \geq \exp\{{-}N_k\delta_1\} \end{align*}

for sufficiently large k, which is a contradiction since $\delta_0 < \varepsilon/2$ .

Using the above theorem, we see that if $\Lambda>0$ , then as N becomes large, it takes longer for the process $\mu_N$ to be close to its invariant measure. This means in particular that metastable states reduce the rates of convergence of $\mu_N$ to its invariant measure. On the other hand, if there is a unique global attractor of the limiting McKean–Vlasov equation (1.1), then we see that $\Lambda = 0$ , and the rate of convergence of $\mu_N$ to its invariant measure does not suffer from such a slowing-down phenomenon.

Note that the spectral expansion in (4.1) is crucial in the proof of Theorem 1.3, to enable the use of the results on the large-time behaviour of $\mu_N$ established in Section 3 to obtain the asymptotics of $\lambda^N_2$ . The main purpose of Theorem 1.3 is to demonstrate that, in the reversible case, the asymptotics of $\lambda^N_2$ can easily be obtained as an application of the study of the large-time behaviour of $\mu_N$ . Even in the non-reversible case, one can obtain asymptotics of the real part of $\lambda^N_2$ via other approaches; see, for example, [47], where the author obtains the asymptotics of the real part of the second-largest eigenvalue of the generator corresponding to a small-noise diffusion process by examining the eigenvalues of a discrete-time chain (with transition probabilities of the form appearing in (3.2)) and transferring them to the operator. Furthermore, the asymptotics of all the eigenvalues of an $l \times l$ transition probability matrix whose (i, j)th entry, for $i \neq j$ , is given by $\exp\!\big\{{-}N\tilde{V}\big(K_i, K_j\big)\big\}$ can also be obtained; the real part of $\big(1-\hat{\lambda}^N_k\big)$ (where $\hat{\lambda}^N_k$ is the kth eigenvalue of the matrix, $2 \leq k \leq l$ ) decays exponentially in N, where the exponent is given by a quantity analogous to $\Lambda$ in (3.6) in which the first minimum is taken over all graphs in G(W) with $|W| = k-1$ and the second minimum is taken over all graphs in G(W) with $|W| = k$ , see Freidlin and Wentzell [20, Chapter 6, Theorem 7.3]. However, it is not clear how to transfer these asymptotics to the eigenvalues of $L^N$ using the large-time behaviour of $\mu_N$ , a question that we leave for the future. This question is also related to the behaviour of $\mu_N$ over times of the order of the inverse of these eigenvalues. For reversible Markov chains with a small parameter, such questions have been studied by Miclo [34, 35]. In particular, it would be interesting to investigate the asymptotics of $\lambda^N_3$ , since the rate of convergence of $\mu_N$ to $\wp_N$ depends on whether $\lambda^N_3$ decays as $\exp\{{-}N\Lambda\}$ or $\lambda^N_3 \gg \exp\{{-}N\Lambda\}$ .

Example 4.1. We provide a simplified Curie–Weiss model of magnetisation for which $L^N$ is reversible with respect to $\wp_N$ for all $N \geq 1$ [13]. Let $\mathcal{Z} = \{{-}1, +1\}$ . The states represent the direction of magnetisation of the particles. For each $N \geq 1$ , consider the following probability measure on $\mathcal{Z}^N$ :

(4.5) \begin{align} \pi_N\big(\mathbf{z}^N\big) = \frac{1}{C_N} \exp\!\left\{N \left(\frac{1}{N}\sum_{n=1}^N z_n\right)^2\right\}, \, \mathbf{z}^N = (z_1,z_2, \ldots, z_N) \in \mathcal{Z}^N, \end{align}

where $C_N$ is a normalisation constant. Given $\xi \in M_1(\mathcal{Z})$ , define the total magnetisation by $\xi_{\text{tot}} = \xi({+}1) - \xi({-}1)$ . Define the transition rates

\begin{align*} \lambda_{z,({-}z)}(\xi) = \exp\{{-}2 z \xi_{\text{tot}}\}, \, z \in \mathcal{Z}, \, \xi \in M_1(\mathcal{Z}). \end{align*}

It is straightforward to verify that the Markov process $\big(X_1^N, \ldots, X_N^N\big)$ that describes the joint evolution of the states of all the particles is reversible with respect to its invariant measure $\pi_N$ in (4.5). That is, for every $\mathbf{z}^N, \tilde{\mathbf{z}}^N \in \mathcal{Z}^N$ that differ on the nth component, we have the following $\big($ recall that $\overline{\mathbf{z}^N} = \frac{1}{N}\sum_{n=1}^N \delta_{z_n}\big)$ :

(4.6) \begin{align} \pi_N\big(\mathbf{z}^N\big) \lambda_{z_n, ({-}z_n)}\big( \overline{\mathbf{z}^N}\big) = \pi_N\big(\tilde{\mathbf{z}}^N\big) \lambda_{({-}z_n), z_n}\big(\overline{\tilde{\mathbf{z}}^N}\big). \end{align}

From the reversibility of $\big(X_1^N, \ldots, X_N^N\big)$ , noting that $\wp_N(\xi)$ is the sum of $\pi_N\big(\mathbf{z}^N\big)$ over all $\mathbf{z}^N$ such that $\overline{\mathbf{z}^N} = \xi$ , it is straightforward to check that $\mu_N$ is reversible. For completeness, we show the reversibility of $\mu_N$ by checking the detailed balance condition. Towards this, we first note that for any $\xi, \tilde{\xi} \in M_1^N(\mathcal{Z})$ such that $\xi(z) = \tilde{\xi}(z)+1/N$ for some $z \in \mathcal{Z}$ (which ensures that $\xi(z) > 0$ , and hence $\tilde{\xi}({-}z) > 0$ ),

(4.7) \begin{align} &\xi(z) \times \big(\text{number of } \mathbf{z}^N \in \mathcal{Z}^N \text{ such that } \overline{\mathbf{z}^N} = \xi\big) \nonumber \\ & \qquad = \tilde{\xi}({-}z) \times \big(\text{number of } \mathbf{z}^N \in \mathcal{Z}^N \text{ such that } \overline{\mathbf{z}^N} = \tilde{\xi}\big). \end{align}

Let $\mathbf{z}^N_\xi \in \mathcal{Z}^N$ $\Big($ resp. $\tilde{\mathbf{z}}^N_{\tilde{\xi}} \in \mathcal{Z}^N\Big)$ be such that $\overline{\mathbf{z}^N} = \xi$ $\big($ resp. $\overline{\tilde{\mathbf{z}}^N} = \tilde{\xi}\big)$ . Noting that $\pi\big(\mathbf{z}^N\big)$ depends only on $\overline{\mathbf{z}^N}$ , for any $z \in \mathcal{Z}$ with $\xi(z) > 0$ , we have

\begin{align*} \wp_N(\xi) N \xi(z) \lambda_{z,({-}z)}(\xi) & = \pi_N\big(\mathbf{z}^N_\xi\big) \big(\text{number of } \mathbf{z}^N \in \mathcal{Z}^N \text{ such that } \overline{\mathbf{z}^N} = \xi\big) N \xi(z) \lambda_{z,({-}z)}(\xi)\\ &= \pi_N\big(\mathbf{z}^N_\xi\big) \big(\text{number of } \mathbf{z}^N \in \mathcal{Z}^N \text{ such that } \overline{\mathbf{z}^N} = \tilde{\xi}\big) N \tilde{\xi}({-}z) \lambda_{z,({-}z)}(\xi) \\ & = \pi_N\big(\mathbf{z}^N_{\tilde{\xi}}\big) \big(\text{number of } \mathbf{z}^N \in \mathcal{Z}^N \text{ such that } \overline{\mathbf{z}^N} = \tilde{\xi}\big) N \tilde{\xi}({-}z) \lambda_{({-}z),z}\big(\tilde{\xi}\big) \\ & = \wp_N\big(\tilde{\xi}\big) N \tilde{\xi}({-}z) \lambda_{({-}z),z}\big(\tilde{\xi}\big), \end{align*}

where we have used (4.7) in the second equality and (4.6) in the third equality. It follows that $\mu_N$ is reversible.

Remark 4.1. Another situation where $\mu_N$ is reversible with respect to $\wp_N$ is in the non-interacting case (i.e., when, for each $(z,z^\prime) \in \mathcal{E}$ , $\lambda_{z,z^\prime}({\cdot})$ is a constant function, which we denote by $\lambda_{z,z^\prime}$ ), where the Markov process on $\mathcal{Z}$ with generator

\begin{align*} f \mapsto \sum_{z^\prime:(z,z^\prime) \in \mathcal{E}} (\,f(z^\prime) - f(z)) \lambda_{z,z^\prime}, \qquad z \in \mathcal{Z}, \end{align*}

is reversible with respect to its invariant measure (i.e., when the Markov process corresponding to a single particle’s evolution on $\mathcal{Z}$ is reversible with respect to its invariant measure). This results in a reversible empirical measure process $\mu_N$ . However, the authors are not aware of a general condition (in terms of the transition rates $\lambda_{z,z^\prime}({\cdot}), (z,z^\prime) \in \mathcal{E}$ ) that characterises reversibility of $\mu_N$ .

5. Convergence to a global minimum via controlled addition of particles

In this section, our goal is to increase the number of particles N over time so as to obtain, with high probability, convergence of the empirical measure process to a global minimum of the rate function s that governs the LDP for the sequence of invariant measure $\{\wp_N\}_{N\geq 1}$ .

Fix $c>0$ . Let $N_0 = \min\{n \in \mathbb{N} \,:\, \exp\{nc\} - 2 \geq 0 \}$ , $t_{N_0} = 0$ , and for each $N > N_0$ , let $t_N = \exp\{Nc\}-2$ . For each $N \geq N_0$ define the generator $L^N_t$ acting on bounded measurable functions f on $M_1(\mathcal{Z})$ by

\begin{align*} L_t^Nf (\xi) \,:\!=\, \sum_{(z,z^\prime) \in \mathcal{E}} N_t \xi(z) \lambda _{z,z^\prime}(\xi) \left[ f\left(\xi+\frac{\delta_{z^\prime}}{N_t}- \frac{\delta_z}{N_t}\right) - f(\xi) \right], \qquad t\in [t_{N}, t_{N+1}),\end{align*}

where $N_t = N$ for $t \in [t_N, t_{N+1})$ . Let $z_0 \in \mathcal{Z}$ be a fixed state and let $\nu \in M_1^{N_0}(\mathcal{Z})$ . We say that a probability measure $\mathbb{P}_{0,\nu}$ on $D([0,\infty),M_1(\mathcal{Z}))$ is a solution to the martingale problem for $\big\{L^N\big\}_{N \geq N_0}$ with initial condition $\nu$ if $\mathbb{P}_{0,\nu}(\bar{\mu}\,:\, \bar{\mu}(0) = \nu)=1$ , for each $N \geq N_0$ , the restriction of $\mathbb{P}_{0,\nu}$ on $D([t_N, t_{N+1}), M_1^{N}(\mathcal{Z}))$ is a solution to the $D([t_N, t_{N+1}), M_1^{N}(\mathcal{Z}))$ -valued martingale problem for $L^N$ , and

\begin{align*} \mathbb{P}_{0,\nu}\!\left(\bar{\mu}\,:\, \bar{\mu}(t_{N+1}) = \frac{N}{1+N}\bar{\mu}\big(t_{N+1}^-\big) + \frac{1}{N+1} \delta_{z_0}\right) =1.\end{align*}

Again, by the boundedness assumption on transition rates (A2), for each $\nu \in M_1^{N_0}(\mathcal{Z})$ , there exists a unique probability measure $\mathbb{P}_{0,\nu}$ that solves the martingale problem for $\big\{L^N\big\}_{N \geq N_0}$ with initial condition $\nu$ . Let $\bar{\mu}$ be the process on $D([0,\infty),M_1(\mathcal{Z}))$ whose law is $\mathbb{P}_{0,\nu}$ . To describe the process in words, we start with $N_0$ particles and follow the mean-field interaction described in Section 1, except that at each time instant $t_N$ , $N > N_0$ , we add a new particle whose state is set to $z_0$ . Similarly, for $t > 0$ and $\nu \in \mathcal{M}_1^{\lfloor \log\! (t+2)\rfloor}$ , let $\mathbb{P}_{t,\nu}$ denote the law of the process $(\bar{\mu}(t^\prime), t^\prime \geq t)$ with $\bar{\mu}(t) = \nu$ .

We anticipate that if c is small, then $N_t$ is so large that the fluid limit kicks in too quickly over time and the process $\bar{\mu}$ converges (over time) to a local minimum of s with positive probability depending on the initial condition $\bar{\mu}(0)$ . When c is sufficiently large, we anticipate that there is enough time for exploration and therefore we will converge to a global minimum of s. Recall that the set of global minimisers of s is denoted by $\tilde{L}_0$ . Our interest in this section is in finding a constant $c^*$ such that for all $c > c^*$ and $\nu \in M_1^{N_0}(\mathcal{Z})$ , we have

(5.1) \begin{align} \mathbb{P}_{0,\nu} \big(\bar{\mu}(t) \text{ lies in a neighbourhood of }\tilde{L}_0\big) \to 1 \end{align}

as $t \to \infty$ .

We use the results in the previous sections to identify the constant $c^*$ . Since $N_t \to \infty$ as $t \to \infty$ , for a fixed $T > 0$ and large enough t, the large deviation properties of the process $(\bar{\mu}(s), t \leq s \leq t+T)$ from the limiting dynamics (1.1) starting at an arbitrary $\bar{\mu}(t)$ can be obtained similarly to the LDP of the process $\mu_N$ studied in Theorem 2.1 and Corollary 2.1. Therefore, the results in the previous sections on the large-time behaviour for the process $(\mu_N(t), t\geq 0)$ are also valid for $(\bar{\mu}(t) , t \geq 0)$ when the t is large enough; we make these precise now.

Lemma 5.1. (See Lemma 3.8.) Let $\pi_1^k$ and $\pi_2^k$ be k-cycles and suppose that $\pi_1^k \to \pi_2^k$ and $\tilde{V}\big(\pi_1^k\big)/c < 1$ . Then, given $\varepsilon > 0$ , there exist $\delta>0$ and $\rho>0$ such that for all $\rho_1 < \rho$ , there is $t^* >0$ such that

\begin{align*} \mathbb{P}_{t,\nu}\Big(\bar{\tau}_{\pi^k_1} \leq t + t^{(\tilde{V}\big(\pi_1^k\big) -\delta)/c}, \bar{\mu}\big(\bar{\tau}_{\pi_1^k}\big) \in \gamma_{\pi_2^k}\Big) \geq t^{-\varepsilon/c} \end{align*}

holds uniformly for all $\nu \in \big[\pi_1^k\big]_{\rho_1} \cap M_1^{N_{t}}(\mathcal{Z})$ and $t \geq t^*$ .

Remark 5.1. The condition $\tilde{V}\big(\pi_1^k\big) /c <1$ in the above lemma ensures that during the time duration $\Big[t, t^{\tilde{V}\big(\pi_1^k\big)/c}\Big]$ , for large enough t, the number of particles does not change, so that Lemma 3.8 for the process $\mu_N$ is applicable for the process $\bar{\mu}$ .

Lemma 5.2. (See Lemma 3.9.) Let $\pi^k$ be a k-cycle and suppose that $\tilde{V}\big(\pi^k\big)/c < 1$ . Then, given $\delta > 0$ such that $\big(\tilde{V}\big(\pi^k\big)+\delta\big)/c < 1$ , there exist $\varepsilon > 0$ and $\rho>0$ such that for all $\rho_1 < \rho$ , there is $t^* > 0$ such that

\begin{align*} \mathbb{P}_{t,\nu}\Big(\bar{\tau}_{\pi^k} & < t + t^{\big(\tilde{V}\big(\pi^k\big) -\delta\big)/c}\Big) \leq t^{-\varepsilon/c} \quad and \\ \mathbb{P}_{t,\nu}\Big(\bar{\tau}_{\pi^k}& > t + t^{\big(\tilde{V}\big(\pi^k\big) +\delta\big)/c}\Big) \leq t^{-\varepsilon/c} \end{align*}

hold uniformly for all $\nu \in \big[\pi^k\big]_{\rho_1} \cap M_1^{N_{t}}(\mathcal{Z})$ and $t \geq t^*$ .

Lemma 5.3. (See Lemma 3.10.) Let $\pi^k$ be a k-cycle and suppose that $\hat{V}\big(\pi^k\big)/c < 1$ . Given $\varepsilon>0$ , there exist $\delta \in \big(0, c-\hat{V}\big(\pi^k\big)\big)$ and $\rho>0$ such that for all $\rho_1 \leq \rho$ , there is $t^* >0$ such that

\begin{align*} \mathbb{P}_{t,\nu}\Big(\bar{\tau}_{\pi^k}\leq t + t^{\big(\hat{V}\big(\pi^k\big)+\delta\big)/c}\Big) \leq t^{-(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big)-\varepsilon)/c} \end{align*}

holds uniformly for all $\nu \in \big[\pi^k\big]_{\rho_1} \cap M_1^{N_{t}}(\mathcal{Z})$ and $t \geq t^*$ .

Recall the definition of the sets L and C from Section 3.

Lemma 5.4. (See Lemma 3.3.) Given $\rho_0 > 0$ and $\rho_1 <\rho_0$ and their associated sets L and C, given $v>0$ , there exist $T^* > 0$ and $t^* >0 $ such that

\begin{align*} \mathbb{P}_{t,\nu}\big(\hat{\tau}_L \geq t + T^*\big) \leq t^{-v/c} \end{align*}

holds uniformly for all $\nu \in C \cap M_1^{N_{t}}(\mathcal{Z})$ and $t \geq t^*$ .

To answer the question on the convergence of $\bar{\mu}$ to a global minimum of s, we define the following quantities, analogously to what is done in Hwang and Sheu [25]. Let m be such that $L_{m+1}$ is a singleton $\big($ denote it by $\big\{\pi^{m+1}\big\}\big)$ . Define

\begin{align*} A_m \,:\!=\, \big\{\pi^m \in L_m\,:\,\tilde{V}(\pi^m) = \hat{V}\big(\pi^{m+1}\big)\big\}.\end{align*}

Inductively define, for each $\pi^{k+1} \in L_{k+1}$ ,

\begin{align*} A_{k}\big(\pi^{k+1}\big) \,:\!=\, \big\{\pi^k \in \pi^{k+1} \,:\, \tilde{V}\big(\pi^k\big) = \hat{V}\big(\pi^{k+1}\big)\big\},\end{align*}

and for each $k \geq 1$ , define

\begin{align*} A_k \,:\!=\, \bigcup_{\pi^{k+1} \in A_{k+1}} A_k\big(\pi^{k+1}\big).\end{align*}

Also, for each $\pi^k \in L_k$ , define

\begin{align*} c_{k-1}\big(\pi^k\big) \,:\!=\, \left\{\begin{array}{l@{\quad}l} 0 \qquad \text{ if } \big\{ \pi^{k-1} \in \pi^k \,:\, \pi^{k-1} \notin A_{k-1}\big(\pi^k\big) \big\} = \emptyset, \\[4pt] \max\!\big\{\tilde{V}\big(\pi^{k-1}\big)\,:\,\pi^{k-1} \notin A_{k-1}\big(\pi^k\big), \pi^{k-1} \in \pi^k\big\} \qquad \text{ otherwise}, \end{array} \right.\end{align*}

and for each $k \geq 1$ , define

\begin{align*} c_{k-1} \,:\!=\, \max\!\big\{c_{k-1}\big(\pi^k\big), \,:\,\pi^k \in A_k\big\}.\end{align*}

Finally, define

\begin{align*} c^* \,:\!=\, \max\{c_k, 0 \leq k \leq m\}.\end{align*}

Figure 1 illustrates these definitions. Similarly to [25, Lemma A.11, Appendix], we can show that $A_0 = \tilde{L}_0$ , the set of minimisers of the rate function s that governs the LDP for the invariant measure $\{\wp_N\}_{N\geq 1}$ . We now prove Theorem 1.4 on the convergence of $\bar{\mu}$ to the set of global minimisers.

Figure 1. An example of the hierarchy of cycles with $|L| = 9$ and $m = 2$ that illustrates the above definitions. There are four 1-cycles and two 2-cycles. The nodes in the bottom row represent the elements of L, and the nodes above it represent the hierarchy of cycles. Dashed and dotted lines indicate the $(k-1)$ -cycles belonging to a k-cycle. Thick lines indicate the $(k-1)$ -cycles that attain $\max_{\pi^{k-1} \in \pi^k} \tilde{V}\!\left(\pi^{k-1}\right)$ for a k-cycle $\pi^{k}$ . Circles indicate the sets $A_k\!\left(\pi^{k+1}\right)$ . Dashed lines indicate the cycle $\pi^{k-1}\notin A_{k-1}\!\left(\pi^k\right)$ that attains the maximum in the second line in the definition of $c_{k-1}\!\left(\pi^k\right)$ ; $c_0\big(\pi_1^1\big) = 0$ (which is not indicated in the figure), and all other $c_{k-1}\!\left(\pi^k\right)$ are positive.

Proof of Theorem 1.4.It suffices to show that, for any $\delta > 0$ with $(c^*+\delta)/c<1$ , there exist $\varepsilon > 0$ , $\rho_1>0$ , and $t^* > 0$ such that

\begin{align*} \mathbb{P}_{t, \nu} \Big(\bar{\mu}\big(t + t^{\big(c^*+\delta\big)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\Big) \geq 1- t^{-\varepsilon/c} \end{align*}

for all $t > t^*$ and $\nu \in M_1^{N_{t}}(\mathcal{Z})$ . Define the stopping time

\begin{align*} \theta \,:\!=\, \inf\!\big\{s>t\,:\, \bar{\mu}(s) \in [L]_{\rho_1}\big\}. \end{align*}

By Lemma 5.4, for any $M >0$ , there exists $T^*>0$ such that for all $\nu \in M_1^{N_0}(\mathcal{Z})$ and large enough t, we have

\begin{align*} \mathbb{P}_{t, \nu} (\theta > t + T^*) \leq t^{-M/c}. \end{align*}

By the strong Markov property, we have

(5.2) \begin{align} \mathbb{P}_{t, \nu}&\Big( \bar{\mu}\big(t + t^{(c^*+\delta)/c}\big)\in \big[\tilde{L}_0\big]_{\rho_1}\Big) \nonumber \\ & \geq \mathbb{E}_{t,\nu} \bigg(1_{\big\{\theta \leq t + T^*\big\}} \cdot \mathbb{E}_{\theta, \bar{\mu}(\theta)} \bigg(1_{\big\{\bar{\mu}(t+t^{(c^*+\delta)/c}) \in \big[\tilde{L}_0\big]_{\rho_1}\big\}}\bigg)\bigg) \nonumber \\ & \geq \inf_{\substack{t \leq t_1 \leq t+T^* \\ \nu_1 \in [L]_{\rho_1}}} \mathbb{P}_{t_1, \nu_1} \Big(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\Big) \big(1-t^{-M/c}\big). \end{align}

To bound the first term above, fix a $t_1$ such that $t \leq t_1 \leq t+T^*$ and $\nu_1 \in [L]_{\rho_1}$ . Define the stopping time $\theta_m \,:\!=\, \inf \{t>t_1\,:\, \bar{\mu}(t) \in [A_m]_{\rho_1}\}$ . We have

(5.3) \begin{align} \mathbb{P}_{t_1, \nu_1}\! &\bigg(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\bigg) \nonumber \\ & \geq \mathbb{E}_{t_1, \nu_1} \bigg(1_{\{\theta_m < t+t^{(c^*+\delta/2)/c}\}} \cdot \mathbb{E}_{\theta_m, \bar{\mu}(\theta_m)}\bigg(1_{\big\{\bar{\mu}(t+t^{(c^*+\delta)/c}) \in \big[\tilde{L}_0\big]_{\rho_1}\big\}}\bigg)\bigg) \nonumber \\ & \geq \inf_{t \leq t_2 \leq t+t^{(c^*+\delta/2)/c}, \nu_2 \in [A_m]_{\rho_1}} \mathbb{P}_{t_2, \nu_2}\bigg(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\bigg) \nonumber \\ & \qquad \times \mathbb{P}_{t_1, \nu_1}\big(\theta_m \leq t+t^{(c^*+\delta/2)/c}\big). \end{align}

We first bound the second term $\mathbb{P}_{t_1, \nu_1}\big(\theta_m \leq t+t^{(c^*+\delta/2)/c}\big)$ . Note that, by Lemma 5.1, for any $M_1>0$ , there exists $\delta_1>0$ such that

\begin{align*} \mathbb{P}_{t_1, \nu_1}\big(\theta_m > t_1+t_1^{(c_m-\delta_1)/c}\big) \leq 1-t_1^{-M_1/c} \end{align*}

for sufficiently large t. Let $T_1 = t_1 + t_1^{(c_m-\delta_1)/c}$ , and define the stopping time $\hat{\theta} \,:\!=\, \inf\{t>T_1\,:\, \bar{\mu}(t) \in [L]_{\rho_1} \}$ . Again, by Lemma 5.4, there exists a $T^*$ large enough so that $\mathbb{P}_{T_1, \nu}(\hat{\theta} > T_1+T^*) \leq T_1^{-M/c}$ for all $\nu \in M_1^{N_{T_1}}(\mathcal{Z})$ . Therefore, using the strong Markov property, we have

(5.4) \begin{align} \mathbb{P}_{t_1, \nu_1}&\big(\theta_m > t+t^{(c^*+\delta/2)/c}\big) \nonumber \\ & \leq \mathbb{E}_{t_1, \nu_1}\Big(1_{\{\theta_m \geq \hat{\theta}, \hat{\theta}< T_1+T^*\}} \cdot \mathbb{E}_{\hat{\theta}, \bar{\mu}(\hat{\theta})}\big(1_{\big\{\theta_m >t+t^{(c^*+\delta/2)/c}\big\}}\big)\Big) + \mathbb{P}_{t_1, \nu_1}\big(\hat{\theta} > T_1+T^*\big) \nonumber \\ & \leq \mathbb{P}_{t_1, \nu_1}(\theta_m > T_1) \sup_{\substack{T_1 \leq t \leq T_1 + T^* \\ \nu \in [L]_{\rho_1}}} \mathbb{P}_{t,\nu}\big(\theta_m > t+t^{(c^*+\delta/2)/c}\big) +t_1^{-M/c} \nonumber\\ & \leq \Big(1-t_1^{-M_1/c} \Big) \sup_{\substack{T_1 \leq t \leq T_1 + T^* \\ \nu \in [L]_{\rho_1}}} \mathbb{P}_{t,\nu}\big(\theta_m > t+t^{(c^*+\delta/2)/c}\big) +t_1^{-M/c}. \end{align}

We now focus on $\mathbb{P}_{t,\nu}\big(\theta_m > t+t^{(c^*+\delta/2)/c}\big)$ for a fixed $t \in [T_1, T_1+T^*]$ and $\nu \in [L]_{\rho_1}$ , and repeat the above steps; this will introduce a multiplication factor of $\big(1-T_1^{-M_1/c}\big)$ along with

\begin{align*} \sup_{\substack{T_2 \leq t \leq T_2 + T^* \\ \nu \in [L]_{\rho_1}}} \mathbb{P}_{t,\nu}\big(\theta_m > t+t^{(c^*+\delta/2)/c}\big), \end{align*}

where $T_2 = T_1 + T_1^{(c_m-\delta_1)/c}$ , in the first term in (5.4), and an addition of $t_1^{-M/c}$ in the second term. Therefore, repeating the above steps $r \sim t_1^{\delta/2c}$ times, we get

\begin{align*} \mathbb{P}_{t_1, \nu_1}\big(\theta_m > t+t^{(c^*+\delta/2)/c}\big) \leq \prod_{n=0}^r \big(1-T_n^{*{-M_1/c}}\big) + rt_1^{-M/c}, \end{align*}

where $T_0^* = t_1$ , and

\begin{align*} T_{n+1}^* = T_n^* + T_n^{*{(c_m-\delta_1)/c}} + T^*. \end{align*}

Note that

(5.5) \begin{align} \prod_{n=0}^r \big(1-T_n^{*{-M_1/c}}\big) & \leq \exp\!\left\{{-}\sum_{n=0}^r T_n^{*{-M_1/c}} \right\} \nonumber \\ & = \exp\!\left\{ -\sum_{n=0}^r T_n^{*{-M_1/c - (c_m-\delta_1)/c}}(T_{n+1}^* - T_n^*) \right\} \nonumber \\ & \leq \exp\!\left\{{-} \int_{T_0^*}^{T_r^*} u^{-(M_1/c) - (c_m-\delta_1)/c} du\right\} \nonumber \\ & = \exp \left\{ - \left( T_r^{*{1-(c_m+M_1-\delta_1)/c}} - t_1^{1-(c_m+M_1-\delta_1)/c} \right)\right\}. \end{align}

Since $T_n \geq t_1$ for all $n \geq 1$ , we see that $T_r^* \geq t_1 + r t_1^{(c_m-\delta_1)/c} \sim t_1 + t_1^{(c_m-\delta_1+\delta/2)/c}$ . Therefore,

\begin{align*} - & \left(T_r^{*{1-(c_m+M_1-\delta_1)/c}} - t_1^{1-(c_m+M_1-\delta_1)/c} \right) \\ & \leq -\left( \big(t_1+t_1^{(c_m-\delta_1+\delta/2)/c}\big)^{1-(c_m+M_1-\delta_1)/c} - t_1^{1-(c_m+M_1-\delta_1)/c}\right) \\ & \leq -\left( t_1^{1-(c_m+M_1-\delta_1)/c} \left( 1+t_1^{(c_m-\delta_1+\delta/2)/c-1}\right)^{1-(c_m+M_1-\delta_1)/c} -1\right) \\ & \leq -c^\prime\! \left(t_1^{1-(c_m+M_1-\delta_1)/c} t_1^{(c_m-\delta_1+\delta/2)/c-1} \right) \\ & = -c^\prime t_1^{(\delta/2 - M_1)/c}, \end{align*}

for some constant $c^\prime >0$ and large enough $t_1$ . Hence, (5.5) becomes

\begin{align*} \prod_{n=0}^r \big(1-T_n^{*^{-M_1/c}}\big) \leq \exp\Big\{{-}c^\prime t_1^{(\delta/2-M_1)/c}\Big\}. \end{align*}

We choose $M_1 = \delta/4$ ; the above and (5.4) then imply

\begin{align*} \mathbb{P}_{t_1, \nu_1}&\big(\theta_m > t+t^{(c^*+\delta/2)/c}\big) \leq \exp\Big\{{-}c^\prime t_1^{\delta/4c}\Big\} + t_1^{-(M-\delta/2)/c}, \end{align*}

and this implies that, for any $M^\prime > 0$ ,

(5.6) \begin{align} \mathbb{P}_{t_1,\nu_1} \big(\theta_m > t+t^{(c^*+\delta/2)/c}\big) \leq t^{-M^\prime/c} \end{align}

for sufficiently large t, $t \leq t_1 \leq t+T^*$ , and for all $\nu \in [L]_{\rho_1}$ .

We now bound the first term in (5.3), $\mathbb{P}_{t_2,\nu_2}\big(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\big)$ where $t \leq t_2 \leq t + t^{(c^*+\delta/2)/c}$ and $\nu_2 \in [A_m]_{\rho_1}$ . Let $\pi_0^m \in A_m$ be the m-cycle such that $\nu_2 \in \big[\pi_0^m\big]_{\rho_1}$ . Define the following quantities:

\begin{align*} \tilde{t}_0 \,:\!=\, t+t^{(c^*+\delta)/c} - t^{(c_{m-1}\big(\pi^m_0\big)+\delta)/c}, \qquad \text{and } \\ \tilde{t}_1 \,:\!=\, t+t^{(c^*+\delta)/c} - t^{(c_{m-1}\big(\pi^m_0\big)+\delta/2)/c}. \end{align*}

Define the stopping time $\theta \,:\!=\, \inf \{t>\tilde{t}_0\,:\, \bar{\mu}(t) \in \big[\pi^m_0\big]_{\rho_1}\}$ , if $c^* > c_{m-1}\big(\pi^m_0\big)$ , and $\theta = t_2$ otherwise. By the strong Markov property,

(5.7) \begin{align} \mathbb{P}_{t_2,\nu_2}& \Big(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\Big) \nonumber \\ & \geq \mathbb{E}_{t_2,\nu_2}\Bigg(1_{\{\theta \leq \tilde{t}_1\}} \cdot \mathbb{E}_{\theta, \bar{\mu}(\theta)}\Bigg(1_{\Big\{\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\Big\}}\Bigg)\Bigg)\nonumber \\ & \geq \mathbb{P}_{t_2, \nu_2} \big(\theta \leq \tilde{t}_1\big) \inf_{\tilde{t}_0 \leq t_3 \leq \tilde{t}_1, \nu_3 \in \big[\pi_0^m\big]_{\rho_1}} \mathbb{P}_{t_3,\nu_3}\Big(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\Big). \end{align}

We first estimate $\mathbb{P}_{t_2, \nu_2}(\theta \leq \tilde{t}_1)$ when $c^* > c_{m-1}(\pi_0^m)$ (if this is not the case, then by definition of $\theta$ , we have $\mathbb{P}_{t_2, \nu_2}(\theta \leq \tilde{t}_1)=1$ ). Note that

\begin{align*} \mathbb{P}_{t_2,\nu_2} \big(\theta > \tilde{t}_1\big) & = \mathbb{P}_{t_2,\nu_2} \big(\bar{\mu}(t) \notin \big[\pi^m_0\big]_{\rho_1} \text{ for all } \tilde{t}_0 \leq t \leq \tilde{t}_1\big) \\ & \leq \mathbb{P}_{t_2,\nu_2} \big(\bar{\mu}(t) \notin [L]_{\rho_1} \text{ for all } \tilde{t}_0 \leq t \leq \tilde{t}_1\big) + \mathbb{P}_{t_2, \nu_2}\Big(\bar{\tau}_{\pi^m_0} \leq \tilde{t}_1\Big). \end{align*}

Lemma 5.2 implies that

\begin{align*} \mathbb{P}_{t_2, \nu_2}\Big(\bar{\tau}_{\pi^m_0} \leq \tilde{t}_1\Big) \leq t^{-\delta/c} \end{align*}

for large t and small enough $\rho_1 > 0$ . Also, with this $\rho_1$ , by using Lemma 5.4, we see that

\begin{align*} \mathbb{P}_{t_2,\nu_2} \big(\bar{\mu}(t) \notin [L]_{\rho_1} \text{ for all } \tilde{t}_0 \leq t \leq \tilde{t}_1\big) \leq t^{-M_1/c} \end{align*}

for large t, where $M_1$ can be chosen as large as we want. This shows that there exists $\varepsilon_1>0$ such that

\begin{align*} \mathbb{P}_{t_2,\nu_2} \big(\theta \leq \tilde{t}_1\big) \geq 1-2t^{-\varepsilon_1/c} \end{align*}

uniformly for all $\nu_2 \in \big[\pi_0^m\big]_{\rho_1}$ and large enough t. Hence, from (5.6), (5.7), and (5.3), we get

\begin{align*} \mathbb{P}_{t_1,\nu_1}\! & \Big(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\Big) \\ & \geq \big(1-t^{-M^\prime/c}\big) \big(1-2t^{-\varepsilon_1/c}\big) \times \inf_{\substack{t_2 \geq \tilde{t}_0, \\ \nu_2 \in \big[\pi_0^m\big]_{\rho_1} \\ \pi_0^m \in A_m \\ \tilde{\delta} \in [\delta/4, \delta]}} \mathbb{P}_{t_2,\nu_2}\bigg(\bar{\mu}\bigg(t_2+t_2^{(c_{m-1}\big(\pi^m_0\big)+\tilde{\delta})/c}\bigg) \in \big[\tilde{L}_0\big]_{\rho_1}\bigg), \end{align*}

and therefore, for some $\varepsilon>0$ , we have

\begin{align*} \inf_{\substack{t \leq t_1 \leq t+T^*, \\ \nu_1 \in [L]_{\rho_1}}}&\mathbb{P}_{t_1,\nu_1}\Big(\bar{\mu}\big(t+t^{(c^*+\delta)/c}\big) \in \big[\tilde{L}_0\big]_{\rho_1}\Big) \\ & \geq \big(1-t^{-\varepsilon/c}\big) \times \inf_{\substack{t_2 \geq \tilde{t}_0 \\ \nu_2 \in \big[\pi^m_0\big]_{\rho_1} \\ \pi_0^m \in A_m \\ \tilde{\delta} \in [\delta/4, \delta]}} \mathbb{P}_{t_2,\nu_2}\bigg(\bar{\mu}\bigg(t_2+t_2^{(c_{m-1}\big(\pi^m_0\big)+\tilde{\delta})/c}\bigg) \in \big[\tilde{L}_0\big]_{\rho_1}\bigg). \end{align*}

We now focus on the second term. This probability inside the infimum can be bounded below using steps similar to those above, starting with (5.7); instead of the random variable $\theta$ , we consider the hitting time of a suitable $(m-1)$ -cycle. Continuing this procedure m times, we eventually reach $A_0$ . Therefore, we can show

\begin{align*} \inf_{\substack{t \leq t_1 \leq t+T^* \\ \nu_1 \in \big[\tilde{L}_0\big]_{\rho_1}}}&\mathbb{P}_{t_1,\nu_1}\big(\bar{\mu}(t+t^{(c^*+\delta)/c}) \in \big[\tilde{L}_0\big]_{\rho_1}\big) \geq \big(1-t^{-\varepsilon/c}\big)^{m+1}, \end{align*}

and the result now follows from (5.2).

We now show that the conclusion of Theorem 1.4 fails if we choose $c < c^*$ . Since $\tilde{L}_0 \neq L$ , we have $c^*>0$ . Given $c < c^*$ , let $\pi^k \in L_k$ be such that $\hat{V}\big(\pi^k\big) \leq c < \tilde{V}\big(\pi^k\big)$ ; this is possible from the definition of $c^*$ . Note that $\tilde{L}_0 \cap \pi^k = \emptyset$ . The result below shows that the exit time from a neighbourhood of $\pi^k$ is infinite with positive probability, and this in particular implies that (5.1) fails.

Proposition 5.1. Let $\pi^k$ be a k-cycle such that $\hat{V}\big(\pi^k\big) \leq c < \tilde{V}\big(\pi^k\big)$ . There exist $\varepsilon \in (0, \tilde{V}\big(\pi^k\big)-c)$ , $c^\prime >0$ , $\rho_1>0$ , and $t^*>0$ such that for all $\nu \in \big[\pi^k\big]_{\rho_1}\cap M_1^{N_{t}}(\mathcal{Z})$ and $t \geq t^*$ , we have

\begin{align*} \mathbb{P}_{t, \nu}\big(\bar{\tau}_{\pi^k} <\infty\big) \leq c^\prime t^{1-(\tilde{V}\big(\pi^k\big) - \varepsilon)/c}. \end{align*}

Proof. We proceed via the steps in Hwang and Sheu [25]. Let $T_0 = t$ , and define, for all $n \geq 1$ ,

\begin{align*} T_{n+1} \,:\!=\, T_n + T_n^{\hat{V}\big(\pi^k\big)/c} \qquad \text{and}\\ T^*_{n+1} \,:\!=\, T_n + \frac{1}{2} T_n^{\hat{V}\big(\pi^k\big)/c}. \end{align*}

(In the above definitions, we assume that $\hat{V}\big(\pi^k\big) > 0$ ; if this is not the case, then we replace $T_n^{\hat{V}\big(\pi^k\big)/c}$ in the above definitions by a sufficiently large constant, and the following arguments will go through.) We have, for any $r \geq 1$ ,

(5.8) \begin{equation} \mathbb{P}_{t, \nu} \big(\bar{\tau}_{\pi^k} <T_r\big) = \mathbb{P}_{t, \nu} \big(\bar{\tau}_{\pi^k} <T_{r-1}\big) + \mathbb{P}_{t, \nu} \big(T_{r-1} \leq \bar{\tau}_{\pi^k} <T_r\big). \end{equation}

To bound the second term, define the stopping time $\theta \,:\!=\, \inf\{t>T^*_{r-1}\,:\,\bar{\mu}(t) \in [L]_{\rho_1}\}$ , where $\rho_1$ is to be chosen later. Then

(5.9) \begin{align} \mathbb{P}_{t, \nu} \big(T_{r-1} \leq \bar{\tau}_{\pi^k} <T_r\big) & = \mathbb{P}_{t, \nu} \big(T_{r-1} \leq \bar{\tau}_{\pi^k} <T_r, \theta \leq T_{r-1}^*+T^* \big) \nonumber \\ &\qquad + \mathbb{P}_{t, \nu} \big(T_{r-1} \leq \bar{\tau}_{\pi^k} <T_r, \theta >T_{r-1}^*+T^*\big) , \end{align}

where $T^*$ is such that the second term above is bounded above by $T_{r-1}^{*^{-M/c}}$ , for some $M>0$ to be chosen later (this is possible by Lemma 5.4). To bound the first term, note that

\begin{align*} \mathbb{P}_{t, \nu} \big(T_{r-1} \leq &\bar{\tau}_{\pi^k} <T_r, \theta \leq T_{r-1}^*+T^* \big) \\ & \leq \mathbb{P}_{t, \nu} \big(\theta\leq \bar{\tau}_{\pi^k} <T_r, \theta \leq T_{r-1}^*+T^* \big) \\ & \leq \mathbb{E}_{t,\nu} \Big(1_{\{\bar{\mu}\big(\theta\big) \in \big[\pi^k\big]_{\rho_1}, \theta \leq T_{r-1}^*+T^*\}} \cdot \mathbb{E}_{\theta, \bar{\mu}\big(\theta\big)}\big(1_{\{\bar{\tau}_{\pi^k} < T_r\}}\big)\Big) \\ & \leq T_{r-1}^{*-\big(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) - \varepsilon\big)/c} \end{align*}

holds for sufficiently large t and small enough $\rho_1$ . Here, the second inequality follows from the strong Markov property and the third from Lemma 5.3. Choose M sufficiently large so that (5.8), (5.9), and the above imply

\begin{align*} \mathbb{P}_{t,\nu}\big(\bar{\tau}_{\pi^k} < T_r\big) \leq \mathbb{P}_{t,\nu}(\bar{\tau}_{\pi^k} < T_{r-1}) + 2T_{r-1}^{*^{-(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) -\varepsilon)/c}}. \end{align*}

Then we have

\begin{align*} \mathbb{P}_{t,\nu}\big(\bar{\tau}_{\pi^k} < T_r\big) &\leq 2\sum_{n=0}^r T_n^{*^{-(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) -\varepsilon)/c}} \\ & \leq c_1^\prime \sum_{n=0}^r T_n^{-(\tilde{V}\big(\pi^k\big) - \hat{V}\big(\pi^k\big) -\varepsilon)/c} \\ & = c_1^\prime \sum_{n=0}^r T_n^{-(\tilde{V}\big(\pi^k\big) - \varepsilon)/c} (T_{n+1} - T_n)\\ & \leq c_1^\prime \int_{t}^{T_r} u^{-(\tilde{V}\big(\pi^k\big)-\varepsilon)/c} du, \end{align*}

where $c_1^\prime $ is a positive constant. Choose $\varepsilon $ such that $\tilde{V}\big(\pi^k\big) - \varepsilon > c$ , so that the above implies

\begin{align*} \mathbb{P}_{t,\nu}\big(\bar{\tau}_{\pi^k} < T_r\big) &\leq c_1^\prime \int_{t}^ \infty u^{-(\tilde{V}\big(\pi^k\big)-\varepsilon)/c} du \\ & \leq c^\prime t^{1-(\tilde{V}\big(\pi^k\big)-\varepsilon)/c}, \end{align*}

where $c^\prime$ is a positive constant. Let $r \to \infty$ , and the result follows since $T_r \to \infty$ .

Example 5.1. We now provide an example where we can choose the transition rates of the particles so as to minimise a given ‘nice’ function U on $M_1(\mathcal{Z})$ . Let $(\mathcal{Z}, \mathcal{E}_{\mathcal{Z}})$ denote the complete graph on $\mathcal{Z}$ . Suppose that for every $\xi \in M_1(\mathcal{Z})$ and $(z,z^\prime) \in \mathcal{E}_\mathcal{Z}$ with $\xi(z) > 0$ , the limit

\begin{align*} \nabla_{z,z^\prime} U(\xi) = \lim_{N \to \infty} \frac{U\!\left(\xi + \frac{\delta_{z^\prime} - \delta_z}{N}\right) - U(\xi)}{1/N} \end{align*}

exists, and is bounded and continuous. Further assume that the above convergence is uniform over $\xi$ . Consider the transition rates

\begin{align*} \lambda_{z,z^\prime}^{(N)}(\xi) = \frac{\exp\biggr\{{-}N \biggr(U\biggr(\xi + \frac{\delta_{z^\prime} - \delta_z}{N}\biggr)- U(\xi)\biggr) \biggr\}}{1+\exp\biggr\{{-}N \biggr(U\biggr(\xi + \frac{\delta_{z^\prime} - \delta_z}{N}\biggr)- U(\xi)\biggr) \biggr\}}, \qquad \xi \in M_1^N(\mathcal{Z}), \ \xi(z) > 0. \end{align*}

Then, by verifying the detailed balance condition, it is straightforward to show that the probability measure

\begin{align*} \frac{1}{c_N} \exp\big\{ -NU\big(\overline{\mathbf{z}^N}\big) \big\}, \qquad \mathbf{z}^N \in \mathcal{Z}^N, \end{align*}

is invariant for the N-particle evolution, where $c_N = \sum_{\mathbf{z}^N \in \mathcal{Z}^N} \exp\!\big\{ -NU\big(\overline{\mathbf{z}^N}\big) \big\}$ . Let $H \,:\, M_1(\mathcal{Z}) \to [0, \infty)$ be the Shannon entropy defined by

\begin{equation*}H(\xi) = - \sum_{z \in \mathcal{Z}} \xi(z) \log \xi(z),\end{equation*}

with the convention that $0 \log 0 = 0$ . Since the number of $\mathbf{z}^N \in \mathcal{Z}^N$ such that $\overline{\mathbf{z}^N} = \xi$ is between $(N+1)^{-|\mathcal{Z}|}\exp\{NH(\xi)\}$ and $\exp\{NH(\xi)\}$ [17, Lemma 2.1.8], $\wp_N$ satisfies

\begin{align*} \frac{(N+1)^{-|\mathcal{Z}|}}{c_N} \exp\{{-}N(U(\xi) - H(\xi))\} \leq \wp_N(\xi) \leq \frac{1}{c_N} \exp\{{-}N(U(\xi) - H(\xi))\}. \end{align*}

Therefore, $\{\wp_N\}$ satisfies the LDP with rate function $U - H$ . Noting that $\lambda_{z,z^\prime}^{(N)}(\xi)$ converges to

\begin{equation*}\lambda_{z,z^\prime}(\xi) = \frac{\exp\{{-}\nabla_{z,z^\prime}U(\xi)\}}{1+\exp\{{-}\nabla_{z,z^\prime} U(\xi)\}}\end{equation*}

as $N \to \infty$ uniformly over $\xi$ , the empirical measure process $\mu_N$ satisfies the process-level LDP; see [27]. Therefore, if we modify U to cU, $c > 0$ , the particle addition algorithm could ensure convergence to a small neighbourhood of a global minimum of $cU - H$ . By choosing c large enough, we can ensure convergence to a neighbourhood of a global minimum of U.