The Galactic radial gradient of velocity dispersion

Extract

The kinematical study of the stars in the solar neighbourhood allows, via the equation of the so-called asymmetrical drift, to deduce the sum of the gradients of the density and the velocity dispersions, 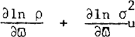. In order to deduce the density gradients in the solar neighbourhood, the second term is generally supposed to be zero. This kind of hypothesis, certainly wrong, comes from the old “ellipsoidal theory”. A velocity dispersion independent of 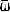is not compatible with the Toomre's local stability. On the contrary, if we suppose 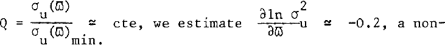negligible value compared with ∂1n 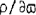(Mayor, 1974). Using Vandervoort's (1975) hydrodynamical approach, Erickson (1975) obtains a similar value for the local velocity-dispersion gradient.