Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T16:57:39.595Z Has data issue: false hasContentIssue false
  • English
  • Français

The Coupling of Modes and the Formation of Population III Objects

Published online by Cambridge University Press:  03 August 2017

J.P. Mücket ,
H.J. Haubold ,
S. Gottlöber  and
V. Müller
J.P. Mücket
Affiliation:
Zentralinstitut für Astrophysik der AdW der DDR, Potsdam, DDR - 1591
H.J. Haubold
Affiliation:
Zentralinstitut für Astrophysik der AdW der DDR, Potsdam, DDR - 1591
S. Gottlöber
Affiliation:
Zentralinstitut für Astrophysik der AdW der DDR, Potsdam, DDR - 1591
V. Müller
Affiliation:
Zentralinstitut für Astrophysik der AdW der DDR, Potsdam, DDR - 1591

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider two density perturbation modes with significantly different length scales λ and L (λ ≪ L) in a homogeneous Universe within Newtonian approximation. For the two modes the coupling terms in the corresponding Euler-Lagrange and Poisson equations are taken into account within lowest order of approximation. We assume that the λ - nods (high-frequency mode) is superimposed on the large-scale mode in such way that by an appropriate averaging procedure, the global behaviour is determined only by the single L-mode. Locally (Δ x ≈ λ ≪ L) the space dependence of the L-mode can be neglected in comparison with the λ -mode, but its time evolution remains important for the evolution of the λ -mode perturbation δ. We obtain for δ the equation: 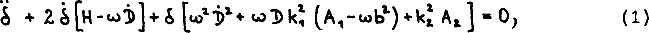where 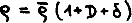, b is the sound velocity with respect to the undisturbed homogeneous natter distribution, H is the Hubble parameter, .

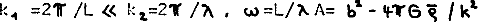Type
Appendix 1: Poster Papers
Information
Symposium - International Astronomical Union , Volume 130: Large Scale Structures of the Universe , 1988 , pp. 591
Copyright
Copyright © Reidel 1988 

References

Mücket, J.P.: Astron.Nachr. 308, 1 (1987)Google Scholar
Haubold, H.J., Mücket, J.P. and Müller, V.: Acta Cosmologica (1987, in press)Google Scholar
Mücket, J.P., Haubold, H.J., Gottlöber, S. and Müller, V.: Publ. of the Centre for Math. Sciences No. 10, Trivandrum (India) (1987, in press)Google Scholar