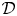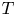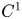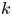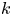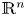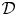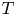1. Introduction
Let us consider a distribution ${\mathcal {D}}$![]() of $k$
of $k$![]() -dimensional planes on an open set $\Omega \subset {\mathbb {R}}^n$
-dimensional planes on an open set $\Omega \subset {\mathbb {R}}^n$![]() and recall that ${\mathcal {D}}$
and recall that ${\mathcal {D}}$![]() is said to be completely integrable if for each $x\in \Omega$
is said to be completely integrable if for each $x\in \Omega$![]() there exists an integral manifold of ${\mathcal {D}}$
there exists an integral manifold of ${\mathcal {D}}$![]() (i.e. a $k$
(i.e. a $k$![]() -dimensional submanifold ${\mathcal {M}}$
-dimensional submanifold ${\mathcal {M}}$![]() of $\Omega$
of $\Omega$![]() such that the tangent plane to ${\mathcal {M}}$
such that the tangent plane to ${\mathcal {M}}$![]() at $y$
at $y$![]() coincides with ${\mathcal {D}} (y)$
coincides with ${\mathcal {D}} (y)$![]() , for each $y\in {\mathcal {M}}$
, for each $y\in {\mathcal {M}}$![]() ) through $x$
) through $x$![]() . It is natural to ask under what assumptions on the defining structure, be it a set of differential forms or a set of vector fields, the distribution ${\mathcal {D}}$
. It is natural to ask under what assumptions on the defining structure, be it a set of differential forms or a set of vector fields, the distribution ${\mathcal {D}}$![]() is completely integrable. In the classical context in which it is assumed that ${\mathcal {D}}$
is completely integrable. In the classical context in which it is assumed that ${\mathcal {D}}$![]() is of class $C^1$
is of class $C^1$![]() and the integral manifolds are of class $C^2$
and the integral manifolds are of class $C^2$![]() , a well-known answer is provided by the following celebrated Frobenius theorem: A distribution is completely integrable if and only if it is involutive at every point of $\Omega$
, a well-known answer is provided by the following celebrated Frobenius theorem: A distribution is completely integrable if and only if it is involutive at every point of $\Omega$![]() (cf. theorems 2.11.9 and 2.11.11 in [Reference Narasimhan14]). In order to avoid technicalities as much as possible, in this introduction we will not recall the definition of involutive distribution (cf. § 2.4), but this will not prevent us from giving an idea of the content of this work.
(cf. theorems 2.11.9 and 2.11.11 in [Reference Narasimhan14]). In order to avoid technicalities as much as possible, in this introduction we will not recall the definition of involutive distribution (cf. § 2.4), but this will not prevent us from giving an idea of the content of this work.
To understand the sense of our main result, we must first point out the following well-known fact, which obviously proves one of the two implications of Frobenius theorem (the easier one): If ${\mathcal {D}}$![]() is of class $C^1$
is of class $C^1$![]() and ${\mathcal {M}}$
and ${\mathcal {M}}$![]() is an integral manifold of ${\mathcal {D}}$
is an integral manifold of ${\mathcal {D}}$![]() , then ${\mathcal {D}}$
, then ${\mathcal {D}}$![]() is involutive at every point of ${\mathcal {M}}$
is involutive at every point of ${\mathcal {M}}$![]() . This property can be generalized through the notion of superdensity. To explain this point, let us consider any $k$
. This property can be generalized through the notion of superdensity. To explain this point, let us consider any $k$![]() -dimensional $C^1$
-dimensional $C^1$![]() submanifold ${\mathcal {M}}$
submanifold ${\mathcal {M}}$![]() of $\Omega$
of $\Omega$![]() and denote by $\tau ({\mathcal {M}},\,{\mathcal {D}})$
and denote by $\tau ({\mathcal {M}},\,{\mathcal {D}})$![]() the tangency set of ${\mathcal {M}}$
the tangency set of ${\mathcal {M}}$![]() with respect to ${\mathcal {D}}$
with respect to ${\mathcal {D}}$![]() , i.e. the set of all points $y\in {\mathcal {M}}$
, i.e. the set of all points $y\in {\mathcal {M}}$![]() such that the tangent plane to ${\mathcal {M}}$
such that the tangent plane to ${\mathcal {M}}$![]() at $y$
at $y$![]() coincides with ${\mathcal {D}} (y)$
coincides with ${\mathcal {D}} (y)$![]() . Furthermore, let ${\mathcal {H}}^k$
. Furthermore, let ${\mathcal {H}}^k$![]() be the $k$
be the $k$![]() -dimensional Hausdorff measure in ${\mathbb {R}}^n$
-dimensional Hausdorff measure in ${\mathbb {R}}^n$![]() and let $B_{\mathcal {M}} (x,\,r)$
and let $B_{\mathcal {M}} (x,\,r)$![]() be the open metric ball of ${\mathcal {M}}$
be the open metric ball of ${\mathcal {M}}$![]() centred at $x\in {\mathcal {M}}$
centred at $x\in {\mathcal {M}}$![]() , of radius $r>0$
, of radius $r>0$![]() (cf. [Reference Chavel4, § 1.6]). The following property holds (cf. [Reference Delladio9, theorem 1.1]): Let $x\in {\mathcal {M}}$
(cf. [Reference Chavel4, § 1.6]). The following property holds (cf. [Reference Delladio9, theorem 1.1]): Let $x\in {\mathcal {M}}$![]() be a $(k+1)$
be a $(k+1)$![]() -superdensity point of $\tau ({\mathcal {M}},\,{\mathcal {D}})$
-superdensity point of $\tau ({\mathcal {M}},\,{\mathcal {D}})$![]() relative to ${\mathcal {M}}$
relative to ${\mathcal {M}}$![]() , i.e.
, i.e.
Then $x\in \tau ({\mathcal {M}},\,{\mathcal {D}})$![]() and ${\mathcal {D}}$
and ${\mathcal {D}}$![]() is involutive at $x$
is involutive at $x$![]() . This property generalizes the ‘fact’ mentioned above. Indeed, if ${\mathcal {M}}$
. This property generalizes the ‘fact’ mentioned above. Indeed, if ${\mathcal {M}}$![]() is an integral manifold of ${\mathcal {D}}$
is an integral manifold of ${\mathcal {D}}$![]() then $\tau ({\mathcal {M}},\,{\mathcal {D}})={\mathcal {M}}$
then $\tau ({\mathcal {M}},\,{\mathcal {D}})={\mathcal {M}}$![]() and hence (1.1) is trivially satisfied. We observe that this generalization is equivalent to the following structure result for the tangency set: If $x\in {\mathcal {M}}$
and hence (1.1) is trivially satisfied. We observe that this generalization is equivalent to the following structure result for the tangency set: If $x\in {\mathcal {M}}$![]() and ${\mathcal {D}}$
and ${\mathcal {D}}$![]() is not involutive at $x$
is not involutive at $x$![]() , then $x$
, then $x$![]() is not a $(k+1)$
is not a $(k+1)$![]() -superdensity point of $\tau ({\mathcal {M}},\,{\mathcal {D}})$
-superdensity point of $\tau ({\mathcal {M}},\,{\mathcal {D}})$![]() relative to ${\mathcal {M}}$
relative to ${\mathcal {M}}$![]() . In particular, if ${\mathcal {D}}$
. In particular, if ${\mathcal {D}}$![]() is nowhere involutive, then there are no $(k+1)$
is nowhere involutive, then there are no $(k+1)$![]() -superdensity points of $\tau ({\mathcal {M}},\,{\mathcal {D}})$
-superdensity points of $\tau ({\mathcal {M}},\,{\mathcal {D}})$![]() relative to ${\mathcal {M}}$
relative to ${\mathcal {M}}$![]() (whatever the choice of the $k$
(whatever the choice of the $k$![]() -dimensional $C^1$
-dimensional $C^1$![]() submanifold ${\mathcal {M}}$
submanifold ${\mathcal {M}}$![]() ). Despite this, $\tau ({\mathcal {M}},\,{\mathcal {D}})$
). Despite this, $\tau ({\mathcal {M}},\,{\mathcal {D}})$![]() may be ordinarily dense, i.e. such that ${\mathcal {H}}^k (B_{\mathcal {M}}(x,\,r)\setminus \tau ({\mathcal {M}},\,{\mathcal {D}})) = o (r^{k})$
may be ordinarily dense, i.e. such that ${\mathcal {H}}^k (B_{\mathcal {M}}(x,\,r)\setminus \tau ({\mathcal {M}},\,{\mathcal {D}})) = o (r^{k})$![]() , as $r\to 0+$
, as $r\to 0+$![]() , for ${\mathcal {H}}^k$
, for ${\mathcal {H}}^k$![]() -a.e. $x\in \tau ({\mathcal {M}},\,{\mathcal {D}})$
-a.e. $x\in \tau ({\mathcal {M}},\,{\mathcal {D}})$![]() . In fact, it can be proved that, for every $x\in \Omega$
. In fact, it can be proved that, for every $x\in \Omega$![]() , there exists a $k$
, there exists a $k$![]() -dimensional $C^1$
-dimensional $C^1$![]() submanifold ${\mathcal {M}}$
submanifold ${\mathcal {M}}$![]() of $\Omega$
of $\Omega$![]() such that $x\in {\mathcal {M}}$
such that $x\in {\mathcal {M}}$![]() and ${\mathcal {H}}^k (\tau ({\mathcal {M}},\,{\mathcal {D}}))>0$
and ${\mathcal {H}}^k (\tau ({\mathcal {M}},\,{\mathcal {D}}))>0$![]() (cf. [Reference Alberti, Massaccesi and Merlo2]).
(cf. [Reference Alberti, Massaccesi and Merlo2]).
In the recent work [Reference Alberti, Massaccesi and Stepanov3] the extension of Frobenius theorem to integral and normal currents is discussed for the first time. One of the main goals of this paper is to prove corollary 4.2, i.e. a generalization of [Reference Delladio9, theorem 1.1] in which, instead of ${\mathcal {M}}$![]() , a normal $k$
, a normal $k$![]() -current on $\Omega$
-current on $\Omega$![]() is considered. Unfortunately, however, its statement (including the definition of normal $k$
is considered. Unfortunately, however, its statement (including the definition of normal $k$![]() -current, cf. § 2.3 below) is too technical to be used effectively in an introduction such as this, which aims to present the results obtained in a simple and informal way. For the purposes of this presentation, it will be sufficient to simply focus on the application of corollary 4.2 to integral $k$
-current, cf. § 2.3 below) is too technical to be used effectively in an introduction such as this, which aims to present the results obtained in a simple and informal way. For the purposes of this presentation, it will be sufficient to simply focus on the application of corollary 4.2 to integral $k$![]() -currents (which constitute a particularly interesting subfamily of normal $k$
-currents (which constitute a particularly interesting subfamily of normal $k$![]() -currents). We recall that an integral $k$
-currents). We recall that an integral $k$![]() -current $T$
-current $T$![]() on $\Omega$
on $\Omega$![]() is a linear functional on the space ${\mathcal {E}}_k$
is a linear functional on the space ${\mathcal {E}}_k$![]() of smooth and compactly supported differential $k$
of smooth and compactly supported differential $k$![]() -forms on $\Omega$
-forms on $\Omega$![]() , with the following properties:
, with the following properties:
(i) It is rectifiable with positive integer multiplicity. This means that $T$
 is representable by integration as follows:
\[ \langle T;\omega\rangle =\int_R\langle\eta;\omega\rangle\theta\, {\rm d}{\mathcal{H}}^k\quad (\text{for all }\omega\in {\mathcal{E}}_k), \]where $R$
is representable by integration as follows:
\[ \langle T;\omega\rangle =\int_R\langle\eta;\omega\rangle\theta\, {\rm d}{\mathcal{H}}^k\quad (\text{for all }\omega\in {\mathcal{E}}_k), \]where $R$
 is a $k$
is a $k$ -rectifiable subset of $\Omega$
-rectifiable subset of $\Omega$ , $\theta$
, $\theta$ is a positive integer-valued function in $L^1({\mathcal {H}}^k\Large \llcorner \text {R})$
is a positive integer-valued function in $L^1({\mathcal {H}}^k\Large \llcorner \text {R})$ and $\eta$
and $\eta$ is a unit simple measurable $k$
is a unit simple measurable $k$ -vectorfield spanning the approximate tangent $k$
-vectorfield spanning the approximate tangent $k$ -plane to $R$
-plane to $R$ at $({\mathcal {H}}^k\Large \llcorner \text {R})$
at $({\mathcal {H}}^k\Large \llcorner \text {R})$ -a.e. point of $R$
-a.e. point of $R$ .
.(ii) The boundary of $T$
 , that is the $(k-1)$
, that is the $(k-1)$ -current $\partial T$
-current $\partial T$ on $\Omega$
on $\Omega$ defined by
\[ \langle \partial T;\omega'\rangle := \langle T;\,{\rm d}\omega'\rangle\quad (\omega' \in{\mathcal{E}}_{k-1}), \]is rectifiable with positive integer multiplicity too. Thus there exist a $(k-1)$
defined by
\[ \langle \partial T;\omega'\rangle := \langle T;\,{\rm d}\omega'\rangle\quad (\omega' \in{\mathcal{E}}_{k-1}), \]is rectifiable with positive integer multiplicity too. Thus there exist a $(k-1)$
 -rectifiable subset $R'$
-rectifiable subset $R'$ of $\Omega$
of $\Omega$ , a positive integer-valued function $\theta '\in L^1({\mathcal {H}}^{k-1} \Large \llcorner \text{R}')$
, a positive integer-valued function $\theta '\in L^1({\mathcal {H}}^{k-1} \Large \llcorner \text{R}')$ and a unit simple measurable $(k-1)$
and a unit simple measurable $(k-1)$ -vectorfield $\eta '$
-vectorfield $\eta '$ spanning the approximate tangent $(k-1)$
spanning the approximate tangent $(k-1)$ -plane to $R'$
-plane to $R'$ at $({\mathcal {H}}^{k-1}\Large \llcorner \text {R}')$
at $({\mathcal {H}}^{k-1}\Large \llcorner \text {R}')$ -a.e. point of $R'$
-a.e. point of $R'$ such that
\[ \langle \partial T;\omega'\rangle =\int_{R'}\langle\eta';\omega'\rangle\theta'\,{\rm d}{\mathcal{H}}^k\quad (\text{for all }\omega'\in {\mathcal{E}}_{k-1}). \]
such that
\[ \langle \partial T;\omega'\rangle =\int_{R'}\langle\eta';\omega'\rangle\theta'\,{\rm d}{\mathcal{H}}^k\quad (\text{for all }\omega'\in {\mathcal{E}}_{k-1}). \]
We now consider a $k$![]() -distribution ${\mathcal {D}}$
-distribution ${\mathcal {D}}$![]() of class $C^1$
of class $C^1$![]() on $\Omega$
on $\Omega$![]() , an integral $k$
, an integral $k$![]() -current $T$
-current $T$![]() on $\Omega$
on $\Omega$![]() and adopt the notation introduced in (i) and (ii) above. Let us denote by $\Gamma (\eta,\, {\mathcal {D}})$
and adopt the notation introduced in (i) and (ii) above. Let us denote by $\Gamma (\eta,\, {\mathcal {D}})$![]() the set of points $x\in R$
the set of points $x\in R$![]() at which the approximate tangent $k$
at which the approximate tangent $k$![]() -plane to $R$
-plane to $R$![]() exists and is equal to ${\mathcal {D}} (x)$
exists and is equal to ${\mathcal {D}} (x)$![]() . Moreover, let $\Gamma (\eta ',\, {\mathcal {D}})$
. Moreover, let $\Gamma (\eta ',\, {\mathcal {D}})$![]() be the set of points $x\in R'$
be the set of points $x\in R'$![]() at which the approximate tangent $(k-1)$
at which the approximate tangent $(k-1)$![]() -plane to $R'$
-plane to $R'$![]() exists and is contained in ${\mathcal {D}} (x)$
exists and is contained in ${\mathcal {D}} (x)$![]() . Then we have the following result (cf. corollary 4.4):
. Then we have the following result (cf. corollary 4.4):
Theorem If $\mathcal {J}$![]() denotes the set of all $x\in \Omega$
denotes the set of all $x\in \Omega$![]() such that
such that
then ${\mathcal {D}}$![]() is involutive at $({\mathcal {H}}^k\Large \llcorner \text {R})$
is involutive at $({\mathcal {H}}^k\Large \llcorner \text {R})$![]() -a.e. $x\in \mathcal {J}$
-a.e. $x\in \mathcal {J}$![]() .
.
2. Basic notation and notions, preliminary results
Throughout this paper $\Omega$![]() denotes an open subset of ${\mathbb {R}}^n$
denotes an open subset of ${\mathbb {R}}^n$![]() (with $n\geq 2$
(with $n\geq 2$![]() ). The standard basis of ${\mathbb {R}}^n$
). The standard basis of ${\mathbb {R}}^n$![]() and its dual will be denoted by $e_1,\, \ldots,\, e_n$
and its dual will be denoted by $e_1,\, \ldots,\, e_n$![]() and $dx_1,\,\ldots,\, dx_n$
and $dx_1,\,\ldots,\, dx_n$![]() , respectively. If $k$
, respectively. If $k$![]() is any positive integer not exceeding $n$
is any positive integer not exceeding $n$![]() , then $I(n,\,k)$
, then $I(n,\,k)$![]() is the family of integer multi-indices ${\bf i}= (i_1,\,\ldots,\, i_k)$
is the family of integer multi-indices ${\bf i}= (i_1,\,\ldots,\, i_k)$![]() such that $1\leq i_1 < \cdots < i_k\leq n$
such that $1\leq i_1 < \cdots < i_k\leq n$![]() . For every ${\bf i}= (i_1,\,\ldots,\, i_k)\in I(n,\,k)$
. For every ${\bf i}= (i_1,\,\ldots,\, i_k)\in I(n,\,k)$![]() , we set
, we set
The linear space of $k$![]() -vectors (resp. $k$
-vectors (resp. $k$![]() -covectors) is denoted by $\wedge _k({\mathbb {R}}^n)$
-covectors) is denoted by $\wedge _k({\mathbb {R}}^n)$![]() (resp. $\wedge ^k({\mathbb {R}}^n)$
(resp. $\wedge ^k({\mathbb {R}}^n)$![]() ). We recall that $\{e_{\bf i}\,\vert \, {\bf i}\in I(n,\,k)\}$
). We recall that $\{e_{\bf i}\,\vert \, {\bf i}\in I(n,\,k)\}$![]() (resp. $\{{\rm d}x_{\bf i}\,\vert \, {\bf i}\in I(n,\,k)\}$
(resp. $\{{\rm d}x_{\bf i}\,\vert \, {\bf i}\in I(n,\,k)\}$![]() ) is the standard basis of $\wedge _k({\mathbb {R}}^n)$
) is the standard basis of $\wedge _k({\mathbb {R}}^n)$![]() (resp. $\wedge ^k({\mathbb {R}}^n)$
(resp. $\wedge ^k({\mathbb {R}}^n)$![]() ). Multivectors and multicovectors are in duality. More precisely, the duality between $\wedge _k({\mathbb {R}}^n)$
). Multivectors and multicovectors are in duality. More precisely, the duality between $\wedge _k({\mathbb {R}}^n)$![]() and $\wedge ^k({\mathbb {R}}^n)$
and $\wedge ^k({\mathbb {R}}^n)$![]() is defined by
is defined by
where $\zeta _{\bf i}$![]() (resp. $\alpha _{\bf i}$
(resp. $\alpha _{\bf i}$![]() ) is the ${\bf i}$
) is the ${\bf i}$![]() -th coefficient in the representation of $\zeta$
-th coefficient in the representation of $\zeta$![]() (resp. $\alpha$
(resp. $\alpha$![]() ) with respect to the standard basis of $\wedge _k({\mathbb {R}}^n)$
) with respect to the standard basis of $\wedge _k({\mathbb {R}}^n)$![]() (resp. $\wedge ^k({\mathbb {R}}^n)$
(resp. $\wedge ^k({\mathbb {R}}^n)$![]() ), that is $\zeta =\sum _{{\bf i}\in I(n,k)}\zeta _{\bf i} e_{\bf i}$
), that is $\zeta =\sum _{{\bf i}\in I(n,k)}\zeta _{\bf i} e_{\bf i}$![]() (resp. $\alpha =\sum _{{\bf i}\in I(n,k)}\alpha _{\bf i}\,{\rm d}x_{\bf i}$
(resp. $\alpha =\sum _{{\bf i}\in I(n,k)}\alpha _{\bf i}\,{\rm d}x_{\bf i}$![]() ). If $h\leq k$
). If $h\leq k$![]() , $\zeta \in \wedge _k({\mathbb {R}}^n)$
, $\zeta \in \wedge _k({\mathbb {R}}^n)$![]() and $\alpha \in \wedge ^h({\mathbb {R}}^n)$
and $\alpha \in \wedge ^h({\mathbb {R}}^n)$![]() , then the interior multiplication $\zeta \Large \llcorner \alpha$
, then the interior multiplication $\zeta \Large \llcorner \alpha$![]() is the $(k-h)$
is the $(k-h)$![]() -vector defined by
-vector defined by
cf. [Reference Federer10, § 1.5.1].
The open ball of radius $r$![]() centred at $x\in {\mathbb {R}}^n$
centred at $x\in {\mathbb {R}}^n$![]() is denoted by $B_r(x)$
is denoted by $B_r(x)$![]() . The Lebesgue measure and the $h$
. The Lebesgue measure and the $h$![]() -dimensional Hausdorff measure on ${\mathbb {R}}^n$
-dimensional Hausdorff measure on ${\mathbb {R}}^n$![]() are denoted by ${\mathcal {L}}^n$
are denoted by ${\mathcal {L}}^n$![]() and ${\mathcal {H}}^h$
and ${\mathcal {H}}^h$![]() , respectively. A subset of ${\mathbb {R}}^n$
, respectively. A subset of ${\mathbb {R}}^n$![]() is said to be $h$
is said to be $h$![]() -rectifiable if it can be covered, except for an ${\mathcal {H}}^h$
-rectifiable if it can be covered, except for an ${\mathcal {H}}^h$![]() -negligible subset, by countably many $h$
-negligible subset, by countably many $h$![]() -dimensional $C^1$
-dimensional $C^1$![]() surfaces. Recall that if $R$
surfaces. Recall that if $R$![]() is a $h$
is a $h$![]() -rectifiable subset of ${\mathbb {R}}^n$
-rectifiable subset of ${\mathbb {R}}^n$![]() , then for ${\mathcal {H}}^h$
, then for ${\mathcal {H}}^h$![]() -a.e. $x\in R$
-a.e. $x\in R$![]() there is the approximate tangent $h$
there is the approximate tangent $h$![]() -plane to $R$
-plane to $R$![]() at $x$
at $x$![]() (cf. [Reference Mattila13, theorem 15.19]).
(cf. [Reference Mattila13, theorem 15.19]).
All measures we will consider below (except for ${\mathcal {L}}^n$![]() and ${\mathcal {H}}^h$
and ${\mathcal {H}}^h$![]() ) will be real-valued and defined on ${\mathcal {B}}(\Omega )$
) will be real-valued and defined on ${\mathcal {B}}(\Omega )$![]() , that is the $\sigma$
, that is the $\sigma$![]() -algebra of Borel subsets of $\Omega$
-algebra of Borel subsets of $\Omega$![]() . The restriction of a measure $\mu$
. The restriction of a measure $\mu$![]() to $E\in {\mathcal {B}}(\Omega )$
to $E\in {\mathcal {B}}(\Omega )$![]() is defined by
is defined by
Recall that the upper $s$![]() -density and the lower $s$
-density and the lower $s$![]() -density of $\mu$
-density of $\mu$![]() at $x\in \Omega$
at $x\in \Omega$![]() (with $0\leq s < +\infty$
(with $0\leq s < +\infty$![]() ) are defined by
) are defined by
respectively (cf. [Reference Mattila13, definition 6.8]). Let us also recall the definition of upper derivative of another locally finite Borel measure $\lambda$![]() on $\Omega$
on $\Omega$![]() with respect to $\mu$
with respect to $\mu$![]() at $x\in \Omega$
at $x\in \Omega$![]() :
:
cf. [Reference Mattila13, definition 2.9]. We have the following result (the proof of which is trivial).
Proposition 2.1 Let $\lambda$![]() and $\mu$
and $\mu$![]() be two locally finite positive Borel measures on $\Omega$
be two locally finite positive Borel measures on $\Omega$![]() . Moreover let $x\in \Omega$
. Moreover let $x\in \Omega$![]() and $s\in [0,\,+\infty )$
and $s\in [0,\,+\infty )$![]() be such that
be such that
Then the following inequality holds$:$![]()
2.1 Vectorfields and differential forms
A map $v:\Omega \to \wedge _k({\mathbb {R}}^n)$![]() is said to be a $k$
is said to be a $k$![]() -vectorfield. Analogously, a map $\omega :\Omega \to \wedge ^k({\mathbb {R}}^n)$
-vectorfield. Analogously, a map $\omega :\Omega \to \wedge ^k({\mathbb {R}}^n)$![]() is said to be a $k$
is said to be a $k$![]() -covectorfield or (more commonly) a differential $k$
-covectorfield or (more commonly) a differential $k$![]() -form. Obviously, a $k$
-form. Obviously, a $k$![]() -vectorfield $v$
-vectorfield $v$![]() (resp. differential $k$
(resp. differential $k$![]() -form $\omega$
-form $\omega$![]() ) can be written in terms of the standard basis of $\wedge _k({\mathbb {R}}^n)$
) can be written in terms of the standard basis of $\wedge _k({\mathbb {R}}^n)$![]() (resp. $\wedge ^k({\mathbb {R}}^n)$
(resp. $\wedge ^k({\mathbb {R}}^n)$![]() ), that is,
), that is,

The regularity of $v$![]() (resp. $\omega$
(resp. $\omega$![]() ) is defined by that of its coefficients $v_{\bf i}$
) is defined by that of its coefficients $v_{\bf i}$![]() (resp. $\omega _{\bf i}$
(resp. $\omega _{\bf i}$![]() ). For example, we will say that $v$
). For example, we will say that $v$![]() (resp. $\omega$
(resp. $\omega$![]() ) is class $C^1$
) is class $C^1$![]() if $v_{\bf i}\in C^1(\Omega )$
if $v_{\bf i}\in C^1(\Omega )$![]() (resp. $\omega _{\bf i}\in C^1(\Omega )$
(resp. $\omega _{\bf i}\in C^1(\Omega )$![]() ) for all ${\bf i}\in I(n,\,k)$
) for all ${\bf i}\in I(n,\,k)$![]() .
.
2.2 Span of a $k$ -vector
-vector
For $v\in \wedge _k({\mathbb {R}}^n)$![]() we define
we define
The span has the following properties (cf. [Reference Alberti and Marchese1, proposition 5.9]):
(1) if $v=0$
 then ${\rm span} (v)=\{0\}$
then ${\rm span} (v)=\{0\}$ ;
;(2) if $v\not =0$
 then $\dim {\rm span}(v)\geq k$
then $\dim {\rm span}(v)\geq k$ ;
;(3) if $v_1,\,\ldots,\,v_k$
 are linearly independent vectors of ${\mathbb {R}}^n$
are linearly independent vectors of ${\mathbb {R}}^n$ and $v=v_1\wedge \cdots \wedge v_k$
and $v=v_1\wedge \cdots \wedge v_k$ , then ${\rm span} (v)$
, then ${\rm span} (v)$ is the $k$
is the $k$ -plane generated by $v_1,\,\ldots,\,v_k$
-plane generated by $v_1,\,\ldots,\,v_k$ . In particular, $\dim {\rm span}(v) = k$
. In particular, $\dim {\rm span}(v) = k$ ;
;(4) conversely, if $\dim {\rm span}(v)= k$
 , then $v$
, then $v$ is simple and $v\not =0$
is simple and $v\not =0$ ;
;(5) ${\rm span}(v)$
 is the smallest of all linear subspaces $W$
is the smallest of all linear subspaces $W$ of ${\mathbb {R}}^n$
of ${\mathbb {R}}^n$ such that $v\in \wedge _k(W)$
such that $v\in \wedge _k(W)$ .
.
We will also need this additional simple property, for which we provide a proof (since we do not have a reference for it).
Proposition 2.2 Let $v\in \wedge _h ({\mathbb {R}}^n)\setminus \{0\}$![]() be simple and let $\beta \in \wedge ^p({\mathbb {R}}^n)$
be simple and let $\beta \in \wedge ^p({\mathbb {R}}^n)$![]() , with $1\leq p\leq h\leq n$
, with $1\leq p\leq h\leq n$![]() . Assume $v \llcorner \beta = 0$
. Assume $v \llcorner \beta = 0$![]() , that is
, that is
Then $\beta \vert _{({\rm span}(v))^p}=0$![]() .
.
Proof. Consider an orthonormal basis $\varepsilon _1,\, \ldots,\,\varepsilon _n$![]() of ${\mathbb {R}}^n$
of ${\mathbb {R}}^n$![]() such that $\varepsilon _1,\, \ldots,\,\varepsilon _h$
such that $\varepsilon _1,\, \ldots,\,\varepsilon _h$![]() generates ${\rm span}(v)$
generates ${\rm span}(v)$![]() . If $\theta _1,\,\ldots,\, \theta _n$
. If $\theta _1,\,\ldots,\, \theta _n$![]() is the dual basis of $\varepsilon _1,\, \ldots,\,\varepsilon _n$
is the dual basis of $\varepsilon _1,\, \ldots,\,\varepsilon _n$![]() and define
and define
then we have $\langle \varepsilon _{\bf i}\, ;\, \beta \rangle$![]() for all ${\bf i}\in I (n,\,p)\setminus I_*(n,\,p)$
for all ${\bf i}\in I (n,\,p)\setminus I_*(n,\,p)$![]() , by (2.1). Then
, by (2.1). Then
hence the conclusion follows.
Remark 2.3 The property established in proposition 2.2 does not hold, in general, if $v$![]() is not simple. For example, let $n=5$
is not simple. For example, let $n=5$![]() , $h=3$
, $h=3$![]() , $p=2$
, $p=2$![]() , $v:=e_1\wedge e_2\wedge e_3 + e_1\wedge e_4\wedge e_5$
, $v:=e_1\wedge e_2\wedge e_3 + e_1\wedge e_4\wedge e_5$![]() and $\beta := {\rm d}x_2 \wedge {\rm d}x_4$
and $\beta := {\rm d}x_2 \wedge {\rm d}x_4$![]() . Then one can easily prove that condition (2.1) is verified and that ${\rm span}(v)={\mathbb {R}}^5$
. Then one can easily prove that condition (2.1) is verified and that ${\rm span}(v)={\mathbb {R}}^5$![]() . Since in this case we have $\beta \vert _{({\rm span}(v))^p}={\rm d}x_2 \wedge {\rm d}x_4$
. Since in this case we have $\beta \vert _{({\rm span}(v))^p}={\rm d}x_2 \wedge {\rm d}x_4$![]() , the above property cannot be validated.
, the above property cannot be validated.
Consider a Borel map $\tau : \Omega \to \wedge _h({\mathbb {R}}^n)$![]() , a Borel differential $l$
, a Borel differential $l$![]() -form $\omega$
-form $\omega$![]() on an open set $U\subset \Omega$
on an open set $U\subset \Omega$![]() (with $1\leq l\leq h-1$
(with $1\leq l\leq h-1$![]() ) and define the Borel set
) and define the Borel set
We observe that in the special case $l=1$![]() , i.e. if $\omega$
, i.e. if $\omega$![]() is a Borel differential $1$
is a Borel differential $1$![]() -form, then we have
-form, then we have
2.3 Currents
An $h$![]() -current on $\Omega$
-current on $\Omega$![]() is a continuous linear functional $T$
is a continuous linear functional $T$![]() on the space ${\mathcal {E}}_h$
on the space ${\mathcal {E}}_h$![]() of smooth and compactly supported differential $h$
of smooth and compactly supported differential $h$![]() -forms on $\Omega$
-forms on $\Omega$![]() . The boundary of $T$
. The boundary of $T$![]() is an $(h-1)$
is an $(h-1)$![]() -current on $\Omega$
-current on $\Omega$![]() denoted with $\partial T$
denoted with $\partial T$![]() and defined by $\langle \partial T ; \omega \rangle := \langle T ; d \omega \rangle$
and defined by $\langle \partial T ; \omega \rangle := \langle T ; d \omega \rangle$![]() for every $\omega \in {\mathcal {E}}_{h-1}$
for every $\omega \in {\mathcal {E}}_{h-1}$![]() . The mass of $T$
. The mass of $T$![]() is defined as
is defined as
Given an $h$![]() -current $T$
-current $T$![]() on $\Omega$
on $\Omega$![]() , the following properties are equivalent (by Riesz theorem):
, the following properties are equivalent (by Riesz theorem):
(1) ${\mathbb {M}} (T)<+\infty$
 ;
;(2) There exist a finite positive measure $\mu$
 on $\Omega$
on $\Omega$ and a Borel $h$
and a Borel $h$ -vectorfield $\tau$
-vectorfield $\tau$ in $L^1(\mu )$
in $L^1(\mu )$ such that $T=\tau \mu$
such that $T=\tau \mu$ , i.e.
\[ \langle T ; \omega\rangle =\int_\Omega \langle \tau ; \omega\rangle\,{\rm d}\mu\quad (\omega\in {\mathcal{E}}_h). \]
, i.e.
\[ \langle T ; \omega\rangle =\int_\Omega \langle \tau ; \omega\rangle\,{\rm d}\mu\quad (\omega\in {\mathcal{E}}_h). \]
Recall from [Reference Giaquinta, Modica and Souček11, Ch. 1, Sect. 1.4] that if $\mu$![]() and $\tau$
and $\tau$![]() are as in (ii), then the total variation of $T=\tau \mu$
are as in (ii), then the total variation of $T=\tau \mu$![]() equals $\vert \tau \vert \mu$
equals $\vert \tau \vert \mu$![]() , namely
, namely
hence also
In particular $\vert \tau \mu \vert$![]() is radon.
is radon.
Remark 2.4 Obviously, the representation $T=\tau \mu$![]() is not unique. In particular, we also have $T=\tau \mu \Large \llcorner S_\tau$
is not unique. In particular, we also have $T=\tau \mu \Large \llcorner S_\tau$![]() , with $S_\tau :=\{x\in \Omega \,\vert \, \tau (x)\not = 0\}$
, with $S_\tau :=\{x\in \Omega \,\vert \, \tau (x)\not = 0\}$![]() . For this reason, it is not restrictive to assume that
. For this reason, it is not restrictive to assume that
hence also ${\rm spt}(T) = {\rm spt}(\mu )$![]() .
.
An $h$![]() -current $T$
-current $T$![]() on $\Omega$
on $\Omega$![]() is said to be:
is said to be:
(i) Normal if ${\mathbb {M}} (T)$
 and ${\mathbb {M}} (\partial T)$
and ${\mathbb {M}} (\partial T)$ are both finite.
are both finite.(ii) Rectifiable if $T=\eta \theta {\mathcal {H}}^h$
 and the following properties hold:
and the following properties hold:
• $\theta \in L^1({\mathcal {H}}^h)$
 ;
;• $R:=\{x\in \Omega \,\vert \, \theta (x)\not =0\}$
 is $k$
is $k$ -rectifiable;
-rectifiable;• $\eta$
 is a unit simple $h$
is a unit simple $h$ -vectorfield such that ${\rm span} (\eta (x))$
-vectorfield such that ${\rm span} (\eta (x))$ is the approximate tangent $h$
is the approximate tangent $h$ -plane to $R$
-plane to $R$ at $x$
at $x$ , for ${\mathcal {H}}^h$
, for ${\mathcal {H}}^h$ -a.e. $x\in R$
-a.e. $x\in R$ .
.
In this case $T$
 is also denoted by $[\hskip -0.6mm [ R,\,\eta,\,\theta ]\hskip -0.6mm ]$
is also denoted by $[\hskip -0.6mm [ R,\,\eta,\,\theta ]\hskip -0.6mm ]$ .
.(iii) Integral if $T$
 is rectifiable and (with the notation above):
is rectifiable and (with the notation above):
• $\theta \vert _R$
 is positive and integer-valued;
is positive and integer-valued;• ${\mathbb {M}} (\partial T) <+\infty$
 (hence $\partial T$
(hence $\partial T$ ).
).
Recall that if $T$![]() is integral then $\partial T$
is integral then $\partial T$![]() is also integral, cf. [Reference Simon15, theorem 30.3].
is also integral, cf. [Reference Simon15, theorem 30.3].
2.4 Distributions
A $k$![]() -distribution on $\Omega$
-distribution on $\Omega$![]() (with $1\leq k\leq n$
(with $1\leq k\leq n$![]() ) is a map ${\mathcal {D}}$
) is a map ${\mathcal {D}}$![]() that to each $x\in \Omega$
that to each $x\in \Omega$![]() associates a $k$
associates a $k$![]() -dimensional plane ${\mathcal {D}} (x)\subset {\mathbb {R}}^n$
-dimensional plane ${\mathcal {D}} (x)\subset {\mathbb {R}}^n$![]() . We say that a $k$
. We say that a $k$![]() -distribution ${\mathcal {D}}$
-distribution ${\mathcal {D}}$![]() on $\Omega$
on $\Omega$![]() is of class $C^p$
is of class $C^p$![]() (with $p\in {\mathbb {N}}$
(with $p\in {\mathbb {N}}$![]() ) if for every $x\in \Omega$
) if for every $x\in \Omega$![]() the following property holds: there exist a neighbourhood $U\subset \Omega$
the following property holds: there exist a neighbourhood $U\subset \Omega$![]() of $x$
of $x$![]() and a family $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$
and a family $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$![]() of $C^p$
of $C^p$![]() differential $1$
differential $1$![]() -forms on $U$
-forms on $U$![]() such that
such that
for all $y\in U$![]() . The forms $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$
. The forms $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$![]() are called defining forms (for ${\mathcal {D}}$
are called defining forms (for ${\mathcal {D}}$![]() ) in $U$
) in $U$![]() .
.
Given an $h$![]() -current with finite mass $T=\tau \mu$
-current with finite mass $T=\tau \mu$![]() and a $k$
and a $k$![]() -distribution ${\mathcal {D}}$
-distribution ${\mathcal {D}}$![]() on $\Omega$
on $\Omega$![]() , with $1\leq h\leq k\leq n$
, with $1\leq h\leq k\leq n$![]() , the tangency set of $T$
, the tangency set of $T$![]() with respect to ${\mathcal {D}}$
with respect to ${\mathcal {D}}$![]() is defined as
is defined as
If ${\mathcal {D}}$![]() is a $k$
is a $k$![]() -distribution of class $C^0$
-distribution of class $C^0$![]() on $\Omega$
on $\Omega$![]() and $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$
and $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$![]() are defining forms (for ${\mathcal {D}}$
are defining forms (for ${\mathcal {D}}$![]() ) in $U\subset \Omega$
) in $U\subset \Omega$![]() , then
, then

that is

Remark 2.5 Let $T=\tau \mu$![]() be a $k$
be a $k$![]() -current with finite mass in $\Omega$
-current with finite mass in $\Omega$![]() , let ${\mathcal {D}}$
, let ${\mathcal {D}}$![]() be a $k$
be a $k$![]() -distribution of class $C^0$
-distribution of class $C^0$![]() on $\Omega$
on $\Omega$![]() and observe that (cf. § 2.2) the following property holds: If $x\in \Gamma (\tau,\,{\mathcal {D}})$
and observe that (cf. § 2.2) the following property holds: If $x\in \Gamma (\tau,\,{\mathcal {D}})$![]() and $\tau (x)\not =0$
and $\tau (x)\not =0$![]() , then $\dim {\rm span} (\tau (x))=k$
, then $\dim {\rm span} (\tau (x))=k$![]() . Hence,
. Hence,
where
Observe that
by (2.2). Moreover, for all $x\in \Gamma _* (\tau,\,{\mathcal {D}})$![]() the $k$
the $k$![]() -vector $\tau (x)$
-vector $\tau (x)$![]() has to be simple (cf. § 2.2). If we assume the non-restrictive condition (2.3), then (2.5) becomes equivalent to $\mu (Z)=0$
has to be simple (cf. § 2.2). If we assume the non-restrictive condition (2.3), then (2.5) becomes equivalent to $\mu (Z)=0$![]() .
.
Recall that a $k$![]() -distribution ${\mathcal {D}}$
-distribution ${\mathcal {D}}$![]() of class $C^1$
of class $C^1$![]() is said to be involutive at $x\in \Omega$
is said to be involutive at $x\in \Omega$![]() if there exists a family $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$
if there exists a family $\omega ^{(1)},\,\ldots,\, \omega ^{(n-k)}$![]() of defining forms in a neighbourhood of $x$
of defining forms in a neighbourhood of $x$![]() such that
such that
One can easily verify that property (2.6) does not depend on the choice of the family of defining forms. The distribution ${\mathcal {D}}$![]() is called involutive (in $\Omega$
is called involutive (in $\Omega$![]() ) if it is involutive at every $x\in \Omega$
) if it is involutive at every $x\in \Omega$![]() .
.
Also recall that, if $p\geq 1$![]() and ${\mathcal {D}}$
and ${\mathcal {D}}$![]() is of class $C^p$
is of class $C^p$![]() , then a non-empty $C^p$
, then a non-empty $C^p$![]() imbedded submanifold $M$
imbedded submanifold $M$![]() of $\Omega$
of $\Omega$![]() such that ${\mathcal {T}}_xM ={\mathcal {D}}(x)$
such that ${\mathcal {T}}_xM ={\mathcal {D}}(x)$![]() for all $x\in M$
for all $x\in M$![]() is called a $C^p$
is called a $C^p$![]() integral manifold of ${\mathcal {D}}$
integral manifold of ${\mathcal {D}}$![]() . As a celebrated theorem established by Frobenius, the involutivity of ${\mathcal {D}}$
. As a celebrated theorem established by Frobenius, the involutivity of ${\mathcal {D}}$![]() is a necessary and sufficient condition for the existence of an integral manifold of ${\mathcal {D}}$
is a necessary and sufficient condition for the existence of an integral manifold of ${\mathcal {D}}$![]() through every point of $\Omega$
through every point of $\Omega$![]() . This topic is extensively covered in many books of differential geometry, for example in [Reference Chern, Chen and Lam5, § 3.2], [Reference Lee12, Ch. 19], [Reference Narasimhan14, § 2.11].
. This topic is extensively covered in many books of differential geometry, for example in [Reference Chern, Chen and Lam5, § 3.2], [Reference Lee12, Ch. 19], [Reference Narasimhan14, § 2.11].
2.5 Superdensity
The following definition generalizes the notion of $m$![]() -density point with respect to ${\mathcal {L}}^n$
-density point with respect to ${\mathcal {L}}^n$![]() (cf. [Reference Delladio6–Reference Delladio8]).
(cf. [Reference Delladio6–Reference Delladio8]).
Definition 2.6 Let $h\in [0,\,+\infty )$![]() and $E\in {\mathcal {B}}(\Omega )$
and $E\in {\mathcal {B}}(\Omega )$![]() . Then $x\in \Omega$
. Then $x\in \Omega$![]() is said to be an $h$
is said to be an $h$![]() -superdensity point of $E$
-superdensity point of $E$![]() with respect to a Borel measure $\lambda$
with respect to a Borel measure $\lambda$![]() if $\lambda (B_r(x)\setminus E)=\lambda (B_r(x))\, o(r^h)$
if $\lambda (B_r(x)\setminus E)=\lambda (B_r(x))\, o(r^h)$![]() , as $r\to 0+$
, as $r\to 0+$![]() . The set of all $h$
. The set of all $h$![]() -superdensity points of $E$
-superdensity points of $E$![]() with respect to $\lambda$
with respect to $\lambda$![]() is denoted by $E^{\lambda,h}$
is denoted by $E^{\lambda,h}$![]() .
.
Remark 2.7 Let $\lambda$![]() be a Borel measure, $h\in [0,\,+\infty )$
be a Borel measure, $h\in [0,\,+\infty )$![]() and $E,\, F\in {\mathcal {B}}(\Omega )$
and $E,\, F\in {\mathcal {B}}(\Omega )$![]() . The following facts hold:
. The following facts hold:
(1) If $\lambda ={\mathcal {L}}^n$
 then the set of all $h$
then the set of all $h$ -superdensity points of $E$
-superdensity points of $E$ with respect to $\lambda$
with respect to $\lambda$ coincides with the set of all $(n+h)$
coincides with the set of all $(n+h)$ -density points of $E$
-density points of $E$ , i.e. $E^{{\mathcal {L}}^n, h}=E^{(n+h)}$
, i.e. $E^{{\mathcal {L}}^n, h}=E^{(n+h)}$ .
.(2) $E^{\lambda,h_2}\subset E^{\lambda,h_1}$
 , whenever $0\leq h_1\leq h_2<+\infty$
, whenever $0\leq h_1\leq h_2<+\infty$ .
.(3) $(E\cap F)^{\lambda, h} = E^{\lambda, h}\cap F^{\lambda, h}$
 .
.(4) $\lambda (E\setminus E^{\lambda, 0}) = \lambda (E^{\lambda, 0}\setminus E)=0$
 (cf. [Reference Mattila13, corollary 2.14]).
(cf. [Reference Mattila13, corollary 2.14]).(5) Let $E$
 be open. Then $E\subset E^{\lambda, h}$
be open. Then $E\subset E^{\lambda, h}$ , where the inclusion can be strict (e.g. for $\lambda ={\mathcal {L}}^n$
, where the inclusion can be strict (e.g. for $\lambda ={\mathcal {L}}^n$ and $E=B_r(x)\setminus \{x\}$
and $E=B_r(x)\setminus \{x\}$ one has $E^{\lambda, h}=B_r(x)$
one has $E^{\lambda, h}=B_r(x)$ ). The equality $E = E^{\lambda, h}$
). The equality $E = E^{\lambda, h}$ occurs instead in the case that all connected components of $E$
occurs instead in the case that all connected components of $E$ are simply connected.
are simply connected.(6) If $x\in \Omega$
 and $\lambda (B_r(x))=0$
and $\lambda (B_r(x))=0$ for some $r>0$
for some $r>0$ , then $x\in E^{\lambda, k}$
, then $x\in E^{\lambda, k}$ for all $k\in [0,\,+\infty )$
for all $k\in [0,\,+\infty )$ .
.(7) $E^{\lambda \Large \llcorner E , k}=\Omega$
 for all $k\in [0,\,+\infty )$
for all $k\in [0,\,+\infty )$ .
.
3. The main result
Let $h,\, n$![]() be integers satisfying $1\leq h \leq n$
be integers satisfying $1\leq h \leq n$![]() and $\Omega$
and $\Omega$![]() be an open subset of ${\mathbb {R}}^n$
be an open subset of ${\mathbb {R}}^n$![]() . Moreover, let $T$
. Moreover, let $T$![]() be a normal $h$
be a normal $h$![]() -current on $\Omega$
-current on $\Omega$![]() . Then $T=\tau \mu$
. Then $T=\tau \mu$![]() and $\partial T=\tau ' \mu '$
and $\partial T=\tau ' \mu '$![]() , where $\mu,\, \mu '$
, where $\mu,\, \mu '$![]() are two finite positive measures on $\Omega$
are two finite positive measures on $\Omega$![]() and
and
are two Borel maps such that $\tau \in L^1(\mu ),\, \tau '\in L^1(\mu ')$![]() , cf. § 2.3. Recall that
, cf. § 2.3. Recall that
by (2.2). In particular, $\vert \tau \mu \vert$![]() and $\vert \tau '\mu '\vert$
and $\vert \tau '\mu '\vert$![]() are Radon.
are Radon.
Remark 3.1 By [Reference Mattila13, corollary 2.14] there exists $N\subset \Omega$![]() such that $\mu (N)=0$
such that $\mu (N)=0$![]() and
and

for all $x\in \Omega \setminus N$![]() .
.
We also consider a continuous differential $l$![]() -form $\omega$
-form $\omega$![]() on an open set $U\subset \Omega$
on an open set $U\subset \Omega$![]() with $1\leq l\leq h-1$
with $1\leq l\leq h-1$![]() and set for simplicity
and set for simplicity
Remark 3.2 We can easily prove that
Indeed, let $x\in K^{\vert \tau \mu \vert, 0}\setminus N$![]() and $\alpha \in \wedge ^{h-l}({\mathbb {R}}^n)$
and $\alpha \in \wedge ^{h-l}({\mathbb {R}}^n)$![]() . Then, denoting by $\theta$
. Then, denoting by $\theta$![]() the constant differential $(h-l)$
the constant differential $(h-l)$![]() -form on $\Omega$
-form on $\Omega$![]() such that $\theta _y=\alpha$
such that $\theta _y=\alpha$![]() for all $y\in \Omega$
for all $y\in \Omega$![]() , we have
, we have

by (3.1). Hence,

by (3.2). Finally, (3.3) follows from the arbitrariness of $x\in K^{\vert \tau \mu \vert, 0}\setminus N$![]() and $\alpha \in \wedge ^{h-l}({\mathbb {R}}^n)$
and $\alpha \in \wedge ^{h-l}({\mathbb {R}}^n)$![]() .
.
Theorem 3.3 Let $T=\tau \mu$![]() , $\partial T=\tau '\mu '$
, $\partial T=\tau '\mu '$![]() , $\omega$
, $\omega$![]() , $K$
, $K$![]() , $K'$
, $K'$![]() and $N$
and $N$![]() be as above with the additional assumption that $\omega$
be as above with the additional assumption that $\omega$![]() is of class $C^1$
is of class $C^1$![]() . Moreover, let $x\in K^{\vert \tau \mu \vert, 1}\setminus N$
. Moreover, let $x\in K^{\vert \tau \mu \vert, 1}\setminus N$![]() and $s\in [0,\,+\infty )$
and $s\in [0,\,+\infty )$![]() be such that
be such that
Finally, let $\alpha$![]() be arbitrarily chosen in $\wedge ^{h-l-1}({\mathbb {R}}^n)$
be arbitrarily chosen in $\wedge ^{h-l-1}({\mathbb {R}}^n)$![]() . Then
. Then
Proof. Let $\rho \in (0,\,1)$![]() and consider $g\in C_c^1(B_1(0))$
and consider $g\in C_c^1(B_1(0))$![]() such that $0\leq g\leq 1$
such that $0\leq g\leq 1$![]() , $g\vert _{B_\rho (0)}\equiv 1$
, $g\vert _{B_\rho (0)}\equiv 1$![]() and
and
For every real number $r$![]() such that $0< r<{\rm dist}(x,\,{\mathbb {R}}^n\setminus U)$
such that $0< r<{\rm dist}(x,\,{\mathbb {R}}^n\setminus U)$![]() , we define $g_r\in C_c^1(B_r(x))$
, we define $g_r\in C_c^1(B_r(x))$![]() as
as
and observe that (for all $y\in B_r(x)$![]() and $i=1,\,\ldots,\,n$
and $i=1,\,\ldots,\,n$![]() )
)
If $\theta$![]() denotes the constant differential $(h-l-1)$
denotes the constant differential $(h-l-1)$![]() -form on $\Omega$
-form on $\Omega$![]() such that $\theta _y=\alpha$
such that $\theta _y=\alpha$![]() , for all $y\in \Omega$
, for all $y\in \Omega$![]() , then
, then
hence
that is
From now on, for simplicity, we will denote $B_r(x)$![]() by $B_r$
by $B_r$![]() and $B_{\rho r}(x)$
and $B_{\rho r}(x)$![]() by $B_{\rho r}$
by $B_{\rho r}$![]() . Recalling the definition of $K$
. Recalling the definition of $K$![]() and $K'$
and $K'$![]() , we obtain
, we obtain
and then, by (3.5),
On the other hand, we have

From (3.6), (3.7) and (3.5) it follows that

hence (also recalling (3.1))

Observe that the constant $C$![]() above is independent from $r$
above is independent from $r$![]() and $\rho$
and $\rho$![]() . Recalling (3.2) and that $x\in K^{\vert \tau \mu \vert, 1}$
. Recalling (3.2) and that $x\in K^{\vert \tau \mu \vert, 1}$![]() , we obtain (letting $r\to 0+$
, we obtain (letting $r\to 0+$![]() )
)

Thus
for all $\rho \in (0,\,1)$![]() . The conclusion follows by letting $\rho \to 1-$
. The conclusion follows by letting $\rho \to 1-$![]() .
.
Remark 3.4 Using proposition 2.1 with $\lambda =\vert \tau '\mu '\vert \Large \llcorner (\Omega \setminus K')$![]() , it is easy to verify that (3.4) is equivalent to the following inequality:
, it is easy to verify that (3.4) is equivalent to the following inequality:
4. Application to the context of distributions
Proposition 4.1 Let $T=\tau \mu$![]() be a $k$
be a $k$![]() -current with finite mass in $\Omega$
-current with finite mass in $\Omega$![]() and let ${\mathcal {D}}$
and let ${\mathcal {D}}$![]() be a $k$
be a $k$![]() -distribution of class $C^0$
-distribution of class $C^0$![]() on $\Omega$
on $\Omega$![]() . Then there exists $N\subset \Omega$
. Then there exists $N\subset \Omega$![]() such that
such that
Proof. We can find a countable family $B_1,\,B_2,\,\ldots$![]() of open balls of ${\mathbb {R}}^n$
of open balls of ${\mathbb {R}}^n$![]() such that:
such that:
(i) $\cup _i B_i=\Omega$
 ;
;(ii) for each $i=1,\,2,\,\ldots$
 there exists a family $\omega ^{(i,1)},\,\ldots,\, \omega ^{(i,n-k)}$
there exists a family $\omega ^{(i,1)},\,\ldots,\, \omega ^{(i,n-k)}$ of defining forms for ${\mathcal {D}}$
of defining forms for ${\mathcal {D}}$ in $B_i$
in $B_i$ (recall from § 2.4 that the $\omega ^{(i,j)}$
(recall from § 2.4 that the $\omega ^{(i,j)}$ are $C^0$
are $C^0$ differential $1$
differential $1$ -forms on $B_i$
-forms on $B_i$ ).
).
For all $i=1,\,2,\,\ldots$![]() and $j=1,\,\ldots,\, n-k$
and $j=1,\,\ldots,\, n-k$![]() , we define
, we define
and recall from (2.4), remarks 3.1 and 3.2 that the following facts hold:
(1) $\Gamma (\tau,\,{\mathcal {D}})\cap B_i=\cap _{j=1}^{n-k} K_{i,j}$
 ;
;(2) $N_{i,j}\subset \Omega$
 has to exist such that
\[ \mu (N_{i,j})=0,\quad K_{i,j}^{\vert\tau\mu\vert , 0}\setminus N_{i,j}\subset K_{i,j}. \]
has to exist such that
\[ \mu (N_{i,j})=0,\quad K_{i,j}^{\vert\tau\mu\vert , 0}\setminus N_{i,j}\subset K_{i,j}. \]
Hence, if we define
we obtain $\mu (N)=0$![]() and, for all $i=1,\,2,\,\ldots$
and, for all $i=1,\,2,\,\ldots$![]() (by also recalling the properties listed in remark 2.7),
(by also recalling the properties listed in remark 2.7),

The conclusion follows by recalling that the balls $B_i$![]() cover $\Omega$
cover $\Omega$![]() .
.
Corollary 4.2 Let $T$![]() be a normal $k$
be a normal $k$![]() -current in $\Omega$
-current in $\Omega$![]() , so we have the usual representations $T=\tau \mu$
, so we have the usual representations $T=\tau \mu$![]() and $\partial T=\tau '\mu '$
and $\partial T=\tau '\mu '$![]() (cf. § 3). Moreover, consider a $k$
(cf. § 3). Moreover, consider a $k$![]() -distribution ${\mathcal {D}}$
-distribution ${\mathcal {D}}$![]() of class $C^1$
of class $C^1$![]() on $\Omega$
on $\Omega$![]() and let $\Upsilon$
and let $\Upsilon$![]() denote the set of all points $x\in \Omega$
denote the set of all points $x\in \Omega$![]() such that:
such that:
(i) $\tau (x)\not =0$
 ;
;(ii) There exists $s(x)\in [0,\,+\infty )$
 such that $\Theta _*^{s(x)} (\mu,\,x)=\Theta ^{*{s(x)}} (\mu,\,x)\in (0,\,+\infty )$
such that $\Theta _*^{s(x)} (\mu,\,x)=\Theta ^{*{s(x)}} (\mu,\,x)\in (0,\,+\infty )$ ;
;(iii) $x\in \Gamma (\tau,\,{\mathcal {D}})^{\vert \tau \mu \vert, 1}$
 (note that $\Gamma (\tau,\,{\mathcal {D}})^{\vert \tau \mu \vert, 1}=\Gamma _* (\tau,\,{\mathcal {D}})^{\vert \tau \mu \vert, 1}$
(note that $\Gamma (\tau,\,{\mathcal {D}})^{\vert \tau \mu \vert, 1}=\Gamma _* (\tau,\,{\mathcal {D}})^{\vert \tau \mu \vert, 1}$ , by remark 2.5);
, by remark 2.5);(iv) $\vert \tau '\mu '\vert (B_r(x)\setminus \Gamma (\tau ',\,{\mathcal {D}})) = o(r^{s(x)})$
 , as $r\to 0+$
, as $r\to 0+$ .
.
If $N$![]() is the $\mu$
is the $\mu$![]() -null set defined in proposition 4.1 and $x\in \Upsilon \setminus N$
-null set defined in proposition 4.1 and $x\in \Upsilon \setminus N$![]() , then the following properties hold:
, then the following properties hold:
(1) The $k$
 -vector $\tau (x)$
-vector $\tau (x)$ is simple and ${\rm span} (\tau (x))={\mathcal {D}}(x)$
is simple and ${\rm span} (\tau (x))={\mathcal {D}}(x)$ ;
;(2) The distribution ${\mathcal {D}}$
 is involutive at $x$
is involutive at $x$ .
.
Proof.
(1) We have $\Gamma (\tau,\,{\mathcal {D}})^{\vert \tau \mu \vert, 1} \subset \Gamma (\tau,\,{\mathcal {D}})^{\vert \tau \mu \vert, 0}$
 , by property (2) in remark 2.7. Hence, $x\in {\rm span} (\tau (x))\subset {\mathcal {D}}(x)$
, by property (2) in remark 2.7. Hence, $x\in {\rm span} (\tau (x))\subset {\mathcal {D}}(x)$ , by proposition 4.1. Since $\tau (x)\not =0$
, by proposition 4.1. Since $\tau (x)\not =0$ , the conclusion follows from properties (2) and (4) in § 2.2.
, the conclusion follows from properties (2) and (4) in § 2.2.(2) Let $\{B_i\}$
 , $\{\omega ^{(i,j)}\}$
, $\{\omega ^{(i,j)}\}$ , $\{K_{i,j}\}$
, $\{K_{i,j}\}$ and $\{N_{i,j}\}$
and $\{N_{i,j}\}$ be the families defined in the proof of proposition 4.1 (here we can obviously assume that the $\omega ^{(i,j)}$
be the families defined in the proof of proposition 4.1 (here we can obviously assume that the $\omega ^{(i,j)}$ are of class $C^1$
are of class $C^1$ ). Without loss of generality we can suppose that $x\in B_1$
). Without loss of generality we can suppose that $x\in B_1$ . Then, by recalling assumption (iii), properties (3) and (5) in remark 2.7 and (2.4), we obtain
(4.1)\begin{align} x\in \Upsilon\cap B_1 \setminus N & \subset \Gamma (\tau,{\mathcal{D}})^{\vert\tau \mu\vert , 1} \cap B_1 \setminus N\nonumber\\ & = \Gamma (\tau,{\mathcal{D}})^{\vert\tau \mu\vert , 1} \cap B_1^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & = \left(\Gamma (\tau,{\mathcal{D}}) \cap B_1\right)^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & = \left(\bigcap_{j=1}^{n-k}K_{1,j}\right)^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & = \bigcap_{j=1}^{n-k}K_{1,j}^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & \subset \bigcap_{j=1}^{n-k}\left( K_{1,j}^{\vert\tau \mu\vert , 1} \setminus N_{1,j}\right). \end{align}Moreover, (by (2.4))
. Then, by recalling assumption (iii), properties (3) and (5) in remark 2.7 and (2.4), we obtain
(4.1)\begin{align} x\in \Upsilon\cap B_1 \setminus N & \subset \Gamma (\tau,{\mathcal{D}})^{\vert\tau \mu\vert , 1} \cap B_1 \setminus N\nonumber\\ & = \Gamma (\tau,{\mathcal{D}})^{\vert\tau \mu\vert , 1} \cap B_1^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & = \left(\Gamma (\tau,{\mathcal{D}}) \cap B_1\right)^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & = \left(\bigcap_{j=1}^{n-k}K_{1,j}\right)^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & = \bigcap_{j=1}^{n-k}K_{1,j}^{\vert\tau \mu\vert , 1} \setminus N\nonumber\\ & \subset \bigcap_{j=1}^{n-k}\left( K_{1,j}^{\vert\tau \mu\vert , 1} \setminus N_{1,j}\right). \end{align}Moreover, (by (2.4)) \[ \Gamma (\tau' , {\mathcal{D}})\cap B_1 =\bigcap_{j=1}^{n-k}K'_{1,j}, \]where
\[ \Gamma (\tau' , {\mathcal{D}})\cap B_1 =\bigcap_{j=1}^{n-k}K'_{1,j}, \]where \[ K_{1,j}':={\mathcal{K}} (\tau' , \omega^{(1,j)})\quad (j=1,\ldots,n-k). \]Hence,
\[ K_{1,j}':={\mathcal{K}} (\tau' , \omega^{(1,j)})\quad (j=1,\ldots,n-k). \]Hence, \[ B_r(x)\setminus K'_{1,j}\subset B_r(x)\setminus \Gamma (\tau' , {\mathcal{D}})\quad (j=1,\ldots, n-k), \]provided $r$
\[ B_r(x)\setminus K'_{1,j}\subset B_r(x)\setminus \Gamma (\tau' , {\mathcal{D}})\quad (j=1,\ldots, n-k), \]provided $r$
 is small enough. Recalling also (iv), we obtain
(4.2)\begin{equation} \vert \tau' \mu'\vert (B_r(x)\setminus K'_{1,j}) =o (r^{s(x)})\quad (j=1,\ldots, n-k) \end{equation}as $r\to 0+$
is small enough. Recalling also (iv), we obtain
(4.2)\begin{equation} \vert \tau' \mu'\vert (B_r(x)\setminus K'_{1,j}) =o (r^{s(x)})\quad (j=1,\ldots, n-k) \end{equation}as $r\to 0+$
 . Now (ii), (4.1), (4.2) and theorem 3.3 yield
\[ \langle\tau(x)\Large\llcorner\alpha ; (d\omega^{(1,j)})_x \rangle =0 \quad (j=1,\ldots, n-k) \]for all $\alpha \in \wedge ^{k-2}({\mathbb {R}}^n)$
. Now (ii), (4.1), (4.2) and theorem 3.3 yield
\[ \langle\tau(x)\Large\llcorner\alpha ; (d\omega^{(1,j)})_x \rangle =0 \quad (j=1,\ldots, n-k) \]for all $\alpha \in \wedge ^{k-2}({\mathbb {R}}^n)$
 . From proposition 2.2 we obtain
\[ ({\rm d}\omega^{(1,j)})_x\vert_{{\rm span} (\tau(x))\times {\rm span} (\tau(x))}=0\quad (j=1,\ldots, n-k). \]Now the conclusion follows from statement (1).
. From proposition 2.2 we obtain
\[ ({\rm d}\omega^{(1,j)})_x\vert_{{\rm span} (\tau(x))\times {\rm span} (\tau(x))}=0\quad (j=1,\ldots, n-k). \]Now the conclusion follows from statement (1).
Remark 4.3 Let ${\mathcal {M}}$![]() be a closed $k$
be a closed $k$![]() -dimensional $C^1$
-dimensional $C^1$![]() submanifold of $\Omega$
submanifold of $\Omega$![]() with $C^1$
with $C^1$![]() boundary such that ${\mathcal {H}}^k ({\mathcal {M}})$
boundary such that ${\mathcal {H}}^k ({\mathcal {M}})$![]() and ${\mathcal {H}}^{k-1}(\partial {\mathcal {M}})$
and ${\mathcal {H}}^{k-1}(\partial {\mathcal {M}})$![]() are finite. Let $\tau _{\mathcal {M}}$
are finite. Let $\tau _{\mathcal {M}}$![]() and $\tau '_{\mathcal {M}}$
and $\tau '_{\mathcal {M}}$![]() be, respectively, a continuous unit simple $k$
be, respectively, a continuous unit simple $k$![]() -vectorfield orienting ${\mathcal {M}}$
-vectorfield orienting ${\mathcal {M}}$![]() and a continuous unit simple $(k-1)$
and a continuous unit simple $(k-1)$![]() -vectorfield orienting $\partial {\mathcal {M}}$
-vectorfield orienting $\partial {\mathcal {M}}$![]() such that the Stoke's identity
such that the Stoke's identity
holds for all $C^1$![]() differential $(k-1)$
differential $(k-1)$![]() -forms with compact support in $\Omega$
-forms with compact support in $\Omega$![]() . Then we consider the maps $\tau :\Omega \to \wedge _k({\mathbb {R}}^n)$
. Then we consider the maps $\tau :\Omega \to \wedge _k({\mathbb {R}}^n)$![]() and $\tau ':\Omega \to \wedge _{k-1}({\mathbb {R}}^n)$
and $\tau ':\Omega \to \wedge _{k-1}({\mathbb {R}}^n)$![]() extending $\tau _{\mathcal {M}}$
extending $\tau _{\mathcal {M}}$![]() and $\tau '_{{\mathcal {M}}}$
and $\tau '_{{\mathcal {M}}}$![]() , respectively, such that $\tau \vert _{\Omega \setminus {\mathcal {M}}}\equiv 0$
, respectively, such that $\tau \vert _{\Omega \setminus {\mathcal {M}}}\equiv 0$![]() and $\tau '\vert _{\Omega \setminus \partial {\mathcal {M}}}\equiv 0$
and $\tau '\vert _{\Omega \setminus \partial {\mathcal {M}}}\equiv 0$![]() . We observe that:
. We observe that:
(1) $T:= \tau \,{\mathcal {H}}^k\Large \llcorner {\mathcal {M}}$
 is a normal $k$
is a normal $k$ -current, with $\partial T = \tau '\, {\mathcal {H}}^{k-1}\Large \llcorner \partial {\mathcal {M}}$
-current, with $\partial T = \tau '\, {\mathcal {H}}^{k-1}\Large \llcorner \partial {\mathcal {M}}$ .
.(2) The equations (3.2) hold for all $x\in {\mathcal {M}}$
 , hence we can assume that the set $N$
, hence we can assume that the set $N$ introduced in § 3 coincides with $\Omega \setminus {\mathcal {M}}$
introduced in § 3 coincides with $\Omega \setminus {\mathcal {M}}$ .
.
Now set for simplicity
and let us consider
We observe that
by (3) and (7) in remark 2.7. Analogously,

Hence, we easily obtain
Now, by applying corollary 4.2, we conclude that ${\rm span}(\tau _{\mathcal {M}} (x))={\mathcal {D}}(x)$![]() and ${\mathcal {D}}$
and ${\mathcal {D}}$![]() is involutive at $x$
is involutive at $x$![]() .
.
The following corollary generalizes the property established in remark 4.3 for the smooth case.
Corollary 4.4 Let ${\mathcal {D}}$![]() and $T$
and $T$![]() be, respectively, a $k$
be, respectively, a $k$![]() -distribution of class $C^1$
-distribution of class $C^1$![]() in $\Omega$
in $\Omega$![]() and an integral $k$
and an integral $k$![]() -current in $\Omega$
-current in $\Omega$![]() . Moreover, if $T=[\hskip -0.6mm [ R,\,\eta,\,\theta ]\hskip -0.6mm ]$
. Moreover, if $T=[\hskip -0.6mm [ R,\,\eta,\,\theta ]\hskip -0.6mm ]$![]() and $\partial T=[\hskip -0.6mm [ R',\,\eta ',\,\theta ']\hskip -0.6mm ]$
and $\partial T=[\hskip -0.6mm [ R',\,\eta ',\,\theta ']\hskip -0.6mm ]$![]() (cf. § 2.3 for the notation), let $\mathcal {J}$
(cf. § 2.3 for the notation), let $\mathcal {J}$![]() be the set of all $x\in \Omega$
be the set of all $x\in \Omega$![]() such that
such that
Then ${\mathcal {D}}$![]() is involutive at $({\mathcal {H}}^k\Large \llcorner \text{R})$
is involutive at $({\mathcal {H}}^k\Large \llcorner \text{R})$![]() -a.e. $x\in \mathcal {J}$
-a.e. $x\in \mathcal {J}$![]() .
.
Proof. Let us define
so that
From [Reference Mattila13, corollary 2.14] and [Reference Mattila13, theorem 17.6] it follows that the following equalities hold at $\mu$![]() -a.e. $x\in \Omega$
-a.e. $x\in \Omega$![]() :
:

hence also
We shall prove the thesis by applying corollary 4.2. To this end, it will suffice to prove that conditions (i–iv) of corollary 4.2 are verified at $\mu$![]() -a.e. $x\in {\mathcal {J}}$
-a.e. $x\in {\mathcal {J}}$![]() (i.e. $\mu ({\mathcal {J}}\setminus \Upsilon )=0$
(i.e. $\mu ({\mathcal {J}}\setminus \Upsilon )=0$![]() ), which we do below:
), which we do below:
• Assumption (i) is verified at $\mu$
 -a.e. $x\in \Omega$
-a.e. $x\in \Omega$ , since $T$
, since $T$ is rectifiable (cf. § 2.3).
is rectifiable (cf. § 2.3).• Assumption (ii) is verified at $\mu$
 -a.e. $x\in \Omega$
-a.e. $x\in \Omega$ (with $s(x)=k$
(with $s(x)=k$ ), by the second equality of (4.4).
), by the second equality of (4.4).• Since $\Gamma _*(\tau,\,{\mathcal {D}})=\Gamma (\eta,\,{\mathcal {D}})$
 , we have
\begin{align*} \frac{\vert \tau\,\mu\vert (B_r(x)\setminus\Gamma_*(\tau,{\mathcal{D}}))}{\vert \tau\,\mu\vert (B_r(x))} & =\frac{\int_{B_r(x)\cap (R\setminus\Gamma (\eta,{\mathcal{D}}))}\theta\, d{\mathcal{H}}^k}{\int_{B_r(x)}\theta\,{\rm d}\mu}\\ & =\frac{\int_{B_r(x)\cap (R\setminus \Gamma (\eta,{\mathcal{D}}))}\theta\,{\rm d}{\mathcal{H}}^k}{r^{k+1}} \cdot\left(\frac{\int_{B_r(x)}\theta\,{\rm d}\mu}{r^k}\right)^{{-}1} r. \end{align*}Hence, recalling also (4.3) and (4.5), we find that assumption (iii) is verified at $\mu$
, we have
\begin{align*} \frac{\vert \tau\,\mu\vert (B_r(x)\setminus\Gamma_*(\tau,{\mathcal{D}}))}{\vert \tau\,\mu\vert (B_r(x))} & =\frac{\int_{B_r(x)\cap (R\setminus\Gamma (\eta,{\mathcal{D}}))}\theta\, d{\mathcal{H}}^k}{\int_{B_r(x)}\theta\,{\rm d}\mu}\\ & =\frac{\int_{B_r(x)\cap (R\setminus \Gamma (\eta,{\mathcal{D}}))}\theta\,{\rm d}{\mathcal{H}}^k}{r^{k+1}} \cdot\left(\frac{\int_{B_r(x)}\theta\,{\rm d}\mu}{r^k}\right)^{{-}1} r. \end{align*}Hence, recalling also (4.3) and (4.5), we find that assumption (iii) is verified at $\mu$
 -a.e. $x\in {\mathcal {J}}$
-a.e. $x\in {\mathcal {J}}$ .
.• If we define $Z':=\{x\in \Omega \,\vert \, \tau '(x)=0\}$
 , then we have
\[ \Gamma (\tau',{\mathcal{D}}) =Z'\bigcup \Gamma (\eta',{\mathcal{D}}),\quad \vert\tau'\mu'\vert (Z')=0. \]Thus,
, then we have
\[ \Gamma (\tau',{\mathcal{D}}) =Z'\bigcup \Gamma (\eta',{\mathcal{D}}),\quad \vert\tau'\mu'\vert (Z')=0. \]Thus, \begin{align*} \vert\tau'\mu'\vert (B_r(x)\setminus \Gamma (\tau',{\mathcal{D}})) & =\vert\tau'\mu'\vert (B_r(x)\setminus \Gamma (\eta',{\mathcal{D}}))\\ & =\int_{B_r(x)\cap (R' \setminus \Gamma (\eta',{\mathcal{D}}))}\theta'\,{\rm d}{\mathcal{H}}^{k-1}. \end{align*}From this equality and (4.3) it follows that assumption (iv) is verified at every $x\in {\mathcal {J}}$
\begin{align*} \vert\tau'\mu'\vert (B_r(x)\setminus \Gamma (\tau',{\mathcal{D}})) & =\vert\tau'\mu'\vert (B_r(x)\setminus \Gamma (\eta',{\mathcal{D}}))\\ & =\int_{B_r(x)\cap (R' \setminus \Gamma (\eta',{\mathcal{D}}))}\theta'\,{\rm d}{\mathcal{H}}^{k-1}. \end{align*}From this equality and (4.3) it follows that assumption (iv) is verified at every $x\in {\mathcal {J}}$
 .
.