Homogeneous sharp Sobolev inequalities on product manifolds

Abstract

Let (M, g) and (N, h) be compact Riemannian manifolds of dimensions m and n, respectively. For p-homogeneous convex functions f(s, t) on [0,∞) × [0, ∞), we study the validity and non-validity of the first-order optimal Sobolev inequality on H^{1, p}(M × N) where 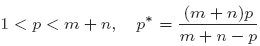and K_f = K_f (m, n, p) is the best constant of the homogeneous Sobolev inequality on D^{1, p} (R^m+n), The proof of the non-validity relies on the knowledge of extremal functions associated with the Sobolev inequality above. In order to obtain such extremals we use mass transportation and convex analysis results. Since variational arguments do not work for general functions f, we investigate the validity in a uniform sense on f and argue with suitable approximations of f which are also essential in the non-validity. Homogeneous Sobolev inequalities on product manifolds are connected to elliptic problems involving a general class of operators.