Duality and compactness results in high-contrast homogenization of incompressible two-dimensional elasticity problems

Abstract

We study incompressible two-dimensional elasticity problems with high-contrast coefficients. The Keller–Dykhne duality relations are extended to the case of Hooke's laws which are equicoercive and uniformly bounded in L¹ but not in L∞. A compactness result is obtained for Hooke's laws which are uniformly bounded from above and such that their inverses are bounded in L¹ but not in L∞, with a refinement in the periodic case. Moreover, we establish a compactness result in 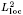for a sequence of two-dimensional vector-valued functions in 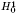which are only bounded in L².