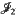Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:43:02.740Z Has data issue: false hasContentIssue false
  • English
  • Français

The -radical in structural matrix near rings, II

Published online by Cambridge University Press:  14 November 2011

Leon van Wyk
Leon van Wyk
Affiliation:
Department of Mathematics, University of Stellenbosch, Stellenbosch 7600, South Africa
Get access Rights & Permissions [Opens in a new window]

Synopsis

Whether the 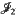-radical of a structural matrix near-ring 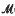(B, R) is the sum of two non-trivial ideals, one of which is nilpotent, is an open problem. However, it is known that 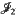((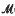B, R)) contains two ideals 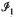and 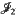, which are respectively precisely the two ideals, the sum of which is the Jacobson radical, in the case where the underlying near-ring is a ring. We strengthen our conjecture that 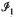and 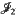are the sought-after ideals by showing that 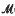(B, R)/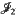≅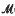(C, R) in the near-ring case, where C is the largest symmetric Boolean matrix such that C≦B, and by showing that 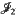is nilpotent.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 122 , Issue 1-2 , 1992 , pp. 53 - 61
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Kim, K. H.. Boolean Matrix Theory and Applications (New York: Marcel Dekker 1982).Google Scholar
2Meldrum, J. D. P.. Near-Rings and their Links with Groups, Research Notes in Mathematics 134 (London: Pitman, 1985).Google Scholar
3Meldrum, J. D. P. and Van der Walt, A. P. J.. Matrix near-rings. Arch. Math. 47 (1986), 312–319.CrossRefGoogle Scholar
4Pilz, G.. Near-Rings, revised edn (Amsterdam: North-Holland, 1983).Google Scholar
5Van der Walt, A. P. J.. Primitivity in matrix near-rings. Quaestiones Math. 9 (1986), 459–469.CrossRefGoogle Scholar
6Van der Walt, A. P. J. and Van Wyk, L.. The J 2-ratlical in structural matrix near-rings. J. Algebra 123 (1989), 248–261.CrossRefGoogle Scholar
7Van Wyk, L.. Special radicals in structural matrix rings. Comm. Algebra 16 (1988), 421–435.CrossRefGoogle Scholar
8Van Wyk, L.. The 2-primitive ideals of structural matrix near-rings. Proc. Edinburgh Math. Soc. 34 (1991), 229–239.CrossRefGoogle Scholar
9Wauters, P. and Jespers, E.. Rings graded by an inverse semigroup with finitely many idempotents. Houston J. Math. 15 (1989), 291–304.Google Scholar