Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Umar, Abdullahi
1993.
On the semigroups of partial one-to-one order-decreasing finite transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 123,
Issue. 2,
p.
355.
Umar, Abdullahi
1996.
Semigroups of Order-decreasing Transformations: The Isomorphism Theorem.
Semigroup Forum,
Vol. 53,
Issue. 1,
p.
220.
Saitô, T.
Aoki, K.
and
Kajitori, K.
1996.
Remarks on isomorphisms of regressive transformation semigroups.
Semigroup Forum,
Vol. 53,
Issue. 1,
p.
129.
Umar, Abdullahi
1997.
On certain infinite semigroups of order-decreasing transformations i.
Communications in Algebra,
Vol. 25,
Issue. 9,
p.
2987.
Araújo, João
and
Konieczny, Janusz
2004.
Semigroups of Transformations Preserving an Equivalence Relation and a Cross-Section.
Communications in Algebra,
Vol. 32,
Issue. 5,
p.
1917.
Laradji, A
and
Umar, A
2004.
Combinatorial results for semigroups of order-preserving partial transformations.
Journal of Algebra,
Vol. 278,
Issue. 1,
p.
342.
Xiuliang, Yang
and
Haobo, Yang
2005.
ℋ
-Trivial Transformation Semibands and Digraphs
.
Communications in Algebra,
Vol. 33,
Issue. 5,
p.
1461.
Yang, Xiuliang
and
Yang, Haobo
2009.
ISOMORPHISMS OF TRANSFORMATION SEMIGROUPS ASSOCIATED WITH SIMPLE DIGRAPHS.
Asian-European Journal of Mathematics,
Vol. 02,
Issue. 04,
p.
727.
Pei, Huisheng
and
Zhou, Huijuan
2011.
Abundant Semigroups of Transformations Preserving an Equivalence Relation.
Algebra Colloquium,
Vol. 18,
Issue. 01,
p.
77.
Almeida, J.
and
Moura, A.
2011.
Idempotent-generated semigroups and pseudovarieties.
Proceedings of the Edinburgh Mathematical Society,
Vol. 54,
Issue. 3,
p.
545.
Yang, Haobo
and
Yang, Xiuliang
2012.
Automorphisms of partition order-decreasing transformation monoids.
Semigroup Forum,
Vol. 85,
Issue. 3,
p.
513.
Zhao, Ping
and
Yang, Mei
2012.
REGULARITY AND GREEN'S RELATIONS ON SEMIGROUPS OF TRANSFORMATION PRESERVING ORDER AND COMPRESSION.
Bulletin of the Korean Mathematical Society,
Vol. 49,
Issue. 5,
p.
1015.
SUN, LEI
and
WANG, LIMIN
2013.
NATURAL PARTIAL ORDER IN SEMIGROUPS OF TRANSFORMATIONS WITH INVARIANT SET.
Bulletin of the Australian Mathematical Society,
Vol. 87,
Issue. 1,
p.
94.
Zhao, Ping
and
Yang, Mei
2013.
MAXIMAL PROPERTIES OF SOME SUBSEMIBANDS OF ORDER-PRESERVING FULL TRANSFORMATIONS.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 2,
p.
627.
SUN, LEI
and
WANG, LIMIN
2014.
ABUNDANCE OF THE SEMIGROUP OF ALL TRANSFORMATIONS OF A SET THAT REFLECT AN EQUIVALENCE RELATION.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 02,
p.
1350088.
SUN, Lei
and
HAN, Xuefeng
2016.
Abundance of $E$-order-preserving transformation semigroups.
TURKISH JOURNAL OF MATHEMATICS,
Vol. 40,
Issue. ,
p.
32.
Sun, Lei
and
Wang, Limin
2016.
Abundance of Semigroups of Transformations Restricted by an Equivalence.
Communications in Algebra,
Vol. 44,
Issue. 5,
p.
1829.
Zhao, Ping
You, Taijie
and
Hu, Huabi
2018.
On the ranks of the semigroup of A-decreasing finite transformations.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 02,
p.
1850036.
Sun, Lei
2020.
A Natural Partial Order on Partition Order-Decreasing Transformation Semigroups.
Bulletin of the Iranian Mathematical Society,
Vol. 46,
Issue. 5,
p.
1357.
Umar, A.
and
Zubairu, M. M.
2021.
On certain semigroups of contraction mappings of a finite chain.
Algebra and Discrete Mathematics,
Vol. 32,
Issue. 2,
p.
299.
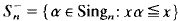 be the subsemigroup of all decreasing maps of Singn. In this paper it is shown that
be the subsemigroup of all decreasing maps of Singn. In this paper it is shown that 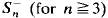 is a non-regular abundant semigroup with n − 1
is a non-regular abundant semigroup with n − 1 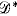 -classes and
-classes and  . Moreover,
. Moreover, 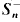 is idempotent-generated and it is generated by the n(n − 1)/2 idempotents in J*n−1. Let
is idempotent-generated and it is generated by the n(n − 1)/2 idempotents in J*n−1. Let