Article contents
Concentration behaviour of normalized ground states of the mass critical fractional Schrödinger equations with ring-shaped potentials
Published online by Cambridge University Press: 14 December 2022
Abstract
We consider $L^{2}$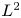 -constraint minimizers of the mass critical fractional Schrödinger energy functional with a ring-shaped potential $V(x)=(|x|-M)^{2}$
-constraint minimizers of the mass critical fractional Schrödinger energy functional with a ring-shaped potential $V(x)=(|x|-M)^{2}$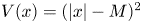 , where $M>0$
, where $M>0$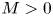 and $x\in \mathbb {R}^{2}$
and $x\in \mathbb {R}^{2}$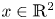 . By analysing some new estimates on the least energy of the mass critical fractional Schrödinger energy functional, we obtain the concentration behaviour of each minimizer of the mass critical fractional Schrödinger energy functional when $a\nearrow a^{\ast }=\|Q\|_{2}^{2s}$
. By analysing some new estimates on the least energy of the mass critical fractional Schrödinger energy functional, we obtain the concentration behaviour of each minimizer of the mass critical fractional Schrödinger energy functional when $a\nearrow a^{\ast }=\|Q\|_{2}^{2s}$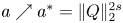 , where $Q$
, where $Q$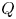 is the unique positive radial solution of $(-\Delta )^{s}u+su-|u|^{2s}u=0$
is the unique positive radial solution of $(-\Delta )^{s}u+su-|u|^{2s}u=0$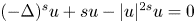 in $\mathbb {R}^{2}$
in $\mathbb {R}^{2}$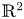 .
.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 6 , December 2023 , pp. 1993 - 2024
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 2
- Cited by



