Introduction
In transmission electron microscopy (TEM), a coherent beam of high-energy electrons is used to illuminate a sample. One of the most commonly used operating TEM modes is diffraction, where the electron wave is imaged in the far-field after scattering. This experiment provides a great deal of information about the sample structure, especially for crystalline samples (De Graef, Reference De Graef2003; Zuo & Spence, Reference Zuo and Spence2017; Zhang et al., Reference Zhang, Zhao, Ding, Chong, Jia, Ophus, Asta, Ritchie and Minor2020). Electron diffraction of nanoscale regions is a powerful characterization technique for several reasons: the strong interaction of free electrons with matter (Shull & Wollan, Reference Shull and Wollan1948), the ability to tune the sample interaction volumes from micrometer to sub-nanometer length scales (Bendersky & Gayle, Reference Bendersky and Gayle2001), the ease of collecting information at high scattering angles including higher-order Laue zones (Bird, Reference Bird1989), and the relative ease of the interpretation of electron diffraction patterns due to their small wavelengths, at least for thin specimens (Vainshtein, Reference Vainshtein2013).
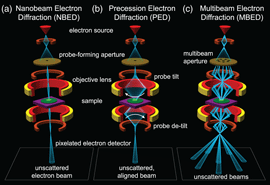
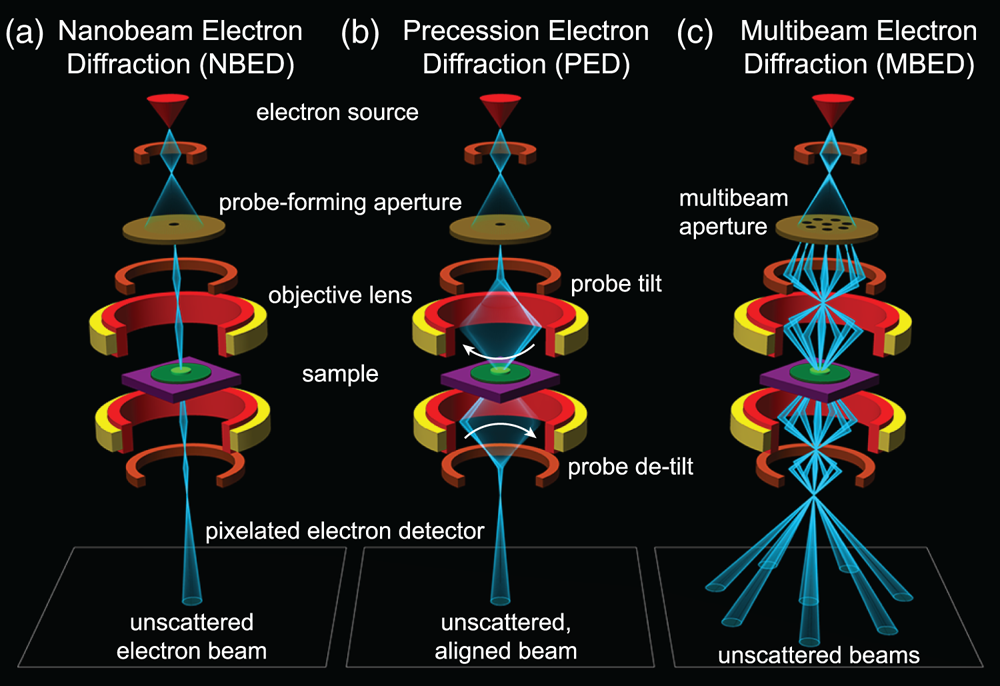
The widespread adoption of modern electron detector technology enables thousands or even millions of scattered electron images to be collected in a single experiment. When combined with scanning transmission electron microscopy (STEM), we can record images of the sample in reciprocal space over a two-dimensional grid of probe positions, generating a four-dimensional output often referred to as a 4D-STEM experiment (Ophus et al., Reference Ophus, Ercius, Sarahan, Czarnik and Ciston2014). One subset of 4D-STEM experiments is nanobeam electron diffraction (NBED), where nanometer-sized electron probes are recorded in diffraction space in order to characterize the sample's structure (Smeaton et al., Reference Cimada da Silva, Smeaton, Dunbar, Xu, Balazs, Kourkoutis and Hanrath2020), degree of short- or medium-range order (Martin et al., Reference Martin, Bøjesen, Petersen, Hu, Biggs, Weyland and Liu2020), local crystal orientation (Panova et al., Reference Panova, Ophus, Takacs, Bustillo, Balhorn, Salleo, Balsara and Minor2019), strain deformation fields (Ozdol et al., Reference Ozdol, Gammer, Jin, Ercius, Ophus, Ciston and Minor2015; Hughes et al., Reference Hughes, Savitzky, Deng, Jin, Lomeli, Chueh, Herring, Ophus and Minor2019), or local electromagnetic fields (Bruas et al., Reference Bruas, Boureau, Conlan, Martinie, Rouviere and Cooper2020). A review of the various 4D-STEM measurement modes is given by Ophus (Reference Ophus2019). The experimental layout of a conventional NBED experiment is shown in Fig. 1a.
Fig. 1. Experimental layout of electron diffraction experiments. (a) Nanobeam electron diffraction, (b) precession electron diffraction, and (c) multibeam electron diffraction.
A major challenge in the interpretation of NBED data is the high sensitivity of the recorded CBED patterns to slight mistilt of the sample from the zone axis (Chen & Gao, Reference Chen and Gao2020) and to dynamical diffraction effects (Donatelli & Spence, Reference Donatelli and Spence2020; Mawson et al., Reference Mawson, Nakamura, Petersen, Shibata, Sasaki, Paganin, Morgan and Findlay2020) in all but the thinnest samples. The presence of multiple crystallites that are not all oriented for strong diffraction also complicates analysis, as many regions of the sample may have an ambiguous interpretation or almost no diffraction signal at all. Traditionally, these challenges could be overcome through precession electron diffraction (PED), shown in Fig. 1b, where the incident beam is precessed about the optical axis by deflector coils as the diffraction pattern is recorded (Oleynikov et al., Reference Oleynikov, Hovmöller and Zou2007; Rouviere et al., Reference Rouviere, Béché, Martin, Denneulin and Cooper2013). This has the effect of incoherently averaging the diffraction patterns from each angle in the precession cone, suppressing dynamical effects and potentially exciting diffraction conditions in off-axis crystals. While this technique has been shown to be highly beneficial in many NBED measurements, particularly strain mapping (Mahr et al., Reference Mahr, Müller-Caspary, Grieb, Schowalter, Mehrtens, Krause, Zillmann and Rosenauer2015), it requires painstaking alignment and often necessitates additional hardware in order to combine precession with STEM. It is also possible to perform diffraction experiments where the precession is applied serially, that is, multiple scans are performed one after the other, where a different initial beam tilt is used for each scan (Beanland et al., Reference Beanland, Thomas, Woodward, Thomas and Roemer2013; Meng & Zuo, Reference Meng and Zuo2016; Hubert et al., Reference Hubert, Römer and Beanland2019). This method removes the need for careful alignment of the different beam tilts since the scans could be aligned during post-processing. It does however require substantially more data collection time when scanning over a sample, and thus is more often applied in crystallography experiments where large real space field-of-view and real space resolution are not required.
In this work, we present an alternative approach using a custom-fabricated amplitude grating in the microscope condenser optics to produce several tilted beams which all simultaneously illuminate the sample and are recorded in parallel as shown in Fig. 1c, which we call multibeam electron diffraction (MBED). Using this unique condenser configuration we produce seven off-axis beams, tilted at up to 60 mrad (approx. 3.5°) with respect to the optical axis, plus one on-axis beam, which are focused to the same location on the sample and record diffraction from each simultaneously. From this data, we compute orientation maps of polycrystalline samples and find substantially improved coverage of reciprocal space as compared to a typical NBED experiment. Since this technique also retains diffraction information from each incident beam direction independently, we further utilize the data to compute tomographic reconstructions of the 3D structure of the sample. Finally, we discuss possible extensions to the MBED technique.
Background and Theory
Multibeam Electron Sources
In this study, we have generated multiple electron probes using a set of spatially separated, fully open apertures situated in the probe-forming condenser plane. There are alternative methods for creating multiple STEM beams such as the two flavors of STEM holography: using diffraction gratings (Harvey et al., Reference Harvey, Yasin, Chess, Pierce, dos Reis, Özdöl, Ercius, Ciston, Feng, Kotov, McMorran and Ophus2018; Yasin et al., Reference Yasin, Harvey, Chess, Pierce, Ophus, Ercius and McMorran2018) or using a biprism to split the beam (Cowley, Reference Cowley2003, Reference Cowley2004). However, diffraction gratings are very difficult to implement with small probe-forming apertures (small q max) due to the very fine grating pitch required to achieve large beam angular separation. Additionally, this technique does not allow for a spatially separated measurement of the individual beams in the diffraction plane, as the beams will recombine in the far field. Biprism beam splitters have even more limitations for MBED applications: the biprism will block part of the beam and cause diffraction at the edges, multiple biprisms are required to form more than two beams, and only powers of two number of total beams can be generated.
Multibeam experiments similar to the experiments described in this paper are more common in scanning electron microscopy (SEM) and electron-beam lithographic patterning instruments. We have taken the same approach for MBED as multibeam SEM, where a single electron source is divided into multiple beams using a patterned aperture (Mohammadi-Gheidari et al., Reference Mohammadi-Gheidari, Hagen and Kruit2010). These systems have demonstrated much higher SEM imaging throughput due to their parallel capabilities (Eberle et al., Reference Eberle, Schalek, Lichtman, Malloy, Thiel and Zeidler2015; Kemen et al., Reference Kemen, Garbowski and Zeidler2015). Similarly, using multiple beams for electron lithography can also improve throughput (Sasaki, Reference Sasaki1981; Yin et al., Reference Yin, Brodie, Tsai, Guo and Parker2000). Multibeam systems have also been implemented for electron-beam induced deposition (Van Bruggen et al., Reference Van Bruggen, Van Someren and Kruit2006).
MBED Experiment Design
In a typical STEM or electron diffraction experiment, the initial probe wavefunction Ψ0(q) is defined as a function of the diffraction space coordinates q = (q x, q y) as
where A(q) is an aperture function defined by
where q max is the maximum scattering vector contained in the probe and χ(q) defines the wavefront phase shifts of the electron probe due to coherent wave aberrations. If we neglect all aberrations except for defocus C 1 and third-order spherical aberration C 3, the coherent wave aberrations are (Kirkland, Reference Kirkland2020)
where λ is the electron wavelength. The scattering angles α of an electron wave are related to the scattering vector by the expression
We can model a multibeam experiment by modifying the aperture function A(q) to contain additional non-zero regions where electrons are allowed to pass through. However, if additional electron beams are created with additional apertures at large scattering angles, these beams can be strongly affected by the coherent wave aberrations. In particular, spherical aberration causes high-angle rays to be focused to a different height than ones near the optical axis. This leads to the outer beams of the MBED probe intersecting the sample plane at a different location than the central beam. To compensate for this effect of spherical aberration on the positions of the beams we operate at a “Scherzer defocus” condition, where a negative C 1 is used to balance the positive C 3 of a TEM without aberration correction (Scherzer, Reference Scherzer1949). This process is depicted schematically in Fig. 2a, where we choose a defocus C 1 so as to yield the flattest phase error across the angle range of the outer beam. The effect of defocus on the alignment of the beams at the sample plane is shown in Fig. 3c, where we label the Scherzer condition that causes all eight beams to overlap as Δf = 0.

Fig. 2. MBED experimental design for outer ring of probes positioned at 60 mrad, for 300 kV. (a) Phase shifts due to defocus and third-order spherical aberration. (b) Aperture geometry. (c) 1D probe size as a function of aperture dimensions. (d,e) Simulated probe intensities in real space, for two geometries where outer probe intensities are matched to the center probe, including aberrations shown in (a).

Fig. 3. MBED aperture fabrication. (a) SEM images of the apertures after FIB fabrication, with enlarged images of two of the apertures. (b) TEM images of the apertures over vacuum, showing enlarged images of all apertures labeled with colored arrows. (c) TEM images in real space showing eight beams generated by the apertures, at four different objective lens defocus values.
For the initial MBED design, we used both a central probe-forming aperture and a ring of apertures at a scattering angle α ring, which corresponds to a scattering vector q ring. The Scherzer condition requires we set C 1 such that the derivative of the aberration function χ(q) with respect to |q| is zero at |q| = q ring, which is met when
Plugging this expression into Eq. (3) yields
This expression is plotted in Fig. 2a, for λ = 0.0197 Å, (300 kV), C 3 = 1.3 mm, and α ring = 60 mrad (which give q ring = 3.05 Å−1 and C 1 = −46,800 Å). Figure 2b shows the 2D geometry of the apertures. The center beam aperture on the optical axis has a circular shape with a radius q max. The outer ring apertures are positioned on the Scherzer ring. They have a rectangular shape, with the sides parallel to the radial and azimuthal directions. In the radial direction, the aperture size q radial needs to be relatively narrow in order to form the smallest possible probe due to the steep curvature of the aberration function along this direction. By contrast, in the annular direction, the aperture size q annular can be made much larger due to the low curvature of the aberration phase surface along this direction.
Figure 2c shows the dependence of real-space probe size on the three relevant aperture dimensions shown in Fig. 2b. The probe size was estimated by first taking 1D inverse Fourier transforms in the relevant direction for a phase surface defined by Eq. (6). Next, the size was measured using the 80% intensity criterion given by Zeltmann et al. (Reference Zeltmann, Müller, Bustillo, Savitzky, Hughes, Minor and Ophus2019). We see that there is an ideal aperture size for all three curves, which will form the smallest probe in real space. All three are diffraction-limited for small dimensions and aberration-limited at large angles. For the center beam, the smallest probe size achievable using these microscope parameters is roughly 40 Å for an aperture with a diameter of 0.04 Å−1, corresponding to a semi-angle of 0.4 mrad. This is smaller than a conventional uncorrected STEM experiment due to the large defocus applied (several micrometers) to reach the Scherzer condition. Similarly, the outer ring aperture will form the smallest probe in real space for a radial size of 0.03 Å−1 and an annular size of 0.6 Å−1. However, as mentioned previously, the probe size is quite insensitive to the annular direction aperture size, which can be tuned from 0.1 to 1 Å−1 without much change.
Figures 2d and 2e show the probe dimensions of the center and outer beams for two possible designs, where the intensity of all beams is approximately constant. Figure 2d prioritizes the smallest possible outer beam, at the cost of making the center beam slightly larger. Figure 2e makes the center beam smaller, at the cost of increasing the annular dimension of the outer beam probes. The latter configuration results in a more desirable set of operating conditions, where the probes are close to isotropic in the radial and annular directions, which will simplify the analysis. In practice however, this analysis is only used as a rough guideline, since the real apertures will never be fabricated perfectly, and the microscope will contain additional misaligned parameters (such as residual tilt, astigmatism, and coma) and aberrations not considered here. We recommend an iterative design process, where aperture geometries can be improved after testing with experiments.
A similar design process can be used to design MBED apertures for aberration-corrected STEM instruments. The main difference is that in an aberration-corrected instrument, C 3 can be deliberately set to a negative value, which when combined with positive C 1 and C 5 aberration coefficients will lead to the flattest possible phase surface (and therefore smallest probes in real space) at large angles. This is similar to the “negative Cs” (C 3) concept for forming the smallest possible sub-Ångstrom probe sizes (Jia et al., Reference Jia, Lentzen and Urban2004).
Methods
Multislice Simulations
All of the simulated diffraction experiments shown in this paper were generated using the methods and atomic potentials given by Kirkland (Reference Kirkland2020). The simulation algorithm employed was the multislice method (Cowley & Moodie, Reference Cowley and Moodie1957), as implemented in the Prismatic simulation code (Ophus, Reference Ophus2017; Pryor et al., Reference Pryor, Ophus and Miao2017; Rangel DaCosta et al., Reference Rangel DaCosta and Ophus2020); simulations were run in parallel through the use of GNU parallel (Tange, Reference Tange2020). Simulations were performed at an acceleration voltage 200 kV, with a beam convergence semi-angle of 0.5 mrad. A single probe was placed at the center of the atomic coordinate cell. Atomic coordinates for the spherical Au nanoparticles were generated using pymatgen (Ong et al., Reference Ong, Richards, Jain, Hautier, Kocher, Cholia, Gunter, Chevrier, Persson and Ceder2013; Togo & Tanaka, Reference Togo and Tanaka2018), and the atomic potential was sampled at a resolution of 0.125 Å and a slice thickness of 2.0 Å. The scattering potentials of individual atoms were radially integrated to 3.0 Å. No thermal effects were applied to perturb the atomic coordinates. A total of 2387 particle orientations were simulated in order to sample diffraction behavior within the [001]-[101]-[111] symmetric projection of the cubic orientation sphere.
FIB Amplitude Aperture Fabrication
The MBED apertures used in this study were fabricated in a silicon nitride membrane TEM window, purchased from Norcada, Canada. The single membrane on the window was 250 μm × 250 μm2 with a thickness of 200 nm. A 1-μm-thick gold thin film was evaporated on one side of the whole window in order to make it opaque to electrons. The MBED aperture was milled into the membrane using the focused ion beam column of an FEI Helios G4 UX system operating at 30 kV with a current of 41 pA. Secondary electron images of the fabricated aperture are shown in Fig. 3a, and a diffraction image obtained with the aperture mounted in the TEM condenser system is shown in Fig. 3b. The aperture used for all experiments in this work has a ring radius of 80 μm, a center beam radius of 0.36 μm, and seven equally spaced outer beams with dimensions 1.52 × 0.2 μm.
Experimental Setup and Alignment
In order to test the MBED method for practical experiments, a set of apertures were installed on the C2 condenser aperture rod of a Thermo Fisher (FEI) TitanX TEM. This Titan was not equipped with an aberration corrector, and the spherical aberration C 3 is estimated to be 1.3 mm. Figure 3b shows TEM diffraction space images of the aperture set, which are identical to the SEM images shown in Fig. 3a. Only the central round aperture and outer rectangular apertures allow electrons to pass through freely. The area outside the eight-aperture set was blocked by using an additional aperture in the C3 condenser position. The insets in Fig. 3b show the different rectangular shapes of the seven outer beams and the circular shape of the center beam. The different shapes of the diffraction space probes make it somewhat easier to distinguish the “parent” beam for diffraction experiments. However, in order to reduce the possible ambiguity of diffracted Bragg spots falling close to the mid-point between adjacent beams, we recommend using a large outer ring convergence semi-angle in order to reduce the overlap of adjacent patterns. The limit for the outer beam semi-angle is given by the maximum scattering angles that can propagate through the TEM column without being occluded, which in our microscope appears to be around 80 mrad.
In order to align the MBED probe, we first set the lens currents in the condenser system of the microscope to select the desired α ring for the experiment. We then perform a standard STEM alignment using a circular aperture, and use the Ronchigram of the amorphous support film to bring the sample to eucentric height and correct the condenser astigmatism. Next, we insert the MBED aperture plate and carefully center it on the optical axis. Slight misalignment of the aperture position is corrected by tilting the beam. We then fine-tune the condenser stigmators and the focus (using both the third condenser lens and the objective lens) to ensure that all of the outer beams are focused to the same point (astigmatism causes rays at different azimuths to be focused to a different plane).
For the experiments shown in this paper, we chose a semi-convergence angle of the outer ring of α ring = 60 mrad, giving a total angular coverage of the outer cone of beams of 6.8°. We used an accelerating voltage of 300 kV for all experiments (i.e., λ = 0.00197 nm), which positions the outer beams at a radius of >38 nm−1, outside the scattering vector limits for most samples. Figure 3c shows the images of the eight probes in real space, at different defocus Δf values. By tuning the defocus, we can produce an imaging condition with either the beams aligned to each other, or spatially separated.
Note that even at Δf = 0 nm, the beams are not perfectly aligned due to residual astigmatism, tilt, or coma in the condenser system. However, for MBED experiments where the probe step size is matched to the probe size (roughly 5 nm), this will not be an issue because the datasets generated from different beams can easily be aligned in post-processing. To perform this post-processing, we first form virtual bright- or dark-field images for each of the parent beams. We then use cross-correlation of the virtual images to determine the offsets between each beam. Typically, the bright-field images give more accurate offsets, as the images are most similar across the different beams. All MBED datasets displayed elliptical distortions similar to those of a typical (uncalibrated) diffraction experiment, on the order of 1–2%. We did not observe strong differences in the pattern distortions for the different beams, and the degree of distortion was negligible for the applications considered in this study. However, due to the large scattering vectors employed in MBED, these measurements may be more sensitive to condenser and projection system aberrations than other electron diffraction experiments, and so should be carefully checked.
Our MBED datasets were acquired using a Gatan Orius CCD camera at 60 mm camera length with 1.5 pA probe current and 50 ms exposure time. Note that all experiments contain a small number of “streak” artifacts in the vertical direction due to errors in the data readout script, These errors consist of duplicate images being read out and do not substantially change the results.
Sample Preparation
The two experimental samples used in this study were both crystalline Au nanoparticles. The sample used for the MBED automated crystal orientation mapping (ACOM) experiments was produced by a chemical synthesis procedure (Nikoobakht & El-Sayed, Reference Nikoobakht and El-Sayed2003). The sample used for the MBED tomography experiments was produced by evaporating Au onto a TEM grid with ultrathin carbon on a lacey support mesh.
Bragg Peak Measurements
Most of the analysis performed in this paper used methods that are standard for NBED experiments (Ophus et al., Reference Ophus, Ercius, Sarahan, Czarnik and Ciston2014; Pekin et al., Reference Pekin, Gammer, Ciston, Minor and Ophus2017; Zeltmann et al., Reference Zeltmann, Müller, Bustillo, Savitzky, Hughes, Minor and Ophus2019). Measurement of the position of all diffracted Bragg disks was performed using the py4DSTEM analysis toolkit (Savitzky et al., Reference Savitzky, Hughes, Zeltmann, Brown, Zhao, Pelz, Barnard, Donohue, Rangel DaCosta, Pekin, Kennedy, Janish, Schneider, Herring, Gopal, Anapolsky, Ercius, Scott, Ciston, Minor and Ophus2020). First, we identified the positions of the eight unscattered electron beams, and then constructed a template image of each of these eight beams by cropping around them. Next, for each STEM probe position, we used cross-correlation of the diffraction image with each of the eight templates to identify candidate Bragg peak locations.
The next analysis steps are more specific to an MBED experiment. In each image, we found the center position of all eight unscattered beams. Each of the scattered beams was then assigned to a given parent beam, which was determined as the minimum distance to an unscattered beam. Note that this will produce a very small number of beams attributed to the wrong parent beam. In the case, where the diffraction patterns from each beam overlap and make assignment of each Bragg disk to its parent beam ambiguous, they can be correctly assigned to a given parent beam by selecting the beam with the highest correlation intensity, since the correlation score will be maximum when the beams are the same shape. Here, we have taken a simpler approach and removed erroneous points by using a smaller radial cutoff around each parent beam. The final result is a list of all detected Bragg peaks, separated into different lists by each parent beam and STEM probe position. The python notebook providing the above analysis, as well as the raw MBED data is available here [link will be added after publication]. https://doi.org/10.18126/7eav-q9vl
MBED Orientation Mapping
In order to determine the local orientation of the sample for a given MBED probe position, we matched a library of kinematic diffraction patterns to each MBED measurement, for all beams independently. This method is usually referred to as automated crystallographic orientation mapping (ACOM) in the literature (Rauch & Véron, Reference Rauch and Véron2014). We computed a library of 8385 kinematic diffraction patterns of FCC Au following the methods given by De Graef (Reference De Graef2003) and Zuo & Spence (Reference Zuo and Spence2017). These patterns spanned an orientation range covering the symmetry-reduced triangular patch of the unit sphere from [001] to [011] to [111]. We assumed an accelerating voltage of 300 kV and used a shape factor given by a 5-nm thick slab. We did not observe a very strong dependence of the results on the assumed thickness, and thus, we used a relatively low thickness in order to include all possible diffraction spots for a given orientation. We have used a 1.3 Å−1 cutoff in reciprocal space here.
To match each pattern, we developed a simple two-step correlation scoring method. Initially, we compared the detected Bragg peak scattering vector lengths to the diffraction library lengths. We summed the absolute 1D distances between each simulated peak position and the nearest experimental peak. From this list, the simulated diffraction patterns with the lowest summed distances were selected for further analysis. The next step was to compare the subset of simulated patterns to the experimental patterns in 2D, rotating the simulated patterns 360° in steps of 2°. For each orientation, we computed a score given by the square root of the simulated peak intensity multiplied by the intensity of the experimental peak, within a cutoff threshold of 0.05 Å−1. This sum overall simulated peaks was normalized by dividing by the total simulated peak intensity, excluding the center unscattered peak. This correlation score is effectively the normalized geometric mean of the simulated and experimental peak intensities, after pairing up each experimentally observed peak with a simulated peak where possible. This score reaches a maximum for the best-fit pattern, which was then assigned as the local orientation. All orientation mapping was performed using custom Matlab scripts.
The above ACOM analysis was carried out for each beam individually, overall STEM probe positions. Once the orientation maps were computed for all eight beams, the orientations of the outer beams were corrected by performing a 3D rotation inwards of 60 mrad to align the best-fit orientations of the outer beams to the center beam. In order to combine the orientation maps for multiple beams, we averaged the orientations by using a weighted median (Brownrigg, Reference Brownrigg1984) of the eight best-fit orientations, using correlation scores as the weights. In this way, beam orientations with low correlation scores were effectively removed from the final result. The primary residual errors are due to overlapping crystallites in the sample, where either individual beams or the union of these beams contained diffraction signal from multiple orientations. These errors could perhaps be removed in the future by combining the orientation mapping with a 3D tomographic reconstruction, such at the method described in the next section.
MBED 3D Tomographic Reconstruction
Our MBED probes contain a center beam along the optical axis, and seven beams arranged along a cone of angles tilted 60 mrad away from this optical axis. We therefore gain a small amount of 3D information about the sample, having covered an angular range of ≈6.8° with the unscattered beams, and ≈10° including the angular range of diffracted Bragg spots from most crystalline samples. Perhaps surprisingly, even these small angular ranges can provide useful information in TEM experiments. One example was shown by Oveisi et al. (Reference Oveisi, Letouzey, Alexander, Jeangros, Schäublin, Lucas, Fua and Hébert2017), who performed 3D reconstructions of dislocations using only two beams, separated by 1.56°. This experiment demonstrated that with sufficiently strong prior assumptions (in their case, assuming a 1D curvilinear object), useful 3D information can be obtained from small angular ranges. In this paper, we demonstrate a simple proof-of-principle MBED tomography experiment by reconstructing just two scalar measurements, the virtual bright-field and virtual dark-field images. These were calculated by summing up the center beam correlation intensities to generate virtual bright-field images, and all scattered Bragg peak correlation intensities to form virtual dark-field images.
We employed the simultaneous iterative reconstruction technique (SIRT) algorithm to perform 3D tomographic reconstructions (Gilbert, Reference Gilbert1972). Because of the extremely large missing wedge present in MBED experiments, we regularize SIRT algorithm in two ways. First, while we set the x–y dimensions of the reconstruction voxels to be equal to the STEM probe step size, we set the z-dimension (along the optical axis) of the reconstruction voxels to be 10 times this size. The factor of 10 was chosen because the largest ray angles from the optical axis for this aspect ratio is approximately 6°, close to the tilt range spanned by the experiment. This aspect ratio also reflects the much-reduced resolution available along the z-direction due to the large missing wedge. Second, we apply a “shrinkage” regularization procedure, where the absolute value of the reconstructed voxels is reduced by a constant value after each SIRT update step (Parikh & Boyd, Reference Parikh and Boyd2014; Ren et al., Reference Ren, Ophus, Chen and Waller2020). We have also included an alignment step between each SIRT update, where the experimental images are aligned using cross-correlation to the projected images from the reconstruction space. The resulting algorithm converges very rapidly to a sparse reconstruction, though it is somewhat sensitive to the strength of the regularization parameter. This reconstruction method was implemented using custom Matlab codes. The MBED dataset used for the tomography experiment is available here https://doi.org/10.18126/7eav-q9vl.
Results and Discussion
Simulations of Diffraction Orientation Dependence
We performed dynamical multislice electron scattering simulations of MBED diffraction experiments for a crystalline gold nanoparticle at many different orientations in order to illustrate the potential benefits of MBED. Figure 4a shows the sample geometry, a 10 nm diameter sphere of Au with the FCC crystal structure. Figures 4c and 4d compare a conventional single-beam NBED experiment to an MBED experiment. In both simulations, the sample is oriented near to the [013] zone axis. The single beam experiment shows only two strongly excited Bragg peaks, with a two additional weakly excited peaks along the same direction. This pattern illustrates the primary issue with ACOM in TEM experiments: even when Bragg diffraction is present, many sample orientations lead to patterns that are essentially one-dimensional, and which cannot be used to uniquely identify the three-dimensional orientation vector [uvw] of the sample. By contrast, the MBED simulation shown in Fig. 4d contains significantly more orientation information. Each of the eight patterns is labeled with the nearest low-index zone axis and taken together give an unambiguous 3D orientation of [013].
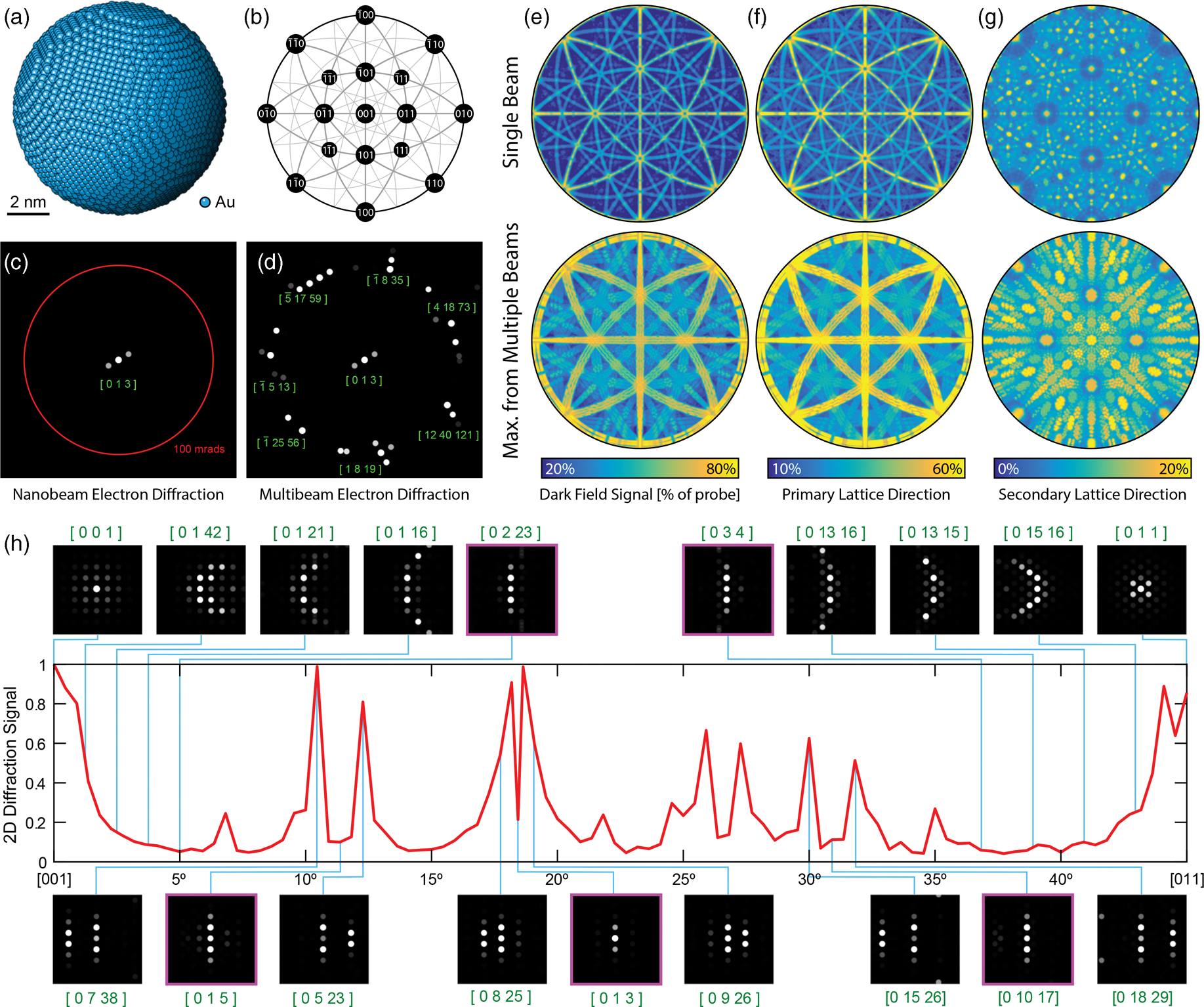
Fig. 4. Multislice simulations demonstrating the benefits of MBED. (a) Coordinates of a 10 nm diameter sphere of FCC Au atoms. (b) Legend of stereographic projections showing the nanoparticle orientation. (c) Single beam diffraction near the [013] zone axis, compared to (d) multibeam diffraction along the same zone axis with the outer beams along a 100 mrad ring, with the closest low-index zone axis labels shown. (e) Total dark-field signal for single beam and eight-beam MBED described in the text. Total 1D diffraction correlation signal along (f) the strongest scattering direction, and (g) perpendicular to the direction used in (f). (h) 2D diffraction signal as a function of particle orientation from [001] to [011] for the single beam case, with various selected diffraction patterns (inset). We have convolved all diffraction pattern images with a circular disk for easier visualization.
We next quantify roughly how often we will encounter a case such as the diffraction pattern shown in Fig. 4c. Figure 4b shows the orientation legend in a stereographic projection for the following figures. Figure 4e compares the total intensity of the diffracted Bragg signals for the single beam case to the maximum diffracted intensity across all eight beams of an MBED experiment, for one center beam and seven outer beams equally spaced around a 60 mrad ring. We note that the darker regions of the single beam case correspond to the orientations that do not produce strong diffraction signals; these regions are much reduced for the multibeam case. However, this analysis does not quantify how well we can overcome the ambiguity shown in Figs. 4c and 4d.
In order to quantify whether a diffraction pattern can be uniquely indexed, we need to estimate how accurately diffraction vector lengths can be estimated in two orthogonal directions. We do this for each simulated diffraction pattern by first measuring the “primary scattering direction” of the diffraction pattern, given by the angle θ 0 corresponding to the highest intensity I(q) angular moment ![]() $M_\theta$
$M_\theta$
 $$\eqalign{M_\theta & = \sum I\lpar {\bf q}\rpar \cos^{2}\lpar \theta_q - \theta_0\rpar \cr & = \sum I\lpar {\bf q}\rpar {\lsqb q_x \cos\lpar \theta_0\rpar + q_y \sin\lpar \theta_0\rpar \rsqb ^{2}\over \vert {\bf q}\vert ^{2}}\comma\; }$$
$$\eqalign{M_\theta & = \sum I\lpar {\bf q}\rpar \cos^{2}\lpar \theta_q - \theta_0\rpar \cr & = \sum I\lpar {\bf q}\rpar {\lsqb q_x \cos\lpar \theta_0\rpar + q_y \sin\lpar \theta_0\rpar \rsqb ^{2}\over \vert {\bf q}\vert ^{2}}\comma\; }$$where θ q is the angular direction of the diffraction space coordinate system q. Once we have determined this direction, we take the autocorrelation of the diffraction pattern
where ![]() ${\cal F}_{{\bf r}\to {\bf q}}$ and
${\cal F}_{{\bf r}\to {\bf q}}$ and ![]() ${\cal F}_{{\bf q}\to {\bf r}}$ represent the forward and inverse 2D Fourier transforms. We then calculate the total correlation intensity along the primary and secondary directions equal to
${\cal F}_{{\bf q}\to {\bf r}}$ represent the forward and inverse 2D Fourier transforms. We then calculate the total correlation intensity along the primary and secondary directions equal to
 $$\matrix{ I_{\hbox{\,primary}} & = \displaystyle\sum I_{\hbox{corr}}\lpar {\bf q}\rpar \cos^{2}\lpar \theta_q - \theta_0\rpar, \cr I_{\hbox{secondary}} & = \displaystyle\sum I_{\hbox{corr}}\lpar {\bf q}\rpar \sin^{2}\lpar \theta_q - \theta_0\rpar \comma\;}$$
$$\matrix{ I_{\hbox{\,primary}} & = \displaystyle\sum I_{\hbox{corr}}\lpar {\bf q}\rpar \cos^{2}\lpar \theta_q - \theta_0\rpar, \cr I_{\hbox{secondary}} & = \displaystyle\sum I_{\hbox{corr}}\lpar {\bf q}\rpar \sin^{2}\lpar \theta_q - \theta_0\rpar \comma\;}$$where θ 0 is the direction which maximizes ![]() $M_\theta$ for each pattern. By definition, I secondary cannot exceed I primary, and these two values should be equal for diffraction patterns which have fourfold or mirror symmetry along both the x- and y-axis. In order to produce accurate results for patterns with a high degree of sixfold symmetry, we have applied some low-pass filtering to the I corr(q) images.
$M_\theta$ for each pattern. By definition, I secondary cannot exceed I primary, and these two values should be equal for diffraction patterns which have fourfold or mirror symmetry along both the x- and y-axis. In order to produce accurate results for patterns with a high degree of sixfold symmetry, we have applied some low-pass filtering to the I corr(q) images.
Figure 4f shows I primary as a function of orientation for both a single beam experiment, and the maximum of all eight beams from an MBED experiment. These signals closely track the total dark-field signals shown in Fig. 4e. The diffraction signal along the secondary direction I secondary is plotted as a function of orientation in Fig. 4g, for both the single beam and MBED cases. These images have a very natural interpretation; a high value indicates strong diffraction signals in two dimensions, indicating diffraction patterns than should be easy to unambiguously index. All of the low-index zones 〈uvw〉 for FCC are represented by signal maxima, including 〈001〉, 〈011〉, 〈111〉, 〈012〉, 〈112〉, 〈113〉, and others. The regions of low I secondary signal indicate orientations that could produce ambiguous diffraction patterns, either with only diffraction vectors excited along one direction or no strong diffraction peaks. The total area fraction of these regions is much-reduced by MBED; the only large remaining orientations are those arranged in a cone around the 〈011〉 zone axes. These regions could be further filled in by increasing the angle of the outer beams beyond 60 mrad.
Finally, to show the potential orientation ambiguity in detail, we have plotted the ratio I secondary/I primary in Fig. 4h, following the orientations from [001] to [011]. As expected, the condition I secondary = I primary is met or nearly met for high-symmetry zone axes such as the two endpoints. Many other orientations also produce strong 2D diffraction signals, such as the insets shown for the [0 7 38], [0 5 23], [0 8 25], and [0 9 26] zone axes. However, the signal is extremely oscillatory, and many orientations produce a very low 2D diffraction signal. In particular, we have highlighted five diffraction patterns with violet boxes, the [0 2 23], [0 1 5], [0 1 3], [0 10 17], and [0 3 4] orientations. These patterns are all essentially one-dimensional, and within the uncertainties given by varying particle thicknesses and shapes in a real experiment, they are effectively identical. Thus, these patterns cannot be assigned an unambiguous orientation from a single-beam diffraction experiment. Figure 4d, however, shows that MBED can be used to easily identify the true orientation in patterns that produce only 1D diffraction signals for single beam experiments.
MBED Orientation Mapping of Polycrystalline Au
In order to test the potential of MBED for crystal orientation mapping studies, we performed an MBED experiment on a sample consisting of highly defected Au nanoparticles with sizes ranging from 5 to 100 nm. Figure 5a shows a 2D histogram of the measured Bragg disk positions from the center beam of an MBED experiment covering a scan area of 128 × 128 STEM probe positions, with a step size of 5 nm. These Bragg peak intensities were used to construct virtual bright-field and dark-field images from the center beam and scattered beams, respectively, which are shown in Figs. 5b and 5c. These images show the wide size distribution and somewhat random morphology of the Au nanoparticles. Figures 5d–5f show the best-fit orientations in all three directions from the center beam. The orientation estimates have been masked by applying an intensity threshold to all diffracted beams, in order to prevent false positives from weak or non-existent diffraction patterns. Comparing these images to Fig. 5b, we see many particles both large and small which have scattered enough to be visible in the bright-field image, but could not be assigned a reliable orientation.
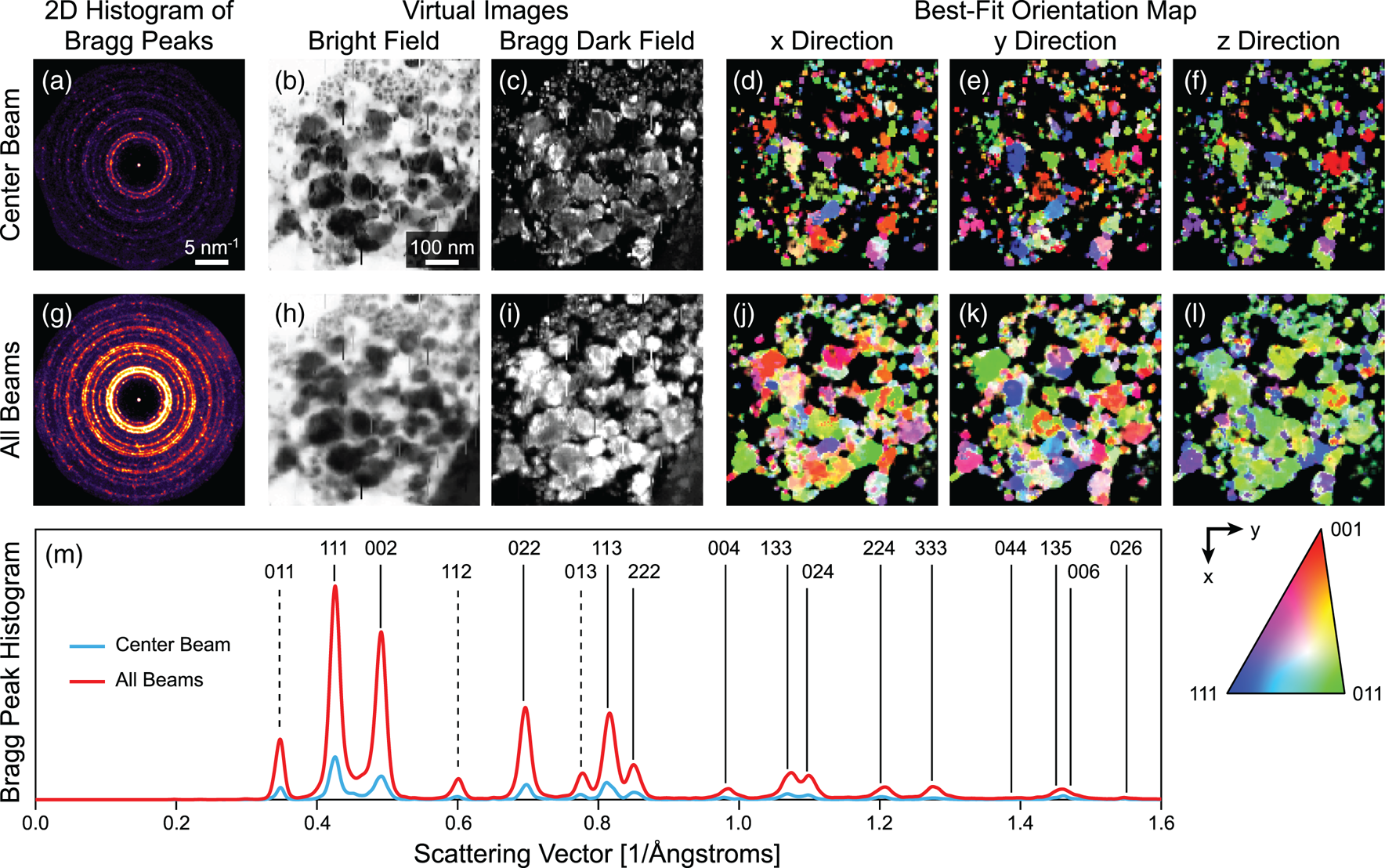
Fig. 5. MBED orientation mapping of Au nanoparticles, comparing center beam to all beams. (a,g) 2D histograms of all detected Bragg peaks. (b,h) Virtual bright-field and (c,i) dark-field images. (d–f) Orientation maps calculated from the center beam, and (j–l) orientation maps calculated from all beams. The x- and y-directions are defined as the in-plane image axes shown in the legend, while the z-direction refers to the out-of-plane orientation. (m) Scattering vector histogram of all Bragg peaks, indexed to FCC Au.
Figure 5g shows a 2D histogram of the measured Bragg disk positions from all eight beams of the MBED experiment. Approximately 5–6 times as many Bragg peaks were detected relative to the center beam measurements. This value is slightly smaller than the factor of 8 that would be expected for an eight-beam experiment. The reduction is due to the reduced intensity of the outer beams, due to their aperture areas being slightly reduced during the FIB machining process. However, the diffraction rings are much more contiguous in the entire MBED dataset; that is, many additional Bragg beams have been excited by the MBED measurement relative to a conventional NBED experiment. Figures 5h and 5i show the virtual bright-field and dark-field images, respectively, averaged over all MBED beams. The bright-field image is virtually identical to the center beam shown in Fig. 5b, though with some additional blurring to the slightly imperfect alignment of all beams. The virtual dark-field image in Fig. 5i, however, shows significantly more constant signal across all grains; this is due to the much higher probability of Bragg excitation for all orientations in an MBED experiment. The orientation maps estimated from all beams (via weighted-median averaging of the eight individual orientations) shown in Figs. 5j–5l bear this out, with a significantly higher fraction of the pixels assigned to an orientation. The overall trend of the particle being biased toward an 〈011〉 orientation is also more clear. The ACOM patterns are also now a very good match to the virtual images shown in Figs. 5h–5i; we can now estimate an orientation for virtually every pixel where the electron beam appears to be strongly scattered. We note that for this sample, the orientation mapping is likely over-determined when using eight beams; for other samples which are more beam-sensitive, using a smaller number of beams could provide almost the same information gain, but for reduced electron dose. For extremely beam-sensitive samples, the optimum pattern is likely three arranged in a triangular pattern with as large a separation angle as possible.
Figure 5m shows a 1D histogram of the scattering vectors for all detected Bragg peaks, for both the center beam and all beams. All Bragg peaks that were observed could be indexed to FCC Au. All low-index peaks occurred with probabilities relatively close to a random distribution, though with some preference for peaks such as (111) and (002) which can occur for a particle oriented along a [011] zone axis, the dominant orientation observed in Fig. 5l. Three strongly excited forbidden reflections were also observed, indexed to (011), (112), and (013), and are marked by dashed lines in the figure. These peaks are likely due to the heavily defected nature of the crystalline grains in this sample. These reflections can also be used for the ACOM measurements, though they were not included in our diffraction library due to the use of kinematic structure factors (which are zero for these peaks).
MBED 3D Reconstruction of Polycrystalline Au
In order to test the potential of MBED experiments to recover 3D information from a sample, we acquired MBED data from 100 × 100 probe positions with a 2 nm step size from an alignment sample consisting of Au nanoparticles on ultrathin carbon with lacey support. Figures 6a and 6b show the virtual bright-field and dark-field images, respectively. The sample morphology consists of small Au particles on both the thin carbon membrane, and thicker carbon support (running diagonally across the field of view). This carbon support is moderately thick and so should displace the Au nanoparticles out of the plane relative to the upper right and lower left corners. A cluster of Au nanoparticles near the center was used for the initial alignment. Unlike the previous section, these virtual images were constructed by using radial integration regions, shown for all beams in Fig. 6d.

Fig. 6. MBED 3D tomography of Au nanoparticles. (a) Virtual bright-field images for all beams. (b) Virtual annular dark-field images from all beams. (c) Comparison between the center beam DF image and the DF images from each of the seven outer beams. (d) Maximum CBED image from all probe positions, with virtual detector ranges overlaid. (e) 3D isosurface plot of the reconstruction. (f) Projections of the maximum intensity along the x-, y-, and z-directions of the reconstructed volume. Note that in both (e) and (f), the z-axis has been scaled to 10× the size of the x- and y-axes. This scaling reflects the limited z-axis resolution of the reconstruction due to the small angular range used.
After completing the tomographic reconstruction, the beams were aligned more precisely to each other. This is shown in Fig. 6c by directly overlaying each outer beam with the center beam, in two different color channels. In each of these images, the signals running across the carbon support are closely aligned. The upper right corner of the field of view shows strong parallax displacement however, where images of the nanoparticles in the outer beams show significant displacement relative to the center beam. Furthermore, these displacements are always in the radial direction for each beam, indicating that this is a true 3D effect, where the different beam angles intersect the sample at different positions for particles displaced out of the focal plane.
We performed a 3D tomographic reconstruction of the dark-field images using the methods described previously. A 3D isosurface plot of the resulting reconstruction is plotted in Fig. 6e. Each isosurface face is colored by the distance along the optical axis, over a range of 240 nm. The small Au nanoparticles show a strongly bimodal height distribution, where the particles on the support arm sit on a plane that is displaced from the plane occupied by the particles in the upper right and lower left of the field of view. This overall geometry is shown even more clearly in Fig. 6f, especially the projection along the x-direction. Here, we can estimate the displacement of the two sets of particles to be 100–140 nm.
Conclusion and Outlook
In this paper, we have introduced MBED, where we position a multiple probe-forming aperture below the second condenser lens of an STEM instrument. These apertures consist of a round center beam, and shaped outer beams falling on a ring of constant radius at a tilt angle which is large relative to the expected diffraction angles, similar to a precession electron diffraction experiment. We have demonstrated the utility of MBED for ACOM of polycrystalline samples using both multislice simulations and experimental measurements of Au nanoparticles. The large angular range of the beams in MBED excites significantly more Bragg diffraction and can thus pick up signals missed by conventional NBED experiments. We have also performed a proof-of-principle 3D tomographic reconstruction of Au nanoparticles using MBED. This experiment was able to show clear evidence of our ability to measure depth information, despite the angular range being small on an absolute scale. While precession electron diffraction can provide many of the same advantages for ACOM as MBED, it cannot provide 3D information due to the angular signals being mixed together.
We believe that MBED can improve virtually any NBED experiment that requires measurement of Bragg diffraction vectors, and so will be useful in many studies. The most promising next steps for development of the MBED technique are to combine crystallographic analysis such as ACOM with 3D tomographic reconstruction. It is possible to reconstruct a full 3D diffraction pattern in each voxel, as demonstrated by Meng & Zuo (Reference Meng and Zuo2016). While the resolution along the optical axis is much lower (both in real and reciprocal space) in MBED, our technique does not require multiple scans over the sample surface or scanning over multiple sample tilts. However, MBED could be easily combined with tilt series measurements and will reduce the number of tilts that need to be collected due to its large range of angles collected in each scan.
Finally, we can also implement MBED in other ways. One idea would be to design MBED probes specifically for an aberration-corrected instrument. One possible route would be to match the symmetry of the aperture layout to that of the non-radially symmetric highest order aberrations. For a hexapole aberration corrector (Haider et al., Reference Haider, Müller and Uhlemann2008), this would mean placing six apertures on the outer ring, positioned along the directions with the flattest phase. With these design principles, aberration-corrected MBED may be able to reach much larger angles than the 60 mrad demonstrated in this paper. To follow a design route targeting electron crystallography of beam-sensitive samples, we could design the beams to be offset from each other on the sample surface, in order to reduce the local dose to the sample. If these beams were offset primarily along a single direction, the measurements would be compatible with sample tilting such that each region of the sample would never see more than one beam. This could improve both micro- and nanoelectron diffraction experiments that already use scanned electron probes (Gallagher-Jones et al., Reference Gallagher-Jones, Ophus, Bustillo, Boyer, Panova, Glynn, Zee, Ciston, Mancia, Minor and Rodriguez2019; Bücker et al., Reference Bücker, Hogan-Lamarre, Mehrabi, Schulz, Bultema, Gevorkov, Brehm, Yefanov, Oberthür, Kassier and Dwayne Miller2020). Any research group can easily pursue these ideas by following the simple fabrication route presented in this paper, using an FIB to machine custom apertures out of Si3N4 membranes with a thick metal layer deposited on one surface.
Acknowledgments
The authors thank Alex Bruefach and Mary Scott for providing the Au nanoparticle sample used for the MBED ACOM experiments. X.H. is support by the National Key Research and Development Program of China (No. 2017YFA0303700), the National Natural Science Foundation of China (No. 11504166), Molecular Foundry Proposal (No. 6463), and China Scholarship Council (No. 201906195020). S.E.Z. was supported by the National Science Foundation under STROBE Grant No. DMR 1548924. B.H.S. and L.R.D. are supported by the Toyota Research Institute. C.O. acknowledges support from the DOE Early Career Research Award program. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.