No CrossRef data available.
Published online by Cambridge University Press: 28 September 2005
The following shows the correction to Equation (3) that appeared on page 356 of Microscopy and Microanalysis, 11:4, August 2005, in the article by Admon et al. The lines, highlighted with gray screen, were inadvertently left out.
In certain cases (e.g., in SEM-to-LM experiments) the sample plane is perpendicular to the viewing direction (z) in both the source and the target instruments. In such cases the dimensions measured on the sample do not require tilt-distortion correction, an inherent feature of the three-point algorithm. Hence, two reference marks, A and B, are sufficient for relocating any particle, P, in the sample plane (Fig. 2). If (x,y) are coordinates measured in the source instrument and (u,v) in the target instrument, then
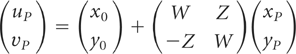
where


In the two-point case the sample plane is perpendicular to the viewing direction (z); hence the transformation from the source to the target instrument reduces to two-dimensional shift and rotation.
The Editor and Cambridge University Press regret the inconvenience that this inadvertent error may have caused.

In the two-point case the sample plane is perpendicular to the viewing direction (z); hence the transformation from the source to the target instrument reduces to two-dimensional shift and rotation.