Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T09:26:39.325Z Has data issue: false hasContentIssue false
  • English
  • Français

Alpha Shape Analysis (ASA) Framework for Post- Clustering Property Determination in Atom Probe Tomographic Data

Published online by Cambridge University Press:  07 January 2021

Evan K. Still Open the ORCID record for Evan K. Still [Opens in a new window] ,
Daniel K. Schreiber ,
Jing Wang  and
Peter Hosemann
Evan K. Still
Affiliation:
Department of Nuclear Engineering, University of California, Berkeley, CA94720, USA
Daniel K. Schreiber
Affiliation:
Energy and Environment Directorate, Pacific Northwest National Laboratory, Richland, WA99354, USA
Jing Wang
Affiliation:
Energy and Environment Directorate, Pacific Northwest National Laboratory, Richland, WA99354, USA
Peter Hosemann*
Affiliation:
Department of Nuclear Engineering, University of California, Berkeley, CA94720, USA
*
*Author for correspondence: Peter Hosemann, E-mail: [email protected]
Get access

Abstract

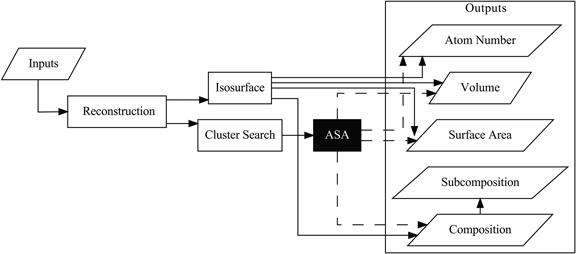
While application of clustering algorithms to atom probe tomography data have enabled quantification of solute clusters in terms of number density, size, and subcomposition there exist other properties (e.g., volume, surface area, and composition) that are better determined by defining an interface between the cluster and the surrounding matrix. The limitation in composition results from an ion selection step where the expected matrix ion types are omitted from the cluster search algorithm to enhance the contrast between the matrix and cluster and to reduce the complexity of the search. Previously, composition determination within solute clusters has utilized a secondary envelopment and erosion step on top of conventional methods such as maximum separation. In this work, we present a novel stochastic method that combines the particle identification fidelity of a conventional clustering algorithm with the analytical flexibility of mesh-based approaches through the generation of alpha shapes for each identified cluster. The corresponding mesh accounts for concave components of the clusters and determines the volume and surface area of the clusters; additionally, the mesh boundary is utilized to update the total composition according to the internal ions.

Keywords

alpha shapesatom probe tomographycluster-analysissurface reconstruction
Type
Software and Instrumentation
Information
Microscopy and Microanalysis , Volume 27 , Issue 2 , April 2021 , pp. 297 - 317
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of the Microscopy Society of America

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akaike, H (2009). Information theory and an extension of the maximum likelihood principle. In 2nd International Symposium on Information Thoery, Petroc BN & Csaki F (Eds.), pp. 267–2816. Budapest, Hungary: Akadémiai Kiadó.Google Scholar
Ankerst, M, Breunig, MM, Kriegel, HP & Sander, J (1999). Optics: Ordering points to identify the clustering structure. SIGMOD Rec 28, 49–60. https://dx.doi.org/10.1145/304181.304187CrossRefGoogle Scholar
Bachhav, M, Odette, G & Marquis, E (2014). α′ precipitation in neutron-irradiated Fe–Cr alloys. Scr Mater 74, 48–51.CrossRefGoogle Scholar
Bailey, NA, Stergar, E, Toloczko, M & Hosemann, P (2015). Atom probe tomography analysis of high dose MA957 at selected irradiation temperatures. J Nucl Mater 459, 225–234.10.1016/j.jnucmat.2015.01.006CrossRefGoogle Scholar
Barber, CB, Dobkin, DP & Huhdanpaa, H (1996). The quickhull algorithm for convex hulls. ACM Trans Math Softw 22, 469–483. https://dx.doi.org/10.1145/235815.235821CrossRefGoogle Scholar
Bas, P, Bostel, A, Deconihout, B & Blavette, D (1995). A general protocol for the reconstruction of 3D atom probe data. Appl Surf Sci 87–88, 298–304.CrossRefGoogle Scholar
Coxeter, HSM (1930). The circumradius of the general simplex. Math Gaz 15, 229–231.CrossRefGoogle Scholar
Edelsbrunner, H, Kirkpatrick, D & Seidel, R (1983). On the shape of a set of points in the plane. IEEE Trans Inf Theory 29, 551–559.10.1109/TIT.1983.1056714CrossRefGoogle Scholar
Edelsbrunner, H & Mücke, EP (1994). Three-dimensional alpha shapes. ACM Trans Graph 13, 43–72. https://dx.doi.org/10.1145/174462.156635CrossRefGoogle Scholar
Ester, M, Kriegel, HP, Sander, J & Xu, X (1996). A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, pp. 226–231. Portland, OR: AAAI Press.Google Scholar
Felfer, P & Cairney, J (2016). A computational geometry framework for the optimisation of atom probe reconstructions. Ultramicroscopy 169, 62–68.CrossRefGoogle ScholarPubMed
Felfer, P, Ceguerra, A, Ringer, S & Cairney, J (2015). Detecting and extracting clusters in atom probe data: A simple, automated method using Voronoi cells. Ultramicroscopy 150, 30–36.CrossRefGoogle ScholarPubMed
Gardiner, JD, Behnsen, J & Brassey, CA (2018). Alpha shapes: Determining 3D shape complexity across morphologically diverse structures. BMC Evol Biol 18, 184. https://dx.doi.org/10.1186/s12862-018-1305-zCrossRefGoogle ScholarPubMed
Gault, B, Moody, MP, Cairney, JM & Ringer, SP (2012). Atom Probe Microscopy. New York, NY: Springer New York.CrossRefGoogle Scholar
Geiser, B, Larson, D, Oltman, E, Gerstl, S, Reinhard, D, Kelly, T & Prosa, T (2009). Wide-field-of-view atom probe reconstruction. Microsc Microanal 15, 292–293.CrossRefGoogle Scholar
Geiser, BP, Kelly, TF, Larson, DJ, Schneir, J & Roberts, JP (2007). Spatial distribution maps for atom probe tomography. Microsc Microanal 13, 437–447.CrossRefGoogle ScholarPubMed
Ghamarian, I & Marquis, E (2019). Hierarchical density-based cluster analysis framework for atom probe tomography data. Ultramicroscopy 200, 28–38.CrossRefGoogle ScholarPubMed
Ghamarian, I, Yu, LJ & Marquis, E (2020). Morphological classification of dense objects in atom probe tomography data. Ultramicroscopy 215, 112996.CrossRefGoogle ScholarPubMed
Guo, Z, Sha, W & Vaumousse, D (2003). Microstructural evolution in a PH13-8 stainless steel after ageing. Acta Mater 51, 101–116.CrossRefGoogle Scholar
Hellman, OC, Vandenbroucke, JA, Rüsing, J, Isheim, D & Seidman, DN (2000). Analysis of three-dimensional atom-probe data by the proximity histogram. Microsc Microanal 6, 437–444.CrossRefGoogle ScholarPubMed
Jenkins, BM, London, AJ, Riddle, N, Hyde, JM, Bagot, PA & Moody, MP (2020). Using alpha hulls to automatically and reproducibly detect edge clusters in atom probe tomography datasets. Mater Charact 160, 110078.CrossRefGoogle Scholar
Karnesky, R, Sudbrack, C & Seidman, D (2007). Best-fit ellipsoids of atom-probe tomographic data to study coalescence of γ′ (l12) precipitates in Ni–Al–Cr. Scr Mater 57, 353–356.CrossRefGoogle Scholar
Lasdon, L, Duarte, A, Glover, F, Laguna, M & Martí, R (2010). Adaptive memory programming for constrained global optimization. Comput Oper Res 37, 1500–1509.CrossRefGoogle Scholar
Marquis, EA, Araullo-Peters, V, Etienne, A, Fedotova, S, Fujii, K, Fukuya, K, Kuleshova, E, Legrand, A, London, A, Lozano-Perez, S, Nagai, Y, Nishida, K, Radiguet, B, Schreiber, D, Soneda, N, Thuvander, M, Toyama, T, Sefta, F & Chou, P (2016). A round robin experiment: Analysis of solute clustering from atom probe tomography data. Microsc Microanal 22, 666–667.10.1017/S1431927616004189CrossRefGoogle Scholar
Marquis, EA & Hyde, JM (2010). Applications of atom-probe tomography to the characterisation of solute behaviours. Mater Sci Eng R: Rep 69, 37–62.CrossRefGoogle Scholar
Mason, DR & London, AJ (2020). Morphological analysis of 3D atom probe data using Minkowski functionals. Ultramicroscopy 211, 112940.CrossRefGoogle ScholarPubMed
Miller, M & Kenik, E (2004). Atom probe tomography: A technique for nanoscale characterization. Microsc Microanal 10, 336–341.CrossRefGoogle ScholarPubMed
Newville, M, Stensitzki, T, Allen, DB & Ingargiola, A (2014). LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python, Software. https://dx.doi.org/10.5281/zenodo.11813.CrossRefGoogle Scholar
Richards, FJ (1959). A flexible growth function for empirical use. J Exp Bot 10, 290–301. https://dx.doi.org/10.1093/jxb/10.2.290CrossRefGoogle Scholar
Sander, J, Qin, X, Lu, Z, Niu, N & Kovarsky, A (2003). Automatic extraction of clusters from hierarchical clustering representations. In Advances in Knowledge Discovery and Data Mining, pp. 75–87. Berlin, Heidelberg: Springer.CrossRefGoogle Scholar
Sommerville, DMY (1958). An Introduction to the Geometry of N Dimensions. New York: Dover.Google Scholar
Thompson, K, Lawrence, D, Larson, D, Olson, J, Kelly, T & Gorman, B (2007). In situ site-specific specimen preparation for atom probe tomography. Ultramicroscopy 107, 131–139.CrossRefGoogle ScholarPubMed
van der Walt, S, Colbert, SC & Varoquaux, G (2011). The NumPy array: A structure for efficient numerical computation. Comput Sci Eng 13, 22–30.CrossRefGoogle Scholar
Vaumousse, D, Cerezo, A & Warren, P (2003). A procedure for quantification of precipitate microstructures from three-dimensional atom probe data. Ultramicroscopy 95, 215–221.CrossRefGoogle ScholarPubMed
Virtanen, P, Gommers, R, Oliphant, TE, Haberland, M, Reddy, T, Cournapeau, D, Burovski, E, Peterson, P, Weckesser, W, Bright, J, van der Walt, SJ, Brett, M, Wilson, J, Jarrod Millman, K, Mayorov, N, Nelson, ARJ, Jones, E, Kern, R, Larson, E, Carey, C, Polat, İ., Feng, Y, Moore, EW, Vand erPlas, J, Laxalde, D, Perktold, J, Cimrman, R, Henriksen, I, Quintero, EA, Harris, CR, Archibald, AM, Ribeiro, AH, Pedregosa, F, van Mulbregt, P & Contributors, S (2020). SciPy 1.0: Fundamental algorithms for scientific computing in python. Nat Methods 17, 261–272.CrossRefGoogle ScholarPubMed
Wang, J, Schreiber, DK, Bailey, N, Hosemann, P & Toloczko, MB (2019). The application of the optics algorithm to cluster analysis in atom probe tomography data. Microsc Microanal 25, 338–348.CrossRefGoogle ScholarPubMed
Wilson, JA, Bender, A, Kaya, T & Clemons, PA (2009). Alpha shapes applied to molecular shape characterization exhibit novel properties compared to established shape descriptors. J Chem Inf Model 49, 2231–2241. https://dx.doi.org/10.1021/ci900190zCrossRefGoogle ScholarPubMed