Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T05:13:39.821Z Has data issue: false hasContentIssue false
  • English
  • Français

THE JUMPING CHAMPION CONJECTURE

Part of: Multiplicative number theory Additive number theory; partitions

Published online by Cambridge University Press:  04 May 2015

Daniel A. Goldston  and
Andrew H. Ledoan
Daniel A. Goldston
Affiliation:
Department of Mathematics, San José State University, 315 MacQuarrie Hall, One Washington Square, San José, CA 95192-0103, U.S.A. email [email protected]
Andrew H. Ledoan
Affiliation:
Department of Mathematics, University of Tennessee at Chattanooga, 415 EMCS Building (Mail Stop 6956), 615 McCallie Avenue, Chattanooga, TN 37403-2598, U.S.A. email [email protected]
Get access

Abstract

An integer 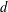$d$ is called a jumping champion for a given $x$ if 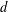$d$ is the most common gap between consecutive primes up to $x$. Occasionally, several gaps are equally common. Hence, there can be more than one jumping champion for the same $x$. In 1999, Odlyzko et al provided convincing heuristics and empirical evidence for the truth of the hypothesis that the jumping champions greater than 1 are 4 and the primorials 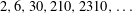$2,6,30,210,2310,\ldots \,$. In this paper, we prove that an appropriate form of the Hardy–Littlewood prime 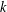$k$-tuple conjecture for prime pairs and prime triples implies that all sufficiently large jumping champions are primorials and that all sufficiently large primorials are jumping champions over a long range of $x$.

MSC classification

Primary: 11N05: Distribution of primes
Secondary: 11P32: Goldbach-type theorems; other additive questions involving primes 11N36: Applications of sieve methods
Type
Research Article
Information
Mathematika , Volume 61 , Issue 3 , September 2015 , pp. 719 - 740
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Erdős, P. and Straus, E. G., Remarks on the differences between consecutive primes. Elem. Math. 35(5) 1980, 115–118.Google Scholar
Ford, K., Simple proof of Gallagher’s singular series sum estimate. Preprint, 2007, available at http://www.math.uiuc.edu/∼ford/gallagher_sum.pdf.Google Scholar
Gallagher, P. X., On the distribution of primes in short intervals. Mathematika 23(1) 1976, 4–9.CrossRefGoogle Scholar
Gallagher, P. X., Corrigendum: On the distribution of primes in short intervals (Mathematika 23(1) (1976), 4–9). Mathematika 28(1) 1981, 86.CrossRefGoogle Scholar
Goldston, D. A. and Ledoan, A. H., Jumping champions and gaps between consecutive primes. Int. J. Number Theory 7(6) 2011, 1–9.CrossRefGoogle Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods (London Mathematical Society Monographs 4), Academic Press (London, New York, San Francisco, 1974).Google Scholar
Hardy, G. H. and Littlewood, J. E., Some problems of ‘Partitio numerorum’; III: On the expression of a number as a sum of primes. Acta Math. 44(1) 1923, 1–70 reprinted as pp. 561–630 in Collected Papers of G. H. Hardy, Vol. I, Clarendon Press (Oxford, 1966).CrossRefGoogle Scholar
Harley, R., Some estimates by Richard Brent applied to the ‘high-jumpers’ problem. Preprint, 1994, available at http://pauillac.inria.fr/∼harley/wnt.html.Google Scholar
Ingham, A. E., The Distribution of Prime Numbers (Cambridge Tracts in Mathematics and Mathematical Physics 30), Cambridge University Press (Cambridge, 1932) reprinted as part of the Cambridge Mathematical Library (with a foreword by R. C. Vaughan), Cambridge University Press (Cambridge, 1990).Google Scholar
Montgomery, H. L. and Soundararajan, K., Primes in short intervals. Comm. Math. Phys. 252 2004, 589–617.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory (Cambridge Studies in Advanced Mathematics 97), Cambridge University Press (Cambridge, 2007).Google Scholar
Odlyzko, A., Rubinstein, M. and Wolf, M., Jumping champions. Experiment. Math. 8(2) 1999, 107–118.CrossRefGoogle Scholar